the analytic concepts of martingale type $p$ and cotype $q$ of a banach space have an intimate relation with the geometric concepts of $p$-concavity and $q$-convexity of the space under consideration, as shown by pisier. in particular, for a banach space $x$, having martingale type $p$ for some $p{>}1$ implies that $x$ has martingale cotype $q$ for some $q{<}\infty$.
the generalisation of these concepts to linear operators was studied by the author, and it turns out that the duality above only holds in a weaker form. an example is constructed showing that this duality result is best possible.
so-called random martingale unconditionality estimates, introduced by garling as a decoupling of the unconditional martingale differences (umd) inequality, are also examined.
it is shown that the random martingale unconditionality constant of $l_\infty^{2^n}$ for martingales of length $n$ asymptotically behaves like $n$. this improves previous estimates by geiss, who needed martingales of length $2^n$ to show this asymptotic. at the same time the order in the paper is the best that can be expected.
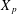 $X_{p}$ INEQUALITIES
$X_{p}$ INEQUALITIES