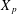Hostname: page-component-5cf477f64f-54txb Total loading time: 0 Render date: 2025-04-04T19:48:00.169Z Has data issue: false hasContentIssue false
  • English
  • Français

METRIC $X_{p}$ INEQUALITIES

Part of: Normed linear spaces and Banach spaces; Banach lattices Special classes of linear operators

Published online by Cambridge University Press:  02 February 2016

ASSAF NAOR  and
GIDEON SCHECHTMAN
ASSAF NAOR
Affiliation:
Mathematics Department, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA; [email protected]
GIDEON SCHECHTMAN
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For every 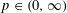$p\in (0,\infty )$ we associate to every metric space 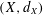$(X,d_{X})$ a numerical invariant 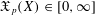$\mathfrak{X}_{p}(X)\in [0,\infty ]$ such that if 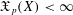$\mathfrak{X}_{p}(X)<\infty$ and a metric space 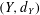$(Y,d_{Y})$ admits a bi-Lipschitz embedding into 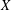$X$ then also 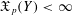$\mathfrak{X}_{p}(Y)<\infty$ . We prove that if 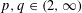$p,q\in (2,\infty )$ satisfy 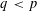$q<p$ then 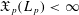$\mathfrak{X}_{p}(L_{p})<\infty$ yet 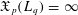$\mathfrak{X}_{p}(L_{q})=\infty$ . Thus, our new bi-Lipschitz invariant certifies that 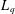$L_{q}$ does not admit a bi-Lipschitz embedding into 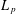$L_{p}$ when 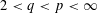$2<q<p<\infty$ . This completes the long-standing search for bi-Lipschitz invariants that serve as an obstruction to the embeddability of 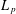$L_{p}$ spaces into each other, the previously understood cases of which were metric notions of type and cotype, which however fail to certify the nonembeddability of 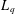$L_{q}$ into 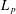$L_{p}$ when 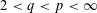$2<q<p<\infty$ . Among the consequences of our results are new quantitative restrictions on the bi-Lipschitz embeddability into 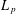$L_{p}$ of snowflakes of 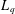$L_{q}$ and integer grids in 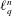$\ell _{q}^{n}$ , for 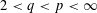$2<q<p<\infty$ . As a byproduct of our investigations, we also obtain results on the geometry of the Schatten 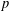$p$ trace class 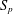$S_{p}$ that are new even in the linear setting.

MSC classification

Primary: 46B80: Nonlinear classification of Banach spaces; nonlinear quotients 46B85: Embeddings of discrete metric spaces into Banach spaces; applications in topology and computer science
Secondary: 46B25: Classical Banach spaces in the general theory 47B10: Operators belonging to operator ideals (nuclear, $p$-summing, in the Schatten-von Neumann classes, etc.)
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 4 , 2016 , e3
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Akemann, C. A., Anderson, J. and Pedersen, G. K., ‘Triangle inequalities in operator algebras’, Linear Multilinear Algebra 11(2) (1982), 167–178.CrossRefGoogle Scholar
Albiac, F. and Baudier, F., ‘Embeddability of snowflaked metrics with applications to the nonlinear geometry of the spaces L p and ℓ p for 0 < p < ∞ ’, J. Geom. Anal. 25(1) (2015), 1–24.CrossRefGoogle Scholar
Ando, T. and Zhan, X., ‘Norm inequalities related to operator monotone functions’, Math. Ann. 315(4) (1999), 771–780.CrossRefGoogle Scholar
Andoni, A., Naor, A. and Neiman, O., ‘Snowflake universality of Wasserstein spaces’, Preprint, 2015, arXiv:1509.08677.Google Scholar
Aronszajn, N., ‘Differentiability of Lipschitzian mappings between Banach spaces’, Studia Math. 57(2) (1976), 147–190.CrossRefGoogle Scholar
Aujla, J. S. and Bourin, J.-C., ‘Eigenvalue inequalities for convex and log-convex functions’, Linear Algebra Appl. 424(1) (2007), 25–35.CrossRefGoogle Scholar
Austin, T. and Naor, A., ‘On the bi-Lipschitz structure of Wasserstein spaces’, Preprint, 2015.Google Scholar
Austin, T., Naor, A. and Peres, Y., ‘The wreath product of ℤ with ℤ has Hilbert compression exponent 2∕3’, Proc. Amer. Math. Soc. 137(1) (2009), 85–90.CrossRefGoogle Scholar
Ball, K., ‘Markov chains, Riesz transforms and Lipschitz maps’, Geom. Funct. Anal. 2(2) (1992), 137–172.CrossRefGoogle Scholar
Ball, K., ‘The Ribe programme’, Astérisque (352): Exp. No. 1047, viii, 147, 159, 2013, Séminaire Bourbaki. Vol. 2011/2012. Exposés 1043–1058.Google Scholar
Ball, K., Carlen, E. A. and Lieb, E. H., ‘Sharp uniform convexity and smoothness inequalities for trace norms’, Invent. Math. 115(3) (1994), 463–482.CrossRefGoogle Scholar
Banach, S., Théorie des opérations linéaires. Éditions Jacques Gabay, Sceaux, 1993. Reprint of the 1932 original.Google Scholar
Bartal, Y., Linial, N., Mendel, M. and Naor, A., ‘On metric Ramsey-type phenomena’, Ann. of Math. (2) 162(2) (2005), 643–709.CrossRefGoogle Scholar
Baudier, F., ‘Quantitative nonlinear embeddings into Lebesgue sequence spaces’, J. Topol. Anal., to appear, Preprint, 2012, arXiv:1210.0588.Google Scholar
Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis, Vol. 1, American Mathematical Society Colloquium Publications, 48 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Bhatia, R., Matrix Analysis, Graduate Texts in Mathematics, 169 (Springer, New York, 1997).CrossRefGoogle Scholar
Bourgain, J., ‘The metrical interpretation of superreflexivity in Banach spaces’, Israel J. Math. 56(2) (1986), 222–230.CrossRefGoogle Scholar
Bourgain, J., ‘Remarks on the extension of Lipschitz maps defined on discrete sets and uniform homeomorphisms’, inGeometrical Aspects of Functional Analysis (1985/86), Lecture Notes in Mathematics, 1267 (Springer, Berlin, 1987), 157–167.CrossRefGoogle Scholar
Bourgain, J., Milman, V. and Wolfson, H., ‘On type of metric spaces’, Trans. Amer. Math. Soc. 294(1) (1986), 295–317.CrossRefGoogle Scholar
Bourin, J.-C. and Uchiyama, M., ‘A matrix subadditivity inequality for f (A + B) and f (A) + f (B)’, Linear Algebra Appl. 423(2–3) (2007), 512–518.CrossRefGoogle Scholar
Bretagnolle, J., Dacunha-Castelle, D. and Krivine, J.-L., ‘Fonctions de type positif sur les espaces L p ’, C. R. Acad. Sci. Paris 261 (1965), 2153–2156.Google Scholar
Brieussel, J. and Zheng, T., ‘Speed of random walks, isoperimetry and compression of finitely generated groups’, Preprint, 2015, arXiv:1510.08040.Google Scholar
Carlen, E., ‘Trace inequalities and quantum entropy: an introductory course’, inEntropy and the Quantum, Contemporary Mathematics, 529 (American Mathematical Society, Providence, RI, 2010), 73–140.Google Scholar
Carlen, E. A. and Lieb, E. H., ‘A Minkowski type trace inequality and strong subadditivity of quantum entropy. II. Convexity and concavity’, Lett. Math. Phys. 83(2) (2008), 107–126.CrossRefGoogle Scholar
Christensen, J. P. R., ‘Measure theoretic zero sets in infinite dimensional spaces and applications to differentiability of Lipschitz mappings’, Publ. Dép. Math. (Lyon) 10(2) (1973), 29–39. Actes du Deuxième Colloque d’Analyse Fonctionnelle de Bordeaux (Univ. Bordeaux, 1973), I, pp. 29–39.Google Scholar
David, G. and Semmes, S., Fractured Fractals and Broken Dreams, Oxford Lecture Series in Mathematics and its Applications, 7 (The Clarendon Press, Oxford University Press, New York, 1997), Self-similar geometry through metric and measure.CrossRefGoogle Scholar
Ding, J., Lee, J. R. and Peres, Y., ‘Markov type and threshold embeddings’, Geom. Funct. Anal. 23(4) (2013), 1207–1229.CrossRefGoogle Scholar
Dixmier, J., ‘Formes linéaires sur un anneau d’opérateurs’, Bull. Soc. Math. France 81 (1953), 9–39.CrossRefGoogle Scholar
Enflo, P., ‘On the nonexistence of uniform homeomorphisms between L p -spaces’, Ark. Mat. 8 (1969), 103–105.CrossRefGoogle Scholar
Enflo, P., ‘Uniform structures and square roots in topological groups. I, II’, Israel J. Math. 8 (1970), 230–252. ibid., 8 (1970), 253–272.CrossRefGoogle Scholar
Enflo, P., ‘Uniform homeomorphisms between Banach spaces’, inSéminaire Maurey-Schwartz (1975–1976), Espaces, L p , applications radonifiantes et géométrie des espaces de Banach, Exp. No. 18 (Centre Math., École Polytech., Palaiseau, 1976), 7.Google Scholar
Epstein, H., ‘Remarks on two theorems of E. Lieb’, Comm. Math. Phys. 31 (1973), 317–325.CrossRefGoogle Scholar
Figiel, T., Johnson, W. B. and Schechtman, G., ‘Random sign embeddings from l r n ,  2 < r < ∞ ’, Proc. Amer. Math. Soc. 102(1) (1988), 102–106.Google Scholar
Giladi, O., Mendel, M. and Naor, A., ‘Improved bounds in the metric cotype inequality for Banach spaces’, J. Funct. Anal. 260(1) (2011), 164–194.CrossRefGoogle Scholar
Giladi, O. and Naor, A., ‘Improved bounds in the scaled Enflo type inequality for Banach spaces’, Extracta Math. 25(2) (2010), 151–164.Google Scholar
Giladi, O., Naor, A. and Schechtman, G., ‘Bourgain’s discretization theorem’, Ann. Fac. Sci. Toulouse Math. (6) 21(4) (2012), 817–837.CrossRefGoogle Scholar
Gluskin, E. D., Pietsch, A. and Puhl, J., ‘A generalization of Khintchine’s inequality and its application in the theory of operator ideals’, Studia Math. 67(2) (1980), 149–155.CrossRefGoogle Scholar
Gromov, M., ‘Filling Riemannian manifolds’, J. Differential Geom. 18(1) (1983), 1–147.CrossRefGoogle Scholar
Hytönen, T. and Naor, A., ‘Pisier’s inequality revisited’, Studia Math. 215(3) (2013), 221–235.CrossRefGoogle Scholar
Johnson, W. B., Maurey, B., Schechtman, G. and Tzafriri, L., ‘Symmetric structures in Banach spaces’, Mem. Amer. Math. Soc. 19(217) (1979), v+298.Google Scholar
Johnson, W. B., Schechtman, G. and Zinn, J., ‘Best constants in moment inequalities for linear combinations of independent and exchangeable random variables’, Ann. Probab. 13(1) (1985), 234–253.CrossRefGoogle Scholar
Kadeć, M. Ĭ., ‘Linear dimension of the spaces L p and l q ’, Uspehi Mat. Nauk 13(6(84)) (1958), 95–98.Google Scholar
Kadec, M. I. and Pełczyński, A., ‘Bases, lacunary sequences and complemented subspaces in the spaces L p ’, Studia Math. 21 (1961/1962), 161–176.CrossRefGoogle Scholar
Kalton, N. J., ‘The nonlinear geometry of Banach spaces’, Rev. Mat. Complut. 21(1) (2008), 7–60.CrossRefGoogle Scholar
Kalton, N. J. and Randrianarivony, N. L., ‘The coarse Lipschitz geometry of l p ⊕l q ’, Math. Ann. 341(1) (2008), 223–237.CrossRefGoogle Scholar
Ledoux, M. and Talagrand, M., Probability in Banach Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 23 (Springer, Berlin, 1991), Isoperimetry and processes.CrossRefGoogle Scholar
Lee, J. R., Naor, A. and Peres, Y., ‘Trees and Markov convexity’, Geom. Funct. Anal. 18(5) (2009), 1609–1659.CrossRefGoogle Scholar
Li, S., ‘Markov convexity and nonembeddability of the Heisenberg group’, Ann. Inst. Fourier, to appear, Preprint, 2014, arXiv:1404.6751.Google Scholar
Lieb, E. H. and Thirring, W. E., ‘Inequalities for the moments of the eigenvalues of the Schrödinger Hamiltonian and their relation to Sobolev inequalities’, inStudies in Mathematical Physics (Princeton University Press, Princeton, NJ, 1976), 269–303.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. I (Springer, Berlin, New York, 1977), Sequence spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 92.CrossRefGoogle Scholar
Linial, N., Magen, A. and Naor, A., ‘Girth and Euclidean distortion’, Geom. Funct. Anal. 12(2) (2002), 380–394.CrossRefGoogle Scholar
Lövblom, G.-M., ‘Uniform homeomorphisms between unit balls in L p -spaces’, Math. Scand. 62(2) (1988), 294–302.CrossRefGoogle Scholar
Lust-Piquard, F., ‘Inégalités de Khintchine dans C p  (1 < p < ∞)’, C. R. Acad. Sci. Paris Sér. I Math. 303(7) (1986), 289–292.Google Scholar
Mankiewicz, P., ‘On Lipschitz mappings between Fréchet spaces’, Studia Math. 41 (1972), 225–241.CrossRefGoogle Scholar
Matoušek, J., Lectures on Discrete Geometry, Graduate Texts in Mathematics, 212 (Springer, New York, 2002).CrossRefGoogle Scholar
Maurey, B., ‘Type, cotype and K-convexity’, inHandbook of the Geometry of Banach Spaces, Vol. 2 (North-Holland, Amsterdam, 2003), 1299–1332.CrossRefGoogle Scholar
McCarthy, C. A., ‘ c p ’, Israel J. Math. 5 (1967), 249–271.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Euclidean quotients of finite metric spaces’, Adv. Math. 189(2) (2004), 451–494.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Some applications of Ball’s extension theorem’, Proc. Amer. Math. Soc. 134(9) (2006), 2577–2584. (electronic).CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Scaled Enflo type is equivalent to Rademacher type’, Bull. Lond. Math. Soc. 39(3) (2007), 493–498.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Metric cotype’, Ann. of Math. (2) 168(1) (2008), 247–298.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Markov convexity and local rigidity of distorted metrics’, J. Eur. Math. Soc. (JEMS) 15(1) (2013), 287–337.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Spectral calculus and Lipschitz extension for barycentric metric spaces’, Anal. Geom. Metr. Spaces 1 (2013), 163–199.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Nonlinear spectral calculus and super-expanders’, Publ. Math. Inst. Hautes Études Sci. 119 (2014), 1–95.CrossRefGoogle Scholar
Mendel, M. and Naor, A., ‘Expanders with respect to Hadamard spaces and random graphs’, Duke Math. J. 164(8) (2015), 1471–1548.CrossRefGoogle Scholar
Naor, A., ‘An introduction to the Ribe program’, Jpn. J. Math. 7(2) (2012), 167–233.CrossRefGoogle Scholar
Naor, A., ‘Comparison of metric spectral gaps’, Anal. Geom. Metr. Spaces 2 (2014), Art. 1.Google Scholar
Naor, A., ‘Discrete Riesz transforms and sharp metric $X_{p}$ inequalities’, Preprint, 2016,arXiv:1601.03332.CrossRefGoogle Scholar
Naor, A. and Peres, Y., ‘Embeddings of discrete groups and the speed of random walks’, Int. Math. Res. Not. IMRN (2008), pages Art. ID rnn 076, 34.CrossRefGoogle Scholar
Naor, A. and Peres, Y., ‘ L p compression, traveling salesmen, and stable walks’, Duke Math. J. 157(1) (2011), 53–108.CrossRefGoogle Scholar
Naor, A., Peres, Y., Schramm, O. and Sheffield, S., ‘Markov chains in smooth Banach spaces and Gromov-hyperbolic metric spaces’, Duke Math. J. 134(1) (2006), 165–197.CrossRefGoogle Scholar
Naor, A. and Schechtman, G., ‘Remarks on non linear type and Pisier’s inequality’, J. Reine Angew. Math. 552 (2002), 213–236.Google Scholar
Naor, A. and Silberman, L., ‘Poincaré inequalities, embeddings, and wild groups’, Compos. Math. 147(5) (2011), 1546–1572.CrossRefGoogle Scholar
Ohta, S.-i., ‘Markov type of Alexandrov spaces of non-negative curvature’, Mathematika 55(1–2) (2009), 177–189.CrossRefGoogle Scholar
Ostrovskii, M. I., Metric Embeddings, De Gruyter Studies in Mathematics, 49 (De Gruyter, Berlin, 2013), Bilipschitz and coarse embeddings into Banach spaces.CrossRefGoogle Scholar
Paley, R. E. A. C., ‘Some theorems on abstract spaces’, Bull. Amer. Math. Soc. 42(4) (1936), 235–240.CrossRefGoogle Scholar
Paley, R. E. A. C. and Zygmund, A., ‘On some series of functions, (1)’, Math. Proc. Cambridge Philos. Soc. 26(3) (1930), 337–357.CrossRefGoogle Scholar
Pisier, G., ‘Some results on Banach spaces without local unconditional structure’, Compos. Math. 37(1) (1978), 3–19.Google Scholar
Pisier, G., ‘Probabilistic methods in the geometry of Banach spaces’, inProbability and Analysis (Varenna, 1985), Lecture Notes in Mathematics, 1206 (Springer, Berlin, 1986), 167–241.CrossRefGoogle Scholar
Pisier, G., ‘Non-commutative vector valued L p -spaces and completely p-summing maps’, Astérisque 247 (1998), vi+131.Google Scholar
Pisier, G. and Xu, Q., ‘Non-commutative L p -spaces’, inHandbook of the Geometry of Banach Spaces, Vol. 2 (North-Holland, Amsterdam, 2003), 1459–1517.CrossRefGoogle Scholar
Ribe, M., ‘On uniformly homeomorphic normed spaces’, Ark. Mat. 14(2) (1976), 237–244.CrossRefGoogle Scholar
Rosenthal, H. P., ‘On the subspaces of L p (p > 2 spanned by sequences of independent random variables’, Israel J. Math. 8 (1970), 273–303.CrossRefGoogle Scholar
Schoenberg, I. J., ‘Metric spaces and positive definite functions’, Trans. Amer. Math. Soc. 44(3) (1938), 522–536.CrossRefGoogle Scholar
Sukochev, F. A., ‘Non-isomorphism of L p -spaces associated with finite and infinite von Neumann algebras’, Proc. Amer. Math. Soc. 124(5) (1996), 1517–1527.CrossRefGoogle Scholar
Talagrand, M., ‘Isoperimetry, logarithmic Sobolev inequalities on the discrete cube, and Margulis’ graph connectivity theorem’, Geom. Funct. Anal. 3(3) (1993), 295–314.CrossRefGoogle Scholar
Veomett, E. and Wildrick, K., ‘Spaces of small metric cotype’, J. Topol. Anal. 2(4) (2010), 581–597.CrossRefGoogle Scholar
Wagner, R., ‘Notes on an inequality by Pisier for functions on the discrete cube’, inGeometric Aspects of Functional Analysis, Lecture Notes in Mathematics, 1745 (Springer, Berlin, 2000), 263–268.CrossRefGoogle Scholar
Wells, J. H. and Williams, L. R., Embeddings and Extensions in Analysis (Springer, New York, Heidelberg, 1975), Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 84.CrossRefGoogle Scholar
Wojtaszczyk, P., Banach Spaces for Analysts, Cambridge Studies in Advanced Mathematics, 25 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar