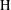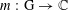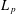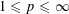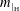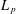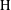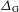2 results
NONCOMMUTATIVE DE LEEUW THEOREMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 12 October 2015, e21
-
- Article
-
- You have access
- Open access
- Export citation
SOME SHARP BOUNDS FOR THE CONE MULTIPLIER OF NEGATIVE ORDER IN ${\mathbb R}^3$
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 12 May 2003, pp. 373-390
- Print publication:
- May 2003
-
- Article
- Export citation