Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T05:01:52.545Z Has data issue: false hasContentIssue false
  • English
  • Français

NONCOMMUTATIVE DE LEEUW THEOREMS

Part of: Locally compact groups and their algebras Harmonic analysis in several variables Selfadjoint operator algebras

Published online by Cambridge University Press:  12 October 2015

MARTIJN CASPERS ,
JAVIER PARCET ,
MATHILDE PERRIN  and
ÉRIC RICARD
MARTIJN CASPERS
Affiliation:
Fachbereich Mathematik und Informatik, Westfälische Wilhelmsuniversität Münster, Einsteinstrasse 62, 48149 Münster, Germany; [email protected]
JAVIER PARCET
Affiliation:
Instituto de Ciencias Matemáticas, Consejo Superior de Investigaciones Científicas, C/Nicolás Cabrera 13-15, 28049 Madrid, Spain; [email protected], [email protected]
MATHILDE PERRIN
Affiliation:
Instituto de Ciencias Matemáticas, Consejo Superior de Investigaciones Científicas, C/Nicolás Cabrera 13-15, 28049 Madrid, Spain; [email protected], [email protected]
ÉRIC RICARD
Affiliation:
Laboratoire de Mathématiques Nicolas Oresme, Université de Caen Normandie, 14032 Caen Cedex, France; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 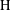$\text{H}$ be a subgroup of some locally compact group 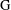$\text{G}$. Assume that 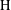$\text{H}$ is approximable by discrete subgroups and that 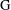$\text{G}$ admits neighborhood bases which are almost invariant under conjugation by finite subsets of 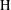$\text{H}$. Let 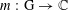$m:\text{G}\rightarrow \mathbb{C}$ be a bounded continuous symbol giving rise to an 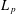$L_{p}$-bounded Fourier multiplier (not necessarily completely bounded) on the group von Neumann algebra of 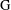$\text{G}$ for some 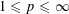$1\leqslant p\leqslant \infty$. Then, 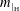$m_{\mid _{\text{H}}}$ yields an 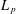$L_{p}$-bounded Fourier multiplier on the group von Neumann algebra of 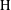$\text{H}$ provided that the modular function 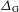${\rm\Delta}_{\text{G}}$ is equal to 1 over 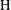$\text{H}$. This is a noncommutative form of de Leeuw’s restriction theorem for a large class of pairs 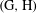$(\text{G},\text{H})$. Our assumptions on 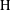$\text{H}$ are quite natural, and they recover the classical result. The main difference with de Leeuw’s original proof is that we replace dilations of Gaussians by other approximations of the identity for which certain new estimates on almost-multiplicative maps are crucial. Compactification via lattice approximation and periodization theorems are also investigated.

MSC classification

Primary: 42B15: Multipliers
Secondary: 22D15: Group algebras of locally compact groups 46L52: Noncommutative function spaces
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e21
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Arhancet, C., ‘Unconditionality, Fourier multipliers and Schur multipliers’, Colloq. Math. 127(1) (2012), 17–37.Google Scholar
Bateman, M., ‘Kakeya sets and directional maximal operators in the plane’, Duke Math. J. 147(1) (2009), 55–77.Google Scholar
Bergh, J. and Löfström, J., Interpolation Spaces. An Introduction, Grundlehren der Mathematischen Wissenschaften, 223 (Springer, Berlin–New York, 1976).Google Scholar
Bhatia, R., Matrix Analysis, Graduate Texts in Mathematics, 169 (Springer, New York, 1997).Google Scholar
Bożejko, M. and Fendler, G., ‘Herz–Schur multipliers and completely bounded multipliers of the Fourier algebra of a locally compact group’, Boll. Unione Mat. Ital. A (6) 3(2) (1984), 297–302.Google Scholar
Calderón, A. P., ‘Ergodic theory and translation-invariant operators’, Proc. Natl Acad. Sci. USA 59 (1968), 349–353.Google Scholar
Caspers, M. and de la Salle, M., ‘Schur and Fourier multipliers of an amenable group acting on non-commutative L p -spaces’, Trans. Amer. Math. Soc. 367(10) (2015), 6997–7013.Google Scholar
Choi, M. D., ‘A Schwarz inequality for positive linear maps on C ∗ -algebras’, Illinois J. Math. 18 (1974), 565–574.Google Scholar
Coifman, R. R. and Weiss, G., Transference Methods in Analysis, Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, 31 (American Mathematical Society, Providence, RI, 1976).Google Scholar
Córdoba, A. and Fefferman, R., ‘On the equivalence between the boundedness of certain classes of maximal and multiplier operators in Fourier analysis’, Proc. Natl Acad. Sci. USA 74(2) (1977), 423–425.Google Scholar
Cotlar, M., ‘A unified theory of Hilbert transforms and ergodic theorems’, Rev. Mat. Cuyana 1 (1955), 105–167.Google Scholar
Cowling, M., ‘Extension of Fourier L p − L q multipliers’, Trans. Amer. Math. Soc. 213 (1975), 1–33.Google Scholar
Cowling, M. and Haagerup, U., ‘Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one’, Invent. Math. 96(3) (1989), 507–549.CrossRefGoogle Scholar
De Cannière, J. and Haagerup, U., ‘Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups’, Amer. J. Math. 107(2) (1985), 455–500.Google Scholar
de Leeuw, K., ‘On L p multipliers’, Ann. of Math. (2) 81 (1965), 364–379.Google Scholar
Derighetti, A., ‘A property of B p(G). Applications to convolution operators’, J. Funct. Anal. 256(3) (2009), 928–939.Google Scholar
Dooley, A. H. and Gaudry, G. I., ‘An extension of de Leeuw’s theorem to the n-dimensional rotation group’, Ann. Inst. Fourier (Grenoble) 34(2) (1984), 111–135.Google Scholar
Fefferman, C., ‘The multiplier problem for the ball’, Ann. of Math. (2) 94 (1971), 330–336.Google Scholar
Figà-Talamanca, A. and Gaudry, G. I., ‘Extensions of multipliers’, Boll. Unione Mat. Ital. (4) 3 (1970), 1003–1014.Google Scholar
Folland, G. B., A Course in Abstract Harmonic Analysis, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
Folland, G. B., ‘Real analysis’, inPure and Applied Mathematics (New York), 2nd edn, Modern techniques and their applications (John Wiley & Sons, Inc., New York, 1999), A Wiley-Interscience Publication.Google Scholar
Goldstein, S. and Lindsay, J. M., ‘Markov semigroups KMS-symmetric for a weight’, Math. Ann. 313(1) (1999), 39–67.Google Scholar
Grafakos, L., Modern Fourier Analysis, 2nd edn, Graduate Texts in Mathematics, 250 (Springer, New York, 2009).Google Scholar
Grosser, S. and Moskowitz, M., ‘On central topological groups’, Trans. Amer. Math. Soc. 127 (1967), 317–340.Google Scholar
Haagerup, U., ‘An example of a nonnuclear C ∗ -algebra, which has the metric approximation property’, Invent. Math. 50(3) (1978/79), 279–293.Google Scholar
Haagerup, U., ‘Group $C^{\ast }$-algebras without the completely bounded approximation property’, 1986.Google Scholar
Haagerup, U., Junge, M. and Xu, Q., ‘A reduction method for noncommutative L p -spaces and applications’, Trans. Amer. Math. Soc. 362(4) (2010), 2125–2165.Google Scholar
Harcharras, A., ‘Fourier analysis, Schur multipliers on S p and non-commutative Λ(p)-sets’, Studia Math. 137(3) (1999), 203–260.Google Scholar
Herz, C., ‘Harmonic synthesis for subgroups’, Ann. Inst. Fourier (Grenoble) 23(3) (1973), 91–123.Google Scholar
Hilsum, M., ‘Les espaces L p d’une algèbre de von Neumann définies par la derivée spatiale’, J. Funct. Anal. 40(2) (1981), 151–169.Google Scholar
Igari, S., Lectures on Fourier Series in Several Variables (University of Wisconsin, 1968).Google Scholar
Jodeit, M. Jr., ‘Restrictions and extensions of Fourier multipliers’, Studia Math. 34 (1970), 215–226.Google Scholar
Junge, M., ‘Fubini’s theorem for ultraproducts of noncommmutative L p -spaces’, Canad. J. Math. 56(5) (2004), 983–1021.Google Scholar
Junge, M. and Mei, T., ‘Noncommutative Riesz transforms—a probabilistic approach’, Amer. J. Math. 132(3) (2010), 611–680.Google Scholar
Junge, M., Mei, T. and Parcet, J., ‘Noncommutative Riesz transforms—dimension free bounds and Fourier multipliers’, J. Eur. Math. Soc. (2015), (to appear) arXiv:1407.2475.Google Scholar
Junge, M., Mei, T. and Parcet, J., ‘Smooth Fourier multipliers on group von Neumann algebras’, Geom. Funct. Anal. 24(6) (2014), 1913–1980.CrossRefGoogle Scholar
Junge, M. and Sherman, D., ‘Noncommutative L p modules’, J. Operator Theory 53(1) (2005), 3–34.Google Scholar
Kosaki, H., ‘Applications of uniform convexity of noncommutative L p -spaces’, Trans. Amer. Math. Soc. 283(1) (1984), 265–282.Google Scholar
Lafforgue, V. and de la Salle, M., ‘Noncommutative L p -spaces without the completely bounded approximation property’, Duke Math. J. 160(1) (2011), 71–116.CrossRefGoogle Scholar
Lebedev, V. and Olevskiĭ, A., ‘Idempotents of Fourier multiplier algebra’, Geom. Funct. Anal. 4(5) (1994), 539–544.Google Scholar
Losert, V., ‘A characterization of SIN-groups’, Math. Ann. 273(1) (1985), 81–88.Google Scholar
Mockenhaupt, G. and Ricker, W. J., ‘Idempotent multipliers for L p(R)’, Arch. Math. (Basel) 74(1) (2000), 61–65.Google Scholar
Neuwirth, S. and Ricard, É., ‘Transfer of Fourier multipliers into Schur multipliers and sumsets in a discrete group’, Canad. J. Math. 63(5) (2011), 1161–1187.Google Scholar
Parcet, J. and Pisier, G., ‘Non-commutative Khintchine type inequalities associated with free groups’, Indiana Univ. Math. J. 54(2) (2005), 531–556.Google Scholar
Parcet, J. and Rogers, K., Twisted Hilbert transforms vs. Kakeya sets of directions, J. reine angew Math. (2013), (to appear) doi:10.1515/crelle-2013-0110.CrossRefGoogle Scholar
Parcet, J. and Rogers, K. M., ‘Differentiation of integrals in higher dimensions’, Proc. Natl Acad. Sci. USA 110(13) (2013), 4941–4944.Google Scholar
Pedersen, G. K., C ∗ -Algebras and their Automorphism Groups, London Mathematical Society Monographs, 14 (Academic Press, Inc., Harcourt Brace Jovanovich, London–New York, 1979).Google Scholar
Pier, J.-P., ‘Amenable locally compact groups’, inPure and Applied Mathematics (New York) (John Wiley & Sons, Inc., New York, 1984), A Wiley-Interscience Publication.Google Scholar
Pisier, G., ‘Non-commutative vector valued L p -spaces and completely p-summing maps’, Astérisque (247) (1998), vi+131.Google Scholar
Pisier, G., Introduction to Operator Space Theory, London Mathematical Society Lecture Note Series, 294 (Cambridge University Press, Cambridge, 2003).Google Scholar
Pisier, G. and Xu, Q., Non-Commutative L p -Spaces, Handbook of the Geometry of Banach Spaces, 2 (North-Holland, Amsterdam, 2003), 1459–1517.Google Scholar
Raghunathan, M. S., Discrete Subgroups of Lie Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 68 (Springer, New York–Heidelberg, 1972).Google Scholar
Ricard, É., ‘Hölder estimates for the noncommutative Mazur maps’, Arch. Math. (Basel) 104(1) (2015), 37–45.Google Scholar
Saeki, S., ‘Translation invariant operators on groups’, Tôhoku Math. J. (2) 22 (1970), 409–419.Google Scholar
Srivastava, S. M., A Course on Borel Sets, Graduate Texts in Mathematics, 180 (Springer, New York, 1998).Google Scholar
Takesaki, M., ‘Theory of operator algebras II’, inEncyclopaedia of Mathematical Sciences, Vol. 125, Operator Algebras and Non-commutative Geometry, 6 (Springer, Berlin, 2003).Google Scholar
Terp, M., $L^{p}$ spaces associated with von neumann algebras, Notes, Københavns Universitets Matematiske Institut (1981).Google Scholar
Terp, M., ‘Interpolation spaces between a von Neumann algebra and its predual’, J. Operator Theory 8(2) (1982), 327–360.Google Scholar
Varopoulos, N. Th., Saloff-Coste, L. and Coulhon, T., Analysis and Geometry on Groups, Cambridge Tracts in Mathematics, 100 (Cambridge University Press, Cambridge, 1992).Google Scholar
Weiss, N. J., ‘A multiplier theorem for SU (n)’, Proc. Amer. Math. Soc. 59(2) (1976), 366–370.Google Scholar