Let 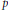 $p$ be prime and let
$p$ be prime and let 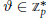 $\vartheta \,\in \,\mathbb{Z}_{p}^{*}$ be of multiplicative order
$\vartheta \,\in \,\mathbb{Z}_{p}^{*}$ be of multiplicative order  $t$ modulo
$t$ modulo 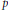 $p$. We consider exponential sums of the form
$p$. We consider exponential sums of the form
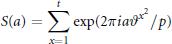 $$S\left( a \right)\,=\,\sum\limits_{x=1}^{t}{\exp \left( 2\pi ia{{\vartheta }^{{{x}^{2}}}}\,/\,p \right)}$$
$$S\left( a \right)\,=\,\sum\limits_{x=1}^{t}{\exp \left( 2\pi ia{{\vartheta }^{{{x}^{2}}}}\,/\,p \right)}$$
and prove that for any 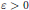 $\varepsilon \,>\,0$
$\varepsilon \,>\,0$
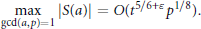 $$\underset{\gcd (a,\,p)\,=\,1}{\mathop{\max }}\,\,\left| S\left( a \right) \right|\,=\,O\left( {{t}^{5/6+\varepsilon }}\,{{p}^{1/8}} \right)$$
$$\underset{\gcd (a,\,p)\,=\,1}{\mathop{\max }}\,\,\left| S\left( a \right) \right|\,=\,O\left( {{t}^{5/6+\varepsilon }}\,{{p}^{1/8}} \right)$$
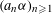 $(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES
$(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES 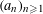 $(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH
$(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH