Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T01:06:57.923Z Has data issue: false hasContentIssue false
  • English
  • Français

On the geometry and regularity of invariant sets of piecewise-affine automorphisms on the Euclidean space

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  07 January 2019

C. SİNAN GÜNTÜRK  and
NGUYEN T. THAO
C. SİNAN GÜNTÜRK
Affiliation:
Courant Institute of Mathematical Sciences, NYU, 251 Mercer Street, New York, NY 10012, USA email [email protected]
NGUYEN T. THAO
Affiliation:
City College of New York, CUNY, Convent Avenue at 138th Street, New York, NY 10031, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we derive geometric and analytic properties of invariant sets, including orbit closures, of a large class of piecewise-affine maps $T$ on 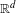$\mathbb{R}^{d}$. We assume that (i) $T$ consists of finitely many affine maps defined on a Borel measurable partition of 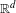$\mathbb{R}^{d}$, (ii) there is a lattice 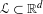$\mathscr{L}\subset \mathbb{R}^{d}$ that contains all of the mutual differences of the translation vectors of these affine maps, and (iii) all of the affine maps have the same linear part that is an automorphism of 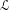$\mathscr{L}$. We prove that finite-volume invariant sets of such piecewise-affine maps always consist of translational tiles relative to this lattice, up to some multiplicity. When the partition is Jordan measurable, we show that closures of bounded orbits of $T$ are invariant and yield Jordan measurable tiles, again up to some multiplicity. In the latter case, we show that compact $T$-invariant sets also consist of Jordan measurable tiles. We then utilize these results to quantify the rate of convergence of ergodic averages for $T$ in the case of bounded single tiles.

Keywords

arithmetic and algebraic dynamicslow-dimensional dynamicstilingstopological dynamics

MSC classification

Secondary: 11K38: Irregularities of distribution, discrepancy
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2183 - 2218
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashwin, P., Fu, X. and Lin, C.. On planar piecewise and two-torus parabolic maps. Internat. J. Bifur. Chaos 19(07) (2009), 2383–2390.CrossRefGoogle Scholar
Ashwin, P., Fu, X.-C., Nishikawa, T. and Zyczkowski, K.. Invariant sets for discontinuous parabolic area-preserving torus maps. Nonlinearity 13(3) (2000), 819.CrossRefGoogle Scholar
Adler, R., Kitchens, B., Martens, M., Pugh, C., Shub, M. and Tresser, C.. Convex dynamics and applications. Ergod. Th. & Dynam. Sys. 25(4) (2005), 321–352.CrossRefGoogle Scholar
Adler, R., Nowicki, T., Świrszcz, G., Tresser, C. and Winograd, S.. Error diffusion on acute simplices: invariant tiles. Israel J. Math. 221 (2017), 445–469.CrossRefGoogle Scholar
Adler, R., Nowicki, T., Świrszcz, G. and Tresser, C.. Convex dynamics with constant input. Ergod. Th. & Dynam. Sys. 30(8) (2010), 957–972.CrossRefGoogle Scholar
Alexander, J. C. and Yorke, J. A.. Fat baker’s transformations. Ergod. Th. & Dynam. Sys. 4(3) (1984), 1–23.CrossRefGoogle Scholar
Blondel, V. D., Bournez, O., Koiran, P. and Tsitsiklis, J. N.. The stability of saturated linear dynamical systems is undecidable. J. Comput. System Sci. 62(3) (2001), 442–462.CrossRefGoogle Scholar
Brandolini, L., Colzani, L., Gigante, G. and Travaglini, G.. On the Koksma–Hlawka inequality. J. Complexity 29(2) (2013), 158–172.CrossRefGoogle Scholar
Boyarsky, A. and Góra, P.. Laws of Chaos (Probability and its Applications). Birkhäuser Boston, Boston, MA, 1997.CrossRefGoogle Scholar
Brown, J. R.. Ergodic Theory and Topological Dynamics (Pure and Applied Mathematics, 70). Academic Press, New York, 1976.Google Scholar
Bruin, H. and Troubetzkoy, S.. The Gauss map on a class of interval translation mappings. Israel J. Math. 137(1) (2003), 125–148.CrossRefGoogle Scholar
Dani, S. G.. Dynamical systems on homogeneous spaces. Dynamical Systems, Ergodic Theory and Applications (Encyclopaedia of Mathematical Sciences, 100), revised edn. Ed. Sinai, Y. G.. Springer, Berlin, 2000, pp. 264–359.Google Scholar
Daubechies, I. and DeVore, R.. Approximating a bandlimited function using very coarsely quantized data: a family of stable sigma-delta modulators of arbitrary order. Ann. of Math. (2) 158(2) (2003), 679–710.CrossRefGoogle Scholar
Daafouz, J., Di Benedetto, M. D., Blondel, V. D., Ferrari-Trecate, G., Hetel, L., Johansson, M., Juloski, A. L., Paoletti, S., Pola, G., Santis, E. De and Vidal, R.. Switched and piecewise affine systems. Handbook of Hybrid Systems Control. Cambridge University Press, Cambridge, 2009, pp. 87–137.CrossRefGoogle Scholar
Daubechies, I., DeVore, R. A., Sinan Güntürk, C. and Vaishampayan, V. A.. A/D conversion with imperfect quantizers. IEEE Trans. Inform. Theory 52(3) (2006), 874–885.CrossRefGoogle Scholar
Daubechies, I., Güntürk, S., Wang, Y. and Yılmaz, Ö.. The golden ratio encoder. IEEE Trans. Inform. Theory 56(10) (2010), 5097–5110.CrossRefGoogle Scholar
Dajani, K. and Kraaikamp, C.. From greedy to lazy expansions and their driving dynamics. Expo. Math. 20(4) (2002), 315–327.CrossRefGoogle Scholar
Federer, H.. Geometric Measure Theory (Die Grundlehren der mathematischen Wissenschaften, Band 153). Springer, New York, 1969.Google Scholar
Góra, P. and Boyarsky, A.. Absolutely continuous invariant measures for piecewise expanding C 2 transformation in RN. Israel J. Math. 67(3) (1989), 272–286.CrossRefGoogle Scholar
Sinan Güntürk, C. and Thao, N. T.. Refined error analysis in second-order 𝛴𝛥 modulation with constant inputs. IEEE Trans. Inform. Theory 50(5) (2004), 839–860.CrossRefGoogle Scholar
Sinan Güntürk, C. and Thao, N. T.. Ergodic dynamics in sigma-delta quantization: tiling invariant sets and spectral analysis of error. Adv. Appl. Math. 34(3) (2005), 523–560.CrossRefGoogle Scholar
Sinan Güntürk, C.. Mathematics of analog-to-digital conversion. Comm. Pure Appl. Math. 65(12) (2012), 1671–1696.CrossRefGoogle Scholar
Hlawka, E.. Discrepancy and Riemann integration. Studies in Pure Mathematics (Presented to Richard Rado). Academic Press, London, 1971, pp. 121–129.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences (Pure and Applied Mathematics). Wiley-Interscience [John Wiley & Sons], New York, 1974.Google Scholar
Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186(1974) (1973), 481–488.CrossRefGoogle Scholar
Masur, H. and Tabachnikov, S.. Rational billiards and flat structures. Handbook Dyn. Sys. 1 (2002), 1015–1089.Google Scholar
Płotka, Krzysztof. On lineability and additivity of real functions with finite preimages. J. Math. Anal. Appl. 421(2) (2015), 1396–1404.CrossRefGoogle Scholar
Tao, T.. Higher Order Fourier Analysis (Graduate Studies in Mathematics, 142). American Mathematical Society, Providence, RI, 2012.CrossRefGoogle Scholar
Veech, W. A. Strict ergodicity in zero dimensional dynamical systems and the Kronecker–Weyl theorem mod 2. Trans. Amer. Math. Soc. 140 (1969), 1–33.Google Scholar
Yılmaz, Ö.. Stability analysis for several second-order sigma-delta methods of coarse quantization of bandlimited functions. Constr. Approx. 18(4) (2002), 599–623.CrossRefGoogle Scholar
Zhang, Y. and Lin, C.. Invariant measures with bounded variation densities for piecewise area preserving maps. Ergod. Th. & Dynam. Sys. 33(4) (2013), 624–642.CrossRefGoogle Scholar