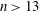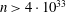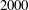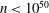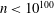We prove an asymptotic formula for squarefree numbers in arithmetic progressions, improving previous results by Prachar and Hooley. As a consequence we improve a lower bound of Heath-Brown for the least squarefree number in an arithmetic progression.

We show that if a Barker sequence of length $n>13$ exists, then either n $=$ 3 979 201 339 721 749 133 016 171 583 224 100, or $n > 4\cdot 10^{33}$. This improves the lower bound on the length of a long Barker sequence by a factor of nearly $2000$. We also obtain eighteen additional integers $n<10^{50}$ that cannot be ruled out as the length of a Barker sequence, and find more than 237 000 additional candidates $n<10^{100}$. These results are obtained by completing extensive searches for Wieferich prime pairs and using them, together with a number of arithmetic restrictions on $n$, to construct qualifying integers below a given bound. We also report on some updated computations regarding open cases of the circulant Hadamard matrix problem.

It is proved that the 3-part of the class number of a quadratic field $\mathbb{Q}(\sqrt{D})$ is $O(|D|^{55/112 + \ep})$ in general and $O(|D|^{5/12+\ep})$ if $|D|$ has a divisor of size $|D|^{5/6}$. These bounds follow as results of nontrivial estimates for the number of solutions to the congruence $x^a \,{\con}\, y^b$ modulo $q$ in the ranges $x \,{\leqslant}\,X$ and $y\,{\leqslant}\, Y$, where $a,b$ are nonzero integers and $q$ is a square-free positive integer. Furthermore, it is shown that the number of elliptic curves over $\Q$ with conductor $N$ is $O(N^{55/112 + \ep})$ in general and $O(N^{5/12 + \ep})$ if $N$ has a divisor of size $N^{5/6}$. These results are the first improvements to the trivial bound $O(|D|^{1/2 + \ep})$ and the resulting bound $O(N^{1/2 + \ep})$ for the 3-part and the number of elliptic curves, respectively.