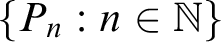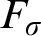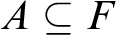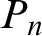2 results
COUNTABLY PERFECTLY MEAGER SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 1214-1227
- Print publication:
- September 2021
-
- Article
- Export citation
Amoeba reals
-
- Journal:
- The Journal of Symbolic Logic / Volume 60 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1168-1185
- Print publication:
- December 1995
-
- Article
- Export citation