Published online by Cambridge University Press: 07 June 2021
We study a strengthening of the notion of a perfectly meager set. We say that a subset A of a perfect Polish space X is countably perfectly meager in X, if for every sequence of perfect subsets 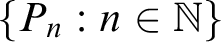 $\{P_n: n \in \mathbb N\}$
of X, there exists an
$\{P_n: n \in \mathbb N\}$
of X, there exists an 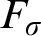 $F_\sigma $
-set F in X such that
$F_\sigma $
-set F in X such that 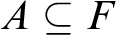 $A \subseteq F$
and
$A \subseteq F$
and  $F\cap P_n$
is meager in
$F\cap P_n$
is meager in 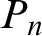 $P_n$
for each n. We give various characterizations and examples of countably perfectly meager sets. We prove that not every universally meager set is countably perfectly meager correcting an earlier result of Bartoszyński.
$P_n$
for each n. We give various characterizations and examples of countably perfectly meager sets. We prove that not every universally meager set is countably perfectly meager correcting an earlier result of Bartoszyński.