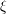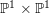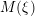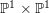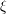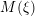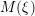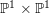1 Introduction
In this paper, we provide an approach to computing extremal rays of the effective cone of moduli spaces of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. In particular, we show that this approach succeeds in computing the entire effective cone on the first fifteen Hilbert schemes of points.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. In particular, we show that this approach succeeds in computing the entire effective cone on the first fifteen Hilbert schemes of points.
The effective cone of a scheme is an important invariant which controls much of the geometry of the scheme [Reference LazarsfeldLaz]. For Mori dream spaces, it determines all of the birational contractions of the space [Reference Hu and KeelHK]. However, in general, determining the effective cone of a scheme is a very difficult question. There has been progress computing the effective cone for certain moduli spaces.
Moduli spaces of sheaves (on a fixed surface) are one kind of moduli space that has been extensively studied (e.g., [Reference Bayer, Craw and ZhangBCZ], [Reference Bolognese, Huizenga, Lin, Riedl, Schmidt, Woolf and ZhaoBHL+], [Reference Choi and ChungCC], [Reference Coskun and HuizengaCH3], [Reference Drézet and NarasimhanDN], [Reference FogartyFog], [Reference GiesekerGie], [Reference Li and QinLQ1], [Reference MaruyamaMar2], [Reference MaruyamaMar1], [Reference Marian and OpreaMO1], [Reference Marian and OpreaMO2], [Reference Matsuki and WentworthMW], [Reference TakemotoTak], [Reference YoshiokaYos3]). In this setting, the geometry of the underlying variety can be used to study the moduli space. In the past decade, Bridgeland stability has motivated a program to compute the effective cones of these moduli spaces by corresponding the edge of the effective cone with the collapsing wall of Bridgeland stability. The recent advances in Bridgeland stability (e.g., [Reference Arcara and BertramAB], [Reference BridgelandBri1], [Reference BridgelandBri2], [Reference Bayer, Bertram, Macrì and TodaBBMT], [Reference Bertram and MartinezBM3], [Reference Bayer and MacrìBM2], [Reference Bayer, Macrì and StellariBMS], [Reference Bayer, Macrì and TodaBMT], [Reference Coskun, Hyeon and ParkCHP], [Reference Lo and QinLQ2], [Reference MacrìMac2], [Reference MaciociaMac1], [Reference Maciocia and MeachanMM], [Reference Maciocia and PiyaratneMP], [Reference Macrì and SchmidtMS], [Reference NuerNue2], [Reference SchmidtSch], [Reference TodaTod3], [Reference TodaTod2], [Reference TodaTod1], [Reference TramelTra], [Reference YoshiokaYos3], [Reference YoshiokaYos4]) have helped this approach be successful in general on K3 surfaces [Reference Bayer and MacrìBM1], Enriques surfaces [Reference NuerNue1], Abelian surfaces [Reference YoshiokaYos2], and
![]() $\mathbb{P}^{2}$
[Reference Coskun, Huizenga and WoolfCHW].
$\mathbb{P}^{2}$
[Reference Coskun, Huizenga and WoolfCHW].
The proof in the last case varies greatly from the proofs in the other cases as it is a surface of negative Kodaira dimension. More generally, there has been a lot of work on
![]() $\mathbb{P}^{2}$
(e.g., [Reference Arcara, Bertram, Coskun and HuizengaABCH], [Reference Bertram, Martinez and WangBMW], [Reference Coskun and HuizengaCH4], [Reference Coskun and HuizengaCH1], [Reference Coskun and HuizengaCH2], [Reference Drézet and Le PotierDLP], [Reference HuizengaHui2], [Reference HuizengaHui1], [Reference Chunyi and ZhaoCZ2], [Reference Chunyi and ZhaoCZ1], [Reference WoolfWoo]). Although much of this work has been extended to more rational and ruled surfaces (e.g., [Reference AbeAbe], [Reference BallicoBal], [Reference GöttscheGöt], [Reference KarpovKar], [Reference MozgovoyMoz], [Reference QinQin]), no general method to compute the entire effective cone of a moduli space of sheaves on
$\mathbb{P}^{2}$
(e.g., [Reference Arcara, Bertram, Coskun and HuizengaABCH], [Reference Bertram, Martinez and WangBMW], [Reference Coskun and HuizengaCH4], [Reference Coskun and HuizengaCH1], [Reference Coskun and HuizengaCH2], [Reference Drézet and Le PotierDLP], [Reference HuizengaHui2], [Reference HuizengaHui1], [Reference Chunyi and ZhaoCZ2], [Reference Chunyi and ZhaoCZ1], [Reference WoolfWoo]). Although much of this work has been extended to more rational and ruled surfaces (e.g., [Reference AbeAbe], [Reference BallicoBal], [Reference GöttscheGöt], [Reference KarpovKar], [Reference MozgovoyMoz], [Reference QinQin]), no general method to compute the entire effective cone of a moduli space of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
has been given. This is because the proof in [Reference Coskun, Huizenga and WoolfCHW] relies heavily on properties that are unique to
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
has been given. This is because the proof in [Reference Coskun, Huizenga and WoolfCHW] relies heavily on properties that are unique to
![]() $\mathbb{P}^{2}$
.
$\mathbb{P}^{2}$
.
This paper provides the general framework to potentially extend the results of [Reference Coskun, Huizenga and WoolfCHW] to del Pezzo and Hirzebruch surfaces and explicitly works out the framework on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Under some additional hypotheses, this framework gives a method to compute the entire effective cone of moduli spaces of sheaves on
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Under some additional hypotheses, this framework gives a method to compute the entire effective cone of moduli spaces of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. The increased ranks of the Picard group and the derived category in the case of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. The increased ranks of the Picard group and the derived category in the case of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
compared to
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
compared to
![]() $\mathbb{P}^{2}$
make the proofs and results significantly harder to obtain.
$\mathbb{P}^{2}$
make the proofs and results significantly harder to obtain.
These difficulties force us to add two new ingredients to the method. The first new addition is putting the choice of an exceptional collection in the context of the work of Rudakov et al. on coils and helices (e.g., [Reference RudakovRud1], [Reference Nogin and ZubeNZ], [Reference GorodentsevGor]). Certain special properties of exceptional collections on
![]() $\mathbb{P}^{2}$
that were used are no longer needed once the choice is put in these terms. The second addition is providing a way to link neighboring extremal rays to show that there are no missing extremal rays in between them. This addition is needed as the Picard rank of the moduli spaces are now higher than two, and it will be essential for expanding these results to other surfaces.
$\mathbb{P}^{2}$
that were used are no longer needed once the choice is put in these terms. The second addition is providing a way to link neighboring extremal rays to show that there are no missing extremal rays in between them. This addition is needed as the Picard rank of the moduli spaces are now higher than two, and it will be essential for expanding these results to other surfaces.
Let
![]() $\unicode[STIX]{x1D709}$
be a Chern character of positive integer rank on
$\unicode[STIX]{x1D709}$
be a Chern character of positive integer rank on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Then there is a nonempty moduli space
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Then there is a nonempty moduli space
![]() $M(\unicode[STIX]{x1D709})$
that parameterizes
$M(\unicode[STIX]{x1D709})$
that parameterizes
![]() $S$
-equivalence classes of semistable sheaves (with respect to the anticanonical divisor) with that Chern character on
$S$
-equivalence classes of semistable sheaves (with respect to the anticanonical divisor) with that Chern character on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
iff
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
iff
![]() $\unicode[STIX]{x1D709}$
satisfies a set of Bogomolov type inequalities given by Rudakov in [Reference RudakovRud2]. It is an irreducible [Reference WalterWal], normal [Reference WalterWal], projective variety [Reference MaruyamaMar3]. We show that these spaces are
$\unicode[STIX]{x1D709}$
satisfies a set of Bogomolov type inequalities given by Rudakov in [Reference RudakovRud2]. It is an irreducible [Reference WalterWal], normal [Reference WalterWal], projective variety [Reference MaruyamaMar3]. We show that these spaces are
![]() $\mathbb{Q}$
-factorial [Proposition 2.14] and, furthermore, are Mori dream spaces [Theorem 2.15].
$\mathbb{Q}$
-factorial [Proposition 2.14] and, furthermore, are Mori dream spaces [Theorem 2.15].
We construct effective Brill–Noether divisors of the form
We create an algorithmic method to produce these divisors. Conjecturally, this method produces a set of divisors spanning the effective cone.
Conjecture.
The method laid out in this paper produces a set of effective divisors spanning the effective cone for
![]() $M(\unicode[STIX]{x1D709})$
for all
$M(\unicode[STIX]{x1D709})$
for all
![]() $\unicode[STIX]{x1D709}$
above Rudakov’s surface.
$\unicode[STIX]{x1D709}$
above Rudakov’s surface.
One reason for this conjecture is that the method computes the entire effective cone of the first fifteen Hilbert schemes of points on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
(which is as many as we applied it to). In the last section of the paper, we explicitly compute the effective cone of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
(which is as many as we applied it to). In the last section of the paper, we explicitly compute the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
for
![]() $n\leqslant 16$
as well as several instances of types of extremal rays that show up in infinite sequences of
$n\leqslant 16$
as well as several instances of types of extremal rays that show up in infinite sequences of
![]() $n$
, and we give a rank two example. Even if this method fails to fully compute the effective cone of every moduli space, it does give a method to produce effective divisors on these moduli spaces.
$n$
, and we give a rank two example. Even if this method fails to fully compute the effective cone of every moduli space, it does give a method to produce effective divisors on these moduli spaces.
The proofs of the steps of the method follow from constructing birational maps or Fano fibrations to simpler, Picard rank one, spaces and analyzing them to find our extremal divisors. Given a birational map or Fano fibration, giving a divisor on an edge of the effective cone follows directly. The difficult part of the process is constructing the maps.
The moduli spaces that we map to are moduli spaces of Kronecker modules,
![]() $Kr_{V}(m,n)$
. The way we construct the map is to find a resolution of the general element of
$Kr_{V}(m,n)$
. The way we construct the map is to find a resolution of the general element of
![]() $M(\unicode[STIX]{x1D709})$
containing a Kronecker module and then to forget the rest of the resolution. The key then is to find resolutions of the general element of the moduli space that contain Kronecker modules. On
$M(\unicode[STIX]{x1D709})$
containing a Kronecker module and then to forget the rest of the resolution. The key then is to find resolutions of the general element of the moduli space that contain Kronecker modules. On
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we have a powerful tool for finding resolutions of sheaves in the form of a generalized Beilinson spectral sequence [Reference GorodentsevGor]. Using this method for finding a resolution makes it clear that the extremal divisors we construct are Brill–Noether divisors as they are defined in terms of the jumping of ranks of cohomology groups appearing in the spectral sequence. Using that spectral sequence, finding resolutions with Kronecker modules is reduced to finding the right collections of exceptional bundles spanning the derived category.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we have a powerful tool for finding resolutions of sheaves in the form of a generalized Beilinson spectral sequence [Reference GorodentsevGor]. Using this method for finding a resolution makes it clear that the extremal divisors we construct are Brill–Noether divisors as they are defined in terms of the jumping of ranks of cohomology groups appearing in the spectral sequence. Using that spectral sequence, finding resolutions with Kronecker modules is reduced to finding the right collections of exceptional bundles spanning the derived category.
We find the elements of the right collections by studying Rudakov’s classification of stable bundles over the hyperbola of Chern characters
![]() $\unicode[STIX]{x1D701}$
with the properties
$\unicode[STIX]{x1D701}$
with the properties
Rudakov’s necessary and sufficient inequalities for a Chern character to be stable each came from an exceptional bundle on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, and the right collections of exceptional bundles are determined by which exceptional bundles have the sharpest inequalities over this curve. Say that
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, and the right collections of exceptional bundles are determined by which exceptional bundles have the sharpest inequalities over this curve. Say that
![]() $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
is an exceptional pair of bundles that have the sharpest inequalities over that curve. Then the resolution we get for the general
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
is an exceptional pair of bundles that have the sharpest inequalities over that curve. Then the resolution we get for the general
![]() $U\in M(\unicode[STIX]{x1D709})$
might look like
$U\in M(\unicode[STIX]{x1D709})$
might look like
Using this resolution, we get the maps we need. There are several cases to be dealt with. On
![]() $\mathbb{P}^{2}$
, there was only two cases. The new cases are a phenomenon that will persist on other surfaces and are not unique to
$\mathbb{P}^{2}$
, there was only two cases. The new cases are a phenomenon that will persist on other surfaces and are not unique to
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
We summarize the approach in the most common case. The resolution of the general object of the moduli space in this case looks like the example resolution above. Then the resolution has four objects and four maps. The map
![]() $W:F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{\ast m_{1}}$
gives the required Kronecker module. We map to the Kronecker moduli space corresponding to it,
$W:F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{\ast m_{1}}$
gives the required Kronecker module. We map to the Kronecker moduli space corresponding to it,
![]() $f:M(\unicode[STIX]{x1D709}){\dashrightarrow}Kr_{V}(m,n)$
. Constructing the Brill–Noether divisor in this case is slightly tricky because the bundle whose corresponding divisor spans the extremal ray is not obviously cohomologically orthogonal to the general object of the moduli space. That orthogonality is established using properties of the Kronecker modules in the resolution of a bundle whose corresponding divisor spans the extremal ray and in the resolution of the general object.
$f:M(\unicode[STIX]{x1D709}){\dashrightarrow}Kr_{V}(m,n)$
. Constructing the Brill–Noether divisor in this case is slightly tricky because the bundle whose corresponding divisor spans the extremal ray is not obviously cohomologically orthogonal to the general object of the moduli space. That orthogonality is established using properties of the Kronecker modules in the resolution of a bundle whose corresponding divisor spans the extremal ray and in the resolution of the general object.
1.1 Organization
In Section 2, we extensively lay out the necessary background and prove two properties of the moduli spaces we want to study. In Section 3, we define primary orthogonal Chern characters via controlling exceptional pairs. In Section 4, we use the controlling pairs and a generalized Beilinson spectral sequence to resolve the general object of our moduli space which constructs effective divisors on our space. In Section 5, we use these resolutions to construct maps from our moduli space to spaces of Kronecker modules that provide the dual moving curves we need. In Section 6, we use these results to compute extremal rays of the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
. Finally, in Section 7, we compute the effective cone of the Hilbert scheme of
$M(\unicode[STIX]{x1D709})$
. Finally, in Section 7, we compute the effective cone of the Hilbert scheme of
![]() $n$
points for
$n$
points for
![]() $n\leqslant 16$
, provide some recurring examples of types of corners, and work out a rank two example.
$n\leqslant 16$
, provide some recurring examples of types of corners, and work out a rank two example.
2 Preliminaries
In this section, we discuss all preliminary material needed to understand the following sections. We base our discussion of the general preliminaries on sections in [Reference Huybrechts and LehnHL] and [Reference Le PotierLP]. For the subsections more specific to
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we also draw on [Reference RudakovRud1] and [Reference RudakovRud2].
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we also draw on [Reference RudakovRud1] and [Reference RudakovRud2].
In this paper, all sheaves are coherent torsion-free sheaves. Other than Proposition 2.14 and Theorem 2.15, we work exclusively on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
and so drop that from labels as convenient. Let
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
and so drop that from labels as convenient. Let
![]() $E$
be a sheaf with Chern character
$E$
be a sheaf with Chern character
![]() $\unicode[STIX]{x1D709}=\left(\operatorname{ch}_{0},\operatorname{ch}_{1},\operatorname{ch}_{2}\right)$
.
$\unicode[STIX]{x1D709}=\left(\operatorname{ch}_{0},\operatorname{ch}_{1},\operatorname{ch}_{2}\right)$
.
2.1 Slopes and the discriminant
Recall that for a locally free sheaf, we have
Using this equality, we define the slope and discriminant of
![]() $E$
to be
$E$
to be
The slope and discriminant are more convenient than the Chern character for us as they have the property that
We should note that these notions are easily extended to Chern characters in
![]() $K\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\otimes \mathbb{R}$
.
$K\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\otimes \mathbb{R}$
.
On a Picard rank one variety, the slope is a generalization of the degree of a line bundle to higher rank vector bundles. On higher Picard rank varieties, we can think of the slope as a generalization of a multi-degree that carries the information of the degree for every choice of embedding. Sometimes we would like an analog to the degree with respect to a specific embedding so we give the following definition. The slope with respect to an ample divisor
![]() $H$
is
$H$
is
We also call this the
![]() $H$
-Slope of
$H$
-Slope of
![]() $E$
. The two ample divisors that we use in this paper are
$E$
. The two ample divisors that we use in this paper are
![]() ${\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(1,1)$
and
${\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(1,1)$
and
![]() ${\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(1,2)$
for which the slopes are denoted
${\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(1,2)$
for which the slopes are denoted
![]() $\unicode[STIX]{x1D707}_{1,1}$
and
$\unicode[STIX]{x1D707}_{1,1}$
and
![]() $\unicode[STIX]{x1D707}_{1,2}$
, respectively.
$\unicode[STIX]{x1D707}_{1,2}$
, respectively.
We want to write the Riemann–Roch formula in terms of these invariants so let us recall the definition of the (reduced) Hilbert polynomial.
Definition 2.1. The Hilbert polynomial of a sheaf
![]() ${\mathcal{F}}$
with respect to an ample line bundle
${\mathcal{F}}$
with respect to an ample line bundle
![]() $H$
is
$H$
is
where
![]() ${\mathcal{F}}(k)={\mathcal{F}}\otimes H^{\otimes k}$
, where the dimension of
${\mathcal{F}}(k)={\mathcal{F}}\otimes H^{\otimes k}$
, where the dimension of
![]() ${\mathcal{F}}$
is
${\mathcal{F}}$
is
![]() $d$
, and where we think of this as a polynomial in the variable
$d$
, and where we think of this as a polynomial in the variable
![]() $k$
.
$k$
.
Definition 2.2. The reduced Hilbert polynomial of a sheaf
![]() ${\mathcal{F}}$
with respect to an ample line bundle
${\mathcal{F}}$
with respect to an ample line bundle
![]() $H$
is defined to be
$H$
is defined to be
where
![]() $d$
is the dimension of
$d$
is the dimension of
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
The Hilbert polynomial, unlike the individual cohomology groups it sums over, is a numerical object that is entirely determined by the Chern character of the sheaf and the Chern character of the ample line bundle.
When
![]() $\operatorname{ch}_{0}(E)>0$
, we can write the Riemann–Roch formula as
$\operatorname{ch}_{0}(E)>0$
, we can write the Riemann–Roch formula as
where
![]() $P(\unicode[STIX]{x1D707})$
is the Hilbert polynomial of
$P(\unicode[STIX]{x1D707})$
is the Hilbert polynomial of
![]() ${\mathcal{O}}$
,
${\mathcal{O}}$
,
2.1.1 Classical stability conditions
Using our notations of slope and the reduced Hilbert polynomial, we can now define the different classical notions of stability that we need.
Definition 2.3. A sheaf
![]() ${\mathcal{F}}$
is slope (semi-)stable with respect to an ample line bundle
${\mathcal{F}}$
is slope (semi-)stable with respect to an ample line bundle
![]() $H$
if for all proper subsheaves
$H$
if for all proper subsheaves
![]() ${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
,
${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
,
A stronger notation of stability is the notion of Gieseker stability.
Definition 2.4. A sheaf
![]() ${\mathcal{F}}$
is Gieseker (semi-)stable with respect to an ample divisor
${\mathcal{F}}$
is Gieseker (semi-)stable with respect to an ample divisor
![]() $H$
if for all proper subsheaves
$H$
if for all proper subsheaves
![]() ${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
,
${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
,
![]() $p_{{\mathcal{F}}^{\prime }}\left({\leqslant}\right)<p_{{\mathcal{F}}}$
where the polynomials are compared for all sufficiently large input values. We also call this
$p_{{\mathcal{F}}^{\prime }}\left({\leqslant}\right)<p_{{\mathcal{F}}}$
where the polynomials are compared for all sufficiently large input values. We also call this
![]() $\unicode[STIX]{x1D6FE}$
(semi-)stability.
$\unicode[STIX]{x1D6FE}$
(semi-)stability.
The ordering on the polynomials could also have been phrased as the lexicographic ordering on their coefficients starting from the highest degree term’s coefficient and working down. The condition on the Hilbert polynomial is equivalent on surfaces to requiring
![]() $\unicode[STIX]{x1D707}_{H}({\mathcal{F}}^{\prime })\leqslant \unicode[STIX]{x1D707}_{H}({\mathcal{F}})$
and, in the case of equality,
$\unicode[STIX]{x1D707}_{H}({\mathcal{F}}^{\prime })\leqslant \unicode[STIX]{x1D707}_{H}({\mathcal{F}})$
and, in the case of equality,
![]() $\unicode[STIX]{x1D6E5}({\mathcal{F}}^{\prime })\left({\geqslant}\right)>\unicode[STIX]{x1D6E5}({\mathcal{F}})$
.
$\unicode[STIX]{x1D6E5}({\mathcal{F}}^{\prime })\left({\geqslant}\right)>\unicode[STIX]{x1D6E5}({\mathcal{F}})$
.
These two notations of stability and semistability are related by a string of implications that seems slightly odd at first, but becomes clear using this last equivalence:
As we are focused on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, one additional notion of stability is relevant.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, one additional notion of stability is relevant.
Definition 2.5. A sheaf
![]() ${\mathcal{F}}$
is
${\mathcal{F}}$
is
![]() $\overline{\unicode[STIX]{x1D6FE}}$
(semi-)stable if it is Gieseker semistable with respect to
$\overline{\unicode[STIX]{x1D6FE}}$
(semi-)stable if it is Gieseker semistable with respect to
![]() ${\mathcal{O}}(1,1)$
and for all proper subsheaves
${\mathcal{O}}(1,1)$
and for all proper subsheaves
![]() ${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
, if
${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
, if
![]() $\unicode[STIX]{x1D707}_{1,1}\left({\mathcal{F}}^{\prime }\right)=\unicode[STIX]{x1D707}_{1,1}\left({\mathcal{F}}\right)$
and
$\unicode[STIX]{x1D707}_{1,1}\left({\mathcal{F}}^{\prime }\right)=\unicode[STIX]{x1D707}_{1,1}\left({\mathcal{F}}\right)$
and
![]() $\unicode[STIX]{x1D6E5}\left({\mathcal{F}}^{\prime }\right)=\unicode[STIX]{x1D6E5}\left({\mathcal{F}}\right)$
, then
$\unicode[STIX]{x1D6E5}\left({\mathcal{F}}^{\prime }\right)=\unicode[STIX]{x1D6E5}\left({\mathcal{F}}\right)$
, then
![]() $\unicode[STIX]{x1D707}_{1,2}\left({\mathcal{F}}^{\prime }\right)\left({\leqslant}\right)<\unicode[STIX]{x1D707}_{1,2}\left({\mathcal{F}}\right)$
.
$\unicode[STIX]{x1D707}_{1,2}\left({\mathcal{F}}^{\prime }\right)\left({\leqslant}\right)<\unicode[STIX]{x1D707}_{1,2}\left({\mathcal{F}}\right)$
.
Again we have implications:
Because Gieseker stability generalizes to all varieties, it might seem odd to add a third, very variety specific, condition. However, adding this third condition allows
![]() $\overline{\unicode[STIX]{x1D6FE}}$
stability to order all Chern characters in a way that was not possible for slope or Gieseker stability. This order is possible with
$\overline{\unicode[STIX]{x1D6FE}}$
stability to order all Chern characters in a way that was not possible for slope or Gieseker stability. This order is possible with
![]() $\overline{\unicode[STIX]{x1D6FE}}$
stability because it has three conditions that can distinguish the three variables for a Chern character on
$\overline{\unicode[STIX]{x1D6FE}}$
stability because it has three conditions that can distinguish the three variables for a Chern character on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
: the two coordinates of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
: the two coordinates of
![]() $c_{1}$
and the coordinate of
$c_{1}$
and the coordinate of
![]() $c_{2}$
.
$c_{2}$
.
2.2 Exceptional bundles
In this subsection, we start with a relative version of Euler characteristic. We eventually see that sheaves
![]() $E$
with relative Euler characteristic
$E$
with relative Euler characteristic
![]() $\unicode[STIX]{x1D712}(E,E)=1$
control the geometry of our moduli spaces.
$\unicode[STIX]{x1D712}(E,E)=1$
control the geometry of our moduli spaces.
2.2.1 The relative Euler characteristic
The relative Euler characteristic of two sheaves on a variety
![]() $X$
of dimension
$X$
of dimension
![]() $n$
is
$n$
is
where
![]() $\operatorname{ext}^{i}(E,F)=\dim (\operatorname{Ext}^{i}(E,F))$
. For locally free sheaves, we can equivalently define it by the formula
$\operatorname{ext}^{i}(E,F)=\dim (\operatorname{Ext}^{i}(E,F))$
. For locally free sheaves, we can equivalently define it by the formula
Restricting to the case where
![]() $n=2$
, we again write out Hirzebruch–Riemann–Roch in order to explicitly compute this as
$n=2$
, we again write out Hirzebruch–Riemann–Roch in order to explicitly compute this as
where
![]() $P(x,y)=(x+1)(y+1)$
is the Euler characteristic of
$P(x,y)=(x+1)(y+1)$
is the Euler characteristic of
![]() ${\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(x,y)$
.
${\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(x,y)$
.
Using the alternate definition of relative Euler characteristic, we define a bilinear pairing on
![]() $K\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)$
by
$K\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)$
by
Then we define the orthogonal complement of
![]() $E$
, denoted
$E$
, denoted
![]() $\operatorname{ch}(E)^{\bot }$
, to be all bundles
$\operatorname{ch}(E)^{\bot }$
, to be all bundles
![]() $F$
such that
$F$
such that
![]() $(E,F)=0$
. Note that the pairing is symmetric so the orthogonal complement does not depend on whether
$(E,F)=0$
. Note that the pairing is symmetric so the orthogonal complement does not depend on whether
![]() $E$
is the first or second element in the pairing.
$E$
is the first or second element in the pairing.
The
![]() $\operatorname{Ext}$
groups we used to define the relative Euler characteristic also allow us to describe a set of vector bundles that control the geometry of
$\operatorname{Ext}$
groups we used to define the relative Euler characteristic also allow us to describe a set of vector bundles that control the geometry of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
Definition 2.6. A sheaf
![]() $E$
is exceptional if
$E$
is exceptional if
![]() $\operatorname{Hom}(E,E)=\mathbb{C}$
and
$\operatorname{Hom}(E,E)=\mathbb{C}$
and
![]() $\operatorname{Ext}^{i}(E,E)=0$
for all
$\operatorname{Ext}^{i}(E,E)=0$
for all
![]() $i>0$
.
$i>0$
.
We say a Chern character (slope) is exceptional if there is an exceptional sheaf with that character (slope). The prototypical exceptional sheaves are the line bundles,
![]() ${\mathcal{O}}(a,b)$
. Many of the properties of line bundles pass to exceptional sheaves on
${\mathcal{O}}(a,b)$
. Many of the properties of line bundles pass to exceptional sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. We list some of these properties without repeating the proofs. Their proofs are in the previously mentioned paper by Gorodentsev [Reference GorodentsevGor].
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. We list some of these properties without repeating the proofs. Their proofs are in the previously mentioned paper by Gorodentsev [Reference GorodentsevGor].
Proposition 2.7. On
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we have the following results.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we have the following results.
∙ Every exceptional sheaf is a vector bundle.
∙ There exists a unique exceptional bundle,
 $E$
, for each exceptional slope.
$E$
, for each exceptional slope.∙ The two coordinates of the first Chern class are coprime with the rank of
 $E$
.
$E$
.∙ The denominator of
 $\unicode[STIX]{x1D707}_{1,1}(E)$
is the rank of
$\unicode[STIX]{x1D707}_{1,1}(E)$
is the rank of
 $E$
.
$E$
.∙ Exceptional bundles are stable with respect to
 ${\mathcal{O}}(1,1)$
.
${\mathcal{O}}(1,1)$
.
Given these properties, it makes sense to define the rank of an exceptional slope
![]() $\unicode[STIX]{x1D708}$
to be the smallest
$\unicode[STIX]{x1D708}$
to be the smallest
![]() $r\in \mathbb{Z}$
such that
$r\in \mathbb{Z}$
such that
![]() $r\unicode[STIX]{x1D707}_{1,1}(\unicode[STIX]{x1D708})\in \mathbb{Z}$
. Also, set the notation
$r\unicode[STIX]{x1D707}_{1,1}(\unicode[STIX]{x1D708})\in \mathbb{Z}$
. Also, set the notation
![]() $E_{\frac{a}{r},\frac{b}{r}}$
for the unique exceptional bundle with slope
$E_{\frac{a}{r},\frac{b}{r}}$
for the unique exceptional bundle with slope
![]() $\left(\frac{a}{r},\frac{b}{r}\right)$
. Given a Chern character
$\left(\frac{a}{r},\frac{b}{r}\right)$
. Given a Chern character
![]() $\unicode[STIX]{x1D709}$
with slope
$\unicode[STIX]{x1D709}$
with slope
![]() $\unicode[STIX]{x1D6FC}=\left(\frac{a}{r},\frac{b}{r}\right)$
, we interchangeably write
$\unicode[STIX]{x1D6FC}=\left(\frac{a}{r},\frac{b}{r}\right)$
, we interchangeably write
![]() $E_{-\unicode[STIX]{x1D6FC}}=E_{\unicode[STIX]{x1D6FC}}^{\ast }=E_{\frac{-a}{r},\frac{-b}{r}}$
. Similarly, we abuse notation and write the slope and the whole Chern character interchangeably.
$E_{-\unicode[STIX]{x1D6FC}}=E_{\unicode[STIX]{x1D6FC}}^{\ast }=E_{\frac{-a}{r},\frac{-b}{r}}$
. Similarly, we abuse notation and write the slope and the whole Chern character interchangeably.
We can characterize exceptional bundles among all stable bundles by the Euler characteristic
![]() $\unicode[STIX]{x1D712}(E,E)$
. For stable
$\unicode[STIX]{x1D712}(E,E)$
. For stable
![]() $E$
, Serre duality implies
$E$
, Serre duality implies
![]() $\operatorname{Ext}^{2}(E,E)=\operatorname{Hom}(E,E(K))=0$
. Similarly, the stability of
$\operatorname{Ext}^{2}(E,E)=\operatorname{Hom}(E,E(K))=0$
. Similarly, the stability of
![]() $E$
implies that
$E$
implies that
![]() $\operatorname{Hom}(E,E)=\mathbb{C}$
. Then for stable
$\operatorname{Hom}(E,E)=\mathbb{C}$
. Then for stable
![]() $E$
we have
$E$
we have
with equality precisely when
![]() $E$
is exceptional. Conversely, we use Hirzebruch–Riemann–Roch to explicitly compute
$E$
is exceptional. Conversely, we use Hirzebruch–Riemann–Roch to explicitly compute
Putting these together, we see that for a stable bundle
For exceptional bundles, this reduces to
Since
![]() $\unicode[STIX]{x1D712}(F,F)\leqslant 0$
for all other stable bundles, we see that exceptional bundles are the only stable bundles with
$\unicode[STIX]{x1D712}(F,F)\leqslant 0$
for all other stable bundles, we see that exceptional bundles are the only stable bundles with
![]() $\unicode[STIX]{x1D6E5}<\frac{1}{2}$
. As there is a unique exceptional bundle for an exceptional slope and there can be no other stable bundles with that discriminant, the moduli space of stable bundles with an exceptional Chern character is a single reduced point [Reference GorodentsevGor]. Giving an explicit description of the exceptional bundles analogous to the description of the exceptional bundles on
$\unicode[STIX]{x1D6E5}<\frac{1}{2}$
. As there is a unique exceptional bundle for an exceptional slope and there can be no other stable bundles with that discriminant, the moduli space of stable bundles with an exceptional Chern character is a single reduced point [Reference GorodentsevGor]. Giving an explicit description of the exceptional bundles analogous to the description of the exceptional bundles on
![]() $\mathbb{P}^{2}$
given in [Reference Coskun, Huizenga and WoolfCHW] and [Reference Le PotierLP] is an open question.
$\mathbb{P}^{2}$
given in [Reference Coskun, Huizenga and WoolfCHW] and [Reference Le PotierLP] is an open question.
2.3 Exceptional collections
Exceptional bundles naturally sit inside of collections.
Definition 2.8. A collection of exceptional bundles
![]() $\left(E_{0},\ldots ,E_{n}\right)$
is an exceptional collection if for all
$\left(E_{0},\ldots ,E_{n}\right)$
is an exceptional collection if for all
![]() $i<j$
,
$i<j$
,
![]() $\operatorname{Ext}^{k}(E_{j},E_{i})=0$
for all
$\operatorname{Ext}^{k}(E_{j},E_{i})=0$
for all
![]() $k$
and there is at most one
$k$
and there is at most one
![]() $k$
such that
$k$
such that
![]() $\operatorname{Ext}^{k}(E_{i},E_{j})\neq 0$
.
$\operatorname{Ext}^{k}(E_{i},E_{j})\neq 0$
.
An exceptional collection is strong if
![]() $k=0$
for all pairs
$k=0$
for all pairs
![]() $(i,j)$
. We say the length an exceptional collection
$(i,j)$
. We say the length an exceptional collection
![]() $\left(E_{0},\ldots ,E_{n}\right)$
is
$\left(E_{0},\ldots ,E_{n}\right)$
is
![]() $n+1$
. An exceptional pair is an exceptional collection of length two. A coil is a maximal exceptional collection, which in the case of
$n+1$
. An exceptional pair is an exceptional collection of length two. A coil is a maximal exceptional collection, which in the case of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
is length four. Our stereotypical (strong) coil is
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
is length four. Our stereotypical (strong) coil is
![]() $\left({\mathcal{O}},{\mathcal{O}}(1,0),{\mathcal{O}}(0,1),{\mathcal{O}}(1,1)\right)$
.
$\left({\mathcal{O}},{\mathcal{O}}(1,0),{\mathcal{O}}(0,1),{\mathcal{O}}(1,1)\right)$
.
Every exceptional bundle sits inside of an exceptional collection, and every exceptional collection can be completed to a coil [Reference RudakovRud2]. Given an exceptional collection of length three
![]() $(E_{0},E_{1},E_{2})$
there are exactly four ways to complete it to a coil:
$(E_{0},E_{1},E_{2})$
there are exactly four ways to complete it to a coil:
In other words, once you pick where you would like the fourth bundle to be, there is a unique way to complete the exceptional collection to a coil. This uniqueness follows as an easy consequence of the requirement that the fourth bundle forms an exceptional pair in the correct way with the other three bundles. First, we require each bundle to be in an exceptional pair which imposes an independent condition on its rank and first Chern classes so they are determined. Then the rank and first Chern class determine its discriminant, and the bundle is uniquely determined by its Chern classes.
Before we can state how to extend an exceptional collection of length two to a coil, we must first explain a process that turns an exceptional collection into different exceptional collections called mutation or reconstruction. We first define mutation for exceptional pairs and then bootstrap this definition into a definition for all exceptional collections. The definitions of mutation that we use are equivalent on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
to the general definitions [Reference GorodentsevGor].
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
to the general definitions [Reference GorodentsevGor].
Definition 2.9. The left mutation of an exceptional pair
![]() $\left(E_{0},E_{1}\right)$
is the exceptional pair
$\left(E_{0},E_{1}\right)$
is the exceptional pair
![]() $L\left(E_{0},E_{1}\right)=\left(L_{E_{0}}E_{1},E_{0}\right)$
where
$L\left(E_{0},E_{1}\right)=\left(L_{E_{0}}E_{1},E_{0}\right)$
where
![]() $L_{E_{0}}E_{1}$
is determined by one of the following short exact sequences:
$L_{E_{0}}E_{1}$
is determined by one of the following short exact sequences:
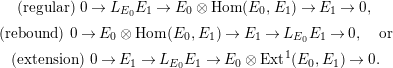 $$\begin{eqnarray}\displaystyle & \displaystyle \text{(regular) }0\rightarrow L_{E_{0}}E_{1}\rightarrow E_{0}\otimes \operatorname{Hom}(E_{0},E_{1})\rightarrow E_{1}\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{(rebound) }0\rightarrow E_{0}\otimes \operatorname{Hom}(E_{0},E_{1})\rightarrow E_{1}\rightarrow L_{E_{0}}E_{1}\rightarrow 0,\quad \text{or} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{(extension) }0\rightarrow E_{1}\rightarrow L_{E_{0}}E_{1}\rightarrow E_{0}\otimes \operatorname{Ext}^{1}(E_{0},E_{1})\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{(regular) }0\rightarrow L_{E_{0}}E_{1}\rightarrow E_{0}\otimes \operatorname{Hom}(E_{0},E_{1})\rightarrow E_{1}\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{(rebound) }0\rightarrow E_{0}\otimes \operatorname{Hom}(E_{0},E_{1})\rightarrow E_{1}\rightarrow L_{E_{0}}E_{1}\rightarrow 0,\quad \text{or} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{(extension) }0\rightarrow E_{1}\rightarrow L_{E_{0}}E_{1}\rightarrow E_{0}\otimes \operatorname{Ext}^{1}(E_{0},E_{1})\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$
One of these sequences exists by Gorodentsev [Reference GorodentsevGor]. By rank considerations only one of the previous short exact sequences is possible so the left mutation is unique. Rebound and extension mutations are called nonregular. Right mutation of an exceptional pair, denoted
![]() $R\left(E_{0},E_{1}\right)=\left(E_{1},R_{E_{1}}E_{0}\right)$
, is defined similarly by tensoring the
$R\left(E_{0},E_{1}\right)=\left(E_{1},R_{E_{1}}E_{0}\right)$
, is defined similarly by tensoring the
![]() $\operatorname{Hom}$
or
$\operatorname{Hom}$
or
![]() $\operatorname{Ext}$
with
$\operatorname{Ext}$
with
![]() $E_{1}$
rather than with
$E_{1}$
rather than with
![]() $E_{0}$
. Note that left and right mutation are inverse operations in the sense that
$E_{0}$
. Note that left and right mutation are inverse operations in the sense that
We can also mutate any part of an exceptional collection. In particular, replacing any adjacent exceptional pair in an exceptional collection with any of its left or right mutations gives another exceptional collection. For example, given an exceptional collection
![]() $\left(E_{0},E_{1},E_{2},E_{3}\right)$
,
$\left(E_{0},E_{1},E_{2},E_{3}\right)$
,
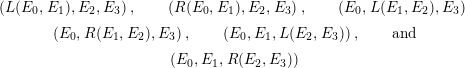 $$\begin{eqnarray}\displaystyle & \displaystyle \left(L(E_{0},E_{1}),E_{2},E_{3}\right),\qquad \left(R(E_{0},E_{1}),E_{2},E_{3}\right),\qquad \left(E_{0},L(E_{1},E_{2}),E_{3}\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(E_{0},R(E_{1},E_{2}),E_{3}\right),\qquad \left(E_{0},E_{1},L(E_{2},E_{3})\right),\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(E_{0},E_{1},R(E_{2},E_{3})\right) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(L(E_{0},E_{1}),E_{2},E_{3}\right),\qquad \left(R(E_{0},E_{1}),E_{2},E_{3}\right),\qquad \left(E_{0},L(E_{1},E_{2}),E_{3}\right) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(E_{0},R(E_{1},E_{2}),E_{3}\right),\qquad \left(E_{0},E_{1},L(E_{2},E_{3})\right),\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(E_{0},E_{1},R(E_{2},E_{3})\right) & \displaystyle \nonumber\end{eqnarray}$$
are all exceptional collections. Rudakov proved that all possible exceptional collections can be gotten from our stereotypical collection via these pairwise reconstructions [Reference RudakovRud1].
Mutating an exceptional collection is then just mutating all of the bundles in a systematic way. We define the left(right) mutation of an exceptional collection
![]() $\left(E_{0},E_{1},E_{2},\ldots ,E_{n}\right)$
as
$\left(E_{0},E_{1},E_{2},\ldots ,E_{n}\right)$
as
For a coil
![]() $(E_{0},E_{1},F_{0},F_{1})$
on
$(E_{0},E_{1},F_{0},F_{1})$
on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, its left mutation is
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, its left mutation is
and its right mutation is
Now, let us return to the problem of completing an exceptional pair to a coil. Say that we could extend
![]() $(E_{0},E_{1})$
to the coil
$(E_{0},E_{1})$
to the coil
![]() $(E_{0},E_{1},F_{0},F_{1})$
, this extension is not unique, even up to placement because
$(E_{0},E_{1},F_{0},F_{1})$
, this extension is not unique, even up to placement because
![]() $(E_{0},E_{1},L(F_{0},F_{1}))$
and
$(E_{0},E_{1},L(F_{0},F_{1}))$
and
![]() $(E_{0},E_{1},R(F_{0},F_{1}))$
are also coils. To make a unique notation of extension, we need the notion of a system.
$(E_{0},E_{1},R(F_{0},F_{1}))$
are also coils. To make a unique notation of extension, we need the notion of a system.
Definition 2.10. Using mutation, each exceptional pair
![]() $\left(E_{0},E_{1}\right)$
generates a system of exceptional bundles
$\left(E_{0},E_{1}\right)$
generates a system of exceptional bundles
![]() $\{E_{i}\}_{i\in \mathbb{Z}}$
where we inductively define
$\{E_{i}\}_{i\in \mathbb{Z}}$
where we inductively define
![]() $E_{i+1}=R_{E_{i}}E_{i-1}$
and
$E_{i+1}=R_{E_{i}}E_{i-1}$
and
![]() $E_{i-1}=L_{E_{i}}E_{i+1}$
.
$E_{i-1}=L_{E_{i}}E_{i+1}$
.
Given an exceptional pair
![]() $\left(E_{0},E_{1}\right)$
, we define the right completion system of it to be the unique system
$\left(E_{0},E_{1}\right)$
, we define the right completion system of it to be the unique system
![]() $\{F_{i}\}$
such that
$\{F_{i}\}$
such that
![]() $\left(E_{0},E_{1},F_{i},F_{i+1}\right)$
is a coil. Left and center completion systems are defined analogously. A left (right,center) completion pair is any pair
$\left(E_{0},E_{1},F_{i},F_{i+1}\right)$
is a coil. Left and center completion systems are defined analogously. A left (right,center) completion pair is any pair
![]() $\left(F_{i},F_{i+1}\right)$
coming from the left (right,center) completion system. By Propositions 4.5 and 4.8 of Rudakov’s paper [Reference RudakovRud1], the completion system is either a system of line bundles or has a minimally ranked completion pair where the minimally ranked completion pair is the pair in the system with the lowest sum of the two ranks of the bundles in the system.
$\left(F_{i},F_{i+1}\right)$
coming from the left (right,center) completion system. By Propositions 4.5 and 4.8 of Rudakov’s paper [Reference RudakovRud1], the completion system is either a system of line bundles or has a minimally ranked completion pair where the minimally ranked completion pair is the pair in the system with the lowest sum of the two ranks of the bundles in the system.
Completing an exceptional collection of length one to a coil can be reduced to the two steps of completing it to an exceptional pair (which is highly not unique) and then completing the pair to a coil. In this paper, we start with pairs and provide a unique way to extend them to a coil.
Given a complex
![]() $W:A^{a}\rightarrow B^{b}$
of powers of an exceptional pair
$W:A^{a}\rightarrow B^{b}$
of powers of an exceptional pair
![]() $(A,B)$
, we extend the idea of mutation to the complex. Define
$(A,B)$
, we extend the idea of mutation to the complex. Define
![]() $LW$
to be the complex
$LW$
to be the complex
and similarly define
![]() $RW$
to be the complex
$RW$
to be the complex
We also define the mutations relative to an exceptional bundle
![]() $C$
where
$C$
where
![]() $\{C,A,B\}\left(\{A,B,C\}\right)$
is an exceptional collection as follows: if
$\{C,A,B\}\left(\{A,B,C\}\right)$
is an exceptional collection as follows: if
![]() $\{C,A,B\}$
is an exceptional collection, define
$\{C,A,B\}$
is an exceptional collection, define
![]() $L_{C}W$
to be the complex
$L_{C}W$
to be the complex
and similarly, if
![]() $\{A,B,C\}$
is an exceptional collection, define
$\{A,B,C\}$
is an exceptional collection, define
![]() $R_{C}W$
to be the complex
$R_{C}W$
to be the complex
We can now state a theorem of Gorodentsev which establishes the spectral sequence that we need on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
Theorem 2.11. [Reference GorodentsevGor]
Let
![]() $U$
be a coherent sheaf on
$U$
be a coherent sheaf on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, and let
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, and let
![]() $\left(E_{0},E_{1},F_{0},F_{1}\right)$
be a coil. Write
$\left(E_{0},E_{1},F_{0},F_{1}\right)$
be a coil. Write
![]() ${\mathcal{A}}=\left(A_{0},A_{1},A_{2},A_{3}\right)=\left(E_{0},E_{1},F_{0},F_{1}\right)$
and
${\mathcal{A}}=\left(A_{0},A_{1},A_{2},A_{3}\right)=\left(E_{0},E_{1},F_{0},F_{1}\right)$
and
![]() ${\mathcal{B}}=\left(B_{-3},B_{-2},B_{-1},B_{0}\right)=\left(F_{1}(K),F_{2}(K),E_{-1},E_{0}\right)$
. There is a spectral sequence with
${\mathcal{B}}=\left(B_{-3},B_{-2},B_{-1},B_{0}\right)=\left(F_{1}(K),F_{2}(K),E_{-1},E_{0}\right)$
. There is a spectral sequence with
![]() $E_{1}^{p,q}$
-page
$E_{1}^{p,q}$
-page
that converges to
![]() $U$
in degree 0 and to 0 in all other degrees where
$U$
in degree 0 and to 0 in all other degrees where
![]() $\unicode[STIX]{x1D6E5}_{p}$
is the number of nonregular mutations in the string
$\unicode[STIX]{x1D6E5}_{p}$
is the number of nonregular mutations in the string
![]() $L_{0}\ldots L_{p-1}A_{p}$
which mutates
$L_{0}\ldots L_{p-1}A_{p}$
which mutates
![]() $A_{p}$
into
$A_{p}$
into
![]() $B_{-p}$
.
$B_{-p}$
.
It should be clear that
![]() $\unicode[STIX]{x1D6E5}_{0}=0$
. Considering the spectral sequence converging to different bundles of the coil allows us to deduce that
$\unicode[STIX]{x1D6E5}_{0}=0$
. Considering the spectral sequence converging to different bundles of the coil allows us to deduce that
![]() $\unicode[STIX]{x1D6E5}_{3}=1$
and that the other two are either 0 or 1 [Reference KarpovKar, Rmk. 1.5.2]. Also, notice that
$\unicode[STIX]{x1D6E5}_{3}=1$
and that the other two are either 0 or 1 [Reference KarpovKar, Rmk. 1.5.2]. Also, notice that
![]() ${\mathcal{B}}$
is the left mutation of
${\mathcal{B}}$
is the left mutation of
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
2.4 Moduli spaces of sheaves
Let
![]() $E$
be exceptional with Chern character
$E$
be exceptional with Chern character
![]() $e$
. Then,
$e$
. Then,
![]() $E$
imposes a numerical condition on stable bundles with “nearby” Chern characters. To see this condition, start with an exceptional bundle
$E$
imposes a numerical condition on stable bundles with “nearby” Chern characters. To see this condition, start with an exceptional bundle
![]() $E$
and another stable bundle
$E$
and another stable bundle
![]() $F$
, we know that there are no maps from
$F$
, we know that there are no maps from
![]() $E$
to
$E$
to
![]() $F$
if the
$F$
if the
![]() $(1,1)$
-slope of
$(1,1)$
-slope of
![]() $E$
is bigger than
$E$
is bigger than
![]() $F$
’s by
$F$
’s by
![]() $F$
’s stability so
$F$
’s stability so
Similarly, there are no maps from
![]() $F$
to
$F$
to
![]() $E$
twisted by the canonical if the
$E$
twisted by the canonical if the
![]() $(1,1)$
-slope of
$(1,1)$
-slope of
![]() $F$
is greater than the
$F$
is greater than the
![]() $(1,1)$
-slope of
$(1,1)$
-slope of
![]() $E(K)$
so
$E(K)$
so
By Serre duality,
Thus, if we have both of these conditions, we know that
This is the numeric condition that
![]() $E$
imposes on nearby stable bundles. Given a fixed exceptional
$E$
imposes on nearby stable bundles. Given a fixed exceptional
![]() $E$
, we can encode this data by saying that the Chern character of
$E$
, we can encode this data by saying that the Chern character of
![]() $F$
must lie on or above a certain surface,
$F$
must lie on or above a certain surface,
![]() $\unicode[STIX]{x1D6FF}_{E}$
, in the
$\unicode[STIX]{x1D6FF}_{E}$
, in the
![]() $(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6E5})$
space. We define
$(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6E5})$
space. We define
![]() $\unicode[STIX]{x1D6FF}_{E}(\unicode[STIX]{x1D707})$
as follows.
$\unicode[STIX]{x1D6FF}_{E}(\unicode[STIX]{x1D707})$
as follows.
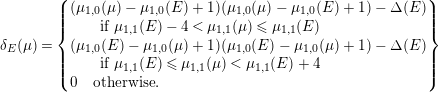 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{E}(\unicode[STIX]{x1D707})=\left\{\begin{array}{@{}l@{}}(\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})-\unicode[STIX]{x1D707}_{1,0}(E)+1)(\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})-\unicode[STIX]{x1D707}_{1,0}(E)+1)-\unicode[STIX]{x1D6E5}(E)\\ \qquad \text{if }\unicode[STIX]{x1D707}_{1,1}(E)-4<\unicode[STIX]{x1D707}_{1,1}(\unicode[STIX]{x1D707})\leqslant \unicode[STIX]{x1D707}_{1,1}(E)\\ (\unicode[STIX]{x1D707}_{1,0}(E)-\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})+1)(\unicode[STIX]{x1D707}_{1,0}(E)-\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})+1)-\unicode[STIX]{x1D6E5}(E)\\ \qquad \text{if }\unicode[STIX]{x1D707}_{1,1}(E)\leqslant \unicode[STIX]{x1D707}_{1,1}(\unicode[STIX]{x1D707})<\unicode[STIX]{x1D707}_{1,1}(E)+4\\ 0\quad \text{otherwise}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{E}(\unicode[STIX]{x1D707})=\left\{\begin{array}{@{}l@{}}(\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})-\unicode[STIX]{x1D707}_{1,0}(E)+1)(\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})-\unicode[STIX]{x1D707}_{1,0}(E)+1)-\unicode[STIX]{x1D6E5}(E)\\ \qquad \text{if }\unicode[STIX]{x1D707}_{1,1}(E)-4<\unicode[STIX]{x1D707}_{1,1}(\unicode[STIX]{x1D707})\leqslant \unicode[STIX]{x1D707}_{1,1}(E)\\ (\unicode[STIX]{x1D707}_{1,0}(E)-\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})+1)(\unicode[STIX]{x1D707}_{1,0}(E)-\unicode[STIX]{x1D707}_{1,0}(\unicode[STIX]{x1D707})+1)-\unicode[STIX]{x1D6E5}(E)\\ \qquad \text{if }\unicode[STIX]{x1D707}_{1,1}(E)\leqslant \unicode[STIX]{x1D707}_{1,1}(\unicode[STIX]{x1D707})<\unicode[STIX]{x1D707}_{1,1}(E)+4\\ 0\quad \text{otherwise}.\end{array}\right\}\end{eqnarray}$$
Then
![]() $F$
’s Chern character lying on or above
$F$
’s Chern character lying on or above
![]() $\unicode[STIX]{x1D6FF}_{E}$
means that
$\unicode[STIX]{x1D6FF}_{E}$
means that
Using these conditions, each exceptional bundle gives an inequality that a Chern character must satisfy in order to be stable. We combine all of these conditions into one by looking at the maximum over all of the inequalities. Formally, let
![]() ${\mathcal{E}}$
be the set of exceptional bundles and define the
${\mathcal{E}}$
be the set of exceptional bundles and define the
![]() $\unicode[STIX]{x1D6FF}$
surface by
$\unicode[STIX]{x1D6FF}$
surface by
Definition 2.12.
Then saying that a stable Chern character,
![]() $\unicode[STIX]{x1D701}$
, must satisfy all of the inequalities from exceptional bundles is equivalent to
$\unicode[STIX]{x1D701}$
, must satisfy all of the inequalities from exceptional bundles is equivalent to
Alternatively, we say that a stable Chern character must lie on or above the
![]() $\unicode[STIX]{x1D6FF}$
-surface.
$\unicode[STIX]{x1D6FF}$
-surface.
Rudakov proved that lying above the
![]() $\unicode[STIX]{x1D6FF}$
surface was not only necessary but also sufficient for a non-semiexceptional Chern character to be stable.
$\unicode[STIX]{x1D6FF}$
surface was not only necessary but also sufficient for a non-semiexceptional Chern character to be stable.
Theorem 2.13. (Main theorem, [Reference RudakovRud2])
Let
![]() $\unicode[STIX]{x1D709}=(r,\unicode[STIX]{x1D707},\unicode[STIX]{x1D6E5})$
be a Chern character of positive integer rank. There exists a positive dimensional moduli space of
$\unicode[STIX]{x1D709}=(r,\unicode[STIX]{x1D707},\unicode[STIX]{x1D6E5})$
be a Chern character of positive integer rank. There exists a positive dimensional moduli space of
![]() $\overline{\unicode[STIX]{x1D6FE}}$
-semistable sheaves
$\overline{\unicode[STIX]{x1D6FE}}$
-semistable sheaves
![]() $M_{\overline{\unicode[STIX]{x1D6FE}}}\left(\unicode[STIX]{x1D709}\right)$
with Chern character
$M_{\overline{\unicode[STIX]{x1D6FE}}}\left(\unicode[STIX]{x1D709}\right)$
with Chern character
![]() $\unicode[STIX]{x1D709}$
if and only if
$\unicode[STIX]{x1D709}$
if and only if
![]() $c_{1}(\unicode[STIX]{x1D707})\cdot (1,1)=r\unicode[STIX]{x1D707}_{1,1}\in \mathbb{Z}$
,
$c_{1}(\unicode[STIX]{x1D707})\cdot (1,1)=r\unicode[STIX]{x1D707}_{1,1}\in \mathbb{Z}$
,
![]() $\unicode[STIX]{x1D712}=r\left(P(\unicode[STIX]{x1D707})-\unicode[STIX]{x1D6E5}\right)\in \mathbb{Z}$
, and
$\unicode[STIX]{x1D712}=r\left(P(\unicode[STIX]{x1D707})-\unicode[STIX]{x1D6E5}\right)\in \mathbb{Z}$
, and
![]() $\unicode[STIX]{x1D6E5}\geqslant \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D707})$
. The same conditions are necessary and sufficient for Gieseker semistability as long as
$\unicode[STIX]{x1D6E5}\geqslant \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D707})$
. The same conditions are necessary and sufficient for Gieseker semistability as long as
![]() $\unicode[STIX]{x1D6E5}>\frac{1}{2}$
and
$\unicode[STIX]{x1D6E5}>\frac{1}{2}$
and
![]() $\unicode[STIX]{x1D707}\notin {\mathcal{E}}\mathbb{Z}$
.
$\unicode[STIX]{x1D707}\notin {\mathcal{E}}\mathbb{Z}$
.
2.5 New basic properties
With this background, we can begin our original work on
![]() $M(\unicode[STIX]{x1D709})$
. In the last subsection, we listed many properties of the nonempty moduli spaces. In this subsection, we prove that the moduli spaces are
$M(\unicode[STIX]{x1D709})$
. In the last subsection, we listed many properties of the nonempty moduli spaces. In this subsection, we prove that the moduli spaces are
![]() $\mathbb{Q}$
-factorial and are Mori dream spaces. In fact, we prove these results for all moduli spaces of Gieseker semistable sheaves on any del Pezzo surface, not just
$\mathbb{Q}$
-factorial and are Mori dream spaces. In fact, we prove these results for all moduli spaces of Gieseker semistable sheaves on any del Pezzo surface, not just
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
Proposition 2.14. Let
![]() $M$
be the moduli space of semistable sheaves with a fixed Chern character on a del Pezzo surface. Then
$M$
be the moduli space of semistable sheaves with a fixed Chern character on a del Pezzo surface. Then
![]() $M$
is
$M$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Proof. By [Reference DrézetDré2],
![]() $M$
is a geometric quotient of a smooth variety. Applying [Reference HausenHau, Thm. 4] immediately allows us to conclude that
$M$
is a geometric quotient of a smooth variety. Applying [Reference HausenHau, Thm. 4] immediately allows us to conclude that
![]() $M$
is
$M$
is
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
The proof that these spaces are Mori dream spaces is slightly more involved, but similar in flavor.
Theorem 2.15. Let
![]() $M$
be the moduli space of semistable sheaves with a fixed Chern character on a del Pezzo surface. Then
$M$
be the moduli space of semistable sheaves with a fixed Chern character on a del Pezzo surface. Then
![]() $M$
is a Mori dream space.
$M$
is a Mori dream space.
Proof. The proof follows the same basic outline as the proof for moduli spaces of sheaves on
![]() $\mathbb{P}^{2}$
[Reference Coskun, Huizenga and WoolfCHW]. By [Reference Birkar, Cascini, Hacon and McKernanBCHM], a log Fano variety is a Mori dream space. This result reduces the theorem to showing that
$\mathbb{P}^{2}$
[Reference Coskun, Huizenga and WoolfCHW]. By [Reference Birkar, Cascini, Hacon and McKernanBCHM], a log Fano variety is a Mori dream space. This result reduces the theorem to showing that
![]() $M$
is a log Fano variety. Since the anticanonical bundle of
$M$
is a log Fano variety. Since the anticanonical bundle of
![]() $M$
is nef [Reference Huybrechts and LehnHL, Thm. 8.2.8 and 8.3.3] and there exists effective divisors
$M$
is nef [Reference Huybrechts and LehnHL, Thm. 8.2.8 and 8.3.3] and there exists effective divisors
![]() $E$
such that
$E$
such that
![]() $-K_{M}-\unicode[STIX]{x1D716}E$
is ample for all sufficiently small
$-K_{M}-\unicode[STIX]{x1D716}E$
is ample for all sufficiently small
![]() $\unicode[STIX]{x1D716}>0$
, showing
$\unicode[STIX]{x1D716}>0$
, showing
![]() $M$
is log Fano reduces to showing that
$M$
is log Fano reduces to showing that
![]() $\left(M,\unicode[STIX]{x1D716}E\right)$
is a klt-pair for all effective divisors
$\left(M,\unicode[STIX]{x1D716}E\right)$
is a klt-pair for all effective divisors
![]() $E$
. Showing that
$E$
. Showing that
![]() $\left(M,\unicode[STIX]{x1D716}E\right)$
is a klt-pair for all effective divisors
$\left(M,\unicode[STIX]{x1D716}E\right)$
is a klt-pair for all effective divisors
![]() $E$
further reduces to showing that
$E$
further reduces to showing that
![]() $M$
has canonical singularities.
$M$
has canonical singularities.
We now show that
![]() $M$
has canonical singularities. By [Reference DrézetDré2],
$M$
has canonical singularities. By [Reference DrézetDré2],
![]() $M$
is also a geometric quotient of a smooth variety. By [Reference BoutotBou], a geometric quotient of a variety with rational singularities has rational singularities so
$M$
is also a geometric quotient of a smooth variety. By [Reference BoutotBou], a geometric quotient of a variety with rational singularities has rational singularities so
![]() $M$
has rational singularities. As a
$M$
has rational singularities. As a
![]() $M$
is 1-Gorenstein [Reference Huybrechts and LehnHL, Thm. 8.3.3], it has canonical singularities [Reference KollárKol, Thm. 11.1].
$M$
is 1-Gorenstein [Reference Huybrechts and LehnHL, Thm. 8.3.3], it has canonical singularities [Reference KollárKol, Thm. 11.1].
2.6 Additional assumptions
There are two previously mentioned properties that we would also like our moduli spaces on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
to have. We want the complement of the stable locus to be codimension at least two, and we want them to have Picard rank 3. The first assumption allows us to ignore the strictly semistable locus when we are working with divisors, and the second assumption lets us use properties of the Picard group that we need. These assumptions are justified for a few reasons. First, they hold for the Hilbert schemes of points, which are the primary examples of such moduli spaces. Second, Yoshioka proved that the second assumption holds for
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
to have. We want the complement of the stable locus to be codimension at least two, and we want them to have Picard rank 3. The first assumption allows us to ignore the strictly semistable locus when we are working with divisors, and the second assumption lets us use properties of the Picard group that we need. These assumptions are justified for a few reasons. First, they hold for the Hilbert schemes of points, which are the primary examples of such moduli spaces. Second, Yoshioka proved that the second assumption holds for
![]() $M(\unicode[STIX]{x1D709})$
where one of the slope components of
$M(\unicode[STIX]{x1D709})$
where one of the slope components of
![]() $\unicode[STIX]{x1D709}$
is an integer and
$\unicode[STIX]{x1D709}$
is an integer and
![]() $\unicode[STIX]{x1D709}$
is above the
$\unicode[STIX]{x1D709}$
is above the
![]() $\unicode[STIX]{x1D6FF}$
surface [Reference YoshiokaYos1]. Lastly, there are no examples of
$\unicode[STIX]{x1D6FF}$
surface [Reference YoshiokaYos1]. Lastly, there are no examples of
![]() $M(\unicode[STIX]{x1D709})$
where
$M(\unicode[STIX]{x1D709})$
where
![]() $\unicode[STIX]{x1D709}$
is above the
$\unicode[STIX]{x1D709}$
is above the
![]() $\unicode[STIX]{x1D6FF}$
surface for which either assumption is known to fail. In fact, both assumptions are believed to be true above the
$\unicode[STIX]{x1D6FF}$
surface for which either assumption is known to fail. In fact, both assumptions are believed to be true above the
![]() $\unicode[STIX]{x1D6FF}$
surface. Proving that they hold in this region is the focus of current research.
$\unicode[STIX]{x1D6FF}$
surface. Proving that they hold in this region is the focus of current research.
We also assume that
![]() $\unicode[STIX]{x1D709}$
is above the
$\unicode[STIX]{x1D709}$
is above the
![]() $\unicode[STIX]{x1D6FF}$
surface and is not a multiple of an exceptional Chern character.
$\unicode[STIX]{x1D6FF}$
surface and is not a multiple of an exceptional Chern character.
2.7 The Picard group of
 $M(\unicode[STIX]{x1D709})$
$M(\unicode[STIX]{x1D709})$
We have a good description of the Picard group of
![]() $M(\unicode[STIX]{x1D709})$
if we assume that the Picard rank is three which we just added as a standing assumption. Linear and numerical equivalence coincide on
$M(\unicode[STIX]{x1D709})$
if we assume that the Picard rank is three which we just added as a standing assumption. Linear and numerical equivalence coincide on
![]() $M(\unicode[STIX]{x1D709})$
, so we have
$M(\unicode[STIX]{x1D709})$
, so we have
As mentioned above, we work with
![]() $M^{s}(\unicode[STIX]{x1D709})$
when it is convenient.
$M^{s}(\unicode[STIX]{x1D709})$
when it is convenient.
![]() $M^{s}(\unicode[STIX]{x1D709})$
is a coarse moduli space for the stable sheaves. In contrast,
$M^{s}(\unicode[STIX]{x1D709})$
is a coarse moduli space for the stable sheaves. In contrast,
![]() $M(\unicode[STIX]{x1D709})$
is not a coarse moduli space, unless
$M(\unicode[STIX]{x1D709})$
is not a coarse moduli space, unless
![]() $\unicode[STIX]{x1D709}$
is a primitive character, as it identifies
$\unicode[STIX]{x1D709}$
is a primitive character, as it identifies
![]() $S$
-equivalence classes of (strictly semistable) sheaves.
$S$
-equivalence classes of (strictly semistable) sheaves.
In order to understand the classes of the divisors that span the effective cone, we have to understand the isomorphism
We construct this isomorphism by uniquely defining a line bundle on families of sheaves for each element of
![]() $\unicode[STIX]{x1D709}^{\bot }$
as done in [Reference Le PotierLP] and [Reference Coskun, Huizenga and WoolfCHW] for the case of
$\unicode[STIX]{x1D709}^{\bot }$
as done in [Reference Le PotierLP] and [Reference Coskun, Huizenga and WoolfCHW] for the case of
![]() $\mathbb{P}^{2}$
.
$\mathbb{P}^{2}$
.
Let
![]() ${\mathcal{U}}/S$
be a flat family of semistable sheaves with Chern character
${\mathcal{U}}/S$
be a flat family of semistable sheaves with Chern character
![]() $\unicode[STIX]{x1D709}$
where
$\unicode[STIX]{x1D709}$
where
![]() $S$
is a smooth variety. Define the two projections
$S$
is a smooth variety. Define the two projections
![]() $p:S\times \mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow S$
and
$p:S\times \mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow S$
and
![]() $q:S\times \mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
. Then consider the composition of maps
$q:S\times \mathbb{P}^{1}\times \mathbb{P}^{1}\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
. Then consider the composition of maps
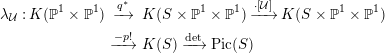 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{{\mathcal{U}}}:K(\mathbb{P}^{1}\times \mathbb{P}^{1}) & \xrightarrow[{}]{q^{\ast }} & \displaystyle K(S\times \mathbb{P}^{1}\times \mathbb{P}^{1})\xrightarrow[{}]{\cdot [{\mathcal{U}}]}K(S\times \mathbb{P}^{1}\times \mathbb{P}^{1})\nonumber\\ \displaystyle & \xrightarrow[{}]{-p!} & \displaystyle K(S)\xrightarrow[{}]{\det }\operatorname{Pic}(S)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{{\mathcal{U}}}:K(\mathbb{P}^{1}\times \mathbb{P}^{1}) & \xrightarrow[{}]{q^{\ast }} & \displaystyle K(S\times \mathbb{P}^{1}\times \mathbb{P}^{1})\xrightarrow[{}]{\cdot [{\mathcal{U}}]}K(S\times \mathbb{P}^{1}\times \mathbb{P}^{1})\nonumber\\ \displaystyle & \xrightarrow[{}]{-p!} & \displaystyle K(S)\xrightarrow[{}]{\det }\operatorname{Pic}(S)\nonumber\end{eqnarray}$$
where
![]() $p!=\sum (-1)^{i}R^{i}p_{\ast }$
. Colloquially, we are taking a sheaf on
$p!=\sum (-1)^{i}R^{i}p_{\ast }$
. Colloquially, we are taking a sheaf on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, pulling it back along the projection to
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, pulling it back along the projection to
![]() $S\times \mathbb{P}^{1}\times \mathbb{P}^{1}$
, restricting it to our family, pushing it forward along the projection onto
$S\times \mathbb{P}^{1}\times \mathbb{P}^{1}$
, restricting it to our family, pushing it forward along the projection onto
![]() $S$
, and then taking its determinant to get a line bundle on
$S$
, and then taking its determinant to get a line bundle on
![]() $S$
.
$S$
.
Tensoring our family
![]() ${\mathcal{U}}$
by
${\mathcal{U}}$
by
![]() $p^{\ast }L$
, where
$p^{\ast }L$
, where
![]() $L$
is a line bundle on
$L$
is a line bundle on
![]() $S$
, does not change the given moduli map
$S$
, does not change the given moduli map
![]() $f:S\rightarrow M(\unicode[STIX]{x1D709})$
, but does change the
$f:S\rightarrow M(\unicode[STIX]{x1D709})$
, but does change the
![]() $\unicode[STIX]{x1D706}$
map as follows:
$\unicode[STIX]{x1D706}$
map as follows:
Now given a class
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D709}^{\bot }$
, we want a
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D709}^{\bot }$
, we want a
![]() $\unicode[STIX]{x1D706}_{M}$
map which commutes with the moduli map in the sense that we should have
$\unicode[STIX]{x1D706}_{M}$
map which commutes with the moduli map in the sense that we should have
for all
![]() ${\mathcal{U}}$
. This equality determines a unique line bundle
${\mathcal{U}}$
. This equality determines a unique line bundle
![]() $\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701})$
on
$\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701})$
on
![]() $M(\unicode[STIX]{x1D709})$
and gives a linear map
$M(\unicode[STIX]{x1D709})$
and gives a linear map
![]() $\unicode[STIX]{x1D706}_{M}:\unicode[STIX]{x1D709}^{\bot }\rightarrow \operatorname{NS}(M(\unicode[STIX]{x1D709}))$
which is an isomorphism under our assumptions.
$\unicode[STIX]{x1D706}_{M}:\unicode[STIX]{x1D709}^{\bot }\rightarrow \operatorname{NS}(M(\unicode[STIX]{x1D709}))$
which is an isomorphism under our assumptions.
Caveat: We have normalized
![]() $\unicode[STIX]{x1D706}_{M}$
using
$\unicode[STIX]{x1D706}_{M}$
using
![]() $-p!$
as in [Reference Coskun, Huizenga and WoolfCHW] rather than
$-p!$
as in [Reference Coskun, Huizenga and WoolfCHW] rather than
![]() $p!$
as in [Reference Huybrechts and LehnHL] and [Reference Le PotierLP] so that the positive rank Chern characters form the “primary half space” that we define later this section.
$p!$
as in [Reference Huybrechts and LehnHL] and [Reference Le PotierLP] so that the positive rank Chern characters form the “primary half space” that we define later this section.
2.8 A basis for the Picard group
Using this isomorphism, we want to construct a basis for the Picard group. Following Huybrechts and Lehn [Reference Huybrechts and LehnHL] and modifying it for
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we define three Chern characters
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, we define three Chern characters
![]() $\unicode[STIX]{x1D701}_{0}$
,
$\unicode[STIX]{x1D701}_{0}$
,
![]() $\unicode[STIX]{x1D701}_{a}$
, and
$\unicode[STIX]{x1D701}_{a}$
, and
![]() $\unicode[STIX]{x1D701}_{b}$
. Bundles with these Chern characters are a basis for the Picard space. These Chern characters depend on the character
$\unicode[STIX]{x1D701}_{b}$
. Bundles with these Chern characters are a basis for the Picard space. These Chern characters depend on the character
![]() $\unicode[STIX]{x1D709}$
of the moduli space. Let
$\unicode[STIX]{x1D709}$
of the moduli space. Let
![]() $a$
be the Chern character of a line of the first ruling and
$a$
be the Chern character of a line of the first ruling and
![]() $b$
be the Chern character of a line of the second ruling on
$b$
be the Chern character of a line of the second ruling on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. We define our Chern characters by the equations
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. We define our Chern characters by the equations
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{0} & = & \displaystyle r(\unicode[STIX]{x1D709}){\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}^{\ast },{\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}){\mathcal{O}}_{p},\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{a} & = & \displaystyle r(\unicode[STIX]{x1D709})a_{1}-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}^{\ast },a){\mathcal{O}}_{p},\qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{b} & = & \displaystyle r(\unicode[STIX]{x1D709})b_{1}-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}^{\ast },b){\mathcal{O}}_{p}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{0} & = & \displaystyle r(\unicode[STIX]{x1D709}){\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}^{\ast },{\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}){\mathcal{O}}_{p},\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{a} & = & \displaystyle r(\unicode[STIX]{x1D709})a_{1}-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}^{\ast },a){\mathcal{O}}_{p},\qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{b} & = & \displaystyle r(\unicode[STIX]{x1D709})b_{1}-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}^{\ast },b){\mathcal{O}}_{p}\nonumber\end{eqnarray}$$
where
![]() ${\mathcal{O}}_{p}$
is the structure sheaf of a point on
${\mathcal{O}}_{p}$
is the structure sheaf of a point on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. (Note the difference from the analogous definition in [Reference Huybrechts and LehnHL] by a sign due to our convention for
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. (Note the difference from the analogous definition in [Reference Huybrechts and LehnHL] by a sign due to our convention for
![]() $\unicode[STIX]{x1D706}_{M}$
.)
$\unicode[STIX]{x1D706}_{M}$
.)
Given that
![]() $(\unicode[STIX]{x1D709},{\mathcal{O}}_{p})=r(\unicode[STIX]{x1D709})$
, it should be clear that they are all in
$(\unicode[STIX]{x1D709},{\mathcal{O}}_{p})=r(\unicode[STIX]{x1D709})$
, it should be clear that they are all in
![]() $\unicode[STIX]{x1D709}^{\bot }$
. They can also be shown to be in
$\unicode[STIX]{x1D709}^{\bot }$
. They can also be shown to be in
![]() $\unicode[STIX]{x1D709}^{\bot }$
by using Riemann–Roch given that the Chern characters
$\unicode[STIX]{x1D709}^{\bot }$
by using Riemann–Roch given that the Chern characters
![]() $(\operatorname{ch}_{0},\operatorname{ch}_{1},\operatorname{ch}_{2})$
of
$(\operatorname{ch}_{0},\operatorname{ch}_{1},\operatorname{ch}_{2})$
of
![]() $\unicode[STIX]{x1D701}_{0},\unicode[STIX]{x1D701}_{a},\unicode[STIX]{x1D701}_{b}$
are
$\unicode[STIX]{x1D701}_{0},\unicode[STIX]{x1D701}_{a},\unicode[STIX]{x1D701}_{b}$
are
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{0} & = & \displaystyle \left(r(\unicode[STIX]{x1D709}),(0,0),-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})\right),\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{a} & = & \displaystyle \left(0,\left(r(\unicode[STIX]{x1D709}),0\right),-r(\unicode[STIX]{x1D709})-c_{1}(\unicode[STIX]{x1D709})\cdot (0,1)\right),\qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{b} & = & \displaystyle \left(0,\left(0,r(\unicode[STIX]{x1D709})\right),-r(\unicode[STIX]{x1D709})-c_{1}(\unicode[STIX]{x1D709})\cdot (1,0)\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}_{0} & = & \displaystyle \left(r(\unicode[STIX]{x1D709}),(0,0),-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})\right),\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{a} & = & \displaystyle \left(0,\left(r(\unicode[STIX]{x1D709}),0\right),-r(\unicode[STIX]{x1D709})-c_{1}(\unicode[STIX]{x1D709})\cdot (0,1)\right),\qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D701}_{b} & = & \displaystyle \left(0,\left(0,r(\unicode[STIX]{x1D709})\right),-r(\unicode[STIX]{x1D709})-c_{1}(\unicode[STIX]{x1D709})\cdot (1,0)\right).\nonumber\end{eqnarray}$$
Using the map from the previous section, define
![]() ${\mathcal{L}}_{0}$
,
${\mathcal{L}}_{0}$
,
![]() ${\mathcal{L}}_{a}$
,
${\mathcal{L}}_{a}$
,
![]() ${\mathcal{L}}_{b}$
by the formulas
${\mathcal{L}}_{b}$
by the formulas
![]() ${\mathcal{L}}_{0}=\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701}_{0})$
,
${\mathcal{L}}_{0}=\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701}_{0})$
,
![]() ${\mathcal{L}}_{a}=\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701}_{a})$
, and
${\mathcal{L}}_{a}=\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701}_{a})$
, and
![]() ${\mathcal{L}}_{b}=\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701}_{b})$
. They are a basis for the Picard space. We know that for
${\mathcal{L}}_{b}=\unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701}_{b})$
. They are a basis for the Picard space. We know that for
![]() $n>>0$
,
$n>>0$
,
![]() ${\mathcal{L}}_{0}\otimes {\mathcal{L}}_{a}^{n}$
and
${\mathcal{L}}_{0}\otimes {\mathcal{L}}_{a}^{n}$
and
![]() ${\mathcal{L}}_{0}\otimes {\mathcal{L}}_{b}^{n}$
are ample [Reference Huybrechts and LehnHL].
${\mathcal{L}}_{0}\otimes {\mathcal{L}}_{b}^{n}$
are ample [Reference Huybrechts and LehnHL].
Now,
![]() $\unicode[STIX]{x1D701}_{a}$
and
$\unicode[STIX]{x1D701}_{a}$
and
![]() $\unicode[STIX]{x1D701}_{b}$
span the plane of rank zero sheaves in
$\unicode[STIX]{x1D701}_{b}$
span the plane of rank zero sheaves in
![]() $\unicode[STIX]{x1D709}^{\bot }$
. Define the primary half space of
$\unicode[STIX]{x1D709}^{\bot }$
. Define the primary half space of
![]() $\unicode[STIX]{x1D709}^{\bot }$
to be the open half space of positive rank Chern characters and the secondary half space to be the closed half space of negative rank and rank zero Chern characters in
$\unicode[STIX]{x1D709}^{\bot }$
to be the open half space of positive rank Chern characters and the secondary half space to be the closed half space of negative rank and rank zero Chern characters in
![]() $\unicode[STIX]{x1D709}^{\bot }$
. Similarly, define the primary and secondary halves of
$\unicode[STIX]{x1D709}^{\bot }$
. Similarly, define the primary and secondary halves of
![]() $\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
as the images of these under the isomorphism
$\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
as the images of these under the isomorphism
![]() $\unicode[STIX]{x1D706}_{M}$
. Every extremal ray of the effective and nef cones sits in one of our halves. Call an extremal ray of the effective or nef cone primary or secondary according to which half it lies in.
$\unicode[STIX]{x1D706}_{M}$
. Every extremal ray of the effective and nef cones sits in one of our halves. Call an extremal ray of the effective or nef cone primary or secondary according to which half it lies in.
We know that the ample cone of
![]() $M(\unicode[STIX]{x1D709})$
lies in the primary half space because
$M(\unicode[STIX]{x1D709})$
lies in the primary half space because
![]() ${\mathcal{L}}_{0}$
lies in that half space.
${\mathcal{L}}_{0}$
lies in that half space.
2.9 Brill–Noether divisors
Now that we have constructed a basis for the Picard space, we discuss the divisors that we construct to span the effective cone. These divisors are examples of Brill–Noether divisors. A Brill–Noether locus in general is the place where the rank of some cohomology group jumps.
Proposition 2.16. Suppose
![]() $V\in M(\unicode[STIX]{x1D701})$
is a stable vector bundle and is cohomologically orthogonal to the general
$V\in M(\unicode[STIX]{x1D701})$
is a stable vector bundle and is cohomologically orthogonal to the general
![]() $U\in M(\unicode[STIX]{x1D709})$
. Put the natural determinantal scheme structure on the locus
$U\in M(\unicode[STIX]{x1D709})$
. Put the natural determinantal scheme structure on the locus
(1)
 $D_{V}$
is an effective divisor.
$D_{V}$
is an effective divisor.(2) If
 $\unicode[STIX]{x1D707}_{1,1}(U\otimes V)>-4$
, then
$\unicode[STIX]{x1D707}_{1,1}(U\otimes V)>-4$
, then
 ${\mathcal{O}}_{M(\unicode[STIX]{x1D709})}(D_{V})\cong \unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701})$
.
${\mathcal{O}}_{M(\unicode[STIX]{x1D709})}(D_{V})\cong \unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701})$
.(3) If
 $\unicode[STIX]{x1D707}_{1,1}(U\otimes V)<0$
, then
$\unicode[STIX]{x1D707}_{1,1}(U\otimes V)<0$
, then
 ${\mathcal{O}}_{M(\unicode[STIX]{x1D709})}(D_{V})\cong \unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701})^{\ast }\cong \unicode[STIX]{x1D706}_{M}(-\unicode[STIX]{x1D701})$
.
${\mathcal{O}}_{M(\unicode[STIX]{x1D709})}(D_{V})\cong \unicode[STIX]{x1D706}_{M}(\unicode[STIX]{x1D701})^{\ast }\cong \unicode[STIX]{x1D706}_{M}(-\unicode[STIX]{x1D701})$
.
Proof. After replacing slope with
![]() $(1,1)$
-slope and
$(1,1)$
-slope and
![]() $-3$
with
$-3$
with
![]() $-4$
(the first is the slope of
$-4$
(the first is the slope of
![]() $K_{\mathbb{P}^{2}}$
while the second is the
$K_{\mathbb{P}^{2}}$
while the second is the
![]() $(1,1)$
-slope of
$(1,1)$
-slope of
![]() $K_{\mathbb{P}^{1}\times \mathbb{P}^{1}}$
), the proof is identical to that of [Reference Coskun, Huizenga and WoolfCHW, Prop. 5.4].
$K_{\mathbb{P}^{1}\times \mathbb{P}^{1}}$
), the proof is identical to that of [Reference Coskun, Huizenga and WoolfCHW, Prop. 5.4].
Given a Brill–Noether divisor, a natural question to ask is whether it lies in the primary or the secondary half of
![]() $\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
. The answer is immediate from the computation of the class of the Brill–Noether divisors.
$\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
. The answer is immediate from the computation of the class of the Brill–Noether divisors.
Corollary 2.17. Keep the notation and hypotheses from Proposition 2.16.
(1) If
 $\unicode[STIX]{x1D707}_{1,1}(U\otimes V)>-4$
, then [
$\unicode[STIX]{x1D707}_{1,1}(U\otimes V)>-4$
, then [
 $D_{V}$
] lies in the primary half of
$D_{V}$
] lies in the primary half of
 $\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
.
$\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
.(2) If
 $\unicode[STIX]{x1D707}_{1,1}(U\otimes V)<0$
, then [
$\unicode[STIX]{x1D707}_{1,1}(U\otimes V)<0$
, then [
 $D_{V}$
] lies in the secondary half of
$D_{V}$
] lies in the secondary half of
 $\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
.
$\operatorname{NS}(M(\unicode[STIX]{x1D709}))$
.
Note that since
![]() $\unicode[STIX]{x1D707}_{1,1}(U\otimes V)$
cannot be between
$\unicode[STIX]{x1D707}_{1,1}(U\otimes V)$
cannot be between
![]() $-4$
and
$-4$
and
![]() $0$
there is no contradiction in these results.
$0$
there is no contradiction in these results.
2.10 The interpolation problem
As we previously mentioned, in order to construct a Brill–Noether divisor, it is necessary to find a sheaf
![]() $V$
for which
$V$
for which
![]() $h^{1}(U\otimes V)=0$
for the general
$h^{1}(U\otimes V)=0$
for the general
![]() $U\in M(\unicode[STIX]{x1D709})$
and the easiest way to do so is to find a sheaf that is cohomologically orthogonal to
$U\in M(\unicode[STIX]{x1D709})$
and the easiest way to do so is to find a sheaf that is cohomologically orthogonal to
![]() $U$
. Cohomological orthogonality implies that
$U$
. Cohomological orthogonality implies that
![]() $\unicode[STIX]{x1D712}(U\otimes V)=0$
. The vanishing of that Euler characteristic is a strictly weaker condition. For example, it might be the case that
$\unicode[STIX]{x1D712}(U\otimes V)=0$
. The vanishing of that Euler characteristic is a strictly weaker condition. For example, it might be the case that
![]() $h^{0}=h^{1}=1$
and
$h^{0}=h^{1}=1$
and
![]() $h^{2}=0$
. We would like an added condition which would make them equivalent. A bundle
$h^{2}=0$
. We would like an added condition which would make them equivalent. A bundle
![]() $V$
is nonspecial with respect to
$V$
is nonspecial with respect to
![]() $U$
if
$U$
if
![]() $\unicode[STIX]{x1D712}(U\otimes V)$
determines the cohomology groups (i.e., they are lowest ranks allowed by the Euler characteristic). We can rephrase cohomological orthogonality as
$\unicode[STIX]{x1D712}(U\otimes V)$
determines the cohomology groups (i.e., they are lowest ranks allowed by the Euler characteristic). We can rephrase cohomological orthogonality as
![]() $V$
having
$V$
having
![]() $\unicode[STIX]{x1D712}(U\otimes V)=0$
and being nonspecial with respect to
$\unicode[STIX]{x1D712}(U\otimes V)=0$
and being nonspecial with respect to
![]() $U$
. In general, there are many such sheaves, but those that interest us are those of “minimum slope”. Finding a sheaf like this is a form of the interpolation problem.
$U$
. In general, there are many such sheaves, but those that interest us are those of “minimum slope”. Finding a sheaf like this is a form of the interpolation problem.
The Interpolation Problem.
Given invariants
![]() $\unicode[STIX]{x1D709}$
of a vector bundle and a polarization
$\unicode[STIX]{x1D709}$
of a vector bundle and a polarization
![]() $H$
of
$H$
of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, find a stable vector bundle
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, find a stable vector bundle
![]() $V$
with minimum
$V$
with minimum
![]() $\unicode[STIX]{x1D707}_{H}$
that is cohomologically orthogonal to the general element of
$\unicode[STIX]{x1D707}_{H}$
that is cohomologically orthogonal to the general element of
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
Note, if we restrict our interest to line bundles on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
and
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
and
![]() $M(\unicode[STIX]{x1D709})=\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[m]}$
, this is the classical interpolation for points lying on
$M(\unicode[STIX]{x1D709})=\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[m]}$
, this is the classical interpolation for points lying on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
: find the “lowest” bidegree
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
: find the “lowest” bidegree
![]() $(a,b)$
such that
$(a,b)$
such that
![]() $m$
points lie on a curve of type
$m$
points lie on a curve of type
![]() $(a,b)$
.
$(a,b)$
.
By construction of the Brill–Noether divisors, any solution of the interpolation problem gives an effective Brill–Noether divisor. Our goal is to give a method to construct Brill–Noether divisors which are sufficient to span the effective cone in many examples. We show that they span in examples by providing an alternate construction of the divisors. This description provides dual moving curves which prove that they are extremal divisors in the effective cone.
The alternate construction starts by using the cohomological vanishing guaranteed by these Brill–Noether divisors to resolve the general objects of
![]() $M(\unicode[STIX]{x1D709})$
. In general, we then use these resolutions to construct maps from
$M(\unicode[STIX]{x1D709})$
. In general, we then use these resolutions to construct maps from
![]() $M(\unicode[STIX]{x1D709})$
to Picard rank one varieties that have positive dimensional fibers. The Brill–Noether divisors match up with the pull backs of an ample divisor on these Picard rank one varieties. We prove the extremality of each divisor using the dual moving curves that cover the fibers of the morphism.
$M(\unicode[STIX]{x1D709})$
to Picard rank one varieties that have positive dimensional fibers. The Brill–Noether divisors match up with the pull backs of an ample divisor on these Picard rank one varieties. We prove the extremality of each divisor using the dual moving curves that cover the fibers of the morphism.
2.11 Kronecker moduli spaces
The simpler varieties that we map to are moduli spaces of Kronecker modules.
Definition 2.18. A quiver with two vertices and arrows in only direction between them is a Kronecker quiver.
Definition 2.19. A Kronecker
![]() $V$
-module is a representation of this quiver and is equivalent to a linear map
$V$
-module is a representation of this quiver and is equivalent to a linear map
![]() $A\otimes V\rightarrow B$
where
$A\otimes V\rightarrow B$
where
![]() $V$
is a vector space of dimension
$V$
is a vector space of dimension
![]() $N$
and
$N$
and
![]() $A$
and
$A$
and
![]() $B$
are arbitrary vector spaces of dimensions
$B$
are arbitrary vector spaces of dimensions
![]() $a$
and
$a$
and
![]() $b$
, respectively.
$b$
, respectively.
Definition 2.20. The moduli space of semistable Kronecker
![]() $V$
-modules with dimension vector
$V$
-modules with dimension vector
![]() $r=(a,b)$
is
$r=(a,b)$
is
![]() $Kr_{N}(a,b)$
.
$Kr_{N}(a,b)$
.
The expected dimension of this space is
For Kronecker moduli spaces, we also know that they are nonempty and of the expected dimension if their expected dimension is nonnegative [Reference ReinekeRei]. Another fact about Kronecker moduli spaces is that they are Picard rank one [Reference DrézetDré1]. We use this fact later when we create effective divisors on our moduli spaces
![]() $M(\unicode[STIX]{x1D709})$
by constructing fibrations from them to these Kronecker moduli spaces and pulling back a generator of the ample cone of
$M(\unicode[STIX]{x1D709})$
by constructing fibrations from them to these Kronecker moduli spaces and pulling back a generator of the ample cone of
![]() $Kr_{N}(a,b)$
. In order to do this, we need to get Kronecker modules from maps between exceptional bundles.
$Kr_{N}(a,b)$
. In order to do this, we need to get Kronecker modules from maps between exceptional bundles.
2.11.1 Kronecker modules from complexes
Given a complex
![]() $W:A^{a}\rightarrow B^{b}$
where
$W:A^{a}\rightarrow B^{b}$
where
![]() $\{A,B\}$
is an exceptional pair, we get a Kronecker
$\{A,B\}$
is an exceptional pair, we get a Kronecker
![]() $\operatorname{Hom}(A,B)$
-module
$\operatorname{Hom}(A,B)$
-module
![]() $R$
with dimension vector
$R$
with dimension vector
![]() $r=(a,b)$
. The properties of exceptional bundles tell us that homomorphisms of the Kronecker module are exactly the homomorphisms of
$r=(a,b)$
. The properties of exceptional bundles tell us that homomorphisms of the Kronecker module are exactly the homomorphisms of
![]() $W$
and that
$W$
and that
![]() $\unicode[STIX]{x1D712}(r,r^{\prime })=\unicode[STIX]{x1D712}(W,W^{\prime })$
where
$\unicode[STIX]{x1D712}(r,r^{\prime })=\unicode[STIX]{x1D712}(W,W^{\prime })$
where
![]() $R^{\prime }$
is the Kronecker module corresponding to a complex
$R^{\prime }$
is the Kronecker module corresponding to a complex
![]() $W^{\prime }:A^{a^{\prime }}\rightarrow B^{b^{\prime }}$
. We get these complexes between exceptional bundles from resolutions of the general objects of our moduli spaces
$W^{\prime }:A^{a^{\prime }}\rightarrow B^{b^{\prime }}$
. We get these complexes between exceptional bundles from resolutions of the general objects of our moduli spaces
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
3 Corresponding exceptional pairs
In this section, we use exceptional pairs to identify the Brill–Noether divisors that we expect to span the effective cone by identifying possible solutions to the interpolation problem.
Let
![]() $U\in M(\unicode[STIX]{x1D709})$
be a general element. Recall that to solve the interpolation problem we wanted to find bundles that were cohomologically orthogonal to
$U\in M(\unicode[STIX]{x1D709})$
be a general element. Recall that to solve the interpolation problem we wanted to find bundles that were cohomologically orthogonal to
![]() $U$
and that being cohomologically orthogonal is equivalent to
$U$
and that being cohomologically orthogonal is equivalent to
![]() $V$
having
$V$
having
![]() $\unicode[STIX]{x1D712}(U\otimes V)=0$
and
$\unicode[STIX]{x1D712}(U\otimes V)=0$
and
![]() $V$
being cohomologically nonspecial with respect to
$V$
being cohomologically nonspecial with respect to
![]() $\unicode[STIX]{x1D709}$
. Now, we are able find all cohomologically orthogonal bundles by imposing each of these two conditions separately.
$\unicode[STIX]{x1D709}$
. Now, we are able find all cohomologically orthogonal bundles by imposing each of these two conditions separately.
3.1 Bundles with vanishing Euler characteristic
First, we find bundles
![]() $V$
with
$V$
with
![]() $\unicode[STIX]{x1D712}(U\otimes V)=0$
. As we are trying to compute the effective cone, scaling Chern characters is relatively unimportant. In particular, we can scale a Chern character so that
$\unicode[STIX]{x1D712}(U\otimes V)=0$
. As we are trying to compute the effective cone, scaling Chern characters is relatively unimportant. In particular, we can scale a Chern character so that
![]() $\operatorname{ch}_{0}=1$
(unless it was 0 to start).
$\operatorname{ch}_{0}=1$
(unless it was 0 to start).
Definition 3.1. When a Chern character
![]() $\unicode[STIX]{x1D709}$
has positive rank, the orthogonal surface to
$\unicode[STIX]{x1D709}$
has positive rank, the orthogonal surface to
![]() $\unicode[STIX]{x1D709}$
is
$\unicode[STIX]{x1D709}$
is
Using the orthogonal surface rather than the full
![]() $\unicode[STIX]{x1D709}^{\bot }$
has the advantage of working in the three dimensional
$\unicode[STIX]{x1D709}^{\bot }$
has the advantage of working in the three dimensional
![]() $\left(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6E5}\right)$
-space instead of in the full four dimensional
$\left(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6E5}\right)$
-space instead of in the full four dimensional
![]() $K(\mathbb{P}^{1}\times \mathbb{P}^{1})$
. We define the reference surface,
$K(\mathbb{P}^{1}\times \mathbb{P}^{1})$
. We define the reference surface,
![]() $Q_{\unicode[STIX]{x1D709}_{0}}$
, to be the orthogonal surface to
$Q_{\unicode[STIX]{x1D709}_{0}}$
, to be the orthogonal surface to
![]() $\unicode[STIX]{x1D709}_{0}=\operatorname{ch}({\mathcal{O}})=(1,(0,0),0)$
.
$\unicode[STIX]{x1D709}_{0}=\operatorname{ch}({\mathcal{O}})=(1,(0,0),0)$
.
Using Hirzebruch–Riemann–Roch to compute the equation of the orthogonal surface to
![]() $\unicode[STIX]{x1D709}$
gives the formula
$\unicode[STIX]{x1D709}$
gives the formula
where
![]() $P(x,y)=(x+1)(y+1)$
. This equation defines a saddle surface that is a shift of the reference surface. It has unique saddle point at the point
$P(x,y)=(x+1)(y+1)$
. This equation defines a saddle surface that is a shift of the reference surface. It has unique saddle point at the point
![]() $\left(-1-x_{0},-1-y_{0}\right)$
where
$\left(-1-x_{0},-1-y_{0}\right)$
where
![]() $(x_{0},y_{0})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D709})$
. Consequently, any two such surfaces intersect in a parabola that lies over a line in the slope plane.
$(x_{0},y_{0})=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D709})$
. Consequently, any two such surfaces intersect in a parabola that lies over a line in the slope plane.
Using this language, the condition that
![]() $\unicode[STIX]{x1D712}(U\otimes V)=0$
can be rephrased as saying that
$\unicode[STIX]{x1D712}(U\otimes V)=0$
can be rephrased as saying that
![]() $V$
must lie on
$V$
must lie on
![]() $Q_{\unicode[STIX]{x1D709}}$
. In other words, we can restrict our search for solutions to the interpolation problem to bundles that lie on the orthogonal surface (to
$Q_{\unicode[STIX]{x1D709}}$
. In other words, we can restrict our search for solutions to the interpolation problem to bundles that lie on the orthogonal surface (to
![]() $\unicode[STIX]{x1D709}$
).
$\unicode[STIX]{x1D709}$
).
As a side note, we can now give an alternative description of each fractal part of the
![]() $\unicode[STIX]{x1D6FF}$
surface using orthogonal surfaces. Given an exceptional bundle
$\unicode[STIX]{x1D6FF}$
surface using orthogonal surfaces. Given an exceptional bundle
![]() $E_{\unicode[STIX]{x1D6FC}}$
,
$E_{\unicode[STIX]{x1D6FC}}$
,
![]() $\unicode[STIX]{x1D6FF}_{E}$
can equivalently be written as
$\unicode[STIX]{x1D6FF}_{E}$
can equivalently be written as
Thus, every saddle subsurface of the surface
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D6E5}$
can be seen to be a portion of some surface
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D707})=\unicode[STIX]{x1D6E5}$
can be seen to be a portion of some surface
![]() $Q_{E}$
.
$Q_{E}$
.
3.2 Cohomologically nonspecial bundles
Now that we have found the bundles with
![]() $\unicode[STIX]{x1D712}(U\otimes V)=0$
, we would like to impose the second condition of cohomological orthogonality, being nonspecial. In some cases, we can find numerical conditions defining being nonspecialty as well. Those conditions are in terms of certain exceptional bundles that we pick out. Picking them out begins with studying
$\unicode[STIX]{x1D712}(U\otimes V)=0$
, we would like to impose the second condition of cohomological orthogonality, being nonspecial. In some cases, we can find numerical conditions defining being nonspecialty as well. Those conditions are in terms of certain exceptional bundles that we pick out. Picking them out begins with studying
![]() $Q_{\unicode[STIX]{x1D709}}$
again.
$Q_{\unicode[STIX]{x1D709}}$
again.
Note that
![]() $Q_{\unicode[STIX]{x1D709}}$
intersects the plane
$Q_{\unicode[STIX]{x1D709}}$
intersects the plane
![]() $\unicode[STIX]{x1D6E5}=\frac{1}{2}$
. The exceptional bundles that we want to pick out are those exceptional bundles that control this intersection.
$\unicode[STIX]{x1D6E5}=\frac{1}{2}$
. The exceptional bundles that we want to pick out are those exceptional bundles that control this intersection.
Definition 3.2. A controlling exceptional bundle of
![]() $\unicode[STIX]{x1D709}$
is an exceptional bundle,
$\unicode[STIX]{x1D709}$
is an exceptional bundle,
![]() $E_{\unicode[STIX]{x1D6FC}}$
, for which there exists a slope
$E_{\unicode[STIX]{x1D6FC}}$
, for which there exists a slope
![]() $\unicode[STIX]{x1D708}$
for which
$\unicode[STIX]{x1D708}$
for which
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{E_{\unicode[STIX]{x1D6FC}}}(\unicode[STIX]{x1D708})$
and
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{E_{\unicode[STIX]{x1D6FC}}}(\unicode[STIX]{x1D708})$
and
![]() $Q_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D708})=\frac{1}{2}$
.
$Q_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D708})=\frac{1}{2}$
.
As promised above, each controlling exceptional bundle provides a necessary condition for a stable Chern character to be nonspecial with respect to the general element of
![]() $M(\unicode[STIX]{x1D709})$
. The condition that a controlling exceptional bundles imposes on a Chern character is that the Chern character must be on or above a surface corresponding to that exceptional bundle.
$M(\unicode[STIX]{x1D709})$
. The condition that a controlling exceptional bundles imposes on a Chern character is that the Chern character must be on or above a surface corresponding to that exceptional bundle.
Definition 3.3. The corresponding surface to an exceptional bundle
![]() $E_{\unicode[STIX]{x1D6FC}}$
for
$E_{\unicode[STIX]{x1D6FC}}$
for
![]() $\unicode[STIX]{x1D709}$
is defined as
$\unicode[STIX]{x1D709}$
is defined as
Then in some, if not all, cases, the Chern characters
![]() $\unicode[STIX]{x1D708}$
such that
$\unicode[STIX]{x1D708}$
such that
![]() $Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D708})>0$
for all controlling bundles
$Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D708})>0$
for all controlling bundles
![]() $E_{\unicode[STIX]{x1D6FC}}$
of
$E_{\unicode[STIX]{x1D6FC}}$
of
![]() $\unicode[STIX]{x1D709}$
are precisely the nonspecial Chern characters with respect to
$\unicode[STIX]{x1D709}$
are precisely the nonspecial Chern characters with respect to
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
3.3 Potential extremal rays
The solutions to interpolation are the intersection of the orthogonal surface and the maximum of the corresponding surfaces. Each part of this intersection is where the orthogonal surface intersects a corresponding surface, that is, where
![]() $Q_{\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}$
for a controlling exceptional
$Q_{\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}$
for a controlling exceptional
![]() $E_{\unicode[STIX]{x1D6FC}}$
of
$E_{\unicode[STIX]{x1D6FC}}$
of
![]() $\unicode[STIX]{x1D709}$
. The corners of the intersection are where the orthogonal surface intersects two different corresponding surfaces, that is, where
$\unicode[STIX]{x1D709}$
. The corners of the intersection are where the orthogonal surface intersects two different corresponding surfaces, that is, where
![]() $Q_{\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
for controlling exceptionals
$Q_{\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
for controlling exceptionals
![]() $E_{\unicode[STIX]{x1D6FC}}$
and
$E_{\unicode[STIX]{x1D6FC}}$
and
![]() $E_{\unicode[STIX]{x1D6FD}}$
of
$E_{\unicode[STIX]{x1D6FD}}$
of
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
As
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FD}$
, and
$\unicode[STIX]{x1D6FD}$
, and
![]() $\unicode[STIX]{x1D709}$
are three linearly independent rational Chern characters,
$\unicode[STIX]{x1D709}$
are three linearly independent rational Chern characters,
![]() $Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
is a single point that corresponds to the intersection of the 3 planes
$Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
is a single point that corresponds to the intersection of the 3 planes
![]() $\unicode[STIX]{x1D6FC}^{\bot }\cap \unicode[STIX]{x1D6FD}^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
,
$\unicode[STIX]{x1D6FC}^{\bot }\cap \unicode[STIX]{x1D6FD}^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
,
![]() $(\unicode[STIX]{x1D6FC}+K)^{\bot }\cap \unicode[STIX]{x1D6FD}^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
,
$(\unicode[STIX]{x1D6FC}+K)^{\bot }\cap \unicode[STIX]{x1D6FD}^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
,
![]() $\unicode[STIX]{x1D6FC}^{\bot }\cap (\unicode[STIX]{x1D6FD}+K)^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
, or
$\unicode[STIX]{x1D6FC}^{\bot }\cap (\unicode[STIX]{x1D6FD}+K)^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
, or
![]() $(\unicode[STIX]{x1D6FC}+K)^{\bot }\cap (\unicode[STIX]{x1D6FD}+K)^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
. We determine which intersection it is by which cases of
$(\unicode[STIX]{x1D6FC}+K)^{\bot }\cap (\unicode[STIX]{x1D6FD}+K)^{\bot }\cap \unicode[STIX]{x1D6FE}^{\bot }$
. We determine which intersection it is by which cases of
![]() $Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}$
and
$Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}$
and
![]() $Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
we are using. We want to find the corners made in this way in order to get effective divisors. To find those divisors, we first define all of the possible triple intersections that might work.
$Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
we are using. We want to find the corners made in this way in order to get effective divisors. To find those divisors, we first define all of the possible triple intersections that might work.
Definition 3.4. The corresponding orthogonal point of a pair of controlling exceptional bundles
![]() $E_{\unicode[STIX]{x1D6FC}}$
and
$E_{\unicode[STIX]{x1D6FC}}$
and
![]() $E_{\unicode[STIX]{x1D6FD}}$
is one of the following
$E_{\unicode[STIX]{x1D6FD}}$
is one of the following
(1) the unique point
 $\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)\in Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
,
$\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)\in Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
,(2)
 $\unicode[STIX]{x1D6FD}$
if
$\unicode[STIX]{x1D6FD}$
if
 $\unicode[STIX]{x1D6FD}\in Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}$
, or
$\unicode[STIX]{x1D6FD}\in Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D709}}$
, or(3)
 $\unicode[STIX]{x1D6FC}$
if
$\unicode[STIX]{x1D6FC}$
if
 $\unicode[STIX]{x1D6FC}\in Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
.
$\unicode[STIX]{x1D6FC}\in Q_{\unicode[STIX]{x1D709}}\cap Q_{\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D709}}$
.
(2) and (3) can occur simultaneously, but you can treat them individually so we say “the orthogonal point”.
Some of the corresponding orthogonal points are not actually what we want, as they can both fail to satisfy interpolation (by being below one of the other corresponding surfaces) or by not being extremal (as they have a slope that is not linearly independent of other solutions). We want to pick out the only the solutions that satisfy interpolation and are extremal among those solutions.
Definition 3.5. A controlling pair of
![]() $\unicode[STIX]{x1D709}$
is an exceptional pair of controlling exceptional bundles
$\unicode[STIX]{x1D709}$
is an exceptional pair of controlling exceptional bundles
![]() $E_{\unicode[STIX]{x1D6FC}}$
and
$E_{\unicode[STIX]{x1D6FC}}$
and
![]() $E_{\unicode[STIX]{x1D6FD}}$
of
$E_{\unicode[STIX]{x1D6FD}}$
of
![]() $\unicode[STIX]{x1D709}$
with a corresponding orthogonal point
$\unicode[STIX]{x1D709}$
with a corresponding orthogonal point
![]() $\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
that is stable.
$\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
that is stable.
We now want to turn these points back into Chern characters for convenience.
Definition 3.6. A potential (primary) orthogonal Chern character
![]() $\unicode[STIX]{x1D709}^{+}$
to
$\unicode[STIX]{x1D709}^{+}$
to
![]() $\unicode[STIX]{x1D709}$
is defined by any character
$\unicode[STIX]{x1D709}$
is defined by any character
![]() $\unicode[STIX]{x1D709}^{+}=\left(r^{+},\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
where
$\unicode[STIX]{x1D709}^{+}=\left(r^{+},\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
where
![]() $r^{+}$
is sufficiently large and divisible and
$r^{+}$
is sufficiently large and divisible and
![]() $(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+})$
is the corresponding orthogonal point of a controlling pair of
$(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+})$
is the corresponding orthogonal point of a controlling pair of
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
We call them potential because we see in the next section that we need a few additional conditions to make sure that they actually span an extremal ray of the effective cone. We give an approach to showing that some of the potential primary orthogonal Chern characters span the solutions of the interpolation problem and that the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
is spanned by the Brill–Noether divisors
$M(\unicode[STIX]{x1D709})$
is spanned by the Brill–Noether divisors
![]() $D_{V}$
for many examples of
$D_{V}$
for many examples of
![]() $M(\unicode[STIX]{x1D709})$
where
$M(\unicode[STIX]{x1D709})$
where
![]() $V$
are bundles whose Chern character is an orthogonal Chern character
$V$
are bundles whose Chern character is an orthogonal Chern character
![]() $\unicode[STIX]{x1D709}^{+}$
.
$\unicode[STIX]{x1D709}^{+}$
.
The behavior of these extremal rays depends on the sign of
![]() $\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FC}}^{\ast },U)$
and
$\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FC}}^{\ast },U)$
and
![]() $\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)$
. Keeping the identification of
$\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)$
. Keeping the identification of
![]() $\operatorname{NS}\left(M(\unicode[STIX]{x1D709})\right)\cong \unicode[STIX]{x1D709}^{\bot }$
in mind, recall that the primary half of the space corresponds to characters of positive rank.
$\operatorname{NS}\left(M(\unicode[STIX]{x1D709})\right)\cong \unicode[STIX]{x1D709}^{\bot }$
in mind, recall that the primary half of the space corresponds to characters of positive rank.
(1) If
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})>0$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})>0$
and
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})>0$
, the ray is spanned by a positive rank Chern character in
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})>0$
, the ray is spanned by a positive rank Chern character in
 $\unicode[STIX]{x1D709}^{\bot }\cap \unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}}^{\bot }\cap \unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}}^{\bot }$
.
$\unicode[STIX]{x1D709}^{\bot }\cap \unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}}^{\bot }\cap \unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}}^{\bot }$
.(2) If
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})<0$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})<0$
and
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})>0$
, the ray is spanned by a positive rank Chern character in
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})>0$
, the ray is spanned by a positive rank Chern character in
 $\unicode[STIX]{x1D709}^{\bot }\cap \left(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}+K}\right)^{\bot }\cap \unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}}^{\bot }$
.
$\unicode[STIX]{x1D709}^{\bot }\cap \left(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}+K}\right)^{\bot }\cap \unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}}^{\bot }$
.(3) If
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})<0$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})<0$
and
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})<0$
, the ray is spanned by a positive rank Chern character in
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})<0$
, the ray is spanned by a positive rank Chern character in
 $\unicode[STIX]{x1D709}^{\bot }\cap \left(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}+K}\right)^{\bot }\cap \left(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}+K}\right)^{\bot }$
.
$\unicode[STIX]{x1D709}^{\bot }\cap \left(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}+K}\right)^{\bot }\cap \left(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}+K}\right)^{\bot }$
.(4) If
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})=0$
or
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D709})=0$
or
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})=0$
, the ray is spanned by
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709}_{-\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D709})=0$
, the ray is spanned by
 $\unicode[STIX]{x1D6FC}$
or
$\unicode[STIX]{x1D6FC}$
or
 $\unicode[STIX]{x1D6FD}$
, respectively.
$\unicode[STIX]{x1D6FD}$
, respectively.
4 The Beilinson spectral sequence
In this section, we find a resolution of the general object
![]() $U\in M(\unicode[STIX]{x1D709})$
for each orthogonal Chern character via a generalized Beilinson spectral sequence. In the next section, we use these resolutions to construct fibrations
$U\in M(\unicode[STIX]{x1D709})$
for each orthogonal Chern character via a generalized Beilinson spectral sequence. In the next section, we use these resolutions to construct fibrations
![]() $M(\unicode[STIX]{x1D709}){\dashrightarrow}Kr_{V}(m,n)$
. In the second last section, these fibrations give us effective divisors on
$M(\unicode[STIX]{x1D709}){\dashrightarrow}Kr_{V}(m,n)$
. In the second last section, these fibrations give us effective divisors on
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
An orthogonal Chern character already has exceptional pairs associated to it. In order to use the spectral sequence, we have to complete each of those exceptional pairs to a coil.
The coil we use to resolve
![]() $U$
depends on the behavior of the extremal ray that we exhibited in the last section.
$U$
depends on the behavior of the extremal ray that we exhibited in the last section.
(1) If
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\geqslant 0$
and
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\geqslant 0$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
, we decompose
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
, we decompose
 $U$
according to the coil
$U$
according to the coil
 $\left(F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}\right)$
where
$\left(F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}\right)$
where
 $(F_{0},F_{1})$
is a minimally ranked right completion pair of
$(F_{0},F_{1})$
is a minimally ranked right completion pair of
 $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
.
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
.(2) If
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
, we decompose
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
, we decompose
 $U$
according to the coil
$U$
according to the coil
 $\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}}\right)$
where
$\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}}\right)$
where
 $(F_{0},F_{1})$
is a minimally ranked right completion pair of
$(F_{0},F_{1})$
is a minimally ranked right completion pair of
 $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
.
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
.(3) If
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\leqslant 0$
, we decompose
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\leqslant 0$
, we decompose
 $U$
according to the coil
$U$
according to the coil
 $\left(E_{-\unicode[STIX]{x1D6FD}}(K),E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast }\right)$
where
$\left(E_{-\unicode[STIX]{x1D6FD}}(K),E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast }\right)$
where
 $(F_{0},F_{1})$
is a minimally ranked right completion pair of
$(F_{0},F_{1})$
is a minimally ranked right completion pair of
 $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
.
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
.
The spectral sequence only gives a resolution under some assumptions on the controlling pairs. These are the additional conditions needed to make a potential orthogonal Chern character span an extremal ray of the effective cone. We call those controlling pairs that satisfy the needed conditions extremal pairs; there is a different definition for if a controlling pair is extremal based on the signs of some Euler characteristics so we defer the definition to the following three subsections.
Extremal pairs pick out the exact Chern characters that correspond to extremal effective divisors using our approach as promised in the previous section.
Definition 4.1. A primary orthogonal Chern character is the potential primary orthogonal Chern character associated to an extremal pair.
It is a current area of research to show the following conjecture for extremal pairs (including those as defined analogously in the next three subsections).
Conjecture 4.2. Every
![]() $\unicode[STIX]{x1D709}$
above the Rudakov
$\unicode[STIX]{x1D709}$
above the Rudakov
![]() $\unicode[STIX]{x1D6FF}$
-surface has an extremal pair and every controlling exceptional bundle of it that is in an extremal pair is in two extremal pairs.
$\unicode[STIX]{x1D6FF}$
-surface has an extremal pair and every controlling exceptional bundle of it that is in an extremal pair is in two extremal pairs.
Proving the conjecture would show that the process laid out in this paper computes the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
for all
$M(\unicode[STIX]{x1D709})$
for all
![]() $\unicode[STIX]{x1D709}$
above the
$\unicode[STIX]{x1D709}$
above the
![]() $\unicode[STIX]{x1D6FF}$
surface. There are two main difficulties in proving this conjecture. First, one would need to show that every orthogonal surface intersects the
$\unicode[STIX]{x1D6FF}$
surface. There are two main difficulties in proving this conjecture. First, one would need to show that every orthogonal surface intersects the
![]() $\unicode[STIX]{x1D6FF}$
surface “nicely” by which we mean that the intersection curve is strictly above the plane
$\unicode[STIX]{x1D6FF}$
surface “nicely” by which we mean that the intersection curve is strictly above the plane
![]() $\unicode[STIX]{x1D6E5}=\frac{1}{2}$
. Note, this is equivalent to the projection of that curve into the slope plane missing the Cantor-like set of points where the
$\unicode[STIX]{x1D6E5}=\frac{1}{2}$
. Note, this is equivalent to the projection of that curve into the slope plane missing the Cantor-like set of points where the
![]() $\unicode[STIX]{x1D6FF}$
surface intersects the plane
$\unicode[STIX]{x1D6FF}$
surface intersects the plane
![]() $\unicode[STIX]{x1D6E5}=\frac{1}{2}$
. Second, one would need to show that each controlling pair gotten from this curve satisfies the necessary hypotheses to be extremal pairs.
$\unicode[STIX]{x1D6E5}=\frac{1}{2}$
. Second, one would need to show that each controlling pair gotten from this curve satisfies the necessary hypotheses to be extremal pairs.
4.1 The “mixed type” spectral sequence
Assume
![]() $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
![]() $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
. Let the right mutated coil of
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
. Let the right mutated coil of
![]() $\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}}\right)$
be
$\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}}\right)$
be
![]() $\left(E_{-\unicode[STIX]{x1D6FD}},E_{-1}^{\ast },E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FC}}\right)$
. Let
$\left(E_{-\unicode[STIX]{x1D6FD}},E_{-1}^{\ast },E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FC}}\right)$
. Let
![]() $\unicode[STIX]{x1D6E5}_{i}$
be as in the spectral sequence with input these two coils.
$\unicode[STIX]{x1D6E5}_{i}$
be as in the spectral sequence with input these two coils.
Definition 4.3. A (mixed type) controlling pair of
![]() $\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D709}$
,
![]() $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
, with corresponding orthogonal slope and discriminant
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
, with corresponding orthogonal slope and discriminant
![]() $\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
is called extremal if it satisfies the following conditions:
$\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
is called extremal if it satisfies the following conditions:
(1) They are within a unit in both slope coordinates.
(2)
 $\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FC}})$
,
$\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FC}})$
,
 $\unicode[STIX]{x1D707}_{1,1}(E_{-2})$
,
$\unicode[STIX]{x1D707}_{1,1}(E_{-2})$
,
 $\unicode[STIX]{x1D707}_{1,1}(E_{-1})$
, and
$\unicode[STIX]{x1D707}_{1,1}(E_{-1})$
, and
 $\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FD}})$
are all greater than
$\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FD}})$
are all greater than
 $\unicode[STIX]{x1D707}_{1,1}(U)-4$
.
$\unicode[STIX]{x1D707}_{1,1}(U)-4$
.(3) (
 $\unicode[STIX]{x1D6E5}_{2}=1$
and
$\unicode[STIX]{x1D6E5}_{2}=1$
and
 $\unicode[STIX]{x1D712}\left(E_{-2}^{\ast },U\right)\geqslant 0$
) or (
$\unicode[STIX]{x1D712}\left(E_{-2}^{\ast },U\right)\geqslant 0$
) or (
 $\unicode[STIX]{x1D6E5}_{2}=0$
and
$\unicode[STIX]{x1D6E5}_{2}=0$
and
 $\unicode[STIX]{x1D712}\left(E_{-2}^{\ast },U\right)\leqslant 0$
).
$\unicode[STIX]{x1D712}\left(E_{-2}^{\ast },U\right)\leqslant 0$
).(4) (
 $\unicode[STIX]{x1D6E5}_{1}=1$
and
$\unicode[STIX]{x1D6E5}_{1}=1$
and
 $\unicode[STIX]{x1D712}\left(E_{-1}^{\ast },U\right)\geqslant 0$
) or (
$\unicode[STIX]{x1D712}\left(E_{-1}^{\ast },U\right)\geqslant 0$
) or (
 $\unicode[STIX]{x1D6E5}_{1}=0$
and
$\unicode[STIX]{x1D6E5}_{1}=0$
and
 $\unicode[STIX]{x1D712}\left(E_{-1}^{\ast },U\right)\geqslant 0$
).
$\unicode[STIX]{x1D712}\left(E_{-1}^{\ast },U\right)\geqslant 0$
).(5)
 $\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast })$
,
$\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast })$
,
 $\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),E_{-\unicode[STIX]{x1D6FD}})$
,
$\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),E_{-\unicode[STIX]{x1D6FD}})$
,
 $\mathscr{H}\!om(F_{0}^{\ast },F_{-1}^{\ast })$
, and
$\mathscr{H}\!om(F_{0}^{\ast },F_{-1}^{\ast })$
, and
 $\mathscr{H}\!om(F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
are all globally generated.
$\mathscr{H}\!om(F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
are all globally generated.(6) Any bundle sitting in a triangle
 $\left(F_{-1}^{\ast }\right)^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}^{m_{0}}\rightarrow U\rightarrow \left(E_{-\unicode[STIX]{x1D6FC}}(K)^{m_{3}}\bigoplus \left(F_{0}^{\ast }\right)^{m_{2}}\right)[1]$
is prioritary.
$\left(F_{-1}^{\ast }\right)^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}^{m_{0}}\rightarrow U\rightarrow \left(E_{-\unicode[STIX]{x1D6FC}}(K)^{m_{3}}\bigoplus \left(F_{0}^{\ast }\right)^{m_{2}}\right)[1]$
is prioritary.
Given an extremal pair, we can resolve the general object of
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
Theorem 4.4. The general
![]() $U\in M(\unicode[STIX]{x1D709})$
admits a resolution of the following form
$U\in M(\unicode[STIX]{x1D709})$
admits a resolution of the following form
Proof. Consider a bundle
![]() $U$
defined by the sequence
$U$
defined by the sequence
where the map
![]() $\unicode[STIX]{x1D719}\in \operatorname{Hom}(E_{-\unicode[STIX]{x1D6FC}}(K)^{m_{3}}\bigoplus \left(F_{0}^{\ast }\right)^{m_{2}}\!,\left(F_{-1}^{\ast }\right)^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}^{m_{0}})$
is general.
$\unicode[STIX]{x1D719}\in \operatorname{Hom}(E_{-\unicode[STIX]{x1D6FC}}(K)^{m_{3}}\bigoplus \left(F_{0}^{\ast }\right)^{m_{2}}\!,\left(F_{-1}^{\ast }\right)^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}^{m_{0}})$
is general.
The proof proceeds in 4 steps: calculate that
![]() $\operatorname{ch}(U)=\unicode[STIX]{x1D709}$
, show
$\operatorname{ch}(U)=\unicode[STIX]{x1D709}$
, show
![]() $\unicode[STIX]{x1D719}$
is injective, confirm the expected vanishings in the spectral sequence, and prove that
$\unicode[STIX]{x1D719}$
is injective, confirm the expected vanishings in the spectral sequence, and prove that
![]() $U$
is stable.
$U$
is stable.
Step 1. Calculate
![]() $\operatorname{ch}(U)=\unicode[STIX]{x1D709}$
. We do not know if
$\operatorname{ch}(U)=\unicode[STIX]{x1D709}$
. We do not know if
![]() $\unicode[STIX]{x1D719}$
is injective yet, but we can compute the Chern character of the mapping cone of
$\unicode[STIX]{x1D719}$
is injective yet, but we can compute the Chern character of the mapping cone of
![]() $\unicode[STIX]{x1D719}$
in the derived category. Assuming
$\unicode[STIX]{x1D719}$
in the derived category. Assuming
![]() $\unicode[STIX]{x1D719}$
is injective, this computes the Chern character of
$\unicode[STIX]{x1D719}$
is injective, this computes the Chern character of
![]() $U$
.
$U$
.
This computation follows from the generalized Beilinson spectral sequence’s convergence to
![]() $U$
. Specifically, we have a spectral sequence with
$U$
. Specifically, we have a spectral sequence with
![]() $E_{1}$
-page
$E_{1}$
-page
 $$\begin{eqnarray}\displaystyle E_{-\unicode[STIX]{x1D6FC}}(K)\otimes \mathbb{C}^{m_{32}} & \rightarrow & \displaystyle F_{0}^{\ast }\otimes \mathbb{C}^{m_{22}}\rightarrow F_{-1}^{\ast }\otimes \mathbb{C}^{m_{12}}\rightarrow 0\nonumber\\ \displaystyle E_{-\unicode[STIX]{x1D6FC}}(K)\otimes \mathbb{C}^{m_{31}} & \rightarrow & \displaystyle F_{0}^{\ast }\otimes \mathbb{C}^{m_{21}}\rightarrow F_{-1}^{\ast }\otimes \mathbb{C}^{m_{11}}\rightarrow E_{-\unicode[STIX]{x1D6FD}}\otimes \mathbb{C}^{m_{01}}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle F_{0}^{\ast }\otimes \mathbb{C}^{m_{20}}\rightarrow F_{-1}^{\ast }\otimes \mathbb{C}^{m_{10}}\rightarrow E_{-\unicode[STIX]{x1D6FD}}\otimes \mathbb{C}^{m_{00}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{-\unicode[STIX]{x1D6FC}}(K)\otimes \mathbb{C}^{m_{32}} & \rightarrow & \displaystyle F_{0}^{\ast }\otimes \mathbb{C}^{m_{22}}\rightarrow F_{-1}^{\ast }\otimes \mathbb{C}^{m_{12}}\rightarrow 0\nonumber\\ \displaystyle E_{-\unicode[STIX]{x1D6FC}}(K)\otimes \mathbb{C}^{m_{31}} & \rightarrow & \displaystyle F_{0}^{\ast }\otimes \mathbb{C}^{m_{21}}\rightarrow F_{-1}^{\ast }\otimes \mathbb{C}^{m_{11}}\rightarrow E_{-\unicode[STIX]{x1D6FD}}\otimes \mathbb{C}^{m_{01}}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle F_{0}^{\ast }\otimes \mathbb{C}^{m_{20}}\rightarrow F_{-1}^{\ast }\otimes \mathbb{C}^{m_{10}}\rightarrow E_{-\unicode[STIX]{x1D6FD}}\otimes \mathbb{C}^{m_{00}}\nonumber\end{eqnarray}$$
that converges in degree 0 to the sheaf
![]() $U$
and to 0 in all other degrees. We omitted all nonzero rows and columns. In particular, row 3 is zero by the vanishing of
$U$
and to 0 in all other degrees. We omitted all nonzero rows and columns. In particular, row 3 is zero by the vanishing of
![]() $h^{2}$
for all the sheaves (follows from Definition 4.3). Also note that either the top or bottom element of each of the middle two rows vanishes (depending on the value of
$h^{2}$
for all the sheaves (follows from Definition 4.3). Also note that either the top or bottom element of each of the middle two rows vanishes (depending on the value of
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
). An easy computation shows that
$\unicode[STIX]{x1D6E5}_{2}$
). An easy computation shows that
In our situation, we see that this gives
where the
![]() $m_{i}$
are defined in the obvious way.
$m_{i}$
are defined in the obvious way.
Step 2. Show
![]() $\unicode[STIX]{x1D719}$
is injective. The sheaves
$\unicode[STIX]{x1D719}$
is injective. The sheaves
![]() $\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast })$
,
$\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast })$
,
![]() $\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),E_{-\unicode[STIX]{x1D6FD}})$
,
$\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),E_{-\unicode[STIX]{x1D6FD}})$
,
![]() $\mathscr{H}\!om(F_{0}^{\ast },F_{-1}^{\ast })$
, and
$\mathscr{H}\!om(F_{0}^{\ast },F_{-1}^{\ast })$
, and
![]() $\mathscr{H}\!om(F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
are all globally generated by the controlling pair being an extremal pair. Those bundles being globally generated immediately implies that
$\mathscr{H}\!om(F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
are all globally generated by the controlling pair being an extremal pair. Those bundles being globally generated immediately implies that
is globally generated as well. Using a Bertini-type theorem [Reference HuizengaHui2, Prop. 2.6] and the fact that the virtually computed rank of
![]() $U$
is positive, we see that
$U$
is positive, we see that
![]() $\unicode[STIX]{x1D719}$
is injective.
$\unicode[STIX]{x1D719}$
is injective.
Step 3. Verify
![]() $U$
’s spectral sequence has the correct vanishings. We know that
$U$
’s spectral sequence has the correct vanishings. We know that
![]() $\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FC}},U)\leqslant 0$
and
$\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FC}},U)\leqslant 0$
and
![]() $\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FD}},U)\geqslant 0$
. We also know that (
$\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FD}},U)\geqslant 0$
. We also know that (
![]() $\unicode[STIX]{x1D712}(E_{-2}^{\ast },U)\leqslant 0$
and
$\unicode[STIX]{x1D712}(E_{-2}^{\ast },U)\leqslant 0$
and
![]() $\unicode[STIX]{x1D6E5}_{2}=0$
) or (
$\unicode[STIX]{x1D6E5}_{2}=0$
) or (
![]() $\unicode[STIX]{x1D712}(E_{-2}^{\ast },U)\geqslant 0$
and
$\unicode[STIX]{x1D712}(E_{-2}^{\ast },U)\geqslant 0$
and
![]() $\unicode[STIX]{x1D6E5}_{2}=1$
). Analogously, we know that (
$\unicode[STIX]{x1D6E5}_{2}=1$
). Analogously, we know that (
![]() $\unicode[STIX]{x1D712}(E_{-1}^{\ast },U)\leqslant 0$
and
$\unicode[STIX]{x1D712}(E_{-1}^{\ast },U)\leqslant 0$
and
![]() $\unicode[STIX]{x1D6E5}_{1}=0$
) or (
$\unicode[STIX]{x1D6E5}_{1}=0$
) or (
![]() $\unicode[STIX]{x1D712}(E_{-1}^{\ast },U)\geqslant 0$
and
$\unicode[STIX]{x1D712}(E_{-1}^{\ast },U)\geqslant 0$
and
![]() $\unicode[STIX]{x1D6E5}_{1}=1$
).
$\unicode[STIX]{x1D6E5}_{1}=1$
).
Since we know that all of the groups other than possibly
![]() $\operatorname{ext}^{1}$
and
$\operatorname{ext}^{1}$
and
![]() $\hom$
vanish, it is enough to check that
$\hom$
vanish, it is enough to check that
These vanishings for the specific
![]() $U$
we have resolved follow from the orthogonality properties of exceptional bundles and the relevant long exact sequences. Once they vanish for a specific
$U$
we have resolved follow from the orthogonality properties of exceptional bundles and the relevant long exact sequences. Once they vanish for a specific
![]() $U$
, they vanish for a general
$U$
, they vanish for a general
![]() $U$
as needed. We show these four vanishings in order.
$U$
as needed. We show these four vanishings in order.
First,
![]() $\hom (E_{-\unicode[STIX]{x1D6FC}},F_{-1}^{\ast })$
,
$\hom (E_{-\unicode[STIX]{x1D6FC}},F_{-1}^{\ast })$
,
![]() $\hom (E_{-\unicode[STIX]{x1D6FC}},E_{-\unicode[STIX]{x1D6FD}})$
, and
$\hom (E_{-\unicode[STIX]{x1D6FC}},E_{-\unicode[STIX]{x1D6FD}})$
, and
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FC}},F_{0}^{\ast })$
all vanish since
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FC}},F_{0}^{\ast })$
all vanish since
![]() $\left(F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}\right)$
is a coil and
$\left(F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}\right)$
is a coil and
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FC}},E_{-\unicode[STIX]{x1D6FC}}(K))$
is equal to
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FC}},E_{-\unicode[STIX]{x1D6FC}}(K))$
is equal to
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FC}}(K),E_{-\unicode[STIX]{x1D6FC}}(K))$
which vanishes since exceptional bundles are rigid. This gives
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FC}}(K),E_{-\unicode[STIX]{x1D6FC}}(K))$
which vanishes since exceptional bundles are rigid. This gives
![]() $\hom (E_{-\unicode[STIX]{x1D6FC}},U)=0$
as desired.
$\hom (E_{-\unicode[STIX]{x1D6FC}},U)=0$
as desired.
For the next vanishing, we have two cases:
![]() $\unicode[STIX]{x1D6E5}_{1}=0$
and
$\unicode[STIX]{x1D6E5}_{1}=0$
and
![]() $\unicode[STIX]{x1D6E5}_{1}=1$
. We assume that
$\unicode[STIX]{x1D6E5}_{1}=1$
. We assume that
![]() $\unicode[STIX]{x1D6E5}_{1}=0$
, and the other case is similar. Assuming
$\unicode[STIX]{x1D6E5}_{1}=0$
, and the other case is similar. Assuming
![]() $\unicode[STIX]{x1D6E5}_{1}=0$
, we need to show that
$\unicode[STIX]{x1D6E5}_{1}=0$
, we need to show that
![]() $\hom (E_{-1}^{\ast },U)=0$
. Next,
$\hom (E_{-1}^{\ast },U)=0$
. Next,
![]() $\operatorname{ext}^{1}(E_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FC}}(K))$
,
$\operatorname{ext}^{1}(E_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FC}}(K))$
,
![]() $\hom (E_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
, and
$\hom (E_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
, and
![]() $\operatorname{ext}^{1}(E_{-1}^{\ast },F_{0}^{\ast })$
all vanish since
$\operatorname{ext}^{1}(E_{-1}^{\ast },F_{0}^{\ast })$
all vanish since
![]() $\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-1}^{\ast }\right)$
is a coil. Then the only remaining vanishing we need to prove is
$\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-1}^{\ast }\right)$
is a coil. Then the only remaining vanishing we need to prove is
![]() $\hom (E_{-1}^{\ast },F_{-1}^{\ast })$
. By assumption on
$\hom (E_{-1}^{\ast },F_{-1}^{\ast })$
. By assumption on
![]() $\unicode[STIX]{x1D6E5}_{1}$
, we can write
$\unicode[STIX]{x1D6E5}_{1}$
, we can write
![]() $0\rightarrow F_{-1}^{\ast }\rightarrow E_{-\unicode[STIX]{x1D6FD}}^{a}\rightarrow E_{-1}^{\ast }\rightarrow 0$
where
$0\rightarrow F_{-1}^{\ast }\rightarrow E_{-\unicode[STIX]{x1D6FD}}^{a}\rightarrow E_{-1}^{\ast }\rightarrow 0$
where
![]() $a=\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FD}},E_{-1})$
. From this resolution, we see
$a=\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FD}},E_{-1})$
. From this resolution, we see
![]() $\hom (E_{-1}^{\ast },F_{-1}^{\ast }){\hookrightarrow}\hom (E_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}})=0$
, and the vanishing follows.
$\hom (E_{-1}^{\ast },F_{-1}^{\ast }){\hookrightarrow}\hom (E_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}})=0$
, and the vanishing follows.
For the next vanishing, we have two cases:
![]() $\unicode[STIX]{x1D6E5}_{1}=0$
and
$\unicode[STIX]{x1D6E5}_{1}=0$
and
![]() $\unicode[STIX]{x1D6E5}_{1}=1$
. We assume that
$\unicode[STIX]{x1D6E5}_{1}=1$
. We assume that
![]() $\unicode[STIX]{x1D6E5}_{1}=0$
, and the other case is similar. Assuming
$\unicode[STIX]{x1D6E5}_{1}=0$
, and the other case is similar. Assuming
![]() $\unicode[STIX]{x1D6E5}_{2}=0$
, we need to show that
$\unicode[STIX]{x1D6E5}_{2}=0$
, we need to show that
![]() $\hom (E_{-2}^{\ast },U)=0$
. Then,
$\hom (E_{-2}^{\ast },U)=0$
. Then,
![]() $\operatorname{ext}^{1}(E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FC}}(K))$
,
$\operatorname{ext}^{1}(E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FC}}(K))$
,
![]() $\hom (E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
, and
$\hom (E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
, and
![]() $\hom (E_{-2}^{\ast },F_{-1}^{\ast })$
all vanish since
$\hom (E_{-2}^{\ast },F_{-1}^{\ast })$
all vanish since
![]() $\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-2}^{\ast }\right)$
is a coil. Then the only remaining vanishing we need to prove is
$\left(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-2}^{\ast }\right)$
is a coil. Then the only remaining vanishing we need to prove is
![]() $\operatorname{ext}^{1}(E_{-2}^{\ast },F_{0}^{\ast })$
. By assumption on
$\operatorname{ext}^{1}(E_{-2}^{\ast },F_{0}^{\ast })$
. By assumption on
![]() $\unicode[STIX]{x1D6E5}_{2}$
, we can write
$\unicode[STIX]{x1D6E5}_{2}$
, we can write
![]() $0\rightarrow F_{0}^{\ast }\rightarrow E_{-\unicode[STIX]{x1D6FD}}^{a}\rightarrow L_{E_{-1}^{\ast }}E_{-2}^{\ast }\rightarrow 0$
where
$0\rightarrow F_{0}^{\ast }\rightarrow E_{-\unicode[STIX]{x1D6FD}}^{a}\rightarrow L_{E_{-1}^{\ast }}E_{-2}^{\ast }\rightarrow 0$
where
![]() $a=\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FD}},L_{E_{-1}^{\ast }}E_{-2}^{\ast })$
. From this resolution we see that
$a=\unicode[STIX]{x1D712}(E_{-\unicode[STIX]{x1D6FD}},L_{E_{-1}^{\ast }}E_{-2}^{\ast })$
. From this resolution we see that
![]() $\operatorname{ext}^{1}(E_{-2}^{\ast },F_{0}^{\ast })\cong \hom (E_{-2}^{\ast },L_{E_{-1}^{\ast }}E_{-2}^{\ast })$
since
$\operatorname{ext}^{1}(E_{-2}^{\ast },F_{0}^{\ast })\cong \hom (E_{-2}^{\ast },L_{E_{-1}^{\ast }}E_{-2}^{\ast })$
since
![]() $\hom (E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FD}})=\operatorname{ext}^{1}(E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FD}})=0$
. Thus, we reduce to showing that
$\hom (E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FD}})=\operatorname{ext}^{1}(E_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FD}})=0$
. Thus, we reduce to showing that
![]() $\hom (E_{-2}^{\ast },L_{E_{-1}^{\ast }}E_{-2}^{\ast })=0$
. Again, by assumption on
$\hom (E_{-2}^{\ast },L_{E_{-1}^{\ast }}E_{-2}^{\ast })=0$
. Again, by assumption on
![]() $\unicode[STIX]{x1D6E5}_{2}$
, we know that we can write
$\unicode[STIX]{x1D6E5}_{2}$
, we know that we can write
![]() $0\rightarrow L_{E_{-1}^{\ast }}E_{-2}^{\ast }\rightarrow (E_{-1}^{\ast })^{a}\rightarrow E_{-2}^{\ast }\rightarrow 0$
from which we can easily see
$0\rightarrow L_{E_{-1}^{\ast }}E_{-2}^{\ast }\rightarrow (E_{-1}^{\ast })^{a}\rightarrow E_{-2}^{\ast }\rightarrow 0$
from which we can easily see
![]() $\hom (E_{-2}^{\ast },L_{E_{-1}^{\ast }}E_{-2}^{\ast }){\hookrightarrow}\hom (E_{-2}^{\ast },E_{-1}^{\ast })=0$
, and the vanishing follows.
$\hom (E_{-2}^{\ast },L_{E_{-1}^{\ast }}E_{-2}^{\ast }){\hookrightarrow}\hom (E_{-2}^{\ast },E_{-1}^{\ast })=0$
, and the vanishing follows.
Finally, we show
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},U)=0$
. Then
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},U)=0$
. Then
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},F_{-1}^{\ast })$
,
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},F_{-1}^{\ast })$
,
![]() $\operatorname{ext}^{2}(E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}(K))$
, and
$\operatorname{ext}^{2}(E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}(K))$
, and
![]() $\operatorname{ext}^{2}(E_{-\unicode[STIX]{x1D6FD}},F_{0}^{\ast })$
all vanish since
$\operatorname{ext}^{2}(E_{-\unicode[STIX]{x1D6FD}},F_{0}^{\ast })$
all vanish since
![]() $(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
is a coil while
$(E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
is a coil while
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FD}})=0$
since exceptional bundles are rigid. This gives the vanishing of
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FD}})=0$
since exceptional bundles are rigid. This gives the vanishing of
![]() $\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},U)$
.
$\operatorname{ext}^{1}(E_{-\unicode[STIX]{x1D6FD}},U)$
.
Step 4. Prove that
![]() $U$
is stable. Let
$U$
is stable. Let
be the open subset of sheaf maps that are injective and have torsion-free cokernels.
By the argument of 5.3 of [Reference Coskun, Huizenga and WoolfCHW], it follows that
![]() $S$
is nonempty.
$S$
is nonempty.
Consider the family
![]() $^{{\mathcal{U}}}\!/_{S}$
of quotients parameterized by
$^{{\mathcal{U}}}\!/_{S}$
of quotients parameterized by
![]() $S$
. We need to show that
$S$
. We need to show that
![]() ${\mathcal{U}}$
is a complete family of prioritary sheaves. Recall that a prioritary sheaf is a torsion-free sheaf
${\mathcal{U}}$
is a complete family of prioritary sheaves. Recall that a prioritary sheaf is a torsion-free sheaf
![]() $U$
such that
$U$
such that
![]() $\operatorname{Ext}^{2}(U,U(0,-1))=0$
or
$\operatorname{Ext}^{2}(U,U(0,-1))=0$
or
![]() $\operatorname{Ext}^{2}(U,U(-1,0))=0$
or, equivalently in our case, that
$\operatorname{Ext}^{2}(U,U(-1,0))=0$
or, equivalently in our case, that
![]() $\operatorname{Hom}(U,U(-1,-2))=0$
or
$\operatorname{Hom}(U,U(-1,-2))=0$
or
![]() $\operatorname{Hom}(U,U(-2,-1))=0$
. By Definition 4.3, the elements of
$\operatorname{Hom}(U,U(-2,-1))=0$
. By Definition 4.3, the elements of
![]() ${\mathcal{U}}$
are prioritary. Again by the general argument of [Reference Coskun, Huizenga and WoolfCHW, 5.3], the family is a complete family. By [Reference WalterWal, Thm. 1], the Artin stack of prioritary sheaves with Chern character
${\mathcal{U}}$
are prioritary. Again by the general argument of [Reference Coskun, Huizenga and WoolfCHW, 5.3], the family is a complete family. By [Reference WalterWal, Thm. 1], the Artin stack of prioritary sheaves with Chern character
![]() $\unicode[STIX]{x1D709}$
is an irreducible stack that contains the stack of semistable sheaves with Chern character
$\unicode[STIX]{x1D709}$
is an irreducible stack that contains the stack of semistable sheaves with Chern character
![]() $\unicode[STIX]{x1D709}$
as a dense open subset. It is then clear that
$\unicode[STIX]{x1D709}$
as a dense open subset. It is then clear that
![]() $S$
parameterizes the general sheaves in
$S$
parameterizes the general sheaves in
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
4.2 The “negative type” spectral sequence
Assume
![]() $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\leqslant 0$
and
![]() $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\leqslant 0$
. Let the right mutated coil of
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\leqslant 0$
. Let the right mutated coil of
![]() $\left(E_{-\unicode[STIX]{x1D6FD}}(K),E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast }\right)$
be
$\left(E_{-\unicode[STIX]{x1D6FD}}(K),E_{-\unicode[STIX]{x1D6FC}}(K),F_{0}^{\ast },F_{-1}^{\ast }\right)$
be
![]() $\left(F_{-1}^{\ast },F_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FE}},E_{-\unicode[STIX]{x1D6FD}}\right)$
. Let
$\left(F_{-1}^{\ast },F_{-2}^{\ast },E_{-\unicode[STIX]{x1D6FE}},E_{-\unicode[STIX]{x1D6FD}}\right)$
. Let
![]() $\unicode[STIX]{x1D6E5}_{i}$
be as in the spectral sequence with input these two coils.
$\unicode[STIX]{x1D6E5}_{i}$
be as in the spectral sequence with input these two coils.
Definition 4.5. A (negative type) controlling pair of
![]() $\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D709}$
,
![]() $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
, with corresponding orthogonal slope and discriminant
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
, with corresponding orthogonal slope and discriminant
![]() $\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
is called extremal if it satisfies the following conditions:
$\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
is called extremal if it satisfies the following conditions:
(1) They are within a unit in both slope coordinates.
(2)
 $\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FC}})$
,
$\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FC}})$
,
 $\unicode[STIX]{x1D707}_{1,1}(F_{-1})$
,
$\unicode[STIX]{x1D707}_{1,1}(F_{-1})$
,
 $\unicode[STIX]{x1D707}_{1,1}(F_{-2})$
, and
$\unicode[STIX]{x1D707}_{1,1}(F_{-2})$
, and
 $\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FD}})$
are all greater than
$\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FD}})$
are all greater than
 $\unicode[STIX]{x1D707}_{1,1}(U)-4$
.
$\unicode[STIX]{x1D707}_{1,1}(U)-4$
.(3) (
 $\unicode[STIX]{x1D6E5}_{2}=0$
and
$\unicode[STIX]{x1D6E5}_{2}=0$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\leqslant 0$
) or (
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\leqslant 0$
) or (
 $\unicode[STIX]{x1D6E5}_{2}=1$
and
$\unicode[STIX]{x1D6E5}_{2}=1$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\geqslant 0$
).
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\geqslant 0$
).(4)
 $\unicode[STIX]{x1D6E5}_{1}=0$
,
$\unicode[STIX]{x1D6E5}_{1}=0$
,
 $\unicode[STIX]{x1D712}\left(F_{-1}^{\ast },U\right)\geqslant 0$
, and
$\unicode[STIX]{x1D712}\left(F_{-1}^{\ast },U\right)\geqslant 0$
, and
 $\unicode[STIX]{x1D712}\left(F_{-2}^{\ast },U\right)\geqslant 0$
.
$\unicode[STIX]{x1D712}\left(F_{-2}^{\ast },U\right)\geqslant 0$
.(5)
 $\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FD}}(K),F_{-1}^{\ast }),\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast })$
, and
$\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FD}}(K),F_{-1}^{\ast }),\mathscr{H}\!om(E_{-\unicode[STIX]{x1D6FC}}(K),F_{-1}^{\ast })$
, and
 $\mathscr{H}\!om(F_{0}^{\ast },F_{-1}^{\ast })$
are all globally generated.
$\mathscr{H}\!om(F_{0}^{\ast },F_{-1}^{\ast })$
are all globally generated.(6) Any bundle sitting in a triangle
 $F_{-1}^{m_{0}}\rightarrow U\rightarrow ((F_{0}^{\ast })^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FC}}(K)^{m_{2}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}(K)^{m_{3}})[1]$
is prioritary.
$F_{-1}^{m_{0}}\rightarrow U\rightarrow ((F_{0}^{\ast })^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FC}}(K)^{m_{2}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}(K)^{m_{3}})[1]$
is prioritary.
Given an extremal pair, we can resolve the general object of
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
Theorem 4.6. The general
![]() $U\in M(\unicode[STIX]{x1D709})$
admits a resolution of the following forms
$U\in M(\unicode[STIX]{x1D709})$
admits a resolution of the following forms
As the proof is similar to the proof of the previous theorem, we omit its proof.
4.3 The “positive type” spectral sequence
Assume
![]() $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\geqslant 0$
and
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FC}},U\right)\geqslant 0$
and
![]() $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
. Let the right mutated coil of
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FD}},U\right)\geqslant 0$
. Let the right mutated coil of
![]() $\left(F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}\right)$
be
$\left(F_{0}^{\ast },F_{-1}^{\ast },E_{-\unicode[STIX]{x1D6FD}},E_{-\unicode[STIX]{x1D6FC}}\right)$
be
![]() $\left(E_{-\unicode[STIX]{x1D6FC}},E_{-\unicode[STIX]{x1D6FE}},F_{1}^{\ast }(-K),F_{0}^{\ast }(-K)\right)$
. Let
$\left(E_{-\unicode[STIX]{x1D6FC}},E_{-\unicode[STIX]{x1D6FE}},F_{1}^{\ast }(-K),F_{0}^{\ast }(-K)\right)$
. Let
![]() $\unicode[STIX]{x1D6E5}_{i}$
be as in the spectral sequence with input these two coils.
$\unicode[STIX]{x1D6E5}_{i}$
be as in the spectral sequence with input these two coils.
Definition 4.7. A (positive type) controlling pair of
![]() $\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D709}$
,
![]() $(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
, with corresponding orthogonal slope and discriminant
$(E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}})$
, with corresponding orthogonal slope and discriminant
![]() $\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
is called extremal if it satisfies the following conditions:
$\left(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+}\right)$
is called extremal if it satisfies the following conditions:
(1) They are within a unit in both slope coordinates.
(2)
 $\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FC}})$
,
$\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FC}})$
,
 $\unicode[STIX]{x1D707}_{1,1}(F_{1}(K))$
,
$\unicode[STIX]{x1D707}_{1,1}(F_{1}(K))$
,
 $\unicode[STIX]{x1D707}_{1,1}(F_{0}(K))$
, and
$\unicode[STIX]{x1D707}_{1,1}(F_{0}(K))$
, and
 $\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FD}})$
are all greater than
$\unicode[STIX]{x1D707}_{1,1}(E_{\unicode[STIX]{x1D6FD}})$
are all greater than
 $\unicode[STIX]{x1D707}_{1,1}(U)-4$
.
$\unicode[STIX]{x1D707}_{1,1}(U)-4$
.(3) (
 $\unicode[STIX]{x1D6E5}_{1}=1$
and
$\unicode[STIX]{x1D6E5}_{1}=1$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\geqslant 0$
) or (
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\geqslant 0$
) or (
 $\unicode[STIX]{x1D6E5}_{1}=0$
and
$\unicode[STIX]{x1D6E5}_{1}=0$
and
 $\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\leqslant 0$
).
$\unicode[STIX]{x1D712}\left(E_{-\unicode[STIX]{x1D6FE}},U\right)\leqslant 0$
).(4)
 $\unicode[STIX]{x1D712}\left(F_{-1}^{\ast }(-K),U\right)\leqslant 0$
,
$\unicode[STIX]{x1D712}\left(F_{-1}^{\ast }(-K),U\right)\leqslant 0$
,
 $\unicode[STIX]{x1D712}\left(F_{0}^{\ast }(-K),U\right)\leqslant 0$
, and
$\unicode[STIX]{x1D712}\left(F_{0}^{\ast }(-K),U\right)\leqslant 0$
, and
 $\unicode[STIX]{x1D6E5}_{2}=1$
.
$\unicode[STIX]{x1D6E5}_{2}=1$
.(5)
 $\mathscr{H}\!om(F_{-0}^{\ast },F_{-1}^{\ast }),\mathscr{H}\!om(F_{-0}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
, and
$\mathscr{H}\!om(F_{-0}^{\ast },F_{-1}^{\ast }),\mathscr{H}\!om(F_{-0}^{\ast },E_{-\unicode[STIX]{x1D6FD}})$
, and
 $\mathscr{H}\!om(F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FC}})$
are all globally generated.
$\mathscr{H}\!om(F_{0}^{\ast },E_{-\unicode[STIX]{x1D6FC}})$
are all globally generated.(6) Any bundle sitting in a triangle
 $F_{-1}^{m_{2}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FC}}^{m_{0}}\rightarrow U\rightarrow \left(F_{0}^{\ast }\right)^{m_{3}}[1]$
is prioritary.
$F_{-1}^{m_{2}}\bigoplus E_{-\unicode[STIX]{x1D6FD}}^{m_{1}}\bigoplus E_{-\unicode[STIX]{x1D6FC}}^{m_{0}}\rightarrow U\rightarrow \left(F_{0}^{\ast }\right)^{m_{3}}[1]$
is prioritary.
Given an extremal pair, we can resolve the general object of
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
Theorem 4.8. The general
![]() $U\in M(\unicode[STIX]{x1D709})$
admits a resolution of the following forms
$U\in M(\unicode[STIX]{x1D709})$
admits a resolution of the following forms
As the proof is similar to the proof of the second previous theorem, we omit its proof.
5 The Kronecker fibration
In this subsection, we use the resolutions constructed in the last section to construct a map to a moduli space of Kronecker modules. In the next section, these maps produce effective divisors on
![]() $M(\unicode[STIX]{x1D709})$
.
$M(\unicode[STIX]{x1D709})$
.
One thing that we need to know in order for this to work is that all the homomorphisms in the derived category are morphisms of complexes. Recall that
![]() $D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the bounded derived category of complexes of sheaves on
$D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the bounded derived category of complexes of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
and
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
and
![]() $Kom(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the category of complexes of sheaves on
$Kom(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the category of complexes of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
.
Lemma 5.1. Consider a pair of two term complexes
and
each sitting in degrees 0 and
![]() $-$
1 where
$-$
1 where
![]() $E^{\ast }$
,
$E^{\ast }$
,
![]() $F_{0}^{\ast }$
, and
$F_{0}^{\ast }$
, and
![]() $F_{-1}^{\ast }$
are all exceptional vector bundles. Every homomorphism
$F_{-1}^{\ast }$
are all exceptional vector bundles. Every homomorphism
![]() $W\rightarrow W^{\prime }$
in the derived category
$W\rightarrow W^{\prime }$
in the derived category
![]() $D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is realized by a homomorphism of the complexes, so
$D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is realized by a homomorphism of the complexes, so
Similarly, consider a pair of two term complexes
and
each sitting in degrees 0 and -1 where
![]() $E^{\ast }$
,
$E^{\ast }$
,
![]() $F_{0}^{\ast }$
, and
$F_{0}^{\ast }$
, and
![]() $F_{-1}^{\ast }$
are all exceptional vector bundles. Every homomorphism
$F_{-1}^{\ast }$
are all exceptional vector bundles. Every homomorphism
![]() $W\rightarrow W^{\prime }$
in the derived category
$W\rightarrow W^{\prime }$
in the derived category
![]() $D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is realized by a homomorphism of the complexes, so
$D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is realized by a homomorphism of the complexes, so
Proof. The proof of each statement are nearly identical to that of [Reference Coskun, Huizenga and WoolfCHW, Lem. 5.5] after switching
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
in place of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
in place of
![]() $\mathbb{P}^{2}$
and noting that
$\mathbb{P}^{2}$
and noting that
![]() $\operatorname{Hom}\left(A^{a}\bigoplus B^{b},A^{a}\bigoplus B^{b}\right)\cong \operatorname{GL}(a)\times \operatorname{GL}(b)\times M_{b,a}(\operatorname{Hom}(A,B))$
where
$\operatorname{Hom}\left(A^{a}\bigoplus B^{b},A^{a}\bigoplus B^{b}\right)\cong \operatorname{GL}(a)\times \operatorname{GL}(b)\times M_{b,a}(\operatorname{Hom}(A,B))$
where
![]() $\{A,B\}$
is an exceptional pair and where
$\{A,B\}$
is an exceptional pair and where
![]() $M_{b,a}(\operatorname{Hom}(A,B))$
is the group of
$M_{b,a}(\operatorname{Hom}(A,B))$
is the group of
![]() $b$
by
$b$
by
![]() $a$
matrices with entries in
$a$
matrices with entries in
![]() $\operatorname{Hom}(A,B)$
.
$\operatorname{Hom}(A,B)$
.
Let
![]() $\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
be an extremal controlling pair to
$\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
be an extremal controlling pair to
![]() $\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D709}$
,
![]() $\{F_{-1},F_{0}\}$
be the left mutation of the minimally ranked right completion pair of
$\{F_{-1},F_{0}\}$
be the left mutation of the minimally ranked right completion pair of
![]() $\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
,
$\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
,
![]() $\unicode[STIX]{x1D709}^{+}$
the primary orthogonal Chern character associated to that exceptional pair
$\unicode[STIX]{x1D709}^{+}$
the primary orthogonal Chern character associated to that exceptional pair
![]() $\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
, and
$\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
, and
![]() $U\in M(\unicode[STIX]{x1D709})$
be a general element. For simplicity, for the rest of the paper, we assume that
$U\in M(\unicode[STIX]{x1D709})$
be a general element. For simplicity, for the rest of the paper, we assume that
![]() $\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\geqslant 0$
and
$\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\geqslant 0$
and
![]() $\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FC}}^{\ast },U)\leqslant 0$
; proving the other cases is similar. In Section 4, we saw that
$\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FC}}^{\ast },U)\leqslant 0$
; proving the other cases is similar. In Section 4, we saw that
![]() $U$
has a resolution of the form
$U$
has a resolution of the form
Using the resolution, we construct dominant rational maps from
![]() $M(\unicode[STIX]{x1D709})$
to different Kronecker moduli spaces.
$M(\unicode[STIX]{x1D709})$
to different Kronecker moduli spaces.
Which Kronecker moduli space we use, as well as the behavior of the map, depends on which, if any, of the
![]() $m_{i}$
are zero. At most two of the
$m_{i}$
are zero. At most two of the
![]() $m_{i}$
are zero because
$m_{i}$
are zero because
![]() $\unicode[STIX]{x1D709}$
is not the Chern class of
$\unicode[STIX]{x1D709}$
is not the Chern class of
![]() $E^{f}$
for any exceptional
$E^{f}$
for any exceptional
![]() $E$
. We break up the cases by the number of
$E$
. We break up the cases by the number of
![]() $m_{i}$
which are zero.
$m_{i}$
which are zero.
If no
![]() $m_{i}$
is zero, we construct a dominant rational map from
$m_{i}$
is zero, we construct a dominant rational map from
![]() $M(\unicode[STIX]{x1D709})$
to
$M(\unicode[STIX]{x1D709})$
to
![]() $Kr_{N}(m_{2},m_{1})$
where
$Kr_{N}(m_{2},m_{1})$
where
![]() $N=\hom (F_{0}^{\ast },F_{-1}^{\ast })$
.
$N=\hom (F_{0}^{\ast },F_{-1}^{\ast })$
.
If exactly one
![]() $m_{i}$
is zero, then we could construct a dominant rational map to a certain Kronecker moduli space, but that space would always be a single point as one part of the dimension vector would be
$m_{i}$
is zero, then we could construct a dominant rational map to a certain Kronecker moduli space, but that space would always be a single point as one part of the dimension vector would be
![]() $0$
. The constant map tells us nothing about our space, so we do not construct it here.
$0$
. The constant map tells us nothing about our space, so we do not construct it here.
If
![]() $m_{i_{0}}$
and
$m_{i_{0}}$
and
![]() $m_{i_{1}}$
are zero, we construct a dominant rational map from
$m_{i_{1}}$
are zero, we construct a dominant rational map from
![]() $M(\unicode[STIX]{x1D709})$
to
$M(\unicode[STIX]{x1D709})$
to
![]() $Kr_{N}(m_{j_{1}},m_{j_{0}})$
where
$Kr_{N}(m_{j_{1}},m_{j_{0}})$
where
![]() $N$
is the dimension of the appropriate group of homomorphisms and
$N$
is the dimension of the appropriate group of homomorphisms and
![]() $\{i_{0},i_{1},j_{0},j_{1}\}$
is some permutation of the set
$\{i_{0},i_{1},j_{0},j_{1}\}$
is some permutation of the set
![]() $\{0,1,2,3,\}$
and
$\{0,1,2,3,\}$
and
![]() $j_{1}<j_{0}$
.
$j_{1}<j_{0}$
.
5.1 The case when two powers vanish
First note that the cases
![]() $m_{3}=m_{2}=0$
and
$m_{3}=m_{2}=0$
and
![]() $m_{1}=m_{0}=0$
cannot occur due to the form of the spectral sequence. This leaves four cases where two exponents vanish to deal with. The proof of the proposition is identical in each case after you replace the two bundles with nonzero exponents so we only explicitly prove the proposition in the first case.
$m_{1}=m_{0}=0$
cannot occur due to the form of the spectral sequence. This leaves four cases where two exponents vanish to deal with. The proof of the proposition is identical in each case after you replace the two bundles with nonzero exponents so we only explicitly prove the proposition in the first case.
5.1.1 When the second and third powers vanish
For this subsubsection, assume that
![]() $m_{2}=0$
and
$m_{2}=0$
and
![]() $m_{1}=0$
in the resolution
$m_{1}=0$
in the resolution
We see that
![]() $U$
determines a complex of the form
$U$
determines a complex of the form
which in turn determines a Kronecker
![]() $\operatorname{Hom}(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast })$
-module.
$\operatorname{Hom}(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast })$
-module.
Conversely, given a general such module and its determined complex,
![]() $W^{\prime }$
, there exists an element
$W^{\prime }$
, there exists an element
![]() $U^{\prime }\in M(\unicode[STIX]{x1D709})$
such that
$U^{\prime }\in M(\unicode[STIX]{x1D709})$
such that
![]() $W^{\prime }$
is the associated complex of
$W^{\prime }$
is the associated complex of
![]() $U^{\prime }$
by Theorem 4.4. Assuming that the Kronecker module associated to a general
$U^{\prime }$
by Theorem 4.4. Assuming that the Kronecker module associated to a general
![]() $W$
is semistable, this constructs a rational map
$W$
is semistable, this constructs a rational map
where
![]() $N=\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast })$
. In order to show that the Kronecker module associated to a general
$N=\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast })$
. In order to show that the Kronecker module associated to a general
![]() $W$
is semistable, it suffices by Section 2.11 to show that
$W$
is semistable, it suffices by Section 2.11 to show that
![]() $Kr_{N}(m_{3},m_{0})$
is positive dimensional.
$Kr_{N}(m_{3},m_{0})$
is positive dimensional.
Proposition 5.2. With the above notation,
![]() $Kr_{N}(m_{3},m_{0})$
is positive dimensional, and the dominant rational map
$Kr_{N}(m_{3},m_{0})$
is positive dimensional, and the dominant rational map
is a birational map.
Proof. By construction, the primary orthogonal Chern characters to
![]() $\unicode[STIX]{x1D709}$
are all semistable so
$\unicode[STIX]{x1D709}$
are all semistable so
![]() $\unicode[STIX]{x1D709}^{+}$
is semistable. By assumption, the general
$\unicode[STIX]{x1D709}^{+}$
is semistable. By assumption, the general
![]() $U\in M(\unicode[STIX]{x1D709})$
has the resolution
$U\in M(\unicode[STIX]{x1D709})$
has the resolution
A general map in a complex of the form
is injective and has a semistable cokernel with Chern character
![]() $\unicode[STIX]{x1D709}$
by Theorem 4.4. We also know that any isomorphism of two general elements of
$\unicode[STIX]{x1D709}$
by Theorem 4.4. We also know that any isomorphism of two general elements of
![]() $M(\unicode[STIX]{x1D709})$
is induced by an isomorphism of their resolutions.
$M(\unicode[STIX]{x1D709})$
is induced by an isomorphism of their resolutions.
Recall from earlier in the section that
![]() $W$
corresponds to a Kronecker
$W$
corresponds to a Kronecker
![]() $\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast })$
-module
$\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast })$
-module
![]() $e$
with dimension vector
$e$
with dimension vector
![]() $(m_{3},m_{0})$
. Then we compute that
$(m_{3},m_{0})$
. Then we compute that
As
![]() $\dim (M(\unicode[STIX]{x1D709}))>0$
, we have that
$\dim (M(\unicode[STIX]{x1D709}))>0$
, we have that
![]() $(\operatorname{edim})Kr_{N}(m_{3},m_{0})>0$
. By the properties of Kronecker moduli spaces,
$(\operatorname{edim})Kr_{N}(m_{3},m_{0})>0$
. By the properties of Kronecker moduli spaces,
![]() $Kr_{N}(m_{3},m_{0})$
is positive dimensional. Thus, the general such module is stable. As isomorphism of complexes corresponds exactly with isomorphism of Kronecker modules, we obtain a birational map
$Kr_{N}(m_{3},m_{0})$
is positive dimensional. Thus, the general such module is stable. As isomorphism of complexes corresponds exactly with isomorphism of Kronecker modules, we obtain a birational map
5.2 When all of the powers are nonzero
For this subsection, assume that
![]() $m_{i}\neq 0$
for all
$m_{i}\neq 0$
for all
![]() $i$
in the resolution
$i$
in the resolution
Forgetting most of the information of the resolution,
![]() $U$
determines a complex of the form
$U$
determines a complex of the form
which in turn determines a Kronecker
![]() $\operatorname{Hom}(F_{0}^{\ast },F_{-1}^{\ast })$
-module.
$\operatorname{Hom}(F_{0}^{\ast },F_{-1}^{\ast })$
-module.
Conversely, given a general such module and its determined complex,
![]() $W^{\prime }$
, there exists an element
$W^{\prime }$
, there exists an element
![]() $U^{\prime }\in M(\unicode[STIX]{x1D709})$
such that
$U^{\prime }\in M(\unicode[STIX]{x1D709})$
such that
![]() $W^{\prime }$
is the associated complex of
$W^{\prime }$
is the associated complex of
![]() $U^{\prime }$
by Theorem 4.4. Assuming that there is a semistable Kronecker module associated to a general
$U^{\prime }$
by Theorem 4.4. Assuming that there is a semistable Kronecker module associated to a general
![]() $W$
, this constructs a rational map
$W$
, this constructs a rational map
where
![]() $N=\hom (F_{0}^{\ast },F_{-1}^{\ast })$
. In order to verify that we get Kronecker modules, we have to prove a result about the map
$N=\hom (F_{0}^{\ast },F_{-1}^{\ast })$
. In order to verify that we get Kronecker modules, we have to prove a result about the map
![]() $E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow U$
and
$E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow U$
and
![]() $U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast m_{3}}(K)[1]$
being canonical. To show that the general associated Kronecker module is semistable, we again have to show that the Kronecker moduli space is nonempty. We now show that the map
$U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast m_{3}}(K)[1]$
being canonical. To show that the general associated Kronecker module is semistable, we again have to show that the Kronecker moduli space is nonempty. We now show that the map
![]() $E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow U$
is canonical.
$E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow U$
is canonical.
Proposition 5.3. With the notation of this subsection, let
![]() $U\in M(\unicode[STIX]{x1D709})$
be general. Let
$U\in M(\unicode[STIX]{x1D709})$
be general. Let
![]() $W^{\prime }\in D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
be the mapping cone of the canonical evaluation map
$W^{\prime }\in D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
be the mapping cone of the canonical evaluation map
so that there is a distinguished triangle
Then
![]() $W^{\prime }$
is isomorphic to a complex of the form
$W^{\prime }$
is isomorphic to a complex of the form
sitting in degrees
![]() $-1$
and
$-1$
and
![]() $0$
.
$0$
.
Furthermore,
![]() $W^{\prime }$
is also isomorphic to the complex
$W^{\prime }$
is also isomorphic to the complex
appearing in the Beilinson spectral sequence for
![]() $U$
.
$U$
.
Proof. It is easy to show that if
is an exact sequence of sheaves, then the mapping cone of
![]() $C\rightarrow D$
is isomorphic to the complex
$C\rightarrow D$
is isomorphic to the complex
![]() $A\rightarrow B$
sitting in degrees
$A\rightarrow B$
sitting in degrees
![]() $-1$
and
$-1$
and
![]() $0$
.
$0$
.
Suppose we have a resolution
of a general
![]() $U$
as in Theorem 4.4. We have
$U$
as in Theorem 4.4. We have
![]() $m_{0}=\hom (E_{\unicode[STIX]{x1D6FD}}^{\ast },U)$
. Then since
$m_{0}=\hom (E_{\unicode[STIX]{x1D6FD}}^{\ast },U)$
. Then since
![]() $U$
is semistable, the map
$U$
is semistable, the map
![]() $E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow U$
can be identified with the canonical evaluation
$E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow U$
can be identified with the canonical evaluation
![]() $E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\rightarrow U$
. Thus, the mapping cone of this evaluation is the complex given by the first component of
$E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\rightarrow U$
. Thus, the mapping cone of this evaluation is the complex given by the first component of
![]() $\unicode[STIX]{x1D719}$
. By Lemma 5.1, any two complexes of the form
$\unicode[STIX]{x1D719}$
. By Lemma 5.1, any two complexes of the form
![]() $E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}\bigoplus F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{m_{1}}$
which are isomorphic in the derived category are in the same orbit of the
$E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}\bigoplus F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{m_{1}}$
which are isomorphic in the derived category are in the same orbit of the
![]() $\operatorname{GL}(m_{3})\times \operatorname{GL}(m_{2})\times M_{m_{2},m_{3}}(\operatorname{Hom}(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),F_{0}^{\ast }))\times \operatorname{GL}(m_{1})$
action.
$\operatorname{GL}(m_{3})\times \operatorname{GL}(m_{2})\times M_{m_{2},m_{3}}(\operatorname{Hom}(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),F_{0}^{\ast }))\times \operatorname{GL}(m_{1})$
action.
Finally, we show that
![]() $W^{\prime }$
is isomorphic to the complex which appears in the Beilinson spectral sequence for
$W^{\prime }$
is isomorphic to the complex which appears in the Beilinson spectral sequence for
![]() $U$
. For simplicity, we assume we are in the case
$U$
. For simplicity, we assume we are in the case
![]() $\unicode[STIX]{x1D6E5}_{1}=\unicode[STIX]{x1D6E5}_{2}=1$
. We recall how to compute the
$\unicode[STIX]{x1D6E5}_{1}=\unicode[STIX]{x1D6E5}_{2}=1$
. We recall how to compute the
![]() $E_{1}^{p,q}$
-page of the spectral sequence. Let
$E_{1}^{p,q}$
-page of the spectral sequence. Let
![]() $p_{i}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
be the projections, and let
$p_{i}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
be the projections, and let
![]() $\unicode[STIX]{x1D6E5}\subset \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)$
be the diagonal. There is a resolution of the diagonal
$\unicode[STIX]{x1D6E5}\subset \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)$
be the diagonal. There is a resolution of the diagonal
We split the resolution of the diagonal into two short exact sequences
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\boxtimes E_{\unicode[STIX]{x1D6FC}}\bigoplus F_{0}^{\ast }\boxtimes E_{0}\rightarrow F_{-1}^{\ast }\boxtimes E_{1}\rightarrow M\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle M\rightarrow E_{\unicode[STIX]{x1D6FD}}^{\ast }\boxtimes E_{\unicode[STIX]{x1D6FD}}\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E5}}\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\boxtimes E_{\unicode[STIX]{x1D6FC}}\bigoplus F_{0}^{\ast }\boxtimes E_{0}\rightarrow F_{-1}^{\ast }\boxtimes E_{1}\rightarrow M\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle M\rightarrow E_{\unicode[STIX]{x1D6FD}}^{\ast }\boxtimes E_{\unicode[STIX]{x1D6FD}}\rightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E5}}\rightarrow 0.\nonumber\end{eqnarray}$$
Tensoring with
![]() $p_{2}^{\ast }(U)$
and applying
$p_{2}^{\ast }(U)$
and applying
![]() $Rp_{1\ast }$
, we get triangles
$Rp_{1\ast }$
, we get triangles
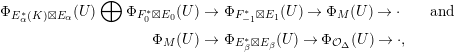 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\boxtimes E_{\unicode[STIX]{x1D6FC}}}(U)\bigoplus \unicode[STIX]{x1D6F7}_{F_{0}^{\ast }\boxtimes E_{0}}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{F_{-1}^{\ast }\boxtimes E_{1}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow \cdot \qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{M}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{E_{\unicode[STIX]{x1D6FD}}^{\ast }\boxtimes E_{\unicode[STIX]{x1D6FD}}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{{\mathcal{O}}_{\unicode[STIX]{x1D6E5}}}(U)\rightarrow \cdot ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\boxtimes E_{\unicode[STIX]{x1D6FC}}}(U)\bigoplus \unicode[STIX]{x1D6F7}_{F_{0}^{\ast }\boxtimes E_{0}}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{F_{-1}^{\ast }\boxtimes E_{1}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow \cdot \qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{M}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{E_{\unicode[STIX]{x1D6FD}}^{\ast }\boxtimes E_{\unicode[STIX]{x1D6FD}}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{{\mathcal{O}}_{\unicode[STIX]{x1D6E5}}}(U)\rightarrow \cdot ,\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F7}_{F}:D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})\rightarrow D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the Fourier–Mukai transform with kernel
$\unicode[STIX]{x1D6F7}_{F}:D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})\rightarrow D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the Fourier–Mukai transform with kernel
![]() $F$
. Computing these transforms using Proposition 4.4, we obtain two different complexes
$F$
. Computing these transforms using Proposition 4.4, we obtain two different complexes
 $$\begin{eqnarray}\displaystyle & & \displaystyle E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\otimes H^{1}(E_{\unicode[STIX]{x1D6FC}}\otimes U)\bigoplus F_{0}^{\ast }\otimes H^{0}(E_{0}\otimes U)\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow F_{-1}^{\ast }\otimes H^{0}(E_{1}\otimes U)\rightarrow \unicode[STIX]{x1D6F7}_{M}(U)[1]\rightarrow \cdot \nonumber\\ \displaystyle & & \displaystyle \text{and}\quad \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\rightarrow U\rightarrow \cdot \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\otimes H^{1}(E_{\unicode[STIX]{x1D6FC}}\otimes U)\bigoplus F_{0}^{\ast }\otimes H^{0}(E_{0}\otimes U)\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow F_{-1}^{\ast }\otimes H^{0}(E_{1}\otimes U)\rightarrow \unicode[STIX]{x1D6F7}_{M}(U)[1]\rightarrow \cdot \nonumber\\ \displaystyle & & \displaystyle \text{and}\quad \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\rightarrow U\rightarrow \cdot \nonumber\end{eqnarray}$$
involving
![]() $\unicode[STIX]{x1D6F7}_{M}(U)$
; notice that the map
$\unicode[STIX]{x1D6F7}_{M}(U)$
; notice that the map
![]() $E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\rightarrow U$
is the canonical one since the map
$E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\rightarrow U$
is the canonical one since the map
is the trace map. Therefore,
![]() $\unicode[STIX]{x1D6F7}_{M}(U)[1]$
is isomorphic to
$\unicode[STIX]{x1D6F7}_{M}(U)[1]$
is isomorphic to
![]() $W$
by the second triangle. On the other hand,
$W$
by the second triangle. On the other hand,
![]() $\unicode[STIX]{x1D6F7}_{M}(U)[1]$
is also isomorphic to the complex in the Beilinson spectral sequence by the first triangle.
$\unicode[STIX]{x1D6F7}_{M}(U)[1]$
is also isomorphic to the complex in the Beilinson spectral sequence by the first triangle.
We now turn to showing that the map
![]() $U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{0}}[1]$
is canonical in order to show that the general
$U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{0}}[1]$
is canonical in order to show that the general
![]() $W$
is associated to a Kronecker module.
$W$
is associated to a Kronecker module.
Proposition 5.4. With the notation of this subsection, let
![]() $U\in M(\unicode[STIX]{x1D709})$
be general. Let
$U\in M(\unicode[STIX]{x1D709})$
be general. Let
![]() $W^{\prime }\in D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
be the mapping cone of the canonical evaluation map
$W^{\prime }\in D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
be the mapping cone of the canonical evaluation map
so that there is a distinguished triangle
Then
![]() $W^{\prime }$
is isomorphic to a complex of the form
$W^{\prime }$
is isomorphic to a complex of the form
sitting in degrees
![]() $-2$
and
$-2$
and
![]() $-1$
.
$-1$
.
Furthermore,
![]() $W^{\prime }$
is also isomorphic to the complex
$W^{\prime }$
is also isomorphic to the complex
![]() $\left(F_{0}^{\ast }\otimes \mathbb{C}^{m_{2}}\right)\rightarrow \left(F_{-1}^{\ast }\otimes \mathbb{C}^{m_{1}}\right)\bigoplus \left(E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \mathbb{C}^{m_{0}}\right)$
appearing in the Beilinson spectral sequence for
$\left(F_{0}^{\ast }\otimes \mathbb{C}^{m_{2}}\right)\rightarrow \left(F_{-1}^{\ast }\otimes \mathbb{C}^{m_{1}}\right)\bigoplus \left(E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \mathbb{C}^{m_{0}}\right)$
appearing in the Beilinson spectral sequence for
![]() $U$
.
$U$
.
Proof. It is easy to show that if
is an exact sequence of sheaves, then the mapping cone of
![]() $D\rightarrow A[1]$
is isomorphic to the complex
$D\rightarrow A[1]$
is isomorphic to the complex
![]() $B\rightarrow C$
sitting in degrees
$B\rightarrow C$
sitting in degrees
![]() $-2$
and
$-2$
and
![]() $-1$
. Suppose we have a resolution
$-1$
. Suppose we have a resolution
of a general
![]() $U$
as in Theorem 4.4. We have
$U$
as in Theorem 4.4. We have
![]() $m_{3}=\hom (U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])$
. Then since
$m_{3}=\hom (U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])$
. Then since
![]() $U$
is semistable, the map
$U$
is semistable, the map
![]() $U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}[1]$
can be identified with the canonical co-evaluation
$U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}[1]$
can be identified with the canonical co-evaluation
![]() $U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1]\otimes \operatorname{Hom}(U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])$
. Thus, the mapping cone of this co-evaluation is the complex given by the second component of
$U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1]\otimes \operatorname{Hom}(U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])$
. Thus, the mapping cone of this co-evaluation is the complex given by the second component of
![]() $\unicode[STIX]{x1D719}$
. By Lemma 5.1, any two complexes of the form
$\unicode[STIX]{x1D719}$
. By Lemma 5.1, any two complexes of the form
![]() $F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{m_{1}}\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}$
which are isomorphic in the derived category are in the same orbit of the
$F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{m_{1}}\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}$
which are isomorphic in the derived category are in the same orbit of the
![]() $\operatorname{GL}(m_{2})\times \operatorname{GL}(m_{1})\times \operatorname{GL}(m_{0})\times M_{m_{0},m_{1}}(\operatorname{Hom}(F_{-1}^{\ast },E_{\unicode[STIX]{x1D6FD}}^{\ast }))$
action.
$\operatorname{GL}(m_{2})\times \operatorname{GL}(m_{1})\times \operatorname{GL}(m_{0})\times M_{m_{0},m_{1}}(\operatorname{Hom}(F_{-1}^{\ast },E_{\unicode[STIX]{x1D6FD}}^{\ast }))$
action.
Finally, we show that
![]() $W^{\prime }$
is isomorphic to the complex which appears in the Beilinson spectral sequence for
$W^{\prime }$
is isomorphic to the complex which appears in the Beilinson spectral sequence for
![]() $U$
. For simplicity, we assume we are in the case
$U$
. For simplicity, we assume we are in the case
![]() $\unicode[STIX]{x1D6E5}_{1}=\unicode[STIX]{x1D6E5}_{2}=0$
. Recall how to compute the
$\unicode[STIX]{x1D6E5}_{1}=\unicode[STIX]{x1D6E5}_{2}=0$
. Recall how to compute the
![]() $E_{1}^{p,q}$
-page of the spectral sequence. Let
$E_{1}^{p,q}$
-page of the spectral sequence. Let
![]() $p_{i}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
be the projections, and let
$p_{i}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
be the projections, and let
![]() $\unicode[STIX]{x1D6E5}\subset \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)$
be the diagonal. There is a resolution of the diagonal
$\unicode[STIX]{x1D6E5}\subset \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)\times \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)$
be the diagonal. There is a resolution of the diagonal
We split the resolution of the diagonal into two short exact sequences
Tensoring with
![]() $p_{2}^{\ast }(U)$
and applying
$p_{2}^{\ast }(U)$
and applying
![]() $Rp_{1\ast }$
, we get triangles
$Rp_{1\ast }$
, we get triangles
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{F_{0}^{\ast }\boxtimes E_{0}}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{F_{-1}^{\ast }\boxtimes E_{1}}(U)\bigoplus \unicode[STIX]{x1D6F7}_{E_{\unicode[STIX]{x1D6FD}}^{\ast }\boxtimes E_{\unicode[STIX]{x1D6FD}}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow \cdot \qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{M}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{{\mathcal{O}}_{\unicode[STIX]{x1D6E5}}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\boxtimes E_{\unicode[STIX]{x1D6FC}})[1]}(U)\rightarrow \cdot ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{F_{0}^{\ast }\boxtimes E_{0}}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{F_{-1}^{\ast }\boxtimes E_{1}}(U)\bigoplus \unicode[STIX]{x1D6F7}_{E_{\unicode[STIX]{x1D6FD}}^{\ast }\boxtimes E_{\unicode[STIX]{x1D6FD}}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow \cdot \qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{M}(U) & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{{\mathcal{O}}_{\unicode[STIX]{x1D6E5}}}(U)\rightarrow \unicode[STIX]{x1D6F7}_{(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\boxtimes E_{\unicode[STIX]{x1D6FC}})[1]}(U)\rightarrow \cdot ,\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F7}_{F}:D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})\rightarrow D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the Fourier–Mukai transform with kernel
$\unicode[STIX]{x1D6F7}_{F}:D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})\rightarrow D^{b}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
is the Fourier–Mukai transform with kernel
![]() $F$
. Computing these transforms using Theorem 4.4, we obtain two different complexes
$F$
. Computing these transforms using Theorem 4.4, we obtain two different complexes
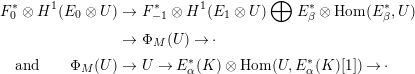 $$\begin{eqnarray}\displaystyle F_{0}^{\ast }\otimes H^{1}(E_{0}\otimes U) & \rightarrow & \displaystyle F_{-1}^{\ast }\otimes H^{1}(E_{1}\otimes U)\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow \cdot \nonumber\\ \displaystyle \text{and}\qquad \unicode[STIX]{x1D6F7}_{M}(U) & \rightarrow & \displaystyle U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\otimes \operatorname{Hom}(U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])\rightarrow \cdot \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{0}^{\ast }\otimes H^{1}(E_{0}\otimes U) & \rightarrow & \displaystyle F_{-1}^{\ast }\otimes H^{1}(E_{1}\otimes U)\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast }\otimes \operatorname{Hom}(E_{\unicode[STIX]{x1D6FD}}^{\ast },U)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \unicode[STIX]{x1D6F7}_{M}(U)\rightarrow \cdot \nonumber\\ \displaystyle \text{and}\qquad \unicode[STIX]{x1D6F7}_{M}(U) & \rightarrow & \displaystyle U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)\otimes \operatorname{Hom}(U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])\rightarrow \cdot \nonumber\end{eqnarray}$$
involving
![]() $\unicode[STIX]{x1D6F7}_{M}(U)$
; notice that the map
$\unicode[STIX]{x1D6F7}_{M}(U)$
; notice that the map
![]() $U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1]\otimes \operatorname{Hom}(U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])$
is the canonical one since the map
$U\rightarrow E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1]\otimes \operatorname{Hom}(U,E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)[1])$
is the canonical one since the map
is the cotrace map. Therefore,
![]() $\unicode[STIX]{x1D6F7}_{M}(U)$
is isomorphic to
$\unicode[STIX]{x1D6F7}_{M}(U)$
is isomorphic to
![]() $W^{\prime }$
by the second triangle. On the other hand,
$W^{\prime }$
by the second triangle. On the other hand,
![]() $\unicode[STIX]{x1D6F7}_{M}(U)$
is also isomorphic to the complex in the Beilinson spectral sequence by the first triangle.
$\unicode[STIX]{x1D6F7}_{M}(U)$
is also isomorphic to the complex in the Beilinson spectral sequence by the first triangle.
We now use that these maps are canonical to establish that each resolution is associated to a Kronecker module.
Proposition 5.5. Let
![]() $U\in M(\unicode[STIX]{x1D709})$
be a general object with the resolution
$U\in M(\unicode[STIX]{x1D709})$
be a general object with the resolution
with subcomplex
Then
![]() $W$
is the complex appearing in the spectral sequence.
$W$
is the complex appearing in the spectral sequence.
Proof. Let
![]() $W^{\prime }:F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{\ast m_{1}}$
be the complex appearing in
$W^{\prime }:F_{0}^{\ast m_{2}}\rightarrow F_{-1}^{\ast m_{1}}$
be the complex appearing in
![]() $U$
’ spectral sequence. By a Bertini-like statement [Reference HuizengaHui2],
$U$
’ spectral sequence. By a Bertini-like statement [Reference HuizengaHui2],
![]() $W^{\prime }$
is either surjective or injective.
$W^{\prime }$
is either surjective or injective.
Assume that it is injective. This means that the
![]() $E_{2}$
page of the spectral sequence is
$E_{2}$
page of the spectral sequence is
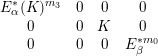 $$\begin{eqnarray}\begin{array}{@{}cccc@{}}E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}} & 0 & 0 & 0\\ 0 & 0 & K & 0\\ 0 & 0 & 0 & E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\\ \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccc@{}}E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}} & 0 & 0 & 0\\ 0 & 0 & K & 0\\ 0 & 0 & 0 & E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\\ \end{array}\end{eqnarray}$$
where
![]() $K=\operatorname{coker}(W^{\prime })$
. In turn this gives that, in the resolution coming from the spectral sequence, the map from
$K=\operatorname{coker}(W^{\prime })$
. In turn this gives that, in the resolution coming from the spectral sequence, the map from
![]() $F_{0}^{\ast m_{2}}$
to
$F_{0}^{\ast m_{2}}$
to
![]() $E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}$
is zero. Then, by Proposition 5.4, we have two short exact sequences
$E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}$
is zero. Then, by Proposition 5.4, we have two short exact sequences
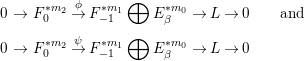 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle F_{0}^{\ast m_{2}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }F_{-1}^{\ast m_{1}}\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow L\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle F_{0}^{\ast m_{2}}\stackrel{\unicode[STIX]{x1D713}}{\rightarrow }F_{-1}^{\ast m_{1}}\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow L\rightarrow 0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle F_{0}^{\ast m_{2}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }F_{-1}^{\ast m_{1}}\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow L\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle F_{0}^{\ast m_{2}}\stackrel{\unicode[STIX]{x1D713}}{\rightarrow }F_{-1}^{\ast m_{1}}\bigoplus E_{\unicode[STIX]{x1D6FD}}^{\ast m_{0}}\rightarrow L\rightarrow 0\nonumber\end{eqnarray}$$
where
![]() $W$
and
$W$
and
![]() $W^{\prime }$
are subcomplexes of the respective sequences and the second component of
$W^{\prime }$
are subcomplexes of the respective sequences and the second component of
![]() $\unicode[STIX]{x1D713}$
is zero. The identity map on
$\unicode[STIX]{x1D713}$
is zero. The identity map on
![]() $L$
induces an isomorphism of its resolutions, which implies that the first component of
$L$
induces an isomorphism of its resolutions, which implies that the first component of
![]() $\unicode[STIX]{x1D719}$
is a scalar multiple of the first component of
$\unicode[STIX]{x1D719}$
is a scalar multiple of the first component of
![]() $\unicode[STIX]{x1D713}$
. This then gives an isomorphism between
$\unicode[STIX]{x1D713}$
. This then gives an isomorphism between
![]() $W$
and
$W$
and
![]() $W^{\prime }$
given by dividing by that scalar multiple in the degree
$W^{\prime }$
given by dividing by that scalar multiple in the degree
![]() $-1$
and the identity in degree
$-1$
and the identity in degree
![]() $0$
. Thus,
$0$
. Thus,
![]() $W$
is the complex in the spectral sequence converging to
$W$
is the complex in the spectral sequence converging to
![]() $U$
.
$U$
.
The case of surjectivity is similar but uses Proposition 5.3.
We now finish the construction of the map
![]() $M(\unicode[STIX]{x1D709}){\dashrightarrow}Kr_{N}(m_{2},m_{1})$
.
$M(\unicode[STIX]{x1D709}){\dashrightarrow}Kr_{N}(m_{2},m_{1})$
.
Proposition 5.6. With the above notation,
![]() $Kr_{N}(m_{2},m_{1})$
is nonempty and there is a dominant rational map
$Kr_{N}(m_{2},m_{1})$
is nonempty and there is a dominant rational map
Proof. By construction, we know that the primary orthogonal Chern characters to
![]() $\unicode[STIX]{x1D709}$
are all semistable so
$\unicode[STIX]{x1D709}$
are all semistable so
![]() $\unicode[STIX]{x1D709}^{+}$
is semistable. Let
$\unicode[STIX]{x1D709}^{+}$
is semistable. Let
![]() $V\in M(\unicode[STIX]{x1D709}^{+})$
be general. Then, by Theorem 4.4,
$V\in M(\unicode[STIX]{x1D709}^{+})$
be general. Then, by Theorem 4.4,
![]() $V$
has the resolution
$V$
has the resolution
or one of the equivalent resolutions which have the same Kronecker module structure. Similarly, the general
![]() $U\in M(\unicode[STIX]{x1D709})$
has the resolution
$U\in M(\unicode[STIX]{x1D709})$
has the resolution
where
![]() $W$
is the complex
$W$
is the complex
As the point
![]() $(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+})$
lies on the surface
$(\unicode[STIX]{x1D707}^{+},\unicode[STIX]{x1D6E5}^{+})$
lies on the surface
![]() $Q_{\unicode[STIX]{x1D709}}$
, we have that
$Q_{\unicode[STIX]{x1D709}}$
, we have that
![]() $\unicode[STIX]{x1D712}(V^{\ast },U)=0$
. By design, the resolution of
$\unicode[STIX]{x1D712}(V^{\ast },U)=0$
. By design, the resolution of
![]() $V$
immediately forces
$V$
immediately forces
![]() $\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FD}}^{\ast })=0$
and
$\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FD}}^{\ast })=0$
and
![]() $\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FC}}^{\ast }(K))=0$
because of the orthogonality properties of the coil
$\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FC}}^{\ast }(K))=0$
because of the orthogonality properties of the coil
![]() $\{E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast },E_{1}^{\ast },E_{0}^{\ast }\}$
. Then vanishings of
$\{E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),E_{\unicode[STIX]{x1D6FD}}^{\ast },E_{1}^{\ast },E_{0}^{\ast }\}$
. Then vanishings of
![]() $\unicode[STIX]{x1D712}(V^{\ast },U)$
,
$\unicode[STIX]{x1D712}(V^{\ast },U)$
,
![]() $\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FD}}^{\ast })$
, and
$\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FD}}^{\ast })$
, and
![]() $\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FC}}^{\ast }(K))$
force
$\unicode[STIX]{x1D712}(V^{\ast },E_{\unicode[STIX]{x1D6FC}}^{\ast }(K))$
force
![]() $\unicode[STIX]{x1D712}(V^{\ast },W)=0$
. Since
$\unicode[STIX]{x1D712}(V^{\ast },W)=0$
. Since
![]() $\unicode[STIX]{x1D712}(V^{\ast },W)=0$
and
$\unicode[STIX]{x1D712}(V^{\ast },W)=0$
and
![]() $\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FD}}^{\ast },W)=0$
, we have that
$\unicode[STIX]{x1D712}(E_{\unicode[STIX]{x1D6FD}}^{\ast },W)=0$
, we have that
![]() $\unicode[STIX]{x1D712}(L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast },W)=0$
. Shifting only shifts the indices so we have
$\unicode[STIX]{x1D712}(L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast },W)=0$
. Shifting only shifts the indices so we have
![]() $\unicode[STIX]{x1D712}(L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1],W)=0$
as well. In the derived category
$\unicode[STIX]{x1D712}(L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1],W)=0$
as well. In the derived category
![]() $L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1]$
is isomorphic to the complex
$L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1]$
is isomorphic to the complex
sitting in degrees
![]() $-1$
and 0. Thus,
$-1$
and 0. Thus,
![]() $L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1]$
and
$L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1]$
and
![]() $W$
both correspond to Kronecker
$W$
both correspond to Kronecker
![]() $\operatorname{Hom}(F_{0}^{\ast },F_{1}^{\ast })$
-modules. Call them
$\operatorname{Hom}(F_{0}^{\ast },F_{1}^{\ast })$
-modules. Call them
![]() $e$
and
$e$
and
![]() $f$
respectively.
$f$
respectively.
Then
![]() $\unicode[STIX]{x1D712}(L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1],W)=0$
tells us that
$\unicode[STIX]{x1D712}(L_{E_{\unicode[STIX]{x1D6FD}}^{\ast }}V^{\ast }[1],W)=0$
tells us that
![]() $\unicode[STIX]{x1D712}(e,f)=0$
which implies that
$\unicode[STIX]{x1D712}(e,f)=0$
which implies that
![]() $\text{}\underline{\dim }\,f$
if a right-orthogonal dimension vector to
$\text{}\underline{\dim }\,f$
if a right-orthogonal dimension vector to
![]() $\text{}\underline{\dim }\,e$
. Since
$\text{}\underline{\dim }\,e$
. Since
![]() $M(V)$
is nonempty, Proposition 5.2 shows that
$M(V)$
is nonempty, Proposition 5.2 shows that
![]() $Kr_{N}(n_{1},n_{2})$
is nonempty. If
$Kr_{N}(n_{1},n_{2})$
is nonempty. If
![]() $Kr_{N}(n_{1},n_{2})$
is positive or
$Kr_{N}(n_{1},n_{2})$
is positive or
![]() $0$
dimensional, the discussion at the end of [Reference Coskun, Huizenga and WoolfCHW, Section 6.1] shows that
$0$
dimensional, the discussion at the end of [Reference Coskun, Huizenga and WoolfCHW, Section 6.1] shows that
![]() $Kr_{N}(m_{2},m_{1})$
is as well. Thus,
$Kr_{N}(m_{2},m_{1})$
is as well. Thus,
![]() $Kr_{N}(m_{2},m_{1})$
is nonempty as promised.
$Kr_{N}(m_{2},m_{1})$
is nonempty as promised.
6 Primary extremal rays of the effective cone
In this section, we use the maps from
![]() $M(\unicode[STIX]{x1D709})$
to Kronecker moduli spaces that we constructed in the previous section to give an alternate description of effective Brill–Noether divisors and to show that they are extremal. Let
$M(\unicode[STIX]{x1D709})$
to Kronecker moduli spaces that we constructed in the previous section to give an alternate description of effective Brill–Noether divisors and to show that they are extremal. Let
![]() $\unicode[STIX]{x1D709}^{+}$
be a primary orthogonal Chern character to
$\unicode[STIX]{x1D709}^{+}$
be a primary orthogonal Chern character to
![]() $M(\unicode[STIX]{x1D709})$
with
$M(\unicode[STIX]{x1D709})$
with
![]() $V\in M(\unicode[STIX]{x1D709}^{+})$
general. The way in which we can express the Brill–Noether divisor
$V\in M(\unicode[STIX]{x1D709}^{+})$
general. The way in which we can express the Brill–Noether divisor
![]() $D_{V}$
depends greatly on the dimension of the Kronecker moduli space,
$D_{V}$
depends greatly on the dimension of the Kronecker moduli space,
![]() $K$
, that we map to (as dictated by the previous section).
$K$
, that we map to (as dictated by the previous section).
If
![]() $\dim (K)=0$
(or a single
$\dim (K)=0$
(or a single
![]() $m_{i}$
is zero so we did not construct a fibration), then the Kronecker fibration is a map to a point so it does not give us any information so we do not use it at all. In this case,
$m_{i}$
is zero so we did not construct a fibration), then the Kronecker fibration is a map to a point so it does not give us any information so we do not use it at all. In this case,
![]() $V$
is an exceptional bundle. This divisor consists exactly of those elements in
$V$
is an exceptional bundle. This divisor consists exactly of those elements in
![]() $M(\unicode[STIX]{x1D709})$
without the specified resolution, and the dual moving curve(s) are found by varying the maps in the resolution.
$M(\unicode[STIX]{x1D709})$
without the specified resolution, and the dual moving curve(s) are found by varying the maps in the resolution.
If
![]() $\dim (K)>0$
, then the Kronecker fibration is far more interesting. In this case,
$\dim (K)>0$
, then the Kronecker fibration is far more interesting. In this case,
![]() $\unicode[STIX]{x1D709}^{+}$
may or may not be exceptional and the Brill–Noether divisor
$\unicode[STIX]{x1D709}^{+}$
may or may not be exceptional and the Brill–Noether divisor
![]() $D_{V}$
is the indeterminacy or exceptional locus of the map from
$D_{V}$
is the indeterminacy or exceptional locus of the map from
![]() $M(\unicode[STIX]{x1D709})$
to the Kronecker moduli space. Either this map is birational, in which case the moving curve is gotten by varying the Kronecker module, or the map has positive dimensional fibers, in which case the moving curve(s) are gotten by varying the other maps in the resolution to cover the fibers of the map. If certain numeric inequalities hold, there are two dual moving curves covering the (positive dimensional) fibers of the map which implies that
$M(\unicode[STIX]{x1D709})$
to the Kronecker moduli space. Either this map is birational, in which case the moving curve is gotten by varying the Kronecker module, or the map has positive dimensional fibers, in which case the moving curve(s) are gotten by varying the other maps in the resolution to cover the fibers of the map. If certain numeric inequalities hold, there are two dual moving curves covering the (positive dimensional) fibers of the map which implies that
![]() $D_{V}$
is the pullback of a generator of the ample cone of the Kronecker moduli space; in the case, the Brill–Noether divisor
$D_{V}$
is the pullback of a generator of the ample cone of the Kronecker moduli space; in the case, the Brill–Noether divisor
![]() $D_{V}$
is also inside the movable cone.
$D_{V}$
is also inside the movable cone.
Let
![]() $\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
be an associated extremal pair to
$\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
be an associated extremal pair to
![]() $\unicode[STIX]{x1D709}$
with orthogonal Chern character
$\unicode[STIX]{x1D709}$
with orthogonal Chern character
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $\{F_{-1},F_{0}\}$
be the left mutation of the minimally ranked right completion pair of
$\{F_{-1},F_{0}\}$
be the left mutation of the minimally ranked right completion pair of
![]() $\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
,
$\{E_{\unicode[STIX]{x1D6FC}},E_{\unicode[STIX]{x1D6FD}}\}$
,
![]() $U\in M(\unicode[STIX]{x1D709})$
be a general element, and
$U\in M(\unicode[STIX]{x1D709})$
be a general element, and
![]() $K$
be the Kronecker moduli space containing the Kronecker module appearing in the resolution of
$K$
be the Kronecker moduli space containing the Kronecker module appearing in the resolution of
![]() $U$
.
$U$
.
6.1 The zero dimensional Kronecker moduli space case
Theorem 6.1. Let
![]() $\unicode[STIX]{x1D709}^{+}$
be a primary orthogonal Chern character to
$\unicode[STIX]{x1D709}^{+}$
be a primary orthogonal Chern character to
![]() $\{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for the Chern character
$\{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for the Chern character
![]() $\unicode[STIX]{x1D709}$
with
$\unicode[STIX]{x1D709}$
with
![]() $\dim (K)=0$
and let
$\dim (K)=0$
and let
![]() $V\in M(\unicode[STIX]{x1D709}^{+})$
be the element. Then the Brill–Noether divisor
$V\in M(\unicode[STIX]{x1D709}^{+})$
be the element. Then the Brill–Noether divisor
is on an edge of the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
. Using the isomorphism
$M(\unicode[STIX]{x1D709})$
. Using the isomorphism
![]() $\operatorname{NS}\left(M(\unicode[STIX]{x1D709})\right)\cong \unicode[STIX]{x1D709}^{\bot }$
,
$\operatorname{NS}\left(M(\unicode[STIX]{x1D709})\right)\cong \unicode[STIX]{x1D709}^{\bot }$
,
![]() $D_{V}$
corresponds to
$D_{V}$
corresponds to
![]() $\unicode[STIX]{x1D709}^{+}$
.
$\unicode[STIX]{x1D709}^{+}$
.
Proof. The general element
![]() $U\in M(\unicode[STIX]{x1D709})$
fits into the short exact sequence
$U\in M(\unicode[STIX]{x1D709})$
fits into the short exact sequence
In order to show that
![]() $D_{V}$
is an effective Brill–Noether divisor, we have to show that
$D_{V}$
is an effective Brill–Noether divisor, we have to show that
![]() $V$
is cohomologically orthogonal to
$V$
is cohomologically orthogonal to
![]() $U$
. This means showing that
$U$
. This means showing that
![]() $U\otimes V=\mathscr{H}\!om(U^{\ast },V)$
has no cohomology. How we show this orthogonality depends upon which if any of the
$U\otimes V=\mathscr{H}\!om(U^{\ast },V)$
has no cohomology. How we show this orthogonality depends upon which if any of the
![]() $m_{i}$
vanish. Note that
$m_{i}$
vanish. Note that
![]() $\dim (K)=0$
implies that at most one of the
$\dim (K)=0$
implies that at most one of the
![]() $m_{i}$
is zero because if two are zero then
$m_{i}$
is zero because if two are zero then
![]() $\dim (K)=\dim (M(\unicode[STIX]{x1D709}))$
.
$\dim (K)=\dim (M(\unicode[STIX]{x1D709}))$
.
Assume that none of the
![]() $m_{i}$
are zero. Then the general element,
$m_{i}$
are zero. Then the general element,
![]() $U\in M(\unicode[STIX]{x1D709})$
, fits into the triangle
$U\in M(\unicode[STIX]{x1D709})$
, fits into the triangle
where
![]() $W$
is the complex
$W$
is the complex
![]() $\left(F_{0}^{\ast }\right)^{m_{2}}\rightarrow \left(F_{-1}^{\ast }\right)^{m_{1}}$
sitting in degrees -1 and 0. Similarly, the general element,
$\left(F_{0}^{\ast }\right)^{m_{2}}\rightarrow \left(F_{-1}^{\ast }\right)^{m_{1}}$
sitting in degrees -1 and 0. Similarly, the general element,
![]() $V\in M(\unicode[STIX]{x1D709}^{+})$
, fits into the triangle
$V\in M(\unicode[STIX]{x1D709}^{+})$
, fits into the triangle
By choice of resolving exceptional bundles,
![]() $\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FD}}^{\ast },\!V)$
and
$\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FD}}^{\ast },\!V)$
and
![]() $\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),\!V)$
have no cohomology. Thus, to construct the divisor it suffices to show that
$\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),\!V)$
have no cohomology. Thus, to construct the divisor it suffices to show that
![]() $\mathscr{H}\!om(W^{\ast },V)$
has no cohomology. As
$\mathscr{H}\!om(W^{\ast },V)$
has no cohomology. As
![]() $\mathscr{H}\!om(W^{\ast },E_{\unicode[STIX]{x1D6FD}})$
has no cohomology, this is equivalent to
$\mathscr{H}\!om(W^{\ast },E_{\unicode[STIX]{x1D6FD}})$
has no cohomology, this is equivalent to
![]() $\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V)$
having no cohomology. We reduce further to showing that
$\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V)$
having no cohomology. We reduce further to showing that
![]() $\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V[1])$
has no cohomology as shifting merely shifts the cohomology. Then if
$\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V[1])$
has no cohomology as shifting merely shifts the cohomology. Then if
![]() $f$
and
$f$
and
![]() $e$
are the Kronecker modules corresponding to
$e$
are the Kronecker modules corresponding to
![]() $W^{\ast }$
and
$W^{\ast }$
and
![]() $R_{\unicode[STIX]{x1D6FD}}V[1]$
, respectively, the vanishing of these cohomologies is equivalent to the vanishing of the
$R_{\unicode[STIX]{x1D6FD}}V[1]$
, respectively, the vanishing of these cohomologies is equivalent to the vanishing of the
![]() $\operatorname{Hom}(f,e)$
, but that vanishing follows directly from [Reference Coskun, Huizenga and WoolfCHW, Thm. 6.1]. Thus, we have the orthogonality that we needed.
$\operatorname{Hom}(f,e)$
, but that vanishing follows directly from [Reference Coskun, Huizenga and WoolfCHW, Thm. 6.1]. Thus, we have the orthogonality that we needed.
If one of the
![]() $m_{i}$
is zero (in which case we have not constructed a Kronecker fibration explicitly), then
$m_{i}$
is zero (in which case we have not constructed a Kronecker fibration explicitly), then
![]() $V$
is one of the exceptional bundles
$V$
is one of the exceptional bundles
![]() $E_{\unicode[STIX]{x1D6FD}}$
,
$E_{\unicode[STIX]{x1D6FD}}$
,
![]() $E_{1}$
,
$E_{1}$
,
![]() $E_{0}$
, or
$E_{0}$
, or
![]() $E_{\unicode[STIX]{x1D6FC}}$
. Then
$E_{\unicode[STIX]{x1D6FC}}$
. Then
![]() $V$
is cohomologically orthogonal to all three bundles that appear in the resolution of
$V$
is cohomologically orthogonal to all three bundles that appear in the resolution of
![]() $U$
so it is automatically cohomologically orthogonal.
$U$
so it is automatically cohomologically orthogonal.
Thus, we have shown the cohomological orthogonality in either case. The class of
![]() $D_{V}$
and the fact that it is effective is computed using Proposition 2.16.
$D_{V}$
and the fact that it is effective is computed using Proposition 2.16.
To show it lies on an edge, we construct a moving curve by varying a map in the resolution.
If
![]() $m_{3}\neq 0$
and
$m_{3}\neq 0$
and
![]() $m_{0}\neq 0$
, fix every map except
$m_{0}\neq 0$
, fix every map except
![]() $E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}\rightarrow \left(E_{\unicode[STIX]{x1D6FD}}^{\ast }\right)^{m_{0}}$
, let
$E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}\rightarrow \left(E_{\unicode[STIX]{x1D6FD}}^{\ast }\right)^{m_{0}}$
, let
and let
![]() ${\mathcal{U}}/S$
be the universal cokernel sheaf (of the fixed map plus the varying part).
${\mathcal{U}}/S$
be the universal cokernel sheaf (of the fixed map plus the varying part).
If
![]() $m_{3}=0$
, fix every map except
$m_{3}=0$
, fix every map except
![]() $F_{0}^{\ast m_{2}}\rightarrow \left(E_{\unicode[STIX]{x1D6FD}}^{\ast }\right)^{m_{0}}$
, let
$F_{0}^{\ast m_{2}}\rightarrow \left(E_{\unicode[STIX]{x1D6FD}}^{\ast }\right)^{m_{0}}$
, let
and let
![]() ${\mathcal{U}}/S$
be the universal cokernel sheaf (of the fixed map plus the varying part).
${\mathcal{U}}/S$
be the universal cokernel sheaf (of the fixed map plus the varying part).
If
![]() $m_{0}=0$
, fix every map except
$m_{0}=0$
, fix every map except
![]() $E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}\rightarrow \left(F_{0}^{\ast }\right)^{m_{1}}$
, let
$E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{3}}\rightarrow \left(F_{0}^{\ast }\right)^{m_{1}}$
, let
and let
![]() ${\mathcal{U}}/S$
be the universal cokernel sheaf (of the fixed map plus the varying part).
${\mathcal{U}}/S$
be the universal cokernel sheaf (of the fixed map plus the varying part).
In any case, we have our
![]() ${\mathcal{U}}$
and our
${\mathcal{U}}$
and our
![]() $S$
. Because
$S$
. Because
![]() $M(\unicode[STIX]{x1D709})$
is positive dimensional and the general sheaf in it has a resolution of this form,
$M(\unicode[STIX]{x1D709})$
is positive dimensional and the general sheaf in it has a resolution of this form,
![]() $S$
is nonempty. Then
$S$
is nonempty. Then
![]() ${\mathcal{U}}$
is a complete family of prioritary sheaves whose fixed Chern character lies above the
${\mathcal{U}}$
is a complete family of prioritary sheaves whose fixed Chern character lies above the
![]() $\unicode[STIX]{x1D6FF}$
surface. Define the open set
$\unicode[STIX]{x1D6FF}$
surface. Define the open set
![]() $S^{\prime }\subset S$
by
$S^{\prime }\subset S$
by
Thus, by assumption, the complement of
![]() $S^{\prime }$
has codimension at least 2 which allows us to find a complete curve in
$S^{\prime }$
has codimension at least 2 which allows us to find a complete curve in
![]() $S^{\prime }$
containing the point corresponding to
$S^{\prime }$
containing the point corresponding to
![]() $U$
for the general element
$U$
for the general element
![]() $U\in M(\unicode[STIX]{x1D709})$
. Notice that this is a moving curve by the codimension statement. Any curve in
$U\in M(\unicode[STIX]{x1D709})$
. Notice that this is a moving curve by the codimension statement. Any curve in
![]() $S^{\prime }$
is disjoint from
$S^{\prime }$
is disjoint from
![]() $D_{V}$
which makes the curve dual to it.
$D_{V}$
which makes the curve dual to it.
This curve makes
![]() $D_{V}$
be on an edge. As the resolution only provides one moving curve, this resolution only shows that it lies on an edge of the cone, not that it is an extremal ray.
$D_{V}$
be on an edge. As the resolution only provides one moving curve, this resolution only shows that it lies on an edge of the cone, not that it is an extremal ray.
6.2 The positive dimensional Kronecker moduli space case
Theorem 6.2. Let
![]() $\unicode[STIX]{x1D709}^{+}$
be a primary orthogonal Chern character to
$\unicode[STIX]{x1D709}^{+}$
be a primary orthogonal Chern character to
![]() $\{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for the Chern character
$\{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for the Chern character
![]() $\unicode[STIX]{x1D709}$
with
$\unicode[STIX]{x1D709}$
with
![]() $\dim (K)>0$
and
$\dim (K)>0$
and
![]() $V\in M(\unicode[STIX]{x1D709}^{+})$
be a general element. Then the Brill–Noether divisor
$V\in M(\unicode[STIX]{x1D709}^{+})$
be a general element. Then the Brill–Noether divisor
lies on the edge of the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
. Using the isomorphism
$M(\unicode[STIX]{x1D709})$
. Using the isomorphism
![]() $\operatorname{NS}\left(M(\unicode[STIX]{x1D709})\right)\cong \unicode[STIX]{x1D709}^{\bot }$
,
$\operatorname{NS}\left(M(\unicode[STIX]{x1D709})\right)\cong \unicode[STIX]{x1D709}^{\bot }$
,
![]() $D_{V}$
corresponds to
$D_{V}$
corresponds to
![]() $\unicode[STIX]{x1D709}^{+}$
.
$\unicode[STIX]{x1D709}^{+}$
.
Proof. Recall that we have a dominant rational map
![]() $\unicode[STIX]{x1D70B}:M(\unicode[STIX]{x1D709}){\dashrightarrow}K$
. There are two possibilities; either
$\unicode[STIX]{x1D70B}:M(\unicode[STIX]{x1D709}){\dashrightarrow}K$
. There are two possibilities; either
![]() $\unicode[STIX]{x1D70B}$
is a birational map or
$\unicode[STIX]{x1D70B}$
is a birational map or
![]() $\unicode[STIX]{x1D70B}$
has positive dimensional fibers.
$\unicode[STIX]{x1D70B}$
has positive dimensional fibers.
Birational case In this case, either zero or two of the
![]() $m_{i}$
can vanish. If zero vanish, we show that
$m_{i}$
can vanish. If zero vanish, we show that
![]() $V$
is cohomologically orthogonal to
$V$
is cohomologically orthogonal to
![]() $U$
by the same arguments as the previous theorem. If two vanish, then
$U$
by the same arguments as the previous theorem. If two vanish, then
![]() $V$
is again one of the exceptional bundles so orthogonality is immediate. The class of
$V$
is again one of the exceptional bundles so orthogonality is immediate. The class of
![]() $D_{V}$
and the fact that it is effective is computed using Proposition 2.16, and
$D_{V}$
and the fact that it is effective is computed using Proposition 2.16, and
![]() $D_{V}$
is the exceptional locus of
$D_{V}$
is the exceptional locus of
![]() $\unicode[STIX]{x1D70B}$
. Using that fact, we get a dual moving curve to
$\unicode[STIX]{x1D70B}$
. Using that fact, we get a dual moving curve to
![]() $D_{V}$
by varying the Kronecker module. Formally, because
$D_{V}$
by varying the Kronecker module. Formally, because
![]() $K$
is Picard rank one, there is a moving curve
$K$
is Picard rank one, there is a moving curve
![]() $C$
. Then
$C$
. Then
![]() $[\unicode[STIX]{x1D70B}^{\ast }(C)]$
is a moving curve which is dual to the exceptional locus of
$[\unicode[STIX]{x1D70B}^{\ast }(C)]$
is a moving curve which is dual to the exceptional locus of
![]() $\unicode[STIX]{x1D70B}$
(i.e., dual to
$\unicode[STIX]{x1D70B}$
(i.e., dual to
![]() $D_{V}$
). Thus,
$D_{V}$
). Thus,
![]() $D_{V}$
is on the edge of the effective cone.
$D_{V}$
is on the edge of the effective cone.
Positive dimensional fiber case In this case, none of the
![]() $m_{i}$
is zero.
$m_{i}$
is zero.
We first show cohomological orthogonality. This means showing that
![]() $U\otimes V=\mathscr{H}\!om(U^{\ast },V)$
has no cohomology. In this case, the general element,
$U\otimes V=\mathscr{H}\!om(U^{\ast },V)$
has no cohomology. In this case, the general element,
![]() $U\in M(\unicode[STIX]{x1D709})$
, fits into the triangle
$U\in M(\unicode[STIX]{x1D709})$
, fits into the triangle
where
![]() $W$
is the complex
$W$
is the complex
![]() $\left(F_{0}^{\ast }\right)^{m_{2}}\rightarrow \left(F_{-1}^{\ast }\right)^{m_{1}}$
sitting in degrees -1 and 0. Similarly, the general element,
$\left(F_{0}^{\ast }\right)^{m_{2}}\rightarrow \left(F_{-1}^{\ast }\right)^{m_{1}}$
sitting in degrees -1 and 0. Similarly, the general element,
![]() $V\in M(\unicode[STIX]{x1D709}^{+})$
, fits into the triangle
$V\in M(\unicode[STIX]{x1D709}^{+})$
, fits into the triangle
By choice of resolving exceptional bundles,
![]() $\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FD}}^{\ast },\!V)$
and
$\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FD}}^{\ast },\!V)$
and
![]() $\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),\!V)$
have no cohomology. Thus, to construct the divisor it suffices to show that
$\mathscr{H}\!om(E_{\unicode[STIX]{x1D6FC}}^{\ast }(K),\!V)$
have no cohomology. Thus, to construct the divisor it suffices to show that
![]() $\mathscr{H}\!om(W^{\ast },V)$
has no cohomology. As
$\mathscr{H}\!om(W^{\ast },V)$
has no cohomology. As
![]() $\mathscr{H}\!om(W^{\ast },E_{\unicode[STIX]{x1D6FD}})$
has no cohomology, we have that this is equivalent to
$\mathscr{H}\!om(W^{\ast },E_{\unicode[STIX]{x1D6FD}})$
has no cohomology, we have that this is equivalent to
![]() $\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V)$
having no cohomology. We reduce further to showing that
$\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V)$
having no cohomology. We reduce further to showing that
![]() $\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V[1])$
has no cohomology as shifting merely shifts the cohomology. Then if
$\mathscr{H}\!om(W^{\ast },R_{\unicode[STIX]{x1D6FD}}V[1])$
has no cohomology as shifting merely shifts the cohomology. Then if
![]() $f$
and
$f$
and
![]() $e$
are the Kronecker modules corresponding to
$e$
are the Kronecker modules corresponding to
![]() $W^{\ast }$
and
$W^{\ast }$
and
![]() $R_{\unicode[STIX]{x1D6FD}}V[1]$
, respectively, the vanishing of these cohomologies is equivalent to the vanishing of the
$R_{\unicode[STIX]{x1D6FD}}V[1]$
, respectively, the vanishing of these cohomologies is equivalent to the vanishing of the
![]() $\operatorname{Hom}(f,e)$
, but that vanishing follows directly from [Reference Coskun, Huizenga and WoolfCHW, Thm. 6.1]
$\operatorname{Hom}(f,e)$
, but that vanishing follows directly from [Reference Coskun, Huizenga and WoolfCHW, Thm. 6.1]
We have now established the cohomological orthogonality. The class of
![]() $D_{V}$
and the fact that it gives an effective divisor are computed using Proposition 2.16.
$D_{V}$
and the fact that it gives an effective divisor are computed using Proposition 2.16.
As the general
![]() $U$
has the given resolution, the fibers of map to
$U$
has the given resolution, the fibers of map to
![]() $K$
are covered by varying the other maps of the resolution as we did in the last proof. As these moving curves sit inside fibers, they are dual to
$K$
are covered by varying the other maps of the resolution as we did in the last proof. As these moving curves sit inside fibers, they are dual to
![]() $D_{V}$
since
$D_{V}$
since
![]() $V$
is dual to the Kronecker modules in
$V$
is dual to the Kronecker modules in
![]() $K$
.
$K$
.
If we can vary two different maps in the resolution other than the Kronecker module independently, than
![]() $D_{V}$
has the same class as the pullback of an ample divisor of
$D_{V}$
has the same class as the pullback of an ample divisor of
![]() $K$
. This immediately implies that
$K$
. This immediately implies that
![]() $D_{V}$
is in the moving cone. We can vary two maps independently if the no
$D_{V}$
is in the moving cone. We can vary two maps independently if the no
![]() $m_{i}$
is zero and no subcomplex of the resolution has enough dimensions to account for all of the dimensions of our moduli space.
$m_{i}$
is zero and no subcomplex of the resolution has enough dimensions to account for all of the dimensions of our moduli space.
These theorems together give an effective divisor on
![]() $M(\unicode[STIX]{x1D709})$
. These conjecturally might give a spanning set of effective divisors for the effective cone of
$M(\unicode[STIX]{x1D709})$
. These conjecturally might give a spanning set of effective divisors for the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
, but even if this method does not do that, it gives a way to construct effective divisors on many of these moduli spaces. In addition, this same method works to give secondary extremal rays when the rank of the moduli space is at least three (for rank less than three all secondary rays have special meaning).
$M(\unicode[STIX]{x1D709})$
, but even if this method does not do that, it gives a way to construct effective divisors on many of these moduli spaces. In addition, this same method works to give secondary extremal rays when the rank of the moduli space is at least three (for rank less than three all secondary rays have special meaning).
In the case that no power in the resolution vanishes, this effective divisor immediately spans an extremal ray if
![]() $\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{0}},K)-m_{0}^{2}<\dim (M(\unicode[STIX]{x1D709}))$
and
$\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{0}},K)-m_{0}^{2}<\dim (M(\unicode[STIX]{x1D709}))$
and
![]() $\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{0}},E_{\unicode[STIX]{x1D6FD}}^{\ast m_{3}})-m_{0}^{2}-m_{3}^{2}<\dim (M(\unicode[STIX]{x1D709}))$
. Otherwise, this divisor is known to span an extremal ray as long as both controlling exceptional bundles are part of another extremal pair.
$\hom (E_{\unicode[STIX]{x1D6FC}}^{\ast }(K)^{m_{0}},E_{\unicode[STIX]{x1D6FD}}^{\ast m_{3}})-m_{0}^{2}-m_{3}^{2}<\dim (M(\unicode[STIX]{x1D709}))$
. Otherwise, this divisor is known to span an extremal ray as long as both controlling exceptional bundles are part of another extremal pair.
7 Examples
The method of the previous section constructs Brill–Noether divisors on the faces of the effective cone for moduli spaces of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. In this section, we work out a series of examples showing the usefulness of our theorems. We work out the effective cones of the first fifteen Hilbert schemes of points as well as some series of extremal rays that occur for infinitely many Hilbert schemes of points on
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. In this section, we work out a series of examples showing the usefulness of our theorems. We work out the effective cones of the first fifteen Hilbert schemes of points as well as some series of extremal rays that occur for infinitely many Hilbert schemes of points on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Lastly, we provide an extremal edge for the effective cone of a moduli space of rank two sheaves with nonsymmetric slope so that we see the theorems are useful in that setting as well.
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Lastly, we provide an extremal edge for the effective cone of a moduli space of rank two sheaves with nonsymmetric slope so that we see the theorems are useful in that setting as well.
7.1 The effective cones of Hilbert schemes of at most sixteen points
The most classical example of a moduli space of sheaves on
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
is Hilbert scheme of
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
is Hilbert scheme of
![]() $n$
points on it. For these Hilbert schemes, the Picard group has a classical basis,
$n$
points on it. For these Hilbert schemes, the Picard group has a classical basis,
![]() $\{B,H_{1},H_{2}\}$
. Each element of this basis has an extremely geometric interpretation.
$\{B,H_{1},H_{2}\}$
. Each element of this basis has an extremely geometric interpretation.
![]() $B$
is the locus of nonreduced schemes or equivalently the schemes supported on
$B$
is the locus of nonreduced schemes or equivalently the schemes supported on
![]() $n-1$
or fewer closed points.
$n-1$
or fewer closed points.
![]() $H_{1}$
is the schemes whose support intersects a fixed line of type
$H_{1}$
is the schemes whose support intersects a fixed line of type
![]() $(1,0)$
. Similarly,
$(1,0)$
. Similarly,
![]() $H_{2}$
is the schemes whose support intersects a fixed line of type
$H_{2}$
is the schemes whose support intersects a fixed line of type
![]() $(0,1)$
.
$(0,1)$
.
Using this basis, every ray in the Néron–Severi space is spanned by a ray of the form
![]() $B$
,
$B$
,
![]() $aH_{1}+bH_{2}+B$
,
$aH_{1}+bH_{2}+B$
,
![]() $aH_{1}+bH_{2}$
, or
$aH_{1}+bH_{2}$
, or
![]() $iH_{1}+jH_{2}-B/2$
. Then we fix the notation for the last two types of ray as
$iH_{1}+jH_{2}-B/2$
. Then we fix the notation for the last two types of ray as
Using this notation, we list the extremal rays of the effective cones of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{\left[n\right]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{\left[n\right]}$
for
![]() $n\leqslant 16$
, explicitly work out the case of
$n\leqslant 16$
, explicitly work out the case of
![]() $n=7$
, prove that some sequences of rays are extremal for varying
$n=7$
, prove that some sequences of rays are extremal for varying
![]() $n$
, and then finally explicitly work out each remaining extremal ray for
$n$
, and then finally explicitly work out each remaining extremal ray for
![]() $n\leqslant 16$
. These are all new results except for the cases of
$n\leqslant 16$
. These are all new results except for the cases of
![]() $n\leqslant 5$
.
$n\leqslant 5$
.

7.2 The effective cone of the Hilbert scheme of
 $7$
points
$7$
points
It is worth showing how the theorem is applied in one of these cases to compute the effective cone. Recall that the general strategy to compute an effective cone has two steps. First, provide effective divisors. Second, provide moving curves which are dual to the effective divisors.
We use our main theorem to do this for the primary extremal rays of the effective cone; we have to deal with the secondary extremal rays separately. There is a single secondary extremal ray which is spanned by
![]() $B$
.
$B$
.
![]() $B$
is clearly an effective divisor as it is the locus of nonreduced schemes. In order to show that
$B$
is clearly an effective divisor as it is the locus of nonreduced schemes. In order to show that
![]() $B$
spans an extremal ray, we just have to construct two distinct dual moving curves.
$B$
spans an extremal ray, we just have to construct two distinct dual moving curves.
We now construct these moving curves,
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
. We construct
$C_{2}$
. We construct
![]() $C_{1}$
by fixing
$C_{1}$
by fixing
![]() $6$
general points and then varying a seventh point along a curve of type
$6$
general points and then varying a seventh point along a curve of type
![]() $(1,0)$
. Similarly, we construct
$(1,0)$
. Similarly, we construct
![]() $C_{2}$
by fixing
$C_{2}$
by fixing
![]() $6$
general points and then varying a seventh point along a curve of type
$6$
general points and then varying a seventh point along a curve of type
![]() $(0,1)$
. Any set of
$(0,1)$
. Any set of
![]() $7$
distinct points lies on at least one curve of type
$7$
distinct points lies on at least one curve of type
![]() $C_{1}$
, so it is a moving curve. Similarly,
$C_{1}$
, so it is a moving curve. Similarly,
![]() $C_{2}$
is a moving curve.
$C_{2}$
is a moving curve.
We now show that
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
are dual to
$C_{2}$
are dual to
![]() $B$
. Starting with six general points, we can find a line
$B$
. Starting with six general points, we can find a line
![]() $l$
of type
$l$
of type
![]() $(1,0)$
that does not contain any of the points. We get a curve
$(1,0)$
that does not contain any of the points. We get a curve
![]() $C^{\prime }$
of type
$C^{\prime }$
of type
![]() $C_{1}$
in the Hilbert scheme by varying the seventh point along
$C_{1}$
in the Hilbert scheme by varying the seventh point along
![]() $l$
. As
$l$
. As
![]() $l$
does not contain any of the six general points, every point in
$l$
does not contain any of the six general points, every point in
![]() $C^{\prime }$
corresponds to seven distinct points, so
$C^{\prime }$
corresponds to seven distinct points, so
![]() $C^{\prime }$
does not intersect
$C^{\prime }$
does not intersect
![]() $B$
. Thus, we get
$B$
. Thus, we get
Similarly, we get that
The only thing left to do in order to show that
![]() $B$
spans an extremal ray is to show that
$B$
spans an extremal ray is to show that
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
have distinct classes. Starting with six general points, we find lines
$C_{2}$
have distinct classes. Starting with six general points, we find lines
![]() $l$
and
$l$
and
![]() $l^{\prime }$
of type
$l^{\prime }$
of type
![]() $(1,0)$
that does not contain any of the points. Again, we get a curve
$(1,0)$
that does not contain any of the points. Again, we get a curve
![]() $C^{\prime }$
of type
$C^{\prime }$
of type
![]() $C_{1}$
in the Hilbert scheme by varying the seventh point along
$C_{1}$
in the Hilbert scheme by varying the seventh point along
![]() $l$
. Analogously, we get a divisor
$l$
. Analogously, we get a divisor
![]() $H^{\prime }$
of type
$H^{\prime }$
of type
![]() $H_{1}$
as the locus of schemes whose support intersects
$H_{1}$
as the locus of schemes whose support intersects
![]() $l^{\prime }$
. As
$l^{\prime }$
. As
![]() $l^{\prime }$
does not contain any of the general fixed points and does not intersect
$l^{\prime }$
does not contain any of the general fixed points and does not intersect
![]() $l$
, we get that
$l$
, we get that
![]() $H_{1}$
and
$H_{1}$
and
![]() $C^{\prime }$
are disjoint. Thus,
$C^{\prime }$
are disjoint. Thus,
Using the same six general points, we find a line
![]() $l_{0}$
of type
$l_{0}$
of type
![]() $(0,1)$
that does not contain any of the points. We get a curve
$(0,1)$
that does not contain any of the points. We get a curve
![]() $C_{0}$
of type
$C_{0}$
of type
![]() $C_{2}$
by varying the seventh point along
$C_{2}$
by varying the seventh point along
![]() $l_{0}$
. Then
$l_{0}$
. Then
![]() $l_{0}$
does not contain any of the six general points by construction but does intersect
$l_{0}$
does not contain any of the six general points by construction but does intersect
![]() $l^{\prime }$
in exactly one point. Thus,
$l^{\prime }$
in exactly one point. Thus,
As
![]() $C_{1}\cdot H_{1}\neq C_{2}\cdot H_{1}$
, we know that
$C_{1}\cdot H_{1}\neq C_{2}\cdot H_{1}$
, we know that
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
are distinct classes. This observation completes the proof that
$C_{2}$
are distinct classes. This observation completes the proof that
![]() $B$
spans an extremal ray.
$B$
spans an extremal ray.
While constructing the primary extremal rays, we construct two moving curves dual to
![]() $B$
. These curves show that
$B$
. These curves show that
![]() $B$
is the only secondary extremal ray. Also as the slope of the ideal sheaf is
$B$
is the only secondary extremal ray. Also as the slope of the ideal sheaf is
![]() $(0,0)$
, the effective cone is symmetric in the coordinates of
$(0,0)$
, the effective cone is symmetric in the coordinates of
![]() $H_{1}$
and
$H_{1}$
and
![]() $H_{2}$
so we only deal with the primary rays spanned by
$H_{2}$
so we only deal with the primary rays spanned by
![]() $X_{i,j}$
where
$X_{i,j}$
where
![]() $i\geqslant j$
. Keeping that in mind, we move to computing the primary extremal rays using our theorem.
$i\geqslant j$
. Keeping that in mind, we move to computing the primary extremal rays using our theorem.
One way to think about the main results of this paper are that they give an algorithm to compute the primary extremal rays of the effective cone of
![]() $M(\unicode[STIX]{x1D709})$
. That algorithm breaks down roughly into four steps: find the extremal pairs, use the extremal pairs to resolve the general object of
$M(\unicode[STIX]{x1D709})$
. That algorithm breaks down roughly into four steps: find the extremal pairs, use the extremal pairs to resolve the general object of
![]() $M(\unicode[STIX]{x1D709})$
, use those resolutions to construct maps to moduli spaces of Kronecker modules, and analyze these maps to find divisors spanning extremal rays. Let us follow those steps in this specific case.
$M(\unicode[STIX]{x1D709})$
, use those resolutions to construct maps to moduli spaces of Kronecker modules, and analyze these maps to find divisors spanning extremal rays. Let us follow those steps in this specific case.
Step 1. As we noted above, the first step is to find all of the extremal pairs. Proceed by finding all controlling exceptional bundles, finding the controlling pairs, and then finding which are extremal pairs.
Controlling exceptional bundles are those controlling the
![]() $\unicode[STIX]{x1D6FF}$
-surface over the locus
$\unicode[STIX]{x1D6FF}$
-surface over the locus
Using Mathematica, we find that these controlling exceptional bundles are
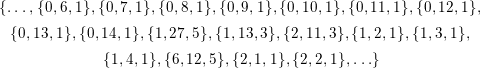 $$\begin{eqnarray}\displaystyle & \displaystyle \{\!\ldots ,\{0,6,1\},\{0,7,1\},\{0,8,1\},\{0,9,1\},\{0,10,1\},\{0,11,1\},\{0,12,1\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \{0,13,1\},\{0,14,1\},\{1,27,5\},\{1,13,3\},\{2,11,3\},\{1,2,1\},\{1,3,1\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \{1,4,1\},\{6,12,5\},\{2,1,1\},\{2,2,1\},\ldots \!\} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \{\!\ldots ,\{0,6,1\},\{0,7,1\},\{0,8,1\},\{0,9,1\},\{0,10,1\},\{0,11,1\},\{0,12,1\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \{0,13,1\},\{0,14,1\},\{1,27,5\},\{1,13,3\},\{2,11,3\},\{1,2,1\},\{1,3,1\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \{1,4,1\},\{6,12,5\},\{2,1,1\},\{2,2,1\},\ldots \!\} & \displaystyle \nonumber\end{eqnarray}$$
where we record an exceptional bundle with Chern character
![]() $\left(r,(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}),\unicode[STIX]{x1D6E5}\right)$
as
$\left(r,(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}),\unicode[STIX]{x1D6E5}\right)$
as
![]() $(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2},r)$
. We truncated the list before and after all bundles which are useful in computing the effective cone. We can see that the ones we have truncated do not matter as our first resolution is dual to
$(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2},r)$
. We truncated the list before and after all bundles which are useful in computing the effective cone. We can see that the ones we have truncated do not matter as our first resolution is dual to
![]() $B$
.
$B$
.
There are many, many controlling exceptional pairs, but we do not need to see all of them.
Finally, we check to see which of these are extremal pairs. They are whittled down by eliminating each pair that does not have each of the properties of an extremal pair. The only four controlling pairs that are extremal pairs are
Each extremal pair controls an extremal ray of the effective cone. Recall that given an extremal pair
![]() $\{A,B\}$
, the extremal ray it corresponds to is spanned by the primary orthogonal Chern character of the pair:
$\{A,B\}$
, the extremal ray it corresponds to is spanned by the primary orthogonal Chern character of the pair:
![]() $\operatorname{ch}(A)$
,
$\operatorname{ch}(A)$
,
![]() $\operatorname{ch}(B)$
, or
$\operatorname{ch}(B)$
, or
Then the primary orthogonal Chern character for our exceptional pairs are
![]() $\left(1,(6,0),0\right)$
,
$\left(1,(6,0),0\right)$
,
![]() $\left(1,(6,0),0\right)$
,
$\left(1,(6,0),0\right)$
,
![]() $\left(5,(12,6),12\right)$
, and
$\left(5,(12,6),12\right)$
, and
![]() $\left(2,(4,3),5\right)$
, respectively. These Chern characters correspond to the extremal rays
$\left(2,(4,3),5\right)$
, respectively. These Chern characters correspond to the extremal rays
![]() $X_{6,0}$
,
$X_{6,0}$
,
![]() $X_{6,0}$
,
$X_{6,0}$
,
![]() $X_{\frac{12}{5},\frac{6}{5}}$
, and
$X_{\frac{12}{5},\frac{6}{5}}$
, and
![]() $X_{2,\frac{3}{2}}$
, respectively. Notice that one of the rays is repeated twice. This repetition is because we need all of these extremal pairs to share each of their elements with another extremal pair in order to link neighboring extremal rays with moving curves.
$X_{2,\frac{3}{2}}$
, respectively. Notice that one of the rays is repeated twice. This repetition is because we need all of these extremal pairs to share each of their elements with another extremal pair in order to link neighboring extremal rays with moving curves.
Step 2. The next step in computing the effective cone is to turn the extremal pairs into resolutions of the general element of the Hilbert scheme. We use Theorems 4.4 and 4.8 to get these resolutions. To apply those theorems, we have to complete the pairs to coils as described in Section 4. This approach gives the coils
 $$\begin{eqnarray}\displaystyle & & \displaystyle \{{\mathcal{O}}(-7,-1),{\mathcal{O}}(-6,-1),{\mathcal{O}}(-7,-0),{\mathcal{O}}(-6,0)\}\nonumber\\ \displaystyle & & \displaystyle \{{\mathcal{O}}(-7,-2),{\mathcal{O}}(-4,-1),{\mathcal{O}}(-3,-1),{\mathcal{O}}(-6,0)\},\nonumber\\ \displaystyle & & \displaystyle \{{\mathcal{O}}(-4,-3),{\mathcal{O}}(-4,-2),{\mathcal{O}}(-3,-2),{\mathcal{O}}(-3,-1)\},\qquad \text{and}\nonumber\\ \displaystyle & & \displaystyle \{{\mathcal{O}}(-4,-3),{\mathcal{O}}(-3,-2),{\mathcal{O}}(-3,-1),{\mathcal{O}}(-2,-2)\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{{\mathcal{O}}(-7,-1),{\mathcal{O}}(-6,-1),{\mathcal{O}}(-7,-0),{\mathcal{O}}(-6,0)\}\nonumber\\ \displaystyle & & \displaystyle \{{\mathcal{O}}(-7,-2),{\mathcal{O}}(-4,-1),{\mathcal{O}}(-3,-1),{\mathcal{O}}(-6,0)\},\nonumber\\ \displaystyle & & \displaystyle \{{\mathcal{O}}(-4,-3),{\mathcal{O}}(-4,-2),{\mathcal{O}}(-3,-2),{\mathcal{O}}(-3,-1)\},\qquad \text{and}\nonumber\\ \displaystyle & & \displaystyle \{{\mathcal{O}}(-4,-3),{\mathcal{O}}(-3,-2),{\mathcal{O}}(-3,-1),{\mathcal{O}}(-2,-2)\},\nonumber\end{eqnarray}$$
respectively.
Given these coils, we get the resolutions we wanted using the spectral sequence as in the proofs of the relevant theorems. Following the proof, we get the resolutions
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-7,-1)^{7}\rightarrow {\mathcal{O}}(-6,-1)^{7}\bigoplus {\mathcal{O}}(-7,0)\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-7,-2)\rightarrow {\mathcal{O}}(-4,-1)\bigoplus {\mathcal{O}}(-3,-1)\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-4,-3)\bigoplus {\mathcal{O}}(-4,-2)^{2}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}(-3,-2)^{3}\bigoplus {\mathcal{O}}(-3,-1)\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-4,-3)\bigoplus {\mathcal{O}}(-3,-2)\rightarrow {\mathcal{O}}(-3,-1)\bigoplus {\mathcal{O}}(-2,-2)^{2}\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-7,-1)^{7}\rightarrow {\mathcal{O}}(-6,-1)^{7}\bigoplus {\mathcal{O}}(-7,0)\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-7,-2)\rightarrow {\mathcal{O}}(-4,-1)\bigoplus {\mathcal{O}}(-3,-1)\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-4,-3)\bigoplus {\mathcal{O}}(-4,-2)^{2}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}(-3,-2)^{3}\bigoplus {\mathcal{O}}(-3,-1)\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-4,-3)\bigoplus {\mathcal{O}}(-3,-2)\rightarrow {\mathcal{O}}(-3,-1)\bigoplus {\mathcal{O}}(-2,-2)^{2}\rightarrow {\mathcal{I}}_{z}\rightarrow 0,\nonumber\end{eqnarray}$$
respectively.
Step 3. We now get to the third step in the process, turning the resolutions into maps to Kronecker moduli spaces. There are no Kronecker modules that are used in the first two resolutions and the Kronecker module in each of the last two resolutions are
respectively.
This means that we have the maps
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{1}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[7]} & {\dashrightarrow} & \displaystyle Kr_{\hom ({\mathcal{O}}(3,2),{\mathcal{O}}(4,2))}(3,2),\qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{2}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[7]} & {\dashrightarrow} & \displaystyle Kr_{\hom ({\mathcal{O}}(3,1),{\mathcal{O}}(3,2))}(1,1),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{1}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[7]} & {\dashrightarrow} & \displaystyle Kr_{\hom ({\mathcal{O}}(3,2),{\mathcal{O}}(4,2))}(3,2),\qquad \text{and}\nonumber\\ \displaystyle \unicode[STIX]{x1D70B}_{2}:\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[7]} & {\dashrightarrow} & \displaystyle Kr_{\hom ({\mathcal{O}}(3,1),{\mathcal{O}}(3,2))}(1,1),\nonumber\end{eqnarray}$$
respectively.
Note that the dimensions of these Kronecker moduli spaces are
![]() $0$
and
$0$
and
![]() $1$
, respectively, so we only consider the map in the last case.
$1$
, respectively, so we only consider the map in the last case.
Step 4. The fourth and final step is actually computing the effective divisors and their dual moving curves. Let
![]() $D=aH_{1}+bH_{2}-cB/2$
be a general effective divisor.
$D=aH_{1}+bH_{2}-cB/2$
be a general effective divisor.
In the first case, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V={\mathcal{O}}(6,0)$
. The moving curve comes from a pencil of maps
$V={\mathcal{O}}(6,0)$
. The moving curve comes from a pencil of maps
![]() ${\mathcal{O}}(-7,-1)^{7}\rightarrow {\mathcal{O}}(-6,-1)^{7}$
. The restriction this moving curve places on
${\mathcal{O}}(-7,-1)^{7}\rightarrow {\mathcal{O}}(-6,-1)^{7}$
. The restriction this moving curve places on
![]() $D$
is that
$D$
is that
![]() $b\geqslant 0$
. In particular,
$b\geqslant 0$
. In particular,
![]() $B$
and
$B$
and
![]() $X_{6,0}$
are dual to this moving curve.
$X_{6,0}$
are dual to this moving curve.
In the second case, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V={\mathcal{O}}(6,0)$
. The moving curve comes from a pencil of maps
$V={\mathcal{O}}(6,0)$
. The moving curve comes from a pencil of maps
![]() ${\mathcal{O}}(-7,-2)\rightarrow {\mathcal{O}}(-4,-1)$
. The restriction this moving curve places on
${\mathcal{O}}(-7,-2)\rightarrow {\mathcal{O}}(-4,-1)$
. The restriction this moving curve places on
![]() $D$
is that
$D$
is that
![]() $3b\geqslant 6-a$
. In particular,
$3b\geqslant 6-a$
. In particular,
![]() $X_{6,0}$
and
$X_{6,0}$
and
![]() $X_{\frac{12}{5},\frac{6}{5}}$
are dual to this moving curve.
$X_{\frac{12}{5},\frac{6}{5}}$
are dual to this moving curve.
For
![]() $\unicode[STIX]{x1D70B}_{1}$
, the Brill–Noether divisor is
$\unicode[STIX]{x1D70B}_{1}$
, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is the exceptional bundle
$V$
is the exceptional bundle
![]() $E_{\frac{12}{5},\frac{6}{5}}$
. Notice that in this case, the Kronecker fibration is a map to a point. This implies that the divisor
$E_{\frac{12}{5},\frac{6}{5}}$
. Notice that in this case, the Kronecker fibration is a map to a point. This implies that the divisor
![]() $D_{V}$
is rigid. The two types of moving curve come from pencils of maps
$D_{V}$
is rigid. The two types of moving curve come from pencils of maps
![]() ${\mathcal{O}}(-4,-3)\rightarrow {\mathcal{O}}(-3,-2)^{3}$
and
${\mathcal{O}}(-4,-3)\rightarrow {\mathcal{O}}(-3,-2)^{3}$
and
![]() ${\mathcal{O}}(-4,-2)^{2}\rightarrow {\mathcal{O}}(-3,-1)$
. These are dual to
${\mathcal{O}}(-4,-2)^{2}\rightarrow {\mathcal{O}}(-3,-1)$
. These are dual to
![]() $D_{V}$
by the resolution
$D_{V}$
by the resolution
since
![]() $\unicode[STIX]{x1D712}((3,2),(4,3))=12+6-2\ast 3\ast 3=0$
. The restriction these two moving curves place on
$\unicode[STIX]{x1D712}((3,2),(4,3))=12+6-2\ast 3\ast 3=0$
. The restriction these two moving curves place on
![]() $D$
are that
$D$
are that
![]() $3b\geqslant 6-a$
and
$3b\geqslant 6-a$
and
![]() $4b\geqslant 12-3a$
. In particular,
$4b\geqslant 12-3a$
. In particular,
![]() $X_{\frac{12}{5},\frac{6}{5}}$
is dual to both moving curves and
$X_{\frac{12}{5},\frac{6}{5}}$
is dual to both moving curves and
![]() $X_{2,\frac{3}{2}}$
is dual to the second moving curve.
$X_{2,\frac{3}{2}}$
is dual to the second moving curve.
For
![]() $\unicode[STIX]{x1D70B}_{2}$
, the Brill–Noether divisor is
$\unicode[STIX]{x1D70B}_{2}$
, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is a bundle
$V$
is a bundle
![]() $F_{2,\frac{3}{2}}$
that has Chern character
$F_{2,\frac{3}{2}}$
that has Chern character
![]() $(2,(4,3),5)$
. The two types of moving curve covering each fiber come from pencils of maps
$(2,(4,3),5)$
. The two types of moving curve covering each fiber come from pencils of maps
![]() ${\mathcal{O}}(-4,-3)\rightarrow K$
and
${\mathcal{O}}(-4,-3)\rightarrow K$
and
![]() ${\mathcal{O}}(-4,-3)\rightarrow {\mathcal{O}}(-2,-2)^{2}$
. These are dual to
${\mathcal{O}}(-4,-3)\rightarrow {\mathcal{O}}(-2,-2)^{2}$
. These are dual to
![]() $D_{V}$
by the resolution
$D_{V}$
by the resolution
since
![]() $\unicode[STIX]{x1D712}((1,1),(1,1))=2\ast 1\ast 1-1\ast 1-1\ast 1+1\ast 1=0$
. The restriction these two moving curve place on
$\unicode[STIX]{x1D712}((1,1),(1,1))=2\ast 1\ast 1-1\ast 1-1\ast 1+1\ast 1=0$
. The restriction these two moving curve place on
![]() $D$
are that
$D$
are that
![]() $4b\geqslant 12-3a$
and
$4b\geqslant 12-3a$
and
![]() $2b\geqslant 7-2a$
. In particular,
$2b\geqslant 7-2a$
. In particular,
![]() $X_{2,\frac{3}{2}}$
is dual to both moving curves,
$X_{2,\frac{3}{2}}$
is dual to both moving curves,
![]() $X_{\frac{12}{5},\frac{6}{5}}$
is dual to the first moving curve, and
$X_{\frac{12}{5},\frac{6}{5}}$
is dual to the first moving curve, and
![]() $X_{\frac{3}{2},2}$
is dual to the second moving curve.
$X_{\frac{3}{2},2}$
is dual to the second moving curve.
We have now exhibited 7 effective divisors
and 7 moving curves that are dual to each pair of extremal rays that span a face of the effective cone. Taken together, these divisors and moving curves determine the effective cone.
7.3 Infinite series of extremal rays
As another example of the power of the methods produced in this paper, we can construct an extremal ray in the Hilbert scheme of
![]() $n$
points for infinite sequences of
$n$
points for infinite sequences of
![]() $n$
. We provide two extremal rays for three such sequences and one extremal ray for a fourth sequence. The strategy for each proof is to first find an extremal pair, then use the process outlined by our theorems to show that they give the desired extremal ray(s).
$n$
. We provide two extremal rays for three such sequences and one extremal ray for a fourth sequence. The strategy for each proof is to first find an extremal pair, then use the process outlined by our theorems to show that they give the desired extremal ray(s).
The first sequence we look at is actually just all
![]() $n$
. For this sequence, we prove what the edges of the effective cone that share the secondary extremal ray are.
$n$
. For this sequence, we prove what the edges of the effective cone that share the secondary extremal ray are.
Proposition 7.1. The edge spanned by
![]() $X_{n-1,0}$
and
$X_{n-1,0}$
and
![]() $B$
is an extremal edge of the effective cone of
$B$
is an extremal edge of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
. Similarly, the edge spanned by
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
. Similarly, the edge spanned by
![]() $X_{0,n-1}$
and
$X_{0,n-1}$
and
![]() $B$
is an extremal edge of the effective cone of
$B$
is an extremal edge of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
.
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
.
Proof. This was proved for
![]() $n\leqslant 5$
in [Reference Bertram and CoskunBC]. It is immediate from the symmetry of the effective cone in terms of
$n\leqslant 5$
in [Reference Bertram and CoskunBC]. It is immediate from the symmetry of the effective cone in terms of
![]() $a$
and
$a$
and
![]() $b$
that the second statement is immediate from the first statement. We now prove the first statement.
$b$
that the second statement is immediate from the first statement. We now prove the first statement.
The first step in proving this edge is an extremal ray is finding an extremal pair. To find an extremal pair, we first have to find the two controlling exceptional bundles that make up the pair. The vector bundle whose Brill–Noether divisor spans the ray
![]() $X_{n-1,0}$
is
$X_{n-1,0}$
is
![]() ${\mathcal{O}}(n-1,0)$
. To find our controlling exceptional bundles, we need to find exceptional bundles cohomologically orthogonal to
${\mathcal{O}}(n-1,0)$
. To find our controlling exceptional bundles, we need to find exceptional bundles cohomologically orthogonal to
![]() ${\mathcal{O}}(n-1,0)$
. Then,
${\mathcal{O}}(n-1,0)$
. Then,
Then it is easy to see that
![]() ${\mathcal{O}}(n-1,1)$
and
${\mathcal{O}}(n-1,1)$
and
![]() ${\mathcal{O}}(n,0)$
are controlling exceptional bundles for the Hilbert scheme, and the pair
${\mathcal{O}}(n,0)$
are controlling exceptional bundles for the Hilbert scheme, and the pair
![]() $\{{\mathcal{O}}(n-1,1),{\mathcal{O}}(n,0)\}$
is an extremal pair.
$\{{\mathcal{O}}(n-1,1),{\mathcal{O}}(n,0)\}$
is an extremal pair.
Once we have the extremal pair, we need to turn it into a resolution of the general object of the Hilbert scheme. We complete the pair to a coil as prescribed by Theorem 4.8. This completion gives the coil
Next, we use the Beilinson spectral sequence to resolve the general ideal sheaf. The spectral sequence gives the resolution
The moving curves are pencils in the space
![]() $\operatorname{Hom}({\mathcal{O}}(-n,-1),{\mathcal{O}}(-n+1,-1))$
. The restriction this moving curve places on
$\operatorname{Hom}({\mathcal{O}}(-n,-1),{\mathcal{O}}(-n+1,-1))$
. The restriction this moving curve places on
![]() $D$
is that
$D$
is that
![]() $b\geqslant 0$
. In particular,
$b\geqslant 0$
. In particular,
![]() $B$
and
$B$
and
![]() $X_{n-1,0}$
are dual to this moving curve.
$X_{n-1,0}$
are dual to this moving curve.
![]() $B$
is known to be an effective divisor. The ray corresponding to
$B$
is known to be an effective divisor. The ray corresponding to
![]() $X_{n-1,0}$
is spanned by the effective Brill–Noether divisor
$X_{n-1,0}$
is spanned by the effective Brill–Noether divisor
![]() $D_{V}$
where
$D_{V}$
where
![]() $V={\mathcal{O}}(n-1,0)$
by Theorem 6.2. By symmetry, it is clear that
$V={\mathcal{O}}(n-1,0)$
by Theorem 6.2. By symmetry, it is clear that
![]() $B$
spans an extremal ray. We have not yet shown that
$B$
spans an extremal ray. We have not yet shown that
![]() $X_{n-1,0}$
spans an extremal ray because we have only provided one moving curve dual to it. The next two propositions complete the proof that it spans an extremal ray by providing a second dual moving curve. The first proposition provides the dual moving curve in the case that
$X_{n-1,0}$
spans an extremal ray because we have only provided one moving curve dual to it. The next two propositions complete the proof that it spans an extremal ray by providing a second dual moving curve. The first proposition provides the dual moving curve in the case that
![]() $n$
is even while the second proposition does so in the case that
$n$
is even while the second proposition does so in the case that
![]() $n$
is odd.
$n$
is odd.
The next proposition provides another edge of the effective cone in the case that
![]() $n$
is even, that is,
$n$
is even, that is,
![]() $n=2k$
. This edge shares an extremal ray with the edge provided by the previous theorem. It provides the second dual moving curve we needed to complete the previous proposition in the case that
$n=2k$
. This edge shares an extremal ray with the edge provided by the previous theorem. It provides the second dual moving curve we needed to complete the previous proposition in the case that
![]() $n$
is even.
$n$
is even.
Proposition 7.2. The edge spanned by
![]() $X_{2k-1,0}$
and
$X_{2k-1,0}$
and
![]() $X_{k-1,1}$
is an extremal edge of the effective cone of
$X_{k-1,1}$
is an extremal edge of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k]}$
for
![]() $k>0$
. Similarly, the edge spanned by
$k>0$
. Similarly, the edge spanned by
![]() $X_{0,2k-1}$
and
$X_{0,2k-1}$
and
![]() $X_{1,k-1}$
is an extremal edge of the effective cone of
$X_{1,k-1}$
is an extremal edge of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k]}$
for
![]() $k>0$
.
$k>0$
.
Proof. This is proved for
![]() $k=1$
and
$k=1$
and
![]() $k=2$
in [Reference Bertram and CoskunBC]. The proof now proceeds analogously as the previous proof. Again, it is immediate from the symmetry of the effective cone in terms of
$k=2$
in [Reference Bertram and CoskunBC]. The proof now proceeds analogously as the previous proof. Again, it is immediate from the symmetry of the effective cone in terms of
![]() $a$
and
$a$
and
![]() $b$
that the second statement immediately follows from the first statement. We now prove the first statement.
$b$
that the second statement immediately follows from the first statement. We now prove the first statement.
The first step in proving this edge is an extremal ray is finding an extremal pair. To find an extremal pair, we first have to find the two controlling exceptional bundles that make up the pair. The vector bundle whose Brill–Noether divisor spans the ray
![]() $X_{2k-1,0}$
is
$X_{2k-1,0}$
is
![]() ${\mathcal{O}}(2k-1,0)$
. The vector bundle whose Brill–Noether divisor spans the ray
${\mathcal{O}}(2k-1,0)$
. The vector bundle whose Brill–Noether divisor spans the ray
![]() $X_{k-1,1}$
is
$X_{k-1,1}$
is
![]() ${\mathcal{O}}(k-1,1)$
. To find our controlling exceptional bundles, we need to find exceptional bundles cohomologically orthogonal to
${\mathcal{O}}(k-1,1)$
. To find our controlling exceptional bundles, we need to find exceptional bundles cohomologically orthogonal to
![]() ${\mathcal{O}}(2k-1,0)$
and
${\mathcal{O}}(2k-1,0)$
and
![]() ${\mathcal{O}}(k-1,1)$
. Then, we have that
${\mathcal{O}}(k-1,1)$
. Then, we have that
Next, it is easy to see that
![]() ${\mathcal{O}}(2k-2,0)$
and
${\mathcal{O}}(2k-2,0)$
and
![]() ${\mathcal{O}}(k,1)$
are controlling exceptional bundles for the Hilbert scheme and that the pair
${\mathcal{O}}(k,1)$
are controlling exceptional bundles for the Hilbert scheme and that the pair
![]() $\{{\mathcal{O}}(2k,0),{\mathcal{O}}(k,1)\}$
is an extremal pair.
$\{{\mathcal{O}}(2k,0),{\mathcal{O}}(k,1)\}$
is an extremal pair.
Once we have the extremal pair, we need to turn it into a resolution of the general object of the Hilbert scheme. We complete the pair to a coil as prescribed by Theorem 4.4. This completion gives the coil
Next, we use the Beilinson spectral sequence to resolve the general ideal sheaf. The spectral sequence gives the resolution
Using this resolution, the third step is again finding a map to a moduli space of Kronecker modules. The Kronecker module in this resolution is
![]() ${\mathcal{O}}(-2k,-2)\rightarrow {\mathcal{O}}(-k,-1)^{2}$
. Then we get a map
${\mathcal{O}}(-2k,-2)\rightarrow {\mathcal{O}}(-k,-1)^{2}$
. Then we get a map
Using this map, we can finally compute the desired part of the effective cone. By a straightforward dimension count, we know that this map is birational. Then the two effective Brill–Noether divisors
![]() $D_{V}$
and
$D_{V}$
and
![]() $D_{V^{\prime }}$
where
$D_{V^{\prime }}$
where
![]() $V={\mathcal{O}}(2k-1,1)$
and
$V={\mathcal{O}}(2k-1,1)$
and
![]() $V^{\prime }={\mathcal{O}}(k-1,1)$
are contracted by this map. Next, any moving curve in the Kronecker moduli space is dual to these contracted divisors. Thus, a pencil in the space
$V^{\prime }={\mathcal{O}}(k-1,1)$
are contracted by this map. Next, any moving curve in the Kronecker moduli space is dual to these contracted divisors. Thus, a pencil in the space
![]() $\operatorname{Hom}({\mathcal{O}}(-2k,-2),{\mathcal{O}}(-k,-1))$
provides a dual moving curve showing that these divisors are on an edge of the effective cone. Alternatively, we could show that this moving curve gives the restriction
$\operatorname{Hom}({\mathcal{O}}(-2k,-2),{\mathcal{O}}(-k,-1))$
provides a dual moving curve showing that these divisors are on an edge of the effective cone. Alternatively, we could show that this moving curve gives the restriction
![]() $kb\geqslant 2k-1-a$
. Coupled with the previous proposition, it is clear that
$kb\geqslant 2k-1-a$
. Coupled with the previous proposition, it is clear that
![]() $X_{2k-1,0}$
spans an extremal ray.
$X_{2k-1,0}$
spans an extremal ray.
In order to show that
![]() $X_{k-1,1}$
is an extremal ray at the other end of the edge, we have to provide another extremal pair. The extremal pair needed is
$X_{k-1,1}$
is an extremal ray at the other end of the edge, we have to provide another extremal pair. The extremal pair needed is
![]() $\{{\mathcal{O}}(k-2,1),{\mathcal{O}}(k-1,1)\}$
. Then we get the coil
$\{{\mathcal{O}}(k-2,1),{\mathcal{O}}(k-1,1)\}$
. Then we get the coil
The spectral sequence gives the resolution
A moving curve is a pencil in the space
![]() $\operatorname{Hom}({\mathcal{O}}(-k,-2),{\mathcal{O}}(-k+1,-2))$
. The restriction this moving curve places on
$\operatorname{Hom}({\mathcal{O}}(-k,-2),{\mathcal{O}}(-k+1,-2))$
. The restriction this moving curve places on
![]() $D$
is that
$D$
is that
![]() $kb\geqslant 4k-3-3a$
. In particular,
$kb\geqslant 4k-3-3a$
. In particular,
![]() $X_{k-1,1}$
is dual to this moving curve which has a different slope than the other moving curve we constructed through this divisor, so we have shown that it is an extremal ray as promised.
$X_{k-1,1}$
is dual to this moving curve which has a different slope than the other moving curve we constructed through this divisor, so we have shown that it is an extremal ray as promised.
We now move on to the analogous proposition for odd
![]() $n$
.
$n$
.
Proposition 7.3. The edge spanned by
![]() $X_{2k,0}$
and
$X_{2k,0}$
and
![]() $X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
is an extremal edge of the effective cone of
$X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
is an extremal edge of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k+1]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k+1]}$
for
![]() $k>1$
. Similarly, the edge spanned by
$k>1$
. Similarly, the edge spanned by
![]() $X_{0,2k}$
and
$X_{0,2k}$
and
![]() $X_{\frac{2k}{2k-1},\frac{2k(k-1)}{2k-1}}$
is an extremal edge of the effective cone of
$X_{\frac{2k}{2k-1},\frac{2k(k-1)}{2k-1}}$
is an extremal edge of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k+1]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[2k+1]}$
for
![]() $k>1$
.
$k>1$
.
Proof. This is shown for
![]() $k=2$
in [Reference Bertram and CoskunBC]. Assume
$k=2$
in [Reference Bertram and CoskunBC]. Assume
![]() $k>2$
. This proof proceeds with all of the same elements as the previous proof, but slightly altered notation due to
$k>2$
. This proof proceeds with all of the same elements as the previous proof, but slightly altered notation due to
![]() $n$
being odd. Due to this, we give a much briefer proof.
$n$
being odd. Due to this, we give a much briefer proof.
The first statement implies the second statement by the symmetry of the effective cone so we prove only the first statement. Then it can be shown that the pair
![]() $\{{\mathcal{O}}(2k-1,0),{\mathcal{O}}(k,1)\}$
is an extremal pair. Then we get the coil
$\{{\mathcal{O}}(2k-1,0),{\mathcal{O}}(k,1)\}$
is an extremal pair. Then we get the coil
The spectral sequence gives the resolution
A moving curve is a pencil in the space
![]() $\operatorname{Hom}({\mathcal{O}}(-2k-1,-2),{\mathcal{O}}(-k,-1))$
. The restriction this moving curve places on
$\operatorname{Hom}({\mathcal{O}}(-2k-1,-2),{\mathcal{O}}(-k,-1))$
. The restriction this moving curve places on
![]() $D$
is that
$D$
is that
![]() $kb\geqslant 2k-a$
. In particular,
$kb\geqslant 2k-a$
. In particular,
![]() $X_{2k,0}$
and
$X_{2k,0}$
and
![]() $X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
are dual to this moving curve.
$X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
are dual to this moving curve.
Then the two effective Brill–Noether divisors
![]() $D_{V}$
and
$D_{V}$
and
![]() $D_{V^{\prime }}$
where
$D_{V^{\prime }}$
where
![]() $V$
is the exceptional bundle
$V$
is the exceptional bundle
![]() ${\mathcal{O}}(2k,0)$
and
${\mathcal{O}}(2k,0)$
and
![]() $V^{\prime }$
is the exceptional bundle
$V^{\prime }$
is the exceptional bundle
![]() $E_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
are shown to be on an edge by this moving curve. Coupled with the previous proposition, it is clear that
$E_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
are shown to be on an edge by this moving curve. Coupled with the previous proposition, it is clear that
![]() $X_{2k-1,0}$
spans an extremal ray.
$X_{2k-1,0}$
spans an extremal ray.
In order to show that
![]() $X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
is an extremal ray at the other end of the edge, we have to provide another extremal pair. The extremal pair needed is
$X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
is an extremal ray at the other end of the edge, we have to provide another extremal pair. The extremal pair needed is
![]() $\{{\mathcal{O}}(k-1,1),{\mathcal{O}}(k,1)\}$
. Then we get the coil
$\{{\mathcal{O}}(k-1,1),{\mathcal{O}}(k,1)\}$
. Then we get the coil
The spectral sequence gives the resolution
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-k-1,-3)\bigoplus {\mathcal{O}}(-k-1,-2)^{k-1}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}(-k,-2)^{k}\bigoplus {\mathcal{O}}(-k,-1)\rightarrow {\mathcal{I}}_{z}\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-k-1,-3)\bigoplus {\mathcal{O}}(-k-1,-2)^{k-1}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}(-k,-2)^{k}\bigoplus {\mathcal{O}}(-k,-1)\rightarrow {\mathcal{I}}_{z}\rightarrow 0.\nonumber\end{eqnarray}$$
Then we get a map
By a dimension count, we see that this Kronecker moduli space is zero dimensional so we disregard it. The moving curves are pencils in the spaces
![]() $\operatorname{Hom}({\mathcal{O}}(-k-1,-3),{\mathcal{O}}(-k,-2))$
and
$\operatorname{Hom}({\mathcal{O}}(-k-1,-3),{\mathcal{O}}(-k,-2))$
and
![]() $\operatorname{Hom}({\mathcal{O}}(-k-1,-2),{\mathcal{O}}(-k,-1))$
. The restrictions these moving curves place on
$\operatorname{Hom}({\mathcal{O}}(-k-1,-2),{\mathcal{O}}(-k,-1))$
. The restrictions these moving curves place on
![]() $D$
are that
$D$
are that
![]() $kb\geqslant 2k-a$
and
$kb\geqslant 2k-a$
and
![]() $(k+1)b\geqslant 4k-3a$
. In particular,
$(k+1)b\geqslant 4k-3a$
. In particular,
![]() $X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
is dual to these moving curve which have different slopes, so we have shown that it is an extremal ray as promised.
$X_{\frac{2k(k-1)}{2k-1},\frac{2k}{2k-1}}$
is dual to these moving curve which have different slopes, so we have shown that it is an extremal ray as promised.
The final sequence we look at is
![]() $n=3k+1$
. We provide this sequence as an example of the large class of extremal rays that can be found in more sporadic sequences.
$n=3k+1$
. We provide this sequence as an example of the large class of extremal rays that can be found in more sporadic sequences.
Proposition 7.4. The ray spanned by
![]() $X_{k-\frac{1}{2},2}$
is an extremal ray of the effective cone of
$X_{k-\frac{1}{2},2}$
is an extremal ray of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[3k+1]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[3k+1]}$
for
![]() $k>1$
. Similarly, the ray spanned by
$k>1$
. Similarly, the ray spanned by
![]() $X_{2,k-\frac{1}{2}}$
is an extremal ray of the effective cone of
$X_{2,k-\frac{1}{2}}$
is an extremal ray of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[3k+1]}$
for
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[3k+1]}$
for
![]() $k>1$
.
$k>1$
.
Proof. This proof again proceeds similarly to the previous proofs so we provide a concise version. Again, the second statement follows from the first by symmetry. The extremal controlling pair is
![]() $\{{\mathcal{O}}(k-1,2),{\mathcal{O}}(k,2)\}$
. This completes to the coil
$\{{\mathcal{O}}(k-1,2),{\mathcal{O}}(k,2)\}$
. This completes to the coil
Then the resolution that we get is
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-k-1,-4)\bigoplus {\mathcal{O}}(-k,-3)^{k-1}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}(-k+1,-3)^{k-1}\bigoplus {\mathcal{O}}(-k,-2)^{2}\rightarrow I_{z}\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-k-1,-4)\bigoplus {\mathcal{O}}(-k,-3)^{k-1}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}(-k+1,-3)^{k-1}\bigoplus {\mathcal{O}}(-k,-2)^{2}\rightarrow I_{z}\rightarrow 0.\nonumber\end{eqnarray}$$
Then we get a map
and
![]() $V$
has the resolution
$V$
has the resolution
Next, the Kronecker modules are dual, so we have cohomological orthogonality. This makes
![]() $D_{V}$
into a divisor. By Proposition 2.16, we know its class is
$D_{V}$
into a divisor. By Proposition 2.16, we know its class is
![]() $X_{k-\frac{1}{2},2}$
. We see that it is an extremal ray by looking at pencils in the spaces
$X_{k-\frac{1}{2},2}$
. We see that it is an extremal ray by looking at pencils in the spaces
![]() $\operatorname{Hom}({\mathcal{O}}(-k-1,-4),{\mathcal{O}}(-k+1,-3))$
and
$\operatorname{Hom}({\mathcal{O}}(-k-1,-4),{\mathcal{O}}(-k+1,-3))$
and
![]() $\operatorname{Hom}({\mathcal{O}}(-k,-3),{\mathcal{O}}(-k,-2))$
which cover the fibers of the Kronecker fibration. The restrictions these moving curve places on
$\operatorname{Hom}({\mathcal{O}}(-k,-3),{\mathcal{O}}(-k,-2))$
which cover the fibers of the Kronecker fibration. The restrictions these moving curve places on
![]() $D$
are
$D$
are
![]() $(1+k)b\geqslant 6k-4a$
and
$(1+k)b\geqslant 6k-4a$
and
![]() $kb\geqslant 4k-1-2a$
. Note, this implies they are distinct curve classes and
$kb\geqslant 4k-1-2a$
. Note, this implies they are distinct curve classes and
![]() $X_{k-\frac{1}{2},2}$
is dual to both moving curves. Thus, the Brill–Noether divisor
$X_{k-\frac{1}{2},2}$
is dual to both moving curves. Thus, the Brill–Noether divisor
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is a bundle with Chern character
$V$
is a bundle with Chern character
![]() $\left(2,(2k-1,4),4k-3\right)$
spans an extremal ray of the effective cone.
$\left(2,(2k-1,4),4k-3\right)$
spans an extremal ray of the effective cone.
There are a couple more infinite families that we mention but do not prove. Their proofs follow similar techniques. Working out their proofs is a good exercise to become comfortable with this type of computation.
These families of rays on a edge require some notation.
Definition 7.5. The symmetric value of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[N]}$
is the value
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[N]}$
is the value
![]() $a$
for which the ray spanned by
$a$
for which the ray spanned by
![]() $X_{a,a}$
is on the edge of the effective cone.
$X_{a,a}$
is on the edge of the effective cone.
Note
![]() $X_{a,a}$
may or may not be an extremal ray. We now state the symmetric value for four infinite sequences of
$X_{a,a}$
may or may not be an extremal ray. We now state the symmetric value for four infinite sequences of
![]() $n$
.
$n$
.
Proposition 7.6. The symmetric value of the effective cone of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
is:
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[n]}$
is:
(I)
 $k-1-\frac{1}{2k-2}$
for
$k-1-\frac{1}{2k-2}$
for
 $n=k^{2}-2,\;k>1$
,
$n=k^{2}-2,\;k>1$
,(II)
 $k-1$
for
$k-1$
for
 $n=k^{2}-1$
or
$n=k^{2}-1$
or
 $k^{2},\;k>1$
,
$k^{2},\;k>1$
,(III)
 $k-1+\frac{1}{k+1}$
for
$k-1+\frac{1}{k+1}$
for
 $n=k^{2}+1,\;k>1$
,
$n=k^{2}+1,\;k>1$
,(IV)
 $k-\frac{1}{2}$
for
$k-\frac{1}{2}$
for
 $n=k^{2}+k,\;k>0$
.
$n=k^{2}+k,\;k>0$
.
7.4 Completing the table
Finally, using our methods, we give brief proofs of each of the five corners in the table at the beginning of this section that do not follow from our general constructions so far. We only state the propositions and proofs for one of each pair of symmetric extremal rays.
Proposition 7.7.
![]() $X_{4,\frac{4}{3}}$
is an extremal ray of
$X_{4,\frac{4}{3}}$
is an extremal ray of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
.
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
.
Proof. Let
![]() $Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
be general. The relevant extremal pair is
$Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
be general. The relevant extremal pair is
![]() $\{{\mathcal{O}}(-4,-1),{\mathcal{O}}(-3,-2)\}$
. The resolving coil then is
$\{{\mathcal{O}}(-4,-1),{\mathcal{O}}(-3,-2)\}$
. The resolving coil then is
since
Then the resolutions we get from the generalized Beilinson spectral sequence are
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-6,-3)\bigoplus {\mathcal{O}}(-4,-2)^{2}\nonumber\\ \displaystyle & \rightarrow & \displaystyle E_{\frac{-11}{3},\frac{-5}{3}}\bigoplus {\mathcal{O}}(-3,-2)\rightarrow {\mathcal{I}}_{Z}\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(2,2)\rightarrow V\rightarrow {\mathcal{O}}(5,1)^{2}\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-6,-3)\bigoplus {\mathcal{O}}(-4,-2)^{2}\nonumber\\ \displaystyle & \rightarrow & \displaystyle E_{\frac{-11}{3},\frac{-5}{3}}\bigoplus {\mathcal{O}}(-3,-2)\rightarrow {\mathcal{I}}_{Z}\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(2,2)\rightarrow V\rightarrow {\mathcal{O}}(5,1)^{2}\rightarrow 0.\nonumber\end{eqnarray}$$
Next, the Kronecker map is
Note that the dimension of this Kronecker moduli space is
![]() $4\ast 2\ast 1-2^{2}-1^{2}+1=4$
.
$4\ast 2\ast 1-2^{2}-1^{2}+1=4$
.
Then, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is a bundle that has Chern character
$V$
is a bundle that has Chern character
![]() $(3,(12,4),14)$
. The two types of moving curves covering each fiber come from pencils of maps
$(3,(12,4),14)$
. The two types of moving curves covering each fiber come from pencils of maps
![]() ${\mathcal{O}}(-6,-3)\rightarrow K$
and
${\mathcal{O}}(-6,-3)\rightarrow K$
and
![]() ${\mathcal{O}}(-6,-3)\rightarrow {\mathcal{O}}(-3,-2)$
. The restrictions these two moving curves place on
${\mathcal{O}}(-6,-3)\rightarrow {\mathcal{O}}(-3,-2)$
. The restrictions these two moving curves place on
![]() $D$
are that
$D$
are that
![]() $3b\geqslant 12-2a$
and
$3b\geqslant 12-2a$
and
![]() $6b\geqslant 20-3a$
. In particular,
$6b\geqslant 20-3a$
. In particular,
![]() $X_{4,\frac{4}{3}}$
is dual to both moving curves,
$X_{4,\frac{4}{3}}$
is dual to both moving curves,
![]() $X_{\frac{40}{9},\frac{10}{9}}$
is dual to the first moving curve, and
$X_{\frac{40}{9},\frac{10}{9}}$
is dual to the first moving curve, and
![]() $X_{\frac{12}{5},\frac{12}{5}}$
is dual to the second moving curve.
$X_{\frac{12}{5},\frac{12}{5}}$
is dual to the second moving curve.
Proposition 7.8.
![]() $X_{\frac{12}{5},\frac{12}{5}}$
is an extremal ray of
$X_{\frac{12}{5},\frac{12}{5}}$
is an extremal ray of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
.
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
.
Proof. Let
![]() $Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
be general. The relevant extremal pair is
$Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[11]}$
be general. The relevant extremal pair is
![]() $\{{\mathcal{O}}(-2,-3),{\mathcal{O}}(-3,-2)\}$
. The resolving coil then is
$\{{\mathcal{O}}(-2,-3),{\mathcal{O}}(-3,-2)\}$
. The resolving coil then is
since
Then the resolutions we get from the generalized Beilinson spectral sequence are
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-4,-4)^{2}\rightarrow {\mathcal{O}}(-3,-3)\bigoplus {\mathcal{O}}(-2,-3)\bigoplus {\mathcal{O}}(-3,-2)\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{I}}_{Z}\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle E_{\frac{7}{3},\frac{7}{3}}^{2}\rightarrow E_{\frac{26}{11},\frac{26}{11}}\rightarrow V\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-4,-4)^{2}\rightarrow {\mathcal{O}}(-3,-3)\bigoplus {\mathcal{O}}(-2,-3)\bigoplus {\mathcal{O}}(-3,-2)\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{I}}_{Z}\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle E_{\frac{7}{3},\frac{7}{3}}^{2}\rightarrow E_{\frac{26}{11},\frac{26}{11}}\rightarrow V\rightarrow 0.\nonumber\end{eqnarray}$$
Next, the Kronecker map is
Note that the dimension of this Kronecker moduli space is
![]() $2\ast 2\ast 1-2^{2}-1^{2}+1=0$
so the map tells us nothing.
$2\ast 2\ast 1-2^{2}-1^{2}+1=0$
so the map tells us nothing.
Then, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is a bundle that has Chern character
$V$
is a bundle that has Chern character
![]() $(5,(12,12),26)$
. There are two types of moving curves coming from pencils of maps
$(5,(12,12),26)$
. There are two types of moving curves coming from pencils of maps
![]() $K\rightarrow {\mathcal{O}}(-2,-3)$
and
$K\rightarrow {\mathcal{O}}(-2,-3)$
and
![]() $K\rightarrow {\mathcal{O}}(-3,-2)$
. The restrictions these two moving curves place on
$K\rightarrow {\mathcal{O}}(-3,-2)$
. The restrictions these two moving curves place on
![]() $D$
are that
$D$
are that
![]() $3b\geqslant 20-6a$
and
$3b\geqslant 20-6a$
and
![]() $6b\geqslant 20-3a$
. In particular,
$6b\geqslant 20-3a$
. In particular,
![]() $X_{\frac{12}{5},\frac{12}{5}}$
is dual to both moving curves,
$X_{\frac{12}{5},\frac{12}{5}}$
is dual to both moving curves,
![]() $X_{4,\frac{4}{3}}$
is dual to the first moving curve, and
$X_{4,\frac{4}{3}}$
is dual to the first moving curve, and
![]() $X_{\frac{4}{3},4}$
is dual to the second moving curve.
$X_{\frac{4}{3},4}$
is dual to the second moving curve.
Proposition 7.9.
![]() $X_{\frac{9}{2},\frac{3}{2}}$
is an extremal ray of
$X_{\frac{9}{2},\frac{3}{2}}$
is an extremal ray of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
.
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
.
Proof. Let
![]() $Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
be general. The relevant extremal pair is
$Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
be general. The relevant extremal pair is
![]() $\{{\mathcal{O}}(-5,-1),{\mathcal{O}}(-4,-2)\}$
. The resolving coil then is
$\{{\mathcal{O}}(-5,-1),{\mathcal{O}}(-4,-2)\}$
. The resolving coil then is
since
Then the resolutions we get from the generalized Beilinson spectral sequence are
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-7,-3)\bigoplus {\mathcal{O}}(-5,-2)^{3}\nonumber\\ \displaystyle & \rightarrow & \displaystyle E_{\frac{-14}{3},\frac{-5}{3}}\bigoplus {\mathcal{O}}(-4,-2)^{2}\rightarrow {\mathcal{I}}_{Z}\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(6,1)\rightarrow V\rightarrow {\mathcal{O}}(3,2)\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(-7,-3)\bigoplus {\mathcal{O}}(-5,-2)^{3}\nonumber\\ \displaystyle & \rightarrow & \displaystyle E_{\frac{-14}{3},\frac{-5}{3}}\bigoplus {\mathcal{O}}(-4,-2)^{2}\rightarrow {\mathcal{I}}_{Z}\rightarrow 0\qquad \text{and}\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle {\mathcal{O}}(6,1)\rightarrow V\rightarrow {\mathcal{O}}(3,2)\rightarrow 0.\nonumber\end{eqnarray}$$
Next, the Kronecker map is
Note that the dimension of this Kronecker moduli space is
![]() $4\ast 1\ast 3-3^{2}-1^{2}+1=3$
.
$4\ast 1\ast 3-3^{2}-1^{2}+1=3$
.
Then, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is a bundle that has Chern character
$V$
is a bundle that has Chern character
![]() $(2,(9,3),12)$
. There are two types of moving curves coming from pencils of maps
$(2,(9,3),12)$
. There are two types of moving curves coming from pencils of maps
![]() ${\mathcal{O}}(-7,-3)\rightarrow K$
and
${\mathcal{O}}(-7,-3)\rightarrow K$
and
![]() ${\mathcal{O}}(-7,-3)\rightarrow {\mathcal{O}}(-4,-2)^{2}$
. The restrictions these two moving curves place on
${\mathcal{O}}(-7,-3)\rightarrow {\mathcal{O}}(-4,-2)^{2}$
. The restrictions these two moving curves place on
![]() $D$
are that
$D$
are that
![]() $4b\geqslant 15-2a$
and
$4b\geqslant 15-2a$
and
![]() $7b\geqslant 24-3a$
. In particular,
$7b\geqslant 24-3a$
. In particular,
![]() $X_{\frac{9}{2},\frac{3}{2}}$
is dual to both moving curves,
$X_{\frac{9}{2},\frac{3}{2}}$
is dual to both moving curves,
![]() $X_{\frac{7}{2},2}$
is dual to the first moving curve, and
$X_{\frac{7}{2},2}$
is dual to the first moving curve, and
![]() $X_{\frac{60}{11},\frac{12}{11}}$
is dual to the second moving curve.
$X_{\frac{60}{11},\frac{12}{11}}$
is dual to the second moving curve.
Proposition 7.10.
![]() $X_{\frac{8}{3},\frac{8}{3}}$
is an extremal ray of
$X_{\frac{8}{3},\frac{8}{3}}$
is an extremal ray of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
.
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
.
Proof. Let
![]() $Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
be general. The relevant extremal pair is
$Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[13]}$
be general. The relevant extremal pair is
![]() $\{{\mathcal{O}}(-2,-3),{\mathcal{O}}(-3,-2)\}$
. The resolving coil then is
$\{{\mathcal{O}}(-2,-3),{\mathcal{O}}(-3,-2)\}$
. The resolving coil then is
since
Then the resolution we get from the generalized Beilinson spectral sequence is
so there is no Kronecker map.
Next, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is the exceptional bundle
$V$
is the exceptional bundle
![]() $E_{\frac{8}{3},\frac{8}{3}}$
. There are two types of moving curves coming from pencils of maps
$E_{\frac{8}{3},\frac{8}{3}}$
. There are two types of moving curves coming from pencils of maps
![]() ${\mathcal{O}}(-4,-5)\rightarrow {\mathcal{O}}(-3,-3)^{3}$
and
${\mathcal{O}}(-4,-5)\rightarrow {\mathcal{O}}(-3,-3)^{3}$
and
![]() ${\mathcal{O}}(-5,-4)\rightarrow {\mathcal{O}}(-3,-3)^{3}$
. The restrictions these two moving curves place on
${\mathcal{O}}(-5,-4)\rightarrow {\mathcal{O}}(-3,-3)^{3}$
. The restrictions these two moving curves place on
![]() $D$
are that
$D$
are that
![]() $5b\geqslant 24-4a$
and
$5b\geqslant 24-4a$
and
![]() $4b\geqslant 24-5a$
. In particular,
$4b\geqslant 24-5a$
. In particular,
![]() $X_{\frac{8}{3},\frac{8}{3}}$
is dual to both moving curves,
$X_{\frac{8}{3},\frac{8}{3}}$
is dual to both moving curves,
![]() $X_{\frac{7}{2},2}$
is dual to the first moving curve, and
$X_{\frac{7}{2},2}$
is dual to the first moving curve, and
![]() $X_{2,\frac{7}{2}}$
is dual to the second moving curve.
$X_{2,\frac{7}{2}}$
is dual to the second moving curve.
Proposition 7.11.
![]() $X_{\frac{10}{3},\frac{7}{3}}$
is an extremal ray of
$X_{\frac{10}{3},\frac{7}{3}}$
is an extremal ray of
![]() $\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[14]}$
.
$\left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[14]}$
.
Proof. Let
![]() $Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[14]}$
be general. The relevant extremal pair is
$Z\in \left(\mathbb{P}^{1}\times \mathbb{P}^{1}\right)^{[14]}$
be general. The relevant extremal pair is
![]() $\{{\mathcal{O}}(-3,-3),{\mathcal{O}}(-4,-2)\}$
. The resolving coil then is
$\{{\mathcal{O}}(-3,-3),{\mathcal{O}}(-4,-2)\}$
. The resolving coil then is
since
Then the resolution we get from the generalized Beilinson spectral sequence is
so there is no Kronecker map.
Next, the Brill–Noether divisor is
![]() $D_{V}$
where
$D_{V}$
where
![]() $V$
is the exceptional bundle
$V$
is the exceptional bundle
![]() $E_{\frac{10}{3},\frac{7}{3}}$
. There are two types of moving curves coming from pencils of maps
$E_{\frac{10}{3},\frac{7}{3}}$
. There are two types of moving curves coming from pencils of maps
![]() ${\mathcal{O}}(-5,-4)^{2}\rightarrow {\mathcal{O}}(-4,-2)$
and
${\mathcal{O}}(-5,-4)^{2}\rightarrow {\mathcal{O}}(-4,-2)$
and
![]() ${\mathcal{O}}(-5,-4)^{2}\rightarrow {\mathcal{O}}(-3,-3)^{2}$
. The restriction these two moving curves place on
${\mathcal{O}}(-5,-4)^{2}\rightarrow {\mathcal{O}}(-3,-3)^{2}$
. The restriction these two moving curves place on
![]() $D$
are that
$D$
are that
![]() $3b\geqslant 17-3a$
and
$3b\geqslant 17-3a$
and
![]() $4b\geqslant 16-2a$
. In particular,
$4b\geqslant 16-2a$
. In particular,
![]() $X_{\frac{10}{3},\frac{7}{3}}$
is dual to both moving curves,
$X_{\frac{10}{3},\frac{7}{3}}$
is dual to both moving curves,
![]() $X_{\frac{7}{3},\frac{10}{3}}$
is dual to the first moving curve, and
$X_{\frac{7}{3},\frac{10}{3}}$
is dual to the first moving curve, and
![]() $X_{6,1}$
is dual to the second moving curve.
$X_{6,1}$
is dual to the second moving curve.
7.5 A rank two example
Let
![]() $\unicode[STIX]{x1D709}=\left(\log (2),(\frac{1}{2},0),2\right)$
. Then, we can find that
$\unicode[STIX]{x1D709}=\left(\log (2),(\frac{1}{2},0),2\right)$
. Then, we can find that
![]() $\{{\mathcal{O}}(-1,2),{\mathcal{O}}(0,1)\}$
is an extremal pair for
$\{{\mathcal{O}}(-1,2),{\mathcal{O}}(0,1)\}$
is an extremal pair for
![]() $M(\unicode[STIX]{x1D709})$
. It gives the resolution
$M(\unicode[STIX]{x1D709})$
. It gives the resolution
where
![]() $U\in M(\unicode[STIX]{x1D709})$
is general. This gives that the divisor
$U\in M(\unicode[STIX]{x1D709})$
is general. This gives that the divisor
![]() $D_{{\mathcal{O}}(-1,3)}$
lies on an edge of the effective cone. In this case, we can actually do two dimension counts to see that varying either map gives a moving curve dual to
$D_{{\mathcal{O}}(-1,3)}$
lies on an edge of the effective cone. In this case, we can actually do two dimension counts to see that varying either map gives a moving curve dual to
![]() $D_{{\mathcal{O}}(-1,3)}$
so it in fact spans an extremal ray of the effective cone.
$D_{{\mathcal{O}}(-1,3)}$
so it in fact spans an extremal ray of the effective cone.
Acknowledgments
We are extremely grateful to Izzet Coskun, Jack Huizenga, Arend Bayer, Lawrence Ein, Daniel Erman, César Lozano Huerta, Emanuele Macrì, Eric Riedl, Alex Stathis, and Kevin Tucker for many useful conversations over the course of this work.