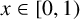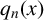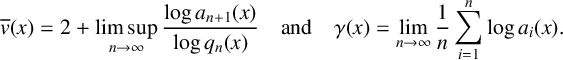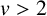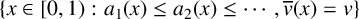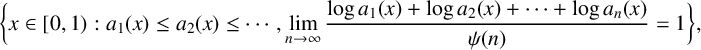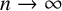1 Introduction
Diophantine approximation is a branch of number theory that can be described as a quantitative analysis of the density of the rational numbers in the real numbers. The first result is due to Dirichlet and is a simple consequence of the pigeonhole principle.
Theorem 1.1 (Dirichlet, 1842).
For any
![]() $x\in [0,1)$
and
$x\in [0,1)$
and
![]() $t>1$
, there exists
$t>1$
, there exists
![]() $(q,p)\in \mathbb {N}^2$
such that
$(q,p)\in \mathbb {N}^2$
such that
 $$ \begin{align*} \bigg|x-\frac{p}{q}\bigg|<\frac{1}{qt}\quad \text{and}\quad 1\leq q\leq t.\end{align*} $$
$$ \begin{align*} \bigg|x-\frac{p}{q}\bigg|<\frac{1}{qt}\quad \text{and}\quad 1\leq q\leq t.\end{align*} $$
Denote
 $$ \begin{align*}J(v)=\bigg\{x\in[0,1): \bigg|x-\frac{p}{q}\bigg|<\frac{1}{q^v}\ \text{for infinitely many}\ (q,p)\in\mathbb{N}^2 \bigg\}.\end{align*} $$
$$ \begin{align*}J(v)=\bigg\{x\in[0,1): \bigg|x-\frac{p}{q}\bigg|<\frac{1}{q^v}\ \text{for infinitely many}\ (q,p)\in\mathbb{N}^2 \bigg\}.\end{align*} $$
Dirichlet’s theorem implies that the set
![]() $J(v)$
equals
$J(v)$
equals
![]() $[0,1)$
for any
$[0,1)$
for any
![]() $v\leq 2$
. Khintchine [Reference Khintchine16] proved that the set
$v\leq 2$
. Khintchine [Reference Khintchine16] proved that the set
![]() $J(v)$
is of Lebesgue measure zero for any
$J(v)$
is of Lebesgue measure zero for any
![]() $v>2$
. Jarník [Reference Jarník13] and Besicovitch [Reference Besicovitch1] independently showed that the Hausdorff dimension of these null sets
$v>2$
. Jarník [Reference Jarník13] and Besicovitch [Reference Besicovitch1] independently showed that the Hausdorff dimension of these null sets
![]() $J(v)$
is
$J(v)$
is
![]() $2/v$
. Since the map
$2/v$
. Since the map
![]() $v\rightarrow J(v)$
is nonincreasing, it is natural to define
$v\rightarrow J(v)$
is nonincreasing, it is natural to define
We call
![]() $\overline {v}(x)$
the irrationality exponent of an irrational number
$\overline {v}(x)$
the irrationality exponent of an irrational number
![]() $x\in [0,1)$
. The irrationality exponent
$x\in [0,1)$
. The irrationality exponent
![]() $\overline {v}(x)$
reflects how well an irrational number x can be approximated by rational numbers: the higher the exponent, the better the approximation.
$\overline {v}(x)$
reflects how well an irrational number x can be approximated by rational numbers: the higher the exponent, the better the approximation.
The theory of continued fractions is closely related to Diophantine approximation. It is well known that continued fraction expansions can be induced by the Gauss map
![]() $T : [0,1)\rightarrow [0,1)$
defined by
$T : [0,1)\rightarrow [0,1)$
defined by
Each irrational number
![]() $x \in [0,1)$
admits a unique continued fraction expansion
$x \in [0,1)$
admits a unique continued fraction expansion
 $$ \begin{align} x = \frac{1}{a_1(x) +\dfrac{1}{a_2(x)+\dfrac{1}{\ddots}}} =[a_1(x), a_2(x),\ldots, a_n(x),\ldots], \end{align} $$
$$ \begin{align} x = \frac{1}{a_1(x) +\dfrac{1}{a_2(x)+\dfrac{1}{\ddots}}} =[a_1(x), a_2(x),\ldots, a_n(x),\ldots], \end{align} $$
where
![]() $a_1(x)=\lfloor {1}/{x}\rfloor $
and
$a_1(x)=\lfloor {1}/{x}\rfloor $
and
![]() $a_n(x)=a_1(T^{n-1}(x))\ (n\geq 2)$
are called the partial quotients of the continued fraction expansion of x. For each
$a_n(x)=a_1(T^{n-1}(x))\ (n\geq 2)$
are called the partial quotients of the continued fraction expansion of x. For each
![]() $n\geq 1$
, let the fraction
$n\geq 1$
, let the fraction
 $$ \begin{align*} \frac{p_n(x)}{q_n(x)}=\dfrac{1}{a_1(x) +\dfrac{1}{a_2(x)+\dfrac{1}{\ddots+\dfrac{1}{a_n(x)}}}}=[a_1(x),a_2(x),\ldots,a_n(x)] \end{align*} $$
$$ \begin{align*} \frac{p_n(x)}{q_n(x)}=\dfrac{1}{a_1(x) +\dfrac{1}{a_2(x)+\dfrac{1}{\ddots+\dfrac{1}{a_n(x)}}}}=[a_1(x),a_2(x),\ldots,a_n(x)] \end{align*} $$
be the nth convergent of the continued fraction expansion of x. Via continued fractions, the irrationality exponent defined in (1.1) can be represented by
 $$ \begin{align} \overline{v}(x)=2+\limsup\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}. \end{align} $$
$$ \begin{align} \overline{v}(x)=2+\limsup\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}. \end{align} $$
From the fundamental work of Khintchine [Reference Khintchine16] (see Bugeaud [Reference Bugeaud3, Ch. 1]),
![]() ${\overline {v}(x)=2}$
for Lebesgue almost all irrational numbers. The Khintchine exponent of x with continued fraction expansion (1.2) is defined (if the limits exist) by
${\overline {v}(x)=2}$
for Lebesgue almost all irrational numbers. The Khintchine exponent of x with continued fraction expansion (1.2) is defined (if the limits exist) by
 $$ \begin{align*} \gamma(x):=\lim\limits_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_i(x)=\lim\limits_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_1(T^{i-1}(x)). \end{align*} $$
$$ \begin{align*} \gamma(x):=\lim\limits_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_i(x)=\lim\limits_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_1(T^{i-1}(x)). \end{align*} $$
The Gauss map T is ergodic (see, for example, [Reference Iosifescu and Kraaikamp11]) with respect to the Gauss measure
![]() $dx/((x+1)\log 2)$
. By Birkhoff’s ergodic theorem, for Lebesgue almost all
$dx/((x+1)\log 2)$
. By Birkhoff’s ergodic theorem, for Lebesgue almost all
![]() $x\in [0,1)$
,
$x\in [0,1)$
,
 $$ \begin{align*}\gamma(x)=\int_{0}^{1}\frac{\log a_1(x)}{(x+1)\log2}\,dx=\log(2.6584\cdots).\end{align*} $$
$$ \begin{align*}\gamma(x)=\int_{0}^{1}\frac{\log a_1(x)}{(x+1)\log2}\,dx=\log(2.6584\cdots).\end{align*} $$
For more details about continued fractions, we refer to [Reference Iosifescu and Kraaikamp11, Reference Khintchine17].
Much attention has been paid to the multifractal analysis of the level sets of the irrationality exponent and Khintchine exponent. For any
![]() $v>2$
, a result of Good [Reference Good10, Theorem 9] implies that the set
$v>2$
, a result of Good [Reference Good10, Theorem 9] implies that the set
![]() $E_{\overline {v}(x)\geq v}(v)=\{x\in [0,1): \overline {v}(x)\geq v\}$
is of Hausdorff dimension
$E_{\overline {v}(x)\geq v}(v)=\{x\in [0,1): \overline {v}(x)\geq v\}$
is of Hausdorff dimension
![]() $2/v$
. The main result of Bugeaud [Reference Bugeaud2, Theorem 1] shows that the set
$2/v$
. The main result of Bugeaud [Reference Bugeaud2, Theorem 1] shows that the set
![]() $E_{\overline {v}(x)=v}(v)=\{x\in [0,1): \overline {v}(x)=v\}$
is also of Hausdorff dimension
$E_{\overline {v}(x)=v}(v)=\{x\in [0,1): \overline {v}(x)=v\}$
is also of Hausdorff dimension
![]() $2/v$
. Sun and Wu [Reference Sun and Wu22] considered the set
$2/v$
. Sun and Wu [Reference Sun and Wu22] considered the set
 $$ \begin{align*}E(v)=\bigg\{x\in[0,1):\ 2+\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}=v\bigg\}\end{align*} $$
$$ \begin{align*}E(v)=\bigg\{x\in[0,1):\ 2+\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}=v\bigg\}\end{align*} $$
and proved that
![]() $E(v)$
has Hausdorff dimension
$E(v)$
has Hausdorff dimension
![]() $1/v$
. Replacing the
$1/v$
. Replacing the
![]() $\limsup $
by
$\limsup $
by
![]() $\liminf $
in (1.3), one can define the corresponding irrationality exponent by
$\liminf $
in (1.3), one can define the corresponding irrationality exponent by
 $$ \begin{align*}\underline{v}(x)=2+\liminf\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}.\end{align*} $$
$$ \begin{align*}\underline{v}(x)=2+\liminf\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}.\end{align*} $$
Tan and Zhou [Reference Tan and Zhou23] calculated the Hausdorff dimension of the intersection of level sets defined by
![]() $\overline {v}(x)$
and
$\overline {v}(x)$
and
![]() $\underline {v}(x)$
, and also showed that the set
$\underline {v}(x)$
, and also showed that the set
![]() $E_{\underline {v}(x)\geq v}(v)=\{x\in [0,1): \underline {v}(x)\geq v\}$
is of Hausdorff dimension
$E_{\underline {v}(x)\geq v}(v)=\{x\in [0,1): \underline {v}(x)\geq v\}$
is of Hausdorff dimension
![]() $1/v$
for any
$1/v$
for any
![]() $v>2$
. Based on these dimensional results for the sets
$v>2$
. Based on these dimensional results for the sets
![]() $E(v)$
and
$E(v)$
and
![]() $E_{\underline {v}(x)\geq v}(v)$
, it follows easily that the set
$E_{\underline {v}(x)\geq v}(v)$
, it follows easily that the set
![]() $E_{\underline {v}(x)=v}(v)=\{x\in [0,1): \underline {v}(x)=v\}$
is of Hausdorff dimension
$E_{\underline {v}(x)=v}(v)=\{x\in [0,1): \underline {v}(x)=v\}$
is of Hausdorff dimension
![]() $1/v$
for any
$1/v$
for any
![]() $v>2$
. For the multifractal analysis of level sets of the Khintchine exponent
$v>2$
. For the multifractal analysis of level sets of the Khintchine exponent
![]() $\gamma (x)$
, Fan et al. [Reference Fan, Liao, Wang and Wu6, Theorem 1.2] presented a complete characterisation for the Hausdorff dimension of the sets
$\gamma (x)$
, Fan et al. [Reference Fan, Liao, Wang and Wu6, Theorem 1.2] presented a complete characterisation for the Hausdorff dimension of the sets
More precisely, they proved that the Hausdorff dimension of the set
![]() $E_{\gamma (x)=\xi }(\xi )$
, as a function of
$E_{\gamma (x)=\xi }(\xi )$
, as a function of
![]() $\xi \in [0,\infty )$
, is neither concave nor convex, and that the set
$\xi \in [0,\infty )$
, is neither concave nor convex, and that the set
![]() $E_{\gamma (x)=\xi }(\infty )$
is of Hausdorff dimension
$E_{\gamma (x)=\xi }(\infty )$
is of Hausdorff dimension
![]() $1/2$
. This shows that there exist uncountably many points with infinite Khintchine exponent. Fan et al. [Reference Fan, Liao, Wang and Wu6, Reference Fan, Liao, Wang and Wu7] gave a more refined classification for the set
$1/2$
. This shows that there exist uncountably many points with infinite Khintchine exponent. Fan et al. [Reference Fan, Liao, Wang and Wu6, Reference Fan, Liao, Wang and Wu7] gave a more refined classification for the set
![]() $E_{\gamma (x)=\xi }(\infty )$
by considering the multifractal spectrum of the level sets of the fast Khintchine exponent defined by
$E_{\gamma (x)=\xi }(\infty )$
by considering the multifractal spectrum of the level sets of the fast Khintchine exponent defined by
 $$ \begin{align*} K(\psi)=\bigg\{x\in[0,1): \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\}, \end{align*} $$
$$ \begin{align*} K(\psi)=\bigg\{x\in[0,1): \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\}, \end{align*} $$
where
![]() $\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
is a function satisfying
$\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
is a function satisfying
![]() $\psi (n)/n\to \infty $
as
$\psi (n)/n\to \infty $
as
![]() $n\to \infty $
.
$n\to \infty $
.
Various related exponents have been investigated. For example, Pollicott and Weiss [Reference Pollicott and Weiss19] studied the Lyapunov exponent of the Gauss map, Kesseböhmer and Stratmann [Reference Kesseböhmer and Stratmann15] the Minkowski’s question mark function, Nicolay and Simons [Reference Nicolay and Simons18] the Hölder exponent, Jaffard and Martin [Reference Jaffard and Martin12] the Brjuno function, Fang et al. [Reference Fang, Ma, Song and Wu8] the convergence exponent and Song et al. [Reference Song, Tan and Zhang21] the irrationality exponent and the convergence exponent.
Multifractal analysis of sets characterised by two (or more) different Diophantine characteristics could potentially show that they are independent or, conversely, help to detect profound links between these characteristics. This paper is mainly concerned with the multifractal spectrum of the irrationality exponent and the Khintchine exponent defined by a nondecreasing sequence of partial quotients. That is, we investigate the Hausdorff dimension of the intersection of the sets
![]() $E_{\overline {v}(x)=v}(v), K(\psi )$
and
$E_{\overline {v}(x)=v}(v), K(\psi )$
and
![]() $\Lambda $
, where
$\Lambda $
, where
By a result of Ramharter [Reference Ramharter20], the set
![]() $\Lambda $
is of Hausdorff dimension
$\Lambda $
is of Hausdorff dimension
![]() $1/2$
(see also Jordan and Rams [Reference Jordan and Rams14] for general results in the setting of infinite iterated function systems).
$1/2$
(see also Jordan and Rams [Reference Jordan and Rams14] for general results in the setting of infinite iterated function systems).
Throughout this paper, we use the notation
![]() $\dim _{\mathrm {H}}$
to denote the Hausdorff dimension (see [Reference Falconer5]). We are now in a position to state our main results.
$\dim _{\mathrm {H}}$
to denote the Hausdorff dimension (see [Reference Falconer5]). We are now in a position to state our main results.
Theorem 1.2. For any
![]() $v>2$
,
$v>2$
,
 $$ \begin{align*} \begin{cases} \dim_{\mathrm{H}}(E(v)\cap\Lambda)=\dim_{\mathrm{H}}(E_{\overline{v}(x)=v}(v)\cap\Lambda)=\dim_{\mathrm{H}}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda)={1}/{v},\cr \dim_{\mathrm{H}}(E_{\underline{v}(x)=v}(v)\cap\Lambda)=\dim_{\mathrm{H}}(E_{\underline{v}(x)\geq v}(v)\cap\Lambda)={1}/{v}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \dim_{\mathrm{H}}(E(v)\cap\Lambda)=\dim_{\mathrm{H}}(E_{\overline{v}(x)=v}(v)\cap\Lambda)=\dim_{\mathrm{H}}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda)={1}/{v},\cr \dim_{\mathrm{H}}(E_{\underline{v}(x)=v}(v)\cap\Lambda)=\dim_{\mathrm{H}}(E_{\underline{v}(x)\geq v}(v)\cap\Lambda)={1}/{v}. \end{cases} \end{align*} $$
We are also interested in the Hausdorff dimension of the intersection of
![]() $\Lambda $
with the sets
$\Lambda $
with the sets
![]() $E_{\overline {v}(x)\leq v}(v)=\{x\in [0,1):\overline {v}(x)\leq v\}$
and
$E_{\overline {v}(x)\leq v}(v)=\{x\in [0,1):\overline {v}(x)\leq v\}$
and
![]() $E_{\underline {v}(x)\leq v}(v)=\{x\in [0,1):\underline {v}(x)\leq v\}$
.
$E_{\underline {v}(x)\leq v}(v)=\{x\in [0,1):\underline {v}(x)\leq v\}$
.
Theorem 1.3. For any
![]() $v>2$
,
$v>2$
,
Let
![]() $\psi $
and
$\psi $
and
![]() $\tilde {\psi }$
be positive functions defined on
$\tilde {\psi }$
be positive functions defined on
![]() $\mathbb {N}$
. We say
$\mathbb {N}$
. We say
![]() $\psi $
and
$\psi $
and
![]() $\tilde {\psi }$
are equivalent if
$\tilde {\psi }$
are equivalent if
![]() $\psi (n)/\tilde {\psi }(n)\to 1$
as
$\psi (n)/\tilde {\psi }(n)\to 1$
as
![]() $n\to \infty $
. Fan et al. [Reference Fan, Liao, Wang and Wu7, Lemma 3.1] proved that
$n\to \infty $
. Fan et al. [Reference Fan, Liao, Wang and Wu7, Lemma 3.1] proved that
![]() $K(\psi )\neq \emptyset $
if and only if
$K(\psi )\neq \emptyset $
if and only if
![]() $\psi $
is equivalent to a nondecreasing function. This also applies to the subset
$\psi $
is equivalent to a nondecreasing function. This also applies to the subset
![]() $K(\psi )\cap \Lambda $
. In the following we always assume that
$K(\psi )\cap \Lambda $
. In the following we always assume that
![]() $\psi $
is nondecreasing.
$\psi $
is nondecreasing.
Theorem 1.4. Let
![]() $\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
be a function satisfying
$\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
be a function satisfying
![]() $\psi (n)\to \infty $
as
$\psi (n)\to \infty $
as
![]() $n\to \infty $
.
$n\to \infty $
.
-
(i) If
 $\psi (n)/(n\log n)\to \alpha \ \ (0\leq \alpha <\infty )$
as
$\psi (n)/(n\log n)\to \alpha \ \ (0\leq \alpha <\infty )$
as
 $n\to \infty $
, then
$n\to \infty $
, then  $$ \begin{align*} \dim_{\mathrm{H}}(K(\psi)\cap\Lambda)= \begin{cases} 0, & 0\leq\alpha<1,\cr {(\alpha-1)}/{2\alpha}, & 1\leq\alpha<\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}(K(\psi)\cap\Lambda)= \begin{cases} 0, & 0\leq\alpha<1,\cr {(\alpha-1)}/{2\alpha}, & 1\leq\alpha<\infty. \end{cases} \end{align*} $$
-
(ii) If
 $\psi (n)/(n\log n)\to \infty $
as
$\psi (n)/(n\log n)\to \infty $
as
 $n\to \infty $
and the sequence
$n\to \infty $
and the sequence
 $\{\psi (n)-\psi (n-1)\}_{n\geq 1}$
is nondecreasing, then
$\{\psi (n)-\psi (n-1)\}_{n\geq 1}$
is nondecreasing, then  $$ \begin{align*}\dim_{\mathrm{H}}(K(\psi)\cap\Lambda)=\frac{1}{1+\limsup\limits_{n\to\infty}{\psi(n+1)}/{\psi(n)}}.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm{H}}(K(\psi)\cap\Lambda)=\frac{1}{1+\limsup\limits_{n\to\infty}{\psi(n+1)}/{\psi(n)}}.\end{align*} $$
From the proof of Theorem 1.4, we can calculate the Hausdorff dimension of the intersection of the level sets of the Khintchine exponent
![]() $\gamma (x)$
and
$\gamma (x)$
and
![]() $\Lambda $
.
$\Lambda $
.
Corollary 1.5. For any
![]() $0\leq \xi \leq \infty $
,
$0\leq \xi \leq \infty $
,
 $$ \begin{align*} \dim_{\mathrm{H}}(E_{\gamma(x)=\xi}(\xi)\cap\Lambda)= \begin{cases} 0,& 0\leq\xi<\infty,\cr {1}/{2},& \xi=\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}(E_{\gamma(x)=\xi}(\xi)\cap\Lambda)= \begin{cases} 0,& 0\leq\xi<\infty,\cr {1}/{2},& \xi=\infty. \end{cases} \end{align*} $$
The Lyapunov exponent of a dynamical system is a quantity that characterises the rate of separation of infinitesimally close trajectories. In the dynamical system of continued fractions, the Lyapunov exponent of orbits of the Gauss map T is defined whenever the limits exist by
 $$ \begin{align*} \lambda(x):=\lim_{n\to\infty}\frac{1}{n}\log |(T^n)'(x))|=\lim_{n\to\infty}\frac{1}{n}\sum_{j=0}^{n-1}\log |T'(T^j(x))| \end{align*} $$
$$ \begin{align*} \lambda(x):=\lim_{n\to\infty}\frac{1}{n}\log |(T^n)'(x))|=\lim_{n\to\infty}\frac{1}{n}\sum_{j=0}^{n-1}\log |T'(T^j(x))| \end{align*} $$
(see Devaney [Reference Devaney4]). The Hausdorff dimension of the level sets
has been completely characterised in Fan et al. [Reference Fan, Liao, Wang and Wu6, Theorem 1.3]. Similarly, we can define the so-called fast Lyapunov exponent of the Gauss map T by
 $$ \begin{align*} \lambda^{\psi}(x):=\lim_{n\to\infty}\frac{1}{\psi(n)}\log |(T^n)'(x))|=\lim_{n\to\infty}\frac{1}{\psi(n)}\sum_{j=0}^{n-1}\log |T'(T^j(x))|, \end{align*} $$
$$ \begin{align*} \lambda^{\psi}(x):=\lim_{n\to\infty}\frac{1}{\psi(n)}\log |(T^n)'(x))|=\lim_{n\to\infty}\frac{1}{\psi(n)}\sum_{j=0}^{n-1}\log |T'(T^j(x))|, \end{align*} $$
where
![]() $\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
is a function satisfying
$\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
is a function satisfying
![]() $\psi (n)/n\to \infty $
as
$\psi (n)/n\to \infty $
as
![]() $n\to \infty $
. Let
$n\to \infty $
. Let
From [Reference Fan, Liao, Wang and Wu6, Lemma 2.7],
The following result follows directly from the proof of Corollary 1.5.
Corollary 1.6. For any
![]() $0\leq \xi \leq \infty $
,
$0\leq \xi \leq \infty $
,
 $$ \begin{align*} \dim_{\mathrm{H}}(E_{\lambda(x)=\xi}(\xi)\cap\Lambda)= \begin{cases} 0,& 0\leq\xi<\infty,\cr {1}/{2},& \xi=\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}(E_{\lambda(x)=\xi}(\xi)\cap\Lambda)= \begin{cases} 0,& 0\leq\xi<\infty,\cr {1}/{2},& \xi=\infty. \end{cases} \end{align*} $$
Under the condition
![]() $\psi (n)/n\to \infty $
as
$\psi (n)/n\to \infty $
as
![]() $n\to \infty $
, we deduce from (1.4) and (2.2) (see below) that
$n\to \infty $
, we deduce from (1.4) and (2.2) (see below) that
![]() $K(\psi )=L(2\psi )$
. Then from Theorem 1.4, the Hausdorff dimension of the intersection of the sets
$K(\psi )=L(2\psi )$
. Then from Theorem 1.4, the Hausdorff dimension of the intersection of the sets
![]() $L(\psi )$
and
$L(\psi )$
and
![]() $\Lambda $
is also determined.
$\Lambda $
is also determined.
Corollary 1.7. Let
![]() $\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
be a function satisfying
$\psi :\mathbb {N}\rightarrow \mathbb {R}^+$
be a function satisfying
![]() $\psi (n)/n\to \infty $
as
$\psi (n)/n\to \infty $
as
![]() $n\to \infty $
.
$n\to \infty $
.
-
(i) If
 $\psi (n)/(n\log n)\to \alpha \ (0\leq \alpha <\infty )$
as
$\psi (n)/(n\log n)\to \alpha \ (0\leq \alpha <\infty )$
as
 $n\to \infty $
, then
$n\to \infty $
, then  $$ \begin{align*} \dim_{\mathrm{H}}(L(\psi)\cap\Lambda)= \begin{cases} 0, & 0\leq\alpha<2,\cr {(\alpha-2)}/{2\alpha}, & 2\leq\alpha<\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}(L(\psi)\cap\Lambda)= \begin{cases} 0, & 0\leq\alpha<2,\cr {(\alpha-2)}/{2\alpha}, & 2\leq\alpha<\infty. \end{cases} \end{align*} $$
-
(ii) If
 $\psi (n)/(n\log n)\to \infty $
as
$\psi (n)/(n\log n)\to \infty $
as
 $n\to \infty $
and the sequence
$n\to \infty $
and the sequence
 $\{\psi (n)-\psi (n-1)\}_{n\geq 1}$
is nondecreasing, then
$\{\psi (n)-\psi (n-1)\}_{n\geq 1}$
is nondecreasing, then  $$ \begin{align*}\dim_{\mathrm{H}}(L(\psi)\cap\Lambda)=\frac{1}{1+\limsup\limits_{n\to\infty}{\psi(n+1)}/{\psi(n)}}.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm{H}}(L(\psi)\cap\Lambda)=\frac{1}{1+\limsup\limits_{n\to\infty}{\psi(n+1)}/{\psi(n)}}.\end{align*} $$
We use
![]() $\mathbb {N}$
to denote the set of all positive integers,
$\mathbb {N}$
to denote the set of all positive integers,
![]() $|\cdot |$
denotes the length of a subinterval of
$|\cdot |$
denotes the length of a subinterval of
![]() $[0,1)$
,
$[0,1)$
,
![]() $\exp (x)$
the natural exponential function,
$\exp (x)$
the natural exponential function,
![]() $\lfloor x\rfloor $
the largest integer not exceeding x and
$\lfloor x\rfloor $
the largest integer not exceeding x and
![]() $\mathcal {H}^{s}$
the s-dimensional Hausdorff measure of a set.
$\mathcal {H}^{s}$
the s-dimensional Hausdorff measure of a set.
The paper is organised as follows. In Section 2 we present some elementary properties and useful lemmas concerning the dimensional results in continued fractions. Section 3 is devoted to the proofs of the main results.
2 Preliminaries
2.1 Elementary properties of continued fractions
For
![]() $n{\kern-1.2pt}\geq{\kern-1.2pt} 1$
and
$n{\kern-1.2pt}\geq{\kern-1.2pt} 1$
and
![]() $(a_1,\ldots , a_n){\kern-1pt}\in{\kern-1pt} \mathbb {N}^{n}$
, we call
$(a_1,\ldots , a_n){\kern-1pt}\in{\kern-1pt} \mathbb {N}^{n}$
, we call
a basic interval of order n for the continued fraction. All points in
![]() $I_{n}(a_1, \ldots , a_n)$
have the same
$I_{n}(a_1, \ldots , a_n)$
have the same
![]() $p_n(x)$
and
$p_n(x)$
and
![]() $q_n(x)$
. Thus, for
$q_n(x)$
. Thus, for
![]() $x\in I_{n}(a_1, \ldots , a_n)$
, we write
$x\in I_{n}(a_1, \ldots , a_n)$
, we write
It is well known (see [Reference Khintchine17, page 4]) that
![]() $ p_n$
and
$ p_n$
and
![]() $q_n$
satisfy the recursive formula:
$q_n$
satisfy the recursive formula:
 $$ \begin{align} \begin{cases} p_{-1}=1,\quad p_0=0,\quad p_n=a_np_{n-1}+p_{n-2}\quad (n\geq1);\cr q_{-1}=0,\quad q_0=1,\quad q_n=a_nq_{n-1}+q_{n-2}\quad (n\geq1). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} p_{-1}=1,\quad p_0=0,\quad p_n=a_np_{n-1}+p_{n-2}\quad (n\geq1);\cr q_{-1}=0,\quad q_0=1,\quad q_n=a_nq_{n-1}+q_{n-2}\quad (n\geq1). \end{cases} \end{align} $$
By the second formula of (2.1),
 $$ \begin{align} \prod_{k=1}^{n}a_k\leq q_n\leq\prod_{k=1}^{n}(a_k+1)\leq2^n\prod_{k=1}^{n}a_k. \end{align} $$
$$ \begin{align} \prod_{k=1}^{n}a_k\leq q_n\leq\prod_{k=1}^{n}(a_k+1)\leq2^n\prod_{k=1}^{n}a_k. \end{align} $$
Proposition 2.1 [Reference Iosifescu and Kraaikamp11, page 18].
For any
![]() $(a_1, a_2,\ldots , a_n)\in \mathbb {N}^{n}$
,
$(a_1, a_2,\ldots , a_n)\in \mathbb {N}^{n}$
,
![]() $I_{n}(a_1, a_2,\ldots , a_n)$
is the interval with the endpoints
$I_{n}(a_1, a_2,\ldots , a_n)$
is the interval with the endpoints
As a result, the length of
![]() $I_{n}(a_1, a_2,\ldots , a_n)$
is
$I_{n}(a_1, a_2,\ldots , a_n)$
is
 $$ \begin{align*} |I_{n}(a_1, a_2,\ldots, a_n)|=\frac{1}{q_n(q_n+q_{n-1})}. \end{align*} $$
$$ \begin{align*} |I_{n}(a_1, a_2,\ldots, a_n)|=\frac{1}{q_n(q_n+q_{n-1})}. \end{align*} $$
Combining (2.2) and Proposition 2.1, we deduce that
 $$ \begin{align} 2^{-2n-1}\bigg(\prod_{k=1}^{n}a_k\bigg)^{-2}\leq |I_{n}(a_1, a_2,\ldots, a_n)| \leq \bigg(\prod_{k=1}^{n}a_k\bigg)^{-2}. \end{align} $$
$$ \begin{align} 2^{-2n-1}\bigg(\prod_{k=1}^{n}a_k\bigg)^{-2}\leq |I_{n}(a_1, a_2,\ldots, a_n)| \leq \bigg(\prod_{k=1}^{n}a_k\bigg)^{-2}. \end{align} $$
2.2 Some useful lemmas
The first lemma below gives a lower bound of the Hausdorff dimension of some sets of points whose partial quotients are nondecreasing.
Lemma 2.2 [Reference Fang, Ma, Song and Wu8, Lemma 3.4].
Let
![]() $\{s_n\}_{n\geq 1}$
be a sequence of positive integers tending to infinity with
$\{s_n\}_{n\geq 1}$
be a sequence of positive integers tending to infinity with
![]() $s_n\geq 2$
for any
$s_n\geq 2$
for any
![]() $n\geq 1$
. Set
$n\geq 1$
. Set
Then
 $$ \begin{align*}\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})=\frac{1}{2+\limsup\limits_{n\to\infty}{(2\log((n+1)!)+ \log s_{n+1})}/{\log(s_1 s_2\cdots s_n)}}.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})=\frac{1}{2+\limsup\limits_{n\to\infty}{(2\log((n+1)!)+ \log s_{n+1})}/{\log(s_1 s_2\cdots s_n)}}.\end{align*} $$
Combining [Reference Fang, Ma, Song and Wu8, Theorem 2.4] and [Reference Fang, Ma, Song and Wu9, Lemma 3.1] immediately yields the Hausdorff dimension of some
![]() $\liminf $
level sets whose partial quotients are nondecreasing.
$\liminf $
level sets whose partial quotients are nondecreasing.
Lemma 2.3. For any
![]() $0\leq \alpha <\infty $
,
$0\leq \alpha <\infty $
,
 $$ \begin{align*} \dim_{\mathrm{H}}\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_n(x)}{\log n}\leq\alpha\bigg\}= \begin{cases} 0,& 0\leq\alpha<1,\cr {(\alpha-1)}/{2\alpha},& 1\leq \alpha<\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_n(x)}{\log n}\leq\alpha\bigg\}= \begin{cases} 0,& 0\leq\alpha<1,\cr {(\alpha-1)}/{2\alpha},& 1\leq \alpha<\infty. \end{cases} \end{align*} $$
3 Proofs of main results
This section is devoted to the proofs of the main results. Our method is inspired by those of Fan et al. [Reference Fan, Liao, Wang and Wu7] and Fang et al. [Reference Fang, Ma, Song and Wu8].
Proof of Theorem 1.2.
For any
![]() $v>2$
, it is clear that
$v>2$
, it is clear that
The next lemma follows from the monotonicity of Hausdorff dimension [Reference Falconer5, page 32].
Lemma 3.1. For any
![]() $v>2$
,
$v>2$
,
 $$ \begin{align*} \begin{cases} \dim_{\mathrm{H}}(E(v)\cap\Lambda)\leq\dim_{\mathrm{H}}(E_{\overline{v}(x)=v}(v)\cap\Lambda)\leq\dim_{\mathrm{H}}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda),\cr \begin{aligned} \dim_{\mathrm{H}}(E(v)\cap\Lambda)\leq\dim_{\mathrm{H}}(E_{\underline{v}(x)=v}(v)\cap\Lambda) & \leq\dim_{\mathrm{H}}(E_{\underline{v}(x)\geq v}(v)\cap\Lambda) \\ & \leq\dim_{\mathrm{H}}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda). \end{aligned} \end{cases}\\[-36pt] \end{align*} $$
$$ \begin{align*} \begin{cases} \dim_{\mathrm{H}}(E(v)\cap\Lambda)\leq\dim_{\mathrm{H}}(E_{\overline{v}(x)=v}(v)\cap\Lambda)\leq\dim_{\mathrm{H}}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda),\cr \begin{aligned} \dim_{\mathrm{H}}(E(v)\cap\Lambda)\leq\dim_{\mathrm{H}}(E_{\underline{v}(x)=v}(v)\cap\Lambda) & \leq\dim_{\mathrm{H}}(E_{\underline{v}(x)\geq v}(v)\cap\Lambda) \\ & \leq\dim_{\mathrm{H}}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda). \end{aligned} \end{cases}\\[-36pt] \end{align*} $$
In view of Lemma 3.1, we divide the proof of Theorem 1.2 into two steps: the upper bound of
![]() $\dim _{\mathrm {H}}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )$
and the lower bound of
$\dim _{\mathrm {H}}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )$
and the lower bound of
![]() $\dim _{\mathrm {H}}(E(v)\cap \Lambda )$
.
$\dim _{\mathrm {H}}(E(v)\cap \Lambda )$
.
The upper bound of
![]() $\dim _{\mathrm {H}}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )$
. Our method is to choose a suitable positive real number s such that
$\dim _{\mathrm {H}}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )$
. Our method is to choose a suitable positive real number s such that
![]() $\mathcal {H}^{s}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )<\infty $
. Let us remark that countable sets are of Hausdorff dimension zero, and the difference of the sets
$\mathcal {H}^{s}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )<\infty $
. Let us remark that countable sets are of Hausdorff dimension zero, and the difference of the sets
![]() $\Lambda $
and
$\Lambda $
and
is a countable set. Thus we only need to consider the Hausdorff dimension of the set
![]() $E_{\overline {v}(x)\geq v}(v)\cap \Lambda _{\infty }$
. For
$E_{\overline {v}(x)\geq v}(v)\cap \Lambda _{\infty }$
. For
![]() $0<\varepsilon <v-2$
and
$0<\varepsilon <v-2$
and
![]() $M\geq 1$
, let
$M\geq 1$
, let
 $$ \begin{align*}J_n(\sigma_1,\ldots,\sigma_n)=\bigcup\limits_{\ell\geq(\sigma_1\cdots\sigma_n)^{v-2-\varepsilon}} I_{n+1}(\sigma_1,\ldots,\sigma_n,\ell)\end{align*} $$
$$ \begin{align*}J_n(\sigma_1,\ldots,\sigma_n)=\bigcup\limits_{\ell\geq(\sigma_1\cdots\sigma_n)^{v-2-\varepsilon}} I_{n+1}(\sigma_1,\ldots,\sigma_n,\ell)\end{align*} $$
and
![]() $C_n=\{(\sigma _1,\ldots ,\sigma _n)\in \mathbb {N}^{n}:\ \sigma _1\cdots \sigma _n\geq M^{n}\}$
. Then by (2.2),
$C_n=\{(\sigma _1,\ldots ,\sigma _n)\in \mathbb {N}^{n}:\ \sigma _1\cdots \sigma _n\geq M^{n}\}$
. Then by (2.2),
 $$ \begin{align} &\ E_{\overline{v}(x)\geq v}(v)\cap\Lambda_{\infty}\nonumber\\ &\quad\subseteq\bigg\{x\in\Lambda_{\infty}:\ \limsup\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log a_1(x)+\cdots+\log a_n(x)}\geq v-2\bigg\}\nonumber\\ &\quad\subseteq\bigcap\limits_{N=1}^{\infty}\bigcup\limits_{n=N}^{\infty}\{x\in[0,1):\ a_{n+1}(x)\geq(a_1(x)\cdots a_n(x))^{v-2-\varepsilon}\ \text{and}\ a_1(x)\cdots a_n(x)\geq M^{n}\}\nonumber\\ &\quad=\bigcap\limits_{N=1}^{\infty}\bigcup\limits_{n=N}^{\infty}\bigcup\limits_{(\sigma_1,\ldots,\sigma_n)\in C_n}J_n(\sigma_1,\ldots,\sigma_n). \end{align} $$
$$ \begin{align} &\ E_{\overline{v}(x)\geq v}(v)\cap\Lambda_{\infty}\nonumber\\ &\quad\subseteq\bigg\{x\in\Lambda_{\infty}:\ \limsup\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log a_1(x)+\cdots+\log a_n(x)}\geq v-2\bigg\}\nonumber\\ &\quad\subseteq\bigcap\limits_{N=1}^{\infty}\bigcup\limits_{n=N}^{\infty}\{x\in[0,1):\ a_{n+1}(x)\geq(a_1(x)\cdots a_n(x))^{v-2-\varepsilon}\ \text{and}\ a_1(x)\cdots a_n(x)\geq M^{n}\}\nonumber\\ &\quad=\bigcap\limits_{N=1}^{\infty}\bigcup\limits_{n=N}^{\infty}\bigcup\limits_{(\sigma_1,\ldots,\sigma_n)\in C_n}J_n(\sigma_1,\ldots,\sigma_n). \end{align} $$
It follows from (2.3) that
 $$ \begin{align} \Big|\!\bigcup\limits_{\ell\geq(\sigma_1\cdots\sigma_n)^{v-2-\varepsilon}}I_{n+1}(\sigma_1,\ldots,\sigma_n,\ell)\Big| \leq\sum\limits_{\ell\geq(\sigma_1\cdots\sigma_n)^{v-2-\varepsilon}}\frac{1}{\ell^2\cdot(\sigma_1\cdots\sigma_n)^{2}} \leq\frac{1}{(\sigma_1\cdots\sigma_n)^{v-\varepsilon}}. \end{align} $$
$$ \begin{align} \Big|\!\bigcup\limits_{\ell\geq(\sigma_1\cdots\sigma_n)^{v-2-\varepsilon}}I_{n+1}(\sigma_1,\ldots,\sigma_n,\ell)\Big| \leq\sum\limits_{\ell\geq(\sigma_1\cdots\sigma_n)^{v-2-\varepsilon}}\frac{1}{\ell^2\cdot(\sigma_1\cdots\sigma_n)^{2}} \leq\frac{1}{(\sigma_1\cdots\sigma_n)^{v-\varepsilon}}. \end{align} $$
We are now in a position to obtain the upper bound of
![]() $\dim _{\mathrm {H}}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )$
. Let
$\dim _{\mathrm {H}}(E_{\overline {v}(x)\geq v}(v)\cap \Lambda )$
. Let
![]() $s,M$
be two real numbers satisfying
$s,M$
be two real numbers satisfying
 $$ \begin{align} s=\frac{1+2\varepsilon}{v-\varepsilon}\quad \text{and}\quad \frac{1}{M^{\varepsilon}}\cdot\sum\limits_{j=1}^{\infty}\frac{1}{j^{1+\varepsilon}}<\frac{1}{2}. \end{align} $$
$$ \begin{align} s=\frac{1+2\varepsilon}{v-\varepsilon}\quad \text{and}\quad \frac{1}{M^{\varepsilon}}\cdot\sum\limits_{j=1}^{\infty}\frac{1}{j^{1+\varepsilon}}<\frac{1}{2}. \end{align} $$
Then we deduce from (3.1), (3.2) and (3.3) that
 $$ \begin{align*} \mathcal{H}^{s}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda_{\infty}) &\leq \liminf_{n\to\infty}\sum\limits_{n=N}^{\infty}\sum\limits_{(\sigma_1,\ldots,\sigma_n)\in C_n} |J_{n}(\sigma_1,\ldots,\sigma_n)|^{s}\\ &\leq\liminf_{n\to\infty}\sum\limits_{n=N}^{\infty}\sum\limits_{(\sigma_1,\ldots,\sigma_n)\in C_n} \frac{1}{(\sigma_1\cdots\sigma_n)^{1+2\varepsilon}}\\ &\leq\liminf_{n\to\infty}\sum\limits_{n=N}^{\infty}\bigg(\frac{1}{M^{\varepsilon}}\cdot \bigg(\sum\limits_{j=1}^{\infty}\frac{1}{j^{1+\varepsilon}}\bigg)\bigg)^{n}=0. \end{align*} $$
$$ \begin{align*} \mathcal{H}^{s}(E_{\overline{v}(x)\geq v}(v)\cap\Lambda_{\infty}) &\leq \liminf_{n\to\infty}\sum\limits_{n=N}^{\infty}\sum\limits_{(\sigma_1,\ldots,\sigma_n)\in C_n} |J_{n}(\sigma_1,\ldots,\sigma_n)|^{s}\\ &\leq\liminf_{n\to\infty}\sum\limits_{n=N}^{\infty}\sum\limits_{(\sigma_1,\ldots,\sigma_n)\in C_n} \frac{1}{(\sigma_1\cdots\sigma_n)^{1+2\varepsilon}}\\ &\leq\liminf_{n\to\infty}\sum\limits_{n=N}^{\infty}\bigg(\frac{1}{M^{\varepsilon}}\cdot \bigg(\sum\limits_{j=1}^{\infty}\frac{1}{j^{1+\varepsilon}}\bigg)\bigg)^{n}=0. \end{align*} $$
This shows that
and letting
![]() $\varepsilon \to 0^+$
gives the desired upper bound.
$\varepsilon \to 0^+$
gives the desired upper bound.
The lower bound of
![]() $\dim _{\mathrm {H}}(E(v)\cap \Lambda )$
. Recall that
$\dim _{\mathrm {H}}(E(v)\cap \Lambda )$
. Recall that
 $$ \begin{align*}E(v)\cap\Lambda=\bigg\{x\in\Lambda:\ \lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}=v-2\bigg\}.\end{align*} $$
$$ \begin{align*}E(v)\cap\Lambda=\bigg\{x\in\Lambda:\ \lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}=v-2\bigg\}.\end{align*} $$
To bound
![]() $\dim _{\mathrm {H}}(E(v)\cap \Lambda )$
from below, we shall construct a Cantor subset of
$\dim _{\mathrm {H}}(E(v)\cap \Lambda )$
from below, we shall construct a Cantor subset of
![]() $E(v)\cap \Lambda $
. Let
$E(v)\cap \Lambda $
. Let
![]() $s_n=\exp ((v-1)^n)$
and
$s_n=\exp ((v-1)^n)$
and
We claim that
If
![]() $x\in \mathbb {F}(\{s_n\}_{n\geq 1})$
, then it is easy to see that
$x\in \mathbb {F}(\{s_n\}_{n\geq 1})$
, then it is easy to see that
![]() $a_n(x)\leq a_{n+1}(x)$
for any
$a_n(x)\leq a_{n+1}(x)$
for any
![]() $n\geq 1$
. Now it remains to show that
$n\geq 1$
. Now it remains to show that
 $$ \begin{align*}\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}=v-2.\end{align*} $$
$$ \begin{align*}\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}=v-2.\end{align*} $$
In fact, we deduce from (2.2) that
 $$ \begin{align*} v-2&=\lim\limits_{n\to\infty}\frac{\log(n+1)+(v-1)^{n+1}}{n\log2+\log(n+1)!+(v-1)+\cdots+(v-1)^{n}}\\ &\leq\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{n\log2+\log a_1(x)+\cdots+\log a_n(x)}\\ &\leq\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}\leq\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log a_1(x)+\cdots+\log a_n(x)}\\ &\leq\lim\limits_{n\to\infty}\frac{\log(n+2)+(v-1)^{n+1}}{\log n!+(v-1)+\cdots+(v-1)^{n}}=v-2. \end{align*} $$
$$ \begin{align*} v-2&=\lim\limits_{n\to\infty}\frac{\log(n+1)+(v-1)^{n+1}}{n\log2+\log(n+1)!+(v-1)+\cdots+(v-1)^{n}}\\ &\leq\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{n\log2+\log a_1(x)+\cdots+\log a_n(x)}\\ &\leq\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}\leq\lim\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log a_1(x)+\cdots+\log a_n(x)}\\ &\leq\lim\limits_{n\to\infty}\frac{\log(n+2)+(v-1)^{n+1}}{\log n!+(v-1)+\cdots+(v-1)^{n}}=v-2. \end{align*} $$
It follows from (3.4) and Lemma 2.2 that
 $$ \begin{align*} \nonumber\dim_{\mathrm{H}}(E(v)\cap\Lambda)\geq\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})&=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log(n+1)!+ (v-1)^{n+1}}{(v-1)+\cdots+(v-1)^n}}\\ &=\frac{1}{2+(v-2)}=\frac{1}{v}. \end{align*} $$
$$ \begin{align*} \nonumber\dim_{\mathrm{H}}(E(v)\cap\Lambda)\geq\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})&=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log(n+1)!+ (v-1)^{n+1}}{(v-1)+\cdots+(v-1)^n}}\\ &=\frac{1}{2+(v-2)}=\frac{1}{v}. \end{align*} $$
Proof of Theorem 1.3.
For any
![]() $v>2$
, recall that
$v>2$
, recall that
 $$ \begin{align*}E_{\overline{v}(x)\leq v}(v)\cap\Lambda=\bigg\{x\in\Lambda:\ 2+\limsup\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}\leq v\bigg\}.\end{align*} $$
$$ \begin{align*}E_{\overline{v}(x)\leq v}(v)\cap\Lambda=\bigg\{x\in\Lambda:\ 2+\limsup\limits_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)}\leq v\bigg\}.\end{align*} $$
It is clear that
![]() $E_{\overline {v}(x)\leq v}(v)\cap \Lambda \subseteq E_{\underline {v}(x)\leq v}(v)\cap \Lambda \subseteq \Lambda $
and so
$E_{\overline {v}(x)\leq v}(v)\cap \Lambda \subseteq E_{\underline {v}(x)\leq v}(v)\cap \Lambda \subseteq \Lambda $
and so
Now it suffices to construct a subset of
![]() $E_{\overline {v}(x)\leq v}(v)\cap \Lambda $
and then show that the subset is of Hausdorff dimension
$E_{\overline {v}(x)\leq v}(v)\cap \Lambda $
and then show that the subset is of Hausdorff dimension
![]() $1/2$
. Let
$1/2$
. Let
![]() $s_n=2^n$
and let
$s_n=2^n$
and let
Then by (2.2), it is easy to prove that
Applying Lemma 2.2, we conclude from (3.5) that
 $$ \begin{align} \dim_{\mathrm{H}}(E_{\overline{v}(x)\leq v}(v)\cap\Lambda)\geq\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log(n+1)!+ (n+1)\log2}{\frac{1}{2}n(n+1)\log2}}=\frac{1}{2}. \end{align} $$
$$ \begin{align} \dim_{\mathrm{H}}(E_{\overline{v}(x)\leq v}(v)\cap\Lambda)\geq\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log(n+1)!+ (n+1)\log2}{\frac{1}{2}n(n+1)\log2}}=\frac{1}{2}. \end{align} $$
Proofs of Theorem 1.4 and Corollary 1.5.
We shall divide the proof of Theorem 1.4 into two cases. Recall that
 $$ \begin{align*}K(\psi)\cap\Lambda=\bigg\{x\in\Lambda:\ \lim\limits_{n\to\infty}\frac{\log a_1(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\}.\end{align*} $$
$$ \begin{align*}K(\psi)\cap\Lambda=\bigg\{x\in\Lambda:\ \lim\limits_{n\to\infty}\frac{\log a_1(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\}.\end{align*} $$
Case 1:
![]() $\psi (n)/(n\log n)\to \alpha \ (0\leq \alpha <\infty )\ \text {as}\ n\to \infty $
. For the upper bound of
$\psi (n)/(n\log n)\to \alpha \ (0\leq \alpha <\infty )\ \text {as}\ n\to \infty $
. For the upper bound of
![]() $\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )$
, we shall construct a larger set containing
$\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )$
, we shall construct a larger set containing
![]() $K(\psi )\cap \Lambda $
by using the general form of the Stolz–Cesàro theorem which states that if
$K(\psi )\cap \Lambda $
by using the general form of the Stolz–Cesàro theorem which states that if
![]() $\{b_n\}_{n\geq 1}$
and
$\{b_n\}_{n\geq 1}$
and
![]() $\{c_n\}_{n\geq 1}$
are two sequences such that
$\{c_n\}_{n\geq 1}$
are two sequences such that
![]() $\{c_n\}_{n\geq 1}$
is monotone and unbounded, then
$\{c_n\}_{n\geq 1}$
is monotone and unbounded, then
It follows from (3.7) that
 $$ \begin{align*} K(\psi)\cap\Lambda&\subseteq\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_1(x)+\cdots+\log a_n(x)}{n\log n}=\alpha\bigg\}\\ &\subseteq\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_n(x)}{\log n}\leq\alpha\bigg\}. \end{align*} $$
$$ \begin{align*} K(\psi)\cap\Lambda&\subseteq\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_1(x)+\cdots+\log a_n(x)}{n\log n}=\alpha\bigg\}\\ &\subseteq\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_n(x)}{\log n}\leq\alpha\bigg\}. \end{align*} $$
Thus we conclude from Lemma 2.3 that
 $$ \begin{align*} \dim_{\mathrm{H}}(K(\psi)\cap\Lambda)\leq \begin{cases} 0,& 0\leq\alpha<1,\cr {(\alpha-1)}/{2\alpha},& \alpha\geq1. \end{cases} \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}(K(\psi)\cap\Lambda)\leq \begin{cases} 0,& 0\leq\alpha<1,\cr {(\alpha-1)}/{2\alpha},& \alpha\geq1. \end{cases} \end{align*} $$
To bound
![]() $\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )$
from below, we shall construct a suitable Cantor subset of
$\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )$
from below, we shall construct a suitable Cantor subset of
![]() $K(\psi )\cap \Lambda $
. By the upper bound estimate, we have
$K(\psi )\cap \Lambda $
. By the upper bound estimate, we have
![]() $\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )=0$
for
$\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )=0$
for
![]() $\alpha =1$
. In what follows, we assume that
$\alpha =1$
. In what follows, we assume that
![]() $\alpha>1$
. Let
$\alpha>1$
. Let
![]() $s_n=2\lfloor n^{\alpha -1}\rfloor $
and let
$s_n=2\lfloor n^{\alpha -1}\rfloor $
and let
Then we claim that
On the one hand, since the sequence of positive integers
![]() $\{s_n\}_{n\geq 1}$
is nondecreasing, the set
$\{s_n\}_{n\geq 1}$
is nondecreasing, the set
![]() $\mathbb {F}(\{s_n\}_{n\geq 1})$
is a subset of
$\mathbb {F}(\{s_n\}_{n\geq 1})$
is a subset of
![]() $\Lambda $
. On the other hand, for each
$\Lambda $
. On the other hand, for each
![]() $x\in \mathbb {F}(\{s_n\}_{n\geq 1})$
,
$x\in \mathbb {F}(\{s_n\}_{n\geq 1})$
,
 $$ \begin{align*} \nonumber\alpha=\lim\limits_{n\to\infty}\frac{\sum_{k=1}^{n}\log(2(k^{\alpha}-k))}{n\log n}&\leq \lim\limits_{n\to\infty} \frac{\log a_1(x)+\cdots+\log a_n(x)}{n\log n}\\ &\leq\lim\limits_{n\to\infty}\frac{\sum_{k=1}^{n}\log(4k^{\alpha})}{n\log n}=\alpha. \end{align*} $$
$$ \begin{align*} \nonumber\alpha=\lim\limits_{n\to\infty}\frac{\sum_{k=1}^{n}\log(2(k^{\alpha}-k))}{n\log n}&\leq \lim\limits_{n\to\infty} \frac{\log a_1(x)+\cdots+\log a_n(x)}{n\log n}\\ &\leq\lim\limits_{n\to\infty}\frac{\sum_{k=1}^{n}\log(4k^{\alpha})}{n\log n}=\alpha. \end{align*} $$
Applying Lemma 2.2, we deduce from (3.7) that
 $$ \begin{align} \nonumber\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log((n+1)!)+ \log s_{n+1}}{\log(s_1 s_2\cdots s_n)}} &\geq\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log(n+2)+ \log s_{n+2}-\log s_{n+1}}{\log s_{n+1}}}\\ &=\frac{1}{2+\frac{2}{\alpha-1}}=\frac{\alpha-1}{2\alpha}. \end{align} $$
$$ \begin{align} \nonumber\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log((n+1)!)+ \log s_{n+1}}{\log(s_1 s_2\cdots s_n)}} &\geq\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log(n+2)+ \log s_{n+2}-\log s_{n+1}}{\log s_{n+1}}}\\ &=\frac{1}{2+\frac{2}{\alpha-1}}=\frac{\alpha-1}{2\alpha}. \end{align} $$
Combining this with (3.8) and (3.9) completes the proof.
Case 2:
![]() $\psi (n)/(n\log n)\to \infty \ \text {as}\ n\to \infty $
. Note that
$\psi (n)/(n\log n)\to \infty \ \text {as}\ n\to \infty $
. Note that
![]() $\psi (n)$
is a nondecreasing function. For the upper bound of
$\psi (n)$
is a nondecreasing function. For the upper bound of
![]() $\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )$
, we deduce from [Reference Fan, Liao, Wang and Wu7, Theorem 1.1] that
$\dim _{\mathrm {H}}(K(\psi )\cap \Lambda )$
, we deduce from [Reference Fan, Liao, Wang and Wu7, Theorem 1.1] that
 $$ \begin{align*}\dim_{\mathrm{H}}(K(\psi)\cap\Lambda)\leq\dim_{\mathrm{H}}K(\psi)=\frac{1}{1+\limsup\limits_{n\to\infty}{\psi(n+1)}/{\psi(n)}}.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm{H}}(K(\psi)\cap\Lambda)\leq\dim_{\mathrm{H}}K(\psi)=\frac{1}{1+\limsup\limits_{n\to\infty}{\psi(n+1)}/{\psi(n)}}.\end{align*} $$
For the lower bound, the strategy is again to construct a suitable Cantor subset. Let
![]() $s_n=2\lfloor \exp (\psi (n)-\psi (n-1))\rfloor $
and set
$s_n=2\lfloor \exp (\psi (n)-\psi (n-1))\rfloor $
and set
![]() $\psi (0)=0$
for convenience. Let
$\psi (0)=0$
for convenience. Let
The sequence
![]() $\{\psi (n)-\psi (n-1)\}_{n\geq 1}$
is nondecreasing and it is easy to check that
$\{\psi (n)-\psi (n-1)\}_{n\geq 1}$
is nondecreasing and it is easy to check that
Before proceeding, we remark that
 $$ \begin{align*}\lim\limits_{n\to\infty}\frac{\psi(n)}{n\log n}=\infty\quad \text{implies}\quad \limsup\limits_{n\to\infty}\frac{\log((n+1)!)}{\psi(n)}=0.\end{align*} $$
$$ \begin{align*}\lim\limits_{n\to\infty}\frac{\psi(n)}{n\log n}=\infty\quad \text{implies}\quad \limsup\limits_{n\to\infty}\frac{\log((n+1)!)}{\psi(n)}=0.\end{align*} $$
Combining these observations, we deduce from Lemma 2.2 that
 $$ \begin{align*} \dim_{\mathrm{H}}(K(\psi)\cap\Lambda)\geq\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})&=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log((n+1)!)+ \log s_{n+1}}{\log(s_1 s_2\cdots s_n)}}\\ &\geq\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log((n+1)!)}{\psi(n)}+ \limsup\limits_{n\to\infty}\frac{\psi(n+1)-\psi(n)}{\psi(n)}}\\ &=\frac{1}{1+\limsup\limits_{n\to\infty}\frac{\psi(n+1)}{\psi(n)}}.\\[-53pt] \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}(K(\psi)\cap\Lambda)\geq\dim_{\mathrm{H}}\mathbb{F}(\{s_n\}_{n\geq1})&=\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log((n+1)!)+ \log s_{n+1}}{\log(s_1 s_2\cdots s_n)}}\\ &\geq\frac{1}{2+\limsup\limits_{n\to\infty}\frac{2\log((n+1)!)}{\psi(n)}+ \limsup\limits_{n\to\infty}\frac{\psi(n+1)-\psi(n)}{\psi(n)}}\\ &=\frac{1}{1+\limsup\limits_{n\to\infty}\frac{\psi(n+1)}{\psi(n)}}.\\[-53pt] \end{align*} $$
Proof of Corollary 1.5.
For the case
![]() $0\leq \xi <\infty $
, we deduce from the definition of the set
$0\leq \xi <\infty $
, we deduce from the definition of the set
![]() $E_{\gamma (x)=\xi }(\xi )$
and (3.7) that
$E_{\gamma (x)=\xi }(\xi )$
and (3.7) that
 $$ \begin{align*} E_{\gamma(x)=\xi}(\xi)\cap\Lambda&\subseteq\bigg\{x\in\Lambda: \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{n\log n}=0\bigg\}\\ &\subseteq\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_n(x)}{\log n}\leq0\bigg\}. \end{align*} $$
$$ \begin{align*} E_{\gamma(x)=\xi}(\xi)\cap\Lambda&\subseteq\bigg\{x\in\Lambda: \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{n\log n}=0\bigg\}\\ &\subseteq\bigg\{x\in\Lambda:\ \liminf\limits_{n\to\infty}\frac{\log a_n(x)}{\log n}\leq0\bigg\}. \end{align*} $$
Then by Lemma 2.3,
For the case
![]() $\xi =\infty $
, clearly
$\xi =\infty $
, clearly
It is easy to prove that the set
![]() $\mathbb {F}(\{s_n\}_{n\geq 1})$
constructed in (3.5) is also a subset of
$\mathbb {F}(\{s_n\}_{n\geq 1})$
constructed in (3.5) is also a subset of
![]() $E_{\gamma (x)=\xi }(\infty )\cap \Lambda $
. Combining this with (3.6) gives
$E_{\gamma (x)=\xi }(\infty )\cap \Lambda $
. Combining this with (3.6) gives