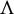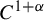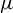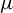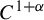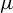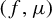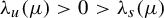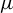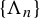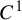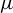1 Introduction
In smooth dynamical systems, a fundamental approximation result asserts that a
![]() $C^{1+\alpha }$
diffeomorphism f which preserves a hyperbolic ergodic measure
$C^{1+\alpha }$
diffeomorphism f which preserves a hyperbolic ergodic measure
![]() $\mu $
of positive entropy can be approximated gradually by compact invariant locally maximal hyperbolic sets–horseshoes
$\mu $
of positive entropy can be approximated gradually by compact invariant locally maximal hyperbolic sets–horseshoes
![]() $\{\Lambda _n\}$
, in the sense that dynamical quantities on the horseshoes such as the topological entropy and pressure, Lyapunov exponents, and averages of continuous functions are approaching those of the measure
$\{\Lambda _n\}$
, in the sense that dynamical quantities on the horseshoes such as the topological entropy and pressure, Lyapunov exponents, and averages of continuous functions are approaching those of the measure
![]() $\mu $
.
$\mu $
.
This type of result is widely referenced to the landmark work by Katok [Reference Katok20] or Katok and Hasselblatt (see [Reference Katok and Hasselblatt21]). Misiurewicz and Szlenk [Reference Misiurewicz and Szlenk28] earlier proved a related result for continuous and for piecewise monotone maps of the interval. Przytycki and Urbański [Reference Przytycki and Urbański34] obtained corresponding properties for holomorphic maps in the case of a measure with only positive Lyapunov exponent. A related setting of dyadic diophantine approximations was established by Persson and Schmeling in [Reference Persson and Schmeling32]. For a general
![]() $C^{1+\alpha }$
diffeomorphism f preserving a hyperbolic ergodic measure
$C^{1+\alpha }$
diffeomorphism f preserving a hyperbolic ergodic measure
![]() $\mu $
with positive entropy, assume that
$\mu $
with positive entropy, assume that
![]() $\mu $
has
$\mu $
has
![]() $\ell $
different Lyapunov exponents
$\ell $
different Lyapunov exponents
![]() $\{\unicode{x3bb} _j\}_{j=1}^{\ell }$
. On each approaching horseshoe
$\{\unicode{x3bb} _j\}_{j=1}^{\ell }$
. On each approaching horseshoe
![]() $\Lambda _n$
, Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson2] obtained a continuous splitting
$\Lambda _n$
, Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson2] obtained a continuous splitting
and showed that the exponential growth of
![]() $D_xf^n|_{E_i}$
is roughly
$D_xf^n|_{E_i}$
is roughly
![]() $\unicode{x3bb} _i$
for each
$\unicode{x3bb} _i$
for each
![]() $i=1, 2, \ldots , \ell $
. A corresponding statement for
$i=1, 2, \ldots , \ell $
. A corresponding statement for
![]() $C^{1+\alpha }$
non-conformal transformations (that is, non-invertible maps) was shown in [Reference Cao, Pesin and Zhao11]. See [Reference Chung12], [Reference Gelfert16, Reference Gelfert17], and [Reference Yang44] for other results related to Katok’s approximation construction of
$C^{1+\alpha }$
non-conformal transformations (that is, non-invertible maps) was shown in [Reference Cao, Pesin and Zhao11]. See [Reference Chung12], [Reference Gelfert16, Reference Gelfert17], and [Reference Yang44] for other results related to Katok’s approximation construction of
![]() $C^{1+\alpha }$
maps.
$C^{1+\alpha }$
maps.
A natural question is how large is that part of the dynamics described by these horseshoes. So, it is interesting to estimate the Hausdorff dimension of the stable and/or unstable Cantor sets of a horseshoe. If
![]() $\mu $
is a Sinai–Ruelle–Bowen (SRB) measure (that is, a measure with a particular absolute continuity property on unstable manifolds; see [Reference Barreira and Pesin6] for precise definitions), it was shown in [Reference Sánchez-Salas36] that
$\mu $
is a Sinai–Ruelle–Bowen (SRB) measure (that is, a measure with a particular absolute continuity property on unstable manifolds; see [Reference Barreira and Pesin6] for precise definitions), it was shown in [Reference Sánchez-Salas36] that
![]() $\mu $
can be approximated by ergodic measures supported on horseshoes with arbitrarily large unstable dimensions, which generalized Mendoza’s result in [Reference Mendoza26] for diffeomorphisms in a higher dimensional manifold. The approach in [Reference Sánchez-Salas36] was based on Markov towers that can be described by horseshoes with infinitely many branches and variable return times. However, there is an essential mistake in the proof of the key proposition [Reference Sánchez-Salas36, Proposition 5.1]. The authors in [Reference Wang, Qu and Cao42] proved the same result by a different method. They used the u-Gibbs property of the conditional measure of the equilibrium measure and the properties of the uniformly hyperbolic dynamical systems. Furthermore, in [Reference Wang, Qu and Cao42], the authors proved that the Hausdorff dimension of
$\mu $
can be approximated by ergodic measures supported on horseshoes with arbitrarily large unstable dimensions, which generalized Mendoza’s result in [Reference Mendoza26] for diffeomorphisms in a higher dimensional manifold. The approach in [Reference Sánchez-Salas36] was based on Markov towers that can be described by horseshoes with infinitely many branches and variable return times. However, there is an essential mistake in the proof of the key proposition [Reference Sánchez-Salas36, Proposition 5.1]. The authors in [Reference Wang, Qu and Cao42] proved the same result by a different method. They used the u-Gibbs property of the conditional measure of the equilibrium measure and the properties of the uniformly hyperbolic dynamical systems. Furthermore, in [Reference Wang, Qu and Cao42], the authors proved that the Hausdorff dimension of
![]() $\mu $
can be approximated gradually by the Hausdorff dimension of the horseshoes
$\mu $
can be approximated gradually by the Hausdorff dimension of the horseshoes
![]() $\{\Lambda _n\}$
provided that the stable direction is one dimension. See also [Reference Luzzatto and Sanchez-Salas24, Reference Mendoza25, Reference Mendoza27, Reference Morris and Shmerkin29, Reference Sánchez-Salas37, Reference Sánchez-Salas38] that represent works close to this topic.
$\{\Lambda _n\}$
provided that the stable direction is one dimension. See also [Reference Luzzatto and Sanchez-Salas24, Reference Mendoza25, Reference Mendoza27, Reference Morris and Shmerkin29, Reference Sánchez-Salas37, Reference Sánchez-Salas38] that represent works close to this topic.
In this work, our main task is to compare the dimension of the horseshoes
![]() $\{\Lambda _n\}$
and the given hyperbolic ergodic measure
$\{\Lambda _n\}$
and the given hyperbolic ergodic measure
![]() $\mu $
of a
$\mu $
of a
![]() $C^{r}$
(
$C^{r}$
(
![]() $r\ge 1$
) diffeomorphism in a more general setting where
$r\ge 1$
) diffeomorphism in a more general setting where
![]() $\mu $
may not be an SRB measure. For a non-conformal repeller
$\mu $
may not be an SRB measure. For a non-conformal repeller
![]() $\Lambda $
of a
$\Lambda $
of a
![]() $C^{1+\alpha }$
map, using the approximation result in [Reference Cao, Pesin and Zhao11], we show that the Lyapunov dimension (see equation (3.1) for the definition) of an f-invariant ergodic measure
$C^{1+\alpha }$
map, using the approximation result in [Reference Cao, Pesin and Zhao11], we show that the Lyapunov dimension (see equation (3.1) for the definition) of an f-invariant ergodic measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\Lambda $
can be approximated gradually by the Carathéodory singular dimension (see equation (3.6) for the definition) of the horseshoes
$\Lambda $
can be approximated gradually by the Carathéodory singular dimension (see equation (3.6) for the definition) of the horseshoes
![]() $\{\Lambda _n\}$
. For a
$\{\Lambda _n\}$
. For a
![]() $C^{1+\alpha }$
diffeomorphism f preserving a hyperbolic ergodic measure
$C^{1+\alpha }$
diffeomorphism f preserving a hyperbolic ergodic measure
![]() $\mu $
of positive entropy, if
$\mu $
of positive entropy, if
![]() $(f, \mu )$
has only two Lyapunov exponents
$(f, \mu )$
has only two Lyapunov exponents
![]() $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
, then the Hausdorff or lower box or upper box dimension of
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
, then the Hausdorff or lower box or upper box dimension of
![]() $\mu $
can be approximated by the corresponding dimension of the horseshoes
$\mu $
can be approximated by the corresponding dimension of the horseshoes
![]() $\{\Lambda _n\}$
. The same statement holds true if f is a
$\{\Lambda _n\}$
. The same statement holds true if f is a
![]() $C^1$
diffeomorphism with a dominated Oseledec’s splitting with respect to
$C^1$
diffeomorphism with a dominated Oseledec’s splitting with respect to
![]() $\mu $
.
$\mu $
.
We arrange the paper as follows. In §2, we give some basic notions and properties about topological and measure theoretic pressures, and dimensions of sets and measures. Statements of our main results will be given in §3. In §4, we will give the detailed proofs of the main results.
2 Definitions and preliminaries
In this section, we recall the definitions of topological pressure and various dimensions of subsets and/or of invariant measures.
2.1 Topological and measure theoretic pressures
Let
![]() $f: X\to X$
be a continuous transformation on a compact metric space X equipped with metric d. A subset
$f: X\to X$
be a continuous transformation on a compact metric space X equipped with metric d. A subset
![]() $F\subset X$
is called an
$F\subset X$
is called an
![]() $(n, \epsilon )$
-separated set with respect to f if for any two different points
$(n, \epsilon )$
-separated set with respect to f if for any two different points
![]() $x,y\in F$
, we have
$x,y\in F$
, we have
![]() $d_n(x,y):=\max _{0\leq k\leq n-1}d(f^k(x), f^k(y))>\epsilon .$
A sequence of continuous functions
$d_n(x,y):=\max _{0\leq k\leq n-1}d(f^k(x), f^k(y))>\epsilon .$
A sequence of continuous functions
![]() $\Phi =\{\phi _n\}_{n\ge 1}$
is called sub-additive if
$\Phi =\{\phi _n\}_{n\ge 1}$
is called sub-additive if
Furthermore, a sequence of continuous functions
![]() $\Psi =\{\psi _n\}_{n\ge 1}$
is called super-additive if
$\Psi =\{\psi _n\}_{n\ge 1}$
is called super-additive if
![]() $-\Psi =\{-\psi _n\}_{n\ge 1}$
is sub-additive.
$-\Psi =\{-\psi _n\}_{n\ge 1}$
is sub-additive.
2.1.1 Topological pressure defined via separated sets
Given a sub-additive potential
![]() $\Phi =\{\phi _n\}_{n\ge 1}$
on X, put
$\Phi =\{\phi _n\}_{n\ge 1}$
on X, put
 $$ \begin{align*}P_n(f, \Phi, \epsilon)=\sup\bigg\{\sum_{x\in F}e^{\phi_n(x)}| F\ \mbox{is an}\ (n, \epsilon)\mbox{-separated subset of } X\bigg\}.\end{align*} $$
$$ \begin{align*}P_n(f, \Phi, \epsilon)=\sup\bigg\{\sum_{x\in F}e^{\phi_n(x)}| F\ \mbox{is an}\ (n, \epsilon)\mbox{-separated subset of } X\bigg\}.\end{align*} $$
Definition 2.1. We call the quantity
the sub-additive topological pressure of
![]() $(f,\Phi )$
.
$(f,\Phi )$
.
Remark 2.2. If
![]() $\varPhi =\{\varphi _n\}_{n\geq 1}$
is additive in the sense that
$\varPhi =\{\varphi _n\}_{n\geq 1}$
is additive in the sense that
![]() $\varphi _n(x)=\varphi (x)+\varphi (fx)+\cdots +\varphi (f^{n-1}x)\triangleq S_n\varphi (x)$
for some continuous function
$\varphi _n(x)=\varphi (x)+\varphi (fx)+\cdots +\varphi (f^{n-1}x)\triangleq S_n\varphi (x)$
for some continuous function
![]() $\varphi : X\to \mathbb {R}$
, we simply denote the topological pressure
$\varphi : X\to \mathbb {R}$
, we simply denote the topological pressure
![]() $P_{\mathrm {top}}(f, \varPhi )$
as
$P_{\mathrm {top}}(f, \varPhi )$
as
![]() $P_{\mathrm {top}}(f, \varphi )$
.
$P_{\mathrm {top}}(f, \varphi )$
.
Let
![]() $\mathcal {M}_f(X)$
denote the space of all f-invariant measures on X. For
$\mathcal {M}_f(X)$
denote the space of all f-invariant measures on X. For
![]() $\mu \in \mathcal {M}_f(X)$
, let
$\mu \in \mathcal {M}_f(X)$
, let
![]() $h_\mu (f)$
denote the metric entropy of f with respect to
$h_\mu (f)$
denote the metric entropy of f with respect to
![]() $\mu $
(see Walters’ book [Reference Walters39] for details of metric entropy), and let
$\mu $
(see Walters’ book [Reference Walters39] for details of metric entropy), and let
The existence of the above limit follows from a sub-additive argument. In [Reference Cao, Feng and Huang9], the authors proved the following variational principle.
Theorem 2.3. Let
![]() $f:X\to X$
be a continuous transformation on a compact metric space X, and
$f:X\to X$
be a continuous transformation on a compact metric space X, and
![]() $\Phi =\{\phi _n\}_{n\ge 1}$
a sub-additive potential on X, then we have
$\Phi =\{\phi _n\}_{n\ge 1}$
a sub-additive potential on X, then we have
Here we take the convention that
![]() $\sup \emptyset =-\infty $
.
$\sup \emptyset =-\infty $
.
Although it is unknown whether the variational principle holds for super-additive topological pressure, Cao, Pesin, and Zhao gave an alternative definition via variational principle in [Reference Cao, Pesin and Zhao11]. Given a sequence of super-additive continuous potentials
![]() $\Psi =\{\psi _n\}_{n\geq 1}$
on a compact dynamical system
$\Psi =\{\psi _n\}_{n\geq 1}$
on a compact dynamical system
![]() $(X, f)$
, the super-additive topological pressure of
$(X, f)$
, the super-additive topological pressure of
![]() $\Psi $
is defined as
$\Psi $
is defined as
where
 $$ \begin{align*}\mathcal{L}_*(\Psi,\mu)=\lim_{n\to\infty}\frac 1n \int\psi_n\,d\mu=\sup_{n\geq1}\frac 1n \int\psi_n\,d\mu.\end{align*} $$
$$ \begin{align*}\mathcal{L}_*(\Psi,\mu)=\lim_{n\to\infty}\frac 1n \int\psi_n\,d\mu=\sup_{n\geq1}\frac 1n \int\psi_n\,d\mu.\end{align*} $$
The second equality is due to the standard sub-additive argument.
2.1.2 Measure theoretic pressure
We first follow the approach in [Reference Pesin33] to give the definitions of topological pressures on arbitrary subsets. Given a sub-additive potential
![]() $\Phi =\{\phi _n\}_{n\ge 1}$
on X, a subset
$\Phi =\{\phi _n\}_{n\ge 1}$
on X, a subset
![]() $Z\subset X$
, and
$Z\subset X$
, and
![]() $\alpha \in \mathbb {R}$
, let
$\alpha \in \mathbb {R}$
, let
 $$ \begin{align*} \begin{aligned} M(Z,\Phi,\alpha,N,\epsilon)=\inf\bigg\{&\sum_i \exp\Big(-\alpha n_i+\sup_{y\in B_{n_i}(x_i,\epsilon)}\phi_{n_i}(y)\Big):\\ &\bigcup_{i}B_{n_i}(x_i,\epsilon)\supset Z, \, x_i\in X \text{ and } n_i\ge N \text{ for all } i\bigg\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} M(Z,\Phi,\alpha,N,\epsilon)=\inf\bigg\{&\sum_i \exp\Big(-\alpha n_i+\sup_{y\in B_{n_i}(x_i,\epsilon)}\phi_{n_i}(y)\Big):\\ &\bigcup_{i}B_{n_i}(x_i,\epsilon)\supset Z, \, x_i\in X \text{ and } n_i\ge N \text{ for all } i\bigg\}. \end{aligned} \end{align*} $$
Since
![]() $M(Z,\Phi ,\alpha ,N,\epsilon )$
is monotonically increasing with N, let
$M(Z,\Phi ,\alpha ,N,\epsilon )$
is monotonically increasing with N, let
We denote the jump-up point of
![]() $m(Z,\Phi ,\alpha ,\epsilon )$
by
$m(Z,\Phi ,\alpha ,\epsilon )$
by
Definition 2.4. We call the quantity
the topological pressure of
![]() $(f, \Phi )$
on the set Z (see [Reference Feng and Huang14] for the weighted version of this quantity).
$(f, \Phi )$
on the set Z (see [Reference Feng and Huang14] for the weighted version of this quantity).
Similarly, for
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $Z\subset X$
, define
$Z\subset X$
, define
 $$ \begin{align*} R(Z,\Phi,\alpha,N,\epsilon)=\inf\bigg\{&\sum_i \exp\Big(-\alpha N+\sup_{y\in B_{N}(x_i,\epsilon)} \phi_N(y) \Big):\\ &\bigcup_{i}B_{N}(x_i,\epsilon)\supset Z,\,x_i\in X\bigg\}. \end{align*} $$
$$ \begin{align*} R(Z,\Phi,\alpha,N,\epsilon)=\inf\bigg\{&\sum_i \exp\Big(-\alpha N+\sup_{y\in B_{N}(x_i,\epsilon)} \phi_N(y) \Big):\\ &\bigcup_{i}B_{N}(x_i,\epsilon)\supset Z,\,x_i\in X\bigg\}. \end{align*} $$
We set
 $$ \begin{align*} \begin{aligned} \underline{r}(Z,\Phi,\alpha,\epsilon) &=\liminf_{N\rightarrow\infty}R(Z,\Phi,\alpha,N,\epsilon), \\ \overline{r}(Z,\Phi,\alpha,\epsilon) &=\limsup_{N\rightarrow\infty}R(Z,\Phi,\alpha,N,\epsilon) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \underline{r}(Z,\Phi,\alpha,\epsilon) &=\liminf_{N\rightarrow\infty}R(Z,\Phi,\alpha,N,\epsilon), \\ \overline{r}(Z,\Phi,\alpha,\epsilon) &=\limsup_{N\rightarrow\infty}R(Z,\Phi,\alpha,N,\epsilon) \end{aligned} \end{align*} $$
and define the jump-up points of
![]() $\underline {r}(Z,\Phi ,\alpha ,\epsilon )$
and
$\underline {r}(Z,\Phi ,\alpha ,\epsilon )$
and
![]() $\overline {r}(Z,\Phi ,\alpha ,\epsilon )$
as
$\overline {r}(Z,\Phi ,\alpha ,\epsilon )$
as
 $$ \begin{align*} \begin{aligned} \underline{CP}_{Z}(f,\Phi,\epsilon)&=\inf\{\alpha: \underline{r}(Z,\Phi,\alpha,\epsilon)=0\} =\sup\{ \alpha: \underline{r}(Z,\Phi,\alpha,\epsilon)=+\infty \},\\ \overline{CP}_{Z}(f,\Phi,\epsilon)&=\inf \{ \alpha: \overline{r}(Z,\Phi,\alpha,\epsilon)=0 \} =\sup\{ \alpha: \overline{r}(Z,\Phi,\alpha,\epsilon)=+\infty\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \underline{CP}_{Z}(f,\Phi,\epsilon)&=\inf\{\alpha: \underline{r}(Z,\Phi,\alpha,\epsilon)=0\} =\sup\{ \alpha: \underline{r}(Z,\Phi,\alpha,\epsilon)=+\infty \},\\ \overline{CP}_{Z}(f,\Phi,\epsilon)&=\inf \{ \alpha: \overline{r}(Z,\Phi,\alpha,\epsilon)=0 \} =\sup\{ \alpha: \overline{r}(Z,\Phi,\alpha,\epsilon)=+\infty\}, \end{aligned} \end{align*} $$
respectively.
Definition 2.5. We call the quantities
the lower and upper topological pressures of
![]() $(f,\Phi )$
on the set Z, respectively.
$(f,\Phi )$
on the set Z, respectively.
Given an f-invariant measure
![]() $\mu $
, let
$\mu $
, let
and then we call the quantity
the measure theoretic pressure of
![]() $(f,\Phi )$
with respect to
$(f,\Phi )$
with respect to
![]() $\mu $
. Let further
$\mu $
. Let further
 $$ \begin{gather*} \underline{CP}_{\mu}(f,\Phi,\epsilon) =\lim_{\delta\to 0}\inf\{\underline{CP}_{Z}(f,\Phi,\epsilon) \colon\mu (Z)\ge 1-\delta\}, \\ \overline{CP}_{\mu}(f,\Phi,\epsilon) =\lim_{\delta\to 0}\inf\{\overline{CP}_{Z}(f,\Phi,\epsilon) \colon\mu (Z)\ge 1-\delta\}. \end{gather*} $$
$$ \begin{gather*} \underline{CP}_{\mu}(f,\Phi,\epsilon) =\lim_{\delta\to 0}\inf\{\underline{CP}_{Z}(f,\Phi,\epsilon) \colon\mu (Z)\ge 1-\delta\}, \\ \overline{CP}_{\mu}(f,\Phi,\epsilon) =\lim_{\delta\to 0}\inf\{\overline{CP}_{Z}(f,\Phi,\epsilon) \colon\mu (Z)\ge 1-\delta\}. \end{gather*} $$
We call the quantities
the lower and upper measure theoretic pressures of
![]() $(f,\Phi )$
with respect to
$(f,\Phi )$
with respect to
![]() $\mu $
, respectively. It is proved in [Reference Cao, Hu and Zhao10, Theorem A] that
$\mu $
, respectively. It is proved in [Reference Cao, Hu and Zhao10, Theorem A] that
for any f-invariant ergodic measure
![]() $\mu $
with
$\mu $
with
![]() $\mathcal {L}_*(\Phi ,\mu )\neq -\infty $
.
$\mathcal {L}_*(\Phi ,\mu )\neq -\infty $
.
Remark 2.6. In fact, one can show that
where
![]() $\mathcal {P}$
denotes either P or
$\mathcal {P}$
denotes either P or
![]() $\underline {CP}$
or
$\underline {CP}$
or
![]() $\overline {CP}$
, see [Reference Zhao46] for a proof.
$\overline {CP}$
, see [Reference Zhao46] for a proof.
2.2 Dimensions of sets and measures
Now we recall the definitions of Hausdorff and box dimensions of subsets and measures. Given a subset
![]() $Z\subset X$
, for any
$Z\subset X$
, for any
![]() $s\ge 0$
, let
$s\ge 0$
, let
 $$ \begin{align*} \mathcal{H}_{\delta}^{s}(Z)=\inf\bigg\{\sum\limits_{i=1}^{\infty}(\mbox{diam}\, U_{i})^{s}:\{U_{i}\}_{i\ge1}\ \mbox{is a cover of } Z \ \mbox{with } \mbox{diam}\,U_{i}\le \delta, \text{ for all } i\ge1 \bigg\} \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\delta}^{s}(Z)=\inf\bigg\{\sum\limits_{i=1}^{\infty}(\mbox{diam}\, U_{i})^{s}:\{U_{i}\}_{i\ge1}\ \mbox{is a cover of } Z \ \mbox{with } \mbox{diam}\,U_{i}\le \delta, \text{ for all } i\ge1 \bigg\} \end{align*} $$
and
The above limit exists, although the limit may be infinity. We call
![]() $\mathcal {H}^{s}(Z)$
the s-dimensional Hausdorff measure of Z.
$\mathcal {H}^{s}(Z)$
the s-dimensional Hausdorff measure of Z.
Definition 2.7. The following jump-up value of
![]() $\mathcal {H}^{s}(Z)$
$\mathcal {H}^{s}(Z)$
is called the Hausdorff dimension of Z. The lower and upper box dimension of Z are defined respectively by
where
![]() $N(Z,\delta )$
denotes the least number of balls of radius
$N(Z,\delta )$
denotes the least number of balls of radius
![]() $\delta $
that are needed to cover the set Z. If
$\delta $
that are needed to cover the set Z. If
![]() $\underline {\dim }_BZ=\overline {\dim }_BZ$
, we will denote the common value by
$\underline {\dim }_BZ=\overline {\dim }_BZ$
, we will denote the common value by
![]() $\dim_{B}{\kern-1pt}Z$
and call it the box dimension of Z.
$\dim_{B}{\kern-1pt}Z$
and call it the box dimension of Z.
The following two results are well known in the field of fractal geometry, e.g. see Falconer’s book [Reference Falconer13] for proofs.
Lemma 2.8. Let X and Y be metric spaces. For any
![]() $r\in (0, 1)$
,
$r\in (0, 1)$
,
![]() $\Phi : X \to Y$
is an onto,
$\Phi : X \to Y$
is an onto,
![]() $(C, r)$
-H
$(C, r)$
-H
![]() $\ddot {o}$
lder continuous map for some
$\ddot {o}$
lder continuous map for some
![]() $C>0$
. Then
$C>0$
. Then
Corollary 2.9. Let X and Y be metric spaces, and let
![]() $\Phi : X \to Y$
be an onto, Lipschitz continuous map. Then
$\Phi : X \to Y$
be an onto, Lipschitz continuous map. Then
Given a Borel probability measure
![]() $\mu $
on X, the quantity
$\mu $
on X, the quantity
 $$ \begin{align*} \begin{aligned} \dim_{H}{\kern-1pt}\mu &=\inf\{\dim_{H}{\kern-1pt}Z: Z\subset X \text{ and }\mu(Z)=1\}\\ &=\lim_{\delta\to 0} \inf\{\dim_{H}{\kern-1pt}Z: Z\subset X \text{ and }\mu(Z)\ge1-\delta\} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \dim_{H}{\kern-1pt}\mu &=\inf\{\dim_{H}{\kern-1pt}Z: Z\subset X \text{ and }\mu(Z)=1\}\\ &=\lim_{\delta\to 0} \inf\{\dim_{H}{\kern-1pt}Z: Z\subset X \text{ and }\mu(Z)\ge1-\delta\} \end{aligned} \end{align*} $$
is called the Hausdorff dimension of the measure
![]() $\mu $
. Similarly, we call the two quantities
$\mu $
. Similarly, we call the two quantities
and
the lower box dimension and upper box dimension of
![]() $\mu $
, respectively.
$\mu $
, respectively.
If
![]() $\mu $
is a finite measure on X and there exists
$\mu $
is a finite measure on X and there exists
![]() $d\geq 0$
such that
$d\geq 0$
such that
for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
, then
$x\in X$
, then
This criterion was established by Young in [Reference Young45].
3 Statements of main results
In this section, we will give the statements of the main results in this paper, and the proof will be postponed to the next section.
3.1 Dimension approximation for uniformly expanding systems
Let
![]() $f:M\to M$
be a smooth map of an
$f:M\to M$
be a smooth map of an
![]() $m_0$
-dimensional compact smooth Riemannian manifold M, and
$m_0$
-dimensional compact smooth Riemannian manifold M, and
![]() $\Lambda $
a compact f-invariant subset of M. Let
$\Lambda $
a compact f-invariant subset of M. Let
![]() $\mathcal {M}_f(\Lambda )$
and
$\mathcal {M}_f(\Lambda )$
and
![]() $\mathcal {E}_f(\Lambda )$
denote respectively the set of all f-invariant measures and ergodic measures on
$\mathcal {E}_f(\Lambda )$
denote respectively the set of all f-invariant measures and ergodic measures on
![]() $\Lambda $
.
$\Lambda $
.
3.1.1 Definitions of repeller and Lyapunov dimension
We call
![]() $\Lambda $
a repeller for f or f is expanding on
$\Lambda $
a repeller for f or f is expanding on
![]() $\Lambda $
if:
$\Lambda $
if:
-
(1) there exists an open neighborhood U of
 $\Lambda $
such that
$\Lambda $
such that
 $\Lambda =\{x\in U: f^n(x)\in U \text {for all}\,\, n\ge 0\}$
;
$\Lambda =\{x\in U: f^n(x)\in U \text {for all}\,\, n\ge 0\}$
; -
(2) there is
 $\kappa> 1 $
such that where
$\kappa> 1 $
such that where $$ \begin{align*} \|D_xf (v) \| \ge \kappa \|v\| \quad \text{for all } x \in \Lambda \text{ and } v \in T_xM, \end{align*} $$
$$ \begin{align*} \|D_xf (v) \| \ge \kappa \|v\| \quad \text{for all } x \in \Lambda \text{ and } v \in T_xM, \end{align*} $$
 $\|\cdot \|$
is the norm induced by the Riemannian metric on M, and
$\|\cdot \|$
is the norm induced by the Riemannian metric on M, and
 $D_xf:T_xM\rightarrow T_{f(x)}M$
is the differential operator.
$D_xf:T_xM\rightarrow T_{f(x)}M$
is the differential operator.
Given an f-invariant ergodic measure
![]() $\mu $
supported on the repeller
$\mu $
supported on the repeller
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $\unicode{x3bb} _1(\mu )\ge \unicode{x3bb} _2(\mu )\ge \cdots \ge \unicode{x3bb} _{m_0}(\mu )$
and
$\unicode{x3bb} _1(\mu )\ge \unicode{x3bb} _2(\mu )\ge \cdots \ge \unicode{x3bb} _{m_0}(\mu )$
and
![]() $h_{\mu }(f)$
denote the Lyapunov exponents and the measure theoretic entropy of
$h_{\mu }(f)$
denote the Lyapunov exponents and the measure theoretic entropy of
![]() $(f,\mu )$
, respectively. We refer the reader to [Reference Barreira and Pesin6, Reference Walters39] for detailed descriptions of Lyapunov exponents and the measure theoretic entropy. We further define the Lyapunov dimension of
$(f,\mu )$
, respectively. We refer the reader to [Reference Barreira and Pesin6, Reference Walters39] for detailed descriptions of Lyapunov exponents and the measure theoretic entropy. We further define the Lyapunov dimension of
![]() $\mu $
as follows:
$\mu $
as follows:

where
![]() $\ell =\max \{i: \unicode{x3bb} _{m_0}(\mu )+\cdots +\unicode{x3bb} _{m_0-i +1}(\mu )\le h_{\mu }(f)\}$
.
$\ell =\max \{i: \unicode{x3bb} _{m_0}(\mu )+\cdots +\unicode{x3bb} _{m_0-i +1}(\mu )\le h_{\mu }(f)\}$
.
The original definition of Lyapunov dimension in [Reference Alexander and Yorke1, Reference Kaplan, Yorke, Peitgen and Walther19, Reference Ledrappier22] is defined only for hyperbolic systems as follows: assume that
![]() $\nu $
is an ergodic measure of a smooth diffeomorphism f with Lyapunov exponents
$\nu $
is an ergodic measure of a smooth diffeomorphism f with Lyapunov exponents
![]() $\unicode{x3bb} _1\ge \cdots \ge \unicode{x3bb} _u>0\ge \unicode{x3bb} _{u+1}\ge \cdots \ge \unicode{x3bb} _{m_0}$
, then the the Lyapunov dimension is
$\unicode{x3bb} _1\ge \cdots \ge \unicode{x3bb} _u>0\ge \unicode{x3bb} _{u+1}\ge \cdots \ge \unicode{x3bb} _{m_0}$
, then the the Lyapunov dimension is
where
![]() $\ell =\max \{i:\unicode{x3bb} _1+\cdots +\unicode{x3bb} _i\ge 0\}$
. Assume further that
$\ell =\max \{i:\unicode{x3bb} _1+\cdots +\unicode{x3bb} _i\ge 0\}$
. Assume further that
![]() $\nu $
is an SRB measure, then
$\nu $
is an SRB measure, then
![]() $h_\nu (f)=\unicode{x3bb} _1+\cdots +\unicode{x3bb} _u$
. As a consequence,
$h_\nu (f)=\unicode{x3bb} _1+\cdots +\unicode{x3bb} _u$
. As a consequence,
and
![]() $\ell =\max \{i:-\unicode{x3bb} _{u+1}-\cdots -\unicode{x3bb} _i\ge h_\nu (f)\}$
. Hence, the definition in equation (3.1) is a reasonable substitute. For a
$\ell =\max \{i:-\unicode{x3bb} _{u+1}-\cdots -\unicode{x3bb} _i\ge h_\nu (f)\}$
. Hence, the definition in equation (3.1) is a reasonable substitute. For a
![]() $C^1$
expanding map f, Feng and Simon [Reference Feng and Simon15] defined the Lyapunov dimension of an ergodic measure as the zero of the measure theoretic pressure
$C^1$
expanding map f, Feng and Simon [Reference Feng and Simon15] defined the Lyapunov dimension of an ergodic measure as the zero of the measure theoretic pressure
![]() $P_\mu (f,\Phi _f(t))=0$
(see equation (3.4)). In this paper, we will prove that the unique solution of the equation
$P_\mu (f,\Phi _f(t))=0$
(see equation (3.4)). In this paper, we will prove that the unique solution of the equation
![]() $P_\mu (f,\Phi _f(t))=0$
is indeed our definition of Lyapunov dimension (see Theorem A). Furthermore, this paper shows that the Lyapunov dimension of an ergodic measure defined in equation (3.1) is equal to its Carathéodory singular dimension (see Proposition 3.2), so the Carathéodory singular dimension (see §3.1.3 for the detailed definition) can be regarded as a geometric explanation of the Lyapunov dimension.
$P_\mu (f,\Phi _f(t))=0$
is indeed our definition of Lyapunov dimension (see Theorem A). Furthermore, this paper shows that the Lyapunov dimension of an ergodic measure defined in equation (3.1) is equal to its Carathéodory singular dimension (see Proposition 3.2), so the Carathéodory singular dimension (see §3.1.3 for the detailed definition) can be regarded as a geometric explanation of the Lyapunov dimension.
3.1.2 Singular valued potentials
Let
![]() $\Lambda $
be a repeller of a smooth map
$\Lambda $
be a repeller of a smooth map
![]() $f:M\to M$
. Given
$f:M\to M$
. Given
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $n\ge 1$
, consider the differentiable operator
$n\ge 1$
, consider the differentiable operator
![]() $D_xf^n: T_xM\to T_{f^n(x)}M$
and denote the singular values of
$D_xf^n: T_xM\to T_{f^n(x)}M$
and denote the singular values of
![]() $D_xf^n$
(square roots of the eigenvalues of
$D_xf^n$
(square roots of the eigenvalues of
![]() $(D_xf^n)^*D_xf^n$
) in the decreasing order by
$(D_xf^n)^*D_xf^n$
) in the decreasing order by
For
![]() $t\in [0,m_0]$
, set
$t\in [0,m_0]$
, set
 $$ \begin{align} \varphi^{t}(x,f^n): =\sum_{i=m_0-[t]+1}^{m_0}\log\alpha_i(x,f^n) +(t-[t])\log\alpha_{m_0-[t]}(x,f^n). \end{align} $$
$$ \begin{align} \varphi^{t}(x,f^n): =\sum_{i=m_0-[t]+1}^{m_0}\log\alpha_i(x,f^n) +(t-[t])\log\alpha_{m_0-[t]}(x,f^n). \end{align} $$
Since f is smooth, the functions
![]() $x\mapsto \alpha _i(x,f^n)$
,
$x\mapsto \alpha _i(x,f^n)$
,
![]() $x\mapsto \varphi ^t(x,f^n)$
are continuous for any
$x\mapsto \varphi ^t(x,f^n)$
are continuous for any
![]() $n\ge 1$
. It is easy to see that for all
$n\ge 1$
. It is easy to see that for all
![]() $n,\ell \in \mathbb {N}$
,
$n,\ell \in \mathbb {N}$
,
It follows that the sequence of functions
is sub-additive, which is called the sub-additive singular valued potentials.
3.1.3 Carathéodory singular dimension
We recall the definition of Carathéodory singular dimension of a repeller which is introduced in [Reference Cao, Pesin and Zhao11].
Let
![]() $\Phi _f(t)=\{-\varphi ^{t}(\cdot ,f^n)\}_{n\ge 1}$
. Given a subset
$\Phi _f(t)=\{-\varphi ^{t}(\cdot ,f^n)\}_{n\ge 1}$
. Given a subset
![]() $Z\subseteq \Lambda $
, for each small number
$Z\subseteq \Lambda $
, for each small number
![]() $r>0$
, let
$r>0$
, let
 $$ \begin{align*} m(Z,t,r):=\lim_{N\to\infty}\inf\bigg\{\sum_i\exp\Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^{t}(y,f^{n_i})\Big)\bigg\}, \end{align*} $$
$$ \begin{align*} m(Z,t,r):=\lim_{N\to\infty}\inf\bigg\{\sum_i\exp\Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^{t}(y,f^{n_i})\Big)\bigg\}, \end{align*} $$
where the infimum is taken over all collections
![]() $\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
$\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
![]() $x_i\in \Lambda $
,
$x_i\in \Lambda $
,
![]() $n_i\ge N$
that cover Z. It is easy to see that there is a jump-up value
$n_i\ge N$
that cover Z. It is easy to see that there is a jump-up value
The quantity
is called the Carathéodory singular dimension of Z. Particularly, the Carathéodory singular dimension of the repeller
![]() $\Lambda $
is independent of the parameter r for small values of
$\Lambda $
is independent of the parameter r for small values of
![]() $r>0$
(see [Reference Cao, Pesin and Zhao11, Theorem 4.1]).
$r>0$
(see [Reference Cao, Pesin and Zhao11, Theorem 4.1]).
For each f-invariant measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\Lambda $
, let
$\Lambda $
, let
and the quantity
is called the Carathéodory singular dimension of the measure
![]() $\mu $
.
$\mu $
.
3.1.4 Approximation of Carathéodory singular dimension of repellers
Given a repeller
![]() $\Lambda $
of a
$\Lambda $
of a
![]() $C^{1+\alpha }$
map f, the following result shows that the zero of the measure theoretic pressure function is exactly the Lyapunov dimension of an ergodic measure
$C^{1+\alpha }$
map f, the following result shows that the zero of the measure theoretic pressure function is exactly the Lyapunov dimension of an ergodic measure
![]() $\mu \in \mathcal {E}_f(\Lambda )$
, and the Lyapunov dimension of an ergodic measure of positive entropy can be approximated by the Carathéodory singular dimension of a sequence of invariant sets. Recall that
$\mu \in \mathcal {E}_f(\Lambda )$
, and the Lyapunov dimension of an ergodic measure of positive entropy can be approximated by the Carathéodory singular dimension of a sequence of invariant sets. Recall that
![]() $ \Phi _f(t):=\{-\varphi ^t(\cdot ,f^n)\}_{n\ge 1} $
is the sub-additive singular valued potentials with respect to f (see the definition in equation (3.4)).
$ \Phi _f(t):=\{-\varphi ^t(\cdot ,f^n)\}_{n\ge 1} $
is the sub-additive singular valued potentials with respect to f (see the definition in equation (3.4)).
The following result gives a measure theoretic version of Bowen’s equation, that is, the unique zero of the measure theoretic pressure is exactly the Lyapunov dimension of an ergodic measure.
Proposition 3.1. Let
![]() $f: M\to M$
be a
$f: M\to M$
be a
![]() $C^{1}$
map of an
$C^{1}$
map of an
![]() $m_0$
-dimensional compact smooth Riemannian manifold M, and
$m_0$
-dimensional compact smooth Riemannian manifold M, and
![]() $\Lambda $
a repeller of f. For every f-invariant ergodic measure
$\Lambda $
a repeller of f. For every f-invariant ergodic measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\Lambda $
, we have that
$\Lambda $
, we have that
where
![]() $s_{\mu }$
is the unique root of the equation
$s_{\mu }$
is the unique root of the equation
![]() $P_\mu (f, \Phi _f(t))=0$
.
$P_\mu (f, \Phi _f(t))=0$
.
For an ergodic measure supported on a repeller with positive entropy, one can find a sequence of compact invariant sets whose Carathéodory singular dimension gradually approaches the Lyapunov dimension of the measure.
Theorem A. Let
![]() $f: M\to M$
be a
$f: M\to M$
be a
![]() $C^{1+\alpha }$
map of an
$C^{1+\alpha }$
map of an
![]() $m_0$
-dimensional compact smooth Riemannian manifold M and
$m_0$
-dimensional compact smooth Riemannian manifold M and
![]() $\Lambda $
a repeller of f, and let
$\Lambda $
a repeller of f, and let
![]() $\mu $
be an f-invariant ergodic measure on
$\mu $
be an f-invariant ergodic measure on
![]() $\Lambda $
with
$\Lambda $
with
![]() $h_{\mu }(f)>0$
. For any
$h_{\mu }(f)>0$
. For any
![]() $\varepsilon>0$
, there exists an f-invariant compact subset
$\varepsilon>0$
, there exists an f-invariant compact subset
![]() $\Lambda _\varepsilon \subset \Lambda $
such that
$\Lambda _\varepsilon \subset \Lambda $
such that
![]() $\dim _C{\kern-1pt} \Lambda _\varepsilon \rightarrow \dim _{\mathrm {L}}{\kern-1pt}\mu $
as
$\dim _C{\kern-1pt} \Lambda _\varepsilon \rightarrow \dim _{\mathrm {L}}{\kern-1pt}\mu $
as
![]() $\varepsilon $
approaches zero.
$\varepsilon $
approaches zero.
Some comments on the previous theorem are in order. First, the map of higher smoothness
![]() $C^{1+\alpha }$
is crucial as it allows us to use some powerful results of Pesin theory. Second, if f is a local diffeomorphism preserving an ergodic expanding measure
$C^{1+\alpha }$
is crucial as it allows us to use some powerful results of Pesin theory. Second, if f is a local diffeomorphism preserving an ergodic expanding measure
![]() $\mu $
of positive entropy, that is,
$\mu $
of positive entropy, that is,
![]() $(f,\mu )$
has only positive Lyapunov exponent, in this case, one can also obtain an approximation result as in [Reference Cao, Pesin and Zhao11] so that we can obtain the second statement in the previous theorem in this setting. In [Reference Sánchez-Salas37], for a
$(f,\mu )$
has only positive Lyapunov exponent, in this case, one can also obtain an approximation result as in [Reference Cao, Pesin and Zhao11] so that we can obtain the second statement in the previous theorem in this setting. In [Reference Sánchez-Salas37], for a
![]() $C^2$
interval map f with finitely many non-degenerate critical points, the author proved that the Hausdorff dimension of an expanding measure
$C^2$
interval map f with finitely many non-degenerate critical points, the author proved that the Hausdorff dimension of an expanding measure
![]() $\mu $
can be approximated gradually by the Hausdorff dimension of a sequence of repellers.
$\mu $
can be approximated gradually by the Hausdorff dimension of a sequence of repellers.
For each f-invariant ergodic measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\Lambda $
, the following result shows that the Carathéodory singular dimension of
$\Lambda $
, the following result shows that the Carathéodory singular dimension of
![]() $\mu $
is exactly its Lyapunov dimension.
$\mu $
is exactly its Lyapunov dimension.
Proposition 3.2. Let
![]() $f: M\to M$
be a
$f: M\to M$
be a
![]() $C^{1}$
map of an
$C^{1}$
map of an
![]() $m_0$
-dimensional compact smooth Riemannian manifold M, and
$m_0$
-dimensional compact smooth Riemannian manifold M, and
![]() $\Lambda $
a repeller for f. Then the following statements hold:
$\Lambda $
a repeller for f. Then the following statements hold:
-
(1) for each subset
 $Z\subset \Lambda $
, we have that where
$Z\subset \Lambda $
, we have that where $$ \begin{align*} \dim_C{\kern-1pt} Z=t_Z, \end{align*} $$
$$ \begin{align*} \dim_C{\kern-1pt} Z=t_Z, \end{align*} $$
 $t_Z$
is the unique root of the equation
$t_Z$
is the unique root of the equation
 $P_Z(f, \Phi _f(t))=0$
;
$P_Z(f, \Phi _f(t))=0$
;
-
(2) for each f-invariant ergodic measure
 $\mu $
supported on
$\mu $
supported on
 $\Lambda $
, we have that
$\Lambda $
, we have that  $$ \begin{align*} \dim_C{\kern-1pt}\mu=\dim_{\mathrm{L}}{\kern-1pt}\mu. \end{align*} $$
$$ \begin{align*} \dim_C{\kern-1pt}\mu=\dim_{\mathrm{L}}{\kern-1pt}\mu. \end{align*} $$
3.2 Dimension approximation in non-uniformly hyperbolic systems
In this section, we first recall an approximation result in non-uniformly hyperbolic systems that is proved by Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson2], then we give the statement of our dimension approximation result in non-uniformly hyperbolic systems.
3.2.1 Lyapunov exponents and holonomy maps
Let
![]() $f: M\to M$
be a diffeomorphism on an
$f: M\to M$
be a diffeomorphism on an
![]() $m_0$
-dimensional compact smooth Riemannian manifold M. By Oseledec’s multiplicative ergodic theorem (see [Reference Oseledec30]), there exists a total measure set
$m_0$
-dimensional compact smooth Riemannian manifold M. By Oseledec’s multiplicative ergodic theorem (see [Reference Oseledec30]), there exists a total measure set
![]() $\mathcal {O}\subset M$
such that for each
$\mathcal {O}\subset M$
such that for each
![]() $x \in \mathcal {O}$
and each invariant measure
$x \in \mathcal {O}$
and each invariant measure
![]() $\mu $
, there exist positive integers
$\mu $
, there exist positive integers
![]() $d_1(x),d_2(x),\ldots , d_{p(x)}(x)$
, numbers
$d_1(x),d_2(x),\ldots , d_{p(x)}(x)$
, numbers
![]() $\unicode{x3bb} _1(x)>\unicode{x3bb} _2(x)>\cdots >\unicode{x3bb} _{p(x)}(x)$
, and a splitting
$\unicode{x3bb} _1(x)>\unicode{x3bb} _2(x)>\cdots >\unicode{x3bb} _{p(x)}(x)$
, and a splitting
which satisfy that:
-
(1)
 $D_xf E_i(x)=E_i(f(x))$
for each i and
$D_xf E_i(x)=E_i(f(x))$
for each i and
 $\sum _{i=1}^{p(x)}d_i(x)=m_0$
;
$\sum _{i=1}^{p(x)}d_i(x)=m_0$
; -
(2) for each
 $0\neq v\in E_i(x)$
, we have that
$0\neq v\in E_i(x)$
, we have that 
Here we call the numbers
![]() $\{\unicode{x3bb} _i(x)\}_{i=1}^{p(x)}$
the Lyapunov exponents of
$\{\unicode{x3bb} _i(x)\}_{i=1}^{p(x)}$
the Lyapunov exponents of
![]() $(f,\mu )$
. In the case that
$(f,\mu )$
. In the case that
![]() $\mu $
is an f-invariant ergodic measure, the numbers
$\mu $
is an f-invariant ergodic measure, the numbers
![]() $p(x)$
,
$p(x)$
,
![]() $\{d_i(x)\}$
, and
$\{d_i(x)\}$
, and
![]() $\{\unicode{x3bb} _i(x)\}$
are constants almost everywhere. We denote them simply by p,
$\{\unicode{x3bb} _i(x)\}$
are constants almost everywhere. We denote them simply by p,
![]() $\{d_i\}_{i=1}^p$
, and
$\{d_i\}_{i=1}^p$
, and
![]() $\{\unicode{x3bb} _i\}_{i=1}^p$
.
$\{\unicode{x3bb} _i\}_{i=1}^p$
.
A compact invariant subset
![]() $\Lambda \subset M$
is called a hyperbolic set if there exists a continuous splitting of the tangent bundle
$\Lambda \subset M$
is called a hyperbolic set if there exists a continuous splitting of the tangent bundle
![]() $T_\Lambda M = E^{s}\oplus E^{u}$
, and constants
$T_\Lambda M = E^{s}\oplus E^{u}$
, and constants
![]() $C> 0,\ 0 < \unicode{x3bb} < 1$
such that for every
$C> 0,\ 0 < \unicode{x3bb} < 1$
such that for every
![]() $x \in \Lambda $
:
$x \in \Lambda $
:
-
(1)
 $D_xf(E^s(x)) = E^s(f(x)),\ D_xf(E^u(x)) = E^u(f(x))$
;
$D_xf(E^s(x)) = E^s(f(x)),\ D_xf(E^u(x)) = E^u(f(x))$
; -
(2) for all
 $n \geq 0, \|D_xf^n(v)\|\leq C\unicode{x3bb} ^n\|v\|$
if
$n \geq 0, \|D_xf^n(v)\|\leq C\unicode{x3bb} ^n\|v\|$
if
 $v \in E^s(x)$
, and
$v \in E^s(x)$
, and
 $\|D_xf^{-n}(v)\|\leq C\unicode{x3bb} ^n\|v\|$
if
$\|D_xf^{-n}(v)\|\leq C\unicode{x3bb} ^n\|v\|$
if
 $v \in E^u(x)$
.
$v \in E^u(x)$
.
Given a point
![]() $x \in \Lambda $
, for each small
$x \in \Lambda $
, for each small
![]() $\beta>0$
, the local stable and unstable manifolds are defined as follows:
$\beta>0$
, the local stable and unstable manifolds are defined as follows:
 $$ \begin{align*} W_\beta^s(f,x)&=\{y \in M : d(f^n(x),f^n(y)) \leq \beta\ \text{ for all } n \geq 0\},\\ W_\beta^u(f,x)&=\{y \in M : d(f^{-n}(x),f^{-n}(y)) \leq \beta\ \text{ for all } n \geq 0\}. \end{align*} $$
$$ \begin{align*} W_\beta^s(f,x)&=\{y \in M : d(f^n(x),f^n(y)) \leq \beta\ \text{ for all } n \geq 0\},\\ W_\beta^u(f,x)&=\{y \in M : d(f^{-n}(x),f^{-n}(y)) \leq \beta\ \text{ for all } n \geq 0\}. \end{align*} $$
The global stable and unstable sets of
![]() $x\in \Lambda $
are given as follows:
$x\in \Lambda $
are given as follows:
A hyperbolic set is called locally maximal if there exists a neighborhood U of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\Lambda =\bigcap _{n\in \mathbb {Z}}f^n(U)$
. Recall that a horseshoe for a diffeomorphism f is a transitive, locally maximal hyperbolic set that is totally disconnected and not finite.
$\Lambda =\bigcap _{n\in \mathbb {Z}}f^n(U)$
. Recall that a horseshoe for a diffeomorphism f is a transitive, locally maximal hyperbolic set that is totally disconnected and not finite.
Let
![]() $W^u$
and
$W^u$
and
![]() $W^s$
be the unstable and stable foliations of a hyperbolic dynamical system
$W^s$
be the unstable and stable foliations of a hyperbolic dynamical system
![]() $(f, \Lambda )$
. For
$(f, \Lambda )$
. For
![]() $x, y\in \Lambda $
with x close to y, let
$x, y\in \Lambda $
with x close to y, let
![]() $W_\beta ^u(f, x)$
and
$W_\beta ^u(f, x)$
and
![]() $W_\beta ^s(f, x)$
be the local stable foliations of x and y. Define the map
$W_\beta ^s(f, x)$
be the local stable foliations of x and y. Define the map
![]() $h: W_\beta ^s(f, x) \to W_\beta ^s(f, y)$
sending z to
$h: W_\beta ^s(f, x) \to W_\beta ^s(f, y)$
sending z to
![]() $h(z)$
by sliding along the leaves of
$h(z)$
by sliding along the leaves of
![]() $W^u$
. The map h is called the holonomy map of
$W^u$
. The map h is called the holonomy map of
![]() $W^u$
. The map h is Lipschitz continuous if
$W^u$
. The map h is Lipschitz continuous if
where
![]() $z_1, z_2 \in W_\beta ^s(f, x)$
and
$z_1, z_2 \in W_\beta ^s(f, x)$
and
![]() $d_x, d_y$
are natural path metrics on
$d_x, d_y$
are natural path metrics on
![]() $W_\beta ^s(f, x)$
,
$W_\beta ^s(f, x)$
,
![]() $W_\beta ^u(f, y)$
with respect to a fixed Riemannian structure on M. The constant L is the Lipschitz constant, and it is independent of the choice of
$W_\beta ^u(f, y)$
with respect to a fixed Riemannian structure on M. The constant L is the Lipschitz constant, and it is independent of the choice of
![]() $W^s$
. The map h is
$W^s$
. The map h is
![]() $\alpha $
-Hölder continuous if
$\alpha $
-Hölder continuous if
where H is the Hölder constant. Similarly, we can define the holonomy map of
![]() $W^s$
.
$W^s$
.
3.2.2 Approximation of Lyapunov exponents and entropy
For a
![]() $C^{1+\alpha }$
diffeomorphism
$C^{1+\alpha }$
diffeomorphism
![]() $f:M\rightarrow M$
, Katok [Reference Katok20] showed that an f-invariant ergodic hyperbolic measure (a measure has no zero Lyapunov exponents) with positive metric entropy can be approximated by horseshoes. However, Katok’s result does not explicitly mention a control of the Oseledets splitting over the horseshoes. Recently, Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson2] showed that there is a dominated splitting over the horseshoes, with approximately the same Lyapunov exponents on each sub-bundle of the splitting.
$f:M\rightarrow M$
, Katok [Reference Katok20] showed that an f-invariant ergodic hyperbolic measure (a measure has no zero Lyapunov exponents) with positive metric entropy can be approximated by horseshoes. However, Katok’s result does not explicitly mention a control of the Oseledets splitting over the horseshoes. Recently, Avila, Crovisier, and Wilkinson [Reference Avila, Crovisier and Wilkinson2] showed that there is a dominated splitting over the horseshoes, with approximately the same Lyapunov exponents on each sub-bundle of the splitting.
Recall that
![]() $Df$
-invariant splitting on a compact f-invariant subset
$Df$
-invariant splitting on a compact f-invariant subset
![]() $\Lambda $
:
$\Lambda $
:
is a dominated splitting if there exists
![]() $N\ge 1$
such that for every
$N\ge 1$
such that for every
![]() $x\in \Lambda $
, any unit vectors
$x\in \Lambda $
, any unit vectors
![]() $v,w\in T_xM$
:
$v,w\in T_xM$
:
We write
![]() $E_1{\kern-1pt}\succeq{\kern-1pt} E_2 {\kern-1pt}\succeq{\kern-1pt} \cdots {\kern-1pt}\succeq{\kern-1pt} E_{\ell }$
. Furthermore, if there are numbers
$E_1{\kern-1pt}\succeq{\kern-1pt} E_2 {\kern-1pt}\succeq{\kern-1pt} \cdots {\kern-1pt}\succeq{\kern-1pt} E_{\ell }$
. Furthermore, if there are numbers
![]() $\unicode{x3bb} _1{\kern-1pt}>{\kern-1pt}\unicode{x3bb} _2{\kern-1pt}>{\kern-1pt}\cdots >\unicode{x3bb} _{\ell }$
, constants
$\unicode{x3bb} _1{\kern-1pt}>{\kern-1pt}\unicode{x3bb} _2{\kern-1pt}>{\kern-1pt}\cdots >\unicode{x3bb} _{\ell }$
, constants
![]() $C>0$
, and
$C>0$
, and
![]() ${0<\varepsilon < \min _{1\leq i < \ell } ({\unicode{x3bb} _{i}-\unicode{x3bb} _{i+1}})/{100}}$
such that for every
${0<\varepsilon < \min _{1\leq i < \ell } ({\unicode{x3bb} _{i}-\unicode{x3bb} _{i+1}})/{100}}$
such that for every
![]() $x\in \Lambda $
,
$x\in \Lambda $
,
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $1\leq j \leq \ell $
and each unit vector
$1\leq j \leq \ell $
and each unit vector
![]() $u\in E_j(x)$
, it holds that
$u\in E_j(x)$
, it holds that
then we say that
is a
![]() $\{\unicode{x3bb} _j\}_{1\leq j \leq \ell }$
-dominated splitting.
$\{\unicode{x3bb} _j\}_{1\leq j \leq \ell }$
-dominated splitting.
For the reader’s convenience, we recall Avila, Crovisier, and Wilkinson’s approximation results in the following, see [Reference Avila, Crovisier and Wilkinson2] for more details.
Theorem 3.3. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism, and
$C^{1+\alpha }$
diffeomorphism, and
![]() $\mu $
an f-invariant ergodic hyperbolic measure with
$\mu $
an f-invariant ergodic hyperbolic measure with
![]() $h_\mu (f)>0$
. For each
$h_\mu (f)>0$
. For each
![]() $\varepsilon>0$
and a weak-
$\varepsilon>0$
and a weak-
![]() $*$
neighborhood
$*$
neighborhood
![]() $\mathcal {V}$
of
$\mathcal {V}$
of
![]() $\mu $
in the space of f-invariant probability measures on M, there exists a compact set
$\mu $
in the space of f-invariant probability measures on M, there exists a compact set
![]() $\Lambda _\varepsilon ^*\subset M$
and a positive integer N such that the following properties hold:
$\Lambda _\varepsilon ^*\subset M$
and a positive integer N such that the following properties hold:
-
(1)
 $\Lambda _\varepsilon ^*$
is a locally maximal hyperbolic set and topologically mixing with respect to
$\Lambda _\varepsilon ^*$
is a locally maximal hyperbolic set and topologically mixing with respect to
 $f^N$
;
$f^N$
; -
(2)
 $h_{\mu }(f){\kern-1pt}-{\kern-1pt}\varepsilon {\kern-1pt}<{\kern-1pt}h_{top}(f,\Lambda _\varepsilon ){\kern-1pt}<{\kern-1pt}h_{\mu }(f)+\varepsilon $
, where
$h_{\mu }(f){\kern-1pt}-{\kern-1pt}\varepsilon {\kern-1pt}<{\kern-1pt}h_{top}(f,\Lambda _\varepsilon ){\kern-1pt}<{\kern-1pt}h_{\mu }(f)+\varepsilon $
, where
 $\Lambda _\varepsilon {\kern-1pt}={\kern-1pt}\Lambda _\varepsilon ^* \cup f(\Lambda _\varepsilon ^*) \cup \cdots f^{N-1}(\Lambda _\varepsilon ^*)$
;
$\Lambda _\varepsilon {\kern-1pt}={\kern-1pt}\Lambda _\varepsilon ^* \cup f(\Lambda _\varepsilon ^*) \cup \cdots f^{N-1}(\Lambda _\varepsilon ^*)$
; -
(3)
 $\Lambda _\varepsilon $
is
$\Lambda _\varepsilon $
is
 $\varepsilon $
-close to the support of
$\varepsilon $
-close to the support of
 $\mu $
in the Hausdorff distance;
$\mu $
in the Hausdorff distance; -
(4) each invariant probability measure supported on the horseshoe
 $\Lambda _\varepsilon $
lies in
$\Lambda _\varepsilon $
lies in
 $\mathcal {V}$
;
$\mathcal {V}$
; -
(5) if
 $\unicode{x3bb} _1>\unicode{x3bb} _2>\cdots >\unicode{x3bb} _{\ell }$
are the distinct Lyapunov exponents of
$\unicode{x3bb} _1>\unicode{x3bb} _2>\cdots >\unicode{x3bb} _{\ell }$
are the distinct Lyapunov exponents of
 $(f,\mu )$
, with multiplicities
$(f,\mu )$
, with multiplicities
 $d_1, d_2,\ldots , d_{\ell }$
, then there exists a
$d_1, d_2,\ldots , d_{\ell }$
, then there exists a
 $\{\unicode{x3bb} _j\}_{1\le j<\ell }$
-dominated splitting
$\{\unicode{x3bb} _j\}_{1\le j<\ell }$
-dominated splitting
 $T_{\Lambda _\varepsilon } M=E_1\oplus E_2\oplus \cdots \oplus E_{\ell }$
with
$T_{\Lambda _\varepsilon } M=E_1\oplus E_2\oplus \cdots \oplus E_{\ell }$
with
 $\dim E_i=d_i$
for each i, and for each
$\dim E_i=d_i$
for each i, and for each
 $x\in \Lambda _\varepsilon $
,
$x\in \Lambda _\varepsilon $
,
 $k\geq 1$
and each vector
$k\geq 1$
and each vector
 $v\in E_i(x)$
$v\in E_i(x)$

Remark 3.4. In the second statement, the original result does not give the inequality of the right-hand side. However, only a slight modification can give the upper bound of the topological entropy of f on the horseshoe.
Remark 3.5. By the estimation in the fifth statement of the above theorem, one can further show that there exists a constant
![]() $C>0$
such that
$C>0$
such that
for all
![]() $x\in \Lambda _\varepsilon $
,
$x\in \Lambda _\varepsilon $
,
![]() $v\in E_i(x)$
, and
$v\in E_i(x)$
, and
![]() $n\ge 1$
. Without loss of generality, one can assume that
$n\ge 1$
. Without loss of generality, one can assume that
![]() $C=1$
by considering an equivalent norm.
$C=1$
by considering an equivalent norm.
3.2.3 Statements of results
Let
![]() $f: M\to M$
be a
$f: M\to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism of a compact Riemannian manifold M, and let
$C^{1+\alpha }$
diffeomorphism of a compact Riemannian manifold M, and let
![]() $\mu $
be a hyperbolic ergodic f-invariant probability measure with positive entropy. Suppose that
$\mu $
be a hyperbolic ergodic f-invariant probability measure with positive entropy. Suppose that
![]() $(f,\mu )$
has only two Lyapunov exponents
$(f,\mu )$
has only two Lyapunov exponents
![]() $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
. Ledrappier, Young [Reference Ledrappier and Young23] and Barreira, Pesin, Schmeling [Reference Barreira, Pesin and Schmeling7] proved that
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
. Ledrappier, Young [Reference Ledrappier and Young23] and Barreira, Pesin, Schmeling [Reference Barreira, Pesin and Schmeling7] proved that
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. Our strategy used to prove the dimension approximation in this setting is as follows. It follows from Theorem 3.3 that
$\overline {\dim }_B$
. Our strategy used to prove the dimension approximation in this setting is as follows. It follows from Theorem 3.3 that
![]() $h_\mu (f)$
can be approximated by the topological entropies of a sequence of horseshoes
$h_\mu (f)$
can be approximated by the topological entropies of a sequence of horseshoes
![]() $\{\Lambda _\varepsilon \}_{\varepsilon>0}$
. Using well-established properties of dimension theory in uniform hyperbolic systems, one can show that
$\{\Lambda _\varepsilon \}_{\varepsilon>0}$
. Using well-established properties of dimension theory in uniform hyperbolic systems, one can show that
for
![]() $i=u, s$
and every
$i=u, s$
and every
![]() $x\in \Lambda $
. Burns and Wilkinson [Reference Burns and Wilkinson8] prove that the holonomy maps of the stable and unstable foliations for
$x\in \Lambda $
. Burns and Wilkinson [Reference Burns and Wilkinson8] prove that the holonomy maps of the stable and unstable foliations for
![]() $(f, \Lambda _\varepsilon )$
are Lipschitz continuous. Consequently, one can show that
$(f, \Lambda _\varepsilon )$
are Lipschitz continuous. Consequently, one can show that
 $$ \begin{align*} \begin{aligned} &\dim_{H}{\kern-1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \dim_{H}{\kern-1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x))\\ &\quad\leq \mathrm{Dim}\Lambda_\varepsilon\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x)) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\dim_{H}{\kern-1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \dim_{H}{\kern-1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x))\\ &\quad\leq \mathrm{Dim}\Lambda_\varepsilon\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x)) \end{aligned} \end{align*} $$
for every
![]() $x\in \Lambda _\varepsilon $
. Hence,
$x\in \Lambda _\varepsilon $
. Hence,
![]() $\mathrm {Dim}\mu $
is approximately equal to
$\mathrm {Dim}\mu $
is approximately equal to
![]() $\mathrm {Dim}\Lambda _\varepsilon $
. The detailed proofs will be given in the next section.
$\mathrm {Dim}\Lambda _\varepsilon $
. The detailed proofs will be given in the next section.
Theorem B. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism, and
$C^{1+\alpha }$
diffeomorphism, and
![]() $\mu $
be an f-invariant ergodic hyperbolic measure with
$\mu $
be an f-invariant ergodic hyperbolic measure with
![]() $h_\mu (f)>0$
. Assume that
$h_\mu (f)>0$
. Assume that
![]() $(f,\mu )$
has only two Lyapunov exponents
$(f,\mu )$
has only two Lyapunov exponents
![]() $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
. For each
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
. For each
![]() $\varepsilon>0$
, there exists a horseshoe
$\varepsilon>0$
, there exists a horseshoe
![]() $\Lambda _\varepsilon $
such that
$\Lambda _\varepsilon $
such that
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
.
$\overline {\dim }_B$
.
In [Reference Wang, Cao and Zou41], the authors relaxed the smoothness of Theorem 3.3 to
![]() $C^1$
under the additional condition that Oseledec’s splitting
$C^1$
under the additional condition that Oseledec’s splitting
![]() $E^u\oplus E^s$
of
$E^u\oplus E^s$
of
![]() $(f,\mu )$
is dominated. In this setting, one does not have Lipschitz continuity of the holonomy map in general. However, using Palis and Viana’s method [Reference Palis, Viana, Bamón, Labarca and Palis31], one can show that for every
$(f,\mu )$
is dominated. In this setting, one does not have Lipschitz continuity of the holonomy map in general. However, using Palis and Viana’s method [Reference Palis, Viana, Bamón, Labarca and Palis31], one can show that for every
![]() $\gamma \in (0, 1)$
, there is some
$\gamma \in (0, 1)$
, there is some
![]() $D_\gamma>0$
such that the holonomy maps of the stable and unstable foliations for the hyperbolic dynamical system
$D_\gamma>0$
such that the holonomy maps of the stable and unstable foliations for the hyperbolic dynamical system
![]() $(f, \Lambda _\varepsilon )$
(see Lemma 4.2) are
$(f, \Lambda _\varepsilon )$
(see Lemma 4.2) are
![]() $(D_\gamma , \gamma )$
-Hölder continuous. Since
$(D_\gamma , \gamma )$
-Hölder continuous. Since
![]() $\gamma $
is arbitrary, using the ideas in [Reference Wang, Wang, Cao and Zhao43], one can prove the following theorem.
$\gamma $
is arbitrary, using the ideas in [Reference Wang, Wang, Cao and Zhao43], one can prove the following theorem.
Theorem C. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1}$
diffeomorphism, and let
$C^{1}$
diffeomorphism, and let
![]() $\mu $
be an f-invariant ergodic hyperbolic measure with
$\mu $
be an f-invariant ergodic hyperbolic measure with
![]() $h_\mu (f)>0$
. Assume that
$h_\mu (f)>0$
. Assume that
![]() $(f,\mu )$
has only two Lyapunov exponents
$(f,\mu )$
has only two Lyapunov exponents
![]() $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
and the corresponding Oseledec’s splitting
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
and the corresponding Oseledec’s splitting
![]() $E^u\oplus E^s$
is dominated. For each
$E^u\oplus E^s$
is dominated. For each
![]() $\varepsilon>0$
, there exists a horseshoe
$\varepsilon>0$
, there exists a horseshoe
![]() $\Lambda _\varepsilon $
such that
$\Lambda _\varepsilon $
such that
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
.
$\overline {\dim }_B$
.
4 Proofs
In this section, we provide the proof of the main results presented in the previous section.
4.1 Proof of Proposition 3.1
Given an f-invariant ergodic measure
![]() $\mu $
, let
$\mu $
, let
![]() $P(t):=P_\mu (f|_\Lambda , \Phi _f(t))$
, it is easy to see that the function
$P(t):=P_\mu (f|_\Lambda , \Phi _f(t))$
, it is easy to see that the function
![]() $t\mapsto P(t)$
is continuous and strictly decreasing on the interval
$t\mapsto P(t)$
is continuous and strictly decreasing on the interval
![]() $[0,m_0]$
. It follows from equation (2.3) that
$[0,m_0]$
. It follows from equation (2.3) that
![]() $P(0)=h_\mu (f)\ge 0$
, and
$P(0)=h_\mu (f)\ge 0$
, and
![]() $P(m_0)\le 0$
by Margulis-Ruelle’s inequality. Consequently, there exists a unique root
$P(m_0)\le 0$
by Margulis-Ruelle’s inequality. Consequently, there exists a unique root
![]() $s_\mu $
of the equation
$s_\mu $
of the equation
![]() $P_\mu (f|_\Lambda , \Phi _f(t))=0$
.
$P_\mu (f|_\Lambda , \Phi _f(t))=0$
.
If
![]() $h_\mu (f)=0$
, it is easy to see that
$h_\mu (f)=0$
, it is easy to see that
![]() $h_\mu (f)=s_\mu =0$
. Hence,
$h_\mu (f)=s_\mu =0$
. Hence,
![]() $\dim _{L}{\kern-1pt}\mu =s_\mu $
.
$\dim _{L}{\kern-1pt}\mu =s_\mu $
.
If
![]() $0<h_\mu (f)< \unicode{x3bb} _{m_0}(\mu )$
, then
$0<h_\mu (f)< \unicode{x3bb} _{m_0}(\mu )$
, then
![]() $P(0)>0$
and
$P(0)>0$
and
![]() $P(1)<0$
. This implies that
$P(1)<0$
. This implies that
![]() $s_\mu \in (0,1)$
and
$s_\mu \in (0,1)$
and
![]() $0=P(s_\mu )=h_\mu (f)-s_\mu \unicode{x3bb} _{m_0}(\mu )$
. As a consequence, we have that
$0=P(s_\mu )=h_\mu (f)-s_\mu \unicode{x3bb} _{m_0}(\mu )$
. As a consequence, we have that

If
![]() $h_\mu (f)\ge \unicode{x3bb} _{m_0}(\mu )$
, note that
$h_\mu (f)\ge \unicode{x3bb} _{m_0}(\mu )$
, note that

Hence,

However, since
![]() $t\mapsto P(t)$
is strictly decreasing in t, we have that
$t\mapsto P(t)$
is strictly decreasing in t, we have that
This yields that
This completes the proof of the proposition.
4.2 Proof of Theorem A
By [Reference Cao, Pesin and Zhao11, Theorem 5.1], for each f-invariant ergodic measure
![]() $\mu $
with positive entropy and for each
$\mu $
with positive entropy and for each
![]() $\varepsilon>0$
, there exists an f-invariant compact subset
$\varepsilon>0$
, there exists an f-invariant compact subset
![]() $\Lambda _\varepsilon \subset \Lambda $
such that the following statements hold:
$\Lambda _\varepsilon \subset \Lambda $
such that the following statements hold:
-
(i)
 $h_{\text {top}}(f|_{\Lambda _\varepsilon })\ge h_{\mu }(f)-\varepsilon $
;
$h_{\text {top}}(f|_{\Lambda _\varepsilon })\ge h_{\mu }(f)-\varepsilon $
; -
(ii) there is a continuous invariant splitting
 $T_x M=E_1(x)\oplus E_2(x)\oplus \cdots \oplus E_\ell (x)$
over
$T_x M=E_1(x)\oplus E_2(x)\oplus \cdots \oplus E_\ell (x)$
over
 $\Lambda _\varepsilon $
and a constant
$\Lambda _\varepsilon $
and a constant
 $C>0$
so that for any unit vector
$C>0$
so that for any unit vector
 $u\in E_j(x)$
, where
$u\in E_j(x)$
, where
 $\unicode{x3bb} _1(\mu )<\dots <\unicode{x3bb} _\ell (\mu )$
are distinct Lyapunov exponents of f with respect to the measure
$\unicode{x3bb} _1(\mu )<\dots <\unicode{x3bb} _\ell (\mu )$
are distinct Lyapunov exponents of f with respect to the measure
 $\mu $
.
$\mu $
.
By modifying the arguments in [Reference Cao, Pesin and Zhao11, Theorem 5.1], one may improve the estimate in statement (i) as follows:
-
(i)′
 $h_{\mu }(f)+\varepsilon \ge h_{\text {top}}(f|_{\Lambda _\varepsilon })\ge h_{\mu }(f)-\varepsilon $
.
$h_{\mu }(f)+\varepsilon \ge h_{\text {top}}(f|_{\Lambda _\varepsilon })\ge h_{\mu }(f)-\varepsilon $
.
Since
![]() $\Lambda _{\varepsilon }$
is a repeller of f, one can choose an f-invariant ergodic measure
$\Lambda _{\varepsilon }$
is a repeller of f, one can choose an f-invariant ergodic measure
![]() $\mu _\varepsilon $
on
$\mu _\varepsilon $
on
![]() $\Lambda _\varepsilon $
so that
$\Lambda _\varepsilon $
so that
![]() $h_{\mu _\varepsilon }(f)=h_{\text {top}}(f|_{\Lambda _\varepsilon })$
yields that
$h_{\mu _\varepsilon }(f)=h_{\text {top}}(f|_{\Lambda _\varepsilon })$
yields that
 $$ \begin{align*} \begin{aligned} P_{\mathrm{top}}(f|_{\Lambda_\varepsilon}, \Phi_f(t))&\ge h_{\mu_\varepsilon}(f)+\mathcal{L}_*(\Phi_f(t), \mu_\varepsilon)\\ &\ge h_{\mu}(f)+\mathcal{L}_*(\Phi_f(t), \mu)-(t+1)\varepsilon\qquad (\text{by statement (ii)})\\ &\ge P_{\mu}(f|_{\Lambda}, \Phi_f(t))-(m_0+1)\varepsilon. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} P_{\mathrm{top}}(f|_{\Lambda_\varepsilon}, \Phi_f(t))&\ge h_{\mu_\varepsilon}(f)+\mathcal{L}_*(\Phi_f(t), \mu_\varepsilon)\\ &\ge h_{\mu}(f)+\mathcal{L}_*(\Phi_f(t), \mu)-(t+1)\varepsilon\qquad (\text{by statement (ii)})\\ &\ge P_{\mu}(f|_{\Lambda}, \Phi_f(t))-(m_0+1)\varepsilon. \end{aligned} \end{align*} $$
However, since f is expanding, by the variational principle, there exists an f-invariant ergodic measure
![]() $\widetilde {\mu }_\varepsilon $
on
$\widetilde {\mu }_\varepsilon $
on
![]() $\Lambda _\varepsilon $
so that
$\Lambda _\varepsilon $
so that
 $$ \begin{align*} \begin{aligned} P_{\mathrm{top}}(f|_{\Lambda_\varepsilon}, \Phi_f(t))&=h_{\widetilde{\mu}_\varepsilon}(f)+\mathcal{L}_*(\Phi_f(t), \widetilde{\mu}_\varepsilon)\\ &\le h_\mu(f)+\mathcal{L}_*(\Phi_f(t), \mu)+(t+1)\varepsilon\\ &\le P_{\mu}(f|_{\Lambda}, \Phi_f(t))+(m_0+1)\varepsilon. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} P_{\mathrm{top}}(f|_{\Lambda_\varepsilon}, \Phi_f(t))&=h_{\widetilde{\mu}_\varepsilon}(f)+\mathcal{L}_*(\Phi_f(t), \widetilde{\mu}_\varepsilon)\\ &\le h_\mu(f)+\mathcal{L}_*(\Phi_f(t), \mu)+(t+1)\varepsilon\\ &\le P_{\mu}(f|_{\Lambda}, \Phi_f(t))+(m_0+1)\varepsilon. \end{aligned} \end{align*} $$
Hence,
By [Reference Cao, Pesin and Zhao11, Theorem 4.1], the Carathéodory singular dimension
![]() $\dim _{C}{\kern-1pt} \Lambda _\varepsilon $
of
$\dim _{C}{\kern-1pt} \Lambda _\varepsilon $
of
![]() $\Lambda _\varepsilon $
is given by the unique root of the following equation:
$\Lambda _\varepsilon $
is given by the unique root of the following equation:
This, together with Proposition 3.1, yields that
 $$ \begin{align*} \begin{aligned} K|\dim_{C}{\kern-1pt}\Lambda_\varepsilon-\dim_{\mathrm{L}}{\kern-1pt}\mu|&\le |P_{\mu}(f|_{\Lambda}, \Phi_f(\dim_{C}{\kern-1pt}\Lambda_\varepsilon))-P_{\mu}(f|_{\Lambda}, \Phi_f(\dim_{\mathrm{L}}{\kern-1pt}\mu)) |\\ &=|P_{\mu}(f|_{\Lambda}, \Phi_f(\dim_{C}{\kern-1pt} \Lambda_\varepsilon))-P_{\mathrm{top}}(f|_{\Lambda_\varepsilon}, \Phi_f(\dim_{C}{\kern-1pt} \Lambda_\varepsilon)) |\\ &\le(m_0+1)\varepsilon, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} K|\dim_{C}{\kern-1pt}\Lambda_\varepsilon-\dim_{\mathrm{L}}{\kern-1pt}\mu|&\le |P_{\mu}(f|_{\Lambda}, \Phi_f(\dim_{C}{\kern-1pt}\Lambda_\varepsilon))-P_{\mu}(f|_{\Lambda}, \Phi_f(\dim_{\mathrm{L}}{\kern-1pt}\mu)) |\\ &=|P_{\mu}(f|_{\Lambda}, \Phi_f(\dim_{C}{\kern-1pt} \Lambda_\varepsilon))-P_{\mathrm{top}}(f|_{\Lambda_\varepsilon}, \Phi_f(\dim_{C}{\kern-1pt} \Lambda_\varepsilon)) |\\ &\le(m_0+1)\varepsilon, \end{aligned} \end{align*} $$
where
![]() $K=\min _{x\in \Lambda }\log m(D_xf)$
and
$K=\min _{x\in \Lambda }\log m(D_xf)$
and
![]() $m(\cdot )$
denotes the minimum norm of an operator. Consequently, we have that
$m(\cdot )$
denotes the minimum norm of an operator. Consequently, we have that
![]() $\dim _{C}{\kern-1pt} \Lambda _\varepsilon \rightarrow \dim _{\mathrm {L}}{\kern-1pt}\mu $
as
$\dim _{C}{\kern-1pt} \Lambda _\varepsilon \rightarrow \dim _{\mathrm {L}}{\kern-1pt}\mu $
as
![]() $\varepsilon $
approaches zero.
$\varepsilon $
approaches zero.
4.3 Proof of Proposition 3.2
Given a subset
![]() $Z\subset \Lambda $
, since
$Z\subset \Lambda $
, since
![]() $P_Z(f|_{\Lambda },\Phi _f(t))$
is continuous and strictly decreasing in t, let
$P_Z(f|_{\Lambda },\Phi _f(t))$
is continuous and strictly decreasing in t, let
![]() $t_Z$
denote the unique root of the equation
$t_Z$
denote the unique root of the equation
![]() $P_Z(f|_{\Lambda },\Phi _f(t))=0$
. For every
$P_Z(f|_{\Lambda },\Phi _f(t))=0$
. For every
![]() $t<t_Z$
, we have that
$t<t_Z$
, we have that
![]() $P_Z(f|_{\Lambda },\Phi _f(t))>0$
. Fix such a number t, and take
$P_Z(f|_{\Lambda },\Phi _f(t))>0$
. Fix such a number t, and take
![]() $\beta>0$
so that
$\beta>0$
so that
![]() $P_Z(f|_{\Lambda },\Phi _f(t))-\beta>0$
. Since
$P_Z(f|_{\Lambda },\Phi _f(t))-\beta>0$
. Since
there exists
![]() $r_0>0$
such that for each
$r_0>0$
such that for each
![]() $0<r<r_0$
, one has
$0<r<r_0$
, one has
Fix such a small
![]() $r>0$
. By the definition of topological pressure on arbitrary subsets, one has
$r>0$
. By the definition of topological pressure on arbitrary subsets, one has
Hence, for each
![]() $\xi>0$
, there exists
$\xi>0$
, there exists
![]() $L\in \mathbb {N}$
so that for any
$L\in \mathbb {N}$
so that for any
![]() $N>L$
, we have that
$N>L$
, we have that
 $$ \begin{align*} \begin{aligned} &\exp(-N(P_Z(f|_{\Lambda},\Phi_f(t))-\beta))\inf \bigg\{ \sum_{i}\exp \Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\Big) \bigg\} \\ &\quad\ge\inf\bigg\{ \sum_{i}\exp (-(P_Z(f|_{\Lambda},\Phi_f(t))-\beta)n_i +\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})) \bigg\}>\xi, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\exp(-N(P_Z(f|_{\Lambda},\Phi_f(t))-\beta))\inf \bigg\{ \sum_{i}\exp \Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\Big) \bigg\} \\ &\quad\ge\inf\bigg\{ \sum_{i}\exp (-(P_Z(f|_{\Lambda},\Phi_f(t))-\beta)n_i +\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})) \bigg\}>\xi, \end{aligned} \end{align*} $$
where the infimum is taken over all collections
![]() $\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
$\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
![]() $n_i\ge N$
, which covers Z. This yields that
$n_i\ge N$
, which covers Z. This yields that
 $$ \begin{align*} \inf \bigg\{ \sum_{i}\exp \big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\big) \bigg\}>\xi \exp(N(P_Z(f|_{\Lambda},\Phi_f(t))-\beta)). \end{align*} $$
$$ \begin{align*} \inf \bigg\{ \sum_{i}\exp \big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\big) \bigg\}>\xi \exp(N(P_Z(f|_{\Lambda},\Phi_f(t))-\beta)). \end{align*} $$
Letting
![]() $N\to \infty $
, we have that
$N\to \infty $
, we have that
Hence,
for all
![]() $0<r<r_0$
. Consequently, since
$0<r<r_0$
. Consequently, since
![]() $t<t_Z$
is arbitrary, we have that
$t<t_Z$
is arbitrary, we have that
However, for each
![]() $t>t_Z$
, one has that
$t>t_Z$
, one has that
![]() $P_Z(f|_{\Lambda },\Phi _f(t))<0$
. Fix such a number t, and take
$P_Z(f|_{\Lambda },\Phi _f(t))<0$
. Fix such a number t, and take
![]() $\widetilde {\beta }>0$
so that
$\widetilde {\beta }>0$
so that
![]() $P_Z(f|_{\Lambda },\Phi _f(t))+\widetilde {\beta }<0$
. By the definition of topological pressure on arbitrary subsets, for any
$P_Z(f|_{\Lambda },\Phi _f(t))+\widetilde {\beta }<0$
. By the definition of topological pressure on arbitrary subsets, for any
![]() $R>0$
, there exists
$R>0$
, there exists
![]() $0<r<R$
such that
$0<r<R$
such that
For such a small
![]() $r>0$
, one has
$r>0$
, one has
Hence, for each small
![]() $\widetilde {\xi }>0$
, there exists
$\widetilde {\xi }>0$
, there exists
![]() $\widetilde {L}\in \mathbb {N}$
so that for any
$\widetilde {L}\in \mathbb {N}$
so that for any
![]() $N>\widetilde {L}$
, we have that
$N>\widetilde {L}$
, we have that
 $$ \begin{align*} \begin{aligned} &\exp(-N(P_Z(f|_{\Lambda},\Phi_f(t))+\widetilde{\beta}))\inf \bigg\{ \sum_{i}\exp \Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\Big) \bigg\} \\ &\quad\le\inf\bigg\{ \sum_{i}\exp \Big(-(P_Z(f|_{\Lambda},\Phi_f(t))+\widetilde{\beta})n_i +\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\Big) \bigg\}\le \widetilde{\xi}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\exp(-N(P_Z(f|_{\Lambda},\Phi_f(t))+\widetilde{\beta}))\inf \bigg\{ \sum_{i}\exp \Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\Big) \bigg\} \\ &\quad\le\inf\bigg\{ \sum_{i}\exp \Big(-(P_Z(f|_{\Lambda},\Phi_f(t))+\widetilde{\beta})n_i +\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\Big) \bigg\}\le \widetilde{\xi}, \end{aligned} \end{align*} $$
where the infimum is taken over all collections
![]() $\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
$\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
![]() $n_i\ge N$
, which covers Z. This yields that
$n_i\ge N$
, which covers Z. This yields that
 $$ \begin{align*} \inf \bigg\{ \sum_{i}\exp \big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\big) \bigg\}\le \widetilde{\xi} \exp(N(P_Z(f|_{\Lambda},\Phi_f(t))+\widetilde{\beta})). \end{align*} $$
$$ \begin{align*} \inf \bigg\{ \sum_{i}\exp \big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^t(y, f^{n_i})\big) \bigg\}\le \widetilde{\xi} \exp(N(P_Z(f|_{\Lambda},\Phi_f(t))+\widetilde{\beta})). \end{align*} $$
Letting
![]() $N\to \infty $
, one has
$N\to \infty $
, one has
Consequently, for such
![]() $r>0$
, one has
$r>0$
, one has
Hence, we have that
It follows from equations (4.1) and (4.2) that
To show the second statement, for a given f-invariant ergodic measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\Lambda $
, and a subset
$\Lambda $
, and a subset
![]() $Z\subset \Lambda $
with
$Z\subset \Lambda $
with
![]() $\mu (Z)=1$
, we have that
$\mu (Z)=1$
, we have that
By item (1) of Theorem A and the first statement, one has
By the definition of Carathéodory singular dimension of arbitrary subsets, one has
for all sufficiently small
![]() $r>0$
. Consequently, we have that
$r>0$
. Consequently, we have that
To prove that
![]() $\dim _{C}{\kern-1pt}\mu =\dim _{L}{\kern-1pt}\mu $
, we assume that
$\dim _{C}{\kern-1pt}\mu =\dim _{L}{\kern-1pt}\mu $
, we assume that
![]() $\dim _{C}{\kern-1pt}\mu>\widetilde {t}>\dim _{L}{\kern-1pt}\mu $
. By the first statement in Theorem A, we have that
$\dim _{C}{\kern-1pt}\mu>\widetilde {t}>\dim _{L}{\kern-1pt}\mu $
. By the first statement in Theorem A, we have that
By the definition of measure theoretic pressure, for each
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $0<r_n< 1/n$
so that
$0<r_n< 1/n$
so that
Hence, there exists a subset
![]() $Z_n\subset \Lambda $
with
$Z_n\subset \Lambda $
with
![]() $\mu (Z_n)=1$
so that
$\mu (Z_n)=1$
so that
Put
![]() $\widetilde {Z}:=\bigcap _{n\ge 1} Z_n$
, then
$\widetilde {Z}:=\bigcap _{n\ge 1} Z_n$
, then
![]() $\mu (\widetilde {Z})=1$
and
$\mu (\widetilde {Z})=1$
and
 $$ \begin{align*} \begin{aligned} P_{\widetilde{Z}}(f|_{\Lambda},\Phi(\widetilde{t}))&=\liminf_{r\to 0}P_{\widetilde{Z}}(f|_{\Lambda},\Phi(\widetilde{t}),r)\\ &\le \liminf_{n\to \infty}P_{Z_n}(f|_{\Lambda},\Phi(\widetilde{t}),r_n)\le 0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} P_{\widetilde{Z}}(f|_{\Lambda},\Phi(\widetilde{t}))&=\liminf_{r\to 0}P_{\widetilde{Z}}(f|_{\Lambda},\Phi(\widetilde{t}),r)\\ &\le \liminf_{n\to \infty}P_{Z_n}(f|_{\Lambda},\Phi(\widetilde{t}),r_n)\le 0. \end{aligned} \end{align*} $$
It follows from the first statement and the definition of Carathéodory singular dimension of
![]() $\mu $
that
$\mu $
that
which yields a contraction. Hence, we have that
![]() $\dim _C{\kern-1pt}\mu =\dim _L{\kern-1pt}\mu $
.
$\dim _C{\kern-1pt}\mu =\dim _L{\kern-1pt}\mu $
.
4.4 Proof of Theorem B
Ledrappier, Young [Reference Ledrappier and Young23] and Barreira, Pesin, Schmeling [Reference Barreira, Pesin and Schmeling7] proved that
where
![]() $\mathrm { Dim}$
denotes either
$\mathrm { Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. Fix a small number
$\overline {\dim }_B$
. Fix a small number
![]() $\varepsilon>0$
. By Theorem 3.3, there exists a horseshoe
$\varepsilon>0$
. By Theorem 3.3, there exists a horseshoe
![]() $\Lambda _\varepsilon $
such that:
$\Lambda _\varepsilon $
such that:
-
(i)
 $|h_{\mathrm {top}}(f,\Lambda _\varepsilon ) - h_{\mu }(f)|<\varepsilon $
;
$|h_{\mathrm {top}}(f,\Lambda _\varepsilon ) - h_{\mu }(f)|<\varepsilon $
; -
(ii) there exists a dominated splitting
 $T_{\Lambda _\varepsilon } M=E^u\oplus E^s$
with
$T_{\Lambda _\varepsilon } M=E^u\oplus E^s$
with
 $\dim E^i=d_i\, (i=u,s)$
, and for each
$\dim E^i=d_i\, (i=u,s)$
, and for each
 $x\in \Lambda _\varepsilon $
, every
$x\in \Lambda _\varepsilon $
, every
 $n\geq 1$
, and each vector
$n\geq 1$
, and each vector
 $v\in E^i(x) (i=s,u)$
, The above estimation can be proven in similar fashion as Remark 3.2.
$v\in E^i(x) (i=s,u)$
, The above estimation can be proven in similar fashion as Remark 3.2.
Fixed any
![]() $k\in \mathbb {N}$
and denote
$k\in \mathbb {N}$
and denote
![]() $F=f^{2^k}$
. Since
$F=f^{2^k}$
. Since
![]() $\Lambda _\varepsilon $
is a locally maximal hyperbolic set for f,
$\Lambda _\varepsilon $
is a locally maximal hyperbolic set for f,
![]() $\Lambda _\varepsilon $
is also a locally maximal hyperbolic set for F. Notice that
$\Lambda _\varepsilon $
is also a locally maximal hyperbolic set for F. Notice that
Let
![]() $\|\cdot \|$
and
$\|\cdot \|$
and
![]() $m(\cdot )$
denote the maximal and minimal norm of an operator. For every
$m(\cdot )$
denote the maximal and minimal norm of an operator. For every
![]() $x\in \Lambda _\varepsilon $
, Barreira [Reference Barreira4] proved that
$x\in \Lambda _\varepsilon $
, Barreira [Reference Barreira4] proved that
where
![]() $\underline {t}_u^k$
,
$\underline {t}_u^k$
,
![]() $\overline {t}_u^k$
are the unique solutions of
$\overline {t}_u^k$
are the unique solutions of
respectively. Using the same arguments as in the proof of [Reference Ban, Cao and Hu3, Theorems 6.2 and 6.3], one can prove that the sequences
![]() $\{\underline {t}_u^k\}$
and
$\{\underline {t}_u^k\}$
and
![]() $\{\overline {t}_u^k\}$
are monotone. Furthermore, setting
$\{\overline {t}_u^k\}$
are monotone. Furthermore, setting
one can show that
![]() $\underline {t}_u$
,
$\underline {t}_u$
,
![]() $\overline {t}_u$
are the unique solutions of the following equations:
$\overline {t}_u$
are the unique solutions of the following equations:
respectively.
Consequently, we have that
and
 $$ \begin{align*}\begin{aligned} \underline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{\displaystyle{\lim_{n\to\infty}} \frac 1n \int \log\|D_xf^n|_{E^u}\|\,d\nu}: \nu\in\mathcal{M}_f(\Lambda_\varepsilon) \bigg\},\\ \overline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{\displaystyle{\lim_{n\to\infty}} \frac 1n \int \log m(D_xf^n|_{E^u})\,d\nu}: \nu\in\mathcal M_f(\Lambda_\varepsilon) \bigg\}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \underline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{\displaystyle{\lim_{n\to\infty}} \frac 1n \int \log\|D_xf^n|_{E^u}\|\,d\nu}: \nu\in\mathcal{M}_f(\Lambda_\varepsilon) \bigg\},\\ \overline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{\displaystyle{\lim_{n\to\infty}} \frac 1n \int \log m(D_xf^n|_{E^u})\,d\nu}: \nu\in\mathcal M_f(\Lambda_\varepsilon) \bigg\}. \end{aligned} \end{align*} $$
Combining with items (i) and (ii), one has
for every
![]() $x\in \Lambda _\varepsilon $
, where
$x\in \Lambda _\varepsilon $
, where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. One can show in a similar fashion that
$\overline {\dim }_B$
. One can show in a similar fashion that
for every
![]() $x\in \Lambda _\varepsilon $
.
$x\in \Lambda _\varepsilon $
.
Lemma 4.1. The holonomy maps of the stable and unstable foliations for
![]() $(f, \Lambda _\varepsilon )$
are Lipschitz continuous.
$(f, \Lambda _\varepsilon )$
are Lipschitz continuous.
Proof. Fix a positive integer N, put
![]() $F:=f^N$
and
$F:=f^N$
and
![]() $\Lambda =\Lambda _\varepsilon $
. Since
$\Lambda =\Lambda _\varepsilon $
. Since
![]() $\Lambda $
is a locally maximal hyperbolic set for f, so is
$\Lambda $
is a locally maximal hyperbolic set for f, so is
![]() $\Lambda $
for F. Notice that
$\Lambda $
for F. Notice that
Let
It follows from item (ii) that
 $$ \begin{align*} 1<\frac{\|D_xF|_{E^i(x)}\|}{m(D_xF|_{E^i(x)})}<e^{2\varepsilon N} \quad\text{for every } x\in \Lambda\text{ and } i\in\{s,u\}. \end{align*} $$
$$ \begin{align*} 1<\frac{\|D_xF|_{E^i(x)}\|}{m(D_xF|_{E^i(x)})}<e^{2\varepsilon N} \quad\text{for every } x\in \Lambda\text{ and } i\in\{s,u\}. \end{align*} $$
Hence,
provided that
![]() $\varepsilon>0$
is sufficiently small such that
$\varepsilon>0$
is sufficiently small such that
![]() $\unicode{x3bb} _s(\mu )+3\varepsilon <0$
. By [Reference Burns and Wilkinson8, Theorem 0.2], we have that the holonomy map of the stable foliation for
$\unicode{x3bb} _s(\mu )+3\varepsilon <0$
. By [Reference Burns and Wilkinson8, Theorem 0.2], we have that the holonomy map of the stable foliation for
![]() $(F, \Lambda )$
is
$(F, \Lambda )$
is
![]() $C^1$
. Similarly, note that
$C^1$
. Similarly, note that
provided that
![]() $\varepsilon>0$
is sufficiently small such that
$\varepsilon>0$
is sufficiently small such that
![]() $\unicode{x3bb} _u(\mu )-3\varepsilon>0$
. It follows from [Reference Burns and Wilkinson8, Theorem 0.2] that the holonomy map of the unstable foliation for
$\unicode{x3bb} _u(\mu )-3\varepsilon>0$
. It follows from [Reference Burns and Wilkinson8, Theorem 0.2] that the holonomy map of the unstable foliation for
![]() $(F, \Lambda )$
is
$(F, \Lambda )$
is
![]() $C^1$
. Combining with equation (4.5), one has the holonomy maps of the stable and unstable foliations for
$C^1$
. Combining with equation (4.5), one has the holonomy maps of the stable and unstable foliations for
![]() $(f, \Lambda )$
are Lipschitz continuous.
$(f, \Lambda )$
are Lipschitz continuous.
By Lemma 4.1 and the fact f is topologically mixing on
![]() $\Lambda _\varepsilon $
, one has
$\Lambda _\varepsilon $
, one has
![]() $\dim _H{\kern-1pt}(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
,
$\dim _H{\kern-1pt}(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
,
![]() $\underline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
, and
$\underline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
, and
![]() $\overline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f,x))$
are independent of
$\overline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f,x))$
are independent of
![]() $\beta $
and x (see the proof of [Reference Barreira5, Theorem 4.3.2] for more details). Let
$\beta $
and x (see the proof of [Reference Barreira5, Theorem 4.3.2] for more details). Let
By the properties of dimension (e.g. see [Reference Falconer13, Reference Pesin33]), one has
 $$ \begin{align} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} A_{\varepsilon, x}\\ &\quad\leq \underline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x)). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} A_{\varepsilon, x}\\ &\quad\leq \underline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x)). \end{aligned} \end{align} $$
Let
![]() $\Phi : A_{\varepsilon ,x} \to \Lambda _\varepsilon $
be given by
$\Phi : A_{\varepsilon ,x} \to \Lambda _\varepsilon $
be given by
It is easy to see
![]() $\Phi $
is a homeomorphism onto a neighborhood
$\Phi $
is a homeomorphism onto a neighborhood
![]() $V_x$
of x in
$V_x$
of x in
![]() $\Lambda _\varepsilon $
. It follows from Lemma 4.1 that
$\Lambda _\varepsilon $
. It follows from Lemma 4.1 that
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi ^{-1}$
are Lipschitz continuous (see [Reference Barreira5, Theorem 4.3.2] for detailed proofs). It follows from Corollary 2.9 that
$\Phi ^{-1}$
are Lipschitz continuous (see [Reference Barreira5, Theorem 4.3.2] for detailed proofs). It follows from Corollary 2.9 that
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. Since
$\overline {\dim }_B$
. Since
![]() $\{V_x: x\in \Lambda _\varepsilon \}$
is an open cover of
$\{V_x: x\in \Lambda _\varepsilon \}$
is an open cover of
![]() $\Lambda _\varepsilon $
, one can choose a finite open cover
$\Lambda _\varepsilon $
, one can choose a finite open cover
![]() $\{V_{x_1}, V_{x_2}, \ldots , V_{x_k}\}$
of
$\{V_{x_1}, V_{x_2}, \ldots , V_{x_k}\}$
of
![]() $\Lambda _\varepsilon $
. It follows from equation (4.6) that
$\Lambda _\varepsilon $
. It follows from equation (4.6) that
 $$ \begin{align*} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} \Lambda_\varepsilon = \max_{1\leq i \leq k} \dim_H{\kern-1pt} V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}\Lambda_\varepsilon =\max_{1\leq i\leq k}\overline{\dim}_{B}{\kern1pt}V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x)), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} \Lambda_\varepsilon = \max_{1\leq i \leq k} \dim_H{\kern-1pt} V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}\Lambda_\varepsilon =\max_{1\leq i\leq k}\overline{\dim}_{B}{\kern1pt}V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x)), \end{aligned} \end{align*} $$
for every
![]() $x\in \Lambda _\varepsilon $
. Combining equations (4.3) and (4.4), we obtain
$x\in \Lambda _\varepsilon $
. Combining equations (4.3) and (4.4), we obtain
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. This completes the proof of Theorem B.
$\overline {\dim }_B$
. This completes the proof of Theorem B.
4.5 Proof of Theorem C
For every pair
![]() $(f,\mu )$
satisfying the assumptions, Wang and Cao [Reference Wang and Cao40, Corollary 1] proved that
$(f,\mu )$
satisfying the assumptions, Wang and Cao [Reference Wang and Cao40, Corollary 1] proved that
Fix a small number
![]() $\varepsilon>0$
. Wang, Cao, and Zou [Reference Wang, Cao and Zou41, Theorem 1.1] proved that there exists a horseshoe
$\varepsilon>0$
. Wang, Cao, and Zou [Reference Wang, Cao and Zou41, Theorem 1.1] proved that there exists a horseshoe
![]() $\Lambda _\varepsilon $
such that:
$\Lambda _\varepsilon $
such that:
-
(i)
 $|h_{\mathrm {top}}(f,\Lambda _\varepsilon ) - h_{\mu }(f)|<\varepsilon $
;
$|h_{\mathrm {top}}(f,\Lambda _\varepsilon ) - h_{\mu }(f)|<\varepsilon $
; -
(ii) there exists a dominated splitting
 $T_{\Lambda _\varepsilon } M=E^u\oplus E^s$
with
$T_{\Lambda _\varepsilon } M=E^u\oplus E^s$
with
 $\dim E^i=d_i\, (i=u,s)$
, and for each
$\dim E^i=d_i\, (i=u,s)$
, and for each
 $x\in \Lambda _\varepsilon $
, every
$x\in \Lambda _\varepsilon $
, every
 $n\geq 1$
, and each vector
$n\geq 1$
, and each vector
 $v\in E^i(x) (i=s, u)$
, The above estimation can be obtained by item (v) of [Reference Wang, Cao and Zou41, Theorem 1.1] and Remark 3.2.
$v\in E^i(x) (i=s, u)$
, The above estimation can be obtained by item (v) of [Reference Wang, Cao and Zou41, Theorem 1.1] and Remark 3.2.
Fix a positive integer
![]() $k\in \mathbb {N}$
, denote
$k\in \mathbb {N}$
, denote
![]() $F=f^{2^k}$
. Since
$F=f^{2^k}$
. Since
![]() $\Lambda _\varepsilon $
is a locally maximal hyperbolic set for f, so is
$\Lambda _\varepsilon $
is a locally maximal hyperbolic set for f, so is
![]() $\Lambda _\varepsilon $
for F. Notice that
$\Lambda _\varepsilon $
for F. Notice that
For every
![]() $x\in \Lambda _\varepsilon $
, it follows from [Reference Wang, Wang, Cao and Zhao43, Lemmas 3.5 and 3.6] that
$x\in \Lambda _\varepsilon $
, it follows from [Reference Wang, Wang, Cao and Zhao43, Lemmas 3.5 and 3.6] that
where
![]() $\underline {t}_u^k$
,
$\underline {t}_u^k$
,
![]() $\overline {t}_u^k$
are the unique roots of
$\overline {t}_u^k$
are the unique roots of
respectively. Using the same arguments as in the proof of [Reference Ban, Cao and Hu3, Theorems 6.2 and 6.3], one can prove that the sequences
![]() $\{\underline {t}_u^k\}$
and
$\{\underline {t}_u^k\}$
and
![]() $\{\overline {t}_u^k\}$
are monotone. Set
$\{\overline {t}_u^k\}$
are monotone. Set
where
![]() $\underline {t}_u$
,
$\underline {t}_u$
,
![]() $\overline {t}_u$
are the unique solutions of the following equations:
$\overline {t}_u$
are the unique solutions of the following equations:
respectively. Hence, we have that
Since
 $$ \begin{align*} \underline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{ \displaystyle{\lim_{n\to\infty}}\frac 1n \int \log\|D_xf^n|_{E^u(x)}\|\,d\nu}: \nu\in\mathcal{M}_f(\Lambda_\varepsilon) \bigg\} \end{align*} $$
$$ \begin{align*} \underline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{ \displaystyle{\lim_{n\to\infty}}\frac 1n \int \log\|D_xf^n|_{E^u(x)}\|\,d\nu}: \nu\in\mathcal{M}_f(\Lambda_\varepsilon) \bigg\} \end{align*} $$
and
 $$ \begin{align*} \overline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{\displaystyle{\lim_{n\to\infty}} \frac 1n \int \log m(D_xf^n|_{E^u(x)})\,d\nu}: \nu\in\mathcal{M}_f(\Lambda_\varepsilon) \bigg\}, \end{align*} $$
$$ \begin{align*} \overline{t}_u &=\sup\bigg\{\frac{h_\nu(f)}{\displaystyle{\lim_{n\to\infty}} \frac 1n \int \log m(D_xf^n|_{E^u(x)})\,d\nu}: \nu\in\mathcal{M}_f(\Lambda_\varepsilon) \bigg\}, \end{align*} $$
using items (i) and (ii), one can show that
for every
![]() $x\in \Lambda _\varepsilon $
, where
$x\in \Lambda _\varepsilon $
, where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. Similarly, we obtain that
$\overline {\dim }_B$
. Similarly, we obtain that
for every
![]() $x\in \Lambda _\varepsilon $
.
$x\in \Lambda _\varepsilon $
.
Lemma 4.2. Let
![]() $\Lambda $
be a locally maximal hyperbolic set of a
$\Lambda $
be a locally maximal hyperbolic set of a
![]() $C^1$
diffeomorphism such that f is topologically mixing on
$C^1$
diffeomorphism such that f is topologically mixing on
![]() $\Lambda $
. Assume that the diffeomorphism
$\Lambda $
. Assume that the diffeomorphism
![]() $f|_\Lambda $
possesses a
$f|_\Lambda $
possesses a
![]() $\{\unicode{x3bb} _u(\mu ), \unicode{x3bb} _s(\mu )\}$
-dominated splitting
$\{\unicode{x3bb} _u(\mu ), \unicode{x3bb} _s(\mu )\}$
-dominated splitting
![]() $T_\Lambda M=E^u\oplus E^s$
with
$T_\Lambda M=E^u\oplus E^s$
with
![]() $E^u\succeq E^s$
and
$E^u\succeq E^s$
and
![]() $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
. Then for every
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
. Then for every
![]() $\gamma \in (0, 1)$
, there exists
$\gamma \in (0, 1)$
, there exists
![]() $D_\gamma>0$
such that the holonomy maps of the stable and unstable foliations for f are
$D_\gamma>0$
such that the holonomy maps of the stable and unstable foliations for f are
![]() $(D_\gamma , \gamma )$
-H
$(D_\gamma , \gamma )$
-H
![]() $\ddot {o}$
lder continuous.
$\ddot {o}$
lder continuous.
Proof. Since the diffeomorphism
![]() $f|_\Lambda $
possesses a
$f|_\Lambda $
possesses a
![]() $\{\unicode{x3bb} _u(\mu ), \unicode{x3bb} _s(\mu )\}$
-dominated splitting
$\{\unicode{x3bb} _u(\mu ), \unicode{x3bb} _s(\mu )\}$
-dominated splitting
![]() $T_\Lambda M=E^u\oplus E^s$
with
$T_\Lambda M=E^u\oplus E^s$
with
![]() $E^u\succeq E^s$
and
$E^u\succeq E^s$
and
![]() $\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
, there exists a constant
$\unicode{x3bb} _u(\mu )>0>\unicode{x3bb} _s(\mu )$
, there exists a constant
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $x\in \Lambda $
,
$x\in \Lambda $
,
![]() $n\in \mathbb {N}$
and each unit vector
$n\in \mathbb {N}$
and each unit vector
![]() $v\in E^i(x)$
(
$v\in E^i(x)$
(
![]() $i=u, s$
),
$i=u, s$
),
As illustrated in Remark 3.2, for simplicity, we assume that
![]() $C=1$
in the rest of the proof. Fix a positive integer N and put
$C=1$
in the rest of the proof. Fix a positive integer N and put
![]() $F:=f^N$
. This implies that for every
$F:=f^N$
. This implies that for every
![]() $x\in \Lambda $
,
$x\in \Lambda $
,
Notice that
![]() $\Lambda $
is also a locally maximal hyperbolic set for F and
$\Lambda $
is also a locally maximal hyperbolic set for F and
for every
![]() $x\in \Lambda $
.
$x\in \Lambda $
.
Let
![]() $\pi ^s$
and
$\pi ^s$
and
![]() $\pi ^u$
be the holonomy maps of stable and unstable foliations for f, that is, for any
$\pi ^u$
be the holonomy maps of stable and unstable foliations for f, that is, for any
![]() $x\in \Lambda $
,
$x\in \Lambda $
,
![]() $x'\in W^s_\beta (f, x)$
, and
$x'\in W^s_\beta (f, x)$
, and
![]() $x"\in W^u_\beta (f, x)$
close to x,
$x"\in W^u_\beta (f, x)$
close to x,
and
Therefore,
![]() $\pi ^s$
is also a map from
$\pi ^s$
is also a map from
![]() $W^u_\beta (F,x)\cap \Lambda $
to
$W^u_\beta (F,x)\cap \Lambda $
to
![]() $W^u_\beta (F, x')\cap \Lambda $
and
$W^u_\beta (F, x')\cap \Lambda $
and
![]() $\pi ^u$
is also a map from
$\pi ^u$
is also a map from
![]() $W^s_\beta (F,x)\cap \Lambda $
to
$W^s_\beta (F,x)\cap \Lambda $
to
![]() $W^s_\beta (F, x")\cap \Lambda $
.
$W^s_\beta (F, x")\cap \Lambda $
.
Let
![]() $U\subset M$
be an open subset such that
$U\subset M$
be an open subset such that
![]() $\Lambda =\bigcap _{n\in \mathbb {Z}}f^n(U)$
, and
$\Lambda =\bigcap _{n\in \mathbb {Z}}f^n(U)$
, and
![]() $\mathcal {U}\subset \mbox {Diff}^{1}(M)$
be a neighborhood of f such that for each
$\mathcal {U}\subset \mbox {Diff}^{1}(M)$
be a neighborhood of f such that for each
![]() $g \in \mathcal {U}$
,
$g \in \mathcal {U}$
,
![]() $\Lambda _g = \bigcap _{n\in \mathbb {Z}} g^n(U)$
is a locally maximal hyperbolic set for g and there is a homeomorphism
$\Lambda _g = \bigcap _{n\in \mathbb {Z}} g^n(U)$
is a locally maximal hyperbolic set for g and there is a homeomorphism
![]() $h_g: \Lambda \rightarrow \Lambda _g$
that satisfies
$h_g: \Lambda \rightarrow \Lambda _g$
that satisfies
![]() $g\circ h_g=h_g\circ f$
, with
$g\circ h_g=h_g\circ f$
, with
![]() $h_g\ C^0$
-close to identity if g is
$h_g\ C^0$
-close to identity if g is
![]() $C^1$
-close to f. For
$C^1$
-close to f. For
![]() $g \in \mathcal {U}$
, let
$g \in \mathcal {U}$
, let
![]() $T_{\Lambda _g}M=E^u_g\oplus E^s_g$
denote the hyperbolic splitting over
$T_{\Lambda _g}M=E^u_g\oplus E^s_g$
denote the hyperbolic splitting over
![]() $\Lambda _g$
. For
$\Lambda _g$
. For
![]() $i\in \{u,s\}$
,
$i\in \{u,s\}$
,
![]() $\{W^i_\beta (g,z):\ z\in \Lambda _g\}$
is continuous on g in the following sense: there is
$\{W^i_\beta (g,z):\ z\in \Lambda _g\}$
is continuous on g in the following sense: there is
![]() $\{\theta _{g,x}^i:\ x\in \Lambda \}$
, where
$\{\theta _{g,x}^i:\ x\in \Lambda \}$
, where
![]() $\theta _{g,x}^i:\ W^i_\beta (f,x)\to W^i_\beta (g,h_g(x))$
is a
$\theta _{g,x}^i:\ W^i_\beta (f,x)\to W^i_\beta (g,h_g(x))$
is a
![]() $C^1$
diffeomorphism with
$C^1$
diffeomorphism with
![]() $\theta _{g,x}^i(x)=h_g(x)$
, such that if g is
$\theta _{g,x}^i(x)=h_g(x)$
, such that if g is
![]() $C^1$
-close to f then, for all
$C^1$
-close to f then, for all
![]() $x\in \Lambda $
,
$x\in \Lambda $
,
![]() $\theta _{g,x}^i$
is uniformly
$\theta _{g,x}^i$
is uniformly
![]() $C^1$
-close to the inclusion of
$C^1$
-close to the inclusion of
![]() $W^i_\beta (f,x)$
in M.
$W^i_\beta (f,x)$
in M.
For any
![]() $\gamma \in (0, 1)$
, let
$\gamma \in (0, 1)$
, let
![]() $\mathcal {U}_\gamma ^F$
be a small
$\mathcal {U}_\gamma ^F$
be a small
![]() $C^1$
neighborhood of F (recall
$C^1$
neighborhood of F (recall
![]() $F=f^N$
). Taking
$F=f^N$
). Taking
![]() $G\in \mathcal {U}_\gamma ^F \cap \mathrm {Diff}^2(M)$
such that for every
$G\in \mathcal {U}_\gamma ^F \cap \mathrm {Diff}^2(M)$
such that for every
![]() $x\in \Lambda _G$
(here
$x\in \Lambda _G$
(here
![]() $\Lambda _G$
is a locally maximal hyperbolic set for G),
$\Lambda _G$
is a locally maximal hyperbolic set for G),
![]() $n\in \mathbb {N}$
, and
$n\in \mathbb {N}$
, and
![]() $i=u, s$
,
$i=u, s$
,
Claim 4.3. The following properties hold:
-
(a)
 $h_G|_{W^u_\beta (F, x)\cap \Lambda }$
and
$h_G|_{W^u_\beta (F, x)\cap \Lambda }$
and
 $(h_G|_{W^u_\beta (F, x)\cap \Lambda })^{-1}$
are
$(h_G|_{W^u_\beta (F, x)\cap \Lambda })^{-1}$
are
 $(C_\gamma , \gamma )$
-Hölder continuous for some
$(C_\gamma , \gamma )$
-Hölder continuous for some
 $C_\gamma>0$
;
$C_\gamma>0$
; -
(b) the stable and unstable foliations
are $$ \begin{align*}\{W^s(G, z): z\in\Lambda_G\}, \quad \{W^u(G, z): z\in\Lambda_G\}\end{align*} $$
$$ \begin{align*}\{W^s(G, z): z\in\Lambda_G\}, \quad \{W^u(G, z): z\in\Lambda_G\}\end{align*} $$
 $C^1$
and invariant for G. Thus the holonomy maps and
$C^1$
and invariant for G. Thus the holonomy maps and $$ \begin{align*} &\pi^s_G: W^u_\beta(G,h_G(x))\cap\Lambda_G\to W^u_\beta(G,h_G(x'))\cap\Lambda_G \quad \text{with}\\& \qquad\,\qquad \pi^s_G(y)=W^s_\beta(G,y)\cap W^u_\beta(G,h_G(x')), \end{align*} $$
are Lipschitz continuous.
$$ \begin{align*} &\pi^s_G: W^u_\beta(G,h_G(x))\cap\Lambda_G\to W^u_\beta(G,h_G(x'))\cap\Lambda_G \quad \text{with}\\& \qquad\,\qquad \pi^s_G(y)=W^s_\beta(G,y)\cap W^u_\beta(G,h_G(x')), \end{align*} $$
are Lipschitz continuous. $$ \begin{align*} &\pi^u_G: W^s_\beta(G,h_G(x))\cap\Lambda_G\to W^s_\beta(G,h_G(x"))\cap\Lambda_G \quad \text{with}\\& \qquad\ \ \qquad \pi^u_G(z)=W^u_\beta(G,z)\cap W^s_\beta(G,h_G(x")) \end{align*} $$
$$ \begin{align*} &\pi^u_G: W^s_\beta(G,h_G(x))\cap\Lambda_G\to W^s_\beta(G,h_G(x"))\cap\Lambda_G \quad \text{with}\\& \qquad\ \ \qquad \pi^u_G(z)=W^u_\beta(G,z)\cap W^s_\beta(G,h_G(x")) \end{align*} $$
Proof. (a) See [Reference Wang, Wang, Cao and Zhao43, Claim 3.1].
(b) Since G satisfies equation (4.9), we conclude

provided that
![]() $\unicode{x3bb} _s(\mu )+6\varepsilon <0$
. By [Reference Hirsch and Pugh18, Theorem 6.3], the stable foliation is
$\unicode{x3bb} _s(\mu )+6\varepsilon <0$
. By [Reference Hirsch and Pugh18, Theorem 6.3], the stable foliation is
![]() $C^1$
. A similar argument shows that the unstable foliation is also
$C^1$
. A similar argument shows that the unstable foliation is also
![]() $C^1$
. Then the corresponding maps are uniformly
$C^1$
. Then the corresponding maps are uniformly
![]() $C^1$
(see [Reference Pugh, Shub and Wilkinson35, pp. 540–541] for more details), which implies the desired result.
$C^1$
(see [Reference Pugh, Shub and Wilkinson35, pp. 540–541] for more details), which implies the desired result.
We proceed to prove Lemma 4.2. For any
![]() $y\in W^u_\beta (F, x)\cap \Lambda $
,
$y\in W^u_\beta (F, x)\cap \Lambda $
,
 $$ \begin{align*} \begin{aligned} h_G(\pi^s(y))&=h_G( W^s_\beta(F,y)\cap W^u_\beta(F, x') )\\ &=W^s_\beta(G, h_G(y)) \cap W^u_\beta(G, h_G(x'))\\ &=\pi^s_G(h_G(y)). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} h_G(\pi^s(y))&=h_G( W^s_\beta(F,y)\cap W^u_\beta(F, x') )\\ &=W^s_\beta(G, h_G(y)) \cap W^u_\beta(G, h_G(x'))\\ &=\pi^s_G(h_G(y)). \end{aligned} \end{align*} $$
For the above
![]() $\gamma $
, by Claim 4.3, there exists
$\gamma $
, by Claim 4.3, there exists
![]() $D_\gamma>0$
such that
$D_\gamma>0$
such that
is
![]() $(D_\gamma , \gamma )$
-Hölder continuous. Using the same arguments, one can prove
$(D_\gamma , \gamma )$
-Hölder continuous. Using the same arguments, one can prove
![]() $(\pi ^s)^{-1}$
,
$(\pi ^s)^{-1}$
,
![]() $\pi ^u$
, and
$\pi ^u$
, and
![]() $(\pi ^u)^{-1}$
are also
$(\pi ^u)^{-1}$
are also
![]() $(D_\gamma , \gamma )$
-Hölder continuous.
$(D_\gamma , \gamma )$
-Hölder continuous.
By Lemma 4.2 and the fact that f is topologically mixing on
![]() $\Lambda _\varepsilon $
, one has
$\Lambda _\varepsilon $
, one has
![]() $\dim _H{\kern-1pt}(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
,
$\dim _H{\kern-1pt}(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
,
![]() $\underline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
, and
$\underline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f, x))$
, and
![]() $\overline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f,x))$
are independent of
$\overline {\dim }_B(\Lambda _\varepsilon \cap W^u_\beta (f,x))$
are independent of
![]() $\beta $
and x (see the proof of [Reference Wang, Wang, Cao and Zhao43, Lemma 3.4] for more details). Let
$\beta $
and x (see the proof of [Reference Wang, Wang, Cao and Zhao43, Lemma 3.4] for more details). Let
be a product space. By the properties of dimension (see [Reference Pesin33, Theorem 6.5] for details), one has
 $$ \begin{align} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} A_{\varepsilon, x}\\ &\quad\leq \underline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x)). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} A_{\varepsilon, x}\\ &\quad\leq \underline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}A_{\varepsilon, x}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon\cap W^s_\beta(f, x)). \end{aligned} \end{align} $$
Let
![]() $\Phi : A_{\varepsilon ,x} \to \Lambda _\varepsilon $
be given by
$\Phi : A_{\varepsilon ,x} \to \Lambda _\varepsilon $
be given by
It is easy to see that
![]() $\Phi $
is a homeomorphism onto a neighborhood
$\Phi $
is a homeomorphism onto a neighborhood
![]() $V_x$
of x in
$V_x$
of x in
![]() $\Lambda _\varepsilon $
. For any
$\Lambda _\varepsilon $
. For any
![]() $\gamma \in (0, 1)$
, by Lemma 4.2, there is
$\gamma \in (0, 1)$
, by Lemma 4.2, there is
![]() $E_\gamma>0$
such that
$E_\gamma>0$
such that
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi ^{-1}$
are
$\Phi ^{-1}$
are
![]() $(E_\gamma , \gamma )$
-Hölder continuous (see Step
$(E_\gamma , \gamma )$
-Hölder continuous (see Step
![]() $2$
in the proof of [Reference Wang, Wang, Cao and Zhao43, Theorem A] for more details). By Lemma 2.8 and the arbitrariness of
$2$
in the proof of [Reference Wang, Wang, Cao and Zhao43, Theorem A] for more details). By Lemma 2.8 and the arbitrariness of
![]() $\gamma $
, one has
$\gamma $
, one has
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. Since
$\overline {\dim }_B$
. Since
![]() $\{V_x: x\in \Lambda _\varepsilon \}$
is an open cover of
$\{V_x: x\in \Lambda _\varepsilon \}$
is an open cover of
![]() $\Lambda _\varepsilon $
, one can choose a finite open cover
$\Lambda _\varepsilon $
, one can choose a finite open cover
![]() $\{V_{x_1}, V_{x_2}, \ldots , V_{x_k}\}$
of
$\{V_{x_1}, V_{x_2}, \ldots , V_{x_k}\}$
of
![]() $\Lambda _\varepsilon $
. It follows from equation (4.10) that
$\Lambda _\varepsilon $
. It follows from equation (4.10) that
 $$ \begin{align*} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} \Lambda_\varepsilon = \max_{1\leq i \leq k} \dim_H{\kern-1pt} V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}\Lambda_\varepsilon =\max_{1\leq i\leq k}\overline{\dim}_{B}{\kern1pt}V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x)), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \dim_H{\kern-1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x))\\ &\quad\leq \dim_H{\kern-1pt} \Lambda_\varepsilon = \max_{1\leq i \leq k} \dim_H{\kern-1pt} V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}\Lambda_\varepsilon =\max_{1\leq i\leq k}\overline{\dim}_{B}{\kern1pt}V_{x_i}\\ &\quad\leq \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^u_\beta(f, x)) + \overline{\dim}_{B}{\kern1pt}(\Lambda_\varepsilon \cap W^s_\beta(f, x)), \end{aligned} \end{align*} $$
for every
![]() $x\in \Lambda _\varepsilon $
. This together with equations (4.7) and (4.8) yields that
$x\in \Lambda _\varepsilon $
. This together with equations (4.7) and (4.8) yields that
where
![]() $\mathrm {Dim}$
denotes either
$\mathrm {Dim}$
denotes either
![]() $\dim _H$
or
$\dim _H$
or
![]() $\underline {\dim }_B$
or
$\underline {\dim }_B$
or
![]() $\overline {\dim }_B$
. This completes the proof of Theorem C.
$\overline {\dim }_B$
. This completes the proof of Theorem C.
Acknowledgements
The authors are grateful to the anonymous referee for valuable comments which helped to improve the manuscript greatly. This work is partially supported by The National Key Research and Development Program of China (2022YFA1005802). Y.C. is partially supported by NSFC (11790274). J.W. is partially supported by NSFC (12271386, U2031145). Y.Z. is partially supported by NSFC (12271386) and Qinglan project of Jiangsu Province.