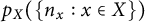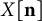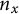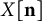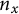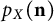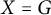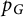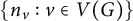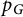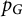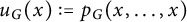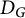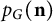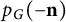1 The blowup-polynomial of a metric space and its distance matrix
This work aims to provide novel connections between metric geometry, the geometry of (real) polynomials, and algebraic combinatorics via partially symmetric functions. In particular, we introduce and study a polynomial graph-invariant for each graph, which to the best of our knowledge, is novel.
1.1 Motivations
The original motivation for our paper came from the study of distance matrices
![]() $D_G$
of graphs G – on both the algebraic and spectral sides:
$D_G$
of graphs G – on both the algebraic and spectral sides:
-
• On the algebraic side, Graham and Pollak [Reference Graham and Pollak21] initiated the study of
 $D_G$
by proving: if
$D_G$
by proving: if
 $T_k$
is a tree on k nodes, then
$T_k$
is a tree on k nodes, then
 $\det D_{T_k}$
is independent of the tree structure and depends only on k. By now, many variants of such results are proved, for trees as well as several other families of graphs, including with q-analogs, weightings, and combinations of both of these. (See, e.g., [Reference Choudhury and Khare16] and its references for a list of such papers, results, and their common unification.)
$\det D_{T_k}$
is independent of the tree structure and depends only on k. By now, many variants of such results are proved, for trees as well as several other families of graphs, including with q-analogs, weightings, and combinations of both of these. (See, e.g., [Reference Choudhury and Khare16] and its references for a list of such papers, results, and their common unification.) -
• Following the above work [Reference Graham and Pollak21], Graham also worked on the spectral side, and with Lovász, studied in [Reference Graham and Lovász20] the distance matrix of a tree, including computing its inverse and characteristic polynomial. This has since led to the intensive study of the roots, i.e., the “distance spectrum,” for trees and other graphs. See, e.g., the survey [Reference Aouchiche and Hansen3] for more on distance spectra.
A well-studied problem in spectral graph theory involves understanding which graphs are distance co-spectral – i.e., for which graphs
![]() $H' \not \cong K'$
, if any, do
$H' \not \cong K'$
, if any, do
![]() $D_{H'}, D_{K'}$
have the same spectra. Many such examples exist; see, e.g., the references in [Reference Drury and Lin18]. In particular, the characteristic polynomial of
$D_{H'}, D_{K'}$
have the same spectra. Many such examples exist; see, e.g., the references in [Reference Drury and Lin18]. In particular, the characteristic polynomial of
![]() $D_G$
does not “detect” the graph G. It is thus natural to seek some other byproduct of
$D_G$
does not “detect” the graph G. It is thus natural to seek some other byproduct of
![]() $D_G$
which does – i.e., which recovers G up to isometry. In this paper, we find such a (to the best of our knowledge) novel graph invariant: a multivariate polynomial, which we call the blowup-polynomial of G, and which does detect G. Remarkably, this polynomial turns out to have several additional attractive properties:
$D_G$
which does – i.e., which recovers G up to isometry. In this paper, we find such a (to the best of our knowledge) novel graph invariant: a multivariate polynomial, which we call the blowup-polynomial of G, and which does detect G. Remarkably, this polynomial turns out to have several additional attractive properties:
-
• It is multi-affine in its arguments.
-
• It is also real-stable, so that its “support” yields a hitherto unexplored delta-matroid.
-
• The blowup-polynomial simultaneously encodes the determinants of all graph-blowups of G (defined presently), thereby connecting with the algebraic side (see the next paragraph).
-
• Its “univariate specialization” is a transformation of the characteristic polynomial of
 $D_G$
, thereby connecting with the spectral side as well.
$D_G$
, thereby connecting with the spectral side as well.
Thus, the blowup-polynomial that we introduce, connects distance spectra for graphs – and more generally, for finite metric spaces – to other well-studied objects, including real-stable/Lorentzian polynomials and delta-matroids.
On the algebraic side, a natural question involves asking if there are graph families
![]() $\{ G_i : i \in I \}$
(like trees on k vertices) for which the scalars
$\{ G_i : i \in I \}$
(like trees on k vertices) for which the scalars
![]() $\det (D_{G_i})$
behave “nicely” as a function of
$\det (D_{G_i})$
behave “nicely” as a function of
![]() $i \in I$
. As stated above, the family of blowups of a fixed graph G (which help answer the preceding “spectral” question) not only answer this question positively as well, but the nature of the answer – multi-affine polynomiality – is desirable in conjunction with its real-stability. In fact, we will obtain many of these results, both spectral and algebraic, in greater generality: for arbitrary finite metric spaces.
$i \in I$
. As stated above, the family of blowups of a fixed graph G (which help answer the preceding “spectral” question) not only answer this question positively as well, but the nature of the answer – multi-affine polynomiality – is desirable in conjunction with its real-stability. In fact, we will obtain many of these results, both spectral and algebraic, in greater generality: for arbitrary finite metric spaces.
The key construction required for all of these contributions is that of a blowup, and we begin by defining it more generally, for arbitrary metric spaces that are discrete (i.e., every point is isolated).
Definition 1.1 Given a metric space
![]() $(X,d)$
with all isolated points, and a function
$(X,d)$
with all isolated points, and a function
![]() $\mathbf {n} : X \to \mathbb {Z}_{>0}$
, the
$\mathbf {n} : X \to \mathbb {Z}_{>0}$
, the
![]() $\mathbf {n}$
-blowup of X is the metric space
$\mathbf {n}$
-blowup of X is the metric space
![]() $X[\mathbf {n}]$
obtained by creating
$X[\mathbf {n}]$
obtained by creating
![]() $n_x := \mathbf {n}(x)$
copies of each point x (also termed blowups of x). Define the distance between copies of distinct points
$n_x := \mathbf {n}(x)$
copies of each point x (also termed blowups of x). Define the distance between copies of distinct points
![]() $x \neq y$
in X to still be
$x \neq y$
in X to still be
![]() $d(x,y)$
, and between distinct copies of the same point to be
$d(x,y)$
, and between distinct copies of the same point to be
![]() $2 d(x,X \setminus \{x\}) = 2 \inf _{y \in X \setminus \{ x \}} d(x,y)$
.
$2 d(x,X \setminus \{x\}) = 2 \inf _{y \in X \setminus \{ x \}} d(x,y)$
.
Also define the distance matrix
![]() $D_X$
and the modified distance matrix
$D_X$
and the modified distance matrix
![]() $\mathcal {D}_X$
of X via:
$\mathcal {D}_X$
of X via:
Notice, for completeness, that the above construction applied to a non-discrete metric space does not yield a metric; and that blowups of X are “compatible” with isometries of X (see (1.3)). We also remark that this notion of blowup seems to be relatively less studied in the literature, and differs from several other variants in the literature – for metric spaces, e.g., [Reference Cheeger, Kleiner and Schioppa14] or for graphs, e.g., [Reference Liu29]. However, the variant studied in this paper was previously studied for the special case of unweighted graphs, see, e.g,. [Reference Hatami, Hirst and Norine24–Reference Komlós, Sárközy and Szemerédi26] in extremal and probabilistic graph theory.
1.2 Defining the blowup-polynomial; Euclidean embeddings
We now describe some of the results in this work, beginning with metric embeddings. Recall that the complete information about a (finite) metric space is encoded into its distance matrix
![]() $D_X$
(or equivalently, in the off-diagonal part of
$D_X$
(or equivalently, in the off-diagonal part of
![]() $\mathcal {D}_X$
). Metric spaces are useful in many sub-disciplines of the mathematical sciences, and have been studied for over a century. For instance, a well-studied question in metric geometry involves understanding metric embeddings. In 1910, Fréchet showed [Reference Fréchet19] that every finite metric space with
$\mathcal {D}_X$
). Metric spaces are useful in many sub-disciplines of the mathematical sciences, and have been studied for over a century. For instance, a well-studied question in metric geometry involves understanding metric embeddings. In 1910, Fréchet showed [Reference Fréchet19] that every finite metric space with
![]() $k+1$
points isometrically embeds into
$k+1$
points isometrically embeds into
![]() $\mathbb R^k$
with the supnorm. Similarly, a celebrated 1935 theorem of Schoenberg [Reference Schoenberg37] (following Menger’s works [Reference Menger32, Reference Menger33]) says the following.
$\mathbb R^k$
with the supnorm. Similarly, a celebrated 1935 theorem of Schoenberg [Reference Schoenberg37] (following Menger’s works [Reference Menger32, Reference Menger33]) says the following.
Theorem 1.2 (Schoenberg [Reference Schoenberg37])
A finite metric space
![]() $X = \{ x_0, \dots , x_k \}$
isometrically embeds inside Euclidean space
$X = \{ x_0, \dots , x_k \}$
isometrically embeds inside Euclidean space
![]() $(\mathbb R^r, \| \cdot \|_2)$
if and only if its modified Cayley–Menger matrix
$(\mathbb R^r, \| \cdot \|_2)$
if and only if its modified Cayley–Menger matrix
is positive semidefinite, with rank at most r.
As an aside, the determinant of this matrix is related to the volume of a polytope with vertices
![]() $x_i$
(beginning with classical work of Cayley [Reference Cayley13]), and the Cayley–Menger matrix itself connects to the principle of trilateration/triangulation that underlies the GPS system.
$x_i$
(beginning with classical work of Cayley [Reference Cayley13]), and the Cayley–Menger matrix itself connects to the principle of trilateration/triangulation that underlies the GPS system.
Returning to the present work, our goal is to study the distance matrix of a finite metric space vis-a-vis its blowups. We begin with a “negative” result from metric geometry. Note that every blowup of a finite metric space embeds into
![]() $\mathbb R^k$
(for some k) equipped with the supnorm, by Fréchet’s aforementioned result. In contrast, we employ Schoenberg’s Theorem 1.2 to show that the same is far from true when considering the Euclidean metric. Namely, given a finite metric space X, we characterize all blowups
$\mathbb R^k$
(for some k) equipped with the supnorm, by Fréchet’s aforementioned result. In contrast, we employ Schoenberg’s Theorem 1.2 to show that the same is far from true when considering the Euclidean metric. Namely, given a finite metric space X, we characterize all blowups
![]() $X[\mathbf {n}]$
that embed in some Euclidean space
$X[\mathbf {n}]$
that embed in some Euclidean space
![]() $(\mathbb R^k, \| \cdot \|_2)$
. Since X embeds into
$(\mathbb R^k, \| \cdot \|_2)$
. Since X embeds into
![]() $X[\mathbf {n}]$
, a necessary condition is that X itself should be Euclidean. With this in mind, we have the following.
$X[\mathbf {n}]$
, a necessary condition is that X itself should be Euclidean. With this in mind, we have the following.
Theorem A Suppose
![]() $X = \{ x_1, \dots , x_k \}$
is a finite metric subspace of Euclidean space
$X = \{ x_1, \dots , x_k \}$
is a finite metric subspace of Euclidean space
![]() $(\mathbb R^r, \| \cdot \|_2)$
. Given positive integers
$(\mathbb R^r, \| \cdot \|_2)$
. Given positive integers
![]() $\{ n_{x_i} : 1 \leqslant i \leqslant k \}$
, not all of which equal
$\{ n_{x_i} : 1 \leqslant i \leqslant k \}$
, not all of which equal
![]() $1$
, the following are equivalent:
$1$
, the following are equivalent:
-
(1) The blowup
 $X[\mathbf {n}]$
isometrically embeds into some Euclidean space
$X[\mathbf {n}]$
isometrically embeds into some Euclidean space
 $(\mathbb R^{r'}, \| \cdot \|_2)$
.
$(\mathbb R^{r'}, \| \cdot \|_2)$
. -
(2) Either
 $k=1$
and
$k=1$
and
 $\mathbf {n}$
is arbitrary (then, by convention,
$\mathbf {n}$
is arbitrary (then, by convention,
 $X[\mathbf {n}]$
is a simplex); or
$X[\mathbf {n}]$
is a simplex); or
 $k>1$
and there exists a unique
$k>1$
and there exists a unique
 $1 \leqslant j \leqslant k$
such that
$1 \leqslant j \leqslant k$
such that
 $n_{x_j} = 2$
. In this case, we moreover have: (a)
$n_{x_j} = 2$
. In this case, we moreover have: (a)
 $n_{x_i} = 1\ \forall i \neq j$
, (b)
$n_{x_i} = 1\ \forall i \neq j$
, (b)
 $x_j$
is not in the affine hull/span V of
$x_j$
is not in the affine hull/span V of
 $\{ x_i : i \neq j \}$
, and (c) the unique point
$\{ x_i : i \neq j \}$
, and (c) the unique point
 $v \in V$
closest to
$v \in V$
closest to
 $x_j$
, lies in X.
$x_j$
, lies in X.
If these conditions hold, one can take
![]() $r' = r$
and
$r' = r$
and
![]() $X[\mathbf {n}] = X \sqcup \{ 2v - x_j \}$
.
$X[\mathbf {n}] = X \sqcup \{ 2v - x_j \}$
.
Given the preceding result, we turn away from metric geometry, and instead focus on studying the family of blowups
![]() $X[\mathbf {n}]$
– through their distance matrices
$X[\mathbf {n}]$
– through their distance matrices
![]() $D_{X[\mathbf {n}]}$
(which contain all of the information on
$D_{X[\mathbf {n}]}$
(which contain all of the information on
![]() $X[\mathbf {n}]$
). Drawing inspiration from Graham and Pollak [Reference Graham and Pollak21], we focus on one of the simplest invariants of this family of matrices: their determinants, and the (possibly algebraic) nature of the dependence of
$X[\mathbf {n}]$
). Drawing inspiration from Graham and Pollak [Reference Graham and Pollak21], we focus on one of the simplest invariants of this family of matrices: their determinants, and the (possibly algebraic) nature of the dependence of
![]() $\det D_{X[\mathbf {n}]}$
on
$\det D_{X[\mathbf {n}]}$
on
![]() $\mathbf {n}$
. In this paper, we show that the function
$\mathbf {n}$
. In this paper, we show that the function
![]() $: \mathbf {n} \mapsto \det D_{X[\mathbf {n}]}$
possesses several attractive properties. First,
$: \mathbf {n} \mapsto \det D_{X[\mathbf {n}]}$
possesses several attractive properties. First,
![]() $\det D_{X[\mathbf {n}]}$
is a polynomial function in the sizes
$\det D_{X[\mathbf {n}]}$
is a polynomial function in the sizes
![]() $n_x$
of the blowup, up to an exponential factor.
$n_x$
of the blowup, up to an exponential factor.
Theorem B Given
![]() $(X,d)$
a finite metric space, and a tuple of positive integers
$(X,d)$
a finite metric space, and a tuple of positive integers
![]() $\mathbf {n} := (n_x)_{x \in X} \in \mathbb {Z}_{>0}^X$
, the function
$\mathbf {n} := (n_x)_{x \in X} \in \mathbb {Z}_{>0}^X$
, the function
![]() $\mathbf {n} \mapsto \det D_{X[\mathbf {n}]}$
is a multi-affine polynomial
$\mathbf {n} \mapsto \det D_{X[\mathbf {n}]}$
is a multi-affine polynomial
![]() $p_X(\mathbf {n})$
in the
$p_X(\mathbf {n})$
in the
![]() $n_x$
(i.e., its monomials are squarefree in the
$n_x$
(i.e., its monomials are squarefree in the
![]() $n_x$
), times the exponential function
$n_x$
), times the exponential function
Moreover, the polynomial
![]() $p_X(\mathbf {n})$
has constant term
$p_X(\mathbf {n})$
has constant term
![]() $p_X(\mathbf {0}) = \prod _{x \in X} (-2 \; d(x, X \setminus \{ x \}))$
, and linear term
$p_X(\mathbf {0}) = \prod _{x \in X} (-2 \; d(x, X \setminus \{ x \}))$
, and linear term
![]() $-p_X(\mathbf {0}) \sum _{x \in X} n_x$
.
$-p_X(\mathbf {0}) \sum _{x \in X} n_x$
.
Theorem B follows from a stronger one proved below. See Theorem 2.3, which shows, in particular, that not only do the conclusions of Theorem B hold over an arbitrary commutative ring, but moreover, the blowup-polynomial
![]() $p_X(\mathbf {n})$
is a polynomial function in the variables
$p_X(\mathbf {n})$
is a polynomial function in the variables
![]() $\mathbf {n} = \{ n_x : x \in X \}$
as well as the entries of the “original” distance matrix
$\mathbf {n} = \{ n_x : x \in X \}$
as well as the entries of the “original” distance matrix
![]() $D_X$
– and moreover, it is squarefree/multi-affine in all of these arguments (where we treat all entries of
$D_X$
– and moreover, it is squarefree/multi-affine in all of these arguments (where we treat all entries of
![]() $D_X$
to be “independent” variables).
$D_X$
to be “independent” variables).
We also refine the final assertions of Theorem B, by isolating in Proposition 2.6, the coefficient of every monomial in
![]() $p_X(\mathbf {n})$
. That proposition moreover provides a sufficient condition under which the coefficients of two monomials in
$p_X(\mathbf {n})$
. That proposition moreover provides a sufficient condition under which the coefficients of two monomials in
![]() $p_X(\mathbf {n})$
are equal.
$p_X(\mathbf {n})$
are equal.
Theorem B leads us to introduce the following notion, for an arbitrary finite metric space (e.g., every finite, connected,
![]() $\mathbb {R}_{>0}$
-weighted graph).
$\mathbb {R}_{>0}$
-weighted graph).
Definition 1.3 Define the (multivariate) blowup-polynomial of a finite metric space
![]() $(X,d)$
to be
$(X,d)$
to be
![]() $p_X(\mathbf {n})$
, where the
$p_X(\mathbf {n})$
, where the
![]() $n_x$
are thought of as indeterminates. We write out a closed-form expression in the proof of Theorem B – see equation (2.2).
$n_x$
are thought of as indeterminates. We write out a closed-form expression in the proof of Theorem B – see equation (2.2).
In this paper, we also study a specialization of this polynomial. Define the univariate blowup-polynomial of
![]() $(X,d)$
to be
$(X,d)$
to be
![]() $u_X(n) := p_X(n,n,\dots ,n)$
, where n is thought of as an indeterminate.
$u_X(n) := p_X(n,n,\dots ,n)$
, where n is thought of as an indeterminate.
Remark 1.4 Definition 1.3 requires a small clarification. The polynomial map (by Theorem B)
can be extended from the Zariski dense subset
![]() $\mathbb {Z}_{>0}^k$
to all of
$\mathbb {Z}_{>0}^k$
to all of
![]() $\mathbb R^k$
. (Zariski density is explained during the proof of Theorem B.) Since
$\mathbb R^k$
. (Zariski density is explained during the proof of Theorem B.) Since
![]() $\mathbb R$
is an infinite field, this polynomial map on
$\mathbb R$
is an infinite field, this polynomial map on
![]() $\mathbb R^k$
may now be identified with a polynomial, which is precisely
$\mathbb R^k$
may now be identified with a polynomial, which is precisely
![]() $p_X(-)$
, a polynomial in
$p_X(-)$
, a polynomial in
![]() $|X|$
variables (which we will denote by
$|X|$
variables (which we will denote by
![]() $\{ n_x : x \in X \}$
throughout the paper, via a mild abuse of notation). Now setting all arguments to be the same indeterminate yields the univariate blowup-polynomial of
$\{ n_x : x \in X \}$
throughout the paper, via a mild abuse of notation). Now setting all arguments to be the same indeterminate yields the univariate blowup-polynomial of
![]() $(X,d)$
.
$(X,d)$
.
1.3 Real-stability
We next discuss the blowup-polynomial
![]() $p_X(\cdot )$
and its univariate specialization
$p_X(\cdot )$
and its univariate specialization
![]() $u_X(\cdot )$
from the viewpoint of root-location properties. As we will see, the polynomial
$u_X(\cdot )$
from the viewpoint of root-location properties. As we will see, the polynomial
![]() $u_X(n) = p_X(n,n,\dots ,n)$
always turns out to be real-rooted in n. In fact, even more is true. Recall that in recent times, the notion of real-rootedness has been studied in a much more powerful avatar: real-stability. Our next result strengthens the real-rootedness of
$u_X(n) = p_X(n,n,\dots ,n)$
always turns out to be real-rooted in n. In fact, even more is true. Recall that in recent times, the notion of real-rootedness has been studied in a much more powerful avatar: real-stability. Our next result strengthens the real-rootedness of
![]() $u_X(\cdot )$
to the second attractive property of
$u_X(\cdot )$
to the second attractive property of
![]() $p_X(\cdot )$
– namely, real-stability.
$p_X(\cdot )$
– namely, real-stability.
Theorem C The blowup-polynomial
![]() $p_X(\mathbf {n})$
of every finite metric space
$p_X(\mathbf {n})$
of every finite metric space
![]() $(X,d)$
is real-stable in
$(X,d)$
is real-stable in
![]() $\{ n_x \}$
. (Hence, its univariate specialization
$\{ n_x \}$
. (Hence, its univariate specialization
![]() $u_X(n) = p_X(n,n,\dots ,n)$
is always real-rooted.)
$u_X(n) = p_X(n,n,\dots ,n)$
is always real-rooted.)
Recall that real-stable polynomials are simply ones with real coefficients, which do not vanish when all arguments are constrained to lie in the (open) upper half-plane
![]() $\Im (z)> 0$
. Such polynomials have been intensively studied in recent years, with a vast number of applications. For instance, they were famously used in celebrated works of Borcea–Brändén (e.g., [Reference Borcea and Brändén5–Reference Borcea and Brändén7]) and Marcus–Spielman–Srivastava [Reference Marcus, Spielman and Srivastava30, Reference Marcus, Spielman and Srivastava31] to prove longstanding conjectures (including of Kadison–Singer, Johnson, Bilu–Linial, Lubotzky, and others), construct expander graphs, and vastly extend the Laguerre–Pólya–Schur program [Reference Laguerre27, Reference Pólya34, Reference Pólya and Schur35] from the turn of the 20th century (among other applications).
$\Im (z)> 0$
. Such polynomials have been intensively studied in recent years, with a vast number of applications. For instance, they were famously used in celebrated works of Borcea–Brändén (e.g., [Reference Borcea and Brändén5–Reference Borcea and Brändén7]) and Marcus–Spielman–Srivastava [Reference Marcus, Spielman and Srivastava30, Reference Marcus, Spielman and Srivastava31] to prove longstanding conjectures (including of Kadison–Singer, Johnson, Bilu–Linial, Lubotzky, and others), construct expander graphs, and vastly extend the Laguerre–Pólya–Schur program [Reference Laguerre27, Reference Pólya34, Reference Pólya and Schur35] from the turn of the 20th century (among other applications).
Theorem C reveals that for all finite metric spaces – in particular, for all finite connected graphs – the blowup-polynomial is indeed multi-affine and real-stable. The class of multi-affine real-stable polynomials has been characterized in [Reference Brändén11, Theorem 5.6] and [Reference Wagner and Wei43, Theorem 3]. (For a connection to matroids, see [Reference Brändén11, Reference Choe, Oxley, Sokal and Wagner15].) To the best of our knowledge, blowup-polynomials
![]() $p_X(\mathbf {n})$
provide novel examples/realizations of multi-affine real-stable polynomials.
$p_X(\mathbf {n})$
provide novel examples/realizations of multi-affine real-stable polynomials.
1.4 Graph metric spaces: symmetries, complete multipartite graphs
We now turn from the metric-geometric Theorem A, the algebraic Theorem B, and the analysis-themed Theorem C, to a more combinatorial theme, by restricting from metric spaces to graphs. Here, we present two “main theorems” and one proposition.
1.4.1 Graph invariants and symmetries
Having shown that
![]() $\det D_{X[\mathbf {n}]}$
is a polynomial in
$\det D_{X[\mathbf {n}]}$
is a polynomial in
![]() $\mathbf {n}$
(times an exponential factor), and that
$\mathbf {n}$
(times an exponential factor), and that
![]() $p_X(\cdot )$
is always real-stable, our next result explains a third attractive property of
$p_X(\cdot )$
is always real-stable, our next result explains a third attractive property of
![]() $p_X(\cdot )$
: The blowup-polynomial of a graph
$p_X(\cdot )$
: The blowup-polynomial of a graph
![]() $X = G$
is indeed a (novel) graph invariant. To formally state this result, we begin by re-examining the blowup-construction for graphs and their distance matrices.
$X = G$
is indeed a (novel) graph invariant. To formally state this result, we begin by re-examining the blowup-construction for graphs and their distance matrices.
A distinguished sub-class of discrete metric spaces is that of finite simple connected unweighted graphs G (so, without parallel/multiple edges or self-loops). Here, the distance between two nodes
![]() $v,w$
is defined to be the (edge-)length of any shortest path joining
$v,w$
is defined to be the (edge-)length of any shortest path joining
![]() $v,w$
. In this paper, we term such objects graph metric spaces. Note that the blowup
$v,w$
. In this paper, we term such objects graph metric spaces. Note that the blowup
![]() $G[\mathbf {n}]$
is a priori only defined as a metric space; we now adjust the definition to make it a graph.
$G[\mathbf {n}]$
is a priori only defined as a metric space; we now adjust the definition to make it a graph.
Definition 1.5 Given a graph metric space
![]() $G = (V,E)$
, and a tuple
$G = (V,E)$
, and a tuple
![]() $\mathbf {n} = (n_v : v \in V)$
, the
$\mathbf {n} = (n_v : v \in V)$
, the
![]() $\mathbf {n}$
-blowup of G is defined to be the graph
$\mathbf {n}$
-blowup of G is defined to be the graph
![]() $G[\mathbf {n}]$
– with
$G[\mathbf {n}]$
– with
![]() $n_v$
copies of each vertex v – such that a copy of v and one of w are adjacent in
$n_v$
copies of each vertex v – such that a copy of v and one of w are adjacent in
![]() $G[\mathbf {n}]$
if and only if
$G[\mathbf {n}]$
if and only if
![]() $v \neq w$
are adjacent in G.
$v \neq w$
are adjacent in G.
(For example, the
![]() $\mathbf {n}$
-blowup of a complete graph is a complete multipartite graph.) Now note that if G is a graph metric space, then so is
$\mathbf {n}$
-blowup of a complete graph is a complete multipartite graph.) Now note that if G is a graph metric space, then so is
![]() $G[\mathbf {n}]$
for all tuples
$G[\mathbf {n}]$
for all tuples
![]() $\mathbf {n} \in \mathbb {Z}_{>0}^{|V|}$
. The results stated above thus apply to every such graph G – more precisely, to the distance matrices of the blowups of G.
$\mathbf {n} \in \mathbb {Z}_{>0}^{|V|}$
. The results stated above thus apply to every such graph G – more precisely, to the distance matrices of the blowups of G.
To motivate our next result, now specifically for graph metric spaces, we first relate the symmetries of the graph with those of its blowup-polynomial
![]() $p_G(\mathbf {n})$
. Suppose a graph metric space
$p_G(\mathbf {n})$
. Suppose a graph metric space
![]() $G = (V,E)$
has a structural (i.e., adjacency-preserving) symmetry
$G = (V,E)$
has a structural (i.e., adjacency-preserving) symmetry
![]() $\Psi : V \to V$
– i.e., an (auto-)isometry as a metric space. Denoting the corresponding relabeled graph metric space by
$\Psi : V \to V$
– i.e., an (auto-)isometry as a metric space. Denoting the corresponding relabeled graph metric space by
![]() $\Psi (G)$
,
$\Psi (G)$
,
It is thus natural to ask if the converse holds – i.e., if
![]() $p_G(\cdot )$
helps recover the group of auto-isometries of G. A stronger result would be if
$p_G(\cdot )$
helps recover the group of auto-isometries of G. A stronger result would be if
![]() $p_G$
recovers G itself (up to isometry). We show that both of these hold.
$p_G$
recovers G itself (up to isometry). We show that both of these hold.
Theorem D Given a graph metric space
![]() $G = (V,E)$
and a bijection
$G = (V,E)$
and a bijection
![]() $\Psi : V \to V$
, the symmetries of the polynomial
$\Psi : V \to V$
, the symmetries of the polynomial
![]() $p_G$
equal the isometries of G. In particular, any (equivalently all) of the statements in (1.3) hold, if and only if
$p_G$
equal the isometries of G. In particular, any (equivalently all) of the statements in (1.3) hold, if and only if
![]() $\Psi $
is an isometry of G. More strongly, the polynomial
$\Psi $
is an isometry of G. More strongly, the polynomial
![]() $p_G(\mathbf {n})$
recovers the graph metric space G (up to isometry). However, this does not hold for the polynomial
$p_G(\mathbf {n})$
recovers the graph metric space G (up to isometry). However, this does not hold for the polynomial
![]() $u_G$
.
$u_G$
.
As the proof reveals, one in fact needs only the homogeneous quadratic part of
![]() $p_G$
, i.e., its Hessian matrix
$p_G$
, i.e., its Hessian matrix
![]() $((\partial _{n_v} \partial _{n_{v'}} p_G)(\mathbf {0}_V))_{v,v' \in V}$
, to recover the graph and its isometries. Moreover, this associates to every graph a partially symmetric polynomial, whose symmetries are precisely the graph-isometries.
$((\partial _{n_v} \partial _{n_{v'}} p_G)(\mathbf {0}_V))_{v,v' \in V}$
, to recover the graph and its isometries. Moreover, this associates to every graph a partially symmetric polynomial, whose symmetries are precisely the graph-isometries.
Our next result works more generally in metric spaces X, hence is stated over them. Note that the polynomial
![]() $p_X(\mathbf {n})$
is “partially symmetric,” depending on the symmetries (or isometries) of the distance matrix (or metric space). Indeed, partial symmetry is as much as one can hope for, because it turns out that “full” symmetry (in all variables
$p_X(\mathbf {n})$
is “partially symmetric,” depending on the symmetries (or isometries) of the distance matrix (or metric space). Indeed, partial symmetry is as much as one can hope for, because it turns out that “full” symmetry (in all variables
![]() $n_x$
) occurs precisely in one situation.
$n_x$
) occurs precisely in one situation.
Proposition 1.6 Given a finite metric space X, the following are equivalent:
-
(1) The polynomial
 $p_X(\mathbf {n})$
is symmetric in the variables
$p_X(\mathbf {n})$
is symmetric in the variables
 $\{ n_x, \ x \in X \}$
.
$\{ n_x, \ x \in X \}$
. -
(2) The metric
 $d_X$
is a rescaled discrete metric:
$d_X$
is a rescaled discrete metric:
 $d_X(x,y) = c \mathbf {1}_{x \neq y}\ \forall x,y \in X$
, for some
$d_X(x,y) = c \mathbf {1}_{x \neq y}\ \forall x,y \in X$
, for some
 $c>0$
.
$c>0$
.
1.4.2 Complete multipartite graphs: novel characterization via stability
The remainder of this section returns back to graphs. We next present an interesting byproduct of the above results: a novel characterization of the class of complete multipartite graphs. Begin by observing from the proof of Theorem C that the polynomials
![]() $p_G(\cdot )$
are stable because of a determinantal representation (followed by inversion). However, they do not enjoy two related properties:
$p_G(\cdot )$
are stable because of a determinantal representation (followed by inversion). However, they do not enjoy two related properties:
-
(1)
 $p_G(\cdot )$
is not homogeneous.
$p_G(\cdot )$
is not homogeneous. -
(2) The coefficients of the multi-affine polynomial
 $p_G(\cdot )$
are not all of the same sign; in particular, they cannot form a probability distribution on the subsets of
$p_G(\cdot )$
are not all of the same sign; in particular, they cannot form a probability distribution on the subsets of
 $\{ 1, \dots , k \}$
(corresponding to the various monomials in
$\{ 1, \dots , k \}$
(corresponding to the various monomials in
 $p_G(\cdot )$
). In fact, even the constant and linear terms have opposite signs, by the final assertion in Theorem B.
$p_G(\cdot )$
). In fact, even the constant and linear terms have opposite signs, by the final assertion in Theorem B.
These two (unavailable) properties of real-stable polynomials are indeed important and well-studied in the literature. Corresponding to the preceding numbering:
-
(1) Very recently, Brändén and Huh [Reference Brändén and Huh12] introduced and studied a distinguished class of homogeneous real polynomials, which they termed Lorentzian polynomials (defined below). Relatedly, Gurvits [Reference Gurvits, Kotsireas and Zima23] / Anari–Oveis Gharan–Vinzant [Reference Anari, Oveis Gharan and Vinzant2] defined strongly/completely log-concave polynomials, also defined below. These classes of polynomials have several interesting properties as well as applications (see, e.g., [Reference Anari, Oveis Gharan and Vinzant1, Reference Anari, Oveis Gharan and Vinzant2, Reference Brändén and Huh12, Reference Gurvits, Kotsireas and Zima23] and related/follow-up works).
-
(2) Recall that strongly Rayleigh measures are probability measures on the power set of
 $\{ 1, \dots , k \}$
whose generating (multi-affine) polynomials are real-stable. These were introduced and studied by Borcea, Brändén, and Liggett in the fundamental work [Reference Borcea, Brändén and Liggett8]. This work developed the theory of negative association/dependence for such measures, and enabled the authors to prove several conjectures of Liggett, Pemantle, and Wagner, among other achievements.
$\{ 1, \dots , k \}$
whose generating (multi-affine) polynomials are real-stable. These were introduced and studied by Borcea, Brändén, and Liggett in the fundamental work [Reference Borcea, Brändén and Liggett8]. This work developed the theory of negative association/dependence for such measures, and enabled the authors to prove several conjectures of Liggett, Pemantle, and Wagner, among other achievements.
Given that
![]() $p_G(\cdot )$
is always real-stable, a natural question is if one can characterize those graphs for which a certain homogenization of
$p_G(\cdot )$
is always real-stable, a natural question is if one can characterize those graphs for which a certain homogenization of
![]() $p_G(\cdot )$
is Lorentzian, or a suitable normalization is strongly Rayleigh. The standard mathematical way to address obstacle (1) above is to “projectivize” using a new variable
$p_G(\cdot )$
is Lorentzian, or a suitable normalization is strongly Rayleigh. The standard mathematical way to address obstacle (1) above is to “projectivize” using a new variable
![]() $z_0$
, while for obstacle (2) we evaluate at
$z_0$
, while for obstacle (2) we evaluate at
![]() $(-z_1, \dots , -z_k)$
, where we use
$(-z_1, \dots , -z_k)$
, where we use
![]() $z_j$
instead of
$z_j$
instead of
![]() $n_{x_j}$
to denote complex variables. Thus, our next result proceeds via homogenization at
$n_{x_j}$
to denote complex variables. Thus, our next result proceeds via homogenization at
![]() $-z_0$
.
$-z_0$
.
Theorem E Say
![]() $G = (V,E)$
with
$G = (V,E)$
with
![]() $|V|=k$
. Define the homogenized blowup-polynomial
$|V|=k$
. Define the homogenized blowup-polynomial
Then the following are equivalent:
-
(1) The polynomial
 $\widetilde {p}_G(z_0, z_1, \dots , z_k)$
is real-stable.
$\widetilde {p}_G(z_0, z_1, \dots , z_k)$
is real-stable. -
(2) The polynomial
 $\widetilde {p}_G(\cdot )$
has all coefficients (of the monomials
$\widetilde {p}_G(\cdot )$
has all coefficients (of the monomials
 $z_0^{k - |J|} \prod _{j \in J} z_j$
) nonnegative.
$z_0^{k - |J|} \prod _{j \in J} z_j$
) nonnegative. -
(3) We have
 $(-1)^k p_G(-1,\dots ,-1)> 0$
, and the normalized “reflected” polynomial is strongly Rayleigh. In other words, this (multi-affine) polynomial is real-stable and has nonnegative coefficients (of all monomials
$(-1)^k p_G(-1,\dots ,-1)> 0$
, and the normalized “reflected” polynomial is strongly Rayleigh. In other words, this (multi-affine) polynomial is real-stable and has nonnegative coefficients (of all monomials $$\begin{align*}(z_1, \dots, z_k) \quad \mapsto \quad \frac{p_G(-z_1, \dots, -z_k)}{p_G(-1,\dots,-1)} \end{align*}$$
$$\begin{align*}(z_1, \dots, z_k) \quad \mapsto \quad \frac{p_G(-z_1, \dots, -z_k)}{p_G(-1,\dots,-1)} \end{align*}$$
 $\prod _{j \in J} z_j$
), which sum up to
$\prod _{j \in J} z_j$
), which sum up to
 $1$
.
$1$
.
-
(4) The modified distance matrix
 $\mathcal {D}_G$
(see Definition 1.1) is positive semidefinite.
$\mathcal {D}_G$
(see Definition 1.1) is positive semidefinite. -
(5) G is a complete multipartite graph.
Theorem E is a novel characterization result of complete multipartite graphs in the literature, in terms of real stability and the strong(ly) Rayleigh property. Moreover, given the remarks preceding Theorem E, we present three further equivalences to these characterizations.
Corollary 1.7 Definitions in Section 4.2. The assertions in Theorem E are further equivalent to:
-
(6) The polynomial
 $\widetilde {p}_G(z_0, \dots , z_k)$
is Lorentzian.
$\widetilde {p}_G(z_0, \dots , z_k)$
is Lorentzian. -
(7) The polynomial
 $\widetilde {p}_G(z_0, \dots , z_k)$
is strongly log-concave.
$\widetilde {p}_G(z_0, \dots , z_k)$
is strongly log-concave. -
(8) The polynomial
 $\widetilde {p}_G(z_0, \dots , z_k)$
is completely log-concave.
$\widetilde {p}_G(z_0, \dots , z_k)$
is completely log-concave.
We quickly explain the corollary. Theorem E(1) implies
![]() $\widetilde {p}_G$
is Lorentzian (see [Reference Brändén and Huh12, Reference Choe, Oxley, Sokal and Wagner15]), which implies Theorem E(2). The other equivalences follow from [Reference Brändén and Huh12, Theorem 2.30], which shows that – for any real homogeneous polynomial – assertions (7), (8) here are equivalent to
$\widetilde {p}_G$
is Lorentzian (see [Reference Brändén and Huh12, Reference Choe, Oxley, Sokal and Wagner15]), which implies Theorem E(2). The other equivalences follow from [Reference Brändén and Huh12, Theorem 2.30], which shows that – for any real homogeneous polynomial – assertions (7), (8) here are equivalent to
![]() $\widetilde {p}_G$
being Lorentzian.
$\widetilde {p}_G$
being Lorentzian.
Remark 1.8 As we see in the proof of Theorem E, when
![]() $\mathcal {D}_G$
is positive semidefinite, the homogeneous polynomial
$\mathcal {D}_G$
is positive semidefinite, the homogeneous polynomial
![]() $\widetilde {p}_G(z_0, \dots , z_k)$
has a determinantal representation, i.e.,
$\widetilde {p}_G(z_0, \dots , z_k)$
has a determinantal representation, i.e.,
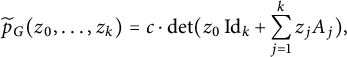 $$\begin{align*}\widetilde{p}_G(z_0, \dots, z_k) = c \cdot \det( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^k z_j A_j), \end{align*}$$
$$\begin{align*}\widetilde{p}_G(z_0, \dots, z_k) = c \cdot \det( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^k z_j A_j), \end{align*}$$
with all
![]() $A_j$
positive semidefinite and
$A_j$
positive semidefinite and
![]() $c \in \mathbb R$
. In Proposition A.2, we further compute the mixed characteristic polynomial of these matrices
$c \in \mathbb R$
. In Proposition A.2, we further compute the mixed characteristic polynomial of these matrices
![]() $A_j$
(see (A.1) for the definition), and show that up to a scalar, it equals the “inversion” of the univariate blowup-polynomial, i.e.,
$A_j$
(see (A.1) for the definition), and show that up to a scalar, it equals the “inversion” of the univariate blowup-polynomial, i.e.,
![]() $z_0^k u_G(z_0^{-1})$
.
$z_0^k u_G(z_0^{-1})$
.
Remark 1.9 We also show that the univariate polynomial
![]() $u_G(x)$
is intimately related to the characteristic polynomial of
$u_G(x)$
is intimately related to the characteristic polynomial of
![]() $D_G$
(i.e., the “distance spectrum” of G), whose study was one of our original motivations. See Proposition 4.2 and the subsequent discussion, for precise statements.
$D_G$
(i.e., the “distance spectrum” of G), whose study was one of our original motivations. See Proposition 4.2 and the subsequent discussion, for precise statements.
1.5 Two novel delta-matroids
We conclude with a related byproduct: two novel constructions of delta-matroids, one for every finite metric space and the other for each tree graph. Recall that a delta-matroid consists of a finite “ground set” E and a nonempty collection of feasible subsets
![]() $\mathcal {F} \subseteq 2^E$
, satisfying
$\mathcal {F} \subseteq 2^E$
, satisfying
![]() $\bigcup _{F \in \mathcal {F}} F = E$
as well as the symmetric exchange axiom: Given
$\bigcup _{F \in \mathcal {F}} F = E$
as well as the symmetric exchange axiom: Given
![]() $A,B \in \mathcal {F}$
and
$A,B \in \mathcal {F}$
and
![]() $x \in A \Delta B$
(their symmetric difference), there exists
$x \in A \Delta B$
(their symmetric difference), there exists
![]() $y \in A \Delta B$
such that
$y \in A \Delta B$
such that
![]() $A \Delta \{ x, y \} \in \mathcal {F}$
. Delta-matroids were introduced by Bouchet in [Reference Bouchet9] as a generalization of the notion of matroids.
$A \Delta \{ x, y \} \in \mathcal {F}$
. Delta-matroids were introduced by Bouchet in [Reference Bouchet9] as a generalization of the notion of matroids.
Each (skew-)symmetric matrix
![]() $A_{k \times k}$
over a field yields a linear delta-matroid
$A_{k \times k}$
over a field yields a linear delta-matroid
![]() $\mathcal {M}_A$
as follows. Given any matrix
$\mathcal {M}_A$
as follows. Given any matrix
![]() $A_{k \times k}$
, let
$A_{k \times k}$
, let
![]() $E := \{ 1, \dots , k \}$
and let a subset
$E := \{ 1, \dots , k \}$
and let a subset
![]() $F \subseteq E$
belong to
$F \subseteq E$
belong to
![]() $\mathcal {M}_A$
if either F is empty or the principal submatrix
$\mathcal {M}_A$
if either F is empty or the principal submatrix
![]() $A_{F \times F}$
is nonsingular. In [Reference Bouchet10], Bouchet showed that if A is (skew-)symmetric, then the set system
$A_{F \times F}$
is nonsingular. In [Reference Bouchet10], Bouchet showed that if A is (skew-)symmetric, then the set system
![]() $\mathcal {M}_A$
is indeed a delta-matroid, which is said to be linear.
$\mathcal {M}_A$
is indeed a delta-matroid, which is said to be linear.
We now return to the blowup-polynomial. First, recall a 2007 result of Brändén [Reference Brändén11]: given a multi-affine real-stable polynomial, the set of monomials with nonzero coefficients forms a delta-matroid. Thus, from
![]() $p_X(\mathbf {n}),$
we obtain a delta-matroid, which as we will explain is linear.
$p_X(\mathbf {n}),$
we obtain a delta-matroid, which as we will explain is linear.
Corollary 1.10 Given a finite metric space
![]() $(X,d)$
, the set of monomials with nonzero coefficients in
$(X,d)$
, the set of monomials with nonzero coefficients in
![]() $p_X(\mathbf {n})$
forms the linear delta-matroid
$p_X(\mathbf {n})$
forms the linear delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_X}$
.
$\mathcal {M}_{\mathcal {D}_X}$
.
Definition 1.11 We term
![]() $\mathcal {M}_{\mathcal {D}_X}$
the blowup delta-matroid of
$\mathcal {M}_{\mathcal {D}_X}$
the blowup delta-matroid of
![]() $(X,d)$
.
$(X,d)$
.
The blowup delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_X}$
is – even for X a finite connected unweighted graph – a novel construction that arises out of metric geometry rather than combinatorics, and one that seems to be unexplored in the literature (and unknown to experts). Of course, it is a simple, direct consequence of Brändén’s result in [Reference Brändén11]. However, the next delta-matroid is less direct to show.
$\mathcal {M}_{\mathcal {D}_X}$
is – even for X a finite connected unweighted graph – a novel construction that arises out of metric geometry rather than combinatorics, and one that seems to be unexplored in the literature (and unknown to experts). Of course, it is a simple, direct consequence of Brändén’s result in [Reference Brändén11]. However, the next delta-matroid is less direct to show.
Theorem F Suppose
![]() $T = (V,E)$
is a finite connected unweighted tree with
$T = (V,E)$
is a finite connected unweighted tree with
![]() $|V| \geqslant 2$
. Define the set system
$|V| \geqslant 2$
. Define the set system
![]() $\mathcal {M}'(T)$
to comprise all subsets
$\mathcal {M}'(T)$
to comprise all subsets
![]() $I \subseteq V$
, except for the ones that contain two vertices
$I \subseteq V$
, except for the ones that contain two vertices
![]() $v_1 \neq v_2$
in I such that the Steiner tree
$v_1 \neq v_2$
in I such that the Steiner tree
![]() $T(I)$
has
$T(I)$
has
![]() $v_1, v_2$
as leaves with a common neighbor. Then
$v_1, v_2$
as leaves with a common neighbor. Then
![]() $\mathcal {M}'(T)$
is a delta-matroid, which does not equal
$\mathcal {M}'(T)$
is a delta-matroid, which does not equal
![]() $\mathcal {M}_{D_T}$
for every path graph
$\mathcal {M}_{D_T}$
for every path graph
![]() $T = P_k$
,
$T = P_k$
,
![]() $k \geqslant 9$
.
$k \geqslant 9$
.
We further prove, this notion of (in)feasible subsets in
![]() $\mathcal {M}'(T)$
does not generalize to all graphs. Thus,
$\mathcal {M}'(T)$
does not generalize to all graphs. Thus,
![]() $\mathcal {M}'(T)$
is a combinatorial (not matrix-theoretic) delta-matroid that is also unstudied in the literature to the best of our knowledge, and which arises from every tree, but interestingly, not from all graphs.
$\mathcal {M}'(T)$
is a combinatorial (not matrix-theoretic) delta-matroid that is also unstudied in the literature to the best of our knowledge, and which arises from every tree, but interestingly, not from all graphs.
As a closing statement here: in addition to further exploring the real-stable polynomials
![]() $p_G(\mathbf {n})$
, it would be interesting to obtain connections between these delta-matroids
$p_G(\mathbf {n})$
, it would be interesting to obtain connections between these delta-matroids
![]() $\mathcal {M}_{\mathcal {D}_G}$
and
$\mathcal {M}_{\mathcal {D}_G}$
and
![]() $\mathcal {M}'(T)$
, and others known in the literature from combinatorics, polynomial geometry, and algebra.
$\mathcal {M}'(T)$
, and others known in the literature from combinatorics, polynomial geometry, and algebra.
1.6 Organization of the paper
The remainder of the paper is devoted to proving the above Theorems A through F; this will require developing several preliminaries along the way. The paper is clustered by theme; thus, the next two sections and the final one respectively involve, primarily:
-
• (commutative) algebraic methods – to prove the polynomiality of
 $p_X(\cdot )$
(Theorem B), and to characterize those X for which it is a symmetric polynomial (Proposition 1.6);
$p_X(\cdot )$
(Theorem B), and to characterize those X for which it is a symmetric polynomial (Proposition 1.6); -
• methods from real-stability and analysis – to show
 $p_X(\cdot )$
is real-stable (Theorem C);
$p_X(\cdot )$
is real-stable (Theorem C); -
• metric geometry – to characterize for a given Euclidean finite metric space X, all blowups that remain Euclidean (Theorem A), and to write down a related “tropical” version of Schoenberg’s Euclidean embedding theorem from [Reference Schoenberg37].
In the remaining Section 4, we prove Theorems D–F. In greater detail: we focus on the special case of
![]() $X = G$
a finite simple connected unweighted graph, with the minimum edge-distance metric. After equating the isometries of G with the symmetries of
$X = G$
a finite simple connected unweighted graph, with the minimum edge-distance metric. After equating the isometries of G with the symmetries of
![]() $p_G(\mathbf {n})$
, and recovering G from
$p_G(\mathbf {n})$
, and recovering G from
![]() $p_G(\mathbf {n})$
, we prove the aforementioned characterization of complete multipartite graphs G in terms of
$p_G(\mathbf {n})$
, we prove the aforementioned characterization of complete multipartite graphs G in terms of
![]() $\widetilde {p}_G$
being real-stable, or
$\widetilde {p}_G$
being real-stable, or
![]() $p_G(-\mathbf {n}) / p_G(-1, \dots , -1)$
being strongly Rayleigh. Next, we discuss a family of blowup-polynomials from this viewpoint of “partial” symmetry. We also connect
$p_G(-\mathbf {n}) / p_G(-1, \dots , -1)$
being strongly Rayleigh. Next, we discuss a family of blowup-polynomials from this viewpoint of “partial” symmetry. We also connect
![]() $u_G(x)$
to the characteristic polynomial of
$u_G(x)$
to the characteristic polynomial of
![]() $D_G$
, hence to the distance spectrum of G. Finally, we introduce the delta-matroid
$D_G$
, hence to the distance spectrum of G. Finally, we introduce the delta-matroid
![]() $\mathcal {M}'(T)$
for every tree, and explore its relation to the blowup delta-matroid
$\mathcal {M}'(T)$
for every tree, and explore its relation to the blowup delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_T}$
(for T a path), as well as extensions to general graphs. We end with Appendices A and B that contain supplementary details and results.
$\mathcal {M}_{\mathcal {D}_T}$
(for T a path), as well as extensions to general graphs. We end with Appendices A and B that contain supplementary details and results.
We conclude this section on a philosophical note. Our approach in this work adheres to the maxim that the multivariate polynomial is a natural, general, and more powerful object than its univariate specialization. This is of course famously manifested in the recent explosion of activity in the geometry of polynomials, via the study of real-stable polynomials by Borcea–Brändén and other researchers; but also shows up in several other settings – we refer the reader to the survey [Reference Sokal and Webb40] by Sokal for additional instances. (E.g., a specific occurrence is in the extreme simplicity of the proof of the multivariate Brown–Colbourn conjecture [Reference Royle and Sokal36, Reference Sokal39], as opposed to the involved proof in the univariate case [Reference Wagner42].)
2 Algebraic results: the blowup-polynomial and its full symmetry
We begin this section by proving Theorem B in “full” algebraic (and greater mathematical) generality, over an arbitrary unital commutative ring R. We require the following notation.
Definition 2.1 Fix positive integers
![]() $k, n_1, \dots , n_k> 0$
, and vectors
$k, n_1, \dots , n_k> 0$
, and vectors
![]() $\mathbf {p}_i, \mathbf {q}_i \in R^{n_i}$
for all
$\mathbf {p}_i, \mathbf {q}_i \in R^{n_i}$
for all
![]() $1 \leqslant i \leqslant k$
.
$1 \leqslant i \leqslant k$
.
-
(1) For these parameters, define the blowup-monoid to be the collection
 $\mathcal {M}_{\mathbf {n}}(R) := R^k \times R^{k \times k}$
. We write a typical element as a pair
$\mathcal {M}_{\mathbf {n}}(R) := R^k \times R^{k \times k}$
. We write a typical element as a pair
 $(\mathbf {a}, D)$
, where in coordinates,
$(\mathbf {a}, D)$
, where in coordinates,
 $\mathbf {a} = (a_i)^T$
and
$\mathbf {a} = (a_i)^T$
and
 $D = (d_{ij})$
.
$D = (d_{ij})$
. -
(2) Given
 $(\mathbf {a}, D) \in \mathcal {M}_{\mathbf {n}}(R)$
, define
$(\mathbf {a}, D) \in \mathcal {M}_{\mathbf {n}}(R)$
, define
 $M(\mathbf {a},D)$
to be the square matrix of dimension
$M(\mathbf {a},D)$
to be the square matrix of dimension
 $n_1 + \cdots + n_k$
with
$n_1 + \cdots + n_k$
with
 $k^2$
blocks, whose
$k^2$
blocks, whose
 $(i,j)$
-block for
$(i,j)$
-block for
 $1 \leqslant i,j \leqslant k$
is
$1 \leqslant i,j \leqslant k$
is
 $\delta _{i,j} a_i \operatorname {\mathrm {Id}}_{n_i} + d_{ij} \mathbf {p}_i \mathbf {q}_j^T$
. Also define
$\delta _{i,j} a_i \operatorname {\mathrm {Id}}_{n_i} + d_{ij} \mathbf {p}_i \mathbf {q}_j^T$
. Also define
 $\Delta _{\mathbf {a}} \in R^{k \times k}$
to be the diagonal matrix with
$\Delta _{\mathbf {a}} \in R^{k \times k}$
to be the diagonal matrix with
 $(i,i)$
entry
$(i,i)$
entry
 $a_i$
, and
$a_i$
, and  $$\begin{align*}N(\mathbf{a},D) := \Delta_{\mathbf{a}} + \operatorname{\mathrm{diag}}(\mathbf{q}_1^T \mathbf{p}_1, \dots, \mathbf{q}_k^T \mathbf{p}_k) \cdot D \ \in R^{k \times k}. \end{align*}$$
$$\begin{align*}N(\mathbf{a},D) := \Delta_{\mathbf{a}} + \operatorname{\mathrm{diag}}(\mathbf{q}_1^T \mathbf{p}_1, \dots, \mathbf{q}_k^T \mathbf{p}_k) \cdot D \ \in R^{k \times k}. \end{align*}$$
-
(3) Given
 $\mathbf {a}, \mathbf {a}' \in R^k$
, define
$\mathbf {a}, \mathbf {a}' \in R^k$
, define
 $\mathbf {a} \circ \mathbf {a}' := (a_1 a^{\prime }_1, \dots , a_k a^{\prime }_k)^T \in R^k$
.
$\mathbf {a} \circ \mathbf {a}' := (a_1 a^{\prime }_1, \dots , a_k a^{\prime }_k)^T \in R^k$
.
The set
![]() $\mathcal {M}_{\mathbf {n}}(R)$
is of course a group under addition, but we are interested in the following non-standard monoid structure on it.
$\mathcal {M}_{\mathbf {n}}(R)$
is of course a group under addition, but we are interested in the following non-standard monoid structure on it.
Lemma 2.2 The set
![]() $\mathcal {M}_{\mathbf {n}}(R)$
is a monoid under the product
$\mathcal {M}_{\mathbf {n}}(R)$
is a monoid under the product
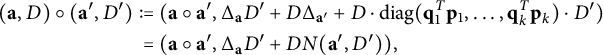 $$ \begin{align*} (\mathbf{a},D) \circ (\mathbf{a}',D') := &\ (\mathbf{a} \circ \mathbf{a}', \Delta_{\mathbf{a}} D' + D \Delta_{\mathbf{a}'} + D \cdot \operatorname{\mathrm{diag}}(\mathbf{q}_1^T \mathbf{p}_1, \dots, \mathbf{q}_k^T \mathbf{p}_k) \cdot D')\\ = &\ (\mathbf{a} \circ \mathbf{a}', \Delta_{\mathbf{a}} D' + D N(\mathbf{a}',D')), \end{align*} $$
$$ \begin{align*} (\mathbf{a},D) \circ (\mathbf{a}',D') := &\ (\mathbf{a} \circ \mathbf{a}', \Delta_{\mathbf{a}} D' + D \Delta_{\mathbf{a}'} + D \cdot \operatorname{\mathrm{diag}}(\mathbf{q}_1^T \mathbf{p}_1, \dots, \mathbf{q}_k^T \mathbf{p}_k) \cdot D')\\ = &\ (\mathbf{a} \circ \mathbf{a}', \Delta_{\mathbf{a}} D' + D N(\mathbf{a}',D')), \end{align*} $$
and with identity element
![]() $((1,\dots ,1)^T, 0_{k \times k})$
.
$((1,\dots ,1)^T, 0_{k \times k})$
.
With this notation in place, we now present the “general” formulation of Theorem B.
Theorem 2.3 Fix integers
![]() $k, n_1, \dots , n_k$
and vectors
$k, n_1, \dots , n_k$
and vectors
![]() $\mathbf {p}_i, \mathbf {q}_i$
as above. Let
$\mathbf {p}_i, \mathbf {q}_i$
as above. Let
![]() $K := n_1 + \cdots + n_k$
.
$K := n_1 + \cdots + n_k$
.
-
(1) The following map is a morphism of monoids:
 $$\begin{align*}\Psi : (\mathcal{M}_{\mathbf{n}}(R), \circ) \to (R^{K \times K}, \cdot), \qquad (\mathbf{a},D) \mapsto M(\mathbf{a},D). \end{align*}$$
$$\begin{align*}\Psi : (\mathcal{M}_{\mathbf{n}}(R), \circ) \to (R^{K \times K}, \cdot), \qquad (\mathbf{a},D) \mapsto M(\mathbf{a},D). \end{align*}$$
-
(2) The determinant of
 $M(\mathbf {a},D)$
equals
$M(\mathbf {a},D)$
equals
 $\prod _i a_i^{n_i - 1}$
times a multi-affine polynomial in
$\prod _i a_i^{n_i - 1}$
times a multi-affine polynomial in
 $a_i, d_{ij}$
, and the entries
$a_i, d_{ij}$
, and the entries
 $\mathbf {q}_i^T \mathbf {p}_i$
. More precisely, (2.1)
$\mathbf {q}_i^T \mathbf {p}_i$
. More precisely, (2.1) $$ \begin{align} \det M(\mathbf{a},D) = \det N(\mathbf{a},D) \prod_{i=1}^k a_i^{n_i - 1}. \end{align} $$
$$ \begin{align} \det M(\mathbf{a},D) = \det N(\mathbf{a},D) \prod_{i=1}^k a_i^{n_i - 1}. \end{align} $$
-
(3) If all
 $a_i \in R^\times $
and
$a_i \in R^\times $
and
 $N(\mathbf {a},D)$
is invertible, then so is
$N(\mathbf {a},D)$
is invertible, then so is
 $M(\mathbf {a},D)$
, and
$M(\mathbf {a},D)$
, and  $$\begin{align*}M(\mathbf{a},D)^{-1} = M((a_1^{-1}, \dots, a_k^{-1})^T, -\Delta_{\mathbf{a}}^{-1} D N(\mathbf{a},D)^{-1}). \end{align*}$$
$$\begin{align*}M(\mathbf{a},D)^{-1} = M((a_1^{-1}, \dots, a_k^{-1})^T, -\Delta_{\mathbf{a}}^{-1} D N(\mathbf{a},D)^{-1}). \end{align*}$$
Instead of using
![]() $N(\mathbf {a},D)$
which involves “post-multiplication” by D, one can also use
$N(\mathbf {a},D)$
which involves “post-multiplication” by D, one can also use
![]() $N(\mathbf {a},D^T)^T$
in the above results, to obtain similar formulas that we leave to the interested reader.
$N(\mathbf {a},D^T)^T$
in the above results, to obtain similar formulas that we leave to the interested reader.
Proof The first assertion is easy, and it implies the third assertion via showing that
![]() $M(\mathbf {a},D)^{-1} M(\mathbf {a},D) = \operatorname {\mathrm {Id}}_K$
. (We show these computations for completeness in the appendix.) Thus, it remains to prove the second assertion. To proceed, we employ Zariski density, as was done in, e.g., our previous work [Reference Choudhury and Khare16]. Namely, we begin by working over the field of rational functions in
$M(\mathbf {a},D)^{-1} M(\mathbf {a},D) = \operatorname {\mathrm {Id}}_K$
. (We show these computations for completeness in the appendix.) Thus, it remains to prove the second assertion. To proceed, we employ Zariski density, as was done in, e.g., our previous work [Reference Choudhury and Khare16]. Namely, we begin by working over the field of rational functions in
![]() $k + k^2 + 2K$
variables
$k + k^2 + 2K$
variables
where
![]() $A_i, D_{ij}$
(with a slight abuse of notation), and
$A_i, D_{ij}$
(with a slight abuse of notation), and
![]() $Q_i^{(l)}, P_i^{(l)}$
– with
$Q_i^{(l)}, P_i^{(l)}$
– with
![]() $1 \leqslant i,j \leqslant k$
and
$1 \leqslant i,j \leqslant k$
and
![]() $1 \leqslant l \leqslant n_i$
– serve as proxies for
$1 \leqslant l \leqslant n_i$
– serve as proxies for
![]() $a_i, d_{ij}$
, and the coordinates of
$a_i, d_{ij}$
, and the coordinates of
![]() $\mathbf {q}_i, \mathbf {p}_i$
, respectively. Over this field, we work with
$\mathbf {q}_i, \mathbf {p}_i$
, respectively. Over this field, we work with
and the matrix
![]() $\mathbf {D} = (D_{ij})$
; note that
$\mathbf {D} = (D_{ij})$
; note that
![]() $\mathbf {D}$
has full rank
$\mathbf {D}$
has full rank
![]() $r=k$
, since
$r=k$
, since
![]() $\det \mathbf {D}$
is a nonzero polynomial over
$\det \mathbf {D}$
is a nonzero polynomial over
![]() $\mathbb {Q}$
, hence is a unit in
$\mathbb {Q}$
, hence is a unit in
![]() $\mathbb {F}$
.
$\mathbb {F}$
.
Let
![]() $\mathbf {D} = \sum _{j=1}^r \mathbf {u}_j \mathbf {v}_j^T$
be any rank-one decomposition. For each
$\mathbf {D} = \sum _{j=1}^r \mathbf {u}_j \mathbf {v}_j^T$
be any rank-one decomposition. For each
![]() $1 \leqslant j \leqslant r$
, write
$1 \leqslant j \leqslant r$
, write
![]() $\mathbf {u}_j = (u_{j1}, \dots , u_{jk})^T$
, and similarly for
$\mathbf {u}_j = (u_{j1}, \dots , u_{jk})^T$
, and similarly for
![]() $\mathbf {v}_j$
. Then
$\mathbf {v}_j$
. Then
![]() $D_{ij} = \sum _{s=1}^r u_{si} v_{sj}$
for all
$D_{ij} = \sum _{s=1}^r u_{si} v_{sj}$
for all
![]() $i,j$
. Now a Schur complement argument (with respect to the
$i,j$
. Now a Schur complement argument (with respect to the
![]() $(2,2)$
block below) yields:
$(2,2)$
block below) yields:

We next compute the determinant on the right alternately: by using the Schur complement with respect to the
![]() $(1,1)$
block instead. This yields:
$(1,1)$
block instead. This yields:
 $$\begin{align*}\det M(\mathbf{A}, \mathbf{D}) = \det ( \operatorname{\mathrm{Id}}_r + M ) \prod_{i=1}^k A_i^{n_i}, \end{align*}$$
$$\begin{align*}\det M(\mathbf{A}, \mathbf{D}) = \det ( \operatorname{\mathrm{Id}}_r + M ) \prod_{i=1}^k A_i^{n_i}, \end{align*}$$
where
![]() $M_{r \times r}$
has
$M_{r \times r}$
has
![]() $(i,j)$
entry
$(i,j)$
entry
![]() $\sum _{l=1}^k v_{il} \; (A_l^{-1} \mathbf {Q}_l^T \mathbf {P}_l) \; u_{jl}$
. But
$\sum _{l=1}^k v_{il} \; (A_l^{-1} \mathbf {Q}_l^T \mathbf {P}_l) \; u_{jl}$
. But
![]() $\det (\operatorname {\mathrm {Id}}_r + M)$
is also the determinant of
$\det (\operatorname {\mathrm {Id}}_r + M)$
is also the determinant of

by taking the Schur complement with respect to its
![]() $(1,1)$
block. Finally, take the Schur complement with respect to the
$(1,1)$
block. Finally, take the Schur complement with respect to the
![]() $(2,2)$
block of
$(2,2)$
block of
![]() $M'$
, to obtain
$M'$
, to obtain
 $$ \begin{align*} \det M(\mathbf{A}, \mathbf{D}) = &\ \det M' \prod_{i=1}^k A_i^{n_i} = \det \left(\operatorname{\mathrm{Id}}_k + \Delta_{\mathbf{A}}^{-1} \operatorname{\mathrm{diag}}( \mathbf{Q}_1^T \mathbf{P}_1, \dots, \mathbf{Q}_k^T \mathbf{P}_k) \mathbf{D} \right) \prod_{i=1}^k A_i^{n_i}\\ = &\ \det N(\mathbf{A}, \mathbf{D}) \prod_{i=1}^k A_i^{n_i - 1}, \end{align*} $$
$$ \begin{align*} \det M(\mathbf{A}, \mathbf{D}) = &\ \det M' \prod_{i=1}^k A_i^{n_i} = \det \left(\operatorname{\mathrm{Id}}_k + \Delta_{\mathbf{A}}^{-1} \operatorname{\mathrm{diag}}( \mathbf{Q}_1^T \mathbf{P}_1, \dots, \mathbf{Q}_k^T \mathbf{P}_k) \mathbf{D} \right) \prod_{i=1}^k A_i^{n_i}\\ = &\ \det N(\mathbf{A}, \mathbf{D}) \prod_{i=1}^k A_i^{n_i - 1}, \end{align*} $$
and this is indeed
![]() $\prod _i A_i^{n_i - 1}$
times a multi-affine polynomial in the claimed variables.
$\prod _i A_i^{n_i - 1}$
times a multi-affine polynomial in the claimed variables.
The above reasoning proves the assertion (2.1) over the field
defined above. We now explain how Zariski density helps prove (2.1) over every unital commutative ring – with the key being that both sides of (2.1) are polynomials in the variables. Begin by observing that (2.1) actually holds over the polynomial (sub)ring
but the above proof used the invertibility of the polynomials
![]() $A_1, \dots , A_k, \det (D_{ij})_{i,j=1}^k$
.
$A_1, \dots , A_k, \det (D_{ij})_{i,j=1}^k$
.
Now use that
![]() $\mathbb {Q}$
is an infinite field; thus, the following result applies.
$\mathbb {Q}$
is an infinite field; thus, the following result applies.
Proposition 2.4 The following are equivalent for a field
![]() $\mathbb {F}$
.
$\mathbb {F}$
.
-
(1) The polynomial ring
 $\mathbb {F}[x_1, \dots , x_n]$
(for some
$\mathbb {F}[x_1, \dots , x_n]$
(for some
 $n \geqslant 1$
) equals the ring of polynomial functions from affine n-space
$n \geqslant 1$
) equals the ring of polynomial functions from affine n-space
 $\mathbb {A}_{\mathbb {F}}^n \cong \mathbb {F}^n$
to
$\mathbb {A}_{\mathbb {F}}^n \cong \mathbb {F}^n$
to
 $\mathbb {F}$
.
$\mathbb {F}$
. -
(2) The preceding statement holds for every
 $n \geqslant 1$
.
$n \geqslant 1$
. -
(3)
 $\mathbb {F}$
is infinite.
$\mathbb {F}$
is infinite.
Moreover, the nonzero-locus
![]() $\mathcal {L}$
of any nonzero polynomial in
$\mathcal {L}$
of any nonzero polynomial in
![]() $\mathbb {F}[x_1, \dots , x_n]$
with
$\mathbb {F}[x_1, \dots , x_n]$
with
![]() $\mathbb {F}$
an infinite field, is Zariski dense in
$\mathbb {F}$
an infinite field, is Zariski dense in
![]() $\mathbb {A}_{\mathbb {F}}^n$
. In other words, if a polynomial in n variables equals zero on
$\mathbb {A}_{\mathbb {F}}^n$
. In other words, if a polynomial in n variables equals zero on
![]() $\mathcal {L}$
, then it vanishes on all of
$\mathcal {L}$
, then it vanishes on all of
![]() $\mathbb {A}_{\mathbb {F}}^n \cong \mathbb {F}^n$
.
$\mathbb {A}_{\mathbb {F}}^n \cong \mathbb {F}^n$
.
Proof-sketch
Clearly
![]() $(2) \implies (1)$
; and that the contrapositive of
$(2) \implies (1)$
; and that the contrapositive of
![]() $(1) \implies (3)$
holds follows from the fact that over a finite field
$(1) \implies (3)$
holds follows from the fact that over a finite field
![]() $\mathbb {F}_q$
, the nonzero polynomial
$\mathbb {F}_q$
, the nonzero polynomial
![]() $x_1^q - x_1$
equals the zero function. The proof of
$x_1^q - x_1$
equals the zero function. The proof of
![]() $(1) \implies (3)$
is by induction on
$(1) \implies (3)$
is by induction on
![]() $n \geqslant 1$
, and is left to the reader (or see, e.g., standard textbooks, or even [Reference Choudhury and Khare16]) – as is the proof of the final assertion.
$n \geqslant 1$
, and is left to the reader (or see, e.g., standard textbooks, or even [Reference Choudhury and Khare16]) – as is the proof of the final assertion.
By the equivalence in Proposition 2.4, the above polynomial ring
![]() $R_0$
equals the ring of polynomial functions in the same number of variables, so (2.1) now holds over the ring of polynomial functions in the above
$R_0$
equals the ring of polynomial functions in the same number of variables, so (2.1) now holds over the ring of polynomial functions in the above
![]() $k + k^2 + 2K$
variables – but only on the nonzero-locus of the polynomial
$k + k^2 + 2K$
variables – but only on the nonzero-locus of the polynomial
![]() $(\det \mathbf {D}) \prod _i A_i$
, since we used
$(\det \mathbf {D}) \prod _i A_i$
, since we used
![]() $A_i^{-1}$
and the invertibility of
$A_i^{-1}$
and the invertibility of
![]() $\mathbf {D}$
in the above proof.
$\mathbf {D}$
in the above proof.
Now for the final touch: as
![]() $(\det \mathbf {D}) \prod _i A_i$
is a nonzero polynomial, its nonzero-locus is Zariski dense in affine space
$(\det \mathbf {D}) \prod _i A_i$
is a nonzero polynomial, its nonzero-locus is Zariski dense in affine space
![]() $\mathbb {A}_{\mathbb {Q}}^{k + k^2 + 2K}$
(by Proposition 2.4). Since the difference of the polynomials in (2.1) (this is where we use that
$\mathbb {A}_{\mathbb {Q}}^{k + k^2 + 2K}$
(by Proposition 2.4). Since the difference of the polynomials in (2.1) (this is where we use that
![]() $\det (\cdot )$
is a polynomial!) vanishes on the above nonzero-locus, it does so for all values of
$\det (\cdot )$
is a polynomial!) vanishes on the above nonzero-locus, it does so for all values of
![]() $A_i$
and the other variables. Therefore, (2.1) holds in the ring
$A_i$
and the other variables. Therefore, (2.1) holds in the ring
![]() $R^{\prime }_0$
of polynomial functions with coefficients in
$R^{\prime }_0$
of polynomial functions with coefficients in
![]() $\mathbb {Q}$
, hence upon restricting to the polynomial subring of
$\mathbb {Q}$
, hence upon restricting to the polynomial subring of
![]() $R^{\prime }_0$
with integer (not just rational) coefficients – since the polynomials on both sides of (2.1) have integer coefficients. Finally, the proof is completed by specializing the variables
$R^{\prime }_0$
with integer (not just rational) coefficients – since the polynomials on both sides of (2.1) have integer coefficients. Finally, the proof is completed by specializing the variables
![]() $A_i$
to specific scalars
$A_i$
to specific scalars
![]() $a_i$
in an arbitrary unital commutative ring R, and similarly for the other variables.
$a_i$
in an arbitrary unital commutative ring R, and similarly for the other variables.
Theorem 2.3, when specialized to
![]() $p_i^{(l)} = q_i^{(l)} = 1$
for all
$p_i^{(l)} = q_i^{(l)} = 1$
for all
![]() $1 \leqslant i \leqslant k$
and
$1 \leqslant i \leqslant k$
and
![]() $1 \leqslant l \leqslant n_i$
, reveals how to convert the sizes
$1 \leqslant l \leqslant n_i$
, reveals how to convert the sizes
![]() $n_{x_i}$
in the blowup-matrix
$n_{x_i}$
in the blowup-matrix
![]() $D_{X[\mathbf {n}]}$
into entries of the related matrix
$D_{X[\mathbf {n}]}$
into entries of the related matrix
![]() $N(\mathbf {a},D)$
. This helps prove a result in the introduction – that
$N(\mathbf {a},D)$
. This helps prove a result in the introduction – that
![]() $\det D_{X[\mathbf {n}]}$
is a polynomial in
$\det D_{X[\mathbf {n}]}$
is a polynomial in
![]() $\mathbf {n}$
.
$\mathbf {n}$
.
Proof of Theorem B
Everything but the final sentence follows from Theorem 2.3, specialized to
 $$ \begin{align*} R = \mathbb{R}, \qquad n_i = n_{x_i}, \qquad d_{ij} = &\ d(x_i, x_j)\ \forall i \neq j, \qquad d_{ii} = 2 d(x_i, X \setminus \{ x_i \}) = -a_i, \\ D = \mathcal{D}_X = &\ (d_{ij})_{i,j=1}^k, \qquad p_i^{(l)} = q_i^{(l)} = 1\ \forall 1 \leqslant l \leqslant n_i. \end{align*} $$
$$ \begin{align*} R = \mathbb{R}, \qquad n_i = n_{x_i}, \qquad d_{ij} = &\ d(x_i, x_j)\ \forall i \neq j, \qquad d_{ii} = 2 d(x_i, X \setminus \{ x_i \}) = -a_i, \\ D = \mathcal{D}_X = &\ (d_{ij})_{i,j=1}^k, \qquad p_i^{(l)} = q_i^{(l)} = 1\ \forall 1 \leqslant l \leqslant n_i. \end{align*} $$
(A word of caution:
![]() $d_{ii} \neq d(x_i, x_i)$
, and hence
$d_{ii} \neq d(x_i, x_i)$
, and hence
![]() $\mathcal {D}_X \neq D_X$
: they differ by a diagonal matrix.)
$\mathcal {D}_X \neq D_X$
: they differ by a diagonal matrix.)
In particular,
![]() $p_X(\mathbf {n})$
is a multi-affine polynomial in
$p_X(\mathbf {n})$
is a multi-affine polynomial in
![]() $\mathbf {q}_i^T \mathbf {p}_i = n_i$
. We also write out the blowup-polynomial, useful here and below:
$\mathbf {q}_i^T \mathbf {p}_i = n_i$
. We also write out the blowup-polynomial, useful here and below:
 $$ \begin{align} p_X(\mathbf{n}) = \det &\ N(\mathbf{a}_X,\mathcal{D}_X), \quad \text{where} \quad \mathbf{a}_X = (D_X - \mathcal{D}_X) (1,1,\dots,1)^T,\\ \text{and so} \quad &\ N(\mathbf{a}_X,\mathcal{D}_X) = \operatorname{\mathrm{diag}}((n_{x_i} - 1) 2 d(x_i, X \setminus \{ x_i \}))_i + (n_{x_i} d(x_i, x_j))_{i,j=1}^k. \notag \end{align} $$
$$ \begin{align} p_X(\mathbf{n}) = \det &\ N(\mathbf{a}_X,\mathcal{D}_X), \quad \text{where} \quad \mathbf{a}_X = (D_X - \mathcal{D}_X) (1,1,\dots,1)^T,\\ \text{and so} \quad &\ N(\mathbf{a}_X,\mathcal{D}_X) = \operatorname{\mathrm{diag}}((n_{x_i} - 1) 2 d(x_i, X \setminus \{ x_i \}))_i + (n_{x_i} d(x_i, x_j))_{i,j=1}^k. \notag \end{align} $$
Now the constant term is obtained by evaluating
![]() $\det N(\mathbf {a}_X, 0_{k \times k})$
, which is easy since
$\det N(\mathbf {a}_X, 0_{k \times k})$
, which is easy since
![]() $N(\mathbf {a}_X, 0_{k \times k})$
is diagonal. Similarly, the coefficient of
$N(\mathbf {a}_X, 0_{k \times k})$
is diagonal. Similarly, the coefficient of
![]() $n_{x_i}$
is obtained by setting all other
$n_{x_i}$
is obtained by setting all other
![]() $n_{x_{i'}} = 0$
in
$n_{x_{i'}} = 0$
in
![]() $\det N(\mathbf {a}_X,\mathcal {D}_X)$
. Expand along the ith column to compute this determinant; now adding these determinants over all i yields the claimed formula for the linear term.
$\det N(\mathbf {a}_X,\mathcal {D}_X)$
. Expand along the ith column to compute this determinant; now adding these determinants over all i yields the claimed formula for the linear term.
As a further refinement of Theorem B, we isolate every term in the multi-affine polynomial
![]() $p_X(\mathbf {n})$
. Two consequences follow: (a) a formula relating the blowup-polynomials for a metric space X and its subspace Y; and (b) a sufficient condition for two monomials in
$p_X(\mathbf {n})$
. Two consequences follow: (a) a formula relating the blowup-polynomials for a metric space X and its subspace Y; and (b) a sufficient condition for two monomials in
![]() $p_X(\mathbf {n})$
to have equal coefficients. In order to state and prove these latter two results, we require the following notion.
$p_X(\mathbf {n})$
to have equal coefficients. In order to state and prove these latter two results, we require the following notion.
Definition 2.5 We say that a metric subspace Y of a finite metric space
![]() $(X,d)$
is admissible if for every
$(X,d)$
is admissible if for every
![]() $y \in Y$
, there exists
$y \in Y$
, there exists
![]() $y' \in Y$
such that
$y' \in Y$
such that
![]() $d(y, X \setminus \{ y \}) = d(y,y')$
.
$d(y, X \setminus \{ y \}) = d(y,y')$
.
For example, in every finite simple connected unweighted graph G with the minimum edge-distance as its metric, a subset Y of vertices is admissible if and only if the induced subgraph in G on Y has no isolated vertices.
Proposition 2.6 Notation as above.
-
(1) Given any subset
 $I \subseteq \{ 1, \dots , k \}$
, the coefficient in
$I \subseteq \{ 1, \dots , k \}$
, the coefficient in
 $p_X(\mathbf {n})$
of
$p_X(\mathbf {n})$
of
 $\prod _{i \in I} n_{x_i}$
is with
$\prod _{i \in I} n_{x_i}$
is with $$\begin{align*}\det (\mathcal{D}_X)_{I \times I} \prod_{j \not\in I} (-2 d(x_j, X \setminus \{ x_j \})) = \det (\mathcal{D}_X)_{I \times I} \prod_{j \not\in I} (-d_{jj}), \end{align*}$$
$$\begin{align*}\det (\mathcal{D}_X)_{I \times I} \prod_{j \not\in I} (-2 d(x_j, X \setminus \{ x_j \})) = \det (\mathcal{D}_X)_{I \times I} \prod_{j \not\in I} (-d_{jj}), \end{align*}$$
 $(\mathcal {D}_X)_{I \times I}$
the principal submatrix of
$(\mathcal {D}_X)_{I \times I}$
the principal submatrix of
 $\mathcal {D}_X$
formed by the rows and columns indexed by I.
$\mathcal {D}_X$
formed by the rows and columns indexed by I.
-
(2) Suppose
 $I \subseteq \{ 1, \dots , k \}$
, and
$I \subseteq \{ 1, \dots , k \}$
, and
 $Y = \{ x_i : i \in I \}$
is an admissible subspace of X. Then, In particular, if a particular monomial
$Y = \{ x_i : i \in I \}$
is an admissible subspace of X. Then, In particular, if a particular monomial $$\begin{align*}p_Y(\{ n_{x_i} : i \in I \}) = p_X(\mathbf{n})|_{n_{x_j} = 0\; \forall j \not\in I} \cdot \prod_{j \not\in I} (-2 d(x_j, X \setminus \{ x_j \}))^{-1}. \end{align*}$$
$$\begin{align*}p_Y(\{ n_{x_i} : i \in I \}) = p_X(\mathbf{n})|_{n_{x_j} = 0\; \forall j \not\in I} \cdot \prod_{j \not\in I} (-2 d(x_j, X \setminus \{ x_j \}))^{-1}. \end{align*}$$
 $\prod _{i \in I_0} n_{x_i}$
does not occur in
$\prod _{i \in I_0} n_{x_i}$
does not occur in
 $p_Y(\cdot )$
for some
$p_Y(\cdot )$
for some
 $I_0 \subseteq I$
, then it does not occur in
$I_0 \subseteq I$
, then it does not occur in
 $p_X(\cdot )$
either.
$p_X(\cdot )$
either.
-
(3) Suppose two admissible subspaces of X, consisting of points
 $(y_1, \dots , y_l)$
and
$(y_1, \dots , y_l)$
and
 $(z_1, \dots , z_l)$
, are isometric (here,
$(z_1, \dots , z_l)$
, are isometric (here,
 $1 \leqslant l \leqslant k$
). If moreover (2.3)then the coefficients in
$1 \leqslant l \leqslant k$
). If moreover (2.3)then the coefficients in $$ \begin{align} \prod_{i=1}^l d(y_i, X \setminus \{ y_i \}) = \prod_{i=1}^l d(z_i, X \setminus \{ z_i \}), \end{align} $$
$$ \begin{align} \prod_{i=1}^l d(y_i, X \setminus \{ y_i \}) = \prod_{i=1}^l d(z_i, X \setminus \{ z_i \}), \end{align} $$
 $p_X(\mathbf {n})$
of
$p_X(\mathbf {n})$
of
 $\prod _{i=1}^l n_{y_i}$
and
$\prod _{i=1}^l n_{y_i}$
and
 $\prod _{i=1}^l n_{z_i}$
are equal.
$\prod _{i=1}^l n_{z_i}$
are equal.
The final assertion strengthens the (obvious) observation that if
![]() $\Psi : X \to X$
is an isometry, then
$\Psi : X \to X$
is an isometry, then
![]() $p_X(\cdot ) \equiv p_{\Psi (X)}(\cdot )$
– in other words, the polynomial
$p_X(\cdot ) \equiv p_{\Psi (X)}(\cdot )$
– in other words, the polynomial
![]() $p_X(\cdot )$
is invariant under the action of the permutation of the variables
$p_X(\cdot )$
is invariant under the action of the permutation of the variables
![]() $( n_x : x \in X )$
induced by
$( n_x : x \in X )$
induced by
![]() $\Psi $
. This final assertion applies to blowup-polynomials of unweighted graphs with “locally homeomorphic neighborhoods,” e.g., to interior points and intervals in path graphs (or more generally, banded graphs). See the opening discussion in Section 4.3, as well as Proposition 4.11.
$\Psi $
. This final assertion applies to blowup-polynomials of unweighted graphs with “locally homeomorphic neighborhoods,” e.g., to interior points and intervals in path graphs (or more generally, banded graphs). See the opening discussion in Section 4.3, as well as Proposition 4.11.
Proof
-
(1) It suffices to compute the coefficient of
 $\prod _{i \in I} n_{x_i}$
in
$\prod _{i \in I} n_{x_i}$
in
 $p_X(\mathbf {n}) = \det N(\mathbf {a}_X,\mathcal {D}_X)$
, where
$p_X(\mathbf {n}) = \det N(\mathbf {a}_X,\mathcal {D}_X)$
, where
 $a_i = -2 d(x_i, X \setminus \{ x_i \})\ \forall 1 \leqslant i \leqslant k$
, and we set all
$a_i = -2 d(x_i, X \setminus \{ x_i \})\ \forall 1 \leqslant i \leqslant k$
, and we set all
 $n_{x_j},\ j \not \in I$
to zero. To evaluate this determinant, notice that for
$n_{x_j},\ j \not \in I$
to zero. To evaluate this determinant, notice that for
 $j \not \in I$
, the jth row contains only one nonzero entry, along the main diagonal. Thus, expand the determinant along the jth row for every
$j \not \in I$
, the jth row contains only one nonzero entry, along the main diagonal. Thus, expand the determinant along the jth row for every
 $j \not \in I$
; this yields
$j \not \in I$
; this yields
 $\prod _{j \not \in I} (-d_{jj})$
times the principal minor
$\prod _{j \not \in I} (-d_{jj})$
times the principal minor
 $N(\mathbf {a}_X,\mathcal {D}_X)_{I \times I}$
. Moreover, the coefficient of
$N(\mathbf {a}_X,\mathcal {D}_X)_{I \times I}$
. Moreover, the coefficient of
 $\prod _{i \in I} n_{x_i}$
in the expansion of
$\prod _{i \in I} n_{x_i}$
in the expansion of
 $\det N(\mathbf {a}_X,\mathcal {D}_X)_{I \times I}$
is the same as that in expanding
$\det N(\mathbf {a}_X,\mathcal {D}_X)_{I \times I}$
is the same as that in expanding
 $\det N(\mathbf {0}, \mathcal {D}_X)_{I \times I}$
, and this is precisely
$\det N(\mathbf {0}, \mathcal {D}_X)_{I \times I}$
, and this is precisely
 $\det (\mathcal {D}_X)_{I \times I}$
.
$\det (\mathcal {D}_X)_{I \times I}$
. -
(2) Let us use
 $\mathbf {a}_X, \mathcal {D}_X$
and
$\mathbf {a}_X, \mathcal {D}_X$
and
 $\mathbf {a}_Y, \mathcal {D}_Y$
for the appropriate data generated from X and
$\mathbf {a}_Y, \mathcal {D}_Y$
for the appropriate data generated from X and
 $Y,$
respectively. Then the admissibility of Y indicates that
$Y,$
respectively. Then the admissibility of Y indicates that
 $(\mathbf {a}_X)_I = \mathbf {a}_Y$
and
$(\mathbf {a}_X)_I = \mathbf {a}_Y$
and
 $(\mathcal {D}_X)_{I \times I} = \mathcal {D}_Y$
. Now a direct computation reveals: This shows the claimed equation, and the final assertion is an immediate consequence of it.
$(\mathcal {D}_X)_{I \times I} = \mathcal {D}_Y$
. Now a direct computation reveals: This shows the claimed equation, and the final assertion is an immediate consequence of it. $$\begin{align*}p_X(\mathbf{n})|_{n_{x_j} = 0\; \forall j \not\in I} = \det(\Delta_{\mathbf{a}_Y} + \Delta_{\mathbf{n}_Y} \mathcal{D}_Y) \prod_{j \not\in I} (-d_{jj}). \end{align*}$$
$$\begin{align*}p_X(\mathbf{n})|_{n_{x_j} = 0\; \forall j \not\in I} = \det(\Delta_{\mathbf{a}_Y} + \Delta_{\mathbf{n}_Y} \mathcal{D}_Y) \prod_{j \not\in I} (-d_{jj}). \end{align*}$$
-
(3) Let
 $I', I" \subseteq \{ 1, \dots , k \}$
index the points
$I', I" \subseteq \{ 1, \dots , k \}$
index the points
 $(y_1, \dots , y_l)$
and
$(y_1, \dots , y_l)$
and
 $(z_1, \dots , z_l)$
, respectively. Similarly, let
$(z_1, \dots , z_l)$
, respectively. Similarly, let
 $\mathcal {D}_Y, \mathcal {D}_Z$
denote the respective
$\mathcal {D}_Y, \mathcal {D}_Z$
denote the respective
 $l \times l$
matrices (e.g., with off-diagonal entries
$l \times l$
matrices (e.g., with off-diagonal entries
 $d(y_i, y_j)$
and
$d(y_i, y_j)$
and
 $d(z_i, z_j),$
respectively). The admissibility of the given subspaces implies that
$d(z_i, z_j),$
respectively). The admissibility of the given subspaces implies that
 $(\mathcal {D}_X)_{I' \times I'} = \mathcal {D}_Y$
and
$(\mathcal {D}_X)_{I' \times I'} = \mathcal {D}_Y$
and
 $(\mathcal {D}_X)_{I" \times I"} = \mathcal {D}_Z$
. Now use the isometry between the
$(\mathcal {D}_X)_{I" \times I"} = \mathcal {D}_Z$
. Now use the isometry between the
 $y_i$
and
$y_i$
and
 $z_i$
(up to relabeling) to deduce that
$z_i$
(up to relabeling) to deduce that
 $\det \mathcal {D}_Y = \det \mathcal {D}_Z$
. Via the first part above, it remains to prove that But this indeed holds, since multiplying the left- and right-hand sides of this equation by the corresponding sides of (2.3) yields
$\det \mathcal {D}_Y = \det \mathcal {D}_Z$
. Via the first part above, it remains to prove that But this indeed holds, since multiplying the left- and right-hand sides of this equation by the corresponding sides of (2.3) yields $$\begin{align*}\prod_{j \not\in I'} (-2 d(x_j, X \setminus \{ x_j \})) = \prod_{j \not\in I"} (-2 d(x_j, X \setminus \{ x_j \})). \end{align*}$$
$$\begin{align*}\prod_{j \not\in I'} (-2 d(x_j, X \setminus \{ x_j \})) = \prod_{j \not\in I"} (-2 d(x_j, X \setminus \{ x_j \})). \end{align*}$$
 $2^{-l} \prod _{x \in X} (-2d(x, X \setminus \{ x \}))$
on both sides (once again using admissibility). here
$2^{-l} \prod _{x \in X} (-2d(x, X \setminus \{ x \}))$
on both sides (once again using admissibility). here
We provide some applications of Proposition 2.6 in later sections; for now, we apply it to prove that the blowup delta-matroid of X is linear.
Proof of Corollary 1.10
It is immediate from Proposition 2.6(1) that the blowup delta-matroid of X is precisely the linear delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_X}$
(see the paragraph preceding Corollary 1.10).
$\mathcal {M}_{\mathcal {D}_X}$
(see the paragraph preceding Corollary 1.10).
We conclude this section by showing another result in the introduction, which studies when
![]() $p_X(\mathbf {n})$
is symmetric in the variables
$p_X(\mathbf {n})$
is symmetric in the variables
![]() $n_x$
.
$n_x$
.
Proof of Proposition 1.6
First suppose
![]() $d_X$
is the discrete metric times a constant
$d_X$
is the discrete metric times a constant
![]() $c> 0$
. Then all
$c> 0$
. Then all
![]() $a_i = -2c = d_{ii}$
. Hence,
$a_i = -2c = d_{ii}$
. Hence,
and this is a rank-one update of the diagonal matrix
![]() $\mathbf {\Delta } := c \operatorname {\mathrm {diag}}(n_{x_1}, \dots , n_{x_k}) -2c \operatorname {\mathrm {Id}}_k$
. Hence,
$\mathbf {\Delta } := c \operatorname {\mathrm {diag}}(n_{x_1}, \dots , n_{x_k}) -2c \operatorname {\mathrm {Id}}_k$
. Hence,
 $$ \begin{align} p_X(\mathbf{n}) = \det N(\mathbf{a}_X,\mathcal{D}_X) = &\ \det (\mathbf{\Delta}) + c \cdot (1,\dots,1) \mathrm{adj} (\mathbf{\Delta}) (n_{x_1}, \dots, n_{x_k})^T\notag\\ = &\ c^k \left( \prod_{i=1}^k (n_{x_i} - 2) + \sum_{i=1}^k n_{x_i} \prod_{i' \neq i} (n_{x_{i'}} - 2) \right), \end{align} $$
$$ \begin{align} p_X(\mathbf{n}) = \det N(\mathbf{a}_X,\mathcal{D}_X) = &\ \det (\mathbf{\Delta}) + c \cdot (1,\dots,1) \mathrm{adj} (\mathbf{\Delta}) (n_{x_1}, \dots, n_{x_k})^T\notag\\ = &\ c^k \left( \prod_{i=1}^k (n_{x_i} - 2) + \sum_{i=1}^k n_{x_i} \prod_{i' \neq i} (n_{x_{i'}} - 2) \right), \end{align} $$
and this is indeed symmetric in the
![]() $n_{x_i}$
.
$n_{x_i}$
.
Conversely, suppose
![]() $p_X(\mathbf {n})$
is symmetric in
$p_X(\mathbf {n})$
is symmetric in
![]() $\mathbf {n}$
. If
$\mathbf {n}$
. If
![]() $|X| = k \leqslant 2,$
then the result is immediate. Also note that the assertion (2) for
$|X| = k \leqslant 2,$
then the result is immediate. Also note that the assertion (2) for
![]() $k \geqslant 3$
follows from that for
$k \geqslant 3$
follows from that for
![]() $k=3$
– since if the distances between any three distinct points are equal, then
$k=3$
– since if the distances between any three distinct points are equal, then
![]() $d(x,y) = d(x,y') = d(x',y')$
for all distinct
$d(x,y) = d(x,y') = d(x',y')$
for all distinct
![]() $x,y,x',y' \in X$
(verifying the remaining cases is easier). Thus, we suppose henceforth that
$x,y,x',y' \in X$
(verifying the remaining cases is easier). Thus, we suppose henceforth that
![]() $|X| = k = 3$
. For ease of exposition, in this proof, we denote
$|X| = k = 3$
. For ease of exposition, in this proof, we denote
![]() $d^{\prime }_{ij} := d(x_i, x_j)$
for
$d^{\prime }_{ij} := d(x_i, x_j)$
for
![]() $1 \leqslant i,j \leqslant 3$
. Also assume by relabeling the
$1 \leqslant i,j \leqslant 3$
. Also assume by relabeling the
![]() $x_i$
(if needed) that
$x_i$
(if needed) that
![]() $0 < d^{\prime }_{12} \leqslant d^{\prime }_{13} \leqslant d^{\prime }_{23}$
. Then
$0 < d^{\prime }_{12} \leqslant d^{\prime }_{13} \leqslant d^{\prime }_{23}$
. Then
 $$\begin{align*}N(\mathbf{a}_X,\mathcal{D}_X) = \begin{pmatrix} (n_{x_1} - 1) 2 d^{\prime}_{12} & n_{x_1} d^{\prime}_{12} & n_{x_1} d^{\prime}_{13} \\ n_{x_2} d^{\prime}_{12} & (n_{x_2} - 1) 2 d^{\prime}_{12} & n_{x_2} d^{\prime}_{23} \\ n_{x_3} d^{\prime}_{13} & n_{x_3} d^{\prime}_{23} & (n_{x_3} - 1) 2 d^{\prime}_{13} \end{pmatrix}. \end{align*}$$
$$\begin{align*}N(\mathbf{a}_X,\mathcal{D}_X) = \begin{pmatrix} (n_{x_1} - 1) 2 d^{\prime}_{12} & n_{x_1} d^{\prime}_{12} & n_{x_1} d^{\prime}_{13} \\ n_{x_2} d^{\prime}_{12} & (n_{x_2} - 1) 2 d^{\prime}_{12} & n_{x_2} d^{\prime}_{23} \\ n_{x_3} d^{\prime}_{13} & n_{x_3} d^{\prime}_{23} & (n_{x_3} - 1) 2 d^{\prime}_{13} \end{pmatrix}. \end{align*}$$
Since
![]() $p_X(\mathbf {n}) = \det N(\mathbf {a}_X,\mathcal {D}_X)$
is symmetric in the
$p_X(\mathbf {n}) = \det N(\mathbf {a}_X,\mathcal {D}_X)$
is symmetric in the
![]() $n_{x_i}$
, we equate the coefficients of
$n_{x_i}$
, we equate the coefficients of
![]() $n_{x_1} n_{x_2}$
and
$n_{x_1} n_{x_2}$
and
![]() $n_{x_2} n_{x_3}$
, to obtain
$n_{x_2} n_{x_3}$
, to obtain
Simplifying this yields:
![]() $d^{\prime }_{12} d^{\prime }_{13} = (d^{\prime }_{23})^2$
, and since
$d^{\prime }_{12} d^{\prime }_{13} = (d^{\prime }_{23})^2$
, and since
![]() $d^{\prime }_{23}$
dominates
$d^{\prime }_{23}$
dominates
![]() $d^{\prime }_{12}, d^{\prime }_{13}$
, the three distances
$d^{\prime }_{12}, d^{\prime }_{13}$
, the three distances
![]() $d^{\prime }_{12}, d^{\prime }_{13}, d^{\prime }_{23}$
are equal. This proves the converse for
$d^{\prime }_{12}, d^{\prime }_{13}, d^{\prime }_{23}$
are equal. This proves the converse for
![]() $|X| = k = 3$
, hence for all
$|X| = k = 3$
, hence for all
![]() $k \geqslant 3$
.
$k \geqslant 3$
.
3 Real-stability of the blowup-polynomial
The proofs in Section 2 were mostly algebraic in nature: although they applied to metric spaces, all but the final proof involved no inequalities. We now show Theorem C:
![]() $p_X(\cdot )$
is always real-stable.
$p_X(\cdot )$
is always real-stable.
We begin by mentioning some properties with respect to which blowups behave well. These include iterated blowups, the blowup-polynomial, and the modified distance matrix
![]() $\mathcal {D}_X$
and its positivity. (As Theorem A indicates, the property of being Euclidean is not such a property.) We first introduce another “well-behaved” matrix
$\mathcal {D}_X$
and its positivity. (As Theorem A indicates, the property of being Euclidean is not such a property.) We first introduce another “well-behaved” matrix
![]() $\mathcal {C}_X$
for a finite metric space, parallel to
$\mathcal {C}_X$
for a finite metric space, parallel to
![]() $\mathcal {D}_X$
and the vector
$\mathcal {D}_X$
and the vector
![]() $\mathbf {a}_X$
, which will be useful here and in later sections.
$\mathbf {a}_X$
, which will be useful here and in later sections.
Definition 3.1 Given a finite metric space
![]() $X = \{ x_1, \dots , x_k \}$
, recall the vector
$X = \{ x_1, \dots , x_k \}$
, recall the vector
![]() $\mathbf {a}_X \in \mathbb R^k$
as in (2.2) and define the symmetric matrix
$\mathbf {a}_X \in \mathbb R^k$
as in (2.2) and define the symmetric matrix
![]() $\mathcal {C}_X \in \mathbb R^{k \times k}$
, via
$\mathcal {C}_X \in \mathbb R^{k \times k}$
, via
 $$ \begin{align} \begin{aligned} \mathbf{a}_X = &\ -2 (d(x_1, X \setminus \{ x_1 \}), \dots, d(x_k, X \setminus \{ x_k \})) = (-2 d(x, X \setminus \{ x \}))_{x \in X}, \\ \mathcal{C}_X := &\ (-\Delta_{\mathbf{a}_X})^{-1/2} \mathcal{D}_X (-\Delta_{\mathbf{a}_X})^{-1/2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbf{a}_X = &\ -2 (d(x_1, X \setminus \{ x_1 \}), \dots, d(x_k, X \setminus \{ x_k \})) = (-2 d(x, X \setminus \{ x \}))_{x \in X}, \\ \mathcal{C}_X := &\ (-\Delta_{\mathbf{a}_X})^{-1/2} \mathcal{D}_X (-\Delta_{\mathbf{a}_X})^{-1/2}. \end{aligned} \end{align} $$
In other words,
![]() $-\mathbf {a}_X$
is the diagonal vector of the modified distance matrix
$-\mathbf {a}_X$
is the diagonal vector of the modified distance matrix
![]() $\mathcal {D}_X$
, and
$\mathcal {D}_X$
, and
 $$ \begin{align} (\mathcal{C}_X)_{ij} = \begin{cases} 1, & \text{if } i = j,\\ \displaystyle \frac{d(x_i, x_j)}{2 \sqrt{d(x_i, X \setminus \{ x_i \}) d(x_j, X \setminus \{ x_j \})}}, \qquad & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} (\mathcal{C}_X)_{ij} = \begin{cases} 1, & \text{if } i = j,\\ \displaystyle \frac{d(x_i, x_j)}{2 \sqrt{d(x_i, X \setminus \{ x_i \}) d(x_j, X \setminus \{ x_j \})}}, \qquad & \text{otherwise}. \end{cases} \end{align} $$
Lemma 3.2 Fix a finite metric space
![]() $(X,d)$
and an integer tuple
$(X,d)$
and an integer tuple
![]() $\mathbf {n} = (n_x : x \in X) \in \mathbb {Z}_{>0}^X$
.
$\mathbf {n} = (n_x : x \in X) \in \mathbb {Z}_{>0}^X$
.
-
(1) Fix a positive integer
 $m_{xi}$
for each
$m_{xi}$
for each
 $x \in X$
and
$x \in X$
and
 $1 \leqslant i \leqslant n_x$
, and let
$1 \leqslant i \leqslant n_x$
, and let
 $\mathbf {m} := (m_{xi})_{x,i}$
denote the entire collection. Then
$\mathbf {m} := (m_{xi})_{x,i}$
denote the entire collection. Then
 $(X[\mathbf {n}])[\mathbf {m}]$
is isometrically isomorphic to
$(X[\mathbf {n}])[\mathbf {m}]$
is isometrically isomorphic to
 $X[\mathbf {n}']$
, where
$X[\mathbf {n}']$
, where
 $\mathbf {n}' = (\sum _{i=1}^{n_x} m_{xi} : x \in X)$
. Here, the ith copy of x in
$\mathbf {n}' = (\sum _{i=1}^{n_x} m_{xi} : x \in X)$
. Here, the ith copy of x in
 $X[\mathbf {n}]$
is copied
$X[\mathbf {n}]$
is copied
 $m_{xi}$
times in
$m_{xi}$
times in
 $(X[\mathbf {n}])[\mathbf { m}]$
.
$(X[\mathbf {n}])[\mathbf { m}]$
. -
(2) In particular, the blowup-polynomial of an iterated blowup is simply the original blowup-polynomial in a larger number of variables, up to a constant:
(3.3)where the coordinates of $$ \begin{align} p_{X[\mathbf{n}]}(\mathbf{m}) \equiv p_X(\mathbf{n}') \prod_{x \in X} a_x^{n_x - 1}, \end{align} $$
$$ \begin{align} p_{X[\mathbf{n}]}(\mathbf{m}) \equiv p_X(\mathbf{n}') \prod_{x \in X} a_x^{n_x - 1}, \end{align} $$
 $\mathbf {n}' = (\sum _{i=1}^{n_x} m_{xi} : x \in X)$
are sums of variables.
$\mathbf {n}' = (\sum _{i=1}^{n_x} m_{xi} : x \in X)$
are sums of variables.
-
(3) Now write
 $X = \{ x_1, \dots , x_k \}$
as above. Then the matrices
$X = \{ x_1, \dots , x_k \}$
as above. Then the matrices
 $\mathcal {D}_{X[\mathbf {n}]}, \mathcal {C}_{X[\mathbf {n}]}$
are both block
$\mathcal {D}_{X[\mathbf {n}]}, \mathcal {C}_{X[\mathbf {n}]}$
are both block
 $k \times k$
matrices, with
$k \times k$
matrices, with
 $(i,j)$
block, respectively, equal to where
$(i,j)$
block, respectively, equal to where $$\begin{align*}d_{ij} \mathbf{1}_{n_{x_i} \times n_{x_j}} \quad \text{and} \quad c_{ij} \mathbf{1}_{n_{x_i} \times n_{x_j}}, \end{align*}$$
$$\begin{align*}d_{ij} \mathbf{1}_{n_{x_i} \times n_{x_j}} \quad \text{and} \quad c_{ij} \mathbf{1}_{n_{x_i} \times n_{x_j}}, \end{align*}$$
 $\mathcal {D}_X = (d_{ij})_{i,j=1}^k, \mathcal {C}_X = (c_{ij})_{i,j=1}^k$
.
$\mathcal {D}_X = (d_{ij})_{i,j=1}^k, \mathcal {C}_X = (c_{ij})_{i,j=1}^k$
.
-
(4) The following are equivalent:
-
(a) The matrix
 $\mathcal {D}_X$
is positive semidefinite.
$\mathcal {D}_X$
is positive semidefinite. -
(b) The matrix
 $\mathcal {D}_{X[\mathbf {n}]}$
is positive semidefinite for some (equivalently, every) tuple
$\mathcal {D}_{X[\mathbf {n}]}$
is positive semidefinite for some (equivalently, every) tuple
 $\mathbf {n}$
of positive integers.
$\mathbf {n}$
of positive integers. -
(c) The matrix
 $\mathcal {C}_X$
is positive semidefinite.
$\mathcal {C}_X$
is positive semidefinite. -
(d) The matrix
 $\mathcal {C}_{X[\mathbf {n}]}$
is positive semidefinite for some (equivalently, every) tuple
$\mathcal {C}_{X[\mathbf {n}]}$
is positive semidefinite for some (equivalently, every) tuple
 $\mathbf {n}$
of positive integers.
$\mathbf {n}$
of positive integers.
-
Proof
-
(1) In studying
 $(X[\mathbf {n}])[\mathbf {m}]$
, for ease of exposition, we write
$(X[\mathbf {n}])[\mathbf {m}]$
, for ease of exposition, we write
 $Y := X[\mathbf {n}], Z := (X[\mathbf {n}])[\mathbf {m}]$
. Also write
$Y := X[\mathbf {n}], Z := (X[\mathbf {n}])[\mathbf {m}]$
. Also write
 $y_{xi}$
for the ith copy of x in Y, and
$y_{xi}$
for the ith copy of x in Y, and
 $z_{xij}$
for the jth copy of
$z_{xij}$
for the jth copy of
 $y_{xi}$
in Z, with
$y_{xi}$
in Z, with
 $1 \leqslant i \leqslant n_x$
and
$1 \leqslant i \leqslant n_x$
and
 $1 \leqslant j \leqslant m_{xi}$
. We now compute
$1 \leqslant j \leqslant m_{xi}$
. We now compute
 $d_Z(z_{xij},z_{x'i'j'})$
, considering three cases. First, if
$d_Z(z_{xij},z_{x'i'j'})$
, considering three cases. First, if
 $x \neq x'$
, then this equals
$x \neq x'$
, then this equals
 $d_Y(y_{xi},y_{x'i'}) = d_X(x,x')$
. Next, if
$d_Y(y_{xi},y_{x'i'}) = d_X(x,x')$
. Next, if
 $x = x'$
but
$x = x'$
but
 $i \neq i'$
, then it equals
$i \neq i'$
, then it equals
 $d_Y(y_{xi}, y_{xi'}) = 2 d(x, X \setminus \{ x \})$
. Finally, suppose
$d_Y(y_{xi}, y_{xi'}) = 2 d(x, X \setminus \{ x \})$
. Finally, suppose
 $x = x'$
and
$x = x'$
and
 $i = i'$
but
$i = i'$
but
 $j \neq j'$
. Then and it is not hard to show, by considering all distances in Y, that this equals
$j \neq j'$
. Then and it is not hard to show, by considering all distances in Y, that this equals $$\begin{align*}d_Z(z_{xij},z_{x'i'j'}) = 2 d_Y(y_{xi}, Y \setminus \{ y_{xi} \}), \end{align*}$$
$$\begin{align*}d_Z(z_{xij},z_{x'i'j'}) = 2 d_Y(y_{xi}, Y \setminus \{ y_{xi} \}), \end{align*}$$
 $2 d_X(x, X \setminus \{ x \})$
. These three cases reveal that
$2 d_X(x, X \setminus \{ x \})$
. These three cases reveal that
 $d_Z(z_{xij}, z_{x'i'j'})$
equals the distance in
$d_Z(z_{xij}, z_{x'i'j'})$
equals the distance in
 $X[\mathbf {n}']$
between the copies of
$X[\mathbf {n}']$
between the copies of
 $x,x' \in X$
, and the proof is complete.
$x,x' \in X$
, and the proof is complete.
-
(2) We show (3.3) using the previous part and the next part, and via Zariski density arguments as in the proof of Theorem 2.3. Define
 $n_j := n_{x_j}$
in this proof for convenience. Thus, we work more generally in the setting where
$n_j := n_{x_j}$
in this proof for convenience. Thus, we work more generally in the setting where
 $X = \{ x_1, \dots , x_k \}$
, but the arrays consist of indeterminates. Let
$X = \{ x_1, \dots , x_k \}$
, but the arrays consist of indeterminates. Let $$\begin{align*}\mathbf{a}_X = (a_{x_1}, \dots, a_{x_k})^T, \qquad \mathcal{D}_X = (d_{rs})_{r,s=1}^k, \qquad \mathbf{m} = (m_{j1}, \dots, m_{jn_j})_{j=1}^k \end{align*}$$
$$\begin{align*}\mathbf{a}_X = (a_{x_1}, \dots, a_{x_k})^T, \qquad \mathcal{D}_X = (d_{rs})_{r,s=1}^k, \qquad \mathbf{m} = (m_{j1}, \dots, m_{jn_j})_{j=1}^k \end{align*}$$
 $K := \sum _{j=1}^k n_j$
, and define
$K := \sum _{j=1}^k n_j$
, and define
 $\mathcal {W}_{K \times k}$
to be the block matrix Now
$\mathcal {W}_{K \times k}$
to be the block matrix Now $$\begin{align*}\mathcal{W} := \begin{pmatrix} \mathbf{1}_{n_1 \times 1} & 0_{n_1 \times 1} & \ldots & 0_{n_1 \times 1} \\ 0_{n_2 \times 1} & \mathbf{1}_{n_2 \times 1} & \ldots & 0_{n_2 \times 1} \\ \vdots & \vdots & \ddots & \vdots \\ 0_{n_k \times 1} & 0_{n_k \times 1} & \ldots & \mathbf{1}_{n_k \times 1} \end{pmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{W} := \begin{pmatrix} \mathbf{1}_{n_1 \times 1} & 0_{n_1 \times 1} & \ldots & 0_{n_1 \times 1} \\ 0_{n_2 \times 1} & \mathbf{1}_{n_2 \times 1} & \ldots & 0_{n_2 \times 1} \\ \vdots & \vdots & \ddots & \vdots \\ 0_{n_k \times 1} & 0_{n_k \times 1} & \ldots & \mathbf{1}_{n_k \times 1} \end{pmatrix}. \end{align*}$$
 $\Delta _{\mathbf {a}_{X[\mathbf {n}]}} = \operatorname {\mathrm {diag}}( a_{x_1} \operatorname {\mathrm {Id}}_{n_1}, \dots , a_{x_k} \operatorname {\mathrm {Id}}_{n_k})$
, and a straightforward computation (using the next part) shows that
$\Delta _{\mathbf {a}_{X[\mathbf {n}]}} = \operatorname {\mathrm {diag}}( a_{x_1} \operatorname {\mathrm {Id}}_{n_1}, \dots , a_{x_k} \operatorname {\mathrm {Id}}_{n_k})$
, and a straightforward computation (using the next part) shows that
 $\mathcal {D}_{X[\mathbf {n}]} = \mathcal {W} \mathcal {D}_X \mathcal {W}^T$
.
$\mathcal {D}_{X[\mathbf {n}]} = \mathcal {W} \mathcal {D}_X \mathcal {W}^T$
.
Notice that if one works over the field
then the following polynomial is nonzero: $$\begin{align*}\mathbb{Q}(\{ a_{x_j}, m_{ji} : 1 \leqslant j \leqslant k, \ 1 \leqslant i \leqslant n_j \}, \{ d_{rs} : 1 \leqslant r,s \leqslant k \}), \end{align*}$$
(3.4)
$$\begin{align*}\mathbb{Q}(\{ a_{x_j}, m_{ji} : 1 \leqslant j \leqslant k, \ 1 \leqslant i \leqslant n_j \}, \{ d_{rs} : 1 \leqslant r,s \leqslant k \}), \end{align*}$$
(3.4) $$ \begin{align} (\det \mathcal{D}_X) \prod_{j=1}^k a_{x_j} \prod_{j=1}^k \prod_{i=1}^{n_j} m_{ji}. \end{align} $$
$$ \begin{align} (\det \mathcal{D}_X) \prod_{j=1}^k a_{x_j} \prod_{j=1}^k \prod_{i=1}^{n_j} m_{ji}. \end{align} $$
Thus, we now compute:
Using (3.4) and Schur complements, this equals $$\begin{align*}p_{X[\mathbf{n}]}(\mathbf{m}) = \det (\Delta_{a_{X[\mathbf{n}]}} + \Delta_{\mathbf{m}} \mathcal{D}_{X[\mathbf{n}]}) = \det (\Delta_{a_{X[\mathbf{n}]}} + \Delta_{\mathbf{m}} \mathcal{W} \mathcal{D}_X \mathcal{W}^T). \end{align*}$$
$$\begin{align*}p_{X[\mathbf{n}]}(\mathbf{m}) = \det (\Delta_{a_{X[\mathbf{n}]}} + \Delta_{\mathbf{m}} \mathcal{D}_{X[\mathbf{n}]}) = \det (\Delta_{a_{X[\mathbf{n}]}} + \Delta_{\mathbf{m}} \mathcal{W} \mathcal{D}_X \mathcal{W}^T). \end{align*}$$
 $$\begin{align*}\det (\Delta_{\mathbf{m}}) \cdot \det \begin{pmatrix} \Delta_{\mathbf{m}}^{-1} \Delta_{a_{X[\mathbf{n}]}} & -\mathcal{W} \\ \mathcal{W}^T & \mathcal{D}_X^{-1} \end{pmatrix} \det (\mathcal{D}_X). \end{align*}$$
$$\begin{align*}\det (\Delta_{\mathbf{m}}) \cdot \det \begin{pmatrix} \Delta_{\mathbf{m}}^{-1} \Delta_{a_{X[\mathbf{n}]}} & -\mathcal{W} \\ \mathcal{W}^T & \mathcal{D}_X^{-1} \end{pmatrix} \det (\mathcal{D}_X). \end{align*}$$
Using an alternate Schur complement, we expand this latter expression as
 $$\begin{align*}\det (\Delta_{\mathbf{m}}) \cdot \det (\Delta_{\mathbf{m}}^{-1}) \det (\Delta_{a_{X[\mathbf{n}]}}) \det( \mathcal{D}_X^{-1} + \mathcal{W}^T \Delta_{\mathbf{m}} \Delta_{a_{X[\mathbf{n}]}}^{-1} \mathcal{W}) \cdot \det(\mathcal{D}_X). \end{align*}$$
$$\begin{align*}\det (\Delta_{\mathbf{m}}) \cdot \det (\Delta_{\mathbf{m}}^{-1}) \det (\Delta_{a_{X[\mathbf{n}]}}) \det( \mathcal{D}_X^{-1} + \mathcal{W}^T \Delta_{\mathbf{m}} \Delta_{a_{X[\mathbf{n}]}}^{-1} \mathcal{W}) \cdot \det(\mathcal{D}_X). \end{align*}$$
Now defining
 $n^{\prime }_j := \sum _{i=1}^{n_j} m_{ji}$
as in the assertion, we have Thus, the above computation can be continued:
$n^{\prime }_j := \sum _{i=1}^{n_j} m_{ji}$
as in the assertion, we have Thus, the above computation can be continued: $$\begin{align*}\mathcal{W}^T \Delta_{\mathbf{m}} \Delta_{a_{X[\mathbf{n}]}}^{-1} \mathcal{W} = \operatorname{\mathrm{diag}}(a_{x_1}^{-1} n^{\prime}_1, \dots, a_{x_k}^{-1} n^{\prime}_k) = \Delta_{a_X}^{-1} \Delta_{\mathbf{n}'}. \end{align*}$$
$$\begin{align*}\mathcal{W}^T \Delta_{\mathbf{m}} \Delta_{a_{X[\mathbf{n}]}}^{-1} \mathcal{W} = \operatorname{\mathrm{diag}}(a_{x_1}^{-1} n^{\prime}_1, \dots, a_{x_k}^{-1} n^{\prime}_k) = \Delta_{a_X}^{-1} \Delta_{\mathbf{n}'}. \end{align*}$$
 $$ \begin{align*} p_{X[\mathbf{n}]}(\mathbf{m}) = &\ \det(\Delta_{a_{X[\mathbf{n}]}}) \det(\mathcal{D}_X^{-1} + \Delta_{a_X}^{-1} \Delta_{\mathbf{n}'}) \det(\mathcal{D}_X)\\ = &\ \prod_{j=1}^k a_{x_j}^{n_j} \cdot \det(\operatorname{\mathrm{Id}}_k + \Delta_{a_X}^{-1} \Delta_{\mathbf{n}'} \mathcal{D}_X)\\ = &\ \prod_{j=1}^k a_{x_j}^{n_j - 1} \cdot \det(\Delta_{a_X} + \Delta_{\mathbf{n}'} \mathcal{D}_X) = p_X(\mathbf{n}') \prod_{j=1}^k a_{x_j}^{n_j - 1}. \end{align*} $$
$$ \begin{align*} p_{X[\mathbf{n}]}(\mathbf{m}) = &\ \det(\Delta_{a_{X[\mathbf{n}]}}) \det(\mathcal{D}_X^{-1} + \Delta_{a_X}^{-1} \Delta_{\mathbf{n}'}) \det(\mathcal{D}_X)\\ = &\ \prod_{j=1}^k a_{x_j}^{n_j} \cdot \det(\operatorname{\mathrm{Id}}_k + \Delta_{a_X}^{-1} \Delta_{\mathbf{n}'} \mathcal{D}_X)\\ = &\ \prod_{j=1}^k a_{x_j}^{n_j - 1} \cdot \det(\Delta_{a_X} + \Delta_{\mathbf{n}'} \mathcal{D}_X) = p_X(\mathbf{n}') \prod_{j=1}^k a_{x_j}^{n_j - 1}. \end{align*} $$
This proves the result over the function field (over
 $\mathbb {Q}$
) in which the entries
$\mathbb {Q}$
) in which the entries
 $a_{x_j}, m_{ji}, d_{rs}$
are variables. Now, we repeat the Zariski density arguments as in the proof of Theorem 2.3, working this time with the nonzero polynomial given in (3.4). This shows the result over an arbitrary commutative ring – in particular, over
$a_{x_j}, m_{ji}, d_{rs}$
are variables. Now, we repeat the Zariski density arguments as in the proof of Theorem 2.3, working this time with the nonzero polynomial given in (3.4). This shows the result over an arbitrary commutative ring – in particular, over
 $\mathbb R$
.
$\mathbb R$
. -
(3) The key observation is that the diagonal entries of
 $\mathcal {D}_{X[\mathbf {n}]}$
corresponding to the copies of
$\mathcal {D}_{X[\mathbf {n}]}$
corresponding to the copies of
 $x \in X$
, all equal
$x \in X$
, all equal
 $2d_X(x, X \setminus \{ x \})$
, which is precisely the corresponding diagonal entry in
$2d_X(x, X \setminus \{ x \})$
, which is precisely the corresponding diagonal entry in
 $\mathcal {D}_X$
. From this, the assertion for
$\mathcal {D}_X$
. From this, the assertion for
 $\mathcal {D}_{X[\mathbf {n}]}$
is immediate, and that for
$\mathcal {D}_{X[\mathbf {n}]}$
is immediate, and that for
 $\mathcal {C}_{X[\mathbf {n}]}$
is also straightforward.
$\mathcal {C}_{X[\mathbf {n}]}$
is also straightforward. -
(4) We first prove the equivalence for the
 $\mathcal {D}$
-matrices. The preceding part implies that
$\mathcal {D}$
-matrices. The preceding part implies that
 $\mathcal {D}_X$
is a principal submatrix of
$\mathcal {D}_X$
is a principal submatrix of
 $\mathcal {D}_{X[\mathbf {n}]}$
, hence is positive semidefinite if
$\mathcal {D}_{X[\mathbf {n}]}$
, hence is positive semidefinite if
 $\mathcal {D}_{X[\mathbf {n}]}$
is. Conversely, given
$\mathcal {D}_{X[\mathbf {n}]}$
is. Conversely, given
 $v \in \mathbb R^{n_{x_1} + \cdots + n_{x_k}}$
, write
$v \in \mathbb R^{n_{x_1} + \cdots + n_{x_k}}$
, write
 $v^T = (v_1^T, \dots , v_k^T)$
, with all
$v^T = (v_1^T, \dots , v_k^T)$
, with all
 $v_i \in \mathbb R^{n_{x_i}}$
. Let
$v_i \in \mathbb R^{n_{x_i}}$
. Let
 $w_i := v_i^T \mathbf {1}_{n_{x_i}}$
, and denote by
$w_i := v_i^T \mathbf {1}_{n_{x_i}}$
, and denote by
 $w := (w_1, \dots , w_k)^T$
the “compression” of v. Now compute and this is nonnegative (for all v) since
$w := (w_1, \dots , w_k)^T$
the “compression” of v. Now compute and this is nonnegative (for all v) since $$\begin{align*}v^T \mathcal{D}_{X[\mathbf{n}]} v = \sum_{i,j=1}^k v_i^T d_{ij} \mathbf{1}_{n_{x_i} \times n_{x_j}} v_j = \sum_{i,j=1}^k w_i d_{ij} w_j = w^T \mathcal{D}_X w, \end{align*}$$
$$\begin{align*}v^T \mathcal{D}_{X[\mathbf{n}]} v = \sum_{i,j=1}^k v_i^T d_{ij} \mathbf{1}_{n_{x_i} \times n_{x_j}} v_j = \sum_{i,j=1}^k w_i d_{ij} w_j = w^T \mathcal{D}_X w, \end{align*}$$
 $\mathcal {D}_X$
is positive semidefinite. Hence so is
$\mathcal {D}_X$
is positive semidefinite. Hence so is
 $\mathcal {D}_{X[\mathbf {n}]}$
.
$\mathcal {D}_{X[\mathbf {n}]}$
.
This proves the equivalence for the
 $\mathcal {D}$
-matrices. Now for any metric space Y (e.g.,
$\mathcal {D}$
-matrices. Now for any metric space Y (e.g.,
 $Y = X$
or
$Y = X$
or
 $X[\mathbf {n}]$
), the matrix
$X[\mathbf {n}]$
), the matrix
 $\mathcal {C}_Y = (-\Delta _{\mathbf {a}_Y})^{-1/2} \mathcal {D}_Y (-\Delta _{\mathbf {a}_Y})^{-1/2}$
is positive semidefinite if and only if
$\mathcal {C}_Y = (-\Delta _{\mathbf {a}_Y})^{-1/2} \mathcal {D}_Y (-\Delta _{\mathbf {a}_Y})^{-1/2}$
is positive semidefinite if and only if
 $\mathcal {D}_Y$
is. This concludes the proof.
$\mathcal {D}_Y$
is. This concludes the proof.
Remark 3.3 The proof of Lemma 3.2(2) using Zariski density indicates a similar, alternate approach to proving the formula for
![]() $\det M(\mathbf {A}, \mathbf {D})$
in Theorem 2.3. The difference, now, is that the rank-one expansion of the matrix
$\det M(\mathbf {A}, \mathbf {D})$
in Theorem 2.3. The difference, now, is that the rank-one expansion of the matrix
![]() $\mathbf {D}$
is no longer needed, and can be replaced by the use of the two block-diagonal matrices
$\mathbf {D}$
is no longer needed, and can be replaced by the use of the two block-diagonal matrices
 $$\begin{align*}\mathcal{W}(\mathbf{p}_1, \dots, \mathbf{p}_k) := \begin{pmatrix} (\mathbf{ p}_1)_{n_1 \times 1} & 0_{n_1 \times 1} & \ldots & 0_{n_1 \times 1} \\ 0_{n_2 \times 1} & (\mathbf{p}_2)_{n_2 \times 1} & \ldots & 0_{n_2 \times 1} \\ \vdots & \vdots & \ddots & \vdots \\ 0_{n_k \times 1} & 0_{n_k \times 1} & \ldots & (\mathbf{p}_k)_{n_k \times 1} \end{pmatrix} \end{align*}$$
$$\begin{align*}\mathcal{W}(\mathbf{p}_1, \dots, \mathbf{p}_k) := \begin{pmatrix} (\mathbf{ p}_1)_{n_1 \times 1} & 0_{n_1 \times 1} & \ldots & 0_{n_1 \times 1} \\ 0_{n_2 \times 1} & (\mathbf{p}_2)_{n_2 \times 1} & \ldots & 0_{n_2 \times 1} \\ \vdots & \vdots & \ddots & \vdots \\ 0_{n_k \times 1} & 0_{n_k \times 1} & \ldots & (\mathbf{p}_k)_{n_k \times 1} \end{pmatrix} \end{align*}$$
and a similar matrix
![]() $\mathcal {W}(\mathbf {q}_1, \dots , \mathbf {q}_k)$
, so that
$\mathcal {W}(\mathbf {q}_1, \dots , \mathbf {q}_k)$
, so that
![]() $M(\mathbf {A}, \mathbf {D}) = \operatorname {\mathrm {diag}}(\{ A_i \cdot \operatorname {\mathrm {Id}}_{n_i} \}) + \mathcal {W}(\{ \mathbf {p}_i \}) \cdot \mathbf {D} \cdot \mathcal {W}(\{ \mathbf {q}_i \})^T$
.
$M(\mathbf {A}, \mathbf {D}) = \operatorname {\mathrm {diag}}(\{ A_i \cdot \operatorname {\mathrm {Id}}_{n_i} \}) + \mathcal {W}(\{ \mathbf {p}_i \}) \cdot \mathbf {D} \cdot \mathcal {W}(\{ \mathbf {q}_i \})^T$
.
Lemma 3.2(2) immediately implies the following consequence (which can also be shown directly).
Corollary 3.4 Fix a finite metric space
![]() $(X,d)$
. For all integer tuples
$(X,d)$
. For all integer tuples
![]() $\mathbf {n} \in \mathbb {Z}_{>0}^X$
, the blowup-polynomial of
$\mathbf {n} \in \mathbb {Z}_{>0}^X$
, the blowup-polynomial of
![]() $X[\mathbf {n}]$
has total degree at most
$X[\mathbf {n}]$
has total degree at most
![]() $|X|$
.
$|X|$
.
In other words, no monomials of degree
![]() $|X|+1$
or higher occur in
$|X|+1$
or higher occur in
![]() $p_{X[\mathbf {n}]}$
, for any tuple
$p_{X[\mathbf {n}]}$
, for any tuple
![]() $\mathbf {n}$
.
$\mathbf {n}$
.
We now prove the real-stability of
![]() $p_X(\cdot )$
.
$p_X(\cdot )$
.
Proof of Theorem C
We continue to use the notation in the proof of Theorem B, with one addition: for expositional clarity, in this proof, we treat
![]() $p_X(\cdot )$
as a polynomial in the complex variables
$p_X(\cdot )$
as a polynomial in the complex variables
![]() $z_j := n_{x_j}$
for
$z_j := n_{x_j}$
for
![]() $j=1,\dots ,k$
. Thus,
$j=1,\dots ,k$
. Thus,
where
![]() $a_j = -2 d(x_j, X \setminus \{ x_j \}) < 0\ \forall j$
and
$a_j = -2 d(x_j, X \setminus \{ x_j \}) < 0\ \forall j$
and
![]() $\Delta _{\mathbf {z}} := \operatorname {\mathrm {diag}}(z_1, \dots , z_k)$
. We compute
$\Delta _{\mathbf {z}} := \operatorname {\mathrm {diag}}(z_1, \dots , z_k)$
. We compute
 $$ \begin{align*} p_X(\mathbf{z}) = &\ \det (\Delta_{\mathbf{z}}) \det (\mathcal{D}_X - (-\Delta_{\mathbf{a}_X}) \Delta_{\mathbf{z}}^{-1})\\ = &\ \prod_{j=1}^k z_j \cdot \det (-\Delta_{\mathbf{a}_X})^{1/2} \det \left( (-\Delta_{\mathbf{a}_X})^{-1/2} \mathcal{D}_X (-\Delta_{\mathbf{a}_X})^{-1/2} - \Delta_{\mathbf{ z}}^{-1} \right) \det (-\Delta_{\mathbf{a}_X})^{1/2}\\ = &\ \det (-\Delta_{\mathbf{a}_X}) \prod_{j=1}^k z_j \cdot \det \left( \mathcal{C}_X + \sum_{j=1}^k (-z_j^{-1}) E_{jj} \right), \end{align*} $$
$$ \begin{align*} p_X(\mathbf{z}) = &\ \det (\Delta_{\mathbf{z}}) \det (\mathcal{D}_X - (-\Delta_{\mathbf{a}_X}) \Delta_{\mathbf{z}}^{-1})\\ = &\ \prod_{j=1}^k z_j \cdot \det (-\Delta_{\mathbf{a}_X})^{1/2} \det \left( (-\Delta_{\mathbf{a}_X})^{-1/2} \mathcal{D}_X (-\Delta_{\mathbf{a}_X})^{-1/2} - \Delta_{\mathbf{ z}}^{-1} \right) \det (-\Delta_{\mathbf{a}_X})^{1/2}\\ = &\ \det (-\Delta_{\mathbf{a}_X}) \prod_{j=1}^k z_j \cdot \det \left( \mathcal{C}_X + \sum_{j=1}^k (-z_j^{-1}) E_{jj} \right), \end{align*} $$
where
![]() $E_{jj}$
is the elementary
$E_{jj}$
is the elementary
![]() $k \times k$
matrix with
$k \times k$
matrix with
![]() $(j,j)$
entry
$(j,j)$
entry
![]() $1$
and all other entries zero.
$1$
and all other entries zero.
We now appeal to two facts. The first is a well-known result of Borcea–Brändén [Reference Borcea and Brändén5, Proposition 2.4] (see also [Reference Brändén11, Lemma 4.1]), which says that if
![]() $A_1, \dots , A_k, B$
are equi-dimensional real symmetric matrices, with all
$A_1, \dots , A_k, B$
are equi-dimensional real symmetric matrices, with all
![]() $A_j$
positive semidefinite, then the polynomial
$A_j$
positive semidefinite, then the polynomial
 $$ \begin{align} f(z_1, \dots, z_k) := \det \left( B + \sum_{j=1}^k z_j A_j \right) \end{align} $$
$$ \begin{align} f(z_1, \dots, z_k) := \det \left( B + \sum_{j=1}^k z_j A_j \right) \end{align} $$
is either real-stable or identically zero. The second is the folklore result that “inversion preserves stability” (since the upper half-plane is preserved under the transformation
![]() $z \mapsto -1/z$
of
$z \mapsto -1/z$
of
![]() $\mathbb {C}^\times $
). That is, if a polynomial
$\mathbb {C}^\times $
). That is, if a polynomial
![]() $g(z_1, \dots , z_k)$
has
$g(z_1, \dots , z_k)$
has
![]() $z_j$
-degree
$z_j$
-degree
![]() $d_j \geqslant 1$
and is real-stable, then so is the polynomial
$d_j \geqslant 1$
and is real-stable, then so is the polynomial
(this actually holds for any
![]() $z_j$
). Apply this latter fact to each variable of the multi-affine polynomial
$z_j$
). Apply this latter fact to each variable of the multi-affine polynomial
![]() $f(\cdot )$
in (3.5) – in which
$f(\cdot )$
in (3.5) – in which
![]() $d_j=1$
,
$d_j=1$
,
![]() $B = \mathcal {C}_X$
, and
$B = \mathcal {C}_X$
, and
![]() $A_j = E_{jj}\ \forall j$
. It follows that the polynomial
$A_j = E_{jj}\ \forall j$
. It follows that the polynomial
 $$ \begin{align*} z_1 \cdots z_k \cdot f(-z_1^{-1}, \dots, -z_k^{-1}) = &\ \prod_{j=1}^k z_j \cdot \det \left( \mathcal{C}_X + \sum_{j=1}^k (-z_j^{-1}) E_{jj} \right)\\ = &\ \det (-\Delta_{\mathbf{a}_X})^{-1} p_X(\mathbf{z}) \end{align*} $$
$$ \begin{align*} z_1 \cdots z_k \cdot f(-z_1^{-1}, \dots, -z_k^{-1}) = &\ \prod_{j=1}^k z_j \cdot \det \left( \mathcal{C}_X + \sum_{j=1}^k (-z_j^{-1}) E_{jj} \right)\\ = &\ \det (-\Delta_{\mathbf{a}_X})^{-1} p_X(\mathbf{z}) \end{align*} $$
is real-stable, and the proof is complete.
Remark 3.5 For completeness, we briefly touch upon other notions of stability that are standard in mathematics (analysis, control theory, differential/difference equations): Hurwitz stability and Schur stability. Recall that a real polynomial in one variable is said to be Hurwitz stable (resp. Schur stable) if all of its roots lie in the open left half-plane (resp. in the open unit disk) in
![]() $\mathbb {C}$
. Now the univariate specializations
$\mathbb {C}$
. Now the univariate specializations
![]() $u_X(n) = p_X(n,n,\dots ,n)$
are not all either Hurwitz or Schur stable. As a concrete example: in the simplest case of the discrete metric on a space X, equation (2.4) implies that
$u_X(n) = p_X(n,n,\dots ,n)$
are not all either Hurwitz or Schur stable. As a concrete example: in the simplest case of the discrete metric on a space X, equation (2.4) implies that
![]() $u_X(n) = (n-2)^{k-1} (n-2 + kn)$
, and this vanishes at
$u_X(n) = (n-2)^{k-1} (n-2 + kn)$
, and this vanishes at
![]() $n=2, \frac {2}{k+1}$
.
$n=2, \frac {2}{k+1}$
.
4 Combinatorics: graphs and their partially symmetric blowup-polynomials
We now take a closer look at a distinguished sub-class of finite metric spaces: unweighted graphs. In this section, we will show Theorems D–F. To avoid having to mention the same quantifiers repeatedly, we introduce the following definition (used in the opening section).
Definition 4.1 A graph metric space is a finite, simple, connected, unweighted graph G, in which the distance between two vertices is the number of edges in a shortest path connecting them.
Every graph metric space G is thus a finite metric space, and so the results in the previous sections apply to it. In particular, to every graph metric space
![]() $G = (V,E)$
are naturally associated a (to the best of our knowledge) novel graph invariant
$G = (V,E)$
are naturally associated a (to the best of our knowledge) novel graph invariant
(which we showed is real-stable), as well as its univariate specialization (which is thus real-rooted)
and its “maximum root”
![]() $\alpha _{\max }(u_G) \in \mathbb R$
. Here,
$\alpha _{\max }(u_G) \in \mathbb R$
. Here,
![]() $D_G$
is the distance matrix of G (with zeros on the diagonal) and
$D_G$
is the distance matrix of G (with zeros on the diagonal) and
![]() $\mathcal {D}_G = D_G + 2 \operatorname {\mathrm {Id}}_V$
is the modified distance matrix.
$\mathcal {D}_G = D_G + 2 \operatorname {\mathrm {Id}}_V$
is the modified distance matrix.
4.1 Connections to the distance spectrum;
 $p_G$
recovers G
$p_G$
recovers G
We begin with an observation (for completeness), which ties into one of our original motivations by connecting the blowup-polynomial
![]() $u_G$
to the distance spectrum of G, i.e., to the eigenvalues of the distance matrix
$u_G$
to the distance spectrum of G, i.e., to the eigenvalues of the distance matrix
![]() $D_G$
. The study of these eigenvalues began with the work of Graham and Lovász [Reference Graham and Lovász20], and by now, is a well-developed program in the literature (see, e.g., [Reference Aouchiche and Hansen3]). Our observation here is the following.
$D_G$
. The study of these eigenvalues began with the work of Graham and Lovász [Reference Graham and Lovász20], and by now, is a well-developed program in the literature (see, e.g., [Reference Aouchiche and Hansen3]). Our observation here is the following.
Proposition 4.2 Suppose
![]() $G = (V,E)$
is a graph metric space. A real number n is a root of the univariate blowup-polynomial
$G = (V,E)$
is a graph metric space. A real number n is a root of the univariate blowup-polynomial
![]() $u_G$
, if and only if
$u_G$
, if and only if
![]() $2n^{-1} - 2$
is an eigenvalue of the distance matrix
$2n^{-1} - 2$
is an eigenvalue of the distance matrix
![]() $D_G$
, with the same multiplicity.
$D_G$
, with the same multiplicity.
Alternately,
![]() $\lambda \neq -2$
is an eigenvalue of
$\lambda \neq -2$
is an eigenvalue of
![]() $D_G$
if and only if
$D_G$
if and only if
![]() $\frac {2}{2 + \lambda }$
is a root of
$\frac {2}{2 + \lambda }$
is a root of
![]() $u_G$
.
$u_G$
.
Proof First, note from the definitions that
![]() $u_G(0) = \det (-2 \operatorname {\mathrm {Id}}_V) \neq 0$
. We now compute
$u_G(0) = \det (-2 \operatorname {\mathrm {Id}}_V) \neq 0$
. We now compute
Thus, n is a (nonzero) root of
![]() $u_G$
if and only if
$u_G$
if and only if
![]() $n^{-1}$
is an eigenvalue of
$n^{-1}$
is an eigenvalue of
![]() $\operatorname {\mathrm {Id}}_V + \frac {1}{2} D_G$
. The result follows from here.
$\operatorname {\mathrm {Id}}_V + \frac {1}{2} D_G$
. The result follows from here.
In the distance spectrum literature, much work has gone into studying the largest eigenvalue of
![]() $D_G$
, called the “distance spectral radius” in the literature, as well as the smallest eigenvalue of
$D_G$
, called the “distance spectral radius” in the literature, as well as the smallest eigenvalue of
![]() $D_G$
. An immediate application of Proposition 4.2 provides an interpretation of another such eigenvalue.
$D_G$
. An immediate application of Proposition 4.2 provides an interpretation of another such eigenvalue.
Corollary 4.3 The smallest eigenvalue of
![]() $D_G$
which is strictly greater than
$D_G$
which is strictly greater than
![]() $-2$
, is precisely
$-2$
, is precisely
![]() $\frac {2}{\alpha _{\max }(u_G)} - 2$
.
$\frac {2}{\alpha _{\max }(u_G)} - 2$
.
We refer the reader to further discussions about
![]() $\alpha _{\max }(u_G)$
in and around Proposition A.4.
$\alpha _{\max }(u_G)$
in and around Proposition A.4.
Following these observations that reinforce our motivating connections between distance spectra and the blowup-polynomial, we now move on to the proof of Theorem D. Recall, this result shows that (the homogeneous quadratic part of)
![]() $p_G$
recovers/detects the graph and its isometries – but
$p_G$
recovers/detects the graph and its isometries – but
![]() $u_G$
does not do so.
$u_G$
does not do so.
Proof of Theorem D
We prove the various assertions in serial order. One implication for the first assertion was described just above the theorem-statement. Conversely, suppose
![]() $p_G(\mathbf {n}) \equiv p_{\Psi (G)}(\mathbf {n})$
. Fix vertices
$p_G(\mathbf {n}) \equiv p_{\Psi (G)}(\mathbf {n})$
. Fix vertices
![]() $v \neq w \in V$
, and equate the coefficient of
$v \neq w \in V$
, and equate the coefficient of
![]() $n_v n_w$
on both sides using Proposition 2.6:
$n_v n_w$
on both sides using Proposition 2.6:
 $$\begin{align*}(-2)^{|V|-2} \det \begin{pmatrix} 2 & d(v,w) \\ d(v,w) & 2 \end{pmatrix} = (-2)^{|V|-2} \det \begin{pmatrix} 2 & d(\Psi(v),\Psi(w)) \\ d(\Psi(v),\Psi(w)) & 2 \end{pmatrix},\\[-6pt] \end{align*}$$
$$\begin{align*}(-2)^{|V|-2} \det \begin{pmatrix} 2 & d(v,w) \\ d(v,w) & 2 \end{pmatrix} = (-2)^{|V|-2} \det \begin{pmatrix} 2 & d(\Psi(v),\Psi(w)) \\ d(\Psi(v),\Psi(w)) & 2 \end{pmatrix},\\[-6pt] \end{align*}$$
since
![]() $d_G(v, V \setminus \{ v \}) = 1\ \forall v \in V$
. Thus
$d_G(v, V \setminus \{ v \}) = 1\ \forall v \in V$
. Thus
![]() $d(\Psi (v), \Psi (w)) = d(v,w)$
for all
$d(\Psi (v), \Psi (w)) = d(v,w)$
for all
![]() $v, w \in V$
, so
$v, w \in V$
, so
![]() $\Psi $
is an isometry.
$\Psi $
is an isometry.
The second assertion is shown as follows. By Proposition 2.6, the vertex set can be obtained from the nonzero monomials
![]() $n_v n_w$
(since every edge yields a nonzero monomial). In particular,
$n_v n_w$
(since every edge yields a nonzero monomial). In particular,
![]() $|V|$
is recovered. Again by Proposition 2.6, there is a bijection between the set of edges
$|V|$
is recovered. Again by Proposition 2.6, there is a bijection between the set of edges
![]() $v \sim w$
in G and the monomials
$v \sim w$
in G and the monomials
![]() $n_v n_w$
in
$n_v n_w$
in
![]() $p_G(\mathbf {n})$
with coefficient
$p_G(\mathbf {n})$
with coefficient
![]() $3(-2)^{|V|-2}$
. Thus, all quadratic monomials in
$3(-2)^{|V|-2}$
. Thus, all quadratic monomials in
![]() $p_G(\mathbf {n})$
with this coefficient reveal the edge set of G as well.
$p_G(\mathbf {n})$
with this coefficient reveal the edge set of G as well.
Finally, to show that
![]() $u_G$
does not detect the graph G, consider the two graphs
$u_G$
does not detect the graph G, consider the two graphs
![]() $H,K$
in Figure 1.
$H,K$
in Figure 1.

Figure 1: Two non-isometric graphs on six vertices with co-spectral blowups.
Both graphs have vertex sets
![]() $\{ 1, \dots , 6 \}$
, and are not isomorphic. Now define (see Remark 4.4):
$\{ 1, \dots , 6 \}$
, and are not isomorphic. Now define (see Remark 4.4):
Then
![]() $H', K'$
are not isometric, but a direct computation reveals:
$H', K'$
are not isometric, but a direct computation reveals:
Remark 4.4 The graphs
![]() $H',K'$
in the preceding proof were not accidental or providential, but stem from the recent paper [Reference Drury and Lin18], which is part of the literature on exploring which graphs are distance co-spectral (see the Introduction). In the discussion preceding [Reference Drury and Lin18, Figure 1], the authors verified that the graphs
$H',K'$
in the preceding proof were not accidental or providential, but stem from the recent paper [Reference Drury and Lin18], which is part of the literature on exploring which graphs are distance co-spectral (see the Introduction). In the discussion preceding [Reference Drury and Lin18, Figure 1], the authors verified that the graphs
![]() $H' \not \cong K'$
used in the preceding proof are indeed distance co-spectral. This result, combined with Proposition 4.2, leads to the above use of
$H' \not \cong K'$
used in the preceding proof are indeed distance co-spectral. This result, combined with Proposition 4.2, leads to the above use of
![]() $H', K'$
in proving that
$H', K'$
in proving that
![]() $u_G$
cannot detect G up to isometry.
$u_G$
cannot detect G up to isometry.
Remark 4.5 As the proof of Theorem D reveals, for any graph metric space
![]() $G = (V,E)$
, the Hessian of the blowup-polynomial carries the same information as the matrix
$G = (V,E)$
, the Hessian of the blowup-polynomial carries the same information as the matrix
![]() $\mathcal {D}_G \in \mathbb {Z}_{>0}^{V \times V}$
:
$\mathcal {D}_G \in \mathbb {Z}_{>0}^{V \times V}$
:
where
![]() $\mathcal {D}_G^{\circ 2}$
is the entrywise square of the modified distance matrix
$\mathcal {D}_G^{\circ 2}$
is the entrywise square of the modified distance matrix
![]() $\mathcal {D}_G$
.
$\mathcal {D}_G$
.
4.2 Complete multipartite graphs via real-stability
The next result we show is Theorem E (described in the title of this subsection). Before doing so, we define the three classes of polynomials alluded to in Corollary 1.7, as promised there (and for the self-sufficiency of this paper).
-
(1) Brändén–Huh [Reference Brändén and Huh12] defined a polynomial
 $p \in \mathbb R[x_1, \dots , x_k]$
to be Lorentzian if
$p \in \mathbb R[x_1, \dots , x_k]$
to be Lorentzian if
 $p(\cdot )$
is homogeneous of some degree d, has nonnegative coefficients, and given any indices
$p(\cdot )$
is homogeneous of some degree d, has nonnegative coefficients, and given any indices
 $0 \leqslant j_1, \dots , j_{d-2} \leqslant k$
, if then the Hessian matrix
$0 \leqslant j_1, \dots , j_{d-2} \leqslant k$
, if then the Hessian matrix $$\begin{align*}g(x_1, \dots, x_k) := \left( \partial_{x_{j_1}} \ldots \partial_{x_{j_{d-2}} } p \right)(x_1, \dots, x_k), \end{align*}$$
$$\begin{align*}g(x_1, \dots, x_k) := \left( \partial_{x_{j_1}} \ldots \partial_{x_{j_{d-2}} } p \right)(x_1, \dots, x_k), \end{align*}$$
 $\mathcal {H}_g := (\partial _{x_i} \partial _{x_j} g)_{i,j=1}^k \in \mathbb R^{k \times k}$
is Lorentzian. (This last term means that
$\mathcal {H}_g := (\partial _{x_i} \partial _{x_j} g)_{i,j=1}^k \in \mathbb R^{k \times k}$
is Lorentzian. (This last term means that
 $\mathcal {H}_g$
is nonsingular and has exactly one positive eigenvalue.)
$\mathcal {H}_g$
is nonsingular and has exactly one positive eigenvalue.)
-
(2) Suppose
 $p \in \mathbb R[x_1, \dots , x_k]$
has nonnegative coefficients. Gurvits [Reference Gurvits, Kotsireas and Zima23] defined p to be strongly log-concave if for all
$p \in \mathbb R[x_1, \dots , x_k]$
has nonnegative coefficients. Gurvits [Reference Gurvits, Kotsireas and Zima23] defined p to be strongly log-concave if for all
 $\alpha \in \mathbb {Z}_{\geqslant 0}^k$
, either the derivative
$\alpha \in \mathbb {Z}_{\geqslant 0}^k$
, either the derivative
 $\displaystyle \partial ^\alpha (p) := \prod _{i=1}^k \partial _{x_i}^{\alpha _i} \cdot p$
is identically zero, or
$\displaystyle \partial ^\alpha (p) := \prod _{i=1}^k \partial _{x_i}^{\alpha _i} \cdot p$
is identically zero, or
 $\log (\partial ^\alpha (p))$
is defined and concave on
$\log (\partial ^\alpha (p))$
is defined and concave on
 $(0,\infty )^k$
.
$(0,\infty )^k$
. -
(3) Suppose
 $p \in \mathbb R[x_1, \dots , x_k]$
has nonnegative coefficients. Anari, Oveis Gharan, and Vinzant [Reference Anari, Oveis Gharan and Vinzant2] defined p to be completely log-concave if for all integers
$p \in \mathbb R[x_1, \dots , x_k]$
has nonnegative coefficients. Anari, Oveis Gharan, and Vinzant [Reference Anari, Oveis Gharan and Vinzant2] defined p to be completely log-concave if for all integers
 $m \geqslant 1$
and matrices
$m \geqslant 1$
and matrices
 $A = (a_{ij}) \in [0,\infty )^{m \times k}$
, either the derivative
$A = (a_{ij}) \in [0,\infty )^{m \times k}$
, either the derivative
 $\displaystyle \partial _A (p) := \prod _{i=1}^m \left ( \sum _{j=1}^k a_{ij} \partial _{x_j} \right ) \cdot p$
is identically zero, or
$\displaystyle \partial _A (p) := \prod _{i=1}^m \left ( \sum _{j=1}^k a_{ij} \partial _{x_j} \right ) \cdot p$
is identically zero, or
 $\log (\partial _A (p))$
is defined and concave on
$\log (\partial _A (p))$
is defined and concave on
 $(0,\infty )^k$
.
$(0,\infty )^k$
.
Having written these definitions, we proceed to the main proof.
Proof of Theorem E
We prove the cyclic chain of implications:
We begin with a short proof of
![]() $(1) \implies (2)$
via Lorentzian polynomials from Corollary 1.7. It was shown in [Reference Brändén and Huh12, pp. 828–829] that if
$(1) \implies (2)$
via Lorentzian polynomials from Corollary 1.7. It was shown in [Reference Brändén and Huh12, pp. 828–829] that if
![]() $(1)$
holds then
$(1)$
holds then
![]() $\widetilde {p}_G$
is Lorentzian (see also [Reference Choe, Oxley, Sokal and Wagner15, Theorem 6.1]), and in turn, this implies
$\widetilde {p}_G$
is Lorentzian (see also [Reference Choe, Oxley, Sokal and Wagner15, Theorem 6.1]), and in turn, this implies
![]() $(2)$
by definition (or by loc. cit.).
$(2)$
by definition (or by loc. cit.).
We next show that
![]() $(3) \implies (2)$
. Observe that
$(3) \implies (2)$
. Observe that
 $$ \begin{align} \frac{p_G(-z_1, \dots, -z_k) \cdot (-1)^k}{p_G(-1, \dots, -1) \cdot (-1)^k} \equiv \frac{\widetilde{p}_G(1, z_1, \dots, z_k)}{\widetilde{p}_G(1,1,\dots,1)}. \end{align} $$
$$ \begin{align} \frac{p_G(-z_1, \dots, -z_k) \cdot (-1)^k}{p_G(-1, \dots, -1) \cdot (-1)^k} \equiv \frac{\widetilde{p}_G(1, z_1, \dots, z_k)}{\widetilde{p}_G(1,1,\dots,1)}. \end{align} $$
Now if
![]() $(3)$
holds, then
$(3)$
holds, then
![]() $\widetilde {p}_G(1,1,\dots ,1) = (-1)^k p_G(-1, \dots , -1)> 0$
, so the polynomial
$\widetilde {p}_G(1,1,\dots ,1) = (-1)^k p_G(-1, \dots , -1)> 0$
, so the polynomial
has all coefficients nonnegative, using
![]() $(3)$
and (4.4). Since
$(3)$
and (4.4). Since
![]() $p_G(\cdot )$
is multi-affine (or by inspecting the form of
$p_G(\cdot )$
is multi-affine (or by inspecting the form of
![]() $\widetilde {p}_G(\cdot )$
), this shows
$\widetilde {p}_G(\cdot )$
), this shows
![]() $(3) \implies (2)$
. Now to show
$(3) \implies (2)$
. Now to show
![]() $\{ (1), (2) \} \implies (3)$
, note that the sum of all coefficients in
$\{ (1), (2) \} \implies (3)$
, note that the sum of all coefficients in
![]() $\widetilde {p}_G(\cdot )$
equals
$\widetilde {p}_G(\cdot )$
equals
and by
![]() $(2)$
, this dominates the “constant term” of
$(2)$
, this dominates the “constant term” of
![]() $p_G$
, i.e.,
$p_G$
, i.e.,
 $$ \begin{align*} (-1)^k p_G(-1,\dots,-1) \geqslant \widetilde{p}_G(1,0,\dots,0) = &\ (-1)^k p_G(0,\dots,0)\\ = &\ (-1)^k \prod_{v \in V} (-2 d(v, V \setminus \{ v \}))> 0. \end{align*} $$
$$ \begin{align*} (-1)^k p_G(-1,\dots,-1) \geqslant \widetilde{p}_G(1,0,\dots,0) = &\ (-1)^k p_G(0,\dots,0)\\ = &\ (-1)^k \prod_{v \in V} (-2 d(v, V \setminus \{ v \}))> 0. \end{align*} $$
In particular,
![]() $(-1)^k p_G(-1,\dots ,-1)> 0$
, proving a part of
$(-1)^k p_G(-1,\dots ,-1)> 0$
, proving a part of
![]() $(3)$
. Hence using
$(3)$
. Hence using
![]() $(2)$
and (4.4), all coefficients of the “reflected” polynomial are nonnegative; and the normalization shows that the coefficients sum to
$(2)$
and (4.4), all coefficients of the “reflected” polynomial are nonnegative; and the normalization shows that the coefficients sum to
![]() $1$
. It remains to show that the “reflected” polynomial
$1$
. It remains to show that the “reflected” polynomial
![]() $p_G(-\mathbf {z}) / p_G(-1,\dots ,-1)$
is real-stable. Once again, using (4.4) and that
$p_G(-\mathbf {z}) / p_G(-1,\dots ,-1)$
is real-stable. Once again, using (4.4) and that
![]() $(-1)^k p_G(-1,\dots ,-1)> 0$
, it suffices to show that
$(-1)^k p_G(-1,\dots ,-1)> 0$
, it suffices to show that
![]() $\widetilde {p}_G(1,z_1, \dots , z_k)$
is real-stable. But this follows from
$\widetilde {p}_G(1,z_1, \dots , z_k)$
is real-stable. But this follows from
![]() $(1)$
by specializing to
$(1)$
by specializing to
![]() $z_0 \mapsto 1 \in \mathbb R$
. This finally shows that
$z_0 \mapsto 1 \in \mathbb R$
. This finally shows that
![]() $(1)$
and
$(1)$
and
![]() $(2)$
together imply
$(2)$
together imply
![]() $(3)$
.
$(3)$
.
We next show the equivalence of
![]() $(4)$
and
$(4)$
and
![]() $(5)$
. If
$(5)$
. If
![]() $G = K_k$
, then
$G = K_k$
, then
![]() $\mathcal {D}_G = \operatorname {\mathrm {Id}}_k + \mathbf {1}_{k \times k}$
is positive semidefinite. Hence so is
$\mathcal {D}_G = \operatorname {\mathrm {Id}}_k + \mathbf {1}_{k \times k}$
is positive semidefinite. Hence so is
![]() $\mathcal {D}_{K_k[\mathbf {n}]}$
for all
$\mathcal {D}_{K_k[\mathbf {n}]}$
for all
![]() $\mathbf {n}$
, by Lemma 3.2(4). The converse follows from [Reference Lin, Hong, Wang and Shu28, Theorem 1.1], since
$\mathbf {n}$
, by Lemma 3.2(4). The converse follows from [Reference Lin, Hong, Wang and Shu28, Theorem 1.1], since
![]() $\mathcal {D}_G = D_G + 2 \operatorname {\mathrm {Id}}_{|V(G)|}$
.
$\mathcal {D}_G = D_G + 2 \operatorname {\mathrm {Id}}_{|V(G)|}$
.
Finally, we will show
![]() $(2) \implies (4) \implies (1)$
. First, assume (2)
$(2) \implies (4) \implies (1)$
. First, assume (2)
![]() $\widetilde {p}_G(\cdot )$
has nonnegative coefficients. Fix a subset
$\widetilde {p}_G(\cdot )$
has nonnegative coefficients. Fix a subset
![]() $J \subseteq \{ 1, \dots , k \}$
; using Proposition 2.6(1), the coefficient of
$J \subseteq \{ 1, \dots , k \}$
; using Proposition 2.6(1), the coefficient of
![]() $z_0^{k - |J|} \prod _{j \in J} z_j$
equals
$z_0^{k - |J|} \prod _{j \in J} z_j$
equals
By the hypotheses, this expression is nonnegative for every
![]() $J \subseteq \{ 1, \dots , k \}$
. Hence,
$J \subseteq \{ 1, \dots , k \}$
. Hence,
![]() $\mathcal {D}_G$
has all principal minors nonnegative (and is symmetric), so is positive semidefinite, proving (4).
$\mathcal {D}_G$
has all principal minors nonnegative (and is symmetric), so is positive semidefinite, proving (4).
Finally, if (4)
![]() $\mathcal {D}_G$
is positive semidefinite, then so is
$\mathcal {D}_G$
is positive semidefinite, then so is
![]() $\mathcal {C}_G$
. As above, write
$\mathcal {C}_G$
. As above, write
![]() $\mathcal {C}_G = (-\Delta _{\mathbf {a}_G})^{-1/2} \mathcal {D}_G (-\Delta _{\mathbf {a}_G})^{-1/2}$
, and compute using that
$\mathcal {C}_G = (-\Delta _{\mathbf {a}_G})^{-1/2} \mathcal {D}_G (-\Delta _{\mathbf {a}_G})^{-1/2}$
, and compute using that
![]() $-\Delta _{\mathbf {a}_G}$
is a positive definite diagonal matrix:
$-\Delta _{\mathbf {a}_G}$
is a positive definite diagonal matrix:
 $$ \begin{align} \widetilde{p}_G(z_0, z_1, \dots, z_k) = &\ \det(z_0 \cdot (-\Delta_{\mathbf{a}_G}) + \Delta_{\mathbf{z}} \mathcal{D}_G)\notag\\ = &\ \det (-\Delta_{\mathbf{a}_G})^{1/2} \det (z_0 \operatorname{\mathrm{Id}}_k + \Delta_{\mathbf{z}} \mathcal{C}_G) \det (-\Delta_{\mathbf{a}_G})^{1/2}\notag\\ = &\ \det (-\Delta_{\mathbf{a}_G}) \det (z_0 \operatorname{\mathrm{Id}}_k + \Delta_{\mathbf{z}} \mathcal{C}_G). \end{align} $$
$$ \begin{align} \widetilde{p}_G(z_0, z_1, \dots, z_k) = &\ \det(z_0 \cdot (-\Delta_{\mathbf{a}_G}) + \Delta_{\mathbf{z}} \mathcal{D}_G)\notag\\ = &\ \det (-\Delta_{\mathbf{a}_G})^{1/2} \det (z_0 \operatorname{\mathrm{Id}}_k + \Delta_{\mathbf{z}} \mathcal{C}_G) \det (-\Delta_{\mathbf{a}_G})^{1/2}\notag\\ = &\ \det (-\Delta_{\mathbf{a}_G}) \det (z_0 \operatorname{\mathrm{Id}}_k + \Delta_{\mathbf{z}} \mathcal{C}_G). \end{align} $$
(As an aside, the second factor in the final expression was termed as the multivariate characteristic polynomial of
![]() $\mathcal {C}_G$
, in [Reference Brändén and Huh12, Section 4.4].)
$\mathcal {C}_G$
, in [Reference Brändén and Huh12, Section 4.4].)
Now
![]() $\mathcal {C}_G$
has a positive semidefinite square root
$\mathcal {C}_G$
has a positive semidefinite square root
![]() $\sqrt {\mathcal {C}_G}$
by the hypotheses. We claim that
$\sqrt {\mathcal {C}_G}$
by the hypotheses. We claim that
this follows by expanding the determinant of
 $\begin {pmatrix} z_0 \operatorname {\mathrm {Id}}_k & -\sqrt {\mathcal {C}_G} \\ \Delta _{\mathbf {z}} \sqrt {\mathcal {C}_G} & \operatorname {\mathrm {Id}}_k \end {pmatrix}$
in two different ways, both using Schur complements. Therefore – and as in the proof of Theorem C – we have
$\begin {pmatrix} z_0 \operatorname {\mathrm {Id}}_k & -\sqrt {\mathcal {C}_G} \\ \Delta _{\mathbf {z}} \sqrt {\mathcal {C}_G} & \operatorname {\mathrm {Id}}_k \end {pmatrix}$
in two different ways, both using Schur complements. Therefore – and as in the proof of Theorem C – we have
 $$ \begin{align} \begin{aligned} \widetilde{p}_G(z_0, z_1, \dots, z_k) = &\ \det (-\Delta_{\mathbf{a}_G}) \det (z_0 \operatorname{\mathrm{Id}}_k + \sqrt{\mathcal{C}_G} \Delta_{\mathbf{z}} \sqrt{\mathcal{C}_G})\\ = &\ \det (-\Delta_{\mathbf{a}_G}) \det \left( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^k z_j \sqrt{\mathcal{C}_G} E_{jj} \sqrt{\mathcal{C}_G} \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \widetilde{p}_G(z_0, z_1, \dots, z_k) = &\ \det (-\Delta_{\mathbf{a}_G}) \det (z_0 \operatorname{\mathrm{Id}}_k + \sqrt{\mathcal{C}_G} \Delta_{\mathbf{z}} \sqrt{\mathcal{C}_G})\\ = &\ \det (-\Delta_{\mathbf{a}_G}) \det \left( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^k z_j \sqrt{\mathcal{C}_G} E_{jj} \sqrt{\mathcal{C}_G} \right). \end{aligned} \end{align} $$
Now the coefficient of each
![]() $z_j, \ j \geqslant 0$
inside the above determinant is a positive semidefinite matrix. It follows by [Reference Borcea and Brändén5, Proposition 2.4] (see the text around (3.5)) that
$z_j, \ j \geqslant 0$
inside the above determinant is a positive semidefinite matrix. It follows by [Reference Borcea and Brändén5, Proposition 2.4] (see the text around (3.5)) that
![]() $\widetilde {p}_G(\cdot )$
is real-stable, proving (1).
$\widetilde {p}_G(\cdot )$
is real-stable, proving (1).
This proves the equivalence. The final assertion is immediate from (4) via Lemma 3.2(4).
Remark 4.6 The assertions in Theorem E and Corollary 1.7 are thus further equivalent to
![]() $\mathcal {C}_G$
being a correlation matrix. Moreover, Theorem C (except the final equivalent assertion (5)) and Corollary 1.7 hold more generally: for arbitrary finite metric spaces. We leave the details to the interested reader.
$\mathcal {C}_G$
being a correlation matrix. Moreover, Theorem C (except the final equivalent assertion (5)) and Corollary 1.7 hold more generally: for arbitrary finite metric spaces. We leave the details to the interested reader.
Remark 4.7 The proof of Theorem E also reveals that inspecting the coefficients in the polynomial
![]() $p_G(\cdot )$
or
$p_G(\cdot )$
or
![]() $\widetilde {p}_G(\cdot )$
helps identify the principal minors of
$\widetilde {p}_G(\cdot )$
helps identify the principal minors of
![]() $\mathcal {D}_G$
(or
$\mathcal {D}_G$
(or
![]() $\mathcal {C}_G$
) that are negative, zero, or positive.
$\mathcal {C}_G$
) that are negative, zero, or positive.
4.3 Symmetries; monomials with zero coefficients
The results in this paper are developed with the goal of being used in proving the main theorems in the opening section. The only exceptions are one of the appendices (below), and this present subsection, in which our goal is to provide further intuition for blowup-polynomials of graph metric spaces G. To do so, we study a concrete family of graph metric spaces
![]() $K^{(l)}_k$
– for which we compute the blowup-polynomials and reveal connections to symmetric functions. In addition, these computations lead to the study of certain monomials whose coefficients in
$K^{(l)}_k$
– for which we compute the blowup-polynomials and reveal connections to symmetric functions. In addition, these computations lead to the study of certain monomials whose coefficients in
![]() $p_G$
vanish – this provides intuition for proving Theorem F.
$p_G$
vanish – this provides intuition for proving Theorem F.
We begin from the proof of Theorem D, which shows that the blowup-polynomial of G is a partially symmetric polynomial, in the sense of being invariant under the subgroup
![]() $\mathrm {Isom}(G)$
(of isometries of G) of
$\mathrm {Isom}(G)$
(of isometries of G) of
![]() $S_{V(G)}$
(the permutations of
$S_{V(G)}$
(the permutations of
![]() $V(G)$
). For instance,
$V(G)$
). For instance,
![]() $p_G(\mathbf {n})$
is symmetric in
$p_G(\mathbf {n})$
is symmetric in
![]() $\mathbf {n}$
for G a complete graph; whereas
$\mathbf {n}$
for G a complete graph; whereas
![]() $p_G$
possesses “cyclic” symmetries for G a cycle; and so on.
$p_G$
possesses “cyclic” symmetries for G a cycle; and so on.
In addition to these global symmetries (i.e., isometries) of G, there also exist “local symmetries.” For example, suppose
![]() $G = P_k$
is a path graph, with vertex
$G = P_k$
is a path graph, with vertex
![]() $x_i$
adjacent to
$x_i$
adjacent to
![]() $x_{i \pm 1}$
for
$x_{i \pm 1}$
for
![]() $1 < i < k$
. For any
$1 < i < k$
. For any
![]() $1 < i \leqslant j < k$
, the coefficient of the monomials
$1 < i \leqslant j < k$
, the coefficient of the monomials
are equal, by Proposition 2.6(3). A similar result holds more generally for banded graphs with bandwidth
![]() $d \geqslant 1$
, in which a vertex
$d \geqslant 1$
, in which a vertex
![]() $x_i$
is adjacent to
$x_i$
is adjacent to
![]() $x_j$
if and only if
$x_j$
if and only if
![]() $0 < |i-j| < d$
and
$0 < |i-j| < d$
and
![]() $1 \leqslant i,j \leqslant k$
.
$1 \leqslant i,j \leqslant k$
.
Example 4.8 We now use this principle of symmetry to compute the blowup-polynomial for a two-parameter family of graph metric spaces
(This will shortly be followed by another application: a sufficient condition for when certain monomials do not occur in
![]() $p_G(\mathbf {n})$
.) Here,
$p_G(\mathbf {n})$
.) Here,
![]() $K_k^{(l)}$
denotes the complete graph
$K_k^{(l)}$
denotes the complete graph
![]() $K_k$
from which the edges
$K_k$
from which the edges
![]() $(1,2), \dots , (1,l+1)$
have been removed. This leads to three types of vertices:
$(1,2), \dots , (1,l+1)$
have been removed. This leads to three types of vertices:
and correspondingly, the isometry group
![]() $\mathrm {Isom}(K_k^{(l)}) \cong S_l \times S_{k-l-1}$
. Notice that the vertices
$\mathrm {Isom}(K_k^{(l)}) \cong S_l \times S_{k-l-1}$
. Notice that the vertices
![]() $2, \dots , k$
form a complete induced subgraph of
$2, \dots , k$
form a complete induced subgraph of
![]() $K_k^{(l)}$
.
$K_k^{(l)}$
.
The graphs
![]() $K_k^{(l)}$
are all chordal (i.e., do not contain an induced m-cycle for any
$K_k^{(l)}$
are all chordal (i.e., do not contain an induced m-cycle for any
![]() $m \geqslant 4$
), and include as special cases: complete graphs (for
$m \geqslant 4$
), and include as special cases: complete graphs (for
![]() $l=0$
) as well as complete graphs with one pendant vertex (for
$l=0$
) as well as complete graphs with one pendant vertex (for
![]() $l=k-2$
). The “almost complete graph”
$l=k-2$
). The “almost complete graph”
![]() $K_k^{(1)}$
(missing exactly one edge) is another special case, important from the viewpoint of matrix positivity: it was crucially used in [Reference Guillot, Khare and Rajaratnam22] to compute a graph invariant which arose out of analysis and positivity, for every chordal graph. This was termed the critical exponent of a graph in [Reference Guillot, Khare and Rajaratnam22], and seems to be a novel graph invariant.
$K_k^{(1)}$
(missing exactly one edge) is another special case, important from the viewpoint of matrix positivity: it was crucially used in [Reference Guillot, Khare and Rajaratnam22] to compute a graph invariant which arose out of analysis and positivity, for every chordal graph. This was termed the critical exponent of a graph in [Reference Guillot, Khare and Rajaratnam22], and seems to be a novel graph invariant.
By the remarks above, the blowup-polynomial in the
![]() $n_{v_i}$
(which we will replace by
$n_{v_i}$
(which we will replace by
![]() $n_i,\ 1 \leqslant i \leqslant k$
for convenience) will be symmetric separately in
$n_i,\ 1 \leqslant i \leqslant k$
for convenience) will be symmetric separately in
![]() $\{ n_2, \dots , n_{l+1} \}$
and in
$\{ n_2, \dots , n_{l+1} \}$
and in
![]() $\{ n_{l+2}, \dots , n_k \}$
. In particular, since the polynomial is multi-affine in the
$\{ n_{l+2}, \dots , n_k \}$
. In particular, since the polynomial is multi-affine in the
![]() $n_i$
, the only terms that appear will be of the form
$n_i$
, the only terms that appear will be of the form
where
![]() $\varepsilon _1 = 0$
or
$\varepsilon _1 = 0$
or
![]() $1$
, and
$1$
, and
![]() $e_r(\cdot )$
is the elementary symmetric (homogeneous, multi-affine, and, in fact, real-stable) polynomial for every
$e_r(\cdot )$
is the elementary symmetric (homogeneous, multi-affine, and, in fact, real-stable) polynomial for every
![]() $r \geqslant 0$
(with
$r \geqslant 0$
(with
![]() $e_0(\cdot ) := 1$
).
$e_0(\cdot ) := 1$
).
With this preparation, we can state and prove the following result for the graphs
![]() $K_k^{(l)}$
.
$K_k^{(l)}$
.
Proposition 4.9 Fix nonnegative integers
![]() $k,l$
such that
$k,l$
such that
![]() $0 \leqslant l \leqslant k-2$
. With
$0 \leqslant l \leqslant k-2$
. With
![]() $K_k^{(l)}$
as defined above, and denoting
$K_k^{(l)}$
as defined above, and denoting
![]() $n_{v_i}$
by
$n_{v_i}$
by
![]() $n_i$
for convenience (with
$n_i$
for convenience (with
![]() $1 \leqslant i \leqslant k$
), we have
$1 \leqslant i \leqslant k$
), we have
 $$ \begin{align*} p_{K_k^{(l)}}(\mathbf{n}) = &\ \sum_{r=0}^l \sum_{s=0}^{k-l-1} \left[ (-2)^{k-r-s} (1 + r + s) \right] e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k)\\ &\ + n_1 \sum_{r=0}^l \sum_{s=0}^{k-l-1} \left[ (-2)^{k-r-s-1} (1 -r) (s+2) \right] e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k). \end{align*} $$
$$ \begin{align*} p_{K_k^{(l)}}(\mathbf{n}) = &\ \sum_{r=0}^l \sum_{s=0}^{k-l-1} \left[ (-2)^{k-r-s} (1 + r + s) \right] e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k)\\ &\ + n_1 \sum_{r=0}^l \sum_{s=0}^{k-l-1} \left[ (-2)^{k-r-s-1} (1 -r) (s+2) \right] e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k). \end{align*} $$
Notice that setting
![]() $n_1=0$
, we obtain the blowup-polynomial of the complete graph
$n_1=0$
, we obtain the blowup-polynomial of the complete graph
![]() $K_{k-1}$
, in the variables
$K_{k-1}$
, in the variables
![]() $n_2, \dots , n_k$
. This clearly equals (via
$n_2, \dots , n_k$
. This clearly equals (via
![]() $r+s \leadsto s$
):
$r+s \leadsto s$
):
 $$\begin{align*}\sum_{s=0}^{k-1} (-2)^{k-s} (1+s) e_s(n_2, \dots, n_k), \end{align*}$$
$$\begin{align*}\sum_{s=0}^{k-1} (-2)^{k-s} (1+s) e_s(n_2, \dots, n_k), \end{align*}$$
and it also equals the expression in (2.4) (modulo relabeling of the variables) since the underlying metric spaces are isometric. A similar computation holds upon working with
![]() $l=0$
.
$l=0$
.
Proof of Proposition 4.9
We begin by exploiting the symmetries in
![]() $K_k^{(l)}$
, which imply that given a subset
$K_k^{(l)}$
, which imply that given a subset
![]() $I \subseteq \{ 1, \dots , k \}$
, the coefficient of
$I \subseteq \{ 1, \dots , k \}$
, the coefficient of
![]() $\prod _{i \in I} n_i$
depends only on the three integers
$\prod _{i \in I} n_i$
depends only on the three integers
Now using (4.7), it follows that the blowup-polynomial indeed has the desired form:
 $$ \begin{align*} p_{K_k^{(l)}}(\mathbf{n}) = &\ \sum_{r=0}^l \sum_{s=0}^{k-l-1} a_{0,r,s} e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k)\\ &\ + n_1 \sum_{r=0}^l \sum_{s=0}^{k-l-1} a_{1,r,s} e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k), \end{align*} $$
$$ \begin{align*} p_{K_k^{(l)}}(\mathbf{n}) = &\ \sum_{r=0}^l \sum_{s=0}^{k-l-1} a_{0,r,s} e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k)\\ &\ + n_1 \sum_{r=0}^l \sum_{s=0}^{k-l-1} a_{1,r,s} e_r(n_2, \dots, n_{l+1}) e_s(n_{l+2}, \dots, n_k), \end{align*} $$
for some coefficients
![]() $a_{\varepsilon _1,r,s} \in \mathbb R$
. It remains to compute these coefficients, and we begin with the coefficients
$a_{\varepsilon _1,r,s} \in \mathbb R$
. It remains to compute these coefficients, and we begin with the coefficients
![]() $a_{0,r,s}$
. By a computation akin to the proof of Proposition 2.6(1), these are obtained by specializing
$a_{0,r,s}$
. By a computation akin to the proof of Proposition 2.6(1), these are obtained by specializing
![]() $n_1 = 0$
, which leads to a power of
$n_1 = 0$
, which leads to a power of
![]() $(-2)$
times a principal minor of
$(-2)$
times a principal minor of
![]() $\mathcal {D}_{K_k^{(l)}}$
not involving its first row or column. But this is the determinant of a principal submatrix of
$\mathcal {D}_{K_k^{(l)}}$
not involving its first row or column. But this is the determinant of a principal submatrix of
of size
![]() $(r+s) \times (r+s)$
, and so a direct computation implies the desired formula:
$(r+s) \times (r+s)$
, and so a direct computation implies the desired formula:
It remains to compute
![]() $a_{1,r,s}$
, which equals
$a_{1,r,s}$
, which equals
![]() $(-2)^{k-r-s-1}$
times the determinant of the block matrix
$(-2)^{k-r-s-1}$
times the determinant of the block matrix
 $$\begin{align*}\mathcal{D}_{r,s} := \begin{pmatrix} 2 & 2 \mathbf{1}_{r \times 1}^T & \mathbf{1}_{s \times 1}^T \\ 2 \mathbf{1}_{r \times 1} & \operatorname{\mathrm{Id}}_r + \mathbf{1}_{r \times r} & \mathbf{1}_{r \times s} \\ \mathbf{1}_{s \times 1} & \mathbf{1}_{s \times r} & \operatorname{\mathrm{Id}}_s + \mathbf{1}_{s \times s} \end{pmatrix} = \begin{pmatrix} 2 & v^T \\ v & C_{r,s} \end{pmatrix} \in \mathbb R^{(1+r+s) \times (1+r+s)}, \end{align*}$$
$$\begin{align*}\mathcal{D}_{r,s} := \begin{pmatrix} 2 & 2 \mathbf{1}_{r \times 1}^T & \mathbf{1}_{s \times 1}^T \\ 2 \mathbf{1}_{r \times 1} & \operatorname{\mathrm{Id}}_r + \mathbf{1}_{r \times r} & \mathbf{1}_{r \times s} \\ \mathbf{1}_{s \times 1} & \mathbf{1}_{s \times r} & \operatorname{\mathrm{Id}}_s + \mathbf{1}_{s \times s} \end{pmatrix} = \begin{pmatrix} 2 & v^T \\ v & C_{r,s} \end{pmatrix} \in \mathbb R^{(1+r+s) \times (1+r+s)}, \end{align*}$$
where
![]() $v := (2 \mathbf {1}_{r \times 1}^T \quad \mathbf {1}_{s \times 1}^T)^T \in \mathbb R^{r+s}$
, and
$v := (2 \mathbf {1}_{r \times 1}^T \quad \mathbf {1}_{s \times 1}^T)^T \in \mathbb R^{r+s}$
, and
![]() $C_{r,s} = \operatorname {\mathrm {Id}}_{r+s} + \mathbf {1}_{(r+s) \times (r+s)}$
denotes the principal submatrix of
$C_{r,s} = \operatorname {\mathrm {Id}}_{r+s} + \mathbf {1}_{(r+s) \times (r+s)}$
denotes the principal submatrix of
![]() $\mathcal {D}_{r,s}$
obtained by removing its first row and column. Now
$\mathcal {D}_{r,s}$
obtained by removing its first row and column. Now
![]() $C_{r,s}^{-1} = \operatorname {\mathrm {Id}} - (1+r+s)^{-1} \mathbf {1}_{(r+s) \times (r+s)}$
, so using Schur complements,
$C_{r,s}^{-1} = \operatorname {\mathrm {Id}} - (1+r+s)^{-1} \mathbf {1}_{(r+s) \times (r+s)}$
, so using Schur complements,
 $$ \begin{align*} &\ \det \mathcal{D}_{r,s}\\ = &\ \det C_{r,s} \cdot \det \left( 2 - v^T C_{r,s}^{-1} v \right)\\ = &\ 2(1+r+s) - \begin{pmatrix} 2 \mathbf{1}_{r \times 1} \\ \mathbf{1}_{s \times 1} \end{pmatrix}^T \begin{pmatrix} (1+r+s) \operatorname{\mathrm{Id}}_r - \mathbf{1}_{r \times r} & - \mathbf{1}_{r \times s} \\ - \mathbf{1}_{s \times r} & (1+r+s) \operatorname{\mathrm{Id}}_s - \mathbf{1}_{s \times s} \end{pmatrix} \begin{pmatrix} 2 \mathbf{1}_{r \times 1} \\ \mathbf{1}_{s \times 1} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} &\ \det \mathcal{D}_{r,s}\\ = &\ \det C_{r,s} \cdot \det \left( 2 - v^T C_{r,s}^{-1} v \right)\\ = &\ 2(1+r+s) - \begin{pmatrix} 2 \mathbf{1}_{r \times 1} \\ \mathbf{1}_{s \times 1} \end{pmatrix}^T \begin{pmatrix} (1+r+s) \operatorname{\mathrm{Id}}_r - \mathbf{1}_{r \times r} & - \mathbf{1}_{r \times s} \\ - \mathbf{1}_{s \times r} & (1+r+s) \operatorname{\mathrm{Id}}_s - \mathbf{1}_{s \times s} \end{pmatrix} \begin{pmatrix} 2 \mathbf{1}_{r \times 1} \\ \mathbf{1}_{s \times 1} \end{pmatrix}, \end{align*} $$
and a straightforward (if careful) calculation reveals this quantity to equal
![]() $(1-r)(s+2)$
.
$(1-r)(s+2)$
.
Example 4.10 As an additional example, we compute the blowup-polynomial for several other graphs at once. The path graph
![]() $P_3$
is a special case of the star graphs
$P_3$
is a special case of the star graphs
![]() $K_{1,k-1}$
, and in turn, these as well as the cycle graph
$K_{1,k-1}$
, and in turn, these as well as the cycle graph
![]() $C_4$
are special cases of complete bipartite graphs
$C_4$
are special cases of complete bipartite graphs
![]() $K_{r,s}$
. As
$K_{r,s}$
. As
![]() $K_{r,s} = K_2[(r,s)]$
is a blowup, we can use Lemma 3.2(2) and equation (2.4) for
$K_{r,s} = K_2[(r,s)]$
is a blowup, we can use Lemma 3.2(2) and equation (2.4) for
![]() $k=2$
, to obtain
$k=2$
, to obtain
 $$ \begin{align} \begin{aligned} &\ p_{K_{r,s}}(n_1, \dots, n_r; m_1, \dots, m_s)\\ = &\ (-2)^{r+s-2} \left( 3 \sum_{i=1}^r n_i \cdot \sum_{j=1}^s m_j - 4 \sum_{i=1}^r n_i - 4 \sum_{j=1}^s m_j + 4 \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\ p_{K_{r,s}}(n_1, \dots, n_r; m_1, \dots, m_s)\\ = &\ (-2)^{r+s-2} \left( 3 \sum_{i=1}^r n_i \cdot \sum_{j=1}^s m_j - 4 \sum_{i=1}^r n_i - 4 \sum_{j=1}^s m_j + 4 \right). \end{aligned} \end{align} $$
As one observes by visual inspection, the coefficient in Proposition 4.9 of
![]() $n_1 n_2$
times any monomial in the (“type-
$n_1 n_2$
times any monomial in the (“type-
![]() $3$
”) node-variables
$3$
”) node-variables
![]() $n_{l+2}, \dots , n_k$
, vanishes. Similarly, in (4.8), there are many coefficients that vanish – in fact, every coefficient of total degree at least
$n_{l+2}, \dots , n_k$
, vanishes. Similarly, in (4.8), there are many coefficients that vanish – in fact, every coefficient of total degree at least
![]() $3$
. These facts can be explained more simply, by the following result about zero terms in the blowup-polynomial.
$3$
. These facts can be explained more simply, by the following result about zero terms in the blowup-polynomial.
Proposition 4.11 Suppose
![]() $G,H$
are graph metric spaces, and
$G,H$
are graph metric spaces, and
![]() $\mathbf {n} \in \mathbb {Z}_{>0}^{V(G)}$
a tuple of positive integers, such that
$\mathbf {n} \in \mathbb {Z}_{>0}^{V(G)}$
a tuple of positive integers, such that
![]() $G[\mathbf {n}]$
isometrically embeds as a subgraph metric space inside H. Also suppose
$G[\mathbf {n}]$
isometrically embeds as a subgraph metric space inside H. Also suppose
![]() $n_v \geqslant 2$
for some
$n_v \geqslant 2$
for some
![]() $v \in V(G)$
, and
$v \in V(G)$
, and
![]() $v_1, v_2 \in G[\mathbf {n}]$
are copies of v. Then for every subset of vertices
$v_1, v_2 \in G[\mathbf {n}]$
are copies of v. Then for every subset of vertices
![]() $\{ v_1, v_2 \} \subseteq S \subseteq V(G[\mathbf {n}])$
, the coefficient of
$\{ v_1, v_2 \} \subseteq S \subseteq V(G[\mathbf {n}])$
, the coefficient of
![]() $\prod _{s \in S} n_s$
in
$\prod _{s \in S} n_s$
in
![]() $p_H(\cdot )$
is zero.
$p_H(\cdot )$
is zero.
For example, for H the path graph
![]() $P_4$
with vertices
$P_4$
with vertices
![]() $a - b - c - d$
, the coefficients of
$a - b - c - d$
, the coefficients of
![]() $n_a n_c, n_a n_b n_c$
, and
$n_a n_c, n_a n_b n_c$
, and
![]() $n_b n_d, n_b n_c n_d$
in
$n_b n_d, n_b n_c n_d$
in
![]() $p_H(\mathbf {n})$
are all zero, since the path subgraphs
$p_H(\mathbf {n})$
are all zero, since the path subgraphs
![]() $a-b-c$
and
$a-b-c$
and
![]() $b-c-d$
are both isomorphic to the graph blowup
$b-c-d$
are both isomorphic to the graph blowup
![]() $K_2[(1,2)]$
.
$K_2[(1,2)]$
.
This result also extends to arbitrary finite metric spaces.
Proof By Proposition 2.6, the coefficient of
![]() $\mathbf {n}^S$
(whose meaning is clear from context) in
$\mathbf {n}^S$
(whose meaning is clear from context) in
![]() $p_H(\{ n_w : w \in V(H) \})$
is a scalar times
$p_H(\{ n_w : w \in V(H) \})$
is a scalar times
![]() $\det (\mathcal {D}_H)_{S \times S}$
. Since
$\det (\mathcal {D}_H)_{S \times S}$
. Since
![]() $G[\mathbf {n}]$
is a metric subspace of H, it suffices to show that
$G[\mathbf {n}]$
is a metric subspace of H, it suffices to show that
![]() $\det (\mathcal {D}_{G[\mathbf {n}]})_{S \times S} = 0$
, since this matrix agrees with
$\det (\mathcal {D}_{G[\mathbf {n}]})_{S \times S} = 0$
, since this matrix agrees with
![]() $(\mathcal {D}_H)_{S \times S}$
. But since
$(\mathcal {D}_H)_{S \times S}$
. But since
![]() $v_1, v_2 \in V(G[\mathbf {n}])$
are copies of
$v_1, v_2 \in V(G[\mathbf {n}])$
are copies of
![]() $v \in V(G)$
, the matrix
$v \in V(G)$
, the matrix
![]() $\mathcal {D}_{G[\mathbf {n}]}$
has two identical rows by Lemma 3.2(3). It follows that
$\mathcal {D}_{G[\mathbf {n}]}$
has two identical rows by Lemma 3.2(3). It follows that
![]() $\det (\mathcal {D}_{G[\mathbf {n}]})_{S \times S} = 0$
, and the proof is complete.
$\det (\mathcal {D}_{G[\mathbf {n}]})_{S \times S} = 0$
, and the proof is complete.
4.4 The tree-blowup delta-matroid
We conclude this section by proving Theorem F about the delta-matroid
![]() $\mathcal {M}'(T)$
for every tree, which seems to be unstudied in the literature. We then explore (a) if this delta-matroid equals the blowup delta-matroid
$\mathcal {M}'(T)$
for every tree, which seems to be unstudied in the literature. We then explore (a) if this delta-matroid equals the blowup delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_T}$
; and (b) if this construction can be extended to arbitrary graphs.
$\mathcal {M}_{\mathcal {D}_T}$
; and (b) if this construction can be extended to arbitrary graphs.
To motivate the construction of
![]() $\mathcal {M}'(T)$
, which we term the tree-blowup delta-matroid, we begin by applying Proposition 4.11 with
$\mathcal {M}'(T)$
, which we term the tree-blowup delta-matroid, we begin by applying Proposition 4.11 with
![]() $G = P_2 = K_2$
and
$G = P_2 = K_2$
and
![]() $G[\mathbf {n}] = P_3$
. An immediate consequence is the following.
$G[\mathbf {n}] = P_3$
. An immediate consequence is the following.
Corollary 4.12 If
![]() $a,b,c \in V(H)$
are such that b is adjacent to
$a,b,c \in V(H)$
are such that b is adjacent to
![]() $a,c$
but
$a,c$
but
![]() $a,c$
are not adjacent, then
$a,c$
are not adjacent, then
![]() $n_a n_c$
and
$n_a n_c$
and
![]() $n_a n_b n_c$
have zero coefficients in
$n_a n_b n_c$
have zero coefficients in
![]() $p_H(\mathbf {n})$
.
$p_H(\mathbf {n})$
.
In light of this, we take a closer look at
![]() $\mathcal {D}_X$
for
$\mathcal {D}_X$
for
![]() $X = P_k$
a path graph. Given an integer
$X = P_k$
a path graph. Given an integer
![]() $k \geqslant 1$
, the path graph
$k \geqslant 1$
, the path graph
![]() $P_k$
has vertex set
$P_k$
has vertex set
![]() $\{ 1, \dots , k \}$
, with vertices
$\{ 1, \dots , k \}$
, with vertices
![]() $i,j$
adjacent if and only if
$i,j$
adjacent if and only if
![]() $|i-j|=1$
.
$|i-j|=1$
.
Recall from [Reference Bouchet10] that the set system
![]() $\mathcal {M}_{\mathcal {D}_X}$
(defined a few lines before Corollary 1.10) is a linear delta-matroid for every finite metric space – in particular, for every graph metric space, such as
$\mathcal {M}_{\mathcal {D}_X}$
(defined a few lines before Corollary 1.10) is a linear delta-matroid for every finite metric space – in particular, for every graph metric space, such as
![]() $P_k$
. It turns out (by inspection) that Corollary 4.12 describes all of the principal minors of
$P_k$
. It turns out (by inspection) that Corollary 4.12 describes all of the principal minors of
![]() $\mathcal {D}_{P_k}$
which vanish – i.e., the complement of the delta-matroid
$\mathcal {D}_{P_k}$
which vanish – i.e., the complement of the delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_{P_k}}$
in the power-set of
$\mathcal {M}_{\mathcal {D}_{P_k}}$
in the power-set of
![]() $\{ 1, \dots , k \}$
– for small values of k. While this may or may not hold for general k, the same construction still defines a delta-matroid, and one that is hitherto unexplored as well.
$\{ 1, \dots , k \}$
– for small values of k. While this may or may not hold for general k, the same construction still defines a delta-matroid, and one that is hitherto unexplored as well.
Proposition 4.13 Given an integer
![]() $k \geqslant 3$
, define the set system
$k \geqslant 3$
, define the set system
Then
![]() $\mathcal {B}(P_k)$
is a delta-matroid.
$\mathcal {B}(P_k)$
is a delta-matroid.
We now strengthen this result to the case of arbitrary trees (for completeness, recall that a tree is a finite connected graph without a cycle
![]() $C_n$
for
$C_n$
for
![]() $n \geqslant 3$
). We begin with a few basic observations on trees, which help in the next proofs. Every pair of vertices in T is connected by a unique path in T. Moreover, every connected sub-graph of T is a tree, and every (nonempty) set I of vertices of T is contained in a unique smallest sub-tree
$n \geqslant 3$
). We begin with a few basic observations on trees, which help in the next proofs. Every pair of vertices in T is connected by a unique path in T. Moreover, every connected sub-graph of T is a tree, and every (nonempty) set I of vertices of T is contained in a unique smallest sub-tree
![]() $T(I)$
, called its Steiner tree. We also recall that a leaf, or a pendant vertex, is any vertex with degree one, i.e., adjacent to exactly one vertex.
$T(I)$
, called its Steiner tree. We also recall that a leaf, or a pendant vertex, is any vertex with degree one, i.e., adjacent to exactly one vertex.
Definition 4.14 Let
![]() $T = (V,E)$
be a finite connected, unweighted, tree with the (unique) edge-distance metric. We say that a subset of vertices
$T = (V,E)$
be a finite connected, unweighted, tree with the (unique) edge-distance metric. We say that a subset of vertices
![]() $I \subseteq V$
is infeasible if there exist vertices
$I \subseteq V$
is infeasible if there exist vertices
![]() $v_1 \neq v_2$
in I, such that the Steiner tree
$v_1 \neq v_2$
in I, such that the Steiner tree
![]() $T(I)$
has
$T(I)$
has
![]() $v_1, v_2$
as leaves, both adjacent to the same (unique) vertex.
$v_1, v_2$
as leaves, both adjacent to the same (unique) vertex.
With this terminology at hand, Theorem F asserts that the feasible subsets of V form a delta-matroid. Note, if
![]() $T = P_k$
is a path graph, then
$T = P_k$
is a path graph, then
![]() $\mathcal {M}'(T)$
equals the delta-matroid
$\mathcal {M}'(T)$
equals the delta-matroid
![]() $\mathcal {B}(P_k)$
above.
$\mathcal {B}(P_k)$
above.
The proof of Theorem F requires a preliminary result, which characterizes when a graph G is a nontrivial blowup, and which then connects this to the distance spectrum of G.
Proposition 4.15 Suppose
![]() $G = (V,E)$
is a graph metric space. Then each of the following statements implies the next:
$G = (V,E)$
is a graph metric space. Then each of the following statements implies the next:
-
(1) G is a nontrivial blowup, i.e., a blowup of a graph metric space H with
 $|V(H)| < |V(G)|$
.
$|V(H)| < |V(G)|$
. -
(2) G contains two vertices
 $v,w$
with the same set of neighbors. (In particular,
$v,w$
with the same set of neighbors. (In particular,
 $d_G(v,w) = 2$
.)
$d_G(v,w) = 2$
.) -
(3)
 $-2$
is an eigenvalue of the distance matrix
$-2$
is an eigenvalue of the distance matrix
 $D_G$
.
$D_G$
. -
(4) The blowup-polynomial has total degree strictly less than
 $|V|$
.
$|V|$
.
In fact
![]() $(1) \Longleftrightarrow (2) \implies (3) \Longleftrightarrow (4)$
, but all four assertions are not equivalent.
$(1) \Longleftrightarrow (2) \implies (3) \Longleftrightarrow (4)$
, but all four assertions are not equivalent.
Proof We show the implications
![]() $(2) {\kern-2pt}\implies{\kern-2pt} (1) {\kern-2pt}\implies{\kern-2pt} (2) {\kern-2pt}\implies{\kern-2pt} (3) {\kern-2pt}\implies{\kern-2pt} (4) {\kern-2pt}\implies{\kern-2pt} (3)$
. If (2) holds, and H is the induced subgraph of G on
$(2) {\kern-2pt}\implies{\kern-2pt} (1) {\kern-2pt}\implies{\kern-2pt} (2) {\kern-2pt}\implies{\kern-2pt} (3) {\kern-2pt}\implies{\kern-2pt} (4) {\kern-2pt}\implies{\kern-2pt} (3)$
. If (2) holds, and H is the induced subgraph of G on
![]() $V(G) \setminus \{ w \}$
, then it is easy to see that
$V(G) \setminus \{ w \}$
, then it is easy to see that
![]() $G = H[\mathbf {n}]$
, where
$G = H[\mathbf {n}]$
, where
![]() $n_{v'} = 1$
for
$n_{v'} = 1$
for
![]() $v' \neq v$
,
$v' \neq v$
,
![]() $n_v = 2$
, and w is the other copy of v. This shows (1); conversely, if (1) holds then there exist two vertices
$n_v = 2$
, and w is the other copy of v. This shows (1); conversely, if (1) holds then there exist two vertices
![]() $v \neq w \in V(G)$
that are copies of one another. But then
$v \neq w \in V(G)$
that are copies of one another. But then
![]() $v,w$
share the same neighbors, so
$v,w$
share the same neighbors, so
![]() $0 < d_G(v,w) \leqslant 2$
. If
$0 < d_G(v,w) \leqslant 2$
. If
![]() $d_G(v,w) = 1$
then
$d_G(v,w) = 1$
then
![]() $v,w$
are neighbors of each other but not of themselves, which contradicts the preceding sentence. This shows that
$v,w$
are neighbors of each other but not of themselves, which contradicts the preceding sentence. This shows that
![]() $(1) \implies (2)$
.
$(1) \implies (2)$
.
Now suppose (2) holds, and hence so does (1). By Lemma 3.2(3),
![]() $\mathcal {D}_G = D_G + 2 \operatorname {\mathrm {Id}}_V$
has two identical rows, so is singular. This shows (3). (This implication is also mentioned in [Reference Aouchiche and Hansen3, Theorem 2.34].) Finally, (3) holds if and only if
$\mathcal {D}_G = D_G + 2 \operatorname {\mathrm {Id}}_V$
has two identical rows, so is singular. This shows (3). (This implication is also mentioned in [Reference Aouchiche and Hansen3, Theorem 2.34].) Finally, (3) holds if and only if
![]() $\mathcal {D}_G$
is singular as above. By Proposition 2.6(1), this is if and only if the coefficient of the unique top-degree monomial
$\mathcal {D}_G$
is singular as above. By Proposition 2.6(1), this is if and only if the coefficient of the unique top-degree monomial
![]() $\prod _{v \in V(G)} n_v$
in
$\prod _{v \in V(G)} n_v$
in
![]() $p_G(\mathbf {n})$
vanishes, which shows that
$p_G(\mathbf {n})$
vanishes, which shows that
![]() $(3) \Longleftrightarrow (4)$
.
$(3) \Longleftrightarrow (4)$
.
To show (3) does not imply (2), consider the path graph
![]() $P_9$
(with edges
$P_9$
(with edges
![]() $\{ i, i+1 \}$
for
$\{ i, i+1 \}$
for
![]() $0 < i < 9$
). It is easy to check that
$0 < i < 9$
). It is easy to check that
![]() $\det \mathcal {D}_{P_9} = 0$
, so that (3) holds; and also that (2) does not hold.
$\det \mathcal {D}_{P_9} = 0$
, so that (3) holds; and also that (2) does not hold.
Specializing Proposition 4.15 to trees, we obtain the following.
Corollary 4.16 A tree T is a blowup of a graph G if and only if (a) G is a sub-tree of T, and (b) the only vertices of G which are “copied” are a set of leaves of G.
Proof One way is easily shown, and for the “only if” part, the key observation is that if a vertex adjacent to at least two others is copied, then this creates a four-cycle in the blowup. (An equally short proof is that this result is a special case of Proposition 4.15
![]() $(1) \Longleftrightarrow (2)$
.)
$(1) \Longleftrightarrow (2)$
.)
Proof of Theorem F
If T has two nodes (so
![]() $T = K_2$
), then
$T = K_2$
), then
![]() $\mathcal {M}'(T) = 2^V$
, which is a delta-matroid. Thus, suppose henceforth that
$\mathcal {M}'(T) = 2^V$
, which is a delta-matroid. Thus, suppose henceforth that
![]() $|V| \geqslant 3$
. Since
$|V| \geqslant 3$
. Since
![]() $\mathcal {M}'(T)$
contains all singleton subsets of V, the only nontrivial step is to verify the symmetric exchange axiom. Suppose
$\mathcal {M}'(T)$
contains all singleton subsets of V, the only nontrivial step is to verify the symmetric exchange axiom. Suppose
![]() $A \neq B \in \mathcal {M}'(T)$
and
$A \neq B \in \mathcal {M}'(T)$
and
![]() $x \in A \Delta B$
. We divide the analysis into two cases; in what follows, given a subset
$x \in A \Delta B$
. We divide the analysis into two cases; in what follows, given a subset
![]() $I \subseteq V$
, we will denote by
$I \subseteq V$
, we will denote by
![]() $T_I$
the subgraph of T induced on the vertex set I, and by
$T_I$
the subgraph of T induced on the vertex set I, and by
![]() $T(I)$
the Steiner tree of I (as above).
$T(I)$
the Steiner tree of I (as above).
-
(1)
 $x \in B \setminus A$
.
$x \in B \setminus A$
.If
 $A \sqcup \{ x \} \in \mathcal {M}'(T)$
, then we simply choose
$A \sqcup \{ x \} \in \mathcal {M}'(T)$
, then we simply choose
 $y=x$
. Otherwise,
$y=x$
. Otherwise,
 $A \sqcup \{ x \}$
is infeasible whereas A is not (i.e., A is feasible). In particular,
$A \sqcup \{ x \}$
is infeasible whereas A is not (i.e., A is feasible). In particular,
 $x \not \in T(A)$
since otherwise
$x \not \in T(A)$
since otherwise
 $T(A \sqcup \{ x \}) = T(A)$
. Now using Corollary 4.16, this yields a unique
$T(A \sqcup \{ x \}) = T(A)$
. Now using Corollary 4.16, this yields a unique
 $v \in A$
such that
$v \in A$
such that
 $v,x$
are leaves in the sub-tree
$v,x$
are leaves in the sub-tree
 $T(A \sqcup \{ x \})$
. Also denote their (unique) common adjacent vertex by
$T(A \sqcup \{ x \})$
. Also denote their (unique) common adjacent vertex by
 $a \in T(A \sqcup \{ x \})$
.
$a \in T(A \sqcup \{ x \})$
.We now proceed. If
 $v \not \in B$
, then compute using
$v \not \in B$
, then compute using
 $y = v$
: Since
$y = v$
: Since $$\begin{align*}A \Delta \{ x, y \} = (A \setminus \{ v \}) \sqcup \{ x \}. \end{align*}$$
$$\begin{align*}A \Delta \{ x, y \} = (A \setminus \{ v \}) \sqcup \{ x \}. \end{align*}$$
 $v,x$
were copies, removing v and adding x produces an isomorphic graph:
$v,x$
were copies, removing v and adding x produces an isomorphic graph:
 $T_{(A \setminus \{ v \}) \sqcup \{ x \}} \cong T_A$
, which is indeed in
$T_{(A \setminus \{ v \}) \sqcup \{ x \}} \cong T_A$
, which is indeed in
 $\mathcal {M}'(T)$
, as desired.
$\mathcal {M}'(T)$
, as desired.
Otherwise,
 $v \in B$
. In this case,
$v \in B$
. In this case,
 $T(B)$
contains
$T(B)$
contains
 $v,x$
and hence a as well. If now
$v,x$
and hence a as well. If now
 $v,x$
are leaves in
$v,x$
are leaves in
 $T(B),$
then B is infeasible, which contradicts the assumption. Hence, there exists
$T(B),$
then B is infeasible, which contradicts the assumption. Hence, there exists
 $y \in B$
which is separated from
$y \in B$
which is separated from
 $a \in V$
by (exactly) one of
$a \in V$
by (exactly) one of
 $v,x \in B$
. Clearly,
$v,x \in B$
. Clearly,
 $y \not \in A \sqcup \{ x \}$
; now note that
$y \not \in A \sqcup \{ x \}$
; now note that
 $A \Delta \{ x, y \} = A \sqcup \{ x, y \}$
, and this belongs to
$A \Delta \{ x, y \} = A \sqcup \{ x, y \}$
, and this belongs to
 $\mathcal {M}'(T)$
by Corollary 4.16 (and the uniqueness of the leaves
$\mathcal {M}'(T)$
by Corollary 4.16 (and the uniqueness of the leaves
 $v,x$
with a common adjacent vertex).
$v,x$
with a common adjacent vertex). -
(2) The other case is when
 $x \in A \setminus B$
.
$x \in A \setminus B$
.Once again, there are two cases, analogous to the two cases above. First, if
 $A \setminus \{ x \} \in \mathcal {M}'(T)$
, then we simply choose
$A \setminus \{ x \} \in \mathcal {M}'(T)$
, then we simply choose
 $y=x$
. Otherwise,
$y=x$
. Otherwise,
 $A \setminus \{ x \}$
is infeasible whereas A is not. Using Corollary 4.16, this yields unique
$A \setminus \{ x \}$
is infeasible whereas A is not. Using Corollary 4.16, this yields unique
 $v,w \in A$
such that:
$v,w \in A$
such that:-
•
 $v,w$
are leaves in
$v,w$
are leaves in
 $T(A \setminus \{ x \})$
,
$T(A \setminus \{ x \})$
, -
•
 $v,w$
are both adjacent to a (unique) vertex
$v,w$
are both adjacent to a (unique) vertex
 $a \in T(A \setminus \{ x \})$
, and
$a \in T(A \setminus \{ x \})$
, and -
• v separates x from w in
 $T(A)$
.
$T(A)$
.
There are now two sub-cases. First, if
 $v,w \in B$
, then
$v,w \in B$
, then
 $T(B)$
contains
$T(B)$
contains
 $v,w$
, hence a. As
$v,w$
, hence a. As
 $B \in \mathcal {M}'(T)$
, there again exists
$B \in \mathcal {M}'(T)$
, there again exists
 $y \in B$
which is separated from
$y \in B$
which is separated from
 $a \in V$
, now by (exactly) one of
$a \in V$
, now by (exactly) one of
 $v,w$
. But then
$v,w$
. But then
 $A \Delta \{ x, y \} = (A \setminus \{ x \}) \sqcup \{ y \}$
, and this is in
$A \Delta \{ x, y \} = (A \setminus \{ x \}) \sqcup \{ y \}$
, and this is in
 $\mathcal {M}'(T)$
as in the preceding case, by Corollary 4.16 (and the uniqueness of the leaves
$\mathcal {M}'(T)$
as in the preceding case, by Corollary 4.16 (and the uniqueness of the leaves
 $v,w$
with a common adjacent vertex).
$v,w$
with a common adjacent vertex).The final sub-case is when not both
 $v,w$
lie in B. Choose an element
$v,w$
lie in B. Choose an element
 $y \in \{ v, w \} \setminus B \subseteq A \setminus B$
. Now
$y \in \{ v, w \} \setminus B \subseteq A \setminus B$
. Now
 $A \Delta \{ x, y \} = (A \setminus \{ x \}) \setminus \{ y \}$
, and by the uniqueness of the leaves
$A \Delta \{ x, y \} = (A \setminus \{ x \}) \setminus \{ y \}$
, and by the uniqueness of the leaves
 $v,w$
(with a common adjacent vertex), this set lacks two leaves at distance
$v,w$
(with a common adjacent vertex), this set lacks two leaves at distance
 $2$
from each other in T. Therefore,
$2$
from each other in T. Therefore,
 $A \Delta \{ x, y \} \in \mathcal {M}'(T)$
, as desired.
$A \Delta \{ x, y \} \in \mathcal {M}'(T)$
, as desired. -
As mentioned above, the delta-matroids
![]() $\mathcal {M}_{\mathcal {D}_{P_k}} = \mathcal {M}'(P_k) = \mathcal {B}(P_k)$
for small values of k. It is natural to seek to know if this result holds for all path graphs, and perhaps even more generally. It turns out that this is false, and the situation is more involved even for path graphs
$\mathcal {M}_{\mathcal {D}_{P_k}} = \mathcal {M}'(P_k) = \mathcal {B}(P_k)$
for small values of k. It is natural to seek to know if this result holds for all path graphs, and perhaps even more generally. It turns out that this is false, and the situation is more involved even for path graphs
![]() $P_k$
with
$P_k$
with
![]() $k \geqslant 9$
.
$k \geqslant 9$
.
Proposition 4.17 Suppose
![]() $k \geqslant 3$
is an integer. The blowup delta-matroid
$k \geqslant 3$
is an integer. The blowup delta-matroid
![]() $\mathcal {M}_{\mathcal {D}_{P_k}}$
of the graph metric space
$\mathcal {M}_{\mathcal {D}_{P_k}}$
of the graph metric space
![]() $P_k$
coincides with the tree-blowup delta-matroid
$P_k$
coincides with the tree-blowup delta-matroid
![]() $\mathcal {B}(P_k)$
, if and only if
$\mathcal {B}(P_k)$
, if and only if
![]() $k \leqslant 8$
.
$k \leqslant 8$
.
Proof An explicit (and longwinded) inspection shows that
![]() $\mathcal {M}_{\mathcal {D}_{P_k}} = \mathcal {B}(P_k)$
for
$\mathcal {M}_{\mathcal {D}_{P_k}} = \mathcal {B}(P_k)$
for
![]() $3 \leqslant k \leqslant 8$
. Another direct computation shows that
$3 \leqslant k \leqslant 8$
. Another direct computation shows that
![]() $\det \mathcal {D}_{P_9} = 0$
. Hence, by Proposition 2.6(2), the coefficient of
$\det \mathcal {D}_{P_9} = 0$
. Hence, by Proposition 2.6(2), the coefficient of
![]() $n_1 n_2 \ldots n_9$
in
$n_1 n_2 \ldots n_9$
in
![]() $p_{P_k}(\mathbf {n})$
also vanishes, for all
$p_{P_k}(\mathbf {n})$
also vanishes, for all
![]() $k \geqslant 9$
. Using Proposition 2.6(3), it follows that
$k \geqslant 9$
. Using Proposition 2.6(3), it follows that
But these sets all lie in
![]() $\mathcal {B}(P_k)$
, so
$\mathcal {B}(P_k)$
, so
![]() $\mathcal {B}(P_k) \supsetneq \mathcal {M}_{\mathcal {D}_{P_k}}$
for
$\mathcal {B}(P_k) \supsetneq \mathcal {M}_{\mathcal {D}_{P_k}}$
for
![]() $k \geqslant 9$
.
$k \geqslant 9$
.
As also promised above, we next explore the question of extending Theorem F from trees to arbitrary graphs. The key observation is that the equivalence
![]() $(1) \Longleftrightarrow (2)$
in Proposition 4.15 extends Corollary 4.16. This suggests how to define a set system in
$(1) \Longleftrightarrow (2)$
in Proposition 4.15 extends Corollary 4.16. This suggests how to define a set system in
![]() $2^{V(G)}$
for every graph metric space G, which specializes to the delta-matroid
$2^{V(G)}$
for every graph metric space G, which specializes to the delta-matroid
![]() $\mathcal {M}'(T)$
when
$\mathcal {M}'(T)$
when
![]() $G = T$
is a tree.
$G = T$
is a tree.
Definition 4.18 Suppose
![]() $G = (V,E)$
is a graph metric space. We say that a subset
$G = (V,E)$
is a graph metric space. We say that a subset
![]() $I \subseteq V$
is:
$I \subseteq V$
is:
-
(1) Infeasible of the first kind if there exist vertices
 $v_1 \neq v_2 \in I$
and a subset
$v_1 \neq v_2 \in I$
and a subset
 $I \subseteq \widetilde {I} \subseteq V$
, such that: (a) the induced subgraph
$I \subseteq \widetilde {I} \subseteq V$
, such that: (a) the induced subgraph
 $G(\widetilde {I})$
on
$G(\widetilde {I})$
on
 $\widetilde {I}$
is connected in G, and (b)
$\widetilde {I}$
is connected in G, and (b)
 $v_1, v_2$
have the same set of neighbors in
$v_1, v_2$
have the same set of neighbors in
 $G(\widetilde {I})$
.
$G(\widetilde {I})$
. -
(2) Infeasible of the second kind if there exist vertices
 $v_1 \neq v_2 \in I$
and a subset
$v_1 \neq v_2 \in I$
and a subset
 $I \subseteq \widetilde {I} \subseteq V$
, such that: (a) the induced subgraph
$I \subseteq \widetilde {I} \subseteq V$
, such that: (a) the induced subgraph
 $G(\widetilde {I})$
on
$G(\widetilde {I})$
on
 $\widetilde {I}$
is a metric subspace of G (hence connected), and (b)
$\widetilde {I}$
is a metric subspace of G (hence connected), and (b)
 $v_1, v_2$
have the same set of neighbors in
$v_1, v_2$
have the same set of neighbors in
 $G(\widetilde {I})$
.
$G(\widetilde {I})$
.
Also define
![]() $\mathcal {M}^{\prime }_1(G)$
(resp.
$\mathcal {M}^{\prime }_1(G)$
(resp.
![]() $\mathcal {M}^{\prime }_2(G)$
) to comprise all subsets of V that are not infeasible of the first (resp. second) kind.
$\mathcal {M}^{\prime }_2(G)$
) to comprise all subsets of V that are not infeasible of the first (resp. second) kind.
For instance, if
![]() $G = T$
is a tree, then it is not hard to see that
$G = T$
is a tree, then it is not hard to see that
![]() $\mathcal {M}^{\prime }_1(T) = \mathcal {M}^{\prime }_2(T) = \mathcal {M}'(T)$
, which was studied in Theorem F. Thus, a question that is natural given that theorem, is whether or not
$\mathcal {M}^{\prime }_1(T) = \mathcal {M}^{\prime }_2(T) = \mathcal {M}'(T)$
, which was studied in Theorem F. Thus, a question that is natural given that theorem, is whether or not
![]() $\mathcal {M}^{\prime }_1(G)$
and/or
$\mathcal {M}^{\prime }_1(G)$
and/or
![]() $\mathcal {M}^{\prime }_2(G)$
is a delta-matroid for every graph G?
$\mathcal {M}^{\prime }_2(G)$
is a delta-matroid for every graph G?
This question is also natural from the viewpoint of the blowup-polynomial, in that if
![]() $I \subseteq V$
is infeasible of the second kind, then the coefficient in
$I \subseteq V$
is infeasible of the second kind, then the coefficient in
![]() $p_G(\mathbf {n})$
of the monomial
$p_G(\mathbf {n})$
of the monomial
![]() $\prod _{i \in I} n_i$
is zero by Proposition 4.11. Nevertheless, our next result shows that this question has a negative answer, already for a graph on seven vertices. Thus, the construction of
$\prod _{i \in I} n_i$
is zero by Proposition 4.11. Nevertheless, our next result shows that this question has a negative answer, already for a graph on seven vertices. Thus, the construction of
![]() $\mathcal {M}'(T)$
does not extend to arbitrary graph metric spaces in either of the above two ways.
$\mathcal {M}'(T)$
does not extend to arbitrary graph metric spaces in either of the above two ways.
Proposition 4.19 There exists a graph G such that neither
![]() $\mathcal {M}^{\prime }_1(G)$
nor
$\mathcal {M}^{\prime }_1(G)$
nor
![]() $\mathcal {M}^{\prime }_2(G)$
is a delta-matroid.
$\mathcal {M}^{\prime }_2(G)$
is a delta-matroid.
Figure 2: A graph on seven vertices.
Proof Let G denote the graph in Figure 2 on the vertex set
![]() $V = \{ u, v_1, v_2, w_1, w_2, x, z \}$
. The definitions show that
$V = \{ u, v_1, v_2, w_1, w_2, x, z \}$
. The definitions show that
![]() $A := V$
and
$A := V$
and
![]() $B := \{v_2 \}$
both lie in
$B := \{v_2 \}$
both lie in
![]() $\mathcal {M}^{\prime }_1(G) \cap \mathcal {M}^{\prime }_2(G)$
, and clearly,
$\mathcal {M}^{\prime }_1(G) \cap \mathcal {M}^{\prime }_2(G)$
, and clearly,
![]() $x \in A \Delta B = A \setminus B$
. Moreover, for all
$x \in A \Delta B = A \setminus B$
. Moreover, for all
![]() $y \in V$
, one can verify that
$y \in V$
, one can verify that
![]() $A \Delta \{ x, y \} = A \setminus \{ x, y \}$
(or
$A \Delta \{ x, y \} = A \setminus \{ x, y \}$
(or
![]() $A \setminus \{ x \}$
if
$A \setminus \{ x \}$
if
![]() $y=x$
) is indeed infeasible of the second kind, hence of the first. (This uses that in the induced subgraph on
$y=x$
) is indeed infeasible of the second kind, hence of the first. (This uses that in the induced subgraph on
![]() $A \setminus \{ x, y \}$
, either
$A \setminus \{ x, y \}$
, either
![]() $v_1, v_2$
are both present, or
$v_1, v_2$
are both present, or
![]() $w_1, w_2$
are, and then they are copies of one another.) Hence, the symmetric exchange axiom fails for both
$w_1, w_2$
are, and then they are copies of one another.) Hence, the symmetric exchange axiom fails for both
![]() $\mathcal {M}^{\prime }_1(G)$
and for
$\mathcal {M}^{\prime }_1(G)$
and for
![]() $\mathcal {M}^{\prime }_2(G)$
, proving the result.
$\mathcal {M}^{\prime }_2(G)$
, proving the result.
5 Metric geometry: Euclidean blowups
In this section, we explore the blowup-polynomial from the viewpoint of metric geometry, and prove the final outstanding theorem. Specifically, we understand which blowups
![]() $X[\mathbf {n}]$
of a given finite metric space X isometrically embed into some Euclidean space
$X[\mathbf {n}]$
of a given finite metric space X isometrically embed into some Euclidean space
![]() $(\mathbb R^r, \| \cdot \|_2)$
.
$(\mathbb R^r, \| \cdot \|_2)$
.
Proof of Theorem A
If
![]() $k=1$
, then the result is immediate, since
$k=1$
, then the result is immediate, since
![]() $X[n_1]$
comprises the vertices of a Euclidean simplex, for any
$X[n_1]$
comprises the vertices of a Euclidean simplex, for any
![]() $n_1 \geqslant 2$
. Thus, we suppose henceforth that
$n_1 \geqslant 2$
. Thus, we suppose henceforth that
![]() $k \geqslant 2$
.
$k \geqslant 2$
.
We first show
![]() $(2) \implies (1)$
. Let
$(2) \implies (1)$
. Let
![]() $j_0 \in [1,k] \setminus \{ j \}$
be such that
$j_0 \in [1,k] \setminus \{ j \}$
be such that
![]() $x_{j_0} = v \in V$
is the closest point in V to
$x_{j_0} = v \in V$
is the closest point in V to
![]() $x_j$
. Now a straightforward computation reveals that
$x_j$
. Now a straightforward computation reveals that
![]() $x^{\prime }_j := 2 x_{j_0} - x_j \in \mathbb R^r$
serves as a blowup of
$x^{\prime }_j := 2 x_{j_0} - x_j \in \mathbb R^r$
serves as a blowup of
![]() $x_j$
in
$x_j$
in
![]() $X[\mathbf {n}]$
. This proves (1).
$X[\mathbf {n}]$
. This proves (1).
The proof of the reverse implication
![]() $(1) \implies (2)$
is in steps. We first suppose
$(1) \implies (2)$
is in steps. We first suppose
![]() $n_{x_1}, n_{x_2} \geqslant 2$
and arrive at a contradiction. Indeed, now the metric subspace
$n_{x_1}, n_{x_2} \geqslant 2$
and arrive at a contradiction. Indeed, now the metric subspace
![]() $Y[(2,2)] \subseteq X[\mathbf {n}]$
is also Euclidean, where
$Y[(2,2)] \subseteq X[\mathbf {n}]$
is also Euclidean, where
![]() $Y = ( x_1, x_2 )$
. Rescale the metric such that
$Y = ( x_1, x_2 )$
. Rescale the metric such that
![]() $d(x_1,x_2) = 1$
, and let
$d(x_1,x_2) = 1$
, and let
![]() $y_i$
be the blowup of
$y_i$
be the blowup of
![]() $x_i$
in
$x_i$
in
![]() $Y[(2,2)]$
for
$Y[(2,2)]$
for
![]() $i=1,2$
. Then the modified Cayley–Menger matrix of
$i=1,2$
. Then the modified Cayley–Menger matrix of
![]() $Y[(2,2)]$
with respect to
$Y[(2,2)]$
with respect to
![]() $(x_1, y_1, x_2, y_2)$
is
$(x_1, y_1, x_2, y_2)$
is
 $$\begin{align*}A = \begin{pmatrix} 8 & 4 & 4 \\ 4 & 2 & -2 \\ 4 & -2 & 2 \end{pmatrix}. \end{align*}$$
$$\begin{align*}A = \begin{pmatrix} 8 & 4 & 4 \\ 4 & 2 & -2 \\ 4 & -2 & 2 \end{pmatrix}. \end{align*}$$
As
![]() $\det A < 0$
, it follows by Theorem 1.2 that
$\det A < 0$
, it follows by Theorem 1.2 that
![]() $Y[(2,2)]$
, and hence
$Y[(2,2)]$
, and hence
![]() $X[\mathbf {n}]$
is not Euclidean.
$X[\mathbf {n}]$
is not Euclidean.
Next, we suppose
![]() $n_{x_2} \geqslant 3$
and again arrive at a contradiction – this time by considering the Euclidean subspace
$n_{x_2} \geqslant 3$
and again arrive at a contradiction – this time by considering the Euclidean subspace
![]() $Y[(1,3)] \subseteq X[\mathbf {n}]$
, where
$Y[(1,3)] \subseteq X[\mathbf {n}]$
, where
![]() $Y = (x_1, x_2)$
. Rescale the metric such that
$Y = (x_1, x_2)$
. Rescale the metric such that
![]() $d(x_1, x_2) = 1$
, let
$d(x_1, x_2) = 1$
, let
![]() $y_2, z_2$
denote the blowups of
$y_2, z_2$
denote the blowups of
![]() $x_2$
in
$x_2$
in
![]() $Y[(1,3)]$
, and consider the modified Cayley–Menger matrix of
$Y[(1,3)]$
, and consider the modified Cayley–Menger matrix of
![]() $Y[(1,3)]$
with respect to
$Y[(1,3)]$
with respect to
![]() $(x_1, x_2, y_2, z_2)$
is
$(x_1, x_2, y_2, z_2)$
is
 $$\begin{align*}A = \begin{pmatrix} 2 & -2 & -2 \\ -2 & 2 & -2 \\ -2 & -2 & 2 \end{pmatrix}. \end{align*}$$
$$\begin{align*}A = \begin{pmatrix} 2 & -2 & -2 \\ -2 & 2 & -2 \\ -2 & -2 & 2 \end{pmatrix}. \end{align*}$$
As
![]() $\det A < 0$
, it follows by Theorem 1.2 that
$\det A < 0$
, it follows by Theorem 1.2 that
![]() $Y[(1,3)]$
, hence
$Y[(1,3)]$
, hence
![]() $X[\mathbf {n}]$
is not Euclidean. (Note, these two uses of Theorem 1.2 can also be avoided by using “visual Euclidean geometry.” For instance, in the latter case,
$X[\mathbf {n}]$
is not Euclidean. (Note, these two uses of Theorem 1.2 can also be avoided by using “visual Euclidean geometry.” For instance, in the latter case,
![]() $x_2, y_2, z_2$
are the vertices of an equilateral triangle with edge-length
$x_2, y_2, z_2$
are the vertices of an equilateral triangle with edge-length
![]() $2$
, and drawing three unit spheres centered at these vertices reveals there is no common intersection point
$2$
, and drawing three unit spheres centered at these vertices reveals there is no common intersection point
![]() $x_1$
.)
$x_1$
.)
This shows the existence of the unique index
![]() $j \in [1,k]$
such that
$j \in [1,k]$
such that
![]() $n_{x_j} = 2$
and (2)(a) all other
$n_{x_j} = 2$
and (2)(a) all other
![]() $n_{x_i} = 1$
. If
$n_{x_i} = 1$
. If
![]() $k=2,$
then the result is easy to show, so we now suppose that
$k=2,$
then the result is easy to show, so we now suppose that
![]() $k \geqslant 3$
. Let
$k \geqslant 3$
. Let
![]() $x_{j_0}$
denote any point in
$x_{j_0}$
denote any point in
![]() $X \setminus \{ x_j \}$
that is closest to
$X \setminus \{ x_j \}$
that is closest to
![]() $x_j$
. Since
$x_j$
. Since
![]() $X[\mathbf {n}]$
is also Euclidean, considering the degenerate (Euclidean) triangle with vertices
$X[\mathbf {n}]$
is also Euclidean, considering the degenerate (Euclidean) triangle with vertices
![]() $x_{j_0}, x_j$
, and the blowup
$x_{j_0}, x_j$
, and the blowup
![]() $x^{\prime }_j$
of
$x^{\prime }_j$
of
![]() $x_j$
shows that these vertices are collinear, and in fact,
$x_j$
shows that these vertices are collinear, and in fact,
![]() $x_{j_0} = (x_j + x^{\prime }_j)/2$
. In turn, this implies that a “closest point”
$x_{j_0} = (x_j + x^{\prime }_j)/2$
. In turn, this implies that a “closest point”
![]() $x_{j_0} \in X$
to
$x_{j_0} \in X$
to
![]() $x_j$
(and hence the index
$x_j$
(and hence the index
![]() $j_0$
) is unique.
$j_0$
) is unique.
Next, denote by
![]() $l \geqslant 1$
the dimension of the span V of
$l \geqslant 1$
the dimension of the span V of
![]() $\{ x_i - x_{j_0} : i \neq j \}$
. Relabel the
$\{ x_i - x_{j_0} : i \neq j \}$
. Relabel the
![]() $x_i$
via:
$x_i$
via:
![]() $y_0 := x_{j_0}, y_1 := x_j$
, and choose any enumeration of the remaining points in X as
$y_0 := x_{j_0}, y_1 := x_j$
, and choose any enumeration of the remaining points in X as
![]() $y_2, \dots , y_{k-1}$
, such that
$y_2, \dots , y_{k-1}$
, such that
![]() $y_2 - y_0, \dots , y_{l+1} - y_0$
form a basis of V. Since X is Euclidean, a simple check shows that the modified Cayley–Menger matrix of X with respect to
$y_2 - y_0, \dots , y_{l+1} - y_0$
form a basis of V. Since X is Euclidean, a simple check shows that the modified Cayley–Menger matrix of X with respect to
![]() $(y_0, \dots , y_{k-1})$
is precisely the Gram matrix
$(y_0, \dots , y_{k-1})$
is precisely the Gram matrix
Now, (2)(b) follows from the claim that if
![]() $y_1 - y_0$
is in the span of
$y_1 - y_0$
is in the span of
![]() $\{ y_i - y_0 : 2 \leqslant i \leqslant l+1 \}$
, then this matrix uniquely determines
$\{ y_i - y_0 : 2 \leqslant i \leqslant l+1 \}$
, then this matrix uniquely determines
![]() $y_1 \in \mathbb R^r$
. To show the claim, write
$y_1 \in \mathbb R^r$
. To show the claim, write
![]() $y_1 - y_0 = \sum _{i=2}^{l+1} c_i (y_i - y_0)$
, and take inner products to obtain the linear system
$y_1 - y_0 = \sum _{i=2}^{l+1} c_i (y_i - y_0)$
, and take inner products to obtain the linear system
 $$\begin{align*}\sum_{i=2}^{l+1} \langle y_{i'} - y_0, y_i - y_0 \rangle c_i = \langle y_{i'} - y_0, y_1 - y_0 \rangle, \qquad 2 \leqslant i' \leqslant l+1. \end{align*}$$
$$\begin{align*}\sum_{i=2}^{l+1} \langle y_{i'} - y_0, y_i - y_0 \rangle c_i = \langle y_{i'} - y_0, y_1 - y_0 \rangle, \qquad 2 \leqslant i' \leqslant l+1. \end{align*}$$
But the left-hand side is the product of the Gram matrix of
![]() $\{ y_{i'} - y_0 : 2 \leqslant i' \leqslant l+1 \}$
against the vector
$\{ y_{i'} - y_0 : 2 \leqslant i' \leqslant l+1 \}$
against the vector
![]() $(c_2, \dots , c_{l+1})^T$
. As the vectors
$(c_2, \dots , c_{l+1})^T$
. As the vectors
![]() $y_{i'} - y_0$
are independent, their Gram matrix is invertible, so this system determines all
$y_{i'} - y_0$
are independent, their Gram matrix is invertible, so this system determines all
![]() $c_i$
uniquely. In particular, if
$c_i$
uniquely. In particular, if
![]() $y_1 = x_j$
is in the affine hull of
$y_1 = x_j$
is in the affine hull of
![]() $X \setminus \{ x_j \}$
, then
$X \setminus \{ x_j \}$
, then
![]() $X[\mathbf {n}]$
cannot be Euclidean since
$X[\mathbf {n}]$
cannot be Euclidean since
![]() $n_{x_j}> 1$
. This proves (2)(b).
$n_{x_j}> 1$
. This proves (2)(b).
Finally, since
![]() $k \geqslant 3$
, we have
$k \geqslant 3$
, we have
![]() $l \geqslant 1$
. Now the definition of the blowup
$l \geqslant 1$
. Now the definition of the blowup
![]() $X[\mathbf {n}]$
implies
$X[\mathbf {n}]$
implies
or in other words,
Simplifying this equality yields that
![]() $y_1 - y_0$
is orthogonal to
$y_1 - y_0$
is orthogonal to
![]() $y_2 - y_0, \dots , y_{l+1} - y_0$
. This implies
$y_2 - y_0, \dots , y_{l+1} - y_0$
. This implies
![]() $y_1 - y_0$
is orthogonal to all of V – which was the assertion (2)(c).
$y_1 - y_0$
is orthogonal to all of V – which was the assertion (2)(c).
5.1 Real-closed analogs
For completeness, we now provide analogs of some of the results proved above, over arbitrary real-closed fields. As this subsection is not used anywhere else in the paper, we will be brief, and also assume familiarity with real-closed fields; we refer the reader to the opening chapter of [Reference Bochnak, Coste and Roy4] for this.
In this part, we suppose
![]() $\mathbb K$
is a real-closed field, where we denote the nonnegative elements in
$\mathbb K$
is a real-closed field, where we denote the nonnegative elements in
![]() $\mathbb K$
by:
$\mathbb K$
by:
![]() $r \geqslant 0$
. Also let
$r \geqslant 0$
. Also let
![]() $\overline {\mathbb K} = \mathbb K[\sqrt {-1}]$
denote an algebraic closure of
$\overline {\mathbb K} = \mathbb K[\sqrt {-1}]$
denote an algebraic closure of
![]() $\mathbb K$
, where we fix a choice of “imaginary” square root
$\mathbb K$
, where we fix a choice of “imaginary” square root
![]() $i = \sqrt {-1}$
in
$i = \sqrt {-1}$
in
![]() $\overline {\mathbb K}$
. Then several “real” notions can be defined over
$\overline {\mathbb K}$
. Then several “real” notions can be defined over
![]() $\mathbb K, \overline {\mathbb K}$
:
$\mathbb K, \overline {\mathbb K}$
:
-
(1) A symmetric matrix
 $A \in \mathbb K^{k \times k}$
is said to be positive semidefinite (resp. positive definite) if
$A \in \mathbb K^{k \times k}$
is said to be positive semidefinite (resp. positive definite) if
 $x^T A x \geqslant 0$
(resp.
$x^T A x \geqslant 0$
(resp.
 $x^T A x> 0$
) for all nonzero vectors
$x^T A x> 0$
) for all nonzero vectors
 $x \in \mathbb K^n$
.
$x \in \mathbb K^n$
. -
(2) A matrix
 $A \in \mathbb K^{k \times k}$
is orthogonal if
$A \in \mathbb K^{k \times k}$
is orthogonal if
 $A A^T = \operatorname {\mathrm {Id}}_k$
.
$A A^T = \operatorname {\mathrm {Id}}_k$
. -
(3) Given
 $z = x + iy \in \overline {\mathbb K}$
with
$z = x + iy \in \overline {\mathbb K}$
with
 $x,y \in \mathbb K$
, we define
$x,y \in \mathbb K$
, we define
 $\Re (z) := x$
and
$\Re (z) := x$
and
 $\Im (z) := y$
.
$\Im (z) := y$
. -
(4) We say that a multivariable polynomial
 $p \in \overline {\mathbb K}[z_1, \dots , z_k]$
is stable if
$p \in \overline {\mathbb K}[z_1, \dots , z_k]$
is stable if
 $p(z_1, \dots , z_k)\ \neq 0$
whenever
$p(z_1, \dots , z_k)\ \neq 0$
whenever
 $\Im (z_j)> 0\ \forall j$
.
$\Im (z_j)> 0\ \forall j$
.
Now (an analog of) the spectral theorem holds for symmetric matrices
![]() $A = A^T \in \mathbb K^{k \times k}$
. Moreover, every such matrix A is positive semidefinite if and only if it has nonnegative eigenvalues in
$A = A^T \in \mathbb K^{k \times k}$
. Moreover, every such matrix A is positive semidefinite if and only if it has nonnegative eigenvalues in
![]() $\mathbb K$
– and if so, then it has a positive semidefinite square root
$\mathbb K$
– and if so, then it has a positive semidefinite square root
![]() $\sqrt {A}$
. One also has the following.
$\sqrt {A}$
. One also has the following.
Proposition 5.1 Fix an integer
![]() $k \geqslant 1$
.
$k \geqslant 1$
.
-
(1) Suppose
 $A_1, \dots , A_m, B \in \mathbb K^{k \times k}$
are symmetric matrices, with all
$A_1, \dots , A_m, B \in \mathbb K^{k \times k}$
are symmetric matrices, with all
 $A_j$
positive semidefinite. Then the polynomial is either stable or identically zero.
$A_j$
positive semidefinite. Then the polynomial is either stable or identically zero. $$\begin{align*}p(z_1, \dots, z_m) := \det \left( B + \sum_{j=1}^m z_j A_j \right) \end{align*}$$
$$\begin{align*}p(z_1, \dots, z_m) := \det \left( B + \sum_{j=1}^m z_j A_j \right) \end{align*}$$
-
(2) Suppose
 $p \in \mathbb K[z_1, \dots , z_m]$
is homogeneous of degree k. If p is stable, then p is Lorentzian (equivalently, strongly/completely log-concave, whenever
$p \in \mathbb K[z_1, \dots , z_m]$
is homogeneous of degree k. If p is stable, then p is Lorentzian (equivalently, strongly/completely log-concave, whenever
 $\log (\cdot )$
is defined over
$\log (\cdot )$
is defined over
 $\mathbb K$
).
$\mathbb K$
).
The two parts of this proposition were proved over
![]() $\mathbb K = \mathbb R$
in [Reference Borcea and Brändén5, Reference Brändén and Huh12], respectively. Thus, they hold over an arbitrary real closed field
$\mathbb K = \mathbb R$
in [Reference Borcea and Brändén5, Reference Brändén and Huh12], respectively. Thus, they hold over an arbitrary real closed field
![]() $\mathbb K$
by Tarski’s principle, since all of these notions can be expressed in the first-order language of ordered fields. Also note that the equivalence in the second part indeed makes sense over some real-closed fields, e.g.,
$\mathbb K$
by Tarski’s principle, since all of these notions can be expressed in the first-order language of ordered fields. Also note that the equivalence in the second part indeed makes sense over some real-closed fields, e.g.,
![]() $\mathbb K = \mathbb R$
, or
$\mathbb K = \mathbb R$
, or
![]() $\mathbb K$
the field of convergent (real) Puiseux series with rational powers, where it was proved in [Reference Brändén and Huh12, Theorem 3.19]. The notions of Lorentzian and strongly/completely log-concave polynomials over the latter field can be found in [Reference Brändén and Huh12] (see page 861).
$\mathbb K$
the field of convergent (real) Puiseux series with rational powers, where it was proved in [Reference Brändén and Huh12, Theorem 3.19]. The notions of Lorentzian and strongly/completely log-concave polynomials over the latter field can be found in [Reference Brändén and Huh12] (see page 861).
Remark 5.2 Schoenberg’s Euclidean embeddability result (Theorem 1.2) – stated and used above – turns out to have an alternate characterization in a specific real-closed field: the convergent generalized Puiseux series
![]() $\mathbb R \{ t \}$
with real powers. Recall, the elements of
$\mathbb R \{ t \}$
with real powers. Recall, the elements of
![]() $\mathbb R \{ t \}$
are series
$\mathbb R \{ t \}$
are series
satisfying: (a) the exponents
![]() $\alpha _0 < \alpha _1 < \cdots $
are real; (b)
$\alpha _0 < \alpha _1 < \cdots $
are real; (b)
![]() $\{ -\alpha _n : n \geqslant 0, \ c_n \neq 0 \}$
is well-ordered; and (c)
$\{ -\alpha _n : n \geqslant 0, \ c_n \neq 0 \}$
is well-ordered; and (c)
![]() $\sum _n c_n t^{\alpha _n}$
is convergent on a punctured open disk around the origin. Such a series is defined to be positive if its leading coefficient is positive. It is known (see, e.g., [Reference Speyer41, Section 1.5]) that this field is real-closed; moreover, its algebraic closure is the degree-
$\sum _n c_n t^{\alpha _n}$
is convergent on a punctured open disk around the origin. Such a series is defined to be positive if its leading coefficient is positive. It is known (see, e.g., [Reference Speyer41, Section 1.5]) that this field is real-closed; moreover, its algebraic closure is the degree-
![]() $2$
extension
$2$
extension
![]() $\mathbb {C} \{ t \}$
, where real coefficients in the definition above are replaced by complex ones. Now, we claim that the following holds.
$\mathbb {C} \{ t \}$
, where real coefficients in the definition above are replaced by complex ones. Now, we claim that the following holds.
Theorem 5.3 A finite metric space
![]() $X = \{ x_0, x_1, \dots , x_k \}$
isometrically embeds inside Hilbert space
$X = \{ x_0, x_1, \dots , x_k \}$
isometrically embeds inside Hilbert space
![]() $\ell ^2$
(over
$\ell ^2$
(over
![]() $\mathbb R$
) if and only if the matrix
$\mathbb R$
) if and only if the matrix
![]() $E_X := (t^{d(x_i, x_j)^2})_{i,j=0}^k$
is positive semidefinite in
$E_X := (t^{d(x_i, x_j)^2})_{i,j=0}^k$
is positive semidefinite in
![]() $\mathbb R \{ t \}$
.
$\mathbb R \{ t \}$
.
Proof This follows from a chain of equivalences: X is Euclidean-embeddable if and only if (by [Reference Schoenberg38], via Theorem 1.2) the matrix
![]() $(-d(x_i,x_j)^2)_{i,j=0}^k$
is conditionally positive semidefinite, if and only if (by [Reference Schoenberg38])
$(-d(x_i,x_j)^2)_{i,j=0}^k$
is conditionally positive semidefinite, if and only if (by [Reference Schoenberg38])
![]() $(\exp (-\lambda d(x_i,x_j)^2))_{i,j=0}^k$
is positive semidefinite for all
$(\exp (-\lambda d(x_i,x_j)^2))_{i,j=0}^k$
is positive semidefinite for all
![]() $\lambda \geqslant 0$
, if and only if (replacing
$\lambda \geqslant 0$
, if and only if (replacing
![]() $e^{-\lambda } \leadsto q \in (0,1)$
and via [Reference Speyer41, Section 1.5])
$e^{-\lambda } \leadsto q \in (0,1)$
and via [Reference Speyer41, Section 1.5])
![]() $E_X$
is positive semidefinite in
$E_X$
is positive semidefinite in
![]() $\mathbb R \{ t \}$
.
$\mathbb R \{ t \}$
.
We conclude this part by formulating the promised tropical version of some of our results above. As the notion of a
![]() $\mathbb K_{\geqslant 0}$
-valued metric (can be easily defined, but) is not very common in the literature, we formulate the next result in greater generality.
$\mathbb K_{\geqslant 0}$
-valued metric (can be easily defined, but) is not very common in the literature, we formulate the next result in greater generality.
Theorem 5.4 Suppose
![]() $\mathbb K$
is a real-closed field, and
$\mathbb K$
is a real-closed field, and
![]() $\Delta , M \in \mathbb K^{k \times k}$
are symmetric matrices, with
$\Delta , M \in \mathbb K^{k \times k}$
are symmetric matrices, with
![]() $\Delta $
a positive definite diagonal matrix.
$\Delta $
a positive definite diagonal matrix.
-
(1) The multi-affine polynomials
are stable, with coefficients in $$\begin{align*}p_\pm(z_1, \dots, z_k) := \det (\pm \Delta + \Delta_{\mathbf{z}} M), \qquad \mathbf{z} \in \overline{\mathbb K}^k \end{align*}$$
$$\begin{align*}p_\pm(z_1, \dots, z_k) := \det (\pm \Delta + \Delta_{\mathbf{z}} M), \qquad \mathbf{z} \in \overline{\mathbb K}^k \end{align*}$$
 $\mathbb K$
.
$\mathbb K$
.
-
(2) Define the homogenization
 $\widetilde {p}(z_0, z_1, \dots , z_k) := p(z_0 \Delta + \Delta _{\mathbf {z}} M)$
. The following are equivalent:
$\widetilde {p}(z_0, z_1, \dots , z_k) := p(z_0 \Delta + \Delta _{\mathbf {z}} M)$
. The following are equivalent:-
(a)
 $\widetilde {p}$
is stable.
$\widetilde {p}$
is stable. -
(b)
 $\widetilde {p}$
is Lorentzian (equivalently, strongly/completely log-concave, whenever
$\widetilde {p}$
is Lorentzian (equivalently, strongly/completely log-concave, whenever
 $\log (\cdot )$
is defined over
$\log (\cdot )$
is defined over
 $\mathbb K$
).
$\mathbb K$
). -
(c) All coefficients of
 $\widetilde {p}$
lie in
$\widetilde {p}$
lie in
 $\mathbb K_{\geqslant 0}$
.
$\mathbb K_{\geqslant 0}$
. -
(d)
 $p(1,\dots ,1)> 0$
, and the polynomial
$p(1,\dots ,1)> 0$
, and the polynomial
 $(z_1, \dots , z_k) \mapsto \displaystyle \frac {p(z_1, \dots , z_k)}{p(1,\dots ,1)}$
is stable and has nonnegative coefficients that sum to
$(z_1, \dots , z_k) \mapsto \displaystyle \frac {p(z_1, \dots , z_k)}{p(1,\dots ,1)}$
is stable and has nonnegative coefficients that sum to
 $1$
.
$1$
. -
(e) The matrix M is positive semidefinite.
-
One can prove this result from the same result over
![]() $\mathbb K = \mathbb R$
, via Tarski’s principle. Alternately, the case of
$\mathbb K = \mathbb R$
, via Tarski’s principle. Alternately, the case of
![]() $\mathbb K = \mathbb R$
was essentially proved in Theorem E; the slightly more general versions here (for
$\mathbb K = \mathbb R$
was essentially proved in Theorem E; the slightly more general versions here (for
![]() $\mathbb K = \mathbb R$
, with M instead of
$\mathbb K = \mathbb R$
, with M instead of
![]() $\mathcal {D}_G$
) require only minimal modifications to the earlier proofs. These proofs (for
$\mathcal {D}_G$
) require only minimal modifications to the earlier proofs. These proofs (for
![]() $\mathbb K = \mathbb R$
) go through over arbitrary real-closed
$\mathbb K = \mathbb R$
) go through over arbitrary real-closed
![]() $\mathbb K$
with minimal further modifications, given Proposition 5.1.
$\mathbb K$
with minimal further modifications, given Proposition 5.1.
6 Concluding remarks
We end the paper with some observations. The results in this work reveal several novel invariants associated with all finite connected unweighted graphs – more generally, to all finite metric spaces X:
-
(1) The (real-stable) blowup-polynomials
 $p_X(\mathbf {n})$
and
$p_X(\mathbf {n})$
and
 $u_X(n)$
.
$u_X(n)$
. -
(2) The degrees of
 $p_X, u_X$
– notice by Proposition 4.17 that the degrees can be strictly less than the number of points in X, even when X is not a blowup of a smaller graph.
$p_X, u_X$
– notice by Proposition 4.17 that the degrees can be strictly less than the number of points in X, even when X is not a blowup of a smaller graph. -
(3) The largest root of
 $u_X(n)$
(which is always positive). By Corollary 4.3, for
$u_X(n)$
(which is always positive). By Corollary 4.3, for
 $X = G$
a graph this equals
$X = G$
a graph this equals
 $\frac {2}{2+\lambda }$
, where
$\frac {2}{2+\lambda }$
, where
 $\lambda $
is the smallest eigenvalue of
$\lambda $
is the smallest eigenvalue of
 $D_G$
above
$D_G$
above
 $-2$
.
$-2$
. -
(4) The blowup delta-matroid
 $\mathcal {M}_{\mathcal {D}_X}$
; and for X an unweighted tree, the delta-matroid
$\mathcal {M}_{\mathcal {D}_X}$
; and for X an unweighted tree, the delta-matroid
 $\mathcal {M}'(X)$
which is combinatorial rather than matrix-theoretic.
$\mathcal {M}'(X)$
which is combinatorial rather than matrix-theoretic.
It would be interesting and desirable to explore if – say for
![]() $X = G$
a graph metric space – these invariants can be related to “traditional” combinatorial graph invariants.
$X = G$
a graph metric space – these invariants can be related to “traditional” combinatorial graph invariants.
A From the matrix
 ${\mathcal {C}}_X$
to the univariate blowup-polynomial
${\mathcal {C}}_X$
to the univariate blowup-polynomial
In this section, we show a few peripheral but related results for completeness. As the proofs of Theorems C and E reveal, the matrix
![]() $\mathcal {C}_G = (-\Delta _{\mathbf {a}_G})^{-1/2} \mathcal {D}_G (-\Delta _{\mathbf {a}_G})^{-1/2}$
plays an important role in determining the real-stability and Lorentzian nature of
$\mathcal {C}_G = (-\Delta _{\mathbf {a}_G})^{-1/2} \mathcal {D}_G (-\Delta _{\mathbf {a}_G})^{-1/2}$
plays an important role in determining the real-stability and Lorentzian nature of
![]() $p_G(\cdot )$
and
$p_G(\cdot )$
and
![]() $\widetilde {p}_G(\cdot )$
, respectively. We thus take a closer look at
$\widetilde {p}_G(\cdot )$
, respectively. We thus take a closer look at
![]() $\mathcal {C}_G$
in its own right. Here, we will work over an arbitrary finite metric space X.
$\mathcal {C}_G$
in its own right. Here, we will work over an arbitrary finite metric space X.
Proposition A.1 Given a finite metric space
![]() $X = \{ x_1, \dots , x_k \}$
with
$X = \{ x_1, \dots , x_k \}$
with
![]() $k \geqslant 2$
, the (real) matrix
$k \geqslant 2$
, the (real) matrix
![]() $\mathcal {C}_X$
has at least two positive eigenvalues, and this bound is sharp. More strongly, for any
$\mathcal {C}_X$
has at least two positive eigenvalues, and this bound is sharp. More strongly, for any
![]() $k \geqslant 3$
, there exists a finite metric space
$k \geqslant 3$
, there exists a finite metric space
![]() $Y = \{ y_1, \dots , y_k \}$
for which
$Y = \{ y_1, \dots , y_k \}$
for which
![]() $\mathcal {C}_Y$
has exactly two positive eigenvalues.
$\mathcal {C}_Y$
has exactly two positive eigenvalues.
Proof Suppose
![]() $i \neq j$
are such that
$i \neq j$
are such that
![]() $d(x_i, x_j)$
is minimal among the off-diagonal entries of the distance matrix
$d(x_i, x_j)$
is minimal among the off-diagonal entries of the distance matrix
![]() $D_X$
(or
$D_X$
(or
![]() $\mathcal {D}_X$
). Using (3.2), the corresponding principal
$\mathcal {D}_X$
). Using (3.2), the corresponding principal
![]() $2 \times 2$
submatrix of
$2 \times 2$
submatrix of
![]() $\mathcal {C}_X$
is
$\mathcal {C}_X$
is
 $\begin {pmatrix} 1 & 1/2 \\ 1/2 & 1 \end {pmatrix}$
. This is positive definite, hence has two positive eigenvalues. But then so does
$\begin {pmatrix} 1 & 1/2 \\ 1/2 & 1 \end {pmatrix}$
. This is positive definite, hence has two positive eigenvalues. But then so does
![]() $\mathcal {C}_X$
, by the Cauchy interlacing theorem.
$\mathcal {C}_X$
, by the Cauchy interlacing theorem.
We now show that this bound is tight, first for
![]() $k=3$
. Consider a Euclidean isosceles triangle with vertices
$k=3$
. Consider a Euclidean isosceles triangle with vertices
![]() $x_1, x_2, x_3$
and edge-lengths
$x_1, x_2, x_3$
and edge-lengths
![]() $1,a,a$
for any fixed scalar
$1,a,a$
for any fixed scalar
![]() $a>3$
. Thus,
$a>3$
. Thus,
![]() $X = \{ x_1, x_2, x_3 \}$
; now a suitable relabeling of the
$X = \{ x_1, x_2, x_3 \}$
; now a suitable relabeling of the
![]() $x_i$
gives
$x_i$
gives
 $$\begin{align*}\mathcal{D}_X = \begin{pmatrix} 2 & 1 & a \\ 1 & 2 & a \\ a & a & 2a \end{pmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{D}_X = \begin{pmatrix} 2 & 1 & a \\ 1 & 2 & a \\ a & a & 2a \end{pmatrix}. \end{align*}$$
Now
![]() $\det \mathcal {D}_X = 2a(3-a) < 0$
, so
$\det \mathcal {D}_X = 2a(3-a) < 0$
, so
![]() $\det \mathcal {C}_X = (3-a)/4 < 0$
. As
$\det \mathcal {C}_X = (3-a)/4 < 0$
. As
![]() $\mathcal {C}_X$
has two positive eigenvalues, the third eigenvalue must be negative.
$\mathcal {C}_X$
has two positive eigenvalues, the third eigenvalue must be negative.
Finally, for
![]() $k> 3$
, we continue to use
$k> 3$
, we continue to use
![]() $X = \{ x_1, x_2, x_3 \}$
as in the preceding paragraph, and consider the blowup
$X = \{ x_1, x_2, x_3 \}$
as in the preceding paragraph, and consider the blowup
![]() $Y := X[(1,1,k-2)]$
. By Lemma 3.2(3),
$Y := X[(1,1,k-2)]$
. By Lemma 3.2(3),
![]() $\mathcal {D}_Y$
is a block
$\mathcal {D}_Y$
is a block
![]() $3 \times 3$
matrix with the
$3 \times 3$
matrix with the
![]() $(3,3)$
block of size
$(3,3)$
block of size
![]() $(k-2) \times (k-2)$
. Let
$(k-2) \times (k-2)$
. Let
![]() $V \subseteq \mathbb R^k$
denote the subspace of vectors whose first two coordinates are zero and the others add up to zero; then
$V \subseteq \mathbb R^k$
denote the subspace of vectors whose first two coordinates are zero and the others add up to zero; then
![]() $V \subseteq \ker \mathcal {D}_Y$
and
$V \subseteq \ker \mathcal {D}_Y$
and
![]() $\dim V = k-3$
. On the ortho-complement
$\dim V = k-3$
. On the ortho-complement
![]() $V^\perp \subseteq \mathbb R^k$
(with basis
$V^\perp \subseteq \mathbb R^k$
(with basis
![]() $e_1, e_2$
, and
$e_1, e_2$
, and
![]() $e_3 + \cdots + e_k$
),
$e_3 + \cdots + e_k$
),
![]() $\mathcal {D}_Y$
acts as the matrix
$\mathcal {D}_Y$
acts as the matrix
![]() $\mathcal {D}_X \cdot \operatorname {\mathrm {diag}} (1, 1, k-2)$
. Thus, the remaining three eigenvalues of
$\mathcal {D}_X \cdot \operatorname {\mathrm {diag}} (1, 1, k-2)$
. Thus, the remaining three eigenvalues of
![]() $\mathcal {D}_Y$
are those of
$\mathcal {D}_Y$
are those of
![]() $\mathcal {D}_X \cdot \operatorname {\mathrm {diag}} (1, 1, k-2)$
, or equivalently, of its conjugate
$\mathcal {D}_X \cdot \operatorname {\mathrm {diag}} (1, 1, k-2)$
, or equivalently, of its conjugate
which is real symmetric. Moreover,
![]() $\mathcal {D}_X$
has a negative eigenvalue, hence is not positive semidefinite. But then the same holds for C, hence for
$\mathcal {D}_X$
has a negative eigenvalue, hence is not positive semidefinite. But then the same holds for C, hence for
![]() $\mathcal {D}_Y$
, and hence for
$\mathcal {D}_Y$
, and hence for
![]() $\mathcal {C}_Y$
. From above,
$\mathcal {C}_Y$
. From above,
![]() $\mathcal {C}_Y$
has at least two positive eigenvalues, and it has a kernel of dimension at least
$\mathcal {C}_Y$
has at least two positive eigenvalues, and it has a kernel of dimension at least
![]() $k-3$
because
$k-3$
because
![]() $\mathcal {D}_Y$
does.
$\mathcal {D}_Y$
does.
The next result starts from the calculation in equation (4.6). The second determinant in the final expression is reminiscent of an important tool used in proving the Kadison–Singer conjecture in [Reference Marcus, Spielman and Srivastava31] (via Weaver’s conjecture
![]() $KS_2$
): the mixed characteristic polynomial of a set of positive semidefinite matrices
$KS_2$
): the mixed characteristic polynomial of a set of positive semidefinite matrices
![]() $A_j \in \mathbb R^{k \times k}$
:
$A_j \in \mathbb R^{k \times k}$
:
 $$ \begin{align} \mu[A_1, \dots, A_m](z_0) := \left. \left( \prod_{j=1}^m (1 - \partial_{z_j}) \right) \det \left( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^m z_j A_j \right) \right|_{z_1 = \cdots = z_m = 0}. \end{align} $$
$$ \begin{align} \mu[A_1, \dots, A_m](z_0) := \left. \left( \prod_{j=1}^m (1 - \partial_{z_j}) \right) \det \left( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^m z_j A_j \right) \right|_{z_1 = \cdots = z_m = 0}. \end{align} $$
In the setting of Theorem E, where
![]() $\mathcal {C}_X$
is positive semidefinite, the matrices
$\mathcal {C}_X$
is positive semidefinite, the matrices
![]() $A_j$
in question – see (4.6) – are
$A_j$
in question – see (4.6) – are
![]() $\sqrt {\mathcal {C}_X} E_{jj} \sqrt {\mathcal {C}_X}$
, which are all positive semidefinite. It turns out that their mixed characteristic polynomial is intimately connected to both
$\sqrt {\mathcal {C}_X} E_{jj} \sqrt {\mathcal {C}_X}$
, which are all positive semidefinite. It turns out that their mixed characteristic polynomial is intimately connected to both
![]() $\mathcal {C}_X$
and to
$\mathcal {C}_X$
and to
![]() $u_X(\cdot )$
.
$u_X(\cdot )$
.
Proposition A.2 Suppose
![]() $(X,d)$
is a finite metric space such that
$(X,d)$
is a finite metric space such that
![]() $\mathcal {D}_X$
(equivalently,
$\mathcal {D}_X$
(equivalently,
![]() $\mathcal {C}_X$
) is positive semidefinite. Up to a real scalar, the mixed characteristic polynomial of the matrices
$\mathcal {C}_X$
) is positive semidefinite. Up to a real scalar, the mixed characteristic polynomial of the matrices
![]() $\{ \sqrt {\mathcal {C}_X} E_{jj} \sqrt {\mathcal {C}_X} : 1 \leqslant j \leqslant k \}$
equals the characteristic polynomial of
$\{ \sqrt {\mathcal {C}_X} E_{jj} \sqrt {\mathcal {C}_X} : 1 \leqslant j \leqslant k \}$
equals the characteristic polynomial of
![]() $\mathcal {C}_X$
, as well as the “inversion”
$\mathcal {C}_X$
, as well as the “inversion”
![]() $z_0^k u_X(z_0^{-1})$
of the univariate blowup-polynomial.
$z_0^k u_X(z_0^{-1})$
of the univariate blowup-polynomial.
Proof We begin with the following claim: If
![]() $p(z_0, z_1, \dots , z_k)$
is a polynomial, then
$p(z_0, z_1, \dots , z_k)$
is a polynomial, then
 $$ \begin{align} \begin{aligned} & \left. \left( \prod_{j=1}^k (1 - \partial_{z_j}) \right) (p) (z_0, z_1, \dots, z_k) \right|_{z_1 = \cdots = z_k = 0}\\ & \quad = \left. MAP_{z_1, \dots, z_k}(p) (z_0, z_1, \dots, z_k) \right|_{z_1 = \cdots = z_k = -1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \left. \left( \prod_{j=1}^k (1 - \partial_{z_j}) \right) (p) (z_0, z_1, \dots, z_k) \right|_{z_1 = \cdots = z_k = 0}\\ & \quad = \left. MAP_{z_1, \dots, z_k}(p) (z_0, z_1, \dots, z_k) \right|_{z_1 = \cdots = z_k = -1}. \end{aligned} \end{align} $$
Here, the operator
![]() $MAP_{z_1, \dots , z_k}$
kills all higher-order terms in
$MAP_{z_1, \dots , z_k}$
kills all higher-order terms in
![]() $z_1, \dots , z_k$
, and retains only the “multi-affine” monomials
$z_1, \dots , z_k$
, and retains only the “multi-affine” monomials
![]() $\prod _{j=0}^k z_j^{m_j}$
with all
$\prod _{j=0}^k z_j^{m_j}$
with all
![]() $m_1, \dots , m_k \leqslant 1$
(but arbitrary
$m_1, \dots , m_k \leqslant 1$
(but arbitrary
![]() $m_0$
).
$m_0$
).
To show the claim, write
 $$\begin{align*}p(z_0, z_1, \dots, z_k) = \sum_{\mathbf{m} \in \mathbb{Z}_{\geqslant 0}^k} a_{\mathbf{m}}(z_0) \prod_{j=1}^k z_j^{m_j}, \end{align*}$$
$$\begin{align*}p(z_0, z_1, \dots, z_k) = \sum_{\mathbf{m} \in \mathbb{Z}_{\geqslant 0}^k} a_{\mathbf{m}}(z_0) \prod_{j=1}^k z_j^{m_j}, \end{align*}$$
where each
![]() $a_{\mathbf {m}}(z_0)$
is a polynomial. Now note that applying a differential “monomial operator” and then specializing at the origin kills all but one monomials:
$a_{\mathbf {m}}(z_0)$
is a polynomial. Now note that applying a differential “monomial operator” and then specializing at the origin kills all but one monomials:
 $$\begin{align*}\left. \prod_{i \in I} \partial_{z_i} \left( \prod_{j=1}^k z_j^{m_j} \right) \right|_{z_1 = \cdots = z_k = 0} = \mathbf{1}(m_i = 1\ \forall i \in I) \cdot \mathbf{1}(m_j = 0\ \forall j \not\in I), \ \forall I \subseteq \{ 1, \dots, k \}. \end{align*}$$
$$\begin{align*}\left. \prod_{i \in I} \partial_{z_i} \left( \prod_{j=1}^k z_j^{m_j} \right) \right|_{z_1 = \cdots = z_k = 0} = \mathbf{1}(m_i = 1\ \forall i \in I) \cdot \mathbf{1}(m_j = 0\ \forall j \not\in I), \ \forall I \subseteq \{ 1, \dots, k \}. \end{align*}$$
Thus, applying
![]() $\prod _{i=1}^k (1 - \partial _{z_i})$
and specializing at the origin will kill all but the multi-affine (in
$\prod _{i=1}^k (1 - \partial _{z_i})$
and specializing at the origin will kill all but the multi-affine (in
![]() $z_1, \dots , z_k$
) monomials in p. Consequently, we may replace p on the left-hand side in (A.2) by
$z_1, \dots , z_k$
) monomials in p. Consequently, we may replace p on the left-hand side in (A.2) by
say, where each
![]() $a_J(z_0)$
is a polynomial as above. Now compute
$a_J(z_0)$
is a polynomial as above. Now compute
 $$ \begin{align*} & \left. \left( \prod_{j=1}^k (1 - \partial_{z_j}) \right) q(z_0, z_1, \dots, z_k) \right|_{z_1 = \cdots = z_k = 0}\\ & \quad = \left. \sum_{I \subseteq \{ 1, \dots, k \}} (-1)^{|I|} \prod_{i \in I} \partial_{z_i} \cdot \sum_{J \subseteq \{ 1, \dots, k \}} a_J(z_0) \prod_{j \in J} z_j \right|_{z_1 = \cdots = z_k = 0}\\ & \quad = \sum_{J \subseteq \{ 1, \dots, k \}} (-1)^{|J|} a_J(z_0) = q(z_0, -1, -1, \dots, -1). \end{align*} $$
$$ \begin{align*} & \left. \left( \prod_{j=1}^k (1 - \partial_{z_j}) \right) q(z_0, z_1, \dots, z_k) \right|_{z_1 = \cdots = z_k = 0}\\ & \quad = \left. \sum_{I \subseteq \{ 1, \dots, k \}} (-1)^{|I|} \prod_{i \in I} \partial_{z_i} \cdot \sum_{J \subseteq \{ 1, \dots, k \}} a_J(z_0) \prod_{j \in J} z_j \right|_{z_1 = \cdots = z_k = 0}\\ & \quad = \sum_{J \subseteq \{ 1, \dots, k \}} (-1)^{|J|} a_J(z_0) = q(z_0, -1, -1, \dots, -1). \end{align*} $$
This shows the claim. Using this, we and assuming that
![]() $\mathcal {D}_X$
is positive semidefinite, we show the first assertion – that the mixed characteristic polynomial of the matrices
$\mathcal {D}_X$
is positive semidefinite, we show the first assertion – that the mixed characteristic polynomial of the matrices
![]() $\sqrt {\mathcal {C}_X} E_{jj} \sqrt {\mathcal {C}_X}$
is the characteristic polynomial of
$\sqrt {\mathcal {C}_X} E_{jj} \sqrt {\mathcal {C}_X}$
is the characteristic polynomial of
![]() $\mathcal {C}_X$
:
$\mathcal {C}_X$
:
 $$ \begin{align*} \mu[\{ \sqrt{\mathcal{C}_X} E_{jj} \sqrt{\mathcal{C}_X} : 1 \leqslant j \leqslant k \}](z_0) = &\ \det \left( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^k (-1) \sqrt{\mathcal{C}_X} E_{jj} \sqrt{\mathcal{C}_X} \right)\\ = &\ \det(z_0 \operatorname{\mathrm{Id}}_k - \mathcal{C}_X). \end{align*} $$
$$ \begin{align*} \mu[\{ \sqrt{\mathcal{C}_X} E_{jj} \sqrt{\mathcal{C}_X} : 1 \leqslant j \leqslant k \}](z_0) = &\ \det \left( z_0 \operatorname{\mathrm{Id}}_k + \sum_{j=1}^k (-1) \sqrt{\mathcal{C}_X} E_{jj} \sqrt{\mathcal{C}_X} \right)\\ = &\ \det(z_0 \operatorname{\mathrm{Id}}_k - \mathcal{C}_X). \end{align*} $$
This shows one assertion. Next, using (4.5) specialized at
![]() $z_1 = \cdots = z_k = -1$
, this expression also equals (up to a scalar) the inversion of
$z_1 = \cdots = z_k = -1$
, this expression also equals (up to a scalar) the inversion of
![]() $u_X$
, as asserted:
$u_X$
, as asserted:
 $$ \begin{align*} = &\ \det(-\Delta_{\mathbf{a}_X})^{-1} \det(z_0 \cdot (-\Delta_{\mathbf{a}_X}) - \mathcal{D}_X) = \det(\Delta_{\mathbf{a}_X})^{-1} z_0^k \det(\Delta_{\mathbf{a}_X} + z_0^{-1} \mathcal{D}_X)\\ = &\ \det(\Delta_{\mathbf{a}_X})^{-1} z_0^k u_X(z_0^{-1}).\\[-31pt] \end{align*} $$
$$ \begin{align*} = &\ \det(-\Delta_{\mathbf{a}_X})^{-1} \det(z_0 \cdot (-\Delta_{\mathbf{a}_X}) - \mathcal{D}_X) = \det(\Delta_{\mathbf{a}_X})^{-1} z_0^k \det(\Delta_{\mathbf{a}_X} + z_0^{-1} \mathcal{D}_X)\\ = &\ \det(\Delta_{\mathbf{a}_X})^{-1} z_0^k u_X(z_0^{-1}).\\[-31pt] \end{align*} $$
We conclude this section by briefly discussing another invariant of the metric space
![]() $(X,d)$
, one that is related to the matrix
$(X,d)$
, one that is related to the matrix
![]() $\mathcal {C}_X$
and the polynomial
$\mathcal {C}_X$
and the polynomial
![]() $u_X(\cdot )$
.
$u_X(\cdot )$
.
Definition A.3 Given a finite metric space
![]() $(X,d)$
, define
$(X,d)$
, define
![]() $\alpha _{\max }(X) \in \mathbb R$
to be the largest root, or “maxroot,” of (the real-rooted polynomial)
$\alpha _{\max }(X) \in \mathbb R$
to be the largest root, or “maxroot,” of (the real-rooted polynomial)
![]() $u_X(\cdot )$
.
$u_X(\cdot )$
.
Notice that
![]() $u_X(x+\alpha _{\max }(X))$
has only nonpositive roots, and (say after dividing by its leading coefficient,) only nonnegative coefficients. In particular, these coefficients yield a (strongly) log-concave sequence for every finite metric space – e.g., for every finite connected unweighted graph.
$u_X(x+\alpha _{\max }(X))$
has only nonpositive roots, and (say after dividing by its leading coefficient,) only nonnegative coefficients. In particular, these coefficients yield a (strongly) log-concave sequence for every finite metric space – e.g., for every finite connected unweighted graph.
Proposition A.4 Given a finite metric space
![]() $X = \{ x_1, \dots , x_k \}$
with
$X = \{ x_1, \dots , x_k \}$
with
![]() $k \geqslant 2$
, the root
$k \geqslant 2$
, the root
![]() $\alpha _{\max }(X)$
is positive. In particular,
$\alpha _{\max }(X)$
is positive. In particular,
![]() $u_X(\cdot )$
has monomials with both positive and negative coefficients.
$u_X(\cdot )$
has monomials with both positive and negative coefficients.
Furthermore, given any integer
![]() $n \geqslant 1$
, we have
$n \geqslant 1$
, we have
For example, for X the k-point discrete metric space (so
![]() $\mathcal {D}_X = \mathbf { 1}_{k \times k} + \operatorname {\mathrm {Id}}_k$
is positive definite) – or equivalently, the complete graph
$\mathcal {D}_X = \mathbf { 1}_{k \times k} + \operatorname {\mathrm {Id}}_k$
is positive definite) – or equivalently, the complete graph
![]() $K_k$
– we have
$K_k$
– we have
![]() $\alpha _{\max }(X) = 2$
, by the computation in equation (2.4).
$\alpha _{\max }(X) = 2$
, by the computation in equation (2.4).
Proof Recall that
![]() $u_X(x) = \det (\Delta _{\mathbf {a}_X} + x \mathcal {D}_X)$
, and so
$u_X(x) = \det (\Delta _{\mathbf {a}_X} + x \mathcal {D}_X)$
, and so
![]() $u_X(0) = \prod _{i=1}^k a_i \neq 0$
. Now, if
$u_X(0) = \prod _{i=1}^k a_i \neq 0$
. Now, if
![]() $\alpha $
is any root of
$\alpha $
is any root of
![]() $u_X$
(hence real and nonzero), we obtain similarly to the preceding proofs in this section:
$u_X$
(hence real and nonzero), we obtain similarly to the preceding proofs in this section:
where
![]() $\mathcal {C}_X = (-\Delta _{\mathbf {a}_X})^{-1/2} \mathcal {D}_X (-\Delta _{\mathbf {a}_X})^{-1/2}$
as above. But since
$\mathcal {C}_X = (-\Delta _{\mathbf {a}_X})^{-1/2} \mathcal {D}_X (-\Delta _{\mathbf {a}_X})^{-1/2}$
as above. But since
![]() $\mathcal {C}_X$
has at least two positive eigenvalues (by Proposition A.1),
$\mathcal {C}_X$
has at least two positive eigenvalues (by Proposition A.1),
![]() $u_X$
has at least two positive roots, and hence
$u_X$
has at least two positive roots, and hence
![]() $\alpha _{\max }(X)> 0$
.
$\alpha _{\max }(X)> 0$
.
The next statement follows directly by Theorem B, which implies that the constant and linear terms in
![]() $u_X$
have opposite signs. More information is obtained by using Descartes’ rule of signs (see, e.g., [Reference Descartes17]), which implies that there are at least two sign changes in the coefficients of
$u_X$
have opposite signs. More information is obtained by using Descartes’ rule of signs (see, e.g., [Reference Descartes17]), which implies that there are at least two sign changes in the coefficients of
![]() $u_X$
.
$u_X$
.
It remains to compute
![]() $\alpha _{\max }(X[n(1,1,\dots ,1)])$
. Using Lemma 3.2(3),
$\alpha _{\max }(X[n(1,1,\dots ,1)])$
. Using Lemma 3.2(3),
the Kronecker products, under a suitable relabeling of indices. In particular, the eigenvalues of the latter Kronecker product are the Minkowski product of the spectra
![]() $\sigma (\mathcal {C}_X)$
and
$\sigma (\mathcal {C}_X)$
and
![]() $\sigma (\mathbf { 1}_{n \times n}) = \{ n, 0, 0, \dots , 0 \}$
. We now make a series of reductions:
$\sigma (\mathbf { 1}_{n \times n}) = \{ n, 0, 0, \dots , 0 \}$
. We now make a series of reductions:
![]() $\alpha \in \mathbb R$
is a positive root of
$\alpha \in \mathbb R$
is a positive root of
![]() $u_{X[n(1,\dots ,1)]}$
,
$u_{X[n(1,\dots ,1)]}$
,
if and only if
![]() $\alpha ^{-1}$
is a positive eigenvalue of
$\alpha ^{-1}$
is a positive eigenvalue of
![]() $\mathcal {C}_{X[n (1,1,\dots ,1)]}$
(using (A.3)),
$\mathcal {C}_{X[n (1,1,\dots ,1)]}$
(using (A.3)),
if and only if (from above)
![]() $\alpha ^{-1}$
equals n times a positive eigenvalue of
$\alpha ^{-1}$
equals n times a positive eigenvalue of
![]() $\mathcal {C}_X$
,
$\mathcal {C}_X$
,
if and only if
![]() $\frac {1}{n \alpha }$
is a positive eigenvalue of
$\frac {1}{n \alpha }$
is a positive eigenvalue of
![]() $\mathcal {C}_X$
,
$\mathcal {C}_X$
,
if and only if
![]() $n \alpha $
is a positive root of
$n \alpha $
is a positive root of
![]() $u_X$
(again using (A.3)).
$u_X$
(again using (A.3)).
Since
![]() $\alpha _{\max }(X)> 0$
, this proves the result.
$\alpha _{\max }(X)> 0$
, this proves the result.
B Monoid morphism computations toward Theorem 2.3
Here, we show parts (1) and (3) of Theorem 2.3, for completeness. For (1), begin by using Lemma 2.2 to check that
![]() $((1,\dots ,1)^T, 0_{k \times k})$
is indeed the identity element of
$((1,\dots ,1)^T, 0_{k \times k})$
is indeed the identity element of
![]() $\mathcal {M}_{\mathbf {n}}(R)$
; clearly, it is sent under the given map
$\mathcal {M}_{\mathbf {n}}(R)$
; clearly, it is sent under the given map
![]() $\Psi : (\mathbf {a}, D) \mapsto M(\mathbf {a},D)$
to
$\Psi : (\mathbf {a}, D) \mapsto M(\mathbf {a},D)$
to
![]() $\operatorname {\mathrm {Id}}_K$
. Next, given
$\operatorname {\mathrm {Id}}_K$
. Next, given
![]() $(\mathbf {a},D),(\mathbf {a}',D') \in \mathcal {M}_{\mathbf {n}}(R)$
, and
$(\mathbf {a},D),(\mathbf {a}',D') \in \mathcal {M}_{\mathbf {n}}(R)$
, and
![]() $1 \leqslant i \leqslant k$
, first compare the
$1 \leqslant i \leqslant k$
, first compare the
![]() $(i,i)$
blocks of their
$(i,i)$
blocks of their
![]() $\Psi $
-images in part (1):
$\Psi $
-images in part (1):
 $$\begin{align*}M((\mathbf{a},D) \circ (\mathbf{a}',D'))_{ii} = a_i a^{\prime}_i \operatorname{\mathrm{Id}}_{n_i} + \left( a_i d^{\prime}_{ii} + d_{ii} a^{\prime}_i + \sum_{l=1}^k d_{il} \cdot \mathbf{q}_l^T \mathbf{p}_l \cdot d^{\prime}_{li} \right) \mathbf{p}_i \mathbf{q}_i^T, \end{align*}$$
$$\begin{align*}M((\mathbf{a},D) \circ (\mathbf{a}',D'))_{ii} = a_i a^{\prime}_i \operatorname{\mathrm{Id}}_{n_i} + \left( a_i d^{\prime}_{ii} + d_{ii} a^{\prime}_i + \sum_{l=1}^k d_{il} \cdot \mathbf{q}_l^T \mathbf{p}_l \cdot d^{\prime}_{li} \right) \mathbf{p}_i \mathbf{q}_i^T, \end{align*}$$
whereas on the other side,
 $$ \begin{align*} & (M(\mathbf{a},D) M(\mathbf{a}',D'))_{ii}\\ & \quad = (a_i \operatorname{\mathrm{Id}}_{n_i} + d_{ii} \mathbf{p}_i \mathbf{q}_i^T) (a^{\prime}_i \operatorname{\mathrm{Id}}_{n_i} + d^{\prime}_{ii} \mathbf{p}_i \mathbf{q}_i^T) + \sum_{l \neq i} d_{il} \mathbf{p}_i \mathbf{q}_l^T \cdot \mathbf{p}_l \mathbf{q}_i^T \cdot d^{\prime}_{li}\\ & \quad = (a_i \operatorname{\mathrm{Id}}_{n_i} + d_{ii} \mathbf{p}_i \mathbf{q}_i^T) (a^{\prime}_i \operatorname{\mathrm{Id}}_{n_i} + d^{\prime}_{ii} \mathbf{p}_i \mathbf{q}_i^T) + \mathbf{p}_i \mathbf{q}_i^T \cdot \sum_{l \neq i} d_{il} \cdot \mathbf{q}_l^T \mathbf{p}_l \cdot d^{\prime}_{li}. \end{align*} $$
$$ \begin{align*} & (M(\mathbf{a},D) M(\mathbf{a}',D'))_{ii}\\ & \quad = (a_i \operatorname{\mathrm{Id}}_{n_i} + d_{ii} \mathbf{p}_i \mathbf{q}_i^T) (a^{\prime}_i \operatorname{\mathrm{Id}}_{n_i} + d^{\prime}_{ii} \mathbf{p}_i \mathbf{q}_i^T) + \sum_{l \neq i} d_{il} \mathbf{p}_i \mathbf{q}_l^T \cdot \mathbf{p}_l \mathbf{q}_i^T \cdot d^{\prime}_{li}\\ & \quad = (a_i \operatorname{\mathrm{Id}}_{n_i} + d_{ii} \mathbf{p}_i \mathbf{q}_i^T) (a^{\prime}_i \operatorname{\mathrm{Id}}_{n_i} + d^{\prime}_{ii} \mathbf{p}_i \mathbf{q}_i^T) + \mathbf{p}_i \mathbf{q}_i^T \cdot \sum_{l \neq i} d_{il} \cdot \mathbf{q}_l^T \mathbf{p}_l \cdot d^{\prime}_{li}. \end{align*} $$
It is easily verified that these two quantities are equal.
For the off-diagonal blocks, fix
![]() $1 \leqslant i \neq j \leqslant k$
and compute
$1 \leqslant i \neq j \leqslant k$
and compute
 $$\begin{align*}M((\mathbf{a},D) \circ (\mathbf{a}',D'))_{ij} = \left( a_i d^{\prime}_{ij} + d_{ij} a^{\prime}_j + \sum_{l=1}^k d_{il} \cdot \mathbf{q}_l^T \mathbf{p}_l \cdot d^{\prime}_{lj} \right) \mathbf{p}_i \mathbf{q}_j^T, \end{align*}$$
$$\begin{align*}M((\mathbf{a},D) \circ (\mathbf{a}',D'))_{ij} = \left( a_i d^{\prime}_{ij} + d_{ij} a^{\prime}_j + \sum_{l=1}^k d_{il} \cdot \mathbf{q}_l^T \mathbf{p}_l \cdot d^{\prime}_{lj} \right) \mathbf{p}_i \mathbf{q}_j^T, \end{align*}$$
whereas on the other side,
 $$ \begin{align*} & (M(\mathbf{a},D) M(\mathbf{a}',D'))_{ij}\\ & \quad = \left( a_{ii} \operatorname{\mathrm{Id}}_{n_i} \cdot d^{\prime}_{ij} \mathbf{p}_i \mathbf{q}_j^T + d_{ii} \mathbf{p}_i \mathbf{q}_i^T \cdot d^{\prime}_{ij} \mathbf{p}_i \mathbf{q}_j^T \right)\\ &\qquad + \left( d_{ij} \mathbf{p}_i \mathbf{q}_j^T \cdot a^{\prime}_{jj} \operatorname{\mathrm{Id}}_{n_j} + d_{ij} \mathbf{p}_i \mathbf{q}_j^T \cdot d^{\prime}_{jj} \mathbf{p}_j \mathbf{q}_j^T \right) + \mathbf{p}_i \mathbf{q}_j^T \cdot \sum_{l \neq i,j} d_{il} d^{\prime}_{li} \mathbf{ q}_l^T \mathbf{p}_l. \end{align*} $$
$$ \begin{align*} & (M(\mathbf{a},D) M(\mathbf{a}',D'))_{ij}\\ & \quad = \left( a_{ii} \operatorname{\mathrm{Id}}_{n_i} \cdot d^{\prime}_{ij} \mathbf{p}_i \mathbf{q}_j^T + d_{ii} \mathbf{p}_i \mathbf{q}_i^T \cdot d^{\prime}_{ij} \mathbf{p}_i \mathbf{q}_j^T \right)\\ &\qquad + \left( d_{ij} \mathbf{p}_i \mathbf{q}_j^T \cdot a^{\prime}_{jj} \operatorname{\mathrm{Id}}_{n_j} + d_{ij} \mathbf{p}_i \mathbf{q}_j^T \cdot d^{\prime}_{jj} \mathbf{p}_j \mathbf{q}_j^T \right) + \mathbf{p}_i \mathbf{q}_j^T \cdot \sum_{l \neq i,j} d_{il} d^{\prime}_{li} \mathbf{ q}_l^T \mathbf{p}_l. \end{align*} $$
Once again, it is easy to check that both expressions are equal.
We now show Theorem 2.3(3); denote the right-hand side in it by
noting that all
![]() $a_i \in R^\times $
. To show (3), using (1) it suffices to show that the composition on the other side yields the identity, i.e.,
$a_i \in R^\times $
. To show (3), using (1) it suffices to show that the composition on the other side yields the identity, i.e.,
The equality of the first components is obvious; now check using Lemma 2.2 that the second component on the left-hand side equals
which concludes the proof.
Acknowledgment
We would like to thank Alexander Belton, Petter Brändén, Carolyn Chun, Karola Meszaros, Aaradhya Pandey, Alan Sokal, and Cynthia Vinzant for useful discussions. We also thank the anonymous referee for carefully reading the manuscript and providing useful feedback.