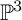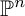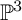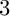1 Introduction
We define a one-parameter family of Euler stability conditions
![]() $\sigma _t=(\mathscr {A}_t, Z_t)$
on
$\sigma _t=(\mathscr {A}_t, Z_t)$
on
![]() $\mathbb {P}^n$
based on [1]. The heart, denoted by
$\mathbb {P}^n$
based on [1]. The heart, denoted by
![]() $\mathscr {A}_t$
, consists of complexes
$\mathscr {A}_t$
, consists of complexes
in which k is the roundup of t to the closest integer, and
![]() $\mathscr {O}_{\mathbb {P}^n}^{a_{-l}}(-k-l)$
(
$\mathscr {O}_{\mathbb {P}^n}^{a_{-l}}(-k-l)$
(
![]() $l=0,1,\ldots ,n$
) denotes the direct sum
$l=0,1,\ldots ,n$
) denotes the direct sum
![]() $\mathscr {O}_{\mathbb {P}^n}(-k-l)^{\bigoplus a_{-l}}$
. With the observation that the Hilbert polynomial
$\mathscr {O}_{\mathbb {P}^n}(-k-l)^{\bigoplus a_{-l}}$
. With the observation that the Hilbert polynomial
![]() $P_t(\mathscr {O}_{\mathbb {P}^n})=\chi (\mathscr {O}_{\mathbb {P}^n}(t))$
of
$P_t(\mathscr {O}_{\mathbb {P}^n})=\chi (\mathscr {O}_{\mathbb {P}^n}(t))$
of
![]() $\mathscr {O}_{\mathbb {P}^n}$
has simple roots
$\mathscr {O}_{\mathbb {P}^n}$
has simple roots
![]() $t = -1, -2, \ldots , -n$
. We define the central charge using the Euler characteristic as follows. For any object
$t = -1, -2, \ldots , -n$
. We define the central charge using the Euler characteristic as follows. For any object
![]() $E\in \mathscr {A}_t$
, let
$E\in \mathscr {A}_t$
, let
![]() $\chi _t(E)$
be the Euler characteristic of the twisted object
$\chi _t(E)$
be the Euler characteristic of the twisted object
![]() $E\otimes \mathscr {O}_{\mathbb {P}^n}(t)$
, that is,
$E\otimes \mathscr {O}_{\mathbb {P}^n}(t)$
, that is,
 $$ \begin{align*}\chi_t(E):=\int_{\mathbb{P}^3} ch(E) \cdot ch(\mathscr{O}_{\mathbb{P}^3})\cdot e^{tH}\cdot Td(\mathbb{P}^3).\end{align*} $$
$$ \begin{align*}\chi_t(E):=\int_{\mathbb{P}^3} ch(E) \cdot ch(\mathscr{O}_{\mathbb{P}^3})\cdot e^{tH}\cdot Td(\mathbb{P}^3).\end{align*} $$
This is the Hilbert polynomial of E, and denote
![]() $\chi ^{\prime }_t(E)$
as the derivative of
$\chi ^{\prime }_t(E)$
as the derivative of
![]() $\chi _t(E)$
with respect to t. Define the central charge as
$\chi _t(E)$
with respect to t. Define the central charge as
![]() $Z_t:=\chi ^{\prime }_t + i\cdot \chi _t$
. We will prove in §3 that the pair
$Z_t:=\chi ^{\prime }_t + i\cdot \chi _t$
. We will prove in §3 that the pair
![]() $\sigma _t=(\mathscr {A}_t, Z_t)$
is a stability condition on
$\sigma _t=(\mathscr {A}_t, Z_t)$
is a stability condition on
![]() $\mathbb {P}^n$
. We conjecture that the moduli space of Euler-stable complexes for large t coincides with the moduli of Gieseker-stable sheaves. Here, we focus on the conjecture for objects in
$\mathbb {P}^n$
. We conjecture that the moduli space of Euler-stable complexes for large t coincides with the moduli of Gieseker-stable sheaves. Here, we focus on the conjecture for objects in
![]() ${D}^b({\mathbb P}^3)$
of class
${D}^b({\mathbb P}^3)$
of class
![]() $v=(0,0,ch_2>0,ch_3)$
, that is, the class of a one-dimensional coherent sheaf.
$v=(0,0,ch_2>0,ch_3)$
, that is, the class of a one-dimensional coherent sheaf.
On
![]() $\mathbb {P}^3$
, there is a construction of Bridgeland stability conditions by the double-tilting approach (see [Reference Bayer, Macrì and Toda6], [Reference Macrì26]). Denote this stability condition by
$\mathbb {P}^3$
, there is a construction of Bridgeland stability conditions by the double-tilting approach (see [Reference Bayer, Macrì and Toda6], [Reference Macrì26]). Denote this stability condition by
![]() $\sigma _{\alpha ,\beta , s}=(\mathscr {A}^{\alpha , \beta }, Z_{\alpha , \beta , s})$
. The heart
$\sigma _{\alpha ,\beta , s}=(\mathscr {A}^{\alpha , \beta }, Z_{\alpha , \beta , s})$
. The heart
![]() $\mathscr {A}^{\alpha , \beta }$
is obtained from tilting
$\mathscr {A}^{\alpha , \beta }$
is obtained from tilting
![]() $Coh(\mathbb {P}^3)$
twice, and the central charge is the following function of twisted Chern characters (Definition 2.9):
$Coh(\mathbb {P}^3)$
twice, and the central charge is the following function of twisted Chern characters (Definition 2.9):
 $$ \begin{align*}Z_{\alpha, \beta, s}:= -ch^{\beta}_3+\left(s+\frac{1}{6}\right)\alpha^2H^2ch^{\beta}_1+i\cdot\left(Hch^{\beta}_2-\frac{\alpha^2}{2}H^3ch^{\beta}_0\right).\end{align*} $$
$$ \begin{align*}Z_{\alpha, \beta, s}:= -ch^{\beta}_3+\left(s+\frac{1}{6}\right)\alpha^2H^2ch^{\beta}_1+i\cdot\left(Hch^{\beta}_2-\frac{\alpha^2}{2}H^3ch^{\beta}_0\right).\end{align*} $$
For
![]() $\alpha =\frac {1}{\sqrt {3}}$
,
$\alpha =\frac {1}{\sqrt {3}}$
,
![]() $\beta =-t-2$
,
$\beta =-t-2$
,
![]() $s=\frac {1}{3}$
, it is straightforward to check that the central charge becomes
$s=\frac {1}{3}$
, it is straightforward to check that the central charge becomes
![]() $Z^{\mathscr {B}_t}_t := Z_{\frac {1}{\sqrt {3}}, -t-2, \frac {1}{3}}=-\chi _t + i \cdot \chi ^{\prime }_t$
. Denote the corresponding heart
$Z^{\mathscr {B}_t}_t := Z_{\frac {1}{\sqrt {3}}, -t-2, \frac {1}{3}}=-\chi _t + i \cdot \chi ^{\prime }_t$
. Denote the corresponding heart
![]() $\mathscr {A}^{\frac {1}{\sqrt {3}}, -t-2}$
by
$\mathscr {A}^{\frac {1}{\sqrt {3}}, -t-2}$
by
![]() $\mathscr {B}_t$
, and this one-dimensional stability condition by
$\mathscr {B}_t$
, and this one-dimensional stability condition by
![]() $\sigma ^{\mathscr {B}_t}_t:=(\mathscr {B}_t, Z^{\mathscr {B}_t}_t)$
. We will show that the two stability conditions
$\sigma ^{\mathscr {B}_t}_t:=(\mathscr {B}_t, Z^{\mathscr {B}_t}_t)$
. We will show that the two stability conditions
![]() $\sigma _t$
(Euler) and
$\sigma _t$
(Euler) and
![]() $\sigma _t^{\mathscr {B}_t}$
(double-tilt) are essentially the same in the sense that
$\sigma _t^{\mathscr {B}_t}$
(double-tilt) are essentially the same in the sense that
![]() $\sigma _t$
is a tilt of
$\sigma _t$
is a tilt of
![]() $\sigma ^{\mathscr {B}_t}_t$
.
$\sigma ^{\mathscr {B}_t}_t$
.
To study the asymptotic behavior of objects in
![]() $\mathscr {A}_t$
, we make use of the finiteness of
$\mathscr {A}_t$
, we make use of the finiteness of
![]() $\mathscr {A}_t$
and the better-behaved walls of
$\mathscr {A}_t$
and the better-behaved walls of
![]() $\mathscr {B}_t$
. We extend the stability condition
$\mathscr {B}_t$
. We extend the stability condition
![]() $\sigma ^{\mathscr {B}_t}_t$
to the “
$\sigma ^{\mathscr {B}_t}_t$
to the “
![]() $(t,u)$
” upper half plane by modifying the central charge to be
$(t,u)$
” upper half plane by modifying the central charge to be
![]() $Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t$
(
$Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t$
(
![]() $\chi ^{\prime \prime }_t$
denotes the second derivative of
$\chi ^{\prime \prime }_t$
denotes the second derivative of
![]() $\chi _t$
, and the
$\chi _t$
, and the
![]() $"u"$
parameter is essentially the
$"u"$
parameter is essentially the
![]() $"s"$
parameter in the double-tilt stability). The pair
$"s"$
parameter in the double-tilt stability). The pair
![]() $\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u})$
is a stability condition, analogous to the construction of tilt stability on surfaces. We start with studying the asymptotic behavior of a fixed object E for
$\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u})$
is a stability condition, analogous to the construction of tilt stability on surfaces. We start with studying the asymptotic behavior of a fixed object E for
![]() $u\gg 0$
.
$u\gg 0$
.
Theorem 1.1 (Theorem 4.7)
For any fixed t, and any object
![]() $E \in \mathscr {B}_t$
with class
$E \in \mathscr {B}_t$
with class
![]() $v(E)=(0,0,ch_2>0,ch_3)$
, there exists a
$v(E)=(0,0,ch_2>0,ch_3)$
, there exists a
![]() $u_E>0$
such that for all
$u_E>0$
such that for all
![]() $u>u_E$
, E is
$u>u_E$
, E is
![]() $\sigma _{t,u}$
-semistable if and only if E is a Gieseker semistable sheaf.
$\sigma _{t,u}$
-semistable if and only if E is a Gieseker semistable sheaf.
Next, we consider the boundedness of the walls for any given class
![]() $v\in K_{num}(\mathbb {P}^3)$
of a one-dimensional sheaf. There are bounded and unbounded parts of potential walls. We find that the bounded walls satisfy
$v\in K_{num}(\mathbb {P}^3)$
of a one-dimensional sheaf. There are bounded and unbounded parts of potential walls. We find that the bounded walls satisfy
![]() $|t-2-ch_3/ch_2|\leq ch_2+2\sqrt {2ch_2}$
. The unbounded walls remain somewhat of a mystery. We expect that unbounded potential walls are not actual walls.
$|t-2-ch_3/ch_2|\leq ch_2+2\sqrt {2ch_2}$
. The unbounded walls remain somewhat of a mystery. We expect that unbounded potential walls are not actual walls.
To support our conjecture, we explicitly compute the wall-crossings for the class
![]() $v=(0,0,3,-5)$
, the class of the structure sheaf of a twisted cubic curve. There was previous work on the class of ideal sheaves of space (rational and elliptic) curves in [Reference Gallardo, Huerta and Schmidt13], [Reference Schmidt33], and [Reference Xia35], and it was shown that the last moduli space was the Hilbert scheme of curves. Our main result is the following.
$v=(0,0,3,-5)$
, the class of the structure sheaf of a twisted cubic curve. There was previous work on the class of ideal sheaves of space (rational and elliptic) curves in [Reference Gallardo, Huerta and Schmidt13], [Reference Schmidt33], and [Reference Xia35], and it was shown that the last moduli space was the Hilbert scheme of curves. Our main result is the following.
Theorem 1.2. For the class
![]() $v=(0,0,3,-5)\in K_{num}{(\mathbb {P}^3)}$
, there are two walls in
$v=(0,0,3,-5)\in K_{num}{(\mathbb {P}^3)}$
, there are two walls in
![]() $\mathscr {A}_1$
(
$\mathscr {A}_1$
(
![]() $t\in (0,1]$
) defined by the short exact sequences:
$t\in (0,1]$
) defined by the short exact sequences:
In the first sequence, Q is a coherent sheaf that can be either
![]() $\mathscr {I}_C$
or
$\mathscr {I}_C$
or
![]() $\mathscr {F}$
, where C is a twisted cubic curve and
$\mathscr {F}$
, where C is a twisted cubic curve and
![]() $\mathscr {F}$
is a sheaf that satisfies the sequence
$\mathscr {F}$
is a sheaf that satisfies the sequence
![]() $0\to \mathscr {O}_{\Lambda }(-3)\to \mathscr {F}\to \mathscr {I}_P(-1) \to 0$
(
$0\to \mathscr {O}_{\Lambda }(-3)\to \mathscr {F}\to \mathscr {I}_P(-1) \to 0$
(
![]() $\Lambda \subset \mathbb {P}^3$
is a plane).
$\Lambda \subset \mathbb {P}^3$
is a plane).
In the second sequence,
![]() $\Lambda \subset {\mathbb P}^3$
is a plane and
$\Lambda \subset {\mathbb P}^3$
is a plane and
![]() $\mathscr {F}_1$
is a complex fitting in the short exact sequence:
$\mathscr {F}_1$
is a complex fitting in the short exact sequence:
![]() $0 \to \mathscr {F}_1\to \mathbb {C}_P\to \mathscr {O}_{\Lambda }(-3)[2] \to 0$
in
$0 \to \mathscr {F}_1\to \mathbb {C}_P\to \mathscr {O}_{\Lambda }(-3)[2] \to 0$
in
![]() $\mathscr {A}_1$
, where
$\mathscr {A}_1$
, where
![]() $\mathbb {C}_P$
is the skyscraper sheaf of a point in
$\mathbb {C}_P$
is the skyscraper sheaf of a point in
![]() $\Lambda $
.
$\Lambda $
.
The moduli spaces in the three corresponding chambers are as follows:
-
1.
 $t\in (0,0.35)$
. The moduli space is empty.
$t\in (0,0.35)$
. The moduli space is empty. -
2.
 $t\in (0.35,0.72)$
. The moduli space consists of two components:
$t\in (0.35,0.72)$
. The moduli space consists of two components:-
(a)
 $K_{(2,3)}$
: a smooth
$K_{(2,3)}$
: a smooth
 $12$
-dimensional Kronecker moduli space.
$12$
-dimensional Kronecker moduli space. -
(b)
 $M_{\mathscr {F}}$
: a
$M_{\mathscr {F}}$
: a
 $\mathbb {P}^3$
bundle over a closed five-dimensional smooth flag variety
$\mathbb {P}^3$
bundle over a closed five-dimensional smooth flag variety
 $H\subset K_{(2,3)}$
.
$H\subset K_{(2,3)}$
.
-
-
3.
 $t\in (0.72,1]$
.
$t\in (0.72,1]$
.
 $M_{\mathscr {F}}$
disappears.
$M_{\mathscr {F}}$
disappears.
 $K_{(2,3)}$
is blown up along H, denoted by
$K_{(2,3)}$
is blown up along H, denoted by
 $\mathbf {B}:=Bl_H(K_{(2,3)})$
. A new component
$\mathbf {B}:=Bl_H(K_{(2,3)})$
. A new component
 $\mathbf {P}$
comes in, glued to
$\mathbf {P}$
comes in, glued to
 $\mathbf {B}$
along the exceptional divisor of
$\mathbf {B}$
along the exceptional divisor of
 $\mathbf {B}$
.
$\mathbf {B}$
.
 $\mathbf {P}$
is the relative Simpson scheme over
$\mathbf {P}$
is the relative Simpson scheme over
 $\mathbb {P}^{3\vee }$
, fibered by the scheme
$\mathbb {P}^{3\vee }$
, fibered by the scheme
 $\mathcal {M}^{3t+1}_{\mathbb {P}^2}$
, which is the moduli space of Gieseker semistable sheaves with Hilbert polynomial
$\mathcal {M}^{3t+1}_{\mathbb {P}^2}$
, which is the moduli space of Gieseker semistable sheaves with Hilbert polynomial
 $P_t=3t+1$
on
$P_t=3t+1$
on
 $\mathbb {P}^2$
. This is the Gieseker moduli space of class v on
$\mathbb {P}^2$
. This is the Gieseker moduli space of class v on
 $\mathbb {P}^3$
.
$\mathbb {P}^3$
.
In [Reference Maican28], Maican proved that the functor
![]() $F: \mathscr {F} \to \mathcal {E}xt^{n-1}(\mathscr {F}, \omega _{\mathbb {P}^n})$
preserves Gieseker stability for sheaves on
$F: \mathscr {F} \to \mathcal {E}xt^{n-1}(\mathscr {F}, \omega _{\mathbb {P}^n})$
preserves Gieseker stability for sheaves on
![]() $\mathbb {P}^n$
. It was generalized to Bridgeland stable complexes on
$\mathbb {P}^n$
. It was generalized to Bridgeland stable complexes on
![]() $\mathbb {P}^2$
in [Reference Martinez29]. We prove the analogous result on
$\mathbb {P}^2$
in [Reference Martinez29]. We prove the analogous result on
![]() $\mathbb {P}^3$
, and a similar duality result holds on
$\mathbb {P}^3$
, and a similar duality result holds on
![]() $\mathbb {P}^n$
(
$\mathbb {P}^n$
(
![]() $n\in \mathbb {Z}_{\geq 0}$
) as well. For a class
$n\in \mathbb {Z}_{\geq 0}$
) as well. For a class
![]() $v\in K_{num}(\mathbb {P}^3)$
and an object
$v\in K_{num}(\mathbb {P}^3)$
and an object
![]() $E\in \mathscr {A}_t$
with this class, define its twisted dual as
$E\in \mathscr {A}_t$
with this class, define its twisted dual as
![]() $E^D:=R\mathscr {H}om(E,\omega _{\mathbb {P}^3})[2]$
.
$E^D:=R\mathscr {H}om(E,\omega _{\mathbb {P}^3})[2]$
.
Theorem 1.3. On
![]() $\mathbb {P}^3$
,
$\mathbb {P}^3$
,
![]() $E\in \mathscr {A}_t$
is (semi)stable with phase
$E\in \mathscr {A}_t$
is (semi)stable with phase
![]() $\phi \in (0,1)$
if and only if
$\phi \in (0,1)$
if and only if
![]() $E^D[1]$
is (semi)stable in
$E^D[1]$
is (semi)stable in
![]() $\mathscr {A}_{-t}$
with phase
$\mathscr {A}_{-t}$
with phase
![]() $1-\phi $
for all
$1-\phi $
for all
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
In the end, we show an example in which an actual wall is built up from two pieces of distinct numerical walls. Unlike surfaces, where walls are nested (see [Reference Maciocia21]), walls on a threefold may intersect (see [Reference Maciocia and Jardim22], [Reference Schmidt33]). Let
![]() $C \subset \mathbb {P}^3$
be a rational quartic curve contained in a quadric surface
$C \subset \mathbb {P}^3$
be a rational quartic curve contained in a quadric surface
![]() $Q \subset \mathbb {P}^3$
. We propose that its actual wall in the
$Q \subset \mathbb {P}^3$
. We propose that its actual wall in the
![]() $(t,u)$
-plane is the outermost part of the numerical walls defined by these two sequences:
$(t,u)$
-plane is the outermost part of the numerical walls defined by these two sequences:
The paper is organized as follows: In §2, we give a brief review of Bridgeland stability conditions. In §3, we introduce the one-dimensional Euler stability condition and show its relation with the double-tilt stability on
![]() $\mathbb {P}^3$
. The §4 is evidence for our main conjecture that for any one-dimensional class
$\mathbb {P}^3$
. The §4 is evidence for our main conjecture that for any one-dimensional class
![]() $v\in K_{num}(\mathbb {P}^3)$
, Euler stable complexes are Gieseker stable sheaves for all large t. We will show the walls for one-dimensional classes and prove some asymptotic results for sheaves and complexes. In §5, we show the duality results for stable objects in
$v\in K_{num}(\mathbb {P}^3)$
, Euler stable complexes are Gieseker stable sheaves for all large t. We will show the walls for one-dimensional classes and prove some asymptotic results for sheaves and complexes. In §5, we show the duality results for stable objects in
![]() $\mathscr {A}_t$
and
$\mathscr {A}_t$
and
![]() $\mathscr {B}_t$
. In §§6 and 7, we will focus on the fixed class
$\mathscr {B}_t$
. In §§6 and 7, we will focus on the fixed class
![]() $v=(0,0,3,-5)$
, finding the walls for the class and describing the moduli spaces in each chamber. Finally, in §8, we show an example in which an actual wall is built up from distinct numerical walls.
$v=(0,0,3,-5)$
, finding the walls for the class and describing the moduli spaces in each chamber. Finally, in §8, we show an example in which an actual wall is built up from distinct numerical walls.
Remark 1.4. There is related recent work on walls and the asymptotic stability for threefolds of Picard rank
![]() $1$
in [Reference Jardim, Maciocia and Martinez16], [Reference Maciocia and Jardim22], and [Reference Pretti31].
$1$
in [Reference Jardim, Maciocia and Martinez16], [Reference Maciocia and Jardim22], and [Reference Pretti31].
Notation: For simplicity, we will denote the direct sum
![]() $\mathscr {O}_{\mathbb {P}^3}(m)^{\bigoplus n}$
(
$\mathscr {O}_{\mathbb {P}^3}(m)^{\bigoplus n}$
(
![]() $m,n\in \mathbb {Z}$
) by
$m,n\in \mathbb {Z}$
) by
![]() $\mathscr {O}^n_{\mathbb {P}^3}(m)$
throughout this paper.
$\mathscr {O}^n_{\mathbb {P}^3}(m)$
throughout this paper.
2 Background on Bridgeland stability conditions
2.1 Stability conditions
In this section, we recall some definitions of Bridgeland stability conditions and the constructions on a smooth threefold X over
![]() $\mathbb {C}$
. We refer to the following articles for more details. [Reference Happel, Reiten and Smalø14] for tilting theory, [Reference Bridgeland9], [Reference Bridgeland10], [Reference Huybrechts15], and [Reference Macrì and Schmidt27] for Bridgeland stability conditions, and [Reference Bayer, Macrì and Stellari5], [Reference Bayer, Macrì and Toda6], and [Reference Macrì26] for stability on a threefold.
$\mathbb {C}$
. We refer to the following articles for more details. [Reference Happel, Reiten and Smalø14] for tilting theory, [Reference Bridgeland9], [Reference Bridgeland10], [Reference Huybrechts15], and [Reference Macrì and Schmidt27] for Bridgeland stability conditions, and [Reference Bayer, Macrì and Stellari5], [Reference Bayer, Macrì and Toda6], and [Reference Macrì26] for stability on a threefold.
Definition 2.1. The heart of a bounded t-structure on
![]() $D^b(X)$
is a full additive subcategory
$D^b(X)$
is a full additive subcategory
![]() $\mathscr {A}\subset D^b(X)$
satisfying the following conditions:
$\mathscr {A}\subset D^b(X)$
satisfying the following conditions:
-
(a) For integers
 $i>j$
and
$i>j$
and
 $A,B \in \mathscr {A}$
, we have
$A,B \in \mathscr {A}$
, we have
 $Hom(A[i], B[j])=0$
.
$Hom(A[i], B[j])=0$
. -
(b) For all
 $E\in D^b(X)$
, there exists integers
$E\in D^b(X)$
, there exists integers
 $k_1>\cdots >k_m$
and objects
$k_1>\cdots >k_m$
and objects
 $E_i\in D^b(X)$
,
$E_i\in D^b(X)$
,
 $A_i\in \mathscr {A}$
for
$A_i\in \mathscr {A}$
for
 $i=1,2,\ldots ,m$
and a diagram consisting of distinguished triangles.
$i=1,2,\ldots ,m$
and a diagram consisting of distinguished triangles.
The heart of a bounded t-structure is indeed an abelian category. The proof can be found in [Reference Beilinson, Bernstein and Deligne7] and [Reference Macrì and Schmidt27].
Let
![]() $\mathscr {A}$
be an abelian category.
$\mathscr {A}$
be an abelian category.
![]() $K_0(\mathscr {A})$
,
$K_0(\mathscr {A})$
,
![]() $K_{num}(\mathscr {A})$
denote the K-group and numerical K-group of
$K_{num}(\mathscr {A})$
denote the K-group and numerical K-group of
![]() $\mathscr {A}$
, respectively.
$\mathscr {A}$
, respectively.
Definition 2.2. A linear function
![]() $Z: K_0(\mathscr {A})\to \mathbb {C}$
is called a central charge (or a stability function) if for every
$Z: K_0(\mathscr {A})\to \mathbb {C}$
is called a central charge (or a stability function) if for every
![]() $E\in \mathscr {A}$
,
$E\in \mathscr {A}$
,
![]() $\mathscr {I}m(Z(E))\geq 0$
, and if
$\mathscr {I}m(Z(E))\geq 0$
, and if
![]() $\mathscr {I}m(Z(E))= 0$
then
$\mathscr {I}m(Z(E))= 0$
then
![]() $\mathscr {R}e(Z(E))<0$
.
$\mathscr {R}e(Z(E))<0$
.
With the heart
![]() $\mathscr {A}$
and the central charge Z, we can define the (semi-)stability of an object in
$\mathscr {A}$
and the central charge Z, we can define the (semi-)stability of an object in
![]() $\mathscr {A}$
as follows:
$\mathscr {A}$
as follows:
Definition 2.3. Let
![]() $Z: K_0(\mathscr {A})\to \mathbb {C}$
be a central charge. Define the slope as
$Z: K_0(\mathscr {A})\to \mathbb {C}$
be a central charge. Define the slope as
![]() $\mu :=-{\mathscr {R}e Z}/{\mathscr {I}m Z}$
. Also, define
$\mu :=-{\mathscr {R}e Z}/{\mathscr {I}m Z}$
. Also, define
![]() $\mu :=+\infty $
if
$\mu :=+\infty $
if
![]() $\mathscr {I}m Z=0$
. A non-zero object
$\mathscr {I}m Z=0$
. A non-zero object
![]() $E\in \mathscr {A}$
is called (semi-)stable if for all non-trivial sub-object
$E\in \mathscr {A}$
is called (semi-)stable if for all non-trivial sub-object
![]() $F\subset E \in \mathscr {A}$
,
$F\subset E \in \mathscr {A}$
,
![]() $\mu (F)(\leq ) < \mu (E)$
holds.
$\mu (F)(\leq ) < \mu (E)$
holds.
Fix a finite rank lattice
![]() $\Lambda $
with a fixed norm
$\Lambda $
with a fixed norm
![]() $||\cdot ||$
on it. Let v be a surjective linear map,
$||\cdot ||$
on it. Let v be a surjective linear map,
![]() $ v: K_0(\mathscr {A})\twoheadrightarrow \Lambda $
. For a Bridgeland stability condition, the central charge Z is required to factor through a finite rank lattice, that is,
$ v: K_0(\mathscr {A})\twoheadrightarrow \Lambda $
. For a Bridgeland stability condition, the central charge Z is required to factor through a finite rank lattice, that is,
![]() $Z: K_0(\mathscr {A})\overset {v}{\to }\Lambda \to \mathbb {C}$
.
$Z: K_0(\mathscr {A})\overset {v}{\to }\Lambda \to \mathbb {C}$
.
Next, we define the Harder–Narasimhan property and the support property. A pair
![]() $\sigma =(\mathscr {A}, Z)$
satisfying the Harder–Narasimhan property is sometimes called a pre-stability. It is a stability condition if it also satisfies the support property.
$\sigma =(\mathscr {A}, Z)$
satisfying the Harder–Narasimhan property is sometimes called a pre-stability. It is a stability condition if it also satisfies the support property.
Definition 2.4. A Bridgeland stability condition on X is a pair
![]() $\sigma =(\mathscr {A}, Z)$
consisting of a heart of a bounded t-structure
$\sigma =(\mathscr {A}, Z)$
consisting of a heart of a bounded t-structure
![]() $\mathscr {A}\subset D^b(X)$
, a central charge
$\mathscr {A}\subset D^b(X)$
, a central charge
![]() $Z: \mathscr {A}\to \Lambda \to \mathbb {C}$
, and two more properties as follows:
$Z: \mathscr {A}\to \Lambda \to \mathbb {C}$
, and two more properties as follows:
-
(a) Every object
 $E\in \mathscr {A}$
satisfies the Harder–Narasimhan property:
$E\in \mathscr {A}$
satisfies the Harder–Narasimhan property:E has a finite filtration
 $0=E_0\subset E_1,\subset \ldots , \subset E_n=E$
, in
$0=E_0\subset E_1,\subset \ldots , \subset E_n=E$
, in
 $\mathscr {A}$
such that the quotients
$\mathscr {A}$
such that the quotients
 $F_i:=E_i/E_{i-1}$
are semi-stable and their slopes are strictly decreasing, that is,
$F_i:=E_i/E_{i-1}$
are semi-stable and their slopes are strictly decreasing, that is,
 $\mu (v(F_1))>\mu (v(F_2))>\cdots >\mu (v(F_n))$
.
$\mu (v(F_1))>\mu (v(F_2))>\cdots >\mu (v(F_n))$
. -
(b)
 $\sigma $
satisfies the support property:
$\sigma $
satisfies the support property:For a fixed norm
 $||\cdot ||$
on
$||\cdot ||$
on
 $\Lambda $
, there exists a
$\Lambda $
, there exists a
 $C>0$
such that for all semi-stable object
$C>0$
such that for all semi-stable object
 $E\in \mathscr {A}$
,
$E\in \mathscr {A}$
,
 $||v(E)||\leq C|Z(E)|$
holds.
$||v(E)||\leq C|Z(E)|$
holds.
The support property can also be defined by a bilinear form Q on the lattice (see [Reference Bayer, Macrì and Stellari5], [Reference Piyaratne and Toda30]).
Lemma 2.5. A pre-stability condition
![]() $\sigma =(\mathscr {A}, Z)$
satisfies the support properly if and only if there is a bilinear form Q on
$\sigma =(\mathscr {A}, Z)$
satisfies the support properly if and only if there is a bilinear form Q on
![]() $\Lambda \otimes \mathbb {R}$
such that:
$\Lambda \otimes \mathbb {R}$
such that:
-
(a) All
 $\sigma $
-semistable objects
$\sigma $
-semistable objects
 $E\in \mathscr {A}$
satisfy the inequality
$E\in \mathscr {A}$
satisfy the inequality
 $Q(v(E),v(E))\geq 0$
.
$Q(v(E),v(E))\geq 0$
. -
(b) All non-zero vectors
 $v\in \Lambda \otimes \mathbb {R}$
with
$v\in \Lambda \otimes \mathbb {R}$
with
 $Z(v)=0$
satisfy
$Z(v)=0$
satisfy
 $Q(v,v)<0$
.
$Q(v,v)<0$
.
Remark 2.6. We say that a pair
![]() $\sigma =(\mathscr {A}, Z)$
is a weak stability condition if Z is a weak central charge in the sense that
$\sigma =(\mathscr {A}, Z)$
is a weak stability condition if Z is a weak central charge in the sense that
![]() $\mathscr {I}m Z\geq 0$
, and if
$\mathscr {I}m Z\geq 0$
, and if
![]() $\mathscr {I}m Z=0,$
then
$\mathscr {I}m Z=0,$
then
![]() $\mathscr {R}e Z\leq 0$
.
$\mathscr {R}e Z\leq 0$
.
The Bridgeland stability condition can be equivalently defined on a triangulated category as well (see [Reference Bridgeland9], [Reference Macrì and Schmidt27]).
Definition 2.7. A slicing
![]() $\mathscr {P}$
of
$\mathscr {P}$
of
![]() $D^b(X)$
is a collection of subcategories
$D^b(X)$
is a collection of subcategories
![]() $\mathscr {P}(\phi )\subset D^b(X)$
for every
$\mathscr {P}(\phi )\subset D^b(X)$
for every
![]() $\phi \in \mathbb {R} $
, such that:
$\phi \in \mathbb {R} $
, such that:
-
(a)
 $\mathscr {P}(\phi )[1]=\mathscr {P}(\phi +1)$
.
$\mathscr {P}(\phi )[1]=\mathscr {P}(\phi +1)$
. -
(b) For
 $A\in \mathscr {P}(\phi _1)$
, and
$A\in \mathscr {P}(\phi _1)$
, and
 $B\in \mathscr {P}(\phi _2)$
, if
$B\in \mathscr {P}(\phi _2)$
, if
 $\phi _1>\phi _2,$
then
$\phi _1>\phi _2,$
then
 $Hom(A,B)=0$
.
$Hom(A,B)=0$
. -
(c) For any
 $E\in D^b(X)$
, there are real numbers
$E\in D^b(X)$
, there are real numbers
 $\phi _1>\cdots >\phi _m$
and distinguished triangles in
$\phi _1>\cdots >\phi _m$
and distinguished triangles in
 $D^b(X):$
such that
$D^b(X):$
such that
 $A_i \in \mathscr {P}(\phi _i)$
.
$A_i \in \mathscr {P}(\phi _i)$
.
The last property is the Harder–Narasimhan filtration of E in
![]() $D^b(X)$
.
$D^b(X)$
.
Definition 2.8. A Bridgeland stability condition on
![]() $D^b(X)$
is a pair
$D^b(X)$
is a pair
![]() $\sigma =(\mathscr {P}, Z),$
where
$\sigma =(\mathscr {P}, Z),$
where
![]() $\mathscr {P}$
is a slicing,
$\mathscr {P}$
is a slicing,
![]() $Z: \Lambda \to \mathbb {C}$
is a linear map (the central charge), satisfying the following two properties:
$Z: \Lambda \to \mathbb {C}$
is a linear map (the central charge), satisfying the following two properties:
-
1. For any non-zero
 $E\in \mathscr {P}(\phi )$
, we have
$E\in \mathscr {P}(\phi )$
, we have  $$ \begin{align*}Z(v(E))\in \mathbb{R}_{>0}\cdot e^{\sqrt{-1}\pi\phi}.\end{align*} $$
$$ \begin{align*}Z(v(E))\in \mathbb{R}_{>0}\cdot e^{\sqrt{-1}\pi\phi}.\end{align*} $$
-
2. (Support property) There exists a constant
 $C>0$
, such that
$C>0$
, such that
 $||v(E)||\leq C|Z(E)|$
for any
$||v(E)||\leq C|Z(E)|$
for any
 $0\neq E \in \mathscr {P}(\phi ), \phi \in \mathbb {R}$
.
$0\neq E \in \mathscr {P}(\phi ), \phi \in \mathbb {R}$
.
Let
![]() $\mathscr {A}:=\mathscr {P}((0,1])$
be the extension closure of slices
$\mathscr {A}:=\mathscr {P}((0,1])$
be the extension closure of slices
![]() $\left \{\mathscr {P}(\phi ):\phi \in (0,1]\right \}$
. The category
$\left \{\mathscr {P}(\phi ):\phi \in (0,1]\right \}$
. The category
![]() $\mathscr {A}$
turns out to be the heart of a bounded t-structure. Moreover, the two stability conditions,
$\mathscr {A}$
turns out to be the heart of a bounded t-structure. Moreover, the two stability conditions,
![]() $\sigma _1=(\mathscr {P}, Z)$
and
$\sigma _1=(\mathscr {P}, Z)$
and
![]() $\sigma _2=(\mathscr {A},Z)$
are equivalent (see [Reference Bridgeland9, Prop. 5.3]).
$\sigma _2=(\mathscr {A},Z)$
are equivalent (see [Reference Bridgeland9, Prop. 5.3]).
2.2 Construction of stability conditions on a smooth threefold
In this subsection, we recall a construction of stability conditions, the tilting approach, and some known results on a smooth variety up to dimension
![]() $3$
.
$3$
.
We start by defining the twisted Chern character.
Definition 2.9. For any
![]() $B\in NS_{\mathbb {R}}(\mathbb {P}^3)$
, define the twisted Chern characters as
$B\in NS_{\mathbb {R}}(\mathbb {P}^3)$
, define the twisted Chern characters as
![]() $ch^B:=ch\cdot e^{-B}$
.
$ch^B:=ch\cdot e^{-B}$
.
By expanding
![]() $ch\cdot e^{-B}$
, we have the first few twisted Chern characters as:
$ch\cdot e^{-B}$
, we have the first few twisted Chern characters as:
 $$ \begin{align*} ch^B_0=&ch_0,\\ ch^B_1=&ch_1-B\cdot ch_0,\\ ch^B_2=&ch_2-B\cdot ch_1+\frac{B^2}{2}ch_0,\\ ch^B_3=&ch_3-B\cdot ch_2+\frac{B^2}{2}ch_1-\frac{B^3}{6}ch_0,\\ \cdots. \end{align*} $$
$$ \begin{align*} ch^B_0=&ch_0,\\ ch^B_1=&ch_1-B\cdot ch_0,\\ ch^B_2=&ch_2-B\cdot ch_1+\frac{B^2}{2}ch_0,\\ ch^B_3=&ch_3-B\cdot ch_2+\frac{B^2}{2}ch_1-\frac{B^3}{6}ch_0,\\ \cdots. \end{align*} $$
A (numerical) stability condition on a smooth curve C is essentially the pair
![]() $\sigma =(Coh(C), Z=-deg+i\cdot rk)$
(see [Reference Bridgeland9], [Reference Macrì25]), which looks like the Mumford stability for vector bundles on curves.
$\sigma =(Coh(C), Z=-deg+i\cdot rk)$
(see [Reference Bridgeland9], [Reference Macrì25]), which looks like the Mumford stability for vector bundles on curves.
For a smooth surface X,
![]() $Coh(X)$
can no longer be used as the heart to define stability conditions. In fact, for dim
$Coh(X)$
can no longer be used as the heart to define stability conditions. In fact, for dim
![]() $X\geq 2$
, the pair
$X\geq 2$
, the pair
![]() $(Coh(X), Z)$
is not a stability condition for any central charge Z. Proof can be found in [Reference Toda34, Lem. 2.7]. To obtain the correct heart, we tilt the category
$(Coh(X), Z)$
is not a stability condition for any central charge Z. Proof can be found in [Reference Toda34, Lem. 2.7]. To obtain the correct heart, we tilt the category
![]() $Coh(X)$
.
$Coh(X)$
.
For the rest of this subsection, we will focus on the construction on
![]() $\mathbb {P}^3$
. A similar approach works for some other smooth varieties as well. ([Reference Arcara and Bertram2], [Reference Bayer and Macrì4], and [Reference Bridgeland10] for surfaces, [Reference Schmidt32] for quadric threefolds, [Reference Bayer, Macrì and Stellari5], [Reference Maciocia and Piyaratne23], and [Reference Maciocia and Piyaratne24] for abelian threefolds, [Reference Bernardara, Macrì, Schmidt and Zhao8] and [Reference Li20] for Fano threefolds, and [Reference Bayer, Macrì and Toda6] for a conjectural construction on all smooth varieties.)
$\mathbb {P}^3$
. A similar approach works for some other smooth varieties as well. ([Reference Arcara and Bertram2], [Reference Bayer and Macrì4], and [Reference Bridgeland10] for surfaces, [Reference Schmidt32] for quadric threefolds, [Reference Bayer, Macrì and Stellari5], [Reference Maciocia and Piyaratne23], and [Reference Maciocia and Piyaratne24] for abelian threefolds, [Reference Bernardara, Macrì, Schmidt and Zhao8] and [Reference Li20] for Fano threefolds, and [Reference Bayer, Macrì and Toda6] for a conjectural construction on all smooth varieties.)
We start with the first tilt of
![]() $Coh(\mathbb {P}^3)$
. Let H be the ample class
$Coh(\mathbb {P}^3)$
. Let H be the ample class
![]() $\mathscr {O}_{\mathbb {P}^3}(1)$
on
$\mathscr {O}_{\mathbb {P}^3}(1)$
on
![]() $\mathbb {P}^3$
.
$\mathbb {P}^3$
.
![]() $B\in NS_{\mathbb {R}}(\mathbb {P}^3)$
is a multiple of H,
$B\in NS_{\mathbb {R}}(\mathbb {P}^3)$
is a multiple of H,
![]() $B=\beta H$
. For simplicity, we write
$B=\beta H$
. For simplicity, we write
![]() $ch^{\beta }$
instead of
$ch^{\beta }$
instead of
![]() $ch^{\beta H}$
.
$ch^{\beta H}$
.
Define the slope function on
![]() $Coh(\mathbb {P}^3)$
as
$Coh(\mathbb {P}^3)$
as
 $$ \begin{align*}\mu_{\beta}:=\frac{ch^{\beta}_1}{ch_0}=\frac{ch_1}{ch_0}-\beta.\end{align*} $$
$$ \begin{align*}\mu_{\beta}:=\frac{ch^{\beta}_1}{ch_0}=\frac{ch_1}{ch_0}-\beta.\end{align*} $$
If
![]() $ch_0=0$
, then define the slope
$ch_0=0$
, then define the slope
![]() $\mu _{\beta }$
to be
$\mu _{\beta }$
to be
![]() $+\infty $
. The slope function defines the following torsion pair:
$+\infty $
. The slope function defines the following torsion pair:
A new heart of a bounded t-structure is defined as the extension closure
![]() $Coh^{\beta }(\mathbb {P}^3):=\left < \mathscr {F}_{\beta }[1], \mathscr {T}_{\beta } \right>$
. Let
$Coh^{\beta }(\mathbb {P}^3):=\left < \mathscr {F}_{\beta }[1], \mathscr {T}_{\beta } \right>$
. Let
![]() $\Gamma $
be the lattice
$\Gamma $
be the lattice
![]() $\Gamma :=(H^3ch_0,H^2ch_1,Hch_2)$
. Define a linear function
$\Gamma :=(H^3ch_0,H^2ch_1,Hch_2)$
. Define a linear function
![]() $Z_{\alpha ,\beta }: \Gamma \to \mathbb {C}$
as
$Z_{\alpha ,\beta }: \Gamma \to \mathbb {C}$
as
 $\displaystyle Z_{\alpha , \beta }:=-Hch^{\beta }_2+\frac {\alpha ^2}{2}H^3ch_0+i\cdot H^2ch^{\beta }_1$
, in which
$\displaystyle Z_{\alpha , \beta }:=-Hch^{\beta }_2+\frac {\alpha ^2}{2}H^3ch_0+i\cdot H^2ch^{\beta }_1$
, in which
![]() $\alpha \in \mathbb {R}_{\geq 0}$
. The pair
$\alpha \in \mathbb {R}_{\geq 0}$
. The pair
![]() $(Coh^{\beta }(\mathbb {P}^3), Z_{\alpha , \beta })$
is called a tilt stability on
$(Coh^{\beta }(\mathbb {P}^3), Z_{\alpha , \beta })$
is called a tilt stability on
![]() $\mathbb {P}^3$
(see [Reference Bayer, Macrì and Toda6]). It is a weak stability condition since
$\mathbb {P}^3$
(see [Reference Bayer, Macrì and Toda6]). It is a weak stability condition since
![]() $Z_{\alpha , \beta }$
maps some non-zero objects (for instance, skyscraper sheaves) to
$Z_{\alpha , \beta }$
maps some non-zero objects (for instance, skyscraper sheaves) to
![]() $0$
.
$0$
.
Let
 $\displaystyle \nu _{\alpha , \beta }:=\frac {Hch^{\beta }_2-\frac {\alpha ^2}{2}H^3ch_0}{H^2ch^{\beta }_1}$
be the slope function defined by
$\displaystyle \nu _{\alpha , \beta }:=\frac {Hch^{\beta }_2-\frac {\alpha ^2}{2}H^3ch_0}{H^2ch^{\beta }_1}$
be the slope function defined by
![]() $Z_{\alpha , \beta }$
. Again, define
$Z_{\alpha , \beta }$
. Again, define
![]() $\nu _{\alpha , \beta }=+\infty $
if
$\nu _{\alpha , \beta }=+\infty $
if
![]() ${H^2ch^{\beta }_1}=0$
. We have the following Bogomolov inequality for tilt-stable objects.
${H^2ch^{\beta }_1}=0$
. We have the following Bogomolov inequality for tilt-stable objects.
Theorem 2.10 ([Reference Bayer, Macrì and Toda6, Cor. 7.3.2])
For any
![]() $\nu _{\alpha , \beta }$
semistable objects
$\nu _{\alpha , \beta }$
semistable objects
![]() $E\in Coh^{\beta }(X)$
, the following inequality holds:
$E\in Coh^{\beta }(X)$
, the following inequality holds:
For smooth surfaces, a single tilt would be sufficient to define stability conditions (see [Reference Arcara and Bertram2], [Reference Bayer and Macrì4], [Reference Bridgeland10]). For a threefold, we need an additional tilt.
Define a torsion pair on
![]() $Coh^{\beta }(\mathbb {P}^3)$
as:
$Coh^{\beta }(\mathbb {P}^3)$
as:
Similarly, we obtain a heart of a bounded t-structure as
![]() $\mathscr {A}^{\alpha , \beta }(\mathbb {P}^3):=\left < \mathscr {F}_{\alpha ,\beta }[1], \mathscr {T}_{\alpha ,\beta } \right>$
. For any
$\mathscr {A}^{\alpha , \beta }(\mathbb {P}^3):=\left < \mathscr {F}_{\alpha ,\beta }[1], \mathscr {T}_{\alpha ,\beta } \right>$
. For any
![]() $s>0$
, the central charge and the bilinear form Q defining the support property are given as follows: (see [Reference Bayer, Macrì and Toda6], [Reference Macrì26], [Reference Schmidt33])
$s>0$
, the central charge and the bilinear form Q defining the support property are given as follows: (see [Reference Bayer, Macrì and Toda6], [Reference Macrì26], [Reference Schmidt33])
 $$\begin{align*}Z_{\alpha, \beta, s}:= & -ch^{\beta}_3+\left(s+\frac{1}{6}\right)\alpha^2H^2ch^{\beta}_1+i\cdot\left(Hch^{\beta}_2-\frac{\alpha^2}{2}H^3ch^{\beta}_0\right)\\Q_{\alpha, \beta, K}(E)= & ((H^2ch_1(E))^2-2(H^3ch_0(E))(Hch_2(E)))(K\alpha^2+\beta^2)+\\&(6(H^3ch_0(E))(Hch_3(E))-2(H^2ch_1(E))(Hch_2(E)))\beta-\\&6(H^2ch_1(E))ch_3(E)+4(Hch_2(E))^2 \end{align*}$$
$$\begin{align*}Z_{\alpha, \beta, s}:= & -ch^{\beta}_3+\left(s+\frac{1}{6}\right)\alpha^2H^2ch^{\beta}_1+i\cdot\left(Hch^{\beta}_2-\frac{\alpha^2}{2}H^3ch^{\beta}_0\right)\\Q_{\alpha, \beta, K}(E)= & ((H^2ch_1(E))^2-2(H^3ch_0(E))(Hch_2(E)))(K\alpha^2+\beta^2)+\\&(6(H^3ch_0(E))(Hch_3(E))-2(H^2ch_1(E))(Hch_2(E)))\beta-\\&6(H^2ch_1(E))ch_3(E)+4(Hch_2(E))^2 \end{align*}$$
for some
![]() $K\in [1,6s+1)$
.
$K\in [1,6s+1)$
.
Theorem 2.11 [Reference Bayer, Macrì and Toda6], [Reference Macrì26]
![]() $(\mathscr {A}^{\alpha ,\beta }((\mathbb {P}^3)), Z_{\alpha , \beta , K})$
is a Bridgeland stability condition on
$(\mathscr {A}^{\alpha ,\beta }((\mathbb {P}^3)), Z_{\alpha , \beta , K})$
is a Bridgeland stability condition on
![]() $\mathbb {P}^3$
for all
$\mathbb {P}^3$
for all
![]() $\beta \in \mathbb {R}$
,
$\beta \in \mathbb {R}$
,
![]() $\alpha ,s>0$
, and
$\alpha ,s>0$
, and
![]() $K\in [1,6s+1)$
. The support property is satisfied with respect to
$K\in [1,6s+1)$
. The support property is satisfied with respect to
![]() $Q_{\alpha , \beta , K}$
.
$Q_{\alpha , \beta , K}$
.
Lastly, for a smooth threefold X and a given class
![]() $v\in K_{num}(X)$
, there is the following continuity result.
$v\in K_{num}(X)$
, there is the following continuity result.
Theorem 2.12 [Reference Bayer, Macrì and Stellari5, Prop. 8.10]
The function
![]() $\displaystyle \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}_{>0} \to Stab(X,v)$
defined by
$\displaystyle \mathbb {R}_{>0}\times \mathbb {R}\times \mathbb {R}_{>0} \to Stab(X,v)$
defined by
![]() $\displaystyle (\alpha , \beta , s) \mapsto (\mathscr {A}^{\alpha , \beta }(X), Z_{\alpha , \beta , s})$
is continuous.
$\displaystyle (\alpha , \beta , s) \mapsto (\mathscr {A}^{\alpha , \beta }(X), Z_{\alpha , \beta , s})$
is continuous.
3 The Euler stability
In this section, we start with defining the Euler stability on
![]() $\mathbb {P}^n$
based on [1]. And then in §
$\mathbb {P}^n$
based on [1]. And then in §
![]() $3.2$
, we focus on the three-dimensional case and show that the Euler stability on
$3.2$
, we focus on the three-dimensional case and show that the Euler stability on
![]() $\mathbb {P}^3$
can also be defined by the tilting approach.
$\mathbb {P}^3$
can also be defined by the tilting approach.
3.1 The Euler stability condition on
 $\mathbb {P}^n$
$\mathbb {P}^n$
We start with defining the category.
Definition 3.1. Define
![]() $\mathscr {A}_m:=\left < \mathscr {O}_{\mathbb {P}^n}(-m-n)[n], \mathscr {O}_{\mathbb {P}^n}(-m-n+1)[n-1], \ldots , \mathscr {O}_{\mathbb {P}^n}(-m) \right>$
(
$\mathscr {A}_m:=\left < \mathscr {O}_{\mathbb {P}^n}(-m-n)[n], \mathscr {O}_{\mathbb {P}^n}(-m-n+1)[n-1], \ldots , \mathscr {O}_{\mathbb {P}^n}(-m) \right>$
(
![]() $m\in \mathbb {Z}$
) to be the extension closure of the exceptional collection
$m\in \mathbb {Z}$
) to be the extension closure of the exceptional collection
![]() $\{ \mathscr {O}_{\mathbb {P}^n}(-m-n)[n], \mathscr {O}_{\mathbb {P}^n}(-m-n+1)[n-1], \ldots , \mathscr {O}_{\mathbb {P}^n}(-m) \}$
on
$\{ \mathscr {O}_{\mathbb {P}^n}(-m-n)[n], \mathscr {O}_{\mathbb {P}^n}(-m-n+1)[n-1], \ldots , \mathscr {O}_{\mathbb {P}^n}(-m) \}$
on
![]() $\mathbb {P}^n$
.
$\mathbb {P}^n$
.
A general element
![]() $E \in \mathscr {A}_m$
is a complex:
$E \in \mathscr {A}_m$
is a complex:
where
![]() $a_i\in \mathbb {Z}_{\geq 0}$
for
$a_i\in \mathbb {Z}_{\geq 0}$
for
![]() $i=0, -1, \ldots , -n$
. The (
$i=0, -1, \ldots , -n$
. The (
![]() $n+$
1)-tuple
$n+$
1)-tuple
![]() $[a_{-n}, \ldots , a_0]$
is called the dimension vector of E in
$[a_{-n}, \ldots , a_0]$
is called the dimension vector of E in
![]() $\mathscr {A}_m$
. We write the dimension vector as
$\mathscr {A}_m$
. We write the dimension vector as
![]() $\underline {dim}(E):=[a_{-n}, \ldots , a_0]$
.
$\underline {dim}(E):=[a_{-n}, \ldots , a_0]$
.
Next, we define the central charge to be
![]() $Z_t:=\chi ^{\prime }_t+i\cdot \chi _t$
, where
$Z_t:=\chi ^{\prime }_t+i\cdot \chi _t$
, where
![]() $\chi _t$
is the twisted Euler characteristic
$\chi _t$
is the twisted Euler characteristic
 $$ \begin{align*}\chi_t(E)=\int_{\mathbb{P}^n}ch(E)\cdot ch(\mathscr{O}_{\mathbb{P}^n})\cdot e^{tH}\cdot Td(\mathbb{P}^n)\end{align*} $$
$$ \begin{align*}\chi_t(E)=\int_{\mathbb{P}^n}ch(E)\cdot ch(\mathscr{O}_{\mathbb{P}^n})\cdot e^{tH}\cdot Td(\mathbb{P}^n)\end{align*} $$
and
![]() $\chi ^{\prime }_t(E)$
is the derivative of
$\chi ^{\prime }_t(E)$
is the derivative of
![]() $\chi _t(E)$
with respect to t.
$\chi _t(E)$
with respect to t.
Proposition 3.2. The pair
![]() $\sigma _t:=(\mathscr {A}_m, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
defines a pre-stability condition for all
$\sigma _t:=(\mathscr {A}_m, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
defines a pre-stability condition for all
![]() $m\in \mathbb {Z}$
,
$m\in \mathbb {Z}$
,
![]() $t\in (m-1,m]$
.
$t\in (m-1,m]$
.
Proof. Firstly, the pair
![]() $(\mathscr {A}_m, Z_t)$
satisfies the Harder–Narasimhan property because
$(\mathscr {A}_m, Z_t)$
satisfies the Harder–Narasimhan property because
![]() $\mathscr {A}_m$
is Artinian, meaning that every descending chain in
$\mathscr {A}_m$
is Artinian, meaning that every descending chain in
![]() $\mathscr {A}_m$
terminates. We prove next that
$\mathscr {A}_m$
terminates. We prove next that
![]() $Z_t$
maps every object in
$Z_t$
maps every object in
![]() $\mathscr {A}_m$
to the upper half-plane. This follows from the observation that the polynomial
$\mathscr {A}_m$
to the upper half-plane. This follows from the observation that the polynomial
![]() $\chi _t(\mathscr {O}_{\mathbb {P}^n})$
has simple roots
$\chi _t(\mathscr {O}_{\mathbb {P}^n})$
has simple roots
![]() $t= -1,\ldots ,-n$
. We show the details below.
$t= -1,\ldots ,-n$
. We show the details below.
It is sufficient to check that
![]() $Z_t$
maps the generators
$Z_t$
maps the generators
![]() $\left \{ \mathscr {O}_{\mathbb {P}^n}(-m-n)[n], \ldots , \mathscr {O}_{\mathbb {P}^n}(-m)\right \}$
of
$\left \{ \mathscr {O}_{\mathbb {P}^n}(-m-n)[n], \ldots , \mathscr {O}_{\mathbb {P}^n}(-m)\right \}$
of
![]() $\mathscr {A}_m$
to the upper plane. More precisely, we will show that
$\mathscr {A}_m$
to the upper plane. More precisely, we will show that
![]() $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i]) \geq 0$
, and if
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i]) \geq 0$
, and if
![]() $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i])=0$
, then
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i])=0$
, then
![]() $\chi ^{\prime }_t(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i])<0$
.
$\chi ^{\prime }_t(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i])<0$
.
The polynomial
![]() $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))=(t+n-m)(t+n-m-1)\cdots (t+1-m)/n!$
has simple roots
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))=(t+n-m)(t+n-m-1)\cdots (t+1-m)/n!$
has simple roots
![]() $t=m-1, m-2, \ldots , m-n$
. The sign of
$t=m-1, m-2, \ldots , m-n$
. The sign of
![]() $\chi _t$
is given as follows:
$\chi _t$
is given as follows:
-
1.
 $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))>0$
for
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))>0$
for $ \begin {array}{lc} t\in (m-n,m-n+1) ,\ldots ,(m-3,m-2), (m-1,\infty ),& \text {if}\quad n= \text {even,} \\ t\in (m-n+1,m-n+2) ,\ldots ,(m-3,m-2), (m-1,\infty ), & \text {if}\quad n= \text {odd.} \end {array} $
$ \begin {array}{lc} t\in (m-n,m-n+1) ,\ldots ,(m-3,m-2), (m-1,\infty ),& \text {if}\quad n= \text {even,} \\ t\in (m-n+1,m-n+2) ,\ldots ,(m-3,m-2), (m-1,\infty ), & \text {if}\quad n= \text {odd.} \end {array} $
-
2.
 $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))<0$
for
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))<0$
for $ \begin {array}{lc} t\in (m-n+1,m-n+2) ,\ldots ,(m-4,m-3), (m-2,m-1),& \text {if}\quad n= \text {even,} \\ t\in (m-n,m-n+1) ,\ldots ,(m-4,m-3), (m-2,m-1), & \text {if}\quad n= \text {odd.} \end {array} $
$ \begin {array}{lc} t\in (m-n+1,m-n+2) ,\ldots ,(m-4,m-3), (m-2,m-1),& \text {if}\quad n= \text {even,} \\ t\in (m-n,m-n+1) ,\ldots ,(m-4,m-3), (m-2,m-1), & \text {if}\quad n= \text {odd.} \end {array} $
-
• For
 $\mathscr {O}_{\mathbb {P}^n}(-m)$
, we have
$\mathscr {O}_{\mathbb {P}^n}(-m)$
, we have
 $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))>0$
when
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m))>0$
when
 $t\in (m-1,m]$
.
$t\in (m-1,m]$
. -
• For
 $\mathscr {O}_{\mathbb {P}^n}(-m-1)[1]$
,
$\mathscr {O}_{\mathbb {P}^n}(-m-1)[1]$
,
 $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-1)[1]=-\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-1))=-\chi _{t-1}(\mathscr {O}_{\mathbb {P}^n}(-m))>0$
when
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-1)[1]=-\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-1))=-\chi _{t-1}(\mathscr {O}_{\mathbb {P}^n}(-m))>0$
when
 $t\in (m-1,m)$
.
$t\in (m-1,m)$
.
 $\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-1)[1]=0$
when
$\chi _t(\mathscr {O}_{\mathbb {P}^n}(-m-1)[1]=0$
when
 $t=m$
, and in this case, we have
$t=m$
, and in this case, we have
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-1)[1])=-\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-1))<0$
.
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-1)[1])=-\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-1))<0$
. -
• For
 $\mathscr {O}_{\mathbb {P}^n}(-m-i)[i]$
,
$\mathscr {O}_{\mathbb {P}^n}(-m-i)[i]$
,
 $i=2,3,\ldots ,n$
, using the sign of
$i=2,3,\ldots ,n$
, using the sign of
 $\chi _t$
above it is straightforward to check that
$\chi _t$
above it is straightforward to check that  $$\begin{align*}\begin{cases} \chi_t(\mathscr{O}_{\mathbb{P}^n}(-m-i)[i])>0, &\ \text{when} \ t\in (m-1,m),\\ \chi_t(\mathscr{O}_{\mathbb{P}^n}(-m-i)[i])=0, &\ \text{when}\ t=m.\\ \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} \chi_t(\mathscr{O}_{\mathbb{P}^n}(-m-i)[i])>0, &\ \text{when} \ t\in (m-1,m),\\ \chi_t(\mathscr{O}_{\mathbb{P}^n}(-m-i)[i])=0, &\ \text{when}\ t=m.\\ \end{cases} \end{align*}$$
The sign of
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i))$
is alternating for
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i))$
is alternating for
 $i=1,2,\ldots ,n$
. So the sign of
$i=1,2,\ldots ,n$
. So the sign of
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i))$
and
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i))$
and
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m))$
are different by
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m))$
are different by
 $(-1)^i$
. On the other hand, the shift by
$(-1)^i$
. On the other hand, the shift by
 $[i]$
will change the sign of
$[i]$
will change the sign of
 $\chi ^{\prime }_t(\mathscr {O}_{\mathbb {P}^n}(-m-i))$
by
$\chi ^{\prime }_t(\mathscr {O}_{\mathbb {P}^n}(-m-i))$
by
 $(-1)^i$
. So the sign of
$(-1)^i$
. So the sign of
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i])$
and
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i)[i])$
and
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m))$
are different by
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m))$
are different by
 $(-1)^i \cdot (-1)^i=1$
. This implies that the signs of
$(-1)^i \cdot (-1)^i=1$
. This implies that the signs of
 $\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i))[i]$
are the same for all
$\chi ^{\prime }_m(\mathscr {O}_{\mathbb {P}^n}(-m-i))[i]$
are the same for all
 $i=0,1,\ldots ,n$
, and they are all negative.
$i=0,1,\ldots ,n$
, and they are all negative.
The proof above indicates that the stability conditions can be extended to the following continuous family.
Definition 3.3. Define
![]() $\mathscr {A}_t:=\mathscr {A}_{\lceil t\rceil }$
(
$\mathscr {A}_t:=\mathscr {A}_{\lceil t\rceil }$
(
![]() $t\in \mathbb {R}$
), where “
$t\in \mathbb {R}$
), where “
![]() $\lceil t \rceil $
” is the roundup of t to the closest integer.
$\lceil t \rceil $
” is the roundup of t to the closest integer.
Corollary 3.4. The pair
![]() $\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
defines a family of pre-stability conditions on
$\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
defines a family of pre-stability conditions on
![]() $\mathbb {P}^n$
for
$\mathbb {P}^n$
for
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
Next, we show that
![]() $\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
satisfies the support property, and then
$\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
satisfies the support property, and then
![]() $\sigma _t$
will be a stability condition. We will show in the next proposition the case of
$\sigma _t$
will be a stability condition. We will show in the next proposition the case of
![]() $\mathbb {P}^3$
when
$\mathbb {P}^3$
when
![]() $t\in (0,1]$
. The proof for all
$t\in (0,1]$
. The proof for all
![]() $\mathbb {P}^n$
(
$\mathbb {P}^n$
(
![]() $n\geq 4$
) and
$n\geq 4$
) and
![]() $t\in \mathbb {R}$
is analogous.
$t\in \mathbb {R}$
is analogous.
Proposition 3.5. The pre-stability condition
![]() $\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
on
$\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
on
![]() $\mathbb {P}^3$
satisfies the support property for
$\mathbb {P}^3$
satisfies the support property for
![]() $t\in (0,1]$
.
$t\in (0,1]$
.
Proof. By definition, we need to find numbers
![]() $C_t>0$
, such that
$C_t>0$
, such that
 $\displaystyle \frac {|Z_t(E)|}{||v(E)||}>C_t$
for any
$\displaystyle \frac {|Z_t(E)|}{||v(E)||}>C_t$
for any
![]() $t\in (0,1]$
. The category is
$t\in (0,1]$
. The category is
![]() $\mathscr {A}_1$
which is generated by these objects:
$\mathscr {A}_1$
which is generated by these objects:

Figure 1 Support property.
Observe that for any
![]() $t\in (0,1]$
, the linear span
$t\in (0,1]$
, the linear span
![]() $U:=\{a_1Z_t(u_1)+a_2Z_t(u_2)+a_3Z_t(u_3)+a_4Z_t(u_4)| a_i\geq 0\}$
is not the entire upper half-plane. For instance, Figure 1 shows the case when
$U:=\{a_1Z_t(u_1)+a_2Z_t(u_2)+a_3Z_t(u_3)+a_4Z_t(u_4)| a_i\geq 0\}$
is not the entire upper half-plane. For instance, Figure 1 shows the case when
![]() $t=0.9$
. We abuse the notation in Figure 1 that
$t=0.9$
. We abuse the notation in Figure 1 that
![]() $u_1,\ldots , u_4$
denote the images
$u_1,\ldots , u_4$
denote the images
![]() $Z_t(u_1), \ldots , Z_t(u_4)$
in the upper half-plane when
$Z_t(u_1), \ldots , Z_t(u_4)$
in the upper half-plane when
![]() $t=0.9$
. The two black rays are passing through
$t=0.9$
. The two black rays are passing through
![]() $Z(u_1)$
(the smallest phase among
$Z(u_1)$
(the smallest phase among
![]() $Z_t(u_1), \ldots , Z_t(u_4)$
) and
$Z_t(u_1), \ldots , Z_t(u_4)$
) and
![]() $Z(u_4)$
(the biggest phase). So for
$Z(u_4)$
(the biggest phase). So for
![]() $t=0.9$
and any object
$t=0.9$
and any object
![]() $u\in \mathscr {A}_t$
,
$u\in \mathscr {A}_t$
,
![]() $Z_t(u)$
must be above the two black rays. It is evident that the region above the black rays does not fill the entire upper half-plane. So we can find a line
$Z_t(u)$
must be above the two black rays. It is evident that the region above the black rays does not fill the entire upper half-plane. So we can find a line
![]() $\Gamma _t$
(the dotted line in Figure 1) such that all the objects in U have a non-zero projection to
$\Gamma _t$
(the dotted line in Figure 1) such that all the objects in U have a non-zero projection to
![]() $\Gamma _t$
. For any object
$\Gamma _t$
. For any object
 $\displaystyle u=\sum _{i=1}^4 a_iu_i$
(
$\displaystyle u=\sum _{i=1}^4 a_iu_i$
(
![]() $a_i\geq 0$
), denote its projection to
$a_i\geq 0$
), denote its projection to
![]() $\Gamma _t$
by
$\Gamma _t$
by
![]() $p_t(u)$
, and let
$p_t(u)$
, and let
![]() $a_t:=min \{ |Z_t(p_t(u_i))| :i=1,2,3,4\}$
,
$a_t:=min \{ |Z_t(p_t(u_i))| :i=1,2,3,4\}$
,
![]() $b_t:=max \{ ||(u_i)|| :i=1,2,3,4\}$
.
$b_t:=max \{ ||(u_i)|| :i=1,2,3,4\}$
.
 $$ \begin{align*}\frac{|Z_t(u)|}{||v(u)||}=\frac{|Z_t(\sum_{i=1}^4 a_iu_i)|}{||\sum_{i=1}^4 a_iu_i||}>\frac{|\sum_{i=1}^4a_ip_t(u_i)|}{\sum_{i=1}^4a_i||u_i||}\geq \frac{(\sum_{i=1}^4a_1)a_t}{(\sum_{i=1}^4a_1)b_t}=\frac{a_t}{b_t}=:C_t>0.\\[-47pt]\end{align*} $$
$$ \begin{align*}\frac{|Z_t(u)|}{||v(u)||}=\frac{|Z_t(\sum_{i=1}^4 a_iu_i)|}{||\sum_{i=1}^4 a_iu_i||}>\frac{|\sum_{i=1}^4a_ip_t(u_i)|}{\sum_{i=1}^4a_i||u_i||}\geq \frac{(\sum_{i=1}^4a_1)a_t}{(\sum_{i=1}^4a_1)b_t}=\frac{a_t}{b_t}=:C_t>0.\\[-47pt]\end{align*} $$
3.2 The Euler stability condition on
 $\mathbb {P}^3$
from tiltings
$\mathbb {P}^3$
from tiltings
In this subsection, we will show that the Euler stability is indeed related to the stability
![]() $\sigma _{\alpha ,\beta ,s}=(\mathscr {A}^{\alpha , \beta }, Z_{\alpha ,\beta ,s})$
in the way that
$\sigma _{\alpha ,\beta ,s}=(\mathscr {A}^{\alpha , \beta }, Z_{\alpha ,\beta ,s})$
in the way that
![]() $\mathscr {A}_t$
is an additional tilt of
$\mathscr {A}_t$
is an additional tilt of
![]() $\mathscr {A}^{\alpha , \beta }$
. We start with reviewing the three tilts of
$\mathscr {A}^{\alpha , \beta }$
. We start with reviewing the three tilts of
![]() $Coh(\mathbb {P}^3)$
, where the central charges for the tilted hearts are defined by derivatives of
$Coh(\mathbb {P}^3)$
, where the central charges for the tilted hearts are defined by derivatives of
![]() $\chi _t$
. And then we show that the heart
$\chi _t$
. And then we show that the heart
![]() $\mathscr {A}_t$
in Euler stability coincides with a one-dimensional slice of the heart obtained by a triple tilt of
$\mathscr {A}_t$
in Euler stability coincides with a one-dimensional slice of the heart obtained by a triple tilt of
![]() $Coh(\mathbb {P}^3)$
.
$Coh(\mathbb {P}^3)$
.
-
1. The first tilt.
The first tilt is made with respect to the first Todd class of
 $\mathbb {P}^3$
(
$\mathbb {P}^3$
(
 $td_1(\mathbb {P}^3)=2H$
). Define the central charge on
$td_1(\mathbb {P}^3)=2H$
). Define the central charge on
 $Coh(\mathbb {P}^3)$
as
$Coh(\mathbb {P}^3)$
as
 $Z_{1,t}=-\chi ^{\prime \prime }_t + i \cdot \chi ^{\prime \prime \prime }_t$
, and the slope function is
$Z_{1,t}=-\chi ^{\prime \prime }_t + i \cdot \chi ^{\prime \prime \prime }_t$
, and the slope function is  $$ \begin{align*}\mu_t:=\frac{\chi^{\prime\prime}_t}{\chi^{\prime\prime\prime}_t}=\frac{ch^{-t-2}_1}{ch_0}=\frac{ch_1+(t+2)ch_0}{ch_0}\end{align*} $$
$$ \begin{align*}\mu_t:=\frac{\chi^{\prime\prime}_t}{\chi^{\prime\prime\prime}_t}=\frac{ch^{-t-2}_1}{ch_0}=\frac{ch_1+(t+2)ch_0}{ch_0}\end{align*} $$
with
 $\mu _t:=+\infty $
if
$\mu _t:=+\infty $
if
 $\chi ^{\prime \prime \prime }_t=ch_0=0$
. This defines the following torsion pair of
$\chi ^{\prime \prime \prime }_t=ch_0=0$
. This defines the following torsion pair of
 $Coh(\mathbb {P}^3):$
$Coh(\mathbb {P}^3):$
 $$ \begin{align*}\mathscr{T}:=\left\{E\in Coh(\mathbb{P}^3): \forall E\twoheadrightarrow Q, \mu_t(Q)>0 \right\},\end{align*} $$
and we obtain the tilted heart as
$$ \begin{align*}\mathscr{T}:=\left\{E\in Coh(\mathbb{P}^3): \forall E\twoheadrightarrow Q, \mu_t(Q)>0 \right\},\end{align*} $$
and we obtain the tilted heart as $$ \begin{align*}\mathscr{F}:=\left\{E\in Coh(\mathbb{P}^3): \forall F\hookrightarrow E, \mu_t(F)\leq 0 \right\},\end{align*} $$
$$ \begin{align*}\mathscr{F}:=\left\{E\in Coh(\mathbb{P}^3): \forall F\hookrightarrow E, \mu_t(F)\leq 0 \right\},\end{align*} $$
 $Coh^{-t-2}(\mathbb {P}^3):=\left < \mathscr {F}[1], \mathscr {T} \right>$
.
$Coh^{-t-2}(\mathbb {P}^3):=\left < \mathscr {F}[1], \mathscr {T} \right>$
.
-
2. The second tilt.
We define the weak stability function
 $Z_{2,t}:=-\chi ^{\prime }_t+i\cdot \chi ^{\prime \prime }_t$
on
$Z_{2,t}:=-\chi ^{\prime }_t+i\cdot \chi ^{\prime \prime }_t$
on
 $Coh^{-t-2}(\mathbb {P}^3)$
and its slope is given by: with
$Coh^{-t-2}(\mathbb {P}^3)$
and its slope is given by: with $$ \begin{align*}\nu_t:=\frac{\chi^{\prime}_t}{\chi^{\prime\prime}_t}=\frac{ch^{-t-2}_2-\frac{1}{6}ch_0}{ch^{-t-2}_1}\end{align*} $$
$$ \begin{align*}\nu_t:=\frac{\chi^{\prime}_t}{\chi^{\prime\prime}_t}=\frac{ch^{-t-2}_2-\frac{1}{6}ch_0}{ch^{-t-2}_1}\end{align*} $$
 $\nu _t:=+\infty $
if
$\nu _t:=+\infty $
if
 $\chi ^{\prime \prime }_t=ch_1^{-t-2}=0$
. We have the torsion pair of the category
$\chi ^{\prime \prime }_t=ch_1^{-t-2}=0$
. We have the torsion pair of the category
 $Coh^{-t-2}(\mathbb {P}^3)$
and the new heart of a bounded t-structure as follows:
$Coh^{-t-2}(\mathbb {P}^3)$
and the new heart of a bounded t-structure as follows:  $$\begin{align*}\begin{array}{l} \mathscr{T}_{\beta}:=\left\{E\in Coh^{-t-2}(\mathbb{P}^3): \forall E\twoheadrightarrow Q, \nu_t(Q)>0 \right\},\\ \mathscr{F}_{\beta}:=\left\{E\in Coh^{-t-2}(\mathbb{P}^3): \forall F\hookrightarrow E, \nu_t(F)\leq 0 \right\},\\ \mathscr{B}_t:=\left< \mathscr{F}_{\beta}[1], \mathscr{T}_{\beta} \right>.\\ \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{l} \mathscr{T}_{\beta}:=\left\{E\in Coh^{-t-2}(\mathbb{P}^3): \forall E\twoheadrightarrow Q, \nu_t(Q)>0 \right\},\\ \mathscr{F}_{\beta}:=\left\{E\in Coh^{-t-2}(\mathbb{P}^3): \forall F\hookrightarrow E, \nu_t(F)\leq 0 \right\},\\ \mathscr{B}_t:=\left< \mathscr{F}_{\beta}[1], \mathscr{T}_{\beta} \right>.\\ \end{array} \end{align*}$$
The central charge for
 $\mathscr {B}_t$
is defined as
$\mathscr {B}_t$
is defined as  $$ \begin{align*}Z_{3,t}=-\chi_t+i\cdot \chi^{\prime}_t=-ch^{-t-2}_3+\frac{1}{6}ch^{-t-2}_1+i\cdot (ch^{-t-2}_2-\frac{1}{6}ch^{-t-2}_0).\end{align*} $$
$$ \begin{align*}Z_{3,t}=-\chi_t+i\cdot \chi^{\prime}_t=-ch^{-t-2}_3+\frac{1}{6}ch^{-t-2}_1+i\cdot (ch^{-t-2}_2-\frac{1}{6}ch^{-t-2}_0).\end{align*} $$
Comparing
 $Z_{3,t}$
to
$Z_{3,t}$
to
 $Z_{\alpha , \beta , s}$
in the previous section, we have
$Z_{\alpha , \beta , s}$
in the previous section, we have
 $\alpha =\frac {1}{\sqrt {3}}$
,
$\alpha =\frac {1}{\sqrt {3}}$
,
 $\beta =-t-2$
, and
$\beta =-t-2$
, and
 $s=\frac {1}{3}$
. So the pair
$s=\frac {1}{3}$
. So the pair
 $(\mathscr {B}_t, Z_t)$
is a one-dimensional family of stability conditions. In this case, the quadratic form
$(\mathscr {B}_t, Z_t)$
is a one-dimensional family of stability conditions. In this case, the quadratic form
 $Q_{\alpha , \beta , K}$
from Theorem 2.11 is given as follows for those specific values
$Q_{\alpha , \beta , K}$
from Theorem 2.11 is given as follows for those specific values
 $\alpha =\frac {1}{\sqrt {3}}$
,
$\alpha =\frac {1}{\sqrt {3}}$
,
 $\beta =-t-2$
,
$\beta =-t-2$
,
 $K=1$
:
$K=1$
:  $$\begin{align*}\begin{array}{rl} Q_t(E)= & ((ch_1(E))^2-2ch_0(E)ch_12(E))(\frac{1}{3}+(t+2)^2)+\\ & (6ch_0(E)ch_3(E)-2ch_1(E)ch_2(E))(-t-2)\\ & -6ch_1(E)ch_3(E)+4(ch_2(E))^2. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{rl} Q_t(E)= & ((ch_1(E))^2-2ch_0(E)ch_12(E))(\frac{1}{3}+(t+2)^2)+\\ & (6ch_0(E)ch_3(E)-2ch_1(E)ch_2(E))(-t-2)\\ & -6ch_1(E)ch_3(E)+4(ch_2(E))^2. \end{array} \end{align*}$$
-
3. The third tilt.
We now make a tilt of the category
 $\mathscr {B}_t$
. The slope on
$\mathscr {B}_t$
. The slope on
 $\mathscr {B}_t$
is defined as
$\mathscr {B}_t$
is defined as
 $\lambda _t=\frac {\chi _t}{\chi ^{\prime }_t}$
, with
$\lambda _t=\frac {\chi _t}{\chi ^{\prime }_t}$
, with
 $\lambda _t=+\infty $
if
$\lambda _t=+\infty $
if
 $\chi ^{\prime }_t=0$
. Similarly, we have the following torsion pair:
$\chi ^{\prime }_t=0$
. Similarly, we have the following torsion pair:  $$ \begin{align*}\mathscr{T}':=\left\{E\in \mathscr{B}_t: \forall E\twoheadrightarrow Q, \lambda_t(Q)>0 \right\},\end{align*} $$
$$ \begin{align*}\mathscr{T}':=\left\{E\in \mathscr{B}_t: \forall E\twoheadrightarrow Q, \lambda_t(Q)>0 \right\},\end{align*} $$
 $$ \begin{align*}\mathscr{F}':=\left\{E\in \mathscr{B}_t: \forall F\hookrightarrow E, \lambda_t(F)\leq 0 \right\}.\end{align*} $$
$$ \begin{align*}\mathscr{F}':=\left\{E\in \mathscr{B}_t: \forall F\hookrightarrow E, \lambda_t(F)\leq 0 \right\}.\end{align*} $$
Define
 $\mathscr {A}^{\prime }_t:=\left <\mathscr {F}'[1],\mathscr {T}'\right>$
to be the new heart of bounded t-structure, and
$\mathscr {A}^{\prime }_t:=\left <\mathscr {F}'[1],\mathscr {T}'\right>$
to be the new heart of bounded t-structure, and
 $Z_t := \chi ^{\prime }_t+i\cdot \chi _t$
.
$Z_t := \chi ^{\prime }_t+i\cdot \chi _t$
.
Remark 3.6. In the above tilting steps, we constructed the heart
![]() $Coh^{-t-2}(\mathbb {P}^3)$
. It is indeed the tilted heart
$Coh^{-t-2}(\mathbb {P}^3)$
. It is indeed the tilted heart
![]() $Coh^{\beta }(\mathbb {P}^3)$
when
$Coh^{\beta }(\mathbb {P}^3)$
when
![]() $\beta =-t-2$
.
$\beta =-t-2$
.
The next proposition shows that
![]() $\mathscr {A}^{\prime }_t$
coincides with
$\mathscr {A}^{\prime }_t$
coincides with
![]() $\mathscr {A}_t$
, so the Euler stability
$\mathscr {A}_t$
, so the Euler stability
![]() $(\mathscr {A}_t, Z_t)=(\mathscr {A}^{\prime }_t, Z_t)$
is a stability condition by tilting
$(\mathscr {A}_t, Z_t)=(\mathscr {A}^{\prime }_t, Z_t)$
is a stability condition by tilting
![]() $Coh(\mathbb {P}^3)$
three times.
$Coh(\mathbb {P}^3)$
three times.
Proposition 3.7. The category
![]() $\mathscr {A}^{\prime }_t$
is the extension closure of the following objects:
$\mathscr {A}^{\prime }_t$
is the extension closure of the following objects:
where
![]() $n:=\lceil t \rceil \in \mathbb {Z}$
.
$n:=\lceil t \rceil \in \mathbb {Z}$
.
Proof.
![]() $\mathscr {A}'$
is the heart of a bounded t-structure since it is obtained from tilting
$\mathscr {A}'$
is the heart of a bounded t-structure since it is obtained from tilting
![]() $Coh(\mathbb {P}^3)$
(see [Reference Happel, Reiten and Smalø14]). The category
$Coh(\mathbb {P}^3)$
(see [Reference Happel, Reiten and Smalø14]). The category
![]() $\mathscr {A}_t$
generated by the objects
$\mathscr {A}_t$
generated by the objects
is also the heart of a bounded t-structure (see [Reference Macrì25, Lem. 3.14]). By [Reference Macrì and Schmidt27, Prop. 5.6], two hearts must coincide if one is contained in another. So it is sufficient to prove that the objects
generating
![]() $\mathscr {A}_t$
are all contained in
$\mathscr {A}_t$
are all contained in
![]() $\mathscr {A}^{\prime }_t$
.
$\mathscr {A}^{\prime }_t$
.
We will prove that the objects
![]() $\left \{ \mathscr {O}_{\mathbb {P}^3}(-3)[3], \mathscr {O}_{\mathbb {P}^3}(-2)[2], \mathscr {O}_{\mathbb {P}^3}(-1)[1], \mathscr {O}_{\mathbb {P}^3}\right \}$
are in the category
$\left \{ \mathscr {O}_{\mathbb {P}^3}(-3)[3], \mathscr {O}_{\mathbb {P}^3}(-2)[2], \mathscr {O}_{\mathbb {P}^3}(-1)[1], \mathscr {O}_{\mathbb {P}^3}\right \}$
are in the category
![]() $\mathscr {A}^{\prime }_t$
where
$\mathscr {A}^{\prime }_t$
where
![]() $t\in (-1,0]$
, and the proof for a general
$t\in (-1,0]$
, and the proof for a general
![]() $t\in \mathbb {R}$
is analogous. We will keep track of the line bundles
$t\in \mathbb {R}$
is analogous. We will keep track of the line bundles
![]() $\mathscr {O}_{\mathbb {P}^3}, \mathscr {O}_{\mathbb {P}^3}(-1), \mathscr {O}_{\mathbb {P}^3}(-2),\mathscr {O}_{\mathbb {P}^3}(-3)$
in
$\mathscr {O}_{\mathbb {P}^3}, \mathscr {O}_{\mathbb {P}^3}(-1), \mathscr {O}_{\mathbb {P}^3}(-2),\mathscr {O}_{\mathbb {P}^3}(-3)$
in
![]() $Coh(\mathbb {P}^{3})$
while we make the three time tiltings.
$Coh(\mathbb {P}^{3})$
while we make the three time tiltings.
The line bundles
![]() $\mathscr {O}_{\mathbb {P}^3}(m)$
are Mumford stable for any
$\mathscr {O}_{\mathbb {P}^3}(m)$
are Mumford stable for any
![]() $m\in \mathbb {Z}$
, so they are also twisted Mumford stable. It is straightforward to check that
$m\in \mathbb {Z}$
, so they are also twisted Mumford stable. It is straightforward to check that
![]() $\mu _t(\mathscr {O}_{\mathbb {P}^3}(k))=k+t+2$
for
$\mu _t(\mathscr {O}_{\mathbb {P}^3}(k))=k+t+2$
for
![]() $k\in \mathbb {Z}$
, and
$k\in \mathbb {Z}$
, and
![]() $\mu _t(\mathscr {O}_{\mathbb {P}^3})>0$
$\mu _t(\mathscr {O}_{\mathbb {P}^3})>0$
![]() $\mu _t(\mathscr {O}_{\mathbb {P}^3}(-1))>0$
$\mu _t(\mathscr {O}_{\mathbb {P}^3}(-1))>0$
![]() $\mu _t(\mathscr {O}_{\mathbb {P}^3}(-2))<0$
$\mu _t(\mathscr {O}_{\mathbb {P}^3}(-2))<0$
![]() $\mu _t(\mathscr {O}_{\mathbb {P}^3}(-3))<0$
for
$\mu _t(\mathscr {O}_{\mathbb {P}^3}(-3))<0$
for
![]() $t\in (-1,0]$
. This implies that the category
$t\in (-1,0]$
. This implies that the category
![]() $Coh^{-t-2}(\mathbb {P}^3)$
(for
$Coh^{-t-2}(\mathbb {P}^3)$
(for
![]() $t\in (-1,0]$
) contains these objects:
$t\in (-1,0]$
) contains these objects:
Then, we use the slope function
![]() $\nu _t=\frac {ch^{-t-2}_2-1/6ch_0}{ch^{-t-2}_1}$
for the second tilt. It was proved in [Reference Macrì26] and [Reference Schmidt33] that line bundles and their shifts (
$\nu _t=\frac {ch^{-t-2}_2-1/6ch_0}{ch^{-t-2}_1}$
for the second tilt. It was proved in [Reference Macrì26] and [Reference Schmidt33] that line bundles and their shifts (
![]() $\mathscr {O}_{\mathbb {P}^3}(m)$
,
$\mathscr {O}_{\mathbb {P}^3}(m)$
,
![]() $\mathscr {O}_{\mathbb {P}^3}(m)[1]$
) are tilt stable when they are in the category. A straightforward computation shows that
$\mathscr {O}_{\mathbb {P}^3}(m)[1]$
) are tilt stable when they are in the category. A straightforward computation shows that
 $\displaystyle \nu _t(\mathscr {O}_{\mathbb {P}^3}(k))=\frac {k^2/2+(t+2)k+(t+2)^2/2-1/6}{k+t+2}$
for
$\displaystyle \nu _t(\mathscr {O}_{\mathbb {P}^3}(k))=\frac {k^2/2+(t+2)k+(t+2)^2/2-1/6}{k+t+2}$
for
![]() $k\in \mathbb {Z}$
, so
$k\in \mathbb {Z}$
, so
![]() $\mathscr {B}_t$
(a tilt of
$\mathscr {B}_t$
(a tilt of
![]() $Coh^{-t-2}(\mathbb {P}^3)$
) contains the following objects for
$Coh^{-t-2}(\mathbb {P}^3)$
) contains the following objects for
![]() $t\in (-1,0]$
:
$t\in (-1,0]$
:

For the last tilt, we have that line bundles and their shifts are Bridgeland stable (see [Reference Macrì26]), that is,
![]() $\mathscr {O}_{\mathbb {P}^3}(m)$
,
$\mathscr {O}_{\mathbb {P}^3}(m)$
,
![]() $\mathscr {O}_{\mathbb {P}^3}(m)[1]$
,
$\mathscr {O}_{\mathbb {P}^3}(m)[1]$
,
![]() $\mathscr {O}_{\mathbb {P}^3}(m)[2]$
are stable in the double tilt
$\mathscr {O}_{\mathbb {P}^3}(m)[2]$
are stable in the double tilt
![]() $\mathscr {B}_t$
.
$\mathscr {B}_t$
.
Using the slope function
 $\displaystyle \lambda _t=\frac {\chi _t}{\chi ^{\prime }_t}=\frac {ch^{-t-2}_3-1/6ch^{-t-2}_1}{ch^{-t-2}_2-1/6ch_0}$
, the claim follows from a direct computation of those
$\displaystyle \lambda _t=\frac {\chi _t}{\chi ^{\prime }_t}=\frac {ch^{-t-2}_3-1/6ch^{-t-2}_1}{ch^{-t-2}_2-1/6ch_0}$
, the claim follows from a direct computation of those
![]() $\lambda _t(\mathscr {O}_{\mathbb {P}^3}(-i)[j])$
’s in the last step. So as expected, the objects
$\lambda _t(\mathscr {O}_{\mathbb {P}^3}(-i)[j])$
’s in the last step. So as expected, the objects
![]() $\mathscr {O}_{\mathbb {P}^3}$
,
$\mathscr {O}_{\mathbb {P}^3}$
,
![]() $\mathscr {O}_{\mathbb {P}^3}(-1)[1]$
,
$\mathscr {O}_{\mathbb {P}^3}(-1)[1]$
,
![]() $\mathscr {O}_{\mathbb {P}^3}(-2)[2]$
,
$\mathscr {O}_{\mathbb {P}^3}(-2)[2]$
,
![]() $\mathscr {O}_{\mathbb {P}^3}(-3)[3]$
are in the category
$\mathscr {O}_{\mathbb {P}^3}(-3)[3]$
are in the category
![]() $\mathscr {A}^{\prime }_t$
.
$\mathscr {A}^{\prime }_t$
.
4 The Gieseker chamber for Euler stability
In this section, we work with a fixed one-dimensional class
![]() $v=(0,0,m=ch_2>0,ch_3)\in K_{num}({\mathbb {P}^3})$
, and show part of the result that there exists a Gieseker chamber for the Euler stability condition
$v=(0,0,m=ch_2>0,ch_3)\in K_{num}({\mathbb {P}^3})$
, and show part of the result that there exists a Gieseker chamber for the Euler stability condition
![]() $\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
on
$\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
on
![]() $\mathbb {P}^3$
. We expect that the Gieseker chamber shows up for
$\mathbb {P}^3$
. We expect that the Gieseker chamber shows up for
![]() $t\gg 0$
, and for
$t\gg 0$
, and for
![]() $t\ll 0$
stable objects are shifted Gieseker stable sheaves
$t\ll 0$
stable objects are shifted Gieseker stable sheaves
![]() $F[1]$
by duality results (in §5). We modify the stability condition on
$F[1]$
by duality results (in §5). We modify the stability condition on
![]() $\mathscr {B}_t$
as
$\mathscr {B}_t$
as
![]() $\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t)$
and work mostly in the
$\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t)$
and work mostly in the
![]() $(t,u)$
plane.
$(t,u)$
plane.
![]() $\sigma _{t,u}$
is indeed a stability condition from [Reference Bayer, Macrì and Toda6] and [Reference Macrì26]. We start with describing the numerical walls and then prove that the Gieseker chamber shows up for
$\sigma _{t,u}$
is indeed a stability condition from [Reference Bayer, Macrì and Toda6] and [Reference Macrì26]. We start with describing the numerical walls and then prove that the Gieseker chamber shows up for
![]() $u\gg 0$
. Finally, we work on the global walls for the class v. We also use the Euler characteristic
$u\gg 0$
. Finally, we work on the global walls for the class v. We also use the Euler characteristic
![]() $\chi =2ch_2+ch_3$
(from Riemann–Roch) of the class v if it is more convenient.
$\chi =2ch_2+ch_3$
(from Riemann–Roch) of the class v if it is more convenient.
4.1 Descriptions of numerical walls
Let
![]() $E\in \mathscr {B}_t$
be an object whose class is v and Hilbert polynomial is
$E\in \mathscr {B}_t$
be an object whose class is v and Hilbert polynomial is
![]() $P_E(t) = mt + \chi $
. Suppose a potential wall is defined by the short exact sequence
$P_E(t) = mt + \chi $
. Suppose a potential wall is defined by the short exact sequence
![]() $0\to A\to E \to B \to 0$
in
$0\to A\to E \to B \to 0$
in
![]() $\mathscr {B}_t$
, then a direct computation shows that the equation of the wall is
$\mathscr {B}_t$
, then a direct computation shows that the equation of the wall is
 $$\begin{align*}\frac{R}{3}(t+2)^3&+\left(\frac{C}{2}+\frac{R\chi}{2m}-R\right)(t+2)^2+\left(\frac{R}{2}u^2+C\left(\frac{\chi}{m}-2\right)\right)(t+2)+\left(\frac{\chi}{m}-2\right)\left(D-\frac{1}{6}R\right)\\[5pt]&+\left(\frac{u^2}{2}+\frac{1}{6}\right)C-E=0, \end{align*}$$
$$\begin{align*}\frac{R}{3}(t+2)^3&+\left(\frac{C}{2}+\frac{R\chi}{2m}-R\right)(t+2)^2+\left(\frac{R}{2}u^2+C\left(\frac{\chi}{m}-2\right)\right)(t+2)+\left(\frac{\chi}{m}-2\right)\left(D-\frac{1}{6}R\right)\\[5pt]&+\left(\frac{u^2}{2}+\frac{1}{6}\right)C-E=0, \end{align*}$$
where
![]() $R,C,D,$
and E denote
$R,C,D,$
and E denote
![]() $ch_0(A), ch_1(A), ch_2(A),$
and
$ch_0(A), ch_1(A), ch_2(A),$
and
![]() $ch_3(A)$
. The term
$ch_3(A)$
. The term
![]() $\frac {R}{2}(u^2(t+2+\frac {C}{R}))$
implies that when
$\frac {R}{2}(u^2(t+2+\frac {C}{R}))$
implies that when
![]() $R\neq 0$
, there is a vertical asymptote
$R\neq 0$
, there is a vertical asymptote
![]() $t=-2-\frac {C}{R}$
. When
$t=-2-\frac {C}{R}$
. When
![]() $R=0$
, the equation reduces to an equation of a circle whose center is
$R=0$
, the equation reduces to an equation of a circle whose center is
![]() $C=(-\frac {\chi }{m}, 0)$
(blue circle in Figure 2a). Indeed, when
$C=(-\frac {\chi }{m}, 0)$
(blue circle in Figure 2a). Indeed, when
![]() $R\neq 0$
, one can prove a similar result that as
$R\neq 0$
, one can prove a similar result that as
![]() $ch(A)$
varies, the “elliptic” part of the numerical wall (bounded part of the red wall in Figures 2a and 2b) is a nested family with respect to the center C as well. Furthermore, a numerical wall falls into the following three possibilities in the
$ch(A)$
varies, the “elliptic” part of the numerical wall (bounded part of the red wall in Figures 2a and 2b) is a nested family with respect to the center C as well. Furthermore, a numerical wall falls into the following three possibilities in the
![]() $(t,u)$
plane:
$(t,u)$
plane:
-
Type 1 Shown as the red walls in Figure 2a. There is a bounded elliptic part of the wall and a “vertical” part whose asymptote is defined by
 $t=-\frac {ch_1(A)}{ch_0(A)}-2$
. The green point in Figure 2a has coordinates
$t=-\frac {ch_1(A)}{ch_0(A)}-2$
. The green point in Figure 2a has coordinates
 $C:=(-\frac {\chi }{m},0)$
. It is the center of the “elliptic part,” which means that all the “elliptic parts” of the walls of Type 1 form a nested family with the center C.
$C:=(-\frac {\chi }{m},0)$
. It is the center of the “elliptic part,” which means that all the “elliptic parts” of the walls of Type 1 form a nested family with the center C. -
Type 2 Shown as the blue wall in Figure 2a. This is when
 $ch_0(A)=0$
and
$ch_0(A)=0$
and
 $ch_1(A)\neq 0$
. (An object
$ch_1(A)\neq 0$
. (An object
 $A\in \mathscr {B}_t$
with
$A\in \mathscr {B}_t$
with
 $ch_0(A)=ch_1(A)=0$
does not define a wall.) The wall is a semi-circle with center C (same C as in Type 1). All the semi-circles form a nested family with the same center C.
$ch_0(A)=ch_1(A)=0$
does not define a wall.) The wall is a semi-circle with center C (same C as in Type 1). All the semi-circles form a nested family with the same center C. -
Type 3 The mirror image of Type 1 (with respect to the vertical line
 $t=-\frac {\chi }{m}$
), as shown in Figure 2b. The asymptote of the vertical part is also defined by
$t=-\frac {\chi }{m}$
), as shown in Figure 2b. The asymptote of the vertical part is also defined by
 $t=-\frac {ch_1(A)}{ch_0(A)}-2$
and the center of the elliptic part is C as well.
$t=-\frac {ch_1(A)}{ch_0(A)}-2$
and the center of the elliptic part is C as well.

Figure 2 Numerical walls
For Types 1 and 3, the “elliptic part” might not show up, but the vertical part always exists.
4.2 Asymptotic results for sheaves and complexes
In this subsection, we show that for a fixed one-dimensional class
![]() $v\in K_{num}(\mathbb {P}^3)$
, the Gieseker chamber appears in the
$v\in K_{num}(\mathbb {P}^3)$
, the Gieseker chamber appears in the
![]() $(t,u)$
-plane when
$(t,u)$
-plane when
![]() $u\gg 0$
. We start with the asymptotic behavior of sheaves for
$u\gg 0$
. We start with the asymptotic behavior of sheaves for
![]() $u\gg 0$
and prove that a sheaf E with class v is Gieseker (semi)stable if and only if it is
$u\gg 0$
and prove that a sheaf E with class v is Gieseker (semi)stable if and only if it is
![]() $\sigma _{t,u}$
(semi)stable when
$\sigma _{t,u}$
(semi)stable when
![]() $u\gg 0$
.
$u\gg 0$
.
Lemma 4.1. For a fixed
![]() $\displaystyle t\in \mathbb {Q}$
and a Gieseker stable sheaf
$\displaystyle t\in \mathbb {Q}$
and a Gieseker stable sheaf
![]() $E\in \mathscr {B}_t$
with class v, there exist
$E\in \mathscr {B}_t$
with class v, there exist
![]() $B_1\in \mathbb {R}$
and
$B_1\in \mathbb {R}$
and
![]() $B_2\in \mathbb {R}^+$
such that for all
$B_2\in \mathbb {R}^+$
such that for all
![]() $A\hookrightarrow E\in \mathscr {B}_t$
, we have
$A\hookrightarrow E\in \mathscr {B}_t$
, we have
 $\displaystyle \frac {\chi _t(A)}{\chi ^{\prime }_t(A)}\leq B_1$
, and
$\displaystyle \frac {\chi _t(A)}{\chi ^{\prime }_t(A)}\leq B_1$
, and
 $\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}\geq B_2>0$
or
$\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}\geq B_2>0$
or
![]() $\chi ^{\prime \prime }_t(A)=0$
.
$\chi ^{\prime \prime }_t(A)=0$
.
Proof. Assume
![]() $t=a/b,$
where
$t=a/b,$
where
![]() $a\in \mathbb {Z}$
,
$a\in \mathbb {Z}$
,
![]() $b\in \mathbb {Z}^+$
, and
$b\in \mathbb {Z}^+$
, and
![]() $g.c.d.(a,b)=1$
.
$g.c.d.(a,b)=1$
.
Let
![]() $B\in \mathscr {B}_t$
be the quotient of the inclusion
$B\in \mathscr {B}_t$
be the quotient of the inclusion
![]() $A\hookrightarrow E$
, that is, defined by the short exact sequence
$A\hookrightarrow E$
, that is, defined by the short exact sequence
![]() $0\to A\to E\to B\to 0$
in
$0\to A\to E\to B\to 0$
in
![]() $\mathscr {B}_t$
. Take the cohomologies in
$\mathscr {B}_t$
. Take the cohomologies in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
, and we have a long exact sequence:
$Coh^{-t-2}(\mathbb {P}^3)$
, and we have a long exact sequence:
where
![]() $\mathscr {H}^{-1}_{\beta }$
and
$\mathscr {H}^{-1}_{\beta }$
and
![]() $\mathscr {H}^{0}_{\beta }$
denote the cohomologies in
$\mathscr {H}^{0}_{\beta }$
denote the cohomologies in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
. Since
$Coh^{-t-2}(\mathbb {P}^3)$
. Since
![]() $E\in Coh(\mathbb {P}^3)$
is a sheaf, we have
$E\in Coh(\mathbb {P}^3)$
is a sheaf, we have
![]() $\mathscr {H}^{-1}_{\beta }(E)=0$
. This implies that
$\mathscr {H}^{-1}_{\beta }(E)=0$
. This implies that
![]() $E\cong \mathscr {H}^{0}_{\beta }(E)$
and
$E\cong \mathscr {H}^{0}_{\beta }(E)$
and
![]() $\mathscr {H}^{-1}_{\beta }(A)=0$
. So
$\mathscr {H}^{-1}_{\beta }(A)=0$
. So
![]() $A\cong \mathscr {H}^{0}_{\beta }(A)$
, and
$A\cong \mathscr {H}^{0}_{\beta }(A)$
, and
![]() $A \in Coh^{-t-2}({\mathbb {P}^3})$
. The long exact sequence above is reduced to the following one:
$A \in Coh^{-t-2}({\mathbb {P}^3})$
. The long exact sequence above is reduced to the following one:
This implies that
![]() $A\in Coh^{-t-2}(\mathbb {P}^3)\subset \mathscr {B}_t$
. So we have
$A\in Coh^{-t-2}(\mathbb {P}^3)\subset \mathscr {B}_t$
. So we have
![]() $\chi ^{\prime \prime }_t(A)\geq 0$
, and
$\chi ^{\prime \prime }_t(A)\geq 0$
, and
![]() $\chi ^{\prime }_t(A)\geq 0$
. Moreover, we have
$\chi ^{\prime }_t(A)\geq 0$
. Moreover, we have
![]() $\chi ^{\prime }_t(B)\geq 0$
and
$\chi ^{\prime }_t(B)\geq 0$
and
![]() $\chi ^{\prime }_t(A)+\chi ^{\prime }_t(B)=\chi ^{\prime }_t(E)=m$
. So
$\chi ^{\prime }_t(A)+\chi ^{\prime }_t(B)=\chi ^{\prime }_t(E)=m$
. So
![]() $\chi ^{\prime }_t(A)\in [0,m]$
, and if
$\chi ^{\prime }_t(A)\in [0,m]$
, and if
![]() $\chi ^{\prime }_t(A)=0,$
then
$\chi ^{\prime }_t(A)=0,$
then
![]() $\chi ^{\prime \prime }_t(A)=0,$
otherwise, the tilt slope
$\chi ^{\prime \prime }_t(A)=0,$
otherwise, the tilt slope
 $\displaystyle \nu (A)=\frac {\chi ^{\prime }_t(A)}{\chi ^{\prime \prime }_t(A)}=0$
will make A shifted in
$\displaystyle \nu (A)=\frac {\chi ^{\prime }_t(A)}{\chi ^{\prime \prime }_t(A)}=0$
will make A shifted in
![]() $\mathscr {B}_t$
(i.e.,
$\mathscr {B}_t$
(i.e.,
![]() $A[1]\in \mathscr {B}_t$
). In this case, A is a sheaf supported on points and this violates the fact that E is Gieseker stable. So
$A[1]\in \mathscr {B}_t$
). In this case, A is a sheaf supported on points and this violates the fact that E is Gieseker stable. So
![]() $\chi ^{\prime }_t(A)>0$
.
$\chi ^{\prime }_t(A)>0$
.
-
1. Lower bound for
 $\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}$
.
$\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}$
. $\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}=\frac {ch_1+(t+2)ch_0}{\chi ^{\prime }_t(A)}\geq \frac {ch_1+(t+2)ch_0}{m}\geq \frac {1/b}{m}=\frac {1}{bm}$
or
$\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}=\frac {ch_1+(t+2)ch_0}{\chi ^{\prime }_t(A)}\geq \frac {ch_1+(t+2)ch_0}{m}\geq \frac {1/b}{m}=\frac {1}{bm}$
or
 $\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}=0$
. We choose
$\displaystyle \frac {\chi ^{\prime \prime }_t(A)}{\chi ^{\prime }_t(A)}=0$
. We choose
 $\displaystyle B_2=\frac {1}{bm}$
. The last inequality holds because
$\displaystyle B_2=\frac {1}{bm}$
. The last inequality holds because
 $ch_0,ch_1\in \mathbb {Z}$
, and
$ch_0,ch_1\in \mathbb {Z}$
, and
 $ch_1+(t+2)ch_0>0$
.
$ch_1+(t+2)ch_0>0$
. -
2. Upper bound for
 $\displaystyle \lambda _t(A)= \frac {\chi _t(A)}{\chi ^{\prime }_t(A)}$
.
$\displaystyle \lambda _t(A)= \frac {\chi _t(A)}{\chi ^{\prime }_t(A)}$
.From the fact that
 $ch_0,ch_1\in \mathbb {Z}$
,
$ch_0,ch_1\in \mathbb {Z}$
,
 $ch_2\in \frac {1}{2}\mathbb {Z}$
, and
$ch_2\in \frac {1}{2}\mathbb {Z}$
, and
 $\chi ^{\prime }_t(A)>0$
, we have
$\chi ^{\prime }_t(A)>0$
, we have
 $\displaystyle \chi ^{\prime }_t(A)=ch_2(A)+(t+2)ch_1(A)+\frac {(t+2)^2}{2}ch_0(A)-\frac {1}{6}ch_0(A)\geq \frac {1}{6b^2}>0$
.
$\displaystyle \chi ^{\prime }_t(A)=ch_2(A)+(t+2)ch_1(A)+\frac {(t+2)^2}{2}ch_0(A)-\frac {1}{6}ch_0(A)\geq \frac {1}{6b^2}>0$
.So we just need an upper bound for
 $\chi _t(A)$
. Consider the Harder–Narasimhan filtration of
$\chi _t(A)$
. Consider the Harder–Narasimhan filtration of
 $A\in \mathscr {B}_t$
with respect to the central charge
$A\in \mathscr {B}_t$
with respect to the central charge
 $Z_t=-\chi _t+i\cdot \chi ^{\prime }_t$
:
$Z_t=-\chi _t+i\cdot \chi ^{\prime }_t$
:  $$ \begin{align*}0=A_0\subset A_1\subset \cdots\subset A_i\subset A_{i+1}\subset \cdots \subset A_{n-1}\subset A_n:=A.\end{align*} $$
$$ \begin{align*}0=A_0\subset A_1\subset \cdots\subset A_i\subset A_{i+1}\subset \cdots \subset A_{n-1}\subset A_n:=A.\end{align*} $$
Let
 $i\in \mathbb {Z}$
be the number such that the semistable factor
$i\in \mathbb {Z}$
be the number such that the semistable factor
 $\displaystyle \frac {A_i}{A_{i-1}}$
is the last one whose slope is positive, that is,
$\displaystyle \frac {A_i}{A_{i-1}}$
is the last one whose slope is positive, that is,
 $\displaystyle \lambda _t(\frac {A_i}{A_{i-1}})>0$
, and
$\displaystyle \lambda _t(\frac {A_i}{A_{i-1}})>0$
, and
 $\displaystyle \lambda _t( \frac {A_{i+1}}{A_{i}})\leq 0$
. If there is no such i, then
$\displaystyle \lambda _t( \frac {A_{i+1}}{A_{i}})\leq 0$
. If there is no such i, then
 $\chi ^{\prime }_t(E)\leq 0$
and we define
$\chi ^{\prime }_t(E)\leq 0$
and we define
 $B_1$
to be
$B_1$
to be
 $0$
.
$0$
.Similarly for the Harder–Narasimhan filtration for
 $E\in \mathscr {B}_t$
:
$E\in \mathscr {B}_t$
:  $$ \begin{align*}0=E_0\subset E_1\subset \cdots\subset E_j\subset E_{j+1}\subset \cdots \subset E.\end{align*} $$
$$ \begin{align*}0=E_0\subset E_1\subset \cdots\subset E_j\subset E_{j+1}\subset \cdots \subset E.\end{align*} $$
Let j be the index such that the Harder–Narasimhan factor is the last one with a positive slope, that is,
 $\displaystyle \lambda _{t}(\frac {E_j}{E_{j-1}})>0$
and
$\displaystyle \lambda _{t}(\frac {E_j}{E_{j-1}})>0$
and
 $\displaystyle \lambda _{t}(\frac {E_{j+1}}{E_{j}})\leq 0$
.
$\displaystyle \lambda _{t}(\frac {E_{j+1}}{E_{j}})\leq 0$
.In the short exact sequence
 $0\to A_i \to A \to \frac {A}{A_i}\to 0,$
we have
$0\to A_i \to A \to \frac {A}{A_i}\to 0,$
we have
 $\chi _t(A_i)>0$
and
$\chi _t(A_i)>0$
and
 $\displaystyle \chi _t(\frac {A}{A_i})\leq 0$
from how we choose i. More precisely, we have
$\displaystyle \chi _t(\frac {A}{A_i})\leq 0$
from how we choose i. More precisely, we have
 $\displaystyle \chi ^{\prime }_t(\frac {A_k}{A_{k-1}})\geq 0$
and
$\displaystyle \chi ^{\prime }_t(\frac {A_k}{A_{k-1}})\geq 0$
and
 $\displaystyle \chi _t(\frac {A_k}{A_{k-1}})>0$
for
$\displaystyle \chi _t(\frac {A_k}{A_{k-1}})>0$
for
 $k=1, 2,\ldots , i$
by the definition of i. Then
$k=1, 2,\ldots , i$
by the definition of i. Then
 $\displaystyle \chi _t(A_i)=\chi _t(A_0)+\chi _t(\frac {A_1}{A_0})+\cdots +\chi _t(\frac {A_i}{A_{i-1}})>0$
. Similarly, we have that
$\displaystyle \chi _t(A_i)=\chi _t(A_0)+\chi _t(\frac {A_1}{A_0})+\cdots +\chi _t(\frac {A_i}{A_{i-1}})>0$
. Similarly, we have that
 $\displaystyle \chi _t(\frac {A}{A_i})=\chi _t(\frac {A_{i+1}}{A_i})+\chi _t(\frac {A_{i+2}}{A_{i+1}})+\cdots +\chi _t(\frac {A}{A_{n-1}})\leq 0$
because
$\displaystyle \chi _t(\frac {A}{A_i})=\chi _t(\frac {A_{i+1}}{A_i})+\chi _t(\frac {A_{i+2}}{A_{i+1}})+\cdots +\chi _t(\frac {A}{A_{n-1}})\leq 0$
because
 $\displaystyle \chi _t(\frac {A_k}{A_{k-1}})\leq 0$
for
$\displaystyle \chi _t(\frac {A_k}{A_{k-1}})\leq 0$
for
 $k=i+1, \ldots , n$
. Therefore, we have
$k=i+1, \ldots , n$
. Therefore, we have
 $\chi _t(A)\leq \chi _t(A_i)$
, and it is sufficient to find an upper bound for
$\chi _t(A)\leq \chi _t(A_i)$
, and it is sufficient to find an upper bound for
 $\chi _t(A_i)$
.
$\chi _t(A_i)$
.Consider the inclusion
 $0\to A_i\xrightarrow {f} E$
in
$0\to A_i\xrightarrow {f} E$
in
 $\mathscr {B}_t$
, and the diagram
$\mathscr {B}_t$
, and the diagram
 $\phi $
is a zero map because the semistable factors of
$\phi $
is a zero map because the semistable factors of
 $A_i$
have
$A_i$
have
 $\lambda _t(A_i)>0$
and the semistable factors of
$\lambda _t(A_i)>0$
and the semistable factors of
 $E/E_j$
have
$E/E_j$
have
 $\lambda _t\leq 0$
. So the morphism f lifts to a morphism
$\lambda _t\leq 0$
. So the morphism f lifts to a morphism
 $f_1$
from
$f_1$
from
 $A_i$
to
$A_i$
to
 $E_j$
, where they are both extended by semistable objects in
$E_j$
, where they are both extended by semistable objects in
 $\mathscr {B}_t$
with positive slope
$\mathscr {B}_t$
with positive slope
 $\lambda _t$
.
$\lambda _t$
.Now, we make another tilt from
 $\mathscr {B}_t$
to
$\mathscr {B}_t$
to
 $\mathscr {A}_t$
and the morphism
$\mathscr {A}_t$
and the morphism
 $0\to A_i \to E_j$
stays the same in
$0\to A_i \to E_j$
stays the same in
 $\mathscr {A}_t$
because they are both generated by objects with positive slopes
$\mathscr {A}_t$
because they are both generated by objects with positive slopes
 $\lambda _t$
. For a fixed E and t, the sub-object
$\lambda _t$
. For a fixed E and t, the sub-object
 $E_j$
and its dimension vector are fixed in
$E_j$
and its dimension vector are fixed in
 $\mathscr {A}_t$
. There are only finitely many choices of sub-objects of
$\mathscr {A}_t$
. There are only finitely many choices of sub-objects of
 $E_j$
in
$E_j$
in
 $\mathscr {A}_t$
, and this implies that
$\mathscr {A}_t$
, and this implies that
 $\chi _t(A_i)$
is bounded from above for all
$\chi _t(A_i)$
is bounded from above for all
 $A\hookrightarrow E$
in
$A\hookrightarrow E$
in
 $\mathscr {B}_t$
. So there exists
$\mathscr {B}_t$
. So there exists
 $B_1\in \mathbb {R}$
such that
$B_1\in \mathbb {R}$
such that
 $\displaystyle \frac {\chi _t(A)}{\chi ^{\prime }_t(A)}\geq B_1$
.
$\displaystyle \frac {\chi _t(A)}{\chi ^{\prime }_t(A)}\geq B_1$
.
Remark 4.2. The above proof (Lemma 4.1) works for all sheaves
![]() $\mathscr {F}\in Coh(\mathbb {P}^3)$
as well. Just replace
$\mathscr {F}\in Coh(\mathbb {P}^3)$
as well. Just replace
![]() $\chi ^{\prime }_t(E)=m$
by
$\chi ^{\prime }_t(E)=m$
by
![]() $\chi ^{\prime }_t(\mathscr {F})$
, which is a fixed number.
$\chi ^{\prime }_t(\mathscr {F})$
, which is a fixed number.
Proposition 4.3. If
![]() $E\in \mathscr {B}_t$
is a sheaf with class v, then E is Gieseker (semi)stable if and only if E is
$E\in \mathscr {B}_t$
is a sheaf with class v, then E is Gieseker (semi)stable if and only if E is
![]() $\sigma _{t,u}$
- (semi)stable for all sufficiently large u (the bound of u can be chosen as
$\sigma _{t,u}$
- (semi)stable for all sufficiently large u (the bound of u can be chosen as
![]() $\frac {2}{B_2}(B_1-t-\frac {\chi }{m})$
).
$\frac {2}{B_2}(B_1-t-\frac {\chi }{m})$
).
Proof. Let
 $\displaystyle \lambda _{t,u}:=\frac {\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t}{\chi ^{\prime }_t}$
be the Bridgeland slope. The “if” part follows from the fact that
$\displaystyle \lambda _{t,u}:=\frac {\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t}{\chi ^{\prime }_t}$
be the Bridgeland slope. The “if” part follows from the fact that
![]() $\lambda _{t,u}(E)=\frac {mt+\chi }{m}=t+{\chi }/{m}$
if E has class v, and the Bridgeland slope is equal to the twisted Mumford slope.
$\lambda _{t,u}(E)=\frac {mt+\chi }{m}=t+{\chi }/{m}$
if E has class v, and the Bridgeland slope is equal to the twisted Mumford slope.
For the “only if” part, suppose the claim is not true, then for any fixed
![]() $u_0\gg 0$
, we can always find an
$u_0\gg 0$
, we can always find an
![]() $A_{u_0}$
, such that
$A_{u_0}$
, such that
![]() $\lambda _{t,u_0}(A_{u_0})\geq (>)\lambda _{t,u_0}(E)$
. More explicitly, we have
$\lambda _{t,u_0}(A_{u_0})\geq (>)\lambda _{t,u_0}(E)$
. More explicitly, we have
 $$ \begin{align*}\lambda_{t,u_0}(A_{u_0})=\frac{\chi_t(A_{u_0})-\frac{u_0^2}{2}\chi^{\prime\prime}_t(A_{u_0})}{\chi^{\prime}_t(A_{u_0})}\geq (>)\frac{\chi_t(E)}{\chi^{\prime}_t(E)}=\frac{mt+\chi}{m}=t+\frac{\chi}{m}.\end{align*} $$
$$ \begin{align*}\lambda_{t,u_0}(A_{u_0})=\frac{\chi_t(A_{u_0})-\frac{u_0^2}{2}\chi^{\prime\prime}_t(A_{u_0})}{\chi^{\prime}_t(A_{u_0})}\geq (>)\frac{\chi_t(E)}{\chi^{\prime}_t(E)}=\frac{mt+\chi}{m}=t+\frac{\chi}{m}.\end{align*} $$
If
![]() $\chi ^{\prime \prime }_t(A_{u_0})\neq 0$
, then
$\chi ^{\prime \prime }_t(A_{u_0})\neq 0$
, then
![]() $\chi ^{\prime \prime }_t(A_{u_0})> 0$
because
$\chi ^{\prime \prime }_t(A_{u_0})> 0$
because
![]() $A_{u_0}\in Coh^{-t-2}(\mathbb {P}^3)$
. The expression of
$A_{u_0}\in Coh^{-t-2}(\mathbb {P}^3)$
. The expression of
![]() $\lambda _{t,u}$
shows that
$\lambda _{t,u}$
shows that
![]() $\displaystyle \lim _{u\to \infty }\lambda _{t,u}(A)=-\infty $
(for
$\displaystyle \lim _{u\to \infty }\lambda _{t,u}(A)=-\infty $
(for
![]() $\chi ^{\prime \prime }_t(A)\neq 0$
). Using the boundedness results from Lemma 4.1, we actually have a universal bound and the following claim:
$\chi ^{\prime \prime }_t(A)\neq 0$
). Using the boundedness results from Lemma 4.1, we actually have a universal bound and the following claim:
There exists a
![]() $u'\in \mathbb {R}$
such that for all
$u'\in \mathbb {R}$
such that for all
![]() $u>u'$
and
$u>u'$
and
![]() $A\hookrightarrow E \in \mathscr {B}_t$
, we have
$A\hookrightarrow E \in \mathscr {B}_t$
, we have
![]() $\lambda _{t,u}(A)<\lambda _{t,u}(E)$
. This violates the assumption that A destabilizes E. So it implies that if E is not Euler stable for all large u (
$\lambda _{t,u}(A)<\lambda _{t,u}(E)$
. This violates the assumption that A destabilizes E. So it implies that if E is not Euler stable for all large u (
![]() $u>u'$
), then we must have
$u>u'$
), then we must have
![]() $ch^{-t-2}_1(A)=\chi ^{\prime \prime }_t(A)=0$
for any destabilizing object
$ch^{-t-2}_1(A)=\chi ^{\prime \prime }_t(A)=0$
for any destabilizing object
![]() $A\hookrightarrow E \in \mathscr {B}_t$
.
$A\hookrightarrow E \in \mathscr {B}_t$
.
We then go back to the short exact sequence
![]() $0\to A\to E\to B\to 0$
in
$0\to A\to E\to B\to 0$
in
![]() $\mathscr {B}_t$
with its long exact sequence in
$\mathscr {B}_t$
with its long exact sequence in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
:
$Coh^{-t-2}(\mathbb {P}^3)$
:

where the morphism
![]() $A\to E$
factors through
$A\to E$
factors through
![]() $Q \in Coh^{-t-2}(\mathbb {P}^3)$
. From the fact that
$Q \in Coh^{-t-2}(\mathbb {P}^3)$
. From the fact that
![]() $\chi ^{\prime \prime }_t(A)=ch^{-t-2}_1(A)=\chi ^{\prime \prime }_t(E)=ch^{-t-2}_1(E)=0$
, and all the objects in the diagram has
$\chi ^{\prime \prime }_t(A)=ch^{-t-2}_1(A)=\chi ^{\prime \prime }_t(E)=ch^{-t-2}_1(E)=0$
, and all the objects in the diagram has
![]() $ch^{-t-2}_1=\chi ^{\prime \prime }_t\geq 0$
(because they are in
$ch^{-t-2}_1=\chi ^{\prime \prime }_t\geq 0$
(because they are in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
), we have
$Coh^{-t-2}(\mathbb {P}^3)$
), we have
![]() $\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(B))=\chi ^{\prime \prime }_t(Q)=\chi ^{\prime \prime }_t(\mathscr {H}^{0}_{\beta }(B))=0$
.
$\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(B))=\chi ^{\prime \prime }_t(Q)=\chi ^{\prime \prime }_t(\mathscr {H}^{0}_{\beta }(B))=0$
.
This implies that
 $\displaystyle \nu (\mathscr {H}^{-1}_{\beta }(B))=\frac {\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(B))}{\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(B))=0}=\infty $
which contradicts with the fact that it is shifted from
$\displaystyle \nu (\mathscr {H}^{-1}_{\beta }(B))=\frac {\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(B))}{\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(B))=0}=\infty $
which contradicts with the fact that it is shifted from
![]() $Coh^{-t-2}(\mathbb {P}^3)$
to
$Coh^{-t-2}(\mathbb {P}^3)$
to
![]() $\mathscr {B}_t$
. So
$\mathscr {B}_t$
. So
![]() $\mathscr {H}^{-1}_{\beta }(B)=0$
, and the short exact sequence
$\mathscr {H}^{-1}_{\beta }(B)=0$
, and the short exact sequence
![]() $0\to A\to E\to B\to 0$
is indeed in
$0\to A\to E\to B\to 0$
is indeed in
![]() $Coh^{-t-2}(\mathbb {P}^3)\subset \mathscr {B}_t$
.
$Coh^{-t-2}(\mathbb {P}^3)\subset \mathscr {B}_t$
.
Similarly, consider its long exact sequence of cohomologies in
![]() $Coh(\mathbb {P}^3)$
as
$Coh(\mathbb {P}^3)$
as
From the fact that
![]() $ch_0(A)=ch_0(E)=0$
and
$ch_0(A)=ch_0(E)=0$
and
![]() $ch^{-t-2}_1(A)=ch^{-t-2}_1(E)=0$
, we have
$ch^{-t-2}_1(A)=ch^{-t-2}_1(E)=0$
, we have
![]() $ch_0(\mathscr {H}^{-1}(B))=ch_0(\mathscr {H}^{0}(B))$
, and
$ch_0(\mathscr {H}^{-1}(B))=ch_0(\mathscr {H}^{0}(B))$
, and
![]() $ch^{-t-2}_1(\mathscr {H}^{-1}(B))=ch^{-t-2}_1(\mathscr {H}^{0}(B))$
. In particular,
$ch^{-t-2}_1(\mathscr {H}^{-1}(B))=ch^{-t-2}_1(\mathscr {H}^{0}(B))$
. In particular,
 $\displaystyle \frac {ch^{-t-2}_1(\mathscr {H}^{-1}(B))}{ch_0(\mathscr {H}^{-1}(B))}=\frac {ch^{-t-2}_1(\mathscr {H}^{0}(B))}{ch_0(\mathscr {H}^{0}(B))}$
, which is a contradiction unless one of
$\displaystyle \frac {ch^{-t-2}_1(\mathscr {H}^{-1}(B))}{ch_0(\mathscr {H}^{-1}(B))}=\frac {ch^{-t-2}_1(\mathscr {H}^{0}(B))}{ch_0(\mathscr {H}^{0}(B))}$
, which is a contradiction unless one of
![]() $\mathscr {H}^{-1}(B)$
and
$\mathscr {H}^{-1}(B)$
and
![]() $\mathscr {H}^{0}(B)$
is zero and the nonzero object has its twisted Mumford slope
$\mathscr {H}^{0}(B)$
is zero and the nonzero object has its twisted Mumford slope
![]() $\infty $
. So
$\infty $
. So
![]() $\mathscr {H}^{-1}(B)=0$
and
$\mathscr {H}^{-1}(B)=0$
and
![]() $\mathscr {H}^{0}(B)\neq 0$
with
$\mathscr {H}^{0}(B)\neq 0$
with
 $\displaystyle \frac {ch^{-t-2}_1(\mathscr {H}^{0}(B))}{ch_0(\mathscr {H}^{0}(B))}=\infty $
.
$\displaystyle \frac {ch^{-t-2}_1(\mathscr {H}^{0}(B))}{ch_0(\mathscr {H}^{0}(B))}=\infty $
.
This shows that B is actually a sheaf, and the short exact sequence
![]() $0 \to A\to E\to B\to 0$
is indeed in
$0 \to A\to E\to B\to 0$
is indeed in
![]() $Coh(\mathbb {P}^3)$
. Now, A is a sub-sheaf of E and they are both one-dimensional. We have that the slope
$Coh(\mathbb {P}^3)$
. Now, A is a sub-sheaf of E and they are both one-dimensional. We have that the slope
![]() $\lambda _{t,u}$
for the class v coincides with the Mumford slope, so the assumption
$\lambda _{t,u}$
for the class v coincides with the Mumford slope, so the assumption
![]() $\lambda _{t,u}(A)\geq (>)\lambda _{t,u}(E)$
is equivalent to E being Mumford (Gieseker) unstable which is a contradiction.
$\lambda _{t,u}(A)\geq (>)\lambda _{t,u}(E)$
is equivalent to E being Mumford (Gieseker) unstable which is a contradiction.
Next, we show that if an object
![]() $E\in \mathscr {B}_t$
with class v is
$E\in \mathscr {B}_t$
with class v is
![]() $\sigma _{t,u}$
- stable for all
$\sigma _{t,u}$
- stable for all
![]() $u\gg 0$
, then E must be a sheaf.
$u\gg 0$
, then E must be a sheaf.
Lemma 4.4. If
![]() $E\in Coh^{\beta }(\mathbb {P}^3)\subset \mathscr {B}_t$
with class v, then E is a sheaf.
$E\in Coh^{\beta }(\mathbb {P}^3)\subset \mathscr {B}_t$
with class v, then E is a sheaf.
Proof. In
![]() $Coh^{\beta }(\mathbb {P}^3),$
we have the short exact sequence:
$Coh^{\beta }(\mathbb {P}^3),$
we have the short exact sequence:
Denote
![]() $(\mathscr {T}_t,\mathscr {F}_t)$
to be the torsion pair on
$(\mathscr {T}_t,\mathscr {F}_t)$
to be the torsion pair on
![]() $Coh(\mathbb {P}^3)$
defined by
$Coh(\mathbb {P}^3)$
defined by
![]() $\mu _t$
.
$\mu _t$
.
Since
![]() $ch_0(E)=ch_1(E)=0$
, we have that
$ch_0(E)=ch_1(E)=0$
, we have that
![]() $ch_0(\mathscr {H}^{-1}(E))=ch_0(\mathscr {H}^{0}(E))$
and
$ch_0(\mathscr {H}^{-1}(E))=ch_0(\mathscr {H}^{0}(E))$
and
![]() $ch_1(\mathscr {H}^{-1}(E))=ch_0(\mathscr {H}^{0}(E))$
. This implies that
$ch_1(\mathscr {H}^{-1}(E))=ch_0(\mathscr {H}^{0}(E))$
. This implies that
![]() $\mu _t(\mathscr {H}^{0}(E))=\mu _t(\mathscr {H}^{-1}(E))$
, but it contradicts with
$\mu _t(\mathscr {H}^{0}(E))=\mu _t(\mathscr {H}^{-1}(E))$
, but it contradicts with
![]() $\mathscr {H}^{-1}(E)\in \mathscr {F}_t$
and
$\mathscr {H}^{-1}(E)\in \mathscr {F}_t$
and
![]() $\mathscr {H}^{0}(E)\in \mathscr {T}_t$
. So one of
$\mathscr {H}^{0}(E)\in \mathscr {T}_t$
. So one of
![]() $\mathscr {H}^{-1}(E)$
and
$\mathscr {H}^{-1}(E)$
and
![]() $\mathscr {H}^{0}(E)$
is zero, and then the twisted Mumford slope
$\mathscr {H}^{0}(E)$
is zero, and then the twisted Mumford slope
![]() $\mu _t$
of the non-zero object will be infinity. This shows that
$\mu _t$
of the non-zero object will be infinity. This shows that
![]() $\mathscr {H}^{-1}(E)=0$
, and
$\mathscr {H}^{-1}(E)=0$
, and
![]() $E\cong \mathscr {H}^{0}(E)$
which is a sheaf.
$E\cong \mathscr {H}^{0}(E)$
which is a sheaf.
Proposition 4.5. For an object
![]() $E\in \mathscr {B}_t$
with class v, if E is
$E\in \mathscr {B}_t$
with class v, if E is
![]() $\sigma _{t,u}$
stable for all
$\sigma _{t,u}$
stable for all
![]() $u\gg 0$
, then E must be a sheaf.
$u\gg 0$
, then E must be a sheaf.
Proof.
E fits into the short exact sequence in
![]() $\mathscr {B}_t$
:
$\mathscr {B}_t$
:
It is sufficient to show that
![]() $\mathscr {H}^{-1}_{\beta }(E)=0$
, and then the claim would follow from Lemma 4.4.
$\mathscr {H}^{-1}_{\beta }(E)=0$
, and then the claim would follow from Lemma 4.4.
Suppose
![]() $\mathscr {H}^{-1}_{\beta }(E)\neq 0$
, then
$\mathscr {H}^{-1}_{\beta }(E)\neq 0$
, then
 $\displaystyle \nu (\mathscr {H}^{-1}_{\beta }(E))=\frac {\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(E))}{\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))}\leq 0$
and
$\displaystyle \nu (\mathscr {H}^{-1}_{\beta }(E))=\frac {\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(E))}{\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))}\leq 0$
and
![]() $\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))>0$
.
$\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))>0$
.
Consider the
![]() $\sigma _{t,u}$
slope of
$\sigma _{t,u}$
slope of
![]() $\mathscr {H}^{-1}_{\beta }(B)[1]$
:
$\mathscr {H}^{-1}_{\beta }(B)[1]$
:
 $$ \begin{align*}\lambda_{t,u}(\mathscr{H}^{-1}_{\beta}(E)[1])=\frac{\chi_t(\mathscr{H}^{-1}_{\beta}(E)[1])-\frac{u^2}{2}\chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E)[1])}{\chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E)[1])},\end{align*} $$
$$ \begin{align*}\lambda_{t,u}(\mathscr{H}^{-1}_{\beta}(E)[1])=\frac{\chi_t(\mathscr{H}^{-1}_{\beta}(E)[1])-\frac{u^2}{2}\chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E)[1])}{\chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E)[1])},\end{align*} $$
![]() $\displaystyle \lim _{u\to \infty }\lambda _{t,u}(\mathscr {H}^{-1}_{\beta }(E)[1])=+\infty $
so E is not stable for
$\displaystyle \lim _{u\to \infty }\lambda _{t,u}(\mathscr {H}^{-1}_{\beta }(E)[1])=+\infty $
so E is not stable for
![]() $u\gg 0$
unless
$u\gg 0$
unless
![]() $\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E)[1])=0$
. But this implies
$\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E)[1])=0$
. But this implies
 $\displaystyle \nu _t(\mathscr {H}^{-1}_{\beta }(E))=\frac {\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(E))}{\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))=0}=+\infty $
and
$\displaystyle \nu _t(\mathscr {H}^{-1}_{\beta }(E))=\frac {\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(E))}{\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))=0}=+\infty $
and
![]() $\mathscr {H}^{-1}_{\beta }(E)\in \mathscr {B}_t$
which is a contradiction. So
$\mathscr {H}^{-1}_{\beta }(E)\in \mathscr {B}_t$
which is a contradiction. So
![]() $\mathscr {H}^{-1}_{\beta }(E)=0$
and this proves the claim.
$\mathscr {H}^{-1}_{\beta }(E)=0$
and this proves the claim.
Lemma 4.6. For a complex
![]() $E\in \mathscr {B}_t$
whose class is v, there exists an
$E\in \mathscr {B}_t$
whose class is v, there exists an
![]() $u_E$
such that for all
$u_E$
such that for all
![]() $u>u_E$
, E is
$u>u_E$
, E is
![]() $\sigma _{t,u}$
-unstable.
$\sigma _{t,u}$
-unstable.
Proof. Consider the short exact sequence in
![]() $\mathscr {B}_t$
as
$\mathscr {B}_t$
as
we must have
![]() $\mathscr {H}_{\beta }^{-1}(E)\neq 0$
and
$\mathscr {H}_{\beta }^{-1}(E)\neq 0$
and
![]() $\mathscr {H}_{\beta }^{0}(E)\neq 0,$
otherwise, Lemma 4.4 will tell us E is a sheaf.
$\mathscr {H}_{\beta }^{0}(E)\neq 0,$
otherwise, Lemma 4.4 will tell us E is a sheaf.
![]() $\mathscr {H}_{\beta }^{-1}(E)\in Coh^{-t-2}(\mathbb {P}^3)$
implies
$\mathscr {H}_{\beta }^{-1}(E)\in Coh^{-t-2}(\mathbb {P}^3)$
implies
![]() $\chi ^{\prime \prime }_t(\mathscr {H}_{\beta }^{-1}(E))>0$
. The claim follows from the observation that:
$\chi ^{\prime \prime }_t(\mathscr {H}_{\beta }^{-1}(E))>0$
. The claim follows from the observation that:
 $$ \begin{align*}\lambda_{t,u}(\mathscr{H}_{\beta}^{-1}(E)[1])=\frac{\chi_t(\mathscr{H}_{\beta}^{-1}(E)[1])-\frac{u^2}{2}\chi^{\prime\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])}{\chi^{\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])}>\lambda_{t,u}(E)=\frac{mt+\chi}{m}\end{align*} $$
$$ \begin{align*}\lambda_{t,u}(\mathscr{H}_{\beta}^{-1}(E)[1])=\frac{\chi_t(\mathscr{H}_{\beta}^{-1}(E)[1])-\frac{u^2}{2}\chi^{\prime\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])}{\chi^{\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])}>\lambda_{t,u}(E)=\frac{mt+\chi}{m}\end{align*} $$
for
![]() $u\gg 0$
. We can also find the critical point for
$u\gg 0$
. We can also find the critical point for
![]() $u_E$
, and this is when the equal sign holds, that is,
$u_E$
, and this is when the equal sign holds, that is,
 $$ \begin{align*}u_E:=\frac{(t+\frac{\chi}{m})\chi^{\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])-\chi_t(\mathscr{H}_{\beta}^{-1}(E)[1])}{-\chi^{\prime\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])}.\\[-50pt]\end{align*} $$
$$ \begin{align*}u_E:=\frac{(t+\frac{\chi}{m})\chi^{\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])-\chi_t(\mathscr{H}_{\beta}^{-1}(E)[1])}{-\chi^{\prime\prime}_t(\mathscr{H}_{\beta}^{-1}(E)[1])}.\\[-50pt]\end{align*} $$
We are now ready to state the main theorem in this subsection.
Theorem 4.7. For any object
![]() $E\in \mathscr {B}_t$
whose class is v, there exists
$E\in \mathscr {B}_t$
whose class is v, there exists
![]() $B_E>0$
such that for all
$B_E>0$
such that for all
![]() $u>B_E$
, E is
$u>B_E$
, E is
![]() $\sigma _{t,u}$
- stable if and only if E is a Gieseker stable sheaf.
$\sigma _{t,u}$
- stable if and only if E is a Gieseker stable sheaf.
Proof. It follows from Propositions 4.3 and 4.5, and Lemma 4.6. We take
![]() $B_E$
to be the maximum of
$B_E$
to be the maximum of
![]() $u_E$
and the bound in Proposition 4.3.
$u_E$
and the bound in Proposition 4.3.
Finally, we show a bound of t for a complex
![]() $E\in \mathscr {B}_t$
to exist in the category.
$E\in \mathscr {B}_t$
to exist in the category.
Lemma 4.8. If
![]() $E\in \mathscr {B}_{t_0}$
is a complex, then E can only exist in
$E\in \mathscr {B}_{t_0}$
is a complex, then E can only exist in
![]() $\mathscr {B}_t$
for
$\mathscr {B}_t$
for
![]() $t\in [a,a+m],$
where
$t\in [a,a+m],$
where
![]() $a\in \mathbb {Z}$
, and
$a\in \mathbb {Z}$
, and
![]() $t_0\in [a,a+m]$
.
$t_0\in [a,a+m]$
.
Proof.
E fits into the short exact sequence in
![]() $\mathscr {B}_t$
as
$\mathscr {B}_t$
as
where
![]() $\mathscr {H}^{-1}_{\beta }(E)$
and
$\mathscr {H}^{-1}_{\beta }(E)$
and
![]() $\mathscr {H}^{0}_{\beta }(E)$
are its cohomologies in
$\mathscr {H}^{0}_{\beta }(E)$
are its cohomologies in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
.
$Coh^{-t-2}(\mathbb {P}^3)$
.
Assume
![]() $ch_0(\mathscr {H}^{0}_{\beta }(E))=R$
,
$ch_0(\mathscr {H}^{0}_{\beta }(E))=R$
,
![]() $ch_1(\mathscr {H}^{0}_{\beta }(E))=C$
and
$ch_1(\mathscr {H}^{0}_{\beta }(E))=C$
and
![]() $ch_2(\mathscr {H}^{0}_{\beta }(E))=D$
then it follows that
$ch_2(\mathscr {H}^{0}_{\beta }(E))=D$
then it follows that
![]() $ch_0(\mathscr {H}^{-1}_{\beta }(E))=R$
,
$ch_0(\mathscr {H}^{-1}_{\beta }(E))=R$
,
![]() $ch_1(\mathscr {H}^{-1}_{\beta }(E))=C$
and
$ch_1(\mathscr {H}^{-1}_{\beta }(E))=C$
and
![]() $ch_2(\mathscr {H}^{-1}_{\beta }(E))=D-m$
.
$ch_2(\mathscr {H}^{-1}_{\beta }(E))=D-m$
.
From the definition of
![]() $Coh^{-t-2}(\mathbb {P}^3)$
, we have the numerical results that
$Coh^{-t-2}(\mathbb {P}^3)$
, we have the numerical results that
 $$ \begin{align*} \left\{ \begin{array}{ll} \chi^{\prime}_t(\mathscr{H}^{0}_{\beta}(E))\geq 0 & \chi^{\prime\prime}_t(\mathscr{H}^{0}_{\beta}(E))\geq 0 \\ \chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E))\leq 0 & \chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E))\geq 0.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} \chi^{\prime}_t(\mathscr{H}^{0}_{\beta}(E))\geq 0 & \chi^{\prime\prime}_t(\mathscr{H}^{0}_{\beta}(E))\geq 0 \\ \chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E))\leq 0 & \chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E))\geq 0.\\ \end{array} \right. \end{align*} $$
A direct computation shows that
 $$ \begin{align*} \left\{ \begin{array}{l} \chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=\chi^{\prime\prime}_t(\mathscr{H}^{0}_{\beta}(E))=C+(t+2)R, \\ \chi^{\prime}_t(\mathscr{H}^{0}_{\beta}(E))=\frac{(t+2)^2}{2}R+(t+2)C+D-\frac{1}{6}R,\\ \chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=\frac{(t+2)^2}{2}R+(t+2)C+D-\frac{1}{6}R-m.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{l} \chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=\chi^{\prime\prime}_t(\mathscr{H}^{0}_{\beta}(E))=C+(t+2)R, \\ \chi^{\prime}_t(\mathscr{H}^{0}_{\beta}(E))=\frac{(t+2)^2}{2}R+(t+2)C+D-\frac{1}{6}R,\\ \chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=\frac{(t+2)^2}{2}R+(t+2)C+D-\frac{1}{6}R-m.\\ \end{array} \right. \end{align*} $$
Observe that, for
![]() $R\neq 0$
, the vertical line
$R\neq 0$
, the vertical line
![]() $\chi ^{\prime \prime }_t(\mathscr {H}^{k}_{\beta }(E))=0$
(
$\chi ^{\prime \prime }_t(\mathscr {H}^{k}_{\beta }(E))=0$
(
![]() $k=0$
or
$k=0$
or
![]() $-1$
) in a
$-1$
) in a
![]() $(t,s)$
-plane is the axis of symmetry of the parabola
$(t,s)$
-plane is the axis of symmetry of the parabola
![]() $f_k(t)=\chi ^{\prime }_t(\mathscr {H}^{k}_{\beta }(E))$
.
$f_k(t)=\chi ^{\prime }_t(\mathscr {H}^{k}_{\beta }(E))$
.
The claim will follow from the following results:
-
1. If
 $R>0$
, then
$R>0$
, then
 $f_1(t):=\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(E))$
, and
$f_1(t):=\chi ^{\prime }_t(\mathscr {H}^{-1}_{\beta }(E))$
, and
 $f_2(t):=\chi ^{\prime }_t(\mathscr {H}^{0}_{\beta }(E))$
are two parabolas and
$f_2(t):=\chi ^{\prime }_t(\mathscr {H}^{0}_{\beta }(E))$
are two parabolas and
 $f_2(t)$
is a shift upward by m from
$f_2(t)$
is a shift upward by m from
 $f_1(t)$
as shown in Figure 3.
$f_1(t)$
as shown in Figure 3.
Figure 3 Function
 $f_i(t)=\chi_t'(\mathcal{H}^i_{\beta}(E))$
for
$f_i(t)=\chi_t'(\mathcal{H}^i_{\beta}(E))$
for
 $R>0$
$R>0$

Figure 4 Function
 $f_i(t)=\chi_t'(\mathcal{H}^i_{\beta}(E))$
for
$f_i(t)=\chi_t'(\mathcal{H}^i_{\beta}(E))$
for
 $R=0$
$R=0$
The inequality
 $\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))=\chi ^{\prime \prime }_t(\mathscr {H}^{0}_{\beta }(E))=C+(t+2)R\geq 0$
corresponds to the region to the right of the dotted line. So the region for t satisfying
$\chi ^{\prime \prime }_t(\mathscr {H}^{-1}_{\beta }(E))=\chi ^{\prime \prime }_t(\mathscr {H}^{0}_{\beta }(E))=C+(t+2)R\geq 0$
corresponds to the region to the right of the dotted line. So the region for t satisfying
 $f_1\leq 0$
and
$f_1\leq 0$
and
 $f_2\geq 0$
is the interval
$f_2\geq 0$
is the interval
 $[A,B]$
. A direct computation shows that
$[A,B]$
. A direct computation shows that
 $\displaystyle |AB|<\sqrt {\frac {2m}{R}}\leq \sqrt {2m}.$
$\displaystyle |AB|<\sqrt {\frac {2m}{R}}\leq \sqrt {2m}.$
-
2. If
 $R<0$
, then the proof is similar to case
$R<0$
, then the proof is similar to case
 $(1)$
.
$(1)$
. -
3. If
 $R=0$
, then
$R=0$
, then
 $C>0$
. We have in this case
$C>0$
. We have in this case  $$ \begin{align*} \left\{ \begin{array}{l} \chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=\chi^{\prime\prime}_t(\mathscr{H}^{0}_{\beta}(E))=C, \\ \chi^{\prime}_t(\mathscr{H}^{0}_{\beta}(E))=(t+2)C+D,\\ \chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=(t+2)C+D-m.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{l} \chi^{\prime\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=\chi^{\prime\prime}_t(\mathscr{H}^{0}_{\beta}(E))=C, \\ \chi^{\prime}_t(\mathscr{H}^{0}_{\beta}(E))=(t+2)C+D,\\ \chi^{\prime}_t(\mathscr{H}^{-1}_{\beta}(E))=(t+2)C+D-m.\\ \end{array} \right. \end{align*} $$
The picture is shown as Figure 4. A simple computation shows
 $|AB|=\frac {m}{C}\leq m$
.
$|AB|=\frac {m}{C}\leq m$
.Finally, when
 $m\geq 3$
,
$m\geq 3$
,
 $\sqrt {2m}<m$
. So for all the possible cases, we have
$\sqrt {2m}<m$
. So for all the possible cases, we have
 $|AB|\leq m$
, and the claim follows.
$|AB|\leq m$
, and the claim follows.
4.3 Boundedness of actual walls
We have shown that for any one-dimensional class
![]() $v\in K_{num}(\mathbb {P}^3)$
,
$v\in K_{num}(\mathbb {P}^3)$
,
![]() $s\gg 0$
and any
$s\gg 0$
and any
![]() $t\in \mathbb {R}$
correspond to the Gieseker chamber in the
$t\in \mathbb {R}$
correspond to the Gieseker chamber in the
![]() $(t,u)$
-plane for
$(t,u)$
-plane for
![]() $\mathscr {B}_t$
. For a complex
$\mathscr {B}_t$
. For a complex
![]() $E\in \mathscr {B}_t$
(E is not a sheaf), it is unstable (resp. does not exist) for
$E\in \mathscr {B}_t$
(E is not a sheaf), it is unstable (resp. does not exist) for
![]() $u\gg 0$
(resp.
$u\gg 0$
(resp.
![]() $t\gg 0$
or
$t\gg 0$
or
![]() $t\ll 0$
). So if actual walls were bounded in both s and t, then the outermost chamber (
$t\ll 0$
). So if actual walls were bounded in both s and t, then the outermost chamber (
![]() $s\gg 0,|t|\gg 0$
) would be the Gieseker chamber. We show some partial results and expectations below.
$s\gg 0,|t|\gg 0$
) would be the Gieseker chamber. We show some partial results and expectations below.
Firstly, we expect the following proposition to be true:
Conjecture 4.9. For any class
![]() $v=(0,0,m=ch_2>0,ch_3)\in K_{num}(\mathbb {P}^3)$
, the actual walls are all from the bounded parts of the numerical walls (Types 1
$v=(0,0,m=ch_2>0,ch_3)\in K_{num}(\mathbb {P}^3)$
, the actual walls are all from the bounded parts of the numerical walls (Types 1
![]() $\sim $
3).
$\sim $
3).
If the proposition were true, then all actual walls would be bounded. This is because the bounded parts of the same type do not intersect. So the outermost wall would at worse consist of three pieces of types 1, 2, and 3 each. Using the fact
![]() $0<\chi ^{\prime }_t(A)<ch_2$
and the same trick in Lemma 4.8, we have that an actual wall will be in a rectangular region
$0<\chi ^{\prime }_t(A)<ch_2$
and the same trick in Lemma 4.8, we have that an actual wall will be in a rectangular region
![]() $\mathcal {R}:=[t_{min},t_{max}]\times [0,u_{max}]$
in the upper half-plane (including the horizontal axis), such that
$\mathcal {R}:=[t_{min},t_{max}]\times [0,u_{max}]$
in the upper half-plane (including the horizontal axis), such that
![]() $t_{max}-t_{min}\leq ch_2+2\sqrt {2ch_2}$
. On the other hand, the center
$t_{max}-t_{min}\leq ch_2+2\sqrt {2ch_2}$
. On the other hand, the center
![]() $C=\frac {\chi }{m}$
is fixed for any fixed v. So we have that any point
$C=\frac {\chi }{m}$
is fixed for any fixed v. So we have that any point
![]() $(t,u)$
on an actual wall satisfies
$(t,u)$
on an actual wall satisfies
![]() $|t-\frac {\chi }{m}|\leq ch_2+2\sqrt {2ch_2}$
. Then,
$|t-\frac {\chi }{m}|\leq ch_2+2\sqrt {2ch_2}$
. Then,
![]() $t>\frac {\chi }{m}+ ch_2+2\sqrt {2ch_2}$
corresponds to the Gieseker chamber for Euler stability.
$t>\frac {\chi }{m}+ ch_2+2\sqrt {2ch_2}$
corresponds to the Gieseker chamber for Euler stability.
Theorem 4.7 implies that any vertical numerical wall can not be an actual wall for
![]() $u\gg 0$
because there are no wall-crossings for
$u\gg 0$
because there are no wall-crossings for
![]() $u\gg 0$
. We expect the following claim which will imply Conjecture 4.9 with the help of the Bogomolov inequality.
$u\gg 0$
. We expect the following claim which will imply Conjecture 4.9 with the help of the Bogomolov inequality.
Conjecture 4.10. For
![]() $E\in \mathscr {B}_t$
whose class is v, any vertical wall defined by
$E\in \mathscr {B}_t$
whose class is v, any vertical wall defined by
![]() $0\to A\to E \to B\to 0$
can not be an actual wall at
$0\to A\to E \to B\to 0$
can not be an actual wall at
![]() $u=0.$
$u=0.$
5 The duality results
In this section, we show some duality properties of objects
![]() $E\in D^b(Coh(\mathbb {P}^3))$
in both
$E\in D^b(Coh(\mathbb {P}^3))$
in both
![]() $\mathscr {A}_t$
and
$\mathscr {A}_t$
and
![]() $\mathscr {B}_t$
. This section is motivated by work in [Reference Maican28] for Gieseker stable sheaves and the results in [Reference Martinez29] for Bridgeland stable complexes in
$\mathscr {B}_t$
. This section is motivated by work in [Reference Maican28] for Gieseker stable sheaves and the results in [Reference Martinez29] for Bridgeland stable complexes in
![]() $D^b(\mathbb {P}^2)$
.
$D^b(\mathbb {P}^2)$
.
Definition 5.1. Define the twisted derived dual of
![]() $E\in D^b(Coh(\mathbb {P}^3))$
to be
$E\in D^b(Coh(\mathbb {P}^3))$
to be
![]() $E^D:=R\mathscr {H}om(E,\omega _{\mathbb {P}^3})[2]$
.
$E^D:=R\mathscr {H}om(E,\omega _{\mathbb {P}^3})[2]$
.
Definition 5.2. For a dimension vector
![]() $\underline {dim}=[a,b,c,d]$
(
$\underline {dim}=[a,b,c,d]$
(
![]() $a,b,c,d\in \mathbb {Z}_{\geq 0}$
), its opposite vector is defined as
$a,b,c,d\in \mathbb {Z}_{\geq 0}$
), its opposite vector is defined as
![]() $\underline {dim}^{op}:=[d,c,b,a]$
.
$\underline {dim}^{op}:=[d,c,b,a]$
.
Proposition 5.3. For the stability condition
![]() $\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i \cdot \chi _t)$
, assume
$\sigma _t=(\mathscr {A}_t, Z_t=\chi ^{\prime }_t+i \cdot \chi _t)$
, assume
![]() $t\notin \mathbb {Z}$
. An object
$t\notin \mathbb {Z}$
. An object
![]() $E\in \mathscr {A}_t$
has its dimension vector
$E\in \mathscr {A}_t$
has its dimension vector
![]() $\underline {dim}(E)$
if and only if
$\underline {dim}(E)$
if and only if
![]() $E^D[1]\in \mathscr {A}_{-t}$
has dimension vector
$E^D[1]\in \mathscr {A}_{-t}$
has dimension vector
![]() $\underline {dim}(E^D[1])=\underline {dim}^{op}(E)$
. Moreover,
$\underline {dim}(E^D[1])=\underline {dim}^{op}(E)$
. Moreover,
![]() $E\in \mathscr {A}_t$
is
$E\in \mathscr {A}_t$
is
![]() $\sigma _t$
- (semi)stable if and only if
$\sigma _t$
- (semi)stable if and only if
![]() $E^D[1]\in \mathscr {A}_{-t}$
is
$E^D[1]\in \mathscr {A}_{-t}$
is
![]() $\sigma _{-t}$
- (semi)stable.
$\sigma _{-t}$
- (semi)stable.
Proof. Let
![]() $n:=\lceil t\rceil $
. For
$n:=\lceil t\rceil $
. For
![]() $E\in \mathscr {A}_t$
, it is quasi-isomorphic to a complex of vector bundles as
$E\in \mathscr {A}_t$
, it is quasi-isomorphic to a complex of vector bundles as
where
![]() $a_i\in \mathbb {Z}_{\geq 0}$
. A direct computation from the definition shows that
$a_i\in \mathbb {Z}_{\geq 0}$
. A direct computation from the definition shows that
which implies that
![]() $E^D[1]\in \mathscr {A}_{-t}$
with dimension vector
$E^D[1]\in \mathscr {A}_{-t}$
with dimension vector
![]() $\underline {dim}(E^D[1])=[a_0,a_1,a_2,a_3]=[a_3,a_2,a_1,a_0]^{op}$
.
$\underline {dim}(E^D[1])=[a_0,a_1,a_2,a_3]=[a_3,a_2,a_1,a_0]^{op}$
.
For the stability, a direct computation shows that
where the derivative in
![]() $\chi ^{\prime }_{-t}(E^D[1])$
is with respect to the parameter “
$\chi ^{\prime }_{-t}(E^D[1])$
is with respect to the parameter “
![]() $-t$
.”
$-t$
.”
A short exact sequence
![]() $0\to A \to E \to B \to 0$
in
$0\to A \to E \to B \to 0$
in
![]() $\mathscr {A}_t$
is essentially a sequence of complexes of vector spaces. Taking the dual of it, we have a dual sequence in
$\mathscr {A}_t$
is essentially a sequence of complexes of vector spaces. Taking the dual of it, we have a dual sequence in
![]() $\mathscr {A}_{-t}$
as
$\mathscr {A}_{-t}$
as
![]() $0\to B^D[1] \to E^D[1] \to A^D[1] \to 0$
. Let
$0\to B^D[1] \to E^D[1] \to A^D[1] \to 0$
. Let
![]() $\lambda _t:=-\frac {\chi ^{\prime }_t}{\chi _t}$
be the slope function of Euler stability. Then the numerical results above imply that for any object
$\lambda _t:=-\frac {\chi ^{\prime }_t}{\chi _t}$
be the slope function of Euler stability. Then the numerical results above imply that for any object
![]() $A\in \mathscr {A}_t$
,
$A\in \mathscr {A}_t$
,
![]() $\lambda _t(A)=-\lambda _{-t}(A^D[1])$
.
$\lambda _t(A)=-\lambda _{-t}(A^D[1])$
.
Now, we have the following correspondence:
![]() $A\hookrightarrow E$
in
$A\hookrightarrow E$
in
![]() $\mathscr {A}_t$
with
$\mathscr {A}_t$
with
![]() $\lambda _t(A)<(\leq )\lambda _t(E)$
is equivalent to
$\lambda _t(A)<(\leq )\lambda _t(E)$
is equivalent to
![]() $E^D[1]\twoheadrightarrow A^D[1]$
in
$E^D[1]\twoheadrightarrow A^D[1]$
in
![]() $\mathscr {A}_{-t}$
with
$\mathscr {A}_{-t}$
with
![]() $\lambda _{-t}(E^D[1])<(\leq )\lambda _{-t}(A^D[1])$
. So this implies that
$\lambda _{-t}(E^D[1])<(\leq )\lambda _{-t}(A^D[1])$
. So this implies that
![]() $E\in \mathscr {A}_t$
is (semi)stable if and only if
$E\in \mathscr {A}_t$
is (semi)stable if and only if
![]() $E^D[1]\in \mathscr {A}_{-t}$
is (semi)stable, and this proves the claim.
$E^D[1]\in \mathscr {A}_{-t}$
is (semi)stable, and this proves the claim.
Remark 5.4. For
![]() $t\in \mathbb {R}\backslash \mathbb {Z}$
, it can be easily checked that the generators
$t\in \mathbb {R}\backslash \mathbb {Z}$
, it can be easily checked that the generators
![]() $\mathscr {O}_{\mathbb {P}^3}(-\lceil t\rceil -i)[i]$
(
$\mathscr {O}_{\mathbb {P}^3}(-\lceil t\rceil -i)[i]$
(
![]() $i=0,1,2,3$
) are all mapped to the strict upper half plane by the central charge
$i=0,1,2,3$
) are all mapped to the strict upper half plane by the central charge
![]() $Z_t:=\chi ^{\prime }_t+i\cdot \chi _t$
, that is,
$Z_t:=\chi ^{\prime }_t+i\cdot \chi _t$
, that is,
![]() $\chi _t(\mathscr {O}_{\mathbb {P}^3}(-\lceil t\rceil -i)[i])>0$
. In particular, there is no stable object
$\chi _t(\mathscr {O}_{\mathbb {P}^3}(-\lceil t\rceil -i)[i])>0$
. In particular, there is no stable object
![]() $E\in \mathscr {A}_t$
with phase
$E\in \mathscr {A}_t$
with phase
![]() $1$
, equivalently,
$1$
, equivalently,
![]() $\mathscr {A}_t\subset \mathscr {P}_t(0,1)$
. So under the duality,
$\mathscr {A}_t\subset \mathscr {P}_t(0,1)$
. So under the duality,
![]() $(\mathscr {A}_t, Z_t)$
is sent to
$(\mathscr {A}_t, Z_t)$
is sent to
![]() $(\mathscr {A}_{-t}, Z_{-t})$
as a stability condition with
$(\mathscr {A}_{-t}, Z_{-t})$
as a stability condition with
![]() $\mathscr {A}_{-t}\subset \mathscr {P}_{-t}(0,1)$
. Indeed, Proposition 5.3 also works for
$\mathscr {A}_{-t}\subset \mathscr {P}_{-t}(0,1)$
. Indeed, Proposition 5.3 also works for
![]() $t\in \mathbb {Z}$
, but we need to modify the heart a bit. We will show it in Remark 5.7.
$t\in \mathbb {Z}$
, but we need to modify the heart a bit. We will show it in Remark 5.7.
Remark 5.5. The duality results in Proposition 5.3 and a similar proof work for all
![]() $\mathbb {P}^n$
(
$\mathbb {P}^n$
(
![]() $n\in \mathbb {Z}_{\geq 0}$
).
$n\in \mathbb {Z}_{\geq 0}$
).
Corollary 5.6. For any
![]() $t\in \mathbb {R}\backslash \mathbb {Z}$
, let
$t\in \mathbb {R}\backslash \mathbb {Z}$
, let
![]() $\mathscr {P}_t(\phi )$
(
$\mathscr {P}_t(\phi )$
(
![]() $\phi \in \mathbb {R}$
) be the slicing such that the heart
$\phi \in \mathbb {R}$
) be the slicing such that the heart
![]() $\mathscr {A}_t$
is given by
$\mathscr {A}_t$
is given by
![]() $\mathscr {P}_t(0,1]$
. We have
$\mathscr {P}_t(0,1]$
. We have
![]() $E\in \mathscr {P}_t(\phi )$
if and only if
$E\in \mathscr {P}_t(\phi )$
if and only if
![]() $E^D[1]\in \mathscr {P}_{-t}(1-\phi )$
for
$E^D[1]\in \mathscr {P}_{-t}(1-\phi )$
for
![]() $\mathscr {A}_{-t}$
.
$\mathscr {A}_{-t}$
.
Proof. It follows from the numerical fact in Proposition 5.3 that for
![]() $E\in \mathscr {A}_t$
, if
$E\in \mathscr {A}_t$
, if
![]() $Z_t(E)=\mathscr {R}e(Z_t(E))+\mathscr {I}m(Z_t(E))$
, then
$Z_t(E)=\mathscr {R}e(Z_t(E))+\mathscr {I}m(Z_t(E))$
, then
![]() $Z_{-t}(E^D[1])=-\mathscr {R}e(Z_t(E))+\mathscr {I}m(Z_t(E))$
. So the phase
$Z_{-t}(E^D[1])=-\mathscr {R}e(Z_t(E))+\mathscr {I}m(Z_t(E))$
. So the phase
![]() $\phi $
(
$\phi $
(
![]() $\phi \in (0,1)$
from Remark 5.4) changes from
$\phi \in (0,1)$
from Remark 5.4) changes from
![]() $\phi $
to
$\phi $
to
![]() $1-\phi $
in the corresponding hearts.
$1-\phi $
in the corresponding hearts.
![]() $\phi $
can be extended to all the real numbers by shifting
$\phi $
can be extended to all the real numbers by shifting
![]() $\mathscr {A}_t$
and
$\mathscr {A}_t$
and
![]() $\mathscr {A}_{-t}$
.
$\mathscr {A}_{-t}$
.
Remark 5.7. Proposition 5.3 and Corollary 5.6 work for
![]() $t\in \mathbb {Z}$
as well. If
$t\in \mathbb {Z}$
as well. If
![]() $t\in \mathbb {Z}$
, then the stability condition
$t\in \mathbb {Z}$
, then the stability condition
![]() $(\mathscr {A}_t, Z_t)$
is supposed to be sent to
$(\mathscr {A}_t, Z_t)$
is supposed to be sent to
![]() $(\mathscr {A}_{1-t}, Z_{-t})$
by the duality. The pair
$(\mathscr {A}_{1-t}, Z_{-t})$
by the duality. The pair
![]() $(\mathscr {A}_{1-t}, Z_{-t})$
is not a stability condition because the stable (simple) objects
$(\mathscr {A}_{1-t}, Z_{-t})$
is not a stability condition because the stable (simple) objects
![]() $\mathscr {O}_{\mathbb {P}^3}(-t-i)[i] \in \mathscr {A}_t$
(
$\mathscr {O}_{\mathbb {P}^3}(-t-i)[i] \in \mathscr {A}_t$
(
![]() $i=1,2,3$
) all have phase
$i=1,2,3$
) all have phase
![]() $1$
, and duality will send them to phase
$1$
, and duality will send them to phase
![]() $0$
in
$0$
in
![]() $\mathscr {A}_{-t}$
which is not in the heart.
$\mathscr {A}_{-t}$
which is not in the heart.
This can be fixed by slightly tilting the upper half-plane. The heart
![]() $\mathscr {A}_t$
(
$\mathscr {A}_t$
(
![]() $t\in \mathbb {Z}$
) is indeed a strict subset of
$t\in \mathbb {Z}$
) is indeed a strict subset of
![]() $\mathscr {P}(0,1]$
, and more precisely,
$\mathscr {P}(0,1]$
, and more precisely,
![]() $\mathscr {A}_t=\mathscr {P}(\phi _1,1]$
where
$\mathscr {A}_t=\mathscr {P}(\phi _1,1]$
where
![]() $\phi _1=\tan ^{-1}(\frac {6}{11})$
. This is because
$\phi _1=\tan ^{-1}(\frac {6}{11})$
. This is because
![]() $Z_t$
sends the generators
$Z_t$
sends the generators
![]() $\mathscr {O}_{\mathbb {P}^3}(-t)$
to
$\mathscr {O}_{\mathbb {P}^3}(-t)$
to
![]() $(\frac {11}{6},1)$
and
$(\frac {11}{6},1)$
and
![]() $\mathscr {O}_{\mathbb {P}^3}(-t-i)[i]$
(
$\mathscr {O}_{\mathbb {P}^3}(-t-i)[i]$
(
![]() $i=1,2,3$
) to
$i=1,2,3$
) to
![]() $(-\frac {1}{3},0)$
or
$(-\frac {1}{3},0)$
or
![]() $(-\frac {1}{6},0)$
. So we just modify the heart to be
$(-\frac {1}{6},0)$
. So we just modify the heart to be
![]() $\mathscr {P}(\phi ,\phi +1]$
as shown in Figure 5 (
$\mathscr {P}(\phi ,\phi +1]$
as shown in Figure 5 (
![]() $\phi := \frac {1}{2}\phi _1$
, and take
$\phi := \frac {1}{2}\phi _1$
, and take
![]() $t=0$
as an example). The new heart under duality is
$t=0$
as an example). The new heart under duality is
![]() $\mathscr {P}_{-t}(-\phi , 1-\phi ]$
and this fixes the issue.
$\mathscr {P}_{-t}(-\phi , 1-\phi ]$
and this fixes the issue.

Figure 5 Image of
![]() $\mathcal{A}_t$
in the upper half-plane
$\mathcal{A}_t$
in the upper half-plane
From Corollary 5.6, we have a duality result for the category
![]() $\mathscr {B}_t$
.
$\mathscr {B}_t$
.
Corollary 5.8. For the stability condition
![]() $\sigma ^{\mathscr {B}_t}_t=(\mathscr {B}_t, Z_t=-\chi _t+i\cdot \chi ^{\prime }_t)$
, an object
$\sigma ^{\mathscr {B}_t}_t=(\mathscr {B}_t, Z_t=-\chi _t+i\cdot \chi ^{\prime }_t)$
, an object
![]() $E\subset \mathscr {P}_{\mathscr {B}_t}(0,1)\subset \mathscr {B}_t$
is (semi)stable if and only if
$E\subset \mathscr {P}_{\mathscr {B}_t}(0,1)\subset \mathscr {B}_t$
is (semi)stable if and only if
![]() $E^D\subset \mathscr {P}_{\mathscr {B}_{-t}}(0,1) \subset \mathscr {B}_{-t} $
is (semi)stable.
$E^D\subset \mathscr {P}_{\mathscr {B}_{-t}}(0,1) \subset \mathscr {B}_{-t} $
is (semi)stable.
Proof. Let
![]() $\mathscr {P}(0,1]=\mathscr {A}_t$
in terms of slicing of
$\mathscr {P}(0,1]=\mathscr {A}_t$
in terms of slicing of
![]() $\mathscr {A}_t$
, then
$\mathscr {A}_t$
, then
![]() $\mathscr {B}_t=\mathscr {P}(-\frac {1}{2},\frac {1}{2}]$
by definition. The claim then follows from Proposition 5.3 and Remark 5.6.
$\mathscr {B}_t=\mathscr {P}(-\frac {1}{2},\frac {1}{2}]$
by definition. The claim then follows from Proposition 5.3 and Remark 5.6.
Finally, we show the duality results for the modified stability condition
![]() $\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t)$
on
$\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t)$
on
![]() $\mathscr {B}_t$
. Before the corollary, we compute the quiver region with respect to the stability condition
$\mathscr {B}_t$
. Before the corollary, we compute the quiver region with respect to the stability condition
![]() $\sigma _{t,u}$
. The quiver region for
$\sigma _{t,u}$
. The quiver region for
![]() $\mathbb {P}^2$
was introduced in [Reference Arcara, Bertram, Coskun and Huizenga3, Sec. 7]. The situation for
$\mathbb {P}^2$
was introduced in [Reference Arcara, Bertram, Coskun and Huizenga3, Sec. 7]. The situation for
![]() $\mathbb {P}^3$
is analogous. For the stability condition
$\mathbb {P}^3$
is analogous. For the stability condition
![]() $\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u})$
on
$\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u})$
on
![]() $\mathscr {B}_t$
, we make a tilt with respect to the slope
$\mathscr {B}_t$
, we make a tilt with respect to the slope
 $$ \begin{align*}\lambda_{t,u}:=-\frac{\mathscr{R}e(Z_{t,u})}{\mathscr{I}m(Z_{t,u})}=\frac{\chi_t-\frac{u^2}{2}\chi^{\prime\prime}_t}{\chi^{\prime}_t},\end{align*} $$
$$ \begin{align*}\lambda_{t,u}:=-\frac{\mathscr{R}e(Z_{t,u})}{\mathscr{I}m(Z_{t,u})}=\frac{\chi_t-\frac{u^2}{2}\chi^{\prime\prime}_t}{\chi^{\prime}_t},\end{align*} $$
and we have the following stability condition
![]() $\sigma ^{\prime }_{t,u} = (\mathscr {A}_{t,u}, Z^{\prime }_{t,u}=\chi ^{\prime }_t+ i \cdot (\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t)).$
$\sigma ^{\prime }_{t,u} = (\mathscr {A}_{t,u}, Z^{\prime }_{t,u}=\chi ^{\prime }_t+ i \cdot (\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t)).$
The quiver region, denoted by
![]() $\mathscr {Q}$
, is a region
$\mathscr {Q}$
, is a region
![]() $\mathscr {Q}\subset (t,u)$
-plane containing all points
$\mathscr {Q}\subset (t,u)$
-plane containing all points
![]() $(t,u)$
such that the following exceptional collection is contained in
$(t,u)$
such that the following exceptional collection is contained in
![]() $\mathscr {A}_{t,u}$
:
$\mathscr {A}_{t,u}$
:
Following the proof of Proposition 3.7, it is straightforward to see the quiver region for
![]() $(-1,0]\times \mathbb {R}_{\geq 0}$
in the
$(-1,0]\times \mathbb {R}_{\geq 0}$
in the
![]() $(t,u)$
-plane is the region below these two hyperbolas
$(t,u)$
-plane is the region below these two hyperbolas
![]() $(t+2)^2-3u^2-1=0$
and
$(t+2)^2-3u^2-1=0$
and
![]() $(t-1)^2-3u^2-1=0$
(including the t-axis), defined by
$(t-1)^2-3u^2-1=0$
(including the t-axis), defined by
![]() $\lambda _{t,u}(\mathscr {O}_{\mathbb {P}^3})=0$
and
$\lambda _{t,u}(\mathscr {O}_{\mathbb {P}^3})=0$
and
![]() $\lambda _{t,u}(\mathscr {O}_{\mathbb {P}^3}(-3))=0$
. Since the quiver regions are periodic (the period is
$\lambda _{t,u}(\mathscr {O}_{\mathbb {P}^3}(-3))=0$
. Since the quiver regions are periodic (the period is
![]() $t=1$
), the entire quiver region is as shown in Figure 6.
$t=1$
), the entire quiver region is as shown in Figure 6.

Figure 6 The quiver region.
Corollary 5.9. For the stability condition
![]() $\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t)$
such that
$\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+i\cdot \chi ^{\prime }_t)$
such that
![]() $(t,u)\in \mathscr {Q}$
,
$(t,u)\in \mathscr {Q}$
,
![]() $E\in \mathscr {P}_{\mathscr {B}_t}(0,1)\subset \mathscr {B}_t$
is
$E\in \mathscr {P}_{\mathscr {B}_t}(0,1)\subset \mathscr {B}_t$
is
![]() $\sigma _{t,u}$
-(semi)stable if and only if
$\sigma _{t,u}$
-(semi)stable if and only if
![]() $E^D\in \mathscr {P}_{\mathscr {B}_{-t}}(0,1) \subset \mathscr {B}_{-t} $
is
$E^D\in \mathscr {P}_{\mathscr {B}_{-t}}(0,1) \subset \mathscr {B}_{-t} $
is
![]() $\sigma _{-t,u}$
-(semi)stable.
$\sigma _{-t,u}$
-(semi)stable.
Proof. The reason that
![]() $E^D\in \mathscr {B}_{-t} $
is the same with Corollary 5.8 or Remark 5.6. For stability, observe that
$E^D\in \mathscr {B}_{-t} $
is the same with Corollary 5.8 or Remark 5.6. For stability, observe that
![]() $\chi _t(E)=\chi _t(E^D)$
,
$\chi _t(E)=\chi _t(E^D)$
,
![]() $\chi ^{\prime \prime }_t(E)=\chi ^{\prime \prime }_t(E^D)$
, and
$\chi ^{\prime \prime }_t(E)=\chi ^{\prime \prime }_t(E^D)$
, and
![]() $\chi ^{\prime }_t(E)=-\chi ^{\prime }_t(E^D)$
. Let
$\chi ^{\prime }_t(E)=-\chi ^{\prime }_t(E^D)$
. Let
![]() $\lambda _{t,u}$
be the slope
$\lambda _{t,u}$
be the slope
 $\displaystyle \lambda _{t,u}:=\frac {\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t}{\chi ^{\prime }_t}$
, then
$\displaystyle \lambda _{t,u}:=\frac {\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t}{\chi ^{\prime }_t}$
, then
![]() $\lambda _{t,u}(E)=-\lambda _{t,u}(E^D)$
. It is obvious that
$\lambda _{t,u}(E)=-\lambda _{t,u}(E^D)$
. It is obvious that
![]() $(t,u)\in \mathscr {Q}$
if and only if
$(t,u)\in \mathscr {Q}$
if and only if
![]() $(-t,u) \in \mathscr {Q}$
. So the claim follows in the same way as the proof in Proposition 5.3.
$(-t,u) \in \mathscr {Q}$
. So the claim follows in the same way as the proof in Proposition 5.3.
6 Walls for the class
 $3t\pm 1$
$3t\pm 1$
In this section, we work with the class
![]() $v=(0,0,3,-5)$
. The class of its twisted dual is
$v=(0,0,3,-5)$
. The class of its twisted dual is
![]() $v(E^{D})=(0,0,3,-7)$
, where
$v(E^{D})=(0,0,3,-7)$
, where
![]() $E\in \mathscr {B}_t$
is any object with
$E\in \mathscr {B}_t$
is any object with
![]() $ch(E)=(0,0,3,-5)$
. It is more convenient to work with the class
$ch(E)=(0,0,3,-5)$
. It is more convenient to work with the class
![]() $v^{\vee }:=v(E^D\otimes \mathscr {O}_{\mathbb {P}^3}(1))=(0,0,3,-4)$
since its actual wall lands in
$v^{\vee }:=v(E^D\otimes \mathscr {O}_{\mathbb {P}^3}(1))=(0,0,3,-4)$
since its actual wall lands in
![]() $\mathcal {A}_1$
. Their Hilbert polynomials are
$\mathcal {A}_1$
. Their Hilbert polynomials are
![]() $P_v(t)=3t+1$
and
$P_v(t)=3t+1$
and
![]() $P_{v^{\vee }}(t)=3t+2,$
respectively. We give two potential walls for v in the
$P_{v^{\vee }}(t)=3t+2,$
respectively. We give two potential walls for v in the
![]() $(t,u)$
plane in §
$(t,u)$
plane in §
![]() $6.1$
. Then, in §
$6.1$
. Then, in §
![]() $6.2$
, we prove that they are actual walls at
$6.2$
, we prove that they are actual walls at
![]() $u=0$
. Finally, in §
$u=0$
. Finally, in §
![]() $6.3$
, we use the duality results to study walls for the dual-class
$6.3$
, we use the duality results to study walls for the dual-class
![]() $v^{\vee }$
.
$v^{\vee }$
.
6.1 Potential walls in the “
 $(t,u)$
” plane
$(t,u)$
” plane
Let
![]() $E\in \mathscr {B}_t$
be a sheaf whose class is v. In [Reference Freiermuth and Trautmann12], the Gieseker moduli space
$E\in \mathscr {B}_t$
be a sheaf whose class is v. In [Reference Freiermuth and Trautmann12], the Gieseker moduli space
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
consists of two components. The general sheaves from those components are
$\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
consists of two components. The general sheaves from those components are
![]() $\mathscr {O}_{C}$
and
$\mathscr {O}_{C}$
and
![]() $L_{C_E}$
, where C is the twisted cubic and
$L_{C_E}$
, where C is the twisted cubic and
![]() $L_{C_E}$
is a degree
$L_{C_E}$
is a degree
![]() $1$
line bundle on the plane cubic curve
$1$
line bundle on the plane cubic curve
![]() $C_E$
.
$C_E$
.
For the stability condition
![]() $\sigma _t=(\mathscr {B}_t, Z_{t,u})$
, there are two walls for those Gieseker stable sheaves which are defined by sheaves
$\sigma _t=(\mathscr {B}_t, Z_{t,u})$
, there are two walls for those Gieseker stable sheaves which are defined by sheaves
![]() $\mathscr {O}_{\mathbb {P}^3}$
and
$\mathscr {O}_{\mathbb {P}^3}$
and
![]() $\mathscr {O}_{\Lambda }$
as follows (
$\mathscr {O}_{\Lambda }$
as follows (
![]() $\Lambda \subset \mathbb {P}^3$
is a plane):
$\Lambda \subset \mathbb {P}^3$
is a plane):
In the first sequence, the quotient object
![]() $Q[1]$
has two possibilities. It can be either the shifted ideal sheaf of a twisted cubic curve
$Q[1]$
has two possibilities. It can be either the shifted ideal sheaf of a twisted cubic curve
![]() $\mathscr {I}_C[1]$
or a shifted sheaf
$\mathscr {I}_C[1]$
or a shifted sheaf
![]() $\mathscr {F}[1]$
where the sheaf
$\mathscr {F}[1]$
where the sheaf
![]() $\mathscr {F}$
fits into the short exact sequence
$\mathscr {F}$
fits into the short exact sequence
![]() $0\to \mathscr {O}_{\Lambda }(-3)\to \mathscr {F}\to \mathscr {I}_P(-1)\to 0 $
(
$0\to \mathscr {O}_{\Lambda }(-3)\to \mathscr {F}\to \mathscr {I}_P(-1)\to 0 $
(
![]() $P\in \Lambda $
is a point in the plane) (see [Reference Freiermuth and Trautmann12], [Reference Xia35]).
$P\in \Lambda $
is a point in the plane) (see [Reference Freiermuth and Trautmann12], [Reference Xia35]).
The second sequence is indeed
![]() $0\to \mathscr {O}_{\Lambda }(-3) \to \mathscr {O}_{\Lambda } \to L_{C_E} \to \mathbb {C}_P\to 0$
in
$0\to \mathscr {O}_{\Lambda }(-3) \to \mathscr {O}_{\Lambda } \to L_{C_E} \to \mathbb {C}_P\to 0$
in
![]() $Coh(\mathbb {P}^3)$
(we will prove it in Proposition 7.9), where P is a point on
$Coh(\mathbb {P}^3)$
(we will prove it in Proposition 7.9), where P is a point on
![]() ${C_E}$
. The first object
${C_E}$
. The first object
![]() $\mathscr {O}_{\Lambda }(-3)$
needs to be shifted so that it is in
$\mathscr {O}_{\Lambda }(-3)$
needs to be shifted so that it is in
![]() $\mathscr {B}_t$
at the wall. The object
$\mathscr {B}_t$
at the wall. The object
![]() $\mathscr {F}_1$
is then a complex extended by
$\mathscr {F}_1$
is then a complex extended by
![]() $\mathbb {C}_P$
and
$\mathbb {C}_P$
and
![]() $\mathscr {O}_{\Lambda }(-3)[1]$
in
$\mathscr {O}_{\Lambda }(-3)[1]$
in
![]() $\mathscr {B}_t$
, that is,
$\mathscr {B}_t$
, that is,
![]() $0\to \mathscr {O}_{\Lambda }(-3)[1] \to \mathscr {F}_1 \to \mathbb {C}_P \to 0$
. The numerical walls are shown in Figure 7 (the bounded parts).
$0\to \mathscr {O}_{\Lambda }(-3)[1] \to \mathscr {F}_1 \to \mathbb {C}_P \to 0$
. The numerical walls are shown in Figure 7 (the bounded parts).

Figure 7 Walls for the class
![]() $v=(0,0,3,-5)$
.
$v=(0,0,3,-5)$
.
6.2 Actual walls in
 $\mathscr {A}_1$
$\mathscr {A}_1$
We will show that those potential walls are actual walls when
![]() $u=0$
. Figure 7 shows that the right endpoints of those walls both land in
$u=0$
. Figure 7 shows that the right endpoints of those walls both land in
![]() $t\in (0,1]$
which corresponds to the category
$t\in (0,1]$
which corresponds to the category
![]() $\mathscr {A}_1$
. The sheaves
$\mathscr {A}_1$
. The sheaves
![]() $\mathscr {O}_{C}$
and
$\mathscr {O}_{C}$
and
![]() $L_{C_E}$
are both in
$L_{C_E}$
are both in
![]() $\mathscr {A}_1$
since they are
$\mathscr {A}_1$
since they are
![]() $1$
-regular (see [Reference Lazarsfeld18, Prop. 1.8.8]). We will prove that the objects
$1$
-regular (see [Reference Lazarsfeld18, Prop. 1.8.8]). We will prove that the objects
![]() $\mathscr {O}_{\mathbb {P}^3}$
,
$\mathscr {O}_{\mathbb {P}^3}$
,
![]() $\mathscr {O}_{\Lambda }$
,
$\mathscr {O}_{\Lambda }$
,
![]() $\mathscr {F}_1$
,
$\mathscr {F}_1$
,
![]() $Q[1]$
which define
$Q[1]$
which define
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are stable in
$W_2$
are stable in
![]() $\mathscr {A}_1$
, and
$\mathscr {A}_1$
, and
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are the only two actual walls in
$W_2$
are the only two actual walls in
![]() $\mathscr {A}_1$
.
$\mathscr {A}_1$
.
6.2.1 Stability of
 $\mathscr {O}_{\mathbb {P}^3}$
and
$\mathscr {O}_{\mathbb {P}^3}$
and
 $\mathscr {O}_{\Lambda }$
$\mathscr {O}_{\Lambda }$
In the category
![]() $\mathscr {A}_1$
,
$\mathscr {A}_1$
,
![]() $\mathscr {O}_{\mathbb {P}^3}$
is resolved by the Koszul complex:
$\mathscr {O}_{\mathbb {P}^3}$
is resolved by the Koszul complex:
and its dimension vector is
![]() $[1464]$
. The object
$[1464]$
. The object
![]() $\mathscr {O}_{\Lambda }$
is a quotient of
$\mathscr {O}_{\Lambda }$
is a quotient of
![]() $\mathscr {O}_{\mathbb {P}^3}$
with dimension vector
$\mathscr {O}_{\mathbb {P}^3}$
with dimension vector
![]() $[1463]$
in
$[1463]$
in
![]() $\mathscr {A}_1$
. Its presentation is obtained by taking off one of the
$\mathscr {A}_1$
. Its presentation is obtained by taking off one of the
![]() $\mathscr {O}_{\mathbb {P}^3}(-1)$
from the presentation of
$\mathscr {O}_{\mathbb {P}^3}(-1)$
from the presentation of
![]() $\mathscr {O}_{\mathbb {P}^3}$
together with all the morphisms mapping to it.
$\mathscr {O}_{\mathbb {P}^3}$
together with all the morphisms mapping to it.
The stability of
![]() $\mathscr {O}_{\mathbb {P}^3}$
(it was also proved in [Reference Macrì26]) and
$\mathscr {O}_{\mathbb {P}^3}$
(it was also proved in [Reference Macrì26]) and
![]() $\mathscr {O}_{\Lambda }$
in
$\mathscr {O}_{\Lambda }$
in
![]() $\mathscr {A}_1$
for all
$\mathscr {A}_1$
for all
![]() $t\in (0,1]$
follows from checking all their sub-complexes. We provide, in Appendix A, a formula for checking the stability of an object. It is in the form of a dot product, which is King’s notation [Reference King17, Defn. 1.1]. This will reduce the amount of computation compared to checking the slopes of all sub-objects.
$t\in (0,1]$
follows from checking all their sub-complexes. We provide, in Appendix A, a formula for checking the stability of an object. It is in the form of a dot product, which is King’s notation [Reference King17, Defn. 1.1]. This will reduce the amount of computation compared to checking the slopes of all sub-objects.
6.2.2 Potential walls
We prove that
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are the only possible walls in
$W_2$
are the only possible walls in
![]() $\mathscr {A}_1$
for the class
$\mathscr {A}_1$
for the class
![]() $v=(0,0,3,-5)$
. Assume that
$v=(0,0,3,-5)$
. Assume that
![]() $E\in \mathscr {A}_1$
with class v, and an actual wall for E in
$E\in \mathscr {A}_1$
with class v, and an actual wall for E in
![]() $\mathscr {A}_1$
is defined by the short exact sequence
$\mathscr {A}_1$
is defined by the short exact sequence
![]() $0\to A\to E\to B\to 0$
. It is straightforward to check that the dimension vector of E in
$0\to A\to E\to B\to 0$
. It is straightforward to check that the dimension vector of E in
![]() $\mathscr { A}_1$
is
$\mathscr { A}_1$
is
![]() $[1694]$
. More precisely,
$[1694]$
. More precisely,
E contains the following sub-complex
and the corresponding quotient is
Serre duality shows that
![]() $Hom(E,\mathscr {O}_{\mathbb {P}^3}(-4)[3])\cong Hom(\mathscr {O}_{\mathbb {P}^3},E)^{\vee }$
. So there is always a non-zero morphism
$Hom(E,\mathscr {O}_{\mathbb {P}^3}(-4)[3])\cong Hom(\mathscr {O}_{\mathbb {P}^3},E)^{\vee }$
. So there is always a non-zero morphism
![]() $\mathscr {O}_{\mathbb {P}^3}\to E$
. Moreover, since
$\mathscr {O}_{\mathbb {P}^3}\to E$
. Moreover, since
![]() $\underline {dim}(E)=[1694]$
and
$\underline {dim}(E)=[1694]$
and
![]() $\underline {dim}(A)+\underline {dim}(B)=\underline {dim}(E)$
, we see that either A or B has dimension vector
$\underline {dim}(A)+\underline {dim}(B)=\underline {dim}(E)$
, we see that either A or B has dimension vector
![]() $[1,a_{-2},a_{-1},a_{0}]$
(
$[1,a_{-2},a_{-1},a_{0}]$
(
![]() $a_0$
,
$a_0$
,
![]() $a_{-1}$
,
$a_{-1}$
,
![]() $a_{-2} \geq 0$
). So without loss of generality, assume A has dimension vector
$a_{-2} \geq 0$
). So without loss of generality, assume A has dimension vector
![]() $[1,a_{-2},a_{-1},a_{0}]$
.
$[1,a_{-2},a_{-1},a_{0}]$
.
Apply Serre duality to
![]() $Hom(E,\mathscr {O}_{\mathbb {P}^3}(-4)[3]) \to Hom(A,\mathscr {O}_{\mathbb {P}^3}(-4)[3])$
. We have
$Hom(E,\mathscr {O}_{\mathbb {P}^3}(-4)[3]) \to Hom(A,\mathscr {O}_{\mathbb {P}^3}(-4)[3])$
. We have
![]() $Hom(\mathscr {O}_{\mathbb {P}^3}, E)^{\vee } \to Hom(\mathscr {O}_{\mathbb {P}^3}, A)^{\vee }$
, which gives
$Hom(\mathscr {O}_{\mathbb {P}^3}, E)^{\vee } \to Hom(\mathscr {O}_{\mathbb {P}^3}, A)^{\vee }$
, which gives
![]() $Hom(\mathscr {O}_{\mathbb {P}^3}, A)\to Hom(\mathscr {O}_{\mathbb {P}^3}, E)$
. This implies that A contains a quotient complex of
$Hom(\mathscr {O}_{\mathbb {P}^3}, A)\to Hom(\mathscr {O}_{\mathbb {P}^3}, E)$
. This implies that A contains a quotient complex of
![]() $\mathscr {O}_{\mathbb {P}^3}$
.
$\mathscr {O}_{\mathbb {P}^3}$
.
Table 1 contains all the quotients of
![]() $\mathscr {O}_{\mathbb {P}^3}$
in
$\mathscr {O}_{\mathbb {P}^3}$
in
![]() $\mathscr {A}_1$
and their stability. If A is one of the quotient complexes in the table, then a direct computation of their walls shows that
$\mathscr {A}_1$
and their stability. If A is one of the quotient complexes in the table, then a direct computation of their walls shows that
![]() $\mathscr {O}_{\mathbb {P}^3}$
and
$\mathscr {O}_{\mathbb {P}^3}$
and
![]() $\mathscr {O}_{\Lambda }$
are the only options for A to define an actual wall in
$\mathscr {O}_{\Lambda }$
are the only options for A to define an actual wall in
![]() $\mathscr {A}_1$
.
$\mathscr {A}_1$
.
Table 1 Quotient complexes of
![]() $\mathscr {O}_{\mathbb {P}^3}$
in
$\mathscr {O}_{\mathbb {P}^3}$
in
![]() $\mathscr {A}_1$
$\mathscr {A}_1$

Next, we show that if A strictly contains one of the quotient complexes T from Table 1, that is,
![]() $T\subsetneq A$
, then A or B will not be semistable at the wall. This implies that an actual wall for the class
$T\subsetneq A$
, then A or B will not be semistable at the wall. This implies that an actual wall for the class
![]() $v=(0,0,3,-5)$
can only be defined by
$v=(0,0,3,-5)$
can only be defined by
![]() $\mathscr {O}_{\mathbb {P}^3}$
or
$\mathscr {O}_{\mathbb {P}^3}$
or
![]() $\mathscr {O}_{\Lambda }$
.
$\mathscr {O}_{\Lambda }$
.
Table 2 consists of all possible dimension vectors of A that satisfy the following constraints:
-
1. A has the desired dimension vector.
 $T \hookrightarrow A \hookrightarrow E$
and
$T \hookrightarrow A \hookrightarrow E$
and
 $dim(T)<dim(A)<dim(E)$
in the lexicographical order in
$dim(T)<dim(A)<dim(E)$
in the lexicographical order in
 $\mathscr {A}_1$
.
$\mathscr {A}_1$
. -
2. The wall falls in
 $\mathscr {A}_1$
.
$\mathscr {A}_1$
. $\lambda ^{Euler}_t :=-\frac {\chi ^{\prime }_t}{\chi _t}$
denotes the slope of the Euler stability. We require that
$\lambda ^{Euler}_t :=-\frac {\chi ^{\prime }_t}{\chi _t}$
denotes the slope of the Euler stability. We require that
 $t_A\in (0,1]$
, where
$t_A\in (0,1]$
, where
 $t_A$
is a solution of
$t_A$
is a solution of
 $\lambda ^{Euler}_t(A)=\lambda ^{Euler}_t(E)$
.
$\lambda ^{Euler}_t(A)=\lambda ^{Euler}_t(E)$
. -
3. A is not destabilized by T at the wall
 $t_A$
, that is,
$t_A$
, that is,
 $\lambda ^{Euler}_{t_A}(T)\leq \lambda ^{Euler}_{t_A}(A)$
.
$\lambda ^{Euler}_{t_A}(T)\leq \lambda ^{Euler}_{t_A}(A)$
.
Table 2 All possibilities of A

Next, we will show that all objects A from Table 2 are unstable at its wall. So none of them can define an actual wall.
-
1.
 $dim(A)=[1564]$
and
$dim(A)=[1564]$
and
 $\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
$\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
In this case, we have
 $$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to \mathscr{O}_{\mathbb{P}^3}(-3)[2]\to 0.\end{align*} $$
$$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to \mathscr{O}_{\mathbb{P}^3}(-3)[2]\to 0.\end{align*} $$
 $Ext^1(\mathscr {O}_{\mathbb {P}^3}(-3)[2],\mathscr {O}_{\mathbb {P}^3})=0$
implies that
$Ext^1(\mathscr {O}_{\mathbb {P}^3}(-3)[2],\mathscr {O}_{\mathbb {P}^3})=0$
implies that
 $A=\mathscr {O}_{\mathbb {P}^3}(-3)[2]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at its wall.
$A=\mathscr {O}_{\mathbb {P}^3}(-3)[2]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at its wall. -
2.
 $dim(A)=[1574]$
and
$dim(A)=[1574]$
and
 $\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
$\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
In this case, we have
 $$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to F\to 0,\end{align*} $$
$$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to F\to 0,\end{align*} $$
where
 $F\in \mathscr {A}_1$
has dimension vector
$F\in \mathscr {A}_1$
has dimension vector
 $[0110]$
.
$[0110]$
.-
(a) If
 $F\overset {qiso}{\cong }[0\to \mathscr {O}_{\mathbb {P}^3}(-3) \overset {0}{\to } \mathscr {O}_{\mathbb {P}^3}(-2) \to 0]$
, then consider the morphism
$F\overset {qiso}{\cong }[0\to \mathscr {O}_{\mathbb {P}^3}(-3) \overset {0}{\to } \mathscr {O}_{\mathbb {P}^3}(-2) \to 0]$
, then consider the morphism  $$ \begin{align*}A \twoheadrightarrow \mathscr{O}_{\mathbb{P}^3}(-3)[2]\bigoplus \mathscr{O}_{\mathbb{P}^3}(-2)[1] \twoheadrightarrow \mathscr{O}_{\mathbb{P}^3}(-2)[1].\end{align*} $$
$$ \begin{align*}A \twoheadrightarrow \mathscr{O}_{\mathbb{P}^3}(-3)[2]\bigoplus \mathscr{O}_{\mathbb{P}^3}(-2)[1] \twoheadrightarrow \mathscr{O}_{\mathbb{P}^3}(-2)[1].\end{align*} $$
Let K be the kernel of the composition
 $A\twoheadrightarrow \mathscr {O}_{\mathbb {P}^3}(-2)[1]$
, then K fits the following short exact sequence:
$A\twoheadrightarrow \mathscr {O}_{\mathbb {P}^3}(-2)[1]$
, then K fits the following short exact sequence:  $$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3}\to K \to \mathscr{O}_{\mathbb{P}^3}(-3)[2] \to 0.\end{align*} $$
$$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3}\to K \to \mathscr{O}_{\mathbb{P}^3}(-3)[2] \to 0.\end{align*} $$
 $Ext^1(\mathscr {O}_{\mathbb {P}^3}(-3)[2], \mathscr {O}_{\mathbb {P}^3}) = 0$
implies that
$Ext^1(\mathscr {O}_{\mathbb {P}^3}(-3)[2], \mathscr {O}_{\mathbb {P}^3}) = 0$
implies that
 $K=\mathscr {O}_{\mathbb {P}^3}\bigoplus \mathscr {O}_{\mathbb {P}^3}(-3)[2]$
. So A fits into the short exact sequence:
$K=\mathscr {O}_{\mathbb {P}^3}\bigoplus \mathscr {O}_{\mathbb {P}^3}(-3)[2]$
. So A fits into the short exact sequence:  $$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3}\bigoplus \mathscr{O}_{\mathbb{P}^3}(-3)[2] \to A \to \mathscr{O}_{\mathbb{P}^3}(-2)[1] \to 0.\end{align*} $$
$$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3}\bigoplus \mathscr{O}_{\mathbb{P}^3}(-3)[2] \to A \to \mathscr{O}_{\mathbb{P}^3}(-2)[1] \to 0.\end{align*} $$
A direct computation shows that
 $\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
destabilizes A at the wall defined by A.
$\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
destabilizes A at the wall defined by A. -
(b) If
 $F\overset {qiso}{\cong }[0\to \mathscr {O}_{\mathbb {P}^3}(-3) \overset {\neq 0}{\to } \mathscr {O}_{\mathbb {P}^3}(-2) \to 0]$
, then
$F\overset {qiso}{\cong }[0\to \mathscr {O}_{\mathbb {P}^3}(-3) \overset {\neq 0}{\to } \mathscr {O}_{\mathbb {P}^3}(-2) \to 0]$
, then
 $F\overset {qiso}{\cong }\mathscr {O}_{\Lambda }(-2)[1]$
, where
$F\overset {qiso}{\cong }\mathscr {O}_{\Lambda }(-2)[1]$
, where
 $\Lambda \subset \mathbb {P}^3$
is a plane.
$\Lambda \subset \mathbb {P}^3$
is a plane. $Ext^1(\mathscr {O}_{\Lambda }(-2)[1], \mathscr {O}_{\mathbb {P}^3})=0$
implies that
$Ext^1(\mathscr {O}_{\Lambda }(-2)[1], \mathscr {O}_{\mathbb {P}^3})=0$
implies that
 $A=\mathscr {O}_{\Lambda }(-2)[1]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at the wall defined by A.
$A=\mathscr {O}_{\Lambda }(-2)[1]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at the wall defined by A.
-
-
3.
 $dim(A)=[1664]$
and
$dim(A)=[1664]$
and
 $\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
In this case, we have
$\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
In this case, we have  $$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to \mathscr{O}^2_{\mathbb{P}^3}(-3)[2]\to 0.\end{align*} $$
$$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to \mathscr{O}^2_{\mathbb{P}^3}(-3)[2]\to 0.\end{align*} $$
 $Ext^1(\mathscr {O}^2_{\mathbb {P}^3}(-3)[2], \mathscr {O}_{\mathbb {P}^3})=0$
implies
$Ext^1(\mathscr {O}^2_{\mathbb {P}^3}(-3)[2], \mathscr {O}_{\mathbb {P}^3})=0$
implies
 $A=\mathscr {O}^2_{\mathbb {P}^3}(-3)[2]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at its wall.
$A=\mathscr {O}^2_{\mathbb {P}^3}(-3)[2]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at its wall.
-
4.
 $dim(A)=[1674]$
and
$dim(A)=[1674]$
and
 $\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
A fits the short exact sequence: where
$\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
A fits the short exact sequence: where $$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to F \to 0,\end{align*} $$
$$ \begin{align*}0\to \mathscr{O}_{\mathbb{P}^3} \to A \to F \to 0,\end{align*} $$
 $dim(F)=[0210]$
.
$dim(F)=[0210]$
.
-
(a) If F has a sub-complex
 $\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
(dimension is
$\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
(dimension is
 $[0100]$
), then let Q be the quotient
$[0100]$
), then let Q be the quotient
 $0\to \mathscr {O}_{\mathbb {P}^3}(-3)[2] \to F \to Q \to 0$
(dim(Q)=
$0\to \mathscr {O}_{\mathbb {P}^3}(-3)[2] \to F \to Q \to 0$
(dim(Q)=
 $[0110]$
).
$[0110]$
).Let K be the kernel of the composition
 $A\twoheadrightarrow F \twoheadrightarrow Q$
. Similarly, we have
$A\twoheadrightarrow F \twoheadrightarrow Q$
. Similarly, we have
 $0\to \mathscr {O}_{\mathbb {P}^3}\to K \to \mathscr {O}_{\mathbb {P}^3}(-3)[2] \to 0$
, and
$0\to \mathscr {O}_{\mathbb {P}^3}\to K \to \mathscr {O}_{\mathbb {P}^3}(-3)[2] \to 0$
, and
 $K=\mathscr {O}_{\mathbb {P}^3}\bigoplus \mathscr {O}_{\mathbb {P}^3}(-3)[2]$
. A direct computations shows that
$K=\mathscr {O}_{\mathbb {P}^3}\bigoplus \mathscr {O}_{\mathbb {P}^3}(-3)[2]$
. A direct computations shows that
 $\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
destabilized A at its wall.
$\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
destabilized A at its wall. -
(b) If
 $\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
is not a sub-complex of F, then F is a complex satisfying the short exact sequence: where
$\mathscr {O}_{\mathbb {P}^3}(-3)[2]$
is not a sub-complex of F, then F is a complex satisfying the short exact sequence: where $$ \begin{align*}0\to F \to \mathscr{O}_{L}[1]\to \mathscr{O}_{\mathbb{P}^3}(-4)[3] \to 0,\end{align*} $$
$$ \begin{align*}0\to F \to \mathscr{O}_{L}[1]\to \mathscr{O}_{\mathbb{P}^3}(-4)[3] \to 0,\end{align*} $$
 $L\subset \mathbb {P}^3$
is a line.
$L\subset \mathbb {P}^3$
is a line.
 $Ext^1(F, \mathscr {O}_{\mathbb {P}^3})=0$
implies that
$Ext^1(F, \mathscr {O}_{\mathbb {P}^3})=0$
implies that
 $A=F\oplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at the wall.
$A=F\oplus \mathscr {O}_{\mathbb {P}^3}$
which is unstable at the wall.
-
-
5.
 $dim(A)=[1684]$
and
$dim(A)=[1684]$
and
 $\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
A fits into the short exact sequence
$\mathscr {O}_{\mathbb {P}^3} \hookrightarrow A$
A fits into the short exact sequence
 $0\to \mathscr {O}_{\mathbb {P}^3} \to A \to F \to 0 $
, where
$0\to \mathscr {O}_{\mathbb {P}^3} \to A \to F \to 0 $
, where
 $dim(F)=[0220]$
.
$dim(F)=[0220]$
.-
(a) If F contains a sub-complex
 $F_1$
whose dimension vector is
$F_1$
whose dimension vector is
 $[0210]$
, that is,
$[0210]$
, that is,
 $0\to F_1 \to F \to \mathscr {O}_{\mathbb {P}^3}(-2)[1] \to 0$
.Let K be the kernel of the composition
$0\to F_1 \to F \to \mathscr {O}_{\mathbb {P}^3}(-2)[1] \to 0$
.Let K be the kernel of the composition
 $A \twoheadrightarrow F \twoheadrightarrow \mathscr {O}_{\mathbb {P}^3}(-2)[1]$
, then K fits into the sequence
$A \twoheadrightarrow F \twoheadrightarrow \mathscr {O}_{\mathbb {P}^3}(-2)[1]$
, then K fits into the sequence
 $0\to \mathscr {O}_{\mathbb {P}^3} \to K \to F_1 \to 0$
.
$0\to \mathscr {O}_{\mathbb {P}^3} \to K \to F_1 \to 0$
.
 $K=F_1\bigoplus \mathscr {O}_{\mathbb {P}^3}$
since the extension class vanishes, and A is destabilized by
$K=F_1\bigoplus \mathscr {O}_{\mathbb {P}^3}$
since the extension class vanishes, and A is destabilized by
 $F_1$
at the wall.
$F_1$
at the wall. -
(b) If F does not contain any sub-complexes whose dimension is
 $[0210]$
. Equivalently,
$[0210]$
. Equivalently,
 $F \cong [0\to \mathscr {O}_{\mathbb {P}^3}^2(-3)\overset {\phi }{\to } \mathscr {O}_{\mathbb {P}^3}^2(-2)\to 0]$
where
$F \cong [0\to \mathscr {O}_{\mathbb {P}^3}^2(-3)\overset {\phi }{\to } \mathscr {O}_{\mathbb {P}^3}^2(-2)\to 0]$
where
 $\phi $
maps to both copies of
$\phi $
maps to both copies of
 $\mathscr {O}_{\mathbb {P}^3}(-2)$
. In this situation, F fits into the sequence where
$\mathscr {O}_{\mathbb {P}^3}(-2)$
. In this situation, F fits into the sequence where $$ \begin{align*}0\to F_1[2] \to F \to T[1] \to 0,\end{align*} $$
$$ \begin{align*}0\to F_1[2] \to F \to T[1] \to 0,\end{align*} $$
 $F_1, T \in Coh(\mathbb {P}^3)$
and T is a torsion sheaf. We have
$F_1, T \in Coh(\mathbb {P}^3)$
and T is a torsion sheaf. We have
 $Ext^1(F, \mathscr {O}_{\mathbb {P}^3})=0$
which implies
$Ext^1(F, \mathscr {O}_{\mathbb {P}^3})=0$
which implies
 $A=F\bigoplus \mathscr {O}_{\mathbb {P}^3}$
. A is unstable at its wall.
$A=F\bigoplus \mathscr {O}_{\mathbb {P}^3}$
. A is unstable at its wall.
-
-
6.
 $dim(A)=[1563]$
and
$dim(A)=[1563]$
and
 $\mathscr {O}_{\Lambda } \hookrightarrow A$
$\mathscr {O}_{\Lambda } \hookrightarrow A$
In this case, we have
 $0\to \mathscr {O}_{\mathbb {P}^3} \to A \to \mathscr {O}_{\mathbb {P}^3}(-3)[2] \to 0$
.
$0\to \mathscr {O}_{\mathbb {P}^3} \to A \to \mathscr {O}_{\mathbb {P}^3}(-3)[2] \to 0$
.
 $Ext^1(\mathscr {O}_{\mathbb {P}^3}(-3)[2], \mathscr {O}_{\mathbb {P}^3})=0$
implies
$Ext^1(\mathscr {O}_{\mathbb {P}^3}(-3)[2], \mathscr {O}_{\mathbb {P}^3})=0$
implies
 $A=\mathscr {O}_{\mathbb {P}^3}(-3)[2]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
, and A is unstable at its wall.
$A=\mathscr {O}_{\mathbb {P}^3}(-3)[2]\bigoplus \mathscr {O}_{\mathbb {P}^3}$
, and A is unstable at its wall.
6.2.3 Stability of
 $Q[1]$
and a description of its quiver moduli
$Q[1]$
and a description of its quiver moduli
![]() $Q[1]\in \mathscr {A}_1$
is the quotient complex in the short exact sequence:
$Q[1]\in \mathscr {A}_1$
is the quotient complex in the short exact sequence:
Its dimension vector is
![]() $[0,2,3,0]$
in
$[0,2,3,0]$
in
![]() $\mathscr {A}_1$
, so Q is presented by the complex
$\mathscr {A}_1$
, so Q is presented by the complex
where
![]() $M\in Hom(\mathbb {C}^3,\mathbb {C}^2)\otimes \mathbb {C}[x_0,\ldots ,x_3]_1$
. For simplicity, we use King’s notation (
$M\in Hom(\mathbb {C}^3,\mathbb {C}^2)\otimes \mathbb {C}[x_0,\ldots ,x_3]_1$
. For simplicity, we use King’s notation (
![]() $\theta $
function, [Reference King17]) for quiver stability. Recall that in our case, a
$\theta $
function, [Reference King17]) for quiver stability. Recall that in our case, a
![]() $\theta $
function is in the form
$\theta $
function is in the form
![]() $\theta (t)=(\theta _{-3}(t),\theta _{-2}(t),\theta _{-1}(t),\theta _{0}(t)),$
where
$\theta (t)=(\theta _{-3}(t),\theta _{-2}(t),\theta _{-1}(t),\theta _{0}(t)),$
where
![]() $\theta _{i}(t)$
(
$\theta _{i}(t)$
(
![]() $i=0,-1,-2,-3)$
) are
$i=0,-1,-2,-3)$
) are
![]() $\mathbb {R}$
-valued functions in t. For any dimension vector
$\mathbb {R}$
-valued functions in t. For any dimension vector
![]() $\underline {a}=(a_{-3},a_{-2},a_{-1},a_{0})$
,
$\underline {a}=(a_{-3},a_{-2},a_{-1},a_{0})$
,
![]() $\theta (t)($
a
$\theta (t)($
a
![]() $):=\theta _{-3}(t)a_{-3}+\theta _{-2}(t)a_{-2}+\theta _{-1}(t)a_{-1}+\theta _{0}(t)a_{0}$
. One can follow the steps in Appendix A to figure out the
$):=\theta _{-3}(t)a_{-3}+\theta _{-2}(t)a_{-2}+\theta _{-1}(t)a_{-1}+\theta _{0}(t)a_{0}$
. One can follow the steps in Appendix A to figure out the
![]() $\theta $
function, but since the dimension vector (
$\theta $
function, but since the dimension vector (
![]() $[0,2,3,0]$
) is relatively easy we can find
$[0,2,3,0]$
) is relatively easy we can find
![]() $\theta $
using the following trick. Indeed, there are only two possibilities for
$\theta $
using the following trick. Indeed, there are only two possibilities for
![]() $\theta $
, and they are independent of t, namely, (1)
$\theta $
, and they are independent of t, namely, (1)
![]() $\theta =(0,3,-2,0)$
and (2)
$\theta =(0,3,-2,0)$
and (2)
![]() $\theta =(0,-3,2,0)$
. Let
$\theta =(0,-3,2,0)$
. Let
![]() $\lambda ^E_t:=-\frac {\chi ^{\prime }_t}{\chi _t}$
be the slope of Euler stability. A direct computation shows that
$\lambda ^E_t:=-\frac {\chi ^{\prime }_t}{\chi _t}$
be the slope of Euler stability. A direct computation shows that
![]() $\lambda ^E_t(\mathscr {O}_{\mathbb {P}^3}(-2)[1])\leq \lambda ^E_t(Q[1])$
for
$\lambda ^E_t(\mathscr {O}_{\mathbb {P}^3}(-2)[1])\leq \lambda ^E_t(Q[1])$
for
![]() $t\in (0,1]$
. This implies that the
$t\in (0,1]$
. This implies that the
![]() $\theta $
function should satisfy
$\theta $
function should satisfy
![]() $\theta ([0,0,1,0,])\geq 0$
, hence
$\theta ([0,0,1,0,])\geq 0$
, hence
![]() $\theta $
should be
$\theta $
should be
![]() $\theta =(0,-3,2,0)$
.
$\theta =(0,-3,2,0)$
.
Let
![]() $\theta :=(0,-3,2,0)$
. For any sub-complex
$\theta :=(0,-3,2,0)$
. For any sub-complex
![]() $F\hookrightarrow Q[1]$
in
$F\hookrightarrow Q[1]$
in
![]() $\mathscr {A}_1$
whose dimension vector is
$\mathscr {A}_1$
whose dimension vector is
![]() $\underline {dim}(F)=[0,a,b,0]$
,
$\underline {dim}(F)=[0,a,b,0]$
,
![]() $\theta ([0,a,b,0]):=(-3)a+(2)b$
by definition.
$\theta ([0,a,b,0]):=(-3)a+(2)b$
by definition.
![]() $Q[1]$
is stable if
$Q[1]$
is stable if
![]() $\theta (F)>0$
for any sub-complex
$\theta (F)>0$
for any sub-complex
![]() $F\hookrightarrow Q[1]$
. The moduli space
$F\hookrightarrow Q[1]$
. The moduli space
![]() $K^{[2,3]}_{\theta }$
(for simplicity, we denote it by
$K^{[2,3]}_{\theta }$
(for simplicity, we denote it by
![]() $K_{\theta }$
) is a GIT quotient of the representation of the generalized Kronecker quiver K with dimension vector
$K_{\theta }$
) is a GIT quotient of the representation of the generalized Kronecker quiver K with dimension vector
![]() $[2,3]$
and stability condition
$[2,3]$
and stability condition
![]() $\theta $
. It is smooth of dimension
$\theta $
. It is smooth of dimension
![]() $12$
from [Reference King17] and [Reference Xia35].
$12$
from [Reference King17] and [Reference Xia35].

Next, we show the stratification of
![]() $K_{\theta }$
. Let
$K_{\theta }$
. Let
![]() $x_0,\ldots ,x_3$
be the coordinates of
$x_0,\ldots ,x_3$
be the coordinates of
![]() $\mathbb {P}^3$
, and
$\mathbb {P}^3$
, and
![]() $C^{\bullet }:=[0\to \mathscr {O}^2_{\mathbb {P}^3}(-3)\overset {M}{\rightarrow } \mathscr {O}^3_{\mathbb {P}^3}(-2) \to 0]$
be a stable complex. It was proved in [Reference Xia35, Th. 4.1] that the moduli space
$C^{\bullet }:=[0\to \mathscr {O}^2_{\mathbb {P}^3}(-3)\overset {M}{\rightarrow } \mathscr {O}^3_{\mathbb {P}^3}(-2) \to 0]$
be a stable complex. It was proved in [Reference Xia35, Th. 4.1] that the moduli space
![]() $K_{\theta }$
contains a five-dimensional smooth sub-variety, denoted by H, such that
$K_{\theta }$
contains a five-dimensional smooth sub-variety, denoted by H, such that
![]() $K_{\theta }\backslash H$
parameterizes twisted cubic curves and the limits of twisted cubics that do not contain embedded points. The sub-variety H parameterizes sheaves
$K_{\theta }\backslash H$
parameterizes twisted cubic curves and the limits of twisted cubics that do not contain embedded points. The sub-variety H parameterizes sheaves
![]() $E\in Coh(\mathbb {P}^3)$
that fit the sequence
$E\in Coh(\mathbb {P}^3)$
that fit the sequence
![]() $0\to \mathscr {O}_V(-3)\to E \to \mathscr {I}_P(-1) \to 0$
. The matrix M defining such a sheaf is the case (
$0\to \mathscr {O}_V(-3)\to E \to \mathscr {I}_P(-1) \to 0$
. The matrix M defining such a sheaf is the case (
![]() $9$
). To see this, we may start with the Koszul complex
$9$
). To see this, we may start with the Koszul complex
where
 $A=\begin {pmatrix}x_3\\ x_1\\ x_2\\\end {pmatrix}$
,
$A=\begin {pmatrix}x_3\\ x_1\\ x_2\\\end {pmatrix}$
,
 $B=\begin {pmatrix}x_2&0&x_3\\x_1&x_3&0\\0&x_2&x_1\\\end {pmatrix}$
, and
$B=\begin {pmatrix}x_2&0&x_3\\x_1&x_3&0\\0&x_2&x_1\\\end {pmatrix}$
, and
![]() $P\in \mathbb {P}^3$
is a point defined by
$P\in \mathbb {P}^3$
is a point defined by
![]() $x_1=x_2=x_3=0$
. Let
$x_1=x_2=x_3=0$
. Let
![]() $E_1$
be the sub-complex
$E_1$
be the sub-complex
![]() $\mathscr {O}^2_{\mathbb {P}^3}(-3)\overset {C}{\to } \mathscr {O}^3_{\mathbb {P}^3}(-2)$
defined by the matrix
$\mathscr {O}^2_{\mathbb {P}^3}(-3)\overset {C}{\to } \mathscr {O}^3_{\mathbb {P}^3}(-2)$
defined by the matrix
 $C=\begin {pmatrix}x_1&0\\0&x_1\\x_2&x_3\\\end {pmatrix}$
. Let G be the quotient complex. We have that
$C=\begin {pmatrix}x_1&0\\0&x_1\\x_2&x_3\\\end {pmatrix}$
. Let G be the quotient complex. We have that
![]() $G\cong [\mathscr {O}_{\mathbb {P}^3}(-4)\overset {D}{\to } \mathscr {O}_{\mathbb {P}^3}(-3)]$
where
$G\cong [\mathscr {O}_{\mathbb {P}^3}(-4)\overset {D}{\to } \mathscr {O}_{\mathbb {P}^3}(-3)]$
where
![]() $D=\begin {pmatrix}x_1\end {pmatrix}$
. This implies that
$D=\begin {pmatrix}x_1\end {pmatrix}$
. This implies that
![]() $G\cong \mathscr {O}_{V}(-3)[2]$
where
$G\cong \mathscr {O}_{V}(-3)[2]$
where
![]() $V\subset \mathbb {P}^3$
is a hyperplane defined by
$V\subset \mathbb {P}^3$
is a hyperplane defined by
![]() $x_1=0$
. Therefore, we have a sequence
$x_1=0$
. Therefore, we have a sequence
![]() $0\to E\to \mathscr {I}_P(-1)\to \mathscr {O}_V(-3)[2]\to 0$
in
$0\to E\to \mathscr {I}_P(-1)\to \mathscr {O}_V(-3)[2]\to 0$
in
![]() $\mathscr {A}_1$
. From the fact
$\mathscr {A}_1$
. From the fact
![]() $Ext^1(\mathscr {I}_P(-1), \mathscr {O}_V(-3))=\mathbb {C}$
(see [Reference Xia35, Lem. 4.2]), we know that it is the shifted sequence
$Ext^1(\mathscr {I}_P(-1), \mathscr {O}_V(-3))=\mathbb {C}$
(see [Reference Xia35, Lem. 4.2]), we know that it is the shifted sequence
![]() $0\to \mathscr {O}_V(-3)\to E\to \mathscr {I}_P(-1)\to 0$
in
$0\to \mathscr {O}_V(-3)\to E\to \mathscr {I}_P(-1)\to 0$
in
![]() $Coh(\mathbb {P}^3),$
where E is the sheaf
$Coh(\mathbb {P}^3),$
where E is the sheaf
![]() $E_1$
. (Here, we skip some details that
$E_1$
. (Here, we skip some details that
![]() $\mathscr {O}_{\Lambda }(-3)$
is stable in
$\mathscr {O}_{\Lambda }(-3)$
is stable in
![]() $Coh(\mathbb {P}^3)$
and
$Coh(\mathbb {P}^3)$
and
![]() $Coh^{-t-2}(\mathbb {P}^3)$
, and
$Coh^{-t-2}(\mathbb {P}^3)$
, and
![]() $\mathscr {O}_{\Lambda }(-3)[1]\in \mathscr {B}_t$
(
$\mathscr {O}_{\Lambda }(-3)[1]\in \mathscr {B}_t$
(
![]() $t\in (0,1]$
),
$t\in (0,1]$
),
![]() $\mathscr {O}_{\Lambda }(-3)[2]\in \mathscr {A}_1$
are also stable. We will show the proof in Lemma 7.7.) The sequence indicates that the locus
$\mathscr {O}_{\Lambda }(-3)[2]\in \mathscr {A}_1$
are also stable. We will show the proof in Lemma 7.7.) The sequence indicates that the locus
![]() $H\subset K_{\theta }$
is the flag variety
$H\subset K_{\theta }$
is the flag variety
![]() $\{P\in V\subset \mathbb {P}^3\}$
which is smooth of dimension
$\{P\in V\subset \mathbb {P}^3\}$
which is smooth of dimension
![]() $5$
. For any curve
$5$
. For any curve
![]() $[C] \in K_{\theta }\backslash H$
, its ideal sheaf
$[C] \in K_{\theta }\backslash H$
, its ideal sheaf
![]() $\mathscr {I}_C$
is one of the cases
$\mathscr {I}_C$
is one of the cases
![]() $(1)-(8)$
in [Reference Freiermuth11, Fig. 1]. So the corresponding matrices M are the cases
$(1)-(8)$
in [Reference Freiermuth11, Fig. 1]. So the corresponding matrices M are the cases
![]() $(1)-(8)$
.
$(1)-(8)$
.
(1)
 $M=\begin {pmatrix}x_0&x_1\\x_1&x_2\\x_2&x_3\\\end {pmatrix}$
(2)
$M=\begin {pmatrix}x_0&x_1\\x_1&x_2\\x_2&x_3\\\end {pmatrix}$
(2)
 $M=\begin {pmatrix}x_1&x_0\\x_0&x_2\\0&x_3\\\end {pmatrix}$
(3)
$M=\begin {pmatrix}x_1&x_0\\x_0&x_2\\0&x_3\\\end {pmatrix}$
(3)
 $M=\begin {pmatrix}x_3&0\\x_0&x_2\\0&x_1\\\end {pmatrix}$
(4)
$M=\begin {pmatrix}x_3&0\\x_0&x_2\\0&x_1\\\end {pmatrix}$
(4)
 $M=\begin {pmatrix}x_2&0\\x_1&x_1\\0&x_0\\\end {pmatrix}$
(5)
$M=\begin {pmatrix}x_2&0\\x_1&x_1\\0&x_0\\\end {pmatrix}$
(5)
 $M=\begin {pmatrix}x_1&x_3\\x_0&x_2\\0&x_0\\\end {pmatrix}$
(6)
$M=\begin {pmatrix}x_1&x_3\\x_0&x_2\\0&x_0\\\end {pmatrix}$
(6)
 $M=\begin {pmatrix}x_3&0\\x_0&x_1\\0&x_0\\\end {pmatrix}$
(7)
$M=\begin {pmatrix}x_3&0\\x_0&x_1\\0&x_0\\\end {pmatrix}$
(7)
 $M=\begin {pmatrix}x_1&x_2\\x_0&x_1\\0&x_0\\\end {pmatrix}$
(8)
$M=\begin {pmatrix}x_1&x_2\\x_0&x_1\\0&x_0\\\end {pmatrix}$
(8)
 $M=\begin {pmatrix}x_1&0\\x_0&x_1\\0&x_0\\\end {pmatrix}$
(9)
$M=\begin {pmatrix}x_1&0\\x_0&x_1\\0&x_0\\\end {pmatrix}$
(9)
 $M=\begin {pmatrix}x_1&0\\0&x_1\\x_2&x_3\\\end {pmatrix}$
$M=\begin {pmatrix}x_1&0\\0&x_1\\x_2&x_3\\\end {pmatrix}$
Remark 6.1. One can also prove directly that a complex
![]() $2\mathscr {O}_{\mathbb {P}^3}(-3)\overset {M}{\to }3\mathscr {O}_{\mathbb {P}^3}(-2)$
is stable with respect to the Theta function
$2\mathscr {O}_{\mathbb {P}^3}(-3)\overset {M}{\to }3\mathscr {O}_{\mathbb {P}^3}(-2)$
is stable with respect to the Theta function
![]() $\theta =(0,-3,2,0)$
if and only if the matrix M falls into cases
$\theta =(0,-3,2,0)$
if and only if the matrix M falls into cases
![]() $(1)-(9)$
above up to a base change.
$(1)-(9)$
above up to a base change.
We make the conclusion that there are two strata on
![]() $K_{\theta }$
: A smooth closed sub-variety of dimension
$K_{\theta }$
: A smooth closed sub-variety of dimension
![]() $5$
parameterizing sheaves
$5$
parameterizing sheaves
![]() $\mathscr {F}$
, and its complement in
$\mathscr {F}$
, and its complement in
![]() $K_{\theta }$
parameterizing the space curves with Hilbert polynomial
$K_{\theta }$
parameterizing the space curves with Hilbert polynomial
![]() $3t+1$
. Correspondingly, there are two general representatives for Q in
$3t+1$
. Correspondingly, there are two general representatives for Q in
![]() $\mathscr {A}_1$
such that
$\mathscr {A}_1$
such that
![]() $Q[1]$
is stable, the ideal sheaf of a space curve
$Q[1]$
is stable, the ideal sheaf of a space curve
![]() $\mathscr {I}_C$
or the sheaf
$\mathscr {I}_C$
or the sheaf
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
6.2.4 Stability of the complex
 $\mathscr {F}_1$
$\mathscr {F}_1$
We start by defining the complex
![]() $\mathscr {F}_1$
and then show that it is the only stable complex in
$\mathscr {F}_1$
and then show that it is the only stable complex in
![]() $\mathscr {A}_1$
with dimension vector
$\mathscr {A}_1$
with dimension vector
![]() $[0231]$
.
$[0231]$
.
Define the complex
![]() $\mathscr {F}_1$
in
$\mathscr {F}_1$
in
![]() $\mathscr {A}_1$
.
$\mathscr {A}_1$
.
We showed that the presentation of the sheaf
![]() $\mathscr {F}$
is
$\mathscr {F}$
is
where
 $M=\begin {pmatrix}x_1&0\\0&x_1\\x_2&x_3\\\end {pmatrix}$
. In fact, the complex
$M=\begin {pmatrix}x_1&0\\0&x_1\\x_2&x_3\\\end {pmatrix}$
. In fact, the complex
![]() $\mathscr {O}^2_{\mathbb {P}^3}(-3)\to \mathscr {O}^3_{\mathbb {P}^3}(-2)$
can be extended to the following complex:
$\mathscr {O}^2_{\mathbb {P}^3}(-3)\to \mathscr {O}^3_{\mathbb {P}^3}(-2)$
can be extended to the following complex:
where
![]() $N=\begin {pmatrix}x_2&x_3&-x_1\end {pmatrix}$
. Define
$N=\begin {pmatrix}x_2&x_3&-x_1\end {pmatrix}$
. Define
![]() $\mathscr {F}_1$
to be this new complex
$\mathscr {F}_1$
to be this new complex
We provide the Koszul complex below that resolves the skyscraper sheaf
![]() $\mathbb {C}_P$
(without loss of generality, we assume that P is defined by
$\mathbb {C}_P$
(without loss of generality, we assume that P is defined by
![]() $x_1=x_2=x_3=0$
in
$x_1=x_2=x_3=0$
in
![]() $\mathbb {P}^3$
). We change the morphisms a bit in order to match the matrix M. Indeed, the complex
$\mathbb {P}^3$
). We change the morphisms a bit in order to match the matrix M. Indeed, the complex
![]() $\mathscr {F}_1$
is a sub-complex of
$\mathscr {F}_1$
is a sub-complex of
![]() $\mathbb {C}_P$
in
$\mathbb {C}_P$
in
![]() $\mathscr {A}_1$
, and we highlight this sub-complex in blue in the Koszul complex.
$\mathscr {A}_1$
, and we highlight this sub-complex in blue in the Koszul complex.

The quotient complex is
![]() $[\mathscr {O}_{\mathbb {P}^3}(-4)\overset {x_1}{\to } \mathscr {O}_{\mathbb {P}^3}(-3)\to 0\to 0] \cong \mathscr {O}_{\Lambda }(-3)[2]$
. So we have the short exact sequence
$[\mathscr {O}_{\mathbb {P}^3}(-4)\overset {x_1}{\to } \mathscr {O}_{\mathbb {P}^3}(-3)\to 0\to 0] \cong \mathscr {O}_{\Lambda }(-3)[2]$
. So we have the short exact sequence
![]() $0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2] \to 0$
in
$0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2] \to 0$
in
![]() $\mathscr {A}_1$
, and
$\mathscr {A}_1$
, and
![]() $\mathscr {F}_1$
is a complex whose cohomologies are:
$\mathscr {F}_1$
is a complex whose cohomologies are:
![]() $\mathscr {H}^{-1}(\mathscr {F}_1)=\mathscr {O}_{\Lambda }(-3)$
,
$\mathscr {H}^{-1}(\mathscr {F}_1)=\mathscr {O}_{\Lambda }(-3)$
,
![]() $\mathscr {H}^{0}(\mathscr {F}_1)=\mathbb {C}_P,$
and
$\mathscr {H}^{0}(\mathscr {F}_1)=\mathbb {C}_P,$
and
![]() $\mathscr {H}^{i}(\mathscr {F}_1)=0$
for
$\mathscr {H}^{i}(\mathscr {F}_1)=0$
for
![]() $i\neq -1, 0$
.
$i\neq -1, 0$
.
Prove that
![]() $\mathscr {F}_1$
is the only stable object with the dimension vector
$\mathscr {F}_1$
is the only stable object with the dimension vector
![]() $[0231]$
.
$[0231]$
.
Assume that G is a complex whose dimension vector is
![]() $[0231]$
in
$[0231]$
in
![]() $\mathscr {A}_1$
, and
$\mathscr {A}_1$
, and
![]() $C^{\bullet }\hookrightarrow G$
is a sub-complex whose dimension vector is
$C^{\bullet }\hookrightarrow G$
is a sub-complex whose dimension vector is
![]() $[0,c,b,a]$
(
$[0,c,b,a]$
(
![]() $c=0,1,2$
,
$c=0,1,2$
,
![]() $b=0,1,2,3$
,
$b=0,1,2,3$
,
![]() $a=0,1$
). The following result is from a direct computation:
$a=0,1$
). The following result is from a direct computation:
-
1. If
 $a=0$
, then
$a=0$
, then
 $\lambda _t(C^{\bullet })>\lambda _t(G)$
for any
$\lambda _t(C^{\bullet })>\lambda _t(G)$
for any
 $b=0,1,2,3$
,
$b=0,1,2,3$
,
 $c=0,1,2$
and
$c=0,1,2$
and
 $t>0.1716$
.
$t>0.1716$
. -
2. If
 $a=1$
, then
$a=1$
, then
 $\lambda _t(C^{\bullet })<\lambda _t(G)$
for any
$\lambda _t(C^{\bullet })<\lambda _t(G)$
for any
 $b=0,1,2,3$
,
$b=0,1,2,3$
,
 $c=0,1,2$
and
$c=0,1,2$
and
 $t>0.1716$
.
$t>0.1716$
.
This result shows that for any
![]() $t\in (0.1716,1]$
in
$t\in (0.1716,1]$
in
![]() $\mathscr {A}_1$
, G is stable if and only if it does not have any sub-complex
$\mathscr {A}_1$
, G is stable if and only if it does not have any sub-complex
![]() $C^{\bullet }$
whose dimension vector is
$C^{\bullet }$
whose dimension vector is
![]() $[0,c,b,0]$
.
$[0,c,b,0]$
.
More explicitly, if
![]() $[0\to \mathscr {O}^2_{\mathbb {P}^3}(-3) \overset {M}{\to } \mathscr {O}^3_{\mathbb {P}^3}(-2) \overset {N}{\to } \mathscr {O}_{\mathbb {P}^3}(-1)]$
is the presentation of G in
$[0\to \mathscr {O}^2_{\mathbb {P}^3}(-3) \overset {M}{\to } \mathscr {O}^3_{\mathbb {P}^3}(-2) \overset {N}{\to } \mathscr {O}_{\mathbb {P}^3}(-1)]$
is the presentation of G in
![]() $\mathscr {A}_1$
, where
$\mathscr {A}_1$
, where
![]() $N=(f_1,f_2,f_3)$
consists of linear functions
$N=(f_1,f_2,f_3)$
consists of linear functions
![]() $f_i$
(
$f_i$
(
![]() $i=1,2,3$
), then
$i=1,2,3$
), then
![]() $f_1,f_2,f_3$
must be linearly independent.
$f_1,f_2,f_3$
must be linearly independent.
Next, we show that the matrix M has to be in the form:
 $\begin {pmatrix}f_3&0\\0&f_3\\-f_1&-f_2\\\end {pmatrix}$
, and this will prove the claim.
$\begin {pmatrix}f_3&0\\0&f_3\\-f_1&-f_2\\\end {pmatrix}$
, and this will prove the claim.
There are two
![]() $\mathscr {O}_{\mathbb {P}^3}(-3)$
’s mapping to
$\mathscr {O}_{\mathbb {P}^3}(-3)$
’s mapping to
![]() $\mathscr {O}^3_{\mathbb {P}^3}(-2)$
, and the morphisms are column vectors of M. Assume the first column of M is
$\mathscr {O}^3_{\mathbb {P}^3}(-2)$
, and the morphisms are column vectors of M. Assume the first column of M is
 $\begin {pmatrix}\phi _1\\\phi _2\\\phi _3\\\end {pmatrix}$
(
$\begin {pmatrix}\phi _1\\\phi _2\\\phi _3\\\end {pmatrix}$
(
![]() $\phi _i$
’s are linear functions), and we have the following diagram.
$\phi _i$
’s are linear functions), and we have the following diagram.

Firstly, we show that
![]() $\phi _i$
’s are linearly dependent. Let
$\phi _i$
’s are linearly dependent. Let
![]() $\langle f_1,f_2\rangle $
be the sub vector space of
$\langle f_1,f_2\rangle $
be the sub vector space of
![]() $\mathbb {C}[x_0,x_1,x_2,x_3]_1$
spanned by
$\mathbb {C}[x_0,x_1,x_2,x_3]_1$
spanned by
![]() $f_1, f_2$
. Since G is a complex, we must have
$f_1, f_2$
. Since G is a complex, we must have
![]() $\phi _1f_1+\phi _2f_2+\phi _3f_3=0$
. Consider the equation mod
$\phi _1f_1+\phi _2f_2+\phi _3f_3=0$
. Consider the equation mod
![]() $\langle f_1,f_2\rangle $
, and we have
$\langle f_1,f_2\rangle $
, and we have
![]() $\bar {\phi _3}\bar {f_3}=0$
in the quotient space
$\bar {\phi _3}\bar {f_3}=0$
in the quotient space
![]() $\mathbb {C}[x_0,x_1,x_2,x_3]_1/\langle f_1,f_2\rangle $
.
$\mathbb {C}[x_0,x_1,x_2,x_3]_1/\langle f_1,f_2\rangle $
.
![]() $f_i$
’s are linearly independent, so
$f_i$
’s are linearly independent, so
![]() $\bar {f_3}\neq 0$
. This implies
$\bar {f_3}\neq 0$
. This implies
![]() $\bar {\phi _3}=0$
and
$\bar {\phi _3}=0$
and
![]() $\phi _3=k_1f_1+k_2f_2$
for some
$\phi _3=k_1f_1+k_2f_2$
for some
![]() $k_1,k_2\in \mathbb {C}$
. The equation now becomes
$k_1,k_2\in \mathbb {C}$
. The equation now becomes
![]() $\phi _1f_1+\phi _2f_2+(k_1f_1+k_2f_2)f_3=0$
which simplifies to
$\phi _1f_1+\phi _2f_2+(k_1f_1+k_2f_2)f_3=0$
which simplifies to
![]() $(\phi _1+k_1f_3)f_1+(\phi _2+k_2f_3)f_2=0$
. Then we have
$(\phi _1+k_1f_3)f_1+(\phi _2+k_2f_3)f_2=0$
. Then we have
![]() $f_2|(\phi _1+k_1f_3)f_1$
and
$f_2|(\phi _1+k_1f_3)f_1$
and
![]() $f_1|(\phi _2+k_2f_3)f_2$
.
$f_1|(\phi _2+k_2f_3)f_2$
.
![]() $f_i$
’s are linearly independent, so we have
$f_i$
’s are linearly independent, so we have
![]() $f_2|\phi _1+k_1f_3$
and
$f_2|\phi _1+k_1f_3$
and
![]() $f_1|\phi _2+k_2f_3$
.
$f_1|\phi _2+k_2f_3$
.
![]() $\phi _i$
’s and
$\phi _i$
’s and
![]() $f_i$
’s are all linear functions, so there is some
$f_i$
’s are all linear functions, so there is some
![]() $k\in \mathbb {C}$
such that
$k\in \mathbb {C}$
such that
![]() $\phi _2+k_2f_3=kf_1$
and
$\phi _2+k_2f_3=kf_1$
and
![]() $\phi _1+k_1f_3=-kf_2$
. Now,
$\phi _1+k_1f_3=-kf_2$
. Now,
![]() $\phi _1=-k_1f_3-kf_2$
,
$\phi _1=-k_1f_3-kf_2$
,
![]() $\phi _2=-k_2f_3+kf_1$
,
$\phi _2=-k_2f_3+kf_1$
,
![]() $\phi _3=k_1f_1+k_2f_2$
, and they satisfy
$\phi _3=k_1f_1+k_2f_2$
, and they satisfy
![]() $k_2\phi _1-k_1\phi _2+k\phi _3=0$
. So
$k_2\phi _1-k_1\phi _2+k\phi _3=0$
. So
![]() $\phi _i$
’s are linearly dependent.
$\phi _i$
’s are linearly dependent.
Therefore, up to a base change, we may assume
![]() $\phi _3=0$
,
$\phi _3=0$
,
![]() $\phi _1=f_2$
, and
$\phi _1=f_2$
, and
![]() $\phi _2=-f_1$
. The presentation of G becomes:
$\phi _2=-f_1$
. The presentation of G becomes:

![]() $\phi _3\neq 0$
in the diagram. Otherwise,
$\phi _3\neq 0$
in the diagram. Otherwise,
![]() $(\phi _1,\phi _2)=c(f_2,-f_1)$
for some
$(\phi _1,\phi _2)=c(f_2,-f_1)$
for some
![]() $c\in \mathbb {C}$
. The map from the second
$c\in \mathbb {C}$
. The map from the second
![]() $\mathscr {O}_{\mathbb {P}^3}(-3)$
to
$\mathscr {O}_{\mathbb {P}^3}(-3)$
to
![]() $\mathscr {O}^3_{\mathbb {P}^3}(-2)$
will be
$\mathscr {O}^3_{\mathbb {P}^3}(-2)$
will be
![]() $0$
by a base change. This implies
$0$
by a base change. This implies
![]() $[ 0\to \mathscr {O}_{\mathbb {P}^3}(-3)\to 0 \to 0]$
is a sub-complex of G, making G unstable.
$[ 0\to \mathscr {O}_{\mathbb {P}^3}(-3)\to 0 \to 0]$
is a sub-complex of G, making G unstable.
If none of those
![]() $\phi _i$
’s is zero, then use
$\phi _i$
’s is zero, then use
![]() $\phi _2$
and
$\phi _2$
and
![]() $\phi _3$
to eliminate
$\phi _3$
to eliminate
![]() $\phi _1$
by a base change. The presentation becomes:
$\phi _1$
by a base change. The presentation becomes:

This diagram is exactly the presentation of
![]() $\mathscr {F}_1$
, and we prove the claim.
$\mathscr {F}_1$
, and we prove the claim.
6.3 Walls for the dual class
Lastly, in this section, we show the walls for the dual class of
![]() $v=(0,0,3,-5)$
. By definition (§5), the dual class
$v=(0,0,3,-5)$
. By definition (§5), the dual class
![]() $v^{\vee }$
is
$v^{\vee }$
is
![]() $(0,0,3,-4)$
(recall that
$(0,0,3,-4)$
(recall that
![]() $v^{\vee }(E):=v(E^D(1))$
, we twist the object
$v^{\vee }(E):=v(E^D(1))$
, we twist the object
![]() $E^D$
by
$E^D$
by
![]() $1$
so that its walls are in
$1$
so that its walls are in
![]() $\mathscr {A}_1$
), and its Hilbert polynomial is
$\mathscr {A}_1$
), and its Hilbert polynomial is
![]() $P_{v^{\vee }}(t) = 3t+2$
.
$P_{v^{\vee }}(t) = 3t+2$
.
Recall that the two general Gieseker stable sheaves with Hilbert polynomial
![]() $P(t)=3t+2$
are: (1)
$P(t)=3t+2$
are: (1)
![]() $E=\mathscr {O}_{C}(P)$
, where C is a space cubic curve and P is a point on C. (2)
$E=\mathscr {O}_{C}(P)$
, where C is a space cubic curve and P is a point on C. (2)
![]() $E=M_{C_E}$
, which is a degree
$E=M_{C_E}$
, which is a degree
![]() $2$
line bundle on a plane cubic curve
$2$
line bundle on a plane cubic curve
![]() $C_E$
. Their walls in
$C_E$
. Their walls in
![]() $\mathscr {A}_t$
are given by the short exact sequences
$\mathscr {A}_t$
are given by the short exact sequences
![]() $W_1'$
and
$W_1'$
and
![]() $W_2'$
below. They are in fact defined by the derived dual of
$W_2'$
below. They are in fact defined by the derived dual of
![]() $W_1$
and
$W_1$
and
![]() $W_2$
for the class
$W_2$
for the class
![]() $3t+1$
.
$3t+1$
.
where the complex
![]() $\left [\mathscr {O}^3_{\mathbb {P}^3}(-1)\to \mathscr {O}^2_{\mathbb {P}^3} \right ]$
is the sub-object of E.
$\left [\mathscr {O}^3_{\mathbb {P}^3}(-1)\to \mathscr {O}^2_{\mathbb {P}^3} \right ]$
is the sub-object of E.
where P is a point in the plane
![]() $\Lambda $
.
$\Lambda $
.
As indicated by the duality result (Corollary 5.9), a sequence
![]() $0\to A\to E\to B\to 0$
in
$0\to A\to E\to B\to 0$
in
![]() $\mathscr {B}_t$
defines an actual wall at
$\mathscr {B}_t$
defines an actual wall at
![]() $(t,u)$
(for some
$(t,u)$
(for some
![]() $(t,u)$
in the quiver region) if and only if the sequence
$(t,u)$
in the quiver region) if and only if the sequence
![]() $0\to B^D \to E^D \to A^D \to 0$
(in
$0\to B^D \to E^D \to A^D \to 0$
(in
![]() $\mathscr {B}_{-t}$
) defines an actual wall at
$\mathscr {B}_{-t}$
) defines an actual wall at
![]() $(-t,u)$
. So their numerical walls are symmetric about the vertical line
$(-t,u)$
. So their numerical walls are symmetric about the vertical line
![]() $t=0$
. Here, we twist the class of
$t=0$
. Here, we twist the class of
![]() $E^D$
by
$E^D$
by
![]() $1$
, that is,
$1$
, that is,
![]() $v^{\vee }=v(E^D(1))$
, therefore, the walls
$v^{\vee }=v(E^D(1))$
, therefore, the walls
![]() $W_1'$
and
$W_1'$
and
![]() $W_2'$
are symmetric to walls
$W_2'$
are symmetric to walls
![]() $W_1$
and
$W_1$
and
![]() $W_2$
with respect to the vertical line
$W_2$
with respect to the vertical line
![]() $t=-\frac {1}{2}$
. We have shown that
$t=-\frac {1}{2}$
. We have shown that
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are actual walls at their right endpoints, so
$W_2$
are actual walls at their right endpoints, so
![]() $W_1'$
and
$W_1'$
and
![]() $W_2'$
must be actual walls at their left endpoints (in
$W_2'$
must be actual walls at their left endpoints (in
![]() $\mathscr {A}_{-1}$
).
$\mathscr {A}_{-1}$
).
Suppose Conjecture 4.9 were proved true, then
![]() $W_1$
(resp.
$W_1$
(resp.
![]() $W_1'$
) and
$W_1'$
) and
![]() $W_2$
(resp.
$W_2$
(resp.
![]() $W_2'$
) would be actual walls everywhere in the
$W_2'$
) would be actual walls everywhere in the
![]() $(t,u)$
plane once we prove that they are actual walls at the other endpoint. This is because there is no possible intersecting of these walls.
$(t,u)$
plane once we prove that they are actual walls at the other endpoint. This is because there is no possible intersecting of these walls.
For the rest of this section, we prove the stability for
![]() $\mathscr {O}_{\Lambda }(-2)[1]$
and
$\mathscr {O}_{\Lambda }(-2)[1]$
and
![]() $\mathscr {I}_{P/\Lambda }(1)$
in
$\mathscr {I}_{P/\Lambda }(1)$
in
![]() $\mathscr {A}_1$
. This will imply that
$\mathscr {A}_1$
. This will imply that
![]() $W_2'$
is an actual wall at the right endpoint. The dimension vector of
$W_2'$
is an actual wall at the right endpoint. The dimension vector of
![]() $\mathscr {O}_{\Lambda }(-2)[1]$
is
$\mathscr {O}_{\Lambda }(-2)[1]$
is
![]() $[0,1,1,0]$
, and
$[0,1,1,0]$
, and
![]() $[0,0,1,0]$
is the only non-trivial sub-complex. It is straightforward to check that
$[0,0,1,0]$
is the only non-trivial sub-complex. It is straightforward to check that
![]() $\mathscr {O}_{\Lambda }(-2)[1]$
is stable in
$\mathscr {O}_{\Lambda }(-2)[1]$
is stable in
![]() $\mathscr {A}_1$
for
$\mathscr {A}_1$
for
![]() $t\in (0,1)$
. The dimension vector of
$t\in (0,1)$
. The dimension vector of
![]() $\mathscr {I}_{P/\Lambda }(1)$
is
$\mathscr {I}_{P/\Lambda }(1)$
is
![]() $[2,8,11,5]$
. Without loss of generality, assume that the coordinates of
$[2,8,11,5]$
. Without loss of generality, assume that the coordinates of
![]() $\mathbb {P}^3$
are
$\mathbb {P}^3$
are
![]() $x,y,z,w$
,
$x,y,z,w$
,
![]() $\Lambda $
is defined by
$\Lambda $
is defined by
![]() $\{x=0\}$
and P is defined by
$\{x=0\}$
and P is defined by
![]() $\{x=y=z=0\}$
. The presentation of
$\{x=y=z=0\}$
. The presentation of
![]() $\mathscr {I}_{P/\Lambda }(1)$
is as follows:
$\mathscr {I}_{P/\Lambda }(1)$
is as follows:
The stability of
![]() $\mathscr {I}_{P/\Lambda }(1)$
follows from a direct computation that the slopes of all its sub-complexes are smaller than the slope of
$\mathscr {I}_{P/\Lambda }(1)$
follows from a direct computation that the slopes of all its sub-complexes are smaller than the slope of
![]() $\mathscr {I}_{P/\Lambda }(1)$
at the wall. See Appendix B for matrices
$\mathscr {I}_{P/\Lambda }(1)$
at the wall. See Appendix B for matrices
![]() $M,N,S$
and the dimension vector of all the sub-complexes.
$M,N,S$
and the dimension vector of all the sub-complexes.
7 The wall-crossings for the class
 $3t+1$
$3t+1$
In this section, we study the wall-crossings for the class
![]() $v=(0,0,3,-5)$
. The moduli space in the last chamber in
$v=(0,0,3,-5)$
. The moduli space in the last chamber in
![]() $\mathscr {A}_1$
(i.e.,
$\mathscr {A}_1$
(i.e.,
![]() $t\in (0.72, 1]$
) turns out to be the Gieseker moduli space. This gives some clue that the last wall in
$t\in (0.72, 1]$
) turns out to be the Gieseker moduli space. This gives some clue that the last wall in
![]() $\mathscr {A}_1$
is expected to be the last wall for all
$\mathscr {A}_1$
is expected to be the last wall for all
![]() $t\in \mathbb {R}$
, and the unbounded chamber containing
$t\in \mathbb {R}$
, and the unbounded chamber containing
![]() $t\gg 0$
is the Gieseker chamber. The main technique we use is the elementary modification. A similar process can be found in [Reference Xia35] and [Reference Arcara and Bertram2].
$t\gg 0$
is the Gieseker chamber. The main technique we use is the elementary modification. A similar process can be found in [Reference Xia35] and [Reference Arcara and Bertram2].
In §6, we found two actual walls in
![]() $\mathscr {A}_1$
for v. These are
$\mathscr {A}_1$
for v. These are
![]() $W_1: 0\to \mathscr {O}_{\mathbb {P}^3}\to E \to Q[1] \to 0$
at
$W_1: 0\to \mathscr {O}_{\mathbb {P}^3}\to E \to Q[1] \to 0$
at
![]() $t=0.35$
, and
$t=0.35$
, and
![]() $W_2: 0\to \mathscr {O}_{\Lambda }\to E \to \mathscr {F}_1 \to 0$
at
$W_2: 0\to \mathscr {O}_{\Lambda }\to E \to \mathscr {F}_1 \to 0$
at
![]() $t=0.72$
. Denote the three chambers in
$t=0.72$
. Denote the three chambers in
![]() $\mathscr {A}_1$
by
$\mathscr {A}_1$
by
![]() $C_1:= \{t\in (0,0.35)\}$
,
$C_1:= \{t\in (0,0.35)\}$
,
![]() $C_2:= \{t\in (0.35,0.72)\},$
and
$C_2:= \{t\in (0.35,0.72)\},$
and
![]() $C_3:= \{t\in (0.72,1]\}$
.
$C_3:= \{t\in (0.72,1]\}$
.
7.1 Moduli space
 $\mathscr {M}_{1}$
in
$\mathscr {M}_{1}$
in
 $C_1$
$C_1$
The moduli space in
![]() $t\in (0,0.35)$
is empty since every object E is destabilized by
$t\in (0,0.35)$
is empty since every object E is destabilized by
![]() $\mathscr {O}_{\mathbb {P}^3} \to E$
. The existence of such a map is given by Serre duality as shown in §6.
$\mathscr {O}_{\mathbb {P}^3} \to E$
. The existence of such a map is given by Serre duality as shown in §6.
7.2 Moduli space
 $\mathscr {M}_{W_1}$
at the first wall
$\mathscr {M}_{W_1}$
at the first wall
 $W_1$
$W_1$
![]() $W_1$
is defined by
$W_1$
is defined by
![]() $0\to \mathscr {O}_{\mathbb {P}^3}\to E \to Q[1] \to 0$
. The moduli space of E at
$0\to \mathscr {O}_{\mathbb {P}^3}\to E \to Q[1] \to 0$
. The moduli space of E at
![]() $W_1$
is the same with the moduli of
$W_1$
is the same with the moduli of
![]() $Q[1]$
which is the Kronecker moduli space
$Q[1]$
which is the Kronecker moduli space
![]() $K_{(2,3)}:=K^{[2,3]}_{\theta }$
(
$K_{(2,3)}:=K^{[2,3]}_{\theta }$
(
![]() $\theta =(-3,2)$
defines the stability condition as we pointed out in §
$\theta =(-3,2)$
defines the stability condition as we pointed out in §
![]() $6.2.2$
). It is a smooth variety of dimension
$6.2.2$
). It is a smooth variety of dimension
![]() $12$
.
$12$
.
7.3 Moduli space
 $\mathscr {M}_{2}$
in
$\mathscr {M}_{2}$
in
 $C_2$
$C_2$
For
![]() $t\in (0.35,0.72)$
. Recall that the quotient
$t\in (0.35,0.72)$
. Recall that the quotient
![]() $Q[1]$
has two general representatives which are stable: (1)
$Q[1]$
has two general representatives which are stable: (1)
![]() $Q=\mathscr {I}_{C}$
or (2)
$Q=\mathscr {I}_{C}$
or (2)
![]() $Q=\mathscr {F}$
, and the locus in
$Q=\mathscr {F}$
, and the locus in
![]() $K_{(2,3)}$
parameterizing
$K_{(2,3)}$
parameterizing
![]() $\mathscr {F}$
is a smooth five-dimensional flag variety. Denote this locus by H. A direct computation shows that
$\mathscr {F}$
is a smooth five-dimensional flag variety. Denote this locus by H. A direct computation shows that
![]() $Ext^1(\mathscr {I}_{C}[1],\mathscr {O}_{\mathbb {P}^3})=\mathbb {C}$
and
$Ext^1(\mathscr {I}_{C}[1],\mathscr {O}_{\mathbb {P}^3})=\mathbb {C}$
and
![]() $Ext^1(\mathscr {F}[1],\mathscr {O}_{\mathbb {P}^3})=\mathbb {C}^4$
. This implies that
$Ext^1(\mathscr {F}[1],\mathscr {O}_{\mathbb {P}^3})=\mathbb {C}^4$
. This implies that
![]() $\mathscr {M}_{2}$
is isomorphic to
$\mathscr {M}_{2}$
is isomorphic to
![]() $ \mathscr {M}_{W_1}$
outside H, and a
$ \mathscr {M}_{W_1}$
outside H, and a
![]() $\mathbb {P}^3$
bundle over H. Denote this
$\mathbb {P}^3$
bundle over H. Denote this
![]() $\mathbb {P}^3$
bundle by
$\mathbb {P}^3$
bundle by
![]() $\mathscr {M}_{\mathscr {F}}$
.
$\mathscr {M}_{\mathscr {F}}$
.
7.4 Moduli space
 $\mathscr {M}_{W_2}$
at the second wall
$\mathscr {M}_{W_2}$
at the second wall
Recall that
![]() $W_2$
is defined by the sequence
$W_2$
is defined by the sequence
![]() $0\to \mathscr {O}_{\Lambda }\to E \to \mathscr {F}_1 \to 0$
. There are two strata on the moduli space
$0\to \mathscr {O}_{\Lambda }\to E \to \mathscr {F}_1 \to 0$
. There are two strata on the moduli space
![]() $\mathscr {M}_{2}$
, which are
$\mathscr {M}_{2}$
, which are
![]() $K_{(2,3)}\backslash H$
and
$K_{(2,3)}\backslash H$
and
![]() $M_{\mathscr {F}}$
.
$M_{\mathscr {F}}$
.
![]() $K_{(2,3)}\backslash H$
parameterizes the structure sheaf of space cubic curves C, and
$K_{(2,3)}\backslash H$
parameterizes the structure sheaf of space cubic curves C, and
![]() $M_{\mathscr {F}}$
parameterizes those objects E which fit into the short exact sequence
$M_{\mathscr {F}}$
parameterizes those objects E which fit into the short exact sequence
![]() $0\to \mathscr {O}_{\mathbb {P}^3}\to E\to \mathscr {F}[1] \to 0$
. Objects E in
$0\to \mathscr {O}_{\mathbb {P}^3}\to E\to \mathscr {F}[1] \to 0$
. Objects E in
![]() $M_{\mathscr {F}}$
satisfy the following sequence as well:
$M_{\mathscr {F}}$
satisfy the following sequence as well:
In the sequence,
![]() $\mathscr {F}_1$
is the complex defined in the last section, and
$\mathscr {F}_1$
is the complex defined in the last section, and
![]() $\mathscr {F}_1$
corresponds to a point
$\mathscr {F}_1$
corresponds to a point
![]() $(P,\Lambda )$
of the Flag variety H.
$(P,\Lambda )$
of the Flag variety H.
![]() $\Lambda '\subset \mathbb {P}^3$
is a plane but not necessarily the same as the plane
$\Lambda '\subset \mathbb {P}^3$
is a plane but not necessarily the same as the plane
![]() $\Lambda $
encoded in
$\Lambda $
encoded in
![]() $\mathscr {F}_1$
. A direct computation shows that
$\mathscr {F}_1$
. A direct computation shows that
 $$ \begin{align*} \left\{ \begin{array}{llc} Ext^1(\mathscr{F}_1, \mathscr{O}_{\Lambda})=\mathbb{C}^9, & Ext^1(\mathscr{O}_{\Lambda}, \mathscr{F}_1)=\mathbb{C,} & {}\\ Ext^1(\mathscr{F}_1, \mathscr{O}_{\Lambda'})=0, & Ext^1(\mathscr{O}_{\Lambda'}, \mathscr{F}_1)=\mathbb{C} & \text{if} \quad \Lambda'\neq \Lambda.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{llc} Ext^1(\mathscr{F}_1, \mathscr{O}_{\Lambda})=\mathbb{C}^9, & Ext^1(\mathscr{O}_{\Lambda}, \mathscr{F}_1)=\mathbb{C,} & {}\\ Ext^1(\mathscr{F}_1, \mathscr{O}_{\Lambda'})=0, & Ext^1(\mathscr{O}_{\Lambda'}, \mathscr{F}_1)=\mathbb{C} & \text{if} \quad \Lambda'\neq \Lambda.\\ \end{array} \right. \end{align*} $$
This implies that
![]() $\mathscr {M}_{W_2}=\mathscr {M}_{2}$
. When varying from
$\mathscr {M}_{W_2}=\mathscr {M}_{2}$
. When varying from
![]() $C_2$
to
$C_2$
to
![]() $W_2$
, objects in the stratum
$W_2$
, objects in the stratum
![]() $K_{(2,3)}\backslash H$
stay stable while objects in
$K_{(2,3)}\backslash H$
stay stable while objects in
![]() $\mathscr {M}_{\mathscr {F}}$
become strictly semi-stable.
$\mathscr {M}_{\mathscr {F}}$
become strictly semi-stable.
Indeed, an object E lies in
![]() $\mathscr {M}_{\mathscr {F}}\backslash H$
if and only if
$\mathscr {M}_{\mathscr {F}}\backslash H$
if and only if
![]() $\Lambda '\neq \Lambda $
in sequence 7.1, and E lies in H if and only if
$\Lambda '\neq \Lambda $
in sequence 7.1, and E lies in H if and only if
![]() $\Lambda '=\Lambda $
. This is implied by the next lemma saying that
$\Lambda '=\Lambda $
. This is implied by the next lemma saying that
![]() $Ext^1(E,E)=\mathbb {C}^8$
for E fitting sequence 7.1 in which
$Ext^1(E,E)=\mathbb {C}^8$
for E fitting sequence 7.1 in which
![]() $\Lambda '\neq \Lambda $
. We will show that
$\Lambda '\neq \Lambda $
. We will show that
![]() $K_{(2,3)}$
intersects
$K_{(2,3)}$
intersects
![]() $\mathscr {M}_{\mathscr {F}}$
transversely in the next subsection.
$\mathscr {M}_{\mathscr {F}}$
transversely in the next subsection.
Lemma 7.1. For an object
![]() $E\in \mathscr {A}_1$
that fits sequence 7.1, in which
$E\in \mathscr {A}_1$
that fits sequence 7.1, in which
![]() $\Lambda '\neq \Lambda $
, we have
$\Lambda '\neq \Lambda $
, we have
![]() $Ext^1(E,E)=\mathbb {C}^8$
.
$Ext^1(E,E)=\mathbb {C}^8$
.
Proof.
Step 1. (Compute
![]() $Ext^1(E,E)$
.) We apply the functor
$Ext^1(E,E)$
.) We apply the functor
![]() $Hom(E, -)$
to sequence 7.1, and we get the following long exact sequence:
$Hom(E, -)$
to sequence 7.1, and we get the following long exact sequence:

Since E is stable for
![]() $t\in C_2$
, we have that
$t\in C_2$
, we have that
![]() $Hom(E,E)=\mathbb {C}$
. This forces
$Hom(E,E)=\mathbb {C}$
. This forces
![]() $Hom(E, \mathscr {F}_1)=0$
. Otherwise, we must have
$Hom(E, \mathscr {F}_1)=0$
. Otherwise, we must have
![]() $Hom(E, \mathscr {F}_1)=\mathbb {C}$
. Then, let
$Hom(E, \mathscr {F}_1)=\mathbb {C}$
. Then, let
![]() $f\in Hom(E, \mathscr {F}_1)$
and
$f\in Hom(E, \mathscr {F}_1)$
and
![]() $id_E\in Hom(E,E)$
be the unique (up to a scalar) morphisms, and let
$id_E\in Hom(E,E)$
be the unique (up to a scalar) morphisms, and let
![]() $0\to \mathscr {F}_1 \xrightarrow {i} E$
be the inclusion. We have that
$0\to \mathscr {F}_1 \xrightarrow {i} E$
be the inclusion. We have that
![]() $i\circ f\circ id_E^{-1}\cong id_E$
(up to a scalar). This implies that sequence 7.1 splits which makes E unstable. Next, we compute
$i\circ f\circ id_E^{-1}\cong id_E$
(up to a scalar). This implies that sequence 7.1 splits which makes E unstable. Next, we compute
![]() $Ext^i(E, \mathscr {F}_1)$
and
$Ext^i(E, \mathscr {F}_1)$
and
![]() $Ext^i(E, \mathscr {O}_{\Lambda '})$
.
$Ext^i(E, \mathscr {O}_{\Lambda '})$
.
Step 2. (Compute
![]() $Ext^i(E, \mathscr {O}_{\Lambda })$
) Apply the functor
$Ext^i(E, \mathscr {O}_{\Lambda })$
) Apply the functor
![]() $Hom(-, \mathscr {O}_{\Lambda '})$
to the sequence
$Hom(-, \mathscr {O}_{\Lambda '})$
to the sequence
![]() $0\to \mathscr {F}_1 \to E \to \mathscr {O}_{\Lambda '} \to 0$
, and we get the following long exact sequence:
$0\to \mathscr {F}_1 \to E \to \mathscr {O}_{\Lambda '} \to 0$
, and we get the following long exact sequence:

We next compute the rightmost column “
![]() $Ext^i(\mathscr {F}_1,\mathscr {O}_{\Lambda '})$
.”
$Ext^i(\mathscr {F}_1,\mathscr {O}_{\Lambda '})$
.”
Step 2-1 (Compute
![]() $Ext^i(\mathscr {F}_1,\mathscr {O}_{\Lambda '})$
.) Apply the functor
$Ext^i(\mathscr {F}_1,\mathscr {O}_{\Lambda '})$
.) Apply the functor
![]() $Hom(-, \mathscr {O}_{\Lambda '})$
to the sequence
$Hom(-, \mathscr {O}_{\Lambda '})$
to the sequence
![]() $0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2]\to 0$
which defines the complex
$0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2]\to 0$
which defines the complex
![]() $\mathscr {F}_1$
. We get the long exact sequence:
$\mathscr {F}_1$
. We get the long exact sequence:

It is straightforward to check that the first and second columns are all zero in the above diagram, and we skip the computations. The diagram implies that
![]() $Hom(\mathscr {F}_1,\mathscr {O}_{\Lambda '})=Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda '})=0$
.
$Hom(\mathscr {F}_1,\mathscr {O}_{\Lambda '})=Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda '})=0$
.
Back to Step 2, we have that
![]() $Hom(E, \mathscr {O}_{\Lambda '})=\mathbb {C}$
, and
$Hom(E, \mathscr {O}_{\Lambda '})=\mathbb {C}$
, and
![]() $Ext^1(E, \mathscr {O}_{\Lambda '})=\mathbb {C}^3$
.
$Ext^1(E, \mathscr {O}_{\Lambda '})=\mathbb {C}^3$
.
Step 3 (Compute
![]() $Ext^i(E, \mathscr {F}_1)$
.) Similarly, we apply the functor
$Ext^i(E, \mathscr {F}_1)$
.) Similarly, we apply the functor
![]() $Hom(-, \mathscr {F}_1)$
to the sequence
$Hom(-, \mathscr {F}_1)$
to the sequence
![]() $0\to \mathscr {F}_1\to E \to \mathscr {O}_{\Lambda '} \to 0$
and we get the following sequence:
$0\to \mathscr {F}_1\to E \to \mathscr {O}_{\Lambda '} \to 0$
and we get the following sequence:

In the above diagram,
![]() $Hom(\mathscr {F}_1,\mathscr {F}_{1})=\mathbb {C}$
and
$Hom(\mathscr {F}_1,\mathscr {F}_{1})=\mathbb {C}$
and
![]() $Ext^1(\mathscr {F}_1,\mathscr {F}_{1})=\mathbb {C}^5$
since
$Ext^1(\mathscr {F}_1,\mathscr {F}_{1})=\mathbb {C}^5$
since
![]() $\mathscr {F}_1$
is stable and the moduli of
$\mathscr {F}_1$
is stable and the moduli of
![]() $\mathscr {F}_1$
is a smooth flag variety of dimension
$\mathscr {F}_1$
is a smooth flag variety of dimension
![]() $5$
.
$5$
.
![]() $Hom(E,\mathscr {F}_{1})=0$
for the same reason that otherwise, the composition
$Hom(E,\mathscr {F}_{1})=0$
for the same reason that otherwise, the composition
![]() $\mathscr {F}_1\hookrightarrow E\to \mathscr {F}_1$
is the identity element in
$\mathscr {F}_1\hookrightarrow E\to \mathscr {F}_1$
is the identity element in
![]() $Hom(\mathscr {F}_1,\mathscr {F}_1)=\mathbb {C}$
(up to a scalar). This implies that
$Hom(\mathscr {F}_1,\mathscr {F}_1)=\mathbb {C}$
(up to a scalar). This implies that
![]() $0\to \mathscr {F}_1\to E \to \mathscr {O}_{\Lambda '} \to 0$
splits, which makes E unstable. Therefore, we also have
$0\to \mathscr {F}_1\to E \to \mathscr {O}_{\Lambda '} \to 0$
splits, which makes E unstable. Therefore, we also have
![]() $Hom(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})=0$
.
$Hom(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})=0$
.
Lastly, we compute
![]() $Ext^i(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})$
.
$Ext^i(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})$
.
Step 3-1 (Compute
![]() $Ext^i(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})$
) Apply the functor
$Ext^i(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})$
) Apply the functor
![]() $Hom(\mathscr {O}_{\Lambda '},-)$
to the sequence
$Hom(\mathscr {O}_{\Lambda '},-)$
to the sequence
![]() $0\to \mathscr {F}_1\to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2] \to 0$
(
$0\to \mathscr {F}_1\to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2] \to 0$
(
![]() $\Lambda '\neq \Lambda $
), and consider the long exact sequence:
$\Lambda '\neq \Lambda $
), and consider the long exact sequence:

The diagram implies
![]() $Ext^2(\mathscr {O}_{\Lambda '},\mathscr {F}_{1})=0$
immediately. Then apply
$Ext^2(\mathscr {O}_{\Lambda '},\mathscr {F}_{1})=0$
immediately. Then apply
![]() $Hom(\mathscr {O}_{\Lambda '}, -)$
to the sequence
$Hom(\mathscr {O}_{\Lambda '}, -)$
to the sequence
![]() $0\to \mathscr {O}_{\mathbb {P}^3}(-1)\to \mathscr {F}_1 \to \mathscr {F}[1]\to 0$
. (This sequence follows from the fact that the complex
$0\to \mathscr {O}_{\mathbb {P}^3}(-1)\to \mathscr {F}_1 \to \mathscr {F}[1]\to 0$
. (This sequence follows from the fact that the complex
![]() $\mathscr {F}_1$
is the extension of the complex of
$\mathscr {F}_1$
is the extension of the complex of
![]() $\mathscr {F}[1]$
in
$\mathscr {F}[1]$
in
![]() $\mathscr {A}_1$
.) We get a long exact sequence:
$\mathscr {A}_1$
.) We get a long exact sequence:
Using the fact that
![]() $\mathscr {F}$
fits the sequence
$\mathscr {F}$
fits the sequence
![]() $0\to \mathscr {O}_{\Lambda }(-3)\to \mathscr {F}\to \mathscr {I}_P(-1)\to 0$
, we get
$0\to \mathscr {O}_{\Lambda }(-3)\to \mathscr {F}\to \mathscr {I}_P(-1)\to 0$
, we get
![]() $Hom(\mathscr {O}_{\Lambda '}, \mathscr {F}[1])=0$
. This implies that
$Hom(\mathscr {O}_{\Lambda '}, \mathscr {F}[1])=0$
. This implies that
![]() $Hom(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})=0$
in the diagram above, hence
$Hom(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})=0$
in the diagram above, hence
![]() $Ext^1(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})=\mathbb {C}$
.
$Ext^1(\mathscr {O}_{\Lambda '}, \mathscr {F}_{1})=\mathbb {C}$
.
Back to Step 3, we get
![]() $Ext^1(E, \mathscr {F}_1)=\mathbb {C}^5$
. With all the above results plugged into the diagram in Step 1, we have that
$Ext^1(E, \mathscr {F}_1)=\mathbb {C}^5$
. With all the above results plugged into the diagram in Step 1, we have that

On one-hand side, the diagram implies that
![]() $5\leq dim(Ext^1(E,E))\leq 8$
, and on the other hand,
$5\leq dim(Ext^1(E,E))\leq 8$
, and on the other hand,
![]() $8\leq dim_{E|\mathscr {M}_2}\leq 15$
geometrically. Therefore, we must have
$8\leq dim_{E|\mathscr {M}_2}\leq 15$
geometrically. Therefore, we must have
![]() $Ext^1(E,E)=\mathbb {C}^8$
.
$Ext^1(E,E)=\mathbb {C}^8$
.
7.5 Moduli space
 $\mathscr {M}_{3}$
in
$\mathscr {M}_{3}$
in
 $C_3$
$C_3$
From the extension classes
we see that extensions E in the sequence
![]() $0\to \mathscr {O}_{\Lambda '}\to E \to \mathscr {F}_1 \to 0 $
are not stable in
$0\to \mathscr {O}_{\Lambda '}\to E \to \mathscr {F}_1 \to 0 $
are not stable in
![]() $C_3$
. The new stable objects are from the extension
$C_3$
. The new stable objects are from the extension
![]() $0\to \mathscr {O}_{\Lambda }\to E \to \mathscr {F}_1 \to 0$
, in which
$0\to \mathscr {O}_{\Lambda }\to E \to \mathscr {F}_1 \to 0$
, in which
![]() $\Lambda $
is the same as the one encoded in the complex
$\Lambda $
is the same as the one encoded in the complex
![]() $\mathscr {F}_1$
.
$\mathscr {F}_1$
.
So when crossing the second wall
![]() $W_2$
from
$W_2$
from
![]() $C_1$
to
$C_1$
to
![]() $C_2$
, the stratum
$C_2$
, the stratum
![]() $K_{(2,3)}\backslash H$
stays, and the
$K_{(2,3)}\backslash H$
stays, and the
![]() $\mathbb {P}^3$
bundle
$\mathbb {P}^3$
bundle
![]() $\mathscr {M}_{\mathscr {F}}$
disappears with only the base H remaining. H then becomes a
$\mathscr {M}_{\mathscr {F}}$
disappears with only the base H remaining. H then becomes a
![]() $\mathbb {P}^8$
bundle over H from the above computation. Denote this bundle by
$\mathbb {P}^8$
bundle over H from the above computation. Denote this bundle by
![]() $\mathbf {P}$
. We will next study this
$\mathbf {P}$
. We will next study this
![]() $\mathbb {P}^8$
bundle
$\mathbb {P}^8$
bundle
![]() $\mathbf {P}$
, and then glue it to
$\mathbf {P}$
, and then glue it to
![]() $K_{(2,3)}\backslash H$
using the elementary modification. The resultant moduli space
$K_{(2,3)}\backslash H$
using the elementary modification. The resultant moduli space
![]() $\mathscr {M}_{3}$
turns out to be the Gieseker moduli space, denoted by
$\mathscr {M}_{3}$
turns out to be the Gieseker moduli space, denoted by
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
.
$\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
.
7.5.1 A description of
 $\mathbf {P}$
$\mathbf {P}$
We show in this subsection that
![]() $\mathbf {P}$
is the fibered space over
$\mathbf {P}$
is the fibered space over
![]() $\mathbb {P}^{3\vee }$
whose fibers are
$\mathbb {P}^{3\vee }$
whose fibers are
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^2}$
.
$\mathscr {M}^{3t+1}_{\mathbb {P}^2}$
.
We have shown that a complex
![]() $\mathscr {F}_1$
corresponds to a point of the flag variety:
$\mathscr {F}_1$
corresponds to a point of the flag variety:
![]() $\{P\in \Lambda \subset \mathbb {P}^3\}$
. Indeed, this flag variety is the same with H since
$\{P\in \Lambda \subset \mathbb {P}^3\}$
. Indeed, this flag variety is the same with H since
![]() $\mathscr {F}_1$
is the unique extension of
$\mathscr {F}_1$
is the unique extension of
![]() $\mathscr {F}$
. Without loss of generality, we fix a complex
$\mathscr {F}$
. Without loss of generality, we fix a complex
![]() $\mathscr {F}_1$
, in which
$\mathscr {F}_1$
, in which
![]() $\Lambda $
is defined by
$\Lambda $
is defined by
![]() $x_1=0$
and the point P is defined by
$x_1=0$
and the point P is defined by
![]() $x_1=x_2=x_3=0$
. We will show that the vector space
$x_1=x_2=x_3=0$
. We will show that the vector space
![]() $Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })$
(up to scalar multiplication) parameterizes plane cubic curves in
$Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })$
(up to scalar multiplication) parameterizes plane cubic curves in
![]() $\Lambda $
that go through P.
$\Lambda $
that go through P.
Let
![]() $\Lambda '$
be an arbitrary plane in
$\Lambda '$
be an arbitrary plane in
![]() $\mathbb {P}^3$
, and we have the extension groups:
$\mathbb {P}^3$
, and we have the extension groups:
 $$ \begin{align*} Ext^1(\mathscr{F}_1,O_{\Lambda'})=\left\{ \begin{array}{ll} 0, & \text{if} \Lambda'\neq \Lambda, \\ \mathbb{C}^9, & \text{if} \Lambda' = \Lambda. \end{array} \right. \end{align*} $$
$$ \begin{align*} Ext^1(\mathscr{F}_1,O_{\Lambda'})=\left\{ \begin{array}{ll} 0, & \text{if} \Lambda'\neq \Lambda, \\ \mathbb{C}^9, & \text{if} \Lambda' = \Lambda. \end{array} \right. \end{align*} $$
In the short exact sequence:
![]() $0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2]\to 0 $
(in
$0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2]\to 0 $
(in
![]() $\mathscr {A}_1$
), the plane
$\mathscr {A}_1$
), the plane
![]() $\Lambda $
encoded in
$\Lambda $
encoded in
![]() $\mathscr {F}_1$
is the same with the plane in the quotient object
$\mathscr {F}_1$
is the same with the plane in the quotient object
![]() $\mathscr {O}_{\Lambda }(-3)[2]$
.
$\mathscr {O}_{\Lambda }(-3)[2]$
.
Apply the functor
![]() $Hom(-,\mathscr {O}_{\Lambda })$
to the sequence:
$Hom(-,\mathscr {O}_{\Lambda })$
to the sequence:
![]() $0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2]\to 0 $
, we have a long exact sequence of cohomologies:
$0\to \mathscr {F}_1 \to \mathbb {C}_P \to \mathscr {O}_{\Lambda }(-3)[2]\to 0 $
, we have a long exact sequence of cohomologies:
in which
![]() $Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })$
is the kernel of
$Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })$
is the kernel of
![]() $\phi $
.
$\phi $
.
One computes that
![]() $Hom(\mathscr {O}_{\Lambda }(-3),\mathscr {O}_{\Lambda })=\mathbb {C}^{10}$
. Consider the twisted Koszul complex
$Hom(\mathscr {O}_{\Lambda }(-3),\mathscr {O}_{\Lambda })=\mathbb {C}^{10}$
. Consider the twisted Koszul complex
![]() $\mathbb {C}_P$
by the complex
$\mathbb {C}_P$
by the complex
![]() $[\mathscr {O}_{\mathbb {P}^3}(-4)\to \mathscr {O}^3_{\mathbb {P}^3}(-3)\to \mathscr {O}^3_{\mathbb {P}^3}(-2)\to \mathscr {O}_{\mathbb {P}^3}(-1)]\to \mathbb {C}_P$
and apply the functor
$[\mathscr {O}_{\mathbb {P}^3}(-4)\to \mathscr {O}^3_{\mathbb {P}^3}(-3)\to \mathscr {O}^3_{\mathbb {P}^3}(-2)\to \mathscr {O}_{\mathbb {P}^3}(-1)]\to \mathbb {C}_P$
and apply the functor
![]() $Hom(-,\mathscr {O}_{\Lambda })$
to it. The cohomology at “
$Hom(-,\mathscr {O}_{\Lambda })$
to it. The cohomology at “
![]() $\mathscr {O}_{\mathbb {P}^3}(-3)$
” gives
$\mathscr {O}_{\mathbb {P}^3}(-3)$
” gives
![]() $Ext^2(\mathbb {C}_P,\mathscr {O}_{\Lambda })=\mathbb {C}$
. (This is because the resolution to
$Ext^2(\mathbb {C}_P,\mathscr {O}_{\Lambda })=\mathbb {C}$
. (This is because the resolution to
![]() $\mathbb {C}_P$
is acyclic for
$\mathbb {C}_P$
is acyclic for
![]() $Hom(-,\mathscr {O}_{\Lambda })$
.) By definition,
$Hom(-,\mathscr {O}_{\Lambda })$
.) By definition,
![]() $Ext^2(\mathbb {C}_P,\mathscr {O}_{\Lambda })={Ker(\alpha )}/{Im(\beta )}$
in the complex:
$Ext^2(\mathbb {C}_P,\mathscr {O}_{\Lambda })={Ker(\alpha )}/{Im(\beta )}$
in the complex:
Define a morphism
![]() $\psi : Hom(\mathscr {O}_{\mathbb {P}^3}(-3)^{\bigoplus 3}, \mathscr {O}_{\Lambda })\to Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })$
which maps a
$\psi : Hom(\mathscr {O}_{\mathbb {P}^3}(-3)^{\bigoplus 3}, \mathscr {O}_{\Lambda })\to Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })$
which maps a
![]() $3$
-tuple
$3$
-tuple
![]() $(f_1, f_2, f_3)$
to
$(f_1, f_2, f_3)$
to
![]() $\psi (f_1, f_2, f_3):=f_1+ f_2+ f_3$
. Let
$\psi (f_1, f_2, f_3):=f_1+ f_2+ f_3$
. Let
![]() $Ker(\psi )$
be the kernel of
$Ker(\psi )$
be the kernel of
![]() $\psi $
, and consider the following diagram.
$\psi $
, and consider the following diagram.

Figure 8 is part of the (twisted) Koszul resolution to
![]() $\mathbb {C}_P$
, and it implies that
$\mathbb {C}_P$
, and it implies that
![]() $(f_1, 0, 0)\in Ker(\alpha )$
for any
$(f_1, 0, 0)\in Ker(\alpha )$
for any
![]() $f_1\in Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })$
. Thus, the restriction
$f_1\in Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })$
. Thus, the restriction
![]() $\psi |_{Ker(\alpha )}: {Ker(\alpha )}\to Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })$
is surjective, and
$\psi |_{Ker(\alpha )}: {Ker(\alpha )}\to Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })$
is surjective, and
![]() $\psi (Ker(\alpha ))=Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })=\mathbb {C}^{10}$
. Moreover, we have a surjective map
$\psi (Ker(\alpha ))=Hom(\mathscr {O}_{\mathbb {P}^3}(-3), \mathscr {O}_{\Lambda })=\mathbb {C}^{10}$
. Moreover, we have a surjective map
![]() $\Phi $
as follows:
$\Phi $
as follows:
 $$\begin{align*}\mathbb{C}=\frac{Ker(\alpha)=\mathbb{C}^{16}}{Im(\beta)=\mathbb{C}^{15}}\overset{\Phi}{\to} \frac{\psi(Ker(\alpha))=\mathbb{C}^{10}}{\psi(Im(\beta))}\to 0. \end{align*}$$
$$\begin{align*}\mathbb{C}=\frac{Ker(\alpha)=\mathbb{C}^{16}}{Im(\beta)=\mathbb{C}^{15}}\overset{\Phi}{\to} \frac{\psi(Ker(\alpha))=\mathbb{C}^{10}}{\psi(Im(\beta))}\to 0. \end{align*}$$
We next show that
![]() $\Phi $
is an isomorphism by showing that the restriction of
$\Phi $
is an isomorphism by showing that the restriction of
![]() $Ker(\psi )$
to
$Ker(\psi )$
to
![]() $Im(\beta )$
, denoted by
$Im(\beta )$
, denoted by
![]() $Ker(\psi )|_{\beta }$
, is
$Ker(\psi )|_{\beta }$
, is
![]() $\mathbb {C}^{6}$
, which will imply
$\mathbb {C}^{6}$
, which will imply
![]() $\psi (Im(\beta ))=\mathbb {C}^{9}$
and
$\psi (Im(\beta ))=\mathbb {C}^{9}$
and
![]() ${\psi (Ker(\alpha ))}/{\psi (Im(\beta ))}=\mathbb {C}$
. For any
${\psi (Ker(\alpha ))}/{\psi (Im(\beta ))}=\mathbb {C}$
. For any
![]() $(Q_1, Q_2, Q_3)\in Hom(\mathscr {O}^3_{\mathbb {P}^3}(-2), \mathscr {O}_{\Lambda })$
,
$(Q_1, Q_2, Q_3)\in Hom(\mathscr {O}^3_{\mathbb {P}^3}(-2), \mathscr {O}_{\Lambda })$
,
![]() $\beta (Q_1, Q_2, Q_3)=(x_3Q_1+x_2Q_2, x_3Q_3, -x_2Q_3)$
. Suppose
$\beta (Q_1, Q_2, Q_3)=(x_3Q_1+x_2Q_2, x_3Q_3, -x_2Q_3)$
. Suppose
![]() $\psi (x_3Q_1+x_2Q_2, x_3Q_3, -x_2Q_3)=0$
, then
$\psi (x_3Q_1+x_2Q_2, x_3Q_3, -x_2Q_3)=0$
, then
![]() $x_3(Q_1+Q_3)+x_2(Q_2-Q_3)=0$
on
$x_3(Q_1+Q_3)+x_2(Q_2-Q_3)=0$
on
![]() $\Lambda =Z(x_1)$
. Therefore, we have
$\Lambda =Z(x_1)$
. Therefore, we have
![]() $Q_1+Q_3=x_2L_1$
and
$Q_1+Q_3=x_2L_1$
and
![]() $Q_2-Q_3=x_3L_2$
for some
$Q_2-Q_3=x_3L_2$
for some
![]() $L_1, L_2\in H^0(\Lambda , \mathscr {O}_{\Lambda }(1))$
, which implies
$L_1, L_2\in H^0(\Lambda , \mathscr {O}_{\Lambda }(1))$
, which implies
![]() $Ker(\psi )|_{\beta }\cong H^0(\Lambda , \mathscr {O}_{\Lambda }(1))\bigoplus H^0(\Lambda , \mathscr {O}_{\Lambda }(1))=\mathbb {C}^6$
.
$Ker(\psi )|_{\beta }\cong H^0(\Lambda , \mathscr {O}_{\Lambda }(1))\bigoplus H^0(\Lambda , \mathscr {O}_{\Lambda }(1))=\mathbb {C}^6$
.

Figure 8 Part of the Koszul resolution to
![]() $\mathbb{C}_P$
$\mathbb{C}_P$
Back to the exact sequence 7.2:
 $$\begin{align*}0\to\begin{matrix} Ext^1(\mathscr{F}_1,\mathscr{O}_{\Lambda})\\=\mathbb{C}^9\end{matrix} \to \begin{matrix}Ext^2(\mathscr{O}_{\Lambda}(-3)[2],\mathscr{O}_{\Lambda})\\=\mathbb{C}^{10}\end{matrix} \overset{\phi}{\to} Ext^2(\mathbb{C}_P,\mathscr{O}_{\Lambda})=\frac{Ker(\alpha)}{Im(\beta)}=\frac{\psi(Ker(\alpha))}{\psi(Im(\beta))}=\mathbb{C} \to 0. \end{align*}$$
$$\begin{align*}0\to\begin{matrix} Ext^1(\mathscr{F}_1,\mathscr{O}_{\Lambda})\\=\mathbb{C}^9\end{matrix} \to \begin{matrix}Ext^2(\mathscr{O}_{\Lambda}(-3)[2],\mathscr{O}_{\Lambda})\\=\mathbb{C}^{10}\end{matrix} \overset{\phi}{\to} Ext^2(\mathbb{C}_P,\mathscr{O}_{\Lambda})=\frac{Ker(\alpha)}{Im(\beta)}=\frac{\psi(Ker(\alpha))}{\psi(Im(\beta))}=\mathbb{C} \to 0. \end{align*}$$
Since
![]() $Ext^2(\mathscr {O}_{\Lambda }(-3)[2],\mathscr {O}_{\Lambda })\cong \psi (Ker(\alpha ))$
, we have that
$Ext^2(\mathscr {O}_{\Lambda }(-3)[2],\mathscr {O}_{\Lambda })\cong \psi (Ker(\alpha ))$
, we have that
![]() $Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })=Ker(\phi )=\psi (Im(\beta ))$
.
$Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })=Ker(\phi )=\psi (Im(\beta ))$
.
![]() $\psi (Im(\beta ))$
is indeed the set
$\psi (Im(\beta ))$
is indeed the set
![]() $\{x_2(Q_2-Q_3)+x_3(Q_1+Q_3)\}$
, where
$\{x_2(Q_2-Q_3)+x_3(Q_1+Q_3)\}$
, where
![]() $Q_1, Q_2, Q_3 \in Hom(\mathscr {O}_{\mathbb {P}^3}(-2),\mathscr {O}_{\Lambda })=H^0(\Lambda , \mathscr {O}_{\Lambda }(2))$
are quadric curves in
$Q_1, Q_2, Q_3 \in Hom(\mathscr {O}_{\mathbb {P}^3}(-2),\mathscr {O}_{\Lambda })=H^0(\Lambda , \mathscr {O}_{\Lambda }(2))$
are quadric curves in
![]() $\Lambda $
. This is exactly the set of all cubic curves in
$\Lambda $
. This is exactly the set of all cubic curves in
![]() $\Lambda $
that go through P (recall that P is defined by
$\Lambda $
that go through P (recall that P is defined by
![]() $x_2= x_3=0$
on
$x_2= x_3=0$
on
![]() $\Lambda $
).
$\Lambda $
).
So we have the following morphism:
in which the fiber at a point
![]() $(P,\Lambda )\in H$
parameterizes all the plane cubic curves in
$(P,\Lambda )\in H$
parameterizes all the plane cubic curves in
![]() $\Lambda $
that go through P.
$\Lambda $
that go through P.
Moreover, consider the morphisms
A point in
![]() $\mathbb {P}^{3\vee }$
corresponds to a plane
$\mathbb {P}^{3\vee }$
corresponds to a plane
![]() $\Lambda \subset \mathbb {P}^3$
, and the fiber over it in
$\Lambda \subset \mathbb {P}^3$
, and the fiber over it in
![]() $\mathbf {P}$
parameterizes the pair
$\mathbf {P}$
parameterizes the pair
![]() $\left \{ C,P \right \}$
, where
$\left \{ C,P \right \}$
, where
![]() $C\subset \Lambda $
is a plane cubic curve passing through the point
$C\subset \Lambda $
is a plane cubic curve passing through the point
![]() $P\in \Lambda $
. So this fiber is the universal cubic curve
$P\in \Lambda $
. So this fiber is the universal cubic curve
![]() $\mathscr {C}\subset |H^0(\mathbb {P}^2, \mathscr {O}_{\mathbb {P}^2}(3))|\times \mathbb {P}^2$
which is the Gieseker moduli space
$\mathscr {C}\subset |H^0(\mathbb {P}^2, \mathscr {O}_{\mathbb {P}^2}(3))|\times \mathbb {P}^2$
which is the Gieseker moduli space
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^2}$
(see [Reference Le Potier19]).
$\mathscr {M}^{3t+1}_{\mathbb {P}^2}$
(see [Reference Le Potier19]).
This proves the claim that
![]() $\mathbf {P}$
is fibered over
$\mathbf {P}$
is fibered over
![]() $\mathbb {P}^{3\vee }$
with fibers
$\mathbb {P}^{3\vee }$
with fibers
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^2}$
. It also matches the result in [Reference Freiermuth and Trautmann12] that
$\mathscr {M}^{3t+1}_{\mathbb {P}^2}$
. It also matches the result in [Reference Freiermuth and Trautmann12] that
![]() $\mathbf {P}$
is a component of the Gieseker moduli space
$\mathbf {P}$
is a component of the Gieseker moduli space
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
parameterizing degree one line bundles on plane curves.
$\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
parameterizing degree one line bundles on plane curves.
7.5.2 The elementary modification
We have shown that when crossing the second wall
![]() $W_2$
, the component
$W_2$
, the component
![]() $\mathscr {M}_{\mathscr {F}}$
disappears, and its base H is replaced by
$\mathscr {M}_{\mathscr {F}}$
disappears, and its base H is replaced by
![]() $\mathbf {P}$
. It is known (see [Reference Freiermuth and Trautmann12]) that
$\mathbf {P}$
. It is known (see [Reference Freiermuth and Trautmann12]) that
![]() $K_{(2,3)}\backslash H$
and
$K_{(2,3)}\backslash H$
and
![]() $\mathbf {P}$
are the components of the Gieseker moduli space
$\mathbf {P}$
are the components of the Gieseker moduli space
![]() $\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
. So it is expected that
$\mathscr {M}^{3t+1}_{\mathbb {P}^3}$
. So it is expected that
![]() $\mathbf {P}$
is glued to
$\mathbf {P}$
is glued to
![]() $K_{(2,3)}$
along the exceptional divisor of its blow-up
$K_{(2,3)}$
along the exceptional divisor of its blow-up
![]() $\mathbf {B}:=Bl_H{(K_{(2,3)})}$
(see [Reference Freiermuth and Trautmann12], [Reference Xia35]).
$\mathbf {B}:=Bl_H{(K_{(2,3)})}$
(see [Reference Freiermuth and Trautmann12], [Reference Xia35]).
We collect some extension groups in the next lemma for later use.
Lemma 7.2. We have the following computational results.
-
1. For any plane
 $\Lambda ' \subset \mathbb {P}^3$
, we have
$\Lambda ' \subset \mathbb {P}^3$
, we have $Hom(\mathscr {O}_{\Lambda '},\mathscr {F}_1) = Ext^2(\mathscr {O}_{\Lambda '},\mathscr {F}_1) = Ext^3(\mathscr {O}_{\Lambda '},\mathscr {F}_1) = 0$
,
$Hom(\mathscr {O}_{\Lambda '},\mathscr {F}_1) = Ext^2(\mathscr {O}_{\Lambda '},\mathscr {F}_1) = Ext^3(\mathscr {O}_{\Lambda '},\mathscr {F}_1) = 0$
,
 $Ext^1(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=\mathbb {C}^{1}$
.
$Ext^1(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=\mathbb {C}^{1}$
. -
2.
 $Hom(\mathscr {F}_1,\mathscr {O}_{\Lambda })=Ext^3(\mathscr {F}_1,\mathscr {O}_{\Lambda }))=0$
,
$Hom(\mathscr {F}_1,\mathscr {O}_{\Lambda })=Ext^3(\mathscr {F}_1,\mathscr {O}_{\Lambda }))=0$
,
 $Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda }))=\mathbb {C}^{9}$
,
$Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda }))=\mathbb {C}^{9}$
,
 $Ext^2(\mathscr {F}_1,\mathscr {O}_{\Lambda }))=\mathbb {C}^{14}$
.
$Ext^2(\mathscr {F}_1,\mathscr {O}_{\Lambda }))=\mathbb {C}^{14}$
.
Proof. We have shown that
![]() $Hom(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=Ext^2(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=0$
and
$Hom(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=Ext^2(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=0$
and
![]() $Ext^1(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=\mathbb {C}$
in Lemma 7.1 for
$Ext^1(\mathscr {O}_{\Lambda '},\mathscr {F}_1)=\mathbb {C}$
in Lemma 7.1 for
![]() $\Lambda '\neq \Lambda $
. For the rest of the extension classes, we use these two sequences in
$\Lambda '\neq \Lambda $
. For the rest of the extension classes, we use these two sequences in
![]() $\mathscr {A}_1:$
$\mathscr {A}_1:$
The proof is similar to the one in Lemma 7.1 (not hard but tedious), and we skip the details.
Some notations:
-
•
 $\mathbf {B}:=Bl_H(K_{(2,3)})\xrightarrow {b} K_{(2,3)}$
where the morphism is denoted by b. Let D be the exceptional divisor, and
$\mathbf {B}:=Bl_H(K_{(2,3)})\xrightarrow {b} K_{(2,3)}$
where the morphism is denoted by b. Let D be the exceptional divisor, and
 $b_H$
:
$b_H$
:
 $D\xrightarrow {b_H} H$
be the restriction of b to the exceptional divisor.
$D\xrightarrow {b_H} H$
be the restriction of b to the exceptional divisor. -
•
 $\pi _H$
,
$\pi _H$
,
 $\pi _{\mathbf {P}}$
, and
$\pi _{\mathbf {P}}$
, and
 $\pi _D$
denote the projections:
$\pi _D$
denote the projections:
 $H\times \mathbb {P}^3 \xrightarrow {\pi _H} H$
,
$H\times \mathbb {P}^3 \xrightarrow {\pi _H} H$
,
 $\mathbf {P}\times \mathbb {P}^3 \xrightarrow {\pi _{\mathbf {P}}} \mathbf {P}$
,
$\mathbf {P}\times \mathbb {P}^3 \xrightarrow {\pi _{\mathbf {P}}} \mathbf {P}$
,
 $D\times \mathbb {P}^3\xrightarrow {\pi _D} D$
.
$D\times \mathbb {P}^3\xrightarrow {\pi _D} D$
. -
• p, q are the projections:
 $H\times \mathbb {P}^3\xrightarrow {p} \mathbb {P}^{3\vee }\times \mathbb {P}^3$
, (where
$H\times \mathbb {P}^3\xrightarrow {p} \mathbb {P}^{3\vee }\times \mathbb {P}^3$
, (where
 $(P\in \Lambda )\mapsto \Lambda $
),
$(P\in \Lambda )\mapsto \Lambda $
),
 $\mathbf {P}\times \mathbb {P}^3\xrightarrow {q} H\times \mathbb {P}^3$
.
$\mathbf {P}\times \mathbb {P}^3\xrightarrow {q} H\times \mathbb {P}^3$
. -
•
 $i,j$
are the inclusions:
$i,j$
are the inclusions:
 $D \times \mathbb {P}^3\xrightarrow {i} \mathbf {B}\times \mathbb {P}^3$
,
$D \times \mathbb {P}^3\xrightarrow {i} \mathbf {B}\times \mathbb {P}^3$
,
 $D\times \mathbb {P}^3\xrightarrow {j} \mathbf {P}\times \mathbb {P}^3$
.
$D\times \mathbb {P}^3\xrightarrow {j} \mathbf {P}\times \mathbb {P}^3$
. -
• Two universal families:
-
1.
 $U_{\mathscr {F}_1}$
on
$U_{\mathscr {F}_1}$
on
 $H\times \mathbb {P}^3$
as the universal family of complexes
$H\times \mathbb {P}^3$
as the universal family of complexes
 $\mathscr {F}_1$
.
$\mathscr {F}_1$
. -
2.
 $U_{\mathscr {O}_{\Lambda }}$
on
$U_{\mathscr {O}_{\Lambda }}$
on
 $\mathbb {P}^{3\vee }\times \mathbb {P}^3$
as the universal family of planes in
$\mathbb {P}^{3\vee }\times \mathbb {P}^3$
as the universal family of planes in
 $\mathbb {P}^3$
.
$\mathbb {P}^3$
.
Proposition 7.3. There exists a universal family of extensions on H of the form
where
![]() $L:=\mathscr {E}xt_{\pi _H}^1(p^*( U_{\mathscr {O}_{\Lambda }}), U_{\mathscr {F}_1})$
is a line bundle on H.
$L:=\mathscr {E}xt_{\pi _H}^1(p^*( U_{\mathscr {O}_{\Lambda }}), U_{\mathscr {F}_1})$
is a line bundle on H.
Proof. Let L be the line bundle
![]() $L:=\mathscr {E}xt_{\pi _H}^1(p^*(U_{\mathscr {O}_{\Lambda }}),U_{\mathscr {F}_1})$
on H. From part 1 in Lemma 7.2 and our assumption, we have that
$L:=\mathscr {E}xt_{\pi _H}^1(p^*(U_{\mathscr {O}_{\Lambda }}),U_{\mathscr {F}_1})$
on H. From part 1 in Lemma 7.2 and our assumption, we have that
![]() $R\mathscr {H}om(p^*(U_{\mathscr {O}_{\Lambda }}), (U_{\mathscr {F}_1}\otimes \pi _H^* L)[1])=R\mathscr {H}om((p^*(U_{\mathscr {O}_{\Lambda }})[-1], U_{\mathscr {F}_1}\otimes \pi _H^* L)$
is a sheaf.
$R\mathscr {H}om(p^*(U_{\mathscr {O}_{\Lambda }}), (U_{\mathscr {F}_1}\otimes \pi _H^* L)[1])=R\mathscr {H}om((p^*(U_{\mathscr {O}_{\Lambda }})[-1], U_{\mathscr {F}_1}\otimes \pi _H^* L)$
is a sheaf.
There is then a canonical identity element:
 $$\begin{align*}\begin{array}{rl} id& \in H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])^{*})\\ &=H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})\otimes L^*)\\ &=H^0(H\times \mathbb{P}^3, p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1] \otimes \pi_H^*L^*)\\ &=H^0(H\times \mathbb{P}^3, R\mathscr{H}om(p^*(U_{\mathscr{O}_{\Lambda}}),U_{\mathscr{F}_1}\otimes\pi_H^*L^*)[1])\\ &=H^0(H\times \mathbb{P}^3, R\mathscr{H}om(p^*(U_{\mathscr{O}_{\Lambda}})[-1],U_{\mathscr{F}_1}\otimes\pi_H^*L^*))\\ \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{rl} id& \in H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])^{*})\\ &=H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})\otimes L^*)\\ &=H^0(H\times \mathbb{P}^3, p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1] \otimes \pi_H^*L^*)\\ &=H^0(H\times \mathbb{P}^3, R\mathscr{H}om(p^*(U_{\mathscr{O}_{\Lambda}}),U_{\mathscr{F}_1}\otimes\pi_H^*L^*)[1])\\ &=H^0(H\times \mathbb{P}^3, R\mathscr{H}om(p^*(U_{\mathscr{O}_{\Lambda}})[-1],U_{\mathscr{F}_1}\otimes\pi_H^*L^*))\\ \end{array} \end{align*}$$
which gives the morphism
![]() $f_{id}:$
$f_{id}:$
The cone
![]() $U_E$
from the triangle is the universal extension we want.
$U_E$
from the triangle is the universal extension we want.
Remark 7.4. Suppose the vector bundle L in Proposition 7.3 has higher rank, where
![]() $L:=\mathscr {E}xt_{\pi _H}^1(p^*(U_{\mathscr {O}_{\Lambda }}),U_{\mathscr {F}_1})$
is a vector bundle on H. Then, we need an extra step to get a universal extension.
$L:=\mathscr {E}xt_{\pi _H}^1(p^*(U_{\mathscr {O}_{\Lambda }}),U_{\mathscr {F}_1})$
is a vector bundle on H. Then, we need an extra step to get a universal extension.
Define
![]() $\pi : \mathbb {P}:=Proj(L^*)\to H$
to be the canonical morphism, and define three other morphisms as follows:
$\pi : \mathbb {P}:=Proj(L^*)\to H$
to be the canonical morphism, and define three other morphisms as follows:
![]() $\pi _1: \mathbb {P}\times \mathbb {P}^3\to H\times \mathbb {P}^3$
,
$\pi _1: \mathbb {P}\times \mathbb {P}^3\to H\times \mathbb {P}^3$
,
![]() $\pi _H: H\times \mathbb {P}^3 \to H,$
and
$\pi _H: H\times \mathbb {P}^3 \to H,$
and
![]() $\pi _{\mathbb {P}}:\mathbb {P}\times \mathbb {P}^3\to \mathbb {P}$
.
$\pi _{\mathbb {P}}:\mathbb {P}\times \mathbb {P}^3\to \mathbb {P}$
.
Following the same steps, we have that there is a canonical identity element:
 $$\begin{align*}\begin{array}{rl} id& \in H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])^{*})\\ &=H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})\otimes L^*)\\ &=H^0(H\times \mathbb{P}^3, p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1] \otimes \pi_H^*L^*)\\ &=H^0(H\times \mathbb{P}^3, \pi_1^*(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes \pi_1^*\pi_H^*L^*)\\ &=H^0(H\times \mathbb{P}^3, R\mathscr{H}om(\pi_1^*(p^*(U_{\mathscr{O}_{\Lambda}})^{*}[-1], \pi_1^*U_{\mathscr{F}_1}\otimes \pi_1^*\pi_H^*L^*)). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{rl} id& \in H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])^{*})\\ &=H^0(H, \pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes\pi_{H*}(p^*(U_{\mathscr{O}_{\Lambda}})\otimes L^*)\\ &=H^0(H\times \mathbb{P}^3, p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1] \otimes \pi_H^*L^*)\\ &=H^0(H\times \mathbb{P}^3, \pi_1^*(p^*(U_{\mathscr{O}_{\Lambda}})^{*}\otimes U_{\mathscr{F}_1}[1])\otimes \pi_1^*\pi_H^*L^*)\\ &=H^0(H\times \mathbb{P}^3, R\mathscr{H}om(\pi_1^*(p^*(U_{\mathscr{O}_{\Lambda}})^{*}[-1], \pi_1^*U_{\mathscr{F}_1}\otimes \pi_1^*\pi_H^*L^*)). \end{array} \end{align*}$$
Then, the surjection on
![]() $\mathbb {P}\times \mathbb {P}^3$
, which is
$\mathbb {P}\times \mathbb {P}^3$
, which is
![]() $\phi : \pi _1^*\pi _H^*L^*\to \pi _{\mathbb {P}}^*\mathscr {O}_{\mathbb {P}}(1)$
, induces a morphism
$\phi : \pi _1^*\pi _H^*L^*\to \pi _{\mathbb {P}}^*\mathscr {O}_{\mathbb {P}}(1)$
, induces a morphism
![]() $f_{id}$
:
$f_{id}$
:
whose cone gives a universal extension
![]() $\mathscr {U}$
$\mathscr {U}$
There is a universal extension on
![]() $\mathbf {P}\times \mathbb {P}^3$
as well which we will state in the next proposition. The proof follows from a similar construction in Proposition 7.3 and Remark 7.4.
$\mathbf {P}\times \mathbb {P}^3$
as well which we will state in the next proposition. The proof follows from a similar construction in Proposition 7.3 and Remark 7.4.
Proposition 7.5. There exists a universal family of extensions on
![]() $\mathbf {P}\times \mathbb {P}^3$
of the form
$\mathbf {P}\times \mathbb {P}^3$
of the form
Next, we show that D is embedded into
![]() $\mathbf {P}$
. This is implied by the commutative diagrams below (7.3 for the local version and 7.4 for the global version). Recall that the locus
$\mathbf {P}$
. This is implied by the commutative diagrams below (7.3 for the local version and 7.4 for the global version). Recall that the locus
![]() $H\subset \mathscr {M}_2$
parameterizes objects E which fit into the short exact sequence:
$H\subset \mathscr {M}_2$
parameterizes objects E which fit into the short exact sequence:
![]() $0\to \mathscr {F}_1 \to E \to \mathscr {O}_{\Lambda } \to 0$
. There is a commutative diagram as follows:
$0\to \mathscr {F}_1 \to E \to \mathscr {O}_{\Lambda } \to 0$
. There is a commutative diagram as follows:

In the above diagram,
![]() $T_{E|H}$
denotes the tangent space at the point E in H, and
$T_{E|H}$
denotes the tangent space at the point E in H, and
![]() $N_{H|\mathscr {M}_2}$
denotes the fiber of the normal bundle of H in
$N_{H|\mathscr {M}_2}$
denotes the fiber of the normal bundle of H in
![]() $\mathscr {M}_2$
at E. The morphism
$\mathscr {M}_2$
at E. The morphism
![]() $\phi $
is the composition
$\phi $
is the composition
![]() $Ext^1(E,E)\xrightarrow {\phi _1}Ext^1(\mathscr {F}_1, E)\xrightarrow {\phi _2}Ext^1(\mathscr {F}_1, \mathscr {O}_{\Lambda })$
, in which
$Ext^1(E,E)\xrightarrow {\phi _1}Ext^1(\mathscr {F}_1, E)\xrightarrow {\phi _2}Ext^1(\mathscr {F}_1, \mathscr {O}_{\Lambda })$
, in which
![]() $\phi _1$
is induced by the injection
$\phi _1$
is induced by the injection
![]() $\mathscr {F}_1\hookrightarrow E$
(in
$\mathscr {F}_1\hookrightarrow E$
(in
![]() $\mathscr {A}_1$
) and
$\mathscr {A}_1$
) and
![]() $\phi _2$
is induced by the surjection
$\phi _2$
is induced by the surjection
![]() $E\twoheadrightarrow \mathscr {O}_{\Lambda }$
. To see that
$E\twoheadrightarrow \mathscr {O}_{\Lambda }$
. To see that
![]() $\phi $
vanishes at
$\phi $
vanishes at
![]() $T_{E|H}$
, consider the following diagram (the two rows are distinguished triangles in
$T_{E|H}$
, consider the following diagram (the two rows are distinguished triangles in
![]() $D^b(\mathbb {P}^3)$
).
$D^b(\mathbb {P}^3)$
).

For any E in H, an extension class
![]() $e\in Ext^1(E,E)$
has image
$e\in Ext^1(E,E)$
has image
![]() $\phi (e)$
as the composition
$\phi (e)$
as the composition
![]() $\phi (e)=b[1]\circ e\circ a=f\circ b \circ a$
, which is
$\phi (e)=b[1]\circ e\circ a=f\circ b \circ a$
, which is
![]() $0$
since
$0$
since
![]() $b \circ a=0$
. This induces a morphism
$b \circ a=0$
. This induces a morphism
![]() $T_{E|H}\to ker(\phi )$
in the above diagram.
$T_{E|H}\to ker(\phi )$
in the above diagram.
Next, we show the computational results in diagram 7.3.
![]() $T_{E|H}=\mathbb {C}^5$
since H is the flag variety
$T_{E|H}=\mathbb {C}^5$
since H is the flag variety
![]() $\{P\in \Lambda \subset \mathbb {P}^3\}$
which is smooth of dimension
$\{P\in \Lambda \subset \mathbb {P}^3\}$
which is smooth of dimension
![]() $5$
.
$5$
.
![]() $Ext^1(\mathscr {F}_1, \mathscr {O}_{\Lambda })=\mathbb {C}^9$
is shown in Lemma 7.2. One can prove that
$Ext^1(\mathscr {F}_1, \mathscr {O}_{\Lambda })=\mathbb {C}^9$
is shown in Lemma 7.2. One can prove that
![]() $Ext^1(E,E)=\mathbb {C}^{15}$
using the method in Lemma 7.1. Here, we show a simpler result in the next lemma that
$Ext^1(E,E)=\mathbb {C}^{15}$
using the method in Lemma 7.1. Here, we show a simpler result in the next lemma that
![]() $Ker(\phi )=\mathbb {C}^8$
. This will imply that
$Ker(\phi )=\mathbb {C}^8$
. This will imply that
![]() $K_{(2,3)}$
intersects
$K_{(2,3)}$
intersects
![]() $\mathscr {M}_{\mathscr {F}}$
transversely. Hence,
$\mathscr {M}_{\mathscr {F}}$
transversely. Hence,
![]() $Ext^1(E,E)=15$
and
$Ext^1(E,E)=15$
and
![]() $N_{H|\mathscr {M}_2}=\mathbb {C}^{10}$
.
$N_{H|\mathscr {M}_2}=\mathbb {C}^{10}$
.
Lemma 7.6. In diagram 7.3,
![]() $Ker(\phi )=\mathbb {C}^{8}$
.
$Ker(\phi )=\mathbb {C}^{8}$
.
Proof. We need two long exact sequences as follows:
Step 1 Apply
![]() $Hom(-, E)$
to the sequence
$Hom(-, E)$
to the sequence
![]() $0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
. We have the following long exact sequence:
$0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
. We have the following long exact sequence:

We can see that
![]() $Hom(E,E)=\mathbb {C}$
since E is stable. This implies that
$Hom(E,E)=\mathbb {C}$
since E is stable. This implies that
![]() $Hom(\mathscr {O}_{\Lambda }, E)=0,$
otherwise, the short exact sequence
$Hom(\mathscr {O}_{\Lambda }, E)=0,$
otherwise, the short exact sequence
![]() $0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
splits.
$0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
splits.
Then, we will show that
![]() $Hom(\mathscr {F}_1, E)=\mathbb {C}$
,
$Hom(\mathscr {F}_1, E)=\mathbb {C}$
,
![]() $Ext^1(\mathscr {O}_{\Lambda }, E)=\mathbb {C}^3$
and
$Ext^1(\mathscr {O}_{\Lambda }, E)=\mathbb {C}^3$
and
![]() $Ext^2(\mathscr {O}_{\Lambda }, E)=0$
in Step 1-1 and Step 1-2 below.
$Ext^2(\mathscr {O}_{\Lambda }, E)=0$
in Step 1-1 and Step 1-2 below.
Step 1-1 (Compute
![]() $Ext^i(\mathscr {O}_{\Lambda }, E)$
). Apply
$Ext^i(\mathscr {O}_{\Lambda }, E)$
). Apply
![]() $Hom(\mathscr {O}_{\Lambda }, -)$
to the sequence
$Hom(\mathscr {O}_{\Lambda }, -)$
to the sequence
![]() $0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
, and consider the long exact sequence:
$0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
, and consider the long exact sequence:

The results for the first column were shown in Lemma 7.2, and it is straightforward to compute the extension groups in the third column. So we have
![]() $Ext^1(\mathscr {O}_{\Lambda },E)=\mathbb {C}^3$
and
$Ext^1(\mathscr {O}_{\Lambda },E)=\mathbb {C}^3$
and
![]() $Ext^2(\mathscr {O}_{\Lambda },E)=0$
.
$Ext^2(\mathscr {O}_{\Lambda },E)=0$
.
Step 1-2 (Compute
![]() $Hom(\mathscr {F}_1, E)$
). Apply
$Hom(\mathscr {F}_1, E)$
). Apply
![]() $Hom(\mathscr {F}_1, -)$
to
$Hom(\mathscr {F}_1, -)$
to
![]() $0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
, and we have
$0\to \mathscr {F}_1\to E\to \mathscr {O}_{\Lambda } \to 0$
, and we have

So
![]() $Hom(\mathscr {F}_1, E)=\mathbb {C}$
.
$Hom(\mathscr {F}_1, E)=\mathbb {C}$
.
Step 2 Now, we have a diagram as follows:

The long column is from the long exact sequence in Step 1 and the long row is from Step 1-2. We see immediately that
![]() $Ker(\phi )=Ker(\phi _1)+Ker(\phi _2)=\mathbb {C}^8$
.
$Ker(\phi )=Ker(\phi _1)+Ker(\phi _2)=\mathbb {C}^8$
.
The global version of diagram 7.3 is the following.

We have that
![]() $N_{H|K_{(2,3)}}=\mathbb {C}^7\hookrightarrow Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })=\mathbb {C}^{9}$
for all points
$N_{H|K_{(2,3)}}=\mathbb {C}^7\hookrightarrow Ext^1(\mathscr {F}_1,\mathscr {O}_{\Lambda })=\mathbb {C}^{9}$
for all points
![]() $E\in H$
. Correspondingly, we have the embedding
$E\in H$
. Correspondingly, we have the embedding
![]() $D=\mathbb {P}(\mathscr {N}_{H|K_{(2,3)}}^*)\hookrightarrow \mathbf {P}:=\mathbb {P}(\mathscr {E}xt_{\pi _H}^1(U_{\mathscr {F}_1}\otimes \pi _H^*L,U_{\mathscr {O}_{\Lambda }})^*)$
.
$D=\mathbb {P}(\mathscr {N}_{H|K_{(2,3)}}^*)\hookrightarrow \mathbf {P}:=\mathbb {P}(\mathscr {E}xt_{\pi _H}^1(U_{\mathscr {F}_1}\otimes \pi _H^*L,U_{\mathscr {O}_{\Lambda }})^*)$
.
By this point, we have that a general point in
![]() $\mathbf {B}$
parameterizes
$\mathbf {B}$
parameterizes
![]() $\mathscr {O}_C$
(
$\mathscr {O}_C$
(
![]() $C\subset \mathbb {P}^3$
is a twisted cubic), and
$C\subset \mathbb {P}^3$
is a twisted cubic), and
![]() $\mathbf {P}$
parameterizes plane cubic curves with an extra point in the curve (equiv. a degree one line bundle on a cubic curve). Recall that the component
$\mathbf {P}$
parameterizes plane cubic curves with an extra point in the curve (equiv. a degree one line bundle on a cubic curve). Recall that the component
![]() $\mathbf {P}$
is created by the second wall:
$\mathbf {P}$
is created by the second wall:
We will show in the next proposition that for a stable object
![]() $E\in \mathscr {A}_1$
that fits the sequence
$E\in \mathscr {A}_1$
that fits the sequence
![]() $W_2$
,
$W_2$
,
![]() $E\cong L_{C_E}$
, where
$E\cong L_{C_E}$
, where
![]() $C_E$
is a cubic curve and
$C_E$
is a cubic curve and
![]() $L_{C_E}$
is a degree one line bundle on that curve. Then, [Reference Freiermuth11, Th. 5.2] implies that
$L_{C_E}$
is a degree one line bundle on that curve. Then, [Reference Freiermuth11, Th. 5.2] implies that
 $$\begin{align*}Ext^1(E,E)= \begin{cases} \mathbb{C}^{13},\quad \text{if }\ supp(E)\ \text{is smooth,}\\ \mathbb{C}^{14},\quad \text{if }\ supp(E)\ \text{is singular.}\\ \end{cases} \end{align*}$$
$$\begin{align*}Ext^1(E,E)= \begin{cases} \mathbb{C}^{13},\quad \text{if }\ supp(E)\ \text{is smooth,}\\ \mathbb{C}^{14},\quad \text{if }\ supp(E)\ \text{is singular.}\\ \end{cases} \end{align*}$$
This indicates the expected gluing, at least set theoretically, that
![]() $\mathbf {B}$
intersects
$\mathbf {B}$
intersects
![]() $\mathbf {P}$
transversely along a divisor in
$\mathbf {P}$
transversely along a divisor in
![]() $\mathbf {B}$
. The intersection parameterizes exactly degree one line bundles supported on some singular cubic curve. We start with the following lemma about tilt stability for
$\mathbf {B}$
. The intersection parameterizes exactly degree one line bundles supported on some singular cubic curve. We start with the following lemma about tilt stability for
![]() $\mathscr {O}_{\Lambda }$
.
$\mathscr {O}_{\Lambda }$
.
Lemma 7.7. For the tilt stability condition
![]() $\sigma _{\alpha , \beta }=(Coh^{\beta }(\mathbb {P}^3), Z_{\alpha , \beta }=-ch_2^{\beta }+\frac {\alpha ^2}{2}ch_0^{\beta }+i\cdot ch_1^{\beta })$
on
$\sigma _{\alpha , \beta }=(Coh^{\beta }(\mathbb {P}^3), Z_{\alpha , \beta }=-ch_2^{\beta }+\frac {\alpha ^2}{2}ch_0^{\beta }+i\cdot ch_1^{\beta })$
on
![]() $\mathbb {P}^3$
, there is a unique tilt wall for
$\mathbb {P}^3$
, there is a unique tilt wall for
![]() $\mathscr {O}_{\Lambda }$
defined by
$\mathscr {O}_{\Lambda }$
defined by
![]() $0\to \mathscr {O}_{\mathbb {P}^3}\to \mathscr {O}_{\Lambda } \to \mathscr {O}_{\mathbb {P}^3}(-1)[1]\to 0 $
with equation
$0\to \mathscr {O}_{\mathbb {P}^3}\to \mathscr {O}_{\Lambda } \to \mathscr {O}_{\mathbb {P}^3}(-1)[1]\to 0 $
with equation
![]() $\alpha ^2+(\beta -1/2)^2=(1/2)^2$
in the
$\alpha ^2+(\beta -1/2)^2=(1/2)^2$
in the
![]() $(\alpha ,\beta )$
plane.
$(\alpha ,\beta )$
plane.
![]() $\mathscr {O}_{\Lambda }$
is tilt stable outside W in the
$\mathscr {O}_{\Lambda }$
is tilt stable outside W in the
![]() $(\alpha ,\beta )$
-plane.
$(\alpha ,\beta )$
-plane.
Proof. Firstly, thanks to [Reference Schmidt33, Th. 5.1], we know that the smallest tilt wall for
![]() $\mathscr {O}_{\Lambda }$
is defined by
$\mathscr {O}_{\Lambda }$
is defined by
![]() $0\to \mathscr {O}_{\mathbb {P}^3}\to \mathscr {O}_{\Lambda } \to \mathscr {O}_{\mathbb {P}^3}(-1)[1]\to 0 $
(denote it by W). Its equation is
$0\to \mathscr {O}_{\mathbb {P}^3}\to \mathscr {O}_{\Lambda } \to \mathscr {O}_{\mathbb {P}^3}(-1)[1]\to 0 $
(denote it by W). Its equation is
![]() $\alpha ^2+(\beta -1/2)^2=(1/2)^2$
. Then, we show that there are no bigger walls.
$\alpha ^2+(\beta -1/2)^2=(1/2)^2$
. Then, we show that there are no bigger walls.
Suppose there is an actual wall
![]() $W'$
defined by
$W'$
defined by
![]() $0\to A \to \mathscr {O}_{\Lambda }\to B \to 0$
in
$0\to A \to \mathscr {O}_{\Lambda }\to B \to 0$
in
![]() $Coh^{\beta }(\mathbb {P}^3)$
. Since numerical tilt walls are nested semicircles, it is known that if there is an actual wall somewhere (say at P in the
$Coh^{\beta }(\mathbb {P}^3)$
. Since numerical tilt walls are nested semicircles, it is known that if there is an actual wall somewhere (say at P in the
![]() $(\alpha ,\beta )$
-plane) then it is an actual wall everywhere along the numerical wall that goes through P. Moreover, since
$(\alpha ,\beta )$
-plane) then it is an actual wall everywhere along the numerical wall that goes through P. Moreover, since
![]() $W'$
is larger than W there is an arc in
$W'$
is larger than W there is an arc in
![]() $W'$
where
$W'$
where
![]() $\beta $
ranges between
$\beta $
ranges between
![]() $-1$
and
$-1$
and
![]() $0$
. So the equation
$0$
. So the equation
![]() $H^2ch^{\beta }_1(A)+H^2ch^{\beta }_1(B)=H^2ch^{\beta }_1(\mathscr {O}_{\Lambda })=1$
holds for all
$H^2ch^{\beta }_1(A)+H^2ch^{\beta }_1(B)=H^2ch^{\beta }_1(\mathscr {O}_{\Lambda })=1$
holds for all
![]() $\beta \in [0,1]$
with
$\beta \in [0,1]$
with
![]() $H^2ch^{\beta }_1(A), H^2ch^{\beta }_1(B)>0$
. When
$H^2ch^{\beta }_1(A), H^2ch^{\beta }_1(B)>0$
. When
![]() $\beta =0$
, we have
$\beta =0$
, we have
![]() $0\leq ch_0(A)\leq 1$
. We must have
$0\leq ch_0(A)\leq 1$
. We must have
![]() $ch_0(A)=1$
(hence
$ch_0(A)=1$
(hence
![]() $ch_0(B)=1$
), since otherwise,
$ch_0(B)=1$
), since otherwise,
![]() $ch_0(A)=ch_0(B)=0$
and there is no such tilt wall. When
$ch_0(A)=ch_0(B)=0$
and there is no such tilt wall. When
![]() $\beta =1$
, we have
$\beta =1$
, we have
![]() $0\leq ch_0(A)+H^2ch_1(A)\leq 1$
and
$0\leq ch_0(A)+H^2ch_1(A)\leq 1$
and
![]() $0\leq ch_0(B)+H^2ch_1(B) \leq 1$
. Using the fact that
$0\leq ch_0(B)+H^2ch_1(B) \leq 1$
. Using the fact that
![]() $H^2ch_1(A)+H^2ch_1(B)=H^2ch_1(\mathscr {O}_{\Lambda })=1$
, we have
$H^2ch_1(A)+H^2ch_1(B)=H^2ch_1(\mathscr {O}_{\Lambda })=1$
, we have
![]() $H^2ch_1(A)=0$
.
$H^2ch_1(A)=0$
.
Then, the Bogomolov inequality for tilt semistable object A implies
![]() $H^2ch^2_1(A)-H^3ch_0(A)Hch_2(A)\geq 0$
, which implies
$H^2ch^2_1(A)-H^3ch_0(A)Hch_2(A)\geq 0$
, which implies
![]() $Hch_2(A)\leq 0$
. On the other hand, the equation for the numerical wall defined by A (
$Hch_2(A)\leq 0$
. On the other hand, the equation for the numerical wall defined by A (
![]() $ch_0(A)=1$
,
$ch_0(A)=1$
,
![]() $ch_1(A)=0$
) is
$ch_1(A)=0$
) is
![]() $\alpha ^2+(\beta +1/2)^2=(1/2)^2+Hch_2(A)\leq 1/4$
. So if
$\alpha ^2+(\beta +1/2)^2=(1/2)^2+Hch_2(A)\leq 1/4$
. So if
![]() $Hch_2(A)<0,$
then
$Hch_2(A)<0,$
then
![]() $W'$
will be smaller than W, which is a contradiction. So we must have
$W'$
will be smaller than W, which is a contradiction. So we must have
![]() $Hch_2(A)=0$
, and
$Hch_2(A)=0$
, and
![]() $W'=W$
.
$W'=W$
.
Finally, it is evident that
![]() $\mathscr {O}_{\Lambda }$
is stable outside the wall W since the tilt slope of
$\mathscr {O}_{\Lambda }$
is stable outside the wall W since the tilt slope of
![]() $\mathscr {O}_{\Lambda }$
is larger than the tilt slope of
$\mathscr {O}_{\Lambda }$
is larger than the tilt slope of
![]() $\mathscr {O}_{\mathbb {P}^3}$
there.
$\mathscr {O}_{\mathbb {P}^3}$
there.
Recall that in §3, we use a one-dimensional family of tilt stability that is
![]() $\sigma ^{tilt}_t:=(Coh^{-t-2}(\mathbb {P}^3), Z_{2,t}:=-\chi ^{\prime }_t+i\cdot \chi ^{\prime \prime }_t)$
. This family is the line
$\sigma ^{tilt}_t:=(Coh^{-t-2}(\mathbb {P}^3), Z_{2,t}:=-\chi ^{\prime }_t+i\cdot \chi ^{\prime \prime }_t)$
. This family is the line
![]() $\alpha =\frac {1}{\sqrt {3}}$
in the
$\alpha =\frac {1}{\sqrt {3}}$
in the
![]() $(\alpha , \beta )$
-plane. Evidently, this line is above the wall W in Lemma 7.7, and
$(\alpha , \beta )$
-plane. Evidently, this line is above the wall W in Lemma 7.7, and
![]() $\mathscr {O}_{\Lambda }\in Coh^{\beta }(\mathbb {P}^3)$
for all
$\mathscr {O}_{\Lambda }\in Coh^{\beta }(\mathbb {P}^3)$
for all
![]() $\beta \in \mathbb {R}$
. So we have the following corollary.
$\beta \in \mathbb {R}$
. So we have the following corollary.
Corollary 7.8.
![]() $\mathscr {O}_{\Lambda }$
is
$\mathscr {O}_{\Lambda }$
is
![]() $\sigma ^{tilt}_t$
-stable for all
$\sigma ^{tilt}_t$
-stable for all
![]() $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
We are now ready to prove that the stable objects created by the second wall are degree-one line bundles on a cubic curve.
Proposition 7.9. For a stable object E that fits the sequence
![]() $0\to \mathscr {O}_{\Lambda }\to E\to \mathscr {F}_1\to 0$
in
$0\to \mathscr {O}_{\Lambda }\to E\to \mathscr {F}_1\to 0$
in
![]() $\mathscr {A}_1$
, E is a sheaf, and more precisely, E is a degree one line bundle on a cubic curve in
$\mathscr {A}_1$
, E is a sheaf, and more precisely, E is a degree one line bundle on a cubic curve in
![]() $\mathbb {P}^3$
.
$\mathbb {P}^3$
.
Proof. For simplicity, we call the sequence
![]() $0\to \mathscr {O}_{\Lambda }\to E\to \mathscr {F}_1\to 0$
“
$0\to \mathscr {O}_{\Lambda }\to E\to \mathscr {F}_1\to 0$
“
![]() $W_2$
” since it defines the second actual wall.
$W_2$
” since it defines the second actual wall.
We have shown in §6 that
![]() $\mathscr {O}_{\Lambda }$
and
$\mathscr {O}_{\Lambda }$
and
![]() $\mathscr {F}_1$
are Euler stable in
$\mathscr {F}_1$
are Euler stable in
![]() $\mathscr {A}_1$
. Recall that the Euler stability
$\mathscr {A}_1$
. Recall that the Euler stability
![]() $\sigma ^{Euler}_t:=(\mathscr {A}_1, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
is a tilt of the stability condition
$\sigma ^{Euler}_t:=(\mathscr {A}_1, Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
is a tilt of the stability condition
![]() $\sigma ^{\mathscr {B}_t}_t=(\mathscr {B}_t, Z^{\prime }_t=-\chi _t+i\cdot \chi ^{\prime }_t)$
. A direct computation shows that
$\sigma ^{\mathscr {B}_t}_t=(\mathscr {B}_t, Z^{\prime }_t=-\chi _t+i\cdot \chi ^{\prime }_t)$
. A direct computation shows that
![]() $\chi ^{\prime }_t(\mathscr {O}_{\Lambda })=t+3/2$
and
$\chi ^{\prime }_t(\mathscr {O}_{\Lambda })=t+3/2$
and
![]() $\chi ^{\prime }_t(\mathscr {F}_{1})=-t+3/2$
which are both positive for
$\chi ^{\prime }_t(\mathscr {F}_{1})=-t+3/2$
which are both positive for
![]() $t\in (0,1]$
. So we have that the sequence
$t\in (0,1]$
. So we have that the sequence
![]() $W_2$
stays the same in
$W_2$
stays the same in
![]() $\mathscr {B}_t$
, that is,
$\mathscr {B}_t$
, that is,
![]() $\mathscr {H}^{-1}_{\mathscr {B}_t}(\mathscr {O}_{\Lambda })=\mathscr {H}^{-1}_{\mathscr {B}_t}(\mathscr {F}_{1})=0$
(
$\mathscr {H}^{-1}_{\mathscr {B}_t}(\mathscr {O}_{\Lambda })=\mathscr {H}^{-1}_{\mathscr {B}_t}(\mathscr {F}_{1})=0$
(
![]() $\mathscr {H}^{-1}_{\mathscr {B}_t}$
denotes the
$\mathscr {H}^{-1}_{\mathscr {B}_t}$
denotes the
![]() $-1$
cohomology in
$-1$
cohomology in
![]() $\mathscr {B}_t$
).
$\mathscr {B}_t$
).
Next, we take the cohomology of
![]() $W_2$
in
$W_2$
in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
. Recall that the stability condition
$Coh^{-t-2}(\mathbb {P}^3)$
. Recall that the stability condition
![]() $\sigma ^{tilt}_t:=(Coh^{-t-2}{(\mathbb {P}^3)}, Z_t=-\chi ^{\prime }_t+i\cdot \chi ^{\prime \prime }_t)$
is a slice of the stability conditions
$\sigma ^{tilt}_t:=(Coh^{-t-2}{(\mathbb {P}^3)}, Z_t=-\chi ^{\prime }_t+i\cdot \chi ^{\prime \prime }_t)$
is a slice of the stability conditions
![]() $\sigma _{\alpha , \beta }:=(Coh^{\beta }(\mathbb {P}^3), Z_{\alpha , \beta }=-ch_2^{\beta }+\frac {\alpha ^2}{2}ch^{\beta }_0+i\cdot ch_1^{\beta })$
, where
$\sigma _{\alpha , \beta }:=(Coh^{\beta }(\mathbb {P}^3), Z_{\alpha , \beta }=-ch_2^{\beta }+\frac {\alpha ^2}{2}ch^{\beta }_0+i\cdot ch_1^{\beta })$
, where
![]() $\alpha =\frac {1}{\sqrt {3}}$
, and
$\alpha =\frac {1}{\sqrt {3}}$
, and
![]() $\beta =-t-2$
.
$\beta =-t-2$
.
![]() $\mathscr {O}_{\Lambda }$
is
$\mathscr {O}_{\Lambda }$
is
![]() $\mu $
-stable, and it is always in
$\mu $
-stable, and it is always in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
for any
$Coh^{-t-2}(\mathbb {P}^3)$
for any
![]() $t\in \mathbb {R}$
. A direct computation shows that
$t\in \mathbb {R}$
. A direct computation shows that
![]() $\nu _t(\mathscr {O}_{\Lambda }):={\chi ^{\prime }_t(\mathscr {O}_{\Lambda })}/{\chi ^{\prime \prime }_t(\mathscr {O}_{\Lambda })}=t+3/2>0$
for
$\nu _t(\mathscr {O}_{\Lambda }):={\chi ^{\prime }_t(\mathscr {O}_{\Lambda })}/{\chi ^{\prime \prime }_t(\mathscr {O}_{\Lambda })}=t+3/2>0$
for
![]() $t\in (0,1]$
, and
$t\in (0,1]$
, and
![]() $\nu _t(\mathscr {O}_{\Lambda }(-3))=t-3/2<0$
for
$\nu _t(\mathscr {O}_{\Lambda }(-3))=t-3/2<0$
for
![]() $t\in (0,1]$
. So we have
$t\in (0,1]$
. So we have
![]() $\mathscr {O}_{\Lambda }, \mathscr {O}_{\Lambda }(-3)$
are
$\mathscr {O}_{\Lambda }, \mathscr {O}_{\Lambda }(-3)$
are
![]() $\mu $
-stable in
$\mu $
-stable in
![]() $Coh(\mathbb {P}^3)$
,
$Coh(\mathbb {P}^3)$
,
![]() $\mathscr {O}_{\Lambda }, \mathscr {O}_{\Lambda }(-3)$
are
$\mathscr {O}_{\Lambda }, \mathscr {O}_{\Lambda }(-3)$
are
![]() $\nu _t$
-stable (by Corollary 7.8) in
$\nu _t$
-stable (by Corollary 7.8) in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
, and
$Coh^{-t-2}(\mathbb {P}^3)$
, and
![]() $\mathscr {O}_{\Lambda }, \mathscr {O}_{\Lambda }(-3)[1]\in \mathscr {B}_t$
for
$\mathscr {O}_{\Lambda }, \mathscr {O}_{\Lambda }(-3)[1]\in \mathscr {B}_t$
for
![]() $t\in (0,1]$
. Then, cohomologies of
$t\in (0,1]$
. Then, cohomologies of
![]() $W_2$
in
$W_2$
in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
are as follows:
$Coh^{-t-2}(\mathbb {P}^3)$
are as follows:
where
![]() $\mathscr {H}_{\beta }^{-1}$
and
$\mathscr {H}_{\beta }^{-1}$
and
![]() $\mathscr {H}_{\beta }^{0}$
denote the cohomology in
$\mathscr {H}_{\beta }^{0}$
denote the cohomology in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
, and recall that we have
$Coh^{-t-2}(\mathbb {P}^3)$
, and recall that we have
![]() $0\to \mathscr {O}_{\Lambda }(-3)[1]\to \mathscr {F}_1\to \mathbb {C}_P\to 0$
in
$0\to \mathscr {O}_{\Lambda }(-3)[1]\to \mathscr {F}_1\to \mathbb {C}_P\to 0$
in
![]() $\mathscr {B}_t$
.
$\mathscr {B}_t$
.
In sequence 7.5, we must have
![]() $\mathscr {H}_{\beta }^{-1}(E)=0$
. Otherwise,
$\mathscr {H}_{\beta }^{-1}(E)=0$
. Otherwise,
![]() $\mathscr {H}_{\beta }^{-1}(E)$
would be a sheaf (since
$\mathscr {H}_{\beta }^{-1}(E)$
would be a sheaf (since
![]() $Im(\theta )$
is a sheaf), and
$Im(\theta )$
is a sheaf), and
![]() $Im(\theta )$
would be a torsion sub-sheaf of
$Im(\theta )$
would be a torsion sub-sheaf of
![]() $\mathscr {O}_{\Lambda }$
which will force
$\mathscr {O}_{\Lambda }$
which will force
![]() $\theta $
to be
$\theta $
to be
![]() $0$
. Then, we have two relations for E, which are (1).
$0$
. Then, we have two relations for E, which are (1).
![]() $\mathscr {H}_{\beta }^{-1}(E) \cong \mathscr {O}_{\Lambda }(-3)$
(2).
$\mathscr {H}_{\beta }^{-1}(E) \cong \mathscr {O}_{\Lambda }(-3)$
(2).
![]() $0\to \mathscr {O}_{\Lambda }\to \mathscr {H}_{\beta }^{0}(E)\to \mathbb {C}_P \to 0$
. Since
$0\to \mathscr {O}_{\Lambda }\to \mathscr {H}_{\beta }^{0}(E)\to \mathbb {C}_P \to 0$
. Since
![]() $Ext^1(\mathbb {C}_P, \mathscr {O}_{\Lambda })=0$
, we have that
$Ext^1(\mathbb {C}_P, \mathscr {O}_{\Lambda })=0$
, we have that
![]() $\mathscr {H}_{\beta }^{0}(E)=\mathscr {O}_{\Lambda }\bigoplus \mathbb {C}_P$
contradiction with E being stable in both
$\mathscr {H}_{\beta }^{0}(E)=\mathscr {O}_{\Lambda }\bigoplus \mathbb {C}_P$
contradiction with E being stable in both
![]() $\mathscr {A}_1$
and
$\mathscr {A}_1$
and
![]() $\mathscr {B}_t$
(
$\mathscr {B}_t$
(
![]() $t\in (0.72,1]$
). (For a simple reason, one sees that there is a morphism
$t\in (0.72,1]$
). (For a simple reason, one sees that there is a morphism
![]() $E\twoheadrightarrow \mathscr {O}_{\Lambda }$
, and a direct computation shows that
$E\twoheadrightarrow \mathscr {O}_{\Lambda }$
, and a direct computation shows that
![]() $\lambda _t(E):=\chi _t(E)/\chi ^{\prime }_t(E)>\lambda _t(\mathscr {O}_{\Lambda })$
for
$\lambda _t(E):=\chi _t(E)/\chi ^{\prime }_t(E)>\lambda _t(\mathscr {O}_{\Lambda })$
for
![]() $t\in (0.9, 1]$
.)
$t\in (0.9, 1]$
.)
Therefore, sequence 7.5 becomes
Assume that the cokernel of
![]() $\theta $
is T, that is, we have two short exact sequences in
$\theta $
is T, that is, we have two short exact sequences in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
as follows:
$Coh^{-t-2}(\mathbb {P}^3)$
as follows:
(1’)
![]() $0\to \mathscr {O}_{\Lambda }(-3) \to \mathscr {O}_{\Lambda }\to T \to 0$
(2’)
$0\to \mathscr {O}_{\Lambda }(-3) \to \mathscr {O}_{\Lambda }\to T \to 0$
(2’)
![]() $0\to T \to E \to \mathbb {C}_P \to 0.$
$0\to T \to E \to \mathbb {C}_P \to 0.$
If T is not a sheaf, then we have
![]() $0\to \mathscr {H}^{-1}(T)\neq 0 \to \mathscr {O}_{\Lambda }(-3) \to \mathscr {O}_{\Lambda }\to \mathscr {H}^{0}(T)\to 0$
. For the same reason, we have
$0\to \mathscr {H}^{-1}(T)\neq 0 \to \mathscr {O}_{\Lambda }(-3) \to \mathscr {O}_{\Lambda }\to \mathscr {H}^{0}(T)\to 0$
. For the same reason, we have
![]() $\mathscr {H}^{-1}(T)\cong \mathscr {O}_{\Lambda }(-3)$
and
$\mathscr {H}^{-1}(T)\cong \mathscr {O}_{\Lambda }(-3)$
and
![]() $\mathscr {O}_{\Lambda }\cong \mathscr {H}^{0}(T)$
. Then,
$\mathscr {O}_{\Lambda }\cong \mathscr {H}^{0}(T)$
. Then,
![]() $0\to \mathscr {O}_{\Lambda }(-3)[1]\to T\to \mathscr {O}_{\Lambda }\to 0$
, which implies
$0\to \mathscr {O}_{\Lambda }(-3)[1]\to T\to \mathscr {O}_{\Lambda }\to 0$
, which implies
![]() $T\cong \mathscr {O}_{\Lambda }(-3)[1]\bigoplus \mathscr {O}_{\Lambda }$
. Then sequence (2’) becomes
$T\cong \mathscr {O}_{\Lambda }(-3)[1]\bigoplus \mathscr {O}_{\Lambda }$
. Then sequence (2’) becomes
![]() $0\to \mathscr {O}_{\Lambda }(-3)[1]\bigoplus \mathscr {O}_{\Lambda } \to E \to \mathbb {C}_P \to 0$
, and it violates the stability of E. So T must be a sheaf, and
$0\to \mathscr {O}_{\Lambda }(-3)[1]\bigoplus \mathscr {O}_{\Lambda } \to E \to \mathbb {C}_P \to 0$
, and it violates the stability of E. So T must be a sheaf, and
![]() $T\cong \mathscr {O}_{C_E}$
in which
$T\cong \mathscr {O}_{C_E}$
in which
![]() $C_E$
is a cubic curve in
$C_E$
is a cubic curve in
![]() $\Lambda $
.
$\Lambda $
.
Lastly, sequence 7.6 becomes
![]() $0\to \mathscr {O}_{C_E}\to E \to \mathbb {C}_P\to 0$
in
$0\to \mathscr {O}_{C_E}\to E \to \mathbb {C}_P\to 0$
in
![]() $Coh^{-t-2}(\mathbb {P}^3)$
. It is easy to see that E is a sheaf, and the sequence stays the same if we take cohomologies in
$Coh^{-t-2}(\mathbb {P}^3)$
. It is easy to see that E is a sheaf, and the sequence stays the same if we take cohomologies in
![]() $Coh(\mathbb {P}^3)$
. This means that we have a sequence in
$Coh(\mathbb {P}^3)$
. This means that we have a sequence in
![]() $Coh(\mathbb {P}^3)$
:
$Coh(\mathbb {P}^3)$
:
![]() $0\to \mathscr {O}_{C_E}\to E \to \mathbb {C}_P\to 0.$
Moreover, since
$0\to \mathscr {O}_{C_E}\to E \to \mathbb {C}_P\to 0.$
Moreover, since
![]() $Ext^1(\mathbb {C}_P, \mathscr {O}_{C_E})=\mathbb {C}$
for
$Ext^1(\mathbb {C}_P, \mathscr {O}_{C_E})=\mathbb {C}$
for
![]() $P\in C_E$
and
$P\in C_E$
and
![]() $Ext^1(\mathbb {C}_P, \mathscr {O}_{C_E})=0$
for
$Ext^1(\mathbb {C}_P, \mathscr {O}_{C_E})=0$
for
![]() $P\not \in C_E$
, we have that E is a degree one line bundle on
$P\not \in C_E$
, we have that E is a degree one line bundle on
![]() $C_E$
.
$C_E$
.
Finally in this section, we show the gluing of
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {P}$
using the Elementary modification.
$\mathbf {P}$
using the Elementary modification.
-
1. Construct a universal family
 $\mathscr {K}$
on the blow up.
$\mathscr {K}$
on the blow up.There are three distinguished triangles (a), (b), and (c) involved (the third one is from the composition of the first two). The octahedral axiom would give the fourth triangle.
 $\mathscr {M}_2$
is a indeed a quiver moduli of the dimension vector
$\mathscr {M}_2$
is a indeed a quiver moduli of the dimension vector
 $[1694]$
. [Reference King17, Prop. 5.3] implies that it is a fine moduli space when
$[1694]$
. [Reference King17, Prop. 5.3] implies that it is a fine moduli space when
 $t\in \mathbb {Q}$
. So
$t\in \mathbb {Q}$
. So
 $\mathscr {M}_2$
and
$\mathscr {M}_2$
and
 $\mathscr {M}_3$
are both fine moduli spaces. Denote the universal family of representation on
$\mathscr {M}_3$
are both fine moduli spaces. Denote the universal family of representation on
 $\mathscr {M}_2$
by
$\mathscr {M}_2$
by
 $U_2$
. When restricting
$U_2$
. When restricting
 $U_2$
to H, there is a line bundle
$U_2$
to H, there is a line bundle
 $L_1$
on H such that
$L_1$
on H such that
 $U_E\cong (U_2|H)\otimes \pi _H^*(L_1)$
. To reduce the complexity of notations, we abuse the notation a bit by assuming that
$U_E\cong (U_2|H)\otimes \pi _H^*(L_1)$
. To reduce the complexity of notations, we abuse the notation a bit by assuming that
 $L_1$
is trivial.
$L_1$
is trivial.-
(a) This is from pulling back the extension in Proposition 7.3 from H to D and then pushforward to the blow-up
 $\mathbf {B}$
.
$\mathbf {B}$
.  $$ \begin{align*}\to i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^* L)\to i_*b_H^*(U_{E}) \xrightarrow{u} i_*b_H^*(p^*( U_{\mathscr{O}_{\Lambda}}))\to.\end{align*} $$
$$ \begin{align*}\to i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^* L)\to i_*b_H^*(U_{E}) \xrightarrow{u} i_*b_H^*(p^*( U_{\mathscr{O}_{\Lambda}}))\to.\end{align*} $$
-
(b)
 $$ \begin{align*}\to b^*(U_2(-D\times \mathbb{P}^3))\to b^*(U_2) \xrightarrow{r} i_*(b^*U_2)_{D\times \mathbb{P}^3}\to.\end{align*} $$
$$ \begin{align*}\to b^*(U_2(-D\times \mathbb{P}^3))\to b^*(U_2) \xrightarrow{r} i_*(b^*U_2)_{D\times \mathbb{P}^3}\to.\end{align*} $$
-
(c) Define
 $\mathscr {K}$
from the following distinguished triangle: (
$\mathscr {K}$
from the following distinguished triangle: (
 $\mathscr {K}$
will be the desired family on
$\mathscr {K}$
will be the desired family on
 $\mathbf {B}$
for the gluing.)
$\mathbf {B}$
for the gluing.)  $$ \begin{align*}\to \mathscr{K} \to b^*U_2\xrightarrow{u\circ r} i_*b_H^*(p^*( U_{\mathscr{O}_{\Lambda}})) \to.\end{align*} $$
$$ \begin{align*}\to \mathscr{K} \to b^*U_2\xrightarrow{u\circ r} i_*b_H^*(p^*( U_{\mathscr{O}_{\Lambda}})) \to.\end{align*} $$
-
(d) Apply the octahedral axiom, we have the following triangle:
 $$ \begin{align*}\to b^*(U_2(-D\times \mathbb{P}^3)) \to \mathscr{K} \to i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^* L)\to.\end{align*} $$
$$ \begin{align*}\to b^*(U_2(-D\times \mathbb{P}^3)) \to \mathscr{K} \to i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^* L)\to.\end{align*} $$
 $\mathscr {K}$
is flat because it is a complex of vector bundles.
$\mathscr {K}$
is flat because it is a complex of vector bundles.
-
-
2. Glue
 $\mathbf {B}$
to the component
$\mathbf {B}$
to the component
 $\mathbf {P}$
using the family
$\mathbf {P}$
using the family
 $\mathscr {K}$
. We will apply the octahedral axiom again to triangles (a’)
$\mathscr {K}$
. We will apply the octahedral axiom again to triangles (a’)
 $\sim $
(c’) below.
$\sim $
(c’) below.-
(a’)
 $$ \begin{align*}\to \mathscr{K}(-D\times \mathbb{P}^3)\to \mathscr{K}\xrightarrow{r} i_*Li^*(\mathscr{K})\to.\end{align*} $$
$$ \begin{align*}\to \mathscr{K}(-D\times \mathbb{P}^3)\to \mathscr{K}\xrightarrow{r} i_*Li^*(\mathscr{K})\to.\end{align*} $$
-
(b’) Define a family
 $\mathscr {K}'$
from the following triangle: Then push it forward to
$\mathscr {K}'$
from the following triangle: Then push it forward to $$ \begin{align*}\to \mathscr{K}'\to Li^*(\mathscr{K})\to b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^*L)\to.\end{align*} $$
$$ \begin{align*}\to \mathscr{K}'\to Li^*(\mathscr{K})\to b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^*L)\to.\end{align*} $$
 $\mathbf {B}$
by
$\mathbf {B}$
by
 $i_*$
:
$i_*$
:  $$ \begin{align*}\to i_*\mathscr{K}'\to i_*Li^*(\mathscr{K})\xrightarrow{v} i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^*L)\to.\end{align*} $$
$$ \begin{align*}\to i_*\mathscr{K}'\to i_*Li^*(\mathscr{K})\xrightarrow{v} i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^*L)\to.\end{align*} $$
-
(c’)
 $$ \begin{align*}b^*U_2(-D\times \mathbb{P}^3) \to \mathscr{K} \xrightarrow{v\circ r}i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^*L).\end{align*} $$
$$ \begin{align*}b^*U_2(-D\times \mathbb{P}^3) \to \mathscr{K} \xrightarrow{v\circ r}i_*b_H^*(U_{\mathscr{F}_1}\otimes \pi_H^*L).\end{align*} $$
-
(d’) Apply the octahedral axiom, and we have the triangle:
 $$ \begin{align*}\to \mathscr{K}(-D\times \mathbb{P}^3)\to b^*U_2(-D\times \mathbb{P}^3) \to i_*\mathscr{K}' \to.\end{align*} $$
$$ \begin{align*}\to \mathscr{K}(-D\times \mathbb{P}^3)\to b^*U_2(-D\times \mathbb{P}^3) \to i_*\mathscr{K}' \to.\end{align*} $$
As desired, we have the following isomorphism, and this completes the proof that
 $\mathbf {B}$
is glued to
$\mathbf {B}$
is glued to
 $\mathbf {P}$
along the exceptional divisor algebraically:
$\mathbf {P}$
along the exceptional divisor algebraically:  $$\begin{align*}\begin{array}{ll} \mathscr{K}'&\cong b_H^*p^*(U_{\mathscr{O}_{\Lambda}})\otimes \mathscr{O}_{D\times \mathbb{P}^3}(-D\times \mathbb{P}^3)\\ {}&\cong b_H^*p^*(U_{\mathscr{O}_{\Lambda}})\otimes \pi_D^* \mathscr{O}_{\mathbb{P}(\mathscr{N}^*_{H|K_{(2,3)}})}(1)\\ {}&\cong b_H^*p^*(U_{\mathscr{O}_{\Lambda}})\otimes \pi_{\mathbf{P}}^* \mathscr{O}_{\mathbf{P}}(1).\\ \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ll} \mathscr{K}'&\cong b_H^*p^*(U_{\mathscr{O}_{\Lambda}})\otimes \mathscr{O}_{D\times \mathbb{P}^3}(-D\times \mathbb{P}^3)\\ {}&\cong b_H^*p^*(U_{\mathscr{O}_{\Lambda}})\otimes \pi_D^* \mathscr{O}_{\mathbb{P}(\mathscr{N}^*_{H|K_{(2,3)}})}(1)\\ {}&\cong b_H^*p^*(U_{\mathscr{O}_{\Lambda}})\otimes \pi_{\mathbf{P}}^* \mathscr{O}_{\mathbf{P}}(1).\\ \end{array} \end{align*}$$
-
8 An example of an actual wall built up from pieces
We have shown the two walls for the class
![]() $v=(0,0,3,-5)$
in the
$v=(0,0,3,-5)$
in the
![]() $(t,u)$
-plane in §6. These two walls, which are expected to be actual walls, do not intersect. However, it is not always the case on a threefold (see [Reference Maciocia and Jardim22], [Reference Schmidt33]) as how they behave on a surface. We give a counter-example in this section.
$(t,u)$
-plane in §6. These two walls, which are expected to be actual walls, do not intersect. However, it is not always the case on a threefold (see [Reference Maciocia and Jardim22], [Reference Schmidt33]) as how they behave on a surface. We give a counter-example in this section.
Let
![]() $C\subset \mathbb {P}^3$
be a rational quartic curve. The wall for
$C\subset \mathbb {P}^3$
be a rational quartic curve. The wall for
![]() $\mathscr {O}_C$
in the
$\mathscr {O}_C$
in the
![]() $(t,u)$
-plane is expected to be the outermost parts of the following two numerical walls:
$(t,u)$
-plane is expected to be the outermost parts of the following two numerical walls:
where
![]() $Q\subset \mathbb {P}^3$
is a quadric surface
$Q\subset \mathbb {P}^3$
is a quadric surface
![]() $Q\subset \mathbb {P}^3$
containing C.
$Q\subset \mathbb {P}^3$
containing C.
In Figure 9, S is the intersection of
![]() $W_1$
and
$W_1$
and
![]() $W_2$
, and the green region
$W_2$
, and the green region
![]() $\mathscr {Q}_1$
is the quiver region for
$\mathscr {Q}_1$
is the quiver region for
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
![]() $T=0.5$
is the right endpoint of
$T=0.5$
is the right endpoint of
![]() $W_2$
, and P is the intersection of
$W_2$
, and P is the intersection of
![]() $W_2$
with the boundary of
$W_2$
with the boundary of
![]() $\mathscr {Q}_1$
. There are two more walls,
$\mathscr {Q}_1$
. There are two more walls,
![]() $W_3$
(purple) and
$W_3$
(purple) and
![]() $W_4$
(brown), which are defined by the short exact sequences
$W_4$
(brown), which are defined by the short exact sequences
![]() $0\to \mathscr {O}_{\mathbb {P}^3} \to \mathscr {O}_{Q}\to \mathscr {O}_{\mathbb {P}^3}(-2)[1]\to 0$
and
$0\to \mathscr {O}_{\mathbb {P}^3} \to \mathscr {O}_{Q}\to \mathscr {O}_{\mathbb {P}^3}(-2)[1]\to 0$
and
![]() $0\to \mathscr {O}_{\mathbb {P}^3}(-2)[1] \to \mathscr {I}_{C}[1]\to \mathscr {I}_{C|Q}[1]\to 0,$
respectively. A direct computation shows that
$0\to \mathscr {O}_{\mathbb {P}^3}(-2)[1] \to \mathscr {I}_{C}[1]\to \mathscr {I}_{C|Q}[1]\to 0,$
respectively. A direct computation shows that
![]() $W_3$
and
$W_3$
and
![]() $W_4$
go through S as well.
$W_4$
go through S as well.

Figure 9 Numerical walls for
![]() $\mathcal{O}_C$
$\mathcal{O}_C$
In fact, it is easy to see that
![]() $W_2$
is not an actual wall to the left of S because
$W_2$
is not an actual wall to the left of S because
![]() $\mathscr {O}_Q$
is unstable, destabilized by
$\mathscr {O}_Q$
is unstable, destabilized by
![]() $\mathscr {O}_{\mathbb {P}^3}$
. Similarly,
$\mathscr {O}_{\mathbb {P}^3}$
. Similarly,
![]() $W_1$
is not an actual wall to the right of S because
$W_1$
is not an actual wall to the right of S because
![]() $\mathscr {I}_C[1]$
is unstable, destabilized by
$\mathscr {I}_C[1]$
is unstable, destabilized by
![]() $\mathscr {O}_{\mathbb {P}^3}(-2)[1]$
.
$\mathscr {O}_{\mathbb {P}^3}(-2)[1]$
.
We prove the following property which implies that the actual wall of
![]() $\mathscr {O}_C$
is built up from more than one numerical wall.
$\mathscr {O}_C$
is built up from more than one numerical wall.
Proposition 8.1. The numerical wall
![]() $W_2$
, defined by
$W_2$
, defined by
![]() $0\to \mathscr {O}_{Q}\to \mathscr {O}_{C} \to \mathscr {I}_{C/Q}[1] \to 0$
, is an actual wall in the quiver region
$0\to \mathscr {O}_{Q}\to \mathscr {O}_{C} \to \mathscr {I}_{C/Q}[1] \to 0$
, is an actual wall in the quiver region
![]() $\mathscr {Q}_1$
and a pseudo wall to the left of S.
$\mathscr {Q}_1$
and a pseudo wall to the left of S.
Proof. Recall that the stability condition in the
![]() $(t,u)$
-plane is the pair
$(t,u)$
-plane is the pair
![]() $\sigma _{t,u}=(\mathscr {B}_t, z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t + i \cdot \chi ^{\prime }_t)$
. Let
$\sigma _{t,u}=(\mathscr {B}_t, z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t + i \cdot \chi ^{\prime }_t)$
. Let
![]() $\lambda _{t,u}$
be the slope function of
$\lambda _{t,u}$
be the slope function of
![]() $Z_{t,u}$
. It is straightforward to check that
$Z_{t,u}$
. It is straightforward to check that
![]() $\lambda _{t,u}(\mathscr {O}_{\mathbb {P}^3})>\lambda _{t,u}(\mathscr {O}_{Q})$
for all
$\lambda _{t,u}(\mathscr {O}_{\mathbb {P}^3})>\lambda _{t,u}(\mathscr {O}_{Q})$
for all
![]() $(t,u)\in W_2$
to the left of S where
$(t,u)\in W_2$
to the left of S where
![]() $W_2$
can not be an actual wall.
$W_2$
can not be an actual wall.
Next, we prove that
![]() $\mathscr {O}_{Q}$
and
$\mathscr {O}_{Q}$
and
![]() $\mathscr {I}_{C/Q}[1]$
are stable in
$\mathscr {I}_{C/Q}[1]$
are stable in
![]() $\mathscr {Q}_1$
.
$\mathscr {Q}_1$
.
-
(a)
 $\mathscr {O}_{Q}$
and
$\mathscr {O}_{Q}$
and
 $\mathscr {I}_{C/Q}[1]$
are stable at T.
$\mathscr {I}_{C/Q}[1]$
are stable at T.We use the Euler stability
 $\sigma _t=(\mathscr {A}_t,Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
with slope
$\sigma _t=(\mathscr {A}_t,Z_t=\chi ^{\prime }_t+i\cdot \chi _t)$
with slope
 $\lambda ^{Euler}_t=-\frac {\chi ^{\prime }_t}{\chi _t}$
at T. (It is the same with the stability condition
$\lambda ^{Euler}_t=-\frac {\chi ^{\prime }_t}{\chi _t}$
at T. (It is the same with the stability condition
 $\sigma _{t,0}$
for
$\sigma _{t,0}$
for
 $\mathscr {B}_t$
.)
$\mathscr {B}_t$
.) $\bullet $
For
$\bullet $
For
 $\mathscr {O}_{Q}$
, it has dimension vector
$\mathscr {O}_{Q}$
, it has dimension vector
 $[1,4,7,4]$
in
$[1,4,7,4]$
in
 $\mathscr {A}_1$
. Without loss of generality, assume Q is defined by the equation
$\mathscr {A}_1$
. Without loss of generality, assume Q is defined by the equation
 $x_0x_3-x_1x_2=0$
. Then the presentation of
$x_0x_3-x_1x_2=0$
. Then the presentation of
 $\mathscr {O}_{Q}$
is given as follows:
$\mathscr {O}_{Q}$
is given as follows:  $$ \begin{align*}\left[\mathscr{O}_{\mathbb{P}^3}(-4) \overset{M}{\to} \mathscr{O}_{\mathbb{P}^3}(-3)^4\overset{N}{\to} \mathscr{O}_{\mathbb{P}^3}(-2)^7 \overset{S}{\to} \mathscr{O}_{\mathbb{P}^3}^4(-1)\right]\cong \mathscr{O}_Q,\end{align*} $$
$$ \begin{align*}\left[\mathscr{O}_{\mathbb{P}^3}(-4) \overset{M}{\to} \mathscr{O}_{\mathbb{P}^3}(-3)^4\overset{N}{\to} \mathscr{O}_{\mathbb{P}^3}(-2)^7 \overset{S}{\to} \mathscr{O}_{\mathbb{P}^3}^4(-1)\right]\cong \mathscr{O}_Q,\end{align*} $$
where
 $N=\begin {pmatrix} x_2&\!\!x_3&\!\!0&\!\!0\\-x_1&\!\!0&\!\!x_3&\!\!0\\x_0&\!\!0&\!\!0&\!\!x_3\\0&\!\!-x_1&\!\!-x_2&\!\!0\\0&\!\!x_0&\!\!0&\!\!-x_2\\0&\!\!0&\!\!x_0&\!\!x_1\\0&\!\!0&\!\!0&\!\!0\\ \end {pmatrix}$
,
$N=\begin {pmatrix} x_2&\!\!x_3&\!\!0&\!\!0\\-x_1&\!\!0&\!\!x_3&\!\!0\\x_0&\!\!0&\!\!0&\!\!x_3\\0&\!\!-x_1&\!\!-x_2&\!\!0\\0&\!\!x_0&\!\!0&\!\!-x_2\\0&\!\!0&\!\!x_0&\!\!x_1\\0&\!\!0&\!\!0&\!\!0\\ \end {pmatrix}$
,
 $S=\begin {pmatrix} -x_1&\!\!-x_2&\!\!0&\!\!-x_3&\!\!0&\!\!0&\!\!x_3\\x_0&\!\!0&\!\!-x_2&\!\!0&\!\!-x_3&\!\!0&\!\!-x_2\\0&\!\!x_0&\!\!x_1&\!\!0&\!\!0&\!\!-x_3&\!\!0\\0&\!\!0&\!\!0&\!\!x_0&\!\!x_1&\!\!x_2&\!\!0\\ \end {pmatrix}$
and
$S=\begin {pmatrix} -x_1&\!\!-x_2&\!\!0&\!\!-x_3&\!\!0&\!\!0&\!\!x_3\\x_0&\!\!0&\!\!-x_2&\!\!0&\!\!-x_3&\!\!0&\!\!-x_2\\0&\!\!x_0&\!\!x_1&\!\!0&\!\!0&\!\!-x_3&\!\!0\\0&\!\!0&\!\!0&\!\!x_0&\!\!x_1&\!\!x_2&\!\!0\\ \end {pmatrix}$
and
 $M=\begin {pmatrix} -x_3&x_2&-x_1&x_0\\ \end {pmatrix}^T. $
$M=\begin {pmatrix} -x_3&x_2&-x_1&x_0\\ \end {pmatrix}^T. $
The stability of
 $\mathscr {O}_Q$
follows from checking the slopes of all its sub-complexes. We reduce the complexity in the following way. The inclusion
$\mathscr {O}_Q$
follows from checking the slopes of all its sub-complexes. We reduce the complexity in the following way. The inclusion
 $\mathscr {O}_{\mathbb {P}^3} \hookrightarrow \mathscr {O}_{Q} $
exists in both
$\mathscr {O}_{\mathbb {P}^3} \hookrightarrow \mathscr {O}_{Q} $
exists in both
 $\mathscr {B}_t$
(
$\mathscr {B}_t$
(
 $t\in (-0.5774, 0.5774)$
) and
$t\in (-0.5774, 0.5774)$
) and
 $\mathscr {A}_1$
, in which the presentation of
$\mathscr {A}_1$
, in which the presentation of
 $\mathscr {O}_{\mathbb {P}^3}$
is its Koszul resolution (dim(
$\mathscr {O}_{\mathbb {P}^3}$
is its Koszul resolution (dim(
 $\mathscr {O}_{\mathbb {P}^3}$
)
$\mathscr {O}_{\mathbb {P}^3}$
)
 $=[1,4,6,4]$
).
$=[1,4,6,4]$
).From the stability of
 $\mathscr {O}_{\mathbb {P}^3}$
in
$\mathscr {O}_{\mathbb {P}^3}$
in
 $\mathscr {A}_1$
, we only need to check the sub-complexes of
$\mathscr {A}_1$
, we only need to check the sub-complexes of
 $\mathscr {O}_{Q}$
that are not sub-complexes of
$\mathscr {O}_{Q}$
that are not sub-complexes of
 $\mathscr {O}_{\mathbb {P}^3}$
. They are given as follows (in dimension vector):
$\mathscr {O}_{\mathbb {P}^3}$
. They are given as follows (in dimension vector):
 $[0143]$
,
$[0143]$
,
 $[0154]$
,
$[0154]$
,
 $[0164]$
,
$[0164]$
,
 $[0174]$
,
$[0174]$
,
 $[0264]$
,
$[0264]$
,
 $[0274]$
,
$[0274]$
,
 $[0374]$
.
$[0374]$
.A direct computation shows that none of those can destabilize
 $\mathscr {O}_Q$
at
$\mathscr {O}_Q$
at
 $(0.5,0)$
.
$(0.5,0)$
. $\bullet $
For
$\bullet $
For
 $\mathscr {I}_{C/Q}[1]$
, its dimension vector in
$\mathscr {I}_{C/Q}[1]$
, its dimension vector in
 $\mathscr {A}_1$
is
$\mathscr {A}_1$
is
 $[0,3,4,1]$
. It is easy to check that a destabilizing sub-object must have dimension vector
$[0,3,4,1]$
. It is easy to check that a destabilizing sub-object must have dimension vector
 $[0,a,b,0]$
, where
$[0,a,b,0]$
, where
 $a=0,\ldots ,3$
and
$a=0,\ldots ,3$
and
 $b=0,\ldots ,4$
. In other words, if we prove that the dimension of a sub-complex must have a
$b=0,\ldots ,4$
. In other words, if we prove that the dimension of a sub-complex must have a
 $"1"$
in the first position from the right, that is,
$"1"$
in the first position from the right, that is,
 $[0,a,b,1]$
, then
$[0,a,b,1]$
, then
 $\mathscr {I}_{C/Q}[1]$
would be stable.
$\mathscr {I}_{C/Q}[1]$
would be stable.It is sufficient to show that there is no sub-complex with dimension vector
 $[0,0,1,0]$
. Suppose
$[0,0,1,0]$
. Suppose
 $[0,0,1,0]=\mathscr {O}_{\mathbb {P}^3}(-2)[1]$
is a sub-complex, then there is a non-zero morphism
$[0,0,1,0]=\mathscr {O}_{\mathbb {P}^3}(-2)[1]$
is a sub-complex, then there is a non-zero morphism
 $\mathscr {O}_{\mathbb {P}^3}(-2)[1] \to \mathscr {I}_{C/Q}[1]$
. But we have a contradiction that
$\mathscr {O}_{\mathbb {P}^3}(-2)[1] \to \mathscr {I}_{C/Q}[1]$
. But we have a contradiction that  $$ \begin{align*}Hom(\mathscr{O}_{\mathbb{P}^3}(-2)[1], \mathscr{I}_{C/Q}[1]) = Hom(\mathscr{O}_{\mathbb{P}^3}(-2), \mathscr{I}_{C/Q}) = H^0(\mathbb{P}^3, \mathscr{I}_{C/Q}(2))=0.\end{align*} $$
$$ \begin{align*}Hom(\mathscr{O}_{\mathbb{P}^3}(-2)[1], \mathscr{I}_{C/Q}[1]) = Hom(\mathscr{O}_{\mathbb{P}^3}(-2), \mathscr{I}_{C/Q}) = H^0(\mathbb{P}^3, \mathscr{I}_{C/Q}(2))=0.\end{align*} $$
This proves that
 $\mathscr {I}_{C/Q}[1]$
is stable in
$\mathscr {I}_{C/Q}[1]$
is stable in
 $\mathscr {A}_1$
.
$\mathscr {A}_1$
. -
(b)
 $\mathscr {O}_{Q}$
and
$\mathscr {O}_{Q}$
and
 $\mathscr {I}_{C/Q}[1]$
are stable along the blue numerical wall between P and T (arc
$\mathscr {I}_{C/Q}[1]$
are stable along the blue numerical wall between P and T (arc
 $\overset {\frown }{PT}$
) in the quiver region.
$\overset {\frown }{PT}$
) in the quiver region.In the quiver region
 $\mathscr {Q}_1$
, the stability condition
$\mathscr {Q}_1$
, the stability condition
 $\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+ i \cdot \chi ^{\prime }_t)$
has essentially the same (up to a shift by
$\sigma _{t,u}=(\mathscr {B}_t, Z_{t,u}=-\chi _t+\frac {u^2}{2}\chi ^{\prime \prime }_t+ i \cdot \chi ^{\prime }_t)$
has essentially the same (up to a shift by
 $[1]$
) slicing with the stability condition
$[1]$
) slicing with the stability condition
 $\sigma ^{Euler}_{t,u} := (\mathscr {A}_t, Z^{Euler}_{t,u}=\chi ^{\prime }_t+i \cdot (\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t))$
. Let
$\sigma ^{Euler}_{t,u} := (\mathscr {A}_t, Z^{Euler}_{t,u}=\chi ^{\prime }_t+i \cdot (\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t))$
. Let
 $\lambda ^{Euler}_{t,u}:=-\frac {\chi ^{\prime }_t}{\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t}$
be the corresponding slope function. It is straightforward to check that the proof in step (a) holds if we replace
$\lambda ^{Euler}_{t,u}:=-\frac {\chi ^{\prime }_t}{\chi _t-\frac {u^2}{2}\chi ^{\prime \prime }_t}$
be the corresponding slope function. It is straightforward to check that the proof in step (a) holds if we replace
 $\lambda ^{Euler}_t$
by
$\lambda ^{Euler}_t$
by
 $\lambda ^{Euler}_{t,u}$
in
$\lambda ^{Euler}_{t,u}$
in
 $\mathscr {Q}_1$
, and this proves the claim.
$\mathscr {Q}_1$
, and this proves the claim.
Remark 8.2. We expect that
![]() $0\to \mathscr {O}_{\mathbb {P}^3}\to \mathscr {O}_{Q} \to \mathscr {O}_{\mathbb {P}^3}(-2)[1]\to 0$
and
$0\to \mathscr {O}_{\mathbb {P}^3}\to \mathscr {O}_{Q} \to \mathscr {O}_{\mathbb {P}^3}(-2)[1]\to 0$
and
![]() $0\to \mathscr {O}_{\mathbb {P}^3}(-2)[1] \to \mathscr {I}_C[1] \to \mathscr {I}_{C|Q}[1] \to 0$
are the unique wall for
$0\to \mathscr {O}_{\mathbb {P}^3}(-2)[1] \to \mathscr {I}_C[1] \to \mathscr {I}_{C|Q}[1] \to 0$
are the unique wall for
![]() $\mathscr {O}_Q$
and
$\mathscr {O}_Q$
and
![]() $\mathscr {I}_{C|Q}$
in the
$\mathscr {I}_{C|Q}$
in the
![]() $(t,u)$
plane, and the outermost parts of
$(t,u)$
plane, and the outermost parts of
![]() $W_1$
and
$W_1$
and
![]() $W_2$
build up the actual wall of
$W_2$
build up the actual wall of
![]() $\mathscr {O}_{C}$
.
$\mathscr {O}_{C}$
.
Acknowledgment
I would like to express my gratitude to my advisor Professor Dr. Aaron Bertram for his support, guidance, and patience during my time as his student at the University of Utah. I would like to thank Professor Emanuele Macrì for his kind suggestions, and my friends Huachen Chen and Ziwen Zhu for their helpful conversations. I am grateful to the Department of Mathematics at the University of Utah for their help and support. I would also like to thank the referees for carefully reading the article.
Appendices
Appendix A. A formula for checking stability
In this appendix, we show a formula to check the stability of an object in the category
![]() $\mathscr {A}_t$
. Here, we may set
$\mathscr {A}_t$
. Here, we may set
![]() $t=1$
to reduce the complexity. The case for a general
$t=1$
to reduce the complexity. The case for a general
![]() $t\in \mathbb {R}$
is analogous.
$t\in \mathbb {R}$
is analogous.
Recall that the category
![]() $\mathscr {A}_1$
consists of complexes of the form
$\mathscr {A}_1$
consists of complexes of the form
For a complex
![]() $E\cong [\mathscr {O}_{\mathbb {P}^3}^{a_{-3}}(-4)\to \mathscr {O}_{\mathbb {P}^3}^{a_{-2}}(-3)\to \mathscr {O}_{\mathbb {P}^3}^{a_{-1}}(-2)\to \mathscr {O}_{\mathbb {P}^3}^{a_{0}}(-1)] $
, we call
$E\cong [\mathscr {O}_{\mathbb {P}^3}^{a_{-3}}(-4)\to \mathscr {O}_{\mathbb {P}^3}^{a_{-2}}(-3)\to \mathscr {O}_{\mathbb {P}^3}^{a_{-1}}(-2)\to \mathscr {O}_{\mathbb {P}^3}^{a_{0}}(-1)] $
, we call
![]() $(a_{-3}, a_{-2}, a_{-1}, a_{0})$
the dimension vector of E, denoted by
$(a_{-3}, a_{-2}, a_{-1}, a_{0})$
the dimension vector of E, denoted by
![]() $\underline {dim}(E)$
.
$\underline {dim}(E)$
.
By definition,
![]() $E\in \mathscr {A}_1$
is Euler semistable if and only if for any sub-object
$E\in \mathscr {A}_1$
is Euler semistable if and only if for any sub-object
![]() $F\hookrightarrow E$
in
$F\hookrightarrow E$
in
![]() $\mathscr {A}_1$
, we have
$\mathscr {A}_1$
, we have
![]() $-\chi _t'(F)/\chi _t(F)\leq -\chi _t'(E)/\chi _t(E)$
. This is equivalent to
$-\chi _t'(F)/\chi _t(F)\leq -\chi _t'(E)/\chi _t(E)$
. This is equivalent to
![]() $\chi ^{\prime }_t(F)\chi _t(E)-\chi ^{\prime }_t(E)\chi _t(F)\geq 0$
. Since
$\chi ^{\prime }_t(F)\chi _t(E)-\chi ^{\prime }_t(E)\chi _t(F)\geq 0$
. Since
![]() $\chi _t(E)=ch_3^{-t-2}(E)-1/6ch_1^{-t-2}(E)$
and
$\chi _t(E)=ch_3^{-t-2}(E)-1/6ch_1^{-t-2}(E)$
and
![]() $\chi ^{\prime }_t(E)=ch_2^{-t-2}(E)-1/6ch_0^{-t-2}(E)$
, the inequality is reduced to the following inequality of matrices:
$\chi ^{\prime }_t(E)=ch_2^{-t-2}(E)-1/6ch_0^{-t-2}(E)$
, the inequality is reduced to the following inequality of matrices:
 $$\begin{align*}\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\frac{1}{6}\chi^{\prime}_t(E)&\chi_t(E)&\chi^{\prime}_t(E) \end{pmatrix} \begin{pmatrix} ch^{-t-2}_0(F)\\ch^{-t-2}_1(F)\\ch^{-t-2}_2(F)\\ch^{-t-2}_3(F)\\ \end{pmatrix} \geq 0. \end{align*}$$
$$\begin{align*}\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\frac{1}{6}\chi^{\prime}_t(E)&\chi_t(E)&\chi^{\prime}_t(E) \end{pmatrix} \begin{pmatrix} ch^{-t-2}_0(F)\\ch^{-t-2}_1(F)\\ch^{-t-2}_2(F)\\ch^{-t-2}_3(F)\\ \end{pmatrix} \geq 0. \end{align*}$$
Moreover, by definition,
![]() $ch^{-t-2}(E)=ch(E)\cdot e^{(t+2)H}$
, so we have that
$ch^{-t-2}(E)=ch(E)\cdot e^{(t+2)H}$
, so we have that
 $$\begin{align*}\begin{pmatrix} ch^{-t-2}_0(F)\\ch^{-t-2}_1(F)\\ch^{-t-2}_2(F)\\ch^{-t-2}_3(F)\\ \end{pmatrix} = \begin{pmatrix} 1&0&0&0\\1&1&0&0\\1/2&1&1&0\\1/6&1/2&1&1\\ \end{pmatrix}^{t+3} \begin{pmatrix} ch^{1}_0(F)\\ch^{1}_1(F)\\ch^{1}_2(F)\\ch^{1}_3(F)\\ \end{pmatrix} = \begin{pmatrix} 1&0&0&0\\t+3&1&0&0\\\frac{(t+3)^2}{2}&t+3&1&0\\\frac{(t+3)^3}{6}&\frac{(t+3)^2}{2}&t+3&1\\ \end{pmatrix} \begin{pmatrix} ch^{1}_0(F)\\ch^{1}_1(F)\\ch^{1}_2(F)\\ch^{1}_3(F)\\ \end{pmatrix}\!. \end{align*}$$
$$\begin{align*}\begin{pmatrix} ch^{-t-2}_0(F)\\ch^{-t-2}_1(F)\\ch^{-t-2}_2(F)\\ch^{-t-2}_3(F)\\ \end{pmatrix} = \begin{pmatrix} 1&0&0&0\\1&1&0&0\\1/2&1&1&0\\1/6&1/2&1&1\\ \end{pmatrix}^{t+3} \begin{pmatrix} ch^{1}_0(F)\\ch^{1}_1(F)\\ch^{1}_2(F)\\ch^{1}_3(F)\\ \end{pmatrix} = \begin{pmatrix} 1&0&0&0\\t+3&1&0&0\\\frac{(t+3)^2}{2}&t+3&1&0\\\frac{(t+3)^3}{6}&\frac{(t+3)^2}{2}&t+3&1\\ \end{pmatrix} \begin{pmatrix} ch^{1}_0(F)\\ch^{1}_1(F)\\ch^{1}_2(F)\\ch^{1}_3(F)\\ \end{pmatrix}\!. \end{align*}$$
Then, for an object
![]() $F\in \mathscr {A}_1$
with dimension vector
$F\in \mathscr {A}_1$
with dimension vector
![]() $\underline {dim}(F)=(a_{-3},a_{-2},a_{-1},a_{0})$
(in
$\underline {dim}(F)=(a_{-3},a_{-2},a_{-1},a_{0})$
(in
![]() $\mathscr {A}_1$
), its (twisted) Chern characters are given by the following equality:
$\mathscr {A}_1$
), its (twisted) Chern characters are given by the following equality:
 $$\begin{align*}\begin{pmatrix} 1&-1&1&-1\\0&1&-2&3\\0&-1/2&2&-9/2\\0&1/6&-4/3&9/2\\ \end{pmatrix} \begin{pmatrix} a_0\\a_{-1}\\a_{-2}\\a_{-3}\\ \end{pmatrix} = \begin{pmatrix} ch^1_0(F)\\ch^1_1(F)\\ch^1_2(F)\\ch^1_3(F)\\ \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} 1&-1&1&-1\\0&1&-2&3\\0&-1/2&2&-9/2\\0&1/6&-4/3&9/2\\ \end{pmatrix} \begin{pmatrix} a_0\\a_{-1}\\a_{-2}\\a_{-3}\\ \end{pmatrix} = \begin{pmatrix} ch^1_0(F)\\ch^1_1(F)\\ch^1_2(F)\\ch^1_3(F)\\ \end{pmatrix}. \end{align*}$$
At this stage, the first inequality becomes
 $$\begin{align*}\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\frac{1}{6}\chi^{\prime}_t(E)&\chi_t(E)&\chi^{\prime}_t(E) \end{pmatrix} \begin{pmatrix} 1&0&0&0\\t+3&1&0&0\\\frac{(t+3)^2}{2}&t+3&1&0\\\frac{(t+3)^3}{6}&\frac{(t+3)^2}{2}&t+3&1\\ \end{pmatrix} \begin{pmatrix} 1&-1&1&-1\\0&1&-2&3\\0&-1/2&2&-9/2\\0&1/6&-4/3&9/2\\ \end{pmatrix} \begin{pmatrix} a_0\\a_{-1}\\a_{-2}\\a_{-3}\\ \end{pmatrix} \geq 0, \end{align*}$$
$$\begin{align*}\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\frac{1}{6}\chi^{\prime}_t(E)&\chi_t(E)&\chi^{\prime}_t(E) \end{pmatrix} \begin{pmatrix} 1&0&0&0\\t+3&1&0&0\\\frac{(t+3)^2}{2}&t+3&1&0\\\frac{(t+3)^3}{6}&\frac{(t+3)^2}{2}&t+3&1\\ \end{pmatrix} \begin{pmatrix} 1&-1&1&-1\\0&1&-2&3\\0&-1/2&2&-9/2\\0&1/6&-4/3&9/2\\ \end{pmatrix} \begin{pmatrix} a_0\\a_{-1}\\a_{-2}\\a_{-3}\\ \end{pmatrix} \geq 0, \end{align*}$$
which is
 $$\begin{align*}\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\frac{1}{6}\chi^{\prime}_t(E)&\chi_t(E)&\chi^{\prime}_t(E) \end{pmatrix} \begin{pmatrix} 1&-1&1&-1\\t+3&-t-2&t+1&-t\\\frac{(t+3)^2}{2}&\frac{-t^2-4t-4}{2}&\frac{t^2+2t+1}{2}&-\frac{t^2}{2}\\\frac{(t+3)^3}{6}&\frac{-t^3-6t^2-12t-8}{6}&\frac{t^3+3t^2+3t+1}{6}&-\frac{t^3}{6}\\ \end{pmatrix} \begin{pmatrix} a_0\\a_{-1}\\a_{-2}\\a_{-3}\\ \end{pmatrix} \geq 0. \end{align*}$$
$$\begin{align*}\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\frac{1}{6}\chi^{\prime}_t(E)&\chi_t(E)&\chi^{\prime}_t(E) \end{pmatrix} \begin{pmatrix} 1&-1&1&-1\\t+3&-t-2&t+1&-t\\\frac{(t+3)^2}{2}&\frac{-t^2-4t-4}{2}&\frac{t^2+2t+1}{2}&-\frac{t^2}{2}\\\frac{(t+3)^3}{6}&\frac{-t^3-6t^2-12t-8}{6}&\frac{t^3+3t^2+3t+1}{6}&-\frac{t^3}{6}\\ \end{pmatrix} \begin{pmatrix} a_0\\a_{-1}\\a_{-2}\\a_{-3}\\ \end{pmatrix} \geq 0. \end{align*}$$
Define a
![]() $1\times 4$
matrix
$1\times 4$
matrix
![]() $\theta _t(E):=(\theta _{t,0}(E), \theta _{t,1}(E), \theta _{t,2}(E), \theta _{t,3}(E))$
as follows:
$\theta _t(E):=(\theta _{t,0}(E), \theta _{t,1}(E), \theta _{t,2}(E), \theta _{t,3}(E))$
as follows:
 $$\begin{align*}\theta_t(E) :=\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\!\frac{1}{6}\chi^{\prime}_t(E)&\!\chi_t(E)&\!\chi^{\prime}_t(E) \end{pmatrix} \!\begin{pmatrix} 1&-1&1&-1\\t+3&-t-2&t+1&-t\\\frac{(t+3)^2}{2}&\frac{-t^2-4t-4}{2}&\frac{t^2+2t+1}{2}&-\frac{t^2}{2}\\\frac{(t+3)^3}{6}&\frac{-t^3-6t^2-12t-8}{6}&\frac{t^3+3t^2+3t+1}{6}&-\frac{t^3}{6}\\ \end{pmatrix}, \end{align*}$$
$$\begin{align*}\theta_t(E) :=\begin{pmatrix} -\frac{1}{6}\chi_t(E)&\!\frac{1}{6}\chi^{\prime}_t(E)&\!\chi_t(E)&\!\chi^{\prime}_t(E) \end{pmatrix} \!\begin{pmatrix} 1&-1&1&-1\\t+3&-t-2&t+1&-t\\\frac{(t+3)^2}{2}&\frac{-t^2-4t-4}{2}&\frac{t^2+2t+1}{2}&-\frac{t^2}{2}\\\frac{(t+3)^3}{6}&\frac{-t^3-6t^2-12t-8}{6}&\frac{t^3+3t^2+3t+1}{6}&-\frac{t^3}{6}\\ \end{pmatrix}, \end{align*}$$
then an object
![]() $E\in \mathscr {A}_1$
is Euler semistable if and only if for any sub-object
$E\in \mathscr {A}_1$
is Euler semistable if and only if for any sub-object
![]() $F\hookrightarrow E \in \mathscr {A}_1$
with
$F\hookrightarrow E \in \mathscr {A}_1$
with
![]() $\underline {dim}(F)=(a_{-3},a_{-2},a_{-1},a_{0})$
, we have
$\underline {dim}(F)=(a_{-3},a_{-2},a_{-1},a_{0})$
, we have
As an example, when
![]() $E\cong \mathscr {O}_{\mathbb {P}^3}$
, a direct computation shows that
$E\cong \mathscr {O}_{\mathbb {P}^3}$
, a direct computation shows that
 $$\begin{align*}\begin{cases} \theta_{t,0}(\mathscr{O}_{\mathbb{P}^3})=\frac{t^5}{6}+\frac{25t^4}{12}+\frac{185t^3}{18}+\frac{299t^2}{12}+\frac{59t}{2}+\frac{27}{2}\\ \theta_{t,1}(\mathscr{O}_{\mathbb{P}^3})=-\frac{t^5}{6}-\frac{5t^4}{3}-\frac{119t^3}{18}-13t^2-\frac{38t}{3}-\frac{44}{9}\\ \theta_{t,2}(\mathscr{O}_{\mathbb{P}^3})=\frac{t^5}{6}+\frac{5t^4}{4}+\frac{65t^3}{18}+\frac{61t^2}{12}+\frac{7t}{2}+\frac{17}{18}\\ \theta_{t,3}(\mathscr{O}_{\mathbb{P}^3})=-\frac{t^5}{8}-\frac{7t^4}{12}-\frac{59t^3}{72}-\frac{5t^2}{12}+\frac{1}{6}.\\ \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} \theta_{t,0}(\mathscr{O}_{\mathbb{P}^3})=\frac{t^5}{6}+\frac{25t^4}{12}+\frac{185t^3}{18}+\frac{299t^2}{12}+\frac{59t}{2}+\frac{27}{2}\\ \theta_{t,1}(\mathscr{O}_{\mathbb{P}^3})=-\frac{t^5}{6}-\frac{5t^4}{3}-\frac{119t^3}{18}-13t^2-\frac{38t}{3}-\frac{44}{9}\\ \theta_{t,2}(\mathscr{O}_{\mathbb{P}^3})=\frac{t^5}{6}+\frac{5t^4}{4}+\frac{65t^3}{18}+\frac{61t^2}{12}+\frac{7t}{2}+\frac{17}{18}\\ \theta_{t,3}(\mathscr{O}_{\mathbb{P}^3})=-\frac{t^5}{8}-\frac{7t^4}{12}-\frac{59t^3}{72}-\frac{5t^2}{12}+\frac{1}{6}.\\ \end{cases} \end{align*}$$
Table 1 provides all the quotient objects of
![]() $\mathscr {O}_{\mathbb {P}^3}$
, hence, it provides the dimension vectors
$\mathscr {O}_{\mathbb {P}^3}$
, hence, it provides the dimension vectors
![]() $\underline {dim}(F)=(a_{-3},a_{-2},a_{-1},a_{0})$
of every sub-object
$\underline {dim}(F)=(a_{-3},a_{-2},a_{-1},a_{0})$
of every sub-object
![]() $F\hookrightarrow \mathscr {O}_{\mathbb {P}^3} \in \mathscr {A}_1$
as well. Stability of
$F\hookrightarrow \mathscr {O}_{\mathbb {P}^3} \in \mathscr {A}_1$
as well. Stability of
![]() $\mathscr {O}_{\mathbb {P}^3}$
follows from checking that
$\mathscr {O}_{\mathbb {P}^3}$
follows from checking that
![]() $\theta _t(\mathscr {O}_{\mathbb {P}^3})\cdot (a_{-3},a_{-2},a_{-1},a_{0})\geq 0$
for all
$\theta _t(\mathscr {O}_{\mathbb {P}^3})\cdot (a_{-3},a_{-2},a_{-1},a_{0})\geq 0$
for all
![]() $\underline {dim}(F),$
where
$\underline {dim}(F),$
where
![]() $F\hookrightarrow \mathscr {O}_{\mathbb {P}^3}$
and all
$F\hookrightarrow \mathscr {O}_{\mathbb {P}^3}$
and all
![]() $t\in (0,1]$
.
$t\in (0,1]$
.
Appendix B. Presentation and sub-complexes of
 $\mathscr {I}_{P/\Lambda }(1)$
$\mathscr {I}_{P/\Lambda }(1)$
The sequence below is the presentation of
![]() $\mathscr {I}_{P/\Lambda }(1)$
in
$\mathscr {I}_{P/\Lambda }(1)$
in
![]() $\mathscr {A}_1$
.
$\mathscr {A}_1$
.
The matrices
![]() $M,N,S$
from the sequence and all the sub-complexes of
$M,N,S$
from the sequence and all the sub-complexes of
![]() $\mathscr {I}_{P/\Lambda }(1)$
are given as follows.
$\mathscr {I}_{P/\Lambda }(1)$
are given as follows.
Matrices
 $N= \begin {pmatrix} z&\!\!0&\!\!w&\!\!0&\!\!0&\!\!0&\!\!0&\!\!0\\-y&\!\!z&\!\!0&\!\!w&\!\!0&\!\!0&\!\!0&\!\!0\\x&\!\!0&\!\!0&\!\!0&\!\!0&\!\!w&\!\!0&\!\!0\\0&\!\!-y&\!\!0&\!\!0&\!\!0&\!\!0&\!\!w&\!\!0\\0&\!\!x&\!\!0&\!\!0&\!\!0&\!\!0&\!\!0&\!\!w\\0&\!\!0&\!\!-y&\!\!-z&\!\!z&\!\!0&\!\!0&\!\!0\\0&\!\!0&\!\!x&\!\!0&\!\!0&\!\!-z&\!\!0&\!\!0\\0&\!\!0&\!\!0&\!\!0&\!\!-y&\!\!0&\!\!-z&\!\!0\\0&\!\!0&\!\!0&\!\!x&\!\!0&\!\!y&\!\!0&\!\!-z\\0&\!\!0&\!\!0&\!\!0&\!\!x&\!\!0&\!\!0&\!\!-z\\0&\!\!0&\!\!0&\!\!0&\!\!0&\!\!0&\!\!x&\!\!y\\ \end {pmatrix} $
$N= \begin {pmatrix} z&\!\!0&\!\!w&\!\!0&\!\!0&\!\!0&\!\!0&\!\!0\\-y&\!\!z&\!\!0&\!\!w&\!\!0&\!\!0&\!\!0&\!\!0\\x&\!\!0&\!\!0&\!\!0&\!\!0&\!\!w&\!\!0&\!\!0\\0&\!\!-y&\!\!0&\!\!0&\!\!0&\!\!0&\!\!w&\!\!0\\0&\!\!x&\!\!0&\!\!0&\!\!0&\!\!0&\!\!0&\!\!w\\0&\!\!0&\!\!-y&\!\!-z&\!\!z&\!\!0&\!\!0&\!\!0\\0&\!\!0&\!\!x&\!\!0&\!\!0&\!\!-z&\!\!0&\!\!0\\0&\!\!0&\!\!0&\!\!0&\!\!-y&\!\!0&\!\!-z&\!\!0\\0&\!\!0&\!\!0&\!\!x&\!\!0&\!\!y&\!\!0&\!\!-z\\0&\!\!0&\!\!0&\!\!0&\!\!x&\!\!0&\!\!0&\!\!-z\\0&\!\!0&\!\!0&\!\!0&\!\!0&\!\!0&\!\!x&\!\!y\\ \end {pmatrix} $
 $ M= \begin {pmatrix} -w&\!\!0\\0&\!\!-w\\z&\!\!0\\-y&\!\!z\\0&\!\!z\\x&\!\!0\\0&\!\!-y\\0&\!\!x\\ \end {pmatrix} $
$ M= \begin {pmatrix} -w&\!\!0\\0&\!\!-w\\z&\!\!0\\-y&\!\!z\\0&\!\!z\\x&\!\!0\\0&\!\!-y\\0&\!\!x\\ \end {pmatrix} $
![]() $ T= \begin {pmatrix} y^2 &\!\! yz &\!\! z^2 &\!\! yw & \!zw\\ \end {pmatrix} $
$ T= \begin {pmatrix} y^2 &\!\! yz &\!\! z^2 &\!\! yw & \!zw\\ \end {pmatrix} $
 $S=\left ( \begin {array}{*{11}c} x&0&-z&0&0&0&-w&0&0&0&0\\ 0&x&y&0&-z&0&0&0&-w&0&0\\ 0&0&0&x&y&0&0&0&0&0&-w\\ 0&0&0&0&0&x&y&0&z&-z&0\\ 0&0&0&0&0&0&0&x&0&y&z\\ \end {array} \right )$
$S=\left ( \begin {array}{*{11}c} x&0&-z&0&0&0&-w&0&0&0&0\\ 0&x&y&0&-z&0&0&0&-w&0&0\\ 0&0&0&x&y&0&0&0&0&0&-w\\ 0&0&0&0&0&x&y&0&z&-z&0\\ 0&0&0&0&0&0&0&x&0&y&z\\ \end {array} \right )$
Sub-complexes of
![]() $\mathscr {I}_{P/\Lambda }(1)$
$\mathscr {I}_{P/\Lambda }(1)$
The dimension vectors of sub-complexes are given in the following table.