1. Introduction
Iceberg calving is one of the most prominent and least understood of the ice-sheet processes, accounting for between half and two-thirds of the mass lost from the Greenland and Antarctic ice sheets (Reference BiggsBiggs, 1999; Reference RignotRignot and others, 2008). Moreover, the highly nonlinear episodic retreat of Greenland outlet glaciers may be analogous to tidewater glacier behavior, where the sustained acceleration and retreat of Columbia Glacier, Alaska, may provide an apt analogy to the more recently observed retreat of Greenland outlet glaciers (Reference Howat, Joughin and ScambosHowat and others, 2007; Reference O’Neel, Marshall, McNamara and PfefferO’Neel and others, 2007). The connection between iceberg calving and dynamics over a wide variety of glaciological domains is further illustrated by the acceleration of tributary glaciers feeding the Larsen B ice shelf, Antarctica, following its demise in 2002 (e.g. Reference Scambos, Bohlander, Shuman and SkvarcaScambos and others, 2004). Despite the important role that iceberg calving plays in the mass balance and dynamics of ice sheets and glaciers, we do not yet have a satisfactory mathematical or physical model of the calving process that can be implemented in numerical ice-sheet models as a seaward boundary condition.
Since iceberg calving is ultimately tied to fracturing of the ice, one approach to developing a mesoscopic (i.e. fracture-level) model of calving is to attempt to simulate the initiation, propagation and interaction of some or all fractures within the ice using, for example, linear elastic fracture mechanics or damage mechanics (Reference WeertmanWeertman, 1977; Reference BahrBahr, 1995; Reference Rist, Sammonds, Oerter and DoakeRist and others, 2002; Reference Pralong and FunkPralong and Funk, 2005). However, due to the large uncertainty in how to treat the fracture process and the enormous computational complexity involved in its simulation, few studies have pursued this approach. Most studies have focused instead on parameterizing mass lost due to calving using calving laws, in which a calving rate, V c, defined as the length lost due to calving divided by a finite time interval, is given as a function of one or more internal or external variables (e.g. Reference Brown, Meier and PostBrown and others, 1982; Reference Van der VeenVan der Veen, 2002; Reference AlleyAlley and others, 2008). The calving law provides a working relationship describing the rate of advance or retreat of the calving front that can be easily incorporated into numerical models as a boundary condition. The computational efficiency, however, comes at a steep price: calving laws tend to be empirically derived with little connection to the underlying physics of fracture. Because of this disconnect, calving laws consist of a patchwork of empirically based, often competing, statistical relationships, each of which is derived for a specific glaciological environment (Reference Brown, Meier and PostBrown and others, 1982; Reference Van der VeenVan der Veen, 2002; Reference Benn, Warren and MottramBenn and others, 2007; Reference AlleyAlley and others, 2008). Without a physical basis, these statistical relationships may fail when extrapolated into the future. This risk is highlighted by the behavior of Columbia Glacier, which, contrary to the previously held belief that temperate ice cannot support buoyancy stresses, has recently developed a floating terminus (Reference Walter, O’Neel, McNamara, Pfeffer, Bassis and FrickerWalter and others, 2010).
Success in incorporating iceberg calving into continental-scale ice-sheet models hinges on formulating (and testing) macroscopic parameterizations of the calving process in which time-averaged mass loss from calving glaciers is related to internal dynamics, geometric variables and/or external mechanical forcings. Some efforts have been made to develop an all-encompassing unified calving law that is valid for all glaciological regimes, including floating and grounded termini and encompassing both tidewater and lacustrine glaciers, in the hope that a general calving law will be less likely to fail when glaciers are pushed into a different climate and/or glaciological regime (Reference Van der VeenVan der Veen, 2002; Reference Benn, Warren and MottramBenn and others, 2007; Reference Amundson and TrufferAmundson and Truffer, 2010). These efforts presuppose that a single calving law that describes calving from all (or at least the most relevant) glaciological regimes exists, an assumption of unknown validity.
If calving is related to fracture, calving laws also should not be entirely independent of the fracture physics. Instead, the calving law should emerge from the fracture physics as a large-spatial-scale/long-temporal-scale limit of the underlying fracture mechanics, akin to the emergence of thermodynamic behavior in the macroscopic limit of many interacting molecules. In this study, I introduce methods rooted in statistical physics not only to verify this conjecture, but also to show that macroscopic calving laws can be derived systematically from the mesoscopic (i.e. fracture-scale physics) as a mean field theory. Key to the methods developed here is that iceberg calving is treated as a stochastic process and that the probability that an iceberg will detach in a given interval of time can be described by a probability distribution. In this approach, it is necessary to specify the probability that an iceberg detaches along a given boundary as a process that only depends on the current state (i.e. a Markov process); fatigue failure is excluded from this approach unless an auxiliary latency variable is introduced. Given that iceberg calving is a sporadic process and the uncertainties in initial conditions and external forcings (winds, ocean swell, etc.) are large, this approach may be unavoidable.
Since I expect many glaciologists have not been exposed to statistical mechanics and may be unfamiliar with much of the terminology and techniques used here, I start by considering a toy model of glacier advance and retreat based on the simplest stochastic system, a discrete random walk. The purpose of this example is to introduce readers to (1) key definitions such as stochastic realizations and transition rates and (2) the concept of ensemble averaging as a replacement for time averaging and as a means of computing probability distribution functions (PDFs) of terminus position. Once the probability distribution of terminus position as a function of time is known, it is possible to compute quantities such as the expected value (and higher-order moments) of terminus position, calving rate and terminus velocity.
The random walk is also used to introduce the reader to the ‘master equation’, a first-order differential equation that directly describes the time evolution of the probability density distribution of terminus position (section 2.3). In section 3, a more general master equation is derived that permits both continuous glacier advance (based on terminus velocity) and calving events of arbitrary size. The theory is then applied, in section 4, to calving from flowline models of (1) freely floating termini, such as ice tongues and ice shelves (with simple geometries), and (2) grounded termini, such as tidewater and lacustrine glaciers. In the first case, the probability of detachment from any place along the ice tongue length is assumed to be approximately equal, giving rise to the sporadic detachment of large tabular icebergs. In the second case, the probability of detachment is assumed to be much greater within a region of approximately one ice thickness from the terminus, giving rise to more frequent smaller calving events and a calving rate that is, under limiting circumstances, proportional to the ice thickness. Finally, in section 5 a systematic expansion of the master equation is shown to provide a more general, universally valid macroscopic calving law. The calving law emerges naturally from the underlying stochastic dynamics as an expansion of the expected value of terminus position over spatial scales that are large compared with the typical iceberg size and for timescales that are long compared with the recurrence interval between calving events. This proves that calving laws, valid for any glaciological regime, can be systematically computed, provided a mesoscopic model of fracture is specified.
2. Introduction to the Stochastic Modeling Approach
2.1. Toy model of glacier calving: discrete asymmetric random walk
In this model, the ‘state’ of the glacier is determined solely by the position of the ice front/terminus, assumed to be confined to discrete, equally spaced nodes (Fig. 1). The notation used throughout is that Pi ,j means the probability of transition from the jth state to the ith state. The random walk proceeds according to the following rules: (1) If the glacier terminus is located at the ith node, the probability itwill ‘hop’ forward or transition to the (i + 1)th node during a (short) time interval, Δt, is Pi +1, i = αi Δt. (2) The probability the terminus will hop backwards (by calving) to the (i − 1)th node is Pi −1, i = βi Δt. (3) The probability that the terminus position neither transitions forward nor backward is Pi , i = 1 − (αi + βi )Δt, since probability mass distribution must sum to unity. The parameters αi and βi are called transition rates and have units of inverse time.

Fig. 1. Illustration showing the discrete geometry used in the asymmetric random walk. The length of the glacier is assumed to be discrete and confined to equally spaced nodes, x = 0, Δx, 2Δx,. . . , NΔx. Transitions are permitted only to adjacent nodes.
The probability of two hops in a single time-step will be of order ![]() , three hops
, three hops ![]() and so on. Taking Δt sufficiently small, these higher-order terms can be neglected. A realization of the model corresponds to a set of N steps, Δx, n = 1,…, N, where Δxn
takes on values of +Δx, 0, −Δx, chosen at random, based on the transition rates αi
and βi
. The αi
and βi
may be functions of position that depend on, for example, ice thickness, stress or strain rate or terminus velocity, but are assumed to be otherwise independent of time.
and so on. Taking Δt sufficiently small, these higher-order terms can be neglected. A realization of the model corresponds to a set of N steps, Δx, n = 1,…, N, where Δxn
takes on values of +Δx, 0, −Δx, chosen at random, based on the transition rates αi
and βi
. The αi
and βi
may be functions of position that depend on, for example, ice thickness, stress or strain rate or terminus velocity, but are assumed to be otherwise independent of time.
The simplest case corresponds to constant αi and βi . Figure 2 shows realizations of the random walk for three different choices of α and β. Units are chosen such that Δx = 1 and the time-step interval Δt = 0.1. In Figure 2a, the probability of advance is equal to the probability of retreat (α = β) and there is no preference for advance or retreat. Nonetheless, it is evident that even though the mean position of the terminus does not change, there are fluctuations in the magnitude of displacement that increase with time. In Figure 2b, α > β and, on average, the glacier advances, although there are again fluctuations that cause the occasional retreat. Similarly, Figure 2c shows that the glacier tends to retreat when α < β, also with occasional fluctuations superimposed on the mean trend.
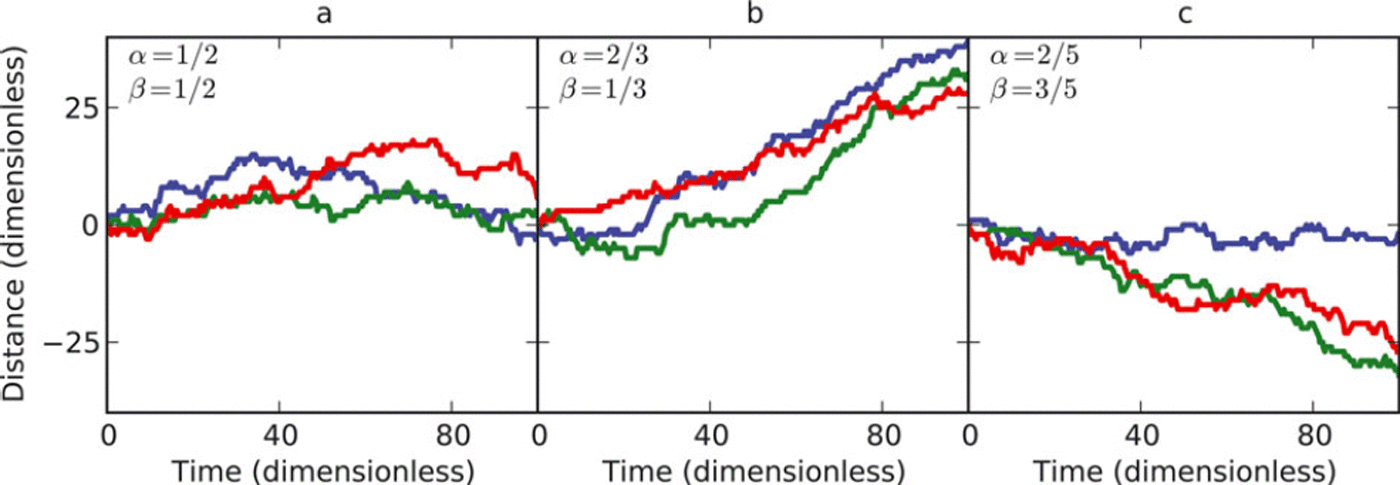
Fig. 2. Three realizations of the random walk for different transition rates. (a) Equal probability of advance and retreat for each time-step. Even though there is no preferred direction, the magnitudes of fluctuations away from x = 0 increase over time. (b) An example of glacier advance where α > β. (c) An example of glacier retreat where α < β.
For this simple example, the rate of terminus advance (negative implies retreat) is undefined during each hop and is zero between hops. This relationship does not particularly illuminate the longer-timescale trends in terminus advance. It is, however, emblematic of the observational problem of determining a calving rate or rate of terminus advance from a time series of individual calving events. Macroscopic variables, such as the rate of terminus advance and calving rate, are only meaningful when considering averages over time, lest the discrete nature of calving events manifests itself in the signal. Moreover, when observations are constrained to a small interval of time it is difficult to distinguish trends from fluctuations. For instance, Figure 2c shows that, although the overall trend is decreasing terminus position, fluctuations about this trend lead to periods of time with a net rate of advance.
2.2. Ensemble averages
It is often useful to calculate the time-averaged rate of terminus advance dL/dt:
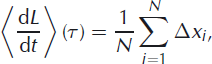
where τ is the averaging interval, N is the number of steps and angle brackets are used to denote averages. Defined this way, the average rate of terminus advance is implicitly a function of the averaging interval, τ; different averaging intervals will yield different rates of terminus advance. Although rarely explicitly stated, this definition is typically implied whenever the terms ‘rate of terminus advance’ or ‘calving rate’ are used. Because of the dependence on averaging interval, τ, Equation (1) is of limited utility, unless, for sufficiently large τ, the average value becomes insensitive to the precise value of τ.
Alternatively, instead of averaging over time, many realizations (such as those in Fig. 2) can be computed and the rate of terminus advance determined by the average of these realizations:
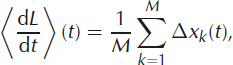
where Δxk are the individual realizations of terminus position (as a function of time) and M is the number of realizations. The system is said to be ergodic if time averaging over a suitably long time is equivalent to ensemble averaging over a large number of realizations. Although many systems are assumed to be ergodic (and this is the fundamental ansatz of statistical mechanics), there is no reason to suppose that glacier retreat/advance is ergodic. Nonetheless, the ensemble averages are often more convenient to perform and it is this expectation value that is used throughout the remainder of this paper, with the understanding that this ensemble-averaged expectation value is only equivalent to the time-averaged expectation value in the special circumstance that the system is ergodic (which it is for the random walk).
The advantage of the ensemble average is illustrated in Figure 3, which shows the probability distribution computed from a normalized histogram of 1000 realizations of the random walk at three different points in time for the same values of a and β as in Figure 2. In all three cases the probability distribution broadens over time, implying a larger probability that the glacier will be found a greater distance from the mean position. Figure 3b and c show that the centroid of the probability distribution drifts over time when a ≠ β with drift velocity determined by a − β. In all examples, fluctuations can constructively add up to drive the glacier terminus away from the expected position. Even when a = β and 〈dL/dt〉 = 0, the expected value of the total change in length of the glacier increases with increasing time, i.e. 〈L 2〉 > 0. This hints that it may be important to determine not only the peak of the distribution, but also its width.
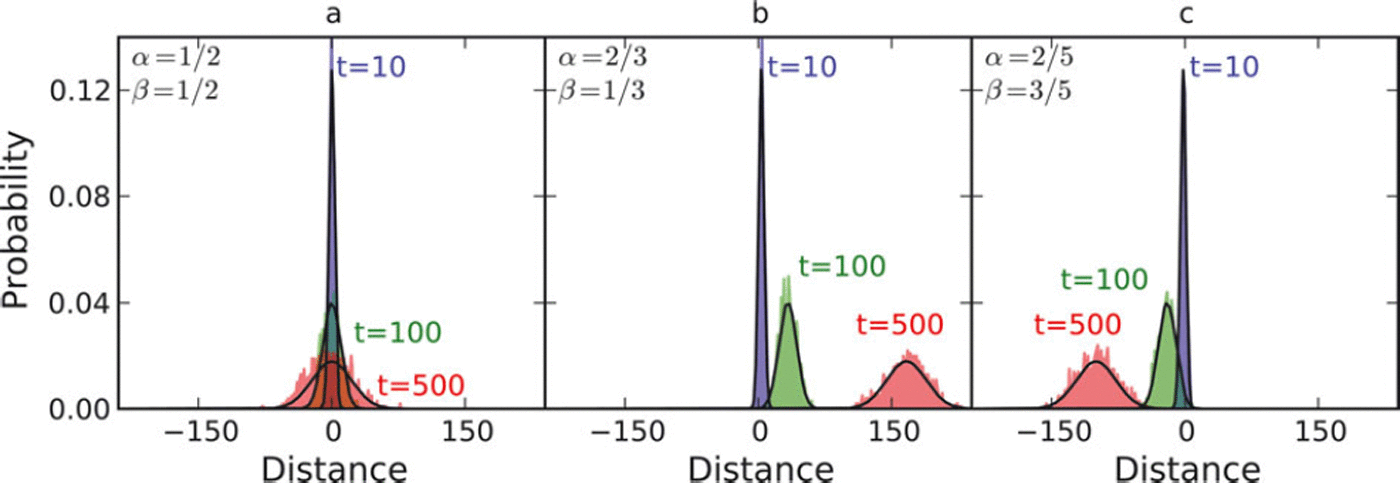
Fig. 3. Normalized probability distribution of terminus position at three points in time. The probability distribution is computed using two different methods. The first method is an ensemble average of 1000 realizations (shaded regions). The second method obtains the PDFs directly by solving the master equation (smooth black curves). The three panels correspond to the three different choices of transition probabilities used in Figure 2.
The advantage of the ensemble method is that individual trajectories can be tracked through time and compared with observations. However, the brute force method of computing the probability distribution by performing thousands of iterations is neither feasible nor desirable for large-scale ice-sheet models, where the computational cost of a single model run may be prohibitive. If individual trajectories are not needed, it is possible to formulate an equation – the so-called master equation – that describes the time evolution of probability density directly.
2.3. The master equation
The master equation (sometimes less prosaically referred to as the ![]() equation) is a differential equation describing the rate of change of probability, obtained in the limit Δt → 0 (e.g. Reference Van KampenVan Kampen, 1992). In the discrete case, it is usually written in the form:
equation) is a differential equation describing the rate of change of probability, obtained in the limit Δt → 0 (e.g. Reference Van KampenVan Kampen, 1992). In the discrete case, it is usually written in the form:
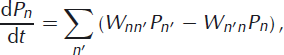
where Pn is the probability that the terminus is located at the nth node at time t and the elements Wnn ′ are transition rates from state n′ to state n (e.g. Reference Van KampenVan Kampen, 1992, p. 96–97). Written this way, it is clear that the first term on the right-hand side of the master equation is a source term, representing the increased probability that the nth state is occupied by transitions from other states into the nth state. The second term on the right-hand side is a loss term, representing the decrease in probability due to transitions out of the nth state into other states. Note that in the master equation formulation, it is not necessary to know Wnn since the change in probability distribution is unaffected by self-transitions as these are neither gains nor losses. Equation (3) represents a linear system of first-order differential equations for the mass probability distribution that the glacier occupies any of the n sites.
For the discrete asymmetric random walk, excluding self-transitions (which do not change the probability), the only nonzero transition rates are:
Substituting these transition rates into Equation (3) provides the master equation for the asymmetric random walk:
The solution of Equation (5) for all n provides the evolution of the probability of finding the terminus at any position as a function of time.
The solid black curve in Figure 3 shows the evolution of the probability distribution, computed by solving Equation (5) numerically using a forward Euler time-step with a delta function initial condition. The initially narrow probability distribution broadens over time and drifts with rate α − β, analogous to what was observed using the brute force method of section 2.2. This time, the probability distribution is a smooth Gaussian, lacking the spikiness of the ensemble method. So long as individual realizations of the process are not what is of interest, solving the master equation is much more accurate and efficient than averaging over realizations. However, even when the mean terminus position is zero (α = β), the PDF does not have a steady-state solution. Instead, it broadens over time, and uncertainty in the location of the terminus position increases until all prognostic information is lost. Crucially, without a steady-state probability distribution, there is no macroscopic calving law that can be extracted from this model. Although simplistic, this model highlights the fundamental difference between the stochastic approach advocated here and fully deterministic approaches. In the absence of a sharply peaked probability distribution, the mean of the distribution may be meaningless. To obtain a useful mean rate of terminus advance, it is also necessary to know something about the width of the distribution and how this changes over time.
The utility of the master equation goes beyond merely being an efficient means of computing the probability distribution. If only the expected value of the probability distribution is sought, it is possible to solve for this (and higher-order moments) directly instead of solving for the entire distribution. This provides the potential for further gains in efficiency and foreshadows the techniques used to obtain calving laws that will be developed later.
The expected value of terminus position can be computed from Equation (5) by multiplying by terminus position, n, and summing over all states:
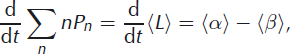
where 〈L〉 denotes the expected value of the terminus position and 〈α〉 and 〈β〉 denote the expected value of the transition rates. (In this case the expected values of αi and βi are trivial since both are constant.)
Equation (6) is valid for unit spacing between discrete nodes. If the nodes are instead spaced a distance Δx apart, the expected rate of change of terminus position is obtained by multiplying Equation (5) by nΔx and summing over all states to find
Equation (7) is a macroscopic equation describing the evolution of the terminus as a function of expected values of forward and backward transition rates and node spacing. Physically, the left-hand side of Equation (7) describes the expected rate of change of terminus position where, unlike previous calving laws, the expected value is an ensemble average instead of a time average. The term 〈αΔx〉 corresponds to the expected value of terminus velocity, u; the term 〈βΔx〉 corresponds to the magnitude of the expected calving rate, V c. With these definitions, Equation (7) can be rewritten in the more familiar form:
The so-called calving law for the random walk is thus
For the random walk, the calving rate has an obvious physical interpretation: it is the expected value of the product of iceberg size and iceberg detachment frequency. With this in mind, the expected value of terminus advance is zero when α ≠ β, as previously demonstrated. When α − β, the expected rate of terminus advance (or retreat) is α − β.
The random walk model can be made more physically relevant by, for example, choosing spatially variable αi and βi that correspond to functions of glacier geometry/dynamics. For instance, the αi must be related to the terminus velocity, u(x), while the probability of calving, βi , may be chosen to be suitable functions of terminus ice thickness, water depth, etc. However, the model will still suffer from the defect that all icebergs have the same size and, in the absence of calving events, the terminus position hops forward discretely rather than continuously advancing. In section 3, a more realistic continuous model is proposed, that permits calving events of arbitrary size while allowing continuous advection of the terminus position (by ice flow).
3. Stochastic Models Of Iceberg Calving
3.1. Continuous advection of the terminus
In the discrete model, during each time-step there are three options: the terminus position either remains fixed, or hops forward a distance Δx or hops back a distance Δx. A more realistic model may assume that while calving is a random process, the terminus still advances every time-step based on the terminus velocity (determined from an ice-sheet model). Replacing the previously random transition rate, α, with a deterministic forward transition rate, u/Δx, where u is the velocity at the terminus, the master equation in the absence of calving is
where Pn = P(xn ), Pn −1 = P(xn − Δx) and so on. In anticipation of taking the limit Δx → 0, the probabilities have been written explicitly as functions of the positions separated by a distance Δx. Writing them this way makes clear the connection with the upwind finite-difference version of the continuity equation.
Taking the limit Δx → 0, while keeping the product u(x) = α(xn )Δx constant, yields an advection equation for probability:
where the lower-case symbol p has been substituted for P to indicate that the discrete probability distribution is now a probability density distribution (probability per unit length). Equation (10) is a probability continuity statement and shows that probability advects forward over time with velocity u. If the initial condition is a very narrow delta-like function, the delta function advects forward over time and the deterministic relationship with ice-front advance in the absence of calving is recovered. Numerical diffusion, associated with discretization of Equation (10) will cause an initially narrow distribution to broaden (or diffuse) over time, in a manner that is analogous to the broadening due to assuming a forward transition rate. Because of this, in some applications it may be convenient to exploit the equivalence of the discretized continuity equation with the discrete stochastic process with transition rates determined by the terminus velocity.
3.2. Icebergs of arbitrary size
To include calving of events of arbitrary size, the master equation can be generalized from discrete to continuous states by replacing the sum in Equation (3) by an integral over all states:

where the notation W(x′|x) indicates the transition rate from state x to x′ (i.e. from terminus position x to x′). In the continuous limit, the transition rates, W(x|x′), have the dimension of inverse time per unit length.
Combining Equations (10) and (11), the master equation can be expressed as an integro-differential equation
Because calving always decreases the length of the glacier, transitions x′ → x are prohibited if x > x′, thus W(x|x′) = 0 for x > x′. Choosing a coordinate system where x measures the length of the glacier so that x ≥ 0, the lower limit of the integrals is zero and the master equation can be more intuitively written
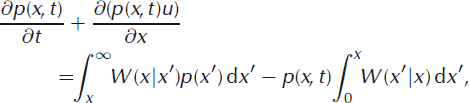
where the first term on the right-hand side represents the probability that a glacier longer than x calves back to x and the second term represents the probability that a glacier with initial length x calves back to x′, a length that is less than x.
It remains to specify the form for the calving transition rates, W(x′|x). Rather than attempting a complete specification of transition rates here, the flexibility of the theory is illustrated using two glaciologically relevant limiting cases to show the theory is able to reproduce (qualitatively at least) both the infrequent, sporadic detachment of large tabular bergs from ice tongues and ice shelves and the more frequent, smaller-sized calving events from tidewater glaciers. These two limiting cases are used in section 4.3 to illustrate how approximate calving laws can be deduced from the master equation, providing the motivation for the more general, systematic expansion of the master equation in section 5, from which universal calving laws are determined.
4. Examples
4.1. Example 1: calving from ice tongues and ice shelves
In this first example, it is assumed that calving from any where along the ice tongue length is permitted and is equally likely everywhere. At first sight this appears to be a severe and unrealistic assumption. However, for ice tongues and ice shelves that protrude beyond their embayments/pinning points it may be justified by noting that, away from the grounding line, ice thickness, strain rate, stress, etc. have small gradients and are nearly constant over length scales that are large compared to the ice thickness. If the transition rates are assumed to be functions of these large-scale internal variables, it is reasonable to suppose that transition rates are also nearly constant. This line of reasoning neglects the small additional bending stresses that occur near the icetongue/ice-shelf terminus that might favor the detachment of ice-thickness-sized bergs (Reference ReehReeh, 1968). However, since mass lost by calving from ice shelves and ice tongues is dominated by large tabular bergs, neglecting these stresses may be a reasonable first approximation. In principle, it is possible to include bending stresses along with structural features such as pre-existing rifts, suture zones that might hinder or favor detachment of icebergs from some places, by allowing for spatially variable transition rates.
The assumption of constant transition rates also corresponds to a modest generalization of a calving law proposed by Reference Benn, Warren and MottramBenn and others (2007). They argued that an iceberg will detach from a glacier anywhere the glaciological stress is sufficient to cause a fracture to either propagate all the way to the bed or, if the glacier terminates in a body of water, to sea or lake level. The latter condition was invoked under the assumption that a well-developed drainage network exists and this causes crevasses that penetrate to water level to immediately fill with water and hydraulically fracture to the bed. This condition is also assumed to be true irrespective of the type of glacier (e.g. freely floating, tidewater, confined or unconfined) and irrespective of whether the body of water is a lake or an ocean. Cold Antarctic ice shelves and ice tongues are unlikely to have a well-developed drainage system. However, one may argue that this condition may be approximately satisfied if basal crevasses intersect with surface crevasses.
In the absence of meltwater, the ratio of the depth to which a surface crevasse will propagate, d, to the ice thickness, H, can be calculated based on the depth when those forces opening a crevasse are exactly balanced by the hydrostatic weight of the ice closing the crevasse (Reference Benn, Warren and MottramBenn and others, 2007):
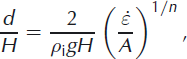
where ![]() is the depth-averaged longitudinal strain rate, ρ
i is the density of ice, g is the acceleration due to gravity, A is the rheological rate parameter and n is the flow-law exponent. A straightforward, heuristic generalization of the crevasse penetration depth criterion supposes that an iceberg detaches when the ratio of surface crevasse depth to ice thickness exceeds a predefined threshold that is ≤1. However, for a freely floating ice tongue, unencumbered by lateral drag or ice rises, the predicted ratio, d/H, in the long-wavelength shallow-shelf approximation is constant. This model then leads to the unsatisfyingly unstable prediction that ice tongues either advance to infinity or retreat to the grounding line, depending on the value chosen for the calving threshold.
is the depth-averaged longitudinal strain rate, ρ
i is the density of ice, g is the acceleration due to gravity, A is the rheological rate parameter and n is the flow-law exponent. A straightforward, heuristic generalization of the crevasse penetration depth criterion supposes that an iceberg detaches when the ratio of surface crevasse depth to ice thickness exceeds a predefined threshold that is ≤1. However, for a freely floating ice tongue, unencumbered by lateral drag or ice rises, the predicted ratio, d/H, in the long-wavelength shallow-shelf approximation is constant. This model then leads to the unsatisfyingly unstable prediction that ice tongues either advance to infinity or retreat to the grounding line, depending on the value chosen for the calving threshold.
In keeping with the spirit of the present work, one might instead assume that the transition rates are functions of the penetration ratio, i.e. λ = f(d/H) = constant. Conceptually, the transition rates would govern the probability that a surface crevasse intersects with a basal crevasse and this probability is controlled by the penetration ratio, d/H. Unlike in the purely deterministic viewpoint, random perturbations to the stress field caused by ocean waves, collisions with passing icebergs, large local variations in basal melt/refreeze rates, etc., may result in basal or surface crevasses that penetrate to a greater (or lesser) depth than one would otherwise expect.
Adopting the hypothesis that transition rates are (nearly) constant implies
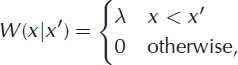
where λ is a constant transition rate. The master equation is then written
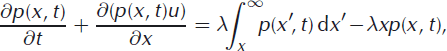
where x = 0 represents the grounding line, a point beyond which the tongue is (for illustrative purposes) prohibited from retreating. For large x, the right-hand side of Equation (15) is negative, implying very long ice tongues are more likely to calve back than to advance. In contrast, for small x, the second term on the right-hand side will be negligible and the right-hand side will be positive. This means short ice tongues will be more likely to advance than retreat. The probability of calving increases (decreases) with increasing (decreasing) ice tongue length. Because of this, a steady-state distribution of ice tongue lengths is possible.
To provide a more concrete visualization of the calving behavior of the ice tongue model, Figure 4a shows an example of a realization of this model, computed using an analytic solution for the ice tongue velocity (e.g. Reference Van der VeenVan der Veen, 1999, p.163, equation (6.6.8)) with ice thickness and ice flow velocity at the grounding line prescribed to be 1000 m and 250 m a−1, softness of the ice B = 108 Pa s1/3 and an initial condition of zero length. For this example, the terminus exhibits a sawtooth pattern of advance and sporadic retreat, reminiscent of the detachment of large, tabular bergs from ice tongues and ice shelves. Although calving events of all sizes are equally likely, large calving events remove more of the ice tongue and dominate the calving portion of the signal.
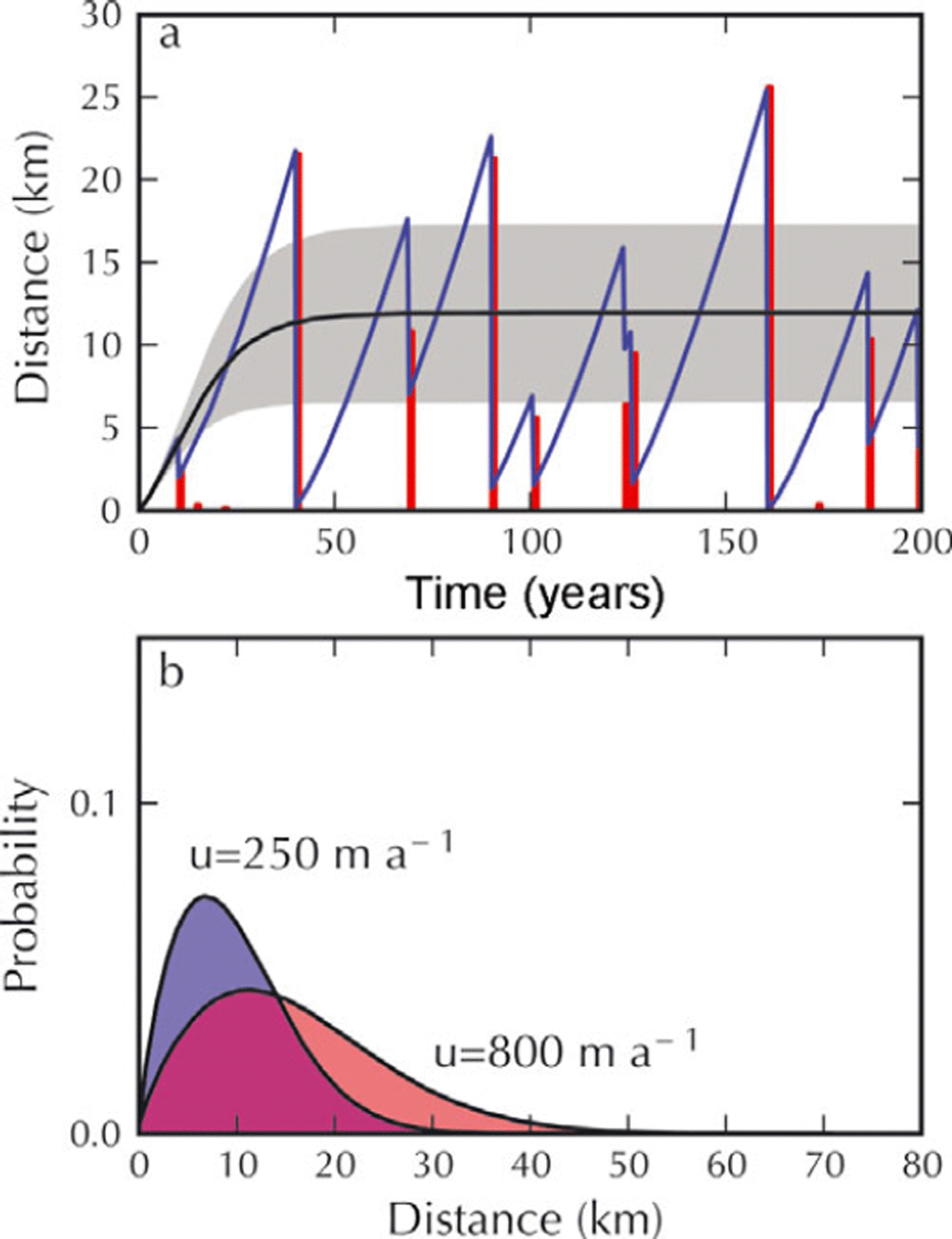
Fig. 4. (a) The blue line shows a realization of the ice-tongue calving model with terminus velocity computed using an analytic solution for terminus velocity (e.g. Reference Van der VeenVan der Veen, 1999, p.163, equation (6.6.8)). For this example, the thickness at the grounding line is 1000 m, the ice-flow velocity at the grounding line is 250 m a−1, the rate factor is B = 108 Pa s1/3 and the (constant) transition rate λ = 0.01 km−1 s−1. The red bars show the size of icebergs that detached. The solid black curve shows the terminus position computed using the macroscopic calving law (Equation (30) with corrections due to fluctuations omitted). The shaded gray area traces out the variance in terminus position, computed using Equation (44). (b) The steady-state probability density distribution, computed from the master equation using the same parameters as in (a) (shaded blue region) and for an increased ice-flow velocity at the grounding line of 800 m a−1 (shaded red region). Here, unlike in the random walk, the PDF shown corresponds to a steady-state solution of the master equation that is reached after a few decades.
The recurrence interval between calving events is determined by the magnitude of the transition rates. Larger transition rates lead to more frequent calving events and a shorter ice tongue. Conversely, a larger terminus velocity will result in faster terminus advance between calving events and hence a greater mean ice tongue length. However, since calving is equally likely from anywhere within the ice tongue, a longer ice tongue permits larger calving events. This will result in a longer-tailed probability distribution. Hence, longer ice tongues have a larger variance and skewness in the probability distribution than smaller tongues. This is illustrated in Figure 4b, which shows the probability distribution computed by solving Equation (15) for two different inflow velocities. In this example, in direct contrast with the random walk, a steady-state probability distribution is reached after a few decades. Furthermore, the shape of the probability density distribution is clearly non-Gaussian, with a long tail that increases with increasing terminus velocity. To reiterate, the prediction of sporadic calving of large tabular bergs emerges in this example solely because transition rates are nearly constant and is independent of any assumptions about the actual physics that governs the transition rates.
4.2. Example 2: calving from tidewater and lacustrine glaciers
In the previous example, stress, strain rate, ice thickness, etc., were all assumed to have relatively small gradients along the entire ice tongue length. In contrast, many calving glaciers (defined here to be any glacier with a grounded terminus, including tidewater and lacustrine) exhibit large variability in strain rate, stress and ice thickness in the near-terminus region, especially as the glacier terminus approaches flotation (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001). In keeping with the previous discussion, it may still be appropriate to assume that transition rates are a function of the penetration ratio, λ = f(d/H). However, it is now assumed that f(d/H) is strongly peaked in a near-terminus region of characteristic size Δx. In this case one might suppose that the characteristic size of this region ought to be approximately proportional to the ice thickness, H. This appears to be reasonable, in that icebergs that calve from calving glaciers tend to be ice-thickness and/or sub-ice-thickness sized rather than tabular.
Assuming the transition rates beyond a distance H are negligibly small, the master equation for near-terminus calving is:
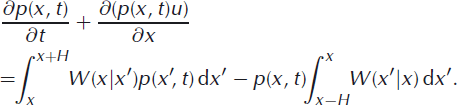
It is further assumed that the probability that an iceberg detaches at point x depends only locally on properties at x (and not the terminus position, x′) and hence the transition rates can be written more simply in the form W(x|x′) = λ(x), where λ(x) is a spatially variable transition rate. The integrals on the right-hand side of Equation (16) can be approximated using the midpoint rule
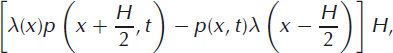
followed by a Taylor series expansion about x ± H/2,
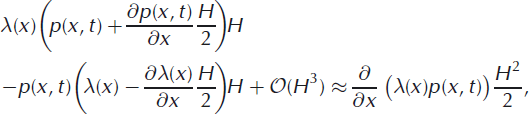
to transform the master equation from an integro-differential equation into a partial differential equation:
The iceberg size vanishes as H → 0, as does the calving rate. This shows that the calving rate is finite for finite ice thickness, but decreases (increases) as the ice thickness decreases (increases) and is analogous to the dependence of calving rate on node spacing, Δx, determined for the random walk (section 2.3).
Finally, the transition rate per unit ice thickness is approximately constant, so defining λ(x) = 2β(x)/H(x), where the factor of two has been introduced for convenience, and making use of the chain rule followed by the product rule, the master equation now becomes
Note that β(x) has units of inverse time, consistent with the discrete transition rates for the discrete random walk discussed previously.
Taking the ice thickness to be approximately constant in the near-terminus region (i.e. averaged over a one-icethickness spatial scale), the last term on the right-hand side of Equation (18) can be dropped and the master equation further approximated as
This last simplification corresponds to neglecting the variability in the characteristic size of icebergs (and hence calving rate) induced by gradients in the near-terminus ice thickness.
If the spatial derivatives are approximated using upwind differences and defining the discrete transition rates
the discretized version of Equation (19) has the same form a the asymmetric random walk with spatially varying transition probabilities:
where Pn = pn Δx. Unlike the random walk, where the terminus can advance, retreat or stay in the same position, here the terminus continually advances, by a distance uΔt each time-step (where u is the terminus velocity).
Figure 5a, shows one realization for this calving model, computed with constant terminus velocity (u = 1 in dimensionless units) and transition rates linearly increasing with distance, α = x/40. This choice is arbitrary, but if the transition rates increase with water depth (increased probability that a surface crevasse intersects with a basal crevasse or plumbing system), this example would correspond to a calving glacier advancing into deeper water. Inspection of Figure 5 shows that there is an initial period of slow terminus advance with superimposed small fluctuations until t ≈ 100, after which the terminus position fluctuates about a steady position. The probability distribution, determined by solving the master equation at three points in time with a delta function initial condition at x = 0, is shown in Figure 5b. The peak of the PDF advances and broadens over time until a steady-state mean and width are reached. Unlike the ice shelf/tongue, the distribution quickly evolves to a (nearly) Gaussian shape with little obvious asymmetry.
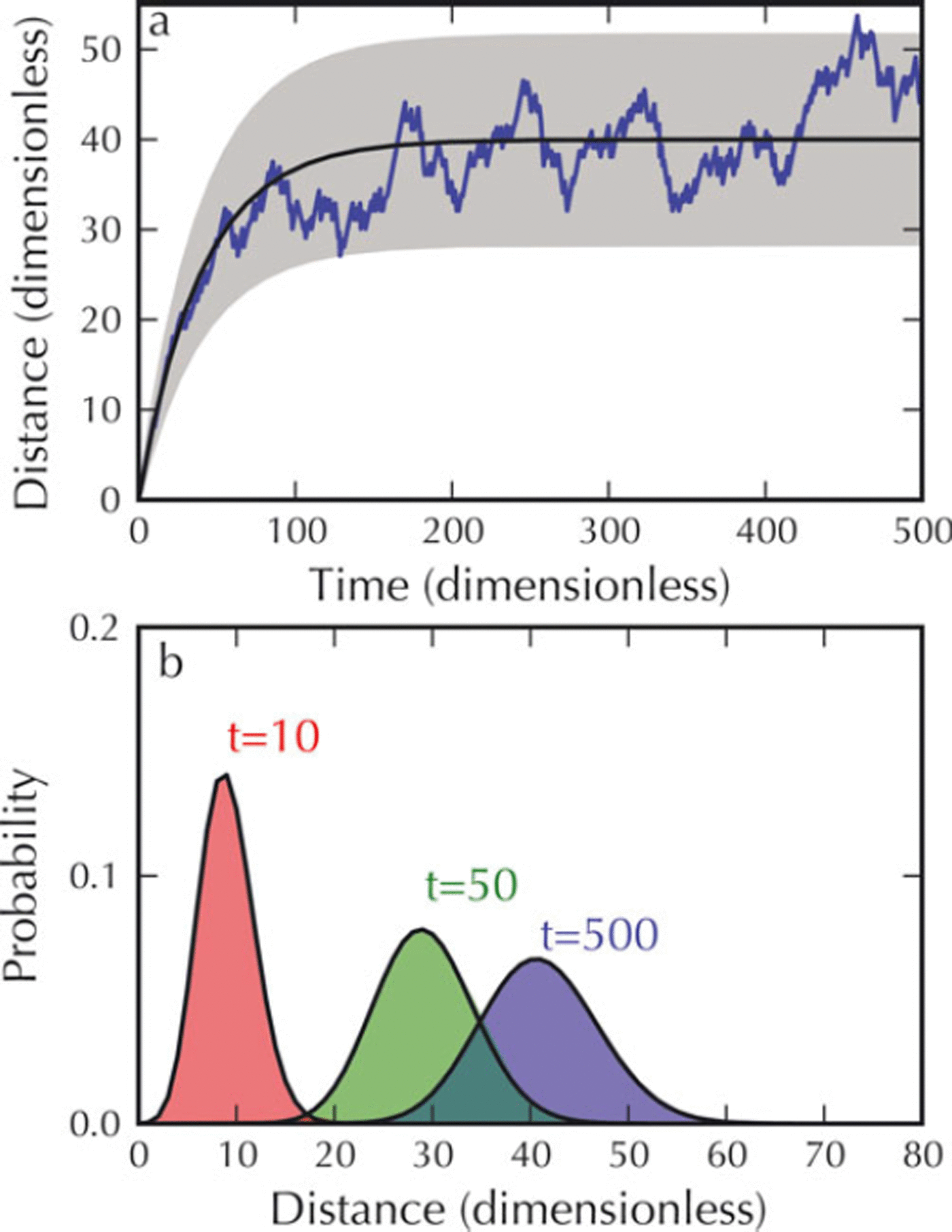
Fig. 5. (a) A single realization of the calving model with constant terminus velocity (u = 1 in dimensionless units) and transition rates linearly increasing with distance, β = x/40. The solid black curve shows the terminus position computed using the macroscopic law (Equation (22)). The shaded gray area traces out the variance in the terminus position, computed using Equation (46). (b) The probability distribution computed from the master equation at three points in time. The initial condition is a delta function centered at x = 0. As in (a), the peak of the PDF advances and broadens over time until a steady-state mean and width are reached. Unlike the ice-shelf/icetongue example, the distribution appears nearly Gaussian at all but the earliest stages of evolution.
4.3. Approximate calving laws
The previous examples showed how the probability distribution for terminus position could be computed directly from the master equation using different limiting assumptions about the form of the underlying transition rates. In this subsection, approximate macroscopic calving laws for both glaciological regimes previously considered are deduced by computing expected values of terminus position directly from the master equations determined for each of the regimes. Calving laws for the two limiting cases are considered separately below. However, the reader should keep in mind that, despite the more involved mathematical manipulations, the procedure used is identical to that used for the random walk discussed previously.
Calving laws for tidewater and lacustrine glaciers
Calving glaciers provide the simplest example, since the discrete master equation is identical to the master equation describing the asymmetric random walk (with spatially variable transition rates). Away from the boundary, substituting Equations (20) and (21) into Equation (7) the expected rate of terminus advance is
where the angle brackets once again denote expected values. As for the random walk model presented in section 2.3, the term 〈u〉 corresponds to the expected value of terminus velocity and 〈βH〉 corresponds to the expected value of calving rate, V c. The calving law consistent with the transition rates assumed is then:
Equation (23) is the macroscopic calving lawfor glaciers with transition rates sharply peaked in the near-terminus region.
Remarkably, the calving rate predicted by Equation (23) is proportional to ice thickness, as found by Brown and others (Reference Brown, Meier and Post1982). However, the ice-thickness dependence of the calving rate is a consequence of the manner in which transition rates were prescribed, and could disappear if β was also allowed to vary. Notice also that since in this example β, H and u are constant, the expected values of u and βH are constant and the expected value of terminus position increases (or decreases) linearly with time until α = β. The solid black curve in Figure 5a shows the expected terminus position, computed from Equation (22) and it is evident that the calving law deduced captures the large-scale trend in terminus position. Furthermore, as for the random walk, the actual terminus position at any point in time fluctuates about the expected value.
Calving laws for ice tongues and ice shelves
This example is slightly more complicated than the previous one, but hints at the difficulty in determining calving laws in the presence of large fluctuations (or large icebergs). The same procedure used to deduce expected values for the random walk (and tidewater glaciers) can be used to find the expected rate of change of terminus position. Multiplying the master equation by terminus position, x, and integrating over all states yields
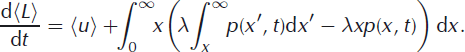
Rather than working with Equation (24), it is convenient to make use of the form (Reference Van KampenVan Kampen, 1992)

With this identity, after noticing that the quantity, r = x’ − x, is just the iceberg size, Equation (24) becomes
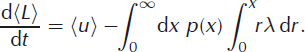
Written in this form, it is clear that the second term on the right-hand side of Equation (25) must be the expected value of the calving rate
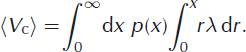
The calving rate must then be
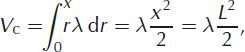
where, as before, L ≡ x denotes the instantaneous terminus position and the quadrature is trivial to evaluate for constant transition rates. The calving rate has a convenient physical interpretation: it is the integral over all possible iceberg sizes, r = x′ − x, weighted by the rate (in this case constant) for which icebergs of each size detach, as determined by the transition rate, λ.
Evaluating the integral in Equation (26), the expected calving rate can be expressed as a function of the expected terminus position and the expected variance in terminus position:
Substituting Equation (28) into Equation (25) provides a macroscopic evolution equation for the terminus position:
The above relationship, however, is problematic. Equation (29) implies that the rate of change of the expected terminus position depends not only on the expected terminus position, but also on the magnitude of the fluctuations (variance) in terminus position. Equation (29) is not a closed system and requires an additional evolution equation for the variance in terminus position. Moreover, since in general 〈u〉 ≠ u(〈L〉), fluctuations (i.e. a nonzero variance) also play a role in determining the expected terminus velocity.
If fluctuations are arbitrarily assumed to be small so that (L − 〈L〉 )2 ≪ 1 and 〈u〉 ≈ u(〈L〉), the macroscopic evolution equation/calving law can be approximated as
The solid black curve in Figure 4a shows the expected terminus position, computed using Equation (30), with corrections due to fluctuations omitted. Despite arbitrarily neglecting fluctuations, the main trend in terminus position (with large fluctuations about the mean) is qualitatively correct. This indicates that the macroscopic equation may still be used cautiously in simulations. However, the limits and approximate nature of the equation need to be recognized when (if) predictions are to be compared with observations.
A more systematic means of deducing the macroscopic calving law, valid for any glaciological regime, is pursued in section 5. The primary advantage of the more cumbersome expansion method pursued next is that the expansion provides a systematic basis for computing not only the calving rate, but also the magnitude of the fluctuations about the expected value. This provides the means of deciding when fluctuations are small and can be neglected and when they cannot. If fluctuations are not small, the expansion also provides a means of maintaining higher-order corrections.
5. Emergence of the Calving Law
5.1. Expansion of the master equation
The previous two examples illustrate that two seemingly different calving laws can be derived from the same underlying master equation, depending on the form of the transition rates. Moreover, these examples hint at one of the limitations of so-called calving laws; they appear to be restricted to cases where fluctuations are small enough that they can be neglected. This fact is exploited in this subsection, where a systematic expansion of the master equation, based on the size of the fluctuations measured relative to the system size, is developed. This systematic expansion reduces the effort of determining the calving law to that of evaluating an integral by quadrature. An additional benefit of the expansion is that it provides a method of determining the magnitude of the fluctuations. The magnitude of fluctuations can then be used to determine when the expansion is expected to fail, indicating when the expansion must either be abandoned or higher-order terms in the expansion retained.
The expansion presented is formidable and readers may wish to skip ahead to subsections 5.2 and 5.3, where the calving law along with an evolution equation for the variance are finally deduced. The expansion closely follows the standard Ω expansion posed by Reference Van KampenVan Kampen (1992), and readers are encouraged to consult this well-written textbook for supplementary descriptions of the arcane sequence of variable transformations and Taylor expansions that follow. The reader should keep in mind that the overarching purpose of the expansion is to (1) formulate an expression for the expected value of terminus position that is independent of the variance or higher-order moments of the distribution and (2) provide a separate evolution equation for the variance in the system.
The expansion proceeds as follows. Let Ω denote the characteristic size of the system. The size may be the characteristic lateral extent of an ice tongue/shelf, glacier or ice sheet or some subsection thereof. Since calving occurs from the ice-sheet margin, the ratio of terminus position (current glacier length) to system size (characteristic glacier length) is a number of order one, irrespective of system size. The size of icebergs (and hence fluctuations in terminus position) will usually be much less than the system size. The smallness of the ratio of fluctuations to system size provides the basis of the expansion method. With this in mind, a coordinate transformation is made to the intensive variable X = x/Ω. Time is simultaneously rescaled by setting τ = t/Ω. Making a transformation to the new variables, the transition rates may be written as a function of starting position and jump size (i.e. initial terminus position and iceberg size)
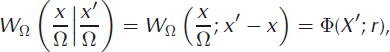
where the dependence on system size has been explicitly retained and r = x′ − x represents the iceberg size. The Ω subscript has been appended to W to emphasize the dependence on system size, and Φ is used to denote transition rates that depend on the intensive variable, X′, and iceberg size, r. Insisting that calving only results in transitions that decrease glacier length implies Φ(X′; r) = 0 unless r > 0 (i.e. negative iceberg size is prohibited).
Noting that W Ω (X′|X) = Φ(X′; −r), because iceberg size in this case is x − x’ = −r, and making use of the fact that X′ = X + r/Ω, the master equation can be written
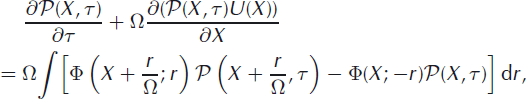
where the symbols U and ![]() are introduced to denote the probability density, p(x, t), and terminus velocity, u(x, t), as functions of the intensive variables, X and τ:
are introduced to denote the probability density, p(x, t), and terminus velocity, u(x, t), as functions of the intensive variables, X and τ:
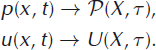
With this rescaling and change of variables, the master equation is now dependent on the ratio of terminus position to system size and on iceberg size. Furthermore, the transition rates and probability densities now have arguments shifted by r/Ω and it is this ratio of iceberg size to system size that can serve as the small parameter in the expansion.
First, however, it is necessary to adopt the ansatz that the non-dimensional terminus position, X, can be represented by
where φ(τ) will be chosen to follow the peak (or some approximation thereof) of the probability density distribution and ξ is a random variable that accounts for fluctuations about the mean terminus position (see, e.g., Van Kampen, Reference Van Kampen1992, for a more detailed motivation of the ansatz). More physically, the change of variables can be viewed as introducing a variable, φ, that follows the ratio of terminus position to system size and a variable, Ω−1/2 ξ, that describes how the width of the distribution fluctuates. These two variables together provide something like a Lagrangian description of the terminus position probability distribution. Note that as Ω → ∞, the width of the distribution (or size of the fluctuations) vanishes and the distribution becomes sharply peaked. This limit, in which icebergs are infinitesimally small compared to the size of the glacier, corresponds to a deterministic calving process. The ansatz is the key step in the expansion.
Denoting the new probability density distribution, Π,
now a function of ξ and τ, and substituting the ansatz into Equation (32) shows that the first term in the integral on the right-hand side can be written in the form
whereas the second term in the integral becomes
The argument in the first integral relative to the second is shifted by Ω−1/2 r. This shift can be accounted for with a Taylor expansion, whence the right-hand side of the master equation becomes
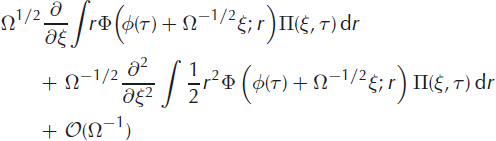
where the first term in the expansion cancelled with the second integral. The integrals can be expressed more concisely by introducing the iceberg jump moments
for ν = 1,2, etc. The iceberg jump moments correspond to integrals of iceberg size, raised to an integer power weighted by the transition rates.
Armed with these simplifications and after making heavy use of the chain rule, Equation (32) can be written in the form
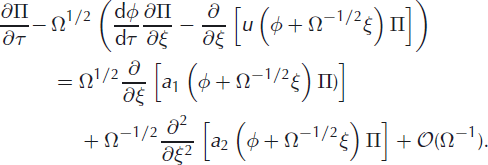
The dependence of ξ apparent in both jump moments and terminus velocity can be removed by yet another Taylor expansion
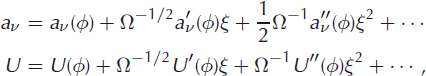
where primes denote differentiation with respect to ξ. Assembling all components, the expansion for the master equation takes the final form
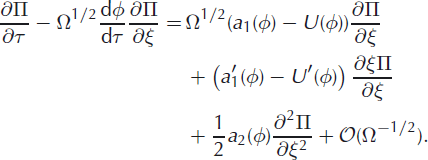
In this form of the master equation an infinite hierarchy of closed equations can be constructed by equating terms of equal size and the series can now be truncated whenever additional terms become small.
5.2. The macroscopic calving law
Examining Equation (36) more closely shows that the expansion will fail unless both of the terms of order Ω1/2 can be arranged so they exactly cancel for arbitrary Π. This can only be arranged if φ is chosen to obey the ordinary differential equation
where the first jump moment (or calving rate) is an integral over transition rates over all iceberg sizes
This, however, is precisely the macroscopic calving law sought in the first place. Recalling that φ is the ratio of terminus position to characteristic system size and U is terminus velocity scaled by characteristic system size, the macroscopic equation can be re-expressed in terms of extensive variables and rescaled back to the original variables:
where the connection between calving rate and the first jump moment has been made explicit and the rescaled version of Equation (38) provides the calving law:
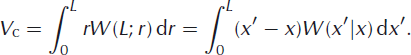
This law, unlike previous laws, is valid for any glacier (floating, grounded, temperate or cold), provided the transition rates can be specified. Furthermore, since the calving rate and terminus velocity now depend on the current terminus position, L, and not at all on the variance of terminus position, the macroscopic equation is an ordinary differential equation that can easily be incorporated into numerical ice-sheet models.
In the extreme case that transition rates are constant, one must integrate over the entire length of the ice shelf/tongue/glacier. Under this assumption, the integral in Equation (38) reduces to the calving rate determined in Equation (27):
In contrast, if the transition rates are strongly peaked near the terminus, evaluating the quadrate under the assumption that the transition rate per unit ice thickness is constant over the ice thickness yields the tidewater calving rate:
where, β is defined as in section 4.2. Equation (40) provides a universally valid calving law. However, the calving law may take on widely disparate forms, including the two examples considered in section 4, depending on the processes that determine the transition rates. Given the wide variety of glaciological conditions in which vigorous calving is observed, it is no wonder that an all-encompassing calving law has not previously been discovered empirically. Despite the fact that Equation (38) provides a convenient recipe to compute the calving law, the accuracy of the calving law hinges on the supposition that the remaining terms in the series are small. To determine if this is true one must proceed to higher-order terms in the expansion.
5.3. Fluctuations and the white-noise approximation
Having determined the macroscopic behavior, it is now possible to proceed to the next order in the expansion. Equating terms of ![]() yields
yields
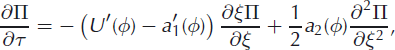
where the reader is reminded that a 2 is the second jump moment of the distribution
and primes denote differentiation with respect to ξ. Equation (41) is a linear Fokker–Planck equation. The equilibrium probability distribution can be shown to be Gaussian and the first and second moments can be found by multiplying Equation (41) by ξ and ξ 2 and integrating over all states (e.g. Reference Van KampenVan Kampen, 1992):
Although not necessary, it is convenient to choose ξ = 0, such that it coincides with φ. With this choice, the first equation can be ignored and the second equation provides the evolution of the width (or variance) about φ. The implication of these equations is most concretely illustrated by returning to the two examples discussed previously.
Fluctuations in terminus position of ice shelves and ice tongues
For the ice-tongue/ice-shelf example with constant transition rates, the equation for the second moment, rescaled back to the original extensive variables, becomes
where I have made use of the fact that u′ is the horizontal strain rate, ![]() . The term λL increases with increasing ice tongue length whereas the term
. The term λL increases with increasing ice tongue length whereas the term ![]() asymptotes to a constant value. Because of this, for large ice tongue lengths, the first term in the evolution equation becomes negative and the variance/fluctuations are guaranteed not to increase without bound. Hence, a stable steady-state solution is possible. This is illustrated in Figure 4, where the shaded gray region shows the variance, computed using Equation (44). That the width of the shaded area is comparable to the ice tongue extent is a testament to the fact that higher-order terms in the expansion that account for non-Gaussian behavior must become important. Despite these misgivings, the shaded gray region at least illustrates where the ice-shelf terminus is most likely to be found, suggesting that the macroscopic calving law can still provide some guidance, even when pushed to the limit of its applicability.
asymptotes to a constant value. Because of this, for large ice tongue lengths, the first term in the evolution equation becomes negative and the variance/fluctuations are guaranteed not to increase without bound. Hence, a stable steady-state solution is possible. This is illustrated in Figure 4, where the shaded gray region shows the variance, computed using Equation (44). That the width of the shaded area is comparable to the ice tongue extent is a testament to the fact that higher-order terms in the expansion that account for non-Gaussian behavior must become important. Despite these misgivings, the shaded gray region at least illustrates where the ice-shelf terminus is most likely to be found, suggesting that the macroscopic calving law can still provide some guidance, even when pushed to the limit of its applicability.
Fluctuations in terminus position of tidewater and lacustrine glaciers
For the calving glacier example, the evolution of ξ 2 can be similarly computed to find:
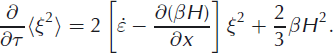
As before, if terminus velocity and ice thickness, H, are assumed constant and non-dimensionalized to unit magnitude and the transition rate, β, is assumed to increase linearly with constant slope, γ, the evolution equation for variance reduces to
The uncertainty in terminus position, as computed from Equation (46), is displayed in Figure 5a as the gray shaded region. The variance provides a much more accurate representation of variability in terminus position than in the ice-shelf case, a consequence of the smaller fluctuations in terminus position.
5.4. Fluctuations, the Langevin equation and steady states
Combining the macroscopic equation with the white-noise approximation provides an equation for the evolution of terminus position:
where η is a source of random, uncorrelated noise with amplitude that varies with L and is determined by solving for ξ 2. If fluctuations are negligible, this equation is entirely deterministic. However, in general, fluctuations do not vanish. To illustrate the potential effect of fluctuations, assume there are two or more steady-state terminus positions, denoted L 0, L 1 and so on. The multiple steady states might be due to bedrock topography, but are otherwise unspecified. The presence of fluctuations means that a glacier with steady-state terminus position L 1 can fluctuate out of state L 1 into L 0 and vice versa. This type of behavior may have important consequences for the episodic retreat and stability of tidewater and outlet glaciers.
6. Discussion
Although the search for a unified calving law that exclusively depends on internal parameters within a few ice thicknesses of the terminus position is flawed, it is possible to find a macroscopic equation that describes how the terminus position varies over large spatial and long temporal scales. This calving law can be determined from a systematic expansion of the master equation, where the calving law corresponds to an integral (first jump moment) of the transition rates. The integral, and hence calving rate, may depend on glacier parameters averaged over an extent that is much larger than the ice thickness. For instance, one might suppose that transition rates are highest in regions where the ice is heavily fractured (or damaged) and integrate over this region to find the calving rate.
Depending on the precise form of the transition rates for each glaciological regime, the quadrature may result in a seemingly endless variety of ‘calving laws’. Nevertheless, according to the present theory, the problem of finding a calving law is reduced to a quadrature of the transition rates and this integration can be performed for any glaciological regime. The calving law determined is universal. As fluctuations (or icebergs) increase in size to become comparable to the system size, the expansion of the master equation from which the calving law was deduced becomes increasingly invalid. Luckily, since it is possible to compute the size of the fluctuations self-consistently, the theory itself provides the information needed to determine its own demise.
As formulated in this study, calving laws are based on a mesoscopic theory of fracture and this must be determined independently of the theory presented here. At first sight, the theoretical approach just presented may seem hollow since, after all, making any concrete predictions requires that transition rates are somehow specified. This might, instead, be one of the greatest strengths of this approach. The advantage arises because the theory described is not tied to any particular flavor of fracture mechanics or hypothesis about the origin of icebergs. Because of this separation, one may focus entirely on formulating a physical theory for the transition rates. Once this is done, the machinery to turn the fracture physics into a calving law has already been determined. Furthermore, because the mesoscopic fracture theory and large-scale calving laws are unified by the calving law they are no longer independent and must be self-consistent. This may be exploited to aid in constructing a theory of mesoscopic fracture. For instance, transition rates could be constructed and/or verified by comparison with seismic, geodetic or imagery observations of calving and fracture propagation (Reference Neave and SavageNeave and Savage, 1970; Reference Bassis, Coleman, Fricker and MinsterBassis and others, 2005, Reference Bassis2007, Reference Bassis, Fricker, Coleman and Minster2008). Calving laws, computed directly from the transition rates, could then be compared with mean calving rates, deduced from satellite imagery or photogrammetry, as an additional test of the theory. Further tests are available if predicted fluctuations about the expected terminus position are compared with observations. Alternatively, it may be possible to invert the process and piece together a self-consistent formulation of transition rates from the known patchwork of empirical calving laws. This may then be compared with seismic and geodetic observations of fracture as an independent prediction. Both procedures have the potential to weed out theories with low explanatory capabilities and focus attention on regions where observations diverge from theoretical predictions.
Although this is promising, several formidable obstacles remain. Foremost amongst these is that the theory currently only applies to one-dimensional problems where the terminus position can be represented by a single degree of freedom. This may be appropriate for long, narrow glaciers that are confined to narrow channels or embayments. However, the large expansive ice shelves of Antarctica have more complicated geometry, and generalizations of the approach to the fully two-dimensional (2-D) problem are not trivial. In the 2-D (map view) generalization of the theory, the terminus position must be represented by a curve, Γ(x, y), rather than a single point. This transforms the quadrature into an integral over an infinitude of transition paths from curve Γ′(x, y) to Γ(x, y). In this limit, the quadrature necessary to find the calving law becomes ill defined. It may be possible to express the quadrature in the form of a path integral. However, given the mathematical complexity and difficulty in evaluating the integrals, this may not be a practical solution unless paths are discretized into a small finite number of discrete states (i.e. terminus position curves) to use in computations. Alternatively, one might seek to discretize the glacier into a series of flowbands. The calving rate could be computed for each flowband independently, using the present theory, and these calculations stitched together to find a 2-D calving rate. This would be easy to implement, but may be too crude an approach. A more satisfying approach may be provided by percolation theory, an approach first advocated by Reference BahrBahr (1995) as a means of modeling iceberg calving. Percolation theory is concerned with estimating the probability that a given group of lattice nodes (or in this case gridpoints) form a cluster that crosses the entire domain (or in this case isolates an iceberg). For a given set of transition rates, this may provide the means of estimating the probability that an iceberg of any given size detaches.
Because the calving law is only valid in the limit of spatial scales that are large compared to the fluctuations in terminus position, the approach advocated here may be an ideal fit for use as the boundary condition of continental-scale ‘shallow’ ice-sheet models with 1–10 km model resolution (e.g. Reference BassisBassis, 2010). However, because the calving law places a much more stringent restriction on the accuracy of spatial scales resolved by ice-sheet models, incorporating it into higher-resolution and/or (non-shallow) full-Stokes models may be problematic; according to the analysis presented here, the concept of a calving law may be inappropriate for a full-Stokes model that seeks to resolve spatial scales much smaller than one ice thickness. Instead, attempts to apply full-Stokes models to simulate the response of calving environments will need to choose between computing many realizations of the calving process (that can then be averaged), or solving the master equation. Given the computational cost of full-Stokes models, this may prove too great a burden.
7. Conclusions
Determining a calving law that is valid for all glaciological regimes has proven to be a vexing problem for glaciologists. Although several unified laws have been proposed over the past few decades, all have so far failed. This study demonstrates, for the first time, that a calving law valid for any glaciological regime can be derived, in a systematic fashion, from an underlying mesoscopic theory of fracture. The calving law constructed may reduce to a number of different forms previously proposed for special cases. Because of this, the approach has the potential to unify the pre-existing patchwork of semi-empirical parameterizations of calving developed for individual glacial regimes. To wit, it has been shown that using different assumptions about the form of the underlying transition rates, the theory is able to reproduce disparate calving styles, including the infrequent sporadic detachment of large tabular bergs from ice tongues and ice shelves and the more continuous calving of smallice-thickness scaled bergs from tidewater and outlet glaciers. The theory also has the appealing feature that it is able to predict its own demise: once fluctuations increase to the point where they are comparable to the system size, the expansion ceases to be valid and the calving law must be abandoned or higher-order corrections computed.
Developing the method advocated here to the point that it can be used as an operational basis in ice-sheet models is not without challenges. For instance, generalizing the theory to two dimensions so it can be applied to the large, expansive ice shelves of Antarctica remains problematic. Moreover, little has been said about how to formulate the transition rates needed to compute the calving law. This will be explored in a separate paper, but a growing number of researchers have postulated different relationships between calving and internal and external variables that provide a foundation for future studies (e.g. Reference Benn, Warren and MottramBenn and others, 2007; Reference Amundson and TrufferAmundson and Truffer, 2010). Once a theory is provided that specifies the transition rates, determining the calving law amounts to a numerical integration to find a calving law which can be integrated into regional- or continental-scale ice-sheet models. Although this study has focused exclusively on iceberg calving, the methods borrowed from statistical physics are remarkably general and powerful and it is likely that similar methods can be applied to additional glaciological processes, such as sliding of glaciers and supra-/subglacial hydrology.
Acknowledgements
This work was supported by NASA through grant NNX08AN59G and US National Science Foundation award ARC-1064535. I thank my colleague J. Barker who inadvertently introduced me to the master equation that forms the basis of this study. J. Johnson and M. Moldwin provided much-needed perspective on an early draft of the manuscript. I also thank J. Amundson and an anonymous reviewer for pointing out an embarrassingly large number of typographic mistakes in an earlier draft and whose comments substantially improved the clarity of the manuscript.







