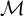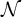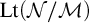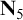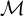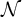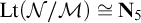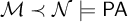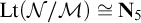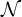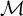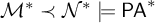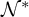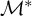Throughout, the (possibly adorned) script letters
![]() ${\mathcal M}, {\mathcal N}, {\mathcal K}$
denote models of Peano Arithmetic (PA) having universes denoted by the (similarly adorned) roman letters
${\mathcal M}, {\mathcal N}, {\mathcal K}$
denote models of Peano Arithmetic (PA) having universes denoted by the (similarly adorned) roman letters
![]() $M,N,K$
, respectively. When we write
$M,N,K$
, respectively. When we write
![]() ${\mathcal M} \prec {\mathcal N}$
, we allow the possibility that
${\mathcal M} \prec {\mathcal N}$
, we allow the possibility that
![]() ${\mathcal M} = {\mathcal N}$
. As usual, we write
${\mathcal M} = {\mathcal N}$
. As usual, we write
![]() ${\mathcal M} \prec _{\mathsf {end}} {\mathcal N}$
if
${\mathcal M} \prec _{\mathsf {end}} {\mathcal N}$
if
![]() ${\mathcal N}$
is an end elementary extension of
${\mathcal N}$
is an end elementary extension of
![]() ${\mathcal M}$
(that is,
${\mathcal M}$
(that is,
![]() $a < b$
whenever
$a < b$
whenever
![]() $a \in M$
and
$a \in M$
and
![]() $b \in N \backslash M$
), and we write
$b \in N \backslash M$
), and we write
![]() ${\mathcal M} \prec _{\mathsf {cf}} {\mathcal N}$
if
${\mathcal M} \prec _{\mathsf {cf}} {\mathcal N}$
if
![]() ${\mathcal N}$
is a cofinal (necessarily elementary) extension of
${\mathcal N}$
is a cofinal (necessarily elementary) extension of
![]() ${\mathcal M}$
(that is, for every
${\mathcal M}$
(that is, for every
![]() $b \in N$
there is
$b \in N$
there is
![]() $a \in M$
such that
$a \in M$
such that
![]() $b < a$
). If the elementary extension is neither end nor cofinal, then we say that it is mixed and write
$b < a$
). If the elementary extension is neither end nor cofinal, then we say that it is mixed and write
![]() ${\mathcal M} \prec _{\mathsf {mix}} {\mathcal N}$
.
${\mathcal M} \prec _{\mathsf {mix}} {\mathcal N}$
.
For a model
![]() ${{\mathcal N}}$
, its substructure lattice
${{\mathcal N}}$
, its substructure lattice
![]() $\operatorname {\mathrm {Lt}}({\mathcal N})$
is the lattice of all those
$\operatorname {\mathrm {Lt}}({\mathcal N})$
is the lattice of all those
![]() ${\mathcal K} \prec {\mathcal N}$
ordered by
${\mathcal K} \prec {\mathcal N}$
ordered by
![]() $\prec $
. More generally, if
$\prec $
. More generally, if
![]() ${\mathcal M} \prec {\mathcal N}$
, then the interstructure lattice
${\mathcal M} \prec {\mathcal N}$
, then the interstructure lattice
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is the sublattice of
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is the sublattice of
![]() $\operatorname {\mathrm {Lt}}({\mathcal N})$
consisting of those
$\operatorname {\mathrm {Lt}}({\mathcal N})$
consisting of those
![]() ${\mathcal K}$
in
${\mathcal K}$
in
![]() $\operatorname {\mathrm {Lt}}({\mathcal N})$
such that
$\operatorname {\mathrm {Lt}}({\mathcal N})$
such that
![]() ${\mathcal M} \prec {\mathcal K}$
. The question of which finite lattices can be substructure (or, equivalently, interstructure, by Corollary 1.2) lattices is discussed in [Reference Kossak and Schmerl1, Chapter 4]. It is still unknown whether there are any finite lattices that are not substructure lattices; however, many lattices are known to be, among which are all the finite distributive lattices. In fact [Reference Kossak and Schmerl1, Corollary 4.3.8], for any
${\mathcal M} \prec {\mathcal K}$
. The question of which finite lattices can be substructure (or, equivalently, interstructure, by Corollary 1.2) lattices is discussed in [Reference Kossak and Schmerl1, Chapter 4]. It is still unknown whether there are any finite lattices that are not substructure lattices; however, many lattices are known to be, among which are all the finite distributive lattices. In fact [Reference Kossak and Schmerl1, Corollary 4.3.8], for any
![]() ${\mathcal M}$
and any finite distributive lattice D, there is
${\mathcal M}$
and any finite distributive lattice D, there is
![]() ${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
such that
${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong D$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong D$
.
Recall that a lattice is distributive iff it embeds neither the pentagon lattice
![]() ${\mathbf N}_5$
nor the diamond lattice
${\mathbf N}_5$
nor the diamond lattice
![]() ${\mathbf M}_3$
, both of which are depicted in Figure 1. A lattice is modular iff it does not embed
${\mathbf M}_3$
, both of which are depicted in Figure 1. A lattice is modular iff it does not embed
![]() ${\mathbf N}_5$
.
${\mathbf N}_5$
.

Figure 1 Lattices
![]() ${\mathbf N}_5$
and
${\mathbf N}_5$
and
![]() ${\mathbf M}_3$
.
${\mathbf M}_3$
.
Paris [Reference Paris2] gave, historically, the first example of a substructure lattice that is not distributive. The following theorem of Wilkie [Reference Wilkie4] gives the first example of a substructure lattice that is not modular.
Theorem 1. For every countable
![]() ${\mathcal M}$
there is
${\mathcal M}$
there is
![]() ${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
such that
${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
.
Incidentally, as proved in [Reference Kossak and Schmerl1, Theorem 4.6.5], for every
![]() ${\mathcal M}_0$
there is
${\mathcal M}_0$
there is
![]() ${\mathcal M} \succ _{\mathsf {end}} {\mathcal M}_0$
for which no
${\mathcal M} \succ _{\mathsf {end}} {\mathcal M}_0$
for which no
![]() ${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
is such that
${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
is such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
. Theorem 1 has the following corollary. (See Theorem 1.1 for the reason.)
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
. Theorem 1 has the following corollary. (See Theorem 1.1 for the reason.)
Corollary 2. For every countable and nonstandard
![]() ${\mathcal M}$
there is
${\mathcal M}$
there is
![]() ${\mathcal N} \succ _{\mathsf {cf}} {\mathcal M}$
such that
${\mathcal N} \succ _{\mathsf {cf}} {\mathcal M}$
such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
.
It is still unresolved if, for every nonstandard
![]() ${\mathcal M}$
, there is
${\mathcal M}$
, there is
![]() ${\mathcal N} \succ _{\mathsf {cf}} {\mathcal M}$
such that
${\mathcal N} \succ _{\mathsf {cf}} {\mathcal M}$
such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
. A positive answer would immediately yield a positive answer to the question [Reference Kossak and Schmerl1, Question 2, Chapter 12] if every uncountable model has a minimal cofinal extension.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong {\mathbf N}_5$
. A positive answer would immediately yield a positive answer to the question [Reference Kossak and Schmerl1, Question 2, Chapter 12] if every uncountable model has a minimal cofinal extension.
Theorem 1 and Corollary 2 together suggest the question of whether the pentagon lattice can be realized by an elementary mixed extension. It was impetuously stated in [Reference Kossak and Schmerl1, p. 123] that
![]() ${\mathbf N}_5$
does have such a representation. There was no published proof at that time, but there was an outline of a proof that later was seen to be flawed.Footnote
1
Mea culpa! In fact, there are no such extensions. That is the content of the next theorem, which is our first main result.
${\mathbf N}_5$
does have such a representation. There was no published proof at that time, but there was an outline of a proof that later was seen to be flawed.Footnote
1
Mea culpa! In fact, there are no such extensions. That is the content of the next theorem, which is our first main result.
Theorem 3. If
![]() ${\mathcal M} \prec _{\mathsf {mix}} {\mathcal N}$
, then
${\mathcal M} \prec _{\mathsf {mix}} {\mathcal N}$
, then
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \not \cong {\mathbf N}_5$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \not \cong {\mathbf N}_5$
.
Despite Theorem 3, there is a sliver of truth to the claim in [Reference Kossak and Schmerl1], as will now be explained. Let
![]() ${\mathcal L}$
be one of the usual finite languages in which PA is formulated; to be definitive, let
${\mathcal L}$
be one of the usual finite languages in which PA is formulated; to be definitive, let
![]() ${\mathcal L} = \{+,\times ,\leq ,0,1\}$
. If
${\mathcal L} = \{+,\times ,\leq ,0,1\}$
. If
![]() ${\mathcal M}$
is a model and
${\mathcal M}$
is a model and
![]() $X \subseteq M$
, then
$X \subseteq M$
, then
![]() ${\mathcal L}(X)$
is the language that, in addition to
${\mathcal L}(X)$
is the language that, in addition to
![]() ${\mathcal L}$
, has constant symbols denoting elements of X; in particular,
${\mathcal L}$
, has constant symbols denoting elements of X; in particular,
![]() ${\mathcal L} = {\mathcal L}(\varnothing )$
. Let
${\mathcal L} = {\mathcal L}(\varnothing )$
. Let
![]() ${\mathcal L}^*$
be the language obtained from
${\mathcal L}^*$
be the language obtained from
![]() ${\mathcal L}$
by adjoining to it the denumerably many new and distinct unary relation symbols
${\mathcal L}$
by adjoining to it the denumerably many new and distinct unary relation symbols
![]() $U_0,U_1,U_2, \ldots $
. Thus,
$U_0,U_1,U_2, \ldots $
. Thus,
![]() ${\mathcal L}^*= {\mathcal L} \cup \{U_i : i < \omega \}$
. Let
${\mathcal L}^*= {\mathcal L} \cup \{U_i : i < \omega \}$
. Let
![]() $\mathsf {PA}^*$
be the
$\mathsf {PA}^*$
be the
![]() ${\mathcal L}^*$
-theory of those structures
${\mathcal L}^*$
-theory of those structures
![]() ${\mathcal M}^* = ({\mathcal M},U_0,U_1,U_2, \ldots )$
, where
${\mathcal M}^* = ({\mathcal M},U_0,U_1,U_2, \ldots )$
, where
![]() ${\mathcal M} \models \mathsf {PA}$
and
${\mathcal M} \models \mathsf {PA}$
and
![]() ${\mathcal M}^*$
satisfies the induction scheme for all
${\mathcal M}^*$
satisfies the induction scheme for all
![]() ${\mathcal L}^*(M)$
-formulas, where
${\mathcal L}^*(M)$
-formulas, where
![]() ${\mathcal L}^*(M) = {\mathcal L}(M) \cup {\mathcal L}^*$
. (From now on,
${\mathcal L}^*(M) = {\mathcal L}(M) \cup {\mathcal L}^*$
. (From now on,
![]() ${\mathcal M}^*,{\mathcal N}^*, \ldots $
always denote models of
${\mathcal M}^*,{\mathcal N}^*, \ldots $
always denote models of
![]() $\mathsf {PA}^*$
that are expansions of
$\mathsf {PA}^*$
that are expansions of
![]() ${\mathcal M}, {\mathcal N}, \ldots $
, respectively.) We can think of
${\mathcal M}, {\mathcal N}, \ldots $
, respectively.) We can think of
![]() $\mathsf {PA}^*$
as a subtheory of
$\mathsf {PA}^*$
as a subtheory of
![]() $\mathsf {PA}$
by identifying
$\mathsf {PA}$
by identifying
![]() $\mathsf {PA}$
with
$\mathsf {PA}$
with
![]() $\mathsf {PA}^* \cup \{U_i = \varnothing : i < \omega \}$
. Many concepts, such as interstructure lattices, that concern models of
$\mathsf {PA}^* \cup \{U_i = \varnothing : i < \omega \}$
. Many concepts, such as interstructure lattices, that concern models of
![]() $\mathsf {PA}$
extend in an obvious and natural way to models of
$\mathsf {PA}$
extend in an obvious and natural way to models of
![]() $\mathsf {PA}^*$
. Also, many results about models of PA, together with their proofs, extend in a straightforward manner to models of
$\mathsf {PA}^*$
. Also, many results about models of PA, together with their proofs, extend in a straightforward manner to models of
![]() $\mathsf {PA}^*$
. Almost all results in [Reference Kossak and Schmerl1] do. Theorem 1 and Corollary 2 also do. In other words, Theorem 1
$\mathsf {PA}^*$
. Almost all results in [Reference Kossak and Schmerl1] do. Theorem 1 and Corollary 2 also do. In other words, Theorem 1
![]() $^*$
and Corollary 2
$^*$
and Corollary 2
![]() $^*$
are valid, where we are adjoining
$^*$
are valid, where we are adjoining
![]() $^*$
to indicate that
$^*$
to indicate that
![]() $\mathsf {PA}^*$
rather than just
$\mathsf {PA}^*$
rather than just
![]() $\mathsf {PA}$
is being considered. But Theorem 3 has the unusual feature that it does not. The next theorem, our second new result, indicates why.
$\mathsf {PA}$
is being considered. But Theorem 3 has the unusual feature that it does not. The next theorem, our second new result, indicates why.
Theorem 4. Every countable, recursively saturated
![]() ${\mathcal M}$
has an expansion
${\mathcal M}$
has an expansion
![]() ${\mathcal M}^*$
for which there is
${\mathcal M}^*$
for which there is
![]() ${\mathcal N}^* \succ _{\mathsf {mix}} {\mathcal M}^*$
such that
${\mathcal N}^* \succ _{\mathsf {mix}} {\mathcal M}^*$
such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N}^*/ {\mathcal M}^*) \cong {\mathbf N}_5$
.
$\operatorname {\mathrm {Lt}}({\mathcal N}^*/ {\mathcal M}^*) \cong {\mathbf N}_5$
.
As far as notation and terminology go, we generally follow what is standard or what can be found in [Reference Kossak and Schmerl1].
There are four numbered sections following this introduction. Section 1 contains some preliminary material much of which is a rehash. Theorem 3 is proved in Section 2. Section 3 is almost purely combinatorial in nature and prepares the way for the proof of Theorem 4, which is then presented in Section 4.
1. Ranked lattices and their representations
This section, comprising three subsections, culminates with a description of how to obtain elementary extensions realizing a given finite ranked lattice. Section 1.1 repeats some material from [Reference Kossak and Schmerl1, Chapter 4]. Section 1.2 extends Section 1.1 and puts a new perspective on it. Finally, Section 1.3 extends Section 1.2 from lattices to ranked lattices.
1.1. Representations of lattices
For any set A, let
![]() $\operatorname {\mathrm {Eq}}(A)$
be the lattice of equivalence relations on A, ordered in such a way that if
$\operatorname {\mathrm {Eq}}(A)$
be the lattice of equivalence relations on A, ordered in such a way that if
![]() $\Theta _1,\Theta _2 \in \operatorname {\mathrm {Eq}}(A)$
, then
$\Theta _1,\Theta _2 \in \operatorname {\mathrm {Eq}}(A)$
, then
![]() $\Theta _1 \leq \Theta _2$
iff
$\Theta _1 \leq \Theta _2$
iff
![]() $\Theta _1 \subseteq \Theta _2$
(that is,
$\Theta _1 \subseteq \Theta _2$
(that is,
![]() $\Theta _1$
refines
$\Theta _1$
refines
![]() $\Theta _2$
). We let
$\Theta _2$
). We let
![]() $0 {\hspace{-6.3pt} 0}_A$
be the discrete equivalence relation on A (that is,
$0 {\hspace{-6.3pt} 0}_A$
be the discrete equivalence relation on A (that is,
![]() $0 {\hspace{-6.3pt} 0}_A$
is the equality relation on A) and
$0 {\hspace{-6.3pt} 0}_A$
is the equality relation on A) and
![]() $1 {\hspace {-3.5pt} 1}_A$
be the trivial equivalence relation (that is,
$1 {\hspace {-3.5pt} 1}_A$
be the trivial equivalence relation (that is,
![]() $1 {\hspace {-3.5pt} 1}_A = A \times A$
). Thus, for any
$1 {\hspace {-3.5pt} 1}_A = A \times A$
). Thus, for any
![]() $\Theta _1, \Theta _2 \in \operatorname {\mathrm {Eq}}(A)$
, we have that
$\Theta _1, \Theta _2 \in \operatorname {\mathrm {Eq}}(A)$
, we have that
and
If
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A)$
and
$\Theta \in \operatorname {\mathrm {Eq}}(A)$
and
![]() $B \subseteq A$
, then
$B \subseteq A$
, then
![]() $\Theta \cap B^2 \in \operatorname {\mathrm {Eq}}(B)$
. If f is a function with domain A, then f induces
$\Theta \cap B^2 \in \operatorname {\mathrm {Eq}}(B)$
. If f is a function with domain A, then f induces
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A)$
if whenever
$\Theta \in \operatorname {\mathrm {Eq}}(A)$
if whenever
![]() $a,b \in A$
, then
$a,b \in A$
, then
![]() $\langle a , b \rangle \in \Theta $
iff
$\langle a , b \rangle \in \Theta $
iff
![]() $f(a) = f(b)$
.
$f(a) = f(b)$
.
Let L be a finite lattice. A representation of L is a one-to-one function
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
such that
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
such that
 $$ \begin{align*}\alpha(0_L) &= 1 {\hspace{-3.5pt} 1}_A, \\\alpha(1_L) &= 0 {\hspace{-6.3pt} 0}_A, \end{align*} $$
$$ \begin{align*}\alpha(0_L) &= 1 {\hspace{-3.5pt} 1}_A, \\\alpha(1_L) &= 0 {\hspace{-6.3pt} 0}_A, \end{align*} $$
and
for each
![]() $r,s \in L$
. (It is not required that
$r,s \in L$
. (It is not required that
![]() $\alpha (r \wedge s ) = \alpha (r) \vee \alpha (s)$
.) We say that
$\alpha (r \wedge s ) = \alpha (r) \vee \alpha (s)$
.) We say that
![]() $\alpha $
is finite if A is a finite set. If
$\alpha $
is finite if A is a finite set. If
![]() $B \subseteq A$
, then
$B \subseteq A$
, then
![]() $\alpha |B : L \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is such that
$\alpha |B : L \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is such that
![]() $(\alpha |B)(r) = \alpha (r) \cap B^2$
for each
$(\alpha |B)(r) = \alpha (r) \cap B^2$
for each
![]() $r \in L$
. The representation
$r \in L$
. The representation
![]() $\beta : L \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is isomorphic to
$\beta : L \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is isomorphic to
![]() $\alpha $
(in symbols:
$\alpha $
(in symbols:
![]() $\alpha \cong \beta $
) if there is a bijection
$\alpha \cong \beta $
) if there is a bijection
![]() $f : A \longrightarrow B$
such that for any
$f : A \longrightarrow B$
such that for any
![]() $x,y \in A$
and
$x,y \in A$
and
![]() $r \in L$
,
$r \in L$
,
![]() $\langle x , y \rangle \in \alpha (r)$
iff
$\langle x , y \rangle \in \alpha (r)$
iff
![]() $\langle f(x) , f(y)\rangle \in \beta (r)$
. If such is the case, then we say that f demonstrates that
$\langle f(x) , f(y)\rangle \in \beta (r)$
. If such is the case, then we say that f demonstrates that
![]() $\alpha \cong \beta $
. If
$\alpha \cong \beta $
. If
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is a representation and
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is a representation and
![]() $\Theta \in \operatorname {\mathrm {Eq}}(B)$
, then
$\Theta \in \operatorname {\mathrm {Eq}}(B)$
, then
![]() $\Theta $
is canonical (for
$\Theta $
is canonical (for
![]() $\alpha $
) if
$\alpha $
) if
![]() $B \subseteq A$
and
$B \subseteq A$
and
![]() $\Theta = \alpha (r) \cap B^2$
for some
$\Theta = \alpha (r) \cap B^2$
for some
![]() $r \in L$
.
$r \in L$
.
Suppose that
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is a representation of the finite lattice L, and
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is a representation of the finite lattice L, and
![]() $\mathcal {B}$
is a set of representations of L. Then
$\mathcal {B}$
is a set of representations of L. Then
![]() $\alpha $
arrows
$\alpha $
arrows
![]() ${\mathcal B}$
(in symbols:
${\mathcal B}$
(in symbols:
![]() $\alpha \longrightarrow {\mathcal B}$
) if whenever
$\alpha \longrightarrow {\mathcal B}$
) if whenever
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A)$
, then there is
$\Theta \in \operatorname {\mathrm {Eq}}(A)$
, then there is
![]() $B \subseteq A$
such that
$B \subseteq A$
such that
![]() $\Theta \cap B^2$
is canonical for
$\Theta \cap B^2$
is canonical for
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha |B \cong \beta $
for some
$\alpha |B \cong \beta $
for some
![]() $\beta \in {\mathcal B}$
. We usually write
$\beta \in {\mathcal B}$
. We usually write
![]() $\alpha \longrightarrow \beta $
instead of
$\alpha \longrightarrow \beta $
instead of
![]() $\alpha \longrightarrow \{\beta \}$
.
$\alpha \longrightarrow \{\beta \}$
.
We next define, by recursion on
![]() $n < \omega $
, when the representation
$n < \omega $
, when the representation
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
of the finite lattice L has the n-canonical partition property (or, briefly, is n-CPP). First,
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
of the finite lattice L has the n-canonical partition property (or, briefly, is n-CPP). First,
![]() $\alpha $
is
$\alpha $
is
![]() $0$
-CPP if for every
$0$
-CPP if for every
![]() $r \in L$
, there do not exist exactly
$r \in L$
, there do not exist exactly
![]() $2\ \alpha (r)$
-classes; next,
$2\ \alpha (r)$
-classes; next,
![]() $\alpha $
is
$\alpha $
is
![]() $(n+1)$
-CPP if there is a set
$(n+1)$
-CPP if there is a set
![]() ${\mathcal B}$
of n-CPP representations of L such that
${\mathcal B}$
of n-CPP representations of L such that
![]() $\alpha \longrightarrow {\mathcal B}$
.
$\alpha \longrightarrow {\mathcal B}$
.
Given
![]() ${\mathcal M}$
, we say that a representation
${\mathcal M}$
, we say that a representation
![]() $\alpha $
of a finite lattice L is an
$\alpha $
of a finite lattice L is an
![]() ${\mathcal M}$
-representation if it is
${\mathcal M}$
-representation if it is
![]() ${\mathcal M}$
-definable. Also, if
${\mathcal M}$
-definable. Also, if
![]() $A \in \operatorname {\mathrm {Def}}({\mathcal M})$
, then we let
$A \in \operatorname {\mathrm {Def}}({\mathcal M})$
, then we let
![]() $\operatorname {\mathrm {Eq}}^{\mathcal M}(A)$
be the set of those
$\operatorname {\mathrm {Eq}}^{\mathcal M}(A)$
be the set of those
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A)$
that are definable in
$\Theta \in \operatorname {\mathrm {Eq}}(A)$
that are definable in
![]() ${\mathcal M}$
. All the definitions in this subsection up to this point make sense when interpreted in a model
${\mathcal M}$
. All the definitions in this subsection up to this point make sense when interpreted in a model
![]() ${\mathcal M}$
and are applied just to
${\mathcal M}$
and are applied just to
![]() ${\mathcal M}$
-representations. In particular, it makes sense to refer to an
${\mathcal M}$
-representations. In particular, it makes sense to refer to an
![]() ${\mathcal M}$
-finite
${\mathcal M}$
-finite
![]() ${\mathcal M}$
-representation
${\mathcal M}$
-representation
![]() $\alpha $
as being a-CPP for
$\alpha $
as being a-CPP for
![]() $a \in M$
. Thus, for every finite lattice L, there is a
$a \in M$
. Thus, for every finite lattice L, there is a
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $cpp_L(x)$
such that for any
$cpp_L(x)$
such that for any
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() $a \in M$
,
$a \in M$
,
![]() ${\mathcal M} \models cpp_L(a)$
iff there is an
${\mathcal M} \models cpp_L(a)$
iff there is an
![]() ${\mathcal M}$
-finite
${\mathcal M}$
-finite
![]() ${\mathcal M}$
-representation of L that
${\mathcal M}$
-representation of L that
![]() ${\mathcal M}$
thinks is a-CPP. The following theorem can be found in [Reference Kossak and Schmerl1, Chapter 4] or [Reference Schmerl3].
${\mathcal M}$
thinks is a-CPP. The following theorem can be found in [Reference Kossak and Schmerl1, Chapter 4] or [Reference Schmerl3].
Theorem 1.1. Let L be a finite lattice and
![]() ${\mathcal M}$
be a nonstandard, countable model. The following are equivalent:
${\mathcal M}$
be a nonstandard, countable model. The following are equivalent:
-
(1) There are
 ${\mathcal N}_0 \succ {\mathcal M}_0 \equiv {\mathcal M}$
such that
${\mathcal N}_0 \succ {\mathcal M}_0 \equiv {\mathcal M}$
such that
 $\operatorname {\mathrm {Lt}}({\mathcal N}_0 / {\mathcal M}_0) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N}_0 / {\mathcal M}_0) \cong L$
. -
(2) For every
 $n < \omega $
,
$n < \omega $
,
 ${\mathcal M} \models cpp_L(n)$
.
${\mathcal M} \models cpp_L(n)$
. -
(3) There is
 ${\mathcal N} \succ _{\mathsf {cf}} {\mathcal M}$
such that
${\mathcal N} \succ _{\mathsf {cf}} {\mathcal M}$
such that
 $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
Notice that Corollary 2 follows from Theorem 1 and
![]() $(1) \Longrightarrow (3)$
of the previous theorem.
$(1) \Longrightarrow (3)$
of the previous theorem.
Corollary 1.2. If L is a finite lattice, then the following are equivalent:
-
(1) There is
 ${\mathcal N}$
such that
${\mathcal N}$
such that
 $\operatorname {\mathrm {Lt}}({\mathcal N}) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N}) \cong L$
. -
(2) There are
 ${\mathcal M} \prec {\mathcal N}$
such that
${\mathcal M} \prec {\mathcal N}$
such that
 $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
Proof Obviously,
![]() $(1) \Longrightarrow (2)$
by letting
$(1) \Longrightarrow (2)$
by letting
![]() ${\mathcal M}$
be the prime elementary submodel of
${\mathcal M}$
be the prime elementary submodel of
![]() ${\mathcal N}$
. The converse
${\mathcal N}$
. The converse
![]() $(2) \Longrightarrow (1)$
follows from Theorem 1.1 as long as
$(2) \Longrightarrow (1)$
follows from Theorem 1.1 as long as
![]() ${\mathcal M}$
is not a model of True Arithmetic (TA) and so its prime elementary submodel is nonstandard. If
${\mathcal M}$
is not a model of True Arithmetic (TA) and so its prime elementary submodel is nonstandard. If
![]() ${\mathcal M}$
is a model of TA, then by
${\mathcal M}$
is a model of TA, then by
![]() $(1) \implies (2)$
of Theorem 1.1,
$(1) \implies (2)$
of Theorem 1.1,
![]() ${\mathcal M} \models cpp_L(n)$
for all
${\mathcal M} \models cpp_L(n)$
for all
![]() $n < \omega $
. Since TA is undecidable, there is a prime, nonstandard
$n < \omega $
. Since TA is undecidable, there is a prime, nonstandard
![]() ${\mathcal M}_0$
such that
${\mathcal M}_0$
such that
![]() ${\mathcal M}_0 \models cpp_L(n)$
for all
${\mathcal M}_0 \models cpp_L(n)$
for all
![]() $n < \omega $
. Then by
$n < \omega $
. Then by
![]() $(1) \implies (2)$
of Theorem 1.1, there is
$(1) \implies (2)$
of Theorem 1.1, there is
![]() ${\mathcal N}_0 \succ _{\mathsf {cf}} {\mathcal M}_0$
such that
${\mathcal N}_0 \succ _{\mathsf {cf}} {\mathcal M}_0$
such that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N}_0) = \operatorname {\mathrm {Lt}}({\mathcal N}_0 / {\mathcal M}_0) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N}_0) = \operatorname {\mathrm {Lt}}({\mathcal N}_0 / {\mathcal M}_0) \cong L$
.
1.2. Correct sets of representations
This subsection consists of a definition followed by a theorem generalizing Theorem 1.1.
Definition 1.3. Let
![]() ${\mathcal M}$
be a model and L be a finite lattice. We say that
${\mathcal M}$
be a model and L be a finite lattice. We say that
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${\mathcal M}$
-correct set of representations of L if each of the following holds.
${\mathcal M}$
-correct set of representations of L if each of the following holds.
-
(1)
 ${\mathcal C}$
is a nonempty set of
${\mathcal C}$
is a nonempty set of
 $0$
-CPP
$0$
-CPP
 ${\mathcal M}$
-representations of L.
${\mathcal M}$
-representations of L. -
(2) Whenever
 $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is in
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is in
 ${\mathcal C}$
and
${\mathcal C}$
and
 $\Theta \in \operatorname {\mathrm {Eq}}^{\mathcal M}(A)$
, then there is a
$\Theta \in \operatorname {\mathrm {Eq}}^{\mathcal M}(A)$
, then there is a
 $B \subseteq A$
such that
$B \subseteq A$
such that
 $\alpha |B \in {\mathcal C}$
and
$\alpha |B \in {\mathcal C}$
and
 $\Theta \cap B^2$
is canonical for
$\Theta \cap B^2$
is canonical for
 $\alpha $
.
$\alpha $
.
Here is an example. Suppose that
![]() ${\mathcal M}$
is nonstandard and that
${\mathcal M}$
is nonstandard and that
![]() ${\mathcal M} \models cpp_L(n)$
for every
${\mathcal M} \models cpp_L(n)$
for every
![]() $n < \omega $
. Let
$n < \omega $
. Let
![]() ${\mathcal C}$
be the set of those
${\mathcal C}$
be the set of those
![]() ${\mathcal M}$
-finite
${\mathcal M}$
-finite
![]() ${\mathcal M}$
-representations
${\mathcal M}$
-representations
![]() $\alpha $
of L such that, for some nonstandard
$\alpha $
of L such that, for some nonstandard
![]() $n \in M$
,
$n \in M$
,
![]() ${\mathcal M}$
thinks that
${\mathcal M}$
thinks that
![]() $\alpha $
is n-CPP. Then,
$\alpha $
is n-CPP. Then,
![]() ${\mathcal C}$
is
${\mathcal C}$
is
![]() ${\mathcal M}$
-correct. With this example, we see that the following theorem generalizes a good portion of Theorem 1.1. It is a consequence of Theorem 1.1 when
${\mathcal M}$
-correct. With this example, we see that the following theorem generalizes a good portion of Theorem 1.1. It is a consequence of Theorem 1.1 when
![]() ${\mathcal M}$
is countable and nonstandard.
${\mathcal M}$
is countable and nonstandard.
Theorem 1.4. Suppose that
![]() ${\mathcal M}$
is a model and L is a finite lattice.
${\mathcal M}$
is a model and L is a finite lattice.
-
(1) If there is
 ${\mathcal N} \succ {\mathcal M}$
such that
${\mathcal N} \succ {\mathcal M}$
such that
 $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
, then there is an
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
, then there is an
 ${\mathcal M}$
-correct set of representations of L.
${\mathcal M}$
-correct set of representations of L. -
(2) If
 ${\mathcal M}$
is countable and there is an
${\mathcal M}$
is countable and there is an
 ${\mathcal M}$
-correct set of representations of L, then there is
${\mathcal M}$
-correct set of representations of L, then there is
 ${\mathcal N} \succ {\mathcal M}$
such that
${\mathcal N} \succ {\mathcal M}$
such that
 $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
Proof
![]() $(1)$
Suppose that
$(1)$
Suppose that
![]() ${\mathcal N} \succ {\mathcal M}$
and that
${\mathcal N} \succ {\mathcal M}$
and that
![]() $F : L \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is an isomorphism. Let
$F : L \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is an isomorphism. Let
![]() $f : L \longrightarrow N$
be such that for
$f : L \longrightarrow N$
be such that for
![]() $r \in L$
,
$r \in L$
,
![]() $f(r)$
generates
$f(r)$
generates
![]() $F(r)$
over
$F(r)$
over
![]() ${\mathcal M}$
. Let
${\mathcal M}$
. Let
![]() $a = f(1_L)$
.
$a = f(1_L)$
.
For each pair of elements
![]() $r,s \in L$
, let
$r,s \in L$
, let
![]() $g_{r,s} : N \longrightarrow N$
and
$g_{r,s} : N \longrightarrow N$
and
![]() $h_{r,s} : N^2 \longrightarrow N$
be functions that are
$h_{r,s} : N^2 \longrightarrow N$
be functions that are
![]() ${\mathcal N}$
-definable using parameters only from M such that
${\mathcal N}$
-definable using parameters only from M such that
-
•
 $g_{r,s}(f(r \vee s)) = f(r)$
,
$g_{r,s}(f(r \vee s)) = f(r)$
, -
•
 $h_{r,s}(f(r),f(s)) = f(r \vee s)$
.
$h_{r,s}(f(r),f(s)) = f(r \vee s)$
.
The functions
![]() $g_{r,s}$
exist since
$g_{r,s}$
exist since
![]() $f(r) \in F(r \vee s)$
; the functions
$f(r) \in F(r \vee s)$
; the functions
![]() $h_{r,s}$
exist for a similar reason. Let
$h_{r,s}$
exist for a similar reason. Let
![]() $g_r = g_{r,1}$
, so that
$g_r = g_{r,1}$
, so that
![]() $g_r(a) = f(r)$
. In particular,
$g_r(a) = f(r)$
. In particular,
![]() $g_1(a) = a$
. The two equalities above become
$g_1(a) = a$
. The two equalities above become
-
•
 $g_{r,s}(g_{r \vee s}(a)) = g_r(a)$
,
$g_{r,s}(g_{r \vee s}(a)) = g_r(a)$
, -
•
 $h_{r,s}(g_r(a),g_s(a)) = g_{r \vee s}(a)$
.
$h_{r,s}(g_r(a),g_s(a)) = g_{r \vee s}(a)$
.
For each
![]() $X \in \operatorname {\mathrm {Def}}({\mathcal M})$
, let
$X \in \operatorname {\mathrm {Def}}({\mathcal M})$
, let
![]() $\alpha _X : L \longrightarrow \operatorname {\mathrm {Eq}}(X)$
be such that whenever
$\alpha _X : L \longrightarrow \operatorname {\mathrm {Eq}}(X)$
be such that whenever
![]() $r \in L$
, then
$r \in L$
, then
![]() $\alpha _X(r)$
is the equivalence relation in
$\alpha _X(r)$
is the equivalence relation in
![]() $\operatorname {\mathrm {Eq}}(X)$
induced by
$\operatorname {\mathrm {Eq}}(X)$
induced by
![]() $g_r \hspace {-4pt} \upharpoonright \hspace {-3pt} X$
. Let B be the set of all
$g_r \hspace {-4pt} \upharpoonright \hspace {-3pt} X$
. Let B be the set of all
![]() $x \in M$
such that
$x \in M$
such that
-
•
 $g_{r,s}(g_{r \vee s}(x)) = g_r(x)$
,
$g_{r,s}(g_{r \vee s}(x)) = g_r(x)$
, -
•
 $h_{r,s}(g_r(x),g_s(x)) = g_{r \vee s}(x)$
,
$h_{r,s}(g_r(x),g_s(x)) = g_{r \vee s}(x)$
, -
•
 $g_1(x) = x$
.
$g_1(x) = x$
.
Clearly,
![]() $B \in \operatorname {\mathrm {Def}}({\mathcal M})$
and
$B \in \operatorname {\mathrm {Def}}({\mathcal M})$
and
![]() $a \in B^{\mathcal N}$
. We claim that
$a \in B^{\mathcal N}$
. We claim that
![]() $\alpha _B$
is an
$\alpha _B$
is an
![]() ${\mathcal M}$
-representation of L. But even more is true. If
${\mathcal M}$
-representation of L. But even more is true. If
![]() $X \subseteq B$
,
$X \subseteq B$
,
![]() $X \in \operatorname {\mathrm {Def}}({\mathcal M})$
and
$X \in \operatorname {\mathrm {Def}}({\mathcal M})$
and
![]() $a \in X^{\mathcal N}$
, then
$a \in X^{\mathcal N}$
, then
![]() $\alpha _X = \alpha _B|X$
.
$\alpha _X = \alpha _B|X$
.
We now claim that each such
![]() $\alpha _X$
is an
$\alpha _X$
is an
![]() ${\mathcal M}$
-representation of L.
${\mathcal M}$
-representation of L.
First,
![]() $\alpha _X$
is one-to-one. For, suppose that
$\alpha _X$
is one-to-one. For, suppose that
![]() $r,s \in L$
and
$r,s \in L$
and
![]() $\alpha _X(r) = \alpha _X(s)$
. Then,
$\alpha _X(r) = \alpha _X(s)$
. Then,
![]() $g_r \hspace {-4pt} \upharpoonright \hspace {-3pt} X$
and
$g_r \hspace {-4pt} \upharpoonright \hspace {-3pt} X$
and
![]() $g_s \hspace {-4pt} \upharpoonright \hspace {-3pt} X$
induce the same equivalence relations on X. It follows that there are
$g_s \hspace {-4pt} \upharpoonright \hspace {-3pt} X$
induce the same equivalence relations on X. It follows that there are
![]() ${\mathcal M}$
-definable functions
${\mathcal M}$
-definable functions
![]() $e_0,e_1 : M \longrightarrow M$
such that for all
$e_0,e_1 : M \longrightarrow M$
such that for all
![]() $x \in X$
,
$x \in X$
,
![]() $e_0(g_r(x)) = g_s(x)$
and
$e_0(g_r(x)) = g_s(x)$
and
![]() $e_1(g_s(x)) = g_r(x)$
. But then
$e_1(g_s(x)) = g_r(x)$
. But then
![]() $e_0^{\mathcal N}(g_r(a)) = g_s(a)$
and
$e_0^{\mathcal N}(g_r(a)) = g_s(a)$
and
![]() $e_1^{\mathcal N}(g_s(a)) = g_r(a)$
, implying that
$e_1^{\mathcal N}(g_s(a)) = g_r(a)$
, implying that
![]() $F(r) = F(s)$
and, therefore,
$F(r) = F(s)$
and, therefore,
![]() $r = s$
.
$r = s$
.
Next, to prove that each
![]() $\alpha _X$
is a representation of L, it is enough to show that
$\alpha _X$
is a representation of L, it is enough to show that
![]() $\alpha _B$
is.
$\alpha _B$
is.
For all
![]() $x \in B$
,
$x \in B$
,
![]() $g_0(x) = f(0)$
and
$g_0(x) = f(0)$
and
![]() $g_1(x) = x$
, so
$g_1(x) = x$
, so
![]() $\alpha _B(0)$
is trivial and
$\alpha _B(0)$
is trivial and
![]() $\alpha _B(1)$
is discrete. Finally, we show that if
$\alpha _B(1)$
is discrete. Finally, we show that if
![]() $r,s \in L$
, then
$r,s \in L$
, then
![]() $\alpha _B(r \vee s) = \alpha _B(r) \wedge \alpha _B(s)$
. To do so, we let
$\alpha _B(r \vee s) = \alpha _B(r) \wedge \alpha _B(s)$
. To do so, we let
![]() $x,y \in X$
, and then show that
$x,y \in X$
, and then show that
![]() $\langle x,y \rangle \in \alpha _B(r \vee s) \Longleftrightarrow \langle x,y \rangle \in \alpha _B(r) \cap \alpha _B(s)$
.
$\langle x,y \rangle \in \alpha _B(r \vee s) \Longleftrightarrow \langle x,y \rangle \in \alpha _B(r) \cap \alpha _B(s)$
.
 $$ \begin{align*} \langle x,y \rangle \in \alpha_B(r \vee s) & \Rightarrow g_{r \vee s}(x) = g_{r \vee s}(y) \nonumber \\ & \Rightarrow g_{r,s}(g_{r \vee s}(x)) = g_{r,s}(g_{r \vee s}(y)) \nonumber \\ & \Rightarrow g_r(x) = g_r(y) \nonumber \\ & \Rightarrow \langle x,y \rangle \in \alpha_B(r). \nonumber \end{align*} $$
$$ \begin{align*} \langle x,y \rangle \in \alpha_B(r \vee s) & \Rightarrow g_{r \vee s}(x) = g_{r \vee s}(y) \nonumber \\ & \Rightarrow g_{r,s}(g_{r \vee s}(x)) = g_{r,s}(g_{r \vee s}(y)) \nonumber \\ & \Rightarrow g_r(x) = g_r(y) \nonumber \\ & \Rightarrow \langle x,y \rangle \in \alpha_B(r). \nonumber \end{align*} $$
Similarly,
![]() $\langle x,y \rangle \in \alpha _B(r \vee s) \Rightarrow \langle x,y \rangle \in \alpha _B(s)$
. Conversely,
$\langle x,y \rangle \in \alpha _B(r \vee s) \Rightarrow \langle x,y \rangle \in \alpha _B(s)$
. Conversely,
 $$ \begin{align*} \langle x,y \rangle \in \alpha_B(r) \cap \alpha_B(s) & \Rightarrow g_r(x) = g_r(y) \ \& \ g_s(x) = g_s(y) \nonumber \\ & \Rightarrow h_{r,s} (g_r(x),g_s(x)) = h_{r,s} (g_r(y),g_s(y)) \nonumber \\ & \Rightarrow g_{r\vee s}(x) = g_{r\vee s}(y) \nonumber \\ & \Rightarrow \langle x,y \rangle \in \alpha_B(r \vee s). \nonumber \end{align*} $$
$$ \begin{align*} \langle x,y \rangle \in \alpha_B(r) \cap \alpha_B(s) & \Rightarrow g_r(x) = g_r(y) \ \& \ g_s(x) = g_s(y) \nonumber \\ & \Rightarrow h_{r,s} (g_r(x),g_s(x)) = h_{r,s} (g_r(y),g_s(y)) \nonumber \\ & \Rightarrow g_{r\vee s}(x) = g_{r\vee s}(y) \nonumber \\ & \Rightarrow \langle x,y \rangle \in \alpha_B(r \vee s). \nonumber \end{align*} $$
Having that each
![]() $\alpha _X$
is a representation of L, we easily see that it is
$\alpha _X$
is a representation of L, we easily see that it is
![]() $0$
-CPP. For if X is partitioned into
$0$
-CPP. For if X is partitioned into
![]() $Y,Z \in \operatorname {\mathrm {Def}}({\mathcal M})$
, then either
$Y,Z \in \operatorname {\mathrm {Def}}({\mathcal M})$
, then either
![]() $a \in Y^{\mathcal N}$
or
$a \in Y^{\mathcal N}$
or
![]() $a \in Z^{\mathcal N}$
, but nodoubling both.
$a \in Z^{\mathcal N}$
, but nodoubling both.
Now let
![]() ${\mathcal C}$
be the set of all such
${\mathcal C}$
be the set of all such
![]() $\alpha _X$
; that is,
$\alpha _X$
; that is,
We have just seen that
![]() ${\mathcal C}$
is a nonempty set of
${\mathcal C}$
is a nonempty set of
![]() $0$
-CPP
$0$
-CPP
![]() ${\mathcal M}$
-representations of L, so that
${\mathcal M}$
-representations of L, so that
![]() $(1)$
of Definition 1.3 is verified. We prove (2) of Definition 1.3. Consider
$(1)$
of Definition 1.3 is verified. We prove (2) of Definition 1.3. Consider
![]() $\alpha _X \in {\mathcal C}$
. Let
$\alpha _X \in {\mathcal C}$
. Let
![]() $\Theta \in \operatorname {\mathrm {Eq}}(X)$
be
$\Theta \in \operatorname {\mathrm {Eq}}(X)$
be
![]() ${\mathcal M}$
-definable. Define
${\mathcal M}$
-definable. Define
![]() $m : X \longrightarrow X$
so that if
$m : X \longrightarrow X$
so that if
![]() $x \in X$
, then
$x \in X$
, then
![]() $m(x) = \min ([x]_\Theta )$
. Let
$m(x) = \min ([x]_\Theta )$
. Let
![]() $r \in L$
be such that
$r \in L$
be such that
![]() $m^{\mathcal N}(a)$
generates
$m^{\mathcal N}(a)$
generates
![]() $F(r)$
over
$F(r)$
over
![]() ${\mathcal M}$
. There are functions
${\mathcal M}$
. There are functions
![]() $e_0,e_1 : N \longrightarrow N$
that are
$e_0,e_1 : N \longrightarrow N$
that are
![]() ${\mathcal N}$
-definable but using parameters only from M such that
${\mathcal N}$
-definable but using parameters only from M such that
![]() $e_0(m^{\mathcal N}(a)) = g_r(a)$
and
$e_0(m^{\mathcal N}(a)) = g_r(a)$
and
![]() $e_1(g_r(a)) = m^{\mathcal N}(a)$
. Let
$e_1(g_r(a)) = m^{\mathcal N}(a)$
. Let
![]() $Y = \{x \in X : e_0(m^{\mathcal N}(x)) = g_r(x)$
and
$Y = \{x \in X : e_0(m^{\mathcal N}(x)) = g_r(x)$
and
![]() $e_1(g_r(x)) = m^{\mathcal N}(x)\}$
. Then
$e_1(g_r(x)) = m^{\mathcal N}(x)\}$
. Then
![]() $m \hspace {-4pt} \upharpoonright \hspace {-3pt} Y$
induces
$m \hspace {-4pt} \upharpoonright \hspace {-3pt} Y$
induces
![]() $\alpha _Y(r)$
. This completes the proof of (1).
$\alpha _Y(r)$
. This completes the proof of (1).
![]() $(2)$
Since
$(2)$
Since
![]() ${\mathcal C} \neq \varnothing $
, let
${\mathcal C} \neq \varnothing $
, let
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
be in
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
be in
![]() ${\mathcal C}$
. Let
${\mathcal C}$
. Let
![]() $\Theta _0,\Theta _1,\Theta _2, \ldots $
enumerate all
$\Theta _0,\Theta _1,\Theta _2, \ldots $
enumerate all
![]() ${\mathcal M}$
-definable equivalence relations on M. By recursion, obtain a sequence
${\mathcal M}$
-definable equivalence relations on M. By recursion, obtain a sequence
![]() $X_0 \supseteq X_1 \supseteq X_2 \supseteq \cdots $
of sets in
$X_0 \supseteq X_1 \supseteq X_2 \supseteq \cdots $
of sets in
![]() $\operatorname {\mathrm {Def}}({\mathcal M})$
as follows. Let
$\operatorname {\mathrm {Def}}({\mathcal M})$
as follows. Let
![]() $X_0 = A$
. Suppose that we have
$X_0 = A$
. Suppose that we have
![]() $X_n$
and that
$X_n$
and that
![]() $\alpha |X_n \in {\mathcal C}$
. Let
$\alpha |X_n \in {\mathcal C}$
. Let
![]() $X_{n+1} \subseteq X_n$
be such that
$X_{n+1} \subseteq X_n$
be such that
![]() $\alpha |X_{n+1} \in {\mathcal C}$
and
$\alpha |X_{n+1} \in {\mathcal C}$
and
![]() $\Theta _n \cap X_{n+1}^2$
is canonical for
$\Theta _n \cap X_{n+1}^2$
is canonical for
![]() $\alpha $
. The
$\alpha $
. The
![]() $X_n$
’s generate a complete type over
$X_n$
’s generate a complete type over
![]() ${\mathcal M}$
(using that each
${\mathcal M}$
(using that each
![]() $\alpha |X_n$
is 0-CPP). Let
$\alpha |X_n$
is 0-CPP). Let
![]() ${\mathcal N}$
be an elementary extension of
${\mathcal N}$
be an elementary extension of
![]() ${\mathcal M}$
generated by an element a realizing this type.
${\mathcal M}$
generated by an element a realizing this type.
For each
![]() $r \in L$
, let
$r \in L$
, let
![]() $t_r : M \longrightarrow M$
be
$t_r : M \longrightarrow M$
be
![]() ${\mathcal M}$
-definable such that whenever
${\mathcal M}$
-definable such that whenever
![]() $x \in X_0$
, then
$x \in X_0$
, then
![]() $t_r(x) = \min ([x]_{\alpha (r)})$
. Define the function F on L so that if
$t_r(x) = \min ([x]_{\alpha (r)})$
. Define the function F on L so that if
![]() $r \in L$
, then
$r \in L$
, then
![]() $F(r)$
is the elementary substructure of
$F(r)$
is the elementary substructure of
![]() ${\mathcal N}$
generated by
${\mathcal N}$
generated by
![]() $t^{\mathcal N}_r(a)$
over
$t^{\mathcal N}_r(a)$
over
![]() ${\mathcal M}$
. One easily checks that
${\mathcal M}$
. One easily checks that
![]() $F : L \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is an isomorphism.
$F : L \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is an isomorphism.
1.3. Ranked lattices
To refine the notions of end/cofinal/mixed extensions, we appeal to rankings of lattices [Reference Kossak and Schmerl1, Definition 4.2.6]. Suppose that L is a finite lattice. A function
![]() $\rho : L \longrightarrow L$
is a ranking of L if for each
$\rho : L \longrightarrow L$
is a ranking of L if for each
![]() $r,s \in L$
:
$r,s \in L$
:
-
(1)
 $\rho (r) \geq r,$
$\rho (r) \geq r,$
-
(2)
 $\rho (\rho (r)) = \rho (r)$
,
$\rho (\rho (r)) = \rho (r)$
, -
(3)
 $\rho (r) \leq \rho (s)$
or
$\rho (r) \leq \rho (s)$
or
 $\rho (s) \leq \rho (r)$
,
$\rho (s) \leq \rho (r)$
, -
(4)
 $\rho (r \vee s) = \rho (r) \vee \rho (s)$
.
$\rho (r \vee s) = \rho (r) \vee \rho (s)$
.
A ranking
![]() $\rho $
of L uniquely determines, and is uniquely determined by, its rankset
$\rho $
of L uniquely determines, and is uniquely determined by, its rankset
![]() $\{\rho (r) : r \in L\}$
. If L is finite and
$\{\rho (r) : r \in L\}$
. If L is finite and
![]() $R \subseteq L$
, then R is a rankset iff R is linearly ordered and
$R \subseteq L$
, then R is a rankset iff R is linearly ordered and
![]() $1_L \in R$
. If
$1_L \in R$
. If
![]() $\rho $
is a ranking of L, then
$\rho $
is a ranking of L, then
![]() $(L,\rho )$
is a ranked lattice.
$(L,\rho )$
is a ranked lattice.
If
![]() ${\mathcal M} \prec {\mathcal N}$
and
${\mathcal M} \prec {\mathcal N}$
and
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is finite, then let
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is finite, then let
![]() $\rho : \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
be such that if
$\rho : \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
be such that if
![]() ${\mathcal K} \in \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
, then
${\mathcal K} \in \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
, then
![]() $\rho ({\mathcal K})$
is uniquely defined by
$\rho ({\mathcal K})$
is uniquely defined by
One easily verifies that
![]() $\rho $
is a ranking of
$\rho $
is a ranking of
![]() $ \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
. We let
$ \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
. We let
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})$
be the ranked lattice
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})$
be the ranked lattice
![]() $(\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}),\rho )$
.
$(\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}),\rho )$
.
Suppose that
![]() $\rho $
is a ranking of the finite lattice L. Then
$\rho $
is a ranking of the finite lattice L. Then
![]() $\rho $
is an end ranking if
$\rho $
is an end ranking if
![]() $\rho (0_L) = 0_L$
, a cofinal ranking if
$\rho (0_L) = 0_L$
, a cofinal ranking if
![]() $\rho (0_L) = 1_L$
and a mixed ranking if
$\rho (0_L) = 1_L$
and a mixed ranking if
![]() $0_L < \rho (0_L) < 1_L$
. Obviously, L has a unique cofinal ranking. If
$0_L < \rho (0_L) < 1_L$
. Obviously, L has a unique cofinal ranking. If
![]() $\rho $
is an end, cofinal, or mixed ranking, then
$\rho $
is an end, cofinal, or mixed ranking, then
![]() $(L,\rho )$
is, respectively, an end, cofinal, or mixed ranked lattice. These definitions are appropriate: if
$(L,\rho )$
is, respectively, an end, cofinal, or mixed ranked lattice. These definitions are appropriate: if
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})$
is an end, cofinal, or mixed ranked lattice, then
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})$
is an end, cofinal, or mixed ranked lattice, then
![]() ${\mathcal N}$
is, respectively, an end, cofinal, or mixed extension of
${\mathcal N}$
is, respectively, an end, cofinal, or mixed extension of
![]() ${\mathcal M}$
.
${\mathcal M}$
.
Of the
![]() $10$
rankings of
$10$
rankings of
![]() $\mathbf {N}_5$
, four are depicted in Figure 2 by letting
$\mathbf {N}_5$
, four are depicted in Figure 2 by letting
![]() $\bullet $
denote those points in the rankset and
$\bullet $
denote those points in the rankset and
![]() $\circ $
those that are not. Of all the ranked pentagons, the four in Figure 2 are the most important for us because of the following.
$\circ $
those that are not. Of all the ranked pentagons, the four in Figure 2 are the most important for us because of the following.

Figure 2 Four ranked pentagon lattices.
Henceforth, we use the labeling of
![]() ${\mathbf N}_5$
as given in Figure 1.
${\mathbf N}_5$
as given in Figure 1.
Proposition 1.5. If
![]() ${\mathcal M} \prec {\mathcal N}$
and
${\mathcal M} \prec {\mathcal N}$
and
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong ({\mathbf N}_5, \rho )$
, then
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong ({\mathbf N}_5, \rho )$
, then
![]() $\rho = \nu _i$
for some
$\rho = \nu _i$
for some
![]() $i \leq 3$
.
$i \leq 3$
.
Proof We first show that
![]() $\rho (c) = 1$
. If
$\rho (c) = 1$
. If
![]() $\rho (c) \neq 1$
, then
$\rho (c) \neq 1$
, then
![]() $\rho (c) = c$
. We apply the Gaifman Condition [Reference Kossak and Schmerl1, Proposition 4.2.12] by letting
$\rho (c) = c$
. We apply the Gaifman Condition [Reference Kossak and Schmerl1, Proposition 4.2.12] by letting
![]() $x = a$
,
$x = a$
,
![]() $y = b$
, and
$y = b$
, and
![]() $z =c$
, to get the contradiction that
$z =c$
, to get the contradiction that
![]() $a = b$
.
$a = b$
.
If
![]() $\rho (0) = 1$
, then
$\rho (0) = 1$
, then
![]() $\rho = \nu _0$
. So, assume that
$\rho = \nu _0$
. So, assume that
![]() $\rho (0) < 1$
. Since
$\rho (0) < 1$
. Since
![]() $\rho (c) = 1$
and
$\rho (c) = 1$
and
![]() $c \wedge b = 0$
, it follows from the Blass Condition [Reference Kossak and Schmerl1, Proposition 4.2.7] that
$c \wedge b = 0$
, it follows from the Blass Condition [Reference Kossak and Schmerl1, Proposition 4.2.7] that
![]() $\rho (b) = b$
. Finally,
$\rho (b) = b$
. Finally,
![]() $\rho (0) \neq b$
by [Reference Kossak and Schmerl1, Theorem 4.6.1]. Thus,
$\rho (0) \neq b$
by [Reference Kossak and Schmerl1, Theorem 4.6.1]. Thus,
![]() $\rho (0) \in \{0,a\}$
, so it must be that
$\rho (0) \in \{0,a\}$
, so it must be that
![]() $\rho \in \{\nu _1,\nu _2, \nu _3\}$
.
$\rho \in \{\nu _1,\nu _2, \nu _3\}$
.
We make some comments about this proposition. First, Proposition 1.5
![]() ${}^*$
is also valid. Theorem 1 can now be restated as: For all countable
${}^*$
is also valid. Theorem 1 can now be restated as: For all countable
![]() ${\mathcal M}$
there are
${\mathcal M}$
there are
![]() $i \in \{1,2\}$
and
$i \in \{1,2\}$
and
![]() ${\mathcal N} \succ {\mathcal M}$
such that
${\mathcal N} \succ {\mathcal M}$
such that
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong ({\mathbf N}_5, \nu _i)$
. In fact, Wilkie’s proof of Theorem 1 yields that
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong ({\mathbf N}_5, \nu _i)$
. In fact, Wilkie’s proof of Theorem 1 yields that
![]() $i = 1$
. A similar proof shows that for every countable
$i = 1$
. A similar proof shows that for every countable
![]() ${\mathcal M}$
there is
${\mathcal M}$
there is
![]() ${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
such that
${\mathcal N} \succ _{\mathsf {end}} {\mathcal M}$
such that
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong ({\mathbf N}_5, \nu _2)$
. Since
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong ({\mathbf N}_5, \nu _2)$
. Since
![]() $\nu _3$
is the only mixed ranking of the four in Figure 2, then in Theorem 4 we get
$\nu _3$
is the only mixed ranking of the four in Figure 2, then in Theorem 4 we get
![]() ${\mathcal N}^*$
such that
${\mathcal N}^*$
such that
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N}^* / {\mathcal M}^*) \cong ({\mathbf N}_5, \nu _3)$
.
$\operatorname {\mathrm {Ltr}}({\mathcal N}^* / {\mathcal M}^*) \cong ({\mathbf N}_5, \nu _3)$
.
The next order of business is to generalize Definition 1.3 and Theorem 1.4 from lattices to ranked lattices.
First, we need some terminology. Suppose that
![]() ${\mathcal M}$
is a model,
${\mathcal M}$
is a model,
![]() $A \in \operatorname {\mathrm {Def}}({\mathcal M})$
, and
$A \in \operatorname {\mathrm {Def}}({\mathcal M})$
, and
![]() $\Theta \in \operatorname {\mathrm {Eq}}^{\mathcal M}(A)$
. We say that a set
$\Theta \in \operatorname {\mathrm {Eq}}^{\mathcal M}(A)$
. We say that a set
![]() ${\mathcal E}$
of
${\mathcal E}$
of
![]() $\Theta $
-classes is
$\Theta $
-classes is
![]() ${\mathcal M}$
-bounded if there is a bounded
${\mathcal M}$
-bounded if there is a bounded
![]() $I \in \operatorname {\mathrm {Def}}({\mathcal M})$
such that
$I \in \operatorname {\mathrm {Def}}({\mathcal M})$
such that
![]() $I \cap X \neq \varnothing $
for each
$I \cap X \neq \varnothing $
for each
![]() $X \in {\mathcal E}$
.
$X \in {\mathcal E}$
.
If
![]() $(L,\rho )$
is a finite ranked lattice, then a representation
$(L,\rho )$
is a finite ranked lattice, then a representation
![]() $\alpha $
of L is a representation of
$\alpha $
of L is a representation of
![]() $(L,\rho )$
if whenever
$(L,\rho )$
if whenever
![]() $r \leq s \in L$
, then
$r \leq s \in L$
, then
![]() $s \leq \rho (r)$
iff every
$s \leq \rho (r)$
iff every
![]() $\alpha (r)$
-class is the union of a finite set of
$\alpha (r)$
-class is the union of a finite set of
![]() $\alpha (s)$
-classes. This definition should help motivate the next definition.
$\alpha (s)$
-classes. This definition should help motivate the next definition.
Definition 1.6. Let
![]() ${\mathcal M}$
be a model and
${\mathcal M}$
be a model and
![]() $(L,\rho )$
a finite ranked lattice.
$(L,\rho )$
a finite ranked lattice.
(1) A representation
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is an
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is an
![]() ${\mathcal M}$
-representation of
${\mathcal M}$
-representation of
![]() $(L,\rho )$
if
$(L,\rho )$
if
![]() $\alpha $
is an
$\alpha $
is an
![]() ${\mathcal M}$
-representation of L and whenever
${\mathcal M}$
-representation of L and whenever
![]() $r \leq s \in L$
, then
$r \leq s \in L$
, then
![]() $s \leq \rho (r)$
iff every
$s \leq \rho (r)$
iff every
![]() $\alpha (r)$
-class is the union of an
$\alpha (r)$
-class is the union of an
![]() ${\mathcal M}$
-bounded set of
${\mathcal M}$
-bounded set of
![]() $\alpha (s)$
-classes.
$\alpha (s)$
-classes.
(2) We say that
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
![]() $(L,\rho )$
if
$(L,\rho )$
if
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${\mathcal M}$
-correct set of representations of L and each
${\mathcal M}$
-correct set of representations of L and each
![]() $\alpha \in {\mathcal C}$
is an
$\alpha \in {\mathcal C}$
is an
![]() ${\mathcal M}$
-representation of
${\mathcal M}$
-representation of
![]() $(L,\rho )$
.
$(L,\rho )$
.
We next generalize Theorem 1.4 from lattices to ranked lattices.
Theorem 1.7. Suppose that
![]() ${\mathcal M}$
is a model and
${\mathcal M}$
is a model and
![]() $(L,\rho )$
is a finite ranked lattice.
$(L,\rho )$
is a finite ranked lattice.
-
(1) If there is
 ${\mathcal N} \succ {\mathcal M}$
such that
${\mathcal N} \succ {\mathcal M}$
such that
 $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong (L,\rho )$
, then there is an
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong (L,\rho )$
, then there is an
 ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
 $(L,\rho )$
.
$(L,\rho )$
. -
(2) If
 ${\mathcal M}$
is countable and there is an
${\mathcal M}$
is countable and there is an
 ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
 $(L,\rho )$
, then there is
$(L,\rho )$
, then there is
 ${\mathcal N} \succ {\mathcal M}$
such that
${\mathcal N} \succ {\mathcal M}$
such that
 $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong (L,\rho )$
.
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M}) \cong (L,\rho )$
.
Proof
![]() $(1)$
Obtain
$(1)$
Obtain
![]() ${\mathcal C}$
as in the proof of Theorem 1.4(1), so that
${\mathcal C}$
as in the proof of Theorem 1.4(1), so that
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${\mathcal M}$
-correct set of representations of L. If
${\mathcal M}$
-correct set of representations of L. If
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is in
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
is in
![]() ${\mathcal C}$
,
${\mathcal C}$
,
![]() $r \leq s$
but not
$r \leq s$
but not
![]() $s \leq \rho (r)$
, then there is some
$s \leq \rho (r)$
, then there is some
![]() $\alpha (r)$
-class that is not the union of an
$\alpha (r)$
-class that is not the union of an
![]() ${\mathcal M}$
-bounded set of
${\mathcal M}$
-bounded set of
![]() $\alpha (s)$
-classes. (For, otherwise, there would be an
$\alpha (s)$
-classes. (For, otherwise, there would be an
![]() ${\mathcal M}$
-definable function
${\mathcal M}$
-definable function
![]() $b : M \longrightarrow M$
such that
$b : M \longrightarrow M$
such that
![]() $b(f(r)) \geq f(s)$
.) However, it could be that
$b(f(r)) \geq f(s)$
.) However, it could be that
![]() $r \leq s \leq \rho (r)$
and some
$r \leq s \leq \rho (r)$
and some
![]() $\alpha (r)$
-class is not the union of an
$\alpha (r)$
-class is not the union of an
![]() ${\mathcal M}$
-bounded set of
${\mathcal M}$
-bounded set of
![]() $\alpha (s)$
-classes. Let
$\alpha (s)$
-classes. Let
![]() ${\mathcal C}_0$
be the set of those
${\mathcal C}_0$
be the set of those
![]() $\alpha \in {\mathcal C}$
that are
$\alpha \in {\mathcal C}$
that are
![]() ${\mathcal M}$
-representations of
${\mathcal M}$
-representations of
![]() $(L, \rho )$
. We will show that this
$(L, \rho )$
. We will show that this
![]() ${\mathcal C}_0$
is an
${\mathcal C}_0$
is an
![]() ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
![]() $(L,\rho )$
. To see this, it suffices to show that for each
$(L,\rho )$
. To see this, it suffices to show that for each
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
in
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
in
![]() ${\mathcal C}$
, there is
${\mathcal C}$
, there is
![]() $B \subseteq A$
such that
$B \subseteq A$
such that
![]() $\alpha |B \in {\mathcal C}_0$
.
$\alpha |B \in {\mathcal C}_0$
.
Suppose that we have
![]() $\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
in
$\alpha : L \longrightarrow \operatorname {\mathrm {Eq}}(A)$
in
![]() ${\mathcal C}$
and that
${\mathcal C}$
and that
![]() $r \leq s \leq \rho (r)$
. Partition A into two sets
$r \leq s \leq \rho (r)$
. Partition A into two sets
![]() $A_0,A_1$
, so that
$A_0,A_1$
, so that
![]() $A_0$
is the union of those
$A_0$
is the union of those
![]() $\alpha (r)$
-classes that are the union of an
$\alpha (r)$
-classes that are the union of an
![]() ${\mathcal M}$
-bounded set of
${\mathcal M}$
-bounded set of
![]() $\alpha (s)$
-classes. Since
$\alpha (s)$
-classes. Since
![]() ${\mathcal C}$
is
${\mathcal C}$
is
![]() ${\mathcal M}$
-correct, then either
${\mathcal M}$
-correct, then either
![]() $\alpha |A_0 \in {\mathcal C}$
or
$\alpha |A_0 \in {\mathcal C}$
or
![]() $\alpha |A_1 \in {\mathcal C}$
. By what was previously said, the latter option is impossible, so we have that
$\alpha |A_1 \in {\mathcal C}$
. By what was previously said, the latter option is impossible, so we have that
![]() $\alpha |A_0 \in {\mathcal C}$
. Repeating this for all such
$\alpha |A_0 \in {\mathcal C}$
. Repeating this for all such
![]() $r,s \in L$
, finally yields
$r,s \in L$
, finally yields
![]() $B \subseteq A$
as required. This completes the proof of (1).
$B \subseteq A$
as required. This completes the proof of (1).
(2) Let
![]() ${\mathcal C}$
be an
${\mathcal C}$
be an
![]() ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
![]() $(L,\rho )$
. Then
$(L,\rho )$
. Then
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${\mathcal M}$
-correct set of representations of L, so we can obtain
${\mathcal M}$
-correct set of representations of L, so we can obtain
![]() ${\mathcal N} \succ {\mathcal M}$
as in the proof of Theorem 1.4(2). Then
${\mathcal N} \succ {\mathcal M}$
as in the proof of Theorem 1.4(2). Then
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong L$
.
We use the notation from the proof of Theorem 1.4(2). Thus,
![]() $F : L \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is an isomorphism and
$F : L \longrightarrow \operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M})$
is an isomorphism and
![]() $F(r)$
is generated by
$F(r)$
is generated by
![]() $t_r(a)$
over
$t_r(a)$
over
![]() ${\mathcal M}$
. We prove that F is also an isomorphism of the ranked lattices
${\mathcal M}$
. We prove that F is also an isomorphism of the ranked lattices
![]() $(L,\rho )$
and
$(L,\rho )$
and
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})$
. It suffices to prove: whenever
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})$
. It suffices to prove: whenever
![]() $r < s \in L$
, then
$r < s \in L$
, then
![]() $s \leq \rho (r)$
iff
$s \leq \rho (r)$
iff
![]() $F(r) \prec _{\mathsf {cf}} F(s)$
. So, let
$F(r) \prec _{\mathsf {cf}} F(s)$
. So, let
![]() $r < s \in L$
.
$r < s \in L$
.
![]() $(\Longrightarrow )$
: Suppose that
$(\Longrightarrow )$
: Suppose that
![]() $s \leq \rho (r)$
. Consider
$s \leq \rho (r)$
. Consider
![]() $\alpha \in {\mathcal C}$
. Every
$\alpha \in {\mathcal C}$
. Every
![]() $\alpha (r)$
-class is the union of an
$\alpha (r)$
-class is the union of an
![]() ${\mathcal M}$
-bounded set of
${\mathcal M}$
-bounded set of
![]() $\alpha (s)$
-classes. Let
$\alpha (s)$
-classes. Let
![]() $g : M \longrightarrow M$
be an
$g : M \longrightarrow M$
be an
![]() ${\mathcal M}$
-definable function such that if
${\mathcal M}$
-definable function such that if
![]() $x \in X$
, then
$x \in X$
, then
![]() $g(x) = \max \{t_s(y) : \langle x,y \rangle \in \alpha (r)\}$
. Clearly,
$g(x) = \max \{t_s(y) : \langle x,y \rangle \in \alpha (r)\}$
. Clearly,
![]() $g(x)$
is well defined for
$g(x)$
is well defined for
![]() $x \in X$
, so there is such an
$x \in X$
, so there is such an
![]() ${\mathcal M}$
-definable g. Thus,
${\mathcal M}$
-definable g. Thus,
![]() $g(t_r(x)) \geq t_s(x)$
for all
$g(t_r(x)) \geq t_s(x)$
for all
![]() $x \in X$
, so that
$x \in X$
, so that
![]() $g^{\mathcal N}(t_r^{\mathcal N}(a)) \geq t_s^{\mathcal N}(a)$
. Therefore,
$g^{\mathcal N}(t_r^{\mathcal N}(a)) \geq t_s^{\mathcal N}(a)$
. Therefore,
![]() $F(r) \prec _{\mathsf {cf}} F(s)$
.
$F(r) \prec _{\mathsf {cf}} F(s)$
.
![]() $(\Longleftarrow )$
: Suppose that
$(\Longleftarrow )$
: Suppose that
![]() $F(r) \prec _{\mathsf {cf}} F(s)$
. Then there is an
$F(r) \prec _{\mathsf {cf}} F(s)$
. Then there is an
![]() ${\mathcal M}$
-definable
${\mathcal M}$
-definable
![]() $g : M \longrightarrow M$
such that
$g : M \longrightarrow M$
such that
![]() $g^{\mathcal N}(t_r^{\mathcal N}(a)) \geq t_s^{\mathcal N}(a)$
. There is
$g^{\mathcal N}(t_r^{\mathcal N}(a)) \geq t_s^{\mathcal N}(a)$
. There is
![]() $X_i$
such that
$X_i$
such that
![]() $g(t_r(x)) \geq t_s(x)$
for all
$g(t_r(x)) \geq t_s(x)$
for all
![]() $x \in X_i$
. Let
$x \in X_i$
. Let
![]() $\alpha _i = \alpha |X_i \in {\mathcal C}$
. Thus, each
$\alpha _i = \alpha |X_i \in {\mathcal C}$
. Thus, each
![]() $\alpha _i(r)$
-class is the union of an
$\alpha _i(r)$
-class is the union of an
![]() ${\mathcal M}$
-bounded set of
${\mathcal M}$
-bounded set of
![]() $\alpha _i(s)$
-classes. Then
$\alpha _i(s)$
-classes. Then
![]() $s \leq \rho (r)$
.
$s \leq \rho (r)$
.
Wilkie’s proof of Theorem 1 made implicit use of Theorem 1.7(2).
2. Proving Theorem 3
This section is devoted to proving Theorem 3.
With the idea of obtaining a contradiction, assume that
![]() ${\mathcal M} \prec _{\mathsf {mix}} {\mathcal N}$
and that
${\mathcal M} \prec _{\mathsf {mix}} {\mathcal N}$
and that
![]() $\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong \mathbf {N}_5$
. Proposition 1.4 implies that
$\operatorname {\mathrm {Lt}}({\mathcal N} / {\mathcal M}) \cong \mathbf {N}_5$
. Proposition 1.4 implies that
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})\ \cong (\mathbf {N}_5, \nu _3)$
. Following Theorem 1.7(1), we let
$\operatorname {\mathrm {Ltr}}({\mathcal N} / {\mathcal M})\ \cong (\mathbf {N}_5, \nu _3)$
. Following Theorem 1.7(1), we let
![]() ${\mathcal C}$
be an
${\mathcal C}$
be an
![]() ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
![]() $({\mathbf N}_5, \nu _3)$
. In the course of this proof, we will see that
$({\mathbf N}_5, \nu _3)$
. In the course of this proof, we will see that
![]() ${\mathcal C}$
must have certain properties. We will also see that there are other properties that
${\mathcal C}$
must have certain properties. We will also see that there are other properties that
![]() ${\mathcal C}$
possibly could have, and we will then assume that
${\mathcal C}$
possibly could have, and we will then assume that
![]() ${\mathcal C}$
does have these properties.
${\mathcal C}$
does have these properties.
Since
![]() ${\mathcal C} \neq \varnothing $
, fix some
${\mathcal C} \neq \varnothing $
, fix some
![]() $\alpha \in {\mathcal C}$
. Thus,
$\alpha \in {\mathcal C}$
. Thus,
![]() $\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
. We can assume:
$\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
. We can assume:
-
(C1) For every
 $\beta \in {\mathcal C}$
, there is
$\beta \in {\mathcal C}$
, there is
 $B \subseteq A$
such that
$B \subseteq A$
such that
 $\beta = \alpha | B$
.
$\beta = \alpha | B$
.
Since
![]() $a \vee c = 1$
, then
$a \vee c = 1$
, then
![]() $\alpha (a) \cap \alpha (c) = 0 {\hspace{-6.3pt} 0}_A$
; therefore, whenever X is an
$\alpha (a) \cap \alpha (c) = 0 {\hspace{-6.3pt} 0}_A$
; therefore, whenever X is an
![]() $\alpha (a)$
-class and Z is an
$\alpha (a)$
-class and Z is an
![]() $\alpha (c)$
-class, then
$\alpha (c)$
-class, then
![]() $|X \cap Z| \leq 1$
. Since
$|X \cap Z| \leq 1$
. Since
![]() $0 < a = \nu _3(0)$
, then, according to Definition 1.6, the set of
$0 < a = \nu _3(0)$
, then, according to Definition 1.6, the set of
![]() $\alpha (a)$
-classes is
$\alpha (a)$
-classes is
![]() ${\mathcal M}$
-bounded; let
${\mathcal M}$
-bounded; let
![]() $n +1\in M$
be the number of
$n +1\in M$
be the number of
![]() $\alpha (a)$
-classes according to
$\alpha (a)$
-classes according to
![]() ${\mathcal M}$
. Then, we can assume:
${\mathcal M}$
. Then, we can assume:
-
(C2)
 $\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
, where
$\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
, where
 $A = [0,n] \times M$
and n is nonstandard, is such that if
$A = [0,n] \times M$
and n is nonstandard, is such that if
 $\langle i,j \rangle , \langle i',j' \rangle \in A$
, then
$\langle i,j \rangle , \langle i',j' \rangle \in A$
, then  $$ \begin{align*} \big\langle \langle i,j \rangle, \langle i',j' \rangle \big\rangle \in \alpha(a) \mbox{ iff } i = i', \end{align*} $$
$$ \begin{align*} \big\langle \langle i,j \rangle, \langle i',j' \rangle \big\rangle \in \alpha(a) \mbox{ iff } i = i', \end{align*} $$
 $$ \begin{align*}\big\langle \langle i,j \rangle, \langle i',j' \rangle \big\rangle \in \alpha(c) \mbox{ iff } j = j'. \end{align*} $$
$$ \begin{align*}\big\langle \langle i,j \rangle, \langle i',j' \rangle \big\rangle \in \alpha(c) \mbox{ iff } j = j'. \end{align*} $$
At first, it may look as if we can only assume that
![]() $A \subseteq [0,n] \times M$
. But it is always possible to enlarge the set A so as to get
$A \subseteq [0,n] \times M$
. But it is always possible to enlarge the set A so as to get
![]() $[0,n] \times M$
.
$[0,n] \times M$
.
For just this proof, let us say that the
![]() ${\mathcal M}$
-representation
${\mathcal M}$
-representation
![]() $\beta $
of
$\beta $
of
![]() ${\mathbf N}_5$
is rectangular if
${\mathbf N}_5$
is rectangular if
![]() $|X \cap Z| = 1$
for each
$|X \cap Z| = 1$
for each
![]() $\beta (a)$
-class X and
$\beta (a)$
-class X and
![]() $\beta (c)$
-class Z. We see from (C2) that
$\beta (c)$
-class Z. We see from (C2) that
![]() $\alpha $
is rectangular. We can even assume:
$\alpha $
is rectangular. We can even assume:
-
(C3) Every
 $\beta \in {\mathcal C}$
is a rectangular representation.
$\beta \in {\mathcal C}$
is a rectangular representation.
To see why, let
![]() ${\mathcal C}_0$
be the set of those rectangular
${\mathcal C}_0$
be the set of those rectangular
![]() ${\mathcal M}$
-representations
${\mathcal M}$
-representations
![]() $\beta $
, where
$\beta $
, where
![]() $B \subseteq A$
and
$B \subseteq A$
and
![]() $\beta = \alpha |B$
, for which there is
$\beta = \alpha |B$
, for which there is
![]() $A_0 \subseteq B$
such that
$A_0 \subseteq B$
such that
![]() $\alpha |A_0 \in {\mathcal C}$
. To prove that this
$\alpha |A_0 \in {\mathcal C}$
. To prove that this
![]() ${\mathcal C}_0$
is an
${\mathcal C}_0$
is an
![]() ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
![]() $({\mathbf N}_5,\nu _3)$
, it suffices to prove that if
$({\mathbf N}_5,\nu _3)$
, it suffices to prove that if
![]() $A_1 \subseteq A$
and
$A_1 \subseteq A$
and
![]() $\alpha | A_1\in {\mathcal C}$
, then there is
$\alpha | A_1\in {\mathcal C}$
, then there is
![]() $B \subseteq A_1$
such that
$B \subseteq A_1$
such that
![]() $\alpha |B \in {\mathcal C}_0$
. To prove this, consider some
$\alpha |B \in {\mathcal C}_0$
. To prove this, consider some
![]() $\alpha _1 = \alpha |A_1 \in {\mathcal C}$
. Define
$\alpha _1 = \alpha |A_1 \in {\mathcal C}$
. Define
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A_1)$
so that if
$\Theta \in \operatorname {\mathrm {Eq}}(A_1)$
so that if
![]() $y,z \in A_1$
, then
$y,z \in A_1$
, then
![]() $\langle y,z \rangle \in \Theta $
iff the following holds for each
$\langle y,z \rangle \in \Theta $
iff the following holds for each
![]() $\alpha _1(a)$
-class X: there is
$\alpha _1(a)$
-class X: there is
![]() $u \in X$
such that
$u \in X$
such that
![]() $\langle u,y \rangle \in \alpha _1(c)$
iff there is
$\langle u,y \rangle \in \alpha _1(c)$
iff there is
![]() $v \in X$
such that
$v \in X$
such that
![]() $\langle v,z \rangle \in \alpha _1(c)$
. Clearly,
$\langle v,z \rangle \in \alpha _1(c)$
. Clearly,
![]() $\alpha _1(c) \subseteq \Theta \in \operatorname {\mathrm {Eq}}(A_1)$
. Since
$\alpha _1(c) \subseteq \Theta \in \operatorname {\mathrm {Eq}}(A_1)$
. Since
![]() ${\mathcal C}$
is
${\mathcal C}$
is
![]() ${\mathcal M}$
-correct, there are
${\mathcal M}$
-correct, there are
![]() $A_0 \subseteq A_1$
and
$A_0 \subseteq A_1$
and
![]() $r \in \{0,c\}$
such that
$r \in \{0,c\}$
such that
![]() $\alpha |A_0 \in {\mathcal C}$
and
$\alpha |A_0 \in {\mathcal C}$
and
![]() $\alpha _1(r) \cap A_0^2 = \Theta \cap A_0^2$
. The number of
$\alpha _1(r) \cap A_0^2 = \Theta \cap A_0^2$
. The number of
![]() $\Theta $
-classes is at most
$\Theta $
-classes is at most
![]() $2^{n+1}$
, so it must be that
$2^{n+1}$
, so it must be that
![]() $r = 0$
. Let B be the union of those
$r = 0$
. Let B be the union of those
![]() $\alpha _1(c)$
-classes that have a nonempty intersection with
$\alpha _1(c)$
-classes that have a nonempty intersection with
![]() $A_0$
. Then
$A_0$
. Then
![]() $A_0 \subseteq B \subseteq A_1$
and
$A_0 \subseteq B \subseteq A_1$
and
![]() $\beta = \alpha |B \in {\mathcal C}_0$
. This proves that
$\beta = \alpha |B \in {\mathcal C}_0$
. This proves that
![]() ${\mathcal C}_0$
is an
${\mathcal C}_0$
is an
![]() ${\mathcal M}$
-correct set of rectangular representations of
${\mathcal M}$
-correct set of rectangular representations of
![]() $({\mathbf N}_5, \nu _3)$
, so we can assume (C3).
$({\mathbf N}_5, \nu _3)$
, so we can assume (C3).
Moreover, we can also assume:
-
(C4) If
 $I \subseteq I' \subseteq [0,n]$
,
$I \subseteq I' \subseteq [0,n]$
,
 $J \subseteq J' \subseteq M$
, and
$J \subseteq J' \subseteq M$
, and
 $\alpha |(I \times J) \in {\mathcal C}$
, then
$\alpha |(I \times J) \in {\mathcal C}$
, then
 $\alpha |(I' \times J') \in {\mathcal C}$
.
$\alpha |(I' \times J') \in {\mathcal C}$
.
Working in
![]() ${\mathcal M}$
, let
${\mathcal M}$
, let
![]() $\langle B_k : k \in M \rangle $
be a one-to-one enumeration of all
$\langle B_k : k \in M \rangle $
be a one-to-one enumeration of all
![]() $\alpha (b)$
-classes. Thus, we let
$\alpha (b)$
-classes. Thus, we let
![]() $\psi (u,v)$
be an
$\psi (u,v)$
be an
![]() ${\mathcal L}(M)$
-formula such that
${\mathcal L}(M)$
-formula such that
We also let
![]() $q : [0,n] \times M \longrightarrow M$
be such that if
$q : [0,n] \times M \longrightarrow M$
be such that if
![]() $\langle i,j \rangle \in A$
, then
$\langle i,j \rangle \in A$
, then
![]() $q(i,j) = k$
, where
$q(i,j) = k$
, where
![]() $\langle i,j \rangle \in B_k$
.
$\langle i,j \rangle \in B_k$
.
If
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
is in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
is in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() $p \in M$
, then there is
$p \in M$
, then there is
![]() $X' \subseteq X$
such that
$X' \subseteq X$
such that
![]() $\beta | X' \in {\mathcal C}$
and if
$\beta | X' \in {\mathcal C}$
and if
![]() $B_k \cap X' \neq \varnothing $
, then
$B_k \cap X' \neq \varnothing $
, then
![]() $k> p$
. To see why, just consider
$k> p$
. To see why, just consider
![]() $\Theta \in \operatorname {\mathrm {Eq}}(X)$
such that
$\Theta \in \operatorname {\mathrm {Eq}}(X)$
such that
![]() $\bigcup \{B_k \cap X : k> p\}$
is a
$\bigcup \{B_k \cap X : k> p\}$
is a
![]() $\Theta $
-class and then apply Definitions 1.3 and 1.6.
$\Theta $
-class and then apply Definitions 1.3 and 1.6.
For each
![]() $j \in M$
, there is a (unique) permutation
$j \in M$
, there is a (unique) permutation
![]() $\pi _j$
of
$\pi _j$
of
![]() $[0,n]$
defined by the following condition: if
$[0,n]$
defined by the following condition: if
![]() $i,i' \leq n$
, then
$i,i' \leq n$
, then
![]() $\pi _j(i) \leq \pi _j(i')$
iff
$\pi _j(i) \leq \pi _j(i')$
iff
![]() $q(i,j) \leq q(I',j)$
. Using these permutations, we define
$q(i,j) \leq q(I',j)$
. Using these permutations, we define
![]() $\Psi \in \operatorname {\mathrm {Eq}}(A)$
so that
$\Psi \in \operatorname {\mathrm {Eq}}(A)$
so that
![]() $\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \in \Psi $
iff
$\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \in \Psi $
iff
![]() $\pi _{j} = \pi _{j'}$
. Clearly,
$\pi _{j} = \pi _{j'}$
. Clearly,
![]() $\beta (c) \subseteq \Psi $
and the set of
$\beta (c) \subseteq \Psi $
and the set of
![]() $\Psi $
-classes is
$\Psi $
-classes is
![]() ${\mathcal M}$
-bounded as
${\mathcal M}$
-bounded as
![]() ${\mathcal M}$
thinks that there are no more than
${\mathcal M}$
thinks that there are no more than
![]() $(n+1)!\ \Psi $
-classes. Thus, there are
$(n+1)!\ \Psi $
-classes. Thus, there are
![]() $I \times J \subseteq [0,n] \times M = A$
and
$I \times J \subseteq [0,n] \times M = A$
and
![]() $\pi $
such that
$\pi $
such that
![]() $\alpha |(I \times J) \in {\mathcal C}$
and
$\alpha |(I \times J) \in {\mathcal C}$
and
![]() $\pi _j = \pi $
whenever
$\pi _j = \pi $
whenever
![]() $\langle i,j \rangle \in I \times J$
. Without loss of generality, we assume that
$\langle i,j \rangle \in I \times J$
. Without loss of generality, we assume that
![]() $J = M$
and that
$J = M$
and that
![]() $\pi $
is the identity permutation. Thus, we can assume:
$\pi $
is the identity permutation. Thus, we can assume:
-
(C5)
 $A = I \times J = [0,n] \times M$
, and if
$A = I \times J = [0,n] \times M$
, and if
 $i,i' \leq n$
and
$i,i' \leq n$
and
 $j \in M$
, then
$j \in M$
, then  $$ \begin{align*}i \leq i' \mbox{ iff } q(i,j) \leq q(i',j). \end{align*} $$
$$ \begin{align*}i \leq i' \mbox{ iff } q(i,j) \leq q(i',j). \end{align*} $$
We now have that
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${\mathcal M}$
-correct set of representations of
${\mathcal M}$
-correct set of representations of
![]() $({\mathbf N}_5,\nu _3)$
satisfying (C1)–(C5).
$({\mathbf N}_5,\nu _3)$
satisfying (C1)–(C5).
With (C5) in mind, we make a couple of definitions concerning a
![]() $\beta \in {\mathcal C}$
, where
$\beta \in {\mathcal C}$
, where
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(I \times J)$
. Suppose that X and Y are
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(I \times J)$
. Suppose that X and Y are
![]() $\beta (b)$
-classes. We say that X is below Y if there are
$\beta (b)$
-classes. We say that X is below Y if there are
![]() $i,i' \in I$
and
$i,i' \in I$
and
![]() $j \in J$
such that
$j \in J$
such that
![]() $\langle i,j \rangle \in X$
,
$\langle i,j \rangle \in X$
,
![]() $\langle i',j \rangle \in Y$
, and
$\langle i',j \rangle \in Y$
, and
![]() $i < i'$
. If X is below Y, then Y is above X. Thus, (C5) says: If
$i < i'$
. If X is below Y, then Y is above X. Thus, (C5) says: If
![]() $B_k$
is below
$B_k$
is below
![]() $B_{k'}$
(as
$B_{k'}$
(as
![]() $\alpha (b)$
-classes), then
$\alpha (b)$
-classes), then
![]() $k < k'$
. The following is a consequence of (C5):
$k < k'$
. The following is a consequence of (C5):
-
(C6) For each
 $\alpha (b)$
-class, the set of
$\alpha (b)$
-class, the set of
 $\alpha (b)$
-classes below it is
$\alpha (b)$
-classes below it is
 ${\mathcal M}$
-bounded.
${\mathcal M}$
-bounded.
We next show that it can be assumed that
![]() $\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
has a very specific form. Recall that if
$\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
has a very specific form. Recall that if
![]() $d \in M$
, then
$d \in M$
, then
![]() $M^d$
is the set (of codes) of all definable sequences of length d. For a given
$M^d$
is the set (of codes) of all definable sequences of length d. For a given
![]() $d \in M$
, with
$d \in M$
, with
![]() $d> 0$
, we will think of
$d> 0$
, we will think of
![]() $M^d = M$
. Also,
$M^d = M$
. Also,
![]() $t \in M^d$
and
$t \in M^d$
and
![]() $i < d$
, then
$i < d$
, then
![]() $t_i$
is the i-th element of the sequence coded by t. If
$t_i$
is the i-th element of the sequence coded by t. If
![]() $t \in M^d$
and
$t \in M^d$
and
![]() $e \leq d$
, then
$e \leq d$
, then
![]() $t \hspace {-4pt} \upharpoonright \hspace {-3pt} e$
is the (code of) the sequence of length e whose i-th element is the same as the i-th element of t.
$t \hspace {-4pt} \upharpoonright \hspace {-3pt} e$
is the (code of) the sequence of length e whose i-th element is the same as the i-th element of t.
We can assume the following, which improves on (C2):
-
(C7)
 $\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
, where
$\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
, where
 $A = [0,n] \times M^n$
, such that, in addition to (C2), we have if
$A = [0,n] \times M^n$
, such that, in addition to (C2), we have if
 $\langle i,t \rangle , \langle i',t' \rangle \in A$
, then
$\langle i,t \rangle , \langle i',t' \rangle \in A$
, then  $$ \begin{align*}\big\langle \langle i,t \rangle, \langle i',t' \rangle \big\rangle\in \alpha(b) {\mbox{ iff }} i = i' {\mbox{ and }} t\hspace{-4pt} \upharpoonright \hspace{-3pt} i = t' \hspace{-4pt} \upharpoonright \hspace{-3pt} i'. \end{align*} $$
$$ \begin{align*}\big\langle \langle i,t \rangle, \langle i',t' \rangle \big\rangle\in \alpha(b) {\mbox{ iff }} i = i' {\mbox{ and }} t\hspace{-4pt} \upharpoonright \hspace{-3pt} i = t' \hspace{-4pt} \upharpoonright \hspace{-3pt} i'. \end{align*} $$
Let
![]() $\alpha $
and A be, for now, as in (C2). Let G be a function on A such that if
$\alpha $
and A be, for now, as in (C2). Let G be a function on A such that if
![]() $\langle i,j \rangle \in A$
, then
$\langle i,j \rangle \in A$
, then
Then G is definable in
![]() ${\mathcal M}$
. Let
${\mathcal M}$
. Let
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A)$
be induced by G. We easily see that
$\Theta \in \operatorname {\mathrm {Eq}}(A)$
be induced by G. We easily see that
![]() $\Theta \subseteq \alpha (b)$
. Thus, there is a definable
$\Theta \subseteq \alpha (b)$
. Thus, there is a definable
![]() $X \subseteq A$
such that
$X \subseteq A$
such that
![]() $X = I \times J$
,
$X = I \times J$
,
![]() $\alpha \hspace {-4pt} \upharpoonright \hspace {-3pt} X \in {\mathcal C}$
and
$\alpha \hspace {-4pt} \upharpoonright \hspace {-3pt} X \in {\mathcal C}$
and
![]() $\alpha (r) \cap X^2 = \Theta \cap X^2$
for some
$\alpha (r) \cap X^2 = \Theta \cap X^2$
for some
![]() $r \in {\mathbf N}_5$
, with
$r \in {\mathbf N}_5$
, with
![]() $r \geq b$
. From (C6) we get that
$r \geq b$
. From (C6) we get that
![]() $r = b$
. We then see that if
$r = b$
. We then see that if
![]() $j \in J$
,
$j \in J$
,
![]() $i,i' \in I$
and
$i,i' \in I$
and
![]() $i < i'$
, then
$i < i'$
, then
![]() $B_{q( i,j )} \cap X \supseteq B_{q( i',j )} $
. It then follows that we can also assume (C7).
$B_{q( i,j )} \cap X \supseteq B_{q( i',j )} $
. It then follows that we can also assume (C7).
A consequence of (C7) is that
![]() $\alpha $
and q are defined by
$\alpha $
and q are defined by
![]() $\Sigma _0\ {\mathcal L}(\{n\})$
-formulas.
$\Sigma _0\ {\mathcal L}(\{n\})$
-formulas.
We saw in (C3) that every
![]() $\beta \in {\mathcal C}$
is rectangular. We also can assume the following:
$\beta \in {\mathcal C}$
is rectangular. We also can assume the following:
-
(C8) If
 $\beta = \alpha |(I \times J) \in {\mathcal C}$
, then
$\beta = \alpha |(I \times J) \in {\mathcal C}$
, then
 $\{\min (I)\} \times J$
is a
$\{\min (I)\} \times J$
is a
 $\beta (b)$
-class.
$\beta (b)$
-class.
To see why, suppose that
![]() $\beta = \alpha |(I \times J) \in {\mathcal C}$
and
$\beta = \alpha |(I \times J) \in {\mathcal C}$
and
![]() $\{\min (I)\} \times J$
is not a
$\{\min (I)\} \times J$
is not a
![]() $\beta (b)$
-class. Let
$\beta (b)$
-class. Let
![]() $\Theta \in \operatorname {\mathrm {Eq}}(I \times J)$
be such that and if
$\Theta \in \operatorname {\mathrm {Eq}}(I \times J)$
be such that and if
![]() $\langle i,j \rangle , \langle i',j' \rangle \in I \times J$
, then
$\langle i,j \rangle , \langle i',j' \rangle \in I \times J$
, then
![]() $\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \in \Theta $
iff
$\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \in \Theta $
iff
![]() $\big \langle \langle \min (I),j \rangle , \langle \min (I),j' \rangle \big \rangle \in \beta (b)$
. Clearly,
$\big \langle \langle \min (I),j \rangle , \langle \min (I),j' \rangle \big \rangle \in \beta (b)$
. Clearly,
![]() $\Theta \in \operatorname {\mathrm {Eq}}^{\mathcal M}(I \times J)$
. Let
$\Theta \in \operatorname {\mathrm {Eq}}^{\mathcal M}(I \times J)$
. Let
![]() $X \subseteq I \times J$
be such that
$X \subseteq I \times J$
be such that
![]() $\beta |X \in {\mathcal C}$
and for some
$\beta |X \in {\mathcal C}$
and for some
![]() $r \in {\mathbf N}_5$
,
$r \in {\mathbf N}_5$
,
![]() $\Theta \cap X^2 = \beta (r) \cap X^2$
. It must be that
$\Theta \cap X^2 = \beta (r) \cap X^2$
. It must be that
![]() $r = 0$
, so there is a
$r = 0$
, so there is a
![]() $\beta (b)$
-class B such that
$\beta (b)$
-class B such that
![]() $X \subseteq B \times J$
. Then, we can assume that
$X \subseteq B \times J$
. Then, we can assume that
![]() $\beta \not \in {\mathcal C}$
and that
$\beta \not \in {\mathcal C}$
and that
![]() $\beta |(B \times J) \in {\mathcal C}$
.
$\beta |(B \times J) \in {\mathcal C}$
.
We will refer to the
![]() $\beta (b)$
-class from (C8) as the root of
$\beta (b)$
-class from (C8) as the root of
![]() $\beta $
.
$\beta $
.
Corollary 2.1. For each
![]() $\beta \in {\mathcal C}$
, there is a
$\beta \in {\mathcal C}$
, there is a
![]() $\beta (b)$
-class X having an
$\beta (b)$
-class X having an
![]() ${\mathcal M}$
-unbounded set of
${\mathcal M}$
-unbounded set of
![]() $\beta (b)$
-classes above it.
$\beta (b)$
-classes above it.
Proof In fact, the root is such
![]() $\beta (b)$
-class.
$\beta (b)$
-class.
Corollary 2.2. If
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
is in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
is in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() $p \in M$
, then there is
$p \in M$
, then there is
![]() $Y \subseteq X$
such that
$Y \subseteq X$
such that
![]() $\beta |Y \in {\mathcal C}$
and if
$\beta |Y \in {\mathcal C}$
and if
![]() $\langle i,j \rangle \in Y$
, then
$\langle i,j \rangle \in Y$
, then
![]() $q(i,j)> p$
.
$q(i,j)> p$
.
Proof Consider
![]() $\Theta \in \operatorname {\mathrm {Eq}}(X)$
such that for
$\Theta \in \operatorname {\mathrm {Eq}}(X)$
such that for
![]() $\langle i,j \rangle , \langle i',j' \rangle \in X$
, then
$\langle i,j \rangle , \langle i',j' \rangle \in X$
, then
![]() $\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \in \Theta $
iff
$\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \in \Theta $
iff
![]() $q(i,j)> p \Longleftrightarrow q(i',j') > p$
. Then apply Corollary 2.1.
$q(i,j)> p \Longleftrightarrow q(i',j') > p$
. Then apply Corollary 2.1.
Consider some
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
in
![]() ${\mathcal C}$
, where
${\mathcal C}$
, where
![]() $X = I \times J \subseteq [0,n] \times M$
. For each
$X = I \times J \subseteq [0,n] \times M$
. For each
![]() $m < \omega $
, we say that
$m < \omega $
, we say that
![]() $\beta $
is m-thick if whenever
$\beta $
is m-thick if whenever
![]() $f : M \longrightarrow M$
is definable, then there are
$f : M \longrightarrow M$
is definable, then there are
![]() $i_0,i_1, \ldots ,i_m \in I$
and
$i_0,i_1, \ldots ,i_m \in I$
and
![]() $j \in J$
such that
$j \in J$
such that
![]() $f(q(i_k,j)) < q(i_{k+1},j)$
for each
$f(q(i_k,j)) < q(i_{k+1},j)$
for each
![]() $k < m$
.
$k < m$
.
Lemma 2.3. If
![]() $ m < \omega $
, then every
$ m < \omega $
, then every
![]() $\beta \in {\mathcal C}$
is m-thick.
$\beta \in {\mathcal C}$
is m-thick.
Proof Notice that every
![]() $\beta \in {\mathcal C}$
is vacuously
$\beta \in {\mathcal C}$
is vacuously
![]() $0$
-thick.
$0$
-thick.
First, we show that every
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(B)$
in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(B)$
in
![]() ${\mathcal C}$
is
${\mathcal C}$
is
![]() $1$
-thick. By Corollary 2.1, there is a
$1$
-thick. By Corollary 2.1, there is a
![]() $\beta (b)$
-class
$\beta (b)$
-class
![]() $B \cap B_{k_0}$
having an
$B \cap B_{k_0}$
having an
![]() ${\mathcal M}$
-unbounded set of
${\mathcal M}$
-unbounded set of
![]() $\beta (b)$
-classes above it. Thus, for any
$\beta (b)$
-classes above it. Thus, for any
![]() ${\mathcal M}$
-definable
${\mathcal M}$
-definable
![]() $f : M \longrightarrow M$
, there is a
$f : M \longrightarrow M$
, there is a
![]() $\beta (b)$
-class
$\beta (b)$
-class
![]() $B \cap B_{k_1}$
above
$B \cap B_{k_1}$
above
![]() $B \cap B_{k_0}$
such that
$B \cap B_{k_0}$
such that
![]() $f(k_0) < k_1$
. Let
$f(k_0) < k_1$
. Let
![]() $i_0,i_1,j$
be such that
$i_0,i_1,j$
be such that
![]() $\langle i_0,j \rangle \in B \cap B_{k_0}$
and
$\langle i_0,j \rangle \in B \cap B_{k_0}$
and
![]() $\langle i_1,j \rangle \in B \cap B_{k_1}$
. Then
$\langle i_1,j \rangle \in B \cap B_{k_1}$
. Then
![]() $f(q(i_0,j)) = k_0 < k_1 = q(i_1,j)$
.
$f(q(i_0,j)) = k_0 < k_1 = q(i_1,j)$
.
Next, we assume that
![]() $1 < m < \omega $
. We will prove that every
$1 < m < \omega $
. We will prove that every
![]() $\beta \in {\mathcal C}$
is m-thick. Actually, we will prove something even stronger:
$\beta \in {\mathcal C}$
is m-thick. Actually, we will prove something even stronger:
If
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() $f : M \longrightarrow M$
is definable, then there is
$f : M \longrightarrow M$
is definable, then there is
![]() $I \times J \subseteq B$
such that
$I \times J \subseteq B$
such that
![]() $\beta | (I \times J) \in {\mathcal C}$
and whenever
$\beta | (I \times J) \in {\mathcal C}$
and whenever
![]() $i,i' \in I$
,
$i,i' \in I$
,
![]() $j \in J$
and
$j \in J$
and
![]() $i < i'$
, then
$i < i'$
, then
![]() $f(q(i,j)) < q(i',j)$
.
$f(q(i,j)) < q(i',j)$
.
To prove this, suppose that
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(B)$
is in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() $f : M \longrightarrow M$
is definable. We assume that
$f : M \longrightarrow M$
is definable. We assume that
![]() $B = I_0 \times J_0$
and, without loss, that whenever
$B = I_0 \times J_0$
and, without loss, that whenever
![]() $i < i' \in M$
, then, then
$i < i' \in M$
, then, then
![]() $\max (i',f(i)) < f(i')$
.
$\max (i',f(i)) < f(i')$
.
We will obtain I and J in two steps.
In the first step, for each
![]() $j \in J_0$
, let
$j \in J_0$
, let
![]() $R_j \subseteq I_0^2$
be such that if
$R_j \subseteq I_0^2$
be such that if
![]() $\langle i,i' \rangle \in I_0^2$
, then
$\langle i,i' \rangle \in I_0^2$
, then
Let
![]() $\Theta _0 \in \operatorname {\mathrm {Eq}}(B)$
be such that if
$\Theta _0 \in \operatorname {\mathrm {Eq}}(B)$
be such that if
![]() $i,i' \in I_0$
and
$i,i' \in I_0$
and
![]() $j,j' \in J_0$
, then
$j,j' \in J_0$
, then
Obviously,
![]() $\beta (c) \subseteq \Theta _0 \in \operatorname {\mathrm {Eq}}^{\mathcal M}(B)$
and the set of
$\beta (c) \subseteq \Theta _0 \in \operatorname {\mathrm {Eq}}^{\mathcal M}(B)$
and the set of
![]() $\Theta _0$
-classes is
$\Theta _0$
-classes is
![]() ${\mathcal M}$
-bounded. Thus, there is
${\mathcal M}$
-bounded. Thus, there is
![]() $B_1 = I_1 \times J_1 \subseteq B$
such that
$B_1 = I_1 \times J_1 \subseteq B$
such that
![]() $\beta | B_1 \in {\mathcal C}$
and
$\beta | B_1 \in {\mathcal C}$
and
![]() $\Theta _0\cap B_1^2 $
is trivial. Notice that if
$\Theta _0\cap B_1^2 $
is trivial. Notice that if
![]() $j,j' \in J_1$
, then
$j,j' \in J_1$
, then
![]() $R_j \cap I_1^2 = R_{j'} \cap I_1^2$
. For some (or all)
$R_j \cap I_1^2 = R_{j'} \cap I_1^2$
. For some (or all)
![]() $j \in J_1$
, let
$j \in J_1$
, let
![]() $R = R_j \cap I_1^2$
.
$R = R_j \cap I_1^2$
.
For the second step, define
![]() $\Theta _1 \in \operatorname {\mathrm {Eq}}(B_1)$
so that if
$\Theta _1 \in \operatorname {\mathrm {Eq}}(B_1)$
so that if
![]() $i,i' \in I_1$
and
$i,i' \in I_1$
and
![]() $j,j' \in J_1$
, then
$j,j' \in J_1$
, then
Obviously,
![]() $(\beta | B_1)(a) \subseteq \Theta _1 \in \operatorname {\mathrm {Eq}}^{\mathcal M}(B_1)$
. Thus, there is
$(\beta | B_1)(a) \subseteq \Theta _1 \in \operatorname {\mathrm {Eq}}^{\mathcal M}(B_1)$
. Thus, there is
![]() $B_2 = I \times J \subseteq B_1$
such that
$B_2 = I \times J \subseteq B_1$
such that
![]() $\beta | B_2 \in {\mathcal C}$
and
$\beta | B_2 \in {\mathcal C}$
and
![]() $\Theta _1 \cap B_2^2 \in \{\beta (a) \cap B_2^2, \beta (0) \cap B_2^2\}$
.
$\Theta _1 \cap B_2^2 \in \{\beta (a) \cap B_2^2, \beta (0) \cap B_2^2\}$
.
We show that
![]() $\Theta _1 \cap B_2^2 \neq \beta (0) \cap B_2^2$
. Assume to the contrary that
$\Theta _1 \cap B_2^2 \neq \beta (0) \cap B_2^2$
. Assume to the contrary that
![]() $\Theta _1 \cap B_2^2 = \beta (0) \cap B_2^2$
. Then, whenever
$\Theta _1 \cap B_2^2 = \beta (0) \cap B_2^2$
. Then, whenever
![]() $i,i' \in I$
and
$i,i' \in I$
and
![]() $i < i'$
, then
$i < i'$
, then
![]() $f(q(i,j)) \geq f(q(i',j))$
. But then
$f(q(i,j)) \geq f(q(i',j))$
. But then
![]() $\beta |((I \backslash \max (I)) \times J)$
is in
$\beta |((I \backslash \max (I)) \times J)$
is in
![]() ${\mathcal C}$
but is not
${\mathcal C}$
but is not
![]() $1$
-thick, which is a contradiction.
$1$
-thick, which is a contradiction.
Therefore,
![]() $\Theta _1 \cap B_2^2 = \beta (0) \cap B_2^2$
. It then follows that
$\Theta _1 \cap B_2^2 = \beta (0) \cap B_2^2$
. It then follows that
![]() $I \times J$
has the desired property.
$I \times J$
has the desired property.
Lemma 2.3 implies a strengthening of itself via Corollary 2.2.
Corollary 2.4. Suppose that
![]() $m < \omega $
,
$m < \omega $
,
![]() $p \in M$
,
$p \in M$
,
![]() $\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
in
$\beta : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(X)$
in
![]() ${\mathcal C}$
, where
${\mathcal C}$
, where
![]() $X = I \times J$
, and
$X = I \times J$
, and
![]() $f : M \longrightarrow M$
is definable. Then there are
$f : M \longrightarrow M$
is definable. Then there are
![]() $i_0,i_1, \ldots ,i_m \in I$
and
$i_0,i_1, \ldots ,i_m \in I$
and
![]() $j \in J$
such that
$j \in J$
such that
![]() $q(i_0,j)> p$
and
$q(i_0,j)> p$
and
![]() $f(q(i_k,j)) < q(i_{k+1},j)$
for each
$f(q(i_k,j)) < q(i_{k+1},j)$
for each
![]() $k < m$
.
$k < m$
.
We need some more notation and terminology. Recall that a cut K (of
![]() ${\mathcal M}$
) is a subset of M such that
${\mathcal M}$
) is a subset of M such that
![]() $0 \in K \neq M$
and that
$0 \in K \neq M$
and that
![]() $x + 1 \in K$
whenever
$x + 1 \in K$
whenever
![]() $x \leq y \in K$
. If
$x \leq y \in K$
. If
![]() $m < \omega $
, then the cut K is
$m < \omega $
, then the cut K is
![]() $\Sigma _m$
-closed iff whenever
$\Sigma _m$
-closed iff whenever
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Sigma _m\ {\mathcal L}(K)$
-formula and
$\Sigma _m\ {\mathcal L}(K)$
-formula and
![]() ${\mathcal M} \models \exists x \varphi (x)$
, then there is
${\mathcal M} \models \exists x \varphi (x)$
, then there is
![]() $d \in K$
such that
$d \in K$
such that
![]() ${\mathcal M} \models \varphi (d)$
. If K is a
${\mathcal M} \models \varphi (d)$
. If K is a
![]() $\Sigma _0$
-closed cut and
$\Sigma _0$
-closed cut and
![]() $\varphi $
is an
$\varphi $
is an
![]() ${\mathcal L}(K)$
-formula, then
${\mathcal L}(K)$
-formula, then
![]() $\ulcorner \varphi \urcorner $
, the Gödel number of
$\ulcorner \varphi \urcorner $
, the Gödel number of
![]() $\varphi $
, is in K.
$\varphi $
, is in K.
Also, recall that
![]() $\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
,
$\alpha : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A)$
,
![]() $A = [0,n] \times M$
and
$A = [0,n] \times M$
and
![]() $\langle B_k : k \in M \rangle $
is a definable, one-to-one enumeration of the
$\langle B_k : k \in M \rangle $
is a definable, one-to-one enumeration of the
![]() $\alpha (b)$
-classes (as defined a few lines after (C3)).
$\alpha (b)$
-classes (as defined a few lines after (C3)).
We work in
![]() ${\mathcal M}$
. For each
${\mathcal M}$
. For each
![]() $k \leq n$
, let
$k \leq n$
, let
![]() $\Lambda _k$
be the set of all prenex
$\Lambda _k$
be the set of all prenex
![]() ${\mathcal L}(M)$
-sentences
${\mathcal L}(M)$
-sentences
![]() $\sigma $
having length at most n and having the form
$\sigma $
having length at most n and having the form
where
![]() $\ell < k$
, each
$\ell < k$
, each
![]() ${\mathsf Q}_i$
is either
${\mathsf Q}_i$
is either
![]() $\exists $
or
$\exists $
or
![]() $\forall $
and
$\forall $
and
![]() $\varphi (\overline x)$
is a
$\varphi (\overline x)$
is a
![]() $\Sigma _0$
formula. If
$\Sigma _0$
formula. If
![]() $\ell < k \leq n$
, then
$\ell < k \leq n$
, then
![]() $\Lambda _\ell \subseteq \Lambda _k$
. Let
$\Lambda _\ell \subseteq \Lambda _k$
. Let
![]() $\Lambda = \Lambda _n = \bigcup _{k \leq n}\Lambda _k$
. If
$\Lambda = \Lambda _n = \bigcup _{k \leq n}\Lambda _k$
. If
![]() $ \ell < n$
,
$ \ell < n$
,
![]() $t = \langle t_0,t_1, \ldots ,t_\ell \rangle \in [0,n]^{\ell +1}$
,
$t = \langle t_0,t_1, \ldots ,t_\ell \rangle \in [0,n]^{\ell +1}$
,
![]() $j \in M$
, and
$j \in M$
, and
![]() $\sigma \in \Lambda $
as in
$\sigma \in \Lambda $
as in
![]() $(*)$
, let
$(*)$
, let
There is an
![]() ${\mathcal L}(\{n\})$
-formula, call it
${\mathcal L}(\{n\})$
-formula, call it
![]() $\varphi _0(x)$
, such that for every standard
$\varphi _0(x)$
, such that for every standard
![]() $\sigma \in \Lambda $
and each t and j as in
$\sigma \in \Lambda $
and each t and j as in
![]() $(**)$
,
$(**)$
,
Let
![]() $g : M \longrightarrow M$
be an increasing,
$g : M \longrightarrow M$
be an increasing,
![]() ${\mathcal L}(\{n\})$
-definable function that is sufficiently fast-growing in the following sense: whenever
${\mathcal L}(\{n\})$
-definable function that is sufficiently fast-growing in the following sense: whenever
![]() $a \in M$
, then there is a
$a \in M$
, then there is a
![]() $\Sigma _0$
-closed cut K such that
$\Sigma _0$
-closed cut K such that
![]() $\{n,a\} \subseteq K \subseteq [0,g(a)]$
. (There is such a g since n is nonstandard.) Notice that
$\{n,a\} \subseteq K \subseteq [0,g(a)]$
. (There is such a g since n is nonstandard.) Notice that
![]() $g(0)> n^n$
; in particular,
$g(0)> n^n$
; in particular,
![]() $g(0)> n^k$
for every
$g(0)> n^k$
for every
![]() $k < \omega $
.
$k < \omega $
.
Continue working in
![]() ${\mathcal M}$
. Define
${\mathcal M}$
. Define
![]() $F : A \longrightarrow M$
so that if
$F : A \longrightarrow M$
so that if
![]() $\langle i,j \rangle \in A$
, then
$\langle i,j \rangle \in A$
, then
![]() $F(\langle i,j \rangle )$
is the set of all pairs
$F(\langle i,j \rangle )$
is the set of all pairs
![]() $\langle t,\sigma \rangle $
such that for some
$\langle t,\sigma \rangle $
such that for some
![]() $\ell < n$
and
$\ell < n$
and
![]() $t \in [0,n]^{\ell +1}$
,
$t \in [0,n]^{\ell +1}$
,
![]() $t_0 = i$
,
$t_0 = i$
,
![]() $\sigma $
is an
$\sigma $
is an
![]() ${\mathcal L}([0,g(q(i,j)])$
in
${\mathcal L}([0,g(q(i,j)])$
in
![]() $\Lambda $
(as in
$\Lambda $
(as in
![]() $(*)$
) and that
$(*)$
) and that
![]() $\sigma ^{(t,j)}$
is true. Let
$\sigma ^{(t,j)}$
is true. Let
![]() $\Theta \in \operatorname {\mathrm {Eq}}(A)$
be induced by F. It is clear that if
$\Theta \in \operatorname {\mathrm {Eq}}(A)$
be induced by F. It is clear that if
![]() $\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \not \in \alpha (b)$
, then
$\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \not \in \alpha (b)$
, then
![]() $F(\langle i,j \rangle ) \neq F(\langle i,j \rangle )$
so that
$F(\langle i,j \rangle ) \neq F(\langle i,j \rangle )$
so that
![]() $\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \not \in \Theta $
. Thus,
$\big \langle \langle i,j \rangle , \langle i',j' \rangle \big \rangle \not \in \Theta $
. Thus,
![]() $\Theta \subseteq \alpha (b)$
. On the other hand, if
$\Theta \subseteq \alpha (b)$
. On the other hand, if
![]() $B_k$
is an
$B_k$
is an
![]() $\alpha (b)$
-class, then the set of possible
$\alpha (b)$
-class, then the set of possible
![]() $F(\langle i,j \rangle )$
for
$F(\langle i,j \rangle )$
for
![]() $\langle i,j \rangle \in B_k$
is
$\langle i,j \rangle \in B_k$
is
![]() ${\mathcal M}$
-bounded. Thus, there is
${\mathcal M}$
-bounded. Thus, there is
![]() $B = I \times J \subseteq A$
such that
$B = I \times J \subseteq A$
such that
![]() $\alpha |B$
is in
$\alpha |B$
is in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() $\alpha (b) \cap B^2 = \Theta \cap B^2$
. Let
$\alpha (b) \cap B^2 = \Theta \cap B^2$
. Let
![]() $\beta = \alpha |B$
.
$\beta = \alpha |B$
.
By Lemma 2.3, there are
![]() $j \in J$
, a sufficiently large
$j \in J$
, a sufficiently large
![]() $\ell < \omega $
,
$\ell < \omega $
,
![]() $t = \langle t_0,t_1, \ldots ,t_\ell \rangle \in I^{\ell + 1}$
and a sufficiently fast-growing, definable
$t = \langle t_0,t_1, \ldots ,t_\ell \rangle \in I^{\ell + 1}$
and a sufficiently fast-growing, definable
![]() $f : M \longrightarrow M$
such that
$f : M \longrightarrow M$
such that
![]() $f(q(t_k,j)) < q(t_{k+1},j)$
. By “sufficiently,” we mean that for every standard
$f(q(t_k,j)) < q(t_{k+1},j)$
. By “sufficiently,” we mean that for every standard
![]() $\Sigma _\ell \ {\mathcal L}([0,g(q(t_0,j))])$
-sentence in
$\Sigma _\ell \ {\mathcal L}([0,g(q(t_0,j))])$
-sentence in
![]() $\Lambda $
, we have that
$\Lambda $
, we have that
Thus, it follows from (1) and (2) that for each such
![]() $\sigma $
, that
$\sigma $
, that
Now let K be the smallest
![]() $\Sigma _0$
-closed cut such that
$\Sigma _0$
-closed cut such that
![]() $n,q(t_0,j) \in K$
. Thus we have that
$n,q(t_0,j) \in K$
. Thus we have that
![]() $K \subseteq [0,g(q(t_0,j))]$
. From (3), we get that there is a
$K \subseteq [0,g(q(t_0,j))]$
. From (3), we get that there is a
![]() $\Sigma _\ell \ {\mathcal L}(K)$
-formula
$\Sigma _\ell \ {\mathcal L}(K)$
-formula
![]() $\varphi (x)$
such that for every
$\varphi (x)$
such that for every
![]() $\Sigma _{\ell -1}\ {\mathcal L}(K)$
-sentence
$\Sigma _{\ell -1}\ {\mathcal L}(K)$
-sentence
![]() $\sigma $
,
$\sigma $
,
But the existence of
![]() $\varphi (x)$
in (4) contradicts the following version of Tarski’s Theorem on the undefinability of truth, which is an immediate consequence of Gödel’s Diagonalization Lemma.
$\varphi (x)$
in (4) contradicts the following version of Tarski’s Theorem on the undefinability of truth, which is an immediate consequence of Gödel’s Diagonalization Lemma.
Theorem 2.5. Suppose that
![]() $1 \leq m < \omega $
,
$1 \leq m < \omega $
,
![]() $K \subseteq M$
is a
$K \subseteq M$
is a
![]() $\Sigma _0$
-closed cut, and
$\Sigma _0$
-closed cut, and
![]() $\varphi (u)$
is an
$\varphi (u)$
is an
![]() ${\mathcal L}(K)$
-formula such that for each
${\mathcal L}(K)$
-formula such that for each
![]() $\Sigma _m\ {\mathcal L}(K)$
-sentence
$\Sigma _m\ {\mathcal L}(K)$
-sentence
![]() $\sigma $
,
$\sigma $
,
![]() ${\mathcal M} \models \varphi (\ulcorner \sigma \urcorner ) \leftrightarrow \sigma $
. Then
${\mathcal M} \models \varphi (\ulcorner \sigma \urcorner ) \leftrightarrow \sigma $
. Then
![]() $\varphi (u)$
is not a
$\varphi (u)$
is not a
![]() $\Pi _m$
formula.
$\Pi _m$
formula.
This contradiction completes the proof of Theorem 3.
3. Representations of
 ${\mathbf N}_5$
${\mathbf N}_5$
For almost all of this section, we ignore PA and concentrate just on representations of
![]() ${\mathbf N}_5$
. Only in the first and last paragraphs is PA considered.
${\mathbf N}_5$
. Only in the first and last paragraphs is PA considered.
Caveat lector: In the next definition, and throughout this paper,
![]() $\omega ^n$
is not an ordinal but is the set of n-tuples of natural numbers. If
$\omega ^n$
is not an ordinal but is the set of n-tuples of natural numbers. If
![]() $s \in \omega ^n$
and
$s \in \omega ^n$
and
![]() $i < n$
, then
$i < n$
, then
![]() $s_i$
is the i-th element of s. Also, remember that if
$s_i$
is the i-th element of s. Also, remember that if
![]() $n < \omega $
, then
$n < \omega $
, then
![]() $n = \{0,1, \ldots , n-1\}$
. If
$n = \{0,1, \ldots , n-1\}$
. If
![]() $s \in \omega ^n$
and
$s \in \omega ^n$
and
![]() $i < m \leq n$
, then
$i < m \leq n$
, then
![]() $s \hspace {-4pt} \upharpoonright \hspace {-3pt} m \in \omega ^m$
and
$s \hspace {-4pt} \upharpoonright \hspace {-3pt} m \in \omega ^m$
and
![]() $(s \hspace {-4pt} \upharpoonright \hspace {-3pt} m)_i = s_i$
.
$(s \hspace {-4pt} \upharpoonright \hspace {-3pt} m)_i = s_i$
.
Definition 3.1. For
![]() $n < \omega $
, let
$n < \omega $
, let
![]() $A_n = (n+2) \times \omega ^{n+1}$
and then define
$A_n = (n+2) \times \omega ^{n+1}$
and then define
![]() $\alpha _n : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A_n)$
so that
$\alpha _n : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}(A_n)$
so that
![]() $\alpha _n(0)$
is trivial,
$\alpha _n(0)$
is trivial,
![]() $\alpha _n(1)$
is discrete, and whenever
$\alpha _n(1)$
is discrete, and whenever
![]() $i,j \leq n+1$
and
$i,j \leq n+1$
and
![]() $s,t \in \omega ^{n+1}$
, then
$s,t \in \omega ^{n+1}$
, then
-
•
 $\big \langle \langle i,s \rangle , \langle j,t \rangle \big \rangle \in \alpha _n(a)$
iff
$\big \langle \langle i,s \rangle , \langle j,t \rangle \big \rangle \in \alpha _n(a)$
iff
 $i = j$
;
$i = j$
; -
•
 $\big \langle \langle i,s \rangle , \langle j,t \rangle \big \rangle \in \alpha _n(b)$
iff
$\big \langle \langle i,s \rangle , \langle j,t \rangle \big \rangle \in \alpha _n(b)$
iff
 $i = j$
and
$i = j$
and
 $s \hspace {-4pt} \upharpoonright \hspace {-3pt} i = t \hspace {-4pt} \upharpoonright \hspace {-3pt} j$
;
$s \hspace {-4pt} \upharpoonright \hspace {-3pt} i = t \hspace {-4pt} \upharpoonright \hspace {-3pt} j$
; -
•
 $\big \langle \langle i,s \rangle , \langle j,t \rangle \big \rangle \in \alpha _n(c)$
iff
$\big \langle \langle i,s \rangle , \langle j,t \rangle \big \rangle \in \alpha _n(c)$
iff
 $s = t$
.
$s = t$
.
It is clear that each
![]() $\alpha _n$
is a representation of
$\alpha _n$
is a representation of
![]() ${\mathbf N}_5$
and that, if
${\mathbf N}_5$
and that, if
![]() $n \geq 1$
, then
$n \geq 1$
, then
![]() $\alpha _n$
is
$\alpha _n$
is
![]() $0$
-CPP. (The representation
$0$
-CPP. (The representation
![]() $\alpha _0$
is not
$\alpha _0$
is not
![]() $0$
-CPP because there are exactly 2
$0$
-CPP because there are exactly 2
![]() $\alpha _0(a)$
-classes.) If
$\alpha _0(a)$
-classes.) If
![]() $n < \omega $
, then
$n < \omega $
, then
![]() $\alpha _n(b) \cap (\{0\} \times \omega ^{n+1})^2$
is trivial whereas
$\alpha _n(b) \cap (\{0\} \times \omega ^{n+1})^2$
is trivial whereas
![]() $\alpha _n(b) \cap (\{n+1\} \times \omega ^{n+1})^2$
is discrete.
$\alpha _n(b) \cap (\{n+1\} \times \omega ^{n+1})^2$
is discrete.
Lemma 3.2. Suppose that
![]() $m \leq n < \omega $
and that
$m \leq n < \omega $
and that
![]() $I \subseteq n+2$
is such that
$I \subseteq n+2$
is such that
![]() $|I| = m+2$
. Then there is
$|I| = m+2$
. Then there is
![]() $D \subseteq \omega ^{n+1}$
such that
$D \subseteq \omega ^{n+1}$
such that
![]() $\alpha _m \cong \alpha _n|(I \times D)$
.
$\alpha _m \cong \alpha _n|(I \times D)$
.
Proof Suppose that
![]() $m,n,I$
are as given. Let
$m,n,I$
are as given. Let
![]() $i_{m+1} = \max (I)$
and
$i_{m+1} = \max (I)$
and
![]() $I \backslash \{i_{m+1}\} = \{i_0,i_1, \ldots , i_m\}$
, where
$I \backslash \{i_{m+1}\} = \{i_0,i_1, \ldots , i_m\}$
, where
![]() $i_0 < i_1 < \cdots < i_m$
. We consider separately the two cases:
$i_0 < i_1 < \cdots < i_m$
. We consider separately the two cases:
![]() ${i_{m+1} < n+1}$
and
${i_{m+1} < n+1}$
and
![]() $i_{m+1} = n+1$
.
$i_{m+1} = n+1$
.
First, suppose that
![]() $i_{m+1} < n+1$
.
$i_{m+1} < n+1$
.
We show that
![]() $\alpha _m \cong \alpha _n|(I \times D)$
. Let
$\alpha _m \cong \alpha _n|(I \times D)$
. Let
![]() $h : (m+2) \times \omega ^{m+1} \longrightarrow (n+2) \times \omega ^{n+1}$
be such that if
$h : (m+2) \times \omega ^{m+1} \longrightarrow (n+2) \times \omega ^{n+1}$
be such that if
![]() $\langle j, s \rangle \in (m+2) \times \omega ^{m+1}$
, then
$\langle j, s \rangle \in (m+2) \times \omega ^{m+1}$
, then
![]() $h(\langle j,s \rangle ) = \langle i_j,t \rangle $
, where
$h(\langle j,s \rangle ) = \langle i_j,t \rangle $
, where
![]() $t \in \omega ^{n+1}$
and
$t \in \omega ^{n+1}$
and
 $$ \begin{align*} t_k = \begin{cases} s_j, {\mbox{ if }} j \leq m {\mbox{ and }} i_j = k, \\ 0, {\mbox{ otherwise, }} \end{cases} \end{align*} $$
$$ \begin{align*} t_k = \begin{cases} s_j, {\mbox{ if }} j \leq m {\mbox{ and }} i_j = k, \\ 0, {\mbox{ otherwise, }} \end{cases} \end{align*} $$
for all
![]() $k \leq n$
. One easily verifies that
$k \leq n$
. One easily verifies that
![]() $h : (m+2) \times \omega ^{m+1} \longrightarrow I \times D$
is a bijection and that whenever
$h : (m+2) \times \omega ^{m+1} \longrightarrow I \times D$
is a bijection and that whenever
![]() $\langle j,s \rangle , \langle j',s' \rangle \in (m+2) \times \omega ^{m+1}$
and
$\langle j,s \rangle , \langle j',s' \rangle \in (m+2) \times \omega ^{m+1}$
and
![]() $r \in {\mathbf N}_5$
, then
$r \in {\mathbf N}_5$
, then
Thus,
![]() $\alpha _m \cong \alpha _n|(I \times D)$
.
$\alpha _m \cong \alpha _n|(I \times D)$
.
Next, suppose that
![]() $i_{m+1} = n+1$
. In this case, let
$i_{m+1} = n+1$
. In this case, let
Showing that
![]() $\alpha _m \cong \alpha _n|(I \times D)$
is much like in the first case.
$\alpha _m \cong \alpha _n|(I \times D)$
is much like in the first case.
Our primary goal in this section is to prove the following theorem, which will be given a more precise formulation in Theorem 3.9.
Theorem 3.3. If
![]() $ m < \omega $
, then there is
$ m < \omega $
, then there is
![]() $n < \omega $
such that
$n < \omega $
such that
![]() $\alpha _n \longrightarrow \alpha _m$
.
$\alpha _n \longrightarrow \alpha _m$
.
To prove this theorem, we will take a detour and visit some other lattices and their representations. These lattices are introduced in Definition 3.4 and their representations in Definition 3.5.
Definition 3.4. Suppose that
![]() $1 \leq m \leq n < \omega $
. Let
$1 \leq m \leq n < \omega $
. Let
![]() $G_{m,n}$
be the set consisting of all pairs
$G_{m,n}$
be the set consisting of all pairs
![]() $\langle \theta , f \rangle $
, where
$\langle \theta , f \rangle $
, where
![]() $\theta \in \operatorname {\mathrm {Eq}}(n+1)$
and
$\theta \in \operatorname {\mathrm {Eq}}(n+1)$
and
![]() $f : n+1 \longrightarrow m+1$
are such that if
$f : n+1 \longrightarrow m+1$
are such that if
![]() $i,j \leq n$
and
$i,j \leq n$
and
![]() $\langle i,j \rangle \in \theta $
, then
$\langle i,j \rangle \in \theta $
, then
![]() $f(i) = f(j)$
. Let
$f(i) = f(j)$
. Let
![]() $\unlhd $
be the partial ordering of
$\unlhd $
be the partial ordering of
![]() $G_{m,n}$
such that if
$G_{m,n}$
such that if
![]() $\langle \theta , f \rangle , \langle \psi , g \rangle \in G_{m,n}$
, then
$\langle \theta , f \rangle , \langle \psi , g \rangle \in G_{m,n}$
, then
Clearly,
![]() $\unlhd $
really is a partial ordering. It should be observed that
$\unlhd $
really is a partial ordering. It should be observed that
![]() $G_{m,n}$
with
$G_{m,n}$
with
![]() $\unlhd $
, as in Definition 3.4, is a lattice in which
$\unlhd $
, as in Definition 3.4, is a lattice in which
where
![]() $\sup (f,g) = h$
iff
$\sup (f,g) = h$
iff
![]() $h(i) = \max (f(i),g(i))$
for all
$h(i) = \max (f(i),g(i))$
for all
![]() $i \leq n$
. In the above equalities, we are identifying
$i \leq n$
. In the above equalities, we are identifying
![]() $k \leq m$
with the function that is constantly k on
$k \leq m$
with the function that is constantly k on
![]() $n+1$
. We will continue to do so.
$n+1$
. We will continue to do so.
Our real concern is with the lattices
![]() $G_n = G_{n,n}$
. The more general
$G_n = G_{n,n}$
. The more general
![]() $G_{m,n}$
are introduced in order to be able to do an inductive proof. One of the reasons for introducing the lattices
$G_{m,n}$
are introduced in order to be able to do an inductive proof. One of the reasons for introducing the lattices
![]() $G_n$
is that there is an embedding
$G_n$
is that there is an embedding
![]() $e_n : {\mathbf N}_5 \longrightarrow G_n$
defined by:
$e_n : {\mathbf N}_5 \longrightarrow G_n$
defined by:
 $$ \begin{align*} e_n(0) & = 0_{G_n}, \\ e_n(a) & = \langle 0 {\hspace{-6.3pt} 0}_{n+1}, 0 \rangle, \\ e_n(b) & = \langle 0 {\hspace{-6.3pt} 0}_{n+1}, \mathsf{id}_{n+1}\rangle, \\ e_n(c) & = \langle 1 {\hspace{-3.5pt} 1} _{n+1},n \rangle, \\ e_n(1) & = 1_{G_n}. \end{align*} $$
$$ \begin{align*} e_n(0) & = 0_{G_n}, \\ e_n(a) & = \langle 0 {\hspace{-6.3pt} 0}_{n+1}, 0 \rangle, \\ e_n(b) & = \langle 0 {\hspace{-6.3pt} 0}_{n+1}, \mathsf{id}_{n+1}\rangle, \\ e_n(c) & = \langle 1 {\hspace{-3.5pt} 1} _{n+1},n \rangle, \\ e_n(1) & = 1_{G_n}. \end{align*} $$
As usual,
![]() $\mathsf {id}_X$
is the identity function on X.
$\mathsf {id}_X$
is the identity function on X.
It is routine to verify that each
![]() $e_n$
is an embedding. Figure 3 depicts the lattice
$e_n$
is an embedding. Figure 3 depicts the lattice
![]() $G_1$
with
$G_1$
with
![]() ${\mathbf N}_5$
embedded in it. If
${\mathbf N}_5$
embedded in it. If
![]() $r \in {\mathbf N}_5$
, then
$r \in {\mathbf N}_5$
, then
![]() $e_1(r)$
is labeled with r. The unlabeled point is
$e_1(r)$
is labeled with r. The unlabeled point is
![]() $\langle 0 {\hspace{-6.3pt} 0}_2, 1-\mathsf {id}_2 \rangle $
, where
$\langle 0 {\hspace{-6.3pt} 0}_2, 1-\mathsf {id}_2 \rangle $
, where
![]() $1-\mathsf {id}_2$
is the function
$1-\mathsf {id}_2$
is the function
![]() $f : 2 \longrightarrow 2$
such that
$f : 2 \longrightarrow 2$
such that
![]() $f(0) = 1$
and
$f(0) = 1$
and
![]() $f(1) = 0$
.
$f(1) = 0$
.

Figure 3 Embedding
![]() ${\mathbf N}_5$
into
${\mathbf N}_5$
into
![]() $G_1$
.
$G_1$
.
Next, we define representations of the
![]() $G_{m,n}$
.
$G_{m,n}$
.
Definition 3.5. Suppose that
![]() $1 \leq m \leq n < \omega $
. Let
$1 \leq m \leq n < \omega $
. Let
![]() $\gamma _{m,n} : G_{m.n} \longrightarrow \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^m\big )$
be such that if
$\gamma _{m,n} : G_{m.n} \longrightarrow \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^m\big )$
be such that if
![]() $\langle \theta , f \rangle \in G_{m,n}$
and
$\langle \theta , f \rangle \in G_{m,n}$
and
![]() $\langle i, s \rangle , \langle j, t \rangle \in (n+1) \times \omega ^m$
, then
$\langle i, s \rangle , \langle j, t \rangle \in (n+1) \times \omega ^m$
, then
![]() $\big \langle \langle i, s \rangle , \langle j, t \rangle \big \rangle \in \gamma _{m,n}( \langle \theta , f \rangle )$
iff
$\big \langle \langle i, s \rangle , \langle j, t \rangle \big \rangle \in \gamma _{m,n}( \langle \theta , f \rangle )$
iff
![]() $\langle i,j \rangle \in \theta $
and
$\langle i,j \rangle \in \theta $
and
![]() $s \hspace {-4pt} \upharpoonright \hspace {-3pt} f(i) = t \hspace {-4pt} \upharpoonright \hspace {-3pt} f(j)$
.
$s \hspace {-4pt} \upharpoonright \hspace {-3pt} f(i) = t \hspace {-4pt} \upharpoonright \hspace {-3pt} f(j)$
.
Observe that
![]() $\gamma _{m,n}$
is indeed a representation of
$\gamma _{m,n}$
is indeed a representation of
![]() $G_{m,n}$
. However, no
$G_{m,n}$
. However, no
![]() $\gamma _{m,n}$
is
$\gamma _{m,n}$
is
![]() $0$
-CPP since if
$0$
-CPP since if
![]() $\theta $
has exactly 2 equivalence classes, then
$\theta $
has exactly 2 equivalence classes, then
![]() $\gamma _{m,n}(\langle \theta , 0 \rangle )$
has exactly 2 equivalence classes. In fact, if E is a
$\gamma _{m,n}(\langle \theta , 0 \rangle )$
has exactly 2 equivalence classes. In fact, if E is a
![]() $\theta $
-class, then
$\theta $
-class, then
![]() $E \times \omega ^m$
is a
$E \times \omega ^m$
is a
![]() $\gamma _{m,n}(\langle \theta , 0 \rangle )$
-class. Thus, the number of
$\gamma _{m,n}(\langle \theta , 0 \rangle )$
-class. Thus, the number of
![]() $\gamma _{m,n}(\langle \theta , 0 \rangle )$
-classes is equal to the number of
$\gamma _{m,n}(\langle \theta , 0 \rangle )$
-classes is equal to the number of
![]() $\theta $
-classes. On the other hand, if
$\theta $
-classes. On the other hand, if
![]() $f : n+1 \longrightarrow m+1$
is not constantly
$f : n+1 \longrightarrow m+1$
is not constantly
![]() $0$
, then there are infinitely many
$0$
, then there are infinitely many
![]() $\gamma _{m,n}(\langle \theta ,f \rangle )$
-classes; specifically, if
$\gamma _{m,n}(\langle \theta ,f \rangle )$
-classes; specifically, if
![]() $f(i)> 0$
and
$f(i)> 0$
and
![]() $s_0 \neq t_0$
, where
$s_0 \neq t_0$
, where
![]() $s,t \in \omega ^m$
, then
$s,t \in \omega ^m$
, then
![]() $\big \langle \langle i,s \rangle , \langle i,t \rangle \big \rangle \not \in \gamma _{m,n}(\langle \theta ,f \rangle )$
.
$\big \langle \langle i,s \rangle , \langle i,t \rangle \big \rangle \not \in \gamma _{m,n}(\langle \theta ,f \rangle )$
.
Let
![]() $\gamma _n = \gamma _{n,n}$
. Note that for
$\gamma _n = \gamma _{n,n}$
. Note that for
![]() $ n < \omega $
, both of the representations
$ n < \omega $
, both of the representations
![]() $\gamma _{n+1}$
and
$\gamma _{n+1}$
and
![]() $\alpha _n$
are into
$\alpha _n$
are into
![]() $\operatorname {\mathrm {Eq}}\big ((n+2) \times \omega ^{n+1}\big )$
. In fact, even more is true.
$\operatorname {\mathrm {Eq}}\big ((n+2) \times \omega ^{n+1}\big )$
. In fact, even more is true.
Lemma 3.6. If
![]() $n < \omega $
, then
$n < \omega $
, then
![]() $\alpha _n = \gamma _{n+1} \circ e_{n+1}$
.
$\alpha _n = \gamma _{n+1} \circ e_{n+1}$
.
Proof The routine proof is left to the reader.
We next come to the main result about the representations
![]() $\gamma _{m,n}$
.
$\gamma _{m,n}$
.
Lemma 3.7. If
![]() $1 \leq m \leq n < \omega $
, then
$1 \leq m \leq n < \omega $
, then
![]() $\gamma _{m,n} \longrightarrow \gamma _{m,n}$
.
$\gamma _{m,n} \longrightarrow \gamma _{m,n}$
.
Proof What this lemma says is that if
![]() $1 \leq m \leq n < \omega $
and
$1 \leq m \leq n < \omega $
and
![]() $\Theta \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^m\big )$
, then there is
$\Theta \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^m\big )$
, then there is
![]() $X \subseteq (n+1) \times \omega ^m$
and
$X \subseteq (n+1) \times \omega ^m$
and
![]() $r \in G_{m,n}$
such that
$r \in G_{m,n}$
such that
![]() $\gamma _{m,n}|X \cong \gamma _{m,n}$
and
$\gamma _{m,n}|X \cong \gamma _{m,n}$
and
![]() $\Theta \cap X^2 = \gamma _{m,n}(r) \cap X^2$
. Observe that if
$\Theta \cap X^2 = \gamma _{m,n}(r) \cap X^2$
. Observe that if
![]() $X \subseteq (n+1) \times \omega ^m$
and
$X \subseteq (n+1) \times \omega ^m$
and
![]() $\gamma _{m,n}|X \cong \gamma _{m,n}$
, then there is
$\gamma _{m,n}|X \cong \gamma _{m,n}$
, then there is
![]() $D \subseteq \omega ^m$
such that
$D \subseteq \omega ^m$
such that
![]() $X = (n+1) \times D$
. This follows from the fact that each
$X = (n+1) \times D$
. This follows from the fact that each
![]() $\gamma _{m,n}(\langle 1 {\hspace {-3.5pt} 1}_{n+1},m \rangle )$
-class has the form
$\gamma _{m,n}(\langle 1 {\hspace {-3.5pt} 1}_{n+1},m \rangle )$
-class has the form
![]() $(n+1) \times \{s\}$
for some
$(n+1) \times \{s\}$
for some
![]() $s \in \omega ^m$
.
$s \in \omega ^m$
.
The proof of the lemma is by induction on
![]() $m \geq 1$
with
$m \geq 1$
with
![]() $n \geq m$
being fixed. The basis step is for
$n \geq m$
being fixed. The basis step is for
![]() $m = 1$
and the inductive step for
$m = 1$
and the inductive step for
![]() $m> 1$
. Both steps start out the same way. So for now, consider
$m> 1$
. Both steps start out the same way. So for now, consider
![]() $n \geq m \geq 1$
and let
$n \geq m \geq 1$
and let
![]() $\Theta \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^m\big )$
.
$\Theta \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^m\big )$
.
Consider an arbitrary
![]() $s \in \omega ^{m-1}$
. (Of course, if
$s \in \omega ^{m-1}$
. (Of course, if
![]() $m = 1$
, then
$m = 1$
, then
![]() $s = \varnothing $
is the only choice.) With the idea of invoking Infinite Ramsey’s Theorem for pairs, we define
$s = \varnothing $
is the only choice.) With the idea of invoking Infinite Ramsey’s Theorem for pairs, we define
![]() $F_s : [\omega ]^2 \longrightarrow \operatorname {\mathrm {Eq}}\big (\{0,1\} \times (n+1)\big )$
so that whenever
$F_s : [\omega ]^2 \longrightarrow \operatorname {\mathrm {Eq}}\big (\{0,1\} \times (n+1)\big )$
so that whenever
![]() $\{k,\ell \} \in [\omega ]^2$
,
$\{k,\ell \} \in [\omega ]^2$
,
![]() $k < \ell $
,
$k < \ell $
,
![]() $e,e' \in \{0,1\}$
and
$e,e' \in \{0,1\}$
and
![]() $i,j \leq n$
, then
$i,j \leq n$
, then
![]() $\big \langle \langle e,i \rangle , \langle e',j \rangle \big \rangle \in F_s(\{k,\ell \})$
iff there are
$\big \langle \langle e,i \rangle , \langle e',j \rangle \big \rangle \in F_s(\{k,\ell \})$
iff there are
![]() $t,t' \in \omega ^m$
such that
$t,t' \in \omega ^m$
such that
![]() ${t_{m-1} = k}$
,
${t_{m-1} = k}$
,
![]() $t^{\prime }_{m-1} = \ell $
,
$t^{\prime }_{m-1} = \ell $
,
![]() $t \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) = t' \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) = s$
and one of the following:
$t \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) = t' \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) = s$
and one of the following:
-
•
 $e = e' = 0$
and
$e = e' = 0$
and
 $\big \langle \langle i,t \rangle , \langle j,t \rangle \big \rangle \in \Theta $
;
$\big \langle \langle i,t \rangle , \langle j,t \rangle \big \rangle \in \Theta $
; -
•
 $e = 0$
,
$e = 0$
,
 $e' = 1$
and
$e' = 1$
and
 $\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
;
$\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
; -
•
 $e = 1$
,
$e = 1$
,
 $e' = 0$
and
$e' = 0$
and
 $\big \langle \langle i,t' \rangle , \langle j,t \rangle \big \rangle \in \Theta $
;
$\big \langle \langle i,t' \rangle , \langle j,t \rangle \big \rangle \in \Theta $
; -
•
 $e = e' = 1$
and
$e = e' = 1$
and
 $\big \langle \langle i,t' \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
.
$\big \langle \langle i,t' \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
.
Now we apply Ramsey to get an infinite
![]() $H_s \subseteq \omega $
such that
$H_s \subseteq \omega $
such that
![]() $F_s \hspace {-4pt} \upharpoonright \hspace {-3pt} [H_s]^2$
is constant. Let
$F_s \hspace {-4pt} \upharpoonright \hspace {-3pt} [H_s]^2$
is constant. Let
Each of the following is true for each
![]() $s \in \omega ^{m-1}$
:
$s \in \omega ^{m-1}$
:
-
(1) If
 $i \leq n$
, then
$i \leq n$
, then
 $\Theta \cap (\{i\} \times Y_s)^2$
is either trivial or discrete.
$\Theta \cap (\{i\} \times Y_s)^2$
is either trivial or discrete. -
(2) If
 $i, j \leq n$
,
$i, j \leq n$
,
 $\Theta \cap ( \{i\} \times Y_s)^2$
is trivial,
$\Theta \cap ( \{i\} \times Y_s)^2$
is trivial,
 $\Theta \cap (\{j\} \times Y_s)^2$
is discrete, and
$\Theta \cap (\{j\} \times Y_s)^2$
is discrete, and
 ${t,t' \in Y_s}$
, then
${t,t' \in Y_s}$
, then
 $\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \not \in \Theta $
.
$\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \not \in \Theta $
. -
(3) If
 $i < j \leq n$
and both
$i < j \leq n$
and both
 $\Theta \cap (\{i\} \times Y_s)^2$
and
$\Theta \cap (\{i\} \times Y_s)^2$
and
 $\Theta \cap (\{j\} \times Y_s)^2$
are discrete, then one of the following:
$\Theta \cap (\{j\} \times Y_s)^2$
are discrete, then one of the following:-
(3a) if
 $t,t' \in Y_s$
, then
$t,t' \in Y_s$
, then
 $\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \not \in \Theta $
;
$\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \not \in \Theta $
; -
(3b) if
 $t,t' \in Y_s$
, then
$t,t' \in Y_s$
, then
 $\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
iff
$\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
iff
 $t = t'$
.
$t = t'$
.
-
A consequence of (1)–(3) is:
-
(4) If
 $i,j \leq n$
and
$i,j \leq n$
and
 $t,t' \in Y_s$
, then
$t,t' \in Y_s$
, then  $$ \begin{align*}\big\langle \langle i,t \rangle, \langle j,t \rangle \big\rangle \in \Theta \Longleftrightarrow \big\langle \langle i,t' \rangle, \langle j,t' \rangle \big\rangle \in \Theta. \end{align*} $$
$$ \begin{align*}\big\langle \langle i,t \rangle, \langle j,t \rangle \big\rangle \in \Theta \Longleftrightarrow \big\langle \langle i,t' \rangle, \langle j,t' \rangle \big\rangle \in \Theta. \end{align*} $$
Let
![]() $T_s = \{i \leq n : \Theta \cap ( \{i\} \times Y_s)^2$
is trivial
$T_s = \{i \leq n : \Theta \cap ( \{i\} \times Y_s)^2$
is trivial
![]() $\}$
. Because of (1),
$\}$
. Because of (1),
![]() $(n+1) \backslash T_s = \{i \leq n : \Theta \cap ( \{i\} \times Y_s)^2$
is discrete
$(n+1) \backslash T_s = \{i \leq n : \Theta \cap ( \{i\} \times Y_s)^2$
is discrete
![]() $\}$
. With (4) in mind, we can let
$\}$
. With (4) in mind, we can let
![]() $\theta _s \in \operatorname {\mathrm {Eq}}(n+1)$
be such that
$\theta _s \in \operatorname {\mathrm {Eq}}(n+1)$
be such that
for each
![]() $t \in Y_s$
. Clearly,
$t \in Y_s$
. Clearly,
![]() $T_s$
is the (possibly empty) union of some
$T_s$
is the (possibly empty) union of some
![]() $\theta _s$
-classes.
$\theta _s$
-classes.
Let
and
It is readily seen that
![]() $\gamma _{m,n} | X_0 \cong \gamma _{m,n}$
.
$\gamma _{m,n} | X_0 \cong \gamma _{m,n}$
.
Basis step
![]() $m = 1$
: Since
$m = 1$
: Since
![]() $m=1$
, it must be that
$m=1$
, it must be that
![]() $s = \varnothing $
. Thus,
$s = \varnothing $
. Thus,
![]() $Y_s$
is an infinite subset of
$Y_s$
is an infinite subset of
![]() $\omega ^1$
and
$\omega ^1$
and
![]() $X_0 = (n+1) \times Y_{\varnothing }$
. We have already noted that
$X_0 = (n+1) \times Y_{\varnothing }$
. We have already noted that
![]() $\gamma _{1,n}|X_0 \cong \gamma _{1,n}$
. To complete this step, we need to show that there is
$\gamma _{1,n}|X_0 \cong \gamma _{1,n}$
. To complete this step, we need to show that there is
![]() $r_0 \in G_{1,n}$
such that
$r_0 \in G_{1,n}$
such that
![]() $\Theta \cap X_0^2 = \gamma _{1,n}(r_0) \cap X_0^2$
.
$\Theta \cap X_0^2 = \gamma _{1,n}(r_0) \cap X_0^2$
.
Let
![]() $f : n+1 \longrightarrow 2$
be such that
$f : n+1 \longrightarrow 2$
be such that
![]() $f(i) = 0$
iff
$f(i) = 0$
iff
![]() $i \in T_{\varnothing }$
. Then we can take
$i \in T_{\varnothing }$
. Then we can take
![]() ${r_0 = \langle \theta _\varnothing ,f \rangle }$
. One easily verifies that
${r_0 = \langle \theta _\varnothing ,f \rangle }$
. One easily verifies that
![]() $\Theta \cap X_0^2 = \gamma _{1,n}(r_0) \cap X_0^2$
.
$\Theta \cap X_0^2 = \gamma _{1,n}(r_0) \cap X_0^2$
.
Inductive step
![]() $m> 1$
: Thus, we are assuming
$m> 1$
: Thus, we are assuming
![]() $\gamma _{m-1,n} \longrightarrow \gamma _{m-1,n}$
. We already have infinite
$\gamma _{m-1,n} \longrightarrow \gamma _{m-1,n}$
. We already have infinite
![]() $Y_s$
for each
$Y_s$
for each
![]() $s \in \omega ^{m-1}$
and that (1)–(4) hold. Also, we have
$s \in \omega ^{m-1}$
and that (1)–(4) hold. Also, we have
![]() $D_0 \subseteq \omega ^m$
and
$D_0 \subseteq \omega ^m$
and
![]() $X_0 = (n+1) \times D_0$
and that
$X_0 = (n+1) \times D_0$
and that
![]() $\gamma _{m,n} | X_0 \cong \gamma _{m,n}$
. Without loss of generality, we assume, for each
$\gamma _{m,n} | X_0 \cong \gamma _{m,n}$
. Without loss of generality, we assume, for each
![]() $s \in \omega ^{m-1}$
, that
$s \in \omega ^{m-1}$
, that
![]() $H_s = \omega $
and then
$H_s = \omega $
and then
![]() $Y_s = \{t \in \omega ^m : t \supseteq s\}$
. Thus,
$Y_s = \{t \in \omega ^m : t \supseteq s\}$
. Thus,
![]() $D_0 = \omega ^m$
and
$D_0 = \omega ^m$
and
![]() $X_0 = (n+1) \times \omega ^m$
.
$X_0 = (n+1) \times \omega ^m$
.
Let
![]() $\Theta _1 \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^{m-1}\big )$
be such that if
$\Theta _1 \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^{m-1}\big )$
be such that if
![]() $i,j \leq n$
and
$i,j \leq n$
and
![]() $s,s' \in \omega ^{m-1}$
, then
$s,s' \in \omega ^{m-1}$
, then
![]() $\big \langle \langle i,s \rangle , \langle j,s' \rangle \big \rangle \in \Theta _1$
iff
$\big \langle \langle i,s \rangle , \langle j,s' \rangle \big \rangle \in \Theta _1$
iff
![]() $T_s = T_{s'}$
and
$T_s = T_{s'}$
and
![]() $\theta _s = \theta _{s'}$
. By the inductive hypothesis, there are
$\theta _s = \theta _{s'}$
. By the inductive hypothesis, there are
![]() $r_1 \in G_{m-1,n}$
,
$r_1 \in G_{m-1,n}$
,
![]() $D_1 \subseteq \omega ^{m-1}$
, and
$D_1 \subseteq \omega ^{m-1}$
, and
![]() $X_1 = (n+1) \times D_1$
such that
$X_1 = (n+1) \times D_1$
such that
![]() $\gamma _{m-1,n} | X_1 \cong \gamma _{m-1,n}$
and
$\gamma _{m-1,n} | X_1 \cong \gamma _{m-1,n}$
and
![]() $\Theta _1 \cap X_1^2 = \gamma _{m-1,n}(r_1) \cap X_1^2$
. Since there are only finitely many
$\Theta _1 \cap X_1^2 = \gamma _{m-1,n}(r_1) \cap X_1^2$
. Since there are only finitely many
![]() $\Theta _1$
-classes, it must be that
$\Theta _1$
-classes, it must be that
![]() $r_1 = \langle \psi ,0 \rangle $
for some
$r_1 = \langle \psi ,0 \rangle $
for some
![]() $\psi \in \operatorname {\mathrm {Eq}}(n+1)$
. Thus, we have, for
$\psi \in \operatorname {\mathrm {Eq}}(n+1)$
. Thus, we have, for
![]() $i,j \leq n$
and
$i,j \leq n$
and
![]() $s,s' \in D_1$
, that
$s,s' \in D_1$
, that
 $$ \begin{align*} \big\langle \langle i,s \rangle, \langle j,s' \rangle \big\rangle \in \Theta_1 & \Longleftrightarrow T_s = T_{s'} {\mbox{ and }} \theta_s = \theta_{s'} \\ & \Longleftrightarrow \langle i,j \rangle \in \psi. \end{align*} $$
$$ \begin{align*} \big\langle \langle i,s \rangle, \langle j,s' \rangle \big\rangle \in \Theta_1 & \Longleftrightarrow T_s = T_{s'} {\mbox{ and }} \theta_s = \theta_{s'} \\ & \Longleftrightarrow \langle i,j \rangle \in \psi. \end{align*} $$
This implies that
![]() $\psi $
is trivial and that there are T and
$\psi $
is trivial and that there are T and
![]() $\theta $
such that
$\theta $
such that
![]() $T_s = T$
and
$T_s = T$
and
![]() $\theta _s = \theta $
whenever
$\theta _s = \theta $
whenever
![]() $s \in D_1$
.
$s \in D_1$
.
Without loss of generality, we will assume that
![]() $D_1 = \omega ^{m-1}$
so that
$D_1 = \omega ^{m-1}$
so that
![]() $X_1 = (n+1) \times \omega ^{m-1}$
. Notice that (1)–(4) remain true and, in addition, the following hold:
$X_1 = (n+1) \times \omega ^{m-1}$
. Notice that (1)–(4) remain true and, in addition, the following hold:
-
(5) If
 $i \leq n$
, then
$i \leq n$
, then
 $\Theta \cap (\{i\} \times Y_s)^2$
is trivial iff
$\Theta \cap (\{i\} \times Y_s)^2$
is trivial iff
 $i \in T$
.
$i \in T$
. -
(6) If
 $i,j \leq n$
and
$i,j \leq n$
and
 $t \in \omega ^m$
, then
$t \in \omega ^m$
, then
 $\langle i,j \rangle \in \theta $
iff
$\langle i,j \rangle \in \theta $
iff
 $\big \langle \langle i,t \rangle , \langle j,t \rangle \big \rangle \in \Theta $
.
$\big \langle \langle i,t \rangle , \langle j,t \rangle \big \rangle \in \Theta $
.
Let
![]() $\Theta _2 \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^{m-1}\big )$
be such that if
$\Theta _2 \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^{m-1}\big )$
be such that if
![]() $i,j \leq n$
and
$i,j \leq n$
and
![]() $s,s' \in \omega ^{m-1}$
, then
$s,s' \in \omega ^{m-1}$
, then
![]() $\big \langle \langle i,s \rangle , \langle j,s' \rangle \big \rangle \in \Theta _2$
iff one of the following:
$\big \langle \langle i,s \rangle , \langle j,s' \rangle \big \rangle \in \Theta _2$
iff one of the following:
-
•
 $i,j \not \in T$
,
$i,j \not \in T$
,
 $\langle i,j \rangle \in \theta $
and
$\langle i,j \rangle \in \theta $
and
 $s = s'$
;
$s = s'$
; -
•
 $i,j \in T$
and for some (or, equivalently, all)
$i,j \in T$
and for some (or, equivalently, all)
 $t \in Y_s$
and
$t \in Y_s$
and
 $t' \in Y_{s'}$
,
$t' \in Y_{s'}$
,
 $\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
.
$\big \langle \langle i,t \rangle , \langle j,t' \rangle \big \rangle \in \Theta $
.
One easily verifies that, indeed,
![]() $\Theta _2 \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^{m-1}\big )$
. By the inductive hypothesis, there are
$\Theta _2 \in \operatorname {\mathrm {Eq}}\big ((n+1) \times \omega ^{m-1}\big )$
. By the inductive hypothesis, there are
![]() $D_2 \subseteq \omega ^{m-1}$
,
$D_2 \subseteq \omega ^{m-1}$
,
![]() $X_2 = (n+1) \times D_2$
and
$X_2 = (n+1) \times D_2$
and
![]() $r_2 \in G_{m-1,n}$
such that
$r_2 \in G_{m-1,n}$
such that
![]() $\gamma _{m-1,n} | X_2 \cong \gamma _{m-1,n}$
and
$\gamma _{m-1,n} | X_2 \cong \gamma _{m-1,n}$
and
![]() $\Theta _2 \cap X_2^2 = \gamma _{m-1,n}(r_2) \cap X_2^2$
. Let
$\Theta _2 \cap X_2^2 = \gamma _{m-1,n}(r_2) \cap X_2^2$
. Let
![]() $r_2 = \langle \varphi , f' \rangle $
. It must be that
$r_2 = \langle \varphi , f' \rangle $
. It must be that
![]() $\varphi = \theta $
.
$\varphi = \theta $
.
Now let
![]() $D_3 = \{t \in \omega ^m : t \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) \in D_2\}$
and
$D_3 = \{t \in \omega ^m : t \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) \in D_2\}$
and
![]() $X_3 = (n+1) \times D_3$
. Then
$X_3 = (n+1) \times D_3$
. Then
![]() $\gamma _{m,n} | X_3 \cong \gamma _{m,n}$
. Let
$\gamma _{m,n} | X_3 \cong \gamma _{m,n}$
. Let
![]() $r_3 = \langle \theta ,f \rangle \in G_{m,n}$
, where
$r_3 = \langle \theta ,f \rangle \in G_{m,n}$
, where
![]() $f(i) = f'(i)$
if
$f(i) = f'(i)$
if
![]() $i \in T$
and
$i \in T$
and
![]() $f(i) = m$
if
$f(i) = m$
if
![]() $i \not \in T$
. Although it is not clear if
$i \not \in T$
. Although it is not clear if
![]() $\Theta \cap X^2_3 = \gamma _{m,n}(r_3) \cap X_3^2$
, we do have
$\Theta \cap X^2_3 = \gamma _{m,n}(r_3) \cap X_3^2$
, we do have
Without loss of generality, let
![]() $D_3 = \omega ^m$
, so that
$D_3 = \omega ^m$
, so that
![]() $X_3 = (n+1) \times \omega ^m$
. Thus, we have, in addition to (1)–(6), that:
$X_3 = (n+1) \times \omega ^m$
. Thus, we have, in addition to (1)–(6), that:
-
(7)
 $\Theta \cap (T \times \omega ^m)^2 = \gamma _{m,n}(r_3) \cap (T \times \omega ^m)^2.$
$\Theta \cap (T \times \omega ^m)^2 = \gamma _{m,n}(r_3) \cap (T \times \omega ^m)^2.$
To complete this inductive step,1 we proceed with what might be called a “thinning” of
![]() $\omega ^m$
. The object is to get
$\omega ^m$
. The object is to get
![]() $D \subseteq \omega ^m$
and
$D \subseteq \omega ^m$
and
![]() $X = (n+1) \times D$
such that
$X = (n+1) \times D$
such that
![]() $\gamma _{m,n} | X \cong \gamma _{m,n}$
and
$\gamma _{m,n} | X \cong \gamma _{m,n}$
and
![]() $\gamma _{m,n}(r_3) \cap X^2 = \Theta \cap X^2$
.
$\gamma _{m,n}(r_3) \cap X^2 = \Theta \cap X^2$
.
Let
![]() $\langle s^k : k < \omega \rangle $
be a one-to-one enumeration of
$\langle s^k : k < \omega \rangle $
be a one-to-one enumeration of
![]() $\omega ^m$
. By recursion on k, choose
$\omega ^m$
. By recursion on k, choose
![]() $t^k \in \omega ^m$
so that:
$t^k \in \omega ^m$
so that:
-
(T1)
 $t^k \not \in \{t^0,t^1, \ldots ,t^{k-1}\}$
,
$t^k \not \in \{t^0,t^1, \ldots ,t^{k-1}\}$
, -
(T2)
 $t^k \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) = s^k \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1)$
,
$t^k \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1) = s^k \hspace {-4pt} \upharpoonright \hspace {-3pt} (m-1)$
, -
(T3)
 $\Theta $
and
$\Theta $
and
 $\gamma _{m,n}(r_3)$
agree on
$\gamma _{m,n}(r_3)$
agree on
 $(n+1) \times \{t^0,t^1, \ldots , t^k\}$
.
$(n+1) \times \{t^0,t^1, \ldots , t^k\}$
.
Clearly,
![]() $t^0 = s^0$
. If
$t^0 = s^0$
. If
![]() $k> 0$
, then there are only finitely many
$k> 0$
, then there are only finitely many
![]() $t \in \omega $
such that (T2) holds but (T3) fails, so it is always possible to get
$t \in \omega $
such that (T2) holds but (T3) fails, so it is always possible to get
![]() $t^k$
.
$t^k$
.
Let
![]() $r = r_3$
,
$r = r_3$
,
![]() $D = \{t^k : k < \omega \}$
, and
$D = \{t^k : k < \omega \}$
, and
![]() $X = (n+1) \times D$
. Then, X and r are as required.
$X = (n+1) \times D$
. Then, X and r are as required.
Corollary 3.8. If
![]() $1 \leq n < \omega $
, then
$1 \leq n < \omega $
, then
![]() $\gamma _n \longrightarrow \gamma _n$
.
$\gamma _n \longrightarrow \gamma _n$
.
Proof Let
![]() $n = m$
in Lemma 3.7.
$n = m$
in Lemma 3.7.
Let
![]() $R : \omega \longrightarrow \omega $
be the Ramsey function such that if
$R : \omega \longrightarrow \omega $
be the Ramsey function such that if
![]() $m < \omega $
, then
$m < \omega $
, then
![]() $R(m)$
is the least
$R(m)$
is the least
![]() $k < \omega $
such that whenever
$k < \omega $
such that whenever
![]() $\chi : [k]^2 \longrightarrow 35$
, then there is
$\chi : [k]^2 \longrightarrow 35$
, then there is
![]() $I \subseteq k$
such that
$I \subseteq k$
such that
![]() $|I| = m$
and
$|I| = m$
and
![]() $\chi $
is constant on
$\chi $
is constant on
![]() $[I]^2$
. (It seems to be right that 35 is large enough for the following proof to work. But if it isn’t, replace it with something that is.)
$[I]^2$
. (It seems to be right that 35 is large enough for the following proof to work. But if it isn’t, replace it with something that is.)
Theorem 3.9. Suppose that
![]() $m < 4R(m+2)^2 \leq n < \omega $
. Then,
$m < 4R(m+2)^2 \leq n < \omega $
. Then,
![]() $\alpha _n \longrightarrow \alpha _m$
.
$\alpha _n \longrightarrow \alpha _m$
.
Proof Let
![]() $m,n$
be as given. Suppose that
$m,n$
be as given. Suppose that
![]() $\Theta \in \operatorname {\mathrm {Eq}}((n+2) \times \omega ^{n+1})$
. By Lemma 3.6 and Corollary 3.8, we can assume that
$\Theta \in \operatorname {\mathrm {Eq}}((n+2) \times \omega ^{n+1})$
. By Lemma 3.6 and Corollary 3.8, we can assume that
![]() $\Theta = \gamma _n(\langle \theta , f \rangle )$
, where
$\Theta = \gamma _n(\langle \theta , f \rangle )$
, where
![]() $\langle \theta ,f \rangle \in G_{n+1}$
. Thus,
$\langle \theta ,f \rangle \in G_{n+1}$
. Thus,
![]() $\theta \in \operatorname {\mathrm {Eq}}(n+2)$
and
$\theta \in \operatorname {\mathrm {Eq}}(n+2)$
and
![]() $f : n+1 \longrightarrow n+1$
. Let
$f : n+1 \longrightarrow n+1$
. Let
![]() $J \subseteq n+2$
be such that
$J \subseteq n+2$
be such that
![]() ${|J| = 2R(m+2)}$
and that
${|J| = 2R(m+2)}$
and that
![]() $\theta \cap J^2$
is either trivial or discrete. We consider each of these possibilities.
$\theta \cap J^2$
is either trivial or discrete. We consider each of these possibilities.
trivial: Since
![]() $\theta \cap J^2$
is trivial, the function
$\theta \cap J^2$
is trivial, the function
![]() $f \hspace {-4pt} \upharpoonright \hspace {-3pt} J$
is constant. Let
$f \hspace {-4pt} \upharpoonright \hspace {-3pt} J$
is constant. Let
![]() $r_0 \leq n+1$
be such that
$r_0 \leq n+1$
be such that
![]() $f(j) = r_0$
for all
$f(j) = r_0$
for all
![]() $j \in J$
. Let
$j \in J$
. Let
![]() $I \subseteq J$
be such that
$I \subseteq J$
be such that
![]() $|I| = m+2$
and either
$|I| = m+2$
and either
![]() $r_0 \leq \min (I)$
or
$r_0 \leq \min (I)$
or
![]() $\max (I) < r_0$
. In either case, invoke Lemma 3.2 to get
$\max (I) < r_0$
. In either case, invoke Lemma 3.2 to get
![]() $D \subseteq \omega ^{n+1}$
such that
$D \subseteq \omega ^{n+1}$
such that
![]() $\alpha _n | (I \times D) \cong \alpha _m$
. Let
$\alpha _n | (I \times D) \cong \alpha _m$
. Let
![]() $X = I \times D$
.
$X = I \times D$
.
If
![]() $r_0 \leq \min (I)$
, then
$r_0 \leq \min (I)$
, then
![]() $\Theta \cap X^2 = \alpha _n(0) \cap X^2$
. If
$\Theta \cap X^2 = \alpha _n(0) \cap X^2$
. If
![]() $\max (I) < r_0$
, then
$\max (I) < r_0$
, then
![]() $\Theta \cap X^2 = \alpha _n(c)$
.
$\Theta \cap X^2 = \alpha _n(c)$
.
discrete: Let
![]() $\chi : [J]^2 \longrightarrow 35$
be such that if
$\chi : [J]^2 \longrightarrow 35$
be such that if
![]() $i,i',j,j' \in J$
,
$i,i',j,j' \in J$
,
![]() $i < j$
,
$i < j$
,
![]() $i' < j'$
and
$i' < j'$
and
![]() $\chi (\{i,j\}) = \chi (\{i',j'\})$
, then
$\chi (\{i,j\}) = \chi (\{i',j'\})$
, then
![]() $\{\langle i,i' \rangle , \langle j,j' \rangle , \langle f(i),f(i') \rangle , \langle f(j),f(j') \rangle \}$
is an order-preserving function. Let
$\{\langle i,i' \rangle , \langle j,j' \rangle , \langle f(i),f(i') \rangle , \langle f(j),f(j') \rangle \}$
is an order-preserving function. Let
![]() $I \subseteq J$
be such that
$I \subseteq J$
be such that
![]() $|I| = m+2$
and
$|I| = m+2$
and
![]() $\chi $
is constant on
$\chi $
is constant on
![]() $[I]^2$
. There are 3 possibilities: (1)
$[I]^2$
. There are 3 possibilities: (1)
![]() $f(i) < j$
for all
$f(i) < j$
for all
![]() $i,j \in I$
; (2)
$i,j \in I$
; (2)
![]() $f(i) = i$
for all
$f(i) = i$
for all
![]() $i \in I$
; (3)
$i \in I$
; (3)
![]() $f(i)> j$
for all
$f(i)> j$
for all
![]() $i,j \in I$
. In any case, invoke Lemma 3.2 to get
$i,j \in I$
. In any case, invoke Lemma 3.2 to get
![]() $D \subseteq \omega ^{n+1}$
such that
$D \subseteq \omega ^{n+1}$
such that
![]() $\alpha _n | (I \times D) \cong \alpha _m$
. Let
$\alpha _n | (I \times D) \cong \alpha _m$
. Let
![]() $X = I \times D$
. If (1), then
$X = I \times D$
. If (1), then
![]() $\Theta \cap X^2 = \alpha _n(a) \cap X^2$
; if (2), then
$\Theta \cap X^2 = \alpha _n(a) \cap X^2$
; if (2), then
![]() $\Theta \cap X^2 = \alpha _n(b) \cap X^2$
; and if (3), then
$\Theta \cap X^2 = \alpha _n(b) \cap X^2$
; and if (3), then
![]() $\Theta \cap X^2 = \alpha _n(1) \cap X^2$
.
$\Theta \cap X^2 = \alpha _n(1) \cap X^2$
.
This completes the proof of the theorem.
A careful inspection of the previous proofs shows that they can be carried out in
![]() $\mathsf {ACA}_0$
. (Keep in mind that
$\mathsf {ACA}_0$
. (Keep in mind that
![]() $({\mathcal M}, \operatorname {\mathrm {Def}}({\mathcal M})) \models \mathsf {ACA}_0$
for every
$({\mathcal M}, \operatorname {\mathrm {Def}}({\mathcal M})) \models \mathsf {ACA}_0$
for every
![]() ${\mathcal M}$
, where
${\mathcal M}$
, where
![]() $\operatorname {\mathrm {Def}}({\mathcal M})$
is the set of definable subsets of M.) For example, we see from the proof of Lemma 3.7 that if
$\operatorname {\mathrm {Def}}({\mathcal M})$
is the set of definable subsets of M.) For example, we see from the proof of Lemma 3.7 that if
![]() $1 \leq m \leq n < \omega $
, then
$1 \leq m \leq n < \omega $
, then
![]() $\mathsf {ACA}_0 \vdash \gamma _{m,n} \longrightarrow \gamma _{m,n}$
. The function R defined just before Theorem 3.9 can defined in any model of
$\mathsf {ACA}_0 \vdash \gamma _{m,n} \longrightarrow \gamma _{m,n}$
. The function R defined just before Theorem 3.9 can defined in any model of
![]() $\mathsf {PA}$
, and then also
$\mathsf {PA}$
, and then also
![]() $\mathsf {ACA}_0$
. Thus, we get the following theorem.
$\mathsf {ACA}_0$
. Thus, we get the following theorem.
Theorem 3.10. If
![]() $m < \omega $
and
$m < \omega $
and
![]() $n = 4R(m+2)^2$
, then
$n = 4R(m+2)^2$
, then
4. Proving Theorem 4
This section is devoted to a proof of Theorem 4. The definitions of
![]() ${\mathcal L}^*$
and the
${\mathcal L}^*$
and the
![]() ${\mathcal L}^*$
-theory
${\mathcal L}^*$
-theory
![]() $\mathsf {PA}^*$
are given in the introduction. For each
$\mathsf {PA}^*$
are given in the introduction. For each
![]() ${\mathcal M}^*$
, observe that
${\mathcal M}^*$
, observe that
![]() $({\mathcal M}, \operatorname {\mathrm {Def}}({\mathcal M}^*)) \models \mathsf {ACA}_0$
. For any countable, recursively saturated
$({\mathcal M}, \operatorname {\mathrm {Def}}({\mathcal M}^*)) \models \mathsf {ACA}_0$
. For any countable, recursively saturated
![]() ${\mathcal M}$
we will obtain
${\mathcal M}$
we will obtain
![]() ${\mathcal M}^*$
and
${\mathcal M}^*$
and
![]() ${\mathcal N}^*$
as in that theorem. First, we isolate a certain class of models of
${\mathcal N}^*$
as in that theorem. First, we isolate a certain class of models of
![]() $\mathsf {PA}^*$
that have such extensions.
$\mathsf {PA}^*$
that have such extensions.
Definition 4.1. A model
![]() ${\mathcal M}^*$
is recursively supersaturated if
${\mathcal M}^*$
is recursively supersaturated if
![]() $({\mathcal M}, \operatorname {\mathrm {Def}}({\mathcal M}^*))$
(qua a two-sorted, first-order model of second-order arithmetic) is recursively saturated.
$({\mathcal M}, \operatorname {\mathrm {Def}}({\mathcal M}^*))$
(qua a two-sorted, first-order model of second-order arithmetic) is recursively saturated.
Proposition 4.2. Every countable, recursively saturated
![]() ${\mathcal M}$
can be expanded to a recursively supersaturated
${\mathcal M}$
can be expanded to a recursively supersaturated
![]() ${\mathcal M}^*$
.
${\mathcal M}^*$
.
Proof Let
![]() $T = \operatorname {\mathrm {Th}}({\mathcal M}) + \mathsf {ACA}_0$
. Then
$T = \operatorname {\mathrm {Th}}({\mathcal M}) + \mathsf {ACA}_0$
. Then
![]() $T \in \operatorname {\mathrm {SSy}}({\mathcal M})$
, so it has a countable
$T \in \operatorname {\mathrm {SSy}}({\mathcal M})$
, so it has a countable
![]() $\operatorname {\mathrm {SSy}}({\mathcal M})$
-saturated model
$\operatorname {\mathrm {SSy}}({\mathcal M})$
-saturated model
![]() $({\mathcal N}, {\mathfrak X})$
. But then
$({\mathcal N}, {\mathfrak X})$
. But then
![]() ${\mathcal N} \equiv {\mathcal M}$
,
${\mathcal N} \equiv {\mathcal M}$
,
![]() $\operatorname {\mathrm {SSy}}({\mathcal N}) = \operatorname {\mathrm {SSy}}({\mathcal M})$
, and
$\operatorname {\mathrm {SSy}}({\mathcal N}) = \operatorname {\mathrm {SSy}}({\mathcal M})$
, and
![]() ${\mathcal N}$
is countable and recursively saturated, so
${\mathcal N}$
is countable and recursively saturated, so
![]() ${\mathcal N} \cong {\mathcal M}$
. We can then let
${\mathcal N} \cong {\mathcal M}$
. We can then let
![]() ${{\mathcal N} = {\mathcal M}}$
. Since
${{\mathcal N} = {\mathcal M}}$
. Since
![]() ${\mathfrak X}$
is countable, we can let
${\mathfrak X}$
is countable, we can let
![]() ${\mathfrak X} = \{U_0,U_1,U_2, \ldots \}$
, and then let
${\mathfrak X} = \{U_0,U_1,U_2, \ldots \}$
, and then let
![]() ${\mathcal M}^* = ({\mathcal M}, U_0,U_1,U_2, \ldots )$
.
${\mathcal M}^* = ({\mathcal M}, U_0,U_1,U_2, \ldots )$
.
Having Proposition 4.2, we see that the following theorem implies Theorem 4.
Theorem 4.3. If
![]() ${\mathcal M}^*$
is countable and recursively supersaturated, then there is
${\mathcal M}^*$
is countable and recursively supersaturated, then there is
![]() ${\mathcal N}^* \succ {\mathcal M}^*$
such that
${\mathcal N}^* \succ {\mathcal M}^*$
such that
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N}^* / {\mathcal M}^*) \cong ({\mathbf N}_5, \nu _3)$
.
$\operatorname {\mathrm {Ltr}}({\mathcal N}^* / {\mathcal M}^*) \cong ({\mathbf N}_5, \nu _3)$
.
Proof For
![]() $n \in M$
, let
$n \in M$
, let
![]() $\alpha _n^{{\mathcal M}^*} : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}\big ((n+2) \times M^{n+1}\big )$
be the function obtained by interpreting Definition 3.1 within
$\alpha _n^{{\mathcal M}^*} : {\mathbf N}_5 \longrightarrow \operatorname {\mathrm {Eq}}\big ((n+2) \times M^{n+1}\big )$
be the function obtained by interpreting Definition 3.1 within
![]() ${\mathcal M}^*$
. Then,
${\mathcal M}^*$
. Then,
![]() $\alpha _n^{{\mathcal M}^*}$
is an
$\alpha _n^{{\mathcal M}^*}$
is an
![]() ${\mathcal M}^*$
-representation of
${\mathcal M}^*$
-representation of
![]() ${\mathbf N} _5$
. Let
${\mathbf N} _5$
. Let
![]() ${\mathcal C}$
be the set of those
${\mathcal C}$
be the set of those
![]() ${\mathcal M}^*$
-representations
${\mathcal M}^*$
-representations
![]() $\alpha $
such that for some nonstandard
$\alpha $
such that for some nonstandard
![]() $n \in M^*$
,
$n \in M^*$
,
![]() ${\mathcal M}^*\models \alpha \cong \alpha _n$
. It is consequence of Theorem 3.10 and the recursive supersaturation of
${\mathcal M}^*\models \alpha \cong \alpha _n$
. It is consequence of Theorem 3.10 and the recursive supersaturation of
![]() ${\mathcal M}^*$
that
${\mathcal M}^*$
that
![]() ${\mathcal C}$
is an
${\mathcal C}$
is an
![]() ${{\mathcal M}^*}$
-correct set (see Definition 1.6
${{\mathcal M}^*}$
-correct set (see Definition 1.6
![]() ${}^*$
) of representations of
${}^*$
) of representations of
![]() $({\mathcal N}_5, \nu _3)$
. Since
$({\mathcal N}_5, \nu _3)$
. Since
![]() ${\mathcal M}^*$
is countable, Theorem 1.7
${\mathcal M}^*$
is countable, Theorem 1.7
![]() ${}^*(2)$
can be applied, yielding
${}^*(2)$
can be applied, yielding
![]() ${\mathcal N}^* \succ {\mathcal M}^*$
such that
${\mathcal N}^* \succ {\mathcal M}^*$
such that
![]() $\operatorname {\mathrm {Ltr}}({\mathcal N}^* / {\mathcal M}^*) \cong ({\mathbf N}_5, \nu _3)$
.
$\operatorname {\mathrm {Ltr}}({\mathcal N}^* / {\mathcal M}^*) \cong ({\mathbf N}_5, \nu _3)$
.