Introduction
The study of the crystal plasticity of ice is in its first stage of development. As this knowledge is fundamental for understanding the behaviour of a polycrystalline aggregate, more information is necessary. As a first attempt we may try a comparison with the behaviour of metals. This can be done by using experiments where the quotient of the temperature of experiment T and the melting point T s , θ = T/T s is the same, since under these conditions most materials behave similarly. It is less interesting to look for slow functions of θ, such as for example strain hardening, than for discontinuous ones. Such a property is recrystallization (the so-called recrystallization temperature has values of θ ≅ 0.35 − 0.5). Above the recrystallization temperature recrystallization after plastic deformation takes place in a fairly short time. Also there appear supplementary glide systems for temperatures above a transition θ, usually of 0.8 or somewhat less. The interesting range for experiments on ice is 0.9 < θ ≤ 1. As regards these discontinuous properties we can assume that experiments at −15° C. will give the same results as at 2° or 0.01° C. below the melting point, e.g. in the whole range we will find recrystallization and also the same glide elements. On the other hand the behaviour of metals in immediate proximity to the melting point is little known and it is certain that phenomena will occur here which cannot be foreseen at lower temperatures. In part the contrary is also valid.
The glide plane for ice, which belongs to one of the crystal classes D 6h , D 3h or C 6v is (0001) (McConnelReference McConnel 1 ; MüggeReference Mügge 2 ; MüggeReference Mügge 3 ; MatsuyamaReference Matsuyama 4 ). A glide direction has not been reported, but Mügge observes: “… dass man einzelne solcher Blätter oder vielmehr Lagen solcher ganz aus dem Eiskristall herausschieben kann, und dass die Richtung, in welcher man schiebt, anscheinend fast gleichgültig ist, wenn sie nur in Basis (also der Ebene der Blättchen) liegt…” The conditions for glide, which relate observed glide elements with the structure of the crystal, give in fact the basal plane (0001) with two bonds per unit cell as the plane with the minimum molecular binding energy and so as the probable glide plane. The direction in which oxygen atoms are most closely spaced is [0001], but if one takes a crumpled sequence, [1120] has higher density and more direct bonds. This is therefore a possible glide direction.
Besides the known slip plane (0001) others have been conjectured.Reference Matsuyama
4
, Reference Rigsby
5
RigsbyReference Rigsby
5
has deduced glide planes from the textures found on Emmons Glacier and the planes (1122) and (1012) or (1124) are given, but the known bisal glide has disappeared. For these planes there are ![]() and more bonds per unit cell.
and more bonds per unit cell.
From recent measurements the plastic behaviour of ice has to be described as quasiviscous (Gerrard, Perutz and Roch,Reference Gerrard, Perutz and Roch
6
Haefeli,Reference Haefeli
7
GlenReference Glen
8
). This means that the shear velocity is related to the shear stress by the formula ![]() , the exponent n being greater than 1; k is a function of temperature. For single crystals a law of this sort has not as yet been proposed.
, the exponent n being greater than 1; k is a function of temperature. For single crystals a law of this sort has not as yet been proposed.
This law is just the same as has been applied by NortonReference Norton 9 to the creep of metals. For polycrystalline ice it is found that the exponent n lies between 3 and 4, in metals the exponent is higher. Strain hardening has never been observed in ice (see BraggReference Bragg 10 ). For metals we know that strain hardening is not so large when a single glide system operates as in multiple glide, and in both cases strain hardening diminishes with increasing temperatures.
The present results form part of a more comprehensive programme which is still going on, so they may seem somewhat disconnected. But it is to be hoped that, read in conjunction with the paper of Glen and Perutz in this issue of the Journal of Glaciology,Reference Glen and Perutz 11 it helps to enlarge our knowledge of ice. Some results presented here confirm their measurements, but the experimental methods are different.
The Production and Description of Single Crystals
In a glacier, nature produces single crystals of nearly all sizes. But conditions of growth, contamination and previous strains are not exactly reproduced in different pieces, as one may conclude from the different measured densities. The differences are discussed by Seligman.Reference Seligman 12 Controlled and reproducible conditions for the growth of single crystals of ice necessitate growth from the melt. Stöber’s methodReference Menzies and Skinner 13 is well suited for these purposes and has already been applied.Reference Jona and Scherrer 14 Because of the reversed density gradient between +4° C. and the freezing point the heat flux is applied from above to the surface of a vessel. A slight heating of the side walls and the bottom prevents nucleation from these parts and enables the temperature gradient to be kept perpendicular to the surface at all stages of growth. At a room temperature of −10° C. a layer consisting of one or a few single crystals will grow on the surface in the form of big flat dendrites. The subsequent growth downwards starts from this “two-dimensional nucleus,” since isothermal surfaces are parallel to the surface and there exists no other possible seed than an ice crystal itself until a supercooling of 2.5° C.Reference Wylie 15 The maximum supercooling in contact with ice is certainly lower than 0.1° C. as WylieReference Wylie 15 points out. The largest single crystals made in this way were of the dimensions of the vessel, i.e. 25×25×20 cm. The deviation of the optic axis from the perpendicular to the surface was seldom more than 20°.
Supercooling, which can be estimated from the linear velocity of growth, influences the appearance of the first layer, the “two-dimensional nucleus.” One may roughly differentiate a dendritic growth with strong main and side branches and a delicate, finely spaced dendritic growth, often also in the form of a leaf. The first type has linear velocities of growth of > 1000 mm./min. and so a supercooling of ~5° C. and more, the second only ~1° C.Reference Tammann and Büchner 16 and this may be attributed to incidental nucleation from an ice-particle in the air. The structure of the “two-dimensional nucleus” remains in the whole crystal, the velocity of growth in the vertical direction not exceeding 3 cm. per day. The second type of “two-dimensional nucleus” always led to the development of good crystals without easily detectable growth faults. Faults are frequent in ice crystals, they are in the form of a lineage structure.Reference Buerger 17 On the other hand the tendency to sub-microscopic faults is extremely low.Reference Owston and Lonsdale 18
In polarized light a strong lineage structure is easily detected as an intensity difference in different branches, if an orientation difference of more than ![]() exists; viewed conoscopically it is even possible that these parts of a crystal produce the characteristic image of a biaxial crystal. Over short distances (1 cm.) an orientation difference in branches as high as 8° has been found. An inspection of the boundaries with Laue diagrams in most cases reveals a jump (double Laue spots), though in some diagrams spirally distorted Laue spots have been found. In the latter cases the lattice of the branches changes continuously to that of another to within the resolving power of X-rays (Figs. 1a
, 1b
, p. 413). A reinspection of all Laue diagrams confirms the observations of Glen and PerutzReference Glen and Perutz
11
in that the Laue spots are seldom sharp, especially in crystals whose first layer had a high velocity of growth. In crystals with the second type of initial layer (fine dendrites), however, they were sometimes exceptionally sharp.
exists; viewed conoscopically it is even possible that these parts of a crystal produce the characteristic image of a biaxial crystal. Over short distances (1 cm.) an orientation difference in branches as high as 8° has been found. An inspection of the boundaries with Laue diagrams in most cases reveals a jump (double Laue spots), though in some diagrams spirally distorted Laue spots have been found. In the latter cases the lattice of the branches changes continuously to that of another to within the resolving power of X-rays (Figs. 1a
, 1b
, p. 413). A reinspection of all Laue diagrams confirms the observations of Glen and PerutzReference Glen and Perutz
11
in that the Laue spots are seldom sharp, especially in crystals whose first layer had a high velocity of growth. In crystals with the second type of initial layer (fine dendrites), however, they were sometimes exceptionally sharp.

Fig. 1 X-ray’ Lane-diagrams of single crystals with growth faults. The X-ray’ beam is nearly parallel to c-axis. Fig. 1 (a) (top): Jumps of orientation. Fig. 1 (b) (middle): A spirally distorted crystal, the change of orientation in the crystal being about 8°
The obvious conclusion is that the production of single crystals has to be effected with care. Every plastic deformation in bad crystals is influenced by the faults, and inhomogeneous strains are generated. One may even say that a bad crystal equals a polycrystal, the fluctuation in orientation being so large.
Means For Complete Orientation Determination of Single Crystal Specimens
The precise determination of the optic axis (1°) conoscopically is easily carried out.
The a-axis, however, is not determinable optically. Without an X-ray apparatus it can nevertheless be found as there exists a correlation between the lattice and growth figures and also Tyndall’s “flowers.”
The X-ray investigation of Glen and PerutzReference Glen and Perutz 11 has fixed the long axis of a dendrite (from water or atmosphere) as the [1120] direction. Thus on the “two-dimensional nucleus” in the crystallization vessel, the direction of the long axis of the dendrites can easily be determined. This has to be done in the initial stage, since evaporation destroys their visibility. Once this direction is marked, giving [1120], it is possible to orient the single crystals to an accuracy of better than 2–3° (as long as the optic axis is not far from being perpendicular to the surface of the bowl) and hence also to know the orientation of specimens cut from this single crystal.
Tyndall’s flowers, caused by melting inside the crystal under radiant heat, are generated at places where there are impurities or irregularities. The cavities thus formed take all the forms of a snowflake: a round plate, a hexagon and also the six spikes. They are, so to speak, negative snowflakes, shaped in the same fashion.Reference Bragg 10 The planes of all the flowers inside a single crystal lie parallel one to another and the spikes all have the same direction. It is known that the plane of the flowers is (0001). A large single crystal, on which the [1120] direction had been marked as described above, was cut into a thin plate and a block of known relative orientation. The thin plate was X-rayed and the large block exposed to the sun. Correlating the observations it was found that the spikes of the dendrites at the surface of water have the same direction as the spikes of Tyndall’s flowers. Tyndall’s flowers are thus “negative snowflakes” of the same orientation as a real snowflake (Fig. 2, p. 413).

Fig. 2 Tyndall’s flowers. The [1120] direction is the direction of the spikes, [0001] is perpendicular to their plane. ×2.5
Orienting a specimen with Tyndall’s flowers is done by cutting a piece of known relation to the main piece, irradiating it and so determining the [1120] directions. Another possibility has also been tried with success. By shading and if possible cooling most of the single crystal while the rest is exposed to radiation, the orientation can be fixed in part of the crystal and this is valid for the whole piece. The accuracy obtained is ~5° with little flowers (diameter 5 mm.), with large flowers and strong irradiation (diameter ≤3 cm.) it is lower than ~2°.
Deformation of Single Crystals with the Basal Plane Clamped
In tension and compression tests, and also in shear, it is possible to cut the crystals in such a way that they will not be deformed by glide on the basal plane. An effective clamping of the basal plane is even possible in a bending test, and even a slight misorientation cannot influence the results if the cross-section is sufficiently large. In such tests it should be possible to make other glide systems active, if they exist.
The arrangement used is shown in Fig. 3 (p. 407). If the ends of the bar are fixed at both the upper and the lower side, the basal planes are clamped, while if the ends are fixed only below, completely free deformation of the bar can occur, by glide on the basal plane, in just the same way as a pack of cards would deform. As the optic axis lies in the plane perpendicular to the axis of bending, besides the clamped basal plane only prismatic planes are precluded from acting.

Fig. 3 The top two diagrams show the effect of a bending test on a free ice crystal in which deformation is possible on the basal plane. The bottom diagram shows that when the basal plane is clamped glide is impossible
The cross-sections of the tested bars were 1×1 cm., the free length 3–4 cm. and the maximum moment 5 kg.cm. Moments higher than 3 kg.cm. caused brittle fracture after a short time, whereas it was possible to maintain moments of 3 kg.cm. for one day or even longer. For these moments the clamped crystal never showed any measurable flexion, while in the non-clamped arrangement a flexion was immediately observable after loading.
The upper and the lower surfaces of the crystals have in this case a tensile or compressive stress of |σ| = |M|/W kg.cm−2 = 18 kg.cm.−2, which is about the stress for fracture. Deformation would have been observed for any other system than the basal one. For example the planes reported by RigsbyReference Rigsby 5 support a tensile or a compressive stress of 7 kg.cm.−2 for (1012) and (1124) and 9 kg.cm.−2 for (1122), as can be seen in a Mohr-diagram. These values are not strongly influenced by the unknown a-direction of the specimen and the particular glide direction. Several specimens of random orientation as regards the a-axis have been tested, but no glide other than that on (0001) was in evidence. Naturally the stresses quoted above are those at the surfaces and vary linearly with height above the neutral zone, but this cannot invalidate the results.
Shearing of Single Crystals in A Bausch Apparatus
An apparatus of this type has been used to study the plastic behaviour. The Bausch apparatus has been adopted to avoid inhomogeneous strains; the crystals are deformed in pure shear along the glide plane (0001).
An objection to this method is the existence of microscopic stresses. But it has been shown that they only occur for short crystals. In long crystals microscopic stresses do not exist and the critical shear stress is lowered; the strain-hardening is also much less than in short crystals.Reference Yamaguchi 19 For these reasons short crystals have never been employed in the experiments.
Single crystals with a cross-section of 15–25 cm.Reference Mügge 2 and a height of 2–5 cm. were frozen onto aluminium plates with small furrows. Before freezing the plates were cleaned in a surface-active agent to secure good adhesion. The crystals were mounted in the apparatus as shown in Fig. 4 (p. 407), the optic axis being perpendicular to the applied force, so that the basal plane is fully active as a glide plane. Shear strain is measured by the factor x/h = γ, the quotient of glide to height expressed as a percentage. The tests reported here were carried out at a temperature of −2.3±0.3° C., other temperatures have also been used but most of the work until now has been done at this temperature. Two views of a deformed crystal are shown in Fig. 5 (p. 413); in Fig. 5 b the glide lines are easily visible on the surface. The distance between the visible glide lines is about 0.6 mm.

Fig. 4 Arrangement in Bausch’s apparatu for direct shear to be applied to ice crystals

Fig. 5 Sheared single crystals. In the upper view (a) the glide is about 50 per cent. In the laser view (b) glide lines are clearly visible
Fig. 6 (p. 409) gives the shear strain as a function of time for several crystals and for different shear stresses. An interesting feature is recognizable. The fresh crystal is hard for a glide of 10–20 per cent and then the creep rate increases but reaches a new linear region. The change is sometimes sharply defined as a kink in the curve, but in most cases there is a smooth transition. No dependence on stress has been found, but the transition always lies at a glide of 10–20 per cent. This can tentatively be described as work softening. The transition is irreversible, the crystal once deformed by a shear greater than 10–20 per cent remains soft, even after several hundred hours. This effect is not due to any diminution of effective cross-section, nor to inhomogeneous strain, since changing the glide direction after having passed the transition does not change the effect, the glide velocity being of the same magnitude as it was in the original direction of glide. No inhomogeneous strains were ever observed in polarized light. Finally experiments have béen made to look for a Bauschinger effect; in these the glide direction was changed three times; no true Bauschinger effect was observable (the true Bauschinger effect on a single crystal is attributed to work hardening on the atomic scale).

Fig. 6. Shear versus time for different shear stresses on a singlec crystal of ice for a temperature of −2.3°
C × Fresh crystal ● Soft crystal
In evaluating creep velocities as a function of stress, one must take the transition into account. For the first stage the minimum creep rate is easily determined. If we plot this for different shear stresses (which are the same as resolved shear stresses, since the optic axis is perpendicular to the shear forces) one finds the known relation ![]() , which has also been given for polycrystalline ice from the pipe experiment on the JungfraufirnReference Gerrard, Perutz and Roch
6
and by Glen.Reference Glen
8
The shear velocity
, which has also been given for polycrystalline ice from the pipe experiment on the JungfraufirnReference Gerrard, Perutz and Roch
6
and by Glen.Reference Glen
8
The shear velocity ![]() is related to the shear stress τ by a power law. Above 10–20 per cent glide, i.e. above the transition, we no longer have a decellerating transient stage followed by a minimum creep rate; nevertheless a straight line can be drawn through the measured points, as has been done in Fig. 6. These later creep velocities also have a power law relation with stress, but the values of n and k are different. The two curves intercept at the maximum shear stress attained in the experiment. In Fig. 7 (p. 409) the results are plotted on a double-logarithmic plot, and the values for n inserted. We also see that the less steep line of the deformed crystals has less scatter than the lines for fresh crystals. Experiments have been conducted by applying a fixed load, determining the steady creep rate and then changing the load to determine the new creep velocity and so on. This can be done on the same crystal to determine several points below or above the transition. If this is done the fluctuations in n are not so great (in Fig. 7 lines are drawn through such points).
is related to the shear stress τ by a power law. Above 10–20 per cent glide, i.e. above the transition, we no longer have a decellerating transient stage followed by a minimum creep rate; nevertheless a straight line can be drawn through the measured points, as has been done in Fig. 6. These later creep velocities also have a power law relation with stress, but the values of n and k are different. The two curves intercept at the maximum shear stress attained in the experiment. In Fig. 7 (p. 409) the results are plotted on a double-logarithmic plot, and the values for n inserted. We also see that the less steep line of the deformed crystals has less scatter than the lines for fresh crystals. Experiments have been conducted by applying a fixed load, determining the steady creep rate and then changing the load to determine the new creep velocity and so on. This can be done on the same crystal to determine several points below or above the transition. If this is done the fluctuations in n are not so great (in Fig. 7 lines are drawn through such points).

Fig. 7 Shear velocity versus shear stress on a single crystal of ice in direct shear for a temperature of −2.3° C
○ Extremely low glide (<1 per cent)
Lowering the stresses always gave the same law, even for shear stresses as low as 0.2 kg.cm.−2; this is valid both for the fresh and the deformed crystal states. If a critical shear stress for ice exists, it must lie below 0.2 kg.cm.−2.
The Glide Direction
The normal method for determining the glide direction is that used by Glen and Perutz,Reference Glen and Perutz 11 i.e. the determination of the crystallographic axis of the specimen by X-rays in relation to the tension axis in an extended single crystal.
Another, older way is also possible. The creep velocity for a fixed stress varies when the shear direction is rotated relative to the glide plane, i.e. when the crystal is rotated in a Bausch apparatus. Such tests have been made. The crystals were of the same dimensions and the temperature the same as in the earlier work. In evaluating the creep velocities for fresh crystals of different known orientation as regards the a-axis, the fluctuations were much too large for any useful deductions to be made, but previously deformed crystals appeared to be isotropic. Doing the experiment on the same crystal in various orientations (unfortunately this has been done only for a soft crystal), the fluctuations are less serious. The creep velocity is plotted as a radius vector for two different stresses and various orientations of the glide direction in Fig. 8. The slight anisotropy for the higher stress cannot, however, at present be attributed to a glide direction, even though it gives the glide direction predicted by the known rules, since it lies within experimental error. Thus the observed glide direction is simply the direction of maximum shear stress in the basal plane, i.e. there is no definite crystallographic slip direction in the basal plane (see also the discussion in the paper of Glen and Perutz Reference Glen and Perutz 11 ).

Fig. 8 Shear velocity plotted as radius vector for a fixed strain and various positions of the glide direction in the basal plane
Recrystallization in Inhomogeneously Deformed Crystals
Recrystallization takes place when crystals are deformed inhomogeneously above a certain amount. In single crystals of bad growth inhomogeneous strains are common, and so one often sees recrystallization in the inhomogeneously strained parts, the rest of the crystal remaining unchanged as it has been strained homogeneously. Recrystallization in these cases always occurs in that part of the crystal whose inhomogeneous deformation is the strongest. The new crystals seldom extend far into the homogeneous part of the sheared crystal; nothing, however, can be said about the crystallization nucleus. Recrystallization took place sometimes during the experiment, sometimes after unloading. Fig. 9 (p. 413) is a thin section of a sheared single crystal which recrystallized during the experiment, the newly formed grains lie completely inside of the crystal. In the figure inhomogeneously strained parts can still be seen; in polarized light they are recognizable as striations.

Fig. 9 Thin section of a sheared crystal in which recrystallization took place viewed in polarized light. The recrystallized parts are completely in the interior of the crystal. Inhomogeneously deformed parts of the single crystal are recognizable as striations in the polarized light. × 3
When crystals are bent recrystallization can easily be generated during or after the experiment if the radius of curvature is lower than 5–20 mm.
Discussion
It now seems to be definitely established, both from the present work and that of Glen and Perutz,Reference Glen and Perutz 11 that (0001) is the only glide plane in ice.
The curious effect of shear on the shear velocity, by which a crystal softens after a certain strain, may lead to various consequences. The process is irreversible until recrystallization occurs, after which the crystal is again hard. To explain this, one has to assume some process within the crystal itself, the exact nature of which is at present completely hypothetical. One possibility is that it arises because of non-crystallographic slip of the various lamellae, as neither a definite glide direction nor a finite critical shear stress have yet been found. Another possible interpretation comes from the local curvatures postulated by Taylor, Yamaguchi and Burgers (see Yamaguchi,Reference Yamaguchi 19 BurgersReference Burgers 20 ) if portions of the lattice rotate about an axis lying in the glide plane and perpendicular to the glide direction.
As ice behaves in this way, pure shear seems to be preferred for experiments, since in tension or compression it is possible that local deformations greater than 10–20 per cent may occur, so producing soft parts into which all the subsequent deformation of the crystal may be concentrated. This process will be further favoured by inhomogeneous strains, which thus tend to be exaggerated. This sort of behaviour has also been observed in shear, especially in bad crystals, and it is possible that the ill-defined nature of the transition is due to this fact.
For metal single crystals the creep law γ = at
m
has been given, where m is a function of temperature and has a value of 0.5 for zinc at room temperature, and an extrapolated value of 1 at 600° C.Reference Thompson
21
A simplified Andrade law ![]() has also been observed in zinc even for strains as large as 40 per cent.Reference Weinberg
22
As the quasiviscous component predominates near the melting point, these two formulae are complementary; the strong quasiviscous component, which is responsible for a linear strain-time relationship, makes a transient undetectable near the melting point. The linearity of the strain-time relation, apart from an observable transient stage, has thus been observed in metals as well as in ice. Shear velocity has not been connected with shear stress in the case of metals, but for ice the analogous relation for polycrystalline material is
has also been observed in zinc even for strains as large as 40 per cent.Reference Weinberg
22
As the quasiviscous component predominates near the melting point, these two formulae are complementary; the strong quasiviscous component, which is responsible for a linear strain-time relationship, makes a transient undetectable near the melting point. The linearity of the strain-time relation, apart from an observable transient stage, has thus been observed in metals as well as in ice. Shear velocity has not been connected with shear stress in the case of metals, but for ice the analogous relation for polycrystalline material is ![]() , n and k being dependent on stress as discussed above.
, n and k being dependent on stress as discussed above.
The consequences of this behaviour as regards a glacier are rather complicated, since many effects can be inferred but few verified.
In a glacier with randomly oriented grains the strains in a single grain have no simple relationship to the macroscopic strain, since a strong differential movement has been observed.Reference Seligman 23 This is analogous to the observations in metals, where the elongation varies from grain to grain and within the individual grain of the aggregate.Reference Urie and Wain 24 In aluminium at a macroscopic strain of 5 per cent of the overall fluctuations in strain between and within grains varies from 1 to 12 per cent, for 10 per cent from 2 to 22 per cent. In ice with the single glide system the difference will be many times greater.
If there were no recrystallization, then even after a slight macroscopic shear, some favourably oriented grains would be sheared by a sufficient amount to be soft, so creating a heterogeneous aggregate. The aggregate itself always constitutes an impediment to absolutely free glide of the grains and so clusters of soft grains would be the next stage. An effect of this sort may account for the observed accelerating stage (tertiary creep), but other explanations are also possible.
On introducing recrystallization one can find the reverse effect. Even an aggregate can remain hard if the recrystallization takes place in sufficient time to prevent the large glide, necessary for softening. An exaggerating effect may also exist, since once the grain has softened it becomes more strongly deformed in an inhomogeneous manner and so is ready for recrystallization in a shorter time. But for this the grains must be deformed inhomogeneously above a certain limiting amount.
If we now take a polycrystalline block with a texture, the situation changes, since inhomogeneous strains are not so pronounced and recrystallization, which is associated with inhomogeneous strains, occurs at a much later stage of macroscopic strain. In an extreme case (a single crystal) the whole block can be softened.
Comparing now laboratory experiments on polycrystalline ice (GlenReference Glen 8 and unpublished work by the present author) with the theoretical arguments above, it has been found that recrystallization takes place during the experiment if the applied stresses are sufficiently high (this may not be necessary, if the time of testing is long enough for the strain to attain the necessary value). The recrystallization began for an elongation of a few per cent. The maximum strain before recrystallization in single grains may be of the order of some 10 per cent and so the polycrystal has only partly softened. The polycrystalline block thus remains hard by recrystallization. If this recrystallization were absent a marked transition followed by a linear part would be expected.
The measured values of k on single crystals are of little significance in a comparison with tests on polycrystalline specimens, but the exponent n is of greater importance. In single crystal measurements the hard crystal has a value of n of 2.3–4, the mean of all measurements being 3.2. The soft crystal above the transition has n=1.3–1.8 with a mean of 1.6. It is of interest to find that the laboratory experiments of GlenReference Glen 8 and glacier measurements of Haefeli and Kasser (Z’Mutt Glacier), Haefeli (Arolla Glacier) and McCall (Vesl-Skautbreen) give n=3.3 or 3.1 (see NyeReference Nye 25 ), and the pipe experiment on the JungfraufirnReference Gerrard, Perutz and Roch 6 gives n=1.5. For the first values one is tempted to say recrystallization accompanies straining and so produces continuous rehardening, but to postulate a soft, strongly deformed crystal and no recrystallization for the Jungfraufirn is rather impossible.
Acknowledgements
I wish to thank Dr. M. de Quervain for his continuous interest in the work. His valuable and stimulating discussions have always been of the greatest help. I also want to thank Dr. J. W. Glen for allowing me to use some unpublished experimental data and also for revising the manuscript.
MS. received 30 December 1953

Ice penitentes up to 30 m. high between the Base Camp and Camp I at about 5000 m.

Ice penitentes at Camp I. In the foreground coolies from Namche Bazar and district. (Autumn 1952)

The upper part of the Khumbu ice fall. At a certain flow rate the glacier breaks up into huge blocks (the Block-Schollen of Finsterwalder). At a still greater speed these blocks themselves break up chaotically

Fluted snow and hanging glaciers on the north-west slope of Nuptse at 7000 m. These formations are due to enormous temperature differences between the shaded surfaces and those exposed to the sun. (Spring 1952). (See text, p. 428–30)

Separation of huge blocks in the upper part of the Khumbu ice fall. Note the two dirt bands in the bottom block. The lower dirt hand probably results from the period of fine weather after the wet monsoon. The layer of snow between the two dirt bands is probably the snow of the dry monsoon. The upper dirt hand probably dates from the period of fine weather preceding the wet monsoon, and the thick layer of snow on top would then be the snow of the wet monsoon

The rope bridge on one of the upper crevasses of the Klzumhu ice fall. The banding of ice allows a rough evaluation of the depth of the annual snow fall. (See text, pp. 428–30)

Fig. 1 The up-arching of slabs of gneiss at the snout of Svellnosbreein, Jotunheimen, after the glacier had uncovered them.

Fig. 2 Pseudo-bedding developed in the gneiss below, and adjacent to, the vertical face of a roche moutonnée at the snout of Svellnosbreein


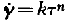 ,
, 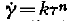 darstellen, wobei
darstellen, wobei 








