Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Balasubramanian, K.
and
Sujith, R. I.
2013.
Non-normality and nonlinearity in combustion–acoustic interaction in diffusion flames – CORRIGENDUM.
Journal of Fluid Mechanics,
Vol. 733,
Issue. ,
p.
680.
Magri, Luca
and
Juniper, Matthew P.
2014.
Adjoint-Based Linear Analysis in Reduced-Order Thermo-Acoustic Models.
International Journal of Spray and Combustion Dynamics,
Vol. 6,
Issue. 3,
p.
225.
Magri, Luca
and
Juniper, Matthew P.
2014.
Global modes, receptivity, and sensitivity analysis of diffusion flames coupled with duct acoustics.
Journal of Fluid Mechanics,
Vol. 752,
Issue. ,
p.
237.
Li, Lei
Zhao, Dan
and
Yang, Xinglin
2016.
Effect of entropy waves on transient energy growth of flow disturbances in triggering thermoacoustic instability.
International Journal of Heat and Mass Transfer,
Vol. 99,
Issue. ,
p.
219.
Singaravelu, Balasubramanian
and
Mariappan, Sathesh
2016.
Stability analysis of thermoacoustic interactions in vortex shedding combustors using Poincaré map.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
597.
Blumenthal, Ralf S
Tangirala, Arun K
Sujith, RI
and
Polifke, Wolfgang
2017.
A systems perspective on non-normality in low-order thermoacoustic models: Full norms, semi-norms and transient growth.
International Journal of Spray and Combustion Dynamics,
Vol. 9,
Issue. 1,
p.
19.
Li, Lei
Zhao, Dan
and
Sun, Xiaofeng
2018.
Nonorthogonality analysis of acoustics and vorticity modes: Should thermoacoustic energy norm be time-invariant?.
Aerospace Science and Technology,
Vol. 77,
Issue. ,
p.
149.
Magina, Nicholas
Acharya, Vishal
and
Lieuwen, Timothy
2019.
Forced response of laminar non-premixed jet flames.
Progress in Energy and Combustion Science,
Vol. 70,
Issue. ,
p.
89.
Sogaro, Francesca M.
Schmid, Peter J.
and
Morgans, Aimee S.
2019.
Thermoacoustic interplay between intrinsic thermoacoustic and acoustic modes: non-normality and high sensitivities.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
190.
Magri, Luca
2019.
Adjoint Methods as Design Tools in Thermoacoustics.
Applied Mechanics Reviews,
Vol. 71,
Issue. 2,
Giannotta, A.
Cherubini, S.
and
De Palma, P.
2022.
Minimal energy thresholds for triggering in the Rijke tube: the effect of the time delay.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Zhao, Dan
2023.
Thermoacoustic Combustion Instability Control.
p.
203.
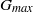 ${G}_{max} $, of the order of
${G}_{max} $, of the order of 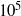 $1{0}^{5} $ to
$1{0}^{5} $ to 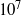 $1{0}^{7} $. However, recent investigations by L. Magri and M. P. Juniper have brought to light certain errors in that paper. When the errors are corrected,
$1{0}^{7} $. However, recent investigations by L. Magri and M. P. Juniper have brought to light certain errors in that paper. When the errors are corrected, 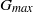 ${G}_{max} $ is found to be of the order of 1 to 10, revealing that non-normality is not as influential as it was thought to be.
${G}_{max} $ is found to be of the order of 1 to 10, revealing that non-normality is not as influential as it was thought to be.

