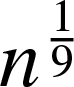1. Introduction
Percolation in infinite graphs is typically studied in the setting where edges (or vertices) are removed uniformly at random and some connectivity-related property is being traced as a function of the percolation probability  $\pi\in(0,1)$ that a randomly chosen edge (or vertex) is present. Conventionally, this property is chosen to describe connected components: maximal vertex sets in which any pair of vertices is connected with a path. Many results about sizes of connected components are known for percolation in infinite lattices [Reference Bollobás and Riordan4] and random graphs [Reference Amini1, Reference Bollobás, Borgs, Chayes and Riordan3, Reference Durrett15, Reference Fountoulakis16, Reference Janson19]. Closely related to percolation are random graph models that depend on a real parameter, such as the well-studied Erdős Rényi random graph
$\pi\in(0,1)$ that a randomly chosen edge (or vertex) is present. Conventionally, this property is chosen to describe connected components: maximal vertex sets in which any pair of vertices is connected with a path. Many results about sizes of connected components are known for percolation in infinite lattices [Reference Bollobás and Riordan4] and random graphs [Reference Amini1, Reference Bollobás, Borgs, Chayes and Riordan3, Reference Durrett15, Reference Fountoulakis16, Reference Janson19]. Closely related to percolation are random graph models that depend on a real parameter, such as the well-studied Erdős Rényi random graph  $G(n,p)$, and also various models for directed random graphs, often referred to as
$G(n,p)$, and also various models for directed random graphs, often referred to as  $D(n,p)$ or
$D(n,p)$ or  $\vec G(n,p)$ [Reference Goldschmidt and Stephenson17, Reference Pittel and Poole26, Reference Łuczak and Cohen29, Reference Łuczak and Seierstad30].
$\vec G(n,p)$ [Reference Goldschmidt and Stephenson17, Reference Pittel and Poole26, Reference Łuczak and Cohen29, Reference Łuczak and Seierstad30].
Fountoulakis [Reference Fountoulakis16] and Janson [Reference Janson19] studied percolation in undirected random graphs with well-behaved degree sequences using techniques that rely on Molloy and Reed’s existence theorem [Reference Molloy and Reed22, Reference Molloy and Reed23], which indicates whether a simple undirected random graph with a given degree sequence contains a giant component and how large it is. These authors showed that if one starts with a simple random graph generated by the configuration model and then removes edges (vertices) uniformly at random, the resulting percolated graph can again be studied with the configuration model, albeit with a modified degree sequence. In this paper, we introduce a similar argument to directed graphs. Although there are several points of analogy, directed graphs generally require a distinct treatment from that of undirected graphs.
In digraphs, there exist several non-equivalent definitions for a connected component, all of which give rise to an interesting percolation problem. Let  $G=(V,E)$ be a simple digraph and
$G=(V,E)$ be a simple digraph and  $n=|V|$. We say that
$n=|V|$. We say that  $\mathcal C \subset V$ is a strongly connected component (SCC) if for all
$\mathcal C \subset V$ is a strongly connected component (SCC) if for all  $v_1,v_2\in \mathcal C $, there are directed paths that connect v 1 with v 2 and v 2 with
$v_1,v_2\in \mathcal C $, there are directed paths that connect v 1 with v 2 and v 2 with  $v_1,$ and no other vertex from V can be added to
$v_1,$ and no other vertex from V can be added to  $\mathcal C$ without losing this property. Suppose G n is uniformly sampled from the set of all digraphs with a fixed graphic degree sequence
$\mathcal C$ without losing this property. Suppose G n is uniformly sampled from the set of all digraphs with a fixed graphic degree sequence
 \begin{align}
\textbf{d}^{n}:=
\left(
({d^-_{1}}, {d^+_{1}}),
({d^-_{2}}, {d^+_{2}}),\dots,
({d^-_{n}}, {d^+_{n}})
\right),
\end{align}
\begin{align}
\textbf{d}^{n}:=
\left(
({d^-_{1}}, {d^+_{1}}),
({d^-_{2}}, {d^+_{2}}),\dots,
({d^-_{n}}, {d^+_{n}})
\right),
\end{align}where  ${d^-_{v}}$ and
${d^-_{v}}$ and  ${d^+_{v}}$ indicate correspondingly the in- and out-degree of vertex
${d^+_{v}}$ indicate correspondingly the in- and out-degree of vertex  $v\in V$. Let additionally the following limits exist,
$v\in V$. Let additionally the following limits exist,  $\mu:= \lim_{n\to \infty} \mu(n)$ and
$\mu:= \lim_{n\to \infty} \mu(n)$ and  $\mu_{11}:=\lim_{n\to \infty} \mu_{11}(n),$ with
$\mu_{11}:=\lim_{n\to \infty} \mu_{11}(n),$ with  $\mu(n):=n^{-1}\sum_{v\in V}{{d^-_{v}}} =n^{-1}\sum_{v\in V}{{d^+_{v}}}$ being the expected number of edges per vertex and
$\mu(n):=n^{-1}\sum_{v\in V}{{d^-_{v}}} =n^{-1}\sum_{v\in V}{{d^+_{v}}}$ being the expected number of edges per vertex and  $ \mu_{11}(n):=n^{-1}\sum_{v\in V}{{d^-_{v}}{d^+_{v}}}$.
$ \mu_{11}(n):=n^{-1}\sum_{v\in V}{{d^-_{v}}{d^+_{v}}}$.
The existence criteria for the giant strongly connected component (GSCC) in directed graphs was formulated for slightly different models by Cooper and Frieze [Reference Cooper and Frieze10], Bloznelis, Götze, and Jaworski [Reference Bloznelis, Götze and Jaworski2], and Penrose [Reference Penrose24]. These results have been subsequently improved by weakening the requirement on the degree sequence by Graf [Reference Graf18] and Coulson [Reference Coulson11], and more recently, further generalized by Cai and Perarnau [Reference Cai and Perarnau7] and Donderwinkel and Xie [Reference Donderwinkel and Xie14]. All in all, the abovementioned authors state that if  $\mu_{11} - \mu \gt 0,$ the size of the largest SCC
$\mu_{11} - \mu \gt 0,$ the size of the largest SCC  $\mathcal{C} (G_n)$ is of the order n,
$\mathcal{C} (G_n)$ is of the order n,
 \begin{align}
\lim_{n\to\infty} \frac{|\mathcal{C}(G_n)|}{n}=c \gt 0,
\end{align}
\begin{align}
\lim_{n\to\infty} \frac{|\mathcal{C}(G_n)|}{n}=c \gt 0,
\end{align}under some regularity conditions on the degree sequences  $(\textbf{d}^{n})_{n\in \mathbb{N}}$. There are also results about the structure of the giant component [Reference Coulson12], its diameter [Reference Cai and Perarnau8], and the properties of the dynamic processes on it [Reference Cai, Caputo, Perarnau and Quattropani5, Reference Cai and Perarnau6]. Sizes of weakly connected components were studied in [Reference Coulson, Perarnau, Nešetřil and Rué13].
$(\textbf{d}^{n})_{n\in \mathbb{N}}$. There are also results about the structure of the giant component [Reference Coulson12], its diameter [Reference Cai and Perarnau8], and the properties of the dynamic processes on it [Reference Cai, Caputo, Perarnau and Quattropani5, Reference Cai and Perarnau6]. Sizes of weakly connected components were studied in [Reference Coulson, Perarnau, Nešetřil and Rué13].
If the limit in equation (2) holds, we say the random graph contains a GSCC. Likewise, if the sign of the inequality is flipped,  $\mu_{11} - \mu \lt 0,$ then the size of all SCCs is
$\mu_{11} - \mu \lt 0,$ then the size of all SCCs is  $\mathcal{O}\left(1\right)$, and the random graph is said to contain no GSCC. This result points out the existence of two classes of limiting degree sequences, those with the size of largest SCC being
$\mathcal{O}\left(1\right)$, and the random graph is said to contain no GSCC. This result points out the existence of two classes of limiting degree sequences, those with the size of largest SCC being  $\Theta(n)$ and those for which this size is
$\Theta(n)$ and those for which this size is  $\mathcal{O}\left(1\right)$.
$\mathcal{O}\left(1\right)$.
In this paper, we study a percolated graph  $G_n^\pi$, in which each edge (vertex) in G n is randomly removed with probability
$G_n^\pi$, in which each edge (vertex) in G n is randomly removed with probability  $1-\pi$. We show that if the GSCC exists in the original graph G n, removing a positive fraction of edges (or vertices) can modify the degree distribution just in the right way to flip the sign of the inequality, while keeping the percolated graph to be uniform in the set of all graphs with a fixed (modified) degree distribution. By combining the latter observation with the theory of Cai and Perarnau [Reference Cai and Perarnau7], we show that the “phase transition” from
$1-\pi$. We show that if the GSCC exists in the original graph G n, removing a positive fraction of edges (or vertices) can modify the degree distribution just in the right way to flip the sign of the inequality, while keeping the percolated graph to be uniform in the set of all graphs with a fixed (modified) degree distribution. By combining the latter observation with the theory of Cai and Perarnau [Reference Cai and Perarnau7], we show that the “phase transition” from  $\mathcal{O}\left(1\right)$ to
$\mathcal{O}\left(1\right)$ to  $\Theta(n)$ takes place at the critical probability
$\Theta(n)$ takes place at the critical probability  $\pi_c= {\mu}/{\mu_{11}}$, such that only for
$\pi_c= {\mu}/{\mu_{11}}$, such that only for  $\pi \gt \pi_c$,
$\pi \gt \pi_c$,  $G_n^\pi$ contains a GSCC with high probability (w.h.p.). The critical threshold π c is the same for bond and site percolation, whereas the fractions of vertices in GSCC, as defined in Eq. (2), are closely related for bond,
$G_n^\pi$ contains a GSCC with high probability (w.h.p.). The critical threshold π c is the same for bond and site percolation, whereas the fractions of vertices in GSCC, as defined in Eq. (2), are closely related for bond,  $c^{\text{bond}}(\pi)$, and site,
$c^{\text{bond}}(\pi)$, and site,  $c^{\text{site}}(\pi)$, percolation models:
$c^{\text{site}}(\pi)$, percolation models:  $c^{\text{site}}(\pi) = \pi{c^{\text{bond}}}(\pi)$. This work and the related proofs are inspired by the results for percolation in undirected graphs by Fountoulakis [Reference Fountoulakis16] and are based on Chapter 4 of Thesis [Reference van Ieperen28]. Similar conclusions were also obtained heuristically by Graf [Reference Graf18] by applying Janson’s exploding method [Reference Janson19].
$c^{\text{site}}(\pi) = \pi{c^{\text{bond}}}(\pi)$. This work and the related proofs are inspired by the results for percolation in undirected graphs by Fountoulakis [Reference Fountoulakis16] and are based on Chapter 4 of Thesis [Reference van Ieperen28]. Similar conclusions were also obtained heuristically by Graf [Reference Graf18] by applying Janson’s exploding method [Reference Janson19].
2. Main result
This section introduces our main theorems for the percolation threshold of the GSCC. We consider two types of percolation models on a simple digraph  $G_n=(V_n,E_n),$
$G_n=(V_n,E_n),$  $n=|V_n|$ that result in a random subgraph
$n=|V_n|$ that result in a random subgraph  $G_{n}^{\pi}$ on the same vertex set:
$G_{n}^{\pi}$ on the same vertex set:
• Bond percolation, fix percolation probability
 $\pi \in (0,1)$, then each edge of G n is removed independently of the other edges with probability
$\pi \in (0,1)$, then each edge of G n is removed independently of the other edges with probability  $1-\pi$.
$1-\pi$.• Site percolation, fix percolation probability
 $\pi \in (0,1)$, then for each vertex of G n, all the edges incident to this vertex are removed together with probability
$\pi \in (0,1)$, then for each vertex of G n, all the edges incident to this vertex are removed together with probability  $1-\pi$ independently of the other vertices. Such a vertex is referred to as a deleted vertex.
$1-\pi$ independently of the other vertices. Such a vertex is referred to as a deleted vertex.
It should be clear from the context which type of percolation is discussed. Strictly speaking, the existence of the GSCC is a limiting property of a sequence of graphs  $(G_n)_{n\in \mathbb{N}}$, in which each element is defined by a finite graphic degree sequence dn. Thus, we refer to an infinite sequence of degree sequences,
$(G_n)_{n\in \mathbb{N}}$, in which each element is defined by a finite graphic degree sequence dn. Thus, we refer to an infinite sequence of degree sequences,  $(\textbf{d}^{n})_{n\in \mathbb{N}},$ as the degree progression, where n is the index and the number of vertices in the nth element of this progression. Although our ultimate goal is to make statements about random graphs satisfying a specific degree distribution in the limit
$(\textbf{d}^{n})_{n\in \mathbb{N}},$ as the degree progression, where n is the index and the number of vertices in the nth element of this progression. Although our ultimate goal is to make statements about random graphs satisfying a specific degree distribution in the limit ![]() $n\to \infty$, the bulk of the paper is spent on determining whether degree progression
$n\to \infty$, the bulk of the paper is spent on determining whether degree progression  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ maintains or acquires some property of interest w.h.p. as
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ maintains or acquires some property of interest w.h.p. as ![]() $n\to \infty$.
$n\to \infty$.
To make valid statements about the GSCC, we need to impose several requirements on the degree progression. We are interested in simple graphs, which indicates that each degree sequence in the progression must be graphic as required by the equivalent of Erdős–Gallai theorem for directed graphs [Reference LaMar20, Theorem 4]. In Section 3.1, we progressively add several more technical constraints on  $(\textbf{d}^{n})_{n\in \mathbb{N}},$ namely Definitions 3.1, 3.2, and 3.3, which we jointly refer to as the requirements for a proper degree progression. Together, these conditions guarantee sufficient regularity of the degree progression, allowing us to reason about the limiting behavior of the corresponding random graphs and their connected components. In this condition, the most restricting requirement is that the maximum degree must be bounded,
$(\textbf{d}^{n})_{n\in \mathbb{N}},$ namely Definitions 3.1, 3.2, and 3.3, which we jointly refer to as the requirements for a proper degree progression. Together, these conditions guarantee sufficient regularity of the degree progression, allowing us to reason about the limiting behavior of the corresponding random graphs and their connected components. In this condition, the most restricting requirement is that the maximum degree must be bounded,  $d_{\max} \leq n^{\frac{1}{9}}$.
$d_{\max} \leq n^{\frac{1}{9}}$.
Definition 2.1. The percolation threshold of a proper degree progression  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is given by
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is given by
 \begin{align}
\pi_{c} = \sup\left\{\pi \in (0,1) \bigm \vert \forall \varepsilon \gt 0, \lim_{n \rightarrow \infty} \mathbb{P}\left[ n^{-1}\left\lvert \mathcal{C}(G_{n}^{\pi})\right\rvert \geq \varepsilon \right] = 0 \right\},
\end{align}
\begin{align}
\pi_{c} = \sup\left\{\pi \in (0,1) \bigm \vert \forall \varepsilon \gt 0, \lim_{n \rightarrow \infty} \mathbb{P}\left[ n^{-1}\left\lvert \mathcal{C}(G_{n}^{\pi})\right\rvert \geq \varepsilon \right] = 0 \right\},
\end{align}with additional superscripts indicating the type of percolation, that is,  ${\pi_c^{{\rm bond}}}$ or
${\pi_c^{{\rm bond}}}$ or  ${\pi_c^{{\rm site}}}$.
${\pi_c^{{\rm site}}}$.
For each n, the probability in this definition is taken with respect to  $G_n^\pi$ – the random graph that results from percolation on a uniform simple random graph that obeys
$G_n^\pi$ – the random graph that results from percolation on a uniform simple random graph that obeys  $(\textbf{d}^{n})_{n\in \mathbb{N}}$.
$(\textbf{d}^{n})_{n\in \mathbb{N}}$.
The following theorems determine the percolation threshold for the existence of the GSCC, and, if this threshold exists, they additionally identify the fraction of the vertices in this component for bond and site percolation. The theorems can be regarded as the extension of [Reference Fountoulakis16, Thm. 1.1] to digraphs.
Theorem 2.2. Consider progression  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper and
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper and  $\mu_{11} \gt \mu $, then the thresholds for the giant component in bond and site percolations are both equal to
$\mu_{11} \gt \mu $, then the thresholds for the giant component in bond and site percolations are both equal to  $ \pi_c = \frac{\mu}{\mu_{11}} \lt 1.$
$ \pi_c = \frac{\mu}{\mu_{11}} \lt 1.$
Let  $N_{{j},{k}}\left(n\right)$ be the number of vertices with in-/out-degree (j, k) in
$N_{{j},{k}}\left(n\right)$ be the number of vertices with in-/out-degree (j, k) in  $G_n,$ and let
$G_n,$ and let  $
p_{j,k}:=\lim\limits_{n \rightarrow \infty}\frac{N_{{j},{k}}\left(n\right)}{n}
$ exist. Let additionally,
$
p_{j,k}:=\lim\limits_{n \rightarrow \infty}\frac{N_{{j},{k}}\left(n\right)}{n}
$ exist. Let additionally,
 \begin{equation*}U_{\pi}^\text{bond}(x,y) := \sum\limits_{j,k\geq0} p_{j,k} (1-\pi +\pi x)^j (1-\pi +\pi y)^k,\end{equation*}
\begin{equation*}U_{\pi}^\text{bond}(x,y) := \sum\limits_{j,k\geq0} p_{j,k} (1-\pi +\pi x)^j (1-\pi +\pi y)^k,\end{equation*} \begin{equation*}U_{\pi}^-(x) := \left(\pi \mu\right)^{-1}\,\frac{\partial}{\partial y}U_{\pi}^\text{bond}(x,y)|_{y=1}\quad \text{and} \quad U_{\pi}^+(y) := \left(\pi \mu\right)^{-1}\,\frac{\partial}{\partial x}U_{\pi}^\text{bond}(x,y)|_{x=1}\end{equation*}
\begin{equation*}U_{\pi}^-(x) := \left(\pi \mu\right)^{-1}\,\frac{\partial}{\partial y}U_{\pi}^\text{bond}(x,y)|_{y=1}\quad \text{and} \quad U_{\pi}^+(y) := \left(\pi \mu\right)^{-1}\,\frac{\partial}{\partial x}U_{\pi}^\text{bond}(x,y)|_{x=1}\end{equation*}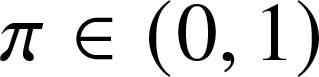 $\pi \in(0,1)$ as a parameter. Here
$\pi \in(0,1)$ as a parameter. Here 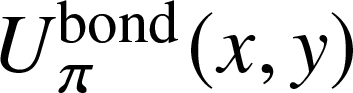 $U_{\pi}^\text{bond}(x,y)$ can be interpreted as the generating function of the degree of a randomly chosen vertex, and
$U_{\pi}^\text{bond}(x,y)$ can be interpreted as the generating function of the degree of a randomly chosen vertex, and 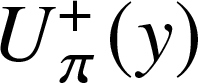 $U_{\pi}^+(y)$ (correspondingly
$U_{\pi}^+(y)$ (correspondingly 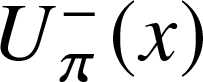 $U_{\pi}^-(x)$) – the generating function for the degree of a vertex at the end of randomly chosen in- (or out-) edge.
$U_{\pi}^-(x)$) – the generating function for the degree of a vertex at the end of randomly chosen in- (or out-) edge.
Theorem 2.3. If  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper and
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper and  $\pi \in( \pi_c,1),$ then for all ɛ > 0,
$\pi \in( \pi_c,1),$ then for all ɛ > 0,
 \begin{equation*} \lim\limits_{n \rightarrow \infty} \mathbb{P}\left[ \left|\frac{\left\lvert \mathcal{C}(G_{n}^{\pi})\right\rvert}{n} -c^{{\rm bond}} (\pi)\right|\geq\varepsilon\right] = 0 \end{equation*}
\begin{equation*} \lim\limits_{n \rightarrow \infty} \mathbb{P}\left[ \left|\frac{\left\lvert \mathcal{C}(G_{n}^{\pi})\right\rvert}{n} -c^{{\rm bond}} (\pi)\right|\geq\varepsilon\right] = 0 \end{equation*}for bond percolation, and
 \begin{equation*} \lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\left|\frac{\left\lvert \mathcal{C}(G_{n}^{\pi})\right\rvert}{n} - c^{{\rm site}}(\pi)\right|\geq \varepsilon\right] = 0 \end{equation*}
\begin{equation*} \lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\left|\frac{\left\lvert \mathcal{C}(G_{n}^{\pi})\right\rvert}{n} - c^{{\rm site}}(\pi)\right|\geq \varepsilon\right] = 0 \end{equation*}for site percolation, with
 \begin{equation*}
c^{\rm{bond}}(\pi) = 1-U_{\pi}^{\rm{bond}}(x^*,1)-U_{\pi}^{\rm bond}(1,y^*)+U_{\pi}^{\rm bond}(x^*,y^*), \qquad c^{{\rm site}}(\pi) = \pi {c^{{\rm bond}}}(\pi)
\end{equation*}
\begin{equation*}
c^{\rm{bond}}(\pi) = 1-U_{\pi}^{\rm{bond}}(x^*,1)-U_{\pi}^{\rm bond}(1,y^*)+U_{\pi}^{\rm bond}(x^*,y^*), \qquad c^{{\rm site}}(\pi) = \pi {c^{{\rm bond}}}(\pi)
\end{equation*}and  $x^*,y^*$ being the smallest positive solutions of
$x^*,y^*$ being the smallest positive solutions of  $x^*= U_{\pi}^-(x^*)$ and
$x^*= U_{\pi}^-(x^*)$ and  $y^*= U_{\pi}^+(y^*)$.
$y^*= U_{\pi}^+(y^*)$.
The remainder of the paper is structured as follows. Section 3 lays out the technical premise: Section 3.1 introduces different classes of degree progressions. Section 3.2 introduces the link between random digraphs and the directed configuration model by repurposing several theorems available for undirected graphs. Section 3.3 gives the definition of a GSCC and formulates Cai and Perarnau’s existence theorem, Theorem 3.11. In Section 3.4, we derive a concentration inequality, Theorem 3.13, enabling the proof of the main result. Section 4 proves Theorems 2.2 and 2.3 separately for the cases of bond and site percolation in, respectively, Sections 4.1 and 4.2. Both subsections have a similar structure: first, we show that the configuration model introduced in Section 3.2 can be used to study percolated digraphs; second, we find the degree distribution after percolation; third, we show that the corresponding degree progression is almost surely feasible in large graphs, and therefore the existence theory from Section 3.3 is applicable.
3. Random digraphs
3.1. Degree sequence, degree progression, and degree distribution
The degree sequence of a given digraph can be uniquely defined by adopting the lexicographic order, as demonstrated in, for example, [Reference LaMar20]. Let  $\mathcal{G}_{\textbf{d}^{n}}$ be the set of all directed multigraphs having degree sequence dn. Since we are interested in sampling from
$\mathcal{G}_{\textbf{d}^{n}}$ be the set of all directed multigraphs having degree sequence dn. Since we are interested in sampling from  $\mathcal{G}_{\textbf{d}^{n}}$, we want to be sure that for given dn,
$\mathcal{G}_{\textbf{d}^{n}}$, we want to be sure that for given dn,  $\mathcal{G}_{\textbf{d}^{n}} \neq \emptyset$. This is always the case for valid degree sequences.
$\mathcal{G}_{\textbf{d}^{n}} \neq \emptyset$. This is always the case for valid degree sequences.
Definition 3.1. A degree sequence dn is called valid if  $
m :=\sum_{i=1}^n {d^-_{i}} = \sum_{i=1}^n {d^+_{i}},
$ where
$
m :=\sum_{i=1}^n {d^-_{i}} = \sum_{i=1}^n {d^+_{i}},
$ where  $m=|E|$ is the number of edges in graph
$m=|E|$ is the number of edges in graph  $G_{\textbf{d}^{n}}$.
$G_{\textbf{d}^{n}}$.
If  $\mathcal{G}_{\textbf{d}^{n}}$ contains a simple graph, dn is called graphical, and Theorem 4 in [Reference LaMar20] gives necessary and sufficient criteria for this property. Suppose dn is graphical and let
$\mathcal{G}_{\textbf{d}^{n}}$ contains a simple graph, dn is called graphical, and Theorem 4 in [Reference LaMar20] gives necessary and sufficient criteria for this property. Suppose dn is graphical and let  $G_{\textbf{d}^{n}}\in\mathcal{G}_{\textbf{d}^{n}}$ be a uniformly chosen simple digraph. To be on the safe side, we need to ensure that the subset of simple graphs in
$G_{\textbf{d}^{n}}\in\mathcal{G}_{\textbf{d}^{n}}$ be a uniformly chosen simple digraph. To be on the safe side, we need to ensure that the subset of simple graphs in  $\mathcal{G}_{\textbf{d}^{n}}$ is not vanishing for large n by imposing restrictions on the limiting behavior of dn. Let
$\mathcal{G}_{\textbf{d}^{n}}$ is not vanishing for large n by imposing restrictions on the limiting behavior of dn. Let
 \begin{align*}
d_{\max}(n) := \max \left\{\max\{{d^-_{1}}, {d^-_{2}}, \ldots, {d^-_{n}}\}, \max\{{d^+_{1}}, {d^+_{2}}, \ldots, {d^+_{n}}\}\right\}
\end{align*}
\begin{align*}
d_{\max}(n) := \max \left\{\max\{{d^-_{1}}, {d^-_{2}}, \ldots, {d^-_{n}}\}, \max\{{d^+_{1}}, {d^+_{2}}, \ldots, {d^+_{n}}\}\right\}
\end{align*}be the largest degree in dn for each index  $n\in \mathbb{N}$. We will refer to this quantity as simply
$n\in \mathbb{N}$. We will refer to this quantity as simply  $d_{\max}$.
$d_{\max}$.
Definition 3.2. A degree progression  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is called feasible if (1) all dn are graphical, (2) the following limits exist yielding bivariate degree distribution
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is called feasible if (1) all dn are graphical, (2) the following limits exist yielding bivariate degree distribution  $ p_{j,k}:= \lim\limits_{n \rightarrow \infty}({N_{{j},{k}}(n)})/{n}$ with finite partial moments up to order 2:
$ p_{j,k}:= \lim\limits_{n \rightarrow \infty}({N_{{j},{k}}(n)})/{n}$ with finite partial moments up to order 2:
 \begin{equation*}
\mu_{ab}:=\lim\limits_{n\rightarrow \infty} \sum_{j,k=0}^\infty \frac{j^ak^bN_{{j},{k}}\left(n\right)}{n} = \sum_{j,k=0}^\infty j^ak^bp_{j,k}\in (0,\infty), \quad 0\leq a+b\leq2,
\end{equation*}
\begin{equation*}
\mu_{ab}:=\lim\limits_{n\rightarrow \infty} \sum_{j,k=0}^\infty \frac{j^ak^bN_{{j},{k}}\left(n\right)}{n} = \sum_{j,k=0}^\infty j^ak^bp_{j,k}\in (0,\infty), \quad 0\leq a+b\leq2,
\end{equation*}and (3)  $d_{\max} = \mathcal{O}\left(\sqrt{n}\right)$. Note that according to Definition 3.1, we have
$d_{\max} = \mathcal{O}\left(\sqrt{n}\right)$. Note that according to Definition 3.1, we have  $\mu:=\mu_{10}=\mu_{01}$.
$\mu:=\mu_{10}=\mu_{01}$.
We refer to  $p_{j,k}$ as the degree distribution of a feasible degree progression. The theorem of Cai and Perarnau [Reference Cai and Perarnau7] holds for feasible degree progressions. However, to show that the degree progression remains feasible after percolation, we need to narrow down the class of initial degree progressions further.
$p_{j,k}$ as the degree distribution of a feasible degree progression. The theorem of Cai and Perarnau [Reference Cai and Perarnau7] holds for feasible degree progressions. However, to show that the degree progression remains feasible after percolation, we need to narrow down the class of initial degree progressions further.
Definition 3.3. A feasible degree progression  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is called proper if
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is called proper if  $d_{\max} \leq n^{\frac{1}{9}}$.
$d_{\max} \leq n^{\frac{1}{9}}$.
Thus far, we have defined a chain of classes for  $(\textbf{d}^{n})_{n\in \mathbb{N}}$: valid
$(\textbf{d}^{n})_{n\in \mathbb{N}}$: valid ![]() $\supset$ graphical
$\supset$ graphical ![]() $\supset$ feasible
$\supset$ feasible ![]() $\supset$ proper, where the definitions of valid and graphical are extended from dn to
$\supset$ proper, where the definitions of valid and graphical are extended from dn to  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ element-wisely.
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ element-wisely.
3.2. Directed configuration model
The behavior of simple random digraphs can be studied with the directed configuration model, as defined below.
Definition 3.4. Let dn be a valid degree sequence. For all vertices enumerated with  $ i \in [n]$, let the set of in-stubs
$ i \in [n]$, let the set of in-stubs  ${W^{-}_{i}}$ consist of
${W^{-}_{i}}$ consist of  ${d^-_{i}}$ unique elements and the set out-stubs
${d^-_{i}}$ unique elements and the set out-stubs  ${W^{+}_{i}}$ contains
${W^{+}_{i}}$ contains  ${d^+_{i}}$ elements. Let
${d^+_{i}}$ elements. Let  ${W^{-}} = \cup_{i \in [n]} {W^{-}_{i}}$ and
${W^{-}} = \cup_{i \in [n]} {W^{-}_{i}}$ and  ${W^{+}} = \cup_{i \in [n]}{W^{+}_{i}}$. Then a configuration
${W^{+}} = \cup_{i \in [n]}{W^{+}_{i}}$. Then a configuration  $\mathcal{M}$ is a random perfect bipartite matching of
$\mathcal{M}$ is a random perfect bipartite matching of  $W^{-}$ and
$W^{-}$ and  $W^{+}$, that is a set of tuples (a, b) such that each tuple contains one element from
$W^{+}$, that is a set of tuples (a, b) such that each tuple contains one element from  $W^{-}$ and one from
$W^{-}$ and one from  $W^{+}$ and each element of
$W^{+}$ and each element of  $W^{-}$ and
$W^{-}$ and  $W^{+}$ appears in exactly one tuple.
$W^{+}$ appears in exactly one tuple.
A configuration  $\mathcal{M}$ prescribes a matching between in-subs and out-stubs and hence defines a multigraph
$\mathcal{M}$ prescribes a matching between in-subs and out-stubs and hence defines a multigraph  $\tilde{G}_{\textbf{d}^{n}}$ with vertex set
$\tilde{G}_{\textbf{d}^{n}}$ with vertex set  $V = [n]$ and edge multiset
$V = [n]$ and edge multiset
 \begin{align}
E = [ (i,j) \mid {W^{+}_{i}} \ni a, {W^{-}_{j}} \ni b\ \text{and}\ (a,b) \in \mathcal{M} ].
\end{align}
\begin{align}
E = [ (i,j) \mid {W^{+}_{i}} \ni a, {W^{-}_{j}} \ni b\ \text{and}\ (a,b) \in \mathcal{M} ].
\end{align} Note that multiple configurations may correspond to the same graph. We will now study the probability that the configuration model generates a specific multigraph  $\tilde{G}_{\textbf{d}^{n}}$.
$\tilde{G}_{\textbf{d}^{n}}$.
Proposition 3.5. Let  $\tilde{G}_{\textbf{d}^{n}}$ be a multigraph with degree sequence dn and
$\tilde{G}_{\textbf{d}^{n}}$ be a multigraph with degree sequence dn and  $\Upsilon_{i,j}$ be the multiplicity of edge (i, j) in
$\Upsilon_{i,j}$ be the multiplicity of edge (i, j) in  $\tilde{G}_{\textbf{d}^{n}}$. Then it holds that
$\tilde{G}_{\textbf{d}^{n}}$. Then it holds that
 \begin{align}
\mathbb{P}\left[CM_{n}\left({\textbf{d}^n}\right) = \tilde{G}_{\textbf{d}^{n}}\right] = \frac{1}{m!}\frac{\prod_{i=1}^n {d^-_{i}}!\prod_{i=1}^n{d^+_{i}}!}{\prod_{1\leq i,j\leq n} \Upsilon_{i,j}!}.
\end{align}
\begin{align}
\mathbb{P}\left[CM_{n}\left({\textbf{d}^n}\right) = \tilde{G}_{\textbf{d}^{n}}\right] = \frac{1}{m!}\frac{\prod_{i=1}^n {d^-_{i}}!\prod_{i=1}^n{d^+_{i}}!}{\prod_{1\leq i,j\leq n} \Upsilon_{i,j}!}.
\end{align}Proof. This proof is based on [Reference van der Hofstad27, Prop. 7.4] formulated for undirected graphs. There are  $m!$ different configurations. As the configuration is chosen uniformly at random,
$m!$ different configurations. As the configuration is chosen uniformly at random,
 \begin{align*}
\mathbb{P}\left[\text{CM}_{n}\left({\textbf{d}^n}\right) = \tilde{G}_{\textbf{d}^{n}}\right] = \frac{1}{m!}N\left(\tilde{G}_{\textbf{d}^{n}}\right),
\end{align*}
\begin{align*}
\mathbb{P}\left[\text{CM}_{n}\left({\textbf{d}^n}\right) = \tilde{G}_{\textbf{d}^{n}}\right] = \frac{1}{m!}N\left(\tilde{G}_{\textbf{d}^{n}}\right),
\end{align*}with  $N\left(\tilde{G}_{\textbf{d}^{n}}\right)$ being the number of distinct configurations inducing
$N\left(\tilde{G}_{\textbf{d}^{n}}\right)$ being the number of distinct configurations inducing  $\tilde{G}_{\textbf{d}^{n}}$. It follows from Eq. (4) that permuting the stub labels results in a different configuration that induces the same multigraph. There are
$\tilde{G}_{\textbf{d}^{n}}$. It follows from Eq. (4) that permuting the stub labels results in a different configuration that induces the same multigraph. There are  $\prod_{i=1}^n {d^-_{i}}!\prod_{i=1}^n{d^+_{i}}!$ such permutations. For
$\prod_{i=1}^n {d^-_{i}}!\prod_{i=1}^n{d^+_{i}}!$ such permutations. For  $a,a^\prime \in {W^{+}_{i}}$ and
$a,a^\prime \in {W^{+}_{i}}$ and  $ b,b^\prime \in {W^{-}_{j}}$ with
$ b,b^\prime \in {W^{-}_{j}}$ with  $(a,b), (a^\prime,b^\prime) \in \mathcal{M}$, any permutation swapping a with aʹ and b with bʹ results in the same configuration. We compensate for this by a factor
$(a,b), (a^\prime,b^\prime) \in \mathcal{M}$, any permutation swapping a with aʹ and b with bʹ results in the same configuration. We compensate for this by a factor  $\Upsilon_{i,j}!$ to obtain
$\Upsilon_{i,j}!$ to obtain
 \begin{equation*}
N\left(\tilde{G}_{\textbf{d}^{n}}\right) = \frac{\prod_{i=1}^n {d^-_{i}}!\prod_{i=1}^n{d^+_{i}}!}{\prod_{1\leq i,j\leq n} \Upsilon_{ij}!},
\end{equation*}
\begin{equation*}
N\left(\tilde{G}_{\textbf{d}^{n}}\right) = \frac{\prod_{i=1}^n {d^-_{i}}!\prod_{i=1}^n{d^+_{i}}!}{\prod_{1\leq i,j\leq n} \Upsilon_{ij}!},
\end{equation*}Corollary 3.6. Conditional on the event that configuration model generates a simple digraph, an element of  $\mathcal{G}_{\textbf{d}^{n}}$ is chosen uniformly.
$\mathcal{G}_{\textbf{d}^{n}}$ is chosen uniformly.
Generally speaking, we are interested in the statements of the form
 \begin{equation}
\lim_{n \rightarrow \infty} \mathbb{P}\left[ \tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \right] =1,
\end{equation}
\begin{equation}
\lim_{n \rightarrow \infty} \mathbb{P}\left[ \tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \right] =1,
\end{equation}where  $\mathcal{A}\left({\textbf{d}^n}\right)$ is the set of all graphs that obey the degree sequence dn and additionally satisfy some desired property. If this limit holds for a given property
$\mathcal{A}\left({\textbf{d}^n}\right)$ is the set of all graphs that obey the degree sequence dn and additionally satisfy some desired property. If this limit holds for a given property  $\mathcal{A}$, then we say that the random graph has this property w.h.p or asymptotically almost surely (a. almost surely). The goal of the remainder of this section is to show that if Eq. (6) holds, then
$\mathcal{A}$, then we say that the random graph has this property w.h.p or asymptotically almost surely (a. almost surely). The goal of the remainder of this section is to show that if Eq. (6) holds, then
 \begin{align*}
\lim_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \mid \tilde{G}_{\textbf{d}^{n}} \,\text{is simple}\right] =1.
\end{align*}
\begin{align*}
\lim_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \mid \tilde{G}_{\textbf{d}^{n}} \,\text{is simple}\right] =1.
\end{align*}First, we show that the probability that the configuration model generates a simple graph is bounded away from zero.
Proposition 3.7. Chen and Olvera-Cravioto [Reference Chen and Olvera-Cravioto9, Thm. 4.3]
Let  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ be a feasible degree progression. The probability that the configuration model generates a simple graph is asymptotically
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ be a feasible degree progression. The probability that the configuration model generates a simple graph is asymptotically  ${\rm e}^{-\frac{\mu_{11}}{\mu} - \frac{\left(\mu_{20} -\mu \right)\left(\mu_{02}-\mu \right)}{\mu} } \gt 0. $
${\rm e}^{-\frac{\mu_{11}}{\mu} - \frac{\left(\mu_{20} -\mu \right)\left(\mu_{02}-\mu \right)}{\mu} } \gt 0. $
Proof. The proof follows from the proof of [Reference Chen and Olvera-Cravioto9, Thm. 4.3]. It suffices to replace Condition 4.1 and Lemma 5.2 from Ref. [Reference Chen and Olvera-Cravioto9] with the requirement of a feasible degree progression.
Lemma 3.8. Let  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ be a feasible degree progression, and let
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ be a feasible degree progression, and let  $\mathcal{A}\left({\textbf{d}^n}\right)$ be a set of multigraphs all satisfying dn. Let
$\mathcal{A}\left({\textbf{d}^n}\right)$ be a set of multigraphs all satisfying dn. Let  $\tilde{G}_{\textbf{d}^{n}}$ be a random multigraph generated by the configuration model.
$\tilde{G}_{\textbf{d}^{n}}$ be a random multigraph generated by the configuration model.
(1) If
 $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[ \tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right)\right] =0,
$ then
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[ \tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right)\right] =0,
$ then  $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \mid \tilde{G}_{\textbf{d}^{n}} \,\textrm{ is simple}\right] =0.
$
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \mid \tilde{G}_{\textbf{d}^{n}} \,\textrm{ is simple}\right] =0.
$(2) If
 $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[ \tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right)\right] =1,
$ then
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[ \tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right)\right] =1,
$ then  $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \big|\, \tilde{G}_{\textbf{d}^{n}} \,\textrm{ is simple}\right] =1.
$
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}} \in \mathcal{A}\left({\textbf{d}^n}\right) \big|\, \tilde{G}_{\textbf{d}^{n}} \,\textrm{ is simple}\right] =1.
$
3.3. Giant strongly connected component in a directed graph
A natural definition of a path in a directed graph requires that a path respects edge directions:
Definition 3.9. Let  $G=(V,E)$ be a digraph. A pair of vertices
$G=(V,E)$ be a digraph. A pair of vertices  $v_1, v_k \in V$ is connected by a directed path if there are distinct vertices
$v_1, v_k \in V$ is connected by a directed path if there are distinct vertices  $v_2,v_3, \ldots ,v_{k-1} \in V$ such that for all
$v_2,v_3, \ldots ,v_{k-1} \in V$ such that for all  $ i \in\{2,3,\ldots, k\},$
$ i \in\{2,3,\ldots, k\},$  $\left(v_{i-1}, v_i\right) \in E$. We refer to such a sequence as a directed
$\left(v_{i-1}, v_i\right) \in E$. We refer to such a sequence as a directed  $v_1-v_k$ path.
$v_1-v_k$ path.
This definition of connectivity can be extended to define connected components:
Definition 3.10. SCC of a directed graph  $G=(V,E)$ is a maximal subset of
$G=(V,E)$ is a maximal subset of  $C\subset V$ such that for any
$C\subset V$ such that for any  $u,v \in C$, there are directed paths u − v and v − u.
$u,v \in C$, there are directed paths u − v and v − u.
Let  $\mathcal{C} (G_n)$ be the largest SCC. The notion of a giant component is introduced as a limiting property of the sequence of
$\mathcal{C} (G_n)$ be the largest SCC. The notion of a giant component is introduced as a limiting property of the sequence of  $\mathcal{C} (G_n)$. Let
$\mathcal{C} (G_n)$. Let  $x^*,y^*$ be the smallest positive solutions of, respectively,
$x^*,y^*$ be the smallest positive solutions of, respectively,  $
x^*= U^-(x^*)
$ and
$
x^*= U^-(x^*)
$ and  $
y^*= U^+(y^*)
$, where
$
y^*= U^+(y^*)
$, where
 \begin{align*}
U^+(y) & := \mu^{-1}\,\frac{\partial}{\partial x}U(x,y)|_{x=1},\\
U^-(x) & := \mu^{-1}\,\frac{\partial}{\partial y}U(x,y)|_{y=1},
\end{align*}
\begin{align*}
U^+(y) & := \mu^{-1}\,\frac{\partial}{\partial x}U(x,y)|_{x=1},\\
U^-(x) & := \mu^{-1}\,\frac{\partial}{\partial y}U(x,y)|_{y=1},
\end{align*}and  $U\left( x, y \right) := \sum_{j,k=0}^{\infty} p_{j,k} {x}^j {y}^k $ is the generating function of
$U\left( x, y \right) := \sum_{j,k=0}^{\infty} p_{j,k} {x}^j {y}^k $ is the generating function of  $p_{j,k}$. Let further,
$p_{j,k}$. Let further,
 \begin{equation*}
\zeta := 1-U(x^*,1)-U(1,y^*)+U(x^*,y^*).
\end{equation*}
\begin{equation*}
\zeta := 1-U(x^*,1)-U(1,y^*)+U(x^*,y^*).
\end{equation*}Theorem 3.11. (Existence of GSCC [Reference Cai and Perarnau7, Theorem 1.2])
Consider a feasible degree progression  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ and a uniformly random sequence of simple graphs
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ and a uniformly random sequence of simple graphs  $\left(G_{\textbf{d}^{n}}\right)_{n\in\mathbb{N}}$. Then,
$\left(G_{\textbf{d}^{n}}\right)_{n\in\mathbb{N}}$. Then,
(1) If
 ${\mu_{11}}/{\mu} \lt 1$, the size of any SCC is
${\mu_{11}}/{\mu} \lt 1$, the size of any SCC is  $\mathcal{O}\left(1\right)$ with high probability.
$\mathcal{O}\left(1\right)$ with high probability.(2) If
 ${\mu_{11}}/{\mu} \gt 1$, then with high probability, the largest SCC has vertex set of size
${\mu_{11}}/{\mu} \gt 1$, then with high probability, the largest SCC has vertex set of size  $|\mathcal{C}(G_n)|\sim\zeta n$.
$|\mathcal{C}(G_n)|\sim\zeta n$.
3.4. Concentration inequality
We introduce a concentration inequality based on McDiarmid’s method of bounded differences, stated below. The inequality is used later in the proof of Theorem 2.2.
Theorem 3.12. [Reference McDiarmid21, Theorem 7.4]
Let  $\left(V,d\right)$ be a finite metric space. Suppose there exists a sequence
$\left(V,d\right)$ be a finite metric space. Suppose there exists a sequence  $\mathcal{P}_0, \mathcal{P}_1, \ldots, \mathcal{P}_s$ of increasingly refined partitions, with
$\mathcal{P}_0, \mathcal{P}_1, \ldots, \mathcal{P}_s$ of increasingly refined partitions, with  $\mathcal{P}_0$ being the trivial partition consisting of V and
$\mathcal{P}_0$ being the trivial partition consisting of V and  $\mathcal{P}_s$ consisting of singletons. Take a sequence of positive integers
$\mathcal{P}_s$ consisting of singletons. Take a sequence of positive integers  $c_1, \ldots, c_s$ such that for all
$c_1, \ldots, c_s$ such that for all  $k \in \{1,2,\ldots, s\}$, whenever
$k \in \{1,2,\ldots, s\}$, whenever  $A,B \in \mathcal{P}_k$ and
$A,B \in \mathcal{P}_k$ and  $A,B\subseteq C \in \mathcal{P}_{k-1}$ for some C, there exists a bijection
$A,B\subseteq C \in \mathcal{P}_{k-1}$ for some C, there exists a bijection  $\phi: A \rightarrow B$ with
$\phi: A \rightarrow B$ with  $d\left(x,\phi(x)\right) \leq c_k$ for all
$d\left(x,\phi(x)\right) \leq c_k$ for all  $x \in A$. Let the function
$x \in A$. Let the function  $f: V \rightarrow \mathbb{R}$ satisfy
$f: V \rightarrow \mathbb{R}$ satisfy  $\lvert f(x) - f(y) \rvert \leq d(x,y)$ for all
$\lvert f(x) - f(y) \rvert \leq d(x,y)$ for all  $x,y,\in V$. Then, for X uniformly distributed over V and any t > 0,
$x,y,\in V$. Then, for X uniformly distributed over V and any t > 0,
 \begin{align*}
\mathbb{P}\left[\lvert f(X) - \mathbb{E}\left[f(X)\right] \rvert \gt t \right] \leq 2\, \exp\left(-\frac{2t^2}{\sum_{k=1}^s c_k^2}\right).
\end{align*}
\begin{align*}
\mathbb{P}\left[\lvert f(X) - \mathbb{E}\left[f(X)\right] \rvert \gt t \right] \leq 2\, \exp\left(-\frac{2t^2}{\sum_{k=1}^s c_k^2}\right).
\end{align*}Theorem 3.13. Consider two finite sets A 0 and A 1 with  $\lvert A_0 \rvert = a_0$ and
$\lvert A_0 \rvert = a_0$ and  $\lvert A_1\rvert = a_1$.
$\lvert A_1\rvert = a_1$.
Let  $ S:= \cup_{i \in \{0,1\}} \{(x,i) \mid x \in A_i\}$. A subset of S containing b 0 elements with i = 0 and b 1 elements with i = 1 is called a
$ S:= \cup_{i \in \{0,1\}} \{(x,i) \mid x \in A_i\}$. A subset of S containing b 0 elements with i = 0 and b 1 elements with i = 1 is called a  $\left(b_0,b_1\right)$-subset of S. Let V be the space of all
$\left(b_0,b_1\right)$-subset of S. Let V be the space of all  $\left(b_0,b_1\right)$-subsets of S. Let
$\left(b_0,b_1\right)$-subsets of S. Let  $f: V \rightarrow \mathbb{R}$ be a function such that for any
$f: V \rightarrow \mathbb{R}$ be a function such that for any  $B,B^\prime \in V$, it holds
$B,B^\prime \in V$, it holds  $\lvert\ f\left(B\right) - f\left(B^\prime\right)\rvert \leq \lvert B \triangle B^\prime \rvert $. Here,
$\lvert\ f\left(B\right) - f\left(B^\prime\right)\rvert \leq \lvert B \triangle B^\prime \rvert $. Here,  $B \triangle B^\prime$ denotes the symmetric difference, that is,
$B \triangle B^\prime$ denotes the symmetric difference, that is,  $B \triangle B^\prime = \left(B\cup B^\prime\right) \setminus \left(B \cap B^\prime\right)$. Then, for X distributed uniformly over V and any t > 0,
$B \triangle B^\prime = \left(B\cup B^\prime\right) \setminus \left(B \cap B^\prime\right)$. Then, for X distributed uniformly over V and any t > 0,
 \begin{align}
\mathbb{P}\left[ \left\lvert f(X) - \mathbb{E}\left[f(X)\right] \right\rvert \gt t\right] \leq 2\,\exp\left(-\frac{t^2}{8(b_0+b_1)}\right).
\end{align}
\begin{align}
\mathbb{P}\left[ \left\lvert f(X) - \mathbb{E}\left[f(X)\right] \right\rvert \gt t\right] \leq 2\,\exp\left(-\frac{t^2}{8(b_0+b_1)}\right).
\end{align}Proof. Consider a  $\left(b_0,b_1\right)$-subset of S. Assign each element a unique number from the index set
$\left(b_0,b_1\right)$-subset of S. Assign each element a unique number from the index set  $\{1,2,\ldots, b_0+b_1\}$ such that for all elements with i = 0, this number is at most b 0. We call a
$\{1,2,\ldots, b_0+b_1\}$ such that for all elements with i = 0, this number is at most b 0. We call a  $\left(b_0,b_1\right)$-subset of S with such a numbering a
$\left(b_0,b_1\right)$-subset of S with such a numbering a  $\left(b_0,b_1\right)$-ordering of S. Define W to be the set of all
$\left(b_0,b_1\right)$-ordering of S. Define W to be the set of all  $\left(b_0,b_1\right)$-orderings of S. The function
$\left(b_0,b_1\right)$-orderings of S. The function  $f: V\rightarrow \mathbb{R}$ naturally gives rise to a function
$f: V\rightarrow \mathbb{R}$ naturally gives rise to a function  $f:W \rightarrow \mathbb{R}$ by regarding each
$f:W \rightarrow \mathbb{R}$ by regarding each  $\left(b_0,b_1\right)$-ordering as
$\left(b_0,b_1\right)$-ordering as  $\left(b_0,b_1\right)$-subset. Note that
$\left(b_0,b_1\right)$-subset. Note that  $\lvert f(x) - f(y)\rvert \leq x \triangle y$, that is, it holds for
$\lvert f(x) - f(y)\rvert \leq x \triangle y$, that is, it holds for  $x,y \in W$ as well. This is true since for any two orderings
$x,y \in W$ as well. This is true since for any two orderings  $x,y$, their symmetric difference as
$x,y$, their symmetric difference as  $\left(b_0,b_1\right)$-orderings is bounded from below by their symmetric difference as
$\left(b_0,b_1\right)$-orderings is bounded from below by their symmetric difference as  $\left(b_0,b_1\right)$-subsets. The next step in proving Eq. (7) is applying Theorem 3.12 to the metric space
$\left(b_0,b_1\right)$-subsets. The next step in proving Eq. (7) is applying Theorem 3.12 to the metric space  $\left(W, \triangle \right)$.
$\left(W, \triangle \right)$.
We will now define a sequence of refined partitions on W using the notion of an i-prefix. An i-prefix determines the first i elements of an ordering. This allows for all  $k \in \{0,1,\ldots, b_0+b_1\}$ to construct the partition
$k \in \{0,1,\ldots, b_0+b_1\}$ to construct the partition  $\mathcal{P}_k$ by defining its elements to be the sets of orderings with the same k-prefix. The partition
$\mathcal{P}_k$ by defining its elements to be the sets of orderings with the same k-prefix. The partition  $\mathcal{P}_0$ is the trivial partition consisting of W. The partition
$\mathcal{P}_0$ is the trivial partition consisting of W. The partition  $\mathcal{P}_{b_0+b_1}$ will be the partition where each element is a single ordering. Next, the values c k need to be determined for
$\mathcal{P}_{b_0+b_1}$ will be the partition where each element is a single ordering. Next, the values c k need to be determined for  $k \in \{1,2,\ldots , b_0+b_1\}$. Take
$k \in \{1,2,\ldots , b_0+b_1\}$. Take  $B,D \in \mathcal{P}_k$ with C satisfying
$B,D \in \mathcal{P}_k$ with C satisfying  $B,D\subset C \in \mathcal{P}_{k-1}$. This implies that any ordering in B has the same k − 1-prefix as an ordering in D. Furthermore, these orderings must differ at the kth element. The remaining
$B,D\subset C \in \mathcal{P}_{k-1}$. This implies that any ordering in B has the same k − 1-prefix as an ordering in D. Furthermore, these orderings must differ at the kth element. The remaining  $b_0+b_1-k$ elements can be any element that is not present in the k-prefix that leads to a valid ordering. Denote the kth element of any ordering in B by
$b_0+b_1-k$ elements can be any element that is not present in the k-prefix that leads to a valid ordering. Denote the kth element of any ordering in B by  $a_{B,k}$. Similarly, let
$a_{B,k}$. Similarly, let  $a_{D,k}$ denote the kth element of any ordering in D. Define the bijection
$a_{D,k}$ denote the kth element of any ordering in D. Define the bijection  $\phi: B \rightarrow D$ by taking
$\phi: B \rightarrow D$ by taking  $x \in B$ and mapping its kth element to
$x \in B$ and mapping its kth element to  $a_{D,k}$. If x contains
$a_{D,k}$. If x contains  $a_{D,k}$ at some position l > k, map the lth element of x to
$a_{D,k}$ at some position l > k, map the lth element of x to  $a_{B,k}$. All the other elements are unchanged by the bijection. By definition, this is an element of D.
$a_{B,k}$. All the other elements are unchanged by the bijection. By definition, this is an element of D.
According to the definition of ϕ, for any  $x \in B$, we have
$x \in B$, we have  $\lvert x \triangle \phi(x) \rvert \leq 4$. Thus, we may take
$\lvert x \triangle \phi(x) \rvert \leq 4$. Thus, we may take  $c_k = 4$ for all
$c_k = 4$ for all  $k \in \{1,2,\ldots , b_0+b_1\}$. Applying Theorem 3.12, we find that Eq. (7) holds for any t > 0 and X distributed uniformly over W. Remark that each element in V gives rise to
$k \in \{1,2,\ldots , b_0+b_1\}$. Applying Theorem 3.12, we find that Eq. (7) holds for any t > 0 and X distributed uniformly over W. Remark that each element in V gives rise to  $b_0!+b_1!$ different orderings. All these orderings have the same value under f. Thus, the probability that
$b_0!+b_1!$ different orderings. All these orderings have the same value under f. Thus, the probability that  $f(X) = c$ does not change when we take X to be a uniformly random element of V instead of W. Together with Eq. (7) being valid for a X uniformly random element of W, this proves the claim.
$f(X) = c$ does not change when we take X to be a uniformly random element of V instead of W. Together with Eq. (7) being valid for a X uniformly random element of W, this proves the claim.
4. Proofs of Theorems 2.2 and 2.3
Theorems 2.2 and 2.3 are proven separately for bond and site percolation using similar techniques as in the proof of [Reference Fountoulakis16, Theorem 1.1], which determines the percolation threshold in undirected graphs. Although these theorems are formulated for simple digraphs, we instead prove the statements on random directed multigraphs introduced in Section 3.2. The results on the multigraphs are then transferred to simple digraphs using Lemma 3.8. After percolation with probability π, dn becomes a random variable  ${\textbf{D}_{\pi}^n}$, which will be considered separately for bond and site percolation.
${\textbf{D}_{\pi}^n}$, which will be considered separately for bond and site percolation.
4.1. Bond percolation
Bond percolation removes edges in a graph, thus in the configuration, it removes in-stubs together with their matched out-stubs. Let  ${W^{-,\pi}}$ and
${W^{-,\pi}}$ and  ${W^{+,\pi}}$ denote the in-stubs and out-stubs surviving percolation. Given that the degree sequence after percolation is fixed,
${W^{+,\pi}}$ denote the in-stubs and out-stubs surviving percolation. Given that the degree sequence after percolation is fixed,  ${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, there is a bijection between the configurations on the surviving stubs
${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, there is a bijection between the configurations on the surviving stubs  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ and the configurations on the stubs of
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ and the configurations on the stubs of  ${\textbf{d}^{n}_{\pi}}$, which we denote
${\textbf{d}^{n}_{\pi}}$, which we denote  $\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$. Let us fix such a bijection. Now, to show that the perfect matching on the remaining stubs (conditional on the degree sequence after percolation) is uniformly distributed on the set of perfect matchings on the stubs that survive percolation, it is sufficient to show that perfect matchings on
$\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$. Let us fix such a bijection. Now, to show that the perfect matching on the remaining stubs (conditional on the degree sequence after percolation) is uniformly distributed on the set of perfect matchings on the stubs that survive percolation, it is sufficient to show that perfect matchings on  $\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$ appear equally likely. Let
$\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$ appear equally likely. Let  $\mathcal{D}_{n}$ be the probability space containing all degree sequences
$\mathcal{D}_{n}$ be the probability space containing all degree sequences  ${\textbf{d}^{n}_{\pi}}$ that can be obtained by applying percolation to a random configuration on
${\textbf{d}^{n}_{\pi}}$ that can be obtained by applying percolation to a random configuration on  $\left({W^{-}}, {W^{+}} \right)$. The probability assigned to each
$\left({W^{-}}, {W^{+}} \right)$. The probability assigned to each  ${\textbf{d}^{n}_{\pi}}$ is the probability that it is induced by
${\textbf{d}^{n}_{\pi}}$ is the probability that it is induced by  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$. The probability space for the degree progression
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$. The probability space for the degree progression  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is the product space
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is the product space  $\mathcal{D} = \prod_{n=1}^\infty \mathcal{D}_{n}$ with the product measure ν.
$\mathcal{D} = \prod_{n=1}^\infty \mathcal{D}_{n}$ with the product measure ν.
The remainder of this section is as follows: in Section 4.1.1, we show that conditional on the degree sequence after percolation, each configuration on  ${W^{-}_{\textbf{d}^{n}_{\pi}}}$ and
${W^{-}_{\textbf{d}^{n}_{\pi}}}$ and  ${W^{+}_{\textbf{d}^{n}_{\pi}}}$ is equally likely. In Section 4.1.2, we determine the limit of the expected number of vertices with degree (j, k) after percolation and show the concentration. Combining these results in Section 4.1.3, the proofs of Theorems 2.2 and 2.3 are completed by showing that an element of
${W^{+}_{\textbf{d}^{n}_{\pi}}}$ is equally likely. In Section 4.1.2, we determine the limit of the expected number of vertices with degree (j, k) after percolation and show the concentration. Combining these results in Section 4.1.3, the proofs of Theorems 2.2 and 2.3 are completed by showing that an element of  $\mathcal{D}$ is ν- almost surely feasible, which authorizes applying Theorem 3.11.
$\mathcal{D}$ is ν- almost surely feasible, which authorizes applying Theorem 3.11.
4.1.1. A percolated configuration is a uniformly random configuration
In this section, we show that conditional on the degree sequence after percolation, the configuration on  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ is also a uniformly random one. The proof is split into two lemmas.
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ is also a uniformly random one. The proof is split into two lemmas.
Lemma 4.1. Apply bond percolation to a uniformly random configuration  $\mathcal{M}$ on
$\mathcal{M}$ on  $\left({W^{-}}, {W^{+}} \right)$. Conditional on the elements of
$\left({W^{-}}, {W^{+}} \right)$. Conditional on the elements of  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$, each configuration on these elements is equally likely.
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$, each configuration on these elements is equally likely.
Proof. Choosing the elements of  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ implies that the configuration
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ implies that the configuration  $\mathcal{M}$ is the union of a configuration on
$\mathcal{M}$ is the union of a configuration on  $\left( {W^{-}} \setminus {W^{-,\pi}}, {W^{+}} \setminus {W^{+,\pi}}\right)$ with one on
$\left( {W^{-}} \setminus {W^{-,\pi}}, {W^{+}} \setminus {W^{+,\pi}}\right)$ with one on  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$. As
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$. As  $\mathcal{M}$ is a uniformly random configuration obeying this split and the elements of
$\mathcal{M}$ is a uniformly random configuration obeying this split and the elements of  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ are fixed, the configuration on
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ are fixed, the configuration on  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ will be a uniformly random one.
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ will be a uniformly random one.
Lemma 4.2. Conditional on having degree sequence  ${\textbf{d}^{n}_{\pi}}$ after bond percolation, that is,
${\textbf{d}^{n}_{\pi}}$ after bond percolation, that is,  ${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, all configurations of
${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, all configurations of  ${W^{-}_{\textbf{d}^{n}_{\pi}}}$ with
${W^{-}_{\textbf{d}^{n}_{\pi}}}$ with  ${W^{+}_{\textbf{d}^{n}_{\pi}}}$ are equally likely.
${W^{+}_{\textbf{d}^{n}_{\pi}}}$ are equally likely.
Proof. Define  $l = \lvert {W^{-, \pi}} \rvert$ and let
$l = \lvert {W^{-, \pi}} \rvert$ and let  $S({\textbf{d}^{n}_{\pi}})$ contain all sets of surviving stubs
$S({\textbf{d}^{n}_{\pi}})$ contain all sets of surviving stubs  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ that induce the degrees sequence
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ that induce the degrees sequence  ${\textbf{d}^{n}_{\pi}}$. Fix a matching
${\textbf{d}^{n}_{\pi}}$. Fix a matching  $\mathcal{M}^{\pi}$ of
$\mathcal{M}^{\pi}$ of  $\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$. Then, using the bijection between
$\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$. Then, using the bijection between  $\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ and
$\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ and  $\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$,
$\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$,
 \begin{align*}
\mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}\right] = \sum_{\left(A,B\right)\in S({\textbf{d}^{n}_{\pi}})} & \mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}, \left({W^{-,\pi}}, {W^{+,\pi}}\right) =
\left(A,B\right) \right] \times \\
&\mathbb{P}\left[ \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right)| {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right].
\end{align*}
\begin{align*}
\mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}\right] = \sum_{\left(A,B\right)\in S({\textbf{d}^{n}_{\pi}})} & \mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}, \left({W^{-,\pi}}, {W^{+,\pi}}\right) =
\left(A,B\right) \right] \times \\
&\mathbb{P}\left[ \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right)| {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right].
\end{align*} Remark that  $\mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}, \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right) \right] = \mathbb{P}\left[\mathcal{M}^{\pi} | \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right) \right]$ by definition of
$\mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}, \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right) \right] = \mathbb{P}\left[\mathcal{M}^{\pi} | \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right) \right]$ by definition of  $S({\textbf{d}^{n}_{\pi}})$. Using Lemma 4.1, we find
$S({\textbf{d}^{n}_{\pi}})$. Using Lemma 4.1, we find
 \begin{equation*}\mathbb{P}\left[\mathcal{M}^{\pi} | \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right) \right] = \frac{1}{l!}.\end{equation*}
\begin{equation*}\mathbb{P}\left[\mathcal{M}^{\pi} | \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right) \right] = \frac{1}{l!}.\end{equation*}Furthermore, combining these observations with
 \begin{equation*}\sum_{\left(A,B\right)\in S({\textbf{d}^{n}_{\pi}})} \mathbb{P}\left[\left({W^{-,\pi}}, {W^{+,\pi}}\right)= \left(A,B\right) | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right] = 1\end{equation*}
\begin{equation*}\sum_{\left(A,B\right)\in S({\textbf{d}^{n}_{\pi}})} \mathbb{P}\left[\left({W^{-,\pi}}, {W^{+,\pi}}\right)= \left(A,B\right) | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right] = 1\end{equation*}following from the definition of  $S({\textbf{d}^{n}_{\pi}})$, we obtain
$S({\textbf{d}^{n}_{\pi}})$, we obtain
 \begin{align*}
\mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}\right] &= \frac{1}{l!} \sum_{\left(A,B\right)\in S({\textbf{d}^{n}_{\pi}})} \mathbb{P}\left[ \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right)| {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right] = \frac{1}{l!},
\end{align*}
\begin{align*}
\mathbb{P}\left[\mathcal{M}^{\pi} | {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}\right] &= \frac{1}{l!} \sum_{\left(A,B\right)\in S({\textbf{d}^{n}_{\pi}})} \mathbb{P}\left[ \left({W^{-,\pi}}, {W^{+,\pi}}\right) = \left(A,B\right)| {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right] = \frac{1}{l!},
\end{align*}completing the proof.
4.1.2. The expected number of vertices with degree (j, k) after bond percolation
In this section, we derive an expression for the degree distribution after bond percolation. This uses the following auxiliary lemma.
Lemma 4.3. Let l out of m edges survive bond percolation applied to a uniformly random configuration  $\mathcal{M}$ on
$\mathcal{M}$ on  $\left({W^{-}}, {W^{+}} \right)$. Then the surviving stubs
$\left({W^{-}}, {W^{+}} \right)$. Then the surviving stubs  ${W^{-, \pi}} {\subset} {W^{-}}$ and
${W^{-, \pi}} {\subset} {W^{-}}$ and  ${W^{+, \pi}} \subset {W^{+}}$ are uniformly distributed among all pairs of subsets of
${W^{+, \pi}} \subset {W^{+}}$ are uniformly distributed among all pairs of subsets of  $W^{-}$ and
$W^{-}$ and  $W^{+}$ of size l.
$W^{+}$ of size l.
Proof. The graph contains m matches of which  $l=\lvert {W^{-, \pi}} \rvert = \lvert {W^{+, \pi}} \rvert $ survive percolation. Thus, the probability that l matches remain is
$l=\lvert {W^{-, \pi}} \rvert = \lvert {W^{+, \pi}} \rvert $ survive percolation. Thus, the probability that l matches remain is  $\frac{1}{{m \choose l}}$. It is left to investigate the probability that all stubs in
$\frac{1}{{m \choose l}}$. It is left to investigate the probability that all stubs in  ${W^{-,\pi}}$ have their match in
${W^{-,\pi}}$ have their match in  ${W^{+,\pi}}$, that is, that
${W^{+,\pi}}$, that is, that  $\mathcal{M}$ can be decomposed into a perfect bipartite matching of
$\mathcal{M}$ can be decomposed into a perfect bipartite matching of  ${W^{-,\pi}}$ with
${W^{-,\pi}}$ with  ${W^{+,\pi}}$ and a perfect bipartite matching of
${W^{+,\pi}}$ and a perfect bipartite matching of  ${W^{-}} \setminus {W^{-, \pi}} $ with
${W^{-}} \setminus {W^{-, \pi}} $ with  ${W^{+}} \setminus {W^{+, \pi}} $. Between two sets of size l, there are
${W^{+}} \setminus {W^{+, \pi}} $. Between two sets of size l, there are ![]() $l!$ perfect bipartite matchings; hence, the probability that
$l!$ perfect bipartite matchings; hence, the probability that  $\mathcal{M}$ decomposes as desired is
$\mathcal{M}$ decomposes as desired is  $l!(m-l)! / m!$. Thus, the probability that
$l!(m-l)! / m!$. Thus, the probability that  $\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ are the stubs surviving percolation is
$\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ are the stubs surviving percolation is  $
\frac{l!\, (m-l)!}{m!}\frac{1}{{m\choose l}} = \frac{1}{{m\choose l}^2}.
$ This is the probability that
$
\frac{l!\, (m-l)!}{m!}\frac{1}{{m\choose l}} = \frac{1}{{m\choose l}^2}.
$ This is the probability that  ${W^{-, \pi}} \!\subset{W^{-}}$ and
${W^{-, \pi}} \!\subset{W^{-}}$ and  ${W^{+, \pi}}\!\subset{W^{+}}$ are uniformly random subsets both of size l.
${W^{+, \pi}}\!\subset{W^{+}}$ are uniformly random subsets both of size l.
Lemma 4.4. Let  $N_{{j},{k}}^{\pi}\left(n\right)$ be the number of vertices in the bond-percolated graph (or configuration) with in-degree j and out-degree k. The following limit exists
$N_{{j},{k}}^{\pi}\left(n\right)$ be the number of vertices in the bond-percolated graph (or configuration) with in-degree j and out-degree k. The following limit exists
 \begin{align}
{p^{{\rm bond}}_{{j}, {k}}}:=\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]}{n} \quad \text{for } j,k\in\mathbb{N}_0
\end{align}
\begin{align}
{p^{{\rm bond}}_{{j}, {k}}}:=\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]}{n} \quad \text{for } j,k\in\mathbb{N}_0
\end{align}and
 \begin{align}
{p^{{\rm bond}}_{{j}, {k}}} = \sum_{d^- = j}^\infty \sum_{d^+ = k}^\infty p_{d^-,d^+} {d^- \choose j}{d^+ \choose k}\pi^{j+k}\left(1-\pi \right)^{d^- - j + d^+ -k}.
\end{align}
\begin{align}
{p^{{\rm bond}}_{{j}, {k}}} = \sum_{d^- = j}^\infty \sum_{d^+ = k}^\infty p_{d^-,d^+} {d^- \choose j}{d^+ \choose k}\pi^{j+k}\left(1-\pi \right)^{d^- - j + d^+ -k}.
\end{align}Proof. When  $j,k \gt d_{\max}$,
$j,k \gt d_{\max}$,  ${p^{{\rm bond}}_{{j}, {k}}}=N_{{j},{k}}^{\pi}\left(n\right)=N_{{j},{k}}\left(n\right) = 0$. Let
${p^{{\rm bond}}_{{j}, {k}}}=N_{{j},{k}}^{\pi}\left(n\right)=N_{{j},{k}}\left(n\right) = 0$. Let  $j,k \leq d_{\max}$ and remark that
$j,k \leq d_{\max}$ and remark that
 \begin{align}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] = \sum_{l=0}^m \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)| \lvert {W^{-, \pi}} \rvert = l\right]\mathbb{P}\left[\lvert {W^{-, \pi}} \rvert = l\right],
\end{align}
\begin{align}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] = \sum_{l=0}^m \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)| \lvert {W^{-, \pi}} \rvert = l\right]\mathbb{P}\left[\lvert {W^{-, \pi}} \rvert = l\right],
\end{align}which, when conditioned on  $\lvert{W^{-, \pi}} \rvert = l$, can be rewritten as
$\lvert{W^{-, \pi}} \rvert = l$, can be rewritten as
 \begin{align*}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)| \lvert {W^{-, \pi}} \rvert = l\right] = \sum_{d^- =j}^{d_{\max}} \sum_{d^+ = k}^{d_{\max}} N_{{d^-},{d^+}}\left(n\right)\mathbb{P}\left[ (d^-,d^+) \to (j, k)\,| \lvert {W^{-, \pi}} \rvert = l\right],
\end{align*}
\begin{align*}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)| \lvert {W^{-, \pi}} \rvert = l\right] = \sum_{d^- =j}^{d_{\max}} \sum_{d^+ = k}^{d_{\max}} N_{{d^-},{d^+}}\left(n\right)\mathbb{P}\left[ (d^-,d^+) \to (j, k)\,| \lvert {W^{-, \pi}} \rvert = l\right],
\end{align*}where event  $(d^-,d^+)\to (j,k)$ is a shorthand for a vertex of degree
$(d^-,d^+)\to (j,k)$ is a shorthand for a vertex of degree  $(d^-,d^+)$ has degree (j, k) after percolation. Since Lemma 4.3 implies that the surviving stubs are chosen uniformly at random, conditional on
$(d^-,d^+)$ has degree (j, k) after percolation. Since Lemma 4.3 implies that the surviving stubs are chosen uniformly at random, conditional on  $|{W^{-, \pi}} |$, we have
$|{W^{-, \pi}} |$, we have
 \begin{align*}
\mathbb{P}\left[ (d^-,d^+) \to(j, k)| \lvert {W^{-, \pi}} \rvert = l\right]= {d^- \choose j}\frac{{{m-d^-} \choose {l-j}}}{{m \choose l}} {d^+ \choose k} \frac{{{m-d^+} \choose {l-k}}}{{m \choose l}}.
\end{align*}
\begin{align*}
\mathbb{P}\left[ (d^-,d^+) \to(j, k)| \lvert {W^{-, \pi}} \rvert = l\right]= {d^- \choose j}\frac{{{m-d^-} \choose {l-j}}}{{m \choose l}} {d^+ \choose k} \frac{{{m-d^+} \choose {l-k}}}{{m \choose l}}.
\end{align*} The edges are removed independently of each other; hence,  $|{W^{-, \pi}} |$ is the sum of m independent Bernoulli variables, each having expectation π. Let
$|{W^{-, \pi}} |$ is the sum of m independent Bernoulli variables, each having expectation π. Let
 \begin{equation}
I_n := \left[ m\pi - \ln n\sqrt{n}, m\pi + \ln n\sqrt{n}\right],
\end{equation}
\begin{equation}
I_n := \left[ m\pi - \ln n\sqrt{n}, m\pi + \ln n\sqrt{n}\right],
\end{equation}applying Hoefdding’s inequality shows that  $\lvert {W^{-, \pi}} \rvert$ concentrates
$\lvert {W^{-, \pi}} \rvert$ concentrates
 \begin{align}
\mathbb{P}\left[ \lvert {W^{-, \pi}} \rvert \notin I_n\right] \leq \exp\left[-\Omega (\ln^2n)\right].
\end{align}
\begin{align}
\mathbb{P}\left[ \lvert {W^{-, \pi}} \rvert \notin I_n\right] \leq \exp\left[-\Omega (\ln^2n)\right].
\end{align} Note that as an immediate consequence of this inequality, we have  $\mathbb{P}\left[l \notin I_n\right] = o\left(n^\alpha\right)$ for any α < 0. Therefore, we have
$\mathbb{P}\left[l \notin I_n\right] = o\left(n^\alpha\right)$ for any α < 0. Therefore, we have
 \begin{align*}
\mathbb{P}\left[ (d^-,d^+) \to(j,k)| \lvert {W^{-, \pi}} \rvert = l\right]
= {{d^-}\choose{j}} {{d^+}\choose{k}} \pi^{j+k}\left(1-\pi \right)^{d^- + d^+ - j - k}\left(1 + \mathcal{O}\left(\frac{\ln n}{n^{7/18}}\right)\right),
\end{align*}
\begin{align*}
\mathbb{P}\left[ (d^-,d^+) \to(j,k)| \lvert {W^{-, \pi}} \rvert = l\right]
= {{d^-}\choose{j}} {{d^+}\choose{k}} \pi^{j+k}\left(1-\pi \right)^{d^- + d^+ - j - k}\left(1 + \mathcal{O}\left(\frac{\ln n}{n^{7/18}}\right)\right),
\end{align*}uniformly for all  $d^-,d^+ \leq d_{\max}\leq n^{\frac{1}{9}}$ and
$d^-,d^+ \leq d_{\max}\leq n^{\frac{1}{9}}$ and  $l \in I_n$. In combination with Eq. (10) and the bound
$l \in I_n$. In combination with Eq. (10) and the bound  $N_{{j},{k}}^{\pi}\left(n\right) \leq n$, we find
$N_{{j},{k}}^{\pi}\left(n\right) \leq n$, we find
 \begin{align}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] &= \left(1 +\mathcal{O}\left(\frac{\ln n}{n^{7/18}}\right)\right)\sum_{d^-=j}^{d_{\max}} \sum_{d^+=k}^{d_{\max}} N_{{d^-},{d^+}}\left(n\right) {{d^-}\choose{j}} {{d^+}\choose{k}} \pi^{j+k}\left(1-\pi \right)^{d^- + d^+ - j - k} +o\left(\frac{1}{n^3}\right),
\end{align}
\begin{align}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] &= \left(1 +\mathcal{O}\left(\frac{\ln n}{n^{7/18}}\right)\right)\sum_{d^-=j}^{d_{\max}} \sum_{d^+=k}^{d_{\max}} N_{{d^-},{d^+}}\left(n\right) {{d^-}\choose{j}} {{d^+}\choose{k}} \pi^{j+k}\left(1-\pi \right)^{d^- + d^+ - j - k} +o\left(\frac{1}{n^3}\right),
\end{align}where we set α = 5 in the estimate for  $\mathbb{P}\left[l \notin I_n\right] $ when calculating the error term. We will now show that for all ϵ > 0, there exist
$\mathbb{P}\left[l \notin I_n\right] $ when calculating the error term. We will now show that for all ϵ > 0, there exist  $\kappa\left(\epsilon\right)$ and
$\kappa\left(\epsilon\right)$ and  $N\left(\epsilon\right)$ such that for all
$N\left(\epsilon\right)$ such that for all  $n \gt N,$
$n \gt N,$
 \begin{align}
\frac{1}{n} \sum_{{\substack{(d^-,d^+) = (j,k)\\
d^- \geq \kappa +1\, {\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} N_{{d^-},{d^+}}\left(n\right) {{d^-} \choose j} {{d^+} \choose k} \pi^{j+k}\left(1-\pi \right)^{d^- + d^+ -j -k} \leq \frac{1}{n} \sum_{{\substack{(d^-,\ d^+) = (j,k)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} N_{{d^-},\ {d^+}}\left(n\right) \lt \epsilon .
\end{align}
\begin{align}
\frac{1}{n} \sum_{{\substack{(d^-,d^+) = (j,k)\\
d^- \geq \kappa +1\, {\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} N_{{d^-},{d^+}}\left(n\right) {{d^-} \choose j} {{d^+} \choose k} \pi^{j+k}\left(1-\pi \right)^{d^- + d^+ -j -k} \leq \frac{1}{n} \sum_{{\substack{(d^-,\ d^+) = (j,k)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} N_{{d^-},\ {d^+}}\left(n\right) \lt \epsilon .
\end{align} The left inequality follows from the binomial theorem, and the right – since  $\lim\limits_{n\rightarrow \infty}\frac{N_{{j},{k}}\left(n\right)}{n} = p_{j,k}$ for
$\lim\limits_{n\rightarrow \infty}\frac{N_{{j},{k}}\left(n\right)}{n} = p_{j,k}$ for  $j,k \geq 0$ and
$j,k \geq 0$ and  $(p_{j,k})$ is a probability distribution, which follows from the degree progression being proper. When combined together, Eqs. (13) and (14) prove the claim.
$(p_{j,k})$ is a probability distribution, which follows from the degree progression being proper. When combined together, Eqs. (13) and (14) prove the claim.
Elementary calculations show that  ${p^{\text{bond}}_{{j}, {k}}}$ is a probability distribution and has the following moments:
${p^{\text{bond}}_{{j}, {k}}}$ is a probability distribution and has the following moments:
 \begin{equation}
\begin{aligned}
\mu^{\pi, \text{bond}}:=&\sum_{j=0}^\infty \sum_{k=0}^\infty j{p^{\text{bond}}_{{j}, {k}}} = \sum_{j=0}^\infty \sum_{k=0}^\infty k{p^{\text{bond}}_{{j}, {k}}} =\pi \mu,\\
\mu_{11}^{\pi, \text{bond}}:=&\sum_{j,k=0}^\infty jk{p^{\text{bond}}_{{j}, {k}}} = \pi^2\sum_{d^-=0}^\infty \sum_{d^+=0}^\infty d^{-}d^{+}p_{d^-,d^+} = \pi^2 \mu_{11}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mu^{\pi, \text{bond}}:=&\sum_{j=0}^\infty \sum_{k=0}^\infty j{p^{\text{bond}}_{{j}, {k}}} = \sum_{j=0}^\infty \sum_{k=0}^\infty k{p^{\text{bond}}_{{j}, {k}}} =\pi \mu,\\
\mu_{11}^{\pi, \text{bond}}:=&\sum_{j,k=0}^\infty jk{p^{\text{bond}}_{{j}, {k}}} = \pi^2\sum_{d^-=0}^\infty \sum_{d^+=0}^\infty d^{-}d^{+}p_{d^-,d^+} = \pi^2 \mu_{11}.
\end{aligned}
\end{equation} The generating function  $U_{\pi}^\text{bond}$ of
$U_{\pi}^\text{bond}$ of  ${p^{\text{bond}}_{{j}, {k}}}$ and auxiliary functions
${p^{\text{bond}}_{{j}, {k}}}$ and auxiliary functions  $U^+_{\pi},U^-_{\pi}$ analogous to those used in Section 3.3 are given by
$U^+_{\pi},U^-_{\pi}$ analogous to those used in Section 3.3 are given by
 \begin{equation}
\begin{aligned}
&U_{\pi}^\text{bond}(x,y) := U(1-\pi +\pi x,1-\pi +\pi y),\\
& U^+_{\pi}(x):=U^+(1-\pi +\pi x),\\
&U^-_{\pi}(y):=U^-(1-\pi +\pi y).
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&U_{\pi}^\text{bond}(x,y) := U(1-\pi +\pi x,1-\pi +\pi y),\\
& U^+_{\pi}(x):=U^+(1-\pi +\pi x),\\
&U^-_{\pi}(y):=U^-(1-\pi +\pi y).
\end{aligned}
\end{equation} The moments (15) and generating functions (16) provide sufficient information for applying Theorem 3.11 to  ${p^{\text{bond}}_{{j}, {k}}}$ and hence formally defining the percolation threshold as such a value of
${p^{\text{bond}}_{{j}, {k}}}$ and hence formally defining the percolation threshold as such a value of  $\pi =\hat{\pi}^{\text{bond}}$ that
$\pi =\hat{\pi}^{\text{bond}}$ that  $\mu^{\pi, \text{bond}}= \mu_{11}^{\pi, \text{bond}}$, that is
$\mu^{\pi, \text{bond}}= \mu_{11}^{\pi, \text{bond}}$, that is
 \begin{align*}
\hat{\pi}^{\text{bond}} = \frac{\mu}{\mu_{11}}.
\end{align*}
\begin{align*}
\hat{\pi}^{\text{bond}} = \frac{\mu}{\mu_{11}}.
\end{align*} In the following section, we will show that this quantity is indeed the desired threshold for bond percolation,  ${\pi_c^{\text{bond}}}=\hat{\pi}^{\text{bond}}$. To this end, we show that
${\pi_c^{\text{bond}}}=\hat{\pi}^{\text{bond}}$. To this end, we show that  ${p^{\text{bond}}_{{j}, {k}}}$ is indeed ν-a.s the limit of the degree distribution of the percolated graph, which itself is a configuration model with the percolated degree sequence.
${p^{\text{bond}}_{{j}, {k}}}$ is indeed ν-a.s the limit of the degree distribution of the percolated graph, which itself is a configuration model with the percolated degree sequence.
4.1.3. Determining  $\pi_{c}^{{\rm bond}}$ and
$\pi_{c}^{{\rm bond}}$ and  $c^{{\rm bond}}$
$c^{{\rm bond}}$
We make use of Lemma 4.2, stating that instead of actually removing edges, one may view the percolated multigraph  $\tilde{G}_{\textbf{d}^{n}}^{\pi}$ as a uniformly random configuration obeying the percolated degree sequence
$\tilde{G}_{\textbf{d}^{n}}^{\pi}$ as a uniformly random configuration obeying the percolated degree sequence  ${\textbf{d}^{n}_{\pi}}$. We show that
${\textbf{d}^{n}_{\pi}}$. We show that  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is indeed ν- almost surely feasible (Lemma 4.5) and hence, Theorem 3.11 is applicable to
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is indeed ν- almost surely feasible (Lemma 4.5) and hence, Theorem 3.11 is applicable to  $\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$. This means that Theorem 3.11 may be applied to almost all degree progressions
$\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$. This means that Theorem 3.11 may be applied to almost all degree progressions  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ to determine
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ to determine  ${\pi_c^{\text{bond}}}$ and c bond for random multigraphs. Conditioning on the graph before percolation being simple will ensure that the percolated graph is simple as well. Finally, we apply a variant of Lemma 3.8 and show that similar assertions hold for a graph progression
${\pi_c^{\text{bond}}}$ and c bond for random multigraphs. Conditioning on the graph before percolation being simple will ensure that the percolated graph is simple as well. Finally, we apply a variant of Lemma 3.8 and show that similar assertions hold for a graph progression  $\left(G_{n}^{\pi}\right)_{n \in \mathbb{N}}$ for percolated simple graphs obeying
$\left(G_{n}^{\pi}\right)_{n \in \mathbb{N}}$ for percolated simple graphs obeying  $(\textbf{d}^{n})_{n\in \mathbb{N}}$, hence proving Theorem 2.3 for the case of bond percolation. In the remainder of this section, we make the above-stated argument formal.
$(\textbf{d}^{n})_{n\in \mathbb{N}}$, hence proving Theorem 2.3 for the case of bond percolation. In the remainder of this section, we make the above-stated argument formal.
Lemma 4.5. The degree progression after bond percolation is feasible ν- almost surely
Proof. By definition, sequence  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is graphical. We need to show that it also satisfies the other requirements of Definition 3.2 ν- almost surely. To demonstrate that
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is graphical. We need to show that it also satisfies the other requirements of Definition 3.2 ν- almost surely. To demonstrate that
 \begin{align}
\lim_{n\rightarrow \infty} \frac{N_{{j},{k}}^{\pi}\left(n\right)}{n} = {p^{{\rm bond}}_{{j}, {k}}},\; \nu\mathrm{-a.s. }\quad {\rm for\ } j,k\in \mathbb{N}_0,
\end{align}
\begin{align}
\lim_{n\rightarrow \infty} \frac{N_{{j},{k}}^{\pi}\left(n\right)}{n} = {p^{{\rm bond}}_{{j}, {k}}},\; \nu\mathrm{-a.s. }\quad {\rm for\ } j,k\in \mathbb{N}_0,
\end{align}it suffices to show (see, e.g., [Reference Petrov25, Lemma 6.8]) that for all  $\epsilon \gt 0,$
$\epsilon \gt 0,$
 \begin{align}
\sum_{n=1}^\infty \mathbb{P}\left[\left\lvert \frac{1}{n}N_{{j},{k}}^{\pi}\left(n\right) - {p^{{\rm bond}}_{{j}, {k}}}\right\rvert \gt \epsilon\right] \lt \infty.
\end{align}
\begin{align}
\sum_{n=1}^\infty \mathbb{P}\left[\left\lvert \frac{1}{n}N_{{j},{k}}^{\pi}\left(n\right) - {p^{{\rm bond}}_{{j}, {k}}}\right\rvert \gt \epsilon\right] \lt \infty.
\end{align} By definition of  ${p^{{\rm bond}}_{{j}, {k}}},$ for any fixed ϵ > 0, there is K such that for all n > K
${p^{{\rm bond}}_{{j}, {k}}},$ for any fixed ϵ > 0, there is K such that for all n > K
 \begin{align*}
\left\lvert \frac{1}{n}\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] - {p^{{\rm bond}}_{{j}, {k}}} \right\rvert \leq \frac{\epsilon}{2}.
\end{align*}
\begin{align*}
\left\lvert \frac{1}{n}\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] - {p^{{\rm bond}}_{{j}, {k}}} \right\rvert \leq \frac{\epsilon}{2}.
\end{align*}This implies that
 \begin{align*}
\mathbb{P}\left[\left\lvert \frac{1}{n}N_{{j},{k}}^{\pi}\left(n\right) - {p^{{\rm bond}}_{{j}, {k}}}\right\rvert \gt \epsilon\right] \leq \mathbb{P}\left[\frac{1}{n}\left\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right \rvert \gt \frac{\epsilon}{2}\right].
\end{align*}
\begin{align*}
\mathbb{P}\left[\left\lvert \frac{1}{n}N_{{j},{k}}^{\pi}\left(n\right) - {p^{{\rm bond}}_{{j}, {k}}}\right\rvert \gt \epsilon\right] \leq \mathbb{P}\left[\frac{1}{n}\left\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right \rvert \gt \frac{\epsilon}{2}\right].
\end{align*} Lemma 4.3 states that conditional on  $\lvert {W^{-, \pi}} \rvert =l$, the stubs surviving percolation
$\lvert {W^{-, \pi}} \rvert =l$, the stubs surviving percolation  $\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ are uniformly distributed among all pairs of subsets of
$\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ are uniformly distributed among all pairs of subsets of  $\left({W^{-}},{W^{+}} \right)$ of size l.
$\left({W^{-}},{W^{+}} \right)$ of size l.  $N_{{j},{k}}^{\pi}\left(n\right)$ is a function of
$N_{{j},{k}}^{\pi}\left(n\right)$ is a function of  ${W^{-, \pi}} \cup {W^{+, \pi}} $. Furthermore, for two sets
${W^{-, \pi}} \cup {W^{+, \pi}} $. Furthermore, for two sets  ${W^{-, \pi}} \cup {W^{+, \pi}} $ and
${W^{-, \pi}} \cup {W^{+, \pi}} $ and  ${W^{'-, \pi}} \cup {W^{'+, \pi}} $, their values of
${W^{'-, \pi}} \cup {W^{'+, \pi}} $, their values of  $N_{{j},{k}}^{\pi}\left(n\right)$ differ by at most the number of elements in their symmetric difference. This implies that the requirements of Theorem 3.13 are fulfilled by setting
$N_{{j},{k}}^{\pi}\left(n\right)$ differ by at most the number of elements in their symmetric difference. This implies that the requirements of Theorem 3.13 are fulfilled by setting  $A_0 = {W^{-}},\ A_1= {W^{+}}{,}\ b_0=b_1=l$, and
$A_0 = {W^{-}},\ A_1= {W^{+}}{,}\ b_0=b_1=l$, and  $N_{{j},{k}}^{\pi}\left(n\right)$ as function f. Applying this theorem gives
$N_{{j},{k}}^{\pi}\left(n\right)$ as function f. Applying this theorem gives
 \begin{align*}
\mathbb{P}\left[\left\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right\rvert \gt \frac{n\epsilon}{2} \,\vert\, \lvert {W^{-, \pi}} \rvert = l\right] \leq 2\,\exp\left(-\frac{{\epsilon}^2n^2}{64l^2}\right).
\end{align*}
\begin{align*}
\mathbb{P}\left[\left\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right\rvert \gt \frac{n\epsilon}{2} \,\vert\, \lvert {W^{-, \pi}} \rvert = l\right] \leq 2\,\exp\left(-\frac{{\epsilon}^2n^2}{64l^2}\right).
\end{align*} For  $l \in I_n$, defined in Eq. (11), this probability is
$l \in I_n$, defined in Eq. (11), this probability is  $o\left(\frac{1}{n^3}\right)$. By Eq. (12), the probability that
$o\left(\frac{1}{n^3}\right)$. By Eq. (12), the probability that  $l \notin I_n$ is
$l \notin I_n$ is  $o\left(\frac{1}{n^3}\right)$. Combining these observations, we find that for all ϵ > 0, the terms in Eq. (18) are vanishing:
$o\left(\frac{1}{n^3}\right)$. Combining these observations, we find that for all ϵ > 0, the terms in Eq. (18) are vanishing:
 \begin{align}
\mathbb{P}\left[\left\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right\rvert \gt n\epsilon\right] = o\left(\frac{1}{n^3}\right),
\end{align}
\begin{align}
\mathbb{P}\left[\left\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right\rvert \gt n\epsilon\right] = o\left(\frac{1}{n^3}\right),
\end{align}which in turn proves that the limit in Eq. (17) holds ν- almost surely
It remains to show that the first, first mixed and second moments of  $\frac{N_{{j},{k}}^{\pi}\left(n\right)}{n}$ converge ν- almost surely to those of
$\frac{N_{{j},{k}}^{\pi}\left(n\right)}{n}$ converge ν- almost surely to those of  ${p^{{\rm bond}}_{{j}, {k}}}$. In Section 4.1.2, we showed that
${p^{{\rm bond}}_{{j}, {k}}}$. In Section 4.1.2, we showed that  $\sum_{j,k=0}^\infty j {p^{{\rm bond}}_{{j}, {k}}}= \sum_{j,k=0}^\infty k {p^{{\rm bond}}_{{j}, {k}}}$, and due to the graph context of the problem,
$\sum_{j,k=0}^\infty j {p^{{\rm bond}}_{{j}, {k}}}= \sum_{j,k=0}^\infty k {p^{{\rm bond}}_{{j}, {k}}}$, and due to the graph context of the problem,  $\sum_{j,k=0}^\infty j N_{{j},{k}}^{\pi}\left(n\right) = \sum_{j,k=0}^\infty k N_{{j},{k}}^{\pi}\left(n\right)$. Therefore, it is sufficient to show that only one of the first moments converges. Define
$\sum_{j,k=0}^\infty j N_{{j},{k}}^{\pi}\left(n\right) = \sum_{j,k=0}^\infty k N_{{j},{k}}^{\pi}\left(n\right)$. Therefore, it is sufficient to show that only one of the first moments converges. Define  $Q_n^\prime:= \frac{1}{n}\sum_{j,k=0}^\infty j N_{{j},{k}}^{\pi}\left(n\right)$, we will then show that
$Q_n^\prime:= \frac{1}{n}\sum_{j,k=0}^\infty j N_{{j},{k}}^{\pi}\left(n\right)$, we will then show that  $
Q:=\lim_{n \rightarrow \infty} Q_n^\prime=\pi \mu,\; \nu\text{-a.s.}
$ Let
$
Q:=\lim_{n \rightarrow \infty} Q_n^\prime=\pi \mu,\; \nu\text{-a.s.}
$ Let  $ X_{\kappa,n} := \frac{1}{n}\sum_{j=0}^{\kappa}\sum_{k=0}^{\kappa} j N_{{j},{k}}^{\pi}\left(n\right)
$ and remark that
$ X_{\kappa,n} := \frac{1}{n}\sum_{j=0}^{\kappa}\sum_{k=0}^{\kappa} j N_{{j},{k}}^{\pi}\left(n\right)
$ and remark that  $X_{\kappa,n} \leq Q_n^\prime$. Since
$X_{\kappa,n} \leq Q_n^\prime$. Since  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is a proper degree progression, for all ϵ > 0, there exists
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is a proper degree progression, for all ϵ > 0, there exists  $\widetilde{\kappa}\left(\epsilon\right), \tilde m\left(\epsilon\right)$ such that for all
$\widetilde{\kappa}\left(\epsilon\right), \tilde m\left(\epsilon\right)$ such that for all  $ \kappa \gt \widetilde{\kappa}$ and
$ \kappa \gt \widetilde{\kappa}$ and  $n \gt \tilde m$
$n \gt \tilde m$
 \begin{align}
\frac{1}{n} \sum_{{\substack{(j,k) = (0,0),\\
j \gt \kappa \,{\rm or}\, k \gt \kappa}}}^{(d_{\max}, d_{\max})} jN_{{j},{k}}\left(n\right) \lt \epsilon.
\end{align}
\begin{align}
\frac{1}{n} \sum_{{\substack{(j,k) = (0,0),\\
j \gt \kappa \,{\rm or}\, k \gt \kappa}}}^{(d_{\max}, d_{\max})} jN_{{j},{k}}\left(n\right) \lt \epsilon.
\end{align} Thus, for  $\kappa \gt \widetilde{\kappa}$, we have
$\kappa \gt \widetilde{\kappa}$, we have  $ X_{\kappa,n} \leq Q_n^\prime \leq X_{\kappa,n} + \epsilon$. This implies that if
$ X_{\kappa,n} \leq Q_n^\prime \leq X_{\kappa,n} + \epsilon$. This implies that if
 \begin{align}
\tilde{X}_{\kappa}:=\lim_{n\rightarrow \infty } X_{\kappa,n} = \sum_{j=0}^{\kappa}\sum_{k=0}^{\kappa} j{p^{{\rm bond}}_{{j}, {k}}} , \; \nu-\text{a.s.},
\end{align}
\begin{align}
\tilde{X}_{\kappa}:=\lim_{n\rightarrow \infty } X_{\kappa,n} = \sum_{j=0}^{\kappa}\sum_{k=0}^{\kappa} j{p^{{\rm bond}}_{{j}, {k}}} , \; \nu-\text{a.s.},
\end{align}then  $\lim\limits_{n\rightarrow \infty } Q_n^\prime = Q$ holds ν- almost surely as well [Reference Fountoulakis16, (3.5)]. Thus, the goal is to prove Eq. (21). Applying [Reference Petrov25, Lemma 6.8], we can show that this limit holds ν- almost surely, if for any ϵ > 0,
$\lim\limits_{n\rightarrow \infty } Q_n^\prime = Q$ holds ν- almost surely as well [Reference Fountoulakis16, (3.5)]. Thus, the goal is to prove Eq. (21). Applying [Reference Petrov25, Lemma 6.8], we can show that this limit holds ν- almost surely, if for any ϵ > 0,
 \begin{align}
\sum_{n=1}^\infty \mathbb{P}\left[\left\lvert X_{\kappa,n} - \tilde{X}_{\kappa} \right \rvert \gt \epsilon\right] \lt \infty.
\end{align}
\begin{align}
\sum_{n=1}^\infty \mathbb{P}\left[\left\lvert X_{\kappa,n} - \tilde{X}_{\kappa} \right \rvert \gt \epsilon\right] \lt \infty.
\end{align} We show this analogously to the proof of Eq. (18). By the definition of  $
X_{\kappa,n}$,
$
X_{\kappa,n}$,  $\tilde{X}_{\kappa}$, and
$\tilde{X}_{\kappa}$, and  ${p^{{\rm bond}}_{{j}, {k}}}$, for all ϵ > 0, there exists
${p^{{\rm bond}}_{{j}, {k}}}$, for all ϵ > 0, there exists  $\widetilde{N}$ such that for all
$\widetilde{N}$ such that for all  $n \gt \widetilde{N}$,
$n \gt \widetilde{N}$,  $
\left\lvert \mathbb{E}\left[X_{\kappa,n}\right] - \tilde{X}_{\kappa} \right\rvert \lt \frac{\epsilon}{2}.
$ Combining this with the reverse triangle inequality, we find for any ϵ > 0,
$
\left\lvert \mathbb{E}\left[X_{\kappa,n}\right] - \tilde{X}_{\kappa} \right\rvert \lt \frac{\epsilon}{2}.
$ Combining this with the reverse triangle inequality, we find for any ϵ > 0,
 \begin{align*}
\mathbb{P}\left[\left\lvert X_{\kappa,n} - \tilde{X}_{\kappa} \right \rvert \gt \epsilon\right] \leq \mathbb{P}\left[\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert \gt \frac{\epsilon}{2}\right].
\end{align*}
\begin{align*}
\mathbb{P}\left[\left\lvert X_{\kappa,n} - \tilde{X}_{\kappa} \right \rvert \gt \epsilon\right] \leq \mathbb{P}\left[\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert \gt \frac{\epsilon}{2}\right].
\end{align*} Remark that  $
\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert = \frac{1}{n}\sum_{j=0}^\kappa \sum_{k=0}^\kappa j \left(N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right).
$ This implies that for
$
\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert = \frac{1}{n}\sum_{j=0}^\kappa \sum_{k=0}^\kappa j \left(N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right).
$ This implies that for  $\epsilon^\prime = \frac{\epsilon}{2\sum_{j \leq \kappa}j}$,
$\epsilon^\prime = \frac{\epsilon}{2\sum_{j \leq \kappa}j}$,
 \begin{align*}
\mathbb{P}\left[\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert \gt \frac{\epsilon}{2}\right] \leq \sum_{j\leq \kappa, k \leq \kappa} \mathbb{P}\left[\frac{1}{n}\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \rvert \gt \epsilon '\right].
\end{align*}
\begin{align*}
\mathbb{P}\left[\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert \gt \frac{\epsilon}{2}\right] \leq \sum_{j\leq \kappa, k \leq \kappa} \mathbb{P}\left[\frac{1}{n}\lvert N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \rvert \gt \epsilon '\right].
\end{align*} Using Eq. (19), we find  $
\mathbb{P}\left[\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert \gt \frac{\epsilon}{2}\right] \leq
\sum_{j\leq \kappa, k \leq \kappa} o\left(\frac{1}{n^3}\right) \leq
o\left(\frac{1}{n^{\frac{25}{9}}}\right).
$ Here we used the fact that
$
\mathbb{P}\left[\left\lvert X_{\kappa,n} - \mathbb{E}\left[X_{\kappa,n}\right] \right \rvert \gt \frac{\epsilon}{2}\right] \leq
\sum_{j\leq \kappa, k \leq \kappa} o\left(\frac{1}{n^3}\right) \leq
o\left(\frac{1}{n^{\frac{25}{9}}}\right).
$ Here we used the fact that  $d_{\max} = O\left(n^{1/9}\right)$ and that
$d_{\max} = O\left(n^{1/9}\right)$ and that  $N_{{j},{k}}^{\pi}\left(n\right) = \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]=0$ when
$N_{{j},{k}}^{\pi}\left(n\right) = \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]=0$ when  $j \gt d_{\max}$ or
$j \gt d_{\max}$ or  $k \gt d_{\max}$ or both. This proves Eq. (22) and hence proves that
$k \gt d_{\max}$ or both. This proves Eq. (22) and hence proves that  $Q_n^\prime$ converges ν- almost surely to Q. Similar derivations hold for the first mixed moment and the second moments. That is, all the moments of interest and the distribution itself converge simultaneously ν- almost surely for an element of
$Q_n^\prime$ converges ν- almost surely to Q. Similar derivations hold for the first mixed moment and the second moments. That is, all the moments of interest and the distribution itself converge simultaneously ν- almost surely for an element of  $\mathcal{D} $. Thus, we have shown that
$\mathcal{D} $. Thus, we have shown that  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is ν- almost surely feasible.
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}}$ is ν- almost surely feasible.
Let  $E \subset \mathcal{D} $ be the event over which the degree progression is feasible. Since any element of
$E \subset \mathcal{D} $ be the event over which the degree progression is feasible. Since any element of  $\mathcal{D} $ is ν- almost surely feasible, we have
$\mathcal{D} $ is ν- almost surely feasible, we have  $\nu\left(E\right) =1$. For any
$\nu\left(E\right) =1$. For any  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}} \in E$, we may apply Theorem 3.11 to a sequence of random multigraphs
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}} \in E$, we may apply Theorem 3.11 to a sequence of random multigraphs  $\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$ arising from uniformly random configurations. Lemma 4.2 states that if we condition
$\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$ arising from uniformly random configurations. Lemma 4.2 states that if we condition  ${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, Theorem 3.11 is applicable for all n. We will now fix
${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, Theorem 3.11 is applicable for all n. We will now fix  $\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}} \in E$ and apply Theorem 3.11 to
$\left({\textbf{d}^{n}_{\pi}}\right)_{n \in \mathbb{N}} \in E$ and apply Theorem 3.11 to  $\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$, distinguishing two cases for π:
$\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$, distinguishing two cases for π:  $ \pi \lt \hat{\pi}^{\text{bond}}$ and
$ \pi \lt \hat{\pi}^{\text{bond}}$ and  $ \pi \gt \hat{\pi}^{\text{bond}}$, with
$ \pi \gt \hat{\pi}^{\text{bond}}$, with  $\hat{\pi}^{\text{bond}} = \frac{\mu}{\mu_{11}}$.
$\hat{\pi}^{\text{bond}} = \frac{\mu}{\mu_{11}}$.
Let  $ \pi \lt \hat{\pi}^{\text{bond}}$ and pick
$ \pi \lt \hat{\pi}^{\text{bond}}$ and pick  $\epsilon \in (0,1)$. Define
$\epsilon \in (0,1)$. Define  $\mathcal{A}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right)$ to be the set of all multigraphs obeying
$\mathcal{A}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right)$ to be the set of all multigraphs obeying  ${\textbf{d}^{n}_{\pi}}$ for which the largest SCC contains no more than
${\textbf{d}^{n}_{\pi}}$ for which the largest SCC contains no more than ![]() $\epsilon n$ vertices. As
$\epsilon n$ vertices. As  $\frac{\mu_{11}^{\pi}}{\mu^{\pi}} = \pi \frac{\mu_{11}}{\mu} \lt 1$, Theorem 3.11 states that for all ϵ:
$\frac{\mu_{11}^{\pi}}{\mu^{\pi}} = \pi \frac{\mu_{11}}{\mu} \lt 1$, Theorem 3.11 states that for all ϵ:
 \begin{align}
\lim_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{A}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right) \,\vert\, {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}\right] = 1.
\end{align}
\begin{align}
\lim_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{A}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right) \,\vert\, {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}\right] = 1.
\end{align} Next consider  $ \pi \gt \hat{\pi}^{\text{bond}}$. Define
$ \pi \gt \hat{\pi}^{\text{bond}}$. Define  $\mathcal{B}_{\theta}\left({\textbf{d}^{n}_{\pi}}\right)$ to be the set of all graphs whose largest SCC has size in
$\mathcal{B}_{\theta}\left({\textbf{d}^{n}_{\pi}}\right)$ to be the set of all graphs whose largest SCC has size in  $((\theta - \varepsilon) n,(\theta + \varepsilon) n)$, with
$((\theta - \varepsilon) n,(\theta + \varepsilon) n)$, with  $\theta \in (0,1)$ and any vanishing ɛ. Since
$\theta \in (0,1)$ and any vanishing ɛ. Since  $\frac{\mu_{11}^{\pi}}{\mu^{\pi}} = \pi \frac{\mu_{11}}{\mu} \gt 1$, Theorem 3.11 states that there exists a unique
$\frac{\mu_{11}^{\pi}}{\mu^{\pi}} = \pi \frac{\mu_{11}}{\mu} \gt 1$, Theorem 3.11 states that there exists a unique  $\theta=c^{\text{bond}}$ such that
$\theta=c^{\text{bond}}$ such that
 \begin{align}
\lim_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{B}_{\theta}\left({\textbf{d}^{n}_{\pi}}\right) \,\vert\, {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right] = 1.
\end{align}
\begin{align}
\lim_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{B}_{\theta}\left({\textbf{d}^{n}_{\pi}}\right) \,\vert\, {\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}} \right] = 1.
\end{align} Moreover, the theorem determines that  $c^{\text{bond}} :=1-U_{\pi}^\text{bond}(x^*,1)-U_{\pi}^\text{bond}(1,y^*)+U_{\pi}^\text{bond}(x^*,y^*),$ where
$c^{\text{bond}} :=1-U_{\pi}^\text{bond}(x^*,1)-U_{\pi}^\text{bond}(1,y^*)+U_{\pi}^\text{bond}(x^*,y^*),$ where  $x^*,y^*$ are the smallest positive solutions of
$x^*,y^*$ are the smallest positive solutions of
 \begin{equation}
\begin{aligned}
x^*= U^-_{\pi}(x^*),\\
y^*= U^+_{\pi}(y^*),
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
x^*= U^-_{\pi}(x^*),\\
y^*= U^+_{\pi}(y^*),
\end{aligned}
\end{equation}and functions  $U_{\pi}^+$,
$U_{\pi}^+$,  $U^-_{\pi}$, and
$U^-_{\pi}$, and  $U_{\pi}^\text{bond}$ are as defined in Eq. (16).
$U_{\pi}^\text{bond}$ are as defined in Eq. (16).
To finalize the proof for Theorems 2.2 and 2.3, we need to supplement Eqs. (23) and (24) with two minor observations. First, the theorem is stated for a percolated multigraph progression  $\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$ without conditioning on the degree progression of the percolated graphs. As
$\left(\tilde{G}_{\textbf{d}^{n}}^{\pi}\right)_{n \in \mathbb{N}}$ without conditioning on the degree progression of the percolated graphs. As  $\nu\left(E\right) =1$, an analogous argument to that of Fountoulakis [Reference Fountoulakis16, p. 348] is applied to show that
$\nu\left(E\right) =1$, an analogous argument to that of Fountoulakis [Reference Fountoulakis16, p. 348] is applied to show that
• If
 $\pi \lt \hat{\pi}^{\text{bond}}, \;
\lim \limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{A}_\epsilon\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$ for all
$\pi \lt \hat{\pi}^{\text{bond}}, \;
\lim \limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{A}_\epsilon\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$ for all  $\epsilon \in (0,1)$.
$\epsilon \in (0,1)$.• If
 $\pi \gt \hat{\pi}^{\text{bond}},\;
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{B}_{c^{\text{bond}}}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$
$\pi \gt \hat{\pi}^{\text{bond}},\;
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{B}_{c^{\text{bond}}}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$and
 $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{B}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 0$ for all
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[\tilde{G}_{\textbf{d}^{n}}^{\pi} \in \mathcal{B}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 0$ for all  $\epsilon \in (0,1), \epsilon \neq c^{\text{bond}}$ .
$\epsilon \in (0,1), \epsilon \neq c^{\text{bond}}$ .
Second, Theorems 2.2 and 2.3 make assertions about uniformly random simple graphs instead of random multigraphs. Lemma 3.8 can also be stated for the graph  $\tilde{G}_{\textbf{d}^{n}}^{\pi}$ conditioning on
$\tilde{G}_{\textbf{d}^{n}}^{\pi}$ conditioning on  $G_{\textbf{d}^{n}}$ (the graph to which percolation is applied) being simple. Applying this variant of Lemma 3.8 to the above limits, we deduce an equivalent statement as above for
$G_{\textbf{d}^{n}}$ (the graph to which percolation is applied) being simple. Applying this variant of Lemma 3.8 to the above limits, we deduce an equivalent statement as above for  $G_{n}^{\pi}$:
$G_{n}^{\pi}$:
• If
 $\pi \lt \hat{\pi}^{\text{bond}}, \;
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[G_{n}^{\pi} \in \mathcal{A}_\epsilon\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$ for all
$\pi \lt \hat{\pi}^{\text{bond}}, \;
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[G_{n}^{\pi} \in \mathcal{A}_\epsilon\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$ for all  $\epsilon \in (0,1)$.
$\epsilon \in (0,1)$.• If
 $\pi \gt \hat{\pi}^{\text{bond}},$
$\pi \gt \hat{\pi}^{\text{bond}},$  $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[G_{n}^{\pi} \in \mathcal{B}_{c^{\text{bond}}}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[G_{n}^{\pi} \in \mathcal{B}_{c^{\text{bond}}}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 1$and
 $
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[G_{n}^{\pi} \in \mathcal{B}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 0$ for all
$
\lim\limits_{n \rightarrow \infty} \mathbb{P}\left[G_{n}^{\pi} \in \mathcal{B}_{\epsilon}\left({\textbf{d}^{n}_{\pi}}\right)\right] = 0$ for all  $\epsilon \in (0,1), \epsilon \neq c^{\text{bond}}$.
$\epsilon \in (0,1), \epsilon \neq c^{\text{bond}}$.
This completes the proofs of Theorems 2.2 and 2.3 for the case of bond percolation.
4.2. Site percolation
The proof of Theorems 2.2 and 2.3 for site percolation has a similar structure as for bond percolation, and we will refer to Section 4.1 where applicable. The proof again is split into three steps. First, in Section 4.2.1, we show that applying site percolation to a uniformly random configuration results in another uniformly random configuration if we condition on the degree sequence after percolation. Second, we determine the limit of the expected number of vertices with degree (j, k) after site percolation, see Section 4.2.2. The proof is completed in Section 4.2.3 by combining the first two steps with the results of Section 4.1.
As mentioned in Section 2, deleting a vertex means that we remove all edges adjacent to this vertex. In the setting of the configuration model, this translates into removing all stubs attached to a deleted vertex. Let us call these stubs  $\left({W^{-, r}}, {W^{+, r}} \right)$. Additionally, the matches of
$\left({W^{-, r}}, {W^{+, r}} \right)$. Additionally, the matches of  $\left({W^{-, r}}, {W^{+, r}} \right)$ are also removed. The situation is further complicated by the fact that a match of a removed stub itself may or may not be attached to a deleted vertex. That is to say, for a deleted edge, both endpoints may be deleted or only one of them. To avoid double counting, we introduce
$\left({W^{-, r}}, {W^{+, r}} \right)$ are also removed. The situation is further complicated by the fact that a match of a removed stub itself may or may not be attached to a deleted vertex. That is to say, for a deleted edge, both endpoints may be deleted or only one of them. To avoid double counting, we introduce  $\left({W^{-, m}}, {W^{+, m}} \right)$ containing all the genuine matches of stubs in
$\left({W^{-, m}}, {W^{+, m}} \right)$ containing all the genuine matches of stubs in  $\left({W^{-, r}}, {W^{+, r}} \right)$ that are not connected to a deleted vertex. Thus,
$\left({W^{-, r}}, {W^{+, r}} \right)$ that are not connected to a deleted vertex. Thus,  ${W^{-, r}} \cup {W^{-, m}} $ (respectively,
${W^{-, r}} \cup {W^{-, m}} $ (respectively,  ${W^{+, r}} \cup {W^{+, m}} $) are all in-stubs (out-stubs) removed by site percolation. The stubs that survive percolation are denoted by
${W^{+, r}} \cup {W^{+, m}} $) are all in-stubs (out-stubs) removed by site percolation. The stubs that survive percolation are denoted by  $\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ as before, allowing us to write the full partition of stubs as
$\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ as before, allowing us to write the full partition of stubs as
 \begin{align}
{W^{-}} = {W^{-, \pi}} \cup {W^{-, r}} \cup {W^{-, m}} \quad \text{and} \quad {W^{+}} = {W^{+, \pi}} \cup {W^{+, r}} \cup {W^{+, m}}.
\end{align}
\begin{align}
{W^{-}} = {W^{-, \pi}} \cup {W^{-, r}} \cup {W^{-, m}} \quad \text{and} \quad {W^{+}} = {W^{+, \pi}} \cup {W^{+, r}} \cup {W^{+, m}}.
\end{align}Hence, the abbreviation is as follows: π – surviving stubs, r – stubs on removed vertices, and m – matches of stubs on removed vertices. These abbreviations will be used throughout the rest of the section.
4.2.1. A site-percolated configuration is a uniformly random configuration
We show in Lemma 4.6 that conditional on the stubs that are removed by the site percolation, the matching on the surviving stubs is uniformly random. This lemma, in turn, allows us to formulate Lemma 4.7 stating that the configuration after percolation is a uniformly random configuration conditional on its degree sequence.
Lemma 4.6. Apply site percolation to a uniformly random configuration  $\mathcal{M}$ on
$\mathcal{M}$ on  $\left({W^{-}}, {W^{+}} \right)$. Conditional on the elements of
$\left({W^{-}}, {W^{+}} \right)$. Conditional on the elements of  $\left({W^{-, r}}, {W^{+, r}} \right)$ and
$\left({W^{-, r}}, {W^{+, r}} \right)$ and  $\left({W^{-, m}},{W^{+, m}} \right)$, each configuration on
$\left({W^{-, m}},{W^{+, m}} \right)$, each configuration on  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ is equally likely.
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ is equally likely.
Proof. According to Eq. (26), fixing the elements of  $\left({W^{-, r}}, {W^{+, r}} \right)$ and
$\left({W^{-, r}}, {W^{+, r}} \right)$ and  $\left({W^{-, m}},{W^{+, m}} \right)$ uniquely determines the elements of
$\left({W^{-, m}},{W^{+, m}} \right)$ uniquely determines the elements of  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$. Choosing the elements of
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$. Choosing the elements of  $\left({W^{-, r}}, {W^{+, r}} \right)$ and
$\left({W^{-, r}}, {W^{+, r}} \right)$ and  $\left({W^{-, m}},{W^{+, m}} \right)$ furthermore implies that the configuration
$\left({W^{-, m}},{W^{+, m}} \right)$ furthermore implies that the configuration  $\mathcal{M}$ is the union of a configuration on
$\mathcal{M}$ is the union of a configuration on  $\left({W^{-, r}} \cup {W^{-, m}}, {W^{+, r}} \cup {W^{-, m}} \right)$ with the one on
$\left({W^{-, r}} \cup {W^{-, m}}, {W^{+, r}} \cup {W^{-, m}} \right)$ with the one on  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$. As
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$. As  $\mathcal{M}$ is a uniformly random configuration obeying this split and the elements of
$\mathcal{M}$ is a uniformly random configuration obeying this split and the elements of  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ are fixed, the configuration on
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ are fixed, the configuration on  $\left({W^{-,\pi}},{W^{+,\pi}}\right)$ will be a uniformly random one.
$\left({W^{-,\pi}},{W^{+,\pi}}\right)$ will be a uniformly random one.
Lemma 4.7. Apply site percolation to a uniformly random configuration on  $\left({W^{-}}, {W^{+}} \right)$. Conditional on
$\left({W^{-}}, {W^{+}} \right)$. Conditional on  ${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, any configuration on
${\textbf{D}_{\pi}^n} = {\textbf{d}^{n}_{\pi}}$, any configuration on  $\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$ is equally likely.
$\left({W^{-}_{\textbf{d}^{n}_{\pi}}}, {W^{+}_{\textbf{d}^{n}_{\pi}}}\right)$ is equally likely.
4.2.2. The expected number of vertices with degree (j, k) after site percolation
The next step in the proof of Theorem 2.2 for the case of site percolation is proving the existence of the limit for  $\frac{N_{{j},{k}}^{\pi}\left(n\right)}{n}$, the fraction of vertices in the site-percolated graph with in-degree j and out-degree k. We then show that the value of this limit, distribution
$\frac{N_{{j},{k}}^{\pi}\left(n\right)}{n}$, the fraction of vertices in the site-percolated graph with in-degree j and out-degree k. We then show that the value of this limit, distribution  ${p^{\text{site}}_{{j}, {k}}}$, is closely related to the corresponding quantity for bond percolation. After this, we determine
${p^{\text{site}}_{{j}, {k}}}$, is closely related to the corresponding quantity for bond percolation. After this, we determine  $\hat{\pi}^{\text{site}}$ and show in Section 4.2.3 that this is indeed the threshold for site percolation.
$\hat{\pi}^{\text{site}}$ and show in Section 4.2.3 that this is indeed the threshold for site percolation.
We introduce the following notation for the sizes of the subsets
 \begin{equation*}
\begin{aligned}
s^-: =& \lvert {W^{-, \pi}} \cup {W^{-, m}}\rvert,\\
s^+: =& \lvert{W^{+, \pi}} \cup {W^{+, m}}\rvert,\\
r^- := &\lvert {W^{-, m}}\rvert,\\
r^+:= &\lvert {W^{+, m}}\rvert.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
s^-: =& \lvert {W^{-, \pi}} \cup {W^{-, m}}\rvert,\\
s^+: =& \lvert{W^{+, \pi}} \cup {W^{+, m}}\rvert,\\
r^- := &\lvert {W^{-, m}}\rvert,\\
r^+:= &\lvert {W^{+, m}}\rvert.
\end{aligned}
\end{equation*} Note that  $ \lvert {W^{-, \pi}} \rvert =s^- - r^- = s^+ - r^+ = \lvert {W^{+, \pi}} \rvert $ and the remaining configuration on
$ \lvert {W^{-, \pi}} \rvert =s^- - r^- = s^+ - r^+ = \lvert {W^{+, \pi}} \rvert $ and the remaining configuration on  $\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ forms a directed multigraph. As before,
$\left({W^{-,\pi}}, {W^{+,\pi}}\right)$ forms a directed multigraph. As before,  $N_{{d^-},{d^+}}\left(n\right)$ is the number of vertices with degree
$N_{{d^-},{d^+}}\left(n\right)$ is the number of vertices with degree  $(d^-,d^+)$ before percolation. Let
$(d^-,d^+)$ before percolation. Let  $N_{{d^-},{d^+}}^{\pi,r}\left(n\right)$ be the number of vertices of original degree
$N_{{d^-},{d^+}}^{\pi,r}\left(n\right)$ be the number of vertices of original degree  $(d^-,d^+)$ that survive site percolation. Then,
$(d^-,d^+)$ that survive site percolation. Then,  $N_{{d^-},{d^+}}\left(n\right)- N_{{d^-},{d^+}}^{\pi,r}\left(n\right)$ is the number of removed vertices of original degree
$N_{{d^-},{d^+}}\left(n\right)- N_{{d^-},{d^+}}^{\pi,r}\left(n\right)$ is the number of removed vertices of original degree  $(d^-,d^+)$. Since each vertex is independently removed with probability
$(d^-,d^+)$. Since each vertex is independently removed with probability  $1-\pi$,
$1-\pi$,
 \begin{align}
&\mathbb{E}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] = \pi N_{{d^-}, {d^+}}\left(n\right),
\end{align}
\begin{align}
&\mathbb{E}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] = \pi N_{{d^-}, {d^+}}\left(n\right),
\end{align} \begin{align}
&\mathbb{E}\left[N_{{d^-},{d^+}}\left(n\right)- N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] = \left(1-\pi \right)N_{{d^-},{d^+}}\left(n\right).
\end{align}
\begin{align}
&\mathbb{E}\left[N_{{d^-},{d^+}}\left(n\right)- N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] = \left(1-\pi \right)N_{{d^-},{d^+}}\left(n\right).
\end{align} We proceed by formulating two lemmas showing that, with high probability,  $s^-,s^+$ remain in some bounded shrinking interval
$s^-,s^+$ remain in some bounded shrinking interval  $I^\prime_n$ and
$I^\prime_n$ and  $r^-,r^+$ in I n.
$r^-,r^+$ in I n.
Lemma 4.8. Let  $I^\prime_n := \left[m\pi - n^{2/3}\,\ln n,\, m\pi + n^{2/3}\ln n\right] $, then
$I^\prime_n := \left[m\pi - n^{2/3}\,\ln n,\, m\pi + n^{2/3}\ln n\right] $, then
 \begin{equation*}\mathbb{P}\left[ s^-,s^+ \in I^\prime_n \right]=1-{\rm e}^{-\Omega\left(\ln^2 n\right)}\end{equation*}
\begin{equation*}\mathbb{P}\left[ s^-,s^+ \in I^\prime_n \right]=1-{\rm e}^{-\Omega\left(\ln^2 n\right)}\end{equation*}holds separately for, respectively,  $s^-$ and
$s^-$ and  $s^+$.
$s^+$.
Proof. By using Eq. (27), we obtain
 \begin{equation*}
\mathbb{E}\left[s^-\right] = \sum_{d^-=0}^{d_{\max}}\sum_{d^+=0}^{d_{\max}} \pi {d}^-N_{{d^-},{d^+}}\left(n\right) = m\pi \end{equation*}
\begin{equation*}
\mathbb{E}\left[s^-\right] = \sum_{d^-=0}^{d_{\max}}\sum_{d^+=0}^{d_{\max}} \pi {d}^-N_{{d^-},{d^+}}\left(n\right) = m\pi \end{equation*}and
 \begin{equation*}\mathbb{E}\left[s^+\right] = \sum_{d^-=0}^{d_{\max}}\sum_{d^+=0}^{d_{\max}} \pi {d}^+ N_{{d^-},{d^+}}\left(n\right) =m\pi.\end{equation*}
\begin{equation*}\mathbb{E}\left[s^+\right] = \sum_{d^-=0}^{d_{\max}}\sum_{d^+=0}^{d_{\max}} \pi {d}^+ N_{{d^-},{d^+}}\left(n\right) =m\pi.\end{equation*} Using Hoeffding’s inequality and the bound on the maximum degree,  $d_{\max} \leq n^{1/9}$ and, we obtain
$d_{\max} \leq n^{1/9}$ and, we obtain
 \begin{align}
\mathbb{P}\left[\left\lvert s^- - \mathbb{E}\left[s^-\right]\right\rvert \gt n^{2/3}\ln n\right] \leq {\rm e}^{-\Omega\left( \ln^2 n\right)} \; \text{and}\; \mathbb{P}\left[\left\lvert s^+ - \mathbb{E}\left[s^+\right]\right\rvert \gt n^{2/3}\ln n\right] \leq {\rm e}^{-\Omega\left( \ln^2 n\right)},
\end{align}
\begin{align}
\mathbb{P}\left[\left\lvert s^- - \mathbb{E}\left[s^-\right]\right\rvert \gt n^{2/3}\ln n\right] \leq {\rm e}^{-\Omega\left( \ln^2 n\right)} \; \text{and}\; \mathbb{P}\left[\left\lvert s^+ - \mathbb{E}\left[s^+\right]\right\rvert \gt n^{2/3}\ln n\right] \leq {\rm e}^{-\Omega\left( \ln^2 n\right)},
\end{align}which proves the claim.
Lemma 4.9. Let  $I_n := \left[m\pi (1-\pi ) - n^{2/3}\,\ln^2 n,\, m\pi (1-\pi ) + n^{2/3}\,\ln^2 n\right]$, then
$I_n := \left[m\pi (1-\pi ) - n^{2/3}\,\ln^2 n,\, m\pi (1-\pi ) + n^{2/3}\,\ln^2 n\right]$, then
 \begin{equation*}\mathbb{P}\left[ r^+,r^- \in I_n \mid s^-, s^+ \in I'_n\right]=1-{\rm e}^{-\Omega\left(\ln^2 n\right)}\end{equation*}
\begin{equation*}\mathbb{P}\left[ r^+,r^- \in I_n \mid s^-, s^+ \in I'_n\right]=1-{\rm e}^{-\Omega\left(\ln^2 n\right)}\end{equation*}holds separately for, respectively, ![]() $r^-$ and
$r^-$ and  $r^+$.
$r^+$.
Proof. We present the proof for ![]() $r^-$. The proof for
$r^-$. The proof for  $r^+$ is then identical up to switching the roles of in-stubs and out-stubs. Since we consider a uniformly random configuration on
$r^+$ is then identical up to switching the roles of in-stubs and out-stubs. Since we consider a uniformly random configuration on  $\left({W^{-}}, {W^{+}} \right)$, the probability that a given in-stub is matched to an out-stub in
$\left({W^{-}}, {W^{+}} \right)$, the probability that a given in-stub is matched to an out-stub in  ${W^{+, r}} $ is
${W^{+, r}} $ is  $\frac{m-s^+}{m}= (1-\pi ) \left( 1+ \mathcal{O}\left(n^{-1/3}\,\ln n\right)\right)$ as
$\frac{m-s^+}{m}= (1-\pi ) \left( 1+ \mathcal{O}\left(n^{-1/3}\,\ln n\right)\right)$ as  $s^-,s^+ \in I^\prime_n$. Since
$s^-,s^+ \in I^\prime_n$. Since ![]() $r^-$ equals the number of in-stubs in
$r^-$ equals the number of in-stubs in  ${W^{-}} \setminus {W^{-, r}} $ with a match in
${W^{-}} \setminus {W^{-, r}} $ with a match in  ${W^{+, r}} $, this implies that
${W^{+, r}} $, this implies that
 \begin{align*}
\mathbb{E}\left[r^-\right] = s^- \frac{m-s^+}{m} = m\pi \left(1-\pi \right) \left(1 + \mathcal{O} \left(n^{2/3}\,\ln n\right)\right).
\end{align*}
\begin{align*}
\mathbb{E}\left[r^-\right] = s^- \frac{m-s^+}{m} = m\pi \left(1-\pi \right) \left(1 + \mathcal{O} \left(n^{2/3}\,\ln n\right)\right).
\end{align*}To complete the proof, we will now show that
 \begin{align*}
\mathbb{P}\left[\lvert r^- - \mathbb{E}\left[r^-\right] \rvert \gt n^{2/3}\,\ln^2 n \right] \leq {\rm e}^{- \Omega\left(\ln^2 n\right)}.
\end{align*}
\begin{align*}
\mathbb{P}\left[\lvert r^- - \mathbb{E}\left[r^-\right] \rvert \gt n^{2/3}\,\ln^2 n \right] \leq {\rm e}^{- \Omega\left(\ln^2 n\right)}.
\end{align*} This is realized by applying Theorem 3.12 to the space of configurations on  $\left({W^{-}}, {W^{+}} \right)$ with the symmetric difference as the metric. The value of
$\left({W^{-}}, {W^{+}} \right)$ with the symmetric difference as the metric. The value of ![]() $r^-$ plays the role of the function f. To partition this space, we order the in-stubs of
$r^-$ plays the role of the function f. To partition this space, we order the in-stubs of  $W^{-}$. Define an i-prefix to be the first i in-stubs together with their match. An element of the partition
$W^{-}$. Define an i-prefix to be the first i in-stubs together with their match. An element of the partition  $\mathcal{P}_k$ consists of all configurations with the same k-prefix for all
$\mathcal{P}_k$ consists of all configurations with the same k-prefix for all  $k \in \{0,1,\ldots, m\}$. For any
$k \in \{0,1,\ldots, m\}$. For any  $A,B \in \mathcal{P}_k$ such that
$A,B \in \mathcal{P}_k$ such that  $A,B\subset C \in \mathcal{P}_{k-1}$, a bijection
$A,B\subset C \in \mathcal{P}_{k-1}$, a bijection  $\phi: A \rightarrow B$ can be defined. Denote the kth pair of a configuration in A by
$\phi: A \rightarrow B$ can be defined. Denote the kth pair of a configuration in A by  $(x,y_A)$ and the kth pair of a configuration in B by
$(x,y_A)$ and the kth pair of a configuration in B by  $(x,y_B)$. Then ϕ maps
$(x,y_B)$. Then ϕ maps  $\mathcal{M} \in A$ to the configuration in B with
$\mathcal{M} \in A$ to the configuration in B with  $(x,y_A)$ replaced by
$(x,y_A)$ replaced by  $(x,y_B)$ and with y A the match of the in-stub in
$(x,y_B)$ and with y A the match of the in-stub in  $\mathcal{M}$ matched to y B. By definition of ϕ, it follows that
$\mathcal{M}$ matched to y B. By definition of ϕ, it follows that  $c_k:=\lvert \mathcal{M} -\phi(\mathcal{M})\rvert = 4 $ for all
$c_k:=\lvert \mathcal{M} -\phi(\mathcal{M})\rvert = 4 $ for all  $k \in \{1,2,\ldots ,m\}$. As the value of
$k \in \{1,2,\ldots ,m\}$. As the value of ![]() $r^-$ changes by at most the symmetric difference of the two matchings, Theorem 3.12 states that
$r^-$ changes by at most the symmetric difference of the two matchings, Theorem 3.12 states that
 \begin{align*}
\mathbb{P}\left[\lvert r^- - \mathbb{E}\left[r^-\right] \rvert \gt n^{2/3}\ln^2 n \right] \leq 2\exp \left(\frac{n^{4/3}\,\ln^2 n}{2m}\right) = {\rm e}^{- \Omega\left(\ln^2 n\right)},
\end{align*}
\begin{align*}
\mathbb{P}\left[\lvert r^- - \mathbb{E}\left[r^-\right] \rvert \gt n^{2/3}\ln^2 n \right] \leq 2\exp \left(\frac{n^{4/3}\,\ln^2 n}{2m}\right) = {\rm e}^{- \Omega\left(\ln^2 n\right)},
\end{align*}as  $m \leq nd_{\max} \leq n^{10/9}$.
$m \leq nd_{\max} \leq n^{10/9}$.
Lemma 4.10. Let  $N_{{j},{k}}^{\pi}\left(n\right)$ be the number of vertices in the site-percolated graph (or configuration) with in-degree j and out-degree k. The following limit exists
$N_{{j},{k}}^{\pi}\left(n\right)$ be the number of vertices in the site-percolated graph (or configuration) with in-degree j and out-degree k. The following limit exists
 \begin{align}
{p^{{\rm site}}_{{j}, {k}}}:=\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]}{n}, \text{for } j,k\in\mathbb{N}_0
\end{align}
\begin{align}
{p^{{\rm site}}_{{j}, {k}}}:=\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]}{n}, \text{for } j,k\in\mathbb{N}_0
\end{align}and
 \begin{align}
{p^{{\rm site}}_{{j}, {k}}} = \begin{cases}
\pi {p^{{\rm bond}}_{j, k}},&(j,k)\neq(0,0),\\
\pi {p^{{\rm bond}}_{0, 0}} + 1-\pi,& (j,k)=(0,0),
\end{cases}
\end{align}
\begin{align}
{p^{{\rm site}}_{{j}, {k}}} = \begin{cases}
\pi {p^{{\rm bond}}_{j, k}},&(j,k)\neq(0,0),\\
\pi {p^{{\rm bond}}_{0, 0}} + 1-\pi,& (j,k)=(0,0),
\end{cases}
\end{align}where  ${p^{{\rm bond}}_{{j}, {k}}}$ is defined in Lemma 4.4.
${p^{{\rm bond}}_{{j}, {k}}}$ is defined in Lemma 4.4.
Proof. If  $j, k \gt d_{\max}$, then
$j, k \gt d_{\max}$, then  ${p^{{\rm site}}_{{j}, {k}}}=N_{{j},{k}}^{\pi}\left(n\right)=N_{{j},{k}}\left(n\right)=0$.
${p^{{\rm site}}_{{j}, {k}}}=N_{{j},{k}}^{\pi}\left(n\right)=N_{{j},{k}}\left(n\right)=0$.
Consider  $0\leq j,k \leq d_{\max}$. A removed vertex will have degree
$0\leq j,k \leq d_{\max}$. A removed vertex will have degree  $(0,0)$ after percolation with probability 1. Let
$(0,0)$ after percolation with probability 1. Let  $P_{j,k}\left(d^-,d^+\right)$ be the probability that a non-removed vertex of degree
$P_{j,k}\left(d^-,d^+\right)$ be the probability that a non-removed vertex of degree  $(d^-,d^+)$ has degree (j, k) after percolation. For
$(d^-,d^+)$ has degree (j, k) after percolation. For  $(j,k) = (0,0)$, we have
$(j,k) = (0,0)$, we have
 \begin{align}
\mathbb{E}\left[N_{{0},{0}}^{\pi}\left(n\right)\right] = \sum_{d^- = 0}^{d_{\max}}\sum_{d^+ = 0}^{d_{\max}}\left( \left(1-\pi \right) N_{{d^-},{d^+}}\left(n\right) + \pi P_{0,0}\left(d^-,d^+\right) N_{{d^-},{d^+}}\left(n\right)\right),
\end{align}
\begin{align}
\mathbb{E}\left[N_{{0},{0}}^{\pi}\left(n\right)\right] = \sum_{d^- = 0}^{d_{\max}}\sum_{d^+ = 0}^{d_{\max}}\left( \left(1-\pi \right) N_{{d^-},{d^+}}\left(n\right) + \pi P_{0,0}\left(d^-,d^+\right) N_{{d^-},{d^+}}\left(n\right)\right),
\end{align}and otherwise,
 \begin{align}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] = \sum_{d^- =j}^{d_{\max}}\sum_{d^+ =k}^{d_{\max}} \pi P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}\left(n\right).
\end{align}
\begin{align}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] = \sum_{d^- =j}^{d_{\max}}\sum_{d^+ =k}^{d_{\max}} \pi P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}\left(n\right).
\end{align} Hence, we need to derive the expression for  $P_{j,k}\left(d^-,d^+\right)$. Let us determine
$P_{j,k}\left(d^-,d^+\right)$. Let us determine  $P_{j,k}\left(d^-,d^+, s^-, s^+, r^-, r^+\right)$, the probability
$P_{j,k}\left(d^-,d^+, s^-, s^+, r^-, r^+\right)$, the probability  $P_{j,k}\left(d^-,d^+\right)$ conditional on the values
$P_{j,k}\left(d^-,d^+\right)$ conditional on the values  $s^-,s^+,r^-,r^+$. Site percolation combines the independent random processes of removing vertices and creating a uniformly random configuration on
$s^-,s^+,r^-,r^+$. Site percolation combines the independent random processes of removing vertices and creating a uniformly random configuration on  $\left({W^{-}}, {W^{+}} \right)$. As these processes are independent, we may first determine the elements of
$\left({W^{-}}, {W^{+}} \right)$. As these processes are independent, we may first determine the elements of  $\left({W^{-, r}},{W^{+, r}} \right)$ and then randomly create a configuration on
$\left({W^{-, r}},{W^{+, r}} \right)$ and then randomly create a configuration on  $\left({W^{-}}, {W^{+}} \right)$. Thus, conditional on the value of
$\left({W^{-}}, {W^{+}} \right)$. Thus, conditional on the value of ![]() $r^-$ (respectively,
$r^-$ (respectively,  $r^+$), each subset of
$r^+$), each subset of  ${W^{-}} \setminus {W^{-, r}} $ (respectively,
${W^{-}} \setminus {W^{-, r}} $ (respectively,  ${W^{+}} \setminus {W^{+, r}} $) of this size is equally likely to be
${W^{+}} \setminus {W^{+, r}} $) of this size is equally likely to be  ${W^{-, m}} $ (respectively,
${W^{-, m}} $ (respectively,  ${W^{+, m}} $). Hence,
${W^{+, m}} $). Hence,
 \begin{align}
P_{j,k}\left(d^-,d^+, r^-, r^+, s^-, s^+\right) = {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \frac{{{s^- - d^-}\choose {r^- - d^- +j}}}{{{s^-}\choose{r^-}}}\frac{{{s^+ - d^+}\choose {r^+ - d^+ +k}}}{{{s^+}\choose{r^+}}}.
\end{align}
\begin{align}
P_{j,k}\left(d^-,d^+, r^-, r^+, s^-, s^+\right) = {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \frac{{{s^- - d^-}\choose {r^- - d^- +j}}}{{{s^-}\choose{r^-}}}\frac{{{s^+ - d^+}\choose {r^+ - d^+ +k}}}{{{s^+}\choose{r^+}}}.
\end{align} Let intervals  $I_n,I_n^\prime$ are as defined in Lemmas 4.8 and 4.9. We have that, uniformly in
$I_n,I_n^\prime$ are as defined in Lemmas 4.8 and 4.9. We have that, uniformly in  $r^-,r^+ \in I_n$ and
$r^-,r^+ \in I_n$ and  $ s^-,s^+ \in I^\prime_n$,
$ s^-,s^+ \in I^\prime_n$,
 \begin{align*}
{d \choose {d-i}}\frac{{{s - d} \choose {r -d +i}}}{{{s}\choose {r}}} = {d \choose {d-i}} \left(1-\pi \right)^{d-i}\pi^i\left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right). \end{align*}
\begin{align*}
{d \choose {d-i}}\frac{{{s - d} \choose {r -d +i}}}{{{s}\choose {r}}} = {d \choose {d-i}} \left(1-\pi \right)^{d-i}\pi^i\left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right). \end{align*}Plugging this equation into Eq. (34) gives
 \begin{align*}
P_{j,k}\left(d^-,d^+, r^-, r^+, s^-, s^+\right) = {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k} \left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right),
\end{align*}
\begin{align*}
P_{j,k}\left(d^-,d^+, r^-, r^+, s^-, s^+\right) = {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k} \left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right),
\end{align*}uniformly for all  $s^-, s^+ \in I^\prime_n$ and
$s^-, s^+ \in I^\prime_n$ and  $r^-,r^+ \in I_n$. It turns out that a violation of the latter condition is unlikely, as
$r^-,r^+ \in I_n$. It turns out that a violation of the latter condition is unlikely, as  $\mathbb{P}\left[s^- \notin I^\prime_n \vee s^+ \notin I^\prime_n \vee r^- \notin I_n \vee r^+ \notin I_n\right]$ is small, which in turn helps to bound the value of
$\mathbb{P}\left[s^- \notin I^\prime_n \vee s^+ \notin I^\prime_n \vee r^- \notin I_n \vee r^+ \notin I_n\right]$ is small, which in turn helps to bound the value of  $\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]$. By applying Hoeffding’s inequality, we have
$\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]$. By applying Hoeffding’s inequality, we have
 \begin{align}
\mathbb{P}\left[\rvert N_{{d^-},{d^+}}^{\pi,r}\left(n\right) - \mathbb{E}\left[N_{{d^+},{d^-}}^{\pi,r}\left(n\right)\right] \rvert \gt \sqrt{n}\,\ln n\right] \lt {\rm e}^{-\Omega\left(\ln^2 n\right)},
\end{align}
\begin{align}
\mathbb{P}\left[\rvert N_{{d^-},{d^+}}^{\pi,r}\left(n\right) - \mathbb{E}\left[N_{{d^+},{d^-}}^{\pi,r}\left(n\right)\right] \rvert \gt \sqrt{n}\,\ln n\right] \lt {\rm e}^{-\Omega\left(\ln^2 n\right)},
\end{align}and in combination with Eq. (27), this gives
 \begin{equation*}N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \in I^{\prime\prime}_n(d^-,d^+) := \left[\pi N_{{d^-}, {d^+}}\left(n\right) - \sqrt{n}\,\ln n, \pi N_{{d^-}, {d^+}}\left(n\right) + \sqrt{n}\,\ln n\right],\end{equation*}
\begin{equation*}N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \in I^{\prime\prime}_n(d^-,d^+) := \left[\pi N_{{d^-}, {d^+}}\left(n\right) - \sqrt{n}\,\ln n, \pi N_{{d^-}, {d^+}}\left(n\right) + \sqrt{n}\,\ln n\right],\end{equation*}with probability  $1-{\rm e}^{-\Omega\left(\ln^2 n\right)}$. Combining this with Lemmas 4.8 and 4.9 gives
$1-{\rm e}^{-\Omega\left(\ln^2 n\right)}$. Combining this with Lemmas 4.8 and 4.9 gives
 \begin{align*}
&\!\!\!\!\!\!\mathbb{P}\left[s^- \notin I^\prime_n \lor s^+ \notin I^\prime_n \lor r^- \notin I_n \lor r^+ \notin I_n \lor N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \notin I^{\prime\prime}_n\left(d^-,d^+\right)\right] \;\;\\
\leq & \mathbb{P}\left[s^- \notin I^\prime_n\right] + \mathbb{P}\left[s^+ \notin I^\prime_n\right] + \mathbb{P}\left[r^- \notin I_n\right] + \mathbb{P}\left[r^+ \notin I_n\right] + \mathbb{P}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \notin I^{\prime\prime}_n\left(d^-,d^+\right)\right]\\
= & o\left(\frac{1}{n^3}\right) + \mathbb{P}\left[r^- \notin I_n\right] + \mathbb{P}\left[r^+ \notin I_n\right],
\end{align*}
\begin{align*}
&\!\!\!\!\!\!\mathbb{P}\left[s^- \notin I^\prime_n \lor s^+ \notin I^\prime_n \lor r^- \notin I_n \lor r^+ \notin I_n \lor N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \notin I^{\prime\prime}_n\left(d^-,d^+\right)\right] \;\;\\
\leq & \mathbb{P}\left[s^- \notin I^\prime_n\right] + \mathbb{P}\left[s^+ \notin I^\prime_n\right] + \mathbb{P}\left[r^- \notin I_n\right] + \mathbb{P}\left[r^+ \notin I_n\right] + \mathbb{P}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \notin I^{\prime\prime}_n\left(d^-,d^+\right)\right]\\
= & o\left(\frac{1}{n^3}\right) + \mathbb{P}\left[r^- \notin I_n\right] + \mathbb{P}\left[r^+ \notin I_n\right],
\end{align*}where  $\mathbb{P}\left[r^- \notin I_n\right]=o\left(n^{-3}\right)$ and
$\mathbb{P}\left[r^- \notin I_n\right]=o\left(n^{-3}\right)$ and  $\mathbb{P}\left[r^+ \notin I_n\right] = o\left(n^{-3}\right)$. Therefore,
$\mathbb{P}\left[r^+ \notin I_n\right] = o\left(n^{-3}\right)$. Therefore,
 \begin{align}
\mathbb{P}\left[s^- \notin I^\prime_n \lor s^+ \notin I^\prime_n \lor r^- \notin I_n \lor r^+ \notin I_n \lor N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \notin I^{\prime\prime}_n\left(d^-,d^+\right)\right] = o\left(n^{-3}\right).
\end{align}
\begin{align}
\mathbb{P}\left[s^- \notin I^\prime_n \lor s^+ \notin I^\prime_n \lor r^- \notin I_n \lor r^+ \notin I_n \lor N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \notin I^{\prime\prime}_n\left(d^-,d^+\right)\right] = o\left(n^{-3}\right).
\end{align} This allows us to determine a lower and upper bound for the value  $\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]$. Since
$\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]$. Since  $N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq N_{{d^-},{d^+}}\left(n\right)$ and
$N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq N_{{d^-},{d^+}}\left(n\right)$ and  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper, for all ϵ > 0, there exist
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper, for all ϵ > 0, there exist  $\kappa\left(\epsilon\right)$ and
$\kappa\left(\epsilon\right)$ and  $N\left(\epsilon\right)$ such that for all n > N
$N\left(\epsilon\right)$ such that for all n > N
 \begin{align}
\sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})}
P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq \sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})}
N_{{d^-},{d^+}}\left(n\right) \leq \epsilon n.
\end{align}
\begin{align}
\sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})}
P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq \sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})}
N_{{d^-},{d^+}}\left(n\right) \leq \epsilon n.
\end{align} In combination with Eq. (33), this implies for  $(j,k) \neq (0,0)$
$(j,k) \neq (0,0)$
 \begin{align}
\sum_{\substack{d^- =j,\\ d^+ =k}}^{\kappa}P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right) \right]\leq \sum_{\substack{d^- =j,\\ d^+ =k}}^{\kappa}P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right) + \epsilon n.
\end{align}
\begin{align}
\sum_{\substack{d^- =j,\\ d^+ =k}}^{\kappa}P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right) \right]\leq \sum_{\substack{d^- =j,\\ d^+ =k}}^{\kappa}P_{j,k}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right) + \epsilon n.
\end{align}Using Eq. (36) on the LHS of the above equation, we find
 \begin{equation*}
\begin{split}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \geq& \sum_{\substack{d^-=j,\\d^+=k}}^{\kappa}\; \sum_{\substack{\tilde r^- \in I^\prime_n,\\\tilde r^+\in I^\prime_n}} \;\sum_{\substack{\tilde s^-\in I_n,\\\tilde s^+ \in I_n}}\;\sum_{\tilde{d}_{d^-,d^+} \in I^{\prime\prime}_n(d^-,d^+)} \tilde{d}_{d^-,d^+}P_{j,k}\left(d^-,d^+,\tilde r^-,\tilde r^+,\tilde s^-,\tilde s^+\right)\\
&\times\mathbb{P}\left[r^-=\tilde r^-, r^+=\tilde r^+, s^- = \tilde s^-, s^+ = \tilde s^+, N_{{d^-},{d^+}}^{\pi,r}\left(n\right) = \tilde{d}_{d^-,d^+}\right] + o \left(\frac{1}{n^2}\right)\\
=&\sum_{\substack{d^- =j,\\ d^+ =k}}^{\kappa}\sum_{\tilde{d}_{d^-,d^+} \in I^{\prime\prime}_n(d^-,d^+)} \tilde{d}_{d^-,d^+}{{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k} \\
&\times\mathbb{P}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right) = \tilde{d}_{d^-,d^+}\right] \left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right)+ o \left(\frac{1}{n^2}\right)
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \geq& \sum_{\substack{d^-=j,\\d^+=k}}^{\kappa}\; \sum_{\substack{\tilde r^- \in I^\prime_n,\\\tilde r^+\in I^\prime_n}} \;\sum_{\substack{\tilde s^-\in I_n,\\\tilde s^+ \in I_n}}\;\sum_{\tilde{d}_{d^-,d^+} \in I^{\prime\prime}_n(d^-,d^+)} \tilde{d}_{d^-,d^+}P_{j,k}\left(d^-,d^+,\tilde r^-,\tilde r^+,\tilde s^-,\tilde s^+\right)\\
&\times\mathbb{P}\left[r^-=\tilde r^-, r^+=\tilde r^+, s^- = \tilde s^-, s^+ = \tilde s^+, N_{{d^-},{d^+}}^{\pi,r}\left(n\right) = \tilde{d}_{d^-,d^+}\right] + o \left(\frac{1}{n^2}\right)\\
=&\sum_{\substack{d^- =j,\\ d^+ =k}}^{\kappa}\sum_{\tilde{d}_{d^-,d^+} \in I^{\prime\prime}_n(d^-,d^+)} \tilde{d}_{d^-,d^+}{{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k} \\
&\times\mathbb{P}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right) = \tilde{d}_{d^-,d^+}\right] \left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right)+ o \left(\frac{1}{n^2}\right)
\end{split}
\end{equation*} Since Eq. (35) and  $N_{d^-,d^+}^{\pi,r}(n)\leq n$ gives
$N_{d^-,d^+}^{\pi,r}(n)\leq n$ gives
 \begin{equation*}\sum_{\tilde{d}_{d^-,d^+} \in I^{\prime\prime}_n(d^-,d^+)}\tilde{d}_{d^-,d^+}\mathbb{P}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right) = \tilde{d}_{d^-,d^+}\right] = \mathbb{E}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] + o\left(\frac{1}{n^2}\right),\end{equation*}
\begin{equation*}\sum_{\tilde{d}_{d^-,d^+} \in I^{\prime\prime}_n(d^-,d^+)}\tilde{d}_{d^-,d^+}\mathbb{P}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right) = \tilde{d}_{d^-,d^+}\right] = \mathbb{E}\left[N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] + o\left(\frac{1}{n^2}\right),\end{equation*}we obtain the lower bound
 \begin{align*}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \geq o\left(\frac{1}{n^2}\right)+ \pi \sum_{d^-=j}^{\kappa}\sum_{d^+=k}^{\kappa} N_{{d^-},{d^+}}\left(n\right) {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \times\\
\pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k}
\left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right).
\end{align*}
\begin{align*}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \geq o\left(\frac{1}{n^2}\right)+ \pi \sum_{d^-=j}^{\kappa}\sum_{d^+=k}^{\kappa} N_{{d^-},{d^+}}\left(n\right) {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}} \times\\
\pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k}
\left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right).
\end{align*}In a similar fashion, using the RHS of Eq. (38) gives the upper bound
 \begin{align*}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \leq \epsilon n + o\left(\frac{1}{n^2}\right)+\pi \sum_{d^-=j}^{\kappa}\sum_{d^+=k}^{\kappa} N_{{d^-},{d^+}}\left(n\right) {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}}
\times\\
\pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k}
\left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right) .
\end{align*}
\begin{align*}
\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \leq \epsilon n + o\left(\frac{1}{n^2}\right)+\pi \sum_{d^-=j}^{\kappa}\sum_{d^+=k}^{\kappa} N_{{d^-},{d^+}}\left(n\right) {{d^-}\choose {d^- -j}} {{d^+}\choose {d^+ -k}}
\times\\
\pi^{j+k}\left(1-\pi \right)^{d^-+d^+-j-k}
\left(1 + \mathcal{O}\left(\frac{\ln^2 n}{n^{1/3}}\right)\right) .
\end{align*} Combining the upper and lower bounds together proves convergence of the limit for  $j,k \gt 0$:
$j,k \gt 0$:
 \begin{align}
{p^{{\rm site}}_{{j}, {k}}}:=\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]}{n} = \pi \sum_{d^- = j}^\infty \sum_{d^+ = k}^\infty p_{d^-,d^+} {d^- \choose j}{d^+ \choose k}\pi^{j+k}\left(1-\pi \right)^{d^- - j + d^+ -k} .
\end{align}
\begin{align}
{p^{{\rm site}}_{{j}, {k}}}:=\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right]}{n} = \pi \sum_{d^- = j}^\infty \sum_{d^+ = k}^\infty p_{d^-,d^+} {d^- \choose j}{d^+ \choose k}\pi^{j+k}\left(1-\pi \right)^{d^- - j + d^+ -k} .
\end{align} For  $(j,k) = (0,0)$, we need to use Eq. (32) instead of Eq. (33). Since
$(j,k) = (0,0)$, we need to use Eq. (32) instead of Eq. (33). Since  $N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq N_{{d^-},{d^+}}\left(n\right)$ and
$N_{{d^-},{d^+}}^{\pi,r}\left(n\right) \leq N_{{d^-},{d^+}}\left(n\right)$ and  $(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper, for all ϵ > 0, there exist
$(\textbf{d}^{n})_{n\in \mathbb{N}}$ is proper, for all ϵ > 0, there exist  $\kappa\left(\epsilon\right)$ and
$\kappa\left(\epsilon\right)$ and  $N\left(\epsilon\right)$ such that for all n > N:
$N\left(\epsilon\right)$ such that for all n > N:
 \begin{align*}
\sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} \left(N_{{d^-},{d^+}}\left(n\right) - N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right) \leq \sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} N_{{d^-},{d^+}}\left(n\right) \leq \epsilon n.
\end{align*}
\begin{align*}
\sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} \left(N_{{d^-},{d^+}}\left(n\right) - N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right) \leq \sum_{{\substack{(d^-,d^+) = (0,0)\\
d^- \geq \kappa +1 \,{\rm or}\, d^+ \geq \kappa +1}}}^{(d_{\max}, d_{\max})} N_{{d^-},{d^+}}\left(n\right) \leq \epsilon n.
\end{align*} Thus, the equivalent of Eq. (38) for  $(j,k) = (0,0)$ becomes
$(j,k) = (0,0)$ becomes
 \begin{align*}
\sum_{d^- =0}^{\kappa}\sum_{d^+ =0}^{\kappa} \left[ \left(N_{{d^-},{d^+}}\left(n\right) - N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right )+P_{0,0}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] \leq \mathbb{E}\left[N_{{0},{0}}^{\pi}\left(n\right) \right] \leq \\ \sum_{d^- =0}^{\kappa}\sum_{d^+ =0}^{\kappa}\left[\left(N_{{d^-},{d^+}}\left(n\right) - N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right) + P_{0,0}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] + 2\epsilon n,
\end{align*}
\begin{align*}
\sum_{d^- =0}^{\kappa}\sum_{d^+ =0}^{\kappa} \left[ \left(N_{{d^-},{d^+}}\left(n\right) - N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right )+P_{0,0}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] \leq \mathbb{E}\left[N_{{0},{0}}^{\pi}\left(n\right) \right] \leq \\ \sum_{d^- =0}^{\kappa}\sum_{d^+ =0}^{\kappa}\left[\left(N_{{d^-},{d^+}}\left(n\right) - N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right) + P_{0,0}\left(d^-,d^+\right) N_{{d^-},{d^+}}^{\pi,r}\left(n\right)\right] + 2\epsilon n,
\end{align*}and the analogous argument as for  $(j,k) \neq (0,0)$ is applied to obtain
$(j,k) \neq (0,0)$ is applied to obtain
 \begin{align}
\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{0},{0}}^{\pi}\left(n\right)\right]}{n} = \left(1-\pi \right) + \pi \sum_{\substack{d^- = j,\\d^+ = k}}^\infty p_{d^-,d^+} {d^- \choose j}{d^+ \choose k}\pi^{j+k}\left(1-\pi \right)^{d^- - j + d^+ -k} = {p^{{\rm site}}_{{0}, {0}}}.
\end{align}
\begin{align}
\lim_{n\rightarrow \infty} \frac{\mathbb{E}\left[N_{{0},{0}}^{\pi}\left(n\right)\right]}{n} = \left(1-\pi \right) + \pi \sum_{\substack{d^- = j,\\d^+ = k}}^\infty p_{d^-,d^+} {d^- \choose j}{d^+ \choose k}\pi^{j+k}\left(1-\pi \right)^{d^- - j + d^+ -k} = {p^{{\rm site}}_{{0}, {0}}}.
\end{align}Comparing Eqs. (39) and (40) with Eq. (9), we obtain Eq. (31).
From Eq. (31), we can see that  ${p^{\text{site}}_{{j}, {k}}}$ is a probability distribution and has moments
${p^{\text{site}}_{{j}, {k}}}$ is a probability distribution and has moments
 \begin{align}
\mu^{\pi, \text{site}}: =\mu_{10}^{\pi, \text{site}} =\mu_{01}^{\pi, \text{site}} = \pi \mu^{\pi, \text{bond}} = \pi^2 \mu \quad \text{and} \quad \mu_{11}^{\pi, \text{site}} = \pi \mu_{11}^{\pi, \text{bond}} = \pi^3\mu_{11}.
\end{align}
\begin{align}
\mu^{\pi, \text{site}}: =\mu_{10}^{\pi, \text{site}} =\mu_{01}^{\pi, \text{site}} = \pi \mu^{\pi, \text{bond}} = \pi^2 \mu \quad \text{and} \quad \mu_{11}^{\pi, \text{site}} = \pi \mu_{11}^{\pi, \text{bond}} = \pi^3\mu_{11}.
\end{align} Additionally, the generating function  $U_{\pi}^\text{site}(x,y)$ for
$U_{\pi}^\text{site}(x,y)$ for  ${p^{\text{site}}_{{j}, {k}}}$ is given by
${p^{\text{site}}_{{j}, {k}}}$ is given by
 \begin{equation}
\begin{aligned}
U^\text{site}_{\pi}(x,y) := 1-\pi +\pi U(1-\pi +\pi x,1-\pi +\pi y),
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
U^\text{site}_{\pi}(x,y) := 1-\pi +\pi U(1-\pi +\pi x,1-\pi +\pi y),
\end{aligned}
\end{equation}and auxiliary functions  $U^+_{\pi},U^-_{\pi}$ are the same as in Eq. (16). It is left to determine
$U^+_{\pi},U^-_{\pi}$ are the same as in Eq. (16). It is left to determine  $\hat{\pi}^{\text{site}}$. Theorem 3.11 states that the percolation threshold is
$\hat{\pi}^{\text{site}}$. Theorem 3.11 states that the percolation threshold is  $\pi =\hat{\pi}^{\text{site}}$ such that
$\pi =\hat{\pi}^{\text{site}}$ such that  $
\sum_{j,k=0}^\infty jk {p^{\text{site}}_{{j}, {k}}} = \sum_{j,k=0}^\infty j{p^{\text{site}}_{{j}, {k}}}.
$ Combining this with Eq. (41), we find that the percolation thresholds for site and bond percolation are equal:
$
\sum_{j,k=0}^\infty jk {p^{\text{site}}_{{j}, {k}}} = \sum_{j,k=0}^\infty j{p^{\text{site}}_{{j}, {k}}}.
$ Combining this with Eq. (41), we find that the percolation thresholds for site and bond percolation are equal:
 \begin{equation*}\hat{\pi}^{\text{site}} = \frac{\mu}{\mu_{11}} = \hat{\pi}^{\text{bond}}.\end{equation*}
\begin{equation*}\hat{\pi}^{\text{site}} = \frac{\mu}{\mu_{11}} = \hat{\pi}^{\text{bond}}.\end{equation*} This can be explained by noting that the expected degree distribution after site percolation is a rescaled version of the degree distribution after bond percolation, exept for  $(0,0)$. Hence, one expects the GSCC to appear under the same conditions. However, the GSCC after site percolation is expected to contain fewer vertices because the probability to find an isolated vertex is larger.
$(0,0)$. Hence, one expects the GSCC to appear under the same conditions. However, the GSCC after site percolation is expected to contain fewer vertices because the probability to find an isolated vertex is larger.
4.2.3. Determining  ${\pi_c^{{\rm site}}}$ and
${\pi_c^{{\rm site}}}$ and  $c^{{\rm site}}$
$c^{{\rm site}}$
To finalize the proof of Theorems 2.2 and 2.3 for the case of site percolation, it remains to show that  ${\pi_c^{\text{site}}} = \hat{\pi}^{\text{site}}$ as well as to determine c site, the fraction of vertices in GSCC. This is done by following a similar exposition as in Section 4.1.3, which covers bond percolation. We therefore focus on explaining the necessary adjustments to be made to apply the derivations in Section 4.1.3 to site percolation.
${\pi_c^{\text{site}}} = \hat{\pi}^{\text{site}}$ as well as to determine c site, the fraction of vertices in GSCC. This is done by following a similar exposition as in Section 4.1.3, which covers bond percolation. We therefore focus on explaining the necessary adjustments to be made to apply the derivations in Section 4.1.3 to site percolation.
First, we need to replace the distribution  ${p^{\text{bond}}_{{j}, {k}}}$ with
${p^{\text{bond}}_{{j}, {k}}}$ with  ${p^{\text{site}}_{{j}, {k}}}$. Lemma 4.7 proves the equivalent statement for site percolation to that of Lemma 4.2 for bond percolation. However, the counterpart of Eq. (22) requires a different proof. Conditional on a certain realization of
${p^{\text{site}}_{{j}, {k}}}$. Lemma 4.7 proves the equivalent statement for site percolation to that of Lemma 4.2 for bond percolation. However, the counterpart of Eq. (22) requires a different proof. Conditional on a certain realization of  $\left( {W^{-, r}}, {W^{+, r}} \right)$ and the values
$\left( {W^{-, r}}, {W^{+, r}} \right)$ and the values  $s^-,s^+ \in I'_n$,
$s^-,s^+ \in I'_n$,  $r^-,r^+ \in I_n$, the value of
$r^-,r^+ \in I_n$, the value of  $N_{{j},{k}}^{\pi}\left(n\right)$ is determined by the random choice of
$N_{{j},{k}}^{\pi}\left(n\right)$ is determined by the random choice of  $\left({W^{-, m}},{W^{+, m}} \right)$. By changing one element of
$\left({W^{-, m}},{W^{+, m}} \right)$. By changing one element of  $\left({W^{-, m}},{W^{+, m}} \right)$, the value of
$\left({W^{-, m}},{W^{+, m}} \right)$, the value of  $N_{{j},{k}}^{\pi}\left(n\right)$ changes by at most 2. Thus, Theorem 3.13 can be applied to obtain
$N_{{j},{k}}^{\pi}\left(n\right)$ changes by at most 2. Thus, Theorem 3.13 can be applied to obtain
 \begin{align*}
\mathbb{P}\left[ \left| N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right| \gt \sqrt{n}\,\ln^2 n \, \mid \,s^-, s^+, r^-, r^+, \left({W^{-, r}}, {W^{+, r}} \right)\right]\\\leq 2\,\exp \left( \frac{n \,\ln^2 n}{\left(m(1-\pi )\pi + n^{2/3}\, \ln^2 n\right)}\right) = {\rm e}^ {-\Omega\left(\ln^2 n\right)}.
\end{align*}
\begin{align*}
\mathbb{P}\left[ \left| N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right| \gt \sqrt{n}\,\ln^2 n \, \mid \,s^-, s^+, r^-, r^+, \left({W^{-, r}}, {W^{+, r}} \right)\right]\\\leq 2\,\exp \left( \frac{n \,\ln^2 n}{\left(m(1-\pi )\pi + n^{2/3}\, \ln^2 n\right)}\right) = {\rm e}^ {-\Omega\left(\ln^2 n\right)}.
\end{align*}Using Lemmas 4.8 and 4.9, it follows that
 \begin{align*}
\mathbb{P}\left[ \left| N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right| \gt \sqrt{n}\,\ln^2 n\right] = o\left(\frac{1}{n^3}\right),
\end{align*}
\begin{align*}
\mathbb{P}\left[ \left| N_{{j},{k}}^{\pi}\left(n\right) - \mathbb{E}\left[N_{{j},{k}}^{\pi}\left(n\right)\right] \right| \gt \sqrt{n}\,\ln^2 n\right] = o\left(\frac{1}{n^3}\right),
\end{align*}and, since κ is bounded, this completes the proof of the counterpart of Eq. (22).
The last change is related to the fact that Theorem 3.11 is now applied to a feasible degree progression with  ${p^{\text{site}}_{{j}, {k}}}$ as degree distribution instead of
${p^{\text{site}}_{{j}, {k}}}$ as degree distribution instead of  ${p^{\text{bond}}_{{j}, {k}}}$. In Section 4.2.2, we found that
${p^{\text{bond}}_{{j}, {k}}}$. In Section 4.2.2, we found that  $\hat{\pi}^{\text{site}} = \frac{\mu}{\mu_{11}}$. Furthermore, in analogy to calculations in Section 4.1.3, we choose
$\hat{\pi}^{\text{site}} = \frac{\mu}{\mu_{11}}$. Furthermore, in analogy to calculations in Section 4.1.3, we choose  $x^*, \;y^*$ to be the solution of Eq. (25) to find that
$x^*, \;y^*$ to be the solution of Eq. (25) to find that
 \begin{equation*}
c^{\text{site}}:=1-U_{\pi}^\text{site}(x^*,1)-U_{\pi}^\text{site}(1,y^*)+U_{\pi}^\text{site}(x^*,y^*)=\pi {c^{\text{bond}}}.
\end{equation*}
\begin{equation*}
c^{\text{site}}:=1-U_{\pi}^\text{site}(x^*,1)-U_{\pi}^\text{site}(1,y^*)+U_{\pi}^\text{site}(x^*,y^*)=\pi {c^{\text{bond}}}.
\end{equation*}which completes the proof of Theorems 2.2 and 2.3 for site percolation.
Acknowledgement
The authors are grateful to Rik Versendaal for corrections and improvements to earlier drafts.