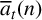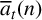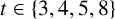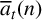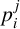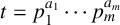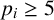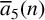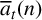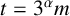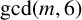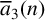1. Introduction and statement of results
A partition
![]() $\pi =\{\pi _1,\pi _2,\ldots ,\pi _k\}$
of a positive integer n is a nonincreasing sequence of natural numbers such that
$\pi =\{\pi _1,\pi _2,\ldots ,\pi _k\}$
of a positive integer n is a nonincreasing sequence of natural numbers such that
![]() $\sum _{i=1}^k \pi _i=n$
. The number of partitions of n is denoted by
$\sum _{i=1}^k \pi _i=n$
. The number of partitions of n is denoted by
![]() $p(n)$
. The Ferrers–Young diagram of
$p(n)$
. The Ferrers–Young diagram of
![]() $\pi $
is an array of nodes with
$\pi $
is an array of nodes with
![]() $\pi _i$
nodes in the ith row. The
$\pi _i$
nodes in the ith row. The
![]() $(i,j)$
hook is the set of nodes directly to the right of the
$(i,j)$
hook is the set of nodes directly to the right of the
![]() $(i,j)$
node, together with the set of nodes directly below it, as well as the
$(i,j)$
node, together with the set of nodes directly below it, as well as the
![]() $(i,j)$
node itself. The hook number,
$(i,j)$
node itself. The hook number,
![]() $H(i,j)$
, is the total number of nodes on the
$H(i,j)$
, is the total number of nodes on the
![]() $(i,j)$
hook. For a positive integer
$(i,j)$
hook. For a positive integer
![]() $t\geq 2$
, a partition of n is called t-core if none of the hook numbers are divisible by t. We illustrate the Ferrers–Young diagram of the partition
$t\geq 2$
, a partition of n is called t-core if none of the hook numbers are divisible by t. We illustrate the Ferrers–Young diagram of the partition
![]() $4+3+1$
of 8 with hook numbers:
$4+3+1$
of 8 with hook numbers:
 $$ \begin{align*} \begin{array}{cccc} {\bullet}^6 & {\bullet}^4 & {\bullet}^3& {\bullet}^1 \\ {\bullet}^4& {\bullet}^2 & {\bullet}^1 & \\ {\bullet}^1 & & & \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cccc} {\bullet}^6 & {\bullet}^4 & {\bullet}^3& {\bullet}^1 \\ {\bullet}^4& {\bullet}^2 & {\bullet}^1 & \\ {\bullet}^1 & & & \\ \end{array} \end{align*} $$
It is clear that the partition
![]() $4+3+1$
of 8 is a t-core partition for
$4+3+1$
of 8 is a t-core partition for
![]() $t\geq 7$
.
$t\geq 7$
.
If
![]() $c_t(n)$
counts the t-core partitions of n, the generating function of
$c_t(n)$
counts the t-core partitions of n, the generating function of
![]() $c_t(n)$
is given by
$c_t(n)$
is given by
 $$ \begin{align*} \displaystyle\sum_{n=0}^{\infty}c_t(n)q^n=\dfrac{(q^t;q^t)_\infty^t}{(q;q)_\infty}=\dfrac{f_t^t}{f_1} \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{n=0}^{\infty}c_t(n)q^n=\dfrac{(q^t;q^t)_\infty^t}{(q;q)_\infty}=\dfrac{f_t^t}{f_1} \end{align*} $$
(see [Reference Garvan, Kim and Stanton6, (2.1)]). Here and throughout the paper, for
![]() $|q| <1$
, we define
$|q| <1$
, we define
![]() $(a;q)_\infty :=\prod _{k=0}^\infty (1-aq^k)$
and for convenience, we set
$(a;q)_\infty :=\prod _{k=0}^\infty (1-aq^k)$
and for convenience, we set
![]() $f_k:=(q^k;q^k)_\infty $
for integers
$f_k:=(q^k;q^k)_\infty $
for integers
![]() $k\geq 1$
. Granville and Ono [Reference Granville and Ono8] proved that if
$k\geq 1$
. Granville and Ono [Reference Granville and Ono8] proved that if
![]() $t\geq 4$
, then
$t\geq 4$
, then
![]() $c_t(n)>0$
for every nonnegative integer n. A survey of t-core partitions can be found in [Reference Cho, Kim, Nam and Sohn4].
$c_t(n)>0$
for every nonnegative integer n. A survey of t-core partitions can be found in [Reference Cho, Kim, Nam and Sohn4].
For an integral power series
![]() $F(q)=\sum _{n=0}^{\infty }a(n)q^n$
and
$F(q)=\sum _{n=0}^{\infty }a(n)q^n$
and
![]() $0\leq r < M$
, we define the arithmetic density
$0\leq r < M$
, we define the arithmetic density
![]() $\delta _r(F,M;X)$
by
$\delta _r(F,M;X)$
by
An integral power series F is called lacunary modulo M if
that is, almost all of the coefficients of F are divisible by M. Arithmetic densities of
![]() $c_t(n)$
modulo arbitrary powers of 2, 3 and for primes greater than or equal to 5 are studied by Jindal and Meher [Reference Jindal and Meher10].
$c_t(n)$
modulo arbitrary powers of 2, 3 and for primes greater than or equal to 5 are studied by Jindal and Meher [Reference Jindal and Meher10].
For
![]() $\vert ab\vert <1$
, Ramanujan’s general theta function
$\vert ab\vert <1$
, Ramanujan’s general theta function
![]() $f(a,b)$
is given by
$f(a,b)$
is given by
 $$ \begin{align*} f(a,b)=\displaystyle\sum_{n=-\infty}^\infty a^{n(n+1)/2}b^{n(n-1)/2}. \end{align*} $$
$$ \begin{align*} f(a,b)=\displaystyle\sum_{n=-\infty}^\infty a^{n(n+1)/2}b^{n(n-1)/2}. \end{align*} $$
In Ramanujan’s notation, the Jacobi triple product identity [Reference Berndt3, page 35, entry 19] takes the shape
Ramanujan introduced two special cases of
![]() $f(a,b)$
:
$f(a,b)$
:
 $$ \begin{align*} \varphi(-q)&:=f(-q,-q)=\displaystyle\sum_{n=-\infty}^\infty (-1)^nq^{n^2}=\dfrac{f_1^2}{f_2},\\ f(-q)&:=f(-q,-q^2)=\displaystyle\sum_{n=-\infty}^\infty (-1)^nq^{n(3n-1)/2}=f_1. \end{align*} $$
$$ \begin{align*} \varphi(-q)&:=f(-q,-q)=\displaystyle\sum_{n=-\infty}^\infty (-1)^nq^{n^2}=\dfrac{f_1^2}{f_2},\\ f(-q)&:=f(-q,-q^2)=\displaystyle\sum_{n=-\infty}^\infty (-1)^nq^{n(3n-1)/2}=f_1. \end{align*} $$
In this notation, the generating function of
![]() $c_t(n)$
may be rewritten as
$c_t(n)$
may be rewritten as
 $$ \begin{align} \displaystyle\sum_{n=0}^{\infty}c_t(n)q^n=\dfrac{f^t(-q^t)}{f(-q)}. \end{align} $$
$$ \begin{align} \displaystyle\sum_{n=0}^{\infty}c_t(n)q^n=\dfrac{f^t(-q^t)}{f(-q)}. \end{align} $$
Recently, Gireesh et al. [Reference Gireesh, Ray and Shivashankar7] considered a new function
![]() $\overline {a}_t(n)$
by substituting
$\overline {a}_t(n)$
by substituting
![]() $\varphi (-q)$
for
$\varphi (-q)$
for
![]() $f(-q)$
in the generating function of
$f(-q)$
in the generating function of
![]() $c_t(n)$
(in (1.1)), namely
$c_t(n)$
(in (1.1)), namely
 $$ \begin{align} \displaystyle\sum_{n=0}^{\infty}\overline{a}_t(n)q^n=\dfrac{\varphi^t(-q^t)}{\varphi(-q)}=\dfrac{f_2f_t^{2t}}{f_1^2f_{2t}^t}. \end{align} $$
$$ \begin{align} \displaystyle\sum_{n=0}^{\infty}\overline{a}_t(n)q^n=\dfrac{\varphi^t(-q^t)}{\varphi(-q)}=\dfrac{f_2f_t^{2t}}{f_1^2f_{2t}^t}. \end{align} $$
They proved several multiplicative formulae and arithmetic identities for
![]() $\overline {a}_t(n)$
for
$\overline {a}_t(n)$
for
![]() $t=$
2, 3, 4 and 8 using Ramanujan’s theta functions and q-series techniques. Using the theory of modular forms, they studied the divisibility of
$t=$
2, 3, 4 and 8 using Ramanujan’s theta functions and q-series techniques. Using the theory of modular forms, they studied the divisibility of
![]() $\overline {a}_t(n)$
modulo arbitrary powers of primes greater than 5. More precisely, they proved the following theorem.
$\overline {a}_t(n)$
modulo arbitrary powers of primes greater than 5. More precisely, they proved the following theorem.
Theorem 1.1. Let
![]() $t=p_1^{a_1}\cdots p_m^{a_m}$
where the
$t=p_1^{a_1}\cdots p_m^{a_m}$
where the
![]() $p_i$
are prime numbers greater than or equal to 5. Then for every positive integer j,
$p_i$
are prime numbers greater than or equal to 5. Then for every positive integer j,
 $$ \begin{align*} \lim_{X\rightarrow\infty}\dfrac{\#\{0\leq n\leq X: \overline{a}_t(n)\equiv 0\pmod{p_i^{\,j}}\}}{X}=1. \end{align*} $$
$$ \begin{align*} \lim_{X\rightarrow\infty}\dfrac{\#\{0\leq n\leq X: \overline{a}_t(n)\equiv 0\pmod{p_i^{\,j}}\}}{X}=1. \end{align*} $$
They also deduced a Ramanujan type congruence for
![]() $\overline {a}_5(n)$
modulo 5 by using an algorithm developed by Radu and Sellers [Reference Radu and Sellers14]. Bandyopadhyay and Baruah [Reference Bandyopadhyay and Baruah2] proved some new identities connecting
$\overline {a}_5(n)$
modulo 5 by using an algorithm developed by Radu and Sellers [Reference Radu and Sellers14]. Bandyopadhyay and Baruah [Reference Bandyopadhyay and Baruah2] proved some new identities connecting
![]() $\overline {a}_5(n)$
and
$\overline {a}_5(n)$
and
![]() $c_5(n)$
. They also found a recurrence relation for
$c_5(n)$
. They also found a recurrence relation for
![]() $\overline {a}_5(n)$
.
$\overline {a}_5(n)$
.
Recently, Cotron et al. [Reference Cotron, Michaelsen, Stamm and Zhu5, Theorem 1.1] proved a strong result regarding lacunarity of eta-quotients modulo arbitrary powers of primes under certain conditions. We observe that the eta-quotients associated with
![]() $\overline {a}_t(n)$
do not satisfy these conditions, which makes the problem of studying lacunarity of
$\overline {a}_t(n)$
do not satisfy these conditions, which makes the problem of studying lacunarity of
![]() $\overline {a}_t(n)$
more interesting. In this article, we study the arithmetic densities of
$\overline {a}_t(n)$
more interesting. In this article, we study the arithmetic densities of
![]() $\overline {a}_{t}(n)$
modulo arbitrary powers of 2 and 3 where
$\overline {a}_{t}(n)$
modulo arbitrary powers of 2 and 3 where
![]() $t=3^\alpha m$
. To be specific, we prove the following theorems.
$t=3^\alpha m$
. To be specific, we prove the following theorems.
Theorem 1.2. Let
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $\alpha \geq 0$
and
$\alpha \geq 0$
and
![]() $m \geq 1$
be integers with gcd
$m \geq 1$
be integers with gcd
![]() $(m, 6)=1$
. Then the set
$(m, 6)=1$
. Then the set
![]() $\{n \in \mathbb {N} : \overline {a}_{3^\alpha m}(n) \equiv 0 \pmod {2^k}\}$
has arithmetic density
$\{n \in \mathbb {N} : \overline {a}_{3^\alpha m}(n) \equiv 0 \pmod {2^k}\}$
has arithmetic density
![]() $1$
.
$1$
.
Theorem 1.3. Let
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $\alpha \geq 0$
and
$\alpha \geq 0$
and
![]() $m \geq 1$
be integers with gcd
$m \geq 1$
be integers with gcd
![]() $(m, 6)=1$
. Then the set
$(m, 6)=1$
. Then the set
![]() $\{n \in \mathbb {N} : \overline {a}_{3^\alpha m}(n) \equiv 0 \pmod {3^k}\}$
has arithmetic density
$\{n \in \mathbb {N} : \overline {a}_{3^\alpha m}(n) \equiv 0 \pmod {3^k}\}$
has arithmetic density
![]() $1$
.
$1$
.
The fact that the action of Hecke algebras on spaces of modular forms of level 1 modulo 2 is locally nilpotent was first observed by Serre and proved by Tate (see [Reference Serre15–Reference Tate, Childress and Jones17]). Later, this result was generalised to higher levels by Ono and Taguchi [Reference Ono and Taguchi13]. We observe that the eta-quotient associated to
![]() $\overline {a}_3(n)$
is a modular form whose level is in the list of Ono and Taguchi. We use a result of Ono and Taguchi to prove the following congruences for
$\overline {a}_3(n)$
is a modular form whose level is in the list of Ono and Taguchi. We use a result of Ono and Taguchi to prove the following congruences for
![]() $\overline {a}_3(n)$
.
$\overline {a}_3(n)$
.
Theorem 1.4. Let n be a nonnegative integer. Then there exists an integer
![]() $c\geq 0$
such that for every
$c\geq 0$
such that for every
![]() $d\geq 1$
and distinct primes
$d\geq 1$
and distinct primes
![]() $p_1,\ldots ,p_{c+d}$
coprime to
$p_1,\ldots ,p_{c+d}$
coprime to
![]() $6$
,
$6$
,
whenever n is coprime to
![]() $p_1,\ldots ,p_{c+d}$
.
$p_1,\ldots ,p_{c+d}$
.
The paper is organised as follows. In Section 2, we state some preliminaries from the theory of modular forms. Then we prove Theorems 1.2–1.4 using the properties of modular forms in Sections 3–5, respectively. We mention some directions for future study in the concluding section.
2. Preliminaries
In this section, we recall some basic facts and definitions for modular forms (for more details, see [Reference Koblitz11, Reference Ono12]).
First, we define the matrix groups
 $$ \begin{align*} \text{SL}_2(\mathbb{Z})&:=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} : a, b, c, d \in \mathbb{Z}, ad-bc=1\bigg\},\\ \Gamma_0(N)&:=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : c\equiv 0 \pmod N\bigg\},\\ \Gamma_1(N)&:=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \Gamma_0(N) : a\equiv d\equiv 1 \pmod N\bigg\}, \end{align*} $$
$$ \begin{align*} \text{SL}_2(\mathbb{Z})&:=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} : a, b, c, d \in \mathbb{Z}, ad-bc=1\bigg\},\\ \Gamma_0(N)&:=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : c\equiv 0 \pmod N\bigg\},\\ \Gamma_1(N)&:=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \Gamma_0(N) : a\equiv d\equiv 1 \pmod N\bigg\}, \end{align*} $$
and
 $$ \begin{align*} \Gamma(N):=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : a\equiv d\equiv 1 \pmod N \text{ and } b\equiv c\equiv 0 \pmod N \bigg\}, \end{align*} $$
$$ \begin{align*} \Gamma(N):=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : a\equiv d\equiv 1 \pmod N \text{ and } b\equiv c\equiv 0 \pmod N \bigg\}, \end{align*} $$
where N is a positive integer. A subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $\text {SL}_2(\mathbb {Z})$
is called a congruence subgroup if
$\text {SL}_2(\mathbb {Z})$
is called a congruence subgroup if
![]() $\Gamma (N)\subseteq \Gamma $
for some N, and the smallest N with this property is called the level of
$\Gamma (N)\subseteq \Gamma $
for some N, and the smallest N with this property is called the level of
![]() $\Gamma $
. For instance,
$\Gamma $
. For instance,
![]() $\Gamma _0(N)$
and
$\Gamma _0(N)$
and
![]() $\Gamma _1(N)$
are congruence subgroups of level N.
$\Gamma _1(N)$
are congruence subgroups of level N.
Let
![]() $\mathbb {H}$
denote the upper half of the complex plane. The group
$\mathbb {H}$
denote the upper half of the complex plane. The group
 $$ \begin{align*} \text{GL}_2^{+}(\mathbb{R}):=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : a, b, c, d \in \mathbb{R} \text{ and } ad-bc>0 \bigg\} \end{align*} $$
$$ \begin{align*} \text{GL}_2^{+}(\mathbb{R}):=\bigg\{\begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : a, b, c, d \in \mathbb{R} \text{ and } ad-bc>0 \bigg\} \end{align*} $$
acts on
![]() $\mathbb {H}$
by
$\mathbb {H}$
by
 $$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} z = \dfrac{az+b}{cz+d}.\end{align*} $$
$$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} z = \dfrac{az+b}{cz+d}.\end{align*} $$
We identify
![]() $\infty $
with
$\infty $
with
![]() ${1}/{0}$
and define
${1}/{0}$
and define
 $$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \dfrac{r}{s} = \dfrac{ar+bs}{cr+ds},\end{align*} $$
$$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \dfrac{r}{s} = \dfrac{ar+bs}{cr+ds},\end{align*} $$
where
![]() ${r}/{s} \in \mathbb {Q} \cup \{ \infty \}$
. This gives an action of
${r}/{s} \in \mathbb {Q} \cup \{ \infty \}$
. This gives an action of
![]() $\text {GL}_2^{+}(\mathbb {R})$
on the extended upper half plane
$\text {GL}_2^{+}(\mathbb {R})$
on the extended upper half plane
![]() $\mathbb {H}^*=\mathbb {H}\cup \mathbb {Q}\cup \{\infty \}$
. Suppose that
$\mathbb {H}^*=\mathbb {H}\cup \mathbb {Q}\cup \{\infty \}$
. Suppose that
![]() $\Gamma $
is a congruence subgroup of
$\Gamma $
is a congruence subgroup of
![]() $\text {SL}_2(\mathbb {Z})$
. A cusp of
$\text {SL}_2(\mathbb {Z})$
. A cusp of
![]() $\Gamma $
is an equivalence class in
$\Gamma $
is an equivalence class in
![]() $\mathbb {P}^1=\mathbb {Q}\cup \{\infty \}$
under the action of
$\mathbb {P}^1=\mathbb {Q}\cup \{\infty \}$
under the action of
![]() $\Gamma $
.
$\Gamma $
.
The group
![]() $\text {GL}_2^{+}(\mathbb {R})$
also acts on functions
$\text {GL}_2^{+}(\mathbb {R})$
also acts on functions
![]() $f:\mathbb {H}\rightarrow \mathbb {C}$
. In particular, if
$f:\mathbb {H}\rightarrow \mathbb {C}$
. In particular, if
![]() $\gamma =[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \text {GL}_2^{+}(\mathbb {R})$
,
$\gamma =[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \text {GL}_2^{+}(\mathbb {R})$
,
![]() $f(z)$
is a meromorphic function on
$f(z)$
is a meromorphic function on
![]() $\mathbb {H}$
and
$\mathbb {H}$
and
![]() $\ell $
is an integer, we define the slash operator
$\ell $
is an integer, we define the slash operator
![]() $|_{\ell }$
by
$|_{\ell }$
by
Definition 2.1. Let
![]() $\Gamma $
be a congruence subgroup of level N. A holomorphic function
$\Gamma $
be a congruence subgroup of level N. A holomorphic function
![]() $f:\mathbb {H}\rightarrow \mathbb {C}$
is called a modular form with integer weight
$f:\mathbb {H}\rightarrow \mathbb {C}$
is called a modular form with integer weight
![]() $\ell $
on
$\ell $
on
![]() $\Gamma $
if the following hold:
$\Gamma $
if the following hold:
-
(1) for all
 $z \in \mathbb {H}$
and all
$z \in \mathbb {H}$
and all
 $[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma $
,
$[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma $
,  $$ \begin{align*} f\bigg(\dfrac{az+b}{cz+d}\bigg)=(cz+d)^{\ell}f(z); \end{align*} $$
$$ \begin{align*} f\bigg(\dfrac{az+b}{cz+d}\bigg)=(cz+d)^{\ell}f(z); \end{align*} $$
-
(2) if
 $\gamma \in \text {SL}_2(\mathbb {Z})$
, then
$\gamma \in \text {SL}_2(\mathbb {Z})$
, then
 $(f|_{\ell }\gamma )(z)$
has a Fourier expansion of the form where
$(f|_{\ell }\gamma )(z)$
has a Fourier expansion of the form where $$ \begin{align*} (f|_{\ell}\gamma)(z)=\displaystyle\sum_{n\geq 0}a_{\gamma}(n)q_{N}^n, \end{align*} $$
$$ \begin{align*} (f|_{\ell}\gamma)(z)=\displaystyle\sum_{n\geq 0}a_{\gamma}(n)q_{N}^n, \end{align*} $$
 $q_N:=e^{2\pi iz/N}$
.
$q_N:=e^{2\pi iz/N}$
.
For a positive integer
![]() $\ell $
, the complex vector space of modular forms of weight
$\ell $
, the complex vector space of modular forms of weight
![]() $\ell $
with respect to a congruence subgroup
$\ell $
with respect to a congruence subgroup
![]() $\Gamma $
is denoted by
$\Gamma $
is denoted by
![]() $M_{\ell }(\Gamma )$
.
$M_{\ell }(\Gamma )$
.
Definition 2.2 [Reference Ono12, Definition 1.15].
If
![]() $\chi $
is a Dirichlet character modulo N, then we say that a modular form
$\chi $
is a Dirichlet character modulo N, then we say that a modular form
![]() $f \in M_{\ell }(\Gamma _{1}(N))$
has Nebentypus character
$f \in M_{\ell }(\Gamma _{1}(N))$
has Nebentypus character
![]() $\chi $
if
$\chi $
if
for all
![]() $z\in \mathbb {H}$
and all
$z\in \mathbb {H}$
and all
![]() $[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _{0}(N)$
. The space of such modular forms is denoted by
$[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _{0}(N)$
. The space of such modular forms is denoted by
![]() $M_{\ell }(\Gamma _{0}(N),\chi )$
.
$M_{\ell }(\Gamma _{0}(N),\chi )$
.
The relevant modular forms for the results of this paper arise from eta-quotients. The Dedekind eta-function
![]() $\eta (z)$
is defined by
$\eta (z)$
is defined by
 $$ \begin{align*} \eta(z):=q^{1/24}(q;q)_{\infty}=q^{1/24}\displaystyle\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$
$$ \begin{align*} \eta(z):=q^{1/24}(q;q)_{\infty}=q^{1/24}\displaystyle\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$
where
![]() $q:=e^{2\pi iz}$
and
$q:=e^{2\pi iz}$
and
![]() $z\in \mathbb {H}$
. A function
$z\in \mathbb {H}$
. A function
![]() $f(z)$
is called an eta-quotient if it is of the form
$f(z)$
is called an eta-quotient if it is of the form
 $$ \begin{align*} f(z)=\displaystyle\prod_{\delta|N}\eta(\delta z)^{r_{\delta}}, \end{align*} $$
$$ \begin{align*} f(z)=\displaystyle\prod_{\delta|N}\eta(\delta z)^{r_{\delta}}, \end{align*} $$
where N is a positive integer and
![]() $r_{\delta }$
is an integer. Now, we recall two important theorems from [Reference Ono12, page 18] that will be used later.
$r_{\delta }$
is an integer. Now, we recall two important theorems from [Reference Ono12, page 18] that will be used later.
Theorem 2.3 [Reference Ono12, Theorem 1.64].
If
![]() $f(z)=\prod _{\delta |N}\eta (\delta z)^{r_{\delta }}$
is an eta-quotient such that
$f(z)=\prod _{\delta |N}\eta (\delta z)^{r_{\delta }}$
is an eta-quotient such that
![]() $\ell ={1}/{2}\sum _{\delta |N}r_{\delta } \in \mathbb {Z}$
,
$\ell ={1}/{2}\sum _{\delta |N}r_{\delta } \in \mathbb {Z}$
,
![]() $\sum _{\delta |N}\delta r_{\delta }\equiv 0 \pmod {24}$
and
$\sum _{\delta |N}\delta r_{\delta }\equiv 0 \pmod {24}$
and
![]() $\sum _{\delta |N}({N}/{\delta }) r_{\delta }\equiv 0 \pmod {24}$
, then
$\sum _{\delta |N}({N}/{\delta }) r_{\delta }\equiv 0 \pmod {24}$
, then
![]() $f(z)$
satisfies
$f(z)$
satisfies
for every
![]() $[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _{0}(N)$
. Here the character
$[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _{0}(N)$
. Here the character
![]() $\chi $
is defined by
$\chi $
is defined by
 $$ \begin{align*}\chi(d) := \bigg(\dfrac{(-1)^{\ell}s}{d}\bigg), \quad\text{where}\ s:= \displaystyle\prod_{\delta|N}\delta^{r_{\delta}}.\end{align*} $$
$$ \begin{align*}\chi(d) := \bigg(\dfrac{(-1)^{\ell}s}{d}\bigg), \quad\text{where}\ s:= \displaystyle\prod_{\delta|N}\delta^{r_{\delta}}.\end{align*} $$
Let f be an eta-quotient that satisfies the conditions of Theorem 2.3 and suppose that the associated weight
![]() $\ell $
is a positive integer. If
$\ell $
is a positive integer. If
![]() $f(z)$
is holomorphic at all the cusps of
$f(z)$
is holomorphic at all the cusps of
![]() $\Gamma _{0}(N)$
, then
$\Gamma _{0}(N)$
, then
![]() $f(z) \in M_{\ell }(\Gamma _{0}(N), \chi )$
. The necessary criterion for determining orders of an eta-quotient at cusps is given by the following theorem.
$f(z) \in M_{\ell }(\Gamma _{0}(N), \chi )$
. The necessary criterion for determining orders of an eta-quotient at cusps is given by the following theorem.
Theorem 2.4 [Reference Ono12, Theorem 1.64].
Let c, d and N be positive integers with
![]() $d \mid N$
and
$d \mid N$
and
![]() $\gcd (c,d)=1$
. If f is an eta-quotient satisfying the conditions of Theorem 2.3 for N, then the order of vanishing of
$\gcd (c,d)=1$
. If f is an eta-quotient satisfying the conditions of Theorem 2.3 for N, then the order of vanishing of
![]() $f(z)$
at the cusp
$f(z)$
at the cusp
![]() $c/d$
is
$c/d$
is
 $$ \begin{align*} \dfrac{N}{24}\displaystyle\sum_{\delta|N}\dfrac{\gcd(d,\delta)^2r_{\delta}}{\gcd(d,N/d)d\delta}. \end{align*} $$
$$ \begin{align*} \dfrac{N}{24}\displaystyle\sum_{\delta|N}\dfrac{\gcd(d,\delta)^2r_{\delta}}{\gcd(d,N/d)d\delta}. \end{align*} $$
We now recall a deep theorem of Serre [see Reference Ono12, page 43] that will be used in proving Theorems 1.2 and 1.3.
Theorem 2.5 [Reference Ono12, page 43].
Let
![]() $g(z) \in M_k(\Gamma _0(N),\chi )$
have Fourier expansion
$g(z) \in M_k(\Gamma _0(N),\chi )$
have Fourier expansion
 $$ \begin{align*} g(z)=\displaystyle\sum_{n=0}^\infty b(n)q^n \in \mathbb{Z}[[q]]. \end{align*} $$
$$ \begin{align*} g(z)=\displaystyle\sum_{n=0}^\infty b(n)q^n \in \mathbb{Z}[[q]]. \end{align*} $$
Then for a positive integer r, there is a constant
![]() $\alpha> 0$
such that
$\alpha> 0$
such that
 $$ \begin{align*} \#\{0<n\leq X: b(n)\not\equiv 0 \pmod r\}=\mathcal{O}\bigg(\dfrac{X}{(\log X)^\alpha}\bigg). \end{align*} $$
$$ \begin{align*} \#\{0<n\leq X: b(n)\not\equiv 0 \pmod r\}=\mathcal{O}\bigg(\dfrac{X}{(\log X)^\alpha}\bigg). \end{align*} $$
Equivalently,
Finally, we recall the definition of Hecke operators. Let m be a positive integer and
![]() $f(z)=\sum _{n=0}^{\infty }a(n)q^n \in M_{\ell }(\Gamma _{0}(N),\chi )$
. Then the action of the Hecke operator
$f(z)=\sum _{n=0}^{\infty }a(n)q^n \in M_{\ell }(\Gamma _{0}(N),\chi )$
. Then the action of the Hecke operator
![]() $T_{m}$
on
$T_{m}$
on
![]() $f(z)$
is defined by
$f(z)$
is defined by
 $$ \begin{align*} f(z)|T_m:=\displaystyle\sum_{n=0}^{\infty}\bigg(\displaystyle\sum_{d|\text{gcd}(n,m)}\chi(d)d^{\ell-1}a\bigg(\dfrac{nm}{d^2}\bigg)\bigg)q^n. \end{align*} $$
$$ \begin{align*} f(z)|T_m:=\displaystyle\sum_{n=0}^{\infty}\bigg(\displaystyle\sum_{d|\text{gcd}(n,m)}\chi(d)d^{\ell-1}a\bigg(\dfrac{nm}{d^2}\bigg)\bigg)q^n. \end{align*} $$
In particular, if
![]() $m=p$
is prime, then
$m=p$
is prime, then
 $$ \begin{align} f(z)|T_p:=\displaystyle\sum_{n=0}^{\infty}\bigg(a(pn)+\chi(p)p^{\ell-1}a\bigg(\dfrac{n}{p}\bigg)\bigg)q^n. \end{align} $$
$$ \begin{align} f(z)|T_p:=\displaystyle\sum_{n=0}^{\infty}\bigg(a(pn)+\chi(p)p^{\ell-1}a\bigg(\dfrac{n}{p}\bigg)\bigg)q^n. \end{align} $$
We note that
![]() $a(n)=0$
unless n is a nonnegative integer.
$a(n)=0$
unless n is a nonnegative integer.
3. Proof of Theorem 1.2
Putting
![]() $t=3^{\alpha }m$
in (1.2),
$t=3^{\alpha }m$
in (1.2),
 $$ \begin{align} \displaystyle\sum_{n=0}^{\infty}\overline{a}_{3^{\alpha}m}(n)q^n=\dfrac{f_2f_{3^{\alpha}m}^{2\cdot3^{\alpha}m}}{f_1^2f_{2\cdot3^{\alpha}m}^{3^{\alpha}m}}. \end{align} $$
$$ \begin{align} \displaystyle\sum_{n=0}^{\infty}\overline{a}_{3^{\alpha}m}(n)q^n=\dfrac{f_2f_{3^{\alpha}m}^{2\cdot3^{\alpha}m}}{f_1^2f_{2\cdot3^{\alpha}m}^{3^{\alpha}m}}. \end{align} $$
We define
 $$ \begin{align*} A_{\alpha,m}(z):=\dfrac{\eta^2\,(2^33^{\alpha+1}mz)}{\eta\,(2^43^{\alpha+1}mz)}. \end{align*} $$
$$ \begin{align*} A_{\alpha,m}(z):=\dfrac{\eta^2\,(2^33^{\alpha+1}mz)}{\eta\,(2^43^{\alpha+1}mz)}. \end{align*} $$
For any prime p and positive integer j,
![]() $(q;q)_{\infty }^{p^j}\equiv (q^p;q^p)_{\infty }^{p^{j-1}}\pmod {p^j}$
. Hence, for any integer
$(q;q)_{\infty }^{p^j}\equiv (q^p;q^p)_{\infty }^{p^{j-1}}\pmod {p^j}$
. Hence, for any integer
![]() $k\geq 1$
,
$k\geq 1$
,
 $$ \begin{align} A^{2^k}_{\alpha,m}(z)=\dfrac{\eta^{2^{k+1}}(2^33^{\alpha+1}mz)}{\eta^{2^k}(2^43^{\alpha+1}mz)}\equiv 1\pmod{2^{k+1}}. \end{align} $$
$$ \begin{align} A^{2^k}_{\alpha,m}(z)=\dfrac{\eta^{2^{k+1}}(2^33^{\alpha+1}mz)}{\eta^{2^k}(2^43^{\alpha+1}mz)}\equiv 1\pmod{2^{k+1}}. \end{align} $$
Next we define
 $$ \begin{align*} B_{\alpha,m,k}(z) :=\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)}A^{2^k}_{\alpha,m}(z) =\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m+2^{k+1}}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m+2^k}(2^43^{\alpha+1}mz)}. \end{align*} $$
$$ \begin{align*} B_{\alpha,m,k}(z) :=\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)}A^{2^k}_{\alpha,m}(z) =\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m+2^{k+1}}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m+2^k}(2^43^{\alpha+1}mz)}. \end{align*} $$
 $$ \begin{align} B_{\alpha,m,k}(z)\equiv\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)} \equiv\dfrac{f_{48}f_{2^33^{\alpha+1}m}^{2\cdot3^{\alpha}m}}{f_{24}^2f_{2^4\cdot3^{\alpha+1}m}^{3^{\alpha}m}} \equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3^{\alpha}m}(n)q^{24n}\pmod{2^{k+1}}. \end{align} $$
$$ \begin{align} B_{\alpha,m,k}(z)\equiv\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)} \equiv\dfrac{f_{48}f_{2^33^{\alpha+1}m}^{2\cdot3^{\alpha}m}}{f_{24}^2f_{2^4\cdot3^{\alpha+1}m}^{3^{\alpha}m}} \equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3^{\alpha}m}(n)q^{24n}\pmod{2^{k+1}}. \end{align} $$
Next, we will show that
![]() $B_{\alpha ,m,k}(z)$
is a modular form. Applying Theorem 2.3, we find that the level of
$B_{\alpha ,m,k}(z)$
is a modular form. Applying Theorem 2.3, we find that the level of
![]() $B_{\alpha ,m,k}(z)$
is
$B_{\alpha ,m,k}(z)$
is
![]() $N=2^43^{\alpha +1}mM$
, where M is the smallest positive integer such that
$N=2^43^{\alpha +1}mM$
, where M is the smallest positive integer such that
 $$ \begin{align*} 2^43^{\alpha+1}mM\bigg(\dfrac{-2}{24}+\dfrac{1}{48}+\dfrac{2\cdot3^{\alpha}m+2^{k+1}}{2^33^{\alpha+1}m}+\dfrac{-3^{\alpha}m-2^k}{2^43^{\alpha+1}m}\bigg)\equiv 0\pmod{24}, \end{align*} $$
$$ \begin{align*} 2^43^{\alpha+1}mM\bigg(\dfrac{-2}{24}+\dfrac{1}{48}+\dfrac{2\cdot3^{\alpha}m+2^{k+1}}{2^33^{\alpha+1}m}+\dfrac{-3^{\alpha}m-2^k}{2^43^{\alpha+1}m}\bigg)\equiv 0\pmod{24}, \end{align*} $$
which implies
Therefore,
![]() $M=4$
and the level of
$M=4$
and the level of
![]() $B_{\alpha ,m,k}(z)$
is
$B_{\alpha ,m,k}(z)$
is
![]() $N=2^6 3^{\alpha +1}m$
.
$N=2^6 3^{\alpha +1}m$
.
The representatives for the cusps of
![]() $\Gamma _0(2^63^{\alpha +1}m)$
are given by fractions
$\Gamma _0(2^63^{\alpha +1}m)$
are given by fractions
![]() $c/d$
where
$c/d$
where
![]() $d \mid 2^63^{\alpha +1}m$
and
$d \mid 2^63^{\alpha +1}m$
and
![]() $\gcd (c, 2^63^{\alpha +1}m) = 1$
(see [Reference Cotron, Michaelsen, Stamm and Zhu5, Proposition 2.1]). By Theorem 2.4,
$\gcd (c, 2^63^{\alpha +1}m) = 1$
(see [Reference Cotron, Michaelsen, Stamm and Zhu5, Proposition 2.1]). By Theorem 2.4,
![]() $B_{\alpha ,m,k}(z)$
is holomorphic at a cusp
$B_{\alpha ,m,k}(z)$
is holomorphic at a cusp
![]() $c/d$
if and only if
$c/d$
if and only if
 $$ \begin{align*} -2 \dfrac{\gcd (d,24)^2}{24} & + \dfrac{\gcd (d,48)^2}{48} \\ &+(3^\alpha m+2^k)\bigg(2\dfrac{ \gcd (d,2^3 3^{\alpha+1} m)^2}{2^3 3^{\alpha+1} m}-\dfrac{\gcd (d,2^4 3^{\alpha+1} m)^2}{2^4 3^{\alpha+1} m}\bigg)\geq 0. \end{align*} $$
$$ \begin{align*} -2 \dfrac{\gcd (d,24)^2}{24} & + \dfrac{\gcd (d,48)^2}{48} \\ &+(3^\alpha m+2^k)\bigg(2\dfrac{ \gcd (d,2^3 3^{\alpha+1} m)^2}{2^3 3^{\alpha+1} m}-\dfrac{\gcd (d,2^4 3^{\alpha+1} m)^2}{2^4 3^{\alpha+1} m}\bigg)\geq 0. \end{align*} $$
Equivalently,
![]() $B_{\alpha ,m,k}(z)$
is holomorphic at a cusp
$B_{\alpha ,m,k}(z)$
is holomorphic at a cusp
![]() $c/d$
if and only if
$c/d$
if and only if
where
 $$ \begin{align*}G_1=\dfrac{\gcd (d,24)^2}{\gcd (d,2^4 3^{\alpha+1} m)^2}, \quad G_2=\dfrac{\gcd (d,48)^2}{\gcd (d,2^43^{\alpha+1} m)^2}, \quad G_3=\dfrac{\gcd (d,2^3 3^{\alpha+1} m)^2}{\gcd (d,2^4 3^{\alpha+1} m)^2}.\end{align*} $$
$$ \begin{align*}G_1=\dfrac{\gcd (d,24)^2}{\gcd (d,2^4 3^{\alpha+1} m)^2}, \quad G_2=\dfrac{\gcd (d,48)^2}{\gcd (d,2^43^{\alpha+1} m)^2}, \quad G_3=\dfrac{\gcd (d,2^3 3^{\alpha+1} m)^2}{\gcd (d,2^4 3^{\alpha+1} m)^2}.\end{align*} $$
Let d be a divisor of
![]() $2^6 3^{\alpha +1} m$
. We can write
$2^6 3^{\alpha +1} m$
. We can write
![]() $d = 2^{r_1}3^{r_2}t$
where
$d = 2^{r_1}3^{r_2}t$
where
![]() $0 \leq r_1 \leq 6$
,
$0 \leq r_1 \leq 6$
,
![]() $0 \leq r_2 \leq \alpha + 1$
and
$0 \leq r_2 \leq \alpha + 1$
and
![]() $t \mid m$
. We now consider two cases depending on
$t \mid m$
. We now consider two cases depending on
![]() $r_1$
.
$r_1$
.
Case 1:
![]() $0\leq r_1\leq 3$
,
$0\leq r_1\leq 3$
,
![]() $0\leq r_2\leq \alpha +1$
. Then
$0\leq r_2\leq \alpha +1$
. Then
![]() $G_1=G_2$
,
$G_1=G_2$
,
![]() ${1}/{3^{2\alpha }t^2}\leq G_1\leq 1$
and
${1}/{3^{2\alpha }t^2}\leq G_1\leq 1$
and
![]() $G_3=1$
. Therefore,
$G_3=1$
. Therefore,
![]() $L= 3^{\alpha +1}m(1-G_1)+3\cdot 2^k\geq 3\cdot 2^k.$
$L= 3^{\alpha +1}m(1-G_1)+3\cdot 2^k\geq 3\cdot 2^k.$
Case 2:
![]() $4\leq r_1\leq 6$
,
$4\leq r_1\leq 6$
,
![]() $0\leq r_2\leq \alpha +1$
. Then
$0\leq r_2\leq \alpha +1$
. Then
![]() $G_2=4G_1$
,
$G_2=4G_1$
,
![]() ${1}/{4\cdot 3^{2\alpha }t^2}\leq G_1\leq {1}/{4}$
and
${1}/{4\cdot 3^{2\alpha }t^2}\leq G_1\leq {1}/{4}$
and
![]() $G_3={1}/{4}$
, which implies
$G_3={1}/{4}$
, which implies
![]() $L= 0.$
$L= 0.$
Hence,
![]() $B_{\alpha ,m,k}(z)$
is holomorphic at every cusp
$B_{\alpha ,m,k}(z)$
is holomorphic at every cusp
![]() $c/d$
. The weight of
$c/d$
. The weight of
![]() $B_{\alpha ,m,k}(z)$
is
$B_{\alpha ,m,k}(z)$
is
![]() $\ell = {1}/{2} (3^\alpha m+2^k-1)$
which is a positive integer and the associated character is given by
$\ell = {1}/{2} (3^\alpha m+2^k-1)$
which is a positive integer and the associated character is given by
 $$ \begin{align*} \chi_1(\bullet)=\bigg(\dfrac{(-1)^\ell 3^{(\alpha+1) (3^\alpha m+2^k)-1} m^{3^\alpha m+2^k}}{\bullet}\bigg). \end{align*} $$
$$ \begin{align*} \chi_1(\bullet)=\bigg(\dfrac{(-1)^\ell 3^{(\alpha+1) (3^\alpha m+2^k)-1} m^{3^\alpha m+2^k}}{\bullet}\bigg). \end{align*} $$
Thus,
![]() $B_{\alpha ,m,k}(z)\in M_\ell (\Gamma _0(N),\chi )$
where
$B_{\alpha ,m,k}(z)\in M_\ell (\Gamma _0(N),\chi )$
where
![]() $\ell $
, N and
$\ell $
, N and
![]() $\chi $
are as above. By Theorem 2.5, the Fourier coefficients of
$\chi $
are as above. By Theorem 2.5, the Fourier coefficients of
![]() $B_{\alpha ,m,k}(z)$
are almost all divisible by
$B_{\alpha ,m,k}(z)$
are almost all divisible by
![]() $r=2^k$
. From (3.3), this holds for
$r=2^k$
. From (3.3), this holds for
![]() $\overline {a}_{3^{\alpha }m}(n)$
also. This completes the proof of Theorem 1.2.
$\overline {a}_{3^{\alpha }m}(n)$
also. This completes the proof of Theorem 1.2.
4. Proof of Theorem 1.3
We proceed along the same lines as in the proof of Theorem 1.2. Here we define
 $$ \begin{align*} C_{\alpha,m}(z):=\dfrac{\eta^3(2^43^{\alpha+1}mz)}{\eta(2^43^{\alpha+2}mz)}. \end{align*} $$
$$ \begin{align*} C_{\alpha,m}(z):=\dfrac{\eta^3(2^43^{\alpha+1}mz)}{\eta(2^43^{\alpha+2}mz)}. \end{align*} $$
By the binomial theorem, for any integer
![]() $k\geq 1$
,
$k\geq 1$
,
 $$ \begin{align} C^{3^k}_{\alpha,m}(z)=\dfrac{\eta^{3^{k+1}}(2^43^{\alpha+1}mz)}{\eta^{3^k}(2^43^{\alpha+2}mz)}\equiv 1\pmod{3^{k+1}}. \end{align} $$
$$ \begin{align} C^{3^k}_{\alpha,m}(z)=\dfrac{\eta^{3^{k+1}}(2^43^{\alpha+1}mz)}{\eta^{3^k}(2^43^{\alpha+2}mz)}\equiv 1\pmod{3^{k+1}}. \end{align} $$
Next we define
 $$ \begin{align*} D_{\alpha,m,k}(z) & :=\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)}C^{3^k}_{\alpha,m}(z) \\ & =\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)\eta^{3^{k+1}-3^{\alpha}m}(2^43^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{k}}(2^43^{\alpha+2}mz)}. \end{align*} $$
$$ \begin{align*} D_{\alpha,m,k}(z) & :=\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)}C^{3^k}_{\alpha,m}(z) \\ & =\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)\eta^{3^{k+1}-3^{\alpha}m}(2^43^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{k}}(2^43^{\alpha+2}mz)}. \end{align*} $$
 $$ \begin{align} D_{\alpha,m,k}(z)\equiv\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)} \equiv\dfrac{f_{48}f_{2^33^{\alpha+1}m}^{2\cdot3^{\alpha}m}}{f_{24}^2f_{2^4\cdot3^{\alpha+1}m}^{3^{\alpha}m}} \equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3^{\alpha}m}(n)q^{24n}\pmod{3^{k+1}}. \end{align} $$
$$ \begin{align} D_{\alpha,m,k}(z)\equiv\dfrac{\eta\,(48z)\eta^{2\cdot3^{\alpha}m}(2^33^{\alpha+1}mz)}{\eta^2(24z)\eta^{3^{\alpha}m}(2^43^{\alpha+1}mz)} \equiv\dfrac{f_{48}f_{2^33^{\alpha+1}m}^{2\cdot3^{\alpha}m}}{f_{24}^2f_{2^4\cdot3^{\alpha+1}m}^{3^{\alpha}m}} \equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3^{\alpha}m}(n)q^{24n}\pmod{3^{k+1}}. \end{align} $$
We now prove that
![]() $D_{\alpha ,m,k}(z)$
is a modular form. Applying Theorem 2.3, we find that the level of
$D_{\alpha ,m,k}(z)$
is a modular form. Applying Theorem 2.3, we find that the level of
![]() $D_{\alpha ,m,k}(z)$
is
$D_{\alpha ,m,k}(z)$
is
![]() $N=2^43^{\alpha +2}mM$
, where M is the smallest positive integer such that
$N=2^43^{\alpha +2}mM$
, where M is the smallest positive integer such that
 $$ \begin{align*} 2^43^{\alpha+2}mM\bigg(\dfrac{-2}{24}+\dfrac{1}{48}+\dfrac{2\cdot3^{\alpha}m}{2^33^{\alpha+1}m}+\dfrac{3^{k+1}-3^{\alpha}m}{2^43^{\alpha+1}m}+\dfrac{-3^k}{2^43^{\alpha+2}m}\bigg)\equiv 0\pmod{24}, \end{align*} $$
$$ \begin{align*} 2^43^{\alpha+2}mM\bigg(\dfrac{-2}{24}+\dfrac{1}{48}+\dfrac{2\cdot3^{\alpha}m}{2^33^{\alpha+1}m}+\dfrac{3^{k+1}-3^{\alpha}m}{2^43^{\alpha+1}m}+\dfrac{-3^k}{2^43^{\alpha+2}m}\bigg)\equiv 0\pmod{24}, \end{align*} $$
which gives
![]() $8\cdot 3^kM\equiv 0\pmod {24}$
. Therefore,
$8\cdot 3^kM\equiv 0\pmod {24}$
. Therefore,
![]() $M=1$
and the level of
$M=1$
and the level of
![]() $D_{\alpha ,m,k}(z)$
is
$D_{\alpha ,m,k}(z)$
is
![]() $N=2^4 3^{\alpha +2}m$
.
$N=2^4 3^{\alpha +2}m$
.
The representatives for the cusps of
![]() $\Gamma _0(2^43^{\alpha +2}m)$
are given by fractions
$\Gamma _0(2^43^{\alpha +2}m)$
are given by fractions
![]() $c/d$
where
$c/d$
where
![]() $d \mid 2^43^{\alpha +2}m$
and
$d \mid 2^43^{\alpha +2}m$
and
![]() $\gcd (c, 2^43^{\alpha +2}m) = 1$
. From Theorem 2.4,
$\gcd (c, 2^43^{\alpha +2}m) = 1$
. From Theorem 2.4,
![]() $D_{\alpha ,m,k}(z)$
is holomorphic at a cusp
$D_{\alpha ,m,k}(z)$
is holomorphic at a cusp
![]() $c/d$
if and only if
$c/d$
if and only if
 $$ \begin{align*} -2 \dfrac{\gcd (d,24)^2}{24} & + \dfrac{\gcd (d,48)^2}{48}+2\cdot 3^{\alpha} m \dfrac{\gcd (d,2^33^{\alpha+1} m)^2}{2^33^{\alpha+1} m} \\ & +(3^{k+1}-3^{\alpha} m) \dfrac{\gcd (d,2^4 3^{\alpha+1} m)^2}{2^43^{\alpha+1} m} -3^k~ \dfrac{\gcd (d,2^4 3^{\alpha+2} m)^2}{2^43^{\alpha+2} m} \geq 0. \end{align*} $$
$$ \begin{align*} -2 \dfrac{\gcd (d,24)^2}{24} & + \dfrac{\gcd (d,48)^2}{48}+2\cdot 3^{\alpha} m \dfrac{\gcd (d,2^33^{\alpha+1} m)^2}{2^33^{\alpha+1} m} \\ & +(3^{k+1}-3^{\alpha} m) \dfrac{\gcd (d,2^4 3^{\alpha+1} m)^2}{2^43^{\alpha+1} m} -3^k~ \dfrac{\gcd (d,2^4 3^{\alpha+2} m)^2}{2^43^{\alpha+2} m} \geq 0. \end{align*} $$
Equivalently,
![]() $D_{\alpha ,m,k}(z)$
is holomorphic at a cusp
$D_{\alpha ,m,k}(z)$
is holomorphic at a cusp
![]() $c/d$
if and only if
$c/d$
if and only if
where
 $$ \begin{align*} & G_1=\dfrac{\gcd (d,24)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}, \quad G_2=\dfrac{\gcd (d,48)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}, \\ & G_3=\dfrac{\gcd (d,2^3 3^{\alpha+1} m)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}, \quad G_4=\dfrac{\gcd (d,2^4 3^{\alpha+1} m)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}. \end{align*} $$
$$ \begin{align*} & G_1=\dfrac{\gcd (d,24)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}, \quad G_2=\dfrac{\gcd (d,48)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}, \\ & G_3=\dfrac{\gcd (d,2^3 3^{\alpha+1} m)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}, \quad G_4=\dfrac{\gcd (d,2^4 3^{\alpha+1} m)^2}{\gcd (d,2^4 3^{\alpha+2} m)^2}. \end{align*} $$
Let d be a divisor of
![]() $2^43^{\alpha +2} m$
. We write
$2^43^{\alpha +2} m$
. We write
![]() $d = 2^{r_1}3^{r_2}t$
where
$d = 2^{r_1}3^{r_2}t$
where
![]() $0 \leq r_1 \leq 4$
,
$0 \leq r_1 \leq 4$
,
![]() $0 \leq r_2 \leq \alpha + 2$
and
$0 \leq r_2 \leq \alpha + 2$
and
![]() $t \mid m$
. We now consider four cases depending on the values of
$t \mid m$
. We now consider four cases depending on the values of
![]() $r_1$
and
$r_1$
and
![]() $r_2$
.
$r_2$
.
Case 1:
![]() $0{\kern-1pt}\leq{\kern-1pt} r_1{\kern-1pt}\leq{\kern-1pt} 3$
,
$0{\kern-1pt}\leq{\kern-1pt} r_1{\kern-1pt}\leq{\kern-1pt} 3$
,
![]() $0\leq r_2\leq \alpha +1$
. Then
$0\leq r_2\leq \alpha +1$
. Then
![]() $G_1{\kern-1pt}={\kern-1pt}G_2$
,
$G_1{\kern-1pt}={\kern-1pt}G_2$
,
![]() ${1}/{3^{2\alpha }t^2}\leq G_1\leq 1$
and
${1}/{3^{2\alpha }t^2}\leq G_1\leq 1$
and
![]() $G_3= G_4=1$
. Hence, we have
$G_3= G_4=1$
. Hence, we have
![]() $L= 3^{\alpha +2}m(1-G_1)+8\cdot 3^k\geq 8\cdot 3^k.$
$L= 3^{\alpha +2}m(1-G_1)+8\cdot 3^k\geq 8\cdot 3^k.$
Case 2:
![]() $0\leq r_1\leq 3$
,
$0\leq r_1\leq 3$
,
![]() $r_2= \alpha +2$
. Then
$r_2= \alpha +2$
. Then
![]() $G_1=G_2$
,
$G_1=G_2$
,
![]() ${1}/{3^{2(\alpha +1)}t^2}\leq G_1\leq {1}/{3^{2(\alpha +1)}}$
and
${1}/{3^{2(\alpha +1)}t^2}\leq G_1\leq {1}/{3^{2(\alpha +1)}}$
and
![]() $G_3=G_4={1}/{9}$
. Therefore,
$G_3=G_4={1}/{9}$
. Therefore,
![]() $L= 3^{\alpha +2}m({1}/{9}-G_1)\geq 0.$
$L= 3^{\alpha +2}m({1}/{9}-G_1)\geq 0.$
Case 3: Let
![]() $r_1=4$
,
$r_1=4$
,
![]() $0\leq r_2 \leq \alpha +1$
. Then
$0\leq r_2 \leq \alpha +1$
. Then
![]() $G_2=4G_1$
,
$G_2=4G_1$
,
![]() ${1}/{4\cdot 3^{(\alpha +1)}t^2}\leq G_1\leq {1}/{4}$
,
${1}/{4\cdot 3^{(\alpha +1)}t^2}\leq G_1\leq {1}/{4}$
,
![]() $G_4=4G_3$
and
$G_4=4G_3$
and
![]() $G_3={1}/{4}$
. Hence, we have
$G_3={1}/{4}$
. Hence, we have
![]() $L=8\cdot 3^k.$
$L=8\cdot 3^k.$
Case 4: Let
![]() $r_1=4$
,
$r_1=4$
,
![]() $ r_2 =\alpha +2$
. Then
$ r_2 =\alpha +2$
. Then
![]() $G_2=4G_1$
,
$G_2=4G_1$
,
![]() ${1}/{4\cdot 3^{(\alpha +1)}t^2}\leq G_1\leq {1}/{4\cdot 3^{2(\alpha +1)}}$
,
${1}/{4\cdot 3^{(\alpha +1)}t^2}\leq G_1\leq {1}/{4\cdot 3^{2(\alpha +1)}}$
,
![]() $G_4=4G_3$
and
$G_4=4G_3$
and
![]() $G_3={1}/{36}$
. Therefore,
$G_3={1}/{36}$
. Therefore,
![]() $L=0.$
$L=0.$
Therefore,
![]() $D_{\alpha ,m,k}(z)$
is holomorphic at every cusp
$D_{\alpha ,m,k}(z)$
is holomorphic at every cusp
![]() $c/d$
. The weight of
$c/d$
. The weight of
![]() $D_{\alpha ,m,k}(z)$
is
$D_{\alpha ,m,k}(z)$
is
![]() $\ell = {1}/{2}{(3^\alpha m-1)}+3^k$
which is a positive integer and the associated character is given by
$\ell = {1}/{2}{(3^\alpha m-1)}+3^k$
which is a positive integer and the associated character is given by
 $$ \begin{align*} \chi_2(\bullet)=\bigg(\dfrac{(-1)^\ell 3^{2 \alpha 3^k+3^\alpha \alpha m+3^\alpha m+3^k-1} m^{3^\alpha m+2\cdot 3^k}}{\bullet}\bigg). \end{align*} $$
$$ \begin{align*} \chi_2(\bullet)=\bigg(\dfrac{(-1)^\ell 3^{2 \alpha 3^k+3^\alpha \alpha m+3^\alpha m+3^k-1} m^{3^\alpha m+2\cdot 3^k}}{\bullet}\bigg). \end{align*} $$
Thus,
![]() $D_{\alpha ,m,k}(z)\in M_\ell (\Gamma _0(N),\chi )$
where
$D_{\alpha ,m,k}(z)\in M_\ell (\Gamma _0(N),\chi )$
where
![]() $\ell $
, N and
$\ell $
, N and
![]() $\chi $
are as above. By Theorem 2.5, the Fourier coefficients of
$\chi $
are as above. By Theorem 2.5, the Fourier coefficients of
![]() $D_{\alpha ,m,k}(z)$
are almost all divisible by
$D_{\alpha ,m,k}(z)$
are almost all divisible by
![]() $r=3^k$
. From (4.2), this holds for
$r=3^k$
. From (4.2), this holds for
![]() $\overline {a}_{3^{\alpha }m}(n)$
also. This completes the proof of Theorem 1.3.
$\overline {a}_{3^{\alpha }m}(n)$
also. This completes the proof of Theorem 1.3.
5. Proof of Theorem 1.4
First we recall the following result of Ono and Taguchi [Reference Ono and Taguchi13] on the nilpotency of Hecke operators.
Theorem 5.1 [Reference Ono and Taguchi13, Theorem 1.3(3)].
Let n be a nonnegative integer and k be a positive integer. Let
![]() $\chi $
be a quadratic Dirichlet character of conductor
$\chi $
be a quadratic Dirichlet character of conductor
![]() $9\cdot 2^a$
. Then there is an integer
$9\cdot 2^a$
. Then there is an integer
![]() $c \geq 0$
such that for every
$c \geq 0$
such that for every
![]() $f(z) \in M_k(\Gamma _0(9\cdot 2^a),\chi ) \cap \mathbb {Z}[[q]]$
and every
$f(z) \in M_k(\Gamma _0(9\cdot 2^a),\chi ) \cap \mathbb {Z}[[q]]$
and every
![]() $t\geq 1$
,
$t\geq 1$
,
whenever the primes
![]() $p_1, \ldots , p_{c+t}$
are coprime to
$p_1, \ldots , p_{c+t}$
are coprime to
![]() $6$
.
$6$
.
We apply this theorem to the modular form
![]() $B_{1,1,k}(z)$
to prove Theorem 1.4. Putting
$B_{1,1,k}(z)$
to prove Theorem 1.4. Putting
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $m=1$
in (3.3), we find that
$m=1$
in (3.3), we find that
 $$ \begin{align*} B_{1,1,k}(z)\equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3}(n)q^{24n}\pmod{2^{k+1}}, \end{align*} $$
$$ \begin{align*} B_{1,1,k}(z)\equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3}(n)q^{24n}\pmod{2^{k+1}}, \end{align*} $$
which yields
 $$ \begin{align} B_{1,1,k}(z):=\displaystyle\sum_{n=0}^{\infty}F_k(n)q^{n}\equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3}\bigg(\dfrac{n}{24}\bigg)q^{n}\pmod{2^{k+1}}. \end{align} $$
$$ \begin{align} B_{1,1,k}(z):=\displaystyle\sum_{n=0}^{\infty}F_k(n)q^{n}\equiv\displaystyle\sum_{n=0}^{\infty}\overline{a}_{3}\bigg(\dfrac{n}{24}\bigg)q^{n}\pmod{2^{k+1}}. \end{align} $$
Now,
![]() $B_{1,1,k}(z)\in M_{2^{k-1}+1}(\Gamma _0(9\cdot 2^6),\chi _3)$
for
$B_{1,1,k}(z)\in M_{2^{k-1}+1}(\Gamma _0(9\cdot 2^6),\chi _3)$
for
![]() $k\geq 1$
where
$k\geq 1$
where
![]() $\chi _3$
is the associated character (which is
$\chi _3$
is the associated character (which is
![]() $\chi _1$
evaluated at
$\chi _1$
evaluated at
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $m=1$
). In view of Theorem 5.1, there is an integer
$m=1$
). In view of Theorem 5.1, there is an integer
![]() $c\geq 0$
such that for any
$c\geq 0$
such that for any
![]() $d\geq 1$
,
$d\geq 1$
,
whenever
![]() $p_1,\ldots , p_{c+d}$
are coprime to 6. It follows from the definition of Hecke operators that if
$p_1,\ldots , p_{c+d}$
are coprime to 6. It follows from the definition of Hecke operators that if
![]() $p_1,\ldots , p_{c+d}$
are distinct primes and if n is coprime to
$p_1,\ldots , p_{c+d}$
are distinct primes and if n is coprime to
![]() $p_1\cdots p_{c+d}$
, then
$p_1\cdots p_{c+d}$
, then
Combining (5.1) and (5.2) completes the proof of the theorem.
6. Concluding remarks
Theorems 1.2 and 1.3 of this paper and [Reference Gireesh, Ray and Shivashankar7, Theorem 1.8] give the arithmetic densities of
![]() $\overline {a}_t(n)$
for odd t, but similar techniques cannot be used to obtain the arithmetic density of
$\overline {a}_t(n)$
for odd t, but similar techniques cannot be used to obtain the arithmetic density of
![]() $\overline {a}_t(n)$
when t is even. It would be interesting to study the arithmetic density of
$\overline {a}_t(n)$
when t is even. It would be interesting to study the arithmetic density of
![]() $\overline {a}_t(n)$
for even values of t.
$\overline {a}_t(n)$
for even values of t.
Computational evidence suggests that there are Ramanujan type congruences for
![]() $\overline {a}_t(n)$
modulo powers of 2, 3 and other primes
$\overline {a}_t(n)$
modulo powers of 2, 3 and other primes
![]() $\geq 5$
for various t that are not covered by the results of [Reference Bandyopadhyay and Baruah2, Reference Gireesh, Ray and Shivashankar7]. It would be of interest to find new congruences for
$\geq 5$
for various t that are not covered by the results of [Reference Bandyopadhyay and Baruah2, Reference Gireesh, Ray and Shivashankar7]. It would be of interest to find new congruences for
![]() $\overline {a}_t(n)$
.
$\overline {a}_t(n)$
.
Asymptotic formulae for partition functions and other related functions have been widely studied in the literature. For instance, the asymptotic formulae for
![]() $p(n)$
and
$p(n)$
and
![]() $c_t(n)$
were obtained by Hardy and Ramanujan [Reference Hardy and Ramanujan9] and Anderson [Reference Anderson1], respectively. It will be desirable to find an asymptotic formula for
$c_t(n)$
were obtained by Hardy and Ramanujan [Reference Hardy and Ramanujan9] and Anderson [Reference Anderson1], respectively. It will be desirable to find an asymptotic formula for
![]() $\overline {a}_t(n)$
.
$\overline {a}_t(n)$
.
Some relations connecting
![]() $\overline {a}_t(n)$
and
$\overline {a}_t(n)$
and
![]() $c_t(n)$
have been discussed in [Reference Bandyopadhyay and Baruah2]. A combinatorial treatment for
$c_t(n)$
have been discussed in [Reference Bandyopadhyay and Baruah2]. A combinatorial treatment for
![]() $\overline {a}_t(n)$
might reveal more interesting partition theoretic connections.
$\overline {a}_t(n)$
might reveal more interesting partition theoretic connections.
Acknowledgements
The author is extremely grateful to his PhD supervisor, Professor Nayandeep Deka Baruah, for his guidance and encouragement. The author is indebted to Professor Rupam Barman for many helpful comments and suggestions. The author thanks the Council of Scientific and Industrial Research, Government of India, for supporting the project. The author would like to thank the anonymous referee for carefully reading the paper.