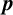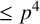1. Introduction
This paper consistently employs the following notation: G for a finite group,
$\mathrm{Irr}(G)$
for the set of all complex irreducible characters of G,
$\mathbb {F}$
for a field with characteristic
$0$
and p for a prime number. In representation theory, a challenging and crucial task is to compute all inequivalent irreducible matrix representations of G over
$\mathbb {F}$
, even for
$\mathbb {F}=\mathbb {C}$
. In this paper, we deal with
$\mathbb {F}=\mathbb {Q}$
. For a given character
$\chi \in \mathrm{Irr}(G)$
, we define
$\Omega (\chi )$
as follows:
$$ \begin{align*} \Omega(\chi) = m_{\mathbb{Q}}(\chi)\sum_{\sigma \in \mathrm{Gal}(\mathbb{Q}(\chi) / \mathbb{Q})}^{}\chi^{\sigma}, \end{align*} $$
where
$m_{\mathbb {Q}}(\chi )$
represents the Schur index of
$\chi $
over
$\mathbb {Q}$
. Note that
$\Omega (\chi )$
corresponds to the character of an irreducible
$\mathbb {Q}$
-representation
$\rho $
of G. Conversely, if
$\rho $
is an irreducible
$\mathbb {Q}$
-representation of G, then there exists
$\chi \in \mathrm{Irr}(G)$
such that
$\Omega (\chi )$
is the character of
$\rho $
. Generally, obtaining an irreducible
$\mathbb {Q}$
-representation
$\rho $
of G that affords the character
$\Omega (\chi )$
is a challenging task. A significant and interesting task is to determine all inequivalent irreducible matrix representations of G over
$\mathbb {Q}$
for several reasons. For example, one problem in rationality concerns the realizability of an
$\mathbb {F}$
-representation of G over its subfields, specially, the realizability of a
$\mathbb {C}$
-representation of G over
$\mathbb {R}$
or
$\mathbb {Q}$
.
In this article, we study irreducible rational matrix representations for some classes of p-groups. In Section 3, for any p-group G, we present Algorithms 15 and 20 for computing an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
, where
$\chi \in \mathrm{Irr}(G)$
. These algorithms rely heavily on results from [Reference Ford9, Reference Yamada31, Reference Yamada32]. To obtain an irreducible rational matrix representation of a finite p-group G affording the character
$\Omega (\chi )$
, where
$\chi \in \mathrm{Irr}(G)$
is equivalent to finding a pair
$(H, \psi )$
, where
$H\leq G$
and
$\psi \in \mathrm{Irr}(H)$
, with some suitable properties (see Algorithms 15 and 20). We refer to
$(H, \psi )$
as a required pair for an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
. Importantly, using a required pair
$(H, \psi )$
, we can also compute an irreducible complex matrix representation of G that affords the character
$\chi $
. In Section 4, we study required pairs for VZ p-groups. A group G is called a VZ-group if all its nonlinear irreducible characters vanish off the centre. VZ-groups have been extensively studied by various researchers in [Reference Fernández-Alcober and Moretó8, Reference Lewis18, Reference Lewis19, Reference Prajapati, Darafsheh and Ghorbani25, Reference Prajapati and Sharma26]. By using our results on VZ p-groups, we explicitly obtain all inequivalent irreducible rational matrix representations of all p-groups of order
$\leq p^4$
(see Sections 5 and 6).
In parallel, this article delves into an investigation of the Wedderburn decomposition of
$\mathbb {Q}G$
with a specific focus on VZ p-groups. For a semisimple group algebra
$\mathbb {F}G$
, the Wedderburn components are matrix algebras over finite extensions of
$\mathbb {F}$
in the case of positive characteristic, and Brauer-equivalent to cyclotomic algebras in the case of zero characteristic, as per the Brauer–Witt theorem (see [Reference Yamada30]). Further, the Wedderburn decomposition of
$\mathbb {F}G$
aids in describing the automorphisms group of
$\mathbb {F}G$
(see [Reference Herman11, Reference Olivieri, del Río and Simón22]) or studying the unit group of the integral group ring
$\mathbb {Z}G$
when
$\mathbb {F}=\mathbb {Q}$
(see [Reference del Río and Ruiz7, Reference Jespers and del Río14, Reference Jespers and Leal16, Reference Ritter and Sehgal28]). The Wedderburn decomposition of
$\mathbb {Q}G$
has been extensively studied in [Reference Bakshi and Kaur2–Reference Bakshi and Maheshwary4, Reference Jespers, Leal and Paques17, Reference Olivieri, del Río and Simón21, Reference Olteanu23, Reference Perlis and Walker24]. They used various concepts such as computation of the field of character values, Shoda pairs, numerical representation of cyclotomic algebras and so forth, to compute simple components of
$\mathbb {Q}G$
. We prove Theorems 1 and 2, which provide a combinatorial description for the Wedderburn decomposition of rational group algebra of a VZ p-group. Our results formulate the computation of the Wedderburn decomposition of a VZ p-group G solely based on computing the number of cyclic subgroups of
$Z(G)$
and
$Z(G)/G'$
, which is similar to the Perlis–Walker theorem for an abelian group (see Lemma 6). Indeed, we prove the following theorems.
Theorem 1. Let G be a finite VZ p-group (odd prime p). Let
$m_1$
,
$m_2$
and
$m_3$
denote the exponents of
$G/G'$
,
$Z(G)$
and
$Z(G)/G'$
, respectively. Then the Wedderburn decomposition of
$\mathbb {Q}G$
is as follows:
$$ \begin{align*}\mathbb{Q}G \cong &\bigoplus_{d_1|m_1}a_{d_1}\mathbb{Q}(\zeta_{d_1})\bigoplus_{d_2\mid m_2, d_2 \nmid m_3} a_{d_2}M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2}))\\ &\bigoplus_{d_2|m_2, d_2|m_3}(a_{d_2}-a_{d_2}')M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2})),\end{align*} $$
where
$a_{d_1}$
,
$a_{d_2}$
and
$a_{d_2}'$
are the number of cyclic subgroups of
$G/G'$
of order
$d_1$
, the number of cyclic subgroups of
$Z(G)$
of order
$d_2$
and the number of cyclic subgroups of
$Z(G)/G'$
of order
$d_2$
, respectively.
Theorem 2. Let G be a VZ
$2$
-group. Let
$m_1$
,
$m_2$
and
$m_3$
denote the exponents of
$G/G'$
,
$Z(G)$
and
$Z(G)/G'$
, respectively. Suppose
$k=|\{\chi \in \mathrm{nl}(G) : m_{\mathbb {Q}}(\chi )=2\}|$
and
$\mathbb {H}(\mathbb {Q})$
represents the standard quaternion algebra over
$\mathbb {Q}$
. Then the Wedderburn decomposition of
$\mathbb {Q}G$
is as follows:
$$ \begin{align*} \mathbb{Q}G \cong &\bigoplus_{d_1\mid m_1}a_{d_1}\mathbb{Q}(\zeta_{d_1}) \bigoplus kM_{{1}/{2}|G/Z(G)|^{{1}/{2}}}(\mathbb{H}(\mathbb{Q})) \bigoplus(a_2-a_2'-k)M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q})\\ &\bigoplus_{d_2\mid m_2, d_2 \nmid m_3} a_{d_2}M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2})) \bigoplus_{d_2\mid m_2, d_2 \mid m_3}(a_{d_2}-a_{d_2}')M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2})), \end{align*} $$
where
$a_{d_1}$
,
$a_{l}$
and
$a_{l}' (l \in \{2, d_2\geq 4\})$
are the number of cyclic subgroups of
$G/G'$
of order
$d_1$
, the number of cyclic subgroups of
$Z(G)$
of order l and the number of cyclic subgroups of
$Z(G)/G'$
of order l, respectively.
In Section 4.2, we derive several consequences from the above theorems. Further, if G is a nonabelian p-group of order
$p^4$
of maximal class, then G has a unique abelian subgroup of index p (see Section 6.2). We prove Theorem 3, which formulates the computation of the Wedderburn decomposition of a non-VZ p-group G of order
$p^4$
.
Theorem 3. Let G be a nonabelian p-group (odd prime p) of order
$p^4$
of nilpotency class
$3$
, and let H be its unique abelian subgroup of index p. Let m and
$m'$
denote the exponents of H and
$H/G'$
, respectively. Then the Wedderburn decomposition of
$\mathbb {Q}G$
is as follows:
$$ \begin{align*}\mathbb{Q}G\cong\bigoplus\mathbb{Q}(G/G')\bigoplus_{d|m, d \nmid m'} \frac{a_{d}}{p}M_p(\mathbb{Q}(\zeta_{d}))\bigoplus_{d|m, d|m'}\frac{a_{d}-a_{d}'}{p}M_p(\mathbb{Q}(\zeta_{d})),\end{align*} $$
where
$a_{d}$
and
$a_{d}'$
are the number of cyclic subgroups of order d of H and
$H/G'$
, respectively.
In this article, we also provide a brief analysis of primitive central idempotents and their corresponding simple components in the Wedderburn decomposition of the rational group ring of a VZ p-group (see Section 4.3).
2. Notation and some basic results
2.1. Notation
For a finite group G, the following notation is used consistently throughout this article.
$$ \begin{align*} \begin{array}{ll} \text{Core}_{G}(H) & \text{the normal core of } H \text{ in } G \text{ for } H \leq G\\ \text{Irr}(G) & \text{the set of irreducible complex characters of }G\\ \text{lin}(G) & \{\chi \in \text{Irr}(G) : \chi(1)=1\}\\ \text{nl}(G) & \{\chi \in \text{Irr}(G) : \chi(1) \neq 1\}\\ \text{FIrr}(G) & \text{the set of faithful irreducible complex characters of }G\\ \text{Irr}^{(m)}(G) & \{\chi \in \text{Irr}(G) : \chi(1)=m\}\\ \text{cd}(G) & \{ \chi(1) : \chi \in \text{Irr}(G) \}\\ \text{Irr}_{\mathbb{Q}}(G) & \text{the set of irreducible rational characters of }G\\\text{Irr}_{\mathbb{Q}}^{(m)}(G) & \{\chi \in \text{Irr}_{\mathbb{Q}}(G) : \chi(1)=m\}\\ \mathbb{F}(\chi) & \text{the field obtained by adjoining the values }\{\chi(g) : g\in G\} \text{ to the}\\ & \text{field }\mathbb{F} \text{ for some }\chi\in \text{Irr}(G) \\ m_{\mathbb{Q}}(\chi) & \text{the Schur index of } \chi \in \text{Irr}(G) \text{ over }\mathbb{Q}\\ \Omega(\chi) & m_{\mathbb{Q}}(\chi)\sum_{\sigma \in \text{Gal}(\mathbb{Q}(\chi) / \mathbb{Q})}^{}\chi^{\sigma} \text{ for }\chi \in \text{Irr}(G)\\ \ker(\chi) & \{g \in G: \chi(g)=\chi(1)\} \text{ for }\chi \in \text{Irr}(G)\\ \text{Irr}(G|N) & \{\chi \in \text{Irr}(G) : N \nsubseteq \ker(\chi)\}, \text{ where }N \trianglelefteq G\\ \psi^G & \text{the induced character of }\psi \text{ to }G, \text{ where }\psi \text{ is a character of }H \text{ for} \\ & \text{some }H \leq G\\ \Psi^G & \text{the induced representation of }\Psi \text{ to }G, \text{ where }\Psi \text{ is a representation}\\ & \text{of }H \text{ for some }H \leq G\\ \chi \downarrow_H & \text{the restriction of a character }\chi \text{ of } G \text{ on }H, \text{ where }H \leq G\\ \mathbb{F}G & \text{the group ring (algebra) of }G \text{ with coefficients in }\mathbb{F}\\ M_{n}(D) & \text{a full matrix ring of order }n \text{ over the skewfield }D\\ Z(B) & \text{the centre of an algebraic structure }B\\ \phi(n) & \text{the Euler phi function}\\ \zeta_m & \text{an }m\, \text{th primitive root of unity }\end{array} \end{align*} $$
2.2. Basic results
In this subsection, we discuss some basic concepts and results, which we use frequently throughout the article.
Let G be a finite group and
$n=|G|$
. Consider
$\mathbb {Q}(\zeta _n)$
, the n th cyclotomic field obtained by adjoining a primitive n th root of unity to
$\mathbb {Q}$
. Let
$\chi \in \mathrm{Irr}(G)$
. If
$\sigma \in \mathrm{Gal}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
, then define the function
$\chi ^{\sigma }: G \mapsto \mathbb {C}$
as
$\chi ^{\sigma }(g)=\sigma (\chi (g))$
for
$g\in G$
. It is easy to observe that
$\chi ^{\sigma }\in \mathrm{Irr}(G)$
and hence,
$\mathrm{Gal}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
acts on
$\mathrm{Irr}(G)$
. Note that
$\mathbb {Q}(\chi )$
is a finite degree Galois extension of
$\mathbb {Q}$
and the Galois group
$\mathrm{Gal}(\mathbb {Q}(\chi )/\mathbb {Q})$
is abelian. It is easy to see that
$\mathrm{Gal}(\mathbb {Q}(\chi )/\mathbb {Q})$
also acts on
$\mathrm{Irr}(G)$
, with action given by
$\sigma \cdot \chi := \chi ^{\sigma }$
. Under the above set-up, we have the following lemma.
Lemma 4 [Reference Isaacs12, Lemma 9.17]
Let
$E(\chi )$
denote the Galois conjugacy class of
$\chi \in \mathrm{Irr}(G)$
under the action of
$\mathrm{Gal}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
. Then,
$$ \begin{align*}|E(\chi)| = [\mathbb{Q}(\chi) : \mathbb{Q}]. \end{align*} $$
Definition 5. Let
$\chi , \psi \in \mathrm{Irr}(G)$
. We say that
$\chi $
and
$\psi $
are Galois conjugates over
$\mathbb {Q}$
if
$\mathbb {Q}(\chi ) = \mathbb {Q}(\psi )$
, and there exists
$\sigma \in \mathrm{Gal}(\mathbb {Q}(\chi ) / \mathbb {Q})$
such that
$\chi ^\sigma = \psi $
.
In [Reference Perlis and Walker24], Perlis and Walker studied the group ring of a finite abelian group G over the field of rational numbers and proved the following result.
Lemma 6 (Perlis–Walker theorem)
Let G be a finite abelian group of exponent m. Then the Wedderburn decomposition of
$\mathbb {Q}G$
is as follows:
$$ \begin{align*}\mathbb{Q}G \cong \bigoplus_{d|m} a_d \mathbb{Q}(\zeta_d),\end{align*} $$
where
$a_d$
is equal to the number of cyclic subgroups of G of order d.
Remark 7. Let G be a finite abelian group of exponent m. Then by Lemma 6:
-
(1) the number of rational irreducible representations of G of degree
$\phi (d)$
is equal to
$a_d$
; and -
(2) the total number of rational irreducible representations of G is equal to
$\sum _{d|m}a_d$
.
Let
$\mathbb {K}$
be an arbitrary field with characteristic zero and
$\mathbb {K}^*$
be the algebraic closure of
$\mathbb {K}$
. Let U be an irreducible
$\mathbb {K}^*$
-representation of G with character
$\chi $
. The Schur index of U with respect to
$\mathbb {K}$
is defined as
$$ \begin{align*}m_{\mathbb{K}}(U) = \text{Min} [\mathbb{L} : \mathbb{K}(\chi)],\end{align*} $$
the minimum being taken over all fields
$\mathbb {L}$
in which U is realizable. Note that
$m_{\mathbb {K}}(\chi )=m_{\mathbb {K}}(U)$
.
Reiner [Reference Reiner27] characterized the simple component of the Wedderburn decomposition of
$\mathbb {K}G$
and proved the following result.
Lemma 8 [Reference Reiner27, Theorem 3]
Let T be an irreducible
$\mathbb {K}$
-representation of G, and extend T (by linearity) to a
$\mathbb {K}$
-representation of
$\mathbb {K}G$
. Set
$$ \begin{align*}A=\{T(x) : x\in \mathbb{K}G\}.\end{align*} $$
Then, A is simple algebra over
$\mathbb {K}$
, and we may write
$A= M_{n}(D)$
, where D is a division ring. Further,
$$ \begin{align*} Z(D)\cong \mathbb{K}(\chi)\quad\text{and}\quad [D : Z(D)]=(m_{\mathbb{K}}(U_i))^2~(1\leq i \leq k), \end{align*} $$
where
$U_i$
are irreducible
$K^{*}$
-representations of G such that
$T=m_{\mathbb {K}(U_i)}\bigoplus _{i=1}^k U_i$
as a
$K^{*}$
-representation.
In this article, we use the classification of p-groups of order
$\leq p^4$
(odd prime p) provided in [Reference James13], which is based on the isoclinism concept.
Definition 9. Two finite groups G and H are said to be isoclinic if there exist isomorphisms
$\theta : G/Z(G)\longrightarrow H/Z(H)$
and
$\phi : G{}'\longrightarrow H{}'$
such that the following diagram is commutative:
where
$a_G(g_1Z(G), g_2Z(G)) = [g_1,g_2]$
for
$g_1,g_2\in G$
, and
$a_H(h_1Z(H), h_2Z(H)) = [h_1,h_2]$
for
$h_1,h_2\in H$
.
The resulting pair
$(\theta , \phi )$
is called an isoclinism of G onto H. Isoclinism was first introduced by Hall [Reference Hall10] for the classification of p-groups. It is a generalization of the concept of isomorphism between two groups. It is well known that two isoclinic nilpotent groups have the same nilpotency class. Now, we end this subsection by quoting the following lemma.
Lemma 10 [Reference Tappe29, Theorem 3.2]
Let G and H be isoclinic groups. Then,
$|H||\mathrm{Irr}^{(k)}(G)| = |G||\mathrm{Irr}^{(k)}(H)|$
.
3. Algorithm
This section outlines the algorithm for computing irreducible rational matrix representations of p-groups. For
$\chi \in \mathrm{Irr}(G)$
, there exists a unique irreducible
$\mathbb {Q}$
-representation
$\rho $
of G such that
$\chi $
occurs as an irreducible constituent of
$\rho \otimes _{\mathbb {Q}}\mathbb {F}$
with multiplicity
$m_{\mathbb{Q}}(\chi)$
, where
$\mathbb {F}$
is a splitting field of G. Therefore, the distinct Galois conjugacy classes give the distinct irreducible rational representations of G.
Lemma 11 [Reference Yamada32, Proposition 1]
Let
$\psi \in \mathrm{lin}(G)$
and
$N = \ker (\psi )$
with
$n = [G : N]$
. Suppose
$G = \bigcup _{i = 0}^{n-1}Ny^i$
. Then,
$$ \begin{align*}\psi(xy^i) = \zeta_n^i,~ (0 \leq i < n;~ x \in N).\end{align*} $$
Now, let
$f(X) = X^s - a_{s-1}X^{s-1} - \cdots -a_1X - a_0$
be the irreducible polynomial over
$\mathbb {Q}$
such that
$f(\zeta _n) = 0$
, where
$s = \phi (n)$
and
$$ \begin{align*}\Psi(xy^i) = \left(\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & \cdots & 0 & 1\\ a_0 & a_1 & \cdots & \cdots & a_{s-1} \end{array}\right)^i,\quad (0 \leq i < n;~ x \in N).\end{align*} $$
Then
$\Psi $
is an irreducible
$\mathbb {Q}$
-representation of G, whose character is
$\Omega (\psi )$
.
Lemma 12 [Reference Yamada32, Proposition 3]
Let H be a subgroup of G and
$\psi \in \mathrm{Irr}(H)$
be such that
$\psi ^G \in \mathrm{Irr}(G)$
. Then
$m_{\mathbb {Q}}(\psi ^G)$
divides
$m_{\mathbb {Q}}(\psi )[\mathbb {Q}(\psi ) : \mathbb {Q}(\psi ^G)]$
. Furthermore, the induced character
$\Omega (\psi )^G$
of G is a character of an irreducible
$\mathbb {Q}$
-representation of G if and only if
$$ \begin{align*}m_{\mathbb{Q}}(\psi^G) = m_{\mathbb{Q}}(\psi)[\mathbb{Q}(\psi) : \mathbb{Q}(\psi^G)].\end{align*} $$
In this case,
$\Omega (\psi )^G = \Omega (\psi ^G)$
.
Lemma 13 [Reference Ford9, Theorem 1]
Let G be a p-group and
$\chi \in \mathrm {Irr}(G)$
. Then, one of the following holds.
-
(1) There exists a subgroup H of G and
$\psi \in \mathrm{lin}(H)$
such that
$\psi ^G = \chi $
and
$\mathbb {Q}(\psi ) = \mathbb {Q}(\chi )$
. -
(2)
$p=2$
and there exist subgroups
$H< K$
in G with
$[K : H] = 2 $
and
$\lambda \in \mathrm{lin}(H)$
such that
$\lambda ^K=\phi $
,
$[\mathbb {Q}(\lambda ) : \mathbb {Q}(\phi ) ]=2$
,
$\phi ^G=\chi $
and
$\mathbb {Q}(\phi ) =\mathbb {Q}(\chi )$
.
Lemma 14 [Reference Isaacs12, Corollary 10.14]
Let G be a p-group and
$\chi \in \mathrm{Irr}(G)$
. If p is an odd prime, then
$m_{\mathbb {Q}}(\chi ) = 1$
; otherwise
$m_{\mathbb {Q}}(\chi )\in \{1,2\}$
.
Let G be a p-group (odd prime p) and
$\chi \in \mathrm{Irr}(G)$
. According to Lemma 14,
$m_{\mathbb {Q}}(\chi )=1$
. By Lemma 13, there exists a subgroup H of G with
$\psi \in \mathrm{lin}(H)$
such that
$\psi ^G = \chi $
and
$\mathbb {Q}(\psi ) = \mathbb {Q}(\chi )$
. Therefore, from Lemma 12, we have
$\Omega (\chi )=\Omega (\psi )^G$
. Now by using Lemma 11, compute an irreducible matrix representation
$\Psi $
of H over
$\mathbb {Q}$
that affords the character
$\Omega (\psi )$
. Then
$\Psi ^G$
is an irreducible
$\mathbb {Q}$
-representation of G that affords the character
$\Omega (\psi )^G = \Omega (\psi ^G) = \Omega (\chi )$
. In summary, an algorithm to find an irreducible rational matrix representation of a p-group G (odd prime p) can be outlined as follows.
Algorithm 15. Input: An irreducible complex character χ of a finite p-group G (odd prime p).
-
(1) Find a pair (H, ψ), where H ≤ G and ψ ∈ lin(H) is such that ψ G = χ and ℚ(ψ) = ℚ(χ).
-
(2) Find an irreducible ℚ-representation Ψ of H that affords the character Ω(ψ).
-
(3) Induce Ψ to G.
Output: Ψ G , an irreducible ℚ-representation of G whose character is Ω(χ).
Remark 16. Obtaining an irreducible rational matrix representation of a finite p-group G (odd prime p) affording the character
$\Omega (\chi )$
, where
$\chi \in \mathrm{Irr}(G)$
is equivalent to finding a pair
$(H, \psi )$
, where H is a subgroup of G and
$\psi \in \mathrm{lin}(H)$
, satisfying
$\psi ^G = \chi $
and
$\mathbb {Q}(\psi ) = \mathbb {Q}(\chi )$
. We refer to this pair
$(H, \psi )$
as a required pair for an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
.
Now, we describe the algorithm for computing irreducible rational matrix representations of
$2$
-groups.
Lemma 17 [Reference Yamada31, Theorem 2.12]
Let G be a
$2$
-group and
$\chi \in \mathrm{Irr}(G)$
. Then there exists a pair
$(H, \psi )$
such that
$H \leq G$
,
$\psi \in \mathrm{Irr}(H)$
,
$\psi ^G = \chi $
,
$\mathbb {Q}(\chi ) = \mathbb {Q}(\psi )$
, and one of the following holds:
-
(1)
$H/\!\ker (\psi )\cong Q_n (n\geq 2)$
,
$m_{\mathbb {Q}}(\chi )=2$
,
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _{2^n}+\zeta ^{-1}_{2^n});$
-
(2)
$H/\!\ker (\psi )\cong D_n (n\geq 3)$
,
$m_{\mathbb {Q}}(\chi )=1$
,
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _{2^n}+\zeta _{2^n}^{-1});$
-
(3)
$H/\!\ker (\psi )\cong SD_n (n\geq 3)$
,
$m_{\mathbb {Q}}(\chi )=1$
,
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _{2^n}-\zeta _{2^n}^{-1});$
-
(4)
$H/\!\ker (\psi )\cong C_n (n\geq 0)$
,
$m_{\mathbb {Q}}(\chi )=1$
,
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _{2^n}),$
where
$Q_n$
,
$D_n$
and
$SD_n$
are respectively the generalized quaternion, dihedral and semidihedral group of order
$2^{n+1}$
, and
$C_n$
is the cyclic group of order
$2^n$
.
Lemma 18 [Reference Yamada32, Example 7 and Proposition 8]
-
(1) Let
$G = Q_n = \langle a, b : a^{2^n} = 1, b^2=a^{2^{n-1}}, bab^{-1}=a^{-1} \rangle $
be the generalized quaternion group of order
$2^{n+1}$
, and let
$\chi \in \mathrm{FIrr}(G)$
. Then,
$\chi = \psi ^G$
, where
$H = \langle a \rangle $
and
$\psi \in \mathrm{lin}(H)$
is such that
$\psi (a)=\zeta _{2^n}$
,
$m_{\mathbb {Q}}(\chi )=2$
and
$\Omega (\chi )=\Omega (\psi )^G$
. -
(2) Let
$G = D_n = \langle a, b : a^{2^n} = b^2=1, bab^{-1}=a^{-1} \rangle $
be the dihedral group of order
$2^{n+ 1}$
or
$G = SD_n = \langle a, b : a^{2^n} = b^2=1, bab^{-1}=a^{2^{n-1}-1} \rangle $
be the semi-dihedral group of order
$2^{n+1}$
, and let
$\chi \in \mathrm{FIrr}(G)$
. Then,
$\Omega (\chi )=\Omega (\psi )^G$
, where
$H = \langle a^{2^{n-1}}, b \rangle $
and
$\psi \in \mathrm{lin}(H)$
is such that
$\psi (a^{2^{n-1}}) = -1$
,
$\psi (b)=1$
.
Remark 19. Let G be a
$2$
-group and let
$\chi \in \mathrm{nl}(G)$
. By Lemma 17, there exists a pair
$(H, \psi )$
, with
$H \leq G$
and
$\psi \in \mathrm{Irr}(H)$
, satisfying the following properties:
$\psi ^G=\chi $
,
$\mathbb {Q}(\chi )=\mathbb {Q}(\psi )$
and
$H/\!\ker (\psi )$
is isomorphic to one of the following groups: cyclic group, generalized quaternion group, dihedral group or semi-dihedral group. We define
$\bar {\psi } \in \mathrm{FIrr}(H/\!\ker (\psi ))$
such that
$\bar {\psi }(h\ker (\psi ))=\psi (h)$
for all
$h \in H$
. Now we have two cases.
Case 1 (
$H/\!\ker (\psi )\cong C_n$
). In this case,
$\psi \in \mathrm{lin}(H)$
and hence by using Lemma 11, we get an irreducible rational matrix representation
$\Psi $
of H that affords the character
$\Omega (\psi )$
. Then by Lemma 12,
$\Psi ^G$
is an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
.
Case 2 (
$H/\!\ker (\psi )\cong Q_n$
, or
$D_n$
, or
$SD_n$
for some
$n \in \mathbb {N}$
). In this case, since
$\bar {\psi } \in \mathrm{FIrr}(H/\!\ker (\psi ))$
, by Lemmas 18 and 11, there exists an irreducible rational matrix representation of
$H/\!\ker (\psi )$
that affords the character
$\Omega (\bar {\psi })$
. Indeed, we get an irreducible rational matrix representation
$\Psi $
of H that affords the character
$\Omega (\psi )$
. Then again by Lemma 12,
$\Psi ^G$
is an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
.
In view of Remark 19, an algorithm to find an irreducible rational matrix representation of a
$2$
-group G can be outlined as follows.
Algorithm 20. Input: An irreducible complex character χ of a finite 2-group G.
-
(1) Find a pair (H, ψ), where H ≤ G and ψ ∈ Irr(H) such that ψ G = χ, ℚ(χ) = ℚ(ψ) and H/ ker(ψ) is a cyclic, generalized quaternion, dihedral or semi-dihedral group.
-
(2) Find an irreducible ℚ-representation Ψ of H that affords the character Ω(ψ).
-
(3) Induce Ψ to G.
Output: Ψ G , an irreducible ℚ-representation of G whose character is Ω(χ).
Here, we call such a pair (H, ψ) a required pair for an irreducible rational matrix representation of G that affords the character Ω(χ).
4. VZ p-group
A group G is called a VZ-group if all its nonlinear complex irreducible characters vanish off centre (see [Reference Lewis19]). In this case,
$G' \subseteq Z(G)$
and hence the nilpotency class of G is
$2$
. The character degree set is given by
$\text {cd}(G) = \{1, |G/Z(G)|^{1/2}\}$
. Furthermore, G has
$|Z(G)| - |Z(G)/G'|$
many inequivalent nonlinear irreducible complex characters, and there is a one-to-one correspondence between the sets
$\mathrm{nl}(G)$
and
$\mathrm{Irr}(Z(G) | G')$
(see [Reference Prajapati and Sharma26, Section 3.1]). For any
$\mu \in \mathrm{Irr}(Z(G) | G')$
, the corresponding
$\chi _\mu \in \mathrm{nl}(G)$
is defined as follows:
$$ \begin{align} \chi_\mu(g) = \begin{cases} |G/Z(G)|^{{1}/{2}}\mu(g) &\text{if } g \in Z(G),\\ 0 & \text{otherwise. } \end{cases} \end{align} $$
Observe that, being a nilpotency class
$2$
group, G can be written as a direct product of its Sylow subgroups. Since
$\text {cd}(G) = \{1, |G/Z(G)|^{1/2}\}$
, all the Sylow subgroups of G, except one, are abelian.
4.1. Rational representations of VZ p-groups
Let G be a VZ-group and let
$\chi _\mu \in \mathrm{nl}(G)$
(as defined in (1)).
Since G is monomial, there exists a subgroup H of G with index
$|G/Z(G)|^{{1}/{2}}$
, and
$\psi \in \mathrm{lin}(H)$
, satisfying
$\psi ^G = \chi _\mu $
. We now present the following results that provide a description of H and
$\psi $
.
Proposition 21. Let G be a VZ-group. Suppose H is a subgroup of G with index
$|G/Z(G)|^{{1}/{2}}$
and
$\psi \in \mathrm{lin}(H)$
. Then,
$\psi ^G = \chi _\mu \in \mathrm{nl}(G)$
(as defined in (1)) if and only if H is normal in G such that
$Z(G)\subset H$
and
$\psi \downarrow _{Z(G)} = \mu $
with
$\mu \in \mathrm{Irr}(Z(G)|G{}')$
.
Proof. Let
$\psi \in \mathrm{lin}(H)$
be such that
$\psi ^G = \chi _\mu $
. Let T be a set of right coset representatives of H in G. Then, for
$g\in G$
, we have
$\psi ^G(g) = \sum _{g_i\in T} {{\psi }^{\circ }}(g_igg_i^{-1})$
, where
${\psi }^{\circ }$
is defined by
$\psi ^\circ (x)=\psi (x)$
if
$x \in H$
and
$\psi ^{\circ }(x)=0$
if
$x\notin H$
. Now, for
$z\in Z(G)$
, we get
$\psi ^G(z) = |G/Z(G)|^{{1}/{2}}{\psi }^\circ (z)$
and since
$\psi ^G = \chi _\mu $
, we obtain
${\psi }^\circ (z) = \mu (z)=\psi (z)$
. This implies that
$Z(G) \subseteq H$
and
$\psi \downarrow _{Z(G)} = \mu $
. Since
$G{}'\subset Z(G)$
, H is normal in G.
Conversely, assume H is a subgroup of G with index
$|G/Z(G)|^{{1}/{2}}$
,
$\psi \in \mathrm{lin}(H)$
and
$Z(G) \subseteq H$
with
$\psi \downarrow _{Z(G)} = \mu $
, where
$\mu \in \mathrm{Irr}(Z(G)|G{}')$
. Claim:
$\psi ^G \in \mathrm{nl}(G)$
. In contrast, suppose that
$\psi ^G \notin \mathrm{nl}(G)$
, then
$\psi ^G$
must be a sum of some linear characters of G. Hence,
$G' \subseteq \ker (\psi ^G)$
, which is a contradiction as
$\psi \downarrow _{Z(G)} = \mu $
, where
$\mu \in \mathrm{Irr}(Z(G) | G')$
. This proves the claim.
We prove Proposition 22 which describes a required pair of a VZ
$2$
-group.
Proposition 22. Let G be a VZ
$2$
-group and
$\chi \in \mathrm{nl}(G)$
. Consider
$(H, \psi )$
as a required pair for an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
. Then
$H/\!\ker (\psi )$
is isomorphic to one of the following groups: cyclic group, quaternion group of order
$8$
denoted as
$Q_8$
or dihedral group of order
$8$
denoted as
$D_8$
.
Proof. Since H is a monomial group, there exists a subgroup K of H such that
$\lambda ^H = \psi $
, where
$\lambda \in \mathrm{lin}(K)$
. Consequently, we have
$\lambda ^G = \chi $
. From Proposition 21, it follows that
$Z(G) \leq K$
, which implies that
$G' \leq Z(G) \leq H$
. It is worth noting that
$H' \leq Z(H)$
and therefore,
$(H/\!\ker (\psi ))' \leq Z(H/\!\ker (\psi ))$
. Hence,
$H/\!\ker (\psi )$
must be isomorphic to one of the groups: cyclic,
$Q_8$
or
$D_8$
.
Let G be a VZ 2-group and
$\chi \in \mathrm{Irr}(G)$
. Consider a required pair
$(H, \psi )$
for a rational representation of G that affords the character
$\Omega (\chi )$
. Then by Proposition 22,
$H/\!\ker (\psi )$
is isomorphic to one of the following: cyclic,
$Q_8$
or
$D_8$
.
Case 1 (
$H/\!\ker (\psi )$
is cyclic). See Case 1 of Remark 19, to get an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
.
Case 2 (
$H/\!\ker (\psi )\hspace{-1pt} \cong\hspace{-1pt} D_8$
). Suppose
$H/\!\ker (\psi )\hspace{-1pt} =\hspace{-1pt} \langle a, b\hspace{-1pt} :\hspace{-1pt} a^4\hspace{-1pt} =\hspace{-1pt} b^2\hspace{-1pt}=\hspace{-1pt}1, bab^{-1}=a^{-1} \rangle $
(that is
$\psi \in \mathrm{nl}(H)$
). Then,
$\bar {\psi }\in \mathrm{FIrr}(H/\!\ker (\psi ))$
and
$\bar {\lambda }\in \mathrm{lin}(K/\!\ker (\psi ))$
are such that
$\bar {\lambda }^{H/\!\ker (\psi )}=\bar {\psi }$
and
$\mathbb {Q}(\bar {\lambda })=\mathbb {Q}(\bar {\psi })=\mathbb {Q}$
, where
$K/\!\ker (\psi )=\langle a^2, b\rangle $
and
$\bar {\lambda }$
is defined as
$\bar {\lambda }(a^2) = -1$
,
$\bar {\lambda }(b)=1$
. This shows that
$(K/\!\ker {\psi }, \bar {\lambda })$
is a required pair for the rational representation of
$H/\!\ker (\psi )$
that affords the character
$\Omega (\bar {\psi })$
. This implies that
$(K, \lambda )$
is also a required pair for the rational representation of G that affords the character
$\Omega (\chi )$
. Note that
$\mathbb {Q}(\lambda )=\mathbb {Q}(\chi )=\mathbb {Q}$
,
$[G:H]=\tfrac 12|G/Z(G)|^{{1}/{2}} $
and
$[G:K]=|G/Z(G)|^{{1}/{2}}$
.
Case 3 (
$H/\!\ker (\psi ) \cong Q_8$
). Suppose
$H/\!\ker (\psi )= \langle a, b : a^4 = b^4=1, bab^{-1}=a^{-1} \rangle $
(that is,
$\psi\hspace{-1pt} \in\hspace{-1pt} \mathrm{nl}(H)$
). Then
$\bar {\psi }\hspace{-1pt}\in\hspace{-1pt} \mathrm{FIrr}(H/\!\ker (\psi ))$
and
$\bar {\lambda }\hspace{-1pt}\in\hspace{-1pt} \mathrm{lin}(K/\!\ker (\psi ))$
are such that
$\bar {\lambda }^{H/\!\ker (\psi )}\hspace{-1pt}=\hspace{-1pt}\bar {\psi }$
and
$[\mathbb {Q}(\bar {\lambda }):\mathbb {Q}(\bar {\psi })]=2$
, where
$K/\!\ker (\psi )=\langle a \rangle $
and
$\bar {\lambda }$
is defined as
$\bar {\lambda }(a) = \zeta _{4}$
. Since
$m_{\mathbb {Q}}(\bar {\psi })=2$
, from Lemma 12, we get
$\Omega (\bar {\lambda })^{H/\!\ker (\psi )}=\Omega (\bar {\psi })$
. This implies that there exists a subgroup K of G and
$\lambda \in \mathrm{lin}(K)$
such that
$\Omega (\lambda )^G=\Omega (\chi )$
. Note that
$[\mathbb {Q}(\lambda ): \mathbb {Q}(\chi )]=2$
,
$[G:H]=\tfrac 12|G/Z(G)|^{{1}/{2}} $
and
$[G:K]=|G/Z(G)|^{{1}/{2}}$
.
Remark 23. In view of the above discussion and Algorithm 15, to obtain an irreducible rational matrix representation of a VZ p-group G (p is any prime) that affords the character
$\Omega (\chi )$
, where
$\chi \in \mathrm{Irr}(G)$
, we need to do the following.
-
(1) If
$m_{\mathbb {Q}}(\chi )=1$
, then find
$H \leq G$
and
$\psi \in \mathrm{lin}(H)$
such that
$\psi ^G = \chi $
,
$\mathbb {Q}(\psi ) = \mathbb {Q}(\chi )$
. -
(2) If
$m_{\mathbb {Q}}(\chi )=2$
, then find
$H \leq G$
and
$\psi \in \mathrm{lin}(H)$
so that
$\psi ^G = \chi $
,
$[\mathbb {Q}(\psi ) : \mathbb {Q}(\chi )]=2$
.
We call such a pair
$(H, \psi )$
a special required pair for an irreducible rational matrix representation of a VZ p-group G that affords the character
$\Omega (\chi )$
, where
$\chi \in \mathrm{Irr}(G)$
.
Now, we prove Lemma 24 which provides a description of the character fields, which is useful to obtain a special required pair of a VZ p-group.
Lemma 24. Let G be a VZ-group and let
$\chi _\mu \in \mathrm{nl}(G)$
(as defined in (1)). Consider a subgroup H of G with index
$|G/Z(G)|^{{1}/{2}}$
and
$\psi _\mu \in \mathrm{lin}(H)$
such that
$\psi _\mu ^G = \chi _\mu $
. Then,
$\mathbb {Q}(\psi _\mu ) = \mathbb {Q}(\chi _\mu )$
if and only if
$|\!\ker (\psi _\mu )/\!\ker (\mu )|=|G/Z(G)|^{{1}/{2}}$
, and
$|\mathbb {Q}(\psi _\mu ) : \mathbb {Q}(\chi _\mu )| = 2$
if and only if
$|\!\ker (\psi _\mu )/\!\ker (\mu )|=\tfrac 12|G/Z(G)|^{{1}/{2}}$
.
Proof. By Proposition 21,
$\psi _{\mu } \downarrow _{Z(G)} = \mu $
with
$\mu \in \mathrm{Irr}(Z(G)|G{}')$
and
$\mathbb {Q}(\chi _\mu )=\mathbb {Q}(\mu )$
. Observe that
$$ \begin{align*} \mathbb{Q}(\psi_\mu) = \mathbb{Q}(\chi_\mu)=\mathbb{Q}(\mu) & \iff \mathbb{Q}(\zeta_{|H/\!\ker(\psi_\mu)|}) = \mathbb{Q}(\zeta_{|Z(G)/\!\ker(\mu)|})\\ & \iff |H/\!\ker(\psi_\mu)| = |Z(G)/\!\ker(\mu)|\\ & \iff |\!\ker(\psi_\mu)| = |H/Z(G)| |\!\ker(\mu)| \\ & \iff |\!\ker(\psi_\mu)| = |G/Z(G)|^{{1}/{2}} |\!\ker(\mu)|. \end{align*} $$
Again,
$$ \begin{align*} [\mathbb{Q}(\psi_\mu) : \mathbb{Q}(\chi_\mu)]=[\mathbb{Q}(\psi_\mu) : \mathbb{Q}(\mu)]= 2 & \iff |\mathbb{Q}(\zeta_{|H/\!\ker(\psi_\mu)|}) : \mathbb{Q}(\zeta_{|Z(G)/\!\ker(\mu)|})|=2\\ & \iff |H/\!\ker(\psi_\mu)| = 2|Z(G)/\!\ker(\mu)|\\ & \iff |\!\ker(\psi_\mu)| = \tfrac{1}{2}|H/Z(G)| |\!\ker(\mu)| \\ & \iff |\!\ker(\psi_\mu)| = \tfrac{1}{2}|G/Z(G)|^{{1}/{2}} |\!\ker(\mu)|. \end{align*} $$
This completes the proof.
Corollary 25. Let G be a VZ-group. Suppose H is a subgroup of G with index
$|G/Z(G)|^{{1}/{2}}$
and
$\psi \in \mathrm{lin}(H)$
is such that
$\psi ^G \in \mathrm{nl}(G)$
. If one of the following is satisfied
-
(a)
$\text {cd}(G)=\{1, p\}$
; -
(b)
$|G'|=p$
,
then H is abelian.
Proof. Let H be a subgroup of G of index
$|G/Z(G)|^{{1}/{2}}$
and let
$\psi \in \mathrm{lin}(G)$
be such that
$\psi ^G \in \mathrm{nl}(G)$
. Then by Proposition 21,
$Z(G) \subseteq H$
and
$\psi \downarrow _{Z(G)} = \mu $
.
Case (a): Suppose
$\text {cd}(G)=\{1, p\}$
. This implies
$|G/Z(G)|=p^2$
and
$|H/Z(G)|=p$
. This shows that H is abelian.
Case (b): Suppose
$|G'|=p$
. In this case,
$|H{}'|\in \{1, p\}$
. Since
$H' \subseteq \ker (\psi ^G) = \text {Core}_G(\ker (\psi ))$
and
$\psi ^G\in \mathrm{nl}(G)$
, we get
$|H{}'|=1$
. Thus, H is abelian.
As we know, for a VZ-group G,
$G'$
is an elementary abelian subgroup, then by Corollary 25, we get the following result.
Corollary 26. Let G be a VZ-group. Suppose H is a subgroup of G with index
$|G/Z(G)|^{{1}/{2}}$
and
$\psi \in \mathrm{lin}(H)$
is such that
$\psi ^G \in \mathrm{nl}(G)$
. If
$Z(G)$
is cyclic, then H is abelian.
Corollary 27. Suppose G is a VZ p-group of order
$\leq p^5$
(p is any prime). Let H be a subgroup G of index
$|G/Z(G)|^{{1}/{2}}$
with
$\psi \in \mathrm{lin}(H)$
such that
$\psi ^G \in \mathrm{nl}(G)$
. Then, H is abelian.
Proof. Suppose G is a VZ p-group of order
$\leq p^5$
. In this case,
$\text {cd}(G) \in \{ \{1, p\}, \{1, p^2 \} \}$
. If
$\text {cd}(G) = \{1, p\}$
, then by Corollary 25, H is abelian. If
$\text {cd}(G) = \{1, p^2\}$
, then
$\sqrt {|G/Z(G)|}=p^2$
and hence,
$|G'| = |Z(G)| = p$
. Again, by Corollary 25, it follows that H is abelian.
Remark 28. The conclusion of Corollary 27 need not hold for higher order VZ p-groups. For instance, consider the group
$$ \begin{align*} G= G_{(15,1)} &= \langle \alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5, \alpha_6 : [\alpha_3, \alpha_5]= \alpha_1, [\alpha_4, \alpha_5]\\ &=\alpha_2, [\alpha_3, \alpha_6]=\alpha_2, [\alpha_4, \alpha_6]=\alpha_1^\nu, \alpha_1^p=\alpha_2^p=\alpha_3^p=\alpha_4^p=\alpha_5^p=\alpha_6^p=1 \rangle, \end{align*} $$
of order
$p^6$
(
$p \geq 7$
), where
$\nu $
denotes the smallest positive integer that is a quadratic nonresidue (mod p) (see [Reference Newman, O’Brien and Vaughan-Lee20]). Here,
$Z(G) = G' = \langle \alpha _1, \alpha _2 \rangle $
. It is easy to observe that G is a VZ p-group and
$\text {cd} (G)=\{1, p^2\}$
. Set
$H = \langle \alpha _1, \alpha _2, \alpha _3, \alpha _5 \rangle $
. Then
$H'=\langle \alpha _1 \rangle $
and
$H/H' = \langle \alpha _2H', \alpha _3H', \alpha _5H' \rangle \cong C_p \times C_p \times C_p$
. Define
$\bar {\psi } \in \mathrm{Irr}(H/H')$
such that
$\bar {\psi }(\alpha _2H')=\zeta _p$
,
$\bar {\psi }(\alpha _3H')=1$
and
$\bar {\psi }(\alpha _5H')=1$
. Now, define a character
$\psi $
of H by taking the lift of
$\bar {\psi } \in \mathrm{Irr}(H/H')$
. Then,
$\psi \in \mathrm{lin}(H)$
and
$\psi {\downarrow }_{Z(G)}\in \mathrm{Irr}(Z(G)| G{}')=\mathrm{Irr}(Z(G))\setminus 1_{Z(G)}$
, where
$1_{Z(G)}$
is the trivial character of
$Z(G)$
. Then by Proposition 21,
$\psi ^G \in \mathrm{nl}(G)$
; however, H is nonabelian.
4.2. Rational group algebra of a VZ p-group
Let G be a VZ-group. Then the Wedderburn decomposition of
$\mathbb {C}G$
is as follows:
$$ \begin{align*}\mathbb{C}G \cong |G/G'|\mathbb{C}\bigoplus (|Z(G)| - |Z(G)/G'|) M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{C}),\end{align*} $$
where
$M_{|G/Z(G)|^{{1}/{2}}}(\mathbb {C})$
denotes the ring of matrices of order
$|G/Z(G)|^{{1}/{2}}$
over
$\mathbb {C}$
. In this subsection, we compute the Wedderburn decomposition of the rational group algebra of a finite VZ p-group.
Let G be a finite group and let
$\chi $
,
$\psi \in \mathrm{Irr}(G)$
. It is well known that if
$\chi $
and
$\psi $
are Galois conjugates over
$\mathbb {Q}$
, then
$\ker (\chi )=\ker (\psi )$
. Now, we begin with the following easy observations.
Lemma 29. Let G be a finite group and let
$\chi , \psi \in \mathrm{lin}(G)$
be such that
$\ker (\chi ) = \ker (\psi )$
. Then,
$\chi $
and
$\psi $
are Galois conjugates over
$\mathbb {Q}$
.
In general, if
$\chi $
,
$\psi \in \mathrm{nl}(G)$
are such that
$\ker (\chi )=\ker (\psi )$
, then
$\chi $
may not be Galois conjugate to
$\psi $
over
$\mathbb {Q}$
. However, in the case of VZ groups, this is true.
Lemma 30. Let G be a VZ-group and let
$\chi , \psi \in \mathrm{Irr}(G)$
. Then
$\chi $
and
$\psi $
are Galois conjugates over
$\mathbb {Q}$
if and only if
$\ker (\chi ) = \ker (\psi )$
.
Proof. If
$\chi , \psi \in \mathrm{lin}(G)$
, then the result follows from Lemma 29. Now let
$\chi , \psi \in \mathrm{nl}(G)$
be such that
$\ker (\chi )=\ker (\psi )$
. Then, in view of (1), there exist
$\mu , \nu \in \mathrm{Irr}(Z(G)~|~G{}')$
such that
$\chi \downarrow _{Z(G)}=\mu $
and
$\psi \downarrow _{Z(G)}=\nu $
. Observe that
$\ker (\chi )=\ker (\mu )$
and
$\ker (\psi )=\ker (\nu )$
. Thus,
$\mu $
and
$\nu $
are Galois conjugates and hence,
$\chi $
and
$\psi $
are Galois conjugates over
$\mathbb {Q}$
. This completes the proof.
Lemma 31. Consider a finite abelian group G, where d divides the exponent of G. Let
$a_d$
denote the number of cyclic subgroups of G with order d. Then the number of non-Galois conjugate characters
$\chi $
satisfying
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _d)$
is precisely
$a_d$
.
Proof. See [Reference Ayoub and Ayoub1, Lemma 1].
Analogously to Lemma 31, we have the following lemma for VZ-groups.
Lemma 32. Consider a VZ-group G. Let
$\chi _\mu \in \mathrm{nl}(G)$
(defined in (1)). Assume that
$a_d$
and
$a_d'$
represent the number of cyclic subgroups of order d of
$Z(G)$
and
$Z(G)/G'$
, respectively. Then the following statements hold.
-
(1) The number of non-Galois conjugate nonlinear characters
$\chi _\mu $
of G satisfying
$\mathbb {Q}(\chi _\mu ) = \mathbb {Q}(\zeta _d)$
, where
$d \mid \exp (Z(G))$
but
$d \nmid \exp (Z(G)/G')$
, is equal to
$a_d$
. -
(2) The number of non-Galois conjugate nonlinear characters
$\chi _\mu $
of G satisfying
$\mathbb {Q}(\chi _\mu ) = \mathbb {Q}(\zeta _d)$
, where
$d \mid \exp (Z(G))$
and
$d \mid \exp (Z(G)/G')$
, is equal to
$a_d - a_d'$
.
Proof. By the one-to-one correspondence between
$\mathrm{nl}(G)$
and
$\mathrm{Irr}(Z(G) | G')$
, we get that
$\ker (\chi _\mu ) = \ker (\mu )$
and
$\mathbb {Q}(\chi _\mu ) = \mathbb {Q}(\mu )$
. Observe that
$\mathrm{Irr}(Z(G))=\mathrm{Irr}(Z(G)|G{}') \sqcup \mathrm{Irr}(Z(G)/G{}')$
. Hence, if
$d \mid \exp (Z(G))$
but
$d\nmid \exp (Z(G)/G')$
, then by Lemma 31, the number of non-Galois conjugate characters
$\mu \in \mathrm{Irr}(Z(G)|G{}')$
such that
$\mathbb {Q}(\mu ) = \mathbb {Q}(\zeta _d)$
is equal to
$a_d$
. This proves Lemma 32(1).
Similarly, if
$d \mid \exp (Z(G))$
and
$d \mid \exp (Z(G)/G')$
, then the number of non-Galois conjugate characters
$\mu \in \mathrm{Irr}(Z(G)|G{}')$
such that
$\mathbb {Q}(\mu ) = \mathbb {Q}(\zeta _d)$
is the difference between the number of non-Galois conjugate characters in
$\mathrm{Irr}(Z(G))$
whose character field is
$\mathbb {Q}(\zeta _d)$
and the number of non-Galois characters in
$\mathrm{Irr}(Z(G)/G')$
whose character field is
$\mathbb {Q}(\zeta _d)$
. Hence, by using Lemma 31, we get Lemma 32(2).
Now, we prove Theorem 1, which provides the Wedderburn decomposition of a VZ p-group, where p is an odd prime.
Proof of Theorem 1
Let G be a finite VZ p-group (odd prime p) and
$\chi \in \mathrm{Irr}(G)$
. Suppose
$\rho $
is an irreducible
$\mathbb {Q}$
-representation of G that affords the character
$\Omega (\chi )$
. Let
$A_{\mathbb {Q}}(\chi )$
be the simple component of the Wedderburn decomposition of
$\mathbb {Q}G$
corresponding to
$\rho $
, that is isomorphic to
$M_n(D)$
for some
$n\in \mathbb {N}$
and a division ring D. From Lemma 14,
$m_{\mathbb {Q}}(\chi ) = 1$
and from Lemma 8, we have
$[D: Z(D)] = m_{\mathbb {Q}}(\chi )^2$
and
$Z(D) = \mathbb {Q}(\chi )$
. Therefore,
$D = Z(D) = \mathbb {Q}(\chi )$
. Now consider
$\rho = {\rho _1} \oplus {\rho _2} \oplus \cdots \oplus {\rho _k}$
, where for
$1\leq i \leq k$
,
$\rho _i$
is a complex irreducible representation of G affording
$\chi ^{\sigma _i}$
for some
$\sigma _i \in \mathrm{Gal}(\mathbb {Q}(\chi ):\mathbb {Q})$
. Here,
$k=[\mathbb {Q}(\chi ): \mathbb {Q}]$
. Since
$m_{\mathbb {Q}}(\chi ) = 1$
, we observe that
$n = \chi (1)$
.
Let
$\chi \in \mathrm{lin}(G)$
and suppose
$\rho $
is the irreducible
$\mathbb {Q}$
-representation of G affording
$\Omega (\chi )$
. Let
$\bar {\chi } \in \mathrm{Irr}(G/G')$
be such that
$\bar {\chi }(gG') = \chi (g)$
. Hence,
$A_{\mathbb {Q}}(\bar {\chi }) \cong \mathbb {Q}(\bar {\chi })$
. Since
$G/G'$
is abelian, according to Lemma 6, the simple components of the Wedderburn decomposition of
$\mathbb {Q}G$
corresponding to all irreducible
$\mathbb {Q}$
-representations of G whose kernels contain
$G'$
contribute
$$ \begin{align*}\bigoplus_{d_1|m_1}a_{d_1}\mathbb{Q}(\zeta_{d_1})\end{align*} $$
in
$\mathbb {Q}G$
, where
$m_1$
is the exponent of
$G/G'$
and
$a_{d_1}$
is the number of cyclic subgroups of
$G/G'$
of order
$d_1$
.
Now, let
$\rho $
be an irreducible
$\mathbb {Q}$
-representation of G that affords the character
$\Omega (\chi _{\mu })$
, where
$\chi _{\mu }\in \mathrm{nl}(G)$
as defined in (1). Here,
$\chi _\mu (1) = |G/Z(G)|^{{1}/{2}}$
and
$\mathbb {Q}(\chi _\mu ) = \mathbb {Q}(\mu )$
. Therefore, by the above discussion,
$A_{\mathbb {Q}}(\chi _\mu ) \cong M_{|G/Z(G)|^{{1}/{2}}}(\mathbb {Q}(\mu ))$
. Observe that
$\mathbb {Q}(\chi _\mu ) = \mathbb {Q}(\mu ) = \mathbb {Q}(\zeta _{d})$
for some
$d \mid \exp (Z(G))$
. Now, we have two cases.
Case 1 (
$d \mid \exp (Z(G))$
but
$d \nmid \exp (Z(G)/G')$
). In this case, from Lemma 32(1), the number of irreducible
$\mathbb {Q}$
representations of G that afford the character
$\Omega (\chi _{\mu })$
is equal to the number of cyclic subgroups of
$Z(G)$
of order d, where
$\mathbb {Q}(\chi _{\mu })=\mathbb {Q}(\mu )=\mathbb {Q}(\zeta _d)$
.
Case 2 (
$d \mid \exp (Z(G))$
and
$d \mid \exp (Z(G)/G')$
). In this case, from Lemma 32(2), the number of irreducible
$\mathbb {Q}$
representations of G that afford the character
$\Omega (\chi _{\mu })$
is equal to the difference of the number of cyclic subgroups of
$Z(G)$
of order d and the number of cyclic subgroups of
$Z(G)/G{}'$
of order d, where
$\mathbb {Q}(\chi _{\mu })=\mathbb {Q}(\mu )=\mathbb {Q}(\zeta _d)$
.
Let
$m_2$
and
$m_3$
be the exponents of
$Z(G)$
and
$Z(G)/G'$
, respectively. Then by the above discussion, the simple components of the Wedderburn decomposition of
$\mathbb {Q}G$
corresponding to all irreducible
$\mathbb {Q}$
-representations of G whose kernels do not contain
$G'$
contribute
$$ \begin{align*}\bigoplus_{d_2|m_2, d_2 \nmid m_3} a_{d_2}M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2}))\bigoplus_{d_2|m_2, d_2|m_3}(a_{d_2}-a_{d_2}')M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2}))\end{align*} $$
in
$\mathbb {Q}G$
, where
$a_{d_2}$
and
$a_{d_2}'$
are the number of cyclic subgroups of
$Z(G)$
of order
$d_2$
and the number of cyclic subgroups of
$Z(G)/G'$
of order
$d_2$
, respectively. Therefore, the result follows.
Corollary 33. Let G be a finite VZ p-group (odd prime p) with cyclic centre
$Z(G)$
. Then the Wedderburn decomposition of the group algebra
$\mathbb {Q}G$
is given by
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q}(G/G') \bigoplus M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{|Z(G)|})). \end{align*} $$
Proof. Let G be a VZ p-group (odd prime p). It is known that
$G' \subseteq Z(G)$
and
$G'$
is an elementary abelian p-group. Since
$Z(G)$
is cyclic,
$|G'|=p$
. Let
$\mu \in \mathrm{Irr}(Z(G) | G')$
. It follows that
$\mu $
is faithful and
$\mathbb {Q}(\mu ) = \mathbb {Q}(\zeta _{|Z(G)|})$
. Therefore, all nonlinear complex irreducible characters G are faithful and Galois conjugate to each other. This completes the proof.
Corollary 34. Let G be an extra special p-group (odd prime p) of order
$p^{1+2n}$
. Then,
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q} \bigoplus (p^{2n-1}+p^{2n-2}+\cdots+p+1) \mathbb{Q}(\zeta_p) \bigoplus M_{p^n}(\mathbb{Q}(\zeta_p)).\end{align*} $$
Proof. One can easily observe that G is a VZ p-group and
$|G/Z(G)|^{{1}/{2}} = p^n=\chi (1)$
, where
$\chi \in \mathrm{nl}(G)$
. Therefore, the result follows from Lemma 6 and Corollary 33.
Remark 35
-
(1) Corollary 34 shows that the rational group algebras of two nonisomorphic groups may be isomorphic.
-
(2) Suppose G is a nonabelian p-group of order
$p^3$
(odd prime p). Then by Corollary 34, This is also computed in [Reference Bakshi and Maheshwary4, Theorems 3 and 4]. The authors computed Wedderburn components of
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q} \bigoplus (p+1) \mathbb{Q}(\zeta_p) \bigoplus M_{p}(\mathbb{Q}(\zeta_p)). \end{align*} $$
$\mathbb {Q}G$
by using the Shoda pair concept.
Corollary 36. Let G and H be two isoclinic VZ p-groups (odd prime p) of the same order. Then the Wedderburn decompositions of
$\mathbb {Q}G$
and
$\mathbb {Q}H$
are isomorphic if and only if
$G/G' \cong H/H'$
and
$Z(G) \cong Z(H)$
.
Proof. The result follows from Theorem 1.
Now, we discuss the rational group algebra of a VZ
$2$
-group.
Lemma 37. Let G be a VZ
$2$
-group. Suppose
$\chi \in \mathrm{nl}(G)$
is such that
$m_{\mathbb {Q}}(\chi ) = 2$
. Then,
$\mathbb {Q}(\chi ) = \mathbb {Q}$
.
Now we prove Theorem 2, which provides a combinatorial description for the Wedderburn decomposition of the rational group algebra of a VZ
$2$
-group.
Proof of Theorem 2
Let
$\chi _{\mu } \in \mathrm{nl}(G)$
as defined in (1). We have two cases for nonlinear irreducible complex characters of G.
Case 1 (
$m_{\mathbb {Q}}(\chi _{\mu })=2, \chi _{\mu }\in \mathrm{nl}(G)$
). By Lemma 37, there are k rational irreducible representations of G, which correspond to k simple components of
$\mathbb {Q}G$
, denoted as
$A_{\mathbb {Q}}(\chi _{\mu })$
. We know that
$A_{\mathbb {Q}}(\chi _{\mu }) \cong M_n(D)$
for some
$n\in \mathbb {N}$
and a division ring D. By [Reference Yamada31, Theorem 2.4], we have
$n = \tfrac 12|G/Z(G)|^{1/2}$
. Now by using Lemmas 8 and 37, we get
$Z(D) = \mathbb {Q}(\chi ) = \mathbb {Q}$
and
$[D : \mathbb {Q}] = 4$
.
Claim.
$A_{\mathbb {Q}}(\chi _{\mu })=M_{1/2|G/Z(G)|^{1/2}}(\mathbb {H}(\mathbb {Q}))$
.
To prove our claim, let
$(H, \psi )$
be a required pair to compute an irreducible rational matrix representation of G that affords the character
$\chi _{\mu }$
. Then,
$H/\!\ker (\psi ) \cong Q_8$
(by Algorithm 20 and Proposition 22). Therefore,
$\bar {\psi } \in \mathrm{FIrr}(H/\!\ker (\psi ))$
and
$\bar {\psi } = \bar {(\lambda )}^{H/\!\ker (\psi )}$
, where
$\bar {(\lambda )} \in \mathrm{FIrr}(N/\!\ker (\psi ))$
and
$N/\!\ker (\psi ) \cong C_4$
. Hence, by Proposition 21,
$N \trianglelefteq G$
with
$\lambda \in \mathrm{lin}(N)$
such that
$\lambda ^G=\chi _{\mu }$
. Now, assume that
$K = \ker (\psi )$
and observe that
$N_G(K)=H$
. Further,
$N/K$
is cyclic and a maximal abelian subgroup of
$H/K$
. Hence,
$(N, K)$
is an extremely strong Shoda pair (see [Reference Bakshi and Maheshwary4]). Furthermore, from [Reference Jespers and del Río15, Theorem 3.5.5],
$$ \begin{align*} A_{\mathbb{Q}}(\chi_{\mu}) = A_{\mathbb{Q}}(G, N, K) \cong M_{{1}/{2}|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_4) * H/N) \cong M_{{1}/{2}|G/Z(G)|^{{1}/{2}}}(\mathbb{H}(\mathbb{Q})). \end{align*} $$
This completes the proof of the above claim and Case 1.
Case 2 (
$m_{\mathbb {Q}}(\chi _{\mu })=1, \chi _{\mu }\in \mathrm{nl}(G)$
). Here,
$A_{\mathbb {Q}}(\chi _{\mu })\cong M_n(D)$
for some
$n\in \mathbb {N}$
and a division ring D. By [Reference Yamada31, Theorem 2.4], we have
$n =|G/Z(G)|^{{1}/{2}}$
. Now again, by using Lemma 8, we get
$D = \mathbb {Q}(\chi _{\mu })$
. Now we have two sub-cases:
Sub-case 2(1)(
${\mathbb {Q}}(\chi _{\mu })={\mathbb {Q}}$
). From Case 1 and Lemma 37, there are
${a_2-a_2{}^{\prime }-k}$
Galois conjugacy classes of complex irreducible characters
$\chi _{\mu }$
such that
$m_{\mathbb {Q}}(\chi _\mu )=1$
and
${\mathbb {Q}}(\chi _{\mu })={\mathbb {Q}}$
. Therefore,
$QG$
contains
$(a_2-a_2^{\prime }-k)M_{|G/Z(G)|^{{1}/{2}}}({\mathbb {Q}})$
.
Sub-case 2(2)(
$\mathbb {Q}(\chi _{\mu })\neq \mathbb {Q}$
). In this sub-case,
$\mathbb {Q}(\chi _{\mu })=\mathbb {Q}(\mu )=\mathbb {Q}(\zeta _d)$
, where
$d\geq 4$
. Observe that either
$d \mid \exp (Z(G))$
but
$d\nmid \exp (Z(G)/G{}')$
, or
$d \mid \exp (Z(G))$
and
$d\mid \exp (Z(G)/G{}')$
. Now by using a similar argument to that mentioned in the proof of Theorem 1,
$\mathbb {Q}G$
contains
$$ \begin{align*}\bigoplus_{d_2\mid m_2, d_2 \nmid m_3} a_{d_2}M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2})) \bigoplus_{d_2\mid m_2, d_2 \mid m_3}(a_{d_2}-a_{d_2}')M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{d_2})).\end{align*} $$
This completes the discussion of Case 2.
Now by using Lemma 6, Case 1 and Case 2, we get the result.
Corollary 38. Let G be a VZ
$2$
-group G such that
$Z(G)$
is cyclic and
$|Z(G)| \geq 4$
. Then the following hold:
-
(1)
$m_{\mathbb {Q}}(\chi ) = 1$
for each
$\chi \in \mathrm{Irr}(G)$
; -
(2)
$\mathbb {Q}G \cong \mathbb {Q}(G/G') \bigoplus M_{|G/Z(G)|^{{1}/{2}}}(\mathbb {Q}(\zeta _{|Z(G)|})).$
Corollary 39. Suppose G is a VZ
$2$
-group with elementary abelian centre. Then,
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q}(G/G') \bigoplus kM_{{1}/{2}|G/Z(G)|^{{1}/{2}}}(\mathbb{H}(\mathbb{Q})) \bigoplus k' M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}),\end{align*} $$
where k and
$k'$
denote the number of nonlinear complex irreducible characters of G with Schur index
$2$
and the number of nonlinear complex irreducible characters of G with Schur index of
$1$
, respectively.
The counting of rational irreducible representations of an abelian group can be determined using Lemma 6 and Remark 7. Corollary 40 provides a characterization for counting irreducible rational representations of VZ-groups.
Corollary 40. For a VZ-group G, let n, x, y and z represent the total numbers of irreducible rational representations of G,
$G/G'$
,
$Z(G)$
and
$Z(G)/G'$
, respectively. It follows that
$n = x + y - z$
.
Proof. Observe that
$|\{ \eta \in \mathrm{Irr}_{\mathbb {Q}}(G) : G' \subseteq \ker (\eta ) \}| = x$
. Further,
$$ \begin{align*} &|\{ \eta \in \mathrm{Irr}_{\mathbb{Q}}(G) : G' \nsubseteq \ker(\eta) \}| \\&\quad= \text{the number of Galois conjugacy classes of } \mathrm{Irr}(Z(G)) \, \, \text{over} \,\, \mathbb{Q}\\ &\qquad- \text{the number of Galois conjugacy classes of } \mathrm{Irr}(Z(G)/G') \, \, \text{over} \, \, \mathbb{Q}. \end{align*} $$
This completes the proof.
In the case of a cyclic centre, we have the following corollary.
Corollary 41. If G is a VZ p-group and
$Z(G)$
is cyclic, then G has only one rational irreducible representation whose kernel does not contain
$G'$
.
4.3. Primitive central idempotents in rational group algebras of VZ-groups
Let G be a finite group. An element e in
$\mathbb {Q}G$
is an idempotent if
$e^2=e$
. A primitive central idempotent e in
$\mathbb {Q}G$
is one that belongs to the centre of
$\mathbb {Q}G$
and cannot be expressed as
$e=e'+e"$
, where
$e'$
and
$e"$
are nonzero idempotents such that
$e'e"=0$
. It is well known that a complete set of primitive central idempotents of
$\mathbb {Q}G$
determines the decomposition of
$\mathbb {Q}G$
into a direct sum of simple sub-algebras. Specifically, if e is a primitive central idempotent of
$\mathbb {Q}G$
, then the corresponding simple component of
$\mathbb {Q}G$
is
$\mathbb {Q}Ge$
. For
$\chi \in \mathrm{Irr}(G)$
, the expression
$$ \begin{align*}e(\chi)=\frac{\chi(1)}{|G|}\sum_{g\in G}\chi(g)g^{-1}\end{align*} $$
defines a primitive central idempotent of
$\mathbb {C}G$
. In fact, the set
$\{e(\chi ) : \chi \in \mathrm{Irr}(G)\}$
forms a complete set of primitive central idempotents of
$\mathbb {C}G$
. Moreover, for
$\chi \in \mathrm{Irr}(G)$
, we define
$$ \begin{align*}e_{\mathbb{Q}}(\chi) := \sum_{\sigma \in \mathrm{Gal}(\mathbb{Q}(\chi) / \mathbb{Q})} e(\chi^{\sigma}).\end{align*} $$
Then
$e_{\mathbb {Q}}(\chi )$
is a primitive central idempotent in
$\mathbb {Q}G$
.
For a subset X of G, define
$$ \begin{align*}\widehat{X}=\frac{1}{|X|}\sum_{x\in X}x \in \mathbb{Q}G,\end{align*} $$
and for a normal subgroup N of G, define
$$ \begin{align*}\epsilon(G, N)= \begin{cases} \widehat{G} & \text{if } G= N;\\ \prod_{D/N \in M(G/N)}(\widehat{N}-\widehat{D}) & \text{otherwise}, \end{cases}\end{align*} $$
where
$M(G/N)$
represents the set of minimal nontrivial normal subgroups
$D/N$
of
$G/N$
, with D being a subgroup of G that contains N. In this subsection, we compute a complete set of primitive central idempotents of the rational group algebra of a VZ-group. Let us start with a general result.
Lemma 42 [Reference Jespers and del Río15, Lemma 3.3.2]
Let G be a finite group. If
$\chi \in \mathrm{lin}(G)$
and
$N=\ker (\chi )$
, then the following hold:
-
(1)
$e_{\mathbb {Q}}(\chi )= \epsilon (G, N)$
; -
(2)
$\mathbb {Q}G\epsilon (G, N) \cong \mathbb {Q}(\zeta _{|G/N|})$
.
Theorem 43 provides a characterization of primitive central idempotents and their corresponding simple components in
$\mathbb {Q}G$
for a VZ p-group.
Theorem 43. Let G be a VZ-group and let
$\chi _\mu \in \mathrm{nl}(G)$
(as defined in (1)) with
$N=\ker (\chi _\mu )=\ker (\mu )$
. Then the following statements hold:
-
(1)
$e_{\mathbb {Q}}(\chi _\mu )= \epsilon (Z(G), N)$
; -
(2) if G is a VZ p-group (odd prime p), then
$\mathbb {Q}G\epsilon (G, N) \cong M_{|G/Z(G)|^{{1}/{2}}}(\mathbb {Q}(\zeta _{|Z(G)/N|}))$
; -
(3) if G is a VZ
$2$
-group, then
$\mathbb {Q}G\epsilon (G, N) \cong M_{|G/Z(G)|^{{1}/{2}}}(\mathbb {Q}(\zeta _{|Z(G)/N|}))$
when
$m_{\mathbb {Q}}(\chi _{\mu })=1$
, and
$\mathbb {Q}G\epsilon (G, N) \cong M_{{1/2}|G/Z(G)|^{{1}/{2}}}(\mathbb {H}(\mathbb {Q}))$
when
$m_{\mathbb {Q}}(\chi _{\mu })=2$
.
Proof. From (1), it is easy to observe that
$e(\chi _\mu )=e(\mu )$
.
Furthermore, we can observe:
$$ \begin{align*} e_{\mathbb{Q}}(\chi_\mu) &= \sum_{\sigma \in \mathrm{Gal}(\mathbb{Q}(\chi_\mu) / \mathbb{Q})} e(\chi_\mu^{\sigma})\\ &= \sum_{\sigma \in \mathrm{Gal}(\mathbb{Q}(\mu) / \mathbb{Q})} e(\chi_{\mu^{\sigma}})\\ &= \sum_{\sigma \in \mathrm{Gal}(\mathbb{Q}(\mu) / \mathbb{Q})} e({\mu^{\sigma}})\\ &= e_{\mathbb{Q}}(\mu)\\ &= \epsilon(Z(G), N) \quad (\text{from Lemma 42}), \end{align*} $$
where
$N=\ker (\mu )$
. Moreover, if G is a VZ p-group (odd prime p), from Theorem 1, the simple component of
$\mathbb {Q}G$
corresponding to
$\chi _\mu \in \mathrm{nl}(G)$
is given by
$$ \begin{align*}A_{\mathbb{Q}}(\chi_\mu)\cong M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\mu))=M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{|Z(G)/N|})).\end{align*} $$
Hence,
$$ \begin{align*}\mathbb{Q}G e_{\mathbb{Q}}(\chi_\mu) = \mathbb{Q}G\epsilon(G, N) \cong M_{|G/Z(G)|^{{1}/{2}}}(\mathbb{Q}(\zeta_{|Z(G)/N|})).\end{align*} $$
Similarly, statement (3) follows from Theorem 2.
Remark 44. In [Reference Bakshi and Passi5, Corollary 2], primitive central idempotents of the rational group algebra of VZ-groups have been computed. However, our approach, which is based on character properties, offers a direct proof.
5. p-group of order
$p^3$
Let G be a nonabelian p-group (odd prime p) of order
$p^3$
. It is well known that G is isomorphic to one of the following two groups:
$$ \begin{align*} \Phi_2(21) &= \langle \alpha, \alpha_1, \alpha_2 : [\alpha_1, \alpha]=\alpha^p=\alpha_2, \alpha_1^p=\alpha_2^p=1 \rangle, \quad\text{and}\\ \Phi_2(111) &= \langle \alpha, \alpha_1, \alpha_2 : [\alpha_1, \alpha]=\alpha_2, \alpha^p=\alpha_1^p=\alpha_2^p=1 \rangle, \end{align*} $$
(see [Reference James13, Section 4.3]). It is easy to check that both the groups are VZ p-groups. In both cases, we have
$Z(G) = G' = \langle \alpha _2 \rangle \cong C_p$
,
$cd(G)=\{1,p\}$
,
$|\mathrm{nl}(G)|=|Z(G)|-1$
and
$G/G' = \langle \alpha G', \alpha _1 G' \rangle \cong C_p \times C_p$
. Since G is a VZ p-group, the nonlinear characters of G can be defined as follows:
$$ \begin{align} \chi_\mu(g) = \begin{cases} p\mu(g) &\text{if } g \in Z(G),\\ 0 &\text{otherwise}, \end{cases} \end{align} $$
where
$\mu \in \mathrm{Irr}(Z(G) | G')$
. The rational representations of G are characterized in Proposition 45.
Proposition 45. Let G be a nonabelian group of order
$p^3$
(odd prime p). Then the following statements hold.
-
(1)
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p+1$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|=1$
. -
(2) A special required pair
$(H, \psi _\mu )$
to determine a rational matrix representation of G whose character is
$\Omega (\chi _\mu )$
(
$\chi _{\mu }$
is defined in (2)) is given by
$H = \langle \alpha _1, \alpha _2 \rangle $
, and
$\psi _\mu \in \mathrm{lin}(H)$
defined by
$\psi _\mu (\alpha _1) = 1$
and
$\psi _\mu (\alpha _2) = \mu (\alpha _2)$
.
Proof. The proof of Proposition 45(1) is obvious. As
$Z(G) \subset H$
and
$\psi _\mu \downarrow _{Z(G)} = \mu $
, we get
$\psi _\mu ^G = \chi _\mu $
(from Proposition 21). Furthermore, since
$\psi _\mu (\alpha _1) = 1$
and
$\psi _\mu (\alpha _2) = \mu (\alpha _2)$
, it follows that
$\mathbb {Q}(\psi _\mu ) = \mathbb {Q}(\mu ) = \mathbb {Q}(\chi _\mu )$
. This completes the Proof of Proposition 45(2).
Remark 46. In general, a required pair to find an irreducible rational matrix representation of G whose character is
$\Omega (\chi )$
may not be unique. For example, consider
$G = \Phi _2(111)$
and
$\chi _\mu \in \mathrm{nl}(G)$
, as defined in (2). Take
$H_{1} = \langle \alpha , \alpha _2 \rangle $
and choose
$\psi ^{\prime }_\mu \in \mathrm{lin}(H_{1})$
such that
$\psi ^{\prime }_\mu (\alpha ) = 1$
and
$\psi ^{\prime }_\mu (\alpha _2) = \mu (\alpha _2)$
. The pair
$(H_{1}, \psi ^{\prime }_\mu )$
is also a special required pair to find an irreducible rational matrix representation of G that affords the character
$\Omega (\chi _\mu )$
.
In Example 47, we show how to find an irreducible rational matrix representation associated with a required pair.
Example 47. Consider
$$ \begin{align*} G= \Phi_2(21) = \langle \alpha, \alpha_1, \alpha_2 : [\alpha_1, \alpha]=\alpha^p=\alpha_2, \alpha_1^p=\alpha_2^p=1 \rangle. \end{align*} $$
We have
$Z(G) = G' = \langle \alpha _2 \rangle \cong C_p$
. Let
$\mu \in \mathrm{Irr}(Z(G) | G')$
be such that
$\mu (\alpha _2) = \zeta _p$
. The character
$\chi _\mu $
defined in (2) is a nonlinear irreducible complex character of G. From Proposition 45, a special required pair to find an irreducible rational matrix representation of G affording the character
$\Omega (\chi _\mu )$
is
$(H, \psi _\mu )$
, where
$H = \langle \alpha _1, \alpha _2 \rangle $
and
$\psi _\mu \in \mathrm{lin}(H)$
is such that
$\psi _\mu (\alpha _1) = 1$
and
$\psi _\mu (\alpha _2) = \mu (\alpha _2)=\zeta _p$
. Now, let
$\Psi _\mu $
denote an irreducible rational matrix representation of degree
$p-1$
of H that affords the character
$\Omega (\psi _\mu )$
. The explicit form of
$\Psi _\mu $
is given by
$$ \begin{align*}\Psi_\mu(\alpha_1)= \left(\begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & \cdots & 1 & 0\\ 0 & 0 & \cdots & \cdots & 1 \end{array}\right) = I, \quad\text{and}\quad ~ \Psi_\mu(\alpha_2)=\left(\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & \cdots & 0 & 1\\ -1 & -1 & \cdots & \cdots & -1 \end{array}\right)\end{align*} $$
(see Lemma 11). Set
$\Psi _\mu (\alpha _2) = P$
, where P denotes a matrix of order
$(p-1)$
, and let O denote the zero matrix of the same order. Then an irreducible rational matrix representation
$\Psi ^G$
of degree
$p^2-p$
of G affording the character
$\Omega (\chi _\mu )$
is given by
$$ \begin{align*}\Psi_\mu^G(\alpha)=\left(\begin{array}{ccccc} O & O & O & \cdots & P\\ I & O & O & \cdots & O\\ O & I & O & \cdots & O\\ \vdots & \vdots & \vdots & \ddots \\ O & O & \cdots & I & 0 \end{array}\right), \quad\text{and}\quad ~ \Psi_\mu^G(\alpha_1)=\left(\begin{array}{ccccc} I & O & O & \cdots & O\\ O & P & O & \cdots & O\\ O & O & P^2 & \cdots & O\\ \vdots & \vdots & \vdots & \ddots \\ O & O & \cdots & \cdots & P^{p-1} \end{array}\right).\end{align*} $$
Here,
$\Psi ^G$
is a rational matrix representation of G whose kernel does not contain
$G{}'$
. Now, use Lemma 11 to compute all irreducible rational matrix representations of G whose kernel contains
$G{}'$
. This gives the complete description of all irreducible rational matrix representations of G.
Remark 48. If G is a nonabelian group of order
$8$
, then either
$G\cong Q_8$
or
$G\cong D_8$
. A special required pair to obtain an irreducible rational matrix representation of G whose kernel does not contain
$G{}'$
is determined in Section 4.1.
6. p-Group of order
$p^4$
In this section, we provide a comprehensive description of all inequivalent irreducible rational matrix representations and the Wedderburn decompositions of the rational group rings for all nonabelian groups of order
$p^4$
. It is easy to observe that if G is a nonabelian group of order
$p^4$
, then
$|Z(G)|=p~\text {or}~p^2$
, and
$\text {cd}(G)=\{1, p\}$
. Moreover, if
$|Z(G)|=p$
, then
$G/Z(G)$
is nonabelian. As we know, a group G is VZ-group if and only if
$\text {cd}(G) = \{1, |G/Z(G)|^{{1}/{2}}\}$
. Hence, a p-group of order
$p^4$
of nilpotency class
$2$
is a VZ p-group. In the subsequent subsections, we separately discuss the cases of groups of order
$p^4$
of nilpotency class
$2$
and nilpotency class
$3$
.
6.1. p-Groups of order
$p^4$
of nilpotency class
$2$
Let G be a p-group of order
$p^4$
of nilpotency class
$2$
. Then
$|G'| = p$
,
$|Z(G)|=p^2$
and
$\text {cd}(G)=\{1,p\}$
. Furthermore,
$|\mathrm{lin}(G)|=p^3$
and
$|\mathrm{nl}(G)|=p^2-p$
. Note that G is a VZ p-group. Then by (1), a nonlinear irreducible complex character is of the form
$\chi _{\mu }$
and is given by
$$ \begin{align} \chi_\mu(g) = \begin{cases} p\mu(g) & \text{if } g \in Z(G),\\ 0 & \text{otherwise }, \end{cases} \end{align} $$
where
$\mu \in \mathrm{Irr}(Z(G) | G')$
.
For an odd prime p, we rely on James’ classification of p-groups of order
$p^4$
(see [Reference James13]). There exist two distinct isoclinic families of nonabelian groups of order
$p^4$
, denoted as
$\Phi _2$
and
$\Phi _3$
(see [Reference James13, Section 4.4]). Prajapati et al. [Reference Prajapati, Darafsheh and Ghorbani25, Proposition 4.2] have proved that all the groups belonging to isoclinic family
$\Phi _2$
are VZ-groups. Note that all the groups belonging to isoclinic family
$\Phi _3$
are non-VZ-groups. Theorem 49 provides a description of all inequivalent irreducible rational matrix representations for all VZ p-groups of order
$p^4$
, where p is an odd prime.
Theorem 49. Let G be a nonabelian p-group (odd prime p) of order
$p^4$
in the isoclinic family
$\Phi _2$
. Then Table 1 determines all inequivalent irreducible rational matrix representations of G whose kernels do not contain
$G'$
.
Table 1 Special required pair
$(H, \psi _\mu )$
to obtain an irreducible rational matrix representation of
$G \in \Phi _{2}$
that affords the character
$\Omega (\chi _{\mu })$
, where
$\chi _{\mu }\in \mathrm{nl}(G)$
(defined in (3)).
Proof. Let
$G \in \Phi _2$
and let
$\chi _\mu \in \mathrm{nl}(G)$
(as defined in (3)). Suppose
$(H, \psi _\mu )$
is a special required pair to obtain an irreducible rational matrix representation of G which affords the character
$\Omega (\chi _\mu )$
. By Proposition 21, it follows that
$Z(G) \subset H$
and
$\psi _\mu \downarrow _{Z(G)} = \mu $
. Further, from Corollary 27, H is abelian. Since
$(H, \psi _\mu )$
is a special required pair,
$\mathbb {Q}(\psi _\mu ) = \mathbb {Q}(\chi _\mu )$
and hence by Lemma 24, we must choose
$\psi _\mu \in \mathrm{lin}(H)$
such that
$|\!\ker (\psi _\mu )| = |G/Z(G)|^{{1}/{2}} |\!\ker (\mu )| = p|\!\ker (\mu )|$
. Consider
$G=\Phi _2(22)$
. Now, for each
$0\leq i\leq (p-1)$
, take
$H=\langle \alpha ^{-i}\alpha _1, \alpha ^p \rangle $
and define
$\mu \in \mathrm{Irr}(Z(G)|G{}')$
as follows:
$$ \begin{align*}\mu(z) = \begin{cases} \zeta_p &\text{if } z=\alpha^p,\\ \zeta_p^i &\text{if } z=\alpha_1^p,\\ \end{cases}\end{align*} $$
where
$z\in Z(G)$
. Observe that
$(\alpha ^{-i}\alpha _1)^p = \alpha ^{-ip}\alpha _1^p$
. Then,
$\psi _\mu \in \mathrm{lin}(H)$
(given in Table 1) satisfies
$\psi _\mu (\alpha _1^p)= ( \psi _\mu (\alpha ^{-i}\alpha _1) )^p(\psi _\mu (\alpha ^p))^i = (\psi _\mu (\alpha ^{p}))^{i}=\mu (\alpha _1^p)$
. It is easy to check that a pair
$(H, \psi _{\mu })$
satisfies the criteria of a special required pair.
It is routine to check that all the pairs
$(H, \psi _{\mu })$
for the rest of the groups mentioned in Table 1 also satisfy the criteria to being special required pairs. This shows that Table 1 presents all of the special required pairs
$(H, \psi _\mu )$
to find all inequivalent irreducible rational matrix representations of G whose kernels do not contain
$G{}'$
, where
$G\in \Phi _2$
. This completes the proof of Theorem 49.
Proposition 50 provides the counting of rational irreducible representations of different degrees for all groups of order
$p^4$
in
$\Phi _2$
.
Proposition 50. Let G be a nonabelian group of order
$p^4$
(odd prime p) in
$\Phi _2$
.
-
(1) If
$G=\Phi _2(211)a$
or
$G=\Phi _2(1^4)$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p^2+p+1$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|=p$
. -
(2) If
$G=\Phi _2(31)$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p+1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|=p$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^3))}(G)|=1$
. -
(3) If
$G=\Phi _2(22)$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p+1$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|=2p$
. -
(4) If
$G=\Phi _2(211)b$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p^2+p+1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^3))} (G)|=1$
. -
(5) If
$G=\Phi _2(211)c$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p+1$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|= p+1$
.
Proof. Suppose
$\chi \in \mathrm{Irr}(G)$
and
$E(\chi )$
denotes the Galois conjugacy class of
$\chi $
over
$\mathbb {Q}$
. Then the degree of the rational representation affording the character
$\Omega (\chi )$
is
$|E(\chi )|\chi (1)$
.
-
(1) For
$G=\Phi _2(211)a$
, we have
$Z(G)=\langle \alpha ^p, \alpha _3 \rangle \cong C_p \times C_p$
,
$G'=\langle \alpha ^p \rangle \cong C_p$
and
$G/G'=\langle \alpha G', \alpha _1 G', \alpha _2 G' \rangle \cong C_p \times C_p \times C_p$
. Observe that in
$\mathrm{Irr}^{(1)}(G)$
, there is a single Galois conjugacy class over
$\mathbb {Q}$
with size
$1$
and
$({p^3-1})/{\phi (p)} = p^2+p+1$
distinct Galois conjugacy classes over
$\mathbb {Q}$
with size
$\phi (p)$
. If
$\mu \in \mathrm{Irr}(Z(G) | G')$
, then
$[\mathbb {Q}(\mu ) : \mathbb {Q}]=\phi (p)$
. Hence, there are
$({p^2-p})/{\phi (p)}=p$
distinct Galois conjugacy classes over
$\mathbb {Q}$
with size
$\phi (p)$
in
$\mathrm{Irr}^{(p)}(G)$
. Similar statements hold for
$G=\Phi _2(1^4)$
. This proves part (1). -
(2) For
$G=\Phi _2(31)$
, we have
$Z(G)=\langle \alpha ^p \rangle \cong C_{p^2}$
,
$G'=\langle \alpha ^{p^2} \rangle \cong C_p$
and
$G/G'=\langle \alpha G', \alpha _1 G' \rangle \cong C_{p^2} \times C_p$
. In
$\mathrm{Irr}^{(1)}(G)$
, there is one Galois conjugacy class over
$\mathbb {Q}$
with size
$1$
,
$({1\times \phi (p)+\phi (p)\times 1+\phi (p)\times \phi (p)})/{\phi (p)} = p+1$
distinct Galois conjugacy classes over
$\mathbb {Q}$
with size
$\phi (p)$
, and
$({\phi (p^2)\times p})/{\phi (p^2)}=p$
distinct Galois conjugacy classes over
$\mathbb {Q}$
with size
$\phi (p^2)$
. If
$\mu \in \mathrm{Irr}(Z(G) | G')$
, then
$[\mathbb {Q}(\mu ) : \mathbb {Q}]=\phi (p^2)$
. Consequently, there is only one (
$({p^2-p})/{\phi (p^2)}=1$
) Galois conjugacy class over
$\mathbb {Q}$
with size
$\phi (p^2)$
in
$\mathrm{Irr}^{(p)}(G)$
. This completes the proof of part (2).Table 2 Special required pair
$(H, \psi _\mu )$
to obtain an irreducible rational matrix representation of a VZ
$2$
-group G of order
$16$
that affords the character
$\Omega (\chi _{\mu })$
, where
$\chi _{\mu }\in \mathrm{nl}(G)$
(defined in (3)).
By using similar arguments, we get the proofs of the remaining parts of Proposition 50.
Remark 51. Let G and H be isoclinic groups with the same order. According to Lemma 10, we have
$|\mathrm{Irr}^{(k)}(G)| = |\mathrm{Irr}^{(k)}(H)|$
. However, it is important to note that
$|\mathrm{Irr}_{\mathbb {Q}}^{(k)}(G)|$
may not be equal to
$|\mathrm{Irr}_{\mathbb {Q}}^{(k)}(H)|$
(see Proposition 50).
Now, let G be a nonabelian 2-group of order
$16$
of nilpotency class
$2$
. Then
$|\mathrm{nl}(G)|=~2$
. We take presentations of
$2$
-groups from Burnside’s book [Reference Burnside6]. Theorem 52 provides a description of all inequivalent irreducible rational matrix representations of G whose kernels do not contain
$G'$
.
Theorem 52. Let G be a nonabelian
$2$
-group of order
$16$
of nilpotency class
$2$
. Then Table 2 determines all inequivalent irreducible rational matrix representations of G whose kernels do not contain
$G'$
.
Proof. Let G be a nonabelian group of order
$16$
of nilpotency class
$2$
. Observe that G is a VZ
$2$
-group. Let
$\chi _\mu \in \mathrm{nl}(G)$
as defined in (3). Suppose
$(H, \psi _\mu )$
is a special required pair to obtain an irreducible rational matrix representation of G that affords the character
$\Omega (\chi _\mu )$
. By Proposition 21, it follows that
$Z(G) \subset H$
and
$\psi _\mu \downarrow _{Z(G)} = \mu $
. Further, from Corollary 27, H is abelian. In view of Remark 23, we have the following: if
$m_{\mathbb {Q}}(\chi _\mu ) =1$
, then
$\mathbb {Q}(\psi _\mu ) = \mathbb {Q}(\chi _\mu )$
and if
$m_{\mathbb {Q}}(\chi _\mu ) =2$
, then
$[\mathbb {Q}(\psi _\mu ) : \mathbb {Q}(\chi _\mu )]=2$
. Therefore, from Lemma 24, we must choose
$\psi _\mu \in \mathrm{lin}(H)$
such that
$|\!\ker (\psi _\mu )| = 2|\!\ker (\mu )|$
whenever
$m_{\mathbb {Q}}(\chi _\mu ) =1$
, and
$\psi _\mu \in \mathrm{lin}(H)$
such that
$|\!\ker (\psi _\mu )| = |\!\ker (\mu )|$
whenever
$m_{\mathbb {Q}}(\chi _\mu ) =2$
. Note that
$m_{\mathbb {Q}}(\chi _\mu )=2$
for
$\chi _\mu \in \mathrm{nl}(G_5)$
, where
$\mu \in \mathrm{Irr}(Z(G_5)|G^{\prime }_5)$
is given by
$\mu (x^2) =-1, \mu (y^2)=-1$
, and
$m_{\mathbb {Q}}(\chi _\mu )=2$
for all
$\chi _\mu \in \mathrm{nl}(G_6)$
, where
$\mu \in \mathrm{Irr}(Z(G_6)|G^{\prime }_6)$
. It is routine to check that the pairs
$(H,\psi _{\mu })$
mentioned in Table 2 are special required pairs. This shows that Table 2 presents special required pairs
$(H, \psi _\mu )$
to find irreducible rational matrix representations of G whose kernels do not contain
$G{}'$
, where
$G\in \Phi _2$
. This completes the proof of Theorem 52.
6.2. p-Groups of order
$p^4$
of nilpotency class
$3$
Let G be a p-group of order
$p^4$
of nilpotency class
$3$
. Then
$|Z(G)| = p$
,
$|G'| = p^2$
and
$Z(G) \subset G{}'$
. Further,
$|\mathrm{lin}(G)|=p^2$
,
$|\mathrm{nl}(G)|=p^2 - 1$
and
$\text {cd}(G)=\{1,p\}$
.
We begin by presenting a few results that enable us to determine all the inequivalent irreducible rational matrix representations of G.
Lemma 53. Let G be a p-group (odd prime p) and let
$1 \neq \chi \in \mathrm{Irr}(G)$
. Then,
$\mathbb {Q}(\chi ) \neq \mathbb {Q}$
.
Proof. The proof is obvious.
Lemma 54. Let G be a nonabelian group with nilpotency class
$\geq 3$
. Suppose that there exists a maximal normal subgroup H of G such that both H and
$G/H$
are abelian. Then H is unique.
Proof. Since
$G/H$
is abelian,
$G' \subseteq H$
. As H is abelian, we get
$C_G(G') \supseteq H$
, where
$C_G(G')$
denotes the centralizer subgroup of
$G'$
. Since nilpotency class of G is
$\geq 3$
,
$G' \nsubseteq Z(G)$
. This implies that
$C_G(G') \neq G$
. Thus, we conclude that
$C_G(G') = H$
, which implies the uniqueness of H.
Corollary 55. If G is a nonabelian group of order
$p^4$
of nilpotency class
$3$
, then G has a unique abelian subgroup of index p, namely
$C_G(G')$
.
Proof. Let G be a nonabelian p-group of order
$p^4$
of nilpotency class
$3$
. Then
$Z(G) \subset G'$
and there exists an abelian subgroup H of G with index p. Therefore, the proof follows from Lemma 54.
For an odd prime p, we follow James’ classification of p-groups of order
$p^4$
(see [Reference James13]). All the relevant groups in this subsection belong to
$\Phi _{3}$
(refer to [Reference James13, Section 4.4]).
Remark 56. Let G be a nonabelian p-group (
$p \geq 5$
) of order
$p^4$
in
$\Phi _3$
(see [Reference James13, Section 4.4]). Then the description of unique abelian subgroup H of G of index p is as follows.
-
• If
$G=\Phi _3(1^4)$
, then
$H=\langle \alpha _1, \alpha _2, \alpha _3 \rangle \cong C_p \times C_p \times C_p$
. -
• If
$G=\Phi _3(211)a$
, then
$H=\langle \alpha ^p, \alpha _1, \alpha _2 \rangle \cong C_p \times C_p \times C_p$
. -
• If
$G=\Phi _3(211)b_r$
(
$r=1, \nu $
), then
$H=\langle \alpha _1, \alpha _2\rangle \cong C_{p^2} \times C_p$
.
Lemma 57. Let G be a nonabelian p-group of order
$p^4$
of nilpotency class
$3$
. Let H be the unique abelian subgroup of G of index p. If
$\psi \in \mathrm{Irr}(H | G')$
, then
$\psi ^G \in \mathrm{nl}(G)$
. Further, for
$\chi \in \mathrm{nl}(G)$
, there exists some
$\psi \in \mathrm{Irr}(H | G')$
such that
$\chi = \psi ^G$
.
Proof. Consider
$\psi \in \mathrm{Irr}(H | G')$
. In contrast, suppose that
$\psi ^G \notin \mathrm{nl}(G)$
. This implies that
$\psi ^G$
is a sum of some linear characters of G. This implies that
$G' \subseteq \ker (\psi ^G)\subseteq \ker (\psi )$
, which is a contradiction.
Now, let
$\psi \in \mathrm{Irr}(H | G')$
. Then
$\psi ^G \in \mathrm{nl}(G)$
, and hence the inertia group
$I_G(\psi )$
of
$\psi $
in G is equal to H [Reference Isaacs12, Problem 6.1]. Furthermore,
${\psi ^{G}}\downarrow _{H} = \sum _{i=1}^{p} \psi _{i}$
, where the
$\psi _{i}$
terms are conjugates of
$\psi $
in G and
$p = |G/I_{G}(\psi )|$
. Hence, there are p conjugates of
$\psi $
and observe that
$\psi ^G=\psi _i^G\in \mathrm{nl}(G)$
for each i. Thus,
$|\mathrm{nl}(G)|={|\mathrm{Irr}(H|G')|}/{p} = p^2-1$
. This completes the proof of Lemma 57.
Theorem 58 provides the necessary information to determine all inequivalent irreducible rational matrix representations for all nonabelian p-groups of order
$p^4$
of nilpotency class
$3$
, where p is an odd prime.
Theorem 58. Let G be a nonabelian p-group (odd prime p) of order
$p^4$
belonging to
$\Phi _3$
. Suppose H is the unique abelian subgroup of G with index p and
$\chi \in \mathrm{nl}(G)$
is such that
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
. Then
$(H, \psi )$
is a required pair to determine an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
.
Proof. Suppose
$p\geq 5$
. If
$G = \Phi _3(1^4)$
or
$\Phi _3(211)a$
, then
$H \cong C_p \times C_p \times C_p$
(see Remark 56). Suppose
$\chi \in \mathrm{nl}(G)$
is such that
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
. Then,
$\mathbb {Q}(\psi )=\mathbb {Q}(\zeta _p)$
. Observe that
$\mathbb {Q}(\chi )=\mathbb {Q}(\psi ^G) \subseteq \mathbb {Q}(\psi )$
. From Lemma 53, we get
$\mathbb {Q}(\chi ) =\mathbb {Q}(\psi ) = \mathbb {Q}(\zeta _p)$
. Next, if
$G = \Phi _3(211)b_r$
(
$r= 1, \nu $
), then
$H = \langle \alpha _1, \alpha _2\rangle \cong C_{p^2} \times C_p $
(see Remark 56). Again, suppose that
$\chi \in \mathrm{nl}(G)$
is such that
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
. Then,
$\mathbb {Q}(\psi ) = \mathbb {Q}(\zeta _p)$
or
$\mathbb {Q}(\zeta _{p^2})$
. If
$\mathbb {Q}(\psi ) = \mathbb {Q}(\zeta _p)$
, then from Lemma 53,
$\mathbb {Q}(\psi ) = \mathbb {Q}(\chi ) = \mathbb {Q}(\zeta _p)$
. Now, suppose
$\mathbb {Q}(\psi ) = \mathbb {Q}(\zeta _{p^2})$
. This implies that
$\psi (\alpha _1) = \zeta _{p^2}$
. Assume that
$G = \bigcup \alpha ^iH (0 \leq i \leq p-1)$
. Then we have the following:
$$ \begin{align*} \psi^G(\alpha_1)&= \sum_{i=0}^{p-1}\psi^{\circ}(\alpha^{-i}\alpha_1\alpha^i), \quad \text{where } {\psi^{\circ}}(g) = \begin{cases} \psi(g) &\text{if } g\in H,\\ 0 &\text{if } g \notin H,\\ \end{cases}\\ &= \psi(\alpha_1) + \psi(\alpha_1\alpha_2)+ \psi(\alpha_1^{1+p}\alpha_2^2)+\psi(\alpha_1^{1+3p}\alpha_2^3)+ \cdots + \psi(\alpha_1^{1+{(p-1)(p-2)}/{2}p}\alpha_2^{p-1})\\ &= \psi(\alpha_1) [1 + \psi(\alpha_2)+ \psi(\alpha_1^{p}\alpha_2^2)+\psi(\alpha_1^{3p}\alpha_2^3)+ \cdots + \psi(\alpha_1^{{(p-1)(p-2)}/{2}p}\alpha_2^{p-1})]\\ &= \theta \zeta_{p^2}, \text{for some}~ 0\neq \theta \in \mathbb{Q}(\zeta_p). \end{align*} $$
Therefore,
$\mathbb {Q}(\psi ) =\mathbb {Q}(\psi ^G) = \mathbb {Q}(\zeta _{p^2})$
. Hence,
$(H,\psi )$
is a required pair. Now, let
$p=3$
. If
$$ \begin{align*} G = \Phi _3(211)b_1=\langle &\alpha , \alpha _1,\alpha _2, \alpha _3 : [\alpha _1, \alpha ]=\alpha _2, [\alpha _2, \alpha ]=\alpha _1^3\alpha _3=\alpha _3,\\ &\hspace{2pt}\alpha ^3=\alpha _2^3=\alpha _3^3=~1\rangle,\end{align*} $$
then
$H = \langle \alpha _1, \alpha _2, \alpha _3 \rangle \cong C_3 \times C_3 \times C_3 $
is the unique normal abelain subgroup of G of index
$3$
(see [Reference James13, Section 4.4]). Suppose
$\chi \in \mathrm{nl}(G)$
is such that
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
. From Lemma 53, we get
$\mathbb {Q}(\chi ) =\mathbb {Q}(\psi ) = \mathbb {Q}(\zeta _3)$
. Next, if G is one of the following groups:
$$ \begin{align*} \Phi_3(211)a= \langle \alpha, \alpha_1,\alpha_2, \alpha_3 : [\alpha_1, \alpha]=\alpha_2, [\alpha_2, \alpha]=\alpha^3=\alpha_3, \alpha_1^3\alpha_3= \alpha_2^3=\alpha_3^3=1\rangle \\ \Phi_3(1^4)= \langle \alpha, \alpha_1,\alpha_2, \alpha_3 : [\alpha_1, \alpha]=\alpha_2, [\alpha_2, \alpha]=\alpha_3, \alpha^3=\alpha_1^{3}\alpha_3= \alpha_2^3=\alpha_3^3=1\rangle \\ \Phi_3(211)b_2=\langle \alpha, \alpha_1,\alpha_2, \alpha_3 : [\alpha_1, \alpha]=\alpha_2, [\alpha_2, \alpha]^2=\alpha_1^3\alpha_3=\alpha_3^2, \alpha^3=\alpha_2^3=\alpha_3^3=1\rangle, \end{align*} $$
then
$H = \langle \alpha _1, \alpha _2\rangle \cong C_{9} \times C_3 $
is the unique normal subgroup of G of index
$3$
(see [Reference James13, Section 4.4]). Again, suppose
$\chi \in \mathrm{nl}(G)$
is such that
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
. By a similar argument as in the case of
$p \geq 5$
, we can establish that
$\mathbb {Q}(\chi ) = \mathbb {Q}(\psi )$
. Hence,
$(H,\psi )$
is a required pair. This completes the proof of Theorem 58.
In Proposition 59, the counting of rational irreducible representations of all p-groups (odd prime p) of order
$p^4$
in
$\Phi _3$
is described.
Proposition 59. Let G be a nonabelian p-group (
$p\geq 5$
) of order
$p^4$
in
$\Phi _3$
. Then we have the following.
-
(1) If
$G=\Phi _3(211)a$
or
$\Phi _3(1^4)$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|=1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|=p+1$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|=p+1$
. -
(2) If
$G{\kern-1.2pt}={\kern-1.2pt}\Phi _3(211)b_r~ (r{\kern-1.2pt}={\kern-1.2pt}1,{\kern-1.2pt} \nu )$
, then
$|\mathrm{Irr}_{\mathbb {Q}}^{(1)}(G)|{\kern-1.2pt}={\kern-1.2pt}1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p))}(G)|{\kern-1.2pt}={\kern-1.2pt}p{\kern-1.2pt}+{\kern-1.2pt}1$
,
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^2))}(G)|{\kern-1.2pt}={\kern-1.2pt}1$
and
$|\mathrm{Irr}_{\mathbb {Q}}^{(\phi (p^3))}(G)|=1$
.
Proof. Suppose
$\chi \in \mathrm{Irr}(G)$
and
$E(\chi )$
denotes the Galois conjugacy class of
$\chi $
over
$\mathbb {Q}$
. Then the degree of the rational representation affording the character
$\Omega (\chi )$
is
$|E(\chi )|\chi (1)$
.
-
(1) Let
Then
$$ \begin{align*} G=\Phi _3(211)a = \langle &\alpha , \alpha _1, \alpha _2, \alpha _3 : [\alpha _1, \alpha ]=\alpha _2, [\alpha _2, \alpha ]=\alpha ^p=\alpha _3,\\ &\hspace{1pt}\alpha _1^p=\alpha _2^p=\alpha _3^p=1 \rangle.\end{align*} $$
$Z(G)= \langle \alpha ^p \rangle \cong C_p$
,
$G'=\langle \alpha ^p, \alpha _2 \rangle \cong C_p \times C_p$
and
$G/G'= \langle \alpha G', \alpha _1 G' \rangle \cong C_p \times C_p$
. Thus, there are one Galois conjugacy class over
$\mathbb {Q}$
of size 1, and
$({p^2-1})/{\phi (p)}=p+1$
distinct Galois conjugacy classes over
$\mathbb {Q}$
of size
$\phi (p)$
in
$\mathrm{Irr}^{(1)}(G)$
. Further,
$H= \langle \alpha ^p, \alpha _1, \alpha _2 \rangle \cong C_p \times C_p \times C_p$
is the abelian subgroup of
$\Phi _3(211)a$
of index p. Suppose
$\chi \in \mathrm{Irr}^{(p)}(G)$
. Then from Theorem 58,
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
and
$\mathbb {Q}(\chi )= \mathbb {Q}(\psi )$
. Moreover, from Lemma 53,
$\mathbb {Q}(\chi )= \mathbb {Q}(\psi )=\mathbb {Q}(\zeta _p)$
. Thus, there are
$({p^2-1})/{\phi (p)}=p+1$
distinct Galois conjugacy classes over
$\mathbb {Q}$
of size
$\phi (p)$
in
$\mathrm{Irr}^{(p)}(G)$
. We get similar results for
$G=\Phi _3(1^4)$
. This completes the proof of part (1) of Proposition 59.
-
(2) Let
Then
$$ \begin{align*}G=\Phi _3(211)b_1= \langle &\alpha , \alpha _1, \alpha _2, \alpha _3 : [\alpha _1, \alpha ]=\alpha _2, [\alpha _2, \alpha ]=\alpha _1^p=\alpha _3,\\ &\hspace{1pt}\alpha ^p=\alpha _2^p=\alpha _3^p=1 \rangle.\end{align*} $$
$Z(G)=\langle \alpha _1^p \rangle = C_p$
,
$G'=\langle \alpha _1^p, \alpha _2 \rangle = C_p \times C_p$
and
$G/G'= \langle \alpha G', \alpha _1 G' \rangle \cong C_p \times C_p$
. Thus, there are one Galois conjugacy class over
$\mathbb {Q}$
of size 1, and
$({p^2-1})/{\phi (p)}=p+1$
distinct Galois conjugacy classes over
$\mathbb {Q}$
of size
$\phi (p)$
in
$\mathrm{Irr}^{(1)}(G)$
. Further,
$H= \langle \alpha _1, \alpha _2 \rangle \cong C_{p^2} \times C_p$
is the abelian subgroup of
$\Phi _3(211)b_1$
of index p. Suppose
$\chi \in \mathrm{Irr}^{(p)}(G)$
. Then from Theorem 58,
$\chi = \psi ^G$
for some
$\psi \in \mathrm{Irr}(H | G')$
and
$\mathbb {Q}(\chi )\hspace{-1pt}=\hspace{-1pt} \mathbb {Q}(\psi )$
. Observe that
$|\{\psi\hspace{-1pt} \in\hspace{-1pt} \mathrm{Irr}(H|G') : \mathbb{Q}(\psi)\hspace{-1pt}=\hspace{-1pt} \mathbb{Q}(\zeta_p)\}|\hspace{-1pt}=\hspace{-1pt} p^2-p$
and
$|\{\psi \in \mathrm{Irr}(H|G') : \mathbb{Q}(\psi)= \mathbb{Q}(\zeta_{p^2})\}|= p^3-p^2$
. Since there are p conjugates of each
$\psi \in \mathrm{Irr}(H | G')$
, the numbers of complex irreducible characters of degree
$p\, (\chi \in \mathrm{Irr}^{(p)})$
such that
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _p)$
and
$\mathbb {Q}(\chi )=\mathbb {Q}(\zeta _{p^2})$
are
$({p^2-p})/{p}=p-1$
and
$({p^3-p^2})/{p}=p^2-p$
, respectively. Thus, there are
$({p-1})/{\phi (p)}=1$
Galois conjugacy classes over
$\mathbb {Q}$
of size
$\phi (p)$
, and
$({p^2-p})/{\phi (p^2)}=1$
Galois conjugacy classes over
$\mathbb {Q}$
of size
$\phi (p^2)$
in
$\mathrm{Irr}^{(p)}(G)$
. We get similar results for
$G=\Phi _3(211)b_\nu $
. This completes the proof of part (2) of Proposition 59.
Now, we prove Theorem 3, which provides the Wedderburn decomposition of
$\mathbb {Q}G$
, where G is a p-group (odd prime p) of order
$p^4$
of nilpotency class
$3$
.
Proof of Theorem 3
Observe that
$G\in \Phi _3$
. Suppose
$\chi \in \mathrm{nl}(G)$
and H is the unique abelian subgroup of G. Then from Lemma 57, there exists
$\psi \in \mathrm{Irr}(H | G')$
such that
$\chi = \psi ^G$
, and if
$\psi \in \mathrm{Irr}(H | G')$
, then
$\psi ^G \in \mathrm{nl}(G)$
. Now by Theorem 58,
$\mathbb {Q}(\chi )=\mathbb {Q}(\psi )$
. Observe that
$\chi ^{\sigma }=(\psi ^{\sigma })^G$
, where
$\sigma \in \mathrm{Gal}(\mathbb {Q}(\chi )/\mathbb {Q})$
and there are exactly p distinct conjugates
$\psi \in \mathrm{Irr}(H|G{}')$
such that
$\chi =\psi ^G$
(see the proof of Lemma 57). Let X and Y be the representative sets of distinct Galois conjugacy classes of
$\mathrm{Irr}(G)$
and
$\mathrm{Irr}(H)$
, respectively. Let d be a divisor of
$\exp (H)$
such that
$\mathbb {Q}(\chi )=\mathbb {Q}(\psi ) = \mathbb {Q}(\zeta _d)$
. Set
$m=\exp (H)$
and
$m{}'=\exp (H/G{}')$
. Then we have two cases.
Case 1 (
$d \mid m$
but
$d \nmid m'$
). In this case,
$$ \begin{align*} |\{\chi \in X : \chi(1)=p, \mathbb{Q}(\chi)=\mathbb{Q}(\zeta_d) \}|&=\frac{1}{p}|\{\psi \in Y : \psi\in \mathrm{Irr}(H|G{}'), ~\mathbb{Q}(\psi)=\mathbb{Q}(\zeta_d) \}|\\ &= \frac{a_d}{p}, \end{align*} $$
where
$a_d$
denotes the number of cyclic subgroups of order d of H (see Lemma 31).
Case 2 (
$d \mid m$
and
$d \mid m'$
). In this case,
$$ \begin{align*} |\{\chi \in X : \chi(1)=p, \mathbb{Q}(\chi)=\mathbb{Q}(\zeta_d) \}|&=\frac{1}{p}|\{\psi \in Y : \psi\in \mathrm{Irr}(H|G{}'), ~\mathbb{Q}(\psi)=\mathbb{Q}(\zeta_d) \}|\\ &= \frac{a_d-a^{\prime}_d}{p}, \end{align*} $$
where
$a_d$
and
$a^{\prime }_d$
denote the numbers of cyclic subgroups of order d of H and
$H/G{}'$
, respectively (see Lemma 31).
Now, let
$A_{\mathbb {Q}}(\chi )$
be the simple component of the Wedderburn decomposition of
$\mathbb {Q}G$
corresponding to the rational representation of G that affords the character
$\Omega (\chi )$
. Then
$A_{\mathbb {Q}}(\chi ) \cong M_n(D)$
for some
$n \in \mathbb {N}$
and a division ring D. Observe that
$n=p$
and
$D = \mathbb {Q}(\chi )$
(see Lemma 8). Therefore, all the irreducible rational representations of G whose kernels do not contain
$G{}'$
contribute
$$ \begin{align*}\bigoplus_{d|m, d \nmid m'} \frac{a_{d}}{p}M_p(\mathbb{Q}(\zeta_{d}))\bigoplus_{d|m, d|m'}\frac{a_{d}-a_{d}'}{p}M_p(\mathbb{Q}(\zeta_{d}))\end{align*} $$
in the Wedderburn decomposition of
$\mathbb {Q}G$
. This completes the proof of Theorem 3.
Corollary 60 immediately follows from Theorem 3.
Corollary 60. Suppose G is a nonabelian p-group (
$p\geq 5$
) of order
$p^4$
in
$\Phi _3$
.
-
(1) If
$G=\Phi _3(211)a$
or
$\Phi _3(1^4)$
, then
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q} \bigoplus (p+1)\mathbb{Q}(\zeta_p) \bigoplus (p+1)M_p(\mathbb{Q}(\zeta_p)).\end{align*} $$
-
(2) If
$G=\Phi _3(211)b_r ~ (r = 1,\nu )$
, then
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q} \bigoplus (p+1)\mathbb{Q}(\zeta_p) \bigoplus M_p(\mathbb{Q}(\zeta_p)) \bigoplus M_p(\mathbb{Q}(\zeta_{p^2})).\end{align*} $$
Remark 61. For
$p=3$
, let
$G\in \Phi _3$
. For
$G = \Phi _3(211)b_1$
,
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q} \bigoplus 4\mathbb{Q}(\zeta_3) \bigoplus 4M_3(\mathbb{Q}(\zeta_3)).\end{align*} $$
Additionally, for
$G = \Phi _3(1^4)$
or
$\Phi _3(211)a$
or
$\Phi _3(211)b_2$
,
$$ \begin{align*}\mathbb{Q}G \cong \mathbb{Q} \bigoplus 4\mathbb{Q}(\zeta_3) \bigoplus M_3(\mathbb{Q}(\zeta_3)) \bigoplus M_3(\mathbb{Q}(\zeta_9)).\end{align*} $$
We end this subsection with the following remark.
Remark 62. It is well known that if G is a
$2$
-group of maximal class, then G is isomorphic to one of the following: a dihedral group, a semi-dihedral group or a generalized quaternion group. Let G be a
$2$
-group of order
$16$
of maximal class (that is, of nilpotency class
$3$
). Then G has two inequivalent irreducible two-dimensional faithful complex representations and one irreducible two-dimensional nonfaithful complex representation. Observe that the irreducible two-dimensional nonfaithful complex representation of G is realizable over
$\mathbb {Q}$
. From Lemma 18, one can compute an irreducible rational matrix representation of G that affords the character
$\Omega (\chi )$
, where
$\chi \in \mathrm{FIrr}(G)$
.
Acknowledgement
We thank the anonymous referee for their comments on the article.
