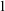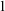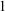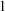1 Introduction
Independence relations are a central notion in model theory. Work on independence in first-order theories was started by Shelah [Reference Shelah30] through the notions of forking and dividing. This was later generalised to simple theories in work by Kim and Pillay [Reference Kim23, Reference Kim and Pillay26]. In NSOP
![]() $_1$
theories dividing is no longer so well-behaved in general. Inspired by ideas from Kim [Reference Kim24], Kaplan and Ramsey developed the notion of Kim-dividing [Reference Kaplan and Ramsey20], which does yield a nice independence relation in NSOP
$_1$
theories dividing is no longer so well-behaved in general. Inspired by ideas from Kim [Reference Kim24], Kaplan and Ramsey developed the notion of Kim-dividing [Reference Kaplan and Ramsey20], which does yield a nice independence relation in NSOP
![]() $_1$
theories. Each of these classes admits a so-called Kim–Pillay style theorem, after a result by Kim and Pillay [Reference Kim and Pillay26, Theorem 4.2]. Roughly the statement is as follows:
$_1$
theories. Each of these classes admits a so-called Kim–Pillay style theorem, after a result by Kim and Pillay [Reference Kim and Pillay26, Theorem 4.2]. Roughly the statement is as follows:
A theory is simple if and only if it admits an independence relation satisfying a certain list of properties. Furthermore, in this case that relation is given by forking independence.
In particular such a theorem gives us canonicity: there can be at most one nice enough independence relation, which must be forking independence.
All of the above takes place in the classical framework of first-order logic. However, there are many interesting classes of structures that do not fit in this framework. Similar work has been done in different and more general logical frameworks. For example, the stable and simple settings have been studied in positive logic [Reference Ben-Yaacov4, Reference Pillay28, Reference Shelah29], continuous logic [Reference Ben-Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and Wilkie6] and AECs [Reference Boney, Grossberg, Kolesnikov and Vasey8, Reference Grossberg and Mazari-Armida13, Reference Hyttinen and Kesälä15, Reference Shelah31, Reference Vasey32]. More recently the NSOP
![]() $_1$
setting has been studied in positive logic [Reference Dobrowolski and Kamsma11, Reference Haykazyan and Kirby14]. It also makes an appearance in continuous logic in [Reference Berenstein, Hyttinen and Villaveces7], where a non-simple NSOP
$_1$
setting has been studied in positive logic [Reference Dobrowolski and Kamsma11, Reference Haykazyan and Kirby14]. It also makes an appearance in continuous logic in [Reference Berenstein, Hyttinen and Villaveces7], where a non-simple NSOP
![]() $_1$
continuous theory is studied. Even then there is a more general category-theoretic approach, unifying all the previously mentioned frameworks. Lieberman, Rosický, and Vasey proved a category-theoretic canonicity theorem for stable independence relations [Reference Lieberman, Rosický and Vasey27]. In [Reference Kamsma18] a category-theoretic canonicity theorem for simple independence relations was proved. In this paper we continue this work and prove a canonicity theorem for NSOP
$_1$
continuous theory is studied. Even then there is a more general category-theoretic approach, unifying all the previously mentioned frameworks. Lieberman, Rosický, and Vasey proved a category-theoretic canonicity theorem for stable independence relations [Reference Lieberman, Rosický and Vasey27]. In [Reference Kamsma18] a category-theoretic canonicity theorem for simple independence relations was proved. In this paper we continue this work and prove a canonicity theorem for NSOP
![]() $_1$
-like independence relations.
$_1$
-like independence relations.
We work in the same framework as in [Reference Kamsma18], namely the framework of Abstract Elementary Categories (AECats) with the amalgamation property. This generalises both the category of models of some first-order theory T and the category of subsets of models of T. The framework can also be applied to positive logic, continuous logic, and AECs (Example 2.3).
An independence relation will be defined as in [Reference Kamsma18] and will be a relation on triples of subobjects, where we use the notation
![]() to say that subobjects
to say that subobjects
![]() $A, B, C$
of M are independent. However, it will be useful to restrict the objects that can appear in the base of the independence relation (i.e., the C in
$A, B, C$
of M are independent. However, it will be useful to restrict the objects that can appear in the base of the independence relation (i.e., the C in
![]() ). For example, we might only want to consider independence over models while allowing arbitrary sets on the sides. We add this flexibility in this paper through the notion of a base class, which will be the class of objects that is allowed in the base.
). For example, we might only want to consider independence over models while allowing arbitrary sets on the sides. We add this flexibility in this paper through the notion of a base class, which will be the class of objects that is allowed in the base.
An independence relation will be called stable, simple, or NSOP
![]() $_1$
-like based on the properties that it satisfies (Definition 4.10). These are the appropriate category-theoretic versions of the properties that we know independence to have in the corresponding classes in the classical first-order setting. In particular this means that any stable independence relation is simple, and any simple independence relation is NSOP
$_1$
-like based on the properties that it satisfies (Definition 4.10). These are the appropriate category-theoretic versions of the properties that we know independence to have in the corresponding classes in the classical first-order setting. In particular this means that any stable independence relation is simple, and any simple independence relation is NSOP
![]() $_1$
-like, reflecting (that part of) the original stability hierarchy.
$_1$
-like, reflecting (that part of) the original stability hierarchy.
In [Reference Kamsma18] the notion of isi-dividing was introduced, and the main result stated that any simple independence relation comes from isi-dividing (i.e., any simple independence relation is non-isi-dividing). As discussed before, in first-order NSOP
![]() $_1$
theories the notion of dividing is no longer so well-behaved, and we should study Kim-dividing instead. So if we think of isi-dividing as the analogue of dividing in AECats, then we will need the right analogue of Kim-dividing to study NSOP
$_1$
theories the notion of dividing is no longer so well-behaved, and we should study Kim-dividing instead. So if we think of isi-dividing as the analogue of dividing in AECats, then we will need the right analogue of Kim-dividing to study NSOP
![]() $_1$
-like independence relations in AECats. To this end we define long Kim-dividing (Definition 6.13). In this definition we need a forking notion based on isi-dividing, which we will then call isi-forking (Definition 6.7).
$_1$
-like independence relations in AECats. To this end we define long Kim-dividing (Definition 6.13). In this definition we need a forking notion based on isi-dividing, which we will then call isi-forking (Definition 6.7).
Before we move on to the main results we make a quick comment about some terminology. Classically being stable or simple is defined as not having the order property (NOP) or not having the tree property (NTP) respectively. In line with this, NSOP
![]() $_1$
means that we do not have SOP
$_1$
means that we do not have SOP
![]() $_1$
, but there is no separate name for NSOP
$_1$
, but there is no separate name for NSOP
![]() $_1$
. We do not consider the combinatorial properties OP, TP, and SOP
$_1$
. We do not consider the combinatorial properties OP, TP, and SOP
![]() $_1$
in this paper. It is not even directly clear what these should look like in settings without compactness. A link between stable independence relations and a form of the order property is established in [Reference Lieberman, Rosický and Vasey27] in a category-theoretic setting. There is also [Reference Grossberg and Mazari-Armida13], which studies the connection between various tree properties and simple independence relations in AECs. For NSOP
$_1$
in this paper. It is not even directly clear what these should look like in settings without compactness. A link between stable independence relations and a form of the order property is established in [Reference Lieberman, Rosický and Vasey27] in a category-theoretic setting. There is also [Reference Grossberg and Mazari-Armida13], which studies the connection between various tree properties and simple independence relations in AECs. For NSOP
![]() $_1$
there is the work [Reference Dobrowolski and Kamsma11, Reference Haykazyan and Kirby14] that does consider the combinatorial property SOP
$_1$
there is the work [Reference Dobrowolski and Kamsma11, Reference Haykazyan and Kirby14] that does consider the combinatorial property SOP
![]() $_1$
in positive logic. However, this is not nearly as general as the category-theoretic setting that we aim for here. This is why we use the term “NSOP
$_1$
in positive logic. However, this is not nearly as general as the category-theoretic setting that we aim for here. This is why we use the term “NSOP
![]() $_1$
-like independence relation”, because it is an independence relation that is classically found in NSOP
$_1$
-like independence relation”, because it is an independence relation that is classically found in NSOP
![]() $_1$
theories, even though we do not consider the relevant combinatorial property.
$_1$
theories, even though we do not consider the relevant combinatorial property.
Main results. Our main result is canonicity of NSOP
![]() $_1$
-like independence relations. In the statement below
$_1$
-like independence relations. In the statement below
![]() denotes the independence relation obtained from long Kim-dividing.
denotes the independence relation obtained from long Kim-dividing.
Theorem 1.1 (Canonicity of NSOP
 $_1$
-like independence).
$_1$
-like independence).
Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and let
$(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and let
![]() $\mathcal {B}$
be some base class. Suppose that
$\mathcal {B}$
be some base class. Suppose that
![]() $(\mathcal {C}, \mathcal {M})$
satisfies the
$(\mathcal {C}, \mathcal {M})$
satisfies the
![]() $\mathcal {B}$
-existence axiom and suppose that there is an NSOP
$\mathcal {B}$
-existence axiom and suppose that there is an NSOP
![]() $_1$
-like independence relation
$_1$
-like independence relation
![]() over
over
![]() $\mathcal {B}$
. Then
$\mathcal {B}$
. Then
![]() over
over
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
For a discussion about the assumption of the
![]() $\mathcal {B}$
-existence axiom we refer to Example 6.16. All we say now is that it is a reasonable, and necessary, assumption, already in the very concrete setting of first-order logic.
$\mathcal {B}$
-existence axiom we refer to Example 6.16. All we say now is that it is a reasonable, and necessary, assumption, already in the very concrete setting of first-order logic.
We also slightly improve the main result from [Reference Kamsma18] on canonicity of simple independence relations. In the statement below
![]() and
and
![]() denote the independence relations obtained from isi-dividing and isi-forking respectively and
denote the independence relations obtained from isi-dividing and isi-forking respectively and
![]() denotes the class of objects that are allowed in the base of
denotes the class of objects that are allowed in the base of
![]() . The slight improvement over [Reference Kamsma18] is the fact that we can restrict the base of our independence relation and the fact that we also get that
. The slight improvement over [Reference Kamsma18] is the fact that we can restrict the base of our independence relation and the fact that we also get that
![]() .
.
Theorem 1.2 (Canonicity of simple independence).
Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property, and suppose that
$(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property, and suppose that
![]() is a simple independence relation. Then
is a simple independence relation. Then
![]() over
over
![]() .
.
Combining the two main theorems we can compare stable, simple, and NSOP
![]() $_1$
-like independence relations, even without assuming the
$_1$
-like independence relations, even without assuming the
![]() $\mathcal {B}$
-existence axiom. This allows us to recover part of the original stability hierarchy based on independence relations, see also Remark 7.5.
$\mathcal {B}$
-existence axiom. This allows us to recover part of the original stability hierarchy based on independence relations, see also Remark 7.5.
Theorem 1.3. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and suppose that
$(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and suppose that
is a stable or a simple independence relation in
![]() $(\mathcal {C}, \mathcal {M})$
. Suppose furthermore that
$(\mathcal {C}, \mathcal {M})$
. Suppose furthermore that
is an NSOP
![]() $_1$
-like independence relation in
$_1$
-like independence relation in
![]() $(\mathcal {C}, \mathcal {M})$
with
$(\mathcal {C}, \mathcal {M})$
with
. Then
Overview. We start by recalling the framework of AECats in Section 2. To make sense of types in this framework we also recall the notion of Galois types.
In Section 3 we will define what we call Lascar strong Galois types, based on the notion of Lascar strong types in first-order logic. These are necessary for a property called Independence Theorem for independence relations later.
We recall the notion of an independence relation in an AECat in Section 4. We also recall the notion of an independent sequence in this section, and prove that these exist assuming only very few basic properties for an independence relation.
In Section 5 we investigate the well-known equivalence between the properties Independence Theorem and 3-amalgamation and we prove this fact for AECats. We also recall that Stationarity implies both of them. All of this is over models.
In Section 6 we recall the notion of isi-dividing and introduce the notions of long dividing, isi-forking, and long Kim-dividing. We also discuss connections to the classical analogues: dividing, forking, and Kim-dividing.
Section 7 contains the main results, the canonicity theorems. After those theorems we discuss how this work extends and brings together previously known results in different (less general) frameworks.
Finally, Section 8 explores the notion of Lascar strong Galois type further. Lascar strong types are known to heavily interact with independence relations in first-order logic and we prove that this is also the case for Lascar strong Galois types.
2 AECats
In this section we recall definitions and basic results for AECats from [Reference Kamsma18]. We assume that the reader is familiar with the framework of accessible categories. A great reference for this is [Reference Adamek and Rosický1].
Convention 2.1. Throughout this paper we are only interested in regular cardinals, which we usually denote by
![]() $\kappa $
,
$\kappa $
,
![]() $\lambda $
, and
$\lambda $
, and
![]() $\mu $
.
$\mu $
.
Definition 2.2 [Reference Kamsma18, Definition 2.5].
An AECat, short for abstract elementary category, consists of a pair
![]() $(\mathcal {C}, \mathcal {M})$
where
$(\mathcal {C}, \mathcal {M})$
where
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {M}$
are accessible categories and
$\mathcal {M}$
are accessible categories and
![]() $\mathcal {M}$
is a full subcategory of
$\mathcal {M}$
is a full subcategory of
![]() $\mathcal {C}$
such that:
$\mathcal {C}$
such that:
-
(i)
 $\mathcal {M}$
has directed colimits, which the inclusion functor into
$\mathcal {M}$
has directed colimits, which the inclusion functor into
 $\mathcal {C}$
preserves.
$\mathcal {C}$
preserves. -
(ii) All arrows in
 $\mathcal {C}$
(and thus in
$\mathcal {C}$
(and thus in
 $\mathcal {M}$
) are monomorphisms.
$\mathcal {M}$
) are monomorphisms.
The objects in
![]() $\mathcal {M}$
are called models. We say that
$\mathcal {M}$
are called models. We say that
![]() $(\mathcal {C}, \mathcal {M})$
has the amalgamation property (or AP) if
$(\mathcal {C}, \mathcal {M})$
has the amalgamation property (or AP) if
![]() $\mathcal {M}$
has the amalgamation property.
$\mathcal {M}$
has the amalgamation property.
We refer to [Reference Kamsma18] for the motivation of this definition and elaborate examples. Below we just summarise some examples of AECats.
Example 2.3. The following are examples of AECats:
-
(i) For a first-order theory T we write
 $\mathbf {Mod}(T)$
for the category of models with elementary embeddings. Then
$\mathbf {Mod}(T)$
for the category of models with elementary embeddings. Then
 $(\mathbf {Mod}(T), \mathbf {Mod}(T))$
is an AECat with AP.
$(\mathbf {Mod}(T), \mathbf {Mod}(T))$
is an AECat with AP. -
(ii) Fix some first-order theory T. Write
 $\mathbf {SubMod}(T)$
for the category of subsets of models of T. That is, objects are pairs
$\mathbf {SubMod}(T)$
for the category of subsets of models of T. That is, objects are pairs
 $(A, M)$
where
$(A, M)$
where
 $A \subseteq M$
and
$A \subseteq M$
and
 $M \models T$
. An arrow
$M \models T$
. An arrow
 $f: (A, M) \to (B, N)$
is an elementary map
$f: (A, M) \to (B, N)$
is an elementary map
 $f: A \to B$
. The inclusion
$f: A \to B$
. The inclusion
 $\mathbf {Mod}(T) \hookrightarrow \mathbf {SubMod}(T)$
sending M to
$\mathbf {Mod}(T) \hookrightarrow \mathbf {SubMod}(T)$
sending M to
 $(M, M)$
is full and faithful. Thus
$(M, M)$
is full and faithful. Thus
 $(\mathbf {SubMod}(T), \mathbf {Mod}(T))$
is an AECat with AP.
$(\mathbf {SubMod}(T), \mathbf {Mod}(T))$
is an AECat with AP. -
(iii) Examples (i) and (ii) generalise to positive logic, because any first-order theory can be seen as a positive theory through Morleyisation. So we use the same notation. That is, for a positive theory T we have the category
 $\mathbf {Mod}(T)$
of existentially closed models and immersions and the category
$\mathbf {Mod}(T)$
of existentially closed models and immersions and the category
 $\mathbf {SubMod}(T)$
of subsets of existentially closed models with immersions between those subsets. Then we have the following AECats with AP:
$\mathbf {SubMod}(T)$
of subsets of existentially closed models with immersions between those subsets. Then we have the following AECats with AP:
 $(\mathbf {Mod}(T), \mathbf {Mod}(T))$
and
$(\mathbf {Mod}(T), \mathbf {Mod}(T))$
and
 $(\mathbf {SubMod}(T), \mathbf {Mod}(T))$
.
$(\mathbf {SubMod}(T), \mathbf {Mod}(T))$
. -
(iv) A similar construction to examples (i) and (ii) is possible for continuous logic. For a continuous theory T we can form categories
 $\mathbf {MetMod}(T)$
of models of T and
$\mathbf {MetMod}(T)$
of models of T and
 $\mathbf {SubMetMod}(T)$
of closed subsets of models of T, see [Reference Kamsma18, Example 2.10] for more details. Then
$\mathbf {SubMetMod}(T)$
of closed subsets of models of T, see [Reference Kamsma18, Example 2.10] for more details. Then
 $(\mathbf {MetMod}(T), \mathbf {MetMod}(T))$
and
$(\mathbf {MetMod}(T), \mathbf {MetMod}(T))$
and
 $(\mathbf {SubMetMod}(T), \mathbf {MetMod}(T))$
are AECats with AP.
$(\mathbf {SubMetMod}(T), \mathbf {MetMod}(T))$
are AECats with AP. -
(v) Let
 $\mathcal {K}$
be an AEC. We view
$\mathcal {K}$
be an AEC. We view
 $\mathcal {K}$
as a category by taking as arrows
$\mathcal {K}$
as a category by taking as arrows
 $\mathcal {K}$
-embeddings. Then
$\mathcal {K}$
-embeddings. Then
 $(\mathcal {K}, \mathcal {K})$
is an AECat and has AP iff
$(\mathcal {K}, \mathcal {K})$
is an AECat and has AP iff
 $\mathcal {K}$
has AP.
$\mathcal {K}$
has AP.
In [Reference Kamsma18, Example 2.11] there is also a construction to consider subsets of the structures in an AEC, similar to the construction of
![]() $\mathbf {SubMod}(T)$
. There is a simpler construction that does not need the assumptions on
$\mathbf {SubMod}(T)$
. There is a simpler construction that does not need the assumptions on
![]() $\mathcal {K}$
in that example.
$\mathcal {K}$
in that example.
Example 2.4. Let
![]() $\mathcal {K}$
be an AEC. We define the category of subsets of
$\mathcal {K}$
be an AEC. We define the category of subsets of
![]() $\mathcal {K}$
, written as
$\mathcal {K}$
, written as
![]() $\mathbf {SubSet}(K)$
, as follows. Objects are pairs
$\mathbf {SubSet}(K)$
, as follows. Objects are pairs
![]() $(A, M)$
where
$(A, M)$
where
![]() $A \subseteq M$
and
$A \subseteq M$
and
![]() $M \in \mathcal {K}$
. An arrow
$M \in \mathcal {K}$
. An arrow
![]() $f: (A, M) \to (B, N)$
is then a
$f: (A, M) \to (B, N)$
is then a
![]() $\mathcal {K}$
-embedding
$\mathcal {K}$
-embedding
![]() $f: M \to N$
such that
$f: M \to N$
such that
![]() $f(A) \subseteq B$
. One easily verifies that
$f(A) \subseteq B$
. One easily verifies that
![]() $(\mathbf {SubSet}(\mathcal {K}), \mathcal {K})$
is an AECat, and it has AP exactly when
$(\mathbf {SubSet}(\mathcal {K}), \mathcal {K})$
is an AECat, and it has AP exactly when
![]() $\mathcal {K}$
has AP.
$\mathcal {K}$
has AP.
Definition 2.5. We call an AECat
![]() $(\mathcal {C}, \mathcal {M})$
a
$(\mathcal {C}, \mathcal {M})$
a
![]() $\kappa $
-AECat if
$\kappa $
-AECat if
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {M}$
are both
$\mathcal {M}$
are both
![]() $\kappa $
-accessible and the inclusion functor preserves
$\kappa $
-accessible and the inclusion functor preserves
![]() $\kappa $
-presentable objects.
$\kappa $
-presentable objects.
Fact 2.6 [Reference Kamsma18, Remark 2.8].
For any AECat
![]() $(\mathcal {C}, \mathcal {M})$
there are arbitrarily large
$(\mathcal {C}, \mathcal {M})$
there are arbitrarily large
![]() $\kappa $
such that
$\kappa $
such that
![]() $(\mathcal {C}, \mathcal {M})$
is a
$(\mathcal {C}, \mathcal {M})$
is a
![]() $\kappa $
-AECat.
$\kappa $
-AECat.
Proposition 2.7. Let
![]() $(\mathcal {C}, \mathcal {M})$
be a
$(\mathcal {C}, \mathcal {M})$
be a
![]() $\kappa $
-AECat and let
$\kappa $
-AECat and let
![]() $\lambda \geq \kappa $
. Then
$\lambda \geq \kappa $
. Then
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\lambda $
-accessible and the inclusion functor preserves and reflects
$\lambda $
-accessible and the inclusion functor preserves and reflects
![]() $\lambda $
-presentable objects.
$\lambda $
-presentable objects.
Proof The claim about
![]() $\lambda $
-accessibility is exactly [Reference Beke and Rosický2, Proposition 4.1]. Preservation and reflection of
$\lambda $
-accessibility is exactly [Reference Beke and Rosický2, Proposition 4.1]. Preservation and reflection of
![]() $\lambda $
-presentable objects follows using the same proofs as [Reference Beke and Rosický2, Proposition 4.3] and [Reference Beke and Rosický2, Lemma 3.6] respectively, where in the latter we use the former and the fact that all arrows in
$\lambda $
-presentable objects follows using the same proofs as [Reference Beke and Rosický2, Proposition 4.3] and [Reference Beke and Rosický2, Lemma 3.6] respectively, where in the latter we use the former and the fact that all arrows in
![]() $\mathcal {C}$
are monomorphisms, so the inclusion functor reflects split epimorphisms (which are isomorphisms).
$\mathcal {C}$
are monomorphisms, so the inclusion functor reflects split epimorphisms (which are isomorphisms).
Definition 2.8. Let M be a model in an AECat. An extension of M is an arrow
![]() $M \to N$
, where N is some model.
$M \to N$
, where N is some model.
Convention 2.9. Usually, there will be only one relevant extension of models. So to prevent cluttering of notation we will not give such an extension a name. Given such an extension
![]() $M \to N$
and some arrow
$M \to N$
and some arrow
![]() $a: A \to M$
we will then denote the arrow
$a: A \to M$
we will then denote the arrow
![]() $A \xrightarrow {a} M \to N$
by a as well.
$A \xrightarrow {a} M \to N$
by a as well.
Definition 2.10. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP. We will use the notation
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP. We will use the notation
![]() $((a_i)_{i \in I}; M)$
to mean that the
$((a_i)_{i \in I}; M)$
to mean that the
![]() $a_i$
are arrows into M and that M is a model.
$a_i$
are arrows into M and that M is a model.
We say that two tuples
![]() $((a_i)_{i \in I}; M)$
and
$((a_i)_{i \in I}; M)$
and
![]() $((a_i')_{i \in I}; M')$
have the same Galois type, and write
$((a_i')_{i \in I}; M')$
have the same Galois type, and write
if
![]() $\operatorname {\mathrm {dom}}(a_i) = \operatorname {\mathrm {dom}}(a_i')$
for all
$\operatorname {\mathrm {dom}}(a_i) = \operatorname {\mathrm {dom}}(a_i')$
for all
![]() $i \in I$
, and there is a common extension
$i \in I$
, and there is a common extension
![]() $M \to N \leftarrow M'$
such that the following commutes for all
$M \to N \leftarrow M'$
such that the following commutes for all
![]() $i \in I$
:
$i \in I$
:

Note that AP ensures that having the same Galois type is an equivalence relation. For this reason, we are only interested in AECats with AP in the rest of this paper.
Fact 2.11 [Reference Kamsma18, Proposition 3.8].
If
![]() $\operatorname {\mathrm {gtp}}((a_i)_{i \in I}; M) = \operatorname {\mathrm {gtp}}((a_i')_{i \in I}; M')$
then
$\operatorname {\mathrm {gtp}}((a_i)_{i \in I}; M) = \operatorname {\mathrm {gtp}}((a_i')_{i \in I}; M')$
then
![]() $:$
$:$
-
(i)
 $($
restriction
$($
restriction
 $)$
we have
$)$
we have
 $\operatorname {\mathrm {gtp}}((a_i)_{i \in I_0}; M) = \operatorname {\mathrm {gtp}}((a_i')_{i \in I_0}; M')$
for any
$\operatorname {\mathrm {gtp}}((a_i)_{i \in I_0}; M) = \operatorname {\mathrm {gtp}}((a_i')_{i \in I_0}; M')$
for any
 $I_0 \subseteq I;$
$I_0 \subseteq I;$
-
(ii)
 $($
monotonicity
$($
monotonicity
 $)$
given an arrow
$)$
given an arrow
 $b_i: B_i \to \operatorname {\mathrm {dom}}(a_i)$
for each
$b_i: B_i \to \operatorname {\mathrm {dom}}(a_i)$
for each
 $i \in I$
, then
$i \in I$
, then  $$\begin{align*}\operatorname{\mathrm{gtp}}((a_i)_{i \in I}, (a_i b_i)_{i \in I}; M) = \operatorname{\mathrm{gtp}}((a_i')_{i \in I}, (a_i' b_i)_{i \in I}; M') \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gtp}}((a_i)_{i \in I}, (a_i b_i)_{i \in I}; M) = \operatorname{\mathrm{gtp}}((a_i')_{i \in I}, (a_i' b_i)_{i \in I}; M') \end{align*}$$
and thus
 $\operatorname {\mathrm {gtp}}((a_i b_i)_{i \in I}; M) = \operatorname {\mathrm {gtp}}((a_i' b_i)_{i \in I}; M')$
;
$\operatorname {\mathrm {gtp}}((a_i b_i)_{i \in I}; M) = \operatorname {\mathrm {gtp}}((a_i' b_i)_{i \in I}; M')$
; -
(iii)
 $($
extension
$($
extension
 $)$
for any
$)$
for any
 $(b; M)$
there is an extension
$(b; M)$
there is an extension
 $M' \to N$
and some
$M' \to N$
and some
 $(b'; N)$
such that
$(b'; N)$
such that
 $\operatorname {\mathrm {gtp}}(b, (a_i)_{i \in I}; M) = \operatorname {\mathrm {gtp}}(b', (a_i')_{i \in I}; N)$
.
$\operatorname {\mathrm {gtp}}(b, (a_i)_{i \in I}; M) = \operatorname {\mathrm {gtp}}(b', (a_i')_{i \in I}; N)$
.
Fact 2.12 [Reference Kamsma18, Proposition 3.9].
If
![]() $\operatorname {\mathrm {gtp}}(a, b; M) = \operatorname {\mathrm {gtp}}(a', b'; M')$
and a factors through b, say as
$\operatorname {\mathrm {gtp}}(a, b; M) = \operatorname {\mathrm {gtp}}(a', b'; M')$
and a factors through b, say as
![]() $a = bi$
, then
$a = bi$
, then
![]() $a'$
factors through
$a'$
factors through
![]() $b'$
in the same way, so as
$b'$
in the same way, so as
![]() $a' = b' i$
.
$a' = b' i$
.
Definition 2.13. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP. For a tuple
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP. For a tuple
![]() $(A_i)_{i \in I}$
of objects in
$(A_i)_{i \in I}$
of objects in
![]() $\mathcal {C}$
, let
$\mathcal {C}$
, let
![]() $S((A_i)_{i \in I})$
be the collection of all tuples
$S((A_i)_{i \in I})$
be the collection of all tuples
![]() $((a_i)_{i \in I}; M)$
such that
$((a_i)_{i \in I}; M)$
such that
![]() $\operatorname {\mathrm {dom}}(a_i) = A_i$
. We define the Galois type set
$\operatorname {\mathrm {dom}}(a_i) = A_i$
. We define the Galois type set
![]() $\mathrm {S}_{\mathrm {gtp}}((A_i)_{i \in I})$
as
$\mathrm {S}_{\mathrm {gtp}}((A_i)_{i \in I})$
as
where
![]() $\sim _{gtp}$
is the equivalence relation of having the same Galois type.
$\sim _{gtp}$
is the equivalence relation of having the same Galois type.
Fact 2.14 [Reference Kamsma18, Proposition 4.6].
![]() $\mathrm {S}_{\mathrm {gtp}}((A_i)_{i \in I})$
is really just a set.
$\mathrm {S}_{\mathrm {gtp}}((A_i)_{i \in I})$
is really just a set.
Definition 2.15. Fix some AECat
![]() $(\mathcal {C}, \mathcal {M})$
with AP.
$(\mathcal {C}, \mathcal {M})$
with AP.
-
(i) A sequence is a tuple
 $((a_i)_{i \in I}; M)$
where every
$((a_i)_{i \in I}; M)$
where every
 $a_i$
has the same domain and I is a linear order.
$a_i$
has the same domain and I is a linear order. -
(ii) A chain is a diagram of ordinal shape. We call a chain
 $(M_i)_{i < \kappa }$
continuous if
$(M_i)_{i < \kappa }$
continuous if
 $M_\ell = \operatorname {\mathrm {colim}}_{i < \ell } M_i$
for all limit
$M_\ell = \operatorname {\mathrm {colim}}_{i < \ell } M_i$
for all limit
 $\ell < \kappa $
. Given a chain
$\ell < \kappa $
. Given a chain
 $(M_i)_{i < \kappa }$
we say that M is a chain bound for
$(M_i)_{i < \kappa }$
we say that M is a chain bound for
 $(M_i)_{i < \kappa }$
if there are arrows
$(M_i)_{i < \kappa }$
if there are arrows
 $m_i: M_i \to M$
forming a cocone for
$m_i: M_i \to M$
forming a cocone for
 $(M_i)_{i < \kappa }$
.
$(M_i)_{i < \kappa }$
. -
(iii) A chain of initial segments for some sequence
 $((a_i)_{i < \kappa }; M)$
is a continuous chain
$((a_i)_{i < \kappa }; M)$
is a continuous chain
 $(M_i)_{i < \kappa }$
of models with chain bound M such that
$(M_i)_{i < \kappa }$
of models with chain bound M such that
 $a_i$
factors through
$a_i$
factors through
 $M_{i+1}$
for all
$M_{i+1}$
for all
 $i < \kappa $
.
$i < \kappa $
. -
(iv) Let
 $(M_i)_{i < \kappa }$
be a chain with chain bound M and let
$(M_i)_{i < \kappa }$
be a chain with chain bound M and let
 $c: C \to M$
be some arrow. We say that c embeds in
$c: C \to M$
be some arrow. We say that c embeds in
 $(M_i)_{i < \kappa }$
if c factors as
$(M_i)_{i < \kappa }$
if c factors as
 $C \to M_0 \to M$
.
$C \to M_0 \to M$
. -
(v) We call a sequence
 $((a_i)_{i < \kappa }; M)$
together with a chain of initial segments
$((a_i)_{i < \kappa }; M)$
together with a chain of initial segments
 $(M_i)_{i < \kappa }$
an isi-sequence (short for initial segment invariant) if for all
$(M_i)_{i < \kappa }$
an isi-sequence (short for initial segment invariant) if for all
 $i \leq j < \kappa $
we have
$i \leq j < \kappa $
we have  $$\begin{align*}\operatorname{\mathrm{gtp}}(a_i, m_i; M) = \operatorname{\mathrm{gtp}}(a_j, m_i; M). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gtp}}(a_i, m_i; M) = \operatorname{\mathrm{gtp}}(a_j, m_i; M). \end{align*}$$
For
 $c: C \to M$
we say this is an isi-sequence over c if c embeds in
$c: C \to M$
we say this is an isi-sequence over c if c embeds in
 $(M_i)_{i < \kappa }$
.
$(M_i)_{i < \kappa }$
.
Convention 2.16. For a chain of initial segments
![]() $(M_i)_{i < \kappa }$
for some sequence
$(M_i)_{i < \kappa }$
for some sequence
![]() $(a_i)_{i < \kappa }$
in M we will abuse notation and view
$(a_i)_{i < \kappa }$
in M we will abuse notation and view
![]() $a_i$
as an arrow into
$a_i$
as an arrow into
![]() $M_j$
for
$M_j$
for
![]() $i < j$
. Similarly, if c embeds in
$i < j$
. Similarly, if c embeds in
![]() $(M_i)_{i < \kappa }$
, we view c as an arrow into
$(M_i)_{i < \kappa }$
, we view c as an arrow into
![]() $M_i$
for all
$M_i$
for all
![]() $i < \kappa $
.
$i < \kappa $
.
Lemma 2.17. Suppose that
![]() $(\mathcal {C}, \mathcal {M})$
is a
$(\mathcal {C}, \mathcal {M})$
is a
![]() $\mu $
-AECat and let
$\mu $
-AECat and let
![]() $\kappa \geq \mu $
. Suppose furthermore that we are given a sequence
$\kappa \geq \mu $
. Suppose furthermore that we are given a sequence
![]() $(a_i)_{i < \kappa }$
in some M with a chain of initial segments
$(a_i)_{i < \kappa }$
in some M with a chain of initial segments
![]() $(M_i)_{i < \kappa }$
and some c that embeds in this chain, such that
$(M_i)_{i < \kappa }$
and some c that embeds in this chain, such that
![]() $\operatorname {\mathrm {dom}}(a_i)$
(which is the same for all i) and
$\operatorname {\mathrm {dom}}(a_i)$
(which is the same for all i) and
![]() $\operatorname {\mathrm {dom}}(c)$
are
$\operatorname {\mathrm {dom}}(c)$
are
![]() $\kappa $
-presentable. Then there is a chain of initial segments
$\kappa $
-presentable. Then there is a chain of initial segments
![]() $(M_i')_{i < \kappa }$
in which c embeds, such that for all
$(M_i')_{i < \kappa }$
in which c embeds, such that for all
![]() $i < \kappa $
the inclusion of
$i < \kappa $
the inclusion of
![]() $M_i'$
into M factors through
$M_i'$
into M factors through
![]() $M_i$
(so
$M_i$
(so
![]() $M_i' \leq M_i$
) and
$M_i' \leq M_i$
) and
![]() $M_i'$
is
$M_i'$
is
![]() $\kappa $
-presentable.
$\kappa $
-presentable.
Proof We build the chain of initial segments
![]() $(M_i')_{i < \kappa }$
by induction. For the base case we note that we can write
$(M_i')_{i < \kappa }$
by induction. For the base case we note that we can write
![]() $M_0$
as a
$M_0$
as a
![]() $\kappa $
-directed colimit of
$\kappa $
-directed colimit of
![]() $\kappa $
-presentable models (using Proposition 2.7). As
$\kappa $
-presentable models (using Proposition 2.7). As
![]() $\operatorname {\mathrm {dom}}(c)$
is
$\operatorname {\mathrm {dom}}(c)$
is
![]() $\kappa $
-presentable, c factors through some
$\kappa $
-presentable, c factors through some
![]() $M_0'$
in this diagram. The successor step is similar, using that
$M_0'$
in this diagram. The successor step is similar, using that
![]() $M_i'$
and
$M_i'$
and
![]() $\operatorname {\mathrm {dom}}(a_i)$
are both
$\operatorname {\mathrm {dom}}(a_i)$
are both
![]() $\kappa $
-presentable and must thus factor through some
$\kappa $
-presentable and must thus factor through some
![]() $\kappa $
-presentable
$\kappa $
-presentable
![]() $M_{i+1}' \leq M_{i+1}$
. In the limit step we just take the colimit
$M_{i+1}' \leq M_{i+1}$
. In the limit step we just take the colimit
![]() $M_\ell ' = \operatorname {\mathrm {colim}}_{i < \ell } M_i'$
and the universal property then yields an arrow
$M_\ell ' = \operatorname {\mathrm {colim}}_{i < \ell } M_i'$
and the universal property then yields an arrow
![]() $M_\ell ' \to M_\ell $
.
$M_\ell ' \to M_\ell $
.
3 Lascar strong Galois types
In this section we will give a definition of Lascar strong Galois type. In the first-order setting this will coincide with Lascar strong types, see Remark 3.2. This notion will be useful later in the property Independence Theorem for independence relations, see Definition 4.9.
To place our definition in context, we recall a possible definition for Lascar strong types in first-order logic. Working in a monster model, tuples a and
![]() $a'$
have the same Lascar strong type over B if there are
$a'$
have the same Lascar strong type over B if there are
![]() $a = a_0, \ldots , a_n = a'$
and models
$a = a_0, \ldots , a_n = a'$
and models
![]() $M_1, \ldots , M_n$
, each containing B, such that
$M_1, \ldots , M_n$
, each containing B, such that
![]() $\operatorname {\mathrm {tp}}(a_i / M_{i+1}) = \operatorname {\mathrm {tp}}(a_{i+1} / M_{i+1})$
for all
$\operatorname {\mathrm {tp}}(a_i / M_{i+1}) = \operatorname {\mathrm {tp}}(a_{i+1} / M_{i+1})$
for all
![]() $0 \leq i < n$
.
$0 \leq i < n$
.
Definition 3.1. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP and fix some
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP and fix some
![]() $((b_j)_{j \in J}; M)$
. We write
$((b_j)_{j \in J}; M)$
. We write
![]() $((a_i)_{i \in I} / (b_j)_{j \in J}; M) \sim _{\operatorname {\mathrm {Lgtp}}} ((a_i')_{i \in I} / (b_j)_{j \in J}; M)$
if there is some extension
$((a_i)_{i \in I} / (b_j)_{j \in J}; M) \sim _{\operatorname {\mathrm {Lgtp}}} ((a_i')_{i \in I} / (b_j)_{j \in J}; M)$
if there is some extension
![]() $M \to N$
and some
$M \to N$
and some
![]() $m_0: M_0 \to N$
, where
$m_0: M_0 \to N$
, where
![]() $M_0$
is a model, such that
$M_0$
is a model, such that
![]() $b_j$
factors through
$b_j$
factors through
![]() $m_0$
for all
$m_0$
for all
![]() $j \in J$
and
$j \in J$
and
![]() $\operatorname {\mathrm {gtp}}((a_i)_{i \in I}, m_0; N) = \operatorname {\mathrm {gtp}}((a_i')_{i \in I}, m_0; N)$
.
$\operatorname {\mathrm {gtp}}((a_i)_{i \in I}, m_0; N) = \operatorname {\mathrm {gtp}}((a_i')_{i \in I}, m_0; N)$
.
We write
for the transitive closure of
![]() $\sim _{\operatorname {\mathrm {Lgtp}}}$
and we say that
$\sim _{\operatorname {\mathrm {Lgtp}}}$
and we say that
![]() $((a_i)_{i \in I}; M)$
and
$((a_i)_{i \in I}; M)$
and
![]() $((a_i')_{i \in I}; M)$
have the same Lascar strong Galois type over
$((a_i')_{i \in I}; M)$
have the same Lascar strong Galois type over
![]() $(b_j)_{j \in J}$
.
$(b_j)_{j \in J}$
.
Remark 3.2. By definition having the same Lascar strong Galois type is the same as having the same Lascar strong type in an AECat based on a first-order theory. That is, they coincide in any AECat of the form
![]() $(\mathbf {SubMod}(T), \mathbf {Mod}(T))$
or
$(\mathbf {SubMod}(T), \mathbf {Mod}(T))$
or
![]() $(\mathbf {Mod}(T), \mathbf {Mod}(T))$
for some first-order theory T. We get a similar statement for continuous logic, because the same standard proofs and definitions go through.
$(\mathbf {Mod}(T), \mathbf {Mod}(T))$
for some first-order theory T. We get a similar statement for continuous logic, because the same standard proofs and definitions go through.
In positive logic the situation is more subtle, but in a broad class of reasonable positive theories Lascar strong types and Lascar strong Galois types coincide. See Fact 7.8 and the surrounding discussion for more details.
Classically multiple equivalent definitions are possible for Lascar strong types. We recall these and prove similar conditions for Lascar strong Galois types in Section 8. Usually these proofs require compactness, but interestingly this can be replaced by the use of a nice enough independence relation.
For ease of notation the following proposition is formulated for single arrows, but everything goes through word for word if we replace those by tuples of arrows.
Proposition 3.3. Suppose that
![]() $\operatorname {\mathrm {gtp}}(a_1, a_2, b; M) = \operatorname {\mathrm {gtp}}(a_1', a_2', b'; M')$
. Then we have
$\operatorname {\mathrm {gtp}}(a_1, a_2, b; M) = \operatorname {\mathrm {gtp}}(a_1', a_2', b'; M')$
. Then we have
![]() $\operatorname {\mathrm {Lgtp}}(a_1 / b; M) = \operatorname {\mathrm {Lgtp}}(a_2 / b; M)$
iff
$\operatorname {\mathrm {Lgtp}}(a_1 / b; M) = \operatorname {\mathrm {Lgtp}}(a_2 / b; M)$
iff
![]() $\operatorname {\mathrm {Lgtp}}(a_1' / b'; M') = \operatorname {\mathrm {Lgtp}}(a_2' / b'; M')$
.
$\operatorname {\mathrm {Lgtp}}(a_1' / b'; M') = \operatorname {\mathrm {Lgtp}}(a_2' / b'; M')$
.
Proof It suffices to prove that
![]() $(a_1 / b; M) \sim _{\operatorname {\mathrm {Lgtp}}} (a_2 / b; M)$
implies
$(a_1 / b; M) \sim _{\operatorname {\mathrm {Lgtp}}} (a_2 / b; M)$
implies
![]() $(a_1' / b'; M') \sim _{\operatorname {\mathrm {Lgtp}}} (a_2' / b'; M')$
. Let
$(a_1' / b'; M') \sim _{\operatorname {\mathrm {Lgtp}}} (a_2' / b'; M')$
. Let
![]() $M \to N$
with
$M \to N$
with
![]() $m_0: M_0 \to N$
witness
$m_0: M_0 \to N$
witness
![]() $(a_1 / b; M) \sim _{\operatorname {\mathrm {Lgtp}}} (a_2 / b; M)$
. So we have that
$(a_1 / b; M) \sim _{\operatorname {\mathrm {Lgtp}}} (a_2 / b; M)$
. So we have that
![]() $b = m_0 b^*$
for some
$b = m_0 b^*$
for some
![]() $b^*: B \to M_0$
, and
$b^*: B \to M_0$
, and
![]() $\operatorname {\mathrm {gtp}}(a_1, m_0; N) = \operatorname {\mathrm {gtp}}(a_2, m_0; N)$
. Let
$\operatorname {\mathrm {gtp}}(a_1, m_0; N) = \operatorname {\mathrm {gtp}}(a_2, m_0; N)$
. Let
![]() $N \to N' \leftarrow M'$
witness
$N \to N' \leftarrow M'$
witness
![]() $\operatorname {\mathrm {gtp}}(a_1, a_2, b; N) = \operatorname {\mathrm {gtp}}(a_1, a_2, b; M) = \operatorname {\mathrm {gtp}}(a_1', a_2', b'; M')$
. Then we get the following commuting diagram:
$\operatorname {\mathrm {gtp}}(a_1, a_2, b; N) = \operatorname {\mathrm {gtp}}(a_1, a_2, b; M) = \operatorname {\mathrm {gtp}}(a_1', a_2', b'; M')$
. Then we get the following commuting diagram:

So we have
![]() $m_0: M_0 \to N'$
and
$m_0: M_0 \to N'$
and
![]() $b'$
factors though
$b'$
factors though
![]() $m_0$
. This follows from the fact that the above diagram commutes, so
$m_0$
. This follows from the fact that the above diagram commutes, so
![]() $b': B \to M' \to N'$
and
$b': B \to M' \to N'$
and
![]() $B \to M_0 \to N \to N'$
are the same arrow. Furthermore, we have that
$B \to M_0 \to N \to N'$
are the same arrow. Furthermore, we have that
![]() $\operatorname {\mathrm {gtp}}(a_1, m_0; N') = \operatorname {\mathrm {gtp}}(a_2, m_0; N')$
and because
$\operatorname {\mathrm {gtp}}(a_1, m_0; N') = \operatorname {\mathrm {gtp}}(a_2, m_0; N')$
and because
![]() $a_1$
and
$a_1$
and
![]() $a_2$
are the same arrows into
$a_2$
are the same arrows into
![]() $N'$
as
$N'$
as
![]() $a_1'$
and
$a_1'$
and
![]() $a_2'$
respectively, we get
$a_2'$
respectively, we get
![]() $\operatorname {\mathrm {gtp}}(a_1', m_0; N') = \operatorname {\mathrm {gtp}}(a_2', m_0; N')$
. So we conclude
$\operatorname {\mathrm {gtp}}(a_1', m_0; N') = \operatorname {\mathrm {gtp}}(a_2', m_0; N')$
. So we conclude
![]() $(a_1' / b'; M') \sim _{\operatorname {\mathrm {Lgtp}}} (a_2' / b'; M')$
, as required.
$(a_1' / b'; M') \sim _{\operatorname {\mathrm {Lgtp}}} (a_2' / b'; M')$
, as required.
Lascar strong Galois types induce a bounded equivalence relation on arrows. We again give a proof for single arrows, which also works for tuples of arrows.
Proposition 3.4. Given objects A and B there is
![]() $\lambda $
such that for any
$\lambda $
such that for any
![]() $b: B \to M$
the relation of having the same Lascar strong Galois type over b partitions
$b: B \to M$
the relation of having the same Lascar strong Galois type over b partitions
![]() $\operatorname {\mathrm {Hom}}(A, M)$
into at most
$\operatorname {\mathrm {Hom}}(A, M)$
into at most
![]() $\lambda $
many equivalence classes.
$\lambda $
many equivalence classes.
Proof We will first prove the following claim: for any
![]() $b: B \to M$
there is
$b: B \to M$
there is
![]() $\lambda _b$
such that for any
$\lambda _b$
such that for any
![]() $b': B \to M'$
with
$b': B \to M'$
with
![]() $\operatorname {\mathrm {gtp}}(b'; M') = \operatorname {\mathrm {gtp}}(b; M)$
there are at most
$\operatorname {\mathrm {gtp}}(b'; M') = \operatorname {\mathrm {gtp}}(b; M)$
there are at most
![]() $\lambda _b$
many equivalence classes of Lascar strong Galois types over
$\lambda _b$
many equivalence classes of Lascar strong Galois types over
![]() $b'$
in
$b'$
in
![]() $\operatorname {\mathrm {Hom}}(A, M')$
. By Fact 2.14 the collection
$\operatorname {\mathrm {Hom}}(A, M')$
. By Fact 2.14 the collection
![]() $\mathrm {S}_{\mathrm {gtp}}(A, M)$
is a set. We pick
$\mathrm {S}_{\mathrm {gtp}}(A, M)$
is a set. We pick
![]() $\lambda _b = |\mathrm {S}_{\mathrm {gtp}}(A, M)|$
. Now let
$\lambda _b = |\mathrm {S}_{\mathrm {gtp}}(A, M)|$
. Now let
![]() $M \to N \leftarrow M'$
witness
$M \to N \leftarrow M'$
witness
![]() $\operatorname {\mathrm {gtp}}(b'; M') = \operatorname {\mathrm {gtp}}(b; M)$
. For any two arrows
$\operatorname {\mathrm {gtp}}(b'; M') = \operatorname {\mathrm {gtp}}(b; M)$
. For any two arrows
![]() $a, a': A \to M'$
we have that
$a, a': A \to M'$
we have that
![]() $\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(a', m; N)$
implies that
$\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(a', m; N)$
implies that
![]() $\operatorname {\mathrm {Lgtp}}(a / b'; M') = \operatorname {\mathrm {Lgtp}}(a' / b'; M')$
, by definition of
$\operatorname {\mathrm {Lgtp}}(a / b'; M') = \operatorname {\mathrm {Lgtp}}(a' / b'; M')$
, by definition of
![]() $\operatorname {\mathrm {Lgtp}}$
. The claim then follows by choice of
$\operatorname {\mathrm {Lgtp}}$
. The claim then follows by choice of
![]() $\lambda _b$
.
$\lambda _b$
.
By the claim we can take
![]() $\lambda $
to be the supremum of
$\lambda $
to be the supremum of
![]() $\lambda _b$
, where b ranges over the representatives of the Galois types in
$\lambda _b$
, where b ranges over the representatives of the Galois types in
![]() $\mathrm {S}_{\mathrm {gtp}}(B)$
.
$\mathrm {S}_{\mathrm {gtp}}(B)$
.
Proposition 3.5. If
![]() $\operatorname {\mathrm {Lgtp}}((a_i)_{i \in I} / b; M) = \operatorname {\mathrm {Lgtp}}((a_i')_{i \in I} / b; M)$
then:
$\operatorname {\mathrm {Lgtp}}((a_i)_{i \in I} / b; M) = \operatorname {\mathrm {Lgtp}}((a_i')_{i \in I} / b; M)$
then:
-
(i) (restriction) we have
 $\operatorname {\mathrm {Lgtp}}((a_i)_{i \in I_0} / b; M) = \operatorname {\mathrm {Lgtp}}((a_i')_{i \in I_0} / b; M)$
for any
$\operatorname {\mathrm {Lgtp}}((a_i)_{i \in I_0} / b; M) = \operatorname {\mathrm {Lgtp}}((a_i')_{i \in I_0} / b; M)$
for any
 $I_0 \subseteq I$
;
$I_0 \subseteq I$
; -
(ii) (monotonicity) given an arrow
 $c_i: C_i \to \operatorname {\mathrm {dom}}(a_i)$
for each
$c_i: C_i \to \operatorname {\mathrm {dom}}(a_i)$
for each
 $i \in I$
, then
$i \in I$
, then  $$\begin{align*}\operatorname{\mathrm{Lgtp}}((a_i)_{i \in I}, (a_i c_i)_{i \in I} / b; M) = \operatorname{\mathrm{Lgtp}}((a_i')_{i \in I}, (a_i' c_i)_{i \in I} / b; M) \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Lgtp}}((a_i)_{i \in I}, (a_i c_i)_{i \in I} / b; M) = \operatorname{\mathrm{Lgtp}}((a_i')_{i \in I}, (a_i' c_i)_{i \in I} / b; M) \end{align*}$$
and thus
 $\operatorname {\mathrm {Lgtp}}((a_i c_i)_{i \in I} / b; M) = \operatorname {\mathrm {Lgtp}}((a_i' c_i)_{i \in I} / b; M)$
;
$\operatorname {\mathrm {Lgtp}}((a_i c_i)_{i \in I} / b; M) = \operatorname {\mathrm {Lgtp}}((a_i' c_i)_{i \in I} / b; M)$
; -
(iii) (extension) for any
 $(c; M)$
there is an extension
$(c; M)$
there is an extension
 $M \to N$
and some
$M \to N$
and some
 $(c'; N)$
such that
$(c'; N)$
such that
 $\operatorname {\mathrm {Lgtp}}(c, (a_i)_{i \in I} / b; N) = \operatorname {\mathrm {Lgtp}}(c', (a_i')_{i \in I} / b; N)$
.
$\operatorname {\mathrm {Lgtp}}(c, (a_i)_{i \in I} / b; N) = \operatorname {\mathrm {Lgtp}}(c', (a_i')_{i \in I} / b; N)$
.
4 Independence relations
Similar to [Reference Kamsma18, Section 6] we define an independence relation in an AECat as a ternary relation on subobjects of models. However, there will be some slight differences in our terminology, see after Definition 4.10.
We write
![]() $\operatorname {\mathrm {Sub}}(X)$
for the poset of subobjects of object X. If
$\operatorname {\mathrm {Sub}}(X)$
for the poset of subobjects of object X. If
![]() $A \leq B$
for
$A \leq B$
for
![]() $A, B \in \operatorname {\mathrm {Sub}}(X)$
we may also consider A to be a subobject of B, that is
$A, B \in \operatorname {\mathrm {Sub}}(X)$
we may also consider A to be a subobject of B, that is
![]() $A \in \operatorname {\mathrm {Sub}}(B)$
. On the other hand, we always have
$A \in \operatorname {\mathrm {Sub}}(B)$
. On the other hand, we always have
![]() $X \in \operatorname {\mathrm {Sub}}(X)$
as the maximal element. So we will use the notation
$X \in \operatorname {\mathrm {Sub}}(X)$
as the maximal element. So we will use the notation
![]() $A \leq X$
to mean that A is a subobject of X.
$A \leq X$
to mean that A is a subobject of X.
Convention 4.1. We extend Convention 2.9 to subobjects: given an extension
![]() $M \to N$
and a subobject
$M \to N$
and a subobject
![]() $A \leq M$
, we will view A as a subobject of N.
$A \leq M$
, we will view A as a subobject of N.
Definition 4.2. In an AECat with AP, an independence relation is a relation on triples of subobjects of models. If such a triple
![]() $(A, B, C)$
of subobjects of a model M is in the relation, we call it independent and write:
$(A, B, C)$
of subobjects of a model M is in the relation, we call it independent and write:

This notation should be read as “A is independent from B over C (in M)”.
We also allow each of the subobjects in the notation to be replaced by an arrow representing them. For example, if a is an arrow representing the subobject A then
![]() means
means
![]() .
.
We may want to restrict the objects that can appear in the base of the independence relation.
Definition 4.3. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP and let
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP and let
![]() $\mathcal {B}$
be a collection of objects in
$\mathcal {B}$
be a collection of objects in
![]() $\mathcal {C}$
, closed under isomorphic objects, with
$\mathcal {C}$
, closed under isomorphic objects, with
![]() $\mathcal {M} \subseteq \mathcal {B}$
. Then we call
$\mathcal {M} \subseteq \mathcal {B}$
. Then we call
![]() $\mathcal {B}$
a base class. An independence relation
$\mathcal {B}$
a base class. An independence relation
![]() is called an independence relation over
is called an independence relation over
![]() $\mathcal {B}$
if it only allows subobjects with their domain in
$\mathcal {B}$
if it only allows subobjects with their domain in
![]() $\mathcal {B}$
in the base. That is,
$\mathcal {B}$
in the base. That is,
![]() implies that the domain of C is in
implies that the domain of C is in
![]() $\mathcal {B}$
. We will also say that
$\mathcal {B}$
. We will also say that
![]() $\mathcal {B}$
is the base class of
$\mathcal {B}$
is the base class of
![]() , written as
, written as
![]() .
.
Convention 4.4. For a base class
![]() $\mathcal {B}$
and some subobject
$\mathcal {B}$
and some subobject
![]() $C \leq M$
we will also write
$C \leq M$
we will also write
![]() $C \in \mathcal {B}$
to mean that the domain of C is in
$C \in \mathcal {B}$
to mean that the domain of C is in
![]() $\mathcal {B}$
, and similarly for
$\mathcal {B}$
, and similarly for
![]() $C \not \in \mathcal {B}$
.
$C \not \in \mathcal {B}$
.
Definition 4.5. We call an independence relation
![]() a basic independence relation if it satisfies the following properties.
a basic independence relation if it satisfies the following properties.
-
Invariance
 and
and
 $\operatorname {\mathrm {gtp}}(a, b, c; M) = \operatorname {\mathrm {gtp}}(a', b', c'; M')$
implies
$\operatorname {\mathrm {gtp}}(a, b, c; M) = \operatorname {\mathrm {gtp}}(a', b', c'; M')$
implies
 .
. -
Monotonicity
 and
and
 $A' \leq A$
implies
$A' \leq A$
implies
 .
. -
Transitivity
 and
and
 with
with
 $B \leq C$
implies
$B \leq C$
implies
 .
. -
Symmetry
 implies
implies
 .
. -
Existence
 for all
for all
 .
. -
Extension If
 and
and
 $(b'; M)$
is such that b factors through
$(b'; M)$
is such that b factors through
 $b'$
then there is an extension
$b'$
then there is an extension
 $M \to N$
with some
$M \to N$
with some
 $(a'; N)$
such that
$(a'; N)$
such that
 $\operatorname {\mathrm {gtp}}(a', b, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
and
$\operatorname {\mathrm {gtp}}(a', b, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
and
 .
. -
Union Let
 $(B_i)_{i \in I}$
be a directed system with a cocone into some model M, and suppose
$(B_i)_{i \in I}$
be a directed system with a cocone into some model M, and suppose
 $B = \operatorname {\mathrm {colim}}_{i \in I} B_i$
exists. Then if
$B = \operatorname {\mathrm {colim}}_{i \in I} B_i$
exists. Then if
 for all
for all
 $i \in I$
, we have
$i \in I$
, we have
 .
.
Before we define some additional properties for independence relations, we first need to translate the notion of a club set to categorical language.
Definition 4.6. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat. For a model M and a regular cardinal
$(\mathcal {C}, \mathcal {M})$
be an AECat. For a model M and a regular cardinal
![]() $\kappa $
we write
$\kappa $
we write
![]() $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
for the poset of
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
for the poset of
![]() $\kappa $
-presentable subobjects of M in
$\kappa $
-presentable subobjects of M in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Note that if we are given a chain
![]() $(M_i)_{i < \theta }$
in
$(M_i)_{i < \theta }$
in
![]() $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
with
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
with
![]() $\theta < \kappa $
then its join in
$\theta < \kappa $
then its join in
![]() $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
exists and is given by
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
exists and is given by
![]() $\operatorname {\mathrm {colim}}_{i < \theta } M_i$
. This is the reason why we restrict ourselves to
$\operatorname {\mathrm {colim}}_{i < \theta } M_i$
. This is the reason why we restrict ourselves to
![]() $\mathcal {M}$
, because there we have directed colimits. If
$\mathcal {M}$
, because there we have directed colimits. If
![]() $\mathcal {C}$
has directed colimits as well then all these definitions would make sense for
$\mathcal {C}$
has directed colimits as well then all these definitions would make sense for
![]() $\mathcal {C}$
as well.
$\mathcal {C}$
as well.
Definition 4.7. Let
![]() $\mathcal {F} \subseteq \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
be a nonempty set.
$\mathcal {F} \subseteq \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
be a nonempty set.
-
(i) We call
 $\mathcal {F}$
unbounded if for every
$\mathcal {F}$
unbounded if for every
 $M_0 \in \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
there is
$M_0 \in \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
there is
 $M_1 \in \mathcal {F}$
such that
$M_1 \in \mathcal {F}$
such that
 $M_0 \leq M_1$
.
$M_0 \leq M_1$
. -
(ii) We call
 $\mathcal {F}$
closed if for any chain
$\mathcal {F}$
closed if for any chain
 $(M_i)_{i < \theta }$
in
$(M_i)_{i < \theta }$
in
 $\mathcal {F}$
with
$\mathcal {F}$
with
 $\theta < \kappa $
its join
$\theta < \kappa $
its join
 $\operatorname {\mathrm {colim}}_{i < \theta } M_i$
is again in
$\operatorname {\mathrm {colim}}_{i < \theta } M_i$
is again in
 $\mathcal {F}$
.
$\mathcal {F}$
. -
(iii) We call
 $\mathcal {F}$
a club set if it is closed and unbounded.
$\mathcal {F}$
a club set if it is closed and unbounded.
Fact 4.8. The following two facts are standard.
-
(i) The intersection of two club sets on
 $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
is again a club set.
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
is again a club set. -
(ii) If
 $M = \operatorname {\mathrm {colim}}_{i < \kappa } M_i$
, where
$M = \operatorname {\mathrm {colim}}_{i < \kappa } M_i$
, where
 $(M_i)_{i < \kappa }$
is a continuous chain of
$(M_i)_{i < \kappa }$
is a continuous chain of
 $\kappa $
-presentable models, then
$\kappa $
-presentable models, then
 $\{M_i : i < \kappa \}$
is a club set on
$\{M_i : i < \kappa \}$
is a club set on
 $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
.
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
.
Proof Fact (i) is standard, see for example [Reference Jech17, Theorem 8.2]. We just apply the argument to the poset
![]() $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
instead of to a cardinal considered as a poset. Fact (ii) is just unfolding definitions. The chain
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
instead of to a cardinal considered as a poset. Fact (ii) is just unfolding definitions. The chain
![]() $(M_i)_{i < \kappa }$
is unbounded because it is
$(M_i)_{i < \kappa }$
is unbounded because it is
![]() $\kappa $
-directed, so any
$\kappa $
-directed, so any
![]() $\kappa $
-presentable
$\kappa $
-presentable
![]() $M' \leq M$
will factor through the chain, and continuity is precisely saying that the chain is a closed set.
$M' \leq M$
will factor through the chain, and continuity is precisely saying that the chain is a closed set.
Definition 4.9. We also define the following properties for an independence relation.
-
Base-Monotonicity:
 and
and
 $C \leq C' \leq B$
with
$C \leq C' \leq B$
with
 implies
implies
 .
. -
Club Local Character: For every regular cardinal
 $\lambda $
there is a regular cardinal
$\lambda $
there is a regular cardinal
 $\Upsilon (\lambda )$
such that the following holds for all regular
$\Upsilon (\lambda )$
such that the following holds for all regular
 $\kappa \geq \Upsilon (\lambda )$
. Let
$\kappa \geq \Upsilon (\lambda )$
. Let
 $A, M \leq N$
, with
$A, M \leq N$
, with
 $A\ \lambda $
-presentable and M a model. Then there is a club set
$A\ \lambda $
-presentable and M a model. Then there is a club set
 $\mathcal {F} \subseteq \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
such that for all
$\mathcal {F} \subseteq \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
such that for all
 $M_0 \in \mathcal {F}$
we have
$M_0 \in \mathcal {F}$
we have
 .
. -
Stationarity: If
 $\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(a', m; N)$
, where the domain of m is a model, then
$\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(a', m; N)$
, where the domain of m is a model, then
 and
and
 implies
implies
 $\operatorname {\mathrm {gtp}}(a, m, b; N) = \operatorname {\mathrm {gtp}}(a', m, b; N)$
.
$\operatorname {\mathrm {gtp}}(a, m, b; N) = \operatorname {\mathrm {gtp}}(a', m, b; N)$
. -
Independence Theorem: Suppose we have
 ,
,
 ,
,
 and also
and also
 $\operatorname {\mathrm {Lgtp}}(a / c; M) = \operatorname {\mathrm {Lgtp}}(a' / c; M)$
. Then there is an extension
$\operatorname {\mathrm {Lgtp}}(a / c; M) = \operatorname {\mathrm {Lgtp}}(a' / c; M)$
. Then there is an extension
 $M \to N$
with
$M \to N$
with
 $(a^*; N)$
such that
$(a^*; N)$
such that
 $\operatorname {\mathrm {Lgtp}}(a^*, b / c; N) = \operatorname {\mathrm {Lgtp}}(a, b / c; N)$
,
$\operatorname {\mathrm {Lgtp}}(a^*, b / c; N) = \operatorname {\mathrm {Lgtp}}(a, b / c; N)$
,
 $\operatorname {\mathrm {Lgtp}}(a^*, b' / c; N) = \operatorname {\mathrm {Lgtp}}(a', b' / c; N)$
and
$\operatorname {\mathrm {Lgtp}}(a^*, b' / c; N) = \operatorname {\mathrm {Lgtp}}(a', b' / c; N)$
and
 .
.
Definition 4.10. Let
![]() be a basic independence relation. We call
be a basic independence relation. We call
![]()
-
•
 $\ldots $
a stable independence relation if it also satisfies Base-Monotonicity, Club Local Character, Stationarity and Independence Theorem.
$\ldots $
a stable independence relation if it also satisfies Base-Monotonicity, Club Local Character, Stationarity and Independence Theorem. -
•
 $\ldots $
a simple independence relation if it also satisfies Base-Monotonicity, Club Local Character and Independence Theorem.
$\ldots $
a simple independence relation if it also satisfies Base-Monotonicity, Club Local Character and Independence Theorem. -
•
 $\ldots $
an NSOP
$\ldots $
an NSOP
 $_1$
-like independence relation if it also satisfies Club Local Character and Independence Theorem;
$_1$
-like independence relation if it also satisfies Club Local Character and Independence Theorem;
We briefly compare the terminology we use here to the terminology in [Reference Kamsma18]. The notion of a base class is entirely new, so properties concerning the subobject in the base have been adjusted accordingly.
The Existence and Transitivity properties are different now, and we have added Extension. However, the formulation of existence and transitivity (together with invariance and monotonicity) in [Reference Kamsma18] implies our new formulation, see [Reference Kamsma18, Proposition 6.11]. The converse is also true: our new formulation of Existence, Transitivity and Extension (together with invariance) implies existence and transitivity there. So ultimately the two approaches are equivalent.
Remark 4.11. In a more traditional definition of local character, such as in simple theories, one would just require that for
![]() $A, M \leq N$
as above there is some
$A, M \leq N$
as above there is some
![]() $\Upsilon (\lambda )$
-presentable
$\Upsilon (\lambda )$
-presentable
![]() $M_0 \leq M$
such that
$M_0 \leq M$
such that
![]() . This is (almost) the definition that was used in [Reference Kamsma18], where we also have access to Base-Monotonicity. We then get Club Local Character by considering the club set
. This is (almost) the definition that was used in [Reference Kamsma18], where we also have access to Base-Monotonicity. We then get Club Local Character by considering the club set
![]() $\mathcal {F} = \{ M_0 \in \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M) : M_0 \leq M \}$
. In NSOP
$\mathcal {F} = \{ M_0 \in \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M) : M_0 \leq M \}$
. In NSOP
![]() $_1$
-like settings we do generally not have Base-Monotonicity. So Club Local Character then still gives us a good amount of Base-Monotonicity, namely on a club set. These ideas are due to [Reference Kaplan, Ramsey and Shelah22].
$_1$
-like settings we do generally not have Base-Monotonicity. So Club Local Character then still gives us a good amount of Base-Monotonicity, namely on a club set. These ideas are due to [Reference Kaplan, Ramsey and Shelah22].
Proposition 4.12 (Strong extension).
Let
![]() be a basic independence relation and suppose that
be a basic independence relation and suppose that
![]() . Then for any
. Then for any
![]() $(d; M)$
there is an extension
$(d; M)$
there is an extension
![]() $M \to N$
and
$M \to N$
and
![]() $(d'; N)$
such that
$(d'; N)$
such that
![]() $\operatorname {\mathrm {Lgtp}}(d'/b,c; N) = \operatorname {\mathrm {Lgtp}}(d/b,c; N)$
and
$\operatorname {\mathrm {Lgtp}}(d'/b,c; N) = \operatorname {\mathrm {Lgtp}}(d/b,c; N)$
and
![]() .
.
Proof We first apply Extension to find
![]() $M \to N_1$
with
$M \to N_1$
with
![]() $m': M \to N_1$
such that
$m': M \to N_1$
such that
![]() and
and
![]() $\operatorname {\mathrm {gtp}}(m', b, c; N_1) = \operatorname {\mathrm {gtp}}(m, b, c; N_1)$
. In particular this means that b and c factor through
$\operatorname {\mathrm {gtp}}(m', b, c; N_1) = \operatorname {\mathrm {gtp}}(m, b, c; N_1)$
. In particular this means that b and c factor through
![]() $m'$
by Fact 2.12. We apply Extension again to find an extension
$m'$
by Fact 2.12. We apply Extension again to find an extension
![]() $n_1: N_1 \to N$
and
$n_1: N_1 \to N$
and
![]() $n_1': N_1 \to N$
with
$n_1': N_1 \to N$
with
![]() and
and
![]() $\operatorname {\mathrm {gtp}}(n_1', m'; N) = \operatorname {\mathrm {gtp}}(n_1, m'; N)$
. We define
$\operatorname {\mathrm {gtp}}(n_1', m'; N) = \operatorname {\mathrm {gtp}}(n_1, m'; N)$
. We define
![]() $d'$
to be the composition
$d'$
to be the composition
![]() $D \xrightarrow {d} M \to N_1 \xrightarrow {n_1'} N$
. By Monotonicity we then have
$D \xrightarrow {d} M \to N_1 \xrightarrow {n_1'} N$
. By Monotonicity we then have
![]() . We also have
. We also have
![]() $\operatorname {\mathrm {gtp}}(d', m'; N) = \operatorname {\mathrm {gtp}}(d, m'; N)$
, so since b and c factor through
$\operatorname {\mathrm {gtp}}(d', m'; N) = \operatorname {\mathrm {gtp}}(d, m'; N)$
, so since b and c factor through
![]() $m'$
, and
$m'$
, and
![]() $m'$
has a model as domain, we indeed get
$m'$
has a model as domain, we indeed get
![]() $\operatorname {\mathrm {Lgtp}}(d'/b,c; N) = \operatorname {\mathrm {Lgtp}}(d/b,c; N)$
.
$\operatorname {\mathrm {Lgtp}}(d'/b,c; N) = \operatorname {\mathrm {Lgtp}}(d/b,c; N)$
.
Corollary 4.13. Let
![]() be a basic independence relation and suppose that
be a basic independence relation and suppose that
![]() . Then for any
. Then for any
![]() $(d; M)$
there is
$(d; M)$
there is
![]() $M \to N$
and
$M \to N$
and
![]() $(a'; N)$
such that
$(a'; N)$
such that
![]() $\operatorname {\mathrm {Lgtp}}(a'/b,c; N) = \operatorname {\mathrm {Lgtp}}(a/b,c; N)$
and
$\operatorname {\mathrm {Lgtp}}(a'/b,c; N) = \operatorname {\mathrm {Lgtp}}(a/b,c; N)$
and
![]() .
.
Proof Apply Proposition 4.12 to find
![]() $M \to N'$
with
$M \to N'$
with
![]() $(d'; N')$
such that
$(d'; N')$
such that
![]() and
and
![]() $\operatorname {\mathrm {Lgtp}}(d'/b,c; N') = \operatorname {\mathrm {Lgtp}}(d/b,c; N')$
. Then just pick
$\operatorname {\mathrm {Lgtp}}(d'/b,c; N') = \operatorname {\mathrm {Lgtp}}(d/b,c; N')$
. Then just pick
![]() $(a'; N)$
in an extension
$(a'; N)$
in an extension
![]() $N' \to N$
such that
$N' \to N$
such that
![]() $\operatorname {\mathrm {Lgtp}}(a',d/b,c; N) = \operatorname {\mathrm {Lgtp}}(a,d'/b,c; N)$
.
$\operatorname {\mathrm {Lgtp}}(a',d/b,c; N) = \operatorname {\mathrm {Lgtp}}(a,d'/b,c; N)$
.
Convention 4.14. We call the class function
![]() $\Upsilon $
for Club Local Character a local character function. For an object A we write
$\Upsilon $
for Club Local Character a local character function. For an object A we write
![]() $\Upsilon (A)$
for
$\Upsilon (A)$
for
![]() $\Upsilon (\lambda )$
where
$\Upsilon (\lambda )$
where
![]() $\lambda $
is the least regular cardinal such that A is
$\lambda $
is the least regular cardinal such that A is
![]() $\lambda $
-presentable.
$\lambda $
-presentable.
Lemma 4.15 (Chain local character).
Let
![]() be an independence relation satisfying Club Local Character. Let
be an independence relation satisfying Club Local Character. Let
![]() $A \leq N$
and
$A \leq N$
and
![]() $\kappa \geq \Upsilon (A)$
. Suppose that we are given a continuous chain
$\kappa \geq \Upsilon (A)$
. Suppose that we are given a continuous chain
![]() $(M_i)_{i < \kappa }$
of
$(M_i)_{i < \kappa }$
of
![]() $\kappa $
-presentable models with
$\kappa $
-presentable models with
![]() $M = \operatorname {\mathrm {colim}}_{i < \kappa } M_i \leq N$
. Then there is
$M = \operatorname {\mathrm {colim}}_{i < \kappa } M_i \leq N$
. Then there is
![]() $i_0 < \kappa $
such that
$i_0 < \kappa $
such that
![]() .
.
Proof Let
![]() $\mathcal {F} \subseteq \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
be the club set from Club Local Character. By Fact 4.8(ii) the chain
$\mathcal {F} \subseteq \operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
be the club set from Club Local Character. By Fact 4.8(ii) the chain
![]() $(M_i)_{i < \kappa }$
forms a club set on
$(M_i)_{i < \kappa }$
forms a club set on
![]() $\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
. So by Fact 4.8(i)
$\operatorname {\mathrm {Sub}}^\kappa _{\mathcal {M}}(M)$
. So by Fact 4.8(i)
![]() $\{ M_i : i < \kappa \} \cap \mathcal {F}$
is nonempty.
$\{ M_i : i < \kappa \} \cap \mathcal {F}$
is nonempty.
Remark 4.16. For all our results we only need chain local character. That is, the conclusion of Lemma 4.15. In particular the canonicity theorems in Section 7 go through even if we would just assume chain local character.
Given that we actually only need chain local character, as per Remark 4.16, it is natural to ask whether the converse of Lemma 4.15 holds. That is, if chain local character implies Club Local Character. This is not so clear, so we leave it at this.
We recall the following from [Reference Kamsma18, Definition 6.13].Footnote 1
Definition 4.17. Suppose we have an independence relation
. Let
![]() $(a_i)_{i < \kappa }$
be a sequence in some M and let
$(a_i)_{i < \kappa }$
be a sequence in some M and let
![]() $c: C \to M$
be an arrow. Suppose that
$c: C \to M$
be an arrow. Suppose that
![]() $(M_i)_{i < \kappa }$
is a chain of initial segments for
$(M_i)_{i < \kappa }$
is a chain of initial segments for
![]() $(a_i)_{i < \kappa }$
and that c embeds in the chain. Then we call
$(a_i)_{i < \kappa }$
and that c embeds in the chain. Then we call
![]() $(M_i)_{i < \kappa }$
witnesses of
$(M_i)_{i < \kappa }$
witnesses of
-independence for
![]() $(a_i)_{i < \kappa }$
if
$(a_i)_{i < \kappa }$
if

for all
![]() $i < \kappa $
. We say that a sequence is
$i < \kappa $
. We say that a sequence is
-independent if it admits a chain of witnesses of
-independence.
The following proposition is the standard argument showing that we can find arbitrarily long independent sequences, assuming very few properties for our independence relation (see, e.g., [Reference Kim25, Proposition 2.2.4]). The proposition after that shows that if we additionally assume Union we can actually get arbitrarily long independent isi-sequences.
Proposition 4.18. Let
![]() be an independence relation satisfying Invariance, Existence and Extension. Then for any
be an independence relation satisfying Invariance, Existence and Extension. Then for any
![]() $(a, c; M)$
with
$(a, c; M)$
with
![]() and any
and any
![]() $\kappa $
there is some extension
$\kappa $
there is some extension
![]() $M \to N$
containing a
$M \to N$
containing a
![]() -independent sequence
-independent sequence
![]() $(a_i)_{i < \kappa }$
with
$(a_i)_{i < \kappa }$
with
![]() $\operatorname {\mathrm {gtp}}(a_i, c; N) = \operatorname {\mathrm {gtp}}(a, c; M)$
for all
$\operatorname {\mathrm {gtp}}(a_i, c; N) = \operatorname {\mathrm {gtp}}(a, c; M)$
for all
![]() $i < \kappa $
.
$i < \kappa $
.
Proof We construct the witnesses of independence
![]() $(M_i)_{i < \kappa }$
and sequence
$(M_i)_{i < \kappa }$
and sequence
![]() $(a_i)_{i < \kappa }$
by induction. At stage i we will construct
$(a_i)_{i < \kappa }$
by induction. At stage i we will construct
![]() $a_i$
and
$a_i$
and
![]() $M_{i+1}$
. By Existence we have
$M_{i+1}$
. By Existence we have
![]() , and so we will have
, and so we will have
![]() for all
for all
![]() $i < \kappa $
. At every stage we will apply Extension to the latter.
$i < \kappa $
. At every stage we will apply Extension to the latter.
For the base case we set
![]() $M_0 = M$
and use Extension to find
$M_0 = M$
and use Extension to find
![]() $a_0$
and
$a_0$
and
![]() $M \to M_1$
with
$M \to M_1$
with
![]() $\operatorname {\mathrm {gtp}}(a_0, c; M_1) = \operatorname {\mathrm {gtp}}(a, c; M)$
and
$\operatorname {\mathrm {gtp}}(a_0, c; M_1) = \operatorname {\mathrm {gtp}}(a, c; M)$
and
![]() . In the successor step we use Extension to find
. In the successor step we use Extension to find
![]() $M_{i+1} \to M_{i+2}$
and
$M_{i+1} \to M_{i+2}$
and
![]() $a_{i+1}$
such that
$a_{i+1}$
such that
![]() and
and
![]() $\operatorname {\mathrm {gtp}}(a_{i+1}, c; M_{i+2}) = \operatorname {\mathrm {gtp}}(a, c; M)$
. Finally, for limit
$\operatorname {\mathrm {gtp}}(a_{i+1}, c; M_{i+2}) = \operatorname {\mathrm {gtp}}(a, c; M)$
. Finally, for limit
![]() $\ell < \kappa $
let
$\ell < \kappa $
let
![]() $M_\ell = \operatorname {\mathrm {colim}}_{i < \ell } M_i$
. We use Extension to find
$M_\ell = \operatorname {\mathrm {colim}}_{i < \ell } M_i$
. We use Extension to find
![]() $M_\ell \to M_{\ell +1}$
and
$M_\ell \to M_{\ell +1}$
and
![]() $a_\ell $
with
$a_\ell $
with
![]() $\operatorname {\mathrm {gtp}}(a_\ell , c; M_{\ell +1}) = \operatorname {\mathrm {gtp}}(a, c; M)$
and
$\operatorname {\mathrm {gtp}}(a_\ell , c; M_{\ell +1}) = \operatorname {\mathrm {gtp}}(a, c; M)$
and
![]() . We finish the construction by taking
. We finish the construction by taking
![]() $N = \operatorname {\mathrm {colim}}_{i < \kappa } M_i$
.
$N = \operatorname {\mathrm {colim}}_{i < \kappa } M_i$
.
Proposition 4.19. Suppose that
![]() is an independence relation satisfying Invariance, Existence, Extension and Union. Then given
is an independence relation satisfying Invariance, Existence, Extension and Union. Then given
![]() $(a, c; M)$
with
$(a, c; M)$
with
![]() and any
and any
![]() $\kappa $
, there is a
$\kappa $
, there is a
![]() -independent isi-sequence
-independent isi-sequence
![]() $(a_i)_{i < \kappa }$
over c in some extension
$(a_i)_{i < \kappa }$
over c in some extension
![]() $M \to N$
such that
$M \to N$
such that
![]() $\operatorname {\mathrm {gtp}}(a_i, c; N) = \operatorname {\mathrm {gtp}}(a, c; M)$
for all
$\operatorname {\mathrm {gtp}}(a_i, c; N) = \operatorname {\mathrm {gtp}}(a, c; M)$
for all
![]() $i < \kappa $
.
$i < \kappa $
.
Proof This is just [Reference Kamsma18, Lemma 6.14]. The differences in terminology are discussed after Definition 4.10. In particular, the monotonicity assumption there is only necessary to get what we call Extension. Finally, there is no notion of base class there, but this is only relevant in the application of Existence, which is only applied with c in the base. Hence the assumption
![]() .
.
5 Independence theorem, 3-amalgamation, and stationarity
It is well known that the property Independence Theorem can also be formulated as an amalgamation property of some independent system. This allows for a more categorical statement without any mention of Lascar strong Galois types. However, we need to restrict ourselves to work only over models. We will give this property its own name and prove its equivalence to Independence Theorem, modulo some basic properties, in Theorem 5.2.
The contents of this section are not necessary for the results in the rest of this paper, but we do refer to them a few times in remarks and discussions.
Definition 5.1 [Reference Kamsma18, Definition 6.7].
An independence relation
has 3-amalgamation if the following holds. Suppose that we have

overloading notation for subobjects of different models. Suppose furthermore that M is a model and that
 $$ \begin{align*} \operatorname{\mathrm{gtp}}(a, m; N_1) &= \operatorname{\mathrm{gtp}}(a, m; N_3), \\ \operatorname{\mathrm{gtp}}(b, m; N_1) &= \operatorname{\mathrm{gtp}}(b, m; N_2), \\ \operatorname{\mathrm{gtp}}(c, m; N_2) &= \operatorname{\mathrm{gtp}}(c, m; N_3), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gtp}}(a, m; N_1) &= \operatorname{\mathrm{gtp}}(a, m; N_3), \\ \operatorname{\mathrm{gtp}}(b, m; N_1) &= \operatorname{\mathrm{gtp}}(b, m; N_2), \\ \operatorname{\mathrm{gtp}}(c, m; N_2) &= \operatorname{\mathrm{gtp}}(c, m; N_3), \end{align*} $$
where a, b, c, and m are representatives for the subobjects A, B, C, and M respectively (again, overloading notation for different models). Then we can find extensions from
![]() $N_1$
,
$N_1$
,
![]() $N_2$
, and
$N_2$
, and
![]() $N_3$
to some N such that the diagram we obtain in that way commutes:
$N_3$
to some N such that the diagram we obtain in that way commutes:

Furthermore, these extensions are such that
.
Theorem 5.2. Let
![]() be a basic independence relation. If
be a basic independence relation. If
![]() satisfies Independence Theorem then it also satisfies 3-amalgamation. Conversely, if
satisfies Independence Theorem then it also satisfies 3-amalgamation. Conversely, if
![]() satisfies 3-amalgamation then it satisfies Independence Theorem over models (i.e., we require the base C to be a model).
satisfies 3-amalgamation then it satisfies Independence Theorem over models (i.e., we require the base C to be a model).
Proof We first prove that Independence Theorem implies 3-amalgamation. Let the set up be as in Definition 5.1. In the diagram below we find the dashed arrows by using
![]() $\operatorname {\mathrm {gtp}}(c, m; N_2) = \operatorname {\mathrm {gtp}}(c, m; N_3)$
and
$\operatorname {\mathrm {gtp}}(c, m; N_2) = \operatorname {\mathrm {gtp}}(c, m; N_3)$
and
![]() $\operatorname {\mathrm {gtp}}(b, m; N_1) = \operatorname {\mathrm {gtp}}(b, m; N_2)$
.
$\operatorname {\mathrm {gtp}}(b, m; N_1) = \operatorname {\mathrm {gtp}}(b, m; N_2)$
.

We write
![]() $a_1$
for the arrow
$a_1$
for the arrow
![]() $A \to N_1 \to N'$
and
$A \to N_1 \to N'$
and
![]() $a_3$
for the arrow
$a_3$
for the arrow
![]() $A \to N_3 \to N'$
. Then we have
$A \to N_3 \to N'$
. Then we have
![]() $\operatorname {\mathrm {Lgtp}}(a_1 / m; N') = \operatorname {\mathrm {Lgtp}}(a_3 / m; N')$
. We can thus apply Independence Theorem to find some extension
$\operatorname {\mathrm {Lgtp}}(a_1 / m; N') = \operatorname {\mathrm {Lgtp}}(a_3 / m; N')$
. We can thus apply Independence Theorem to find some extension
![]() $N' \to N^*$
with some
$N' \to N^*$
with some
![]() $a^*: A \to N^*$
such that
$a^*: A \to N^*$
such that
![]() $\operatorname {\mathrm {Lgtp}}(a^*,b/m; N^*) = \operatorname {\mathrm {Lgtp}}(a_1,b/m; N^*)$
,
$\operatorname {\mathrm {Lgtp}}(a^*,b/m; N^*) = \operatorname {\mathrm {Lgtp}}(a_1,b/m; N^*)$
,
![]() $\operatorname {\mathrm {Lgtp}}(a^*,c/m; N^*) = \operatorname {\mathrm {Lgtp}}(a_3,c/m; N^*)$
and
$\operatorname {\mathrm {Lgtp}}(a^*,c/m; N^*) = \operatorname {\mathrm {Lgtp}}(a_3,c/m; N^*)$
and
. So in particular we have
by Monotonicity. Using
![]() $\operatorname {\mathrm {gtp}}(a, b, m; N_1) = \operatorname {\mathrm {gtp}}(a_1, b, m; N^*) = \operatorname {\mathrm {gtp}}(a^*, b, m; N^*)$
and
$\operatorname {\mathrm {gtp}}(a, b, m; N_1) = \operatorname {\mathrm {gtp}}(a_1, b, m; N^*) = \operatorname {\mathrm {gtp}}(a^*, b, m; N^*)$
and
![]() $\operatorname {\mathrm {gtp}}(a, c, m; N_3) = \operatorname {\mathrm {gtp}}(a_3, c, m; N^*) = \operatorname {\mathrm {gtp}}(a^*, c, m; N^*)$
after each other we find an extension
$\operatorname {\mathrm {gtp}}(a, c, m; N_3) = \operatorname {\mathrm {gtp}}(a_3, c, m; N^*) = \operatorname {\mathrm {gtp}}(a^*, c, m; N^*)$
after each other we find an extension
![]() $N^* \to N$
together with extensions from
$N^* \to N$
together with extensions from
![]() $N_1$
and
$N_1$
and
![]() $N_3$
to N and we just forget about the previous extensions from
$N_3$
to N and we just forget about the previous extensions from
![]() $N_1$
and
$N_1$
and
![]() $N_3$
to
$N_3$
to
![]() $N^*$
. These two new extensions, together with
$N^*$
. These two new extensions, together with
![]() $N_2 \to N^* \to N$
, then form the solution to our 3-amalgamation problem.
$N_2 \to N^* \to N$
, then form the solution to our 3-amalgamation problem.
Now we prove the converse. So we assume 3-amalgamation and we prove Independence Theorem over models. So suppose that
,
and
and
![]() $\operatorname {\mathrm {Lgtp}}(a / m; N) = \operatorname {\mathrm {Lgtp}}(a' / m; N)$
. Then we can form the commuting diagram as below, where we find the dashed arrows by 3-amalgamation.
$\operatorname {\mathrm {Lgtp}}(a / m; N) = \operatorname {\mathrm {Lgtp}}(a' / m; N)$
. Then we can form the commuting diagram as below, where we find the dashed arrows by 3-amalgamation.

We take the extension
![]() $N \to N^*$
to be h and write
$N \to N^*$
to be h and write
![]() $a^*$
for
$a^*$
for
![]() $fa = ga'$
. The application of 3-amalgamation yields
$fa = ga'$
. The application of 3-amalgamation yields
![]() . Furthermore,
. Furthermore,
![]() $\operatorname {\mathrm {gtp}}(a^*, b, m; N^*) = \operatorname {\mathrm {gtp}}(a, b, m; N) = \operatorname {\mathrm {gtp}}(a, b, m; N^*)$
, so
$\operatorname {\mathrm {gtp}}(a^*, b, m; N^*) = \operatorname {\mathrm {gtp}}(a, b, m; N) = \operatorname {\mathrm {gtp}}(a, b, m; N^*)$
, so
![]() $\operatorname {\mathrm {Lgtp}}(a^*, b / m; N^*) = \operatorname {\mathrm {Lgtp}}(a, b / m; N^*)$
because the domain of m is a model. Similarly, we also find
$\operatorname {\mathrm {Lgtp}}(a^*, b / m; N^*) = \operatorname {\mathrm {Lgtp}}(a, b / m; N^*)$
because the domain of m is a model. Similarly, we also find
![]() $\operatorname {\mathrm {Lgtp}}(a^*, c / m; N^*) = \operatorname {\mathrm {Lgtp}}(a', c / m; N^*)$
, which concludes the proof.
$\operatorname {\mathrm {Lgtp}}(a^*, c / m; N^*) = \operatorname {\mathrm {Lgtp}}(a', c / m; N^*)$
, which concludes the proof.
We recall that 3-amalgamation follows from Stationarity. This might for example be useful in the case where
![]() , so one does not need to verify the Independence Theorem property for a stable independence relation, as it follows automatically. In particular this means that a stable independence relation in the sense of [Reference Lieberman, Rosický and Vasey27] also yields a stable independence relation in our setting and vice versa, see also [Reference Kamsma18, Remark 6.7] for further comparison.
, so one does not need to verify the Independence Theorem property for a stable independence relation, as it follows automatically. In particular this means that a stable independence relation in the sense of [Reference Lieberman, Rosický and Vasey27] also yields a stable independence relation in our setting and vice versa, see also [Reference Kamsma18, Remark 6.7] for further comparison.
Fact 5.3 [Reference Kamsma18, Proposition 6.16].
Let
![]() be a basic independence relation satisfying Stationarity then it also satisfies 3-amalgamation.
be a basic independence relation satisfying Stationarity then it also satisfies 3-amalgamation.
6 Long dividing, isi-dividing, and long Kim-dividing
In this section we introduce various notions of dividing, each yielding its own independence relation. These notions are based on the classical notion of dividing, as we know it from first-order logic. For the convenience of the reader, and to compare it to the new definitions, we recall the definition of dividing.
Definition 6.1. In the classical setting of first-order logic, we say that a type
![]() $p(x, b) = \operatorname {\mathrm {tp}}(a/Cb)$
divides over C if there is a C-indiscernible sequence
$p(x, b) = \operatorname {\mathrm {tp}}(a/Cb)$
divides over C if there is a C-indiscernible sequence
![]() $(b_i)_{i < \omega }$
such that
$(b_i)_{i < \omega }$
such that
![]() $\operatorname {\mathrm {tp}}(b_i/C) = \operatorname {\mathrm {tp}}(b/C)$
for all
$\operatorname {\mathrm {tp}}(b_i/C) = \operatorname {\mathrm {tp}}(b/C)$
for all
![]() $i < \omega $
and
$i < \omega $
and
![]() $\bigcup _{i < \omega } p(x, b_i)$
is inconsistent.
$\bigcup _{i < \omega } p(x, b_i)$
is inconsistent.
In many proofs, to use this definition, one has to apply compactness in one way or another. For example to elongate the sequence
![]() $(b_i)_{i < \omega }$
, or to find a finite subsequence along which p is inconsistent. This is generally an issue in AECats, because we do not have compactness there. To solve this we introduce the notion of long dividing. The name is due to the fact that we consider arbitrarily long sequences in the definition, something that we would normally have to use compactness for. This is very close to the notion of isi-dividing from [Reference Kamsma18, Definition 5.7]. In fact, isi-dividing is just long dividing but then restricted to isi-sequences, so that we have some homogeneity in the sequences involved. Of course, indiscernible sequences would be even more homogeneous, but the little bit that isi-sequences offer us turns out to be enough.
$(b_i)_{i < \omega }$
, or to find a finite subsequence along which p is inconsistent. This is generally an issue in AECats, because we do not have compactness there. To solve this we introduce the notion of long dividing. The name is due to the fact that we consider arbitrarily long sequences in the definition, something that we would normally have to use compactness for. This is very close to the notion of isi-dividing from [Reference Kamsma18, Definition 5.7]. In fact, isi-dividing is just long dividing but then restricted to isi-sequences, so that we have some homogeneity in the sequences involved. Of course, indiscernible sequences would be even more homogeneous, but the little bit that isi-sequences offer us turns out to be enough.
We remind the reader of Fact 2.1, namely that all cardinals considered are regular. So in the following definition we only quantify over regular cardinals.
Definition 6.2. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP and fix some
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP and fix some
![]() $(a, b, c; M)$
.
$(a, b, c; M)$
.
-
(i) Suppose that we have some sequence
 $((b_i)_{i \in I}; M)$
such that
$((b_i)_{i \in I}; M)$
such that
 $\operatorname {\mathrm {gtp}}(b_i, c; M) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i, c; M) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
 $i \in I$
. We say that
$i \in I$
. We say that
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
 $(b_i)_{i \in I}$
if there is an extension
$(b_i)_{i \in I}$
if there is an extension
 $M \to N$
and an arrow
$M \to N$
and an arrow
 $(a'; N)$
such that
$(a'; N)$
such that  $$\begin{align*}\operatorname{\mathrm{gtp}}(a, b, c; M) = \operatorname{\mathrm{gtp}}(a', b_i, c; N) \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gtp}}(a, b, c; M) = \operatorname{\mathrm{gtp}}(a', b_i, c; N) \end{align*}$$
for all
 $i \in I$
. We call
$i \in I$
. We call
 $a'$
a realisation of
$a'$
a realisation of
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
for
 $(b_i)_{i \in I}$
.
$(b_i)_{i \in I}$
.Being inconsistent is the negation of the above. So
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
 $(b_i)_{i \in I}$
if there is no extension of M with a realisation
$(b_i)_{i \in I}$
if there is no extension of M with a realisation
 $a'$
of
$a'$
of
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
for
 $(b_i)_{i \in I}$
.
$(b_i)_{i \in I}$
. -
(ii) We say that
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
long divides over c if there is
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
long divides over c if there is
 $\mu $
such that for every
$\mu $
such that for every
 $\lambda \geq \mu $
there is a sequence
$\lambda \geq \mu $
there is a sequence
 $(b_i)_{i < \lambda }$
in some extension
$(b_i)_{i < \lambda }$
in some extension
 $M \to N$
with
$M \to N$
with
 $\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
 $i < \lambda $
, such that for some
$i < \lambda $
, such that for some
 $\kappa < \lambda $
and every
$\kappa < \lambda $
and every
 $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
 $|I| = \kappa $
we have that
$|I| = \kappa $
we have that
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
 $(b_i)_{i \in I}$
.
$(b_i)_{i \in I}$
. -
(iii) We say that
 $\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-divides if it long divides with respect to isi-sequences over c. That is, we require the sequence
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-divides if it long divides with respect to isi-sequences over c. That is, we require the sequence
 $(b_i)_{i < \lambda }$
to be an isi-sequence over c.
$(b_i)_{i < \lambda }$
to be an isi-sequence over c.
Remark 6.3. We discussed how long dividing and isi-dividing are inspired by dividing. A natural question would be whether or not they are actually the same. This was discussed in [Reference Kamsma18] from Remark 5.8 and onwards. The discussion there is just about isi-dividing but applies to long dividing as well. The summary is as follows, restricting ourselves to AECats obtained from a first-order theory.
-
(i) Dividing implies isi-dividing implies long dividing.
-
(ii) Long dividing (and thus isi-dividing) implies dividing if we assume the existence of a proper class of Ramsey cardinals.
-
(iii) Using the canonicity theorem, Theorem 1.2, we can actually drop the large cardinal assumption and conclude that isi-dividing implies dividing in simple theories.
-
(iv) The question remains: does long dividing (and thus isi-dividing) generally imply dividing, without the large cardinal assumption?
In fact, dividing makes sense in positive logic as well (see [Reference Ben-Yaacov4, Reference Pillay28]), and the above discussion applies to AECats obtained from a positive theory as well. There is an even more general setting, namely that of finitely short AECats, where this discussion applies. These are AECats where a Galois type of an infinite tuple of arrows is determined by the Galois types of the finite subtuples, see [Reference Kamsma19, Section 4]. This is more or less the same framework as that of homogeneous model theory in the sense of [Reference Buechler and Lessmann9] (see [Reference Kamsma18, Example 4.4]).
The point of these dividing notions is that they yield independence relations. We can already prove some basic properties about these independence relations in arbitrary AECats, similar to the basic properties that dividing always has.
Proposition 6.4. Let
![]() $A, B, C \leq M$
be subobjects. Let
$A, B, C \leq M$
be subobjects. Let
![]() $(a, b, c; M)$
and
$(a, b, c; M)$
and
![]() $(a', b', c'; M)$
be two sets of representatives. Then
$(a', b', c'; M)$
be two sets of representatives. Then
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
long divides over c if and only if
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
long divides over c if and only if
![]() $\operatorname {\mathrm {gtp}}(a', b', c'; M)$
long divides over
$\operatorname {\mathrm {gtp}}(a', b', c'; M)$
long divides over
![]() $c'$
. The same statement holds for isi-dividing.
$c'$
. The same statement holds for isi-dividing.
Proof This comes down to checking all the definitions, which is lengthy to do in detail. However, there is only one trick that we repeatedly use, and that is Fact 2.11(ii). To apply this trick we let
![]() $f, g, h$
be isomorphisms such that
$f, g, h$
be isomorphisms such that
![]() $a' = af$
,
$a' = af$
,
![]() $b' = bg$
and
$b' = bg$
and
![]() $c' = ch$
. Then, using the above trick, we easily see that for any sequence
$c' = ch$
. Then, using the above trick, we easily see that for any sequence
![]() $(b_i)_{i < \lambda }$
witnessing long dividing of
$(b_i)_{i < \lambda }$
witnessing long dividing of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
we have that
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
we have that
![]() $(b_i g)_{i < \lambda }$
witnesses long dividing for
$(b_i g)_{i < \lambda }$
witnesses long dividing for
![]() $\operatorname {\mathrm {gtp}}(a, b g, c; M) = \operatorname {\mathrm {gtp}}(a, b', c; M)$
. Similarly we can replace c by
$\operatorname {\mathrm {gtp}}(a, b g, c; M) = \operatorname {\mathrm {gtp}}(a, b', c; M)$
. Similarly we can replace c by
![]() $ch = c'$
and a by
$ch = c'$
and a by
![]() $af = a'$
. The same holds for isi-dividing, noting that any isi-sequence over c is also an isi-sequence over
$af = a'$
. The same holds for isi-dividing, noting that any isi-sequence over c is also an isi-sequence over
![]() $ch = c'$
.
$ch = c'$
.
Definition 6.5. For subobjects
![]() $A, B, C \leq M$
we write
$A, B, C \leq M$
we write
![]() if
if
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not long divide for all (equivalently: some) representatives
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not long divide for all (equivalently: some) representatives
![]() $a, b, c$
of
$a, b, c$
of
![]() $A, B, C$
. Similarly, we write
$A, B, C$
. Similarly, we write
![]() if
if
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-divide.
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-divide.
As
![]() and
and
![]() do not generally satisfy Symmetry we have to distinguish between “left” and “right” versions of certain properties, as we do below.
do not generally satisfy Symmetry we have to distinguish between “left” and “right” versions of certain properties, as we do below.
Proposition 6.6. Long dividing and isi-dividing always satisfy the following
![]() $:$
Invariance, Left-Monotonicity, Existence, and Base-Monotonicity. In addition, long dividing also satisfies Right-Monotonicity.
$:$
Invariance, Left-Monotonicity, Existence, and Base-Monotonicity. In addition, long dividing also satisfies Right-Monotonicity.
Proof Everything is direct from the definition, except for Right-Monotonicity for long dividing and Base-Monotonicity. For both we will prove the contraposition.
For Base-Monotonicity let
![]() $(a, b, c, c'; M)$
be such that
$(a, b, c, c'; M)$
be such that
![]() $\operatorname {\mathrm {gtp}}(a, b, c'; M)$
long divides over
$\operatorname {\mathrm {gtp}}(a, b, c'; M)$
long divides over
![]() $c'$
and
$c'$
and
![]() $C \leq C' \leq B$
, where
$C \leq C' \leq B$
, where
![]() $C, C', B$
are the subobjects represented by
$C, C', B$
are the subobjects represented by
![]() $c, c', b$
respectively. Let
$c, c', b$
respectively. Let
![]() $\mu $
be as in the definition of long dividing and let
$\mu $
be as in the definition of long dividing and let
![]() $\lambda \geq \mu $
. Then there is
$\lambda \geq \mu $
. Then there is
![]() $(b_i)_{i < \lambda }$
in some N that witnesses long dividing of
$(b_i)_{i < \lambda }$
in some N that witnesses long dividing of
![]() $\operatorname {\mathrm {gtp}}(a, b, c'; M)$
over
$\operatorname {\mathrm {gtp}}(a, b, c'; M)$
over
![]() $c'$
. We will prove that it also witnesses long dividing of
$c'$
. We will prove that it also witnesses long dividing of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
. Indeed we have for all
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
. Indeed we have for all
![]() $i < \lambda $
that
$i < \lambda $
that
![]() $\operatorname {\mathrm {gtp}}(b_i, c'; N) = \operatorname {\mathrm {gtp}}(b, c'; M)$
and thus
$\operatorname {\mathrm {gtp}}(b_i, c'; N) = \operatorname {\mathrm {gtp}}(b, c'; M)$
and thus
![]() $\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
, because
$\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
, because
![]() $C \leq C'$
. Let
$C \leq C'$
. Let
![]() $\kappa < \lambda $
be such that for
$\kappa < \lambda $
be such that for
![]() $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
![]() $|I| = \kappa $
we have that
$|I| = \kappa $
we have that
![]() $\operatorname {\mathrm {gtp}}(a, b, c'; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b, c'; M)$
is inconsistent for
![]() $(b_i)_{i \in I}$
. We claim that for such I we also have that
$(b_i)_{i \in I}$
. We claim that for such I we also have that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
![]() $(b_i)_{i \in I}$
. Suppose that there would be a realisation
$(b_i)_{i \in I}$
. Suppose that there would be a realisation
![]() $(a'; N')$
for some extension
$(a'; N')$
for some extension
![]() $N \to N'$
, then
$N \to N'$
, then
![]() $\operatorname {\mathrm {gtp}}(a', b_i, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(a', b_i, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
for all
![]() $i \in I$
. Since
$i \in I$
. Since
![]() $c'$
factors through b and
$c'$
factors through b and
![]() $b_i$
in the same way for all
$b_i$
in the same way for all
![]() $i < \lambda $
, see Fact 2.12, we then have
$i < \lambda $
, see Fact 2.12, we then have
![]() $\operatorname {\mathrm {gtp}}(a', b_i, c'; N') = \operatorname {\mathrm {gtp}}(a, b, c'; M)$
for all
$\operatorname {\mathrm {gtp}}(a', b_i, c'; N') = \operatorname {\mathrm {gtp}}(a, b, c'; M)$
for all
![]() $i \in I$
, contradicting that
$i \in I$
, contradicting that
![]() $\operatorname {\mathrm {gtp}}(a, b, c'; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b, c'; M)$
is inconsistent for
![]() $(b_i)_{i \in I}$
. This proves Base-Monotonicity for long dividing. We have shown that the same sequences that witness long dividing of
$(b_i)_{i \in I}$
. This proves Base-Monotonicity for long dividing. We have shown that the same sequences that witness long dividing of
![]() $\operatorname {\mathrm {gtp}}(a, b, c'; M)$
also witness long dividing of
$\operatorname {\mathrm {gtp}}(a, b, c'; M)$
also witness long dividing of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
. As any isi-sequence over
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
. As any isi-sequence over
![]() $c'$
is an isi-sequence over c, the same proof shows that isi-dividing has Base-Monotonicity.
$c'$
is an isi-sequence over c, the same proof shows that isi-dividing has Base-Monotonicity.
Now we prove Right-Monotonicity for long dividing. Let
![]() $(a, b, b', c; M)$
be such that
$(a, b, b', c; M)$
be such that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
long divides over c and b factors through
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
long divides over c and b factors through
![]() $b'$
. For any sequence
$b'$
. For any sequence
![]() $(b_i)_{i < \lambda }$
in some N witnessing long dividing we can form
$(b_i)_{i < \lambda }$
in some N witnessing long dividing we can form
![]() $(b_i')_{i < \lambda }$
by letting
$(b_i')_{i < \lambda }$
by letting
![]() $b_i'$
be such that
$b_i'$
be such that
![]() $\operatorname {\mathrm {gtp}}(b_i', b_i, c; N) = \operatorname {\mathrm {gtp}}(b', b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i', b_i, c; N) = \operatorname {\mathrm {gtp}}(b', b, c; M)$
for all
![]() $i < \lambda $
(possibly replacing N by an extension in the process). Then for
$i < \lambda $
(possibly replacing N by an extension in the process). Then for
![]() $I \subseteq \lambda $
a realisation of
$I \subseteq \lambda $
a realisation of
![]() $\operatorname {\mathrm {gtp}}(a, b', c; M)$
for
$\operatorname {\mathrm {gtp}}(a, b', c; M)$
for
![]() $(b_i')_{i \in I}$
would also be a realisation of
$(b_i')_{i \in I}$
would also be a realisation of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
for
![]() $(b_i)_{i \in I}$
. So if we let
$(b_i)_{i \in I}$
. So if we let
![]() $\kappa < \lambda $
be such that for every
$\kappa < \lambda $
be such that for every
![]() $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
![]() $|I| = \kappa $
we have that
$|I| = \kappa $
we have that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is inconsistent for
![]() $(b_i)_{i \in I}$
, we also get that
$(b_i)_{i \in I}$
, we also get that
![]() $\operatorname {\mathrm {gtp}}(a, b', c; M)$
is inconsistent for
$\operatorname {\mathrm {gtp}}(a, b', c; M)$
is inconsistent for
![]() $(b_i')_{i \in I}$
for any such I. We conclude that
$(b_i')_{i \in I}$
for any such I. We conclude that
![]() $\operatorname {\mathrm {gtp}}(a, b', c; M)$
long divides over c.
$\operatorname {\mathrm {gtp}}(a, b', c; M)$
long divides over c.
We note that in the above proof we did not have to change the sequence involved for Base-Monotonicity, which was why the same proof also works for isi-dividing. In the proof of Right-Monotonicity we had to build a new sequence, which might not be an isi-sequence again. This is why that proof only works for long dividing.
An important property that misses in Proposition 6.6 is Extension. Classically (working in a monster model) this is fixed by considering forking instead of dividing. This forces the Extension property as follows. Suppose that Extension fails for some type
![]() $p = \operatorname {\mathrm {tp}}(a/Cb)$
. Then there is some parameter set, say D, such that every extension of p to D divides over C. In other words, p implies a disjunction of types over D such that every type in that disjunction divides over C. Classically we could even further reformulate this by using compactness and having p actually imply a finite disjunction of dividing formulas, but that is not necessary and we want to avoid compactness in our definitions. So our definition of isi-forking will be the semantical way of saying “implies a (possibly infinite) disjunction of types that each isi-divide”.
$p = \operatorname {\mathrm {tp}}(a/Cb)$
. Then there is some parameter set, say D, such that every extension of p to D divides over C. In other words, p implies a disjunction of types over D such that every type in that disjunction divides over C. Classically we could even further reformulate this by using compactness and having p actually imply a finite disjunction of dividing formulas, but that is not necessary and we want to avoid compactness in our definitions. So our definition of isi-forking will be the semantical way of saying “implies a (possibly infinite) disjunction of types that each isi-divide”.
Definition 6.7. We say that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c if there is some extension
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c if there is some extension
![]() $M \to N$
with
$M \to N$
with
![]() $((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
such that:
$((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
such that:
-
(i)
 $\operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
isi-divides over c for each
$\operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
isi-divides over c for each
 $j \in J$
;
$j \in J$
; -
(ii) given an extension
 $N \to N'$
with some
$N \to N'$
with some
 $(a'; N')$
such that
$(a'; N')$
such that
 $\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; N)$
there is
$\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; N)$
there is
 $j \in J$
such that
$j \in J$
such that
 $\operatorname {\mathrm {gtp}}(a', d_j, c; N') = \operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
.
$\operatorname {\mathrm {gtp}}(a', d_j, c; N') = \operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
.
Note that we do not require that b actually factors through the
![]() $d_j$
. This is because we also want to force in Right-Monotonicity.
$d_j$
. This is because we also want to force in Right-Monotonicity.
Of course, one could also define a notion of long forking by replacing isi-dividing by long dividing in the above. However, we will have no use for this.
Remark 6.8. The definition of isi-forking is just the semantical way of saying “
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
implies a (possibly infinite) disjunction of Galois types that each isi-divide over c”. In the first-order setting and in the positive setting (see [Reference Pillay28]) forking has been defined and can be formulated as follows: a type forks over C if it implies a (possibly infinite) disjunction of types that each divide over C. It should then be clear that forking implies isi-forking. This uses the fact that dividing implies isi-dividing, see Remark 6.3(i). If isi-dividing and dividing coincide then the converse is true, so isi-forking would then imply forking.
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
implies a (possibly infinite) disjunction of Galois types that each isi-divide over c”. In the first-order setting and in the positive setting (see [Reference Pillay28]) forking has been defined and can be formulated as follows: a type forks over C if it implies a (possibly infinite) disjunction of types that each divide over C. It should then be clear that forking implies isi-forking. This uses the fact that dividing implies isi-dividing, see Remark 6.3(i). If isi-dividing and dividing coincide then the converse is true, so isi-forking would then imply forking.
As before, we will prove various basic properties of isi-forking.
Proposition 6.9. Let
![]() $A, B, C \leq M$
be subobjects. Let
$A, B, C \leq M$
be subobjects. Let
![]() $(a, b, c; M)$
and
$(a, b, c; M)$
and
![]() $(a', b', c'; M)$
be two sets of representatives. Then
$(a', b', c'; M)$
be two sets of representatives. Then
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c if and only if
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c if and only if
![]() $\operatorname {\mathrm {gtp}}(a', b', c'; M)$
isi-forks over
$\operatorname {\mathrm {gtp}}(a', b', c'; M)$
isi-forks over
![]() $c'$
.
$c'$
.
Proof We use the same trick as we did in Proposition 6.4. Let f be the isomorphism such that
![]() $a' = af$
. Let
$a' = af$
. Let
![]() $M \to N$
be an extension with
$M \to N$
be an extension with
![]() $((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
witnessing isi-forking of
$((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
witnessing isi-forking of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
. Then using Proposition 6.4 we have that
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
. Then using Proposition 6.4 we have that
![]() $\operatorname {\mathrm {gtp}}(a_j f, d_j, c'; N)$
isi-divides over
$\operatorname {\mathrm {gtp}}(a_j f, d_j, c'; N)$
isi-divides over
![]() $c'$
for all
$c'$
for all
![]() $j \in J$
. We claim that isi-forking of
$j \in J$
. We claim that isi-forking of
![]() $\operatorname {\mathrm {gtp}}(a', b', c'; M)$
is witnessed by
$\operatorname {\mathrm {gtp}}(a', b', c'; M)$
is witnessed by
![]() $((a_j f)_{j \in J}, (d_j)_{j \in J}; N)$
, for which we are now left to check (ii) from Definition 6.7.
$((a_j f)_{j \in J}, (d_j)_{j \in J}; N)$
, for which we are now left to check (ii) from Definition 6.7.
Let g and h be isomorphisms such that
![]() $b' = bg$
and
$b' = bg$
and
![]() $c' = ch$
. Let
$c' = ch$
. Let
![]() $N \to N^*$
be an extension with some
$N \to N^*$
be an extension with some
![]() $(a^*; N^*)$
such that
$(a^*; N^*)$
such that
![]() $\operatorname {\mathrm {gtp}}(a^*, b', c'; N^*) = \operatorname {\mathrm {gtp}}(a', b', c'; N)$
. Then
$\operatorname {\mathrm {gtp}}(a^*, b', c'; N^*) = \operatorname {\mathrm {gtp}}(a', b', c'; N)$
. Then
 $$ \begin{align*} \operatorname{\mathrm{gtp}}(a^* f^{-1}, b, c; N^*) &= \operatorname{\mathrm{gtp}}(a^* f^{-1}, b' g^{-1}, c' h^{-1}; N^*) \\ &= \operatorname{\mathrm{gtp}}(a' f^{-1}, b' g^{-1}, c' h^{-1}; N) \\ &= \operatorname{\mathrm{gtp}}(a, b, c; N), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gtp}}(a^* f^{-1}, b, c; N^*) &= \operatorname{\mathrm{gtp}}(a^* f^{-1}, b' g^{-1}, c' h^{-1}; N^*) \\ &= \operatorname{\mathrm{gtp}}(a' f^{-1}, b' g^{-1}, c' h^{-1}; N) \\ &= \operatorname{\mathrm{gtp}}(a, b, c; N), \end{align*} $$
so there is
![]() $j \in J$
with
$j \in J$
with
![]() $\operatorname {\mathrm {gtp}}(a^* f^{-1}, d_j, c; N^*) = \operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
. We conclude that
$\operatorname {\mathrm {gtp}}(a^* f^{-1}, d_j, c; N^*) = \operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
. We conclude that
![]() $\operatorname {\mathrm {gtp}}(a^*, d_j, c'; N^*) = \operatorname {\mathrm {gtp}}(a^* f^{-1} f, d_j, c h; N^*) = \operatorname {\mathrm {gtp}}(a_j f, d_j, c'; N)$
.
$\operatorname {\mathrm {gtp}}(a^*, d_j, c'; N^*) = \operatorname {\mathrm {gtp}}(a^* f^{-1} f, d_j, c h; N^*) = \operatorname {\mathrm {gtp}}(a_j f, d_j, c'; N)$
.
Definition 6.10. For
![]() $A, B, C \leq M$
we write
$A, B, C \leq M$
we write
![]() if
if
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-fork for all (equivalently: some) representatives
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-fork for all (equivalently: some) representatives
![]() $a, b, c$
of
$a, b, c$
of
![]() $A, B, C$
.
$A, B, C$
.
Proposition 6.11. Isi-forking satisfies the following: Invariance, Monotonicity on both sides, Extension and Base-Monotonicity.
Proof The properties Invariance and Right-Monotonicity are direct from the definition. We prove the contraposition of the remaining three.
For Left-Monotonicity suppose that
![]() $\operatorname {\mathrm {gtp}}(a', b, c; M)$
isi-forks over c and let
$\operatorname {\mathrm {gtp}}(a', b, c; M)$
isi-forks over c and let
![]() $(a; M)$
be such that
$(a; M)$
be such that
![]() $a'$
factors through a. Let
$a'$
factors through a. Let
![]() $((a^{\prime }_j)_{j \in J}, (d_j)_{j \in J}; N)$
in some extension
$((a^{\prime }_j)_{j \in J}, (d_j)_{j \in J}; N)$
in some extension
![]() $M \to N$
witness the isi-forking. Let f be such that
$M \to N$
witness the isi-forking. Let f be such that
![]() $af = a'$
. The following is a set by Fact 2.14:
$af = a'$
. The following is a set by Fact 2.14:
 $$ \begin{align*} F = \{\operatorname{\mathrm{gtp}}(a^*, d_j, c; N^*) :\, &N^* \text{ is an extension of } N \text{ and } j \in J \text{ and} \\ &\operatorname{\mathrm{gtp}}(a^*, b, c; N^*) = \operatorname{\mathrm{gtp}}(a, b, c; M) \text{ and } \\ &\operatorname{\mathrm{gtp}}(a^* f, d_j, c; N^*) = \operatorname{\mathrm{gtp}}(a_j', d_j, c; N)\}. \end{align*} $$
$$ \begin{align*} F = \{\operatorname{\mathrm{gtp}}(a^*, d_j, c; N^*) :\, &N^* \text{ is an extension of } N \text{ and } j \in J \text{ and} \\ &\operatorname{\mathrm{gtp}}(a^*, b, c; N^*) = \operatorname{\mathrm{gtp}}(a, b, c; M) \text{ and } \\ &\operatorname{\mathrm{gtp}}(a^* f, d_j, c; N^*) = \operatorname{\mathrm{gtp}}(a_j', d_j, c; N)\}. \end{align*} $$
By Left-Monotonicity of isi-dividing, every Galois type in F isi-divides over c. By inductively amalgamating things we find one extension
![]() $N \to N^*$
with
$N \to N^*$
with
![]() $((a_k)_{k \in K}, (d_k)_{k \in K}; N^*)$
such that every Galois type in F is realised by
$((a_k)_{k \in K}, (d_k)_{k \in K}; N^*)$
such that every Galois type in F is realised by
![]() $(a_k, d_k, c; N^*)$
for some
$(a_k, d_k, c; N^*)$
for some
![]() $k \in K$
. This then witnesses isi-forking of
$k \in K$
. This then witnesses isi-forking of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
over c.
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
over c.
For Extension let
![]() $(a, b, b', c; M)$
be such that b factors through
$(a, b, b', c; M)$
be such that b factors through
![]() $b'$
and for every
$b'$
and for every
![]() $(a'; N)$
in some extension
$(a'; N)$
in some extension
![]() $M \to N$
with
$M \to N$
with
![]() $\operatorname {\mathrm {gtp}}(a', b, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
we have that
$\operatorname {\mathrm {gtp}}(a', b, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
we have that
![]() $\operatorname {\mathrm {gtp}}(a', b', c; N)$
isi-forks over c. So the conclusion of the Extension property for
$\operatorname {\mathrm {gtp}}(a', b', c; N)$
isi-forks over c. So the conclusion of the Extension property for
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
fails. We have to prove that then
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
fails. We have to prove that then
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c.
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c.
For each Galois type in
![]() $\mathrm {S}_{\mathrm {gtp}}(\operatorname {\mathrm {dom}}(a), \operatorname {\mathrm {dom}}(b'), \operatorname {\mathrm {dom}}(c))$
we fix some witnesses of isi-forking. By Fact 2.14 and the definition of isi-forking, the following is a set:
$\mathrm {S}_{\mathrm {gtp}}(\operatorname {\mathrm {dom}}(a), \operatorname {\mathrm {dom}}(b'), \operatorname {\mathrm {dom}}(c))$
we fix some witnesses of isi-forking. By Fact 2.14 and the definition of isi-forking, the following is a set:
 $$ \begin{align*} F = \{&\operatorname{\mathrm{gtp}}(a', d, c; N) : N \text{ is an extension of } M \text{ and}\\ &\quad \operatorname{\mathrm{gtp}}(a', b, c; N) = \operatorname{\mathrm{gtp}}(a, b, c; M) \text{ and } \\ &\quad \operatorname{\mathrm{gtp}}(a', d, c; N) \text{ is a fixed witness of isi-forking of } \operatorname{\mathrm{gtp}}(a', b', c; N)\}. \end{align*} $$
$$ \begin{align*} F = \{&\operatorname{\mathrm{gtp}}(a', d, c; N) : N \text{ is an extension of } M \text{ and}\\ &\quad \operatorname{\mathrm{gtp}}(a', b, c; N) = \operatorname{\mathrm{gtp}}(a, b, c; M) \text{ and } \\ &\quad \operatorname{\mathrm{gtp}}(a', d, c; N) \text{ is a fixed witness of isi-forking of } \operatorname{\mathrm{gtp}}(a', b', c; N)\}. \end{align*} $$
By inductively amalgamating things we find one extension
![]() $N \to N^*$
together with
$N \to N^*$
together with
![]() $((a_j)_{j \in J}, (d_j)_{j \in J}; N^*)$
such that every Galois type in F is realised by
$((a_j)_{j \in J}, (d_j)_{j \in J}; N^*)$
such that every Galois type in F is realised by
![]() $(a_j, d_j, c; N^*)$
for some
$(a_j, d_j, c; N^*)$
for some
![]() $j \in J$
. This then witnesses isi-forking of
$j \in J$
. This then witnesses isi-forking of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
over c.
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
over c.
Finally, for Base-Monotonicity let
![]() $(a, b, c, c'; M)$
be such that
$(a, b, c, c'; M)$
be such that
![]() $\operatorname {\mathrm {gtp}}(a, b, c'; M)$
isi-forks over
$\operatorname {\mathrm {gtp}}(a, b, c'; M)$
isi-forks over
![]() $c'$
and
$c'$
and
![]() $C \leq C' \leq B$
, where
$C \leq C' \leq B$
, where
![]() $C, C', B$
are the subobjects represented by
$C, C', B$
are the subobjects represented by
![]() $c, c', b$
respectively. Let
$c, c', b$
respectively. Let
![]() $((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
witness this in some extension
$((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
witness this in some extension
![]() $M \to N$
. We claim that this also witnesses isi-forking of
$M \to N$
. We claim that this also witnesses isi-forking of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
over c. Indeed, let
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
over c. Indeed, let
![]() $a': A \to N'$
for some extension
$a': A \to N'$
for some extension
![]() $N \to N'$
be such that
$N \to N'$
be such that
![]() $\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; N)$
. We have
$\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; N)$
. We have
![]() $C' \leq B$
, so
$C' \leq B$
, so
![]() $\operatorname {\mathrm {gtp}}(a', b, c'; N') = \operatorname {\mathrm {gtp}}(a, b, c'; N)$
. So there must be some
$\operatorname {\mathrm {gtp}}(a', b, c'; N') = \operatorname {\mathrm {gtp}}(a, b, c'; N)$
. So there must be some
![]() $j \in J$
such that
$j \in J$
such that
![]() $\operatorname {\mathrm {gtp}}(a', d_j, c'; N') = \operatorname {\mathrm {gtp}}(a_j, d_j, c'; N)$
. As
$\operatorname {\mathrm {gtp}}(a', d_j, c'; N') = \operatorname {\mathrm {gtp}}(a_j, d_j, c'; N)$
. As
![]() $C \leq C'$
this restricts to
$C \leq C'$
this restricts to
![]() $\operatorname {\mathrm {gtp}}(a', d_j, c; N') = \operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
, which concludes the proof.
$\operatorname {\mathrm {gtp}}(a', d_j, c; N') = \operatorname {\mathrm {gtp}}(a_j, d_j, c; N)$
, which concludes the proof.
Proposition 6.12. For any
![]() $A, B, C \leq M$
we always have
$A, B, C \leq M$
we always have

The converse holds if and only if isi-dividing satisfies Right-Monotonicity and Extension.
Proof The first implication is just the contrapositive of the trivial statement that isi-dividing implies isi-forking. If the converse of this implication holds, then isi-dividing and isi-forking coincide and so isi-dividing satisfies Right-Monotonicity and Extension by Proposition 6.11.
We are left to prove that if isi-dividing satisfies Right-Monotonicity and Extension then isi-forking implies isi-dividing. Suppose for a contradiction that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c but does not isi-divide over c. Let
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
isi-forks over c but does not isi-divide over c. Let
![]() $((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
for some extension
$((a_j)_{j \in J}, (d_j)_{j \in J}; N)$
for some extension
![]() $M \to N$
witness the isi-forking of
$M \to N$
witness the isi-forking of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
. By Extension for isi-dividing we find an extension
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
. By Extension for isi-dividing we find an extension
![]() $N \to N'$
with
$N \to N'$
with
![]() $(a'; N')$
such that
$(a'; N')$
such that
![]() $\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; N)$
and
$\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; N)$
and
![]() $\operatorname {\mathrm {gtp}}(a', N, c; N')$
does not isi-divide. By isi-forking, there must be
$\operatorname {\mathrm {gtp}}(a', N, c; N')$
does not isi-divide. By isi-forking, there must be
![]() $j \in J$
such that
$j \in J$
such that
![]() $\operatorname {\mathrm {gtp}}(a', d_j, c; N')$
isi-divides over c contradicting Right-Monotonicity of isi-dividing.
$\operatorname {\mathrm {gtp}}(a', d_j, c; N')$
isi-divides over c contradicting Right-Monotonicity of isi-dividing.
When considering NSOP
![]() $_1$
-theories in first-order logic the useful notion of independence is given by Kim-dividing, see for example [Reference Dobrowolski, Kim and Ramsey12, Reference Kaplan and Ramsey20]. The idea is to only consider dividing with respect to Morley sequences, that is, with respect to indiscernible nonforking sequences. We adapt that definition to our earlier ideas.
$_1$
-theories in first-order logic the useful notion of independence is given by Kim-dividing, see for example [Reference Dobrowolski, Kim and Ramsey12, Reference Kaplan and Ramsey20]. The idea is to only consider dividing with respect to Morley sequences, that is, with respect to indiscernible nonforking sequences. We adapt that definition to our earlier ideas.
Definition 6.13. We say that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
long Kim-divides over c if it long divides over c with respect to
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
long Kim-divides over c if it long divides over c with respect to
![]() -independent sequences. That is, the definition is exactly as long dividing, but we require the sequence
-independent sequences. That is, the definition is exactly as long dividing, but we require the sequence
![]() $(b_i)_{i < \lambda }$
to be
$(b_i)_{i < \lambda }$
to be
![]() -independent. We write
-independent. We write
![]() if
if
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not long Kim-divide over c for all (equivalently: some) representatives
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not long Kim-divide over c for all (equivalently: some) representatives
![]() $a, b, c$
of the subobjects
$a, b, c$
of the subobjects
![]() $A, B, C$
.
$A, B, C$
.
We implicitly used a combination of Proposition 6.4 and Proposition 6.9 to conclude that long Kim-dividing is invariant under taking different representatives of subobjects.
We have defined
![]() -independence using
-independence using
![]() -independent sequences, but these may not exist. For this we define the following axiom, from which the existence of such sequences follows.
-independent sequences, but these may not exist. For this we define the following axiom, from which the existence of such sequences follows.
Definition 6.14. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat and let
$(\mathcal {C}, \mathcal {M})$
be an AECat and let
![]() $\mathcal {B}$
be a base class. We say that
$\mathcal {B}$
be a base class. We say that
![]() $(\mathcal {C}, \mathcal {M})$
satisfies the
$(\mathcal {C}, \mathcal {M})$
satisfies the
![]() $\mathcal {B}$
-existence axiom if
$\mathcal {B}$
-existence axiom if
![]() with its base restricted to
with its base restricted to
![]() $\mathcal {B}$
satisfies Existence. That is, for all
$\mathcal {B}$
satisfies Existence. That is, for all
![]() $A, C \leq M$
with
$A, C \leq M$
with
![]() $C \in \mathcal {B}$
we have
$C \in \mathcal {B}$
we have
![]() .
.
Corollary 6.15. If
![]() $(\mathcal {C}, \mathcal {M})$
satisfies the
$(\mathcal {C}, \mathcal {M})$
satisfies the
![]() $\mathcal {B}$
-existence axiom then for any
$\mathcal {B}$
-existence axiom then for any
![]() $(a, c; M)$
with
$(a, c; M)$
with
![]() $\operatorname {\mathrm {dom}}(c) \in \mathcal {B}$
and any
$\operatorname {\mathrm {dom}}(c) \in \mathcal {B}$
and any
![]() $\kappa $
there is some extension
$\kappa $
there is some extension
![]() $M \to N$
containing a
$M \to N$
containing a
![]() -independent sequence
-independent sequence
![]() $(a_i)_{i < \kappa }$
with
$(a_i)_{i < \kappa }$
with
![]() $\operatorname {\mathrm {gtp}}(a_i, c; N) = \operatorname {\mathrm {gtp}}(a, c; M)$
for all
$\operatorname {\mathrm {gtp}}(a_i, c; N) = \operatorname {\mathrm {gtp}}(a, c; M)$
for all
![]() $i < \kappa $
.
$i < \kappa $
.
Example 6.16. We discuss some examples of the
![]() $\mathcal {B}$
-existence axiom. These are either settings where we have the axiom, or where it is natural to assume the axiom.
$\mathcal {B}$
-existence axiom. These are either settings where we have the axiom, or where it is natural to assume the axiom.
-
(i) For any first-order theory T we have the
 $\mathbf {Mod}(T)$
-existence axiom. This is because any type over a model can be extended to a global invariant type, which can then be used in a standard argument to show that such a type does not isi-fork over M as follows.
$\mathbf {Mod}(T)$
-existence axiom. This is because any type over a model can be extended to a global invariant type, which can then be used in a standard argument to show that such a type does not isi-fork over M as follows.Let
 $q(x) \supseteq \operatorname {\mathrm {tp}}(a/M)$
be a global M-invariant extension. Let
$q(x) \supseteq \operatorname {\mathrm {tp}}(a/M)$
be a global M-invariant extension. Let
 $\alpha \models q$
, which then lives in some bigger monster model. Suppose that
$\alpha \models q$
, which then lives in some bigger monster model. Suppose that
 $\operatorname {\mathrm {tp}}(a/M)$
isi-forks. Then there is d such that
$\operatorname {\mathrm {tp}}(a/M)$
isi-forks. Then there is d such that
 $r(x, d) = \operatorname {\mathrm {tp}}(\alpha / Md)$
isi-divides over M. However, we will show that
$r(x, d) = \operatorname {\mathrm {tp}}(\alpha / Md)$
isi-divides over M. However, we will show that
 $r(x, d)$
cannot even long divide. So let
$r(x, d)$
cannot even long divide. So let
 $(d_i)_{i < \lambda }$
be any infinite sequence in
$(d_i)_{i < \lambda }$
be any infinite sequence in
 $\operatorname {\mathrm {tp}}(d/M)$
. Then by M-invariance
$\operatorname {\mathrm {tp}}(d/M)$
. Then by M-invariance
 $\operatorname {\mathrm {tp}}(\alpha d_i/M) = \operatorname {\mathrm {tp}}(\alpha d/M)$
for all
$\operatorname {\mathrm {tp}}(\alpha d_i/M) = \operatorname {\mathrm {tp}}(\alpha d/M)$
for all
 $i < \lambda $
. So
$i < \lambda $
. So
 $\bigcup _{i < \lambda } r(x, d_i)$
is consistent, and so we conclude that
$\bigcup _{i < \lambda } r(x, d_i)$
is consistent, and so we conclude that
 $r(x, d)$
does not long divide.
$r(x, d)$
does not long divide. -
(ii) Analogous to the previous point, for a continuous theory T we have the
 $\mathbf {MetMod}(T)$
-existence axiom.
$\mathbf {MetMod}(T)$
-existence axiom. -
(iii) For positive logic something similar to (i) is true, but we need an extra assumption on T. We recall these assumptions in more detail in Definition 7.6. For now we just summarise what we get from them in terms of the existence axiom. In a semi-Hausdorff positive theory T any type over an e.c. model can be extended to a global invariant type (see [Reference Ben-Yaacov5, Lemma 3.11]), so the proof in (i) goes through and we have the
 $\mathbf {Mod}(T)$
-existence axiom. In the more general class of thick theories we still have the
$\mathbf {Mod}(T)$
-existence axiom. In the more general class of thick theories we still have the
 $\mathbf {Mod}(T)$
-existence axiom, but we have to use global Lascar-invariant types instead, see [Reference Dobrowolski and Kamsma11, Lemmas 3.11 and 9.11].
$\mathbf {Mod}(T)$
-existence axiom, but we have to use global Lascar-invariant types instead, see [Reference Dobrowolski and Kamsma11, Lemmas 3.11 and 9.11]. -
(iv) For an NSOP
 $_1$
theory T in first-order logic it is common to assume the existence axiom for forking. It is still an open problem whether or not the existence axiom for forking holds in every NSOP
$_1$
theory T in first-order logic it is common to assume the existence axiom for forking. It is still an open problem whether or not the existence axiom for forking holds in every NSOP
 $_1$
theory T, but it has been proved in many specific instances, see [Reference Dobrowolski, Kim and Ramsey12, Fact 2.14].
$_1$
theory T, but it has been proved in many specific instances, see [Reference Dobrowolski, Kim and Ramsey12, Fact 2.14].If for such T we take
 $(\mathcal {C}, \mathcal {M}) = (\mathbf {SubMod}(T), \mathbf {Mod}(T))$
then we are very close to having the
$(\mathcal {C}, \mathcal {M}) = (\mathbf {SubMod}(T), \mathbf {Mod}(T))$
then we are very close to having the
 $\mathcal {C}$
-existence axiom. The only difference is that we work with isi-forking, see Remark 6.8 for a comparison. In particular, the
$\mathcal {C}$
-existence axiom. The only difference is that we work with isi-forking, see Remark 6.8 for a comparison. In particular, the
 $\mathcal {C}$
-existence axiom implies the existence axiom for forking. Furthermore, if there is a proper class of Ramsey cardinals then isi-forking and forking coincide and so the converse would hold as well. Additionally, it is quite likely that techniques to prove existence for forking also work for isi-forking. For example, in [Reference Dobrowolski, Kim and Ramsey12, Remark 2.15] it is shown that in the theory of parametrised equivalence relations any type over any set A can be extended to a global A-invariant type. Following point (i) we then see that such a type does not isi-fork over A.
$\mathcal {C}$
-existence axiom implies the existence axiom for forking. Furthermore, if there is a proper class of Ramsey cardinals then isi-forking and forking coincide and so the converse would hold as well. Additionally, it is quite likely that techniques to prove existence for forking also work for isi-forking. For example, in [Reference Dobrowolski, Kim and Ramsey12, Remark 2.15] it is shown that in the theory of parametrised equivalence relations any type over any set A can be extended to a global A-invariant type. Following point (i) we then see that such a type does not isi-fork over A. -
(v) If
 $(\mathcal {C}, \mathcal {M})$
is an AECat with a simple independence relation
$(\mathcal {C}, \mathcal {M})$
is an AECat with a simple independence relation
 then it will satisfy the
then it will satisfy the
 -existence axiom. This follows from canonicity, Theorem 1.2, because then
-existence axiom. This follows from canonicity, Theorem 1.2, because then
 over
over
 . This mirrors the fact that simple theories in first-order logic (and even simple thick positive theories, see [Reference Ben-Yaacov5]) have the existence axiom for forking, see also the previous point.
. This mirrors the fact that simple theories in first-order logic (and even simple thick positive theories, see [Reference Ben-Yaacov5]) have the existence axiom for forking, see also the previous point.
Remark 6.17. The usual definition of Kim-dividing states that a type Kim-divides if it divides with respect to nonforking Morley sequences, see, e.g., [Reference Dobrowolski, Kim and Ramsey12, Reference Kaplan and Ramsey20]. To compare this to long Kim-dividing we first note that by Remark 6.8 any
![]() -independent sequence is also a forking-independent sequence, and the converse is true if isi-dividing coincides with dividing. As before, if we assume that there is a proper class of Ramsey cardinals then long Kim-dividing and Kim-dividing coincide, using the same arguments as for long dividing and isi-dividing versus dividing.
-independent sequence is also a forking-independent sequence, and the converse is true if isi-dividing coincides with dividing. As before, if we assume that there is a proper class of Ramsey cardinals then long Kim-dividing and Kim-dividing coincide, using the same arguments as for long dividing and isi-dividing versus dividing.
If we do not want to assume large cardinals then we can again use canonicity, this time Theorem 1.1, to see that long Kim-dividing and Kim-dividing coincide in NSOP
![]() $_1$
-theories where it has been developed.
$_1$
-theories where it has been developed.
7 Canonicity
In this section we prove the main results, namely the canonicity theorems for simple (Theorem 1.2) and NSOP
![]() $_1$
-like (Theorem 1.1) independence relations. The former is just a slightly improved version of [Reference Kamsma18, Theorem 1.1]. The results in this section up to and including Theorem 1.2 are then essentially just the proof of [Reference Kamsma18, Theorem 1.1] cut up in smaller parts. However, we cannot really just refer to that proof again. First of all because we work with slightly different definitions. More importantly, the results here are actually improved versions. Most notably Lemma 7.2 gives a lot more information, where the proof of [Reference Kamsma18, Theorem 1.1] only used the last sentence of that lemma.
$_1$
-like (Theorem 1.1) independence relations. The former is just a slightly improved version of [Reference Kamsma18, Theorem 1.1]. The results in this section up to and including Theorem 1.2 are then essentially just the proof of [Reference Kamsma18, Theorem 1.1] cut up in smaller parts. However, we cannot really just refer to that proof again. First of all because we work with slightly different definitions. More importantly, the results here are actually improved versions. Most notably Lemma 7.2 gives a lot more information, where the proof of [Reference Kamsma18, Theorem 1.1] only used the last sentence of that lemma.
Theorem 7.1. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP and let
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP and let
![]() be a basic independence relation that also satisfies Club Local Character. Then
be a basic independence relation that also satisfies Club Local Character. Then
![]() implies
implies
![]() for any
for any
![]() .
.
If
![]() satisfies the same assumptions, except possibly Union, then we still have that
satisfies the same assumptions, except possibly Union, then we still have that
![]() implies
implies
![]() for any
for any
![]() .
.
Proof Suppose that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-divide over c. Let
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-divide over c. Let
![]() $\kappa \geq \Upsilon (A)$
such that
$\kappa \geq \Upsilon (A)$
such that
![]() $(\mathcal {C}, \mathcal {M})$
is a
$(\mathcal {C}, \mathcal {M})$
is a
![]() $\kappa $
-AECat and
$\kappa $
-AECat and
![]() $\operatorname {\mathrm {dom}}(a)$
and
$\operatorname {\mathrm {dom}}(a)$
and
![]() $\operatorname {\mathrm {dom}}(c)$
are
$\operatorname {\mathrm {dom}}(c)$
are
![]() $\kappa $
-presentable. By Proposition 4.19 we find a long enough
$\kappa $
-presentable. By Proposition 4.19 we find a long enough
-independent isi-sequence
![]() $(b_i)_{i < \lambda }$
over c in some
$(b_i)_{i < \lambda }$
over c in some
![]() $M \to N$
with
$M \to N$
with
![]() $\lambda> \kappa $
and
$\lambda> \kappa $
and
![]() $\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
![]() $i < \lambda $
. Let
$i < \lambda $
. Let
![]() $(M_i)_{i < \lambda }$
be witnesses of independence. Since
$(M_i)_{i < \lambda }$
be witnesses of independence. Since
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-divide over c there is
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
does not isi-divide over c there is
![]() $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
![]() $|I| = \kappa $
such that
$|I| = \kappa $
such that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
![]() $(b_i)_{i \in I}$
. Let
$(b_i)_{i \in I}$
. Let
![]() $a'$
be a realisation for
$a'$
be a realisation for
![]() $(b_i)_{i \in I}$
, which for convenience we may assume to be in N. By possibly deleting an end segment from I we may assume that I has the order type of
$(b_i)_{i \in I}$
, which for convenience we may assume to be in N. By possibly deleting an end segment from I we may assume that I has the order type of
![]() $\kappa $
. Using Lemma 2.17 we may assume that each object in the chain
$\kappa $
. Using Lemma 2.17 we may assume that each object in the chain
![]() $(M_i)_{i \in I}$
is
$(M_i)_{i \in I}$
is
![]() $\kappa $
-presentable, where Monotonicity implies that these are still witnesses of independence. Then by chain local character, Lemma 4.15, we find
$\kappa $
-presentable, where Monotonicity implies that these are still witnesses of independence. Then by chain local character, Lemma 4.15, we find
![]() $i_0 \in I$
such that
$i_0 \in I$
such that
where
![]() $M_I = \operatorname {\mathrm {colim}}_{i \in I} M_i$
. By Monotonicity and Symmetry we then have
$M_I = \operatorname {\mathrm {colim}}_{i \in I} M_i$
. By Monotonicity and Symmetry we then have

We also have

So by Transitivity we have
and the result follows by Symmetry and because
![]() $\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
.
$\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
.
For the final claim we just note that if we do not have Union we can still apply Proposition 4.18 instead of Proposition 4.19 to get an arbitrarily long
![]() -independent sequence. It might just not be an isi-sequence. Then the rest of the proof goes through as written.
-independent sequence. It might just not be an isi-sequence. Then the rest of the proof goes through as written.
The following lemma generalises the Independence Theorem property to independent sequences of any length. The original Independence Theorem can roughly be viewed as just considering an independent sequence of length two.
Lemma 7.2 (Generalised independence theorem).
Suppose that
![]() is a basic independence relation satisfying Independence Theorem. Let
is a basic independence relation satisfying Independence Theorem. Let
![]() $\delta $
be any (possibly finite) ordinal. Suppose we have
$\delta $
be any (possibly finite) ordinal. Suppose we have
![]() $(a, b, c; N)$
such that
$(a, b, c; N)$
such that
![]() and a
and a
![]() -independent sequence
-independent sequence
![]() $(b_i)_{i < \delta }$
in N with
$(b_i)_{i < \delta }$
in N with
![]() $\operatorname {\mathrm {Lgtp}}(b_i / c; N) = \operatorname {\mathrm {Lgtp}}(b / c; N)$
for all
$\operatorname {\mathrm {Lgtp}}(b_i / c; N) = \operatorname {\mathrm {Lgtp}}(b / c; N)$
for all
![]() $i < \delta $
. Then there is an extension
$i < \delta $
. Then there is an extension
![]() $N \to N'$
with
$N \to N'$
with
![]() $(a'; N')$
such that
$(a'; N')$
such that
![]() and
and
![]() $\operatorname {\mathrm {Lgtp}}(a', b_i / c; N') = \operatorname {\mathrm {Lgtp}}(a, b / c; N')$
for all
$\operatorname {\mathrm {Lgtp}}(a', b_i / c; N') = \operatorname {\mathrm {Lgtp}}(a, b / c; N')$
for all
![]() $i < \delta $
.
$i < \delta $
.
In particular,
![]() $\operatorname {\mathrm {gtp}}(a, b, c; N)$
is consistent for
$\operatorname {\mathrm {gtp}}(a, b, c; N)$
is consistent for
![]() $(b_i)_{i < \delta }$
.
$(b_i)_{i < \delta }$
.
Proof Let
![]() $(M_i)_{i < \delta }$
be witnesses of independence for
$(M_i)_{i < \delta }$
be witnesses of independence for
![]() $(b_i)_{i < \delta }$
, which we may assume to be subobjects of N. We will add one more link
$(b_i)_{i < \delta }$
, which we may assume to be subobjects of N. We will add one more link
![]() $M_\delta $
to the chain. If
$M_\delta $
to the chain. If
![]() $\delta $
is a limit ordinal we set
$\delta $
is a limit ordinal we set
![]() $M_\delta = \operatorname {\mathrm {colim}}_{i < \delta } M_i$
. If
$M_\delta = \operatorname {\mathrm {colim}}_{i < \delta } M_i$
. If
![]() $\delta $
is a successor ordinal we set
$\delta $
is a successor ordinal we set
![]() $M_\delta = N$
.
$M_\delta = N$
.
We will by induction construct a chain
![]() $(N_i)_{i \leq \delta }$
with
$(N_i)_{i \leq \delta }$
with
![]() $N_0$
extending N, together with extensions
$N_0$
extending N, together with extensions
![]() $\{m_i': M_i \to N_i\}_{i \leq \delta }$
and an arrow
$\{m_i': M_i \to N_i\}_{i \leq \delta }$
and an arrow
![]() $(a"; N_0)$
such that
$(a"; N_0)$
such that
![]() $m_0' = m_0$
and
$m_0' = m_0$
and
![]() $\operatorname {\mathrm {Lgtp}}(a" / c; N_0) = \operatorname {\mathrm {Lgtp}}(a / c; N_0)$
while at stage i we have:
$\operatorname {\mathrm {Lgtp}}(a" / c; N_0) = \operatorname {\mathrm {Lgtp}}(a / c; N_0)$
while at stage i we have:
-
(i) the extensions
 $\{m_j': M_j \to N_j\}_{j \leq i}$
are natural in the sense that
$\{m_j': M_j \to N_j\}_{j \leq i}$
are natural in the sense that 
commutes for all
 $j \leq i$
;
$j \leq i$
; -
(ii) if i is a successor, say
 $i = j + 1$
, then
$i = j + 1$
, then
 $\operatorname {\mathrm {Lgtp}}(a", b_j' / c; N_i) = \operatorname {\mathrm {Lgtp}}(a, b / c; N_i)$
, where
$\operatorname {\mathrm {Lgtp}}(a", b_j' / c; N_i) = \operatorname {\mathrm {Lgtp}}(a, b / c; N_i)$
, where
 $b_j'$
is the composition
$b_j'$
is the composition
 $B \xrightarrow {b_j} M_i \xrightarrow {m_i'} N_i$
;
$B \xrightarrow {b_j} M_i \xrightarrow {m_i'} N_i$
; -
(iii)
 .
.
Base case. By Existence we have
![]() , so we can apply strong extension (Corollary 4.13) to find
, so we can apply strong extension (Corollary 4.13) to find
![]() $N \to N_0$
and
$N \to N_0$
and
![]() $(a"; N_0)$
with
$(a"; N_0)$
with
![]() and
and
![]() $\operatorname {\mathrm {Lgtp}}(a" / c; N_0) = \operatorname {\mathrm {Lgtp}}(a / c; N_0)$
.
$\operatorname {\mathrm {Lgtp}}(a" / c; N_0) = \operatorname {\mathrm {Lgtp}}(a / c; N_0)$
.
Successor step. Suppose we have constructed
![]() $N_i$
and
$N_i$
and
![]() $m_i'$
. As
$m_i'$
. As
![]() $M_i$
is an amalgamation base we have
$M_i$
is an amalgamation base we have
![]() $\operatorname {\mathrm {gtp}}(m_i; N_i) = \operatorname {\mathrm {gtp}}(m_i'; N_i)$
. By (i) we have that
$\operatorname {\mathrm {gtp}}(m_i; N_i) = \operatorname {\mathrm {gtp}}(m_i'; N_i)$
. By (i) we have that
![]() $m_0'$
factors through
$m_0'$
factors through
![]() $m_i'$
in the same way that
$m_i'$
in the same way that
![]() $m_0$
factors through
$m_0$
factors through
![]() $m_i$
, so
$m_i$
, so
![]() $\operatorname {\mathrm {gtp}}(m_i', m_0'; N_i) = \operatorname {\mathrm {gtp}}(m_i, m_0; N_i)$
. Since
$\operatorname {\mathrm {gtp}}(m_i', m_0'; N_i) = \operatorname {\mathrm {gtp}}(m_i, m_0; N_i)$
. Since
![]() $m_0' = m_0$
have
$m_0' = m_0$
have
![]() $\operatorname {\mathrm {gtp}}(m_i', m_0; N_i) = \operatorname {\mathrm {gtp}}(m_i, m_0; N_i)$
, so
$\operatorname {\mathrm {gtp}}(m_i', m_0; N_i) = \operatorname {\mathrm {gtp}}(m_i, m_0; N_i)$
, so
![]() $\operatorname {\mathrm {Lgtp}}(m_i' / c; N_i) = \operatorname {\mathrm {Lgtp}}(m_i / c; N_i)$
. We thus find
$\operatorname {\mathrm {Lgtp}}(m_i' / c; N_i) = \operatorname {\mathrm {Lgtp}}(m_i / c; N_i)$
. We thus find
![]() $(a^*, m_{i+1}^*; N^*)$
for some
$(a^*, m_{i+1}^*; N^*)$
for some
![]() $N_i \to N^*$
such that
$N_i \to N^*$
such that
![]() $\operatorname {\mathrm {Lgtp}}(m_{i+1}^*, m_i' / c; N^*) = \operatorname {\mathrm {Lgtp}}(m_{i+1}, m_i / c; N^*)$
and
$\operatorname {\mathrm {Lgtp}}(m_{i+1}^*, m_i' / c; N^*) = \operatorname {\mathrm {Lgtp}}(m_{i+1}, m_i / c; N^*)$
and
![]() $\operatorname {\mathrm {Lgtp}}(a^*, b_i^* / c; N^*) = \operatorname {\mathrm {Lgtp}}(a, b / c; N^*)$
, where
$\operatorname {\mathrm {Lgtp}}(a^*, b_i^* / c; N^*) = \operatorname {\mathrm {Lgtp}}(a, b / c; N^*)$
, where
![]() $b_i^*$
is given by
$b_i^*$
is given by
![]() $B \xrightarrow {b_i} M_{i+1} \xrightarrow {m_{i+1}^*} N^*$
. For this last construction we used that
$B \xrightarrow {b_i} M_{i+1} \xrightarrow {m_{i+1}^*} N^*$
. For this last construction we used that
![]() $\operatorname {\mathrm {Lgtp}}(b_i / c; N) = \operatorname {\mathrm {Lgtp}}(b / c; N)$
and that
$\operatorname {\mathrm {Lgtp}}(b_i / c; N) = \operatorname {\mathrm {Lgtp}}(b / c; N)$
and that
![]() $b_i$
factors through
$b_i$
factors through
![]() $m_{i+1}$
. Then
$m_{i+1}$
. Then
![]() ,
,
![]() and
and
![]() . So by Independence Theorem we find
. So by Independence Theorem we find
![]() $N^* \to N_{i+1}$
and
$N^* \to N_{i+1}$
and
![]() $(a^{**}; N_{i+1})$
with
$(a^{**}; N_{i+1})$
with
![]() $\operatorname {\mathrm {Lgtp}}(a^{**}, b_i^* / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a^*, b_i^* / c; N_{i+1})$
,
$\operatorname {\mathrm {Lgtp}}(a^{**}, b_i^* / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a^*, b_i^* / c; N_{i+1})$
,
![]() $\operatorname {\mathrm {Lgtp}}(a^{**}, m_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_i' / c; N_{i+1})$
and
$\operatorname {\mathrm {Lgtp}}(a^{**}, m_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_i' / c; N_{i+1})$
and
![]() . By Monotonicity we get
. By Monotonicity we get
![]() . Using
. Using
![]() $\operatorname {\mathrm {Lgtp}}(a^{**}, m_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_i' / c; N_{i+1})$
we find
$\operatorname {\mathrm {Lgtp}}(a^{**}, m_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_i' / c; N_{i+1})$
we find
![]() $m_{i+1}': M_{i+1} \to N_{i+1}$
(after replacing
$m_{i+1}': M_{i+1} \to N_{i+1}$
(after replacing
![]() $N_{i+1}$
by an extension) such that
$N_{i+1}$
by an extension) such that
![]() $\operatorname {\mathrm {Lgtp}}(a^{**}, m_{i+1}^*, m_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_{i+1}', m_i' / c; N_{i+1})$
. We verify the induction hypothesis:
$\operatorname {\mathrm {Lgtp}}(a^{**}, m_{i+1}^*, m_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_{i+1}', m_i' / c; N_{i+1})$
. We verify the induction hypothesis:
-
(i) we have by construction that
 $\operatorname {\mathrm {gtp}}(m_{i+1}', m_i'; N_{i+1}) = \operatorname {\mathrm {gtp}}(m_{i+1}^*, m_i'; N_{i+1}) = \operatorname {\mathrm {gtp}}(m_{i+1}, m_i: N_{i+1})$
, so
$\operatorname {\mathrm {gtp}}(m_{i+1}', m_i'; N_{i+1}) = \operatorname {\mathrm {gtp}}(m_{i+1}^*, m_i'; N_{i+1}) = \operatorname {\mathrm {gtp}}(m_{i+1}, m_i: N_{i+1})$
, so
 $m_i'$
factors through
$m_i'$
factors through
 $m_{i+1}'$
in the same way that
$m_{i+1}'$
in the same way that
 $m_i$
factors through
$m_i$
factors through
 $m_{i+1}$
by Fact 2.12, and naturality follows;
$m_{i+1}$
by Fact 2.12, and naturality follows; -
(ii) using
 $\operatorname {\mathrm {Lgtp}}(a^{**}, m_{i+1}^* / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_{i+1}' / c; N_{i+1})$
and that
$\operatorname {\mathrm {Lgtp}}(a^{**}, m_{i+1}^* / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a", m_{i+1}' / c; N_{i+1})$
and that
 $b_i^*$
and
$b_i^*$
and
 $b_i'$
are
$b_i'$
are
 $B \xrightarrow {b_i} M_{i+1} \xrightarrow {m_{i+1}^*} N_{i+1}$
and
$B \xrightarrow {b_i} M_{i+1} \xrightarrow {m_{i+1}^*} N_{i+1}$
and
 $B \xrightarrow {b_i} M_{i+1} \xrightarrow {m_{i+1}'} N_{i+1}$
respectively by definition, we have
$B \xrightarrow {b_i} M_{i+1} \xrightarrow {m_{i+1}'} N_{i+1}$
respectively by definition, we have
 $\operatorname {\mathrm {Lgtp}}(a", b_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a^{**}, b_i^*/ c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a^*, b_i^* / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a, b / c; N_{i+1})$
;
$\operatorname {\mathrm {Lgtp}}(a", b_i' / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a^{**}, b_i^*/ c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a^*, b_i^* / c; N_{i+1}) = \operatorname {\mathrm {Lgtp}}(a, b / c; N_{i+1})$
; -
(iii) by
 and Invariance.
and Invariance.
Limit step. For limit
![]() $\ell $
let
$\ell $
let
![]() $N_\ell = \operatorname {\mathrm {colim}}_{i < \ell } N_i$
. By (i) from the induction hypothesis the arrows
$N_\ell = \operatorname {\mathrm {colim}}_{i < \ell } N_i$
. By (i) from the induction hypothesis the arrows
![]() $m_i'$
composed with the coprojections
$m_i'$
composed with the coprojections
![]() $N_i \to N_\ell $
form a cocone on
$N_i \to N_\ell $
form a cocone on
![]() $(M_i)_{i < \ell }$
. By continuity
$(M_i)_{i < \ell }$
. By continuity
![]() $M_\ell = \operatorname {\mathrm {colim}}_{i < \ell } M_i$
, so there is a universal arrow
$M_\ell = \operatorname {\mathrm {colim}}_{i < \ell } M_i$
, so there is a universal arrow
![]() $m_\ell ': M_\ell \to N_\ell $
. This directly establishes (i). Property (ii) is vacuous. Property (iii) follows from the induction hypothesis and Union.
$m_\ell ': M_\ell \to N_\ell $
. This directly establishes (i). Property (ii) is vacuous. Property (iii) follows from the induction hypothesis and Union.
Having finished the inductive construction, we have two arrows
![]() $M_\delta \to N_\delta $
, namely
$M_\delta \to N_\delta $
, namely
![]() $m_\delta : M_\delta \to N \to N_\delta $
and the
$m_\delta : M_\delta \to N \to N_\delta $
and the
![]() $m_\delta '$
we just constructed. By (i) from the induction hypothesis we have
$m_\delta '$
we just constructed. By (i) from the induction hypothesis we have
![]() $\operatorname {\mathrm {gtp}}(m_\delta , m_0; N_\delta ) = \operatorname {\mathrm {gtp}}(m_\delta ', m_0; N_\delta )$
. So we find an extension
$\operatorname {\mathrm {gtp}}(m_\delta , m_0; N_\delta ) = \operatorname {\mathrm {gtp}}(m_\delta ', m_0; N_\delta )$
. So we find an extension
![]() $N_\delta \to N'$
and some
$N_\delta \to N'$
and some
![]() $(a'; N')$
such that
$(a'; N')$
such that
![]() $\operatorname {\mathrm {gtp}}(a', m_\delta , m_0; N') = \operatorname {\mathrm {gtp}}(a", m_\delta ', m_0; N_\delta )$
. Using that c factors through
$\operatorname {\mathrm {gtp}}(a', m_\delta , m_0; N') = \operatorname {\mathrm {gtp}}(a", m_\delta ', m_0; N_\delta )$
. Using that c factors through
![]() $m_0$
and (ii) from the induction hypothesis, we find that for any
$m_0$
and (ii) from the induction hypothesis, we find that for any
![]() $i < \delta $
we have
$i < \delta $
we have
![]() $\operatorname {\mathrm {Lgtp}}(a', b_i / c; N') = \operatorname {\mathrm {Lgtp}}(a", b_i' / c; N') = \operatorname {\mathrm {Lgtp}}(a, b / c; N')$
. By (iii) from the induction hypothesis we also have
$\operatorname {\mathrm {Lgtp}}(a', b_i / c; N') = \operatorname {\mathrm {Lgtp}}(a", b_i' / c; N') = \operatorname {\mathrm {Lgtp}}(a, b / c; N')$
. By (iii) from the induction hypothesis we also have
![]() . So if
. So if
![]() $\delta $
was a successor ordinal we had
$\delta $
was a successor ordinal we had
![]() $M_\delta = N$
and we are done. Otherwise we can just apply Extension and relabel things to get
$M_\delta = N$
and we are done. Otherwise we can just apply Extension and relabel things to get
![]() .
.
The final claim follows because
![]() $a'$
is a realisation of
$a'$
is a realisation of
![]() $\operatorname {\mathrm {gtp}}(a, b, c; N)$
for
$\operatorname {\mathrm {gtp}}(a, b, c; N)$
for
![]() $(b_i)_{i < \delta }$
.
$(b_i)_{i < \delta }$
.
Remark 7.3. In the context of Lemma 7.2 if C is a model then there is no need to concern ourselves with Lascar strong Galois types. That is, the proof as written then goes through if we replace “Lascar strong Galois type” by just “Galois type” everywhere. We also only apply Independence Theorem with C in the base. So if C is a model then it would be enough to just have Independence Theorem over models. Or equivalently, to have 3-amalgamation, see Theorem 5.2.
The following is a slightly improved version of [Reference Kamsma18, Theorem 1.1]. The improvement is in the fact that we can restrict our independence relation to a base class and the fact that we also get
![]() .
.
Theorem 1.2, repeated. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property, and suppose that
$(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property, and suppose that
![]() is a simple independence relation. Then
is a simple independence relation. Then
![]() over
over
![]() .
.
Proof The implication
is already given by Theorem 7.1. For the converse we will assume that
and we will prove that
. Pick some representatives
![]() $a, b, c$
of
$a, b, c$
of
![]() $A, B, C$
. Let
$A, B, C$
. Let
![]() $\mu $
be such that
$\mu $
be such that
![]() $(\mathcal {C}, \mathcal {M})$
is a
$(\mathcal {C}, \mathcal {M})$
is a
![]() $\mu $
-AECat and let
$\mu $
-AECat and let
![]() $\lambda> \Upsilon (B) + \mu $
. Let
$\lambda> \Upsilon (B) + \mu $
. Let
![]() $(b_i)_{i < \lambda }$
be an isi-sequence over c in some
$(b_i)_{i < \lambda }$
be an isi-sequence over c in some
![]() $M \to N$
, with chain of initial segments
$M \to N$
, with chain of initial segments
![]() $(M_i)_{i < \lambda }$
and
$(M_i)_{i < \lambda }$
and
![]() $\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
![]() $i < \lambda $
. Let
$i < \lambda $
. Let
![]() $\Upsilon (B) + \mu \leq \kappa < \lambda $
. By Lemma 2.17 we may assume that
$\Upsilon (B) + \mu \leq \kappa < \lambda $
. By Lemma 2.17 we may assume that
![]() $M_i$
is
$M_i$
is
![]() $\kappa $
-presentable for all
$\kappa $
-presentable for all
![]() $i < \kappa $
. We can thus apply chain local character, Lemma 4.15, to find
$i < \kappa $
. We can thus apply chain local character, Lemma 4.15, to find
![]() $i_0 < \kappa $
such that
$i_0 < \kappa $
such that
. We will aim to show that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
![]() $(b_i)_{i_0 \leq i < \kappa }$
. We use
$(b_i)_{i_0 \leq i < \kappa }$
. We use
![]() $\operatorname {\mathrm {gtp}}(b_{i_0}, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
to find a common extension
$\operatorname {\mathrm {gtp}}(b_{i_0}, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
to find a common extension
![]() $M \to N' \leftarrow N$
where
$M \to N' \leftarrow N$
where
![]() $b = b_{i_0}$
as arrows into
$b = b_{i_0}$
as arrows into
![]() $N'$
. By applying Extension to the assumption
$N'$
. By applying Extension to the assumption
we then find
![]() $(a'; N')$
(possibly after replacing
$(a'; N')$
(possibly after replacing
![]() $N'$
by an extension) such that
$N'$
by an extension) such that
and
![]() $\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
. Then by Base-Monotonicity and Monotonicity we find
$\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
. Then by Base-Monotonicity and Monotonicity we find
. For any
![]() $i_0 \leq i < \kappa $
we have
$i_0 \leq i < \kappa $
we have
![]() $\operatorname {\mathrm {gtp}}(b_i, m_i, m_{i_0}; N') = \operatorname {\mathrm {gtp}}(b_\kappa , m_i, m_{i_0}; N')$
because
$\operatorname {\mathrm {gtp}}(b_i, m_i, m_{i_0}; N') = \operatorname {\mathrm {gtp}}(b_\kappa , m_i, m_{i_0}; N')$
because
![]() $(b_i)_{i < \lambda }$
is an isi-sequence. So by Monotonicity and Invariance and the earlier fact that
$(b_i)_{i < \lambda }$
is an isi-sequence. So by Monotonicity and Invariance and the earlier fact that
, we find

for all
![]() $i_0 \leq i < \kappa $
. So
$i_0 \leq i < \kappa $
. So
![]() $(b_i)_{i_0 \leq i < \kappa }$
is a
$(b_i)_{i_0 \leq i < \kappa }$
is a
-independent sequence. We can thus apply the generalised independence theorem, Lemma 7.2, to conclude that
![]() $\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
is indeed consistent for
$\operatorname {\mathrm {gtp}}(a', b, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
is indeed consistent for
![]() $(b_i)_{i_0 \leq i < \kappa }$
. As
$(b_i)_{i_0 \leq i < \kappa }$
. As
![]() $\kappa $
was arbitrarily large below
$\kappa $
was arbitrarily large below
![]() $\lambda $
,
$\lambda $
,
![]() $\lambda $
itself was arbitarily large and
$\lambda $
itself was arbitarily large and
![]() $(b_i)_{i_0 \leq i < \kappa }$
is a subsequence of an arbitrary isi-sequence of length
$(b_i)_{i_0 \leq i < \kappa }$
is a subsequence of an arbitrary isi-sequence of length
![]() $\lambda $
we conclude that indeed
$\lambda $
we conclude that indeed
.
Finally, the claim
![]() follows from Proposition 6.12 because
follows from Proposition 6.12 because
![]() has Extension and Right-Monotonicity.
has Extension and Right-Monotonicity.
Remark 7.4. For the canonicity theorem for simple independence relations, Theorem 1.2, we only need 3-amalgamation. Or equivalently, by Theorem 5.2, Independence Theorem over models. Even if
![]() is more than just
is more than just
![]() $\mathcal {M}$
, e.g.,
$\mathcal {M}$
, e.g.,
![]() . In the proof of Theorem 1.2 we only applied the Independence Theorem indirectly through Lemma 7.2. The base, i.e., C in that lemma, is by construction always a model. So by Remark 7.3 it would be enough to only assume 3-amalgamation instead of Independence Theorem.
. In the proof of Theorem 1.2 we only applied the Independence Theorem indirectly through Lemma 7.2. The base, i.e., C in that lemma, is by construction always a model. So by Remark 7.3 it would be enough to only assume 3-amalgamation instead of Independence Theorem.
Theorem 1.1, repeated. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and let
$(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and let
![]() $\mathcal {B}$
be some base class. Suppose that
$\mathcal {B}$
be some base class. Suppose that
![]() $(\mathcal {C}, \mathcal {M})$
satisfies the
$(\mathcal {C}, \mathcal {M})$
satisfies the
![]() $\mathcal {B}$
-existence axiom and suppose that there is an NSOP
$\mathcal {B}$
-existence axiom and suppose that there is an NSOP
![]() $_1$
-like independence relation
$_1$
-like independence relation
![]() over
over
![]() $\mathcal {B}$
. Then
$\mathcal {B}$
. Then
![]() over
over
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Proof Suppose that
![]() with
with
![]() $C \in \mathcal {B}$
and pick some representatives
$C \in \mathcal {B}$
and pick some representatives
![]() $a, b, c$
of
$a, b, c$
of
![]() $A, B, C$
. There is a bound
$A, B, C$
. There is a bound
![]() $\mu $
on the cardinality of the set of Lascar strong Galois types compatible with
$\mu $
on the cardinality of the set of Lascar strong Galois types compatible with
![]() $(b, c; M)$
, see Proposition 3.4. Let
$(b, c; M)$
, see Proposition 3.4. Let
![]() $\lambda> \mu $
and let
$\lambda> \mu $
and let
![]() $(b_i)_{i < \lambda }$
be a
$(b_i)_{i < \lambda }$
be a
![]() -independent sequence in some
-independent sequence in some
![]() $M \to N$
with
$M \to N$
with
![]() $\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
![]() $i < \lambda $
. Then
$i < \lambda $
. Then
![]() $(b_i)_{i < \lambda }$
is also
$(b_i)_{i < \lambda }$
is also
![]() -independent, by Theorem 7.1 and Proposition 6.12. We have to show that for every
-independent, by Theorem 7.1 and Proposition 6.12. We have to show that for every
![]() $\kappa < \lambda $
there is
$\kappa < \lambda $
there is
![]() $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
![]() $|I| = \kappa $
such that
$|I| = \kappa $
such that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
$\operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
![]() $(b_i)_{i \in I}$
. So let
$(b_i)_{i \in I}$
. So let
![]() $\kappa < \lambda $
. Then by the choice of
$\kappa < \lambda $
. Then by the choice of
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
there must be some
$\lambda $
there must be some
![]() $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
![]() $|I| = \kappa $
such that
$|I| = \kappa $
such that
![]() $\operatorname {\mathrm {Lgtp}}(b_i / c; N) = \operatorname {\mathrm {Lgtp}}(b_j / c; N)$
for all
$\operatorname {\mathrm {Lgtp}}(b_i / c; N) = \operatorname {\mathrm {Lgtp}}(b_j / c; N)$
for all
![]() $i,j \in I$
. Let
$i,j \in I$
. Let
![]() $i_0$
be the least element of I. Let
$i_0$
be the least element of I. Let
![]() $(a'; N')$
for some extension
$(a'; N')$
for some extension
![]() $N \to N'$
be such that
$N \to N'$
be such that
![]() $\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
. Then we can apply the generalised independence theorem, Lemma 7.2, to see that
$\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
. Then we can apply the generalised independence theorem, Lemma 7.2, to see that
![]() $\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
$\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N') = \operatorname {\mathrm {gtp}}(a, b, c; M)$
is consistent for
![]() $(b_i)_{i \in I}$
. We conclude that indeed
$(b_i)_{i \in I}$
. We conclude that indeed
![]() .
.
For the other direction, suppose that
with
![]() $C \in \mathcal {B}$
. Let
$C \in \mathcal {B}$
. Let
![]() $\kappa \geq \Upsilon (A)$
be such that
$\kappa \geq \Upsilon (A)$
be such that
![]() $(\mathcal {C}, \mathcal {M})$
is a
$(\mathcal {C}, \mathcal {M})$
is a
![]() $\kappa $
-AECat and A and C are
$\kappa $
-AECat and A and C are
![]() $\kappa $
-presentable. Let
$\kappa $
-presentable. Let
![]() $(b_i)_{i < \lambda }$
be a long enough
$(b_i)_{i < \lambda }$
be a long enough
-independent sequence in some extension
![]() $M \to N$
, with
$M \to N$
, with
![]() $\lambda> \kappa $
, witnesses of independence
$\lambda> \kappa $
, witnesses of independence
![]() $(M_i)_{i < \lambda }$
and
$(M_i)_{i < \lambda }$
and
![]() $\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
$\operatorname {\mathrm {gtp}}(b_i, c; N) = \operatorname {\mathrm {gtp}}(b, c; M)$
for all
![]() $i < \lambda $
. Such a sequence exists by Corollary 6.15, because we assumed the
$i < \lambda $
. Such a sequence exists by Corollary 6.15, because we assumed the
![]() $\mathcal {B}$
-existence axiom. By Theorem 7.1 and Proposition 6.12 this is also a
$\mathcal {B}$
-existence axiom. By Theorem 7.1 and Proposition 6.12 this is also a
-independent sequence. By definition of long Kim-dividing there is
![]() $I \subseteq \lambda $
with
$I \subseteq \lambda $
with
![]() $|I| = \kappa $
such that
$|I| = \kappa $
such that
![]() $\operatorname {\mathrm {gtp}}(a, b, c; N)$
is consistent for
$\operatorname {\mathrm {gtp}}(a, b, c; N)$
is consistent for
![]() $(b_i)_{i \in I}$
. Let
$(b_i)_{i \in I}$
. Let
![]() $a'$
be a realisation for this (we may assume
$a'$
be a realisation for this (we may assume
![]() $a'$
is an arrow into N). By possibly deleting an end segment from I we may assume that I has the order type of
$a'$
is an arrow into N). By possibly deleting an end segment from I we may assume that I has the order type of
![]() $\kappa $
. Using Lemma 2.17 we may assume that each object in the chain
$\kappa $
. Using Lemma 2.17 we may assume that each object in the chain
![]() $(M_i)_{i \in I}$
is
$(M_i)_{i \in I}$
is
![]() $\kappa $
-presentable, where Monotonicity guarantees that these are still witnesses of independence. Then by chain local character, Lemma 4.15, we find
$\kappa $
-presentable, where Monotonicity guarantees that these are still witnesses of independence. Then by chain local character, Lemma 4.15, we find
![]() $i_0 \in I$
such that
$i_0 \in I$
such that
where
![]() $M_I = \operatorname {\mathrm {colim}}_{i \in I} M_i$
. So by Monotonicity and Symmetry we have
$M_I = \operatorname {\mathrm {colim}}_{i \in I} M_i$
. So by Monotonicity and Symmetry we have

Furthermore, we have

So by Transitivity we have
. The result then follows by Symmetry and the fact that
![]() $\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
.
$\operatorname {\mathrm {gtp}}(a', b_{i_0}, c; N) = \operatorname {\mathrm {gtp}}(a, b, c; M)$
.
By definition any stable independence relation is also simple, and any simple independence relation is also NSOP
![]() $_1$
-like. The canonicity theorems then tell us that these are indeed unique in a given AECat with AP and with what notion of dividing they coincide. We make this precise in the following theorem.
$_1$
-like. The canonicity theorems then tell us that these are indeed unique in a given AECat with AP and with what notion of dividing they coincide. We make this precise in the following theorem.
Theorem 1.3, repeated. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and suppose that
$(\mathcal {C}, \mathcal {M})$
be an AECat with the amalgamation property and suppose that
is a stable or a simple independence relation in
![]() $(\mathcal {C}, \mathcal {M})$
. Suppose furthermore that
$(\mathcal {C}, \mathcal {M})$
. Suppose furthermore that
is an NSOP
![]() $_1$
-like independence relation in
$_1$
-like independence relation in
![]() $(\mathcal {C}, \mathcal {M})$
with
$(\mathcal {C}, \mathcal {M})$
with
. Then
Proof This follows directly from Theorem 1.2 and Theorem 1.1. To apply the latter we need the
![]() -existence axiom. This is automatic, as
-existence axiom. This is automatic, as
![]() over
over
![]() by Theorem 1.2 and we have Existence by assumption.
by Theorem 1.2 and we have Existence by assumption.
Remark 7.5. We can classify AECats based on the existence of certain independence relations, just as we can classify theories in first-order logic in that way. For example, suppose that we have an AECat
![]() $(\mathcal {C}, \mathcal {M})$
with AP and an NSOP
$(\mathcal {C}, \mathcal {M})$
with AP and an NSOP
![]() $_1$
-like independence relation
$_1$
-like independence relation
![]() where Base-Monotonicity fails. Then we can never find a simple independence relation in
where Base-Monotonicity fails. Then we can never find a simple independence relation in
![]() $(\mathcal {C}, \mathcal {M})$
(with the same base class). Because if we would have such a simple independence relation
$(\mathcal {C}, \mathcal {M})$
(with the same base class). Because if we would have such a simple independence relation
![]() then by Theorem 1.3 we would have
then by Theorem 1.3 we would have
![]() , but that is impossible because a simple independence relation must satisfy Base-Monotonicity. So we can classify
, but that is impossible because a simple independence relation must satisfy Base-Monotonicity. So we can classify
![]() $(\mathcal {C}, \mathcal {M})$
as NSOP
$(\mathcal {C}, \mathcal {M})$
as NSOP
![]() $_1$
, but non-simple.
$_1$
, but non-simple.
We close out this section by discussing how this work extends and brings together previously known results in the settings of first-order, positive and continuous logic. We also describe precisely how to apply the canonicity theorems in these more concrete settings.
We first recall some useful terminology for positive logic from [Reference Ben-Yaacov3, Reference Ben-Yaacov5].
Definition 7.6. Let T be a positive theory. We call T:
-
• semi-Hausdorff if equality of types is type-definable;
-
• thick if being an indiscernible sequence is type-definable.
It quickly follows that any first-order theory is semi-Hausdorff as a positive theory and that any semi-Hausdorff theory is thick. So whenever we mention semi-Hausdorff or thick theories in the examples below this automatically includes the first-order setting.
In a semi-Hausdorff theory T we have that having the same type over an e.c. model implies having the same Lascar strong type (see [Reference Ben-Yaacov5, Proposition 3.13]), just as we have for first-order theories. If T is thick this is no longer generally true, see [Reference Dobrowolski and Kamsma11, Section 10.1]. In [Reference Dobrowolski and Kamsma11, Lemma 2.20] this is solved by considering
![]() $\lambda _T$
-saturated models, where
$\lambda _T$
-saturated models, where
![]() $\lambda _T = \beth _{(2^{|T|})^+ }$
. The problem for AECats is then that the full subcategory of
$\lambda _T = \beth _{(2^{|T|})^+ }$
. The problem for AECats is then that the full subcategory of
![]() $\lambda _T$
-saturated models in
$\lambda _T$
-saturated models in
![]() $\mathbf {Mod}(T)$
is not closed under directed colimits. We solve this with the following notion.
$\mathbf {Mod}(T)$
is not closed under directed colimits. We solve this with the following notion.
Definition 7.7. We call an e.c. model M of some positive theory T finitely
![]() $\lambda $
-saturated if for every finite tuple
$\lambda $
-saturated if for every finite tuple
![]() $a \in M$
there is a
$a \in M$
there is a
![]() $\lambda $
-saturated e.c. model
$\lambda $
-saturated e.c. model
![]() $M_0 \subseteq M$
with
$M_0 \subseteq M$
with
![]() $a \in M_0$
.
$a \in M_0$
.
Clearly any
![]() $\lambda $
-saturated model is also finitely
$\lambda $
-saturated model is also finitely
![]() $\lambda $
-saturated. The point is that the full subcategory of finitely
$\lambda $
-saturated. The point is that the full subcategory of finitely
![]() $\lambda $
-saturated models in
$\lambda $
-saturated models in
![]() $\mathbf {Mod}(T)$
is then closed under directed colimits for any
$\mathbf {Mod}(T)$
is then closed under directed colimits for any
![]() $\lambda $
. At the same time this notion is strong enough to give us the following fact.
$\lambda $
. At the same time this notion is strong enough to give us the following fact.
Fact 7.8 [Reference Kamsma19, Proposition 2.39].
In a thick positive theory T having the same Lascar strong type over some parameter set C is the transitive closure of having the same type over finitely
![]() $\lambda _T$
-saturated models containing C.
$\lambda _T$
-saturated models containing C.
Example 7.9. Let T be a thick theory. Let
![]() $\mathcal {C}$
be either
$\mathcal {C}$
be either
![]() $\mathbf {SubMod}(T)$
or
$\mathbf {SubMod}(T)$
or
![]() $\mathbf {Mod}(T)$
. Following Fact 7.8 we take
$\mathbf {Mod}(T)$
. Following Fact 7.8 we take
![]() $\mathcal {M}$
to be the category of finitely
$\mathcal {M}$
to be the category of finitely
![]() $\lambda _T$
-saturated models, so that Lascar strong types and Lascar strong Galois types coincide. If T is semi-Hausdorff, we can instead just take
$\lambda _T$
-saturated models, so that Lascar strong types and Lascar strong Galois types coincide. If T is semi-Hausdorff, we can instead just take
![]() $\mathcal {M} = \mathbf {Mod}(T)$
.
$\mathcal {M} = \mathbf {Mod}(T)$
.
If T is stable or simple then there is respectively a stable or simple independence relation
![]() in
in
![]() $(\mathcal {C}, \mathcal {M})$
with
$(\mathcal {C}, \mathcal {M})$
with
![]() . This follows from a combination of [Reference Ben-Yaacov4, Reference Ben-Yaacov5]. So Theorem 1.2 applies.
. This follows from a combination of [Reference Ben-Yaacov4, Reference Ben-Yaacov5]. So Theorem 1.2 applies.
The Stationarity property in a stable theory follows from [Reference Ben-Yaacov4, Theorem 2.8]. In their statement the base model M is assumed to be
![]() $|T|^+$
-saturated, which they need for only two reasons. The first reason is that types over M should coincide with Lascar strong types over M, but by our choice of
$|T|^+$
-saturated, which they need for only two reasons. The first reason is that types over M should coincide with Lascar strong types over M, but by our choice of
![]() $\mathcal {M}$
and the thickness assumption this happens for all
$\mathcal {M}$
and the thickness assumption this happens for all
![]() $M \in \mathcal {M}$
. The second reason is that types over M should be what they call extendible, but in a simple thick theory every type is extendible, see [Reference Ben-Yaacov5, Theorem 1.15].
$M \in \mathcal {M}$
. The second reason is that types over M should be what they call extendible, but in a simple thick theory every type is extendible, see [Reference Ben-Yaacov5, Theorem 1.15].
Example 7.10. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat based on some semi-Hausdorff or thick theory T as in Example 7.9. By Example 6.16(iii) we have the
$(\mathcal {C}, \mathcal {M})$
be an AECat based on some semi-Hausdorff or thick theory T as in Example 7.9. By Example 6.16(iii) we have the
![]() $\mathbf {Mod}(T)$
-existence axiom. If T is NSOP
$\mathbf {Mod}(T)$
-existence axiom. If T is NSOP
![]() $_1$
then it has an NSOP
$_1$
then it has an NSOP
![]() $_1$
-like independence relation
$_1$
-like independence relation
![]() with
with
![]() . For first-order logic this was proved in [Reference Kaplan and Ramsey20–Reference Kaplan, Ramsey and Shelah22], which was extended to thick positive theories in [Reference Dobrowolski and Kamsma11]. So Theorem 1.1 applies.
. For first-order logic this was proved in [Reference Kaplan and Ramsey20–Reference Kaplan, Ramsey and Shelah22], which was extended to thick positive theories in [Reference Dobrowolski and Kamsma11]. So Theorem 1.1 applies.
Here we had to restrict the base class to e.c. models, simply because Kim-independence in positive logic has only been developed over e.c. models. For theories in first-order logic Kim-independence has been extended to arbitrary base sets, see [Reference Chernikov, Kim and Ramsey10, Reference Dobrowolski, Kim and Ramsey12]. To make this work we need to assume the existence axiom, see also Example 6.16(iv). So let T be an NSOP
![]() $_1$
theory in first-order logic and set
$_1$
theory in first-order logic and set
![]() $(\mathcal {C}, \mathcal {M}) = (\mathbf {SubMod}(T), \mathbf {Mod}(T))$
, which we assume to satisfy the
$(\mathcal {C}, \mathcal {M}) = (\mathbf {SubMod}(T), \mathbf {Mod}(T))$
, which we assume to satisfy the
![]() $\mathcal {C}$
-existence axiom. Then the aforementioned sources show that there is an NSOP
$\mathcal {C}$
-existence axiom. Then the aforementioned sources show that there is an NSOP
![]() $_1$
-like independence relation
$_1$
-like independence relation
![]() with
with
![]() and so Theorem 1.1 applies.
and so Theorem 1.1 applies.
Finally we note that there is a Kim–Pillay style theorem in [Reference Chernikov, Kim and Ramsey10, Theorem 5.1] for Kim-independence over arbitrary sets. They still rely on a syntactical property “strong finite character”, which could be replaced by just “finite character”. Theorem 1.1 gives us just the canonicity part. To conclude that a theory with such an independence relation is NSOP
![]() $_1$
, without using strong finite character, we can restrict ourselves to work over models and use the proof from [Reference Dobrowolski and Kamsma11, Theorem 9.1].
$_1$
, without using strong finite character, we can restrict ourselves to work over models and use the proof from [Reference Dobrowolski and Kamsma11, Theorem 9.1].
Example 7.11. Let T be a continuous theory, in the sense of [Reference Ben-Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and Wilkie6]. Let
![]() $\mathcal {C}$
be either
$\mathcal {C}$
be either
![]() $\mathbf {SubMetMod}(T)$
or
$\mathbf {SubMetMod}(T)$
or
![]() $\mathbf {MetMod}(T)$
, and let
$\mathbf {MetMod}(T)$
, and let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\mathbf {MetMod}(T)$
. If T is stable or simple then there is respectively a stable or simple independence relation
$\mathbf {MetMod}(T)$
. If T is stable or simple then there is respectively a stable or simple independence relation
![]() in
in
![]() $(\mathcal {C}, \mathcal {M})$
with
$(\mathcal {C}, \mathcal {M})$
with
![]() . Every continuous theory is in particular a Hausdorff compact abstract theory, and so the machinery of [Reference Ben-Yaacov4, Reference Ben-Yaacov5] applies. This shows we can indeed find an appropriate independence relation in any simple or stable continuous theory. There is also [Reference Ben-Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and Wilkie6, Section 14] for a further discussion about stability specifically in continuous theories. So Theorem 1.2 applies.
. Every continuous theory is in particular a Hausdorff compact abstract theory, and so the machinery of [Reference Ben-Yaacov4, Reference Ben-Yaacov5] applies. This shows we can indeed find an appropriate independence relation in any simple or stable continuous theory. There is also [Reference Ben-Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and Wilkie6, Section 14] for a further discussion about stability specifically in continuous theories. So Theorem 1.2 applies.
In [Reference Ben-Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and Wilkie6] some examples of stable continuous theories and their corresponding independence relations are given, including Hilbert spaces and atomless probability spaces.
Example 7.12. In this example we consider the continuous theory
![]() $T_N$
of Hilbert spaces with a distance function to a random subset, as studied in [Reference Berenstein, Hyttinen and Villaveces7]. They prove that this theory has TP
$T_N$
of Hilbert spaces with a distance function to a random subset, as studied in [Reference Berenstein, Hyttinen and Villaveces7]. They prove that this theory has TP
![]() $_2$
and thus cannot be simple. They also define an independence relation
$_2$
and thus cannot be simple. They also define an independence relation
![]() over arbitrary sets that has all the properties of an NSOP
over arbitrary sets that has all the properties of an NSOP
![]() $_1$
-like independence relation. Except that they do not prove the full Independence Theorem, but enough for 3-amalgamation (i.e., over models, see Theorem 5.2). So setting
$_1$
-like independence relation. Except that they do not prove the full Independence Theorem, but enough for 3-amalgamation (i.e., over models, see Theorem 5.2). So setting
![]() $\mathcal {C} = \mathbf {SubMetMod}(T_N)$
and
$\mathcal {C} = \mathbf {SubMetMod}(T_N)$
and
![]() $\mathcal {M} = \mathbf {MetMod}(T_N)$
, and taking
$\mathcal {M} = \mathbf {MetMod}(T_N)$
, and taking
![]() , we have that
, we have that
![]() is an NSOP
is an NSOP
![]() $_1$
-like independence relation in
$_1$
-like independence relation in
![]() $(\mathcal {C}, \mathcal {M})$
. By Example 6.16(ii) we also have the
$(\mathcal {C}, \mathcal {M})$
. By Example 6.16(ii) we also have the
![]() $\mathbf {MetMod}(T)$
-existence axiom. So Theorem 1.1 applies.
$\mathbf {MetMod}(T)$
-existence axiom. So Theorem 1.1 applies.
8 More on Lascar strong Galois types
In this section we will show that in the presence of a nice enough independence relation there are some equivalent definitions of Lascar strong Galois types, matching those we classically have for Lascar strong types. To place this all in context we recall the relevant equivalent definitions of Lascar strong types in first-order logic (see, e.g., [Reference Kim25, Proposition 3.1.5]).
Definition 8.1. Let a and b be tuples in some monster model of a first-order theory and let C be some parameter set. We say that a and b have the same Lascar strong type over C if the following equivalent conditions hold.
-
(i) There are
 $a = a_0, a_1, \ldots , a_n = b$
and models
$a = a_0, a_1, \ldots , a_n = b$
and models
 $M_1, \ldots , M_n$
, each containing C, such that
$M_1, \ldots , M_n$
, each containing C, such that
 $\operatorname {\mathrm {tp}}(a_i / M_{i+1}) = \operatorname {\mathrm {tp}}(a_{i+1} / M_{i+1})$
for all
$\operatorname {\mathrm {tp}}(a_i / M_{i+1}) = \operatorname {\mathrm {tp}}(a_{i+1} / M_{i+1})$
for all
 $0 \leq i < n$
.
$0 \leq i < n$
. -
(ii) We have
 $a \sim b$
for any bounded C-invariant equivalence relation
$a \sim b$
for any bounded C-invariant equivalence relation
 $\sim $
.
$\sim $
. -
(iii) There are
 $a = a_0, a_1, \ldots , a_n = b$
such that
$a = a_0, a_1, \ldots , a_n = b$
such that
 $a_i$
and
$a_i$
and
 $a_{i+1}$
are on a C-indiscernible sequence for all
$a_{i+1}$
are on a C-indiscernible sequence for all
 $0 \leq i < n$
. In this case we say that a and b have Lascar distance at most n (over C).
$0 \leq i < n$
. In this case we say that a and b have Lascar distance at most n (over C).
It is well known that Lascar strong types heavily interact with independence relations in first-order logic. For example, independence relations can be used to show that having the same Lascar strong type is type-definable in any simple theory by showing that the Lascar distance within a Lascar strong type is at most
![]() $2$
, see [Reference Kim25, Proposition 5.1.11]. The same technique applies to any NSOP
$2$
, see [Reference Kim25, Proposition 5.1.11]. The same technique applies to any NSOP
![]() $_1$
theory in first-order logic that satisfies the existence axiom [Reference Dobrowolski, Kim and Ramsey12, Corollary 5.9]. We essentially adapt this technique in this section, while at the same time using independence relations to build what we call “strongly 2-indiscernible” sequences (Definition 8.5), which take the role of the usual indiscernible sequences.
$_1$
theory in first-order logic that satisfies the existence axiom [Reference Dobrowolski, Kim and Ramsey12, Corollary 5.9]. We essentially adapt this technique in this section, while at the same time using independence relations to build what we call “strongly 2-indiscernible” sequences (Definition 8.5), which take the role of the usual indiscernible sequences.
Throughout this section we will work with single arrows
![]() $a, b, c$
and objects A and C, where
$a, b, c$
and objects A and C, where
![]() $\operatorname {\mathrm {dom}}(a) = \operatorname {\mathrm {dom}}(b) = A$
and
$\operatorname {\mathrm {dom}}(a) = \operatorname {\mathrm {dom}}(b) = A$
and
![]() $\operatorname {\mathrm {dom}}(c) = C$
. This leads to cleaner notation and when working with independence relations we can only work with single arrows anyway (i.e., the sides and base of an independence relation do not allow tuples of arrows in our definition). However, it is not too difficult to extend the main result of this section (Theorem 8.7) to arbitrary tuples, see Remark 8.13.
$\operatorname {\mathrm {dom}}(c) = C$
. This leads to cleaner notation and when working with independence relations we can only work with single arrows anyway (i.e., the sides and base of an independence relation do not allow tuples of arrows in our definition). However, it is not too difficult to extend the main result of this section (Theorem 8.7) to arbitrary tuples, see Remark 8.13.
Definition 8.2. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP and fix some objects A and C. Suppose that for each M and each
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP and fix some objects A and C. Suppose that for each M and each
![]() $c: C \to M$
we are given an equivalence relation
$c: C \to M$
we are given an equivalence relation
![]() $\equiv _{c,M}$
on
$\equiv _{c,M}$
on
![]() $\operatorname {\mathrm {Hom}}(A, M)$
. Then we say that the family
$\operatorname {\mathrm {Hom}}(A, M)$
. Then we say that the family
![]() $\equiv $
is an equivalence relation over C.
$\equiv $
is an equivalence relation over C.
We call
![]() $\equiv $
a bounded equivalence relation if there is
$\equiv $
a bounded equivalence relation if there is
![]() $\lambda $
such that
$\lambda $
such that
![]() $\equiv _{c,M}$
has at most
$\equiv _{c,M}$
has at most
![]() $\lambda $
many equivalence classes for any M and
$\lambda $
many equivalence classes for any M and
![]() $c: C \to M$
.
$c: C \to M$
.
We call
![]() $\equiv $
an invariant equivalence relation if it is invariant under equality of Galois types over C. That is, if
$\equiv $
an invariant equivalence relation if it is invariant under equality of Galois types over C. That is, if
![]() $\operatorname {\mathrm {gtp}}(a, b, c; M) = \operatorname {\mathrm {gtp}}(a', b', c'; M')$
then we have that
$\operatorname {\mathrm {gtp}}(a, b, c; M) = \operatorname {\mathrm {gtp}}(a', b', c'; M')$
then we have that
![]() $a \equiv _{c, M} b$
if and only if
$a \equiv _{c, M} b$
if and only if
![]() $a' \equiv _{c', M'} b'$
.
$a' \equiv _{c', M'} b'$
.
Convention 8.3. We will only deal with invariant equivalence relations. To further simplify the notation we will drop the M from the notation. So we write
![]() $a \equiv _c b$
instead of
$a \equiv _c b$
instead of
![]() $a \equiv _{c, M} b$
. Because of invariance it does not matter if we consider a and b as arrows into M or as arrows into an extension of M.
$a \equiv _{c, M} b$
. Because of invariance it does not matter if we consider a and b as arrows into M or as arrows into an extension of M.
Example 8.4. We give some familiar examples.
-
(i) Taking just equality as equivalence relation is an equivalence relation over any C. This relation is invariant, but generally not bounded because
 $\operatorname {\mathrm {Hom}}(A, M)$
may become arbitrarily large.
$\operatorname {\mathrm {Hom}}(A, M)$
may become arbitrarily large. -
(ii) The trivial equivalence where everything is equivalent is a bounded invariant equivalence relation over any C.
-
(iii) Having the same Galois type is a bounded invariant equivalence relation over any C. That is, we define
 $\equiv $
as
$\equiv $
as
 $a \equiv _c b$
if and only if
$a \equiv _c b$
if and only if
 $\operatorname {\mathrm {gtp}}(a, c; M) = \operatorname {\mathrm {gtp}}(b, c; M)$
. Clearly
$\operatorname {\mathrm {gtp}}(a, c; M) = \operatorname {\mathrm {gtp}}(b, c; M)$
. Clearly
 $\equiv $
is invariant, and by Fact 2.14 it is bounded.
$\equiv $
is invariant, and by Fact 2.14 it is bounded. -
(iv) Having the same Lascar strong Galois type is a bounded invariant equivalence relation. Similar to the previous point we define
 $\equiv $
as
$\equiv $
as
 $a \equiv _c b$
if and only if
$a \equiv _c b$
if and only if
 $\operatorname {\mathrm {Lgtp}}(a / c; M) = \operatorname {\mathrm {Lgtp}}(a' / c; M)$
. This is invariant by Proposition 3.3 and bounded by Proposition 3.4.
$\operatorname {\mathrm {Lgtp}}(a / c; M) = \operatorname {\mathrm {Lgtp}}(a' / c; M)$
. This is invariant by Proposition 3.3 and bounded by Proposition 3.4. -
(v) In any (positive or first-order) theory T, any hyperimaginary yields an invariant equivalence relation. That is, if
 $E(x, y)$
is a set of formulas that defines an equivalence relation modulo T then we can define an invariant equivalence relation
$E(x, y)$
is a set of formulas that defines an equivalence relation modulo T then we can define an invariant equivalence relation
 $\equiv ^E$
over
$\equiv ^E$
over
 $\emptyset $
as follows: for tuples
$\emptyset $
as follows: for tuples
 $a, b \in M$
we set
$a, b \in M$
we set
 $a \equiv ^E b$
iff
$a \equiv ^E b$
iff
 $M \models E(a, b)$
.
$M \models E(a, b)$
.
Usually bounded invariant equivalence relations are linked to Lascar strong types using indiscernible sequences. This requires some compactness, which we generally do not have. To solve this we will adapt the idea of strongly indiscernible sequences from [Reference Hyttinen and Lessmann16].
Definition 8.5. We call sequence
![]() $(a_i)_{i < \kappa }$
in some M 2-c-indiscernible if for any
$(a_i)_{i < \kappa }$
in some M 2-c-indiscernible if for any
![]() $i_1 < i_2 < \kappa $
and any
$i_1 < i_2 < \kappa $
and any
![]() $j_1 < j_2 < \kappa $
we have
$j_1 < j_2 < \kappa $
we have
![]() $\operatorname {\mathrm {gtp}}(a_{i_1}, c; M) = \operatorname {\mathrm {gtp}}(a_{i_2}, c; M)$
and
$\operatorname {\mathrm {gtp}}(a_{i_1}, c; M) = \operatorname {\mathrm {gtp}}(a_{i_2}, c; M)$
and
![]() $\operatorname {\mathrm {gtp}}(a_{i_1}, a_{i_2}, c; M) = \operatorname {\mathrm {gtp}}(a_{j_1}, a_{j_2}, c; M)$
. We call such a sequence strongly 2-c-indiscernible if it can be extended to a 2-c-indiscernible sequence (possibly in some extension model) of arbitrary length.
$\operatorname {\mathrm {gtp}}(a_{i_1}, a_{i_2}, c; M) = \operatorname {\mathrm {gtp}}(a_{j_1}, a_{j_2}, c; M)$
. We call such a sequence strongly 2-c-indiscernible if it can be extended to a 2-c-indiscernible sequence (possibly in some extension model) of arbitrary length.
Given an independence relation
![]() we define a 2-
we define a 2-
![]() -Morley sequence to be a 2-c-indiscernible sequence that is also
-Morley sequence to be a 2-c-indiscernible sequence that is also
![]() -independent. Such a sequence is called a strong 2-
-independent. Such a sequence is called a strong 2-
![]() -Morley sequence if it can be extended to a 2-
-Morley sequence if it can be extended to a 2-
![]() -Morley sequence (possibly in some extension model) of arbitrary length.
-Morley sequence (possibly in some extension model) of arbitrary length.
Definition 8.6. For
![]() $(a, b, c; M)$
we write
$(a, b, c; M)$
we write
![]() $a \sim ^2_c b$
if a and b are on some strongly 2-c-indiscernible sequence. We write
$a \sim ^2_c b$
if a and b are on some strongly 2-c-indiscernible sequence. We write
![]() $\equiv ^2_c$
for the transitive closure of
$\equiv ^2_c$
for the transitive closure of
![]() $\sim ^2_c$
. Similarly, given an independence relation
$\sim ^2_c$
. Similarly, given an independence relation
![]() , we write
, we write
![]() if a and b are on some strong 2-
if a and b are on some strong 2-
![]() -Morley sequence and
-Morley sequence and
![]() for its transitive closure. Finally, we write
for its transitive closure. Finally, we write
![]() $a \equiv ^B_c b$
if a and b are equivalent for every bounded invariant relation over c.
$a \equiv ^B_c b$
if a and b are equivalent for every bounded invariant relation over c.
One easily verifies that
![]() $\equiv ^2$
and
$\equiv ^2$
and
![]() $\equiv ^B$
are equivalence relations over any C. For
$\equiv ^B$
are equivalence relations over any C. For
![]() we may generally not have reflexivity, but we will have that in the situations we are interested in. In particular, Lemma 8.11 shows that
we may generally not have reflexivity, but we will have that in the situations we are interested in. In particular, Lemma 8.11 shows that
![]() has reflexivity over models.
has reflexivity over models.
Theorem 8.7. Let
![]() $(\mathcal {C}, \mathcal {M})$
be an AECat with AP, and suppose that
$(\mathcal {C}, \mathcal {M})$
be an AECat with AP, and suppose that
![]() is a basic independence relation that also satisfies 3-amalgamation. Then the following are equivalent for any
is a basic independence relation that also satisfies 3-amalgamation. Then the following are equivalent for any
![]() $(a, b, c; M)$
:
$(a, b, c; M)$
:
-
(i)
 $\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
;
$\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
; -
(ii)
 $a \equiv ^B_c b$
, so a and b are equivalent under every bounded invariant equivalence relation over C;
$a \equiv ^B_c b$
, so a and b are equivalent under every bounded invariant equivalence relation over C; -
(iii)
 $a \equiv ^2_c b$
, so a and b can be connected by strongly 2-c-indiscernible sequences.
$a \equiv ^2_c b$
, so a and b can be connected by strongly 2-c-indiscernible sequences.
Comparing the above statement to Definition 8.1 we see great similarity, but to prove the equivalence in Definition 8.1 no independence relation was needed. In this very general setting we use the independence relation as a replacement for the uses compactness. Proving the equivalence of the above conditions without a nice independence relation seems a lot harder, if not impossible in this generality.
Remark 8.8. In Theorem 8.7 we only required
![]() to have 3-amalgamation. So the assumptions of the theorem do not mention anything about Lascar strong Galois types. That means that, in the presence of such an independence relation, we can take any of the equivalent conditions in Theorem 8.7 as the definition for Lascar strong Galois types, without any circularity in the definitions.
to have 3-amalgamation. So the assumptions of the theorem do not mention anything about Lascar strong Galois types. That means that, in the presence of such an independence relation, we can take any of the equivalent conditions in Theorem 8.7 as the definition for Lascar strong Galois types, without any circularity in the definitions.
The remainder of this section is devoted to proving Theorem 8.7.
Lemma 8.9. For any
![]() $(a, b, c; M)$
and any independence relation
$(a, b, c; M)$
and any independence relation
we always have
Proof The first implication follows because any strong 2-
![]() -Morley sequence is in particular strongly 2-c-indiscernible. The final implication follows because having the same Lascar strong Galois type is a bounded invariant equivalence relation, see Example 8.4(iv). We prove the middle implication. So let
-Morley sequence is in particular strongly 2-c-indiscernible. The final implication follows because having the same Lascar strong Galois type is a bounded invariant equivalence relation, see Example 8.4(iv). We prove the middle implication. So let
![]() $\equiv $
be a bounded invariant equivalence relation over C. It is enough to prove that
$\equiv $
be a bounded invariant equivalence relation over C. It is enough to prove that
![]() $a \sim ^2_c b$
implies
$a \sim ^2_c b$
implies
![]() $a \equiv _c b$
. Let
$a \equiv _c b$
. Let
![]() $\kappa $
be the bound of
$\kappa $
be the bound of
![]() $\equiv $
. Since
$\equiv $
. Since
![]() $a \sim ^2_c b$
we find a 2-c-indiscernible sequence
$a \sim ^2_c b$
we find a 2-c-indiscernible sequence
![]() $(a_i)_{i < \kappa ^+}$
in some extension N of M with a and b on it. Without loss of generality we may assume
$(a_i)_{i < \kappa ^+}$
in some extension N of M with a and b on it. Without loss of generality we may assume
![]() $a_0 = a$
and
$a_0 = a$
and
![]() $a_1 = b$
. By boundedness we find
$a_1 = b$
. By boundedness we find
![]() $i < j < \kappa ^+$
such that
$i < j < \kappa ^+$
such that
![]() $a_i \equiv _c a_j$
. By 2-c-indiscernibility we have
$a_i \equiv _c a_j$
. By 2-c-indiscernibility we have
![]() $\operatorname {\mathrm {gtp}}(a, b, c; N) = \operatorname {\mathrm {gtp}}(a_i, a_j, c; N)$
. So
$\operatorname {\mathrm {gtp}}(a, b, c; N) = \operatorname {\mathrm {gtp}}(a_i, a_j, c; N)$
. So
![]() $a \equiv _c b$
follows from invariance.
$a \equiv _c b$
follows from invariance.
Lemma 8.10. Suppose that
![]() is a basic independence relation that also satisfies 3-amalgamation. Let m be an arrow with a model as domain and let
is a basic independence relation that also satisfies 3-amalgamation. Let m be an arrow with a model as domain and let
![]() $\delta \geq 2$
be any ordinal (possibly finite). Then any 2-
$\delta \geq 2$
be any ordinal (possibly finite). Then any 2-
![]() -Morley sequence
-Morley sequence
![]() $(a_i)_{i < \delta }$
is a strong 2-
$(a_i)_{i < \delta }$
is a strong 2-
![]() -Morley sequence. In particular
-Morley sequence. In particular
![]() and
and
![]() $\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(b, m; N)$
implies
$\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(b, m; N)$
implies
![]() .
.
Proof By Remark 7.3 we can apply Lemma 7.2, the generalised independence theorem, while avoiding referring to Lascar strong Galois types. We can thus inductively apply Lemma 7.2 to elongate
![]() $(a_i)_{i < \delta }$
to any length we want. We do this by letting
$(a_i)_{i < \delta }$
to any length we want. We do this by letting
![]() $a_0$
,
$a_0$
,
![]() $a_1$
and m play the roles of b, a and c respectively. The final claim follows because in that case
$a_1$
and m play the roles of b, a and c respectively. The final claim follows because in that case
![]() $(a, b)$
is a 2-
$(a, b)$
is a 2-
![]() -Morley sequence of length two.
-Morley sequence of length two.
Lemma 8.11. Suppose that
![]() is a basic independence relation that also satisfies 3-amalgamation. If
is a basic independence relation that also satisfies 3-amalgamation. If
![]() $\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(b, m; N)$
, where
$\operatorname {\mathrm {gtp}}(a, m; N) = \operatorname {\mathrm {gtp}}(b, m; N)$
, where
![]() $\operatorname {\mathrm {dom}}(m)$
is a model, then
$\operatorname {\mathrm {dom}}(m)$
is a model, then
![]() .
.
Proof By Existence we have
![]() , so we can apply Extension to find
, so we can apply Extension to find
![]() $N \to N'$
and some
$N \to N'$
and some
![]() $(a'; N')$
such that
$(a'; N')$
such that
![]() while
while
![]() $\operatorname {\mathrm {gtp}}(a', m; N') = \operatorname {\mathrm {gtp}}(a, m; N')$
. By Monotonicity we then have
$\operatorname {\mathrm {gtp}}(a', m; N') = \operatorname {\mathrm {gtp}}(a, m; N')$
. By Monotonicity we then have
![]() and
and
![]() . So by Lemma 8.10 we have
. So by Lemma 8.10 we have
![]() , and we are done.
, and we are done.
Proof of Theorem 8.7
By Lemma 8.9 we only need to prove that
![]() $\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
implies
$\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
implies
![]() $a \equiv ^2_c b$
. It is enough to prove that
$a \equiv ^2_c b$
. It is enough to prove that
![]() $(a/c; M) \sim _{\operatorname {\mathrm {Lgtp}}} (b/c; M)$
implies
$(a/c; M) \sim _{\operatorname {\mathrm {Lgtp}}} (b/c; M)$
implies
![]() $a \equiv ^2_c b$
. So let
$a \equiv ^2_c b$
. So let
![]() $M \to N$
be an extension and let
$M \to N$
be an extension and let
![]() $m_0: M_0 \to N$
be such that c factors through
$m_0: M_0 \to N$
be such that c factors through
![]() $m_0$
,
$m_0$
,
![]() $M_0$
is a model and
$M_0$
is a model and
![]() $\operatorname {\mathrm {gtp}}(a, m_0; N) = \operatorname {\mathrm {gtp}}(b, m_0; N)$
. Then by Lemma 8.11 we get
$\operatorname {\mathrm {gtp}}(a, m_0; N) = \operatorname {\mathrm {gtp}}(b, m_0; N)$
. Then by Lemma 8.11 we get
![]() . So by Lemma 8.9 we have
. So by Lemma 8.9 we have
![]() $a \equiv ^2_{m_0} b$
. Any strongly 2-
$a \equiv ^2_{m_0} b$
. Any strongly 2-
![]() $m_0$
-indiscernible sequence is also strongly 2-c-indiscernible, because c factors through
$m_0$
-indiscernible sequence is also strongly 2-c-indiscernible, because c factors through
![]() $m_0$
. So we conclude that indeed
$m_0$
. So we conclude that indeed
![]() $a \equiv ^2_c b$
.
$a \equiv ^2_c b$
.
Remark 8.12. The proof of Theorem 8.7 also shows that if
![]() $\operatorname {\mathrm {dom}}(c)$
is a model then
$\operatorname {\mathrm {dom}}(c)$
is a model then
![]() $\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
is further equivalent to
$\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
is further equivalent to
![]() .
.
Remark 8.13. We have stated Theorem 8.7 for single arrows, rather than for tuples of arrows. We briefly sketch how we can get the result for tuples of arrows as well. That is, if we replace a, b and c by
![]() $(a_i)_{i \in I}$
,
$(a_i)_{i \in I}$
,
![]() $(b_i)_{i \in I}$
and
$(b_i)_{i \in I}$
and
![]() $(c_j)_{j \in J}$
respectively.
$(c_j)_{j \in J}$
respectively.
First we extend the definitions of (strongly) 2-indiscernible,
![]() $\equiv ^2$
and
$\equiv ^2$
and
![]() $\equiv ^B$
to tuples of arrows in a straightforward way. Then following the same proof as in Lemma 8.9 we get:
$\equiv ^B$
to tuples of arrows in a straightforward way. Then following the same proof as in Lemma 8.9 we get:
 $$ \begin{align*} &(a_i)_{i \in I} \equiv^2_{(c_j)_{j \in J}} (b_i)_{i \in I} &\implies \\ &(a_i)_{i \in I} \equiv^B_{(c_j)_{j \in J}} (b_i)_{i \in I} &\implies \\ &\operatorname{\mathrm{Lgtp}}((a_i)_{i \in I} / (c_j)_{j \in J}; M) = \operatorname{\mathrm{Lgtp}}((b_i)_{i \in I} / (c_j)_{j \in J}; M). \end{align*} $$
$$ \begin{align*} &(a_i)_{i \in I} \equiv^2_{(c_j)_{j \in J}} (b_i)_{i \in I} &\implies \\ &(a_i)_{i \in I} \equiv^B_{(c_j)_{j \in J}} (b_i)_{i \in I} &\implies \\ &\operatorname{\mathrm{Lgtp}}((a_i)_{i \in I} / (c_j)_{j \in J}; M) = \operatorname{\mathrm{Lgtp}}((b_i)_{i \in I} / (c_j)_{j \in J}; M). \end{align*} $$
So we are left to prove that
![]() $\operatorname {\mathrm {Lgtp}}((a_i)_{i \in I} / (c_j)_{j \in J}; M) = \operatorname {\mathrm {Lgtp}}((b_i)_{i \in I} / (c_j)_{j \in J}; M)$
implies
$\operatorname {\mathrm {Lgtp}}((a_i)_{i \in I} / (c_j)_{j \in J}; M) = \operatorname {\mathrm {Lgtp}}((b_i)_{i \in I} / (c_j)_{j \in J}; M)$
implies
![]() $(a_i)_{i \in I} \equiv ^2_{(c_j)_{j \in J}} (b_i)_{i \in I}$
. It is enough to prove that
$(a_i)_{i \in I} \equiv ^2_{(c_j)_{j \in J}} (b_i)_{i \in I}$
. It is enough to prove that
![]() $((a_i)_{i \in I} / (c_j)_{j \in J}; M) \sim _{\operatorname {\mathrm {Lgtp}}} ((b_i)_{i \in I} / (c_j)_{j \in J}; M)$
implies
$((a_i)_{i \in I} / (c_j)_{j \in J}; M) \sim _{\operatorname {\mathrm {Lgtp}}} ((b_i)_{i \in I} / (c_j)_{j \in J}; M)$
implies
![]() $(a_i)_{i \in I} \equiv ^2_{(c_j)_{j \in J}} (b_i)_{i \in I}$
. So let
$(a_i)_{i \in I} \equiv ^2_{(c_j)_{j \in J}} (b_i)_{i \in I}$
. So let
![]() $M \to N$
be an extension and let
$M \to N$
be an extension and let
![]() $m_0: M_0 \to N$
be such that all arrows in
$m_0: M_0 \to N$
be such that all arrows in
![]() $(c_j)_{j \in J}$
factor through
$(c_j)_{j \in J}$
factor through
![]() $m_0$
,
$m_0$
,
![]() $M_0$
is a model and
$M_0$
is a model and
![]() $\operatorname {\mathrm {gtp}}((a_i)_{i \in I}, m_0; N) = \operatorname {\mathrm {gtp}}((b_i)_{i \in I}, m_0; N)$
. Pick some
$\operatorname {\mathrm {gtp}}((a_i)_{i \in I}, m_0; N) = \operatorname {\mathrm {gtp}}((b_i)_{i \in I}, m_0; N)$
. Pick some
![]() $d: D \to N$
such that every arrow in
$d: D \to N$
such that every arrow in
![]() $(a_i)_{i \in I}$
factors through d. We then find an extension
$(a_i)_{i \in I}$
factors through d. We then find an extension
![]() $N \to N'$
and
$N \to N'$
and
![]() $d': D \to N'$
such that every arrow in
$d': D \to N'$
such that every arrow in
![]() $(b_i)_{i \in I}$
factors through
$(b_i)_{i \in I}$
factors through
![]() $d'$
and
$d'$
and
![]() $\operatorname {\mathrm {gtp}}(d, m_0; N') = \operatorname {\mathrm {gtp}}(d', m_0; N')$
. Now we can apply the original result Theorem 8.7 to obtain
$\operatorname {\mathrm {gtp}}(d, m_0; N') = \operatorname {\mathrm {gtp}}(d', m_0; N')$
. Now we can apply the original result Theorem 8.7 to obtain
![]() $d \equiv ^2_{m_0} d'$
and hence
$d \equiv ^2_{m_0} d'$
and hence
![]() $(a_i)_{i \in I} \equiv ^2_{(c_j)_{j \in J}} (b_i)_{i \in I}$
, as required.
$(a_i)_{i \in I} \equiv ^2_{(c_j)_{j \in J}} (b_i)_{i \in I}$
, as required.
Remark 8.14. We only assumed 3-amalgamation. If we also assume Independence Theorem together with
![]() we get a little bit more, namely that
we get a little bit more, namely that
![]() $\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
is further equivalent to
$\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
is further equivalent to
![]() . This happens for example in any simple thick positive theory where
. This happens for example in any simple thick positive theory where
![]() is the usual dividing independence (see Example 7.9).
is the usual dividing independence (see Example 7.9).
The proof of this is largely the same as the proof in this section. We sketch where some changes would need to be made. We adjust Lemma 8.10 as follows: any 2-
![]() -Morley sequence
-Morley sequence
![]() $(a_i)_{i < \delta }$
such that
$(a_i)_{i < \delta }$
such that
![]() $\operatorname {\mathrm {Lgtp}}(a_i / c; M) = \operatorname {\mathrm {Lgtp}}(a_j / c; M)$
for all
$\operatorname {\mathrm {Lgtp}}(a_i / c; M) = \operatorname {\mathrm {Lgtp}}(a_j / c; M)$
for all
![]() $i < j < \delta $
is a strong 2-
$i < j < \delta $
is a strong 2-
![]() -Morley sequence. Here the extra assumption “
-Morley sequence. Here the extra assumption “
![]() $\operatorname {\mathrm {Lgtp}}(a_i / c; M) = \operatorname {\mathrm {Lgtp}}(a_j / c; M)$
” is necessary to still apply Lemma 7.2, and so the proof goes through. Then Lemma 8.11 can be restated as
$\operatorname {\mathrm {Lgtp}}(a_i / c; M) = \operatorname {\mathrm {Lgtp}}(a_j / c; M)$
” is necessary to still apply Lemma 7.2, and so the proof goes through. Then Lemma 8.11 can be restated as
![]() $\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
implies
$\operatorname {\mathrm {Lgtp}}(a/c; M) = \operatorname {\mathrm {Lgtp}}(b/c; M)$
implies
![]() . The only change in the proof is that we need to apply strong extension, Corollary 4.13. This then already concludes the proof.
. The only change in the proof is that we need to apply strong extension, Corollary 4.13. This then already concludes the proof.
This also tells us that in this case we will need at most two strong 2-
![]() -Morley sequences to connect a and b, whenever they have the same Lascar strong Galois type. That is, there is some
-Morley sequences to connect a and b, whenever they have the same Lascar strong Galois type. That is, there is some
![]() $a'$
in an extension of M such that
$a'$
in an extension of M such that
![]() . In particular this also means that we need at most two strongly 2-c-indiscernible sequences to connect a and b, because strong 2-
. In particular this also means that we need at most two strongly 2-c-indiscernible sequences to connect a and b, because strong 2-
![]() -Morley sequences are in particular strongly 2-c-indiscernible.
-Morley sequences are in particular strongly 2-c-indiscernible.
Acknowledgements
I would like to thank Jonathan Kirby for his feedback which greatly improved the presentation of this paper. I would also like to thank the anonymous referee whose remarks further helped to improve the presentation of this paper.
Funding
This paper is part of a PhD project at the University of East Anglia (UEA), and as such is supported by a scholarship from the UEA.