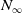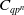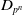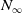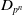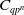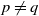1. Introduction
Throughout,
![]() $D_{p^n}$
denotes the dihedral group of order
$D_{p^n}$
denotes the dihedral group of order
![]() $2p^n$
,
$2p^n$
,
![]() $p\gt 2$
prime, and
$p\gt 2$
prime, and
![]() $C_{qp^n}$
the cyclic group of order
$C_{qp^n}$
the cyclic group of order
![]() $qp^n$
, for
$qp^n$
, for
![]() $q,p$
distinct primes. (We allow
$q,p$
distinct primes. (We allow
![]() $p=2$
in the cyclic case.)
$p=2$
in the cyclic case.)
This paper—at its heart—is concerned with the combinatorial data arising when studying commutative
![]() $G$
-equivariant spectra for
$G$
-equivariant spectra for
![]() $G$
either
$G$
either
![]() $D_{p^n}$
or
$D_{p^n}$
or
![]() $C_{qp^n}$
. In particular, we wish to study the set of
$C_{qp^n}$
. In particular, we wish to study the set of
![]() $N_\infty$
operads for these groups, as introduced by Blumberg–Hill [Reference Blumberg and Hill2], which govern the ways in which the commutativity respects the group action.
$N_\infty$
operads for these groups, as introduced by Blumberg–Hill [Reference Blumberg and Hill2], which govern the ways in which the commutativity respects the group action.
Such an exploration of
![]() $N_\infty$
operads for
$N_\infty$
operads for
![]() $G= C_{p^n}$
was undertaken in [Reference Balchin, Barnes and Roitzheim1], where it was proved that the collection of these operads (up to homotopy) was in bijection with the Tamari lattice, and in particular, there are
$G= C_{p^n}$
was undertaken in [Reference Balchin, Barnes and Roitzheim1], where it was proved that the collection of these operads (up to homotopy) was in bijection with the Tamari lattice, and in particular, there are
![]() $\mathrm{Cat}(n+1)$
many of them, where
$\mathrm{Cat}(n+1)$
many of them, where
![]() $\mathrm{Cat}(k)$
is the
$\mathrm{Cat}(k)$
is the
![]() $k$
-th Catalan number. This was achieved using an explicit representation of
$k$
-th Catalan number. This was achieved using an explicit representation of
![]() $N_\infty$
operads as combinatorial structures called transfer systems on the subgroup lattice of
$N_\infty$
operads as combinatorial structures called transfer systems on the subgroup lattice of
![]() $C_{p^n}$
. As such, one is led to study transfer systems on arbitrary finite lattices. We refer the reader to [Reference Franchere, Ormsby, Osorno, Qin and Waugh9, Section 4] and Definition2.1 for definitions in this context.
$C_{p^n}$
. As such, one is led to study transfer systems on arbitrary finite lattices. We refer the reader to [Reference Franchere, Ormsby, Osorno, Qin and Waugh9, Section 4] and Definition2.1 for definitions in this context.
Note that the subgroup lattice for
![]() $C_{p^n}$
is isomorphic to
$C_{p^n}$
is isomorphic to
![]() $[n] = \{0\lt 1\lt \cdots \lt n\}$
. A key method employed in [Reference Balchin, Barnes and Roitzheim1] was a recursive method for building all transfer systems on
$[n] = \{0\lt 1\lt \cdots \lt n\}$
. A key method employed in [Reference Balchin, Barnes and Roitzheim1] was a recursive method for building all transfer systems on
![]() $[n]$
from ones on
$[n]$
from ones on
![]() $[i]$
where
$[i]$
where
![]() $i \lt n$
. It is this powerful point of view that we will generalize in this paper. In particular, in Section 2, we shall exhibit an extremely general method of iteratively building all transfer systems on a finite lattice
$i \lt n$
. It is this powerful point of view that we will generalize in this paper. In particular, in Section 2, we shall exhibit an extremely general method of iteratively building all transfer systems on a finite lattice
![]() $L$
.
$L$
.
We will then implement the algorithm of Section 2 in the case of
![]() $L = [1] \times [n]$
. From a homotopical viewpoint, we observe that
$L = [1] \times [n]$
. From a homotopical viewpoint, we observe that
![]() $[1] \times [n] \cong \operatorname{Sub}(C_{qp^n})$
, and as such, transfer systems on
$[1] \times [n] \cong \operatorname{Sub}(C_{qp^n})$
, and as such, transfer systems on
![]() $[1] \times [n]$
correspond to
$[1] \times [n]$
correspond to
![]() $N_\infty$
operads for
$N_\infty$
operads for
![]() $C_{qp^n}$
. To do so, we will first begin by considering a restricted collection of transfer systems, namely the liftable transfer systems (Definition3.1). From the work of the authors in [Reference Balchin, MacBrough and Ormsby5], liftable transfer systems on
$C_{qp^n}$
. To do so, we will first begin by considering a restricted collection of transfer systems, namely the liftable transfer systems (Definition3.1). From the work of the authors in [Reference Balchin, MacBrough and Ormsby5], liftable transfer systems on
![]() $[1] \times [n]$
are in bijection with
$[1] \times [n]$
are in bijection with
![]() $N_\infty$
operads for
$N_\infty$
operads for
![]() $D_{p^n}$
(provided
$D_{p^n}$
(provided
![]() $p \neq 2$
). A recursive formula for computing the number of liftable transfer systems appears as the main result in Theorem3.12.
$p \neq 2$
). A recursive formula for computing the number of liftable transfer systems appears as the main result in Theorem3.12.
We are then able to exploit the self-duality of transfer systems on
![]() $[1] \times [n]$
as observed in [Reference Franchere, Ormsby, Osorno, Qin and Waugh9, Theorem 4.21] to complete the computation for
$[1] \times [n]$
as observed in [Reference Franchere, Ormsby, Osorno, Qin and Waugh9, Theorem 4.21] to complete the computation for
![]() $C_{qp^n}$
almost immediately from the case of
$C_{qp^n}$
almost immediately from the case of
![]() $D_{p^n}$
. This leads to Theorem4.3 where we provide a recursive formula for computing the number of transfer systems on
$D_{p^n}$
. This leads to Theorem4.3 where we provide a recursive formula for computing the number of transfer systems on
![]() $[1] \times [n]$
.Footnote 1 Thus, we obtain a (recursive) formula for a second and third infinite family of groups following the work of [Reference Balchin, Barnes and Roitzheim1].Footnote 2
$[1] \times [n]$
.Footnote 1 Thus, we obtain a (recursive) formula for a second and third infinite family of groups following the work of [Reference Balchin, Barnes and Roitzheim1].Footnote 2
Following these enumerative results, we begin to explore some of the combinatorial structures appearing in the recursions that we have provided. In Section 5, we study the notion of restricted Tamari intervals, which form an important part of the recursions for
![]() $C_{qp^n}$
and
$C_{qp^n}$
and
![]() $D_{p^n}$
and see that this is related to certain triangulations of polygons.
$D_{p^n}$
and see that this is related to certain triangulations of polygons.
Finally, in Section 6, we will restrict ourselves to what we call maximally extendable transfer systems. In terms of the lattice
![]() $[1] \times [n]$
, these are those transfer systems whose restriction to the bottom row is the maximal transfer system on
$[1] \times [n]$
, these are those transfer systems whose restriction to the bottom row is the maximal transfer system on
![]() $[n]$
. We shall see that in the liftable case these have specific combinatorial interpretation (in terms of large Schröder numbers), and we make a conjecture relating the general case to rooted subtrees of a rooted planar tree. Returning to the world of homotopy theory, these maximally extendable transfer systems have a meaninful interpretation. Indeed, they are precisely those transfer systems cooresponding to
$[n]$
. We shall see that in the liftable case these have specific combinatorial interpretation (in terms of large Schröder numbers), and we make a conjecture relating the general case to rooted subtrees of a rooted planar tree. Returning to the world of homotopy theory, these maximally extendable transfer systems have a meaninful interpretation. Indeed, they are precisely those transfer systems cooresponding to
![]() $N_\infty$
operads which restrict to the genuine
$N_\infty$
operads which restrict to the genuine
![]() $G$
-
$G$
-
![]() $E_\infty$
operad on
$E_\infty$
operad on
![]() $C_{p^n}$
.
$C_{p^n}$
.
2. Transfer systems and a generalized
 $\odot$
construction
$\odot$
construction
We begin by recalling the definition of a transfer system on a poset from [Reference Balchin, MacBrough and Ormsby5, Reference Franchere, Ormsby, Osorno, Qin and Waugh9].
Definition 2.1.
Let
![]() $\mathcal{P} = (\mathcal{P}, \leqslant )$
be a poset. A (categorical) transfer system on
$\mathcal{P} = (\mathcal{P}, \leqslant )$
be a poset. A (categorical) transfer system on
![]() $\mathcal{P}$
consists of a partial order
$\mathcal{P}$
consists of a partial order
![]() $\mathcal{R}$
on
$\mathcal{R}$
on
![]() $\mathcal{P}$
that refines
$\mathcal{P}$
that refines
![]() $\leqslant$
and such that whenever
$\leqslant$
and such that whenever
![]() $x \, \mathcal{R} \, y$
and
$x \, \mathcal{R} \, y$
and
![]() $z\leqslant y$
, then for all maximal
$z\leqslant y$
, then for all maximal
![]() $w\in x^{\downarrow }\cap z^{\downarrow }$
we have
$w\in x^{\downarrow }\cap z^{\downarrow }$
we have
![]() $w \, \mathcal{R} \, z$
where
$w \, \mathcal{R} \, z$
where
![]() $x^{\downarrow }$
denotes the set of all
$x^{\downarrow }$
denotes the set of all
![]() $y \leqslant x$
.
$y \leqslant x$
.
For a lattice
![]() $L$
, we write
$L$
, we write
![]() $\mathsf{Tr}(L)$
for the collection of all transfer systems of
$\mathsf{Tr}(L)$
for the collection of all transfer systems of
![]() $L$
. In [Reference Balchin, Barnes and Roitzheim1], it was proved that
$L$
. In [Reference Balchin, Barnes and Roitzheim1], it was proved that
![]() $|\mathsf{Tr}([n])|$
coincides with the
$|\mathsf{Tr}([n])|$
coincides with the
![]() $(n+1)$
-th Catalan number. The proof for this proceeded in a recursive fashion which was governed by an operation denoted
$(n+1)$
-th Catalan number. The proof for this proceeded in a recursive fashion which was governed by an operation denoted
![]() $\odot$
in loc. cit.
$\odot$
in loc. cit.
Let
![]() $\mathcal{R}$
be a transfer system on
$\mathcal{R}$
be a transfer system on
![]() $[n]$
. Denote by
$[n]$
. Denote by
![]() $x$
the minimal element such that
$x$
the minimal element such that
![]() $x\, \mathcal{R}\, n$
, and consider the partition of
$x\, \mathcal{R}\, n$
, and consider the partition of
![]() $[n]$
as
$[n]$
as
![]() $[0,x-1] \amalg [x,n]$
. The key observation is that the restriction of
$[0,x-1] \amalg [x,n]$
. The key observation is that the restriction of
![]() $\mathcal{R}$
to
$\mathcal{R}$
to
![]() $[0,x-1]$
and
$[0,x-1]$
and
![]() $[x,n]$
yields two transfer systems, and moreover,
$[x,n]$
yields two transfer systems, and moreover,
![]() $\mathcal{R}$
can be recovered from the disjoint union of these two transfer systems. To retrieve the aforementioned
$\mathcal{R}$
can be recovered from the disjoint union of these two transfer systems. To retrieve the aforementioned
![]() $\odot$
operation from this, we note that the pivot element in [Reference Balchin, Barnes and Roitzheim1] is simply
$\odot$
operation from this, we note that the pivot element in [Reference Balchin, Barnes and Roitzheim1] is simply
![]() $x$
.
$x$
.
In this section, we will follow a suggestion of Mike Hill to extend this observation to transfer systems on an arbitrary finite lattice
![]() $L$
, which provides a method for producing recursive formulas for counting transfer systems. To this end, let
$L$
, which provides a method for producing recursive formulas for counting transfer systems. To this end, let
![]() $L$
be a finite lattice equipped with a transfer system
$L$
be a finite lattice equipped with a transfer system
![]() $\mathcal{R}$
. Let
$\mathcal{R}$
. Let
![]() $m$
be the maximal element of
$m$
be the maximal element of
![]() $L$
, we will say that
$L$
, we will say that
![]() $x \in L$
is fibrant if
$x \in L$
is fibrant if
![]() $x\, \mathcal{R}\, m$
. (This terminology is inspired by the corresponding statement under the equivalence of transfer systems to weak factorization systems.)
$x\, \mathcal{R}\, m$
. (This terminology is inspired by the corresponding statement under the equivalence of transfer systems to weak factorization systems.)
Lemma 2.2.
Let
![]() $L$
and
$L$
and
![]() $\mathcal{R}$
be as above. Then
$\mathcal{R}$
be as above. Then
![]() $\mathcal{R}$
has a unique minimal fibrant element.
$\mathcal{R}$
has a unique minimal fibrant element.
Proof. Let
![]() $\{x_i\}_i$
be the collection of fibrant elements of
$\{x_i\}_i$
be the collection of fibrant elements of
![]() $\mathcal{R}$
. Then by the definition of transfer systems, it follows that
$\mathcal{R}$
. Then by the definition of transfer systems, it follows that
![]() $(\bigwedge _i x_i)\, \mathcal{R}\, m$
. In particular,
$(\bigwedge _i x_i)\, \mathcal{R}\, m$
. In particular,
![]() $\bigwedge _i x_i$
is a fibrant element and
$\bigwedge _i x_i$
is a fibrant element and
![]() $(\bigwedge _i x_i) \leqslant x_j$
for all
$(\bigwedge _i x_i) \leqslant x_j$
for all
![]() $j$
as required.
$j$
as required.
Definition 2.3.
Let
![]() $L$
be a lattice, and
$L$
be a lattice, and
![]() $x \in L$
. We denote by
$x \in L$
. We denote by
![]() $x_{\uparrow }$
the set of all
$x_{\uparrow }$
the set of all
![]() $y \geqslant x$
. The set theoretic complement of
$y \geqslant x$
. The set theoretic complement of
![]() $x_{\uparrow }$
in
$x_{\uparrow }$
in
![]() $L$
will be denoted
$L$
will be denoted
![]() $x_{\uparrow }^{\mathsf{c}}$
.
$x_{\uparrow }^{\mathsf{c}}$
.
The following is a standard result in the theory of finite lattices.
Lemma 2.4.
Let
![]() $L$
be a finite lattice and
$L$
be a finite lattice and
![]() $x \in L$
. Then the collection
$x \in L$
. Then the collection
![]() $x_{\uparrow }$
is a sublattice of
$x_{\uparrow }$
is a sublattice of
![]() $L$
, and
$L$
, and
![]() $x_{\uparrow }^{\mathsf{c}}$
is a sub-meet-semilattice of
$x_{\uparrow }^{\mathsf{c}}$
is a sub-meet-semilattice of
![]() $L$
.
$L$
.
Via Lemma2.4, one sees that there is a well-defined notion of transfer system for
![]() $x_{\uparrow }$
and
$x_{\uparrow }$
and
![]() $x_{\uparrow }^{\mathsf{c}}$
. Indeed, the axioms for a categorical transfer system only depend on the meet operation, so we can use the same definition for meet-semilattices like
$x_{\uparrow }^{\mathsf{c}}$
. Indeed, the axioms for a categorical transfer system only depend on the meet operation, so we can use the same definition for meet-semilattices like
![]() $x_\uparrow ^{\mathsf{c}}$
. In particular, for
$x_\uparrow ^{\mathsf{c}}$
. In particular, for
![]() $L$
a finite lattice and
$L$
a finite lattice and
![]() $\mathcal{R}$
a transfer system on
$\mathcal{R}$
a transfer system on
![]() $L$
, if
$L$
, if
![]() $x$
is the unique minimal fibrant element, then
$x$
is the unique minimal fibrant element, then
![]() $\mathcal{R}$
restricts to transfer systems
$\mathcal{R}$
restricts to transfer systems
![]() $\mathcal{R}_2$
and
$\mathcal{R}_2$
and
![]() $\mathcal{R}_1$
on
$\mathcal{R}_1$
on
![]() $x_{\uparrow }$
and
$x_{\uparrow }$
and
![]() $x_{\uparrow }^{\mathsf{c}}$
, respectively.
$x_{\uparrow }^{\mathsf{c}}$
, respectively.
Given
![]() $\mathcal{R}_1$
and
$\mathcal{R}_1$
and
![]() $\mathcal{R}_2$
as above, we can construct a candidate transfer system
$\mathcal{R}_2$
as above, we can construct a candidate transfer system
![]() $\mathcal{R}_1 \amalg \mathcal{R}_2$
by simply taking their disjoint union over
$\mathcal{R}_1 \amalg \mathcal{R}_2$
by simply taking their disjoint union over
![]() $L$
. The following lemma proves that this retrieves the starting transfer system
$L$
. The following lemma proves that this retrieves the starting transfer system
![]() $\mathcal{R}$
.
$\mathcal{R}$
.
Lemma 2.5.
Let
![]() $\mathcal{R}$
,
$\mathcal{R}$
,
![]() $\mathcal{R}_1$
, and
$\mathcal{R}_1$
, and
![]() $\mathcal{R}_2$
be as above. Then
$\mathcal{R}_2$
be as above. Then
![]() $\mathcal{R} = \mathcal{R}_1 \amalg \mathcal{R}_2$
.
$\mathcal{R} = \mathcal{R}_1 \amalg \mathcal{R}_2$
.
Proof. Assume that there is some
![]() $y \in x_\uparrow ^{\mathsf{c}}$
and
$y \in x_\uparrow ^{\mathsf{c}}$
and
![]() $z \in x_\uparrow$
such that
$z \in x_\uparrow$
such that
![]() $y\, \mathcal{R}\, z$
. By the property of a transfer system, we have
$y\, \mathcal{R}\, z$
. By the property of a transfer system, we have
![]() $(x \wedge y )\, \mathcal{R}\, x$
, and by transitivity we have
$(x \wedge y )\, \mathcal{R}\, x$
, and by transitivity we have
![]() $(x \wedge y )\, \mathcal{R}\, x \mathcal{R}\, m$
, that is,
$(x \wedge y )\, \mathcal{R}\, x \mathcal{R}\, m$
, that is,
![]() $x \wedge y$
is fibrant. However, as
$x \wedge y$
is fibrant. However, as
![]() $y \in x_\uparrow ^{\mathsf{c}}$
,
$y \in x_\uparrow ^{\mathsf{c}}$
,
![]() $(x \wedge y ) \lt x$
, violating the assumed minimality of
$(x \wedge y ) \lt x$
, violating the assumed minimality of
![]() $x$
.
$x$
.
Example 2.6.
Let
![]() $L = [1] \times [3]$
, and consider the following transfer system.
Footnote 3
$L = [1] \times [3]$
, and consider the following transfer system.
Footnote 3

The minimal fibrant element
![]() $(0,1)$
is highlighted in red. One clearly sees pictorially that
$(0,1)$
is highlighted in red. One clearly sees pictorially that
![]() $\mathcal{R}$
splits as a transfer system
$\mathcal{R}$
splits as a transfer system
![]() $\mathcal{R}_2$
on
$\mathcal{R}_2$
on
![]() $(0,1)_{\uparrow } \cong [1] \times [2]$
and a transfer system
$(0,1)_{\uparrow } \cong [1] \times [2]$
and a transfer system
![]() $\mathcal{R}_1$
on
$\mathcal{R}_1$
on
![]() $(0,1)_{\uparrow }^{\mathsf{c}} \cong [1] \times [0] \cong [1]$
.
$(0,1)_{\uparrow }^{\mathsf{c}} \cong [1] \times [0] \cong [1]$
.
As such, every transfer system
![]() $\mathcal{R}$
on
$\mathcal{R}$
on
![]() $L$
can be split into a pair of transfer systems
$L$
can be split into a pair of transfer systems
![]() $\mathcal{R}_1, \mathcal{R}_2$
on sub-(semi-)lattices
$\mathcal{R}_1, \mathcal{R}_2$
on sub-(semi-)lattices
![]() $x_\uparrow ^{\mathsf{c}}$
and
$x_\uparrow ^{\mathsf{c}}$
and
![]() $x_\uparrow$
of
$x_\uparrow$
of
![]() $L$
where
$L$
where
![]() $\mathcal{R}_2$
has minimal fibrant element
$\mathcal{R}_2$
has minimal fibrant element
![]() $x$
. In the converse direction, given two transfer systems
$x$
. In the converse direction, given two transfer systems
![]() $\mathcal{R}_1$
and
$\mathcal{R}_1$
and
![]() $\mathcal{R}_2$
on
$\mathcal{R}_2$
on
![]() $x_\uparrow ^{\mathsf{c}}$
and
$x_\uparrow ^{\mathsf{c}}$
and
![]() $x_\uparrow$
, respectively, we can ask when
$x_\uparrow$
, respectively, we can ask when
![]() $\mathcal{R}_1 \amalg \mathcal{R}_2$
is a transfer system for
$\mathcal{R}_1 \amalg \mathcal{R}_2$
is a transfer system for
![]() $L$
. This happens if and only if the relations in
$L$
. This happens if and only if the relations in
![]() $\mathcal{R}_2$
when restricted to
$\mathcal{R}_2$
when restricted to
![]() $x_{\uparrow }^{\mathsf{c}}$
(i.e., those relations that are forced by the relations of
$x_{\uparrow }^{\mathsf{c}}$
(i.e., those relations that are forced by the relations of
![]() $\mathcal{R}_2$
under the restriction property of a transfer system on the larger lattice
$\mathcal{R}_2$
under the restriction property of a transfer system on the larger lattice
![]() $L$
) are relations in
$L$
) are relations in
![]() $\mathcal{R}_1$
. We will say that such an
$\mathcal{R}_1$
. We will say that such an
![]() $\mathcal{R}_1$
and
$\mathcal{R}_1$
and
![]() $\mathcal{R}_2$
is a restriction closed pair over
$\mathcal{R}_2$
is a restriction closed pair over
![]() $L$
.
$L$
.
Example 2.7.
If we modify Example
2.6 so that
![]() $\mathcal{R}_1$
is the empty transfer system on
$\mathcal{R}_1$
is the empty transfer system on
![]() $[1]$
, then this pair is not restriction closed and
$[1]$
, then this pair is not restriction closed and
![]() $\mathcal{R}_1 \amalg \mathcal{R}_2$
does not form a transfer system for
$\mathcal{R}_1 \amalg \mathcal{R}_2$
does not form a transfer system for
![]() $[1] \times [3]$
.
$[1] \times [3]$
.
From this discussion, we can form the basis of a recursive formula for computing
![]() $\mathsf{Tr}(L)$
based on the geometry of
$\mathsf{Tr}(L)$
based on the geometry of
![]() $L$
. We summarize this in the following theorem.
$L$
. We summarize this in the following theorem.
Theorem 2.8.
Let
![]() $L$
be a finite lattice. Then there is a bijection between transfer systems on
$L$
be a finite lattice. Then there is a bijection between transfer systems on
![]() $L$
and triples
$L$
and triples
![]() $(x,\mathcal{R}_1,\mathcal{R}_2)$
where
$(x,\mathcal{R}_1,\mathcal{R}_2)$
where
![]() $x\in L$
,
$x\in L$
,
![]() $\mathcal{R}_1$
is a transfer system on
$\mathcal{R}_1$
is a transfer system on
![]() $x_\uparrow ^{\mathsf c}$
,
$x_\uparrow ^{\mathsf c}$
,
![]() $\mathcal{R}_2$
is a transfer system on
$\mathcal{R}_2$
is a transfer system on
![]() $x_\uparrow$
with minimal fibrant element
$x_\uparrow$
with minimal fibrant element
![]() $x$
, and
$x$
, and
![]() $\mathcal{R}_1,\mathcal{R}_2$
form a restriction closed pair.
$\mathcal{R}_1,\mathcal{R}_2$
form a restriction closed pair.
Remark 2.9.
The condition that
![]() $\mathcal{R}_2$
has minimal fibrant element
$\mathcal{R}_2$
has minimal fibrant element
![]() $x$
is equivalent to
$x$
is equivalent to
![]() $\mathcal{R}_2$
being connected when its relations are considered as edges in an undirected graph.
$\mathcal{R}_2$
being connected when its relations are considered as edges in an undirected graph.
Construction 2.10.
To rephrase this strategy in the form of an
![]() $\odot$
operation, we use the observation from the beginning of this section that the pivot element of the
$\odot$
operation, we use the observation from the beginning of this section that the pivot element of the
![]() $\odot$
operation for
$\odot$
operation for
![]() $[n]$
was given by the minimal fibrant element of
$[n]$
was given by the minimal fibrant element of
![]() $\mathcal{R}$
. If
$\mathcal{R}$
. If
![]() $L$
is now an arbitrary finite lattice with
$L$
is now an arbitrary finite lattice with
![]() $\mathcal{R}$
,
$\mathcal{R}$
,
![]() $\mathcal{R}_1$
, and
$\mathcal{R}_1$
, and
![]() $\mathcal{R}_2$
as above, we let
$\mathcal{R}_2$
as above, we let
![]() $\mathcal{R}_2 \smallsetminus \{x\}$
be the collection of relations where we have removed the initial element (i.e., we remove the fibrant element
$\mathcal{R}_2 \smallsetminus \{x\}$
be the collection of relations where we have removed the initial element (i.e., we remove the fibrant element
![]() $x$
). Then we could sensibly define
$x$
). Then we could sensibly define
![]() $\mathcal{R} = \mathcal{R}_1 \odot (\mathcal{R}_2 \smallsetminus \{x\}$
), where the operation
$\mathcal{R} = \mathcal{R}_1 \odot (\mathcal{R}_2 \smallsetminus \{x\}$
), where the operation
![]() $\odot$
inserts a new element
$\odot$
inserts a new element
![]() $x$
and adds in the relation
$x$
and adds in the relation
![]() $x\, \mathcal{R}\, m$
and all relations induced by this.
$x\, \mathcal{R}\, m$
and all relations induced by this.
In this notation, one would decompose the
![]() $\mathcal{R}$
of Example
2.6 as
$\mathcal{R}$
of Example
2.6 as

3. Enumerating transfer systems for
 $D_{p^n}$
$D_{p^n}$
The eventual goal of this paper is to provide a recursive formula for transfer systems on
![]() $[1] \times [n]$
which we realize as the subgroup lattice of
$[1] \times [n]$
which we realize as the subgroup lattice of
![]() $G = C_{qp^n}$
for
$G = C_{qp^n}$
for
![]() $p,q$
distinct primes. We will begin with a slightly more tame count, that of liftable transfer systems of
$p,q$
distinct primes. We will begin with a slightly more tame count, that of liftable transfer systems of
![]() $[1] \times [n]$
as we now define.
$[1] \times [n]$
as we now define.
Definition 3.1.
A transfer system
![]() $\mathcal{R}$
on
$\mathcal{R}$
on
![]() $[1] \times [n]$
is liftable if
$[1] \times [n]$
is liftable if
![]() $\mathcal{R}$
additionally satisfies
$\mathcal{R}$
additionally satisfies
We write
![]() $L(n)$
to denote the collection of liftable transfer systems on
$L(n)$
to denote the collection of liftable transfer systems on
![]() $[1] \times [n]$
.
$[1] \times [n]$
.
The relevance of liftable transfer systems in the general machinery of
![]() $N_\infty$
operads is provided by the following key result of [Reference Balchin, MacBrough and Ormsby5].
$N_\infty$
operads is provided by the following key result of [Reference Balchin, MacBrough and Ormsby5].
Proposition 3.2 ([Reference Balchin, MacBrough and Ormsby5, Section 4]). Let
![]() $n \geqslant 0$
. Then there is a bijection between liftable transfer systems on
$n \geqslant 0$
. Then there is a bijection between liftable transfer systems on
![]() $[1] \times [n]$
and transfer systems for the group
$[1] \times [n]$
and transfer systems for the group
![]() $G = D_{p^n}$
.
$G = D_{p^n}$
.
The link between liftable transfer systems and dihedral transfer systems arises via the lattice isomorphism
![]() $\operatorname{Sub}(D_{p^n})/D_{p^n} \cong [1] \times [n]$
. (Here the quotient is with respect to the conjugation action of
$\operatorname{Sub}(D_{p^n})/D_{p^n} \cong [1] \times [n]$
. (Here the quotient is with respect to the conjugation action of
![]() $D_{p^n}$
on its subgroups.) Once we have given a recursive formula for
$D_{p^n}$
on its subgroups.) Once we have given a recursive formula for
![]() $L(n)$
, we will, in the following section, exploit the involution on transfer systems as uncovered in [Reference Franchere, Ormsby, Osorno, Qin and Waugh9] to prove a recursion for
$L(n)$
, we will, in the following section, exploit the involution on transfer systems as uncovered in [Reference Franchere, Ormsby, Osorno, Qin and Waugh9] to prove a recursion for
![]() $\mathsf{Tr}([1] \times [n])$
.
$\mathsf{Tr}([1] \times [n])$
.
As a warmup, let us see how the liftable condition
![]() $(L)$
allows us to enumerate the number of saturated transfer systems in
$(L)$
allows us to enumerate the number of saturated transfer systems in
![]() $L(n)$
. Recall that a transfer system is said to be saturated if it satisfies 2-out-of-3.
$L(n)$
. Recall that a transfer system is said to be saturated if it satisfies 2-out-of-3.
Proposition 3.3.
There are
![]() $(n+2)2^n$
saturated transfer systems for
$(n+2)2^n$
saturated transfer systems for
![]() $D_{p^n}$
.
$D_{p^n}$
.
Proof. In [Reference Hafeez, Marcus, Ormsby and Osorno10], it was proved that there are
![]() $2^n$
saturated transfer systems on
$2^n$
saturated transfer systems on
![]() $[n]$
. Consider the bottom row of
$[n]$
. Consider the bottom row of
![]() $[1]\times [n]$
given by the coordinates
$[1]\times [n]$
given by the coordinates
![]() $(0,i)$
, then we can freely pick any saturated transfer system to fill this in. Let
$(0,i)$
, then we can freely pick any saturated transfer system to fill this in. Let
![]() $j$
be the maximal number such that
$j$
be the maximal number such that
![]() $(0,j) \, \mathcal{R} \, (1,j)$
. Clearly there are
$(0,j) \, \mathcal{R} \, (1,j)$
. Clearly there are
![]() $n+2$
such choices (including the possibility of no such
$n+2$
such choices (including the possibility of no such
![]() $j$
existing). We then claim that this data uniquely determines a saturated transfer system on
$j$
existing). We then claim that this data uniquely determines a saturated transfer system on
![]() $[1] \times [n]$
which moreover satisfies
$[1] \times [n]$
which moreover satisfies
![]() $(L)$
.
$(L)$
.
We begin by observing that if
![]() $j^{\prime},j^{\prime\prime} \gt j$
, we cannot have
$j^{\prime},j^{\prime\prime} \gt j$
, we cannot have
![]() $(1, j^{\prime}) \, \mathcal{R} \, (1, j^{\prime\prime})$
. If this were the case then by
$(1, j^{\prime}) \, \mathcal{R} \, (1, j^{\prime\prime})$
. If this were the case then by
![]() $(L)$
, we would be forced to have
$(L)$
, we would be forced to have
![]() $(0,j^{\prime}) \, \mathcal{R} \, (1,j^{\prime})$
which contradicts the maximality of
$(0,j^{\prime}) \, \mathcal{R} \, (1,j^{\prime})$
which contradicts the maximality of
![]() $j$
. Instead consider the existence of
$j$
. Instead consider the existence of
![]() $(1,j) \, \mathcal{R} \, (1, j+1)$
. By restriction, we must have
$(1,j) \, \mathcal{R} \, (1, j+1)$
. By restriction, we must have
![]() $(0,j) \, \mathcal{R} \, (1, j+1)$
as well as
$(0,j) \, \mathcal{R} \, (1, j+1)$
as well as
![]() $(0,j) \, \mathcal{R} \, (0, j+1)$
. As saturated transfer systems satisfy two-out-of-three, it would imply that we moreover have
$(0,j) \, \mathcal{R} \, (0, j+1)$
. As saturated transfer systems satisfy two-out-of-three, it would imply that we moreover have
![]() $(0,j+1) \, \mathcal{R} \, (1,j+1)$
, once again contradicting the maximality of
$(0,j+1) \, \mathcal{R} \, (1,j+1)$
, once again contradicting the maximality of
![]() $j$
. As such, everything to the right of
$j$
. As such, everything to the right of
![]() $j$
on the top row of
$j$
on the top row of
![]() $[1] \times [n]$
must be empty.
$[1] \times [n]$
must be empty.
As we have
![]() $(0,j) \, \mathcal{R} \, (1,j)$
, by restriction we also have
$(0,j) \, \mathcal{R} \, (1,j)$
, by restriction we also have
![]() $(0, \ell ) \, \mathcal{R} \, (1, \ell )$
for all
$(0, \ell ) \, \mathcal{R} \, (1, \ell )$
for all
![]() $0 \leqslant \ell \leqslant j$
. By the saturation condition, this forces the top row to the left of
$0 \leqslant \ell \leqslant j$
. By the saturation condition, this forces the top row to the left of
![]() $j$
to be identical to the bottom row.
$j$
to be identical to the bottom row.
Assembling everything, it follows that there are
![]() $(n+2)2^n$
possibilities as claimed.
$(n+2)2^n$
possibilities as claimed.
Remark 3.4. Saturated transfer systems have a simple description as those transfer systems which satisfy the 2-out-of-3 property; however, they are extremely important in the realm of commutative equivariant homotopy theory. Indeed, they are related to the equivariant linear isometry operads. Every linear isometry operad arises from a saturated transfer system, but this relation need not be bijective. We refer the reader to [Reference MacBrough13, Reference Rubin16] for more details.
We will use the strategy outlined in Section 2 to give a recursion for
![]() $L(n)$
. In particular, we begin by considering the partition of
$L(n)$
. In particular, we begin by considering the partition of
![]() $L(n)$
as:
$L(n)$
as:
where
![]() $L(n,(a,b))$
is the set of liftable transfer systems such that
$L(n,(a,b))$
is the set of liftable transfer systems such that
![]() $(a,b)$
is the minimal fibrant element (i.e.,
$(a,b)$
is the minimal fibrant element (i.e.,
![]() $(a,b)$
is minimal such that
$(a,b)$
is minimal such that
![]() $(a,b)\, \mathcal{R}\, (1,n)$
).
$(a,b)\, \mathcal{R}\, (1,n)$
).
We will find it advantageous to further split up the elements
![]() $L(n,(a,b))$
based on further partitioning properties of transfer systems.
$L(n,(a,b))$
based on further partitioning properties of transfer systems.
Definition 3.5.
Let
![]() $\mathcal{R}$
be a transfer system on
$\mathcal{R}$
be a transfer system on
![]() $[1] \times [n]$
. We say that
$[1] \times [n]$
. We say that
![]() $(a,b) \in [1] \times [n]$
is
$(a,b) \in [1] \times [n]$
is
-
• Stationary if
 $a=1$
and there exists no
$a=1$
and there exists no
 $d \gt b \geqslant c$
with
$d \gt b \geqslant c$
with
 $(1,c)\, \mathcal{R}\, (1,d)$
.
$(1,c)\, \mathcal{R}\, (1,d)$
. -
• Extendable if
 $a=0$
and
$a=0$
and
 $(a,b)\, \mathcal{R}\, (0,n)$
.
$(a,b)\, \mathcal{R}\, (0,n)$
.
It is clear that any transfer system possesses at least one stationary and at least one extendable element, namely
![]() $(1,n)$
and
$(1,n)$
and
![]() $(0,n)$
respectively. We now have a different partition of
$(0,n)$
respectively. We now have a different partition of
![]() $L(n)$
as:
$L(n)$
as:
where
![]() $L(n,k)$
is the collection of transfer systems such that exactly
$L(n,k)$
is the collection of transfer systems such that exactly
![]() $k$
elements are stationary. We then further refine each
$k$
elements are stationary. We then further refine each
![]() $L(n,k)$
as:
$L(n,k)$
as:
where
![]() $L(n,k,\ell ) \subseteq L(n,k)$
is the subset of those transfer system where exactly
$L(n,k,\ell ) \subseteq L(n,k)$
is the subset of those transfer system where exactly
![]() $\ell$
elements are extendable.
$\ell$
elements are extendable.
Finally, we can define
![]() $L(n,k,\ell, (a,b))$
to be
$L(n,k,\ell, (a,b))$
to be
![]() $L(n,k,\ell ) \cap L(n,(a,b))$
. We provide a full description of these transfer systems in the following definition.
$L(n,k,\ell ) \cap L(n,(a,b))$
. We provide a full description of these transfer systems in the following definition.
Definition 3.6.
Let
![]() $n \geqslant 0$
,
$n \geqslant 0$
,
![]() $1 \leqslant k, \ell \leqslant n+1, (a,b) \in [1] \times [n]$
. We define
$1 \leqslant k, \ell \leqslant n+1, (a,b) \in [1] \times [n]$
. We define
![]() $L(n,k,\ell, (a,b))$
to be the collection of liftable transfer systems
$L(n,k,\ell, (a,b))$
to be the collection of liftable transfer systems
![]() $\mathcal{R}$
on
$\mathcal{R}$
on
![]() $[1] \times [n]$
such that:
$[1] \times [n]$
such that:
-
•
 $\mathcal{R}$
has
$\mathcal{R}$
has
 $k$
stationary elements.
$k$
stationary elements.
-
•
 $\mathcal{R}$
has
$\mathcal{R}$
has
 $\ell$
extendable elements.
$\ell$
extendable elements.
-
•
 $(a,b)$
is the minimal fibrant element of
$(a,b)$
is the minimal fibrant element of
 $\mathcal{R}$
.
$\mathcal{R}$
.
In the next collection of propositions, we will provide recursions for
![]() $L(n,k,\ell, (a,b))$
for varying families of
$L(n,k,\ell, (a,b))$
for varying families of
![]() $(a,b) \in [1] \times [n]$
. We require one more definition before continuing to the first case.
$(a,b) \in [1] \times [n]$
. We require one more definition before continuing to the first case.
Definition 3.7.
We denote by
![]() $\mathrm{Tam}(n) \subset L(n)$
the set of all transfer systems
$\mathrm{Tam}(n) \subset L(n)$
the set of all transfer systems
![]() $\mathcal{R}$
with
$\mathcal{R}$
with
![]() $(0,n)\, \mathcal{R}\, (1,n)$
and
$(0,n)\, \mathcal{R}\, (1,n)$
and
![]() $\mathrm{Tam}(n,k) =\mathrm{Tam}(n) \cap L(n,k)$
.
$\mathrm{Tam}(n,k) =\mathrm{Tam}(n) \cap L(n,k)$
.
We will provide an in-depth exploration of
![]() $\mathrm{Tam}(n,k)$
in Section 5. In particular, we will explain their namesake (Tamari intervals) and provide explicit formulæ for
$\mathrm{Tam}(n,k)$
in Section 5. In particular, we will explain their namesake (Tamari intervals) and provide explicit formulæ for
![]() $|\mathrm{Tam}(n)|$
and
$|\mathrm{Tam}(n)|$
and
![]() $|\mathrm{Tam}(n,k)|$
; see Proposition5.2.
$|\mathrm{Tam}(n,k)|$
; see Proposition5.2.
Proposition 3.8.
Let
![]() $b \gt 0$
. Then
$b \gt 0$
. Then
Proof. Let
![]() $\mathcal{R} \in L(n, (0,b))$
. Then by restriction to
$\mathcal{R} \in L(n, (0,b))$
. Then by restriction to
![]() $(0,b)_{\uparrow }^{\mathrm{c}} \cong [1] \times [b-1]$
, we obtain a transfer system
$(0,b)_{\uparrow }^{\mathrm{c}} \cong [1] \times [b-1]$
, we obtain a transfer system
![]() $\mathcal{R}_1 \in L(b-1)$
, and by restricting to
$\mathcal{R}_1 \in L(b-1)$
, and by restricting to
![]() $(0,b)_\uparrow \cong [1] \times [n-b]$
, we obtain a transfer system
$(0,b)_\uparrow \cong [1] \times [n-b]$
, we obtain a transfer system
![]() $\mathcal{R}_2 \in L(n-b)$
.
$\mathcal{R}_2 \in L(n-b)$
.
Since
![]() $(0,b)$
is fibrant in
$(0,b)$
is fibrant in
![]() $\mathcal{R}$
and the minimal element of
$\mathcal{R}$
and the minimal element of
![]() $(0,b)_\uparrow$
, we see that
$(0,b)_\uparrow$
, we see that
![]() $\mathcal{R}_2 \in L(n-b,(0,0))$
. Similarly, since
$\mathcal{R}_2 \in L(n-b,(0,0))$
. Similarly, since
![]() $(0,b)\, \mathcal{R}\, (1,b)$
by assumption, we also have
$(0,b)\, \mathcal{R}\, (1,b)$
by assumption, we also have
![]() $(0,b-1)\, \mathcal{R}\, (1,b-1)$
. As such,
$(0,b-1)\, \mathcal{R}\, (1,b-1)$
. As such,
![]() $(1,b-1)$
is fibrant in
$(1,b-1)$
is fibrant in
![]() $\mathcal{R}_1$
. In particular, we conclude that
$\mathcal{R}_1$
. In particular, we conclude that
and
Conversely, given an arbitrary
![]() $\mathcal{R}_1 \in \mathrm{Tam}(b-1)$
and
$\mathcal{R}_1 \in \mathrm{Tam}(b-1)$
and
![]() $\mathcal{R}_2 \in L(n-b,(0,0))$
, we can construct a relation
$\mathcal{R}_2 \in L(n-b,(0,0))$
, we can construct a relation
![]() $\mathcal{R}$
on
$\mathcal{R}$
on
![]() $[1] \times [n]$
by placing
$[1] \times [n]$
by placing
![]() $\mathcal{R}_2$
to the right of
$\mathcal{R}_2$
to the right of
![]() $\mathcal{R}_1$
(i.e., we reindex
$\mathcal{R}_1$
(i.e., we reindex
![]() $\mathcal{R}_2$
via a horizontal shift of
$\mathcal{R}_2$
via a horizontal shift of
![]() $b$
). We will show that
$b$
). We will show that
![]() $\mathcal{R}_1$
and
$\mathcal{R}_1$
and
![]() $\mathcal{R}_2$
form a restriction closed pair.
$\mathcal{R}_2$
form a restriction closed pair.
Clearly such an
![]() $\mathcal{R}$
is transitive and satisfies the lifting condition. Suppose that
$\mathcal{R}$
is transitive and satisfies the lifting condition. Suppose that
![]() $(c,d)\, \mathcal{R}\, (e,f)$
and
$(c,d)\, \mathcal{R}\, (e,f)$
and
![]() $(g,h) \leqslant (e,f)$
. If
$(g,h) \leqslant (e,f)$
. If
![]() $(e,f) \leqslant (1,b-1)$
, then we know that
$(e,f) \leqslant (1,b-1)$
, then we know that
![]() $(c,d)\wedge (g,h)\, \mathcal{R}\, (g,h)$
by the virtue of
$(c,d)\wedge (g,h)\, \mathcal{R}\, (g,h)$
by the virtue of
![]() $\mathcal{R}_1$
being a transfer system.
$\mathcal{R}_1$
being a transfer system.
Else, if
![]() $(e,f) \not \leqslant (1,b-1)$
, then we must have
$(e,f) \not \leqslant (1,b-1)$
, then we must have
![]() $(e,f) \geqslant (0,b)$
, and since
$(e,f) \geqslant (0,b)$
, and since
![]() $(c,d)\, \mathcal{R}\, (e,f)$
and we have no relations from
$(c,d)\, \mathcal{R}\, (e,f)$
and we have no relations from
![]() $(0,b)_{\uparrow }^{\mathsf{c}}$
to
$(0,b)_{\uparrow }^{\mathsf{c}}$
to
![]() $(0,b)_\uparrow$
, we must also have
$(0,b)_\uparrow$
, we must also have
![]() $(c,d) \geqslant (0,b)$
. If
$(c,d) \geqslant (0,b)$
. If
![]() $(g,h) \geqslant (0,b)$
as well, then
$(g,h) \geqslant (0,b)$
as well, then
![]() $(c,d) \wedge (g,h)\, \mathcal{R}\, (g,h)$
from that fact that
$(c,d) \wedge (g,h)\, \mathcal{R}\, (g,h)$
from that fact that
![]() $\mathcal{R}_2$
is a transfer system.
$\mathcal{R}_2$
is a transfer system.
The last remaining case is
![]() $(0,b) \leqslant (c,d)$
and
$(0,b) \leqslant (c,d)$
and
![]() $(g,h) \leqslant (1,b-1)$
, then
$(g,h) \leqslant (1,b-1)$
, then
![]() $(c,d) \wedge (g,h) = (c \wedge g, h)$
. If
$(c,d) \wedge (g,h) = (c \wedge g, h)$
. If
![]() $c \wedge g = g$
, then we have
$c \wedge g = g$
, then we have
![]() $(c \wedge g, h ) \mathcal{R}(g,h)$
. Otherwise,
$(c \wedge g, h ) \mathcal{R}(g,h)$
. Otherwise,
![]() $c=0$
and
$c=0$
and
![]() $g=1$
, so that we just need to ensure that
$g=1$
, so that we just need to ensure that
![]() $(0,h)\, \mathcal{R}\, (1,h)$
fo all
$(0,h)\, \mathcal{R}\, (1,h)$
fo all
![]() $h \leqslant b$
, but this follows from that fact that
$h \leqslant b$
, but this follows from that fact that
![]() $(0,b-1)$
is fibrant in
$(0,b-1)$
is fibrant in
![]() $\mathcal{R}_1$
.
$\mathcal{R}_1$
.
As such, we have shown that
Now we note that
![]() $(1,d)$
is stationary in
$(1,d)$
is stationary in
![]() $\mathcal{R}$
if and only if
$\mathcal{R}$
if and only if
![]() $d \leqslant b-1$
, and
$d \leqslant b-1$
, and
![]() $(1,d)$
is stationary in
$(1,d)$
is stationary in
![]() $\mathcal{R}_1$
, or
$\mathcal{R}_1$
, or
![]() $d \geqslant b$
and
$d \geqslant b$
and
![]() $(1,d-b)$
is stationary in
$(1,d-b)$
is stationary in
![]() $\mathcal{R}_2$
. Furthermore,
$\mathcal{R}_2$
. Furthermore,
![]() $(0,d)$
is extendable in
$(0,d)$
is extendable in
![]() $\mathcal{R}$
if and only if
$\mathcal{R}$
if and only if
![]() $d \geqslant b$
and
$d \geqslant b$
and
![]() $(0,d-b)$
is extendable in
$(0,d-b)$
is extendable in
![]() $\mathcal{R}_2$
. As such, we can refine the above formula to the desired result.
$\mathcal{R}_2$
. As such, we can refine the above formula to the desired result.
Proposition3.8 is valid whenever
![]() $b \gt 0$
. However, we see that the formula is trivial if
$b \gt 0$
. However, we see that the formula is trivial if
![]() $b=0$
, even though there are liftable transfer systems on
$b=0$
, even though there are liftable transfer systems on
![]() $[1] \times [n]$
where the minimal fibrant element is
$[1] \times [n]$
where the minimal fibrant element is
![]() $(0,0)$
(in particular the maximal transfer system is such). The next proposition resolves that case of
$(0,0)$
(in particular the maximal transfer system is such). The next proposition resolves that case of
![]() $b=0$
.
$b=0$
.
Proposition 3.9.
Proof. Let
![]() $\mathcal{R} \in L(n,k,(0,0))$
, and
$\mathcal{R} \in L(n,k,(0,0))$
, and
![]() $\mathcal{R}^{\prime} \in L(n-1)$
be the restriction to
$\mathcal{R}^{\prime} \in L(n-1)$
be the restriction to
![]() $(0,1)_\uparrow \cong [1] \times [n-1]$
. Let
$(0,1)_\uparrow \cong [1] \times [n-1]$
. Let
![]() $b \leqslant n$
be the maximal such that
$b \leqslant n$
be the maximal such that
![]() $(1,0)\, \mathcal{R}\, (1,b)$
. Then
$(1,0)\, \mathcal{R}\, (1,b)$
. Then
![]() $\mathcal{R}$
is determined by
$\mathcal{R}$
is determined by
![]() $\mathcal{R}^{\prime}$
and
$\mathcal{R}^{\prime}$
and
![]() $b$
. Further, the only constraint that we have on
$b$
. Further, the only constraint that we have on
![]() $\mathcal{R}^{\prime}$
and
$\mathcal{R}^{\prime}$
and
![]() $b$
is that if
$b$
is that if
![]() $b \neq 0$
then
$b \neq 0$
then
![]() $(1,b-1)$
must be stationary in
$(1,b-1)$
must be stationary in
![]() $\mathcal{R}^{\prime}$
.
$\mathcal{R}^{\prime}$
.
We then note that an element
![]() $(1,d)$
is stationary in
$(1,d)$
is stationary in
![]() $\mathcal{R}$
if and only if
$\mathcal{R}$
if and only if
![]() $d \geqslant b$
, and either
$d \geqslant b$
, and either
![]() $d=b=0$
or
$d=b=0$
or
![]() $(1,d-1)$
is stationary in
$(1,d-1)$
is stationary in
![]() $\mathcal{R}^{\prime}$
. Conversely, an element
$\mathcal{R}^{\prime}$
. Conversely, an element
![]() $(0,d)$
is extendable if and only if
$(0,d)$
is extendable if and only if
![]() $d=0$
or
$d=0$
or
![]() $(0,d-1)$
is extendable in
$(0,d-1)$
is extendable in
![]() $\mathcal{R}^{\prime}$
. The result follows.
$\mathcal{R}^{\prime}$
. The result follows.
Via Propositions3.8 and 3.9, we have now computed
![]() $|L(n,k,\ell, (0,b))|$
for all possible values of
$|L(n,k,\ell, (0,b))|$
for all possible values of
![]() $b$
. As such we now turn our attention to computing
$b$
. As such we now turn our attention to computing
![]() $|L(n,k,\ell, (1,b))|$
. The case where
$|L(n,k,\ell, (1,b))|$
. The case where
![]() $b \lt n$
is trivial as we now prove.
$b \lt n$
is trivial as we now prove.
Proposition 3.10.
Let
![]() $b \lt n$
, then
$b \lt n$
, then
Proof. Recall that
![]() $L(n)$
consists of the liftable transfer systems. Assume that
$L(n)$
consists of the liftable transfer systems. Assume that
![]() $\mathcal{R} \in L(n,k,\ell, (1,b))$
then by assumption we have
$\mathcal{R} \in L(n,k,\ell, (1,b))$
then by assumption we have
![]() $(1,b)\, \mathcal{R}\, (1,n)$
. However, by the lifting condition, this implies that
$(1,b)\, \mathcal{R}\, (1,n)$
. However, by the lifting condition, this implies that
![]() $(0,b)\, \mathcal{R}\, (1,b)\, \mathcal{R}\, (1,n)$
, violating the minimality of
$(0,b)\, \mathcal{R}\, (1,b)\, \mathcal{R}\, (1,n)$
, violating the minimality of
![]() $(1,b)$
. Therefore, no such
$(1,b)$
. Therefore, no such
![]() $\mathcal{R}$
exists.
$\mathcal{R}$
exists.
The simplicity of the case of
![]() $(1,b)$
where
$(1,b)$
where
![]() $b \lt n$
is one of the reasons why working with liftable transfer systems is simpler than the general case. Given Proposition3.10, it now suffices to compute
$b \lt n$
is one of the reasons why working with liftable transfer systems is simpler than the general case. Given Proposition3.10, it now suffices to compute
![]() $L(n,k,\ell, (1,n))$
:
$L(n,k,\ell, (1,n))$
:
Proposition 3.11. We have
Proof. Let
![]() $\mathcal{R} \in L(n,k,(1,n))$
, and
$\mathcal{R} \in L(n,k,(1,n))$
, and
![]() $\mathcal{R}^{\prime} \in L(n,-1)$
be the restriction to
$\mathcal{R}^{\prime} \in L(n,-1)$
be the restriction to
![]() $[1] \times [n-1]$
. Clearly there are no constraints on
$[1] \times [n-1]$
. Clearly there are no constraints on
![]() $\mathcal{R}^{\prime}$
except from that it must have
$\mathcal{R}^{\prime}$
except from that it must have
![]() $k-1$
stationary elements.
$k-1$
stationary elements.
We begin by assuming that there are no relations
![]() $(0,d)\, \mathcal{R}\, (0,n)$
for
$(0,d)\, \mathcal{R}\, (0,n)$
for
![]() $d \lt n$
, that is,
$d \lt n$
, that is,
![]() $\mathcal{R}$
has a single extendable element. Thus, all relations in
$\mathcal{R}$
has a single extendable element. Thus, all relations in
![]() $\mathcal{R}$
are contained in
$\mathcal{R}$
are contained in
![]() $(0,n)^{\mathsf{c}}_{\uparrow }$
and hence
$(0,n)^{\mathsf{c}}_{\uparrow }$
and hence
![]() $\mathcal{R}$
is determined solely by
$\mathcal{R}$
is determined solely by
![]() $\mathcal{R}^{\prime}$
. In particular, we have
$\mathcal{R}^{\prime}$
. In particular, we have
We now move to the case where
![]() $\mathcal{R}$
has more than a single extendable element. That is, we assume that there exists some
$\mathcal{R}$
has more than a single extendable element. That is, we assume that there exists some
![]() $d \lt n$
with
$d \lt n$
with
![]() $(0,d)\, \mathcal{R}\, (0,n)$
for
$(0,d)\, \mathcal{R}\, (0,n)$
for
![]() $d \lt n$
. The set of all
$d \lt n$
. The set of all
![]() $d \lt n$
admitting arrows
$d \lt n$
admitting arrows
![]() $(0,d)\, \mathcal{R}\, (0,n)$
is determined by the maximal such
$(0,d)\, \mathcal{R}\, (0,n)$
is determined by the maximal such
![]() $d$
, which we denote
$d$
, which we denote
![]() $b$
. Indeed, if
$b$
. Indeed, if
![]() $(0,d)\, \mathcal{R}\, (0,n)$
then by restriction we also have
$(0,d)\, \mathcal{R}\, (0,n)$
then by restriction we also have
![]() $(0,d)\, \mathcal{R}\, (0,b)$
, and hence by definition
$(0,d)\, \mathcal{R}\, (0,b)$
, and hence by definition
![]() $(0,d) \mathcal{R}^{\prime} (0,b)$
. Conversely if
$(0,d) \mathcal{R}^{\prime} (0,b)$
. Conversely if
![]() $(0,d) \mathcal{R}^{\prime} (0,b)$
, then by transitivity we have
$(0,d) \mathcal{R}^{\prime} (0,b)$
, then by transitivity we have
![]() $(0,d)\, \mathcal{R}\, (0,b)\, \mathcal{R}\, (0,n)$
. The only constraint that we have on
$(0,d)\, \mathcal{R}\, (0,b)\, \mathcal{R}\, (0,n)$
. The only constraint that we have on
![]() $b$
is that
$b$
is that
![]() $(0,b)$
must be extendable in
$(0,b)$
must be extendable in
![]() $\mathcal{R}^{\prime}$
. Note that if
$\mathcal{R}^{\prime}$
. Note that if
![]() $b$
is the
$b$
is the
![]() $i$
-th smallest extendable element in
$i$
-th smallest extendable element in
![]() $\mathcal{R}^{\prime}$
, then
$\mathcal{R}^{\prime}$
, then
![]() $\mathcal{R}$
has
$\mathcal{R}$
has
![]() $i+1$
extendable elements. If
$i+1$
extendable elements. If
![]() $\mathcal{R}^{\prime}$
has
$\mathcal{R}^{\prime}$
has
![]() $k$
stationary elements, then
$k$
stationary elements, then
![]() $\mathcal{R}$
has
$\mathcal{R}$
has
![]() $k+1$
stationary elements. Thus we have shown that
$k+1$
stationary elements. Thus we have shown that
as required. We note that this retrieves the above formula when
![]() $\ell = 1$
.
$\ell = 1$
.
We are now in a position to combine the above results into the main theorem of this section which provides an explicit recursive algorithm for computing
![]() $|L(n)|$
.
$|L(n)|$
.
Theorem 3.12.
Let
![]() $n \geqslant 0$
. Then for
$n \geqslant 0$
. Then for
![]() $1 \leqslant \ell, k \leqslant n+1$
and
$1 \leqslant \ell, k \leqslant n+1$
and
![]() $(a,b) \in [1] \times [n]$
we have
$(a,b) \in [1] \times [n]$
we have
 \begin{align*} |L(n,k,\ell, (0,0))| = & \sum _{k-1 \leqslant k^{\prime} \leqslant n} |L(n-1,k^{\prime},\ell -1)|&\\ |L(n,k,\ell, (1,n))| = & \sum _{\ell -1 \leqslant \ell ^{\prime} \leqslant n} |L(n-1,k-1,\ell ^{\prime})|&\\ |L(n,k,\ell, (0,b))| = & \sum _{0 \leqslant i \leqslant k} |\mathrm{Tam}(b-1,i)| \cdot |L(n-b,k-i,\ell, (0,0))|& (b\gt 0)\\ |L(n,k,\ell, (1,b))| = &{\hspace{1ex}} 0 & (b\lt n). \end{align*}
\begin{align*} |L(n,k,\ell, (0,0))| = & \sum _{k-1 \leqslant k^{\prime} \leqslant n} |L(n-1,k^{\prime},\ell -1)|&\\ |L(n,k,\ell, (1,n))| = & \sum _{\ell -1 \leqslant \ell ^{\prime} \leqslant n} |L(n-1,k-1,\ell ^{\prime})|&\\ |L(n,k,\ell, (0,b))| = & \sum _{0 \leqslant i \leqslant k} |\mathrm{Tam}(b-1,i)| \cdot |L(n-b,k-i,\ell, (0,0))|& (b\gt 0)\\ |L(n,k,\ell, (1,b))| = &{\hspace{1ex}} 0 & (b\lt n). \end{align*}
By convention, set
![]() $|L(n,k, \ell, (a,b))| = 0$
when
$|L(n,k, \ell, (a,b))| = 0$
when
![]() $k, \ell$
are out of range. Then
$k, \ell$
are out of range. Then
Corollary 3.13.
Let
![]() $n \geqslant 0$
. Then the number of homotopically distinct
$n \geqslant 0$
. Then the number of homotopically distinct
![]() $N_\infty$
operads for
$N_\infty$
operads for
![]() $D_{p^n}$
is given by the recursion in Theorem
3.12.
$D_{p^n}$
is given by the recursion in Theorem
3.12.
Remark 3.14.
Note that in Theorem
3.12, it is only the computation
![]() $|L(n,k,\ell, (1,b))| = 0$
for
$|L(n,k,\ell, (1,b))| = 0$
for
![]() $b \lt n$
where we use the fact that we are working with liftable transfer systems. This will be relevant in the next section we consider transfer systems for
$b \lt n$
where we use the fact that we are working with liftable transfer systems. This will be relevant in the next section we consider transfer systems for
![]() $C_{qp^n}$
.
$C_{qp^n}$
.
Computation 3.15.
By starting at
![]() $m=0$
, we inductively store the values of
$m=0$
, we inductively store the values of
![]() $|L (m, k, \ell, (a,b))|$
for all
$|L (m, k, \ell, (a,b))|$
for all
![]() $m \leqslant n$
,
$m \leqslant n$
,
![]() $1 \leqslant k, \ell \leqslant m+1$
and
$1 \leqslant k, \ell \leqslant m+1$
and
![]() $(a,b) \in [1] \times [m]$
. The entries for all
$(a,b) \in [1] \times [m]$
. The entries for all
![]() $m \lt m^{\prime}$
allow us to compute the values for
$m \lt m^{\prime}$
allow us to compute the values for
![]() $m=m^{\prime}$
via Theorem
3.12 and Proposition
5.2
; some small values are recorded in Table
1, and large-scale structure appears at the end of the paper in Figure 1
.
$m=m^{\prime}$
via Theorem
3.12 and Proposition
5.2
; some small values are recorded in Table
1, and large-scale structure appears at the end of the paper in Figure 1
.
Table 1. Values of
![]() $|L(n)|$
, the number of transfer systems for
$|L(n)|$
, the number of transfer systems for
![]() $D_{p^n}$
(
$D_{p^n}$
(
![]() $p\ne 2$
), computed via Theorem3.12.
$p\ne 2$
), computed via Theorem3.12.


Figure 1. A (nonlogarithmic) plot of
![]() $|L(n)|/|T(n)|$
for
$|L(n)|/|T(n)|$
for
![]() $0\leqslant n\leqslant 80$
. The semilogarithmic plot appears approximately linear.
$0\leqslant n\leqslant 80$
. The semilogarithmic plot appears approximately linear.
Remark 3.16.
We leave open the challenge of finding a closed formula for
![]() $|L(n)|$
. One might begin with a five-variable generating function and the functional equation implied by Theorem
3.12. Of course, a bijective enumeration would be even more desirable.
$|L(n)|$
. One might begin with a five-variable generating function and the functional equation implied by Theorem
3.12. Of course, a bijective enumeration would be even more desirable.
Remark 3.17.
In Proposition
6.11, we deduce a nontrivial lower bound on the asymptotics of
![]() $|L(n)|$
.
$|L(n)|$
.
4. Enumerating transfer systems for
 $C_{qp^n}$
$C_{qp^n}$
In the previous section, we enumerated the liftable transfer systems on
![]() $[1] \times [n]$
. We will now move to the general case. For clarity, we will write
$[1] \times [n]$
. We will now move to the general case. For clarity, we will write
![]() $T(n)$
for the collection of all transfer systems
$T(n)$
for the collection of all transfer systems
![]() $[1] \times [n]$
(i.e.,
$[1] \times [n]$
(i.e.,
![]() $L(n) \subseteq T(n)$
). We will employ the same strategy as before, and
$L(n) \subseteq T(n)$
). We will employ the same strategy as before, and
![]() $T(n,k, \ell, (a,b))$
will be as before (but without the lifting condition).
$T(n,k, \ell, (a,b))$
will be as before (but without the lifting condition).
From Remark3.14, we see that we need only consider how to resolve the case of
![]() $T(n,k,\ell, (1,b))$
for
$T(n,k,\ell, (1,b))$
for
![]() $b \lt n$
, and in the other cases the recursion for
$b \lt n$
, and in the other cases the recursion for
![]() $T(n,k, \ell, (a,b))$
is the same as the recursion for
$T(n,k, \ell, (a,b))$
is the same as the recursion for
![]() $L(n,k, \ell, (a,b))$
. To resolve this remaining case, we will use a powerful observation regarding the duality of transfer systems as described in [Reference Franchere, Ormsby, Osorno, Qin and Waugh9] which we now recall. For a transfer system
$L(n,k, \ell, (a,b))$
. To resolve this remaining case, we will use a powerful observation regarding the duality of transfer systems as described in [Reference Franchere, Ormsby, Osorno, Qin and Waugh9] which we now recall. For a transfer system
![]() $\mathcal{R}$
on a finite lattice
$\mathcal{R}$
on a finite lattice
![]() $L$
, we write
$L$
, we write
for the downward closure of
![]() $\mathcal{R}$
.
$\mathcal{R}$
.
We recall that a lattice
![]() $L$
admits a self-duality if there exists a bijection
$L$
admits a self-duality if there exists a bijection
![]() $\nabla : L \to L$
such that
$\nabla : L \to L$
such that
![]() $ x \leqslant y$
if and only if
$ x \leqslant y$
if and only if
![]() $y^\nabla \leqslant x^\nabla$
for all
$y^\nabla \leqslant x^\nabla$
for all
![]() $x,y \in L$
.
$x,y \in L$
.
Definition 4.1.
Let
![]() $L$
be a finite lattice admitting a self-duality
$L$
be a finite lattice admitting a self-duality
![]() $\nabla$
and let
$\nabla$
and let
![]() $\mathcal{R}$
be a transfer system on
$\mathcal{R}$
be a transfer system on
![]() $L$
. The dual of
$L$
. The dual of
![]() $\mathcal{R}$
is the transfer system
$\mathcal{R}$
is the transfer system
![]() $\mathcal{R}^\ast$
defined as:
$\mathcal{R}^\ast$
defined as:
From [Reference Franchere, Ormsby, Osorno, Qin and Waugh9, Theorem 4.21], we have that
![]() $(\mathcal{R}^\ast )^\ast = \mathcal{R}$
so this provides an involution on the set
$(\mathcal{R}^\ast )^\ast = \mathcal{R}$
so this provides an involution on the set
![]() $\mathsf{Tr}(L)$
. In the case that
$\mathsf{Tr}(L)$
. In the case that
![]() $L = [1] \times [n]$
, we use the canonical duality given by
$L = [1] \times [n]$
, we use the canonical duality given by ![]() . In particular, we have
. In particular, we have
![]() $(a,b) \, \mathcal{R} \, (c,d)$
if and only if
$(a,b) \, \mathcal{R} \, (c,d)$
if and only if ![]() .
.
Proposition 4.2.
The duality on
![]() $\mathsf{Tr}([1] \times [n])$
restricts to a duality:
$\mathsf{Tr}([1] \times [n])$
restricts to a duality:
This duality does not preserve the property of being liftable.
Proof. Let
![]() $\mathcal{R} \in T(n,k,\ell, (a,b))$
. We first observe that
$\mathcal{R} \in T(n,k,\ell, (a,b))$
. We first observe that
![]() $(1-a,n-b)$
is the minimal fibrant element in
$(1-a,n-b)$
is the minimal fibrant element in
![]() $\mathcal{R}^\ast$
. Indeed, we have
$\mathcal{R}^\ast$
. Indeed, we have
![]() $(a,b)$
as the minimal element such that
$(a,b)$
as the minimal element such that
![]() $(a,b)\, \mathcal{R}\, (1,n)$
. From the definition, we see that
$(a,b)\, \mathcal{R}\, (1,n)$
. From the definition, we see that
![]() $(1-a,n-b)\, \mathcal{R}^\ast \, (1,n)$
if and only if
$(1-a,n-b)\, \mathcal{R}^\ast \, (1,n)$
if and only if ![]() . Assume that we have
. Assume that we have
![]() $(0,0)\, \mathcal{E}(\mathcal{R}) \, (a,b)$
, then this implies the existence of some
$(0,0)\, \mathcal{E}(\mathcal{R}) \, (a,b)$
, then this implies the existence of some
![]() $(i,j) \lt (a,b)$
such that
$(i,j) \lt (a,b)$
such that
![]() $(i,j)\, \mathcal{R}\, (a,b)$
, but by transitivity we would get
$(i,j)\, \mathcal{R}\, (a,b)$
, but by transitivity we would get
![]() $(i,j)\, \mathcal{R}\, (a,b)\, \mathcal{R}\, (1,n)$
, contradicting the minimality of
$(i,j)\, \mathcal{R}\, (a,b)\, \mathcal{R}\, (1,n)$
, contradicting the minimality of
![]() $(a,b)$
. The minimality of
$(a,b)$
. The minimality of
![]() $(1-a,n-b)$
as a fibrant element of
$(1-a,n-b)$
as a fibrant element of
![]() $\mathcal{R}^\ast$
is afforded by the minimality of
$\mathcal{R}^\ast$
is afforded by the minimality of
![]() $(a,b)$
in
$(a,b)$
in
![]() $\mathcal{R}$
.
$\mathcal{R}$
.
We will now explore the duality between the extendable and stationary elements. Let
![]() $y \geqslant 1$
, we will show that
$y \geqslant 1$
, we will show that
![]() $(1,y-1)$
is stationary in
$(1,y-1)$
is stationary in
![]() $\mathcal{R}$
if and only if
$\mathcal{R}$
if and only if
![]() $(0,n-y)$
is extendable in
$(0,n-y)$
is extendable in
![]() $\mathcal{R}^\ast$
. Again by definition, this happens if and only if
$\mathcal{R}^\ast$
. Again by definition, this happens if and only if ![]() . Assume that
. Assume that
![]() $(1,0)\, \mathcal{E}(\mathcal{R})\, (1,y)$
, then this implies the existence of some
$(1,0)\, \mathcal{E}(\mathcal{R})\, (1,y)$
, then this implies the existence of some
![]() $0 \leqslant z \lt y$
with
$0 \leqslant z \lt y$
with
![]() $(1,z)\, \mathcal{R}\, (1,y)$
. However, we have assumed that
$(1,z)\, \mathcal{R}\, (1,y)$
. However, we have assumed that
![]() $y-1$
is stationary, so no such
$y-1$
is stationary, so no such
![]() $z$
can exist.
$z$
can exist.
The remaining case of
![]() $y=0$
is covered by the fact that
$y=0$
is covered by the fact that
![]() $(1,n)$
is always stationary and
$(1,n)$
is always stationary and
![]() $(0,n)$
is always extendable.
$(0,n)$
is always extendable.
Combining Proposition4.2, Theorem3.12, and Remark3.14, we arrive at our desired result.
Theorem 4.3.
Let
![]() $n \geqslant 0$
. Then for
$n \geqslant 0$
. Then for
![]() $1 \leqslant \ell, k \leqslant n+1$
and
$1 \leqslant \ell, k \leqslant n+1$
and
![]() $(a,b) \in [1] \times [n]$
, we have
$(a,b) \in [1] \times [n]$
, we have
 \begin{align*} |T(n,k,\ell, (0,0))| = & \sum _{k-1 \leqslant k^{\prime} \leqslant n} |T(n-1,k^{\prime},\ell -1)|&\\ |T(n,k,\ell, (0,b))| = & \sum _{0 \leqslant i \leqslant k} |\mathrm{Tam}(b-1,i)| \cdot |T(n-b,k-i,\ell, (0,0))|& (b\gt 0)\\ |T(n,k,\ell, (1,b))| = &{\hspace{1ex}} |T(n,\ell, k,(0,n-b))|. & \end{align*}
\begin{align*} |T(n,k,\ell, (0,0))| = & \sum _{k-1 \leqslant k^{\prime} \leqslant n} |T(n-1,k^{\prime},\ell -1)|&\\ |T(n,k,\ell, (0,b))| = & \sum _{0 \leqslant i \leqslant k} |\mathrm{Tam}(b-1,i)| \cdot |T(n-b,k-i,\ell, (0,0))|& (b\gt 0)\\ |T(n,k,\ell, (1,b))| = &{\hspace{1ex}} |T(n,\ell, k,(0,n-b))|. & \end{align*}
By convention, set
![]() $|T(n,k, \ell, (a,b))| = 0$
when
$|T(n,k, \ell, (a,b))| = 0$
when
![]() $k, \ell$
are out of range. Then
$k, \ell$
are out of range. Then
Corollary 4.4.
Let
![]() $n \geqslant 0$
. Then the number of homotopically distinct
$n \geqslant 0$
. Then the number of homotopically distinct
![]() $N_\infty$
operads for
$N_\infty$
operads for
![]() $C_{qp^n}$
is given by the recursion in Theorem
4.3.
$C_{qp^n}$
is given by the recursion in Theorem
4.3.
Computation 4.5.
Following the methods of Computation
3.15, we are once again able to efficiently compute values of
![]() $|T(n)|$
; for small values of
$|T(n)|$
; for small values of
![]() $n$
, these are presented in Table
2, and larger-scale behavior appears at the end of the paper in Figure 1
.
$n$
, these are presented in Table
2, and larger-scale behavior appears at the end of the paper in Figure 1
.
Table 2. Values of
![]() $|T(n)|$
, the number of transfer systems for
$|T(n)|$
, the number of transfer systems for
![]() $C_{qp^n}$
, computed via Theorem4.3.
$C_{qp^n}$
, computed via Theorem4.3.

Remark 4.6.
The strategy outlined Section
2 is extremely general, and one could envisage running the machine for other fundamental lattices such as
![]() $[m] \times [n]$
and
$[m] \times [n]$
and
![]() $[1]^n$
. What is evident from the discussions in Sections
3 and
4 is that the power of the computation can be improved by understanding the inherent structures of transfer systems and how they arise (e.g., the existence of suitable liftable families and dualities).
$[1]^n$
. What is evident from the discussions in Sections
3 and
4 is that the power of the computation can be improved by understanding the inherent structures of transfer systems and how they arise (e.g., the existence of suitable liftable families and dualities).
Remark 4.7.
As with
![]() $|L(n)|$
, it would be desirable to derive a closed formula for
$|L(n)|$
, it would be desirable to derive a closed formula for
![]() $|T(n)|$
via generating function or bijective techniques.
$|T(n)|$
via generating function or bijective techniques.
5. Restricted Tamari intervals
In this section, we will study the term
![]() $\mathrm{Tam}(n,k)$
which appears in Proposition3.8, Theorems3.12, and 4.3.
$\mathrm{Tam}(n,k)$
which appears in Proposition3.8, Theorems3.12, and 4.3.
We begin by recalling from Definition3.7 that we denote by
![]() $\mathrm{Tam}(n)$
the set of all transfer systems
$\mathrm{Tam}(n)$
the set of all transfer systems
![]() $\mathcal{R}$
with
$\mathcal{R}$
with
![]() $(0,n)\, \mathcal{R}\, (1,n)$
and
$(0,n)\, \mathcal{R}\, (1,n)$
and
![]() $\mathrm{Tam}(n,k) =\mathrm{Tam}(n) \cap L(n,k)$
.
$\mathrm{Tam}(n,k) =\mathrm{Tam}(n) \cap L(n,k)$
.
Recall from [Reference Balchin, Ormsby, Osorno and Roitzheim6, Proposition 2.23, Proposition 4.17] that
![]() $\mathsf{Tr}([n])$
admits a lattice bijection to the Tamari lattice. As such for
$\mathsf{Tr}([n])$
admits a lattice bijection to the Tamari lattice. As such for
![]() $\mathcal{R}$
and
$\mathcal{R}$
and
![]() $\mathcal{R}^{\prime}$
transfer systems on
$\mathcal{R}^{\prime}$
transfer systems on
![]() $[n]$
, we say that
$[n]$
, we say that
![]() $\mathcal{R} \leqslant \mathcal{R}^{\prime}$
is a Tamari interval. The next lemma justifies our choice of notation for
$\mathcal{R} \leqslant \mathcal{R}^{\prime}$
is a Tamari interval. The next lemma justifies our choice of notation for
![]() $\mathrm{Tam}(n)$
. We note that if
$\mathrm{Tam}(n)$
. We note that if
![]() $\mathcal{R}$
is a transfer system on
$\mathcal{R}$
is a transfer system on
![]() $[n]$
, then we—analogously to the
$[n]$
, then we—analogously to the
![]() $[1] \times [n]$
case—say that
$[1] \times [n]$
case—say that
![]() $b \in [n]$
is stationary for
$b \in [n]$
is stationary for
![]() $\mathcal{R}$
if there exists no
$\mathcal{R}$
if there exists no
![]() $d \gt b \geqslant c$
with
$d \gt b \geqslant c$
with
![]() $(1,c)\, \mathcal{R}\, (1,d)$
.
$(1,c)\, \mathcal{R}\, (1,d)$
.
Lemma 5.1.
Let
![]() $n \geq 0$
. Then
$n \geq 0$
. Then
![]() $\mathrm{Tam}(n)$
is in bijection with Tamari intervals in
$\mathrm{Tam}(n)$
is in bijection with Tamari intervals in
![]() $\mathsf{Tr}[n]$
. In particular,
$\mathsf{Tr}[n]$
. In particular,
![]() $\mathrm{Tam}(n,k)$
is in bijection with the Tamari intervals
$\mathrm{Tam}(n,k)$
is in bijection with the Tamari intervals
![]() $\mathcal{R} \leqslant \mathcal{R}^{\prime}$
in
$\mathcal{R} \leqslant \mathcal{R}^{\prime}$
in
![]() $\mathsf{Tr}[n]$
such that
$\mathsf{Tr}[n]$
such that
![]() $\mathcal{R}$
has
$\mathcal{R}$
has
![]() $k$
stationary elements.
$k$
stationary elements.
Proof.
By restriction, a transfer system in
![]() $\mathrm{Tam}(n)$
has all vertical relations
$\mathrm{Tam}(n)$
has all vertical relations
![]() $(0,a)\, \mathcal{R}$
$(0,a)\, \mathcal{R}$
![]() $(1,a)$
for
$(1,a)$
for
![]() $0 \leqslant a \leqslant n$
. We have the diagonal
$0 \leqslant a \leqslant n$
. We have the diagonal
![]() $(0,b)\, \mathcal{R}\, (1,c)$
if and only if
$(0,b)\, \mathcal{R}\, (1,c)$
if and only if
![]() $(0,b)\, \mathcal{R}\, (0,c)$
. Indeed, the forward implication follows by pullback closure, and the reverse implication is given by composition with
$(0,b)\, \mathcal{R}\, (0,c)$
. Indeed, the forward implication follows by pullback closure, and the reverse implication is given by composition with
![]() $(0,c)\, \mathcal{R}\, (1,c)$
. Therefore, such an
$(0,c)\, \mathcal{R}\, (1,c)$
. Therefore, such an
![]() $\mathcal{R}$
restricted to the bottom row determines all diagonals. In particular,
$\mathcal{R}$
restricted to the bottom row determines all diagonals. In particular,
![]() $\mathcal{R}$
is determined uniquely by its restriction to the top and bottom and is therefore the data of a Tamari interval.
$\mathcal{R}$
is determined uniquely by its restriction to the top and bottom and is therefore the data of a Tamari interval.
From work of Chapoton [Reference Chapoton8], we know that the cardinality of the set of Tamari intervals for
![]() $[n]$
has closed form given by:
$[n]$
has closed form given by:
(We warn the reader that our indexing conventions differ from those of [Reference Chapoton8]). The following proposition provides a closed formula for
![]() $|\mathrm{Tam}(n,k)|$
.
$|\mathrm{Tam}(n,k)|$
.
Proposition 5.2.
Let
![]() $n \geqslant 0$
and
$n \geqslant 0$
and
![]() $1 \leqslant k \leqslant n+1$
. Then
$1 \leqslant k \leqslant n+1$
. Then
Proof. An explicit bijection between transfer systems on
![]() $[n]$
and rooted binary trees with
$[n]$
and rooted binary trees with
![]() $(n+1)$
internal nodes was constructed in [Reference Balchin, Barnes and Roitzheim1]. One can check that under this bijection that the number of stationary elements of a transfer system
$(n+1)$
internal nodes was constructed in [Reference Balchin, Barnes and Roitzheim1]. One can check that under this bijection that the number of stationary elements of a transfer system
![]() $\mathcal{R}$
on
$\mathcal{R}$
on
![]() $[n]$
is equal to the number of elements on the corresponding binary tree whose path from the root is a straight line to the left.
$[n]$
is equal to the number of elements on the corresponding binary tree whose path from the root is a straight line to the left.
Using the classical bijection between binary trees with
![]() $n+1$
nodes and Dyck paths of length
$n+1$
nodes and Dyck paths of length
![]() $2n+2$
, we see that the number of stationary elements is also given by one less than the number of times the corresponding Dyck path touches the horizontal axis.
$2n+2$
, we see that the number of stationary elements is also given by one less than the number of times the corresponding Dyck path touches the horizontal axis.
The result then follows from [Reference Bousquet-Mélou, Fusy and Préville-Ratelle4, Corollary 11] and the first remark following it.
Table 3. Values of
![]() $|\mathrm{Tam}(n,k)|$
for small values of
$|\mathrm{Tam}(n,k)|$
for small values of
![]() $n$
and
$n$
and
![]() $k$
using Proposition5.2.
$k$
using Proposition5.2.

Remark 5.3.
The values appearing in Table
3 make up some very well-known number sequences as we now outline. The triangular array
![]() $|\mathrm{Tam}(n,k)|$
appears in a reindexed form in [Reference Brown7] where one enumerates triangulations of
$|\mathrm{Tam}(n,k)|$
appears in a reindexed form in [Reference Brown7] where one enumerates triangulations of
![]() $k+3$
-gons with
$k+3$
-gons with
![]() $n+1$
-internal vertices. In particular, we have:
$n+1$
-internal vertices. In particular, we have:
-
• The major diagonal where
 $k=n+1$
retrieves the Catalan numbers.
$k=n+1$
retrieves the Catalan numbers.
-
• The sum of the row
 $|\mathrm{Tam}(n,-)|$
computes the number of Tamari intervals for
$|\mathrm{Tam}(n,-)|$
computes the number of Tamari intervals for
 $[n]$
.
$[n]$
. -
• The column
 $|\mathrm{Tam}(-,1)|$
is the number of Tamari intervals for
$|\mathrm{Tam}(-,1)|$
is the number of Tamari intervals for
 $[n-1]$
.
$[n-1]$
. -
• The column
 $|\mathrm{Tam}(-,k)|$
is the number of triangulations of a
$|\mathrm{Tam}(-,k)|$
is the number of triangulations of a
 $(k+2)$
-gon with
$(k+2)$
-gon with
 $n$
internal nodes.
$n$
internal nodes.
6. Maximally extendable
 $D_{p^n}$
transfer systems and Schröder numbers
$D_{p^n}$
transfer systems and Schröder numbers
In the remainder of this paper, we will explore a certain type of transfer system on
![]() $[1] \times [n]$
in the liftable and nonliftable cases, the enumeration of which retrieve interesting number sequences. We begin by introducing the class that we are interested in.
$[1] \times [n]$
in the liftable and nonliftable cases, the enumeration of which retrieve interesting number sequences. We begin by introducing the class that we are interested in.
Definition 6.1.
A (liftable) transfer system
![]() $\mathcal{R}$
for
$\mathcal{R}$
for
![]() $[1] \times [n]$
is maximally extendable if it has
$[1] \times [n]$
is maximally extendable if it has
![]() $n+1$
extendable elements.
$n+1$
extendable elements.
Remark 6.2.
In a more intuitive description, a transfer system is maximally extendable if and only if its restriction to the bottom row is the maximal transfer system on
![]() $[n]$
. As such, for
$[n]$
. As such, for
![]() $G = D_{p^n}$
or
$G = D_{p^n}$
or
![]() $C_{qp^n}$
(in the liftable and general scenarios, respectively) these are the transfer systems associated with
$C_{qp^n}$
(in the liftable and general scenarios, respectively) these are the transfer systems associated with
![]() $G$
-
$G$
-
![]() $N_\infty$
operads restricting to genuine
$N_\infty$
operads restricting to genuine
![]() $G$
-
$G$
-
![]() $E_\infty$
operads on
$E_\infty$
operads on
![]() $C_{p^n}\leqslant G$
.
$C_{p^n}\leqslant G$
.
We will once again begin with the case of liftable transfer systems.
Definition 6.3.
Let
![]() $n \geqslant 0$
. Then
$n \geqslant 0$
. Then
![]() $\mathfrak{S}_n$
, the
$\mathfrak{S}_n$
, the
![]() $n^{\mathrm{th}}$
(large) Schröder number, is the number of lattice paths from the southwest corner
$n^{\mathrm{th}}$
(large) Schröder number, is the number of lattice paths from the southwest corner
![]() $(0,0)$
of an
$(0,0)$
of an
![]() $n \times n$
grid to the northeast corner
$n \times n$
grid to the northeast corner
![]() $(n,n)$
using single steps north
$(n,n)$
using single steps north
![]() $(0,1)$
, northeast
$(0,1)$
, northeast
![]() $(1,1)$
, or east
$(1,1)$
, or east
![]() $(1,0)$
, that do not rise above the
$(1,0)$
, that do not rise above the
![]() $SW$
-
$SW$
-
![]() $NE$
diagonal. (Such paths are called royal (
$NE$
diagonal. (Such paths are called royal (
![]() $n$
-)paths.)
$n$
-)paths.)
Proposition 6.4 ([Reference Qi and Guo15]). If
![]() $n = 0$
then
$n = 0$
then
![]() $\mathfrak{S}_n = 1$
. For
$\mathfrak{S}_n = 1$
. For
![]() $n\ge 1$
, the large Schröder numbers satisfy the recurrence:
$n\ge 1$
, the large Schröder numbers satisfy the recurrence:
Additionally, for
![]() $n \geqslant 1$
we have
$n \geqslant 1$
we have
where
![]() $\mathrm{Nar}(n,k)$
is the
$\mathrm{Nar}(n,k)$
is the
![]() $(n,k)$
-th Narayana number.
$(n,k)$
-th Narayana number.
Computation 6.5.
Table
4 provides a calculation of
![]() $\mathfrak{S}_n$
for small values of
$\mathfrak{S}_n$
for small values of
![]() $n$
.
$n$
.
Table 4. Values of
![]() $\mathfrak{S}_n$
computed via Proposition6.4.
$\mathfrak{S}_n$
computed via Proposition6.4.

We can produce refined statistics on royal paths by tracking the number of diagonal returns each path has, using the convention that a northeast step on the diagonal counts as a return. Let
![]() $\mathfrak S_n(k)$
denote the number of royal
$\mathfrak S_n(k)$
denote the number of royal
![]() $n$
-paths with
$n$
-paths with
![]() $k$
returns to the diagonal; call these the refined Schröder numbers.
$k$
returns to the diagonal; call these the refined Schröder numbers.
Proposition 6.6 ([14]). The refined Schröder numbers take the values
 \begin{equation*} \mathfrak S_n(k) = \begin {cases} 0 &\text {if }n\lt k,\\ 2^n &\text {if }n=k,\\ 2^k\frac {k}{n-k}\sum _{p=1}^{n-k}\binom {n-k}{p}\binom {n-1+p}{p-1}&\text {if }n\gt k. \end {cases} \end{equation*}
\begin{equation*} \mathfrak S_n(k) = \begin {cases} 0 &\text {if }n\lt k,\\ 2^n &\text {if }n=k,\\ 2^k\frac {k}{n-k}\sum _{p=1}^{n-k}\binom {n-k}{p}\binom {n-1+p}{p-1}&\text {if }n\gt k. \end {cases} \end{equation*}
Furthermore,
Computation 6.7.
Table
5 provides a calculation of
![]() $\mathfrak{S}_n(k)$
for small values of
$\mathfrak{S}_n(k)$
for small values of
![]() $n$
and
$n$
and
![]() $k$
.
$k$
.
Table 5. Values of
![]() $\mathfrak{S}_n(k)$
computed via Proposition6.6.
$\mathfrak{S}_n(k)$
computed via Proposition6.6.

While the above result is standard, we were unable to find a proof of the following recurrence in the literature. It will be extremely useful in linking large Schröder numbers with transfer systems.
Lemma 6.8. The refined Schröder numbers satisfy the recurrence relation:
for
![]() $1\le k\le n$
.
$1\le k\le n$
.
Proof. Write
![]() $E$
for east steps,
$E$
for east steps,
![]() $N$
for north steps, and
$N$
for north steps, and
![]() $D$
for diagonal steps. Given a royal
$D$
for diagonal steps. Given a royal
![]() $n$
-path, consider the location of its first diagonal return. If this return is in position
$n$
-path, consider the location of its first diagonal return. If this return is in position
![]() $(1,1)$
, then the path begins
$(1,1)$
, then the path begins
![]() $EN$
or
$EN$
or
![]() $D$
and the rest of the path may be filled in by any royal
$D$
and the rest of the path may be filled in by any royal
![]() $(n-1)$
-path with
$(n-1)$
-path with
![]() $k-1$
returns. This accounts for the
$k-1$
returns. This accounts for the
![]() $2\mathfrak S_n(k-1)$
term. If the first return is in position
$2\mathfrak S_n(k-1)$
term. If the first return is in position
![]() $(r,r)$
with
$(r,r)$
with
![]() $r\gt 1$
, then we may write our path as
$r\gt 1$
, then we may write our path as
![]() $EPNQ$
where
$EPNQ$
where
![]() $P$
is a royal
$P$
is a royal
![]() $(r-1)$
-path and
$(r-1)$
-path and
![]() $Q$
is a royal
$Q$
is a royal
![]() $(n-r)$
-path. The path
$(n-r)$
-path. The path
![]() $PQ$
is then a royal
$PQ$
is then a royal
![]() $(n-1)$
-path with at least
$(n-1)$
-path with at least
![]() $k$
diagonal returns. This decomposition is unique and each such royal
$k$
diagonal returns. This decomposition is unique and each such royal
![]() $(n-1)$
-path arises in this fashion, so this accounts for the term
$(n-1)$
-path arises in this fashion, so this accounts for the term
![]() $\sum _{p=k}^n \mathfrak S_{n-1}(p)$
.
$\sum _{p=k}^n \mathfrak S_{n-1}(p)$
.
We are now prepared to demonstrate the connection between (refined) large Schröder numbers and maximally extendable transfer systems on
![]() $D_{p^n}$
.
$D_{p^n}$
.
Theorem 6.9.
Let
![]() $n \geqslant 0$
. Then the number of maximally extendable transfer systems in
$n \geqslant 0$
. Then the number of maximally extendable transfer systems in
![]() $L(n)$
is given by
$L(n)$
is given by
![]() $\mathfrak{S}_{n+1}$
, and the number of maximally extendable transfer systems in
$\mathfrak{S}_{n+1}$
, and the number of maximally extendable transfer systems in
![]() $L(n)$
with exactly
$L(n)$
with exactly
![]() $k$
stationary nodes is
$k$
stationary nodes is
![]() $\mathfrak S_{n+1}(k)$
.
$\mathfrak S_{n+1}(k)$
.
Proof. It suffices to prove the second statement since the refined Schröder numbers
![]() $\mathfrak S_{n+1}(k)$
add up to
$\mathfrak S_{n+1}(k)$
add up to
![]() $\mathfrak S_{n+1}$
. Write
$\mathfrak S_{n+1}$
. Write
![]() $\mathfrak m(n,k) := |L(n,k,n+1)|$
for the number of maximally exetndable transfer systems on
$\mathfrak m(n,k) := |L(n,k,n+1)|$
for the number of maximally exetndable transfer systems on
![]() $D_{p^n}$
with exactly
$D_{p^n}$
with exactly
![]() $k$
stationary nodes. Clearly
$k$
stationary nodes. Clearly
![]() $\mathfrak m(0,1) = 2 = \mathfrak S_1(1)$
, so it suffices to prove that
$\mathfrak m(0,1) = 2 = \mathfrak S_1(1)$
, so it suffices to prove that
![]() $\mathfrak m(n,k)$
satisfies the recurrence of Lemma6.8, that is,
$\mathfrak m(n,k)$
satisfies the recurrence of Lemma6.8, that is,
This is a direct consequence of Theorem3.12 specialized to the case
![]() $\ell = n+1$
.
$\ell = n+1$
.
Remark 6.10.
In [
Reference Stanley18, Exercise 6.39], Stanley provides a list of nineteen classical structures counted by Schröder numbers. The challenge of finding an explicit bijection between maximally extendable transfer systems on
![]() $D_{p^n}$
and one of these structures remains open.
$D_{p^n}$
and one of these structures remains open.
Proposition 6.11.
Let
![]() $L^{\mathrm{max}}(n)$
denote the collection of maximally extendable liftable transfer systems on
$L^{\mathrm{max}}(n)$
denote the collection of maximally extendable liftable transfer systems on
![]() $[1]\times [n]$
. The asymptotics of
$[1]\times [n]$
. The asymptotics of
![]() $|L^{\mathrm{max}}(n)|$
satisfy
$|L^{\mathrm{max}}(n)|$
satisfy
where
 \begin{equation*} C = \frac {\sqrt {2}(3+2\sqrt {2})}{2\sqrt {\pi ({-}4+3\sqrt {2})}}\approx 4.720408926. \end{equation*}
\begin{equation*} C = \frac {\sqrt {2}(3+2\sqrt {2})}{2\sqrt {\pi ({-}4+3\sqrt {2})}}\approx 4.720408926. \end{equation*}
This provides a lower bound on the asymptotic behavior of
![]() $|L(n)|$
.
$|L(n)|$
.
Proof. This follows directly from Theorem6.9 and the asymptotics of the large Schröder numbers (see for instance Exercise 12 on p. 539 of [Reference Knuth12]).
We now shift our attention back to all transfer systems on
![]() $[1] \times [n]$
, and consider the maximally extendable transfer systems here. Recall from Proposition4.2 that there is a duality:
$[1] \times [n]$
, and consider the maximally extendable transfer systems here. Recall from Proposition4.2 that there is a duality:
In particular, by summing up over all elements
![]() $(a,b) \in [1] \times [n]$
we obtain a duality:
$(a,b) \in [1] \times [n]$
we obtain a duality:
Definition 6.12.
A transfer system
![]() $\mathcal{R}$
for
$\mathcal{R}$
for
![]() $[1] \times [n]$
is maximally stationary if it has
$[1] \times [n]$
is maximally stationary if it has
![]() $n+1$
stationary elements.
$n+1$
stationary elements.
Remark 6.13.
In a more intuitive description, a transfer system is maximally stationary if and only if its restriction to the top row is the minimal transfer system on
![]() $[n]$
.
$[n]$
.
Corollary 6.14.
Let
![]() $n \geqslant 0$
. Then the number of maximally extendable transfer systems in
$n \geqslant 0$
. Then the number of maximally extendable transfer systems in
![]() $T(n)$
is the same as the number of maximally stationary transfer systems in
$T(n)$
is the same as the number of maximally stationary transfer systems in
![]() $T(n)$
(and indeed the same as the number of maximally stationary transfer systems in
$T(n)$
(and indeed the same as the number of maximally stationary transfer systems in
![]() $L(n)$
).
$L(n)$
).
Definition 6.15.
Let
![]() $n \geqslant 1$
. Then
$n \geqslant 1$
. Then
![]() $\mathfrak{A}_n$
is the number of rooted subtrees in rooted planar tree with
$\mathfrak{A}_n$
is the number of rooted subtrees in rooted planar tree with
![]() $n$
nodes.
$n$
nodes.
Remark 6.16. Rooted subtrees of a fixed planar tree are in bijection with nonempty antichains in the same tree (with the canonical partial order in which the root is minimal and edges are covering relations). Rooted subtrees are analyzed in [Reference Ruskey17], while [Reference Klazar11] studies the same problem in the language of antichains.
Proposition 6.17 ([Reference Ruskey17, Reference Klazar11]]). Let
![]() $n \geqslant 1$
. Then
$n \geqslant 1$
. Then
 \begin{equation*} \mathfrak {A}_n = \dfrac {\displaystyle {\sum _{0 \leqslant i \lt n}} \binom {2i+1}{i} \binom {2n-1}{n-i-1}}{2n-1}. \end{equation*}
\begin{equation*} \mathfrak {A}_n = \dfrac {\displaystyle {\sum _{0 \leqslant i \lt n}} \binom {2i+1}{i} \binom {2n-1}{n-i-1}}{2n-1}. \end{equation*}
Moreover,
![]() $\mathfrak{A}_n$
satisfies the recurrence
$\mathfrak{A}_n$
satisfies the recurrence
![]() $\mathfrak{A}_1 = 1$
and
$\mathfrak{A}_1 = 1$
and
 \begin{equation*} \mathfrak {A}_{n} = \sum _{j=1}^{n-1} \mathfrak {A}_{n-j} \mathfrak {A}_{j} + \mathfrak {A}_{n-j} \mathrm{Cat}(j-1) \end{equation*}
\begin{equation*} \mathfrak {A}_{n} = \sum _{j=1}^{n-1} \mathfrak {A}_{n-j} \mathfrak {A}_{j} + \mathfrak {A}_{n-j} \mathrm{Cat}(j-1) \end{equation*}
where
![]() $\mathrm{Cat}(j)$
is the
$\mathrm{Cat}(j)$
is the
![]() $j$
-th Catalan number.
$j$
-th Catalan number.
Computation 6.18.
Table
6 provides a calculation of
![]() $\mathfrak{A}_n$
for small values of
$\mathfrak{A}_n$
for small values of
![]() $n$
.
$n$
.
Table 6. Values of
![]() $\mathfrak{A}_n$
computed via Proposition6.17.
$\mathfrak{A}_n$
computed via Proposition6.17.

Numerical experiments lead us to conjecture that maximally extendable transfer systems in
![]() $T(n)$
are counted by
$T(n)$
are counted by
![]() $\mathfrak A_{n+2}$
. By Corollary6.14, we conjecture the same count for maximally stationary transfer systems in
$\mathfrak A_{n+2}$
. By Corollary6.14, we conjecture the same count for maximally stationary transfer systems in
![]() $T(n)$
and maximally stationary transfer systems in
$T(n)$
and maximally stationary transfer systems in
![]() $L(n)$
.
$L(n)$
.
Conjecture 6.19.
For
![]() $n \geqslant 0$
, the number of maximally extendable transfer systems in
$n \geqslant 0$
, the number of maximally extendable transfer systems in
![]() $T(n)$
is given by
$T(n)$
is given by
![]() $\mathfrak{A}_{n+2}$
.
$\mathfrak{A}_{n+2}$
.
The authors’ attempts to prove this conjecture by standard enumerative methods (both bijective and inductive) have been spoiled by the subtle effects of restriction on relations joining the bottom and top rows. Following the argument of [Reference Klazar11], we note that it would suffice to decompose the top row
![]() $r$
of each maximally extendable transfer system in
$r$
of each maximally extendable transfer system in
![]() $T(n)$
into “primary components”
$T(n)$
into “primary components”
![]() $r_1,\ldots, r_k$
for which
$r_1,\ldots, r_k$
for which
where
![]() $w(s)$
measures the number of maximally extendable transfer systems with top row
$w(s)$
measures the number of maximally extendable transfer systems with top row
![]() $s$
.
$s$
.
6.1. Figures
We conclude by plotting of the behavior of our enumerations related to transfer systems for
![]() $D_{p^n}$
and
$D_{p^n}$
and
![]() $C_{qp^n}$
. All of the data for these figures was produced using code available at https://github.com/bifibrant/recursion/.
$C_{qp^n}$
. All of the data for these figures was produced using code available at https://github.com/bifibrant/recursion/.
The graph in Figure 1 suggests that
![]() $|L(n)|$
and
$|L(n)|$
and
![]() $|T(n)|$
might have subexponential growth rates of a shape similar to the asymptotics of
$|T(n)|$
might have subexponential growth rates of a shape similar to the asymptotics of
![]() $|L^{\mathrm{max}}(n)|$
from Proposition6.11.
$|L^{\mathrm{max}}(n)|$
from Proposition6.11.
Finally, in Figure 2, we plot
![]() $|L(n)|/|T(n)|$
and observe that the fraction of liftable transfer systems appears to approach
$|L(n)|/|T(n)|$
and observe that the fraction of liftable transfer systems appears to approach
![]() $0$
.
$0$
.

Figure 2. A semilog plot of the values of
![]() $|L(n)|$
(blue dots),
$|L(n)|$
(blue dots),
![]() $|T(n)|$
(red dots),
$|T(n)|$
(red dots),
![]() $|L^{\mathrm{max}}(n)|$
(blue squares), and
$|L^{\mathrm{max}}(n)|$
(blue squares), and
![]() $|T^{\mathrm{max}}(n)|$
(red squares) for
$|T^{\mathrm{max}}(n)|$
(red squares) for
![]() $0\leqslant n\leqslant 80$
. Here, the superscript
$0\leqslant n\leqslant 80$
. Here, the superscript
![]() $\mathrm{max}$
indicates maximally extendable transfer systems.
$\mathrm{max}$
indicates maximally extendable transfer systems.
Acknowledgments
The authors thank Mike Hill for suggesting the construction presented in Section 2. They also thank Angélica Osorno and the anonymous referees for helpful feedback.
The first author would like to thank the Max Planck Institute for Mathematics for its hospitality and was partially supported by the European Research Council (ERC) under Horizon Europe (grant No. 101042990). The second author thanks Coil Technologies for their generous donation to fund his tuition, which enabled him to conduct this research. The third author’s work was supported by the National Science Foundation under Grant No. DMS-2204365.
Competing interests
The authors declare none.