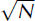List of Symbols
Introduction
Objectives
Mountain-glacier mass balances are excellent indicators of climate change over the last few centuries (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992; Haeberli, 1995). However, the investigation of climate trends requires the measurement of mass balance over several decades (Reference VincentVincent, 2002), and long series are also useful for the modelling of glacier dynamics (e.g. Reference Le Meur and VincentLe Meur and Vincent, 2003). Unfortunately, throughout the world, only 33 glaciers have annual mass-balance series longer than 40 years (Reference Dyurgerov and MeierDyurgerov and Meier, 1999). Given the limited number of long balance series, the quality of such data is very important.
The traditional field-measurement method is the glaciological method, in which yearly point mass balances are obtained from stakes inserted in ice and from cores drilled in firn. When extrapolated to the whole surface of the glacier and added year after year, the resulting cumulative glacier-wide balance is likely to be very sensitive to systematic errors which accumulate linearly with the number of measurement years (denoted as N; see List of symbols). Such systematic errors will determine the exactness (veracity) of the method. Its precision (reproducibility) will depend on random errors that increase in the cumulative mass balance only with
. Discerning these two types of errors requires an independent method for which the intrinsic error is as small as possible and not time-dependent.
The volumetric mass-balance method, in which changes in the surface elevation of a glacier are calculated from photogrammetry, can be used to this end, as its intrinsic errors are mostly random (Reference KrimmelKrimmel, 1999; Reference Østrem and HaakensenØstrem and Haakensen, 1999; Reference Cox and MarchCox and March, 2004). The comparison of measurements is a classical problem in metrology, requiring detailed error analysis to determine possible significant discrepancies within their natural scatter. Surprisingly, very few studies have focused on this point.
Previous studies
Reference Meier, Tangborn, Mayo and PostMeier and others (1971) indicated errors between ±0.1 and ±0.34 m w.e. for balances determined by the glaciological method. Reference LliboutryLliboutry (1974) calculated an error of ±0.19 m w.e. for ablation measured with stakes, whereas Reference Vallon and LeivaVallon and Leiva (1981) indicated ±0.3 m w.e. for mass balances obtained by drilling in the accumulation area. Most authors have proposed error estimates between ±0.2 and ±0.4 m w.e. (Reference BraithwaiteBraithwaite, 1986; Reference Braithwaite, Konzelmann, Marty and OlesenBraithwaite and others, 1998; Reference Cogley and AdamsCogley and Adams, 1998; Reference Cox and MarchCox and March, 2004). In a recent study, Reference Gerbaux, Genthon, Etchevers, Vincent and DedieuGerbeaux and others (2005) attempted to discern winter and summer balance measurements and their locations (accumulation/ablation areas). They estimated an error of ±0.10 m w.e. for ablation measured in ice and between −0.25 and +0.4 m w.e. for ablation measured in firn. Errors owing to spatial sampling and to area integration have been investigated by Reference Vallon and LeivaVallon and Leiva (1981). Using three integration methods, they concluded that the integration error is about ±0.07 m w.e. and the sampling error is approximately ±0.07 m w.e. The relation linking the measurement error at a site to the error in the glacier total balance has also been treated by Reference Fountain and VecchiaFountain and Vecchia (1999).
When assessing potential biases related to the sampling and area-integration method, it is of interest to compare results with the balance obtained from maps, given that photogrammetry integrates the overall spatial variability. Several studies have undertaken such a comparison and provided estimates of the error in the volumetric method (Reference KrimmelKrimmel, 1999; Reference AndreassenAndreassen, 1999; Reference Cox and MarchCox and March, 2004). The reported errors are consistent, about ±1 to 2 m w.e., depending on map quality and photograph condition. Only Reference KrimmelKrimmel (1999) reports a significant discrepancy between the two types of measurements and suggests the water-equivalent conversion and the area integration as possible sources of bias.
Here we compare the two methods based on the long mass-balance series of Glacier de Sarennes, France (45°07′ N; 6°07′ E; Fig. 1) initiated in 1949. Preceding studies show a discrepancy of 18% (Reference Valla and PiedalluValla and Piedallu, 1997). This led us to carry out a new estimate of the volumetric mass balance together with a careful error analysis that is also developed for field data. Possible sources of systematic errors are discussed by a variance analysis.
Fig. 1. (a) Location of stakes, drilling sites and control points used for photogrammetric restitution. Contour lines on bedrock and on the glacier are at 25 m intervals. (b) Spatial repartition of the 51 year altitude variations obtained from photogrammetry. Contour lines of altitude change are at 10 m intervals.
Volumetric Mass Balance
Principle of calculation
In this method, digital elevation models (DEMs) of the glacier are subtracted to calculate volume changes. The volumetric balance calculation between two dates (initial state 1, final state 2) requires knowledge of the altitude, Z(x, y), of the glacier and the bedrock margins that may have been covered or uncovered. Calculations also require the density function, ρ(x, y, z), so the water-equivalent mass of the glacier at date 1 (covering the space S1) will be expressed as:
where subscript 0 refers to the glacier bedrock and 1 to initial state 1. As the density function is generally unknown, we apply Sorge’s law and accordingly assume that the density remains constant between two dates (i.e. ρ 1 = ρ 2 = ρ; Reference BaderBader, 1954), so the mass variation, Δm vol can be written as:
Method of calculation
The volumetric mass balance of Glacier de Sarennes has been measured between 1952 and 2003 using aerial photogrammetry. Table 1 gives photogrammetry-related information. In order to orient the images, a stereopreparation was performed in 2005 using geodetic differential GPS (global positioning system) on control points (Fig. 1). Obvious features were used as control points. Moreover, as the relative orientation of the images between the two dates is more important than the absolute ground orientation, nearly 150 tie points on the common 1952 and 2003 bedrock were added to improve consistency. The photogrammetric restitution was performed on a Leica DSR15 analytical plotter with plotted points every 20 m on flat surfaces of the glacier, up to one point per metre in bumpy areas. Then three methods were used to build the DEM: (1) linear interpolations between plotted points, (2) kriging analysis and (3) a triangular irregular network (TIN) based on Delauney’s algorithm (Reference MauneMaune, 2007). Each is followed by a re-sampling on a 10 m grid.
Table 1. Characteristics of the aerial photographs
The subtraction of the DEMs yields altitudinal variations that must be converted to water equivalent using a density assumption. This can lead to an error which might depend on time, as glaciers losing mass have increasing mean densities and deviate from Sorge’s law (Reference Krimmel and OerlemansKrimmel, 1989). Field data are helpful in investigating the choice of the density function at Sarennes. The 4 years of field mass-balance data available before 1952 reveal a clear negative cumulative budget of −5.99 m w.e. (Reference VallaValla, 1989). For previous years, meteorological mass-balance computation can be used (Reference Torinesi, Letréguilly and VallaTorinesi and others, 2002). We estimate a strong negative cumulative balance of −16 m w.e. for Glacier de Sarennes between 1930 and 1950. Considering the low altitude and the southerly aspect of the glacier, the density of the material that forms its upper layers in 1952 is probably very close to the density of bulk ice. In 2003, the glacier was completely free of snow and firn on the date the photographs were taken, and it has shown a strong deficit since 1981. We may therefore assume a density of ρ = 900 ± (σρ = 15) kg m−3 in Equation (2) and in all ice-depth to water-equivalent conversions.
The net volumetric mass balance is obtained by dividing the mass variation by a mean surface area, S m, and is expressed using the height variations of the Q (= 8464) nodes of the grid as:
where Δhj is the altitude variation at node j, and s grid is the elementary surface area of the grid (10 m × 10 m).
Error analysis
Errors are quantified (standard deviation) and combined assuming they are uncorrelated (CETAMA, 1986).
Surface roughness
The surface roughness of the glacier acts as a source of error in stereoscopic measurements. Field observations suggest that surface roughness can be described as waves with peakto-peak amplitudes, δh
p−p, of ∼0.5 m and wavelengths ∼1 to 2 m. As the spatial sampling of the stereoscopic measurement is 20 m, which is one order of magnitude larger than the estimated wavelength, the roughness is analogous to noise in the altitude signal. Assuming a sinusoidal shape for the roughness function (first component of a Fourier series), the standard deviation will be
for both years, which is in good agreement with laser-scan values reported for a metric wavelength by Reference Rees and ArnoldRees and Arnold (2006).
Internal stereoscopic measurement error
The stereoscopic measurement has intrinsic planimetric and altimetric errors which depend on: (1) the scale, s, of the photographs, (2) the sighting error on the stereotypes, σ phot, depending on the visibility of the sighted point, (3) the focal length, T, and (4) the stereoscopic base, B (Reference Kraus and WaldhäuslKraus and Waldhäusl, 1998). The planimetric error, σ stereo.xy , is:
where the sighting uncertainty typically ranges from 10 μm for control and tie points to 30 μm for any point on the surface of the glacier. Similarly, the altimetric error, σ stereo.z , is:
As explained by Reference Thibert, Faure and VincentThibert and others (2005), the planimetric error, σ stereo.xy , also results in an additional altimetric error due to the slope of the ground, given by:
where Z(x, y) is the height function provided by the DEM. Using the scale of stereotypes at mean altitudes of the glacier, a mean sighting error of 30 μm and mean slopes of, respectively, 27.7% and 30.6% in 1952 and 2003, planimetric errors of ±1.32 and ±0.87 m are obtained along with a total altimetric error of ±2.10 and ±1.26 m in 1952 and 2003, respectively.
For a single point, the altimetric error accounts for stereoscopic and roughness errors. When repeated every 20 m, the mean error is divided by the square root of the number, P, of sighted points and expressed as the internal altimetric error,
:
giving 0.047 (1952) and 0.029 m (2003) using P = 2116.
Stereotype orientation error
The absolute orientation of the stereotype itself leads to an error in altitude that does not depend on the number of measurement points. As explained by Reference Thibert, Faure and VincentThibert and others (2005), errors associated with the absolute orientation of the photographs depend on (1) the height residuals, σz , of the ground control points, (2) the planimetric residuals, σx , σy , which lead to a height error related to the slope of the DEM and (3) the DEM resolution. As shown in this paper, where analogous methods were used to build the DEM, the error related to its resolution appears to be negligible, as the contour lines computed from the DEM merge perfectly with those obtained from the analytical plotter. The overall standard deviation of the height measurement, σ a.o, associated with the absolute orientation of the photographs is therefore given by:
Using orientation residuals and mean slopes provided by the DEM, σ a.o is 0.34 and 0.22 m in 1952 and 2003, respectively (Table 2).
Table 2. Random and systematic errors in the volumetric and glaciological mass-balance measurements
Correction of Systematic Errors
Over and above the random errors detailed in the previous section and the density assumption, the volumetric method also includes systematic errors.
Lack of stereoscopic measurements
The lack of contrast and the evenness of the texture of snow can prevent stereoscopic measurements. In the 1952 photographs this occurs in three regions, of 13.1 ha, of the accumulation zone where altitudes have not been measured but interpolated. Although encircled by reliably measured points, such altitudes are overestimated because concavities are not taken into account by linear interpolations. These altitude differences have been estimated using the concavity of the 2003 DEM where measurements were possible. We found a mean difference in altitude of 1.62 m over 13.1 ha. Considering surface ratios, the overall error on the 1952 DEM is +0.23 m w.e.
Mean surface area used for volume to net balance reduction
For comparison with the balance obtained from field measurements, a water-equivalent balance (b vol) is estimated from Equation (3). The mean surface area (S m) is generally taken as the arithmetic mean, which can lead to an error, as it assumes that surface and mass balance trends are linear. If both volumetric and glaciological methods provide the same measurements, i.e. Δm vol = Δm gla, S m used in the expression b vol = Δm vol/S m = Δm gla/S m = Σbt is therefore:
where bt denotes the yearly net balances and St the surface area of the glacier for year t among the N years (note that if the cumulative mass balance is zero, there is no error associated with the choice of S m). Evaluating S m from Equation (9) using field annual mass balances and annual surfaces given by three segmental linear trends between 1952, 1981, 1991 and 2003 (Reference Valla and PiedalluValla and Piedallu, 1997) gives 0.595 km2. An arithmetic averaging of 1952 and 2003 surface values gives 0.631 km2 whereas an arithmetic averaging of segmental linear surfaces gives a higher value of 0.659 km2. Figure 2 shows the change of S m with time for intermediate years between 1952 and 2003, together with other surface estimations. Using the 1952–2003 arithmetic mean therefore results in a 6% underestimation of the net balance in absolute values. In order to preserve the independence of both methods, we have nevertheless used this value to calculate the volumetric net balance, and a note of caution should be associated with this choice. The only error that will be considered hereafter in relation to the mean surface is a random error linked to the determination of the glacier extent on 1952 photographs. Because snow covered the upper part of the glacier, an error of ±0.0286 km2 affects its measurement. As this error concerns only 1952, it affects only half of S m uncertainty. This results in S m = 0.6313 ± (σ s = 0.0143) km2.
Fig. 2. Surface evolution of Glacier de Sarennes between 1951 and 2003. Possible surface values for net balance reduction from photogrammetry volume changes are indicated.
Results and overall random error
Mass balance
During the 51 years, altitude variations over the glacier range from 0 to −70 m (Fig. 1). The mean altitude variations obtained from the three interpolation methods are very close: −36 m (kriging), −36.11 m (linear interpolation) and −36.22 m (TIN). When analyzing the mean difference between the kriging-interpolated nodes and points measured with the plotter, the linear-interpolation method seems to better fit the source data. In addition, this interpolation provides a balance which is the mean of the three tested methods. Considering that it probably minimizes errors, this method is preferred. The overall error, σ vol, on the volumetric balance is:
which gives ±1.04 m w.e. (surface area, density and photogrammetric errors each contribute nearly a third). Using the correction due to areas without measurement, the volumetric mass balance is b vol = −32.30 ± (σ vol = 1.04) m w.e. for the period 1 August 1952 to 20 September 2003.
Mass-balance spatial variability
The overall variability of the mass balance, σ
sp, can be calculated from the spatial distribution of altitude changes obtained from photogrammetry (Fig. 1). We assume that the flow of ice is negligible (static glacier) so the water equivalent of the local altitude variation between 1952 and 2003 equals the cumulative local balance. Such an assumption is confirmed by comparing altitude changes given by photogrammetry with local cumulative balances that are negative over the entire altitude range of the glacier. The discrepancy is very small, <0.08 m w.e. a−1 as a mean over the 51 years. Furthermore, the error introduced when assimilating annual height variations, ∂Z/∂t, to the mass balance, b(x,y), can be estimated from the horizontal flux difference over the ice thickness based on the continuity equation (Reference Kääb and FunkKääb and Funk, 1999). At a fixed point of the surface in the case of no basal sliding, it can be written as a function of the vertical strain rate
integration through the ice thickness, h, between the glacier bedrock, Z
0, and the surface Z
s:
where subscript s refers to the glacier surface. An upper limit of the error can therefore be estimated using the vertical strain at the surface, the ice incompressibility, velocities, u s , v s, of ablation stakes (0.2–0.4 m a−1),slopes provided by the DEM and a mean depth of 45 m inferred from Reference Valla and PiedalluValla and Piedallu (1997). We obtain a small error of <3 cm a−1,and therefore consider that the water equivalent of height variations given by photogrammetry are a reliable proxy of the local balance values within the 2003 glacier extent that has been continuously covered by ice since 1952. As a consequence, the overall spatial variability of annual balances is given by the standard deviation of height variations over the 2003 glacier extent which is σ sp = 0.27 m w.e.a−1.
Glaciological Mass Balance
Data and adjustments
The method used on Glacier de Sarennes measures the yearly net balance (end of ablation season) at five sites using emergence variations of stakes inserted in ice and cores drilled in firn (Fig. 1). Some balances have not been measured, so the experimental table (51 years × 5 sites) is an incomplete set of 243/255 data. Local balances are extrapolated using the area–altitude distribution, which results in a cumulative balance of −34.62 m w.e. (4 September 1952 to 29 September 2003).
For comparison with the volumetric balance, the data have to be adjusted to the same period. Field measurements performed on 23 July and 6 August 1952 can be used to calculate a daily ablation rate close to the date of the aerial photographs (1 August 1952). The adjustment applied to the cumulative balance is then calculated from this rate and from the ablation measured up to the end of the ablation period (20 September 2003). This gives −0.8 m w.e., so the adjusted cumulative balance is −35.42 m w.e. between 1 August 1952 and 20 September 2003, and, considering the adjustment as an additional measurement, the corresponding experimental table is a set of 248/260 data (52 dates × 5 sites).
Random-error analysis
The quantification of the error associated with the glaciological balance requires a distinction between years and sites of negative budget (71%) and those of positive mass balance (29%).
Positive mass balance
Positive balance measurements at the end of the ablation season are based on density and height determinations. These are performed with an auger that provides a single core through the whole depth of the snow.
-
1. Density measurement. Density is mainly affected by the presence of liquid water which may reach up to 20–30% during the ablation period (Reference Vallon and LeivaVallon and Leiva, 1981) and lead to a 50% overestimation of the density. However, in a summer–autumn firn (density 0.6), as melting ceases, the liquid-water content decreases to reach a non-zero minimum (4%) which depends on the porosity (0.33; Reference Schneider and JanssonSchneider and Jansson, 2004). Such water content represents only 2.4 cm of water for a 1 m depth firn. Densities are therefore not highly affected by the liquid-water content at the end of the ablation season. Errors, mainly related to the size and weight of the cores, have been estimated using another auger (PICO (Polar Ice Coring Office); Reference Kelley, Stanford, Koci, Wumkes and ZagorodnovKelley and others, 1994) showing that the density is measured within 5%, with no systematic discrepancy. As a result, the uncertainty for firn with a density of 0.6 is σ d = 0.03.
-
2. Snow height measurement. The accuracy of the snow height depends on the roughness of the glacier and on the detection of the underlying material. When this material is ice (39 times), the accuracy is generally good, within a few centimetres. When it is firn (33 times), a stratigraphic error is possible despite favourable indicators (hardness, grain size) and can lead to an overestimation of the mass balance if part of the firn of the previous year is accidentally included. Because strati-graphic error is a bias, it has not been included in the present random-error calculation. The overall uncertainty on a positive balance, σb +, combining density and height contributions is therefore given by:
(12)
which gives 0.21 m w.e. using d = 0.6 and a mean value of snow height of l= 0.73 m measured for the 72 positive-balance situations over the period 1952–2003.
Negative mass balance
For a negative budget, the mass balance is measured as an ablation in ice or in firn with an age of 1 year or more.
-
1. There are 153 ablation values measured as a variation of stake length inserted in ice. The error due to the creep of ice is negligible at Glacier de Sarennes because of the very low flow of ice. Errors are therefore essentially linked to the mechanical play of the jointed stakes and the inaccurate surface at the bottom of stakes due to the anchorage hole. Repeatability tests show that this error is ∼15 cm, which results in an uncertainty of
in a balance measured as ablation in ice. -
2. The 23 ablation measurements in firn were performed in two ways: (a) with stakes inserted in the underlying ice but emerging from the residual firn of previous year(s) and (b) by drilling in order to reconstruct the stratigraphy when no stakes were found. Errors in observations of type (a) are the same as those for ablation measured in ice (with d = 0.7) which gives ±0.11 m w.e. Errors in observations of type (b) are the same as those for positive mass balance but using l = 0.66 m as a mean which gives ±0.25 m w.e. Combining the errors from both,
, the uncertainty for negative mass balances measured in firn is ±0.27 m w.e.
Sampling error
The finite number of sampling sites results in a sampling error, σ samp, a function of the number of sites, n, and of the overall spatial variability of the mass balance, σ sp, and expressed as:
in which σ sp is unknown from the data, but is estimated from photogrammetry. Using a mean value of 4.76 sites sampled each year, this gives a sampling error of ±0.12 m w.e. a−1 and results in an error of ±0.89 m w.e. in the cumulative mass balance.
Correction of systematic errors and results
Although negligible on an annual basis, some corrections are required when calculating the cumulative mass balance over decades.
Internal accumulation
Internal accumulation results from the refreezing of percolating water in cold firn and the freezing of capillary-trapped water in snow and firn cooled by the winter cold wave (sensible heat). Both processes are able to account for a significant part of accumulation (Reference Schneider and JanssonSchneider and Jansson, 2004). The occurrence of such processes has been studied using computations developed for Glacier de Saint-Sorlin, which is located at a distance of 3 km (Reference Gerbaux, Genthon, Etchevers, Vincent and DedieuGerbeaux and others, 2005). These use a mass-balance reconstruction based on the Crocus snow model developed by Reference Brun, Martin, Simon, Gendre and ColéouBrun and others (1989). The model estimates a mean sensible heat of 5000 kJ m−2, stored each winter in the firn of the accumulation area for the period 1981–2004. Using a specific latent heat of fusion of ice of 335 kJ kg−1 (Reference HobbsHobbs, 1974), this results in a mean internal accumulation of 0.015 m w.e. a−1 at Glacier de Saint-Sorlin. Using the same mean value at Glacier de Sarennes over the period of record, and an equivalent number of 14 years of positive balance covering the overall glacier, internal accumulation accounts for an underestimate of the mass balance of 0.22 m w.e.
Internal ablation
As ice motion is negligible at Glacier de Sarennes, internal ablation is only caused by two sources of subglacial energy: geothermal heat and heat conversion of the potential energy loss from water flow through and under the glacier.
The geothermal flux is ∼90 mW m−2 in this part of the Alps (Reference Gable, Goguel and SouquetGable and Goguel, 1981), which results in a basal melting of 0.94 cm a−1. This ablation rate accounts, consequently, for −0.48 m w.e. over the 51 years of the cumulative balance.
The principle of calculation of ablation from water flow has been described by Reference March and TrabantMarch and Trabant (1997, equation (9)). Such ablation is divided into two sources. The first is the alpine (non-glacial) runoff over the 0.63 km2 hydrologic basin. For the 38 years of negative mass balance, melting is estimated from the mean winter balance as 1.60 m w.e. a−1. For the 13 years of positive balance, it is equal to the mean ablation which is 1.50 m w.e.a−1. The second is the glacial runoff over the glacier area (mean 0.63 km2 over the period), equal to the mean summer balance which is 2.36 m w.e. a−1 during 1952–2003.
Assuming that flowing water and ice are at the melting point and form an isolated system, then according to the first law of thermodynamics, the potential energy lost by water flow is totally converted into heat. Assuming that 100% of the alpine runoff flows under the glacier, the heat per unit area per year can be calculated from the altitude lost by water from the glacier surface to its terminus which is 130 m as obtained from an average 1952–2003 DEM. This gives a heat flux of 158 mW m−2. Nearly half of this is diffused toward the glacier, inducing a melt rate of 0.83 cm a−1 accounting for an ablation of 0.42 m w.e. between 1952 and 2003. This estimation of internal ablation is of the same order of magnitude as ablation due to geothermal heat. However, because it is subject to a number of unverifiable assumptions, such as internal and subglacial water flows, we have not used it to correct the mass balance in the present calculations and prefer to discuss it in the following section.
Updating of the weighting law
As proposed by Reference Cox and MarchCox and March (2004), we have established a linear time-variable area–altitude distribution (AAD) based on 1952 and 2003 DEMs to update the weighting relationship established in 1959 (Reference de Crécyde Crécy, 1963). The correction to the cumulative mass balance is +0.8 m w.e. (see coefficients in Table 3).
Table 3. Altitude and area–altitude distribution based weighting coefficients of the five sampling sites in 1952 and 2003. Over the period, coefficients have a linear time variation between initial and final values
Random uncertainties on point mass balances have been combined in a variance table using the above weighting relationship to give the uncertainty for the whole glacier. It results in an error of 0.7 m w.e. in the cumulative mass balance. Taking into account the sampling error, the error of the cumulative balance is therefore 1.15 m w.e. After correction for the internal accumulation and the geothermal ablation annually distributed, the yearly glacier-wide balance, bt , is shown in Figure 3. The cumulative balance is b gla = Σbt = −34.89 ± (σ gla = 1.15) m w.e. for the period 1 August 1952 to 20 September 2003.
Fig. 3. Glaciological mass balances: upper curve is the glacier-wide yearly balances measured by the glaciological method and its annually calculated random errors according to the type of measurement. Lower curve is the cumulative glaciological mass balance and its comparison to the volumetric balance. No significant discrepancy between the two methods can be admitted at the α = 5% type I error risk. Error bars are 1.96 standard deviations.
Discussion
Comparison
The 2.59 m w.e. discrepancy between the two methods is small, representing <10% of the signal. It equals an annual value of less than 6 cm w.e. a−1 over 51 years which is far less than the intrinsic random errors of each method. Assuming normally distributed measurements (Fig. 4), in a type I error risk of α = 5%, the discrepancy is not significant, as the condition
is fulfilled by our data, and the hypothesis H0: b vol = b gla can therefore be accepted. However, the ability to detect a bias in the glaciological method is given by the test ability to reject H0 when it is actually false. This is the probability of not committing a type II error which is 1 − β (Table 4). Quantifying β requires choosing the alternative true hypothesis. Assuming that the discrepancy of δb = 2.59 m w.e. corresponds to a true bias in the glaciological balance, β will then be
where F is the repartition function of the normal law, so that it results in a high risk of a wrong conclusion with β = 61.4%. This shows that there is a low probability (38.6%) of making the correct selection in this case. This is mainly due to the high common standard deviation of both methods (1.55 m w.e.) which reaches 40% of the measured discrepancy.
Fig. 4. Normal distribution of results. The solid curve is the volumetric mass balance and the dashed curve is the glaciological mass balance. The dotted curve is the lowest detectable biased glaciological mass balance for 5% type I and II error risks.
Table 4. Type I and II errors associated with the detection of a significant discrepancy between glaciological and volumetric balances. From our data, the tested hypothesis, H0: b vol = b gla, is not rejected at the α = 5% type I probability of error. However, if H0 is false, and the true hypothesis is b gla = b vol + 2.59 m w.e., there is a probability of β = 61.4% of a wrong acceptance of H0
We may therefore ask, with fixed type I and II errors, what the detectable bias, δb, is. This is given by
where uγ, is given by the normal distribution law as F(uγ ) =γ. For α = β = 5% admissible errors, δb is 5.6 m w.e. (0.11 m w.e. a−1; Fig. 4). For α = β = 10%, δb is 0.06 m w.e.a−1 . These biases are smaller than the mean annual random error of the glaciological balance (0.16 m w.e.a−1) and therefore are very difficult to detect, showing that the ability of the volumetric method to test field data is not all that important. Moreover, corrections of results from the estimation of possible systematic errors are critical to support any conclusions derived from the comparison. If corrected for all possible and quantifiable biases (volume to net balance reduction, subglacial melting from water flow), the discrepancy would be 1.07 m w.e., giving β = 75%. If present in the glaciological balance, biases are low and therefore cannot be reliably detected and quantified by such a comparison. However, a variance analysis allows the extraction of spatial effects from field data and the potential systematic errors remaining to be quantified. This is the topic of the next subsection.
Variance analysis
The natural spatial variability of the mass balance is a potential source of systematic error through an erroneous weighting relationship or insufficient spatial sampling. Considering that it is estimated from photogrammetry as 0.27 m w.e.a−1, it is important to check whether field data hold all or part of this variability. This can be performed with the variance analysis proposed by Reference LliboutryLliboutry (1974). By comparison with more descriptive analyses such as principal components, a variance analysis allows an explicit separation of overall space and time effects, non-linear effects and random errors, at the cost of a hypothesis of identically centred and normally distributed residuals and temporal control factors.
The model specifies that bi,t , the mass balance recorded at stake i for year tand corrected by the systematic annual bias, is decomposed in four terms as:
The αi terms are mean annual balances at each stake, and their standard deviation is the spatial variability of the data. The βt term represents an amount of mass balance, constant over all the glacier, which differs from year to year. Under the constraint Σβt = 0, βt is called the centred mass balance and can be interpreted as the annual and uniform response of all stakes to climate fluctuations. The cross-term, γiδt , under the constraints Σ γi = 0 and Σ δt = 0, represents additional effects that deviate from the time and space variability separation. The εi,t term represents residuals corresponding to both measurement errors and discrepancies between the model and data. Variances, σα , σβ and σδ , need to be estimated together with the missing values of the experimental table. Inference is carried out in a Bayesian framework using a Markov chain Monte Carlo scheme (Reference Gilks, Richardson and SpiegelhalterGilks and others, 1996).
The variance analysis results are presented in Table 5. The modelling hypotheses are not rejected at good confidence levels by standard tests such as Snedecor’s and χ2 on the period of record (51 years, 5 stakes and 12 missing values). In particular, the hypothesis of identically normally distributed residuals is fulfilled, indicating that a variance-analysis model is well suited to the studied glacier. The standard deviation of the residual is 0.24 m w.e. a−1, which is just slightly greater than the mean measurement error at each stake (±0.17 m w.e. a−1) and indicates that the model fits well the space and time variability of the data.
Table 5. Variance analysis results for the glaciological mass-balance data over the period 1952–2003 (values in m w.e.)
Three main conclusions result from this variance analysis.
-
1. Regarding the temporal variability, the balance at each stake differs from year to year by an amount which is nearly uniform over the entire glacier. This is shown in Figure 5, where the mean balance measured over the period of record at each stake is plotted versus altitude (αi curve). Yearly net balances are simply shifted with the βt annual value from the αi spatial distribution curve (as plotted for the year 1975). This linear shift fits 94.5% of the data. This linear behaviour has been reported for other glaciers (Reference Meier and TangbornMeier and Tangborn, 1965; Reference LliboutryLliboutry, 1974; Reference KuhnKuhn 1984; Reference RasmussenRasmussen, 2004) and is not surprising for Glacier de Sarennes which is a small size glacier with a small altitude range. However, non-linear effects explain some of the variability of the data, as 14 cross-terms among 255 are significantly different from 0 at the 95% confidence level. Figure 5 illustrates this for stake 1 in 2002 where a cross-term, γ 1 δ 2002, must be added to correctly fit the data. Note that non-linearity does not play any role in the quantification of the space and time effects because of the modelling constraints, and a pure linear model would have led to the same αi and βt .
-
2. Regarding the spatial variability, the deviation from the mean glaciological balance caused by the sampling at five sites is significant, showing that sampling on more than one is worthwhile (Table 5). However, sampling on four sites would be acceptable, as the discrepancy between the αi spatial terms is not significant for stakes 1 and 3. The standard deviation between the αi is 0.26 m w.e.a−1 and therefore very close to the 0.27 m w.e.a−1 overall spatial variability estimated from photogrammetry. This point suggests that all the spatial variability is recorded by the adopted sampling.
-
3. The final point is related to the linear composition of time and space variabilities. It results in only needing one stake to record the annual βt deviation which is the same at each stake. This can also be shown by the very high staketo-stake (>69%) and stake-to- βt (>85%) correlations. Best estimators are stakes 2 and 4, as the data from each explain 97% and 96% of βt , respectively. Nevertheless, the number of sites should not be reduced excessively. Firstly, despite low spatial variability and small differences between the αi , their distribution is needed to calculate the glacier-wide balance. Secondly, random errors related to the sampling and to point measurements are divided by the square root of the number of sites. Thirdly, the risk of losing some data increases for a low number of sites (stake not found or broken). Even if the linear model makes it possible to estimate missing values in the experimental table, at least one is needed every year, and the standard deviation while estimating βt is higher for years with missing values.
Fig. 5. Variance decomposition (αi , βt , γiδt ) of balances, bi , t , through the linear model (see text).
To complete the assessment regarding possible sources of systematic errors, the reliability of the spatial integration must be considered. The low spatial variability of the mass balance estimated from photogrammetry (0.27 m w.e. a−1) is reasonable given the small size and small altitude range (165 m) of the glacier. Small size and altitude range result in a reduced sensitivity of the glacier-wide balance to variable weighting parameters: using the same weight at each site would have led to a cumulative mass balance different by 4.5 m w.e. over 51 years which corresponds to <0.09 m w.e. a−1.This suggests that any systematic error in the weighting law, if it exists, would not be significant.
Nevertheless, given that the occurrence of such a systematic error cannot be totally ruled out and that the true distribution of the mass balance over the glacier is unknown, preference is given to photogrammetry to estimate the cumulative glacier-wide balance. The cumulative balance (adjusted to 4 September 1952 to 29 September 2003) that we recommend is therefore −31.5 m w.e.
. Regarding yearly balances, it seems also preferable to combine both methods. As αi
terms represent mean annual balances at each stake, the best possible estimate of their spatial integration is given by the mean annual volumetric balance, which is b
vol
/N = −0.62 m w.e.a−1 over the adjusted period. Considering that the αi
to altitude correlation is poor (r2
= 0.42), this seems more reliable than using the AAD integration relationship. Glacier-wide balance, bt
, can therefore be expressed for any years of the period by:
where βt is the centred mass balance obtained from the variance analysis (Table 6).
Table 6. Centred mass balance, βt , estimated from variance analysis, and glacier-wide balance, bt , combining photogrammetry and variance analysis using Equation (17) over the period 1952–2003
Conclusion and Recommendations
The purpose of this paper is to compare glaciological and volumetric mass-balance methods in search of systematic errors. When corrected for biases due to quantifiable systematic errors, the two measurements differ by only 2.59 m w.e. and no significant discrepancy can be detected at the 95% confidence level (type I error). However, the hypothesis that the discrepancy is linked to a systematic difference can only be accepted at a confidence level of 39% (type II error). Nevertheless, even if they are hardly detectable in the glaciological balance, potential residual systematic errors seem to be small. A variance analysis shows that the spatial sampling of field data covers the low overall spatial variability of the mass balance (0.27 m w.e.) over the small (0.5 km2) Glacier de Sarennes. All the spatial information is therefore accounted for by sampling sites.
As a result of the comparison and the variance analysis, the two methods should be considered complementary, and we propose to combine them in future work according to the following recommendations:
-
1. The investigation of climate variations requires the extraction of the centred mass balance, βt , which accounts for the temporal variability and is free of effects related to the geometry and the dynamics of the glacier. This should be based on a variance analysis of the glaciological balance data, with a linear separation of spatial and temporal variables. Such a variance analysis also makes it possible to discard superfluous stakes and retain a reduced network. Although not discussed in the present paper, both winter and summer balances may be analyzed this way (Reference Rasmussen and AndreassenRasmussen and Andreassen, 2005).
-
2. Given that the occurrence of systematic errors in the glaciological method cannot be totally ruled out, we recommend using photogrammetry to find the cumulative balance over a long period of monitoring. We conclude that the cumulative balance for Glacier de Sarennes is −31.5 (±1.07) m w.e., when adjusted to the end of both ablation seasons (4 September 1952 to 29 September 2003), and that the best possible estimate of yearly glacier-wide balances is a combination of the photogrammetric mean annual balance (−0.62 m w.e. a−1) and the centred mass balance resulting from the variance analysis.
Acknowledgements
This work was supported by GLACIOCLIM Observatoire de Recherce en Environnement (ORE), Programme d’Observation des Glaciers (POG) and Observatoire des Sciences de l’Univers de Grenoble (OSUG) (Institut National des Sciences de l’Univers, France (INSU)) funding. We thank L. de Crécy and F. Valla who have maintained the long balance series of Glacier de Sarennes over decades, and the many people who have helped collect field data since 1949. We thank M. Gerbaux for help with the calculations of internal accumulation and M. Vallon for constructive discussions. We also thank W. Wang (Scientific Editor), T.H. Jacka (Chief Editor) and an anonymous reviewer for helpful comments and suggestions.
