1. Introduction
We consider the linear reaction-diffusion (or growth-diffusion) problem:
where $\psi \geq 0$![]() (representing a population or concentration, for example). Here, $D>0$
(representing a population or concentration, for example). Here, $D>0$![]() is the diffusion coefficient, the constant $f_0>0$
is the diffusion coefficient, the constant $f_0>0$![]() describes the growth, and there are homogeneous Dirichlet boundary conditions at the endpoints. Both the start of the interval, $A(t)$
describes the growth, and there are homogeneous Dirichlet boundary conditions at the endpoints. Both the start of the interval, $A(t)$![]() , and the length of the interval, $L(t)$
, and the length of the interval, $L(t)$![]() , are prescribed functions of time, and we assume that both $A(t)$
, are prescribed functions of time, and we assume that both $A(t)$![]() and $L(t)$
and $L(t)$![]() are twice continuously differentiable.
are twice continuously differentiable.
The scenario of a domain with moving boundaries is relevant in the context of, for example, a species population in a habitat which changes over time. This could be due to factors such as flooding, climate change, habitat destruction, forest fire, loss of snow cover, or ‘re-wilding’ or ‘re-greening’ areas of land. Such phenomena mean that the habitat's size, as well as location, can change with time (and not necessarily at a constant rate). For such an application, the relevant climatological or ecological data could be used to choose an appropriate $A(t)$![]() and $L(t)$
and $L(t)$![]() for the mathematical model. While changing habitats are one motivation, there are numerous other physical applications of diffusion equations, and this work is relevant whenever these processes occur within a spatial domain whose boundary moves due to some external influence. (It is worth remarking that this is not the same as a free boundary problem, in which the moving boundary would be determined as part of the solution.)
for the mathematical model. While changing habitats are one motivation, there are numerous other physical applications of diffusion equations, and this work is relevant whenever these processes occur within a spatial domain whose boundary moves due to some external influence. (It is worth remarking that this is not the same as a free boundary problem, in which the moving boundary would be determined as part of the solution.)
We treat a linear growth term: $f_0\psi$![]() for some $f_0>0$
for some $f_0>0$![]() . This allows for certain exact solutions and precise bounds on behaviour, which are useful for understanding and evaluating the effects of a time-dependent domain, as well as having mathematical interest. Following this study, we intend to treat the case of a so-called FKPP-type nonlinear term (named from the initials of the authors of [Reference Fisher17, Reference Petrowsky, Kolmogorov and Piskunov21]), where $f(0)=f(1)=0$
. This allows for certain exact solutions and precise bounds on behaviour, which are useful for understanding and evaluating the effects of a time-dependent domain, as well as having mathematical interest. Following this study, we intend to treat the case of a so-called FKPP-type nonlinear term (named from the initials of the authors of [Reference Fisher17, Reference Petrowsky, Kolmogorov and Piskunov21]), where $f(0)=f(1)=0$![]() , $f>0$
, $f>0$![]() on $(0,1)$
on $(0,1)$![]() , and $f(k)\leq f'(0)k$
, and $f(k)\leq f'(0)k$![]() . This has applications to population dynamics. The results for the nonlinear case will be discussed elsewhere. An important property of such nonlinear terms is that the solution to the linear problem (with $f_0=f'(0)$
. This has applications to population dynamics. The results for the nonlinear case will be discussed elsewhere. An important property of such nonlinear terms is that the solution to the linear problem (with $f_0=f'(0)$![]() ) is a supersolution. Moreover, a linearization around the zero state can be used as an approximation to the nonlinear equation when the population density is small enough. Therefore, a thorough understanding of this linear problem (with the full time-dependence) will also be an important tool in the analysis of nonlinear problems in time-dependent domains.
) is a supersolution. Moreover, a linearization around the zero state can be used as an approximation to the nonlinear equation when the population density is small enough. Therefore, a thorough understanding of this linear problem (with the full time-dependence) will also be an important tool in the analysis of nonlinear problems in time-dependent domains.
Due to the importance of climate change and its consequences for the migration of species, the topic of habitat movement in a reaction-diffusion model has been considered by several authors (see, for example, [Reference Alfaro, Berestycki and Raoul1, Reference Berestycki and Rossi3–Reference Berestycki, Desvillettes and Diekmann6, Reference Bouhours and Giletti8, Reference Bouhours and Nadin9, Reference Potapov and Lewis22, Reference Roques, Roques, Berestycki and Kretzschmar23, Reference Wu, Wang and Zou29].) To our knowledge, all of these make the mathematically convenient assumption that climate change translates the habitat at a constant speed $c$![]() . Here, we consider not only the case of a fixed length $L$
. Here, we consider not only the case of a fixed length $L$![]() and constant speed $c$
and constant speed $c$![]() but also several other much more general moving boundaries. The domain length is able to vary with time. The results presented here will focus, primarily, on some particular cases of $A(t)$
but also several other much more general moving boundaries. The domain length is able to vary with time. The results presented here will focus, primarily, on some particular cases of $A(t)$![]() and $L(t)$
and $L(t)$![]() for which exact results can be given: explicit expressions for the solution for certain forms of $L(t)$
for which exact results can be given: explicit expressions for the solution for certain forms of $L(t)$![]() , and precise boundary behaviour in a ‘critical’ case. We also extend the methods to much more general forms of $A(t)$
, and precise boundary behaviour in a ‘critical’ case. We also extend the methods to much more general forms of $A(t)$![]() , $L(t)$
, $L(t)$![]() , making use of a comparison principle on a transformed version of the equation. This provides useful upper or lower bounds on the solution for a range of cases.
, making use of a comparison principle on a transformed version of the equation. This provides useful upper or lower bounds on the solution for a range of cases.
This paper is split into two main sections. Section 2 treats the cases which can be solved exactly, deriving the explicit expressions and studying some of their implications. In § 3, we construct a supersolution and an Airy function subsolution, to prove precise bounds on the solution near a boundary moving with $A(t)=-2\sqrt {Df_0}t+\alpha \log (t+1)+O(1)$![]() . This describes a ‘critical’ case, in the sense that as $\alpha$
. This describes a ‘critical’ case, in the sense that as $\alpha$![]() varies, a transition occurs between growth and decay, with the solution near the boundary behaving like a power law in $t$
varies, a transition occurs between growth and decay, with the solution near the boundary behaving like a power law in $t$![]() .
.
We begin by transforming onto a fixed spatial domain. We change variables from $\psi (x,t)$![]() to $u(\xi,t)$
to $u(\xi,t)$![]() where $\xi =\frac {(x-A(t))}{L(t)}L_0$
where $\xi =\frac {(x-A(t))}{L(t)}L_0$![]() , with $L_0=L(0)$
, with $L_0=L(0)$![]() and obtain the variable-coefficient PDE
and obtain the variable-coefficient PDE
In § 2, we introduce a further change of variables and thus deduce conditions under which the transformed equation can be solved exactly by separation of variables, reducing to a Sturm–Liouville problem on a fixed interval. These conditions are that $\ddot {L}L^{3}$![]() and $\ddot {A}L^{3}$
and $\ddot {A}L^{3}$![]() are constants, which is when the length varies as $L(t)=\sqrt {at^{2} + 2bt+L_0^{2}}$
are constants, which is when the length varies as $L(t)=\sqrt {at^{2} + 2bt+L_0^{2}}$![]() . The forms of $A(t)$
. The forms of $A(t)$![]() , and of the exact solutions, depend on whether $a$
, and of the exact solutions, depend on whether $a$![]() is zero or non-zero and on the sign of $aL_0^{2}-b^{2}$
is zero or non-zero and on the sign of $aL_0^{2}-b^{2}$![]() . We derive the explicit expressions for $u(\xi,t)$
. We derive the explicit expressions for $u(\xi,t)$![]() in each exactly solvable case and describe several implications of the results. We also extend the same method to a ball in $\mathbb {R}^{n}$
in each exactly solvable case and describe several implications of the results. We also extend the same method to a ball in $\mathbb {R}^{n}$![]() with moving centre and time-dependent radius $R(t)$
with moving centre and time-dependent radius $R(t)$![]() , giving exact solutions when $\ddot {R}R^{3}$
, giving exact solutions when $\ddot {R}R^{3}$![]() is constant, i.e. $R(t)=\sqrt {at^{2} + 2bt+R_0^{2}}$
is constant, i.e. $R(t)=\sqrt {at^{2} + 2bt+R_0^{2}}$![]() .
.
The exact solutions show directly each of the individual factors involved in determining the overall behaviour, and they determine precisely how any initial condition will evolve over time. This is very instructive in understanding the effect of each time-dependent domain. One also sees the effect of each parameter, which gives useful insight into how any changes or uncertainty in the parameters would alter the solution. We suggest that these exact solutions could be a useful tool in comparing theoretical with ecological observations. Finally, they are a means of deducing the long-time asymptotic behaviour: we show that, in some cases, the solution tends uniformly to zero, in other cases, it becomes arbitrarily large at each interior point, while there are also cases for which the solution grows exponentially on part of the domain while decaying elsewhere. This third sort of behaviour occurs when the interface (between the regions for growth and decay) can travel at an asymptotic speed $c_*=2\sqrt {Df_0}$![]() while staying within the domain. We recall that this speed $c_*$
while staying within the domain. We recall that this speed $c_*$![]() is also the asymptotic spreading speed for solutions to the linear and nonlinear FKPP equations on the real line with compactly supported initial conditions (see [Reference Aronson and Weinberger2, Reference Petrowsky, Kolmogorov and Piskunov21]), and it is the minimum wave speed for travelling wave solutions to the FKPP equation.
is also the asymptotic spreading speed for solutions to the linear and nonlinear FKPP equations on the real line with compactly supported initial conditions (see [Reference Aronson and Weinberger2, Reference Petrowsky, Kolmogorov and Piskunov21]), and it is the minimum wave speed for travelling wave solutions to the FKPP equation.
In § 2.6, we use comparison principles to deduce upper and lower bounds on the solution for other forms of $L(t)$![]() and $A(t)$
and $A(t)$![]() . One application gives bounds whenever the domain $(A(t), A(t)+L(t))$
. One application gives bounds whenever the domain $(A(t), A(t)+L(t))$![]() encloses, or is enclosed by, one of the exactly solvable cases. A second method allows us to derive bounds whenever $\ddot {L}L^{3}$
encloses, or is enclosed by, one of the exactly solvable cases. A second method allows us to derive bounds whenever $\ddot {L}L^{3}$![]() and $\ddot {A}L^{3}$
and $\ddot {A}L^{3}$![]() are bounded.
are bounded.
Our exact solutions are (it would seem) previously unknown. A linear growth-diffusion on an expanding domain was analysed by Simpson in [Reference Simpson25] (and extended to a coupled system in [Reference Simpson, Sharp, Morrow and Baker26]). In that model, the domain was itself expanding at each position $x$![]() , to model the uniform growth of living tissue. This differs from the case considered here, where the physical points inside the domain are not being expanded, but rather the boundary of the domain is moving. This led to a different reaction-diffusion equation in [Reference Simpson25]:
, to model the uniform growth of living tissue. This differs from the case considered here, where the physical points inside the domain are not being expanded, but rather the boundary of the domain is moving. This led to a different reaction-diffusion equation in [Reference Simpson25]:
In our own model, the additional terms in Equation (1.3) mean that more changes of variables are required in order to get the equation into a separable form (see Equation (2.5)). Moreover, the dependence of these terms on both space and time means that it is only separable under the extra conditions that $\ddot {L}L^{3}$![]() and $\ddot {A}L^{3}$
and $\ddot {A}L^{3}$![]() are constants. Our explicit solutions appear more intricate than those in [Reference Simpson25], although the principle is the same. Note, also, the paper [Reference Jana and Roy20] which considered the Schrödinger equation on an interval $(0,L(t))$
are constants. Our explicit solutions appear more intricate than those in [Reference Simpson25], although the principle is the same. Note, also, the paper [Reference Jana and Roy20] which considered the Schrödinger equation on an interval $(0,L(t))$![]() of changing length and derived necessary conditions to solve it by separation of variables.
of changing length and derived necessary conditions to solve it by separation of variables.
On the topic of exact solutions to certain parabolic equations, let us also mention the works [Reference Suazo, Suslov and Vega-Guzmán27, Reference Suazo, Suslov and Vega-Guzmán28] by Suazo, Suslov and Vega-Guzmán. They used transformations of variables to convert between a diffusion-type equation with variable coefficients and the heat equation, and thus they derived the fundamental solution for their class of equation. This was given in terms of the solution $\mu (t)$![]() to a second-order ODE, and a set of six coefficients which were themselves defined by integrals involving $\mu$
to a second-order ODE, and a set of six coefficients which were themselves defined by integrals involving $\mu$![]() , $\mu '$
, $\mu '$![]() and the time-dependent coefficients of the parabolic equation.
and the time-dependent coefficients of the parabolic equation.
Reaction-diffusion models on domains subject to translation at a constant speed $c$![]() have been considered by several authors. We note, in particular, the paper by Potapov and Lewis [Reference Potapov and Lewis22] on a two-species competition, and the paper of Berestycki (H.), Diekmann, Nagelkerke and Zegeling [Reference Berestycki, Diekmann, Nagelkerke and Zegeling5] for a single species (see also [Reference Alfaro, Berestycki and Raoul1, Reference Berestycki and Rossi3, Reference Berestycki and Rossi4, Reference Berestycki, Desvillettes and Diekmann6, Reference Bouhours and Giletti8, Reference Bouhours and Nadin9, Reference Roques, Roques, Berestycki and Kretzschmar23, Reference Wu, Wang and Zou29]). These two papers considered a nonlinear reaction term and a model on the real line with growth in a favourable region – of a fixed length $L$
have been considered by several authors. We note, in particular, the paper by Potapov and Lewis [Reference Potapov and Lewis22] on a two-species competition, and the paper of Berestycki (H.), Diekmann, Nagelkerke and Zegeling [Reference Berestycki, Diekmann, Nagelkerke and Zegeling5] for a single species (see also [Reference Alfaro, Berestycki and Raoul1, Reference Berestycki and Rossi3, Reference Berestycki and Rossi4, Reference Berestycki, Desvillettes and Diekmann6, Reference Bouhours and Giletti8, Reference Bouhours and Nadin9, Reference Roques, Roques, Berestycki and Kretzschmar23, Reference Wu, Wang and Zou29]). These two papers considered a nonlinear reaction term and a model on the real line with growth in a favourable region – of a fixed length $L$![]() and moving at a constant speed $c$
and moving at a constant speed $c$![]() – and decay elsewhere. The case of Dirichlet boundary conditions on a finite interval was included as a limiting case. Several interesting results were proved regarding the dynamics on a moving domain as opposed to a stationary one. (See, especially, the observations in [Reference Potapov and Lewis22] regarding invasibility in a moving domain.) Both papers proved the existence of a minimal domain length $L$
– and decay elsewhere. The case of Dirichlet boundary conditions on a finite interval was included as a limiting case. Several interesting results were proved regarding the dynamics on a moving domain as opposed to a stationary one. (See, especially, the observations in [Reference Potapov and Lewis22] regarding invasibility in a moving domain.) Both papers proved the existence of a minimal domain length $L$![]() needed for survival and expressed this as a function of $c$
needed for survival and expressed this as a function of $c$![]() . If $c$
. If $c$![]() was greater than a certain critical value then the solution decayed exponentially to zero regardless of the domain length. The implication was that if the climate changes too rapidly then the species is unable to keep up and goes extinct. This critical speed, $c_*=2\sqrt {Df_0}$
was greater than a certain critical value then the solution decayed exponentially to zero regardless of the domain length. The implication was that if the climate changes too rapidly then the species is unable to keep up and goes extinct. This critical speed, $c_*=2\sqrt {Df_0}$![]() , features in our solutions in a similar manner.
, features in our solutions in a similar manner.
Another moving boundary reaction-diffusion problem which has received much attention is the free boundary problem
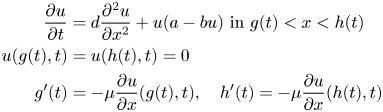
where $a$![]() , $b$
, $b$![]() , and $\mu$
, and $\mu$![]() are given positive constants. Note that here $g(t)$
are given positive constants. Note that here $g(t)$![]() and $h(t)$
and $h(t)$![]() are monotonic functions of $t$
are monotonic functions of $t$![]() . The reader is referred to [Reference Bunting, Du and Krakowski10, Reference Du and Lin13, Reference Du and Lin14], where Du, Lin, Bunting and Krakowski proved a vanishing/spreading dichotomy: either $g(t)\rightarrow g_{\infty }$
. The reader is referred to [Reference Bunting, Du and Krakowski10, Reference Du and Lin13, Reference Du and Lin14], where Du, Lin, Bunting and Krakowski proved a vanishing/spreading dichotomy: either $g(t)\rightarrow g_{\infty }$![]() , $h(t)\rightarrow h_{\infty }$
, $h(t)\rightarrow h_{\infty }$![]() with $h_{\infty }-g_{\infty } \leq \pi \sqrt {d/a}$
with $h_{\infty }-g_{\infty } \leq \pi \sqrt {d/a}$![]() and $u\rightarrow 0$
and $u\rightarrow 0$![]() , or $g(t)\rightarrow -\infty$
, or $g(t)\rightarrow -\infty$![]() , $h(t)\rightarrow +\infty$
, $h(t)\rightarrow +\infty$![]() and $u$
and $u$![]() spreads at an asymptotically constant speed in both directions. In the vanishing case, their domain is enclosed by a stationary domain of the critical length, $\pi \sqrt {d/a}$
spreads at an asymptotically constant speed in both directions. In the vanishing case, their domain is enclosed by a stationary domain of the critical length, $\pi \sqrt {d/a}$![]() , and the solution decays to zero. In the spreading case, the asymptotic speed $c(\mu )$
, and the solution decays to zero. In the spreading case, the asymptotic speed $c(\mu )$![]() is strictly less than the critical speed $c_*=2\sqrt {da}$
is strictly less than the critical speed $c_*=2\sqrt {da}$![]() , and it is crucially determined by the parameter $\mu$
, and it is crucially determined by the parameter $\mu$![]() which occurs in their free boundary condition. Certain properties of the solution in the case of spreading have been proved in [Reference Du, Matsuzawa and Zhou15, Reference El-Hachem, McCue, Jin, Du and Simpson16] and may provide a useful and interesting point of comparison in the intended extension of our own problem to include a nonlinear reaction term. In the current study, we focus our attention on the case with a linear reaction term.
which occurs in their free boundary condition. Certain properties of the solution in the case of spreading have been proved in [Reference Du, Matsuzawa and Zhou15, Reference El-Hachem, McCue, Jin, Du and Simpson16] and may provide a useful and interesting point of comparison in the intended extension of our own problem to include a nonlinear reaction term. In the current study, we focus our attention on the case with a linear reaction term.
In § 3, we consider the behaviour on a domain whose endpoints move close to the critical speed $c_*$![]() . An analysis of one of our exact solutions suggests that a logarithmic-in-time adjustment may be the key to this. This is further motivated by the well-known result regarding Bramson's logarithmic correction in relation to the nonlinear FKPP equation on the real line with compactly supported initial conditions. In that case, it has been proven that the positions $x=\pm (c_*t - \frac {3D}{c_*}\log (t+1)+O(1))$
. An analysis of one of our exact solutions suggests that a logarithmic-in-time adjustment may be the key to this. This is further motivated by the well-known result regarding Bramson's logarithmic correction in relation to the nonlinear FKPP equation on the real line with compactly supported initial conditions. In that case, it has been proven that the positions $x=\pm (c_*t - \frac {3D}{c_*}\log (t+1)+O(1))$![]() are the asymptotic positions at which the solution takes on any value strictly between zero and the finite stable equilibrium. Moreover, there is locally uniform convergence, at this shifted position, to the profile of the minimum speed travelling wave. This result is known as Bramson's logarithmic correction. (See [Reference Bramson11, Reference Bramson12] for Bramson's original proof using probabilistic arguments, or [Reference Hamel, Nolen, Roquejoffre and Ryzhik19] for an alternative proof using PDEs by Hamel, Nolen, Roquejoffre and Ryzhik.)
are the asymptotic positions at which the solution takes on any value strictly between zero and the finite stable equilibrium. Moreover, there is locally uniform convergence, at this shifted position, to the profile of the minimum speed travelling wave. This result is known as Bramson's logarithmic correction. (See [Reference Bramson11, Reference Bramson12] for Bramson's original proof using probabilistic arguments, or [Reference Hamel, Nolen, Roquejoffre and Ryzhik19] for an alternative proof using PDEs by Hamel, Nolen, Roquejoffre and Ryzhik.)
Here, we study the behaviour near the boundary when
We construct super- and sub-solutions to demonstrate that when $\alpha >0$![]() , the solution at $x=A(t)+y$
, the solution at $x=A(t)+y$![]() (for $y=O(1)$
(for $y=O(1)$![]() ) is ‘exactly of order’ $y t^{-\frac {3}{2}+\frac {\alpha c_*}{2D}}$
) is ‘exactly of order’ $y t^{-\frac {3}{2}+\frac {\alpha c_*}{2D}}$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() . (A precise statement can be found in § 3.) In particular, the ‘critical’ boundary motion, for which the solution at $A(t)+y$
. (A precise statement can be found in § 3.) In particular, the ‘critical’ boundary motion, for which the solution at $A(t)+y$![]() remains exactly of order $y$
remains exactly of order $y$![]() , is $A(t)=-c_*t+\frac {3D}{c_*}\log (t+1)+O(1)$
, is $A(t)=-c_*t+\frac {3D}{c_*}\log (t+1)+O(1)$![]() . This precisely matches Bramson's logarithmic term.
. This precisely matches Bramson's logarithmic term.
Our analysis uses a change of variables; a supersolution based on the principal eigenfunction of the Laplacian; and a subsolution constructed from a space-and-time-dependent Airy function $\textrm{Ai}$![]() and its tangent at the position $\textrm {Ai}(0)$
and its tangent at the position $\textrm {Ai}(0)$![]() .
.
Bramson's logarithmic term (or similar) has been seen to arise in several other circumstances. We note, in particular, the paper [Reference Gärtner18], by Gärtner, which generalized the result to the multi-dimensional case (see also [Reference Roquejoffre, Rossi and Roussier-Michon24]), and the paper [Reference Berestycki, Brunet and Derrida7], by Berestycki (J.), Brunet and Derrida, which derived the term in the setting of a linear equation on a semi-infinite interval with a free boundary. They prescribed constant values of the function and its gradient at the free boundary and then calculated the precise asymptotics of the boundary motion for which the prescribed conditions would be satisfied. Again, the leading term was $c_*t$![]() and the next term was of order $\log (t)$
and the next term was of order $\log (t)$![]() . For initial conditions with suitable decay, the coefficient of the logarithmic term was the same as in Bramson's correction. (Many subsequent terms were also calculated; see [Reference Berestycki, Brunet and Derrida7].)
. For initial conditions with suitable decay, the coefficient of the logarithmic term was the same as in Bramson's correction. (Many subsequent terms were also calculated; see [Reference Berestycki, Brunet and Derrida7].)
To our knowledge, our current study is the first time that such a term has appeared in the context of the linear equation on a finite, but time-dependent, interval with Dirichlet boundary conditions. In contrast to our own method of super- and sub-solutions, the logarithmic correction term in [Reference Hamel, Nolen, Roquejoffre and Ryzhik19] was derived using bounds on some approximate solutions together with parabolic estimates in the function spaces $L^{2}$![]() and $H_0^{1}$
and $H_0^{1}$![]() , and in [Reference Berestycki, Brunet and Derrida7], it was derived using a clever integral transform method and a singularity analysis in a small parameter. These three derivations of the term are completely different; nevertheless, the same logarithmic term appears in each different setting. It is possible that some useful insight into this somewhat ‘universal’ logarithmic term may be gained from our change of variables — which is the source of the factor $t^{-\frac {1}{2}+\frac {\alpha c_*}{2D}}$
, and in [Reference Berestycki, Brunet and Derrida7], it was derived using a clever integral transform method and a singularity analysis in a small parameter. These three derivations of the term are completely different; nevertheless, the same logarithmic term appears in each different setting. It is possible that some useful insight into this somewhat ‘universal’ logarithmic term may be gained from our change of variables — which is the source of the factor $t^{-\frac {1}{2}+\frac {\alpha c_*}{2D}}$![]() in the critical behaviour — or from our super- and sub-solutions — the source of the $yt^{-1}$
in the critical behaviour — or from our super- and sub-solutions — the source of the $yt^{-1}$![]() factor.
factor.
We also discuss, in § 3.3, the extensions of this result to a ball in $\mathbb {R}^{n}$![]() with radius $R(t)=c_*t-\alpha \log (t+1)+O(1)$
with radius $R(t)=c_*t-\alpha \log (t+1)+O(1)$![]() .
.
2. Exact solutions
In this section, we state and prove the form of each exact solution.
Theorem 1 Suppose that
Then, for any given initial conditions $u(\xi,0)$![]() in $L^{2}([0,L_0]),$
in $L^{2}([0,L_0]),$![]() the solution for $u(\xi,t)$
the solution for $u(\xi,t)$![]() can be obtained exactly, as a sum of $u_n(\xi,t)$
can be obtained exactly, as a sum of $u_n(\xi,t)$![]() with coefficients depending only on the initial conditions. The functions $u_n$
with coefficients depending only on the initial conditions. The functions $u_n$![]() are given by
are given by
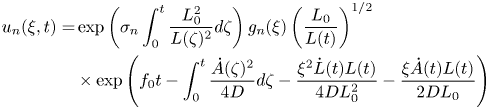
where $g_n(\xi )$![]() satisfies the Sturm–Liouville problem in equations (2.9), (2.10) with $\gamma _{0}=aL_0^{2}-b^{2},$
satisfies the Sturm–Liouville problem in equations (2.9), (2.10) with $\gamma _{0}=aL_0^{2}-b^{2},$![]() with eigenvalue $\sigma _n$
with eigenvalue $\sigma _n$![]() . The explicit expressions for these exact solutions depend on whether $a$
. The explicit expressions for these exact solutions depend on whether $a$![]() is zero or non-zero, and on the sign of $aL_0^{2}-b^{2}$
is zero or non-zero, and on the sign of $aL_0^{2}-b^{2}$![]() . They are given in full in Equations (2.17), (2.21), (2.28), (2.32), (2.33), and (2.34).
. They are given in full in Equations (2.17), (2.21), (2.28), (2.32), (2.33), and (2.34).
These explicit expressions determine precisely how any initial condition will evolve over time and demonstrate each factor contributing to the behaviour. We can compare Equation (2.3) (or the specific formulae in Equations (2.17), (2.21), (2.28), (2.32), (2.33), and (2.34)) with the more standard case of a Fourier series solution on a fixed domain, for which
The comparison is very instructive in understanding the precise effects of the time-dependent domain on the way the solution develops — the subtleties of which would otherwise have been non-obvious.
Proof. We begin with a useful change of variables. With $u(\xi,t)$![]() satisfying Equation (1.3), let
satisfying Equation (1.3), let

This removes the terms in $\frac {\partial u}{\partial \xi }$![]() , shifting the effects of the time-dependent domain into the factors in (2.5) and the zero-order term in the equation satisfied by $w(\xi, t)$
, shifting the effects of the time-dependent domain into the factors in (2.5) and the zero-order term in the equation satisfied by $w(\xi, t)$![]() :
:
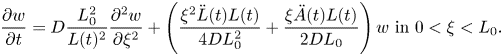
Next, change the time variable from $t$![]() to $s(t)= \int_0^ t \frac {L_0^{2}}{L(\zeta )^{2}}d\zeta$
to $s(t)= \int_0^ t \frac {L_0^{2}}{L(\zeta )^{2}}d\zeta$![]() , and write $v(\xi,s)=w(\xi, t)$
, and write $v(\xi,s)=w(\xi, t)$![]() . Then
. Then

Notice that the $v(\xi,s)$![]() equation is separable if and only if $\ddot {L}L^{3}=\gamma _{0}=$
equation is separable if and only if $\ddot {L}L^{3}=\gamma _{0}=$![]() constant and $\ddot {A}L^{3}=\gamma _{1}={\rm constant}$
constant and $\ddot {A}L^{3}=\gamma _{1}={\rm constant}$![]() . This corresponds to $L(t)$
. This corresponds to $L(t)$![]() given by Equation (2.1), with $\gamma _{0}=aL_0^{2}-b^{2}$
given by Equation (2.1), with $\gamma _{0}=aL_0^{2}-b^{2}$![]() , and $A(t)$
, and $A(t)$![]() satisfying Equation (2.2) (which can be integrated twice to give $A(t)$
satisfying Equation (2.2) (which can be integrated twice to give $A(t)$![]() ). The $v(\xi,s)$
). The $v(\xi,s)$![]() equation is then separable, with solutions of the form $v(\xi,s)=\exp (\sigma s)g(\xi )$
equation is then separable, with solutions of the form $v(\xi,s)=\exp (\sigma s)g(\xi )$![]() where $g(\xi )$
where $g(\xi )$![]() satisfies the related Sturm–Liouville problem:
satisfies the related Sturm–Liouville problem:
The Sturm–Liouville theory gives that there is a countably infinite set of eigenfunctions $g_{n}$![]() with eigenvalues $\sigma _{n}$
with eigenvalues $\sigma _{n}$![]() , and that $v(\xi,s)$
, and that $v(\xi,s)$![]() has an eigenfunction expansion in terms of $v_n(\xi,s):=\exp (\sigma _n s)g_n(\xi )$
has an eigenfunction expansion in terms of $v_n(\xi,s):=\exp (\sigma _n s)g_n(\xi )$![]() , with coefficients depending only on the initial conditions. Thus, the solution for $u(\xi,t)$
, with coefficients depending only on the initial conditions. Thus, the solution for $u(\xi,t)$![]() is given exactly by a sum of
is given exactly by a sum of
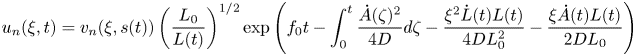
where $s(t)= \int_0^ t \frac {L_0^{2}}{L(\zeta )^{2}}d\zeta$![]() . Thus, Equation (2.3) is proved.
. Thus, Equation (2.3) is proved.
The required integrals (for $A(t)$![]() , $s(t)$
, $s(t)$![]() ) depend on the specific form of $L(t)$
) depend on the specific form of $L(t)$![]() : namely whether $a$
: namely whether $a$![]() is zero or non-zero and on the sign of $aL_0^{2}-b^{2}$
is zero or non-zero and on the sign of $aL_0^{2}-b^{2}$![]() . They can each be done by standard calculus, resulting in the expressions for $u_n$
. They can each be done by standard calculus, resulting in the expressions for $u_n$![]() in Equations (2.17), (2.21), (2.28), (2.32), (2.33), and (2.34).
in Equations (2.17), (2.21), (2.28), (2.32), (2.33), and (2.34).
In the following sections, the long-time behaviour of each solution is extracted based on the leading order terms. In certain cases, the governing term depends on the eigenvalue $\sigma _n$![]() . Recall that, by Sturm–Liouville theory, the eigenvalues satisfy $\sigma _{n+1} \leq \sigma _{n}$
. Recall that, by Sturm–Liouville theory, the eigenvalues satisfy $\sigma _{n+1} \leq \sigma _{n}$![]() , and the largest eigenvalue, $\sigma _1$
, and the largest eigenvalue, $\sigma _1$![]() , corresponds to an eigenfunction which is positive. We know already that when $\gamma _0=\gamma _1=0$
, corresponds to an eigenfunction which is positive. We know already that when $\gamma _0=\gamma _1=0$![]() then $\sigma _1=-\frac {D\pi ^{2}}{L_0^{2}}$
then $\sigma _1=-\frac {D\pi ^{2}}{L_0^{2}}$![]() . In cases when $\gamma _0<0$
. In cases when $\gamma _0<0$![]() , we need the following lemma when inferring the asymptotic behaviour.
, we need the following lemma when inferring the asymptotic behaviour.
Lemma 1 If $\gamma _{0}=-\rho ^{2}<0,$![]() then
then
Proof. Write $\displaystyle {g_1(\xi )=e^{-\frac {1}{2}(\eta -\eta _0)^{2}}h(\eta )}$![]() , where $\displaystyle {\eta =\sqrt {\frac {\vert \rho \vert }{2D}}\frac {\xi }{L_0}}$
, where $\displaystyle {\eta =\sqrt {\frac {\vert \rho \vert }{2D}}\frac {\xi }{L_0}}$![]() and $\displaystyle {\eta _0=\frac {\gamma _{1}}{\vert \rho \vert ^{3/2}\sqrt {2D}}}$
and $\displaystyle {\eta _0=\frac {\gamma _{1}}{\vert \rho \vert ^{3/2}\sqrt {2D}}}$![]() . This puts the equation into self-adjoint form
. This puts the equation into self-adjoint form
where
Integrate Equation (2.13) over the interval and recall that $h$![]() is positive, to deduce $\lambda <0$
is positive, to deduce $\lambda <0$![]() . This is equivalent to equation (2.12).
. This is equivalent to equation (2.12).
The following sections give the full expressions for $u_n(\xi,t)$![]() , as well as their long-time behaviour. An exact formula is obtained for each form of $L(t)$
, as well as their long-time behaviour. An exact formula is obtained for each form of $L(t)$![]() (depending on $a$
(depending on $a$![]() and $aL_0^{2}-b^{2}$
and $aL_0^{2}-b^{2}$![]() ). The integrals (for $A(t)$
). The integrals (for $A(t)$![]() , $s(t)$
, $s(t)$![]() ) and the expressions occurring in Equation (2.3) differ between the cases. Thus, the formulae given below are the result of performing the necessary calculations and integrals and substituting the relevant expressions into Equation (2.3).
) and the expressions occurring in Equation (2.3) differ between the cases. Thus, the formulae given below are the result of performing the necessary calculations and integrals and substituting the relevant expressions into Equation (2.3).
2.1. $L(t)=L_0$
For a fixed domain length $L_0$![]() , we have $\ddot {L}L^{3}=\gamma _0=0$
, we have $\ddot {L}L^{3}=\gamma _0=0$![]() and the separable cases are those where
and the separable cases are those where
The separable solutions then have the form

If $\gamma _{1}\neq 0$![]() then, as $t\rightarrow \infty$
then, as $t\rightarrow \infty$![]() , $u(\xi,t)\rightarrow 0$
, $u(\xi,t)\rightarrow 0$![]() since the behaviour is dominated by the term
since the behaviour is dominated by the term
If $\gamma _{1}=0$![]() then, as $t\rightarrow \infty$
then, as $t\rightarrow \infty$![]() , there is exponential growth or decay in the cases $f_0>\frac {D\pi ^{2}}{L_0^{2}}+\frac {c^{2}}{4D}$
, there is exponential growth or decay in the cases $f_0>\frac {D\pi ^{2}}{L_0^{2}}+\frac {c^{2}}{4D}$![]() or $f_0<\frac {D\pi ^{2}}{L_0^{2}}+\frac {c^{2}}{4D}$
or $f_0<\frac {D\pi ^{2}}{L_0^{2}}+\frac {c^{2}}{4D}$![]() respectively. Indeed, the long time behaviour of $u_n$
respectively. Indeed, the long time behaviour of $u_n$![]() is governed by
is governed by
where $\sigma _n =-\frac {Dn^{2}\pi ^{2}}{L_0^{2}}$![]() .
.
2.2. $L(t)=L_0+\alpha t$ with $\alpha \neq 0$
with $\alpha \neq 0$
When $L(t)=L_0+\alpha t$![]() then again $\ddot {L}L^{3}=\gamma _0=0$
then again $\ddot {L}L^{3}=\gamma _0=0$![]() , but now the separable cases are those where
, but now the separable cases are those where
The separable solutions then have the form

If $\alpha >0$![]() then as $t\rightarrow \infty$
then as $t\rightarrow \infty$![]() , the behaviour is asymptotically governed by
, the behaviour is asymptotically governed by

Recall that we defined
Thus, if $-\alpha -c_* < c < c_*$![]() , then there is a region of $\xi$
, then there is a region of $\xi$![]() in which there is exponential growth: namely, where
in which there is exponential growth: namely, where
Otherwise, $u(\xi,t)$![]() decays to zero everywhere in $(0,L_0)$
decays to zero everywhere in $(0,L_0)$![]() .
.
If instead $\alpha <0$![]() , then $L(t)\rightarrow 0$
, then $L(t)\rightarrow 0$![]() as $t\rightarrow -L_0/\alpha$
as $t\rightarrow -L_0/\alpha$![]() , and in this limit, $u(\xi,t)\rightarrow 0$
, and in this limit, $u(\xi,t)\rightarrow 0$![]() . Indeed, if $\gamma _{1}\neq 0$
. Indeed, if $\gamma _{1}\neq 0$![]() , then the behaviour is governed by
, then the behaviour is governed by
which decays exponentially since $\alpha <0$![]() . If $\gamma _{1}=0$
. If $\gamma _{1}=0$![]() then the governing term is
then the governing term is
where $\sigma _n =-\frac {Dn^{2}\pi ^{2}}{L_0^{2}}<0$![]() and so, again, $u(\xi,t)\rightarrow 0$
and so, again, $u(\xi,t)\rightarrow 0$![]() .
.
2.3. $L(t)=\sqrt {L_0^{2}+2\rho t}$ with $\rho \neq 0$
with $\rho \neq 0$
If $L(t)^{2}=L_0^{2}+2\rho t$![]() then $\ddot {L}L^{3}=\gamma _{0}=-\rho ^{2}<0$
then $\ddot {L}L^{3}=\gamma _{0}=-\rho ^{2}<0$![]() and the separable cases are those where
and the separable cases are those where
The separable solutions then have the form

Therefore, if $\rho >0$![]() then, as $t\rightarrow \infty$
then, as $t\rightarrow \infty$![]() , there is exponential growth or decay in the cases $f_0>\frac {c^{2}}{4D}$
, there is exponential growth or decay in the cases $f_0>\frac {c^{2}}{4D}$![]() or $f_0<\frac {c^{2}}{4D}$
or $f_0<\frac {c^{2}}{4D}$![]() respectively. Indeed, the long-time behaviour in this case is governed by
respectively. Indeed, the long-time behaviour in this case is governed by
If instead $\rho <0$![]() then $L(t)\rightarrow 0$
then $L(t)\rightarrow 0$![]() as $t\rightarrow -L_0^{2}/2\rho$
as $t\rightarrow -L_0^{2}/2\rho$![]() , and in this limit $u(\xi,t)\rightarrow 0$
, and in this limit $u(\xi,t)\rightarrow 0$![]() . This follows because the behaviour of each $u_n$
. This follows because the behaviour of each $u_n$![]() is governed by
is governed by

This implies that $u(\xi,t)\rightarrow 0$![]() , by using the bound in equation (2.12).
, by using the bound in equation (2.12).
2.4. $L(t)=\sqrt {a t^{2} + 2b t + L_0^{2}}$ with $a\neq 0$
with $a\neq 0$ and $aL_0^{2}-b^{2} \neq 0$
and $aL_0^{2}-b^{2} \neq 0$
If $L(t)^{2}=a t^{2} + 2b t + L_0^{2}$![]() then $\ddot {L}L^{3}=\gamma _{0}=aL_0^{2}-b^{2}$
then $\ddot {L}L^{3}=\gamma _{0}=aL_0^{2}-b^{2}$![]() , and for $aL_0^{2}-b^{2} \neq 0$
, and for $aL_0^{2}-b^{2} \neq 0$![]() , the separable cases are those where
, the separable cases are those where
The separable solutions have the form

where if $\gamma _0=aL_0^{2}-b^{2} < 0$![]() ,
,

and if $\gamma _0=aL_0^{2}-b^{2} >0$![]() then
then
If $L(t)$![]() remains positive for all $t>0$
remains positive for all $t>0$![]() , then $a>0$
, then $a>0$![]() and the behaviour as $t\rightarrow \infty$
and the behaviour as $t\rightarrow \infty$![]() is governed by
is governed by

So, if $\displaystyle {-c_*+\frac {\gamma _{1}\sqrt {a}}{(b^{2}-aL_0^{2})}-\sqrt {a}< c< c_*+\frac {\gamma _{1}\sqrt {a}}{(b^{2}-aL_0^{2})}}$![]() , then there is a region of $\xi$
, then there is a region of $\xi$![]() in which there is exponential growth: namely, where
in which there is exponential growth: namely, where
Otherwise, there is exponential decay everywhere.
If instead $L(t)\rightarrow 0$![]() in a finite time, then it must be that $aL_0^{2}-b^{2} < 0$
in a finite time, then it must be that $aL_0^{2}-b^{2} < 0$![]() and that $L(t)\rightarrow 0$
and that $L(t)\rightarrow 0$![]() as
as
In this limit, $u(\xi,t)\rightarrow 0$![]() since the behaviour is governed by
since the behaviour is governed by

This implies that $u(\xi,t)\rightarrow 0$![]() , by using the bound in equation (2.12) with $\rho ^{2}=b^{2}- aL_0^{2}=-\gamma _{0}$
, by using the bound in equation (2.12) with $\rho ^{2}=b^{2}- aL_0^{2}=-\gamma _{0}$![]() .
.
2.5. Observed properties of the solutions
These expressions are very instructive in understanding the effects of a time-dependent domain on the solution. From them, one can observe the ways in which the exact nature of the time-dependence influences the solution in both short and long time.
One may choose specific parameter values and, after solving the relevant Sturm–Liouville problem, plot the solutions. An illustrative example is given in Figure 1, with $D=L_0=1$![]() , $f_0=10$
, $f_0=10$![]() , $L(t)=\sqrt {1+6t}$
, $L(t)=\sqrt {1+6t}$![]() and $A(t)\equiv 0$
and $A(t)\equiv 0$![]() . Using the notation of Lemma 1, the principal eigenfunction is proportional to $e^{-\frac {1}{2}\eta ^{2}}H_3(\eta )$
. Using the notation of Lemma 1, the principal eigenfunction is proportional to $e^{-\frac {1}{2}\eta ^{2}}H_3(\eta )$![]() where $\eta =\sqrt {\frac {3}{2}}\frac {\xi }{L_0}$
where $\eta =\sqrt {\frac {3}{2}}\frac {\xi }{L_0}$![]() and $H_3$
and $H_3$![]() is the third Hermite polynomial. We use a multiple of this for our initial condition: $v(\xi,0)=g_1(\xi )=e^{-\frac {3}{4}\xi ^{2}}(\xi -\xi ^{3})$
is the third Hermite polynomial. We use a multiple of this for our initial condition: $v(\xi,0)=g_1(\xi )=e^{-\frac {3}{4}\xi ^{2}}(\xi -\xi ^{3})$![]() . The principal eigenvalue is $\sigma _1=-\frac {21}{2}$
. The principal eigenvalue is $\sigma _1=-\frac {21}{2}$![]() . The solution is calculated using the exact expression in Equation (2.28) and plotted both on the fixed domain (as a function of the scaled variable $\xi$
. The solution is calculated using the exact expression in Equation (2.28) and plotted both on the fixed domain (as a function of the scaled variable $\xi$![]() ) and on the time-dependent domain (as a function of the original variable $x$
) and on the time-dependent domain (as a function of the original variable $x$![]() ). It is noted that, at small positive times, the solution decreases relative to its initial value, before the eventual exponential growth. This can be inferred from the formula in Equation (2.28) with the chosen parameter values. This is in contrast to the (more familiar) behaviour on a fixed domain, for which (in a separable solution) each of the eigenfunctions simply either grows or decays exponentially for $t>0$
). It is noted that, at small positive times, the solution decreases relative to its initial value, before the eventual exponential growth. This can be inferred from the formula in Equation (2.28) with the chosen parameter values. This is in contrast to the (more familiar) behaviour on a fixed domain, for which (in a separable solution) each of the eigenfunctions simply either grows or decays exponentially for $t>0$![]() .
.
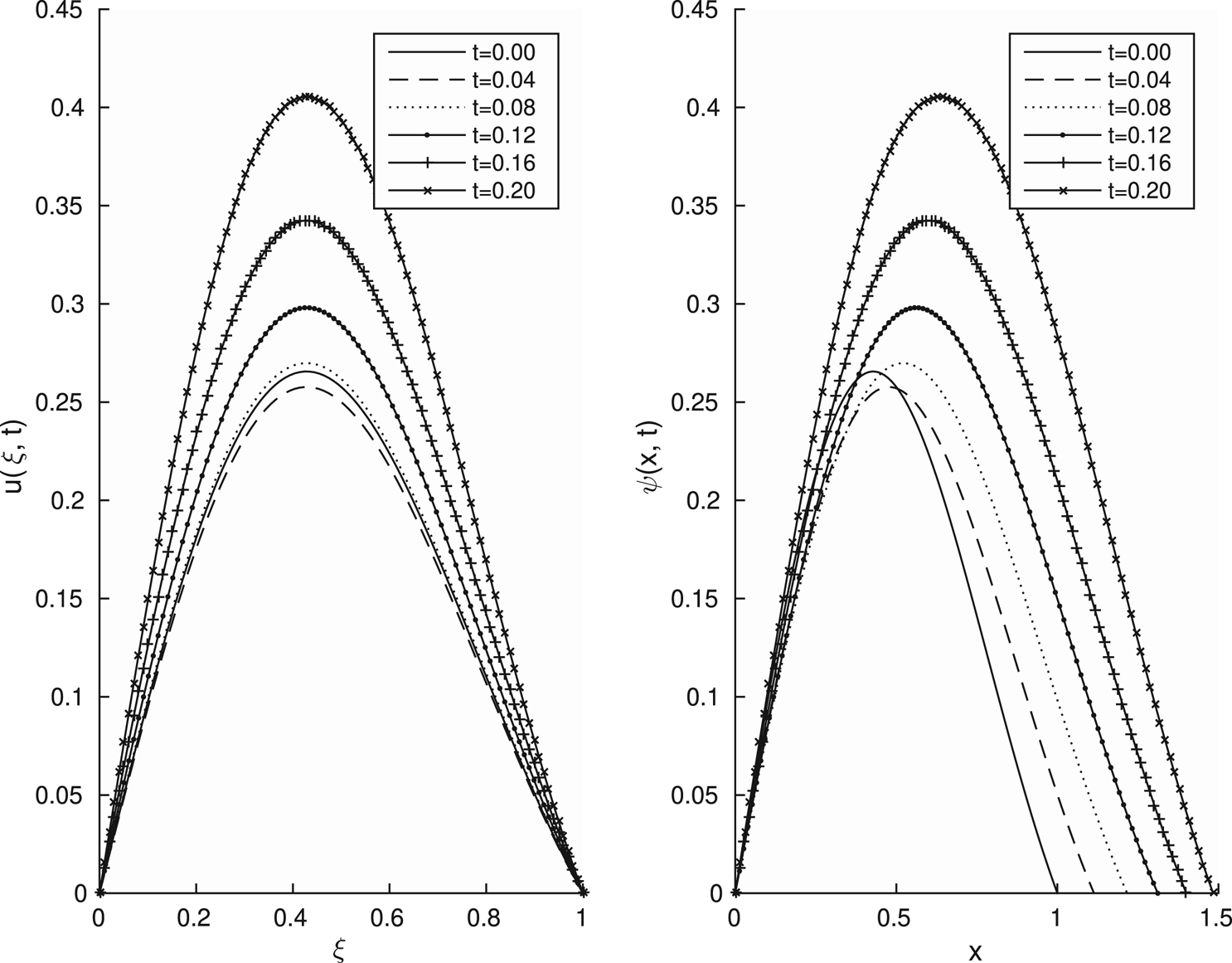
Figure 1. Exact solution on a time-dependent interval $0< x<\sqrt {1+6t}$![]() , calculated using Equation (2.28). Left: solution $u(\xi,t)$
, calculated using Equation (2.28). Left: solution $u(\xi,t)$![]() as a function of the scaled variable $\xi$
as a function of the scaled variable $\xi$![]() . Right: solution $\psi (x,t)$
. Right: solution $\psi (x,t)$![]() on the time-dependent domain.
on the time-dependent domain.
Although the formulae in Equations (2.17), (2.21), (2.28), (2.32), (2.33), and (2.34) differ, we note some common behaviour of these exact solutions in the asymptotic large time (or finite time) limit.
Firstly, whenever the domain length tends to zero in a finite time, the solution also tends to zero uniformly in $\xi$![]() (see § 2.3 and § 2.4). In each case, this follows from an upper bound on the eigenvalue $\sigma _1$
(see § 2.3 and § 2.4). In each case, this follows from an upper bound on the eigenvalue $\sigma _1$![]() .
.
Note, also, that in the separable cases with $L(t)\rightarrow \infty$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() , the long-time behaviour does not depend on the eigenvalue $\sigma _1$
, the long-time behaviour does not depend on the eigenvalue $\sigma _1$![]() . In these cases, $s(t)=o(t)$
. In these cases, $s(t)=o(t)$![]() and the term $\exp (\sigma _1 s(t))$
and the term $\exp (\sigma _1 s(t))$![]() is not of leading order.
is not of leading order.
Next, note that the separable solutions share the property that there is exponential growth at any $\xi \in (0,L_0)$![]() such that
such that
whereas there is exponential decay if
(Here $x(\xi,t)=\frac {\xi }{L_0}L(t)+A(t)$![]() is the original variable.) This is, in some sense, similar to the behaviour of the solution, $\tilde {\psi }$
is the original variable.) This is, in some sense, similar to the behaviour of the solution, $\tilde {\psi }$![]() say, on the whole real line with initial conditions compactly supported in $[a,b]$
say, on the whole real line with initial conditions compactly supported in $[a,b]$![]() :
:
This spreads at the asymptotic speed $c_*$![]() , in the sense that for $\vert c\vert < c_*$
, in the sense that for $\vert c\vert < c_*$![]() , $\tilde {\psi }(ct,t)\rightarrow \infty$
, $\tilde {\psi }(ct,t)\rightarrow \infty$![]() whereas $\sup _{\vert x\vert \geq c_*t}\tilde {\psi }(x,t)\rightarrow 0$
whereas $\sup _{\vert x\vert \geq c_*t}\tilde {\psi }(x,t)\rightarrow 0$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() . It is well known that $c_*$
. It is well known that $c_*$![]() is also the minimum wave speed for travelling wave solutions to the nonlinear FKPP equation and that it is the asymptotic spreading speed for solutions to the same equation on the real line with compactly supported initial conditions (see [Reference Aronson and Weinberger2, Reference Petrowsky, Kolmogorov and Piskunov21]). Much work has been done on determining the exact behaviour associated with this spreading and especially with respect to Bramson's logarithmic correction term (see [Reference Bramson11, Reference Bramson12, Reference Hamel, Nolen, Roquejoffre and Ryzhik19]). It is natural, therefore, to be interested in the exact behaviour of our solution $\psi (x,t)$
is also the minimum wave speed for travelling wave solutions to the nonlinear FKPP equation and that it is the asymptotic spreading speed for solutions to the same equation on the real line with compactly supported initial conditions (see [Reference Aronson and Weinberger2, Reference Petrowsky, Kolmogorov and Piskunov21]). Much work has been done on determining the exact behaviour associated with this spreading and especially with respect to Bramson's logarithmic correction term (see [Reference Bramson11, Reference Bramson12, Reference Hamel, Nolen, Roquejoffre and Ryzhik19]). It is natural, therefore, to be interested in the exact behaviour of our solution $\psi (x,t)$![]() (in terms of the original variable $x$
(in terms of the original variable $x$![]() ), at this critical interface between growth and decay. This is considered in § 3.
), at this critical interface between growth and decay. This is considered in § 3.
Finally, note that in § 2.1 and the particular sub-case where $\gamma _1=0$![]() , the problem has become that of an interval of fixed length $L_0$
, the problem has become that of an interval of fixed length $L_0$![]() moving at a constant speed $c$
moving at a constant speed $c$![]() . Our result is in agreement with [Reference Berestycki, Diekmann, Nagelkerke and Zegeling5, Reference Potapov and Lewis22] in deriving a critical domain length, which is defined by the equation $f_0=\frac {D\pi ^{2}}{L_0^{2}}+\frac {c^{2}}{4D}$
. Our result is in agreement with [Reference Berestycki, Diekmann, Nagelkerke and Zegeling5, Reference Potapov and Lewis22] in deriving a critical domain length, which is defined by the equation $f_0=\frac {D\pi ^{2}}{L_0^{2}}+\frac {c^{2}}{4D}$![]() , and represents a threshold between decay and growth.
, and represents a threshold between decay and growth.
2.6. Applications to more general $A(t)$ , $L(t)$
, $L(t)$
The preceding results are relevant not only to those specific forms of $A(t)$![]() , $L(t)$
, $L(t)$![]() which led to the exact solutions. The explicit expressions can also be used to deduce bounds on the solution for other, more general, forms of $A(t)$
which led to the exact solutions. The explicit expressions can also be used to deduce bounds on the solution for other, more general, forms of $A(t)$![]() and $L(t)$
and $L(t)$![]() .
.
The parabolic comparison principle leads to the following result.
Proposition 1 Let $\psi _1(x,t)$![]() and $\psi _2(x,t)$
and $\psi _2(x,t)$![]() be the solutions with $A_1(t),$
be the solutions with $A_1(t),$![]() $L_1(t),$
$L_1(t),$![]() and $A_2(t),$
and $A_2(t),$![]() $L_2(t)$
$L_2(t)$![]() respectively. If (for each $t$
respectively. If (for each $t$![]() ) $(A_1(t), A_1(t)+L_1(t))\subseteq (A_2(t), A_2(t)+L_2(t)),$
) $(A_1(t), A_1(t)+L_1(t))\subseteq (A_2(t), A_2(t)+L_2(t)),$![]() then $\psi _1(x,t) \leq \psi _2(x,t)$
then $\psi _1(x,t) \leq \psi _2(x,t)$![]() for $x \in (A_1(t), A_1(t)+L_1(t))$
for $x \in (A_1(t), A_1(t)+L_1(t))$![]() .
.
This, therefore, provides an explicit lower [or upper] bound for the solution $\psi$![]() , whenever the domain contains [or is contained by] one of the separable cases.
, whenever the domain contains [or is contained by] one of the separable cases.
A rather different extension of the method is to consider cases for which $\ddot {L}L^{3}$![]() and $\ddot {A}L^{3}$
and $\ddot {A}L^{3}$![]() are each bounded above or bounded below. In this case, we can bound the solution by expressions involving $A(t)$
are each bounded above or bounded below. In this case, we can bound the solution by expressions involving $A(t)$![]() and $L(t)$
and $L(t)$![]() , together with the same Sturm–Liouville eigenfunctions and eigenvalues that occurred in the preceding sections.
, together with the same Sturm–Liouville eigenfunctions and eigenvalues that occurred in the preceding sections.
Proposition 2 Suppose that
for some constants $\gamma _{0}^{+},$![]() $\gamma _{1}^{+}$
$\gamma _{1}^{+}$![]() . Then, for any given initial conditions $u(\xi,0)$
. Then, for any given initial conditions $u(\xi,0)$![]() in $L^{2}([0,L_0]),$
in $L^{2}([0,L_0]),$![]() the solution $u(\xi,t)$
the solution $u(\xi,t)$![]() can be bounded above by a sum of the $u_n(\xi,t)$
can be bounded above by a sum of the $u_n(\xi,t)$![]() in equation (2.3), where now the $g_n(\xi ),$
in equation (2.3), where now the $g_n(\xi ),$![]() $\sigma _n$
$\sigma _n$![]() satisfy the Sturm–Liouville problem in Equations (2.9), (2.10) with $\gamma _{0}=\gamma _{0}^{+}$
satisfy the Sturm–Liouville problem in Equations (2.9), (2.10) with $\gamma _{0}=\gamma _{0}^{+}$![]() and $\gamma _{1}=\gamma _{1}^{+}$
and $\gamma _{1}=\gamma _{1}^{+}$![]() . If equation (2.42) holds with both inequalities reversed, then the solution $u(\xi,t)$
. If equation (2.42) holds with both inequalities reversed, then the solution $u(\xi,t)$![]() can instead be bounded below by a sum of the $u_n(\xi,t)$
can instead be bounded below by a sum of the $u_n(\xi,t)$![]() .
.
Proof. The same changes of variables as in Theorem 1 leads to Equations (2.7), (2.8) for $v(\xi,s)$![]() . Let $v^{+}(\xi,s)$
. Let $v^{+}(\xi,s)$![]() satisfy these same equations but with $\gamma _{0}^{+}$
satisfy these same equations but with $\gamma _{0}^{+}$![]() in place of $\ddot {L}L^{3}$
in place of $\ddot {L}L^{3}$![]() , and $\gamma _{1}^{+}$
, and $\gamma _{1}^{+}$![]() in place of $\ddot {A}L^{3}$
in place of $\ddot {A}L^{3}$![]() . (This is the separable problem which has just been considered.) Now, due to the special form Equation (2.7) and the positivity of the solutions, $v^{+}$
. (This is the separable problem which has just been considered.) Now, due to the special form Equation (2.7) and the positivity of the solutions, $v^{+}$![]() is a supersolution for $v$
is a supersolution for $v$![]() . The comparison principle can be applied to $v$
. The comparison principle can be applied to $v$![]() , to deduce that if $v(\xi,0)\leq v^{+}(\xi,0)$
, to deduce that if $v(\xi,0)\leq v^{+}(\xi,0)$![]() , then $v(\xi,s)\leq v^{+}(\xi,s)$
, then $v(\xi,s)\leq v^{+}(\xi,s)$![]() for all $s$
for all $s$![]() . On changing variables back, we obtain the stated upper bound on $u(\xi,t)$
. On changing variables back, we obtain the stated upper bound on $u(\xi,t)$![]() .
.
If the inequalities in Equation (2.42) are reversed, and if $v^{+}(\xi,0)\leq v(\xi,0)$![]() , then $v^{+}(\xi,s)$
, then $v^{+}(\xi,s)$![]() is instead a subsolution, and thus we obtain the lower bound on $u(\xi,t)$
is instead a subsolution, and thus we obtain the lower bound on $u(\xi,t)$![]() . □
. □
For the sake of completeness, we make the remark that, in the level of generality considered (i.e. $A(t)$![]() and $L(t)$
and $L(t)$![]() twice continuously differentiable), the domains — and consequently the solutions — will be hard to describe in any very general terms. Indeed, examples can be constructed with alternating growth and decay, such that the solution becomes both arbitrarily large and arbitrarily small over time. Such examples are not the focus of this paper.
twice continuously differentiable), the domains — and consequently the solutions — will be hard to describe in any very general terms. Indeed, examples can be constructed with alternating growth and decay, such that the solution becomes both arbitrarily large and arbitrarily small over time. Such examples are not the focus of this paper.
2.7. Exact solutions on a ball in higher dimension
To conclude this section, we demonstrate that a similar process can lead to exact solutions to the problem on a ball in $\mathbb {R}^{n}$![]() with radius $R(t)$
with radius $R(t)$![]() and centre $\textbf {A}(t)$
and centre $\textbf {A}(t)$![]() . Consider the problem
. Consider the problem
A change of variables from $\textbf {x}$![]() to $\textbf {z}=\frac {(\textbf {x}-\textbf {A}(t))}{R(t)}R_0$
to $\textbf {z}=\frac {(\textbf {x}-\textbf {A}(t))}{R(t)}R_0$![]() , with $R_0=R(0)$
, with $R_0=R(0)$![]() , and from $\psi (\textbf {x},t)$
, and from $\psi (\textbf {x},t)$![]() to
to

followed by $s(t)= \int_0^{t} \frac {R_0^{2}}{R(\zeta )^{2}}d\zeta$![]() , and $v(\textbf {z}, s)=w(\textbf {z}, t)$
, and $v(\textbf {z}, s)=w(\textbf {z}, t)$![]() , leads to the equation
, leads to the equation

This is separable in $s$![]() , $r=\vert \textbf {z} \vert$
, $r=\vert \textbf {z} \vert$![]() , and $\theta$
, and $\theta$![]() (the angular co-ordinates) if $\ddot {R}R^{3}=\gamma _{0}=$
(the angular co-ordinates) if $\ddot {R}R^{3}=\gamma _{0}=$![]() constant and $\ddot {\textbf {A}}R^{3}=\textbf {0}$
constant and $\ddot {\textbf {A}}R^{3}=\textbf {0}$![]() . This corresponds to $R(t)^{2}=at^{2}+2bt+R_0^{2}$
. This corresponds to $R(t)^{2}=at^{2}+2bt+R_0^{2}$![]() for some constants $a$
for some constants $a$![]() ,$b$
,$b$![]() and $\gamma _{0}=aR_0^{2}-b^{2}$
and $\gamma _{0}=aR_0^{2}-b^{2}$![]() ; and $\textbf{A}(t)=\textbf{A}_\textbf{0}+\textbf{c}t$
; and $\textbf{A}(t)=\textbf{A}_\textbf{0}+\textbf{c}t$![]() for some constant vectors $\textbf{A}_\textbf{0}$
for some constant vectors $\textbf{A}_\textbf{0}$![]() and $\textbf {c}$
and $\textbf {c}$![]() . The solutions can then be expressed in terms of a sum of the eigenfunctions $v_l(r,\theta )=H_l(\theta )X_l(r)$
. The solutions can then be expressed in terms of a sum of the eigenfunctions $v_l(r,\theta )=H_l(\theta )X_l(r)$![]() of
of
which satisfy the correct periodicity in $\theta$![]() and which are non-singular at the origin $r=0$
and which are non-singular at the origin $r=0$![]() . This leads to the following theorem.
. This leads to the following theorem.
Theorem 2 Let $\psi (\textbf {x},t)$![]() satisfy Equations (2.43), (2.44) on the ball in $\mathbb {R}^{n}$
satisfy Equations (2.43), (2.44) on the ball in $\mathbb {R}^{n}$![]() with radius $R(t)=\sqrt {at^{2}+2bt+R_0^{2}}$
with radius $R(t)=\sqrt {at^{2}+2bt+R_0^{2}}$![]() and centre $\textbf {A}(t)=\textbf {A}_\textbf{0}+\textbf {c}t$
and centre $\textbf {A}(t)=\textbf {A}_\textbf{0}+\textbf {c}t$![]() . Then, for any suitable initial conditions $\psi (\textbf {x},0),$
. Then, for any suitable initial conditions $\psi (\textbf {x},0),$![]() the solution for $\psi (\textbf {x},t)$
the solution for $\psi (\textbf {x},t)$![]() can be obtained exactly, as a sum of $\psi _l(\textbf {x},t)$
can be obtained exactly, as a sum of $\psi _l(\textbf {x},t)$![]() with coefficients depending only on the initial conditions. The $\psi _l$
with coefficients depending only on the initial conditions. The $\psi _l$![]() are expressed purely in terms of $\textbf {c}$
are expressed purely in terms of $\textbf {c}$![]() , the constants occurring in $R(t)$
, the constants occurring in $R(t)$![]() , and the eigenfunctions and eigenvalues ($v_l,$
, and the eigenfunctions and eigenvalues ($v_l,$![]() $\sigma _l$
$\sigma _l$![]() ) of the eigenvalue problem (2.48), (2.49) with $\gamma _{0}=aR_0^{2}-b^{2}$
) of the eigenvalue problem (2.48), (2.49) with $\gamma _{0}=aR_0^{2}-b^{2}$![]() .
.
The explicit expressions are similar to the one-dimensional case, but note the dependence on $n$![]() in the factor $\left (\frac {R(t)}{R_0}\right )^{\frac {n}{2}}$
in the factor $\left (\frac {R(t)}{R_0}\right )^{\frac {n}{2}}$![]() in Equation (2.45) as well as, of course, the dependence on $n$
in Equation (2.45) as well as, of course, the dependence on $n$![]() in the eigenfunctions and eigenvalues. In $n$
in the eigenfunctions and eigenvalues. In $n$![]() dimensions, we have the bound $\sigma _1 <-\frac {n\rho }{2R_0^{2}}$
dimensions, we have the bound $\sigma _1 <-\frac {n\rho }{2R_0^{2}}$![]() on the principal eigenvalue when $\gamma _0=-\rho ^{2}<0$
on the principal eigenvalue when $\gamma _0=-\rho ^{2}<0$![]() .
.
3. Critical boundary motion
3.1. Behaviour near the critical speed
In this section, we take up the question mentioned in § 2.5, regarding the exact behaviour of our solution $\psi (x,t)$![]() at the critical interface between growth and decay. Recall that we defined
at the critical interface between growth and decay. Recall that we defined
and that, in the separable solutions, there was an exponential growth of $u(\xi,t)$![]() at any $\xi \in (0,L_0)$
at any $\xi \in (0,L_0)$![]() such that Equation (2.39) held, and exponential decay at any $\xi$
such that Equation (2.39) held, and exponential decay at any $\xi$![]() where Equation (2.40) held (i.e. $x(\xi,t)$
where Equation (2.40) held (i.e. $x(\xi,t)$![]() travelling slower or faster than $c_*$
travelling slower or faster than $c_*$![]() , respectively). It is natural to seek a more precise description of this changeover between regions of growth and decay. Given $A(t)$
, respectively). It is natural to seek a more precise description of this changeover between regions of growth and decay. Given $A(t)$![]() , $L(t)$
, $L(t)$![]() , are we able to track the position $x(t)$
, are we able to track the position $x(t)$![]() at which the solution $\psi (x,t)$
at which the solution $\psi (x,t)$![]() is equal to some a constant, $O(1)$
is equal to some a constant, $O(1)$![]() , value? For which choices of $A(t)$
, value? For which choices of $A(t)$![]() , $L(t)$
, $L(t)$![]() will the solution be exactly of order $1$
will the solution be exactly of order $1$![]() near the boundary (neither growing to $\infty$
near the boundary (neither growing to $\infty$![]() nor decaying to $0$
nor decaying to $0$![]() )?
)?
Initially, let us make use of an exact solution from § 2. Let $\hat {\psi }(x,t)$![]() be the solution on the interval
be the solution on the interval
This is given by Equation (2.21) with $c=-c_*$![]() , $\alpha =2c_*$
, $\alpha =2c_*$![]() , $\gamma _1=0$
, $\gamma _1=0$![]() , $\sigma _n=-\frac {Dn^{2}\pi ^{2}}{L_0^{2}}$
, $\sigma _n=-\frac {Dn^{2}\pi ^{2}}{L_0^{2}}$![]() and $g_n(\xi )=\sin \left (\frac {n\pi \xi }{L_0}\right )$
and $g_n(\xi )=\sin \left (\frac {n\pi \xi }{L_0}\right )$![]() . Without loss of generality (and for simplicity) take the initial conditions to be $\sin \left (\frac {\pi \xi }{L_0}\right )$
. Without loss of generality (and for simplicity) take the initial conditions to be $\sin \left (\frac {\pi \xi }{L_0}\right )$![]() . Then (recalling that $f_0=\frac {c_*^{2}}{4D}$
. Then (recalling that $f_0=\frac {c_*^{2}}{4D}$![]() ) this exact solution is:
) this exact solution is:

Therefore at $x=-c_*t - L_0/2 +y$![]() , we have
, we have

If $y=O(1)$![]() then as $t\rightarrow \infty$
then as $t\rightarrow \infty$![]() ,
,
Observe that the choice $y(t)=\frac {3D}{c_*}\log (t+1)$![]() in equation (3.3) removes all the powers of $t$
in equation (3.3) removes all the powers of $t$![]() and gives (as $t\rightarrow \infty$
and gives (as $t\rightarrow \infty$![]() ):
):
The form of this exact solution for $\hat {\psi }$![]() suggests that the critical choices of $A(t)$
suggests that the critical choices of $A(t)$![]() , $L(t)$
, $L(t)$![]() (where the solution near to the boundary remains exactly of order $1$
(where the solution near to the boundary remains exactly of order $1$![]() ) may occur when the endpoints move as $\pm c_* t$
) may occur when the endpoints move as $\pm c_* t$![]() plus a logarithmic term (plus smaller order corrections). Furthermore, the fact that the choice $y(t)=\frac {3D}{c_*}\log (t+1)$
plus a logarithmic term (plus smaller order corrections). Furthermore, the fact that the choice $y(t)=\frac {3D}{c_*}\log (t+1)$![]() removes all the powers of $t$
removes all the powers of $t$![]() suggests the likely coefficient of such a term. The following section will give the precise statement of the behaviour on an interval which does include a logarithmic adjustment to the endpoints.
suggests the likely coefficient of such a term. The following section will give the precise statement of the behaviour on an interval which does include a logarithmic adjustment to the endpoints.
3.2. Precise behaviour in the critical case
From now on, we restrict attention to cases where $A(t)=-\frac {L(t)}{2}$![]() . Our change of variables from Equation (2.5) becomes
. Our change of variables from Equation (2.5) becomes

Let us give a precise definition of the behaviour we are interested in and the notation we shall use for it.
Definition 1 Given two functions $F_1$![]() , $F_2$
, $F_2$![]() , one will be referred to as being exactly of the order the other (in a given limit), and denoted by $F_1=\overline {\underline {O}}(F_2)$
, one will be referred to as being exactly of the order the other (in a given limit), and denoted by $F_1=\overline {\underline {O}}(F_2)$![]() , when $F_2=O(F_1)$
, when $F_2=O(F_1)$![]() and $F_1=O(F_2)$
and $F_1=O(F_2)$![]() (in the limit under consideration). In other words, there are positive constants $0< \beta _0 \leq \beta _1$
(in the limit under consideration). In other words, there are positive constants $0< \beta _0 \leq \beta _1$![]() such that $\beta _0 \vert F_2 \vert \leq \vert F_1 \vert \leq \beta _1 \vert F_2 \vert$
such that $\beta _0 \vert F_2 \vert \leq \vert F_1 \vert \leq \beta _1 \vert F_2 \vert$![]() .
.
The following theorem is the main result which is proved in the remainder of this section. The proof relies on the construction of a supersolution and a subsolution, both having the specified behaviour.
Theorem 3 Let
where $c_*=2\sqrt {Df_0},$![]() $\alpha >0,$
$\alpha >0,$![]() and
and
Then
Remark 1 Any function $\eta (t)$![]() satisfying the assumptions in equation 3.9 will suffice to give the conclusion of Theorem 3. Note that these conditions on $\eta (t)$
satisfying the assumptions in equation 3.9 will suffice to give the conclusion of Theorem 3. Note that these conditions on $\eta (t)$![]() allow, for example, $\eta (t)=\eta _0=$
allow, for example, $\eta (t)=\eta _0=$![]() constant, or $\eta (t)=(t+1)^{k}$
constant, or $\eta (t)=(t+1)^{k}$![]() for $k<0$
for $k<0$![]() , but not $\eta (t)=\log \log (t)$
, but not $\eta (t)=\log \log (t)$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() .
.
This theorem gives asymptotic bounds on $\psi (x,t)$![]() for $x$
for $x$![]() within $O(1)$
within $O(1)$![]() of the moving boundary. Hence, it also bounds the asymptotic behaviour of the gradient at the moving boundary itself:
of the moving boundary. Hence, it also bounds the asymptotic behaviour of the gradient at the moving boundary itself:
In particular, at the critical value
we have that $\psi \left (\frac {-L(t)}{2}+y,t\right )= \overline {\underline {O}}(y)$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() , and that the gradient at the boundary is bounded above and below independently of time: $\frac {\partial \psi }{\partial x}\left (\frac {-L(t)}{2},t\right )=\overline {\underline {O}}(1)$
, and that the gradient at the boundary is bounded above and below independently of time: $\frac {\partial \psi }{\partial x}\left (\frac {-L(t)}{2},t\right )=\overline {\underline {O}}(1)$![]() .
.
The derivation of the $\frac {3D}{c_{*}}\log (t+1)$![]() term in this context is completely different from the proofs in the other settings in which such a term arises. In this case (of a linear equation on a finite interval with moving boundaries), our derivation of the term is relatively straightforward, or accessible, being based solely on explicit super- and sub-solutions to a linear equation. Moreover, the bulk of our proof is in fact taken up in showing that the function $w(\xi,t)$
term in this context is completely different from the proofs in the other settings in which such a term arises. In this case (of a linear equation on a finite interval with moving boundaries), our derivation of the term is relatively straightforward, or accessible, being based solely on explicit super- and sub-solutions to a linear equation. Moreover, the bulk of our proof is in fact taken up in showing that the function $w(\xi,t)$![]() is exactly of order $\xi$
is exactly of order $\xi$![]() (or $y/t$
(or $y/t$![]() ). The other factor, $t^{-\frac {1}{2}+\frac {\alpha c_*}{2D}}$
). The other factor, $t^{-\frac {1}{2}+\frac {\alpha c_*}{2D}}$![]() , in the critical behaviour comes straight from the change of variables. This observation and the exact expression used in the change of variables (Equation (3.7)) may therefore help to give insight into the source of the logarithmic term in other settings.
, in the critical behaviour comes straight from the change of variables. This observation and the exact expression used in the change of variables (Equation (3.7)) may therefore help to give insight into the source of the logarithmic term in other settings.
Recall that the function $w$![]() now satisfies
now satisfies
where
The following two propositions give a supersolution and a subsolution for $w(\xi,t)$![]() under certain conditions on $P(t)$
under certain conditions on $P(t)$![]() . It is worth noting that Proposition 3 and Proposition 4 apply in general whenever $w(\xi,t)$
. It is worth noting that Proposition 3 and Proposition 4 apply in general whenever $w(\xi,t)$![]() satisfies Equations (3.13), (3.14) for any function $P(t)$
satisfies Equations (3.13), (3.14) for any function $P(t)$![]() (satisfying the conditions of the proposition). They do not rely at all on the specific form of $P(t)$
(satisfying the conditions of the proposition). They do not rely at all on the specific form of $P(t)$![]() that we are interested in here, given by Equation (3.15). In the case where $P(t)$
that we are interested in here, given by Equation (3.15). In the case where $P(t)$![]() is given by Equation (3.15), the condition (3.21) in Proposition 4 becomes simply
is given by Equation (3.15), the condition (3.21) in Proposition 4 becomes simply
Proposition 3 (Supersolution)
Let $w(\xi,t)\geq 0$![]() satisfy Equations (3.13), (3.14). If $P(t)\geq 0$
satisfy Equations (3.13), (3.14). If $P(t)\geq 0$![]() then (up to multiplication by a constant) $w(\xi,t)\leq \overline {w}(\xi,t)$
then (up to multiplication by a constant) $w(\xi,t)\leq \overline {w}(\xi,t)$![]() where
where
Moreover, if
then $w(\xi,t)=O(\xi )$![]() independently of time as $t\rightarrow \infty$
independently of time as $t\rightarrow \infty$![]() , in the sense that given $B_1\in (0,L_0),$
, in the sense that given $B_1\in (0,L_0),$![]() there exists $\beta _1$
there exists $\beta _1$![]() such that
such that
Proof. The function $\overline {w}(\xi,t)$![]() satisfies the boundary conditions and, since $P(t)\geq 0$
satisfies the boundary conditions and, since $P(t)\geq 0$![]() , it satisfies the inequality
, it satisfies the inequality

and so it is a supersolution for $w(\xi,t)$![]() . Hence, up to multiplication by a constant, $w(\xi,t)\leq \overline {w}(\xi,t)$
. Hence, up to multiplication by a constant, $w(\xi,t)\leq \overline {w}(\xi,t)$![]() . Moreover, if equation (3.18) holds, then $\overline {w}(\xi,t)=O(\xi )$
. Moreover, if equation (3.18) holds, then $\overline {w}(\xi,t)=O(\xi )$![]() (independently of time as $t\rightarrow \infty$
(independently of time as $t\rightarrow \infty$![]() ) and so equation (3.19) is proved.
) and so equation (3.19) is proved.
Next, we construct a subsolution using the Airy function $\textrm{Ai}$![]() and its tangent at the position $\textrm{Ai} (0)$
and its tangent at the position $\textrm{Ai} (0)$![]() .
.
Proposition 4 (Subsolution)
Let $w(\xi,t)\geq 0$![]() satisfy Equations (3.13), (3.14). If $P(t)\rightarrow \infty$
satisfy Equations (3.13), (3.14). If $P(t)\rightarrow \infty$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() and $\dot {P}(t)\geq 0,$
and $\dot {P}(t)\geq 0,$![]() then (up to multiplication by a constant) $w(\xi,t)\geq \tilde {w}(\xi,t)= \underline {w}(\xi,t)a(t)$
then (up to multiplication by a constant) $w(\xi,t)\geq \tilde {w}(\xi,t)= \underline {w}(\xi,t)a(t)$![]() where $\underline {w}(\xi,t)$
where $\underline {w}(\xi,t)$![]() and $a(t)$
and $a(t)$![]() are given by equations (3.23) and (3.33). Moreover, if
are given by equations (3.23) and (3.33). Moreover, if
then for $P(t)^{1/3} \frac {\xi }{L_0}$![]() sufficiently small, $w(\xi,t)$
sufficiently small, $w(\xi,t)$![]() can be bounded below by a positive multiple of $\xi$
can be bounded below by a positive multiple of $\xi$![]() (independently of $t$
(independently of $t$![]() ) as $t\rightarrow \infty$
) as $t\rightarrow \infty$![]() . In other words, for $B_0>0$
. In other words, for $B_0>0$![]() small enough, there exists $\beta _0>0$
small enough, there exists $\beta _0>0$![]() such that
such that
Proof. Let $c_1$![]() be the largest real zero of the Airy function $\textrm{Ai}$
be the largest real zero of the Airy function $\textrm{Ai}$![]() . Note, for reference, the facts that $c_1<0$
. Note, for reference, the facts that $c_1<0$![]() , $\textrm{Ai} '(c_1)>0$
, $\textrm{Ai} '(c_1)>0$![]() , $\textrm{Ai} (0)>0$
, $\textrm{Ai} (0)>0$![]() , $\textrm{Ai} '(0)<0$
, $\textrm{Ai} '(0)<0$![]() , and $\textrm{Ai} ''(0)=0$
, and $\textrm{Ai} ''(0)=0$![]() . Define $\underline {w}(\xi,t)$
. Define $\underline {w}(\xi,t)$![]() by:
by:

Note that $\underline {w}$![]() is continuous and non-negative on $[0,L_0]$
is continuous and non-negative on $[0,L_0]$![]() and satisfies the boundary conditions. Furthermore, both $\frac {\partial \underline {w}}{\partial \xi }$
and satisfies the boundary conditions. Furthermore, both $\frac {\partial \underline {w}}{\partial \xi }$![]() and $\frac {\partial ^{2} \underline {w}}{\partial \xi ^{2}}$
and $\frac {\partial ^{2} \underline {w}}{\partial \xi ^{2}}$![]() are continuous across Regions I-II, including at the point where they meet, since at this point, the left and right limits both give $\frac {\partial \underline {w}}{\partial \xi }=\frac {\textrm{Ai} '(0)}{L_0}$
are continuous across Regions I-II, including at the point where they meet, since at this point, the left and right limits both give $\frac {\partial \underline {w}}{\partial \xi }=\frac {\textrm{Ai} '(0)}{L_0}$![]() and $\frac {\partial ^{2} \underline {w}}{\partial \xi ^{2}}=0$
and $\frac {\partial ^{2} \underline {w}}{\partial \xi ^{2}}=0$![]() . In each Region I and Region II, $\frac {\partial \underline {w}}{\partial t}$
. In each Region I and Region II, $\frac {\partial \underline {w}}{\partial t}$![]() satisfies
satisfies
and so it follows from the continuity of each term that $\frac {\partial \underline {w}}{\partial t}$![]() is also continuous across Regions I–II.
is also continuous across Regions I–II.
In Region I:


Note that $\frac {\partial ^{2} \underline {w}}{\partial \xi ^{2}}\leq 0$![]() in Region I, since $\textrm{Ai} ''(x)=x\textrm{Ai} (x)\leq 0$
in Region I, since $\textrm{Ai} ''(x)=x\textrm{Ai} (x)\leq 0$![]() on $[c_1,0]$
on $[c_1,0]$![]() . Therefore, using $\underline {w}(0,t)=0$
. Therefore, using $\underline {w}(0,t)=0$![]() , it holds that
, it holds that
Thus, Equation (3.27) together with the assumption that $P(t)\geq 0$![]() and $\dot {P}(t)\geq 0$
and $\dot {P}(t)\geq 0$![]() implies that, in Region I,
implies that, in Region I,
In Region II, since $P(t)\geq 0$![]() , $\dot {P}(t)\geq 0$
, $\dot {P}(t)\geq 0$![]() , and $\textrm{Ai} '(0)<0$
, and $\textrm{Ai} '(0)<0$![]() ,
,

This leads us to define $\tilde {w}(\xi,t)= \underline {w}(\xi,t)a(t)$![]() where
where
Then in Regions I–II, the function $\tilde {w}(\xi,t)$![]() is $C^{2}$
is $C^{2}$![]() in $\xi$
in $\xi$![]() , $C^{1}$
, $C^{1}$![]() in $t$
in $t$![]() and it satisfies
and it satisfies
so it is a classical subsolution for $0\leq \xi \leq -\left ( \frac {\textrm{Ai} (0)}{\textrm{Ai} '(0)} +c_1 \right ) P(t)^{-1/3}L_0$![]() (Regions I-II).
(Regions I-II).
It is clear that $\tilde {w}\equiv 0$![]() is also a classical subsolution in Region III. At the point where Region II and Region III meet, $\tilde {w}$
is also a classical subsolution in Region III. At the point where Region II and Region III meet, $\tilde {w}$![]() is continuous, it is a classical subsolution on either side, and $\frac {\partial \tilde {w}}{\partial \xi }$
is continuous, it is a classical subsolution on either side, and $\frac {\partial \tilde {w}}{\partial \xi }$![]() has a jump discontinuity from a negative value on the left (Region II) to zero on the right (Region III). It follows that $\tilde {w}(\xi,t)$
has a jump discontinuity from a negative value on the left (Region II) to zero on the right (Region III). It follows that $\tilde {w}(\xi,t)$![]() is a weak subsolution to the parabolic problem on $(0,L_0)$
is a weak subsolution to the parabolic problem on $(0,L_0)$![]() . Therefore, up to multiplication by some constant,
. Therefore, up to multiplication by some constant,
If Equation (3.21) holds, then $a(t)$![]() converges to a strictly positive value as $t\rightarrow \infty$
converges to a strictly positive value as $t\rightarrow \infty$![]() . Then, since
. Then, since
it follows that for $P(t)^{1/3} \frac {\xi }{L_0}$![]() sufficiently small, $\tilde {w}(\xi,t)$
sufficiently small, $\tilde {w}(\xi,t)$![]() can be bounded above and below by positive multiples of $\xi$
can be bounded above and below by positive multiples of $\xi$![]() (independently of time as $t\rightarrow \infty$
(independently of time as $t\rightarrow \infty$![]() ). In particular, for $B_0>0$
). In particular, for $B_0>0$![]() small enough, there exists $\beta _0>0$
small enough, there exists $\beta _0>0$![]() such that
such that
Equation (3.22) follows and the proposition is proved.
Next, we use the super- and sub-solutions for $w(\xi,t)$![]() to prove Theorem 3:
to prove Theorem 3:
Proof of Theorem 3. Recall from Equation (3.8) that
Thus, as $t\rightarrow \infty$![]() the function $\displaystyle {P(t)=\frac {\ddot {L}(t)L(t)^{3}}{4D^{2}}}$
the function $\displaystyle {P(t)=\frac {\ddot {L}(t)L(t)^{3}}{4D^{2}}}$![]() obeys
obeys
Moreover, since $L(t)\sim 2c_* t$![]() and $\ddot {L}(t)\sim 2\alpha t^{-2}$
and $\ddot {L}(t)\sim 2\alpha t^{-2}$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() , it also holds that
, it also holds that
So, both Proposition 3 and 4 apply to this case, giving that (for some positive constants) $C_1\underline {w}(\xi,t)a(t)\leq w(\xi,t)\leq C_2\overline {w}(\xi,t)$![]() , and that for $B_0>0$
, and that for $B_0>0$![]() small enough, there exist $0<\beta _0\leq \beta _1$
small enough, there exist $0<\beta _0\leq \beta _1$![]() such that
such that
Hence, we have shown that $w(\xi,t)$![]() is exactly of order $\xi$
is exactly of order $\xi$![]() :
:
In terms of the original function $\psi (x,t)$![]() , recall that
, recall that

and note that with $L(t)$![]() given by Equation (3.38),
given by Equation (3.38),
Consider $x=\frac {-L(t)}{2}+y$![]() with $y=O(1)$
with $y=O(1)$![]() . Then $\xi =\frac {yL_0}{L(t)}=O\left (\frac {1}{t+1}\right )$
. Then $\xi =\frac {yL_0}{L(t)}=O\left (\frac {1}{t+1}\right )$![]() is certainly $O(P(t)^{-1/3} )$
is certainly $O(P(t)^{-1/3} )$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() , and so
, and so

which concludes the proof of Theorem 3.
3.3. Critical case in higher dimensions
To conclude this section, we note that a similar analysis can also be applied to a ball in $\mathbb {R}^{n}$![]() .
.
Theorem 4 Let $\psi$![]() satisfy
satisfy
where
with $\alpha >0,$![]() and $\eta$
and $\eta$![]() satisfying Equation (3.9), and where $n\leq 3$
satisfying Equation (3.9), and where $n\leq 3$![]() . Then
. Then
Remark 2 Hence, the ‘critical value’ of $\alpha$![]() , for which the solution behaves exactly as order $y$
, for which the solution behaves exactly as order $y$![]() , is now
, is now
As in the one-dimensional case, this appears to match the coefficient of the logarithmic correction term in the nonlinear FKPP problem on $\mathbb {R}^{n}$![]() , with compactly supported initial conditions (see [Reference Gärtner18, Reference Roquejoffre, Rossi and Roussier-Michon24]).
, with compactly supported initial conditions (see [Reference Gärtner18, Reference Roquejoffre, Rossi and Roussier-Michon24]).
Proof. The change of variables $\textbf {z}=\frac {\textbf {x}}{R(t)}R_0$![]() and
and

leads to the equation
where $r=\vert \textbf {z} \vert$![]() and
and
which satisfies $Q(t)>0$![]() , $Q(t)\rightarrow \infty$
, $Q(t)\rightarrow \infty$![]() , $\dot {Q}\geq 0$
, $\dot {Q}\geq 0$![]() as $t\rightarrow \infty$
as $t\rightarrow \infty$![]() .
.
Let $h_0(r)$![]() be the radially symmetric principal eigenfunction of
be the radially symmetric principal eigenfunction of
in the $n$![]() -dimensional ball, with eigenvalue $\lambda _0$
-dimensional ball, with eigenvalue $\lambda _0$![]() . Then the function
. Then the function
is a supersolution for $W$![]() . Thus, up to multiplication by a constant, $W \leq \overline {W}$
. Thus, up to multiplication by a constant, $W \leq \overline {W}$![]() .
.
Next consider the function
where $\tilde {w}(\xi,t)= \underline {w}(\xi,t)a(t)$![]() is given in equations (3.23) and (3.33) with $L(t)=2R(t)$
is given in equations (3.23) and (3.33) with $L(t)=2R(t)$![]() , $L_0=2R_0$
, $L_0=2R_0$![]() , $\xi =R_0-r$
, $\xi =R_0-r$![]() , and $P(t)=\frac {\ddot {L}(t)L(t)^{3}}{4D^{2}}$
, and $P(t)=\frac {\ddot {L}(t)L(t)^{3}}{4D^{2}}$![]() . Note that
. Note that

Therefore (for $t$![]() large enough), this function $w_1(r,t)$
large enough), this function $w_1(r,t)$![]() satisfies
satisfies
Next, using the form of the Laplacian in $n$![]() dimensions, we claim that the function
dimensions, we claim that the function
is a subsolution in the $n$![]() -dimensional case when $n\leq 3$
-dimensional case when $n\leq 3$![]() . Certainly the boundary condition (at $r=R_0$
. Certainly the boundary condition (at $r=R_0$![]() ) and the non-singular condition (at $r=0$
) and the non-singular condition (at $r=0$![]() ) will be satisfied, since $w_1(R_0,t)=0$
) will be satisfied, since $w_1(R_0,t)=0$![]() , and $w_1(r,t)=0$
, and $w_1(r,t)=0$![]() on some neighbourhood $[0,r_0)$
on some neighbourhood $[0,r_0)$![]() of $r=0$
of $r=0$![]() . Moreover,
. Moreover,
where the equality follows from the form of the Laplacian in $n$![]() dimensions and the final inequality holds for $n=1$
dimensions and the final inequality holds for $n=1$![]() ,$2$
,$2$![]() ,$3$
,$3$![]() . Thus, $\hat {w}$
. Thus, $\hat {w}$![]() is a subsolution and, up to multiplication by a constant, we obtain $\hat {w}\leq W$
is a subsolution and, up to multiplication by a constant, we obtain $\hat {w}\leq W$![]() .
.
We are interested in $y = R(t)-\vert \textbf {x} \vert =O(1)$![]() . This corresponds to $\vert \textbf {z} \vert = r=R_0-\frac {yR_0}{R(t)}$
. This corresponds to $\vert \textbf {z} \vert = r=R_0-\frac {yR_0}{R(t)}$![]() with $y=O(1)$
with $y=O(1)$![]() , for which the above supersolution and subsolution ($C_1\hat {w}\leq W \leq C_2\overline {W}$
, for which the above supersolution and subsolution ($C_1\hat {w}\leq W \leq C_2\overline {W}$![]() ) provide the bounds $w(\textbf {z}, t)=\overline {\underline {O}}(R_0-\vert \textbf {z} \vert ) = \overline {\underline {O}}\left (\frac {yR_0}{R(t)}\right )$
) provide the bounds $w(\textbf {z}, t)=\overline {\underline {O}}(R_0-\vert \textbf {z} \vert ) = \overline {\underline {O}}\left (\frac {yR_0}{R(t)}\right )$![]() , independently of $t$
, independently of $t$![]() . Therefore, the same calculations as in the one-dimensional case give:
. Therefore, the same calculations as in the one-dimensional case give:
Remark 3 The proof of Theorem 4 shows that, in any dimension $n$![]() ,
,
This follows from the supersolution. However, the subsolution $\hat {w}$![]() used in the proof only satisfies the required inequality when $n\leq 3$
used in the proof only satisfies the required inequality when $n\leq 3$![]() . One may conjecture that the full result of Theorem 4 actually applies in all dimensions $n$
. One may conjecture that the full result of Theorem 4 actually applies in all dimensions $n$![]() .
.
Acknowledgements
I am very grateful to my PhD supervisor, Professor Elaine Crooks. I am also grateful for an EPSRC-funded studentship (project reference 2227486).








