INTRODUCTION
The World Health Organization (WHO) recommends that first-line antimalarial treatment policies be changed when a drug's cure rate falls below 90%, and that new treatments should not be recommended unless they have a cure rate greater than 95% [1]. However, defining the antimalarial cure rate is difficult in falciparum malaria clinical trials because recurrent parasitaemias can result from either recrudescence (drug failure) or re-infection during follow-up.
One tool used to distinguish between re-infection and recrudescence is polymerase chain reaction (PCR)-correction (or PCR-adjustment). PCR-correction most often uses nested PCR (nPCR) to categorize recurrences by comparing the size of polymorphisms in genetic markers [merozoite surface proteins 1 and 2 (msp1, msp2) and glutamate-rich protein (glurp)] before and after treatment. PCR-correction of cure rates has been in use for more than 20 years and there is an extensive literature on the substantial impact it can have on estimates of treatment efficacy, as previously reviewed [Reference Collins2, Reference Guthmann3]. Variations in PCR-correction techniques exist, especially with regard to the interpretation of results. In response to this variability, the Medicines for Malaria Venture (MMV) collaborated with the WHO to generate guidelines for PCR-correction including a definition of a recrudescent infection, i.e. a recurrence in which one or more allelic variants are shared in the pre-treatment (day 0) sample and the recurrent (day R) parasitaemia [4].
PCR-correction is fallible. Incorrect identification of a re-infection as a recrudescence occurs when the patient is infected with same variant before and after treatment; this is more likely to occur in an area with limited allelic diversity or high transmission intensity [Reference Greenhouse5, Reference Kwiek6]. This type of misclassification results in underestimation of the cure rate. Additionally, there are often multiple genetically distinct allelic variants present within a single host and nPCR is not capable of detecting minority variants representing <20% of the population [Reference Juliano, Taylor and Meshnick7]. Thus, PCR-correction could misclassify a recrudescence as a re-infection because an apparently ‘new’ variant which appears in the day-R sample was present, but not detected, in the day-0 sample [Reference Juliano8]. This may be particularly important if drug-resistant variants are at levels below detection initially but become more prevalent in the patient as other variants are cleared by the treatment. This type of misclassification results in overestimation of the cure rate.
This present work has two aims. First, to demonstrate the effect of the distribution of allelic variants, transmission intensity, and multiplicity of infection (MOI) on the probability of misclassification of recurrent infections. Second, to develop a practical approach for adjusting PCR-corrected results for misclassification of both re-infections and recrudescences. A worked example using data from areas of both high- and low-transmission intensity is provided.
METHODS
Characteristics affecting the probability of false positives
We used simulations of the infection, cure, and re-infection process to demonstrate the effect of allelic diversity, transmission intensity and MOI on the probability of a false positive. In this context, a false positive refers to a re-infection that is misclassified as a recrudescence because allelic variants in the day-0 and day-R samples match by chance. We used Matlab R2008a (USA) software to simulate infections (and re-infections) of individual patients after specifying the population-wide distribution of allelic variants. For each of 100 000 simulated patients, we assigned a specified number of day-0 variants drawn randomly from the distribution. We set treatment success at 100% and assigned a specified number of day-R variants the same way. We tested all patients for a match of day-0 and day-R variants, and calculated the probability of a false positive as the number of patients with a match divided by 100 000, the number of simulated patients.
We first assessed the effect of allelic diversity in the parasite population on the probability of a false positive. We simulated allelic distributions by assuming that length variation followed a normal distribution:
We generated ten distributions, each with a mean (μ) equal to 350 bp (a relevant value based on the size of bands amplified during genotyping of msp1). Each distribution had a different variance; we included variances (σ2) within the range of values observed in natural populations as well as extremes to demonstrate the effect of allelic diversity on false positives (the variances ranged from 1575 to 6475). The resulting distributions are shown in Figure 1. For each distribution, we simulated the infection and re-infection of 100 000 patients by assigning each a single day-0 variant and a single day-R variant drawn randomly from the distribution. As in routine PCR-correction, allelic variants were distinguished by the number of base pairs; due to the insensitivity of nPCR to small variations in the number of base pairs, variants that were different by no more than 20 bp were considered to be the same in order to replicate the degree of precision routinely allowed.

Fig. 1. The ten normal distributions of base pairs used for simulations. These distributions all have the same mean (350 bp); the variance increases from top to bottom. Each plot represents 100 000 randomly assigned number of base pairs selected from the distribution.
We assessed the effect of transmission intensity on the probability of a false positive by assigning each patient one day-0 variant and one, two, three or four day-R variants, each reflecting an infectious bite (for simplicity, we assumed each infectious bite transmitted a single variant). We simulated the effect of MOI similarly, assigning each patient 1–4 day-0 variants and the same number of day-R variants.
Monte Carlo uncertainty analysis
To accurately measure treatment success, estimates of the cure rate need to be adjusted for two types of misclassification: false positives (re-infections incorrectly classified as recrudescent) and false negatives (true recrudescent infections misclassified as re-infections because a minority variant in the day-0 sample was not detected by nPCR). To adjust for this misclassification, we developed an uncertainty analysis that requires two sources of external, or prior, information: the distributions of false positives and false negatives. These distributions can be estimated using data from antimalarial efficacy studies.
We developed a method for estimating the distribution of false positives that reflects our understanding of the factors that influence the probability of a chance match and exploits characteristics of the study data, allowing the probability of a false positive to appropriately be tailored to the study setting. False-positive probabilities were calculated using the same simulation procedure described above, except that the number of allelic variants observed in each patient at day 0 and day R, and the population-wide distribution of allelic variants were set to match study data. We used Matlab R2008a (USA) to simulate the infection and re-infection of N patients, where N was the number of patients who participated in the study. Each patient was assigned X day-0 and Y day-R infections from the observed day-0 and day-R distributions of allelic variants (X for each patient was randomly selected from the observed distribution of the number of day-0 infections, Y was randomly selected from the distribution of the number of day-R infections) and tested for matches. The false-positive probability for this simulated study was then calculated as the number of chance matches divided by N. We repeated this process 10 000 times (generating 10 000 false-positive probabilities) and fit a normal distribution to their values; this provided the mean and variance for the distribution of the proportion of recrudescent infections that were false positives.
To estimate the distribution of false negatives, we made use of the observation that nPCR has limited sensitivity to variants comprising <20% of a patient's parasite population [Reference Juliano, Taylor and Meshnick7]. Misclassification of a recrudescence as a re-infection, a false negative, requires that each day-R variant be undetected in the day-0 variants, as a single shared variant will result in the classification of the recurrence as a recrudescence according to the MMV/WHO guidelines [4]. To our knowledge, the only published information on the role of false negatives comes from Juliano et al. who used heteroduplex tracking assays (HTAs), a molecular method more sensitive to minority variants and genetic variation than nPCR, and found that five of six new infections (83%) identified by PCR-correction were truly recrudescent infections [Reference Juliano8]. However, their study population was at negligible risk of re-infection, probably making their results an overestimate in the context of an average antimalarial trial. Therefore, to estimate the proportion of re-infections that were false negatives we used the median number of variants observed in the day-R samples, assumed each variant carried with it a 20% chance of being missed in the day-0 sample, and calculated the probability that all were missed at day 0 resulting in a false negative using the formula: proportion of false negatives=(0·2)v, where v is the median number of variants. The 20% chance was based on existing literature and expert opinion. Figure 2 shows our estimate of the effect of the number of variants in the day-R sample on the probability that a recrudescence was misclassified as a re-infection (a false negative). We also conducted a sensitivity analysis varying the probability of a band being missed in the day-0 sample from 0% to 80%.
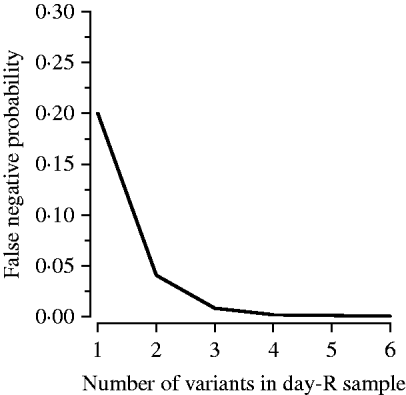
Fig. 2. Multiplicity of infection and its effect on the probability of a false negative. A false negative, or a recrudescent infection misclassified as a re-infection, occurs as a result of nPCR insensitivity to minority variants (those comprising <20% of a patient's infection).
We conducted a Monte Carlo uncertainty analysis to adjust the observed number of recrudescent infections as determined by PCR-correction after genotyping msp2 by the estimated distributions of false positives and false negatives. Using an approach similar to that described by Jurek et al. [Reference Jurek9], we calculated the adjusted cure rate using the formula:
where N t is the total number of patients, N rec is the number of recrudescent infections identified by PCR-correction, FP is the proportion of recrudescent infections that were false positives, N new is the number of re-infections identified by PCR-correction, and FN is the proportion of re-infections that were false negatives.
We used Oracle Crystal Ball, Fusion Edition (USA) software to run 100 000 trials in which the number of recrudescent infections as determined by PCR-correction after genotyping msp2 in each study area was adjusted and the cure rate calculated using formula (1) (above). As the last step in each trial, we included a bootstrap procedure to allow for sampling error by generating a random value from a binomial distribution [Reference Vose10]. The binomial distribution is parameterized by n, the number of trials, and p, the probability of success. In this case, the number of trials equalled the number of patients in the study and the probability of success was the uncertainty-adjusted probability of treatment failure. We drew a single random value from the distribution and treated it as the number of recrudescences which allowed us to calculate the final cure rate, adjusted for both uncertainty and sampling error. We also ran 100 000 trials without the bootstrap step to explore the effect of uncertainty in the absence of sampling error, and finally, also calculated traditional 95% confidence intervals around the PCR-corrected cure rate with no adjustment for outcome misclassification to demonstrate the effect of sampling error in the absence of uncertainty about the outcome.
Example data
To provide an example of our proposed uncertainty analysis, we used genotyping data from two randomized antimalarial efficacy trials conducted in areas of differing transmission intensity. The data from the high-transmission area came from a study in Tororo, Uganda (N=401); the researchers were comparing the efficacy of an amodiaquine plus artesunate regimen compared to an atemether-lumefantrine regimen [Reference Bukirwa11]. The data from the low-transmission area were generated by a study conducted in Bobo-Dioulasso, Burkina Faso (N=827); the researchers were comparing the efficacy of amodiaquine, sulfadoxine-pyrimethamine and amodiaquine plus sulfadoxine-pyrimethamine [Reference Zongo12]. In both studies, the different therapies did demonstrate different levels of efficacy [Reference Bukirwa11, Reference Zongo12]; however, because we are not interested in a particular treatment's efficacy, and instead are simply providing an example of the uncertainty analysis, we did not stratify by treatment arm. The data for each patient included the number and identity of allelic variants. Greenhouse et al. used two sets of primers for amplification to capture two allelic families of msp2, IC3D7 and FC27 [Reference Greenhouse5]. Alleles were considered different if they were from different allelic families or if they were not the same length.
RESULTS
Characteristics affecting the probability of false positives
The simulations compared the effect of transmission intensity and MOI on the probability of a false positive across ten normal distributions comprising alleles with the same mean size (350 bp) but different variances (Fig. 1); increased variance signified higher levels of genetic diversity in the population under study. We drew 100 000 samples of allelic variants from each distribution, assumed 100% treatment success, and drew a second variant to allow us to calculate the probability of a false positive. We calculated these probabilities at different levels of transmission intensity and different MOI.
At any level of allelic variance, the greater the number of post-treatment bites, or the more variants a patient had at day 0 and day R, the more likely a false positive. Conversely, higher levels of allelic diversity had lower probabilities of false positives regardless of transmission intensity or MOI (Fig. 3).
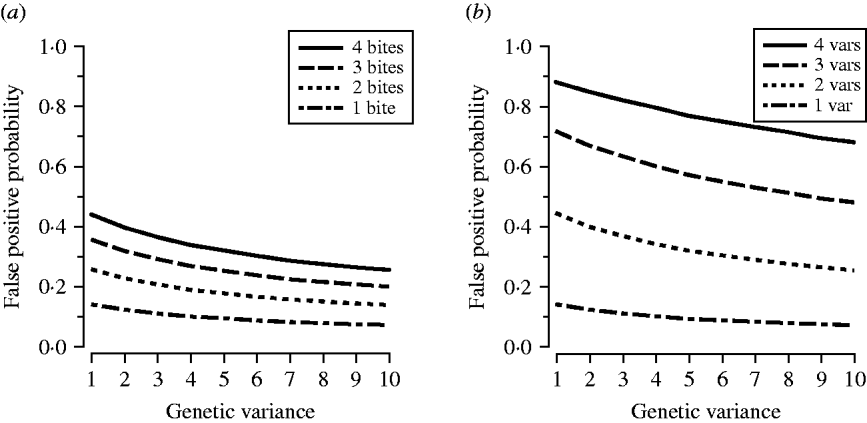
Fig. 3. (a) The effect of transmission intensity on the probability of a false positive. (b) The effect of multiplicity of infection on the probability of a false positive. The x-axis indicates a measure of allelic variation in the parasite population (1=least variance, as seen in Fig. 1); the y-axis indicates the probability of a false positive (a false positive occurs when a day-0 and a day-R variant match by chance); var=variant.
Example of Monte Carlo uncertainty analysis
We used two datasets to provide examples of our Monte Carlo uncertainty analysis, which adjusted the number of recrudescent infections identified by PCR-correction by false positives (the proportion of nPCR-identified recrudescent infections misclassified due to a variant in the day-0 and day-R samples matching by chance) and false negatives (the proportion of nPCR re-infections misclassified due to nPCR insensitivity).
Patients from Tororo, the high transmission area, had 1–8 day-0 variants (median of four) and 1–8 day-R variants (median of three). There were 40 variants in the day-0 sample when divided into 20-bp bins with variants ranging in size from 181 to 611 bp. There were 38 variants in the day-R sample with sizes ranging from 212 to 663 bp.
Patients from Bobo-Dioulasso, the low-transmission area, had 1–8 day-0 variants (median of two) and 1–6 day-R variants (median of two). There were 39 variants in the day-0 sample with sizes ranging from 195 to 637 bp. There were 25 variants in the day-R sample with sizes ranging from 232 to 565 bp.
False positives
There was slightly less allelic diversity in Bobo-Dioulasso; however, individuals with single pre-treatment and post-treatment variants had very similar probabilities of a false positive (in Tororo the probability was 0·050 vs. 0·045 in Bobo-Dioulasso). In patients with the sites' median numbers of pre-treatment and post-treatment variants (four and three, respectively, in Tororo; two and two in Bobo-Dioulasso), the probability of a false positive was considerably higher in Tororo (0·327) compared to Bobo-Dioulasso (0·163).
We used the probability of a day-0 and a day-R variant matching by chance to inform our distribution of false positives. We did this by running 10 000 simulations, each with the number of participants in the study. Each participant was assigned X day-0 and Y day-R variants from the observed day-0 and day-R distributions of allelic variants (X for each patient was randomly selected from the observed distribution of the number of day-0 variants, Y was randomly selected from the distribution of the number of day-R variants) and tested for matches. We created a distribution of these 10 000 probabilities and determined its mean and standard error. The mean proportion of recrudescent infections that were false positives was 0·423 in Tororo (s.e.=0·0007) and 0·193 in Bobo-Dioulasso (s.e.=0·0004).
False negatives
False negatives occur when a minority variant is undetected by nPCR and results in misclassification of a recrudescent infection as a re-infection. The proportion of variants likely to be false negatives was equal to (0·2)v, where 0·2 is the probability that a variant was missed in day 0 and v is the median number of variants in the site's day-R samples (Fig. 2). The proportion of re-infections that were false negatives was 0·008 in Tororo and 0·04 in Bobo-Dioulasso.
Adjusted number of recrudescent infections
There were 232 recurrent parasitaemias in the 401 study participants from Tororo. After genotyping msp2, 145 were classified as recrudescent and 87 as re-infection, corresponding to a cure rate of 63·8%. After conducting our uncertainty analysis, we determined that the 95% simulation interval of likely cure rates ranged from 74·6% to 83·3% (Table 1).
Table 1. Results from the uncertainty analysis: estimates of cure rates from studies in Bobo-Dioulasso, Burkina Faso, and Tororo, Uganda

CI, Confidence interval; SI, simulation interval.
Of the 827 study participants from Bobo-Dioulasso, there were 75 recurrent parasitaemias. After genotyping msp2, 50 were classified as recrudescent and 25 as re-infection, corresponding to a cure rate of 94·0%. After conducting our uncertainty analysis, we determined that the 95% simulation interval of likely cure rates ranged from 93·5% to 96·5% (Table 1).
We evaluated the effect of uncertainty due to outcome misclassification and sampling error independently. The adjustment for uncertainty regarding outcome misclassification was responsible for the upward shift of the cure rate (indicating greater efficacy) and sampling error increased the width of the simulation interval (Table 1).
DISCUSSION
Our simulations demonstrated the effect of allelic diversity, transmission intensity and MOI on the probability of a chance match between a day-0 and a day-R variant. False positives were more common in areas with less diverse parasite populations and high transmission levels which would lead to underestimation of cure rates in those areas. The most dramatic increase in the probability of a false positive was associated with increased MOI (Fig. 3 b).
The results of the proposed uncertainty analysis indicated false positives (re-infections misclassified as recrudescences) were responsible for the majority of misclassification in both examples. Selecting variants at random from the observed distributions in Tororo resulted in false positives in more than one-third of the recrudescent infections, while in Bobo-Dioulasso the probability that a recrudescence was a false positive was <20%. The discrepancy is primarily the result of the lower median day-0 and day-R MOI in Bobo-Dioulasso, as both areas had similar levels of allelic diversity. In Tororo, false positives resulted in an uncertainty interval of the cure rate that indicated greater efficacy than the original point estimate calculated after genotyping msp2.
False negatives (recrudescences misclassified as re-infections) resulted in only a small amount of misclassification for two reasons. First, multiple variants in the day-R sample (observed in both study sites) decreased the probability of this type of misclassification exponentially (Fig. 2). Our sensitivity analysis indicated that even with a 30% chance that a day-0 variant was not detected, the impact of the observed number of variants in the day-R samples resulted in a negligible effect of false negatives (data not shown). As the chance a day-0 variant was not detected increased past 40%, the impact began to increase more rapidly; however, values ⩾30% are highly unlikely. Second, using PCR-correction there were very few recurrences identified as re-infections; regardless of the probability that a re-infection was truly a recrudescence, the contribution of this type of misclassification to overall uncertainty would be low. However, in areas of low transmission, such as South East Asia, where few variants are present at day R, false negatives may be an important source of misclassification [Reference Juliano8].
The uncertainty analysis was based on PCR-correction of a single marker. Although the use of multiple markers to perform PCR-correction (a common practice) may reduce the probability of false positives, it increases the probability of false negatives because the MMV/WHO guidelines state that a single marker classified as a re-infection results in the recurrence being classified as such, regardless of the classification of other markers genotyped. As additional information is generated regarding the probability of false negatives and how it changes with the use of multiple markers, it will be possible to refine this uncertainty analysis to accommodate multiple markers.
The impact of misclassification with regard to WHO efficacy thresholds varied between the two sites. Although ultimately the range of likely cure rates in Tororo did not cross a WHO cut-point, it did demonstrate that misclassification plays an important role. In Bobo-Dioulasso, the area of low transmission, a WHO cut-point was included in the interval of likely cure rates (i.e. 93·5–96·5%). The relatively few patients who had recurrent parasitaemia in Bobo-Dioulasso resulted in a narrow interval of cure rates with values similar to the PCR-corrected point estimate; however, a drug whose cure rate, calculated the traditional way, would have been just below the level of efficacy required for new drugs may have been rejected when it should be eligible for consideration. Misclassification should always be considered when policy decisions are made based on estimates of efficacy.
Our approach to generating the distribution of false positives is probably not practical for use in all antimalarial efficacy studies. However, we are optimistic that it is possible to generate three reasonable ‘stock’ distributions of false positives, one for high, medium, and low transmission areas. The uncertainty analysis itself is quite straightforward and can easily be carried out in Crystal Ball, a relatively inexpensive addition to Microsoft Excel, and perhaps eventually in a free web-based tool. It is our hope that future molecular research will allow us to provide researchers with distributions of false positives and false negatives, making this uncertainty analysis available for wide use.
Misclassification of recurrent parasitaemias resulting from PCR-correction has been previously described. Adjustments of PCR-corrected trial results have been made using the distribution of allelic variants to calculate the probability of false positives leading to incorrect classification of the recurrence as a recrudescence when it is a re-infection [Reference Greenhouse5, Reference Kwiek6, Reference Brockman13, Reference Gatton and Cheng14]. HTAs, which use radiolabelled probes to bind to host amplicons, are more sensitive to minority variants and genetic variation than nPCR [Reference Kwiek6, Reference Juliano15–Reference Ngrenngarmlert17] and have been used to demonstrate that nPCR insensitivity can result in recrudescent infections being misclassified as re-infections [Reference Juliano8]. To our knowledge, simultaneous adjustment for both types of misclassification has not been undertaken previously.
Traditional confidence intervals summarize only the effect of random error and do not capture or reveal any uncertainty resulting from bias, including misclassification or measurement error, in the study. Adjusting results for misclassification has been illustrated in previous work [Reference Jurek9] and is grounded in methods proposed to estimate intervals that are an extension of traditional confidence intervals through use of simulations [Reference Greenland18]. Some researchers are uncomfortable with the explicit assumptions about misclassification that are required for uncertainty analyses. However, this approach is far preferable to assuming misclassification is entirely absent, an implicit assumption in the traditional estimation of a PCR-corrected cure rate.
A point estimate of the cure rate, the traditional outcome measure in antimalarial efficacy studies, is insufficient given the limitations of PCR-correction. This insufficiency is even more important given the policy implications of efficacy estimates. A 95% simulation interval for the cure rate, instead of an estimate likely to be biased by outcome misclassification, may encourage more careful assessment of a treatment's utility before policy decisions are made. This work provides a template for adjusting for outcome misclassification in antimalarial efficacy studies that addresses both types of misclassification and can be applied to any study data that include information on the variants present in the patient population.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge Dr Brian Greenhouse for provision and explanation of the genotyping data, Dr Joseph Eron for critical review of the study proposal, Dr Anne Jurek for helpful input regarding the uncertainty analysis, Ben Baragiola for assistance with Matlab programming, and Andrew Edmonds for his critique of the manuscript. K. A. Porter received support from a National Research Service Award from the National Institute of Allergy and Infectious Diseases (grant no. 1-T32-AI070114-01A1).
DECLARATION OF INTEREST
None.






