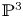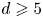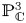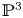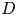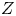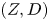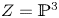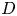1. Introduction
The aim of this paper is to construct a compactification of the moduli space of degree-![]() $d$ surfaces in
$d$ surfaces in ![]() ${{\mathbb {P}}}^{3}$. In the case of plane curves, using the Hilbert scheme or geometric invariant theory (GIT) techniques, one can find a compactification of the space parameterizing smooth degree-
${{\mathbb {P}}}^{3}$. In the case of plane curves, using the Hilbert scheme or geometric invariant theory (GIT) techniques, one can find a compactification of the space parameterizing smooth degree-![]() $d$ curves in
$d$ curves in ![]() ${{\mathbb {P}}}^{2}$, but the boundary does not always have a good modular interpretation. For instance, there are points on the boundary that correspond to several different limits of families of plane curves. In [Reference HassettHas99] for the degree-four case and [Reference HackingHac04] for general degree, instead of studying curves
${{\mathbb {P}}}^{2}$, but the boundary does not always have a good modular interpretation. For instance, there are points on the boundary that correspond to several different limits of families of plane curves. In [Reference HassettHas99] for the degree-four case and [Reference HackingHac04] for general degree, instead of studying curves ![]() $C$, the authors worked with pairs
$C$, the authors worked with pairs ![]() $({{\mathbb {P}}}^{2}, C)$ and certain allowable degenerations. Remembering the embedding of
$({{\mathbb {P}}}^{2}, C)$ and certain allowable degenerations. Remembering the embedding of ![]() $C$ in
$C$ in ![]() ${{\mathbb {P}}}^{2}$ and extracting certain properties yielded a compactification with a modular interpretation.
${{\mathbb {P}}}^{2}$ and extracting certain properties yielded a compactification with a modular interpretation.
This paper stems from the natural generalization of Hacking's work: find a good compactification of the moduli space of degree-![]() $d$ surfaces
$d$ surfaces ![]() $S$ in
$S$ in ![]() ${{\mathbb {P}}}^{3}$ using pairs. In fact, because the framework is not specific to
${{\mathbb {P}}}^{3}$ using pairs. In fact, because the framework is not specific to ![]() ${{\mathbb {P}}}^{3}$, we solve a more general problem and find a modular compactification of anticanonical divisors
${{\mathbb {P}}}^{3}$, we solve a more general problem and find a modular compactification of anticanonical divisors ![]() $D_Z$ on a fixed Fano variety
$D_Z$ on a fixed Fano variety ![]() $Z$ using degenerations of the pair
$Z$ using degenerations of the pair ![]() $(Z,D_Z)$.
$(Z,D_Z)$.
For ![]() $Z = {{\mathbb {P}}}^{3}$ and
$Z = {{\mathbb {P}}}^{3}$ and ![]() $D$ a surface of degree
$D$ a surface of degree ![]() $d = 5$, the moduli space of smooth surfaces has been understood by [Reference HorikawaHor73]. However, even for smooth surfaces, this moduli space is not irreducible. When fixing the numerical invariants
$d = 5$, the moduli space of smooth surfaces has been understood by [Reference HorikawaHor73]. However, even for smooth surfaces, this moduli space is not irreducible. When fixing the numerical invariants ![]() $K_S^{5} = 5$,
$K_S^{5} = 5$, ![]() $p_g = 4$, and
$p_g = 4$, and ![]() $q = 0$ of quintic surfaces, even in the smooth case, one obtains a moduli space with two components. These details will be further explored in § 5, but we mention it here to indicate the increase in complexity when passing from curves to surfaces and motivate our focus on smoothable pairs.
$q = 0$ of quintic surfaces, even in the smooth case, one obtains a moduli space with two components. These details will be further explored in § 5, but we mention it here to indicate the increase in complexity when passing from curves to surfaces and motivate our focus on smoothable pairs.
To find a meaningful compactification of the moduli space of degree-![]() $d$ surfaces in
$d$ surfaces in ![]() ${{\mathbb {P}}}^{3}$, and more generally, divisors
${{\mathbb {P}}}^{3}$, and more generally, divisors ![]() $D_Z$ that are a rational multiple of the anticanonical divisor on a fixed Fano variety
$D_Z$ that are a rational multiple of the anticanonical divisor on a fixed Fano variety ![]() $Z$, we follow Hacking's approach and study pairs
$Z$, we follow Hacking's approach and study pairs ![]() $(X,D)$ that arise as limits of pairs
$(X,D)$ that arise as limits of pairs ![]() $(Z,D_Z)$. In fact, we only consider what we call
$(Z,D_Z)$. In fact, we only consider what we call ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs
${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs ![]() $(X,D)$ (see Definition 2.1) which have prescribed singularities and satisfy the relationship
$(X,D)$ (see Definition 2.1) which have prescribed singularities and satisfy the relationship ![]() $pK_X + qD \sim 0$ and admit a smoothing to
$pK_X + qD \sim 0$ and admit a smoothing to ![]() $Z$. As in Hacking's work, this class of pairs is particularly well-behaved. In the case of
$Z$. As in Hacking's work, this class of pairs is particularly well-behaved. In the case of ![]() $Z = {{\mathbb {P}}}^{3}$, remembering the embedding of
$Z = {{\mathbb {P}}}^{3}$, remembering the embedding of ![]() $D$ into
$D$ into ![]() ${{\mathbb {P}}}^{3}$ allows us to not only have a modular compactification of a space parameterizing
${{\mathbb {P}}}^{3}$ allows us to not only have a modular compactification of a space parameterizing ![]() $({{\mathbb {P}}}^{3}, D)$ but also to classify the pairs appearing on the boundary of the moduli space. The first result is that the class of pairs defined does actually give a compactification of the moduli space of pairs
$({{\mathbb {P}}}^{3}, D)$ but also to classify the pairs appearing on the boundary of the moduli space. The first result is that the class of pairs defined does actually give a compactification of the moduli space of pairs ![]() $(Z, D_Z)$.
$(Z, D_Z)$.
Theorem 1.1 The moduli space of ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs is a proper Deligne–Mumford stack.
${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs is a proper Deligne–Mumford stack.
Although the smoothability assumption restricts us to one component of the moduli space, we can remove the assumption in the case of odd degree surfaces in ![]() ${{\mathbb {P}}}^{3}$. However, this moduli space is not irreducible.
${{\mathbb {P}}}^{3}$. However, this moduli space is not irreducible.
Theorem 1.2 For odd degree ![]() $d$, the moduli space of three-dimensional
$d$, the moduli space of three-dimensional ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs is a proper Deligne–Mumford stack.
${(\mathbb {P}^{3},d,4)}$ H-stable pairs is a proper Deligne–Mumford stack.
The reason for requiring oddness of degree is that, without the smoothability assumption, the class of pairs defined is not obviously a bounded family. If boundedness was known, Hacking's arguments in the plane curve case [Reference HackingHac04] would imply that the moduli space is a Deligne–Mumford stack and properness would follow from a relatively standard arguments. Hacon, McKernan, and Xu proved a strong result about boundedness of families of certain pairs ![]() $(X,D)$. It requires the coefficients of the divisors appearing in
$(X,D)$. It requires the coefficients of the divisors appearing in ![]() $D$ to belong to a set satisfying the descending chain condition (DCC). Here, in the definition of a
$D$ to belong to a set satisfying the descending chain condition (DCC). Here, in the definition of a ![]() ${(Z,p,q)}$ H-stable pair, one requires that
${(Z,p,q)}$ H-stable pair, one requires that ![]() $(X, ({q}/{p} + \epsilon ) D)$ is semi-log-canonical (slc) for
$(X, ({q}/{p} + \epsilon ) D)$ is semi-log-canonical (slc) for ![]() $\epsilon$ sufficiently small. However,
$\epsilon$ sufficiently small. However, ![]() $\epsilon$ is not bounded from below, so results on boundedness such as those in [Reference Hacon, McKernan and XuHMX14b] do not directly apply. If
$\epsilon$ is not bounded from below, so results on boundedness such as those in [Reference Hacon, McKernan and XuHMX14b] do not directly apply. If ![]() $\epsilon$ was required to belong to a DCC set, [Reference Hacon, McKernan and XuHMX14b, Theorem 1.1] would apply to show the given pairs belong to a bounded family.
$\epsilon$ was required to belong to a DCC set, [Reference Hacon, McKernan and XuHMX14b, Theorem 1.1] would apply to show the given pairs belong to a bounded family.
In a different direction, an initial goal of this project was to classify the singular pairs appearing on the boundary of the moduli space of ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs. In working on this problem, the classification results gave enough control of the singularities of the boundary of the moduli space for odd degree
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs. In working on this problem, the classification results gave enough control of the singularities of the boundary of the moduli space for odd degree ![]() $d$ to obtain boundedness even for non-smoothable pairs. In other words, regardless of what set
$d$ to obtain boundedness even for non-smoothable pairs. In other words, regardless of what set ![]() $\epsilon$ lives in, the classification results for odd degree
$\epsilon$ lives in, the classification results for odd degree ![]() $d$ actually imply boundedness. Therefore, for
$d$ actually imply boundedness. Therefore, for ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs, the following theorems serve two purposes: explicit classification of singular threefolds appearing in the moduli space and a means to achieve boundedness without carefully studying the numbers
${(\mathbb {P}^{3},d,4)}$ H-stable pairs, the following theorems serve two purposes: explicit classification of singular threefolds appearing in the moduli space and a means to achieve boundedness without carefully studying the numbers ![]() $\epsilon$ that appear in H-stable pairs. The first result is about ambient spaces
$\epsilon$ that appear in H-stable pairs. The first result is about ambient spaces ![]() $X$ with mild singularities. Because
$X$ with mild singularities. Because ![]() $D \sim _{\mathbb {Q}} -({d}/{4}) K_{X}$, classifying all the possible threefolds
$D \sim _{\mathbb {Q}} -({d}/{4}) K_{X}$, classifying all the possible threefolds ![]() $X$ appearing is the first step toward understanding
$X$ appearing is the first step toward understanding ![]() $D$.
$D$.
Theorem 1.3 Given a ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pair
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pair ![]() $(X,D)$, if
$(X,D)$, if ![]() $d$ is odd and
$d$ is odd and ![]() $X$ has canonical singularities, then:
$X$ has canonical singularities, then:
(a)
 $X \cong {{\mathbb {P}}}^{3}$;
$X \cong {{\mathbb {P}}}^{3}$;(b)
 $X$ is isomorphic to the cone over the anticanonical embedding of the quadric surface
$X$ is isomorphic to the cone over the anticanonical embedding of the quadric surface  ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$; or
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$; or(c)
 $X \cong {{\mathbb {P}}}(1,1,2,4)$, the cone over the anticanonical embedding of the singular quadric surface;
$X \cong {{\mathbb {P}}}(1,1,2,4)$, the cone over the anticanonical embedding of the singular quadric surface;
and ![]() $D \in | \mathcal {O}_{X}(-({d}/{4})K_X) |$ such that
$D \in | \mathcal {O}_{X}(-({d}/{4})K_X) |$ such that ![]() $(X, ({4}/{d})D)$ is log-terminal.
$(X, ({4}/{d})D)$ is log-terminal.
Certainly there are other examples of threefolds ![]() $X$ with canonical singularities and
$X$ with canonical singularities and ![]() $-K_X$ ample that do not appear in the previous list, even some appearing in the boundary for even degree. However, in the odd-degree case, the boundary is very special. For any degree, the previous theorem gives a divisorial component of the boundary of the moduli space.
$-K_X$ ample that do not appear in the previous list, even some appearing in the boundary for even degree. However, in the odd-degree case, the boundary is very special. For any degree, the previous theorem gives a divisorial component of the boundary of the moduli space.
Theorem 1.4 Let ![]() $X$ be the cone over the anticanonical embedding of
$X$ be the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. For any degree
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. For any degree ![]() $d > 4$, (the closure of) the locus of
$d > 4$, (the closure of) the locus of ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs ![]() $(X,D)$ in the moduli space forms a divisor
$(X,D)$ in the moduli space forms a divisor ![]() ${{\mathcal {D}}}_Q$ in
${{\mathcal {D}}}_Q$ in ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and the moduli space is smooth at the generic point of
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and the moduli space is smooth at the generic point of ![]() ${{\mathcal {D}}}_Q$.
${{\mathcal {D}}}_Q$.
More generally, in the moduli space of ![]() $(d,n+1) {{\mathbb {P}}}^{n}$-smoothable H-stable pairs, the locus parameterizing divisors on a cone over a quadric always forms a divisor.
$(d,n+1) {{\mathbb {P}}}^{n}$-smoothable H-stable pairs, the locus parameterizing divisors on a cone over a quadric always forms a divisor.
Theorem 1.5 Let ![]() $X \subset {{\mathbb {P}}}(1^{n+1}, 2)$ be the cone over the degree-two embedding of a smooth quadric
$X \subset {{\mathbb {P}}}(1^{n+1}, 2)$ be the cone over the degree-two embedding of a smooth quadric ![]() $Q \in | {{\mathcal {O}}}_{{{\mathbb {P}}}^{n}}(2) |$. For any degree
$Q \in | {{\mathcal {O}}}_{{{\mathbb {P}}}^{n}}(2) |$. For any degree ![]() $d > n+1$, (the closure of) the locus of
$d > n+1$, (the closure of) the locus of ![]() $(d, n+1) {{\mathbb {P}}}^{n}$-smoothable H-stable pairs
$(d, n+1) {{\mathbb {P}}}^{n}$-smoothable H-stable pairs ![]() $(X,D)$ forms a divisor
$(X,D)$ forms a divisor ![]() ${{\mathcal {D}}}_Q$ in the moduli space
${{\mathcal {D}}}_Q$ in the moduli space ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{n\text {-sm}}, (d,n+1)}$.
${{\mathcal {M}}}_{{{\mathbb {P}}}^{n\text {-sm}}, (d,n+1)}$.
In the case of ![]() ${{\mathbb {P}}}^{3}$-smoothable H-stable pairs, we also study more complicated singularities. In order to guarantee a proper moduli space, we consider slc pairs. In § 4, we show that pairs with strictly slc singularities can only appear in the moduli space of pairs with even degree
${{\mathbb {P}}}^{3}$-smoothable H-stable pairs, we also study more complicated singularities. In order to guarantee a proper moduli space, we consider slc pairs. In § 4, we show that pairs with strictly slc singularities can only appear in the moduli space of pairs with even degree ![]() $d$. Therefore, for odd degree, we only need to consider semi-log-terminal pairs to construct the moduli space.
$d$. Therefore, for odd degree, we only need to consider semi-log-terminal pairs to construct the moduli space.
Theorem 1.6 Given a ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pair with
${(\mathbb {P}^{3},d,4)}$ H-stable pair with ![]() $d$ odd,
$d$ odd, ![]() $(X,({4}/{d})D)$, each component of the normalization of
$(X,({4}/{d})D)$, each component of the normalization of ![]() $(X,({4}/{d})D)$ is divisorial log-terminal (dlt).
$(X,({4}/{d})D)$ is divisorial log-terminal (dlt).
Considering for a moment the H-stable pairs ![]() $(X,D)$ with
$(X,D)$ with ![]() $X$ normal, the canonical threefolds
$X$ normal, the canonical threefolds ![]() $X$ appearing are described in Theorem 1.3. From Theorem 1.6, it remains to classify the (non-canonical) log-terminal threefolds appearing as H-stable pairs. Partial progress toward this goal is obtained in § 4.5. We hope to continue this study and classify non-normal threefolds (via a similar analysis of their normalization) in future work.
$X$ appearing are described in Theorem 1.3. From Theorem 1.6, it remains to classify the (non-canonical) log-terminal threefolds appearing as H-stable pairs. Partial progress toward this goal is obtained in § 4.5. We hope to continue this study and classify non-normal threefolds (via a similar analysis of their normalization) in future work.
1.1 A map of this paper
In the first half of the paper, we study ![]() ${(Z,p,q)}$ H-stable pairs for an arbitrary smooth Fano variety
${(Z,p,q)}$ H-stable pairs for an arbitrary smooth Fano variety ![]() $Z$. We begin in § 2 with a brief explanation of motivating ideas for this paper, we define H-stable pairs, and use the existence of minimal models to prove that a family of pairs over a punctured curve can be extended in an essentially unique way, justifying the definition. In § 3, we study deformation theory of H-stable pairs and further analyze the moduli space
$Z$. We begin in § 2 with a brief explanation of motivating ideas for this paper, we define H-stable pairs, and use the existence of minimal models to prove that a family of pairs over a punctured curve can be extended in an essentially unique way, justifying the definition. In § 3, we study deformation theory of H-stable pairs and further analyze the moduli space ![]() ${{\mathcal {M}}}_{{(Z^{\mathrm{sm}},p,q)}}$, proving that it is a proper Deligne–Mumford stack. In the case of
${{\mathcal {M}}}_{{(Z^{\mathrm{sm}},p,q)}}$, proving that it is a proper Deligne–Mumford stack. In the case of ![]() $Z = {{\mathbb {P}}}^{3}$, we remove the smoothability assumption for odd degree
$Z = {{\mathbb {P}}}^{3}$, we remove the smoothability assumption for odd degree ![]() $d$ and prove that
$d$ and prove that ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ is a proper Deligne–Mumford stack. In the second half of the paper, we focus primarily on the case
${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ is a proper Deligne–Mumford stack. In the second half of the paper, we focus primarily on the case ![]() $Z = {{\mathbb {P}}}^{3}$ to obtain finer classification results, generalizing to
$Z = {{\mathbb {P}}}^{3}$ to obtain finer classification results, generalizing to ![]() $Z = {{\mathbb {P}}}^{n}$ when possible. In § 4, we prove a number of technical lemmas about extremal contractions in the minimal model program, use them to understand log-canonical singularities appearing in degree
$Z = {{\mathbb {P}}}^{n}$ when possible. In § 4, we prove a number of technical lemmas about extremal contractions in the minimal model program, use them to understand log-canonical singularities appearing in degree ![]() $d {{\mathbb {P}}}^{3}$ H-stable pairs, and build up the necessary machinery to prove Theorem 1.6. We prove a number of related results on the structure of slc Fano varieties and their connections to boundedness of odd degree
$d {{\mathbb {P}}}^{3}$ H-stable pairs, and build up the necessary machinery to prove Theorem 1.6. We prove a number of related results on the structure of slc Fano varieties and their connections to boundedness of odd degree ![]() ${{\mathbb {P}}}^{3}$ H-stable pairs. We also discuss canonical and log-terminal Fano degenerations of
${{\mathbb {P}}}^{3}$ H-stable pairs. We also discuss canonical and log-terminal Fano degenerations of ![]() ${{\mathbb {P}}}^{n}$ as a step toward classifying all
${{\mathbb {P}}}^{n}$ as a step toward classifying all ![]() ${{\mathbb {P}}}^{n}$-smoothable H-stable pairs. Finally, in § 5, we explicitly study
${{\mathbb {P}}}^{n}$-smoothable H-stable pairs. Finally, in § 5, we explicitly study ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm}, (5,4)}$, the moduli space of quintic surfaces in
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm}, (5,4)}$, the moduli space of quintic surfaces in ![]() ${{\mathbb {P}}}^{3}$. We compare this to existing compactifications and discuss the differences between
${{\mathbb {P}}}^{3}$. We compare this to existing compactifications and discuss the differences between ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ and
${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ and ![]() $\mathcal{M}_{{(\mathbb {P}^{3,\mathrm{sm}},d,4)}}$.
$\mathcal{M}_{{(\mathbb {P}^{3,\mathrm{sm}},d,4)}}$.
2. H-stable pairs
Throughout, we work with varieties over ![]() $\mathbb{C}$. A pair
$\mathbb{C}$. A pair ![]() $(X,D)$ is a variety
$(X,D)$ is a variety ![]() $X$ with a divisor
$X$ with a divisor ![]() $D = \sum a_iD_i$ that is a formal linear combination of prime divisors. We restrict to the case
$D = \sum a_iD_i$ that is a formal linear combination of prime divisors. We restrict to the case ![]() $a_i \in \mathbb {Q}$. We use the standard definitions for (log-)terminal and (log-)canonical singularities found, for example, in [Reference Kollár and MoriKM98, § 2.3].
$a_i \in \mathbb {Q}$. We use the standard definitions for (log-)terminal and (log-)canonical singularities found, for example, in [Reference Kollár and MoriKM98, § 2.3].
2.1 Previous work
We will construct a compactification of the moduli space of degree ![]() $d$ surfaces in
$d$ surfaces in ![]() ${{\mathbb {P}}}^{3}$ using ideas first introduced in [Reference Kollár and Shepherd-BarronKS-B88] and mention here the relationship between this compactification and related ones. The Kollár–Shepherd-Barron (KSB) compactification is a construction of a parameter space for stable objects with slc singularities. Our precise definition of stable objects appears in § 2. One can consider these compactifications as higher-dimensional analogues of
${{\mathbb {P}}}^{3}$ using ideas first introduced in [Reference Kollár and Shepherd-BarronKS-B88] and mention here the relationship between this compactification and related ones. The Kollár–Shepherd-Barron (KSB) compactification is a construction of a parameter space for stable objects with slc singularities. Our precise definition of stable objects appears in § 2. One can consider these compactifications as higher-dimensional analogues of ![]() $\bar {M}_{g,n}$, the moduli space of stable genus
$\bar {M}_{g,n}$, the moduli space of stable genus ![]() $g$ curves with
$g$ curves with ![]() $n$ marked points [Reference AlexeevAle96].
$n$ marked points [Reference AlexeevAle96].
The framework motivating this definition of the compactification comes from earlier work of Hassett and Hacking, studying moduli spaces of degree ![]() $d$ plane curves by considering them as pairs
$d$ plane curves by considering them as pairs ![]() $({{\mathbb {P}}}^{2}, C)$. A compactification of the moduli space of the space of pairs
$({{\mathbb {P}}}^{2}, C)$. A compactification of the moduli space of the space of pairs ![]() $({{\mathbb {P}}}^{2}, C_4)$, where
$({{\mathbb {P}}}^{2}, C_4)$, where ![]() $C_4$ has degree four was studied in [Reference HassettHas99] and, more generally, for any degree
$C_4$ has degree four was studied in [Reference HassettHas99] and, more generally, for any degree ![]() $d \geqslant 4$, a compactification of pairs
$d \geqslant 4$, a compactification of pairs ![]() $({{\mathbb {P}}}^{2}, C_d)$ was constructed in [Reference HackingHac04]. The work in [Reference HackingHac04] provides much of the foundation for this paper as the study of pairs
$({{\mathbb {P}}}^{2}, C_d)$ was constructed in [Reference HackingHac04]. The work in [Reference HackingHac04] provides much of the foundation for this paper as the study of pairs ![]() $({{\mathbb {P}}}^{3}, S_d)$ is a natural generalization. In a different direction, one could generalize [Reference HackingHac04] to study pairs
$({{\mathbb {P}}}^{3}, S_d)$ is a natural generalization. In a different direction, one could generalize [Reference HackingHac04] to study pairs ![]() $(S,D)$ for other del Pezzo surfaces. In particular, a compactification of the space of pairs
$(S,D)$ for other del Pezzo surfaces. In particular, a compactification of the space of pairs ![]() $({{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}, C_{3,3})$ using similar machinery is described in [Reference Deopurkar and HanDH21]. In general, Kollár and Xu show that one can make a coarse moduli space of polarized log Calabi Yau pairs where each irreducible component is projective [Reference Kollár and XuKX20].
$({{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}, C_{3,3})$ using similar machinery is described in [Reference Deopurkar and HanDH21]. In general, Kollár and Xu show that one can make a coarse moduli space of polarized log Calabi Yau pairs where each irreducible component is projective [Reference Kollár and XuKX20].
There is another approach to the study of plane curves and surfaces in ![]() ${{\mathbb {P}}}^{3}$ using the tools provided by GIT. However, as discussed in [Reference Wang and XuWX14], GIT begins to fail for higher degree
${{\mathbb {P}}}^{3}$ using the tools provided by GIT. However, as discussed in [Reference Wang and XuWX14], GIT begins to fail for higher degree ![]() $d$. In the GIT construction, the moduli space depends on the power
$d$. In the GIT construction, the moduli space depends on the power ![]() $r$ of
$r$ of ![]() $\omega _S$ (or other ample line bundle) being used to embed smooth surfaces into projective space and it is shown that the moduli spaces in this construction do not stabilize. In particular, in [Reference Wang and XuWX14, Theorem 1 (2)], there are families of degree
$\omega _S$ (or other ample line bundle) being used to embed smooth surfaces into projective space and it is shown that the moduli spaces in this construction do not stabilize. In particular, in [Reference Wang and XuWX14, Theorem 1 (2)], there are families of degree ![]() $d > 30$ smooth surfaces over a punctured base whose limit does not stabilize as
$d > 30$ smooth surfaces over a punctured base whose limit does not stabilize as ![]() $r$ increases. Therefore, it benefits us to approach the problem for general degree
$r$ increases. Therefore, it benefits us to approach the problem for general degree ![]() $d$ surfaces using the framework of stable pairs instead of GIT. Some comparison to the GIT case for degree
$d$ surfaces using the framework of stable pairs instead of GIT. Some comparison to the GIT case for degree ![]() $d = 5$ will be given in § 5.
$d = 5$ will be given in § 5.
2.2 Definitions
We are interested in studying the moduli space of hypersurfaces ![]() $S$ (of a fixed degree) in
$S$ (of a fixed degree) in ![]() $\mathbb {P}^{3}$. As motivated in the introduction, instead of studying moduli of such
$\mathbb {P}^{3}$. As motivated in the introduction, instead of studying moduli of such ![]() $S$ directly, we study moduli of pairs
$S$ directly, we study moduli of pairs ![]() $(X, D)$ where
$(X, D)$ where ![]() $X$ is a degeneration of
$X$ is a degeneration of ![]() $\mathbb {P}^{3}$ and
$\mathbb {P}^{3}$ and ![]() $D$ is a degeneration of
$D$ is a degeneration of ![]() $S$. The motivating work for plane curves in [Reference HackingHac04] considered moduli of pairs
$S$. The motivating work for plane curves in [Reference HackingHac04] considered moduli of pairs ![]() $(X,D)$ where
$(X,D)$ where ![]() $X$ was a slc surface that smoothed to
$X$ was a slc surface that smoothed to ![]() $\mathbb {P}^{2}$ and
$\mathbb {P}^{2}$ and ![]() $D$ was a divisor such that
$D$ was a divisor such that ![]() $d K_X + 3 D \sim 0$ and
$d K_X + 3 D \sim 0$ and ![]() $K_X + ({3}/{d} + \epsilon ) D$ was ample for some (and hence all)
$K_X + ({3}/{d} + \epsilon ) D$ was ample for some (and hence all) ![]() $\epsilon$ sufficiently small. Hacking was able to show that, for
$\epsilon$ sufficiently small. Hacking was able to show that, for ![]() $d$ not a multiple of 3, this moduli stack is proper, separated, and smooth, and was also able to explicitly determine the surfaces
$d$ not a multiple of 3, this moduli stack is proper, separated, and smooth, and was also able to explicitly determine the surfaces ![]() $X$ (and thus the divisors
$X$ (and thus the divisors ![]() $D$) appearing on the boundary of the moduli space.
$D$) appearing on the boundary of the moduli space.
Now, consider the direct generalization of [Reference HackingHac04]: a compactification of the moduli space of degree ![]() $d$ hypersurfaces in
$d$ hypersurfaces in ![]() $\mathbb {P}^{3}$. We present the following definitions. This paper will focus on dimension 3, but the definitions make sense for general Fano varieties and divisors of arbitrary dimension. First, we define a
$\mathbb {P}^{3}$. We present the following definitions. This paper will focus on dimension 3, but the definitions make sense for general Fano varieties and divisors of arbitrary dimension. First, we define a ![]() ${(Z,p,q)}$ stable pair.
${(Z,p,q)}$ stable pair.
Definition 2.1 For a given Fano variety ![]() $Z$, let
$Z$, let ![]() $n = \dim Z$, and fix integers
$n = \dim Z$, and fix integers ![]() $p,q> 0$ such that
$p,q> 0$ such that ![]() ${q}/{p} <1$. A pair
${q}/{p} <1$. A pair ![]() $(X,D)$, where
$(X,D)$, where ![]() $X$ is an
$X$ is an ![]() $n$-fold and
$n$-fold and ![]() $D$ is an effective
$D$ is an effective ![]() $\mathbb {Q}$-Cartier
$\mathbb {Q}$-Cartier ![]() $\mathbb {Z}$-divisor, is said to be
$\mathbb {Z}$-divisor, is said to be ![]() ${(Z,p,q)}$ stable in the sense of Hacking, or
${(Z,p,q)}$ stable in the sense of Hacking, or ![]() ${(Z,p,q)}$ H-stable, if:
${(Z,p,q)}$ H-stable, if:
(i) the pair
 $(X, ({q}/{p}+\epsilon )D)$ is slc and the divisor
$(X, ({q}/{p}+\epsilon )D)$ is slc and the divisor  $K_X + ({q}/{p} + \epsilon )D$ is ample for some
$K_X + ({q}/{p} + \epsilon )D$ is ample for some  $\epsilon > 0$;
$\epsilon > 0$;(ii) the divisor
 $pK_X + qD$ is linearly equivalent to zero;
$pK_X + qD$ is linearly equivalent to zero;(iii)
 $K_X^{n} = K_{Z}^{n}$ and
$K_X^{n} = K_{Z}^{n}$ and  $X$ is Cohen–Macaulay.
$X$ is Cohen–Macaulay.
Note that this definition does not require that ![]() $Z$ admits a deformation to
$Z$ admits a deformation to ![]() $X$.
$X$.
Next, we define ![]() $Z$-smoothable pairs. Note that the last condition implies the last condition in the non-smoothable definition by Proposition 4.2.
$Z$-smoothable pairs. Note that the last condition implies the last condition in the non-smoothable definition by Proposition 4.2.
Definition 2.2 Fix a smooth Fano variety ![]() $Z$ and integers
$Z$ and integers ![]() $p,q> 0$ such that
$p,q> 0$ such that ![]() ${q}/{p} <1$. A pair
${q}/{p} <1$. A pair ![]() $(X,D)$, where
$(X,D)$, where ![]() $X$ is an
$X$ is an ![]() $n$-fold and
$n$-fold and ![]() $D$ is an effective
$D$ is an effective ![]() $\mathbb {Q}$-Cartier
$\mathbb {Q}$-Cartier ![]() $\mathbb {Z}$-divisor, is said to be
$\mathbb {Z}$-divisor, is said to be ![]() ${(Z^{\mathrm{sm}},p,q)}$ stable in the sense of Hacking, or
${(Z^{\mathrm{sm}},p,q)}$ stable in the sense of Hacking, or ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable if:
${(Z^{\mathrm{sm}},p,q)}$ H-stable if:
(i) the pair
 $(X, ({q}/{p}+\epsilon )D)$ is slc and the divisor
$(X, ({q}/{p}+\epsilon )D)$ is slc and the divisor  $K_X + ({q}/{p} + \epsilon )D$ is ample for some
$K_X + ({q}/{p} + \epsilon )D$ is ample for some  $\epsilon > 0$;
$\epsilon > 0$;(ii) the divisor
 $pK_X + qD$ is linearly equivalent to zero;
$pK_X + qD$ is linearly equivalent to zero;(iii) there is a deformation
 $(\mathcal {X}, \mathcal {D})/T$ of
$(\mathcal {X}, \mathcal {D})/T$ of  $(X,D)$ over the germ of a curve such that the general fiber
$(X,D)$ over the germ of a curve such that the general fiber  $\mathcal {X}_t$ is smooth,
$\mathcal {X}_t$ is smooth,  $\mathcal {X}_t$ admits a smooth deformation to
$\mathcal {X}_t$ admits a smooth deformation to  $Z$, and the divisors
$Z$, and the divisors  $K_{\mathcal {X}/T}$ and
$K_{\mathcal {X}/T}$ and  $\mathcal {D}$ are
$\mathcal {D}$ are  $\mathbb {Q}$-Cartier.
$\mathbb {Q}$-Cartier.
Note that the last condition in Definition 2.2 serves two purposes: one, to ensure that ![]() $X$ is smoothable (restricting to certain components of the moduli space) but two, to ensure that
$X$ is smoothable (restricting to certain components of the moduli space) but two, to ensure that ![]() $X$ is smoothable to a fixed component of the moduli space. For example, the Fano surfaces
$X$ is smoothable to a fixed component of the moduli space. For example, the Fano surfaces ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ and
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ and ![]() $\mathbb {F}_1$ have the same volume, but are not deformation equivalent, and correspond to two different components of a moduli space. If, for example,
$\mathbb {F}_1$ have the same volume, but are not deformation equivalent, and correspond to two different components of a moduli space. If, for example, ![]() $Z = {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, we would require that
$Z = {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, we would require that ![]() $X$ admits a smoothing to
$X$ admits a smoothing to ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. If
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. If ![]() $Z$ itself has moduli (for example,
$Z$ itself has moduli (for example, ![]() $Z$ a cubic surface in
$Z$ a cubic surface in ![]() ${{\mathbb {P}}}^{3}$), we require that
${{\mathbb {P}}}^{3}$), we require that ![]() $X$ admit a smoothing to a smooth cubic surface, deformation equivalent to
$X$ admit a smoothing to a smooth cubic surface, deformation equivalent to ![]() $Z$.
$Z$.
Our goal is to construct a moduli space ![]() ${{\mathcal {M}}}_{{(Z^{\mathrm{sm}},p,q)}}$ of these pairs.
${{\mathcal {M}}}_{{(Z^{\mathrm{sm}},p,q)}}$ of these pairs.
Remark 2.3 Note that the relationship ![]() $pK_X + qD \sim 0$ implies that, if
$pK_X + qD \sim 0$ implies that, if ![]() $K_X^{n}$ is fixed, so is the volume of the pair
$K_X^{n}$ is fixed, so is the volume of the pair ![]() $(K_X + D)^{n}$. The condition that
$(K_X + D)^{n}$. The condition that ![]() $X$ is Cohen–Macaulay potentially restricts us to some components of the general moduli space, but by [Reference Kollár and KovácsKK10, Corollary 7.13], the components parameterizing non-Cohen–Macaulay pairs are disconnected from these components.
$X$ is Cohen–Macaulay potentially restricts us to some components of the general moduli space, but by [Reference Kollár and KovácsKK10, Corollary 7.13], the components parameterizing non-Cohen–Macaulay pairs are disconnected from these components.
Remark 2.4 In [Reference Deopurkar and HanDH21], for del Pezzo surfaces ![]() $S$ and curves
$S$ and curves ![]() $C$, the authors make the natural generalization of Hacking's definition and refer to pairs
$C$, the authors make the natural generalization of Hacking's definition and refer to pairs ![]() $(S,C)$ as almost K3 stable. This definition coincides with their definition.
$(S,C)$ as almost K3 stable. This definition coincides with their definition.
There are trivial advantages to studying ![]() ${(Z,p,q)}$ (and
${(Z,p,q)}$ (and ![]() ${(Z^{\mathrm{sm}},p,q)}$) H-stable pairs, summarized in the following lemma. These are the primary reasons
${(Z^{\mathrm{sm}},p,q)}$) H-stable pairs, summarized in the following lemma. These are the primary reasons ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs are classifiable.
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs are classifiable.
Lemma 2.5 If ![]() $(X,D)$ is an H-stable pair, the following hold:
$(X,D)$ is an H-stable pair, the following hold:
(a)
 $K_X$ is anti-ample;
$K_X$ is anti-ample;(b)
 $D$ is ample;
$D$ is ample;(c) both
 $K_X$ and
$K_X$ and  $D$ are
$D$ are  ${{\mathbb {Q}}}$-Cartier;
${{\mathbb {Q}}}$-Cartier;(d) if
 $X$ is strictly slc, the strictly slc locus of
$X$ is strictly slc, the strictly slc locus of  $X$ is not contained in the support of
$X$ is not contained in the support of  $D$.
$D$.
2.3 Limits of H-stable pairs exist
In recent work [Reference Kollár and XuKX20], János Kollár and Chenyang Xu prove the following theorem.
Theorem 2.6 [Reference Kollár and XuKX20, Theorem 2]
The irreducible components of the coarse moduli space of ![]() ${(Z,p,q)}$ H-stable pairs are projective.
${(Z,p,q)}$ H-stable pairs are projective.
We are very grateful to János Kollár for pointing our attention to this result and the crucial steps of the proof. In particular, this implies that each component of the moduli stack ![]() ${{\mathcal {M}}}_{{(Z,p,q)}}$ is proper.
${{\mathcal {M}}}_{{(Z,p,q)}}$ is proper.
Theorem 2.7 Let ![]() $0 \in T$ be the germ of a curve and write
$0 \in T$ be the germ of a curve and write ![]() $T^{\times } = T - 0$. Let
$T^{\times } = T - 0$. Let ![]() $X$ be a smooth Fano variety and
$X$ be a smooth Fano variety and ![]() $\mathcal {D}^{\times } \subset X^{\times } \times T^{\times }$ be a family of smooth hypersurfaces over
$\mathcal {D}^{\times } \subset X^{\times } \times T^{\times }$ be a family of smooth hypersurfaces over ![]() $T^{\times }$ such that
$T^{\times }$ such that ![]() $pK_X + qD \sim 0$,
$pK_X + qD \sim 0$, ![]() $0 < {q}/{p} < 1$. Then, there exists a finite surjective base change
$0 < {q}/{p} < 1$. Then, there exists a finite surjective base change ![]() $T' \to T$ and a family
$T' \to T$ and a family ![]() $(\mathcal {X}, \mathcal {D})/T'$ of H-stable pairs extending the pullback of the family
$(\mathcal {X}, \mathcal {D})/T'$ of H-stable pairs extending the pullback of the family ![]() $(X \times T^{\times }, \mathcal {D}^{\times })/T^{\times }$ such that the divisors
$(X \times T^{\times }, \mathcal {D}^{\times })/T^{\times }$ such that the divisors ![]() $K_\mathcal {X}$ and
$K_\mathcal {X}$ and ![]() $\mathcal {D}$ are
$\mathcal {D}$ are ![]() $\mathbb {Q}$-Cartier. Any two such families become isomorphic after a further finite surjective base change.
$\mathbb {Q}$-Cartier. Any two such families become isomorphic after a further finite surjective base change.
Proof. (Sketch.) This is a consequence of Kollár and Xu's Theorem, although we provide a brief sketch of the proof for convenience of the reader. By [Reference Abramovich and KaruAK00, Theorem 0.3], we can complete ![]() $(X \times T^{\times }, \mathcal {D}^{\times })/T^{\times }$ to a locally stable family
$(X \times T^{\times }, \mathcal {D}^{\times })/T^{\times }$ to a locally stable family ![]() $(\mathcal {X}, \mathcal {D})/T'$. Let
$(\mathcal {X}, \mathcal {D})/T'$. Let ![]() $r = {q}/{p}$. Choosing an appropriate ample divisor
$r = {q}/{p}$. Choosing an appropriate ample divisor ![]() $L$ on
$L$ on ![]() $\mathcal {X}$, one can run a relative minimal model program with scaling of
$\mathcal {X}$, one can run a relative minimal model program with scaling of ![]() $L + \mathcal {D}$ to obtain a minimal family over a smooth base, which is locally stable by [Reference Kollár, Nicaise and XuKNX18, Corollary 10]. Furthermore, the total space is
$L + \mathcal {D}$ to obtain a minimal family over a smooth base, which is locally stable by [Reference Kollár, Nicaise and XuKNX18, Corollary 10]. Furthermore, the total space is ![]() $\mathbb {Q}$-factorial and one can show that
$\mathbb {Q}$-factorial and one can show that ![]() $K_{\mathcal {X}^{\mathrm{min}}} + r\mathcal {D}^{\mathrm{min}}$ is relatively trivial and
$K_{\mathcal {X}^{\mathrm{min}}} + r\mathcal {D}^{\mathrm{min}}$ is relatively trivial and ![]() $\mathcal {D}^{\mathrm {min}}$ is relatively big, so by [Reference Hacon and XuHX13, Theorem 1.1] one can find a relative canonical model
$\mathcal {D}^{\mathrm {min}}$ is relatively big, so by [Reference Hacon and XuHX13, Theorem 1.1] one can find a relative canonical model ![]() $(\mathcal {X}^{\rm c}, (r+\epsilon )\mathcal {D}^{\rm c})$. This is a stable family and one can show that
$(\mathcal {X}^{\rm c}, (r+\epsilon )\mathcal {D}^{\rm c})$. This is a stable family and one can show that ![]() $K_{\mathcal {X}^{\rm c}} + r\mathcal {D}^{\rm c}$ is relatively semiample and trivial on the generic fiber, so trivial on the central fiber. Because both
$K_{\mathcal {X}^{\rm c}} + r\mathcal {D}^{\rm c}$ is relatively semiample and trivial on the generic fiber, so trivial on the central fiber. Because both ![]() $K_{\mathcal {X}^{\rm c}} + r\mathcal {D}^{\rm c}$ and
$K_{\mathcal {X}^{\rm c}} + r\mathcal {D}^{\rm c}$ and ![]() $K_{\mathcal {X}^{\rm c}} + (r + \epsilon ) \mathcal {D}^{\rm c}$ are
$K_{\mathcal {X}^{\rm c}} + (r + \epsilon ) \mathcal {D}^{\rm c}$ are ![]() $\mathbb {Q}$-Cartier, we have
$\mathbb {Q}$-Cartier, we have ![]() $K_{\mathcal {X}^{\rm c}}$ and
$K_{\mathcal {X}^{\rm c}}$ and ![]() $\mathcal {D}^{\rm c}$ are both
$\mathcal {D}^{\rm c}$ are both ![]() $\mathbb {Q}$-Cartier. Therefore,
$\mathbb {Q}$-Cartier. Therefore, ![]() $(\mathcal {X}^{\rm c}, \mathcal {D}^{\rm c})$ is the desired family of H-stable pairs. Uniqueness follows from uniqueness of canonical models.
$(\mathcal {X}^{\rm c}, \mathcal {D}^{\rm c})$ is the desired family of H-stable pairs. Uniqueness follows from uniqueness of canonical models.
3. The moduli space
3.1 Boundedness
First, we show the moduli functor is bounded. This argument is inspired by that in [Reference KaruKar00, Theorem 1.1] and is similar to the proof of Kollár and Xu's Theorem (Theorem 2.6). As before, this is also a consequence of Theorem 2.6.
Theorem 3.1 For a given Fano variety ![]() $Z$, the set of
$Z$, the set of ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs
${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs ![]() $(X,D)$ form a bounded family.
$(X,D)$ form a bounded family.
Proof. By a theorem of Matsusaka [Reference MatsusakaMat86, Theorem 2.4], there is a fixed integer ![]() $m$ such that all smooth Fano varieties
$m$ such that all smooth Fano varieties ![]() $X$ with fixed anticanonical Hilbert polynomial
$X$ with fixed anticanonical Hilbert polynomial ![]() $H_X(l) = \chi (X,-lK_X) = \chi (Z,-lK_Z)$ have
$H_X(l) = \chi (X,-lK_X) = \chi (Z,-lK_Z)$ have ![]() $-mK_X$ very ample with no higher cohomology, hence a fixed projective space
$-mK_X$ very ample with no higher cohomology, hence a fixed projective space ![]() ${{\mathbb {P}}}^{n}$ containing all such
${{\mathbb {P}}}^{n}$ containing all such ![]() $X$. In particular,
$X$. In particular, ![]() $Z$ is one such
$Z$ is one such ![]() $X$, as is any smooth variety
$X$, as is any smooth variety ![]() $W$ deformation equivalent to
$W$ deformation equivalent to ![]() $Z$. Let
$Z$. Let ![]() $r = {q}/{p}$. Similarly, we can choose
$r = {q}/{p}$. Similarly, we can choose ![]() $m$ such that
$m$ such that ![]() $-mK_W|_D$ is very ample with no higher cohomology for any smooth
$-mK_W|_D$ is very ample with no higher cohomology for any smooth ![]() $D \sim _{\mathbb {Q}} -r^{-1}K_W$. We can find a product
$D \sim _{\mathbb {Q}} -r^{-1}K_W$. We can find a product ![]() $\mathrm {Hilb}$ of Hilbert schemes parameterizing embeddings
$\mathrm {Hilb}$ of Hilbert schemes parameterizing embeddings ![]() $D \subset W \subset {{\mathbb {P}}}^{n}$. Let
$D \subset W \subset {{\mathbb {P}}}^{n}$. Let ![]() $B_0 \subset \mathrm {Hilb}$ be the subscheme parameterizing such pairs. Taking its closure
$B_0 \subset \mathrm {Hilb}$ be the subscheme parameterizing such pairs. Taking its closure ![]() $B_0 \subset B \subset \mathrm {Hilb}$, there is a universal family
$B_0 \subset B \subset \mathrm {Hilb}$, there is a universal family ![]() $(\mathcal {X}, \mathcal {D}) \to B$ whose general fiber is deformation equivalent to the smooth Fano variety
$(\mathcal {X}, \mathcal {D}) \to B$ whose general fiber is deformation equivalent to the smooth Fano variety ![]() $Z$ with a smooth divisor
$Z$ with a smooth divisor ![]() $D$. By [Reference Abramovich and KaruAK00, Theorem 0.3], we can apply weak semistable reduction to obtain a locally stable family
$D$. By [Reference Abramovich and KaruAK00, Theorem 0.3], we can apply weak semistable reduction to obtain a locally stable family ![]() $(\mathcal {Y}, \mathcal {D}_{\mathcal {Y}}) \to B'$, where
$(\mathcal {Y}, \mathcal {D}_{\mathcal {Y}}) \to B'$, where ![]() $B' \to B$ is a modification of
$B' \to B$ is a modification of ![]() $B$ and
$B$ and ![]() $\mathcal {Y} \to \mathcal {X}' = \mathcal {X} \times _B B'$ is a modification of
$\mathcal {Y} \to \mathcal {X}' = \mathcal {X} \times _B B'$ is a modification of ![]() $\mathcal {X}'$. We can apply the techniques of proof of Theorems 2.6 and 2.7 to find the
$\mathcal {X}'$. We can apply the techniques of proof of Theorems 2.6 and 2.7 to find the ![]() $K_{\mathcal {Y}} + (r + \epsilon ) \mathcal {D}_{\mathcal {Y}}$ canonical model over
$K_{\mathcal {Y}} + (r + \epsilon ) \mathcal {D}_{\mathcal {Y}}$ canonical model over ![]() $B'$ for any
$B'$ for any ![]() $\epsilon$ sufficiently small; call it
$\epsilon$ sufficiently small; call it ![]() $(\mathcal {Y}^{\rm c}, \mathcal {D}^{\rm c})$. It is straightforward to show that every fiber satisfies the conditions of being an H-stable pair; now it suffices to show that every H-stable pair appears as a fiber.
$(\mathcal {Y}^{\rm c}, \mathcal {D}^{\rm c})$. It is straightforward to show that every fiber satisfies the conditions of being an H-stable pair; now it suffices to show that every H-stable pair appears as a fiber.
Because the weak semistable reduction potentially modifies even smooth fibers, we first need to show the generic smooth fibers are isomorphic to the generic fibers of the canonical model. Let ![]() $(\mathcal {X}^{0}, \mathcal {D}^{0})$ be the universal family over
$(\mathcal {X}^{0}, \mathcal {D}^{0})$ be the universal family over ![]() $B_0$ and let
$B_0$ and let ![]() $({\mathcal {X}^{0}}', {\mathcal {D}^{0}}')$ be the family over the preimage
$({\mathcal {X}^{0}}', {\mathcal {D}^{0}}')$ be the family over the preimage ![]() $B_0' \subset B'$. Let
$B_0' \subset B'$. Let ![]() $(\mathcal {Y}^{0,c}, \mathcal {D}^{0,c}) \to B_0'$ be the fibers of the canonical model over
$(\mathcal {Y}^{0,c}, \mathcal {D}^{0,c}) \to B_0'$ be the fibers of the canonical model over ![]() $B_0'$. Because the fibers of
$B_0'$. Because the fibers of ![]() $({\mathcal {X}^{0}}', {\mathcal {D}^{0}}') \to B_0'$ are smooth Fano varieties with smooth divisors
$({\mathcal {X}^{0}}', {\mathcal {D}^{0}}') \to B_0'$ are smooth Fano varieties with smooth divisors ![]() $D$ over a smooth base, it follows that
$D$ over a smooth base, it follows that ![]() $({\mathcal {X}^{0}}', {\mathcal {D}^{0}}')$ is its own relative canonical model, and birational to
$({\mathcal {X}^{0}}', {\mathcal {D}^{0}}')$ is its own relative canonical model, and birational to ![]() $(\mathcal {Y}^{0,c}, \mathcal {D}^{0,c})$ by construction. Therefore, by uniqueness of canonical models, we must have
$(\mathcal {Y}^{0,c}, \mathcal {D}^{0,c})$ by construction. Therefore, by uniqueness of canonical models, we must have ![]() $({\mathcal {X}^{0}}', {\mathcal {D}^{0}}') \cong (\mathcal {Y}^{0,c}, \mathcal {D}^{0,c}).$
$({\mathcal {X}^{0}}', {\mathcal {D}^{0}}') \cong (\mathcal {Y}^{0,c}, \mathcal {D}^{0,c}).$
Now, let ![]() $(Y,D_Y)$ be any H-stable pair. By the smoothability assumption,
$(Y,D_Y)$ be any H-stable pair. By the smoothability assumption, ![]() $(Y,D_Y)$ admits a smoothing over the germ of a curve to
$(Y,D_Y)$ admits a smoothing over the germ of a curve to ![]() $(W,D_W)$ for some
$(W,D_W)$ for some ![]() $D_W$, so
$D_W$, so ![]() $(Y, D_Y)$ is the central fiber of some family
$(Y, D_Y)$ is the central fiber of some family ![]() $(\mathcal {X}, \mathcal {D}) \to T$, where
$(\mathcal {X}, \mathcal {D}) \to T$, where ![]() $T$ is a discrete valuation ring. Up to a finite base change, the generic fiber
$T$ is a discrete valuation ring. Up to a finite base change, the generic fiber ![]() $(\mathcal {X}^{\times }, \mathcal {D}^{\times }) \to T^{\times }$ gives an embedding
$(\mathcal {X}^{\times }, \mathcal {D}^{\times }) \to T^{\times }$ gives an embedding ![]() $T^{\times } \to B'$ which can be completed to a curve
$T^{\times } \to B'$ which can be completed to a curve ![]() $T' \subset B'$. The family over
$T' \subset B'$. The family over ![]() $T'$ has the same generic fiber as
$T'$ has the same generic fiber as ![]() $(\mathcal {X}, \mathcal {D}) \to T$, but up to a finite base change, both families are canonical models of a common semistable resolution. Therefore, their central fibers are isomorphic.
$(\mathcal {X}, \mathcal {D}) \to T$, but up to a finite base change, both families are canonical models of a common semistable resolution. Therefore, their central fibers are isomorphic.
As mentioned in § 2, one could define an alternate class of pairs, omitting the condition that each pair admits a smoothing. Indeed, even for quintic surfaces in ![]() ${{\mathbb {P}}}^{3}$, there should be a second component of the moduli space of smooth surfaces as discussed in § 5, so it seems natural to relax this condition. Although we do not have boundedness of non-smoothable pairs in general, we can prove boundedness of
${{\mathbb {P}}}^{3}$, there should be a second component of the moduli space of smooth surfaces as discussed in § 5, so it seems natural to relax this condition. Although we do not have boundedness of non-smoothable pairs in general, we can prove boundedness of ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs when
${(\mathbb {P}^{3},d,4)}$ H-stable pairs when ![]() $d$ is odd. This is further discussed in § 4 and proven in Theorem 4.32.
$d$ is odd. This is further discussed in § 4 and proven in Theorem 4.32.
3.2 Algebraicity
Using recent results, we can further analyze the structure of the moduli space of H-stable pairs. We study Kollár families of pairs, ![]() $\mathbb {Q}$-Gorenstein families where
$\mathbb {Q}$-Gorenstein families where ![]() $\omega _{\mathcal {X}}^{[n]}$ commutes with base change for all
$\omega _{\mathcal {X}}^{[n]}$ commutes with base change for all ![]() $n$. In fact, we will require a stronger condition that both
$n$. In fact, we will require a stronger condition that both ![]() $\omega _{\mathcal {X}}^{[n]}$ and
$\omega _{\mathcal {X}}^{[n]}$ and ![]() ${{\mathcal {O}}}_{\mathcal {X}}(nD)$ commute with base change for all
${{\mathcal {O}}}_{\mathcal {X}}(nD)$ commute with base change for all ![]() $n$. Using [Reference HackingHac04, c.f. Theorem 4.4] and following his work, one can show that the moduli space is indeed an algebraic stack.
$n$. Using [Reference HackingHac04, c.f. Theorem 4.4] and following his work, one can show that the moduli space is indeed an algebraic stack.
Definition 3.2 Let ![]() $p \in X$ be a germ of an slc variety. Define the index of
$p \in X$ be a germ of an slc variety. Define the index of ![]() $p$ in
$p$ in ![]() $X$ to be the minimal
$X$ to be the minimal ![]() $N > 0$ such that
$N > 0$ such that ![]() $NK_X$ is Cartier. Let
$NK_X$ is Cartier. Let ![]() $V \to X$ be the canonical covering
$V \to X$ be the canonical covering ![]() $V = \text {Spec}_X \mathcal {O} \oplus \mathcal {O}(K_X) \oplus \cdots \oplus \mathcal {O}((N-1)K_X)$, a
$V = \text {Spec}_X \mathcal {O} \oplus \mathcal {O}(K_X) \oplus \cdots \oplus \mathcal {O}((N-1)K_X)$, a ![]() $\mu _N$ quotient (cf. [Reference ReidRei87]). A deformation
$\mu _N$ quotient (cf. [Reference ReidRei87]). A deformation ![]() $\mathcal {X}/S$ of
$\mathcal {X}/S$ of ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-Gorenstein if there is a
$\mathbb {Q}$-Gorenstein if there is a ![]() $\mu _N$-equivariant deformation
$\mu _N$-equivariant deformation ![]() $\mathcal {V}/S$ of
$\mathcal {V}/S$ of ![]() $V$ whose quotient is
$V$ whose quotient is ![]() $\mathcal {X}/S$.
$\mathcal {X}/S$.
Definition 3.3 Let ![]() $\mathcal {X}/S$ be a flat family of slc varieties. We say that
$\mathcal {X}/S$ be a flat family of slc varieties. We say that ![]() $\mathcal {X}$ is weakly
$\mathcal {X}$ is weakly ![]() $\mathbb {Q}$-Gorenstein if, for some
$\mathbb {Q}$-Gorenstein if, for some ![]() $N > 0, \omega _{\mathcal {X}/S}^{[N]}$ is invertible. The minimal such
$N > 0, \omega _{\mathcal {X}/S}^{[N]}$ is invertible. The minimal such ![]() $N$ is called the index of
$N$ is called the index of ![]() $\mathcal {X}$.
$\mathcal {X}$.
The following lemmas show that ![]() $\mathbb {Q}$-Gorenstein implies weakly
$\mathbb {Q}$-Gorenstein implies weakly ![]() $\mathbb {Q}$-Gorenstein and that the conditions are equivalent if the general fiber is canonical and the base is a curve.
$\mathbb {Q}$-Gorenstein and that the conditions are equivalent if the general fiber is canonical and the base is a curve.
Lemma 3.4 Let ![]() $p \in X$ be a germ of an slc variety. A
$p \in X$ be a germ of an slc variety. A ![]() $\mathbb {Q}$-Gorenstein deformation
$\mathbb {Q}$-Gorenstein deformation ![]() $\mathcal {X}/S$ of
$\mathcal {X}/S$ of ![]() $X$ of index
$X$ of index ![]() $N$ is weakly
$N$ is weakly ![]() $\mathbb {Q}$-Gorenstein of index
$\mathbb {Q}$-Gorenstein of index ![]() $N$.
$N$.
Proof. This follows directly from [Reference HackingHac04, Lemma 3.3].
Lemma 3.5 Let ![]() $\mathcal {X}/T$ be a flat family of slc varieties over the germ of a curve. If the general fiber has canonical singularities and
$\mathcal {X}/T$ be a flat family of slc varieties over the germ of a curve. If the general fiber has canonical singularities and ![]() $K_{\mathcal {X}}$ is
$K_{\mathcal {X}}$ is ![]() $\mathbb {Q}$-Cartier, then
$\mathbb {Q}$-Cartier, then ![]() $\mathcal {X}/S$ is a
$\mathcal {X}/S$ is a ![]() $\mathbb {Q}$-Gorenstein deformation of
$\mathbb {Q}$-Gorenstein deformation of ![]() $\mathcal {X}_0$.
$\mathcal {X}_0$.
Proof. Using the stronger inversion of adjunction result in [Reference PatakfalviPat16, Lemma 2.10], the proof of Lemma 3.4 in [Reference HackingHac04] applies directly.
Many properties of ![]() $\mathbb {Q}$-Gorenstein deformations are collected in [Reference HackingHac04, § 3]. In fact,
$\mathbb {Q}$-Gorenstein deformations are collected in [Reference HackingHac04, § 3]. In fact, ![]() $\mathbb {Q}$-Gorenstein deformations
$\mathbb {Q}$-Gorenstein deformations ![]() $X$ are exactly the deformations
$X$ are exactly the deformations ![]() ${{\mathcal {X}}}$ of
${{\mathcal {X}}}$ of ![]() $X$ satisfying the Kollár condition that
$X$ satisfying the Kollár condition that ![]() $\omega _{{\mathcal {X}}}^{[n]}$ commutes with base change for all
$\omega _{{\mathcal {X}}}^{[n]}$ commutes with base change for all ![]() $n$ (see [Reference HackingHac12, 2.4]). However, the presence of the divisor
$n$ (see [Reference HackingHac12, 2.4]). However, the presence of the divisor ![]() $D$ can cause further obstructions to deforming
$D$ can cause further obstructions to deforming ![]() $X$. In particular, taking the canonical cover
$X$. In particular, taking the canonical cover ![]() $V$ of
$V$ of ![]() $X$, the associated divisor
$X$, the associated divisor ![]() $D_V$ does not have to be a Cartier divisor.
$D_V$ does not have to be a Cartier divisor.
Example 3.6 Let ![]() $X$ be the cone over the anticanonical embedding of
$X$ be the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, a section of
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, a section of ![]() ${{\mathcal {O}}}_W(2)$ in
${{\mathcal {O}}}_W(2)$ in ![]() $W = {{\mathbb {P}}}(1,1,1,1,2)$. This is a
$W = {{\mathbb {P}}}(1,1,1,1,2)$. This is a ![]() $\mathbb {Q}$-Gorenstein deformation of
$\mathbb {Q}$-Gorenstein deformation of ![]() ${{\mathbb {P}}}^{3}$ as computed in Example 4.34 and appears in
${{\mathbb {P}}}^{3}$ as computed in Example 4.34 and appears in ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs. Note that
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs. Note that ![]() $X$ has canonical singularities, so the canonical cover of
$X$ has canonical singularities, so the canonical cover of ![]() $X$ is
$X$ is ![]() $X$ itself and
$X$ itself and ![]() ${{\mathcal {O}}}_X(K_X) = {{\mathcal {O}}}_W(-4)|_X$. A general surface
${{\mathcal {O}}}_X(K_X) = {{\mathcal {O}}}_W(-4)|_X$. A general surface ![]() $D$ such that
$D$ such that ![]() $dK_X + 4D \sim 0$ is an element of
$dK_X + 4D \sim 0$ is an element of ![]() ${{\mathcal {O}}}_W(d)|_X$. If
${{\mathcal {O}}}_W(d)|_X$. If ![]() $d$ is odd,
$d$ is odd, ![]() $D$ is not a Cartier divisor.
$D$ is not a Cartier divisor.
This contrasts the picture for plane curves, ![]() $(d,3) {{\mathbb {P}}}^{2}$ H-stable pairs: in [Reference HackingHac04, Theorem 3.12], it is shown that
$(d,3) {{\mathbb {P}}}^{2}$ H-stable pairs: in [Reference HackingHac04, Theorem 3.12], it is shown that ![]() $D_V$, the induced divisor on the canonical cover, is always Cartier. In order to avoid obstructions coming from the divisor
$D_V$, the induced divisor on the canonical cover, is always Cartier. In order to avoid obstructions coming from the divisor ![]() $D$, we consider higher-index covers. By considering the canonical covering of slightly higher index, we can show that studying deformations of the pair
$D$, we consider higher-index covers. By considering the canonical covering of slightly higher index, we can show that studying deformations of the pair ![]() $(X,D)$ amounts to studying deformations of
$(X,D)$ amounts to studying deformations of ![]() $X$ because the presence of the divisor
$X$ because the presence of the divisor ![]() $D$ does not add any further obstructions. In fact, this can be done by taking the canonical covering
$D$ does not add any further obstructions. In fact, this can be done by taking the canonical covering ![]() $V$ corresponding to
$V$ corresponding to ![]() $N'K_X$, where
$N'K_X$, where ![]() $N'$ is the index of the
$N'$ is the index of the ![]() $\mathbb {Q}$-divisor
$\mathbb {Q}$-divisor ![]() $({1}/{q})K_X$: the relationship
$({1}/{q})K_X$: the relationship ![]() $pK_X + qD \sim 0$ implies that
$pK_X + qD \sim 0$ implies that ![]() $D_V$ is Cartier on
$D_V$ is Cartier on ![]() $V$. We call such a cover a
$V$. We call such a cover a ![]() $q$-canonical cover and such a deformation a
$q$-canonical cover and such a deformation a ![]() $q$-
$q$-![]() $\mathbb {Q}$-Gorenstein deformation. By the same proof as in [Reference HackingHac12, 2.4], these deformations are exactly those such that both
$\mathbb {Q}$-Gorenstein deformation. By the same proof as in [Reference HackingHac12, 2.4], these deformations are exactly those such that both ![]() $K_{\mathcal {X}}$ and
$K_{\mathcal {X}}$ and ![]() $\mathcal {D}$ commute with base change.
$\mathcal {D}$ commute with base change.
Theorem 3.7 Let ![]() $(\mathcal {X}, \mathcal {D})/A$ be a
$(\mathcal {X}, \mathcal {D})/A$ be a ![]() $\mathbb {Q}$-Gorenstein family H-stable pairs. Let
$\mathbb {Q}$-Gorenstein family H-stable pairs. Let ![]() $A' \to A$ be an infinitesimal extension and
$A' \to A$ be an infinitesimal extension and ![]() $\mathcal {X}' \to A'$ a
$\mathcal {X}' \to A'$ a ![]() $q$-
$q$-![]() $\mathbb {Q}$-Gorenstein deformation of
$\mathbb {Q}$-Gorenstein deformation of ![]() $\mathcal {X}/A$. Then, there exists a
$\mathcal {X}/A$. Then, there exists a ![]() $\mathbb {Q}$-Gorenstein deformation
$\mathbb {Q}$-Gorenstein deformation ![]() $(\mathcal {X}',\mathcal {D}')/A'$ of
$(\mathcal {X}',\mathcal {D}')/A'$ of ![]() $(\mathcal {X}, \mathcal {D})/A$.
$(\mathcal {X}, \mathcal {D})/A$.
Proof. Using the following lemma in place of Lemma 3.14 in the proof of Theorem 3.12 in [Reference HackingHac04], the same proof holds.
Lemma 3.8 Let ![]() $(X,D)$ be an H-stable pair. Then,
$(X,D)$ be an H-stable pair. Then, ![]() $H^{1}(X, \mathcal {O}_X(D)) = 0$.
$H^{1}(X, \mathcal {O}_X(D)) = 0$.
Proof. Recall that ![]() $D$ is an ample
$D$ is an ample ![]() $\mathbb {Q}$-Cartier
$\mathbb {Q}$-Cartier ![]() $\mathbb {Z}$-divisor. Although this is a standard consequence of Kawamata–Viehweg vanishing when
$\mathbb {Z}$-divisor. Although this is a standard consequence of Kawamata–Viehweg vanishing when ![]() $X$ is log-terminal, for the general case we apply [Reference FujinoFuj14, Theorem 1.7] to
$X$ is log-terminal, for the general case we apply [Reference FujinoFuj14, Theorem 1.7] to ![]() $(X,0)$, noting that
$(X,0)$, noting that ![]() $D$ and
$D$ and ![]() $-K_X$ are ample, so
$-K_X$ are ample, so ![]() $D-K_X$ is ample. Note that the hypotheses in [Reference FujinoFuj14, Theorem 1.7] are satisfied because
$D-K_X$ is ample. Note that the hypotheses in [Reference FujinoFuj14, Theorem 1.7] are satisfied because ![]() $(X,({q}/{p})D)$ is slc and, by definition,
$(X,({q}/{p})D)$ is slc and, by definition, ![]() $D$ does not contain any component of the conductor of
$D$ does not contain any component of the conductor of ![]() $X$ (see [Reference KollárKol13, Definition-Lemma 5.10]).
$X$ (see [Reference KollárKol13, Definition-Lemma 5.10]).
We continue Example 3.6 and compute the ![]() $4$-canonical covering.
$4$-canonical covering.
Example 3.9 Let ![]() $X$ be the cone over the anticanonical embedding of
$X$ be the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, a section of
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, a section of ![]() ${{\mathcal {O}}}_W(2)$ in
${{\mathcal {O}}}_W(2)$ in ![]() $W = {{\mathbb {P}}}(1,1,1,1,2)$, so
$W = {{\mathbb {P}}}(1,1,1,1,2)$, so ![]() ${{\mathcal {O}}}_X(K_X) = {{\mathcal {O}}}_W(-4)|_X$. Therefore,
${{\mathcal {O}}}_X(K_X) = {{\mathcal {O}}}_W(-4)|_X$. Therefore, ![]() ${{\mathcal {O}}}_X(\frac {1}{2}K_X) = {{\mathcal {O}}}_X(-2)$ is Cartier, so we need to construct a
${{\mathcal {O}}}_X(\frac {1}{2}K_X) = {{\mathcal {O}}}_X(-2)$ is Cartier, so we need to construct a ![]() $2:1$ cover to make
$2:1$ cover to make ![]() $\frac {1}{4}K_X$ a Cartier divisor. Alternatively, we are taking a cover to make
$\frac {1}{4}K_X$ a Cartier divisor. Alternatively, we are taking a cover to make ![]() ${{\mathcal {O}}}_X(1)$ a Cartier divisor. Let
${{\mathcal {O}}}_X(1)$ a Cartier divisor. Let ![]() $X' \subset {{\mathbb {P}}}^{4}$ be the cone over the quadric surface in
$X' \subset {{\mathbb {P}}}^{4}$ be the cone over the quadric surface in ![]() ${{\mathbb {P}}}^{3}$, so
${{\mathbb {P}}}^{3}$, so ![]() $X'$ is the cone over the
$X'$ is the cone over the ![]() $(1,1)$-embedding of
$(1,1)$-embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Because
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Because ![]() $X$ is the cone over the
$X$ is the cone over the ![]() $(2,2)$-embedding of the same surface, there is a finite morphism
$(2,2)$-embedding of the same surface, there is a finite morphism ![]() $X' \to X$ which is the desired cover near the singular point of
$X' \to X$ which is the desired cover near the singular point of ![]() $X$.
$X$.
In [Reference HackingHac04, § 3], the author computes the deformation and obstruction spaces for these pairs. We can use this and Examples 3.6 and 3.9 to show that the moduli space ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ is generically smooth along the locus parameterizing pairs
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ is generically smooth along the locus parameterizing pairs ![]() $(X,D)$ where
$(X,D)$ where ![]() $X$ is the cone over the anticanonical embedding of
$X$ is the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Later, in Proposition 4.41, we show that this locus is actually a divisor in
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Later, in Proposition 4.41, we show that this locus is actually a divisor in ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$.
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$.
Proposition 3.10 Let ![]() $X$ be the cone over the anticanonical embedding of
$X$ be the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Then,
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Then, ![]() $X$ has unobstructed
$X$ has unobstructed ![]() $4$-
$4$-![]() $\mathbb {Q}$-Gorenstein deformations. In particular, the moduli space
$\mathbb {Q}$-Gorenstein deformations. In particular, the moduli space ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ is smooth at the generic point of the locus parameterizing surfaces on
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ is smooth at the generic point of the locus parameterizing surfaces on ![]() $X$.
$X$.
Proof. By [Reference HackingHac04, Remark after 3.9], the obstructions to extending ![]() $4$-
$4$-![]() $\mathbb {Q}$-Gorenstein deformations of
$\mathbb {Q}$-Gorenstein deformations of ![]() $X$ are contained in sheaves
$X$ are contained in sheaves ![]() $T^{2}_{QG,X}$ (see [Reference HackingHac04, Notation 3.6]). Furthermore, there is a spectral sequence
$T^{2}_{QG,X}$ (see [Reference HackingHac04, Notation 3.6]). Furthermore, there is a spectral sequence ![]() $H^{p}({{\mathcal {T}}}^{q}_{QG,X}) \Rightarrow T^{p+q}_{QG,X}$. If, locally,
$H^{p}({{\mathcal {T}}}^{q}_{QG,X}) \Rightarrow T^{p+q}_{QG,X}$. If, locally, ![]() $\pi : V \to X$ is the
$\pi : V \to X$ is the ![]() $4$-canonical cover where
$4$-canonical cover where ![]() $X$ is the quotient by a group
$X$ is the quotient by a group ![]() $G$, we can compute
$G$, we can compute ![]() ${{\mathcal {T}}}^{q}_{QG,X} = (\pi _*{{\mathcal {T}}}^{q}_V)^{G}$. Furthermore,
${{\mathcal {T}}}^{q}_{QG,X} = (\pi _*{{\mathcal {T}}}^{q}_V)^{G}$. Furthermore, ![]() ${{\mathcal {T}}}^{0}_{QG,X} = {{\mathcal {T}}}^{0}_X, {{\mathcal {T}}}^{1}_V$ is supported on the singular locus of
${{\mathcal {T}}}^{0}_{QG,X} = {{\mathcal {T}}}^{0}_X, {{\mathcal {T}}}^{1}_V$ is supported on the singular locus of ![]() $V$, and
$V$, and ![]() ${{\mathcal {T}}}^{2}_V$ is supported where
${{\mathcal {T}}}^{2}_V$ is supported where ![]() $V$ is not a local complete intersection. By Example 3.9, if
$V$ is not a local complete intersection. By Example 3.9, if ![]() $X$ is the cone over the anticanonical embedding of
$X$ is the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, then
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, then ![]() $V$ is the cone over the quadric surface. Because the singular locus of
$V$ is the cone over the quadric surface. Because the singular locus of ![]() $V$ is a single point and
$V$ is a single point and ![]() $V$ is a hypersurface, we have
$V$ is a hypersurface, we have ![]() $H^{1}({{\mathcal {T}}}^{1}_V) = 0$ and
$H^{1}({{\mathcal {T}}}^{1}_V) = 0$ and ![]() $H^{0}({{\mathcal {T}}}^{2}_V) = 0$. A computation shows that
$H^{0}({{\mathcal {T}}}^{2}_V) = 0$. A computation shows that ![]() $H^{2}({{\mathcal {T}}}^{0}_X) = 0$, hence
$H^{2}({{\mathcal {T}}}^{0}_X) = 0$, hence ![]() $T^{2}_{QG,X} = 0$.
$T^{2}_{QG,X} = 0$.
Finally, we aim to describe the moduli functor. In the definition of ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs, we require that
${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs, we require that ![]() $(X,D)$ has a smoothing to
$(X,D)$ has a smoothing to ![]() $(W, D_W)$, where
$(W, D_W)$, where ![]() $W$ is a smooth Fano variety deformation equivalent to
$W$ is a smooth Fano variety deformation equivalent to ![]() $Z$. Therefore, we are interested only in certain ‘smoothable’ deformations of
$Z$. Therefore, we are interested only in certain ‘smoothable’ deformations of ![]() $(X,D)$, made precise in the following.
$(X,D)$, made precise in the following.
Definition 3.11 Let ![]() $(X,D)/\mathbb {C}$ be a
$(X,D)/\mathbb {C}$ be a ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable pair. Let
${(Z^{\mathrm{sm}},p,q)}$ H-stable pair. Let ![]() $(\mathcal {X}^{u}, \mathcal {D}^{u})/S_0$ be a versal
$(\mathcal {X}^{u}, \mathcal {D}^{u})/S_0$ be a versal ![]() $\mathbb {Q}$-Gorenstein deformation of
$\mathbb {Q}$-Gorenstein deformation of ![]() $(X,D)$, where
$(X,D)$, where ![]() $S_0$ is finite type over
$S_0$ is finite type over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $S_1 \subset S_0$ be the open subscheme where the fibers of
$S_1 \subset S_0$ be the open subscheme where the fibers of ![]() $\mathcal {X}^{u}$ over
$\mathcal {X}^{u}$ over ![]() $S_0$ are smooth and deformation equivalent to
$S_0$ are smooth and deformation equivalent to ![]() $Z$ and
$Z$ and ![]() $S_2$ the (scheme-theoretic) closure of
$S_2$ the (scheme-theoretic) closure of ![]() $S_1$ in
$S_1$ in ![]() $S_0$. A
$S_0$. A ![]() $q$-
$q$-![]() $\mathbb {Q}$-Gorenstein deformation of
$\mathbb {Q}$-Gorenstein deformation of ![]() $(X,D)$ is said to be smoothable if it can be obtained by pullback from the deformation
$(X,D)$ is said to be smoothable if it can be obtained by pullback from the deformation ![]() $(\mathcal {X}^{u}, \mathcal {D}^{u}) \times _{S_0} S_2 \to 0 \in S_2$.
$(\mathcal {X}^{u}, \mathcal {D}^{u}) \times _{S_0} S_2 \to 0 \in S_2$.
Remark 3.12 In [Reference HackingHac04], it is shown that this condition is vacuous for ![]() $(d,3) {{\mathbb {P}}}^{2}$-smoothable H-stable pairs when
$(d,3) {{\mathbb {P}}}^{2}$-smoothable H-stable pairs when ![]() $d$ is not a multiple of
$d$ is not a multiple of ![]() $3$, but non-trivial when
$3$, but non-trivial when ![]() $3$ divides
$3$ divides ![]() $d$.
$d$.
For the definition of family of ![]() $\mathbb {Q}$-Gorenstein smoothable pairs, and more technicalities on the necessary conditions for the divisor
$\mathbb {Q}$-Gorenstein smoothable pairs, and more technicalities on the necessary conditions for the divisor ![]() ${{\mathcal {D}}}$ to be well-behaved, we refer the reader to the recent paper [Reference KollárKol19] of Kollár. We include the necessary definition here (see [Reference KollárKol19, Definition 10]). Note that the idea of K-flatness over a reduced base is equivalent to the usual definition of family of stable pairs [Reference KollárKol17].
${{\mathcal {D}}}$ to be well-behaved, we refer the reader to the recent paper [Reference KollárKol19] of Kollár. We include the necessary definition here (see [Reference KollárKol19, Definition 10]). Note that the idea of K-flatness over a reduced base is equivalent to the usual definition of family of stable pairs [Reference KollárKol17].
Definition 3.13 A family of stable pairs is a morphism ![]() $f : (X, cD) \to S$, where:
$f : (X, cD) \to S$, where:
(i)
 $f: X \to S$ is flat and projective;
$f: X \to S$ is flat and projective;(ii)
 $D$ is a K-flat family of divisors on
$D$ is a K-flat family of divisors on  $X$ (see [Reference KollárKol19, Definition 2]);
$X$ (see [Reference KollárKol19, Definition 2]);(iii)
 $K_X + cD$ is
$K_X + cD$ is  $\mathbb {Q}$ Cartier and relatively ample; and
$\mathbb {Q}$ Cartier and relatively ample; and(iv) the fibers
 $(X_s, cD_s)$ are slc.
$(X_s, cD_s)$ are slc.
Definition 3.14 Let ![]() $Sch$ be the category of noetherian schemes over
$Sch$ be the category of noetherian schemes over ![]() $\mathbb {C}$. For a smooth Fano variety
$\mathbb {C}$. For a smooth Fano variety ![]() $Z$ and
$Z$ and ![]() $(p,q)\in \mathbb {N}^{2}$, we define a moduli pseudofunctor over a reduced base
$(p,q)\in \mathbb {N}^{2}$, we define a moduli pseudofunctor over a reduced base ![]() $S$ as
$S$ as ![]() $\mathcal {M}_{{(Z^{\mathrm{sm}},p,q)}} \to Sch$ by
$\mathcal {M}_{{(Z^{\mathrm{sm}},p,q)}} \to Sch$ by
As stated previously, in [Reference HackingHac04], it is shown that the ![]() $\mathbb {Q}$-Gorenstein deformation condition is equivalent to requiring the Kollár condition on families. Using the deformation theory in [Reference HackingHac04, § 3], Theorem 2.7, and the finiteness of automorphism groups [Reference KollárKol13, Corollary 10.69] we deduce the following theorem.
$\mathbb {Q}$-Gorenstein deformation condition is equivalent to requiring the Kollár condition on families. Using the deformation theory in [Reference HackingHac04, § 3], Theorem 2.7, and the finiteness of automorphism groups [Reference KollárKol13, Corollary 10.69] we deduce the following theorem.
Theorem 3.15 The moduli space of ![]() ${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs is a proper Deligne–Mumford stack.
${(Z^{\mathrm{sm}},p,q)}$ H-stable pairs is a proper Deligne–Mumford stack.
Remark 3.16 As mentioned in § 2, one could remove the condition that H-stable pairs admit a smoothing to ![]() $Z$ and define an analogous moduli functor
$Z$ and define an analogous moduli functor ![]() ${{\mathcal {M}}}_{{(Z,p,q)}}$ of pairs, although the class of arbitrary
${{\mathcal {M}}}_{{(Z,p,q)}}$ of pairs, although the class of arbitrary ![]() ${(Z,p,q)}$ H-stable pairs is not obviously bounded. However, Theorem 4.32 says that
${(Z,p,q)}$ H-stable pairs is not obviously bounded. However, Theorem 4.32 says that ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs are bounded for odd degree
${(\mathbb {P}^{3},d,4)}$ H-stable pairs are bounded for odd degree ![]() $d$, and this moduli space is still proper. Although the proof of properness was given for pairs that admit a smoothing, the same proof applies more generally. By Hacking's work in [Reference HackingHac04, § 3] and the boundedness theorem, we obtain the following.
$d$, and this moduli space is still proper. Although the proof of properness was given for pairs that admit a smoothing, the same proof applies more generally. By Hacking's work in [Reference HackingHac04, § 3] and the boundedness theorem, we obtain the following.
Theorem 3.17 For odd degree ![]() $d$, the moduli space
$d$, the moduli space ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ is a proper Deligne–Mumford stack.
${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ is a proper Deligne–Mumford stack.
We explore ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ in §§ 4 and 5. As a final remark, note that one could define an alternative moduli functor via the work of Abramovich and Hasset [Reference Abramovich and HassettAH11]. We can consider the substack of the algebraic stack
${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$ in §§ 4 and 5. As a final remark, note that one could define an alternative moduli functor via the work of Abramovich and Hasset [Reference Abramovich and HassettAH11]. We can consider the substack of the algebraic stack ![]() $\mathcal {K}^{\omega }_{\text {slc}}$ (cf. [Reference Abramovich and HassettAH11, § 5]) satisfying the locally closed condition
$\mathcal {K}^{\omega }_{\text {slc}}$ (cf. [Reference Abramovich and HassettAH11, § 5]) satisfying the locally closed condition ![]() $dK_X+4D \sim 0$ (see [Reference KovácsKov09, Lemma 5.8]). This condition is algebraic, so we could define a variant
$dK_X+4D \sim 0$ (see [Reference KovácsKov09, Lemma 5.8]). This condition is algebraic, so we could define a variant ![]() ${{\mathcal {P}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ of
${{\mathcal {P}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ of ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ as this substack. It is not clear if the presence of the divisor
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ as this substack. It is not clear if the presence of the divisor ![]() $D$ has an effect on the structure of this stack.
$D$ has an effect on the structure of this stack.
4. Classification
Now, we turn our attention to ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs. We begin an explicit classification of the threefolds appearing in this moduli space. We dedicate our attention only to the threefolds
${(\mathbb {P}^{3},d,4)}$ H-stable pairs. We begin an explicit classification of the threefolds appearing in this moduli space. We dedicate our attention only to the threefolds ![]() $X$, not the pair
$X$, not the pair ![]() $(X,D)$, since the ample divisor
$(X,D)$, since the ample divisor ![]() $D$ must be in a linear system determined by a multiple of
$D$ must be in a linear system determined by a multiple of ![]() $K_X$. As a starting point, we have the following result of de Fernex and Fusi that implies any log-terminal degenerations are rational.
$K_X$. As a starting point, we have the following result of de Fernex and Fusi that implies any log-terminal degenerations are rational.
Theorem 4.1 [Reference de Fernex and FusidFF13, Theorem 1.3]
Rationality specializes in families of complex Kawamata log-terminal (klt) varieties of dimension at most three.
A partial classification of rational, log-terminal varieties that admit a smoothing to ![]() $\mathbb {P}^{3}$ is discussed in § 4.5. One necessary criterion is that
$\mathbb {P}^{3}$ is discussed in § 4.5. One necessary criterion is that ![]() $(-K_X)^{3} = 64$ (see the following). We point out that such a classification is known in dimension two (log-terminal surfaces that smooth to
$(-K_X)^{3} = 64$ (see the following). We point out that such a classification is known in dimension two (log-terminal surfaces that smooth to ![]() ${{\mathbb {P}}}^{2}$) by [Reference ManettiMan91] and is recalled in § 4.5.
${{\mathbb {P}}}^{2}$) by [Reference ManettiMan91] and is recalled in § 4.5.
Proposition 4.2 Let ![]() $f: \mathcal {X} \to C$ be a flat family of
$f: \mathcal {X} \to C$ be a flat family of ![]() $n$-dimensional projective varieties over a pointed curve
$n$-dimensional projective varieties over a pointed curve ![]() $0\in C$. Assume that
$0\in C$. Assume that ![]() $K_{\mathcal {X}/C}$ is
$K_{\mathcal {X}/C}$ is ![]() $\mathbb {Q}$-Cartier, the general fiber
$\mathbb {Q}$-Cartier, the general fiber ![]() $X_t$ is smooth, and the special fiber
$X_t$ is smooth, and the special fiber ![]() $X_0$ is slc. Then,
$X_0$ is slc. Then, ![]() $(K_{X_0})^{n} = (K_{X_t})^{n}$. In particular, if
$(K_{X_0})^{n} = (K_{X_t})^{n}$. In particular, if ![]() $X_t \cong \mathbb {P}^{3}, (K_{X_0})^{3} = -64$.
$X_t \cong \mathbb {P}^{3}, (K_{X_0})^{3} = -64$.
Proof. Let ![]() $l$ be an integer such that
$l$ be an integer such that ![]() $lK_{\mathcal {X}}$ is Cartier. Then, for any
$lK_{\mathcal {X}}$ is Cartier. Then, for any ![]() $t \in C, \mathcal {O}_{X_t}(lK_{X_t}) \cong \omega _{X_t}^{[l]} \cong (\omega _{\mathcal {X}}^{[l]})_t$. By definition,
$t \in C, \mathcal {O}_{X_t}(lK_{X_t}) \cong \omega _{X_t}^{[l]} \cong (\omega _{\mathcal {X}}^{[l]})_t$. By definition, ![]() $(lK_{X_t})^{n}$ is the coefficient of
$(lK_{X_t})^{n}$ is the coefficient of ![]() $m_1m_2\ldots m_n$ in
$m_1m_2\ldots m_n$ in ![]() $\chi (X_t, \mathcal {O}_{X_t}((m_1+m_2+\cdots +m_n)lK_{X_t}) )$. Because
$\chi (X_t, \mathcal {O}_{X_t}((m_1+m_2+\cdots +m_n)lK_{X_t}) )$. Because ![]() $f$ is flat, this polynomial is constant, so
$f$ is flat, this polynomial is constant, so ![]() $(lK_{X_t})^{n} = l^{n}K_{X_t}^{n}$ is constant. Therefore,
$(lK_{X_t})^{n} = l^{n}K_{X_t}^{n}$ is constant. Therefore, ![]() $K_{X_t}^{n}$ is constant, as desired.
$K_{X_t}^{n}$ is constant, as desired.
Remark 4.3 The assumption that ![]() $K_{\mathcal {X}}$ is
$K_{\mathcal {X}}$ is ![]() $\mathbb {Q}$-Cartier is essential; see [Reference Kollár and MoriKM98, Example 7.61].
$\mathbb {Q}$-Cartier is essential; see [Reference Kollár and MoriKM98, Example 7.61].
It is also easy to construct a non-rational (normal) degeneration of ![]() $\mathbb {P}^{3}$, as shown by the following example. Any such example is at least log-canonical, in light of Theorem 4.1.
$\mathbb {P}^{3}$, as shown by the following example. Any such example is at least log-canonical, in light of Theorem 4.1.
Example 4.4 Given a projectively normal variety ![]() $V \subset \mathbb {P}^{N}$, there is a standard degeneration of
$V \subset \mathbb {P}^{N}$, there is a standard degeneration of ![]() $V$ to a cone over its hyperplane section [Reference Kollár and MoriKM98, 7.61]. Thus, taking the
$V$ to a cone over its hyperplane section [Reference Kollár and MoriKM98, 7.61]. Thus, taking the ![]() $4$-uple embedding
$4$-uple embedding ![]() $\mathbb {P}^{3} \hookrightarrow \mathbb {P}^{34}$, the general hyperplane section of the image corresponds to a K3 surface in
$\mathbb {P}^{3} \hookrightarrow \mathbb {P}^{34}$, the general hyperplane section of the image corresponds to a K3 surface in ![]() $\mathbb {P}^{3}$, which has trivial canonical divisor. The cone
$\mathbb {P}^{3}$, which has trivial canonical divisor. The cone ![]() $X$ over such a surface
$X$ over such a surface ![]() $S$ is log-canonical: let
$S$ is log-canonical: let ![]() $Y$ be the blow up of
$Y$ be the blow up of ![]() $X$ at the vertex,
$X$ at the vertex, ![]() $f: Y \to X$. Then,
$f: Y \to X$. Then, ![]() $f$ is birational with exceptional divisor isomorphic to
$f$ is birational with exceptional divisor isomorphic to ![]() $S$, so
$S$, so ![]() $K_Y \sim f^{*} K_X + a S$. By adjunction,
$K_Y \sim f^{*} K_X + a S$. By adjunction, ![]() $K_S \sim (K_Y + S)|_S$, so
$K_S \sim (K_Y + S)|_S$, so ![]() $0 \sim K_S \sim (f^{*}K_X + (a+1)S)|_S$. Given any curve
$0 \sim K_S \sim (f^{*}K_X + (a+1)S)|_S$. Given any curve ![]() $C \subset S, 0 = K_S \cdot C = (a+1)S|_S \cdot C$, hence
$C \subset S, 0 = K_S \cdot C = (a+1)S|_S \cdot C$, hence ![]() $a = -1$ and
$a = -1$ and ![]() $X$ is log-canonical. A calculation shows that
$X$ is log-canonical. A calculation shows that ![]() $-K_Y-S$ is nef and zero exactly on curves contained in the exceptional locus
$-K_Y-S$ is nef and zero exactly on curves contained in the exceptional locus ![]() $S$, so
$S$, so ![]() $-K_X$ is ample. However, for
$-K_X$ is ample. However, for ![]() $X$ to occur as a threefold in a pair
$X$ to occur as a threefold in a pair ![]() $(X,D)$ on the boundary of the moduli space above, we must have
$(X,D)$ on the boundary of the moduli space above, we must have ![]() $-({d}/{4})K_X \equiv D$. By the previous discussion,
$-({d}/{4})K_X \equiv D$. By the previous discussion, ![]() $K_X\cdot C \in \mathbb {Z}$ for any curve
$K_X\cdot C \in \mathbb {Z}$ for any curve ![]() $C \subset X$, and a calculation shows that
$C \subset X$, and a calculation shows that ![]() $K_X \cdot \Gamma = -1$ for a ruling of the cone. As the singularity of
$K_X \cdot \Gamma = -1$ for a ruling of the cone. As the singularity of ![]() $X$ is not klt, in order for
$X$ is not klt, in order for ![]() $(X,({4}/{d}+\epsilon ) D)$ to also be log-canonical,
$(X,({4}/{d}+\epsilon ) D)$ to also be log-canonical, ![]() $D$ must miss the singularity of
$D$ must miss the singularity of ![]() $X$. Hence,
$X$. Hence, ![]() $D$ is contained in the smooth locus of
$D$ is contained in the smooth locus of ![]() $X$ and is therefore Cartier, so
$X$ and is therefore Cartier, so ![]() $D\cdot C \in \mathbb {Z}$, which implies
$D\cdot C \in \mathbb {Z}$, which implies ![]() ${d}/{4}\in \mathbb {Z}$. Therefore, for
${d}/{4}\in \mathbb {Z}$. Therefore, for ![]() $d$ not divisible by four,
$d$ not divisible by four, ![]() $X$ cannot occur as a boundary threefold.
$X$ cannot occur as a boundary threefold.
From this observation and the comment on boundedness, we first focus on the log-canonical but non-klt threefolds appearing in the moduli problem. The main result is that, for odd degree ![]() $d$, there are none.
$d$, there are none.
4.1 Non-klt Fano threefolds
The inspiration for classification of the non-klt threefolds in this moduli problem is the following.
Theorem 4.5 [Reference IshiiIsh91]
If ![]() $X$ is a normal, Gorenstein variety of dimension
$X$ is a normal, Gorenstein variety of dimension ![]() $n$ with
$n$ with ![]() $K_X$ anti-ample and with finite (non-empty) irrational locus, then
$K_X$ anti-ample and with finite (non-empty) irrational locus, then ![]() $X$ is a cone over a variety
$X$ is a cone over a variety ![]() $S$ with canonical singularities and
$S$ with canonical singularities and ![]() $K_S \sim 0$.
$K_S \sim 0$.
Following Ishii, we refer to the log-canonical but non-klt locus as the strictly log-canonical locus. If ![]() $X$ is a normal, Gorenstein, log-canonical variety with
$X$ is a normal, Gorenstein, log-canonical variety with ![]() $K_X$ anti-ample, the strictly log-canonical locus coincides with the irrational locus [Reference Kollár and MoriKM98, Corollary 5.24]. Therefore, this theorem implies that if a normal, Gorenstein threefold
$K_X$ anti-ample, the strictly log-canonical locus coincides with the irrational locus [Reference Kollár and MoriKM98, Corollary 5.24]. Therefore, this theorem implies that if a normal, Gorenstein threefold ![]() $X$ has a finite (non-empty) non-klt locus, it is either a cone over a K3 surface or two-dimensional Abelian variety. Note that the Gorenstein hypothesis implies that any klt singularity must be canonical, so the klt but non-canonical locus is empty in this case. We provide the following generalization.
$X$ has a finite (non-empty) non-klt locus, it is either a cone over a K3 surface or two-dimensional Abelian variety. Note that the Gorenstein hypothesis implies that any klt singularity must be canonical, so the klt but non-canonical locus is empty in this case. We provide the following generalization.
Theorem 4.6 Let ![]() $X$ be a log-canonical projective variety with a finite number of strictly log-canonical singularities
$X$ be a log-canonical projective variety with a finite number of strictly log-canonical singularities ![]() $\{p_1, \ldots, p_n \}$ and
$\{p_1, \ldots, p_n \}$ and ![]() $-K_X$ ample. If
$-K_X$ ample. If ![]() $a(E,X) \in \{-1, \mathbb {R}^{\geqslant 0} \}$ for every exceptional divisor
$a(E,X) \in \{-1, \mathbb {R}^{\geqslant 0} \}$ for every exceptional divisor ![]() $E$ over
$E$ over ![]() $X$ with
$X$ with ![]() $\text {center}_X(E)\subset \{p_1, \ldots, p_n \}$, then
$\text {center}_X(E)\subset \{p_1, \ldots, p_n \}$, then ![]() $X$ is a cone over a variety
$X$ is a cone over a variety ![]() $Z$ with
$Z$ with ![]() $K_Z \equiv 0$.
$K_Z \equiv 0$.
The extra hypotheses in this result arise from removing the Gorenstein hypotheses in Theorem 4.5. In order to ensure ![]() $X$ is a cone, there needs to be a certain extremal ray in the cone of curves. Before getting to the proof, we provide a few definitions and technical lemmas. In all cases, we consider dlt pairs
$X$ is a cone, there needs to be a certain extremal ray in the cone of curves. Before getting to the proof, we provide a few definitions and technical lemmas. In all cases, we consider dlt pairs ![]() $(X,D)$ and study properties of various
$(X,D)$ and study properties of various ![]() $K_X$-negative and
$K_X$-negative and ![]() $K_X + D$-negative contractions. The motivating idea is to study contractions that happen ‘over’
$K_X + D$-negative contractions. The motivating idea is to study contractions that happen ‘over’ ![]() $D$: divisorial contractions that are
$D$: divisorial contractions that are ![]() $K_X + D$-negative and
$K_X + D$-negative and ![]() $D$-positive must have a certain structure.
$D$-positive must have a certain structure.
Definition 4.7 Given a proper variety ![]() $X$, the effective cone
$X$, the effective cone ![]() $NE(X)$ is the collection of effective 1-cycles on
$NE(X)$ is the collection of effective 1-cycles on ![]() $X$ modulo numerical equivalence, and its closure is denoted
$X$ modulo numerical equivalence, and its closure is denoted ![]() $\overline {NE}(X)$. If
$\overline {NE}(X)$. If ![]() $R$ is an extremal ray in
$R$ is an extremal ray in ![]() $\overline {NE}(X)$, we say that the contraction of
$\overline {NE}(X)$, we say that the contraction of ![]() $R$ is an elementary extremal contraction. In what follows, we refer to the contraction of
$R$ is an elementary extremal contraction. In what follows, we refer to the contraction of ![]() $R$ as simply an extremal contraction and always mean the contraction of an extremal ray.
$R$ as simply an extremal contraction and always mean the contraction of an extremal ray.
We begin with the negativity of ![]() $K_X$ in certain
$K_X$ in certain ![]() $K_X$-negative contractions. Namely, the next lemma shows that
$K_X$-negative contractions. Namely, the next lemma shows that ![]() $K_X$ cannot be ‘too’ negative on fibers.
$K_X$ cannot be ‘too’ negative on fibers.
Lemma 4.8 Let ![]() $X$ be a normal, log-terminal projective variety such that
$X$ be a normal, log-terminal projective variety such that ![]() $K_X$ is
$K_X$ is ![]() $\mathbb {Q}$-Cartier. If
$\mathbb {Q}$-Cartier. If ![]() $\phi : X \to Y$ is a birational contraction of a
$\phi : X \to Y$ is a birational contraction of a ![]() $K_X$-negative extremal ray with fibers of dimension at most one, then each fiber
$K_X$-negative extremal ray with fibers of dimension at most one, then each fiber ![]() $F$ is a chain of
$F$ is a chain of ![]() $\mathbb {P}^{1}$ whose configuration is a tree such that
$\mathbb {P}^{1}$ whose configuration is a tree such that ![]() $-1 \leqslant K_X \cdot C < 0$ for each irreducible component
$-1 \leqslant K_X \cdot C < 0$ for each irreducible component ![]() $C$ of
$C$ of ![]() $F$.
$F$.
Proof. By assumption, ![]() $R^{2} \phi _* \mathcal {F} = 0$ for any coherent sheaf
$R^{2} \phi _* \mathcal {F} = 0$ for any coherent sheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $X$. By Grauert–Riemenschneider vanishing [Reference KollárKol13, Corollary 10.38],
$X$. By Grauert–Riemenschneider vanishing [Reference KollárKol13, Corollary 10.38], ![]() $R^{1} \phi _* \omega _X = 0$, and by [Reference Kawamata, Matsuda and MatsukiKMM87, Theorem 1-2-5], because
$R^{1} \phi _* \omega _X = 0$, and by [Reference Kawamata, Matsuda and MatsukiKMM87, Theorem 1-2-5], because ![]() $-K_X$ is
$-K_X$ is ![]() $\phi$-ample,
$\phi$-ample, ![]() $R^{1} \phi _* \mathcal {O}_X = 0$. Then, consider any sheaf of ideals
$R^{1} \phi _* \mathcal {O}_X = 0$. Then, consider any sheaf of ideals ![]() $J$ such that
$J$ such that ![]() $\mathcal {O}_X / J$ is supported on a fiber
$\mathcal {O}_X / J$ is supported on a fiber ![]() $F$ of
$F$ of ![]() $\phi$:
$\phi$:
Pushing forward to ![]() $Y$, we see that
$Y$, we see that ![]() $R^{1}\phi _* (\mathcal {O}_X / J) = H^{1}(F, \mathcal {O}_X / J |_F) = 0$. Similarly, we see that
$R^{1}\phi _* (\mathcal {O}_X / J) = H^{1}(F, \mathcal {O}_X / J |_F) = 0$. Similarly, we see that ![]() $H^{1}(F, \omega _X / J\omega _X |_F) = 0$ so
$H^{1}(F, \omega _X / J\omega _X |_F) = 0$ so ![]() $H^{1}(F, (\omega _X / J\omega _X)|_F /T) = 0$, where
$H^{1}(F, (\omega _X / J\omega _X)|_F /T) = 0$, where ![]() $T \subset (\omega _X / J\omega _X)|_F$ denotes torsion. Taking
$T \subset (\omega _X / J\omega _X)|_F$ denotes torsion. Taking ![]() $J$ to be the ideal of
$J$ to be the ideal of ![]() $F$, we see that
$F$, we see that ![]() $F$ is a chain of
$F$ is a chain of ![]() $\mathbb {P}^{1}$s whose configuration is a tree. Then, consider an irreducible component
$\mathbb {P}^{1}$s whose configuration is a tree. Then, consider an irreducible component ![]() $C \subset F$ and the sheaf
$C \subset F$ and the sheaf ![]() $(\omega _X \otimes \mathcal {O}_C) / T$, where
$(\omega _X \otimes \mathcal {O}_C) / T$, where ![]() $T$ is the torsion in
$T$ is the torsion in ![]() $\omega _X \otimes \mathcal {O}_C$. This is a torsion-free sheaf on
$\omega _X \otimes \mathcal {O}_C$. This is a torsion-free sheaf on ![]() $\mathbb {P}^{1}$, so must be a vector bundle of the form
$\mathbb {P}^{1}$, so must be a vector bundle of the form ![]() $(\omega _X \otimes \mathcal {O}_C) / T \cong \oplus \mathcal {O}_{\mathbb {P}^{1}}(a_i)$. The vanishing of
$(\omega _X \otimes \mathcal {O}_C) / T \cong \oplus \mathcal {O}_{\mathbb {P}^{1}}(a_i)$. The vanishing of ![]() $H^{1}$ given previously implies that
$H^{1}$ given previously implies that ![]() $a_i \geqslant -1$ for each
$a_i \geqslant -1$ for each ![]() $i$. If
$i$. If ![]() $m$ is an integer such that
$m$ is an integer such that ![]() $\omega _X^{[m]}$ is Cartier, we must have that
$\omega _X^{[m]}$ is Cartier, we must have that ![]() $\omega _X^{[m]}\otimes \mathcal {O}_C = \mathcal {O}_{\mathbb {P}^{1}}(b)$ is a negative degree line bundle. However, there is a non-zero morphism from taking the double dual of
$\omega _X^{[m]}\otimes \mathcal {O}_C = \mathcal {O}_{\mathbb {P}^{1}}(b)$ is a negative degree line bundle. However, there is a non-zero morphism from taking the double dual of ![]() $\omega _X$:
$\omega _X$:
and ![]() $a_i \geqslant -1$ implies that
$a_i \geqslant -1$ implies that ![]() $b \geqslant -1$. Therefore,
$b \geqslant -1$. Therefore, ![]() $-1 \leqslant K_X \cdot C < 0$.
$-1 \leqslant K_X \cdot C < 0$.
The previous lemma bounds the negativity of ![]() $K_X$. If curves
$K_X$. If curves ![]() $C$ are contained in the smooth locus, because
$C$ are contained in the smooth locus, because ![]() $K_X \cdot C \geqslant -1$ for contracted curves, if
$K_X \cdot C \geqslant -1$ for contracted curves, if ![]() $C \cap D \ne \emptyset$, that should force
$C \cap D \ne \emptyset$, that should force ![]() $(K_X + D) \cdot C \geqslant 0$. Certainly this could be false if
$(K_X + D) \cdot C \geqslant 0$. Certainly this could be false if ![]() $X$ was highly singular and
$X$ was highly singular and ![]() $D \cdot C \notin {{\mathbb {Z}}}$, but with a few restrictions on the singularities, we can apply the lemma to our advantage.
$D \cdot C \notin {{\mathbb {Z}}}$, but with a few restrictions on the singularities, we can apply the lemma to our advantage.
Lemma 4.9 If ![]() $(X,D)$ is dlt,
$(X,D)$ is dlt, ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial, and
$\mathbb {Q}$-factorial, and ![]() $D$ is an effective prime
$D$ is an effective prime ![]() $\mathbb {Z}$-divisor that is Cartier in codimension two, then any
$\mathbb {Z}$-divisor that is Cartier in codimension two, then any ![]() $K_X+D$-negative extremal divisorial contraction is an isomorphism on
$K_X+D$-negative extremal divisorial contraction is an isomorphism on ![]() $D$ if and only if the exceptional divisor does not intersect
$D$ if and only if the exceptional divisor does not intersect ![]() $D$.
$D$.
Proof. Let ![]() $\phi : X \to Y$ be the given contraction. Because
$\phi : X \to Y$ be the given contraction. Because ![]() $\phi$ is
$\phi$ is ![]() $K_X + D$ negative and divisorial, the negativity lemma implies that
$K_X + D$ negative and divisorial, the negativity lemma implies that
where ![]() $D_Y = \phi _*D, E$ is the (irreducible) exceptional divisor, and
$D_Y = \phi _*D, E$ is the (irreducible) exceptional divisor, and ![]() $a > 0$. Because
$a > 0$. Because ![]() $D$ is Cartier in codimension 2 and normal by [Reference KollárKol13, Theorem 4.16],
$D$ is Cartier in codimension 2 and normal by [Reference KollárKol13, Theorem 4.16], ![]() $K_X + D |_D = K_D$. By [Reference Kollár and MoriKM98, Corollary 3.44] and [Reference KollárKol13, Theorem 4.16],
$K_X + D |_D = K_D$. By [Reference Kollár and MoriKM98, Corollary 3.44] and [Reference KollárKol13, Theorem 4.16], ![]() $D_Y$ is also normal, so restricting to
$D_Y$ is also normal, so restricting to ![]() $D$ (where, by abuse of notation, we still denote by
$D$ (where, by abuse of notation, we still denote by ![]() $\phi$ the induced map
$\phi$ the induced map ![]() $D \to D_Y$):
$D \to D_Y$):
where ![]() $\mathrm {Diff}_{D_Y}(0)$ is the correction term to the adjunction formula. This correction term is effective by [Reference KollárKol13, Proposition 4.5], and
$\mathrm {Diff}_{D_Y}(0)$ is the correction term to the adjunction formula. This correction term is effective by [Reference KollárKol13, Proposition 4.5], and ![]() $aE|_D$ is effective, so
$aE|_D$ is effective, so ![]() $\phi |_D: D \to D_Y$ is an isomorphism if and only if
$\phi |_D: D \to D_Y$ is an isomorphism if and only if ![]() $E|_D = 0$. This also shows that
$E|_D = 0$. This also shows that ![]() $\mathrm {Diff}_{D_Y}(0) = 0$.
$\mathrm {Diff}_{D_Y}(0) = 0$.
From this observation and Lemma 4.8, we see that given a ‘nice’ contraction that is an isomorphism on ![]() $D$, the map is forced to be a fibration. However, one should be cautious; this lemma (and the corollaries) are false without the hypothesis that
$D$, the map is forced to be a fibration. However, one should be cautious; this lemma (and the corollaries) are false without the hypothesis that ![]() $D$ is Cartier in codimension two.
$D$ is Cartier in codimension two.
Example 4.10 Let ![]() $X = {{\mathbb {P}}}^{2}$ and let
$X = {{\mathbb {P}}}^{2}$ and let ![]() $\pi : Y \to X$ be the
$\pi : Y \to X$ be the ![]() $(n,1)$ weighted blow up of the point
$(n,1)$ weighted blow up of the point ![]() $(0,0)$ in linear coordinates
$(0,0)$ in linear coordinates ![]() $(x/z, y/z)$ for any
$(x/z, y/z)$ for any ![]() $n > 1$. Let
$n > 1$. Let ![]() $L = (y = 0)$ be a line in
$L = (y = 0)$ be a line in ![]() ${{\mathbb {P}}}^{2}$ and let
${{\mathbb {P}}}^{2}$ and let ![]() $L_Y$ be the strict transform. Denote the exceptional divisor of
$L_Y$ be the strict transform. Denote the exceptional divisor of ![]() $\pi$ by
$\pi$ by ![]() $E$ and note that
$E$ and note that ![]() $E^{2} = -{1}/{n}$. By construction,
$E^{2} = -{1}/{n}$. By construction, ![]() $L_Y$ and
$L_Y$ and ![]() $E$ intersect at the unique
$E$ intersect at the unique ![]() $({1}/{n})(1, n-1)$ singularity of
$({1}/{n})(1, n-1)$ singularity of ![]() $Y$ and are not Cartier at that point. We can compute
$Y$ and are not Cartier at that point. We can compute
and
so that ![]() $K_Y \cdot E = -1$ and
$K_Y \cdot E = -1$ and ![]() $L_Y \cdot E = {1}/{n}$. Then,
$L_Y \cdot E = {1}/{n}$. Then,
so the contraction ![]() $\pi : Y \to X$ of
$\pi : Y \to X$ of ![]() $E$ is
$E$ is ![]() $K_Y + L_Y$-negative and is an isomorphism on
$K_Y + L_Y$-negative and is an isomorphism on ![]() $L_Y$, but
$L_Y$, but ![]() $L_Y \cap E \ne \emptyset$.
$L_Y \cap E \ne \emptyset$.
If ![]() $D$ is Cartier in codimension two, however, we avoid the behavior in the previous example.
$D$ is Cartier in codimension two, however, we avoid the behavior in the previous example.
Corollary 4.11 If ![]() $(X,D)$ is dlt and
$(X,D)$ is dlt and ![]() $D$ is an effective, prime divisor that is Cartier in codimension two, then any
$D$ is an effective, prime divisor that is Cartier in codimension two, then any ![]() $K_X+D$-negative,
$K_X+D$-negative, ![]() $D$-positive extremal contraction that contracts a divisor but contracts no curves in
$D$-positive extremal contraction that contracts a divisor but contracts no curves in ![]() $D$ is a Fano fiber contraction
$D$ is a Fano fiber contraction ![]() $X \to D$.
$X \to D$.
Proof. Let ![]() $\pi : X \to Y$ be the contraction. If a divisor is contracted, then the morphism is either a divisorial contraction or Fano fiber contraction onto a variety with strictly lower dimension. If no curves in
$\pi : X \to Y$ be the contraction. If a divisor is contracted, then the morphism is either a divisorial contraction or Fano fiber contraction onto a variety with strictly lower dimension. If no curves in ![]() $D$ are contracted, the induced map
$D$ are contracted, the induced map ![]() $D \to \pi (D)$ is finite, but
$D \to \pi (D)$ is finite, but ![]() $(Y, \pi _*D)$ is dlt by [Reference Kollár and MoriKM98, Corollary 3.44] and
$(Y, \pi _*D)$ is dlt by [Reference Kollár and MoriKM98, Corollary 3.44] and ![]() $D$ is a prime divisor, hence
$D$ is a prime divisor, hence ![]() $\pi _*D$ is normal by [Reference KollárKol13, Theorem 4.16]. Furthermore, because no curves in
$\pi _*D$ is normal by [Reference KollárKol13, Theorem 4.16]. Furthermore, because no curves in ![]() $D$ are contracted, the fibers have dimension at most one. Indeed, let
$D$ are contracted, the fibers have dimension at most one. Indeed, let ![]() $F$ be a fiber of
$F$ be a fiber of ![]() $\pi$. Because
$\pi$. Because ![]() $\pi$ contracts no curves in
$\pi$ contracts no curves in ![]() $D, F \cap D$ must be a collection of points. However,
$D, F \cap D$ must be a collection of points. However, ![]() $\pi$ is a
$\pi$ is a ![]() $D$-positive contraction, so
$D$-positive contraction, so ![]() $D|_F$ is ample, hence must be a divisor on
$D|_F$ is ample, hence must be a divisor on ![]() $F$. Therefore,
$F$. Therefore, ![]() $F$ has dimension at most one.
$F$ has dimension at most one.
However, if ![]() $\pi$ is divisorial, Lemma 4.8 implies
$\pi$ is divisorial, Lemma 4.8 implies ![]() $K_X \cdot C \geqslant -1$ for any irreducible curve
$K_X \cdot C \geqslant -1$ for any irreducible curve ![]() $C$ contracted by
$C$ contracted by ![]() $\pi$. Suppose that
$\pi$. Suppose that ![]() $C$ is an irreducible component of a general fiber of dimension one. By assumption,
$C$ is an irreducible component of a general fiber of dimension one. By assumption, ![]() $D\cdot C > 0$, and because
$D\cdot C > 0$, and because ![]() $D$ is Cartier in codimension two,
$D$ is Cartier in codimension two, ![]() $D$ is Cartier when restricted to
$D$ is Cartier when restricted to ![]() $C$, so
$C$, so ![]() $D \cdot C \in \mathbb {Z}$. Therefore,
$D \cdot C \in \mathbb {Z}$. Therefore, ![]() $(K_X + D) \cdot C \geqslant 0$, a contradiction. Thus, the contraction cannot be birational and must be a fibration with general fiber
$(K_X + D) \cdot C \geqslant 0$, a contradiction. Thus, the contraction cannot be birational and must be a fibration with general fiber ![]() $\mathbb {P}^{1}$. In this case, for general fiber
$\mathbb {P}^{1}$. In this case, for general fiber ![]() $C, K_X \cdot C = -2$, so we must have
$C, K_X \cdot C = -2$, so we must have ![]() $D \cdot C = 1$, so
$D \cdot C = 1$, so ![]() $\pi |_D: D \to \pi (D)$ is generically of degree one. Therefore, by Zariski's main theorem, and because
$\pi |_D: D \to \pi (D)$ is generically of degree one. Therefore, by Zariski's main theorem, and because ![]() $D$ is prime,
$D$ is prime, ![]() $\pi _*D$ must be isomorphic to
$\pi _*D$ must be isomorphic to ![]() $D$ and
$D$ and ![]() $\pi : X \to Y$ is a Fano fiber contraction and
$\pi : X \to Y$ is a Fano fiber contraction and ![]() $Y \cong D$.
$Y \cong D$.
Corollary 4.12 If ![]() $X$ is a variety with terminal singularities and
$X$ is a variety with terminal singularities and ![]() $(X,D)$ is dlt for some effective prime divisor
$(X,D)$ is dlt for some effective prime divisor ![]() $D$ where
$D$ where ![]() $-D|_D$ is nef, then any
$-D|_D$ is nef, then any ![]() $K_X+D$-negative
$K_X+D$-negative ![]() $D$-positive contraction gives a Fano fibration
$D$-positive contraction gives a Fano fibration ![]() $X \to D$.
$X \to D$.
Proof. If ![]() $X$ is terminal, the singular set has codimension at least three in
$X$ is terminal, the singular set has codimension at least three in ![]() $X$ (see [Reference KollárKol13, Corollary 2.30]), hence
$X$ (see [Reference KollárKol13, Corollary 2.30]), hence ![]() $D$ is Cartier in codimension two. If
$D$ is Cartier in codimension two. If ![]() $-D|_D$ is nef, then any
$-D|_D$ is nef, then any ![]() $D$-positive contraction contracts no curves in
$D$-positive contraction contracts no curves in ![]() $D$, so by Corollary 4.11, the contraction of such a ray gives a Fano fibration
$D$, so by Corollary 4.11, the contraction of such a ray gives a Fano fibration ![]() $X \to D$.
$X \to D$.
We should point out that Lemma 4.8 does not require the contraction be divisorial; it could be a small contraction and the result would still hold. In particular, the next lemma shows that ![]() $K_X+D$-negative and
$K_X+D$-negative and ![]() $D$-positive small contractions cannot exist with certain assumptions on the singularities of
$D$-positive small contractions cannot exist with certain assumptions on the singularities of ![]() $(X,D)$.
$(X,D)$.
Lemma 4.13 If ![]() $X$ has terminal,
$X$ has terminal, ![]() $\mathbb {Q}$-factorial singularities and
$\mathbb {Q}$-factorial singularities and ![]() $(X,D)$ is a pair with log-terminal singularities such that
$(X,D)$ is a pair with log-terminal singularities such that ![]() $D$ is an effective prime divisor, then the contraction of a
$D$ is an effective prime divisor, then the contraction of a ![]() $K_X + D$-negative,
$K_X + D$-negative, ![]() $D$-positive extremal ray
$D$-positive extremal ray ![]() $R$ that contracts no curves in
$R$ that contracts no curves in ![]() $D$ cannot be a small contraction.
$D$ cannot be a small contraction.
Proof. Assume such a small contraction exists. Because this is a ![]() $K_X$-negative contraction, we consider the flip of
$K_X$-negative contraction, we consider the flip of ![]() $\phi$ as in the following diagram, where
$\phi$ as in the following diagram, where ![]() $Z$ is a log resolution of the rational map
$Z$ is a log resolution of the rational map ![]() $X \dashrightarrow X^{+}$ (so both
$X \dashrightarrow X^{+}$ (so both ![]() $Z$ and the strict transform of
$Z$ and the strict transform of ![]() $D$ are smooth). The flip exists by [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.1].
$D$ are smooth). The flip exists by [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.1].

Note that the fiber of the contraction ![]() $\phi : X \to Y$ is not contained in
$\phi : X \to Y$ is not contained in ![]() $D$, by assumption. Because every
$D$, by assumption. Because every ![]() $\pi$ exceptional divisor
$\pi$ exceptional divisor ![]() $E$ has non-negative discrepancy
$E$ has non-negative discrepancy ![]() $a(E,X,D)$, if
$a(E,X,D)$, if ![]() $D_Z = \pi ^{-1}_* D$, we have
$D_Z = \pi ^{-1}_* D$, we have
where ![]() $a_i > -1$ for each
$a_i > -1$ for each ![]() $i$, and
$i$, and ![]() $a_i \geqslant 0$ for any exceptional divisor
$a_i \geqslant 0$ for any exceptional divisor ![]() $E_i$ such that
$E_i$ such that ![]() $\text {center}_X(E_i) \not \subset D$. Restricting to
$\text {center}_X(E_i) \not \subset D$. Restricting to ![]() $D$, because
$D$, because ![]() $D$ is Cartier in codimension two, we obtain
$D$ is Cartier in codimension two, we obtain
However, by [Reference Kollár and MoriKM98, Lemma 3.38], flips can only improve singularities, so
where ![]() $c_i \geqslant 0$. Because the flip was
$c_i \geqslant 0$. Because the flip was ![]() $K_X$-negative, by the same lemma,
$K_X$-negative, by the same lemma, ![]() $X^{+}$ is also terminal, so
$X^{+}$ is also terminal, so ![]() $D^{+}$ is Cartier in codimension two. Then, restricting to
$D^{+}$ is Cartier in codimension two. Then, restricting to ![]() $D$ and
$D$ and ![]() $D^{+}$ we see that
$D^{+}$ we see that
Substituting, we see that
Because no curves in ![]() $D$ are contracted, the map
$D$ are contracted, the map ![]() $D \to \phi (D)$ is finite, and because
$D \to \phi (D)$ is finite, and because ![]() $\phi$ is a small contraction, the map has degree one, so either
$\phi$ is a small contraction, the map has degree one, so either ![]() $D \cong \phi (D)$ or
$D \cong \phi (D)$ or ![]() $D$ is its normalization. In either case, because
$D$ is its normalization. In either case, because ![]() $X^{+}$ is dlt,
$X^{+}$ is dlt, ![]() $D^{+}$ is normal by [Reference KollárKol13, Theorem 4.16], so there is a morphism
$D^{+}$ is normal by [Reference KollárKol13, Theorem 4.16], so there is a morphism ![]() $f:D^{+} \to D$ making the diagram
$f:D^{+} \to D$ making the diagram

commute. Observe that ![]() $f$ cannot be an isomorphism: if
$f$ cannot be an isomorphism: if ![]() $D^{+} \cong D$, then
$D^{+} \cong D$, then ![]() $f^{*}(K_D) = K_{D^{+}}$, and hence
$f^{*}(K_D) = K_{D^{+}}$, and hence ![]() $\pi |_D^{*}(K_D) = \pi ^{+}|_{D^{+}}^{*}(K_{D^{+}})$. However, this implies that
$\pi |_D^{*}(K_D) = \pi ^{+}|_{D^{+}}^{*}(K_{D^{+}})$. However, this implies that ![]() $c_i = 0$ for all
$c_i = 0$ for all ![]() $i$. By [Reference Kollár and MoriKM98, Lemma 3.38], this implies that, for any exceptional divisor
$i$. By [Reference Kollár and MoriKM98, Lemma 3.38], this implies that, for any exceptional divisor ![]() $E$ over
$E$ over ![]() $X, \phi \circ \pi = \phi ^{+} \circ \pi ^{+}$ is an isomorphism over the generic point of
$X, \phi \circ \pi = \phi ^{+} \circ \pi ^{+}$ is an isomorphism over the generic point of ![]() $\mathrm {center}_Y E$. This implies that neither
$\mathrm {center}_Y E$. This implies that neither ![]() $\pi$ nor
$\pi$ nor ![]() $\pi ^{+}$ extract any divisors, so by normality of
$\pi ^{+}$ extract any divisors, so by normality of ![]() $X, Z,$ and
$X, Z,$ and ![]() $X^{+}$, and
$X^{+}$, and ![]() $\mathbb {Q}$-factoriality of
$\mathbb {Q}$-factoriality of ![]() $X$ and
$X$ and ![]() $X^{+}, X \cong X^{+}$, a contradiction.
$X^{+}, X \cong X^{+}$, a contradiction.
Therefore, there is some exceptional divisor ![]() $E_0$ such
$E_0$ such ![]() $E_0|_{D_Z}$ is not contracted by
$E_0|_{D_Z}$ is not contracted by ![]() $\pi ^{+}|_{D_Z}$ but is contracted by
$\pi ^{+}|_{D_Z}$ but is contracted by ![]() $\pi |_{D_Z}$. In this case, we must have
$\pi |_{D_Z}$. In this case, we must have ![]() $c_0 > 0$. If we can show that
$c_0 > 0$. If we can show that ![]() $\text {center}_X(E_0) \not \subset D$, this is a contradiction because it would imply the coefficient of
$\text {center}_X(E_0) \not \subset D$, this is a contradiction because it would imply the coefficient of ![]() $E_0|_{D_Z}$ in (1) is non-zero, but
$E_0|_{D_Z}$ in (1) is non-zero, but ![]() $E_0|_{D_Z}$ is not an exceptional divisor of
$E_0|_{D_Z}$ is not an exceptional divisor of ![]() $\pi ^{+}|_{D_Z}$.
$\pi ^{+}|_{D_Z}$.
To conclude the proof, assume for contradiction that ![]() $\text {center}_X(E_0) \subset D$ for any such divisor
$\text {center}_X(E_0) \subset D$ for any such divisor ![]() $E_0$. Then, for any exceptional divisor
$E_0$. Then, for any exceptional divisor ![]() $E_0$ contracted to a curve in
$E_0$ contracted to a curve in ![]() $D^{+}$, it must be contracted to a point in
$D^{+}$, it must be contracted to a point in ![]() $D$, as the small contraction did not contract any curves in
$D$, as the small contraction did not contract any curves in ![]() $D$. By definition of
$D$. By definition of ![]() $Z$, there must exist a divisor
$Z$, there must exist a divisor ![]() $E_1$ whose image is a one-dimensional component of
$E_1$ whose image is a one-dimensional component of ![]() $C$, i.e.
$C$, i.e. ![]() $\text {center}_X{E_1} \not \subset D$. By assumption, for any such divisor
$\text {center}_X{E_1} \not \subset D$. By assumption, for any such divisor ![]() $E_1, \pi ^{+}(E_1) \cap D^{+}$ must be finite. However, let us compute discrepancies. Because
$E_1, \pi ^{+}(E_1) \cap D^{+}$ must be finite. However, let us compute discrepancies. Because ![]() $\pi (E_1)$ is a curve not contained in
$\pi (E_1)$ is a curve not contained in ![]() $D$ and
$D$ and ![]() $X$ has only isolated singularities,
$X$ has only isolated singularities, ![]() $K_Z = \pi ^{*}(K_X) + b_1E_1 + \text{other terms}$, where
$K_Z = \pi ^{*}(K_X) + b_1E_1 + \text{other terms}$, where ![]() $b_1 \in \mathbb {Z}, b_1 > 0$. In addition,
$b_1 \in \mathbb {Z}, b_1 > 0$. In addition, ![]() $\pi ^{*}(D) = D_Z + 0 \cdot E_1 + \text { other terms}$. Thus, the discrepancy
$\pi ^{*}(D) = D_Z + 0 \cdot E_1 + \text { other terms}$. Thus, the discrepancy ![]() $a_1$ of
$a_1$ of ![]() $E_1$ in the map
$E_1$ in the map ![]() $\pi$ is
$\pi$ is ![]() $a_1 = b_1 \in \mathbb {Z} > 0$. However, on
$a_1 = b_1 \in \mathbb {Z} > 0$. However, on ![]() $D^{+}$, we then obtain that
$D^{+}$, we then obtain that ![]() $K_{D_Z} = \pi ^{+}|_{D^{+}}^{*}(K_{D^{+}}) + (1+c_1)E_1 + \text { other terms}$, where the other terms by assumption correspond to divisors with positive discrepancy in the same fashion as
$K_{D_Z} = \pi ^{+}|_{D^{+}}^{*}(K_{D^{+}}) + (1+c_1)E_1 + \text { other terms}$, where the other terms by assumption correspond to divisors with positive discrepancy in the same fashion as ![]() $E_1$. All discrepancies in the extraction
$E_1$. All discrepancies in the extraction ![]() $D_Z$ to
$D_Z$ to ![]() $D^{+}$ are thus at least one. By assumption,
$D^{+}$ are thus at least one. By assumption, ![]() $D_Z$ was smooth, so
$D_Z$ was smooth, so ![]() $D^{+}$ is therefore smooth. As
$D^{+}$ is therefore smooth. As ![]() $D_Z \to D^{+}$ can be factored as blow ups of smooth points [Reference HartshorneHar77, Chapter 5.5], the discrepancy of some
$D_Z \to D^{+}$ can be factored as blow ups of smooth points [Reference HartshorneHar77, Chapter 5.5], the discrepancy of some ![]() $E_i$ (without loss of generality, assume it is
$E_i$ (without loss of generality, assume it is ![]() $E_1$) must be
$E_1$) must be ![]() $1$, and
$1$, and ![]() $c_1 = 0$. However, this contradicts the fact that
$c_1 = 0$. However, this contradicts the fact that ![]() $\phi : X \to Y$ is not an isomorphism above the generic point of
$\phi : X \to Y$ is not an isomorphism above the generic point of ![]() $\text {center}_Y(E_1)$, as
$\text {center}_Y(E_1)$, as ![]() $E_1$ is contracted to a curve via
$E_1$ is contracted to a curve via ![]() $\pi$ (see [Reference Kollár and MoriKM98, Lemma 3.38]). Therefore, we have reached a contradiction and, thus, there exists an
$\pi$ (see [Reference Kollár and MoriKM98, Lemma 3.38]). Therefore, we have reached a contradiction and, thus, there exists an ![]() $E_0$ such that
$E_0$ such that ![]() $\text {center}_X(E_0) \not \subset D$.
$\text {center}_X(E_0) \not \subset D$.
We can tie the previous lemmas together in the following result, seemingly technical but the key ingredient in the proof of Theorem 4.6.
Lemma 4.14 Let ![]() $X$ be a variety with terminal singularities and
$X$ be a variety with terminal singularities and ![]() $(X,D)$ a pair with canonical singularities with
$(X,D)$ a pair with canonical singularities with ![]() $D$ an effective prime divisor such that
$D$ an effective prime divisor such that ![]() $K_X|_D$ is nef. If the class of a
$K_X|_D$ is nef. If the class of a ![]() $K_X+ D$-negative extremal ray
$K_X+ D$-negative extremal ray ![]() $R$ contains a curve
$R$ contains a curve ![]() $C$ such that
$C$ such that ![]() $C\cap D$ is finite and non-empty (hence,
$C\cap D$ is finite and non-empty (hence, ![]() $R$ is
$R$ is ![]() $D$-positive), and the contraction of
$D$-positive), and the contraction of ![]() $R$ has fiber dimension at most one, then it must be a Fano fibration
$R$ has fiber dimension at most one, then it must be a Fano fibration ![]() $X\to Y$ such that the general fiber is isomorphic to
$X\to Y$ such that the general fiber is isomorphic to ![]() $\mathbb {P}^{1}$ and
$\mathbb {P}^{1}$ and ![]() $Y \cong D$.
$Y \cong D$.
Proof. Because varieties with terminal singularities are singular only in codimension ![]() $\geqslant 3$,
$\geqslant 3$, ![]() $D$ is Cartier in codimension two. By hypothesis, any curve
$D$ is Cartier in codimension two. By hypothesis, any curve ![]() $C \subset D$ has
$C \subset D$ has ![]() $K_X \cdot C \geqslant 0$, hence the contraction
$K_X \cdot C \geqslant 0$, hence the contraction ![]() $\phi : X \to Y$ of a
$\phi : X \to Y$ of a ![]() $K_X + D$-negative
$K_X + D$-negative ![]() $D$-positive extremal ray cannot contract any curves in
$D$-positive extremal ray cannot contract any curves in ![]() $D$. By Lemma 4.13, the contraction of
$D$. By Lemma 4.13, the contraction of ![]() $R$ cannot be a small contraction, so must contract a divisor. Applying Corollary 4.11, we obtain that
$R$ cannot be a small contraction, so must contract a divisor. Applying Corollary 4.11, we obtain that ![]() $X\to Y$ is a Fano fibration and
$X\to Y$ is a Fano fibration and ![]() $Y \cong D$.
$Y \cong D$.
We are now ready to prove Theorem 4.6.
Proof. By a result of Hacon [Reference Kollár and KovácsKK10, Theorem 3.1], there is a minimal ![]() $\mathbb {Q}$-factorial dlt model of
$\mathbb {Q}$-factorial dlt model of ![]() $Y \to X$. More precisely, there is a
$Y \to X$. More precisely, there is a ![]() $\mathbb {Q}$-factorial variety
$\mathbb {Q}$-factorial variety ![]() $Y$ and a morphism
$Y$ and a morphism ![]() $\pi : Y \to X$ extracting all divisors
$\pi : Y \to X$ extracting all divisors ![]() $E_i$ with discrepancy
$E_i$ with discrepancy ![]() $a(E_i, X) = -1$ such that
$a(E_i, X) = -1$ such that ![]() $K_Y$ is relatively nef. Let
$K_Y$ is relatively nef. Let ![]() $E = \sum E_i$ and observe that
$E = \sum E_i$ and observe that ![]() $K_Y + E = \pi ^{*}K_X$. Because
$K_Y + E = \pi ^{*}K_X$. Because ![]() $-K_X$ is ample and
$-K_X$ is ample and ![]() $K_Y + E$ is numerically trivial on
$K_Y + E$ is numerically trivial on ![]() $E$ and negative on all curves not contained in
$E$ and negative on all curves not contained in ![]() $E$, there must exist a
$E$, there must exist a ![]() $K_Y + E$ negative,
$K_Y + E$ negative, ![]() $E$ positive extremal ray
$E$ positive extremal ray ![]() $R$ in
$R$ in ![]() $\overline {NE}(Y)$. In fact, because
$\overline {NE}(Y)$. In fact, because ![]() $E \cdot R > 0$, there must be some component
$E \cdot R > 0$, there must be some component ![]() $E_0 \subset E$ such that
$E_0 \subset E$ such that ![]() $E_0 \cdot R >0$ and
$E_0 \cdot R >0$ and ![]() $(K_Y + E_0) \cdot R < 0$. Indeed, if
$(K_Y + E_0) \cdot R < 0$. Indeed, if ![]() $(K_Y + E_0) \cdot R \geqslant 0$, for any curve
$(K_Y + E_0) \cdot R \geqslant 0$, for any curve ![]() $[C] \in R$, we would have
$[C] \in R$, we would have ![]() $C \subset E$, so
$C \subset E$, so ![]() $(K_Y+E) \cdot C = 0$, a contradiction.
$(K_Y+E) \cdot C = 0$, a contradiction.
Let ![]() $\phi : Y \to S$ be the contraction of
$\phi : Y \to S$ be the contraction of ![]() $R$. By assumption, the pair
$R$. By assumption, the pair ![]() $(Y,E)$ is canonical along the components of
$(Y,E)$ is canonical along the components of ![]() $E$ (because
$E$ (because ![]() $a(F,Y,E) = a(F,X)$ for any exceptional divisor
$a(F,Y,E) = a(F,X)$ for any exceptional divisor ![]() $F$ over
$F$ over ![]() $X$). By Corollary 4.11 applied to
$X$). By Corollary 4.11 applied to ![]() $(Y, E_0), \phi : Y \to S$ is a fiber contraction of relative dimension one and
$(Y, E_0), \phi : Y \to S$ is a fiber contraction of relative dimension one and ![]() $S \cong E_0$. Note that, for a general fiber
$S \cong E_0$. Note that, for a general fiber ![]() $l$ of
$l$ of ![]() $\phi, K_Y \cdot l = -2$ and
$\phi, K_Y \cdot l = -2$ and ![]() $[l] \in R$, so
$[l] \in R$, so ![]() $(K_Y + E) \cdot l < 0$. Choosing an appropriate fiber
$(K_Y + E) \cdot l < 0$. Choosing an appropriate fiber ![]() $l$ that misses the singular points of
$l$ that misses the singular points of ![]() $Y$, one sees that
$Y$, one sees that ![]() $E_i \cdot l \in \mathbb {Z}$ for each
$E_i \cdot l \in \mathbb {Z}$ for each ![]() $i$ because
$i$ because ![]() $l$ is contained in the smooth locus of
$l$ is contained in the smooth locus of ![]() $Y$, and
$Y$, and ![]() $E_i$ cannot be contracted by
$E_i$ cannot be contracted by ![]() $\phi$ as curves in
$\phi$ as curves in ![]() $E_i$ are
$E_i$ are ![]() $K_Y+E$-trivial. Therefore, because
$K_Y+E$-trivial. Therefore, because ![]() $K_Y\cdot l = -2$ and
$K_Y\cdot l = -2$ and ![]() $(K_Y + E) \cdot l < 0$, there is only one exceptional divisor
$(K_Y + E) \cdot l < 0$, there is only one exceptional divisor ![]() $E_0 = E$. Because
$E_0 = E$. Because ![]() $(Y,E)$ is dlt,
$(Y,E)$ is dlt, ![]() $E$ is normal and
$E$ is normal and ![]() $\phi$ contracts no curves in
$\phi$ contracts no curves in ![]() $E$, hence
$E$, hence ![]() $S \cong E$, giving
$S \cong E$, giving ![]() $\phi : Y \to S$ the structure of a
$\phi : Y \to S$ the structure of a ![]() $\mathbb {P}^{1}$ bundle. However, as
$\mathbb {P}^{1}$ bundle. However, as ![]() $E$ is contractible by
$E$ is contractible by ![]() $\pi : Y \to X$, we see that
$\pi : Y \to X$, we see that ![]() $X$ is a cone over
$X$ is a cone over ![]() $E$ (where ‘cone’ is only defined as the contraction of a section of a
$E$ (where ‘cone’ is only defined as the contraction of a section of a ![]() $\mathbb {P}^{1}$-bundle over
$\mathbb {P}^{1}$-bundle over ![]() $E$ to a point). We can further characterize
$E$ to a point). We can further characterize ![]() $E$ by observing that
$E$ by observing that ![]() $(K_Y + E)|_E = K_E$, hence
$(K_Y + E)|_E = K_E$, hence ![]() $K_E$ is numerically trivial.
$K_E$ is numerically trivial.
As one cannot guarantee that the exceptional divisors over a variety are in the set given in Theorem 4.6, we first make an easy observation, that follows from the proof of Theorem 4.6.
Proposition 4.15 Let ![]() $X$ be a log-canonical projective variety with a finite number of strictly log-canonical singularities
$X$ be a log-canonical projective variety with a finite number of strictly log-canonical singularities ![]() $\{p_1, \ldots, p_n \}$ and
$\{p_1, \ldots, p_n \}$ and ![]() $-K_X$ ample. Consider a minimal dlt modification
$-K_X$ ample. Consider a minimal dlt modification ![]() $\pi : Y \to X$ extracting the
$\pi : Y \to X$ extracting the ![]() $-1$ divisors of
$-1$ divisors of ![]() $X$, so
$X$, so ![]() $K_Y + E = \pi ^{*}(K_X)$. If there exists an extremal ray
$K_Y + E = \pi ^{*}(K_X)$. If there exists an extremal ray ![]() $R \in \overline {NE}(Y)$ such that a curve
$R \in \overline {NE}(Y)$ such that a curve ![]() $C \not \subset E, [C]\in R$, intersects
$C \not \subset E, [C]\in R$, intersects ![]() $E$ at a smooth point of
$E$ at a smooth point of ![]() $Y$, then
$Y$, then ![]() $X$ is a cone over a numerically Calabi–Yau variety.
$X$ is a cone over a numerically Calabi–Yau variety.
To remove the restrictions on the discrepancies in Theorem 4.6, we would like to say there always exists a ray as in Proposition 4.15. However, it is not obvious why this is true or even clear that it should be true. Instead, we proceed to use the ideas in Theorem 4.6 to study the given moduli problem. Note first that many standard examples of log-canonical singularities have resolutions where an exceptional divisor is not rational or ruled. If that is the case, the following result characterizes these singularities.
Theorem 4.16 If ![]() $X$ is a projective log-canonical threefold with a finite number of strictly log-canonical singularities and
$X$ is a projective log-canonical threefold with a finite number of strictly log-canonical singularities and ![]() $-K_X$ ample such that at least one exceptional divisor
$-K_X$ ample such that at least one exceptional divisor ![]() $E$ over
$E$ over ![]() $X$ with discrepancy
$X$ with discrepancy ![]() $a(E,X) = -1$ is not rational or birationally ruled, then there is only one such
$a(E,X) = -1$ is not rational or birationally ruled, then there is only one such ![]() $E$ and
$E$ and ![]() $X$ is birational to a
$X$ is birational to a ![]() $\mathbb {P}^{1}$ bundle over
$\mathbb {P}^{1}$ bundle over ![]() $E$.
$E$.
Proof. We proceed in a similar fashion as in the previous proof. By [Reference KollárKol13, Theorem 1.33, Corollary 1.37], there is a terminal model of ![]() $X$; a
$X$; a ![]() $\mathbb {Q}$-factorial variety
$\mathbb {Q}$-factorial variety ![]() $Y$ and a morphism
$Y$ and a morphism ![]() $\pi : Y\to X$ extracting divisors
$\pi : Y\to X$ extracting divisors ![]() $\Delta _i$ with discrepancy
$\Delta _i$ with discrepancy ![]() $a(\Delta _i,X) \leqslant 0$ such that
$a(\Delta _i,X) \leqslant 0$ such that ![]() $Y$ is terminal and
$Y$ is terminal and ![]() $K_Y$ is relatively nef. Let
$K_Y$ is relatively nef. Let ![]() $E = \sum \Delta _j$ be the sum over divisors
$E = \sum \Delta _j$ be the sum over divisors ![]() $\Delta _j$ with discrepancy
$\Delta _j$ with discrepancy ![]() $-1$ and
$-1$ and ![]() $F = \sum -a(\Delta _k,X)\Delta _k$ be the sum over divisors with discrepancy larger than
$F = \sum -a(\Delta _k,X)\Delta _k$ be the sum over divisors with discrepancy larger than ![]() $-1$. By construction of
$-1$. By construction of ![]() $Y$ (which is terminal, hence has finitely many singular points), these effective divisors are Cartier in codimension two,
$Y$ (which is terminal, hence has finitely many singular points), these effective divisors are Cartier in codimension two, ![]() $\pi ^{*}(K_X) = K_Y + E + F$, and for any curves
$\pi ^{*}(K_X) = K_Y + E + F$, and for any curves ![]() $C\subset \operatorname {Supp} (E+F)$ contracted by
$C\subset \operatorname {Supp} (E+F)$ contracted by ![]() $\pi$,
$\pi$, ![]() $K_Y\cdot C \geqslant 0$. By assumption on
$K_Y\cdot C \geqslant 0$. By assumption on ![]() $X$, the general curve through
$X$, the general curve through ![]() $E$ has negative
$E$ has negative ![]() $K_X$-degree.
$K_X$-degree.
We would like to find an ![]() $E$ positive and
$E$ positive and ![]() $K_Y + E$ negative extremal ray in the cone of curves. If so, we proceed exactly as in the proof of Theorem 4.6 to conclude that the contraction of such a ray gives a Fano fibration
$K_Y + E$ negative extremal ray in the cone of curves. If so, we proceed exactly as in the proof of Theorem 4.6 to conclude that the contraction of such a ray gives a Fano fibration ![]() $\phi : Y \to E$ (and
$\phi : Y \to E$ (and ![]() $E$ consists of only one component, necessarily not rational nor ruled by assumption). Then, we conclude as in Theorem 4.6 that the log-canonical locus in
$E$ consists of only one component, necessarily not rational nor ruled by assumption). Then, we conclude as in Theorem 4.6 that the log-canonical locus in ![]() $X$ consists of a single point
$X$ consists of a single point ![]() $x\in X$,
$x\in X$, ![]() $E$ is a single component, and
$E$ is a single component, and ![]() $X$ is birational to a
$X$ is birational to a ![]() ${{\mathbb {P}}}^{1}$ bundle over
${{\mathbb {P}}}^{1}$ bundle over ![]() $E$.
$E$.
In more generality, run a ![]() $K_Y$-minimal model program (MMP) (contracting
$K_Y$-minimal model program (MMP) (contracting ![]() $K_Y$ negative extremal rays) on
$K_Y$ negative extremal rays) on ![]() $Y$. If at any point in the MMP we reach an intermediate variety
$Y$. If at any point in the MMP we reach an intermediate variety ![]() $Y'$ with a
$Y'$ with a ![]() $K_{Y'} + E'$-negative
$K_{Y'} + E'$-negative ![]() $E'$-positive extremal ray
$E'$-positive extremal ray ![]() $R$ in
$R$ in ![]() $\overline {NE}(Y')$, the arguments in the previous paragraph imply that the MMP terminates in a fibration of dimension one over
$\overline {NE}(Y')$, the arguments in the previous paragraph imply that the MMP terminates in a fibration of dimension one over ![]() $E'$. As we show in the following arguments, the only components that could have been contracted in running the MMP up to this point are rational or ruled, so we obtain the desired result.
$E'$. As we show in the following arguments, the only components that could have been contracted in running the MMP up to this point are rational or ruled, so we obtain the desired result.
Finally, assume that we do not find such a ray in the course of the MMP. Because ![]() $X$ was a Fano threefold, the MMP must terminate with a Fano fibration
$X$ was a Fano threefold, the MMP must terminate with a Fano fibration ![]() $f: Y' \to S$ such that
$f: Y' \to S$ such that ![]() $\dim S < 3$. Because
$\dim S < 3$. Because ![]() $Y$ has terminal singularities and at each stage of the MMP as we are contracting
$Y$ has terminal singularities and at each stage of the MMP as we are contracting ![]() $K_Y$-negative extremal rays, by [Reference Kollár and MoriKM98, Corollary 3.43(2)],
$K_Y$-negative extremal rays, by [Reference Kollár and MoriKM98, Corollary 3.43(2)], ![]() $Y'$ also has terminal singularities. We claim that the only components of
$Y'$ also has terminal singularities. We claim that the only components of ![]() $E$ that could be contracted by an MMP are rational or ruled.
$E$ that could be contracted by an MMP are rational or ruled.
In running the ![]() $K_Y$-MMP, first consider the case that in one of the steps one obtains a divisorial contraction
$K_Y$-MMP, first consider the case that in one of the steps one obtains a divisorial contraction ![]() $\phi : Y' \to Y''$ of a component
$\phi : Y' \to Y''$ of a component ![]() $\Delta$ of
$\Delta$ of ![]() $E'$. Because
$E'$. Because ![]() $(Y,E)$ is at worst log-canonical (and, hence,
$(Y,E)$ is at worst log-canonical (and, hence, ![]() $(Y', E')$ is at worst log-canonical),
$(Y', E')$ is at worst log-canonical), ![]() $\Delta$ is a log-canonical surface, contracted by
$\Delta$ is a log-canonical surface, contracted by ![]() $\phi$ to a point or curve. If the divisorial contraction
$\phi$ to a point or curve. If the divisorial contraction ![]() $\phi : Y' \to Y''$ contracted
$\phi : Y' \to Y''$ contracted ![]() $\Delta$ to a curve, the general fiber is
$\Delta$ to a curve, the general fiber is ![]() ${{\mathbb {P}}}^{1}$, so it is birationally ruled. Thus, in this case, the result follows. If instead
${{\mathbb {P}}}^{1}$, so it is birationally ruled. Thus, in this case, the result follows. If instead ![]() $\Delta$ is contracted to a point,
$\Delta$ is contracted to a point, ![]() $\Delta$ is Fano, and a normal log-canonical surface, so only singular at points. By [Reference KollárKol92, Theorem 17.4], the locus of strictly log-canonical non-klt singularities is connected and hence a single point. Therefore, [Reference Hacon and MckernanHM07, Theorem 1.2] implies that
$\Delta$ is Fano, and a normal log-canonical surface, so only singular at points. By [Reference KollárKol92, Theorem 17.4], the locus of strictly log-canonical non-klt singularities is connected and hence a single point. Therefore, [Reference Hacon and MckernanHM07, Theorem 1.2] implies that ![]() $\Delta$ is rationally chain connected. Finally, by [Reference KollárKol96, Proposition 3.3.4], this implies that
$\Delta$ is rationally chain connected. Finally, by [Reference KollárKol96, Proposition 3.3.4], this implies that ![]() $\Delta$ must be uniruled, and any uniruled surface is birationally ruled by [Reference KollárKol96, Exercise 1.1.6.2], so the result follows.
$\Delta$ must be uniruled, and any uniruled surface is birationally ruled by [Reference KollárKol96, Exercise 1.1.6.2], so the result follows.
Now, suppose no component of ![]() $E'$ is contracted until the termination of the MMP
$E'$ is contracted until the termination of the MMP ![]() $f': Y' \to S$. If
$f': Y' \to S$. If ![]() $Y'$ is a terminal Fano variety of Picard rank one, because
$Y'$ is a terminal Fano variety of Picard rank one, because ![]() $K_{Y} + E = \pi ^{*}(K_X)$ was negative on the generic curve in
$K_{Y} + E = \pi ^{*}(K_X)$ was negative on the generic curve in ![]() $Y$, we must have
$Y$, we must have ![]() $K_{Y'} + E'$ negative. Hence, for any component
$K_{Y'} + E'$ negative. Hence, for any component ![]() $\Delta$ of
$\Delta$ of ![]() $E', K_{Y'} + \Delta$ is negative and
$E', K_{Y'} + \Delta$ is negative and ![]() $\Delta$ is a log-canonical Fano surface, hence rationally connected, hence rational or birationally ruled by the previous argument.
$\Delta$ is a log-canonical Fano surface, hence rationally connected, hence rational or birationally ruled by the previous argument.
If ![]() $Y'$ has Picard rank two and
$Y'$ has Picard rank two and ![]() $S$ is a curve, if
$S$ is a curve, if ![]() $\Delta$ is a fiber of
$\Delta$ is a fiber of ![]() $f'$, because
$f'$, because ![]() $Y'$ is terminal,
$Y'$ is terminal, ![]() $\Delta$ must be log-terminal and Fano, and hence rational. If instead
$\Delta$ must be log-terminal and Fano, and hence rational. If instead ![]() $f'|_{\Delta }: \Delta \to S$ is surjective,
$f'|_{\Delta }: \Delta \to S$ is surjective, ![]() $\Delta$ is birationally ruled. Finally, if
$\Delta$ is birationally ruled. Finally, if ![]() $\dim S = 2$,
$\dim S = 2$, ![]() $\dim f'(\Delta ) = 0$ implies
$\dim f'(\Delta ) = 0$ implies ![]() $\Delta$ is Fano and therefore rational or birationally ruled by the previous arguments. If
$\Delta$ is Fano and therefore rational or birationally ruled by the previous arguments. If ![]() $\dim f'(\Delta ) = 1$,
$\dim f'(\Delta ) = 1$, ![]() $\Delta$ is again birationally ruled.
$\Delta$ is again birationally ruled.
Therefore, if there exists a non-rational or birationally ruled component ![]() $\Delta$ of
$\Delta$ of ![]() $E'$, it cannot be contracted in any way described previously, and thus we must be in the final remaining case:
$E'$, it cannot be contracted in any way described previously, and thus we must be in the final remaining case: ![]() $f': Y' \to S$ is a Fano fibration and
$f': Y' \to S$ is a Fano fibration and ![]() $\dim f'(\Delta ) = 2$. Because
$\dim f'(\Delta ) = 2$. Because ![]() $f'$ is the contraction of a
$f'$ is the contraction of a ![]() $K_{Y'}$-negative ray (and necessarily
$K_{Y'}$-negative ray (and necessarily ![]() $K_{Y'} + E'$-negative, by consideration of the general fiber
$K_{Y'} + E'$-negative, by consideration of the general fiber ![]() $l$, whose transform in
$l$, whose transform in ![]() $Y$ must be
$Y$ must be ![]() $K_Y+E$-negative), we have
$K_Y+E$-negative), we have ![]() $K_{Y'}\cdot l = -2$ and, hence, must have
$K_{Y'}\cdot l = -2$ and, hence, must have ![]() $E' \cdot l = \Delta \cdot l = 1$, so
$E' \cdot l = \Delta \cdot l = 1$, so ![]() $\Delta$ is birational to
$\Delta$ is birational to ![]() $S$. In particular, we are in the case of the Fano fibration over a surface birational to
$S$. In particular, we are in the case of the Fano fibration over a surface birational to ![]() $\Delta$. By the computation
$\Delta$. By the computation ![]() $E' \cdot l = \Delta \cdot l = 1$, we see that
$E' \cdot l = \Delta \cdot l = 1$, we see that ![]() $\Delta$ is the only such component that can map birationally to
$\Delta$ is the only such component that can map birationally to ![]() $S$, which implies the result.
$S$, which implies the result.
To relate this to the moduli problem, exactly as in Example 4.4, we can show that varieties satisfying the hypotheses of Theorem 4.6, Proposition 4.15 or Theorem 4.16 do not appear as ![]() ${(\mathbb {P}^{3},d,4)}$ stable pairs.
${(\mathbb {P}^{3},d,4)}$ stable pairs.
Corollary 4.17 If ![]() $X$ is a threefold satisfying the hypotheses of Theorem 4.6, Proposition 4.15, or Theorem 4.16, and
$X$ is a threefold satisfying the hypotheses of Theorem 4.6, Proposition 4.15, or Theorem 4.16, and ![]() $D$ is a
$D$ is a ![]() $\mathbb {Q}$-Cartier
$\mathbb {Q}$-Cartier ![]() $\mathbb {Z}$ divisor on
$\mathbb {Z}$ divisor on ![]() $X$ that does not contain the locus of strictly log-canonical singularities such that
$X$ that does not contain the locus of strictly log-canonical singularities such that ![]() $dK_X + 4D \sim 0$, then
$dK_X + 4D \sim 0$, then ![]() $d$ is even.
$d$ is even.
Proof. By Theorem 4.6, Proposition 4.15, or Theorem 4.16, there is a birational model ![]() $Y \to X$ such that
$Y \to X$ such that ![]() $\pi ^{*}K_X = K_Y + E + F$ and the minimal model program on
$\pi ^{*}K_X = K_Y + E + F$ and the minimal model program on ![]() $Y$ terminates in a Fano fibration
$Y$ terminates in a Fano fibration ![]() $Y' \to S$, where
$Y' \to S$, where ![]() $S$ is a surface birational to
$S$ is a surface birational to ![]() $E_0$, a component of
$E_0$, a component of ![]() $E$.
$E$.
If ![]() $X$ is as in Theorem 4.6 or Proposition 4.15, from their proofs, we have
$X$ is as in Theorem 4.6 or Proposition 4.15, from their proofs, we have ![]() $Y' = Y$. Consider a general fiber
$Y' = Y$. Consider a general fiber ![]() $l \subset Y$: we have
$l \subset Y$: we have ![]() $K_{Y} \cdot l = -2$, and
$K_{Y} \cdot l = -2$, and ![]() $E \cdot l = 1$, so
$E \cdot l = 1$, so ![]() $\pi ^{*}(K_X)\cdot l = (K_Y+E)\cdot l = -1$. Hence, if
$\pi ^{*}(K_X)\cdot l = (K_Y+E)\cdot l = -1$. Hence, if ![]() $\bar {l}$ is the image of
$\bar {l}$ is the image of ![]() $l$ on
$l$ on ![]() $X$,
$X$, ![]() $K_X \cdot \bar {l} = -1$. However,
$K_X \cdot \bar {l} = -1$. However, ![]() $D$ does not contain the strictly log-canonical locus of
$D$ does not contain the strictly log-canonical locus of ![]() $X$, so choosing
$X$, so choosing ![]() $l$ sufficiently generally implies that
$l$ sufficiently generally implies that ![]() $D \cdot \bar {l} = n \in \mathbb {Z}$, hence the relationship
$D \cdot \bar {l} = n \in \mathbb {Z}$, hence the relationship ![]() $dK_X + 4D \sim 0$ implies
$dK_X + 4D \sim 0$ implies ![]() $d(-1) + 4n = 0$, so
$d(-1) + 4n = 0$, so ![]() $d$ is even.
$d$ is even.
In the next case, suppose ![]() $X$ is as in Theorem 4.16. Following the notation and proof, we obtain that the MMP results in a Fano fibration
$X$ is as in Theorem 4.16. Following the notation and proof, we obtain that the MMP results in a Fano fibration ![]() $f': Y' \to S$, where
$f': Y' \to S$, where ![]() $S$ is birational to the unique non-rational or ruled component of
$S$ is birational to the unique non-rational or ruled component of ![]() $E'$ (and this component is generically a section of
$E'$ (and this component is generically a section of ![]() $f'$). Now, consider
$f'$). Now, consider ![]() $F'$, the image of the divisors
$F'$, the image of the divisors ![]() $F$ in
$F$ in ![]() $Y$ with discrepancy
$Y$ with discrepancy ![]() $> -1$. By [Reference Hacon and MckernanHM07, Theorem 1.2], these divisors are all rational or ruled. Hence, they cannot be birational to
$> -1$. By [Reference Hacon and MckernanHM07, Theorem 1.2], these divisors are all rational or ruled. Hence, they cannot be birational to ![]() $S$, so for each component
$S$, so for each component ![]() $\Delta _F \subset \operatorname {Supp} F'$, we have
$\Delta _F \subset \operatorname {Supp} F'$, we have ![]() $\dim f'(\Delta _F) < 2$. Therefore, choosing a sufficiently general fiber
$\dim f'(\Delta _F) < 2$. Therefore, choosing a sufficiently general fiber ![]() $l$ of
$l$ of ![]() $f'$,
$f'$, ![]() $l$ does not intersect any component of
$l$ does not intersect any component of ![]() $\operatorname {Supp} F'$ and
$\operatorname {Supp} F'$ and ![]() $(K_{Y'} + E') \cdot l = -1$. Therefore, if
$(K_{Y'} + E') \cdot l = -1$. Therefore, if ![]() $l'$ is the pre-image of
$l'$ is the pre-image of ![]() $l$ in
$l$ in ![]() $Y$,
$Y$, ![]() $\pi ^{*} K_X \cdot l' = (K_Y+E+F)\cdot l' = -1$, and if
$\pi ^{*} K_X \cdot l' = (K_Y+E+F)\cdot l' = -1$, and if ![]() $\bar {l}$ is the image of
$\bar {l}$ is the image of ![]() $l'$ on
$l'$ on ![]() $X$,
$X$, ![]() $K_X \cdot \bar {l} = -1$. However,
$K_X \cdot \bar {l} = -1$. However, ![]() $D$ does not contain the strictly log-canonical locus of
$D$ does not contain the strictly log-canonical locus of ![]() $X$, so choosing
$X$, so choosing ![]() $l$ sufficiently generally implies that
$l$ sufficiently generally implies that ![]() $D \cdot \bar {l} = n \in \mathbb {Z}$, hence the relationship
$D \cdot \bar {l} = n \in \mathbb {Z}$, hence the relationship ![]() $dK_X + 4D \sim 0$ implies
$dK_X + 4D \sim 0$ implies ![]() $d(-1) + 4n = 0$, so
$d(-1) + 4n = 0$, so ![]() $d$ is even.
$d$ is even.
With great care and analysis of the MMP, we can obtain the same result for strictly log-canonical (non-klt) Fano threefolds in more generality.
Theorem 4.18 If ![]() $X$ is a strictly log-canonical Cohen–Macaulay threefold such that
$X$ is a strictly log-canonical Cohen–Macaulay threefold such that ![]() $-K_X$ is ample,
$-K_X$ is ample, ![]() $dK_X + 4D \sim 0$ for some
$dK_X + 4D \sim 0$ for some ![]() $\mathbb {Q}$-Cartier
$\mathbb {Q}$-Cartier ![]() $\mathbb {Z}$-divisor
$\mathbb {Z}$-divisor ![]() $D$, and
$D$, and ![]() $D$ does not contain the locus of strictly log-canonical singularities, then
$D$ does not contain the locus of strictly log-canonical singularities, then ![]() $d$ is even.
$d$ is even.
Proof. By [Reference KollárKol13, Theorem 1.33], there is a ![]() $\mathbb {Q}$-factorial variety
$\mathbb {Q}$-factorial variety ![]() $Y$ and a morphism
$Y$ and a morphism ![]() $\pi : Y \to X$ extracting divisors
$\pi : Y \to X$ extracting divisors ![]() $\Delta _j$ with discrepancy
$\Delta _j$ with discrepancy ![]() $a(\Delta _i,X) \leqslant 0$ such that
$a(\Delta _i,X) \leqslant 0$ such that ![]() $Y$ is terminal and
$Y$ is terminal and ![]() $K_Y$ is relatively nef. Let
$K_Y$ is relatively nef. Let ![]() $E = \sum \Delta _j$ be the sum over divisors
$E = \sum \Delta _j$ be the sum over divisors ![]() $\Delta _j$ with discrepancy
$\Delta _j$ with discrepancy ![]() $-1$ and
$-1$ and ![]() $F = \sum -a(\Delta _k,X)\Delta _k$ be the sum over divisors with discrepancy larger than
$F = \sum -a(\Delta _k,X)\Delta _k$ be the sum over divisors with discrepancy larger than ![]() $-1$. By construction of
$-1$. By construction of ![]() $Y$ (which is terminal, hence has finitely many singular points), these effective divisors are Cartier in codimension two,
$Y$ (which is terminal, hence has finitely many singular points), these effective divisors are Cartier in codimension two, ![]() $\pi ^{*}(K_X) = K_Y + E + F$, and for any curves
$\pi ^{*}(K_X) = K_Y + E + F$, and for any curves ![]() $C\subset \operatorname {Supp} (E+F)$ contracted by
$C\subset \operatorname {Supp} (E+F)$ contracted by ![]() $\pi$,
$\pi$, ![]() $K_Y\cdot C \geqslant 0$.
$K_Y\cdot C \geqslant 0$.
We run a ![]() $K_Y$-MMP to obtain the result. The proof is somewhat technical, so we first provide a sketch, pointing out the necessary technicalities. If there is a component of
$K_Y$-MMP to obtain the result. The proof is somewhat technical, so we first provide a sketch, pointing out the necessary technicalities. If there is a component of ![]() $E_0$ that is not contracted by the MMP, the MMP terminates in a fibration
$E_0$ that is not contracted by the MMP, the MMP terminates in a fibration ![]() $Y' \to S$ and one can show that
$Y' \to S$ and one can show that ![]() $S$ is birational to
$S$ is birational to ![]() $E_0$. Now, to conclude that
$E_0$. Now, to conclude that ![]() $d$ is even, we wish to perform a similar intersection theoretic computation to that above, finding a sufficiently generic fiber
$d$ is even, we wish to perform a similar intersection theoretic computation to that above, finding a sufficiently generic fiber ![]() $l$ of
$l$ of ![]() $Y' \to S$ such that its preimage
$Y' \to S$ such that its preimage ![]() $l'$ in
$l'$ in ![]() $Y$ satisfies
$Y$ satisfies ![]() $(K_Y+E_0)\cdot l' = -1$. However, to conclude that
$(K_Y+E_0)\cdot l' = -1$. However, to conclude that ![]() $\pi ^{*}(K_X)\cdot l' = -1$, we must show that either there do not exist other components of
$\pi ^{*}(K_X)\cdot l' = -1$, we must show that either there do not exist other components of ![]() $\operatorname {Supp} E$ or
$\operatorname {Supp} E$ or ![]() $\operatorname {Supp} F$ that map finitely to
$\operatorname {Supp} F$ that map finitely to ![]() $S$ or we can use the other components to conclude that
$S$ or we can use the other components to conclude that ![]() $d$ is even.
$d$ is even.
If instead all components of ![]() $E$ are contracted by the MMP, we prove the necessary existence of certain components of
$E$ are contracted by the MMP, we prove the necessary existence of certain components of ![]() $\operatorname {Supp} F$ intersecting
$\operatorname {Supp} F$ intersecting ![]() $E$ so that the curves in
$E$ so that the curves in ![]() $E$ (which, initially may be
$E$ (which, initially may be ![]() $K_Y$-positive) become
$K_Y$-positive) become ![]() $K_Y$-negative and thus contractible. Then, we make the following observation: because
$K_Y$-negative and thus contractible. Then, we make the following observation: because ![]() $dK_X + 4D \sim 0$ and the strictly log-canonical (non-klt) locus of
$dK_X + 4D \sim 0$ and the strictly log-canonical (non-klt) locus of ![]() $X$ is not contained in
$X$ is not contained in ![]() $D$, for any component
$D$, for any component ![]() $\Delta$ of
$\Delta$ of ![]() $\operatorname {Supp} F$ that maps into the non-klt locus of
$\operatorname {Supp} F$ that maps into the non-klt locus of ![]() $X$, the discrepancy of
$X$, the discrepancy of ![]() $\Delta$ must be of the form
$\Delta$ must be of the form ![]() ${a}/{d}$ for some
${a}/{d}$ for some ![]() $a \in \mathbb {Z}$. Furthermore, on curves contained in components of
$a \in \mathbb {Z}$. Furthermore, on curves contained in components of ![]() $\Delta$ of
$\Delta$ of ![]() $E$ contracted by
$E$ contracted by ![]() $\pi$, we have
$\pi$, we have ![]() $(K_Y + E + F)|_{\Delta } = 0$, so if
$(K_Y + E + F)|_{\Delta } = 0$, so if ![]() $C_E = (E-\Delta )|_\Delta$ and
$C_E = (E-\Delta )|_\Delta$ and ![]() $C_F = F|_\Delta$, we know
$C_F = F|_\Delta$, we know ![]() $K_{\Delta } + C_E + C_F = 0$. If
$K_{\Delta } + C_E + C_F = 0$. If ![]() $\Delta$ is sufficiently nice, we use this relationship to show that either
$\Delta$ is sufficiently nice, we use this relationship to show that either ![]() $d$ must be even or the discrepancies of the components of
$d$ must be even or the discrepancies of the components of ![]() $F$ must be in a finite collection of exceptional possibilities, and we rule out these possibilities by hand.
$F$ must be in a finite collection of exceptional possibilities, and we rule out these possibilities by hand.
We begin in the simpler case, when there exists a component ![]() $E_0 \subset E$ that is not contracted by the MMP.
$E_0 \subset E$ that is not contracted by the MMP.
Lemma 4.19 If there is a component ![]() $E_0 \subset E$ that is not contracted by the MMP (including the final step as a Fano fibration), then
$E_0 \subset E$ that is not contracted by the MMP (including the final step as a Fano fibration), then ![]() $d$ is even.
$d$ is even.
Proof. In this case, the MMP must terminate with a morphism ![]() $Y \dashrightarrow Y' \to S$, and
$Y \dashrightarrow Y' \to S$, and ![]() $\dim S = 2$. Exactly as in the proof of Theorem 4.6, we obtain that
$\dim S = 2$. Exactly as in the proof of Theorem 4.6, we obtain that ![]() $S$ is birational to
$S$ is birational to ![]() $E_0'$, where
$E_0'$, where ![]() $E_0'$ is the image of
$E_0'$ is the image of ![]() $E_0$ in
$E_0$ in ![]() $Y'$, and by negativity of
$Y'$, and by negativity of ![]() $K_Y + E = \pi ^{*}K_X$, the general fiber
$K_Y + E = \pi ^{*}K_X$, the general fiber ![]() $l$ of
$l$ of ![]() $Y' \to S$ cannot intersect other components of
$Y' \to S$ cannot intersect other components of ![]() $E$. We are done by the same argument as in Corollary 4.17 if
$E$. We are done by the same argument as in Corollary 4.17 if ![]() $l$ intersects no components of
$l$ intersects no components of ![]() $\operatorname {Supp} F$. However, a priori,
$\operatorname {Supp} F$. However, a priori, ![]() $l$ could intersect components of
$l$ could intersect components of ![]() $\operatorname {Supp} F$: suppose
$\operatorname {Supp} F$: suppose ![]() $\Delta _0' \to S$ is generically finite, where
$\Delta _0' \to S$ is generically finite, where ![]() $\Delta _0'$ is the image of some
$\Delta _0'$ is the image of some ![]() $\Delta _0 \subset \operatorname {Supp} F$. Because
$\Delta _0 \subset \operatorname {Supp} F$. Because ![]() $\Delta _0$ is contracted by
$\Delta _0$ is contracted by ![]() $\pi$, let
$\pi$, let ![]() $C \subset S$ be the image of a general fiber of
$C \subset S$ be the image of a general fiber of ![]() $\pi |_{\Delta _0}$, noting that
$\pi |_{\Delta _0}$, noting that ![]() $C$ must be rational as
$C$ must be rational as ![]() $\Delta _0$ contracts to a log-terminal singularity [Reference Hacon and MckernanHM07, Theorem 1.2]. Because
$\Delta _0$ contracts to a log-terminal singularity [Reference Hacon and MckernanHM07, Theorem 1.2]. Because ![]() $Y'$ is terminal, it has isolated singularities, so choosing
$Y'$ is terminal, it has isolated singularities, so choosing ![]() $C$ sufficiently generally, we may assume that the pre-image of
$C$ sufficiently generally, we may assume that the pre-image of ![]() $C$ is a smooth ruled surface
$C$ is a smooth ruled surface ![]() $P \to C$ with multi-section
$P \to C$ with multi-section ![]() $\Delta _0'|_P$. As
$\Delta _0'|_P$. As ![]() $E_0'$ is a section of
$E_0'$ is a section of ![]() $P$, and all fibers of
$P$, and all fibers of ![]() $P$ are numerically equivalent with respect to
$P$ are numerically equivalent with respect to ![]() $E_0'$, we see that there cannot be any singular fibers (using that
$E_0'$, we see that there cannot be any singular fibers (using that ![]() $P$ is smooth). However, because
$P$ is smooth). However, because ![]() $\Delta _0'|_P$ is a contractible multi-section in the smooth ruled surface
$\Delta _0'|_P$ is a contractible multi-section in the smooth ruled surface ![]() $P$, it must, in fact, be a section. As there is only one contractible section in
$P$, it must, in fact, be a section. As there is only one contractible section in ![]() $P$, we see that
$P$, we see that ![]() $E_0'|_P$ cannot be contractible. Similar analysis implies, for any other component
$E_0'|_P$ cannot be contractible. Similar analysis implies, for any other component ![]() $\Delta _1$ of
$\Delta _1$ of ![]() $\operatorname {Supp} F$ mapping finitely to
$\operatorname {Supp} F$ mapping finitely to ![]() $S, \Delta _1'|_P$ cannot be contractible.
$S, \Delta _1'|_P$ cannot be contractible.
However, for any such ![]() $\Delta _1'$, reversing roles of
$\Delta _1'$, reversing roles of ![]() $\Delta _1'$ and
$\Delta _1'$ and ![]() $\Delta _0'$, we find a surface
$\Delta _0'$, we find a surface ![]() $P'$ with contractible section
$P'$ with contractible section ![]() $\Delta _1'|_{P'}$ and non-contractible sections
$\Delta _1'|_{P'}$ and non-contractible sections ![]() $\Delta _0'|_{P'}$ and
$\Delta _0'|_{P'}$ and ![]() $E_0'|_{P'}$. Computation shows that this would imply that
$E_0'|_{P'}$. Computation shows that this would imply that ![]() $E_0$ is, in fact, not contractible in
$E_0$ is, in fact, not contractible in ![]() $Y$, a contradiction. Therefore, there can be at most one component
$Y$, a contradiction. Therefore, there can be at most one component ![]() $\Delta _0$ of
$\Delta _0$ of ![]() $\operatorname {Supp}(F)$ that maps birationally onto
$\operatorname {Supp}(F)$ that maps birationally onto ![]() $S$.
$S$.
Thus, in the smooth ruled surface ![]() $P$, we may assume that
$P$, we may assume that ![]() $E_0'|_P$ is a positive section,
$E_0'|_P$ is a positive section, ![]() $(E_0'|_P)^{2} = n$. Choosing another section
$(E_0'|_P)^{2} = n$. Choosing another section ![]() $\gamma$ such that
$\gamma$ such that ![]() $\gamma \cap \Delta _0'|_P = \emptyset$,
$\gamma \cap \Delta _0'|_P = \emptyset$, ![]() $\gamma ^{2} = E_0' \cdot \gamma = n$, and
$\gamma ^{2} = E_0' \cdot \gamma = n$, and ![]() $K_P \cdot \gamma = K_{Y'} \cdot \gamma = -2 - n$, so that
$K_P \cdot \gamma = K_{Y'} \cdot \gamma = -2 - n$, so that ![]() $K_X \cdot \gamma ' = (K_{Y'} + E_0')\cdot \gamma = -2$, where
$K_X \cdot \gamma ' = (K_{Y'} + E_0')\cdot \gamma = -2$, where ![]() $\gamma '$ is the image of
$\gamma '$ is the image of ![]() $\gamma$ on
$\gamma$ on ![]() $X$. Provided that
$X$. Provided that ![]() $C$ and
$C$ and ![]() $\gamma$ are chosen generically,
$\gamma$ are chosen generically, ![]() $D \cdot \gamma ' = n \in \mathbb {Z}$, hence the relationship
$D \cdot \gamma ' = n \in \mathbb {Z}$, hence the relationship ![]() $dK_X + 4D \sim 0$ implies that
$dK_X + 4D \sim 0$ implies that ![]() $d(-2) + 4n = 0$ and
$d(-2) + 4n = 0$ and ![]() $d$ is even.
$d$ is even.
Now, assume that all components of ![]() $E$ are contracted by the MMP. Let
$E$ are contracted by the MMP. Let ![]() $E_0$ be the first component of
$E_0$ be the first component of ![]() $E$ contracted, and assume for contradiction that
$E$ contracted, and assume for contradiction that ![]() $d$ is odd.
$d$ is odd.
Consider the dlt model of the pair ![]() $(K_Y, E + F)$ over
$(K_Y, E + F)$ over ![]() $X, (X^{\mathrm {dlt}}, E^{\mathrm {dlt}}) \to X$. By [Reference KollárKol13, Corollary 1.36], this contracts all components of
$X, (X^{\mathrm {dlt}}, E^{\mathrm {dlt}}) \to X$. By [Reference KollárKol13, Corollary 1.36], this contracts all components of ![]() $\operatorname {Supp} F$.
$\operatorname {Supp} F$.
Lemma 4.20 Suppose that ![]() $F_1$ is a component of
$F_1$ is a component of ![]() $F$ whose image in
$F$ whose image in ![]() $X^{\mathrm {dlt}}$ is a curve
$X^{\mathrm {dlt}}$ is a curve ![]() $C$ contained in
$C$ contained in ![]() $E$. Then, the generic point of
$E$. Then, the generic point of ![]() $C$ in
$C$ in ![]() $E$ is a cyclic quotient singularity of index
$E$ is a cyclic quotient singularity of index ![]() $n$, and the discrepancy
$n$, and the discrepancy ![]() $-a(F_1, X) = {a_1}/{n}$. If
$-a(F_1, X) = {a_1}/{n}$. If ![]() $F_i \cap E \ne \emptyset$, then the discrepancy is
$F_i \cap E \ne \emptyset$, then the discrepancy is ![]() $-a(F_1, X) = 1 - {1}/{n}$. Furthermore, if
$-a(F_1, X) = 1 - {1}/{n}$. Furthermore, if ![]() $E_0$ is the component of
$E_0$ is the component of ![]() $E$ containing
$E$ containing ![]() $C$, the collection of exceptional divisors
$C$, the collection of exceptional divisors ![]() $E_0$ and those
$E_0$ and those ![]() $\{ F_i \}$ mapping to
$\{ F_i \}$ mapping to ![]() $C$ form a chain (i.e. above the generic point of
$C$ form a chain (i.e. above the generic point of ![]() $C$, the divisors can be written
$C$, the divisors can be written ![]() $E_0 \cup F_1 \cup F_2 \cup \cdots \cup F_k$ where each divisor only meets the adjacent divisors in the list and each intersection is only one point).
$E_0 \cup F_1 \cup F_2 \cup \cdots \cup F_k$ where each divisor only meets the adjacent divisors in the list and each intersection is only one point).
Proof. Because ![]() $F$ is contracted to a curve and the discrepancy of the divisor
$F$ is contracted to a curve and the discrepancy of the divisor ![]() $F$ is greater than
$F$ is greater than ![]() $-1$, at the generic point of
$-1$, at the generic point of ![]() $C$, we reduce to studying log-terminal surface singularities. Because this curve is contained in
$C$, we reduce to studying log-terminal surface singularities. Because this curve is contained in ![]() $E_0$, these are cyclic quotient singularities [Reference Kollár and MoriKM98, Theorem 4.15]. Let
$E_0$, these are cyclic quotient singularities [Reference Kollár and MoriKM98, Theorem 4.15]. Let ![]() $n$ be the index (and note that, by the previous discussion,
$n$ be the index (and note that, by the previous discussion, ![]() $n \mid d$, so
$n \mid d$, so ![]() $n$ is odd). Then, the Cartier index of the divisor
$n$ is odd). Then, the Cartier index of the divisor ![]() $K_{X^{\mathrm{dlt}}} + E^{\mathrm {dlt}}$ is a divisor of
$K_{X^{\mathrm{dlt}}} + E^{\mathrm {dlt}}$ is a divisor of ![]() $n$, so all discrepancies take the form
$n$, so all discrepancies take the form ![]() ${a_i}/{n}$.
${a_i}/{n}$.
Consider the map ![]() $g: E \dashrightarrow E^{\mathrm {dlt}}$. At the generic point of
$g: E \dashrightarrow E^{\mathrm {dlt}}$. At the generic point of ![]() $C$, this is an isomorphism, so a local computation of the discrepancy of
$C$, this is an isomorphism, so a local computation of the discrepancy of ![]() $F_i$ can be done using adjunction. Near the generic point of
$F_i$ can be done using adjunction. Near the generic point of ![]() $C$, we have
$C$, we have ![]() $K_Y + E + \sum a_i F_i = g^{*}(K_{X^{\mathrm {dlt}}} + E^{\mathrm {dlt}})$, and restricting to
$K_Y + E + \sum a_i F_i = g^{*}(K_{X^{\mathrm {dlt}}} + E^{\mathrm {dlt}})$, and restricting to ![]() $E$, we obtain
$E$, we obtain ![]() $K_E + \sum a_i F_i|_E = K_E + \mathrm {Diff}$, where
$K_E + \sum a_i F_i|_E = K_E + \mathrm {Diff}$, where ![]() $\mathrm {Diff}$ is supported on the codimension one part of singular locus of
$\mathrm {Diff}$ is supported on the codimension one part of singular locus of ![]() $X^{\mathrm {dlt}}$ contained in
$X^{\mathrm {dlt}}$ contained in ![]() $E$, which is
$E$, which is ![]() $C$. By [Reference KollárKol13, 4.4], the coefficients of the different are precisely
$C$. By [Reference KollárKol13, 4.4], the coefficients of the different are precisely ![]() $1 - {1}/{n}$. Thus, for
$1 - {1}/{n}$. Thus, for ![]() $F_1$ such that
$F_1$ such that ![]() $F_1 \cap E \ne \emptyset$, the discrepancy is as claimed.
$F_1 \cap E \ne \emptyset$, the discrepancy is as claimed.
Finally, the description of the divisors as a chain is [Reference Kollár and MoriKM98, Theorem 4.15(3)].
We divide the divisors ![]() $F_i$ in
$F_i$ in ![]() $\operatorname {Supp} F$ into two groups: those whose image in
$\operatorname {Supp} F$ into two groups: those whose image in ![]() $X^{\mathrm {dlt}}$ is a curve in
$X^{\mathrm {dlt}}$ is a curve in ![]() $E$, which we continue to denote by
$E$, which we continue to denote by ![]() $F_i$, and those whose image is not, which we denote by
$F_i$, and those whose image is not, which we denote by ![]() $G_j$, and write
$G_j$, and write ![]() $F = \sum -a(X,F_i)F_i$, respectively
$F = \sum -a(X,F_i)F_i$, respectively ![]() $G = \sum -a(X,G_j)G_j$, so we have the relationship
$G = \sum -a(X,G_j)G_j$, so we have the relationship ![]() $K_Y + E + F + G = \pi ^{*}(K_X)$. The exceptional divisors
$K_Y + E + F + G = \pi ^{*}(K_X)$. The exceptional divisors ![]() $F_i$ play an important role in what follows. Label the steps of the MMP
$F_i$ play an important role in what follows. Label the steps of the MMP ![]() $Y \dashrightarrow Y_1 \dashrightarrow \cdots \dashrightarrow Y_{m+1} \dashrightarrow$, where
$Y \dashrightarrow Y_1 \dashrightarrow \cdots \dashrightarrow Y_{m+1} \dashrightarrow$, where ![]() $Y_m \to Y_{m+1}$ is the contraction of the image of
$Y_m \to Y_{m+1}$ is the contraction of the image of ![]() $E_0$, and
$E_0$, and ![]() $\dim Y_{m+1} \leqslant 3$. We denote the image of a divisor
$\dim Y_{m+1} \leqslant 3$. We denote the image of a divisor ![]() $H \subset Y$ in
$H \subset Y$ in ![]() $Y_k$ by
$Y_k$ by ![]() $H^{k}$.
$H^{k}$.
Lemma 4.21 Let ![]() $Y_l \dashrightarrow Y_{l+1}$ be the first contraction of a curve
$Y_l \dashrightarrow Y_{l+1}$ be the first contraction of a curve ![]() $C$ in
$C$ in ![]() $E_0^{l}$ (so
$E_0^{l}$ (so ![]() $E_0 \cong E_0^{l}$). Then, the only steps of the minimal model program up to this point were contractions that did not intersect
$E_0 \cong E_0^{l}$). Then, the only steps of the minimal model program up to this point were contractions that did not intersect ![]() $E_0$ or contractions of components of the exceptional locus of
$E_0$ or contractions of components of the exceptional locus of ![]() $\pi$. If
$\pi$. If ![]() $E_0^{l} \to E_0^{l+1}$ is birational, then
$E_0^{l} \to E_0^{l+1}$ is birational, then ![]() $C$ is not contained in any component of the exceptional locus of
$C$ is not contained in any component of the exceptional locus of ![]() $\pi$ other than
$\pi$ other than ![]() $E_0$ and
$E_0$ and ![]() $C$ is a fiber of
$C$ is a fiber of ![]() $\pi |_{E_0}: E_0 \to \pi (E_0)$.
$\pi |_{E_0}: E_0 \to \pi (E_0)$.
Proof. Because ![]() $E_0 \cong E_0^{l}$, we write
$E_0 \cong E_0^{l}$, we write ![]() $E_0$ in what follows. Assume that
$E_0$ in what follows. Assume that ![]() $C$ is the first curve in
$C$ is the first curve in ![]() $E_0$ contracted by the MMP. Near
$E_0$ contracted by the MMP. Near ![]() $E_0$, prior to the contraction of
$E_0$, prior to the contraction of ![]() $C$, we could only have contracted divisors
$C$, we could only have contracted divisors ![]() $\Delta$ onto
$\Delta$ onto ![]() $E_0$ (i.e. the image of any contraction that intersects
$E_0$ (i.e. the image of any contraction that intersects ![]() $E_0$ is a curve in
$E_0$ is a curve in ![]() $E_0$) or flipped curves into
$E_0$) or flipped curves into ![]() $E_0$ because
$E_0$ because ![]() $C$ was the first curve contracted. However, if this was a divisor that intersected
$C$ was the first curve contracted. However, if this was a divisor that intersected ![]() $E$ or a flip not contained in the exceptional locus, the curves contracted would indeed be
$E$ or a flip not contained in the exceptional locus, the curves contracted would indeed be ![]() $K+E$-negative, so the induced contraction could not be birational because it contracts no curves in
$K+E$-negative, so the induced contraction could not be birational because it contracts no curves in ![]() $E_0$ (Lemma 4.13, Corollary 4.11). Therefore, the only contractions near
$E_0$ (Lemma 4.13, Corollary 4.11). Therefore, the only contractions near ![]() $E_0$ before this curve
$E_0$ before this curve ![]() $C$ were be divisorial and contracted divisors in the exceptional locus of
$C$ were be divisorial and contracted divisors in the exceptional locus of ![]() $\pi$. Furthermore, they must all be contracted to curves in
$\pi$. Furthermore, they must all be contracted to curves in ![]() $E_0$ by assumption that
$E_0$ by assumption that ![]() $C$ is the first curve contracted. If
$C$ is the first curve contracted. If ![]() $E_0$ is contracted to a curve
$E_0$ is contracted to a curve ![]() $\pi (E_0)$ by
$\pi (E_0)$ by ![]() $\pi$, and the first curve
$\pi$, and the first curve ![]() $C$ contracted is a (multi-)section of
$C$ contracted is a (multi-)section of ![]() $\pi |_{E_0}: E_0 \to \pi (E_0)$, we divide into cases based on if the contraction of
$\pi |_{E_0}: E_0 \to \pi (E_0)$, we divide into cases based on if the contraction of ![]() $C$ is birational on
$C$ is birational on ![]() $E_0$. If it is not birational, then we find that
$E_0$. If it is not birational, then we find that ![]() $E_0$ must be
$E_0$ must be ![]() ${{\mathbb {P}}}^{1} \times C'$ by considering the projections from the contraction of
${{\mathbb {P}}}^{1} \times C'$ by considering the projections from the contraction of ![]() $C$ and contraction
$C$ and contraction ![]() $\pi |_{E_0}$. (There cannot be any singular fibers: they would have been flipped into
$\pi |_{E_0}$. (There cannot be any singular fibers: they would have been flipped into ![]() $E_0$, but we then find a contradiction to
$E_0$, but we then find a contradiction to ![]() $K$-negativity of the contraction of
$K$-negativity of the contraction of ![]() $C$.) If the contraction of
$C$.) If the contraction of ![]() $C$ is birational, we can obtain a contradiction to contractibility of
$C$ is birational, we can obtain a contradiction to contractibility of ![]() $E_0^{m}$ by considering a general curve
$E_0^{m}$ by considering a general curve ![]() $\Gamma \subset E_0^{n}$ that is contracted when
$\Gamma \subset E_0^{n}$ that is contracted when ![]() $E_0^{m}$ is contracted. By a intersection-theoretic computation,
$E_0^{m}$ is contracted. By a intersection-theoretic computation, ![]() $\Gamma$ cannot be a fiber of
$\Gamma$ cannot be a fiber of ![]() $\pi |_{E_0}$, so its (reduced) image in
$\pi |_{E_0}$, so its (reduced) image in ![]() $X$ is the same as that of
$X$ is the same as that of ![]() $C$. Considering the intersection of these two curves with
$C$. Considering the intersection of these two curves with ![]() $\pi ^{*}(K_X)$ (which should be multiples of each other) gives a contradiction.
$\pi ^{*}(K_X)$ (which should be multiples of each other) gives a contradiction.
Thus, we may assume that the first curve ![]() $C$ in
$C$ in ![]() $E_0$ contracted is a fiber of
$E_0$ contracted is a fiber of ![]() $\pi |_{E_0}$. In the MMP, we are only contracting
$\pi |_{E_0}$. In the MMP, we are only contracting ![]() $K_Y$-negative,
$K_Y$-negative, ![]() $(K_Y + E)$-non-positive curves. In order to contract such a curve
$(K_Y + E)$-non-positive curves. In order to contract such a curve ![]() $C$ in
$C$ in ![]() $E_0$ in a step of the MMP, we must have first performed contractions over
$E_0$ in a step of the MMP, we must have first performed contractions over ![]() $E_0$ to change the positivity of
$E_0$ to change the positivity of ![]() $C$. By the previous paragraph, these contractions must be those of divisors contained in the exceptional locus of
$C$. By the previous paragraph, these contractions must be those of divisors contained in the exceptional locus of ![]() $\pi$. Suppose
$\pi$. Suppose ![]() $\Delta$ is such a divisor contracted to
$\Delta$ is such a divisor contracted to ![]() $E_0$. If it is contracted to a curve in
$E_0$. If it is contracted to a curve in ![]() $E_0$, the contraction would not change the sign of
$E_0$, the contraction would not change the sign of ![]() $(K_Y+E)\cdot C$. If it is contracted to a point in
$(K_Y+E)\cdot C$. If it is contracted to a point in ![]() $E_0$, there must have been a prior contraction changing the positivity of the curve
$E_0$, there must have been a prior contraction changing the positivity of the curve ![]() $\Delta \cap E_0$, contradicting that this is the first curve contracted.
$\Delta \cap E_0$, contradicting that this is the first curve contracted.
If ![]() $C$ was an intersection curve
$C$ was an intersection curve ![]() $G_j \cap E_0$, where
$G_j \cap E_0$, where ![]() $G_j$ is a component of the exceptional locus that is contracted to a point in
$G_j$ is a component of the exceptional locus that is contracted to a point in ![]() $E$ in the dlt model, either it is contracted to a canonical point of
$E$ in the dlt model, either it is contracted to a canonical point of ![]() $X^{\mathrm {dlt}}$, in which case the curves in
$X^{\mathrm {dlt}}$, in which case the curves in ![]() $G_j$ are
$G_j$ are ![]() $K_Y$-non-positive, but
$K_Y$-non-positive, but ![]() $K_Y+E$-positive, because
$K_Y+E$-positive, because ![]() $E^{\mathrm {dlt}}$ is not canonical at the point. Otherwise, if it is contracted to a non-canonical point (or non-terminal curve not contained in
$E^{\mathrm {dlt}}$ is not canonical at the point. Otherwise, if it is contracted to a non-canonical point (or non-terminal curve not contained in ![]() $E$), the curves in
$E$), the curves in ![]() $G_j$ are
$G_j$ are ![]() $K_Y$-positive (non-negative) and
$K_Y$-positive (non-negative) and ![]() $K_Y+E$ positive. In order for
$K_Y+E$ positive. In order for ![]() $C$ to be contracted, the positivity with respect to
$C$ to be contracted, the positivity with respect to ![]() $K+E$ must change, but for any divisor contracted to a curve in
$K+E$ must change, but for any divisor contracted to a curve in ![]() $E_0$, the contraction would not change the sign of
$E_0$, the contraction would not change the sign of ![]() $(K_Y+E)\cdot C$. Therefore,
$(K_Y+E)\cdot C$. Therefore, ![]() $C$ cannot be the intersection of a component
$C$ cannot be the intersection of a component ![]() $G_j \cap E_0$.
$G_j \cap E_0$.
Next, we emphasize the importance of the relative nef-ness of ![]() $K_Y$ and the coefficients of
$K_Y$ and the coefficients of ![]() $F_i$.
$F_i$.
Lemma 4.22 In the map ![]() $\pi : Y \to X$, let
$\pi : Y \to X$, let ![]() $C$ be a fiber of
$C$ be a fiber of ![]() $\pi |_{E_0}$. If the contraction of
$\pi |_{E_0}$. If the contraction of ![]() $E_0^{m}$ contracts a generic fiber
$E_0^{m}$ contracts a generic fiber ![]() $C$, before the contraction of
$C$, before the contraction of ![]() $E_0$, there must have been a contraction of some
$E_0$, there must have been a contraction of some ![]() $F_i$ such that
$F_i$ such that ![]() $F_i \cap E_0 \ne \emptyset$. In particular, the coefficient of such an
$F_i \cap E_0 \ne \emptyset$. In particular, the coefficient of such an ![]() $F_i$ in
$F_i$ in ![]() $\pi ^{*}(K_X)$ is
$\pi ^{*}(K_X)$ is ![]() $1 - {1}/{n}$.
$1 - {1}/{n}$.
Proof. By construction of ![]() $Y, K_Y$ is relatively nef, so for any fiber
$Y, K_Y$ is relatively nef, so for any fiber ![]() $C \subset E_0, K_Y \cdot C \geqslant 0$. Therefore, in order for
$C \subset E_0, K_Y \cdot C \geqslant 0$. Therefore, in order for ![]() $C$ to be contracted in the course of the MMP
$C$ to be contracted in the course of the MMP ![]() $Y \dashrightarrow Y_m \to Y_{m+1}$ as a
$Y \dashrightarrow Y_m \to Y_{m+1}$ as a ![]() $K_{Y_m}$-negative extremal ray, we must have performed a contraction
$K_{Y_m}$-negative extremal ray, we must have performed a contraction ![]() $Y_l \to Y_{l+1}$ of a divisor that intersected
$Y_l \to Y_{l+1}$ of a divisor that intersected ![]() $E_0$ to change the positivity of
$E_0$ to change the positivity of ![]() $K_Y$ on
$K_Y$ on ![]() $C$. If the contraction was not a component of
$C$. If the contraction was not a component of ![]() $\operatorname {Supp} F$, a generic contracted curve would necessarily be
$\operatorname {Supp} F$, a generic contracted curve would necessarily be ![]() $K_{Y_l} + E_0^{l}$ negative (because its transform in
$K_{Y_l} + E_0^{l}$ negative (because its transform in ![]() $Y$ satisfies the same negativity), so Corollary 4.11 and Lemma 4.13 imply that it would have been a contraction onto a lower-dimensional variety, giving
$Y$ satisfies the same negativity), so Corollary 4.11 and Lemma 4.13 imply that it would have been a contraction onto a lower-dimensional variety, giving ![]() $Y_l$ the structure of a Fano fibration, which is a contradiction, or the contraction of a component
$Y_l$ the structure of a Fano fibration, which is a contradiction, or the contraction of a component ![]() $G_i^{j}$ onto a curve in
$G_i^{j}$ onto a curve in ![]() $E_0^{j}$ for some
$E_0^{j}$ for some ![]() $j < l$ followed by more contractions or flips. However, because each
$j < l$ followed by more contractions or flips. However, because each ![]() $G_i$ is contracted to a point in the dlt model, by
$G_i$ is contracted to a point in the dlt model, by ![]() $\mathbb {Q}$-factoriality, we must have performed a flip into
$\mathbb {Q}$-factoriality, we must have performed a flip into ![]() $G_i$ before the contraction (otherwise,
$G_i$ before the contraction (otherwise, ![]() $G_i$ would already admit a contraction to a curve followed by a small contraction to
$G_i$ would already admit a contraction to a curve followed by a small contraction to ![]() $X^{\mathrm {dlt}}$). However, using the relative nef-ness of the canonical divisor on
$X^{\mathrm {dlt}}$). However, using the relative nef-ness of the canonical divisor on ![]() $G_i$, a computation using the formulas for discrepancies as in Lemma 4.13 shows that, after a flip,
$G_i$, a computation using the formulas for discrepancies as in Lemma 4.13 shows that, after a flip, ![]() $G_i^{j}$ could not admit a fibration over a curve because we could not have
$G_i^{j}$ could not admit a fibration over a curve because we could not have ![]() $K_{Y_j} \cdot l = -1$ and
$K_{Y_j} \cdot l = -1$ and ![]() $G_i^{j}\cdot l = -1$ for a generic fiber
$G_i^{j}\cdot l = -1$ for a generic fiber ![]() $l$ of the contraction. Therefore, we must have performed a contraction of such an
$l$ of the contraction. Therefore, we must have performed a contraction of such an ![]() $F_i$ that intersects
$F_i$ that intersects ![]() $E_0$ in a curve.
$E_0$ in a curve.
Now, we separate into two cases based on the non-klt locus of ![]() $X$.
$X$.
Case 1:  $E_0$ is contracted to a point in
$E_0$ is contracted to a point in  $X$
$X$
By the previous lemma, before contracting ![]() $E_0^{m}$, we must have contracted a component of
$E_0^{m}$, we must have contracted a component of ![]() $\operatorname {Supp} F$ onto
$\operatorname {Supp} F$ onto ![]() $E_0$. Let
$E_0$. Let ![]() $F_1$ be this component, with discrepancy
$F_1$ be this component, with discrepancy ![]() $a(X,F_1) = 1 - {1}/{n}$, and suppose it is contracted at the step of the MMP
$a(X,F_1) = 1 - {1}/{n}$, and suppose it is contracted at the step of the MMP ![]() $Y_l \to Y_{l+1}$. Because
$Y_l \to Y_{l+1}$. Because ![]() $n \mid d$, we may assume
$n \mid d$, we may assume ![]() $n \geqslant 3$ (if
$n \geqslant 3$ (if ![]() $n = 2, d$ would be even, as desired). Note that
$n = 2, d$ would be even, as desired). Note that ![]() $F_1$ is contractible in
$F_1$ is contractible in ![]() $Y$ to a curve (via the map to
$Y$ to a curve (via the map to ![]() $X^{\mathrm {dlt}}$), so must have the structure of a (possibly singular) ruled surface. Consider a generic fiber
$X^{\mathrm {dlt}}$), so must have the structure of a (possibly singular) ruled surface. Consider a generic fiber ![]() $f$ of this contraction, which is also a generic fiber of
$f$ of this contraction, which is also a generic fiber of ![]() $F_1^{l}$. Because
$F_1^{l}$. Because ![]() $K_Y$ was relatively nef to begin with, we must have contracted some collection of divisors
$K_Y$ was relatively nef to begin with, we must have contracted some collection of divisors ![]() $\Delta$ onto
$\Delta$ onto ![]() $F_1$ before contracting
$F_1$ before contracting ![]() $F_1^{l}$ to change the positivity of
$F_1^{l}$ to change the positivity of ![]() $K_Y$ on
$K_Y$ on ![]() $F_1$. In particular,
$F_1$. In particular, ![]() $K_{Y_l} \cdot f^{l} = -1$ and
$K_{Y_l} \cdot f^{l} = -1$ and ![]() $F_1^{l} \cdot f^{l} = -1$. Furthermore, by Lemma 4.20,
$F_1^{l} \cdot f^{l} = -1$. Furthermore, by Lemma 4.20, ![]() $E_0 \cdot f = E_0^{l} \cdot f^{l} = 1$, and
$E_0 \cdot f = E_0^{l} \cdot f^{l} = 1$, and ![]() $f$ can meet only one other component
$f$ can meet only one other component ![]() $F_2$ of the exceptional locus of
$F_2$ of the exceptional locus of ![]() $\pi$. Furthermore, if
$\pi$. Furthermore, if ![]() $F_2$ exists, the intersection curves
$F_2$ exists, the intersection curves ![]() $E_0 \cap F_1$ and
$E_0 \cap F_1$ and ![]() $F_1 \cap F_2$ must be disjoint (if they were not disjoint, the intersection curve
$F_1 \cap F_2$ must be disjoint (if they were not disjoint, the intersection curve ![]() $E_0 \cap F_2$ would necessarily be
$E_0 \cap F_2$ would necessarily be ![]() $K_Y$-negative, but we are assuming
$K_Y$-negative, but we are assuming ![]() $K_Y$ is relatively nef).
$K_Y$ is relatively nef).
Note that a component ![]() $\Delta$ contracted onto
$\Delta$ contracted onto ![]() $F_1$ cannot intersect
$F_1$ cannot intersect ![]() $E_0$ because its contraction would necessarily contract a
$E_0$ because its contraction would necessarily contract a ![]() $K_Y\geqslant 0$ curve in
$K_Y\geqslant 0$ curve in ![]() $E_0$, and similarly, if
$E_0$, and similarly, if ![]() $F_2$ exists and was not contracted before
$F_2$ exists and was not contracted before ![]() $\Delta, \Delta$ cannot intersect
$\Delta, \Delta$ cannot intersect ![]() $F_2$. If it did, because
$F_2$. If it did, because ![]() $\Delta$ was contracted by a
$\Delta$ was contracted by a ![]() $K$-negative extremal MMP contraction, all the fibers are numerically equivalent, however
$K$-negative extremal MMP contraction, all the fibers are numerically equivalent, however ![]() $F_2$ is contractible in
$F_2$ is contractible in ![]() $\Delta$ (to
$\Delta$ (to ![]() $X$, so the curve
$X$, so the curve ![]() $\Delta \cap F_2$ must be a component of some fiber. However, the other component of the fiber would then be
$\Delta \cap F_2$ must be a component of some fiber. However, the other component of the fiber would then be ![]() $F_2$-positive, but the generic fiber of
$F_2$-positive, but the generic fiber of ![]() $\Delta$ is
$\Delta$ is ![]() $F_2$-trivial; a contradiction. Therefore, if
$F_2$-trivial; a contradiction. Therefore, if ![]() $F_2$ exists,
$F_2$ exists, ![]() $\Delta \cap F_1$ is disjoint from both
$\Delta \cap F_1$ is disjoint from both ![]() $E_0 \cap F_1$ and
$E_0 \cap F_1$ and ![]() $F_1 \cap F_2$. In addition, in this setting where
$F_1 \cap F_2$. In addition, in this setting where ![]() $\Delta$ is contracted before
$\Delta$ is contracted before ![]() $F_2$, in the contraction of
$F_2$, in the contraction of ![]() $F_1$, there cannot be any reducible fibers: the fibers must be numerically equivalent, but
$F_1$, there cannot be any reducible fibers: the fibers must be numerically equivalent, but ![]() $F_1 \cap F_2$ and
$F_1 \cap F_2$ and ![]() $E_0 \cap F_1$ are disjoint sections of the ruled surface
$E_0 \cap F_1$ are disjoint sections of the ruled surface ![]() $F_1$, so any component of a singular fiber must pass through both sections. Because they are disjoint, a reducible fiber would have genus larger than zero, a contradiction. Therefore, if
$F_1$, so any component of a singular fiber must pass through both sections. Because they are disjoint, a reducible fiber would have genus larger than zero, a contradiction. Therefore, if ![]() $\Delta$ is contracted before
$\Delta$ is contracted before ![]() $F_2, \Delta \cap F_1$ is a multi-section of the ruled surface
$F_2, \Delta \cap F_1$ is a multi-section of the ruled surface ![]() $F_1$ (with no singular fibers, so Picard rank two) that is disjoint from the other two disjoint sections of
$F_1$ (with no singular fibers, so Picard rank two) that is disjoint from the other two disjoint sections of ![]() $F_1$:
$F_1$: ![]() $E_0 \cap F_1$ and
$E_0 \cap F_1$ and ![]() $F_1 \cap F_2$. This implies that, in fact,
$F_1 \cap F_2$. This implies that, in fact, ![]() $F_1$ is
$F_1$ is ![]() $\mathbb {P}^{1} \times C$, where
$\mathbb {P}^{1} \times C$, where ![]() $C$ is a smooth genus
$C$ is a smooth genus ![]() $g$ curve and
$g$ curve and ![]() $\Delta \cap F_1$ is a section. Taking a generic horizontal section
$\Delta \cap F_1$ is a section. Taking a generic horizontal section ![]() ${pt} \times C$, near
${pt} \times C$, near ![]() $C$, we have the relationship
$C$, we have the relationship ![]() $0 = \pi ^{*}(K_X) \cdot C = (K_Y + F_1 - ({1}/{n})F_1) \cdot C$, so
$0 = \pi ^{*}(K_X) \cdot C = (K_Y + F_1 - ({1}/{n})F_1) \cdot C$, so ![]() $n(2g - 2) = F_1\cdot C$ and, hence,
$n(2g - 2) = F_1\cdot C$ and, hence, ![]() $K_Y \cdot C = - (n-1)(2g-2)$. By relative nef-ness of the canonical divisor, this implies
$K_Y \cdot C = - (n-1)(2g-2)$. By relative nef-ness of the canonical divisor, this implies ![]() $g = 0$ or
$g = 0$ or ![]() $g = 1$. Finally, note that this analysis applies for any
$g = 1$. Finally, note that this analysis applies for any ![]() $\Delta$ contracted onto any
$\Delta$ contracted onto any ![]() $F_i$ in the chain of divisors above the curve
$F_i$ in the chain of divisors above the curve ![]() $E_0 \cap F_1$. The following lemma shows that this behavior is impossible when
$E_0 \cap F_1$. The following lemma shows that this behavior is impossible when ![]() $d$ is odd.
$d$ is odd.
Lemma 4.23 If ![]() $F_i$ is
$F_i$ is ![]() ${{\mathbb {P}}}^{1} \times C$ and
${{\mathbb {P}}}^{1} \times C$ and ![]() $\Delta$ a non-exceptional divisor of
$\Delta$ a non-exceptional divisor of ![]() $\pi$ contracted onto
$\pi$ contracted onto ![]() $F_i$, then
$F_i$, then ![]() $i = 1$.
$i = 1$.
Proof. Because ![]() $\Delta$ is contracted onto
$\Delta$ is contracted onto ![]() $F_i$ in an extremal contraction of the minimal model program, it is a ruled surface, and
$F_i$ in an extremal contraction of the minimal model program, it is a ruled surface, and ![]() $F_i$ is smooth, so there cannot be any singularities along
$F_i$ is smooth, so there cannot be any singularities along ![]() $F_i \cap \Delta$. Therefore, there cannot be any singular fibers of the ruled surface
$F_i \cap \Delta$. Therefore, there cannot be any singular fibers of the ruled surface ![]() $\Delta$, and cannot be any singularities on
$\Delta$, and cannot be any singularities on ![]() $\Delta$ because curves through the singular points would have
$\Delta$ because curves through the singular points would have ![]() $-(K+\Delta )\cdot C$ less than that of the generic fiber, but
$-(K+\Delta )\cdot C$ less than that of the generic fiber, but ![]() $F_i \cdot C$ equal to that of a generic fiber, impossible by relative numerical equivalence. Thus,
$F_i \cdot C$ equal to that of a generic fiber, impossible by relative numerical equivalence. Thus, ![]() $\Delta$ is a smooth ruled surface. Because
$\Delta$ is a smooth ruled surface. Because ![]() $F_i$ is contractible to a point, the section
$F_i$ is contractible to a point, the section ![]() $F_i \cap \Delta$ is the negative section
$F_i \cap \Delta$ is the negative section ![]() $\sigma _0$, and let
$\sigma _0$, and let ![]() $\sigma _{\infty }$ be generic positive section that does not intersect
$\sigma _{\infty }$ be generic positive section that does not intersect ![]() $\sigma _0$, and let
$\sigma _0$, and let ![]() $f$ be a generic fiber.
$f$ be a generic fiber.
If ![]() $g = 1$, by the previous computation, we see that
$g = 1$, by the previous computation, we see that ![]() $K_Y \cdot \sigma _0 = F_i \cdot \sigma _0 = \Delta \cdot \sigma _0 = 0,$ and as
$K_Y \cdot \sigma _0 = F_i \cdot \sigma _0 = \Delta \cdot \sigma _0 = 0,$ and as ![]() $F_i \cdot \sigma _0 = \sigma _0^{2}$, this implies that
$F_i \cdot \sigma _0 = \sigma _0^{2}$, this implies that ![]() $\Delta$ is in fact
$\Delta$ is in fact ![]() ${{\mathbb {P}}}^{1} \times C_1$, where
${{\mathbb {P}}}^{1} \times C_1$, where ![]() $C_1 \cong \sigma _0$ is genus 1, so choosing a generic section
$C_1 \cong \sigma _0$ is genus 1, so choosing a generic section ![]() $C_1$, we see that
$C_1$, we see that ![]() $(K_Y+ \Delta )\cdot C_1 = 0$. Because
$(K_Y+ \Delta )\cdot C_1 = 0$. Because ![]() $\Delta$ is contractible, when
$\Delta$ is contractible, when ![]() $\Delta$ is contracted
$\Delta$ is contracted ![]() $Y_m \to Y_{m+1}$ in the minimal model program, near the generic section
$Y_m \to Y_{m+1}$ in the minimal model program, near the generic section ![]() $C_1$, the pullback of
$C_1$, the pullback of ![]() $K_{Y_m}$ to
$K_{Y_m}$ to ![]() $Y$ is
$Y$ is ![]() $K_Y - \Delta -\sum \Gamma _i$, where
$K_Y - \Delta -\sum \Gamma _i$, where ![]() $\Gamma _i$ are the other divisors contracted in the course of the MMP. However, the image of each
$\Gamma _i$ are the other divisors contracted in the course of the MMP. However, the image of each ![]() $\Gamma _i$ must be a point in
$\Gamma _i$ must be a point in ![]() $Y_m$: if it was a curve, either it is an entire fiber (and, hence, would have intersected
$Y_m$: if it was a curve, either it is an entire fiber (and, hence, would have intersected ![]() $F_i$; contracting a curve in
$F_i$; contracting a curve in ![]() $F_i$, which is impossible), or a (multi-)section of
$F_i$, which is impossible), or a (multi-)section of ![]() $\Delta$ (which would have forced the fibers of
$\Delta$ (which would have forced the fibers of ![]() $\Delta$ to be
$\Delta$ to be ![]() $K_Y$-non-negative, impossible as they are not contained in the exceptional locus of
$K_Y$-non-negative, impossible as they are not contained in the exceptional locus of ![]() $\pi$). None of these
$\pi$). None of these ![]() $\Gamma _i$ intersect
$\Gamma _i$ intersect ![]() $\sigma _0$ and none intersect the generic
$\sigma _0$ and none intersect the generic ![]() $C_1$, and
$C_1$, and ![]() $\sigma _0$ and
$\sigma _0$ and ![]() $C_1$ have the same image in
$C_1$ have the same image in ![]() $Y_{m+1}$, so
$Y_{m+1}$, so
Thus, ![]() $(2K_Y) \cdot C_1 = 0$, so
$(2K_Y) \cdot C_1 = 0$, so ![]() $K_Y \cdot C_1 \geqslant 0$. This is impossible as
$K_Y \cdot C_1 \geqslant 0$. This is impossible as ![]() $C_1$ is not contained in the exceptional locus of
$C_1$ is not contained in the exceptional locus of ![]() $\pi$. Therefore,
$\pi$. Therefore, ![]() $g\ne 1$.
$g\ne 1$.
If ![]() $g = 0$, we perform a similar computation: we find that
$g = 0$, we perform a similar computation: we find that ![]() $\Delta$ is a smooth ruled surface over a rational curve
$\Delta$ is a smooth ruled surface over a rational curve ![]() $\sigma _0$ and no
$\sigma _0$ and no ![]() $\Gamma _i$ as described previously intersect
$\Gamma _i$ as described previously intersect ![]() $\sigma _0$ or the generic section, and the computations before the proof of this lemma say
$\sigma _0$ or the generic section, and the computations before the proof of this lemma say ![]() $K_Y\cdot \sigma _0 = 2(n-1)$,
$K_Y\cdot \sigma _0 = 2(n-1)$, ![]() $F\cdot \sigma _0 = -2n$, and
$F\cdot \sigma _0 = -2n$, and ![]() $\Delta \cdot \sigma _0 = 0$. Therefore, for a generic section
$\Delta \cdot \sigma _0 = 0$. Therefore, for a generic section ![]() $\sigma _\infty$ of
$\sigma _\infty$ of ![]() $\Delta$,
$\Delta$, ![]() $(K_Y+\Delta ) \cdot \sigma _0 = -2(n+1)$, and as previously, because
$(K_Y+\Delta ) \cdot \sigma _0 = -2(n+1)$, and as previously, because ![]() $\sigma _0$ and
$\sigma _0$ and ![]() $\sigma _{\infty }$ have the same image when
$\sigma _{\infty }$ have the same image when ![]() $\Delta$ is contracted,
$\Delta$ is contracted,
so ![]() $2K_Y\cdot \sigma _{\infty } = -4$ and
$2K_Y\cdot \sigma _{\infty } = -4$ and ![]() $K_Y\cdot \sigma _{\infty } = -2$. Therefore, if
$K_Y\cdot \sigma _{\infty } = -2$. Therefore, if ![]() $\sigma _{\infty }$ intersects no other exceptional divisors of
$\sigma _{\infty }$ intersects no other exceptional divisors of ![]() $\pi$, as it is contained in the smooth locus of
$\pi$, as it is contained in the smooth locus of ![]() $Y$, and
$Y$, and ![]() $dK_X + 4D \sim 0$ implies that
$dK_X + 4D \sim 0$ implies that ![]() $d$ is even.
$d$ is even.
Finally, suppose that ![]() $\sigma _{\infty }$ intersects some other exceptional divisor
$\sigma _{\infty }$ intersects some other exceptional divisor ![]() $G_j \in \operatorname {Supp} G$ whose discrepancy
$G_j \in \operatorname {Supp} G$ whose discrepancy ![]() $-a(G_j,X,({4}/{d})D) = {a}/{d}$. Because
$-a(G_j,X,({4}/{d})D) = {a}/{d}$. Because ![]() $G_j$ and
$G_j$ and ![]() $D$ do not intersect
$D$ do not intersect ![]() $\sigma _0$, their restrictions to
$\sigma _0$, their restrictions to ![]() $\Delta$ are
$\Delta$ are ![]() $G_{\Delta } \equiv p\sigma _{\infty }$ and
$G_{\Delta } \equiv p\sigma _{\infty }$ and ![]() $D_{\Delta } = q\sigma _{\infty }$. For the generic fiber
$D_{\Delta } = q\sigma _{\infty }$. For the generic fiber ![]() $f$ of
$f$ of ![]() $\Delta$,
$\Delta$, ![]() $f$ intersects a single
$f$ intersects a single ![]() $F_i$ and the discrepancy of
$F_i$ and the discrepancy of ![]() $F_i$ is
$F_i$ is ![]() $({n-r})/{n}$ for some integer
$({n-r})/{n}$ for some integer ![]() $r$. Thus, the relationship
$r$. Thus, the relationship ![]() $dK_X + 4D\sim 0$ pulled back to
$dK_X + 4D\sim 0$ pulled back to ![]() $Y$ implies that
$Y$ implies that
Intersecting with a generic fiber ![]() $f$ and the generic section
$f$ and the generic section ![]() $\sigma _0$, we find that
$\sigma _0$, we find that ![]() $r=1$ and such a
$r=1$ and such a ![]() $\Delta$ can only occur on
$\Delta$ can only occur on ![]() $F_1$.
$F_1$.
Now, in the set-up described previously, the proof is complete by the following lemma.
Lemma 4.24 If ![]() $\Delta$ is contracted by an extremal contraction onto a curve contained in
$\Delta$ is contracted by an extremal contraction onto a curve contained in ![]() $F_1$, followed by an extremal contraction of
$F_1$, followed by an extremal contraction of ![]() $F_1$, and
$F_1$, and ![]() $\Delta$ is not an exceptional divisor of
$\Delta$ is not an exceptional divisor of ![]() $\pi$, then
$\pi$, then ![]() $d$ is even.
$d$ is even.
Proof. Suppose the generic fiber of ![]() $\Delta$ does not intersect any other exceptional divisor of
$\Delta$ does not intersect any other exceptional divisor of ![]() $\pi$. Because the contraction of
$\pi$. Because the contraction of ![]() $\Delta$ is a
$\Delta$ is a ![]() $K$-negative extremal contraction, for general fiber
$K$-negative extremal contraction, for general fiber ![]() $f_g$,
$f_g$, ![]() $K_{Y_l} \cdot f_g = -1$, and the same is true for the strict transform in
$K_{Y_l} \cdot f_g = -1$, and the same is true for the strict transform in ![]() $Y$, so
$Y$, so ![]() $K_Y \cdot f_g = -1$. Then,
$K_Y \cdot f_g = -1$. Then, ![]() $\pi ^{*}(K_X)\cdot f_g = K_Y\cdot f_g + (1 - {1}/{n}) F_1 \cdot f_l = -1 + 1 - {1}/{n} = -{1}/{n}$ because
$\pi ^{*}(K_X)\cdot f_g = K_Y\cdot f_g + (1 - {1}/{n}) F_1 \cdot f_l = -1 + 1 - {1}/{n} = -{1}/{n}$ because ![]() $f_g$ intersects no other exceptional components. Let
$f_g$ intersects no other exceptional components. Let ![]() $f$ be the image of
$f$ be the image of ![]() $f_g$ in
$f_g$ in ![]() $X$. This curve meets
$X$. This curve meets ![]() $D$ in the smooth locus of
$D$ in the smooth locus of ![]() $X$, so
$X$, so ![]() $0 = (dK_X + 4D)\cdot f = - {d}/{n} + 4 k$ for some
$0 = (dK_X + 4D)\cdot f = - {d}/{n} + 4 k$ for some ![]() $k \in \mathbb {Z}$. Therefore,
$k \in \mathbb {Z}$. Therefore, ![]() $d = 4nk$ so
$d = 4nk$ so ![]() $d$ is even.
$d$ is even.
Now suppose ![]() $f_g \subset \Delta$ intersects some other exceptional divisor of
$f_g \subset \Delta$ intersects some other exceptional divisor of ![]() $\pi$. Call this divisor
$\pi$. Call this divisor ![]() $G_j$ as previously. Because
$G_j$ as previously. Because ![]() $G_j$ must be contracted to its image
$G_j$ must be contracted to its image ![]() $G_{\Delta }$ in
$G_{\Delta }$ in ![]() $X, G_j$ is a fibration over the curve
$X, G_j$ is a fibration over the curve ![]() $G_{\Delta }$. Consider a generic fiber
$G_{\Delta }$. Consider a generic fiber ![]() $f_g$ of
$f_g$ of ![]() $G_j$, and suppose
$G_j$, and suppose ![]() $G_j\cdot f_g = -k$ (so
$G_j\cdot f_g = -k$ (so ![]() $K_Y\cdot f_g = k-2$). Intersecting with
$K_Y\cdot f_g = k-2$). Intersecting with ![]() $\pi ^{*}(K_X)$, we see that
$\pi ^{*}(K_X)$, we see that ![]() $k-2 + ({a}/{d})(-k) + s = 0$, where
$k-2 + ({a}/{d})(-k) + s = 0$, where ![]() $s \geqslant 0$ is the intersection of
$s \geqslant 0$ is the intersection of ![]() $f_g$ with other divisors in the formula
$f_g$ with other divisors in the formula ![]() $\pi ^{*}(K_X)$. Because
$\pi ^{*}(K_X)$. Because ![]() ${a}/{d} < {1}/{n}$ and
${a}/{d} < {1}/{n}$ and ![]() $n \geqslant 3$, this implies that
$n \geqslant 3$, this implies that ![]() $k = 2$.
$k = 2$.
Now, because our MMP contracts ![]() $\Delta$ and then
$\Delta$ and then ![]() $F_1$, we can study what happens to
$F_1$, we can study what happens to ![]() $G_j$ in these contractions. After these contractions in the threefold
$G_j$ in these contractions. After these contractions in the threefold ![]() $Y_{l+1}$, the images of the curves
$Y_{l+1}$, the images of the curves ![]() $f$ in
$f$ in ![]() $G_j^{l+1}$ are
$G_j^{l+1}$ are ![]() $K_{Y_{l+1}}$-negative,
$K_{Y_{l+1}}$-negative, ![]() $E^{l+1}$-positive, and
$E^{l+1}$-positive, and ![]() $K_{Y_{l+1}} + E^{l+1}$-negative. In addition, they are
$K_{Y_{l+1}} + E^{l+1}$-negative. In addition, they are ![]() $G_j^{l}$-trivial. From the description of the exceptional divisors of
$G_j^{l}$-trivial. From the description of the exceptional divisors of ![]() $Y \to X$, this implies that there must be an extremal ray
$Y \to X$, this implies that there must be an extremal ray ![]() $R$ in the cone of curves of
$R$ in the cone of curves of ![]() $Y_{l+1}$ that is
$Y_{l+1}$ that is ![]() $K_{Y_{l+1}}$-negative,
$K_{Y_{l+1}}$-negative, ![]() $E^{l+1}$-positive, and
$E^{l+1}$-positive, and ![]() $K_{Y_{l+1}} + E^{l+1}$-negative, and
$K_{Y_{l+1}} + E^{l+1}$-negative, and ![]() $G_j^{l+1}$-trivial, and its contraction cannot contract any curves in
$G_j^{l+1}$-trivial, and its contraction cannot contract any curves in ![]() $E^{l+1}$ (the only curves in
$E^{l+1}$ (the only curves in ![]() $E^{l+1}$ that are
$E^{l+1}$ that are ![]() $G_j^{l+1}$ trivial are those that do not intersect
$G_j^{l+1}$ trivial are those that do not intersect ![]() $G_j^{l+1}$, but then their positivity is the same as that in
$G_j^{l+1}$, but then their positivity is the same as that in ![]() $Y$, so they are
$Y$, so they are ![]() $K_{Y_{l+1}}$-positive). Therefore, choosing an alternate path in the MMP and contracting
$K_{Y_{l+1}}$-positive). Therefore, choosing an alternate path in the MMP and contracting ![]() $R$, the MMP terminates at this contraction with a fibration over
$R$, the MMP terminates at this contraction with a fibration over ![]() $E^{l+1}$, which implies that
$E^{l+1}$, which implies that ![]() $d$ is even by Lemma 4.19.
$d$ is even by Lemma 4.19.
Now, we consider the case that ![]() $\Delta$ contracted onto the chain of divisors is such that no
$\Delta$ contracted onto the chain of divisors is such that no ![]() $F_i$ is
$F_i$ is ![]() ${{\mathbb {P}}}^{1} \times C$, but
${{\mathbb {P}}}^{1} \times C$, but ![]() $\Delta$ is disjoint from
$\Delta$ is disjoint from ![]() $F_{i-1}$ and
$F_{i-1}$ and ![]() $F_{i+1}$, so the previous arguments imply that
$F_{i+1}$, so the previous arguments imply that ![]() $\Delta$ is only connected to
$\Delta$ is only connected to ![]() $F_k$, the last divisor in the chain (cf. Lemma 4.20). Therefore, to reach the extremal contraction of the (image of)
$F_k$, the last divisor in the chain (cf. Lemma 4.20). Therefore, to reach the extremal contraction of the (image of) ![]() $F_1$ in the MMP, we contract
$F_1$ in the MMP, we contract ![]() $\Delta$ onto
$\Delta$ onto ![]() $F_k$, then
$F_k$, then ![]() $F_k$ onto
$F_k$ onto ![]() $F_{k-1}, \ldots, F_i$ onto
$F_{k-1}, \ldots, F_i$ onto ![]() $F_{i-1}, \ldots$, and ultimately,
$F_{i-1}, \ldots$, and ultimately, ![]() $F_1$ onto
$F_1$ onto ![]() $E$. If any other surface
$E$. If any other surface ![]() $G_j$ is contracted onto
$G_j$ is contracted onto ![]() $F_i$ for any
$F_i$ for any ![]() $i$, it must be some component of
$i$, it must be some component of ![]() $\operatorname {Supp} G$ (because some curve in it must begin
$\operatorname {Supp} G$ (because some curve in it must begin ![]() $K_Y$-non-negative). A brief computation with the discrepancies as in Lemma 4.37 and using that
$K_Y$-non-negative). A brief computation with the discrepancies as in Lemma 4.37 and using that ![]() $\Delta, F_i$ are ruled surfaces (albeit possibly singular) and that the curves
$\Delta, F_i$ are ruled surfaces (albeit possibly singular) and that the curves ![]() $C$ in
$C$ in ![]() $F_i$ must satisfy the relationship
$F_i$ must satisfy the relationship ![]() $\pi ^{*}(K_X) \cdot C = 0$, one can show that there are no flips into and out of
$\pi ^{*}(K_X) \cdot C = 0$, one can show that there are no flips into and out of ![]() $F_i$. At this point, we work backwards from the contraction of
$F_i$. At this point, we work backwards from the contraction of ![]() $F_1$. We have reduced to the case that we performed several divisorial contractions of divisors in
$F_1$. We have reduced to the case that we performed several divisorial contractions of divisors in ![]() $\operatorname {Supp} F$, possibly with some divisors in
$\operatorname {Supp} F$, possibly with some divisors in ![]() $\operatorname {Supp} G$, after beginning with a divisorial contraction of a component
$\operatorname {Supp} G$, after beginning with a divisorial contraction of a component ![]() $\Delta$ not contained in the exceptional locus onto a curve
$\Delta$ not contained in the exceptional locus onto a curve ![]() $C$ in
$C$ in ![]() $F_k$ (the last divisor in the chain). It is not hard to show that, if the generic fiber of
$F_k$ (the last divisor in the chain). It is not hard to show that, if the generic fiber of ![]() $\Delta$ intersects some exceptional divisor
$\Delta$ intersects some exceptional divisor ![]() $G_j$ other than
$G_j$ other than ![]() $F_k$, then
$F_k$, then ![]() $G_j\cap \Delta$ is not contractible in
$G_j\cap \Delta$ is not contractible in ![]() $\Delta$; i.e.
$\Delta$; i.e. ![]() $G_j$ contracts onto the curve
$G_j$ contracts onto the curve ![]() $G_j \cap \Delta$ in the morphism
$G_j \cap \Delta$ in the morphism ![]() $\pi : Y \to X$. We begin with a specific case,
$\pi : Y \to X$. We begin with a specific case, ![]() $n = 3$.
$n = 3$.
Lemma 4.25 Suppose ![]() $n = 3$. Then,
$n = 3$. Then, ![]() $d$ is even.
$d$ is even.
Proof. If ![]() $n = 3$, the chain
$n = 3$, the chain ![]() $F_i$ is either one component
$F_i$ is either one component ![]() $F_1$ with discrepancy
$F_1$ with discrepancy ![]() $-\frac {2}{3}$ or two components
$-\frac {2}{3}$ or two components ![]() $F_1, F_2$ with discrepancies
$F_1, F_2$ with discrepancies ![]() $-\frac {2}{3}$ and
$-\frac {2}{3}$ and ![]() $-\frac {1}{3}$. Suppose we are in the first case; then the generic fiber
$-\frac {1}{3}$. Suppose we are in the first case; then the generic fiber ![]() $f_g$ of
$f_g$ of ![]() $\Delta$ contracted by the first step of the MMP intersects
$\Delta$ contracted by the first step of the MMP intersects ![]() $F_1$ so
$F_1$ so ![]() $\pi ^{*}(K_X)\cdot f_g = (K_Y + \frac {2}{3} F_1 + \sum ({a_i}/{d}) G_i) \cdot f_g = -\frac {1}{3} + \sum ({a_i}/{d}) m_i$ for some
$\pi ^{*}(K_X)\cdot f_g = (K_Y + \frac {2}{3} F_1 + \sum ({a_i}/{d}) G_i) \cdot f_g = -\frac {1}{3} + \sum ({a_i}/{d}) m_i$ for some ![]() $m_i$. If there are no components
$m_i$. If there are no components ![]() $G_i$ intersecting
$G_i$ intersecting ![]() $f_g$,
$f_g$, ![]() $K_X\cdot \pi (f_g) = - \frac {1}{3}$, and the relationship
$K_X\cdot \pi (f_g) = - \frac {1}{3}$, and the relationship ![]() $dK_X + 4D$ then implies
$dK_X + 4D$ then implies ![]() $d$ is even. If there do exist
$d$ is even. If there do exist ![]() $G_i$, the equation implies each coefficient
$G_i$, the equation implies each coefficient ![]() ${a_i}/{d} < \frac {1}{3}$. For a component
${a_i}/{d} < \frac {1}{3}$. For a component ![]() $G_j$ intersecting
$G_j$ intersecting ![]() $f_g$, this implies the general fiber
$f_g$, this implies the general fiber ![]() $l_g$ of the ruled surface
$l_g$ of the ruled surface ![]() $G_j$ satisfies
$G_j$ satisfies ![]() $G_j \cdot l_g = -2$, so by the same argument in Lemma 4.24, after contracting
$G_j \cdot l_g = -2$, so by the same argument in Lemma 4.24, after contracting ![]() $\Delta$ and
$\Delta$ and ![]() $F_1$, there exists a
$F_1$, there exists a ![]() $K+E$-negative
$K+E$-negative ![]() $E$-positive extremal ray in the cone of curves, and we can choose the MMP to terminate with a fibration over
$E$-positive extremal ray in the cone of curves, and we can choose the MMP to terminate with a fibration over ![]() $E$.
$E$.
In the second case, we contract ![]() $\Delta$ onto
$\Delta$ onto ![]() $F_2$ and then
$F_2$ and then ![]() $F_2$ onto
$F_2$ onto ![]() $F_1$, followed by
$F_1$, followed by ![]() $F_1$ onto
$F_1$ onto ![]() $E_0$. Again considering a generic fiber
$E_0$. Again considering a generic fiber ![]() $f_g$ of
$f_g$ of ![]() $\Delta$, if
$\Delta$, if ![]() $f_g$ intersects no components
$f_g$ intersects no components ![]() $G_i$, we find that
$G_i$, we find that ![]() $K_X\cdot \pi (f_g) = - \frac {2}{3}$ and the relationship
$K_X\cdot \pi (f_g) = - \frac {2}{3}$ and the relationship ![]() $dK_X + 4D$ implies
$dK_X + 4D$ implies ![]() $d$ is even. Suppose there are components
$d$ is even. Suppose there are components ![]() $G_i$ intersecting
$G_i$ intersecting ![]() $f_g$. Let
$f_g$. Let ![]() $G_j$ be such a component and let
$G_j$ be such a component and let ![]() $l_g$ be a general fiber of the ruled surface
$l_g$ be a general fiber of the ruled surface ![]() $G_j$. If
$G_j$. If ![]() $G_j \cdot l_g = -3$ or
$G_j \cdot l_g = -3$ or ![]() $-2$, after contracting some of the components
$-2$, after contracting some of the components ![]() $\Delta$,
$\Delta$, ![]() $F_2$, and
$F_2$, and ![]() $F_1$, we find a
$F_1$, we find a ![]() $\pi ^{*}(K_X)$-negative but
$\pi ^{*}(K_X)$-negative but ![]() $E_0 + F$-positive extremal ray. The contraction of such a ray terminates in a fibration over
$E_0 + F$-positive extremal ray. The contraction of such a ray terminates in a fibration over ![]() $E_0$ or one component
$E_0$ or one component ![]() $F_i$. Note that
$F_i$. Note that ![]() $E_0$ cannot be contracted (as the curves in
$E_0$ cannot be contracted (as the curves in ![]() $E_0$ are not
$E_0$ are not ![]() $K$-negative) so by Lemma 4.19,
$K$-negative) so by Lemma 4.19, ![]() $d$ is even.
$d$ is even.
Suppose then all components ![]() $G$ meeting
$G$ meeting ![]() $f_g$ have
$f_g$ have ![]() $G\cdot l_g \geqslant -4$. Using that
$G\cdot l_g \geqslant -4$. Using that ![]() $\pi ^{*}(K_X)\cdot f_g = (K_Y + \frac {2}{3} F_1 + \sum ({a_i}/{d}) G_i) \cdot f_g < 0$, we know that the coefficient of any such
$\pi ^{*}(K_X)\cdot f_g = (K_Y + \frac {2}{3} F_1 + \sum ({a_i}/{d}) G_i) \cdot f_g < 0$, we know that the coefficient of any such ![]() $G$ is less than
$G$ is less than ![]() $\frac {2}{3}$. Given this bound on the discrepancy and that
$\frac {2}{3}$. Given this bound on the discrepancy and that ![]() $G\cdot l_g \leqslant -4$, we can compute all possible configurations of divisors
$G\cdot l_g \leqslant -4$, we can compute all possible configurations of divisors ![]() $G_j$. By taking a generic hyperplane section
$G_j$. By taking a generic hyperplane section ![]() $H$ meeting the image of
$H$ meeting the image of ![]() $G$ in
$G$ in ![]() $X$ and noting that this is log-terminal at the generic point of
$X$ and noting that this is log-terminal at the generic point of ![]() $\pi (G)$, we reduce to studying configurations
$\pi (G)$, we reduce to studying configurations ![]() $C$ of curves on
$C$ of curves on ![]() $H_Y = \pi ^{-1}_*H$ that contract to a log-terminal singularity with at least one
$H_Y = \pi ^{-1}_*H$ that contract to a log-terminal singularity with at least one ![]() $-n$ curve,
$-n$ curve, ![]() $n \geqslant 4$, with coefficient of that curve less than
$n \geqslant 4$, with coefficient of that curve less than ![]() $\frac {2}{3}$. We find only the following possibilities:
$\frac {2}{3}$. We find only the following possibilities: ![]() $C$ is one
$C$ is one ![]() $-5$ curve, with coefficient
$-5$ curve, with coefficient ![]() $\frac {3}{5}, C$ is a
$\frac {3}{5}, C$ is a ![]() $-4$ curve meeting a
$-4$ curve meeting a ![]() $-3$ curve, with coefficient
$-3$ curve, with coefficient ![]() $\frac {7}{11}$ on the
$\frac {7}{11}$ on the ![]() $-4$ curve, or
$-4$ curve, or ![]() $C$ is a
$C$ is a ![]() $-4$ curve meeting a chain of
$-4$ curve meeting a chain of ![]() $k-1 -2$ curves, with coefficient
$k-1 -2$ curves, with coefficient ![]() ${2k}/({3k+1})$ on the
${2k}/({3k+1})$ on the ![]() $-4$ curve. From this description, we see that
$-4$ curve. From this description, we see that ![]() $\pi ^{*}(K_X)\cdot f_g = (K_Y + \frac {2}{3} F_1 + \sum ({a_i}/{d}) G_i) \cdot f_g < 0$ implies that there is only one
$\pi ^{*}(K_X)\cdot f_g = (K_Y + \frac {2}{3} F_1 + \sum ({a_i}/{d}) G_i) \cdot f_g < 0$ implies that there is only one ![]() $G$ meeting
$G$ meeting ![]() $f_g$, and plugging in the given discrepancies in each of the three cases, we see that
$f_g$, and plugging in the given discrepancies in each of the three cases, we see that ![]() $K_X \cdot \pi (f_g) = -1 + \frac {1}{3} + {a}/{d}$, which is either
$K_X \cdot \pi (f_g) = -1 + \frac {1}{3} + {a}/{d}$, which is either ![]() $-\frac {1}{15}, -\frac {1}{33}$, or
$-\frac {1}{15}, -\frac {1}{33}$, or ![]() $-{2}/{3(3k+1)}$. With the relationship
$-{2}/{3(3k+1)}$. With the relationship ![]() $dK_X+4D \sim 0$, each case implies that
$dK_X+4D \sim 0$, each case implies that ![]() $d$ is even.
$d$ is even.
Now, suppose ![]() $n > 3$, so
$n > 3$, so ![]() $n \geqslant 5$ because
$n \geqslant 5$ because ![]() $n$ is odd. We perform contractions of
$n$ is odd. We perform contractions of ![]() $\Delta$ and
$\Delta$ and ![]() $F_i$ ultimately contracting
$F_i$ ultimately contracting ![]() $F_1$ onto
$F_1$ onto ![]() $E$. In our final contraction
$E$. In our final contraction ![]() $F_1$ contracting onto
$F_1$ contracting onto ![]() $E$, say
$E$, say ![]() $Y_l \to Y_{l+1}$, along the image of
$Y_l \to Y_{l+1}$, along the image of ![]() $F_1$ in
$F_1$ in ![]() $E^{l+1}$, the threefold
$E^{l+1}$, the threefold ![]() $Y_{l+1}$ has only index one singularities. Indeed, as these are all divisorial contractions, all of the fibers are numerically equivalent, i.e. all multiple of the general fiber
$Y_{l+1}$ has only index one singularities. Indeed, as these are all divisorial contractions, all of the fibers are numerically equivalent, i.e. all multiple of the general fiber ![]() $f_g$ which satisfies
$f_g$ which satisfies ![]() $K_{Y_l} \cdot f_g = -1, F_1^{l} \cdot f_g = -1$, and
$K_{Y_l} \cdot f_g = -1, F_1^{l} \cdot f_g = -1$, and ![]() $E_0^{l} \cdot f_g = 1$, and the pullbacks of both the general fiber
$E_0^{l} \cdot f_g = 1$, and the pullbacks of both the general fiber ![]() $f_0$ and
$f_0$ and ![]() $f_g$ must satisfy
$f_g$ must satisfy ![]() $0 = \pi ^{*}(K_X) \cdot f$. Because
$0 = \pi ^{*}(K_X) \cdot f$. Because ![]() $\pi ^{*}(K_X) = K_Y + E_0 + (1-{1}/{n})F_1+\cdots$, for a special fiber
$\pi ^{*}(K_X) = K_Y + E_0 + (1-{1}/{n})F_1+\cdots$, for a special fiber ![]() $f_0$, we can use the wealth of information on divisorial extremal neighborhoods [Reference MoriMor88, Reference Kollár and MoriKM92, Reference Mori and ProkhorovMP11, Reference TziolasTzi05] and formulas for intersection with
$f_0$, we can use the wealth of information on divisorial extremal neighborhoods [Reference MoriMor88, Reference Kollár and MoriKM92, Reference Mori and ProkhorovMP11, Reference TziolasTzi05] and formulas for intersection with ![]() $-K_{Y_l}$ (and its numerical equivalence with
$-K_{Y_l}$ (and its numerical equivalence with ![]() $F_i^{l}$ and
$F_i^{l}$ and ![]() $E_0^{l}$) along with adjunction on the ruled surface
$E_0^{l}$) along with adjunction on the ruled surface ![]() $F_1$ to compute that
$F_1$ to compute that ![]() $-K_{Y_l} \cdot f_0$ must be
$-K_{Y_l} \cdot f_0$ must be ![]() $-{1}/{r}$, where
$-{1}/{r}$, where ![]() $r$ is the index of the threefold singularity on the fiber
$r$ is the index of the threefold singularity on the fiber ![]() $f_0$. Then, [Reference TziolasTzi05, Theorem 5.5] implies that
$f_0$. Then, [Reference TziolasTzi05, Theorem 5.5] implies that ![]() $Y_{l+1}$ has only index one singularities and
$Y_{l+1}$ has only index one singularities and ![]() $Y_{l+1}$ is factorial. Therefore,
$Y_{l+1}$ is factorial. Therefore, ![]() $K_{Y_{l+1}}$ and
$K_{Y_{l+1}}$ and ![]() $E^{l+1}$ are both Cartier, so, by adjunction,
$E^{l+1}$ are both Cartier, so, by adjunction, ![]() $E_0^{l+1}$ has only Du Val singularities along the image of
$E_0^{l+1}$ has only Du Val singularities along the image of ![]() $F_1$. Let
$F_1$. Let ![]() $C_F$ be the curve that is the image of
$C_F$ be the curve that is the image of ![]() $F_1$. By [Reference TziolasTzi05, Lemma 5.1],
$F_1$. By [Reference TziolasTzi05, Lemma 5.1], ![]() $C_F$ is a smooth curve and cannot intersect any exceptional divisors of
$C_F$ is a smooth curve and cannot intersect any exceptional divisors of ![]() $\pi$ other than
$\pi$ other than ![]() $E_0^{l+1}$ (if it did, the very first contraction of
$E_0^{l+1}$ (if it did, the very first contraction of ![]() $\Delta$ would necessarily have contracted a
$\Delta$ would necessarily have contracted a ![]() $K$-non-negative curve in one of these divisors, a contradiction). By comparing
$K$-non-negative curve in one of these divisors, a contradiction). By comparing ![]() $C_F$ to
$C_F$ to ![]() $\pi ^{*}(K_X)|_{E_0}$, we find that
$\pi ^{*}(K_X)|_{E_0}$, we find that ![]() $C_F$ satisfies
$C_F$ satisfies ![]() $(K_{E_0} + (({n-1})/{n})C_F)\cdot C_F = 0$, i.e.
$(K_{E_0} + (({n-1})/{n})C_F)\cdot C_F = 0$, i.e. ![]() $(K_{E_0} + C_F)\cdot C_F = ({1}/{n})C_F^{2}$. In particular,
$(K_{E_0} + C_F)\cdot C_F = ({1}/{n})C_F^{2}$. In particular, ![]() $C_F$ is contractible in
$C_F$ is contractible in ![]() $E_0$ if and only if it is rational with at most three singularities. However, if
$E_0$ if and only if it is rational with at most three singularities. However, if ![]() $C_F^{2} < 0$, then it is not hard to show it is extremal in the cone of curves of
$C_F^{2} < 0$, then it is not hard to show it is extremal in the cone of curves of ![]() $Y_{l+1}$, so we may contract (and possibly flip)
$Y_{l+1}$, so we may contract (and possibly flip) ![]() $C_F$ before continuing the MMP. This is certainly a
$C_F$ before continuing the MMP. This is certainly a ![]() $K_{Y_{l+1}} + E_0^{l+1}$-positive contraction, but the flip exists because the divisor
$K_{Y_{l+1}} + E_0^{l+1}$-positive contraction, but the flip exists because the divisor ![]() $D^{l+1}$ (the image of
$D^{l+1}$ (the image of ![]() $\pi ^{-1}_*D$) satisfies
$\pi ^{-1}_*D$) satisfies ![]() $(Y_{l+1}, E^{l+1} + ({4}/{d} - \epsilon )D^{l+1})$ is log-terminal but the log-canonical divisor is negative on
$(Y_{l+1}, E^{l+1} + ({4}/{d} - \epsilon )D^{l+1})$ is log-terminal but the log-canonical divisor is negative on ![]() $C_F$ for
$C_F$ for ![]() $\epsilon$ sufficiently small. Because this ray is
$\epsilon$ sufficiently small. Because this ray is ![]() $K_{Y_{l+1}}+E_0^{l+1}$-positive, the contraction/flip may create worse singularities on the threefold
$K_{Y_{l+1}}+E_0^{l+1}$-positive, the contraction/flip may create worse singularities on the threefold ![]() $Y_{l+2}$, but
$Y_{l+2}$, but ![]() $E_0^{l+2}$ is still Cartier in codimension two, so our earlier results (cf. Lemmas 4.9 and 4.37) still apply. In this case, after the contraction of
$E_0^{l+2}$ is still Cartier in codimension two, so our earlier results (cf. Lemmas 4.9 and 4.37) still apply. In this case, after the contraction of ![]() $C_F$, the curves in
$C_F$, the curves in ![]() $E_0^{l+2}$ are still
$E_0^{l+2}$ are still ![]() $K_{Y_{l+2}}$-non-negative, so if
$K_{Y_{l+2}}$-non-negative, so if ![]() $E_0^{l+2}$ is contracted by the MMP, following the logic in Lemmas 4.21 and 4.22, there must exist another chain of contractions of components of
$E_0^{l+2}$ is contracted by the MMP, following the logic in Lemmas 4.21 and 4.22, there must exist another chain of contractions of components of ![]() $\operatorname {Supp} F$ changing the positivity of these curves. Therefore, by repeating this process, we may assume that the curve
$\operatorname {Supp} F$ changing the positivity of these curves. Therefore, by repeating this process, we may assume that the curve ![]() $C_F$ has non-negative self-intersection. If
$C_F$ has non-negative self-intersection. If ![]() $C_F^{2} = 0$, then there exists a morphism
$C_F^{2} = 0$, then there exists a morphism ![]() $E_0 \to C$ fibering
$E_0 \to C$ fibering ![]() $E_0$ over a curve with
$E_0$ over a curve with ![]() $C_F$ as one of its fibers. However, as
$C_F$ as one of its fibers. However, as ![]() $C_F$ does not intersect any other exceptional divisors, the same is true for the generic fiber, so the generic fiber
$C_F$ does not intersect any other exceptional divisors, the same is true for the generic fiber, so the generic fiber ![]() $f_g$ of this map would satisfy
$f_g$ of this map would satisfy ![]() $K_{E_0} \cdot f_g = -2$ so
$K_{E_0} \cdot f_g = -2$ so ![]() $0 = \pi ^{*}(K_X)\cdot f_g = (K_X + E_0 + \cdots )\cdot f_g = -2$ (where
$0 = \pi ^{*}(K_X)\cdot f_g = (K_X + E_0 + \cdots )\cdot f_g = -2$ (where ![]() $\cdots$ indicate the other exceptional divisors which by assumption do not intersect
$\cdots$ indicate the other exceptional divisors which by assumption do not intersect ![]() $f_g$), a contradiction.
$f_g$), a contradiction.
Therefore, we may assume that ![]() $C_F^{2} > 0$ which implies that
$C_F^{2} > 0$ which implies that ![]() $C_F$ is a big divisor on the surface
$C_F$ is a big divisor on the surface ![]() $E_0$. Because
$E_0$. Because ![]() $-K_{E_0} = (({n-1})/{n})C_F, -K_{E_0}$ is also big. Because
$-K_{E_0} = (({n-1})/{n})C_F, -K_{E_0}$ is also big. Because ![]() $C_F$ is a smooth curve through at worst Du Val singularities that does not intersect any other exceptional divisors of
$C_F$ is a smooth curve through at worst Du Val singularities that does not intersect any other exceptional divisors of ![]() $\pi$, the pair
$\pi$, the pair ![]() $(E_0, C_F + \sum -a(\Delta _i, X) \Delta _i|_{E_0})$ is dlt, where the
$(E_0, C_F + \sum -a(\Delta _i, X) \Delta _i|_{E_0})$ is dlt, where the ![]() $\Delta _i$ are the other exceptional divisors of
$\Delta _i$ are the other exceptional divisors of ![]() $\pi$, so we may consider the
$\pi$, so we may consider the ![]() $K_{E_0} + C_F + \sum -a(\Delta _i, X) \Delta _i|_{E_0}$ MMP on
$K_{E_0} + C_F + \sum -a(\Delta _i, X) \Delta _i|_{E_0}$ MMP on ![]() $E_0$. Here, the divisor
$E_0$. Here, the divisor ![]() $K_{E_0} + (({n-1})/{n}) C_F + \sum -a(\Delta _i, X) \Delta _i|_{E_0} = 0$ and the components
$K_{E_0} + (({n-1})/{n}) C_F + \sum -a(\Delta _i, X) \Delta _i|_{E_0} = 0$ and the components ![]() $\Delta _i$ do not intersect
$\Delta _i$ do not intersect ![]() $C_F$, so this contracts all components
$C_F$, so this contracts all components ![]() $\Delta _i$ along with any additional curves that do not intersect
$\Delta _i$ along with any additional curves that do not intersect ![]() $C_F$. Denote the image of this surface by
$C_F$. Denote the image of this surface by ![]() $S$. This is an isomorphism on
$S$. This is an isomorphism on ![]() $C_F$, so we continue to denote
$C_F$, so we continue to denote ![]() $C_F$ in the same way. By construction,
$C_F$ in the same way. By construction, ![]() $C_F$ is ample on
$C_F$ is ample on ![]() $S$ and
$S$ and ![]() $-K_S = (({n-1})/{n}) C_F$, so
$-K_S = (({n-1})/{n}) C_F$, so ![]() $S$ is Fano. If
$S$ is Fano. If ![]() $S$ has any strictly log-canonical (non-klt) singularities, then
$S$ has any strictly log-canonical (non-klt) singularities, then ![]() $S$ has index of
$S$ has index of ![]() $-K_S$ equal to 1, 2, 3, 4, or 6 (see Lemma 4.28), and the index divides
$-K_S$ equal to 1, 2, 3, 4, or 6 (see Lemma 4.28), and the index divides ![]() $d \geqslant 5$, so we must have index 1 or 3. It the index is 1,
$d \geqslant 5$, so we must have index 1 or 3. It the index is 1, ![]() $K_S$ is Gorenstein near the non-klt singularity. Because
$K_S$ is Gorenstein near the non-klt singularity. Because ![]() $-K_S$ is ample, by Theorem 4.6,
$-K_S$ is ample, by Theorem 4.6, ![]() $S$ is an elliptic cone, in which case it is impossible for
$S$ is an elliptic cone, in which case it is impossible for ![]() $-K_S = (({n-1})/{n})C_F$ unless
$-K_S = (({n-1})/{n})C_F$ unless ![]() $n =2$, which implies that
$n =2$, which implies that ![]() $d$ is even. If the index is 3, then
$d$ is even. If the index is 3, then ![]() $S$ is rational [Reference HackingHac04, Theorem 8.5], so we assume that
$S$ is rational [Reference HackingHac04, Theorem 8.5], so we assume that ![]() $S$ is a rational Fano surface.
$S$ is a rational Fano surface.
Now, we proceed by comparing the minimal resolution of ![]() $S$ and its minimal model. Let
$S$ and its minimal model. Let ![]() $\phi : M \to S$ be the minimal resolution, and let
$\phi : M \to S$ be the minimal resolution, and let ![]() $M \to Z$ be the minimal model of
$M \to Z$ be the minimal model of ![]() $M$ (with respect to
$M$ (with respect to ![]() $K_M$). By [Reference NakayamaNak07, Corollary 3.4] any curve
$K_M$). By [Reference NakayamaNak07, Corollary 3.4] any curve ![]() $C \subset M$ with
$C \subset M$ with ![]() $C^{2} < 0$ is either contained in the exceptional locus of
$C^{2} < 0$ is either contained in the exceptional locus of ![]() $M \to S$ or is a
$M \to S$ or is a ![]() $-1$ curve. By the ampleness of
$-1$ curve. By the ampleness of ![]() $C_F$, any
$C_F$, any ![]() $-1$ curve in
$-1$ curve in ![]() $M$ must intersect the pullback of
$M$ must intersect the pullback of ![]() $C_F$.
$C_F$.
Following the ideas in [Reference NakayamaNak07, Reference FujitaFuj16], we can classify such surfaces. Although their work is in the case when ![]() $C_F$ is Cartier and
$C_F$ is Cartier and ![]() $S$ is klt, the Du Val singularities do not provide a significant complication. For example, suppose that
$S$ is klt, the Du Val singularities do not provide a significant complication. For example, suppose that ![]() $S$ is singular at a point
$S$ is singular at a point ![]() $p\in C_F$. By assumption, this is a Du Val singularity. Let
$p\in C_F$. By assumption, this is a Du Val singularity. Let ![]() $P$ be the chain of
$P$ be the chain of ![]() $-$2 curves above
$-$2 curves above ![]() $p$ in the minimal resolution
$p$ in the minimal resolution ![]() $M$. If
$M$. If ![]() $C \subset M$ is a
$C \subset M$ is a ![]() $-1$ curve that intersects the chain
$-1$ curve that intersects the chain ![]() $P$, we can contract
$P$, we can contract ![]() $C$ and then contract the curves in
$C$ and then contract the curves in ![]() $P$ until we find either a degree-zero curve (in which case, the MMP can terminate with a fibration) or produce a
$P$ until we find either a degree-zero curve (in which case, the MMP can terminate with a fibration) or produce a ![]() $-1$ curve connected to only smooth points of
$-1$ curve connected to only smooth points of ![]() $C_F$ and then follow the ideas of [Reference FujitaFuj16]. For brevity, we only sketch the idea here. We first reduce to
$C_F$ and then follow the ideas of [Reference FujitaFuj16]. For brevity, we only sketch the idea here. We first reduce to ![]() $S$ only having
$S$ only having ![]() $A_1$ singularities along
$A_1$ singularities along ![]() $C_F$: if there were larger
$C_F$: if there were larger ![]() $A_n$ singularities, there must be a
$A_n$ singularities, there must be a ![]() $-1$ curve connected somewhere to the chain, and contracting the
$-1$ curve connected somewhere to the chain, and contracting the ![]() $-1$ curve and connected
$-1$ curve and connected ![]() $-2$ curves yields a fibration where
$-2$ curves yields a fibration where ![]() $\phi ^{*}(K_S + (({n-1})/{n})C_F)$ is not trivial. Then, we note that any
$\phi ^{*}(K_S + (({n-1})/{n})C_F)$ is not trivial. Then, we note that any ![]() $-2$ curve must meet a
$-2$ curve must meet a ![]() $-1$ curve (it cannot be a section in
$-1$ curve (it cannot be a section in ![]() $Z$ as a general fiber of the fibration would also not satisfy
$Z$ as a general fiber of the fibration would also not satisfy ![]() $\phi ^{*}(K_S + (({n-1})/{n})C_F)$ trivial), and such a
$\phi ^{*}(K_S + (({n-1})/{n})C_F)$ trivial), and such a ![]() $-1$ curve cannot meet
$-1$ curve cannot meet ![]() $C_F$ in any other point (because if it did, and because
$C_F$ in any other point (because if it did, and because ![]() $n \geqslant 5$, that
$n \geqslant 5$, that ![]() $-1$ curve would not satisfy
$-1$ curve would not satisfy ![]() $\phi ^{*}(K_S + (({n-1})/{n})C_F)$ triviality). Therefore, we find
$\phi ^{*}(K_S + (({n-1})/{n})C_F)$ triviality). Therefore, we find ![]() $-1$ curves meeting a
$-1$ curves meeting a ![]() $-2$ curve and any other negative curves attached to the
$-2$ curve and any other negative curves attached to the ![]() $-1$ curves have discrepancy at most
$-1$ curves have discrepancy at most ![]() $({n-1})/{2n}$. Ultimately, this is impossible to satisfy while simultaneously maintaining
$({n-1})/{2n}$. Ultimately, this is impossible to satisfy while simultaneously maintaining ![]() $\phi ^{*}(K_S + (({n-1})/{n})C_F) = 0$. Therefore, we conclude that there are no singularities along
$\phi ^{*}(K_S + (({n-1})/{n})C_F) = 0$. Therefore, we conclude that there are no singularities along ![]() $C_F$. Then, we show that
$C_F$. Then, we show that ![]() $S$ must be klt: if
$S$ must be klt: if ![]() $S$ has a log-canonical singularity of Cartier index 3, we show that the unique fork of the dual graph in the minimal resolution must be the negative section of the minimal model, but then
$S$ has a log-canonical singularity of Cartier index 3, we show that the unique fork of the dual graph in the minimal resolution must be the negative section of the minimal model, but then ![]() $C_F$ must also be a section and hence rational. However, from the formula
$C_F$ must also be a section and hence rational. However, from the formula ![]() $K_S + F = ({1}/{n})C_F$, this is only possible if
$K_S + F = ({1}/{n})C_F$, this is only possible if ![]() $C_F^{2} = -2n <0$, which is a contradiction. Therefore, we find that
$C_F^{2} = -2n <0$, which is a contradiction. Therefore, we find that ![]() $S$ is a klt Fano surface with
$S$ is a klt Fano surface with ![]() $C_F$ Cartier, and we can apply Fujita's results directly.
$C_F$ Cartier, and we can apply Fujita's results directly.
Thus, we assume ![]() $S$ is a log-terminal Fano surface, and
$S$ is a log-terminal Fano surface, and ![]() $C_F$ is a Cartier divisor on
$C_F$ is a Cartier divisor on ![]() $S$ satisfying
$S$ satisfying ![]() $K_{S} + (({n-1})/{n})C_F =0$ for some
$K_{S} + (({n-1})/{n})C_F =0$ for some ![]() $n \geqslant 5$, and we use the classification in [Reference FujitaFuj16]) to bound its fractional index and prove that there is only one possibility for
$n \geqslant 5$, and we use the classification in [Reference FujitaFuj16]) to bound its fractional index and prove that there is only one possibility for ![]() $S$.
$S$.
Definition 4.26 For a ![]() $\mathbb {Q}$-Fano log-terminal variety
$\mathbb {Q}$-Fano log-terminal variety ![]() $Z$, define the fractional index as
$Z$, define the fractional index as
Lemma 4.27 In the setting described previously, the index must in fact be ![]() $(({n-1})/{n})$.
$(({n-1})/{n})$.
Proof. Indeed, if it were less than this, computations show that we would find a smaller ample divisor ![]() $L$ and
$L$ and ![]() $kL = C_F, k \geqslant 2$, but this would imply that the fractional index is at least one, but then by [Reference FujitaFuj16]
$kL = C_F, k \geqslant 2$, but this would imply that the fractional index is at least one, but then by [Reference FujitaFuj16] ![]() $S$ is either
$S$ is either ![]() ${{\mathbb {P}}}(1,1,q)$ or has at worst Du Val singularities. If
${{\mathbb {P}}}(1,1,q)$ or has at worst Du Val singularities. If ![]() $S$ is
$S$ is ![]() ${{\mathbb {P}}}(1,1,q)$, using the relationship
${{\mathbb {P}}}(1,1,q)$, using the relationship ![]() $K_S + (({n-1})/{n})C_F = 0$, the fact that
$K_S + (({n-1})/{n})C_F = 0$, the fact that ![]() $C_F$ misses the singular point of
$C_F$ misses the singular point of ![]() $S$, a short computation shows that
$S$, a short computation shows that ![]() $n \leqslant 4$, contradicting our assumption that
$n \leqslant 4$, contradicting our assumption that ![]() $n \geqslant 5$. If instead
$n \geqslant 5$. If instead ![]() $S$ has Du Val singularities, then we can find a curve
$S$ has Du Val singularities, then we can find a curve ![]() $l$ such that
$l$ such that ![]() $K_S \cdot l = -1$,
$K_S \cdot l = -1$, ![]() $-2,$ or
$-2,$ or ![]() $-3$, and then use the relationship
$-3$, and then use the relationship ![]() $K_S + (({n-1})/{n})C_F = 0$ to get a contradiction if
$K_S + (({n-1})/{n})C_F = 0$ to get a contradiction if ![]() $n \geqslant 5$.
$n \geqslant 5$.
Thus, given that the fractional index is ![]() $({n-1})/{n}$,
$({n-1})/{n}$, ![]() $n \geqslant 5$, we can apply the results in [Reference FujitaFuj16]. From the classification in that paper, we see that the only possible fractional index of this form is
$n \geqslant 5$, we can apply the results in [Reference FujitaFuj16]. From the classification in that paper, we see that the only possible fractional index of this form is ![]() $\frac {4}{5}$. By Fujita's classification,
$\frac {4}{5}$. By Fujita's classification, ![]() $S$ must have a singularity of type
$S$ must have a singularity of type ![]() $\frac {1}{5}(1,2)$ away from
$\frac {1}{5}(1,2)$ away from ![]() $C_F$. Here
$C_F$. Here ![]() $S$ is constructed as a birational model of
$S$ is constructed as a birational model of ![]() $\mathbb {F}_3$: blow up two points on a fiber
$\mathbb {F}_3$: blow up two points on a fiber ![]() $l$ away from the negative section of
$l$ away from the negative section of ![]() $\mathbb {F}_3$, and let
$\mathbb {F}_3$, and let ![]() $M \to \mathbb {F}_3$ be the resulting surface. Then, contract the strict transform of
$M \to \mathbb {F}_3$ be the resulting surface. Then, contract the strict transform of ![]() $l$ and the strict transform of the negative section to obtain
$l$ and the strict transform of the negative section to obtain ![]() $M \to S$, with an isolated
$M \to S$, with an isolated ![]() $\frac {1}{5}(1,2)$ singularity on
$\frac {1}{5}(1,2)$ singularity on ![]() $S$. The curve
$S$. The curve ![]() $C_F$ is obtained as the image of the strict transform of the degree-two multi-section of
$C_F$ is obtained as the image of the strict transform of the degree-two multi-section of ![]() $\mathbb {F}_3$ that passes through the two points blown up. Let
$\mathbb {F}_3$ that passes through the two points blown up. Let ![]() $l_1$ and
$l_1$ and ![]() $l_2$ be the images of the two
$l_2$ be the images of the two ![]() $-1$ curves in
$-1$ curves in ![]() $S$. Then, by construction, either
$S$. Then, by construction, either ![]() $E_0 = S$,
$E_0 = S$, ![]() $E_0 = M$, or
$E_0 = M$, or ![]() $E_0$ is obtained from
$E_0$ is obtained from ![]() $M$ by blowing down either the
$M$ by blowing down either the ![]() $-2$ or the
$-2$ or the ![]() $-3$ curve (but not both). Note that this implies that
$-3$ curve (but not both). Note that this implies that ![]() $E = E_0$ (there are no divisors with discrepancy one) and there are no other components of
$E = E_0$ (there are no divisors with discrepancy one) and there are no other components of ![]() $\operatorname {Supp} F$ that intersect
$\operatorname {Supp} F$ that intersect ![]() $E$ (no divisors have discrepancy of the form
$E$ (no divisors have discrepancy of the form ![]() $({n-1})/{n}$).
$({n-1})/{n}$).
At this point, the problem becomes purely computational, studying the positivity and negativity of ![]() $K_{Y_{l+1}}$ and
$K_{Y_{l+1}}$ and ![]() $E^{l+1}$. Suppose we are in the first case,
$E^{l+1}$. Suppose we are in the first case, ![]() $E = S$ (the other cases are similar, with extra divisors
$E = S$ (the other cases are similar, with extra divisors ![]() $G_i$ attached along the exceptional curves in
$G_i$ attached along the exceptional curves in ![]() $E$). Because
$E$). Because ![]() $C_F$ is contained in the smooth locus of
$C_F$ is contained in the smooth locus of ![]() $E$, the contraction of each component of the exceptional chain
$E$, the contraction of each component of the exceptional chain ![]() $F_1 \cup \cdots \cup F_k$ is the contraction of a smooth ruled surface. Because
$F_1 \cup \cdots \cup F_k$ is the contraction of a smooth ruled surface. Because ![]() $n = 5$, there are only three possibilities for the chain itself (as the generic point contracts to a cyclic quotient singularity of index five): either there is one surface
$n = 5$, there are only three possibilities for the chain itself (as the generic point contracts to a cyclic quotient singularity of index five): either there is one surface ![]() $F_1$ with coefficient
$F_1$ with coefficient ![]() $\frac {4}{5}$ in
$\frac {4}{5}$ in ![]() $\pi ^{*}(K_X)$; two surfaces
$\pi ^{*}(K_X)$; two surfaces ![]() $F_1 \cup F_2$ with coefficient either
$F_1 \cup F_2$ with coefficient either ![]() $\frac {4}{5}$ and
$\frac {4}{5}$ and ![]() $\frac {2}{5}$ or
$\frac {2}{5}$ or ![]() $\frac {4}{5}$ and
$\frac {4}{5}$ and ![]() $\frac {3}{5}$; or four surfaces
$\frac {3}{5}$; or four surfaces ![]() $F_1 \cup F_2 \cup F_3 \cup F_4$ with coefficient (of
$F_1 \cup F_2 \cup F_3 \cup F_4$ with coefficient (of ![]() $F_i$)
$F_i$) ![]() $1 - {1}/{n}$. Therefore, thus far the MMP has been the contraction of a smooth ruled surface
$1 - {1}/{n}$. Therefore, thus far the MMP has been the contraction of a smooth ruled surface ![]() $\Delta$ onto
$\Delta$ onto ![]() $F_k$ (the last divisor in the chain) followed by the contractions of each
$F_k$ (the last divisor in the chain) followed by the contractions of each ![]() $F_i$. By computation,
$F_i$. By computation, ![]() $(K_{Y_{l+1}} + E^{l+1})\cdot C_F = -8$ and
$(K_{Y_{l+1}} + E^{l+1})\cdot C_F = -8$ and ![]() $C_F^{2} = 10$ (as a curve in
$C_F^{2} = 10$ (as a curve in ![]() $E^{l+1}$). Denote by
$E^{l+1}$). Denote by ![]() $E^{l+1} \cdot C_F = -d$ and
$E^{l+1} \cdot C_F = -d$ and ![]() $K_{Y_{l+1}}\cdot C_F = d-8$. Let
$K_{Y_{l+1}}\cdot C_F = d-8$. Let ![]() $\phi : Y \to Y_l$ be the composition of the contractions thus far. We can compute
$\phi : Y \to Y_l$ be the composition of the contractions thus far. We can compute ![]() $\phi ^{*}K_{Y_{l+1}}$ and
$\phi ^{*}K_{Y_{l+1}}$ and ![]() $\phi ^{*}E^{l+1}$ and, together with the hypotheses that curves in
$\phi ^{*}E^{l+1}$ and, together with the hypotheses that curves in ![]() $\operatorname {Supp} F$ are
$\operatorname {Supp} F$ are ![]() $K$-non-negative but the generic curves in
$K$-non-negative but the generic curves in ![]() $\Delta$ are
$\Delta$ are ![]() $K$-negative and that all components of
$K$-negative and that all components of ![]() $\operatorname {Supp} F$ and
$\operatorname {Supp} F$ and ![]() $\Delta$ are smooth ruled surfaces, computation implies that
$\Delta$ are smooth ruled surfaces, computation implies that ![]() $d > 8$ and there can be no extra exceptional components
$d > 8$ and there can be no extra exceptional components ![]() $G_i \in \operatorname {Supp} G$ of
$G_i \in \operatorname {Supp} G$ of ![]() $\pi$ attached to
$\pi$ attached to ![]() $\Delta$. (In fact, this already rules out the first two possibilities for the chains
$\Delta$. (In fact, this already rules out the first two possibilities for the chains ![]() $F_i$: the generic fiber
$F_i$: the generic fiber ![]() $f_g$ of
$f_g$ of ![]() $\Delta$ would then have image in
$\Delta$ would then have image in ![]() $X$ satisfying
$X$ satisfying ![]() $K_X \cdot \pi (f_g) = {i}/{5}$,
$K_X \cdot \pi (f_g) = {i}/{5}$, ![]() $i = 1, 2$, or
$i = 1, 2$, or ![]() $3$, so we use
$3$, so we use ![]() $dK_X + 4D \sim 0$ to conclude
$dK_X + 4D \sim 0$ to conclude ![]() $d$ is even.)
$d$ is even.)
Now, from the computation that ![]() $d > 8$, we see that
$d > 8$, we see that ![]() $E^{l+1} \cdot C_F < 0$ and
$E^{l+1} \cdot C_F < 0$ and ![]() $K_{Y_{l+1}}\cdot C_F > 0$. There must exist a
$K_{Y_{l+1}}\cdot C_F > 0$. There must exist a ![]() $K$-negative extremal ray somewhere in
$K$-negative extremal ray somewhere in ![]() $Y_{l+1}$, and the only contractible curves in
$Y_{l+1}$, and the only contractible curves in ![]() $E^{l+1}$ are
$E^{l+1}$ are ![]() $l_1$ and
$l_1$ and ![]() $l_2$. If at this point of the MMP we find another
$l_2$. If at this point of the MMP we find another ![]() $K$-negative,
$K$-negative, ![]() $E^{l+1}$-positive extremal ray that does not contain
$E^{l+1}$-positive extremal ray that does not contain ![]() $l_1$ or
$l_1$ or ![]() $l_2$, because there were no extra exceptional components
$l_2$, because there were no extra exceptional components ![]() $G$ of
$G$ of ![]() $\pi$ attached to
$\pi$ attached to ![]() $\Delta$, this ray is necessarily
$\Delta$, this ray is necessarily ![]() $K+E^{l+1}$-negative, and the MMP terminates in a fibration, so we are done by previous arguments. If there are
$K+E^{l+1}$-negative, and the MMP terminates in a fibration, so we are done by previous arguments. If there are ![]() $K$-negative rays away from
$K$-negative rays away from ![]() $E^{l+1}$ (i.e. are
$E^{l+1}$ (i.e. are ![]() $E$-trivial and do not contain
$E$-trivial and do not contain ![]() $l_1$ or
$l_1$ or ![]() $l_2$), we contract and continue the MMP.
$l_2$), we contract and continue the MMP.
The only other possibility is that we find only ![]() $K$-negative rays that contain
$K$-negative rays that contain ![]() $l_1$ or
$l_1$ or ![]() $l_2$, and we show that this is not possible. These cannot both be
$l_2$, and we show that this is not possible. These cannot both be ![]() $K$-negative: it is straightforward to show
$K$-negative: it is straightforward to show ![]() $C_F$ in the face spanned by these curves, and
$C_F$ in the face spanned by these curves, and ![]() $K_{Y_{l+1}}\cdot C_F > 0$. Suppose the only
$K_{Y_{l+1}}\cdot C_F > 0$. Suppose the only ![]() $K$-negative ray contains
$K$-negative ray contains ![]() $l_1$. Let
$l_1$. Let ![]() $\phi _{l+1}: Y_{l+1} \dashrightarrow Y_{l+2}$ be the associated step of the MMP. At this stage,
$\phi _{l+1}: Y_{l+1} \dashrightarrow Y_{l+2}$ be the associated step of the MMP. At this stage, ![]() $E^{l+2} \cong \mathbb {P}(1,1,2)$, so at the next stage of the MMP,
$E^{l+2} \cong \mathbb {P}(1,1,2)$, so at the next stage of the MMP, ![]() $l_2$ and
$l_2$ and ![]() $C_F$ must be numerically equivalent. However, on
$C_F$ must be numerically equivalent. However, on ![]() $E^{l+1}, \phi _{l+1}$ is a morphism, so we can compute the pullback of
$E^{l+1}, \phi _{l+1}$ is a morphism, so we can compute the pullback of ![]() $K_{Y_{l+2}}$ to
$K_{Y_{l+2}}$ to ![]() $E^{l+1}$. Using the numerical equivalence of
$E^{l+1}$. Using the numerical equivalence of ![]() $l_2$ and
$l_2$ and ![]() $C_F$ after the contraction, we find that
$C_F$ after the contraction, we find that ![]() $K_{Y_{l+1}} \cdot l_2 < 0$, contradicting that both curves were not
$K_{Y_{l+1}} \cdot l_2 < 0$, contradicting that both curves were not ![]() $K$-negative. This concludes the proof in the case that
$K$-negative. This concludes the proof in the case that ![]() $E_0$ is contracted to a point in
$E_0$ is contracted to a point in ![]() $X$.
$X$.
Case 2:  $E_0$ is contracted to a curve in
$E_0$ is contracted to a curve in  $X$
$X$
This case uses that the generic point of the image of ![]() $E_0$ is a log-canonical surface singularity, so we have a classification. The following result is well-known by classification of log-canonical surface singularities (for example, [Reference Kollár and MoriKM98, Theorem 4.7] or [Reference KollárKol92, Chapter 3]).
$E_0$ is a log-canonical surface singularity, so we have a classification. The following result is well-known by classification of log-canonical surface singularities (for example, [Reference Kollár and MoriKM98, Theorem 4.7] or [Reference KollárKol92, Chapter 3]).
Lemma 4.28 If ![]() $X$ is a threefold with a one-dimensional locus of log-canonical singularities
$X$ is a threefold with a one-dimensional locus of log-canonical singularities ![]() $C$, over the generic point
$C$, over the generic point ![]() $p$ of a component of
$p$ of a component of ![]() $C$, the pre-image of
$C$, the pre-image of ![]() $p$ in the terminalization is:
$p$ in the terminalization is:
(i) a smooth elliptic or nodal curve, or a cycle of smooth rational curves;
(ii) a tree with exactly one fork, which has three branches with lengths
 $n_1 - 1$,
$n_1 - 1$,  $n_2 - 1,$ and
$n_2 - 1,$ and  $n_3 - 1$; the possible values for
$n_3 - 1$; the possible values for  $(n_1, n_2, n_3)$ are
$(n_1, n_2, n_3)$ are  $(2,3,6), (2,4,4)$, or
$(2,3,6), (2,4,4)$, or  $(3,3,3)$;
$(3,3,3)$;(iii) a tree with exactly two forks as pictured in [Reference Kollár and MoriKM98, Theorem 4.7(3)].
In each case, the index of the canonical divisor near ![]() $p$ is
$p$ is ![]() $1, 2, 3, 4,$ or
$1, 2, 3, 4,$ or ![]() $6$.
$6$.
Because the index of ![]() $K_X$ divides
$K_X$ divides ![]() $d$, we immediately obtain the following.
$d$, we immediately obtain the following.
Corollary 4.29 If ![]() $X$ is log-canonical along a curve and
$X$ is log-canonical along a curve and ![]() $d$ is odd, the index at the generic point must be
$d$ is odd, the index at the generic point must be ![]() $1$ or
$1$ or ![]() $3$.
$3$.
The only cases that have index ![]() $1$ or
$1$ or ![]() $3$ are case (i) or the
$3$ are case (i) or the ![]() $(3,3,3)$ case of case (ii). Suppose
$(3,3,3)$ case of case (ii). Suppose ![]() $C$ in
$C$ in ![]() $E_0$ is the first curve contracted. By Lemma 4.21 and its proof, if
$E_0$ is the first curve contracted. By Lemma 4.21 and its proof, if ![]() $C$ is not a fiber of
$C$ is not a fiber of ![]() $\pi |_{E_0}$, then
$\pi |_{E_0}$, then ![]() $E_0 = {{\mathbb {P}}}^{1} \times C'$. If
$E_0 = {{\mathbb {P}}}^{1} \times C'$. If ![]() $C$ intersects no other exceptional components of
$C$ intersects no other exceptional components of ![]() $\pi$, then
$\pi$, then ![]() $K_X\cdot \pi (C) = -2$, so the relationship
$K_X\cdot \pi (C) = -2$, so the relationship ![]() $dK_X + 4D$ implies that
$dK_X + 4D$ implies that ![]() $D$ is even. If
$D$ is even. If ![]() $C$ does intersect other exceptional components, they must be components of
$C$ does intersect other exceptional components, they must be components of ![]() $\operatorname {Supp} F$ with discrepancy
$\operatorname {Supp} F$ with discrepancy ![]() $(({n-1})/{n})$. In this case, if any component of
$(({n-1})/{n})$. In this case, if any component of ![]() $\operatorname {Supp} F$ is not supported on fibers of
$\operatorname {Supp} F$ is not supported on fibers of ![]() $\pi |_{E_0}$, then we must be in case (ii),
$\pi |_{E_0}$, then we must be in case (ii), ![]() $(3,3,3)$, which implies
$(3,3,3)$, which implies ![]() $C' = {{\mathbb {P}}}^{1}$ so
$C' = {{\mathbb {P}}}^{1}$ so ![]() $E_0 = {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ and
$E_0 = {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ and ![]() $n = 3$. In this case, the configuration of divisors above the log-canonical singularity consists of one fork and three branches, each with length two, and the branches contract to cyclic quotient singularities of type
$n = 3$. In this case, the configuration of divisors above the log-canonical singularity consists of one fork and three branches, each with length two, and the branches contract to cyclic quotient singularities of type ![]() $\frac {1}{3}(1,2)$ along the generic point. The discrepancies of the
$\frac {1}{3}(1,2)$ along the generic point. The discrepancies of the ![]() $F_i$ meeting
$F_i$ meeting ![]() $E$ are therefore
$E$ are therefore ![]() $\frac {2}{3}$, and because
$\frac {2}{3}$, and because ![]() $C \cong {{\mathbb {P}}}^{1}$, we find that
$C \cong {{\mathbb {P}}}^{1}$, we find that ![]() $K_X \cdot \pi (C) = -2 + \frac {2}{3}k$, where
$K_X \cdot \pi (C) = -2 + \frac {2}{3}k$, where ![]() $k$ is the number of components
$k$ is the number of components ![]() $F_i$ that
$F_i$ that ![]() $C$ intersects. This implies
$C$ intersects. This implies ![]() $d$ is even provided
$d$ is even provided ![]() $k \ne 1$. If
$k \ne 1$. If ![]() $k = 1$, then
$k = 1$, then ![]() $C$ intersects
$C$ intersects ![]() $F_1$ but not
$F_1$ but not ![]() $F_2$ or
$F_2$ or ![]() $F_3$, so
$F_3$, so ![]() $F_1|_{E_0}$ is a section of
$F_1|_{E_0}$ is a section of ![]() ${{\mathcal {O}}}(1,1)$ and
${{\mathcal {O}}}(1,1)$ and ![]() $F_2$ and
$F_2$ and ![]() $F_3$ restrict to fibers proportional to
$F_3$ restrict to fibers proportional to ![]() $C$. However, considering the fiber of
$C$. However, considering the fiber of ![]() $\pi$ over the intersection point of
$\pi$ over the intersection point of ![]() $F_1$ and
$F_1$ and ![]() $F_2$, these surfaces intersect along some curve
$F_2$, these surfaces intersect along some curve ![]() $f$ that is contracted to
$f$ that is contracted to ![]() $X$. However, computing
$X$. However, computing ![]() $0 = \pi ^{*}(K_X)\cdot f$, we find a contradiction that
$0 = \pi ^{*}(K_X)\cdot f$, we find a contradiction that ![]() $K_Y \cdot f \geqslant 0$. Therefore,
$K_Y \cdot f \geqslant 0$. Therefore, ![]() $C$ only intersects components of
$C$ only intersects components of ![]() $\operatorname {Supp} F$ supported on the fibers of
$\operatorname {Supp} F$ supported on the fibers of ![]() $\pi |_{E_0}$, and it is easy to see that there must exist another
$\pi |_{E_0}$, and it is easy to see that there must exist another ![]() $K$-negative
$K$-negative ![]() $E$-positive extremal ray (other than
$E$-positive extremal ray (other than ![]() $C$) and it cannot be contained in the exceptional locus of
$C$) and it cannot be contained in the exceptional locus of ![]() $\pi$, so must be
$\pi$, so must be ![]() $K+E$-negative, so its contraction results in a fibration and we see that
$K+E$-negative, so its contraction results in a fibration and we see that ![]() $d$ is even.
$d$ is even.
Otherwise, the first curve in ![]() $E_0$ contracted must be a fiber of
$E_0$ contracted must be a fiber of ![]() $\pi |_{E_0}$. The only contractions thus far did not contract curves in
$\pi |_{E_0}$. The only contractions thus far did not contract curves in ![]() $E_0$, and this is the first curve contracted, so there must have been a contraction of some component of
$E_0$, and this is the first curve contracted, so there must have been a contraction of some component of ![]() $\operatorname {Supp} F$ onto
$\operatorname {Supp} F$ onto ![]() $E_0$ (Lemma 4.22). The existence of such a component
$E_0$ (Lemma 4.22). The existence of such a component ![]() $F_i$ implies that we are in the
$F_i$ implies that we are in the ![]() $(3,3,3)$ case in case (ii), and the contraction of divisors
$(3,3,3)$ case in case (ii), and the contraction of divisors ![]() $F_i$ means we can apply the arguments in the contracted to a point case about contractions of chains of divisors in
$F_i$ means we can apply the arguments in the contracted to a point case about contractions of chains of divisors in ![]() $\operatorname {Supp} F$. However, in order for the singularity to be log-canonical with the appropriate configuration, not only is the index 3, but this discrepancy of the divisor
$\operatorname {Supp} F$. However, in order for the singularity to be log-canonical with the appropriate configuration, not only is the index 3, but this discrepancy of the divisor ![]() $F$ must be
$F$ must be ![]() $\frac {2}{3}$, so we must have
$\frac {2}{3}$, so we must have ![]() $n = 3$. This is impossible by Lemma 4.25. This concludes the proof in the case that
$n = 3$. This is impossible by Lemma 4.25. This concludes the proof in the case that ![]() $E_0$ is contracted to a curve.
$E_0$ is contracted to a curve.
Lastly, we can immediately generalize this result to the case of non-normal slc varieties with anti-ample canonical sheaf and whose normalizations have non-log-terminal singularities. By normalizing the variety and considering each component ![]() $(X^{\nu },\Delta )$ (where
$(X^{\nu },\Delta )$ (where ![]() $X^{\nu }$ is a component of the normalization and
$X^{\nu }$ is a component of the normalization and ![]() $\Delta$ is the double locus), this is equivalent to studying the case of a pair
$\Delta$ is the double locus), this is equivalent to studying the case of a pair ![]() $(X^{\nu },\Delta )$ where
$(X^{\nu },\Delta )$ where ![]() $- (K_{X^{\nu }} + \Delta )$ is ample and the
$- (K_{X^{\nu }} + \Delta )$ is ample and the ![]() $1$-dimensional locus of log-canonical singularities intersects
$1$-dimensional locus of log-canonical singularities intersects ![]() $\Delta$. Because the locus of log-canonical singularities must intersect
$\Delta$. Because the locus of log-canonical singularities must intersect ![]() $\Delta$ (see [Reference KollárKol92]) but cannot be contained in
$\Delta$ (see [Reference KollárKol92]) but cannot be contained in ![]() $\Delta, X^{\nu }$ must, in fact, have a log-canonical singularity along a curve. Then, a terminal modification
$\Delta, X^{\nu }$ must, in fact, have a log-canonical singularity along a curve. Then, a terminal modification ![]() $X'$ of
$X'$ of ![]() $X^{\nu }$ and minimal model program on
$X^{\nu }$ and minimal model program on ![]() $X'$ gives the same conclusion, where
$X'$ gives the same conclusion, where ![]() $\Delta$ is not considered as a component of
$\Delta$ is not considered as a component of ![]() $E$ (but we instead use the relationship
$E$ (but we instead use the relationship ![]() $d(K_{X^{\nu }} + \Delta ) + 4D \sim 0$).
$d(K_{X^{\nu }} + \Delta ) + 4D \sim 0$).
4.2 Applications to  ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and  ${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$
${{\mathcal {M}}}_{{(\mathbb {P}^{3},d,4)}}$
We can use Theorem 4.18 to obtain boundedness of ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs without the smoothability assumption and other interesting corollaries. First, we slightly rephrase Theorem 4.18 and combine this with the discussion in the previous paragraph.
${(\mathbb {P}^{3},d,4)}$ H-stable pairs without the smoothability assumption and other interesting corollaries. First, we slightly rephrase Theorem 4.18 and combine this with the discussion in the previous paragraph.
Theorem 4.30 If ![]() $(X,D)$ is a
$(X,D)$ is a ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pair and
${(\mathbb {P}^{3},d,4)}$ H-stable pair and ![]() $d$ is odd, then any component of the normalization of
$d$ is odd, then any component of the normalization of ![]() $(X,({4}/{d})D)$ is dlt.
$(X,({4}/{d})D)$ is dlt.
For quintic surfaces, we can be even more precise (see Theorem 5.3).
In what follows, we make a careful distinction in each statement between smoothable and non-smoothable pairs. First, we give a corollary of Theorem 4.1.
Corollary 4.31 For ![]() $d$ odd, the normal varieties
$d$ odd, the normal varieties ![]() $X$ occurring in a
$X$ occurring in a ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pair are rational.
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pair are rational.
Finally, using Theorem 4.30, we are also able to obtain boundedness for ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs when
${(\mathbb {P}^{3},d,4)}$ H-stable pairs when ![]() $d$ is odd, not just smoothable ones. The following theorem is a special case of [Reference Hacon, McKernan and XuHMX14a, Corollary 1.7] for threefolds.
$d$ is odd, not just smoothable ones. The following theorem is a special case of [Reference Hacon, McKernan and XuHMX14a, Corollary 1.7] for threefolds.
Theorem 4.32 For fixed odd degree ![]() $d$, the set of
$d$, the set of ![]() ${(\mathbb {P}^{3},d,4)}$ H-stable pairs form a bounded family.
${(\mathbb {P}^{3},d,4)}$ H-stable pairs form a bounded family.
Proof. Restricting to the normal case, by Theorem 3.1, ![]() $(X,({4}/{d})D)$ is klt, and because of the assumption that
$(X,({4}/{d})D)$ is klt, and because of the assumption that ![]() $dK_X + 4D \sim 0$, the pairs
$dK_X + 4D \sim 0$, the pairs ![]() $(X,({4}/{d})D)$ are
$(X,({4}/{d})D)$ are ![]() $\epsilon$-log-terminal because
$\epsilon$-log-terminal because ![]() $dK_X + 4D \sim 0$ is linear equivalence (not just numerical). Then,
$dK_X + 4D \sim 0$ is linear equivalence (not just numerical). Then, ![]() $-K_X$ is ample and
$-K_X$ is ample and ![]() $K_X + ({4}/{d}) D$ is numerically trivial by assumption, hence by [Reference Hacon, McKernan and XuHMX14a, Corollary 1.7], form a bounded family. We can restrict to the normal case because the non-normal pairs are in bijection with normal pairs and a certain involution as in [Reference KollárKol13, Theorem 5.13] and, by Theorem 4.30, the normalization is
$K_X + ({4}/{d}) D$ is numerically trivial by assumption, hence by [Reference Hacon, McKernan and XuHMX14a, Corollary 1.7], form a bounded family. We can restrict to the normal case because the non-normal pairs are in bijection with normal pairs and a certain involution as in [Reference KollárKol13, Theorem 5.13] and, by Theorem 4.30, the normalization is ![]() $\epsilon$-log-terminal.
$\epsilon$-log-terminal.
Next, we study log-terminal Fano degenerations of ![]() ${{\mathbb {P}}}^{3}$ to determine the boundary of the moduli space of
${{\mathbb {P}}}^{3}$ to determine the boundary of the moduli space of ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs, generalizing from
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs, generalizing from ![]() ${{\mathbb {P}}}^{3}$ to
${{\mathbb {P}}}^{3}$ to ![]() ${{\mathbb {P}}}^{n}$ when possible. We first focus on threefolds with canonical singularities appearing in the moduli problem.
${{\mathbb {P}}}^{n}$ when possible. We first focus on threefolds with canonical singularities appearing in the moduli problem.
4.3 Canonical Fano threefolds
A standard reference for canonical threefolds is [Reference ReidRei87]. In the Fano case, particularly when ![]() $X$ is Gorenstein, such threefolds can be classified by invariants like
$X$ is Gorenstein, such threefolds can be classified by invariants like ![]() $K_X^{3}$ and the Fano index. If
$K_X^{3}$ and the Fano index. If ![]() $X$ has at worst canonical singularities, the Fletcher–Reid plurigenus formula [Reference ReidRei87, Theorem 10.2] gives the plurigenera of
$X$ has at worst canonical singularities, the Fletcher–Reid plurigenus formula [Reference ReidRei87, Theorem 10.2] gives the plurigenera of ![]() $X$ in terms of
$X$ in terms of ![]() $K_X^{3}, \chi ({{\mathcal {O}}}_X)$, and coefficients
$K_X^{3}, \chi ({{\mathcal {O}}}_X)$, and coefficients ![]() $c_P$ determined by a basket of singularities
$c_P$ determined by a basket of singularities ![]() $\{ Q_i \}$ for
$\{ Q_i \}$ for ![]() $X$. In [Reference FletcherFle89, Theorem 1.1], Fletcher shows the plurigenus formula is exact, meaning that any two canonical threefolds with the same plurigenera have the same
$X$. In [Reference FletcherFle89, Theorem 1.1], Fletcher shows the plurigenus formula is exact, meaning that any two canonical threefolds with the same plurigenera have the same ![]() $K_X^{3}, \chi ({{\mathcal {O}}}_X)$, and basket of singularities are the same. The contribution from the singularities is non-zero precisely when there are points
$K_X^{3}, \chi ({{\mathcal {O}}}_X)$, and basket of singularities are the same. The contribution from the singularities is non-zero precisely when there are points ![]() $Q_i$ such that
$Q_i$ such that ![]() $K_{X'}$ is not Cartier at
$K_{X'}$ is not Cartier at ![]() $Q_i$. In the case at hand,
$Q_i$. In the case at hand, ![]() $X$ is a flat degeneration of
$X$ is a flat degeneration of ![]() ${{\mathbb {P}}}^{3}$, the plurigenera of
${{\mathbb {P}}}^{3}$, the plurigenera of ![]() $X$ and
$X$ and ![]() ${{\mathbb {P}}}^{3}$ are the same, so this inversion of the plurigenus formula implies that
${{\mathbb {P}}}^{3}$ are the same, so this inversion of the plurigenus formula implies that ![]() $X'$ must be a terminal Gorenstein variety. Because
$X'$ must be a terminal Gorenstein variety. Because ![]() $X' \to X$ is any crepant partial resolution such that
$X' \to X$ is any crepant partial resolution such that ![]() $X'$ has only terminal singularities,
$X'$ has only terminal singularities, ![]() $K_{X'}^{3} = -64$ and we can take
$K_{X'}^{3} = -64$ and we can take ![]() $X'$ to be
$X'$ to be ![]() ${{\mathbb {Q}}}$-factorial. Thus, we obtain the following.
${{\mathbb {Q}}}$-factorial. Thus, we obtain the following.
Theorem 4.33 If ![]() $X$ is a terminal variety that admits a smoothing to
$X$ is a terminal variety that admits a smoothing to ![]() ${{\mathbb {P}}}^{3}$, then
${{\mathbb {P}}}^{3}$, then ![]() $X \cong {{\mathbb {P}}}^{3}$.
$X \cong {{\mathbb {P}}}^{3}$.
Proof. The Fletcher–Reid plurigenus formula shows that if ![]() $X$ is not Gorenstein, it does not admit a smoothing to
$X$ is not Gorenstein, it does not admit a smoothing to ![]() ${{\mathbb {P}}}^{3}$, so it suffices to consider Gorenstein threefolds
${{\mathbb {P}}}^{3}$, so it suffices to consider Gorenstein threefolds ![]() $X$. In this case, [Reference Casagrande, Jahnke and RadloffCJR08, Theorem 2.1] implies that the Fano index of
$X$. In this case, [Reference Casagrande, Jahnke and RadloffCJR08, Theorem 2.1] implies that the Fano index of ![]() $X$, the maximal integer
$X$, the maximal integer ![]() $r$ such that
$r$ such that ![]() $K_X \sim -rH$ for
$K_X \sim -rH$ for ![]() ${{\mathcal {O}}}(H) \in \operatorname {Pic}(X)$, is equal to that of
${{\mathcal {O}}}(H) \in \operatorname {Pic}(X)$, is equal to that of ![]() ${{\mathbb {P}}}^{3}$. Therefore, the Fano index of
${{\mathbb {P}}}^{3}$. Therefore, the Fano index of ![]() $X$ is four. Then, [Reference Casagrande, Jahnke and RadloffCJR08, Theorem 3.1] says that, because the Fano index is maximal,
$X$ is four. Then, [Reference Casagrande, Jahnke and RadloffCJR08, Theorem 3.1] says that, because the Fano index is maximal, ![]() $X \cong {{\mathbb {P}}}^{3}$.
$X \cong {{\mathbb {P}}}^{3}$.
There do exist non-trivial canonical degenerations of ![]() ${{\mathbb {P}}}^{3}$.
${{\mathbb {P}}}^{3}$.
Example 4.34 Observe that the standard embedding of the quadric surface ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1} \subset {{\mathbb {P}}}^{3}$ is an element of the linear system
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1} \subset {{\mathbb {P}}}^{3}$ is an element of the linear system ![]() ${{\mathcal {O}}}_{{{\mathbb {P}}}^{3}}(2)$. Let
${{\mathcal {O}}}_{{{\mathbb {P}}}^{3}}(2)$. Let ![]() $Z$ be the image of the degree-two embedding of
$Z$ be the image of the degree-two embedding of ![]() ${{\mathbb {P}}}^{3} \hookrightarrow {{\mathbb {P}}}^{9}$. There is a standard degeneration from
${{\mathbb {P}}}^{3} \hookrightarrow {{\mathbb {P}}}^{9}$. There is a standard degeneration from ![]() $Z$ to the cone over a hyperplane section of
$Z$ to the cone over a hyperplane section of ![]() $Z$ by taking the cone over
$Z$ by taking the cone over ![]() $Z$ (see, for example, [Reference Kollár and MoriKM98, Example 7.61]). In this case, the hyperplane section of
$Z$ (see, for example, [Reference Kollár and MoriKM98, Example 7.61]). In this case, the hyperplane section of ![]() $Z$ corresponds to an element of
$Z$ corresponds to an element of ![]() ${{\mathcal {O}}}_{{{\mathbb {P}}}^{3}}(2)$, and is the
${{\mathcal {O}}}_{{{\mathbb {P}}}^{3}}(2)$, and is the ![]() ${{\mathcal {O}}}(2,2)$ embedding of the quadric surface in
${{\mathcal {O}}}(2,2)$ embedding of the quadric surface in ![]() ${{\mathbb {P}}}^{8}$. A computation shows that the cone over this is indeed Gorenstein as it is the cone over the anticanonical embedding of
${{\mathbb {P}}}^{8}$. A computation shows that the cone over this is indeed Gorenstein as it is the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. A check shows that this has canonical singularities; for details, see [Reference KollárKol13, Lemma 3.1]. Therefore, this gives an example of a flat degeneration of
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. A check shows that this has canonical singularities; for details, see [Reference KollárKol13, Lemma 3.1]. Therefore, this gives an example of a flat degeneration of ![]() ${{\mathbb {P}}}^{3}$ to a Gorenstein canonical variety.
${{\mathbb {P}}}^{3}$ to a Gorenstein canonical variety.
A priori there may be many canonical degenerations of ![]() ${{\mathbb {P}}}^{3}$, but the following theorem shows that if
${{\mathbb {P}}}^{3}$, but the following theorem shows that if ![]() $d$ is odd, they must be closely related to the previous example. In fact, they must be
$d$ is odd, they must be closely related to the previous example. In fact, they must be ![]() ${{\mathbb {P}}}^{3}$ or cones over the anticanonical embeddings of elements of the linear system
${{\mathbb {P}}}^{3}$ or cones over the anticanonical embeddings of elements of the linear system ![]() $|{{\mathcal {O}}}_{\mathbb {P}^{3}}(2)|$, which have a simple description.
$|{{\mathcal {O}}}_{\mathbb {P}^{3}}(2)|$, which have a simple description.
Theorem 4.35 For odd degree ![]() $d$, if
$d$, if ![]() $X$ is a canonical threefold appearing in a
$X$ is a canonical threefold appearing in a ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pair
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pair ![]() $(X,D)$, then
$(X,D)$, then ![]() $X$ is either
$X$ is either ![]() ${{\mathbb {P}}}^{3}$, the cone over the anticanonical embedding of
${{\mathbb {P}}}^{3}$, the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, or the cone over the anticanonical embedding of the quadric cone,
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, or the cone over the anticanonical embedding of the quadric cone, ![]() ${{\mathbb {P}}}(1,1,2,4)$.
${{\mathbb {P}}}(1,1,2,4)$.
If ![]() $X$ has only terminal singularities, Theorem 4.33 implies the result. If
$X$ has only terminal singularities, Theorem 4.33 implies the result. If ![]() $X$ has canonical singularities, consider a crepant partial resolution
$X$ has canonical singularities, consider a crepant partial resolution ![]() $X' \to X$ such that
$X' \to X$ such that ![]() $X'$ is terminal and
$X'$ is terminal and ![]() ${{\mathbb {Q}}}$-factorial. Before giving the proof, we give a sketch of the argument.
${{\mathbb {Q}}}$-factorial. Before giving the proof, we give a sketch of the argument.
By [Reference FletcherFle89], if ![]() $K_{X'}$ is not Cartier, there is a non-zero contribution to a basket of singularities on
$K_{X'}$ is not Cartier, there is a non-zero contribution to a basket of singularities on ![]() $X$, so
$X$, so ![]() $X$ is not isomorphic to
$X$ is not isomorphic to ![]() $\mathbb {P}^{3}$. It then suffices to consider the case where
$\mathbb {P}^{3}$. It then suffices to consider the case where ![]() $X'$ is a terminal,
$X'$ is a terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein variety with
${{\mathbb {Q}}}$-factorial Gorenstein variety with ![]() $-K_{X'}$ nef. Running a minimal model program on
$-K_{X'}$ nef. Running a minimal model program on ![]() $X'$, if it terminates in a morphism
$X'$, if it terminates in a morphism ![]() $X' \dashrightarrow Y \to \operatorname {Spec} k$, then
$X' \dashrightarrow Y \to \operatorname {Spec} k$, then ![]() $Y$ must be a terminal Fano threefold with
$Y$ must be a terminal Fano threefold with ![]() $\rho (Y) = 1$. Studying the pseudo-index of
$\rho (Y) = 1$. Studying the pseudo-index of ![]() $Y$ as in [Reference Casagrande, Jahnke and RadloffCJR08] and combining this with the fact that
$Y$ as in [Reference Casagrande, Jahnke and RadloffCJR08] and combining this with the fact that ![]() $K_{X'}^{3} = -64$ would imply that
$K_{X'}^{3} = -64$ would imply that ![]() $X'$ itself must have been
$X'$ itself must have been ![]() ${{\mathbb {P}}}^{3}$, so
${{\mathbb {P}}}^{3}$, so ![]() $X\cong {{\mathbb {P}}}^{3}$. If a run of the minimal model program on
$X\cong {{\mathbb {P}}}^{3}$. If a run of the minimal model program on ![]() $X'$ terminates in a morphism
$X'$ terminates in a morphism ![]() $X' \dashrightarrow Y \to C$, where
$X' \dashrightarrow Y \to C$, where ![]() $C$ is a curve, the generic fiber of
$C$ is a curve, the generic fiber of ![]() $Y \to C$ must be a smooth del Pezzo surface, so there are sufficiently general curves
$Y \to C$ must be a smooth del Pezzo surface, so there are sufficiently general curves ![]() $L \subset X'$ such that
$L \subset X'$ such that ![]() $K_{X'} \cdot L = -3$ or
$K_{X'} \cdot L = -3$ or ![]() $-2$, and if the termination is in a surface
$-2$, and if the termination is in a surface ![]() $W$, there are sufficiently general curves
$W$, there are sufficiently general curves ![]() $L \subset X'$ such that
$L \subset X'$ such that ![]() $K_{X'} \cdot L = -2$. If any of these curves miss the exceptional divisors of the partial resolution
$K_{X'} \cdot L = -2$. If any of these curves miss the exceptional divisors of the partial resolution ![]() $\pi : X'\to X$, then
$\pi : X'\to X$, then ![]() $D\cdot \pi (L) \in {{\mathbb {Z}}}$, and we can argue as in the previous example to show that
$D\cdot \pi (L) \in {{\mathbb {Z}}}$, and we can argue as in the previous example to show that ![]() $d$ must be even. Similarly, we can reach the same conclusion if
$d$ must be even. Similarly, we can reach the same conclusion if ![]() $D$ does not pass through the strictly canonical singularities of
$D$ does not pass through the strictly canonical singularities of ![]() $X$. The remaining case is when
$X$. The remaining case is when ![]() $D$ contains the strictly canonical singularities of
$D$ contains the strictly canonical singularities of ![]() $X$ and the general fiber
$X$ and the general fiber ![]() $L$ intersects the exceptional divisors of
$L$ intersects the exceptional divisors of ![]() $\pi : X' \to X$, because it is not obvious that
$\pi : X' \to X$, because it is not obvious that ![]() $D \cdot \pi (L) \in {{\mathbb {Z}}}$. However, we can explicitly understand the fibration when this occurs.
$D \cdot \pi (L) \in {{\mathbb {Z}}}$. However, we can explicitly understand the fibration when this occurs.
First, let us recall results of Cutkosky on contractions of extremal rays on terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein threefolds.
${{\mathbb {Q}}}$-factorial Gorenstein threefolds.
Lemma 4.36 [Reference CutkoskyCut88, Lemma 2]
Suppose that ![]() $X$ is a terminal,
$X$ is a terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein threefold. Then,
${{\mathbb {Q}}}$-factorial Gorenstein threefold. Then, ![]() $X$ is factorial.
$X$ is factorial.
Lemma 4.37 [Reference CutkoskyCut88, Lemma 3]
Suppose that ![]() $X$ is a terminal,
$X$ is a terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein threefold and
${{\mathbb {Q}}}$-factorial Gorenstein threefold and ![]() $\phi : X \to Y$ is the contraction of a
$\phi : X \to Y$ is the contraction of a ![]() $K_X$-negative extremal ray with at most one-dimensional fibers. Then,
$K_X$-negative extremal ray with at most one-dimensional fibers. Then, ![]() $Y$ is factorial. In particular,
$Y$ is factorial. In particular, ![]() $Y$ is a terminal,
$Y$ is a terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein threefold, and
${{\mathbb {Q}}}$-factorial Gorenstein threefold, and ![]() $\phi$ cannot be a small contraction.
$\phi$ cannot be a small contraction.
Theorem 4.38 [Reference CutkoskyCut88, Theorem 4]
Suppose that ![]() $X$ is a terminal,
$X$ is a terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein threefold and
${{\mathbb {Q}}}$-factorial Gorenstein threefold and ![]() $\phi : X \to Y$ is a birational contraction of a surface
$\phi : X \to Y$ is a birational contraction of a surface ![]() $W \subset X$ to a curve
$W \subset X$ to a curve ![]() $C \subset Y$. Then,
$C \subset Y$. Then, ![]() $Y$ is smooth near
$Y$ is smooth near ![]() $C$.
$C$.
Theorem 4.39 [Reference CutkoskyCut88, Theorem 5]
Suppose that ![]() $X$ is a terminal,
$X$ is a terminal, ![]() ${{\mathbb {Q}}}$-factorial Gorenstein threefold and
${{\mathbb {Q}}}$-factorial Gorenstein threefold and ![]() $\phi : X \to Y$ is a birational contraction of a surface
$\phi : X \to Y$ is a birational contraction of a surface ![]() $W \subset X$ to a point
$W \subset X$ to a point ![]() $p \subset Y$. Then, one of the following four cases occurs:
$p \subset Y$. Then, one of the following four cases occurs:
(i)
 $Y$ is non-singular near
$Y$ is non-singular near  $p, W \cong \mathbb {P}^{2}$, and
$p, W \cong \mathbb {P}^{2}$, and  ${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{2}}(-1)$;
${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{2}}(-1)$;(ii)
 $W \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ and
$W \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ and  ${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}}(-1,-1)$;
${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}}(-1,-1)$;(iii)
 $W$ is isomorphic to a reduced, irreducible singular quadric surface
$W$ is isomorphic to a reduced, irreducible singular quadric surface  $D$ in
$D$ in  ${{\mathbb {P}}}^{3}$ and
${{\mathbb {P}}}^{3}$ and  ${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{3}}(-1)\otimes {{\mathcal {O}}}_D$;
${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{3}}(-1)\otimes {{\mathcal {O}}}_D$;(iv)
 $Y$ is singular at
$Y$ is singular at  $p, W \cong \mathbb {P}^{2}$, and
$p, W \cong \mathbb {P}^{2}$, and  ${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{2}}(-2)$.
${{\mathcal {O}}}_W(W) \cong {{\mathcal {O}}}_{{{\mathbb {P}}}^{2}}(-2)$.
Now we can prove Theorem 4.35.
Proof. Let us begin with the simplest case: no component of the locus of canonical singularities is contained in ![]() $D$. Then, the contraction of a
$D$. Then, the contraction of a ![]() $K_{X'}$ negative extremal ray must be birational
$K_{X'}$ negative extremal ray must be birational ![]() $X' \to Y$ or a Fano fibration
$X' \to Y$ or a Fano fibration ![]() $X' \to S$ or
$X' \to S$ or ![]() $X' \to C$, where
$X' \to C$, where ![]() $\dim S = 2$ or
$\dim S = 2$ or ![]() $\dim C = 1$. Because
$\dim C = 1$. Because ![]() $-K_{X'}$ is nef and non-trivial, the contraction cannot be
$-K_{X'}$ is nef and non-trivial, the contraction cannot be ![]() $X' \to \operatorname {Spec} k$. Also, by Lemma 4.37,
$X' \to \operatorname {Spec} k$. Also, by Lemma 4.37, ![]() $X' \to Y$ is necessarily a divisorial contraction. Therefore, in every case, the generic curve contracted has
$X' \to Y$ is necessarily a divisorial contraction. Therefore, in every case, the generic curve contracted has ![]() $K_{X'} \cdot C = -1, -2$, or
$K_{X'} \cdot C = -1, -2$, or ![]() $-3$, so the image of
$-3$, so the image of ![]() $C$ on
$C$ on ![]() $X$ has
$X$ has ![]() $K_X \cdot \pi (C) = -1, -2$, or
$K_X \cdot \pi (C) = -1, -2$, or ![]() $-3$. Because
$-3$. Because ![]() $D$ does not contain the locus of canonical singularities, for a sufficiently generic curve
$D$ does not contain the locus of canonical singularities, for a sufficiently generic curve ![]() $C, D \cdot \pi (C) \in \mathbb {Z}$. Therefore, the relationship
$C, D \cdot \pi (C) \in \mathbb {Z}$. Therefore, the relationship ![]() $dK_X + 4D \sim 0$ implies
$dK_X + 4D \sim 0$ implies ![]() $d$ is even. If a component
$d$ is even. If a component ![]() $\Delta$ of the locus of canonical singularities is contained in
$\Delta$ of the locus of canonical singularities is contained in ![]() $D$, we can separate into two cases: either
$D$, we can separate into two cases: either ![]() $\Delta$ is one- or zero-dimensional.
$\Delta$ is one- or zero-dimensional.
Case 1: ![]() ${\dim \Delta = 1}$
${\dim \Delta = 1}$
If ![]() $\Delta$ is one-dimensional, consider the partial resolution
$\Delta$ is one-dimensional, consider the partial resolution ![]() $\pi : X' \to X$. Because
$\pi : X' \to X$. Because ![]() $X$ has only canonical singularities, the fibers of
$X$ has only canonical singularities, the fibers of ![]() $\pi$ must be chains of rational curves. We can study the pullback
$\pi$ must be chains of rational curves. We can study the pullback ![]() $\pi ^{*}D$: in particular,
$\pi ^{*}D$: in particular, ![]() $\pi ^{*}D = \tilde {D} + \sum a_i F_i$, where
$\pi ^{*}D = \tilde {D} + \sum a_i F_i$, where ![]() $\tilde {D}$ is the strict transform of
$\tilde {D}$ is the strict transform of ![]() $D$ and
$D$ and ![]() $F = \bigcup F_i$ is the fiber over
$F = \bigcup F_i$ is the fiber over ![]() $\Delta$. Let
$\Delta$. Let ![]() $F_0$ be a component of
$F_0$ be a component of ![]() $F$ such that
$F$ such that ![]() $\dim \pi (F_0) = 1$. For a generic curve
$\dim \pi (F_0) = 1$. For a generic curve ![]() $C \subset F_0$ contracted by
$C \subset F_0$ contracted by ![]() $\pi$,
$\pi$, ![]() $K_{X'} \cdot C = 0$ and
$K_{X'} \cdot C = 0$ and ![]() $F \cdot C < 0$. However,
$F \cdot C < 0$. However, ![]() $-2 = K_{F_0} \cdot C = (K_{X'} + F_0) \cdot C$, so there can be at most one component
$-2 = K_{F_0} \cdot C = (K_{X'} + F_0) \cdot C$, so there can be at most one component ![]() $F_i$ meeting
$F_i$ meeting ![]() $C$ with
$C$ with ![]() $F_i \cdot C = 1$. Therefore, either there is no such
$F_i \cdot C = 1$. Therefore, either there is no such ![]() $F_i$ and
$F_i$ and
for some ![]() $n \in \mathbb {Z}$ so
$n \in \mathbb {Z}$ so ![]() $a_0 \in \frac {1}{2}{{\mathbb {Z}}}$ or there is some
$a_0 \in \frac {1}{2}{{\mathbb {Z}}}$ or there is some ![]() $F_i$ that meets
$F_i$ that meets ![]() $C$ and a contracted curve
$C$ and a contracted curve ![]() $C' \subset F_i$ meeting
$C' \subset F_i$ meeting ![]() $F_0$ so
$F_0$ so
 \begin{gather*} 0 = \pi^{*}D \cdot C = \tilde{D} \cdot C + \sum a_i F_i \cdot C = n + a_0 (-2) + a_i(1),\\ 0 = \pi^{*}D \cdot C' = \tilde{D} \cdot C' + \sum a_i F_i \cdot C' = m + a_0(1) + a_i(-2), \end{gather*}
\begin{gather*} 0 = \pi^{*}D \cdot C = \tilde{D} \cdot C + \sum a_i F_i \cdot C = n + a_0 (-2) + a_i(1),\\ 0 = \pi^{*}D \cdot C' = \tilde{D} \cdot C' + \sum a_i F_i \cdot C' = m + a_0(1) + a_i(-2), \end{gather*}
so ![]() $a_0, a_i \in \frac {1}{3}{{\mathbb {Z}}}$. This shows that, for generic curves in
$a_0, a_i \in \frac {1}{3}{{\mathbb {Z}}}$. This shows that, for generic curves in ![]() $X$ meeting
$X$ meeting ![]() $D$, the intersection with
$D$, the intersection with ![]() $D$ is in
$D$ is in ![]() $\frac {1}{6}{{\mathbb {Z}}}$. With this in mind, now contract a
$\frac {1}{6}{{\mathbb {Z}}}$. With this in mind, now contract a ![]() $K_{X'}$ negative extremal ray on
$K_{X'}$ negative extremal ray on ![]() $X'$. As previously, we have the following options: (A)
$X'$. As previously, we have the following options: (A) ![]() $X' \to Y$ is divisorial; (B)
$X' \to Y$ is divisorial; (B) ![]() $X' \to S$ is a Fano fibration over a surface; or (C)
$X' \to S$ is a Fano fibration over a surface; or (C) ![]() $X' \to C$ is a Fano fibration over a curve.
$X' \to C$ is a Fano fibration over a curve.
Case 1A. Assume first that ![]() $X' \to Y$ is divisorial. If
$X' \to Y$ is divisorial. If ![]() $X' \to Y$ is divisorial and with at most one-dimensional fibers, the generic fiber
$X' \to Y$ is divisorial and with at most one-dimensional fibers, the generic fiber ![]() $C$ has
$C$ has ![]() $K_{X'} \cdot C = -1$, so the image in
$K_{X'} \cdot C = -1$, so the image in ![]() $X$ has
$X$ has ![]() $K_{X} \cdot \pi (C) = -1$. For sufficiently generic
$K_{X} \cdot \pi (C) = -1$. For sufficiently generic ![]() $C$,
$C$, ![]() $D \cdot \pi (C) \in \frac {1}{6}{{\mathbb {Z}}}$. Therefore, the relationship
$D \cdot \pi (C) \in \frac {1}{6}{{\mathbb {Z}}}$. Therefore, the relationship ![]() $dK_X + 4D \sim 0$ implies
$dK_X + 4D \sim 0$ implies ![]() $d$ must be even. If
$d$ must be even. If ![]() $X' \to Y$ is divisorial but contracts a surface to a point, if any case other than case (i) as in Theorem 4.39 occurs, we still find a generic curve
$X' \to Y$ is divisorial but contracts a surface to a point, if any case other than case (i) as in Theorem 4.39 occurs, we still find a generic curve ![]() $C$ in the fiber with
$C$ in the fiber with ![]() $K_{X'} \cdot C = -1$.
$K_{X'} \cdot C = -1$.
If case (i) occurs, the threefold ![]() $Y$ is still terminal,
$Y$ is still terminal, ![]() $\mathbb {Q}$-factorial, and Gorenstein, so we can contract a new
$\mathbb {Q}$-factorial, and Gorenstein, so we can contract a new ![]() $K_Y$ negative extremal ray and repeat. If at any point our contraction one of the cases (ii), (iii), or (iv), by the same argument, we are done. If we perform a divisorial contraction with at most one-dimensional fibers, again the output is terminal,
$K_Y$ negative extremal ray and repeat. If at any point our contraction one of the cases (ii), (iii), or (iv), by the same argument, we are done. If we perform a divisorial contraction with at most one-dimensional fibers, again the output is terminal, ![]() $\mathbb {Q}$-factorial and Gorenstein, so we can continue. Therefore, it suffices to analyze the possible fibrations that arise as minimal models of a terminal,
$\mathbb {Q}$-factorial and Gorenstein, so we can continue. Therefore, it suffices to analyze the possible fibrations that arise as minimal models of a terminal, ![]() $\mathbb {Q}$-factorial, Gorenstein variety
$\mathbb {Q}$-factorial, Gorenstein variety ![]() $X'$ where, at each step of the minimal model program, the resulting variety is also terminal,
$X'$ where, at each step of the minimal model program, the resulting variety is also terminal, ![]() $\mathbb {Q}$-factorial, and Gorenstein.
$\mathbb {Q}$-factorial, and Gorenstein.
However, after some number of divisorial contractions, we reach the point of a fibration, then the divisorial contractions were blow ups of some point(s) on the fibration. Therefore, either the general fiber of the fibration does not intersect ![]() $F$, or after blowing up, a fiber of the divisorial contraction does not intersect
$F$, or after blowing up, a fiber of the divisorial contraction does not intersect ![]() $F$. Therefore, its image on
$F$. Therefore, its image on ![]() $X$ has
$X$ has ![]() $D \cdot C \in \mathbb {Z}$. Arguing as before implies
$D \cdot C \in \mathbb {Z}$. Arguing as before implies ![]() $d$ is even. Therefore, the only two cases that remain to be studied are if the only possible
$d$ is even. Therefore, the only two cases that remain to be studied are if the only possible ![]() $K_{X'}$ negative contraction yields a fibration.
$K_{X'}$ negative contraction yields a fibration.
Case 1B. If ![]() $\phi : X' \to S$ is a fibration with general fiber
$\phi : X' \to S$ is a fibration with general fiber ![]() $\cong \mathbb {P}^{1}$, either there are
$\cong \mathbb {P}^{1}$, either there are ![]() $F$-trivial fibers
$F$-trivial fibers ![]() $C$ or
$C$ or ![]() $F$ is relatively ample. In the first case,
$F$ is relatively ample. In the first case, ![]() $K_X \cdot \pi (C) = -2$ and
$K_X \cdot \pi (C) = -2$ and ![]() $D \cdot \pi (C) \in \mathbb {Z}$, so
$D \cdot \pi (C) \in \mathbb {Z}$, so ![]() $d$ be even. Assume then that
$d$ be even. Assume then that ![]() $F$ is relatively ample. By [Reference CutkoskyCut88, Theorem 7],
$F$ is relatively ample. By [Reference CutkoskyCut88, Theorem 7], ![]() $S$ must be smooth and
$S$ must be smooth and ![]() $X'$ must be a conic bundle over
$X'$ must be a conic bundle over ![]() $S$. If
$S$. If ![]() $X' \to S$ has any singular fibers, then there exist curves
$X' \to S$ has any singular fibers, then there exist curves ![]() $C$ such that
$C$ such that ![]() $K_{X'} \cdot C = -1$, and we argue as before to show
$K_{X'} \cdot C = -1$, and we argue as before to show ![]() $d$ must be even. Therefore, we may assume every fiber is smooth and
$d$ must be even. Therefore, we may assume every fiber is smooth and ![]() $X' \to S$ is a smooth
$X' \to S$ is a smooth ![]() $\mathbb {P}^{1}$-bundle over a smooth surface
$\mathbb {P}^{1}$-bundle over a smooth surface ![]() $S$. Furthermore, by [Reference Casagrande, Jahnke and RadloffCJR08, Lemma 2.5],
$S$. Furthermore, by [Reference Casagrande, Jahnke and RadloffCJR08, Lemma 2.5], ![]() $-K_S$ is big and nef. Because
$-K_S$ is big and nef. Because ![]() $F$ is relatively ample, for some component
$F$ is relatively ample, for some component ![]() $F_0$ of
$F_0$ of ![]() $F$, the induced morphism
$F$, the induced morphism ![]() $F_0 \to S$ must be finite. However,
$F_0 \to S$ must be finite. However, ![]() $F_0$ is contractible on
$F_0$ is contractible on ![]() $X'$, so we have the following diagram.
$X'$, so we have the following diagram.

Consider a smooth curve ![]() $C \subset S$ such that
$C \subset S$ such that ![]() $Z = \phi ^{-1}(C)$ contains a contracted curve in
$Z = \phi ^{-1}(C)$ contains a contracted curve in ![]() $F_0$. Because every fiber of
$F_0$. Because every fiber of ![]() $\phi$ is
$\phi$ is ![]() $\mathbb {P}^{1}, Z$ is a ruled surface over
$\mathbb {P}^{1}, Z$ is a ruled surface over ![]() $C$ and because
$C$ and because ![]() $F_0 \to S$ is finite,
$F_0 \to S$ is finite, ![]() $F_0|_Z$ is a multi-section of
$F_0|_Z$ is a multi-section of ![]() $\phi |_Z: Z \to C$. However, this multi-section is contractible in
$\phi |_Z: Z \to C$. However, this multi-section is contractible in ![]() $Z$ to a surface
$Z$ to a surface ![]() $\bar {Z} \subset X$. For generic
$\bar {Z} \subset X$. For generic ![]() $Z, Z$ is not contracted by
$Z, Z$ is not contracted by ![]() $\pi$, so intersection theory on ruled surfaces implies that
$\pi$, so intersection theory on ruled surfaces implies that ![]() $F_0|_Z$ is actually a section. This is true for any such
$F_0|_Z$ is actually a section. This is true for any such ![]() $Z$, so the degree of
$Z$, so the degree of ![]() $\phi |_{F_0}: F_0 \to S$ must be 1, hence
$\phi |_{F_0}: F_0 \to S$ must be 1, hence ![]() $S\cong F_0$ and
$S\cong F_0$ and ![]() $F_0$ is a section of
$F_0$ is a section of ![]() $\phi$.
$\phi$.
Assume first that ![]() $F_0$ is contracted to a curve via
$F_0$ is contracted to a curve via ![]() $\pi : X' \to X$. Then,
$\pi : X' \to X$. Then, ![]() $S \cong F_0$ must be a ruled surface over
$S \cong F_0$ must be a ruled surface over ![]() $C$ with
$C$ with ![]() $-K_S$ big and nef, so
$-K_S$ big and nef, so ![]() $S$ must be
$S$ must be ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}, \mathbb {F}_1$, or
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}, \mathbb {F}_1$, or ![]() $\mathbb {F}_2$. Because each of these surfaces have
$\mathbb {F}_2$. Because each of these surfaces have ![]() $\rho (S) = 2$, it follows that
$\rho (S) = 2$, it follows that ![]() $\rho (X') = 3$ and there are at most two components of
$\rho (X') = 3$ and there are at most two components of ![]() $F$. If there is only one component of
$F$. If there is only one component of ![]() $F$, there is exactly one contraction
$F$, there is exactly one contraction ![]() $X' \to X$ that is
$X' \to X$ that is ![]() $K_{X'}$ trivial, but
$K_{X'}$ trivial, but ![]() $\rho (X') \geqslant 3$ implies that there are at least two
$\rho (X') \geqslant 3$ implies that there are at least two ![]() $K_{X'}$-negative contractions. One corresponds to the map
$K_{X'}$-negative contractions. One corresponds to the map ![]() $\phi : X' \to S \cong F$ and the other must correspond to another case, so we use the argument in the other cases to find a contradiction or show
$\phi : X' \to S \cong F$ and the other must correspond to another case, so we use the argument in the other cases to find a contradiction or show ![]() $X \cong {{\mathbb {P}}}(1,1,2,4)$.
$X \cong {{\mathbb {P}}}(1,1,2,4)$.
If there are two components of ![]() $F$, so
$F$, so ![]() $F = F_0 \cup F_1$, then
$F = F_0 \cup F_1$, then ![]() $F_1$ must also be relatively ample as it is covered by
$F_1$ must also be relatively ample as it is covered by ![]() $K_{X'}$-trivial curves so cannot be contracted by
$K_{X'}$-trivial curves so cannot be contracted by ![]() $\phi$. Therefore,
$\phi$. Therefore, ![]() $S \cong F_0 \cong F_1$. However, this is only possible if both
$S \cong F_0 \cong F_1$. However, this is only possible if both ![]() $F_0$ and
$F_0$ and ![]() $F_1$ are contracted to a curve via
$F_1$ are contracted to a curve via ![]() $\pi$; otherwise, say
$\pi$; otherwise, say ![]() $F_1$ is contracted to a point, then there exist
$F_1$ is contracted to a point, then there exist ![]() $F_1$ trivial curves intersecting
$F_1$ trivial curves intersecting ![]() $F_0$, so
$F_0$, so ![]() $F_1$ is not relatively ample. Now, as before, consider a smooth curve
$F_1$ is not relatively ample. Now, as before, consider a smooth curve ![]() $C \subset S$ such that
$C \subset S$ such that ![]() $Z = \phi ^{-1}(C)$ contains a contracted curve in
$Z = \phi ^{-1}(C)$ contains a contracted curve in ![]() $F_0$. Because every fiber of
$F_0$. Because every fiber of ![]() $\phi$ is
$\phi$ is ![]() $\mathbb {P}^{1}$, by the previous argument,
$\mathbb {P}^{1}$, by the previous argument, ![]() $Z$ is a ruled surface over
$Z$ is a ruled surface over ![]() $C$ with a contractible section. However,
$C$ with a contractible section. However, ![]() $Z$ must also contain a contracted curve in
$Z$ must also contain a contracted curve in ![]() $F_1$, hence
$F_1$, hence ![]() $Z$ has two contractible sections. However, this is a contraction, as it would imply
$Z$ has two contractible sections. However, this is a contraction, as it would imply ![]() $\pi |_Z: Z \to \pi (Z)$ contracts
$\pi |_Z: Z \to \pi (Z)$ contracts ![]() $Z$ to a curve.
$Z$ to a curve.
Therefore, we can assume that ![]() $F_0$ is contracted to a point via
$F_0$ is contracted to a point via ![]() $\pi : X' \to X$. If each
$\pi : X' \to X$. If each ![]() $\phi$-ample divisor
$\phi$-ample divisor ![]() $F_i$ does not intersect
$F_i$ does not intersect ![]() $\tilde {D}$, we find curves
$\tilde {D}$, we find curves ![]() $C$ such that
$C$ such that ![]() $D\cdot C \in {{\mathbb {Z}}}$ and
$D\cdot C \in {{\mathbb {Z}}}$ and ![]() $K_X \cdot C = -2$ so
$K_X \cdot C = -2$ so ![]() $d$ is even. Therefore, it suffices to consider only
$d$ is even. Therefore, it suffices to consider only ![]() $F_i$ that intersect
$F_i$ that intersect ![]() $\tilde {D}$. Because
$\tilde {D}$. Because ![]() $D$ contains
$D$ contains ![]() $\Delta$, there is some
$\Delta$, there is some ![]() $F_1$ that is contacted to a curve via
$F_1$ that is contacted to a curve via ![]() $\pi$ such that
$\pi$ such that ![]() $F_1 \cap D \ne \emptyset$ and
$F_1 \cap D \ne \emptyset$ and ![]() $F_1 \cap F_0 \ne \emptyset$. The intersection
$F_1 \cap F_0 \ne \emptyset$. The intersection ![]() $F_1 \cap F_0$ must be a fiber of the ruled surface
$F_1 \cap F_0$ must be a fiber of the ruled surface ![]() $F_1$, hence
$F_1$, hence ![]() $F_0$ contains a curve
$F_0$ contains a curve ![]() $C$ such that
$C$ such that ![]() $K_{X'} \cdot C = 0, F_1 \cdot C = -2$, and
$K_{X'} \cdot C = 0, F_1 \cdot C = -2$, and ![]() $F_0 \cdot C = 0$. Therefore,
$F_0 \cdot C = 0$. Therefore, ![]() $K_{F_0} \cdot C = 0$ so
$K_{F_0} \cdot C = 0$ so ![]() $F_0 \cong \mathbb {F}_2$.
$F_0 \cong \mathbb {F}_2$.
This implies that ![]() $\rho (X') = 3$ because
$\rho (X') = 3$ because ![]() $\phi : X' \to S \cong \mathbb {F}_2$ is a
$\phi : X' \to S \cong \mathbb {F}_2$ is a ![]() ${{\mathbb {P}}}^{1}$ bundle, hence there is only one exceptional divisor
${{\mathbb {P}}}^{1}$ bundle, hence there is only one exceptional divisor ![]() $F_1$ with
$F_1$ with ![]() $\dim \pi (F_1) = 1$. If
$\dim \pi (F_1) = 1$. If ![]() $F_1$ were also
$F_1$ were also ![]() $\phi$-ample, we must have
$\phi$-ample, we must have ![]() $F_1 \cong \mathbb {F}_2$ also be a section. However, the intersection curve
$F_1 \cong \mathbb {F}_2$ also be a section. However, the intersection curve ![]() $C = F_0 \cap F_1$ is a section of
$C = F_0 \cap F_1$ is a section of ![]() $F_0$ but a fiber of
$F_0$ but a fiber of ![]() $F_1$, a contradiction. Therefore,
$F_1$, a contradiction. Therefore, ![]() $F_1$ is not
$F_1$ is not ![]() $\phi$-ample, so we must have
$\phi$-ample, so we must have ![]() $F_1 \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Contracting
$F_1 \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. Contracting ![]() $F_0$ and
$F_0$ and ![]() $F_1$ to
$F_1$ to ![]() $X$ shows
$X$ shows ![]() $\rho (X) = 1$ and
$\rho (X) = 1$ and ![]() $X$ has a
$X$ has a ![]() $\frac {1}{4}(1,1,2)$ singularity, hence we must have
$\frac {1}{4}(1,1,2)$ singularity, hence we must have ![]() $X \cong {{\mathbb {P}}}(1,1,2,4)$.
$X \cong {{\mathbb {P}}}(1,1,2,4)$.
Case 1C. If ![]() $\phi : X' \to C$ is a fibration with general fiber a smooth del Pezzo surface and
$\phi : X' \to C$ is a fibration with general fiber a smooth del Pezzo surface and ![]() $C \cong \mathbb {P}^{1}$, we can first note that if the general fiber is a surface other than
$C \cong \mathbb {P}^{1}$, we can first note that if the general fiber is a surface other than ![]() $\mathbb {P}^{2}$ or
$\mathbb {P}^{2}$ or ![]() $\mathbb {P}^{1} \times \mathbb {P}^{1}$, there exist curves
$\mathbb {P}^{1} \times \mathbb {P}^{1}$, there exist curves ![]() $C$ with
$C$ with ![]() $K_{X'} \cdot C = -1$, so we argue as before to conclude
$K_{X'} \cdot C = -1$, so we argue as before to conclude ![]() $d$ is even. Similarly, if the fiber is
$d$ is even. Similarly, if the fiber is ![]() $\mathbb {P}^{2}$, there exist curves
$\mathbb {P}^{2}$, there exist curves ![]() $C$ with
$C$ with ![]() $K_{X'} \cdot C = -3$, and again we can conclude
$K_{X'} \cdot C = -3$, and again we can conclude ![]() $d$ is even. Therefore, it suffices to analyze the case when the general fiber is
$d$ is even. Therefore, it suffices to analyze the case when the general fiber is ![]() $\mathbb {P}^{1} \times \mathbb {P}^{1}$. Because
$\mathbb {P}^{1} \times \mathbb {P}^{1}$. Because ![]() $\rho (C) = 1$ and
$\rho (C) = 1$ and ![]() $\phi$ was an extremal contraction,
$\phi$ was an extremal contraction, ![]() $\rho (X') = 2$. There is then only one component of
$\rho (X') = 2$. There is then only one component of ![]() $F$. We would like to show that there are divisors
$F$. We would like to show that there are divisors ![]() $D_1$ and
$D_1$ and ![]() $D_2$ whose restriction to each fiber are the different rulings. Those are not linearly equivalent nor are they linearly equivalent to the general fiber
$D_2$ whose restriction to each fiber are the different rulings. Those are not linearly equivalent nor are they linearly equivalent to the general fiber ![]() $F$, hence it would imply
$F$, hence it would imply ![]() $\rho (X') \geqslant 3$, a contradiction.
$\rho (X') \geqslant 3$, a contradiction.
Suppose for contradiction ![]() $X'$ does exist. If
$X'$ does exist. If ![]() $F$ was contained in a fiber of
$F$ was contained in a fiber of ![]() $\phi$, then there exist many
$\phi$, then there exist many ![]() $F$-trivial curves with
$F$-trivial curves with ![]() $K_{X'} \cdot C = -2$, and on
$K_{X'} \cdot C = -2$, and on ![]() $X, D \cdot \pi (C) \in {{\mathbb {Z}}}$. As usual, we consider the relation
$X, D \cdot \pi (C) \in {{\mathbb {Z}}}$. As usual, we consider the relation ![]() $dK_X + 4D \sim 0$, so find that
$dK_X + 4D \sim 0$, so find that ![]() $d$ must be even. Now consider the case that
$d$ must be even. Now consider the case that ![]() $F$ is
$F$ is ![]() $\phi$-ample, so
$\phi$-ample, so ![]() $\phi |_F: F \to C$ gives
$\phi |_F: F \to C$ gives ![]() $F$ the structure of a ruled surface over
$F$ the structure of a ruled surface over ![]() $C$ and contracts only
$C$ and contracts only ![]() $K_{X'}$-negative curves. Because
$K_{X'}$-negative curves. Because ![]() $\pi |_F$ also contracts
$\pi |_F$ also contracts ![]() $F$ to a curve but contracts only
$F$ to a curve but contracts only ![]() $K_{X'}$-trivial curves,
$K_{X'}$-trivial curves, ![]() $F$ must have the structure of a product, so
$F$ must have the structure of a product, so ![]() $F \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$.
$F \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$.
Let ![]() $\Gamma \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ be a fiber of
$\Gamma \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ be a fiber of ![]() $\phi$. We claim that
$\phi$. We claim that ![]() $F$,
$F$, ![]() $\Gamma$, and
$\Gamma$, and ![]() $K_{X'}$ in
$K_{X'}$ in ![]() $N^{1}(X)$ are independent so we must have
$N^{1}(X)$ are independent so we must have ![]() $\rho (X') \geqslant 3$, a contradiction. To see the claim, note that
$\rho (X') \geqslant 3$, a contradiction. To see the claim, note that ![]() $\Gamma |_F$ must be a ruling of
$\Gamma |_F$ must be a ruling of ![]() $F$, so
$F$, so ![]() $\Gamma |_F \in | {{\mathcal {O}}}_F(1,0) |$. Next, observe that
$\Gamma |_F \in | {{\mathcal {O}}}_F(1,0) |$. Next, observe that ![]() $K_{X'}|_F$ is negative on the fibers contracted by
$K_{X'}|_F$ is negative on the fibers contracted by ![]() $\phi$ and trivial on the fibers contracted by
$\phi$ and trivial on the fibers contracted by ![]() $\pi$. However, these are the two rulings of
$\pi$. However, these are the two rulings of ![]() $F$, so
$F$, so ![]() $K_{X'}|_F \in | {{\mathcal {O}}}_F(-2,0) |$. Furthermore,
$K_{X'}|_F \in | {{\mathcal {O}}}_F(-2,0) |$. Furthermore, ![]() $K_{X'}$ and
$K_{X'}$ and ![]() $\Gamma$ are certainly not linearly equivalent. Finally, consider
$\Gamma$ are certainly not linearly equivalent. Finally, consider ![]() $F|_F$. On the fibers of
$F|_F$. On the fibers of ![]() $F$ contracted by
$F$ contracted by ![]() $\pi$, by the negativity lemma, this must be negative, so
$\pi$, by the negativity lemma, this must be negative, so ![]() $F|_F \in |{{\mathcal {O}}}_F(a, -b)|$ for
$F|_F \in |{{\mathcal {O}}}_F(a, -b)|$ for ![]() $b >0$. Therefore,
$b >0$. Therefore, ![]() $F$ cannot be linearly equivalent to any linear combination of
$F$ cannot be linearly equivalent to any linear combination of ![]() $\Gamma$ and
$\Gamma$ and ![]() $K_{X'}$, so
$K_{X'}$, so ![]() $\rho (X') \geqslant 3$, so
$\rho (X') \geqslant 3$, so ![]() $X'$ cannot exist.
$X'$ cannot exist.
Case 2: ![]() ${\dim \Delta = 0}$
${\dim \Delta = 0}$
Finally, suppose the locus of log-canonical singularities is a point contained in ![]() $D$. We can study the same contractions: (A)
$D$. We can study the same contractions: (A) ![]() $X' \to Y$ is divisorial; (B)
$X' \to Y$ is divisorial; (B) ![]() $X' \to S$ is a Fano fibration over a surface; or (C)
$X' \to S$ is a Fano fibration over a surface; or (C) ![]() $X' \to C$ is a Fano fibration over a curve. In this case, if
$X' \to C$ is a Fano fibration over a curve. In this case, if ![]() $F$ is the exceptional locus of the map
$F$ is the exceptional locus of the map ![]() $\pi : X' \to X$, the curves in
$\pi : X' \to X$, the curves in ![]() $F$ are all
$F$ are all ![]() $K_{X'}$-trivial, so none can be contracted by a
$K_{X'}$-trivial, so none can be contracted by a ![]() $K_{X'}$-negative contraction. Therefore, the third arrow (case (C))
$K_{X'}$-negative contraction. Therefore, the third arrow (case (C)) ![]() $X' \to C$ is not possible.
$X' \to C$ is not possible.
Case 2A. Because the curves in ![]() $F$ are all
$F$ are all ![]() $K_{X'}$ -trivial, the only possible
$K_{X'}$ -trivial, the only possible ![]() $K$-negative divisorial contraction over
$K$-negative divisorial contraction over ![]() $F$ is
$F$ is ![]() $X' \to Y$ that has at most one-dimensional fibers. However, then
$X' \to Y$ that has at most one-dimensional fibers. However, then ![]() $Y$ would be terminal, Gorenstein, and
$Y$ would be terminal, Gorenstein, and ![]() $\mathbb {Q}$-factorial, so we can continue the minimal model program on
$\mathbb {Q}$-factorial, so we can continue the minimal model program on ![]() $Y$. Much of this argument is the same as case 1A. If divisorial contractions happen first, there exist curves with
$Y$. Much of this argument is the same as case 1A. If divisorial contractions happen first, there exist curves with ![]() $K_{X'} \cdot C$ equal to
$K_{X'} \cdot C$ equal to ![]() $-1, -2,$ or
$-1, -2,$ or ![]() $-3$ that do not intersect
$-3$ that do not intersect ![]() $F$, and (invoking factoriality of
$F$, and (invoking factoriality of ![]() $X'$),
$X'$), ![]() $D \cdot \pi (C) \in \mathbb {Z}$, and we can conclude
$D \cdot \pi (C) \in \mathbb {Z}$, and we can conclude ![]() $d$ is even.
$d$ is even.
Case 2B. The remaining case is if the only ![]() $K_{X'}$ negative contraction is a fibration
$K_{X'}$ negative contraction is a fibration ![]() $X' \to S$, and as in case 1B, we can assume every fiber is smooth and isomorphic to
$X' \to S$, and as in case 1B, we can assume every fiber is smooth and isomorphic to ![]() $\mathbb {P}^{1}$. Therefore, we find ourselves in the situation where
$\mathbb {P}^{1}$. Therefore, we find ourselves in the situation where ![]() $\phi : X' \to S$ is a smooth
$\phi : X' \to S$ is a smooth ![]() $\mathbb {P}^{1}$-bundle over a smooth surface
$\mathbb {P}^{1}$-bundle over a smooth surface ![]() $S$ and by [Reference Casagrande, Jahnke and RadloffCJR08, Lemma 2.5],
$S$ and by [Reference Casagrande, Jahnke and RadloffCJR08, Lemma 2.5], ![]() $-K_S$ is big and nef. Exactly as before, we can conclude
$-K_S$ is big and nef. Exactly as before, we can conclude ![]() $S \cong F_0$ for some component
$S \cong F_0$ for some component ![]() $F_0$ of
$F_0$ of ![]() $F$ and
$F$ and ![]() $F_0$ is a section of
$F_0$ is a section of ![]() $\phi$. Furthermore, for any component
$\phi$. Furthermore, for any component ![]() $F_i$ of
$F_i$ of ![]() $F$, because
$F$, because ![]() $\pi (F_i)$ is a point,
$\pi (F_i)$ is a point, ![]() $K_{X'}\cdot C_i = 0$ for any
$K_{X'}\cdot C_i = 0$ for any ![]() $C_i \subset F_i$, so
$C_i \subset F_i$, so ![]() $C_i$ cannot be contracted by
$C_i$ cannot be contracted by ![]() $\phi$. Therefore, every component
$\phi$. Therefore, every component ![]() $F_i$ of
$F_i$ of ![]() $F$ is
$F$ is ![]() $\phi$-ample and
$\phi$-ample and ![]() $S \cong F_i$ for all
$S \cong F_i$ for all ![]() $i$.
$i$.
Briefly turning our attention to the map ![]() $\pi : X' \to X$, because components of
$\pi : X' \to X$, because components of ![]() $F$ are contracted to points by
$F$ are contracted to points by ![]() $\pi$, every curve in
$\pi$, every curve in ![]() $F$ is
$F$ is ![]() $K_{X'}$-trivial and
$K_{X'}$-trivial and ![]() $F$-negative. By adjunction, for
$F$-negative. By adjunction, for ![]() $C\in F_i$,
$C\in F_i$, ![]() $(K_{X'} + F_i) \cdot C = K_{F_i} \cdot C$, so
$(K_{X'} + F_i) \cdot C = K_{F_i} \cdot C$, so ![]() $F_i \cdot C = K_{F_i} \cdot C$. Therefore, not only is
$F_i \cdot C = K_{F_i} \cdot C$. Therefore, not only is ![]() $-K_S = -K_{F_i}$ big and nef, but it is ample, so
$-K_S = -K_{F_i}$ big and nef, but it is ample, so ![]() $S \cong F_i$ is a Fano surface. If there are any
$S \cong F_i$ is a Fano surface. If there are any ![]() $-1$ curves on
$-1$ curves on ![]() $F$, taking the intersection product with
$F$, taking the intersection product with ![]() $\pi ^{*}D = \tilde {D} + aF$ implies
$\pi ^{*}D = \tilde {D} + aF$ implies ![]() $a \in \mathbb {Z}$, so for any curve
$a \in \mathbb {Z}$, so for any curve ![]() $C$ on
$C$ on ![]() $X, D \cdot C \in {{\mathbb {Z}}}$. Therefore, for a fiber of
$X, D \cdot C \in {{\mathbb {Z}}}$. Therefore, for a fiber of ![]() $\phi$ with
$\phi$ with ![]() $K_{X'} \cdot C = -2$, we find that
$K_{X'} \cdot C = -2$, we find that ![]() $d$ must be even. Similarly, if
$d$ must be even. Similarly, if ![]() $F_i \cong {{\mathbb {P}}}^{2}$, we find lines with
$F_i \cong {{\mathbb {P}}}^{2}$, we find lines with ![]() $F \cdot C = -3$, so
$F \cdot C = -3$, so ![]() $D \cdot C \in \frac {1}{3}{{\mathbb {Z}}}$ and the same conclusion holds.
$D \cdot C \in \frac {1}{3}{{\mathbb {Z}}}$ and the same conclusion holds.
Therefore, the only remaining case is if ![]() $F_i \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ for all
$F_i \cong {{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ for all ![]() $i$:
$i$:

and ![]() $\pi : X' \to X$ contracts
$\pi : X' \to X$ contracts ![]() $F$. Consider
$F$. Consider ![]() $Z = \phi ^{-1}(C)$ for a generic ruling
$Z = \phi ^{-1}(C)$ for a generic ruling ![]() $C$ on
$C$ on ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. By construction, each
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. By construction, each ![]() $F_i|_Z$ is a contractible section of the smooth ruled surface
$F_i|_Z$ is a contractible section of the smooth ruled surface ![]() $Z$. Because
$Z$. Because ![]() $Z$ is not contracted by
$Z$ is not contracted by ![]() $\pi$, this implies that there is only one
$\pi$, this implies that there is only one ![]() $F_i$ and
$F_i$ and ![]() $F = F_0$. Then,
$F = F_0$. Then, ![]() $X$ is locally isomorphic to the cone over the anticanonically embedded
$X$ is locally isomorphic to the cone over the anticanonically embedded ![]() $\mathbb {P}^{1} \times \mathbb {P}^{1}$, Example 4.34. However,
$\mathbb {P}^{1} \times \mathbb {P}^{1}$, Example 4.34. However, ![]() $\rho (X) = 1$, so
$\rho (X) = 1$, so ![]() $X$ must actually be isomorphic to that cone.
$X$ must actually be isomorphic to that cone.
Ultimately, the odd-degree pairs are behaving in a very special way: oddness of the degree is forcing constraints on the threefolds ![]() $X$ that can appear. Summarizing the previous two sections, no log-canonical threefolds
$X$ that can appear. Summarizing the previous two sections, no log-canonical threefolds ![]() $X$ can appear and there are only three possibilities if the threefold
$X$ can appear and there are only three possibilities if the threefold ![]() $X$ has canonical singularities.
$X$ has canonical singularities.
4.4 A divisor in the moduli space
By a simple dimension count, we obtain the following.
Proposition 4.40 Let ![]() $X$ be the cone over the anticanonical embedding of
$X$ be the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, considered as a hypersurface in
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, considered as a hypersurface in ![]() $W = {{\mathbb {P}}}(1,1,1,1,2)$ (c.f. 4.65), so
$W = {{\mathbb {P}}}(1,1,1,1,2)$ (c.f. 4.65), so ![]() ${{\mathcal {O}}}(K_X) = {{\mathcal {O}}}_W(-4)|_X$. If the pair
${{\mathcal {O}}}(K_X) = {{\mathcal {O}}}_W(-4)|_X$. If the pair ![]() $( X, ({4}/{d}) D )$ is log-terminal for the general member
$( X, ({4}/{d}) D )$ is log-terminal for the general member ![]() $D$ in the linear system
$D$ in the linear system ![]() $|{{\mathcal {O}}}_X(d)|$, then there is a divisor
$|{{\mathcal {O}}}_X(d)|$, then there is a divisor ![]() ${{\mathcal {D}}}_Q$ in the moduli space
${{\mathcal {D}}}_Q$ in the moduli space ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ parameterizing surfaces on
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ parameterizing surfaces on ![]() $X$.
$X$.
To show that surfaces on ![]() $X$ appear as a divisor in the moduli space for any degree
$X$ appear as a divisor in the moduli space for any degree ![]() $d$, we show that the general member
$d$, we show that the general member ![]() $D \in |{{\mathcal {O}}}_X(d)|$ is such that
$D \in |{{\mathcal {O}}}_X(d)|$ is such that ![]() $(X, ({4}/{d}) D)$ has log-terminal singularities. In fact, because the log-canonical threshold is upper semicontinuous, it suffices to show this for a particular member
$(X, ({4}/{d}) D)$ has log-terminal singularities. In fact, because the log-canonical threshold is upper semicontinuous, it suffices to show this for a particular member ![]() $D \in |{{\mathcal {O}}}_X(d)|$. For even degree
$D \in |{{\mathcal {O}}}_X(d)|$. For even degree ![]() $d$, we can find a smooth member
$d$, we can find a smooth member ![]() $D \in |{{\mathcal {O}}}_X(d)|$ missing the unique singular point of
$D \in |{{\mathcal {O}}}_X(d)|$ missing the unique singular point of ![]() $X$, and because
$X$, and because ![]() $X$ has canonical singularities, certainly
$X$ has canonical singularities, certainly ![]() $(X, ({4}/{d}) D)$ is log-terminal. For odd degree
$(X, ({4}/{d}) D)$ is log-terminal. For odd degree ![]() $d$, consider
$d$, consider ![]() $D_0 = D_1 \cup D_{(d-1)/2}$, where
$D_0 = D_1 \cup D_{(d-1)/2}$, where ![]() $D_1 \in |{{\mathcal {O}}}_X(1)|$ and
$D_1 \in |{{\mathcal {O}}}_X(1)|$ and ![]() $D_{(d-1)/2} \in |{{\mathcal {O}}}_X((d-1)/2)|$ are general members meeting transversally.
$D_{(d-1)/2} \in |{{\mathcal {O}}}_X((d-1)/2)|$ are general members meeting transversally. ![]() $D_1$ has a unique
$D_1$ has a unique ![]() $\frac {1}{4}(1,1)$ singularity at the vertex of
$\frac {1}{4}(1,1)$ singularity at the vertex of ![]() $X$ and
$X$ and ![]() $D_2$ is smooth, missing the vertex of
$D_2$ is smooth, missing the vertex of ![]() $X$, and a computation shows
$X$, and a computation shows ![]() $(X, ({4}/{d}) D_0)$ is log-terminal. Therefore, we have proven the following.
$(X, ({4}/{d}) D_0)$ is log-terminal. Therefore, we have proven the following.
Proposition 4.41 Let ![]() $X$ be the cone over the anticanonical embedding of
$X$ be the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. For any degree
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. For any degree ![]() $d > 4$, there is a divisor
$d > 4$, there is a divisor ![]() ${{\mathcal {D}}}_Q$ in the moduli space
${{\mathcal {D}}}_Q$ in the moduli space ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ parameterizing surfaces on
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ parameterizing surfaces on ![]() $X$. Furthermore, by Proposition 3.10,
$X$. Furthermore, by Proposition 3.10, ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ is smooth generically along
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ is smooth generically along ![]() ${{\mathcal {D}}}_Q$.
${{\mathcal {D}}}_Q$.
In higher dimensions, the same proof gives the existence of a divisor in the moduli space of ![]() $(d,n+1) {{\mathbb {P}}}^{n}$-smoothable H-stable pairs.
$(d,n+1) {{\mathbb {P}}}^{n}$-smoothable H-stable pairs.
Theorem 4.42 Let ![]() $X_n \subset {{\mathbb {P}}}(1^{n+1}, 2)$ be the cone over the degree
$X_n \subset {{\mathbb {P}}}(1^{n+1}, 2)$ be the cone over the degree ![]() $2$ embedding of a smooth quadric
$2$ embedding of a smooth quadric ![]() $Q \in | {{\mathcal {O}}}_{{{\mathbb {P}}}^{n}}(2) |$. For any degree
$Q \in | {{\mathcal {O}}}_{{{\mathbb {P}}}^{n}}(2) |$. For any degree ![]() $d > n+1$, there is a divisor
$d > n+1$, there is a divisor ![]() ${{\mathcal {D}}}_Q$ in the moduli space
${{\mathcal {D}}}_Q$ in the moduli space ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{n}\text {-sm},(d,n+1)}$ parameterizing hypersurfaces on
${{\mathcal {M}}}_{{{\mathbb {P}}}^{n}\text {-sm},(d,n+1)}$ parameterizing hypersurfaces on ![]() $X_n$.
$X_n$.
In fact, we can describe the singularities of the generic degree ![]() $d$ hypersurface on
$d$ hypersurface on ![]() $X_n$.
$X_n$.
Proposition 4.43 For a generic point ![]() $(X_n,D)$ on the divisor
$(X_n,D)$ on the divisor ![]() ${{\mathcal {D}}}_Q$, where
${{\mathcal {D}}}_Q$, where ![]() $X_n \subset {{\mathbb {P}}}(1^{n+1}, 2)$ is the cone over the degree-two embedding of a smooth quadric
$X_n \subset {{\mathbb {P}}}(1^{n+1}, 2)$ is the cone over the degree-two embedding of a smooth quadric ![]() $Q \subset {{\mathbb {P}}}^{n}$, we can describe
$Q \subset {{\mathbb {P}}}^{n}$, we can describe ![]() $D$ as follows.
$D$ as follows.
(i) If
 $d$ is even,
$d$ is even,  $D$ is smooth.
$D$ is smooth.(ii) If
 $d$ is odd,
$d$ is odd,  $D$ passes through the vertex of the cone
$D$ passes through the vertex of the cone  $X_n$ and is locally isomorphic to the vertex of the cone
$X_n$ and is locally isomorphic to the vertex of the cone  $X_{n-1}$.
$X_{n-1}$.
Remark 4.44 For ![]() $(d,3) {{\mathbb {P}}}^{2}$-smoothable H-stable pairs, there is a divisor parameterizing curves on
$(d,3) {{\mathbb {P}}}^{2}$-smoothable H-stable pairs, there is a divisor parameterizing curves on ![]() $X_2 = {{\mathbb {P}}}(1,1,4)$, the cone over the degree-two embedding of a conic in
$X_2 = {{\mathbb {P}}}(1,1,4)$, the cone over the degree-two embedding of a conic in ![]() ${{\mathbb {P}}}^{2}$. If
${{\mathbb {P}}}^{2}$. If ![]() $d$ is even, the curves are smooth and miss the singular point, and if
$d$ is even, the curves are smooth and miss the singular point, and if ![]() $d$ is odd, the curves are nodal at the singular point. The node can be interpreted as the singularity of a cone over two points,
$d$ is odd, the curves are nodal at the singular point. The node can be interpreted as the singularity of a cone over two points, ![]() $X_1$. For three-dimensional pairs, there is a divisor parameterizing surfaces on
$X_1$. For three-dimensional pairs, there is a divisor parameterizing surfaces on ![]() $X_3$, the cone over the anticanonical embedding of
$X_3$, the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. If
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. If ![]() $d$ is even, again the generic surface misses the singular point of
$d$ is even, again the generic surface misses the singular point of ![]() $X_3$, but if
$X_3$, but if ![]() $d$ is odd, the generic surface has a singularity of type
$d$ is odd, the generic surface has a singularity of type ![]() $\frac {1}{4}(1,1)$ at the vertex of
$\frac {1}{4}(1,1)$ at the vertex of ![]() $X_3$, matching the singularity type of
$X_3$, matching the singularity type of ![]() $X_2$. Proposition 4.43 shows that this behavior persists in all dimensions.
$X_2$. Proposition 4.43 shows that this behavior persists in all dimensions.
4.5 Log-terminal degenerations of  $\mathbb {P}^{n}$
$\mathbb {P}^{n}$
To completely classify normal varieties appears as ![]() ${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs when
${(\mathbb {P}^{3,\mathrm {sm}},d,4)}$ H-stable pairs when ![]() $d$ is odd, it remains to understand log-terminal threefolds
$d$ is odd, it remains to understand log-terminal threefolds ![]() $X$ that are degenerations of
$X$ that are degenerations of ![]() $\mathbb {P}^{3}$. We approach this in general (not only in the
$\mathbb {P}^{3}$. We approach this in general (not only in the ![]() $d$ odd case) and state results for
$d$ odd case) and state results for ![]() ${{\mathbb {P}}}^{n}$ whenever possible. There are natural log-terminal varieties to consider: weighted projective spaces. We summarize the case in dimension two, due to Hacking and Prokhorov.
${{\mathbb {P}}}^{n}$ whenever possible. There are natural log-terminal varieties to consider: weighted projective spaces. We summarize the case in dimension two, due to Hacking and Prokhorov.
Theorem 4.45 [Reference Hacking and ProkhorovHP10]
If ![]() $X$ is a normal, log-terminal degeneration of
$X$ is a normal, log-terminal degeneration of ![]() $\mathbb {P}^{2}$ such that the total space is
$\mathbb {P}^{2}$ such that the total space is ![]() $\mathbb {Q}$-Gorenstein, then
$\mathbb {Q}$-Gorenstein, then ![]() $X \cong {{\mathbb {P}}}(p^{2}, q^{2}, r^{2})$ or a smoothing of such a space, where
$X \cong {{\mathbb {P}}}(p^{2}, q^{2}, r^{2})$ or a smoothing of such a space, where
Furthermore, all such varieties admit a ![]() $\mathbb {Q}$-Gorenstein smoothing to
$\mathbb {Q}$-Gorenstein smoothing to ![]() $\mathbb {P}^{2}$.
$\mathbb {P}^{2}$.
In addition to the theorem, we can describe all solutions with an infinite graph.
Theorem 4.46 All solutions to
can be obtained by starting with the obvious solution ![]() $(1,1,1)$ and performing a sequence of mutations: if
$(1,1,1)$ and performing a sequence of mutations: if ![]() $(p,q,r)$ is a solution, then
$(p,q,r)$ is a solution, then ![]() $(p,q,3pq-r)$ is a solution.
$(p,q,3pq-r)$ is a solution.
One could hope for an analogue of the description of degenerations in the three-dimensional case, although that seems far out of reach. However, there are partial results, using properties of weighted projective spaces. Recall that a weighted projective space ![]() ${{\mathbb {P}}}(a_0, \ldots, a_n)$ is called well-formed if every subset of
${{\mathbb {P}}}(a_0, \ldots, a_n)$ is called well-formed if every subset of ![]() $n$ of the
$n$ of the ![]() $a_i$ has no common factors. We call the set of integers
$a_i$ has no common factors. We call the set of integers ![]() $(a_0, \ldots, a_n)$ well-formed if the associated weighted projective space is.
$(a_0, \ldots, a_n)$ well-formed if the associated weighted projective space is.
Proposition 4.47 If ![]() ${{\mathbb {P}}}(a,b,c,d)$ is well-formed and admits a
${{\mathbb {P}}}(a,b,c,d)$ is well-formed and admits a ![]() $\mathbb {Q}$-Gorenstein smoothing to
$\mathbb {Q}$-Gorenstein smoothing to ![]() ${{\mathbb {P}}}^{3}$, then
${{\mathbb {P}}}^{3}$, then
Proof. In order for ![]() $X = {{\mathbb {P}}}(a,b,c,d)$ to have a
$X = {{\mathbb {P}}}(a,b,c,d)$ to have a ![]() ${{\mathbb {Q}}}$-Gorenstein smoothing, necessarily
${{\mathbb {Q}}}$-Gorenstein smoothing, necessarily ![]() $K_X^{3} = K_{{{\mathbb {P}}}^{3}}^{3} = -64$ by Proposition 4.2. However,
$K_X^{3} = K_{{{\mathbb {P}}}^{3}}^{3} = -64$ by Proposition 4.2. However, ![]() ${{\mathcal {O}}}(K_X) = {{\mathcal {O}}}(-a-b-c-d)$, and
${{\mathcal {O}}}(K_X) = {{\mathcal {O}}}(-a-b-c-d)$, and
Therefore, we must have ![]() $64abcd = (a + b + c + d)^{3}$.
$64abcd = (a + b + c + d)^{3}$.
One could make the immediate generalization to ![]() $n$-dimensional weighted projective spaces as follows.
$n$-dimensional weighted projective spaces as follows.
Proposition 4.48 If ![]() ${{\mathbb {P}}}(a_0, a_1, \ldots, a_n)$ is well-formed and admits a
${{\mathbb {P}}}(a_0, a_1, \ldots, a_n)$ is well-formed and admits a ![]() $\mathbb {Q}$-Gorenstein smoothing to
$\mathbb {Q}$-Gorenstein smoothing to ![]() ${{\mathbb {P}}}^{n}$, then
${{\mathbb {P}}}^{n}$, then
Remark 4.49 Although this formula appears different from the formula in Theorem 4.46, the equation ![]() $9abc = (a+b+c)^{2}$ simplifies to
$9abc = (a+b+c)^{2}$ simplifies to ![]() $3pqr = p^{2} + q^{2} + r^{2}$ (where
$3pqr = p^{2} + q^{2} + r^{2}$ (where ![]() $a = p^{2}, b = q^{2}, c = r^{2}$) when
$a = p^{2}, b = q^{2}, c = r^{2}$) when ![]() $(a,b,c)$ is well formed.
$(a,b,c)$ is well formed.
Given the equation, one must ask how to find solutions. There is certainly an infinite family of solutions, which makes sense geometrically. If we have a degeneration of ![]() $\mathbb {P}^{2}$ to such a weighted projective space, it should induce a degeneration of
$\mathbb {P}^{2}$ to such a weighted projective space, it should induce a degeneration of ![]() $\mathbb {P}^{3}$ to an appropriate cone over that weighted projective space. This is the content of the following proposition, stated first in the three-dimensional case and then in general, whose proof is simple arithmetic.
$\mathbb {P}^{3}$ to an appropriate cone over that weighted projective space. This is the content of the following proposition, stated first in the three-dimensional case and then in general, whose proof is simple arithmetic.
Proposition 4.50 If ![]() ${{\mathbb {P}}}(a,b,c)$ admits a smoothing to
${{\mathbb {P}}}(a,b,c)$ admits a smoothing to ![]() ${{\mathbb {P}}}^{2}$, then
${{\mathbb {P}}}^{2}$, then ![]() $d =\sqrt {abc} = ({a + b + c})/{3} \in \mathbb {Z}$ and
$d =\sqrt {abc} = ({a + b + c})/{3} \in \mathbb {Z}$ and ![]() $P(a,b,c,d)$ satisfies the condition
$P(a,b,c,d)$ satisfies the condition
Example 4.51 The first non-trivial example of a solution is ![]() ${{\mathbb {P}}}(1,1,2,4)$. Because this can be embedded as a degree-two section of
${{\mathbb {P}}}(1,1,2,4)$. Because this can be embedded as a degree-two section of ![]() ${{\mathbb {P}}}(1,1,1,1,2)$, it clearly admits a smoothing to
${{\mathbb {P}}}(1,1,1,1,2)$, it clearly admits a smoothing to ![]() ${{\mathbb {P}}}^{3}$.
${{\mathbb {P}}}^{3}$.
We have the following immediate generalization to ![]() ${{\mathbb {P}}}^{n}$.
${{\mathbb {P}}}^{n}$.
Proposition 4.52 If ![]() ${{\mathbb {P}}}(a_0, a_1, \ldots, a_n)$ satisfies
${{\mathbb {P}}}(a_0, a_1, \ldots, a_n)$ satisfies
then ![]() $b = (\Pi a_i)^{1/n} = {\sum a_i}/({n+1}) \in \mathbb {Z}$ and
$b = (\Pi a_i)^{1/n} = {\sum a_i}/({n+1}) \in \mathbb {Z}$ and ![]() ${{\mathbb {P}}}(a_0, a_1, \ldots, a_n, b)$ satisfies
${{\mathbb {P}}}(a_0, a_1, \ldots, a_n, b)$ satisfies
Let us further investigate the three-dimensional case. Using a computer, one can list the integer solutions to the equation ![]() $64abcd = (a + b + c + d)^{3}$ such that the associated weighted projective space is well-formed, and finds the following weighted projective spaces as the first few solutions:
$64abcd = (a + b + c + d)^{3}$ such that the associated weighted projective space is well-formed, and finds the following weighted projective spaces as the first few solutions:
 \[ \begin{array}{lll} {{\mathbb{P}}}(1,1,1,1) & {{\mathbb{P}}}(1,1,2,4) & {{\mathbb{P}}}(1,2,9,12) \\ {{\mathbb{P}}}(1,4,10,25) & {{\mathbb{P}}}(1,4,16,27) & {{\mathbb{P}}}(1,6,9,32) \\ {{\mathbb{P}}}(1,7,27,49) & {{\mathbb{P}}}(1,9,50,60) & {{\mathbb{P}}}(1,22,32,121)\\ \end{array} \]
\[ \begin{array}{lll} {{\mathbb{P}}}(1,1,1,1) & {{\mathbb{P}}}(1,1,2,4) & {{\mathbb{P}}}(1,2,9,12) \\ {{\mathbb{P}}}(1,4,10,25) & {{\mathbb{P}}}(1,4,16,27) & {{\mathbb{P}}}(1,6,9,32) \\ {{\mathbb{P}}}(1,7,27,49) & {{\mathbb{P}}}(1,9,50,60) & {{\mathbb{P}}}(1,22,32,121)\\ \end{array} \]
We can immediately determine that some of these threefolds do not admit smoothings to ![]() ${{\mathbb {P}}}^{3}$, using the following theorem of Schlessinger [Reference SchlessingerSch71, Theorem 3].
${{\mathbb {P}}}^{3}$, using the following theorem of Schlessinger [Reference SchlessingerSch71, Theorem 3].
Theorem 4.53 [Reference SchlessingerSch71]
Assume ![]() $Y$ is smooth of dimension
$Y$ is smooth of dimension ![]() $\geqslant 3$,
$\geqslant 3$, ![]() $G$ is a finite group, and
$G$ is a finite group, and ![]() $X = Y / G$. Let
$X = Y / G$. Let ![]() $p: Y \to X$ be the quotient map. If
$p: Y \to X$ be the quotient map. If ![]() $y \in Y$ is the only fixed point of
$y \in Y$ is the only fixed point of ![]() $G$, then
$G$, then ![]() $X$ is rigid.
$X$ is rigid.
In the list of weighted projective spaces, it implies that neither ![]() ${{\mathbb {P}}}(1,4,16,27)$ nor
${{\mathbb {P}}}(1,4,16,27)$ nor ![]() ${{\mathbb {P}}}(1,7,27,49)$ are smoothable, so we see that, in dimension
${{\mathbb {P}}}(1,7,27,49)$ are smoothable, so we see that, in dimension ![]() $\geqslant 3$, satisfying the equation is not a sufficient condition to admit a smoothing (contrasting with the case for dimension two). For the remaining candidates, in light of Proposition 4.50, there are some solutions
$\geqslant 3$, satisfying the equation is not a sufficient condition to admit a smoothing (contrasting with the case for dimension two). For the remaining candidates, in light of Proposition 4.50, there are some solutions ![]() ${{\mathbb {P}}}(a,b,c,d)$ arising from the degenerations
${{\mathbb {P}}}(a,b,c,d)$ arising from the degenerations ![]() ${{\mathbb {P}}}(a,b,c)$ of
${{\mathbb {P}}}(a,b,c)$ of ![]() ${{\mathbb {P}}}^{2}$ where
${{\mathbb {P}}}^{2}$ where ![]() $d = ({a+b+c})/{3}$ is the average of
$d = ({a+b+c})/{3}$ is the average of ![]() $a, b$, and
$a, b$, and ![]() $c$. The only three that appear in this truncated list are
$c$. The only three that appear in this truncated list are ![]() ${{\mathbb {P}}}(1,1,1,1)$,
${{\mathbb {P}}}(1,1,1,1)$, ![]() ${{\mathbb {P}}}(1,1,2,4)$, and
${{\mathbb {P}}}(1,1,2,4)$, and ![]() ${{\mathbb {P}}}(1,4,10,25)$. These solutions are well understood and, following work of Hacking, Prokhorov, and Manetti, we have the following result. This is simply a restatement of Theorem 4.46, adding in the fourth variable
${{\mathbb {P}}}(1,4,10,25)$. These solutions are well understood and, following work of Hacking, Prokhorov, and Manetti, we have the following result. This is simply a restatement of Theorem 4.46, adding in the fourth variable ![]() $d$.
$d$.
Proposition 4.54 There is an infinite family of well-formed solutions to the equation ![]() $64abcd = (a + b + c + d)^{3}$ given by
$64abcd = (a + b + c + d)^{3}$ given by ![]() $(a,b,c,d) = (\alpha ^{2}, \beta ^{2}, \gamma ^{2}, \alpha \beta \gamma ) = (\alpha ^{2}, \beta ^{2}, \gamma ^{2}, ({\alpha ^{2} + \beta ^{2} + \gamma ^{2}})/{3})$. All such
$(a,b,c,d) = (\alpha ^{2}, \beta ^{2}, \gamma ^{2}, \alpha \beta \gamma ) = (\alpha ^{2}, \beta ^{2}, \gamma ^{2}, ({\alpha ^{2} + \beta ^{2} + \gamma ^{2}})/{3})$. All such ![]() $\alpha, \beta$, and
$\alpha, \beta$, and ![]() $\gamma$ lie on an infinite tree and are obtained by a mutation of the form
$\gamma$ lie on an infinite tree and are obtained by a mutation of the form ![]() $(\alpha, \beta, \gamma ) \to (\alpha, \beta, 3\alpha \beta - \gamma )$ starting from
$(\alpha, \beta, \gamma ) \to (\alpha, \beta, 3\alpha \beta - \gamma )$ starting from ![]() $(1,1,1)$.
$(1,1,1)$.
Definition 4.55 We call a solution of this form ![]() ${{\mathbb {P}}}^{2}$-type because it arises from a degeneration of
${{\mathbb {P}}}^{2}$-type because it arises from a degeneration of ![]() ${{\mathbb {P}}}^{2}$.
${{\mathbb {P}}}^{2}$.
The deformation theory of these weighted projective spaces is in general quite complicated, but we can show that all solutions of ![]() ${{\mathbb {P}}}^{2}$-type admit a smoothing to
${{\mathbb {P}}}^{2}$-type admit a smoothing to ![]() ${{\mathbb {P}}}^{3}$.
${{\mathbb {P}}}^{3}$.
Proposition 4.56 [Reference HackingHac12]
The weighted projective spaces appearing as solutions of ![]() ${{\mathbb {P}}}^{2}$-type can be connected as a family of threefolds over a two-parameter base, and are each
${{\mathbb {P}}}^{2}$-type can be connected as a family of threefolds over a two-parameter base, and are each ![]() $\mathbb {Q}$-Gorenstein deformations of a common smoothing.
$\mathbb {Q}$-Gorenstein deformations of a common smoothing.
Proof. This is proved in [Reference HackingHac12, Example 7.7]. We relate the weighted projective spaces one step apart on the infinite tree over a two-parameter base. Let ![]() ${{\mathbb {P}}}(a,b,c,d)$ and
${{\mathbb {P}}}(a,b,c,d)$ and ![]() ${{\mathbb {P}}}(a,b,c',d')$ be two solutions to
${{\mathbb {P}}}(a,b,c',d')$ be two solutions to ![]() $64abcd = (a + b + c + d)^{3}$ of
$64abcd = (a + b + c + d)^{3}$ of ![]() ${{\mathbb {P}}}^{2}$-type related by one mutation so that
${{\mathbb {P}}}^{2}$-type related by one mutation so that
and
Using the fact that ![]() $3\alpha \beta \gamma = \alpha ^{2} + \beta ^{2} + \gamma ^{2}$ (and similarly for
$3\alpha \beta \gamma = \alpha ^{2} + \beta ^{2} + \gamma ^{2}$ (and similarly for ![]() $\gamma '$), we can form the two-parameter family
$\gamma '$), we can form the two-parameter family
of weighted degree ![]() $\alpha ^{2} + \beta ^{2} = \gamma \gamma '$ threefolds in
$\alpha ^{2} + \beta ^{2} = \gamma \gamma '$ threefolds in ![]() ${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma, \gamma ', \alpha \beta ).$
${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma, \gamma ', \alpha \beta ).$
When ![]() $s = t = 0$, we obtain a non-normal threefold
$s = t = 0$, we obtain a non-normal threefold ![]() ${{\mathbb {P}}}(\alpha ^{2}, \gamma, \gamma ', \alpha \beta ) \cup {{\mathbb {P}}}(\beta ^{2}, \gamma, \gamma ', \alpha \beta )$.
${{\mathbb {P}}}(\alpha ^{2}, \gamma, \gamma ', \alpha \beta ) \cup {{\mathbb {P}}}(\beta ^{2}, \gamma, \gamma ', \alpha \beta )$.
When ![]() $s = 0$ but
$s = 0$ but ![]() $t \ne 0$, we obtain
$t \ne 0$, we obtain ![]() ${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma ^{2}, \alpha \beta \gamma )$ via the degree
${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma ^{2}, \alpha \beta \gamma )$ via the degree ![]() $\gamma$ embedding
$\gamma$ embedding
given by
When ![]() $s \ne 0$ but
$s \ne 0$ but ![]() $t = 0$, we obtain
$t = 0$, we obtain ![]() ${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma '^{2}, \alpha \beta \gamma ')$ via the degree
${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma '^{2}, \alpha \beta \gamma ')$ via the degree ![]() $\gamma '$ embedding
$\gamma '$ embedding
given by
Finally, for ![]() $s \ne 0$ and
$s \ne 0$ and ![]() $t \ne 0$, we obtain a smoothing of the singularities of index
$t \ne 0$, we obtain a smoothing of the singularities of index ![]() $c$ and
$c$ and ![]() $c'$, respectively. Because this is taking place as a complete intersection in weighted projective space, which is
$c'$, respectively. Because this is taking place as a complete intersection in weighted projective space, which is ![]() ${{\mathbb {Q}}}$-factorial, the total space of these smoothings is
${{\mathbb {Q}}}$-factorial, the total space of these smoothings is ![]() ${{\mathbb {Q}}}$-Gorenstein.
${{\mathbb {Q}}}$-Gorenstein.
Remark 4.57 Because ![]() ${{\mathbb {P}}}^{3}$ is the ‘linear cone’ over the anticanonically embedded
${{\mathbb {P}}}^{3}$ is the ‘linear cone’ over the anticanonically embedded ![]() ${{\mathbb {P}}}^{2}$, it makes sense that ‘cones’ (the weighted projective spaces
${{\mathbb {P}}}^{2}$, it makes sense that ‘cones’ (the weighted projective spaces ![]() ${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma ^{2}, d)$) over degenerations of
${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, \gamma ^{2}, d)$) over degenerations of ![]() ${{\mathbb {P}}}^{2}$ are appearing as degenerations of
${{\mathbb {P}}}^{2}$ are appearing as degenerations of ![]() ${{\mathbb {P}}}^{3}$. Analogously, the equation
${{\mathbb {P}}}^{3}$. Analogously, the equation ![]() $4\alpha \beta \gamma = \alpha ^{2} + \beta ^{2} + 2\gamma ^{2}$ parameterizes weighted projective spaces
$4\alpha \beta \gamma = \alpha ^{2} + \beta ^{2} + 2\gamma ^{2}$ parameterizes weighted projective spaces ![]() ${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, 2\gamma ^{2})$ that appear as degenerations of
${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, 2\gamma ^{2})$ that appear as degenerations of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ (see [Reference Hacking and ProkhorovHP10, Theorem 1.2]). Because
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ (see [Reference Hacking and ProkhorovHP10, Theorem 1.2]). Because ![]() ${{\mathbb {P}}}^{3}$ is a smoothing of the cone over the anticanonical embedding of
${{\mathbb {P}}}^{3}$ is a smoothing of the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, it makes sense that ‘cones’ (weighted projective spaces
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, it makes sense that ‘cones’ (weighted projective spaces ![]() ${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, 2\gamma ^{2}, d)$) over degenerations of
${{\mathbb {P}}}(\alpha ^{2}, \beta ^{2}, 2\gamma ^{2}, d)$) over degenerations of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ should be appearing as degenerations of
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ should be appearing as degenerations of ![]() ${{\mathbb {P}}}^{3}$. This allows us to find a second infinite tree of solutions to the equation.
${{\mathbb {P}}}^{3}$. This allows us to find a second infinite tree of solutions to the equation.
Proposition 4.58 There is an infinite family of well-formed solutions to the equation ![]() $64abcd = (a + b + c + d)^{3}$ given by
$64abcd = (a + b + c + d)^{3}$ given by ![]() $(a,b,c,d) = (a,b,c, a+b+c)$. All such
$(a,b,c,d) = (a,b,c, a+b+c)$. All such ![]() $(a,b,c,d)$ lie on an infinite tree and are obtained by a mutation of the form
$(a,b,c,d)$ lie on an infinite tree and are obtained by a mutation of the form ![]() $(a,b,c,d) \to (a,b,8ab-a-b-d,8ab-d)$ starting from
$(a,b,c,d) \to (a,b,8ab-a-b-d,8ab-d)$ starting from ![]() $(1,1,2,4)$.
$(1,1,2,4)$.
Proof. If ![]() $a + b + c = d$, the equation
$a + b + c = d$, the equation ![]() $64abcd = (a+ b+ c+d)^{3}$ simplifies to
$64abcd = (a+ b+ c+d)^{3}$ simplifies to ![]() $8abc = (a+b+c)^{2}$. If desired, one can simplify this further by showing
$8abc = (a+b+c)^{2}$. If desired, one can simplify this further by showing ![]() $a = \alpha ^{2}$,
$a = \alpha ^{2}$, ![]() $b = \beta ^{2}$, and
$b = \beta ^{2}$, and ![]() $c = 2\gamma ^{2}$ so the equation becomes
$c = 2\gamma ^{2}$ so the equation becomes ![]() $4\alpha \beta \gamma = \alpha ^{2} + \beta ^{2} + 2\gamma ^{2}$. These parametrize weighted projective degenerations of
$4\alpha \beta \gamma = \alpha ^{2} + \beta ^{2} + 2\gamma ^{2}$. These parametrize weighted projective degenerations of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, and we use the mutation process in [Reference Hacking and ProkhorovHP10, Theorem 1.2] to obtain the result.
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$, and we use the mutation process in [Reference Hacking and ProkhorovHP10, Theorem 1.2] to obtain the result.
In the list of weighted projective spaces, one sees that ![]() ${{\mathbb {P}}}(1,1,2,4)$,
${{\mathbb {P}}}(1,1,2,4)$, ![]() ${{\mathbb {P}}}(1,2,9,12)$, and
${{\mathbb {P}}}(1,2,9,12)$, and ![]() ${{\mathbb {P}}}(1,9,50,60)$ are all of this form.
${{\mathbb {P}}}(1,9,50,60)$ are all of this form.
Definition 4.59 We call a solution of this form ![]() $Q$-type because it arises from a degeneration of the quadric.
$Q$-type because it arises from a degeneration of the quadric.
One can prove a simple lemma showing that ![]() $(1,1,2,4)$ is the only overlap between the types.
$(1,1,2,4)$ is the only overlap between the types.
Lemma 4.60 The only solution to the equation ![]() $64abcd = (a + b + c + d)^{3}$ that is both of
$64abcd = (a + b + c + d)^{3}$ that is both of ![]() ${{\mathbb {P}}}^{2}$-type and
${{\mathbb {P}}}^{2}$-type and ![]() $Q$-type is
$Q$-type is ![]() $(1,1,2,4)$.
$(1,1,2,4)$.
As in the case of solutions of ![]() ${{\mathbb {P}}}^{2}$-type, we can relate two weighted projective spaces of
${{\mathbb {P}}}^{2}$-type, we can relate two weighted projective spaces of ![]() $Q$-type that are one mutation apart.
$Q$-type that are one mutation apart.
Proposition 4.61 Given two weighted projective spaces that are solutions of ![]() $Q$-type one mutation apart, there is a two-parameter
$Q$-type one mutation apart, there is a two-parameter ![]() ${{\mathbb {Q}}}$-Gorenstein family connecting them and each are
${{\mathbb {Q}}}$-Gorenstein family connecting them and each are ![]() $\mathbb {Q}$-Gorenstein deformations of a common smoothing.
$\mathbb {Q}$-Gorenstein deformations of a common smoothing.
Proof. Let ![]() $(a,b,c,d)$ be the first solution and
$(a,b,c,d)$ be the first solution and ![]() $(a,b,c',d') = (a,b,8ab-a-b-d,8ab-d)$ be the second. Without loss of generality, assume
$(a,b,c',d') = (a,b,8ab-a-b-d,8ab-d)$ be the second. Without loss of generality, assume ![]() $d < d'$. First, because
$d < d'$. First, because ![]() $d = a + b + c$, we have
$d = a + b + c$, we have ![]() $8abc = (a + b + c)^{2} = d^{2}$. Then, observe that
$8abc = (a + b + c)^{2} = d^{2}$. Then, observe that ![]() $d(a+b) = d(d - c) = d^{2} - dc = 8abc - dc = c(8ab-d) = cd'$, hence
$d(a+b) = d(d - c) = d^{2} - dc = 8abc - dc = c(8ab-d) = cd'$, hence ![]() $a+b = {cd'}/{d}$, and similarly,
$a+b = {cd'}/{d}$, and similarly, ![]() $a+b = {c'd}/{d'}$. Using this relationship repeatedly, we can form the desired family.
$a+b = {c'd}/{d'}$. Using this relationship repeatedly, we can form the desired family.
Then, we can consider the family
When ![]() $s = 0$ and
$s = 0$ and ![]() $t = 0$, this is a non-normal threefold
$t = 0$, this is a non-normal threefold ![]() ${{\mathbb {P}}}(ac,c,a+b,d) \cup {{\mathbb {P}}}(bc,c,a+b,d)$.
${{\mathbb {P}}}(ac,c,a+b,d) \cup {{\mathbb {P}}}(bc,c,a+b,d)$.
For ![]() $t =0$ but
$t =0$ but ![]() $s \ne 0$, this is the image of the degree
$s \ne 0$, this is the image of the degree ![]() $c$ embedding of
$c$ embedding of
given by
When ![]() $s = 0$ but
$s = 0$ but ![]() $t \ne 0$, this is the image of the degree
$t \ne 0$, this is the image of the degree ![]() $a+b$ embedding of
$a+b$ embedding of
given by
Finally, for ![]() $s \ne 0$ and
$s \ne 0$ and ![]() $t \ne 0$, this gives a partial smoothing of the singularities of index
$t \ne 0$, this gives a partial smoothing of the singularities of index ![]() $c$ and
$c$ and ![]() $d$ and
$d$ and ![]() $c'$ and
$c'$ and ![]() $d'$. Because the total space is a complete intersection in weighted projective space, it is
$d'$. Because the total space is a complete intersection in weighted projective space, it is ![]() ${{\mathbb {Q}}}$-Gorenstein.
${{\mathbb {Q}}}$-Gorenstein.
Remark 4.62 Although one could write the smoothings in Propositions 4.56 and 4.61 over a one-parameter base, the family over the two-dimensional base shows how to degenerate each pair of normal threefolds to a non-normal threefold, which can also appear in the moduli problem.
Remark 4.63 The fact that there are two essentially distinct families of solutions to the equation ![]() $64abcd = (a + b + c + d)^{3}$ indicates the increase in complexity when studying degenerations of
$64abcd = (a + b + c + d)^{3}$ indicates the increase in complexity when studying degenerations of ![]() ${{\mathbb {P}}}^{3}$ versus those of
${{\mathbb {P}}}^{3}$ versus those of ![]() ${{\mathbb {P}}}^{2}$. Although we do not know smoothability for all solutions, Propositions 4.56 and 4.61 show that weighted projective spaces of
${{\mathbb {P}}}^{2}$. Although we do not know smoothability for all solutions, Propositions 4.56 and 4.61 show that weighted projective spaces of ![]() ${{\mathbb {P}}}^{2}$ or
${{\mathbb {P}}}^{2}$ or ![]() $Q$ type are smoothable to
$Q$ type are smoothable to ![]() ${{\mathbb {P}}}^{3}$.
${{\mathbb {P}}}^{3}$.
Furthermore, based on preliminary computation we make the following conjecture.
Conjecture 4.64 The only weighted projective spaces ![]() ${{\mathbb {P}}}(a,b,c,d)$ that admit
${{\mathbb {P}}}(a,b,c,d)$ that admit ![]() $\mathbb {Q}$-Gorenstein smoothings to
$\mathbb {Q}$-Gorenstein smoothings to ![]() ${{\mathbb {P}}}^{3}$ are solutions of
${{\mathbb {P}}}^{3}$ are solutions of ![]() ${{\mathbb {P}}}^{2}$ type or
${{\mathbb {P}}}^{2}$ type or ![]() $Q$ type.
$Q$ type.
4.6 Examples of log-terminal degenerations and their smoothings
Example 4.65 Let ![]() $X$ be the cone over the anticanonically embedded
$X$ be the cone over the anticanonically embedded ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. In other words,
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. In other words, ![]() $X$ is the cone over the anticanonical embedding of the quadric surface in
$X$ is the cone over the anticanonical embedding of the quadric surface in ![]() ${{\mathbb {P}}}^{3}$. By construction,
${{\mathbb {P}}}^{3}$. By construction, ![]() $X$ is a hyperplane section of
$X$ is a hyperplane section of ![]() ${{\mathbb {P}}}(1,1,1,1,2)$, the cone over the anticanonical embedding of
${{\mathbb {P}}}(1,1,1,1,2)$, the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{3}$. However, we could apply the same construction to the cone over the anticanonical embedding of the singular quadric
${{\mathbb {P}}}^{3}$. However, we could apply the same construction to the cone over the anticanonical embedding of the singular quadric ![]() $(xy- z^{2} = 0) \subset {{\mathbb {P}}}^{3}$ to realize the cone
$(xy- z^{2} = 0) \subset {{\mathbb {P}}}^{3}$ to realize the cone ![]() ${{\mathbb {P}}}(1,1,2,4)$ as another hyperplane section of
${{\mathbb {P}}}(1,1,2,4)$ as another hyperplane section of ![]() ${{\mathbb {P}}}(1,1,1,1,2)$. Taking an appropriate pencil of these hyperplanes, we realize
${{\mathbb {P}}}(1,1,1,1,2)$. Taking an appropriate pencil of these hyperplanes, we realize ![]() $X$ as a
$X$ as a ![]() ${{\mathbb {Q}}}$-Gorenstein smoothing of
${{\mathbb {Q}}}$-Gorenstein smoothing of ![]() ${{\mathbb {P}}}(1,1,2,4)$.
${{\mathbb {P}}}(1,1,2,4)$.
Example 4.66 The weighted projective space ![]() ${{\mathbb {P}}}(1,4,10,25)$ admits at least seven different partial smoothings that all admit smoothings to
${{\mathbb {P}}}(1,4,10,25)$ admits at least seven different partial smoothings that all admit smoothings to ![]() ${{\mathbb {P}}}^{3}$. For the construction of the smoothings and a discussion of the applications to the study of moduli of quintic surfaces, see § 5. Here, we draw a rough sketch of some smoothings. First, we observe that
${{\mathbb {P}}}^{3}$. For the construction of the smoothings and a discussion of the applications to the study of moduli of quintic surfaces, see § 5. Here, we draw a rough sketch of some smoothings. First, we observe that ![]() ${{\mathbb {P}}}(1,4,10,25)$ has singular locus
${{\mathbb {P}}}(1,4,10,25)$ has singular locus ![]() ${{\mathbb {P}}}^{1} \cup {{\mathbb {P}}}^{1}$. At the general point of the first component
${{\mathbb {P}}}^{1} \cup {{\mathbb {P}}}^{1}$. At the general point of the first component ![]() ${{\mathbb {P}}}^{1}$, it is isomorphic to
${{\mathbb {P}}}^{1}$, it is isomorphic to ![]() $\frac {1}{2}(1,1) \times {{\mathbb {A}}}^{1}$. At the general point of the second component
$\frac {1}{2}(1,1) \times {{\mathbb {A}}}^{1}$. At the general point of the second component ![]() ${{\mathbb {P}}}^{1}$, it is isomorphic to
${{\mathbb {P}}}^{1}$, it is isomorphic to ![]() $\frac {1}{5}(1,4) \times {{\mathbb {A}}}^{1}$. This has canonical singularities at all points except the unique
$\frac {1}{5}(1,4) \times {{\mathbb {A}}}^{1}$. This has canonical singularities at all points except the unique ![]() $\frac {1}{25}(1,4,10)$ singularity. There is a partial smoothing
$\frac {1}{25}(1,4,10)$ singularity. There is a partial smoothing ![]() $Y_{26}$ that smooths the
$Y_{26}$ that smooths the ![]() $\frac {1}{4}(1,1,2)$ singularity to a singularity of type
$\frac {1}{4}(1,1,2)$ singularity to a singularity of type ![]() $v$, isomorphic to the vertex of the cone over the anticanonical embedding of
$v$, isomorphic to the vertex of the cone over the anticanonical embedding of ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ (as in Example 4.65). There is a different partial smoothing
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$ (as in Example 4.65). There is a different partial smoothing ![]() $W_{26}$ of
$W_{26}$ of ![]() ${{\mathbb {P}}}(1,4,10,25)$ that partially smooths the
${{\mathbb {P}}}(1,4,10,25)$ that partially smooths the ![]() $\frac {1}{25}(1,4,10)$ singularity to a non-isolated singularity
$\frac {1}{25}(1,4,10)$ singularity to a non-isolated singularity ![]() $q$ isomorphic to the quotient of
$q$ isomorphic to the quotient of ![]() $ab - c^{3}d = 0 \subset \mathbb {A}^{4}$ by the
$ab - c^{3}d = 0 \subset \mathbb {A}^{4}$ by the ![]() $\mu _5$ action
$\mu _5$ action ![]() $(a,b,c,d) \sim (\zeta _5 a, \zeta _5^{4} b, \zeta _5 c, \zeta _5^{2} d)$. We can further smooth
$(a,b,c,d) \sim (\zeta _5 a, \zeta _5^{4} b, \zeta _5 c, \zeta _5^{2} d)$. We can further smooth ![]() $W_{26}$ to a threefold
$W_{26}$ to a threefold ![]() $Z_{26}$ that has an isolated singularity
$Z_{26}$ that has an isolated singularity ![]() $p$ in place of
$p$ in place of ![]() $q$. This singularity
$q$. This singularity ![]() $p$ is the quotient of the isolated singularity
$p$ is the quotient of the isolated singularity ![]() $ab - c(d^{2}-c^{4}) = 0 \subset \mathbb {A}^{4}$, a perturbation of a cone over a
$ab - c(d^{2}-c^{4}) = 0 \subset \mathbb {A}^{4}$, a perturbation of a cone over a ![]() $D_6$ singularity, by the same
$D_6$ singularity, by the same ![]() $\mu _5$ action.
$\mu _5$ action.

Furthermore, the isolated singularities ![]() $p$ and
$p$ and ![]() $v$ are themselves smoothable. Because the local to global deformation theory is unobstructed, we can combine the partial smoothings of each component of the singular locus of
$v$ are themselves smoothable. Because the local to global deformation theory is unobstructed, we can combine the partial smoothings of each component of the singular locus of ![]() ${{\mathbb {P}}}(1,4,10,25)$ in every possible way to obtain seven different partial smoothings.
${{\mathbb {P}}}(1,4,10,25)$ in every possible way to obtain seven different partial smoothings.
Let ![]() $X_{26}$ be the partial smoothing of
$X_{26}$ be the partial smoothing of ![]() ${{\mathbb {P}}}(1,4,10,25)$ with only one singular point, a unique singularity of type
${{\mathbb {P}}}(1,4,10,25)$ with only one singular point, a unique singularity of type ![]() $p$. By a careful dimension count, we obtain the following analogue of Proposition 4.41.
$p$. By a careful dimension count, we obtain the following analogue of Proposition 4.41.
Proposition 4.67 Let ![]() $X_{26}$ be the partial smoothing of
$X_{26}$ be the partial smoothing of ![]() ${{\mathbb {P}}}(1,4,10,25)$ with a unique singularity of type
${{\mathbb {P}}}(1,4,10,25)$ with a unique singularity of type ![]() $p$. If the pair
$p$. If the pair ![]() $( X_{26}, ({4}/{d}) D )$ is log-terminal for the general member
$( X_{26}, ({4}/{d}) D )$ is log-terminal for the general member ![]() $D$ in the
$D$ in the ![]() $\mathbb {Q}$-linear system
$\mathbb {Q}$-linear system ![]() $|{-}({d}/{4}) K_{X_{26}}|$, then there is a divisor in the moduli space of H-stable pairs of degree
$|{-}({d}/{4}) K_{X_{26}}|$, then there is a divisor in the moduli space of H-stable pairs of degree ![]() $d$ parameterizing surfaces on
$d$ parameterizing surfaces on ![]() $X_{26}$.
$X_{26}$.
Remark 4.68 Propositions 4.41 and 4.67 are the higher-dimensional versions of calculations in [Reference HackingHac04]: curves on the surfaces ![]() ${{\mathbb {P}}}(1,1,4)$ and
${{\mathbb {P}}}(1,1,4)$ and ![]() $X_{26}$, the smoothing of the
$X_{26}$, the smoothing of the ![]() $\frac {1}{4}(1,1)$ singularity on
$\frac {1}{4}(1,1)$ singularity on ![]() ${{\mathbb {P}}}(1,4,25)$, form divisors in the moduli space of degree
${{\mathbb {P}}}(1,4,25)$, form divisors in the moduli space of degree ![]() $d$ plane curves, provided the curves have appropriate singularities.
$d$ plane curves, provided the curves have appropriate singularities.
5. Quintic surfaces
Because ![]() ${{\mathbb {P}}}(H^{0}({{\mathbb {P}}}^{3}, {{\mathcal {O}}}(5)) \cong {{\mathbb {P}}}^{55}$ and
${{\mathbb {P}}}(H^{0}({{\mathbb {P}}}^{3}, {{\mathcal {O}}}(5)) \cong {{\mathbb {P}}}^{55}$ and ![]() $\dim \operatorname {Aut} {{\mathbb {P}}}^{3} = 15$, we have a
$\dim \operatorname {Aut} {{\mathbb {P}}}^{3} = 15$, we have a ![]() $40$-dimensional space of quintic surfaces in
$40$-dimensional space of quintic surfaces in ![]() ${{\mathbb {P}}}^{3}$. However, just fixing numerical invariants, we obtain a moduli space of smooth quintic surfaces with an additional component [Reference HorikawaHor73]. Smooth quintic surfaces have numerical invariants
${{\mathbb {P}}}^{3}$. However, just fixing numerical invariants, we obtain a moduli space of smooth quintic surfaces with an additional component [Reference HorikawaHor73]. Smooth quintic surfaces have numerical invariants ![]() $K_S^{5} = 5$,
$K_S^{5} = 5$, ![]() $p_g = 4$, and
$p_g = 4$, and ![]() $q = 0$ and the moduli space parameterizing these surfaces has two
$q = 0$ and the moduli space parameterizing these surfaces has two ![]() $40$-dimensional components. The first component, consisting of type I surfaces, parameterizes traditional quintic surfaces
$40$-dimensional components. The first component, consisting of type I surfaces, parameterizes traditional quintic surfaces ![]() $S$ such that
$S$ such that ![]() $K_S$ is very ample and defines an embedding
$K_S$ is very ample and defines an embedding ![]() $S \subset {{\mathbb {P}}}^{3}$. The second component parameterizes type IIa surfaces such that
$S \subset {{\mathbb {P}}}^{3}$. The second component parameterizes type IIa surfaces such that ![]() $|K_S|$ has a base-point and
$|K_S|$ has a base-point and ![]() $S$ admits a generically two-to-one morphism to
$S$ admits a generically two-to-one morphism to ![]() ${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. The two components meet along a divisor of dimension
${{\mathbb {P}}}^{1} \times {{\mathbb {P}}}^{1}$. The two components meet along a divisor of dimension ![]() $39$ parameterizing type IIb surfaces such that
$39$ parameterizing type IIb surfaces such that ![]() $|K_S|$ has a base-point and
$|K_S|$ has a base-point and ![]() $S$ admits a generically two-to-one morphism to
$S$ admits a generically two-to-one morphism to ![]() ${{\mathbb {F}}}_2$. For an image of the moduli space and the construction of type II surfaces, see [Reference RanaRan17]. One might naturally ask how the moduli space of pairs defined in this paper encompasses surfaces of type II. To describe the type II surfaces, we recall how to embed surfaces them into weighted projective spaces, worked out in [Reference GriffinGri85]. There is a typographical error in the main theorem in [Reference GriffinGri85] in the first relation
${{\mathbb {F}}}_2$. For an image of the moduli space and the construction of type II surfaces, see [Reference RanaRan17]. One might naturally ask how the moduli space of pairs defined in this paper encompasses surfaces of type II. To describe the type II surfaces, we recall how to embed surfaces them into weighted projective spaces, worked out in [Reference GriffinGri85]. There is a typographical error in the main theorem in [Reference GriffinGri85] in the first relation ![]() $r_1$, but it is stated correctly as follows.
$r_1$, but it is stated correctly as follows.
Theorem 5.1 (Griffin)
Let ![]() $S$ be a numerical quintic surface of type II. Then,
$S$ be a numerical quintic surface of type II. Then,
where ![]() ${{\mathbb {P}}}(1,1,1,1,2,3,3)$ has coordinates
${{\mathbb {P}}}(1,1,1,1,2,3,3)$ has coordinates ![]() $(x_0,x_1,x_2,x_3,y,z_1,z_2)$ and
$(x_0,x_1,x_2,x_3,y,z_1,z_2)$ and ![]() $I$ is generated by the relations
$I$ is generated by the relations

where ![]() $Q$ and
$Q$ and ![]() $e_i$ are weight-five polynomials satisfying certain conditions. The surface
$e_i$ are weight-five polynomials satisfying certain conditions. The surface ![]() $S$ is of type IIb if
$S$ is of type IIb if ![]() $\beta = 0$ and type IIa if
$\beta = 0$ and type IIa if ![]() $\beta \ne 0$.
$\beta \ne 0$.
The simplest example is ![]() $\beta = \gamma = \delta = \lambda = e_i = 0$. In this case, we show that
$\beta = \gamma = \delta = \lambda = e_i = 0$. In this case, we show that ![]() $S$ is a hypersurface of degree
$S$ is a hypersurface of degree ![]() $50$ on
$50$ on ![]() $X = {{\mathbb {P}}}(1,4, 10, 25)$, so it satisfies
$X = {{\mathbb {P}}}(1,4, 10, 25)$, so it satisfies ![]() $5K_X + 4S \sim 0$.
$5K_X + 4S \sim 0$.
Example 5.2 Let ![]() $X = {{\mathbb {P}}}(1,4,10,25)$ with coordinates
$X = {{\mathbb {P}}}(1,4,10,25)$ with coordinates ![]() $a_0, a_1, a_2, a_3$. First, consider the embedding
$a_0, a_1, a_2, a_3$. First, consider the embedding
given by
so that, if ![]() ${{\mathbb {P}}}(1,2,5,13,25)$ has coordinates
${{\mathbb {P}}}(1,2,5,13,25)$ has coordinates ![]() $b_0,b_1,b_2,b_3,b_4$, then
$b_0,b_1,b_2,b_3,b_4$, then
Then, consider the embedding
given by
If ![]() ${{\mathbb {P}}}(1,1,1,1,2,3,3,5)$ has coordinates
${{\mathbb {P}}}(1,1,1,1,2,3,3,5)$ has coordinates ![]() $x_0,x_1,x_2,x_3,y,z_1,z_2,$ and
$x_0,x_1,x_2,x_3,y,z_1,z_2,$ and ![]() $t$, in the composition
$t$, in the composition
we find that ![]() $X$ is defined almost exactly by the equations in Theorem 5.1, with
$X$ is defined almost exactly by the equations in Theorem 5.1, with ![]() $\beta = \gamma = \delta = \lambda = e_i = 0$, the only difference is that
$\beta = \gamma = \delta = \lambda = e_i = 0$, the only difference is that ![]() $t = Q(x_i,y)$. To obtain the surface
$t = Q(x_i,y)$. To obtain the surface ![]() $S$, let
$S$, let ![]() $S$ be
$S$ be ![]() $t = Q(x_i,y)$ in
$t = Q(x_i,y)$ in ![]() ${{\mathbb {P}}}(1,1,1,1,2,3,3,5)|_X$. As desired,
${{\mathbb {P}}}(1,1,1,1,2,3,3,5)|_X$. As desired, ![]() $S$ has degree
$S$ has degree ![]() $50$ on
$50$ on ![]() $X$.
$X$.
By using various partial smoothings of ![]() ${{\mathbb {P}}}(1,4,10,25)$, we can obtain all surfaces of type IIb as a hypersurface on one smoothing of
${{\mathbb {P}}}(1,4,10,25)$, we can obtain all surfaces of type IIb as a hypersurface on one smoothing of ![]() ${{\mathbb {P}}}(1,4,10,25)$, with the generic one on
${{\mathbb {P}}}(1,4,10,25)$, with the generic one on ![]() $X_{26}$.
$X_{26}$.
Returning to ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$, the previous result shows that pairs
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$, the previous result shows that pairs ![]() $(X_{26},S)$ form a divisor
$(X_{26},S)$ form a divisor ![]() ${{\mathcal {D}}}_1$ in the moduli space: it parameterizes the surfaces of type IIb. By Proposition 4.41, we know there is a second divisor
${{\mathcal {D}}}_1$ in the moduli space: it parameterizes the surfaces of type IIb. By Proposition 4.41, we know there is a second divisor ![]() ${{\mathcal {D}}}_2$ in
${{\mathcal {D}}}_2$ in ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ parameterizing surfaces on
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ parameterizing surfaces on ![]() $X$, the cone over the anticanonical embedding of the quadric surface. Because
$X$, the cone over the anticanonical embedding of the quadric surface. Because ![]() $X$ is a section of
$X$ is a section of ![]() ${{\mathcal {O}}}_W(2)$ for the weighted projective space
${{\mathcal {O}}}_W(2)$ for the weighted projective space ![]() $W = {{\mathbb {P}}}(1,1,1,1,2)$, we compute that
$W = {{\mathbb {P}}}(1,1,1,1,2)$, we compute that ![]() ${{\mathcal {O}}}_X(K_X) = {{\mathcal {O}}}_W(-4)|_X$ and generic
${{\mathcal {O}}}_X(K_X) = {{\mathcal {O}}}_W(-4)|_X$ and generic ![]() $D$ satisfying
$D$ satisfying ![]() $5 K_X + 4D \sim 0$ is a section of
$5 K_X + 4D \sim 0$ is a section of ![]() ${{\mathcal {O}}}_X(D) = {{\mathcal {O}}}_W(5)|_X$. For general
${{\mathcal {O}}}_X(D) = {{\mathcal {O}}}_W(5)|_X$. For general ![]() $D \in {{\mathcal {O}}}_W(5)|_X$, because
$D \in {{\mathcal {O}}}_W(5)|_X$, because ![]() $D$ is a complete intersection in
$D$ is a complete intersection in ![]() ${{\mathbb {P}}}(1,1,1,1,2)$, we can compute the singularities as in [Reference Iano-FletcherI-F00, § 1.7]. The computation shows that
${{\mathbb {P}}}(1,1,1,1,2)$, we can compute the singularities as in [Reference Iano-FletcherI-F00, § 1.7]. The computation shows that ![]() $D$ has a unique
$D$ has a unique ![]() $\frac {1}{4}(1,1)$ singularity at the vertex of
$\frac {1}{4}(1,1)$ singularity at the vertex of ![]() $X$ (cf. Proposition 4.43). Furthermore, by Proposition 3.10, we know
$X$ (cf. Proposition 4.43). Furthermore, by Proposition 3.10, we know ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ is smooth at the generic point of
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ is smooth at the generic point of ![]() ${{\mathcal {D}}}_2$. In [Reference RanaRan17, Theorem 1.5], it is shown that there is a divisor
${{\mathcal {D}}}_2$. In [Reference RanaRan17, Theorem 1.5], it is shown that there is a divisor ![]() ${{\mathcal {D}}}'$ in the moduli space of stable quintic surfaces parameterizing surfaces whose unique non-Du Val singularity is of type
${{\mathcal {D}}}'$ in the moduli space of stable quintic surfaces parameterizing surfaces whose unique non-Du Val singularity is of type ![]() $\frac {1}{4}(1,1)$. The component
$\frac {1}{4}(1,1)$. The component ![]() ${{\mathcal {D}}}_2$ in
${{\mathcal {D}}}_2$ in ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ found here parameterizes the surfaces Rana calls ‘type 1’ (appearing as a divisor on the component parameterizing surfaces of type I). In other words, for general
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ found here parameterizes the surfaces Rana calls ‘type 1’ (appearing as a divisor on the component parameterizing surfaces of type I). In other words, for general ![]() $S$ such that
$S$ such that ![]() $[S] \in {{\mathcal {D}}}'$ in Rana's work,
$[S] \in {{\mathcal {D}}}'$ in Rana's work, ![]() $S$ appears as a divisor on the threefold
$S$ appears as a divisor on the threefold ![]() $X$ where
$X$ where ![]() $[(X,S)] \in {{\mathcal {D}}}_2$ in this interpretation.
$[(X,S)] \in {{\mathcal {D}}}_2$ in this interpretation.
We can describe components of higher codimension using the work in § 4.5. From Example 4.65, we know that ![]() ${{\mathbb {P}}}(1,1,2,4)$ admits a smoothing to
${{\mathbb {P}}}(1,1,2,4)$ admits a smoothing to ![]() $X$, so should correspond to a higher-codimension piece of
$X$, so should correspond to a higher-codimension piece of ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$. Indeed, a toric computation shows that the projective dimension of the automorphism group of
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$. Indeed, a toric computation shows that the projective dimension of the automorphism group of ![]() ${{\mathbb {P}}}(1,1,2,4)$ is
${{\mathbb {P}}}(1,1,2,4)$ is ![]() $17$, and surfaces on
$17$, and surfaces on ![]() $Z = {{\mathbb {P}}}(1,1,2,4)$ satisfying
$Z = {{\mathbb {P}}}(1,1,2,4)$ satisfying ![]() $5K_Z + 4D \sim 0$ are elements of the linear system
$5K_Z + 4D \sim 0$ are elements of the linear system ![]() $| {{\mathcal {O}}}_Z(10)|$. This linear system has projective dimension
$| {{\mathcal {O}}}_Z(10)|$. This linear system has projective dimension ![]() $55$, so the space parameterizing surfaces on
$55$, so the space parameterizing surfaces on ![]() ${{\mathbb {P}}}(1,1,2,4)$ has dimension 38. This is a codimension-two component of
${{\mathbb {P}}}(1,1,2,4)$ has dimension 38. This is a codimension-two component of ![]() ${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ that is codimension one inside
${{\mathcal {M}}}_{{{\mathbb {P}}}^{3}\text {-sm},(5,4)}$ that is codimension one inside ![]() ${{\mathcal {D}}}_2$. Furthermore, a computation as in [Reference Iano-FletcherI-F00, § 1.7] shows that the surfaces appearing on
${{\mathcal {D}}}_2$. Furthermore, a computation as in [Reference Iano-FletcherI-F00, § 1.7] shows that the surfaces appearing on ![]() ${{\mathbb {P}}}(1,1,2,4)$ have two singularities:
${{\mathbb {P}}}(1,1,2,4)$ have two singularities: ![]() $\frac {1}{4}(1,1)$ and
$\frac {1}{4}(1,1)$ and ![]() $\frac {1}{2}(1,1)$. We could continue further: there is a 37-dimensional (or codimension-3) component parameterizing surfaces on
$\frac {1}{2}(1,1)$. We could continue further: there is a 37-dimensional (or codimension-3) component parameterizing surfaces on ![]() ${{\mathbb {P}}}(1,2,9,12)$. This admits a smoothing to
${{\mathbb {P}}}(1,2,9,12)$. This admits a smoothing to ![]() ${{\mathbb {P}}}(1,1,2,4)$ (see § 4.5) and the surfaces appearing on
${{\mathbb {P}}}(1,1,2,4)$ (see § 4.5) and the surfaces appearing on ![]() ${{\mathbb {P}}}(1,2,9,12)$ have an additional
${{\mathbb {P}}}(1,2,9,12)$ have an additional ![]() $\frac {1}{9}(1,2)$ singularity.
$\frac {1}{9}(1,2)$ singularity.
We can also describe some non-normal threefolds appearing using Propositions 4.56 and 4.61. For instance, considering the mutations going from ![]() $(1,1,1,1)$ to
$(1,1,1,1)$ to ![]() $(1,1,2,4)$, from
$(1,1,2,4)$, from ![]() $(1,1,2,4)$ to
$(1,1,2,4)$ to ![]() $(1,4,10,25)$, and from
$(1,4,10,25)$, and from ![]() $(1,1,2,4)$ to
$(1,1,2,4)$ to ![]() $(1,2,9,12)$, we obtain the non-normal threefolds
$(1,2,9,12)$, we obtain the non-normal threefolds ![]() ${{\mathbb {P}}}(1,1,1,2)\cup {{\mathbb {P}}}(1,1,1,2), {{\mathbb {P}}}(1,1,2,5) \cup {{\mathbb {P}}}(1,4,2,5)$, and
${{\mathbb {P}}}(1,1,1,2)\cup {{\mathbb {P}}}(1,1,1,2), {{\mathbb {P}}}(1,1,2,5) \cup {{\mathbb {P}}}(1,4,2,5)$, and ![]() ${{\mathbb {P}}}(1,1,3,4) \cup {{\mathbb {P}}}(1,2,3,4)$.
${{\mathbb {P}}}(1,1,3,4) \cup {{\mathbb {P}}}(1,2,3,4)$.
In fact, we can strengthen the result on non-normal threefolds as follows. Theorem 4.30 implies that any threefold ![]() $X$ appearing in one of these pairs is semi-dlt. In the case of quintic surfaces, it is, in fact, semi-plt (purely log-terminal).
$X$ appearing in one of these pairs is semi-dlt. In the case of quintic surfaces, it is, in fact, semi-plt (purely log-terminal).
Theorem 5.3 The varieties ![]() $X$ occurring in a
$X$ occurring in a ![]() $(\mathbb {P}^{3},5,4)$ H-stable pair have at most two components, so each component
$(\mathbb {P}^{3},5,4)$ H-stable pair have at most two components, so each component ![]() $(X^{\nu }, \Delta )$ of the normalization is plt.
$(X^{\nu }, \Delta )$ of the normalization is plt.
Proof. If ![]() $X$ is not normal and the double locus
$X$ is not normal and the double locus ![]() $\Delta$ on
$\Delta$ on ![]() $X^{\nu }$ has more than one component,
$X^{\nu }$ has more than one component, ![]() $\Delta$ must be connected by [Reference KollárKol92, Theorem 17.4]. In particular, if
$\Delta$ must be connected by [Reference KollárKol92, Theorem 17.4]. In particular, if ![]() $(X^{\nu }, \Delta )$ is not plt, two components
$(X^{\nu }, \Delta )$ is not plt, two components ![]() $\Delta _i$ and
$\Delta _i$ and ![]() $\Delta _j$ meet along a curve [Reference KollárKol13, Theorem 4.16(2)]. Call this curve
$\Delta _j$ meet along a curve [Reference KollárKol13, Theorem 4.16(2)]. Call this curve ![]() $C$. By hypothesis,
$C$. By hypothesis, ![]() $-(K_{X^{\nu }} +\Delta )$ is ample, and writing
$-(K_{X^{\nu }} +\Delta )$ is ample, and writing ![]() $\Delta ' = \Delta \setminus (\Delta _1 + \Delta _2)$, we compute
$\Delta ' = \Delta \setminus (\Delta _1 + \Delta _2)$, we compute ![]() $-(K_{X^{\nu }} + \Delta _1 + \Delta _2 + \Delta ')\cdot C = -2 + \sum (1 - {1}/{m_i}) + \Delta '\cdot C < 0$, where
$-(K_{X^{\nu }} + \Delta _1 + \Delta _2 + \Delta ')\cdot C = -2 + \sum (1 - {1}/{m_i}) + \Delta '\cdot C < 0$, where ![]() $m_i$ is the index of any singularities along
$m_i$ is the index of any singularities along ![]() $C$. If
$C$. If ![]() $\Delta '$ is not empty, then there is at most one such singularity and
$\Delta '$ is not empty, then there is at most one such singularity and ![]() $-(K_{X^{\nu }} + \Delta )\cdot C = -{1}/{m}$ or
$-(K_{X^{\nu }} + \Delta )\cdot C = -{1}/{m}$ or ![]() $-1$, and
$-1$, and ![]() $D \cdot C \in ({1}/{m}) \mathbb {Z}$, so the relationship
$D \cdot C \in ({1}/{m}) \mathbb {Z}$, so the relationship ![]() $dK_X + 4D \sim 0$ implies that
$dK_X + 4D \sim 0$ implies that ![]() $d$ is even. Assume then
$d$ is even. Assume then ![]() $\Delta '$ is empty. If there are no singular points of index
$\Delta '$ is empty. If there are no singular points of index ![]() $m_i >1$ along
$m_i >1$ along ![]() $C$, we also get that
$C$, we also get that ![]() $d$ is even. However, there may be one or two singularities along
$d$ is even. However, there may be one or two singularities along ![]() $C$, in which case
$C$, in which case ![]() $-(K_{X^{\nu }} + \Delta _1 + \Delta _2) \cdot C = -1 - {1}/{m}$ or
$-(K_{X^{\nu }} + \Delta _1 + \Delta _2) \cdot C = -1 - {1}/{m}$ or ![]() $-{1}/{m_1} - {1}/{m_2}$. Note that these do not necessarily violate the condition that
$-{1}/{m_1} - {1}/{m_2}$. Note that these do not necessarily violate the condition that ![]() $dK_X + 4D \sim 0$ (for example, if there is only singular point of index three). Assume that
$dK_X + 4D \sim 0$ (for example, if there is only singular point of index three). Assume that ![]() $dK_X + 4D \sim 0$ and
$dK_X + 4D \sim 0$ and ![]() $d$ is odd. Then, we must have
$d$ is odd. Then, we must have ![]() $m = 3 \mod 4$ in the case of one singular point, or
$m = 3 \mod 4$ in the case of one singular point, or ![]() $m_1+m_2 = 0 \mod 4$.
$m_1+m_2 = 0 \mod 4$.
Consider the first case (one singular point of index ![]() $m$) and now assume
$m$) and now assume ![]() $d = 5$. The second is similar. If
$d = 5$. The second is similar. If ![]() $D$ misses the singular point, then
$D$ misses the singular point, then ![]() $m$ divides
$m$ divides ![]() $d$ because
$d$ because ![]() $dK_X$ is Cartier in a neighborhood of the point, but
$dK_X$ is Cartier in a neighborhood of the point, but ![]() $m = 3 \mod 4$, so this is impossible. If
$m = 3 \mod 4$, so this is impossible. If ![]() $D$ passes through the singular point, the pair
$D$ passes through the singular point, the pair ![]() $(X, \frac {4}{5}D)$ is slc, so
$(X, \frac {4}{5}D)$ is slc, so ![]() $(X^{\nu }, \Delta + D^{\nu })$ is log-canonical and resolving the point
$(X^{\nu }, \Delta + D^{\nu })$ is log-canonical and resolving the point ![]() $\pi : Y \to X^{\nu }$, we find that this is possible only if the curve
$\pi : Y \to X^{\nu }$, we find that this is possible only if the curve ![]() $D|_{\Delta _i}$ passes through the singular point with multiplicity one. Restricting to
$D|_{\Delta _i}$ passes through the singular point with multiplicity one. Restricting to ![]() $\Delta _i$, suppose the singular point is of type
$\Delta _i$, suppose the singular point is of type ![]() $({1}/{m})(1,a)$, and
$({1}/{m})(1,a)$, and ![]() $m = 3 \mod 4$. Using local coordinates
$m = 3 \mod 4$. Using local coordinates ![]() $D|_{\Delta _i} = x^{i}y^{j} + \cdots$ and the relationship
$D|_{\Delta _i} = x^{i}y^{j} + \cdots$ and the relationship ![]() $4D|_{\Delta _i} = -5(K_{\Delta _i} + C)$, we find that
$4D|_{\Delta _i} = -5(K_{\Delta _i} + C)$, we find that ![]() $5 = 1 \mod m$, but
$5 = 1 \mod m$, but ![]() $m = 3 \mod 4$, and this is impossible.
$m = 3 \mod 4$, and this is impossible.
Remark 5.4 For larger degree ![]() $d$, even when
$d$, even when ![]() $d$ is odd, the threefolds need not be semi-plt: there is a degeneration of
$d$ is odd, the threefolds need not be semi-plt: there is a degeneration of ![]() ${{\mathbb {P}}}^{3}$ that is a union of six components, isomorphic to
${{\mathbb {P}}}^{3}$ that is a union of six components, isomorphic to ![]() ${{\mathbb {P}}}(1,1,2,3)$, glued in a cycle such that the double locus in each component is
${{\mathbb {P}}}(1,1,2,3)$, glued in a cycle such that the double locus in each component is ![]() $\Delta _1 + \Delta _2 , \Delta _1 \cong {{\mathbb {P}}}(1,1,3)$ and
$\Delta _1 + \Delta _2 , \Delta _1 \cong {{\mathbb {P}}}(1,1,3)$ and ![]() $\Delta _2 \cong {{\mathbb {P}}}(1,2,3)$. On each component,
$\Delta _2 \cong {{\mathbb {P}}}(1,2,3)$. On each component, ![]() $D \in |\mathcal {O} (d)|$ (and this can occur for odd degree
$D \in |\mathcal {O} (d)|$ (and this can occur for odd degree ![]() $d$; even, for instance,
$d$; even, for instance, ![]() $d = 7$).
$d = 7$).
For general degree, to explicitly describe all threefolds appearing in ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$, we must complete the classification begun in § 4.5. Furthermore, if we denote by
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$, we must complete the classification begun in § 4.5. Furthermore, if we denote by ![]() ${{\mathcal {M}}}_d^{\rm GIT}$ the GIT moduli space of degree
${{\mathcal {M}}}_d^{\rm GIT}$ the GIT moduli space of degree ![]() $d$ surfaces, one expects a rational map
$d$ surfaces, one expects a rational map
although understanding this map would require a better understanding of both ![]() ${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and
${{\mathcal {M}}}_{{(\mathbb {P}^{3,\mathrm {sm}},d,4)}}$ and ![]() ${{\mathcal {M}}}_d^{\rm GIT}$. This will be explored in future work.
${{\mathcal {M}}}_d^{\rm GIT}$. This will be explored in future work.
Acknowledgements
This paper is based on my PhD thesis. I would like to thank my advisor, S. Kovács, for suggesting this problem and for his years of generous guidance, encouragement, and insight. I also benefited from conversations with M. Lieblich, C. Godfrey, S. Mathur, and K. Ascher. I would also like to thank P. Hacking for comments on an earlier version of this paper. I would like to thank J. Kollár for comments on an earlier draft and the crucial ideas for extending the proof of Theorem 1.1 to arbitrary smooth Fano varieties. Finally, I thank the referee for their detailed and careful comments greatly improving the exposition of this paper.