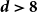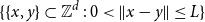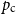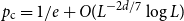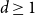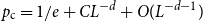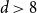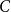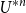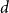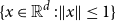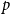1. Introduction and the main result
Given an 
$L\in{\mathbb N}$, we consider spread-out lattice animals 
$A=(V_A,E_A)$, where the vertex set 
$V_A$ is a finite subset of 
$\mathbb{Z}^d$ and any pair of vertices in 
$V_A$ are connected by a path of spread-out edges 
$E_A\subset \{\{x,y\}\;:\;0\lt \|x-y\|\le L\}$; 
$\|\cdot \|$ is an arbitrary fixed norm on 
$\mathbb R^d$. A lattice tree is a lattice animal with no loops. Both models are statistical-mechanical models for branched polymers.
To investigate their statistical properties, we consider the following generating functions. Let
\begin{align} \Lambda =\{x\in \mathbb{Z}^d\;:\;0\lt \|x\|\le L\},&& D(x)=\frac 1{|\Lambda |}\mathbb{1}_{\{x\in \Lambda \}}, \end{align}
where 
$\mathbb{1}_{E}$ is the indicator function of 
$E$, being 1 or 0 depending on whether or not 
$E$ is true. The function 
$D$ will be used as a transition probability of the underlying random walk. Then, we define the weight function for a tree 
$T$ as
\begin{align} W_p(T)=\prod _{\{x,y\}\in E_T}pD(x-y)={\bigg (\frac{p}{|\Lambda |}\bigg )}^{|E_T|}, \end{align}
and similarly for a lattice animal 
$A$ as 
$W_p(A)$. For a finite set 
$X\subset \mathbb{Z}^d$, we denote by 
$\mathcal{T}_X$ (resp., 
$\mathcal{A}_X$) the set of lattice trees 
$T$ with 
$X\subset V_T$ (resp., lattice animals 
$A$ with 
$X\subset V_A$); if 
$X$ consists of a vertex or two, we simply write, e.g., 
$\mathcal{T}_o$ (for 
$X=\{o\}$; see Fig. 1) or 
$\mathcal{T}_{o,x}$ (for 
$X=\{o,x\}$; see Fig. 2). The generating functions we want to investigate are the 1-point and 2-point functions, defined respectively as
\begin{align} g_p=\sum _{T\in \mathcal{T}_o}W_p(T),&& \tau _p(x)=\sum _{T\in \mathcal{T}_{o,x}}W_p(T), \end{align}
for lattice trees, and similarly defined for lattice animals. The susceptibility 
$\chi _p$ is the sum of the 2-point function, defined as
\begin{align} \chi _p=\sum _{x\in \mathbb{Z}^d}\tau _p(x)=\sum _{x\in \mathbb{Z}^d}\sum _{T\in \mathcal{T}_o}\mathbb{1}_{\{x\in V_T\}}\, W_p(T)=\sum _{T\in \mathcal{T}_o}|V_T|\,W_p(T), \end{align}
for lattice trees, and similarly for lattice animals. It has been known (see [Reference Madras and Slade18] and references therein) that there is a model-dependent critical point 
$p_{\textrm{c}}$ such that 
$\chi _p$ is finite if and only if 
$p\lt p_{\textrm{c}}$ and diverges as 
$p\uparrow p_{\textrm{c}}$. The goal of this paper is to reveal the asymptotics of 
$p_{\textrm{c}}$ as 
$L\uparrow \infty$ for both models.
Figure 1. A sample 
$T$ of 
$\mathcal{T}_o$. Removal of all edges 
$\{o,y_j\}\in E_T$ leaves disjoint subtrees 
$R_j$ rooted at 
$y_j$: 
$V_T\setminus \{o\}=\bigcup _jV_{R_j}$ and 
$E_T\setminus \bigcup _j\{\{o,y_j\}\}=\bigcup _jE_{R_j}$.
Figure 2. A sample tree in 
$\mathcal{T}_{o,x}$. Removal of the backbone edges (in blue) yields disjoint subtrees 
$\{R_j\}$, called ribs. In this example, 
$R_1,R_3$ and 
$R_6$ are single-vertex trees.
The best estimate so far on 
$p_{\textrm{c}}$ for the spread-out model was achieved by Penrose [Reference Penrose23]. He investigated the growth constant, which is defined by the 
$n\uparrow \infty$ limit of the 
$n$th root of the number 
$t_n=\frac 1n\sum _{T\in \mathcal{T}_o}\mathbb{1}{\{|V_T|=n\}}$ of 
$n$-vertex unrooted lattice trees. Since 
$\{t_n\}_{n\in{\mathbb N}}$ is a supermultiplicative sequence, i.e., 
$t_{n+m}\ge t_n\,t_m$ (see, e.g., [Reference Klein16]), 
$\lim _{n\uparrow \infty }t_n^{1/n}$ exists and is asymptotically 
$e|\Lambda |+O(|\Lambda |^{5/7}\log |\Lambda |)$ as 
$|\Lambda |\uparrow \infty$ [Reference Penrose23]. Since 
$|E_T|=|V_T|-1$ for each lattice tree, we can rewrite 
$\chi _p$ as
\begin{align} \chi _p\stackrel{\text{(1.4)}}=\sum _{n=1}^\infty n\sum _{T\in \mathcal{T}_o} \mathbb{1}_{\{|V_T|=n\}}\,W_p(T)=\sum _{n=1}^\infty n^2{\bigg (\frac{p}{|\Lambda |}\bigg )}^{n -1}t_n. \end{align}
Therefore, for large 
$|\Lambda |$,
\begin{align} p_{\textrm{c}}=\lim _{n\uparrow \infty }{\bigg (\frac{n^2}{|\Lambda |^{n-1}}\,t_n\bigg )}^{-1/n} =\frac{|\Lambda |}{e|\Lambda |+O(|\Lambda |^{5/7}\log |\Lambda |)}=\frac 1e +O(|\Lambda |^{-2/7}\log |\Lambda |), \end{align}
which is true for all dimensions 
$d\ge 1$. Penrose also claimed in [Reference Penrose23, Section 3.1] that 
$p_{\textrm{c}}$ for lattice animals obeys the same bound, due to the result of Klarner [Reference Klarner15].
A weaker estimate, 
$p_{\textrm{c}}=1/e+o(1)$ as 
$L\uparrow \infty$ for all 
$d$ bigger than the critical dimension 
$d_{\textrm{c}}=8$, was obtained by Miranda and Slade [Reference Miranda and Slade20]. In fact, their main concern was to obtain 
$1/d$ expansions of 
$p_{\textrm{c}}$ for the nearest-neighbor models. In [Reference Miranda19, Reference Miranda and Slade21], they showed that,
\begin{align} p_{\textrm{c}}=\frac 1e+\frac 3{2e}|\Lambda |^{-1}+ \begin{cases} \dfrac{115}{24e}|\Lambda |^{-2}+o(|\Lambda |^{-2})&[\text{lattice trees}],\\[1pc] \bigg (\dfrac{115}{24e}-\dfrac 1{2e^2}\bigg )|\Lambda |^{-2}+o(|\Lambda |^{-2}) &[\text{lattice animals}], \end{cases} \end{align}
as 
$|\Lambda |=2d\uparrow \infty$. The proof is based on the lace expansion for the 2-point function 
$\tau _p(x)$ and an expansion for the 1-point function 
$g_p$ based on inclusion-exclusion. Notice that the model-dependence appears only from the 
$O(|\Lambda |^{-2})$ term. This is due to unit squares that are in 
$g_p$ for lattice animals, but not in 
$g_p$ for lattice trees. The lace expansion has been successful in showing mean-field critical behaviour in high dimensions for various models, including lattice trees and lattice animals for 
$d\gt 8$ (e.g., [Reference Hara, Hofstad and Slade6, Reference Hara and Slade8, Reference Hara and Slade10]). The other models are self-avoiding walk for 
$d\gt 4$ (e.g., [Reference Brydges and Spencer2, Reference Hara, Hofstad and Slade6, Reference Hara and Slade9]), percolation for 
$d\gt 6$ (e.g., [Reference Hara, Hofstad and Slade6, Reference Hara and Slade7]), oriented percolation and the contact process for the spatial dimension 
$d\gt 4$ (e.g., [Reference Nguyen and Yang22, Reference Sakai24]), and the Ising and 
$\varphi ^4$ models for 
$d\gt 4$ (e.g., [Reference Brydges, Helmuth and Holmes1, Reference Sakai25–Reference Sakai27]).
For the nearest-neighbor lattice trees and lattice animals, in particular, Hara and Slade [Reference Hara, Hofstad and Slade6, Reference Hara and Slade8, Reference Hara and Slade10] show mean-field behaviour for both models in dimensions higher than an unspecified number bigger than 
$8$. In contrast, Fitzner and van der Hofstad [Reference Fitzner and van der Hofstad5] prove that 
$d\gt 16$ is enough for lattice trees, and 
$d\gt 17$ for lattice animals to exhibit mean-field behaviour. The proof is based on the so-called non-backtracking lace expansion (NoBLE) that is different from the standard lace expansion by Hara and Slade.
In [Reference Hofstad and Sakai12], van der Hofstad and the second-named author of the current paper applied the lace expansion to the spread-out models [defined by 
$D$ in equation (1.1)] of self-avoiding walk, percolation, oriented percolation and the contact process, and showed that, for all 
$d$ bigger than the respective critical dimension 
$d_{\textrm{c}}$,
\begin{align} p_{\textrm{c}}=1+CL^{-d}+O(L^{-d-1}), \end{align}
as 
$L\uparrow \infty$, where 1 is the mean-field value, and the model-dependent constant 
$C$ has the following random-walk representation:
\begin{align} C= \begin{cases} \displaystyle \sum _{n=2}^\infty U^{*n}(o) &[\text{self-avoiding walk, the contact process}],\\[1pc] \displaystyle \frac 12\sum _{n=2}^\infty U^{*2n}(o)&[\text{oriented percolation}],\\ \displaystyle U^{*2}(o)+\sum _{n=3}^\infty \frac{n+1}2U^{*n}(o)&[\text{percolation}], \end{cases} \end{align}
where 
$U^{*n}$ is the 
$n$-fold convolution in 
${\mathbb R}^d$ of the uniform probability distribution 
$U$ on 
$\{x\in{\mathbb R}^d\;:\;\|x\|\le 1\}$. For example, if 
$\|x\|=\|x\|_\infty \;:\!=\;\max _j|x_j|$, then, for all 
$n\in{\mathbb N}$,
\begin{align} U(x)=\frac{\mathbb{1}_{\{\|x\|_\infty \le 1\}}}{2^d},&& U^{*(n+1)}(x)=\int _{{\mathbb R}^d}U^{*n}(y)\, U(x-y)\, \textrm{d}^dy. \end{align}
These quantities are the spread-out limit of the underlying random walk generated by 
$D$ [Reference Hofstad and Sakai12, Section 4]. For example, for 
$d\gt 4$,
\begin{align} \sum _{n=2}^\infty \frac{n+1}2D^{*n}(o)=L^{-d}\sum _{n=2}^\infty \frac{n+1}2 U^{*n}(o)+O(L^{-d-1}), \end{align}
where we have used the same notation 
$*$ to represent convolutions on 
$\mathbb{Z}^d$ as well. The error term 
$O(L^{-d-1})$ is due to Riemann-sum approximation.
We want to achieve a similar result for lattice trees and lattice animals, i.e., a random-walk representation for the difference between 
$p_{\textrm{c}}$ and its mean-field value 
$1/e$, and see how the model-dependence arises in it. In the rest of the paper, we will show the following:
Theorem 1.1. For both lattice trees and lattice animals with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} p_{\textrm{c}}=\frac 1e+CL^{-d}+O(L^{-d-1}), \end{align}
where the model-dependent constant 
$C$ has the following random-walk representation:
\begin{align} C_{\textrm{LT}}=\sum _{n=2}^\infty \frac{n+1}{2e}U^{*n}(o),&& C_{\textrm{LA}}=C_{\textrm{LT}}-\frac 1{2e^2}\sum _{n=3}^\infty U^{*n}(o), \end{align}
The difference in 
$p_{\textrm{c}}$ already shows up in the first error term of order 
$L^{-d}$ for the spread-out models, while it appears in (1.7) from the second error term of order 
$d^{-2}$ for the nearest-neighbor models, as mentioned earlier. This is due to closed loops of length bigger than 2 in 
$g_p$ for lattice animals. The smallest among such loops for the spread-out model is of length 3 and of order 
$L^{-d}$, while that for the nearest-neighbor model is of length 4 and of order 
$d^{-2}$ (see Lemma 4.1 below). Identifying coefficients of the higher-order terms for the spread-out models may need more work since they are absorbed in the error term 
$O(L^{-d-1})$ in (1.12), which is inherent in Riemann-sum approximation, just as mentioned below (1.11).
The proof of the above theorem is based on the lace expansion for the 2-point function and detailed analysis of the 1-point function, similarly to the previous work by Miranda and Slade [Reference Miranda and Slade21]. The key to our analysis is to introduce a new base point 
$p_1$ defined in (2.1) below, as 
$p_1g_{p_1}=1$. It is to estimate various generating functions in terms of massless random walks. For the spread-out models of self-avoiding walk, percolation, oriented percolation and the contact process, van der Hofstad and Sakai [Reference Hofstad and Sakai12] use the base point 
$p_1=1$, because of the unity of the 
$1$-point function for those models. Since the analysis in terms of the underlying random walks is very simple, we do not have to know in detail the lace expansion; the exception is in Lemma 2.1 below, where we investigate the first lace-expansion coefficient 
$\hat \pi _p^{\scriptscriptstyle (1)}$ to prove 
$p_{\textrm{c}}-p_1=O(L^{-2d})$. However, the basic facts (summarized in Proposition 2.2 below) and a minimum definition about the lace-expansion coefficients should be enough to read the proof, which we hope makes this paper more accessible to wider audience.
Our method can be applied to the nearest-neighbor models as well to identify the coefficient of 
$(2d)^{-1}$, as we can use the same method (i.e., Lemma 2.1 below) to conclude 
$p_{\textrm{c}}-p_1=O(d^{-2})$, but this limits the accuracy our method can achieve. Therefore, to identify the higher-order coefficients, we may need investigate the lace-expansion coefficients at 
$p_c$ more carefully as in Miranda and Slade [Reference Miranda and Slade21].
The rest of the paper is organized as follows. In Section 2, we show that 
$p_{\textrm{c}}$ is close (up to order 
$L^{-2d}$) to 
$p_1$ that satisfies the identity 
$p_1g_{p_1}=1$, which is heavily used in the analysis in Sections 3 and 4. Section 3 is devoted to evaluating 
$g_{p_1}$ for lattice trees. The 1-point function is split into two parts, 
$G$ and 
$H$, which are investigated in Sections 3.1 and 3.2, respectively. Finally, in Section 4, we demonstrate how to evaluate the difference between lattice trees and lattice animals.
2. Results due to the lace expansion
In this section, we approximate 
$p_{\textrm{c}}$ by 
$p_1$ that is defined for both models by the identity
\begin{align} p_1g_{p_1}=1. \end{align}
From now on, we frequently use
\begin{align} \beta =L^{-d}. \end{align}
Lemma 2.1. For both lattice trees and lattice animals with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} 0\lt p_{\textrm{c}}-p_1=O(\beta ^2). \end{align}
The key to the proof is the following collection of the lace-expansion results [Reference Hara, Hofstad and Slade6, Reference Liang17], in which we use
\begin{align} h_p(x)= \begin{cases} 0&[\text{lattice trees}],\\[5pt] \displaystyle (1-\delta _{o,x})\sum _{A\in \mathcal{A}_o}\mathbb{1}_{\{o\Longleftrightarrow x\}}\,W_p(A)\quad &[\text{lattice animals}], \end{cases} \end{align}
where 
$o\Longleftrightarrow x$ means that (
$o=x$ or) there is at least one pair of edge-disjoint paths from 
$o$ to 
$x$ in an animal 
$A$. Let 
$\hat h_p$ denote the sum of 
$h_p(x)$ over 
$x\in \mathbb{Z}^d$:
\begin{align} \hat h_p=\sum _{x\in \mathbb{Z}^d}h_p(x). \end{align}
Proposition 2.2 ([Reference Hara, Hofstad and Slade6, Reference Liang17]). For both lattice trees and lattice animals with 
$d\gt 8$, there is a model-dependent 
$L_0\lt \infty$ such that, for all 
$L\ge L_0$, the following holds for all 
$p\le p_{\textrm{c}}$:
1. The
$1$-point function is bounded away from zero and infinity. In fact,
(2.6)
\begin{align} 1\le g_p\le 4. \end{align}
-
2. There are nonnegative lace-expansion coefficients
$\pi _p^{\scriptscriptstyle (n)}(x)$, $n\in{\mathbb N}$, such that
(2.7)and that, by defining
\begin{align} \exists K\lt \infty,\quad \forall x\in \mathbb{Z}^d,\quad \pi _p^{\scriptscriptstyle (n)}(x)\le \frac{KL^{-6}(K\beta )^{n-1}}{(\|x\|\vee L)^{2d-6}}, \end{align}
$\pi _p(x)=\sum _{n\in{\mathbb N}}(\!-\!1)^n\pi _p^{\scriptscriptstyle (n)}(x)$, the recursion equation
(2.8)holds for all
\begin{align} \tau _p(x)&=g_p\delta _{o,x}+h_p(x)+\pi _p(x)\nonumber \\ &\quad +\sum _{u,v}\Big (g_p\delta _{o,u}+h_p(u)+\pi _p(u)\Big )\,pD(v-u)\, \tau _p(x-v) \end{align}
$x\in \mathbb{Z}^d$.
Consequently, there is a 
$K'\lt \infty$ such that
\begin{align} \forall x\ne o,\quad \tau _{p_{\textrm{c}}}(x)\le \frac{K'L^{-2}}{(\|x\|\vee L)^{d-2}},&& \chi _p\underset{p\uparrow p_{\textrm{c}}}\asymp (p_{\textrm{c}}-p)^{-1/2}, \end{align}
where the latter means 
$\chi _p/(p_{\textrm{c}}-p)^{-1/2}$ is bounded away from 0 and 
$\infty$ as 
$p\uparrow p_{\textrm{c}}$, and
\begin{align} p_{\textrm{c}}=\frac 1{g_{p_{\textrm{c}}}+\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}={\bigg (g_{p_{\textrm{c}}}+\sum _{x\ne o} h_{p_{\textrm{c}}}(x)+\sum _x\pi _{p_{\textrm{c}}}(x)\bigg )}^{-1}. \end{align}
The above results for lattice trees are proven in [Reference Liang17] by following the same line of proof as in [Reference Hara, Hofstad and Slade6] and using the convolution bounds in [Reference Chen and Sakai4, Lemma 3.2] instead of the weaker ones in [Reference Hara, Hofstad and Slade6, Proposition 1.7]. The same strategy applies to lattice animals, and we refrain from showing details.
Consequently, for any 
$p\le p_{\textrm{c}}$,
\begin{align} \hat \pi _p^{\scriptscriptstyle (n)}=\sum _{x\in \mathbb{Z}^d}\pi _p^{\scriptscriptstyle (n)}(x) \stackrel{\text{(2.7)}}\le K(K\beta )^{n-1}\bigg (\sum _{x:\|x\|\le L} L^{-2d}+\sum _{x:\|x\|\gt L}\frac{L^{-6}}{\|x\|^{2d-6}}\bigg )=O(\beta )^n. \end{align}
Moreover, by subadditivity (i.e., forgetting edge-disjointness among paths from 
$o$ to 
$x$),
\begin{align} \hat h_p\le \sum _{x\ne o}\tau _p(x)^2\stackrel{\text{(2.9)}}\le (K'L^{-2})^2\bigg (\sum _{x:\|x\|\le L}L^{2(2-d)}+\sum _{x:\|x\|\gt L}\|x\|^{2(2-d)} \bigg )=O(\beta ). \end{align}
The identity (2.10) is obtained by summing (2.8) over 
$x\in \mathbb{Z}^d$, solving the resulting equation for 
$\chi _p$ and then using the fact that 
$\chi _p$ diverges as 
$p\uparrow p_{\textrm{c}}$. Substituting (2.11)–(2.12) to (2.10) yieldsFootnote 1
\begin{align} p_{\textrm{c}}=\frac 1{g_{p_{\textrm{c}}}}{\bigg (1+\frac{\hat h_{p_{\textrm{c}}}-\hat \pi _{p_{\textrm{c}}}^{\scriptscriptstyle (1)}}{g_{p_{\textrm{c}}}} +O(\beta ^2)\bigg )}^{-1}=\frac 1{g_{p_{\textrm{c}}}}\bigg (1+\frac{\hat \pi _{p_{\textrm{c}}}^{\scriptscriptstyle (1)} -\hat h_{p_{\textrm{c}}}}{g_{p_{\textrm{c}}}}\bigg )+O(\beta ^2), \end{align}
which is the starting point of the analysis.
Proof of Lemma 2.1. First we show 
$p_1\lt p_{\textrm{c}}$. Since 
$pg_p$ is increasing in 
$p$ with 
$p_1g_{p_1}=1$, it suffices to show 
$p_{\textrm{c}} g_{p_{\textrm{c}}}\gt 1$. By (2.6) and (2.14), it then suffices to show that 
$\hat \pi _{p_{\textrm{c}}}^{\scriptscriptstyle (1)}-\hat h_{p_{\textrm{c}}}$ is bounded from below by 
$\beta$ times a positive constant for large 
$L$. Here, and only here, we use the actual definition of the lace-expansion coefficient 
$\hat \pi _p^{\scriptscriptstyle (1)}$ (see, e.g., [Reference Hara and Slade8]). We can easily check that 
$\hat \pi _p^{\scriptscriptstyle (1)}$ for both models is larger than the sum of triangles consisting only of three distinct edges: 
$\hat \pi _p^{\scriptscriptstyle (1)}\ge |\Lambda |(|\Lambda |-1)(p/|\Lambda |)^3$, which is enough for lattice trees because 
$\hat h _p \equiv 0$. For lattice animals, we show below 
$\hat h_p\le \frac 14\hat \pi _p^{\scriptscriptstyle (1)}+O(\beta ^2)$ for 
$p \le p_c$ in high dimensions 
$d\gt 8$. The aforementioned sufficient condition for 
$p_{\textrm{c}} g_{p_{\textrm{c}}}\gt 1$ is now verified.
Next we show 
$p_{\textrm{c}}-p_1=O(\beta ^2)$ for lattice animals by induction. The same induction also works for lattice trees with 
$A=T$ and 
$\hat h_{p_c} \equiv 0$. Let 
$\{\ell _n\}_{n\in{\mathbb N}}$ be the following increasing sequence bounded above by 2:
\begin{align} \ell _1=1,&& \ell _{j+1}=1+\frac{\ell _j}2\qquad [j\in{\mathbb N}]. \end{align}
Since 
$p_c=O(1)$ (see, e.g., (1.6) or [Reference Hara, Hofstad and Slade6, Proposition 2.2]) and 
$p_1g_{p_1}=p_{\textrm{c}}(g_{p_{\textrm{c}}}+\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}})=1$, we have
\begin{align} 0\lt 1-\frac{p_1}{p_{\textrm{c}}}=1-\frac{g_{p_{\textrm{c}}}+\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}} =-\underbrace{\frac{g_{p_{\textrm{c}}}-g_{p_1}}{g_{p_1}}}_{\ge 0}-\frac{\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}}, \end{align}
which is bounded above by 
$-\hat \pi _{p_{\textrm{c}}}/g_{p_1}=O(\beta )$ [due to (2.11)], confirming 
$p_{\textrm{c}}-p_1=O(\beta ^{\ell _1})$.
Now we suppose 
$p_{\textrm{c}}-p_1=O(\beta ^{\ell _j})$. Notice that 
$g_{p_c}-g_{p_1}$ can be rewritten as
\begin{align} g_{p_{\textrm{c}}}-g_{p_1}=\sum _{A\in \mathcal{A}_o}\bigg (1-\Big (\frac{p_1}{p_{\textrm{c}}}\Big )^{|E_A|} \bigg )W_{p_{\textrm{c}}}(A)&=\bigg (1-\frac{p_1}{p_{\textrm{c}}}\bigg )\underbrace{\sum _{A\in \mathcal{A}_o} \sum _{n=0}^{|E_A|-1}\Big (\frac{p_1}{p_{\textrm{c}}}\Big )^nW_{p_{\textrm{c}}}(A)}_{=:F}\nonumber \\ &\!\stackrel{\text{(2.16)}}=\bigg (\!-\!\frac{g_{p_{\textrm{c}}}-g_{p_1}}{g_{p_1}} -\frac{\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}}\bigg )F. \end{align}
Solving this for 
$g_{p_{\textrm{c}}}-g_{p_1}$ yields
\begin{align} g_{p_{\textrm{c}}}-g_{p_1}=-\frac{\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}+F}F, \end{align}
which is bounded above by 
$-\hat \pi _{p_{\textrm{c}}}=O(\beta )$ [due to (2.11)] for both models. By substituting (2.18) to (2.16), we obtain
\begin{align} p_c-p_1=p_c\left (\frac{1}{g_{p_1}}\frac{\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}+F}F-\frac{\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}}\right )&=-p_c\frac{\hat h_{p_{\textrm{c}}}+\hat \pi _{p_{\textrm{c}}}}{g_{p_1}+F}\nonumber \\ &\overset{(2.11)}{=}p_c\frac{\hat \pi _{p_{\textrm{c}}}^{\scriptscriptstyle (1)}-\hat h_{p_{\textrm{c}}}}{g_{p_1}+F}+O(\beta ^2). \end{align}
Recall the definition of 
$F$ in (2.17). Since 
$(p_1/p_{\textrm{c}})^nW_{p_{\textrm{c}}}(A)=(p_{\textrm{c}}/p_1)^{|E_A|-n}W_{p_1}(A)$, which is also true for lattice trees, we have
\begin{align} F=\sum _{A\in \mathcal{A}_o}\sum _{n=1}^{|E_A|}\Big (\frac{p_{\textrm{c}}}{p_1}\Big )^nW_{p_1}(A) \stackrel{p_1\lt p_{\textrm{c}}}\ge \sum _{A\in \mathcal{A}_o}|E_A|W_{p_1}(A)\stackrel{\scriptscriptstyle |V_A| \le 2|E_A|}\ge \frac{\chi _{p_1}}2. \end{align}
By (2.19) and (2.20), we can estimate 
$p_c-p_1$ as
\begin{align} p_c-p_1=p_c\frac{\hat \pi _{p_{\textrm{c}}}^{\scriptscriptstyle (1)}-\hat h_{p_{\textrm{c}}}}{g_{p_1}F^{-1}+1}F^{-1}+O(\beta ^2)&= O(\beta )\chi _p^{-1}+O(\beta ^2)\nonumber \\ &= O(\beta )(p_c-p_1)^{\frac{1}{2}}+O(\beta ^2), \end{align}
where, for the last inequality, we use 
$\chi _{p_1}\asymp (p_{\textrm{c}}-p_1)^{-1/2}$ for both models in dimensions 
$d\gt 8$. Applying the inductive hypothesis 
$p_c-p_1=O(\beta ^{\ell _j})$ to (2.21), we obtain 
$p_c-p_1=O(\beta ^{\ell _{j+1}})$, which completes the induction. Since 
$\lim _{j\uparrow \infty }\ell _j=2$, this proves 
$p_{\textrm{c}}-p_1=O(\beta ^2)$, as required.
Proof of 
$\hat h_p\le \frac 14\hat \pi _p^{\scriptscriptstyle (1)}+O(\beta ^2)$ for lattice animals. First we recall that
\begin{align} \hat h_p&=\sum _{x\ne o}\sum _{A\in \mathcal{A}_o}{\bigg (\frac{p}{|\Lambda |}\bigg )}^{|E_A|} \mathbb{1}_{\{o\Longleftrightarrow x\}}. \end{align}
We split the sum into two depending on whether or not there are distinct vertices 
$y,z\in V_A$ such that 
$o\longleftrightarrow y$, 
$y\longleftrightarrow x$, 
$o\longleftrightarrow z$, 
$z\longleftrightarrow x$ and 
$y\longleftrightarrow z$ occur in 
$A$ edge-disjointly, i.e., those connections occur in distinct sets of 
$E_A$. (We note that, if 
$y=o$, for example, then we should interpret this as 
$o\longleftrightarrow x$, 
$o\Longleftrightarrow z$ and 
$z\longleftrightarrow x$ occurring edge-disjointly.) Intuitively,
Using submultiplicativity and the 
$x$-space bound in (2.9), we can show that the contribution from this case is 
$O(\beta ^2)$. On the other hand, if there are no such vertices 
$y,z\in V_A$, i.e.,
then there are exactly two edge-disjoint connections between 
$o$ and 
$x$, with two pivotal edges from 
$o$, say 
$\{o,u\},\{o,u'\}$, and two from 
$x$, say 
$\{v,x\},\{v',x\}$, one of which may coincide with either 
$\{o,u\}$ or 
$\{o,u'\}$, for the double connection 
$o\Longleftrightarrow x$ in 
$A$. Suppose that there is order among vertices in 
$\Lambda$. If 
$u\in \Lambda$ is earlier than 
$u'\in \Lambda$ in this order, we write 
$u\prec u'$. Let 
$\Lambda (x)=\{v\in V\;:\;v-x\in \Lambda \}$. Then, the contribution to 
$\hat h_p$ from (2.24) is bounded above by (see Fig. 3)
\begin{align} &\sum _{x\ne o}\sum _{\substack{A_1\in \mathcal{A}_o\\ A_2\in \mathcal{A}_x}}W_p(A_1)\,W_p(A_2) \Bigg (\mathbb{1}_{\{x\in \Lambda \}}\frac{p}{|\Lambda |}\sum _{\substack{u\in \Lambda \\ (x\prec u)}}\sum _{\substack{v\in \Lambda (x)\\ (v\ne o)}}{\bigg (\frac{p}{|\Lambda |} \bigg )}^2\sum _{A_3\in \mathcal{A}_{u,v}}W_p(A_3)\nonumber \\ &\quad+\mathbb{1}_{\{x\in \Lambda \}}\frac{p}{|\Lambda |}\sum _{\substack{u\in \Lambda \\ (u\prec x)}} \sum _{\substack{v\in \Lambda (x)\\ (v\ne o)}}{\bigg (\frac{p}{|\Lambda |}\bigg )}^2 \sum _{A_3\in \mathcal{A}_{u,v}}W_p(A_3)\nonumber \\ &\quad+\sum _{\substack{u,u'\in \Lambda \\ (u\prec u')}}\sum _{\substack{v,v'\in \Lambda (x)\\ (v\ne v')}}{\bigg (\frac{p}{|\Lambda |}\bigg )}^4\sum _{\substack{A_3\in \mathcal{A}_{u,v}\\ A_4\in \mathcal{A}_{u',v'}}}W_p(A_3)\,W_p(A_4)\Bigg )\prod _{i\ne j} \mathbb{1}_{\{V_{A_i}\cap V_{A_j}=\varnothing \}}. \end{align}
Since 
$\Lambda$ is symmetric with respect to the underlying lattice symmetry, the first and second terms are the same. Due to the same reason, the third term remains unchanged when the restriction 
$u\prec u'$ is replaced by 
$u'\prec u$. Therefore, (2.25) equals
\begin{align} &\sum _{x\ne o}\sum _{\substack{A_1\in \mathcal{A}_o\\ A_2\in \mathcal{A}_x}}W_p(A_1)\,W_p(A_2) \Bigg (\mathbb{1}_{\{x\in \Lambda \}}\frac{p}{|\Lambda |}\sum _{\substack{u\in \Lambda \\ (u\ne x)}}\sum _{\substack{v\in \Lambda (x)\\ (v\ne o)}}{\bigg (\frac{p}{|\Lambda |} \bigg )}^2\sum _{A_3\in \mathcal{A}_{u,v}}W_p(A_3)\nonumber \\ & \quad +\frac 12\sum _{\substack{u,u'\in \Lambda \\ (u\ne u')}}\sum _{\substack{v,v'\in \Lambda (x)\\ (v\ne v')}}{\bigg (\frac{p}{|\Lambda |}\bigg )}^4\sum _{\substack{A_3\in \mathcal{A}_{u,v}\\ A_4\in \mathcal{A}_{u',v'}}}W_p(A_3)\,W_p(A_4)\Bigg )\prod _{i\ne j} \mathbb{1}_{\{V_{A_i}\cap V_{A_j}=\varnothing \}}. \end{align}
Figure 3. Schematic representations of the three terms in (2.25). The black line segments are pivotal for 
$o\Longleftrightarrow x$ in 
$A$. Removal of those edges results in the animals 
$\{A_j\}_{j=1}^3$ or 
$\{A_j\}_{j=1}^4$ that are mutually avoiding, as indicated by the red arrows. The vertices in 
$\Lambda$ are ordered in an arbitrary way (counter-clockwise in the above 2-dimensional figures).
Figure 4. Schematic representation of 
$\pi _p^{\scriptscriptstyle (1)}(x)$. The sequence of edges 
$\omega _1,\dots,\omega _{|\omega |}$ joined by the animals 
$B_0,\dots,B_{|\omega |}$ form the backbone from 
$o$ to 
$x$ in 
$A$. The terminal animals 
$B_0$ and 
$B_{|\omega |}$ share a vertex [due to 
${\mathbb{1}}_{B_0\cap B_{|\omega |}\ne \varnothing }$ in (2.27)], otherwise those animals are mutually avoiding [due to the product of indicators in (2.27)]. Each animal 
$B_j$ contains a double connection between 
$\overline \omega _j$ and 
$\underline \omega _{j+1}$.
Now we compare (2.26) with 
$\hat \pi _p^{\scriptscriptstyle (1)}$ for lattice animals, which is defined as (see Fig. 4)
\begin{align} \hat \pi _p^{\scriptscriptstyle (1)}&=\sum _x\sum _{\substack{\omega =\{(\underline \omega _i, \overline \omega _i)\}_{i=1}^{|\omega |}\\ (|\omega |\ge 1)}}{\bigg (\frac{p}{|\Lambda |}\bigg )}^{|\omega |}\prod _{j=0}^{|\omega |}\sum _{B_j\in \mathcal{A}_{\overline \omega _j,\underline \omega _{j+1}}}W_p(B_j)\,\mathbb{1}_{\{\overline \omega _j\Longleftrightarrow \underline \omega _{j+1}\text{ in }B_j\}}\nonumber \\ & \quad \times \mathbb{1}_{\{B_0\cap B_{|\omega |}\ne \varnothing \}}\prod _{\substack{0\le k\lt l\le |\omega |\\ ((k,l)\ne (0,|\omega |))}}\mathbb{1}_{\{B_k\cap B_l=\varnothing \}}, \end{align}
where we have abused the notation 
$\overline \omega _0=o$ and 
$\underline \omega _{|\omega |+1}=x$. This can be bounded below by restricting the sum over 
$\omega$ to those satisfying 
$\underline \omega _1=o$ and 
$\overline \omega _{|\omega |}=x$ (so that 
$\mathcal{A}_{\overline \omega _0,\underline \omega _1}=\mathcal{A}_o$ and 
$\mathcal{A}_{\overline \omega _{|\omega |},\,\underline \omega _{|\omega |+1}}=\mathcal{A}_x$) and then by restricting the sum over 
$B_0\in \mathcal{A}_o$ to 
$B_0=\{o\}$ (so that 
$\mathbb{1}_{\{B_0\cap B_{|\omega |}\ne \varnothing \}}=\mathbb{1}_{\{o\in B_{|\omega |}\}}$) or restricting the sum over 
$B_{|\omega |}\in \mathcal{A}_x$ to 
$B_{|\omega |}=\{x\}$ (so that 
$\mathbb{1}_{\{B_0\cap B_{|\omega |}\ne \varnothing \}}=\mathbb{1}_{\{x\in B_0\}}$):
Those two terms are basically the same. Splitting the sum over 
$\omega$ into two depending on whether 
$|\omega |=1$ (so that 
$\omega =\{\omega _1\}$, where 
$\omega _1=(o,x)$) or 
$|\omega |\ge 2$ and then, for the latter, by summing over the animals 
$B_1,\dots,B_{|\omega |-1}$ (to form an animal 
$A_3\in \mathcal{A}_{\overline \omega _1,\,\underline \omega _{|\omega |}}$), we obtain
\begin{align} \hat \pi _p^{\scriptscriptstyle (1)}\ge& 2\sum _{x\ne o}\sum _{B\in \mathcal{A}_{o,x}}W_p(B)\Bigg (\mathbb{1}_{\{(o, x)\notin E_B\}}\mathbb{1}_{\{x\in \Lambda \}}\frac{p}{|\Lambda |}\nonumber \\ &+\sum _{\substack{u\in \Lambda \\ (u\ne x)}}\sum _{\substack{v\in \Lambda (x)\\ (v\ne o)}}{\bigg (\frac{p}{|\Lambda |}\bigg )}^2\sum _{A_3\in \mathcal{A}_{u,v}}W_p(A_3)\, \mathbb{1}_{\{V_B\cap V_{A_3}=\varnothing \}}\Bigg ). \end{align}
We further bound this below by restricting the sum over 
$B\in \mathcal{A}_{o,x}$ to smaller animals 
$B=(V_B,E_B)$ with either
(i)
$V_B=V_{A_1}\cup V_{A_2}$, $E_B=E_{A_1}\cup \{(o,x)\}\cup E_{A_2}$ for some $A_1\in \mathcal{A}_o$, $A_2\in \mathcal{A}_x$ (as in the left and middle figures of Fig. 3), or-
(ii)
$V_B=V_{A_1}\cup V_{A_2}\cup V_{A_4}$, $E_B=E_{A_1}\cup \{(o,u')\}\cup E_{A_4}\cup \{(v',x)\}\cup E_{A_2}$ for some $A_1\in \mathcal{A}_o$, $A_2\in \mathcal{A}_x$, $u'\in \Lambda$, $v'\in \Lambda (x)$, $A_4\in \mathcal{A}_{u',v'}$ (as in the right figure of Fig. 3).
The contribution from (i) to the right-hand side of (2.29) is
\begin{align} 2\sum _{x\ne o}\sum _{\substack{A_1\in \mathcal{A}_o\\ A_2\in \mathcal{A}_x}}W_p(A_1)\,W_p(A_2) \mathbb{1}_{\{x\in \Lambda \}}\frac{p}{|\Lambda |}\sum _{\substack{u\in \Lambda \\ (u\ne x)}} \sum _{\substack{v\in \Lambda (x)\\ (v\ne o)}}{\bigg (\frac{p}{|\Lambda |}\bigg )}^2 \sum _{A_3\in \mathcal{A}_{u,v}}W_p(A_3)\prod _{i\ne j}\mathbb{1}_{\{V_{A_i}\cap V_{A_j}=\varnothing \}}, \end{align}
while the contribution from (ii) is
\begin{align} & 2\sum _{x\ne o}\sum _{\substack{A_1\in \mathcal{A}_o\\ A_2\in \mathcal{A}_x}}W_p(A_1)\,W_p(A_2) \Bigg (\mathbb{1}_{\{x\in \Lambda \}}\frac{p}{|\Lambda |}\sum _{\substack{u\in \Lambda \\ (u\ne x)}}\sum _{\substack{v\in \Lambda (x)\\ (v\ne o)}}{\bigg (\frac{p}{|\Lambda |} \bigg )}^2\sum _{A_3\in \mathcal{A}_{u,v}}W_p(A_3)\nonumber \\ & \quad +\sum _{\substack{u,u'\in \Lambda \\ (u\ne u')}}\sum _{\substack{v,v'\in \Lambda (x)\\ (v\ne v')}}\bigg (\frac{p}{|\Lambda |}\bigg )^4\sum _{\substack{A_3\in \mathcal{A}_{u,v}\\ A_4\in \mathcal{A}_{u',v'}}}W_p(A_3)\,W_p(A_4)\Bigg )\prod _{i\ne j} \mathbb{1}_{\{V_{A_i}\cap V_{A_j}=\varnothing \}}. \end{align}
Notice that the sum of (2.30) and (2.31) is four times as large as (2.26). This completes the proof of 
$\hat h_p\le \frac 14\hat \pi _p^{\scriptscriptstyle (1)}+O(\beta ^2)$.
3. Detailed analysis of the 1-point function for lattice trees
To complete the proof of Theorem 1.1, it remains to investigate 
$p_1=1/g_{p_1}$ (due to (2.1) and Lemma 2.1). In this section, we concentrate our attention to lattice trees and show the following:
Lemma 3.1. For lattice trees with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} g_{p_1}=e\bigg (1-\sum _{n=2}^\infty \frac{n+1}2D^{*n}(o)\bigg ) +O(\beta ^2). \end{align}
Consequently,
\begin{align} p_1=\frac 1e+\sum _{n=2}^\infty \frac{n+1}{2e}D^{*n}(o)+O(\beta ^2). \end{align}
To prove Lemma 3.1, we first rewrite 
$g_{p_1}$ by identifying the connected neighbours 
$Y$ of the origin as
\begin{align} g_{p_1}&=\sum _{T\in \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_T|}\nonumber \\ &=1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\sum _{T\in \mathcal{T}_{Y\cup \{o\}}} \bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_T|}\nonumber \\ &=1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\prod _{\substack{u,v\in Y\\ (u\ne v)}}\mathbb{1}_{\{V_{R_u} \cap V_{R_v}=\varnothing \}}, \end{align}
where, and from now on, 
$\sum _{Y\subset \Lambda }$ is the sum over sets 
$Y$ of distinct vertices of 
$\Lambda$ (we recall that 
$o$ is not included in 
$\Lambda$) and
\begin{align} \prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}(p_1/|\Lambda |)^{|E_{R_y}|} =\sum _{R_{y_1}\in \mathcal{T}_{y_1}\setminus \mathcal{T}_o}(p_1/|\Lambda |)^{|E_{R_{y_1}}|} \cdots \sum _{R_{y_n}\in \mathcal{T}_{y_n}\setminus \mathcal{T}_o}(p_1/|\Lambda |)^{|E_{R_{y_n}}|} \end{align}
for 
$Y=\{y_1,\dots,y_n\}$. By convention, 
$\prod _{u\ne v}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}=\varnothing \}}$ is regarded as 1 when 
$|Y|=1$. Let (see Fig. 5)
\begin{align} g_{p_1}=G-H, \end{align}
where
\begin{align} G&=1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}, \end{align}
\begin{align} H&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 2)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\bigg (1-\prod _{\substack{u,v\in Y\\ (u\ne v)}} \mathbb{1}_{\{V_{R_u}\cap V_{R_v}=\varnothing \}}\bigg ). \end{align}
We investigate those 
$G$ and 
$H$ in Sections 3.1 and 3.2, respectively (cf., Lemmas 3.2 and 3.4 below).
Figure 5. Intuitive explanation of (3.5). The double-headed arrows on the left (
$=g_{p_1}$) represents mutual avoidance among subtrees. In the first term on the right (
$=G$), those subtrees are independently summed over 
$\mathcal{T}_y\setminus \mathcal{T}_o$, 
$y\in Y$, where 
$Y$ is the set of connected neighbours of the origin. In the second term on the right (
$=H$), there is at least one pair of subtrees that share vertices.
3.1 Detailed analysis of $G$
From now on, we frequently use
\begin{align} S_{\ge t}(x)=\sum _{n=t}^\infty D^{*n}(x), \end{align}
where 
$D^{*0}(x)=\delta _{o,x}$ by convention. The following is what we are going to show in this section:
Lemma 3.2. For lattice trees with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} G=e\bigg (1-\frac 12D^{*2}(o)-S_{\ge 2}(o)\bigg )+O(\beta ^2). \end{align}
Proof. Since 
$p_1g_{p_1}=1$, we can rewrite 
$G$ as
\begin{align} G&=1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\Bigg (\underbrace{\sum _{R_y\in \mathcal{T}_y}\bigg ( \frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}}_{g_{p_1}}-\underbrace{\sum _{R_y\in \mathcal{T}_{o,y}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}}_{\tau _{p_1}(y)} \Bigg )\nonumber \\ &=1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac 1{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\bigg (1-\frac{\tau _{p_1}(y)}{g_{p_1}}\bigg ). \end{align}
If we replace 
$\prod _{y\in Y}(1-\tau _{p_1}(y)/g_{p_1})$ by 1, then we obtain
\begin{align} G_0\;:\!=\;1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac 1{|\Lambda |} \bigg )^{|Y|}=\bigg (1+\frac 1{|\Lambda |}\bigg )^{|\Lambda |}. \end{align}
Since 
$k\log (1+1/k)=1-1/(2k)+O(k^{-2})$ as 
$k\uparrow \infty$, and since 
$|\Lambda |^{-1}=D^{*2}(o)$, we obtain
\begin{align} G_0=e\bigg (1-\frac 1{2|\Lambda |}\bigg )+O(|\Lambda |^{-2}) =e\bigg (1-\frac 12D^{*2}(o)\bigg )+O(\beta ^2). \end{align}
Next we consider the remainder, which is
\begin{align} G-G_0&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac 1{|\Lambda |} \bigg )^{|Y|}\Bigg (\prod _{y\in Y}\bigg (1-\frac{\tau _{p_1}(y)}{g_{p_1}}\bigg )-1 \Bigg )\nonumber \\ &=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac 1{|\Lambda |} \bigg )^{|Y|}\sum _{\substack{Z\subset Y\\ (|Z|\ge 1)}}\prod _{y\in Z}\frac{- \tau _{p_1}(y)}{g_{p_1}}. \end{align}
Changing the order of sums yields
\begin{align} G-G_0&=\sum _{\substack{Z\subset \Lambda \\ (|Z|\ge 1)}}\prod _{y\in Z}\frac{- \tau _{p_1}(y)}{g_{p_1}}\bigg (\frac 1{|\Lambda |}\bigg )^{|Z|}\sum _{Z\subset Y \subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^{|Y\setminus Z|}\nonumber \\ &=\sum _{\substack{Z\subset \Lambda \\ (|Z|\ge 1)}}\prod _{y\in Z}\frac{-\tau _{p_1} (y)\,D(y)}{g_{p_1}}\bigg (1+\frac 1{|\Lambda |}\bigg )^{|\Lambda \setminus Z|}\nonumber \\ &=G_1+G_2, \end{align}
where
\begin{align} G_1&=\sum _{\substack{Z\subset \Lambda \\ (|Z|=1)}}\prod _{y\in Z}\frac{-\tau _{p_1} (y)\,D(y)}{g_{p_1}}\bigg (1+\frac 1{|\Lambda |}\bigg )^{|\Lambda \setminus Z|} =\frac{-(\tau _{p_1}*D)(o)}{g_{p_1}}\frac{G_0}{(1+1/|\Lambda |)}, \end{align}
\begin{align} G_2&=\sum _{\substack{Z\subset \Lambda \\ (|Z|\ge 2)}}\prod _{y\in Z}\frac{- \tau _{p_1}(y)\,D(y)}{g_{p_1}}\bigg (1+\frac 1{|\Lambda |}\bigg )^{|\Lambda \setminus Z|}. \end{align}
We have made use of reflection symmetry in (3.14)–(3.16), such as 
$\tau _p(\!-\!y)=\tau _p(y)$ and 
$D(\!-\!y)=D(y)$; we will frequently the symmetry without mentioning each time. To estimate 
$G_1$ and 
$G_2$, we use the following lemma, which will be proven after the proof of Lemma 3.2 is completed.
Lemma 3.3. For any 
$d\gt 2$ and 
$x\ne o$, the lattice tree 2-point function satisfies
\begin{align} 0\le S_{\ge 1}(x)-\frac{\tau _{p_1}(x)}{g_{p_1}}\le \sum _{\substack{y,z\in \mathbb{Z}^d\\ (y\ne z)}}S_{\ge 0}^{*2}(z-y)\,S_{\ge 0}(y)\,S_{\ge 1}(z-y)\,S_{\ge 0}(x-z). \end{align}
Remark. The right-hand side of ( 3.17) is diagrammatically represented by
where an unslashed (resp., slashed) line represents 
$S_{\ge 0}$ (resp., 
$S_{\ge 1}$) and an unlabelled vertex is summed over 
$\mathbb{Z}^d$. Due to translation invariance, we can change the order of terms in ( 3.17) for a given 
$x\ne o$. Then ( 3.18) is also equal to
These diagrammatic representations will be used in the proof of Lemma 3.4 below.
First we estimate 
$G_2$. By the first inequality in (3.17) and the heat-kernel bound (see, e.g., [Reference Chen and Sakai3, (1.6)]):
\begin{align} \|D^{*n}\|_\infty =O(\beta )n^{-d/2}\qquad [n\in{\mathbb N}], \end{align}
we can show
\begin{align} \frac{(\tau _{p_1}*D)(o)}{g_{p_1}}\le \sup _{x\in \Lambda }\frac{\tau _{p_1}(x)}{g_{p_1}}\le \sup _{x\in \Lambda }S_{\ge 1}(x)\le \sum _{n=1}^\infty \|D^{*n}\|_\infty \stackrel{d\gt 2}=O(\beta ). \end{align}
Therefore,
\begin{align} |G_2|&\le G_0\sum _{n=2}^{|\Lambda |}\sum _{\substack{Z\subset \Lambda \\ (|Z|=n)}} \prod _{y\in Z}\frac{\tau _{p_1}(y)\,D(y)}{g_{p_1}}\le G_0\sum _{n=2}^\infty \bigg (\frac{(\tau _{p_1}*D)(o)}{g_{p_1}}\bigg )^n=O(\beta ^2). \end{align}
Next we estimate 
$G_1$ in (3.15). By using (3.17), we have
\begin{align} 0\le S_{\ge 2}(o)-\frac{(\tau _{p_1}*D)(o)}{g_{p_1}}&=\sum _{x \in \mathbb{Z}^d}D(x)\left (S_{\ge 1}(x)-\frac{\tau _{p_1}(x)}{g_{p_1}}\right )\nonumber \\ &\overset{(3.17)}{\le } \sum _{x \in \mathbb{Z}^d}D(x)\sum _{\substack{y,z\in \mathbb{Z}^d\\ (y\ne z)}}S_{\ge 0}^{*2}(z-y)\,S_{\ge 0}(y)\,S_{\ge 1}(z-y)\,S_{\ge 0}(x-z)\nonumber \\ &\le \sum _{\substack{y,z\in \mathbb{Z}^d\\ (y\ne z)}}S_{\ge 0}^{*2}(z-y)\,S_{\ge 0}(y)\, S_{\ge 1}(z-y)\,S_{\ge 1}(z)\nonumber \\ &\le \sup _{w\ne o}S_{\ge 0}^{*2}(w)\, \big (S_{\ge 0}*S_{\ge 1}^{*2}\big )(o). \end{align}
By the heat-kernel bound (3.20), we can estimate each term as
\begin{align} S_{\ge 0}^{*2}(w)&=\sum _{s,t=0}^\infty D^{*(s+t)}(w)\stackrel{w\ne o}\le \sum _{n=1}^\infty (n+1)D^{*n}(w)\stackrel{d\gt 4}=O(\beta ), \end{align}
\begin{align} \big (S_{\ge 0}*S_{\ge 1}^{*2}\big )(o)&=\sum _{s=0}^\infty \sum _{t,u=1}^\infty D^{*(s+t+u)}(o)=\sum _{n=2}^\infty \binom{n}2D^{*n}(o)\stackrel{d\gt 6}=O(\beta ), \end{align}
so that
\begin{align} 0\le S_{\ge 2}(o)-\frac{(\tau _{p_1}*D)(o)}{g_{p_1}}=O(\beta ^2). \end{align}
Therefore, by (3.12),
\begin{align} G_1&=(\!-\!\underbrace{S_{\ge 2}(o)}_{\overset{(3.21)}{=}O(\beta )}+\;O(\beta ^2))\bigg (e-\underbrace{\frac{e}{2}D^{*2}(o)}_{\overset{(3.20)}{=}O(\beta )}+\;O(\beta ^2)\bigg )\nonumber \\ &=-eS_{\ge 2}(o)+O(\beta ^2). \end{align}
Summarizing (3.12), (3.14), (3.22) and (3.27), we complete the proof of Lemma 3.2.
Proof of Lemma 3.3. First we recall
\begin{align} \frac{\tau _{p_1}(x)}{g_{p_1}}=\frac 1{g_{p_1}}\sum _{T\in \mathcal{T}_{o,x}} \bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_T|}. \end{align}
Since a tree 
$T\in \mathcal{T}_{o,x}$ can be divided into a unique path 
$\omega =(\omega _0,\omega _1,\dots,\omega _{|\omega |})$ from 
$\omega _0=o$ to 
$\omega _{|\omega |}=x$, called a backbone, and disjoint subtrees 
$R_j\in \mathcal{T}_{\omega _j}$, called ribs (see Fig. 2), we can rewrite the above expression as
\begin{align} \frac{\tau _{p_1}(x)}{g_{p_1}}=\frac 1{g_{p_1}}\sum _{\omega :o\to x}\bigg ( \frac{p_1}{|\Lambda |}\bigg )^{|\omega |}\prod _{j=0}^{|\omega |}\sum _{R_j\in \mathcal{T}_{\omega _j}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_j}|}\prod _{s\lt t} \mathbb{1}_{\{V_{R_s}\cap V_{R_t}=\varnothing \}}. \end{align}
If we replace the indicator 
$\prod _{s\lt t}\mathbb{1}_{\{V_{R_s}\cap V_{R_t}=\varnothing \}}$ by 1, then we obtain
\begin{align} \frac 1{g_{p_1}}\sum _{\omega :o\to x}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|\omega |} \prod _{j=0}^{|\omega |}\underbrace{\sum _{R_j\in \mathcal{T}_{\omega _j}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_j}|}}_{g_{p_1}}\stackrel{\text{(2.1)}} =\sum _{\omega :o\to x}\bigg (\frac 1{|\Lambda |}\bigg )^{|\omega |} \stackrel{x\ne o}=S_{\ge 1}(x). \end{align}
Next we consider the remainder. Since 
$1-\prod _{j=1}^na_j\le \sum _{j=1}^n(1-a_j)$ as long as 
$0\le a_j\le 1$ for all 
$j$, we can bound the remainder as
\begin{align} S_{\ge 1}(x)-\frac{\tau _{p_1}(x)}{g_{p_1}}&=\frac 1{g_{p_1}} \sum _{\omega :o\to x}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|\omega |}\prod _{j =0}^{|\omega |}\sum _{R_j\in \mathcal{T}_{\omega _j}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_j}|}\bigg (1-\prod _{s\lt t}\mathbb{1}_{\{V_{R_s}\cap V_{R_t}=\varnothing \}}\bigg )\nonumber \\ &\le \frac 1{g_{p_1}}\sum _{\omega :o\to x}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|\omega |}\prod _{j=0}^{|\omega |}\sum _{R_j\in \mathcal{T}_{\omega _j}}\bigg ( \frac{p_1}{|\Lambda |}\bigg )^{|E_{R_j}|}\sum _{s\lt t}\mathbb{1}_{\{V_{R_s}\cap V_{R_t}\ne \varnothing \}}. \end{align}
If 
$V_{R_s}\cap V_{R_t}\ne \varnothing$, then there must be a 
$w\in \mathbb{Z}^d$ that is shared by those two ribs. Therefore, the remainder is further bounded above as
\begin{align} S_{\ge 1}(x)-\frac{\tau _{p_1}(x)}{g_{p_1}} &\le \frac 1{g_{p_1}}\sum _{\omega :o\to x}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|\omega |}\sum _{s\lt t}\underbrace{\prod _{j\ne s,t}\sum _{R_j\in \mathcal{T}_{\omega _j}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_j}|}}_{g_{p_1} ^{|\omega |-1}}\nonumber \\[9pt] & \quad\times \sum _{w\in \mathbb{Z}^d}\underbrace{\sum _{R_s\in \mathcal{T}_{\omega _s,w}} \bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_s}|}}_{\tau _{p_1}(w-\omega _s)}\, \underbrace{\sum _{R_t\in \mathcal{T}_{\omega _t,w}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_t}|}}_{\tau _{p_1}(\omega _t-w)}\nonumber \\[9pt] &=\frac 1{g_{p_1}^2}\sum _{\omega :o\to x}\bigg (\frac 1{|\Lambda |}\bigg )^{|\omega |} \sum _{s\lt t}\sum _{w\in \mathbb{Z}^d}\tau _{p_1}(w-\omega _s)\,\tau _{p_1}(\omega _t-w)\nonumber \\[9pt] &=\sum _{\substack{y,z\in \mathbb{Z}^d\\ (y\ne z)}}\frac{\tau _{p_1}^{*2}(z-y)}{g_{p_1}^2} \sum _{\omega :o\to y\to z\to x}\bigg (\frac 1{|\Lambda |}\bigg )^{|\omega |}\nonumber \\[9pt] &=\sum _{\substack{y,z\in \mathbb{Z}^d\\ (y\ne z)}}\frac{\tau _{p_1}^{*2}(z-y)}{g_{p_1}^2}\, S_{\ge 0}(y)\,S_{\ge 1}(z-y)\,S_{\ge 0}(x-z). \end{align}
The proof of (3.17) is completed by applying (3.29)–(3.30) to 
$(\tau _{p_1}/g_{p_1})^{*2}$ in the above bound.
3.2 Detailed analysis of $H$
To complete the proof of Lemma 3.1, it suffices to show the following:
Lemma 3.4. For lattice trees with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} H=e\sum _{n=3}^\infty \frac{n-1}2D^{*n}(o)+O(\beta ^2). \end{align}
Proof. Recall the definition (3.7) of 
$H$:
\begin{align} H&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 2)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\bigg (1-\prod _{\substack{u,v\in Y\\ (u\ne v)}} \mathbb{1}_{\{V_{R_u}\cap V_{R_v}=\varnothing \}}\bigg ). \end{align}
First we split the indicator 
$1-\prod _{u\ne v}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}=\varnothing \}}$ in (3.7) by introducing order among pairs of distinct vertices in 
$\Lambda$, called bonds. If a bond 
$b$ is earlier than another bond 
$b'$ in that order, we denote it by 
$b\lt b'$. Then we have
\begin{align} &1-\prod _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}=\varnothing \}}\nonumber \\ &\quad=\sum _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\prod _{\substack{\{u',v'\}\subset Y\\ (\{u', v'\}\lt \{u,v\})}}\mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}=\varnothing \}}\nonumber \\ &\quad=\sum _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}-\sum _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\bigg (1-\prod _{\substack{\{u',v'\}\subset Y\\ (\{u',v'\}\lt \{u,v\})}}\mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}=\varnothing \}}\bigg ), \end{align}
where the second sum on the right is zero when 
$|Y|=2$. Let 
$H_1$ be the contribution from the first sum on the right:
\begin{align} H_1=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 2)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\sum _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v} \ne \varnothing \}}. \end{align}
We will later show [after the derivation of (3.33); see (3.54)] that
\begin{align} H_2\;:\!=\;H_1-H=O(\beta ^2). \end{align}
Next we investigate 
$H_1$. Let 
$H'_{1}$ be the contribution from the case of 
$|Y|=2$:
\begin{align} H'_{1}=\sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2 \sum _{\substack{R_u\in \mathcal{T}_u\setminus \mathcal{T}_o \\ R_v\in \mathcal{T}_v\setminus \mathcal{T}_o}}{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^{|E_{R_u}|+|E_{R_v}|}\mathbb{1}_{\{V_{R_u}\cap V_{R_v} \ne \varnothing \}}. \end{align}
By subadditivity, we already know that 
$H'_{1}=O(\beta )$ for 
$d\gt 4$. By changing the order of sums, we can rewrite 
$H_1-H'_{1}$ as
\begin{align} H_1-H'_{1}&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}{\bigg ( \frac{p_1}{|\Lambda |}\bigg )}^{|E_{R_y}|}\sum _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\nonumber \\[5pt] &=\underbrace{\sum _{\{u,v\}\subset \Lambda }{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^2 \sum _{\substack{R_u\in \mathcal{T}_u\setminus \mathcal{T}_o \\R_v\in \mathcal{T}_v\setminus \mathcal{T}_o}}{ \bigg (\frac{p_1}{|\Lambda |}\bigg )}^{|E_{R_u}|+|E_{R_v}|}\mathbb{1}_{\{V_{R_u}\cap V_{R_v} \ne \varnothing \}}}_{H'_{1}}\nonumber \\[5pt] & \quad \times \sum _{\substack{Y'\subset \Lambda \setminus \{u,v\}\\ (|Y'|\ge 1)}}{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^{|Y'|}\prod _{y'\in Y'}\underbrace{\sum _{ R_{y'}\in \mathcal{T}_{y'}\setminus \mathcal{T}_o}{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^{|E_{R_{y'}}|}}_{g_{p_1}-\tau _{p_1}(y')}. \end{align}
Similarly to the proof of Lemma 3.2, we can show that the last line is estimated as
\begin{align} &\sum _{\substack{Y' \subset \Lambda \setminus \{u,v\} \\ (|Y'|\ge 1) }}\bigg ( \frac 1{|\Lambda |}\bigg )^{|Y'|}\prod _{y'\in Y'}\bigg (1-\frac{\tau _{p_1}(y')}{g_{p_1}}\bigg )\nonumber \\ &\quad=\bigg (1+\frac 1{|\Lambda |}\bigg )^{|\Lambda |-2}-1+\sum _{\substack{Y'\subset \Lambda \setminus \{u,v\} \\ (|Y'|\ge 1) }}\bigg (\frac 1{|\Lambda |}\bigg )^{|Y'|} \Bigg (\prod _{y'\in Y'}\bigg (1-\frac{\tau _{p_1}(y')}{g_{p_1}}\bigg )-1\Bigg )\nonumber \\ &\quad=e-1+O(\beta ). \end{align}
Therefore,
\begin{align} H_1-H'_{1}=H'_{1}\big (e-1+O(\beta )\big ), \end{align}
or equivalently
\begin{align} H_1=eH'_{1}+O(\beta ^2). \end{align}
Next we investigate 
$H'_{1}$. To do so, we first rewrite 
$\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}$ in (3.38) by introducing order among vertices in 
$\mathbb{Z}^d$. For a vertex set 
$V$ and an element 
$x\in V$, we denote by 
$V^{\lt x}$ the set of vertices in 
$V$ that are earlier than 
$x$ in that order. By identifying the earliest element 
$x$ among 
$V_{R_u}$ that is also in 
$V_{R_v}$ (so that 
$V^{\lt x}_{R_u}\cap V_{R_v}=\varnothing$), we can rewrite 
$\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}$ as
\begin{align} \mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}&=\sum _{x\in V_{R_u}}\mathbb{1}_{\{x\in V_{R_v}\}}\, \mathbb{1}_{\{V^{\lt x}_{R_u}\cap V_{R_v}=\varnothing \}}\nonumber \\ &=\sum _{x\in \mathbb{Z}^d}\mathbb{1}_{\{x\in V_{R_u}\cap V_{R_v}\}}-\sum _{x\in V_{R_u} \cap V_{R_v}}\Big (1-\mathbb{1}_{\{V^{\lt x}_{R_{u}} \cap V_{R_{v}}= \varnothing \}}\Big ). \end{align}
Let 
${H'_{1}}'$ be the contribution from the first sum in the last line:
\begin{align} {H'_{1}}'&=\sum _{\{u,v\}\subset \Lambda }{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^2\sum _{x \in \mathbb{Z}^d}\sum _{\substack{R_u\in \mathcal{T}_{u,x}\setminus \mathcal{T}_o \\R_v\in \mathcal{T}_{v,x} \setminus \mathcal{T}_o}}{\bigg (\frac{p_1}{|\Lambda |}\bigg )}^{|E_{R_u}|+|E_{R_v}|}\nonumber \\ &=\sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d}{\Big (\tau _{p_1}(u-x)-\tau _{p_1}^{\scriptscriptstyle (3)}(o,u,x)\Big )}{\Big (\tau _{p_1}(v-x) -\tau _{p_1}^{\scriptscriptstyle (3)}(o,v,x)\Big )}\nonumber \\ &\stackrel{\text{(2.1)}}=\sum _{\{u,v\}\subset \Lambda }{\bigg (\frac 1{|\Lambda |}\bigg )}^2\sum _{x\in \mathbb{Z}^d}{\bigg (\frac{\tau _{p_1}(u-x)}{g_{p_1}} -\frac{\tau _{p_1}^{\scriptscriptstyle (3)}(o,u,x)}{g_{p_1}}\bigg )}{\bigg (\frac{\tau _{p_1}(v-x)}{g_{p_1}}-\frac{\tau _{p_1}^{\scriptscriptstyle (3)}(o,v,x)}{g_{p_1}}\bigg )}, \end{align}
where 
$\tau _p^{\scriptscriptstyle (3)}(o,u,x)$ is a 3-point function, defined as
\begin{align} \tau _p^{\scriptscriptstyle (3)}(o,u,x)=\sum _{T\in{\mathcal{T}}_{o,u,x}}W_p(T). \end{align}
We will later show that
\begin{align} {H'_{2}}'\;:\!=\;H_{1}''-H_{1}'=O(\beta ^2). \end{align}
Finally we investigate 
${H'_{1}}'$. The dominant contribution to 
${H'_{1}}'$ comes from the product of 2-point functions:
\begin{align} {H'_{1}}''&\;:\!=\;\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d} \frac{\tau _{p_1}(u-x)}{g_{p_1}}\frac{\tau _{p_1}(v-x)}{g_{p_1}}\nonumber \\ &=2\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\frac{\tau _{p_1} (u-v)}{g_{p_1}}+\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2 \sum _{x\ne u,v}\frac{\tau _{p_1}(u-x)}{g_{p_1}}\frac{\tau _{p_1}(v-x)}{g_{p_1}}, \end{align}
where we have used the identity 
$\tau _p(o)=g_p$. We will later show that the other contribution to 
${H'_{1}}'$ which involves 3-point functions is estimated as
\begin{align} {H'_{2}}''\;:\!=\;{H'_{1}}'-{H'_{1}}''=O(\beta ^2). \end{align}
By Lemma 3.3, the first term in (3.47) is estimated as
where a gap next to the origin in the last diagram represents 
$1/|\Lambda |$. By translation invariance and (3.24)–(3.25), the last term is bounded above by
Similarly, the second term in (3.47) is estimated as
By Lemma 3.3, (3.19) and the translation invariance, the last term of (3.51) is bounded above by
Therefore,
\begin{align} {H'_{1}}''=S_{\ge 3}(o)+\frac 12S_{\ge 2}^{*2}(o)+O(\beta ^2)&=\sum _{n=3}^\infty D^{*n} (o)+\frac 12\sum _{n,m=2}^\infty D^{*(n+m)}(o)+O(\beta ^2)\nonumber \\[5pt] &=\sum _{n=3}^\infty \frac{n-1}2D^{*n}(o)+O(\beta ^2). \end{align}
Summarizing all the above estimates, we arrive at
\begin{align} H\stackrel{\text{(3.37)}}=H_1+O(\beta ^2) \stackrel{\text{(3.42)}}=eH'_{1}+O(\beta ^2) \stackrel{\text{(3.46)}}=e{H'_{1}}'+O(\beta ^2) \stackrel{\text{(3.48)}}=e{H'_{1}}''+O(\beta ^2)\nonumber \\[5pt] \stackrel{\text{(3.53)}}=e\sum _{n=3}^\infty \frac{n-1}2D^{*n}(o) +O(\beta ^2), \end{align}
Proof of (3.37): bounding 
$H_2$. First we recall that 
$H_2$ is the contribution from the second sum on the right of (3.35):
\begin{align} H_2=&\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\sum _{\{u,v\}\subset Y}\mathbb{1}_{\{V_{R_u}\cap V_{R_v} \ne \varnothing \}}\nonumber \\[5pt] &\times \bigg (1-\prod _{\substack{\{u',v'\}\subset Y\\ (\{u',v'\}\lt \{u,v\})}} \mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}=\varnothing \}}\bigg ), \end{align}
which is nonnegative. Since we get an upper bound
\begin{align} 1-\prod _{\substack{\{u',v'\}\subset Y\\ (\{u',v'\}\lt \{u,v\})}} \mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}=\varnothing \}}\le \sum _{\substack{ \{u',v'\} \subset Y\\ (\{u',v'\}\lt \{u,v\})}}\mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}\ne \varnothing \}} \end{align}
in a same manner as (3.35), we can bound 
$H_2$ as
\begin{align} H_2&\le \sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\sum _{\substack{\{u,v\}\subset Y\\ \{u',v'\} \subset Y\\ (\{u',v'\}\lt \{u,v\})}}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\, \mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}\ne \varnothing \}}\nonumber \\ &=\frac{1}{2}\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\sum _{\substack{\{u,v\}\subset Y\\ \{u',v'\} \subset Y\\ (\{u',v'\}\neq \{u,v\})}}\mathbb{1}{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\, \mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}\ne \varnothing \}}. \end{align}
Since 
$\{u,v\}\ne \{u',v'\}$, the union 
$\{u,v\}\cup \{u',v'\}$ consists of either three or four distinct vertices. We denote the contribution from the former by 
$H_{2,3}$, and that from the latter by 
$H_{2,4}$ and then we obtain
\begin{align} H_2\le \frac{1}{2}(H_{2,3}+H_{2,4}). \end{align}
Figure 6. Schematic representation of 
$H_{2,4}$.
First we investigate 
$H_{2,4}$, which is bounded as (see Fig. 6)
\begin{align} H_{2,4}&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 4)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\sum _{\substack{u,v,u',v'\in Y\\ (\text{distinct})}}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}\ne \varnothing \}}\nonumber \\ &=\sum _{\substack{u,v,u',v'\in \Lambda \\ (\text{distinct})}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^4\sum _{\substack{R_u\in \mathcal{T}_u\setminus \mathcal{T}_o\\ R_v\in \mathcal{T}_v\setminus \mathcal{T}_o\\ R_{u'}\in \mathcal{T}_{u'}\setminus \mathcal{T}_o\\ R_{v'}\in \mathcal{T}_{v'}\setminus \mathcal{T}_o}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_u}| +|E_{R_v}|+|E_{R_{u'}}|+|E_{R_{v'}}|}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}} \mathbb{1}_{\{V_{R_{u'}}\cap V_{R_{v'}}\ne \varnothing \}}\nonumber \\ & \quad \times \Bigg (1+\sum _{\substack{Y'\subset \Lambda \setminus \{u,v,u',v'\}\\ (|Y'|\ge 1)}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y'|}\prod _{y\in Y'}\underbrace{ \sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{ R_y}|}}_{g_{p_1}-\tau _{p_1}(y)}\Bigg ). \end{align}
By (2.1) (i.e., 
$p_1g_{p_1}=1$), the last line is equal to
\begin{align} 1+\sum _{\substack{Y'\subset \Lambda \setminus \{u,v,u',v'\}\\ (|Y'|\ge 1)}}\bigg ( \frac 1{|\Lambda |}\bigg )^{|Y'|}=\bigg (1+\frac 1{|\Lambda |}\bigg )^{|\Lambda |-4} =e+O(\beta ). \end{align}
Then, by ignoring the constraint that 
$\{u,v\}$ and 
$\{u',v'\}$ are disjoint pairs and using the trivial inequality 
$\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\le \sum _x\mathbb{1}_{\{x\in V_{R_u}\cap V_{R_v}\}}$ as well as the relation 
$\mathcal{T}_{u,x}\setminus \mathcal{T}_o\subset \mathcal{T}_{u,x}$, 
$H_{2,4}$ is further bounded above as
\begin{align} H_{2,4}&\le \big (e+O(\beta )\big )\Bigg (\sum _{\{u,v\}\subset \Lambda } \bigg (\frac{p_1}{|\Lambda |}\bigg )^2\sum _{\substack{R_u\in \mathcal{T}_u\setminus \mathcal{T}_o\\ R_v\in \mathcal{T}_v\setminus \mathcal{T}_o}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_u}|+|E_{R_v}|}\mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\Bigg )^2\nonumber \\ &\le \big (e+O(\beta )\big )\Bigg (\sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d}\underbrace{\sum _{\substack{R_u\in \mathcal{T}_{u,x}\\ R_v\in \mathcal{T}_{v,x}}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_u}| +|E_{R_v}|}}_{\tau _{p_1}(u-x)\,\tau _{p_1}(v-x)}\Bigg )^2\nonumber \\ &\stackrel{\text{(2.1)}}=\big (e+O(\beta )\big )\Bigg (\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d}\frac{\tau _{p_1}(u-x)}{g_{p_1}}\frac{\tau _{p_1}(v-x)}{g_{p_1}}\Bigg )^2. \end{align}
Finally, by using 
$\tau _{p_1}(u-x)/g_{p_1}\le S_{\ge 1}(u-x)$ for 
$x\ne u$ [cf., the first inequality in (3.17)] and 
$\tau _p(o)=g_p$ for 
$x=u$, we arrive at
\begin{align} H_{2,4}&\le \big (e+O(\beta )\big )\Bigg (\sum _{u,v\in \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2S_{\ge 0}^{*2}(u-v)\Bigg )^2\le \big (e+O(\beta )\big )\,S_{\ge 1}^{*2}(o)^2\,\stackrel{d\gt 4}=O(\beta ^2). \end{align}
Figure 7. Schematic representation of 
$H_{2,3}$.
Next we investigate 
$H_{2,3}$, which is bounded in a similar way to (3.61) as (see Fig. 7)
\begin{align} H_{2,3}&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\prod _{y\in Y}\sum _{R_y\in \mathcal{T}_y\setminus \mathcal{T}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_y}|}\sum _{\substack{u,v,v'\in Y\\ (\text{distinct})}} \mathbb{1}_{\{V_{R_u}\cap V_{R_v}\ne \varnothing \}}\,\mathbb{1}_{\{V_{R_u}\cap V_{R_{v'}}\ne \varnothing \}}\nonumber \\ &\le \big (e+O(\beta )\big )\sum _{\substack{u,v,v'\in \Lambda \\ (\text{distinct})}} \bigg (\frac{p_1}{|\Lambda |}\bigg )^3\sum _{x,x'\in \mathbb{Z}^d}\sum _{ \substack{R_u\in \mathcal{T}_{u,x,x'}\\ R_v\in \mathcal{T}_{v,x}\\ R_{v'}\in \mathcal{T}_{v',x'}}} \bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_u}|+|E_{R_v}|+|E_{R_{v'}}|}\nonumber \\ &=\big (e+O(\beta )\big )g_{p_1}^2\sum _{\substack{u,v,v'\in \Lambda \\ (\text{distinct})}}\bigg (\frac 1{|\Lambda |}\bigg )^3\sum _{x,x'\in \mathbb{Z}^d} \frac{\tau _{p_1}^{\scriptscriptstyle (3)}(u,x,x')}{g_{p_1}^3}\frac{\tau _{p_1}(v-x)}{g_{p_1}} \frac{\tau _{p_1}(v'-x')}{g_{p_1}}. \end{align}
Due to submultiplicativity, we can bound 
$\tau _p^{\scriptscriptstyle (3)}(u,x,x')$ as
\begin{align} \tau _p^{\scriptscriptstyle (3)}(u,x,x')\le \sum _{y\in \mathbb{Z}^d}\tau _p(u-y)\,\tau _p(x-y)\,\tau _p(x'-y). \end{align}
Then, by using 
$\tau _{p_1}(u-x)/g_{p_1}\le S_{\ge 1}(u-x)$ for 
$x\ne u$ and 
$\tau _p(o)=g_p$ for 
$x=u$, we can bound the sum in (3.63) as
\begin{align} &\sum _{\substack{u,v,v'\in \Lambda \\ (\text{distinct})}}\bigg (\frac 1{|\Lambda |}\bigg )^3\sum _{y,x,x'\in \mathbb{Z}^d}\frac{\tau _{p_1}(u-y)}{g_{p_1}} \frac{\tau _{p_1}(x-y)}{g_{p_1}}\frac{\tau _{p_1}(x'-y)}{g_{p_1}}\frac{\tau _{p_1} (v-x)}{g_{p_1}}\frac{\tau _{p_1}(v'-x')}{g_{p_1}}\nonumber \\ &\le \sum _{y,x,x'\in \mathbb{Z}^d}S_{\ge 0}(x-y)\,S_{\ge 0}(x'-y)\underbrace{ \sum _{u,v,v'\in \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^3S_{\ge 0}(u-y)\,S_{\ge 0}(v-x)\,S_{\ge 0}(v'-x')}_{S_{\ge 1}(y)\,S_{\ge 1}(x)\,S_{\ge 1}(x')}\nonumber \\ &=\sum _{y\in \mathbb{Z}^d}(S_{\ge 0}*S_{\ge 1})(y)^2\, S_{\ge 1}(y)\nonumber \\ &\le \|S_{\ge 0}*S_{\ge 1}\|_\infty \,(S_{\ge 0}*S_{\ge 1}^{*2})(o)\stackrel{d\gt 6}= O(\beta ^2). \end{align}
This together with (3.58) and (3.62) implies
\begin{align} H_2\le \frac{1}{2}(H_{2,3}+H_{2,4})=O(\beta ^2), \end{align}
as required.
Figure 8. Schematic representation of the bound on 
${H'_{2}}'$ due to (3.68).
Proof of (3.46): bounding 
${H'_{2}}'$. First we recall that 
${H'_{2}}'$ is the contribution to 
$H'_{1}$ from the second sum on the right of (3.43):
\begin{align} {H'_{2}}'=\sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2\sum _{x \in \mathbb{Z}^d}\sum _{\substack{R_u\in \mathcal{T}_{u,x}\setminus \mathcal{T}_o \\R_v\in \mathcal{T}_{v,x} \setminus \mathcal{T}_o}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_u}|+|E_{R_v}|}\Big (1 -\mathbb{1}_{\{V^{\lt x}_{R_{u}} \cap V_{R_{v}}= \varnothing \}}\Big ). \end{align}
Notice that
\begin{align} 1-\mathbb{1}_{\{V^{\lt x}_{R_{u}} \cap V_{R_v}=\varnothing \}}\le \sum _{x'\in \mathbb{Z}^d\setminus \{x\}} \mathbb{1}_{\{x'\in V_{R_u}\cap V_{R_v}\}}. \end{align}
By the inclusion relation 
$\mathcal{T}_{u,x,x'}\setminus \mathcal{T}_o\subset \mathcal{T}_{u,x,x'}$ and using (3.64), (2.1) and (3.17), we can bound 
${H'_{2}}'$ as (see Fig. 8)
\begin{align} {H'_{2}}'&\le \sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2 \sum _{\substack{x,x'\in \mathbb{Z}^d\\ (x\ne x')}}\underbrace{\sum _{\substack{R_u\in \mathcal{T}_{u,x,x'}\\ R_v\in \mathcal{T}_{v,x,x'}}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{ |E_{R_u}|+|E_{R_v}|}}_{\tau _{p_1}^{\scriptscriptstyle (3)}(u,x,x')\,\tau _{p_1}^{\scriptscriptstyle (3)}(v,x, x')}\nonumber \\ &\le g_{p_1}^4\sum _{\substack{x,x',y,y'\in \mathbb{Z}^d\\ (x\ne x')}}\frac{\tau _{p_1}(y -x)}{g_{p_1}}\frac{\tau _{p_1}(y-x')}{g_{p_1}}\frac{\tau _{p_1}(y'-x)}{g_{p_1}} \frac{\tau _{p_1}(y'-x')}{g_{p_1}}\nonumber \\ & \quad \times \frac 12\sum _{u,v\in \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2 \frac{\tau _{p_1}(u-y)}{g_{p_1}}\frac{\tau _{p_1}(v-y')}{g_{p_1}}\nonumber \\ &\le \frac{g_{p_1}^4}2\sum _{\substack{x,x',y,y'\in \mathbb{Z}^d\\ (x\ne x')}}S_{\ge 0}(y-x)\,S_{\ge 0}(y-x')\,S_{\ge 0}(y'-x)\,S_{\ge 0}(y'-x')\,S_{\ge 1}(y)\,S_{\ge 1} (y'). \end{align}
Shifting the variables by 
$-x'$ and changing the variables 
$x-x',y-x',y'-x'$ to the new ones 
$w,z,z'$, respectively, we can rewrite the above sum as
\begin{align} \sum _{\substack{w,z,z'\in \mathbb{Z}^d\\ (w\ne o)}}S_{\ge 0}(z-w)\,S_{\ge 0}(z)\,S_{\ge 0} (z'-w)\,S_{\ge 0}(z')\underbrace{\sum _{x'\in \mathbb{Z}^d}S_{\ge 1}(z+x')\,S_{\ge 1}(z' +x')}_{S_{\ge 1}^{*2}(z-z')}, \end{align}
which is bounded above by
\begin{align} \|S_{\ge 1}^{*2}\|_\infty \sum _{w\ne o}S_{\ge 0}^{*2}(w)^2 &=\|S_{\ge 1}^{*2}\|_\infty \sum _{w\ne o}\bigg (\sum _{n=1}^\infty (n+1)D^{*n}(w) \bigg )^2\nonumber \\ &\le \|S_{\ge 1}^{*2}\|_\infty \sum _{t=2}^\infty D^{*t}(o)\underbrace{\sum _{n=1}^{t -1}(n+1)(t-n+1)}_{O(t^3)}\, \stackrel{d\gt 8}=O(\beta ^2), \end{align}
as required.
Proof of (3.48): bounding 
${H'_{2}}''$. First we recall that 
${H'_{2}}''$ is the contribution to 
${H'_{1}}'$ which involves 3-point functions [cf., (3.44)]:
\begin{align} {H'_{2}}''&=\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d}\frac{\tau _{p_1}^{\scriptscriptstyle (3)}(o,u,x)}{g_{p_1}}\bigg (\frac{\tau _{p_1}^{\scriptscriptstyle (3)} (o,v,x)}{g_{p_1}}-2\frac{\tau _{p_1}(v-x)}{g_{p_1}}\bigg ). \end{align}
By (2.1), (3.64) and (3.17), we can readily conclude that
\begin{align} |{H'_{2}}''|&\le \frac{g_{p_1}^2}2\sum _{u,v\in \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2 \sum _{x,y\in \mathbb{Z}^d}\frac{\tau _{p_1}(y)}{g_{p_1}}\frac{\tau _{p_1}(y-u)}{g_{p_1}}\frac{\tau _{p_1}(y-x)}{g_{p_1}}\nonumber \\ & \quad\times \bigg (g_{p_1}^2\sum _{z\in \mathbb{Z}^d}\frac{\tau _{p_1}(z)}{g_{p_1}} \frac{\tau _{p_1}(z-v)}{g_{p_1}}\frac{\tau _{p_1}(z-x)}{g_{p_1}} +2\frac{\tau _{p_1}(v-x)}{g_{p_1}}\bigg )\nonumber \\ &\le g_{p_1}^2\sum _{x,y\in \mathbb{Z}^d}S_{\ge 0}(y)\,S_{\ge 1}(y)\,S_{\ge 0}(y-x)\nonumber \\ & \quad\times \bigg (\frac{g_{p_1}^2}2\sum _{z\in \mathbb{Z}^d}S_{\ge 0}(z)\,S_{\ge 1}(z)\, S_{\ge 0}(z-x)+S_{\ge 1}(x)\bigg )\nonumber \\ &=g_{p_1}^2\sum _{y\in \mathbb{Z}^d}S_{\ge 0}(y)\,S_{\ge 1}(y)\bigg (\frac{g_{p_1}^2}2 \sum _{z\in \mathbb{Z}^d}S_{\ge 0}(z)\,S_{\ge 1}(z)\,S_{\ge 0}^{*2}(y-z)+(S_{\ge 0}*S_{\ge 1}) (y)\bigg )\nonumber \\ &\le g_{p_1}^2\underbrace{(S_{\ge 0}*S_{\ge 1})(o)}_{O(\beta )\text{ for }d\gt 4} \bigg (\frac{g_{p_1}^2}2(S_{\ge 0}*S_{\ge 1})(o)\underbrace{\|S_{\ge 0}^{*2} \|_\infty }_{O(1)\text{ for }d\gt 4}+\underbrace{\|S_{\ge 0}*S_{\ge 1}\|_\infty }_{O (\beta )\text{ for }d\gt 4}\bigg )\nonumber \\ &=O(\beta ^2), \end{align}
as required.
4. Difference between lattice trees and lattice animals
Finally we prove Theorem 1.1 for lattice animals. Recall that, by Lemma 2.1, it suffices to investigate 
$p_1=1/g_{p_1}$ [cf., (2.1)]. The following is the key lemma:
Lemma 4.1. For lattice animals with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} g_{p_1}=e\bigg (1-\sum _{n=2}^\infty \frac{n+1}2D^{*n}(o)\bigg ) +\frac 12S_{\ge 3}(o)+O(\beta ^2). \end{align}
Consequently,
\begin{align} p_1=\frac 1e+\sum _{n=2}^\infty \frac{n+1}{2e}D^{*n}(o)-\frac 1{2e^2}S_{\ge 3}(o)+O(\beta ^2). \end{align}
Proof. As a first step, we want a similar decomposition to (3.3) for lattice animals. To do so, we identify the connected neighbours 
$Y$ of the origin, just as done in (3.3). Then, we introduce 
$\Gamma (Y)$, which is the set of all partitions of 
$Y$. For example, if 
$Y=\{1,2,3\}$, then
\begin{align} \Gamma (Y)=\bigg \{\{Y\},\, \big \{\{1,2\},\{3\}\big \},\, \big \{\{1,3\},\{2\}\big \},\, \big \{\{1\},\{2,3\}\big \},\, \big \{\{1\},\{2\},\{3\}\big \}\bigg \}. \end{align}
For a partition 
$\gamma \in \Gamma (Y)$, we denote by 
$|\gamma |$ the number of sets in 
$\gamma$, so that 
$\gamma =\{\gamma _j\}_{j=1}^{|\gamma |}$. We can rewrite 
$g_{p_1}$ as
\begin{align} g_{p_1}&=1+\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 1)}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y|}\sum _{\gamma \in \Gamma (Y)}\,\prod _{j=1}^{|\gamma |}\, \sum _{R_j\in \mathcal{A}_{\gamma _j}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_j}|}\prod _{i\lt j}\mathbb{1}_{\{V_{R_i}\cap V_{R_j}=\varnothing \}}. \end{align}
The contribution from the maximum partition 
$\bar \gamma =\{\{y\}\}_{y\in Y}$ (i.e., 
$|\bar \gamma |=|Y|$) is equal to (3.3) (with 
$\mathcal{T}$ replaced by 
$\mathcal{A}$) and can be decomposed into 
$G$ and 
$H$ as in (3.5) (with 
$R_y$ regarded as animals instead of trees). Let 
$I$ be the contribution from the remaining partitions 
$\gamma \in \Gamma (Y)$ with 
$|\gamma |\lt |Y|$, which is zero for lattice trees:
\begin{align} I&=g_{p_1}-(G-H)\nonumber \\ &=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 2)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\sum _{\substack{\gamma \in \Gamma (Y)\\ (|\gamma |\lt |Y|)}}\prod _{j =1}^{|\gamma |}\sum _{R_j\in \mathcal{A}_{\gamma _j}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_j}|}\prod _{i\lt j}\mathbb{1}_{\{V_{R_i}\cap V_{R_j}=\varnothing \}}. \end{align}
To evaluate 
$G, H$ and 
$I$ for lattice animals, we cannot apply Lemma 3.3, which is a powerful tool for lattice trees to identify the coefficients of 
$\beta$ as well as to estimate the error terms of 
$O(\beta ^2)$. For the latter purpose for lattice animals, we will use the infrared bound (2.9) (and monotonicity in 
$p$, i.e., 
$\tau _{p_1}\le \tau _{p_{\textrm{c}}}$); for the former purpose, we will use the following bounds that correspond to (3.26), (3.49) and (3.51), respectively:
Lemma 4.2. For lattice animals with 
$d\gt 8$ and 
$L\uparrow \infty$,
\begin{align} \bigg |\sum _{u\in \Lambda }\frac 1{|\Lambda |}\frac{\tau _{p_1}(u)}{g_{p_1}} -S_{\ge 2}(o)\bigg |=O(\beta ^2), \end{align}
\begin{align} \bigg |\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2 \frac{\tau _{p_1}(u-v)}{g_{p_1}}-\frac 12S_{\ge 3}(o)\bigg |=O(\beta ^2), \end{align}
\begin{align} \bigg |\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{x\ne u,v} \frac{\tau _{p_1}(u-x)}{g_{p_1}}\frac{\tau _{p_1}(x-v)}{g_{p_1}}-\frac 12S_{\ge 2}^{*2}(o)\bigg |=O(\beta ^2). \end{align}
We will prove Lemma 4.2 after the proof of Lemma 4.1 is completed.
Now we resume the proof of Lemma 4.1 assuming the bounds in Lemma 4.2. First we recall 
$G=G_0+G_1+G_2$ [cf., (3.14)], where 
$G_0$ is independent of the models and estimated as (3.12); 
$G_1$ is defined as (3.15) and here we use (4.6) to show (3.27); 
$G_2$ is defined as (3.16) and obeys the same bound as (3.22). As a result, Lemma 3.2 also holds for lattice animals. Similarly, we can show 
$H=e({H'_{1}}''+{H'_{2}}''-{H'_{2}}'-H_2)+O(\beta ^2)$ [cf., (3.37), (3.42), (3.46) and (3.48)], where 
${H'_{1}}''$ is defined in (3.47) and here we use (4.7)–(4.8) to show (3.53); 
$H_2$ is bounded by 
$H_{2,3}+H_{2,4}$, and 
$H_{2,3}$ and 
$H_{2,4}$ are further bounded as (3.59)–(3.61) and (3.63)–(3.65) (with 
$\mathcal{T}$ replaced by 
$\mathcal{A}$), and here we use the infrared bound (2.9) and the convolution bound on power functions [Reference Chen and Sakai4, Lemma 3.2(i)] to show 
$H_2=O(\beta ^2)$, such as
\begin{align} &\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d} \tau _{p_1}(u-x)\,\tau _{p_1}(v-x)\nonumber \\[5pt] &\le \sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{x\in \mathbb{Z}^d} \frac{O(L^{-2})}{(\|u-x\|\vee L)^{d-2}}\frac{O(L^{-2})}{(\|v-x\|\vee L)^{d-2}} \nonumber \\[5pt] &\le \sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\frac{O(L^{-4})}{(\|u-v\|\vee L)^{d-4}}\, =O(\beta ^2). \end{align}
Similarly we can show that 
${H'_{2}}'$ and 
${H'_{2}}''$ are both 
$O(\beta ^2)$ by using the infrared bound and the convolution bound, instead of bounding 
$\tau _{p_1}/g_{p_1}$ by 
$S_{\ge 0}$ or 
$S_{\ge 1}$, just as done for lattice trees. As a result, Lemma 3.4 also holds for lattice animals.
Figure 9. Schematic representation of the dominant contribution to 
$I'_{1}$.
Next we investigate 
$I$, which is unique for lattice animals. Let 
$I_1$ be the contribution from 
$\gamma \in \Gamma (Y)$ with 
$|\gamma |=|Y|-1$, i.e., consisting of a pair 
$\{u,v\}$ and 
$|Y|-2$ singletons 
$\{y\}_{y\in Y\setminus \{u,v\}}$:
\begin{align} I_1&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 2)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\sum _{\{u,v\}\subset Y}\sum _{R\in \mathcal{A}_{u,v}\setminus \mathcal{A}_o} \bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_R|}\prod _{y\in Y\setminus \{u,v\}} \sum _{R_y\in \mathcal{A}_y\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_y}|}\nonumber \\[5pt] &\quad\times \prod _{y\in Y\setminus \{u,v\}}\mathbb{1}_{\{V_R\cap V_{R_y}=\varnothing \}} \prod _{\substack{y,z\in Y\setminus \{u,v\}\\ (y\ne z)}}\mathbb{1}_{\{V_{R_y}\cap V_{R_z} =\varnothing \}}, \end{align}
where an empty product is regarded as 1. The dominant contribution to 
$I_1$, denoted 
$I'_1$, comes from when the last line is replaced by 1. By the tree-graph inequality (3.64), which is also true for lattice animals due to subadditivity, and then using the infrared bound (2.9), it is estimated as (see Fig. 9)
\begin{align} I'_{1}&\, =\sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2\Big ( \tau _{p_1}(u-v)-\tau _{p_1}^{\scriptscriptstyle (3)}(o,u,v)\Big )\underbrace{\sum _{Y'\subset \Lambda \setminus \{u,v\}}\bigg (\frac 1{|\Lambda |}\bigg )^{|Y'|}\prod _{y\in Y'} \bigg (1-\frac{\tau _{p_1}(y)}{g_{p_1}}\bigg )}_{e+O(\beta )}\nonumber \\ &\, =\, \underbrace{p_1\big (e+O(\beta )\big )}_{1+O(\beta )}\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\bigg (\frac{\tau _{p_1}(u-v)}{g_{p_1}} -\frac{\tau _{p_1}^{\scriptscriptstyle (3)}(o,u,v)}{g_{p_1}}\bigg )\nonumber \\ &\, =\sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\frac{\tau _{p_1}(u-v)}{g_{p_1}}+O(\beta ^2)\nonumber \\ &\stackrel{\text{(4.7)}}=\, \frac 12S_{\ge 3}(o)+O(\beta ^2). \end{align}
On the other hand, by using 
$1-ab\le (1-a)+(1-b)$ for any 
$a,b\in \{0,1\}$, we can bound the difference 
$I'_1-I_1\, (\ge 0)$ as
\begin{align} I'_1-I_1 &\le \sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2\sum _{R\in \mathcal{A}_{u,v}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_R|} \sum _{Y'\subset \Lambda \setminus \{u,v\}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y'|} \prod _{y\in Y'}\sum _{R_y\in \mathcal{A}_y\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_y}|}\nonumber \\ &\quad\times \bigg (1-\prod _{y\in Y'}\mathbb{1}_{\{V_R\cap V_{R_y}=\varnothing \}}+1-\prod _{ \substack{y,z\in Y' \\ (y\ne z)}}\mathbb{1}_{\{V_{R_y}\cap V_{R_z}=\varnothing \}}\bigg )\nonumber \\ &\le \sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^2\sum _{R\in \mathcal{A}_{u,v}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_R|} \sum _{Y'\subset \Lambda \setminus \{u,v\}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y'|} \prod _{y\in Y'}\sum _{R_y\in \mathcal{A}_y\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_y}|}\nonumber \\ &\quad\times \bigg (\sum _{y\in Y'}\mathbb{1}_{\{V_R\cap V_{R_y}\ne \varnothing \}}+\sum _{ \substack{y,z\in Y'\\ (y\ne z)}}\mathbb{1}_{\{V_{R_y}\cap V_{R_z}\ne \varnothing \}}\bigg ). \end{align}
This is 
$O(\beta ^2)$, as the contribution from the former (resp., latter) sum in the last line can be estimated in a similar way to showing 
$H_{2,3}=O(\beta ^2)$ (resp., 
$H_{2,4}=O(\beta ^2)$); see Fig. 10.
Figure 10. Schematic representation of the bound on (4.12).
As a result,
\begin{align} I_1=\frac 12S_{\ge 3}(o)+O(\beta ^2). \end{align}
Finally we estimate the difference 
$I-I_1$:
\begin{align} I-I_1&=\sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|Y|}\sum _{\substack{\gamma \in \Gamma (Y)\\ (|\gamma |\le |Y|-2)}}\prod _{j =1}^{|\gamma |}\sum _{R_j\in \mathcal{A}_{\gamma _j}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_{R_j}|}\prod _{i\lt j}\mathbb{1}_{\{V_{R_i}\cap V_{R_j}=\varnothing \}}. \end{align}
Since 
$|\gamma |\le |Y|-2$, there are two possibilities: (i) there is a set in 
$\gamma$ which includes at least three distinct neighbours of the origin, or (ii) there are at least two disjoint sets in 
$\gamma$ both of which include exactly two distinct neighbours of the origin. Therefore,
\begin{align} I-I_1&\le \sum _{\substack{Y\subset \Lambda \\ (|Y|\ge 3)}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y|}\sum _{\gamma \in \Gamma (Y)}\prod _{j=1}^{|\gamma |} \sum _{R_j\in \mathcal{A}_{\gamma _j}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_j}|}\prod _{i\lt j}\mathbb{1}_{\{V_{R_i}\cap V_{R_j}=\varnothing \}}\nonumber \\ &\quad\times \Big (\mathbb{1}_{\{\exists j,\;|\gamma _j|\ge 3\}}+\mathbb{1}_{\{\exists i\ne j,\; |\gamma _i|=|\gamma _j|=2\}}\Big )\nonumber \\ &=I_3+I_2, \end{align}
where 
$I_3$ and 
$I_2$ are the contributions from 
$\mathbb{1}_{\{\exists j,\;|\gamma _j|\ge 3\}}$ and 
$\mathbb{1}_{\{\exists i\ne j,\;|\gamma _i|=|\gamma _j|=2\}}$, respectively.
For 
$I_2$, we split the set 
$Y$ of neighbours of the origin into 
$U$, 
$V$ and 
$Y'=Y\setminus (U\cup V)$, where 
$U\cap V=\varnothing$ and 
$|U|=|V|=2$. Partially ignoring the avoidance constraint among animals, we can bound 
$I_2$ as
\begin{align} I_2&\le \sum _{\substack{U\subset \Lambda \\ (|U|=2)}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^2\sum _{R\in \mathcal{A}_U\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_R|}\sum _{\substack{V\subset \Lambda \setminus U \\ (|V|=2)}}\bigg ( \frac{p_1}{|\Lambda |}\bigg )^2\sum _{R'\in \mathcal{A}_V\setminus \mathcal{A}_o}\bigg ( \frac{p_1}{|\Lambda |}\bigg )^{|E_{R'}|}\nonumber \\ & \quad \times \sum _{Y'\subset \Lambda \setminus (U\cup V)}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y'|}\sum _{\gamma \in \Gamma (Y')}\prod _{j=1}^{|\gamma |} \sum _{R_j\in \mathcal{A}_{\gamma _j}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_j}|}\prod _{i\lt j}\mathbb{1}_{\{V_{R_i}\cap V_{R_j}=\varnothing \}}. \end{align}
Notice that the second line is almost identical to 
$g_{p_1}$; the only difference is the domain of summation over 
$Y'$, and therefore it is bounded above by 
$g_{p_1}$. Since 
$p_1g_{p_1}=1$, we obtain
\begin{align} I_2\le g_{p_1}\Bigg (\sum _{\{u,v\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |} \bigg )^2\underbrace{\sum _{R\in \mathcal{A}_{u,v}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_R|}}_{\tau _{p_1}(u-v)}\Bigg )^2 \stackrel{\text{(4.7)}}\le p_1\bigg (\frac 12S_{\ge 3}(o) +O(\beta ^2)\bigg )^2=O(\beta ^2). \end{align}
For 
$I_3$, we split the set 
$Y$ into 
$X$ and 
$Y'=Y\setminus X$, where 
$X$ includes at least 3 distinct vertices 
$x,y,z\in \Lambda$. Again, by partially ignoring the avoidance constraint among animals, we can bound 
$I_3$ as
\begin{align} I_3&\le \sum _{\{x,y,z\}\subset \Lambda }\sum _{\substack{X \subset \Lambda \\ (X\ni x,y,z)}}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|X|}\sum _{R \in \mathcal{A}_X\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|E_R|}\nonumber \\ & \quad \times \sum _{Y'\subset \Lambda \setminus X}\bigg (\frac{p_1}{|\Lambda |}\bigg )^{|Y'|}\sum _{\gamma \in \Gamma (Y')}\prod _{j=1}^{|\gamma |} \sum _{R_j\in \mathcal{A}_{\gamma _j}\setminus \mathcal{A}_o}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|E_{R_j}|}\prod _{i\lt j}\mathbb{1}_{\{V_{R_i}\cap V_{R_j}=\varnothing \}}. \end{align}
Notice again that the second line is bounded above by 
$g_{p_1}$. Using the relation 
$\mathcal{A}_X\setminus \mathcal{A}_o\subset \mathcal{A}_{x,y,z}$ and splitting 
$X$ into 
$\{x,y,z\}$ and 
$X'=X\setminus \{x,y,z\}$, we obtain
\begin{align} I_3&\le g_{p_1}\sum _{\{x,y,z\}\subset \Lambda }\bigg ( \frac{p_1}{|\Lambda |}\bigg )^3\underbrace{\sum _{R\in \mathcal{A}_{x,y,z}}\bigg ( \frac{p_1}{|\Lambda |}\bigg )^{|E_R|}}_{\tau _{p_1}^{(3)}(x,y,z)}\, \underbrace{ \sum _{X'\subset \Lambda \setminus \{x,y,z\}}\bigg (\frac{p_1}{|\Lambda |} \bigg )^{|X'|}}_{\le \,(1+p_1/|\Lambda |)^{|\Lambda |}}. \end{align}
By the tree-graph inequality (3.64), we can show that
\begin{align} &\sum _{\{x,y,z\}\subset \Lambda }\bigg (\frac{p_1}{|\Lambda |}\bigg )^3 \tau _{p_1}^{\scriptscriptstyle (3)}(x,y,z)\nonumber \\ &\quad\le \sum _{\{x,y,z\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^3\sum _{w\in \mathbb{Z}^d} \frac{\tau _{p_1}(x-w)}{g_{p_1}}\frac{\tau _{p_1}(y-w)}{g_{p_1}}\frac{\tau _{p_1} (z-w)}{g_{p_1}}\nonumber \\ &\quad=\sum _{\{x,y,z\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^3\bigg (\sum _{w \ne x,y,z}\frac{\tau _{p_1}(x-w)}{g_{p_1}}\frac{\tau _{p_1}(y-w)}{g_{p_1}} \frac{\tau _{p_1}(z-w)}{g_{p_1}}+\frac 3{g_{p_1}}\frac{\tau _{p_1}(x-z)}{g_{p_1}} \frac{\tau _{p_1}(y-z)}{g_{p_1}}\bigg )\nonumber \\ &\quad\le \frac 3{g_{p_1}}\Big (\underbrace{\|D*\tau _{p_1}\|_\infty +\|D\|_\infty }_{O (\beta )\, (\because \text{(2.9)})}\Big )\underbrace{\sum _{\{x,y\} \subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\sum _{w\ne x,y}\frac{\tau _{p_1} (x-w)}{g_{p_1}}\frac{\tau _{p_1}(y-w)}{g_{p_1}}}_{O(\beta )\, (\because \text{(4.8)})}, \end{align}
hence 
$I_3=O(\beta ^2)$. This completes the proof of 
$I=\frac 12S_{\ge 3}(o)+O(\beta ^2)$, hence the proof of Lemma 4.1.
Proof of Lemma 4.2. First we prove (4.6). By the inverse Fourier transform, we have the rewrite
\begin{align} \sum _{u\in \Lambda }\frac 1{|\Lambda |}\frac{\tau _{p_1}(u)}{g_{p_1}}=\bigg (D* \frac{\tau _{p_1}(u)}{g_{p_1}}\bigg )(o)=\int _{[-\pi,\pi ]^d}\hat D(k)\,\frac{\hat \tau _{p_1}(k)}{g_{p_1}}\frac{\textrm{d}^dk}{(2\pi )^d}. \end{align}
Notice that the Fourier transform of the recursion equation (2.8) yields
\begin{align} \hat \tau _p(k) =\frac{g_p+\hat h_p(k)+\hat \pi _p(k)}{1-(g_p+\hat h_p(k)+\hat \pi _p(k))p\hat D(k)}. \end{align}
We use this identity at 
$p_1=1/g_{p_1}$. Let
\begin{align} H(x)=\frac{h_{p_1}(x)+\pi _{p_1}(x)}{g_{p_1}}. \end{align}
Thanks to the symmetry, the Fourier transform 
$\hat H(k)$ is real. Moreover, by (2.11)–(2.12), we can show that, for 
$d\gt 8$ and 
$L\gg 1$, 
$|\hat H(k)|=O(\beta )$ uniformly in 
$k$. Then, we can rewrite 
$\hat \tau _{p_1}(k)/g_{p_1}$ as
\begin{align} \frac{\hat \tau _{p_1}(k)}{g_{p_1}} &=\frac{1+\hat H(k)}{1-(1+\hat H(k))\hat D(k)}\nonumber \\ &=\frac 1{1-\hat D(k)}+\frac{\hat H(k)}{1-\hat D(k)}\underbrace{\frac 1{1-(1+\hat H(k))\hat D(k)}}_{=:\hat F(k)}. \end{align}
Applying this to (4.21) yields the main term 
$S_{\ge 2}(o)$ as
\begin{align} \sum _{u\in \Lambda }\frac 1{|\Lambda |}\frac{\tau _{p_1}(u)}{g_{p_1}} &=\underbrace{\int _{[-\pi,\pi ]^d}\frac{\hat D(k)}{1-\hat D(k)}\frac{\textrm{d}^dk}{(2\pi )^d}}_{\hskip 4pc S_{\ge 1}(o)\, (=S_{\ge 2}(o))}+\int _{[-\pi,\pi ]^d} \frac{\hat D(k)\hat H(k)}{1-\hat D(k)}\hat F(k)\frac{\textrm{d}^dk}{(2\pi )^d}. \end{align}
It remains to show that the second term on the right is 
$O(\beta ^2)$. To do so, we want an effective bound on 
$\hat F(k)$. We will show at the end of the proof that, for 
$d\gt 8$ and 
$L\gg 1$, there is an 
$L$-independent constant 
$C\lt \infty$ such that
\begin{align} 0\lt \hat F(k)\le \frac{C}{1-\hat D(k)}, \end{align}
uniformly in 
$k$. However, this results in a weaker bound than (4.6), because 
$\int \frac{|\hat D(k)|}{(1-\hat D(k))^2} \frac{\textrm{d}^dk}{(2\pi )^d}=O(\beta ^{1/2})$. Instead, we first rewrite 
$\hat F(k)$ as
\begin{align} \hat F(k)=\frac 1{1-\hat D(k)}+\frac{\hat D(k)\hat H(k)}{1-\hat D(k)}\hat F(k). \end{align}
Then, the second term on the right of (4.25) equals
\begin{align} \underbrace{\int _{[-\pi,\pi ]^d}\frac{\hat D(k)\hat H(k)}{(1-\hat D(k))^2} \frac{\textrm{d}^dk}{(2\pi )^d}}_{(D*S_{\ge 0}^{*2}*H)(o)}+\int _{[-\pi,\pi ]^d}\bigg ( \frac{\hat D(k)\hat H(k)}{1-\hat D(k)}\bigg )^2\hat F(k)\frac{\textrm{d}^dk}{(2\pi )^d}. \end{align}
Notice that, due to the identity (4.27), we have 
$\hat D(k)^2$ in the numerator of the second integrand in (4.28). The first term is readily bounded by 
$\|D*S_{\ge 0}^{*2}\|_\infty \hat H(0)=O(\beta ^2)$. For the second term, we use 
$|\hat H(k)|=O(\beta )$ and (4.26) to obtain that
\begin{align} \int _{[-\pi,\pi ]^d}\bigg (\frac{\hat D(k)\hat H(k)}{1-\hat D(k)}\bigg )^2\hat F(k) \frac{\textrm{d}^dk}{(2\pi )^d}&\le O(\beta ^2)\underbrace{\int _{[-\pi,\pi ]^d} \frac{\hat D(k)^2}{(1-\hat D(k))^3}\frac{\textrm{d}^dk}{(2\pi )^d}}_{(D^{*2}*S_{\ge 0}^{*3})(o)}=O(\beta ^3). \end{align}
This completes the proof of (4.6).
We can also prove (4.7)–(4.8) in a similar manner by assuming (4.26). Hence we here prove only (4.7). By the inverse Fourier transform, we can rewrite the sum in (4.7) as
\begin{align} \sum _{\{u,v\}\subset \Lambda }\bigg (\frac 1{|\Lambda |}\bigg )^2\frac{\tau _{p_1} (u-v)}{g_{p_1}}&=\frac 12\left (D^{*2}*\frac{\tau _{p_1}}{g_{p_1}} \right )(o) -\frac 12D^{*2}(o)\nonumber \\ &=\frac 12\int _{[-\pi,\pi ]^d}\hat D(k)^2\frac{\hat \tau _{p_1}(k)}{g_{p_1}} \frac{\textrm{d}^dk}{(2\pi )^d}-\frac 12D^{*2}(o). \end{align}
Then, by the identity (4.24), we can extract the main term 
$\frac 12S_{\ge 3}(o)$ as
\begin{align} \underbrace{\frac 12\int _{[-\pi,\pi ]^d}\frac{\hat D(k)^2}{1-\hat D(k)} \frac{\textrm{d}^dk}{(2\pi )^d}-\frac 12D^{*2}(o)}_{\frac 12S_{\ge 3}(o)}+\,\frac 12 \int _{[-\pi,\pi ]^d}\frac{\hat D(k)^2\hat H(k)}{1-\hat D(k)}\hat F(k) \frac{\textrm{d}^dk}{(2\pi )^d}. \end{align}
Similarly to (4.29), the second term is bounded as
\begin{align} \bigg |\frac 12\int _{[-\pi,\pi ]^d}\frac{\hat D(k)^2\hat H(k)}{1-\hat D(k)}\hat F(k)\frac{\textrm{d}^dk}{(2\pi )^d}\bigg |\stackrel{\text{(4.26)}}\le O(\beta )\underbrace{\int _{[-\pi,\pi ]^d}\frac{\hat D(k)^2}{(1-\hat D(k))^2} \frac{\textrm{d}^dk}{(2\pi )^d}}_{(D^{*2}*S_{\ge 0}^{*2})(o)}=O(\beta ^2), \end{align}
hence the completion of the proof of (4.7).
Finally we prove the inequality (4.26), for 
$\|k\|\ge \frac 1L$ and 
$\|k\|\le \frac 1L$ separately. We begin with the former case. It is known (cf., e.g., [Reference Hofstad and Sakai12]) that our 
$D$ satisfies [Reference van der Hofstad and Slade14, Assumption D]; in particular, there is an 
$L$-independent constant 
$\eta \in (0,1)$ such that
\begin{align} -1+\eta \, \stackrel{\forall k}\le \, \hat D(k)\stackrel{\|k\|\ge \frac 1L}\le 1-\eta . \end{align}
Since 
$|\hat H(k)|=O(\beta )$, we obtain that, for 
$L\gg 1$,
\begin{align} -1+\frac \eta 2\, \stackrel{\forall k}\le \, \big (1+\hat H(k)\big )\hat D(k) \stackrel{\|k\|\ge \frac 1L}\le 1-\frac \eta 2, \end{align}
hence
\begin{align} 0\lt \frac 1{2-\eta/2}\, \stackrel{\forall k}\le \, \hat F(k)\stackrel{\|k\|\ge \frac 1L} \le \frac 2\eta \, \stackrel{\forall k}\le \, \frac 2\eta \frac{2-\eta }{1-\hat D(k)}. \end{align}
It remains to show that 
$\hat F(k)$ is bounded above by a multiple of 
$(1-\hat D(k))^{-1}$ uniformly in 
$\|k\|\le \frac 1L$. We note that
\begin{align} \hat F(k)^{-1}&=1-\big (1+\hat H(0)\big )+\big (1+\hat H(0)\big )\big (1-\hat D(k) \big )+\big (\hat H(0)-\hat H(k)\big )\hat D(k)\nonumber \\ &=-\hat H(0)+\bigg (1+\hat H(0)+\frac{\hat H(0)-\hat H(k)}{1-\hat D(k)}\hat D(k)\bigg )\big (1-\hat D(k)\big ). \end{align}
Since 
$-\hat H(0)$ is bounded below by a positive multiple of 
$\beta$ (as explained in the beginning of the proof of Lemma 2.1), ignoring this term yields a lower bound on 
$\hat F(k)^{-1}$. Moreover, since 
$|k\cdot x|\le \|k\|\|x\|\le 1$ for 
$x\in \Lambda$ and 
$\|k\|\le \frac 1L$, and since 
$1-\cos t\ge \frac 2{\pi ^2}t^2$ for 
$|t|\le 1$, there is a 
$c\gt 0$ such that
\begin{align} 1-\hat D(k)=\sum _{x\in \Lambda }\frac{1-\cos (k\cdot x)}{|\Lambda |}\ge \frac 2{\pi ^2}\sum _{x\in \Lambda }\frac{(k\cdot x)^2}{|\Lambda |}=\frac{2\|k\|^2}{d\pi ^2} \underbrace{\sum _{x\in \Lambda }\frac{\|x\|^2}{|\Lambda |}}_{\ge cL^2}. \end{align}
On the other hand, by 
$1-\cos t\le \frac 12t^2$ for any 
$t$ and using the 
$x$-space bounds (2.7) and (2.12), we have
\begin{align} |\hat H(0)-\hat H(k)|\le \sum _x\frac{(k\cdot x)^2}2|H(x)|\le \frac{\|k\|^2}{2d} \underbrace{\sum _x\|x\|^2|H(x)|}_{O(L^2\beta )}. \end{align}
Therefore, by taking 
$L$ sufficiently large, 
$\hat F(k)^{-1}$ is bounded below by a positive multiple of 
$1-\hat D(k)$, uniformly in 
$\|k\|\le \frac 1L$. Combined with (4.35), this completes the proof of the inequality (4.26), hence the completion of the proof of Lemma 4.2.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Number 18K03406. We are grateful to Yinshuang Liang for working together in the early stage of this project. We would also like to thank Gordon Slade for comments to an earlier version of this paper. We are grateful to the two anonymous referees for thorough reviewing and many valuable suggestions to the previous version of the manuscript.
