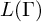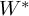1 Introduction
In [Reference Murray and von NeumannMvN43], Murray and von Neumann associated in a natural way a von Neumann algebra, denoted by
![]() $L(\Gamma )$
, to every countable discrete group
$L(\Gamma )$
, to every countable discrete group
![]() $\Gamma $
. Precisely,
$\Gamma $
. Precisely,
![]() $L(\Gamma )$
is defined as the weak operator closure of the complex group algebra
$L(\Gamma )$
is defined as the weak operator closure of the complex group algebra
![]() $\mathbb C[\Gamma ]$
acting by left convolution on the Hilbert space
$\mathbb C[\Gamma ]$
acting by left convolution on the Hilbert space
![]() $\ell ^2(\Gamma )$
of square-summable functions on
$\ell ^2(\Gamma )$
of square-summable functions on
![]() $\Gamma $
. The classification of group von Neumann algebras has since been a central theme in operator algebras, driven by the following fundamental question: What aspects of the group
$\Gamma $
. The classification of group von Neumann algebras has since been a central theme in operator algebras, driven by the following fundamental question: What aspects of the group
![]() $\Gamma $
are remembered by
$\Gamma $
are remembered by
![]() $L(\Gamma )$
? This is a challenging problem, as von Neumann algebras tend to forget a lot of the information about the groups from which they were constructed. An excellent illustration of this is Connes’ theorem, which asserts that II
$L(\Gamma )$
? This is a challenging problem, as von Neumann algebras tend to forget a lot of the information about the groups from which they were constructed. An excellent illustration of this is Connes’ theorem, which asserts that II
![]() $_1$
factors arising from amenable groups are isomorphic to the hyperfinite II
$_1$
factors arising from amenable groups are isomorphic to the hyperfinite II
![]() $_1$
factor [Reference ConnesCo76]. Hence, group von Neumann algebras of infinite conjucacy classes (icc) amenable groups have no memory of the algebraic structure of the underlying group. In sharp contrast, the nonamenable case is far more complex. The emergence of Popa’s deformation/rigidity theory [Reference PopaPo06] has led to the discovery of groups with certain canonical algebraic properties, which are completely retained by their von Neumann algebra. We highlight here only a few of these developments and refer the reader to the surveys [Reference PopaPo06, Reference VaesVa10b, Reference IoanaIo12, Reference IoanaIo17] for a more complete account in this direction. Popa’s strong rigidity theorem [Reference PopaPo03, Reference PopaPo04] asserts that wreath product groups
$_1$
factor [Reference ConnesCo76]. Hence, group von Neumann algebras of infinite conjucacy classes (icc) amenable groups have no memory of the algebraic structure of the underlying group. In sharp contrast, the nonamenable case is far more complex. The emergence of Popa’s deformation/rigidity theory [Reference PopaPo06] has led to the discovery of groups with certain canonical algebraic properties, which are completely retained by their von Neumann algebra. We highlight here only a few of these developments and refer the reader to the surveys [Reference PopaPo06, Reference VaesVa10b, Reference IoanaIo12, Reference IoanaIo17] for a more complete account in this direction. Popa’s strong rigidity theorem [Reference PopaPo03, Reference PopaPo04] asserts that wreath product groups
![]() $\mathbb Z/2\mathbb Z\wr \Gamma $
, where
$\mathbb Z/2\mathbb Z\wr \Gamma $
, where
![]() $\Gamma $
is an icc property (T) group, are completely recognizable from the category of all von Neumann algebras arising from arbitrary wreath product groups with Abelian base and icc acting group. Several years later Ioana, Popa and Vaes discovered in [Reference Ioana, Popa and VaesIPV10] the first examples of W
$\Gamma $
is an icc property (T) group, are completely recognizable from the category of all von Neumann algebras arising from arbitrary wreath product groups with Abelian base and icc acting group. Several years later Ioana, Popa and Vaes discovered in [Reference Ioana, Popa and VaesIPV10] the first examples of W
![]() $^*$
-superrigid groups, that is, groups that can be entirely reconstructed from their von Neumann algebras. Several additional classes of examples were unveiled subsequently [Reference Berbec and VaesBV12, Reference BerbecBe14, Reference Chifan and IoanaCI17, Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference Chifan, Diaz-Arias and DrimbeCD-AD21, Reference Chifan, Ioana, Osin and SunCIOS21]. In this paper, we study superrigidity aspects of von Neumann algebras of graph product groups [Reference GreenGr90]. These groups are natural generalizations of right-angled Artin and Coxeter groups and play an important role in several subareas of topology and group theory. These groups display a rich structure and have been investigated intensively over the last two decades using deep methods in geometric group theory. In this direction, several landmark results have been discovered (see [Reference Haglund and WiseHW08, Reference Antolín and MinasyanAM10, Reference WiseWi11, Reference Minasyan and OsinMO13, Reference AgolAg13]). More recently, certain classes of graph product groups, including many right-angled Artin groups, have been studied through the lens of measured group theory and led to strong rigidity results in the orbit equivalence setting [Reference Horbez and HuangHH20, Reference Horbez and HuangHH21].
$^*$
-superrigid groups, that is, groups that can be entirely reconstructed from their von Neumann algebras. Several additional classes of examples were unveiled subsequently [Reference Berbec and VaesBV12, Reference BerbecBe14, Reference Chifan and IoanaCI17, Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference Chifan, Diaz-Arias and DrimbeCD-AD21, Reference Chifan, Ioana, Osin and SunCIOS21]. In this paper, we study superrigidity aspects of von Neumann algebras of graph product groups [Reference GreenGr90]. These groups are natural generalizations of right-angled Artin and Coxeter groups and play an important role in several subareas of topology and group theory. These groups display a rich structure and have been investigated intensively over the last two decades using deep methods in geometric group theory. In this direction, several landmark results have been discovered (see [Reference Haglund and WiseHW08, Reference Antolín and MinasyanAM10, Reference WiseWi11, Reference Minasyan and OsinMO13, Reference AgolAg13]). More recently, certain classes of graph product groups, including many right-angled Artin groups, have been studied through the lens of measured group theory and led to strong rigidity results in the orbit equivalence setting [Reference Horbez and HuangHH20, Reference Horbez and HuangHH21].
Graph product groups have also been considered in the analytic framework of von Neumann algebras [Reference Caspers and FimaCF14, Reference CaspersCa16, Reference Chifan, de Santiago and SucpikarnonCdSS17, Reference Ding and Kunnawalkam ElayavalliDK-E21, Reference Chifan and Kunnawalkam-ElyavalliCK-E21, Reference Chifan, Davis and DrimbeCDD22], where various structural and rigidity results of von Neumann algebras of graph product groups have been obtained. In [Reference Chifan, Davis and DrimbeCDD22], we further developed some of Popa’s powerful deformation/rigidity theoretic methods [Reference PopaPo06] which enabled us to completely describe the structure of all
![]() $\ast $
-isomorphisms between von Neumann algebras arising from the fairly large class of graph product groups associated with flower-shaped graphs (see class
$\ast $
-isomorphisms between von Neumann algebras arising from the fairly large class of graph product groups associated with flower-shaped graphs (see class
![]() $\mathrm {CC}_1$
in Definition 1.1 below) and vertex groups which are property (T) wreath-like product groups introduced in [Reference Chifan, Ioana, Osin and SunCIOS21]. In essence, our result can be viewed as a von Neumann algebraic counterpart of the group theoretic result of Genevois-Martin [Reference Genevois and MartinGM19].
$\mathrm {CC}_1$
in Definition 1.1 below) and vertex groups which are property (T) wreath-like product groups introduced in [Reference Chifan, Ioana, Osin and SunCIOS21]. In essence, our result can be viewed as a von Neumann algebraic counterpart of the group theoretic result of Genevois-Martin [Reference Genevois and MartinGM19].
This paper continues the study initiated in [Reference Chifan, Davis and DrimbeCDD22], the main goal being to establish strong rigidity results for the aforementioned graph product groups. For example, we show that any graph product group associated with an asymmetric
![]() $\mathrm {CC}_1$
graph and vertex groups that are property (T) wreath-like product groups is completely recognizable from the category of all von Neumann algebras arising from an arbitrary nontrivial graph product group with infinite vertex groups (see Theorem C). Along the way, we also extend the main W
$\mathrm {CC}_1$
graph and vertex groups that are property (T) wreath-like product groups is completely recognizable from the category of all von Neumann algebras arising from an arbitrary nontrivial graph product group with infinite vertex groups (see Theorem C). Along the way, we also extend the main W
![]() $^*$
-superrigidity result from [Reference Chifan, Ioana, Osin and SunCIOS21] to direct product groups, consequently obtaining new examples of groups satisfying Connes rigidity conjecture (see Corollary B).
$^*$
-superrigidity result from [Reference Chifan, Ioana, Osin and SunCIOS21] to direct product groups, consequently obtaining new examples of groups satisfying Connes rigidity conjecture (see Corollary B).
1.1 Statements of the main results
Before stating our results, we recall the construction of graph product groups [Reference GreenGr90]. Let
![]() $\mathscr {G}=(\mathscr V,\mathscr E)$
be a finite graph without loops or multiple edges. The graph product group
$\mathscr {G}=(\mathscr V,\mathscr E)$
be a finite graph without loops or multiple edges. The graph product group
![]() $\Gamma ={\mathscr {G}}\{\Gamma _v\}$
of a given family of vertex groups
$\Gamma ={\mathscr {G}}\{\Gamma _v\}$
of a given family of vertex groups
![]() $\{\Gamma _v\}_{v\in \mathscr V}$
is the quotient of the free product
$\{\Gamma _v\}_{v\in \mathscr V}$
is the quotient of the free product
![]() $\ast _{v\in \mathscr V} \Gamma _v$
by the relations
$\ast _{v\in \mathscr V} \Gamma _v$
by the relations
![]() $[\Gamma _u,\Gamma _v]=1$
, whenever
$[\Gamma _u,\Gamma _v]=1$
, whenever
![]() $(u,v)\in \mathscr E$
. Note that graph products can be seen as groups that ‘interpolate’ between the direct product
$(u,v)\in \mathscr E$
. Note that graph products can be seen as groups that ‘interpolate’ between the direct product
![]() $\times _{v\in \mathscr V} \Gamma _v$
(when
$\times _{v\in \mathscr V} \Gamma _v$
(when
![]() $\mathscr {G}$
is complete) and the free product
$\mathscr {G}$
is complete) and the free product
![]() $\ast _{v\in \mathscr V} \Gamma _v$
(when
$\ast _{v\in \mathscr V} \Gamma _v$
(when
![]() $\mathscr {G}$
has no edges). For any subgraph
$\mathscr {G}$
has no edges). For any subgraph
![]() $\mathscr {H}= (\mathscr U,\mathscr F)$
of
$\mathscr {H}= (\mathscr U,\mathscr F)$
of
![]() $\mathscr {G}$
, we denote by
$\mathscr {G}$
, we denote by
![]() $\Gamma _{\mathscr {H}}$
the subgroup generated by
$\Gamma _{\mathscr {H}}$
the subgroup generated by
![]() $\langle \Gamma _u \,:\,u\in \mathscr U\rangle $
, and we call it the full subgroup of
$\langle \Gamma _u \,:\,u\in \mathscr U\rangle $
, and we call it the full subgroup of
![]() $\mathscr {G}\{\Gamma _v\}$
corresponding to
$\mathscr {G}\{\Gamma _v\}$
corresponding to
![]() $\mathscr {H}$
. A clique
$\mathscr {H}$
. A clique
![]() $\mathscr {C}$
of
$\mathscr {C}$
of
![]() $\mathscr {G}$
is a maximal, complete subgraph of
$\mathscr {G}$
is a maximal, complete subgraph of
![]() $\mathscr {G}$
. The set of cliques of
$\mathscr {G}$
. The set of cliques of
![]() $\mathscr {G}$
will be denoted by
$\mathscr {G}$
will be denoted by
![]() $\mathrm {cliq}(\mathscr {G})$
. The full subgroups
$\mathrm {cliq}(\mathscr {G})$
. The full subgroups
![]() $\Gamma _{\mathscr {C}}$
for
$\Gamma _{\mathscr {C}}$
for
![]() $\mathscr {C}\in \mathrm {cliq}(\mathscr {G})$
are called the clique subgroups of
$\mathscr {C}\in \mathrm {cliq}(\mathscr {G})$
are called the clique subgroups of
![]() $\mathscr {G}\{\Gamma _v\}$
.
$\mathscr {G}\{\Gamma _v\}$
.
We are now ready to recall the class of graphs
![]() $\mathrm {CC}_1$
that was introduced in [Reference Chifan, Davis and DrimbeCDD22] and which is used for our main results.
$\mathrm {CC}_1$
that was introduced in [Reference Chifan, Davis and DrimbeCDD22] and which is used for our main results.
Definition 1.1. A graph
![]() $\mathscr {G}$
is called a simple cycle of cliques
$\mathscr {G}$
is called a simple cycle of cliques
![]() $(\mathrm {CC}_1)$
if there is an enumeration of its clique set
$(\mathrm {CC}_1)$
if there is an enumeration of its clique set
![]() $ \mathrm {cliq}(\mathscr {G})= \{\mathscr {C}_1, ..., \mathscr {C}_n\} $
with
$ \mathrm {cliq}(\mathscr {G})= \{\mathscr {C}_1, ..., \mathscr {C}_n\} $
with
![]() $n\geq 4$
, such that the subgraphs
$n\geq 4$
, such that the subgraphs
![]() $\mathscr {C}_{i,j} :=\mathscr {C}_i \cap \mathscr {C}_j$
satisfy:
$\mathscr {C}_{i,j} :=\mathscr {C}_i \cap \mathscr {C}_j$
satisfy:
 $$ \begin{align*} &\mathscr{C}_{i,j}=\begin{cases} \emptyset, \text{ if } \hat i-\hat j\in \mathbb Z_{n} \setminus \{ \hat 1, \widehat {n-1}\}\\ \neq \emptyset, \text{ if } \hat i-\hat j\in \{\hat 1, \widehat {n-1}\} \end{cases} \text{ and }\\ &\mathscr{C}^{\mathrm{int}}_i:=\mathscr{C}_i \setminus \left(\mathscr{C}_{i-1,i} \cup \mathscr{C}_{i,i+1}\right) \neq \emptyset\text{, for all }1\leq k\leq n, \text{ with conventions } 0=n \text{ and } n+1=1. \end{align*} $$
$$ \begin{align*} &\mathscr{C}_{i,j}=\begin{cases} \emptyset, \text{ if } \hat i-\hat j\in \mathbb Z_{n} \setminus \{ \hat 1, \widehat {n-1}\}\\ \neq \emptyset, \text{ if } \hat i-\hat j\in \{\hat 1, \widehat {n-1}\} \end{cases} \text{ and }\\ &\mathscr{C}^{\mathrm{int}}_i:=\mathscr{C}_i \setminus \left(\mathscr{C}_{i-1,i} \cup \mathscr{C}_{i,i+1}\right) \neq \emptyset\text{, for all }1\leq k\leq n, \text{ with conventions } 0=n \text{ and } n+1=1. \end{align*} $$
Note, this automatically implies the cardinality
![]() $|\mathscr {C}_i |\geq 3$
for all i. Also, such an enumeration
$|\mathscr {C}_i |\geq 3$
for all i. Also, such an enumeration
![]() $ \mathrm {cliq}(\mathscr {G})= \{\mathscr {C}_1,..., \mathscr {C}_n\} $
is called a consecutive clique’s enumeration.
$ \mathrm {cliq}(\mathscr {G})= \{\mathscr {C}_1,..., \mathscr {C}_n\} $
is called a consecutive clique’s enumeration.
Example 1.2. A basic example of such a graph is any simple, length n, cycle of triangles
![]() $\mathscr F_n=(\mathscr V_n,\mathscr E_n)$
, which essentially looks like a flower-shaped graph with n petals:
$\mathscr F_n=(\mathscr V_n,\mathscr E_n)$
, which essentially looks like a flower-shaped graph with n petals:
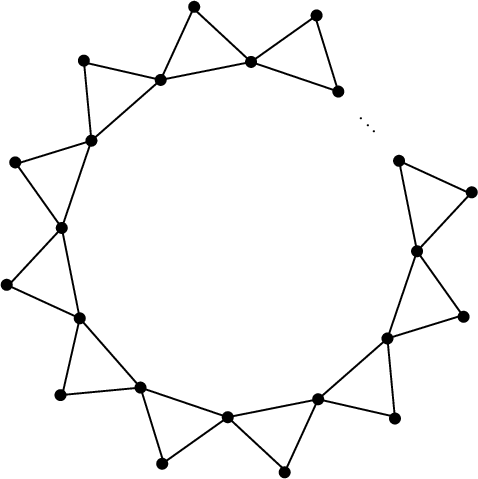
In fact, any graph from
![]() $\mathrm {CC}_1$
is a two-level clustered graph that is a specific retraction of
$\mathrm {CC}_1$
is a two-level clustered graph that is a specific retraction of
![]() $\mathscr F_n$
; for more details, the reader may consult [Reference Chifan, Davis and DrimbeCDD22, Section 2].
$\mathscr F_n$
; for more details, the reader may consult [Reference Chifan, Davis and DrimbeCDD22, Section 2].
In this paper, we investigate various superrigidity aspects for group von Neumann algebras of the aforementioned graph product groups. Since the underlying groups are essentially built-up from collections of large clique groups that are just direct product groups, it is natural to first tackle the superrigidity question for these types of groups. One could think of this as being the degenerate case. In this direction, we were able to establish a product rigidity result for property (T) wreath-like product groups in the same spirit with [Reference Chifan, de Santiago and SinclairCdSS15, Theorem A] or the more recent results [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference DrimbeDr20]. Specifically, we have the following:
Theorem A. For every
![]() $1\leq k\leq n$
, let
$1\leq k\leq n$
, let
![]() $\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
$\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
![]() $A_k$
is Abelian,
$A_k$
is Abelian,
![]() $B_k$
is an icc subgroup of a hyperbolic group,
$B_k$
is an icc subgroup of a hyperbolic group,
![]() $B_k \curvearrowright I_k$
has amenable stabilizers and denote
$B_k \curvearrowright I_k$
has amenable stabilizers and denote
![]() $\Gamma = \Gamma _1\times \dots \times \Gamma _n$
.
$\Gamma = \Gamma _1\times \dots \times \Gamma _n$
.
Assume that
![]() $t>0$
is a scalar and
$t>0$
is a scalar and
![]() $\Lambda $
is an arbitrary group satisfying
$\Lambda $
is an arbitrary group satisfying
![]() ${\mathcal M}={\mathcal L}(\Gamma )^t={\mathcal L}(\Lambda )$
.
${\mathcal M}={\mathcal L}(\Gamma )^t={\mathcal L}(\Lambda )$
.
Then one can find a direct product decomposition
![]() $\Lambda = \Lambda _1\times \dots \times \Lambda _n$
, some scalars
$\Lambda = \Lambda _1\times \dots \times \Lambda _n$
, some scalars
![]() $t_1,\dots ,t_n>0$
with
$t_1,\dots ,t_n>0$
with
![]() $t_1\cdots t_n=t$
and a unitary
$t_1\cdots t_n=t$
and a unitary
![]() $u\in {\mathcal M}$
satisfying
$u\in {\mathcal M}$
satisfying
![]() ${\mathcal L}(\Gamma _{i})^{t_i}=u{\mathcal L}(\Lambda _i) u^*$
, for any
${\mathcal L}(\Gamma _{i})^{t_i}=u{\mathcal L}(\Lambda _i) u^*$
, for any
![]() $1\leq i \leq n.$
$1\leq i \leq n.$
This theorem in conjunction with the W
![]() $^*$
-superrigidity result from [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 9.9] immediately yields that essentially all finite direct products of property (T) wreath-like product groups covered by the prior theorem are completely recognizable from their von Neumann algebras. Before we introduce the result, we recall the notion of group-like
$^*$
-superrigidity result from [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 9.9] immediately yields that essentially all finite direct products of property (T) wreath-like product groups covered by the prior theorem are completely recognizable from their von Neumann algebras. Before we introduce the result, we recall the notion of group-like
![]() $*$
-isomorphism between von Neumann algebras. Let
$*$
-isomorphism between von Neumann algebras. Let
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Lambda $
be countable groups. Let
$\Lambda $
be countable groups. Let
![]() $\eta :\Gamma \rightarrow \mathbb T$
be a multiplicative character and
$\eta :\Gamma \rightarrow \mathbb T$
be a multiplicative character and
![]() $\delta : \Gamma \rightarrow \Lambda $
a group isomorphism. Consider the group von Neumann algebras
$\delta : \Gamma \rightarrow \Lambda $
a group isomorphism. Consider the group von Neumann algebras
![]() ${\mathcal L}(\Gamma )$
, and
${\mathcal L}(\Gamma )$
, and
![]() ${\mathcal L}(\Lambda )$
and denote by
${\mathcal L}(\Lambda )$
and denote by
![]() $\{u_g \,:\, g\in \Gamma \}$
and
$\{u_g \,:\, g\in \Gamma \}$
and
![]() $\{v_\lambda \,:\, \lambda \in \Lambda \}$
their corresponding canonical group unitaries. Then the map
$\{v_\lambda \,:\, \lambda \in \Lambda \}$
their corresponding canonical group unitaries. Then the map
![]() $\Gamma \ni u_g\rightarrow \eta (g)v_{\delta (g)}\in \Lambda $
canonically extends to a
$\Gamma \ni u_g\rightarrow \eta (g)v_{\delta (g)}\in \Lambda $
canonically extends to a
![]() $\ast $
-isomorphism denoted by
$\ast $
-isomorphism denoted by
![]() $\Psi _{\eta ,\delta }: {\mathcal L}(\Gamma )\rightarrow {\mathcal L}(\Lambda )$
.
$\Psi _{\eta ,\delta }: {\mathcal L}(\Gamma )\rightarrow {\mathcal L}(\Lambda )$
.
Corollary B. For every
![]() $1\leq k\leq n$
, let
$1\leq k\leq n$
, let
![]() $\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
$\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
![]() $A_k$
is Abelian,
$A_k$
is Abelian,
![]() $B_k$
is an icc subgroup of a hyperbolic group,
$B_k$
is an icc subgroup of a hyperbolic group,
![]() $B_k \curvearrowright I_k$
has amenable stabilizers and the set
$B_k \curvearrowright I_k$
has amenable stabilizers and the set
![]() $\{i\in I \; | \; g\cdot i\neq i\}$
is infinite for any
$\{i\in I \; | \; g\cdot i\neq i\}$
is infinite for any
![]() $g\in B_k\setminus \{1\}$
. Denote
$g\in B_k\setminus \{1\}$
. Denote
![]() $\Gamma = \Gamma _1\times \dots \times \Gamma _n$
.
$\Gamma = \Gamma _1\times \dots \times \Gamma _n$
.
Let
![]() $t>0$
be any scalar,
$t>0$
be any scalar,
![]() $\Lambda $
be an arbitrary group and
$\Lambda $
be an arbitrary group and
![]() $\theta : {\mathcal L}(\Gamma )^t\rightarrow {\mathcal L}(\Lambda )$
be any
$\theta : {\mathcal L}(\Gamma )^t\rightarrow {\mathcal L}(\Lambda )$
be any
![]() $\ast $
-isomorphism.
$\ast $
-isomorphism.
Then
![]() $t=1$
, and one can find a character
$t=1$
, and one can find a character
![]() $\eta :\Gamma \to \mathbb T$
, a group isomorphism
$\eta :\Gamma \to \mathbb T$
, a group isomorphism
![]() $\delta :\Gamma \to \Lambda $
and a unitary
$\delta :\Gamma \to \Lambda $
and a unitary
![]() $u\in {\mathcal L}(\Lambda )$
satisfying
$u\in {\mathcal L}(\Lambda )$
satisfying
![]() $\theta =\mathrm {ad}(u)\circ \Psi _{\eta ,\delta }$
.
$\theta =\mathrm {ad}(u)\circ \Psi _{\eta ,\delta }$
.
We mention in passing that since property (T) passes to (finite) direct products of groups, Corollary B provides new examples of property (T) groups which satisfy Popa’s strengthening of Connes rigidity conjecture [Reference ConnesCo82, Reference PopaPo06]. In particular, the result also shows that these property (T) factors have trivial fundamental group and also verify Jones’s outer automorphism problem [Reference Jones, Arnold, Atiyah, Lax and MazurJo00], providing additional examples to recent similar results [Reference Chifan, Das, Houdayer and KhanCDHK20, Reference Chifan, Ioana, Osin and SunCIOS21, Reference Chifan, Ioana, Osin and SunCIOS23].
To tackle the problem of reconstructing the above graph product groups
![]() $\Gamma $
from their factors
$\Gamma $
from their factors
![]() ${\mathcal L}(\Gamma )$
, we develop new aspects of a more conceptual principle from [Reference Chifan and IoanaCI17, Reference Chifan, Diaz-Arias and DrimbeCD-AD20] called peripheral reconstruction
${\mathcal L}(\Gamma )$
, we develop new aspects of a more conceptual principle from [Reference Chifan and IoanaCI17, Reference Chifan, Diaz-Arias and DrimbeCD-AD20] called peripheral reconstruction
![]() $W^*$
-method; this consists of exploiting the natural tension that occurs between ‘a peripheral structure’ and a ‘direct product structure’ in the group. In our specific situation, this means that if
$W^*$
-method; this consists of exploiting the natural tension that occurs between ‘a peripheral structure’ and a ‘direct product structure’ in the group. In our specific situation, this means that if
![]() $\Lambda $
is any group, such that
$\Lambda $
is any group, such that
![]() $\mathcal L(\Gamma )=\mathcal L(\Lambda )$
, then the main strategy is to first identify in
$\mathcal L(\Gamma )=\mathcal L(\Lambda )$
, then the main strategy is to first identify in
![]() $\Lambda $
collections of subgroups that play the same role as the ‘peripheral structure’ of
$\Lambda $
collections of subgroups that play the same role as the ‘peripheral structure’ of
![]() $\Gamma $
given by its full subgroups associated to the cliques in the underlying graph.
$\Gamma $
given by its full subgroups associated to the cliques in the underlying graph.
In this direction, using an approach combining the comultiplication map [Reference IoanaIo10, Reference Ioana, Popa and VaesIPV10, Reference Popa and VaesPV11], the ultrapower methods from [Reference IoanaIo11] (see also [Reference Drimbe, Hoff and IoanaDHI16, Reference Chifan, de Santiago and SinclairCdSS15, Reference Krogager and VaesKV15]), a method for reconstructing malnormal groups from [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference Chifan and IoanaCI17] and Corollary B, we are able to show that the clique subgroups of our graph product groups are, in fact, completely recognizable under the W
![]() $^*$
-equivalence. For the precise statement, the reader may consult Theorem 7.1. While this result does not show complete reconstruction of these graph products from the category of all group von Neumann algebras, it can be used effectively to show these groups are recognizable from the von Neumann algebras associated with an extensive family of groups—all nontrivial graph products with infinite vertex groups.
$^*$
-equivalence. For the precise statement, the reader may consult Theorem 7.1. While this result does not show complete reconstruction of these graph products from the category of all group von Neumann algebras, it can be used effectively to show these groups are recognizable from the von Neumann algebras associated with an extensive family of groups—all nontrivial graph products with infinite vertex groups.
Theorem C. Let
![]() $\mathscr {G}\in \mathrm {CC}_1$
, let
$\mathscr {G}\in \mathrm {CC}_1$
, let
![]() $\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1, \ldots , \mathscr {C}_n\}$
be its consecutive cliques enumeration and assume that
$\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1, \ldots , \mathscr {C}_n\}$
be its consecutive cliques enumeration and assume that
![]() $|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
$|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group where all vertex groups
$\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group where all vertex groups
![]() $\Gamma _v$
are property (T) wreath-like product groups
$\Gamma _v$
are property (T) wreath-like product groups
![]() $\Gamma _v\in \mathcal W\mathcal R(A_v,B_v)$
with
$\Gamma _v\in \mathcal W\mathcal R(A_v,B_v)$
with
![]() $A_v$
Abelian and
$A_v$
Abelian and
![]() $B_v$
an icc subgroup of a hyperbolic group.
$B_v$
an icc subgroup of a hyperbolic group.
Then, for any nontrivial graph product group
![]() $\Lambda $
with infinite vertex groups satisfying
$\Lambda $
with infinite vertex groups satisfying
![]() ${\mathcal L}(\Gamma )\cong {\mathcal L}(\Lambda )$
, we have
${\mathcal L}(\Gamma )\cong {\mathcal L}(\Lambda )$
, we have
![]() $\Gamma \cong \Lambda $
.
$\Gamma \cong \Lambda $
.
In fact, we have obtained a more precise version of the above result (see Theorem 7.6). Not only can we derive an isomorphism of the underlying groups, but we can, in fact, completely describe all isomorphisms between
![]() ${\mathcal L}(\Gamma )$
and
${\mathcal L}(\Gamma )$
and
![]() ${\mathcal L}(\Lambda )$
. Namely, they appear as compositions between the canonical group-like isomorphisms
${\mathcal L}(\Lambda )$
. Namely, they appear as compositions between the canonical group-like isomorphisms
![]() $\Psi _{\eta , \delta }$
induced by a group isomorphism
$\Psi _{\eta , \delta }$
induced by a group isomorphism
![]() $\delta :\Gamma \to \Lambda $
, a character
$\delta :\Gamma \to \Lambda $
, a character
![]() $\eta :\Gamma \to \mathbb T$
and the local automorphisms of graph product group von Neumann algebras introduced in [Reference Chifan, Davis and DrimbeCDD22] (see also Section 2.3).
$\eta :\Gamma \to \mathbb T$
and the local automorphisms of graph product group von Neumann algebras introduced in [Reference Chifan, Davis and DrimbeCDD22] (see also Section 2.3).
The result yields new applications towards rigidity in the
![]() $C^*$
-algebraic framework. Since these graph product groups have trivial amenable radical (see [Reference Chifan, Davis and DrimbeCDD22, Lemma 4.3]) using [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO14, Theorem 1.3], it follows that their reduced C
$C^*$
-algebraic framework. Since these graph product groups have trivial amenable radical (see [Reference Chifan, Davis and DrimbeCDD22, Lemma 4.3]) using [Reference Breuillard, Kalantar, Kennedy and OzawaBKKO14, Theorem 1.3], it follows that their reduced C
![]() $^*$
-algebras have unique trace. Therefore, the conclusion of Theorem C still holds true for reduced group
$^*$
-algebras have unique trace. Therefore, the conclusion of Theorem C still holds true for reduced group
![]() $C^*$
-algebras. Moreover, if one assumes, in addition, these groups are torsion free, then the previous theorem actually yields a formally stronger reconstruction statement allowing us to drop the hypothesis assumption that the vertex groups of the target
$C^*$
-algebras. Moreover, if one assumes, in addition, these groups are torsion free, then the previous theorem actually yields a formally stronger reconstruction statement allowing us to drop the hypothesis assumption that the vertex groups of the target
![]() $\Lambda $
are infinite.
$\Lambda $
are infinite.
Corollary D. Let
![]() $\mathscr {G}\in \mathrm {CC}_1$
, let
$\mathscr {G}\in \mathrm {CC}_1$
, let
![]() $\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1,\ldots , \mathscr {C}_n\}$
be a consecutive clique’s enumeration and assume that
$\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1,\ldots , \mathscr {C}_n\}$
be a consecutive clique’s enumeration and assume that
![]() $|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
$|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group where all vertex groups
$\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group where all vertex groups
![]() $\Gamma _v$
are torsion free, property (T) wreath-like product groups
$\Gamma _v$
are torsion free, property (T) wreath-like product groups
![]() $\Gamma _v\in \mathcal W\mathcal R(A_v,B_v)$
with
$\Gamma _v\in \mathcal W\mathcal R(A_v,B_v)$
with
![]() $A_v$
Abelian and
$A_v$
Abelian and
![]() $B_v$
an icc subgroup of a hyperbolic group.
$B_v$
an icc subgroup of a hyperbolic group.
Then, for any nontrivial graph product group
![]() $\Lambda $
satisfying
$\Lambda $
satisfying
![]() $C^*_r(\Gamma )\cong C^*_r(\Lambda )$
, we have
$C^*_r(\Gamma )\cong C^*_r(\Lambda )$
, we have
![]() $\Gamma \cong \Lambda $
.
$\Gamma \cong \Lambda $
.
To see this, just notice that the graph product groups
![]() $\Gamma $
covered by this corollary are torsion free and also satisfy the Baum-Connes conjecture (see Proposition 2.2, [Reference Oyono-OyonoO-O01b, Theorem 7.7] and [Reference Mineyev and YuMY02, Theorem 20]). Hence, their reduced
$\Gamma $
covered by this corollary are torsion free and also satisfy the Baum-Connes conjecture (see Proposition 2.2, [Reference Oyono-OyonoO-O01b, Theorem 7.7] and [Reference Mineyev and YuMY02, Theorem 20]). Hence, their reduced
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $C^*_r(\Gamma )$
are projectionless and so are
$C^*_r(\Gamma )$
are projectionless and so are
![]() $C^*_r(\Lambda )$
. This further entails that
$C^*_r(\Lambda )$
. This further entails that
![]() $\Lambda $
is also torsion free; in particular, the vertex subgroups of
$\Lambda $
is also torsion free; in particular, the vertex subgroups of
![]() $\Lambda $
are automatically infinite. Thus, the conclusion follows from Theorem C.
$\Lambda $
are automatically infinite. Thus, the conclusion follows from Theorem C.
2 Preliminaries
2.1 Terminology
Throughout this article, all von Neumann algebras are denoted by calligraphic letters, for example,
![]() ${\mathcal M}$
,
${\mathcal M}$
,
![]() $\mathcal N$
,
$\mathcal N$
,
![]() $\mathcal P$
,
$\mathcal P$
,
![]() $\mathcal {Q}$
, etc. All von Neumann algebras
$\mathcal {Q}$
, etc. All von Neumann algebras
![]() ${\mathcal M}$
will be tracial, that is, endowed with a unital, faithful, normal linear functional
${\mathcal M}$
will be tracial, that is, endowed with a unital, faithful, normal linear functional
![]() $\tau :{\mathcal M}\rightarrow \mathbb C$
satisfying
$\tau :{\mathcal M}\rightarrow \mathbb C$
satisfying
![]() $\tau (xy)=\tau (yx)$
, for all
$\tau (xy)=\tau (yx)$
, for all
![]() $x,y\in {\mathcal M}$
. This induces a norm on
$x,y\in {\mathcal M}$
. This induces a norm on
![]() ${\mathcal M}$
given by the formula
${\mathcal M}$
given by the formula
![]() $\|x\|_2=\tau (x^*x)^{1/2}$
, for any
$\|x\|_2=\tau (x^*x)^{1/2}$
, for any
![]() $x\in {\mathcal M}$
. The
$x\in {\mathcal M}$
. The
![]() $\|\cdot \|_2$
-completion of
$\|\cdot \|_2$
-completion of
![]() ${\mathcal M}$
will be denoted by
${\mathcal M}$
will be denoted by
![]() $L^2({\mathcal M})$
. Given a von Neumann algebra
$L^2({\mathcal M})$
. Given a von Neumann algebra
![]() ${\mathcal M}$
, we will denote by
${\mathcal M}$
, we will denote by
![]() $\mathscr U({\mathcal M})$
its unitary group, by
$\mathscr U({\mathcal M})$
its unitary group, by
![]() $\mathcal P({\mathcal M})$
its projections set and by
$\mathcal P({\mathcal M})$
its projections set and by
![]() $\mathcal Z({\mathcal M})$
its center. Given a unital inclusion
$\mathcal Z({\mathcal M})$
its center. Given a unital inclusion
![]() ${\mathcal N}\subset {\mathcal M}$
of von Neumann algebras, we denote by
${\mathcal N}\subset {\mathcal M}$
of von Neumann algebras, we denote by
![]() $E_{\mathcal N}:{\mathcal M}\to \mathcal N$
the unique
$E_{\mathcal N}:{\mathcal M}\to \mathcal N$
the unique
![]() $\tau $
-preserving conditional expectation from
$\tau $
-preserving conditional expectation from
![]() ${\mathcal M}$
onto
${\mathcal M}$
onto
![]() $\mathcal N$
, by
$\mathcal N$
, by
![]() $e_{\mathcal N}:L^2({\mathcal M})\to L^2(\mathcal N)$
the orthogonal projection onto
$e_{\mathcal N}:L^2({\mathcal M})\to L^2(\mathcal N)$
the orthogonal projection onto
![]() $L^2(\mathcal N)$
and by
$L^2(\mathcal N)$
and by
![]() $\langle {\mathcal M},e_{\mathcal {N}}\rangle $
the Jones’s basic construction of
$\langle {\mathcal M},e_{\mathcal {N}}\rangle $
the Jones’s basic construction of
![]() $\mathcal N\subset {\mathcal M}$
. Also, we denote by
$\mathcal N\subset {\mathcal M}$
. Also, we denote by
![]() $\mathcal N'\cap {\mathcal M} =\{ x\in {\mathcal M} \,:\, [x, \mathcal N]=0\}$
the relative commmutant of
$\mathcal N'\cap {\mathcal M} =\{ x\in {\mathcal M} \,:\, [x, \mathcal N]=0\}$
the relative commmutant of
![]() $\mathcal N$
inside
$\mathcal N$
inside
![]() ${\mathcal M}$
and by
${\mathcal M}$
and by
![]() $\mathscr N_{\mathcal M}(\mathcal N)=\{ u\in \mathscr U({\mathcal M})\,:\, u\mathcal N u^*=\mathcal N\}$
the normalizer of
$\mathscr N_{\mathcal M}(\mathcal N)=\{ u\in \mathscr U({\mathcal M})\,:\, u\mathcal N u^*=\mathcal N\}$
the normalizer of
![]() $\mathcal N$
inside
$\mathcal N$
inside
![]() ${\mathcal M}$
. We say that the inclusion
${\mathcal M}$
. We say that the inclusion
![]() $\mathcal N$
is regular in
$\mathcal N$
is regular in
![]() ${\mathcal M}$
if
${\mathcal M}$
if
![]() $\mathscr N_{{\mathcal M}}(\mathcal N)"={\mathcal M}$
and irreducible if
$\mathscr N_{{\mathcal M}}(\mathcal N)"={\mathcal M}$
and irreducible if
![]() $\mathcal N'\cap {\mathcal M}=\mathbb C 1$
.
$\mathcal N'\cap {\mathcal M}=\mathbb C 1$
.
For a group inclusion
![]() $\Sigma < \Gamma $
, we denote by
$\Sigma < \Gamma $
, we denote by
![]() $C_{\Gamma }(\Sigma )=\{ g\in \Gamma \,|\, [g,\Sigma ]=1\}$
its centralizer in
$C_{\Gamma }(\Sigma )=\{ g\in \Gamma \,|\, [g,\Sigma ]=1\}$
its centralizer in
![]() $\Gamma $
and by
$\Gamma $
and by
![]() $vC_{\Gamma }(\Sigma )=\{ g\in \Gamma \,|\, |g^\Sigma |<\infty \}$
its virtual centralizer. Note that
$vC_{\Gamma }(\Sigma )=\{ g\in \Gamma \,|\, |g^\Sigma |<\infty \}$
its virtual centralizer. Note that
![]() $vC_\Gamma (\Gamma )=1$
precisely when
$vC_\Gamma (\Gamma )=1$
precisely when
![]() $\Gamma $
is icc. We denote by
$\Gamma $
is icc. We denote by
![]() $N_\Gamma (\Sigma )=\{ g\in \Gamma \,|\, g\Sigma g^{-1}=\Sigma \}$
the normalizer of
$N_\Gamma (\Sigma )=\{ g\in \Gamma \,|\, g\Sigma g^{-1}=\Sigma \}$
the normalizer of
![]() $\Sigma $
in
$\Sigma $
in
![]() $\Gamma $
.
$\Gamma $
.
2.2 Graph product groups
We now recall the notion of graph product groups introduced by Green [Reference GreenGr90] while also highlighting some of their properties that are relevant to our work. Let
![]() $\mathscr {G}=(\mathscr V,\mathscr E)$
be a finite simple graph, where
$\mathscr {G}=(\mathscr V,\mathscr E)$
be a finite simple graph, where
![]() $\mathscr V$
and
$\mathscr V$
and
![]() $\mathscr E$
denote its vertex and edge sets, respectively. Let
$\mathscr E$
denote its vertex and edge sets, respectively. Let
![]() $\{\Gamma _v\}_{v\in \mathscr V}$
be a family of groups called vertex groups. The graph product group associated with these data, denoted by
$\{\Gamma _v\}_{v\in \mathscr V}$
be a family of groups called vertex groups. The graph product group associated with these data, denoted by
![]() $\mathscr {G}\{\Gamma _v,v \in \mathscr V\}$
or simply
$\mathscr {G}\{\Gamma _v,v \in \mathscr V\}$
or simply
![]() $\mathscr {G}\{\Gamma _v\}$
, is the group generated by
$\mathscr {G}\{\Gamma _v\}$
, is the group generated by
![]() $\Gamma _v$
,
$\Gamma _v$
,
![]() $v\in \mathscr V$
with the only relations being
$v\in \mathscr V$
with the only relations being
![]() $[\Gamma _u, \Gamma _v] = 1$
, whenever
$[\Gamma _u, \Gamma _v] = 1$
, whenever
![]() $(u,v)\in \mathscr E$
. Given any subset
$(u,v)\in \mathscr E$
. Given any subset
![]() $\mathscr U\subset \mathscr V$
, the subgroup
$\mathscr U\subset \mathscr V$
, the subgroup
![]() $\Gamma _{\mathscr {U}} =\langle \Gamma _u \,:\,u\in \mathscr {U}\rangle $
of
$\Gamma _{\mathscr {U}} =\langle \Gamma _u \,:\,u\in \mathscr {U}\rangle $
of
![]() $\mathscr {G}\{\Gamma _v,v\in \mathscr V\}$
is called a full subgroup. This can be identified with the graph product
$\mathscr {G}\{\Gamma _v,v\in \mathscr V\}$
is called a full subgroup. This can be identified with the graph product
![]() $\mathscr {G}_{\mathscr {U}}\{\Gamma _u,u \in \mathscr {U}\}$
corresponding to the subgraph
$\mathscr {G}_{\mathscr {U}}\{\Gamma _u,u \in \mathscr {U}\}$
corresponding to the subgraph
![]() $\mathscr {G}_{\mathscr {U}}$
of
$\mathscr {G}_{\mathscr {U}}$
of
![]() $\mathscr {G}$
, spanned by the vertices of
$\mathscr {G}$
, spanned by the vertices of
![]() $\mathscr {U}$
. For every
$\mathscr {U}$
. For every
![]() $v \in \mathscr V$
, we denote by
$v \in \mathscr V$
, we denote by
![]() $\mathrm {lk}(v)$
the subset of vertices
$\mathrm {lk}(v)$
the subset of vertices
![]() $w\neq v$
so that
$w\neq v$
so that
![]() $(w,v)\in \mathscr E$
. Similarly, for every
$(w,v)\in \mathscr E$
. Similarly, for every
![]() $\mathscr {U} \subseteq \mathscr V$
, we denote by
$\mathscr {U} \subseteq \mathscr V$
, we denote by
![]() ${\mathrm {lk}(\mathscr {U}) = \cap _{u\in \mathscr {U}}\mathrm {lk}(u)}$
. Also, we make the convention that
${\mathrm {lk}(\mathscr {U}) = \cap _{u\in \mathscr {U}}\mathrm {lk}(u)}$
. Also, we make the convention that
![]() $\mathrm {lk}(\emptyset ) = \mathscr V$
. Notice that
$\mathrm {lk}(\emptyset ) = \mathscr V$
. Notice that
![]() $\mathscr {U} \cap \mathrm {lk}(\mathscr {U}) = \emptyset $
.
$\mathscr {U} \cap \mathrm {lk}(\mathscr {U}) = \emptyset $
.
Graph product groups naturally admit many amalgamated free product decompositions as follows (see [Reference GreenGr90, Lemma 3.20]). For any
![]() $w \in \mathscr V$
, we have
$w \in \mathscr V$
, we have
where
![]() $\mathrm {st} (w) = \{w\} \cup \mathrm {lk} (w)$
. Notice that
$\mathrm {st} (w) = \{w\} \cup \mathrm {lk} (w)$
. Notice that
![]() $\Gamma _{\mathrm {lk}(w)}\lneqq \Gamma _{\mathrm {st}(w)}$
, but it could be the case that
$\Gamma _{\mathrm {lk}(w)}\lneqq \Gamma _{\mathrm {st}(w)}$
, but it could be the case that
![]() $\Gamma _{\mathrm {lk}(w)}=\Gamma _{\mathscr V\setminus \{w\}} $
, when
$\Gamma _{\mathrm {lk}(w)}=\Gamma _{\mathscr V\setminus \{w\}} $
, when
![]() $\mathscr V=\mathrm {st}(w)$
. In this case, the amalgam decomposition is called degenerate.
$\mathscr V=\mathrm {st}(w)$
. In this case, the amalgam decomposition is called degenerate.
Similarly, for every subgraph
![]() $\mathscr {U}\subset \mathscr {G}$
, we denote by
$\mathscr {U}\subset \mathscr {G}$
, we denote by
![]() $\mathrm {st}(\mathscr {U})= \mathscr {U} \cup \mathrm {lk}(\mathscr {U} )$
. A maximal complete subgraph
$\mathrm {st}(\mathscr {U})= \mathscr {U} \cup \mathrm {lk}(\mathscr {U} )$
. A maximal complete subgraph
![]() $\mathscr {C}\subseteq \mathscr {G}$
is called a clique, and the collections of all cliques of
$\mathscr {C}\subseteq \mathscr {G}$
is called a clique, and the collections of all cliques of
![]() $\mathscr {G}$
will be denoted by
$\mathscr {G}$
will be denoted by
![]() $\mathrm {cliq}(\mathscr {G})$
. Below, we highlight various properties of full subgroups that will be useful in this paper.
$\mathrm {cliq}(\mathscr {G})$
. Below, we highlight various properties of full subgroups that will be useful in this paper.
Proposition 2.1. Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups,
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups,
![]() $g\in \Gamma $
and let
$g\in \Gamma $
and let
![]() $\mathscr {S},\mathscr {T}\subseteq \mathscr {G}$
be any subgraphs. Then the following hold.
$\mathscr {S},\mathscr {T}\subseteq \mathscr {G}$
be any subgraphs. Then the following hold.
-
1. [Reference Antolín and MinasyanAM10, Lemma 3.9] If
 $g \Gamma _{\mathscr {T}} g^{-1}\subset \Gamma _{\mathscr {T}}$
, then
$g \Gamma _{\mathscr {T}} g^{-1}\subset \Gamma _{\mathscr {T}}$
, then
 $g \Gamma _{\mathscr {T}} g^{-1}=\Gamma _{\mathscr {T}}$
.
$g \Gamma _{\mathscr {T}} g^{-1}=\Gamma _{\mathscr {T}}$
. -
2. [Reference Antolín and MinasyanAM10, Proposition 3.13]
 $N_{\Gamma }(\Gamma _{\mathscr {T}})=\Gamma _{\mathscr {T}\cup \mathrm {link}(\mathscr {T})}$
.
$N_{\Gamma }(\Gamma _{\mathscr {T}})=\Gamma _{\mathscr {T}\cup \mathrm {link}(\mathscr {T})}$
. -
3. [Reference Antolín and MinasyanAM10, Proposition 3.4] There exist
 $\mathscr {D}\subseteq \mathscr {S}\cap \mathscr {T}$
and
$\mathscr {D}\subseteq \mathscr {S}\cap \mathscr {T}$
and
 $h\in \Gamma _{\mathscr {T}}$
, such that
$h\in \Gamma _{\mathscr {T}}$
, such that
 $g \Gamma _{\mathscr {S}} g^{-1}\cap \Gamma _{\mathscr {T}}=h \Gamma _{\mathscr {D}} h^{-1}$
.
$g \Gamma _{\mathscr {S}} g^{-1}\cap \Gamma _{\mathscr {T}}=h \Gamma _{\mathscr {D}} h^{-1}$
.
For further use, we also record the following easy consequence of results in [Reference Oyono-OyonoO-O01b, Reference Oyono-OyonoO-O98].
Proposition 2.2. Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups. Then the following hold:
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups. Then the following hold:
-
1. If
 $\Gamma _v$
is torsion free for all
$\Gamma _v$
is torsion free for all
 $v\in \mathscr V$
, then
$v\in \mathscr V$
, then
 $\Gamma $
is also torsion free;
$\Gamma $
is also torsion free; -
2. If
 $\Gamma _v$
is torsion free and satisfies Baum-Connes conjecture for all
$\Gamma _v$
is torsion free and satisfies Baum-Connes conjecture for all
 $v\in \mathscr V$
, then so is
$v\in \mathscr V$
, then so is
 $\Gamma $
.
$\Gamma $
.
Proof. Torsion free passes to both direct products and free product with amalgamation. Thus, using either product decomposition or (2.1), the statement follows by induction on the number of vertices in
![]() $\mathscr {G}$
.
$\mathscr {G}$
.
To see part 2, notice that the class of torsion free groups that satisfies Baum-Connes property is closed under taking finite direct products [Reference Oyono-OyonoO-O01b] and also undertaking free product with amalgamation [Reference Oyono-OyonoO-O98]. Once again, using either product decomposition or (2.1), the statement follows by induction on the number of vertices in
![]() $\mathscr {G}$
.
$\mathscr {G}$
.
2.3 Cycles of cliques graphs and their von Neumann algebras
In the first part of this section, we recall from [Reference Chifan, Davis and DrimbeCDD22, Section 7] a canonical family of
![]() $*$
-isomorphisms between graph product group von Neumann algebras when the underlying graphs belong to
$*$
-isomorphisms between graph product group von Neumann algebras when the underlying graphs belong to
![]() $\mathrm { CC}_1$
. Let
$\mathrm { CC}_1$
. Let
![]() $\mathscr {G},\mathscr {H} \in \mathrm {CC}_1$
be isomorphic graphs, and fix
$\mathscr {G},\mathscr {H} \in \mathrm {CC}_1$
be isomorphic graphs, and fix
![]() $\sigma : \mathscr {G} \rightarrow \mathscr {H}$
an isometry. Let
$\sigma : \mathscr {G} \rightarrow \mathscr {H}$
an isometry. Let
![]() $\mathrm {cliq}( \mathscr {G}) =\{ \mathscr {C}_1, \ldots ,\mathscr {C}_n\}$
be an enumeration of consecutive cliques. Let
$\mathrm {cliq}( \mathscr {G}) =\{ \mathscr {C}_1, \ldots ,\mathscr {C}_n\}$
be an enumeration of consecutive cliques. Let
![]() $\Gamma _{\mathscr {G}}$
and
$\Gamma _{\mathscr {G}}$
and
![]() $\Lambda _{\mathscr {H}}$
be graph product groups, and assume that for every
$\Lambda _{\mathscr {H}}$
be graph product groups, and assume that for every
![]() $1\leq i\leq n $
, there are
$1\leq i\leq n $
, there are
![]() $\ast $
-isomorphisms
$\ast $
-isomorphisms
![]() $\theta _{i-1,i}: {\mathcal L}(\Gamma _{\mathscr {C}_{i-1,i}})\rightarrow \mathcal L(\Lambda _{\mathscr {C}_{\sigma (\mathscr {C}_{i-1,i})}}) $
,
$\theta _{i-1,i}: {\mathcal L}(\Gamma _{\mathscr {C}_{i-1,i}})\rightarrow \mathcal L(\Lambda _{\mathscr {C}_{\sigma (\mathscr {C}_{i-1,i})}}) $
,
![]() $\xi _{i}:\mathcal L(\Gamma _{\mathscr {C}^{\mathrm {int}}_i})\rightarrow \mathcal L(\Lambda _{\sigma (\mathscr {C}^{\mathrm { int}}_i)})$
and
$\xi _{i}:\mathcal L(\Gamma _{\mathscr {C}^{\mathrm {int}}_i})\rightarrow \mathcal L(\Lambda _{\sigma (\mathscr {C}^{\mathrm { int}}_i)})$
and
![]() $\theta _{i,i+1}:{\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}})\rightarrow {\mathcal L}(\Lambda _{\mathscr {C}_{\sigma (\mathscr {C}_{i,i+1})}}) $
; here, and in what follows, we convene as before that
$\theta _{i,i+1}:{\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}})\rightarrow {\mathcal L}(\Lambda _{\mathscr {C}_{\sigma (\mathscr {C}_{i,i+1})}}) $
; here, and in what follows, we convene as before that
![]() $n=0$
and
$n=0$
and
![]() $n+1=1$
. By [Reference Chifan, Davis and DrimbeCDD22, Theorem 7.1] (see also [Reference Caspers and FimaCF14]), these
$n+1=1$
. By [Reference Chifan, Davis and DrimbeCDD22, Theorem 7.1] (see also [Reference Caspers and FimaCF14]), these
![]() $\ast $
-isomorphisms induce a unique
$\ast $
-isomorphisms induce a unique
![]() $\ast $
-isomorphism
$\ast $
-isomorphism
![]() $\phi _{\theta ,\xi , \sigma }:{\mathcal L}(\Gamma _{\mathscr {G}})\rightarrow {\mathcal L}(\Lambda _{\mathscr {H}})$
defined as
$\phi _{\theta ,\xi , \sigma }:{\mathcal L}(\Gamma _{\mathscr {G}})\rightarrow {\mathcal L}(\Lambda _{\mathscr {H}})$
defined as
 $$ \begin{align} \phi_{\theta,\xi, \sigma}(x)=\begin{cases} \theta_{i-1,i}(x), \text{ if } x\in {\mathcal L}(\Gamma_{\mathscr{C}_{i-1,i}})\\ \xi_i(x), \qquad \text{if } x\in {\mathcal L}(\Gamma_{\mathscr{C}^{\mathrm{int}}_i }) \end{cases} \end{align} $$
$$ \begin{align} \phi_{\theta,\xi, \sigma}(x)=\begin{cases} \theta_{i-1,i}(x), \text{ if } x\in {\mathcal L}(\Gamma_{\mathscr{C}_{i-1,i}})\\ \xi_i(x), \qquad \text{if } x\in {\mathcal L}(\Gamma_{\mathscr{C}^{\mathrm{int}}_i }) \end{cases} \end{align} $$
for all
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
When
![]() $\Gamma _{\mathscr {G}} =\Lambda _{\mathscr {H}}$
, this construction yields a group of
$\Gamma _{\mathscr {G}} =\Lambda _{\mathscr {H}}$
, this construction yields a group of
![]() $\ast $
-automorphisms of
$\ast $
-automorphisms of
![]() ${\mathcal L}(\Gamma _{\mathscr {G}})$
, denoted by
${\mathcal L}(\Gamma _{\mathscr {G}})$
, denoted by
![]() $\mathrm {Loc}_{\mathrm {c,g}}({\mathcal L}(\Gamma _{\mathscr {G}}))$
. We also denote by
$\mathrm {Loc}_{\mathrm {c,g}}({\mathcal L}(\Gamma _{\mathscr {G}}))$
. We also denote by
![]() $\mathrm {Loc}_{\mathrm {c}}({\mathcal L}(\Gamma _{\mathscr {G}}))$
the subgroup of all local automorphisms satisfying
$\mathrm {Loc}_{\mathrm {c}}({\mathcal L}(\Gamma _{\mathscr {G}}))$
the subgroup of all local automorphisms satisfying
![]() $\sigma =\mathrm {Id}$
. Next, we highlight a class of automorphisms in
$\sigma =\mathrm {Id}$
. Next, we highlight a class of automorphisms in
![]() $\mathrm {Loc}_{\mathrm {c}}({\mathcal L}(\Gamma _{\mathscr {G}}))$
needed to state Theorem 7.6. Consider n-tuples
$\mathrm {Loc}_{\mathrm {c}}({\mathcal L}(\Gamma _{\mathscr {G}}))$
needed to state Theorem 7.6. Consider n-tuples
![]() $a =(a_{i,i+1})_i$
and
$a =(a_{i,i+1})_i$
and
![]() $b= (b_i)_i$
of nontrivial unitaries
$b= (b_i)_i$
of nontrivial unitaries
![]() $a_{i,i+1} \in \mathcal L(\Gamma _{\mathscr {C}_{i-1,i}})$
and
$a_{i,i+1} \in \mathcal L(\Gamma _{\mathscr {C}_{i-1,i}})$
and
![]() $b_i\in \mathcal L(\Gamma _{\mathscr {C}^{\mathrm {int}}_i})$
, for every
$b_i\in \mathcal L(\Gamma _{\mathscr {C}^{\mathrm {int}}_i})$
, for every
![]() $1\leq i\leq n$
. If in (2.2) we let
$1\leq i\leq n$
. If in (2.2) we let
![]() $\theta _{i,i+1}= \mathrm {ad} (a_{i,i+1}) $
and
$\theta _{i,i+1}= \mathrm {ad} (a_{i,i+1}) $
and
![]() $\xi _i =\mathrm {ad} (b_i)$
, then the corresponding local automorphism
$\xi _i =\mathrm {ad} (b_i)$
, then the corresponding local automorphism
![]() $\phi _{\theta ,\xi , \mathrm {Id}}$
is, in general, an outer automorphism of
$\phi _{\theta ,\xi , \mathrm {Id}}$
is, in general, an outer automorphism of
![]() $\mathcal L(\Gamma )$
(see [Reference Chifan, Davis and DrimbeCDD22, Proposition 7.4]) and will be denoted by
$\mathcal L(\Gamma )$
(see [Reference Chifan, Davis and DrimbeCDD22, Proposition 7.4]) and will be denoted by
![]() $\phi _{a,b}$
throughout the paper.
$\phi _{a,b}$
throughout the paper.
We conclude this subsection by recording an important result from [Reference Chifan, Davis and DrimbeCDD22] that is essential for deriving Theorem C.
Theorem 2.3 [Reference Chifan, Davis and DrimbeCDD22, Theorem 5.2].
Let
![]() $\mathscr {G}=\{\mathscr V,\mathscr E\}$
be a graph in the class
$\mathscr {G}=\{\mathscr V,\mathscr E\}$
be a graph in the class
![]() $\mathrm {CC}_1$
, and let
$\mathrm {CC}_1$
, and let
![]() $\mathscr {C}_1,...,\mathscr {C}_n$
be an enumeration of its consecutive cliques. Let {
$\mathscr {C}_1,...,\mathscr {C}_n$
be an enumeration of its consecutive cliques. Let {
![]() $\Gamma _v|\;v\in \mathscr V\}$
be a collection of icc groups, and let
$\Gamma _v|\;v\in \mathscr V\}$
be a collection of icc groups, and let
![]() $\Gamma _{\mathscr {G}}$
be the corresponding graph product group. For each
$\Gamma _{\mathscr {G}}$
be the corresponding graph product group. For each
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $a_{i,i+1}\in \mathscr {U}({\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}))$
,
$a_{i,i+1}\in \mathscr {U}({\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}))$
,
![]() $b_{i,i+1}\in \mathscr {U}(\mathcal L(\Gamma _{\mathscr {C}_i \cup \mathscr {C}_{i+1}\setminus \mathscr {C}_{i,i+1}})$
and denote
$b_{i,i+1}\in \mathscr {U}(\mathcal L(\Gamma _{\mathscr {C}_i \cup \mathscr {C}_{i+1}\setminus \mathscr {C}_{i,i+1}})$
and denote
![]() $x_{i,i+1}= a_{i,i+1} b_{i,i+1}$
.
$x_{i,i+1}= a_{i,i+1} b_{i,i+1}$
.
If
![]() $x_{1,2} x_{2,3}\cdots x_{n-1,n}x_{n,1}=1$
, then for each
$x_{1,2} x_{2,3}\cdots x_{n-1,n}x_{n,1}=1$
, then for each
![]() $1\leq i\leq n $
, one can find
$1\leq i\leq n $
, one can find
![]() $a_i \in \mathscr {U}({\mathcal L}(\Gamma _{\mathscr {C}_{i-1,i}}))$
,
$a_i \in \mathscr {U}({\mathcal L}(\Gamma _{\mathscr {C}_{i-1,i}}))$
,
![]() $b_i \in \mathscr {U}({\mathcal L}(\Gamma _{\mathscr {C}^{\mathrm {int}}_i}))$
and
$b_i \in \mathscr {U}({\mathcal L}(\Gamma _{\mathscr {C}^{\mathrm {int}}_i}))$
and
![]() $c_i \in \mathscr {U}(\mathcal L (\Gamma _{\mathscr {C}_{i,i+1}}))$
so that
$c_i \in \mathscr {U}(\mathcal L (\Gamma _{\mathscr {C}_{i,i+1}}))$
so that
![]() $x_{i,i+1}= a_i b_i c_i b^*_{i+1} a^*_{i+2}c^*_{i+1}$
. Here, we convene that
$x_{i,i+1}= a_i b_i c_i b^*_{i+1} a^*_{i+2}c^*_{i+1}$
. Here, we convene that
![]() $n+1=1$
,
$n+1=1$
,
![]() $n+2=2$
, etc.
$n+2=2$
, etc.
2.4 Wreath-like product groups
In [Reference Chifan, Ioana, Osin and SunCIOS21], a new category of groups called wreath-like product groups was introduced. To recall their construction, let A and B be any countable groups, and let
![]() $B \curvearrowright I$
be an action on a countable set. One says W is a wreath-like product of A and
$B \curvearrowright I$
be an action on a countable set. One says W is a wreath-like product of A and
![]() $B\curvearrowright I$
if it can be realized as a group extension
$B\curvearrowright I$
if it can be realized as a group extension
which satisfies the following properties:
-
a)
 $A_i\cong A$
for all
$A_i\cong A$
for all
 $i\in I$
, and
$i\in I$
, and -
b) the action by conjugation of W on
 $\bigoplus _{i\in I} A_i$
permutes the direct summands according to the rule
$\bigoplus _{i\in I} A_i$
permutes the direct summands according to the rule  $$ \begin{align*}w A_i w^{-1}= A_{\varepsilon(w)i}\text{ for all }w\in W, i\in I.\end{align*} $$
$$ \begin{align*}w A_i w^{-1}= A_{\varepsilon(w)i}\text{ for all }w\in W, i\in I.\end{align*} $$
The class of all such wreath-like groups is denoted by
![]() $\mathcal W\mathcal R(A, B\curvearrowright I)$
. When
$\mathcal W\mathcal R(A, B\curvearrowright I)$
. When
![]() $I= B$
and the action
$I= B$
and the action
![]() $B\curvearrowright I$
is by translation, this consists of so-called regular wreath-like product groups, and we simply denote their class by
$B\curvearrowright I$
is by translation, this consists of so-called regular wreath-like product groups, and we simply denote their class by
![]() $\mathcal W\mathcal R(A, B)$
.
$\mathcal W\mathcal R(A, B)$
.
Notice that every classical generalized wreath product
![]() $A\wr _I B \in \mathcal W\mathcal R (A,B\curvearrowright I)$
. However, building examples of nonsplit wreath-like products is far more involved. Indeed, using deep methods in group theoretic Dehn filling and Cohen-Lyndon subgroups, it was shown in [Reference Chifan, Ioana, Osin and SunCIOS21] that large classes of such wreath-like products exist, including many with property (T).
$A\wr _I B \in \mathcal W\mathcal R (A,B\curvearrowright I)$
. However, building examples of nonsplit wreath-like products is far more involved. Indeed, using deep methods in group theoretic Dehn filling and Cohen-Lyndon subgroups, it was shown in [Reference Chifan, Ioana, Osin and SunCIOS21] that large classes of such wreath-like products exist, including many with property (T).
Theorem 2.4 [Reference Chifan, Ioana, Osin and SunCIOS21].
Let G be a hyperbolic group. For every finitely generated group A, there exists a quotient W of G, such that
![]() $W\in \mathcal W\mathcal R (A,B)$
for some hyperbolic group B. In particular, when G has property (T) (e.g. any uniform lattice in
$W\in \mathcal W\mathcal R (A,B)$
for some hyperbolic group B. In particular, when G has property (T) (e.g. any uniform lattice in
![]() $Sp(n,1)$
,
$Sp(n,1)$
,
![]() $n\geq 2$
), then so does W.
$n\geq 2$
), then so does W.
2.5 Popa’s intertwining-by-bimodules techniques
We next recall from [Reference PopaPo03, Theorem 2.1, Corollary 2.3] Popa’s intertwining-by-bimodules technique. Let
![]() $\mathcal {Q}\subset {\mathcal M}$
be a von Neumann subalgebra. Jones’s basic construction
$\mathcal {Q}\subset {\mathcal M}$
be a von Neumann subalgebra. Jones’s basic construction
![]() $\langle {\mathcal M},e_{\mathcal {Q}}\rangle $
is defined as the von Neumann subalgebra of
$\langle {\mathcal M},e_{\mathcal {Q}}\rangle $
is defined as the von Neumann subalgebra of
![]() $\mathbb B(L^2({\mathcal M}))$
generated by
$\mathbb B(L^2({\mathcal M}))$
generated by
![]() ${\mathcal M}$
and the orthogonal projection
${\mathcal M}$
and the orthogonal projection
![]() $e_{\mathcal {Q}}$
from
$e_{\mathcal {Q}}$
from
![]() $L^2({\mathcal M})$
onto
$L^2({\mathcal M})$
onto
![]() $L^2(\mathcal {Q})$
. The basic construction
$L^2(\mathcal {Q})$
. The basic construction
![]() $\langle {\mathcal M},e_{\mathcal {Q}}\rangle $
has a faithful semi-finite trace given by
$\langle {\mathcal M},e_{\mathcal {Q}}\rangle $
has a faithful semi-finite trace given by
![]() $\text {Tr}(xe_{\mathcal {Q}} y)=\tau (xy)$
, for every
$\text {Tr}(xe_{\mathcal {Q}} y)=\tau (xy)$
, for every
![]() $x,y\in {\mathcal M}$
. We denote by
$x,y\in {\mathcal M}$
. We denote by
![]() $L^2(\langle {\mathcal M},e_{\mathcal {Q}}\rangle )$
the associated Hilbert space and endow it with the natural
$L^2(\langle {\mathcal M},e_{\mathcal {Q}}\rangle )$
the associated Hilbert space and endow it with the natural
![]() ${\mathcal M}$
-bimodule structure.
${\mathcal M}$
-bimodule structure.
Theorem 2.5 [Reference PopaPo03].
Let
![]() $({\mathcal M},\tau )$
be a tracial von Neumann algebra and
$({\mathcal M},\tau )$
be a tracial von Neumann algebra and
![]() $\mathcal P\subset p{\mathcal M} p, \mathcal {Q}\subset q{\mathcal M} q$
be von Neumann subalgebras. Then the following are equivalent:
$\mathcal P\subset p{\mathcal M} p, \mathcal {Q}\subset q{\mathcal M} q$
be von Neumann subalgebras. Then the following are equivalent:
-
1. There exist projections
 $p_0\in \mathcal P, q_0\in \mathcal {Q}$
, a
$p_0\in \mathcal P, q_0\in \mathcal {Q}$
, a
 $*$
-homomorphism
$*$
-homomorphism
 $\theta :p_0\mathcal P p_0\rightarrow q_0\mathcal {Q} q_0$
and a nonzero partial isometry
$\theta :p_0\mathcal P p_0\rightarrow q_0\mathcal {Q} q_0$
and a nonzero partial isometry
 $v\in q_0{\mathcal M} p_0$
, such that
$v\in q_0{\mathcal M} p_0$
, such that
 $\theta (x)v=vx$
, for all
$\theta (x)v=vx$
, for all
 $x\in p_0\mathcal P p_0$
.
$x\in p_0\mathcal P p_0$
. -
2. There is no sequence
 $(u_n)_{n\ge 1}\subset \mathcal U(\mathcal P)$
satisfying
$(u_n)_{n\ge 1}\subset \mathcal U(\mathcal P)$
satisfying
 $\|E_{\mathcal {Q}}(x^*u_ny)\|_2\rightarrow 0$
, for all
$\|E_{\mathcal {Q}}(x^*u_ny)\|_2\rightarrow 0$
, for all
 $x,y\in p{\mathcal M}$
.
$x,y\in p{\mathcal M}$
.
If one of these equivalent conditions holds true, we write
![]() $\mathcal P\prec _{{\mathcal M}}\mathcal {Q}$
, and say that a corner of
$\mathcal P\prec _{{\mathcal M}}\mathcal {Q}$
, and say that a corner of
![]() $\mathcal P$
embeds into
$\mathcal P$
embeds into
![]() $\mathcal {Q}$
inside
$\mathcal {Q}$
inside
![]() ${\mathcal M}$
. Moreover, if
${\mathcal M}$
. Moreover, if
![]() $\mathcal P p'\prec _{{\mathcal M}}\mathcal {Q}$
for any nonzero projection
$\mathcal P p'\prec _{{\mathcal M}}\mathcal {Q}$
for any nonzero projection
![]() $p'\in \mathcal P'\cap p{\mathcal M} p$
, then we write
$p'\in \mathcal P'\cap p{\mathcal M} p$
, then we write
![]() $\mathcal P\prec ^{s}_{{\mathcal M}}\mathcal {Q}$
.
$\mathcal P\prec ^{s}_{{\mathcal M}}\mathcal {Q}$
.
We continue by recording several elementary facts about intertwining results in group von Neumann algebras (of graph product groups).
Lemma 2.6 [Reference Chifan and IoanaCI17, Lemma 2.2].
Let
![]() $\Gamma _1, \Gamma _2 < \Gamma $
be countable groups, such that
$\Gamma _1, \Gamma _2 < \Gamma $
be countable groups, such that
![]() ${\mathcal L}(\Gamma _1) \prec _{{\mathcal L}(\Gamma )} {\mathcal L}(\Gamma _2)$
. Then one can find
${\mathcal L}(\Gamma _1) \prec _{{\mathcal L}(\Gamma )} {\mathcal L}(\Gamma _2)$
. Then one can find
![]() $g \in \Gamma $
, such that
$g \in \Gamma $
, such that
![]() $[\Gamma _1 : \Gamma _1 \cap g \Gamma _2g^{-1}] < \infty $
.
$[\Gamma _1 : \Gamma _1 \cap g \Gamma _2g^{-1}] < \infty $
.
Corollary 2.7 [Reference Chifan, Davis and DrimbeCDD22, Lemma 2.3].
Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of infinite groups, and let
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of infinite groups, and let
![]() $\mathscr {S},\mathscr {T}\subseteq \mathscr {G}$
be any subgraphs. If
$\mathscr {S},\mathscr {T}\subseteq \mathscr {G}$
be any subgraphs. If
![]() ${\mathcal L}(\Gamma _{\mathscr {S}})\prec _{{\mathcal L}(\Gamma )} \mathcal L(\Gamma _{\mathscr {T}})$
, then
${\mathcal L}(\Gamma _{\mathscr {S}})\prec _{{\mathcal L}(\Gamma )} \mathcal L(\Gamma _{\mathscr {T}})$
, then
![]() $\mathscr {S}\subset \mathscr {T}$
.
$\mathscr {S}\subset \mathscr {T}$
.
We also recall the following result, which classifies all rigid subalgebras of von Neumann algebras associated to graph product groups.
Theorem 2.8 [Reference Chifan, Davis and DrimbeCDD22, Theorem 6.1].
Let
![]() $\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group, let
$\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group, let
![]() $\Gamma \curvearrowright \mathcal P$
be any trace preserving action and denote by
$\Gamma \curvearrowright \mathcal P$
be any trace preserving action and denote by
![]() ${\mathcal M}=\mathcal P\rtimes \Gamma $
the corresponding crossed product von Neumann algebra. Let
${\mathcal M}=\mathcal P\rtimes \Gamma $
the corresponding crossed product von Neumann algebra. Let
![]() $r\in {\mathcal M}$
be a projection, and let
$r\in {\mathcal M}$
be a projection, and let
![]() $\mathcal {Q}\subset r{\mathcal M} r$
be a property (T) von Neumann subalgebra.
$\mathcal {Q}\subset r{\mathcal M} r$
be a property (T) von Neumann subalgebra.
Then one can find a clique
![]() $\mathscr {C}\in \mathrm {cliq}(\mathscr {G})$
, such that
$\mathscr {C}\in \mathrm {cliq}(\mathscr {G})$
, such that
![]() $\mathcal {Q}\prec _{\mathcal M} \mathcal P\rtimes \Gamma _{\mathscr {C}}$
. Moreover, if
$\mathcal {Q}\prec _{\mathcal M} \mathcal P\rtimes \Gamma _{\mathscr {C}}$
. Moreover, if
![]() $Q\nprec \mathcal P \rtimes \Gamma _{\mathscr {C} \setminus \{c\}}$
for all
$Q\nprec \mathcal P \rtimes \Gamma _{\mathscr {C} \setminus \{c\}}$
for all
![]() $c\in \mathscr {C}$
, then one can find projections
$c\in \mathscr {C}$
, then one can find projections
![]() $q\in \mathcal {Q}$
,
$q\in \mathcal {Q}$
,
![]() $q'\in \mathcal {Q}'\cap r{\mathcal M} r$
with
$q'\in \mathcal {Q}'\cap r{\mathcal M} r$
with
![]() $qq'\neq 0$
and a unitary
$qq'\neq 0$
and a unitary
![]() $u\in {\mathcal M}$
, such that
$u\in {\mathcal M}$
, such that
![]() $u q\mathcal {Q} q q'u^{*}\subseteq \mathcal P \rtimes \Gamma _{\mathscr {C}}$
. In particular, if
$u q\mathcal {Q} q q'u^{*}\subseteq \mathcal P \rtimes \Gamma _{\mathscr {C}}$
. In particular, if
![]() $\mathcal P\rtimes \Gamma _{\mathscr {C}}$
is a factor, then one can take
$\mathcal P\rtimes \Gamma _{\mathscr {C}}$
is a factor, then one can take
![]() $q=1$
above.
$q=1$
above.
The following result is a direct corollary of [Reference Ioana, Peterson and PopaIPP05, Theorem 1.2.1]. For completeness, we provide all the details.
Corollary 2.9. Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of infinite groups, and let
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of infinite groups, and let
![]() ${\mathcal M}={\mathcal L}(\Gamma )$
. Let
${\mathcal M}={\mathcal L}(\Gamma )$
. Let
![]() $\mathcal A\subset {\mathcal L}(\Gamma _v)$
be a diffuse von Neumann subalgebra, for some
$\mathcal A\subset {\mathcal L}(\Gamma _v)$
be a diffuse von Neumann subalgebra, for some
![]() $v\in \mathscr {G}$
. Then
$v\in \mathscr {G}$
. Then
![]() $\mathcal A '\cap {\mathcal M} = {\mathcal L}(\Gamma _{\mathrm {link}(v)})\bar \otimes (\mathcal A'\cap {\mathcal L}(\Gamma _v))$
.
$\mathcal A '\cap {\mathcal M} = {\mathcal L}(\Gamma _{\mathrm {link}(v)})\bar \otimes (\mathcal A'\cap {\mathcal L}(\Gamma _v))$
.
Proof. From definitions, we have
![]() $\mathcal A '\cap {\mathcal M} \supset {\mathcal L}(\Gamma _{\mathrm {link}(v)})\bar \otimes (\mathcal A'\cap {\mathcal L}(\Gamma _v))$
. For proving the reverse containment, we note that we can write
$\mathcal A '\cap {\mathcal M} \supset {\mathcal L}(\Gamma _{\mathrm {link}(v)})\bar \otimes (\mathcal A'\cap {\mathcal L}(\Gamma _v))$
. For proving the reverse containment, we note that we can write
![]() ${\mathcal M}$
as an amalgamated free product
${\mathcal M}$
as an amalgamated free product
![]() ${{\mathcal M}= {\mathcal L}(\Gamma _{\mathrm {star} (v)})\ast _{{\mathcal L}(\Gamma _{\mathrm {link} (v)})} {\mathcal L}(\Gamma _{\mathscr {G}\setminus \{v\}})}$
. Since
${{\mathcal M}= {\mathcal L}(\Gamma _{\mathrm {star} (v)})\ast _{{\mathcal L}(\Gamma _{\mathrm {link} (v)})} {\mathcal L}(\Gamma _{\mathscr {G}\setminus \{v\}})}$
. Since
![]() $\mathcal A$
is diffuse, it follows that
$\mathcal A$
is diffuse, it follows that
![]() $\mathcal A\nprec _{{\mathcal L}(\Gamma _{\mathrm {star} (v)})} {\mathcal L}(\Gamma _{\mathrm {link} (v)}) $
. By [Reference Ioana, Peterson and PopaIPP05, Theorem 1.2.1], it follows that
$\mathcal A\nprec _{{\mathcal L}(\Gamma _{\mathrm {star} (v)})} {\mathcal L}(\Gamma _{\mathrm {link} (v)}) $
. By [Reference Ioana, Peterson and PopaIPP05, Theorem 1.2.1], it follows that
![]() $\mathcal A '\cap {\mathcal M}\subset \mathcal A '\cap {\mathcal L}(\Gamma _{\mathrm {star} (v)}) ={\mathcal L}(\Gamma _{\mathrm {link}(v)})\bar \otimes (\mathcal A'\cap {\mathcal L}(\Gamma _v)).$
$\mathcal A '\cap {\mathcal M}\subset \mathcal A '\cap {\mathcal L}(\Gamma _{\mathrm {star} (v)}) ={\mathcal L}(\Gamma _{\mathrm {link}(v)})\bar \otimes (\mathcal A'\cap {\mathcal L}(\Gamma _v)).$
Lemma 2.10. Let
![]() $\Sigma <\Gamma $
be countable groups, and denote
$\Sigma <\Gamma $
be countable groups, and denote
![]() ${\mathcal M}={\mathcal L} (\Gamma )$
. Assume that
${\mathcal M}={\mathcal L} (\Gamma )$
. Assume that
![]() ${\mathcal P\subset p{\mathcal M} p}$
and
${\mathcal P\subset p{\mathcal M} p}$
and
![]() $\mathcal {Q}\subset q{\mathcal M} q$
are von Neumann subalgebras satisfying
$\mathcal {Q}\subset q{\mathcal M} q$
are von Neumann subalgebras satisfying
![]() $\mathcal P\prec _{{\mathcal M}} {\mathcal L}(\Sigma )$
and
$\mathcal P\prec _{{\mathcal M}} {\mathcal L}(\Sigma )$
and
![]() ${\mathcal L}(\Sigma )\prec _{{\mathcal M}} \mathcal {Q}$
.
${\mathcal L}(\Sigma )\prec _{{\mathcal M}} \mathcal {Q}$
.
If
![]() $\mathcal P'\cap p{\mathcal M} p$
is amenable, then
$\mathcal P'\cap p{\mathcal M} p$
is amenable, then
![]() $\mathcal {Q} '\cap q{\mathcal M} q$
has an amenable direct summand.
$\mathcal {Q} '\cap q{\mathcal M} q$
has an amenable direct summand.
Proof. Note that one can find an increasing sequence of groups
![]() $\Omega _1 \leqslant \Omega _{2}\leqslant \cdots \leqslant \mathrm {vC}_\Gamma (\Sigma )$
normalized by
$\Omega _1 \leqslant \Omega _{2}\leqslant \cdots \leqslant \mathrm {vC}_\Gamma (\Sigma )$
normalized by
![]() $\Sigma $
with
$\Sigma $
with
![]() $\cup _{n\ge 1} \Omega _n=\mathrm { vC}_\Gamma (\Sigma )$
whose centralizers form a descending sequence
$\cup _{n\ge 1} \Omega _n=\mathrm { vC}_\Gamma (\Sigma )$
whose centralizers form a descending sequence
![]() $\Sigma \geqslant C_\Sigma (\Omega _1)\geqslant \cdots \geqslant C_\Sigma (\Omega _n )\geqslant C_\Sigma (\Omega _{n+1})\geqslant \cdots $
of finite index subgroups. Indeed, recall that
$\Sigma \geqslant C_\Sigma (\Omega _1)\geqslant \cdots \geqslant C_\Sigma (\Omega _n )\geqslant C_\Sigma (\Omega _{n+1})\geqslant \cdots $
of finite index subgroups. Indeed, recall that
![]() $\mathrm {vC}_\Gamma (\Sigma )=\{g\in \Gamma |\; g^\Sigma \text { is finite} \}$
, and let
$\mathrm {vC}_\Gamma (\Sigma )=\{g\in \Gamma |\; g^\Sigma \text { is finite} \}$
, and let
![]() $\{\mathcal O_n\}_{n\ge 1}$
be a countable enumeration of all the finite orbits of the action by conjugation of
$\{\mathcal O_n\}_{n\ge 1}$
be a countable enumeration of all the finite orbits of the action by conjugation of
![]() $\Sigma $
on on
$\Sigma $
on on
![]() $\Gamma $
. Note that
$\Gamma $
. Note that
![]() $\Omega _n:=\langle \cup _{1\leq k\leq n} \mathcal O_k \rangle $
satisfies the assumption.
$\Omega _n:=\langle \cup _{1\leq k\leq n} \mathcal O_k \rangle $
satisfies the assumption.
Next, since
![]() $[\Sigma : C_\Sigma (\Omega _n )]<\infty $
, we get from the assumption that
$[\Sigma : C_\Sigma (\Omega _n )]<\infty $
, we get from the assumption that
![]() $\mathcal P\prec _{{\mathcal M}} {\mathcal L}(C_\Sigma (\Omega _n ))$
, for all
$\mathcal P\prec _{{\mathcal M}} {\mathcal L}(C_\Sigma (\Omega _n ))$
, for all
![]() $n\ge 1$
. By passing to relative commutants, we derive from [Reference VaesVa08, Lemma 3.5] that
$n\ge 1$
. By passing to relative commutants, we derive from [Reference VaesVa08, Lemma 3.5] that
![]() ${\mathcal L}(\Omega _n)\prec _{{\mathcal M}} \mathcal P'\cap p{\mathcal M} p$
, which implies that
${\mathcal L}(\Omega _n)\prec _{{\mathcal M}} \mathcal P'\cap p{\mathcal M} p$
, which implies that
![]() $L(\Omega _n)$
has an amenable direct summand for any
$L(\Omega _n)$
has an amenable direct summand for any
![]() $n\ge 1$
. This further implies that there exists a nonzero projection
$n\ge 1$
. This further implies that there exists a nonzero projection
![]() $z_n\in \mathcal Z(L(\Omega _n))$
, such that
$z_n\in \mathcal Z(L(\Omega _n))$
, such that
![]() $L(\Omega _n)z_n$
is amenable (see [Reference Ioana, Ioana and VaesIo12b, Remark 2.2]). Standard arguments now imply that
$L(\Omega _n)z_n$
is amenable (see [Reference Ioana, Ioana and VaesIo12b, Remark 2.2]). Standard arguments now imply that
![]() $\Omega _n$
is amenable for any
$\Omega _n$
is amenable for any
![]() $n\ge 1$
. This shows that
$n\ge 1$
. This shows that
![]() $\mathrm {vC}_\Gamma (\Sigma )$
is amenable. Finally, since
$\mathrm {vC}_\Gamma (\Sigma )$
is amenable. Finally, since
![]() ${\mathcal L}(\Sigma )\prec _{{\mathcal M}} \mathcal {Q}$
, we pass to relative commutants and apply [Reference VaesVa08, Lemma 3.5] to get that
${\mathcal L}(\Sigma )\prec _{{\mathcal M}} \mathcal {Q}$
, we pass to relative commutants and apply [Reference VaesVa08, Lemma 3.5] to get that
![]() $\mathcal {Q}'\cap q{\mathcal M} q\prec _{{\mathcal M}} {\mathcal L}(\mathrm {vC}_\Gamma (\Sigma ))$
. Since
$\mathcal {Q}'\cap q{\mathcal M} q\prec _{{\mathcal M}} {\mathcal L}(\mathrm {vC}_\Gamma (\Sigma ))$
. Since
![]() $\mathrm {vC}_\Gamma (\Sigma )$
is amenable, the conclusion follows.
$\mathrm {vC}_\Gamma (\Sigma )$
is amenable, the conclusion follows.
2.6 Relative amenability
A tracial von Neumann algebra
![]() $({\mathcal M},\tau )$
is amenable if there exists a positive linear functional
$({\mathcal M},\tau )$
is amenable if there exists a positive linear functional
![]() $\Phi :\mathbb B(L^2({\mathcal M}))\to \mathbb C$
satisfying
$\Phi :\mathbb B(L^2({\mathcal M}))\to \mathbb C$
satisfying
![]() $\Phi _{|{\mathcal M}}=\tau $
and
$\Phi _{|{\mathcal M}}=\tau $
and
![]() $\Phi $
is
$\Phi $
is
![]() ${\mathcal M}$
-central, meaning
${\mathcal M}$
-central, meaning
![]() $\Phi (xT)=\Phi (Tx),$
for all
$\Phi (xT)=\Phi (Tx),$
for all
![]() $x\in {\mathcal M}$
and
$x\in {\mathcal M}$
and
![]() $T\in \mathbb B(L^2({\mathcal M}))$
. By Connes’s celebrated theorem [Reference ConnesCo76], it follows that
$T\in \mathbb B(L^2({\mathcal M}))$
. By Connes’s celebrated theorem [Reference ConnesCo76], it follows that
![]() ${\mathcal M}$
is amenable if and only if
${\mathcal M}$
is amenable if and only if
![]() ${\mathcal M}$
is approximately finite dimensional.
${\mathcal M}$
is approximately finite dimensional.
We continue by recalling the notion of relative amenability introduced by Ozawa and Popa in [Reference Ozawa and PopaOP07]. Let
![]() $({\mathcal M},\tau )$
be a tracial von Neumann algebra. Let
$({\mathcal M},\tau )$
be a tracial von Neumann algebra. Let
![]() $p\in {\mathcal M}$
be a projection and
$p\in {\mathcal M}$
be a projection and
![]() $\mathcal P\subset p{\mathcal M} p,\mathcal {Q}\subset {\mathcal M}$
be von Neumann subalgebras. Following [Reference Ozawa and PopaOP07, Definition 2.2], we say that
$\mathcal P\subset p{\mathcal M} p,\mathcal {Q}\subset {\mathcal M}$
be von Neumann subalgebras. Following [Reference Ozawa and PopaOP07, Definition 2.2], we say that
![]() $\mathcal P$
is amenable relative to
$\mathcal P$
is amenable relative to
![]() $\mathcal {Q}$
inside
$\mathcal {Q}$
inside
![]() ${\mathcal M}$
if there exists a positive linear functional
${\mathcal M}$
if there exists a positive linear functional
![]() $\Phi :p\langle {\mathcal M},e_{\mathcal {Q}} \rangle p\to \mathbb C$
, such that
$\Phi :p\langle {\mathcal M},e_{\mathcal {Q}} \rangle p\to \mathbb C$
, such that
![]() $\Phi _{|p{\mathcal M} p}=\tau $
and
$\Phi _{|p{\mathcal M} p}=\tau $
and
![]() $\Phi $
is
$\Phi $
is
![]() $\mathcal P$
-central. We say that
$\mathcal P$
-central. We say that
![]() $\mathcal P$
is strongly nonamenable relative to
$\mathcal P$
is strongly nonamenable relative to
![]() $\mathcal {Q}$
inside
$\mathcal {Q}$
inside
![]() ${\mathcal M}$
if
${\mathcal M}$
if
![]() $\mathcal P p'$
is nonamenable relative to
$\mathcal P p'$
is nonamenable relative to
![]() $\mathcal {Q}$
inside
$\mathcal {Q}$
inside
![]() ${\mathcal M}$
for any nonzero projection
${\mathcal M}$
for any nonzero projection
![]() $p'\in \mathcal P '\cap p{\mathcal M} p$
.
$p'\in \mathcal P '\cap p{\mathcal M} p$
.
In this section, we prove a result (Proposition 2.12) that is inspired by [Reference Popa and VaesPV12, Proposition 3.2]; its proof is similar to the approach from [Dr19a, Lemma 2.10]. First, we show the following well-known result, which computes the basic construction of natural inclusions of subalgebras arising from trace preserving actions of countable groups (see also [Reference BerbecBe14, Lemma 2.5]).
Lemma 2.11. Let
![]() $\Gamma \curvearrowright {\mathcal D}$
be a trace preserving action of a countable group. Let
$\Gamma \curvearrowright {\mathcal D}$
be a trace preserving action of a countable group. Let
![]() $\Sigma <\Gamma $
be a subgroup, and denote
$\Sigma <\Gamma $
be a subgroup, and denote
![]() ${\mathcal M}={\mathcal D}\rtimes \Gamma $
and
${\mathcal M}={\mathcal D}\rtimes \Gamma $
and
![]() $\mathcal N={\mathcal D}\rtimes \Sigma $
. Denote by
$\mathcal N={\mathcal D}\rtimes \Sigma $
. Denote by
![]() $\mathcal {Q}=({\mathcal D}\bar \otimes \ell ^\infty (\Gamma /\Sigma ))\rtimes \Gamma $
the semifinite von Neumann algebra arising from the diagonal action
$\mathcal {Q}=({\mathcal D}\bar \otimes \ell ^\infty (\Gamma /\Sigma ))\rtimes \Gamma $
the semifinite von Neumann algebra arising from the diagonal action
![]() $\Gamma \curvearrowright {\mathcal D}\bar \otimes \ell ^\infty (\Gamma /\Sigma )$
.
$\Gamma \curvearrowright {\mathcal D}\bar \otimes \ell ^\infty (\Gamma /\Sigma )$
.
Then there exists a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta : \langle {\mathcal M},e_{\mathcal N} \rangle \to \mathcal {Q}$
satisfying
$\theta : \langle {\mathcal M},e_{\mathcal N} \rangle \to \mathcal {Q}$
satisfying
![]() $\theta (x)=x$
, for all
$\theta (x)=x$
, for all
![]() $x\in {\mathcal M}$
, and
$x\in {\mathcal M}$
, and
![]() $\theta (e_{\mathcal N})=1\otimes \delta _{e\Sigma }\in {\mathcal D}\bar \otimes \ell ^\infty (\Gamma /\Sigma )$
.
$\theta (e_{\mathcal N})=1\otimes \delta _{e\Sigma }\in {\mathcal D}\bar \otimes \ell ^\infty (\Gamma /\Sigma )$
.
Proof. We denote by
![]() $\tau $
the trace on
$\tau $
the trace on
![]() ${\mathcal M}$
and by
${\mathcal M}$
and by
![]() $\mathrm {Tr}$
the natural faithful normal semifinite trace on
$\mathrm {Tr}$
the natural faithful normal semifinite trace on
![]() $\mathcal {Q}$
, so that the restriction of
$\mathcal {Q}$
, so that the restriction of
![]() $(\mathcal {Q}, \mathrm {Tr})$
to
$(\mathcal {Q}, \mathrm {Tr})$
to
![]() ${\mathcal M}$
is
${\mathcal M}$
is
![]() $({\mathcal M},\tau )$
. By letting
$({\mathcal M},\tau )$
. By letting
![]() $f=1\otimes \delta _{e\Sigma }$
, note that the following properties hold:
$f=1\otimes \delta _{e\Sigma }$
, note that the following properties hold:
-
(i)
 $\mathcal {Q}$
is the weak closure of the
$\mathcal {Q}$
is the weak closure of the
 $*$
-subspace
$*$
-subspace
 ${\mathcal M} f{\mathcal M}$
,
${\mathcal M} f{\mathcal M}$
, -
(ii)
 $\mathrm {Tr}(f)=1$
and
$\mathrm {Tr}(f)=1$
and
 $\mathrm {Tr}(xf)=\tau (x)$
, for any
$\mathrm {Tr}(xf)=\tau (x)$
, for any
 $x\in {\mathcal M}$
,
$x\in {\mathcal M}$
, -
(iii)
 $f\mathcal {Q} f=f\mathcal N=\mathcal N f$
.
$f\mathcal {Q} f=f\mathcal N=\mathcal N f$
.
By using [Reference Sinclair and SmithSS10, Theorem 4.3.15], we derive from properties (i)–(iii) that there is a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta : \langle {\mathcal M},e_{\mathcal N} \rangle \to \mathcal {Q}$
with
$\theta : \langle {\mathcal M},e_{\mathcal N} \rangle \to \mathcal {Q}$
with
![]() $\theta (x)=x$
, for all
$\theta (x)=x$
, for all
![]() $x\in {\mathcal M}$
, and
$x\in {\mathcal M}$
, and
![]() $\theta (e_{\mathcal N})=f$
.
$\theta (e_{\mathcal N})=f$
.
Proposition 2.12. Let
![]() $\varepsilon :\Gamma \rightarrow \Lambda $
be an epimorphism between countable groups, and let
$\varepsilon :\Gamma \rightarrow \Lambda $
be an epimorphism between countable groups, and let
![]() $\Gamma \curvearrowright {\mathcal D}$
be a trace preserving action. Let
$\Gamma \curvearrowright {\mathcal D}$
be a trace preserving action. Let
![]() ${\mathcal M} = {\mathcal D}\rtimes \Gamma $
and
${\mathcal M} = {\mathcal D}\rtimes \Gamma $
and
![]() $\mathcal N= {\mathcal L}(\Lambda )$
and denote by
$\mathcal N= {\mathcal L}(\Lambda )$
and denote by
![]() $\Delta : {\mathcal M}\rightarrow {\mathcal M}\bar \otimes \mathcal N$
be the
$\Delta : {\mathcal M}\rightarrow {\mathcal M}\bar \otimes \mathcal N$
be the
![]() $\ast $
-embedding given by
$\ast $
-embedding given by
![]() $\Delta (au_g)=au_g\otimes v_{\varepsilon (g)}$
for all
$\Delta (au_g)=au_g\otimes v_{\varepsilon (g)}$
for all
![]() $a\in {\mathcal D},g\in \Gamma $
. Here, we denoted by
$a\in {\mathcal D},g\in \Gamma $
. Here, we denoted by
![]() $\{u_g\}_{g\in \Gamma }$
the canonical unitaries that implement the action
$\{u_g\}_{g\in \Gamma }$
the canonical unitaries that implement the action
![]() $\Gamma \curvearrowright {\mathcal D}$
and by
$\Gamma \curvearrowright {\mathcal D}$
and by
![]() $\{v_\lambda \}_{\lambda \in \Lambda }$
the canonical generating unitaries of
$\{v_\lambda \}_{\lambda \in \Lambda }$
the canonical generating unitaries of
![]() ${\mathcal L}(\Lambda )$
.
${\mathcal L}(\Lambda )$
.
If
![]() $\mathcal P\subseteq p {\mathcal M} p$
is a von Neumann subalgebra, such that
$\mathcal P\subseteq p {\mathcal M} p$
is a von Neumann subalgebra, such that
![]() $\Delta (\mathcal P)$
is amenable relative to
$\Delta (\mathcal P)$
is amenable relative to
![]() ${\mathcal M}\otimes 1$
inside
${\mathcal M}\otimes 1$
inside
![]() ${\mathcal M} \bar \otimes \mathcal N$
, then
${\mathcal M} \bar \otimes \mathcal N$
, then
![]() $\mathcal P$
is amenable relative to
$\mathcal P$
is amenable relative to
![]() ${\mathcal D}\rtimes \ker (\varepsilon )$
inside
${\mathcal D}\rtimes \ker (\varepsilon )$
inside
![]() ${\mathcal M}$
.
${\mathcal M}$
.
Proof. First, we claim that there is an injective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\theta : \langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle \to \langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle $
which satisfies
$\theta : \langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle \to \langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle $
which satisfies
![]() $\theta (x)=\Delta (x)$
, for any
$\theta (x)=\Delta (x)$
, for any
![]() $x\in {\mathcal M}$
, and
$x\in {\mathcal M}$
, and
![]() $\theta (e_{{\mathcal D}\rtimes \ker (\varepsilon )})=e_{{\mathcal M}\otimes 1}$
. To see that the above claim holds, we use Lemma 2.11 to obtain a
$\theta (e_{{\mathcal D}\rtimes \ker (\varepsilon )})=e_{{\mathcal M}\otimes 1}$
. To see that the above claim holds, we use Lemma 2.11 to obtain a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta _1: \langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle \to ({\mathcal D}\bar \otimes \ell ^{\infty }(\Gamma /\ker (\varepsilon )))\rtimes \Gamma $
which satisfies
$\theta _1: \langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle \to ({\mathcal D}\bar \otimes \ell ^{\infty }(\Gamma /\ker (\varepsilon )))\rtimes \Gamma $
which satisfies
![]() $\theta _1(au_g)=(a\otimes 1)u_g$
, for all
$\theta _1(au_g)=(a\otimes 1)u_g$
, for all
![]() $a\in {\mathcal D},g\in \Gamma $
and
$a\in {\mathcal D},g\in \Gamma $
and
![]() $\theta _1(e_{{\mathcal D}\rtimes \ker (\varepsilon )})=1\otimes \delta _{e \ker (\varepsilon )}$
. By applying once again Lemma 2.11, it follows that there is a
$\theta _1(e_{{\mathcal D}\rtimes \ker (\varepsilon )})=1\otimes \delta _{e \ker (\varepsilon )}$
. By applying once again Lemma 2.11, it follows that there is a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\theta _2: \langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle \to ({\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda ))\rtimes \Lambda $
which satisfies
$\theta _2: \langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle \to ({\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda ))\rtimes \Lambda $
which satisfies
![]() $\theta _2(au_g\otimes v_\lambda )=(au_g\otimes 1)v_\lambda $
, for all
$\theta _2(au_g\otimes v_\lambda )=(au_g\otimes 1)v_\lambda $
, for all
![]() $a\in {\mathcal D},g\in \Gamma ,\lambda \in \Lambda $
and
$a\in {\mathcal D},g\in \Gamma ,\lambda \in \Lambda $
and
![]() $\theta _2(e_{{\mathcal M}\otimes 1})=1\otimes \delta _e$
. Here,
$\theta _2(e_{{\mathcal M}\otimes 1})=1\otimes \delta _e$
. Here,
![]() $({\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda ))\rtimes \Lambda $
arises from the diagonal action of
$({\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda ))\rtimes \Lambda $
arises from the diagonal action of
![]() $\Lambda $
on
$\Lambda $
on
![]() ${\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda )$
, where
${\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda )$
, where
![]() $\Lambda $
acts trivially on
$\Lambda $
acts trivially on
![]() ${\mathcal M}$
and by left translations on
${\mathcal M}$
and by left translations on
![]() $\ell ^\infty (\Lambda )$
.
$\ell ^\infty (\Lambda )$
.
Next, since the epimorphism
![]() $\varepsilon :\Gamma \to \Lambda $
naturally defines a group isomorphism between
$\varepsilon :\Gamma \to \Lambda $
naturally defines a group isomorphism between
![]() $\Gamma /\ker (\varepsilon )$
and
$\Gamma /\ker (\varepsilon )$
and
![]() $\Lambda $
, there is a
$\Lambda $
, there is a
![]() $*$
-isomorphism between
$*$
-isomorphism between
![]() $\ell ^{\infty }(\Gamma /\ker (\varepsilon ))$
and
$\ell ^{\infty }(\Gamma /\ker (\varepsilon ))$
and
![]() $\ell ^\infty (\Lambda )$
which sends
$\ell ^\infty (\Lambda )$
which sends
![]() $\delta _{e \mathrm {ker}(\epsilon )}$
to
$\delta _{e \mathrm {ker}(\epsilon )}$
to
![]() $\delta _e$
. Therefore, we can define an injective
$\delta _e$
. Therefore, we can define an injective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\varphi : ({\mathcal D}\bar \otimes \ell ^{\infty }(\Gamma /\ker (\varepsilon )))\rtimes \Gamma \to ({\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda ))\rtimes \Lambda $
by letting
$\varphi : ({\mathcal D}\bar \otimes \ell ^{\infty }(\Gamma /\ker (\varepsilon )))\rtimes \Gamma \to ({\mathcal M}\bar \otimes \ell ^{\infty }(\Lambda ))\rtimes \Lambda $
by letting
![]() $\varphi ((a\otimes f)u_g)=(au_g\otimes f)v_{\varepsilon (g)}$
, for all
$\varphi ((a\otimes f)u_g)=(au_g\otimes f)v_{\varepsilon (g)}$
, for all
![]() $a\in D,g\in \Gamma $
and
$a\in D,g\in \Gamma $
and
![]() $f\in \ell ^{\infty }(\Gamma /\ker (\varepsilon ))$
. Altogether, it implies that we can define an injective
$f\in \ell ^{\infty }(\Gamma /\ker (\varepsilon ))$
. Altogether, it implies that we can define an injective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\theta : \langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle \to \langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle $
by letting
$\theta : \langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle \to \langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle $
by letting
![]() $\theta =\theta _2^{-1}\circ \varphi \circ \theta _1$
. In this way,
$\theta =\theta _2^{-1}\circ \varphi \circ \theta _1$
. In this way,
![]() $\theta (au_g)=\theta _2^{-1} (\varphi ((a\otimes 1)u_g))=\theta _2^{-1}((au_g\otimes 1)v_{\varepsilon (g)})=\Delta (au_g)$
, for all
$\theta (au_g)=\theta _2^{-1} (\varphi ((a\otimes 1)u_g))=\theta _2^{-1}((au_g\otimes 1)v_{\varepsilon (g)})=\Delta (au_g)$
, for all
![]() $a\in {\mathcal D}$
and
$a\in {\mathcal D}$
and
![]() $g\in \Gamma $
. Note that we also have
$g\in \Gamma $
. Note that we also have
![]() $\theta (e_{{\mathcal D}\rtimes \ker (\varepsilon )})=\theta _2^{-1}(\varphi (1\otimes \delta _{e \ker (\varepsilon )}))=\theta _2^{-1}(1\otimes \delta _e)= e_{{\mathcal M}\otimes 1}$
, hence, proving the above claim.
$\theta (e_{{\mathcal D}\rtimes \ker (\varepsilon )})=\theta _2^{-1}(\varphi (1\otimes \delta _{e \ker (\varepsilon )}))=\theta _2^{-1}(1\otimes \delta _e)= e_{{\mathcal M}\otimes 1}$
, hence, proving the above claim.
Finally, denote
![]() $\tilde p=\Delta (p)$
. The assumption implies that there exists a
$\tilde p=\Delta (p)$
. The assumption implies that there exists a
![]() $\Delta (\mathcal P)$
-central positive linear functional
$\Delta (\mathcal P)$
-central positive linear functional
![]() $\Phi : \tilde p\langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle \tilde p\to \mathbb C$
, such that the restriction of
$\Phi : \tilde p\langle {\mathcal M}\bar \otimes \mathcal N, e_{{\mathcal M}\otimes 1} \rangle \tilde p\to \mathbb C$
, such that the restriction of
![]() $\Phi $
to
$\Phi $
to
![]() $\tilde p ({\mathcal M}\bar \otimes \mathcal N) \tilde p$
equals the trace on
$\tilde p ({\mathcal M}\bar \otimes \mathcal N) \tilde p$
equals the trace on
![]() $\tilde p ({\mathcal M}\bar \otimes \mathcal N) \tilde p$
. Define now the positive linear functional
$\tilde p ({\mathcal M}\bar \otimes \mathcal N) \tilde p$
. Define now the positive linear functional
![]() $\Psi : p\langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle p \to \mathbb C$
by
$\Psi : p\langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle p \to \mathbb C$
by
![]() $\Psi (x)=(\Phi \circ \theta )(x)$
, for all
$\Psi (x)=(\Phi \circ \theta )(x)$
, for all
![]() $x\in p\langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle p$
, and note that the restriction of
$x\in p\langle {\mathcal M}, e_{{\mathcal D}\rtimes \ker (\varepsilon )} \rangle p$
, and note that the restriction of
![]() $\Psi $
to
$\Psi $
to
![]() $p{\mathcal M} p$
equals the trace on
$p{\mathcal M} p$
equals the trace on
![]() $p{\mathcal M} p$
and
$p{\mathcal M} p$
and
![]() $\Psi $
is
$\Psi $
is
![]() $\mathcal P$
-central. This shows that
$\mathcal P$
-central. This shows that
![]() $\mathcal P$
is amenable relative to
$\mathcal P$
is amenable relative to
![]() ${\mathcal D}\rtimes \ker (\varepsilon )$
inside
${\mathcal D}\rtimes \ker (\varepsilon )$
inside
![]() ${\mathcal M}$
.
${\mathcal M}$
.
2.7 Quasi-normalizers of von Neumann algebras
Given a group inclusion
![]() $\Sigma <\Gamma $
, the one-sided quasi-normalizer
$\Sigma <\Gamma $
, the one-sided quasi-normalizer
![]() $\mathrm {QN}^{(1)}_\Gamma (\Sigma )$
is the semigroup of all
$\mathrm {QN}^{(1)}_\Gamma (\Sigma )$
is the semigroup of all
![]() $g\in \Gamma $
for which there exists a finite set
$g\in \Gamma $
for which there exists a finite set
![]() $F\subset \Gamma $
, such that
$F\subset \Gamma $
, such that
![]() $\Sigma g\subset F \Sigma $
[Reference Fang, Gao and SmithFGS10, Section 5]; equivalently,
$\Sigma g\subset F \Sigma $
[Reference Fang, Gao and SmithFGS10, Section 5]; equivalently,
![]() $g\in \mathrm {QN}^{(1)}_\Gamma (\Sigma )$
if and only if
$g\in \mathrm {QN}^{(1)}_\Gamma (\Sigma )$
if and only if
![]() $[\Sigma : g \Sigma g^{-1}\cap \Sigma ]<\infty $
. The quasi-normalizer
$[\Sigma : g \Sigma g^{-1}\cap \Sigma ]<\infty $
. The quasi-normalizer
![]() $\mathrm { QN}_\Gamma (\Sigma )$
is the group of all
$\mathrm { QN}_\Gamma (\Sigma )$
is the group of all
![]() $g\in \Gamma $
for which exists a finite set
$g\in \Gamma $
for which exists a finite set
![]() $F\subset \Gamma $
, such that
$F\subset \Gamma $
, such that
![]() $\Sigma g\subset F\Sigma $
and
$\Sigma g\subset F\Sigma $
and
![]() $g \Sigma \subset \Sigma F$
.
$g \Sigma \subset \Sigma F$
.
Given an inclusion
![]() $\mathcal P \subseteq {\mathcal M}$
of finite von Neumann algebra, we define the quasi-normalizer
$\mathcal P \subseteq {\mathcal M}$
of finite von Neumann algebra, we define the quasi-normalizer
![]() $\mathscr {QN}_{{\mathcal M}}(\mathcal P)$
as the set of all elements
$\mathscr {QN}_{{\mathcal M}}(\mathcal P)$
as the set of all elements
![]() $x\in {\mathcal M}$
for which there exist
$x\in {\mathcal M}$
for which there exist
![]() $x_1,...,x_n\in {\mathcal M}$
, such that
$x_1,...,x_n\in {\mathcal M}$
, such that
![]() $\mathcal P x\subseteq \sum x_i \mathcal P$
and
$\mathcal P x\subseteq \sum x_i \mathcal P$
and
![]() $x\mathcal P \subseteq \sum \mathcal P x_i$
(see [Reference PopaPo99, Definition 4.8]). Also, the one-sided quasi-normalizer
$x\mathcal P \subseteq \sum \mathcal P x_i$
(see [Reference PopaPo99, Definition 4.8]). Also, the one-sided quasi-normalizer
![]() $\mathscr {QN}^{(1)}_{{\mathcal M}}(\mathcal P)$
is defined as the set of all elements
$\mathscr {QN}^{(1)}_{{\mathcal M}}(\mathcal P)$
is defined as the set of all elements
![]() $x\in {\mathcal M}$
for which there exist
$x\in {\mathcal M}$
for which there exist
![]() $x_1,...,x_n\in {\mathcal M}$
such that
$x_1,...,x_n\in {\mathcal M}$
such that
![]() $\mathcal P x\subseteq \sum x_i \mathcal P$
[Reference Fang, Gao and SmithFGS10]. We continue by recalling from [Reference PopaPo03, Reference Fang, Gao and SmithFGS10] some basic properties of (one-sided) quasi-normalizing algebras.
$\mathcal P x\subseteq \sum x_i \mathcal P$
[Reference Fang, Gao and SmithFGS10]. We continue by recalling from [Reference PopaPo03, Reference Fang, Gao and SmithFGS10] some basic properties of (one-sided) quasi-normalizing algebras.
Lemma 2.13 [Reference PopaPo03, Reference Fang, Gao and SmithFGS10].
Let
![]() $\mathcal P\subset {\mathcal M}$
be tracial von Neumann algebras. For any projection
$\mathcal P\subset {\mathcal M}$
be tracial von Neumann algebras. For any projection
![]() $p\in \mathcal P$
, the following hold:
$p\in \mathcal P$
, the following hold:
-
1.
 $W^*({\mathscr {QN}^{(1)}_{p{\mathcal M} p}}(p\mathcal P p))=pW^*(\mathrm {\mathscr {QN}^{(1)}_{{\mathcal M}}}(\mathcal P))p$
.
$W^*({\mathscr {QN}^{(1)}_{p{\mathcal M} p}}(p\mathcal P p))=pW^*(\mathrm {\mathscr {QN}^{(1)}_{{\mathcal M}}}(\mathcal P))p$
. -
2.
 $W^*({ \mathscr {QN}_{p{\mathcal M} p}}(p\mathcal P p))=pW^*(\mathrm {\mathscr {QN}_{M}}(\mathcal P))p$
.
$W^*({ \mathscr {QN}_{p{\mathcal M} p}}(p\mathcal P p))=pW^*(\mathrm {\mathscr {QN}_{M}}(\mathcal P))p$
.
We continue by recording the following remark, which can be deduced directly from the definition.
Remark 2.14. Let
![]() $\mathcal P\subset {\mathcal M}$
be tracial von Neumann algebras. For any projection
$\mathcal P\subset {\mathcal M}$
be tracial von Neumann algebras. For any projection
![]() ${p\in \mathcal P'\cap {\mathcal M}}$
, we have
${p\in \mathcal P'\cap {\mathcal M}}$
, we have
![]() $W^*(\mathrm {\mathscr {QN}_{p'{\mathcal M} p'}}(\mathcal P p'))=p'W^*(\mathrm { \mathscr {QN}_{{\mathcal M}}}(\mathcal P))p'$
.
$W^*(\mathrm {\mathscr {QN}_{p'{\mathcal M} p'}}(\mathcal P p'))=p'W^*(\mathrm { \mathscr {QN}_{{\mathcal M}}}(\mathcal P))p'$
.
Finally, we record the following result, which provides a relation between the group theoretical quasi-normalizer and the von Neumann algebraic one.
Lemma 2.15 (Corollary 5.2 in [Reference Fang, Gao and SmithFGS10]).
Let
![]() $\Sigma <\Gamma $
be countable groups. Then the following hold:
$\Sigma <\Gamma $
be countable groups. Then the following hold:
-
1.
 $W^*(\mathscr {QN}^{(1)}_{{\mathcal L}(\Gamma )}(\mathcal L(\Sigma )))=\mathcal L(K)$
, where
$W^*(\mathscr {QN}^{(1)}_{{\mathcal L}(\Gamma )}(\mathcal L(\Sigma )))=\mathcal L(K)$
, where
 $K<\Gamma $
is the subgroup generated by
$K<\Gamma $
is the subgroup generated by
 $\mathrm {QN}^{(1)}_\Gamma (\Sigma )$
. In particular, if
$\mathrm {QN}^{(1)}_\Gamma (\Sigma )$
. In particular, if
 $\mathrm { QN}^{(1)}_\Gamma (\Sigma )=\Sigma $
, then
$\mathrm { QN}^{(1)}_\Gamma (\Sigma )=\Sigma $
, then
 $\mathscr {QN}^{(1)}_{{\mathcal L}(\Gamma )}({\mathcal L}(\Sigma ))={\mathcal L}(\Sigma )$
.
$\mathscr {QN}^{(1)}_{{\mathcal L}(\Gamma )}({\mathcal L}(\Sigma ))={\mathcal L}(\Sigma )$
. -
2.
 $W^*(\mathscr {QN}_{{\mathcal L}(\Gamma )}({\mathcal L}(\Sigma )))=\mathcal L(\mathrm {QN}_\Gamma (\Sigma ))$
.
$W^*(\mathscr {QN}_{{\mathcal L}(\Gamma )}({\mathcal L}(\Sigma )))=\mathcal L(\mathrm {QN}_\Gamma (\Sigma ))$
.
For further use, we briefly recall some results from [Reference Chifan, Davis and DrimbeCDD22] that provide control of quasi-normalizers of certain von Neumann subalgebras in von Neumann algebras of general graph product groups.
Theorem 2.16 [Reference Chifan, Davis and DrimbeCDD22, Theorem 2.7].
Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups, and let
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups, and let
![]() $\mathscr {S},\mathscr {T}\subseteq \mathscr {G}$
be any subgraphs. Denote by
$\mathscr {S},\mathscr {T}\subseteq \mathscr {G}$
be any subgraphs. Denote by
![]() ${\mathcal M}= {\mathcal L}(\Gamma )$
, and assume there exist
${\mathcal M}= {\mathcal L}(\Gamma )$
, and assume there exist
![]() $x,x_1,x_2,...,x_n \in {\mathcal M}$
, such that
$x,x_1,x_2,...,x_n \in {\mathcal M}$
, such that
![]() ${\mathcal L}(\Gamma _{\mathscr {S}})x\subseteq \sum ^n_{k=1} x_k \mathcal L(\Gamma _{\mathscr {T}})$
. Then
${\mathcal L}(\Gamma _{\mathscr {S}})x\subseteq \sum ^n_{k=1} x_k \mathcal L(\Gamma _{\mathscr {T}})$
. Then
![]() $\mathscr {S}\subseteq \mathscr {T}$
and
$\mathscr {S}\subseteq \mathscr {T}$
and
![]() $x\in \mathcal L(\Gamma _{\mathscr {T} \cup \mathrm {lk}(\mathscr {S}) })$
.
$x\in \mathcal L(\Gamma _{\mathscr {T} \cup \mathrm {lk}(\mathscr {S}) })$
.
Corollary 2.17. Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups, and let
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be any graph product of groups, and let
![]() $\mathscr {C}\in \mathrm {cliq}( \mathscr {G})$
be a clique with at least two vertices. Fix a vertex
$\mathscr {C}\in \mathrm {cliq}( \mathscr {G})$
be a clique with at least two vertices. Fix a vertex
![]() $v\in \mathscr {C}$
, such that
$v\in \mathscr {C}$
, such that
![]() $\mathrm {lk}(\mathscr {C} \setminus \{v\})=\{v\}$
. Denote by
$\mathrm {lk}(\mathscr {C} \setminus \{v\})=\{v\}$
. Denote by
![]() ${\mathcal M}= {\mathcal L}(\Gamma )$
, and assume there exist
${\mathcal M}= {\mathcal L}(\Gamma )$
, and assume there exist
![]() $x,x_1,x_2,...,x_n \in {\mathcal M}$
, such that
$x,x_1,x_2,...,x_n \in {\mathcal M}$
, such that
![]() $\mathcal L(\Gamma _{\mathscr {C} \setminus \{v\}})x\subseteq \sum ^n_{k=1} x_k {\mathcal L}(\Gamma _{\mathscr {C}})$
. Then
$\mathcal L(\Gamma _{\mathscr {C} \setminus \{v\}})x\subseteq \sum ^n_{k=1} x_k {\mathcal L}(\Gamma _{\mathscr {C}})$
. Then
![]() $x\in {\mathcal L}(\Gamma _{\mathscr {C} })$
.
$x\in {\mathcal L}(\Gamma _{\mathscr {C} })$
.
Proof. Follows applying Theorem 2.16 for
![]() $\mathscr {S} =\mathscr {C} \setminus \{v\} $
and
$\mathscr {S} =\mathscr {C} \setminus \{v\} $
and
![]() $\mathscr {T} =\mathscr {C}$
.
$\mathscr {T} =\mathscr {C}$
.
Lemma 2.18 [Reference Chifan, Davis and DrimbeCDD22, Lemma 2.9].
Let
![]() $\Gamma =\mathscr {G} \{\Gamma _v\}$
be a graph product of groups, and let
$\Gamma =\mathscr {G} \{\Gamma _v\}$
be a graph product of groups, and let
![]() $\mathscr {C}\in \mathrm {cliq}(\mathscr {G})$
be a clique. Let
$\mathscr {C}\in \mathrm {cliq}(\mathscr {G})$
be a clique. Let
![]() $\mathcal P\subset p{\mathcal L}(\Gamma _{\mathscr {C}})p$
be a von Neumann subalgebra, such that
$\mathcal P\subset p{\mathcal L}(\Gamma _{\mathscr {C}})p$
be a von Neumann subalgebra, such that
![]() $\mathcal P\nprec _{{\mathcal L}(\Gamma _{\mathscr {C}})} L(\Gamma _{\mathscr {C} \setminus \{v\}})$
, for any
$\mathcal P\nprec _{{\mathcal L}(\Gamma _{\mathscr {C}})} L(\Gamma _{\mathscr {C} \setminus \{v\}})$
, for any
![]() $v\in \mathscr {C}$
. If
$v\in \mathscr {C}$
. If
![]() $x\in {\mathcal L}(\Gamma )$
satisfies
$x\in {\mathcal L}(\Gamma )$
satisfies
![]() $x\mathcal P\subset \sum _{i=1}^n {\mathcal L}(\Gamma _{\mathscr {C}})x_i$
for some
$x\mathcal P\subset \sum _{i=1}^n {\mathcal L}(\Gamma _{\mathscr {C}})x_i$
for some
![]() $x_1,\dots ,x_n\in {\mathcal L}(\Gamma )$
, then
$x_1,\dots ,x_n\in {\mathcal L}(\Gamma )$
, then
![]() $xp\in {\mathcal L}(\Gamma _{\mathscr {C}})$
.
$xp\in {\mathcal L}(\Gamma _{\mathscr {C}})$
.
3 A version of Popa-Vaes dichotomy for normalizers of subalgebras in crossed-product von Neumann algebras
In [Reference Popa and VaesPV12, Theorem 1.4], Popa and Vaes established a remarkably deep dichotomy for normalizers of von Neumann subalgebras in crossed-product von Neumann algebras,
![]() ${\mathcal A\rtimes \Gamma} $
, arising from trace preserving actions
${\mathcal A\rtimes \Gamma} $
, arising from trace preserving actions
![]() $\Gamma \curvearrowright {\mathcal D}$
of biexact weakly amenable groups
$\Gamma \curvearrowright {\mathcal D}$
of biexact weakly amenable groups
![]() $\Gamma $
on tracial von Neumann algebras
$\Gamma $
on tracial von Neumann algebras
![]() ${\mathcal D}$
. For further use, we present, next, a version of this result for actions of groups which surject onto biexact, weakly amenable groups.
${\mathcal D}$
. For further use, we present, next, a version of this result for actions of groups which surject onto biexact, weakly amenable groups.
Theorem 3.1. Let
![]() $\Sigma $
be a biexact weakly amenable group, and let
$\Sigma $
be a biexact weakly amenable group, and let
![]() $\Gamma $
be a group which admits an epimorphism
$\Gamma $
be a group which admits an epimorphism
![]() $\varepsilon : \Gamma \rightarrow \Sigma $
. Let
$\varepsilon : \Gamma \rightarrow \Sigma $
. Let
![]() ${\mathcal D}$
be a tracial von Neumann algebra, and let
${\mathcal D}$
be a tracial von Neumann algebra, and let
![]() $\Gamma \curvearrowright ^{\sigma } {\mathcal D}$
be a trace-preserving action. Denote by
$\Gamma \curvearrowright ^{\sigma } {\mathcal D}$
be a trace-preserving action. Denote by
![]() ${\mathcal M} ={\mathcal D} \rtimes _{\sigma } \Gamma $
the corresponding crossed-product von Neumann algebra, and let
${\mathcal M} ={\mathcal D} \rtimes _{\sigma } \Gamma $
the corresponding crossed-product von Neumann algebra, and let
![]() $0\neq p\in {\mathcal M}$
be a projection. Then, for any von Neumann subalgebra
$0\neq p\in {\mathcal M}$
be a projection. Then, for any von Neumann subalgebra
![]() $\mathcal P \subset p{\mathcal M} p$
that is amenable relative to
$\mathcal P \subset p{\mathcal M} p$
that is amenable relative to
![]() ${\mathcal D}$
inside
${\mathcal D}$
inside
![]() ${\mathcal M}$
, one of the following must hold:
${\mathcal M}$
, one of the following must hold:
-
1.
 $\mathcal P \prec _{\mathcal M} {\mathcal D}\rtimes \ker (\varepsilon )$
, or
$\mathcal P \prec _{\mathcal M} {\mathcal D}\rtimes \ker (\varepsilon )$
, or -
2.
 $\mathscr N_{p{\mathcal M} p}(\mathcal P)"$
is amenable relative to
$\mathscr N_{p{\mathcal M} p}(\mathcal P)"$
is amenable relative to
 ${\mathcal D}\rtimes \ker (\varepsilon ) $
inside
${\mathcal D}\rtimes \ker (\varepsilon ) $
inside
 ${\mathcal M}$
.
${\mathcal M}$
.
Proof. Denote
![]() $\mathcal {Q}=\mathscr N_{p{\mathcal M} p}(\mathcal P)"$
. Following [Reference Chifan, Ioana and KidaCIK13, Section 3], consider the
$\mathcal {Q}=\mathscr N_{p{\mathcal M} p}(\mathcal P)"$
. Following [Reference Chifan, Ioana and KidaCIK13, Section 3], consider the
![]() $\ast $
-embedding
$\ast $
-embedding
![]() $\Delta : {\mathcal M} \rightarrow {\mathcal M} \bar \otimes {\mathcal L}(\Sigma )$
given by
$\Delta : {\mathcal M} \rightarrow {\mathcal M} \bar \otimes {\mathcal L}(\Sigma )$
given by
![]() $\Delta (au_g)=(au_g) \otimes v_{\varepsilon (g)}$
for all
$\Delta (au_g)=(au_g) \otimes v_{\varepsilon (g)}$
for all
![]() $a\in {\mathcal D}$
and
$a\in {\mathcal D}$
and
![]() $g\in \Gamma $
, where
$g\in \Gamma $
, where
![]() $(v_g)_{g\in \Gamma }$
are the canonical group unitaries in
$(v_g)_{g\in \Gamma }$
are the canonical group unitaries in
![]() ${\mathcal L}(\Sigma )$
. Then, using [Reference Popa and VaesPV12, Theorem 1.4], one of the following must hold:
${\mathcal L}(\Sigma )$
. Then, using [Reference Popa and VaesPV12, Theorem 1.4], one of the following must hold:
-
a)
 $\Delta (\mathcal P)\prec _{{\mathcal M}\bar \otimes {\mathcal L}(\Sigma )} {\mathcal M}\otimes 1$
, or
$\Delta (\mathcal P)\prec _{{\mathcal M}\bar \otimes {\mathcal L}(\Sigma )} {\mathcal M}\otimes 1$
, or -
b)
 $\Delta (\mathcal {Q})$
is amenable relative to
$\Delta (\mathcal {Q})$
is amenable relative to
 ${\mathcal M} \otimes 1$
inside
${\mathcal M} \otimes 1$
inside
 ${\mathcal M}\bar \otimes {\mathcal L}(\Sigma )$
.
${\mathcal M}\bar \otimes {\mathcal L}(\Sigma )$
.
Using [Reference Chifan, Ioana and KidaCIK13, Proposition 3.4], one can see that case a) implies 1. Moreover, using Proposition 2.12, case b) yields 2.
4 Solidity results for von Neumann algebras of wreath-like product groups
We start this section by recording the following result, which follows from Popa and Vaes’s structure theorem [Reference Popa and VaesPV12, Theorem 1.4] for normalizers inside crossed products of hyperbolic groups, as in [Reference Chifan, Ioana and KidaCIK13].
Proposition 4.1. Let
![]() $\Gamma \in \mathcal W\mathcal R (A, B \curvearrowright I)$
, where A is Abelian and B is a subgroup of a hyperbolic group. Let
$\Gamma \in \mathcal W\mathcal R (A, B \curvearrowright I)$
, where A is Abelian and B is a subgroup of a hyperbolic group. Let
![]() $\Gamma \curvearrowright {\mathcal D}$
be a trace preserving action, and denote
$\Gamma \curvearrowright {\mathcal D}$
be a trace preserving action, and denote
![]() ${\mathcal M}={\mathcal D}\rtimes \Gamma .$
Let
${\mathcal M}={\mathcal D}\rtimes \Gamma .$
Let
![]() $\mathcal A,\mathcal B\subset p {\mathcal M} p$
be commuting von Neumann subalgebras.
$\mathcal A,\mathcal B\subset p {\mathcal M} p$
be commuting von Neumann subalgebras.
Then, either
![]() $\mathcal A\prec _{{\mathcal M}} {\mathcal D}\rtimes A^{I}$
or
$\mathcal A\prec _{{\mathcal M}} {\mathcal D}\rtimes A^{I}$
or
![]() $\mathcal B$
is amenable relative to
$\mathcal B$
is amenable relative to
![]() ${\mathcal D}$
inside
${\mathcal D}$
inside
![]() ${\mathcal M}$
.
${\mathcal M}$
.
Proof. Let
![]() $\varepsilon :\Gamma \to B$
be the quotient homomorphism given by
$\varepsilon :\Gamma \to B$
be the quotient homomorphism given by
![]() $\Gamma \in \mathcal W\mathcal R (A, B \curvearrowright I)$
, and let
$\Gamma \in \mathcal W\mathcal R (A, B \curvearrowright I)$
, and let
![]() $\{u_g\}_{g\in \Gamma }$
and
$\{u_g\}_{g\in \Gamma }$
and
![]() $\{v_h\}_{h\in B}$
be the canonical generating unitaries of
$\{v_h\}_{h\in B}$
be the canonical generating unitaries of
![]() ${\mathcal L}(\Gamma )$
and
${\mathcal L}(\Gamma )$
and
![]() ${\mathcal L}(B)$
, respectively. Denote by
${\mathcal L}(B)$
, respectively. Denote by
![]() $\Delta :{\mathcal M}\to {\mathcal M}\bar \otimes \mathcal L(B)$
the
$\Delta :{\mathcal M}\to {\mathcal M}\bar \otimes \mathcal L(B)$
the
![]() $*$
-homomorphism given by
$*$
-homomorphism given by
![]() $\Delta (au_g)=au_g\otimes v_{\varepsilon (g)}$
, for all
$\Delta (au_g)=au_g\otimes v_{\varepsilon (g)}$
, for all
![]() $a\in {\mathcal D},g\in \Gamma $
. From [Reference Krogager and VaesKV15, Lemma 5.2], we derive that either
$a\in {\mathcal D},g\in \Gamma $
. From [Reference Krogager and VaesKV15, Lemma 5.2], we derive that either
![]() $\Delta (\mathcal A)\prec _{{\mathcal M}\bar \otimes {\mathcal L}(B)} {\mathcal M}\otimes 1$
or
$\Delta (\mathcal A)\prec _{{\mathcal M}\bar \otimes {\mathcal L}(B)} {\mathcal M}\otimes 1$
or
![]() $\Delta (\mathcal B)$
is amenable relative to
$\Delta (\mathcal B)$
is amenable relative to
![]() ${\mathcal M}\bar \otimes 1$
. The first possibility implies by [Reference Chifan, Ioana and KidaCIK13, Proposition 3.4] that
${\mathcal M}\bar \otimes 1$
. The first possibility implies by [Reference Chifan, Ioana and KidaCIK13, Proposition 3.4] that
![]() $\mathcal A\prec _{{\mathcal M}} {\mathcal D}\rtimes A^{I}$
, while the second one implies by Proposition 2.12 that
$\mathcal A\prec _{{\mathcal M}} {\mathcal D}\rtimes A^{I}$
, while the second one implies by Proposition 2.12 that
![]() $\mathcal B$
is amenable relative to
$\mathcal B$
is amenable relative to
![]() ${\mathcal D}\rtimes A^{I}$
inside
${\mathcal D}\rtimes A^{I}$
inside
![]() ${\mathcal M}$
. Since A is amenable, the conclusion follows from [Reference Ozawa and PopaOP07, Proposition 2.4].
${\mathcal M}$
. Since A is amenable, the conclusion follows from [Reference Ozawa and PopaOP07, Proposition 2.4].
We recall that a II
![]() $_1$
factor
$_1$
factor
![]() ${\mathcal M}$
is called solid if for any projection
${\mathcal M}$
is called solid if for any projection
![]() $p\in {\mathcal M}$
and any diffuse von Neumann subalgebra
$p\in {\mathcal M}$
and any diffuse von Neumann subalgebra
![]() $\mathcal A \subset p {\mathcal M} p$
the relative commutant
$\mathcal A \subset p {\mathcal M} p$
the relative commutant
![]() $\mathcal A'\cap p{\mathcal M} p$
is amenable. We note that if
$\mathcal A'\cap p{\mathcal M} p$
is amenable. We note that if
![]() ${\mathcal M}$
is solid, then any amplification
${\mathcal M}$
is solid, then any amplification
![]() ${\mathcal M}^t$
, where
${\mathcal M}^t$
, where
![]() $t>0$
, is also solid.
$t>0$
, is also solid.
Theorem 4.2. Let
![]() $\Gamma \in \mathcal W\mathcal R (A, B \curvearrowright I)$
where A is Abelian, B is a subgroup of a hyperbolic group and the action
$\Gamma \in \mathcal W\mathcal R (A, B \curvearrowright I)$
where A is Abelian, B is a subgroup of a hyperbolic group and the action
![]() $B\curvearrowright I$
has amenable stabilizers. Then
$B\curvearrowright I$
has amenable stabilizers. Then
![]() ${\mathcal L}(\Gamma )$
is solid.
${\mathcal L}(\Gamma )$
is solid.
Proof. Let
![]() $\mathcal A \subset p{\mathcal L}(\Gamma )p$
be a diffuse von Neumann subalgebra, and assume by contradiction that
$\mathcal A \subset p{\mathcal L}(\Gamma )p$
be a diffuse von Neumann subalgebra, and assume by contradiction that
![]() $\mathcal B:=\mathcal A'\cap p{\mathcal L}(\Gamma )p$
is nonamenable. Thus, there exists a nonzero projection
$\mathcal B:=\mathcal A'\cap p{\mathcal L}(\Gamma )p$
is nonamenable. Thus, there exists a nonzero projection
![]() ${z\in \mathcal Z(\mathcal B)}$
, such that
${z\in \mathcal Z(\mathcal B)}$
, such that
![]() $ q \mathcal B q$
is nonamenable for every projection
$ q \mathcal B q$
is nonamenable for every projection
![]() $q \in \mathcal B z$
. By applying Proposition 4.1, we deduce that
$q \in \mathcal B z$
. By applying Proposition 4.1, we deduce that
![]() $\mathcal A z\prec ^s_{{\mathcal L}(\Gamma )} {\mathcal L}(A^{I})$
, and hence, by using [Reference Chifan, Ioana, Osin and SunCIOS21, Corollary 4.7] (for
$\mathcal A z\prec ^s_{{\mathcal L}(\Gamma )} {\mathcal L}(A^{I})$
, and hence, by using [Reference Chifan, Ioana, Osin and SunCIOS21, Corollary 4.7] (for
![]() $m=1$
) and also [Reference Chifan, Ioana, Osin and SunCIOS21, Lemma 4.11], we get that
$m=1$
) and also [Reference Chifan, Ioana, Osin and SunCIOS21, Lemma 4.11], we get that
![]() $\mathcal B z$
is amenable, contradiction.
$\mathcal B z$
is amenable, contradiction.
Remark 4.3. Notice that this result generalizes some of the results obtained in [Reference Chifan, Ioana, Osin and SunCIOS21, Section 9.2].
Proposition 4.4. For any
![]() $1\leq i\leq n$
, we consider
$1\leq i\leq n$
, we consider
![]() $\Gamma _i\in \mathcal W\mathcal R (A_i, B_i \curvearrowright I_i)$
where
$\Gamma _i\in \mathcal W\mathcal R (A_i, B_i \curvearrowright I_i)$
where
![]() $A_i$
is Abelian,
$A_i$
is Abelian,
![]() $B_i$
is a subgroup of a hyperbolic group and denote
$B_i$
is a subgroup of a hyperbolic group and denote
![]() $\Gamma = \Gamma _1\times \cdots \times \Gamma _n$
. Let
$\Gamma = \Gamma _1\times \cdots \times \Gamma _n$
. Let
![]() $\Lambda $
be a countable group, and denote
$\Lambda $
be a countable group, and denote
![]() ${\mathcal M}={\mathcal L}(\Lambda )$
. Assume that
${\mathcal M}={\mathcal L}(\Lambda )$
. Assume that
![]() ${\mathcal L}(\Gamma )\subset {\mathcal M}$
is a von Neumann subalgebra.
${\mathcal L}(\Gamma )\subset {\mathcal M}$
is a von Neumann subalgebra.
Let
![]() $\mathcal P_1,\dots ,\mathcal P_{m}\subset p{\mathcal M} p$
be commuting nonamenable factors and
$\mathcal P_1,\dots ,\mathcal P_{m}\subset p{\mathcal M} p$
be commuting nonamenable factors and
![]() $\Lambda _0<\Lambda $
a subgroup, such that
$\Lambda _0<\Lambda $
a subgroup, such that
![]() $\mathcal P_1\vee \dots \vee \mathcal P_{m}\prec _{{\mathcal M}} {\mathcal L}(\Lambda _0)$
and
$\mathcal P_1\vee \dots \vee \mathcal P_{m}\prec _{{\mathcal M}} {\mathcal L}(\Lambda _0)$
and
![]() $\mathcal L(\Lambda _0)\prec _{{\mathcal M}} \mathcal L(\Gamma _1\times \dots \times \Gamma _n)$
. Then,
$\mathcal L(\Lambda _0)\prec _{{\mathcal M}} \mathcal L(\Gamma _1\times \dots \times \Gamma _n)$
. Then,
![]() $m\leq n$
.
$m\leq n$
.
Throughout the proof, we use the following notation. If
![]() $\mathcal P\subset p{\mathcal M} p, \mathcal {Q}\subset q {\mathcal M} q$
are subalgebras, such that
$\mathcal P\subset p{\mathcal M} p, \mathcal {Q}\subset q {\mathcal M} q$
are subalgebras, such that
![]() $\mathcal P\prec _{{\mathcal M}} \mathcal {Q} q'$
, for all projections
$\mathcal P\prec _{{\mathcal M}} \mathcal {Q} q'$
, for all projections
![]() $0\neq q'\in \mathcal {Q}'\cap q{\mathcal M} q$
, we write
$0\neq q'\in \mathcal {Q}'\cap q{\mathcal M} q$
, we write
![]() $\mathcal P\prec _{{\mathcal M}}^{s'} \mathcal {Q}$
.
$\mathcal P\prec _{{\mathcal M}}^{s'} \mathcal {Q}$
.
Proof. Denote
![]() $\Gamma =\Gamma _1\times \dots \times \Gamma _n$
and
$\Gamma =\Gamma _1\times \dots \times \Gamma _n$
and
![]() $\mathcal P=\mathcal P_1\vee \dots \vee \mathcal P_{m}$
. Following the augmentation technique from [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Section 3], we consider a Bernoulli action with Abelian base
$\mathcal P=\mathcal P_1\vee \dots \vee \mathcal P_{m}$
. Following the augmentation technique from [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Section 3], we consider a Bernoulli action with Abelian base
![]() $\Lambda \curvearrowright {\mathcal D}^\Lambda $
, and let
$\Lambda \curvearrowright {\mathcal D}^\Lambda $
, and let
![]() $\tilde {\mathcal M}={\mathcal D}^\Lambda \rtimes \Lambda $
. Let
$\tilde {\mathcal M}={\mathcal D}^\Lambda \rtimes \Lambda $
. Let
![]() $\Delta :\tilde {{\mathcal M}}\to \tilde {{\mathcal M}}\bar \otimes {\mathcal M}$
be the
$\Delta :\tilde {{\mathcal M}}\to \tilde {{\mathcal M}}\bar \otimes {\mathcal M}$
be the
![]() $*$
-homomorphism given by
$*$
-homomorphism given by
![]() $\Delta (dv_h)=dv_h\otimes v_h$
, for all
$\Delta (dv_h)=dv_h\otimes v_h$
, for all
![]() $d\in {\mathcal D}^\Lambda , h\in \Lambda $
. The assumption implies that
$d\in {\mathcal D}^\Lambda , h\in \Lambda $
. The assumption implies that
![]() $\mathcal P\prec ^{s'}_{\tilde {\mathcal M}} {\mathcal D}^\Lambda \rtimes \Lambda _0$
, and hence, by applying [Reference DrimbeDr19b, Lemma 2.3], we get that
$\mathcal P\prec ^{s'}_{\tilde {\mathcal M}} {\mathcal D}^\Lambda \rtimes \Lambda _0$
, and hence, by applying [Reference DrimbeDr19b, Lemma 2.3], we get that
![]() $\Delta (\mathcal P)\prec _{\tilde {\mathcal M}\bar \otimes {\mathcal M}}^{s'} \tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Lambda _0)$
. Next, from [Reference DrimbeDr19b, Lemma 2.4(2)], we derive that
$\Delta (\mathcal P)\prec _{\tilde {\mathcal M}\bar \otimes {\mathcal M}}^{s'} \tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Lambda _0)$
. Next, from [Reference DrimbeDr19b, Lemma 2.4(2)], we derive that
![]() $\Delta (\mathcal P)\prec _{\tilde {\mathcal M}\bar \otimes {\mathcal M}} \tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )$
.
$\Delta (\mathcal P)\prec _{\tilde {\mathcal M}\bar \otimes {\mathcal M}} \tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )$
.
Thus, there exist projections
![]() $r\in \mathcal P, q\in \tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )$
, a nonzero partial isometry
$r\in \mathcal P, q\in \tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )$
, a nonzero partial isometry
![]() ${v\in q(\tilde {{\mathcal M}}\bar \otimes {\mathcal M})\Delta (r)}$
and a
${v\in q(\tilde {{\mathcal M}}\bar \otimes {\mathcal M})\Delta (r)}$
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\theta : \Delta (r\mathcal P r)\to q (\tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )) q$
, such that
$\theta : \Delta (r\mathcal P r)\to q (\tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )) q$
, such that
![]() $\theta (x)v=vx$
, for any
$\theta (x)v=vx$
, for any
![]() $x\in \Delta (rPr)$
, and the support projection of
$x\in \Delta (rPr)$
, and the support projection of
![]() $E_{\tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )}(vv^*)$
equals q. Using [Reference Chifan, de Santiago and SucpikarnonCdSS17, Lemma 4.5], we can assume that
$E_{\tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )}(vv^*)$
equals q. Using [Reference Chifan, de Santiago and SucpikarnonCdSS17, Lemma 4.5], we can assume that
![]() $r\in \mathcal P_1$
. Denote
$r\in \mathcal P_1$
. Denote
![]() $\mathcal N=\tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )$
and
$\mathcal N=\tilde {{\mathcal M}} \bar \otimes {\mathcal L}(\Gamma )$
and
![]() $\mathcal {Q}_i=\Delta (r\mathcal P_i r)$
for any
$\mathcal {Q}_i=\Delta (r\mathcal P_i r)$
for any
![]() $1\leq i\leq m$
. From [Reference Ioana, Popa and VaesIPV10, Lemma 10.2], it follows that
$1\leq i\leq m$
. From [Reference Ioana, Popa and VaesIPV10, Lemma 10.2], it follows that
![]() $\Delta (\mathcal P_i)$
is strongly nonamenable relative to
$\Delta (\mathcal P_i)$
is strongly nonamenable relative to
![]() $\tilde {{\mathcal M}}\otimes 1$
inside
$\tilde {{\mathcal M}}\otimes 1$
inside
![]() $\tilde {{\mathcal M}}\bar \otimes {\mathcal M}$
, for any
$\tilde {{\mathcal M}}\bar \otimes {\mathcal M}$
, for any
![]() $1\leq i\leq m$
. Therefore,
$1\leq i\leq m$
. Therefore,
![]() $\mathcal {Q}_i$
is nonamenable relative to
$\mathcal {Q}_i$
is nonamenable relative to
![]() $\tilde {{\mathcal M}}\otimes 1$
inside
$\tilde {{\mathcal M}}\otimes 1$
inside
![]() $\mathcal N$
for any
$\mathcal N$
for any
![]() $1\leq i\leq m$
. In particular, we derive from [Reference Popa and VaesPV11, Proposition 2.7] that there exists
$1\leq i\leq m$
. In particular, we derive from [Reference Popa and VaesPV11, Proposition 2.7] that there exists
![]() $1\leq j\leq n$
, such that
$1\leq j\leq n$
, such that
![]() $\mathcal {Q}_m$
is nonamenable relative to
$\mathcal {Q}_m$
is nonamenable relative to
![]() $\tilde {{\mathcal M}}\otimes {\mathcal L}(\Gamma _{\widehat {j}})$
inside
$\tilde {{\mathcal M}}\otimes {\mathcal L}(\Gamma _{\widehat {j}})$
inside
![]() $\mathcal N$
. Without loss of generality, we may assume that
$\mathcal N$
. Without loss of generality, we may assume that
![]() $j=n$
. By applying Proposition 4.1, it follows that
$j=n$
. By applying Proposition 4.1, it follows that
![]() $\bigvee _{i=1}^{m-1} Q_i\prec _{\mathcal N} \tilde {{\mathcal M}}\otimes \mathcal L(\Gamma _{\widehat {n}}\times A_{n}),$
where
$\bigvee _{i=1}^{m-1} Q_i\prec _{\mathcal N} \tilde {{\mathcal M}}\otimes \mathcal L(\Gamma _{\widehat {n}}\times A_{n}),$
where
![]() $A_n<\Gamma _{n}$
is an amenable subgroup. Thus,
$A_n<\Gamma _{n}$
is an amenable subgroup. Thus,
![]() $ \Delta (\bigvee _{i=1}^{m-1} \mathcal P_i)\prec _{\tilde {{\mathcal M}}\bar \otimes {\mathcal M}} \tilde {{\mathcal M}}\bar \otimes {\mathcal L}(\Gamma _{\widehat {n}}\times A_{n}). $
$ \Delta (\bigvee _{i=1}^{m-1} \mathcal P_i)\prec _{\tilde {{\mathcal M}}\bar \otimes {\mathcal M}} \tilde {{\mathcal M}}\bar \otimes {\mathcal L}(\Gamma _{\widehat {n}}\times A_{n}). $
Assume, by contradiction, that
![]() $m>n$
. By repeating the previous argument finitely many times, we obtain that there exists an amenable subgroup
$m>n$
. By repeating the previous argument finitely many times, we obtain that there exists an amenable subgroup
![]() $A<\Gamma $
with the property that
$A<\Gamma $
with the property that
![]() $\Delta (\bigvee _{i=1}^{m-n} \mathcal P_i)\prec _{\tilde {{\mathcal M}}\bar \otimes {\mathcal M}}\tilde {{\mathcal M}}\bar \otimes {\mathcal L}(A)$
. By applying [Reference Ioana, Popa and VaesIPV10, Lemma 10.2], it follows that
$\Delta (\bigvee _{i=1}^{m-n} \mathcal P_i)\prec _{\tilde {{\mathcal M}}\bar \otimes {\mathcal M}}\tilde {{\mathcal M}}\bar \otimes {\mathcal L}(A)$
. By applying [Reference Ioana, Popa and VaesIPV10, Lemma 10.2], it follows that
![]() $\mathcal P_1$
is amenable, contradiction.
$\mathcal P_1$
is amenable, contradiction.
Proposition 4.5. For any
![]() $1\leq i\leq n$
, we consider
$1\leq i\leq n$
, we consider
![]() $\Gamma _i\in \mathcal W\mathcal R (A_i, B_i \curvearrowright I_i)$
where
$\Gamma _i\in \mathcal W\mathcal R (A_i, B_i \curvearrowright I_i)$
where
![]() $A_i$
is Abelian,
$A_i$
is Abelian,
![]() $B_i$
is a subgroup of a hyperbolic group and denote
$B_i$
is a subgroup of a hyperbolic group and denote
![]() $\Gamma = \Gamma _1\times \cdots \times \Gamma _n$
. Let
$\Gamma = \Gamma _1\times \cdots \times \Gamma _n$
. Let
![]() $\mathcal P_0,\mathcal P_1,..., \mathcal P_n\subseteq p {\mathcal L}(\Gamma ) p$
be commuting von Neumann subalgebras, such that
$\mathcal P_0,\mathcal P_1,..., \mathcal P_n\subseteq p {\mathcal L}(\Gamma ) p$
be commuting von Neumann subalgebras, such that
![]() $\mathcal P_n$
has no amenable direct summand and
$\mathcal P_n$
has no amenable direct summand and
![]() $\mathcal P_i$
is a nonamenable factor for any
$\mathcal P_i$
is a nonamenable factor for any
![]() $1\leq i\leq n-1$
.
$1\leq i\leq n-1$
.
Then
![]() $\mathcal P_0$
is completely atomic.
$\mathcal P_0$
is completely atomic.
Proof. Throughout the proof, we denote by
![]() $\Gamma _S=\times _{i\in S}\Gamma _i$
the subproduct supported on a subset
$\Gamma _S=\times _{i\in S}\Gamma _i$
the subproduct supported on a subset
![]() $S\subset \{1,\dots , n\}$
. We also denote by
$S\subset \{1,\dots , n\}$
. We also denote by
![]() $\widehat S$
the complement of S inside
$\widehat S$
the complement of S inside
![]() $\{1,\dots , n\}$
. Denote
$\{1,\dots , n\}$
. Denote
![]() ${\mathcal M}={\mathcal L}(\Gamma )$
. Since
${\mathcal M}={\mathcal L}(\Gamma )$
. Since
![]() $\mathcal P_n$
has no amenable direct summand, it follows that
$\mathcal P_n$
has no amenable direct summand, it follows that
![]() $\mathcal P_n z$
is nonamenable for any nonzero projection
$\mathcal P_n z$
is nonamenable for any nonzero projection
![]() $z\in (\bigvee _{i=0}^n \mathcal P_i)'\cap pMp$
. By [Reference Popa and VaesPV11, Proposition 2.7], we get that there exists
$z\in (\bigvee _{i=0}^n \mathcal P_i)'\cap pMp$
. By [Reference Popa and VaesPV11, Proposition 2.7], we get that there exists
![]() $1\leq j\leq n$
, such that
$1\leq j\leq n$
, such that
![]() $\mathcal P_n z$
is nonamenable relative to
$\mathcal P_n z$
is nonamenable relative to
![]() ${\mathcal L}(\Gamma _{\widehat j})$
inside
${\mathcal L}(\Gamma _{\widehat j})$
inside
![]() ${\mathcal M}$
. Without loss of generalization, assume
${\mathcal M}$
. Without loss of generalization, assume
![]() $j=n$
. Using Proposition 4.1, we get that
$j=n$
. Using Proposition 4.1, we get that
![]() $(\bigvee _{i=0}^{n-1} \mathcal P_i)z\prec _{{\mathcal M}} {\mathcal L}(\Gamma _{\widehat n})\bar \otimes {\mathcal L}(A_n^{(I_n)})$
. Thus, there exist projections
$(\bigvee _{i=0}^{n-1} \mathcal P_i)z\prec _{{\mathcal M}} {\mathcal L}(\Gamma _{\widehat n})\bar \otimes {\mathcal L}(A_n^{(I_n)})$
. Thus, there exist projections
![]() $r\in \bigvee _{i=0}^{n-1} \mathcal P_i, q\in {\mathcal L}(\Gamma _{\widehat n})\bar \otimes \mathcal L(A_n^{(I_n)})$
with
$r\in \bigvee _{i=0}^{n-1} \mathcal P_i, q\in {\mathcal L}(\Gamma _{\widehat n})\bar \otimes \mathcal L(A_n^{(I_n)})$
with
![]() $rz\neq 0$
, a nonzero partial isometry
$rz\neq 0$
, a nonzero partial isometry
![]() $v\in q{\mathcal M} r$
and a
$v\in q{\mathcal M} r$
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\theta : r(\bigvee _{i=0}^{n-1} \mathcal P_i)rz \to q({\mathcal L}(\Gamma _{\widehat n})\bar \otimes \mathcal L(A_n^{(I_n)}))q$
, such that
$\theta : r(\bigvee _{i=0}^{n-1} \mathcal P_i)rz \to q({\mathcal L}(\Gamma _{\widehat n})\bar \otimes \mathcal L(A_n^{(I_n)}))q$
, such that
![]() $\theta (x)v=vx$
and the support projection of
$\theta (x)v=vx$
and the support projection of
![]() $E_{\mathcal L(\Gamma _{\widehat n})\bar \otimes \mathcal L(A_n^{(I_n)})}(vv^*)$
equals q. Since
$E_{\mathcal L(\Gamma _{\widehat n})\bar \otimes \mathcal L(A_n^{(I_n)})}(vv^*)$
equals q. Since
![]() $\mathcal P_{n-1}$
is a II
$\mathcal P_{n-1}$
is a II
![]() $_1$
factor, by using [Reference Chifan, de Santiago and SucpikarnonCdSS17, Lemma 4.5], we can assume that
$_1$
factor, by using [Reference Chifan, de Santiago and SucpikarnonCdSS17, Lemma 4.5], we can assume that
![]() $r\in \mathcal P_{n-1}$
. Denote
$r\in \mathcal P_{n-1}$
. Denote
![]() $\mathcal N=q({\mathcal L}(\Gamma _{\widehat n})\bar \otimes {\mathcal L}(A_n^{(I_n)}))q$
and
$\mathcal N=q({\mathcal L}(\Gamma _{\widehat n})\bar \otimes {\mathcal L}(A_n^{(I_n)}))q$
and
![]() $\mathcal {Q}_i=\theta (r\mathcal P_irz)$
for any
$\mathcal {Q}_i=\theta (r\mathcal P_irz)$
for any
![]() $0\leq i\leq n-1$
. Since
$0\leq i\leq n-1$
. Since
![]() $\mathcal {Q}_{n-1}$
is nonamenable, we use [Reference Popa and VaesPV11, Proposition 2.7] and derive that exists
$\mathcal {Q}_{n-1}$
is nonamenable, we use [Reference Popa and VaesPV11, Proposition 2.7] and derive that exists
![]() $1\leq k\leq n-1$
, such that
$1\leq k\leq n-1$
, such that
![]() $\mathcal {Q}_{n-1}$
is nonamenable relative to
$\mathcal {Q}_{n-1}$
is nonamenable relative to
![]() $\mathcal L( \Gamma _{\widehat {k,n}})\bar \otimes {\mathcal L}(A_k^{(I_k)}\times A_n^{(I_n)})$
inside
$\mathcal L( \Gamma _{\widehat {k,n}})\bar \otimes {\mathcal L}(A_k^{(I_k)}\times A_n^{(I_n)})$
inside
![]() $\mathcal N$
. Without loss of generalization, we assume
$\mathcal N$
. Without loss of generalization, we assume
![]() $k=n-1$
. By applying Proposition 4.1, we derive that
$k=n-1$
. By applying Proposition 4.1, we derive that
![]() $ \bigvee _{i=0}^{n-2} \mathcal {Q}_i\prec _{\mathcal N} {\mathcal L}( \Gamma _{\widehat {n-1,n}})\bar \otimes {\mathcal L}(A_{n-1}^{(I_{n-1})}\times A_n^{(I_n)}). $
Using that
$ \bigvee _{i=0}^{n-2} \mathcal {Q}_i\prec _{\mathcal N} {\mathcal L}( \Gamma _{\widehat {n-1,n}})\bar \otimes {\mathcal L}(A_{n-1}^{(I_{n-1})}\times A_n^{(I_n)}). $
Using that
![]() $\mathcal {Q}_i v=v r\mathcal P_i rz$
, we derive that
$\mathcal {Q}_i v=v r\mathcal P_i rz$
, we derive that
![]() $(\bigvee _{i=0}^{n-2} \mathcal P_i)z\prec _{{\mathcal M}} {\mathcal L}(\Gamma _{\widehat {n-1,n}})\bar \otimes {\mathcal L}(A_{n-1}^{(I_{n-1})}\times A_n^{(I_n)})$
. By using the previous argument finitely many times, we obtain
$(\bigvee _{i=0}^{n-2} \mathcal P_i)z\prec _{{\mathcal M}} {\mathcal L}(\Gamma _{\widehat {n-1,n}})\bar \otimes {\mathcal L}(A_{n-1}^{(I_{n-1})}\times A_n^{(I_n)})$
. By using the previous argument finitely many times, we obtain
![]() $\mathcal P_0z\prec _{{\mathcal M}}{\mathcal L}(\times _{i=1}^n A_i^{(I_i)})$
.
$\mathcal P_0z\prec _{{\mathcal M}}{\mathcal L}(\times _{i=1}^n A_i^{(I_i)})$
.
Assume, by contradiction, that
![]() $\mathcal P_0z\nprec _{{\mathcal M}} \mathbb C1$
. The previous paragraph implies that there exists a nonempty subset
$\mathcal P_0z\nprec _{{\mathcal M}} \mathbb C1$
. The previous paragraph implies that there exists a nonempty subset
![]() $F\subset \{1,\dots ,n\}$
, such that
$F\subset \{1,\dots ,n\}$
, such that
Therefore, there exist projections
![]() $p_0\in P_0, s\in {\mathcal L}(\times _{i\in F} A_i^{(I_i)})$
with
$p_0\in P_0, s\in {\mathcal L}(\times _{i\in F} A_i^{(I_i)})$
with
![]() $p_0z\neq 0$
, a nonzero partial isometry
$p_0z\neq 0$
, a nonzero partial isometry
![]() $w\in s{\mathcal M} p_0$
, a
$w\in s{\mathcal M} p_0$
, a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\Psi : p_0P_0p_0z\to s{\mathcal L}(\times _{i\in F} A_i^{(I_i)})s$
, such that
$\Psi : p_0P_0p_0z\to s{\mathcal L}(\times _{i\in F} A_i^{(I_i)})s$
, such that
![]() $\Psi (x)w=wx$
, for any
$\Psi (x)w=wx$
, for any
![]() $x\in p_0P_0p_0z$
, and the support projection of
$x\in p_0P_0p_0z$
, and the support projection of
![]() $E_{\mathcal L(\times _{i\in F} A_i^{(I_i)})}(ww^*)$
equals s. By letting
$E_{\mathcal L(\times _{i\in F} A_i^{(I_i)})}(ww^*)$
equals s. By letting
![]() $T=\Psi (p_0P_0z)$
and
$T=\Psi (p_0P_0z)$
and
![]() $A=\times _{i\in F} A_i^{(I_i)}$
, one can check that (4.1) implies that
$A=\times _{i\in F} A_i^{(I_i)}$
, one can check that (4.1) implies that
By applying [Reference Chifan, Ioana, Osin and SunCIOS21, Corollary 4.7 and Lemma 4.11], we have
![]() $T'\cap s {\mathcal L}(\Gamma _{F}) s$
is amenable. Note that the
$T'\cap s {\mathcal L}(\Gamma _{F}) s$
is amenable. Note that the
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $\mathrm {Ad}(w): w^*w {\mathcal M} w^*w\to ww^* {\mathcal M} ww^*$
sends
$\mathrm {Ad}(w): w^*w {\mathcal M} w^*w\to ww^* {\mathcal M} ww^*$
sends
![]() $w^*w (p_0P_0p_0z'\cap p_0z{\mathcal M} p_0z) w^*w$
onto
$w^*w (p_0P_0p_0z'\cap p_0z{\mathcal M} p_0z) w^*w$
onto
![]() $ww^* (T'\cap s{\mathcal M} s) ww^*$
. Hence,
$ww^* (T'\cap s{\mathcal M} s) ww^*$
. Hence,
Since
![]() $\bigvee _{i=1}^n \mathcal P_i\subset \mathcal P_0'\cap p{\mathcal M} p$
, it follows that
$\bigvee _{i=1}^n \mathcal P_i\subset \mathcal P_0'\cap p{\mathcal M} p$
, it follows that
![]() $\bigvee _{i=1}^n \mathcal P_i\prec _{{\mathcal M}} (T'\cap s {\mathcal L}(\Gamma _{F}) s)\bar \otimes \mathcal L(\Gamma _{\widehat F})s $
. Since
$\bigvee _{i=1}^n \mathcal P_i\prec _{{\mathcal M}} (T'\cap s {\mathcal L}(\Gamma _{F}) s)\bar \otimes \mathcal L(\Gamma _{\widehat F})s $
. Since
![]() $\widehat F$
has at most
$\widehat F$
has at most
![]() $n-1$
elements and
$n-1$
elements and
![]() $T'\cap s \mathcal L(\Gamma _{F}) s$
is amenable, we can apply the previous arguments finitely many times and derive that there exists an amenable subalgebra
$T'\cap s \mathcal L(\Gamma _{F}) s$
is amenable, we can apply the previous arguments finitely many times and derive that there exists an amenable subalgebra
![]() $S\subset {\mathcal M} $
, such that
$S\subset {\mathcal M} $
, such that
![]() $\mathcal P_n\prec _{{\mathcal M}} S$
. This shows that
$\mathcal P_n\prec _{{\mathcal M}} S$
. This shows that
![]() $\mathcal P_n$
has an amenable direct summand, contradiction.
$\mathcal P_n$
has an amenable direct summand, contradiction.
Finally, we conclude that
![]() $\mathcal P_0z\prec _{{\mathcal M}} \mathbb C1$
, for all nonzero projections
$\mathcal P_0z\prec _{{\mathcal M}} \mathbb C1$
, for all nonzero projections
![]() $z\in (\bigvee _{i=0}^n \mathcal P_i)'\cap p{\mathcal M} p$
. Using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4], we conclude that
$z\in (\bigvee _{i=0}^n \mathcal P_i)'\cap p{\mathcal M} p$
. Using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4], we conclude that
![]() $\mathcal P_0\prec ^s_{{\mathcal M}} \mathbb C1$
, which implies that
$\mathcal P_0\prec ^s_{{\mathcal M}} \mathbb C1$
, which implies that
![]() $\mathcal P_0$
is completely atomic.
$\mathcal P_0$
is completely atomic.
5 Product rigidity results for von Neumann algebras of wreath-like product groups
The goal of this section is to prove Theorem A and consequently derive Corollary B. We first prove the following proposition.
Proposition 5.1 [Reference Chifan and UdreaCU18, Reference Chifan, de Santiago and SinclairCdSS15].
Let
![]() $\Gamma $
be an icc group, denote
$\Gamma $
be an icc group, denote
![]() ${\mathcal M}=L(\Gamma )$
and assume that
${\mathcal M}=L(\Gamma )$
and assume that
![]() ${\mathcal M}=\mathcal A \bar \otimes \mathcal B$
where
${\mathcal M}=\mathcal A \bar \otimes \mathcal B$
where
![]() $\mathcal B$
is solid. Let
$\mathcal B$
is solid. Let
![]() $ \Omega <\Gamma $
be a subgroup with nonamenable centralizer
$ \Omega <\Gamma $
be a subgroup with nonamenable centralizer
![]() $C_\Lambda (\Omega )$
, such that
$C_\Lambda (\Omega )$
, such that
![]() $\mathcal A\prec {\mathcal L}(\Omega )$
.
$\mathcal A\prec {\mathcal L}(\Omega )$
.
Then there exist projections
![]() $e\in {\mathcal L}(\Omega )$
and
$e\in {\mathcal L}(\Omega )$
and
![]() $r \in {\mathcal L}(\Omega )'\cap {\mathcal M}$
with
$r \in {\mathcal L}(\Omega )'\cap {\mathcal M}$
with
![]() $e r\neq 0$
, such that
$e r\neq 0$
, such that
![]() $ e(\mathcal L(\Omega )e r \vee r(\mathcal L(\Omega )'\cap {\mathcal M})r e\subseteq er{\mathcal M} er $
is a finite index inclusion of II
$ e(\mathcal L(\Omega )e r \vee r(\mathcal L(\Omega )'\cap {\mathcal M})r e\subseteq er{\mathcal M} er $
is a finite index inclusion of II
![]() $_1$
factors.
$_1$
factors.
Proof. Let
![]() $\mathcal {Q}={\mathcal L}(\Omega )$
as
$\mathcal {Q}={\mathcal L}(\Omega )$
as
![]() $\mathcal A\prec \mathcal {Q}$
, then using [Reference Chifan, Kida and PantCKP14, Proposition 2.4] and its proof, one can find nonzero projections
$\mathcal A\prec \mathcal {Q}$
, then using [Reference Chifan, Kida and PantCKP14, Proposition 2.4] and its proof, one can find nonzero projections
![]() $a \in \mathcal A$
,
$a \in \mathcal A$
,
![]() $q \in \mathcal {Q}$
, a partial isometry
$q \in \mathcal {Q}$
, a partial isometry
![]() $v\in q {\mathcal M} a$
, a subalgebra
$v\in q {\mathcal M} a$
, a subalgebra
![]() ${\mathcal D} \subseteq q\mathcal {Q} q$
and a
${\mathcal D} \subseteq q\mathcal {Q} q$
and a
![]() $\ast $
-isomorphism
$\ast $
-isomorphism
![]() $\phi : a\mathcal A a \rightarrow {\mathcal D} $
, such that
$\phi : a\mathcal A a \rightarrow {\mathcal D} $
, such that
-
1.
 ${\mathcal D} \vee ({\mathcal D}'\cap q\mathcal {Q} q) \subseteq q\mathcal {Q} q$
has finite index, and
${\mathcal D} \vee ({\mathcal D}'\cap q\mathcal {Q} q) \subseteq q\mathcal {Q} q$
has finite index, and -
2.
 $\phi (x)v = vx$
for all
$\phi (x)v = vx$
for all
 $x \in a\mathcal A a$
.
$x \in a\mathcal A a$
.
The intertwining relation 2. implies that
![]() $vv^* \in {\mathcal D}' \cap q{\mathcal M} q$
and
$vv^* \in {\mathcal D}' \cap q{\mathcal M} q$
and
![]() $v^*v \in (a\mathcal A a)' \cap a{\mathcal M} a = a \otimes \mathcal B.$
Hence, there is a projection
$v^*v \in (a\mathcal A a)' \cap a{\mathcal M} a = a \otimes \mathcal B.$
Hence, there is a projection
![]() $b \in \mathcal B$
satisfying
$b \in \mathcal B$
satisfying
![]() $v ^*v = a \otimes b$
. Choosing
$v ^*v = a \otimes b$
. Choosing
![]() $u \in \mathscr {U}({\mathcal M} )$
, such that
$u \in \mathscr {U}({\mathcal M} )$
, such that
![]() $v = u(a \otimes b) $
then relation 2. entails that
$v = u(a \otimes b) $
then relation 2. entails that
Using this relation and passing to the relative commutants, we obtain
![]() $vv^* ({\mathcal D}' \cap q{\mathcal M} q)vv^* = u(a \otimes b\mathcal B b)u ^*$
. Thus, one can find scalars
$vv^* ({\mathcal D}' \cap q{\mathcal M} q)vv^* = u(a \otimes b\mathcal B b)u ^*$
. Thus, one can find scalars
![]() $s_1,s_2> 0$
satisfying
$s_1,s_2> 0$
satisfying
Here, z denotes the central support projection of
![]() $vv^*$
in
$vv^*$
in
![]() ${\mathcal D}'\cap q{\mathcal M} q$
. Now notice that
${\mathcal D}'\cap q{\mathcal M} q$
. Now notice that
where
![]() ${\mathcal L}(C_\Lambda (\Omega ))$
has no amenable direct summand since
${\mathcal L}(C_\Lambda (\Omega ))$
has no amenable direct summand since
![]() $C_\Lambda (\Omega )$
is a nonamenable group. Moreover, we also have
$C_\Lambda (\Omega )$
is a nonamenable group. Moreover, we also have
![]() ${\mathcal D}' \cap q{\mathcal M} q \supseteq {\mathcal D}' \cap q \mathcal {Q} q$
. Thus,
${\mathcal D}' \cap q{\mathcal M} q \supseteq {\mathcal D}' \cap q \mathcal {Q} q$
. Thus,
![]() $(\mathcal {Q} ' \cap {\mathcal M} )z$
and
$(\mathcal {Q} ' \cap {\mathcal M} )z$
and
![]() $({\mathcal D}' \cap q\mathcal {Q} q)z$
are commuting subalgebras of
$({\mathcal D}' \cap q\mathcal {Q} q)z$
are commuting subalgebras of
![]() $({\mathcal D}' \cap q {\mathcal M} q)z$
where
$({\mathcal D}' \cap q {\mathcal M} q)z$
where
![]() $(\mathcal {Q}' \cap {\mathcal M} )z$
has no amenable direct summand. Since
$(\mathcal {Q}' \cap {\mathcal M} )z$
has no amenable direct summand. Since
![]() $\mathcal B^{s_2}$
is solid, then
$\mathcal B^{s_2}$
is solid, then
![]() $({\mathcal D}' \cap q\mathcal {Q} q)z$
must be purely atomic. Thus, cutting by a central projection
$({\mathcal D}' \cap q\mathcal {Q} q)z$
must be purely atomic. Thus, cutting by a central projection
![]() $0\neq r \in {\mathcal D}' \cap q\mathcal {Q} q$
, we may assume that
$0\neq r \in {\mathcal D}' \cap q\mathcal {Q} q$
, we may assume that
![]() ${\mathcal D} \subseteq q\mathcal {Q} q$
is a finite index inclusion of algebras. Since
${\mathcal D} \subseteq q\mathcal {Q} q$
is a finite index inclusion of algebras. Since
![]() ${\mathcal D}$
is a factor, shrinking r if necessary, we can actually assume that
${\mathcal D}$
is a factor, shrinking r if necessary, we can actually assume that
![]() ${\mathcal D} \subseteq q\mathcal {Q} q$
is an irreducible inclusion of finite index II
${\mathcal D} \subseteq q\mathcal {Q} q$
is an irreducible inclusion of finite index II
![]() $_1$
factors. Moreover, one can check that if one replaces v by the partial isometry of the polar decomposition of
$_1$
factors. Moreover, one can check that if one replaces v by the partial isometry of the polar decomposition of
![]() $r v \neq 0$
, then all relations (5.1), (5.2) and (5.3) are still satisfied. In addition, we can assume without any loss of generality that the support projection satisfies
$r v \neq 0$
, then all relations (5.1), (5.2) and (5.3) are still satisfied. In addition, we can assume without any loss of generality that the support projection satisfies
![]() $s(E_{\mathcal {Q}}(vv^*)) = q$
.
$s(E_{\mathcal {Q}}(vv^*)) = q$
.
Using [Reference JonesJo81, Lemma 3.1], one can find a projection
![]() $e\in q\mathcal {Q} q$
and a subfactor
$e\in q\mathcal {Q} q$
and a subfactor
![]() $\mathcal R \subseteq {\mathcal D} \subseteq q \mathcal {Q} q$
, such that
$\mathcal R \subseteq {\mathcal D} \subseteq q \mathcal {Q} q$
, such that
![]() $e \mathcal {Q} e =\mathcal R e$
and the index
$e \mathcal {Q} e =\mathcal R e$
and the index
![]() $[{\mathcal D}:\mathcal R]=[q \mathcal {Q} q: {\mathcal D}]$
. Now, notice the restriction
$[{\mathcal D}:\mathcal R]=[q \mathcal {Q} q: {\mathcal D}]$
. Now, notice the restriction
![]() $\phi ^{-1}: \mathcal R \rightarrow a\mathcal A a$
is an injective
$\phi ^{-1}: \mathcal R \rightarrow a\mathcal A a$
is an injective
![]() $\ast $
-homomorphism, such that
$\ast $
-homomorphism, such that
![]() $\mathcal T:= \phi ^{-1}(\mathcal R)\subseteq a\mathcal A a$
is finite index and
$\mathcal T:= \phi ^{-1}(\mathcal R)\subseteq a\mathcal A a$
is finite index and
Let
![]() $\phi ': \mathcal R e \rightarrow \mathcal R$
be the
$\phi ': \mathcal R e \rightarrow \mathcal R$
be the
![]() $\ast $
-homomorphism given by
$\ast $
-homomorphism given by
![]() $\phi '(y e)=y$
, for any
$\phi '(y e)=y$
, for any
![]() $y\in \mathcal R$
. Since e has full support in
$y\in \mathcal R$
. Since e has full support in
![]() $\langle {\mathcal D}, e\rangle =q\mathcal {Q} q$
, we have
$\langle {\mathcal D}, e\rangle =q\mathcal {Q} q$
, we have
![]() $ev\neq 0$
. Letting
$ev\neq 0$
. Letting
![]() $w_0$
be a partial isometry, such that
$w_0$
be a partial isometry, such that
![]() $w_0 |v^*e |=v^*e$
, the (5.4) gives that
$w_0 |v^*e |=v^*e$
, the (5.4) gives that
![]() $\theta = \phi ^{-1} \circ \phi ': e \mathcal {Q} e \rightarrow a\mathcal A a$
is an injective
$\theta = \phi ^{-1} \circ \phi ': e \mathcal {Q} e \rightarrow a\mathcal A a$
is an injective
![]() $\ast $
-isomorphism satisfying
$\ast $
-isomorphism satisfying
![]() $\theta (e \mathcal {Q} e)= \mathcal T$
and
$\theta (e \mathcal {Q} e)= \mathcal T$
and
Notice that
![]() $w_0^*w_0\in \mathcal T'\cap (a \mathcal A a \bar \otimes \mathcal B)=(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B $
. Since we have
$w_0^*w_0\in \mathcal T'\cap (a \mathcal A a \bar \otimes \mathcal B)=(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B $
. Since we have
![]() $\mathcal T'\cap (a\mathcal A a\bar \otimes \mathcal B )\supseteq \mathscr Z(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B$
and these von Neumann algebras have the same center then proceeding as in the proof of [Reference Ozawa and PopaOP03, Proposition 12], one can see that
$\mathcal T'\cap (a\mathcal A a\bar \otimes \mathcal B )\supseteq \mathscr Z(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B$
and these von Neumann algebras have the same center then proceeding as in the proof of [Reference Ozawa and PopaOP03, Proposition 12], one can see that
![]() $w_0^*w_0$
is equivalent in
$w_0^*w_0$
is equivalent in
![]() ${\mathcal T'\cap (a \mathcal A a \bar \otimes \mathcal B)}$
with projection in
${\mathcal T'\cap (a \mathcal A a \bar \otimes \mathcal B)}$
with projection in
![]() $\mathscr Z(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B$
. Thus, one can assume without any loss of generality that
$\mathscr Z(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B$
. Thus, one can assume without any loss of generality that
![]() $w_0^*w_0\in \mathscr Z(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B$
. As
$w_0^*w_0\in \mathscr Z(\mathcal T'\cap a \mathcal A a) \bar \otimes \mathcal B$
. As
![]() $[a\mathcal A a:\mathcal T]<\infty $
, then
$[a\mathcal A a:\mathcal T]<\infty $
, then
![]() $\mathcal T'\cap a\mathcal A a$
is finite-dimensional. Thus, replacing
$\mathcal T'\cap a\mathcal A a$
is finite-dimensional. Thus, replacing
![]() $w_0$
by
$w_0$
by
![]() $w=w_0r_0$
for a minimal projection
$w=w_0r_0$
for a minimal projection
![]() $r_0\in \mathscr Z(\mathcal T'\cap a \mathcal A a)$
with
$r_0\in \mathscr Z(\mathcal T'\cap a \mathcal A a)$
with
![]() $r_0 w_0^*|v^*e|\neq 0$
, we see all previous relations are satisfied, including (5.5). Moreover, we can assume that
$r_0 w_0^*|v^*e|\neq 0$
, we see all previous relations are satisfied, including (5.5). Moreover, we can assume that
![]() $w^*w= z_1\otimes z_2$
for some
$w^*w= z_1\otimes z_2$
for some
![]() $z_1\in \mathscr Z(\mathcal T'\cap a \mathcal A a)$
and
$z_1\in \mathscr Z(\mathcal T'\cap a \mathcal A a)$
and
![]() $z_2\in B$
. Hence, (5.5) implies
$z_2\in B$
. Hence, (5.5) implies
Since
![]() $\mathcal T \subseteq a \mathcal A a$
is a finite index inclusion of II
$\mathcal T \subseteq a \mathcal A a$
is a finite index inclusion of II
![]() $_1$
factors, using the local index formula [Reference JonesJo81, Lemma 2.2.1], we have that
$_1$
factors, using the local index formula [Reference JonesJo81, Lemma 2.2.1], we have that
![]() $\mathcal T z_1\subseteq z_1 \mathcal A z_1$
is a finite index inclusion of II
$\mathcal T z_1\subseteq z_1 \mathcal A z_1$
is a finite index inclusion of II
![]() $_1$
factors as well. In addition, we have
$_1$
factors as well. In addition, we have
Altogether, the previous relations (5.6) and (5.7) imply that
 $$ \begin{align} \begin{aligned} \mathcal T z_1 \bar\otimes z_2 \mathcal B z_2& \subset \mathcal T z_1 \vee (\mathcal T z_1'\cap z_1 \mathcal A a)\bar\otimes z_2 \mathcal B z_2\\ &= w^* \mathcal{Q} w\vee (w^* \mathcal{Q} w)'\cap (z_1\otimes z_2) {\mathcal M} (z_1\otimes z_2)\\ &\subseteq z_1 \mathcal A z_1\bar\otimes z_2 \mathcal B z_2 = (z_1\otimes z_2) {\mathcal M} (z_1\otimes z_2). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal T z_1 \bar\otimes z_2 \mathcal B z_2& \subset \mathcal T z_1 \vee (\mathcal T z_1'\cap z_1 \mathcal A a)\bar\otimes z_2 \mathcal B z_2\\ &= w^* \mathcal{Q} w\vee (w^* \mathcal{Q} w)'\cap (z_1\otimes z_2) {\mathcal M} (z_1\otimes z_2)\\ &\subseteq z_1 \mathcal A z_1\bar\otimes z_2 \mathcal B z_2 = (z_1\otimes z_2) {\mathcal M} (z_1\otimes z_2). \end{aligned} \end{align} $$
Since
![]() $\mathcal T z_1\subseteq z_1 \mathcal A z_1$
is a finite index inclusion of II
$\mathcal T z_1\subseteq z_1 \mathcal A z_1$
is a finite index inclusion of II
![]() $_1$
factors, then so is
$_1$
factors, then so is
![]() $\mathcal T z_1 \bar \otimes z_2 \mathcal B z_2\subseteq z_1 \mathcal A z_1\bar \otimes z_2 \mathcal B z_2$
. Let
$\mathcal T z_1 \bar \otimes z_2 \mathcal B z_2\subseteq z_1 \mathcal A z_1\bar \otimes z_2 \mathcal B z_2$
. Let
![]() $f= ww^*$
, and note that
$f= ww^*$
, and note that
![]() $f=re$
for some projection
$f=re$
for some projection
![]() $r\in \mathcal {Q}'\cap {\mathcal M}$
. Now notice (5.8) implies that
$r\in \mathcal {Q}'\cap {\mathcal M}$
. Now notice (5.8) implies that
is a finite index inclusion of von Neumann algebras. Since
![]() ${\mathcal M}$
is a factor, the finite index condition implies that the center
${\mathcal M}$
is a factor, the finite index condition implies that the center
![]() $\mathscr Z(r(\mathcal {Q}'\cap {\mathcal M} )r)$
is completely atomic (see [Reference Chifan, de Santiago and SucpikarnonCdSS17, Proposition 2.1(3)]). Thus, compressing r more if necessary, we further obtain that
$\mathscr Z(r(\mathcal {Q}'\cap {\mathcal M} )r)$
is completely atomic (see [Reference Chifan, de Santiago and SucpikarnonCdSS17, Proposition 2.1(3)]). Thus, compressing r more if necessary, we further obtain that
![]() $e\mathcal {Q} e r \vee r (\mathcal {Q} '\cap {\mathcal M})r e \subseteq f {\mathcal M} f$
is a finite index inclusion of II
$e\mathcal {Q} e r \vee r (\mathcal {Q} '\cap {\mathcal M})r e \subseteq f {\mathcal M} f$
is a finite index inclusion of II
![]() $_1$
factors, as desired.
$_1$
factors, as desired.
In this section, we show that various direct products of wreath-like groups give rise to
![]() $W^*$
-superrigid groups. To show this, we first establish a product rigidity result in the same spirit of [Reference Chifan, de Santiago and SinclairCdSS15] (see also [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference DrimbeDr20] for more recent similar results).
$W^*$
-superrigid groups. To show this, we first establish a product rigidity result in the same spirit of [Reference Chifan, de Santiago and SinclairCdSS15] (see also [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference DrimbeDr20] for more recent similar results).
Theorem 5.2. For every
![]() $1\leq k\leq n$
, let
$1\leq k\leq n$
, let
![]() $\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
$\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
![]() $A_k$
is Abelian,
$A_k$
is Abelian,
![]() $B_k$
is an icc subgroup of a hyperbolic group and
$B_k$
is an icc subgroup of a hyperbolic group and
![]() $B_k \curvearrowright I_k$
has amenable stabilizers. Denote
$B_k \curvearrowright I_k$
has amenable stabilizers. Denote
![]() $\Gamma = \Gamma _1\times \dots \times \Gamma _n$
, and assume that
$\Gamma = \Gamma _1\times \dots \times \Gamma _n$
, and assume that
![]() $t>0$
is a scalar and
$t>0$
is a scalar and
![]() $\Lambda $
is an arbitrary group satisfying
$\Lambda $
is an arbitrary group satisfying
![]() ${\mathcal M}={\mathcal L}(\Gamma )^t={\mathcal L}(\Lambda )$
.
${\mathcal M}={\mathcal L}(\Gamma )^t={\mathcal L}(\Lambda )$
.
Then one can find a product decomposition
![]() $\Lambda = \Lambda _1\times \dots \times \Lambda _n$
, some scalars
$\Lambda = \Lambda _1\times \dots \times \Lambda _n$
, some scalars
![]() $t_1,\dots ,t_n>0$
with
$t_1,\dots ,t_n>0$
with
![]() $t_1\cdots t_n=t$
and a unitary
$t_1\cdots t_n=t$
and a unitary
![]() $u\in \mathscr {U}({\mathcal M})$
so that
$u\in \mathscr {U}({\mathcal M})$
so that
![]() ${\mathcal L}(\Gamma _{i})^{t_i}=u{\mathcal L}(\Lambda _i) u^*$
for any
${\mathcal L}(\Gamma _{i})^{t_i}=u{\mathcal L}(\Lambda _i) u^*$
for any
![]() $1\leq i\leq n $
.
$1\leq i\leq n $
.
Proof. Without any loss of generality, we can assume that
![]() $t=1$
, as the other cases do not hide any difficulties. Throughout the proof, we denote by
$t=1$
, as the other cases do not hide any difficulties. Throughout the proof, we denote by
![]() $\Gamma _S=\times _{i\in S}\Gamma _i$
the subproduct supported on a subset
$\Gamma _S=\times _{i\in S}\Gamma _i$
the subproduct supported on a subset
![]() $S\subset \{1,\dots , n\}$
. We also denote by
$S\subset \{1,\dots , n\}$
. We also denote by
![]() $\widehat S$
the complement of S inside
$\widehat S$
the complement of S inside
![]() $\{1,\dots , n\}$
.
$\{1,\dots , n\}$
.
Let
![]() $\Delta : {\mathcal M}\rightarrow {\mathcal M}\bar \otimes {\mathcal M}$
be the
$\Delta : {\mathcal M}\rightarrow {\mathcal M}\bar \otimes {\mathcal M}$
be the
![]() $\ast $
-embedding given by
$\ast $
-embedding given by
![]() $\Delta (v_h)=v_h\otimes v_h$
for all
$\Delta (v_h)=v_h\otimes v_h$
for all
![]() $h\in \Lambda $
. Let
$h\in \Lambda $
. Let
![]() $1\leq i,j\leq n $
, and observe that
$1\leq i,j\leq n $
, and observe that
![]() $\Delta ({\mathcal L}(\Gamma _{\hat i})), \Delta (\mathcal L(\Gamma _i))\subset {\mathcal M} \bar \otimes \mathcal L(\Gamma _{\hat j})\bar \otimes \mathcal L(\Gamma _j)$
are commuting subalgebras. Using Proposition 4.1 (see also [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 6.15]), we have either
$\Delta ({\mathcal L}(\Gamma _{\hat i})), \Delta (\mathcal L(\Gamma _i))\subset {\mathcal M} \bar \otimes \mathcal L(\Gamma _{\hat j})\bar \otimes \mathcal L(\Gamma _j)$
are commuting subalgebras. Using Proposition 4.1 (see also [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 6.15]), we have either
![]() $\Delta ({\mathcal L}(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})\bar \otimes L(A^{(I_j)}_j)$
or
$\Delta ({\mathcal L}(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})\bar \otimes L(A^{(I_j)}_j)$
or
![]() $\Delta ({\mathcal L}(\Gamma _{i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})\bar \otimes {\mathcal L}(A^{(I_j)}_j)$
. Since
$\Delta ({\mathcal L}(\Gamma _{i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})\bar \otimes {\mathcal L}(A^{(I_j)}_j)$
. Since
![]() ${\mathcal L}(A^{(I_j)}_j)$
is Abelian and
${\mathcal L}(A^{(I_j)}_j)$
is Abelian and
![]() $\Delta ({\mathcal L}(\Gamma _{\hat i}))$
,
$\Delta ({\mathcal L}(\Gamma _{\hat i}))$
,
![]() $\Delta ({\mathcal L}(\Gamma _{i}))$
have property (T), the prior intertwining relations further imply that either
$\Delta ({\mathcal L}(\Gamma _{i}))$
have property (T), the prior intertwining relations further imply that either
![]() $\Delta ({\mathcal L}(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})$
or
$\Delta ({\mathcal L}(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})$
or
![]() $\Delta (\mathcal L(\Gamma _{i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
. Moreover, using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4(3)], we have either
$\Delta (\mathcal L(\Gamma _{i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
. Moreover, using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4(3)], we have either
![]() $\Delta (\mathcal L(\Gamma _{\hat i}))\prec ^s_{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
or
$\Delta (\mathcal L(\Gamma _{\hat i}))\prec ^s_{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
or
![]() $\Delta (\mathcal L(\Gamma _{i}))\prec ^s_{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
. If the former would hold for all
$\Delta (\mathcal L(\Gamma _{i}))\prec ^s_{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
. If the former would hold for all
![]() $1\leq j\leq n$
, then by using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.8(2)], we would get
$1\leq j\leq n$
, then by using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.8(2)], we would get
![]() $\Delta ({\mathcal L}(\Gamma _{i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} \bigcap ^n_{j=1} ({\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})) ={\mathcal M}\otimes 1$
. This contradicts [Reference Ioana, Popa and VaesIPV10, Lemma 7.2]. Hence, for every
$\Delta ({\mathcal L}(\Gamma _{i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} \bigcap ^n_{j=1} ({\mathcal M}\bar \otimes {\mathcal L}(\Gamma _{\hat j})) ={\mathcal M}\otimes 1$
. This contradicts [Reference Ioana, Popa and VaesIPV10, Lemma 7.2]. Hence, for every
![]() $1\leq i\leq n$
, there is
$1\leq i\leq n$
, there is
![]() $1\leq j\leq n$
so that
$1\leq j\leq n$
so that
![]() $\Delta (\mathcal L(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
. Furthermore, using [Reference DrimbeDr20, Theorem 4.3], we actually have that
$\Delta (\mathcal L(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat j})$
. Furthermore, using [Reference DrimbeDr20, Theorem 4.3], we actually have that
![]() $\Delta (\mathcal L(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat i})$
for all
$\Delta (\mathcal L(\Gamma _{\hat i}))\prec _{{\mathcal M}\bar \otimes {\mathcal M}} {\mathcal M}\bar \otimes \mathcal L(\Gamma _{\hat i})$
for all
![]() $1\leq i\leq n$
. Now, since
$1\leq i\leq n$
. Now, since
![]() $\mathcal L(\Gamma _i)$
has property (T), Theorem 6.1 shows that there is a subgroup
$\mathcal L(\Gamma _i)$
has property (T), Theorem 6.1 shows that there is a subgroup
![]() $\Sigma <\Lambda $
, such that
$\Sigma <\Lambda $
, such that
Since
![]() ${\mathcal L}(\Gamma _i)$
is solid, (5.10) allows to apply Proposition 5.1 and find a projection
${\mathcal L}(\Gamma _i)$
is solid, (5.10) allows to apply Proposition 5.1 and find a projection
![]() ${0\neq p= qr}$
with
${0\neq p= qr}$
with
![]() $q\in {\mathcal L}(\Sigma ), r \in {\mathcal L}(\Sigma )'\cap {\mathcal M}$
, such that
$q\in {\mathcal L}(\Sigma ), r \in {\mathcal L}(\Sigma )'\cap {\mathcal M}$
, such that
![]() $p({\mathcal L}(\Sigma )\vee ({\mathcal L}(\Sigma )'\cap {\mathcal M}))p \subseteq p{\mathcal M} p$
is a finite index inclusion of II
$p({\mathcal L}(\Sigma )\vee ({\mathcal L}(\Sigma )'\cap {\mathcal M}))p \subseteq p{\mathcal M} p$
is a finite index inclusion of II
![]() $_1$
factors. In particular,
$_1$
factors. In particular,
![]() $p{\mathcal L}(\Sigma \mathrm {vC}_\Lambda (\Sigma ))p \subseteq p{\mathcal M} p$
is also a finite index inclusion of von Neumann algebras, and thus,
$p{\mathcal L}(\Sigma \mathrm {vC}_\Lambda (\Sigma ))p \subseteq p{\mathcal M} p$
is also a finite index inclusion of von Neumann algebras, and thus,
![]() $[\Lambda : \Sigma \mathrm {vC}_\Lambda (\Sigma )]<\infty $
. Since
$[\Lambda : \Sigma \mathrm {vC}_\Lambda (\Sigma )]<\infty $
. Since
![]() $\Lambda $
is icc property (T), then so is
$\Lambda $
is icc property (T), then so is
![]() $\Sigma \mathrm {vC}_\Lambda (\Sigma )$
. Now, observe that one can find an increasing sequence of groups
$\Sigma \mathrm {vC}_\Lambda (\Sigma )$
. Now, observe that one can find an increasing sequence of groups
![]() $\cdots \leqslant \Omega _n \leqslant \Omega _{n+1}\leqslant \cdots \leqslant \mathrm {vC}_\Lambda (\Sigma )$
normalized by
$\cdots \leqslant \Omega _n \leqslant \Omega _{n+1}\leqslant \cdots \leqslant \mathrm {vC}_\Lambda (\Sigma )$
normalized by
![]() $\Sigma $
with
$\Sigma $
with
![]() $\cup _n \Omega _n=\mathrm {vC}_\Lambda (\Sigma )$
whose centralizers form a descending sequence
$\cup _n \Omega _n=\mathrm {vC}_\Lambda (\Sigma )$
whose centralizers form a descending sequence
![]() $\Sigma \geqslant C_\Sigma (\Omega _1)\geqslant \cdots \geqslant C_\Sigma (\Omega _n )\geqslant C_\Sigma (\Omega _{n+1}) \cdots $
of finite index subgroups. Therefore,
$\Sigma \geqslant C_\Sigma (\Omega _1)\geqslant \cdots \geqslant C_\Sigma (\Omega _n )\geqslant C_\Sigma (\Omega _{n+1}) \cdots $
of finite index subgroups. Therefore,
![]() $\Sigma \Omega _n \nearrow \Sigma \mathrm {vC}_\Lambda (\Sigma )$
, and using property (T), there is n so that
$\Sigma \Omega _n \nearrow \Sigma \mathrm {vC}_\Lambda (\Sigma )$
, and using property (T), there is n so that
![]() ${\Sigma \Omega _n = \Sigma \mathrm {vC}_\Lambda (\Sigma )}$
. Since
${\Sigma \Omega _n = \Sigma \mathrm {vC}_\Lambda (\Sigma )}$
. Since
![]() $C_\Sigma (\Omega _n) \Omega _n \leqslant \Sigma \Omega _n$
has finite index, we conclude that
$C_\Sigma (\Omega _n) \Omega _n \leqslant \Sigma \Omega _n$
has finite index, we conclude that
![]() $C_\Lambda (\Omega _n) \Omega _n\leq \Lambda $
has finite index as well. Denote
$C_\Lambda (\Omega _n) \Omega _n\leq \Lambda $
has finite index as well. Denote
![]() $\Sigma _0=C_\Lambda (\Omega _n)$
, and note that
$\Sigma _0=C_\Lambda (\Omega _n)$
, and note that
![]() $C_\Lambda (\Sigma )\leq C_\Lambda (\Sigma _0)$
. From (5.10), it follows that
$C_\Lambda (\Sigma )\leq C_\Lambda (\Sigma _0)$
. From (5.10), it follows that
By passing to relative commutants in (5.11), we get that
![]() ${\mathcal L}(\Sigma _0)\prec _{\mathcal M} \mathcal L(\Gamma _{\hat i})$
and
${\mathcal L}(\Sigma _0)\prec _{\mathcal M} \mathcal L(\Gamma _{\hat i})$
and
![]() $\mathcal L(C_{\Lambda }(\Sigma _0))\prec _{\mathcal M} \mathcal L(\Gamma _i)$
. Since
$\mathcal L(C_{\Lambda }(\Sigma _0))\prec _{\mathcal M} \mathcal L(\Gamma _i)$
. Since
![]() $[\Lambda :\Sigma _0 C_\Lambda (\Sigma _0)]<\infty $
, we derive that
$[\Lambda :\Sigma _0 C_\Lambda (\Sigma _0)]<\infty $
, we derive that
![]() $\mathcal L(\Sigma C_\Lambda (\Sigma ))'\cap {\mathcal M}=\mathbb C 1$
. Therefore, using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4(3)], we see that
$\mathcal L(\Sigma C_\Lambda (\Sigma ))'\cap {\mathcal M}=\mathbb C 1$
. Therefore, using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4(3)], we see that
By using (5.11), (5.12) together with [Reference Drimbe, Hoff and IoanaDHI16, Theorem 6.1] and a standard inductive argument, we obtain the desired conclusion.
Corollary 5.3. For every
![]() $1\leq k\leq n$
, let
$1\leq k\leq n$
, let
![]() $\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
$\Gamma _k\in \mathcal W\mathcal R (A_k, B_k \curvearrowright I_k)$
be property (T) groups where
![]() $A_k$
is Abelian,
$A_k$
is Abelian,
![]() $B_k$
is an icc subgroup of a hyperbolic group,
$B_k$
is an icc subgroup of a hyperbolic group,
![]() $B_k \curvearrowright I_k$
has amenable stabilizers and the set
$B_k \curvearrowright I_k$
has amenable stabilizers and the set
![]() $\{i\in I \; | \; g\cdot i\neq i\}$
is infinite for any
$\{i\in I \; | \; g\cdot i\neq i\}$
is infinite for any
![]() $g\in B_k\setminus \{1\}$
. Denote
$g\in B_k\setminus \{1\}$
. Denote
![]() $\Gamma = \Gamma _1\times \dots \times \Gamma _n$
, and assume that
$\Gamma = \Gamma _1\times \dots \times \Gamma _n$
, and assume that
![]() $t>0$
is any scalar,
$t>0$
is any scalar,
![]() $\Lambda $
is an arbitrary group and
$\Lambda $
is an arbitrary group and
![]() $\theta : {\mathcal L}(\Gamma )^t\rightarrow {\mathcal L}(\Lambda )$
is any
$\theta : {\mathcal L}(\Gamma )^t\rightarrow {\mathcal L}(\Lambda )$
is any
![]() $\ast $
-isomorphism.
$\ast $
-isomorphism.
Then
![]() $t=1$
, and one can find a character
$t=1$
, and one can find a character
![]() $\eta :\Gamma \to \mathbb T$
, a group isomorphism
$\eta :\Gamma \to \mathbb T$
, a group isomorphism
![]() $\delta :\Gamma \to \Lambda $
and a unitary
$\delta :\Gamma \to \Lambda $
and a unitary
![]() $u\in {\mathcal L}(\Lambda )$
, such that
$u\in {\mathcal L}(\Lambda )$
, such that
![]() $\theta (u_g)= \eta (g) u v_{\delta (g)} u^*$
, for all
$\theta (u_g)= \eta (g) u v_{\delta (g)} u^*$
, for all
![]() $g\in \Gamma $
.
$g\in \Gamma $
.
Proof. This follows directly from Theorem 5.2 and [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 9.1].
6 Reconstruction of clique subgroups under
 $W^*$
-equivalence
$W^*$
-equivalence
Towards establishing superrigidity results for graph products, the first major step is to identify in the mystery group
![]() $\Lambda $
collections of subgroups that play the same role as the full subgroups associated to clique subgraphs in the source group
$\Lambda $
collections of subgroups that play the same role as the full subgroups associated to clique subgraphs in the source group
![]() $\Gamma $
. This will be achieved using the commultiplication map [Reference IoanaIo10, Reference Popa and VaesPV11] in combination with an ultrapower method from [Reference IoanaIo11] (see also [Reference Drimbe, Hoff and IoanaDHI16, Reference Chifan, de Santiago and SinclairCdSS15]) and a technique for reconstructing malnormal group structure developed in [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference Chifan and IoanaCI17]. Our result is a new manifestation of a more conceptual principle called peripheral reconstruction
$\Gamma $
. This will be achieved using the commultiplication map [Reference IoanaIo10, Reference Popa and VaesPV11] in combination with an ultrapower method from [Reference IoanaIo11] (see also [Reference Drimbe, Hoff and IoanaDHI16, Reference Chifan, de Santiago and SinclairCdSS15]) and a technique for reconstructing malnormal group structure developed in [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Reference Chifan and IoanaCI17]. Our result is a new manifestation of a more conceptual principle called peripheral reconstruction
![]() $W^*$
-method, which consists of exploiting the natural tension that occurs between ‘a peripheral structure’ and a ‘direct product structure’ in the group. For completeness, we include all the details.
$W^*$
-method, which consists of exploiting the natural tension that occurs between ‘a peripheral structure’ and a ‘direct product structure’ in the group. For completeness, we include all the details.
We start by recalling an ultrapower technique which is essentially contained in the proof of [Reference IoanaIo11, Theorem 3.1] (see also [Reference Chifan, de Santiago and SinclairCdSS15, Theorem 3.3]) and the statement that will be used is a particular case of [Reference Drimbe, Hoff and IoanaDHI16, Theorem 4.1].
Theorem 6.1 [Reference IoanaIo11].
Let
![]() $\Lambda $
be a countable icc group and denote by
$\Lambda $
be a countable icc group and denote by
![]() ${\mathcal M}={\mathcal L}(\Lambda )$
. Let
${\mathcal M}={\mathcal L}(\Lambda )$
. Let
![]() $\Delta :{\mathcal M}\to {\mathcal M}\bar \otimes {\mathcal M}$
be the
$\Delta :{\mathcal M}\to {\mathcal M}\bar \otimes {\mathcal M}$
be the
![]() $*$
-homomorphism given by
$*$
-homomorphism given by
![]() $\Delta (v_\lambda )=v_\lambda \otimes v_\lambda $
, for all
$\Delta (v_\lambda )=v_\lambda \otimes v_\lambda $
, for all
![]() $\lambda \in \Lambda .$
Let
$\lambda \in \Lambda .$
Let
![]() $\mathcal P,\mathcal {Q}\subset {\mathcal M}$
be von Neumann subalgebras, such that
$\mathcal P,\mathcal {Q}\subset {\mathcal M}$
be von Neumann subalgebras, such that
![]() $\Delta (\mathcal P)\prec _{{\mathcal M}\bar \otimes {\mathcal M}}{\mathcal M}\bar \otimes \mathcal {Q}$
.
$\Delta (\mathcal P)\prec _{{\mathcal M}\bar \otimes {\mathcal M}}{\mathcal M}\bar \otimes \mathcal {Q}$
.
Then there exists a decreasing sequence of subgroups
![]() $\Sigma _k<\Lambda $
, such that
$\Sigma _k<\Lambda $
, such that
![]() $\mathcal P\prec _{\mathcal M} {\mathcal L}(\Sigma _k)$
, for every
$\mathcal P\prec _{\mathcal M} {\mathcal L}(\Sigma _k)$
, for every
![]() $k\ge 1$
, and
$k\ge 1$
, and
![]() $\mathcal {Q}'\cap {\mathcal M}\prec _{\mathcal M} {\mathcal L}(\cup _{k\ge 1} C_\Lambda (\Sigma _k)).$
$\mathcal {Q}'\cap {\mathcal M}\prec _{\mathcal M} {\mathcal L}(\cup _{k\ge 1} C_\Lambda (\Sigma _k)).$
We continue with the following result, which contains a consequence of Theorem 6.1 and solidity type result to certain von Neumann algebras of graph product groups. Throughout this article, if
![]() $\mathscr {C}\in \mathrm {cliq} (\mathscr {G})$
is a clique of a graph, then for every
$\mathscr {C}\in \mathrm {cliq} (\mathscr {G})$
is a clique of a graph, then for every
![]() $v\in \mathscr {C}$
, we denote by
$v\in \mathscr {C}$
, we denote by
![]() $\hat v= \mathscr {C}\setminus \{v\}$
.
$\hat v= \mathscr {C}\setminus \{v\}$
.
Theorem 6.2. Let
![]() $\Gamma = \mathscr {G} \{\Gamma _v\}$
be a graph product of groups, such that
$\Gamma = \mathscr {G} \{\Gamma _v\}$
be a graph product of groups, such that
![]() $\mathscr {G}\in \mathrm {CC}_1$
, and denote
$\mathscr {G}\in \mathrm {CC}_1$
, and denote
![]() ${\mathcal M}={\mathcal L}(\Gamma )$
. Assume that for any
${\mathcal M}={\mathcal L}(\Gamma )$
. Assume that for any
![]() $v\in \mathscr V$
,
$v\in \mathscr V$
,
![]() $\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
$\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
![]() $A_v$
is Abelian,
$A_v$
is Abelian,
![]() $B_v$
is an icc subgroup of a hyperbolic group.
$B_v$
is an icc subgroup of a hyperbolic group.
Let
![]() $\Lambda $
be an arbitrary group, such that
$\Lambda $
be an arbitrary group, such that
![]() ${\mathcal M}={\mathcal L}(\Lambda )$
, and let
${\mathcal M}={\mathcal L}(\Lambda )$
, and let
![]() $\mathscr {C} \in \mathrm {cliq} (\mathscr G)$
and
$\mathscr {C} \in \mathrm {cliq} (\mathscr G)$
and
![]() $v\in \mathscr {C}$
. Then the following hold:
$v\in \mathscr {C}$
. Then the following hold:
-
1. There is a subgroup
 $\Lambda _{\hat v} < \Lambda $
, such that
$\Lambda _{\hat v} < \Lambda $
, such that
 $C_\Lambda (\Lambda _{\hat v})$
is nonamenable and
$C_\Lambda (\Lambda _{\hat v})$
is nonamenable and
 ${\mathcal L}(\Gamma _{\hat v})\prec _{{\mathcal M}} L(\Lambda _{\hat v})$
.
${\mathcal L}(\Gamma _{\hat v})\prec _{{\mathcal M}} L(\Lambda _{\hat v})$
. -
2. If
 $\mathcal P, \mathcal {Q}, \mathcal R\subset p{\mathcal L}(\Gamma _{\mathscr {C}}) p$
are commuting von Neumann subalgebras, such that
$\mathcal P, \mathcal {Q}, \mathcal R\subset p{\mathcal L}(\Gamma _{\mathscr {C}}) p$
are commuting von Neumann subalgebras, such that
 $\mathcal {Q}$
has no amenable direct summand and
$\mathcal {Q}$
has no amenable direct summand and
 $\mathcal R$
is isomorphic to a corner of
$\mathcal R$
is isomorphic to a corner of
 ${\mathcal L}(\Gamma _{\hat v})$
, then
${\mathcal L}(\Gamma _{\hat v})$
, then
 $\mathcal P$
is completely atomic.
$\mathcal P$
is completely atomic.
Proof. 1. Following [Reference Ioana, Popa and VaesIPV10, Reference IoanaIo10], consider the
![]() $\ast $
-embedding
$\ast $
-embedding
![]() $\Delta : {\mathcal M} \rightarrow {\mathcal M} \bar \otimes {\mathcal M}$
given by
$\Delta : {\mathcal M} \rightarrow {\mathcal M} \bar \otimes {\mathcal M}$
given by
![]() $\Delta (v_h)=v_h\otimes v_h$
for all
$\Delta (v_h)=v_h\otimes v_h$
for all
![]() $h\in \Lambda $
. Fix
$h\in \Lambda $
. Fix
![]() $\mathscr {C} \in \mathrm {cliq} (\mathscr G)$
. From assumptions, we have
$\mathscr {C} \in \mathrm {cliq} (\mathscr G)$
. From assumptions, we have
![]() $\Delta ({\mathcal L}(\Gamma _{\mathscr {C}}))\subseteq {\mathcal M} \bar \otimes {\mathcal M} = \mathcal L(\Gamma \times \Gamma )$
is a property (T) von Neumann algebra. Thus, applying Theorem 2.8, one can find cliques
$\Delta ({\mathcal L}(\Gamma _{\mathscr {C}}))\subseteq {\mathcal M} \bar \otimes {\mathcal M} = \mathcal L(\Gamma \times \Gamma )$
is a property (T) von Neumann algebra. Thus, applying Theorem 2.8, one can find cliques
![]() $\mathscr {C}_1,\mathscr {C}_2\in \mathrm {cliq}(\mathscr {G})$
, such that
$\mathscr {C}_1,\mathscr {C}_2\in \mathrm {cliq}(\mathscr {G})$
, such that
![]() $\Delta (\mathcal L(\Gamma _{\mathscr {C}}))\prec _{{\mathcal M} \bar \otimes {\mathcal M}} \mathcal L(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2})$
. This implies that one find projections
$\Delta (\mathcal L(\Gamma _{\mathscr {C}}))\prec _{{\mathcal M} \bar \otimes {\mathcal M}} \mathcal L(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2})$
. This implies that one find projections
![]() $q\in \Delta (\mathcal L(\Gamma _{\mathscr {C}})) p\in \mathcal L(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2})$
, partial isometry
$q\in \Delta (\mathcal L(\Gamma _{\mathscr {C}})) p\in \mathcal L(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2})$
, partial isometry
![]() ${w\in {\mathcal M}\bar \otimes {\mathcal M} }$
and a
${w\in {\mathcal M}\bar \otimes {\mathcal M} }$
and a
![]() $\ast $
-isomorphism onto its image
$\ast $
-isomorphism onto its image
![]() $\theta : q\Delta (\mathcal L(\Gamma _{\mathscr {C}})) q\rightarrow \mathcal R:= \theta (q\Delta (\mathcal L(\Gamma _{\mathscr {C}})) q)\subseteq p \mathcal L(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2}) p$
, such that
$\theta : q\Delta (\mathcal L(\Gamma _{\mathscr {C}})) q\rightarrow \mathcal R:= \theta (q\Delta (\mathcal L(\Gamma _{\mathscr {C}})) q)\subseteq p \mathcal L(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2}) p$
, such that
![]() $\theta (x)w=wx$
for all
$\theta (x)w=wx$
for all
![]() $x\in q \Delta (\mathcal L(\Gamma _{\mathscr {C}})) q$
. Notice that
$x\in q \Delta (\mathcal L(\Gamma _{\mathscr {C}})) q$
. Notice that
![]() $ww^*\in \mathcal R'\cap q({\mathcal M} \bar \otimes {\mathcal M})q $
and
$ww^*\in \mathcal R'\cap q({\mathcal M} \bar \otimes {\mathcal M})q $
and
![]() $w^*w\in (\Delta ({\mathcal L}(\Gamma _{\mathscr {C}}))'\cap {\mathcal M}\bar \otimes {\mathcal M} )q$
. Moreover, we can assume without loss of generality that the support of
$w^*w\in (\Delta ({\mathcal L}(\Gamma _{\mathscr {C}}))'\cap {\mathcal M}\bar \otimes {\mathcal M} )q$
. Moreover, we can assume without loss of generality that the support of
![]() $E_{\mathcal L(\Gamma _{\mathscr {C}_1} \times \Gamma _{\mathscr {C}_2})}(ww^*)$
equals p.
$E_{\mathcal L(\Gamma _{\mathscr {C}_1} \times \Gamma _{\mathscr {C}_2})}(ww^*)$
equals p.
Since
![]() $\Gamma _t, t\in \mathscr V$
, are icc, we can assume without loss of generality that
$\Gamma _t, t\in \mathscr V$
, are icc, we can assume without loss of generality that
![]() $q\in \Delta ({\mathcal L}(\Gamma _{v_0}))$
for some
$q\in \Delta ({\mathcal L}(\Gamma _{v_0}))$
for some
![]() $v_0\in \mathscr {C}$
. For every
$v_0\in \mathscr {C}$
. For every
![]() $\mathscr {D} \subseteq \mathscr {C}$
, we denote
$\mathscr {D} \subseteq \mathscr {C}$
, we denote
![]() $\mathcal R_{\mathscr {D}}= \theta (q\Delta (\mathcal L(\Gamma _{\mathscr {D}}))q)$
. Thus,
$\mathcal R_{\mathscr {D}}= \theta (q\Delta (\mathcal L(\Gamma _{\mathscr {D}}))q)$
. Thus,
![]() $\mathcal R= \vee _{t\in \mathscr {C}} \mathcal R_v$
where
$\mathcal R= \vee _{t\in \mathscr {C}} \mathcal R_v$
where
![]() $\mathcal R_t= \theta (q\Delta (\mathcal L(\Gamma _t))q)$
are mutually commuting nonamenable II
$\mathcal R_t= \theta (q\Delta (\mathcal L(\Gamma _t))q)$
are mutually commuting nonamenable II
![]() $_1$
factors.
$_1$
factors.
Now, fix
![]() $\emptyset \neq \mathscr {D} \subseteq \mathscr {C}$
, and notice that
$\emptyset \neq \mathscr {D} \subseteq \mathscr {C}$
, and notice that
![]() $\mathcal R_{\mathscr {D}} \vee \mathcal R_{\mathrm {lk}(\mathscr {D})} = \mathcal R\subset {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2})=:\tilde {\mathcal N}$
are commuting nonamenable factors. Since
$\mathcal R_{\mathscr {D}} \vee \mathcal R_{\mathrm {lk}(\mathscr {D})} = \mathcal R\subset {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2})=:\tilde {\mathcal N}$
are commuting nonamenable factors. Since
![]() $\mathcal R_{\mathscr {D}}$
and
$\mathcal R_{\mathscr {D}}$
and
![]() $\mathcal R_{\mathrm {lk}(\mathscr {D})}$
are commuting property (T) algebras, then [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 6.15] implies that for every
$\mathcal R_{\mathrm {lk}(\mathscr {D})}$
are commuting property (T) algebras, then [Reference Chifan, Ioana, Osin and SunCIOS21, Theorem 6.15] implies that for every
![]() $t \in \mathscr {C}_2$
, either
$t \in \mathscr {C}_2$
, either
![]() $\mathcal R_{\mathscr {D}}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}}\times A^{(B_t)}_t ) $
or
$\mathcal R_{\mathscr {D}}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}}\times A^{(B_t)}_t ) $
or
![]() $\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}}\times A^{(B_t)}_t ) $
. However, since
$\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}}\times A^{(B_t)}_t ) $
. However, since
![]() $R_{\mathscr {D}}, \mathcal R_{\mathrm { lk}(\mathscr {D})}$
have property (T) and
$R_{\mathscr {D}}, \mathcal R_{\mathrm { lk}(\mathscr {D})}$
have property (T) and
![]() $A_t^{(B_t)}$
is amenable, we further conclude that either
$A_t^{(B_t)}$
is amenable, we further conclude that either
![]() $\mathcal R_{\mathscr {D}}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
or
$\mathcal R_{\mathscr {D}}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
or
![]() $\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
, and using factoriality, we actually have either a)
$\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec _{\tilde {\mathcal N}} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
, and using factoriality, we actually have either a)
![]() $\mathcal R_{\mathscr {D}}\prec ^s {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
or b)
$\mathcal R_{\mathscr {D}}\prec ^s {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
or b)
![]() $\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec ^s {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
. Assume by contradiction that b) holds for all
$\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec ^s {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )$
. Assume by contradiction that b) holds for all
![]() $t\in \mathscr {C}_2$
. By [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.6], this would imply that
$t\in \mathscr {C}_2$
. By [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.6], this would imply that
![]() $\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec \cap _{t\in \mathscr {C}_2} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )= {\mathcal L}(\Gamma _{\mathscr {C}_1})\otimes 1$
. Using [Reference Ioana, Popa and VaesIPV10, Proposition 7.2], this entails that
$\mathcal R_{\mathrm {lk}(\mathscr {D})}\prec \cap _{t\in \mathscr {C}_2} {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}} )= {\mathcal L}(\Gamma _{\mathscr {C}_1})\otimes 1$
. Using [Reference Ioana, Popa and VaesIPV10, Proposition 7.2], this entails that
![]() $\mathcal R_{\mathrm {lk}(\mathscr {D})}$
is atomic, a contradiction. Hence, there is
$\mathcal R_{\mathrm {lk}(\mathscr {D})}$
is atomic, a contradiction. Hence, there is
![]() $t\in \mathscr {C}_2$
, such that
$t\in \mathscr {C}_2$
, such that
![]() $\mathcal R_{\mathscr {D}}\prec ^s {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{v\}} )$
. Combining this with the first part, we get again that
$\mathcal R_{\mathscr {D}}\prec ^s {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{v\}} )$
. Combining this with the first part, we get again that
![]() $\Delta ({\mathcal L}(\Gamma _{\mathscr {D}}))\prec {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}}) )$
. The conclusion of the first part follows from Theorem 6.1 by letting
$\Delta ({\mathcal L}(\Gamma _{\mathscr {D}}))\prec {\mathcal L}(\Gamma _{\mathscr {C}_1}\times \Gamma _{\mathscr {C}_2 \setminus \{t\}}) )$
. The conclusion of the first part follows from Theorem 6.1 by letting
![]() $\mathscr {D}=\mathscr {C}\setminus \{v\}$
.
$\mathscr {D}=\mathscr {C}\setminus \{v\}$
.
2. The conclusion follows from Proposition 4.5.
Next, by using similar methods to [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Theorem 9.1], we identify up to corners the clique subgroups in the mystery subgroup.
Theorem 6.3. Let
![]() $\Gamma = \mathscr {G} \{\Gamma _v\}$
be a graph product of icc groups, such that
$\Gamma = \mathscr {G} \{\Gamma _v\}$
be a graph product of icc groups, such that
![]() $\mathscr {G}\in \mathrm {CC}_1$
, and denote
$\mathscr {G}\in \mathrm {CC}_1$
, and denote
![]() ${\mathcal M}={\mathcal L}(\Gamma )$
. Let
${\mathcal M}={\mathcal L}(\Gamma )$
. Let
![]() $\mathscr {C} \in \mathrm {cliq} (\mathscr G)$
and
$\mathscr {C} \in \mathrm {cliq} (\mathscr G)$
and
![]() $v\in \mathscr {C}$
with
$v\in \mathscr {C}$
with
![]() $\mathrm {lk}( \hat {v})=\{v\}$
. Assume that whenever
$\mathrm {lk}( \hat {v})=\{v\}$
. Assume that whenever
![]() $\mathcal P, \mathcal {Q}, \mathcal R\subset p{\mathcal L}(\Gamma _{\mathscr {C}}) p$
are commuting von Neumann subalgebras, such that
$\mathcal P, \mathcal {Q}, \mathcal R\subset p{\mathcal L}(\Gamma _{\mathscr {C}}) p$
are commuting von Neumann subalgebras, such that
![]() $\mathcal {Q}$
has no amenable direct summand and
$\mathcal {Q}$
has no amenable direct summand and
![]() $\mathcal R$
is isomorphic to a corner of
$\mathcal R$
is isomorphic to a corner of
![]() ${\mathcal L}(\Gamma _{\hat v})$
, then
${\mathcal L}(\Gamma _{\hat v})$
, then
![]() $\mathcal P$
is completely atomic.
$\mathcal P$
is completely atomic.
Let
![]() $\Lambda $
be an arbitrary group, such that
$\Lambda $
be an arbitrary group, such that
![]() ${\mathcal M}={\mathcal L}(\Lambda )$
, and assume that there exists a subgroup
${\mathcal M}={\mathcal L}(\Lambda )$
, and assume that there exists a subgroup
![]() $\Lambda _{\hat v}< \Lambda $
with nonamenable centralizer
$\Lambda _{\hat v}< \Lambda $
with nonamenable centralizer
![]() $C_\Lambda (\Lambda _{\hat v})$
, such that
$C_\Lambda (\Lambda _{\hat v})$
, such that
![]() ${\mathcal L}(\Gamma _{\hat v})\prec _{{\mathcal M}} {\mathcal L}(\Lambda _{\hat v})$
.
${\mathcal L}(\Gamma _{\hat v})\prec _{{\mathcal M}} {\mathcal L}(\Lambda _{\hat v})$
.
Then there exist a subgroup
![]() $\Lambda _{\hat v} C_\Lambda (\Lambda _{\hat v}) \leqslant \Sigma _{\mathscr {C}}<\Lambda $
with
$\Lambda _{\hat v} C_\Lambda (\Lambda _{\hat v}) \leqslant \Sigma _{\mathscr {C}}<\Lambda $
with
![]() $[\Sigma : \Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v})]<\infty $
and
$[\Sigma : \Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v})]<\infty $
and
![]() $\mathrm { QN}^{(1)}_\Lambda (\Sigma _{\mathscr {C}})=\Sigma _{\mathscr {C}}$
, a nonzero projection
$\mathrm { QN}^{(1)}_\Lambda (\Sigma _{\mathscr {C}})=\Sigma _{\mathscr {C}}$
, a nonzero projection
![]() $c\in \mathcal Z({\mathcal L}(\Sigma _{\mathscr {C}}))$
and
$c\in \mathcal Z({\mathcal L}(\Sigma _{\mathscr {C}}))$
and
![]() $w_0\in \mathscr {U}({\mathcal M})$
with
$w_0\in \mathscr {U}({\mathcal M})$
with
![]() $w_0c w^*_0=n\in \mathcal L(\Gamma _{\mathscr {C}})$
, such that
$w_0c w^*_0=n\in \mathcal L(\Gamma _{\mathscr {C}})$
, such that
![]() $w_0 \mathcal L(\Sigma _{\mathscr {C}})c w^*_0= n\mathcal L (\Gamma _{\mathscr {C}})n$
.
$w_0 \mathcal L(\Sigma _{\mathscr {C}})c w^*_0= n\mathcal L (\Gamma _{\mathscr {C}})n$
.
Proof. Since
![]() ${\mathcal L}(\Gamma _{\hat v})\prec _{\mathcal M} {\mathcal L}(\Lambda _{\hat v})$
, one can find projections
${\mathcal L}(\Gamma _{\hat v})\prec _{\mathcal M} {\mathcal L}(\Lambda _{\hat v})$
, one can find projections
![]() $a\in {\mathcal L}(\Gamma _{\hat v})$
,
$a\in {\mathcal L}(\Gamma _{\hat v})$
,
![]() $f\in {\mathcal L}(\Lambda _{\hat v})$
, a nonzero partial isometry
$f\in {\mathcal L}(\Lambda _{\hat v})$
, a nonzero partial isometry
![]() $v\in f{\mathcal M} a$
and a
$v\in f{\mathcal M} a$
and a
![]() $\ast $
-isomorphism onto its image
$\ast $
-isomorphism onto its image
![]() $\phi :a \mathcal L(\Gamma _{\hat v})a \rightarrow \mathcal B:=\phi (a\mathcal L(\Gamma _{\hat v})a) \subseteq f\mathcal L(\Lambda _{\hat v})f $
, such that
$\phi :a \mathcal L(\Gamma _{\hat v})a \rightarrow \mathcal B:=\phi (a\mathcal L(\Gamma _{\hat v})a) \subseteq f\mathcal L(\Lambda _{\hat v})f $
, such that
Notice that
![]() $vv^*\in \mathcal B'\cap f{\mathcal M} f$
and
$vv^*\in \mathcal B'\cap f{\mathcal M} f$
and
![]() $v^*v\in a{\mathcal L}(\Gamma _{\hat v})a'\cap a{\mathcal M} a$
. Since the virtual centralizer satisfies
$v^*v\in a{\mathcal L}(\Gamma _{\hat v})a'\cap a{\mathcal M} a$
. Since the virtual centralizer satisfies
![]() $\mathrm {vC}_\Gamma (\Gamma _{\hat v})= C_\Gamma (\Gamma _{\hat v}) = \Gamma _v$
, then
$\mathrm {vC}_\Gamma (\Gamma _{\hat v})= C_\Gamma (\Gamma _{\hat v}) = \Gamma _v$
, then
![]() ${\mathcal L}(\Gamma _{\hat v})'\cap {\mathcal M} = {\mathcal L}(\Gamma _v)$
. Thus, we can write
${\mathcal L}(\Gamma _{\hat v})'\cap {\mathcal M} = {\mathcal L}(\Gamma _v)$
. Thus, we can write
![]() ${v^*v=aa_0}$
for a projection
${v^*v=aa_0}$
for a projection
![]() $a_0\in {\mathcal L}(\Gamma _v)$
. Equation (6.1) implies that
$a_0\in {\mathcal L}(\Gamma _v)$
. Equation (6.1) implies that
![]() $\mathcal B vv^* = v {\mathcal L}(\Gamma _{\hat v})v^* = u_1 {\mathcal L}(\Gamma _{\hat v}) v^*v u^*_1$
, where
$\mathcal B vv^* = v {\mathcal L}(\Gamma _{\hat v})v^* = u_1 {\mathcal L}(\Gamma _{\hat v}) v^*v u^*_1$
, where
![]() $u_1\in {\mathcal M}$
is a unitary extending v. Taking relative commutants, we get
$u_1\in {\mathcal M}$
is a unitary extending v. Taking relative commutants, we get
![]() $vv^*(\mathcal B' \cap f{\mathcal M} f)vv^*= u_1 v^*v( a{\mathcal L}(\Gamma _{\hat v})a'\cap a{\mathcal M} a )v^*v u^*_1= u_1 v^*v\mathcal L(\Gamma _{v} ) v^*v u^*_1$
. Hence,
$vv^*(\mathcal B' \cap f{\mathcal M} f)vv^*= u_1 v^*v( a{\mathcal L}(\Gamma _{\hat v})a'\cap a{\mathcal M} a )v^*v u^*_1= u_1 v^*v\mathcal L(\Gamma _{v} ) v^*v u^*_1$
. Hence,
![]() $vv^*(\mathcal B \vee \mathcal B'\cap f{\mathcal M} f)vv^*=\mathcal B vv^*\vee vv^*(\mathcal B' \cap f{\mathcal M} f)vv^*= u_1 v^*v\mathcal L(\Gamma _{\mathscr {C}}) v^*vu^*_1$
. Therefore, since
$vv^*(\mathcal B \vee \mathcal B'\cap f{\mathcal M} f)vv^*=\mathcal B vv^*\vee vv^*(\mathcal B' \cap f{\mathcal M} f)vv^*= u_1 v^*v\mathcal L(\Gamma _{\mathscr {C}}) v^*vu^*_1$
. Therefore, since
![]() $\mathcal L(\Gamma _{\mathscr {C}})$
is a factor, one can find a new unitary
$\mathcal L(\Gamma _{\mathscr {C}})$
is a factor, one can find a new unitary
![]() $u_2 \in \mathscr {U}({\mathcal M})$
, such that
$u_2 \in \mathscr {U}({\mathcal M})$
, such that
here,
![]() $z_2$
is the central support of
$z_2$
is the central support of
![]() $vv^*$
in
$vv^*$
in
![]() $\mathcal B \vee \mathcal B'\cap f{\mathcal M} f$
. In particular, we have
$\mathcal B \vee \mathcal B'\cap f{\mathcal M} f$
. In particular, we have
![]() $z_2\in \mathcal Z(\mathcal B'\cap f{\mathcal M} f )$
and
$z_2\in \mathcal Z(\mathcal B'\cap f{\mathcal M} f )$
and
![]() $vv^*\leq z_2 \leq f$
.
$vv^*\leq z_2 \leq f$
.
Now, observe that (6.2) implies that
Next, we will show the following containment
Since we have
![]() ${\mathcal M}= u_2{\mathcal L}(\Gamma _{\mathscr V\setminus \{v\}} \ast _{\Gamma _{\hat v}} \Gamma _{\mathscr {C}} ) u^*_2=u_2{\mathcal L}(\Gamma _{\mathscr V\setminus \{v\}})u_2^* \ast _{u_2{\mathcal L}(\Gamma _{\hat v})u_2^*} u_2\mathcal L (\Gamma _{\mathscr {C}} ) u^*_2$
, then by [Reference Ioana, Peterson and PopaIPP05, Theorem 1.2.1] and (6.3) to get (6.4), it suffices to show that
${\mathcal M}= u_2{\mathcal L}(\Gamma _{\mathscr V\setminus \{v\}} \ast _{\Gamma _{\hat v}} \Gamma _{\mathscr {C}} ) u^*_2=u_2{\mathcal L}(\Gamma _{\mathscr V\setminus \{v\}})u_2^* \ast _{u_2{\mathcal L}(\Gamma _{\hat v})u_2^*} u_2\mathcal L (\Gamma _{\mathscr {C}} ) u^*_2$
, then by [Reference Ioana, Peterson and PopaIPP05, Theorem 1.2.1] and (6.3) to get (6.4), it suffices to show that
Since
![]() $\Gamma _v$
is icc, it follows that
$\Gamma _v$
is icc, it follows that
![]() $vv^*(\mathcal B' \kern1.3pt{\cap}\kern1.3pt f{\mathcal M} f)vv^*{=} u_1 v^*v{\mathcal L}(\Gamma _{v} ) v^*v u^*_1{=} u_1 a_0(\mathcal L(\Gamma _{v} ) )a_0 a u^*_1$
is a factor. Since
$vv^*(\mathcal B' \kern1.3pt{\cap}\kern1.3pt f{\mathcal M} f)vv^*{=} u_1 v^*v{\mathcal L}(\Gamma _{v} ) v^*v u^*_1{=} u_1 a_0(\mathcal L(\Gamma _{v} ) )a_0 a u^*_1$
is a factor. Since
![]() $z_2$
is the central support of
$z_2$
is the central support of
![]() $vv^*$
in
$vv^*$
in
![]() $\mathcal B' \cap f{\mathcal M} f$
, then
$\mathcal B' \cap f{\mathcal M} f$
, then
![]() $(\mathcal B' \cap f{\mathcal M} f) z_2$
is a factor as well.
$(\mathcal B' \cap f{\mathcal M} f) z_2$
is a factor as well.
Assume that (6.5) does not hold. Thus, one can find projections
![]() $t\in {\mathcal L}(C_\Lambda (\Lambda _{\hat v})), r\in u_2 \mathcal L(\Gamma _{\hat v})u_2^*$
, a partial isometry
$t\in {\mathcal L}(C_\Lambda (\Lambda _{\hat v})), r\in u_2 \mathcal L(\Gamma _{\hat v})u_2^*$
, a partial isometry
![]() $w\in ru_2{\mathcal L}(\Gamma _{\mathscr {C}})u_2^* tz_2$
and a
$w\in ru_2{\mathcal L}(\Gamma _{\mathscr {C}})u_2^* tz_2$
and a
![]() $\ast $
-isomorphism onto its image
$\ast $
-isomorphism onto its image
![]() $\psi : t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2\rightarrow ru_2\mathcal L(\Gamma _{\hat v})u_2^* r$
, such that
$\psi : t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2\rightarrow ru_2\mathcal L(\Gamma _{\hat v})u_2^* r$
, such that
Notice that
![]() $t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2\subseteq t(\mathcal B'\cap f {\mathcal M} f)tz_2\subseteq u_2 {\mathcal L}(\Gamma _{\mathscr {C}})u_2^*$
, and observe one can pick t small enough so that
$t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2\subseteq t(\mathcal B'\cap f {\mathcal M} f)tz_2\subseteq u_2 {\mathcal L}(\Gamma _{\mathscr {C}})u_2^*$
, and observe one can pick t small enough so that
![]() $tz_2$
is subequivalent to
$tz_2$
is subequivalent to
![]() $v^*v$
inside
$v^*v$
inside
![]() $(\mathcal B'\cap f {\mathcal M} f)z_2$
. Using this, one can find a unitary
$(\mathcal B'\cap f {\mathcal M} f)z_2$
. Using this, one can find a unitary
![]() $u_3\in {\mathcal M}$
, such that
$u_3\in {\mathcal M}$
, such that
![]() $t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2\subseteq u_3 v^*v \mathcal L(\Gamma _v)v^*v u_3^*$
. Hence, using this in combination with relation (6.6), we see that for all unitaries
$t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2\subseteq u_3 v^*v \mathcal L(\Gamma _v)v^*v u_3^*$
. Hence, using this in combination with relation (6.6), we see that for all unitaries
![]() $x\in t\mathcal L(C_\Lambda (\Lambda _{\hat v}))tz_2$
, we have that
$x\in t\mathcal L(C_\Lambda (\Lambda _{\hat v}))tz_2$
, we have that
![]() $\psi (x)$
is a unitary in
$\psi (x)$
is a unitary in
![]() $r u_2 \mathcal L(\Gamma _{\mathscr {C}}) u_2^* r$
, and therefore,
$r u_2 \mathcal L(\Gamma _{\mathscr {C}}) u_2^* r$
, and therefore,
 $$ \begin{align} \begin{aligned} \|E_{u_2 {\mathcal L}(\Gamma_{\hat v}) u_2^*}(ww^*)\|_2&=\|E_{u_2 {\mathcal L}(\Gamma_{\hat v}) u_2^*}(\psi(x)ww^*)\|_2= \| E_{u_2{\mathcal L}(\Gamma_{\hat v})u_2^*}(wxw^*)\|_2\\ &=\| E_{u_2{\mathcal L}(\Gamma_{\hat v})u_2^*}(wE_{u_3 {\mathcal L}(\Gamma_v)u_3^*}(x)w^*)\|_2\\ &=\| E_{{\mathcal L}(\Gamma_{\hat v})}(u_2^*w u_3E_{{\mathcal L}(\Gamma_v)}(u_3^*x u_3)u_3^*w^* u_2)\|_2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \|E_{u_2 {\mathcal L}(\Gamma_{\hat v}) u_2^*}(ww^*)\|_2&=\|E_{u_2 {\mathcal L}(\Gamma_{\hat v}) u_2^*}(\psi(x)ww^*)\|_2= \| E_{u_2{\mathcal L}(\Gamma_{\hat v})u_2^*}(wxw^*)\|_2\\ &=\| E_{u_2{\mathcal L}(\Gamma_{\hat v})u_2^*}(wE_{u_3 {\mathcal L}(\Gamma_v)u_3^*}(x)w^*)\|_2\\ &=\| E_{{\mathcal L}(\Gamma_{\hat v})}(u_2^*w u_3E_{{\mathcal L}(\Gamma_v)}(u_3^*x u_3)u_3^*w^* u_2)\|_2. \end{aligned} \end{align} $$
Since
![]() $w\neq 0$
, then (6.7) and basic approximations of
$w\neq 0$
, then (6.7) and basic approximations of
![]() $u_2^*w u_3$
and
$u_2^*w u_3$
and
![]() $u_3$
imply the existence of a finite subset
$u_3$
imply the existence of a finite subset
![]() $F\subset \Gamma $
and a constant
$F\subset \Gamma $
and a constant
![]() $C>0$
, such that for all unitaries
$C>0$
, such that for all unitaries
![]() $x\in t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2$
, we have
$x\in t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2$
, we have
However, we see that for all
![]() $x\in t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2$
, we have
$x\in t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2$
, we have
 $$ \begin{align*}\begin{aligned}\sum_{g,h,k,l\in F }| E_{{\mathcal L}(\Gamma_{\hat v})}(u_gE_{{\mathcal L}(\Gamma_v)}(u_hx u_k) u_l)\|_2&= \sum_{g,h,k,l\in F }| P_{ g^{-1}\Gamma_{\hat v}l^{-1}\cap \Gamma_v}(u_hx u_k)\|_2 \\&= \sum_{g,h,k,l\in F, gl^{-1}\in \Gamma_v }| P_{ (g^{-1}\Gamma_{\hat v}g^{-1}\cap \Gamma_v)gl^{-1}}(u_hx u_k)\|_2\\&= \sum_{g,h,k,l\in F, gl^{-1}\in \Gamma_v }| E_{ {\mathcal L}(g^{-1}\Gamma_{\hat v}g^{-1}\cap \Gamma_v)}(u_hx u_{klg^{-1}})\|_2\\ &=\sum_{g,h,k,l\in F, gl^{-1}\in \Gamma_v }| \tau(x u_{klg^{-1}h})|.\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned}\sum_{g,h,k,l\in F }| E_{{\mathcal L}(\Gamma_{\hat v})}(u_gE_{{\mathcal L}(\Gamma_v)}(u_hx u_k) u_l)\|_2&= \sum_{g,h,k,l\in F }| P_{ g^{-1}\Gamma_{\hat v}l^{-1}\cap \Gamma_v}(u_hx u_k)\|_2 \\&= \sum_{g,h,k,l\in F, gl^{-1}\in \Gamma_v }| P_{ (g^{-1}\Gamma_{\hat v}g^{-1}\cap \Gamma_v)gl^{-1}}(u_hx u_k)\|_2\\&= \sum_{g,h,k,l\in F, gl^{-1}\in \Gamma_v }| E_{ {\mathcal L}(g^{-1}\Gamma_{\hat v}g^{-1}\cap \Gamma_v)}(u_hx u_{klg^{-1}})\|_2\\ &=\sum_{g,h,k,l\in F, gl^{-1}\in \Gamma_v }| \tau(x u_{klg^{-1}h})|.\end{aligned}\end{align*} $$
Here, we denoted by
![]() $P_S:\ell ^2(\Gamma )\to \ell ^2(\Gamma )$
the orthogonal projection onto the
$P_S:\ell ^2(\Gamma )\to \ell ^2(\Gamma )$
the orthogonal projection onto the
![]() $\|\cdot \|_2$
-closure of the
$\|\cdot \|_2$
-closure of the
![]() $\mathrm {span}\{u_g|g\in S\}$
for any subset
$\mathrm {span}\{u_g|g\in S\}$
for any subset
![]() $S\subset \Gamma $
. As F is finite and
$S\subset \Gamma $
. As F is finite and
![]() $t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2$
is diffuse, there is a sequence of unitaries
$t{\mathcal L}(C_\Lambda (\Lambda _{\hat v}))tz_2$
is diffuse, there is a sequence of unitaries
![]() $x_n \in t\mathcal L(C_\Lambda (\Lambda _{\hat v}))tz_2$
, such that
$x_n \in t\mathcal L(C_\Lambda (\Lambda _{\hat v}))tz_2$
, such that
![]() $\sum _{g,h,k,l\in F, gl^{-1}\in \Gamma _v }| \tau (x_n u_{klg^{-1}h})|\rightarrow 0$
as
$\sum _{g,h,k,l\in F, gl^{-1}\in \Gamma _v }| \tau (x_n u_{klg^{-1}h})|\rightarrow 0$
as
![]() $n\rightarrow \infty $
. This, however, contradicts (6.8). Hence, (6.5) must hold.
$n\rightarrow \infty $
. This, however, contradicts (6.8). Hence, (6.5) must hold.
Thus, (6.4) implies that
![]() $z_2 ({\mathcal L}(C_\Lambda (\Lambda _{\hat v}))f\vee {\mathcal L}(C_\Lambda (\Lambda _{\hat v}))f'\cap f{\mathcal M} f) z_2\subseteq u_2\mathcal L(\Gamma _{\mathscr {C}})u_2^*$
. Again, since
$z_2 ({\mathcal L}(C_\Lambda (\Lambda _{\hat v}))f\vee {\mathcal L}(C_\Lambda (\Lambda _{\hat v}))f'\cap f{\mathcal M} f) z_2\subseteq u_2\mathcal L(\Gamma _{\mathscr {C}})u_2^*$
. Again, since
![]() $\mathcal L(\Gamma _{\mathscr {C}})$
is a factor, there is
$\mathcal L(\Gamma _{\mathscr {C}})$
is a factor, there is
![]() $u\in \mathscr {U}({\mathcal M})$
so that
$u\in \mathscr {U}({\mathcal M})$
so that
where z is the central support of
![]() $z_2$
in
$z_2$
in
![]() $(\mathcal L(C_\Lambda (\Lambda _{\hat v}))f\vee \mathcal L(C_\Lambda (\Lambda _{\hat v}))f'\cap f{\mathcal M} f)$
. In particular, we have
$(\mathcal L(C_\Lambda (\Lambda _{\hat v}))f\vee \mathcal L(C_\Lambda (\Lambda _{\hat v}))f'\cap f{\mathcal M} f)$
. In particular, we have
![]() $vv^*\leq z_2 \leq z \leq f$
. Now since
$vv^*\leq z_2 \leq z \leq f$
. Now since
![]() $f\mathcal L(\Lambda _{\hat v} )f\subseteq \mathcal L(C_\Lambda (\Lambda _{\hat v}))f'\cap f{\mathcal M} f$
, then by (6.9), we get
$f\mathcal L(\Lambda _{\hat v} )f\subseteq \mathcal L(C_\Lambda (\Lambda _{\hat v}))f'\cap f{\mathcal M} f$
, then by (6.9), we get
![]() $(f{\mathcal L}(\Lambda _{\hat v} )f\vee {\mathcal L}(C_\Lambda (\Lambda _{\hat v}))f)z\subseteq u{\mathcal L}(\Gamma _{\mathscr {C}})u^*$
, and hence
$(f{\mathcal L}(\Lambda _{\hat v} )f\vee {\mathcal L}(C_\Lambda (\Lambda _{\hat v}))f)z\subseteq u{\mathcal L}(\Gamma _{\mathscr {C}})u^*$
, and hence
In particular, (6.10) implies that
![]() $u^*f{\mathcal L}(\Lambda _{\hat v})fzu\subseteq {\mathcal L}(\Gamma _{\mathscr {C}})$
. Since
$u^*f{\mathcal L}(\Lambda _{\hat v})fzu\subseteq {\mathcal L}(\Gamma _{\mathscr {C}})$
. Since
![]() $vv^*\leq z\in f{\mathcal L}(C_\Lambda (\Lambda _{\hat v})) f'\cap f{\mathcal M} f$
and
$vv^*\leq z\in f{\mathcal L}(C_\Lambda (\Lambda _{\hat v})) f'\cap f{\mathcal M} f$
and
![]() $\mathcal B$
is a factor, then the map
$\mathcal B$
is a factor, then the map
![]() $\phi ': a\mathcal L(\Gamma _{\hat v})a \rightarrow u^* \mathcal B z u \subseteq u^*f \mathcal L(\Lambda _{\hat v})fz u$
given by
$\phi ': a\mathcal L(\Gamma _{\hat v})a \rightarrow u^* \mathcal B z u \subseteq u^*f \mathcal L(\Lambda _{\hat v})fz u$
given by
![]() $\phi '(x)=u^* \phi (x)z u$
still defines a
$\phi '(x)=u^* \phi (x)z u$
still defines a
![]() $\ast $
-isomorphism that satisfies
$\ast $
-isomorphism that satisfies
![]() $\phi '(x) w=wx$
, for any
$\phi '(x) w=wx$
, for any
![]() $x\in a\mathcal L(\Gamma _{\hat v})a$
, where
$x\in a\mathcal L(\Gamma _{\hat v})a$
, where
![]() $w= u^*zv$
is a nonzero partial isometry. Hence,
$w= u^*zv$
is a nonzero partial isometry. Hence,
![]() $\mathcal L(\Gamma _{\hat v}) \prec _{{\mathcal M}} u^*f\mathcal L(\Lambda _{\hat v})fzu$
. Thus, by Corollary 2.17, it follows that
$\mathcal L(\Gamma _{\hat v}) \prec _{{\mathcal M}} u^*f\mathcal L(\Lambda _{\hat v})fzu$
. Thus, by Corollary 2.17, it follows that
![]() $\mathcal L(\Gamma _{\hat v})\prec _{\mathcal L(\Gamma _{\mathscr {C}})} u^*f\mathcal L(\Lambda _{\hat v})fzu$
.
$\mathcal L(\Gamma _{\hat v})\prec _{\mathcal L(\Gamma _{\mathscr {C}})} u^*f\mathcal L(\Lambda _{\hat v})fzu$
.
To this end, using [Reference Chifan, Kida and PantCKP14, Proposition 2.4] and its proof, we can find nonzero
![]() ${p \in \mathscr P({\mathcal L}(\Gamma _{\hat v}))}$
,
${p \in \mathscr P({\mathcal L}(\Gamma _{\hat v}))}$
,
![]() $r=u^*ezu \in u^*f{\mathcal L}(\Lambda _{\hat v})fzu$
with
$r=u^*ezu \in u^*f{\mathcal L}(\Lambda _{\hat v})fzu$
with
![]() $e\in \mathscr P(f{\mathcal L}(\Lambda _{\hat v})f)$
, a von Neumann subalgebra
$e\in \mathscr P(f{\mathcal L}(\Lambda _{\hat v})f)$
, a von Neumann subalgebra
![]() $\mathcal C \subseteq u^*e\mathcal L(\Lambda _{\hat v})ezu $
and a
$\mathcal C \subseteq u^*e\mathcal L(\Lambda _{\hat v})ezu $
and a
![]() $\ast $
-isomorphism
$\ast $
-isomorphism
![]() $\theta : p\mathcal L(\Gamma _{\hat v})p \rightarrow \mathcal C$
, such that:
$\theta : p\mathcal L(\Gamma _{\hat v})p \rightarrow \mathcal C$
, such that:
-
a) the inclusion
 $\mathcal C \vee (\mathcal C' \cap u^*e{\mathcal L}(\Lambda _{\hat v})ezu ) \subseteq u^*e{\mathcal L}(\Lambda _{\hat v})ezu $
has finite index;
$\mathcal C \vee (\mathcal C' \cap u^*e{\mathcal L}(\Lambda _{\hat v})ezu ) \subseteq u^*e{\mathcal L}(\Lambda _{\hat v})ezu $
has finite index; -
b) there is a nonzero partial isometry
 $y \in {\mathcal L}(\Gamma _{\mathscr {C}})$
, such that
$y \in {\mathcal L}(\Gamma _{\mathscr {C}})$
, such that
 $\theta (x) y =y x$
for all
$\theta (x) y =y x$
for all
 ${x\in p{\mathcal L}(\Gamma _{\hat v})p}$
, where
${x\in p{\mathcal L}(\Gamma _{\hat v})p}$
, where
 $y^*y\in p{\mathcal L}(\Gamma _{\hat v})p'\cap p{\mathcal M} p$
and
$y^*y\in p{\mathcal L}(\Gamma _{\hat v})p'\cap p{\mathcal M} p$
and
 $yy^*\in \mathcal C '\cap r{\mathcal M} r$
.
$yy^*\in \mathcal C '\cap r{\mathcal M} r$
.
Note that
![]() $r\in {\mathcal L}(\Gamma _{\mathscr {C}})$
and
$r\in {\mathcal L}(\Gamma _{\mathscr {C}})$
and
![]() $\mathcal C$
,
$\mathcal C$
,
![]() $\mathcal C' \cap u^* r{\mathcal L}(\Lambda _{\hat v})r z u$
and
$\mathcal C' \cap u^* r{\mathcal L}(\Lambda _{\hat v})r z u$
and
![]() $u^*\mathcal L(C_\Lambda (\Lambda _{\hat v}))r z u$
are commuting von Neumann subalgebras of
$u^*\mathcal L(C_\Lambda (\Lambda _{\hat v}))r z u$
are commuting von Neumann subalgebras of
![]() $r {\mathcal L}(\Gamma _{\mathscr {C}})r$
. Since
$r {\mathcal L}(\Gamma _{\mathscr {C}})r$
. Since
![]() $\mathcal C$
is isomorphic to a corner of
$\mathcal C$
is isomorphic to a corner of
![]() $\mathcal L(\Gamma _{\hat v})$
and
$\mathcal L(\Gamma _{\hat v})$
and
![]() $u^*\mathcal L(C_\Lambda (\Lambda _{\hat v}))ezu$
has no amenable direct summand, then the assumption implies that
$u^*\mathcal L(C_\Lambda (\Lambda _{\hat v}))ezu$
has no amenable direct summand, then the assumption implies that
![]() $\mathcal C' \cap u^* e\mathcal L(\Lambda _{\hat v})ezu$
is purely atomic. Thus, one can find a nonzero projection
$\mathcal C' \cap u^* e\mathcal L(\Lambda _{\hat v})ezu$
is purely atomic. Thus, one can find a nonzero projection
![]() $q \in \mathcal Z(\mathcal C' \cap u^* e{\mathcal L}(\Lambda _{\hat v})e zu )$
, such that after compressing the containment in a) by q and replacing
$q \in \mathcal Z(\mathcal C' \cap u^* e{\mathcal L}(\Lambda _{\hat v})e zu )$
, such that after compressing the containment in a) by q and replacing
![]() $\mathcal C$
by
$\mathcal C$
by
![]() $\mathcal C q$
, y by
$\mathcal C q$
, y by
![]() $qy$
and
$qy$
and
![]() $\theta (x)$
by
$\theta (x)$
by
![]() $\theta (x) q$
in b), we can assume in addition that
$\theta (x) q$
in b), we can assume in addition that
![]() $\mathcal C \subseteq u^*e{\mathcal L}(\Lambda _{\hat v})ezu $
is a finite index inclusion of nonamenable II
$\mathcal C \subseteq u^*e{\mathcal L}(\Lambda _{\hat v})ezu $
is a finite index inclusion of nonamenable II
![]() $_1$
factors. By [Reference Pimsner and PopaPP86, Proposition 1.3], it follows that
$_1$
factors. By [Reference Pimsner and PopaPP86, Proposition 1.3], it follows that
![]() $\mathcal C \subseteq u^*e{\mathcal L}(\Lambda _{\hat v})ezu $
admits a finite Pimsner-Popa basis, which implies that there exist
$\mathcal C \subseteq u^*e{\mathcal L}(\Lambda _{\hat v})ezu $
admits a finite Pimsner-Popa basis, which implies that there exist
![]() $x_1,\dots ,x_m\in u^*e{\mathcal L}(\Lambda _{\hat v})ezu$
, such that
$x_1,\dots ,x_m\in u^*e{\mathcal L}(\Lambda _{\hat v})ezu$
, such that
![]() $u^*e{\mathcal L}(\Lambda _{\hat v})ezu=\sum _{i=1}^m x_i \mathcal C$
. Note also that
$u^*e{\mathcal L}(\Lambda _{\hat v})ezu=\sum _{i=1}^m x_i \mathcal C$
. Note also that
![]() $u^*e{\mathcal L}(\Lambda _{\hat v})ezu \subset r{\mathcal M} r$
since
$u^*e{\mathcal L}(\Lambda _{\hat v})ezu \subset r{\mathcal M} r$
since
![]() $r=u^*ezu$
. Hence,
$r=u^*ezu$
. Hence,
Also, the intertwining relation in b) shows that
![]() $\mathcal C yy^*= y p{\mathcal L}(\Gamma _{\hat v})p y^*= l p{\mathcal L}(\Gamma _{\hat v})p y^*y l$
where
$\mathcal C yy^*= y p{\mathcal L}(\Gamma _{\hat v})p y^*= l p{\mathcal L}(\Gamma _{\hat v})p y^*y l$
where
![]() $yy^*\in \mathcal C'\cap r {\mathcal M} r$
and
$yy^*\in \mathcal C'\cap r {\mathcal M} r$
and
![]() $l\in {\mathcal L}(\Gamma _{\mathscr {C}})$
is a unitary extending y, meaning
$l\in {\mathcal L}(\Gamma _{\mathscr {C}})$
is a unitary extending y, meaning
![]() $y=ly^*y$
. Therefore, using the quasi-normalizer formulas for group von Neumann algebras and for compressions, Lemmas 2.15 and 2.13 (and Remark 2.14), respectively, we deduce that
$y=ly^*y$
. Therefore, using the quasi-normalizer formulas for group von Neumann algebras and for compressions, Lemmas 2.15 and 2.13 (and Remark 2.14), respectively, we deduce that
 $$ \begin{align}\begin{aligned} ly^*y {\mathcal L}(\Gamma_{\mathscr{C}}) y^*yl^* & = ly^*y {\mathcal L}(\mathrm{QN}_\Gamma (\Gamma_{\hat v})) y^*yl^* \overset{L.2.15}{=} l y^*y \mathcal{QN}_{{\mathcal M}}({\mathcal L}(\Gamma_{\hat v}))"y^*yl^*\\ & \overset{L.2.13}{=}\mathcal {QN}_{l y^*y {\mathcal M} y^*yl}(l p{\mathcal L}(\Gamma_{\hat v})p y^*y l)"= \mathcal {QN}_{yy^*{\mathcal M} yy^*}(\mathcal C yy^*)" \\ &\overset{R.2.14}{=}yy^*\mathcal {QN}_{ r{\mathcal M} r}(\mathcal C ) "yy^*\overset{(6.11)}{=}yy^*\mathcal {QN}_{ r{\mathcal M} r}( u^* e{\mathcal L}(\Lambda_{\hat v})ezu )" yy^*\\ &\overset{L.2.13}{=} yy^* u^*z e\mathcal {QN}_{ {\mathcal L}(\Lambda)}({\mathcal L}(\Lambda_{\hat v}) )"ez u yy^*\overset{L.2.15}{=}yy^* u^* z e{\mathcal L} (\mathrm{QN}_{\Lambda}(\Lambda_{\hat v}) )e zu yy^*. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} ly^*y {\mathcal L}(\Gamma_{\mathscr{C}}) y^*yl^* & = ly^*y {\mathcal L}(\mathrm{QN}_\Gamma (\Gamma_{\hat v})) y^*yl^* \overset{L.2.15}{=} l y^*y \mathcal{QN}_{{\mathcal M}}({\mathcal L}(\Gamma_{\hat v}))"y^*yl^*\\ & \overset{L.2.13}{=}\mathcal {QN}_{l y^*y {\mathcal M} y^*yl}(l p{\mathcal L}(\Gamma_{\hat v})p y^*y l)"= \mathcal {QN}_{yy^*{\mathcal M} yy^*}(\mathcal C yy^*)" \\ &\overset{R.2.14}{=}yy^*\mathcal {QN}_{ r{\mathcal M} r}(\mathcal C ) "yy^*\overset{(6.11)}{=}yy^*\mathcal {QN}_{ r{\mathcal M} r}( u^* e{\mathcal L}(\Lambda_{\hat v})ezu )" yy^*\\ &\overset{L.2.13}{=} yy^* u^*z e\mathcal {QN}_{ {\mathcal L}(\Lambda)}({\mathcal L}(\Lambda_{\hat v}) )"ez u yy^*\overset{L.2.15}{=}yy^* u^* z e{\mathcal L} (\mathrm{QN}_{\Lambda}(\Lambda_{\hat v}) )e zu yy^*. \end{aligned}\end{align} $$
Denote
![]() $\Upsilon = \mathrm {QN}_\Lambda (\Lambda _{\hat v})$
and
$\Upsilon = \mathrm {QN}_\Lambda (\Lambda _{\hat v})$
and
![]() $\Sigma = \langle \mathrm {QN}^{(1)}_\Lambda (\Upsilon ))\rangle <\Lambda $
. As
$\Sigma = \langle \mathrm {QN}^{(1)}_\Lambda (\Upsilon ))\rangle <\Lambda $
. As
![]() $\mathrm {QN}^{(1)}_\Gamma (\Gamma _{\mathscr {C}})= \Gamma _{\mathscr {C}}$
, then formula (6.12) together with the corresponding formulas for one-sided quasi-normalizers, Lemmas 2.13 and 2.15, show that
$\mathrm {QN}^{(1)}_\Gamma (\Gamma _{\mathscr {C}})= \Gamma _{\mathscr {C}}$
, then formula (6.12) together with the corresponding formulas for one-sided quasi-normalizers, Lemmas 2.13 and 2.15, show that
In particular, by [Reference Chifan and IoanaCI17, Lemma 2.2], we have
![]() $[\Sigma :\Upsilon ]<\infty $
, and one can also check that
$[\Sigma :\Upsilon ]<\infty $
, and one can also check that
![]() $\mathrm {QN}^{(1)}_\Lambda (\Sigma )=\Sigma $
.
$\mathrm {QN}^{(1)}_\Lambda (\Sigma )=\Sigma $
.
Notice the above relations also show that
![]() $yy^*= u^* d u$
for some projection
$yy^*= u^* d u$
for some projection
![]() $d\in ze{\mathcal L} (\Sigma )ez$
. Thus, relation (6.13) entails that
$d\in ze{\mathcal L} (\Sigma )ez$
. Thus, relation (6.13) entails that
![]() $ u^* d{\mathcal L} (\Sigma ) d u = ly^*y {\mathcal L}(\Gamma _{\mathscr {C}}) y^*yl^*$
, and letting
$ u^* d{\mathcal L} (\Sigma ) d u = ly^*y {\mathcal L}(\Gamma _{\mathscr {C}}) y^*yl^*$
, and letting
![]() $w_0:=ul \in \mathscr {U}({\mathcal M})$
and
$w_0:=ul \in \mathscr {U}({\mathcal M})$
and
![]() $t=y^*y$
, we conclude that
$t=y^*y$
, we conclude that
![]() $w^*_0 d {\mathcal L}(\Sigma )d w_0= t {\mathcal L}(\Gamma _{\mathscr {C}}) t$
. Moreover, if we replace
$w^*_0 d {\mathcal L}(\Sigma )d w_0= t {\mathcal L}(\Gamma _{\mathscr {C}}) t$
. Moreover, if we replace
![]() $w^*_0 \Sigma w_0$
by
$w^*_0 \Sigma w_0$
by
![]() $\Sigma $
and we use
$\Sigma $
and we use
![]() $w^*_0 d w_0= t$
, we have that
$w^*_0 d w_0= t$
, we have that
![]() $t {\mathcal L}(\Sigma )t = t {\mathcal L}(\Gamma _{\mathscr {C}})t$
. As
$t {\mathcal L}(\Sigma )t = t {\mathcal L}(\Gamma _{\mathscr {C}})t$
. As
![]() $\mathcal L(\Gamma _{\mathscr {C}})$
is a factor, one can find a unitary
$\mathcal L(\Gamma _{\mathscr {C}})$
is a factor, one can find a unitary
![]() $w_1 \in {\mathcal M}$
so that if c denotes the central support of
$w_1 \in {\mathcal M}$
so that if c denotes the central support of
![]() $t \in {\mathcal L}(\Sigma )$
, we have that
$t \in {\mathcal L}(\Sigma )$
, we have that
![]() ${\mathcal L}(\Sigma ) c \subseteq w_1\mathcal L(\Gamma _{\mathscr {C}})w_1^*$
. This implies that there exists a projection
${\mathcal L}(\Sigma ) c \subseteq w_1\mathcal L(\Gamma _{\mathscr {C}})w_1^*$
. This implies that there exists a projection
![]() $h \in {\mathcal L}(\Gamma _{\mathscr {C}})$
, such that
$h \in {\mathcal L}(\Gamma _{\mathscr {C}})$
, such that
![]() $t= w_1 hw_1^*$
. Moreover, since
$t= w_1 hw_1^*$
. Moreover, since
![]() ${\mathcal L}(\Gamma _{\mathscr {C}})$
is a factor, there is a unitary
${\mathcal L}(\Gamma _{\mathscr {C}})$
is a factor, there is a unitary
![]() $w_2 \in \mathcal L(\Gamma _{\mathscr {C}})$
so that
$w_2 \in \mathcal L(\Gamma _{\mathscr {C}})$
so that
![]() $t = w_2 hw^*_2$
. Altogether, these relations show that
$t = w_2 hw^*_2$
. Altogether, these relations show that
![]() $wt=tw$
where
$wt=tw$
where
![]() $w :=w_1 w_2^*$
. Also, we have that
$w :=w_1 w_2^*$
. Also, we have that
![]() ${\mathcal L}(\Sigma )c\subseteq w {\mathcal L}(\Gamma _{\mathscr {C}})w^*$
. Multiplying on both sides by t, we get
${\mathcal L}(\Sigma )c\subseteq w {\mathcal L}(\Gamma _{\mathscr {C}})w^*$
. Multiplying on both sides by t, we get
![]() $t {\mathcal L}(\Gamma _{\mathscr {C}})t=t\mathcal L(\Sigma )t\subseteq t w\mathcal L(\Gamma _{\mathscr {C}})w^* t$
, and hence
$t {\mathcal L}(\Gamma _{\mathscr {C}})t=t\mathcal L(\Sigma )t\subseteq t w\mathcal L(\Gamma _{\mathscr {C}})w^* t$
, and hence
![]() $tw^*t \mathcal L(\Gamma _{\mathscr {C}}) t\subseteq t \mathcal L(\Gamma _{\mathscr {C}})t w^* t$
. In particular, using Corollary 2.17, we get
$tw^*t \mathcal L(\Gamma _{\mathscr {C}}) t\subseteq t \mathcal L(\Gamma _{\mathscr {C}})t w^* t$
. In particular, using Corollary 2.17, we get
![]() $w^*t =tw^*t\in \mathcal {QN}^{(1)}_{t{\mathcal M} t}(t{\mathcal L}(\Gamma _{\mathscr {C}})t)=t {\mathcal L}(\Gamma _{\mathscr {C}})t$
, and hence
$w^*t =tw^*t\in \mathcal {QN}^{(1)}_{t{\mathcal M} t}(t{\mathcal L}(\Gamma _{\mathscr {C}})t)=t {\mathcal L}(\Gamma _{\mathscr {C}})t$
, and hence
![]() $wt \in t {\mathcal L}(\Gamma _{\mathscr {C}})t$
. Altogether, these relations imply that
$wt \in t {\mathcal L}(\Gamma _{\mathscr {C}})t$
. Altogether, these relations imply that
![]() $t {\mathcal L}(\Sigma )t= t{\mathcal L}(\Gamma _{\mathscr {C}})t=w t \mathcal L(\Gamma _{\mathscr {C}})t w^*$
. Since
$t {\mathcal L}(\Sigma )t= t{\mathcal L}(\Gamma _{\mathscr {C}})t=w t \mathcal L(\Gamma _{\mathscr {C}})t w^*$
. Since
![]() $\mathcal L(\Sigma ) c\subseteq w \mathcal L(\Gamma _{\mathscr {C}})w^*$
, we apply the ‘moreover’ part in [Reference Chifan and IoanaCI17, Lemma 2.6] and derive that
$\mathcal L(\Sigma ) c\subseteq w \mathcal L(\Gamma _{\mathscr {C}})w^*$
, we apply the ‘moreover’ part in [Reference Chifan and IoanaCI17, Lemma 2.6] and derive that
![]() $\mathcal L(\Sigma ) c= c \mathcal L(\Gamma _{\mathscr {C}})c$
.
$\mathcal L(\Sigma ) c= c \mathcal L(\Gamma _{\mathscr {C}})c$
.
In conclusion, we showed there is a subgroup
![]() $\Lambda _{\hat v} \mathrm {C}_\Lambda (\Lambda _{\hat v})<\mathrm {QN}_\Lambda (\Lambda _{\hat v})<\Sigma <\Lambda $
, such that
$\Lambda _{\hat v} \mathrm {C}_\Lambda (\Lambda _{\hat v})<\mathrm {QN}_\Lambda (\Lambda _{\hat v})<\Sigma <\Lambda $
, such that
![]() $[\Sigma :\mathrm {QN}_\Lambda (\Lambda _{\hat v})]<\infty $
, and
$[\Sigma :\mathrm {QN}_\Lambda (\Lambda _{\hat v})]<\infty $
, and
![]() $\mathrm {QN}^{(1)}_\Lambda (\Sigma )=\Sigma $
. Moreover, there are
$\mathrm {QN}^{(1)}_\Lambda (\Sigma )=\Sigma $
. Moreover, there are
![]() $r\in \mathscr P(\mathscr Z({\mathcal L}(\Sigma )))$
,
$r\in \mathscr P(\mathscr Z({\mathcal L}(\Sigma )))$
,
![]() $v_0\in \mathscr {U}({\mathcal M})$
and
$v_0\in \mathscr {U}({\mathcal M})$
and
![]() $n\in \mathscr P(\mathcal L(\Gamma _{\mathscr {C}}))$
so that
$n\in \mathscr P(\mathcal L(\Gamma _{\mathscr {C}}))$
so that
Finally, we show that
![]() $[\Sigma : \Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v})]<\infty $
. Let
$[\Sigma : \Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v})]<\infty $
. Let
![]() $u^*qzu=s\in u^* e {\mathcal L}(\Lambda _{\hat v})e z u$
be a projection, and let
$u^*qzu=s\in u^* e {\mathcal L}(\Lambda _{\hat v})e z u$
be a projection, and let
![]() $\mathcal C_1\subseteq \mathcal C \subseteq u^* e {\mathcal L}(\Lambda _{\hat v})e z u$
be a subfactor, such that
$\mathcal C_1\subseteq \mathcal C \subseteq u^* e {\mathcal L}(\Lambda _{\hat v})e z u$
be a subfactor, such that
![]() $u^* e {\mathcal L}(\Lambda _{\hat v})e z u=\langle \mathcal C, s \rangle $
is the basic construction for
$u^* e {\mathcal L}(\Lambda _{\hat v})e z u=\langle \mathcal C, s \rangle $
is the basic construction for
![]() $\mathcal C_1\subseteq \mathcal C$
. Notice that
$\mathcal C_1\subseteq \mathcal C$
. Notice that
![]() ${\mathcal D}_1 := \theta ^{-1}(\mathcal C_1)\subseteq p\mathcal L(\Gamma _{\hat v})p$
is a finite index subfactor. Let
${\mathcal D}_1 := \theta ^{-1}(\mathcal C_1)\subseteq p\mathcal L(\Gamma _{\hat v})p$
is a finite index subfactor. Let
![]() $\Theta : {\mathcal D}_1 \rightarrow \mathcal C_1s= u^*q \mathcal L(\Lambda _{\hat v})qzu$
be the isomorphism given by
$\Theta : {\mathcal D}_1 \rightarrow \mathcal C_1s= u^*q \mathcal L(\Lambda _{\hat v})qzu$
be the isomorphism given by
![]() $\Theta (x)=\theta (x)s$
for all
$\Theta (x)=\theta (x)s$
for all
![]() $x\in {\mathcal D}_1$
. Using b), we have that
$x\in {\mathcal D}_1$
. Using b), we have that
![]() $\Theta (x) sy=sy x$
for all
$\Theta (x) sy=sy x$
for all
![]() $x\in {\mathcal D}_1$
. Since s is a Jones’s projection for
$x\in {\mathcal D}_1$
. Since s is a Jones’s projection for
![]() $\mathcal C_1\subseteq \mathcal C$
, one can check that
$\mathcal C_1\subseteq \mathcal C$
, one can check that
![]() $sy\neq 0$
. Letting w be the polar decomposition of
$sy\neq 0$
. Letting w be the polar decomposition of
![]() $sy$
, we further have that
$sy$
, we further have that
![]() $\Theta (x) w=w x$
for all
$\Theta (x) w=w x$
for all
![]() $x\in {\mathcal D}_1$
. By Corollary 2.17, we have
$x\in {\mathcal D}_1$
. By Corollary 2.17, we have
![]() $s\in {\mathcal L}(\Gamma _{\mathscr {C}})$
,
$s\in {\mathcal L}(\Gamma _{\mathscr {C}})$
,
![]() $ww^*\in u^*q\mathcal L(\Lambda _{\hat v})qzu'\cap s{\mathcal M} s \subset s\mathcal L(\Gamma _{\mathscr {C}})s$
and
$ww^*\in u^*q\mathcal L(\Lambda _{\hat v})qzu'\cap s{\mathcal M} s \subset s\mathcal L(\Gamma _{\mathscr {C}})s$
and
![]() $w^*w \in p{\mathcal D}_1 p' \cap p{\mathcal M} p\subset p{\mathcal D}_1 p' \cap pL(\Gamma _{\mathscr {C}}) p$
. Letting
$w^*w \in p{\mathcal D}_1 p' \cap p{\mathcal M} p\subset p{\mathcal D}_1 p' \cap pL(\Gamma _{\mathscr {C}}) p$
. Letting
![]() $w_o$
be a unitary extending w and using the previous intertwining relation, we see that
$w_o$
be a unitary extending w and using the previous intertwining relation, we see that
![]() $u^* q{\mathcal L}(\Lambda _{\hat v})qzu ww^*= w_o {\mathcal D}_1 w^*_o$
. By taking relative commutants, we obtain that
$u^* q{\mathcal L}(\Lambda _{\hat v})qzu ww^*= w_o {\mathcal D}_1 w^*_o$
. By taking relative commutants, we obtain that
![]() $ ww^*(u^* q\mathcal L(\Lambda _{\hat v})qzu'\cap s {\mathcal M} s)ww^*=w_o {\mathcal D}_1'\cap p\mathcal L(\Gamma _{\mathscr {C}})p w_o^* $
, and hence,
$ ww^*(u^* q\mathcal L(\Lambda _{\hat v})qzu'\cap s {\mathcal M} s)ww^*=w_o {\mathcal D}_1'\cap p\mathcal L(\Gamma _{\mathscr {C}})p w_o^* $
, and hence,
 $$ \begin{align}\begin{aligned} &w_o ({\mathcal D}_1\vee \mathcal L(\Gamma_v)p )w_o^*\subset w_o ({\mathcal D}_1\vee {\mathcal D}_1'\cap p\mathcal L(\Gamma_{\mathscr{C}})p )w_o^*=\\ &=ww^*(u^* q{\mathcal L}(\Lambda_{\hat v})qzu \vee u^* qL(\Lambda_{\hat v})qzu'\cap s {\mathcal M} s)ww^* \\ &=ww^*u^* qz ({\mathcal L}(\Lambda_{\hat v}) \vee {\mathcal L}(\Lambda_{\hat v})'\cap {\mathcal M} ) qzu ww^*\subseteq ww^* {\mathcal L}(\Gamma_{\mathscr{C}})ww^*.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &w_o ({\mathcal D}_1\vee \mathcal L(\Gamma_v)p )w_o^*\subset w_o ({\mathcal D}_1\vee {\mathcal D}_1'\cap p\mathcal L(\Gamma_{\mathscr{C}})p )w_o^*=\\ &=ww^*(u^* q{\mathcal L}(\Lambda_{\hat v})qzu \vee u^* qL(\Lambda_{\hat v})qzu'\cap s {\mathcal M} s)ww^* \\ &=ww^*u^* qz ({\mathcal L}(\Lambda_{\hat v}) \vee {\mathcal L}(\Lambda_{\hat v})'\cap {\mathcal M} ) qzu ww^*\subseteq ww^* {\mathcal L}(\Gamma_{\mathscr{C}})ww^*.\end{aligned}\end{align} $$
Since
![]() $\Gamma _{\mathscr {C}}$
is malnormal in
$\Gamma _{\mathscr {C}}$
is malnormal in
![]() $\Gamma $
, the containment
$\Gamma $
, the containment
![]() $w_o ({\mathcal D}_1\vee {\mathcal L}(\Gamma _v)p )w_o^*\subseteq ww^* {\mathcal L}(\Gamma _{\mathscr {C}})ww^*$
implies that
$w_o ({\mathcal D}_1\vee {\mathcal L}(\Gamma _v)p )w_o^*\subseteq ww^* {\mathcal L}(\Gamma _{\mathscr {C}})ww^*$
implies that
![]() $w=w_o p\in {\mathcal L}(\Gamma _{\mathscr {C}})$
, and hence
$w=w_o p\in {\mathcal L}(\Gamma _{\mathscr {C}})$
, and hence
![]() $ww^* {\mathcal L}(\Gamma _{\mathscr {C}})ww^*= w{\mathcal L}(\Gamma _{\mathscr {C}})w^*= w_o p{\mathcal L}(\Gamma _{\mathscr {C}})pw_o^*$
. Therefore, since
$ww^* {\mathcal L}(\Gamma _{\mathscr {C}})ww^*= w{\mathcal L}(\Gamma _{\mathscr {C}})w^*= w_o p{\mathcal L}(\Gamma _{\mathscr {C}})pw_o^*$
. Therefore, since
![]() ${\mathcal D}_1\vee {\mathcal L}(\Gamma _v)p\subseteq p\mathcal L(\Gamma _{\mathscr {C}})p$
has finite index, then so does
${\mathcal D}_1\vee {\mathcal L}(\Gamma _v)p\subseteq p\mathcal L(\Gamma _{\mathscr {C}})p$
has finite index, then so does
![]() $w_o ({\mathcal D}_1\vee \mathcal L(\Gamma _v)p )w_o^*\subset ww^*\mathcal L(\Gamma _{\mathscr {C}}) ww^*$
. In particular, all inclusions in (6.15) are of finite index. Hence, we have
$w_o ({\mathcal D}_1\vee \mathcal L(\Gamma _v)p )w_o^*\subset ww^*\mathcal L(\Gamma _{\mathscr {C}}) ww^*$
. In particular, all inclusions in (6.15) are of finite index. Hence, we have
![]() ${\mathcal L}(\Gamma _{\mathscr {C}})\prec _{\mathcal M} {\mathcal L}(\Lambda _{\hat v})\vee \mathcal L(\Lambda _{\hat v})'\cap {\mathcal M}$
and since
${\mathcal L}(\Gamma _{\mathscr {C}})\prec _{\mathcal M} {\mathcal L}(\Lambda _{\hat v})\vee \mathcal L(\Lambda _{\hat v})'\cap {\mathcal M}$
and since
![]() $\mathcal L(\Lambda _{\hat v})\vee \mathcal L(\Lambda _{\hat v})'\cap {\mathcal M}\subseteq \mathcal L(\Lambda _{\hat v} vC_\Lambda (\Lambda _{\hat v}))$
, we get
$\mathcal L(\Lambda _{\hat v})\vee \mathcal L(\Lambda _{\hat v})'\cap {\mathcal M}\subseteq \mathcal L(\Lambda _{\hat v} vC_\Lambda (\Lambda _{\hat v}))$
, we get
![]() $\mathcal L(\Gamma _{\mathscr {C}})\prec _{\mathcal M} \mathcal L(\Lambda _{\hat v} vC_\Lambda (\Lambda _{\hat v}))$
. Using (6.14), this further implies that
$\mathcal L(\Gamma _{\mathscr {C}})\prec _{\mathcal M} \mathcal L(\Lambda _{\hat v} vC_\Lambda (\Lambda _{\hat v}))$
. Using (6.14), this further implies that
![]() $\mathcal L(\Sigma )\prec _{\mathcal M} \mathcal L(\Lambda _{\hat v} \mathrm { vC}_\Lambda (\Lambda _{\hat v}))$
. Moreover, since
$\mathcal L(\Sigma )\prec _{\mathcal M} \mathcal L(\Lambda _{\hat v} \mathrm { vC}_\Lambda (\Lambda _{\hat v}))$
. Moreover, since
![]() $\Lambda _{\hat v}\mathrm {vC}_\Lambda (\Lambda _{\hat v})<\Sigma $
and
$\Lambda _{\hat v}\mathrm {vC}_\Lambda (\Lambda _{\hat v})<\Sigma $
and
![]() $\mathrm {QN}^{(1)}(\Sigma )=\Sigma $
, we actually have that
$\mathrm {QN}^{(1)}(\Sigma )=\Sigma $
, we actually have that
![]() ${\mathcal L}(\Sigma )\prec _{{\mathcal L}(\Sigma )} {\mathcal L}(\Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v}))$
. Using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.5], this implies that
${\mathcal L}(\Sigma )\prec _{{\mathcal L}(\Sigma )} {\mathcal L}(\Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v}))$
. Using [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.5], this implies that
![]() $[\Sigma : \Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v})]<\infty $
, as claimed.
$[\Sigma : \Lambda _{\hat v} \mathrm {vC}_\Lambda (\Lambda _{\hat v})]<\infty $
, as claimed.
We continue with the following technical result which goes back to [Reference Chifan and IoanaCI17, Theorem 3.2]. The proof goes along the same lines with the proof of [Reference Chifan, Diaz-Arias and DrimbeCD-AD20, Theorem 9.2], and we include all the details for completeness.
Theorem 6.4. Assume that
![]() $\Gamma = \mathscr {G} \{\Gamma _v\}$
is a graph product of groups, such that
$\Gamma = \mathscr {G} \{\Gamma _v\}$
is a graph product of groups, such that
![]() $\mathscr {G}\in \mathrm {CC}_1$
and all vertex groups
$\mathscr {G}\in \mathrm {CC}_1$
and all vertex groups
![]() $\Gamma _v$
are icc, nonamenable. Let
$\Gamma _v$
are icc, nonamenable. Let
![]() $\mathscr {C}_1,\dots ,\mathscr {C}_n$
be an enumeration of its consecutive cliques, and denote
$\mathscr {C}_1,\dots ,\mathscr {C}_n$
be an enumeration of its consecutive cliques, and denote
![]() $\Gamma _i=\Gamma _{\mathscr {C}_i}$
, for any
$\Gamma _i=\Gamma _{\mathscr {C}_i}$
, for any
![]() $i\in \overline {1,n}$
.
$i\in \overline {1,n}$
.
Let
![]() $\Lambda $
be an arbitrary group, such that
$\Lambda $
be an arbitrary group, such that
![]() ${\mathcal M}={\mathcal L}(\Gamma )=\mathcal L(\Lambda )$
. Assume that for any
${\mathcal M}={\mathcal L}(\Gamma )=\mathcal L(\Lambda )$
. Assume that for any
![]() ${i\in \{1,\dots ,n\}}$
, there exist
${i\in \{1,\dots ,n\}}$
, there exist
![]() $\Lambda _i<\Lambda $
with
$\Lambda _i<\Lambda $
with
![]() $\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
and a subset
$\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
and a subset
![]() $i\in J_i\subset \overline {1,n}$
satisfying:
$i\in J_i\subset \overline {1,n}$
satisfying:
-
1. For any
 $k\in J_i$
, there exists a projection
$k\in J_i$
, there exists a projection
 $0\neq z_i^k\in \mathcal Z({\mathcal L}(\Lambda _i))$
, such that
$0\neq z_i^k\in \mathcal Z({\mathcal L}(\Lambda _i))$
, such that
 $\sum _{k\in J _i}z_i^k=1$
;
$\sum _{k\in J _i}z_i^k=1$
; -
2. For any
 $k\in J_i$
, there exists
$k\in J_i$
, there exists
 $u_i^k\in \mathcal U({\mathcal M})$
, such that:
$u_i^k\in \mathcal U({\mathcal M})$
, such that:-
a.
 $u_i^i {\mathcal L}(\Lambda _i) z_i^i (u_i^i)^*=p_i{\mathcal L}(\Gamma _i)p_i$
, where
$u_i^i {\mathcal L}(\Lambda _i) z_i^i (u_i^i)^*=p_i{\mathcal L}(\Gamma _i)p_i$
, where
 $p_i=u_i^i z_i^i (u_i^i)^*$
;
$p_i=u_i^i z_i^i (u_i^i)^*$
; -
b.
 $u_i^k {\mathcal L}(\Lambda _i) z_i^k (u_i^k)^*\subset {\mathcal L}(\Gamma _k)$
.
$u_i^k {\mathcal L}(\Lambda _i) z_i^k (u_i^k)^*\subset {\mathcal L}(\Gamma _k)$
.
-
Then there exists a partition
![]() $T_1\sqcup \dots \sqcup T_l= \{1,...,n\}$
and a subgroup
$T_1\sqcup \dots \sqcup T_l= \{1,...,n\}$
and a subgroup
![]() $\tilde \Lambda _i<\Lambda $
with
$\tilde \Lambda _i<\Lambda $
with
![]() $\mathrm {QN_\Lambda ^{(1)}}(\tilde \Lambda _i)=\tilde \Lambda _i$
for any
$\mathrm {QN_\Lambda ^{(1)}}(\tilde \Lambda _i)=\tilde \Lambda _i$
for any
![]() $1\leq i\leq l$
, such that:
$1\leq i\leq l$
, such that:
-
1. For any
 $k\in T_i$
, there exists a projection
$k\in T_i$
, there exists a projection
 $0\neq \tilde z_i^k\in \mathcal Z({\mathcal L}(\tilde \Lambda _i))$
satisfying
$0\neq \tilde z_i^k\in \mathcal Z({\mathcal L}(\tilde \Lambda _i))$
satisfying
 $\sum _{k\in T _i}\tilde z_i^k=1$
;
$\sum _{k\in T _i}\tilde z_i^k=1$
; -
2. For any
 $k\in T_i$
, there exists
$k\in T_i$
, there exists
 $\tilde u_i^k\in \mathcal U({\mathcal M})$
, such that
$\tilde u_i^k\in \mathcal U({\mathcal M})$
, such that
 $\tilde u_i^k {\mathcal L}(\tilde \Lambda _i) \tilde z_i^k (\tilde u_i^k)^* = \tilde p_k^i{\mathcal L}(\Gamma _k) \tilde p_k^i$
, where
$\tilde u_i^k {\mathcal L}(\tilde \Lambda _i) \tilde z_i^k (\tilde u_i^k)^* = \tilde p_k^i{\mathcal L}(\Gamma _k) \tilde p_k^i$
, where
 $\tilde p_k^i=\tilde u_i^k \tilde z_i^k (\tilde u_i^k)^*$
.
$\tilde p_k^i=\tilde u_i^k \tilde z_i^k (\tilde u_i^k)^*$
.
Proof. We fix an arbitrary
![]() $k\in J_1\setminus \{1\}$
. Note that the assumption 2. implies that
$k\in J_1\setminus \{1\}$
. Note that the assumption 2. implies that
![]() ${\mathcal L}(\Lambda _1)\prec _{{\mathcal M}} \mathcal L (\Gamma _k)$
and
${\mathcal L}(\Lambda _1)\prec _{{\mathcal M}} \mathcal L (\Gamma _k)$
and
![]() $\mathcal L(\Gamma _k)\prec ^s_{{\mathcal M}} \mathcal L(\Lambda _k)$
since
$\mathcal L(\Gamma _k)\prec ^s_{{\mathcal M}} \mathcal L(\Lambda _k)$
since
![]() $\mathcal L(\Gamma _k)'\cap {\mathcal M}=\mathbb C1.$
Using [Reference VaesVa08, Lemma 3.7], we deduce that
$\mathcal L(\Gamma _k)'\cap {\mathcal M}=\mathbb C1.$
Using [Reference VaesVa08, Lemma 3.7], we deduce that
![]() ${\mathcal L}(\Lambda _1)\prec _{{\mathcal M}} {\mathcal L}(\Lambda _k)$
. Using [Reference Chifan and IoanaCI17, Lemma 2.2], there exists
${\mathcal L}(\Lambda _1)\prec _{{\mathcal M}} {\mathcal L}(\Lambda _k)$
. Using [Reference Chifan and IoanaCI17, Lemma 2.2], there exists
![]() $h_k\in \Lambda $
, such that
$h_k\in \Lambda $
, such that
![]() $[\Lambda _1: h_k\Lambda _kh_k^{-1}\cap \Lambda _1]<\infty $
. Up to replacing
$[\Lambda _1: h_k\Lambda _kh_k^{-1}\cap \Lambda _1]<\infty $
. Up to replacing
![]() $\Lambda _k$
by
$\Lambda _k$
by
![]() $h_k \Lambda _k h^{-1}_k$
, we may assume that
$h_k \Lambda _k h^{-1}_k$
, we may assume that
![]() $h_k=1$
.
$h_k=1$
.
We continue by showing that for all
![]() $i\in J_1, j\in J_k$
with
$i\in J_1, j\in J_k$
with
![]() $i\neq j$
, we have
$i\neq j$
, we have
![]() $z_1^i z_k^j=0$
. By assuming the contrary, we consider some
$z_1^i z_k^j=0$
. By assuming the contrary, we consider some
![]() $i\in J_1,j\in J_k$
with
$i\in J_1,j\in J_k$
with
![]() $i\neq j$
satisfying
$i\neq j$
satisfying
![]() $z_1^i z_k^j\neq 0$
. Assumption 2. gives that
$z_1^i z_k^j\neq 0$
. Assumption 2. gives that
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1) z_1^i\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _i)$
and
${\mathcal L}(\Lambda _k\cap \Lambda _1) z_1^i\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _i)$
and
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1) z_k^j\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _j)$
. From [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4], there exist maximal projections
${\mathcal L}(\Lambda _k\cap \Lambda _1) z_k^j\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _j)$
. From [Reference Drimbe, Hoff and IoanaDHI16, Lemma 2.4], there exist maximal projections
![]() $a_1^i, a_k^j\in \mathcal Z({\mathcal L}(\Lambda _k\cap \Lambda _1)'\cap {\mathcal M})$
, such that
$a_1^i, a_k^j\in \mathcal Z({\mathcal L}(\Lambda _k\cap \Lambda _1)'\cap {\mathcal M})$
, such that
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1) a_1^i\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _i)$
and
${\mathcal L}(\Lambda _k\cap \Lambda _1) a_1^i\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _i)$
and
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1) a_k^j\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _j)$
. Since
${\mathcal L}(\Lambda _k\cap \Lambda _1) a_k^j\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _j)$
. Since
![]() $z_1^i z_k^j\neq 0$
, we deduce that
$z_1^i z_k^j\neq 0$
, we deduce that
![]() $a_1^i a_k^j\in \mathcal Z({\mathcal L}(\Lambda _k\cap \Lambda _1)'\cap {\mathcal M})$
is a nonzero projection. Thus, we can apply [Reference VaesVa10a, Lemma 2.7] to get that
$a_1^i a_k^j\in \mathcal Z({\mathcal L}(\Lambda _k\cap \Lambda _1)'\cap {\mathcal M})$
is a nonzero projection. Thus, we can apply [Reference VaesVa10a, Lemma 2.7] to get that
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1) a_1^i a_k^j\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _i\cap g \Gamma _j g^{-1})$
for some
${\mathcal L}(\Lambda _k\cap \Lambda _1) a_1^i a_k^j\prec _{{\mathcal M}}^s {\mathcal L}(\Gamma _i\cap g \Gamma _j g^{-1})$
for some
![]() $g\in \Gamma $
. Since
$g\in \Gamma $
. Since
![]() $[\Lambda _1: \Lambda _k\cap \Lambda _1]<\infty $
, we therefore deduce that
$[\Lambda _1: \Lambda _k\cap \Lambda _1]<\infty $
, we therefore deduce that
![]() ${\mathcal L}(\Gamma _1)\prec _{{\mathcal M}} {\mathcal L}(\Lambda _k\cap \Lambda _1)$
and
${\mathcal L}(\Gamma _1)\prec _{{\mathcal M}} {\mathcal L}(\Lambda _k\cap \Lambda _1)$
and
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1)\prec _{{\mathcal M}} \mathcal L(\Gamma _{\hat v})$
for some
${\mathcal L}(\Lambda _k\cap \Lambda _1)\prec _{{\mathcal M}} \mathcal L(\Gamma _{\hat v})$
for some
![]() $v\in \mathscr {C}_{i}$
. By Lemma 2.10, we get that
$v\in \mathscr {C}_{i}$
. By Lemma 2.10, we get that
![]() $\Gamma _v$
is amenable, contradiction.
$\Gamma _v$
is amenable, contradiction.
Thus, we have
![]() $J_k=J_1$
and
$J_k=J_1$
and
![]() $z_1^i=z_k^i$
for all
$z_1^i=z_k^i$
for all
![]() $i\in J_1$
. Indeed, if
$i\in J_1$
. Indeed, if
![]() $i\in J_1$
, then there exists
$i\in J_1$
, then there exists
![]() $l\in J_k$
, such that
$l\in J_k$
, such that
![]() $z_1^i z_k^l\neq 0$
. The previous paragraph shows that
$z_1^i z_k^l\neq 0$
. The previous paragraph shows that
![]() $l=i$
. This shows, in particular, that
$l=i$
. This shows, in particular, that
![]() $J_1\subset J_k$
. By symmetry, we also get that
$J_1\subset J_k$
. By symmetry, we also get that
![]() $J_k\subset J_1$
. The previous paragraph also implies that
$J_k\subset J_1$
. The previous paragraph also implies that
![]() $z_1^i z_k^{i'}= 0$
for all
$z_1^i z_k^{i'}= 0$
for all
![]() $i'\in J_k$
with
$i'\in J_k$
with
![]() $i'\neq i$
. This implies that
$i'\neq i$
. This implies that
![]() $z_1^i\leq z_k^i$
, and the conclusion follows again by symmetry reasons.
$z_1^i\leq z_k^i$
, and the conclusion follows again by symmetry reasons.
Next, we show that
![]() $\Lambda _k=\Lambda _1$
. Assumption 2. gives that
$\Lambda _k=\Lambda _1$
. Assumption 2. gives that
![]() $\text {for all } i\in J_1=J_k$
, we have
$\text {for all } i\in J_1=J_k$
, we have
Fix an element
![]() $w_i\in \mathscr {C}_i$
, and note that
$w_i\in \mathscr {C}_i$
, and note that
![]() $\Gamma = \Gamma _{\mathscr V\setminus \{w_i\}} \ast _{\Gamma _{\hat {w_i}}} \Gamma _i$
, where
$\Gamma = \Gamma _{\mathscr V\setminus \{w_i\}} \ast _{\Gamma _{\hat {w_i}}} \Gamma _i$
, where
![]() $\Gamma =\mathscr {G}\{\Gamma _v,v \in \mathscr V\}$
. As before, Lemma 2.10 implies that
$\Gamma =\mathscr {G}\{\Gamma _v,v \in \mathscr V\}$
. As before, Lemma 2.10 implies that
By letting
![]() $a^i=u_1^i z_1^i (u_k^i)^*$
, we note that
$a^i=u_1^i z_1^i (u_k^i)^*$
, we note that
By using (6.16), (6.17), (6.18) and by applying [Reference Ioana, Peterson and PopaIPP05, Theorem 1.2.1], we get that
![]() $a^i\in {\mathcal L}(\Gamma _i)$
. Assumption 2. implies that
$a^i\in {\mathcal L}(\Gamma _i)$
. Assumption 2. implies that
By noticing that
![]() $z_1^1=z_k^1$
and by conjugating the previous inclusion by
$z_1^1=z_k^1$
and by conjugating the previous inclusion by
![]() $a^1\in {\mathcal L}(\Gamma _1)$
, we derive that
$a^1\in {\mathcal L}(\Gamma _1)$
, we derive that
Hence,
![]() $u_1^1 z_1^1 (u_1^1)^*=p_1$
, and therefore,
$u_1^1 z_1^1 (u_1^1)^*=p_1$
, and therefore,
![]() ${\mathcal L}(\Lambda _k\cap \Lambda _1)z_1^1\subset {\mathcal L}(\Lambda _k)z_1^1\subset \mathcal L(\Lambda _1)z_1^1$
. Since
${\mathcal L}(\Lambda _k\cap \Lambda _1)z_1^1\subset {\mathcal L}(\Lambda _k)z_1^1\subset \mathcal L(\Lambda _1)z_1^1$
. Since
![]() ${[\Lambda _1: \Lambda _k\cap \Lambda _1]<\infty }$
, we deduce that
${[\Lambda _1: \Lambda _k\cap \Lambda _1]<\infty }$
, we deduce that
![]() $\mathcal L(\Lambda _k\cap \Lambda _1)z_1^1\subset \mathcal L(\Lambda _k)z_1^1$
admits a finite Pimsner-Popa basis. By applying [Reference Chifan, de Santiago and SinclairCdSS15, Proposition 2.6], we derive that
$\mathcal L(\Lambda _k\cap \Lambda _1)z_1^1\subset \mathcal L(\Lambda _k)z_1^1$
admits a finite Pimsner-Popa basis. By applying [Reference Chifan, de Santiago and SinclairCdSS15, Proposition 2.6], we derive that
![]() $[\Lambda _k: \Lambda _k\cap \Lambda _1]<\infty $
. In combination with
$[\Lambda _k: \Lambda _k\cap \Lambda _1]<\infty $
. In combination with
![]() $[\Lambda _1: \Lambda _k\cap \Lambda _1]<\infty $
, we get that
$[\Lambda _1: \Lambda _k\cap \Lambda _1]<\infty $
, we get that
Therefore, we have
![]() $u_1^1{\mathcal L}(\Lambda _1) z_1^1 (u_1^1)^*=p_1\mathcal L(\Gamma _1) p_1$
and
$u_1^1{\mathcal L}(\Lambda _1) z_1^1 (u_1^1)^*=p_1\mathcal L(\Gamma _1) p_1$
and
![]() $u_k^k\mathcal L(\Lambda _1) z_k^k (u_k^k)^*=p_k\mathcal L(\Gamma _k) p_k$
. Since
$u_k^k\mathcal L(\Lambda _1) z_k^k (u_k^k)^*=p_k\mathcal L(\Gamma _k) p_k$
. Since
![]() $z_1^k=z_k^k$
and all these work for all
$z_1^k=z_k^k$
and all these work for all
![]() $k\in J_1$
, we get the conclusion of the proof for the first element of the partition. Namely, we let
$k\in J_1$
, we get the conclusion of the proof for the first element of the partition. Namely, we let
![]() $\tilde \Lambda _1=\Lambda _1$
,
$\tilde \Lambda _1=\Lambda _1$
,
![]() $T_1=J_1$
,
$T_1=J_1$
,
![]() $\tilde u_1^k= u_k^k $
and
$\tilde u_1^k= u_k^k $
and
![]() $\tilde z_1^k= z_k^k$
. Finally, if
$\tilde z_1^k= z_k^k$
. Finally, if
![]() $T_1=\{1,\dots ,n\}$
, then the proof is completed. Otherwise, pick an element
$T_1=\{1,\dots ,n\}$
, then the proof is completed. Otherwise, pick an element
![]() $t\in \{1,\dots ,n\}\setminus T_1$
, and repeat the above arguments, starting with
$t\in \{1,\dots ,n\}\setminus T_1$
, and repeat the above arguments, starting with
![]() $J_t$
.
$J_t$
.
Theorem 6.5. Let
![]() $\Gamma = \mathscr {G} \{\Gamma _v\}$
be a graph product of groups, such that
$\Gamma = \mathscr {G} \{\Gamma _v\}$
be a graph product of groups, such that
![]() $\mathscr {G}\in \mathrm {CC}_1$
and for any
$\mathscr {G}\in \mathrm {CC}_1$
and for any
![]() $v\in \mathscr V$
,
$v\in \mathscr V$
,
![]() $\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
$\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
![]() $A_v$
is Abelian,
$A_v$
is Abelian,
![]() $B_v$
is an icc subgroup of a hyperbolic group. Assume that
$B_v$
is an icc subgroup of a hyperbolic group. Assume that
![]() $|\mathscr {C}|\neq |\mathscr {D}|$
for any two distinct cliques
$|\mathscr {C}|\neq |\mathscr {D}|$
for any two distinct cliques
![]() $\mathscr {C},\mathscr {D}\in \mathrm {cliq}(\mathscr {G})$
.
$\mathscr {C},\mathscr {D}\in \mathrm {cliq}(\mathscr {G})$
.
Let
![]() $\Lambda $
be an arbitrary group, such that
$\Lambda $
be an arbitrary group, such that
![]() ${\mathcal L}(\Gamma )={\mathcal L}(\Lambda )$
. Thus, for every clique
${\mathcal L}(\Gamma )={\mathcal L}(\Lambda )$
. Thus, for every clique
![]() $\mathscr {C}\in \mathrm {cliq}( \mathscr {G})$
, there exist a unitary
$\mathscr {C}\in \mathrm {cliq}( \mathscr {G})$
, there exist a unitary
![]() $u_{\mathscr {C}} \in {\mathcal M}$
and a subgroup
$u_{\mathscr {C}} \in {\mathcal M}$
and a subgroup
![]() $\Lambda _{\mathscr {C}} \leqslant \Lambda $
, such that
$\Lambda _{\mathscr {C}} \leqslant \Lambda $
, such that
![]() $u_{\mathscr {C}} \mathcal L(\Gamma _{\mathscr {C}}) u_{\mathscr {C}}^*= \mathcal L(\Lambda _{\mathscr {C}})$
.
$u_{\mathscr {C}} \mathcal L(\Gamma _{\mathscr {C}}) u_{\mathscr {C}}^*= \mathcal L(\Lambda _{\mathscr {C}})$
.
Proof. The proof is using several techniques from [Reference Chifan and IoanaCI17, CD-AD20]. First, let
![]() $\mathscr {C}_1,\dots ,\mathscr {C}_n$
be an enumeration of its consecutive cliques, and denote
$\mathscr {C}_1,\dots ,\mathscr {C}_n$
be an enumeration of its consecutive cliques, and denote
![]() $\Gamma _i=\Gamma _{\mathscr {C}_i}$
, for any
$\Gamma _i=\Gamma _{\mathscr {C}_i}$
, for any
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Claim 6.6. For any
![]() $1\leq i\leq n$
, there exist
$1\leq i\leq n$
, there exist
![]() $\Lambda _i<\Lambda $
with
$\Lambda _i<\Lambda $
with
![]() $\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
and a subset
$\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
and a subset
![]() $i\in J_i\subset \{1,...,n\}$
satisfying:
$i\in J_i\subset \{1,...,n\}$
satisfying:
-
1. For any
 $k\in J_i$
, there exists a projection
$k\in J_i$
, there exists a projection
 $0\neq z_i^k\in \mathcal Z({\mathcal L}(\Lambda _i))$
, such that
$0\neq z_i^k\in \mathcal Z({\mathcal L}(\Lambda _i))$
, such that
 $\sum _{k\in J _i}z_i^k=1$
;
$\sum _{k\in J _i}z_i^k=1$
; -
2. For any
 $k\in J_i$
, there exists
$k\in J_i$
, there exists
 $u_i^k\in \mathcal U({\mathcal M})$
, such that:
$u_i^k\in \mathcal U({\mathcal M})$
, such that:-
a.
 $u_i^i {\mathcal L}(\Lambda _i) z_i^i (u_i^i)^*=p_i{\mathcal L}(\Gamma _i)p_i$
, where
$u_i^i {\mathcal L}(\Lambda _i) z_i^i (u_i^i)^*=p_i{\mathcal L}(\Gamma _i)p_i$
, where
 $p_i=u_i^i z_i^i (u_i^i)^*$
;
$p_i=u_i^i z_i^i (u_i^i)^*$
; -
b.
 $u_i^k {\mathcal L}(\Lambda _i) z_i^k (u_i^k)^*\subset {\mathcal L}(\Gamma _k)$
.
$u_i^k {\mathcal L}(\Lambda _i) z_i^k (u_i^k)^*\subset {\mathcal L}(\Gamma _k)$
.
-
Proof of the Claim 6.6.
Fix
![]() $1\leq i\leq n$
. By applying Theorems 6.2 and 6.3, there exist a subgroup
$1\leq i\leq n$
. By applying Theorems 6.2 and 6.3, there exist a subgroup
![]() $\Lambda _i<\Lambda $
with
$\Lambda _i<\Lambda $
with
![]() $\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
, a projection
$\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
, a projection
![]() $0\neq z_i\in \mathcal Z({\mathcal L}(\Lambda _i))$
and
$0\neq z_i\in \mathcal Z({\mathcal L}(\Lambda _i))$
and
![]() $u_i\in \mathscr {U}({\mathcal M})$
with
$u_i\in \mathscr {U}({\mathcal M})$
with
![]() $p_i=u_iz_i (u_i)^*\in {\mathcal L} (\Gamma _i)$
, such that
$p_i=u_iz_i (u_i)^*\in {\mathcal L} (\Gamma _i)$
, such that
Since
![]() $\Gamma _i$
has property (T), then (6.19) together with [Reference Chifan and IoanaCI17, Lemma 2.13] imply that
$\Gamma _i$
has property (T), then (6.19) together with [Reference Chifan and IoanaCI17, Lemma 2.13] imply that
![]() $\Lambda _i$
has property (T) as well. Using
$\Lambda _i$
has property (T) as well. Using
![]() $\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
and
$\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
and
![]() ${\mathcal L}(\Lambda _i)'\cap {\mathcal M}\subset {\mathcal L}(\mathrm {vC}_{\Lambda }(\Lambda _i))$
, it follows that
${\mathcal L}(\Lambda _i)'\cap {\mathcal M}\subset {\mathcal L}(\mathrm {vC}_{\Lambda }(\Lambda _i))$
, it follows that
Since
![]() ${\mathcal L}(\Gamma _j)$
is a II
${\mathcal L}(\Gamma _j)$
is a II
![]() $_1$
factor for any
$_1$
factor for any
![]() $1\leq j\leq n$
, by using (6.20), there is a maximal projection
$1\leq j\leq n$
, by using (6.20), there is a maximal projection
![]() $z_j^i\in \mathscr Z({\mathcal L}(\Lambda _i))$
, such that
$z_j^i\in \mathscr Z({\mathcal L}(\Lambda _i))$
, such that
![]() ${\mathcal L}(\Lambda _i)z_j^i$
can be unitarily conjugated into
${\mathcal L}(\Lambda _i)z_j^i$
can be unitarily conjugated into
![]() $\mathcal L(\Gamma _j)$
; hence, we take
$\mathcal L(\Gamma _j)$
; hence, we take
![]() $u_j^i\in \mathscr {U}({\mathcal M})$
, such that
$u_j^i\in \mathscr {U}({\mathcal M})$
, such that
![]() $u_j^i\mathcal L(\Lambda _i)z_j^i (u_j^i)^*\subset \mathcal L(\Gamma _j).$
We continue by showing that
$u_j^i\mathcal L(\Lambda _i)z_j^i (u_j^i)^*\subset \mathcal L(\Gamma _j).$
We continue by showing that
![]() $\bigvee _{j=1}^n z_j^i=1$
. By assuming the contrary, then
$\bigvee _{j=1}^n z_j^i=1$
. By assuming the contrary, then
![]() $z=1-\bigvee _{j=1}^n z_j^i$
is a nonzero projection of
$z=1-\bigvee _{j=1}^n z_j^i$
is a nonzero projection of
![]() $\mathscr Z({\mathcal L}(\Lambda _i))$
. Since
$\mathscr Z({\mathcal L}(\Lambda _i))$
. Since
![]() ${\mathcal L}(\Lambda _i)z$
has property (T), Theorem 2.8 implies that there exists
${\mathcal L}(\Lambda _i)z$
has property (T), Theorem 2.8 implies that there exists
![]() $j\in \overline {1,n}$
, such that
$j\in \overline {1,n}$
, such that
![]() ${\mathcal L}(\Lambda _i)z\prec _{{\mathcal M}} \mathcal L(\Gamma _j)$
. Note that
${\mathcal L}(\Lambda _i)z\prec _{{\mathcal M}} \mathcal L(\Gamma _j)$
. Note that
![]() $\mathcal L(\Lambda _i)z\nprec _{{\mathcal M}} \mathcal L(\Gamma _{\mathscr {C}_j\setminus \{v\}})$
, for any
$\mathcal L(\Lambda _i)z\nprec _{{\mathcal M}} \mathcal L(\Gamma _{\mathscr {C}_j\setminus \{v\}})$
, for any
![]() $v\in \mathscr {C}_j$
. Indeed, otherwise, there is
$v\in \mathscr {C}_j$
. Indeed, otherwise, there is
![]() $v\in \mathscr {C}_j$
, such that
$v\in \mathscr {C}_j$
, such that
![]() $\mathcal L(\Lambda _i)\prec _{{\mathcal M}} \mathcal L(\Gamma _{\mathscr {C}_j\setminus \{v\}})$
. By using [Reference VaesVa08, Lemma 3.5] and (6.20), we get
$\mathcal L(\Lambda _i)\prec _{{\mathcal M}} \mathcal L(\Gamma _{\mathscr {C}_j\setminus \{v\}})$
. By using [Reference VaesVa08, Lemma 3.5] and (6.20), we get
![]() ${\mathcal L}(\Gamma _{v})\prec _{{\mathcal M}} \mathcal L(\Lambda _i)'\cap {\mathcal M}=\mathscr Z(\mathcal L(\Lambda _i))$
, which is impossible since
${\mathcal L}(\Gamma _{v})\prec _{{\mathcal M}} \mathcal L(\Lambda _i)'\cap {\mathcal M}=\mathscr Z(\mathcal L(\Lambda _i))$
, which is impossible since
![]() $\Gamma _v$
is nonamenable. Therefore, the ‘moreover’ part of Theorem 2.8 gives a nonzero projection
$\Gamma _v$
is nonamenable. Therefore, the ‘moreover’ part of Theorem 2.8 gives a nonzero projection
![]() $z_0\in \mathscr Z (\mathcal L(\Lambda _i))$
and
$z_0\in \mathscr Z (\mathcal L(\Lambda _i))$
and
![]() $u_0\in \mathscr {U}({\mathcal M})$
, such that
$u_0\in \mathscr {U}({\mathcal M})$
, such that
![]() $u_0 \mathcal L(\Lambda _i)z_0 u_0^*\subset \mathcal L(\Gamma _j)$
. Recall that
$u_0 \mathcal L(\Lambda _i)z_0 u_0^*\subset \mathcal L(\Gamma _j)$
. Recall that
![]() $u_j^i{\mathcal L}(\Lambda _i)z_j^i (u_j^i)^*\subset {\mathcal L}(\Gamma _j).$
Since
$u_j^i{\mathcal L}(\Lambda _i)z_j^i (u_j^i)^*\subset {\mathcal L}(\Gamma _j).$
Since
![]() ${\mathcal L}(\Gamma _j)$
is a II
${\mathcal L}(\Gamma _j)$
is a II
![]() $_1$
factor, we can perturb
$_1$
factor, we can perturb
![]() $u_0$
by a different unitary and assume that
$u_0$
by a different unitary and assume that
![]() $u_0z_0 u_0^*$
and
$u_0z_0 u_0^*$
and
![]() $u_j^iz_j^i (u_j^i)^*$
are orthogonal projections in
$u_j^iz_j^i (u_j^i)^*$
are orthogonal projections in
![]() $\mathcal L(\Gamma _j)$
. By letting
$\mathcal L(\Gamma _j)$
. By letting
![]() $u=u_0z_0+u_j^iz_j^i$
, we note that
$u=u_0z_0+u_j^iz_j^i$
, we note that
![]() $u^*u=z_0+z_j^i$
and let
$u^*u=z_0+z_j^i$
and let
![]() $v\in \mathscr {U}({\mathcal M})$
, such that
$v\in \mathscr {U}({\mathcal M})$
, such that
![]() $vu^*u=u$
. Therefore,
$vu^*u=u$
. Therefore,
![]() $v \mathcal L(\Lambda _i)(z_0+z_j^i) v^*\subset \mathcal L(\Gamma _j)$
, which contradicts the maximality of
$v \mathcal L(\Lambda _i)(z_0+z_j^i) v^*\subset \mathcal L(\Gamma _j)$
, which contradicts the maximality of
![]() $z_j^i$
. This shows that
$z_j^i$
. This shows that
![]() $\bigvee _{j=1}^n z_j^i=1$
.
$\bigvee _{j=1}^n z_j^i=1$
.
Next, we prove that
![]() $z_i^i=z_i$
. By assuming the contrary, the maximality of
$z_i^i=z_i$
. By assuming the contrary, the maximality of
![]() $z_i^i$
implies that
$z_i^i$
implies that
![]() $c:=z_i^i-z_i$
is a nonzero projection in
$c:=z_i^i-z_i$
is a nonzero projection in
![]() $\mathscr Z({\mathcal L}(\Lambda _i))$
. By using (6.19) and
$\mathscr Z({\mathcal L}(\Lambda _i))$
. By using (6.19) and
![]() $u_i^i{\mathcal L}(\Lambda _i)c (u_i^i)^*\subset {\mathcal L}(\Gamma _j)$
, we can proceed as in the previous paragraph and assume that
$u_i^i{\mathcal L}(\Lambda _i)c (u_i^i)^*\subset {\mathcal L}(\Gamma _j)$
, we can proceed as in the previous paragraph and assume that
![]() $p_i$
and
$p_i$
and
![]() $p:=u_i^i c (u_i^i)^*$
are orthogonal projections of
$p:=u_i^i c (u_i^i)^*$
are orthogonal projections of
![]() ${\mathcal L}(\Gamma _i)$
. Hence, by letting
${\mathcal L}(\Gamma _i)$
. Hence, by letting
![]() $u=u_i^i c + u_i z_i$
, we derive that
$u=u_i^i c + u_i z_i$
, we derive that
![]() $uu^*=p+p_i$
,
$uu^*=p+p_i$
,
![]() $u^*u=c+z_i$
and
$u^*u=c+z_i$
and
Since
![]() $\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
, we obtain from Lemmas 2.13 and 2.15 that
$\mathrm {QN_\Lambda ^{(1)}}(\Lambda _i)=\Lambda _i$
, we obtain from Lemmas 2.13 and 2.15 that
Relations (6.19), (6.21) and (6.22) and the fact that
![]() $(p+p_i){\mathcal L}(\Gamma _j)(p+p_i)$
is a II
$(p+p_i){\mathcal L}(\Gamma _j)(p+p_i)$
is a II
![]() $_1$
factor allow to apply the ‘moreover’ part of [Reference Chifan and IoanaCI17, Lemma 2.6] and deduce that
$_1$
factor allow to apply the ‘moreover’ part of [Reference Chifan and IoanaCI17, Lemma 2.6] and deduce that
![]() $u{\mathcal L}(\Lambda _i)(c+z_i) u^*= (p+p_i){\mathcal L}(\Gamma _j)(p+p_i).$
This is a contradiction, since the center of
$u{\mathcal L}(\Lambda _i)(c+z_i) u^*= (p+p_i){\mathcal L}(\Gamma _j)(p+p_i).$
This is a contradiction, since the center of
![]() $u\mathcal L(\Lambda _i)(c+z_i) u^*$
is at least two-dimensional. This shows that
$u\mathcal L(\Lambda _i)(c+z_i) u^*$
is at least two-dimensional. This shows that
![]() $z_i^i=z_i$
.
$z_i^i=z_i$
.
Finally, since
![]() $\bigvee _{j=1}^n z_j^i=1$
, for any
$\bigvee _{j=1}^n z_j^i=1$
, for any
![]() $1\leq i\leq n$
, we can eventually replace
$1\leq i\leq n$
, we can eventually replace
![]() $z_j^i$
by a smaller projection in
$z_j^i$
by a smaller projection in
![]() $\mathscr Z({\mathcal L}(\Lambda _i))$
and assume that
$\mathscr Z({\mathcal L}(\Lambda _i))$
and assume that
![]() $\{z_j^i\}_{j=1}^n$
are mutually orthogonal. The claim follows by letting
$\{z_j^i\}_{j=1}^n$
are mutually orthogonal. The claim follows by letting
![]() $J_i=\{1\leq k\leq n\,:\, z_k^i\neq 0 \}$
.
$J_i=\{1\leq k\leq n\,:\, z_k^i\neq 0 \}$
.
Next, we can apply Theorem 6.4 and obtain a partition there exist a partition
![]() $T_1\sqcup \dots \sqcup T_l= \{1,...,n\}$
and a subgroup
$T_1\sqcup \dots \sqcup T_l= \{1,...,n\}$
and a subgroup
![]() $\tilde \Lambda _i<\Lambda $
with
$\tilde \Lambda _i<\Lambda $
with
![]() $\mathrm {QN_\Lambda ^{(1)}}(\tilde \Lambda _i)=\tilde \Lambda _i$
for any
$\mathrm {QN_\Lambda ^{(1)}}(\tilde \Lambda _i)=\tilde \Lambda _i$
for any
![]() $1\leq i\leq l$
, such that:
$1\leq i\leq l$
, such that:
-
1. For any
 $k\in T_i$
, there exists a projection
$k\in T_i$
, there exists a projection
 $0\neq \tilde z_i^k\in \mathcal Z({\mathcal L}(\tilde \Lambda _i))$
satisfying
$0\neq \tilde z_i^k\in \mathcal Z({\mathcal L}(\tilde \Lambda _i))$
satisfying
 $\sum _{k\in T _i}\tilde z_i^k=1$
;
$\sum _{k\in T _i}\tilde z_i^k=1$
; -
2. For any
 $k\in T_i$
, there exists
$k\in T_i$
, there exists
 $\tilde u_i^k\in \mathcal U({\mathcal M})$
, such that
$\tilde u_i^k\in \mathcal U({\mathcal M})$
, such that
 $\tilde u_i^k {\mathcal L}(\tilde \Lambda _i) \tilde z_i^k (\tilde u_i^k)^* = \tilde p_k^i{\mathcal L}(\Gamma _k) \tilde p_k^i$
, where
$\tilde u_i^k {\mathcal L}(\tilde \Lambda _i) \tilde z_i^k (\tilde u_i^k)^* = \tilde p_k^i{\mathcal L}(\Gamma _k) \tilde p_k^i$
, where
 $\tilde p_k^i=\tilde u_i^k \tilde z_i^k (\tilde u_i^k)^*$
.
$\tilde p_k^i=\tilde u_i^k \tilde z_i^k (\tilde u_i^k)^*$
.
Note that it is enough to show that
![]() $|T_i|=1$
, for all
$|T_i|=1$
, for all
![]() $1\leq i\leq l$
. Hence, we fix an arbitrary
$1\leq i\leq l$
. Hence, we fix an arbitrary
![]() $1\leq i\leq l$
and assume by contradiction that
$1\leq i\leq l$
and assume by contradiction that
![]() $|T_i|>2$
. Take
$|T_i|>2$
. Take
![]() $k,j \in T_i$
, two distinct elements, such that
$k,j \in T_i$
, two distinct elements, such that
![]() $|\mathscr {C}_k|>|\mathscr {C}_j|$
. Note that we have
$|\mathscr {C}_k|>|\mathscr {C}_j|$
. Note that we have
![]() ${\mathcal L}(\Gamma _k)\prec _{{\mathcal M}} {\mathcal L}(\tilde \Lambda _i)$
and
${\mathcal L}(\Gamma _k)\prec _{{\mathcal M}} {\mathcal L}(\tilde \Lambda _i)$
and
![]() $\mathcal L(\tilde \Lambda _i)\prec _{{\mathcal M}} \mathcal L(\Gamma _j)$
. Proposition 4.4 implies that
$\mathcal L(\tilde \Lambda _i)\prec _{{\mathcal M}} \mathcal L(\Gamma _j)$
. Proposition 4.4 implies that
![]() $|\mathscr {C}_k|\leq |\mathscr {C}_j|$
, contradiction. This shows that
$|\mathscr {C}_k|\leq |\mathscr {C}_j|$
, contradiction. This shows that
![]() $|T_i|=1$
, for all
$|T_i|=1$
, for all
![]() $1\leq i\leq l$
, and the conclusion follows.
$1\leq i\leq l$
, and the conclusion follows.
7 Superrigidity results within the category of graph product groups
In this final section, we derive a strong rigidity result for factors arising from graph product groups considered in Section 5 (see Theorem 7.6). Building upon the results in the prior sections, we show that the graph product groups considered in Theorem 6.5 are completely recognizable from the category of all von Neumann algebras associated to any nontrivial graph product group with infinite vertex groups. Notice that unlike previous strong rigidity results [Reference Ioana, Peterson and PopaIPP05, Reference Chifan and HoudayerCH08], in our case, we do not need any other additional a priori assumptions on the vertex groups or on the underlying graph.
To prove our theorem, we first establish a result which asserts that the click subgroups of the graph products from Theorem 6.5 along with various other aspects of their ‘position’ in the ambient group are features which are completely recognizable from the von Neumann algebra framework. The result relies heavily on Theorem 6.5, and for the proof, we only explain how it follows from this. Although, for deriving Theorem 7.6 we do not need all the parts of the conclusion, we decided to state it here in its complete and somewhat technical form as this could be instrumental for further attempts to establish
![]() $W^*$
-superrigidity of these groups.
$W^*$
-superrigidity of these groups.
Theorem 7.1. Let
![]() $\mathscr {G}\in \mathrm {CC}_1$
, let
$\mathscr {G}\in \mathrm {CC}_1$
, let
![]() $\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1, \ldots , \mathscr {C}_n\}$
be a consecutive cliques enumeration and assume that
$\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1, \ldots , \mathscr {C}_n\}$
be a consecutive cliques enumeration and assume that
![]() $|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
$|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group, such that for any
$\Gamma = \mathscr {G}\{\Gamma _v\}$
be a graph product group, such that for any
![]() $v\in \mathscr V$
,
$v\in \mathscr V$
,
![]() $\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
$\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
![]() $A_v$
is Abelian,
$A_v$
is Abelian,
![]() $B_v$
is an icc subgroup of a hyperbolic group and the set
$B_v$
is an icc subgroup of a hyperbolic group and the set
![]() $\{i\in I_v \; | \; g\cdot i\neq i\}$
is infinite for any
$\{i\in I_v \; | \; g\cdot i\neq i\}$
is infinite for any
![]() $g\in B_v\setminus \{1\}$
. Denote
$g\in B_v\setminus \{1\}$
. Denote
![]() ${\mathcal M}={\mathcal L}(\Gamma )$
.
${\mathcal M}={\mathcal L}(\Gamma )$
.
Let
![]() $\Lambda $
be an arbitrary group, such that
$\Lambda $
be an arbitrary group, such that
![]() ${\mathcal M}={\mathcal L}(\Lambda )$
. Then for any
${\mathcal M}={\mathcal L}(\Lambda )$
. Then for any
![]() $1\leq i\leq n$
, one can find a unitary
$1\leq i\leq n$
, one can find a unitary
![]() $w_i\in {\mathcal M}$
and a subgroup
$w_i\in {\mathcal M}$
and a subgroup
![]() $\Lambda _i<\Lambda $
satisfying the following relations:
$\Lambda _i<\Lambda $
satisfying the following relations:
-
1.
 $\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T \Lambda _i$
for all
$\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T \Lambda _i$
for all
 $1\leq i\leq n$
;
$1\leq i\leq n$
; -
2.
 $\mathbb T w_i \Gamma _{\mathscr {C}_{i,i+1}} w_i^*= \mathbb T w_{i+1} \Gamma _{\mathscr {C}_{i,i+1}} w_{i+1}^*= \mathbb T \Lambda _{i,i+1}$
where
$\mathbb T w_i \Gamma _{\mathscr {C}_{i,i+1}} w_i^*= \mathbb T w_{i+1} \Gamma _{\mathscr {C}_{i,i+1}} w_{i+1}^*= \mathbb T \Lambda _{i,i+1}$
where
 $\Lambda _{i,i+1}= \Lambda _i\cap \Lambda _{i+1}$
for all
$\Lambda _{i,i+1}= \Lambda _i\cap \Lambda _{i+1}$
for all
 $1\leq i\leq n-1$
;
$1\leq i\leq n-1$
; -
3. There is an
 $s\in \Lambda $
, such that
$s\in \Lambda $
, such that
 $\mathbb T w_n \Gamma _{\mathscr {C}_{n,1}} w_n^*= \mathbb T v_s w_{1} \Gamma _{\mathscr {C}_{n,1}} w_{1}^* v_{s^{-1}}= \mathbb T \Lambda _{n}\cap s \Lambda _1 s^{-1}$
;
$\mathbb T w_n \Gamma _{\mathscr {C}_{n,1}} w_n^*= \mathbb T v_s w_{1} \Gamma _{\mathscr {C}_{n,1}} w_{1}^* v_{s^{-1}}= \mathbb T \Lambda _{n}\cap s \Lambda _1 s^{-1}$
; -
4.
 $w_i{\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})w_i^*=w_{i+1}{\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})w_{i+1}^* = {\mathcal L}(\Lambda _{i,i+1} C_\Lambda (\Lambda _{i,i+1}))$
, and hence
$w_i{\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})w_i^*=w_{i+1}{\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})w_{i+1}^* = {\mathcal L}(\Lambda _{i,i+1} C_\Lambda (\Lambda _{i,i+1}))$
, and hence
 $w^*_{i+1}w_i\in {\mathcal L} (\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})$
, for all
$w^*_{i+1}w_i\in {\mathcal L} (\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})$
, for all
 $1\leq i\leq n-1$
;
$1\leq i\leq n-1$
; -
5.
 $\vee ^{n-1}_{i=1} \left (\Lambda _{i,i+1} C_\Lambda (\Lambda _{i,i+1})\right )=\Lambda $
.
$\vee ^{n-1}_{i=1} \left (\Lambda _{i,i+1} C_\Lambda (\Lambda _{i,i+1})\right )=\Lambda $
.
Proof. Using Theorem 6.5 and Corollary 5.3, one can find for any
![]() $1\leq i\leq n$
, a unitary
$1\leq i\leq n$
, a unitary
![]() $x_i\in {\mathcal M}$
and a subgroup
$x_i\in {\mathcal M}$
and a subgroup
![]() $\Lambda _i<\Lambda $
satisfying
$\Lambda _i<\Lambda $
satisfying
![]() $\mathbb T x_i \Gamma _{\mathscr {C}_i} x_i^* =\mathbb T \Lambda _i$
. The prior relations show that
$\mathbb T x_i \Gamma _{\mathscr {C}_i} x_i^* =\mathbb T \Lambda _i$
. The prior relations show that
![]() $\mathbb T x_1 \Gamma _{\mathscr {C}_{1,2}} x_1^* =\mathbb T \Lambda ^{\prime }_1$
and
$\mathbb T x_1 \Gamma _{\mathscr {C}_{1,2}} x_1^* =\mathbb T \Lambda ^{\prime }_1$
and
![]() $\mathbb T x_2 \Gamma _{\mathscr {C}_{1,2}} x_2^* =\mathbb T \Lambda ^{\prime }_2$
for two subproduct groups
$\mathbb T x_2 \Gamma _{\mathscr {C}_{1,2}} x_2^* =\mathbb T \Lambda ^{\prime }_2$
for two subproduct groups
![]() $\Lambda ^{\prime }_1<\Lambda _1$
and
$\Lambda ^{\prime }_1<\Lambda _1$
and
![]() $\Lambda ^{\prime }_2<\Lambda _2$
. Thus, for every
$\Lambda ^{\prime }_2<\Lambda _2$
. Thus, for every
![]() $i=1,2$
, there exist a group isomorphism
$i=1,2$
, there exist a group isomorphism
![]() $\delta _i: \Gamma _{\mathscr {C}_{1,2}}\rightarrow \Lambda _i'$
and a multiplicative character
$\delta _i: \Gamma _{\mathscr {C}_{1,2}}\rightarrow \Lambda _i'$
and a multiplicative character
![]() $\eta _i :\mathscr {C}_{1,2}\to \mathbb T$
, such that
$\eta _i :\mathscr {C}_{1,2}\to \mathbb T$
, such that
Letting
![]() $\eta (g)=\overline {\eta _2(g)}\eta _1(g)$
, one can see that altogether these relations imply that
$\eta (g)=\overline {\eta _2(g)}\eta _1(g)$
, one can see that altogether these relations imply that
![]() $\eta (g) x_2x_1^* v_{\delta _1(g)}= \overline {\eta _2(g)} x_2 u_g x_1^*= v_{\delta _2(g)} x_2x_1^\ast $
or all
$\eta (g) x_2x_1^* v_{\delta _1(g)}= \overline {\eta _2(g)} x_2 u_g x_1^*= v_{\delta _2(g)} x_2x_1^\ast $
or all
![]() $g\in \Gamma _{\mathscr {C}_{1,2}} $
. Hence,
$g\in \Gamma _{\mathscr {C}_{1,2}} $
. Hence,
![]() $\eta (g) x_2x_1^* = v_{\delta _2(g)} x_2x_1^*v_{\delta _1(g^{-1})}$
, for all
$\eta (g) x_2x_1^* = v_{\delta _2(g)} x_2x_1^*v_{\delta _1(g^{-1})}$
, for all
![]() $g\in \Gamma _{\mathscr {C}_{1,2}} $
. If we consider the Fourier decomposition of
$g\in \Gamma _{\mathscr {C}_{1,2}} $
. If we consider the Fourier decomposition of
![]() $x_2x_1^*$
in
$x_2x_1^*$
in
![]() ${\mathcal M}={\mathcal L}(\Lambda )$
, then basic analysis together with the previous relation show that
${\mathcal M}={\mathcal L}(\Lambda )$
, then basic analysis together with the previous relation show that
![]() $x_2x_1^*$
is supported on the set of those
$x_2x_1^*$
is supported on the set of those
![]() $h\in \Lambda $
for which the orbit
$h\in \Lambda $
for which the orbit
![]() $\{ \delta _2(g) h \delta _1(g^{-1}) \,:\, g\in \Gamma _{\mathscr {C}_{1,2}}\}$
is finite. This finiteness condition yields that for any such h, one can find a finite index subgroup
$\{ \delta _2(g) h \delta _1(g^{-1}) \,:\, g\in \Gamma _{\mathscr {C}_{1,2}}\}$
is finite. This finiteness condition yields that for any such h, one can find a finite index subgroup
![]() $\Sigma _h\leqslant \Gamma _{\mathscr {C}_{1,2}}$
, such that
$\Sigma _h\leqslant \Gamma _{\mathscr {C}_{1,2}}$
, such that
![]() $\delta _2(g) h \delta _1(g^{-1})=h$
, and hence,
$\delta _2(g) h \delta _1(g^{-1})=h$
, and hence,
![]() $\delta _1(g) = h^{-1}\delta _2(g)h$
, for all
$\delta _1(g) = h^{-1}\delta _2(g)h$
, for all
![]() $g\in \Sigma _h$
. Thus, replacing
$g\in \Sigma _h$
. Thus, replacing
![]() $\delta _2$
by
$\delta _2$
by
![]() $\mathrm {ad}(h^{-1})\circ \delta _2$
,
$\mathrm {ad}(h^{-1})\circ \delta _2$
,
![]() $x_2$
by
$x_2$
by
![]() $v_{h^{-1}} x_2$
and
$v_{h^{-1}} x_2$
and
![]() $\Lambda _2$
by
$\Lambda _2$
by
![]() $h^{-1}\Lambda _2 h$
, we can assume that
$h^{-1}\Lambda _2 h$
, we can assume that
![]() ${\delta _1}_{|_{\Sigma _h}}= {\delta _2}_{|_{\Sigma _h}}$
. Moreover, using this combined with (7.1), we deduce that
${\delta _1}_{|_{\Sigma _h}}= {\delta _2}_{|_{\Sigma _h}}$
. Moreover, using this combined with (7.1), we deduce that
![]() $u_g x u_{g^{-1}}= \eta (g) x$
where
$u_g x u_{g^{-1}}= \eta (g) x$
where
![]() $x=x_1^*x_2$
. However, this shows that x is supported on elements
$x=x_1^*x_2$
. However, this shows that x is supported on elements
![]() $h\in \Gamma $
with finite
$h\in \Gamma $
with finite
![]() $\Sigma _h$
-conjugation orbits. Using the icc condition and the graph product structure, we can see that such elements belong to
$\Sigma _h$
-conjugation orbits. Using the icc condition and the graph product structure, we can see that such elements belong to
![]() $\Gamma _{\mathscr {C}_1\triangle \mathscr {C}_2}$
, and hence,
$\Gamma _{\mathscr {C}_1\triangle \mathscr {C}_2}$
, and hence,
![]() $x\in {\mathcal L}(\Gamma _{\mathscr {C}_1\triangle \mathscr {C}_2})$
. Therefore, it follows from (7.1) that
$x\in {\mathcal L}(\Gamma _{\mathscr {C}_1\triangle \mathscr {C}_2})$
. Therefore, it follows from (7.1) that
![]() $\eta _1(g)v_{\delta _1(g)}=x_1 u_g x_1^*= x_2 u_g x_2^*= \eta _2(g)v_{\delta _2(g)}$
for all
$\eta _1(g)v_{\delta _1(g)}=x_1 u_g x_1^*= x_2 u_g x_2^*= \eta _2(g)v_{\delta _2(g)}$
for all
![]() $g\in \Gamma _{\mathscr {C}_{1,2}}$
. In particular,
$g\in \Gamma _{\mathscr {C}_{1,2}}$
. In particular,
![]() $\delta _1=\delta _2$
on
$\delta _1=\delta _2$
on
![]() $ \Gamma _{\mathscr {C}_{1,2}}$
; altogether, this implies the conclusion for
$ \Gamma _{\mathscr {C}_{1,2}}$
; altogether, this implies the conclusion for
![]() $i=1$
. Continuing by induction, after conjugating the
$i=1$
. Continuing by induction, after conjugating the
![]() $\Lambda _i$
’s by elements in
$\Lambda _i$
’s by elements in
![]() $\Lambda $
, we obtain the conclusion of the first three parts.
$\Lambda $
, we obtain the conclusion of the first three parts.
Next, we prove 4. First notice that 2. implies
By using the graph product structure and by taking quasi-normalizers in (7.2), we apply Lemma 2.15 to derive that
![]() $w_i{\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})w_i^*= w_i {\mathcal L}(\mathrm {QN}_\Gamma (\Gamma _{\mathscr {C}_{i,i+1}})) w_i^*=w_{i} \mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}))"w_i^*\kern1.3pt{=}\kern1.3ptw_{i+1} \mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}))" w_{i+1}^*\kern1.3pt{=}\kern1.3pt w_{i+1} ({\mathcal L}(\mathrm {QN}_\Gamma (\Gamma _{\mathscr {C}_{i,i+1}})) w_{i+1}^*\kern1.3pt{=} w_{i+1} {\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}}\kern-0.1pt) w_{i+1}^* $
. The same quasi-normalizer formula also implies that
$w_i{\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}})w_i^*= w_i {\mathcal L}(\mathrm {QN}_\Gamma (\Gamma _{\mathscr {C}_{i,i+1}})) w_i^*=w_{i} \mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}))"w_i^*\kern1.3pt{=}\kern1.3ptw_{i+1} \mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}))" w_{i+1}^*\kern1.3pt{=}\kern1.3pt w_{i+1} ({\mathcal L}(\mathrm {QN}_\Gamma (\Gamma _{\mathscr {C}_{i,i+1}})) w_{i+1}^*\kern1.3pt{=} w_{i+1} {\mathcal L}(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}}\kern-0.1pt) w_{i+1}^* $
. The same quasi-normalizer formula also implies that
![]() $w_i\mathcal L(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}}\kern-0.1pt) w_i^*=w_{i+1} \mathcal L(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}}) w_{i+1}^*= \mathcal L(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})$
. In particular,
$w_i\mathcal L(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}}\kern-0.1pt) w_i^*=w_{i+1} \mathcal L(\Gamma _{\mathscr {C}_i\cup \mathscr {C}_{i+1}}) w_{i+1}^*= \mathcal L(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})$
. In particular,
![]() $\mathcal L(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})$
is a II
$\mathcal L(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})$
is a II
![]() $_1$
factor. Taking relative commutants in 2. we also have that
$_1$
factor. Taking relative commutants in 2. we also have that
![]() $w_i\mathcal L(\Gamma _{\mathscr {C}_{i}\triangle \mathscr {C}_{i+1}})w_i^*=w_{i+1} \mathcal L(\Gamma _{\mathscr {C}_{i}\triangle \mathscr {C}_{i+1}}) w_{i+1}^*= \mathcal L(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda )$
. Altogether, these relations imply that
$w_i\mathcal L(\Gamma _{\mathscr {C}_{i}\triangle \mathscr {C}_{i+1}})w_i^*=w_{i+1} \mathcal L(\Gamma _{\mathscr {C}_{i}\triangle \mathscr {C}_{i+1}}) w_{i+1}^*= \mathcal L(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda )$
. Altogether, these relations imply that
![]() ${\mathcal L}(\Lambda _{i,i+1})'\cap {\mathcal L}(\Lambda ) \vee {\mathcal L}(\Lambda _{i,i+1})={\mathcal L}(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})) $
. In particular, we have
${\mathcal L}(\Lambda _{i,i+1})'\cap {\mathcal L}(\Lambda ) \vee {\mathcal L}(\Lambda _{i,i+1})={\mathcal L}(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})) $
. In particular, we have
![]() $\mathrm {QN}_\Lambda (\Lambda _{i,i+1})= \Lambda _i vC_\Lambda (\Lambda _{i,i+1})$
.
$\mathrm {QN}_\Lambda (\Lambda _{i,i+1})= \Lambda _i vC_\Lambda (\Lambda _{i,i+1})$
.
Moreover, factoriality also shows that
![]() $({\mathcal L}(\Lambda _{i,i+1})'\cap {\mathcal L}(\Lambda )) \bar \otimes {\mathcal L}(\Lambda _{i,i+1})={\mathcal L}(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})) $
. As
$({\mathcal L}(\Lambda _{i,i+1})'\cap {\mathcal L}(\Lambda )) \bar \otimes {\mathcal L}(\Lambda _{i,i+1})={\mathcal L}(\mathrm {QN}_\Lambda (\Lambda _{i,i+1})) $
. As
![]() ${\mathcal L}(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda )\subseteq \mathcal L(vC_{\Lambda }(\Lambda _{i,i+1}))$
, then Ge’s tensor splitting theorem [Reference GeGe95, Theorem A] further implies that
${\mathcal L}(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda )\subseteq \mathcal L(vC_{\Lambda }(\Lambda _{i,i+1}))$
, then Ge’s tensor splitting theorem [Reference GeGe95, Theorem A] further implies that
![]() ${\mathcal L}(vC_{\Lambda }(\Lambda _{i,i+1}))=\left ( \mathcal L(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda ) \right )\bar \otimes B$
, where
${\mathcal L}(vC_{\Lambda }(\Lambda _{i,i+1}))=\left ( \mathcal L(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda ) \right )\bar \otimes B$
, where
![]() $B= \mathcal L(vC_{\Lambda }(\Lambda _{i,i+1}))\cap \mathcal L(\Lambda _{i,i+1})$
. However, we can see that
$B= \mathcal L(vC_{\Lambda }(\Lambda _{i,i+1}))\cap \mathcal L(\Lambda _{i,i+1})$
. However, we can see that
![]() $B = {\mathcal L}(vC_{\Lambda }(\Lambda _{i,i+1}))\cap {\mathcal L}(\Lambda _{i,i+1})={\mathcal L}(vC_{\Lambda }(\Lambda _{i,i+1})\cap \Lambda _{i,i+1})= \mathbb C 1$
, as
$B = {\mathcal L}(vC_{\Lambda }(\Lambda _{i,i+1}))\cap {\mathcal L}(\Lambda _{i,i+1})={\mathcal L}(vC_{\Lambda }(\Lambda _{i,i+1})\cap \Lambda _{i,i+1})= \mathbb C 1$
, as
![]() $\Lambda _{i,i+1}$
is icc. In conclusion, we have shown that
$\Lambda _{i,i+1}$
is icc. In conclusion, we have shown that
![]() $\mathcal L(vC_{\Lambda }(\Lambda _{i,i+1}))=\mathcal L(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda )$
which implies that
$\mathcal L(vC_{\Lambda }(\Lambda _{i,i+1}))=\mathcal L(\Lambda _{i,i+1})'\cap \mathcal L(\Lambda )$
which implies that
![]() $vC_{\Lambda }(\Lambda _{i,i+1})=C_\Lambda (\Lambda _{i,i+1})$
. Hence,
$vC_{\Lambda }(\Lambda _{i,i+1})=C_\Lambda (\Lambda _{i,i+1})$
. Hence,
![]() $\mathrm {QN}_\Lambda (\Lambda _{i,i+1})= \Lambda _{i,i+1} C_\Lambda (\Lambda _{i,i+1})$
. Then the remaining part of 4. follows from (7.2) and Lemma 2.15 because of the graph product structure of
$\mathrm {QN}_\Lambda (\Lambda _{i,i+1})= \Lambda _{i,i+1} C_\Lambda (\Lambda _{i,i+1})$
. Then the remaining part of 4. follows from (7.2) and Lemma 2.15 because of the graph product structure of
![]() $\mathscr {G}$
.
$\mathscr {G}$
.
Part 5. follows from part 4. Indeed, since
![]() $w_2{\mathcal L}(\Gamma _{\mathscr {C}_1\cup \mathscr {C}_{2}})w_2^*= {\mathcal L}(\Lambda _{1,2} C_\Lambda (\Lambda _{1,2}))$
and
$w_2{\mathcal L}(\Gamma _{\mathscr {C}_1\cup \mathscr {C}_{2}})w_2^*= {\mathcal L}(\Lambda _{1,2} C_\Lambda (\Lambda _{1,2}))$
and
![]() $w_{2}{\mathcal L}(\Gamma _{\mathscr {C}_2\cup \mathscr {C}_{3}})w_{2}^* \kern1pt{=}\kern1pt {\mathcal L}(\Lambda _{2,3} C_\Lambda (\Lambda _{2,3}))$
, we further get
$w_{2}{\mathcal L}(\Gamma _{\mathscr {C}_2\cup \mathscr {C}_{3}})w_{2}^* \kern1pt{=}\kern1pt {\mathcal L}(\Lambda _{2,3} C_\Lambda (\Lambda _{2,3}))$
, we further get
![]() $w_2 {\mathcal L}(\Gamma _{\mathscr {C}_1\cup \mathscr {C}_2\cup \mathscr {C}_{3} }) w_2^*\kern1pt{=}\kern1pt \mathcal L(\Lambda _{1,2} C_\Lambda (\Lambda _{1,2})\kern1pt{\vee} \Lambda _{2,3} C_\Lambda (\Lambda _{2,3}))$
. Since
$w_2 {\mathcal L}(\Gamma _{\mathscr {C}_1\cup \mathscr {C}_2\cup \mathscr {C}_{3} }) w_2^*\kern1pt{=}\kern1pt \mathcal L(\Lambda _{1,2} C_\Lambda (\Lambda _{1,2})\kern1pt{\vee} \Lambda _{2,3} C_\Lambda (\Lambda _{2,3}))$
. Since
![]() $w_3^*w_2\in \mathcal L (\Gamma _{\mathscr {C}_2\cup \mathscr {C}_3})$
, we deduce
$w_3^*w_2\in \mathcal L (\Gamma _{\mathscr {C}_2\cup \mathscr {C}_3})$
, we deduce
![]() $w_3 \mathcal L(\Gamma _{\mathscr {C}_1\cup \mathscr {C}_2\cup \mathscr {C}_{3} }) w_3^*= \mathcal L(\Lambda _{1,2} C_\Lambda (\Lambda _{1,2})\vee \Lambda _{2,3} C_\Lambda (\Lambda _{2,3}))$
. Continuing in this fashion, we get the desired conclusion by induction.
$w_3 \mathcal L(\Gamma _{\mathscr {C}_1\cup \mathscr {C}_2\cup \mathscr {C}_{3} }) w_3^*= \mathcal L(\Lambda _{1,2} C_\Lambda (\Lambda _{1,2})\vee \Lambda _{2,3} C_\Lambda (\Lambda _{2,3}))$
. Continuing in this fashion, we get the desired conclusion by induction.
Remark 7.2. We observe that, if in item 3., one could better control where the element s is located, then the statement will actually imply superrigidity of these groups. For example, this is the case if s can be picked in the subgroups
![]() $\Lambda _1$
or
$\Lambda _1$
or
![]() $\Lambda _n$
. This, however, seems difficult to establish at this time. We also note that the control of the elements s is closely related with relating the consecutive unitaries
$\Lambda _n$
. This, however, seems difficult to establish at this time. We also note that the control of the elements s is closely related with relating the consecutive unitaries
![]() $w_i$
’s, which, as we have seen in the previous results, is key in the reconstruction problem.
$w_i$
’s, which, as we have seen in the previous results, is key in the reconstruction problem.
From a different perspective, if one assumes a priori that the mysterious subgroup
![]() $\Lambda $
has a nontrivial graph product structure, the analysis can be enhanced and a reconstruction statement can be obtained. Moreover, in this case, we do not even need to use the full conclusion of Theorem 7.1. Before proceeding to the result, we need three elementary lemmas.
$\Lambda $
has a nontrivial graph product structure, the analysis can be enhanced and a reconstruction statement can be obtained. Moreover, in this case, we do not even need to use the full conclusion of Theorem 7.1. Before proceeding to the result, we need three elementary lemmas.
Lemma 7.3. Let
![]() $A,B$
be countable groups, and let
$A,B$
be countable groups, and let
![]() $C\subset \mathscr {U}({\mathcal L}(A))$
be a countable subgroup of unitaries. Assume there exists a unitary
$C\subset \mathscr {U}({\mathcal L}(A))$
be a countable subgroup of unitaries. Assume there exists a unitary
![]() $x\in {\mathcal L}(A\times B)$
, such that
$x\in {\mathcal L}(A\times B)$
, such that
![]() $\mathbb T xCx^*< \mathbb T (A\times B)$
. Then there exists a finite index subgroup
$\mathbb T xCx^*< \mathbb T (A\times B)$
. Then there exists a finite index subgroup
![]() $C_0\leqslant C$
, such that
$C_0\leqslant C$
, such that
![]() $\mathbb T xC_0x^*< \mathbb T A$
.
$\mathbb T xC_0x^*< \mathbb T A$
.
Proof. From the assumption there exist group homomorphisms
![]() $\alpha : C\rightarrow A$
,
$\alpha : C\rightarrow A$
,
![]() $\beta : C\rightarrow B$
and a character
$\beta : C\rightarrow B$
and a character
![]() $\mu \in C\to \mathbb T$
, such that for all
$\mu \in C\to \mathbb T$
, such that for all
![]() $c\in C$
, we have
$c\in C$
, we have
We denoted by
![]() $\{u_a\}_{a\in A}$
and
$\{u_a\}_{a\in A}$
and
![]() $\{v_b\}_{b\in B}$
the canonical unitaries that generate
$\{v_b\}_{b\in B}$
the canonical unitaries that generate
![]() ${\mathcal L}(A)$
and
${\mathcal L}(A)$
and
![]() ${\mathcal L}(B)$
, respectively. Letting
${\mathcal L}(B)$
, respectively. Letting
![]() $x= \sum _{b\in B}x_b \otimes v_b$
be the Fourier expansion, where
$x= \sum _{b\in B}x_b \otimes v_b$
be the Fourier expansion, where
![]() $x_b\in {\mathcal L}(A),b\in B$
, and using (7.3), we see that
$x_b\in {\mathcal L}(A),b\in B$
, and using (7.3), we see that
for any
![]() $c\in C$
. Identifying the coefficients above, we get
$c\in C$
. Identifying the coefficients above, we get
![]() $x_b c= \mu (c) u_{\alpha (c)} x_{\beta (c) ^{-1}b}$
for all
$x_b c= \mu (c) u_{\alpha (c)} x_{\beta (c) ^{-1}b}$
for all
![]() $b\in B,c\in C$
. In particular, we have
$b\in B,c\in C$
. In particular, we have
![]() $\|x_b\|_2= \| x_{\beta (c) ^{-1}b}\|_2$
, for all
$\|x_b\|_2= \| x_{\beta (c) ^{-1}b}\|_2$
, for all
![]() $b\in B,c\in C$
. Thus, if we denote the image group by
$b\in B,c\in C$
. Thus, if we denote the image group by
![]() $B_0 := \beta (C)<B$
, we get that
$B_0 := \beta (C)<B$
, we get that
![]() $\|x_b\|_2$
is constant on each left coset
$\|x_b\|_2$
is constant on each left coset
![]() $B/B_0$
. This implies that
$B/B_0$
. This implies that
![]() $B_0$
is finite, and letting
$B_0$
is finite, and letting
![]() $C_0:= \mathrm {ker} (\beta )$
, we get the desired conclusion.
$C_0:= \mathrm {ker} (\beta )$
, we get the desired conclusion.
Lemma 7.4. Let
![]() $\Gamma _1,\Gamma _2$
be countable groups, and assume
$\Gamma _1,\Gamma _2$
be countable groups, and assume
![]() $\Sigma <\Gamma _1\times \Gamma _2$
is a subgroup.
$\Sigma <\Gamma _1\times \Gamma _2$
is a subgroup.
If there is a finite index subgroup
![]() $\Gamma _1^0<\Gamma _1$
with
$\Gamma _1^0<\Gamma _1$
with
![]() $\Gamma _1^0<\Sigma $
, then there is a subgroup
$\Gamma _1^0<\Sigma $
, then there is a subgroup
![]() $\Gamma _2^0<\Gamma _2$
, such that
$\Gamma _2^0<\Gamma _2$
, such that
![]() $\Gamma _1^0\times \Gamma _2^0<\Sigma $
has finite index.
$\Gamma _1^0\times \Gamma _2^0<\Sigma $
has finite index.
Proof. Let
![]() $\pi :\Sigma \to \Gamma _1/\Gamma _1^0$
be the composition between the restriction to
$\pi :\Sigma \to \Gamma _1/\Gamma _1^0$
be the composition between the restriction to
![]() $\Sigma $
of the projection map
$\Sigma $
of the projection map
![]() $\Gamma _1\times \Gamma _2 \ni (g_1,g_2)\to g_1\in \Gamma _1$
with the quotient map
$\Gamma _1\times \Gamma _2 \ni (g_1,g_2)\to g_1\in \Gamma _1$
with the quotient map
![]() $\Gamma _1\to \Gamma _1/\Gamma _1^0$
. Since the kernel of
$\Gamma _1\to \Gamma _1/\Gamma _1^0$
. Since the kernel of
![]() $\pi $
equals
$\pi $
equals
![]() $\Sigma \cap (\Gamma _1^0\times \Gamma _2)$
and the image of
$\Sigma \cap (\Gamma _1^0\times \Gamma _2)$
and the image of
![]() $\pi $
is finite, it follows that
$\pi $
is finite, it follows that
![]() $[\Sigma : \Sigma \cap (\Gamma _1^0\times \Gamma _2)]<\infty $
. Since
$[\Sigma : \Sigma \cap (\Gamma _1^0\times \Gamma _2)]<\infty $
. Since
![]() $\Gamma _1^0<\Sigma $
, we get
$\Gamma _1^0<\Sigma $
, we get
![]() $[\Sigma : \Gamma _1^0\times (\Sigma \cap \Gamma _2)]<\infty $
.
$[\Sigma : \Gamma _1^0\times (\Sigma \cap \Gamma _2)]<\infty $
.
For the following lemma, we introduce the following ad hoc definition. We say that a countable group
![]() $\Gamma $
is virtually prime if
$\Gamma $
is virtually prime if
![]() $\Gamma $
does not admit a finite index subgroup
$\Gamma $
does not admit a finite index subgroup
![]() $\Gamma _0$
, which is generated by two infinite commuting subgroups. The next lemma shows that products of virtually prime groups satisfy a unique prime factorization result.
$\Gamma _0$
, which is generated by two infinite commuting subgroups. The next lemma shows that products of virtually prime groups satisfy a unique prime factorization result.
Lemma 7.5. Let
![]() $\Gamma =\Gamma _1\times \dots \times \Gamma _n$
be a product of countable groups that are virtually prime.
$\Gamma =\Gamma _1\times \dots \times \Gamma _n$
be a product of countable groups that are virtually prime.
If
![]() $\Sigma _1\times \Sigma _2<\Gamma $
is a finite index product subgroup, then there exist finite index subgroups
$\Sigma _1\times \Sigma _2<\Gamma $
is a finite index product subgroup, then there exist finite index subgroups
![]() $\Sigma ^0_i<\Sigma _i, 1\leq i\leq 2$
, and
$\Sigma ^0_i<\Sigma _i, 1\leq i\leq 2$
, and
![]() $\Gamma ^0_j<\Gamma _j$
,
$\Gamma ^0_j<\Gamma _j$
,
![]() $1\leq j\leq n$
, and a partition
$1\leq j\leq n$
, and a partition
![]() $T_1\sqcup T_2=\{1,\dots ,n\}$
, such that
$T_1\sqcup T_2=\{1,\dots ,n\}$
, such that
![]() $\Sigma _i^0=\times _{j\in T_i}\Gamma _j^0$
, for any
$\Sigma _i^0=\times _{j\in T_i}\Gamma _j^0$
, for any
![]() $1\leq i\leq 2$
.
$1\leq i\leq 2$
.
Proof. For any
![]() $j\in \overline {1,n}$
, let
$j\in \overline {1,n}$
, let
![]() $\pi _j:\Gamma \to \Gamma _j$
be the canonical projection. Since
$\pi _j:\Gamma \to \Gamma _j$
be the canonical projection. Since
![]() $\Gamma _j$
is virtually prime and
$\Gamma _j$
is virtually prime and
![]() $\pi _j(\Sigma _1)$
and
$\pi _j(\Sigma _1)$
and
![]() $\pi _j(\Sigma _2)$
are commuting subgroups of
$\pi _j(\Sigma _2)$
are commuting subgroups of
![]() $\Gamma _j$
, it follows that either
$\Gamma _j$
, it follows that either
![]() $\pi _j(\Sigma _1)$
or
$\pi _j(\Sigma _1)$
or
![]() $\pi _j(\Sigma _2)$
is finite. Hence, there exist finite index subgroups
$\pi _j(\Sigma _2)$
is finite. Hence, there exist finite index subgroups
![]() $\Sigma _1^0<\Sigma _1$
and
$\Sigma _1^0<\Sigma _1$
and
![]() $ \Sigma _2^0<\Sigma _2$
and a map
$ \Sigma _2^0<\Sigma _2$
and a map
![]() $\sigma :\{1,...,n\}\to \{1,2\}$
, such that
$\sigma :\{1,...,n\}\to \{1,2\}$
, such that
![]() $\pi _j(\Sigma _{\sigma (j)}^0)<\Gamma _j$
has finite index and
$\pi _j(\Sigma _{\sigma (j)}^0)<\Gamma _j$
has finite index and
![]() $\pi _j(\Sigma ^0_{\sigma (j)+1})=1$
for any
$\pi _j(\Sigma ^0_{\sigma (j)+1})=1$
for any
![]() $1\leq j\leq n$
. Here, we use the notation that
$1\leq j\leq n$
. Here, we use the notation that
![]() $\Sigma _{3}=\Sigma _1$
. By letting
$\Sigma _{3}=\Sigma _1$
. By letting
![]() $T_1=\sigma ^{-1}(1), T_2=\sigma ^{-1}(2)$
, we derive that
$T_1=\sigma ^{-1}(1), T_2=\sigma ^{-1}(2)$
, we derive that
![]() $\Sigma _i^0=\times _{j\in T_i} \pi _j(\Sigma ^0_{i})$
, for any
$\Sigma _i^0=\times _{j\in T_i} \pi _j(\Sigma ^0_{i})$
, for any
![]() $1\leq i\leq 2$
, which ends the proof.
$1\leq i\leq 2$
, which ends the proof.
With these preparations at hand, we are now ready to state and prove our main result.
Theorem 7.6. Let
![]() $\mathscr {G}\in \mathrm {CC}_1$
, let
$\mathscr {G}\in \mathrm {CC}_1$
, let
![]() $\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1, \ldots , \mathscr {C}_n\}$
be a consecutive cliques enumeration and assume that
$\mathrm {cliq}(\mathscr {G})=\{ \mathscr {C}_1, \ldots , \mathscr {C}_n\}$
be a consecutive cliques enumeration and assume that
![]() $|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
$|\mathscr {C}_i|\neq |\mathscr {C}_j|$
whenever
![]() $i\neq j$
. Let
$i\neq j$
. Let
![]() $\Gamma = \mathscr {G}\{\Gamma _v\}$
, be a graph product group, such that for any
$\Gamma = \mathscr {G}\{\Gamma _v\}$
, be a graph product group, such that for any
![]() $v\in \mathscr V$
,
$v\in \mathscr V$
,
![]() $\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
$\Gamma _v\in \mathcal W\mathcal R (A_v, B_v \curvearrowright I_v)$
where
![]() $A_v$
is Abelian,
$A_v$
is Abelian,
![]() $B_v$
is an icc subgroup of a hyperbolic group and the set
$B_v$
is an icc subgroup of a hyperbolic group and the set
![]() $\{i\in I_v \; | \; g\cdot i\neq i\}$
is infinite for any
$\{i\in I_v \; | \; g\cdot i\neq i\}$
is infinite for any
![]() $g\in B_v\setminus \{1\}$
.
$g\in B_v\setminus \{1\}$
.
Let
![]() $\theta : {\mathcal L}(\Gamma )\rightarrow {\mathcal L}(\Lambda )$
be any
$\theta : {\mathcal L}(\Gamma )\rightarrow {\mathcal L}(\Lambda )$
be any
![]() $\ast $
-isomorphism where
$\ast $
-isomorphism where
![]() $\Lambda $
is any nontrivial graph product group whose vertex groups are infinite.
$\Lambda $
is any nontrivial graph product group whose vertex groups are infinite.
Then, one can find a character
![]() $\eta : \Gamma \to \mathbb T$
, a group isomorphism
$\eta : \Gamma \to \mathbb T$
, a group isomorphism
![]() $\delta :\Gamma \to \Lambda $
, an automorphism of
$\delta :\Gamma \to \Lambda $
, an automorphism of
![]() ${\mathcal L}(\Lambda )$
of the form
${\mathcal L}(\Lambda )$
of the form
![]() $\phi _{a,b}$
(see the notation after equation (2.2) in Section 2) and a unitary
$\phi _{a,b}$
(see the notation after equation (2.2) in Section 2) and a unitary
![]() $u\in {\mathcal L}(\Lambda )$
, such that
$u\in {\mathcal L}(\Lambda )$
, such that
![]() $\theta = \mathrm {ad}(u)\circ \phi _{a,b}\circ \Psi _{\eta , \delta }$
.
$\theta = \mathrm {ad}(u)\circ \phi _{a,b}\circ \Psi _{\eta , \delta }$
.
Proof. Assume that
![]() $\Lambda = \Lambda _{\mathscr {H}}$
, and let
$\Lambda = \Lambda _{\mathscr {H}}$
, and let
![]() $\mathrm {cliq}(\mathscr {H})=\{\mathscr {D}_1,\ldots ,\mathscr {D}_m\}$
be the cliques of
$\mathrm {cliq}(\mathscr {H})=\{\mathscr {D}_1,\ldots ,\mathscr {D}_m\}$
be the cliques of
![]() $\mathscr {H}$
. To simplify the notation, assume that
$\mathscr {H}$
. To simplify the notation, assume that
![]() ${\mathcal L}(\Gamma )={\mathcal L}(\Lambda )={\mathcal M}$
. Then, by Theorem 7.1, for any
${\mathcal L}(\Gamma )={\mathcal L}(\Lambda )={\mathcal M}$
. Then, by Theorem 7.1, for any
![]() $1\leq i\leq n$
, one can find a unitary
$1\leq i\leq n$
, one can find a unitary
![]() $w_i\in {\mathcal M}$
and a subgroup
$w_i\in {\mathcal M}$
and a subgroup
![]() $\Lambda _i<\Lambda $
satisfying the following relations:
$\Lambda _i<\Lambda $
satisfying the following relations:
-
1.
 $\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T \Lambda _i$
for all
$\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T \Lambda _i$
for all
 $1\leq i\leq n$
;
$1\leq i\leq n$
; -
2. The virtual centralizers satisfy
 $vC_\Lambda (\Lambda _i)= 1$
for all
$vC_\Lambda (\Lambda _i)= 1$
for all
 $1\leq i\leq n$
.
$1\leq i\leq n$
. -
3.
 $\mathbb T w_i \Gamma _{\mathscr {C}_{i,i+1}} w_i^*= \mathbb T w_{i+1} \Gamma _{\mathscr {C}_{i,i+1}} w_{i+1}^*= \mathbb T \Lambda _{i,i+1}$
where
$\mathbb T w_i \Gamma _{\mathscr {C}_{i,i+1}} w_i^*= \mathbb T w_{i+1} \Gamma _{\mathscr {C}_{i,i+1}} w_{i+1}^*= \mathbb T \Lambda _{i,i+1}$
where
 $\Lambda _{i,i+1}= \Lambda _i\cap \Lambda _{i+1}$
for all
$\Lambda _{i,i+1}= \Lambda _i\cap \Lambda _{i+1}$
for all
 $1\leq i\leq n-1$
;
$1\leq i\leq n-1$
; -
4. There is an
 $s\in \Lambda $
, such that
$s\in \Lambda $
, such that
 $\mathbb T w_n \Gamma _{\mathscr {C}_{n,1}} w_n^*= \mathbb T v_s w_{1} \Gamma _{\mathscr {C}_{n,1}} w_{1}^*= \mathbb T \Lambda _{n}\cap s \Lambda _1 s^{-1}$
;
$\mathbb T w_n \Gamma _{\mathscr {C}_{n,1}} w_n^*= \mathbb T v_s w_{1} \Gamma _{\mathscr {C}_{n,1}} w_{1}^*= \mathbb T \Lambda _{n}\cap s \Lambda _1 s^{-1}$
;
Items 1., 3. and 4. are clear. We only have to justify 2. For seeing this, note that Lemma 2.15 and Theorem 2.16 give
![]() ${\mathcal L}(\mathrm {QN}_\Lambda (\Lambda _i))=\mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Lambda _i))"= w_i \mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Gamma _{\mathscr {C}_i}))" w_i^*= w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^*={\mathcal L}(\Lambda _i)$
. Since
${\mathcal L}(\mathrm {QN}_\Lambda (\Lambda _i))=\mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Lambda _i))"= w_i \mathscr {QN}_{{\mathcal M}}({\mathcal L}(\Gamma _{\mathscr {C}_i}))" w_i^*= w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^*={\mathcal L}(\Lambda _i)$
. Since
![]() $vC_{\Lambda }(\Lambda _i) < \mathrm {QN}_\Lambda (\Lambda _i)$
, we deduce that
$vC_{\Lambda }(\Lambda _i) < \mathrm {QN}_\Lambda (\Lambda _i)$
, we deduce that
![]() $vC_{\Lambda }(\Lambda _i)<\Lambda _i$
, and hence, by using that
$vC_{\Lambda }(\Lambda _i)<\Lambda _i$
, and hence, by using that
![]() $\Lambda _i$
is icc, we derive
$\Lambda _i$
is icc, we derive
![]() $vC_{\Lambda }(\Lambda _i)=vC_{\Lambda _i}(\Lambda _i)=1$
.
$vC_{\Lambda }(\Lambda _i)=vC_{\Lambda _i}(\Lambda _i)=1$
.
Claim 7.7. There exist a map
![]() $\sigma :\{1,\dots ,n\}\to \{1,\dots ,m\}$
and elements
$\sigma :\{1,\dots ,n\}\to \{1,\dots ,m\}$
and elements
![]() $h_1,\dots ,h_n \in \Lambda $
so that
$h_1,\dots ,h_n \in \Lambda $
so that
![]() $\Lambda _i\leqslant h_i\Lambda _{\mathscr {D}_{\sigma (i)}} h^{-1}_i$
, for any
$\Lambda _i\leqslant h_i\Lambda _{\mathscr {D}_{\sigma (i)}} h^{-1}_i$
, for any
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Proof of Claim 7.7.
Let
![]() $1\leq i\leq n$
be arbitrary. Since
$1\leq i\leq n$
be arbitrary. Since
![]() $\Gamma _{\mathscr {C}_i}$
has property (T), then
$\Gamma _{\mathscr {C}_i}$
has property (T), then
![]() $\Lambda _i< \Lambda $
has property (T) as well. By applying Theorem 2.8, one can find
$\Lambda _i< \Lambda $
has property (T) as well. By applying Theorem 2.8, one can find
![]() $1\leq k\leq m$
, such that
$1\leq k\leq m$
, such that
![]() ${\mathcal L}(\Lambda _i)\prec _{{\mathcal M}} {\mathcal L}(\Lambda _{\mathscr {D}_k}).$
Using Lemma 2.6, there is
${\mathcal L}(\Lambda _i)\prec _{{\mathcal M}} {\mathcal L}(\Lambda _{\mathscr {D}_k}).$
Using Lemma 2.6, there is
![]() $h\in \Lambda $
, such that
$h\in \Lambda $
, such that
![]() $[\Lambda _i: \Lambda _i \cap h \Lambda _{\mathscr {D}_k} h^{-1}]<\infty $
. Thus, there is a finite index normal subgroup
$[\Lambda _i: \Lambda _i \cap h \Lambda _{\mathscr {D}_k} h^{-1}]<\infty $
. Thus, there is a finite index normal subgroup
![]() $\Lambda _i'\lhd \Lambda _i$
, such that
$\Lambda _i'\lhd \Lambda _i$
, such that
![]() $\Lambda ^{\prime }_i\leqslant h\Lambda _{\mathscr {D}_k} h^{-1}$
. We continue by proving that
$\Lambda ^{\prime }_i\leqslant h\Lambda _{\mathscr {D}_k} h^{-1}$
. We continue by proving that
![]() $\Lambda _i\leqslant h\Lambda _{\mathscr {D}_k} h^{-1}$
. To this end, fix
$\Lambda _i\leqslant h\Lambda _{\mathscr {D}_k} h^{-1}$
. To this end, fix
![]() $t\in \Lambda _i$
. Hence,
$t\in \Lambda _i$
. Hence,
![]() $\Lambda _i'\leqslant h\Lambda _{\mathscr {D}_k} h^{-1} \cap th\Lambda _{\mathscr {D}_k} h^{-1}t^{-1}$
, and by Proposition 2.1, we have that
$\Lambda _i'\leqslant h\Lambda _{\mathscr {D}_k} h^{-1} \cap th\Lambda _{\mathscr {D}_k} h^{-1}t^{-1}$
, and by Proposition 2.1, we have that
Since
![]() $[\Lambda _i:\Lambda _i']<\infty $
, condition 2. implies that
$[\Lambda _i:\Lambda _i']<\infty $
, condition 2. implies that
![]() $vC_{\Lambda }(\Lambda _i')=vC_{\Lambda }(\Lambda _i)=1$
. It follows from (7.4) that
$vC_{\Lambda }(\Lambda _i')=vC_{\Lambda }(\Lambda _i)=1$
. It follows from (7.4) that
![]() $vC_{\Lambda }(h_0 h\Lambda _{\mathscr {T}} h^{-1} h_0^{-1})=1$
, and hence,
$vC_{\Lambda }(h_0 h\Lambda _{\mathscr {T}} h^{-1} h_0^{-1})=1$
, and hence,
![]() $\mathscr {T}$
is a clique. This forces that
$\mathscr {T}$
is a clique. This forces that
![]() $\mathscr {T}=\mathscr {D}_k$
, and hence, (7.4) implies that
$\mathscr {T}=\mathscr {D}_k$
, and hence, (7.4) implies that
![]() $th\Lambda _{\mathscr {D}_k} h^{-1}t^{-1} \geqslant h\Lambda _{\mathscr {D}_k} h^{-1}$
. Using Proposition 2.1, we derive that
$th\Lambda _{\mathscr {D}_k} h^{-1}t^{-1} \geqslant h\Lambda _{\mathscr {D}_k} h^{-1}$
. Using Proposition 2.1, we derive that
![]() $th\Lambda _{\mathscr {D}_k} h^{-1}t^{-1} = h\Lambda _{\mathscr {D}_k} h^{-1}$
, and hence,
$th\Lambda _{\mathscr {D}_k} h^{-1}t^{-1} = h\Lambda _{\mathscr {D}_k} h^{-1}$
, and hence,
![]() $h^{-1}t h\in \Lambda _{\mathscr {D}_k\cup \mathrm {link}(\mathscr {D}_k)}$
. Since
$h^{-1}t h\in \Lambda _{\mathscr {D}_k\cup \mathrm {link}(\mathscr {D}_k)}$
. Since
![]() $\mathscr {D}_k$
is a clique, we conclude that
$\mathscr {D}_k$
is a clique, we conclude that
![]() $t\in h\Lambda _{\mathscr {D}_k} h^{-1}$
.
$t\in h\Lambda _{\mathscr {D}_k} h^{-1}$
.
We continue with the following claim.
Claim 7.8. For every
![]() $1\leq i\leq n$
, we have
$1\leq i\leq n$
, we have
![]() $[h_i\Lambda _{\mathscr {D}_{\sigma (i)}} h^{-1}_i: \Lambda _i]<\infty $
.
$[h_i\Lambda _{\mathscr {D}_{\sigma (i)}} h^{-1}_i: \Lambda _i]<\infty $
.
Proof of Claim 7.8.
Fix
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $v\in \mathscr {C}_i^{\mathrm {int}}$
, and note that
$v\in \mathscr {C}_i^{\mathrm {int}}$
, and note that
![]() $\mathrm {star}(v)=\mathscr {C}_i$
. Let
$\mathrm {star}(v)=\mathscr {C}_i$
. Let
![]() $j=\sigma (i)$
. Next, we briefly argue that
$j=\sigma (i)$
. Next, we briefly argue that
![]() $|\mathscr {D}_j|\geqslant 2$
. Assume by contradiction that
$|\mathscr {D}_j|\geqslant 2$
. Assume by contradiction that
![]() $\mathscr {D}_j=\{s\}$
. As
$\mathscr {D}_j=\{s\}$
. As
![]() $\Lambda $
is a nontrivial graph product, there is a nontrivial group
$\Lambda $
is a nontrivial graph product, there is a nontrivial group
![]() $\Sigma $
so that
$\Sigma $
so that
![]() $\Lambda =\Lambda _s \ast \Sigma $
; thus,
$\Lambda =\Lambda _s \ast \Sigma $
; thus,
![]() ${\mathcal M} = {\mathcal L}(\Lambda _s\ast \Sigma )$
. Since
${\mathcal M} = {\mathcal L}(\Lambda _s\ast \Sigma )$
. Since
![]() ${\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}})$
is diffuse, then using Claim 7.7 and relation 1. we get
${\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}})$
is diffuse, then using Claim 7.7 and relation 1. we get
![]() $x {\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}) x^*\subseteq \mathcal L(\Lambda _s)$
where we have denoted by
$x {\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}}) x^*\subseteq \mathcal L(\Lambda _s)$
where we have denoted by
![]() $x:= u_{h_i^{-1}}w_i\in \mathscr {U}({\mathcal M})$
. Using Lemma 2.18 and the graph product structure of
$x:= u_{h_i^{-1}}w_i\in \mathscr {U}({\mathcal M})$
. Using Lemma 2.18 and the graph product structure of
![]() $\Gamma $
, this further implies that
$\Gamma $
, this further implies that
![]() $x \mathcal L(\Gamma _{\mathscr {C}_{i}\cup \mathscr {C}_{i+1}}) x^*= \mathscr N_{{\mathcal M}} (x \mathcal L(\Gamma _{\mathscr {C}_{i,i+1}}) x^*)"\subseteq \mathcal L(\Lambda _s)$
. In particular, we have
$x \mathcal L(\Gamma _{\mathscr {C}_{i}\cup \mathscr {C}_{i+1}}) x^*= \mathscr N_{{\mathcal M}} (x \mathcal L(\Gamma _{\mathscr {C}_{i,i+1}}) x^*)"\subseteq \mathcal L(\Lambda _s)$
. In particular, we have
![]() $ x {\mathcal L}(\Gamma _{\mathscr {C}_{i+1,i+2}}) x^*\subseteq \mathcal L(\Lambda _s)$
. Thus, taking the normalizer and repeating the previous argument, we get
$ x {\mathcal L}(\Gamma _{\mathscr {C}_{i+1,i+2}}) x^*\subseteq \mathcal L(\Lambda _s)$
. Thus, taking the normalizer and repeating the previous argument, we get
![]() $ x \mathcal L(\Gamma _{\mathscr {C}_{i+1}\cup \mathscr {C}_{i+2}}) x^*= \mathscr N_{{\mathcal M}} (x \mathcal L(\Gamma _{\mathscr {C}_{i+1,i+2}}) x^*)"\subseteq {\mathcal L}(\Lambda _s)$
. Therefore, proceeding by induction, we have
$ x \mathcal L(\Gamma _{\mathscr {C}_{i+1}\cup \mathscr {C}_{i+2}}) x^*= \mathscr N_{{\mathcal M}} (x \mathcal L(\Gamma _{\mathscr {C}_{i+1,i+2}}) x^*)"\subseteq {\mathcal L}(\Lambda _s)$
. Therefore, proceeding by induction, we have
![]() $ x {\mathcal L}(\Gamma _{\mathscr {C}_{k}\cup \mathscr {C}_{l}}) x^*\subseteq \mathcal L(\Lambda _s)$
for all
$ x {\mathcal L}(\Gamma _{\mathscr {C}_{k}\cup \mathscr {C}_{l}}) x^*\subseteq \mathcal L(\Lambda _s)$
for all
![]() $1\leqslant k,l\leqslant m$
satisfying
$1\leqslant k,l\leqslant m$
satisfying
![]() $\hat k-\hat l \in \{ \hat 1,\widehat {n-1}\}$
; here, the classes are considered in
$\hat k-\hat l \in \{ \hat 1,\widehat {n-1}\}$
; here, the classes are considered in
![]() $\mathbb Z_m$
. Altogether, these relations imply that
$\mathbb Z_m$
. Altogether, these relations imply that
 $ {\mathcal M} = x_i {\mathcal L}(\Gamma ) x^*= x \mathcal L(\vee _{k,l, \hat k-\hat l \in \{\hat 1,\widehat {n-1}\}} \Gamma _{\mathscr {C}_{k}\cup \mathscr {C}_{l}}) x^*=\bigvee _{k,l, \hat k-\hat l \in \{\hat 1,\widehat {n-1}\}}x {\mathcal L}(\Gamma _{\mathscr {C}_{k}\cup \mathscr {C}_{l}}) x^*\subseteq {\mathcal L}(\Lambda _s) $
, contradicting
$ {\mathcal M} = x_i {\mathcal L}(\Gamma ) x^*= x \mathcal L(\vee _{k,l, \hat k-\hat l \in \{\hat 1,\widehat {n-1}\}} \Gamma _{\mathscr {C}_{k}\cup \mathscr {C}_{l}}) x^*=\bigvee _{k,l, \hat k-\hat l \in \{\hat 1,\widehat {n-1}\}}x {\mathcal L}(\Gamma _{\mathscr {C}_{k}\cup \mathscr {C}_{l}}) x^*\subseteq {\mathcal L}(\Lambda _s) $
, contradicting
![]() $\Sigma \neq 1$
.
$\Sigma \neq 1$
.
Now, fix an arbitrary
![]() $w\in \mathscr {D}_j$
. By letting
$w\in \mathscr {D}_j$
. By letting
![]() $\mathcal P_1= {\mathcal L}(\Lambda _{\mathscr {D}_{j} \setminus \{w\}})$
and
$\mathcal P_1= {\mathcal L}(\Lambda _{\mathscr {D}_{j} \setminus \{w\}})$
and
![]() $\mathcal P_2= {\mathcal L}(\Lambda _w)$
, we have
$\mathcal P_2= {\mathcal L}(\Lambda _w)$
, we have
![]() $\mathcal P_1\bar \otimes \mathcal P_2={\mathcal L}(\Lambda _{\mathscr {D}_j})$
. Since the vertex groups of
$\mathcal P_1\bar \otimes \mathcal P_2={\mathcal L}(\Lambda _{\mathscr {D}_j})$
. Since the vertex groups of
![]() $\Lambda $
are infinite, then by [Reference Chifan, de Santiago and SucpikarnonCdSS17, Theorem 3.1], one of the following must hold:
$\Lambda $
are infinite, then by [Reference Chifan, de Santiago and SucpikarnonCdSS17, Theorem 3.1], one of the following must hold:
-
1.
 $\mathcal P_1\vee \mathcal P_2$
is amenable relative to
$\mathcal P_1\vee \mathcal P_2$
is amenable relative to
 $ {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
inside
$ {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
inside
 ${\mathcal M}$
;
${\mathcal M}$
; -
2.
 $\mathcal P_1\vee \mathcal P_2 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathscr {G}\setminus \{v\}})$
;
$\mathcal P_1\vee \mathcal P_2 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathscr {G}\setminus \{v\}})$
; -
3.
 $\mathcal P_1\vee \mathcal P_2 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {star}(v)})$
;
$\mathcal P_1\vee \mathcal P_2 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {star}(v)})$
; -
4.
 $\mathcal P_i \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
, for some
$\mathcal P_i \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
, for some
 $1 \leq i\leq 2$
;
$1 \leq i\leq 2$
;
First, assume 1. holds. Since
![]() $\mathbb T h_i^{-1} w_i \Gamma _{\mathscr {C}_i} w_i^* h_i=\mathbb T h_i^{-1} \Lambda _i h_i\subset \mathcal P_1\vee \mathcal P_2$
, we derive that
$\mathbb T h_i^{-1} w_i \Gamma _{\mathscr {C}_i} w_i^* h_i=\mathbb T h_i^{-1} \Lambda _i h_i\subset \mathcal P_1\vee \mathcal P_2$
, we derive that
![]() $h_i^{-1} w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^* h_i$
is amenable relative to
$h_i^{-1} w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^* h_i$
is amenable relative to
![]() $ {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
inside
$ {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
inside
![]() ${\mathcal M}$
. Since
${\mathcal M}$
. Since
![]() ${\mathcal L}(\Gamma _{\mathscr {C}_i})$
has property (T), then
${\mathcal L}(\Gamma _{\mathscr {C}_i})$
has property (T), then
![]() $h_i^{-1} w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^* h_i\prec _{{\mathcal M}} {\mathcal L} (\Gamma _{\mathrm {link}(v)})$
. By applying Corollary 2.7, it follows that
$h_i^{-1} w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^* h_i\prec _{{\mathcal M}} {\mathcal L} (\Gamma _{\mathrm {link}(v)})$
. By applying Corollary 2.7, it follows that
![]() $\mathscr {C}_i\subset \mathrm {link}(v)$
, contradiction.
$\mathscr {C}_i\subset \mathrm {link}(v)$
, contradiction.
Now, assume 2. holds. Since
![]() $\mathbb T h_i^{-1} w_i \Gamma _{\mathscr {C}_i} w_i^* h_i=\mathbb T h_i^{-1} \Lambda _i h_i\subset \mathcal P_1\vee \mathcal P_2$
, we derive that
$\mathbb T h_i^{-1} w_i \Gamma _{\mathscr {C}_i} w_i^* h_i=\mathbb T h_i^{-1} \Lambda _i h_i\subset \mathcal P_1\vee \mathcal P_2$
, we derive that
![]() ${\mathcal L}(\Gamma _{\mathscr {C}_i})\prec _{\mathcal M} {\mathcal L} (\Gamma _{\mathscr {G}\setminus \{v\}})$
. As in the previous case, we apply Corollary 2.7 and derive that
${\mathcal L}(\Gamma _{\mathscr {C}_i})\prec _{\mathcal M} {\mathcal L} (\Gamma _{\mathscr {G}\setminus \{v\}})$
. As in the previous case, we apply Corollary 2.7 and derive that
![]() $\mathscr {C}_i\subset \mathscr {G} \setminus \{v\}$
, contradiction.
$\mathscr {C}_i\subset \mathscr {G} \setminus \{v\}$
, contradiction.
Next, assume 3. holds. As
![]() $\mathrm {star}(v)=\mathscr {C}_i$
and
$\mathrm {star}(v)=\mathscr {C}_i$
and
![]() $\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T\Lambda _i $
, we derive that
$\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T\Lambda _i $
, we derive that
![]() ${\mathcal L} (\Lambda _{\mathscr {D}_j})\prec _{\mathcal M} {\mathcal L} (h_i^{-1} \Lambda _i h_i)$
. This implies that there exist projections
${\mathcal L} (\Lambda _{\mathscr {D}_j})\prec _{\mathcal M} {\mathcal L} (h_i^{-1} \Lambda _i h_i)$
. This implies that there exist projections
![]() $p\in {\mathcal L} (\Lambda _{\mathscr {D}_j}), q\in \mathcal L (h_i^{-1} \Lambda _i h_i)$
, a nonzero partial isometry
$p\in {\mathcal L} (\Lambda _{\mathscr {D}_j}), q\in \mathcal L (h_i^{-1} \Lambda _i h_i)$
, a nonzero partial isometry
![]() $w\in q {\mathcal M} p$
and a
$w\in q {\mathcal M} p$
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\theta : p\mathcal L (\Lambda _{\mathscr {D}_j})p\to q\mathcal L (h_i^{-1} \Lambda _i h_i)q$
, such that
$\theta : p\mathcal L (\Lambda _{\mathscr {D}_j})p\to q\mathcal L (h_i^{-1} \Lambda _i h_i)q$
, such that
![]() $\theta (x)w=wx$
. Since
$\theta (x)w=wx$
. Since
![]() $\Lambda _i\leqslant h_i\Lambda _{\mathscr {D}_{j}} h^{-1}_i$
, it follows that
$\Lambda _i\leqslant h_i\Lambda _{\mathscr {D}_{j}} h^{-1}_i$
, it follows that
![]() $w p\mathcal L (\Lambda _{\mathscr {D}_j})p\subset q \mathcal L (\Lambda _{\mathscr {D}_j})qw$
. Since
$w p\mathcal L (\Lambda _{\mathscr {D}_j})p\subset q \mathcal L (\Lambda _{\mathscr {D}_j})qw$
. Since
![]() ${\mathcal D}_j$
is a clique, it follows from Lemma 2.18 that
${\mathcal D}_j$
is a clique, it follows from Lemma 2.18 that
![]() $w\in \mathcal L (\Lambda _{\mathscr {D}_j})$
. This shows that
$w\in \mathcal L (\Lambda _{\mathscr {D}_j})$
. This shows that
![]() ${\mathcal L} (\Lambda _{\mathscr {D}_j})\prec _{{\mathcal L} (\Lambda _{\mathscr {D}_j})} {\mathcal L} (h_i^{-1} \Lambda _i h_i)$
, which further implies that
${\mathcal L} (\Lambda _{\mathscr {D}_j})\prec _{{\mathcal L} (\Lambda _{\mathscr {D}_j})} {\mathcal L} (h_i^{-1} \Lambda _i h_i)$
, which further implies that
![]() $[\Lambda _{\mathscr {D}_j}: h_i^{-1} \Lambda _i h_i]<\infty $
. This proves the claim.
$[\Lambda _{\mathscr {D}_j}: h_i^{-1} \Lambda _i h_i]<\infty $
. This proves the claim.
Before completing Claim 7.8 by assuming that 4. holds, we first establish the following notation and prove the following subclaim. Since
![]() $\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^*=\mathbb T \Lambda _i$
, we define the subgroups
$\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^*=\mathbb T \Lambda _i$
, we define the subgroups
![]() $\Lambda ^i_v, \Lambda ^i_{\hat v}<\Lambda _i$
by
$\Lambda ^i_v, \Lambda ^i_{\hat v}<\Lambda _i$
by
![]() $\mathbb T w_i \Gamma _{v} w_i^*=\mathbb T \Lambda ^i_{ v}$
and
$\mathbb T w_i \Gamma _{v} w_i^*=\mathbb T \Lambda ^i_{ v}$
and
![]() $\mathbb T w_i \Gamma _{\mathrm {link}(v)} w_i^*=\mathbb T \Lambda ^i_{\hat v}$
, respectively. Note that
$\mathbb T w_i \Gamma _{\mathrm {link}(v)} w_i^*=\mathbb T \Lambda ^i_{\hat v}$
, respectively. Note that
![]() $\Lambda _i= \Lambda ^i_{v}\times \Lambda ^i_{\hat v}$
since
$\Lambda _i= \Lambda ^i_{v}\times \Lambda ^i_{\hat v}$
since
![]() $v\in \mathscr {C}_i^{\mathrm {int}}$
.
$v\in \mathscr {C}_i^{\mathrm {int}}$
.
Subclaim 1. For any subset
![]() $\mathscr {D}_0\subset \mathscr {D}_j$
satisfying
$\mathscr {D}_0\subset \mathscr {D}_j$
satisfying
![]() ${\mathcal L}(\Lambda _{\mathscr {D}_0})\prec _{{\mathcal M}} {\mathcal L} (\Gamma _{\mathrm {link}(v)})$
, the subgroup
${\mathcal L}(\Lambda _{\mathscr {D}_0})\prec _{{\mathcal M}} {\mathcal L} (\Gamma _{\mathrm {link}(v)})$
, the subgroup
![]() $(\Lambda _0)_{\mathscr {D}_0}:= h_i \Lambda _{\mathscr {D}_0} h_i^{-1}\cap \Lambda ^i_{\hat v} $
satisfies
$(\Lambda _0)_{\mathscr {D}_0}:= h_i \Lambda _{\mathscr {D}_0} h_i^{-1}\cap \Lambda ^i_{\hat v} $
satisfies
![]() $[h_i \Lambda _{\mathscr {D}_0} h_i^{-1}:(\Lambda _0)_{\mathscr {D}_0}]<\infty $
.
$[h_i \Lambda _{\mathscr {D}_0} h_i^{-1}:(\Lambda _0)_{\mathscr {D}_0}]<\infty $
.
Proof of Subclaim 1.
For proving the subclaim, we consider a subset
![]() $\mathscr {D}_0\subset \mathscr {D}_j$
satisfying
$\mathscr {D}_0\subset \mathscr {D}_j$
satisfying
![]() ${\mathcal L}(\Lambda _{\mathscr {D}_0})\prec _{{\mathcal M}} \mathcal L (\Gamma _{\mathrm {link}(v)})$
. By applying Lemma 2.6, there is
${\mathcal L}(\Lambda _{\mathscr {D}_0})\prec _{{\mathcal M}} \mathcal L (\Gamma _{\mathrm {link}(v)})$
. By applying Lemma 2.6, there is
![]() $k\in \Lambda $
, such that
$k\in \Lambda $
, such that
Set
![]() $\Lambda _0= k^{-1}h_i \Lambda _{\mathscr {D}_0} h_i^{-1}k\cap \Lambda ^i_{\hat v}$
. We continue by showing that k normalizes
$\Lambda _0= k^{-1}h_i \Lambda _{\mathscr {D}_0} h_i^{-1}k\cap \Lambda ^i_{\hat v}$
. We continue by showing that k normalizes
![]() $h_i \Lambda _{\mathscr {D}_0} h_i^{-1}$
. Recall that
$h_i \Lambda _{\mathscr {D}_0} h_i^{-1}$
. Recall that
![]() $\Lambda ^i_{\hat v}<\Lambda _i< h_i \Lambda _{\mathscr {D}_j} h_i^{-1}$
. From (7.5), we get that
$\Lambda ^i_{\hat v}<\Lambda _i< h_i \Lambda _{\mathscr {D}_j} h_i^{-1}$
. From (7.5), we get that
![]() $[h_i \Lambda _{\mathscr {D}_0} h_i^{-1}: k \Lambda _0 k^{-1}]<\infty $
, and consequently, there is a finite subset
$[h_i \Lambda _{\mathscr {D}_0} h_i^{-1}: k \Lambda _0 k^{-1}]<\infty $
, and consequently, there is a finite subset
![]() $S\subset \Lambda $
satisfying
$S\subset \Lambda $
satisfying
![]() $(h_i \Lambda _{\mathscr {D}_0} h_i^{-1})k\subset \cup _{s\in S} sk \Lambda _0 \subset \cup _{s\in S} sk h_i \Lambda _{\mathscr {D}_j}h_i^{-1}$
. By applying Theorem 2.16 we derive that
$(h_i \Lambda _{\mathscr {D}_0} h_i^{-1})k\subset \cup _{s\in S} sk \Lambda _0 \subset \cup _{s\in S} sk h_i \Lambda _{\mathscr {D}_j}h_i^{-1}$
. By applying Theorem 2.16 we derive that
![]() $h_i^{-1}k h_i\in \Lambda _{\mathscr {D}_j\cup \mathrm {link}(\mathscr {D}_0)}$
, which implies that k is normalizing
$h_i^{-1}k h_i\in \Lambda _{\mathscr {D}_j\cup \mathrm {link}(\mathscr {D}_0)}$
, which implies that k is normalizing
![]() $h_i \Lambda _{\mathscr {D}_0} h_i^{-1}$
. In combination with (7.5), this shows that
$h_i \Lambda _{\mathscr {D}_0} h_i^{-1}$
. In combination with (7.5), this shows that
![]() ${\Lambda _0=(\Lambda _0)_{\mathscr {D}_0}}$
is a finite index subgroup of
${\Lambda _0=(\Lambda _0)_{\mathscr {D}_0}}$
is a finite index subgroup of
![]() $h_i \Lambda _{\mathscr {D}_0} h_i^{-1}$
. This proves the subclaim.
$h_i \Lambda _{\mathscr {D}_0} h_i^{-1}$
. This proves the subclaim.
Now, we can assume that 4. holds for all
![]() $w\in \mathscr {D}_j$
. Namely, one of the following holds: a)
$w\in \mathscr {D}_j$
. Namely, one of the following holds: a)
![]() $\mathcal P_1 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
or b)
$\mathcal P_1 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
or b)
![]() $\mathcal P_2 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
. We continue by considering the following cases.
$\mathcal P_2 \prec _{\mathcal M} {\mathcal L}(\Gamma _{\mathrm {link}(v) })$
. We continue by considering the following cases.
Case 1. Suppose there are
![]() $w_1\neq w_2\in \mathscr {D}_j$
, such that a) holds. The subclaim implies that
$w_1\neq w_2\in \mathscr {D}_j$
, such that a) holds. The subclaim implies that
![]() $[h_i \Lambda _{\mathscr {D}_j\setminus \{w_1\}} h_i^{-1}:(\Lambda _0)_{\mathscr {D}_j\setminus \{w_1\}}]<\infty $
and
$[h_i \Lambda _{\mathscr {D}_j\setminus \{w_1\}} h_i^{-1}:(\Lambda _0)_{\mathscr {D}_j\setminus \{w_1\}}]<\infty $
and
![]() $[h_i \Lambda _{\mathscr {D}_j\setminus \{w_2\}} h_i^{-1}:(\Lambda _0)_{\mathscr {D}_j\setminus \{w_2\}}]<\infty $
. Since
$[h_i \Lambda _{\mathscr {D}_j\setminus \{w_2\}} h_i^{-1}:(\Lambda _0)_{\mathscr {D}_j\setminus \{w_2\}}]<\infty $
. Since
![]() ${w_1\in \mathscr {D}_j\setminus \{w_2\}}$
, it follows that
${w_1\in \mathscr {D}_j\setminus \{w_2\}}$
, it follows that
![]() $[h_i\Lambda _{w_1}h_i^{-1}: h_i\Lambda _{w_1}h_i^{-1}\cap \Lambda ^i_{\hat v}]<\infty $
. Consequently, the inclusion
$[h_i\Lambda _{w_1}h_i^{-1}: h_i\Lambda _{w_1}h_i^{-1}\cap \Lambda ^i_{\hat v}]<\infty $
. Consequently, the inclusion
![]() $(h_i\Lambda _{w_1}h_i^{-1}\cap \Lambda ^i_{\hat v})\vee (\Lambda _0)_{\mathscr {D}_j\setminus \{w_1\}}<\Lambda _i<h_i \mathscr {D}_j h_i^{-1}$
is of finite index. This proves the claim.
$(h_i\Lambda _{w_1}h_i^{-1}\cap \Lambda ^i_{\hat v})\vee (\Lambda _0)_{\mathscr {D}_j\setminus \{w_1\}}<\Lambda _i<h_i \mathscr {D}_j h_i^{-1}$
is of finite index. This proves the claim.
Case 2. Next, we suppose that
![]() $b)$
holds for any
$b)$
holds for any
![]() $w\in \mathscr {D}_j$
. Using the subclaim, we get that
$w\in \mathscr {D}_j$
. Using the subclaim, we get that
![]() $(\Lambda _0)_{w}<h_i \Lambda _{w} h_i^{-1}$
has finite index for any
$(\Lambda _0)_{w}<h_i \Lambda _{w} h_i^{-1}$
has finite index for any
![]() $w\in \mathscr {D}_j$
. Hence, the inclusion
$w\in \mathscr {D}_j$
. Hence, the inclusion
![]() $\vee _{w\in \mathscr {D}_j}(\Lambda _0)_{w}<\Lambda _i<\vee _{w\in \mathscr {D}_j}h_i \Lambda _{w} h_i^{-1}=h_i \Lambda _{\mathscr {D}_j} h_i ^{-1}$
has finite index as well, which again proves the claim.
$\vee _{w\in \mathscr {D}_j}(\Lambda _0)_{w}<\Lambda _i<\vee _{w\in \mathscr {D}_j}h_i \Lambda _{w} h_i^{-1}=h_i \Lambda _{\mathscr {D}_j} h_i ^{-1}$
has finite index as well, which again proves the claim.
Case 3. Finally, assume that there is
![]() $w_0\in \mathscr {D}_j$
, such that a) holds and for any
$w_0\in \mathscr {D}_j$
, such that a) holds and for any
![]() ${w\in \mathscr {D}_j\setminus \{w_0\}}$
, we have that b) holds. We note in passing that in this situation, b) does not provide any additional information besides a). Note that Subclaim 1 provides
${w\in \mathscr {D}_j\setminus \{w_0\}}$
, we have that b) holds. We note in passing that in this situation, b) does not provide any additional information besides a). Note that Subclaim 1 provides
We continue by showing the following.
Subclaim 2. The group
![]() $(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
is icc and
$(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
is icc and
![]() $ vC_{h_i\Lambda _{\mathscr {D}_j \setminus \{w_0\}}h_i^{-1} }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})=1$
. Also, there exists a subgroup
$ vC_{h_i\Lambda _{\mathscr {D}_j \setminus \{w_0\}}h_i^{-1} }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})=1$
. Also, there exists a subgroup
![]() $\Upsilon < h_i \Lambda _{w_0} h_i^{-1}$
satisfying
$\Upsilon < h_i \Lambda _{w_0} h_i^{-1}$
satisfying
![]() $[\Lambda _i: (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon ]<\infty $
.
$[\Lambda _i: (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon ]<\infty $
.
Proof of Subclaim 2.
Using
![]() $(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}<\Lambda ^i_{\hat v}<h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1}\times h_i \Lambda _{w_0} h_i^{-1}$
, we apply Lemma 7.4 and deduce that there is a subgroup
$(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}<\Lambda ^i_{\hat v}<h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1}\times h_i \Lambda _{w_0} h_i^{-1}$
, we apply Lemma 7.4 and deduce that there is a subgroup
![]() $\Lambda '< h_i \Lambda _{w_0} h_i^{-1}\cap \Lambda _{\hat v}^i$
, such that
$\Lambda '< h_i \Lambda _{w_0} h_i^{-1}\cap \Lambda _{\hat v}^i$
, such that
Since
![]() $\Lambda _{\hat v}^i$
is icc, (7.7) implies that
$\Lambda _{\hat v}^i$
is icc, (7.7) implies that
![]() $(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
is icc as well. Next, we argue that there is a finite index subgroup
$(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
is icc as well. Next, we argue that there is a finite index subgroup
![]() $\Lambda " \leqslant h_i \Lambda _{w_0} h_i^{-1}\cap \Lambda _v^i$
, such that
$\Lambda " \leqslant h_i \Lambda _{w_0} h_i^{-1}\cap \Lambda _v^i$
, such that
Indeed, as
![]() $(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
is icc, one can see from (7.6) that
$(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
is icc, one can see from (7.6) that
![]() $C_{h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1}}((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})=1$
, and thus,
$C_{h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1}}((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})=1$
, and thus,
![]() $\Lambda _v^i\leqslant C_{h_i\Lambda _{\mathscr {D}_j}h_i^{-1}}(\Lambda ^i_{\hat v} ) \leqslant C_{h_i \Lambda _{\mathscr {D}_j}h_i^{-1}}((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}} ) \leqslant h_i \Lambda _{w_0}h_i^{-1}$
. This shows that we can actually choose
$\Lambda _v^i\leqslant C_{h_i\Lambda _{\mathscr {D}_j}h_i^{-1}}(\Lambda ^i_{\hat v} ) \leqslant C_{h_i \Lambda _{\mathscr {D}_j}h_i^{-1}}((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}} ) \leqslant h_i \Lambda _{w_0}h_i^{-1}$
. This shows that we can actually choose
![]() $\Lambda "=\Lambda _v^i$
to satisfy (7.8).
$\Lambda "=\Lambda _v^i$
to satisfy (7.8).
Altogether, (7.7) and (7.8) imply the existence of
![]() $\Upsilon := \Lambda '\times \Lambda "< h_i \Lambda _{w_0} h_i^{-1}$
, such that
$\Upsilon := \Lambda '\times \Lambda "< h_i \Lambda _{w_0} h_i^{-1}$
, such that
![]() $[\Lambda _i: (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon ]<\infty $
. Together with condition 2., we deduce that
$[\Lambda _i: (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon ]<\infty $
. Together with condition 2., we deduce that
![]() $1= vC_{\Lambda }(\Lambda _i)= vC_{\Lambda }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon )\geq vC_{h_i\Lambda _{\mathscr {D}_j \setminus \{w_0\}}h_i^{-1} }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})\times vC_{h_i\Lambda _{w_0}h_i^{-1} }( \Upsilon )$
. In particular, this shows that
$1= vC_{\Lambda }(\Lambda _i)= vC_{\Lambda }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon )\geq vC_{h_i\Lambda _{\mathscr {D}_j \setminus \{w_0\}}h_i^{-1} }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})\times vC_{h_i\Lambda _{w_0}h_i^{-1} }( \Upsilon )$
. In particular, this shows that
![]() $ vC_{h_i\Lambda _{\mathscr {D}_j \setminus \{w_0\}}h_i^{-1} }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})=1.$
$ vC_{h_i\Lambda _{\mathscr {D}_j \setminus \{w_0\}}h_i^{-1} }((\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}})=1.$
We continue by applying Lemma 7.5 and find a subgraph
![]() $v\in \mathscr {C}^1_i\subset \mathscr {C}_i$
, a finite index subgroup
$v\in \mathscr {C}^1_i\subset \mathscr {C}_i$
, a finite index subgroup
![]() $\Upsilon _0\leqslant \Upsilon $
and finite index subgroups
$\Upsilon _0\leqslant \Upsilon $
and finite index subgroups
![]() $\Gamma ^{\prime }_w\leqslant \Gamma _w$
, for any
$\Gamma ^{\prime }_w\leqslant \Gamma _w$
, for any
![]() $w\in \mathscr {C}^1_i$
, such that if
$w\in \mathscr {C}^1_i$
, such that if
![]() $\Gamma ^{\prime }_{\mathscr {C}_i^1}:= \times _{w\in \mathscr {C}_i^1} \Gamma ^{\prime }_w$
, then
$\Gamma ^{\prime }_{\mathscr {C}_i^1}:= \times _{w\in \mathscr {C}_i^1} \Gamma ^{\prime }_w$
, then
By Lemma 7.5, we consider some finite index subgroups
![]() $\Gamma ^{\prime }_{\mathscr {C}_i \setminus \mathscr {C}_i^1}\leqslant \Gamma _{\mathscr {C}_i\setminus \mathscr {C}_i^1}$
and
$\Gamma ^{\prime }_{\mathscr {C}_i \setminus \mathscr {C}_i^1}\leqslant \Gamma _{\mathscr {C}_i\setminus \mathscr {C}_i^1}$
and
![]() $(\Lambda ^0_0)_{\mathscr {D}_j\setminus \{w_0\}}< (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
, such that
$(\Lambda ^0_0)_{\mathscr {D}_j\setminus \{w_0\}}< (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}$
, such that
Since
![]() $\Gamma ^{\prime }_{\mathscr {C}_i^1}\leqslant \Gamma _{\mathscr {C}_i^1}$
has finite index and
$\Gamma ^{\prime }_{\mathscr {C}_i^1}\leqslant \Gamma _{\mathscr {C}_i^1}$
has finite index and
![]() $v\in \mathscr {C}_i^1\cap \mathscr {C}_i^{\mathrm {int}}$
, we obtain from Theorem 2.16 that
$v\in \mathscr {C}_i^1\cap \mathscr {C}_i^{\mathrm {int}}$
, we obtain from Theorem 2.16 that
![]() ${\mathcal L}(\Gamma _{\mathscr {C}_i \setminus \mathscr {C}_i^1})= \mathcal L(\Gamma ^{\prime }_{\mathscr {C}_i^1})' \cap {\mathcal M}$
. Hence, by taking relative commutants in (7.9) and using
${\mathcal L}(\Gamma _{\mathscr {C}_i \setminus \mathscr {C}_i^1})= \mathcal L(\Gamma ^{\prime }_{\mathscr {C}_i^1})' \cap {\mathcal M}$
. Hence, by taking relative commutants in (7.9) and using
![]() $\Upsilon _0<\Upsilon < h_i\Lambda _{w_0}h_i^{-1}$
, we deduce that
$\Upsilon _0<\Upsilon < h_i\Lambda _{w_0}h_i^{-1}$
, we deduce that
![]() $w_i \mathcal L(\Gamma _{\mathscr {C}_i \setminus \mathscr {C}_i^1}) w_i^*= w_i \mathcal L(\Gamma ^{\prime }_{\mathscr {C}_i^1})' w_i^*\cap {\mathcal M} = \mathcal L(\Upsilon _0)'\cap {\mathcal M} \supseteq \mathcal L(h_i\Lambda _{\mathrm {link}(w_0)}h_i^{-1}) $
. Since
$w_i \mathcal L(\Gamma _{\mathscr {C}_i \setminus \mathscr {C}_i^1}) w_i^*= w_i \mathcal L(\Gamma ^{\prime }_{\mathscr {C}_i^1})' w_i^*\cap {\mathcal M} = \mathcal L(\Upsilon _0)'\cap {\mathcal M} \supseteq \mathcal L(h_i\Lambda _{\mathrm {link}(w_0)}h_i^{-1}) $
. Since
![]() $(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\leqslant h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1}$
, then relation (7.10) entails
$(\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\leqslant h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1}$
, then relation (7.10) entails
![]() $w_i \mathcal L(\Gamma ^{\prime }_{\mathscr {C}_i \setminus \mathscr {C}_i^1}) w_i^*\subseteq \mathcal L(h_i \Lambda _{\mathscr {D}_j }h_i^{-1})$
, and hence, by combining this with the prior containment, it follows that
$w_i \mathcal L(\Gamma ^{\prime }_{\mathscr {C}_i \setminus \mathscr {C}_i^1}) w_i^*\subseteq \mathcal L(h_i \Lambda _{\mathscr {D}_j }h_i^{-1})$
, and hence, by combining this with the prior containment, it follows that
![]() ${\mathcal L}(h_i\Lambda _{\mathrm { link}(w_0)}h_i^{-1})\prec _{{\mathcal M}} {\mathcal L}(h_i \Lambda _{\mathscr {D}_j }h_i^{-1})$
. Using Corollary 2.7, we further deduce that
${\mathcal L}(h_i\Lambda _{\mathrm { link}(w_0)}h_i^{-1})\prec _{{\mathcal M}} {\mathcal L}(h_i \Lambda _{\mathscr {D}_j }h_i^{-1})$
. Using Corollary 2.7, we further deduce that
![]() $\mathrm {link}(w_0)\subset \mathscr {D}_j$
.
$\mathrm {link}(w_0)\subset \mathscr {D}_j$
.
Next, we claim that
Assume, by contradiction, that (7.11) does not hold. Without loss of generality, we may assume there is
![]() $v_0\in \mathscr {C}^1_i\cap \mathscr {C}_{i+1}$
. Note that
$v_0\in \mathscr {C}^1_i\cap \mathscr {C}_{i+1}$
. Note that
![]() $\mathbb T w_i \Gamma ^{\prime }_{v_0} w_i^*= \mathbb T \Upsilon _1$
for some subgroup
$\mathbb T w_i \Gamma ^{\prime }_{v_0} w_i^*= \mathbb T \Upsilon _1$
for some subgroup
![]() $\Upsilon _1< \Upsilon _0< h_i \Lambda _{w_o}h_i^{-1}$
, and hence,
$\Upsilon _1< \Upsilon _0< h_i \Lambda _{w_o}h_i^{-1}$
, and hence,
![]() $ w_i{\mathcal L}(\Gamma ^{\prime }_{v_0}) w_i^*= {\mathcal L}(\Upsilon _1)$
. By taking relative commutants and using Corollary 2.9 and
$ w_i{\mathcal L}(\Gamma ^{\prime }_{v_0}) w_i^*= {\mathcal L}(\Upsilon _1)$
. By taking relative commutants and using Corollary 2.9 and
![]() $\mathrm {link}(w_0)=\mathscr {D}_j\setminus \{w_0\}$
, we see that
$\mathrm {link}(w_0)=\mathscr {D}_j\setminus \{w_0\}$
, we see that
 $$ \begin{align}\begin{aligned} \mathcal{Q}:=w_i{\mathcal L}(\Gamma_{\mathrm{link}(v_0) })w_i^*&= (w_i{\mathcal L}(\Gamma^{\prime}_{v_0}) w_i^*)'\cap {\mathcal M} = {\mathcal L}(\Upsilon_1)'\cap {\mathcal M}\\ &= {\mathcal L}(h_i\Lambda_{\mathscr{D}_j\setminus \{w_0\}} h_i^{-1})\bar\otimes ({\mathcal L}(\Upsilon_1)'\cap {\mathcal L}(h_i \Lambda_{w_0}h_i^{-1})).\end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \mathcal{Q}:=w_i{\mathcal L}(\Gamma_{\mathrm{link}(v_0) })w_i^*&= (w_i{\mathcal L}(\Gamma^{\prime}_{v_0}) w_i^*)'\cap {\mathcal M} = {\mathcal L}(\Upsilon_1)'\cap {\mathcal M}\\ &= {\mathcal L}(h_i\Lambda_{\mathscr{D}_j\setminus \{w_0\}} h_i^{-1})\bar\otimes ({\mathcal L}(\Upsilon_1)'\cap {\mathcal L}(h_i \Lambda_{w_0}h_i^{-1})).\end{aligned} \end{align} $$
Since
![]() $\mathrm {link}(v_0)=(\mathscr {C}_i\cup \mathscr {C}_{i+1})\setminus \{v_0\}$
, we note that
$\mathrm {link}(v_0)=(\mathscr {C}_i\cup \mathscr {C}_{i+1})\setminus \{v_0\}$
, we note that
Since
![]() $ {\mathcal L} (h_i\Lambda _{\mathscr D_j\setminus \{w_0\}} h_i^{-1})$
is a regular property (T) von Neumann subalgebra of
$ {\mathcal L} (h_i\Lambda _{\mathscr D_j\setminus \{w_0\}} h_i^{-1})$
is a regular property (T) von Neumann subalgebra of
![]() $\mathcal {Q}$
, it follows from the main technical result of [Reference Ioana, Peterson and PopaIPP05] (see also [Reference Popa and VaesPV09, Theorem 5.4]) that
$\mathcal {Q}$
, it follows from the main technical result of [Reference Ioana, Peterson and PopaIPP05] (see also [Reference Popa and VaesPV09, Theorem 5.4]) that
![]() ${\mathcal L} (h_i\Lambda _{\mathscr D_j\setminus \{w_0\}} h_i^{-1})\prec _{\mathcal {Q}} w_i{\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}\setminus \{v_0\} })w_i^*$
. Thus, relation (7.10) and Corollary 2.7 entail
${\mathcal L} (h_i\Lambda _{\mathscr D_j\setminus \{w_0\}} h_i^{-1})\prec _{\mathcal {Q}} w_i{\mathcal L}(\Gamma _{\mathscr {C}_{i,i+1}\setminus \{v_0\} })w_i^*$
. Thus, relation (7.10) and Corollary 2.7 entail
Using (7.10), we have
![]() $w_i {\mathcal L}(\Gamma ^{\prime }_{\mathscr {C}_{i} \setminus \mathscr {C}_{i}^{1}} ) w_i^*=\mathcal L((\Lambda _0^0)_{\mathscr {D}_j\setminus \{w_0\}})$
. By taking relative commutants in (7.12) inside
$w_i {\mathcal L}(\Gamma ^{\prime }_{\mathscr {C}_{i} \setminus \mathscr {C}_{i}^{1}} ) w_i^*=\mathcal L((\Lambda _0^0)_{\mathscr {D}_j\setminus \{w_0\}})$
. By taking relative commutants in (7.12) inside
![]() $\mathcal {Q}$
and using Subclaim 2 and (7.13), we further get
$\mathcal {Q}$
and using Subclaim 2 and (7.13), we further get
In particular, we have
Since we also have
![]() $\mathbb T w_{i+1}\Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} }w_{i+1}^*< \mathbb T h_{i+1}\Lambda _{\mathscr {D}_{\sigma (i+1)}} h_{i+1}^{-1} $
, we obtain that
$\mathbb T w_{i+1}\Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} }w_{i+1}^*< \mathbb T h_{i+1}\Lambda _{\mathscr {D}_{\sigma (i+1)}} h_{i+1}^{-1} $
, we obtain that
![]() $w_0\in \mathscr {D}_{\sigma (i+1)}$
. Indeed, by [Reference VaesVa10a, Lemma 2.7], there is
$w_0\in \mathscr {D}_{\sigma (i+1)}$
. Indeed, by [Reference VaesVa10a, Lemma 2.7], there is
![]() $\lambda \in \Lambda $
, such that
$\lambda \in \Lambda $
, such that
![]() ${\mathcal L}(\Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} })\prec _{{\mathcal M}}^s \mathcal L (\lambda \Lambda _{w_0} \lambda ^{-1} \cap \Lambda _{\mathscr {D}_{\sigma (i+1)}} )$
, and hence,
${\mathcal L}(\Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} })\prec _{{\mathcal M}}^s \mathcal L (\lambda \Lambda _{w_0} \lambda ^{-1} \cap \Lambda _{\mathscr {D}_{\sigma (i+1)}} )$
, and hence,
![]() $\lambda \Lambda _{w_0} \lambda ^{-1} \cap \Lambda _{\mathscr {D}_{\sigma (i+1)}}$
is an infinite group. By Proposition 2.1, we get that
$\lambda \Lambda _{w_0} \lambda ^{-1} \cap \Lambda _{\mathscr {D}_{\sigma (i+1)}}$
is an infinite group. By Proposition 2.1, we get that
![]() $w_0\in \mathscr {D}_{\sigma (i+1)}$
. Now, using that
$w_0\in \mathscr {D}_{\sigma (i+1)}$
. Now, using that
![]() $\mathrm {link}(w_0)\subset \mathscr {D}_j$
, we get
$\mathrm {link}(w_0)\subset \mathscr {D}_j$
, we get
![]() $\sigma (i+1)=j$
. In particular, we have that
$\sigma (i+1)=j$
. In particular, we have that
![]() $\mathbb T w_{i+1}\Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} }w_{i+1}^*=\mathbb T \Lambda _{i+1}< \mathbb T h_{i+1}\Lambda _{\mathscr {D}_{j}} h_{i+1}^{-1}.$
This further implies that
$\mathbb T w_{i+1}\Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} }w_{i+1}^*=\mathbb T \Lambda _{i+1}< \mathbb T h_{i+1}\Lambda _{\mathscr {D}_{j}} h_{i+1}^{-1}.$
This further implies that
Using Theorem 2.16, (7.15) and (7.16) further imply that
![]() $x:=h_i h^{-1}_{i+1}w_{i+1} w_i^*\in \mathscr {U}({\mathcal L}(h_i \Lambda _{\mathscr {D}_j} h_i^{-1}))$
. Thus, using Lemma 7.3, (7.15) and (7.16) further entail the existence of a finite index subgroup
$x:=h_i h^{-1}_{i+1}w_{i+1} w_i^*\in \mathscr {U}({\mathcal L}(h_i \Lambda _{\mathscr {D}_j} h_i^{-1}))$
. Thus, using Lemma 7.3, (7.15) and (7.16) further entail the existence of a finite index subgroup
![]() $\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1}}\leqslant \Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1}}$
, such that
$\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1}}\leqslant \Gamma _{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1}}$
, such that
![]() $\mathbb T x( w_i\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} } w_i^*) x^* < \mathbb T h_{i}\Lambda _{w_0} h_{i}^{-1}$
. In particular, there exist a finite index subgroup
$\mathbb T x( w_i\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1} \setminus \mathscr {C}_{i,i+1} } w_i^*) x^* < \mathbb T h_{i}\Lambda _{w_0} h_{i}^{-1}$
. In particular, there exist a finite index subgroup
![]() $\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1,i+2}}\leqslant \Gamma _{\mathscr {C}_{i+1,i+2}}$
and a subgroup
$\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1,i+2}}\leqslant \Gamma _{\mathscr {C}_{i+1,i+2}}$
and a subgroup
![]() $\Lambda _2<h_i \Lambda _{w_0} h_i^{-1}$
, such that
$\Lambda _2<h_i \Lambda _{w_0} h_i^{-1}$
, such that
![]() $\mathbb T x( w_i\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1,i+2}} w_i^*) x^* =\mathbb T \Lambda _2$
. Taking relative commutants and using Corollary 2.9, we get
$\mathbb T x( w_i\Gamma ^{\prime \prime }_{\mathscr {C}_{i+1,i+2}} w_i^*) x^* =\mathbb T \Lambda _2$
. Taking relative commutants and using Corollary 2.9, we get
However, we canonically have the free product decomposition
From (7.17), we derive that
![]() ${\mathcal L}(h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1})$
is a regular property (T) von Neumann subalgebra of
${\mathcal L}(h_i \Lambda _{\mathscr {D}_j\setminus \{w_0\}} h_i^{-1})$
is a regular property (T) von Neumann subalgebra of
![]() $x{\mathcal L}(\Gamma _{\mathscr {C}_{i+1}\cup \mathscr {C}_{i+2} \setminus \mathscr {C}_{i+1,i+2}})x^*$
. Hence, we obtain a contradiction by applying [Reference Popa and VaesPV09, Theorem 5.4] (see also [Reference Ioana, Peterson and PopaIPP05]) to relation (7.18). Thus, relation (7.11) holds.
$x{\mathcal L}(\Gamma _{\mathscr {C}_{i+1}\cup \mathscr {C}_{i+2} \setminus \mathscr {C}_{i+1,i+2}})x^*$
. Hence, we obtain a contradiction by applying [Reference Popa and VaesPV09, Theorem 5.4] (see also [Reference Ioana, Peterson and PopaIPP05]) to relation (7.18). Thus, relation (7.11) holds.
Using (7.11) and taking relative commutants in (7.10), we obtain that
![]() $w_i {\mathcal L}(\Gamma _{\mathscr {C}_i^1})w_i^*= {\mathcal L} (h_i \Lambda _{w_0}h_i^{-1})$
. Combining this with (7.9), we conclude that
$w_i {\mathcal L}(\Gamma _{\mathscr {C}_i^1})w_i^*= {\mathcal L} (h_i \Lambda _{w_0}h_i^{-1})$
. Combining this with (7.9), we conclude that
![]() $[h_i \Lambda _{w_0} h_i^{-1}: \Upsilon _0]<\infty $
. Thus,
$[h_i \Lambda _{w_0} h_i^{-1}: \Upsilon _0]<\infty $
. Thus,
![]() $[h_i\Lambda _{\mathscr {D}_j} h_i^{-1}: (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon _0 ]<\infty $
. Since
$[h_i\Lambda _{\mathscr {D}_j} h_i^{-1}: (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon _0 ]<\infty $
. Since
![]() $ (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon _0 <\Lambda _i< h_i\Lambda _{\mathscr {D}_j} h_i^{-1}$
, we conclude the proof of our claim in case 3.
$ (\Lambda _0)_{\mathscr {D}_j\setminus \{w_0\}}\times \Upsilon _0 <\Lambda _i< h_i\Lambda _{\mathscr {D}_j} h_i^{-1}$
, we conclude the proof of our claim in case 3.
Next, we prove the following claim.
Claim 7.9. For any
![]() $1\leq i\leq n$
, there exists a unitary
$1\leq i\leq n$
, there exists a unitary
![]() $y_i \in {\mathcal M}$
, such that
$y_i \in {\mathcal M}$
, such that
![]() $\mathbb T y_i \Gamma _{\mathscr {C}_i} y_i^*= \mathbb T \Lambda _{\mathscr {D}_{\sigma (i)}}$
.
$\mathbb T y_i \Gamma _{\mathscr {C}_i} y_i^*= \mathbb T \Lambda _{\mathscr {D}_{\sigma (i)}}$
.
Proof of Claim 7.9.
Fix
![]() $1\leq i\leq n$
. From Claim 7.8, we have
$1\leq i\leq n$
. From Claim 7.8, we have
![]() $[h_i\Lambda _{\mathscr {D}_{\sigma (i)}} h^{-1}_i: \Lambda _i]<\infty $
. Recall also that
$[h_i\Lambda _{\mathscr {D}_{\sigma (i)}} h^{-1}_i: \Lambda _i]<\infty $
. Recall also that
![]() $\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T \Lambda _i$
, which clearly implies that
$\mathbb T w_i \Gamma _{\mathscr {C}_i} w_i^* =\mathbb T \Lambda _i$
, which clearly implies that
![]() $w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^* = \mathcal L(\Lambda _i)$
. Taking quasi-normalizers of these algebras and using successively part 2. in Lemma 2.15, we have
$w_i {\mathcal L}(\Gamma _{\mathscr {C}_i}) w_i^* = \mathcal L(\Lambda _i)$
. Taking quasi-normalizers of these algebras and using successively part 2. in Lemma 2.15, we have
 $$ \begin{align*} \begin{aligned}w_i {\mathcal L}(\Gamma_{\mathscr{C}_i}) w_i^*&= w_i {\mathcal L}(\mathrm{QN}_\Gamma(\Gamma_{\mathscr{C}_i})) w_i^*= w_i \mathscr Q\mathscr N ({\mathcal L}(\Gamma_{\mathscr{C}_i}))" w_i^*\\&= \mathscr Q\mathscr N (w_i{\mathcal L}(\Gamma_{\mathscr{C}_i})w_i^*)"= \mathscr{QN}_{\mathcal M}({\mathcal L}(\Lambda_i))"= {\mathcal L}(\mathrm{QN}_\Lambda(\Lambda_i)) \\& ={\mathcal L}(\mathrm{QN}_\Lambda(h_i \Lambda_{\mathscr{D}_{\sigma(i)}}h_i^{-1}))= {\mathcal L}(\mathrm{QN}_\Lambda(h_i \Lambda_{\mathscr{D}_{\sigma(i)}}h_i^{-1}))={\mathcal L}(h_i \Lambda_{\mathscr{D}_{\sigma(i)}}h_i^{-1})\\&= v_{h_i}{\mathcal L}(\Lambda_{\mathscr{D}_{\sigma(i)}}) v_{h_i^{-1}}.\end{aligned}\end{align*} $$
$$ \begin{align*} \begin{aligned}w_i {\mathcal L}(\Gamma_{\mathscr{C}_i}) w_i^*&= w_i {\mathcal L}(\mathrm{QN}_\Gamma(\Gamma_{\mathscr{C}_i})) w_i^*= w_i \mathscr Q\mathscr N ({\mathcal L}(\Gamma_{\mathscr{C}_i}))" w_i^*\\&= \mathscr Q\mathscr N (w_i{\mathcal L}(\Gamma_{\mathscr{C}_i})w_i^*)"= \mathscr{QN}_{\mathcal M}({\mathcal L}(\Lambda_i))"= {\mathcal L}(\mathrm{QN}_\Lambda(\Lambda_i)) \\& ={\mathcal L}(\mathrm{QN}_\Lambda(h_i \Lambda_{\mathscr{D}_{\sigma(i)}}h_i^{-1}))= {\mathcal L}(\mathrm{QN}_\Lambda(h_i \Lambda_{\mathscr{D}_{\sigma(i)}}h_i^{-1}))={\mathcal L}(h_i \Lambda_{\mathscr{D}_{\sigma(i)}}h_i^{-1})\\&= v_{h_i}{\mathcal L}(\Lambda_{\mathscr{D}_{\sigma(i)}}) v_{h_i^{-1}}.\end{aligned}\end{align*} $$
Thus, the claim follows from the
![]() $W^*$
-superrigidity of
$W^*$
-superrigidity of
![]() $\Gamma _{\mathscr {C}_i}$
(see Corollary 5.3).
$\Gamma _{\mathscr {C}_i}$
(see Corollary 5.3).
In particular, Claim 7.9 implies that
![]() $y_i{\mathcal L}(\Gamma _{\mathscr {C}_i})y_i^*= {\mathcal L}(\Lambda _{\mathscr {D}_{\sigma (i)}})$
. Then, using Theorem 2.3 and the same argument from the proof of [Reference Chifan, Davis and DrimbeCDD22, Theorem 7.9], one can find a unitary
$y_i{\mathcal L}(\Gamma _{\mathscr {C}_i})y_i^*= {\mathcal L}(\Lambda _{\mathscr {D}_{\sigma (i)}})$
. Then, using Theorem 2.3 and the same argument from the proof of [Reference Chifan, Davis and DrimbeCDD22, Theorem 7.9], one can find a unitary
![]() $u\in {\mathcal M}$
, such that
$u\in {\mathcal M}$
, such that
![]() $u{\mathcal L}(\Gamma _{\mathscr {C}_i})u^*= \mathcal L(\Lambda _{\mathscr {D}_{\sigma (i)}})$
for all i. Thus, without any loss of generality, we can assume that
$u{\mathcal L}(\Gamma _{\mathscr {C}_i})u^*= \mathcal L(\Lambda _{\mathscr {D}_{\sigma (i)}})$
for all i. Thus, without any loss of generality, we can assume that
![]() ${\mathcal L}(\Gamma _{\mathscr {C}_i})= {\mathcal L}(\Lambda _{\mathscr {D}_{\sigma (i)}})=:{\mathcal M}_i$
for all i. Since
${\mathcal L}(\Gamma _{\mathscr {C}_i})= {\mathcal L}(\Lambda _{\mathscr {D}_{\sigma (i)}})=:{\mathcal M}_i$
for all i. Since
![]() $\Gamma _{\mathscr {C}_i}$
is
$\Gamma _{\mathscr {C}_i}$
is
![]() $W^*$
-superrigid, we can find unitaries
$W^*$
-superrigid, we can find unitaries
![]() $x_i\in {\mathcal M}_i$
, such that
$x_i\in {\mathcal M}_i$
, such that
These relations already show that
![]() $\Lambda = \vee _i \Lambda _{\mathscr {D}_{\sigma (i)}}$
and also
$\Lambda = \vee _i \Lambda _{\mathscr {D}_{\sigma (i)}}$
and also
![]() $\sigma : \mathrm {cliq}(\mathscr {G}) \rightarrow \mathrm {cliq}(\mathscr {H})$
are bijections. Moreover, one can see that the graph
$\sigma : \mathrm {cliq}(\mathscr {G}) \rightarrow \mathrm {cliq}(\mathscr {H})$
are bijections. Moreover, one can see that the graph
![]() $\mathscr {H}\in \mathrm {CC}_1$
. This and relations (7.19) show that
$\mathscr {H}\in \mathrm {CC}_1$
. This and relations (7.19) show that
![]() $\Lambda $
can be represented as a graph product
$\Lambda $
can be represented as a graph product
![]() $\Lambda _{\mathscr {H}'}$
, where the vertex groups
$\Lambda _{\mathscr {H}'}$
, where the vertex groups
![]() $\Lambda _w$
are property (T) wreath-like products as in Theorem 5.2 and the underlying graph
$\Lambda _w$
are property (T) wreath-like products as in Theorem 5.2 and the underlying graph
![]() $\mathscr {H}'$
is isometric to
$\mathscr {H}'$
is isometric to
![]() $\mathscr {G}$
. Hence, the desired conclusion follows from [Reference Chifan, Davis and DrimbeCDD22, Theorem 7.10].
$\mathscr {G}$
. Hence, the desired conclusion follows from [Reference Chifan, Davis and DrimbeCDD22, Theorem 7.10].
Acknowledgements
We are grateful to the referee for all the comments and remarks that significantly improved the exposition of the paper.
Competing interests
The authors have no competing interest to declare.