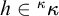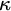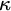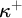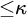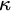In an effort to generalise the cardinal characteristics related to the null ideal from the context of the continuum
![]() ${}^{\omega }\omega $
to the generalised Baire space
${}^{\omega }\omega $
to the generalised Baire space
![]() ${}^{\kappa }\kappa $
, the authors of [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] considered localisation cardinals. These cardinals were first described in the context of
${}^{\kappa }\kappa $
, the authors of [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] considered localisation cardinals. These cardinals were first described in the context of
![]() ${}^{\omega }\omega $
by Bartoszyński [Reference Bartoszyński1] and are defined using the concept of slaloms.
${}^{\omega }\omega $
by Bartoszyński [Reference Bartoszyński1] and are defined using the concept of slaloms.
Definition 0.1. Let
![]() $\kappa $
be a regular strong limit cardinal (hence
$\kappa $
be a regular strong limit cardinal (hence
![]() $\kappa $
is inaccessible or equal to
$\kappa $
is inaccessible or equal to
![]() $\omega $
) and let
$\omega $
) and let
![]() $h\in {}^{\kappa }\kappa $
be increasing, then an h-slalom is a function
$h\in {}^{\kappa }\kappa $
be increasing, then an h-slalom is a function
![]() $\varphi :\kappa \to [\kappa ]^{<\kappa }$
such that
$\varphi :\kappa \to [\kappa ]^{<\kappa }$
such that
![]() $|\varphi (\alpha )|\leq |h(\alpha )|$
for all
$|\varphi (\alpha )|\leq |h(\alpha )|$
for all
![]() $\alpha \in \kappa $
. A slalom
$\alpha \in \kappa $
. A slalom
![]() $\varphi $
localises a function
$\varphi $
localises a function
![]() $f\in {}^{\kappa }\kappa $
, written symbolically as
$f\in {}^{\kappa }\kappa $
, written symbolically as
![]() $f\in ^*\varphi $
, if there exists some
$f\in ^*\varphi $
, if there exists some
![]() $\xi \in \kappa $
such that
$\xi \in \kappa $
such that
![]() $f(\alpha )\in \varphi (\alpha )$
for all
$f(\alpha )\in \varphi (\alpha )$
for all
![]() $\alpha \in [\xi ,\kappa )$
. We denote the set of h-slaloms as
$\alpha \in [\xi ,\kappa )$
. We denote the set of h-slaloms as
![]() $\mathrm {Loc}_h$
.
$\mathrm {Loc}_h$
.
We can define the following two cardinal characteristics, sometimes called localisation cardinals, having an increasing function
![]() $h\in {}^{\kappa }\kappa $
as parameter:
$h\in {}^{\kappa }\kappa $
as parameter:
 $$ \begin{align*} \mathfrak b_\kappa^h(\in^*) &= \text{the least cardinality of a family }\mathcal F\subseteq {}^{\kappa}\kappa\text{ such that }\forall \varphi\in \mathrm{Loc}_h \exists f\in\mathcal F(f\notin^*\varphi),\\ \mathfrak d_\kappa^h(\in^*) &= \text{the least cardinality of a family }\Phi\subseteq \mathrm{Loc}_h\text{ such that }\forall f\in {}^{\kappa}\kappa \exists \varphi\in\Phi(f\in^*\varphi). \end{align*} $$
$$ \begin{align*} \mathfrak b_\kappa^h(\in^*) &= \text{the least cardinality of a family }\mathcal F\subseteq {}^{\kappa}\kappa\text{ such that }\forall \varphi\in \mathrm{Loc}_h \exists f\in\mathcal F(f\notin^*\varphi),\\ \mathfrak d_\kappa^h(\in^*) &= \text{the least cardinality of a family }\Phi\subseteq \mathrm{Loc}_h\text{ such that }\forall f\in {}^{\kappa}\kappa \exists \varphi\in\Phi(f\in^*\varphi). \end{align*} $$
In the case that
![]() $\kappa =\omega $
these cardinals give a combinatorial definition of two of the cardinal invariants of the Lebesgue null ideal
$\kappa =\omega $
these cardinals give a combinatorial definition of two of the cardinal invariants of the Lebesgue null ideal
![]() $\mathcal N$
:
$\mathcal N$
:
 $$ \begin{align*} \mathrm{add}(\mathcal N) &= \text{the least cardinality of a family }\mathcal A\subseteq \mathcal N\text{ such that } \textstyle\bigcup \mathcal A\notin \mathcal N,\\ \mathrm{cof}(\mathcal N) &= \text{the least cardinality of a family }\mathcal C\subseteq \mathcal N\text{ such that }\forall N\in\mathcal N\exists C\in \mathcal C(N\subseteq C). \end{align*} $$
$$ \begin{align*} \mathrm{add}(\mathcal N) &= \text{the least cardinality of a family }\mathcal A\subseteq \mathcal N\text{ such that } \textstyle\bigcup \mathcal A\notin \mathcal N,\\ \mathrm{cof}(\mathcal N) &= \text{the least cardinality of a family }\mathcal C\subseteq \mathcal N\text{ such that }\forall N\in\mathcal N\exists C\in \mathcal C(N\subseteq C). \end{align*} $$
Bartoszyński [Reference Bartoszyński1] introduced localisation cardinals to give the following characterisation.
Fact 0.2.
![]() $\mathrm {add}(\mathcal N)=\mathfrak b_\omega ^h(\in ^*)$
and
$\mathrm {add}(\mathcal N)=\mathfrak b_\omega ^h(\in ^*)$
and
![]() $\mathrm {cof}(\mathcal N)=\mathfrak d_\omega ^h(\in ^*)$
.
$\mathrm {cof}(\mathcal N)=\mathfrak d_\omega ^h(\in ^*)$
.
It is clear from this fact that the choice of the parameter
![]() $h\in {}^{\omega }\omega $
is irrelevant, as it does not influence the cardinalities of
$h\in {}^{\omega }\omega $
is irrelevant, as it does not influence the cardinalities of
![]() $\mathfrak b_\omega ^h(\in ^*)$
and
$\mathfrak b_\omega ^h(\in ^*)$
and
![]() $\mathfrak d_\omega ^h(\in ^*)$
. This turns out to be different in the generalised case. Recently, it was proved in [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] that
$\mathfrak d_\omega ^h(\in ^*)$
. This turns out to be different in the generalised case. Recently, it was proved in [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] that
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
can consistently have different values for different
${\mathfrak d_\kappa ^{h}(\in ^*)}$
can consistently have different values for different
![]() $h\in {}^{\kappa }\kappa $
. In particular, it was shown that
$h\in {}^{\kappa }\kappa $
. In particular, it was shown that
![]() ${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}<{\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
is consistent, where
${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}<{\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
is consistent, where
![]() $\mathsf {pow}:\alpha \mapsto 2^{|\alpha |}$
and
$\mathsf {pow}:\alpha \mapsto 2^{|\alpha |}$
and
![]() $\mathsf {id}:\alpha \mapsto |\alpha |$
. This consistency was proved using a generalisation of Sacks forcing on
$\mathsf {id}:\alpha \mapsto |\alpha |$
. This consistency was proved using a generalisation of Sacks forcing on
![]() ${}^{\kappa }2$
that has the generalised
${}^{\kappa }2$
that has the generalised
![]() $\mathsf {pow}$
-Sacks property, but not the generalised
$\mathsf {pow}$
-Sacks property, but not the generalised
![]() $\mathsf {id}$
-Sacks property.
$\mathsf {id}$
-Sacks property.
Definition 0.3. Let
![]() $h\in {}^{\kappa }\kappa $
. A forcing
$h\in {}^{\kappa }\kappa $
. A forcing
![]() $\mathbb P$
has the generalised h-Sacks property if for every
$\mathbb P$
has the generalised h-Sacks property if for every
![]() $\mathbb P$
-name
$\mathbb P$
-name
![]() $\dot f$
and
$\dot f$
and
![]() $p\in \mathbb P$
such that
$p\in \mathbb P$
such that
![]() $p\Vdash \text {"}\,\dot f:\check \kappa \to \check \kappa \,\text {"}$
there exists an h-slalom
$p\Vdash \text {"}\,\dot f:\check \kappa \to \check \kappa \,\text {"}$
there exists an h-slalom
![]() $\varphi $
and
$\varphi $
and
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $q\Vdash \text {"}\,\dot f(\check \alpha )\in \check \varphi (\check \alpha )\,\text {"}$
for all
$q\Vdash \text {"}\,\dot f(\check \alpha )\in \check \varphi (\check \alpha )\,\text {"}$
for all
![]() $\alpha \in \kappa $
. We will from now on simply say h-Sacks property and omit “generalised”.
$\alpha \in \kappa $
. We will from now on simply say h-Sacks property and omit “generalised”.
Hence, if
![]() $\Phi \subseteq \mathrm {Loc}_h$
is a family as in the definition of
$\Phi \subseteq \mathrm {Loc}_h$
is a family as in the definition of
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
in the ground model, then
${\mathfrak d_\kappa ^{h}(\in ^*)}$
in the ground model, then
![]() $\Phi $
will still witness the size of
$\Phi $
will still witness the size of
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
in extensions by forcings with the h-Sacks property. Specifically, the generalised Sacks forcing is unable to increase the size of
${\mathfrak d_\kappa ^{h}(\in ^*)}$
in extensions by forcings with the h-Sacks property. Specifically, the generalised Sacks forcing is unable to increase the size of
![]() ${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}$
. Meanwhile, it is possible to increase the size of
${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}$
. Meanwhile, it is possible to increase the size of
![]() ${\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
by using an iteration or a product of the generalised Sacks forcing.
${\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
by using an iteration or a product of the generalised Sacks forcing.
In this article we will answer an open question from [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] and prove that there exist functions
![]() $h_\xi \in {}^{\kappa }\kappa $
and cardinals
$h_\xi \in {}^{\kappa }\kappa $
and cardinals
![]() $\lambda _\xi $
with
$\lambda _\xi $
with
![]() $\mathrm {cf}(\lambda _\xi )>\kappa $
for each
$\mathrm {cf}(\lambda _\xi )>\kappa $
for each
![]() $\xi \in \kappa ^+$
such that it is simultaneously consistent that
$\xi \in \kappa ^+$
such that it is simultaneously consistent that
![]() ${\mathfrak d_\kappa ^{h_\xi }(\in ^*)}=\lambda _\xi $
for all
${\mathfrak d_\kappa ^{h_\xi }(\in ^*)}=\lambda _\xi $
for all
![]() $\xi \in \kappa $
. The strategy will be the same as the strategy used to separate
$\xi \in \kappa $
. The strategy will be the same as the strategy used to separate
![]() ${\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
from
${\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
from
![]() ${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}$
, in that we consider a product of Sacks-like forcings that have the
${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}$
, in that we consider a product of Sacks-like forcings that have the
![]() $h_\xi $
-Sacks property, but not the
$h_\xi $
-Sacks property, but not the
![]() $h_\eta $
-Sacks property for different
$h_\eta $
-Sacks property for different
![]() $\xi $
and
$\xi $
and
![]() $\eta $
. In the first section, we introduce the Sacks-like forcing
$\eta $
. In the first section, we introduce the Sacks-like forcing
![]() ${\mathbb S^{h}_\kappa }$
. We will prove that it preserves cardinals and cofinalities and use fusion to show that it satisfies certain Sacks properties. In the second section we consider products of such forcings. We show that properties such as the preservation of cardinals and cofinalities and the relevant Sacks properties are preserved under
${\mathbb S^{h}_\kappa }$
. We will prove that it preserves cardinals and cofinalities and use fusion to show that it satisfies certain Sacks properties. In the second section we consider products of such forcings. We show that properties such as the preservation of cardinals and cofinalities and the relevant Sacks properties are preserved under
![]() ${\leq }\kappa $
-support products and we use this to prove the consistency of
${\leq }\kappa $
-support products and we use this to prove the consistency of
![]() $\kappa $
many different cardinals. Finally, in the third section we will show that with a preparatory forcing, we can use our approach to prove the consistency of
$\kappa $
many different cardinals. Finally, in the third section we will show that with a preparatory forcing, we can use our approach to prove the consistency of
![]() $\kappa ^+$
many different cardinals.
$\kappa ^+$
many different cardinals.
For the sake of brevity, from now on we will assume that
![]() $\kappa $
denotes a strongly inaccessible cardinal. We will also fix the convention that
$\kappa $
denotes a strongly inaccessible cardinal. We will also fix the convention that
![]() $h,H,F\in {}^{\kappa }\kappa $
denote increasing cofinal cardinal functions (i.e.,
$h,H,F\in {}^{\kappa }\kappa $
denote increasing cofinal cardinal functions (i.e.,
![]() $\mathrm {ran}(h)$
is cofinal in
$\mathrm {ran}(h)$
is cofinal in
![]() $\kappa $
and
$\kappa $
and
![]() $h(\alpha )$
is a cardinal for each
$h(\alpha )$
is a cardinal for each
![]() $\alpha \in \kappa $
). This convention extends to
$\alpha \in \kappa $
). This convention extends to
![]() $h_\xi $
,
$h_\xi $
,
![]() $F_0$
, and other subscripts.
$F_0$
, and other subscripts.
1 The forcing
Let us establish some notation to discuss trees on
![]() ${}^{\kappa }\kappa $
before we define our forcing notion.
${}^{\kappa }\kappa $
before we define our forcing notion.
A subset
![]() $T\subseteq {}^{<\kappa }\kappa $
is called a
$T\subseteq {}^{<\kappa }\kappa $
is called a
![]() $\kappa $
-tree if for every
$\kappa $
-tree if for every
![]() $u\in T$
and
$u\in T$
and
![]() $\beta \in \mathrm {dom}(u)$
we have
$\beta \in \mathrm {dom}(u)$
we have
![]() $u\restriction \beta \in T$
. A subset
$u\restriction \beta \in T$
. A subset
![]() $C\subseteq T$
is a chain if for any
$C\subseteq T$
is a chain if for any
![]() $u,v\in C$
we have
$u,v\in C$
we have
![]() $u\subseteq v$
or
$u\subseteq v$
or
![]() $v\subseteq u$
, and C is called maximal if there exists no chain
$v\subseteq u$
, and C is called maximal if there exists no chain
![]() $C'\subseteq T$
with
$C'\subseteq T$
with
![]() $C\subsetneq C'$
. A function
$C\subsetneq C'$
. A function
![]() $b:\alpha \to \kappa $
where
$b:\alpha \to \kappa $
where
![]() $\alpha \leq \kappa $
is called a branch of T if there exists a maximal chain
$\alpha \leq \kappa $
is called a branch of T if there exists a maximal chain
![]() $C\subseteq T$
such that
$C\subseteq T$
such that
![]() $b=\textstyle \bigcup C$
. The set of branches of T is denoted by
$b=\textstyle \bigcup C$
. The set of branches of T is denoted by
![]() $[T]$
. We define the subtree of T generated by
$[T]$
. We define the subtree of T generated by
![]() $u\in T$
as
$u\in T$
as
Given
![]() $u\in {}^{<\kappa }\kappa $
and
$u\in {}^{<\kappa }\kappa $
and
![]() $\beta \in \kappa $
, we write
$\beta \in \kappa $
, we write
![]() $u^\frown \beta $
for the extension of the sequence u with the term
$u^\frown \beta $
for the extension of the sequence u with the term
![]() $\beta $
. If
$\beta $
. If
![]() $u\in T$
, let
$u\in T$
, let
![]() $v\in T$
be a successor of u if there exists
$v\in T$
be a successor of u if there exists
![]() $\beta \in \kappa $
such that
$\beta \in \kappa $
such that
![]() $v=u^\frown \beta $
. We denote the set of successors of u in T by
$v=u^\frown \beta $
. We denote the set of successors of u in T by
![]() $\mathrm {suc}(u,T)$
.
$\mathrm {suc}(u,T)$
.
We call u a
![]() $\lambda $
-splitting node (of T), if
$\lambda $
-splitting node (of T), if
![]() $\lambda \leq \left |\mathrm {suc}(u,T)\right |$
. We say u is a splitting node if it is a 2-splitting node, and a non-splitting node otherwise. If u is a
$\lambda \leq \left |\mathrm {suc}(u,T)\right |$
. We say u is a splitting node if it is a 2-splitting node, and a non-splitting node otherwise. If u is a
![]() $\lambda $
-splitting node, but not a
$\lambda $
-splitting node, but not a
![]() $\mu $
-splitting node for any cardinal
$\mu $
-splitting node for any cardinal
![]() $\mu $
with
$\mu $
with
![]() $\lambda <\mu $
, then we say that u is a sharp
$\lambda <\mu $
, then we say that u is a sharp
![]() $\lambda $
-splitting node.
$\lambda $
-splitting node.
We let
![]() $\mathrm {Split}_\alpha (T)$
be the set of all
$\mathrm {Split}_\alpha (T)$
be the set of all
![]() $u\in T$
such that u splitting and
$u\in T$
such that u splitting and
where
![]() $\mathrm {ot}(X)$
denotes the order-type of X.
$\mathrm {ot}(X)$
denotes the order-type of X.
Definition 1.1. The conditions of the forcing
![]() ${\mathbb S^{h}_\kappa }$
are
${\mathbb S^{h}_\kappa }$
are
![]() $\kappa $
-trees
$\kappa $
-trees
![]() $T\subseteq {}^{<\kappa }\kappa $
that satisfy the following properties:
$T\subseteq {}^{<\kappa }\kappa $
that satisfy the following properties:
-
(i) For any
 $u\in T$
there exists
$u\in T$
there exists
 $v\in T$
such that
$v\in T$
such that
 $u\subseteq v$
and v is splitting.
$u\subseteq v$
and v is splitting. -
(ii) If
 $u\in \mathrm {Split}_\alpha (T)$
, then u is an
$u\in \mathrm {Split}_\alpha (T)$
, then u is an
 $h(\alpha )$
-splitting node in T.
$h(\alpha )$
-splitting node in T. -
(iii) If
 $C\subseteq T$
is a chain of splitting nodes with
$C\subseteq T$
is a chain of splitting nodes with
 $|C|<\kappa $
, then
$|C|<\kappa $
, then
 $\textstyle \bigcup C$
is a splitting node in T.
$\textstyle \bigcup C$
is a splitting node in T.
The order is defined as
![]() $T\leq _{{\mathbb S^{h}_\kappa }} S$
(here T provides more information than S) iff:
$T\leq _{{\mathbb S^{h}_\kappa }} S$
(here T provides more information than S) iff:
-
•
 $T\subseteq S$
and
$T\subseteq S$
and -
• for every
 $u\in T$
, if
$u\in T$
, if
 $\mathrm {suc}(u,T)\neq \mathrm {suc}(u,S)$
, then
$\mathrm {suc}(u,T)\neq \mathrm {suc}(u,S)$
, then
 $|\mathrm {suc}(u,T)|<|\mathrm {suc}(u,S)|$
.
$|\mathrm {suc}(u,T)|<|\mathrm {suc}(u,S)|$
.
If the forcing notion is clear from context, we will write
![]() $T\leq S$
in place of
$T\leq S$
in place of
![]() $T\leq _{{\mathbb S^{h}_\kappa }}S$
.
$T\leq _{{\mathbb S^{h}_\kappa }}S$
.
The generalised Sacks forcing from [Reference Kanamori6], which was used in [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] to separate
![]() ${\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
from
${\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
from
![]() ${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}$
, is a special case of the forcing
${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}$
, is a special case of the forcing
![]() $\mathbb S^h_\kappa $
. Indeed, the only difference is that splitting nodes split into
$\mathbb S^h_\kappa $
. Indeed, the only difference is that splitting nodes split into
![]() $h(\alpha )$
successors in our forcing, instead of only two successors in the Sacks forcing. That is, if
$h(\alpha )$
successors in our forcing, instead of only two successors in the Sacks forcing. That is, if
![]() $f:\kappa \to {\left \{2\right \}}$
is the constant function that sends every
$f:\kappa \to {\left \{2\right \}}$
is the constant function that sends every
![]() $\alpha \in \kappa $
to
$\alpha \in \kappa $
to
![]() $2$
, then the generalised Sacks forcing is equivalent to
$2$
, then the generalised Sacks forcing is equivalent to
![]() $\mathbb S^{f}_\kappa $
.
$\mathbb S^{f}_\kappa $
.
However, contrary to the constant function f, we will assume that h is an increasing cofinal cardinal function, and thus (as a consequence of the next lemma) any node can be extended to a
![]() $\lambda $
-splitting node for arbitrarily large
$\lambda $
-splitting node for arbitrarily large
![]() $\lambda <\kappa $
. In this sense we can also view
$\lambda <\kappa $
. In this sense we can also view
![]() $\mathbb S^h_\kappa $
as a bounded version of Miller forcing, where the set of successors of a node is
$\mathbb S^h_\kappa $
as a bounded version of Miller forcing, where the set of successors of a node is
![]() $<\kappa $
but eventually arbitrarily large. On
$<\kappa $
but eventually arbitrarily large. On
![]() ${}^{\omega }\omega $
, such a forcing has first been studied in [Reference Geschke4] as Miller Lite forcing.
${}^{\omega }\omega $
, such a forcing has first been studied in [Reference Geschke4] as Miller Lite forcing.
Lemma 1.2. If
![]() $T\in {\mathbb S^{h}_\kappa }$
and
$T\in {\mathbb S^{h}_\kappa }$
and
![]() $b\in [T]$
is a branch of T, then
$b\in [T]$
is a branch of T, then
![]() $\mathrm {dom}(b)=\kappa $
. In particular, if
$\mathrm {dom}(b)=\kappa $
. In particular, if
![]() $\alpha \in \kappa $
is limit and
$\alpha \in \kappa $
is limit and
![]() $u\in {}^\alpha \kappa $
is such that
$u\in {}^\alpha \kappa $
is such that
![]() $u\restriction \beta \in T$
for all
$u\restriction \beta \in T$
for all
![]() $\beta \in \alpha $
, then
$\beta \in \alpha $
, then
![]() $u\in T$
.
$u\in T$
.
Proof Suppose that
![]() $C\subseteq T$
is a chain such that
$C\subseteq T$
is a chain such that
![]() $u=\textstyle \bigcup C$
and
$u=\textstyle \bigcup C$
and
![]() $\mathrm {dom}(u)\in \kappa $
. If we show that
$\mathrm {dom}(u)\in \kappa $
. If we show that
![]() $u\in T$
, then
$u\in T$
, then
![]() $\mathrm {suc}(u,T)\neq \varnothing $
by (i) of Definition 1.1, thus it follows that C is not a branch. Let
$\mathrm {suc}(u,T)\neq \varnothing $
by (i) of Definition 1.1, thus it follows that C is not a branch. Let
From (i) of Definition 1.1 we can conclude that either
![]() $\textstyle \bigcup C'=u$
or there is some splitting node
$\textstyle \bigcup C'=u$
or there is some splitting node
![]() $v\in T$
with
$v\in T$
with
![]() $w\subseteq v$
for all
$w\subseteq v$
for all
![]() $w\in C$
. In the first case it follows that
$w\in C$
. In the first case it follows that
![]() $u\in T$
by (iii) of Definition 1.1, and in the second case
$u\in T$
by (iii) of Definition 1.1, and in the second case
![]() $v\restriction \mathrm {dom}(u)=u\in T$
since T is a
$v\restriction \mathrm {dom}(u)=u\in T$
since T is a
![]() $\kappa $
-tree.
$\kappa $
-tree.
We naturally want
![]() ${\mathbb S^{h}_\kappa }$
to preserve cardinalities. If we assume that
${\mathbb S^{h}_\kappa }$
to preserve cardinalities. If we assume that
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, then it is clear that
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, then it is clear that
![]() ${\mathbb S^{h}_\kappa }$
has the
${\mathbb S^{h}_\kappa }$
has the
![]() ${<}\kappa ^{++}$
-chain condition, since
${<}\kappa ^{++}$
-chain condition, since
![]() $|{\mathbb S^{h}_\kappa }|\leq |\mathcal P({}^{<\kappa }\kappa )|= 2^\kappa =\kappa ^+$
, where the former equality is implied by
$|{\mathbb S^{h}_\kappa }|\leq |\mathcal P({}^{<\kappa }\kappa )|= 2^\kappa =\kappa ^+$
, where the former equality is implied by
![]() $\kappa ^{<\kappa }=\kappa $
, which in turn follows from
$\kappa ^{<\kappa }=\kappa $
, which in turn follows from
![]() $\kappa $
being inaccessible. Therefore cardinalities above
$\kappa $
being inaccessible. Therefore cardinalities above
![]() $\kappa ^+$
are preserved under assumption of
$\kappa ^+$
are preserved under assumption of
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
.
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
.
To preserve cardinalities less than or equal to
![]() $\kappa $
, we show that
$\kappa $
, we show that
![]() ${\mathbb S^{h}_\kappa }$
is
${\mathbb S^{h}_\kappa }$
is
![]() ${<}\kappa $
-closed.
${<}\kappa $
-closed.
Lemma 1.3.
![]() ${\mathbb S^{h}_\kappa }$
is
${\mathbb S^{h}_\kappa }$
is
![]() ${<}\kappa $
-closed. That is, for any
${<}\kappa $
-closed. That is, for any
![]() $\lambda <\kappa $
, if
$\lambda <\kappa $
, if
![]() $\left \langle T_\xi \mid \xi \in \lambda \right \rangle $
is a descending chain of conditions, then there exists a condition T such that
$\left \langle T_\xi \mid \xi \in \lambda \right \rangle $
is a descending chain of conditions, then there exists a condition T such that
![]() $T\leq T_\xi $
for all
$T\leq T_\xi $
for all
![]() $\xi \in \lambda $
.
$\xi \in \lambda $
.
The condition T that is below all
![]() $T_\xi $
will simply be
$T_\xi $
will simply be
![]() $T=\textstyle \bigcap _{\xi \in \lambda }T_\xi $
, which can easily be seen to be a
$T=\textstyle \bigcap _{\xi \in \lambda }T_\xi $
, which can easily be seen to be a
![]() $\kappa $
-tree as well. We will make use of the following claim to prove the lemma.
$\kappa $
-tree as well. We will make use of the following claim to prove the lemma.
Claim 1.4. If
![]() $u\in T=\textstyle \bigcap _{\xi \in \lambda } T_\xi $
, then there is
$u\in T=\textstyle \bigcap _{\xi \in \lambda } T_\xi $
, then there is
![]() $\eta \in \lambda $
such that
$\eta \in \lambda $
such that
![]() $\mathrm {suc}(u,T)=\mathrm {suc}(u,T_\eta )$
.
$\mathrm {suc}(u,T)=\mathrm {suc}(u,T_\eta )$
.
Proof Suppose that
![]() $u\in T$
, and let
$u\in T$
, and let
![]() $\lambda _\xi =|\mathrm {suc}(u,T_{\xi })|$
, then the ordering on
$\lambda _\xi =|\mathrm {suc}(u,T_{\xi })|$
, then the ordering on
![]() ${\mathbb S^{h}_\kappa }$
dictates that
${\mathbb S^{h}_\kappa }$
dictates that
![]() $\left \langle \lambda _\xi \mid \xi \in \lambda \right \rangle $
is a descending sequence of cardinals, hence there is
$\left \langle \lambda _\xi \mid \xi \in \lambda \right \rangle $
is a descending sequence of cardinals, hence there is
![]() $\eta \in \lambda $
such that
$\eta \in \lambda $
such that
![]() $\lambda _\xi =\lambda _\eta $
for all
$\lambda _\xi =\lambda _\eta $
for all
![]() $\xi \in [\eta ,\lambda )$
. But then
$\xi \in [\eta ,\lambda )$
. But then
![]() $\mathrm {suc}(u,T_\xi )=\mathrm {suc}(u,T_\eta )$
for all
$\mathrm {suc}(u,T_\xi )=\mathrm {suc}(u,T_\eta )$
for all
![]() $\xi \in [\eta ,\lambda )$
by the ordering of
$\xi \in [\eta ,\lambda )$
by the ordering of
![]() ${\mathbb S^{h}_\kappa }$
.
${\mathbb S^{h}_\kappa }$
.
Proof of Lemma 1.3
We show that
![]() $T=\textstyle \bigcap _{\xi \in \lambda } T_\xi $
satisfies the lemma by verifying points (i)–(iii) from Definition 1.1 and showing that
$T=\textstyle \bigcap _{\xi \in \lambda } T_\xi $
satisfies the lemma by verifying points (i)–(iii) from Definition 1.1 and showing that
![]() $T\leq T_\xi $
for all
$T\leq T_\xi $
for all
![]() $\xi \in \lambda $
.
$\xi \in \lambda $
.
(i) Let
![]() $u\in T$
, and let
$u\in T$
, and let
![]() $f\in [T]$
be a branch for which
$f\in [T]$
be a branch for which
![]() $u\subseteq f$
. If
$u\subseteq f$
. If
![]() $\mathrm {ot}(f)<\kappa $
, then
$\mathrm {ot}(f)<\kappa $
, then
![]() $f\in T_\xi $
for each
$f\in T_\xi $
for each
![]() $\xi $
, thus by Claim 1.4 there is some
$\xi $
, thus by Claim 1.4 there is some
![]() $\eta \in \lambda $
for which
$\eta \in \lambda $
for which
![]() $\mathrm {suc}(f,T_\eta )=\mathrm {suc}(f,T)=\varnothing $
. Then clearly
$\mathrm {suc}(f,T_\eta )=\mathrm {suc}(f,T)=\varnothing $
. Then clearly
![]() $T_\eta \notin {\mathbb S^{h}_\kappa }$
, which is a contradiction, hence
$T_\eta \notin {\mathbb S^{h}_\kappa }$
, which is a contradiction, hence
![]() $\mathrm {ot}(f)=\kappa $
.
$\mathrm {ot}(f)=\kappa $
.
Let
![]() $C_\xi ={\left \{{\alpha \in [\mathrm {ot}(u),\kappa )\mid f\restriction \alpha \text { is splitting in }T_\xi }\right \}}$
, then since
$C_\xi ={\left \{{\alpha \in [\mathrm {ot}(u),\kappa )\mid f\restriction \alpha \text { is splitting in }T_\xi }\right \}}$
, then since
![]() $T_\xi \in {\mathbb S^{h}_\kappa }$
satisfies (i) and (iii), we see that
$T_\xi \in {\mathbb S^{h}_\kappa }$
satisfies (i) and (iii), we see that
![]() $ C_\xi $
is a club set. But then
$ C_\xi $
is a club set. But then
![]() $\textstyle \bigcap _{\xi \in \lambda } C_\xi $
is club. Any
$\textstyle \bigcap _{\xi \in \lambda } C_\xi $
is club. Any
![]() $v\in \textstyle \bigcap _{\xi \in \lambda } C_\xi $
is splitting in all
$v\in \textstyle \bigcap _{\xi \in \lambda } C_\xi $
is splitting in all
![]() $T_\xi $
, thus by Claim 1.4 it is splitting in T, and by definition of
$T_\xi $
, thus by Claim 1.4 it is splitting in T, and by definition of
![]() $ C_\xi $
it follows that
$ C_\xi $
it follows that
![]() $u\subseteq v$
.
$u\subseteq v$
.
(ii) If
![]() $u\in \mathrm {Split}_\alpha (T)$
, then by Claim 1.4 there is
$u\in \mathrm {Split}_\alpha (T)$
, then by Claim 1.4 there is
![]() $\eta \in \lambda $
such that
$\eta \in \lambda $
such that
![]() $\mathrm {suc}(u,T_\eta )=\mathrm {suc}(u,T)$
. Therefore
$\mathrm {suc}(u,T_\eta )=\mathrm {suc}(u,T)$
. Therefore
![]() $u\in \mathrm {Split}_\beta (T_\eta )$
for some
$u\in \mathrm {Split}_\beta (T_\eta )$
for some
![]() $\beta \geq \alpha $
, hence u is a
$\beta \geq \alpha $
, hence u is a
![]() $h(\beta )$
-splitting in T. Remember that we assume h is increasing, so u is also
$h(\beta )$
-splitting in T. Remember that we assume h is increasing, so u is also
![]() $h(\alpha )$
-splitting in T.
$h(\alpha )$
-splitting in T.
(iii) Let
![]() $C\subseteq T$
be a chain of splitting nodes, then for every
$C\subseteq T$
be a chain of splitting nodes, then for every
![]() $\xi \in \lambda $
we also see that C is a chain of splitting nodes in
$\xi \in \lambda $
we also see that C is a chain of splitting nodes in
![]() $T_\xi $
, and thus
$T_\xi $
, and thus
![]() $\textstyle \bigcup C$
is a splitting node in all
$\textstyle \bigcup C$
is a splitting node in all
![]() $T_\xi $
, hence by Claim 1.4,
$T_\xi $
, hence by Claim 1.4,
![]() $\textstyle \bigcup C$
is splitting in T.
$\textstyle \bigcup C$
is splitting in T.
(
![]() $\leq $
) Clearly
$\leq $
) Clearly
![]() $T\subseteq T_\xi $
for each
$T\subseteq T_\xi $
for each
![]() $\xi \in \lambda $
, and if
$\xi \in \lambda $
, and if
![]() $u\in T$
and
$u\in T$
and
![]() $\mathrm {suc}(u,T)\neq \mathrm {suc}(u,T_\xi )$
, then by Claim 1.4 there exists
$\mathrm {suc}(u,T)\neq \mathrm {suc}(u,T_\xi )$
, then by Claim 1.4 there exists
![]() $\eta \in \lambda $
such that
$\eta \in \lambda $
such that
![]() $\mathrm {suc}(u,T)=\mathrm {suc}(u,T_\eta )$
, and clearly
$\mathrm {suc}(u,T)=\mathrm {suc}(u,T_\eta )$
, and clearly
![]() $\xi <\eta $
. Since
$\xi <\eta $
. Since
![]() $T_\xi \leq T_\eta $
by assumption, then
$T_\xi \leq T_\eta $
by assumption, then
![]() $|\mathrm {suc}(u,T)|=|\mathrm {suc}(u,T_\eta )|<|\mathrm {suc}(u,T_\xi )|$
. Hence
$|\mathrm {suc}(u,T)|=|\mathrm {suc}(u,T_\eta )|<|\mathrm {suc}(u,T_\xi )|$
. Hence
![]() $T\leq T_\xi $
.
$T\leq T_\xi $
.
Corollary 1.5.
![]() ${\mathbb S^{h}_\kappa }$
preserves all cardinalities and cofinalities
${\mathbb S^{h}_\kappa }$
preserves all cardinalities and cofinalities
![]() $\leq \kappa $
.
$\leq \kappa $
.
What is left, is to show that
![]() $\kappa ^+$
is also preserved. This will be a consequence of the proof that
$\kappa ^+$
is also preserved. This will be a consequence of the proof that
![]() ${\mathbb S^{h}_\kappa }$
has the F-Sacks property for some suitably large
${\mathbb S^{h}_\kappa }$
has the F-Sacks property for some suitably large
![]() $F\in {}^{\kappa }\kappa $
, so we will prove this first. But before that, we will need to show that
$F\in {}^{\kappa }\kappa $
, so we will prove this first. But before that, we will need to show that
![]() ${\mathbb S^{h}_\kappa }$
is closed under fusion. It will be helpful to establish the notion of sharp trees.
${\mathbb S^{h}_\kappa }$
is closed under fusion. It will be helpful to establish the notion of sharp trees.
Let a
![]() $\kappa $
-tree
$\kappa $
-tree
![]() $T\in {\mathbb S^{h}_\kappa }$
be called sharp if every
$T\in {\mathbb S^{h}_\kappa }$
be called sharp if every
![]() $u\in \mathrm {Split}_\alpha (T)$
is a sharp
$u\in \mathrm {Split}_\alpha (T)$
is a sharp
![]() $h(\alpha )$
-splitting node. It is clear that by pruning we may find a sharp
$h(\alpha )$
-splitting node. It is clear that by pruning we may find a sharp
![]() $T^*$
below any condition
$T^*$
below any condition
![]() $T\in {\mathbb S^{h}_\kappa }$
such that
$T\in {\mathbb S^{h}_\kappa }$
such that
![]() $\mathrm {Split}_\alpha (T^*)\subseteq \mathrm {Split}_\alpha (T)$
for every
$\mathrm {Split}_\alpha (T^*)\subseteq \mathrm {Split}_\alpha (T)$
for every
![]() $\alpha \in \kappa $
. We may assume that we can canonically do so, thus we will hereby fix the notation
$\alpha \in \kappa $
. We may assume that we can canonically do so, thus we will hereby fix the notation
![]() $T^*$
to denote a canonical sharp
$T^*$
to denote a canonical sharp
![]() $\kappa $
-tree below condition T. We will write
$\kappa $
-tree below condition T. We will write
![]() $({\mathbb S^{h}_\kappa })^*={\left \{{T\in {\mathbb S^{h}_\kappa }\mid T\text { is sharp}}\right \}}$
, which embeds densely into
$({\mathbb S^{h}_\kappa })^*={\left \{{T\in {\mathbb S^{h}_\kappa }\mid T\text { is sharp}}\right \}}$
, which embeds densely into
![]() ${\mathbb S^{h}_\kappa }$
.
${\mathbb S^{h}_\kappa }$
.
Definition 1.6. For
![]() $T,S\in {\mathbb S^{h}_\kappa }$
, we let
$T,S\in {\mathbb S^{h}_\kappa }$
, we let
![]() $T\leq _\alpha S$
iff
$T\leq _\alpha S$
iff
![]() $T\leq S$
and
$T\leq S$
and
![]() $\mathrm {Split}_\alpha (T)=\mathrm {Split}_\alpha (S)$
. A fusion sequence is a sequence
$\mathrm {Split}_\alpha (T)=\mathrm {Split}_\alpha (S)$
. A fusion sequence is a sequence
![]() $\left \langle T_\alpha \in {\mathbb S^{h}_\kappa }\mid \alpha \in \kappa \right \rangle $
such that
$\left \langle T_\alpha \in {\mathbb S^{h}_\kappa }\mid \alpha \in \kappa \right \rangle $
such that
![]() $T_{\beta }\leq _\alpha T_\alpha $
for all
$T_{\beta }\leq _\alpha T_\alpha $
for all
![]() $\alpha \leq \beta \in \kappa $
.
$\alpha \leq \beta \in \kappa $
.
Lemma 1.7. If
![]() $\left \langle T_\alpha \in {\mathbb S^{h}_\kappa }\mid \alpha \in \kappa \right \rangle $
is a fusion sequence, then
$\left \langle T_\alpha \in {\mathbb S^{h}_\kappa }\mid \alpha \in \kappa \right \rangle $
is a fusion sequence, then
![]() $T=\textstyle \bigcap _{\alpha \in \kappa }T_\alpha \in {\mathbb S^{h}_\kappa }$
.
$T=\textstyle \bigcap _{\alpha \in \kappa }T_\alpha \in {\mathbb S^{h}_\kappa }$
.
Proof Clearly T is a
![]() $\kappa $
-tree on
$\kappa $
-tree on
![]() ${}^{<\kappa }\kappa $
. We check conditions (i)–(iii) of Definition 1.1.
${}^{<\kappa }\kappa $
. We check conditions (i)–(iii) of Definition 1.1.
(i) Let
![]() $u\in T$
and
$u\in T$
and
![]() $\alpha =\mathrm {ot}(u)$
, then for any
$\alpha =\mathrm {ot}(u)$
, then for any
![]() $\beta \geq \alpha $
we see that
$\beta \geq \alpha $
we see that
![]() $\mathrm {Split}_\alpha (T_\beta )=\mathrm {Split}_\alpha (T_\alpha )$
. Since
$\mathrm {Split}_\alpha (T_\beta )=\mathrm {Split}_\alpha (T_\alpha )$
. Since
![]() $\alpha =\mathrm {ot}(u)$
, necessarily there exists some
$\alpha =\mathrm {ot}(u)$
, necessarily there exists some
![]() $v\in \mathrm {Split}_\alpha (T_\alpha )$
such that
$v\in \mathrm {Split}_\alpha (T_\alpha )$
such that
![]() $u\subseteq v$
, and since
$u\subseteq v$
, and since
![]() $v\in \mathrm {Split}_\alpha (T_\beta )$
for all
$v\in \mathrm {Split}_\alpha (T_\beta )$
for all
![]() $\beta>\alpha $
we see that
$\beta>\alpha $
we see that
![]() $v\in \mathrm {Split}_\alpha (T)$
.
$v\in \mathrm {Split}_\alpha (T)$
.
(ii) Let
![]() $u\in \mathrm {Split}_\alpha (T)$
, then u is
$u\in \mathrm {Split}_\alpha (T)$
, then u is
![]() $h(\alpha )$
-splitting in
$h(\alpha )$
-splitting in
![]() $T_{\alpha +1}$
. Let
$T_{\alpha +1}$
. Let
![]() $\lambda _u=|\mathrm {suc}(u,T_{\alpha +1})|\geq h(\alpha )$
and let
$\lambda _u=|\mathrm {suc}(u,T_{\alpha +1})|\geq h(\alpha )$
and let
![]() $\left \langle v_\xi \mid \xi \in \lambda _u\right \rangle $
enumerate those
$\left \langle v_\xi \mid \xi \in \lambda _u\right \rangle $
enumerate those
![]() $v\supseteq u$
such that
$v\supseteq u$
such that
![]() $v\in \mathrm {Split}_{\alpha +1}(T_{\alpha +1})$
. For all
$v\in \mathrm {Split}_{\alpha +1}(T_{\alpha +1})$
. For all
![]() $\beta \geq \alpha +1$
we have
$\beta \geq \alpha +1$
we have
![]() $\mathrm {Split}_{\alpha +1}(T_{\beta })=\mathrm {Split}_{\alpha +1}(T_{\alpha +1})$
, therefore for each
$\mathrm {Split}_{\alpha +1}(T_{\beta })=\mathrm {Split}_{\alpha +1}(T_{\alpha +1})$
, therefore for each
![]() $\xi \in \lambda _u$
we see that
$\xi \in \lambda _u$
we see that
![]() $v_\xi \in T_\beta $
for all
$v_\xi \in T_\beta $
for all
![]() $\beta>\alpha $
, thus
$\beta>\alpha $
, thus
![]() $v_\xi \in T$
. Therefore u is
$v_\xi \in T$
. Therefore u is
![]() $h(\alpha )$
-splitting in T.
$h(\alpha )$
-splitting in T.
(iii) Let
![]() $C\subseteq T$
be a chain of splitting nodes with
$C\subseteq T$
be a chain of splitting nodes with
![]() $|C|<\kappa $
and let
$|C|<\kappa $
and let
![]() $\gamma \in \kappa $
be large enough such that
$\gamma \in \kappa $
be large enough such that
![]() $C\subseteq \textstyle \bigcup _{\alpha <\gamma }\mathrm {Split}_\alpha (T)$
. It follows that
$C\subseteq \textstyle \bigcup _{\alpha <\gamma }\mathrm {Split}_\alpha (T)$
. It follows that
![]() $C\subseteq \textstyle \bigcup _{\alpha <\gamma }\mathrm {Split}_\alpha (T_\gamma )$
, and thus
$C\subseteq \textstyle \bigcup _{\alpha <\gamma }\mathrm {Split}_\alpha (T_\gamma )$
, and thus
![]() $\textstyle \bigcup C\in \mathrm {Split}_\beta (T_\gamma )$
for some
$\textstyle \bigcup C\in \mathrm {Split}_\beta (T_\gamma )$
for some
![]() $\beta \leq \gamma $
. Then also
$\beta \leq \gamma $
. Then also
![]() $\textstyle \bigcup C\in \mathrm {Split}_\beta (T_{\gamma '})$
for all
$\textstyle \bigcup C\in \mathrm {Split}_\beta (T_{\gamma '})$
for all
![]() $\gamma '>\gamma $
, hence
$\gamma '>\gamma $
, hence
![]() $\textstyle \bigcup C\in \mathrm {Split}_\beta (T)$
.
$\textstyle \bigcup C\in \mathrm {Split}_\beta (T)$
.
(
![]() $\leq $
) Clearly
$\leq $
) Clearly
![]() $T\subseteq T_\alpha $
for all
$T\subseteq T_\alpha $
for all
![]() $\alpha \in \kappa $
. Given
$\alpha \in \kappa $
. Given
![]() $u\in T$
and
$u\in T$
and
![]() $\alpha \in \kappa $
such that
$\alpha \in \kappa $
such that
![]() $\mathrm {suc}(u,T)\neq \mathrm {suc}(u,T_\alpha )$
, we will show that
$\mathrm {suc}(u,T)\neq \mathrm {suc}(u,T_\alpha )$
, we will show that
![]() $|\mathrm {suc}(u,T)|<|\mathrm {suc}(u,T_\alpha )|$
. We may assume without loss of generality that u is splitting in T, so let
$|\mathrm {suc}(u,T)|<|\mathrm {suc}(u,T_\alpha )|$
. We may assume without loss of generality that u is splitting in T, so let
![]() $\beta \in \kappa $
be such that
$\beta \in \kappa $
be such that
![]() $u\in \mathrm {Split}_\beta (T)$
. Since
$u\in \mathrm {Split}_\beta (T)$
. Since
![]() $\mathrm {Split}_\gamma (T)=\mathrm {Split}_\gamma (T_\alpha )$
for all
$\mathrm {Split}_\gamma (T)=\mathrm {Split}_\gamma (T_\alpha )$
for all
![]() $\gamma \leq \alpha $
, we see that
$\gamma \leq \alpha $
, we see that
![]() $\beta \geq \alpha $
. We have
$\beta \geq \alpha $
. We have
![]() $\mathrm {Split}_{\beta +1}(T_{\beta +1})=\mathrm {Split}_{\beta +1}(T)$
, and thus
$\mathrm {Split}_{\beta +1}(T_{\beta +1})=\mathrm {Split}_{\beta +1}(T)$
, and thus
![]() $\mathrm {suc}(u,T_{\beta +1})=\mathrm {suc}(u,T)$
. Finally
$\mathrm {suc}(u,T_{\beta +1})=\mathrm {suc}(u,T)$
. Finally
![]() $T_{\beta +1}\leq T_\alpha $
gives us
$T_{\beta +1}\leq T_\alpha $
gives us
![]() $|\mathrm {suc}(u,T)|=|\mathrm {suc}(u,T_{\beta +1})|<|\mathrm {suc}(u,T_\alpha )|$
.
$|\mathrm {suc}(u,T)|=|\mathrm {suc}(u,T_{\beta +1})|<|\mathrm {suc}(u,T_\alpha )|$
.
We are now ready to prove the two main ingredients necessary for separating the localisation cardinals. We will show that for any h there is some faster growing F such that
![]() ${\mathbb S^{h}_\kappa }$
has the F-Sacks property, and reversely that for any F there exists some faster growing h such that
${\mathbb S^{h}_\kappa }$
has the F-Sacks property, and reversely that for any F there exists some faster growing h such that
![]() ${\mathbb S^{h}_\kappa }$
does not have the F-Sacks property. In other words, for any
${\mathbb S^{h}_\kappa }$
does not have the F-Sacks property. In other words, for any
![]() $F_0$
we may find h and
$F_0$
we may find h and
![]() $F_1$
such that
$F_1$
such that
![]() ${\mathbb S^{h}_\kappa }$
does not have the
${\mathbb S^{h}_\kappa }$
does not have the
![]() $F_0$
-Sacks property, but does have the
$F_0$
-Sacks property, but does have the
![]() $F_1$
-Sacks property.
$F_1$
-Sacks property.
If T is a
![]() $\kappa $
-tree and
$\kappa $
-tree and
![]() $u\in T$
, let
$u\in T$
, let
![]() $(T)_u={\left \{{v\in T\mid u\subseteq v\lor v\subseteq u}\right \}}$
. It is clear that
$(T)_u={\left \{{v\in T\mid u\subseteq v\lor v\subseteq u}\right \}}$
. It is clear that
![]() $(T)_u\leq T$
.
$(T)_u\leq T$
.
Theorem 1.8. For any h there exists F such that
![]() $h\leq ^* F$
and
$h\leq ^* F$
and
![]() $\mathbb S^{h}_\kappa $
has the F-Sacks property.
$\mathbb S^{h}_\kappa $
has the F-Sacks property.
Proof We will let
![]() $F:\alpha \mapsto h(\alpha )^{|\alpha |}$
and show that
$F:\alpha \mapsto h(\alpha )^{|\alpha |}$
and show that
![]() ${\mathbb S^{h}_\kappa }$
has the F-Sacks property.
${\mathbb S^{h}_\kappa }$
has the F-Sacks property.
Let
![]() $T_0\in {\mathbb S^{h}_\kappa }$
and let
$T_0\in {\mathbb S^{h}_\kappa }$
and let
![]() $\dot f$
be a name such that
$\dot f$
be a name such that
![]() $T_0\Vdash \text {"}\,\dot f:\check \kappa \to \check \kappa \,\text {"}$
. If
$T_0\Vdash \text {"}\,\dot f:\check \kappa \to \check \kappa \,\text {"}$
. If
![]() $T_0\Vdash \text {"}\,\dot f\in \check {\mathbf V}\,\text {"}$
, then the existence of an appropriate F-slalom is obvious, so we assume that
$T_0\Vdash \text {"}\,\dot f\in \check {\mathbf V}\,\text {"}$
, then the existence of an appropriate F-slalom is obvious, so we assume that
![]() $T_0\Vdash \text {"}\,\dot f\notin \check {\mathbf V}\,\text {"}$
. We will construct a fusion sequence
$T_0\Vdash \text {"}\,\dot f\notin \check {\mathbf V}\,\text {"}$
. We will construct a fusion sequence
![]() $\left \langle T_\xi \mid \xi \in \kappa \right \rangle $
and sets
$\left \langle T_\xi \mid \xi \in \kappa \right \rangle $
and sets
![]() ${\left \{{D_\xi \subseteq \kappa \mid \xi \in \kappa }\right \}}$
with
${\left \{{D_\xi \subseteq \kappa \mid \xi \in \kappa }\right \}}$
with
![]() $|D_\xi |\leq F(\xi )$
such that
$|D_\xi |\leq F(\xi )$
such that
for each
![]() $\xi \in \kappa $
. Consequently, we can define the F-slalom
$\xi \in \kappa $
. Consequently, we can define the F-slalom
![]() $\varphi :\xi \mapsto D_\xi $
in the ground model, then it follows that
$\varphi :\xi \mapsto D_\xi $
in the ground model, then it follows that
![]() $T\Vdash \text {"}\,\dot f(\check \xi )\in \check \varphi (\check \xi )\,\text {"}$
for all
$T\Vdash \text {"}\,\dot f(\check \xi )\in \check \varphi (\check \xi )\,\text {"}$
for all
![]() $\xi \in \kappa $
.
$\xi \in \kappa $
.
In general, we will assume each
![]() $T_\xi $
has the following property:
$T_\xi $
has the following property:
This is vacuously true for
![]() $T_0$
, and by using sharp
$T_0$
, and by using sharp
![]() $\kappa $
-trees at successor stages of our construction,
$\kappa $
-trees at successor stages of our construction,
![]() $(*)$
will follow by induction. If
$(*)$
will follow by induction. If
![]() $\gamma $
is limit, we will let
$\gamma $
is limit, we will let
![]() $T_\gamma =\textstyle \bigcap _{\xi \in \gamma }T_\xi $
, which will be a condition by the proof of Lemma 1.3.
$T_\gamma =\textstyle \bigcap _{\xi \in \gamma }T_\xi $
, which will be a condition by the proof of Lemma 1.3.
![]() $T_\gamma $
need not necessarily be a sharp
$T_\gamma $
need not necessarily be a sharp
![]() $\kappa $
-tree, but it is at least sharp for all splitting levels less than
$\kappa $
-tree, but it is at least sharp for all splitting levels less than
![]() $\gamma $
, which is enough for
$\gamma $
, which is enough for
![]() $(*)$
.
$(*)$
.
Suppose
![]() $T_\xi $
has been defined, then we will define
$T_\xi $
has been defined, then we will define
![]() $T_{\xi +1}$
such that it limits the possible values of
$T_{\xi +1}$
such that it limits the possible values of
![]() $\dot f(\xi )$
and such that
$\dot f(\xi )$
and such that
![]() $T_{\xi +1}\leq _\xi T_\xi $
. First note that if
$T_{\xi +1}\leq _\xi T_\xi $
. First note that if
![]() $T_\xi $
has property
$T_\xi $
has property
![]() $(*)$
, then
$(*)$
, then
![]() $T_\xi ^*\leq _\xi T_\xi $
: If u is splitting in
$T_\xi ^*\leq _\xi T_\xi $
: If u is splitting in
![]() $T_\xi $
and
$T_\xi $
and
![]() $u\notin T_\xi ^*$
, then u was removed because there is some
$u\notin T_\xi ^*$
, then u was removed because there is some
![]() $v\subseteq u$
such that
$v\subseteq u$
such that
![]() $\mathrm {suc}(v,T_\xi )$
is too large for sharpness. But then by
$\mathrm {suc}(v,T_\xi )$
is too large for sharpness. But then by
![]() $(*)$
it follows that
$(*)$
it follows that
![]() $v\in \mathrm {Split}_\alpha (T_\xi )$
for some
$v\in \mathrm {Split}_\alpha (T_\xi )$
for some
![]() $\alpha \geq \xi $
, hence
$\alpha \geq \xi $
, hence
![]() $u\in \mathrm {Split}_\beta (T_\xi )$
for some
$u\in \mathrm {Split}_\beta (T_\xi )$
for some
![]() $\beta>\xi $
.
$\beta>\xi $
.
We define a set
![]() $V_\xi $
of successor nodes of the
$V_\xi $
of successor nodes of the
![]() $\xi $
-th splitting level, that is,
$\xi $
-th splitting level, that is,
Our goal is to find a stronger condition below each subtree
![]() $(T^*_\xi )_v$
with
$(T^*_\xi )_v$
with
![]() $v\in V_\xi $
that decides
$v\in V_\xi $
that decides
![]() $\dot f(\check \xi )$
, and glue these conditions back together to get a condition stronger than
$\dot f(\check \xi )$
, and glue these conditions back together to get a condition stronger than
![]() $T^*_\xi $
. Since the size of
$T^*_\xi $
. Since the size of
![]() $V_\xi $
is limited, this limits the possible values of
$V_\xi $
is limited, this limits the possible values of
![]() $\dot f(\check \xi )$
to a small set.
$\dot f(\check \xi )$
to a small set.
For each
![]() $v\in V_\xi $
find a condition
$v\in V_\xi $
find a condition
![]() $T^v\leq (T_\xi ^*)_v$
such that
$T^v\leq (T_\xi ^*)_v$
such that
![]() $T^v\Vdash \text {"}\,\dot f(\check \xi )=\check \beta _\xi ^v\,\text {"}$
for some
$T^v\Vdash \text {"}\,\dot f(\check \xi )=\check \beta _\xi ^v\,\text {"}$
for some
![]() $\beta _\xi ^v\in \kappa $
. Choose some arbitrary
$\beta _\xi ^v\in \kappa $
. Choose some arbitrary
![]() $u\in \mathrm {Split}_\xi (T^v )$
and
$u\in \mathrm {Split}_\xi (T^v )$
and
![]() $w\in \mathrm {suc}(u,T^v )$
, and consider the subtree
$w\in \mathrm {suc}(u,T^v )$
, and consider the subtree
![]() $(T^v)_{w}$
of
$(T^v)_{w}$
of
![]() $T^v $
generated by the initial segment w. We let
$T^v $
generated by the initial segment w. We let
![]() $G_\xi :V_\xi \to \mathcal P(T_\xi )$
send
$G_\xi :V_\xi \to \mathcal P(T_\xi )$
send
![]() $v\mapsto (T^v)_w$
. Note that the
$v\mapsto (T^v)_w$
. Note that the
![]() $\alpha $
-th splitting level of
$\alpha $
-th splitting level of
![]() $G_\xi (v)=(T^v)_w$
corresponds to the
$G_\xi (v)=(T^v)_w$
corresponds to the
![]() $(\xi +1+\alpha )$
-th splitting level of
$(\xi +1+\alpha )$
-th splitting level of
![]() $T^v$
.
$T^v$
.
Now we define
 $$ \begin{align*} T_{\xi+1}&= \textstyle\bigcup G_\xi[V_\xi ]= \textstyle\bigcup {\left\{{G_\xi(v)\mid v\in V_\xi }\right\}},\\ D_{\xi}&={\left\{{\beta_\xi^v\mid v\in V_\xi }\right\}}. \end{align*} $$
$$ \begin{align*} T_{\xi+1}&= \textstyle\bigcup G_\xi[V_\xi ]= \textstyle\bigcup {\left\{{G_\xi(v)\mid v\in V_\xi }\right\}},\\ D_{\xi}&={\left\{{\beta_\xi^v\mid v\in V_\xi }\right\}}. \end{align*} $$
For each
![]() $v\in V_\xi $
we have
$v\in V_\xi $
we have
![]() $v\in G_\xi (v)$
, thus each successor of a splitting node in
$v\in G_\xi (v)$
, thus each successor of a splitting node in
![]() $\mathrm {Split}_\xi (T_\xi )$
is in
$\mathrm {Split}_\xi (T_\xi )$
is in
![]() $T_{\xi +1}$
. Therefore we see that
$T_{\xi +1}$
. Therefore we see that
![]() $\mathrm {Split}_{\xi }(T_{\xi +1})=\mathrm {Split}_\xi (T_\xi )$
. If
$\mathrm {Split}_{\xi }(T_{\xi +1})=\mathrm {Split}_\xi (T_\xi )$
. If
![]() $u\in \mathrm {Split}_{\xi +1+\alpha } (T_{\xi +1})$
for some
$u\in \mathrm {Split}_{\xi +1+\alpha } (T_{\xi +1})$
for some
![]() $\alpha \in \kappa $
, then
$\alpha \in \kappa $
, then
![]() $u\in \mathrm {Split}_{\alpha }(G_\xi (v))$
, thus
$u\in \mathrm {Split}_{\alpha }(G_\xi (v))$
, thus
![]() $u\in \mathrm {Split}_{\xi +1+\alpha }(T^v)$
, and since
$u\in \mathrm {Split}_{\xi +1+\alpha }(T^v)$
, and since
![]() $T^v \in {\mathbb S^{h}_\kappa }$
, we see that u is
$T^v \in {\mathbb S^{h}_\kappa }$
, we see that u is
![]() $h(\xi +1+\alpha )$
-splitting. Therefore
$h(\xi +1+\alpha )$
-splitting. Therefore
![]() $T_{\xi +1}$
satisfies (ii) of Definition 1.1. It is easy to check (i) and (iii), thus we can conclude that
$T_{\xi +1}$
satisfies (ii) of Definition 1.1. It is easy to check (i) and (iii), thus we can conclude that
![]() $T_{\xi +1}\in {\mathbb S^{h}_\kappa }$
and that
$T_{\xi +1}\in {\mathbb S^{h}_\kappa }$
and that
![]() $T_{\xi +1}\leq _\xi T_\xi $
.
$T_{\xi +1}\leq _\xi T_\xi $
.
Note that the set
![]() $D_\xi $
is indeed small enough:
$D_\xi $
is indeed small enough:
For each
![]() $v\in V_\xi $
we have
$v\in V_\xi $
we have
![]() $T^v \Vdash \text {"}\,\dot f(\check \xi )\in \check D_\xi \,\text {"}$
, and
$T^v \Vdash \text {"}\,\dot f(\check \xi )\in \check D_\xi \,\text {"}$
, and
![]() ${\left \{{T^v \mid v\in V_\xi }\right \}}$
is predense below
${\left \{{T^v \mid v\in V_\xi }\right \}}$
is predense below
![]() $T_{\xi +1}$
; thus,
$T_{\xi +1}$
; thus,
Let
![]() $T=\textstyle \bigcap _{\xi \in \kappa }T_\xi $
, then by the fusion lemma
$T=\textstyle \bigcap _{\xi \in \kappa }T_\xi $
, then by the fusion lemma
![]() $T\in {\mathbb S^{h}_\kappa }$
, and
$T\in {\mathbb S^{h}_\kappa }$
, and
![]() $T\Vdash \text {"}\,\dot f(\check \xi )\in \check D_\xi \,\text {"}$
for all
$T\Vdash \text {"}\,\dot f(\check \xi )\in \check D_\xi \,\text {"}$
for all
![]() $\xi \in \kappa $
.
$\xi \in \kappa $
.
As a corollary of
![]() ${\mathbb S^{h}_\kappa }$
having the F-Sacks property, we immediately get that
${\mathbb S^{h}_\kappa }$
having the F-Sacks property, we immediately get that
![]() $\kappa ^+$
is preserved.
$\kappa ^+$
is preserved.
Corollary 1.9.
![]() ${\mathbb S^{h}_\kappa }$
preserves
${\mathbb S^{h}_\kappa }$
preserves
![]() $\kappa ^+$
.
$\kappa ^+$
.
Proof Given an
![]() ${\mathbb S^{h}_\kappa }$
-name
${\mathbb S^{h}_\kappa }$
-name
![]() $\dot f$
and
$\dot f$
and
![]() $T\in {\mathbb S^{h}_\kappa }$
such that
$T\in {\mathbb S^{h}_\kappa }$
such that
![]() $T\Vdash \text {"}\,\dot f:\check \kappa \to \check \kappa ^+\,\text {"}$
, then using (the proof of) the F-Sacks property we may produce sets
$T\Vdash \text {"}\,\dot f:\check \kappa \to \check \kappa ^+\,\text {"}$
, then using (the proof of) the F-Sacks property we may produce sets
![]() $D_\xi $
with
$D_\xi $
with
![]() $|D_\xi |=F(\xi )<\kappa $
for each
$|D_\xi |=F(\xi )<\kappa $
for each
![]() $\xi \in \kappa $
such that
$\xi \in \kappa $
such that
![]() $T'\Vdash \text {"}\,\dot f(\check \xi )\in \check D_\xi \,\text {"}$
for some stronger
$T'\Vdash \text {"}\,\dot f(\check \xi )\in \check D_\xi \,\text {"}$
for some stronger
![]() $T'\leq T$
, and thus
$T'\leq T$
, and thus
![]() $\dot f$
is forced to have a range contained in
$\dot f$
is forced to have a range contained in
![]() $\textstyle \bigcup _{\xi \in \kappa } D_\xi $
and cannot be cofinal in
$\textstyle \bigcup _{\xi \in \kappa } D_\xi $
and cannot be cofinal in
![]() $\kappa ^+$
.
$\kappa ^+$
.
The second ingredient is to find a suitably fast growing h for a given function F such that
![]() ${\mathbb S^{h}_\kappa }$
does not have the F-Sacks property. We will need the following lemma.
${\mathbb S^{h}_\kappa }$
does not have the F-Sacks property. We will need the following lemma.
Lemma 1.10. Let
![]() $T\in {\mathbb S^{h}_\kappa }$
and let
$T\in {\mathbb S^{h}_\kappa }$
and let
![]() $C_T={\left \{{\alpha \in \kappa \mid \mathrm {Split}_\alpha (T)=T\cap {}^\alpha \kappa }\right \}}$
, then
$C_T={\left \{{\alpha \in \kappa \mid \mathrm {Split}_\alpha (T)=T\cap {}^\alpha \kappa }\right \}}$
, then
![]() $C_T$
is a club set.
$C_T$
is a club set.
Proof For
![]() $\alpha _0\in \kappa $
we can recursively define
$\alpha _0\in \kappa $
we can recursively define
![]() $\alpha _{n+1}$
large enough such that
$\alpha _{n+1}$
large enough such that
![]() $\mathrm {Split}_{\alpha _n}(T)\subseteq {}^{\leq \alpha _{n+1}}\kappa $
for each
$\mathrm {Split}_{\alpha _n}(T)\subseteq {}^{\leq \alpha _{n+1}}\kappa $
for each
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $\alpha =\textstyle \bigcup _{n\in \omega }\alpha _n$
, then
$\alpha =\textstyle \bigcup _{n\in \omega }\alpha _n$
, then
![]() $\alpha \in C_T$
, hence
$\alpha \in C_T$
, hence
![]() $C_T$
is unbounded. It is easy to see that
$C_T$
is unbounded. It is easy to see that
![]() $C_T$
is continuous.
$C_T$
is continuous.
Theorem 1.11. Let
![]() $F\in {}^\kappa \kappa $
, then there exists h such that
$F\in {}^\kappa \kappa $
, then there exists h such that
![]() $\mathbb S^{h}_\kappa $
does not have the F-Sacks property.
$\mathbb S^{h}_\kappa $
does not have the F-Sacks property.
Proof Let h be such that
![]() $F(\alpha )<h(\alpha )$
for all
$F(\alpha )<h(\alpha )$
for all
![]() $\alpha \in S$
, where S is a stationary subset of
$\alpha \in S$
, where S is a stationary subset of
![]() $\kappa $
. We will show that
$\kappa $
. We will show that
![]() $\mathbb S^h_\kappa $
does not have the F-Sacks property.
$\mathbb S^h_\kappa $
does not have the F-Sacks property.
Let
![]() $\dot f$
be a name for the generic
$\dot f$
be a name for the generic
![]() $\mathbb S^h_\kappa $
-real in
$\mathbb S^h_\kappa $
-real in
![]() ${}^{\kappa }\kappa $
, let
${}^{\kappa }\kappa $
, let
![]() $\varphi $
be an F-slalom, let
$\varphi $
be an F-slalom, let
![]() $T\in \mathbb S^h_\kappa $
and let
$T\in \mathbb S^h_\kappa $
and let
![]() $\alpha _0\in \kappa $
. We want to find some
$\alpha _0\in \kappa $
. We want to find some
![]() $\alpha \geq \alpha _0$
and
$\alpha \geq \alpha _0$
and
![]() $S\leq T$
such that
$S\leq T$
such that
![]() $S\Vdash \text {"}\,\dot f(\check \alpha )\notin \check \varphi (\check \alpha )\,\text {"}$
. If we can find
$S\Vdash \text {"}\,\dot f(\check \alpha )\notin \check \varphi (\check \alpha )\,\text {"}$
. If we can find
![]() $u\in T\cap {}^{\alpha +1}\kappa $
such that
$u\in T\cap {}^{\alpha +1}\kappa $
such that
![]() $u(\alpha )\notin \varphi (\alpha )$
, then
$u(\alpha )\notin \varphi (\alpha )$
, then
![]() $(T)_u$
will be sufficient.
$(T)_u$
will be sufficient.
Let
![]() $C_T$
be as defined in Lemma 1.10 and
$C_T$
be as defined in Lemma 1.10 and
![]() $\alpha \in C_T\cap S$
such that
$\alpha \in C_T\cap S$
such that
![]() $\alpha _0\leq \alpha $
, then
$\alpha _0\leq \alpha $
, then
![]() $\mathrm {Split}_\alpha (T)=T\cap {}^\alpha \kappa $
, thus each
$\mathrm {Split}_\alpha (T)=T\cap {}^\alpha \kappa $
, thus each
![]() $t\in T\cap {}^\alpha \kappa $
is an
$t\in T\cap {}^\alpha \kappa $
is an
![]() $h(\alpha )$
-splitting node. Hence, there is a set
$h(\alpha )$
-splitting node. Hence, there is a set
![]() $X\subseteq \kappa $
with
$X\subseteq \kappa $
with
![]() $|X|=h(\alpha )$
such that
$|X|=h(\alpha )$
such that
![]() $t^\frown \gamma \in T$
for all
$t^\frown \gamma \in T$
for all
![]() $\gamma \in X$
. Since
$\gamma \in X$
. Since
![]() $|\varphi (\alpha )|=F(\alpha )<h(\alpha )$
, there is some
$|\varphi (\alpha )|=F(\alpha )<h(\alpha )$
, there is some
![]() $\gamma \in X$
such that
$\gamma \in X$
such that
![]() $\gamma \notin \varphi (\alpha )$
, and thus
$\gamma \notin \varphi (\alpha )$
, and thus
![]() $u=t^\frown \gamma $
is as desired.
$u=t^\frown \gamma $
is as desired.
As a final part of this section, we will discuss the relation between parameters that are almost equal. For functions
![]() $f,g\in {}^{\kappa }\kappa $
, we say that f and g are almost equal, written as
$f,g\in {}^{\kappa }\kappa $
, we say that f and g are almost equal, written as
![]() $f=^*g$
, if there exists
$f=^*g$
, if there exists
![]() $\xi \in \kappa $
such that
$\xi \in \kappa $
such that
![]() $f(\alpha )=g(\alpha )$
for all
$f(\alpha )=g(\alpha )$
for all
![]() $\alpha \in [\xi ,\kappa )$
. A related notion is that g dominates f, written as
$\alpha \in [\xi ,\kappa )$
. A related notion is that g dominates f, written as
![]() $f\leq ^*g$
, if there exists
$f\leq ^*g$
, if there exists
![]() $\xi \in \kappa $
such that
$\xi \in \kappa $
such that
![]() $f(\alpha )\leq g(\alpha )$
for all
$f(\alpha )\leq g(\alpha )$
for all
![]() $\alpha \in [\xi ,\kappa )$
.
$\alpha \in [\xi ,\kappa )$
.
Fact 1.12. If
![]() $h=^*h'$
, then
$h=^*h'$
, then
![]() ${\mathbb S^{h}_\kappa }$
and
${\mathbb S^{h}_\kappa }$
and
![]() ${\mathbb S^{h'}_\kappa }$
are forcing equivalent.
${\mathbb S^{h'}_\kappa }$
are forcing equivalent.
Proof Since
![]() ${\mathbb S^{h}_\kappa }\cap {\mathbb S^{h'}_\kappa }$
is dense in both
${\mathbb S^{h}_\kappa }\cap {\mathbb S^{h'}_\kappa }$
is dense in both
![]() ${\mathbb S^{h}_\kappa }$
and
${\mathbb S^{h}_\kappa }$
and
![]() ${\mathbb S^{h'}_\kappa }$
.
${\mathbb S^{h'}_\kappa }$
.
2 Products
We see that for any
![]() $F_0$
, we can find a faster growing
$F_0$
, we can find a faster growing
![]() $F_1$
and some suitable h such that the forcing
$F_1$
and some suitable h such that the forcing
![]() ${\mathbb S^{h}_\kappa }$
has the
${\mathbb S^{h}_\kappa }$
has the
![]() $F_1$
-Sacks property and not the
$F_1$
-Sacks property and not the
![]() $F_0$
-Sacks property, thus forcing with
$F_0$
-Sacks property, thus forcing with
![]() ${\mathbb S^{h}_\kappa }$
will not increase
${\mathbb S^{h}_\kappa }$
will not increase
![]() ${\mathfrak d_\kappa ^{F_1}(\in ^*)}$
, but has the potential to increase
${\mathfrak d_\kappa ^{F_1}(\in ^*)}$
, but has the potential to increase
![]() ${\mathfrak d_\kappa ^{F_0}(\in ^*)}$
.
${\mathfrak d_\kappa ^{F_0}(\in ^*)}$
.
In order to increase
![]() ${\mathfrak d_\kappa ^{F_0}(\in ^*)}$
we will need to add many
${\mathfrak d_\kappa ^{F_0}(\in ^*)}$
we will need to add many
![]() ${\mathbb S^{h}_\kappa }$
-generic
${\mathbb S^{h}_\kappa }$
-generic
![]() $\kappa $
-reals to the ground model. This can be either done with an iteration, or with a product. Iteration has the drawback that once we have forced
$\kappa $
-reals to the ground model. This can be either done with an iteration, or with a product. Iteration has the drawback that once we have forced
![]() $2^\kappa $
to be of size
$2^\kappa $
to be of size
![]() $\kappa ^{++}$
, the forcing
$\kappa ^{++}$
, the forcing
![]() ${\mathbb S^{h}_\kappa }$
no longer has the
${\mathbb S^{h}_\kappa }$
no longer has the
![]() ${<}\kappa ^{++}$
-c.c., and thus we cannot sufficiently control the iteration past this point. While this does not form a problem to prove the consistency of
${<}\kappa ^{++}$
-c.c., and thus we cannot sufficiently control the iteration past this point. While this does not form a problem to prove the consistency of
![]() $\kappa ^+={\mathfrak d_\kappa ^{F_1}(\in ^*)}<{\mathfrak d_\kappa ^{F_0}(\in ^*)}=\kappa ^{++}$
, iteration proves to be an obstacle when we wish to force localisation cardinals to be larger than
$\kappa ^+={\mathfrak d_\kappa ^{F_1}(\in ^*)}<{\mathfrak d_\kappa ^{F_0}(\in ^*)}=\kappa ^{++}$
, iteration proves to be an obstacle when we wish to force localisation cardinals to be larger than
![]() $\kappa ^{++}$
. In particular, our goal to simultaneously assign multiple localisation cardinals to different cardinalities requires a product.
$\kappa ^{++}$
. In particular, our goal to simultaneously assign multiple localisation cardinals to different cardinalities requires a product.
Definition 2.1. Let A be a set of ordinals and
![]() $\mathbb P_\xi $
a forcing notion for each
$\mathbb P_\xi $
a forcing notion for each
![]() $\xi \in A$
. Let
$\xi \in A$
. Let
![]() $\mathcal C$
be the set of functions p with
$\mathcal C$
be the set of functions p with
![]() $\mathrm {dom}(p)=A$
such that
$\mathrm {dom}(p)=A$
such that
![]() $p(\xi )\in \mathbb P_\xi $
for each
$p(\xi )\in \mathbb P_\xi $
for each
![]() $\xi \in A$
. For any
$\xi \in A$
. For any
![]() $p\in \mathcal C$
, the support of p is defined as
$p\in \mathcal C$
, the support of p is defined as
We define the
![]() ${<}\lambda $
-support product as follows:
${<}\lambda $
-support product as follows:
This is a forcing poset under the ordering
![]() $q\leq _{\overline {\mathbb P}} p$
iff
$q\leq _{\overline {\mathbb P}} p$
iff
![]() $q\leq _{\mathbb P_\xi }p$
for all
$q\leq _{\mathbb P_\xi }p$
for all
![]() $\xi \in A$
. Generally we will say “
$\xi \in A$
. Generally we will say “
![]() ${\leq }\kappa $
-support” instead of “
${\leq }\kappa $
-support” instead of “
![]() ${<}\kappa ^+$
-support”.
${<}\kappa ^+$
-support”.
Let us fix a set of ordinals A, parameters
![]() $\left \langle h_\xi \mid \xi \in A\right \rangle $
for the forcings
$\left \langle h_\xi \mid \xi \in A\right \rangle $
for the forcings
![]() ${\mathbb S^{h_\xi }_\kappa }$
and the set
${\mathbb S^{h_\xi }_\kappa }$
and the set
![]() $\mathcal C$
of functions p such that
$\mathcal C$
of functions p such that
![]() $p(\xi )\in {\mathbb S^{h_\xi }_\kappa }$
for each
$p(\xi )\in {\mathbb S^{h_\xi }_\kappa }$
for each
![]() $\xi \in A$
. For the remainder of this section we will also fix the shorthand
$\xi \in A$
. For the remainder of this section we will also fix the shorthand
![]() $\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
. If
$\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
. If
![]() $p,q\in \overline {\mathbb S}$
, we will often write
$p,q\in \overline {\mathbb S}$
, we will often write
![]() $q\leq p$
instead of
$q\leq p$
instead of
![]() $q\leq _{\overline {\mathbb S}}p$
when the forcing
$q\leq _{\overline {\mathbb S}}p$
when the forcing
![]() $\overline {\mathbb S}$
is clear from context.
$\overline {\mathbb S}$
is clear from context.
If
![]() $\left \langle p_\alpha \mid \alpha \in \gamma \right \rangle $
is a sequence of conditions in
$\left \langle p_\alpha \mid \alpha \in \gamma \right \rangle $
is a sequence of conditions in
![]() $\overline {\mathbb S}$
such that
$\overline {\mathbb S}$
such that
![]() $p_{\alpha '}\leq _{\overline {\mathbb S}} p_\alpha $
for all
$p_{\alpha '}\leq _{\overline {\mathbb S}} p_\alpha $
for all
![]() $\alpha \leq \alpha '$
, define
$\alpha \leq \alpha '$
, define
Lemma 2.2.
![]() $\overline {\mathbb S}$
is
$\overline {\mathbb S}$
is
![]() ${<}\kappa $
-closed.
${<}\kappa $
-closed.
Proof If
![]() $\left \langle p_\alpha \mid \alpha \in \gamma \right \rangle $
is a descending sequence in
$\left \langle p_\alpha \mid \alpha \in \gamma \right \rangle $
is a descending sequence in
![]() $\overline {\mathbb S}$
and
$\overline {\mathbb S}$
and
![]() $\gamma \in \kappa $
, then
$\gamma \in \kappa $
, then
![]() $\textstyle \bigwedge \!_{\alpha \in \gamma }p_\alpha $
is a condition below each
$\textstyle \bigwedge \!_{\alpha \in \gamma }p_\alpha $
is a condition below each
![]() $p_\alpha $
, since each
$p_\alpha $
, since each
![]() ${\mathbb S^{h_\xi }_\kappa }$
is
${\mathbb S^{h_\xi }_\kappa }$
is
![]() ${<}\kappa $
-closed.
${<}\kappa $
-closed.
We will also need a generalisation of the fusion lemma to work on product forcings. The generalisation of fusion described here is analogous to what is described in [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] or [Reference Kanamori6].
Definition 2.3. Given
![]() $p,q\in \overline {\mathbb S}$
,
$p,q\in \overline {\mathbb S}$
,
![]() $\alpha \in \kappa $
, and
$\alpha \in \kappa $
, and
![]() $Z\subseteq A$
with
$Z\subseteq A$
with
![]() $|Z|<\kappa $
, let
$|Z|<\kappa $
, let
![]() $q\leq _{Z,\alpha }p$
iff
$q\leq _{Z,\alpha }p$
iff
![]() $q\leq p$
and for each
$q\leq p$
and for each
![]() $\xi \in Z$
we have
$\xi \in Z$
we have
![]() $q(\xi )\leq _\alpha p(\xi )$
.
$q(\xi )\leq _\alpha p(\xi )$
.
A generalised fusion sequence is a sequence
![]() $\left \langle (p_\alpha ,Z_\alpha )\mid \alpha \in \kappa \right \rangle $
such that:
$\left \langle (p_\alpha ,Z_\alpha )\mid \alpha \in \kappa \right \rangle $
such that:
-
(1)
 $p_\alpha \in \overline {\mathbb S}$
and
$p_\alpha \in \overline {\mathbb S}$
and
 $Z_\alpha \in [A]^{<\kappa }$
for each
$Z_\alpha \in [A]^{<\kappa }$
for each
 $\alpha \in \kappa $
.
$\alpha \in \kappa $
. -
(2)
 $p_{\beta }\leq _{Z_\alpha ,\alpha }p_\alpha $
and
$p_{\beta }\leq _{Z_\alpha ,\alpha }p_\alpha $
and
 $Z_\alpha \subseteq Z_{\beta }$
for all
$Z_\alpha \subseteq Z_{\beta }$
for all
 $\alpha \leq \beta \in \kappa $
.
$\alpha \leq \beta \in \kappa $
. -
(3) For limit
 $\delta $
we have
$\delta $
we have
 $Z_\delta =\textstyle \bigcup _{\alpha \in \delta } Z_\alpha $
.
$Z_\delta =\textstyle \bigcup _{\alpha \in \delta } Z_\alpha $
. -
(4)
 $\textstyle \bigcup _{\alpha \in \kappa } Z_\alpha =\textstyle \bigcup _{\alpha \in \kappa }\mathrm {supp}(p_\alpha )$
.
$\textstyle \bigcup _{\alpha \in \kappa } Z_\alpha =\textstyle \bigcup _{\alpha \in \kappa }\mathrm {supp}(p_\alpha )$
.
Lemma 2.4. If
![]() $\left \langle (p_\alpha ,Z_\alpha )\mid \alpha \in \kappa \right \rangle $
is a generalised fusion sequence, then
$\left \langle (p_\alpha ,Z_\alpha )\mid \alpha \in \kappa \right \rangle $
is a generalised fusion sequence, then
![]() $\textstyle \bigwedge \!_{\alpha \in \kappa }p_\alpha \in \overline {\mathbb S}$
.
$\textstyle \bigwedge \!_{\alpha \in \kappa }p_\alpha \in \overline {\mathbb S}$
.
Proof Suppose that
![]() $\left \langle (p_\alpha ,Z_\alpha )\mid \alpha \in \kappa \right \rangle $
is a generalised fusion sequence, and let
$\left \langle (p_\alpha ,Z_\alpha )\mid \alpha \in \kappa \right \rangle $
is a generalised fusion sequence, and let
![]() $p=\textstyle \bigwedge \!_{\alpha \in \kappa }p_\alpha $
. Point (4) of Definition 2.3 implies that every
$p=\textstyle \bigwedge \!_{\alpha \in \kappa }p_\alpha $
. Point (4) of Definition 2.3 implies that every
![]() $\xi \in \mathrm {supp}(p)$
is an element of
$\xi \in \mathrm {supp}(p)$
is an element of
![]() $Z_{\eta _\xi }$
for some
$Z_{\eta _\xi }$
for some
![]() $\eta _\xi \in \kappa $
. This means that if
$\eta _\xi \in \kappa $
. This means that if
![]() $\beta \geq \alpha \geq \eta _\xi $
, then
$\beta \geq \alpha \geq \eta _\xi $
, then
![]() $p_\beta (\xi )\leq _\alpha p_\alpha (\xi )$
, and thus
$p_\beta (\xi )\leq _\alpha p_\alpha (\xi )$
, and thus
![]() $\left \langle p_\alpha (\xi )\mid \alpha>\eta _\xi \right \rangle $
is a fusion sequence in
$\left \langle p_\alpha (\xi )\mid \alpha>\eta _\xi \right \rangle $
is a fusion sequence in
![]() ${\mathbb S^{h_\xi }_\kappa }$
. Since
${\mathbb S^{h_\xi }_\kappa }$
. Since
![]() ${\mathbb S^{h_\xi }_\kappa }$
is closed under fusion sequences (Lemma 1.7), we can conclude that
${\mathbb S^{h_\xi }_\kappa }$
is closed under fusion sequences (Lemma 1.7), we can conclude that
Since
![]() $\mathrm {supp}(p)=\textstyle \bigcup _{\alpha \in \kappa } Z_\alpha $
, we see that
$\mathrm {supp}(p)=\textstyle \bigcup _{\alpha \in \kappa } Z_\alpha $
, we see that
![]() $|\mathrm {supp}(p)|\leq \kappa $
, thus we can conclude that
$|\mathrm {supp}(p)|\leq \kappa $
, thus we can conclude that
![]() $p\in \overline {\mathbb S}$
.
$p\in \overline {\mathbb S}$
.
By Lemma 2.2,
![]() $\overline {\mathbb S}$
preserves all cardinalities up to and including
$\overline {\mathbb S}$
preserves all cardinalities up to and including
![]() $\kappa $
. Suppose that each
$\kappa $
. Suppose that each
![]() ${\mathbb S^{h_\xi }_\kappa }$
has the F-Sacks property for some suitably large F. We will show in the next lemma that this implies that
${\mathbb S^{h_\xi }_\kappa }$
has the F-Sacks property for some suitably large F. We will show in the next lemma that this implies that
![]() $\overline {\mathbb S}$
has the F-Sacks property and therefore preserves
$\overline {\mathbb S}$
has the F-Sacks property and therefore preserves
![]() $\kappa ^+$
. Finally, if we assume that
$\kappa ^+$
. Finally, if we assume that
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, then a standard
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, then a standard
![]() $\Delta $
-system argument (see, e.g., [Reference Jech5, Lemma 15.4]) shows that
$\Delta $
-system argument (see, e.g., [Reference Jech5, Lemma 15.4]) shows that
![]() $\overline {\mathbb S}$
is
$\overline {\mathbb S}$
is
![]() ${<}\kappa ^{++}$
-c.c. as well. Thus,
${<}\kappa ^{++}$
-c.c. as well. Thus,
![]() $\overline {\mathbb S}$
preserves all cardinals and cofinalities assuming that there exists some fixed
$\overline {\mathbb S}$
preserves all cardinals and cofinalities assuming that there exists some fixed
![]() $F\in {}^{\kappa }\kappa $
such that each
$F\in {}^{\kappa }\kappa $
such that each
![]() ${\mathbb S^{h_\xi }_\kappa }$
has the F-Sacks property.
${\mathbb S^{h_\xi }_\kappa }$
has the F-Sacks property.
Before we prove the lemma, let us introduce some notation related to the product of forcings. Suppose
![]() $\overline {\mathbb P}=\prod _{\xi \in A}\mathbb P_\xi $
is a product with
$\overline {\mathbb P}=\prod _{\xi \in A}\mathbb P_\xi $
is a product with
![]() ${\leq }\kappa $
-support,
${\leq }\kappa $
-support,
![]() $X\subseteq \overline {\mathbb P}$
and
$X\subseteq \overline {\mathbb P}$
and
![]() $B\subseteq A$
, we define
$B\subseteq A$
, we define
Let
![]() $B^c=A\setminus B$
and
$B^c=A\setminus B$
and
![]() $G\subseteq \overline {\mathbb P}$
be
$G\subseteq \overline {\mathbb P}$
be
![]() $\overline {\mathbb P}$
-generic over
$\overline {\mathbb P}$
-generic over
![]() $\mathbf V$
, then clearly
$\mathbf V$
, then clearly
![]() $\overline {\mathbb P}$
and
$\overline {\mathbb P}$
and
![]() $(\overline {\mathbb P}\restriction B)\times (\overline {\mathbb P}\restriction B^c)$
are forcing equivalent,
$(\overline {\mathbb P}\restriction B)\times (\overline {\mathbb P}\restriction B^c)$
are forcing equivalent,
![]() $(G\restriction B)\times (G\restriction B^c)$
is
$(G\restriction B)\times (G\restriction B^c)$
is
![]() $(\overline {\mathbb P}\restriction B)\times (\overline {\mathbb P}\restriction B^c)$
-generic and
$(\overline {\mathbb P}\restriction B)\times (\overline {\mathbb P}\restriction B^c)$
-generic and
Lemma 2.5. Let
![]() $B\subseteq A$
be sets of ordinals and
$B\subseteq A$
be sets of ordinals and
![]() $B^c=A\setminus B$
, and consider a sequence of functions
$B^c=A\setminus B$
, and consider a sequence of functions
![]() $\left \langle h_\xi \mid \xi \in A\right \rangle $
. We define the
$\left \langle h_\xi \mid \xi \in A\right \rangle $
. We define the
![]() ${\leq }\kappa $
-support product
${\leq }\kappa $
-support product
![]() $\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
, we assume G is an
$\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
, we assume G is an
![]() $\overline {\mathbb S}$
-generic filter. If there exists
$\overline {\mathbb S}$
-generic filter. If there exists
![]() $F\in {}^{\kappa }\kappa $
such that
$F\in {}^{\kappa }\kappa $
such that
![]() $F(\alpha )^{|\alpha |}=F(\alpha )$
for all
$F(\alpha )^{|\alpha |}=F(\alpha )$
for all
![]() $\alpha \in \kappa $
and
$\alpha \in \kappa $
and
![]() $h_\xi \leq ^*F$
for all
$h_\xi \leq ^*F$
for all
![]() $\xi \in B^c$
, then for each
$\xi \in B^c$
, then for each
![]() $f\in ({}^{\kappa }\kappa )^{\mathbf V[G]}$
there is
$f\in ({}^{\kappa }\kappa )^{\mathbf V[G]}$
there is
![]() $\varphi \in (\mathrm {Loc}_F)^{\mathbf V[G\restriction B]}$
such that
$\varphi \in (\mathrm {Loc}_F)^{\mathbf V[G\restriction B]}$
such that
![]() $f\in ^*\varphi $
.
$f\in ^*\varphi $
.
Proof Note that Fact 1.12 implies that we can assume without loss of generality that
![]() $h_\xi \leq F$
for each
$h_\xi \leq F$
for each
![]() $\xi \in A$
. Let
$\xi \in A$
. Let
![]() $p\in \overline {\mathbb S}$
and
$p\in \overline {\mathbb S}$
and
![]() $\dot f$
be a name such that
$\dot f$
be a name such that
![]() $p\Vdash _{\overline {\mathbb S}}\text {"}\,\dot f:\check \kappa \to \check \kappa \,\text {"}$
, then we will construct a name
$p\Vdash _{\overline {\mathbb S}}\text {"}\,\dot f:\check \kappa \to \check \kappa \,\text {"}$
, then we will construct a name
![]() $\dot \varphi $
and a condition
$\dot \varphi $
and a condition
![]() $p'\leq p$
such that
$p'\leq p$
such that
![]() $p'\Vdash \text {"}\,\dot \varphi \in (\mathrm {Loc}_{\check F})^{\mathbf V[\dot G\restriction \check B]}\,\text {"}$
.
$p'\Vdash \text {"}\,\dot \varphi \in (\mathrm {Loc}_{\check F})^{\mathbf V[\dot G\restriction \check B]}\,\text {"}$
.
The proof is essentially the same as the proof of Theorem 1.8, except that we work with generalised fusion sequences and have to construct a name
![]() $\dot \varphi $
for the appropriate F-slalom in
$\dot \varphi $
for the appropriate F-slalom in
![]() $\mathbf V[G\restriction B]$
, since such a slalom is not generally present in the ground model. That is, we will construct a sequence
$\mathbf V[G\restriction B]$
, since such a slalom is not generally present in the ground model. That is, we will construct a sequence
![]() $\left \langle (p_\xi ,Z_\xi )\mid \xi \in \kappa \right \rangle $
with each
$\left \langle (p_\xi ,Z_\xi )\mid \xi \in \kappa \right \rangle $
with each
![]() $p_\xi \in \overline {\mathbb S}$
that is a generalised fusion sequence in
$p_\xi \in \overline {\mathbb S}$
that is a generalised fusion sequence in
![]() $\overline {\mathbb S}$
and names
$\overline {\mathbb S}$
and names
![]() $\dot D_\xi $
for sets of ordinals
$\dot D_\xi $
for sets of ordinals
![]() $D_\xi \in \mathbf V[G\restriction B]$
with
$D_\xi \in \mathbf V[G\restriction B]$
with
![]() $|D_\xi |\leq F(\xi )$
, such that
$|D_\xi |\leq F(\xi )$
, such that
![]() $p_{\xi +1}\Vdash \text {"}\,\dot f(\check \xi )\in \dot D_\xi \,\text {"}$
.
$p_{\xi +1}\Vdash \text {"}\,\dot f(\check \xi )\in \dot D_\xi \,\text {"}$
.
For each
![]() $\xi \in \kappa $
and
$\xi \in \kappa $
and
![]() $\beta \in Z_\xi $
we will make sure that
$\beta \in Z_\xi $
we will make sure that
![]() $p_\xi (\beta )\in ({\mathbb S^{h_\beta }_\kappa })^*$
is sharp. To start, we let
$p_\xi (\beta )\in ({\mathbb S^{h_\beta }_\kappa })^*$
is sharp. To start, we let
![]() $p_0= p$
and we let
$p_0= p$
and we let
![]() $Z_0=\varnothing $
. At limit stages
$Z_0=\varnothing $
. At limit stages
![]() $\delta $
we can define
$\delta $
we can define
![]() $p_\delta '=\textstyle \bigwedge \!_{\xi \in \delta }p_\xi $
and let
$p_\delta '=\textstyle \bigwedge \!_{\xi \in \delta }p_\xi $
and let
![]() $p_\delta \leq p_\delta '$
be defined elementwise such that
$p_\delta \leq p_\delta '$
be defined elementwise such that
![]() $p_\delta (\beta )=(p_\delta '(\beta ))^*$
is sharp for each
$p_\delta (\beta )=(p_\delta '(\beta ))^*$
is sharp for each
![]() $\beta \in Z_\delta $
.
$\beta \in Z_\delta $
.
Suppose we have defined
![]() $p_\xi \in \overline {\mathbb S}$
and
$p_\xi \in \overline {\mathbb S}$
and
![]() $Z_\xi $
and that
$Z_\xi $
and that
![]() $|Z_\xi |\leq |\xi |$
. As in the proof of Theorem 1.8, we will consider the successor nodes of the
$|Z_\xi |\leq |\xi |$
. As in the proof of Theorem 1.8, we will consider the successor nodes of the
![]() $\xi $
-th splitting level, find subtrees that decide the value of
$\xi $
-th splitting level, find subtrees that decide the value of
![]() $\dot f(\check \xi )$
, and glue the subtrees together. However, in this situation we have to deal with multiple trees at once, namely with each
$\dot f(\check \xi )$
, and glue the subtrees together. However, in this situation we have to deal with multiple trees at once, namely with each
![]() $p_\xi (\beta )$
such that
$p_\xi (\beta )$
such that
![]() $\beta \in Z_\xi $
. For each
$\beta \in Z_\xi $
. For each
![]() $\beta \in Z_\xi $
we define the set of successor nodes of the
$\beta \in Z_\xi $
we define the set of successor nodes of the
![]() $\xi $
-th splitting level of
$\xi $
-th splitting level of
![]() $p_\xi (\beta )$
:
$p_\xi (\beta )$
:
To deal with
![]() $p_\xi (\beta )$
for all
$p_\xi (\beta )$
for all
![]() $\beta \in Z_\xi $
simultaneously, we have to consider combinations of elements of
$\beta \in Z_\xi $
simultaneously, we have to consider combinations of elements of
![]() $V^\beta _\xi $
for
$V^\beta _\xi $
for
![]() $\beta \in Z_\xi $
, and for each combination we will define a condition that decides
$\beta \in Z_\xi $
, and for each combination we will define a condition that decides
![]() $\dot f(\check \xi )$
. These combinations are given by functions
$\dot f(\check \xi )$
. These combinations are given by functions
![]() $g:Z_\xi \to \textstyle \bigcup _{\beta \in Z_\xi }V^\beta _\xi $
with the property that
$g:Z_\xi \to \textstyle \bigcup _{\beta \in Z_\xi }V^\beta _\xi $
with the property that
![]() $g(\beta )\in V^\beta _\xi $
. We will refer to such g as choice functions, since g chooses an element of
$g(\beta )\in V^\beta _\xi $
. We will refer to such g as choice functions, since g chooses an element of
![]() $V^\beta _\xi $
for each
$V^\beta _\xi $
for each
![]() $\beta \in Z_\xi $
.
$\beta \in Z_\xi $
.
Let
![]() $\mathcal V_\xi $
be the set of choice functions on
$\mathcal V_\xi $
be the set of choice functions on
![]() $\{V_\xi ^\beta \mid \beta \in Z_\xi \}$
and
$\{V_\xi ^\beta \mid \beta \in Z_\xi \}$
and
![]() $\mathcal V_\xi '$
the set of choice functions on
$\mathcal V_\xi '$
the set of choice functions on
![]() $\{V_\xi ^\beta \mid \beta \in Z_\xi \setminus B\}$
, that is,
$\{V_\xi ^\beta \mid \beta \in Z_\xi \setminus B\}$
, that is,
![]() $\mathcal V_\xi '$
is the set of
$\mathcal V_\xi '$
is the set of
![]() $g\restriction (Z_\xi \setminus B)$
with
$g\restriction (Z_\xi \setminus B)$
with
![]() $g\in \mathcal V_\xi $
.
$g\in \mathcal V_\xi $
.
By induction hypothesis
![]() $p_\xi (\beta )\in ({\mathbb S^{h_\beta }_\kappa })^*$
for each
$p_\xi (\beta )\in ({\mathbb S^{h_\beta }_\kappa })^*$
for each
![]() $\beta \in Z_\xi \setminus B$
, hence we know that
$\beta \in Z_\xi \setminus B$
, hence we know that
and thus
![]() $|V_\xi ^\beta |\leq F(\xi )$
for all
$|V_\xi ^\beta |\leq F(\xi )$
for all
![]() $\beta \in Z_\xi \setminus B$
. Since we assume that
$\beta \in Z_\xi \setminus B$
. Since we assume that
![]() $|Z_\xi |\leq |\xi |$
, we therefore have
$|Z_\xi |\leq |\xi |$
, we therefore have
![]() $|\mathcal V_\xi '|\leq F(\xi )^{|\xi |}=F(\xi )$
(assuming without loss of generality that
$|\mathcal V_\xi '|\leq F(\xi )^{|\xi |}=F(\xi )$
(assuming without loss of generality that
![]() $F(\xi )$
is infinite). Hence, if we restrict our attention to
$F(\xi )$
is infinite). Hence, if we restrict our attention to
![]() $Z_\xi \setminus B$
, we have a small number of choice functions. Consequently, we can describe a name
$Z_\xi \setminus B$
, we have a small number of choice functions. Consequently, we can describe a name
![]() $\dot D_\xi $
depending only on the support in B, i.e.,
$\dot D_\xi $
depending only on the support in B, i.e.,
![]() $\dot D_\xi $
names a set in
$\dot D_\xi $
names a set in
![]() $\mathbf V[G\restriction B]$
, such that
$\mathbf V[G\restriction B]$
, such that
![]() $\dot D_\xi $
is bounded in cardinality by
$\dot D_\xi $
is bounded in cardinality by
![]() $F(\xi )$
.
$F(\xi )$
.
For any choice function
![]() $g\in \mathcal V_\xi $
, let
$g\in \mathcal V_\xi $
, let
![]() $(p_\xi )_g$
be the condition defined by
$(p_\xi )_g$
be the condition defined by
 $$ \begin{align*} (p_\xi)_g(\beta)=\begin{cases}p_\xi(\beta), &\text{if }\beta\notin Z_\xi,\\ ({p_\xi(\beta)})_{g(\beta)}, &\text{if }\beta\in Z_\xi. \end{cases} \end{align*} $$
$$ \begin{align*} (p_\xi)_g(\beta)=\begin{cases}p_\xi(\beta), &\text{if }\beta\notin Z_\xi,\\ ({p_\xi(\beta)})_{g(\beta)}, &\text{if }\beta\in Z_\xi. \end{cases} \end{align*} $$
Here
![]() $({p_\xi (\beta )})_{g(\beta )}$
is the subtree of
$({p_\xi (\beta )})_{g(\beta )}$
is the subtree of
![]() $p_\xi (\beta )$
generated by the initial segment
$p_\xi (\beta )$
generated by the initial segment
![]() $g(\beta )\in V^\beta _\xi $
.
$g(\beta )\in V^\beta _\xi $
.
Let
![]() $\zeta =|\mathcal V_\xi |$
then
$\zeta =|\mathcal V_\xi |$
then
![]() $\zeta <\kappa $
by inaccessibility of
$\zeta <\kappa $
by inaccessibility of
![]() $\kappa $
. Fix some enumeration
$\kappa $
. Fix some enumeration
![]() $\left \langle g_\eta \mid \eta \in \zeta \right \rangle $
of
$\left \langle g_\eta \mid \eta \in \zeta \right \rangle $
of
![]() $\mathcal V_\xi $
, which we will use to recursively define a decreasing sequence of conditions
$\mathcal V_\xi $
, which we will use to recursively define a decreasing sequence of conditions
![]() $r_\eta $
with
$r_\eta $
with
![]() $r_\eta \leq _{Z_\xi ,\xi }p_\xi $
for each
$r_\eta \leq _{Z_\xi ,\xi }p_\xi $
for each
![]() $\eta \in \zeta $
. Essentially, our recursive construction will result in
$\eta \in \zeta $
. Essentially, our recursive construction will result in
![]() $r_{\eta +1}$
being like
$r_{\eta +1}$
being like
![]() $r_\eta $
, except that
$r_\eta $
, except that
![]() $(r_\eta )_{g_\eta }$
is replaced by a stronger condition that decides
$(r_\eta )_{g_\eta }$
is replaced by a stronger condition that decides
![]() $\dot f(\check \xi )$
. At the end of the recursion, we will be left with a condition
$\dot f(\check \xi )$
. At the end of the recursion, we will be left with a condition
![]() $r_\zeta $
such that
$r_\zeta $
such that
![]() $(r_\zeta )_{g}$
decides
$(r_\zeta )_{g}$
decides
![]() $\dot f(\check \xi )$
for every
$\dot f(\check \xi )$
for every
![]() $g\in \mathcal V_\xi $
. We then gather the possible values of
$g\in \mathcal V_\xi $
. We then gather the possible values of
![]() $\dot f(\check \xi )$
to construct the name
$\dot f(\check \xi )$
to construct the name
![]() $\dot D_\xi $
.
$\dot D_\xi $
.
Let
![]() $r_0=p_\xi $
. For limit
$r_0=p_\xi $
. For limit
![]() $\delta \in \zeta $
let
$\delta \in \zeta $
let
![]() $r_\delta =\textstyle \bigwedge \!_{\eta \in \delta }r_\eta $
, which is a condition by
$r_\delta =\textstyle \bigwedge \!_{\eta \in \delta }r_\eta $
, which is a condition by
![]() ${<}\kappa $
-closure (Lemma 2.2). Assuming that
${<}\kappa $
-closure (Lemma 2.2). Assuming that
![]() $r_\eta \leq _{Z_\xi ,\xi }p_\xi $
for each
$r_\eta \leq _{Z_\xi ,\xi }p_\xi $
for each
![]() $\eta \in \delta $
, it is easy to see that
$\eta \in \delta $
, it is easy to see that
![]() $r_\delta \leq _{Z_\xi ,\xi }p_\xi $
as well.
$r_\delta \leq _{Z_\xi ,\xi }p_\xi $
as well.
Suppose
![]() $r_\eta $
is defined and
$r_\eta $
is defined and
![]() $r_\eta \leq _{Z_\xi ,\xi } p_\xi $
, then in particular
$r_\eta \leq _{Z_\xi ,\xi } p_\xi $
, then in particular
![]() $r_\eta (\beta )\leq _\xi p_\xi (\beta )$
for all
$r_\eta (\beta )\leq _\xi p_\xi (\beta )$
for all
![]() $\beta \in Z_\xi $
, and thus
$\beta \in Z_\xi $
, and thus
![]() $\mathrm {Split}_\xi (r_\eta (\beta ))=\mathrm {Split}_\xi (p_\xi (\beta ))$
for all
$\mathrm {Split}_\xi (r_\eta (\beta ))=\mathrm {Split}_\xi (p_\xi (\beta ))$
for all
![]() $\beta \in Z_\xi $
. Therefore by definition of the ordering on
$\beta \in Z_\xi $
. Therefore by definition of the ordering on
![]() ${\mathbb S^{h_\beta }_\kappa }$
and the fact that
${\mathbb S^{h_\beta }_\kappa }$
and the fact that
![]() $p_\xi (\beta )$
is sharp, we see that
$p_\xi (\beta )$
is sharp, we see that
![]() $V_\xi ^\beta $
is exactly the set of successors of nodes at the
$V_\xi ^\beta $
is exactly the set of successors of nodes at the
![]() $\xi $
-th splitting level of
$\xi $
-th splitting level of
![]() $r_\eta (\beta )$
. Take the
$r_\eta (\beta )$
. Take the
![]() $\eta $
-th choice function
$\eta $
-th choice function
![]() $g_\eta \in \mathcal V_\xi $
, and let
$g_\eta \in \mathcal V_\xi $
, and let
![]() $r^{\prime }_{\eta }\leq (r_\eta )_{g_\eta }$
be such that
$r^{\prime }_{\eta }\leq (r_\eta )_{g_\eta }$
be such that
![]() $r^{\prime }_{\eta }\Vdash \text {"}\,\dot f(\check \xi )=\check \beta ^\eta _\xi \,\text {"}$
for some ordinal
$r^{\prime }_{\eta }\Vdash \text {"}\,\dot f(\check \xi )=\check \beta ^\eta _\xi \,\text {"}$
for some ordinal
![]() $\beta ^\eta _\xi $
. We define
$\beta ^\eta _\xi $
. We define
![]() $r_{\eta +1}$
elementwise.
$r_{\eta +1}$
elementwise.
If
![]() $\beta \notin Z_\xi $
, then we simply take
$\beta \notin Z_\xi $
, then we simply take
![]() $r_{\eta +1}(\beta )=r_{\eta }'(\beta )$
.
$r_{\eta +1}(\beta )=r_{\eta }'(\beta )$
.
If
![]() $\beta \in Z_\xi $
, fix some
$\beta \in Z_\xi $
, fix some
![]() $w\in \mathrm {suc}(u,r^{\prime }_{\eta }(\beta ))$
for some
$w\in \mathrm {suc}(u,r^{\prime }_{\eta }(\beta ))$
for some
![]() $u\in \mathrm {Split}_\xi (r^{\prime }_{\eta }(\beta ))$
and consider the subtree
$u\in \mathrm {Split}_\xi (r^{\prime }_{\eta }(\beta ))$
and consider the subtree
![]() $(r^{\prime }_{\eta }(\beta ))_w$
generated by the initial segment w. Now we are ready to define
$(r^{\prime }_{\eta }(\beta ))_w$
generated by the initial segment w. Now we are ready to define
![]() $r_{\eta +1}(\beta )$
as
$r_{\eta +1}(\beta )$
as
In words,
![]() $r_{\eta +1}(\beta )$
is the result of replacing the extensions of
$r_{\eta +1}(\beta )$
is the result of replacing the extensions of
![]() $g_\eta (\beta )\in r_\eta (\beta )$
by
$g_\eta (\beta )\in r_\eta (\beta )$
by
![]() $(r^{\prime }_\eta (\beta ))_w$
that decides
$(r^{\prime }_\eta (\beta ))_w$
that decides
![]() $\dot f(\check \xi )$
, where we use the subtree
$\dot f(\check \xi )$
, where we use the subtree
![]() $(r^{\prime }_\eta (\beta ))_w$
instead of
$(r^{\prime }_\eta (\beta ))_w$
instead of
![]() $r_\eta '(\beta )$
to make sure that
$r_\eta '(\beta )$
to make sure that
![]() $r_{\eta +1}(\beta )$
has enough successors at each splitting level to be in
$r_{\eta +1}(\beta )$
has enough successors at each splitting level to be in
![]() ${\mathbb S^{h_\beta }_\kappa }$
(compare this to the role of
${\mathbb S^{h_\beta }_\kappa }$
(compare this to the role of
![]() $(T^v)_w$
instead of
$(T^v)_w$
instead of
![]() $T^v$
in the proof of Theorem 1.8).
$T^v$
in the proof of Theorem 1.8).
To finish the construction of the next condition in the fusion sequence, we use
![]() ${<}\kappa $
-closure to define
${<}\kappa $
-closure to define
![]() $p_{\xi +1}'=\textstyle \bigwedge \!_{\eta \in \zeta }\ r_\eta $
and let
$p_{\xi +1}'=\textstyle \bigwedge \!_{\eta \in \zeta }\ r_\eta $
and let
![]() $p_{\xi +1}=(p^{\prime }_{\xi +1})^*$
be sharp. To see that
$p_{\xi +1}=(p^{\prime }_{\xi +1})^*$
be sharp. To see that
![]() $p_{\xi +1}\leq _{Z_\xi ,\xi }p_\xi $
, note that for every
$p_{\xi +1}\leq _{Z_\xi ,\xi }p_\xi $
, note that for every
![]() $\beta \in Z_\xi $
and
$\beta \in Z_\xi $
and
![]() $v\in V^\beta _\xi $
we have
$v\in V^\beta _\xi $
we have
![]() $v\in r_\eta (\beta )$
for all
$v\in r_\eta (\beta )$
for all
![]() $\eta \in \zeta $
, hence
$\eta \in \zeta $
, hence
![]() $v\in p_{\xi +1}(\beta )$
. This implies by definition of
$v\in p_{\xi +1}(\beta )$
. This implies by definition of
![]() $V^\beta _\xi $
that
$V^\beta _\xi $
that
![]() $p_{\xi +1}(\beta )\leq _\xi p_\xi (\beta )$
for all
$p_{\xi +1}(\beta )\leq _\xi p_\xi (\beta )$
for all
![]() $\beta \in Z_\xi $
. Finally, we can let
$\beta \in Z_\xi $
. Finally, we can let
![]() $Z_{\xi +1}=Z_\xi \cup {\left \{{\delta }\right \}}$
for some ordinal
$Z_{\xi +1}=Z_\xi \cup {\left \{{\delta }\right \}}$
for some ordinal
![]() $\delta $
, using bookkeeping to make sure that
$\delta $
, using bookkeeping to make sure that
![]() $\textstyle \bigcup _{\xi \in \kappa }Z_\xi =\textstyle \bigcup _{\xi \in \kappa }\mathrm {supp}(p_\xi )$
.
$\textstyle \bigcup _{\xi \in \kappa }Z_\xi =\textstyle \bigcup _{\xi \in \kappa }\mathrm {supp}(p_\xi )$
.
Note that the set of conditions
![]() $r\leq p_{\xi +1}$
with
$r\leq p_{\xi +1}$
with
![]() $|r(\beta )\cap V_\xi ^\beta |=1$
for all
$|r(\beta )\cap V_\xi ^\beta |=1$
for all
![]() $\beta \in Z_\xi $
, is dense below
$\beta \in Z_\xi $
, is dense below
![]() $p_{\xi +1}$
. For any such r, let g map
$p_{\xi +1}$
. For any such r, let g map
![]() $\beta $
to the unique element of
$\beta $
to the unique element of
![]() $r(\beta )\cap V_\xi ^\beta $
for each
$r(\beta )\cap V_\xi ^\beta $
for each
![]() $\beta \in Z_\xi $
, then
$\beta \in Z_\xi $
, then
![]() $g\in \mathcal V_\xi $
is a choice function, so we see that there exists
$g\in \mathcal V_\xi $
is a choice function, so we see that there exists
![]() $\eta \in \zeta $
such that
$\eta \in \zeta $
such that
![]() $g=g_\eta $
. We will show that
$g=g_\eta $
. We will show that
![]() $r\leq r_\eta '$
, which implies that
$r\leq r_\eta '$
, which implies that
![]() $r\Vdash \text {"}\,\dot f(\check \xi )=\check \beta _\xi ^\eta \,\text {"}$
.
$r\Vdash \text {"}\,\dot f(\check \xi )=\check \beta _\xi ^\eta \,\text {"}$
.
For any
![]() $\beta $
we have
$\beta $
we have
![]() $r(\beta )\leq p_{\xi +1}(\beta )\leq r_{\eta +1}(\beta )$
. If
$r(\beta )\leq p_{\xi +1}(\beta )\leq r_{\eta +1}(\beta )$
. If
![]() $\beta \notin Z_\xi $
, then we simply have
$\beta \notin Z_\xi $
, then we simply have
![]() $r_{\eta +1}(\beta )=r_\eta '(\beta )$
, thus we are done. Otherwise
$r_{\eta +1}(\beta )=r_\eta '(\beta )$
, thus we are done. Otherwise
![]() $\beta \in Z_\xi $
, and we know that
$\beta \in Z_\xi $
, and we know that
![]() $g(\beta )$
is an initial segment of the stem of
$g(\beta )$
is an initial segment of the stem of
![]() $r(\beta )$
, hence
$r(\beta )$
, hence
where w is as in the definition of
![]() $r_{\eta +1}(\beta )$
above. Since
$r_{\eta +1}(\beta )$
above. Since
![]() $r(\beta )\leq r_{\eta +1}(\beta )$
, we also have
$r(\beta )\leq r_{\eta +1}(\beta )$
, we also have
and thus
![]() $r(\beta )\leq r^{\prime }_\eta (\beta )$
.
$r(\beta )\leq r^{\prime }_\eta (\beta )$
.
We are now ready to construct the names
![]() $\dot D_\xi $
such that
$\dot D_\xi $
such that
For any
![]() $g\in \mathcal V_\xi $
, we define
$g\in \mathcal V_\xi $
, we define
 $$ \begin{align*} g"&=g\restriction (Z_\xi\cap B),\\ E_g&={\left\{{\eta\in\zeta\mid \exists g'\in \mathcal V_\xi'(g'\cup g"=g_\eta)}\right\}},\\ D_\xi^g&={\left\{{\beta_\xi^\eta\mid \eta\in E_g}\right\}}. \end{align*} $$
$$ \begin{align*} g"&=g\restriction (Z_\xi\cap B),\\ E_g&={\left\{{\eta\in\zeta\mid \exists g'\in \mathcal V_\xi'(g'\cup g"=g_\eta)}\right\}},\\ D_\xi^g&={\left\{{\beta_\xi^\eta\mid \eta\in E_g}\right\}}. \end{align*} $$
Since
![]() $|\mathcal V_\xi '|\leq F(\xi )$
, we see that
$|\mathcal V_\xi '|\leq F(\xi )$
, we see that
![]() $|E_g|\leq F(\xi )$
, hence
$|E_g|\leq F(\xi )$
, hence
![]() $|D_\xi ^g|\leq F(\xi )$
. Clearly, if
$|D_\xi ^g|\leq F(\xi )$
. Clearly, if
![]() $g,\tilde g\in \mathcal V_\xi $
and
$g,\tilde g\in \mathcal V_\xi $
and
![]() $g\restriction (Z_\xi \cap B)=\tilde g\restriction (Z_\xi \cap B)$
, then
$g\restriction (Z_\xi \cap B)=\tilde g\restriction (Z_\xi \cap B)$
, then
![]() $D_\xi ^g=D_\xi ^{\tilde g}$
.
$D_\xi ^g=D_\xi ^{\tilde g}$
.
Let
![]() $\mathcal A_\xi $
be an antichain below
$\mathcal A_\xi $
be an antichain below
![]() $p_{\xi +1}$
such that
$p_{\xi +1}$
such that
![]() $r\in \mathcal A_\xi $
implies
$r\in \mathcal A_\xi $
implies
![]() $|r(\beta )\cap V_\xi ^\beta |=1$
for all
$|r(\beta )\cap V_\xi ^\beta |=1$
for all
![]() $\beta \in Z_\xi $
, and let
$\beta \in Z_\xi $
, and let
![]() $g_r\in \mathcal V_\xi $
be such that
$g_r\in \mathcal V_\xi $
be such that
![]() $g_r(\beta )$
is the single element of
$g_r(\beta )$
is the single element of
![]() $r(\beta )\cap V_\xi ^\beta $
for each
$r(\beta )\cap V_\xi ^\beta $
for each
![]() $\beta \in Z_\xi $
. We define
$\beta \in Z_\xi $
. We define
It is clear by the above that for each
![]() $r\in \mathcal A_\xi $
and
$r\in \mathcal A_\xi $
and
![]() $\eta $
such that
$\eta $
such that
![]() $g_r=g_\eta $
we have
$g_r=g_\eta $
we have
so by denseness
To see that
![]() $p_{\xi +1}\Vdash \text {"}\, \dot D_\xi \in \mathbf V[\dot G\restriction \check B]\,\text {"}$
, we argue within
$p_{\xi +1}\Vdash \text {"}\, \dot D_\xi \in \mathbf V[\dot G\restriction \check B]\,\text {"}$
, we argue within
![]() $\mathbf V[ G\restriction B]$
. For every
$\mathbf V[ G\restriction B]$
. For every
![]() $r,\tilde r\in \mathcal A_\xi $
such that both
$r,\tilde r\in \mathcal A_\xi $
such that both
![]() $r\restriction B$
and
$r\restriction B$
and
![]() $\tilde r\restriction B$
are elements of
$\tilde r\restriction B$
are elements of
![]() $G\restriction B$
we see that the corresponding
$G\restriction B$
we see that the corresponding
![]() $g_r$
and
$g_r$
and
![]() $g_{\tilde r}$
have the property that
$g_{\tilde r}$
have the property that
![]() $g_r\restriction (Z_\xi \cap B)=g_{\tilde r}\restriction (Z_\xi \cap B)$
, and therefore
$g_r\restriction (Z_\xi \cap B)=g_{\tilde r}\restriction (Z_\xi \cap B)$
, and therefore
![]() $D_\xi ^{g_r}=D_\xi ^{g_{\tilde r}}$
. Thus, we can fix any arbitrary such
$D_\xi ^{g_r}=D_\xi ^{g_{\tilde r}}$
. Thus, we can fix any arbitrary such
![]() $r\in \mathcal A_\xi $
for which
$r\in \mathcal A_\xi $
for which
![]() $r\restriction B\in G\restriction B$
holds, and see that
$r\restriction B\in G\restriction B$
holds, and see that
Let
![]() $p'=\textstyle \bigwedge \!_{\xi \in \kappa }p_\xi $
be the limit of the generalised fusion sequence, and let
$p'=\textstyle \bigwedge \!_{\xi \in \kappa }p_\xi $
be the limit of the generalised fusion sequence, and let
![]() $\dot \varphi $
be a name such that
$\dot \varphi $
be a name such that
![]() $p'\Vdash \text {"}\,\dot \varphi :\check \xi \mapsto \dot D_\xi \,\text {"}$
, then
$p'\Vdash \text {"}\,\dot \varphi :\check \xi \mapsto \dot D_\xi \,\text {"}$
, then
![]() $\dot \varphi $
names an F-slalom in
$\dot \varphi $
names an F-slalom in
![]() $\mathbf V[G\restriction B]$
and
$\mathbf V[G\restriction B]$
and
![]() $p'\Vdash \text {"}\,\dot f\in ^*\dot \varphi \,\text {"}$
.
$p'\Vdash \text {"}\,\dot f\in ^*\dot \varphi \,\text {"}$
.
If we let
![]() $B=\varnothing $
in the definition of the lemma, then we can simplify this lemma to the following corollary, providing us with the preservation of the Sacks property.
$B=\varnothing $
in the definition of the lemma, then we can simplify this lemma to the following corollary, providing us with the preservation of the Sacks property.
Corollary 2.6. If
![]() $\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
and each
$\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
and each
![]() $h_\xi \leq ^*h$
and
$h_\xi \leq ^*h$
and
![]() $F:\alpha \mapsto h(\alpha )^{|\alpha |}$
, then
$F:\alpha \mapsto h(\alpha )^{|\alpha |}$
, then
![]() $\overline {\mathbb S}$
has the F-Sacks property.
$\overline {\mathbb S}$
has the F-Sacks property.
Finally the following lemma is based on Theorem 1.11 and shows how we can use products of forcings
![]() ${\mathbb S^{h_\xi }_\kappa }$
to increase the cardinality of
${\mathbb S^{h_\xi }_\kappa }$
to increase the cardinality of
![]() ${\mathfrak d_\kappa ^{F}(\in ^*)}$
.
${\mathfrak d_\kappa ^{F}(\in ^*)}$
.
Lemma 2.7. Let
![]() $B\subseteq A$
be sets of ordinals, and consider a sequence of functions
$B\subseteq A$
be sets of ordinals, and consider a sequence of functions
![]() $\left \langle h_\xi \mid \xi \in A\right \rangle $
. We define the
$\left \langle h_\xi \mid \xi \in A\right \rangle $
. We define the
![]() ${\leq }\kappa $
-support product
${\leq }\kappa $
-support product
![]() $\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
and we assume G is an
$\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
and we assume G is an
![]() $\overline {\mathbb S}$
-generic filter. Let
$\overline {\mathbb S}$
-generic filter. Let
![]() $\left \langle S_\xi \mid \xi \in B\right \rangle $
be a sequence of stationary sets. If F is such that for each
$\left \langle S_\xi \mid \xi \in B\right \rangle $
be a sequence of stationary sets. If F is such that for each
![]() $\xi \in B$
we have
$\xi \in B$
we have
![]() $F(\alpha )<h_\xi (\alpha )$
for all
$F(\alpha )<h_\xi (\alpha )$
for all
![]() $\alpha \in S_\xi $
, then
$\alpha \in S_\xi $
, then
![]() $\mathbf V[G]\vDash \text {"}\,|B|\leq {\mathfrak d_\kappa ^{F}(\in ^*)}\,\text {"}$
.
$\mathbf V[G]\vDash \text {"}\,|B|\leq {\mathfrak d_\kappa ^{F}(\in ^*)}\,\text {"}$
.
Proof The lemma is trivial if
![]() $|B|\leq \kappa ^+$
, so we will assume that
$|B|\leq \kappa ^+$
, so we will assume that
![]() $|B|\geq \kappa ^{++}$
.
$|B|\geq \kappa ^{++}$
.
We work in
![]() $\mathbf V[G]$
. Let
$\mathbf V[G]$
. Let
![]() $\mu <|B|$
and let
$\mu <|B|$
and let
![]() ${\left \{{\varphi _\xi \mid \xi \in \mu }\right \}}$
be a family of F-slaloms, then we want to describe some
${\left \{{\varphi _\xi \mid \xi \in \mu }\right \}}$
be a family of F-slaloms, then we want to describe some
![]() $f\in {}^{\kappa }\kappa $
such that
$f\in {}^{\kappa }\kappa $
such that
![]() $f\notin ^*\varphi _\xi $
for each
$f\notin ^*\varphi _\xi $
for each
![]() $\xi \in \mu $
. Since
$\xi \in \mu $
. Since
![]() $\overline {\mathbb S}$
is
$\overline {\mathbb S}$
is
![]() ${<}\kappa ^{++}$
-c.c., we could find
${<}\kappa ^{++}$
-c.c., we could find
![]() $A_\xi \subseteq A$
with
$A_\xi \subseteq A$
with
![]() $|A_\xi |\leq \kappa ^+$
for each
$|A_\xi |\leq \kappa ^+$
for each
![]() $\xi \in \mu $
such that
$\xi \in \mu $
such that
![]() $\varphi _\xi \in \mathbf V[G\restriction A_\xi ]$
. Since
$\varphi _\xi \in \mathbf V[G\restriction A_\xi ]$
. Since
![]() $|B|>\mu \cdot \kappa ^+$
, we may fix some
$|B|>\mu \cdot \kappa ^+$
, we may fix some
![]() $\beta \in B\setminus \textstyle \bigcup _{\xi \in \mu }A_\xi $
for the remainder of this proof. Let
$\beta \in B\setminus \textstyle \bigcup _{\xi \in \mu }A_\xi $
for the remainder of this proof. Let
![]() $f=\textstyle \bigcap _{p\in G}p(\beta )$
, then
$f=\textstyle \bigcap _{p\in G}p(\beta )$
, then
![]() $f\in {}^{\kappa }\kappa $
is the generic
$f\in {}^{\kappa }\kappa $
is the generic
![]() $\kappa $
-real added by the
$\kappa $
-real added by the
![]() $\beta $
-th term of the product
$\beta $
-th term of the product
![]() $\overline {\mathbb S}$
.
$\overline {\mathbb S}$
.
Continuing the proof in the ground model, let
![]() $\dot f$
be an
$\dot f$
be an
![]() $\overline {\mathbb S}$
-name for f and
$\overline {\mathbb S}$
-name for f and
![]() $\dot \varphi _\xi $
be an
$\dot \varphi _\xi $
be an
![]() $\overline {\mathbb S}$
-name for
$\overline {\mathbb S}$
-name for
![]() $\varphi _\xi $
, let
$\varphi _\xi $
, let
![]() $p\in \overline {\mathbb S}$
and
$p\in \overline {\mathbb S}$
and
![]() $\alpha _0\in \kappa $
. We want to find some
$\alpha _0\in \kappa $
. We want to find some
![]() $\alpha \geq \alpha _0$
and
$\alpha \geq \alpha _0$
and
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $q\Vdash \text {"}\,\dot f(\check \alpha )\notin \dot \varphi _\xi (\check \alpha )\,\text {"}$
.
$q\Vdash \text {"}\,\dot f(\check \alpha )\notin \dot \varphi _\xi (\check \alpha )\,\text {"}$
.
Let
![]() $C={\left \{{\alpha \in \kappa \mid p(\beta )\cap {}^\alpha \kappa =\mathrm {Split}_\alpha (p(\beta ))}\right \}}$
, which is a club set by Lemma 1.10. Since
$C={\left \{{\alpha \in \kappa \mid p(\beta )\cap {}^\alpha \kappa =\mathrm {Split}_\alpha (p(\beta ))}\right \}}$
, which is a club set by Lemma 1.10. Since
![]() $S_\beta $
is stationary, there exists some
$S_\beta $
is stationary, there exists some
![]() $\alpha \geq \alpha _0$
such that
$\alpha \geq \alpha _0$
such that
![]() $\alpha \in C\cap S_\beta $
. Choose some
$\alpha \in C\cap S_\beta $
. Choose some
![]() $p_0\leq p$
such that
$p_0\leq p$
such that
![]() $p_0(\beta )=p(\beta )$
and such that there is a
$p_0(\beta )=p(\beta )$
and such that there is a
![]() $Y\in [\kappa ]^{\leq F(\alpha )}$
for which
$Y\in [\kappa ]^{\leq F(\alpha )}$
for which
![]() $p_0\Vdash \text {"}\,\dot \varphi _\xi (\check \alpha )=\check Y\,\text {"}$
. This is possible, since
$p_0\Vdash \text {"}\,\dot \varphi _\xi (\check \alpha )=\check Y\,\text {"}$
. This is possible, since
![]() $\varphi _\xi \in \mathbf V[G\restriction A_\xi ]$
and
$\varphi _\xi \in \mathbf V[G\restriction A_\xi ]$
and
![]() $\beta \notin A_\xi $
, therefore we could find
$\beta \notin A_\xi $
, therefore we could find
![]() $p_0'\in \overline {\mathbb S}\restriction A_\xi $
with
$p_0'\in \overline {\mathbb S}\restriction A_\xi $
with
![]() $p_0'\leq p\restriction A_\xi $
and Y with the aforementioned property, and then let
$p_0'\leq p\restriction A_\xi $
and Y with the aforementioned property, and then let
![]() $p_0(\eta )=p^{\prime }_0(\eta )$
if
$p_0(\eta )=p^{\prime }_0(\eta )$
if
![]() $\eta \in A_\xi $
and
$\eta \in A_\xi $
and
![]() $p_0(\eta )=p(\eta )$
otherwise.
$p_0(\eta )=p(\eta )$
otherwise.
Each
![]() $t\in p_0(\beta )\cap {}^\alpha \kappa $
is a
$t\in p_0(\beta )\cap {}^\alpha \kappa $
is a
![]() $h_\beta (\alpha )$
-splitting node, hence the set
$h_\beta (\alpha )$
-splitting node, hence the set
![]() $X=\left \{\chi \in \kappa \mid t^\frown \chi \in p_0(\beta )\right \}$
has cardinality
$X=\left \{\chi \in \kappa \mid t^\frown \chi \in p_0(\beta )\right \}$
has cardinality
![]() $|X|\geq h_\beta (\alpha )$
. Because
$|X|\geq h_\beta (\alpha )$
. Because
![]() $\alpha \in S_\beta $
and
$\alpha \in S_\beta $
and
![]() $\beta \in B$
, we have by our assumptions on F that
$\beta \in B$
, we have by our assumptions on F that
![]() $|Y|\leq F(\alpha )<h_\beta (\alpha )\leq |X|$
. We can therefore find some
$|Y|\leq F(\alpha )<h_\beta (\alpha )\leq |X|$
. We can therefore find some
![]() $\chi \in X$
such that
$\chi \in X$
such that
![]() $\chi \notin Y$
. Let
$\chi \notin Y$
. Let
![]() $q\leq p_0$
be defined as
$q\leq p_0$
be defined as
 $$ \begin{align*} q(\eta)=\begin{cases} (p_0(\beta))_{t^\frown \chi},&\text{if }\eta=\beta,\\ p_0(\eta),&\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} q(\eta)=\begin{cases} (p_0(\beta))_{t^\frown \chi},&\text{if }\eta=\beta,\\ p_0(\eta),&\text{otherwise}. \end{cases} \end{align*} $$
Here
![]() $(p_0(\beta ))_{t^\frown \chi }$
is the subtree of
$(p_0(\beta ))_{t^\frown \chi }$
is the subtree of
![]() $p_0(\beta )$
generated by the initial segment
$p_0(\beta )$
generated by the initial segment
![]() $t^\frown \chi $
. Then
$t^\frown \chi $
. Then
![]() $q\leq p_0\leq p$
and
$q\leq p_0\leq p$
and
![]() $q\Vdash \text {"}\,\dot f(\check \alpha )\notin \check Y=\dot \varphi _\xi (\check \alpha )\,\text {"}$
.
$q\Vdash \text {"}\,\dot f(\check \alpha )\notin \check Y=\dot \varphi _\xi (\check \alpha )\,\text {"}$
.
Lemma 2.8. Let A be a set of ordinals such that
![]() $\kappa <\mathrm {cf}(|A|)$
, let
$\kappa <\mathrm {cf}(|A|)$
, let
![]() $\left \langle h_\xi \mid \xi \in A\right \rangle $
be a sequence of functions, let
$\left \langle h_\xi \mid \xi \in A\right \rangle $
be a sequence of functions, let
![]() $\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
with
$\overline {\mathbb S}=\prod _{\xi \in A}{\mathbb S^{h_\xi }_\kappa }$
with
![]() $\overline {\mathbb S}$
-generic G, and let
$\overline {\mathbb S}$
-generic G, and let
![]() $F\in {}^{\kappa }\kappa $
. Assuming
$F\in {}^{\kappa }\kappa $
. Assuming
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, it follows that
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, it follows that
Proof This is a standard argument of counting names.
We are now ready to use our product forcing to separate
![]() $\kappa $
many cardinals of the form
$\kappa $
many cardinals of the form
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
.
${\mathfrak d_\kappa ^{h}(\in ^*)}$
.
Theorem 2.9. There exists a family of functions
![]() ${\left \{{g_\eta \mid \eta \in \kappa }\right \}}\subseteq {}^{\kappa }\kappa $
such that for any
${\left \{{g_\eta \mid \eta \in \kappa }\right \}}\subseteq {}^{\kappa }\kappa $
such that for any
![]() $\gamma \in \kappa ^+$
and any increasing sequence
$\gamma \in \kappa ^+$
and any increasing sequence
![]() $\left \langle \lambda _\xi \mid \xi \in \gamma \right \rangle $
of cardinals with
$\left \langle \lambda _\xi \mid \xi \in \gamma \right \rangle $
of cardinals with
![]() $\kappa <\mathrm {cf}(\lambda _\xi )$
for all
$\kappa <\mathrm {cf}(\lambda _\xi )$
for all
![]() $\xi \in \gamma $
and any
$\xi \in \gamma $
and any
![]() $\sigma :\kappa \to \gamma $
, there exists a forcing extension in which
$\sigma :\kappa \to \gamma $
, there exists a forcing extension in which
![]() ${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}=\lambda _{\sigma (\eta )}$
for all
${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}=\lambda _{\sigma (\eta )}$
for all
![]() $\eta \in \kappa $
.
$\eta \in \kappa $
.
Proof We assume that
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, or otherwise we first use a forcing to collapse
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, or otherwise we first use a forcing to collapse
![]() $2^\kappa $
to become
$2^\kappa $
to become
![]() $\kappa ^+$
. By a result of Solovay (Theorem 8.10 in [Reference Jech5]) there exists a family of
$\kappa ^+$
. By a result of Solovay (Theorem 8.10 in [Reference Jech5]) there exists a family of
![]() $\kappa $
many disjoint stationary subsets of
$\kappa $
many disjoint stationary subsets of
![]() $\kappa $
, thus let
$\kappa $
, thus let
![]() ${\left \{{S_\eta \mid \eta \in \kappa }\right \}}$
be such a family. Let
${\left \{{S_\eta \mid \eta \in \kappa }\right \}}$
be such a family. Let
![]() $\kappa \leq \gamma \in \kappa ^+$
and
$\kappa \leq \gamma \in \kappa ^+$
and
![]() $\sigma :\kappa \to \gamma $
be given. We will assume without loss of generality that
$\sigma :\kappa \to \gamma $
be given. We will assume without loss of generality that
![]() $\sigma $
is bijective, and hence that
$\sigma $
is bijective, and hence that
![]() $\sigma ^{-1}:\gamma \to \kappa $
is a well-defined bijection. Let
$\sigma ^{-1}:\gamma \to \kappa $
is a well-defined bijection. Let
![]() $\left \langle \lambda _\xi \mid \xi \in \gamma \right \rangle $
be an increasing sequence of cardinals with
$\left \langle \lambda _\xi \mid \xi \in \gamma \right \rangle $
be an increasing sequence of cardinals with
![]() $\mathrm {cf}(\lambda _\xi )>\kappa $
for all
$\mathrm {cf}(\lambda _\xi )>\kappa $
for all
![]() $\xi \in \gamma $
.
$\xi \in \gamma $
.
Fix some
![]() $F\in {}^{\kappa }\kappa $
such that
$F\in {}^{\kappa }\kappa $
such that
![]() $F(\alpha )^{|\alpha |}=F(\alpha )$
and
$F(\alpha )^{|\alpha |}=F(\alpha )$
and
![]() $2^{F(\alpha )}\leq F(\beta )$
for any
$2^{F(\alpha )}\leq F(\beta )$
for any
![]() $\alpha <\beta $
. For each
$\alpha <\beta $
. For each
![]() $\eta \in \kappa $
we define a function
$\eta \in \kappa $
we define a function
![]() $g_\eta $
as follows:
$g_\eta $
as follows:
 $$ \begin{align*} g_\eta(\alpha)=\begin{cases} F(\alpha),&\text{ if }\alpha\in S_\eta,\\ 2^{F(\alpha)},&\text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} g_\eta(\alpha)=\begin{cases} F(\alpha),&\text{ if }\alpha\in S_\eta,\\ 2^{F(\alpha)},&\text{ otherwise}. \end{cases} \end{align*} $$
For each
![]() $\xi \in \gamma $
we define
$\xi \in \gamma $
we define
![]() $H_\xi \in {}^{\kappa }\kappa $
as follows:
$H_\xi \in {}^{\kappa }\kappa $
as follows:
 $$ \begin{align*} H_\xi(\alpha)=\begin{cases} F(\alpha),&\text{ if }\alpha\in\textstyle\bigcup_{\zeta\in\xi}S_{\sigma^{-1}(\zeta)},\\ 2^{F(\alpha)},&\text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} H_\xi(\alpha)=\begin{cases} F(\alpha),&\text{ if }\alpha\in\textstyle\bigcup_{\zeta\in\xi}S_{\sigma^{-1}(\zeta)},\\ 2^{F(\alpha)},&\text{ otherwise}. \end{cases} \end{align*} $$
For each
![]() $\xi \in \gamma $
let
$\xi \in \gamma $
let
![]() $A_\xi $
be a set of ordinals with
$A_\xi $
be a set of ordinals with
![]() $|A_\xi |=\lambda _\xi $
, such that
$|A_\xi |=\lambda _\xi $
, such that
![]() $\left \langle A_\xi \mid \xi \in \gamma \right \rangle $
is a sequence of mutually disjoint sets, and let
$\left \langle A_\xi \mid \xi \in \gamma \right \rangle $
is a sequence of mutually disjoint sets, and let
![]() $A=\textstyle \bigcup _{\xi \in \gamma } A_\xi $
. For each
$A=\textstyle \bigcup _{\xi \in \gamma } A_\xi $
. For each
![]() $\xi \in \gamma $
and
$\xi \in \gamma $
and
![]() $\beta \in A_\xi $
, we define
$\beta \in A_\xi $
, we define
![]() $h_\beta =H_{\xi }$
.
$h_\beta =H_{\xi }$
.
We now consider the product forcing
![]() $\overline {\mathbb S}=\prod _{\beta \in A}{\mathbb S^{h_\beta }_\kappa }$
with
$\overline {\mathbb S}=\prod _{\beta \in A}{\mathbb S^{h_\beta }_\kappa }$
with
![]() ${\leq }\kappa $
-support. Let G be
${\leq }\kappa $
-support. Let G be
![]() $\overline {\mathbb S}$
-generic. We will fix some
$\overline {\mathbb S}$
-generic. We will fix some
![]() $\eta \in \kappa $
, and let
$\eta \in \kappa $
, and let
![]() $B=\textstyle \bigcup _{\xi \in {\sigma (\eta )}+1}A_{\xi }$
and
$B=\textstyle \bigcup _{\xi \in {\sigma (\eta )}+1}A_{\xi }$
and
![]() $B^c=A\setminus B$
. By Lemma 2.8 we see that
$B^c=A\setminus B$
. By Lemma 2.8 we see that
![]() $(\mathrm {Loc}_{g_\eta })^{\mathbf V[G\restriction B]}$
has cardinality
$(\mathrm {Loc}_{g_\eta })^{\mathbf V[G\restriction B]}$
has cardinality
To use Lemma 2.5, we need that
![]() $h_\beta \leq ^* g_\eta $
for all
$h_\beta \leq ^* g_\eta $
for all
![]() $\beta \in B^c$
, equivalently, that
$\beta \in B^c$
, equivalently, that
![]() $H_{\xi }\leq ^*g_\eta $
for all
$H_{\xi }\leq ^*g_\eta $
for all
![]() $\xi \in ({\sigma (\eta )},\gamma )$
. But this is true for any
$\xi \in ({\sigma (\eta )},\gamma )$
. But this is true for any
![]() $\xi \in ({\sigma (\eta )},\gamma )$
, since
$\xi \in ({\sigma (\eta )},\gamma )$
, since
![]() $g_\eta =F(\alpha )$
iff
$g_\eta =F(\alpha )$
iff
![]() $\alpha \in S_\eta =S_{\sigma ^{-1}({\sigma (\eta )})}$
and because
$\alpha \in S_\eta =S_{\sigma ^{-1}({\sigma (\eta )})}$
and because
![]() ${\sigma (\eta )}\in \xi $
we see that
${\sigma (\eta )}\in \xi $
we see that
![]() $H_{\xi }(\alpha )=F(\alpha )$
as well. Meanwhile for all
$H_{\xi }(\alpha )=F(\alpha )$
as well. Meanwhile for all
![]() $\alpha \notin S_\eta $
we have
$\alpha \notin S_\eta $
we have
![]() $g_\eta (\alpha )=2^{F(\alpha )}\geq H_{\xi }(\alpha )$
. Therefore Lemma 2.5 shows that
$g_\eta (\alpha )=2^{F(\alpha )}\geq H_{\xi }(\alpha )$
. Therefore Lemma 2.5 shows that
![]() $(\mathrm {Loc}_{g_\eta })^{\mathbf V[G\restriction B]}$
is a family in
$(\mathrm {Loc}_{g_\eta })^{\mathbf V[G\restriction B]}$
is a family in
![]() $\mathbf V[G]$
of size
$\mathbf V[G]$
of size
![]() $\lambda _{\sigma (\eta )}$
that forms a witness for
$\lambda _{\sigma (\eta )}$
that forms a witness for
On the other hand, if
![]() $\beta \in A_{{\sigma (\eta )}}$
, then
$\beta \in A_{{\sigma (\eta )}}$
, then
![]() $h_\beta =H_{{\sigma (\eta )}}$
and thus for any
$h_\beta =H_{{\sigma (\eta )}}$
and thus for any
![]() $\alpha \in S_\eta =S_{\sigma ^{-1}({\sigma (\eta )})}$
we see that
$\alpha \in S_\eta =S_{\sigma ^{-1}({\sigma (\eta )})}$
we see that
![]() $g_\eta (\alpha )<H_{\sigma (\eta )}(\alpha )$
. Therefore by Lemma 2.7 we see that
$g_\eta (\alpha )<H_{\sigma (\eta )}(\alpha )$
. Therefore by Lemma 2.7 we see that
In conclusion, we get for every
![]() $\eta \in \kappa $
that
$\eta \in \kappa $
that
Corollary 2.10. There exists functions
![]() $h_\xi $
for each
$h_\xi $
for each
![]() $\xi \in \kappa $
such that for any cardinals
$\xi \in \kappa $
such that for any cardinals
![]() $\lambda _\xi>\kappa $
with
$\lambda _\xi>\kappa $
with
![]() $\mathrm {cf}(\lambda _\xi )>\kappa $
it is consistent that simultaneously
$\mathrm {cf}(\lambda _\xi )>\kappa $
it is consistent that simultaneously
![]() ${\mathfrak d_\kappa ^{h_\xi }(\in ^*)}=\lambda _\xi $
for all
${\mathfrak d_\kappa ^{h_\xi }(\in ^*)}=\lambda _\xi $
for all
![]() $\xi \in \kappa $
.
$\xi \in \kappa $
.
3 Separating
 $\kappa ^+$
many cardinals
$\kappa ^+$
many cardinals
We saw in the previous section that we can use a partition of
![]() $\kappa $
into disjoint stationary sets
$\kappa $
into disjoint stationary sets
![]() ${\left \{{S_\eta \mid \eta \in \kappa }\right \}}$
, and associate a function
${\left \{{S_\eta \mid \eta \in \kappa }\right \}}$
, and associate a function
![]() $g_\eta $
with each stationary
$g_\eta $
with each stationary
![]() $S_\eta $
such that the cardinals
$S_\eta $
such that the cardinals
![]() ${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
can consistently be put in any arbitrary well-order.
${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
can consistently be put in any arbitrary well-order.
It is natural to ask if we can do better than this, and separate
![]() $\kappa ^+$
many cardinalities. Clearly we cannot do this using a disjoint family of stationary sets, since no such family of size
$\kappa ^+$
many cardinalities. Clearly we cannot do this using a disjoint family of stationary sets, since no such family of size
![]() $\kappa ^+$
exists. Fortunately we can work around this by using an almost disjoint family of stationary sets, that is, a family
$\kappa ^+$
exists. Fortunately we can work around this by using an almost disjoint family of stationary sets, that is, a family
![]() $\mathcal S$
of stationary subsets of
$\mathcal S$
of stationary subsets of
![]() $\kappa $
, such that
$\kappa $
, such that
![]() $|S\cap S'|<\kappa $
for any distinct
$|S\cap S'|<\kappa $
for any distinct
![]() $S,S'\in \mathcal S$
. Let us refer to such families as stationary almost disjoint families, or sad families.
$S,S'\in \mathcal S$
. Let us refer to such families as stationary almost disjoint families, or sad families.
The existence of a sad family of size
![]() $2^\kappa $
is a consequence of
$2^\kappa $
is a consequence of
![]() $\Diamond _\kappa $
. Let
$\Diamond _\kappa $
. Let
![]() $\left \langle A_\alpha \mid \alpha \in \kappa \right \rangle $
be a
$\left \langle A_\alpha \mid \alpha \in \kappa \right \rangle $
be a
![]() $\Diamond _\kappa $
-sequence, that is, a sequence such that for any
$\Diamond _\kappa $
-sequence, that is, a sequence such that for any
![]() $X\in \mathcal P(\kappa )$
the following set is stationary:
$X\in \mathcal P(\kappa )$
the following set is stationary:
If
![]() $X,Y\in \mathcal P(\kappa )$
are distinct, and
$X,Y\in \mathcal P(\kappa )$
are distinct, and
![]() $\xi $
is the least element of the symmetric difference
$\xi $
is the least element of the symmetric difference
![]() $X\mathord \triangle Y$
, then it is easy to see that
$X\mathord \triangle Y$
, then it is easy to see that
![]() $S_X\cap S_{Y}\subseteq \xi +1$
, thus
$S_X\cap S_{Y}\subseteq \xi +1$
, thus
![]() ${\left \{{S_X\mid X\in \mathcal P(\kappa )}\right \}}$
is a sad family of size
${\left \{{S_X\mid X\in \mathcal P(\kappa )}\right \}}$
is a sad family of size
![]() $2^\kappa $
.
$2^\kappa $
.
However, generalising the proof of Theorem 2.9 to work with a sad family is not as straightforward as it seems. As we have seen in Lemmas 2.5 and 2.7, the forcing
![]() ${\mathbb S^{h}_\kappa }$
will not increase
${\mathbb S^{h}_\kappa }$
will not increase
![]() ${\mathfrak d_\kappa ^{g}(\in ^*)}$
if
${\mathfrak d_\kappa ^{g}(\in ^*)}$
if
![]() ${\mathbb S^{h}_\kappa }$
has the F-Sacks property for some
${\mathbb S^{h}_\kappa }$
has the F-Sacks property for some
![]() $F\leq ^* g$
, but it will increase
$F\leq ^* g$
, but it will increase
![]() ${\mathfrak d_\kappa ^{g}(\in ^*)}$
if there exists a stationary set S such that
${\mathfrak d_\kappa ^{g}(\in ^*)}$
if there exists a stationary set S such that
![]() $g(\alpha )<h(\alpha )$
for all
$g(\alpha )<h(\alpha )$
for all
![]() $\alpha \in S$
.
$\alpha \in S$
.
Let us assume
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\text { and }\Diamond _\kappa \,\text {"}$
and fix a sad family
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\text { and }\Diamond _\kappa \,\text {"}$
and fix a sad family
![]() ${\left \{{S_\eta \mid \eta \in \kappa ^+}\right \}}$
. We assume that
${\left \{{S_\eta \mid \eta \in \kappa ^+}\right \}}$
. We assume that
![]() $F\in {}^{\kappa }\kappa $
is some arbitrary function such that
$F\in {}^{\kappa }\kappa $
is some arbitrary function such that
![]() $F(\alpha )^{|\alpha |}=F(\alpha )$
and
$F(\alpha )^{|\alpha |}=F(\alpha )$
and
![]() $2^{F(\alpha )}\leq F(\beta )$
for all
$2^{F(\alpha )}\leq F(\beta )$
for all
![]() $\alpha <\beta $
. For every
$\alpha <\beta $
. For every
![]() $\eta \in \kappa ^+$
we can define the functions
$\eta \in \kappa ^+$
we can define the functions
![]() $g_\eta $
, forming the parameters of
$g_\eta $
, forming the parameters of
![]() ${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
:
${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
:
 $$ \begin{align*} g_\eta(\alpha)=\begin{cases} F(\alpha), & \text{if }\alpha\in S_\eta.\\ 2^{F(\alpha)}, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} g_\eta(\alpha)=\begin{cases} F(\alpha), & \text{if }\alpha\in S_\eta.\\ 2^{F(\alpha)}, & \text{otherwise}. \end{cases} \end{align*} $$
In analogy with Theorem 2.9, we want to define functions
![]() $H_\xi $
such that
$H_\xi $
such that
![]() ${\mathbb S^{H_\xi }_\kappa }$
keeps
${\mathbb S^{H_\xi }_\kappa }$
keeps
![]() ${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
small when
${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
small when
![]() $\eta \in X$
and increases
$\eta \in X$
and increases
![]() ${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
when
${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}$
when
![]() $\eta \in Y$
, where
$\eta \in Y$
, where
![]() ${\left \{{X,Y}\right \}}$
forms a partition of
${\left \{{X,Y}\right \}}$
forms a partition of
![]() $\kappa ^+$
. Assuming
$\kappa ^+$
. Assuming
![]() $H_\xi (\alpha )=H_\xi (\alpha )^{|\alpha |}$
for all
$H_\xi (\alpha )=H_\xi (\alpha )^{|\alpha |}$
for all
![]() $\alpha \in \kappa $
, this means that we want to define
$\alpha \in \kappa $
, this means that we want to define
![]() $H_\xi $
such that:
$H_\xi $
such that:
 $$ \begin{align*}\text{ when }\eta\in X:\qquad&H_\xi\leq^* g_\eta,\\\text{ when }\eta\in Y:\qquad&g_\eta(\alpha)<H_\xi(\alpha)\text{ for all }\alpha\in S\text{, where }S\text{ is stationary}. \end{align*} $$
$$ \begin{align*}\text{ when }\eta\in X:\qquad&H_\xi\leq^* g_\eta,\\\text{ when }\eta\in Y:\qquad&g_\eta(\alpha)<H_\xi(\alpha)\text{ for all }\alpha\in S\text{, where }S\text{ is stationary}. \end{align*} $$
Note that
![]() $g_\eta (\alpha )$
can only have two possible values, either
$g_\eta (\alpha )$
can only have two possible values, either
![]() $F(\alpha )$
or
$F(\alpha )$
or
![]() $2^{F(\alpha )}$
, regardless of
$2^{F(\alpha )}$
, regardless of
![]() $\eta \in \kappa ^+$
. We can therefore assume without loss of generality that the same holds for
$\eta \in \kappa ^+$
. We can therefore assume without loss of generality that the same holds for
![]() $H_\xi (\alpha )$
. Let z be the set on which
$H_\xi (\alpha )$
. Let z be the set on which
![]() $H_\xi $
is small:
$H_\xi $
is small:
If
![]() $\eta \in X$
, then
$\eta \in X$
, then
![]() $H_\xi (\alpha )\leq g_\eta (\alpha )$
is true for all
$H_\xi (\alpha )\leq g_\eta (\alpha )$
is true for all
![]() $\alpha \notin S_\eta $
, but since
$\alpha \notin S_\eta $
, but since
![]() $H_\xi (\alpha )\leq g_\eta (\alpha )$
has to hold for almost all
$H_\xi (\alpha )\leq g_\eta (\alpha )$
has to hold for almost all
![]() $\alpha \in \kappa $
, we also need
$\alpha \in \kappa $
, we also need
![]() $\left |{\left \{{\alpha \in S_\eta \mid \alpha \notin z}\right \}}\right |<\kappa $
. Let us fix the notation that
$\left |{\left \{{\alpha \in S_\eta \mid \alpha \notin z}\right \}}\right |<\kappa $
. Let us fix the notation that
![]() $a\subseteq ^* b$
iff
$a\subseteq ^* b$
iff
![]() $a\setminus c\subseteq b$
for some c with
$a\setminus c\subseteq b$
for some c with
![]() $|c|<\kappa $
, then our condition above states that
$|c|<\kappa $
, then our condition above states that
![]() $S_\eta \subseteq ^* z$
should hold.
$S_\eta \subseteq ^* z$
should hold.
On the other hand, if
![]() $\eta \in Y$
, then
$\eta \in Y$
, then
![]() $g_\eta (\alpha )<H_\xi (\alpha )$
is possible if
$g_\eta (\alpha )<H_\xi (\alpha )$
is possible if
Thus
![]() $(\kappa \setminus z)\cap S_\eta $
needs to be stationary. The assumption that
$(\kappa \setminus z)\cap S_\eta $
needs to be stationary. The assumption that
![]() $|z\cap S_\eta |<\kappa $
is sufficient for this.
$|z\cap S_\eta |<\kappa $
is sufficient for this.
Given our sad family
![]() $\mathcal S=\left \langle S_\eta \mid \eta \in \kappa ^+\right \rangle $
, the existence of a set z such that
$\mathcal S=\left \langle S_\eta \mid \eta \in \kappa ^+\right \rangle $
, the existence of a set z such that
![]() $S_\eta \subseteq ^*z$
for all
$S_\eta \subseteq ^*z$
for all
![]() $\eta \in X$
and
$\eta \in X$
and
![]() $|z\cap S_\eta |<\kappa $
for all
$|z\cap S_\eta |<\kappa $
for all
![]() $\eta \in Y$
, is not immediately clear, but we can add such z generically through forcing.
$\eta \in Y$
, is not immediately clear, but we can add such z generically through forcing.
We define the forcing
![]() ${\mathbb W^{X,Y}_\kappa }$
(where
${\mathbb W^{X,Y}_\kappa }$
(where
![]() $\mathbb W$
stands for wedge). If
$\mathbb W$
stands for wedge). If
![]() $s\in [\kappa ]^{<\kappa }$
, let
$s\in [\kappa ]^{<\kappa }$
, let
![]() $\sigma _s$
be the least ordinal such that
$\sigma _s$
be the least ordinal such that
![]() $s\subseteq \sigma _s$
.
$s\subseteq \sigma _s$
.
Definition 3.1. Given a sequence
![]() $\mathcal S={\left \{{S_\eta \mid \eta \in \kappa ^+}\right \}}$
of almost disjoint subsets of
$\mathcal S={\left \{{S_\eta \mid \eta \in \kappa ^+}\right \}}$
of almost disjoint subsets of
![]() $\kappa $
and a partition
$\kappa $
and a partition
![]() ${\left \{{X,Y}\right \}}$
of
${\left \{{X,Y}\right \}}$
of
![]() $\kappa ^+$
, we define
$\kappa ^+$
, we define
![]() ${\mathbb W^{X,Y}_\kappa }$
to have tuples
${\mathbb W^{X,Y}_\kappa }$
to have tuples
![]() $p=(s_p,A_p,B_p)$
as conditions, where
$p=(s_p,A_p,B_p)$
as conditions, where
![]() $s_p\in [\kappa ]^{<\kappa }$
and
$s_p\in [\kappa ]^{<\kappa }$
and
![]() $A_p\in [X]^{<\kappa }$
and
$A_p\in [X]^{<\kappa }$
and
![]() $B_p\in [Y]^{<\kappa }$
are such that
$B_p\in [Y]^{<\kappa }$
are such that
The ordering on
![]() ${\mathbb W^{X,Y}_\kappa }$
is given by
${\mathbb W^{X,Y}_\kappa }$
is given by
![]() $(s_q,A_q,B_q)\leq (s_p,A_p,B_p)$
if all of the following hold:
$(s_q,A_q,B_q)\leq (s_p,A_p,B_p)$
if all of the following hold:
-
(i)
 $A_p\subseteq A_q$
,
$A_p\subseteq A_q$
, -
(ii)
 $B_p\subseteq B_q$
,
$B_p\subseteq B_q$
, -
(iii)
 $s_p=s_q\cap \sigma _{s_p},$
$s_p=s_q\cap \sigma _{s_p},$
-
(iv)
 $s_q\cap [\sigma _{s_p},\sigma _{s_q})\supseteq \textstyle \bigcup _{\eta \in A_p}S_\eta \cap [\sigma _{s_p},\sigma _{s_q})$
,
$s_q\cap [\sigma _{s_p},\sigma _{s_q})\supseteq \textstyle \bigcup _{\eta \in A_p}S_\eta \cap [\sigma _{s_p},\sigma _{s_q})$
, -
(v)
 $s_q\cap \textstyle \bigcup _{\eta \in B_p}S_\eta \subseteq \sigma _{s_p}$
.
$s_q\cap \textstyle \bigcup _{\eta \in B_p}S_\eta \subseteq \sigma _{s_p}$
.
If
![]() $G\subseteq {\mathbb W^{X,Y}_\kappa }$
is a generic filter, then let
$G\subseteq {\mathbb W^{X,Y}_\kappa }$
is a generic filter, then let
![]() $z_G=\textstyle \bigcup _{p\in G} s_p$
. It is not hard to see that
$z_G=\textstyle \bigcup _{p\in G} s_p$
. It is not hard to see that
![]() $z_G$
indeed has the desired properties.
$z_G$
indeed has the desired properties.
Lemma 3.2. If
![]() $\eta \in X$
, then
$\eta \in X$
, then
![]() $S_\eta \subseteq ^* z_G$
. If
$S_\eta \subseteq ^* z_G$
. If
![]() $\eta \in Y$
, then
$\eta \in Y$
, then
![]() $|S_\eta \cap z_G|<\kappa $
.
$|S_\eta \cap z_G|<\kappa $
.
Proof Let
![]() $p\in {\mathbb W^{X,Y}_\kappa }$
. It is clear from the way we have defined the forcing that for any
$p\in {\mathbb W^{X,Y}_\kappa }$
. It is clear from the way we have defined the forcing that for any
![]() $\eta \in A_p$
we have
$\eta \in A_p$
we have
![]() $p\Vdash \text {"}\,\check S_\eta \subseteq ^*\dot z_G\,\text {"}$
and for any
$p\Vdash \text {"}\,\check S_\eta \subseteq ^*\dot z_G\,\text {"}$
and for any
![]() $\eta \in B_p$
we have
$\eta \in B_p$
we have
![]() $p\Vdash \text {"}\,\check S_\eta \cap \dot z_G\subseteq \check \sigma _p\in \kappa \,\text {"}$
. Therefore, we are done if we prove that:
$p\Vdash \text {"}\,\check S_\eta \cap \dot z_G\subseteq \check \sigma _p\in \kappa \,\text {"}$
. Therefore, we are done if we prove that:
-
(1) for every
 $\eta \in X$
there is
$\eta \in X$
there is
 $q\leq p$
such that
$q\leq p$
such that
 $\eta \in A_q$
, and
$\eta \in A_q$
, and -
(2) for every
 $\eta \in Y$
there is
$\eta \in Y$
there is
 $q\leq p$
such that
$q\leq p$
such that
 $\eta \in B_q$
.
$\eta \in B_q$
.
Proving (1) and (2) happens in the same way, so we only prove (1) below.
Fix some
![]() $\eta \in X$
. Since
$\eta \in X$
. Since
![]() $S_\eta $
is almost disjoint from
$S_\eta $
is almost disjoint from
![]() $S_\xi $
for all
$S_\xi $
for all
![]() $\xi \in B_p$
, we can define
$\xi \in B_p$
, we can define
![]() $\gamma _\xi \in \kappa $
such that
$\gamma _\xi \in \kappa $
such that
![]() $S_\xi \cap S_\eta \subseteq \gamma _\xi $
for each
$S_\xi \cap S_\eta \subseteq \gamma _\xi $
for each
![]() $\xi \in B_p$
. Since
$\xi \in B_p$
. Since
![]() $|B_p|<\kappa $
we see that
$|B_p|<\kappa $
we see that
![]() $\textstyle \bigcup _{\xi \in B_p}\gamma _\xi \in \kappa $
. Pick some
$\textstyle \bigcup _{\xi \in B_p}\gamma _\xi \in \kappa $
. Pick some
![]() $\gamma \in \textstyle \bigcup _{\xi \in A_p}S_\xi $
such that
$\gamma \in \textstyle \bigcup _{\xi \in A_p}S_\xi $
such that
![]() $\gamma \geq \sigma _{s_p}\cup \textstyle \bigcup _{\xi \in B_p}\gamma _\xi $
.
$\gamma \geq \sigma _{s_p}\cup \textstyle \bigcup _{\xi \in B_p}\gamma _\xi $
.
We define
![]() $q\leq p$
by
$q\leq p$
by
 $$ \begin{align*} s_q&=s_p\cup \left( \textstyle\bigcup_{\xi\in A_p}S_\xi\cap [\sigma_{s_p},\gamma]\right),\\ A_q&=A_p\cup{\left\{{\eta}\right\}},\\ B_q&=B_p. \end{align*} $$
$$ \begin{align*} s_q&=s_p\cup \left( \textstyle\bigcup_{\xi\in A_p}S_\xi\cap [\sigma_{s_p},\gamma]\right),\\ A_q&=A_p\cup{\left\{{\eta}\right\}},\\ B_q&=B_p. \end{align*} $$
Note that
![]() $\gamma \in s_q$
, thus
$\gamma \in s_q$
, thus
![]() $\sigma _{s_q}=\gamma +1$
. Furthermore, note that
$\sigma _{s_q}=\gamma +1$
. Furthermore, note that
 $$ \begin{align*} \textstyle\bigcup_{\xi\in A_p}S_\xi\cap \textstyle\bigcup_{\xi\in B_p}S_\xi\subseteq \sigma_{s_p}&\leq\gamma,\quad\text{ and}\\ S_\eta\cap \textstyle\bigcup_{\xi\in B_p}S_\xi\subseteq \textstyle\bigcup_{\xi\in B_p}\gamma_\xi&\leq \gamma. \end{align*} $$
$$ \begin{align*} \textstyle\bigcup_{\xi\in A_p}S_\xi\cap \textstyle\bigcup_{\xi\in B_p}S_\xi\subseteq \sigma_{s_p}&\leq\gamma,\quad\text{ and}\\ S_\eta\cap \textstyle\bigcup_{\xi\in B_p}S_\xi\subseteq \textstyle\bigcup_{\xi\in B_p}\gamma_\xi&\leq \gamma. \end{align*} $$
Therefore, q is indeed a condition.
We need to show that our forcing has several nice properties to satisfy our needs. Firstly, it is essential that the sad family
![]() ${\left \{{S_\eta \mid \eta \in \kappa ^+}\right \}}$
will remain a sad family, in particular, the forcing should not destroy any stationary sets. Secondly, our forcing needs to preserve cardinals. In particular, we may not collapse
${\left \{{S_\eta \mid \eta \in \kappa ^+}\right \}}$
will remain a sad family, in particular, the forcing should not destroy any stationary sets. Secondly, our forcing needs to preserve cardinals. In particular, we may not collapse
![]() $\kappa ^+$
to
$\kappa ^+$
to
![]() $\kappa $
, since our goal of proving the consistency of
$\kappa $
, since our goal of proving the consistency of
![]() $\kappa ^+$
many distinct cardinal characteristics requires our sad family to have cardinality
$\kappa ^+$
many distinct cardinal characteristics requires our sad family to have cardinality
![]() $\kappa ^+$
. Thirdly, our forcing should preserve
$\kappa ^+$
. Thirdly, our forcing should preserve
![]() $2^\kappa =\kappa ^+$
, which we need for the forcings of type
$2^\kappa =\kappa ^+$
, which we need for the forcings of type
![]() ${\mathbb S^{h}_\kappa }$
afterwards.
${\mathbb S^{h}_\kappa }$
afterwards.
All of these properties hold for
![]() ${\mathbb W^{X,Y}_\kappa }$
under the assumption that
${\mathbb W^{X,Y}_\kappa }$
under the assumption that
![]() $|X|=\kappa $
, since we can show that the forcing is
$|X|=\kappa $
, since we can show that the forcing is
![]() ${<}\kappa $
-closed and
${<}\kappa $
-closed and
![]() $\kappa $
-centred in this case, and our forcing is small enough that it does not increase
$\kappa $
-centred in this case, and our forcing is small enough that it does not increase
![]() $2^\kappa $
.
$2^\kappa $
.
Lemma 3.3.
![]() ${\mathbb W^{X,Y}_\kappa }$
is
${\mathbb W^{X,Y}_\kappa }$
is
![]() ${<}\kappa $
-closed.
${<}\kappa $
-closed.
Proof Let
![]() $\gamma \in \kappa $
be limit and let
$\gamma \in \kappa $
be limit and let
![]() $\left \langle p_\eta \mid \eta <\gamma \right \rangle $
be a descending sequence of conditions. We will write
$\left \langle p_\eta \mid \eta <\gamma \right \rangle $
be a descending sequence of conditions. We will write
![]() $p_\eta =(s_\eta ,A_\eta ,B_\eta )$
. Let
$p_\eta =(s_\eta ,A_\eta ,B_\eta )$
. Let
![]() $p=(s_p,A_p,B_p)$
be given by
$p=(s_p,A_p,B_p)$
be given by
![]() $s_p=\textstyle \bigcup _{\eta \in \gamma }s_\eta $
and
$s_p=\textstyle \bigcup _{\eta \in \gamma }s_\eta $
and
![]() $A_p=\textstyle \bigcup _{\eta \in \gamma }A_\eta $
and
$A_p=\textstyle \bigcup _{\eta \in \gamma }A_\eta $
and
![]() $B_p=\textstyle \bigcup _{\eta \in \gamma }B_\eta $
. That p is a condition and that
$B_p=\textstyle \bigcup _{\eta \in \gamma }B_\eta $
. That p is a condition and that
![]() $p\leq p_\eta $
for each
$p\leq p_\eta $
for each
![]() $\eta \in \gamma $
are easy to check.
$\eta \in \gamma $
are easy to check.
Corollary 3.4.
![]() ${\mathbb W^{X,Y}_\kappa }$
preserves stationary sets.
${\mathbb W^{X,Y}_\kappa }$
preserves stationary sets.
Proof See, for example, Lemma 23.7 in [Reference Jech5].
Definition 3.5. Let
![]() $\mathbb P$
be a forcing. We will call a set
$\mathbb P$
be a forcing. We will call a set
![]() $P\subseteq \mathbb P$
centred if for every
$P\subseteq \mathbb P$
centred if for every
![]() $Q\in [P]^{<\kappa }$
there exists
$Q\in [P]^{<\kappa }$
there exists
![]() $q\in \mathbb P$
such that
$q\in \mathbb P$
such that
![]() $q\leq p$
for all
$q\leq p$
for all
![]() $p\in Q$
. We say that
$p\in Q$
. We say that
![]() $\mathbb P$
is
$\mathbb P$
is
![]() $\kappa $
-centred if
$\kappa $
-centred if
![]() $\mathbb P=\textstyle \bigcup _{\alpha \in \kappa }P_\alpha $
where each
$\mathbb P=\textstyle \bigcup _{\alpha \in \kappa }P_\alpha $
where each
![]() $P_\alpha $
is centred.
$P_\alpha $
is centred.
Note that our notion of a centred set is not the usual definition: more commonly P is called centred if every finite
![]() $Q\subseteq P$
has a common extension, but since we are working in the context of
$Q\subseteq P$
has a common extension, but since we are working in the context of
![]() ${}^{\kappa }\kappa $
we have to replace “finite” by “
${}^{\kappa }\kappa $
we have to replace “finite” by “
![]() ${<}\kappa $
” to have a proper analogy.
${<}\kappa $
” to have a proper analogy.
Clearly if
![]() $A\subseteq \mathbb P$
is an antichain and
$A\subseteq \mathbb P$
is an antichain and
![]() $\mathbb P=\textstyle \bigcup _{\alpha \in \kappa }P_\alpha $
is
$\mathbb P=\textstyle \bigcup _{\alpha \in \kappa }P_\alpha $
is
![]() $\kappa $
-centred, then
$\kappa $
-centred, then
![]() $|A|\leq \kappa $
, since
$|A|\leq \kappa $
, since
![]() $|P_\alpha \cap A|\leq 1$
for every
$|P_\alpha \cap A|\leq 1$
for every
![]() $\alpha \in \kappa $
. Therefore, if
$\alpha \in \kappa $
. Therefore, if
![]() $\mathbb P$
is
$\mathbb P$
is
![]() $\kappa $
-centred, it is
$\kappa $
-centred, it is
![]() ${<}\kappa ^+$
-c.c. as well.
${<}\kappa ^+$
-c.c. as well.
Lemma 3.6. If
![]() $|X|\leq \kappa $
, then
$|X|\leq \kappa $
, then
![]() ${\mathbb W^{X,Y}_\kappa }$
is
${\mathbb W^{X,Y}_\kappa }$
is
![]() $\kappa $
-centred.
$\kappa $
-centred.
Proof For any
![]() $s\in [\kappa ]^{<\kappa }$
and
$s\in [\kappa ]^{<\kappa }$
and
![]() $A\in [X]^{<\kappa }$
we define
$A\in [X]^{<\kappa }$
we define
Since
![]() $|X|\leq \kappa $
implies that
$|X|\leq \kappa $
implies that
![]() $\left |[\kappa ]^{<\kappa }\times [X]^{<\kappa }\right |=\kappa $
, we are done if we show that each
$\left |[\kappa ]^{<\kappa }\times [X]^{<\kappa }\right |=\kappa $
, we are done if we show that each
![]() $W_{s,A}$
is centred. Let
$W_{s,A}$
is centred. Let
![]() $Q\in [ W_{s,A}]^{<\kappa }$
and
$Q\in [ W_{s,A}]^{<\kappa }$
and
![]() $B=\textstyle \bigcup _{p\in Q}B_p$
. We claim that
$B=\textstyle \bigcup _{p\in Q}B_p$
. We claim that
![]() $q=\left \langle s,A,B\right \rangle $
is a condition and that
$q=\left \langle s,A,B\right \rangle $
is a condition and that
![]() $q\leq p$
for all
$q\leq p$
for all
![]() $p\in Q$
.
$p\in Q$
.
Suppose that
![]() $\alpha \in \textstyle \bigcup _{\eta \in A} S_\eta \cap \textstyle \bigcup _{\eta \in B}S_\eta $
, then there is
$\alpha \in \textstyle \bigcup _{\eta \in A} S_\eta \cap \textstyle \bigcup _{\eta \in B}S_\eta $
, then there is
![]() $p\in Q$
such that
$p\in Q$
such that
![]() $\alpha \in \textstyle \bigcup _{\eta \in A} S_\eta \cap \textstyle \bigcup _{\eta \in B_p}S_\eta $
, and since p is a condition it follows that
$\alpha \in \textstyle \bigcup _{\eta \in A} S_\eta \cap \textstyle \bigcup _{\eta \in B_p}S_\eta $
, and since p is a condition it follows that
![]() $\alpha \in \sigma _{s_p}=\sigma _s$
. Hence q is a condition. To check that
$\alpha \in \sigma _{s_p}=\sigma _s$
. Hence q is a condition. To check that
![]() $q\leq p$
for each
$q\leq p$
for each
![]() $p\in Q$
, note that (i)–(iii) of Definition 3.1 are immediate, while (iv) and (v) hold vacuously by
$p\in Q$
, note that (i)–(iii) of Definition 3.1 are immediate, while (iv) and (v) hold vacuously by
![]() $s_p=s_q$
.
$s_p=s_q$
.
Corollary 3.7. If
![]() $|X|\leq \kappa $
, then
$|X|\leq \kappa $
, then
![]() ${\mathbb W^{X,Y}_\kappa }$
preserves all cardinalities.
${\mathbb W^{X,Y}_\kappa }$
preserves all cardinalities.
Finally, we have to look at adding multiple generics of forcings of the type
![]() ${\mathbb W^{X,Y}_\kappa }$
. Our goal is to define functions
${\mathbb W^{X,Y}_\kappa }$
. Our goal is to define functions
![]() $H_\xi $
for each
$H_\xi $
for each
![]() $\xi \in \kappa ^+$
. Fix some bijection
$\xi \in \kappa ^+$
. Fix some bijection
![]() $\sigma :\kappa ^+\to \kappa ^+$
, then we want to add a generic set z for the forcing
$\sigma :\kappa ^+\to \kappa ^+$
, then we want to add a generic set z for the forcing
![]() ${\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
for each
${\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
for each
![]() $\xi \in \kappa ^+$
, where
$\xi \in \kappa ^+$
, where
![]() $X_\xi =\sigma (\xi )$
and
$X_\xi =\sigma (\xi )$
and
![]() $Y_\xi =\kappa ^+\setminus X$
. This means that we also need to guarantee that a
$Y_\xi =\kappa ^+\setminus X$
. This means that we also need to guarantee that a
![]() ${<}\kappa $
-support products of size
${<}\kappa $
-support products of size
![]() $\kappa ^+$
of forcings of the form
$\kappa ^+$
of forcings of the form
![]() ${\mathbb W^{X,Y}_\kappa }$
behaves nicely, in the sense that it preserves cardinals, stationary sets and
${\mathbb W^{X,Y}_\kappa }$
behaves nicely, in the sense that it preserves cardinals, stationary sets and
![]() $2^\kappa =\kappa ^+$
.
$2^\kappa =\kappa ^+$
.
Lemma 3.8. Let
![]() $\left \langle {\left \{{X_\xi ,Y_\xi }\right \}}\mid \xi \in \kappa ^+\right \rangle $
be a sequence of partitions of
$\left \langle {\left \{{X_\xi ,Y_\xi }\right \}}\mid \xi \in \kappa ^+\right \rangle $
be a sequence of partitions of
![]() $\kappa ^+$
such that
$\kappa ^+$
such that
![]() $|X_\xi |\leq \kappa $
for each
$|X_\xi |\leq \kappa $
for each
![]() $\xi \in \kappa ^+$
and let
$\xi \in \kappa ^+$
and let
![]() $\overline {\mathbb W}=\prod _{\xi \in \kappa ^+}{\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
be the
$\overline {\mathbb W}=\prod _{\xi \in \kappa ^+}{\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
be the
![]() ${<}\kappa $
-support product of the forcings
${<}\kappa $
-support product of the forcings
![]() ${\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
. Then
${\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
. Then
![]() $\overline {\mathbb W}$
is
$\overline {\mathbb W}$
is
![]() ${<}\kappa $
-closed,
${<}\kappa $
-closed,
![]() ${<}\kappa ^+$
-c.c. and if G is
${<}\kappa ^+$
-c.c. and if G is
![]() $\overline {\mathbb W}$
-generic over
$\overline {\mathbb W}$
-generic over
![]() $\mathbf V$
and
$\mathbf V$
and
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, then
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
, then
![]() $\mathbf V[G]\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
.
$\mathbf V[G]\vDash \text {"}\,2^\kappa =\kappa ^+\,\text {"}$
.
Proof Note that each term
![]() ${\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
is
${\mathbb W^{X_\xi ,Y_\xi }_\kappa }$
is
![]() ${<}\kappa $
-closed and
${<}\kappa $
-closed and
![]() ${<}\kappa ^+$
-c.c. (the latter as a consequence of
${<}\kappa ^+$
-c.c. (the latter as a consequence of
![]() $\kappa $
-centredness), thus a
$\kappa $
-centredness), thus a
![]() ${<}\kappa $
-support product of length
${<}\kappa $
-support product of length
![]() $\kappa ^+$
is also
$\kappa ^+$
is also
![]() ${<}\kappa $
-closed, which is easily proved, and
${<}\kappa $
-closed, which is easily proved, and
![]() ${<}\kappa ^+$
-c.c., which is proved using a
${<}\kappa ^+$
-c.c., which is proved using a
![]() $\Delta $
-system argument. That
$\Delta $
-system argument. That
![]() $2^\kappa =\kappa ^+$
will remain true, follows from an argument by counting names, using that
$2^\kappa =\kappa ^+$
will remain true, follows from an argument by counting names, using that
![]() $|{\mathbb W^{X_\xi ,Y_\xi }_\kappa }|=\kappa ^+$
for each
$|{\mathbb W^{X_\xi ,Y_\xi }_\kappa }|=\kappa ^+$
for each
![]() $\xi \in \kappa ^+$
, and that the product has
$\xi \in \kappa ^+$
, and that the product has
![]() $\kappa ^+$
many terms, thus
$\kappa ^+$
many terms, thus
![]() $|\overline {\mathbb W}|=\kappa ^+$
.
$|\overline {\mathbb W}|=\kappa ^+$
.
Corollary 3.9.
![]() $\overline {\mathbb W}$
preserves cardinals and stationary sets.
$\overline {\mathbb W}$
preserves cardinals and stationary sets.
Now we are finally ready to prove our last theorem, which is an extension of Theorem 2.9, and shows that there can be consistently
![]() $\kappa ^+$
many distinct cardinal characteristics of the form
$\kappa ^+$
many distinct cardinal characteristics of the form
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
.
${\mathfrak d_\kappa ^{h}(\in ^*)}$
.
Theorem 3.10. Assuming
![]() $2^\kappa =\kappa ^+$
and
$2^\kappa =\kappa ^+$
and
![]() $\Diamond _\kappa $
, there exists a family of functions
$\Diamond _\kappa $
, there exists a family of functions
![]() ${\left \{{g_\eta \mid \eta \in \kappa ^+}\right \}}\subseteq {}^{\kappa }\kappa $
such that for any increasing sequence
${\left \{{g_\eta \mid \eta \in \kappa ^+}\right \}}\subseteq {}^{\kappa }\kappa $
such that for any increasing sequence
![]() $\left \langle \lambda _\xi \mid \xi \in \kappa ^+\right \rangle $
of cardinals with
$\left \langle \lambda _\xi \mid \xi \in \kappa ^+\right \rangle $
of cardinals with
![]() $\kappa <\mathrm {cf}(\lambda _\xi )$
and any function
$\kappa <\mathrm {cf}(\lambda _\xi )$
and any function
![]() $\sigma :\kappa ^+\to \kappa ^+$
, there exists a forcing extension in which
$\sigma :\kappa ^+\to \kappa ^+$
, there exists a forcing extension in which
![]() ${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}=\lambda _{\sigma (\eta )}$
for all
${\mathfrak d_\kappa ^{g_\eta }(\in ^*)}=\lambda _{\sigma (\eta )}$
for all
![]() $\eta \in \kappa ^{+}$
.
$\eta \in \kappa ^{+}$
.
Proof We start with a model
![]() $\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\text { and }\Diamond _\kappa \,\text {"}$
containing a sad family
$\mathbf V\vDash \text {"}\,2^\kappa =\kappa ^+\text { and }\Diamond _\kappa \,\text {"}$
containing a sad family
![]() $\mathcal S=\left \langle S_\eta \mid \eta \in \kappa ^+\right \rangle $
, and we will assume without loss of generality that
$\mathcal S=\left \langle S_\eta \mid \eta \in \kappa ^+\right \rangle $
, and we will assume without loss of generality that
![]() $\sigma :\kappa ^+\to \kappa ^+$
is a bijection. We define the functions
$\sigma :\kappa ^+\to \kappa ^+$
is a bijection. We define the functions
![]() $g_\eta $
for each
$g_\eta $
for each
![]() $\eta \in \kappa ^+$
as
$\eta \in \kappa ^+$
as
 $$ \begin{align*} g_\eta(\alpha)=\begin{cases} F(\alpha), & \text{if }\alpha\in S_\eta,\\ 2^{F(\alpha)}, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} g_\eta(\alpha)=\begin{cases} F(\alpha), & \text{if }\alpha\in S_\eta,\\ 2^{F(\alpha)}, & \text{otherwise}. \end{cases} \end{align*} $$
For each
![]() $\eta \in \kappa ^+$
we define the partition
$\eta \in \kappa ^+$
we define the partition
![]() ${\left \{{X_\eta ,Y_\eta }\right \}}$
of
${\left \{{X_\eta ,Y_\eta }\right \}}$
of
![]() $\kappa ^+$
by
$\kappa ^+$
by
 $$ \begin{align*} X_\eta&=\sigma^{-1}[\sigma(\eta)]={\left\{{\zeta\in\kappa^+\mid \sigma(\zeta)\in\sigma(\eta)}\right\}},\\ Y_\eta&=\kappa^+\setminus X_\eta. \end{align*} $$
$$ \begin{align*} X_\eta&=\sigma^{-1}[\sigma(\eta)]={\left\{{\zeta\in\kappa^+\mid \sigma(\zeta)\in\sigma(\eta)}\right\}},\\ Y_\eta&=\kappa^+\setminus X_\eta. \end{align*} $$
We then force with a
![]() ${<}\kappa $
-support product
${<}\kappa $
-support product
![]() $\overline {\mathbb W}=\prod _{\eta \in \kappa ^+}{\mathbb W^{X_\eta ,Y_\eta }_\kappa }$
. Note, in particular, that
$\overline {\mathbb W}=\prod _{\eta \in \kappa ^+}{\mathbb W^{X_\eta ,Y_\eta }_\kappa }$
. Note, in particular, that
![]() $|X_\eta |\leq \kappa $
. Let G be
$|X_\eta |\leq \kappa $
. Let G be
![]() $\overline {\mathbb W}$
-generic, then we will work in
$\overline {\mathbb W}$
-generic, then we will work in
![]() $\mathbf V[G]$
. We define
$\mathbf V[G]$
. We define
![]() $z_ {\sigma (\eta )}=\textstyle \bigcup _{p\in G}s_{p(\eta )}$
, then
$z_ {\sigma (\eta )}=\textstyle \bigcup _{p\in G}s_{p(\eta )}$
, then
![]() $z_{\sigma (\eta )}$
is
$z_{\sigma (\eta )}$
is
![]() ${\mathbb W^{X_\eta ,Y_\eta }_\kappa }$
-generic over
${\mathbb W^{X_\eta ,Y_\eta }_\kappa }$
-generic over
![]() $\mathbf V$
.
$\mathbf V$
.
By Lemma 3.8, we know that
![]() $\mathbf V[G]\vDash \text {"}\,2^\kappa =\kappa ^+\text { + }\check {\mathcal S}\text { is a sad family}\,\text {"}$
. Therefore by Lemma 3.2, if
$\mathbf V[G]\vDash \text {"}\,2^\kappa =\kappa ^+\text { + }\check {\mathcal S}\text { is a sad family}\,\text {"}$
. Therefore by Lemma 3.2, if
![]() $\eta \in \kappa ^+$
, then we have
$\eta \in \kappa ^+$
, then we have
![]() $S_\zeta \subseteq ^* z_{\sigma (\eta )}$
for all
$S_\zeta \subseteq ^* z_{\sigma (\eta )}$
for all
![]() $\zeta \in X_\eta $
and
$\zeta \in X_\eta $
and
![]() $|S_\zeta \cap z_{\sigma (\eta )}|<\kappa $
for all
$|S_\zeta \cap z_{\sigma (\eta )}|<\kappa $
for all
![]() $\zeta \in Y_\eta $
. Equivalently, using the definition of
$\zeta \in Y_\eta $
. Equivalently, using the definition of
![]() $X_\eta $
and
$X_\eta $
and
![]() $Y_\eta $
, if
$Y_\eta $
, if
![]() $\xi \in \kappa ^+$
, then we have
$\xi \in \kappa ^+$
, then we have
![]() $S_\zeta \subseteq ^* z_\xi $
for all
$S_\zeta \subseteq ^* z_\xi $
for all
![]() $\zeta \in \kappa ^+$
such that
$\zeta \in \kappa ^+$
such that
![]() $\sigma (\zeta )\in \xi $
and
$\sigma (\zeta )\in \xi $
and
![]() $|S_\zeta \cap z_{\xi }|<\kappa $
for all
$|S_\zeta \cap z_{\xi }|<\kappa $
for all
![]() $\zeta \in \kappa ^+$
such that
$\zeta \in \kappa ^+$
such that
![]() $\sigma (\zeta )\in [\xi ,\kappa ^+)$
.
$\sigma (\zeta )\in [\xi ,\kappa ^+)$
.
For each
![]() $\xi \in \kappa ^+$
we define
$\xi \in \kappa ^+$
we define
![]() $H_\xi \in {}^{\kappa }\kappa $
as follows:
$H_\xi \in {}^{\kappa }\kappa $
as follows:
 $$ \begin{align*} H_\xi(\alpha)=\begin{cases} F(\alpha),&\text{ if }\alpha\in z_\xi,\\ 2^{F(\alpha)},&\text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} H_\xi(\alpha)=\begin{cases} F(\alpha),&\text{ if }\alpha\in z_\xi,\\ 2^{F(\alpha)},&\text{ otherwise}. \end{cases} \end{align*} $$
The remainder of the proof mirrors the proof of Theorem 2.9 almost exactly.
For each
![]() $\xi \in \kappa ^+$
let
$\xi \in \kappa ^+$
let
![]() $A_\xi $
be a set of ordinals with
$A_\xi $
be a set of ordinals with
![]() $|A_\xi |=\lambda _\xi $
, such that
$|A_\xi |=\lambda _\xi $
, such that
![]() $\left \langle A_\xi \mid \xi \in \kappa ^+\right \rangle $
is a sequence of mutually disjoint sets, and let
$\left \langle A_\xi \mid \xi \in \kappa ^+\right \rangle $
is a sequence of mutually disjoint sets, and let
![]() $A=\textstyle \bigcup _{\xi \in \kappa ^+} A_\xi $
. For each
$A=\textstyle \bigcup _{\xi \in \kappa ^+} A_\xi $
. For each
![]() $\xi \in \kappa ^+$
and
$\xi \in \kappa ^+$
and
![]() $\beta \in A_\xi $
, we define
$\beta \in A_\xi $
, we define
![]() $h_\beta =H_{\xi }$
.
$h_\beta =H_{\xi }$
.
We now consider the product forcing
![]() $\overline {\mathbb S}=\prod _{\beta \in A}{\mathbb S^{h_\beta }_\kappa }$
with
$\overline {\mathbb S}=\prod _{\beta \in A}{\mathbb S^{h_\beta }_\kappa }$
with
![]() ${\leq }\kappa $
-support. Let K be
${\leq }\kappa $
-support. Let K be
![]() $\overline {\mathbb S}$
-generic. We will fix some
$\overline {\mathbb S}$
-generic. We will fix some
![]() $\eta \in \kappa ^+$
, and let
$\eta \in \kappa ^+$
, and let
![]() $B=\textstyle \bigcup _{\xi \in \sigma (\eta )+1}A_{\xi }$
and
$B=\textstyle \bigcup _{\xi \in \sigma (\eta )+1}A_{\xi }$
and
![]() $B^c=A\setminus B$
. By Lemma 2.8 we see that
$B^c=A\setminus B$
. By Lemma 2.8 we see that
![]() $(\mathrm {Loc}_{g_\eta })^{\mathbf V[G][K\restriction B]}$
has cardinality
$(\mathrm {Loc}_{g_\eta })^{\mathbf V[G][K\restriction B]}$
has cardinality
To use Lemma 2.5, we need that
![]() $h_\beta \leq ^* g_\eta $
for all
$h_\beta \leq ^* g_\eta $
for all
![]() $\beta \in B^c$
, equivalently, that
$\beta \in B^c$
, equivalently, that
![]() $H_{\xi }\leq ^*g_\eta $
for all
$H_{\xi }\leq ^*g_\eta $
for all
![]() $\xi \in ({\sigma (\eta )},\kappa ^+)$
. But this is true for any
$\xi \in ({\sigma (\eta )},\kappa ^+)$
. But this is true for any
![]() $\xi \in ({\sigma (\eta )},\kappa ^+)$
, since
$\xi \in ({\sigma (\eta )},\kappa ^+)$
, since
![]() $g_\eta =F(\alpha )$
iff
$g_\eta =F(\alpha )$
iff
![]() $\alpha \in S_\eta $
, while
$\alpha \in S_\eta $
, while
![]() $H_{\xi }(\alpha )=F(\alpha )$
iff
$H_{\xi }(\alpha )=F(\alpha )$
iff
![]() $\alpha \in z_{\xi }$
, and because
$\alpha \in z_{\xi }$
, and because
![]() ${\sigma (\eta )}\in \xi $
we have
${\sigma (\eta )}\in \xi $
we have
![]() $S_\eta \subseteq ^*z_{\xi }$
. Therefore Lemma 2.5 shows that
$S_\eta \subseteq ^*z_{\xi }$
. Therefore Lemma 2.5 shows that
![]() $(\mathrm {Loc}_{g_\eta })^{\mathbf V[G][K\restriction B]}$
is a family in
$(\mathrm {Loc}_{g_\eta })^{\mathbf V[G][K\restriction B]}$
is a family in
![]() $\mathbf V[G][K]$
of size
$\mathbf V[G][K]$
of size
![]() $\lambda _{\sigma (\eta )}$
that forms a witness for
$\lambda _{\sigma (\eta )}$
that forms a witness for
On the other hand, if
![]() $\beta \in A_{{\sigma (\eta )}}$
, then
$\beta \in A_{{\sigma (\eta )}}$
, then
![]() $h_\beta =H_{{\sigma (\eta )}}$
and thus
$h_\beta =H_{{\sigma (\eta )}}$
and thus
![]() $\sigma (\eta )\in [{\sigma (\eta )},\kappa ^+)$
implies that
$\sigma (\eta )\in [{\sigma (\eta )},\kappa ^+)$
implies that
![]() $|S_\eta \cap z_{\sigma (\eta )}|<\kappa $
. In particular,
$|S_\eta \cap z_{\sigma (\eta )}|<\kappa $
. In particular,
![]() $S_\eta \setminus z_{\sigma (\eta )}$
is stationary and if
$S_\eta \setminus z_{\sigma (\eta )}$
is stationary and if
![]() $\alpha \in S_\eta \setminus z_{\sigma (\eta )}$
, then
$\alpha \in S_\eta \setminus z_{\sigma (\eta )}$
, then
![]() $g_\eta (\alpha )<H_{\sigma (\eta )}(\alpha )$
. Hence by Lemma 2.7 we see that
$g_\eta (\alpha )<H_{\sigma (\eta )}(\alpha )$
. Hence by Lemma 2.7 we see that
In conclusion, we get for every
![]() $\eta \in \kappa $
that
$\eta \in \kappa $
that
4 Concluding remarks
With Theorem 3.10 we improved the known consistency of
![]() ${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}<{\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
to a family of
${\mathfrak d_\kappa ^{\mathsf {pow}}(\in ^*)}<{\mathfrak d_\kappa ^{\mathsf {id}}(\in ^*)}$
to a family of
![]() $\kappa ^+$
many cardinal invariants that are mutually independent in the sense that any ordering of the cardinals with order-type
$\kappa ^+$
many cardinal invariants that are mutually independent in the sense that any ordering of the cardinals with order-type
![]() $\kappa ^+$
is consistent. This answers Questions 72 and 73 from [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] positively. Moreover, we have shown that there exist functions
$\kappa ^+$
is consistent. This answers Questions 72 and 73 from [Reference Brendle, Brooke-Taylor, Friedman and Montoya3] positively. Moreover, we have shown that there exist functions
![]() $h,h'\in {}^{\kappa }\kappa $
for which it is consistent that
$h,h'\in {}^{\kappa }\kappa $
for which it is consistent that
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}<{\mathfrak d_\kappa ^{h'}(\in ^*)}$
, but also that it is consistent that
${\mathfrak d_\kappa ^{h}(\in ^*)}<{\mathfrak d_\kappa ^{h'}(\in ^*)}$
, but also that it is consistent that
![]() ${\mathfrak d_\kappa ^{h'}(\in ^*)}<{\mathfrak d_\kappa ^{h}(\in ^*)}$
.
${\mathfrak d_\kappa ^{h'}(\in ^*)}<{\mathfrak d_\kappa ^{h}(\in ^*)}$
.
It is natural to ask if we can do better than this.
Question 4.1. Is it consistent that there exists a family of functions
![]() ${\left \{{h_\xi \mid \xi \in \kappa ^{++}}\right \}}$
such that each
${\left \{{h_\xi \mid \xi \in \kappa ^{++}}\right \}}$
such that each
![]() ${\mathfrak d_\kappa ^{h_\xi }(\in ^*)}$
has a distinct value? Is it consistent that there is a model with
${\mathfrak d_\kappa ^{h_\xi }(\in ^*)}$
has a distinct value? Is it consistent that there is a model with
![]() $2^\kappa $
many distinct values for cardinals of the form
$2^\kappa $
many distinct values for cardinals of the form
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
?
${\mathfrak d_\kappa ^{h}(\in ^*)}$
?
Our method of separating cardinals uses a forcing
![]() ${\mathbb S^{h}_\kappa }$
that requires
${\mathbb S^{h}_\kappa }$
that requires
![]() $2^\kappa =\kappa ^+$
in the ground model to have the
$2^\kappa =\kappa ^+$
in the ground model to have the
![]() ${<}\kappa ^{++}$
-c.c., hence if we start with a family of functions of size
${<}\kappa ^{++}$
-c.c., hence if we start with a family of functions of size
![]() $\kappa ^{++}$
, our forcing may collapse
$\kappa ^{++}$
, our forcing may collapse
![]() $\kappa ^{++}$
. This makes it hard to answer the above question using the method presented in this paper.
$\kappa ^{++}$
. This makes it hard to answer the above question using the method presented in this paper.
Another limitation of our method, is that we restrict our attention to forcings that have the F-Sacks properties where
![]() $F(\alpha )=F(\alpha )^{|\alpha |}$
. Essentially, we know how to separate cardinals with a parameter h from cardinals with a parameter
$F(\alpha )=F(\alpha )^{|\alpha |}$
. Essentially, we know how to separate cardinals with a parameter h from cardinals with a parameter
![]() $2^h$
, and thus we make a jump on the order of a power set operation. It is unclear whether a finer structure can be discovered between these cardinals, motivating the following question:
$2^h$
, and thus we make a jump on the order of a power set operation. It is unclear whether a finer structure can be discovered between these cardinals, motivating the following question:
Question 4.2. Is it consistent that there exist
![]() $h_0,h_1,h_2\in {}^{\kappa }\kappa $
such that
$h_0,h_1,h_2\in {}^{\kappa }\kappa $
such that
![]() $|h_0(\alpha )|<|h_1(\alpha )|<2^{|h_0(\alpha )|}=h_2(\alpha )$
and
$|h_0(\alpha )|<|h_1(\alpha )|<2^{|h_0(\alpha )|}=h_2(\alpha )$
and
![]() ${\mathfrak d_\kappa ^{h_2}(\in ^*)}<{\mathfrak d_\kappa ^{h_1}(\in ^*)}<{\mathfrak d_\kappa ^{h_0}(\in ^*)}$
?
${\mathfrak d_\kappa ^{h_2}(\in ^*)}<{\mathfrak d_\kappa ^{h_1}(\in ^*)}<{\mathfrak d_\kappa ^{h_0}(\in ^*)}$
?
The localisation cardinals
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
have a natural dual form
${\mathfrak d_\kappa ^{h}(\in ^*)}$
have a natural dual form
![]() $\mathfrak b_\kappa ^{h}(\in ^*)$
defined in the introduction, where duality is taken with respect to relational systems, as described in [Reference Blass, Foreman and Kanamori2]. In general, for many cardinal characteristics
$\mathfrak b_\kappa ^{h}(\in ^*)$
defined in the introduction, where duality is taken with respect to relational systems, as described in [Reference Blass, Foreman and Kanamori2]. In general, for many cardinal characteristics
![]() $\mathfrak x,\mathfrak y$
with duals
$\mathfrak x,\mathfrak y$
with duals
![]() $\mathfrak x',\mathfrak y'$
it is the case that if
$\mathfrak x',\mathfrak y'$
it is the case that if
![]() $\mathfrak x<\mathfrak y$
is consistent, then
$\mathfrak x<\mathfrak y$
is consistent, then
![]() $\mathfrak y'<\mathfrak x'$
is consistent as well. This motivates the following question, which has also been asked as Question 71 from [Reference Brendle, Brooke-Taylor, Friedman and Montoya3]:
$\mathfrak y'<\mathfrak x'$
is consistent as well. This motivates the following question, which has also been asked as Question 71 from [Reference Brendle, Brooke-Taylor, Friedman and Montoya3]:
Question 4.3. Do there exist functions
![]() $h,h'$
such that
$h,h'$
such that
![]() $\mathfrak b_\kappa ^{h}(\in ^*)<\mathfrak b_\kappa ^{h'}(\in ^*)$
is consistent?
$\mathfrak b_\kappa ^{h}(\in ^*)<\mathfrak b_\kappa ^{h'}(\in ^*)$
is consistent?
Indeed, despite being able to separate
![]() $\kappa ^+$
many cardinals of the form
$\kappa ^+$
many cardinals of the form
![]() ${\mathfrak d_\kappa ^{h}(\in ^*)}$
, it is currently unknown how to separate even two cardinals of the form
${\mathfrak d_\kappa ^{h}(\in ^*)}$
, it is currently unknown how to separate even two cardinals of the form
![]() $\mathfrak b_\kappa ^{h}(\in ^*)$
. The main obstacle to this is the lack of preservation theorems for forcings related to the generalised Baire space. Without such theorems, the preservation of, for example,
$\mathfrak b_\kappa ^{h}(\in ^*)$
. The main obstacle to this is the lack of preservation theorems for forcings related to the generalised Baire space. Without such theorems, the preservation of, for example,
![]() $\mathfrak b_\kappa ^{\mathsf {id}}(\in ^*)=\kappa ^+$
under a forcing that increases
$\mathfrak b_\kappa ^{\mathsf {id}}(\in ^*)=\kappa ^+$
under a forcing that increases
![]() $\mathfrak b_\kappa ^{\mathsf {pow}}(\in ^*)$
needs an analogue of Lemma 2.5. However, it is unclear what this forcing should be.
$\mathfrak b_\kappa ^{\mathsf {pow}}(\in ^*)$
needs an analogue of Lemma 2.5. However, it is unclear what this forcing should be.
Acknowledgement
The author wishes to thank Jörg Brendle for valuable discussions, suggestions, and extensive comments.