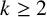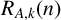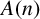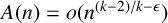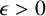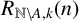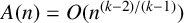1 Introduction
Let
$\mathbb {N}$
be the set of nonnegative integers and let A be a subset of nonnegative integers. We use
$A^n$
to denote the Cartesian product of n sets A, that is,
$$ \begin{align*}A^n=\{(a_1,a_2,\ldots,a_n):~a_1,a_2,\ldots,a_n\in A\}.\end{align*} $$
Let
$$ \begin{align*}R_{A,k}(n)=|\{ (a_{1}, a_2,\dots{}, a_{k})\in A^k: a_{1} +a_2+\cdots + a_{k} = n \}|, \end{align*} $$
$$ \begin{align*}R^{<}_{A,k}(n)=|\{ (a_{1}, a_2,\dots{}, a_{k})\in A^k: a_{1} + a_2+\cdots+ a_{k} = n, a_{1} <a_2< \cdots{} < a_{k} \}|, \end{align*} $$
$$ \begin{align*}R^{\le}_{A,k}(n)=|\{ (a_{1},a_2, \dots{} a_{k})\in A^k:a_{1} +a_2+ \cdots + a_{k} = n, a_{1} \le a_2\le \cdots{} \le a_{k} \}|, \end{align*} $$
where
$|\cdot |$
denotes the cardinality of a finite set. We say that
$R_{A,k}(n)$
is monotonically increasing in n from a certain point on (or eventually monotone increasing) if there exists an integer
$n_{0}$
such that
$R_{A,k}(n+1) \ge R_{A,k}(n)$
for all integers
$n\ge n_0$
. We define the monotonicity of the other two representation functions
$R^{<}_{A,k}(n)$
and
$R^{\le }_{A,k}(n)$
in the same way.
We denote the counting function of the set A by
$$ \begin{align*} A(n) = \sum_{\overset{a \in A}{a \le n}}1. \end{align*} $$
We define the lower asymptotic density of a set A of natural numbers by
$$ \begin{align*} \liminf_{n \rightarrow \infty}\frac{A(n)}{n} \end{align*} $$
and the asymptotic density by
$$ \begin{align*} \lim_{n \rightarrow \infty}\frac{A(n)}{n} \end{align*} $$
whenever the limit exists. The generating function of a set A of natural numbers is denoted by
$$ \begin{align*} G_{A}(x) = \sum_{a\in A}x^{a}. \end{align*} $$
Obviously, if
$\mathbb {N}\setminus A$
is finite, then each of the functions
$R_{A,2}(n), R^{<}_{A,2}(n)$
and
$R^{\le }_{A,2}(n)$
is eventually monotone increasing. In [Reference Erdős, Sárközy, Sós and Alladi4, Reference Erdős, Sárközy and Sós5], Erdős et al. investigated whether there exists a set A for which
$\mathbb {N}\setminus A$
is infinite and the representation functions are monotone increasing from a certain point on. They proved the following theorems.
Theorem A. The function
$R_{A,2}(n)$
is monotonically increasing from a certain point on if and only if the sequence A contains all the integers from a certain point on, that is, there exists an integer
$n_{1}$
with
$$ \begin{align*} A \cap \{n_{1}, n_{1}+1, n_{1}+2, \dots{} \} = \{n_{1}, n_{1}+1, n_{1}+2, \dots{} \}. \end{align*} $$
Theorem B. There exists an infinite set
$A\subseteq \mathbb {N}$
such that
$A(n) < n - cn^{1/3}$
for
$n> n_{0}$
and
$R^{<}_{A,2}(n)$
is monotone increasing from a certain point on.
Theorem C. If
$$ \begin{align*}A(n) = o\bigg(\frac{n}{\log n}\bigg),\end{align*} $$
then the functions
$R^{<}_{A,2}(n)$
and
$R^{\le }_{A,2}(n)$
cannot be monotonically increasing in n from a certain point on.
Theorem D. If
$A\subseteq \mathbb {N}$
is an infinite set with
$$ \begin{align*}\lim_{n\rightarrow \infty}\frac{n-A(n)}{\log n} = \infty, \end{align*} $$
then
$R^{\le }_{A,2}(n)$
cannot be monotone increasing from a certain point on.
The last theorem was proved independently by Balasubramanian [Reference Balasubramanian1]. Very little is known when
$k> 2$
. The following result was proved many years ago in [Reference Tang8] and independently in [Reference Kiss6].
Theorem E. If k is an integer with
$k> 2$
,
$A \subseteq \mathbb {N}$
and
$R_{A,k}(n)$
is monotonically increasing in n from a certain point on, then
$$ \begin{align*} A(n) = o\bigg(\frac{n^{2/k}}{(\log n)^{2/k}}\bigg) \end{align*} $$
cannot hold.
Dombi [Reference Dombi3] constructed sets A of asymptotic density
$\tfrac 12$
such that for
$k> 4$
, the function
$R_{A,k}(n)$
is monotone increasing from a certain point on. His constructions are based on the Rudin–Shapiro sets and Thue–Morse sequences. However, Dombi gave the following conjecture.
Dombi’s conjecture. If
$\mathbb {N}\setminus A$
is infinite, then
$R_{A,k}(n)$
cannot be strictly increasing.
For
$k \ge 3$
, Bell and Shallit [Reference Bell and Shallit2] recently gave a counterexample of Dombi’s conjecture by applying tools from automata theory and logic. They also proved the following result.
Theorem F. Let k be an integer with
$k\ge 3$
and let
$F\subseteq \mathbb {N}$
with
$0\notin F$
. If
$F(n) = o(n^{\alpha })$
for
$\alpha < (k-2)/k$
and
$A = \mathbb {N}\setminus F$
, then
$R_{A,k}(n)$
is eventually strictly increasing.
In this paper, we improve this result in the following theorem.
Theorem 1.1. Let k be an integer with
$k\ge 3$
. If
$A \subseteq \mathbb {N}$
satisfies
$$ \begin{align*}A(n) \leqslant \frac{n^{{(k-2)}/{(k-1)}}}{\sqrt[k-1]{(k-2)!}} - 2\end{align*} $$
for all sufficiently large integers n, then
$R_{\mathbb {N}\setminus A,k}(n)$
is eventually strictly increasing.
In particular, for
$k = 3$
, this gives the following corollary.
Corollary 1.2. If
$A \subseteq \mathbb {N}$
satisfies
$A(n) \leqslant \sqrt {n} - 2$
for all sufficiently large integers n, then
$R_{\mathbb {N}\setminus A,3}(n)$
is eventually strictly increasing.
After we uploaded our paper to arXiv, we were informed that Mihalis Kolountzakis proved in an unpublished note that if
$A \subseteq \mathbb {N}$
satisfies
$A(n) \leqslant c\sqrt {n}$
for a sufficiently small positive constant c, then
$R_{\mathbb {N}\setminus A,3}(n)$
is eventually strictly increasing. We improve the constant factor in the following result.
Theorem 1.3. If
$A \subseteq \mathbb {N}$
satisfies
$A(n) \leqslant ({2}/{\sqrt {3}}) \sqrt {n}-2$
for all sufficiently large integers n, then
$R_{\mathbb {N}\setminus A,3}(n)$
is eventually strictly increasing.
It turns out from the next theorem that the upper bound for the counting function of A in Theorem 1.1 is tight up to a constant factor.
Theorem 1.4. Suppose that
$f(n)$
is a function satisfying
$f(n)\rightarrow \infty $
as
$n\rightarrow \infty $
. Then there is a set
$A\subseteq \mathbb {N}$
such that
$A(n)<\!\!\sqrt [k-1]{k-1}\cdot n^{{(k-2)}/{(k-1)}}+f(n)$
for all sufficiently large integers n and
$R_{\mathbb {N}\setminus A,k}(n)<R_{\mathbb {N}\setminus A,k}(n-1)$
for infinitely many positive integers n.
Shallit [Reference Shallit7] recently constructed a set A with positive lower asymptotic density such that the function
$R_{\mathbb {N}\setminus A,3}(n)$
is strictly increasing.
2 Proofs
The proofs of the theorems are based on the next lemma, coming from Bell and Shallit’s paper [Reference Bell and Shallit2] although not explicitly stated there.
Lemma 2.1. For any positive integers n and k with
$k\ge 3$
,
$$ \begin{align*}R_{\mathbb{N}\setminus A,k}(n)-R_{\mathbb{N}\setminus A,k}(n-1) &=\binom{n+k-2}{k-2}+\sum_{i=1}^{k-2}\binom{k}{i}(-1)^{i}\Bigg(\sum_{m=0}^{n}\binom{m+k-i-2}{k-i-2}R_{A,i}(n-m)\Bigg)\\ &\quad + (-1)^{k-1}kR_{A,k-1}(n)+(-1)^{k}(R_{A,k}(n)-R_{A,k}(n-1)). \end{align*} $$
Proof. Observe that
$$ \begin{align*} (1-x)(G_{\mathbb{N}\setminus A}(x))^{k}& = \sum_{n=0}^{\infty}R_{\mathbb{N}\setminus A,k}(n)x^{n}-\sum_{n=0}^{\infty}R_{\mathbb{N}\setminus A,k}(n)x^{n+1}\\ &=R_{\mathbb{N}\setminus A,k}(0)+\sum_{n=1}^{\infty}(R_{\mathbb{N}\setminus A,k}(n)-R_{\mathbb{N}\setminus A,k}(n-1))x^{n}. \end{align*} $$
However,
$$ \begin{align*} &(1-x)((G_{\mathbb{N}\setminus A)}(x))^{k} = (1-x)\bigg(\frac{1}{1-x}-G_{A}(x)\bigg)^{k} = (1-x)\sum_{i=0}^{k}\binom{k}{i}\frac{(-1)^{i}}{(1-x)^{k-i}}G_{A}(x)^{i}\\ &=\frac{1}{(1-x)^{k-1}} + \sum_{i=1}^{k-2}\binom{k}{i}\frac{(-1)^{i}}{(1-x)^{k-i-1}}G_{A}(x)^{i}+(-1)^{k-1}kG_{A}(x)^{k-1}+(-1)^{k}(1-x)G_{A}(x)^{k}. \end{align*} $$
It is well known that
$$ \begin{align*} \frac{1}{(1-x)^{m}} = \sum_{n=0}^{\infty}\binom{n+m-1}{m-1}x^{n}. \end{align*} $$
It follows that
$$ \begin{align*} &R_{\mathbb{N}\setminus A,k}(0)+\sum_{n=1}^{\infty}(R_{\mathbb{N}\setminus A,k}(n)-R_{\mathbb{N}\setminus A,k}(n-1))x^{n}\\ &\quad=\sum_{n=0}^{\infty}\binom{n+k-2}{k-2}x^{n} + \sum_{i=1}^{k-2}(-1)^{i}\binom{k}{i}\sum_{n=0}^{\infty}\Bigg(\sum_{m=0}^{n}\binom{m+k-i-2}{k-i-2}R_{A,i}(n-m)\Bigg)x^{n}\\ &\qquad +(-1)^{k-1}k\sum_{n=0}^{\infty}R_{A,k-1}(n)x^{n}+(-1)^{k}R_{A,k}(0)+(-1)^{k}\sum_{n=0}^{\infty}(R_{A,k}(n)-R_{A,k}(n-1))x^{n}. \end{align*} $$
By comparing the coefficient of
$x^{n}$
on both sides of this equation, Lemma 2.1 follows immediately.
Proof of Theorem 1.1.
Clearly,
$$ \begin{align*} R_{A,i}(n) & =|\{ (a_{1}, a_2,\dots{}, a_{i})\in A^i: a_{1} + a_2+\cdots{} + a_{i} = n \}|\\ &\le |\{ (a_{1},a_2, \dots{},a_{i-1})\in A^{i-1}: a_{1},a_2, \dots{} ,a_{i-1} \le n \}| = A(n)^{i-1}. \end{align*} $$
By Lemma 2.1, there exist constants
$c_{1},c_{2},c_{3}, c_{4}$
only depending on k such that
$$ \begin{align*} &R_{\mathbb{N}\setminus A,k}(n)-R_{\mathbb{N}\setminus A,k}(n-1)\\ &\quad= \binom{n+k-2}{k-2}+\sum_{i=1}^{k-2}\binom{k}{i}(-1)^{i}\Bigg(\sum_{m=0}^{n}\binom{m+k-i-2}{k-i-2}R_{A,i}(n-m)\Bigg)\\ &\qquad +(-1)^{k-1}kR_{A,k-1}(n)+(-1)^{k}(R_{A,k}(n)-R_{A,k}(n-1))\\ &\quad\ge \frac{n^{k-2}}{(k-2)!}-\sum_{i=1}^{k-2}2^{k}\sum_{m=0}^{n}\binom{m+k-i-2}{k-i-2}A(n)^{i-1}-kR_{A,k-1}(n)-A(n)^{k-1}\\ &\quad\ge \frac{n^{k-2}}{(k-2)!}-\sum_{i=1}^{k-2}2^{k}A(n)^{i-1}\binom{n+k-i-1}{k-i-2}\\ &\qquad -k\bigg(\frac{n^{{(k-2)}/{(k-1)}}}{\sqrt[k-1]{(k-2)!}}\bigg)^{k-2} -\bigg(\frac{n^{{(k-2)}/{(k-1)}}}{\sqrt[k-1]{(k-2)!}}-2\bigg)^{k-1}\\ &\quad\ge \frac{n^{k-2}}{(k-2)!}-c_{1}\sum_{i=1}^{k-2}A(n)^{i-1}n^{k-i-2}-k\cdot\frac{n^{{(k-2)^{2}}/{(k-1)}}}{((k-2)!)^{{(k-2)}/{(k-1)}}}\\ &\qquad -\bigg(\frac{n^{k-2}}{(k-2)!}-2(k-1)\frac{n^{{(k-2)^2}/{(k-1)}}} {((k-2)!)^{{(k-2)}/{(k-1)}}}+c_{2}n^{{(k-2)(k-3)}/{(k-1)}}\bigg)\\ &\quad\ge \frac{n^{k-2}}{(k-2)!}-c_{3}n^{k-3}-k\frac{n^{{(k-2)^{2}}/{(k-1)}}}{((k-2)!)^{{(k-2)}/{(k-1)}}} \\ &\qquad -\bigg(\frac{n^{k-2}}{(k-2)!}-\frac{2(k-1)n^{{(k-2)^{2}}/{(k-1)}}}{((k-2)!)^{{(k-2)}/{(k-1)}}} +c_{2}n^{{(k-2)(k-3)}/{(k-1)}}\bigg)\\ &\quad= \frac{k-2}{((k-2)!)^{{(k-2)}/{(k-1)}}}\cdot n^{{(k-2)^{2}}/{(k-1)}}-c_{4}n^{k-3}. \end{align*} $$
Hence,
$R_{\mathbb {N}\setminus A,k}(n)-R_{\mathbb {N}\setminus A,k}(n-1)>0$
when n is large enough.
Lemma 2.2. For any set A of natural numbers and for any natural number n, one has
$R_{A, 3}(n) \leqslant \tfrac 34 A(n)^2+\{\tfrac 14A(n)^{2}\},$
where
$\{x\}$
denotes the fractional part of x.
Note that Lemma 2.2 is sharp: if
$A = \{0,1,\dots {} ,m\}$
, then
$$ \begin{align*} R_{A, 3}\bigg(\bigg \lfloor \frac{3m}{2} \bigg \rfloor \bigg) = \frac{3}{4} A\bigg(\bigg \lfloor \frac{3m}{2} \bigg \rfloor\bigg)^2+\bigg\{\frac{A( \lfloor {3m}/{2} \rfloor)^{2}}{4}\bigg\}, \end{align*} $$
where
$\lfloor y\rfloor $
denotes the maximal integer not greater than y.
Proof of Lemma 2.2.
Fix a natural number n. Let
$A \cap [1, n]=\{a_1<a_2<\cdots <a_m\}$
and
$\overline {A}=\{n-a_m<n-a_{m-1}<\cdots <n-a_1\}$
. For
$i=1,2,\ldots ,m$
, we define
$$ \begin{align*}A_i=\{a_i+a_1<a_i+a_2<\cdots<a_i+a_{m+1-i}<a_{i+1}+a_{m+1-i}<\cdots<a_m+a_{m+1-i}\}.\end{align*} $$
Clearly,
$$ \begin{align*} R_{A, 3}(n)=\sum_{i=1}^m|A_i\cap \overline{A}| & \leqslant \sum_{i=1}^m \min \{2 m-2 i+1, m\}\\ &=\sum_{i=1}^{\lfloor{m}/{2}\rfloor} m+\sum_{i=\lfloor{m}/{2}\rfloor+1}^m(2 m-2 i+1)\\ &=m\bigg\lfloor\frac{m}{2}\bigg\rfloor+\bigg(m-\bigg\lfloor\frac{m}{2}\bigg\rfloor\bigg)^2=\frac{3}{4} m^2+\bigg\{\frac{m^2}{4}\bigg\}. \\[-3.4pc] \end{align*} $$
Proof of Theorem 1.3.
Applying Lemma 2.1 for
$k = 3$
,
$$ \begin{align*} &R_{\mathbb{N} \backslash A,3}(n) -R_{\mathbb{N} \backslash A,3}(n-1) \\ &\quad = n + 1 -3\sum_{m=0}^{n}R_{A,1}(n-m)+3R_{A,2}(n)-(R_{A,3}(n)-R_{A,3}(n-1)) \\ &\quad = n + 1 - 3A(n) + 3R_{A,2}(n) - (R_{A, 3}(n) - R_{A, 3}(n-1)). \end{align*} $$
Hence, by Lemma 2.2,
$$ \begin{align*} &R_{\mathbb{N} \backslash A,3}(n) -R_{\mathbb{N} \backslash A,3}(n-1)\ge n + 1 - 3A(n) - R_{A,3}(n) \\ &\quad \ge n+1-3\bigg(\frac{2}{\sqrt{3}}\sqrt{n}-2\bigg) -\frac{3}{4}\bigg(\frac{2}{\sqrt{3}}\sqrt{n}-2\bigg)^{2}-\frac{1}{4}=\frac{15}{4}> 0, \end{align*} $$
which completes the proof.
Proof of Theorem 1.4.
We may suppose that
$f(n)<\!\!\sqrt [k-1]{k-1}\cdot n^{{(k-2)}/{(k-1)}}$
. We define an infinite sequence of natural numbers
$N_{1}, N_{2}, \dots {}$
by induction. Let
$N_{1} = 100k^4$
. Assume that
$N_{1}, \dots {} ,N_{j}$
are already defined. Let
$N_{j+1}$
be an even number with
$N_{j+1}> 100k^4N_{j}^{k-1}$
and
$f(n)> (k-1)(N_{1}^{k-2} + \cdots {} + N_{j}^{k-2})$
for every
$n \ge N_{j+1}$
. We define the set A by
$$ \begin{align*} A = \bigcup_{j=1}^{\infty}\{N_{j}, 2N_{j}, 3N_{j}, \dots{} ,(k-1)N_{j}^{k-1}\}. \end{align*} $$
First, we give an upper estimation for
$A(n)$
. Let
$n\ge 100k^4$
. Then there exists an index j such that
$N_{j} \le n < N_{j+1}$
. Define l as the largest integer with
$l \le (k-1)N_{j}^{k-2}$
and
$lN_{j} \le n$
. Then,
$$ \begin{align*} &A(n) -\!\!\sqrt[k-1]{k-1}n^{{(k-2)}/{(k-1)}} \\ &\quad\le (k-1)(N_{1}^{k-2} + \cdots{} + N_{j}^{k-2}) + l - \!\!\sqrt[k-1]{k-1}(lN_{j})^{{(k-2)}/{(k-1)}}\\ &\quad=(k-1)(N_{1}^{k-2} + \cdots{} + N_{j}^{k-2}) + l^{{(k-2)}/{(k-1)}}(l^{{1}/{(k-1)}}-(k-1)^{{1}/{(k-1)}}N_{j}^{{(k-2)}/{(k-1)}})\\ &\quad \le f(n), \end{align*} $$
which implies that
$$ \begin{align*}A(n)<\!\!\sqrt[k-1]{k-1}\cdot n^{{(k-2)}/{(k-1)}}+f(n). \end{align*} $$
Next, we shall prove that there exist infinitely many positive integers n such that
$R_{\mathbb {N}\setminus A,k}(n)<R_{\mathbb {N}\setminus A,k}(n-1)$
. To prove this, we divide into two cases according to the parity of k.
Suppose that k is an odd integer. For
$j=1,2,\ldots ,$
we define
$$ \begin{align*}u_j=(k-1)N_{j}^{k-1} + 100(k-2)(k-1)^3N_{j}^{k-2}. \end{align*} $$
Now, we show that
$R_{\mathbb {N}\setminus A,k}(u_j) < R_{\mathbb {N}\setminus A,k}(u_j-1)$
when j is large enough.
Since all the elements of A are even and
$u_j-1$
is odd, it follows that
$R_{A,k}(u_j-1)=0$
. By Lemma 2.1,
$$ \begin{align} &\nonumber R_{\mathbb{N}\setminus A,k}(u_j) - R_{\mathbb{N}\setminus A,k}(u_j-1)\\ &\quad=\nonumber \binom{u_j+k-2}{k-2}+\sum_{i=1}^{k-2}\binom{k}{i}(-1)^{i}\Bigg(\sum_{m=0}^{u_j}\binom{m+k-i-2}{k-i-2}R_{A,i}(u_j-m)\Bigg)\\ &\qquad \nonumber + (-1)^{k-1}kR_{A,k-1}(u_j)+ (-1)^{k}(R_{A,k}(u_j)-R_{A,k}(u_j-1))\\ &\quad\le \nonumber\binom{u_j+k-2}{k-2}+k^2\Bigg(\sum_{m=0}^{u_j}\binom{m+k-4}{k-4}R_{A,2}(u_j-m)\Bigg)\\ &\qquad +\sum_{i=3}^{k-2}2^{k}\sum_{m=0}^{u_j}\binom{m+k-i-2}{k-i-2}A(u_j)^{i-1}+ kR_{A,k-1}(u_j)-R_{A,k}(u_j). \end{align} $$
Next we shall give a bound for each term of the right-hand side of (2.1). There exists a constant
$c_5$
only depending on k such that
$$ \begin{align} \binom{u_j+k-2}{k-2} \le \frac{(k-1)^{k-2}N_{j}^{k^{2}-3k+2}+100(k-2)^2(k-1)^{k}N_{j}^{k^{2}-3k+1}+c_{5}N_{j}^{k^{2}-3k}}{(k-2)!} \end{align} $$
and
$$ \begin{align} & k^2\sum_{m=0}^{u_j}\binom{m+k-4}{k-4}R_{A,2}(u_j-m)\le k^2\sum_{m=0}^{u_j}\binom{m+k-4}{k-4}A(u_j-m) \nonumber\\ &\quad\le \nonumber k^2\sum_{m=0}^{u_j}\binom{m+k-4}{k-4}A(kN_{j}^{k-1})\le k^2\sum_{m=0}^{u_j}\binom{m+k-4}{k-4}2\sqrt[k-1]{k-1}(kN_j^{k-1})^{{(k-2)}/{(k-1)}} \\ &\quad\le \nonumber k^2\sum_{m=0}^{u_j}\binom{m+k-4}{k-4}2k N_j^{k-2}=2k^3N_j^{k-2}\binom{u_j+k-3}{k-3}\\ &\quad\le 2k^3N_j^{k-2}\binom{kN_j^{k-1}}{k-3}\le \frac{2k^k}{(k-3)!}N_j^{k^2-3k+1}. \end{align} $$
Furthermore,
$$ \begin{align} &\nonumber\sum_{i=3}^{k-2}2^{k}\sum_{m=0}^{u_j}\binom{m+k-i-2}{k-i-2}A(u_j)^{i-1}\\ &\quad\le \nonumber c_{6}\sum_{i=3}^{k-2}2^{k}\sum_{m=0}^{u_j}\binom{m+k-i-2}{k-i-2}((N_{j}^{k-1})^{{(k-2)}/{(k-1)}})^{i-1}\\ &\quad\le\nonumber c_{6}\sum_{i=3}^{k-2}2^{k}N_{j}^{(k-2)(i-1)}\sum_{m=0}^{u_j}\binom{m+k-i-2}{k-i-2}\\ &\quad= \nonumber c_{6}\sum_{i=3}^{k-2}2^{k}N_{j}^{(k-2)(i-1)}\binom{u_j+k-i-1}{k-i-1}\\ &\quad\le c_{7}\sum_{i=3}^{k-2}N_{j}^{(k-2)(i-1)}\cdot N_{j}^{(k-1)(k-i-1)} =c_{7}\sum_{i=3}^{k-2}N_{j}^{k^{2}-3k-i+3} \le c_{8}N_{i}^{k^{2}-3k}, \end{align} $$
where
$c_{6}, c_{7}$
and
$c_{8}$
are constants only depending on k. Moreover,
$$ \begin{align} R_{A,k-1}(u_j))&\le \nonumber A(u_j)^{k-2} \le A(kN_{j}^{k-1})^{k-2}\\ & \le (2\sqrt[k-1]{k-1}(kN_{j}^{k-1})^{{(k-2)}/{(k-1)}})^{k-2} \le (2k)^{k-2}N_{j}^{(k-2)^{2}}. \end{align} $$
Obviously,
$$ \begin{align*} &R_{A,k}(u_j) \\ &\quad\ge \bigg|\bigg\{(x_{1}, \dots{} ,x_{k})\in (\mathbb{Z}^+)^k: \sum_{t=1}^k x_t=u_j, N_{j}\mid x_{t}, x_{t} \le (k-1)N_{j}^{k-1}~\text{for}~t=1,\ldots,k\bigg\}\bigg|\\ &\quad=\bigg|\bigg\{(y_{1}, \dots{} ,y_{k})\in (\mathbb{Z}^+)^k: \sum_{t=1}^k y_t = \frac{u_j}{N_j}, y_{t} \le (k-1)N_{j}^{k-2}~\text{for}~t=1,\ldots,k\bigg\}\bigg|\\ &\quad=\bigg|\bigg\{(y_{1}, \dots{} ,y_{k})\in (\mathbb{Z}^+)^k: \sum_{t=1}^k y_t = \frac{u_j}{N_j}\bigg\} \bigg|\\ &\qquad - \bigg|\bigg\{(y_{1}, \dots{} ,y_{k})\in (\mathbb{Z}^+)^k: \sum_{t=1}^k y_t = \frac{u_j}{N_j},~y_{t}> (k-1)N_{j}^{k-2}~\text{for some}~t\in \{1,\ldots,k\}\bigg\}\bigg|. \end{align*} $$
We see that
$$ \begin{align*} &\bigg|\bigg\{(y_{1}, \dots{} ,y_{k})\in (\mathbb{Z}^+)^k: y_{1} + \cdots{} + y_{k} = \frac{u_j}{N_j}\bigg\}\bigg|\\ &\quad= \binom{{u_j}/{N_j}-1}{k-1} \ge \frac{N_{j}^{k^{2}-3k+2}+100(k-2)(k-1)^{k+2}N_{j}^{k^{2}-3k+1}+c_{9}N_{j}^{k^{2}-3k}}{(k-1)!}, \end{align*} $$
where
$c_{9}$
is a constant only depending on k, and
$$ \begin{align*} &\bigg|\bigg\{(y_{1}, \dots{} ,y_{k})\in (\mathbb{Z}^+)^k: \sum_{t=1}^k y_t = \frac{u_j}{N_j},~y_{t}> (k-1)N_{j}^{k-2}~\text{for some}~t\in \{1,\ldots,k\}\bigg\}\bigg|\\ &\quad= k|\{(z_{1}, \dots{} ,z_{k})\in (\mathbb{Z}^+)^k: z_{1} + \cdots{} + z_{k} = 100(k-2)(k-1)^3N_{j}^{k-3}\}|\\ &\quad\le k(100(k-2)(k-1)^3)^kN_{j}^{k^{2}-3k}. \end{align*} $$
The last equality holds because if
$y_{1} + \cdots {} + y_{k} = {u_j}/{N_j}$
with
$y_{t}> (k-1)N_{j}^{k-1}$
, then
$$ \begin{align*}y_{1} + \cdots{} + y_{t-1} + (y_{t}-(k-1)N_{j}^{k-2}) + y_{t+1} + \cdots{} + y_{k} = 100(k-2)(k-1)^3N_{j}^{k-3},\end{align*} $$
where every term is positive. Furthermore, if
$z_{1} + \cdots {} + z_{k} = 100(k-2)(k-1)^3N_{j}^{k-3}$
,
$z_{i}\in \mathbb {Z}^{+}$
, then one can create k different sums of the form
$ y_{1} + \cdots {} + y_{k} = {u_j}/{N_j}$
with
$y_{i} = z_{i}$
if
$i\neq t$
and
$y_{t} = z_{t} + (k-1)N_{j}^{k-2}$
. Therefore,
$$ \begin{align} R_{A,k}(u_j) \ge \frac{(k-1)^{k-1}N_{j}^{k^{2}-3k+2}+100(k-2)(k-1)^{k+2}N_{j}^{k^{2}-3k+1}+c_{10}N_{j}^{k^{2}-3k}}{(k-1)!}, \end{align} $$
where
$c_{10}$
is a constant. In view of (2.1)–(2.6),
$$ \begin{align*} &R_{\mathbb{N}\setminus A,k}(u_j) - R_{\mathbb{N}\setminus A,k}(u_j-1)\\ & \quad\le \frac{(k-1)^{k-2}N_{j}^{k^{2}-3k+2}+100(k-2)^2(k-1)^k N_{j}^{k^{2}-3k+1}+c_{5}N_{j}^{k^{2}-3k}}{(k-2)!}\\ &\qquad +\frac{2k^k}{(k-3)!}N_j^{k^2-3k+1} + c_{8}N_{i}^{k^{2}-3k} + (2k)^{k-2}N_{j}^{(k-2)^{2}}\\ &\qquad -\frac{(k-1)^{k-1}N_{j}^{k^{2}-3k+2}+100(k-2)(k-1)^{k+2}N_{j}^{k^{2}-3k+1}+c_{10}N_{j}^{k^{2}-3k}}{(k-1)!}\\ &\quad=\bigg( \frac{2k^k}{(k-3)!} -100\frac{(k-1)^{k}}{(k-3)!} \bigg)N_{j}^{k^{2}-3k+1} + (2k)^{k-2}N_{j}^{(k-2)^{2}} + c_{11}N_{j}^{k^{2}-3k}, \end{align*} $$
where
$c_{11}$
is a constant. Thus, we have
$R_{\mathbb {N}\setminus A,k}(u_j) < R_{\mathbb {N}\setminus A,k}(u_j-1)$
when j is large enough.
If k is even, then the same argument shows that
$R_{\mathbb {N}\setminus A,k}(u_j+1) < R_{\mathbb {N}\setminus A,k}(u_j)$
when j is large enough.
