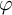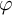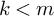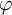1 Introduction
Let
![]() $(X^{n},\omega )$
be a closed Kähler manifold, and let
$(X^{n},\omega )$
be a closed Kähler manifold, and let
![]() $m\mathrm{SH}(X, \omega )$
be the space of
$m\mathrm{SH}(X, \omega )$
be the space of
![]() $(m, \omega )$
-sh functions on X,
$(m, \omega )$
-sh functions on X,
![]() $1 \leqslant m\leqslant n$
. m-sh functions were introduced by Błocki [Reference Błocki9] as the natural space of weak solutions to the complex m-Hessian equation on domains in
$1 \leqslant m\leqslant n$
. m-sh functions were introduced by Błocki [Reference Błocki9] as the natural space of weak solutions to the complex m-Hessian equation on domains in
![]() $\mathbb{C}^n$
, and they naturally interpolate between plurisubharmonic (psh) and subharmonic (sh) functions as m varies.
$\mathbb{C}^n$
, and they naturally interpolate between plurisubharmonic (psh) and subharmonic (sh) functions as m varies.
As such, m-sh functions share many similarities with psh functions. Both support a robust potential theory which has been the subject of much interest in recent years (see, e.g., [Reference Bedford and Taylor7, Reference Bedford and Taylor8, Reference Błocki9, Reference Åhag, Cegrell, Czyż and Hiệp1, Reference Dinew and Kołodziej19, Reference Lu and Nguyên28, Reference Darvas, Di Nezza and Lu12]). One major difference however is the lack of a strong relation between m-sh functions and analytic geometry, something which can be seen, for instance, in our inability to solve the
![]() $\overline {\partial }$
-problem with generic m-sh weights. This geometric connection is utilized to great effect in the study of psh functions, and is largely responsible for our understanding of what singularities of psh functions can look like, for example, Demailly approximation [Reference Demailly16] and Siu’s theorem [Reference Siu32].
$\overline {\partial }$
-problem with generic m-sh weights. This geometric connection is utilized to great effect in the study of psh functions, and is largely responsible for our understanding of what singularities of psh functions can look like, for example, Demailly approximation [Reference Demailly16] and Siu’s theorem [Reference Siu32].
Our goal in this paper is to develop a better understanding of the singularities of m-sh functions, proceeding in a more ad-hoc manner. A natural starting place is to study their behaviour along complex submanifolds:
Theorem 1.1. Let
![]() $V\subset X$
be a closed, complex submanifold of codimension k and
$V\subset X$
be a closed, complex submanifold of codimension k and
![]() $\Omega $
a sufficiently small m-hyperconvex neighborhood of V.
$\Omega $
a sufficiently small m-hyperconvex neighborhood of V.
For each
![]() $m \leqslant k$
, there exists an
$m \leqslant k$
, there exists an
![]() $(m,\omega )$
-sh function
$(m,\omega )$
-sh function
![]() $\psi_V$
on X, locally bounded and maximal on
$\psi_V$
on X, locally bounded and maximal on
![]() $\Omega \setminus V$
, with the same singularity type as
$\Omega \setminus V$
, with the same singularity type as
 $$\begin{align*}G_m(r) := \begin{cases} \log r &\text{ when }m=k\\ -r^{-2\left(\frac{k}{m}-1\right)} & \text{ when }m < k,\end{cases} \end{align*}$$
$$\begin{align*}G_m(r) := \begin{cases} \log r &\text{ when }m=k\\ -r^{-2\left(\frac{k}{m}-1\right)} & \text{ when }m < k,\end{cases} \end{align*}$$
where here
![]() $r := \mathrm{dist}_\omega (\cdot , V)$
is the
$r := \mathrm{dist}_\omega (\cdot , V)$
is the
![]() $\omega $
-distance to V.
$\omega $
-distance to V.
With the function
![]() $\psi_V$
in hand, we can study generalized Lelong numbers, in the sense of Demailly [Reference Demailly17], and relative types, in the sense of Rashkovskii [Reference Rashkovskii30], of arbitrary m-sh functions along V.
$\psi_V$
in hand, we can study generalized Lelong numbers, in the sense of Demailly [Reference Demailly17], and relative types, in the sense of Rashkovskii [Reference Rashkovskii30], of arbitrary m-sh functions along V.
Corollary 1.2. Let V,
![]() $\psi_V$
and r be as in Theorem 1.1. Then for any
$\psi_V$
and r be as in Theorem 1.1. Then for any
![]() $\varphi \in m\mathrm{SH}(X, \omega )$
, the limit
$\varphi \in m\mathrm{SH}(X, \omega )$
, the limit
 $$\begin{align*}\nu(\varphi, \psi_V) := \lim_{s\rightarrow 0} \frac{C_{k,m}}{s^{2k - 2k/m}} \int_{\{r < s\}} \sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} r^2)^{m-1}\wedge\omega^{n-m} \end{align*}$$
$$\begin{align*}\nu(\varphi, \psi_V) := \lim_{s\rightarrow 0} \frac{C_{k,m}}{s^{2k - 2k/m}} \int_{\{r < s\}} \sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} r^2)^{m-1}\wedge\omega^{n-m} \end{align*}$$
exists and is both finite and nonnegative. Here,
![]() $C_{k,m}$
is a constant depending only on k and m.
$C_{k,m}$
is a constant depending only on k and m.
Corollary 1.3. Let V and
![]() $\psi_V$
be as in Theorem 1.1. Let
$\psi_V$
be as in Theorem 1.1. Let
![]() $W_{s} := \{\psi_V < s\}$
. Then for any
$W_{s} := \{\psi_V < s\}$
. Then for any
![]() $\varphi \in m\mathrm{SH}(X, \omega )$
, the limit
$\varphi \in m\mathrm{SH}(X, \omega )$
, the limit
exists and is both finite and nonnegative.
Note that, if
![]() $m> k$
, then we can still apply Corollaries 1.2 and 1.3 by just considering
$m> k$
, then we can still apply Corollaries 1.2 and 1.3 by just considering
![]() $\varphi \in m\mathrm{SH}(X,\omega )\subset k\mathrm{SH}(X,\omega )$
.
$\varphi \in m\mathrm{SH}(X,\omega )\subset k\mathrm{SH}(X,\omega )$
.
Corollaries 1.2 and 1.3 are the first such results about the singularities of m-sh functions along submanifolds of positive dimension – for more information about Lelong numbers of m-sh functions at points, we refer the reader to [Reference Dinew and Kołodziej19], and also [Reference Harvey and Lawson22, Reference Harvey and Lawson23, Reference Chu11]. As one sees from Theorem 1.1 and Corollary 1.2, the natural scaling changes with the codimension k when
![]() $k \geqslant m$
, something quite different from the psh case.
$k \geqslant m$
, something quite different from the psh case.
The scaling we obtain agrees with what one might naively expect if they were to assume that the restriction of
![]() $\varphi $
to any k-dimensional submanifold transverse to V were still m-sh. This assumption is very much not true;
$\varphi $
to any k-dimensional submanifold transverse to V were still m-sh. This assumption is very much not true;
![]() $\varphi $
will generally lose positivity when restricted to a submanifold since
$\varphi $
will generally lose positivity when restricted to a submanifold since
![]() $\sqrt {-1}\partial \overline {\partial } \varphi $
can have negative eigenvalues. That we still recover this optimal scaling may seem surprising in light of this.
$\sqrt {-1}\partial \overline {\partial } \varphi $
can have negative eigenvalues. That we still recover this optimal scaling may seem surprising in light of this.
This loss of positivity also means that we cannot use a slicing argument to reduce our situation to the case of studying the singularity of
![]() $\varphi $
at the origin, as one does in the psh case. Instead, we show Theorem 1.1 by constructing smooth sub- and supersolutions (essentially) to the equation
$\varphi $
at the origin, as one does in the psh case. Instead, we show Theorem 1.1 by constructing smooth sub- and supersolutions (essentially) to the equation
![]() $H^m(\varphi ) = 0$
on
$H^m(\varphi ) = 0$
on
![]() $\Omega \setminus V$
. This is done by taking small perturbations of
$\Omega \setminus V$
. This is done by taking small perturbations of
![]() $G_m(r)$
, using the computations of Tam-Yu [Reference Tam and Yu33] for the Hessian of r. The function
$G_m(r)$
, using the computations of Tam-Yu [Reference Tam and Yu33] for the Hessian of r. The function
![]() $\psi_V$
is then realized as a singularity type envelope; the sub- and supersolutions guarantee that
$\psi_V$
is then realized as a singularity type envelope; the sub- and supersolutions guarantee that
![]() $\psi_V$
has the correct singularity type.
$\psi_V$
has the correct singularity type.
We show that our construction of subsolutions can be modified in Proposition 3.7 to produce m-sh functions whose behaviour near V is roughly like
for any smooth
![]() $\theta \geqslant 0$
(see Proposition 3.7 for a precise statement). This behaviour is predicted by Åhag-Cegrell-Czyż-Hiệp’s [Reference Åhag, Cegrell, Czyż and Hiệp1], and Hung-Phu’s [Reference Hung and Van Phu24], solutions to certain highly degenerate complex Monge-Ampère (resp. complex Hessian) equations. Their solutions are constructed as a sequence of envelopes, and the resulting behaviour of the solutions near V is not easily seen. Our examples provide constraints on what that behaviour can be (which can be quite strong in fact – see Remark 3.8), but without corresponding supersolutions, we cannot deduce the exact singularity types of the solutions.
$\theta \geqslant 0$
(see Proposition 3.7 for a precise statement). This behaviour is predicted by Åhag-Cegrell-Czyż-Hiệp’s [Reference Åhag, Cegrell, Czyż and Hiệp1], and Hung-Phu’s [Reference Hung and Van Phu24], solutions to certain highly degenerate complex Monge-Ampère (resp. complex Hessian) equations. Their solutions are constructed as a sequence of envelopes, and the resulting behaviour of the solutions near V is not easily seen. Our examples provide constraints on what that behaviour can be (which can be quite strong in fact – see Remark 3.8), but without corresponding supersolutions, we cannot deduce the exact singularity types of the solutions.
In the context of this paper, the examples in Proposition 3.7 are interesting in that they show that
![]() $\sigma (\varphi , \psi_V) \not = \nu (\varphi , \psi_V)$
in general, unlike the more classical case when the weight is singular only at a point. Indeed, these examples show that it is possible to have
$\sigma (\varphi , \psi_V) \not = \nu (\varphi , \psi_V)$
in general, unlike the more classical case when the weight is singular only at a point. Indeed, these examples show that it is possible to have
![]() $\sigma (\varphi , \psi_V) = 0$
but
$\sigma (\varphi , \psi_V) = 0$
but
![]() $\nu (\varphi , \psi_V)> 0$
– the reverse is impossible (see Corollary 2.12).
$\nu (\varphi , \psi_V)> 0$
– the reverse is impossible (see Corollary 2.12).
We conclude that we cannot expect constraints which are significantly stronger than Corollaries 1.2 and 1.3 when V has codimension
![]() $\geqslant m$
. When the codimension is less than m, however, our next result finds that the situation is much closer to the psh case:
$\geqslant m$
. When the codimension is less than m, however, our next result finds that the situation is much closer to the psh case:
Theorem 1.4. Suppose that
![]() $V\subset X$
is a complex submanifold of codimension k and
$V\subset X$
is a complex submanifold of codimension k and
![]() $\varphi \in m\mathrm{SH}(X,\omega )$
. Suppose that
$\varphi \in m\mathrm{SH}(X,\omega )$
. Suppose that
![]() $k < m$
, and let
$k < m$
, and let
![]() $\psi_V\in k\mathrm{SH}(X,\omega )$
be the function constructed in Theorem 1.1. Then the function
$\psi_V\in k\mathrm{SH}(X,\omega )$
be the function constructed in Theorem 1.1. Then the function
 $$\begin{align*}L_{\psi_V}(\varphi)(z) := \liminf_{\substack{z'\rightarrow z\\ z'\not\in V}} \frac{\varphi(z')}{\psi_V(z')}\quad z\in V \end{align*}$$
$$\begin{align*}L_{\psi_V}(\varphi)(z) := \liminf_{\substack{z'\rightarrow z\\ z'\not\in V}} \frac{\varphi(z')}{\psi_V(z')}\quad z\in V \end{align*}$$
is constant along V.
Theorem 1.4 can be seen as a version of Siu’s theorem in our context. Note in particular that it implies a certain propagation of singularities along V since the function
![]() $L_{\psi_V}(\varphi )$
is defined pointwise.
$L_{\psi_V}(\varphi )$
is defined pointwise.
Since the analyticity of V is already assumed, the proof of Theorem 1.4 is pleasantly elementary and boils down to essentially the weak Harnack inequality and Corollary 1.3.
Taken together, our results indicate a stark dichotomy in the behaviour of m-sh functions, depending on the size of their singular set. The situation where the singular set is small appears to be easier since it can be ‘selected’ by assuming that
![]() $\varphi $
has a well-defined complex Hessian measure – specifically, one sees that, if we assume that
$\varphi $
has a well-defined complex Hessian measure – specifically, one sees that, if we assume that
![]() $\varphi \in \mathcal {E}^m$
(the m-subharmonic version of Cegrell’s class) then
$\varphi \in \mathcal {E}^m$
(the m-subharmonic version of Cegrell’s class) then
![]() $\nu (\varphi , \psi_V) = 0$
for all
$\nu (\varphi , \psi_V) = 0$
for all
![]() $k \leqslant m$
. The small codimension case is likely to be more interesting from a geometric point of view however, and it is unclear if there is a similar potential theoretic assumption one can make to limit to this situation. Finding conditions which work well in both cases appears challenging.
$k \leqslant m$
. The small codimension case is likely to be more interesting from a geometric point of view however, and it is unclear if there is a similar potential theoretic assumption one can make to limit to this situation. Finding conditions which work well in both cases appears challenging.
We conclude this introduction with an outline of the rest of the paper. In Section 2, we recall some background results, which should be more-or-less standard to experts. Since we will need to utilize the lack of boundary of V at several points, it is important that we do not restrict ourselves to domains in
![]() $\mathbb{C}^n$
and work rather on abstract m-hyperconvex manifolds. In Section 3, we prove Theorem 1.1 (Theorem 3.4), as well as Corollary 1.2 (Proposition 3.6). The examples in Proposition 3.7 are constructed in Subsection 3.4. Theorem 1.4 is finally shown in Section 4 (Theorem 4.2).
$\mathbb{C}^n$
and work rather on abstract m-hyperconvex manifolds. In Section 3, we prove Theorem 1.1 (Theorem 3.4), as well as Corollary 1.2 (Proposition 3.6). The examples in Proposition 3.7 are constructed in Subsection 3.4. Theorem 1.4 is finally shown in Section 4 (Theorem 4.2).
2 Background and notation
Throughout, we shall assume that
![]() $(X^n, \omega )$
is a closed Kähler manifold of complex dimension n, with Kähler form
$(X^n, \omega )$
is a closed Kähler manifold of complex dimension n, with Kähler form
![]() $\omega $
.
$\omega $
.
![]() $(\Omega ^n, \omega )$
will always denote a compact Kähler manifold with boundary. In this paper, we will always assume that
$(\Omega ^n, \omega )$
will always denote a compact Kähler manifold with boundary. In this paper, we will always assume that
![]() $\Omega \subset X$
, mostly as a matter of convenience. We always assume that
$\Omega \subset X$
, mostly as a matter of convenience. We always assume that
![]() $V^{n-k}\subset \Omega $
is a compact submanifold without boundary and (complex) codimension k (so that V has complex dimension
$V^{n-k}\subset \Omega $
is a compact submanifold without boundary and (complex) codimension k (so that V has complex dimension
![]() $n - k$
).
$n - k$
).
Definition 2.1. Suppose that
![]() $(\Omega ^n, \omega )$
is a Kähler manifold, with boundary, and let m be an integer between
$(\Omega ^n, \omega )$
is a Kähler manifold, with boundary, and let m be an integer between
![]() $1$
and n. We say a smooth
$1$
and n. We say a smooth
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\alpha $
is m-subharmonic (or m-sh) if
$\alpha $
is m-subharmonic (or m-sh) if
We denote the set of all m-sh forms by
![]() $\Gamma ^m(\Omega )$
, or
$\Gamma ^m(\Omega )$
, or
![]() $\Gamma _\omega ^m(\Omega )$
if the metric needs to be specified.
$\Gamma _\omega ^m(\Omega )$
if the metric needs to be specified.
In [Reference Błocki9], Błocki defines a real
![]() $(1, 1)$
-current T to be m-sh if
$(1, 1)$
-current T to be m-sh if
By Gårding’s inequality [Reference Gårding20], the above definitions are consistent. Additionally, we shall say that T is strictly m-sh if
![]() $T - \delta \omega $
is m-sh for some
$T - \delta \omega $
is m-sh for some
![]() $\delta> 0$
.
$\delta> 0$
.
We say a function
![]() $\rho $
on
$\rho $
on
![]() $\Omega $
is m-sh if the
$\Omega $
is m-sh if the
![]() $(1,1)$
-current
$(1,1)$
-current
![]() $dd^c\rho $
is m-sh and write
$dd^c\rho $
is m-sh and write
![]() $m\mathrm{SH}(\Omega )$
for the space of m-sh functions on
$m\mathrm{SH}(\Omega )$
for the space of m-sh functions on
![]() $\Omega $
(or
$\Omega $
(or
![]() $m\mathrm{SH}_\omega (\Omega )$
, if the metric needs to be specified). We will also say that
$m\mathrm{SH}_\omega (\Omega )$
, if the metric needs to be specified). We will also say that
![]() $\rho $
is strictly m-sh if
$\rho $
is strictly m-sh if
![]() $i\partial \overline {\partial }\rho $
is.
$i\partial \overline {\partial }\rho $
is.
Given a closed, real
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\theta $
, we say that a function u is
$\theta $
, we say that a function u is
![]() $(m,\theta )$
-sh if
$(m,\theta )$
-sh if
![]() $\theta _u := \theta + dd^c u$
is m-sh and write
$\theta _u := \theta + dd^c u$
is m-sh and write
![]() $m\mathrm{SH}(X, \theta )$
for the set of all
$m\mathrm{SH}(X, \theta )$
for the set of all
![]() $(m, \theta )$
-sh functions on X.
$(m, \theta )$
-sh functions on X.
Classically, the case which has been most studied is when
![]() $\theta = \omega $
; however, it is easy to check that essentially all standard results hold when
$\theta = \omega $
; however, it is easy to check that essentially all standard results hold when
![]() $\theta $
is any closed, strictly m-sh form.
$\theta $
is any closed, strictly m-sh form.
2.1 m-hyperconvex manifolds
We have the following m-sh analogue of hyperconvex manifolds.
Definition 2.2. We say a compact Kähler manifold
![]() $(\Omega , \omega )$
is m-hyperconvex if there exists a strictly m-sh exhaustion function on
$(\Omega , \omega )$
is m-hyperconvex if there exists a strictly m-sh exhaustion function on
![]() $\Omega ^\circ $
which is smooth up to the boundary, that is, a strictly m-sh function
$\Omega ^\circ $
which is smooth up to the boundary, that is, a strictly m-sh function
![]() $0> \rho \in C^\infty (\overline {\Omega })$
such that
$0> \rho \in C^\infty (\overline {\Omega })$
such that
![]() $\Omega _c := \{\rho < c\} \Subset \Omega $
for each
$\Omega _c := \{\rho < c\} \Subset \Omega $
for each
![]() $c < 0$
.
$c < 0$
.
It is easy to see that m-hyperconvex manifolds can contain nontrivial closed subvarieties. This basic observation is key to our setting, so it is important that we do not restrict our definition to domains in
![]() $\mathbb{C}^n$
, which has been the primary case considered in much of the literature. Many of those previous results do not heavily utilize this assumption, however, and can be shown to hold for arbitrary hyperconvex domains with only minor changes to their proofs.
$\mathbb{C}^n$
, which has been the primary case considered in much of the literature. Many of those previous results do not heavily utilize this assumption, however, and can be shown to hold for arbitrary hyperconvex domains with only minor changes to their proofs.
One difference between the two settings which is worth pointing out is that it is crucial for
![]() $\rho $
to be strictly m-subharmonic in Definition 2.2. Without this, the complex Hessian operator may fail to be well-defined; for example, consider a neighborhood U of a smooth, ample divisor
$\rho $
to be strictly m-subharmonic in Definition 2.2. Without this, the complex Hessian operator may fail to be well-defined; for example, consider a neighborhood U of a smooth, ample divisor
![]() $D \subset \mathbb{CP}^n$
. If we let s be a holomorphic section of
$D \subset \mathbb{CP}^n$
. If we let s be a holomorphic section of
![]() $\mathcal {O}_{\mathbb{CP}^n}(D)$
with
$\mathcal {O}_{\mathbb{CP}^n}(D)$
with
![]() ${\{s = 0\} = D}$
, and h a positive metric on
${\{s = 0\} = D}$
, and h a positive metric on
![]() $\mathcal {O}_{\mathbb{CP}^n}(D)$
, then it is well-known that the product
$\mathcal {O}_{\mathbb{CP}^n}(D)$
, then it is well-known that the product
![]() $(\sqrt {-1}\partial \overline {\partial } \log |s|_h)^2\wedge \omega ^{n-m}$
is not well-defined, even though there exists a smooth, psh exhaustion function on U. For positive results in this direction, see the recent papers [Reference Andersson3, Reference Andersson and Wulcan6, Reference Andersson, Błocki and Wulcan4, Reference Błocki10, Reference Andersson, Witt Nyström and Wulcan5], which define product currents which retain some of the singular nature of
$(\sqrt {-1}\partial \overline {\partial } \log |s|_h)^2\wedge \omega ^{n-m}$
is not well-defined, even though there exists a smooth, psh exhaustion function on U. For positive results in this direction, see the recent papers [Reference Andersson3, Reference Andersson and Wulcan6, Reference Andersson, Błocki and Wulcan4, Reference Błocki10, Reference Andersson, Witt Nyström and Wulcan5], which define product currents which retain some of the singular nature of
![]() $\log |s|_h$
.
$\log |s|_h$
.
Since we repeatedly make use of the fact that codimension m-subvarieties admit m-hyperconvex neighborhoods, we record this fact here:
Proposition 2.3. Suppose that
![]() $(X^n, \omega )$
is a compact Kähler manifold and that
$(X^n, \omega )$
is a compact Kähler manifold and that
![]() $V\subset X$
is a compact submanifold of codimension m. Then there exists an m-hyperconvex neighborhood U of V with smooth boundary.
$V\subset X$
is a compact submanifold of codimension m. Then there exists an m-hyperconvex neighborhood U of V with smooth boundary.
Proof. Let
![]() $r(z) := \mathrm{dist}_\omega (z, V)$
be the Riemannian distance function to V. When r is sufficiently small,
$r(z) := \mathrm{dist}_\omega (z, V)$
be the Riemannian distance function to V. When r is sufficiently small,
![]() $r^{2}$
is smooth. By [Reference Tam and Yu33],
$r^{2}$
is smooth. By [Reference Tam and Yu33],
 $$\begin{align*}\sqrt{-1}\partial\overline{\partial} r^2 = \begin{pmatrix}I_m & 0\\ 0 & 0 \end{pmatrix} + o(1), \end{align*}$$
$$\begin{align*}\sqrt{-1}\partial\overline{\partial} r^2 = \begin{pmatrix}I_m & 0\\ 0 & 0 \end{pmatrix} + o(1), \end{align*}$$
where
![]() $o(1)$
denotes a term satisfying
$o(1)$
denotes a term satisfying
![]() $\lim _{r\rightarrow 0}o(1)=0$
. It is clear that the leading term belongs to
$\lim _{r\rightarrow 0}o(1)=0$
. It is clear that the leading term belongs to
![]() $\Gamma ^{m}$
. Then we can take any sublevel set of
$\Gamma ^{m}$
. Then we can take any sublevel set of
![]() $r^{2}$
to be the desired m-hyperconvex neighborhood of V.
$r^{2}$
to be the desired m-hyperconvex neighborhood of V.
2.2 The complex Hessian operator
For later use, we recall some basic facts about the complex Hessian operator on m-hyperconvex domains – see, for example, [Reference Wan and Wang34], which draws heavily from the work of Demailly [Reference Demailly13, Reference Demailly14, Reference Demailly15, Reference Demailly17, Reference Demailly18] in the psh case. The above papers phrase their results in terms of a weight function
![]() $\psi $
, and they required the unbounded locus of
$\psi $
, and they required the unbounded locus of
![]() $\psi $
to be a discrete set. However, it is easy to see that this assumption is superfluous for the results we will need below – all that is needed is for the unbounded locus of
$\psi $
to be a discrete set. However, it is easy to see that this assumption is superfluous for the results we will need below – all that is needed is for the unbounded locus of
![]() $\psi $
to be compact and that it not intersect the boundary of
$\psi $
to be compact and that it not intersect the boundary of
![]() $\Omega $
, as in [Reference Demailly18].
$\Omega $
, as in [Reference Demailly18].
Throughout, we will be assuming that
![]() $(\Omega ^n, \omega )$
is an m-hyperconvex manifold (which recall we assume to be compact with boundary). We start by defining the classes of weights which we will study:
$(\Omega ^n, \omega )$
is an m-hyperconvex manifold (which recall we assume to be compact with boundary). We start by defining the classes of weights which we will study:
Definition 2.4. We say that
![]() $\psi $
is a weight on
$\psi $
is a weight on
![]() $\Omega $
if
$\Omega $
if
![]() $\psi $
satisfies the following:
$\psi $
satisfies the following:
-
(1)
 $\psi $
is bounded above.
$\psi $
is bounded above. -
(2)
 $\mathrm{Sing}(\psi ) := \{\psi = -\infty \}$
is closed.
$\mathrm{Sing}(\psi ) := \{\psi = -\infty \}$
is closed. -
(3) the level sets
 $W_s := \{z\in \Omega \ |\ \psi (z)< s\}$
are connected and relatively compact for all s sufficiently negative.
$W_s := \{z\in \Omega \ |\ \psi (z)< s\}$
are connected and relatively compact for all s sufficiently negative.
Additionally, we will require our weights to satisfy a differential inequality.
-
• We say
 $\psi $
is an m
-subweight if
$\psi $
is an m
-subweight if
 $\psi $
is m-sh.
$\psi $
is m-sh. -
• We say
 $\psi $
is an m
-superweight if
$\psi $
is an m
-superweight if
 $\psi \in C^\infty (\Omega \setminus \mathrm{Sing}(\psi ))$
and
$\psi \in C^\infty (\Omega \setminus \mathrm{Sing}(\psi ))$
and
 $(\sqrt {-1}\partial \overline {\partial } \psi )^m\wedge \omega ^{n-m} \leqslant 0$
there.
$(\sqrt {-1}\partial \overline {\partial } \psi )^m\wedge \omega ^{n-m} \leqslant 0$
there. -
• We say
 $\psi $
is a maximal m
-weight if
$\psi $
is a maximal m
-weight if
 $\psi $
is m-sh such that
$\psi $
is m-sh such that
 $(\sqrt {-1}\partial \overline {\partial }\psi )^m\wedge \omega ^{n-m} = 0$
on
$(\sqrt {-1}\partial \overline {\partial }\psi )^m\wedge \omega ^{n-m} = 0$
on
 $\Omega \setminus \mathrm{Sing}(\psi )$
.
$\Omega \setminus \mathrm{Sing}(\psi )$
.
Sub- and superweights are suited to different measurements of the singularities of m-sh functions; subweights work well for Lelong numbers, while superweights are required when working with the relative type. Maximal m-weights are precisely those weights for which these two types of measurements can be compared.
Now, by [Reference Demailly18, Reference Wan and Wang34], for any m-subweight
![]() $\psi $
, the complex Hessian operator
$\psi $
, the complex Hessian operator
is a well-defined, positive Borel measure on
![]() $\Omega $
, with locally finite mass, which is continuous along decreasing sequences (that is to say that
$\Omega $
, with locally finite mass, which is continuous along decreasing sequences (that is to say that
![]() $\psi \in \mathcal {E}^m(\Omega )$
, the m-sh version of the Cegrell class [Reference Lu26]). More generally, if
$\psi \in \mathcal {E}^m(\Omega )$
, the m-sh version of the Cegrell class [Reference Lu26]). More generally, if
![]() $\psi_1, \ldots , \psi_{m-1}$
are all m-subweights and
$\psi_1, \ldots , \psi_{m-1}$
are all m-subweights and
![]() $\varphi \in m\mathrm{SH}(\Omega )$
is arbitrary, then the mixed measure:
$\varphi \in m\mathrm{SH}(\Omega )$
is arbitrary, then the mixed measure:
shares these same properties and is moreover multilinear in each argument.
Definition 2.5. [Reference Demailly18, Reference Wan and Wang34] Suppose that
![]() $\psi $
is an m-subweight on
$\psi $
is an m-subweight on
![]() $\Omega $
such that
$\Omega $
such that
![]() $\{\psi < -1\}\Subset \Omega $
. Let
$\{\psi < -1\}\Subset \Omega $
. Let
![]() $\varphi \in m\mathrm{SH}(\Omega )$
be such that
$\varphi \in m\mathrm{SH}(\Omega )$
be such that
![]() $\varphi \leqslant -1$
. For any
$\varphi \leqslant -1$
. For any
![]() $s < -1$
, set
$s < -1$
, set
Then we define:
 $$ \begin{align} \nu_m(\varphi, \psi) &:= \lim_{s\rightarrow -\infty} \int_{W_s} \sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} \psi)^{m-1}\wedge \omega^{n-m} \\ &= \int_{\{\psi = -\infty\}} \sqrt{-1}\partial\overline{\partial} \varphi\wedge(\sqrt{-1}\partial\overline{\partial} \psi)^{m-1}\wedge \omega^{n-m}.\notag \end{align} $$
$$ \begin{align} \nu_m(\varphi, \psi) &:= \lim_{s\rightarrow -\infty} \int_{W_s} \sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} \psi)^{m-1}\wedge \omega^{n-m} \\ &= \int_{\{\psi = -\infty\}} \sqrt{-1}\partial\overline{\partial} \varphi\wedge(\sqrt{-1}\partial\overline{\partial} \psi)^{m-1}\wedge \omega^{n-m}.\notag \end{align} $$
We call
![]() $\nu _m(\varphi , \psi )$
the generalized m
-Lelong number of
$\nu _m(\varphi , \psi )$
the generalized m
-Lelong number of
![]() $\varphi $
with respect to
$\varphi $
with respect to
![]() $\psi $
or, more compactly, the
$\psi $
or, more compactly, the
![]() $(m, \psi )$
-Lelong number of
$(m, \psi )$
-Lelong number of
![]() $\varphi $
. By standard results,
$\varphi $
. By standard results,
![]() $\nu _m(\varphi , \psi )$
is always finite and nonnegative, and the sequence in Equation (2.1) is monotone decreasing.
$\nu _m(\varphi , \psi )$
is always finite and nonnegative, and the sequence in Equation (2.1) is monotone decreasing.
The following comparison theorem for m-polar measures is standard, and can be obtained by following the proof of [Reference Åhag, Cegrell, Czyż and Hiệp1, Lemma 4.1] (see also [Reference Demailly17, Reference Hung and Van Phu24]):
Proposition 2.6. Suppose that
![]() $\psi_1, \psi_2$
are m-subweights and
$\psi_1, \psi_2$
are m-subweights and
![]() $\varphi _1, \varphi _2\in m\mathrm{SH}(\Omega )$
are such that
$\varphi _1, \varphi _2\in m\mathrm{SH}(\Omega )$
are such that
![]() $\psi_1 \leqslant \psi_2 + C$
and
$\psi_1 \leqslant \psi_2 + C$
and
![]() $\varphi _1\leqslant \varphi _2 + C$
for some constant C. Let
$\varphi _1\leqslant \varphi _2 + C$
for some constant C. Let
![]() $S := \mathrm{Sing}(\psi_2)\cap \mathrm{Sing}(\varphi _2)$
. Then
$S := \mathrm{Sing}(\psi_2)\cap \mathrm{Sing}(\varphi _2)$
. Then
2.3 Relative types
Relative-types were first studied by Rashkovskii in [Reference Rashkovskii30]. The natural generalization of his original definition is the following lower semicontinuous function defined on
![]() $\mathrm{Sing}(\psi )$
:
$\mathrm{Sing}(\psi )$
:
Definition 2.7. Suppose that
![]() $\psi \leqslant -1$
is an m-superweight (or a maximal m-weight) and
$\psi \leqslant -1$
is an m-superweight (or a maximal m-weight) and
![]() $\varphi \in m\mathrm{SH}(\Omega )$
. We define
$\varphi \in m\mathrm{SH}(\Omega )$
. We define
 $$\begin{align*}L_\psi(\varphi)(z_0) := \liminf_{\substack{z\rightarrow z_0 \\ z\not\in \mathrm{Sing}(\psi)}} \frac{\varphi(z)}{\psi(z)}. \end{align*}$$
$$\begin{align*}L_\psi(\varphi)(z_0) := \liminf_{\substack{z\rightarrow z_0 \\ z\not\in \mathrm{Sing}(\psi)}} \frac{\varphi(z)}{\psi(z)}. \end{align*}$$
It is easy to see that
![]() $L_{\psi }(\varphi )$
is a lower-semincontinous function on
$L_{\psi }(\varphi )$
is a lower-semincontinous function on
![]() $\mathrm{Sing}(\psi )$
(Proposition 2.11).
$\mathrm{Sing}(\psi )$
(Proposition 2.11).
For a general
![]() $\psi $
, this definition is somewhat lacking on its own. One of the main applications of the relative type is to get bounds of the form
$\psi $
, this definition is somewhat lacking on its own. One of the main applications of the relative type is to get bounds of the form
![]() $\varphi \leqslant L_{\psi }(\varphi )\cdot \psi + C$
on a neighbourhood of
$\varphi \leqslant L_{\psi }(\varphi )\cdot \psi + C$
on a neighbourhood of
![]() $\mathrm{Sing}(\psi )$
– but since
$\mathrm{Sing}(\psi )$
– but since
![]() $L_{\psi }(\varphi )$
is nonconstant, the right-hand side is only defined up to fixing an extension of
$L_{\psi }(\varphi )$
is nonconstant, the right-hand side is only defined up to fixing an extension of
![]() $L_{\psi }(\varphi )$
to a neighborhood of
$L_{\psi }(\varphi )$
to a neighborhood of
![]() $\mathrm{Sing}(\psi )$
. Since
$\mathrm{Sing}(\psi )$
. Since
![]() $L_{\psi }(\varphi )$
is only lower semicontinuous and
$L_{\psi }(\varphi )$
is only lower semicontinuous and
![]() $\mathrm{Sing}(\psi )$
can be very poorly behaved, it seems possible to us that this inequality may fail to hold if
$\mathrm{Sing}(\psi )$
can be very poorly behaved, it seems possible to us that this inequality may fail to hold if
![]() $L_{\psi }(\varphi )$
is extended haphazardly.
$L_{\psi }(\varphi )$
is extended haphazardly.
A definition which can be more easily applied to get upper bounds for
![]() $\varphi $
is the following, which recovers the minimum of
$\varphi $
is the following, which recovers the minimum of
![]() $L_{\psi }(\varphi )$
(although we will see later that this definition has drawbacks of its own):
$L_{\psi }(\varphi )$
(although we will see later that this definition has drawbacks of its own):
Definition 2.8. Suppose that
![]() $(\Omega ^n, \omega )\subset (X^n, \omega )$
is an m-hyperconvex manifold. Let
$(\Omega ^n, \omega )\subset (X^n, \omega )$
is an m-hyperconvex manifold. Let
![]() $\psi $
be an m-superweight (or maximal m-weight) on
$\psi $
be an m-superweight (or maximal m-weight) on
![]() $\Omega $
. Suppose that
$\Omega $
. Suppose that
![]() $W_0 = \{z\in \Omega \ |\ \psi (z)< 0\} \Subset \Omega $
.
$W_0 = \{z\in \Omega \ |\ \psi (z)< 0\} \Subset \Omega $
.
There exists a constant
![]() $A> 0$
such that for any
$A> 0$
such that for any
![]() $\varphi \in m\mathrm{SH}(X,\omega )$
, we have
$\varphi \in m\mathrm{SH}(X,\omega )$
, we have
Define
Then we define the relative type of
![]() $\varphi $
with respect to
$\varphi $
with respect to
![]() $\psi $
to be
$\psi $
to be
That
![]() $\sigma (\varphi , \psi )$
is well-defined comes from the following three-circles type result (see, e.g., [Reference Liu25] for similar results in the psh case):
$\sigma (\varphi , \psi )$
is well-defined comes from the following three-circles type result (see, e.g., [Reference Liu25] for similar results in the psh case):
Proposition 2.9. The function
![]() $M_s(\varphi +A\rho )$
in Definition 2.8 is convex on
$M_s(\varphi +A\rho )$
in Definition 2.8 is convex on
![]() $(-\infty , -1)$
. It follows that the limit (
2.2
) exists, and
$(-\infty , -1)$
. It follows that the limit (
2.2
) exists, and
![]() $\sigma (\varphi , \psi )$
is always finite and nonnegative.
$\sigma (\varphi , \psi )$
is always finite and nonnegative.
Proof. Suppose first that
![]() $\psi $
is a superweight and that
$\psi $
is a superweight and that
![]() $\varphi $
is also smooth on
$\varphi $
is also smooth on
![]() $\Omega $
. Let
$\Omega $
. Let
![]() $\rho \leqslant 0$
be a strictly m-sh function on
$\rho \leqslant 0$
be a strictly m-sh function on
![]() $\Omega $
, and define
$\Omega $
, and define
![]() $\varphi _\varepsilon := \varphi + (A + \varepsilon )\rho $
. Let
$\varphi _\varepsilon := \varphi + (A + \varepsilon )\rho $
. Let
![]() $-\infty < s_1 < s_2 < -1$
, and consider the function
$-\infty < s_1 < s_2 < -1$
, and consider the function
defined on
![]() $W := W_{s_2}\setminus \overline {W}_{s_1}$
. We seek to show that
$W := W_{s_2}\setminus \overline {W}_{s_1}$
. We seek to show that
It is clear this inequality holds on
![]() $\partial W$
, so suppose for the sake of a contradiction that
$\partial W$
, so suppose for the sake of a contradiction that
![]() $\varphi _\varepsilon - F$
admits an interior maximum at some
$\varphi _\varepsilon - F$
admits an interior maximum at some
![]() $z_0\in W$
. It follows that
$z_0\in W$
. It follows that
But this is impossible, as F is a superweight. Taking the limit as
![]() $\varepsilon \rightarrow 0$
finishes the proof in this case.
$\varepsilon \rightarrow 0$
finishes the proof in this case.
The case of a general
![]() $\varphi $
follows now by using a decreasing sequence of smooth m-sh functions which converge to
$\varphi $
follows now by using a decreasing sequence of smooth m-sh functions which converge to
![]() $\varphi $
[Reference Lu and Nguyên27, Reference Pliś29].
$\varphi $
[Reference Lu and Nguyên27, Reference Pliś29].
If
![]() $\psi $
is instead a maximal subweight, we may bypass the smooth approximation argument and instead appeal to the comparison principle directly since in this case, F will be a maximal m-sh function on
$\psi $
is instead a maximal subweight, we may bypass the smooth approximation argument and instead appeal to the comparison principle directly since in this case, F will be a maximal m-sh function on
![]() $W_{s_2}\setminus \overline {W}_{s_1}$
.
$W_{s_2}\setminus \overline {W}_{s_1}$
.
An immediate consequence of Proposition 2.9 is the following alternative definition for
![]() $\sigma (\varphi , \psi )$
:
$\sigma (\varphi , \psi )$
:
Proposition 2.10.
![]() $\sigma (\varphi , \psi ) = \max \{\gamma \geqslant 0\ |\ \varphi \leqslant \gamma \,\psi + O(1)\}$
.
$\sigma (\varphi , \psi ) = \max \{\gamma \geqslant 0\ |\ \varphi \leqslant \gamma \,\psi + O(1)\}$
.
Proof. The proof is standard – it suffices to check that
Let
![]() $A> 0$
be such that
$A> 0$
be such that
![]() $\varphi + A\rho \in m\mathrm{SH}(\Omega )$
. Convexity of
$\varphi + A\rho \in m\mathrm{SH}(\Omega )$
. Convexity of
![]() $M_s(\varphi + A\rho )$
implies that
$M_s(\varphi + A\rho )$
implies that
![]() $\sigma (\varphi , \psi )$
can be computed by the slopes of the secant lines
$\sigma (\varphi , \psi )$
can be computed by the slopes of the secant lines
for any fixed
![]() $s_0 < -1$
. Since
$s_0 < -1$
. Since
![]() $M_s(\varphi + A\rho )$
is also decreasing as
$M_s(\varphi + A\rho )$
is also decreasing as
![]() $s\rightarrow -\infty $
, the sequence in Equation (2.3) is decreasing, and we have
$s\rightarrow -\infty $
, the sequence in Equation (2.3) is decreasing, and we have
for all
![]() $s < s_0$
. From this, we see that
$s < s_0$
. From this, we see that
For later use, we record the following facts:
Proposition 2.11. The function
![]() $L_{\psi }(\varphi )$
is lower semicontinuous on
$L_{\psi }(\varphi )$
is lower semicontinuous on
![]() $S_\psi := \mathrm{Sing}(\psi )$
, and
$S_\psi := \mathrm{Sing}(\psi )$
, and
Proof. We first show the lower semicontinuity of
![]() $L_{\psi }(\varphi )$
. Fix a point
$L_{\psi }(\varphi )$
. Fix a point
![]() $z_{0}\in S_\psi $
, and let
$z_{0}\in S_\psi $
, and let
![]() $z_{i}\in S_\psi $
be a sequence of points converging to
$z_{i}\in S_\psi $
be a sequence of points converging to
![]() $z_{0}$
. For any
$z_{0}$
. For any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $x_{i}\in X\setminus S_\psi $
such that
$x_{i}\in X\setminus S_\psi $
such that
 $$\begin{align*}\mathrm{dist}_{\omega}(x_{i},z_{i}) \leqslant i^{-1}, \quad \frac{\varphi(x_{i})}{\psi(x_{i})} \leqslant L_\psi(\varphi)(z_{i})+\varepsilon. \end{align*}$$
$$\begin{align*}\mathrm{dist}_{\omega}(x_{i},z_{i}) \leqslant i^{-1}, \quad \frac{\varphi(x_{i})}{\psi(x_{i})} \leqslant L_\psi(\varphi)(z_{i})+\varepsilon. \end{align*}$$
It is clear that
![]() $x_{i}\to z_{0}$
. By definition,
$x_{i}\to z_{0}$
. By definition,
 $$\begin{align*}L_\psi(\varphi)(z_{0}) \leqslant \liminf_{i\to\infty}\frac{\varphi(x_{i})}{\psi(x_{i})} \leqslant \liminf_{i\to\infty}L_{\psi}(\varphi)(z_{i})+\varepsilon. \end{align*}$$
$$\begin{align*}L_\psi(\varphi)(z_{0}) \leqslant \liminf_{i\to\infty}\frac{\varphi(x_{i})}{\psi(x_{i})} \leqslant \liminf_{i\to\infty}L_{\psi}(\varphi)(z_{i})+\varepsilon. \end{align*}$$
Letting
![]() $\varepsilon \rightarrow 0$
concludes.
$\varepsilon \rightarrow 0$
concludes.
Now, it is clear from the definitions that
![]() $L_{\psi }(\varphi ) \geqslant \sigma (\varphi , \psi )$
. To see that it is the minimum, using that
$L_{\psi }(\varphi ) \geqslant \sigma (\varphi , \psi )$
. To see that it is the minimum, using that
![]() $\varphi $
is upper semicontinuous, we can find a sequence of points
$\varphi $
is upper semicontinuous, we can find a sequence of points
![]() $z_i\in W_{-i} = \{\psi \leqslant -i\}$
such that
$z_i\in W_{-i} = \{\psi \leqslant -i\}$
such that
![]() $\varphi (z_i) = \max _{W_{-i}} \varphi $
. It follows from compactness of
$\varphi (z_i) = \max _{W_{-i}} \varphi $
. It follows from compactness of
![]() $S_\psi $
that there exists a convergent subsequence
$S_\psi $
that there exists a convergent subsequence
![]() $z_i \rightarrow z_0\in S_\psi $
, and so we see that
$z_i \rightarrow z_0\in S_\psi $
, and so we see that
![]() $L_{\psi }(\varphi )(z_0) \leqslant \sigma (\varphi ,\psi )$
, finishing the proof.
$L_{\psi }(\varphi )(z_0) \leqslant \sigma (\varphi ,\psi )$
, finishing the proof.
Again, following Demailly [Reference Demailly18], Proposition 2.6 can be used to compare
![]() $\sigma (\varphi , \psi )$
and
$\sigma (\varphi , \psi )$
and
![]() $\nu _m(\varphi , \psi )$
. For notational convenience, we set
$\nu _m(\varphi , \psi )$
. For notational convenience, we set
Note that
![]() $\mathrm{Supp}(\mu _\psi )\subseteq S_\psi $
, but the inclusion may be proper; indeed, as Example 2.1 of [Reference Åhag, Cegrell and Hiệp2] shows,
$\mathrm{Supp}(\mu _\psi )\subseteq S_\psi $
, but the inclusion may be proper; indeed, as Example 2.1 of [Reference Åhag, Cegrell and Hiệp2] shows,
![]() $\mathrm{Supp}(\mu _\psi )$
can be quite small inside
$\mathrm{Supp}(\mu _\psi )$
can be quite small inside
![]() $S_\psi $
.
$S_\psi $
.
Corollary 2.12. Suppose that
![]() $\psi \leqslant -1$
is a maximal m-weight such that
$\psi \leqslant -1$
is a maximal m-weight such that
![]() $\mu _\psi (S_\psi )> 0$
. Then
$\mu _\psi (S_\psi )> 0$
. Then
Proof. By Corollary 2.10, we have that
in some neighborhood of
![]() $S_\psi $
. By Proposition 2.6, it follows that
$S_\psi $
. By Proposition 2.6, it follows that
Integrating over
![]() $S_\psi $
finishes the proof.
$S_\psi $
finishes the proof.
Remark 2.13. Proposition 2.6 allows us to define the Radon–Nikodym derivative of
![]() $\chi _{S_\psi } \sqrt {-1}\partial \overline {\partial } \varphi \wedge (\sqrt {-1}\partial \overline {\partial }\psi )^{m-1}\wedge \omega ^{n-m}$
with respect to
$\chi _{S_\psi } \sqrt {-1}\partial \overline {\partial } \varphi \wedge (\sqrt {-1}\partial \overline {\partial }\psi )^{m-1}\wedge \omega ^{n-m}$
with respect to
![]() $\mu _\psi $
in certain cases, for example, when
$\mu _\psi $
in certain cases, for example, when
![]() $\varphi \in \mathcal {E}^m(\Omega )$
(see [Reference Åhag, Cegrell, Czyż and Hiệp1, Lem. 4.4]). It is interesting to ask how different this function is from
$\varphi \in \mathcal {E}^m(\Omega )$
(see [Reference Åhag, Cegrell, Czyż and Hiệp1, Lem. 4.4]). It is interesting to ask how different this function is from
![]() $L_{\psi }(\varphi )$
.
$L_{\psi }(\varphi )$
.
3 Construction of m-Weights along submanifolds
In this section, we construct our maximal m-weights
![]() $\psi_V$
, associated to the complex submanifold V.
$\psi_V$
, associated to the complex submanifold V.
3.1 Construction of the m-subweight associated to V
Let
![]() $V\subseteq X$
be a smooth submanifold of codimension k. Let
$V\subseteq X$
be a smooth submanifold of codimension k. Let
![]() $r(z) := \mathrm{dist}_\omega (z, V)$
be the Riemannian distance function to V, and choose
$r(z) := \mathrm{dist}_\omega (z, V)$
be the Riemannian distance function to V, and choose
![]() $0 < s_V < 1$
sufficiently small so that
$0 < s_V < 1$
sufficiently small so that
![]() $\Omega := \{z\in X\ |\ r(z) < s_V\}$
does not intersect the cut-locus of V.
$\Omega := \{z\in X\ |\ r(z) < s_V\}$
does not intersect the cut-locus of V.
It follows that r will be smooth on
![]() $\Omega \setminus V$
, so that
$\Omega \setminus V$
, so that
will be smooth on all of
![]() $\Omega $
for any
$\Omega $
for any
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
Define
![]() $G_m: \mathbb{R}_{\geqslant 0}\rightarrow \mathbb{R}\cup \{-\infty \}$
:
$G_m: \mathbb{R}_{\geqslant 0}\rightarrow \mathbb{R}\cup \{-\infty \}$
:
 $$\begin{align*}G_m(t) := \begin{cases} \log t &\text{ if } m = k \\ -t^{2 - \frac{2k}{m}} &\text{ if }m < k.\end{cases} \end{align*}$$
$$\begin{align*}G_m(t) := \begin{cases} \log t &\text{ if } m = k \\ -t^{2 - \frac{2k}{m}} &\text{ if }m < k.\end{cases} \end{align*}$$
![]() $G_m$
will be the natural scaling of a maximal m-weight near V – by perturbing it slightly, we will be able to produce sub- and superweights. Our perturbations will be of the form
$G_m$
will be the natural scaling of a maximal m-weight near V – by perturbing it slightly, we will be able to produce sub- and superweights. Our perturbations will be of the form
where
![]() $\max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \} < \delta $
will be a uniform constant for all s sufficiently small. We will also have
$\max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \} < \delta $
will be a uniform constant for all s sufficiently small. We will also have
![]() $A = \pm 1$
, depending on if we are constructing the sub- or supersolution. Note that as long as
$A = \pm 1$
, depending on if we are constructing the sub- or supersolution. Note that as long as
![]() $\max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \} < \delta $
,
$\max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \} < \delta $
,
![]() $G_m(h(r))$
and
$G_m(h(r))$
and
![]() $G_m(r)$
will have the same singularity type on
$G_m(r)$
will have the same singularity type on
![]() $\Omega $
, for either choice of A.
$\Omega $
, for either choice of A.
We will need to choose suitable coordinates for our computations, which we fix once and for all. Let
![]() $z\in \Omega \setminus V$
, and let
$z\in \Omega \setminus V$
, and let
![]() $x\in V$
be the unique nearest point to z. Consider the geodesic connecting these points, which will be normal to V at x. Choose a unitary frame
$x\in V$
be the unique nearest point to z. Consider the geodesic connecting these points, which will be normal to V at x. Choose a unitary frame
![]() $\{e_{i}\}_{i=1}^{n}$
at x such that
$\{e_{i}\}_{i=1}^{n}$
at x such that
the
![]() $e_{2},\ldots ,e_{k}$
are perpendicular to V, and the
$e_{2},\ldots ,e_{k}$
are perpendicular to V, and the
![]() $e_{k+1},\ldots ,e_{n}$
are tangent to V; we also write
$e_{k+1},\ldots ,e_{n}$
are tangent to V; we also write
![]() $\{e_{i}\}_{i=1}^{n}$
for the parallel transport of this frame to z. Then, according to [Reference Tam and Yu33, Lemma 2.2], in these coordinates we have that
$\{e_{i}\}_{i=1}^{n}$
for the parallel transport of this frame to z. Then, according to [Reference Tam and Yu33, Lemma 2.2], in these coordinates we have that
 $$\begin{align*}r_{i\overline{j}}= \begin{pmatrix} \frac{1}{2r} & 0 & 0 \\ 0 & \frac{1}{r}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} +o(1), \end{align*}$$
$$\begin{align*}r_{i\overline{j}}= \begin{pmatrix} \frac{1}{2r} & 0 & 0 \\ 0 & \frac{1}{r}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} +o(1), \end{align*}$$
where
![]() $o(1)$
denotes a term satisfying
$o(1)$
denotes a term satisfying
![]() $\lim _{r\rightarrow 0}o(1)=0$
(see in particular Equation (2.22) in [Reference Tam and Yu33]).
$\lim _{r\rightarrow 0}o(1)=0$
(see in particular Equation (2.22) in [Reference Tam and Yu33]).
In what follows, it suffices to restrict to the case
![]() $m \leqslant k$
, since, if
$m \leqslant k$
, since, if
![]() $m> k$
, then the m-sh functions we construct will also be k-sh.
$m> k$
, then the m-sh functions we construct will also be k-sh.
Proposition 3.1. Suppose that
![]() $z\in \Omega \setminus V$
and that
$z\in \Omega \setminus V$
and that
![]() $m \leqslant k$
. Let
$m \leqslant k$
. Let
![]() $D_{k, m} = \left (\frac {2k}{m} - 2\right )^{-1}$
if
$D_{k, m} = \left (\frac {2k}{m} - 2\right )^{-1}$
if
![]() $k\not = m$
and
$k\not = m$
and
![]() $D_{k,m} = 1$
if
$D_{k,m} = 1$
if
![]() $k = m$
.
$k = m$
.
Then for any
![]() $\varepsilon> 0$
, we have
$\varepsilon> 0$
, we have
 $$ \begin{align} D_{k,m}h^{\frac{2k}{m}}(\sqrt{-1}\partial\overline{\partial} G_m(h(r_\varepsilon)))_{i\overline{j}} &= \begin{pmatrix} 1 - \frac{k}{m} + AB_1r_\varepsilon^\delta & 0 & 0 \\ 0 & \left(1 + AB_2 r_\varepsilon^\delta\right)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix}\notag \\ &+ \frac{\varepsilon}{r_\varepsilon^2}\begin{pmatrix} \frac{k}{m} + A B_3 r_\varepsilon^\delta + o(r_\varepsilon^\delta) & 0 & 0\\ 0& 0 & 0 \\ 0 & 0 & 0\end{pmatrix} + o(r_\varepsilon^\delta), \end{align} $$
$$ \begin{align} D_{k,m}h^{\frac{2k}{m}}(\sqrt{-1}\partial\overline{\partial} G_m(h(r_\varepsilon)))_{i\overline{j}} &= \begin{pmatrix} 1 - \frac{k}{m} + AB_1r_\varepsilon^\delta & 0 & 0 \\ 0 & \left(1 + AB_2 r_\varepsilon^\delta\right)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix}\notag \\ &+ \frac{\varepsilon}{r_\varepsilon^2}\begin{pmatrix} \frac{k}{m} + A B_3 r_\varepsilon^\delta + o(r_\varepsilon^\delta) & 0 & 0\\ 0& 0 & 0 \\ 0 & 0 & 0\end{pmatrix} + o(r_\varepsilon^\delta), \end{align} $$
where we define the constants
 $$\begin{align*}B_{1} =2\left[1-\frac{k}{m}+\left(1-\frac{k}{m}\right)\delta+\frac{\delta^{2}}{4}\right] \end{align*}$$
$$\begin{align*}B_{1} =2\left[1-\frac{k}{m}+\left(1-\frac{k}{m}\right)\delta+\frac{\delta^{2}}{4}\right] \end{align*}$$
and
 $$\begin{align*}B_2 := 2 + \delta,\quad \quad B_3 := 2\left[\frac{k}{m} + \delta\left(\frac{k}{m} - \frac{1}{2}\right) - \frac{\delta^2}{4}\right]. \end{align*}$$
$$\begin{align*}B_2 := 2 + \delta,\quad \quad B_3 := 2\left[\frac{k}{m} + \delta\left(\frac{k}{m} - \frac{1}{2}\right) - \frac{\delta^2}{4}\right]. \end{align*}$$
The terms
![]() $o(r_\varepsilon ^\delta )$
satisfy
$o(r_\varepsilon ^\delta )$
satisfy
![]() $o(r_\varepsilon ^\delta ) \leqslant c r_\varepsilon ^\delta $
for any
$o(r_\varepsilon ^\delta ) \leqslant c r_\varepsilon ^\delta $
for any
![]() $0 < c$
and all
$0 < c$
and all
![]() $0 < r_\varepsilon ^\delta < r_c$
, where
$0 < r_\varepsilon ^\delta < r_c$
, where
![]() $r_c$
depends on both c and an upper bound for
$r_c$
depends on both c and an upper bound for
![]() $\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
.
$\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
.
Since the constant
![]() $D_{k,m}> 0$
, it will have no bearing on the positivity/negativity of
$D_{k,m}> 0$
, it will have no bearing on the positivity/negativity of
![]() $\sqrt {-1}\partial \overline {\partial } G_m(h(r_\varepsilon ))$
, and we will omit it in all of the below computations.
$\sqrt {-1}\partial \overline {\partial } G_m(h(r_\varepsilon ))$
, and we will omit it in all of the below computations.
For later use, we also remark that it will be clear from the below proof that (3.1) still holds if either
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $z\in V$
or if
$z\in V$
or if
![]() $\varepsilon = 0$
and
$\varepsilon = 0$
and
![]() $z\not \in V$
(replacing
$z\not \in V$
(replacing
![]() $o(r_\varepsilon )$
with
$o(r_\varepsilon )$
with
![]() $o(r)$
in this case).
$o(r)$
in this case).
Proof. The proof is a computation. To start, if
![]() $m < k$
, then we have
$m < k$
, then we have
 $$\begin{align*}(G_m(h(r_\varepsilon)))_{i\overline{j}} = \left(\frac{2k}{m}-2\right)\cdot h^{-\frac{2k}{m}}\cdot\left( h h' (r_\varepsilon)_{i\overline{j}} + \left(h h" + \left(1-\frac{2k}{m}\right)(h')^2\right)(r_\varepsilon)_{i}(r_\varepsilon)_{\overline{j}}\right), \end{align*}$$
$$\begin{align*}(G_m(h(r_\varepsilon)))_{i\overline{j}} = \left(\frac{2k}{m}-2\right)\cdot h^{-\frac{2k}{m}}\cdot\left( h h' (r_\varepsilon)_{i\overline{j}} + \left(h h" + \left(1-\frac{2k}{m}\right)(h')^2\right)(r_\varepsilon)_{i}(r_\varepsilon)_{\overline{j}}\right), \end{align*}$$
while if
![]() $m = k$
$m = k$
Thus, we may deal with both cases simultaneously by computing
 $$ \begin{align} h h' (r_\varepsilon)_{i\overline{j}} + \left(h h" + \left(1-\frac{2k}{m}\right)(h')^2\right)(r_\varepsilon)_{i}(r_\varepsilon)_{\overline{j}}. \end{align} $$
$$ \begin{align} h h' (r_\varepsilon)_{i\overline{j}} + \left(h h" + \left(1-\frac{2k}{m}\right)(h')^2\right)(r_\varepsilon)_{i}(r_\varepsilon)_{\overline{j}}. \end{align} $$
We now compute
 $$\begin{align*}(r_{\varepsilon})_{i} = \frac{rr_{i}}{\sqrt{r^{2}+\varepsilon}} = \frac{rr_{i}}{r_{\varepsilon}}, \quad (r_{\varepsilon})_{i}(r_{\varepsilon})_{\overline{j}} = \frac{r^{2}r_{i}r_{\overline{j}}}{r_{\varepsilon}^{2}} \end{align*}$$
$$\begin{align*}(r_{\varepsilon})_{i} = \frac{rr_{i}}{\sqrt{r^{2}+\varepsilon}} = \frac{rr_{i}}{r_{\varepsilon}}, \quad (r_{\varepsilon})_{i}(r_{\varepsilon})_{\overline{j}} = \frac{r^{2}r_{i}r_{\overline{j}}}{r_{\varepsilon}^{2}} \end{align*}$$
and
 $$ \begin{align*} (r_{\varepsilon})_{i\overline{j}} = {} & \frac{rr_{i\overline{j}}}{\sqrt{r^{2}+\varepsilon}}+\frac{r_{i}r_{\overline{j}}}{\sqrt{r^{2}+\varepsilon}}-\frac{r^{2}r_{i}r_{\overline{j}}}{(r^{2}+\varepsilon)^{\frac{3}{2}}} \\ ={} & \frac{r r_{i\overline{j}}}{r_\varepsilon} + \frac{\varepsilon r_i r_{\overline{j}}}{r_\varepsilon^3}. \end{align*} $$
$$ \begin{align*} (r_{\varepsilon})_{i\overline{j}} = {} & \frac{rr_{i\overline{j}}}{\sqrt{r^{2}+\varepsilon}}+\frac{r_{i}r_{\overline{j}}}{\sqrt{r^{2}+\varepsilon}}-\frac{r^{2}r_{i}r_{\overline{j}}}{(r^{2}+\varepsilon)^{\frac{3}{2}}} \\ ={} & \frac{r r_{i\overline{j}}}{r_\varepsilon} + \frac{\varepsilon r_i r_{\overline{j}}}{r_\varepsilon^3}. \end{align*} $$
Hence, in our coordinates, we have
 $$\begin{align*}(r_{\varepsilon})_{i}(r_{\varepsilon})_{\overline{j}} = \frac{r^{2}r_{i}r_{\overline{j}}}{r_{\varepsilon}^{2}} = \begin{pmatrix} \frac{r^{2}}{2r_{\varepsilon}^{2}} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \end{align*}$$
$$\begin{align*}(r_{\varepsilon})_{i}(r_{\varepsilon})_{\overline{j}} = \frac{r^{2}r_{i}r_{\overline{j}}}{r_{\varepsilon}^{2}} = \begin{pmatrix} \frac{r^{2}}{2r_{\varepsilon}^{2}} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \end{align*}$$
and
 $$ \begin{align*} (r_{\varepsilon})_{i\overline{j}} = \frac{rr_{i\overline{j}}}{r_{\varepsilon}}+\frac{\varepsilon r_{i}r_{\overline{j}}}{r_{\varepsilon}^{3}} &= \begin{pmatrix} \frac{1}{2r_{\varepsilon}}+\frac{\varepsilon}{2r_{\varepsilon}^{3}} & 0 & 0 \\ 0 & \frac{1}{r_{\varepsilon}}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} +\frac{r}{r_\varepsilon}\cdot o(1).\\ \end{align*} $$
$$ \begin{align*} (r_{\varepsilon})_{i\overline{j}} = \frac{rr_{i\overline{j}}}{r_{\varepsilon}}+\frac{\varepsilon r_{i}r_{\overline{j}}}{r_{\varepsilon}^{3}} &= \begin{pmatrix} \frac{1}{2r_{\varepsilon}}+\frac{\varepsilon}{2r_{\varepsilon}^{3}} & 0 & 0 \\ 0 & \frac{1}{r_{\varepsilon}}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} +\frac{r}{r_\varepsilon}\cdot o(1).\\ \end{align*} $$
Applying this to Equation (3.2) gives
 $$ \begin{align*} & h h' (r_\varepsilon)_{i\overline{j}} + \left(h h" + \left(1-\frac{2k}{m}\right)(h')^2\right)(r_\varepsilon)_{i}(r_\varepsilon)_{\overline{j}} \\ = & \begin{pmatrix} (h h')\left(\frac{1}{2r_\varepsilon}+\frac{\varepsilon}{2r_\varepsilon^3}\right) + \frac{r^2}{2r_\varepsilon^2}h h" + \left(\frac{1}{2}-\frac{k}{m}\right)\frac{r^2}{r_\varepsilon^2}(h')^2 & 0 & 0 \\ 0 & (h h')\frac{1}{r_\varepsilon}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r) \end{align*} $$
$$ \begin{align*} & h h' (r_\varepsilon)_{i\overline{j}} + \left(h h" + \left(1-\frac{2k}{m}\right)(h')^2\right)(r_\varepsilon)_{i}(r_\varepsilon)_{\overline{j}} \\ = & \begin{pmatrix} (h h')\left(\frac{1}{2r_\varepsilon}+\frac{\varepsilon}{2r_\varepsilon^3}\right) + \frac{r^2}{2r_\varepsilon^2}h h" + \left(\frac{1}{2}-\frac{k}{m}\right)\frac{r^2}{r_\varepsilon^2}(h')^2 & 0 & 0 \\ 0 & (h h')\frac{1}{r_\varepsilon}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r) \end{align*} $$
as
![]() $hh' = r_\varepsilon + o(r_\varepsilon )$
.
$hh' = r_\varepsilon + o(r_\varepsilon )$
.
We simplify this matrix. Recalling that
![]() $h(s) = s + As^{1+\delta }$
, we have
$h(s) = s + As^{1+\delta }$
, we have
It follows that
 $$ \begin{align*} h h' &= s + (2+\delta)A s^{1+\delta} + (1+\delta)A^2s^{1+2\delta}\\ h h" &= (1+\delta)\delta A s^\delta + (1+\delta)\delta A^2 s^{2\delta}\\ (h')^2 &= 1 + 2(1+\delta)As^\delta + (1+\delta)^2A^2 s^{2\delta} \end{align*} $$
$$ \begin{align*} h h' &= s + (2+\delta)A s^{1+\delta} + (1+\delta)A^2s^{1+2\delta}\\ h h" &= (1+\delta)\delta A s^\delta + (1+\delta)\delta A^2 s^{2\delta}\\ (h')^2 &= 1 + 2(1+\delta)As^\delta + (1+\delta)^2A^2 s^{2\delta} \end{align*} $$
so that the first entry simplifies to
 $$ \begin{align*} &(h h')\left(\frac{1}{2r_\varepsilon} + \frac{\varepsilon}{2r_\varepsilon^3}\right) + \frac{r^2}{2r_\varepsilon^2}h h" + \left(\frac{1}{2}-\frac{k}{m}\right)\frac{r^2}{r_\varepsilon^2}(h')^2\\ &= \left(r_\varepsilon + (2+\delta)A r_\varepsilon^{1+\delta} + (1+\delta)A^2r_\varepsilon^{1+2\delta}\right)\left(\frac{1}{2r_\varepsilon} + \frac{\varepsilon}{2r_\varepsilon^3}\right)\\ &\quad \quad + \left(\frac{1}{2} - \frac{\varepsilon}{2r_\varepsilon^2}\right)\left((1+\delta)\delta A r_\varepsilon^\delta + (1+\delta)\delta A^2 r_\varepsilon^{2\delta}\right)\\ &\quad \quad + \left(\frac{1}{2}-\frac{\varepsilon}{2r_\varepsilon^2}\right)\left(1 - \frac{2k}{m}\right)\left(1 + 2(1+\delta)Ar_\varepsilon^\delta + (1+\delta)^2A^2 r_\varepsilon^{2\delta}\right)\\ &= \left(\frac{1}{2} + \frac{\varepsilon}{2r_\varepsilon^2}\right)\left(1 + (2+\delta)A r_\varepsilon^{\delta} + (1+\delta)A^2r_\varepsilon^{2\delta}\right)\\ &\quad \quad + \left(\frac{1}{2} - \frac{\varepsilon}{2r_\varepsilon^2}\right)\left((1+\delta)\delta A r_\varepsilon^\delta + (1+\delta)\delta A^2 r_\varepsilon^{2\delta}\right)\\ &\quad \quad + \left(\frac{1}{2} - \frac{\varepsilon}{2r_\varepsilon^2}\right)\left(1-\frac{2k}{m}\right)\left(1 + 2(1+\delta)Ar_\varepsilon^\delta + (1+\delta)^2A^2 r_\varepsilon^{2\delta}\right)\\ &= 1 - \frac{k}{m} + 2A\left[1 - \frac{k}{m} + \left(1 - \frac{k}{m}\right)\delta + \frac{\delta^2}{4}\right]r_\varepsilon^\delta + o(r_\varepsilon^{\delta})\\ &\quad \quad +\frac{\varepsilon}{r_\varepsilon^2} \left(\frac{k}{m} + 2A\left(\frac{k}{m} + \delta \left(\frac{k}{m} - \frac{1}{2}\right) - \frac{\delta^2}{4}\right)r_\varepsilon^\delta + o(r_\varepsilon^\delta)\right)\\ &= 1 - \frac{k}{m} + AB_1 r_\varepsilon^\delta + \frac{\varepsilon}{r_\varepsilon^2}\left(\frac{k}{m} + AB_3r_\varepsilon^\delta + o(r_\varepsilon^\delta)\right) + o(r_\varepsilon^\delta). \end{align*} $$
$$ \begin{align*} &(h h')\left(\frac{1}{2r_\varepsilon} + \frac{\varepsilon}{2r_\varepsilon^3}\right) + \frac{r^2}{2r_\varepsilon^2}h h" + \left(\frac{1}{2}-\frac{k}{m}\right)\frac{r^2}{r_\varepsilon^2}(h')^2\\ &= \left(r_\varepsilon + (2+\delta)A r_\varepsilon^{1+\delta} + (1+\delta)A^2r_\varepsilon^{1+2\delta}\right)\left(\frac{1}{2r_\varepsilon} + \frac{\varepsilon}{2r_\varepsilon^3}\right)\\ &\quad \quad + \left(\frac{1}{2} - \frac{\varepsilon}{2r_\varepsilon^2}\right)\left((1+\delta)\delta A r_\varepsilon^\delta + (1+\delta)\delta A^2 r_\varepsilon^{2\delta}\right)\\ &\quad \quad + \left(\frac{1}{2}-\frac{\varepsilon}{2r_\varepsilon^2}\right)\left(1 - \frac{2k}{m}\right)\left(1 + 2(1+\delta)Ar_\varepsilon^\delta + (1+\delta)^2A^2 r_\varepsilon^{2\delta}\right)\\ &= \left(\frac{1}{2} + \frac{\varepsilon}{2r_\varepsilon^2}\right)\left(1 + (2+\delta)A r_\varepsilon^{\delta} + (1+\delta)A^2r_\varepsilon^{2\delta}\right)\\ &\quad \quad + \left(\frac{1}{2} - \frac{\varepsilon}{2r_\varepsilon^2}\right)\left((1+\delta)\delta A r_\varepsilon^\delta + (1+\delta)\delta A^2 r_\varepsilon^{2\delta}\right)\\ &\quad \quad + \left(\frac{1}{2} - \frac{\varepsilon}{2r_\varepsilon^2}\right)\left(1-\frac{2k}{m}\right)\left(1 + 2(1+\delta)Ar_\varepsilon^\delta + (1+\delta)^2A^2 r_\varepsilon^{2\delta}\right)\\ &= 1 - \frac{k}{m} + 2A\left[1 - \frac{k}{m} + \left(1 - \frac{k}{m}\right)\delta + \frac{\delta^2}{4}\right]r_\varepsilon^\delta + o(r_\varepsilon^{\delta})\\ &\quad \quad +\frac{\varepsilon}{r_\varepsilon^2} \left(\frac{k}{m} + 2A\left(\frac{k}{m} + \delta \left(\frac{k}{m} - \frac{1}{2}\right) - \frac{\delta^2}{4}\right)r_\varepsilon^\delta + o(r_\varepsilon^\delta)\right)\\ &= 1 - \frac{k}{m} + AB_1 r_\varepsilon^\delta + \frac{\varepsilon}{r_\varepsilon^2}\left(\frac{k}{m} + AB_3r_\varepsilon^\delta + o(r_\varepsilon^\delta)\right) + o(r_\varepsilon^\delta). \end{align*} $$
As
![]() $\frac {h h'}{r_\varepsilon } = 1 + A B_2 r_\varepsilon ^\delta + o(r_\varepsilon ^\delta )$
and
$\frac {h h'}{r_\varepsilon } = 1 + A B_2 r_\varepsilon ^\delta + o(r_\varepsilon ^\delta )$
and
![]() $0 < \max \{r, \sqrt {\varepsilon }\} \leqslant r_\varepsilon $
, we conclude Equation (3.1).
$0 < \max \{r, \sqrt {\varepsilon }\} \leqslant r_\varepsilon $
, we conclude Equation (3.1).
We may now construct our m-subweights.
Proposition 3.2. Suppose that
![]() $m\leqslant k$
. Then for any
$m\leqslant k$
. Then for any
![]() $\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
, there exists a
$\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
, there exists a
![]() $0 < \underline {s} < s_V/2$
such that for all
$0 < \underline {s} < s_V/2$
such that for all
![]() $0 < \varepsilon < s_V/2$
we have that
$0 < \varepsilon < s_V/2$
we have that
where
![]() $\underline {h}(s) := s + s^{1 + \delta }$
. Moreover, as
$\underline {h}(s) := s + s^{1 + \delta }$
. Moreover, as
![]() $\varepsilon \rightarrow 0$
, we have that
$\varepsilon \rightarrow 0$
, we have that
The constant
![]() $\underline {s}$
depends on
$\underline {s}$
depends on
![]() $k, m, \omega , V,$
and an upper bound for
$k, m, \omega , V,$
and an upper bound for
![]() $\delta $
.
$\delta $
.
Proof. Since
![]() $G_m(\underline {h}(r_\varepsilon ))$
is smooth on
$G_m(\underline {h}(r_\varepsilon ))$
is smooth on
![]() $\Omega $
, it will be sufficient to check that it is m-sh at an arbitrary
$\Omega $
, it will be sufficient to check that it is m-sh at an arbitrary
![]() $z\in \Omega \setminus V$
(though the computations translate easily to the case when
$z\in \Omega \setminus V$
(though the computations translate easily to the case when
![]() $z\in V$
). Choose coordinates as before, so that Proposition 3.1 with
$z\in V$
). Choose coordinates as before, so that Proposition 3.1 with
![]() $A = 1$
gives
$A = 1$
gives
 $$ \begin{align} D_{k,m}\underline{h}^{\frac{2k}{m}}(\sqrt{-1}\partial\overline{\partial} \underline{\psi}_{V,\varepsilon})_{i\overline{j}} &= \begin{pmatrix} 1 - \frac{k}{m} + B_1r_\varepsilon^\delta & 0 & 0 \\ 0 & \left(1 + B_2 r_\varepsilon^\delta\right)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix}\notag \\ &+ \frac{\varepsilon}{r_\varepsilon^2}\begin{pmatrix} \frac{k}{m} + B_3 r_\varepsilon^\delta + o(r_\varepsilon^\delta) & 0 & 0\\ 0& 0 & 0 \\ 0 & 0 & 0\end{pmatrix} + o(r_\varepsilon^\delta). \end{align} $$
$$ \begin{align} D_{k,m}\underline{h}^{\frac{2k}{m}}(\sqrt{-1}\partial\overline{\partial} \underline{\psi}_{V,\varepsilon})_{i\overline{j}} &= \begin{pmatrix} 1 - \frac{k}{m} + B_1r_\varepsilon^\delta & 0 & 0 \\ 0 & \left(1 + B_2 r_\varepsilon^\delta\right)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix}\notag \\ &+ \frac{\varepsilon}{r_\varepsilon^2}\begin{pmatrix} \frac{k}{m} + B_3 r_\varepsilon^\delta + o(r_\varepsilon^\delta) & 0 & 0\\ 0& 0 & 0 \\ 0 & 0 & 0\end{pmatrix} + o(r_\varepsilon^\delta). \end{align} $$
![]() $B_3$
can be bounded using an upper bound on
$B_3$
can be bounded using an upper bound on
![]() $\delta $
, so long as
$\delta $
, so long as
![]() $\underline {s}$
is sufficiently small the second matrix will be positive semidefinite for any
$\underline {s}$
is sufficiently small the second matrix will be positive semidefinite for any
![]() $\varepsilon> 0$
and can be dropped from all further computations.
$\varepsilon> 0$
and can be dropped from all further computations.
When
![]() $k = m$
, Equation (3.3) now simplifies to
$k = m$
, Equation (3.3) now simplifies to
 $$ \begin{align*} \underline{h}^{2}(\sqrt{-1}\partial\overline{\partial} \underline{\psi}_{V,\varepsilon})_{i\overline{j}} &\geqslant \begin{pmatrix} \frac{\delta^2}{2}r_\varepsilon^\delta & 0 & 0 \\ 0 & \mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r_\varepsilon^\delta). \end{align*} $$
$$ \begin{align*} \underline{h}^{2}(\sqrt{-1}\partial\overline{\partial} \underline{\psi}_{V,\varepsilon})_{i\overline{j}} &\geqslant \begin{pmatrix} \frac{\delta^2}{2}r_\varepsilon^\delta & 0 & 0 \\ 0 & \mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r_\varepsilon^\delta). \end{align*} $$
The error term can be controlled by shrinking
![]() $\underline {s}$
if necessary, again depending on
$\underline {s}$
if necessary, again depending on
![]() $\delta $
, completing this case.
$\delta $
, completing this case.
We now deal with the case when
![]() $m < k$
. We compute the leading term of the j-th symmetric polynomial (
$m < k$
. We compute the leading term of the j-th symmetric polynomial (
![]() $1 \leqslant j \leqslant m$
) of Equation (3.3) to be
$1 \leqslant j \leqslant m$
) of Equation (3.3) to be
 $$ \begin{align*} &\left(1 - \frac{k}{m} + B_1 r_\varepsilon^{\delta}\right)(1+ B_2r_\varepsilon^{\delta})^{j-1} + \left(\frac{k}{j}-1\right) (1+ B_2r_\varepsilon^{\delta})^j\\ &= \frac{k}{j} - \frac{k}{m} + \left[B_1 + \left( \left(1-\frac{k}{m}\right)(j-1) + \left(\frac{k}{j} - 1\right)j\right)B_2\right]r_\varepsilon^{\delta} + o(r_\varepsilon^{\delta}), \end{align*} $$
$$ \begin{align*} &\left(1 - \frac{k}{m} + B_1 r_\varepsilon^{\delta}\right)(1+ B_2r_\varepsilon^{\delta})^{j-1} + \left(\frac{k}{j}-1\right) (1+ B_2r_\varepsilon^{\delta})^j\\ &= \frac{k}{j} - \frac{k}{m} + \left[B_1 + \left( \left(1-\frac{k}{m}\right)(j-1) + \left(\frac{k}{j} - 1\right)j\right)B_2\right]r_\varepsilon^{\delta} + o(r_\varepsilon^{\delta}), \end{align*} $$
omitting a multiplicative factor of
![]() $j \cdot (k-1)\ldots (k-j+1)$
. When
$j \cdot (k-1)\ldots (k-j+1)$
. When
![]() $j < m$
, the leading term is positive. When
$j < m$
, the leading term is positive. When
![]() $j = m$
, this term is zero, so the leading order term becomes
$j = m$
, this term is zero, so the leading order term becomes
 $$ \begin{align*} &\left[B_1 + \left( \left(1-\frac{k}{m}\right)(m-1) + \left(\frac{k}{m} - 1\right)m\right)B_2\right]r_\varepsilon^{\delta}\\[1mm] = {} & \left[B_1 + \left(\frac{k}{m}-1\right)B_2\right]r_\varepsilon^{\delta}\\[1mm] = {} & \delta\left[\frac{\delta}{2}-\left(\frac{k}{m}-1\right)\right]r_\varepsilon^{\delta} \end{align*} $$
$$ \begin{align*} &\left[B_1 + \left( \left(1-\frac{k}{m}\right)(m-1) + \left(\frac{k}{m} - 1\right)m\right)B_2\right]r_\varepsilon^{\delta}\\[1mm] = {} & \left[B_1 + \left(\frac{k}{m}-1\right)B_2\right]r_\varepsilon^{\delta}\\[1mm] = {} & \delta\left[\frac{\delta}{2}-\left(\frac{k}{m}-1\right)\right]r_\varepsilon^{\delta} \end{align*} $$
since we have assumed
 $$\begin{align*}\delta> 2\left(\frac{k}{m} - 1\right). \end{align*}$$
$$\begin{align*}\delta> 2\left(\frac{k}{m} - 1\right). \end{align*}$$
By taking
![]() $\underline {s}$
sufficiently small depending on the above constant, we can control the error term, showing that
$\underline {s}$
sufficiently small depending on the above constant, we can control the error term, showing that
![]() $\sqrt {-1}\partial \overline {\partial }\underline {\psi }_{V,\varepsilon }$
is an m-subweight. Letting
$\sqrt {-1}\partial \overline {\partial }\underline {\psi }_{V,\varepsilon }$
is an m-subweight. Letting
![]() $\varepsilon \rightarrow 0$
shows the secondary statement in the proposition immediately.
$\varepsilon \rightarrow 0$
shows the secondary statement in the proposition immediately.
3.2 Construction of the m-superweight
We may now construct our m-superweight by very similar considerations:
Proposition 3.3. Suppose that
![]() $m\leqslant k$
. Then for any
$m\leqslant k$
. Then for any
![]() $\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
, there exists a
$\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
, there exists a
![]() $0 < \overline {s} < s_V/2$
, depending on
$0 < \overline {s} < s_V/2$
, depending on
![]() $k, m, \omega , V,$
and an upper bound for
$k, m, \omega , V,$
and an upper bound for
![]() $\delta $
so that if
$\delta $
so that if
![]() $\overline {h}(s) := s - s^{1 + \delta }$
, then
$\overline {h}(s) := s - s^{1 + \delta }$
, then
is an m-superweight on
![]() $W_{\overline {s}}$
.
$W_{\overline {s}}$
.
Proof. By the remark immediately following Proposition 3.1, we have
 $$ \begin{align} \overline{h}^{\frac{2k}{m}}(\sqrt{-1}\partial\overline{\partial} \overline{\psi}_V)_{i\overline{j}} &= \begin{pmatrix} 1 - \frac{k}{m} - B_1r^\delta & 0 & 0 \\ 0 & \left(1 - B_2 r^\delta\right)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r^\delta). \end{align} $$
$$ \begin{align} \overline{h}^{\frac{2k}{m}}(\sqrt{-1}\partial\overline{\partial} \overline{\psi}_V)_{i\overline{j}} &= \begin{pmatrix} 1 - \frac{k}{m} - B_1r^\delta & 0 & 0 \\ 0 & \left(1 - B_2 r^\delta\right)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r^\delta). \end{align} $$
When
![]() $k = m$
, Equation (3.4) simplifies to
$k = m$
, Equation (3.4) simplifies to
 $$ \begin{align*} \overline{h}^2(\sqrt{-1}\partial\overline{\partial} \overline{\psi}_V)_{i\overline{j}} &= \begin{pmatrix} -\frac{\delta^2}{2}r^\delta & 0 & 0 \\ 0 & (1 - (2 + \delta)r^\delta)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r^\delta). \end{align*} $$
$$ \begin{align*} \overline{h}^2(\sqrt{-1}\partial\overline{\partial} \overline{\psi}_V)_{i\overline{j}} &= \begin{pmatrix} -\frac{\delta^2}{2}r^\delta & 0 & 0 \\ 0 & (1 - (2 + \delta)r^\delta)\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + o(r^\delta). \end{align*} $$
Choosing
![]() $\overline {s}$
sufficiently small relative to
$\overline {s}$
sufficiently small relative to
![]() $\delta $
again controls the error term so that this is a superweight.
$\delta $
again controls the error term so that this is a superweight.
When
![]() $m < k$
, we again compute the leading terms of the j-th symmetric polynomials of the matrix in Equation (3.4). When
$m < k$
, we again compute the leading terms of the j-th symmetric polynomials of the matrix in Equation (3.4). When
![]() $j < m$
, the leading order term is the same as the leading term in Proposition 3.2; when
$j < m$
, the leading order term is the same as the leading term in Proposition 3.2; when
![]() $m = j$
, it becomes the negation of the term in Proposition 3.2 and hence will be negative as long as
$m = j$
, it becomes the negation of the term in Proposition 3.2 and hence will be negative as long as
![]() $\delta> 2\left (\frac {k}{m} - 1\right )$
. Again, the error terms are an order of magnitude smaller than the leading order term and so can be controlled assuming an upper bound for
$\delta> 2\left (\frac {k}{m} - 1\right )$
. Again, the error terms are an order of magnitude smaller than the leading order term and so can be controlled assuming an upper bound for
![]() $\delta $
.
$\delta $
.
3.3 The maximal m-weight along V
We now show Theorem 1.1, and construct
![]() $\psi_V$
from
$\psi_V$
from
![]() $\underline {\psi }_V$
and
$\underline {\psi }_V$
and
![]() $\overline {\psi }_V$
by using an envelope to make the complex Hessian measure vanish.
$\overline {\psi }_V$
by using an envelope to make the complex Hessian measure vanish.
Theorem 3.4. Suppose that
![]() $m\leqslant k$
, and
$m\leqslant k$
, and
![]() $\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
. Let
$\delta> \max \left \{1, 2\left (\frac {k}{m} - 1\right )\right \}$
. Let
![]() $\underline {\psi }_V$
and
$\underline {\psi }_V$
and
![]() $\overline {\psi }_V$
be the m-subweight and m-superweights constructed in Propositions 3.2 and 3.3, respectively, for the given
$\overline {\psi }_V$
be the m-subweight and m-superweights constructed in Propositions 3.2 and 3.3, respectively, for the given
![]() $\delta $
. Set
$\delta $
. Set
![]() $s_0 := \min \{\underline {s}, \overline {s}\}$
. Then the function
$s_0 := \min \{\underline {s}, \overline {s}\}$
. Then the function
is a maximal m-weight on
![]() $W_{s_0}$
, which moreover has the same singularity type as
$W_{s_0}$
, which moreover has the same singularity type as
![]() $\underline {\psi }_V, \overline {\psi }_V$
, and
$\underline {\psi }_V, \overline {\psi }_V$
, and
![]() $G_m(r)$
.
$G_m(r)$
.
Proof. As mentioned at the beginning of this section, the three functions
![]() $\underline {\psi }_V, \overline {\psi }_V,$
and
$\underline {\psi }_V, \overline {\psi }_V,$
and
![]() $G_m(r)$
have the same singularity type so that
$G_m(r)$
have the same singularity type so that
for some sufficiently large constant
![]() $C_0$
. Since it is clear that the definition of
$C_0$
. Since it is clear that the definition of
![]() $\psi_V$
only depends on the singularity type of
$\psi_V$
only depends on the singularity type of
![]() $G_m(r)$
, we have that
$G_m(r)$
, we have that
Since
![]() $\underline {\psi }_V \leqslant 0$
, the envelopes
$\underline {\psi }_V \leqslant 0$
, the envelopes
satisfy
for all
![]() $C \geqslant C_0$
. Recall that the
$C \geqslant C_0$
. Recall that the
![]() $\psi_{V,C}$
increase to
$\psi_{V,C}$
increase to
![]() $\psi_V$
as
$\psi_V$
as
![]() $C\rightarrow \infty $
so that
$C\rightarrow \infty $
so that
![]() $\underline {\psi }_V \leqslant \psi_{V}$
as well.
$\underline {\psi }_V \leqslant \psi_{V}$
as well.
Let
![]() $A> 0$
be such that
$A> 0$
be such that
![]() $\overline {\psi }_V + A \geqslant 0$
on
$\overline {\psi }_V + A \geqslant 0$
on
![]() $\partial W_{s_0}$
. By Lemma 3.5 below, we have that
$\partial W_{s_0}$
. By Lemma 3.5 below, we have that
Letting
![]() $C\rightarrow \infty $
now shows that
$C\rightarrow \infty $
now shows that
![]() $\psi_{V} \leqslant \overline {\psi }_V + A$
, so
$\psi_{V} \leqslant \overline {\psi }_V + A$
, so
![]() $\psi_V$
has the same singularity type as
$\psi_V$
has the same singularity type as
![]() $G_m(r)$
.
$G_m(r)$
.
The conclusion about vanishing mass follows from a standard balayage argument – see, for example, [Reference Bedford and Taylor7].
The following lemma is just a restatement of [Reference Rashkovskii and Sigurdsson31, Lemma 4.1].
Lemma 3.5. Suppose that
![]() $\psi \leqslant 0$
is an m-superweight (or a maximal m-weight) and
$\psi \leqslant 0$
is an m-superweight (or a maximal m-weight) and
![]() $\varphi \in m\mathrm{SH}(X, \omega )$
,
$\varphi \in m\mathrm{SH}(X, \omega )$
,
![]() $\varphi \leqslant 0$
, is such that
$\varphi \leqslant 0$
, is such that
![]() $\sigma (\varphi , \psi ) \geqslant 1$
. If
$\sigma (\varphi , \psi ) \geqslant 1$
. If
![]() $\varphi \leqslant \psi \text { on }\partial \Omega $
, then there exists a constant, independent of
$\varphi \leqslant \psi \text { on }\partial \Omega $
, then there exists a constant, independent of
![]() $\varphi $
so that
$\varphi $
so that
![]() $\varphi \leqslant \psi + C$
on all of
$\varphi \leqslant \psi + C$
on all of
![]() $\Omega $
.
$\Omega $
.
Proof. Let
![]() $s_0 \leqslant 0$
be such that
$s_0 \leqslant 0$
be such that
![]() $W_{s_0} := \{\psi (z) < s_0\} \Subset \Omega $
. Since
$W_{s_0} := \{\psi (z) < s_0\} \Subset \Omega $
. Since
![]() $\sigma (\varphi , \psi ) \geqslant 1$
, we can use Proposition 2.9 to see that
$\sigma (\varphi , \psi ) \geqslant 1$
, we can use Proposition 2.9 to see that
for all
![]() $z\in W_{s_0}$
.
$z\in W_{s_0}$
.
It follows that
![]() $\varphi +A\rho \leqslant \psi - s_{0}$
on
$\varphi +A\rho \leqslant \psi - s_{0}$
on
![]() $\partial (\Omega \setminus W_{s_0})$
. We can now conclude by the maximum/comparison principle, as in Proposition 2.9 (depending on if
$\partial (\Omega \setminus W_{s_0})$
. We can now conclude by the maximum/comparison principle, as in Proposition 2.9 (depending on if
![]() $\psi $
is a super/maximal weight).
$\psi $
is a super/maximal weight).
We now show Corollary 1.2, proving a formula for
![]() $\nu (\varphi , \psi_V)$
as a density of a weighted Laplacian of
$\nu (\varphi , \psi_V)$
as a density of a weighted Laplacian of
![]() $\varphi $
, which has been averaged over V.
$\varphi $
, which has been averaged over V.
Proposition 3.6. Suppose that we are in the setting of the previous section so that r is the geodesic distance to
![]() $V^{n-k}\subset \Omega ^n$
. Let
$V^{n-k}\subset \Omega ^n$
. Let
![]() $\varphi \in m\mathrm{SH}(\Omega )$
with
$\varphi \in m\mathrm{SH}(\Omega )$
with
![]() $m \leqslant k$
. Then
$m \leqslant k$
. Then
 $$\begin{align*}\nu_{m}(\varphi, \psi_V) = \lim_{s\rightarrow 0}\frac{C_{k,m}}{s^{2k - 2k/m}}\int_{\{r < s\}} \sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} r^2)^{m-1}\wedge\omega^{n-m} \end{align*}$$
$$\begin{align*}\nu_{m}(\varphi, \psi_V) = \lim_{s\rightarrow 0}\frac{C_{k,m}}{s^{2k - 2k/m}}\int_{\{r < s\}} \sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} r^2)^{m-1}\wedge\omega^{n-m} \end{align*}$$
for some constant
![]() $C_{k, m}$
depending only on
$C_{k, m}$
depending only on
![]() $k, m$
.
$k, m$
.
Proof. For the sake of convenience, we only give the proof when
![]() $k> m$
. Let
$k> m$
. Let
![]() $H_m(t) := \left (-t\right )^{-\frac {m}{k-m}}$
. Note that
$H_m(t) := \left (-t\right )^{-\frac {m}{k-m}}$
. Note that
![]() $H_m$
is convex and increasing on
$H_m$
is convex and increasing on
![]() $(-\infty , 0)$
and that
$(-\infty , 0)$
and that
Since
![]() $\{\underline {\psi }_V < G_m(s)\} = \{\underline {h}(r) < s\}$
, by [Reference Demailly18, Chapter III, Formula (5.5)], we have that
$\{\underline {\psi }_V < G_m(s)\} = \{\underline {h}(r) < s\}$
, by [Reference Demailly18, Chapter III, Formula (5.5)], we have that
 $$ \begin{align*} \int_{\{\underline{h} < s\}} &\sqrt{-1}\partial\overline{\partial}\varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{h}^2)^{m-1}\wedge\omega^{n-m} \\&\!\!\!\!= (H^{\prime}m(G_m(s)))^{m-1} \int_{\{\underline{\psi}_V \leqslant G_m(s)\}} \sqrt{-1}\partial\overline{\partial} \varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{\psi}_V)^{m-1}\wedge \omega^{n-m}\\ &\!\!\!\!=\left(\frac{m}{k-m}\right)^{m-1}\left(s^{\frac{2(m-k)}{m}}\right)^{\frac{-k(m-1)}{k-m}}\int_{\{\underline{\psi}_V \leqslant G_m(s)\}} \sqrt{-1}\partial\overline{\partial} \varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{\psi}_V)^{m-1}\wedge \omega^{n-m} \end{align*} $$
$$ \begin{align*} \int_{\{\underline{h} < s\}} &\sqrt{-1}\partial\overline{\partial}\varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{h}^2)^{m-1}\wedge\omega^{n-m} \\&\!\!\!\!= (H^{\prime}m(G_m(s)))^{m-1} \int_{\{\underline{\psi}_V \leqslant G_m(s)\}} \sqrt{-1}\partial\overline{\partial} \varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{\psi}_V)^{m-1}\wedge \omega^{n-m}\\ &\!\!\!\!=\left(\frac{m}{k-m}\right)^{m-1}\left(s^{\frac{2(m-k)}{m}}\right)^{\frac{-k(m-1)}{k-m}}\int_{\{\underline{\psi}_V \leqslant G_m(s)\}} \sqrt{-1}\partial\overline{\partial} \varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{\psi}_V)^{m-1}\wedge \omega^{n-m} \end{align*} $$
so that
 $$\begin{align*}\nu_{m}(\varphi, \underline{\psi}_V) = \left(\frac{k-m}{m}\right)^{m-1}\lim_{s\rightarrow 0}\frac{1}{s^{2k-2k/m}} \int_{\{\underline{h} < s\}} \sqrt{-1}\partial\overline{\partial}\varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{h}^2)^{m-1}\wedge\omega^{n-m}. \end{align*}$$
$$\begin{align*}\nu_{m}(\varphi, \underline{\psi}_V) = \left(\frac{k-m}{m}\right)^{m-1}\lim_{s\rightarrow 0}\frac{1}{s^{2k-2k/m}} \int_{\{\underline{h} < s\}} \sqrt{-1}\partial\overline{\partial}\varphi\wedge (\sqrt{-1}\partial\overline{\partial} \underline{h}^2)^{m-1}\wedge\omega^{n-m}. \end{align*}$$
Since
![]() $\underline {h}$
is only a small perturbation of r, we can replace it with r in the above expression by the following argument. By [Reference Tam and Yu33],
$\underline {h}$
is only a small perturbation of r, we can replace it with r in the above expression by the following argument. By [Reference Tam and Yu33],
 $\sqrt {-1}\partial \overline {\partial } r^2 = \begin {pmatrix}I_{k} & 0 \\ 0 & 0 \end {pmatrix} + o(1)$
is smooth and m-sh on any sufficiently small neighborhood of V. By possibly increasing
$\sqrt {-1}\partial \overline {\partial } r^2 = \begin {pmatrix}I_{k} & 0 \\ 0 & 0 \end {pmatrix} + o(1)$
is smooth and m-sh on any sufficiently small neighborhood of V. By possibly increasing
![]() $\delta $
, we may assume that it is a large integer so that
$\delta $
, we may assume that it is a large integer so that
![]() $\underline {h}^2$
is also smooth.
$\underline {h}^2$
is also smooth.
Let
![]() $T := \sqrt {-1}\partial \overline {\partial } \varphi \wedge (\sqrt {-1}\partial \overline {\partial } \underline {h}^2)^{m-2}\wedge \omega ^{n-m}$
. We have that
$T := \sqrt {-1}\partial \overline {\partial } \varphi \wedge (\sqrt {-1}\partial \overline {\partial } \underline {h}^2)^{m-2}\wedge \omega ^{n-m}$
. We have that
so away from V
 $$ \begin{align*} \sqrt{-1}\partial\overline{\partial} r^{2+\delta} & = (2+ \delta)\sqrt{-1}\partial \left( r^{1+\delta} \overline{\partial} r\right)\\[1mm] & = (2+\delta)r^{1+\delta}\sqrt{-1}\partial\overline{\partial} r + (2 + \delta)(1+\delta)r^{\delta}\sqrt{-1}\partial r\wedge \overline{\partial} r\\[1mm] & = \frac{2+\delta}{2} r^\delta \sqrt{-1}\partial\overline{\partial} r^2 + \delta(2+\delta) r^\delta\sqrt{-1}\partial r\wedge \overline{\partial} r. \end{align*} $$
$$ \begin{align*} \sqrt{-1}\partial\overline{\partial} r^{2+\delta} & = (2+ \delta)\sqrt{-1}\partial \left( r^{1+\delta} \overline{\partial} r\right)\\[1mm] & = (2+\delta)r^{1+\delta}\sqrt{-1}\partial\overline{\partial} r + (2 + \delta)(1+\delta)r^{\delta}\sqrt{-1}\partial r\wedge \overline{\partial} r\\[1mm] & = \frac{2+\delta}{2} r^\delta \sqrt{-1}\partial\overline{\partial} r^2 + \delta(2+\delta) r^\delta\sqrt{-1}\partial r\wedge \overline{\partial} r. \end{align*} $$
Since both sides are continuous across V, however, the above expression holds there as well. Then
 $$ \begin{align*} \sqrt{-1}\partial\overline{\partial} \underline{h}^2 - \sqrt{-1}\partial\overline{\partial} r^2 = {} & \left((2+\delta)r^\delta + (1+\delta)r^{2\delta}\right)\sqrt{-1}\partial\overline{\partial} r^2 \\ & + 2\delta\left((2+\delta)r^\delta + (2+2\delta)r^{2\delta}\right)\sqrt{-1}\partial r\wedge \overline{\partial} r \end{align*} $$
$$ \begin{align*} \sqrt{-1}\partial\overline{\partial} \underline{h}^2 - \sqrt{-1}\partial\overline{\partial} r^2 = {} & \left((2+\delta)r^\delta + (1+\delta)r^{2\delta}\right)\sqrt{-1}\partial\overline{\partial} r^2 \\ & + 2\delta\left((2+\delta)r^\delta + (2+2\delta)r^{2\delta}\right)\sqrt{-1}\partial r\wedge \overline{\partial} r \end{align*} $$
and so
where the above
![]() $\leqslant $
’s are understood as meaning that the difference between the two sides is m-sh. It follows that
$\leqslant $
’s are understood as meaning that the difference between the two sides is m-sh. It follows that
 $$ \begin{align*} 0 &\leqslant\frac{\chi_{\{\underline{h} < s\}}}{s^{2k - 2k/m}}\left( T\wedge \sqrt{-1}\partial\overline{\partial} \underline{h}^2 - T\wedge \sqrt{-1}\partial\overline{\partial} r^2\right)\\ & \leqslant C_{\delta}s^\delta \left(\frac{\chi_{\{\underline{h} < s\}}}{s^{2k - 2k/m}} T\wedge \sqrt{-1}\partial\overline{\partial} \underline{h}^2\right) \end{align*} $$
$$ \begin{align*} 0 &\leqslant\frac{\chi_{\{\underline{h} < s\}}}{s^{2k - 2k/m}}\left( T\wedge \sqrt{-1}\partial\overline{\partial} \underline{h}^2 - T\wedge \sqrt{-1}\partial\overline{\partial} r^2\right)\\ & \leqslant C_{\delta}s^\delta \left(\frac{\chi_{\{\underline{h} < s\}}}{s^{2k - 2k/m}} T\wedge \sqrt{-1}\partial\overline{\partial} \underline{h}^2\right) \end{align*} $$
since the measure
![]() $T\wedge \sqrt {-1}\partial \overline {\partial }\underline {h}^2 \geqslant 0$
. Taking
$T\wedge \sqrt {-1}\partial \overline {\partial }\underline {h}^2 \geqslant 0$
. Taking
![]() $s\rightarrow 0$
now implies that
$s\rightarrow 0$
now implies that
 $$\begin{align*}\lim_{s\rightarrow 0} \frac{1}{s^{2k - 2k/m}}\int_{\{\underline{h} < s\}} T \wedge \sqrt{-1}\partial\overline{\partial} \underline{h}^{2} = \lim_{s\rightarrow 0} \frac{1}{s^{2k - 2k/m}}\int_{\{\underline{h} < s\}} T \wedge \sqrt{-1}\partial\overline{\partial} r^2, \end{align*}$$
$$\begin{align*}\lim_{s\rightarrow 0} \frac{1}{s^{2k - 2k/m}}\int_{\{\underline{h} < s\}} T \wedge \sqrt{-1}\partial\overline{\partial} \underline{h}^{2} = \lim_{s\rightarrow 0} \frac{1}{s^{2k - 2k/m}}\int_{\{\underline{h} < s\}} T \wedge \sqrt{-1}\partial\overline{\partial} r^2, \end{align*}$$
and it is easy to see that, by repeating the above argument
![]() $m-2$
more times, we have that
$m-2$
more times, we have that
 $$\begin{align*}\nu(\varphi, \underline{\psi}_V) = \left(\frac{k-m}{m}\right)^{m-1}\lim_{s\rightarrow 0} \frac{1}{s^{2k - 2k/m}}\int_{\{\underline{h} < s\}}\sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} r^2)^{m-1}\wedge \omega^{n-m}. \end{align*}$$
$$\begin{align*}\nu(\varphi, \underline{\psi}_V) = \left(\frac{k-m}{m}\right)^{m-1}\lim_{s\rightarrow 0} \frac{1}{s^{2k - 2k/m}}\int_{\{\underline{h} < s\}}\sqrt{-1}\partial\overline{\partial} \varphi \wedge (\sqrt{-1}\partial\overline{\partial} r^2)^{m-1}\wedge \omega^{n-m}. \end{align*}$$
By noting that
![]() $\{r < (1-\varepsilon )s\} \subset \{\underline {h} < s\} \subset \{r < s\}$
as long as s is sufficiently small (depending on
$\{r < (1-\varepsilon )s\} \subset \{\underline {h} < s\} \subset \{r < s\}$
as long as s is sufficiently small (depending on
![]() $\varepsilon $
), we can also replace the set
$\varepsilon $
), we can also replace the set
![]() $\{\underline {h} < s\}$
with
$\{\underline {h} < s\}$
with
![]() $\{r < s\}$
in the above limit.
$\{r < s\}$
in the above limit.
Finally, since
![]() $\underline {\psi }_V$
and
$\underline {\psi }_V$
and
![]() $\psi_V$
have the same singularity type, we can conclude by using Proposition 2.6.
$\psi_V$
have the same singularity type, we can conclude by using Proposition 2.6.
3.4 Subweights with localized singularities
We now construct explicit m-subweights,
![]() $\psi_\theta $
, which have ‘nonconstant’ behavior along V when
$\psi_\theta $
, which have ‘nonconstant’ behavior along V when
![]() $k \geqslant m$
. It is easy to see from the construction that these subweights will satisfy
$k \geqslant m$
. It is easy to see from the construction that these subweights will satisfy
![]() $\sigma (\psi_\theta , \psi_V) = 0$
and
$\sigma (\psi_\theta , \psi_V) = 0$
and
![]() $\nu (\psi_\theta , \psi_V)> 0$
(Remark 3.9).
$\nu (\psi_\theta , \psi_V)> 0$
(Remark 3.9).
For any real number
![]() $\nu \in \mathbb{R}$
, define
$\nu \in \mathbb{R}$
, define
![]() $F_\nu : \mathbb{R}_{\geqslant 0}\rightarrow \mathbb{R}\cup \{-\infty \}$
by
$F_\nu : \mathbb{R}_{\geqslant 0}\rightarrow \mathbb{R}\cup \{-\infty \}$
by
 $$\begin{align*}F_\nu(t) := \begin{cases} t^{2 - 2\nu} &\text{ if }\nu < 1 \\ \log t &\text{ if } \nu = 1 \\ -t^{2 - 2\nu} &\text{ if }\nu> 1.\end{cases} \end{align*}$$
$$\begin{align*}F_\nu(t) := \begin{cases} t^{2 - 2\nu} &\text{ if }\nu < 1 \\ \log t &\text{ if } \nu = 1 \\ -t^{2 - 2\nu} &\text{ if }\nu> 1.\end{cases} \end{align*}$$
We additionally define
![]() $D_\nu := |2\nu - 2|$
if
$D_\nu := |2\nu - 2|$
if
![]() $\nu \not =1$
, and
$\nu \not =1$
, and
![]() $D_\nu = 1$
if
$D_\nu = 1$
if
![]() $\nu = 1$
. If
$\nu = 1$
. If
![]() $m \leqslant k$
, then for any
$m \leqslant k$
, then for any
![]() $\nu < \frac {k}{m}$
we have that
$\nu < \frac {k}{m}$
we have that
![]() $G_m < F_{\nu }$
.
$G_m < F_{\nu }$
.
Proposition 3.7. Suppose we are in the setting of the previous subsections and
![]() $\delta $
is sufficiently large, depending only on k and m. Let
$\delta $
is sufficiently large, depending only on k and m. Let
![]() $\theta $
be a smooth, nonnegative function on V, and suppose that
$\theta $
be a smooth, nonnegative function on V, and suppose that
![]() $m \leqslant k$
. Then for any
$m \leqslant k$
. Then for any
![]() $\frac {k}{m} - \frac {1}{2} \leqslant \nu < \frac {k}{m}$
, there exists a
$\frac {k}{m} - \frac {1}{2} \leqslant \nu < \frac {k}{m}$
, there exists a
![]() $C> 0$
such that
$C> 0$
such that
where
![]() $\underline {\theta }$
is a smooth extension of
$\underline {\theta }$
is a smooth extension of
![]() $\theta $
with compact support. When
$\theta $
with compact support. When
![]() $m = 1$
, we can take
$m = 1$
, we can take
![]() $k - 1\leqslant \nu < k$
.
$k - 1\leqslant \nu < k$
.
The construction is local and so works if V is only locally defined in
![]() $\overline {\Omega }$
.
$\overline {\Omega }$
.
Remark 3.8. The bounds on
![]() $\nu $
seem to be optimal. Note that when
$\nu $
seem to be optimal. Note that when
![]() $k < \frac {3}{2}m$
, we can choose
$k < \frac {3}{2}m$
, we can choose
![]() $\nu < 1$
so that the
$\nu < 1$
so that the
![]() $F_{\nu }$
term is bounded from below.
$F_{\nu }$
term is bounded from below.
Proof. The proof is a computation which is very similar to Proposition 3.1, so we omit several details. Working in the same geodesic normal coordinates as before, it follows that
 $$ \begin{align*} \sqrt{-1}\partial\overline{\partial}(\underline{\theta\psi}_V(\underline{h}(r_\varepsilon))) = {} & \underline{\theta}\sqrt{-1}\partial\overline{\partial} G_m(\underline{h}(r_\varepsilon)) + \sqrt{-1} \partial \underline{\theta} \wedge \overline{\partial} G_m(\underline{h}(r_\varepsilon))\\[3mm] & +\sqrt{-1} \partial G_m(\underline{h}(r_\varepsilon))\wedge \overline{\partial} \underline{\theta} + G_m(\underline{h}(r_\varepsilon)) \sqrt{-1}\partial\overline{\partial}\underline{\theta}\\[3mm] \geqslant {} & \begin{pmatrix} 0 & 0 & \frac{D_{k,m}^{-1} r}{r_\varepsilon^{\frac{2k}{m}}}\overline{\partial} \underline{\theta} \\ 0 & 0 & 0 \\ \frac{D_{k,m}^{-1} r}{r_\varepsilon^{\frac{2k}{m}}}\partial \underline{\theta} & 0 & \frac{-1}{r_\varepsilon^{\frac{2k}{m}-2}}\sqrt{-1}\partial\overline{\partial} \underline{\theta} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \sqrt{-1}\partial\overline{\partial}(\underline{\theta\psi}_V(\underline{h}(r_\varepsilon))) = {} & \underline{\theta}\sqrt{-1}\partial\overline{\partial} G_m(\underline{h}(r_\varepsilon)) + \sqrt{-1} \partial \underline{\theta} \wedge \overline{\partial} G_m(\underline{h}(r_\varepsilon))\\[3mm] & +\sqrt{-1} \partial G_m(\underline{h}(r_\varepsilon))\wedge \overline{\partial} \underline{\theta} + G_m(\underline{h}(r_\varepsilon)) \sqrt{-1}\partial\overline{\partial}\underline{\theta}\\[3mm] \geqslant {} & \begin{pmatrix} 0 & 0 & \frac{D_{k,m}^{-1} r}{r_\varepsilon^{\frac{2k}{m}}}\overline{\partial} \underline{\theta} \\ 0 & 0 & 0 \\ \frac{D_{k,m}^{-1} r}{r_\varepsilon^{\frac{2k}{m}}}\partial \underline{\theta} & 0 & \frac{-1}{r_\varepsilon^{\frac{2k}{m}-2}}\sqrt{-1}\partial\overline{\partial} \underline{\theta} \end{pmatrix}, \end{align*} $$
where we again understand
![]() $\geqslant $
as meaning the difference of the two sides is m-sh in this proof. Here, we are also interpreting
$\geqslant $
as meaning the difference of the two sides is m-sh in this proof. Here, we are also interpreting
![]() $\overline {\partial }\underline {\theta }$
as a
$\overline {\partial }\underline {\theta }$
as a
![]() $1\times k$
matrix and
$1\times k$
matrix and
![]() $\partial \underline {\theta }$
as its conjugate transpose.
$\partial \underline {\theta }$
as its conjugate transpose.
From the previous proposition, we also have
 $$ \begin{align*} (\sqrt{-1}\partial\overline{\partial} F_{\nu}(\underline{h}(r_\varepsilon)))_{i\overline{j}} &\geqslant D_{\nu}^{-1}\underline{h}^{-2\nu}\begin{pmatrix} 1 - \nu & 0 & 0 \\ 0 & \mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + O(r_\varepsilon^{\delta - 2\nu}). \end{align*} $$
$$ \begin{align*} (\sqrt{-1}\partial\overline{\partial} F_{\nu}(\underline{h}(r_\varepsilon)))_{i\overline{j}} &\geqslant D_{\nu}^{-1}\underline{h}^{-2\nu}\begin{pmatrix} 1 - \nu & 0 & 0 \\ 0 & \mathrm{Id}_{k-1} & 0 \\ 0 & 0 & 0 \end{pmatrix} + O(r_\varepsilon^{\delta - 2\nu}). \end{align*} $$
This leading order matrix will be strictly m-sh as long as
![]() $\nu < \frac {k}{m},$
by previous computations.
$\nu < \frac {k}{m},$
by previous computations.
We now have that
 $$\begin{align*}\sqrt{-1}\partial\overline{\partial}(\underline{\theta\psi}_V + C F_{\nu}(\underline{h}(r)))\geqslant \begin{pmatrix} \frac{C}{r_\varepsilon^{2\nu}}\left(1 - \nu\right) & 0 & \frac{r}{r_\varepsilon^{\frac{2k}{m}}}\overline{\partial} \underline{\theta} \\ 0 & \frac{C}{r_\varepsilon^{2\nu}}\mathrm{Id}_{k-1} & 0 \\ \frac{r}{r_\varepsilon^{\frac{2k}{m}}}\partial \underline{\theta} & 0 & \frac{-1}{r_\varepsilon^{\frac{2k}{m}-2}}\sqrt{-1}\partial\overline{\partial} \underline{\theta} \end{pmatrix} + O(r_\varepsilon^{\delta - 2\nu}), \end{align*}$$
$$\begin{align*}\sqrt{-1}\partial\overline{\partial}(\underline{\theta\psi}_V + C F_{\nu}(\underline{h}(r)))\geqslant \begin{pmatrix} \frac{C}{r_\varepsilon^{2\nu}}\left(1 - \nu\right) & 0 & \frac{r}{r_\varepsilon^{\frac{2k}{m}}}\overline{\partial} \underline{\theta} \\ 0 & \frac{C}{r_\varepsilon^{2\nu}}\mathrm{Id}_{k-1} & 0 \\ \frac{r}{r_\varepsilon^{\frac{2k}{m}}}\partial \underline{\theta} & 0 & \frac{-1}{r_\varepsilon^{\frac{2k}{m}-2}}\sqrt{-1}\partial\overline{\partial} \underline{\theta} \end{pmatrix} + O(r_\varepsilon^{\delta - 2\nu}), \end{align*}$$
ignoring some multiplicative constants. This leading matrix will be (strictly) m-sh with a positive term of order
![]() $r^{2\nu }_\varepsilon $
if we choose
$r^{2\nu }_\varepsilon $
if we choose
![]() $\nu $
appropriately. This can be done by choosing
$\nu $
appropriately. This can be done by choosing
![]() $\nu $
so that the strict m-subharmonicity of the
$\nu $
so that the strict m-subharmonicity of the
![]() $F_\nu $
term beats the powers coming from the
$F_\nu $
term beats the powers coming from the
![]() $\underline {\theta }$
terms. This can be seen by noting that
$\underline {\theta }$
terms. This can be seen by noting that
![]() $r < r_\varepsilon $
so that, when
$r < r_\varepsilon $
so that, when
![]() $m> 1$
, we need
$m> 1$
, we need
giving the combined constraints
when
![]() $m = 1$
, we only need the trace to be positive, so we only require
$m = 1$
, we only need the trace to be positive, so we only require
Remark 3.9. For
![]() $\varphi $
in Cegrell’s class
$\varphi $
in Cegrell’s class
![]() $\mathcal {E}^m$
, we denote the complex Hessian operator of
$\mathcal {E}^m$
, we denote the complex Hessian operator of
![]() $\varphi $
by
$\varphi $
by
![]() $\mathrm{H}^m(\varphi ) := \left (\sqrt {-1}\partial \overline {\partial }\varphi \right )^m\wedge \omega ^{n-m}$
. We claim that the
$\mathrm{H}^m(\varphi ) := \left (\sqrt {-1}\partial \overline {\partial }\varphi \right )^m\wedge \omega ^{n-m}$
. We claim that the
![]() $\underline {\psi }_\theta \in \mathcal {E}^m$
constructed in Proposition 3.7 satisfies
$\underline {\psi }_\theta \in \mathcal {E}^m$
constructed in Proposition 3.7 satisfies
Indeed, on any sufficiently small open B near
![]() $z\in V$
, we have
$z\in V$
, we have
so Proposition 2.6 implies that
Covering V with a disjoint collection of such B and then letting
![]() $\varepsilon \rightarrow 0$
produces the claimed equality.
$\varepsilon \rightarrow 0$
produces the claimed equality.
Taking
![]() $\theta $
such that
$\theta $
such that
![]() $\min _V \theta = 0$
but
$\min _V \theta = 0$
but
![]() $\theta \not = 0$
now gives a function such that
$\theta \not = 0$
now gives a function such that
Additionally, we can use Proposition 2.6 to see that
![]() $\chi _{V} \mathrm{H}^m(\underline {\psi }_{\theta }) = \chi _V\theta ^m\mathrm{H}^m\left (\psi_V\right ).$
Solutions to
$\chi _{V} \mathrm{H}^m(\underline {\psi }_{\theta }) = \chi _V\theta ^m\mathrm{H}^m\left (\psi_V\right ).$
Solutions to
![]() $\mathrm{H}^m(v) = \chi _V \theta ^m \mathrm{H}^m(\varphi )$
for any given
$\mathrm{H}^m(v) = \chi _V \theta ^m \mathrm{H}^m(\varphi )$
for any given
![]() $\varphi \in \mathcal {E}^m(\Omega )$
were constructed in [Reference Hung and Van Phu24], following the work of [Reference Åhag, Cegrell, Czyż and Hiệp1] in the psh case, as a nested sequence of envelopes. Our
$\varphi \in \mathcal {E}^m(\Omega )$
were constructed in [Reference Hung and Van Phu24], following the work of [Reference Åhag, Cegrell, Czyż and Hiệp1] in the psh case, as a nested sequence of envelopes. Our
![]() $\underline {\psi }_\theta $
can be seen as explicit contenders in these envelopes for
$\underline {\psi }_\theta $
can be seen as explicit contenders in these envelopes for
![]() $\varphi = \psi_V$
.
$\varphi = \psi_V$
.
Let
![]() $\psi_\theta $
be the solution to
$\psi_\theta $
be the solution to
![]() $\mathrm{H}^m(\psi_\theta ) = \chi _V\theta ^m\mathrm{H}^m(\psi_V)$
constructed in [Reference Hung and Van Phu24]. If
$\mathrm{H}^m(\psi_\theta ) = \chi _V\theta ^m\mathrm{H}^m(\psi_V)$
constructed in [Reference Hung and Van Phu24]. If
![]() $k \leqslant \frac {3}{2}m$
, our examples show that
$k \leqslant \frac {3}{2}m$
, our examples show that
![]() $\psi_\theta $
is actually bounded on
$\psi_\theta $
is actually bounded on
![]() $V\setminus \mathrm{Supp}(\theta )$
. We suspect our examples actually compute the exact singularity type of
$V\setminus \mathrm{Supp}(\theta )$
. We suspect our examples actually compute the exact singularity type of
![]() $\psi_\theta $
on all of V.
$\psi_\theta $
on all of V.
3.5 Subharmonic functions and minimal submanifolds
We conclude this section with the observation that the above method can be copied directly when V is only a minimal submanifold of X (which we still assume to be Kähler), provided that we take
![]() $m=1$
. Subharmonic functions have long been known to be intimately related with minimal submanifolds, and as such, we are unsure if a similar construction is already present in the literature.
$m=1$
. Subharmonic functions have long been known to be intimately related with minimal submanifolds, and as such, we are unsure if a similar construction is already present in the literature.
Proposition 3.10. Suppose that V is a minimal submanifold of X of (real) codimension k. Then there exists an
![]() $\omega $
-subharmonic function
$\omega $
-subharmonic function
![]() $\psi_V$
on a neighborhood
$\psi_V$
on a neighborhood
![]() $\Omega $
of V, which is moreover
$\Omega $
of V, which is moreover
![]() $\omega $
-harmonic on
$\omega $
-harmonic on
![]() $\Omega \setminus V$
, such that
$\Omega \setminus V$
, such that
![]() $\psi_V$
has the same singularity type as
$\psi_V$
has the same singularity type as
Proof. Construct real coordinates at a point z near V in the same way as done at the beginning of this section so that
![]() $e_1$
is in the direction of the geodesic connecting z and V. By [Reference Tam and Yu33, Lemma 2.2], we have
$e_1$
is in the direction of the geodesic connecting z and V. By [Reference Tam and Yu33, Lemma 2.2], we have
 $$\begin{align*}r_{ij}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & \frac{1}{r}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & h_{ij} \end{pmatrix} +o(1), \end{align*}$$
$$\begin{align*}r_{ij}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & \frac{1}{r}\cdot\mathrm{Id}_{k-1} & 0 \\ 0 & 0 & h_{ij} \end{pmatrix} +o(1), \end{align*}$$
where here
![]() $(h_{ij})_{k+1\leqslant i,j \leqslant 2n}$
are the components of the second fundamental form of V evaluated against
$(h_{ij})_{k+1\leqslant i,j \leqslant 2n}$
are the components of the second fundamental form of V evaluated against
![]() $e_1$
. All of the computations in Proposition 3.1 go through verbatim, with the exception that the second fundamental form term becomes
$e_1$
. All of the computations in Proposition 3.1 go through verbatim, with the exception that the second fundamental form term becomes
![]() $rh_{ij} + o(r_\varepsilon )$
. Since V is minimal, this bad term disappears when we take the trace of
$rh_{ij} + o(r_\varepsilon )$
. Since V is minimal, this bad term disappears when we take the trace of
![]() $\sqrt {-1}\partial \overline {\partial } r_\varepsilon ^{k-2}$
, and the computations in Propositions 3.2 and 3.3 can then be repeated.
$\sqrt {-1}\partial \overline {\partial } r_\varepsilon ^{k-2}$
, and the computations in Propositions 3.2 and 3.3 can then be repeated.
Once a sub- and superweight have been produced, Proposition 3.4 is standard.
4 A Siu-type theorem
We now present our Siu-type theorem, stated as Theorem 1.4 in the introduction. We will need the following weak Harnack inequality:
Proposition 4.1 (Theorem 8.18 of [Reference Gilbarg and Trudinger21])
Let
![]() $\Omega \subset \mathbb{R}^{2n}$
be a domain. Suppose that
$\Omega \subset \mathbb{R}^{2n}$
be a domain. Suppose that
![]() $\varphi $
is a nonpositive smooth subsolution of a linear elliptic operator
$\varphi $
is a nonpositive smooth subsolution of a linear elliptic operator
![]() $L = a^{ij}\partial _{i}\partial _{j}$
, that is,
$L = a^{ij}\partial _{i}\partial _{j}$
, that is,
and
![]() $\lambda I_{2n} \leqslant (a^{ij}) \leqslant \Lambda I_{2n}$
for positive constants
$\lambda I_{2n} \leqslant (a^{ij}) \leqslant \Lambda I_{2n}$
for positive constants
![]() $\lambda $
and
$\lambda $
and
![]() $\Lambda $
. Then for any ball
$\Lambda $
. Then for any ball
![]() $B_{2}(y)\subset \Omega $
and
$B_{2}(y)\subset \Omega $
and
![]() $p\in [1,n/(n-1))$
, we have
$p\in [1,n/(n-1))$
, we have
 $$\begin{align*}\varphi(y) \leqslant -\frac{1}{C(\lambda,\Lambda,p,n)}\int_{B_{1}(y)}(-\varphi)^{p} \leqslant 0. \end{align*}$$
$$\begin{align*}\varphi(y) \leqslant -\frac{1}{C(\lambda,\Lambda,p,n)}\int_{B_{1}(y)}(-\varphi)^{p} \leqslant 0. \end{align*}$$
Theorem 4.2. Suppose that V is a compact, complex submanifold of codimension k. If
![]() $\varphi \in m\mathrm{SH}(\Omega )$
is such that
$\varphi \in m\mathrm{SH}(\Omega )$
is such that
![]() $k < m$
, then
$k < m$
, then
![]() $L_{\psi_V}(\varphi ) \equiv \sigma (\varphi , \psi_V)$
.
$L_{\psi_V}(\varphi ) \equiv \sigma (\varphi , \psi_V)$
.
Proof. For convenience, set
![]() $\sigma := \sigma (\varphi , \psi_V)$
. We will show that the set of points where
$\sigma := \sigma (\varphi , \psi_V)$
. We will show that the set of points where
![]() $L_{\psi_V}(\varphi ) = \sigma $
is open in V – since
$L_{\psi_V}(\varphi ) = \sigma $
is open in V – since
![]() $L_{\psi_V}(\varphi )$
is lower semicontinuous, it is clear that this set is closed and nonempty, by Proposition 2.11.
$L_{\psi_V}(\varphi )$
is lower semicontinuous, it is clear that this set is closed and nonempty, by Proposition 2.11.
Let
![]() $z_0\in V$
be such that
$z_0\in V$
be such that
![]() $L_{\psi_V}(\varphi )(z_0) = \sigma $
. Choose local holomorphic coordinates
$L_{\psi_V}(\varphi )(z_0) = \sigma $
. Choose local holomorphic coordinates
![]() $z = (z', z")$
centered at
$z = (z', z")$
centered at
![]() $z_0$
such that
$z_0$
such that
![]() $V = \{z' = 0\}$
in these coordinates. Let
$V = \{z' = 0\}$
in these coordinates. Let
![]() $B_{R}$
be the coordinate ball of radius
$B_{R}$
be the coordinate ball of radius
![]() $0 < R\leqslant 2$
, centered at
$0 < R\leqslant 2$
, centered at
![]() $z_0 = (0, 0)$
. Fix a uniform constant C such that
$z_0 = (0, 0)$
. Fix a uniform constant C such that
Further, let
![]() $\rho (z)$
be a smooth potential for
$\rho (z)$
be a smooth potential for
![]() $\omega $
on
$\omega $
on
![]() $B_2$
such that
$B_2$
such that
![]() $-C \leqslant \rho (z) \leqslant 0$
.
$-C \leqslant \rho (z) \leqslant 0$
.
By definition, there exists a sequence
![]() $z_i = (z_i', z_i") \rightarrow z_0$
, with
$z_i = (z_i', z_i") \rightarrow z_0$
, with
![]() $z_i \in \Omega \setminus V$
, such that
$z_i \in \Omega \setminus V$
, such that
 $$\begin{align*}\lim_{i\rightarrow\infty} \frac{\varphi(z_i)}{\psi_V(z_i)} = \sigma. \end{align*}$$
$$\begin{align*}\lim_{i\rightarrow\infty} \frac{\varphi(z_i)}{\psi_V(z_i)} = \sigma. \end{align*}$$
We assume without loss of generality that
![]() $\log |z_i'|, \log r(z_i), \psi_V(z_i) \leqslant -1$
. Since
$\log |z_i'|, \log r(z_i), \psi_V(z_i) \leqslant -1$
. Since
![]() $\psi_V$
and
$\psi_V$
and
![]() $\log r$
have the same singularity type, by Equation (4.1), we have that
$\log r$
have the same singularity type, by Equation (4.1), we have that
 $$\begin{align*}\lim_{i\rightarrow\infty} \frac{\varphi(z_i)}{\log |z_i'|} = \sigma \end{align*}$$
$$\begin{align*}\lim_{i\rightarrow\infty} \frac{\varphi(z_i)}{\log |z_i'|} = \sigma \end{align*}$$
also. It follows that, for any
![]() $\varepsilon> 0$
, we have
$\varepsilon> 0$
, we have
for all i sufficiently large.
Define the functions
![]() $\eta _{i, \varepsilon }$
on
$\eta _{i, \varepsilon }$
on
![]() $V_2 := V\cap B_2$
by
$V_2 := V\cap B_2$
by
 $$\begin{align*}\eta_{i, \varepsilon}(z") := \frac{\varphi(z_i', z") + \rho(z_i', z") - \varphi(z_i) + 3\varepsilon\log|z_i'|}{-\log|z_i'|}. \end{align*}$$
$$\begin{align*}\eta_{i, \varepsilon}(z") := \frac{\varphi(z_i', z") + \rho(z_i', z") - \varphi(z_i) + 3\varepsilon\log|z_i'|}{-\log|z_i'|}. \end{align*}$$
Note that
![]() $\eta _{i, \varepsilon }$
is subharmonic on
$\eta _{i, \varepsilon }$
is subharmonic on
![]() $V_2$
with respect to the metric
$V_2$
with respect to the metric
![]() $\omega |_{\{z' = z^{\prime }i\}}$
since we have assumed that
$\omega |_{\{z' = z^{\prime }i\}}$
since we have assumed that
![]() $m> k$
.
$m> k$
.
We will show that
![]() $\eta _{i_j, \varepsilon _j}\rightarrow 0$
pointwise a.e. for some subsequence
$\eta _{i_j, \varepsilon _j}\rightarrow 0$
pointwise a.e. for some subsequence
![]() $i_j\rightarrow \infty $
of the i and an associated sequence of
$i_j\rightarrow \infty $
of the i and an associated sequence of
![]() $\varepsilon _j\rightarrow 0$
by using the Harnack inequality. To utilize this, we need to first verify that
$\varepsilon _j\rightarrow 0$
by using the Harnack inequality. To utilize this, we need to first verify that
![]() $\sup \eta _{i, \varepsilon } \leqslant 0$
. Increasing C if necessary, we have that
$\sup \eta _{i, \varepsilon } \leqslant 0$
. Increasing C if necessary, we have that
so by the definition of
![]() $\sigma $
we have
$\sigma $
we have
Combining this with Equation (4.2) and our choice of
![]() $\rho $
gives
$\rho $
gives
 $$ \begin{align} \sup_{V_2}\eta_{i,\varepsilon} \leqslant -(\sigma - \varepsilon) + (\sigma + \varepsilon) - 3\varepsilon + \frac{(\sigma - \varepsilon)C}{-\log|z_i|} \leqslant -\varepsilon + \frac{(\sigma - \varepsilon)C}{-\log|z_i|} < 0 \end{align} $$
$$ \begin{align} \sup_{V_2}\eta_{i,\varepsilon} \leqslant -(\sigma - \varepsilon) + (\sigma + \varepsilon) - 3\varepsilon + \frac{(\sigma - \varepsilon)C}{-\log|z_i|} \leqslant -\varepsilon + \frac{(\sigma - \varepsilon)C}{-\log|z_i|} < 0 \end{align} $$
for
![]() $\varepsilon $
fixed and i sufficiently large.
$\varepsilon $
fixed and i sufficiently large.
Let
![]() $\varepsilon _{j}>0$
be a sequence such that
$\varepsilon _{j}>0$
be a sequence such that
![]() $\varepsilon _{j}\to 0$
as
$\varepsilon _{j}\to 0$
as
![]() $j\to \infty $
. By Equation (4.3), for each j there exists a sufficiently large
$j\to \infty $
. By Equation (4.3), for each j there exists a sufficiently large
![]() $i_{j}$
such that
$i_{j}$
such that
![]() $i_{j}\to \infty $
as
$i_{j}\to \infty $
as
![]() $j\to \infty $
and
$j\to \infty $
and
Letting
![]() $V_1 := V\cap B_1$
, Proposition 4.1 now implies that
$V_1 := V\cap B_1$
, Proposition 4.1 now implies that
for any
![]() $p \in [1, n/(n-1))$
(up to increasing C again, depending on p and
$p \in [1, n/(n-1))$
(up to increasing C again, depending on p and
![]() $\omega $
). Fixing some
$\omega $
). Fixing some
![]() $p>1$
, it is clear that
$p>1$
, it is clear that
Hence, we see that
![]() $\eta _{i_{j},\varepsilon _{j}}\rightarrow 0$
in
$\eta _{i_{j},\varepsilon _{j}}\rightarrow 0$
in
![]() $L^p$
as
$L^p$
as
![]() $j\rightarrow \infty $
, and so after passing to a subsequence of the j, we have that
$j\rightarrow \infty $
, and so after passing to a subsequence of the j, we have that
Now, from our definition of
![]() $\eta _{i, \varepsilon }$
, we see that
$\eta _{i, \varepsilon }$
, we see that
 $$\begin{align*}\frac{\varphi(z^{\prime}{i_{j}}, z")}{\log|z_{i_{j}}'|} = \frac{\varphi(z_{i_{j}}', z_{i_{j}}")}{\log|z_{i_{j}}'|} -\eta_{{i_{j}}, \varepsilon_{j}}(z") - 3\varepsilon_{j} - \frac{\rho(z^{\prime}{i_{j}}, z")}{\log|z^{\prime}{i_{j}}|}. \end{align*}$$
$$\begin{align*}\frac{\varphi(z^{\prime}{i_{j}}, z")}{\log|z_{i_{j}}'|} = \frac{\varphi(z_{i_{j}}', z_{i_{j}}")}{\log|z_{i_{j}}'|} -\eta_{{i_{j}}, \varepsilon_{j}}(z") - 3\varepsilon_{j} - \frac{\rho(z^{\prime}{i_{j}}, z")}{\log|z^{\prime}{i_{j}}|}. \end{align*}$$
Using Equation (4.4) and taking the limit as
![]() $j\rightarrow \infty $
gives
$j\rightarrow \infty $
gives
 $$\begin{align*}\lim_{j\rightarrow\infty} \frac{\varphi(z^{\prime}{i_{j}}, z")}{\log|z_{i_{j}}'|} = \sigma \end{align*}$$
$$\begin{align*}\lim_{j\rightarrow\infty} \frac{\varphi(z^{\prime}{i_{j}}, z")}{\log|z_{i_{j}}'|} = \sigma \end{align*}$$
for almost all
![]() $z"\in V_1$
. Then we conclude that
$z"\in V_1$
. Then we conclude that
 $$\begin{align*}L_{\psi_V}(\varphi)(0, z") \leqslant \lim_{j\rightarrow\infty} \frac{\varphi(z^{\prime}{i_{j}}, z")}{\log|z_{i_{j}}'|} = \sigma \end{align*}$$
$$\begin{align*}L_{\psi_V}(\varphi)(0, z") \leqslant \lim_{j\rightarrow\infty} \frac{\varphi(z^{\prime}{i_{j}}, z")}{\log|z_{i_{j}}'|} = \sigma \end{align*}$$
for almost every
![]() $z"\in V_1$
. It follows now from Proposition 2.11 that in fact
$z"\in V_1$
. It follows now from Proposition 2.11 that in fact
![]() $L_{\psi_V}(\varphi ) \equiv \sigma $
on
$L_{\psi_V}(\varphi ) \equiv \sigma $
on
![]() $V_1$
, finishing the proof.
$V_1$
, finishing the proof.
Acknowledgements
We would like to thank M. Jonsson for his interest in the present work. J. Chu was partially supported by the Fundamental Research Funds for the Central Universities, Peking University.
Competing interests
The authors have no competing interest to declare.