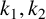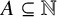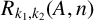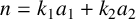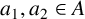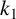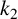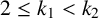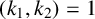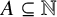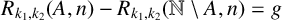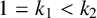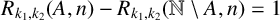1 Introduction
Let
$\mathbb {N}$
be the set of all nonnegative integers. For a set
$A\subseteq \mathbb {N}$
, let
$R_{1}(A,n)$
,
$R_{2}(A,n)$
and
$R_{3}(A,n)$
denote the number of solutions of
$a_1+a_2=n, a_1,a_2\in A$
;
$a_1+a_2=n, a_1, a_2\in A, a_1<a_2$
and
$a_1+a_2=n, a_1,a_2\in A, a_1\leq a_2$
, respectively. For
$i=1,2,3$
, Sárközy asked whether there exist two sets A and B with
$|(A\cup B)\setminus (A\cap B)|=+\infty $
such that
$R_{i}(A,n)=R_{i}(B,n)$
for all sufficiently large integers n. We call this problem the Sárközy problem. In 2002, Dombi [Reference Dombi2] proved that the answer is negative for
$i=1$
and positive for
$i=2$
. For
$i=3$
, Chen and Wang [Reference Chen and Wang1] proved that the answer is also positive. In 2004, Lev [Reference Lev3] provided a new proof by using generating functions. Later, Sándor [Reference Sándor5] determined the partitions of
$\mathbb {N}$
into two sets with the same representation functions by using generating functions. In 2008, Tang [Reference Tang6] provided a simple proof by using the characteristic function.
In 2012, Yang and Chen [Reference Yang and Chen7] first considered the Sárközy problem with weighted representation functions. For any positive integers
$k_1,\ldots ,k_t$
and any set
$A\subseteq \mathbb {N}$
, let
$R_{k_1,\ldots ,k_t}(A,n)$
be the number of solutions of the equation
$n=k_1a_1+\cdots +k_ta_t$
with
$a_1,\ldots ,a_t\in A$
. They posed the following question.
Problem 1.1 [Reference Yang and Chen7, Problem 1]
Does there exist a set
$A\subseteq \mathbb {N}$
such that
$R_{k_1,\ldots ,k_t}(A,n)=R_{k_1,\ldots ,k_t}(\mathbb {N}\setminus A,n)$
for all
$n\geq n_0$
?
They answered this question for
$t=2$
and proved the following results.
Theorem 1.2 [Reference Yang and Chen7, Theorem 1].
If
$k_1$
and
$k_2$
are two integers with
$k_2>k_1\geq 2$
and
$(k_1,k_2)=1$
, then there does not exist any set
$A\subseteq \mathbb {N}$
such that
$R_{k_1,k_2}(A,n)=R_{k_1,k_2} (\mathbb {N}\setminus A,n)$
for all sufficiently large integers n.
Theorem 1.3 [Reference Yang and Chen7, Theorem 2].
If k is an integer with
$k>1$
, then there exists a set
$A\subseteq \mathbb {N}$
such that
$$ \begin{align} R_{1,k}(A,n)=R_{1,k}(\mathbb{N}\setminus A,n) \end{align} $$
for all integers
$n\geq 1$
.
Furthermore, if
$0\in A$
, then (1.1) holds for all integers
$n\geq 1$
if and only if
$$ \begin{align*}A=\{0\}\bigcup\bigg(\bigcup_{i=0}^{\infty}[(k+1)k^{2i},(k+1)k^{2i+1}-1]\bigg),\end{align*} $$
where
$[x,y]=\{n:n\in \mathbb {Z},x\leq n\leq y\}$
.
Later, Li and Ma [Reference Li and Ma4] proved the same results by using generating functions.
Let g be a fixed integer. In this paper, we consider whether there exists a set
$A\subseteq \mathbb {N}$
such that
$R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=g$
for all
$n\geq n_0$
. First, we answer this problem in the negative if
$k_1$
and
$k_2$
are two integers with
$2\le k_1<k_2$
and
$(k_1,k_2)=1$
.
Theorem 1.4. Let g be a fixed integer. If
$k_1$
and
$k_2$
are two integers with
$2\le k_1<k_2$
and
$(k_1,k_2)=1$
, then there does not exist any set
$A\subseteq \mathbb {N}$
such that
$$ \begin{align*}R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb{N}\setminus A,n)=g\end{align*} $$
for all sufficiently large integers n.
Similar to Theorem 1.3, we seek a set
$A\subseteq \mathbb {N}$
such that
$R_{1,k}(A,n)-R_{1,k}(\mathbb {N}\setminus A,n)=g$
for all integers
$n\geq 1$
. In fact, if
$|g|>1$
, then such a set A does not exist by the simple observation that
$0\le R_{1,k}(A,n)\le 1$
and
$0\le R_{1,k}(\mathbb {N}\setminus A,n)\le 1$
for all positive integers
$n<k$
. So we only need to consider the case
$g=1$
.
Theorem 1.5. If k is an integer with
$k>1$
, then there exists a set
$A\subseteq \mathbb {N}$
such that
$$ \begin{align} R_{1,k}(A,n)-R_{1,k}(\mathbb{N}\setminus A,n)=1 \end{align} $$
for all integers
$n\ge 1$
.
Furthermore, (1.2) holds for all integers
$n\geq 1$
if and only if
$$ \begin{align*}A=\{0\}\bigcup\bigg(\bigcup_{i=0}^{\infty}[k^{2i},k^{2i+1}-1]\bigg).\end{align*} $$
2 Proofs
Lemma 2.1. Let
$k_1<k_2$
be two positive integers,
$\{a(n)\}_{n=-\infty }^{+\infty }$
be a sequence of integers with
$a(n)=0$
for
$n<0$
and
$A\subseteq \mathbb {N}$
. Then the equality
$$ \begin{align} R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb{N}\setminus A,n)=a(n)\end{align} $$
holds for all nonnegative integers n if and only if
$$ \begin{align*}\chi_{A}\bigg(\bigg[\frac{n}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{n}{k_2}\bigg]\bigg)=1+\sum_{j=0}^{k_1-1}(a(n-j)-a(n-k_2-j))\end{align*} $$
holds for all nonnegative integers n, where
$\chi _A(i)$
is the characteristic function of A, that is,
$\chi _A(i) = 1$
if
$i\in A$
and
$\chi _A(i) = 0$
if
$i\notin A$
.
Proof. Let
$f(x)$
be the generating function associated with A, that is,
$$ \begin{align*}f(x)=\sum_{a\in A}x^{a}=\sum_{i=0}^{\infty}\chi_A(i)x^i.\end{align*} $$
Then,
$$ \begin{align*} &\sum_{n=0}^\infty (R_{k_1,k_2}(A,n) -R_{k_1,k_2}(\mathbb{N}\setminus A,n))x^n \\ &\quad=f(x^{k_1})f(x^{k_2})-\bigg(\frac{1}{1-x^{k_1}}-f(x^{k_1})\bigg)\bigg(\frac{1}{1-x^{k_2}}-f(x^{k_2})\bigg)\\ &\quad=\frac{f(x^{k_1})}{1-x^{k_2}}+\frac{f(x^{k_2})}{1-x^{k_1}}-\frac{1}{(1-x^{k_1})(1-x^{k_2})}. \end{align*} $$
Let
$$ \begin{align*}p(x)=\sum_{n=0}^{\infty}a(n)x^n.\end{align*} $$
It follows that (2.1) holds for all nonnegative integers n if and only if
$$ \begin{align*}\frac{f(x^{k_1})}{1-x^{k_2}}+\frac{f(x^{k_2})}{1-x^{k_1}}-\frac{1}{(1-x^{k_1})(1-x^{k_2})}=p(x),\end{align*} $$
that is,
$$ \begin{align} f(x^{k_1})\frac{1-x^{k_1}}{1-x}+f(x^{k_2})\frac{1-x^{k_2}}{1-x}=\frac{1}{1-x}+(1-x^{k_2})\frac{1-x^{k_1}}{1-x}p(x). \end{align} $$
Note that
$$ \begin{align*} f(x^{k_1})\dfrac{1-x^{k_1}}{1-x}=(1+x+\cdots+x^{k_1-1})\displaystyle\sum_{n=0}^{\infty}\chi_A(n)x^{k_1n}=\displaystyle\sum_{n=0}^{\infty}\chi_{A}\bigg(\bigg[\dfrac{n}{k_1}\bigg]\bigg)\kern0.8pt x^n, \end{align*} $$
$$ \begin{align*} f(x^{k_2})\dfrac{1-x^{k_2}}{1-x}=(1+x+\cdots+x^{k_2-1})\displaystyle\sum_{n=0}^{\infty}\chi_A(n)x^{k_2n}=\displaystyle\sum_{n=0}^{\infty}\chi_{A}\bigg(\bigg[\dfrac{n}{k_2}\bigg]\bigg)\kern0.8pt x^n, \end{align*} $$
$$ \begin{align*} \dfrac{1}{1-x}=\displaystyle\sum_{n=0}^{\infty}x^n \end{align*} $$
and
$$ \begin{align*} (1-x^{k_2})\frac{1-x^{k_1}}{1-x}p(x) &=(1-x^{k_2})(1+x+\cdots+x^{k_1-1})\sum_{n=0}^{\infty}a(n)x^n\\ &=\sum_{n=0}^{\infty}\bigg(\sum_{j=0}^{k_1-1}(a(n-j)-a(n-k_2-j))\bigg)\kern0.8pt x^n. \end{align*} $$
It follows from (2.2) that for all nonnegative integers n,
$$ \begin{align*}\chi_{A}\bigg(\bigg[\frac{n}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{n}{k_2}\bigg]\bigg)=1+\sum_{j=0}^{k_1-1}(a(n-j)-a(n-k_2-j)).\end{align*} $$
This completes the proof of Lemma 2.1.
Lemma 2.2. Let
$n_0$
be a positive integer and
$k_1<k_2$
be two positive integers with
$(k_1,k_2)=1$
and
$A\subseteq \mathbb {N}$
be a set with
$$ \begin{align} \chi_{A}\bigg(\bigg[\frac{i}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{i}{k_2}\bigg]\bigg)=1 \quad \text{for~all}~i\ge k_1+k_2+n_0. \end{align} $$
If
$n\ge k_1+k_2+n_0$
and
$\chi _{A}(n)+\chi _{A}(n+1)=1$
, then
$k_2\mid n+1$
.
Proof. Since
$\chi _{A}(n)+\chi _{A}(n+1)=1$
, it follows that
$$ \begin{align} \chi_{A}\bigg(\bigg[\frac{(n+1)k_1-1}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{(n+1)k_1}{k_1}\bigg]\bigg)=\chi_{A}(n)+\chi_{A}(n+1)=1. \end{align} $$
By (2.3),
$$ \begin{align*}\chi_{A}\bigg(\bigg[\frac{(n+1)k_1-1}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{(n+1)k_1-1}{k_2}\bigg]\bigg)=1\end{align*} $$
and
$$ \begin{align*}\chi_{A}\bigg(\bigg[\frac{(n+1)k_1}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{(n+1)k_1}{k_2}\bigg]\bigg)=1.\end{align*} $$
It follows from (2.4) that
$$ \begin{align*}\chi_{A}\bigg(\bigg[\frac{(n+1)k_1-1}{k_2}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{(n+1)k_1}{k_2}\bigg]\bigg)=1.\end{align*} $$
Let t and r be integers with
$$ \begin{align*}(n+1)k_1=tk_2+r, \quad 0\le r\le k_2-1.\end{align*} $$
If
$r\ge 1$
, then
$$ \begin{align*}1=\chi_{A}\bigg(\bigg[\frac{(n+1)k_1-1}{k_2}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{(n+1)k_1}{k_2}\bigg]\bigg)=2\chi_{A}(t),\end{align*} $$
which is a contradiction. Hence,
$r=0$
and
$(n+1)k_1=tk_2$
. Noting that
$(k_1,k_2)=1$
, we have
$k_2\mid n+1$
. This completes the proof of Lemma 2.2.
Proof of Theorem 1.4.
Let g be an integer and let
$k_1,k_2$
be integers with
$2\le k_1<k_2$
and
$(k_1,k_2)=1$
. Suppose that
$$ \begin{align} R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb{N}\setminus A,n)=g \end{align} $$
for all integers
$n\ge n_0$
. Let
$\{a(n)\}_{n=-\infty }^{+\infty }$
be a sequence of integers with
$a(n)=0$
for
$n<0$
and
$a(n)=g$
for all integers
$n\ge n_0$
. It follows from Lemma 2.1 that for all integers
$i\ge k_1+k_2+n_0$
,
$$ \begin{align} \chi_{A}\bigg(\bigg[\frac{i}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{i}{k_2}\bigg]\bigg)=1. \end{align} $$
If A is a finite set, then
$R_{k_1,k_2}(A,n)=0$
for all sufficiently large integers n, and
$R_{k_1,k_2} (\mathbb {N}\setminus A,n)$
cannot be a fixed constant as
$n\rightarrow +\infty $
, which implies that (2.5) cannot hold. So A is an infinite set. Similarly,
$\mathbb {N}\setminus A$
is also an infinite set.
Since
$2\le k_1<k_2$
, it follows that there exists an integer
$t>1$
such that
$k_2< k_1^{t}$
. Note that both A and
$\mathbb {N}\setminus A$
are infinite sets. So there exists an integer
$n=k_1^{\alpha }k_2^{\beta }h-1>(k_1+k_2+n_0)^{t+1}$
such that
$n\in A$
and
$n+1\notin A$
, where
$\alpha $
and
$\beta $
are nonnegative integers and h is a positive integer with
$(h,k_1k_2)=1$
. It follows from (2.6) and Lemma 2.2 that
$k_2\mid n+1$
and
$\beta \ge 1$
. Since
$$ \begin{align*}(k_1+k_2+n_0)^{t+1}<n<k_1^{\alpha}k_2^{\beta}h<k_1^{t(\alpha+\beta)}h,\end{align*} $$
it follows that
$k_1^{\alpha +\beta }>k_1+k_2+n_0$
or
$h>k_1+k_2+n_0$
. Hence, for any
$0\le i\le \beta $
,
$$ \begin{align} k_1^{\alpha+i}k_2^{\beta-i}h\ge k_1^{\alpha+\beta}h>k_1+k_2+n_0. \end{align} $$
By (2.6),
$$ \begin{align} \chi_{A}\bigg(\bigg[\frac{k_1^{\alpha+1}k_2^{\beta}h}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{k_1^{\alpha+1}k_2^{\beta}h}{k_2}\bigg]\bigg)=1 \end{align} $$
and
$$ \begin{align} \chi_{A}\bigg(\bigg[\frac{k_1^{\alpha+1}k_2^{\beta}h-k_1}{k_1}\bigg]\bigg)+\chi_{A}\bigg(\bigg[\frac{k_1^{\alpha+1}k_2^{\beta}h-k_1}{k_2}\bigg]\bigg)=1. \end{align} $$
Since
$k_1^{\alpha }k_2^{\beta }h=n+1\notin A$
and
$k_1^{\alpha }k_2^{\beta }h-1=n\in A$
, it follows from (2.8) and (2.9) that
$$ \begin{align*}\chi_{A}(k_1^{\alpha+1}k_2^{\beta-1}h-1)+\chi_{A}(k_1^{\alpha+1}k_2^{\beta-1}h)=1. \end{align*} $$
By Lemma 2.2,
$k_2\mid k_1^{\alpha +1}k_2^{\beta -1}h$
and so
$\beta \ge 2$
. Continuing this procedure yields
$$ \begin{align*}\chi_{A}(k_1^{\alpha+\beta}h-1)+\chi_{A}(k_1^{\alpha+\beta}h)=1.\end{align*} $$
By (2.7) and Lemma 2.2, we also have
$k_2\mid k_1^{\alpha +\beta }h$
, which is impossible. Hence, there does not exist any set
$A\subseteq \mathbb {N}$
such that (2.5) holds for all sufficiently large integers n. This completes the proof of Theorem 1.4.
Proof of Theorem 1.5.
Suppose that there is a set A such that
$$ \begin{align} R_{1,k}(A,n)-R_{1,k}(\mathbb{N}\setminus A,n)=1 \end{align} $$
for all integers
$n\ge 1$
. Then
$0 \in A$
and (2.10) holds for all integers
$n\ge 0$
. Let
$\{a(n)\}_{n=-\infty }^{+\infty }$
be a sequence of integers with
$a(n)=0$
for
$n<0$
and
$a(n)=1$
for
$n\ge 0$
. By Lemma 2.1,
$$ \begin{align*} R_{1,k}(A,n)-R_{1,k}(\mathbb{N}\setminus A,n)=a(n)\end{align*} $$
for all nonnegative integers n if and only if
$$ \begin{align*}\chi_{A}(n)+\chi_{A}\bigg(\bigg[\frac{n}{k}\bigg]\bigg)=1+a(n)-a(n-k)\end{align*} $$
for all nonnegative integers n, that is,
$$ \begin{align*} \chi_{A}(n)+\chi_{A}(0) & =2 \quad\text{for}~0\le n\le k-1, \\ \chi_{A}(n)+\chi_{A}\bigg(\bigg[\frac{n}{k}\bigg]\bigg) & =1 \quad\text{for}~n\ge k. \end{align*} $$
Thus,
$$ \begin{align*} A=\{0\}\bigcup\bigg(\bigcup_{i=0}^{\infty}[k^{2i},k^{2i+1}-1]\bigg).\\[-45pt] \end{align*} $$
