Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-22T20:44:41.467Z Has data issue: false hasContentIssue false
  • English
  • Français

SPANNING TREES IN 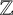$\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES

Part of: Sequences and sets Graph theory Algebraic number theory: global fields

Published online by Cambridge University Press:  28 October 2024

RICCARDO PENGO Open the ORCID record for RICCARDO PENGO [Opens in a new window]  and
DANIEL VALLIÈRES Open the ORCID record for DANIEL VALLIÈRES [Opens in a new window]
RICCARDO PENGO
Affiliation:
IAZD, Fakultät für Mathematik und Physik, Leibniz Universität Hannover, Welfengarten 1, 30167 Hannover, Germany e-mail: pengo@math.uni-hannover.de
DANIEL VALLIÈRES*
Affiliation:
Mathematics and Statistics Department, California State University, Chico, 400 West First Street, Chico, CA 95929, USA
*
e-mail: dvallieres@csuchico.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Using the special value at 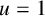$u=1$ of Artin–Ihara L-functions, we associate to every 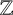$\mathbb {Z}$-cover of a finite connected graph a polynomial, which we call the Ihara polynomial. We show that the number of spanning trees for the finite intermediate graphs of such a cover can be expressed in terms of the Pierce–Lehmer sequence associated to a factor of the Ihara polynomial. This allows us to express the asymptotic growth of the number of spanning trees in terms of the Mahler measure of this polynomial. Specialising to the situation where the base graph is a bouquet or the dumbbell graph gives us back previous results in the literature for circulant and I-graphs (including the generalised Petersen graphs). We also express the p-adic valuation of the number of spanning trees of the finite intermediate graphs in terms of the p-adic Mahler measure of the Ihara polynomial. When applied to a particular 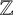$\mathbb {Z}$-cover, our result gives us back Lengyel’s calculation of the p-adic valuations of Fibonacci numbers.

Keywords

Artin–Ihara L-funtionabelian cover of finite graphsnumber of spanning treesMahler measure

MSC classification

Primary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Secondary: 11B83: Special sequences and polynomials 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 118 , Issue 1 , February 2025 , pp. 108 - 144
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement number 945714). Moreover, the first author thanks the research projects ‘Motivic homotopy, quadratic invariants and diagonal classes’ (ANR-21-CE40-0015) and IRN GANDA for their financial support. Both authors are grateful to the Max Planck Institute for Mathematics in Bonn for providing excellent working conditions, great hospitality and financial support.

Communicated by Michael Giudici

References

Bambury, H., Campagna, F. and Pazuki, F., ‘Ordinary isogeny graphs over $\mathbb{F}_p$ : the inverse volcano problem’, Ann. Sc. Norm. Super. di Pisa Cl. Sci. (5), to appear.Google Scholar
Bass, H., ‘The Ihara–Selberg zeta function of a tree lattice’, Internat. J. Math. 3(6) (1992), 717–797.CrossRefGoogle Scholar
Besser, A. and Deninger, C., ‘ $p$ -adic Mahler measures’, J. reine angew. Math. 517 (1999), 19–50.CrossRefGoogle Scholar
Bilu, Y., Luca, F., Nieuwveld, J., Ouaknine, J. and Worrell, J., ‘On the $p$ -adic zeros of the Tribonacci sequence’, Math. Comp. 93 (2023), 21 pages.CrossRefGoogle Scholar
Cohen, H., A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138 (Springer-Verlag, Berlin, 1993).CrossRefGoogle Scholar
Corry, S. and Perkinson, D., Divisors and Sandpiles: An Introduction to Chip–Firing, AMS Non-Series Monographs, 114 (American Mathematical Society, Providence, RI, 2018).CrossRefGoogle Scholar
Cuoco, A. A. and Monsky, P., ‘Class numbers in ${Z}_p^d$ -extensions’, Math. Ann. 255(2) (1981), 235–258.CrossRefGoogle Scholar
DeGroot, M. H. and Schervish, M. J., Probability and Statistics, 4th edn (Addison-Wesley, Boston, MA, 2012).Google Scholar
DuBose, S. and Vallières, D., ‘On ${\mathbb{Z}}_{\ell}^d$ -towers of graphs’, Algebr. Comb. 6(5) (2023), 1331–1346.Google Scholar
Einsiedler, M., Everest, G. and Ward, T., ‘Primes in sequences associated to polynomials (after Lehmer)’, LMS J. Comput. Math. 3 (2000), 125–139.CrossRefGoogle Scholar
Everest, G. and Ward, T., Heights of Polynomials and Entropy in Algebraic Dynamics, Universitext (Springer-Verlag, London, 1999).CrossRefGoogle Scholar
Flatters, A., ‘Primitive divisors of some Lehmer–Pierce sequences’, J. Number Theory 129(1) (2009), 209–219.CrossRefGoogle Scholar
Friedman, E. C., ‘Ideal class groups in basic $\mathbb{Z}_{p_{1}}\times \cdots \times \mathbb{Z}_{p_{s}}$ -extensions of abelian number fields’, Invent. Math. 65(3) (1981/82), 425–440.CrossRefGoogle Scholar
Fukaya, T. and Kato, K., A Formulation of Conjectures on $p$ -adic Zeta Functions in Noncommutative Iwasawa Theory (American Mathematical Society, Providence, RI, 2006), 1–85.Google Scholar
Gonet, S. R., ‘Iwasawa theory of Jacobians of graphs’, Algebr. Comb. 5(5) (2022), 827–848.Google Scholar
Gonet, S. R., ‘Jacobians of finite and infinite voltage covers of graphs’, PhD Thesis, The University of Vermont and State Agricultural College, 2021.Google Scholar
González-Acuña, F. and Short, H., ‘Cyclic branched coverings of knots and homology spheres’, Rev. Mat. Complut. 4(1) (1991), 97–120.Google Scholar
Greenberg, R., ‘Iwasawa theory—past and present’, in: Class Field Theory—Its Centenary and Prospect (Tokyo, 1998), Advanced Studies in Pure Mathematics, 30 (ed. Miyake, K.) (Mathematical Society of Japan, Tokyo, 2001), 335–385.CrossRefGoogle Scholar
Gross, J. L., ‘Voltage graphs’, Discrete Math. 9 (1974), 239–246.CrossRefGoogle Scholar
Hashimoto, K., ‘On zeta and $L$ -functions of finite graphs’, Internat. J. Math. 1(4) (1990), 381–396.CrossRefGoogle Scholar
Hillman, J., Matei, D. and Morishita, M., Pro-p Link Groups and p-Homology Groups, Contemporary Mathematics, 416 (American Mathematical Society, Providence, RI, 2006), 121–136.Google Scholar
Iwasawa, K., ‘On $\varGamma$ -extensions of algebraic number fields’, Bull. Amer. Math. Soc. (N.S.) 65 (1959), 183–226.CrossRefGoogle Scholar
Ji, Q. and Qin, H., ‘The numerical factors of ${\varDelta}_n\left(f,g\right)$ ’, Indian J. Pure Appl. Math. 46(5) (2015), 701–714.CrossRefGoogle Scholar
Kadokami, T. and Mizusawa, Y., ‘Iwasawa type formula for covers of a link in a rational homology sphere’, J. Knot Theory Ramifications 17(10) (2008), 1199–1221.CrossRefGoogle Scholar
Kakde, M., ‘From the classical to the noncommutative Iwasawa theory (for totally real number fields)’, in: Non-abelian Fundamental Groups and Iwasawa Theory, London Mathematical Society Lecture Note Series, 393 (eds. Pop, F., Coates, J., Kim, M., Saïdi, M., and Schneider, P.) (Cambridge University Press, Cambridge, 2011), 107–131.CrossRefGoogle Scholar
Kataoka, T., ‘Fitting ideals of Jacobian groups of graphs’, Algebr. Comb. 7 (2024), 597–625.Google Scholar
Kleine, S. and Müller, K., ‘On the growth of the Jacobian in ${\mathbb{Z}}_p^l$ -voltage covers of graphs’, Algebr. Comb. 7 (2024), 1011–1038.Google Scholar
Kleine, S. and Müller, K., ‘On the non-commutative Iwasawa main conjecture for voltage covers of graphs’, Israel J. Math., to appear; arXiv:2307.15395.Google Scholar
Kotani, M. and Sunada, T., ‘Zeta functions of finite graphs’, J. Math. Sci. Univ. Tokyo 7(1) (2000), 7–25.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences, Pure and Applied Mathematics (Wiley, New York–London–Sydney, 1974).Google Scholar
Kwon, Y. S., Mednykh, A. D. and Mednykh, I. A., ‘On Jacobian group and complexity of the generalized Petersen graph $GP\left(n,k\right)$ through Chebyshev polynomials’, Linear Algebra Appl. 529 (2017), 355–373.CrossRefGoogle Scholar
Lehmer, D. H., ‘Factorization of certain cyclotomic functions’, Ann. of Math. (2) 34(3) (1933), 461–479.CrossRefGoogle Scholar
Lei, A. and Müller, K., ‘On ordinary isogeny graphs with level structure’, Expo. Math. 42 (2024), 125589.CrossRefGoogle Scholar
Lei, A. and Müller, K., ‘On towers of isogeny graphs with full level structure’, Preprint, 2023, arXiv:2309.00524.CrossRefGoogle Scholar
Lei, A. and Vallières, D., ‘The non- $\ell$ -part of the number of spanning trees in abelian $\ell$ -towers of multigraphs’, Res. Number Theory 9(1) (2023), Paper no. 18, 16 pages.CrossRefGoogle Scholar
Lengyel, T., ‘The order of the Fibonacci and Lucas numbers’, Fibonacci Quart. 33(3) (1995), 234–239.CrossRefGoogle Scholar
Lenstra, H. W., ‘On Artin’s conjecture and Euclid’s algorithm in global fields’, Invent. Math. 42(1) (1977), 201–224.CrossRefGoogle Scholar
Mahler, K., ‘On some inequalities for polynomials in several variables’, J. Lond. Math. Soc. (2) s1–37(1) (1962), 341–344.CrossRefGoogle Scholar
McGown, K. and Vallières, D., ‘On abelian $\ell$ -towers of multigraphs II’, Ann. Math. Qué. 47(2) (2023), 461–473.CrossRefGoogle Scholar
McGown, K. and Vallières, D., ‘On abelian $\ell$ -towers of multigraphs III’, Ann. Math. Qué. 48(1) (2024), 1–19.CrossRefGoogle Scholar
Mednykh, A. D. and Mednykh, I. A., ‘The number of spanning trees in circulant graphs, its arithmetic properties and asymptotic’, Discrete Math. 342(6) (2019), 1772–1781.CrossRefGoogle Scholar
Mednykh, I. A., ‘On Jacobian group and complexity of the $I$ -graph $I\left(n,k,l\right)$ through Chebyshev polynomials’, Ars Math. Contemp. 15(2) (2018), 467–485.CrossRefGoogle Scholar
Morishita, M., Knots and Primes. An Introduction to Arithmetic Topology. Based on the Japanese Original (Springer, 2009), Universitext (Springer, Berlin, 2012).CrossRefGoogle Scholar
Pierce, T. A., ‘The numerical factors of the arithmetic forms $\prod \nolimits_{i=1}^n(1\pm {\alpha}_i^m)$ ’, Ann. of Math. (2) 18(2) (1916), 53–64.CrossRefGoogle Scholar
Ray, A. and Vallières, D., ‘An analogue of Kida’s formula in graph theory’, Preprint, 2022, arXiv:2209.04890.Google Scholar
Riley, R., ‘Growth of order of homology of cyclic branched covers of knots’, Bull. Lond. Math. Soc. 22(3) (1990), 287–297.CrossRefGoogle Scholar
Rosen, M., Number Theory in Function Fields, Graduate Texts in Mathematics, 210 (Springer-Verlag, New York, 2002).CrossRefGoogle Scholar
Serre, J.-P., Arbres, Amalgames, $\mathrm{SL}_2$ , Astérisque, 46, Avec un sommaire anglais, Rédigé avec la collaboration de Hyman Bass (Société Mathématique de France, Paris, 1977).Google Scholar
Serre, J.-P., Linear Representations of Finite Groups, Graduate Texts in Mathematics, 42 (Springer-Verlag, New York–Heidelberg, 1977).CrossRefGoogle Scholar
Silver, D. S. and Williams, S. G., ‘Lehmer’s question, graph complexity growth and links’, New York J. Math. 27 (2021), 981–1008.Google Scholar
Stark, H. M. and Terras, A. A., ‘Zeta functions of finite graphs and coverings. II’, Adv. Math. 154(1) (20000), 132–195.CrossRefGoogle Scholar
Sunada, T., Topological Crystallography, Surveys and Tutorials in the Applied Mathematical Sciences, 6 (Springer, Tokyo, 2013); with a view towards discrete geometric analysis.CrossRefGoogle Scholar
Terras, A., Zeta Functions of Graphs: A Stroll Through the Garden, Cambridge Studies in Advanced Mathematics, 128 (Cambridge University Press, Cambridge, 2011).Google Scholar
The Sage Developers, Sagemath, the Sage Mathematics Software System (Version 9.5). https://www.sagemath.org.Google Scholar
Ueki, J., ‘On the Iwasawa invariants for links and Kida’s formula’, Int. J. Math. Anal. (N.S.) 28(6) (2017), 1750035.Google Scholar
Ueki, J., ‘ $p$ -adic Mahler measure and $\mathbb{Z}$ -covers of links’, Ergodic Theory Dynam. Systems 40(1) (2020), 272–288.CrossRefGoogle Scholar
Vallières, D., ‘On abelian $\ell$ -towers of multigraphs’, Ann. Math. Qué. 45(2) (2021), 433–452.CrossRefGoogle Scholar
Washington, L. C., ‘The non- $p$ -part of the class number in a cyclotomic Zp -extension’, Invent. Math. 49(1) (1978), 87–97.CrossRefGoogle Scholar
Weber, C., ‘Sur une formule de R. H. Fox concernant l’homologie des revêtements cycliques’, Enseign. Math. (2) 25(3–4) (1979), 261–272 (1980).Google Scholar