Dorfberg: channeled slope characteristics

The Dorfberg area, located near Davos-Dorf, eastern Switzerland, has very diverse topographic characteristics. It ranges from the top of Salezer Horn (2536ma.s.l.) to the valley bottom covered by Davos lake at 1560 ma.s.l. (Fig. 1). Every year, numerous dry and wet snow avalanches occur on its southeast, exposed, 30–40˚ slopes. The very steep, ∼1km long Salezer gully often channels the flow of avalanches releasing at the steep southeastern slope of the Salezer Horn. A large wet snow avalanche occurred at the end of March 2008. Run-out distance and depositions were accurately documented using aerial imagery, helicopter-based lidar and GPS measurements. Using these datasets, critical input parameters such as release area and release height, as well as the avalanche run-out distance, can be estimated.

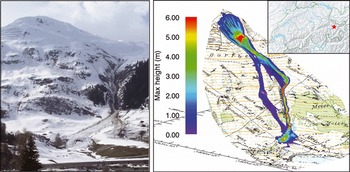
Fig. 1. Photograph of the Salezertobel avalanche (March 2008) within the test site Dorfberg and the corresponding RAMMS simulation. (Topographic map © swisstopo (DV033492.2).)

Vallée de la Sionne: open slope characteristics

In the Vallée de la Sionne the WSL Institute for Snow and Avalanche Research SLF has been operating a test site for large-scale snow avalanches since 1997 (Reference AmmannAmmann, 1999). Many avalanche events have been recorded using different techniques, such as airborne laser scanning, photogrammetry, videogrammetry, frequency-modulated continuous-wave (FMCW) radar and pressure sensors (Reference Sovilla, Schaer, Kern and BarteltSovilla and others, 2008). The slopes are less channeled than at the Dorfberg test site, and a long run-out zone is missing as large avalanches are stopped by the steep counterslope (Fig. 2). On 6 March 2006 two large mixed flowing/powder avalanches (Nos. 816 and 817) were triggered one after the other using explosives. Helicopter-based lidar data were acquired before and after the dry snow avalanche events to accurately document the release areas, release heights, mass balance and run-out distances (Reference Sovilla, McElwaine, Schaer and ValletSovilla and others, 2010).

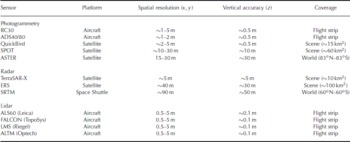
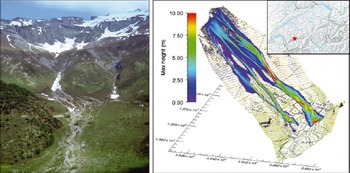
Fig. 2. Photograph of the Vallée de la Sionne test site and the RAMMS simulation of the large dry snow avalanche (6 March 2006) used for this study. (Topographic map © swisstopo (DV033492.2).)

Investigated digital elevation models

For this study we use high-resolution DEMs widespread in Switzerland (DTM-AV and DHM25) that are representative of DEM datasets available in countries with advanced geo-data coverage. Freely available DEMs, covering large parts of the Earth’s surface (ASTER, global DEM (GDEM) and SRTM) are also investigated. Such datasets may be used in countries where no high-resolution accurate DEM data are available. The ASTER and SRTM datasets were taken as delivered; no error corrections were performed. Figure 3 shows the shaded reliefs of the investigated DEMs, which have the following characteristics.

Fig. 3. Hillshades of the investigated DEM datasets (top: Dorfberg; bottom: Vallée de la Sionne,) showing the differing representation of terrain features with changing spatial resolution.

DTM 2m

This dataset has the best spatial resolution available for both test sites. For areas <2000ma.s.l., airborne lidar data with a spatial resolution of 2 m and a vertical accuracy of ∼0.5m are used (swisstopo, http://www.swisstopo.admin.ch/internet/swisstopo/de/home/products/height/domdtm-av.html). The elevation information for areas >2000ma.s.l. is derived from airborne optical scanner data (sensor ADS40, Leica HGeosystems, http://www.leica-geosystems.com/en/Leica-ADS80-Airborne-Digital-Sensor86846.htm) with similar spatial resolution and vertical accuracy of ∼1m in alpine terrain. This sensor has shown its usefulness for other applications in mountainous terrain, such as automated avalanche deposit detection (Reference Bühler, Hüni, Christen, Meister and KellenbergerBühler and others, 2009). Unlike the lidar technology, the optical scanner derives only DSMs. Even though there is only sparse elevated vegetation >2000ma.s.l., the ADS40 DSM has been smoothed using a low-pass filter to minimize the increased roughness caused by single trees, bushes and tussocks.

DHM 25m

The DHM 25m is derived from the 1 : 25 000 topographic map of Switzerland and was carefully checked for errors (swisstopo, unpublished information). It has a spatial resolution of 25 m and vertical accuracies of ∼2m within non-alpine terrain and of ∼3m within the Alps. Because of its long-time availability in Switzerland and its proven quality, the DHM 25m was used for the majority of studies in need of topographic information within Switzerland.

ASTER 30m

The ASTER sensor aboard the Terra satellite was launched in 1999. The visible/near-infrared subsystem acquires data at nadir (0˚ looking angle) and 27.7˚ backward-looking angle with a spatial resolution of 15m (Reference Yamaguchi, Kahle, Tsu, Kawakami and PnielYamaguchi and others, 1998). These data were used in 2009 to generate a GDEM covering the Earth’s surface between 83˚N and 83˚ S (ASTER GDEM Validation Team, http://www.ersdac.or.jp/GDEM/E/image/ASTERGDEMValidation Summary ReportVer1.pdf). The worldwide availability free of charge and the comparatively good spatial resolution make this DEM product very valuable for regions where no better national elevation models are available. Nevertheless, the ASTER DEM contains numerous errors in areas covered by clouds, in cast shadow or hidden by steep slopes. Therefore it must be checked carefully before using it for numerical simulations.

SRTM 90m

The SRTM was accomplished in February 2000 and generated a GDEM dataset covering 60˚ N–60˚ S with a spatial resolution of 1 arcsecond (∼90m). It was the first GDEM dataset freely available. The interferometric SAR (InSAR) technology is able to acquire data unaffected by cloud cover, which is particularly important in tropical areas (Reference FarrFarr and others, 2007). Due to the low backscatter signal over smooth surfaces (e.g. calm water bodies) and further constraints (e.g. radar shadow in mountainous terrain), the dataset is affected by numerous errors and must be checked carefully.

Numerical avalanche dynamics model, RAMMS

The following four depth-averaged equations are solved governing mass balance, momentum balance (Reference Pudasaini and HutterPudasaini and Hutter, 2007) and random kinetic energy production and decay (Reference Bartelt, Buser and PlatzerBartelt and others, 2006; Reference Buser and BarteltBuser and Bartelt, 2009):

The DEM is given as the function Z(X, Y) in a fixed Cartesian coordinate system X, Y, Z. The independent variables x and y denote the arc-length along the surface topography. The z-coordinate is perpendicular to the profile. Gravitational acceleration is given by the vector (gx , gy , gz ). The field variables of interest are the avalanche flow height, H(x, y, t ), the mean avalanche velocity, U(x, y, t)=(Ux (x, y, t ),Uy (x, y, t ))^T, and the specific random kinetic energy density, R(x, y, t ). The magnitude and direction of the flow velocity are given by ∥U∥ = and the unit vector, respectively. We neglect centripetal accelerations (Reference Gray, M. and K.Gray and others, 1999), as we cannot define the exact running surface of the avalanche. High-curvature terrain features are often filled with snow, producing flat running surfaces of low curvature.

The effective snow entrainment rate, Q̇(x, y, t ), is given by

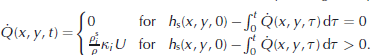
and controlled by the dimensionless entrainment coefficient κ. The initial value h _s(x, y, 0) is given by the total height of the snow cover at position (x, y) and time t = 0 s. Because a naturally occurring snow cover exhibits a strong vertical structure, we allow bulk parameters, such as density and hardness, to vary with vertical position in the snow cover. We assume that the ith snow layer has height hi with constant snow density so h _s = ∑ hi .

The right-hand side terms of the momentum equations, Equations (2) and (3), add up to an effective acceleration. The gravitational accelerations in the x- and y-directions are

The friction, S _f = (S _f, x , S _f, y )^T, is given by the extended Voellmy model which considers the effect of random kinetic energy, R, on frictional processes (Reference Bartelt and BuserBartelt and Buser, 2010):

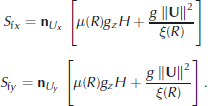
Bartelt and Buser have found (Reference Bartelt, Buser and PlatzerBartelt and others, 2007)

indicating exponential relationships between the mean random kinetic energy and the frictional coefficients, μ and ξ:

when each constitutive process (Coulomb and turbulent) is considered individually. The frictional processes giving rise to μ(R) and ξ(R) depend on R, which is governed in Equation (4) by the production coefficient, α ∈ [0, 1], which defines the amount of granule scattering induced by shear, while the coefficient β > 0 can be considered the inverse

mean lifetime of the random kinetic energy. The constant, R ₀, defines the exponential growth rate of friction as a function of the mean random kinetic energy density. The friction coefficients, μ ₀ and ξ ₀, are now constants that represent the static dry Coulomb and turbulent friction values

Measurements in Vallée de la Sionne show 4 ≤ R ₀ ≤ 7kJm ^{− 3} (Reference Bartelt and BuserBartelt and Buser, 2010), depending on the granulometric dimensions of the avalanches (Reference Bartelt and McArdellBartelt and McArdell, 2009). This provides μ values in good agreement with snow-chute experiments (Reference Platzer, Bartelt and KernPlatzer and others, 2007). Static dry Coulomb values can be deduced from deposition angles at the front of the avalanche, typically 0.40 ≤ μ ₀ ≤ 0.55 (20–30 ^˚ ), and ξ ₀ (300 ≤ ξ ₀ ≤ 800 ms ^{− 2}) is determined from avalanche tail velocities. The standard Voellmy–Salm model (Reference VoellmyVoellmy, 1955; Reference SalmSalm, 1993) can be recovered from the extended system by choosing α = 0. Due to the initial fluctuation energy being zero R(t = 0) = 0, this always ensures that R ≡ 0.

The governing differential equations are solved with second-order numerical schemes (Reference Christen, Kowalski and BarteltChristen and others, 2010b).

Simulation set-up

To investigate the influence of the DEM quality and resolution, we perform RAMMS calculations keeping all flow parameters constant, varying only the input DEM. For the Dorfberg test site we applied the standard Voellmy–Salm model (α = 0), generating the μ and ξ values for a large avalanche with a 10 year return period using a procedure documented by Reference Gruber and BarteltGruber and Bartelt (2007) and specified ‘no entrainment’, Q̇(x, y, t)=0.We simulated Vallée de la Sionne avalanches 816 and 817 using the extended Voellmy–Salm model with α = 0.1 and and β = 0.7 s ^{− 1}. These values were determined from velocity profile measurements (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009). We first simulated avalanche 816 on a 5 m grid, updating the DEM for avalanche 817. The results reported below are for the simulation of avalanche 817. The static friction coefficients, μ ₀ and ξ ₀, were taken to be μ ₀ = 0.57 and ξ ₀ = 550 ms ^{− 2} (Reference Christen, Kowalski and BarteltChristen and others, 2010b). R ₀ was set to 5 kJm³, in accordance with Reference Bartelt and BuserBartelt and Buser (2010). Avalanche 817 entrained 0.95 m of snow (κ = 1). For each case study, we use exactly the same release areas and release heights, calculation grid sizes, return periods, volume categories, snow densities, numerical calculation schemes and erosion parameters for the simulations within one test site. This approach ensures that the only source of differences between the simulations is the DEM.

Flow path

The simulation results at the Dorfberg test site show an evident influence of the DEM resolution on the flow path. While the results of the DTM 2m and the DHM 25m simulations are very similar, the southwestern sub-branches of the avalanches, which were observed in the field, disappear in the ASTER 30m and SRTM 90m simulations. Such changes in flow path can be observed within both test sites (Fig. 4 and 5).

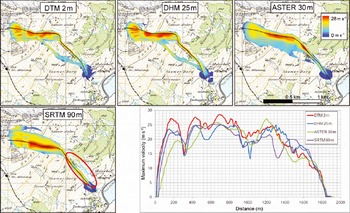
Fig. 4. Maximum velocity of the different simulations and comparison of the maximum velocity values within the Dorfberg test site. The black lines indicate the location of the profiles following the main flow path and indicate the line used to plot velocity vs distance. The flow path in the SRTM 90m simulation is shifted up to 100 m away from the gully (red circle). Note that profile paths had to be changed for the 30 and 90 m simulations due to divergence in the flow path. (Topographic map © swisstopo (DV033492.2).)

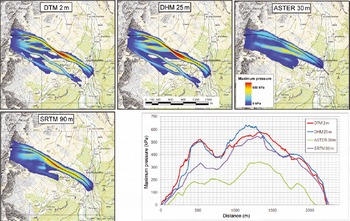
Fig. 5. Maximum pressure of the different simulations and comparison of the maximum pressure values within the Vallée de la Sionne test site. The black lines indicate the location of the profiles. Note that profile paths had to be changed for the 30 and 90 m simulations. (Topographic map © swisstopo (DV033492.2).)

At both test sites, the complex topography of the release and transition zones, containing many small channels and ridges, cannot be represented by the two coarsely resolved DEM datasets. Within the strongly channeled topography of Dorfberg, the avalanche path in the SRTM 90m simulation is shifted up to 100 m away from the gully (Fig. 4). The steep gully is not correctly represented and located by the coarse DEM resolution of 90 m. At Vallée de la Sionne, the flow path of the ASTER 30 m simulations is shifted up to 100m to the north and is stopped >300m too soon (Fig. 6). Clouds, cast shadows and steep slopes cause errors in the ASTER 30m DEM product (Fig. 7). The quality assessment file (QA), delivered with every ASTER GDEM tile, can help identify areas likely to be affected by errors (ASTER GDEM Validation Team, http://www.ersdac.or.jp/GDEM/E/image/ASTERGDEMValidation Summary ReportVer1.pdf). However, such anomalies and artifacts are hard to identify, and limit the usability of the ASTER 30m DEM as well as the SRTM 90 m.

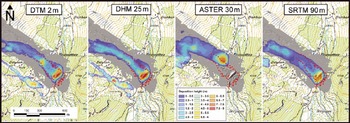
Fig. 6. Simulated avalanche deposits superimposed on helicopter-based lidar data (in gray) of the Vallée de la Sionne avalanche acquired in March 2006. The dotted red line indicates the reference deposition outline derived from the lidar data. The southwestern arm of the avalanche was not covered by the lidar data acquisition but was observed in the field. (Topographic map © swisstopo (DV033492.2).)

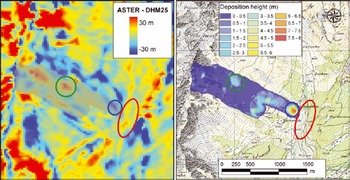
Fig. 7. Height deviations (left) of the ASTER 30 mm and the DHM 25mm DEM. The river bed is represented ∼25mm too high (red circle) and area to the northwest ∼30mm too low (blue circle) in the ASTER elevation model. Therefore the ASTER 30 mm RAMMS simulation (right image and outline superimposed in gray on the left image) deposits most of its material in the dump and stops before the avalanche reaches the valley bottom. Furthermore a false bump of ∼30mm in the middle of the slope (green circle) retains mass and leads to an incorrect deposition. (Topographic map © swisstopo (DV033492.2).)

Run-out distance and deposit

The comparison of the model results with measurements of observed reference avalanche events demonstrates the achieved accuracy of the DTM 2m and the DHM 25m simulations. Figure 8 shows that even small arms of the avalanche deposit are well represented. The break-out on the western part of the deposit can be explained by the levee, built up by the wet snow avalanche during its flow. This change in topography is not implementable without advance information. The shape of the deposit and the run-out distance are modeled significantly worse by the ASTER 30 m and SRTM 90m simulations on the open run-out slope at the Dorfberg test site. The material is sedimented in a circular deposit reaching further than the reference avalanche. The branches of the deposit are not modeled correctly.

Fig. 8. Aerial imagery of the Salezertobel avalanche deposition with the simulation results superposed. The dotted red line indicates the reference deposition outline derived from aerial imagery.

The differences in run-out distance and deposit of the main avalanche branch are less obvious between the different simulations on the confined run-out zone at the Vallée de la Sionne test site. The main part of the material is deposited within the river bed at the bottom of the valley (Fig. 6). The sole exception is the ASTER 30 m simulation where the avalanche stops before it reaches the river bed. This change in run-out distance is caused by an incorrect representation of the river gully in the ASTER 30 m DEM. Figure 7 illustrates the deviations of the defective ASTER DEM, compared to the quality-checked DHM 25m DEM. The gully bottom is up to 30 m too high, damming the avalanche and stopping its flow. An incorrect dump just before the valley bottom leads to a precipitated deposition of the material. Such DEM anomalies and artifacts substantially limit the reliability of numerical avalanche simulations.

Flow velocities and impact pressure

Flow velocity and dynamic impact pressure are important parameters for hazard mapping, mitigationmeasure planning and safety assessment for buildings and infrastructure (Reference Margreth and AmmannMargreth and Ammann, 2004). Figure 5 illustrates the maximum pressure for the avalanche simulations at the Vallée de la Sionne test site. The profile graph along the main flow path of the simulations demonstrates the good agreement between the DTM 2m and DHM 25m simulations. The maximal pressure values and the shapes of the curves match well. The SRTM 90m simulation shows lower pressure values, especially within the upper part of the avalanche. The pressure values resulting from the ASTER 30 msimulation are only half of the DTM 2m and DHM 25m simulations. Due to errors in the DEM (see Fig. 7), a new avalanche branch, not existing within the other simulations, developed south of the main branch, dividing the available amount of snow and lowering the pressure. This example shows that such DEM errors can cause major failures in pressure simulations and could therefore lead to serious misclassifications in hazard maps.