1. Introduction
In a recent paper, we presented an analysis of the formation and the evolution with meteorological conditions (essentially air temperatures) of the ephemeral waterfall ice structures that form from the freezing of liquid water seeping on steep rock (Reference MontagnatMontagnat and others, 2010). To our knowledge, with the exception of one internal report (Reference BianchiBianchi, 2004), this was the first scientific study of waterfall ice in the literature. From an automatic photographic survey of two typical vertical frozen waterfalls situated near Glacier d’Argentière, France, meteorological measurements from a nearby automatic weather station and a microstructural analysis of ice samples, we showed that the growth of these structures occurred through the aggregation of stalactites and could be related to the cumulative effect of negative air temperatures from the beginning of the season (expressed as a ‘freezing potential’). This leads to a rapid initial growth rate, which then decreases progressively, with the volume of the structure reaching an asymptotic value when the previously formed ice isolates the water flowing inside the structure from the atmosphere.
While the formation of the waterfall ice structures, driven by thermodynamical processes, occurs progressively, their collapse generally occurs abruptly through a mechanical instability. The nature of these instabilities as well as their triggering factors are the subject of the present paper. A better understanding of this process is important for ice climbers: from 2000 to 2006, 22 ice climbers were killed in France and the rescue services performed 148 rescues. Possible reasons for these accidents, as reported by the rescue services, can be various, including climbers’ inexperience or snow avalanches. The fall of ice blocks or the collapse of the structure cause 20% of reported accidents, but a larger proportion of deaths. Mechanical instabilities are a concern for the climbing community and professional mountain guides, as several experienced climbers have been killed in the past few years while climbing vertical structures during supposedly favorable meteorological conditions, i.e. low temperatures favoring ice formation. Many climbers have also informally reported frightening climbing conditions (crack propagation within the structure, brittle ice and/or ice-block falls) during periods of abrupt cooling. If prolonged warm weather conditions with air temperatures above 0°C are easily recognized as being unfavorable for climbing, the situations briefly described above (low temperatures, rapid cooling) are more difficult to associate with dangerous conditions. As shown below, the initiation and propagation of cracks triggered by thermal tensile stresses is likely to explain how temperatures well below freezing can trigger collapse of waterfall ice structures.
This work was performed in the European Alps, where air temperatures below −20°C are extremely rare at altitudes below 2000 m. Most waterfall ice climbing sites are located below this altitude. Over the two winters of analysis, the lowest temperature recorded at the Glacier d’Argentière meteorological station (2400 m a.s.l.), situated above the waterfall structures studied (see section 3), was −19°C. The vocabulary used in this paper to describe temperature conditions refers to this situation: ‘cold’ means below −10°C; ‘mild’ means ∼0°C.
2. Potential Sources of Stresses Within Waterfall Ice Structures
We focus mainly on the mechanical stability of vertical, or even sometimes slightly overhanging, ice structures. Following the terminology used in the climbing community, we distinguish ‘stalactites’ hanging at the top, ‘free standings’ separated from the rock cliff between their extremities, and ‘ice columns’ attached to the cliff (Fig. 1). The less steep walls of ice (≤80° to 85°), anchored to the rock over most of the ice/bedrock interface, are only briefly mentioned, as they are supposed to be less prone to abrupt mechanical instability.

Fig. 1. Sketch of (a) a stalactite, (b) a free standing and (c) a column section of a frozen waterfall.
There are several potential sources of stress within waterfall ice structures:
-
1. For a hanging stalactite, the weight of the ice leads essentially to vertical tensile stresses, maximum near the top. As an order of magnitude, for an idealized conical stalactite of length h, this gives a tensile stress of ρgh/3, where ρ is the ice density and g = 9.81 m s−2 is the acceleration due to gravity. For h = 15 m, we obtain a stress of ∼45 kPa, far below the tensile strength of ice at −10°C (∼1 MPa; Reference Schulson and DuvalSchulson and Duval, 2009). In this situation, the additional weight of a climber appears negligible (<0.2 kPa for a weight of 80 kg and a stalactite’s diameter of 3 m at the top). The bending stress induced by a climber hitting the stalactite along a horizontal direction with an ice axe or crampons, though slightly larger, remains small (a few tens of kPa at most; see Appendix).
-
2. For a free-standing structure (Fig. 1b), the weight of the ice leads to vertical tensile stresses in the top half, and, by symmetry, compressive stresses in the bottom half. For an idealized vertical structure of constant horizontal section and h of 15 m, the tensile stress at the top and the compressive stress at the bottom would both have a magnitude of 1/2ρgh ≈ 70 kPa, i.e. still far below the tensile strength of ice. However, the action of the climber, through the initiation of cracks when hitting the structure with an ice axe, might be an aggravating factor if such a crack propagates unstably through a structure submitted to tensile stresses. From linear elastic fracture mechanics (LEFM), such instability occurs if

where the stress intensity factor K I depends on the applied tensile stress σ and the crack depth a, B is a geometrical factor close to 1, and K IC is the fracture toughness. Using B = 1, σ = 70 kPa and K IC = 100 kPam1/2 (Reference Schulson and DuvalSchulson and Duval, 2009), we obtain a critical crack depth of ∼0.65 m. Such a large value suggests that, for the situation described above, a climber by himself is unlikely to trigger the collapse of the structure.
-
3. Thermal stresses, induced by thermal fluctuations and gradients, are an important potential source of stresses within waterfall ice structures. This is particularly the case for free standings. Considering a free standing of constant section and a thermal expansion coefficient α ≈ 5.3 × 10−5 K−1 in the temperature range of interest (−20°C to 0°C) (Reference HobbsHobbs, 1974), a temperature drop of ΔT = 10°C will lead to a vertical tensile stress σ = αEΔT ≈ 5 MPa, where E = 9.3 MPa is the bulk modulus of granular ice (Reference Gammon, Kiefte, Clouter and DennerGammon and others, 1983). Such a tensile stress is much larger than the tensile strength of ice, and is of the order of magnitude of the compressive strength (respectively, about 1 and 5 MPa; Reference Schulson and DuvalSchulson and Duval, 2009). This rough calculation, however, considers the temperature drop to occur instantaneously in the entire structure, i.e. considers neither the thermal diffusivity of the ice nor the rate of air cooling. For slow temperature changes, these thermal stresses will be relaxed by creep, i.e. a ductile-to-brittle transition will occur. Despite these approximations, this calculation illuminates the role of thermal stresses in the mechanical stability of waterfall ice, which is discussed in more detail in sections 4.1 and 5. This role will be enhanced in the presence of climbers fracturing the ice with their axes. As an example, using the same LEFM criterion as above, a crack of depth a = 3 cm is expected to propagate unstably under a tensile stress of only 320 kPa.
-
4. Another possible source of internal stresses could be water$ice phase transitions. Water circulates within most of these structures throughout the season (Mont-agnat and others, 2010), along complex channel networks. The freezing of water inside confined channels might generate internal stresses. We expect these to be essentially local (see below).
3. Situation and Measurements
To analyze the stresses within frozen waterfalls and their mechanical (in)stability, different observations and measurements were performed on a few typical vertical structures. During the 2007/08 and 2008/09 boreal winters, we focused on two frozen waterfalls situated on the left and right sides of Glacier d′Argentière, the icefall (45°58′ N, 6°58′ E), at ∼2100 m a.s.l. (top of the structures) (Reference MontagnatMontagnat and others, 2010). The so-called ‘Nuit Blanche’ is a very steep frozen waterfall 120 m in length, with the last two-thirds nearly vertical. It is oriented north-northeast and remains in the shade nearly all winter. We focused on the top of the frozen waterfall consisting of a vertical ice pillar of 16.5 ± 1 m generally separated from the rock cliff between its extremities, i.e. a ‘free standing’ (Fig. 2a). However, during winter 2008/09, as a result of sustained cold, this ice pillar became very large and anchored to the rock cliff during the second part of the season, i.e. it became an ‘ice column’ (Fig. 2b). One pressure sensor was installed at the bottom of the Nuit Blanche ice pillar during these two winters, just above the bottom anchor point. This sensor measured the internal pressure within the ice as well as the ice temperature at the same location, with a 10 min periodicity. At the date of installation, pressure and temperature were recorded at a horizontal distance of ∼10 cm from the surface, but this distance increased during the season as the sensor was covered by newly grown ice, up to about 50–70 cm (Figs 2a and 3). As a pressure sensor, it does not give any information about the tensorial nature of the stress, and is unable to record tensile loading. The stress state at the bottom of the column is likely a superposition of different loadings (see section 2). Therefore, if the recorded pressure is difficult to interpret quantitatively, its fluctuations through time and with air-temperature conditions can be interpreted in terms of the relative roles of these different loadings. To follow the global evolution of the Nuit Blanche ice pillar, a digital camera was installed on its right side, at a distance of ∼10 m and taking pictures at regular time intervals (six photographs a day, with a periodicity of 90 min, starting from 0830 h; see examples in Fig. 2). Reference MontagnatMontagnat and others (2010) used these images to follow the formation and the evolution of the ice pillar through the season.

Fig. 2. View of the ‘Nuit Blanche’ frozen waterfall free standing, near Glacier d’Argentière, Mont Blanc massif. As (a) a free standing, January 2008, and (b) an ice column, February 2009. The arrow in (a) indicates the approximate location of the pressure sensor.

Fig. 3. Extraction of the pressure sensor from the ice of the Nuit Blanche free standing at the end of the season (picture taken on 13 March 2008). The sensor was embedded inside ∼60 cm of ice
The second surveyed frozen waterfall was ‘Shiva Lingam′, on the other side of the glacier canyon. Shiva Lingam (orientation west, 120 m long) terminates in an impressive vertical free standing of 35 ± 1 m at the top (Fig. 7, further below). Owing to its orientation, it is affected by the sun for part of the afternoon, even in December. Shiva Lingam was only surveyed with an automatic digital camera situated in the front of the structure, with the same periodicity as for Nuit Blanche.
To follow the local meteorological conditions at Glacier d’Argentière, we used a meteorological station installed within the framework of the project GLACIOCLIM (http://www-lgge.obs.ujf-grenoble.fr/ServiceObs/index.htm) at 2400 m a.s.l., on the moraine on the right-hand side of the glacier just above the serac fall (Reference MontagnatMontagnat and others, 2010). We focused here essentially on air-temperature data, sampled with a 30 min periodicity, which have been corrected by a temperature/elevation gradient of 0.6°C (100 m)−1 to obtain the temperatures at 2100 m a.s.l. (top of the waterfalls).
During winter 2009/10, a pressure sensor was installed at the bottom of a free standing in Rovenaud, Valsavarenche valley, Italy (45°36′ N, 7°12′ E; 1600 m a.s.l.). This free standing is oriented west, i.e. affected by the sun during the afternoon. Owing to the strongly overhanging rock, this free standing is typical, never fixed on the rock along its length of 15 m (Fig. 4). To follow the local air-temperature conditions near this site, we used data from a meteorological station of the Centro Funzionale, Regione Autonoma Valle d’Aosta, situated in Pont, 9.2 km upstream in the Valsavarenche valley, at 1950 m a.s.l. The same temperature correction, 0.6°C (100 m)−1, was applied to obtain the air temperature at this frozen waterfall.

Fig. 4. Overall view of the Rovenaud’s free standing, Valsavarenche valley, Italy. Photograph taken 26 January 2010.
4. Results and Observations
In Figure 5a–c, we show the air temperature, ice temperature and pressure records obtained for, respectively, Nuit Blanche during winter 2007/08, Nuit Blanche during winter 2008/09 and the Rovenaud free standing during winter 2009/10. Before we focus on the pressure record during specific periods and its relation to air temperature, we make several general remarks.
-
1. The pressures measured at the bottom of the free standings are, on average, of the correct order of magnitude (few tens of kPa) compared with the overburden pressure estimated in section 3.
-
2. During winter 2007/08, the average pressure measured on Nuit Blanche slowly increased during the first part of the record, roughly up to early February (days of year 35–40; Fig. 5a) before saturation. This can be interpreted as a result of growth/thickening of the structure, which shows a similar evolution throughout the season (significant growth during the first part of the season, followed by an asymptotic behavior; Reference MontagnatMontagnat and others, 2010).
-
3. During winter 2008/09, the recorded situation was different: after an initial increasing stage, roughly up to 22 January, the average pressure decreased slowly to reach very small values from early March (about one-fifth of the value recorded in March 2008; Fig. 5b). This, we believe, is due to the change of configuration observed in the field during that winter (see section 3). As a result of sustained cold, the Nuit Blanche ice pillar became anchored to the rock cliff (Fig. 2b). This change of boundary conditions suppressed most of the overburden stress.
-
4. A diurnal cycle, which attenuates throughout the season, is clearly observed on all ice-temperature records. As deduced from a cross-covariance analysis between ice-and air-temperature records (not shown), fluctuations at larger timescales are correlated with air-temperature fluctuations (correlation coefficient around 0.4–0.5), but with a time lag that increases through the season, from ∼8 hours in early January to slightly more than 1 day at the end of the season. These observations can be explained by thermal conduction within the ice. As the ice pillar thickens, the ice surface moves away from the sensor, and air-temperature variations are increasingly lagged and attenuated at the level of the sensor.

Fig. 5. Ice pressure recorded at the bottom of the free standings, in relation to air- and ice-temperature records. (a) Nuit Blanche, winter 2008. (b) Nuit Blanche, winter 2009. (c) Rovenaud’s free standing, winter 2010.
We focus now on some specific periods of these records in order to discuss the generation of ice internal stresses.
4.1. Thermal stresses
Figure 6 shows examples of episodes of rapid air cooling, typically a drop of 10°C within 24 hours or less, followed, with a time lag of several hours (see above), by a dramatic cooling of the ice. This ice cooling generates a sudden drop in the ice pressure measured at the bottom of the free standing. This, we believe, is the signature of tensile thermal stresses that partly compensate the overburden stress at the bottom of the structure, although the amplitude of these fluctuations is difficult to interpret quantitatively, for the reasons given in section 2. At the top of the structures, where the overburden stress vanishes, this mechanism generates vertical tensile stresses that are a potential source of fracturing, and possibly the collapse of the structure.

Fig. 6. Episodes of dramatic cooling, indicated by arrows. (a) Nuit Blanche, February 2008. (b) Nuit Blanche, January 2009. (c) Rovenaud’s free standing, January–February 2010.
The photographic surveys of Shiva Lingam clearly illustrate this scenario. On 20–21 January 2008, a dramatic air cooling of 15°C (from +6°C to −9°C) during the night resulted in the sudden collapse of the entire structure, triggered by the propagation of a large horizontal crack, just below the upper anchor point of the free standing (Fig. 7a). Depending on the configuration of the structure, such upper crack propagation does not necessarily lead to the structure’s collapse. In 2009 a crack propagation occurred on 1 March (day 60), after an air-temperature drop of 7°C overnight (from +4°C to −3°C). Probably in relation to a much larger development of the free standing’s basement in this season compared to the previous one, as a result of sustained cold (Reference MontagnatMontagnat and others, 2010), this crack did not immediately result in a general failure. Instead, just after another dramatic cooling (14°C in 24 hours, from +1°C to −13°C), this crack reopened and triggered the collapse of the structure on 10 March (day 69) (Fig. 7b).

Fig. 7. Fracturing and collapse of Shiva Lingam’s free standing, in relation to dramatic air cooling. (a) 2008: 20 January (left) and 21 January (right). (b) 2009: 1 March (left), 8 March (middle) and 10 March (right).
Because the photographic survey of Nuit Blanche was conducted from the side, it did not allow us to follow the very top of the structure (Reference MontagnatMontagnat and others, 2010). Therefore we were unable to correlate possible fracturing events with temperature profiles. In 2008 the presence of a horizontal crack at the top was noted during fieldwork on 5 March (day 64) just after an air-temperature drop of 14°C in 14 hours. Two days later, a subsequent severe cooling episode, with air temperature as low as −19°C and a significant decrease of ice temperature, did not result in any significant modification of the ice internal pressure (Fig. 5a), a possible illustration of tensile stress relaxation as a result of fracturing. We also note that in 2009, from late January to early February when Nuit Blanche became anchored to the rock cliff (section 3; Fig. 2b) and was no longer a free standing, the relationship between rapid cooling and ice pressure drop vanished, in relation to this change of boundary conditions (Fig. 5b).
From these examples, if the amplitude of the temperature drop is essential to explain crack initiation and propagation, the rate of cooling also seems important. This is illustrated in Figure 8, where a significant ice-temperature drop of ∼5°C, however spread over 6 days, did not result in significant internal pressure drop. As discussed in section 5, this can be explained by a creep relaxation of these tensile thermal stresses.

Fig. 8. An episode of significant but slow cooling of the ice within the Nuit Blanche free standing during February 2008.
4.2. Phase transitions
Figure 9 shows episodes, late in the winter, characterized by a marked diurnal air-temperature cycle and temperatures well above 0°C during the day. Consequently, the ice temperature fluctuates between a fraction of a degree below 0°C during the night, and the melting point during the day. We expect water ↔ ice phase transitions to occur with the same periodicity along the complex channel networks where water circulates within the waterfall ice structure. This is accompanied by dramatic ice pressure fluctuations every day, especially around 1000 and 1800 h, which are likely the signature of these phase transitions.

Fig. 9. Episodes of mild days followed by cool nights in Nuit Blanche, with the ice temperature fluctuating between a fraction of a degree below 0°C during the night, and the melting point during the day. These episodes are associated with ice pressure fluctuations triggered by water ↔ ice phase transitions within the structure. (a) February–March, 2008; (b) April 2009.
Although the amplitude of these fluctuations is of the same order of magnitude as those described in section 4.1, we expect them to be localized around pores and channels where water circulates. In other words, the sensor’s measurements in this case give information at a local scale, not representative of the loading at the global scale. In addition, warm and wet ice is extremely ductile (Reference DuvalDuval, 1977; Reference De la Chapelle, Milsch, Castelnau and DuvalDe la Chapelle and others, 1999), therefore allowing rapid relaxation of these stresses and preventing crack propagation. We did not observe large-scale mechanical instabilities or fracturing associated with these episodes.
5. Discussion
The observations and measurements described in section 4 illustrate the role of two mechanisms in the generation of internal stress fluctuations within vertical waterfall ice structures: water ↔ ice phase transitions and tensile stresses induced by thermal contraction, the latter being a major instability factor for free standings.
The simple calculation presented in section 2 for freestanding structures showed that an instantaneous ice-temperature drop of 10°C will generate tensile stresses well above the tensile strength of freshwater granular ice, of ∼1 MPa (Reference Schulson, Lim and LeeSchulson and others, 1984; Reference Lee and SchulsonLee and Schulson, 1988; Reference Schulson and DuvalSchulson and Duval, 2009). Considering the same thermal expansion coefficient (α ≈ 5.3 × 10−5 K−1) and bulk modulus (E = 9.3 MPa) as above, an ice temperature drop as low as 2°C should theoretically be sufficient to generate tensile failure.
This, however, neglects the role of loading rate, i.e. of temperature change in our specific case. For freshwater polycrystalline ice at −10°C, a brittle-to-ductile transition occurs under tension around a strain rate
![]() of 10−7 s−1 (Reference Schulson and DuvalSchulson and Duval, 2009). Below
of 10−7 s−1 (Reference Schulson and DuvalSchulson and Duval, 2009). Below
![]() , visco-plastic processes take place to relax the elastic stress build-up responsible for crack initiation. Translated for waterfall-ice free standings in terms of ice-temperature change rate, this gives
, visco-plastic processes take place to relax the elastic stress build-up responsible for crack initiation. Translated for waterfall-ice free standings in terms of ice-temperature change rate, this gives
![]() . Such large temperature drop rates were hardly ever observed in our ice-temperature records. However, as noted above, the ice thermal fluctuations measured inside the ice structure were necessarily attenuated compared with air-temperature fluctuations, as a result of ice thermal diffusivity, and we can expect stronger fluctuations for the ice in contact with the atmosphere. It is worth noting that air-temperature change rates as large as 7°C h−1 are not unusual in our records. In addition, as emphasized in section 2, the initiation of cracks by climbers hitting the structure with ice axes will be an aggravating factor in this case. The most critical situation will be encountered when the climber reaches the top of the structure where tensile stresses are maximum. From these considerations, air-temperature drops of the order of several °C h−1 over several hours could be considered as a rule-ofthumb warning for dangerous climbing conditions on freestanding structures. A priori, similar meteorological conditions will be less critical for other vertical structures such as stalactites or ice columns (Fig. 1). For stalactites, the boundary conditions allow the structure to respond freely to thermal contraction. For ice columns, the boundary conditions, i.e. ice anchored to the rock face along its length, suppress most of the overburden stress and/or vertical thermal stresses, as observed for Nuit Blanche during the second part of the season (see section 4.1). In these cases however, less directional thermal stresses could still take place as a result of thermal gradients between the cold outside ice and the warmer inside ice, favoring the climber’s feeling of ‘brittleness’ of the ice. We believe this climber’s feeling is a combination of such thermal stresses related to shallow thermal gradients, and brittle behavior. When a climber hits cold outside ice, the impact creates a compressive wave that bounces off the back surface of the ice. This wave then reflects as a tensile wave which, helped by superficial thermal stresses, causes the ice surface to spall off (the so-called ‘dinner-plating’ phenomenon).
. Such large temperature drop rates were hardly ever observed in our ice-temperature records. However, as noted above, the ice thermal fluctuations measured inside the ice structure were necessarily attenuated compared with air-temperature fluctuations, as a result of ice thermal diffusivity, and we can expect stronger fluctuations for the ice in contact with the atmosphere. It is worth noting that air-temperature change rates as large as 7°C h−1 are not unusual in our records. In addition, as emphasized in section 2, the initiation of cracks by climbers hitting the structure with ice axes will be an aggravating factor in this case. The most critical situation will be encountered when the climber reaches the top of the structure where tensile stresses are maximum. From these considerations, air-temperature drops of the order of several °C h−1 over several hours could be considered as a rule-ofthumb warning for dangerous climbing conditions on freestanding structures. A priori, similar meteorological conditions will be less critical for other vertical structures such as stalactites or ice columns (Fig. 1). For stalactites, the boundary conditions allow the structure to respond freely to thermal contraction. For ice columns, the boundary conditions, i.e. ice anchored to the rock face along its length, suppress most of the overburden stress and/or vertical thermal stresses, as observed for Nuit Blanche during the second part of the season (see section 4.1). In these cases however, less directional thermal stresses could still take place as a result of thermal gradients between the cold outside ice and the warmer inside ice, favoring the climber’s feeling of ‘brittleness’ of the ice. We believe this climber’s feeling is a combination of such thermal stresses related to shallow thermal gradients, and brittle behavior. When a climber hits cold outside ice, the impact creates a compressive wave that bounces off the back surface of the ice. This wave then reflects as a tensile wave which, helped by superficial thermal stresses, causes the ice surface to spall off (the so-called ‘dinner-plating’ phenomenon).
Less-than-vertical ice walls frozen on rock slabs are, for similar reasons, weakly sensitive to dramatic air cooling in midwinter. However, thermal stresses may play a role in destabilizing these structures at the end of the season, when still, cold nights are intercalated between warm days favoring ice and snow melting. Under these conditions, water starts to flow between the ice layer and the rock slab, inducing decohesion. This modifies the boundary conditions and might allow the propagation of horizontal cracks and the destabilization of the structure, as illustrated in Figure 10 for an ice wall situated on the right side of Glacier d’Argentière, the so-called ‘Grand Bleu’. This point merits further observations and analyses.

Fig. 10. The ‘Grand Bleu’ ice wall, situated on the right side of Glacier d’Argentière, in front of Nuit Blanche. Photograph taken 23 March 2009, corresponding to the end of the climbing season. Horizontal cracks (green arrows) as well as water seeping on the rock slabs (orange arrow) are clearly visible.
Although the pressure fluctuations recorded by the sensors in relation to phase transitions (Fig. 9) are of the same order of magnitude as those related to thermal contraction, we were not able to associate them with mechanical instabilities at the structure’s scale. Therefore, we believe that, in terms of risks for climbers, the associated meteorological conditions (mild days, cool nights) are less critical than those associated with thermal contraction (dramatic cooling, cold temperatures), especially for freestanding structures. This is reinforced by the fact that in warm ice, close to the melting point (so-called ‘sorbet ice’), the water content of the ice strongly enhances its ductility (Reference DuvalDuval, 1977; Reference De la Chapelle, Milsch, Castelnau and DuvalDe La Chapelle and others, 1999), preventing crack propagation from ice-axe impact, dinner-plating and the associated climber’s feeling of brittleness.
6. Conclusion
We performed an analysis of the mechanical (in)stability of vertical waterfall ice structures, in relation to meteorological (mainly temperature) conditions. Our goal was not to build a scale of risk in a way similar to that developed, for example, for snow avalanches (Reference Greene, Wiesinger, Birkeland, Coléou, Jones, Statham and GleasonGreene and others, 2006), but we hope that the conclusions of this work might to some extent help the climbing community in decision making concerning climbing conditions.
Prolonged (≥3 days) warm weather conditions, with air temperatures above 0°C including during the night are easily recognized as favoring the destabilization of waterfall structures, either the vertical structures sketched in Figure 1 or those lying on rock slabs. On the other hand, situations with mild days (air temperatures between 0°C and +5°C) and relatively cool nights (e.g. air temperatures around −5°C), although favorable for local internal stress build-up as a result of water ↔ ice phase transition, do not seem critical in terms of large-scale instability. Indeed, these local stress concentrations are presumably relaxed by the extreme ductility of wet ice, preventing crack propagation.
Low temperatures (<−10°C) are favorable for waterfall ice formation (Reference MontagnatMontagnat and others, 2010). The situation might be different, however, for extreme cold events, below −20°C, when water is presumably no longer available, a situation very unusual in the Alps. It might therefore be assumed that low temperatures also favor waterfall ice structure stability, and thus ice climbing. However, we have shown here that dramatic air cooling, of the order of several °Ch−1 over several hours, generates important tensile stresses within vertical ice structures such as free standings. This can trigger a sudden collapse of the entire structure. In addition, cold ice is more brittle than warm ice (Reference Schulson and DuvalSchulson and Duval, 2009), i.e. cracks initiated by climbers with ice axes are more prone to propagate further. Therefore, dramatic cooling and cold weather are not favorable conditions for climbing. As this is counterintuitive, ignoring this might be particularly dangerous.
To our knowledge, this work is the first study of the mechanical (in)stability of waterfall ice structures. Consequently, it can be considered as preliminary, and further work is needed to confirm the scenarios detailed above, or to test their relevance to climatological conditions different from those in the Alps. This is particularly true for regions with very cold average winter temperatures, such as exist in Canada.
Acknowledgements
This work has been funded by the Petzl Foundation. The Société d’Electricité d’Emosson S.A. and the Compagnie du Mont Blanc are acknowledged for their logistic support for fieldwork. Meteorological data for Glacier d’Argentière are provided by Argentière Meteorological Station which is part of the French Observatory GLACIOCLIM (les GLACIers, un Observatoire du CLIMat) supported by CNRS-INSU and the French Ministry of Research. We thank the ‘centro funzionale’ of the Department of Public Works, Soil Conservation and Public Housing of the Regione Autonoma Valle d’Aosta for kindly providing us with the meteorological data for the Valsavarenche valley. We thank E.M. Schulson for interesting discussions, as well as M. Funk and another reviewer for fruitful comments on the manuscript.
Appendix
Estimation of the bending tensile stress induced by a climber hitting a hanging stalactite with an ice axe
We consider a stalactite of length h and a circular section of diameter d at the top (Fig. 11). If the climber exerts a horizontal force F at the bottom, the maximum tensile stress is obtained at the top, on the stalactite’s surface, and is given by
To estimate the impact force F, the impact energy E has to be considered first. As a rough estimate of this energy, we consider a pendular hammer of length L = 1 m with an indentor of mass m = 2 kg at its extremity, which falls from a horizontal position to hit the vertical ice structure (Fig. 12). The corresponding impact energy is given by
This energy is transmitted to the stalactite over a penetration depth l of the indentor, i.e.
Combining Equations (A1), (A2) and (A3), we obtain
Taking h = 15 m (a rather large hanging structure), d = 3 m and l = 1 cm, we obtain σ max = 11 kPa.
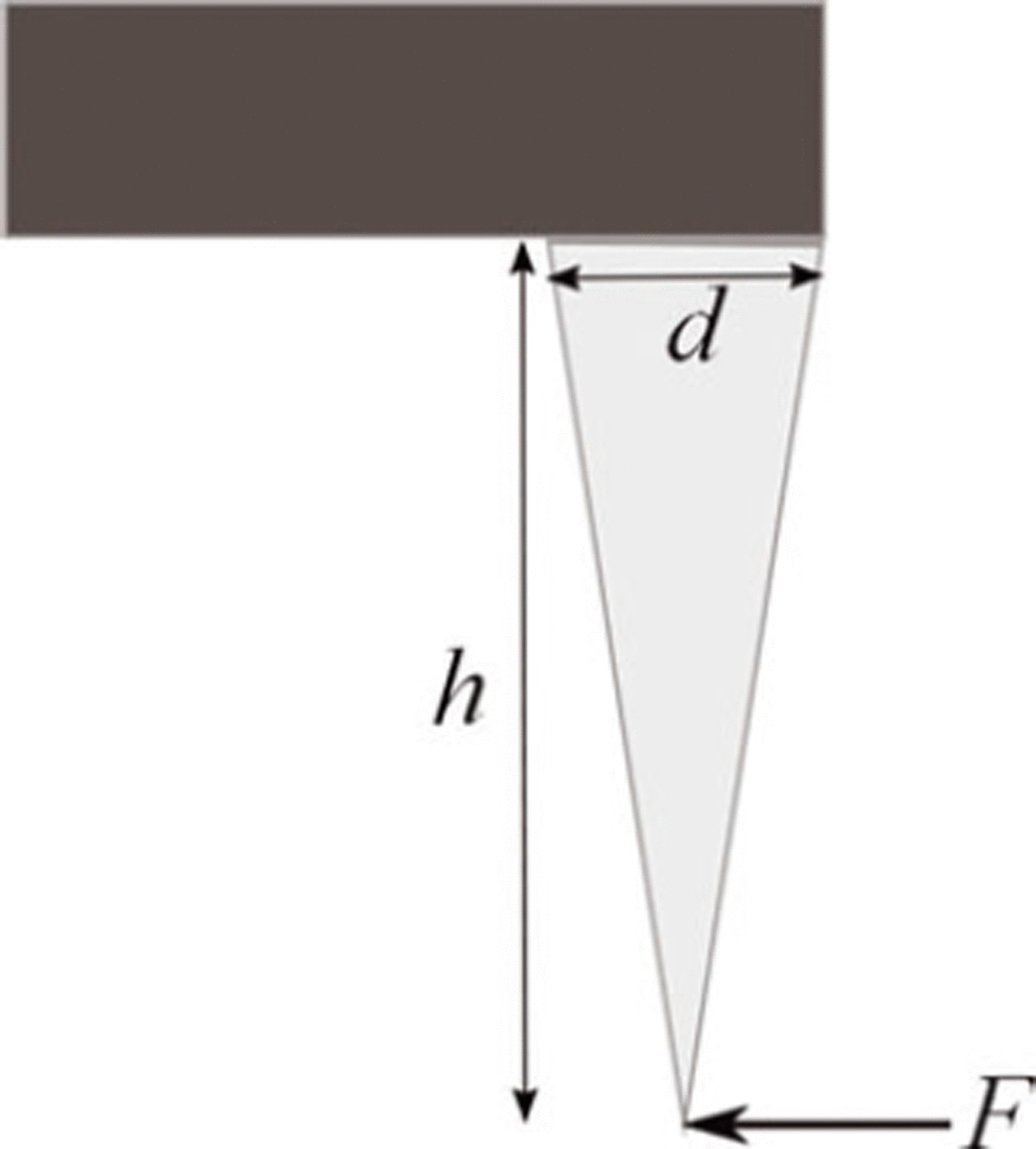
Fig. 11. Sketch showing an idealized conical stalactite, with a horizontal force F exerted by the climber at its bottom.

Fig. 12. Sketch showing a pendular hammer of mass m hitting the ice after a 90° rotation.
This simple calculation shows that the impact force will be likely larger when the ice is colder, i.e. more brittle and less penetrable, but the resulting maximum bending tensile stress will remain small relative to the tensile strength of the ice.