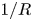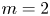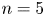Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T13:15:08.374Z Has data issue: false hasContentIssue false
  • English
  • Français

Global fluid turbulence simulations in the scrape-off layer of a stellarator island divertor

Published online by Cambridge University Press:  22 April 2024

B. Shanahan Open the ORCID record for B. Shanahan [Opens in a new window] ,
D. Bold  and
B. Dudson
B. Shanahan*
Affiliation:
Max-Planck-Institut für Plasmaphysik, Wendelsteinstr. 1, 17491 Greifswald, Deutschland
D. Bold
Affiliation:
Max-Planck-Institut für Plasmaphysik, Wendelsteinstr. 1, 17491 Greifswald, Deutschland
B. Dudson
Affiliation:
Lawrence Livermore National Laboratory, 7000 East Avenue, Livermore 94550, CA, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Isothermal fluid turbulence simulations have been performed in the edge and scrape-off layer (SOL) of an analytic stellarator configuration with an island divertor, thereby providing numerical insight into edge turbulence in regions around islands in a stellarator. The steady-state transport follows the a curvature drive that is inverse to the major radius ($1/R$) toward the outboard side, but large fluctuations are present throughout the island divertor region, with the average wavelength of similar size to the island width. The system exhibits a prominent $m=2$, $n=5$ mode, where m is the poloidal mode number and n is the toroidal mode number, although other modes are present. The amplitude and radial extent of the density fluctuations are similar throughout the edge and SOL, but can decrease near island O-points. The fluctuations exhibit a predominantly positive skewness on the outboard midplane, indicating blob-like perturbations for the transport into the outer SOL. It is determined that a point on the separatrix is generally more correlated with regions outside of the SOL than a nearby reference point which does not lie on the separatrix.

Keywords

plasma nonlinear phenomenaplasma simulationfusion plasma
Type
Research Article
Information
Journal of Plasma Physics , Volume 90 , Issue 2 , April 2024 , 905900216
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press

1 Introduction

Advances in stellarator optimization have led to unprecedented improvement in neoclassical transport in Wendelstein 7-X (W7-X) (Beidler et al. Reference Beidler, Smith, Alonso, Andreeva, Baldzuhn, Beurskens, Borchardt, Bozhenkov, Brunner and Damm2021) such that anomalous transport is now contributing a significant portion of the transport, especially in the scrape-off layer (SOL) (Pablant et al. Reference Pablant, Langenberg, Alonso, Beidler, Bitter, Bozhenkov, Burhenn, Beurskens, Delgado-Aparicio and Dinklage2018). The island divertor concept, originally proposed nearly five decades ago (Karger & Lackner Reference Karger and Lackner1977), utilizes low-order magnetic islands which intersect the wall to manage heat and particle exhaust (Feng et al. Reference Feng, Sardei, Grigull, McCormick, Kisslinger and Reiter2006; Feng & W7-X-team Reference Feng2022). The island divertor is advantageous in that it potentially provides a higher whetted area, and has been able to enter very stable detachment regimes (Pedersen et al. Reference Pedersen, König, Jakubowski, Krychowiak, Gradic, Killer, Niemann, Szepesi, Wenzel and Ali2019). Due to this island divertor, the SOL of W7-X provides a unique environment for SOL physics, as the toroidally discontinuous intersection of magnetic islands creates complicated topologies which can inhibit numerical investigation. As such, turbulence simulations in stellarators have focused on the core transport using either a gyrokinetic (Xanthopoulos et al. Reference Xanthopoulos, Merz, Görler and Jenko2007; Bañón Navarro et al. Reference Bañón Navarro, Merlo, Plunk, Xanthopoulos, von Stechow, Di Siena, Maurer, Hindenlang, Wilms and Jenko2020; Maurer et al. Reference Maurer, Bañón Navarro, Dannert, Restelli, Hindenlang, Görler, Told, Jarema, Merlo and Jenko2020; Singh et al. Reference Singh, Nicolau, Lin, Sharma, Sen and Kuley2022) or, less commonly, a fluid approach (Kleiber & Scott Reference Kleiber and Scott2005). Recent work using local fluid simulations has informed interpretation of experimental measurements (Shanahan, Dudson & Hill Reference Shanahan, Dudson and Hill2018; Killer et al. Reference Killer, Shanahan, Grulke, Endler, Hammond and Rudischhauser2020; Shanahan et al. Reference Shanahan, Killer, Pechstein, Henneberg, Fuchert and Grulke2021; Huslage et al. Reference Huslage, Birkenmeier, Shanahan and Killer2023), without requiring modelling of the complex and numerically challenging SOL topology. Developments of numerical methods have provided the opportunity for global fluid turbulence simulations in stellarator geometries (Shanahan, Dudson & Hill Reference Shanahan, Dudson and Hill2019; Coelho et al. Reference Coelho, Loizu, Ricci and Giacomin2022), but a general understanding of global phenomena at the edge and SOL of stellarators is only in its infancy. In this work, we utilize an isothermal model in the BOUT++ (Dudson et al. Reference Dudson, Umansky, Xu, Snyder and Wilson2009) framework to explore the nature of turbulence in the island divertor region at the edge of an analytic stellarator configuration (Coelho et al. Reference Coelho, Loizu, Ricci and Giacomin2022).

Section 2 details the methods used in this work, including the plasma model, geometry and computational grid. Section 3 discusses the simulation results, and is divided into two subsections; the steady-state transport properties of the system and the dynamics of the fluctuations in the island SOL. The implications of this work and its context within previous work are discussed in § 4.

2 Methods

The strength of BOUT++ (Dudson et al. Reference Dudson, Umansky, Xu, Snyder and Wilson2009) is its flexibility: models and numerical methods can be easily changed to suit the problem to be addressed. Here, we use an isothermal plasma model in a complex numerical scheme, as the turbulent dynamics is available despite numerous assumptions, but the geometry is necessarily complicated.

2.1 Isothermal plasma model

In this work we exploit a reduced magnetohydrodynamic model from the Hermes family of models (Dudson & Leddy Reference Dudson and Leddy2017; Leddy et al. Reference Leddy, Dudson, Romanelli, Shanahan and Walkden2017; Huslage et al. Reference Huslage, Birkenmeier, Shanahan and Killer2023), which do not separate fluctuations from the background. The simulations here are isothermal, and evolve number density $n$, vorticity $\omega$, parallel ion momentum $m_inv_\parallel$ and Ohm's law $J_\parallel = en(v_{\parallel,i} - v_{\parallel,e}) = -({1}/{\nu }) \partial _\parallel \phi - ({1}/{n_e}) \partial _\parallel p_e$, where $p_e$ is the electron pressure, $e$ is the electron charge, $m_{i}$ is the ion mass and $\phi$ is the plasma potential, for the parallel electron velocity $v_{\|e}$. Quasineutrality is assumed, so that the electron and ion densities are equal: $n_e = n_i = n$. Here, $\nu =1.96 \tau _{ei} ({m_i}/{m_e})$ is the resistivity. The thin layer (Oberbeck–Boussinesq (Oberbeck Reference Oberbeck1879)) approximation is made in calculating the potential $\phi$ from vorticity $\omega$ such that

(2.1)\begin{equation} \omega = \boldsymbol{\nabla}\boldsymbol{\cdot}\left[\frac{en_0}{\varOmega B}\boldsymbol{\nabla}_\perp\phi\right], \end{equation}

where $\varOmega = eB/m_i$ is the ion cyclotron frequency, where B is the magnetic field strength and $n_0$ is a constant typical number density, in this work set to be $n_0 = 1\times 10^{18}\,\mathrm {m}^{-3}$. The resulting equations for (electron) number density $n$, vorticity $\omega$ and parallel momentum $m_in v_{\parallel i}$ are

(2.2)\begin{gather} \frac{\partial n}{\partial t} ={-}\boldsymbol{\nabla}\boldsymbol{\cdot}\left(n\boldsymbol{v}_{E\times B} + n\boldsymbol{v}_{{\rm mag},e}\right) - \boldsymbol{\nabla}_{\|}\left(n v_{\|e}\right) + S_n, \end{gather}
(2.3)\begin{gather} \frac{\partial \omega}{\partial t} = \boldsymbol{\nabla}\boldsymbol{\cdot}\left[e\left(p_e + p_i\right)\boldsymbol{\nabla}\times\frac{\boldsymbol{b}}{B}\right] + \boldsymbol{\nabla}_{\|}j_{\|} - \boldsymbol{\nabla} \boldsymbol{\cdot} \left(\omega\boldsymbol{v}_{E\times B}\right), \end{gather}
(2.4)\begin{gather} \frac{\partial}{\partial t}\left(m_inv_{\|i}\right) ={-}\boldsymbol{\nabla}\boldsymbol{\cdot}\left[m_inv_{\|i}\left(\boldsymbol{v}_{E\times B} + \boldsymbol{b}v_{\|i} + \boldsymbol{v}_{{\rm mag},i}\right)\right] - \partial_{\|}p_e - \partial_{\|}p_i, \end{gather}

where $S_n$ is the density source, $p_{e/i}$ is the pressure for electrons and ions, respectively, and the drift terms for $E\times B$, $\boldsymbol {v}_{E\times B}$ and ion and electron magnetic drifts, $\boldsymbol {v}_{{\rm mag},e/i}$, are defined as

(2.5)\begin{equation} \boldsymbol{v}_{E\times B} = \frac{\boldsymbol{b}\times\boldsymbol{\nabla} \phi}{B} \quad \boldsymbol{v}_{{\rm mag},e} ={-}\frac{T_e}{e}\boldsymbol{\nabla}\times\frac{\boldsymbol{b}}{B} \quad \boldsymbol{v}_{{\rm mag},i} = \frac{T_i}{e}\boldsymbol{\nabla}\times\frac{\boldsymbol{b}}{B}. \end{equation}

where E is the electric field, $T_{e,i}$ is the electron and ion temperature, respectively, $\boldsymbol{b}$ is a unit vector in the direction of the magnetic field, and f is an arbitrary function. Here, the notation is such that $\boldsymbol {\nabla }_\perp = \boldsymbol {\nabla } - \boldsymbol {bb}\boldsymbol {\cdot } \boldsymbol {\nabla }$, $\partial _\parallel f = {\boldsymbol {b}}\boldsymbol {\cdot }\boldsymbol {\nabla } f$ and $\boldsymbol {\nabla }_\parallel f = \boldsymbol {\nabla } \boldsymbol {\cdot } ({\boldsymbol {b}}f)$. While the model allows terms for anomalous diffusion, these terms are not necessary for numerical stability and, as the nature of their origin is unknown, are neglected in this work. An imposed parallel diffusion of $4.2\,\mathrm {m}^2\,\mathrm {s}^{-1}$ is used in Ohm's law to suppress numerical instability.

2.2 BSTING and BOUT++

The BSTING project (Shanahan et al. Reference Shanahan, Dudson and Hill2019) has recently allowed for simulations of stellarator geometries using the BOUT++ framework (Dudson et al. Reference Dudson, Umansky, Xu, Snyder and Wilson2009), in which exploitation of the flux-coordinate-independent (FCI) method for parallel derivatives (Hariri & Ottaviani Reference Hariri and Ottaviani2013; Hariri et al. Reference Hariri, Hill, Ottaviani and Sarazin2014; Hill, Hariri & Ottaviani Reference Hill, Hariri and Ottaviani2015; Shanahan, Hill & Dudson Reference Shanahan, Hill and Dudson2016; Stegmeir et al. Reference Stegmeir, Coster, Maj, Hallatschek and Lackner2016; Hill, Shanahan & Dudson Reference Hill, Shanahan and Dudson2017) allows for simulation of complex magnetic geometries including magnetic islands and chaotic field regions. The implementation of three-dimensional metric tensor components in BOUT++ has allowed for poloidally curvilinear FCI grids (Shanahan et al. Reference Shanahan, Dudson and Hill2019) that do not include grid points in the core of the plasma – where the fluid approximation due to high collisionality can break down – and allow for the poloidal grid alignment to flux surfaces or plasma-facing components. As such, FCI simulations can be performed with resolutions comparable to field-aligned tokamak simulations.

2.3 Geometry and initial conditions

The simulation geometry used here is similar to that in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022). Namely, a stellarator magnetic field with an outer $m=9$ island chain was created using the same Dommaschk potential (Dommaschk Reference Dommaschk1986) as in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022), where the magnetic field varies to lowest order by $1/R$, where R is the major radius – similar to (for instance) a tokamak. The BSTING framework utilizes curvilinear grids, however, meaning that, in contrast to the work presented in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022), here, the core is neglected, and the outer poloidal surface is an ellipse with the same maximum dimensions of the outer boundary as used in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022). The inner surface is aligned to a vacuum flux surface, and the elliptical outer surface provides a plasma-facing component which intersects islands at discrete toroidal locations (for instance, figure 1b), as in an island divertor.

Figure 1. Poincaré plots (black) of the magnetic field using parameters from Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022), including the inner (red) and outer (blue) surfaces of the grid.

The numerical grid utilized in this work was of the size (radial, toroidal, poloidal) $(nx,ny,nz) = (68,128,256)$ with an average resolution of $({{\rm d} x},{{\rm d} y},{\rm d}z) \approx (1,75,1)\rho _i$, where $\rho _i$ is the ion Larmor radius. The simulation domain spans the entire toroidal extent ($0$ to $2{\rm \pi}$). Despite the difference in numerical implementation, the magnetic field is identical to that in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022), including the outer magnetic islands, as shown in figure 1. The radial extent of the SOL can be as small as 10 Larmor radii, and perturbations often exhibit a similar perpendicular size. As such, fluctuations cannot be categorized as edge or SOL localized. A more detailed discussion of the fluctuations follows in § 3.2.

The simulations are flux driven, with a particle source of the form

(2.6)\begin{equation} S_n(r) = S_0\frac{1}{w\sqrt{2{\rm \pi}}} \exp\left(\frac{-(r-r_0)^2}{(2w^2)}\right) \,\mathrm{m}^{{-}3}\,\mathrm{s}^{{-}1}, \end{equation}

where $S_0$ is a prescribed constant used to balance the sinks, $r_0$ is the radial location the peak and $w$ is the Gaussian root-mean-square width. Here, $r_0$ and $w$ are chosen such that the source peaks at the same radial location in the closed-field-line region as the source in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022). Since the particle source introduces an external drive into the system, the dynamics which originates farther inward (toward the core) must be carefully treated – and is therefore not included in the computational domain. The equilibrium parameters – the background density ($n_0 = 1\times 10^{18}\,{\rm m}^{-3}$), the magnetic field ($B_0 \approx 0.3T$) and the background temperature ($T_0 = 10\,{\rm eV}$) have been chosen to most closely align with Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022). These parameters are similar to those found in university-scale experiments, such as TORPEX (Furno et al. Reference Furno, Labit, Podestà, Fasoli, Müller, Poli, Ricci, Theiler, Brunner and Diallo2008; Shanahan & Dudson Reference Shanahan and Dudson2016). Parallel sheath boundary conditions (Walkden et al. Reference Walkden, Easy, Militello and Omotani2016) are imposed such that the species are accelerated to the local sound speed and implemented using the leg-boundary-fill method at the ends of magnetic field lines (Hill et al. Reference Hill, Shanahan and Dudson2017). Perpendicular boundary conditions, with the exception of plasma potential, are zero gradient, allowing flows into the domain from the inner boundary and out of the domain at the outer boundary. The plasma potential is calculated from vorticity using PETSc (Balay et al. Reference Balay, Gropp, McInnes and Smith1997) with Dirichlet boundary conditions such that $\phi _{{\rm boundary}} = 2.8T_e$. The density is set to an approximate initial profile, and an initial perturbation in vorticity is added to the system; after a transient phase, the simulation settles into a state where the particle source is balanced by the sinks in the sheath, characterized by fluctuations throughout the domain. The simulation is then run such that the time scale exceeds 1 ms, which is calculated in approximately 30 000 core hours.

3 Results

The dynamics simulated here can be separated into two scales; large-scale, steady-state flows of the plasma and the perturbations on top of these macroscopic aspects. The following two subsections will look into this dynamics in more detail.

3.1 Macroscopic transport and steady-state flows

On longer time scales ($t > 100\,\mathrm {\mu }{\rm s}$), the plasma advects with a dominant motion toward the outboard side. This motion is visualized by plotting the contours of the time-averaged plasma potential, figure 2, as the flows follow the contours of $\langle \phi \rangle$ via $E\times B$ motion. Throughout this work, the angled brackets ($\langle \rangle$) will always indicate a time average, and tilde ($\,\tilde{}\,$) will indicate a perturbed quantity around the time average. The time-averaged transport indicates predominantly radial transport in the edge and SOL, with a return flow antiparallel to the curvature drive in the low-density region – near the outer boundary – best visualized in figure 2(a). The dynamics is more complicated in the verticalcross-section, figure 2(b), due to the sheath connection that introduces a discontinuity between the inboard and outboard. A return flow is seen on the outboard midplane of the vertical cross-section, and can also be seen when plotting the radial flux (Shanahan & Dudson Reference Shanahan and Dudson2014), $\varGamma _r = \langle nv_r\rangle$, as is shown in figure 3. The most prominent areas of radial flux coincide with the strongest gradients in potential contours shown in figure 2 – for instance on the inboard side of figure 2(a). These areas of large radial flux can be attributed to steady-state flows due to the $1/R$ curvature drive; a radially inward flux is seen on the inboard side of figure 3(a) in blue, and a strong radially outward flux on the outboard side in red. The vertical cross-section, figure 3(b), diverges from this curvature-driven nature, with flux on the inboard side prominent near X-points – including a flux antiparallel to the curvature drive at the midplane – and significant outward radial flux near the intersection with the outer boundary.

Figure 2. Time-averaged plasma potential; the contour lines indicate flows due to $E\times B$ advection. Transport towards the outboard side due to $1/R$ curvature drive is the dominant flow within the system. In this figure, the magnetic field is predominantly into the page.

Figure 3. Time-averaged radial flux, indicating regions of radial transport. A negative radial flux indicates radially inward flux, whereas a positive flux is outward.

To further examine the flows in the island SOL presented here, one can plot the Pearson correlation coefficient (Freedman, Pisani & Purves Reference Freedman, Pisani and Purves2007) of density signals relative to a given point in the SOL, as is done in Shanahan & Dudson (Reference Shanahan and Dudson2014). In this work, we correlate the time trace of every point in the domain to a reference point, defining the Pearson correlation coefficient $P_{fg}$ between a reference point $f$ and a sample point $g$ as

(3.1)\begin{equation} P_{fg} = \frac{\mathrm{cov}(f,g)}{\sigma_f \sigma_g} = \sum^{N_t-1}_{t=0}\left(f_t - \left\langle f\right\rangle\right)\left(g_t - \left\langle g\right\rangle\right) \left\{\left[\sum^{N_t-1}_{t=0}\left(f_t - \left\langle f\right\rangle\right)^2\right]\left[\sum^{N_t-1}_{t=0}\left(g_t - \left\langle g\right\rangle\right)^2\right]\right\}^{-{1}/{2}}, \end{equation}

where $\mathrm {cov}(f,g)$ indicates the covariance of $f$ and $g$, $\sigma _f$ and $\sigma _g$ are the standard deviations of $f$ and $g$, respectively, the angled brackets ($\langle \ \rangle$) indicate a time average, $t$ is the time index for each time trace and $N_t$ is the number of time points in the time trace. A higher correlation of a point in space to a reference point indicates a better correlation between fluctuations at these positions. Due to the large-scale fluctuations, the correlation $P_{fg}$ often has a similar structure regardless of the reference point chosen, see figure 4.

Figure 4. The Pearson correlation coefficients when considering a reference point (a) in the separatrix, $P_{{\rm sep}}$, and (b) when choosing a reference point at a magnetic O-point, $P_O$. These reference points are marked with a white X and a white dot, respectively. A positive value indicates positive correlation with the reference point.

The Pearson correlations shown in figure 4 are very similar in structure, inhibiting a clear conclusion for the role of the separatrix in providing a channel for flows in the SOL. For this reason, we will look at the relative correlation when choosing two reference points; one correlation with a reference point at the separatrix $P_{{\rm sep}}$ , and one with a reference point at an island O-point, $P_O$.

Figure 5 shows the difference of two correlations given by (3.1); one where the reference point is in the separatrix, $f_{{\rm sep}}$, and one where the reference point is at an O-point, $f_O$. The reference points are shown as white markers in figure 5(a). By plotting their difference, $P_{{\rm sep}} - P_O$, where the higher correlation of the separatrix to the outer edges of the domain is illustrated by the positive difference of the two correlations, one can obtain a clearer picture of the correlation within the SOL. Figure 5(a) indicates an increased relative correlation of the edge SOL to the separatrix – even on the outboard side – while the strongest relative correlation to the O-point is seen nearest the O-point reference location. The vertical cross-section, figure 5(b), does not indicate such strong correlation with the separatrix reference location, except at the edges near the boundary. The higher relative correlations of the boundary on the vertical cross-section indicate that the separatrix could provide a transport channel to the boundary.

Figure 5. The relative Pearson correlation coefficients when considering a reference point in the separatrix, $P_{{\rm sep}}$, and when choosing a reference point at a magnetic O-point, $P_O$. These reference points are marked with a white X and and circle in figure 5(a). A positive value indicates stronger correlations with fluctuations at the separatrix, whereas a negative value indicates correlation with fluctuations at an island O-point.

3.2 Perturbations near the edge and SOL

Having examined the characteristics of the large-scale dynamics, attention is now turned to the dynamics of the perturbations. The system exhibits a strong $m=2$, $n=5$ mode, although other modes are present. The fluctuations are large – $k_\perp \rho _s$ is generally less than 1, as indicated in figure 6. As the magnetic islands are, at widest, only a couple of tens of $\rho _i$ the fluctuations can at times exceed the width of the island SOL.

Figure 6. (a) Average radial fluctuation size and (b) average poloidal fluctuation size on a flux surface indicated by the dashed surface in figure 1.

To determine the nature of the fluctuations, we examine central moments of the time signal, where the $n{\mathrm {th}}$ central moment of a quantity $x$ is given by $\mu _n = \langle (x -\langle x\rangle )^n\rangle$, where the angled brackets ($\langle \ \rangle$) indicate a time average. The standard deviation of $x$, $\sigma _x$, is the square root of the second moment ($n=2$) and the skewness, which will be used later, is proportional to the third moment ($n=3$) normalized to the standard deviation. The standard deviation of the density signal, $\sigma _n$ is shown in figure 7. Figure 7 indicates that fluctuations are present throughout the domain. The vertical cross-section, figure 7(b), indicates a decrease in $\sigma _n$ outside the outer midplane island O-point relative to the neighbouring X-point regions, suggesting that fluctuations are reduced here. Figure 7 indicates that the fluctuations, despite their large scale relative to the system size, fall off radially. Using the correlation coefficient, (3.1), it is determined that the fluctuations have radial correlation lengths which vary from approximately $8\rho _i$ on the outboard midplane of the verticalcross-section (figure 5b) to approximately $50\rho _i$ on the inboard side of the horizontal cross-section (figure 5a). Since the islands in the SOL are wider at the locations of longer correlation lengths, this poloidal variation in correlation length could be related to the island width. Furthermore, the standard deviation of the vorticity perturbations, $\sigma _\omega$, also shows fluctuations present throughout the domain, figure 8. Figure 8(b) indicates again that the outboard midplane island O-point in the vertical cross-section exhibits reduced fluctuation amplitudes, whereas the neighbouring X-points show stronger fluctuations. Vorticity localized to islands can in turn lead to transport around the island separatrices. Island-localized potentials leading to flows around the island separatrix have been seen in W7-X (Killer et al. Reference Killer, Grulke, Drews, Gao, Jakubowski, Knieps, Nicolai, Niemann, Sitjes and Satheeswaran2019). It is also possible to plot the radial flux of the perturbations, $\tilde {\varGamma }_\perp = \langle \tilde {n}\tilde {v}_r\rangle$, illustrated in figure 9. The radial perturbation flux can increase near X-points, and is indeed seen in several studies in other geometries (Poli, Bottino & Peeters Reference Poli, Bottino and Peeters2009; Hill et al. Reference Hill, Hariri and Ottaviani2015; Choi Reference Choi2021), but this phenomenon is not universal in the simulations presented here and a concrete conclusion cannot be drawn. The radial perturbation flux shown in figure 9(b) indicates stronger outboard activity, with a change in the sign of the radial flux near the outboard midplane.

Figure 7. Standard deviation of the density; perturbations are apparent at all poloidal locations, with a slight increase on the outboard side.

Figure 8. Standard deviation of vorticity. The horizontal cross-section (a) indicates better poloidal symmetry compared with the vertical cross-section (b).

Figure 9. Time average of the radial perturbation flux.

To determine the transport nature of the fluctuations, the skewness of the profiles is plotted in figure 10, where a positive skewness indicates blob-like transport (Walkden et al. Reference Walkden, Militello, Harrison, Farley, Silburn and Young2017), and negative skewness indicates areas dominated by the propagation of negative perturbations (holes). From figure 10, it is apparent that the transport near the outer boundary, at the inboard and outboard midplane locations mostly include positive perturbations, whereas in the middle of the domain, particularly the top and bottom of the configuration exhibit a predominantly negative skewness, where negative perturbations are more prevalent.

Figure 10. Density skewness; a positive skewness (red) indicates positive perturbations (blob like), while negative skewness (blue) indicates the prominence of negative perturbations (holes).

4 Summary and implications

In this work, a detailed analysis of fluid turbulence in a stellarator island divertor is presented. An isothermal fluid turbulence model was used to simulate turbulence in an analytic stellarator geometry, finding that the fluctuations are present throughout the island divertor region. It was determined that the steady-state dynamics is mostly consistent with the $1/R$ curvature drive, but the sheath connection in the cross-sections which intersect the boundary introduces a discontinuity. The plasma outside the SOL is more highly correlated with the point on the separatrix than the island O-point, indicating the separatrix as a transport channel into the private flux region. The fluctuations are exhibited throughout the domain, with a smaller amplitude near the outboard midplane island in the vertical cross-section. The radial perturbation flux can, but must not necessarily manifest near island X-points.

4.1 Context within previous work

The results shown previously in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022) suggest that despite a ballooning-dominant configuration, fluctuations are dominated by an $m=4$, $n=5$ mode and localized to the inboard side of the torus. The results presented herein indicate the fluctuation amplitudes are higher on the outboard side of the torus in the same geometry, see figure 11. Furthermore, the dominant $m=4$ mode seen in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022) is present but not dominant. Rather, there exists several modes – the most prominent of which is an $m=2$, $n=5$. Generally, there does not seem to be higher-amplitude fluctuations at the inboard side. There are a few methodological differences in between this work and that shown in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022) which could contribute to the discrepancies. Firstly, we do not simulate the core region in this work. We have chosen not to simulate the core due to the applied source at the outside of the closed-field-line region (chosen in Coelho et al. Reference Coelho, Loizu, Ricci and Giacomin2022), which could potentially influence the dynamics, but future work could, in principle, simulate this area. Additionally, the simulation model in Coelho et al. (Reference Coelho, Loizu, Ricci and Giacomin2022) was non-isothermal, and therefore included other effects which cannot be captured here.

Figure 11. Standard deviation of the density fluctuations on the last closed flux surface; fluctuations have a higher amplitude on the outboard side.

Future work will look to relax the isothermal approximation and remove the islands from the geometry in order to more fully assess the impact of islands on the transport and perturbation dynamics, although this is a laborious task due to the non-intuitive nature of Dommaschk potentials. While it is true that by adjusting higher-order coefficients one can almost remove islands, this process is described by the author in Dommaschk (Reference Dommaschk1986) as only achieved ‘by trial.’ It could be more interesting, therefore, to explore more realistic geometries, such as the various W7-X configurations which have been more extensively investigated.

Acknowledgements

The authors would like to thank A. Coelho and J. Loizu for many interesting discussions and providing the coefficients for the Dommaschk potential. The efforts of the BOUT++ development team have been crucial to this work. BOUT++ is an open-source framework available at boutproject.github.io.

Editor T. Carter thanks the referees for their advice in evaluating this article.

Funding

This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. Prepared in part by LLNL under Contract DE-AC52-07NA27344. LLNL-JRNL-849204.

Declaration of interests

The authors report no conflict of interest.

Data availability statement

All of the requisite files for this work are open source and can be obtained either from the lead author or at github.com/bshanahan/papers.

References

Balay, S., Gropp, W.D., McInnes, L.C. & Smith, B.F. 1997 Efficient management of parallelism in object-oriented numerical software libraries. In Modern Software Tools for Scientific Computing, pp. 163–202. Springer.CrossRefGoogle Scholar
Bañón Navarro, A., Merlo, G., Plunk, G.G., Xanthopoulos, P., von Stechow, A., Di Siena, A., Maurer, M., Hindenlang, F., Wilms, F. & Jenko, F. 2020 Global gyrokinetic simulations of ITG turbulence in the magnetic configuration space of the Wendelstein 7-X stellarator. Plasma Phys. Control. Fusion 62 (10), 105005.CrossRefGoogle Scholar
Beidler, C.D., Smith, H.M., Alonso, A., Andreeva, T., Baldzuhn, J., Beurskens, M.N.A., Borchardt, M., Bozhenkov, S.A., Brunner, K.J., Damm, H., et al. 2021 Demonstration of reduced neoclassical energy transport in Wendelstein 7-X. Nature 596 (7871), 221–226.CrossRefGoogle ScholarPubMed
Choi, M.J. 2021 Interaction between a magnetic island and turbulence. Rev. Mod. Plasma Phys. 5 (1), 9.CrossRefGoogle Scholar
Coelho, A.J., Loizu, J., Ricci, P. & Giacomin, M. 2022 Global fluid simulation of plasma turbulence in a stellarator with an island divertor. Nucl. Fusion 62 (7), 074004.CrossRefGoogle Scholar
Dommaschk, W. 1986 Representations for vacuum potentials in stellarators. Comput. Phys. Commun. 40 (2), 203–218.CrossRefGoogle Scholar
Dudson, B.D. & Leddy, J. 2017 Hermes: global plasma edge fluid turbulence simulations. Plasma Phys. Control. Fusion 59 (5), 054010.CrossRefGoogle Scholar
Dudson, B.D., Umansky, M.V., Xu, X.Q., Snyder, P.B. & Wilson, H.R. 2009 BOUT++: a framework for parallel plasma fluid simulations. Comput. Phys. Commun. 180, 1467–1480.CrossRefGoogle Scholar
Feng, Y. W7-X-team 2022 Review of magnetic islands from the divertor perspective and a simplified heat transport model for the island divertor. Plasma Phys. Control. Fusion 64 (12), 125012.CrossRefGoogle Scholar
Feng, Y., Sardei, F., Grigull, P., McCormick, K., Kisslinger, J. & Reiter, D. 2006 Physics of island divertors as highlighted by the example of W7-AS. Nucl. Fusion 46 (8), 807.CrossRefGoogle Scholar
Freedman, D., Pisani, R. & Purves, R. 2007 Statistics. W.W. Norton & Company.Google Scholar
Furno, I., Labit, B., Podestà, M., Fasoli, A., Müller, S.H., Poli, F.M., Ricci, P., Theiler, C., Brunner, S., Diallo, A., et al. 2008 Experimental observation of the blob-generation mechanism from interchange waves in a plasma. Phys. Rev. Lett. 100, 055004.CrossRefGoogle ScholarPubMed
Hariri, F., Hill, P., Ottaviani, M. & Sarazin, Y. 2014 The flux-coordinate independent approach applied to x-point geometries. Phys. Plasmas 21 (8), 082509.CrossRefGoogle Scholar
Hariri, F. & Ottaviani, M. 2013 A flux-coordinate independent field-aligned approach to plasma turbulence simulations. Comput. Phys. Commun. 184 (11), 2419–2429.CrossRefGoogle Scholar
Hill, P., Hariri, F. & Ottaviani, M. 2015 The effect of magnetic islands on ion temperature gradient turbulence driven transport. Phys. Plasmas 22 (4), 042308.CrossRefGoogle Scholar
Hill, P., Shanahan, B. & Dudson, B. 2017 Dirichlet boundary conditions for arbitrary-shaped boundaries in stellarator-like magnetic fields for the flux-coordinate independent method. Comput. Phys. Commun. 213, 9–18.CrossRefGoogle Scholar
Huslage, P., Birkenmeier, G., Shanahan, B. & Killer, C. 2023 Coherence of turbulent structures with varying drive in stellarator edge plasmas. Plasma Phys. Control. Fusion 66 (1), 015006.CrossRefGoogle Scholar
Karger, F. & Lackner, K. 1977 Resonant helical divertor. Phys. Lett. A 61 (6), 385–387.CrossRefGoogle Scholar
Killer, C., Grulke, O., Drews, P., Gao, Y., Jakubowski, M., Knieps, A., Nicolai, D., Niemann, H., Sitjes, A.P. & Satheeswaran, G. 2019 Characterization of the W7-X scrape-off layer using reciprocating probes. Nucl. Fusion 59 (8), 086013.CrossRefGoogle Scholar
Killer, C., Shanahan, B., Grulke, O., Endler, M., Hammond, K. & Rudischhauser, L. 2020 Plasma filaments in the scrape-off layer of Wendelstein 7-X. Plasma Phys. Control. Fusion 62 (8), 085003.CrossRefGoogle Scholar
Kleiber, R. & Scott, B. 2005 Fluid simulations of edge turbulence for stellarators and axisymmetric configurations. Phys. Plasmas 12 (10), 102507.CrossRefGoogle Scholar
Leddy, J., Dudson, B., Romanelli, M., Shanahan, B. & Walkden, N. 2017 A novel flexible field-aligned coordinate system for tokamak edge plasma simulation. Comput. Phys. Commun. 212, 59–68.CrossRefGoogle Scholar
Maurer, M., Bañón Navarro, A., Dannert, T., Restelli, M., Hindenlang, F., Görler, T., Told, D., Jarema, D., Merlo, G. & Jenko, F. 2020 Gene-3D: a global gyrokinetic turbulence code for stellarators. J. Comput. Phys. 420, 109694.CrossRefGoogle Scholar
Oberbeck, A. 1879 Über die wärmeleitung der flüssigkeiten bei berücksichtigung der strömungen infolge von temperaturdifferenzen. Ann. Phys. 243 (6), 271–292.CrossRefGoogle Scholar
Pablant, N.A., Langenberg, A., Alonso, A., Beidler, C.D., Bitter, M., Bozhenkov, S., Burhenn, R., Beurskens, M., Delgado-Aparicio, L., Dinklage, A., et al. 2018 Core radial electric field and transport in Wendelstein 7-X plasmas. Phys. Plasmas 25 (2), 022508.CrossRefGoogle Scholar
Pedersen, T.S., König, R., Jakubowski, M., Krychowiak, M., Gradic, D., Killer, C., Niemann, H., Szepesi, T., Wenzel, U., Ali, A., et al. 2019 First divertor physics studies in Wendelstein 7-X. Nucl. Fusion 59 (9), 096014.CrossRefGoogle Scholar
Poli, E., Bottino, A. & Peeters, A.G. 2009 Behaviour of turbulent transport in the vicinity of a magnetic island. Nucl. Fusion 49 (7), 075010.CrossRefGoogle Scholar
Shanahan, B.W. & Dudson, B.D. 2014 X-point modelling in linear configurations using BOUT++. J. Phys.: Conf. Ser. 561 (1), 012015.Google Scholar
Shanahan, B.W. & Dudson, B.D. 2016 Blob dynamics in TORPEX poloidal null configurations. Plasma Phys. Control. Fusion 58 (12), 125003.CrossRefGoogle Scholar
Shanahan, B., Dudson, B. & Hill, P. 2018 The effects of non-uniform drive on plasma filaments. J. Phys.: Conf. Ser. 1125, 012018.Google Scholar
Shanahan, B., Dudson, B. & Hill, P. 2019 Fluid simulations of plasma filaments in stellarator geometries with BSTING. Plasma Phys. Control. Fusion 61 (2), 025007.CrossRefGoogle Scholar
Shanahan, B., Hill, P. & Dudson, B. 2016 Towards nonaxisymmetry; initial results using the flux coordinate independent method in BOUT++. J. Phys.: Conf. Ser. 775 (1), 012012.Google Scholar
Shanahan, B., Killer, C., Pechstein, G., Henneberg, S.A., Fuchert, G. & Grulke, O. 2021 Estimating the error in filament propagation measurement using a synthetic probe. Plasma Phys. Control. Fusion 63 (12), 125018.CrossRefGoogle Scholar
Singh, T., Nicolau, J.H., Lin, Z., Sharma, S., Sen, A. & Kuley, A. 2022 Global gyrokinetic simulations of electrostatic microturbulent transport using kinetic electrons in LHD stellarator. Nucl. Fusion 62 (12), 126006.CrossRefGoogle Scholar
Stegmeir, A., Coster, D., Maj, O., Hallatschek, K. & Lackner, K. 2016 The field line map approach for simulations of magnetically confined plasmas. Comput. Phys. Commun. 198, 139–153.CrossRefGoogle Scholar
Walkden, N.R., Easy, L., Militello, F. & Omotani, J.T. 2016 Dynamics of 3D isolated thermal filaments. Plasma Phys. Control. Fusion 58 (11), 115010.CrossRefGoogle Scholar
Walkden, N.R., Militello, F., Harrison, J., Farley, T., Silburn, S. & Young, J. 2017 Identification of intermittent transport in the scrape-off layer of mast through high speed imaging. Nucl. Mater. Energy 12, 175–180, proceedings of the 22nd International Conference on Plasma Surface Interactions 2016, 22nd PSI.CrossRefGoogle Scholar
Xanthopoulos, P., Merz, F., Görler, T. & Jenko, F. 2007 Nonlinear gyrokinetic simulations of ion-temperature-gradient turbulence for the optimized Wendelstein 7-X stellarator. Phys. Rev. Lett. 99, 035002.CrossRefGoogle ScholarPubMed
Figure 0

Figure 1. Poincaré plots (black) of the magnetic field using parameters from Coelho et al. (2022), including the inner (red) and outer (blue) surfaces of the grid.

Figure 1

Figure 2. Time-averaged plasma potential; the contour lines indicate flows due to $E\times B$ advection. Transport towards the outboard side due to $1/R$ curvature drive is the dominant flow within the system. In this figure, the magnetic field is predominantly into the page.

Figure 2

Figure 3. Time-averaged radial flux, indicating regions of radial transport. A negative radial flux indicates radially inward flux, whereas a positive flux is outward.

Figure 3

Figure 4. The Pearson correlation coefficients when considering a reference point (a) in the separatrix, $P_{{\rm sep}}$, and (b) when choosing a reference point at a magnetic O-point, $P_O$. These reference points are marked with a white X and a white dot, respectively. A positive value indicates positive correlation with the reference point.

Figure 4

Figure 5. The relative Pearson correlation coefficients when considering a reference point in the separatrix, $P_{{\rm sep}}$, and when choosing a reference point at a magnetic O-point, $P_O$. These reference points are marked with a white X and and circle in figure 5(a). A positive value indicates stronger correlations with fluctuations at the separatrix, whereas a negative value indicates correlation with fluctuations at an island O-point.

Figure 5

Figure 6. (a) Average radial fluctuation size and (b) average poloidal fluctuation size on a flux surface indicated by the dashed surface in figure 1.

Figure 6

Figure 7. Standard deviation of the density; perturbations are apparent at all poloidal locations, with a slight increase on the outboard side.

Figure 7

Figure 8. Standard deviation of vorticity. The horizontal cross-section (a) indicates better poloidal symmetry compared with the vertical cross-section (b).

Figure 8

Figure 9. Time average of the radial perturbation flux.

Figure 9

Figure 10. Density skewness; a positive skewness (red) indicates positive perturbations (blob like), while negative skewness (blue) indicates the prominence of negative perturbations (holes).

Figure 10

Figure 11. Standard deviation of the density fluctuations on the last closed flux surface; fluctuations have a higher amplitude on the outboard side.