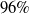1. Introduction
The granular medium is a typical terrain that appears on some planet surfaces, especially the Mars and lunar surfaces. This type of terrain usually consists of gravel, dust, and other materials. It is deformable and has fluid-like properties [Reference Reina, Ojeda, Milella and Borenstein1], and these special characteristics could lead the robot to excessive sinkage (losing mobility) and slippage (falling down or difficult to localize). To overcome these challenges, conducting an in-depth study of the robot-terrain contact process and interaction characteristics is necessary. Slippage and sinkage are the two main phenomena during robot-terrain interaction [Reference Li, Wu, Di, Angelova, Arvidson, Lee, Maimone, Matthies, Richer and Robert, H. Michael, G. Tebecca and W. Steven2]. Thus, it is important to characterize these two phenomena using proper parameters, which will be very useful for modeling and control of robot-terrain contact problems.
Mobile robots that work in a granular medium environment have different forms [Reference Ocón, Buckley, Colmenero, Bensalem, Dragomir, Karachalios, Woods, Pommerening and Keller3], for example, wheeled vehicles (i.e., rovers), walking robots (e.g., quadruped and hexapod robots), and hybrid wheel-leg robots. It is obvious that the form of contact interaction is strictly related to the robot’s locomotion modality, that is, its motion mode. The sinkage for all motion modes can be represented by a distance or displacement value. However, it is unfortunate that the definition of slippage varies with robot motion mode. The movement of a vehicle depends on the wheel rotation; its slippage is represented by the slip ratio [Reference Ding, Gao, Deng, Yoshida and Nagatani4]. Some wheeled robots may move in a distinct peristaltic manner [Reference Andrade, Amar, Bidaud and Chatila5]; their slippages can be expressed in terms of distance. The walking robot’s movement depends on the switching of supporting feet; its slippage is represented by a distance as well [Reference Focchi, Barasuol, Frigerio, Caldwell and Semini6]. For a hybrid wheel-leg robot (e.g., the robot shown in Fig. 1), its actual locomotion modality depends on the motion mode of each wheel-leg module, whose exact motion mode dictates the corresponding slippage definitions. An extreme case is that the robot shown in Fig. 1 operates two of its limbs in foot mode and the other two in the wheel mode. In this case, it is hard to estimate or control the contact state of the limbs in various motion modes, because of the different contact parameter definitions. We would like to adopt a unified contact parameter definition for different motion modalities, so that we can provide a unified measurement or evaluation standard for hybrid wheel-leg robots, which often have better mobility and adaptability to various working scenes [Reference Bjelonic, Sankar, Bellicoso, Vallery and Hutter7].

Figure 1. Our framework for terrain contact parameter estimation process for hybrid wheel-leg mobile robots. (a) This paper studies three types of motion modalities: driving-wheel mode, locked-wheel foot mode, and planar foot mode. We use DWT to process the sensor signals to reduce the scale of raw data and feed them into a trained CNN, as shown in (b). We can compare the predicted results with the experiment ground truth, as shown in (c).
2. Related works
There are many studies on contact parameter estimation for robot-terrain interactions. The traditional estimation methods are to use wheel-terrain or foot-terrain interaction models [Reference Inotsume, Sutoh, Nagaoka, Nagatani and Yoshida8–Reference Lyu, Zhang, Yao, Zhu and Jia10]. To extract the contact parameter, these model-based methods often need to inversely solve the physical contact model or terramechanics model using a large amount of experiment data. These methods have two major problems: (a) the wheel/foot-terrain contact model can be very complicated, making it very challenging to model the entire contact process in detail; (b) uncertainties introduced by the terrain’s physical properties will have a significant effect on the results, as discussed in ref. [Reference Inotsume, Sutoh, Nagaoka, Nagatani and Yoshida8]. Moreover, these studies mostly focus on estimating the parameters when the contact process reaches a stable state, while the description of dynamic processes, such as making and breaking contact, is very limited in the literature.
Some researches use other methods such as machine learning and image processing to investigate the contact process [Reference Hu, Wang, Liu, Ding and Knoll11]. For wheeled robots, a variety of learning methods have been used for slippage estimation, as summarized in ref. [Reference Gonzalez, Apostolopoulos and Iagnemma12]. Ref. [Reference Gonzalez, Fiacchini and Iagnemma13] classifies the slippage into three categories (high slip, moderate slip, and low slip) to predict possible slip states. This obviously is a rough estimation. The studies on non-model-based sinkage estimation mostly use vision methods [Reference Yao, Xue, Wang, Yuan, Zhu, Ding and Jia14] (some scholars also use LiDAR), which focus on real-time detection of wheel sinkage [Reference Reina15]. However, these vision-based methods are sensitive to light, terrain, obstacles, and many other factors. There are also some strict constraints on the pose of the installed camera. So, we need a robust method (preferably using intrinsic sensors) that can give detailed quantitative results that can be used to control the multi-modal hybrid robot.
For walking robots, contact parameter estimation usually is part of the entire robot state estimation procedure. Ref. [Reference Buchanan, Camurri, Dellaert and Fallon16] uses IMU (inertia measurement unit) data to estimate the robot slippage and sinkage. Other sensors such as the F/T sensors can also be used for robot state estimation, as shown in ref. [Reference Fink and Semini17]. However, these methods may cause mobility or safety issues when traveling over soft granular terrain. This is because the robots have already moved onto the soft soil when the contact parameter is estimated. In this case, the robots may sink or even fall over. So, we need to separate out the contact estimation process and estimate possible contact parameters before the robot moves to soft terrain, and our method can meet these requirements well. An example is shown in ref. [Reference Zhang, Lyu, Xue, Yao, Zhu and Jia18]; we can use our method by the remote articulated wheeled bevameter to detect the contact parameters. Furthermore, these methods only focus on the start and terminal states while ignoring the contact information during the contact process. Actually, these ignoring information is very important for the study of the contact surface properties [Reference Walas, Kanoulas and Kryczka19]. Ref. [Reference Buchanan, Bednarek, Camurri, Nowicki, Walas and Fallon20] uses the intermediate results of terrain perception and classification to estimate the contact parameters. However, this indirect method will cause uncertainties to accumulate.
To mitigate these problems, we propose to use the intrinsic IMU and force sensors that are installed on the distal end of the wheel/foot module (as shown in Fig. 1) to directly estimate the contact parameters. To this end, we propose a unified wheel-terrain contact parameterization approach to represent the (dynamic) contact process. Then, we can use unified parameters to control or describe the hybrid robot motion. As the main idea is to use the intrinsic sensor signals to describe the contact process, we can effectively mitigate the influence of environmental factors (e.g., illumination, occlusion). The main contributions are as follows:
We propose a unified contact parameters that can describe the dynamic phenomena of contact event for hybrid robots.
Based on our unified parameters, we develop an estimation algorithm using DWT and CNN, achieving very high prediction accuracy. Using only intrinsic signals, this method is very robust in different environmental conditions, as demonstrated by our experiments.
Compared to other methods, we show that the proposed method can get the same or even better performance. Furthermore, our method can not only estimate the dynamic contact process but also can be sensitive enough to measure small slippage and sinkage.
The remainder of this paper is organized as follows. Section 3 introduces our test facility and hybrid wheel-leg module. Section 4 presents the methods for data processing. Section 5 verifies our methods via experimental results. Section 6 shows the conclusion and future work.
3. Experimental setup
As the purpose of this paper is to estimate the contact parameters for the multi-modal robot locomotion on deformable granular terrains, we need to collect these contact parameters (i.e., slippage and sinkage) first. As these parameters are related to the interaction forms (i.e., the robot motion mode), the terrain condition (e.g., slope, and terrain types), and robot states (e.g., velocity, load, and moving direction), we need a testbed to meet these conditions to collect a representative dataset. In the following subsections, we will introduce a multi-freedom testbed to collect interaction data, and the testbed is equipped with a wheel/foot module that can automatically switch its motion modes.
3.1. Testbed for robot-terrain interaction
In order to collect robot-terrain contact data, we build a multi-DoF (degree of freedom) testbed. The lightweight testbed is shown in Fig. 2. It includes two parts: a hybrid wheel-leg test module and a robot-terrain adjustment system. The adjustment system includes a linear motion module, a yaw motion module, and an adaptive tilt module. The hybrid wheel-leg test module can be operated at three motion modes: driving-wheel mode, locked-wheel mode, and planar foot mode, as shown in Fig. 1.

Figure 2. The experimental testbed consists of a wheel-leg test module and a robot-terrain adjustment system. We use a computer for data acquisition and actuator controls.
As shown in Fig. 2, the robot-terrain adjustment system is
![]() $1.2\,{\rm m}\times 0.8\,{\rm m}\times 0.8\,{\rm m}$
(height
$1.2\,{\rm m}\times 0.8\,{\rm m}\times 0.8\,{\rm m}$
(height
![]() $\times$
length
$\times$
length
![]() $\times$
width). To acquire more scenarios of wheel/foot-terrain contact events, we can adjust the yaw motion module to change the movement direction of the wheel-leg test module. This is an important factor for wheel/foot-terrain contact parameter, as discussed in ref. [Reference Prágr, Čížek and Faigl21]. The linear motion module can move the wheel-leg module with a velocity that equals the robot’s forward velocity. The terrain slope angle
$\times$
width). To acquire more scenarios of wheel/foot-terrain contact events, we can adjust the yaw motion module to change the movement direction of the wheel-leg test module. This is an important factor for wheel/foot-terrain contact parameter, as discussed in ref. [Reference Prágr, Čížek and Faigl21]. The linear motion module can move the wheel-leg module with a velocity that equals the robot’s forward velocity. The terrain slope angle
![]() $\alpha$
(
$\alpha$
(
![]() $\alpha \subseteq [{-}20^\circ, 20^\circ ]$
), which is measured by the inclinometer, can be adjusted by the linear stage. During test, we can manually loosen the terrain and level its surface, ensuring the uniformity of the terrain medium among multiple experiments. We use two Realsense D435i cameras to record details of the wheel/foot-terrain interaction process and use two AprilTags to measure the contact parameters of the wheel-leg module. As shown in Fig. 3, one AprilTag is mounted on the center of the wheel’s side surface, while the other one is mounted on the F/T sensor. There is another USB camera recording the entire experiment.
$\alpha \subseteq [{-}20^\circ, 20^\circ ]$
), which is measured by the inclinometer, can be adjusted by the linear stage. During test, we can manually loosen the terrain and level its surface, ensuring the uniformity of the terrain medium among multiple experiments. We use two Realsense D435i cameras to record details of the wheel/foot-terrain interaction process and use two AprilTags to measure the contact parameters of the wheel-leg module. As shown in Fig. 3, one AprilTag is mounted on the center of the wheel’s side surface, while the other one is mounted on the F/T sensor. There is another USB camera recording the entire experiment.

Figure 3. Three motion modes in our experiments. The wheel-leg module can switch between planar foot configuration (a) and wheel model configuration (b); the latter can be operated as the driving-wheel mode or locked-wheel mode (c).
This wheel-leg module uses a 5-DOF series linkage design, with the last joint driving the wheel, as shown in Fig. 3. All joints are powered by high-quality Dynamixel servos. By adjusting the pose of robot joints, we can switch the test module between two-foot shapes: planar foot and locked-wheel foot. The F/T sensor (SRI M3813D, frequency:200 HZ) can acquire the contact forces between the wheel/foot and granular medium. We also attach an IMU (WIT-HWT 906, frequency:400 HZ) on the wheel to record signals during the contact process.
3.2. Granular medium selection
Four types of granular medium are selected for our contact experiments, as shown in Fig. 4. We select desert sand because deserts and beaches are the most common terrain with a granular medium in nature. This sand’s granularity is not uniform, and its particle size is ranging from
![]() $0.25$
to
$0.25$
to
![]() $0.6\,{\rm mm}$
. In order to study the effect of different particle sizes on contact estimation, we also choose two other kinds of sand: the garnet sand with a particle size around
$0.6\,{\rm mm}$
. In order to study the effect of different particle sizes on contact estimation, we also choose two other kinds of sand: the garnet sand with a particle size around
![]() $0.25\,{\rm mm}$
, and the quartz sand with a particle size around
$0.25\,{\rm mm}$
, and the quartz sand with a particle size around
![]() $1.5\,{\rm mm}$
. Moreover, we also select millet as an extremely granular medium, due to its special characteristics of uniform particle size and smooth surface. These properties would cause a great challenge to field rovers because excessive sinkage and slippage often cause mission failure [Reference Richard22].
$1.5\,{\rm mm}$
. Moreover, we also select millet as an extremely granular medium, due to its special characteristics of uniform particle size and smooth surface. These properties would cause a great challenge to field rovers because excessive sinkage and slippage often cause mission failure [Reference Richard22].

Figure 4. Four types of granular medium selected for our experiments.
4. Methodology
4.1. Slippage and sinkage definition
In order to describe the robot-terrain contact process of the hybrid wheel-leg mobile robots in a unified manner, we provide a unified contact parameterization, as shown in Fig. 5. We analyze the dynamic contact processes corresponding to the three locomotion modalities: driving-wheel, locked-wheel foot, and planar foot. For each motion modality, the contact process during one gait period
![]() $T$
can be described by three contact states:
$T$
can be described by three contact states:

Figure 5. Explanation of the three contact states defined for the multi-modal hybrid wheel-leg robot. The green arrow indicates the order of the motion sequences during the contact process. The wheel-leg module’s color depth indicates the movement order, that is, the deeper color represents the most recent position.
(1) State 1: The state that the wheel or foot makes its first contact with the terrain surface.
(2) State 2: The state when the supporting force of the wheel/foot along the gravity direction reaches its maximum value for the first time.
(3) State 3: For planar foot or locked-wheel foot modes, this represents the state when the foot breaks contact with the terrain and the supporting force becomes zero. Note that some portion of the foot may be still below the ground level of the terrain due to the plastic deformation during the contact process, as shown in Fig. 5. For driving-wheel mode, this state represents the end of a typical motion period
![]() $T$
.
$T$
.
For both foot modes, the entire motion period
![]() $T$
equals to the period of one walking gait. For the driving-wheel mode, it is difficult to define a gait time similar to that of a legged robot, because the wheel maintains contact with the terrain during movement (continuous process). In order to ensure that the driving-wheel mode can also experience the three-state process during the movement period
$T$
equals to the period of one walking gait. For the driving-wheel mode, it is difficult to define a gait time similar to that of a legged robot, because the wheel maintains contact with the terrain during movement (continuous process). In order to ensure that the driving-wheel mode can also experience the three-state process during the movement period
![]() $T$
, we choose
$T$
, we choose
![]() $T=6\pi/\omega$
. We can also select other values for
$T=6\pi/\omega$
. We can also select other values for
![]() $T$
as long as
$T$
as long as
![]() $T\gt T_{\min}=4\pi/\omega$
. Note that most legged robots may use point foot, its contact process and parameterization are similar to those of the planar or locked-wheel foot.
$T\gt T_{\min}=4\pi/\omega$
. Note that most legged robots may use point foot, its contact process and parameterization are similar to those of the planar or locked-wheel foot.
As shown in Fig. 5, we use
![]() $h$
to represent the sinkage, which refers to the distance perpendicular to the terrain between state 1 and state 2.
$h$
to represent the sinkage, which refers to the distance perpendicular to the terrain between state 1 and state 2.
![]() $d_1$
denotes the distance between state 1 and state 2 which is parallel to the terrain surface, and the used time is
$d_1$
denotes the distance between state 1 and state 2 which is parallel to the terrain surface, and the used time is
![]() $t_1$
.
$t_1$
.
![]() $d_2$
denotes the distance between state 2 and state 3 which is parallel to terrain surface too, and the used time is
$d_2$
denotes the distance between state 2 and state 3 which is parallel to terrain surface too, and the used time is
![]() $t_2$
.
$t_2$
.
 \begin{equation} \left \{ \begin{array}{c} D_x= wrt_x-d_x \qquad,x\subseteq \{1,2\}\\[5pt] H=h \qquad \\ \end{array} \right. \end{equation}
\begin{equation} \left \{ \begin{array}{c} D_x= wrt_x-d_x \qquad,x\subseteq \{1,2\}\\[5pt] H=h \qquad \\ \end{array} \right. \end{equation}
where
![]() $D_x$
is the slippage, and
$D_x$
is the slippage, and
![]() $H$
is the sinkage.
$H$
is the sinkage.
![]() $r$
is the wheel’s radius (
$r$
is the wheel’s radius (
![]() $r=0.07\,{\rm m}$
), and
$r=0.07\,{\rm m}$
), and
![]() $\omega$
is the angular velocity. We define the contact time period
$\omega$
is the angular velocity. We define the contact time period
![]() $t$
during a gait period
$t$
during a gait period
![]() $T$
. In other words,
$T$
. In other words,
![]() $t_1+t_2=t$
. In the Eq. (1), when the subscript
$t_1+t_2=t$
. In the Eq. (1), when the subscript
![]() $x=1$
, we call
$x=1$
, we call
![]() $D_1$
“transitional slippage.” Transitional slippage represents the slip process from state 1 to state 2. During this process, the wheel-leg module gradually acquires enough support force form the terrain, successfully achieving the stable standing state. It is an gradual stabilization process, so it is referred to as transitional slippage. When
$D_1$
“transitional slippage.” Transitional slippage represents the slip process from state 1 to state 2. During this process, the wheel-leg module gradually acquires enough support force form the terrain, successfully achieving the stable standing state. It is an gradual stabilization process, so it is referred to as transitional slippage. When
![]() $x=2$
, we call
$x=2$
, we call
![]() $D_2$
“stable slippage.” Stable slippage represents the slip process while the leg module working as a supporting leg during period
$D_2$
“stable slippage.” Stable slippage represents the slip process while the leg module working as a supporting leg during period
![]() $t_2$
(from state 2 to state 3), that is, the phase when the supporting force is stable, as shown in Fig. 6(b). For the driving-wheel mode, the supporting force is stable during this period, so we can also treat the driving wheel as a supporting wheel.
$t_2$
(from state 2 to state 3), that is, the phase when the supporting force is stable, as shown in Fig. 6(b). For the driving-wheel mode, the supporting force is stable during this period, so we can also treat the driving wheel as a supporting wheel.
Most of the literature studies pay more attention to the information about stable slippage, for example, in the field of planetary exploration and terrain-vehicle interactions. In these researches (e.g., ref. [Reference Inotsume, Kubota and Wettergreen23]), people often use slip ratio to describe the slippage of a driving wheel:
where
![]() $V$
is the linear velocity of the wheel-leg module,
$V$
is the linear velocity of the wheel-leg module,
![]() $s$
is the unitless slip ratio. The slip ratio
$s$
is the unitless slip ratio. The slip ratio
![]() $s$
and the slippage
$s$
and the slippage
![]() $D_2$
in Eq. (1) are equivalent; their conversion is shown in Eq. (3).
$D_2$
in Eq. (1) are equivalent; their conversion is shown in Eq. (3).
Unfortunately, there is little literature about transitional slippage, which is as important as stable slippage for contact event research. For example, the transitional slippage is highly dependent on the granular medium if the motion mode is fixed, so that it is useful for terrain classification problem. Here, our unified contact parameterization approach covers both transitional slippage and stable slippage, thereby providing a solid foundation to study the dynamic contact process of wheel-leg-terrain interactions.

Figure 6. The controller that regulates the wheel/foot motion for experiments. (a) The initial setup for typical driving-wheel or locked-wheel modes. The planar foot mode will have a similar setup. (b) Motion sequence of the locked-wheel foot mode. The planar foot mode will have a similar sequence. (c) Motion sequence of the driving-wheel mode. In fig. (b) and fig. (c),
![]() $A$
is the starting state (note: not state 1),
$A$
is the starting state (note: not state 1),
![]() $B$
is state 2,
$B$
is state 2,
![]() $C$
is state 3.
$C$
is state 3.
![]() $A\to B\to C$
is the planned reference trajectory of the wheel/foot motion (initial state:
$A\to B\to C$
is the planned reference trajectory of the wheel/foot motion (initial state:
![]() $H=L$
) using kinematics, without knowing the geometry of the terrain profile. During the actual experiment, the wheel/foot first executes this reference trajectory; however, when the wheel/foot makes contact with the terrain and the actual supporting force
$H=L$
) using kinematics, without knowing the geometry of the terrain profile. During the actual experiment, the wheel/foot first executes this reference trajectory; however, when the wheel/foot makes contact with the terrain and the actual supporting force
![]() $F_d$
reaches the prescribed threshold
$F_d$
reaches the prescribed threshold
![]() $F_g$
(i.e., point
$F_g$
(i.e., point
![]() $B^\prime$
), we need to use Algorithm 1 to replan the trajectory with
$B^\prime$
), we need to use Algorithm 1 to replan the trajectory with
![]() $H$
replaced with
$H$
replaced with
![]() $H_{now}$
. The new trajectory is
$H_{now}$
. The new trajectory is
![]() $A^\prime \to B^\prime \to C^\prime$
.
$A^\prime \to B^\prime \to C^\prime$
.
4.2. Motion controller
During the data collection process, we need to change the motion modality of the hybrid wheel-leg robot and control its motion during each motion mode. For each mode, our control variables are the forward velocity
![]() $V$
, and the supporting force
$V$
, and the supporting force
![]() $F_g$
of the wheel/foot module.
$F_g$
of the wheel/foot module.
Figure 6(a) shows the initial state of wheel-leg module.
![]() $l$
is an constant value (
$l$
is an constant value (
![]() $l=0.10\,{\rm m}$
) that represents the initial distance from the wheel/foot center to the terrain surface along the gravity direction.
$l=0.10\,{\rm m}$
) that represents the initial distance from the wheel/foot center to the terrain surface along the gravity direction.
![]() $L$
represents the maximum distance that the wheel-leg module can reach in the gravity direction.
$L$
represents the maximum distance that the wheel-leg module can reach in the gravity direction.
Algorithm 1
outlines the detailed control strategy. It is worth noting that the kinematics in Algorithm 1
will be different for different motion modes.
![]() $J_{now}(\theta )$
is the joint angles at the sampling time, and
$J_{now}(\theta )$
is the joint angles at the sampling time, and
![]() $t_{now}$
is the system time during sampling.
$t_{now}$
is the system time during sampling.
![]() $J_{next}(\theta )$
is the target joint angles that can be calculated using kinematics, and
$J_{next}(\theta )$
is the target joint angles that can be calculated using kinematics, and
![]() $t_{next}$
is the system time when the robot joints begin the next action.
$t_{next}$
is the system time when the robot joints begin the next action.
![]() $F_g$
is the excepted supporting force, and
$F_g$
is the excepted supporting force, and
![]() $F_d$
is the actual supporting force measured by the F/T sensor.
$F_d$
is the actual supporting force measured by the F/T sensor.
![]() $H_{now}$
is the distance along the gravity direction when the wheel-leg module’s supporting force satisfies
$H_{now}$
is the distance along the gravity direction when the wheel-leg module’s supporting force satisfies
![]() $F_d \ge F_g\ \&\ flag =0$
. We use PID control to keep the wheel/foot supporting force at the desired level, that is,
$F_d \ge F_g\ \&\ flag =0$
. We use PID control to keep the wheel/foot supporting force at the desired level, that is,
![]() $F_d = F_g$
. Note that phase
$F_d = F_g$
. Note that phase
![]() $A$
is not state 1 defined in Fig. 5. It is our initial experiment setup that is used to simplify control logic. This does not affect the data collection process.
$A$
is not state 1 defined in Fig. 5. It is our initial experiment setup that is used to simplify control logic. This does not affect the data collection process.
Algorithm 1 Motion Control Algorithm

Following Algorithm 1
, the controller firstly collects the information of recent joint angle
![]() $J_{now}(\theta )$
and supporting force
$J_{now}(\theta )$
and supporting force
![]() $F_d$
. The controller needs to detect if supporting force
$F_d$
. The controller needs to detect if supporting force
![]() $F_d$
reaches threshold
$F_d$
reaches threshold
![]() $F_g$
. If
$F_g$
. If
![]() $F_d \ge F_g$
, the controller sets the distance
$F_d \ge F_g$
, the controller sets the distance
![]() $H_{now}$
as
$H_{now}$
as
![]() $H$
which is largest distance the robot can reach in the gravity direction, and
$H$
which is largest distance the robot can reach in the gravity direction, and
![]() $flag =1$
. Then, the controller calculates robot joint angle
$flag =1$
. Then, the controller calculates robot joint angle
![]() $J_{next}(\theta )$
for the next step action based on robotic inverse kinematics. If flag does not equal
$J_{next}(\theta )$
for the next step action based on robotic inverse kinematics. If flag does not equal
![]() $1$
or time
$1$
or time
![]() $t$
does not in support phase
$t$
does not in support phase
![]() $[t_1,t]$
, the controller just drives robot by
$[t_1,t]$
, the controller just drives robot by
![]() $J_{next}(\theta )$
. Otherwise, the controller drives the robot with
$J_{next}(\theta )$
. Otherwise, the controller drives the robot with
![]() $J_{next}({\theta })$
while using a PID function to keep
$J_{next}({\theta })$
while using a PID function to keep
![]() $F_d$
near the threshold
$F_d$
near the threshold
![]() $F_d$
. The controller would continue the above process during entire motion period
$F_d$
. The controller would continue the above process during entire motion period
![]() $T$
. The final motion trajectories for different robotic modes are shown in Fig. 6(b)(c).
$T$
. The final motion trajectories for different robotic modes are shown in Fig. 6(b)(c).
4.3. Dataset collection
In this paper, we collect two datasets: the normal medium dataset (Nm-dataset) and the extreme medium dataset (Em-dataset). Both datasets are collected on our experiment platform shown in Fig. 3. The Nm-dataset contains
![]() $9$
groups of data, each of which is a combination of terrain medium (desert sand, quartz sand, and garnet sand) and motion modes. The Em-dataset contains
$9$
groups of data, each of which is a combination of terrain medium (desert sand, quartz sand, and garnet sand) and motion modes. The Em-dataset contains
![]() $3$
sub-datasets, each of which corresponds to one specific motion mode.
$3$
sub-datasets, each of which corresponds to one specific motion mode.
In order to explore multiple experiment scenarios such as slope ascending and descending, we test
![]() $5$
slope angles
$5$
slope angles
![]() $\{-10^\circ, -5^\circ, 0^\circ, 5^\circ, 10^\circ \}$
. We can adjust the terrain slope angle by controlling the pitch angle of the small sandbox using linear stage actuators. Various studies (e.g., ref. [Reference Prágr, Čížek and Faigl21]) have shown that the movement direction during wheel/foot-terrain contact will directly affect energy consumption and contact states. So we control the yaw motion actuator shown in Fig. 3 and select four directions
$\{-10^\circ, -5^\circ, 0^\circ, 5^\circ, 10^\circ \}$
. We can adjust the terrain slope angle by controlling the pitch angle of the small sandbox using linear stage actuators. Various studies (e.g., ref. [Reference Prágr, Čížek and Faigl21]) have shown that the movement direction during wheel/foot-terrain contact will directly affect energy consumption and contact states. So we control the yaw motion actuator shown in Fig. 3 and select four directions
![]() $\{0^\circ,30^\circ,60^\circ,90^\circ \}$
. In each experiment, the control variables are the linear velocity (driving-wheel mode:
$\{0^\circ,30^\circ,60^\circ,90^\circ \}$
. In each experiment, the control variables are the linear velocity (driving-wheel mode:
![]() $0.05\,{\rm m/s}$
$0.05\,{\rm m/s}$
![]() $\sim$
$\sim$
![]() $0.2\,{\rm m/s}$
; foot modes:
$0.2\,{\rm m/s}$
; foot modes:
![]() $0\,{\rm m/s}$
$0\,{\rm m/s}$
![]() $\sim$
$\sim$
![]() $0.3\,{\rm m/s}$
) and the load (
$0.3\,{\rm m/s}$
) and the load (
![]() $25.5\,{\rm N}$
$25.5\,{\rm N}$
![]() $\sim$
$\sim$
![]() $60\,{\rm N}$
) of the wheel/foot.
$60\,{\rm N}$
) of the wheel/foot.
The total impacts of the Nm-dataset include two parts. The first part is the contact data for the locked-wheel foot and planar foot modes. We consider these two motion modes and four motion directions over three types of terrains, whose inclination can be set at five slope angles. For each combination, we measure
![]() $10$
contacts. Hence, the first part contains
$10$
contacts. Hence, the first part contains
![]() $1200$
impacts. The second part is the contact data for the driving-wheel mode. The test scenarios are similar to those of the first part, except that we cannot perform the
$1200$
impacts. The second part is the contact data for the driving-wheel mode. The test scenarios are similar to those of the first part, except that we cannot perform the
![]() $10^\circ$
and
$10^\circ$
and
![]() $-10^\circ$
inclination angle experiments. The main reason is that the wheel-leg module’s reachable space in the gravity direction is limited, so that the control variable
$-10^\circ$
inclination angle experiments. The main reason is that the wheel-leg module’s reachable space in the gravity direction is limited, so that the control variable
![]() $F_g$
cannot be stabilized in the driving-wheel mode if the slope angle is too large. The second part contains
$F_g$
cannot be stabilized in the driving-wheel mode if the slope angle is too large. The second part contains
![]() $360$
impacts.
$360$
impacts.
For the Em-dataset, the range of control variable
![]() $F_g$
and the slope angle are different from the Nm-dataset. Recall that the special characteristics of extreme granular medium (millet) will cause excessive slippage and sinkage, we have to limit
$F_g$
and the slope angle are different from the Nm-dataset. Recall that the special characteristics of extreme granular medium (millet) will cause excessive slippage and sinkage, we have to limit
![]() $F_g$
in
$F_g$
in
![]() $22.5\,{\rm N} \sim 32\,{\rm N}$
range (about half of other terrain values). This extreme medium dataset contains three slope angles
$22.5\,{\rm N} \sim 32\,{\rm N}$
range (about half of other terrain values). This extreme medium dataset contains three slope angles
![]() $\{-5^\circ, 0^\circ, 5^\circ \}$
, as the driving-wheel mode will not work in
$\{-5^\circ, 0^\circ, 5^\circ \}$
, as the driving-wheel mode will not work in
![]() $10^\circ$
and
$10^\circ$
and
![]() $-10^\circ$
inclinations using our facility, as discussed above. The total impacts are
$-10^\circ$
inclinations using our facility, as discussed above. The total impacts are
![]() $360$
.
$360$
.
For each impact, we need to record the interaction signals (synchronized by software synchronization) and the motion sequence images of the test module. The interaction signals consist of two parts. The first part is the signals collected by the force sensor, and they are the 3-axis force and 3-axis torque. The second part is the signals collected by the IMU, and they are the 3-axis velocity and 3-axis acceleration. The above signals are the input of our learning model, and annotations are contact parameters, and these parameters are measured by the camera (calculated by Eq. (1)).
4.4. Feature selection
Different from refs. [Reference Camurri, Fallon, Bazeille, Radulescu, Barasuol, Caldwell and Semini24] and [Reference Nisticò, Fahmi, Pallottino, Semini and Fink25], we extract the contact information from the IMU and F/T signals in this part manually. Firstly, we detect the z-axis force signal during each impact experiment and mark the interaction time (the time for entering and breaking the terrain) manually. Then, we use the marked interaction time to extract the interaction signals from all the signals collected by the sensors as all the signals are collected through software synchronization. Compared to the method used in refs. [Reference Camurri, Fallon, Bazeille, Radulescu, Barasuol, Caldwell and Semini24] and [Reference Nisticò, Fahmi, Pallottino, Semini and Fink25], the interaction signals segmented manually have higher confidence.
Taking the time domain and frequency domain information into consideration for feature selection process, discrete wavelet transformation (DWT) is more suitable for processing discretely sampled sensor signals than other techniques (for feature selection in this situation, as discussed in ref. [Reference Kolvenbach, Bärtschi, Wellhausen, Grandia and Hutter26]). We use MATLAB Discrete Wavelet Transform Toolbox and select daubechies wavelet with four vanishing moments (db4) to process the signal. To reduce the size of selected features, we need to choose the appropriate number of decomposition levels for DWT. Generally, as the decomposition level increases, the number of features selected from the extracted signal decreases. In this paper, we have chosen to use five levels of decomposition. Corresponding to each segmentation signal processed by DWT, we select the detail coefficients (features) and linearly regroup these parameters.
We list the number of features for each signal in Table I. Each number in Table I is the features we got from the DWT processing for each impart signal. It is obvious that the feature numbers are different for different motion modes, so we select the largest number of the features as
![]() $N$
to regroup the matrix with size of
$N$
to regroup the matrix with size of
![]() $M*N$
. Based on the Table I, the
$M*N$
. Based on the Table I, the
![]() $N$
equals 852. The
$N$
equals 852. The
![]() $M$
refers to the signal channels and equals
$M$
refers to the signal channels and equals
![]() $12$
(
$12$
(
![]() $3$
forces
$3$
forces
![]() $+$
$+$
![]() $3$
torque
$3$
torque
![]() $+$
$+$
![]() $3$
velocity
$3$
velocity
![]() $+3$
acceleration). The problem with regrouping the matrix is that the numbers of signals for motion modes are different. To solve this problem, we add
$+3$
acceleration). The problem with regrouping the matrix is that the numbers of signals for motion modes are different. To solve this problem, we add
![]() $0$
in the selected features of the signals to make sure they are as big as the feature numbers of the biggest one (
$0$
in the selected features of the signals to make sure they are as big as the feature numbers of the biggest one (
![]() $N=852$
), so that we can get the matrix (
$N=852$
), so that we can get the matrix (
![]() $M*N$
). As shown in Fig. 7, we collect multiple signals during a single contact process. We try to process every signal using DWT and regroup the features into a matrix, so that our CNN network can use these features to estimate the contact parameters.
$M*N$
). As shown in Fig. 7, we collect multiple signals during a single contact process. We try to process every signal using DWT and regroup the features into a matrix, so that our CNN network can use these features to estimate the contact parameters.
Table I. Feature numbers selected through signals.


Figure 7. The feature selection process of multiple F/T and IMU sensor signals (all signals are synchronized). This process contains three parts: segmentation, DWT, and regrouping.

Figure 8. The pipeline of the network for contact parameter estimation. The input is the feature matrix created in feature selection section, and the output is three contact parameters, that is, sinkage, transitional slippage, and stable slippage.
4.5. Regression
Inspired by ref. [Reference Gonzalez, Apostolopoulos and Iagnemma12], we select CNN for contact data regression because it is simpler but useful for this problem. Our network structure is shown in Fig. 8. As the feature information between IMU and F/T is complementary, we divide the feature matrix into two parts, that is, the IMU part and F/T part, and use two sub-pipelines to handle them. For each sub-pipeline, the matrix is reshaped and processed by the convolutional and fully connected layer. We combine the output of the two sub-pipelines and use a fully connected layer to get the three contact parameters, that is, sinkage, transitional slippage, and stable slippage. The Conv block in Fig. 8 consists of two convolutional layers and pooling layers. For detail information, please see Table II. We use the
![]() $L_2$
loss function (squared error) to calculate the loss function in our network, and the loss function is shown in Eq. (4). The
$L_2$
loss function (squared error) to calculate the loss function in our network, and the loss function is shown in Eq. (4). The
![]() $H$
represents the actual sinkage of the ground truth, while the
$H$
represents the actual sinkage of the ground truth, while the
![]() $\hat{H}$
represents the estimated sinkage by our network. The
$\hat{H}$
represents the estimated sinkage by our network. The
![]() $D_i$
represents the two instances of ground truth slippages, and the
$D_i$
represents the two instances of ground truth slippages, and the
![]() $\hat{D_i}$
represents the estimated two slippages by our network.
$\hat{D_i}$
represents the estimated two slippages by our network.
One net is trained for three granular terrains (shown in Fig. 5) to estimate the contact parameters, and one net is trained to evaluate the movement capability of three motion modes on extreme granular medium (millet). We build the network based on the Machine Learning Toolbox on MATLAB-2021b. We use Statistics Toolbox and Machine Learning Toolbox to train the network using 80
![]() $\%$
of the data of each dataset with 5-fold cross-validation, while the other
$\%$
of the data of each dataset with 5-fold cross-validation, while the other
![]() $20\%$
data is used for validation [Reference Kolvenbach, Bärtschi, Wellhausen, Grandia and Hutter26].
$20\%$
data is used for validation [Reference Kolvenbach, Bärtschi, Wellhausen, Grandia and Hutter26].
Table II. The layers and parameters in the Conv block are in Fig. 8.


Figure 9. The contact parameters for planar foot mode on four types of granular terrains, which are color-coded using shaded squares (blue: quartz sand, green: garnet sand, orange: desert sand, yellow: millet). For each terrain, that is, each color-coded square, we use the transparency value of each tall rectangle to represent different slope angles. Each rectangle (combination of slope angle and terrain type) contains results corresponding to four different heading angles.
5. Experimental results and discussions
5.1. Nm-dataset results
Figure 9 shows the contact parameters for planar foot mode on four types of granular terrains. From the figure, we see that the sinkage and slippage contact parameters and their variation tendencies are different for different terrain types and different slope angles. These observations indicate that the terrain medium classification and contact parameter prediction problems are solvable using learning algorithms based on our unified definition.
As shown in Fig. 9, during the contact process of planar foot on four types of terrains, both the stable slippage and sinkage are smaller than the transitional slippage. Specifically, Fig. 10 shows the typical motion trajectories and three states from a set of experiments corresponding to the planar foot mode, locked-wheel foot, and driving-wheel mode. Similar conclusion can be drawn for the other two motion modes. One can refer to our dataset for more details.

Figure 10. The typical motion trajectories for the locked-wheel mode (first row), planar foot mode (second row), and wheel mode (third row). The granular medium is desert sand, the slope angle is
![]() $10^\circ$
(
$10^\circ$
(
![]() $5^\circ$
for wheel mode), and the heading angle is
$5^\circ$
for wheel mode), and the heading angle is
![]() $0^\circ$
. The motion sequence of trajectories is from lift to right, while the three contact states are marked in the figure.
$0^\circ$
. The motion sequence of trajectories is from lift to right, while the three contact states are marked in the figure.

Figure 11. The three blue lines refer to the test module trajectory measured on the same condition (desert sand,
![]() $5^\circ$
slope, motion direction is
$5^\circ$
slope, motion direction is
![]() $30^\circ$
, heading angle is
$30^\circ$
, heading angle is
![]() $0^\circ$
).
$0^\circ$
).
The three states (defined in Fig. 5) are the key points during the robot-terrain contact process, and related parameters in our definition are influenced by the robot motion modes. So we use the contact parameters to estimate the robot wheel/foot trajectory during the interaction. In Fig. 11, We draw the true trajectories (the blue lines) of three motion modes, and the trajectories are measured by the fixed Realsense D435i(2) camera (see Fig. 2). As the test module moves along the linear direction, the depth values of the trajectory in the
![]() $z$
direction (D435i-2 coordinate system) are nearly the same. So that we can think that the test module moves in the
$z$
direction (D435i-2 coordinate system) are nearly the same. So that we can think that the test module moves in the
![]() $x-y$
plane, and we show the trajectories in Fig. 11. The red lines are the estimated trajectories, and they are calculated by the polynomial fitting method. As shown in Fig. 11, the estimated trajectories can represent the true one, and the mean errors of the positions (selected in the trajectory for polynomial fitting) between the estimated trajectories and ground truth are
$x-y$
plane, and we show the trajectories in Fig. 11. The red lines are the estimated trajectories, and they are calculated by the polynomial fitting method. As shown in Fig. 11, the estimated trajectories can represent the true one, and the mean errors of the positions (selected in the trajectory for polynomial fitting) between the estimated trajectories and ground truth are
![]() $1.28e-04m$
for the planar foot,
$1.28e-04m$
for the planar foot,
![]() $4.46e-05m$
for the locker wheel foot, and
$4.46e-05m$
for the locker wheel foot, and
![]() $3.68e-05m$
for the driving wheel. So, the estimated trajectories can be useful to handle the robot state estimation problems. This is another potential use of our definition and method for contact parameter estimation.
$3.68e-05m$
for the driving wheel. So, the estimated trajectories can be useful to handle the robot state estimation problems. This is another potential use of our definition and method for contact parameter estimation.
For contact parameter estimation, we assume that the predicted results are acceptable if the difference between the predicted parameter and the ground truth is less than a
![]() $1\,{\rm mm}$
threshold. The network we trained has great accuracy for contact parameter prediction. As shown in Fig. 12, it achieves an average accuracy better than
$1\,{\rm mm}$
threshold. The network we trained has great accuracy for contact parameter prediction. As shown in Fig. 12, it achieves an average accuracy better than
![]() $96\%$
. For more details about prediction accuracy, please see Table III (left). The results show that our method is accurate enough to estimate the contact parameter on different granular mediums. This method is also robust enough to predict contact parameter for different wheel-leg-terrain contact scenes on the same medium. Obviously, the prediction accuracy of the driving-wheel mode is much stable than other two motion modes in our Nm-dataset. The reason is that the movement of the driving-wheel mode is the simplest one among all three motion modes. For the driving-wheel mode, the percentage of the steady-state (i.e., the supporting force and friction of the driving wheel remains constant) duration over the entire motion period
$96\%$
. For more details about prediction accuracy, please see Table III (left). The results show that our method is accurate enough to estimate the contact parameter on different granular mediums. This method is also robust enough to predict contact parameter for different wheel-leg-terrain contact scenes on the same medium. Obviously, the prediction accuracy of the driving-wheel mode is much stable than other two motion modes in our Nm-dataset. The reason is that the movement of the driving-wheel mode is the simplest one among all three motion modes. For the driving-wheel mode, the percentage of the steady-state (i.e., the supporting force and friction of the driving wheel remains constant) duration over the entire motion period
![]() $T$
is large. This helps to reduce the measurement error. In contrast, for the other two motion modes, the wheel/foot is almost in constant motion with varying contact forces, which often cause large measurement error in the sensor signals. This makes accurate estimation of the contact parameter challenging.
$T$
is large. This helps to reduce the measurement error. In contrast, for the other two motion modes, the wheel/foot is almost in constant motion with varying contact forces, which often cause large measurement error in the sensor signals. This makes accurate estimation of the contact parameter challenging.
Table III. The average prediction accuracy for two datasets and mixture terrain.


Figure 12. The prediction accuracy of three motion modes over three types of terrains. The figure arrangement and color code are similar to Fig. 9.
5.2. Em-dataset results
The contact parameters of three motion modes on extreme granular medium are shown in Table IV. The contact parameters are much larger than those of grit medium as shown in Fig. 9. This is because the millet grain has a rounder shape and smoother surface. Moreover, its density is lower than the sands, making it more fluid-like. The slippage and sinkage of the driving-wheel mode are larger than those of the other two motion modes. This can be explained as follows:
For the planar foot mode, its terrain contact area is larger than those of the other two motion modes. Hence, under the same load, it has the smallest contact pressure, which results in smallest slippage and sinkage.
In the driving-wheel mode, the wheel keeps rotating, thereby continuously cutting the terrain that lies along the motion direction. This phenomenon will increase the fluidity of the medium, resulting in larger slippage and sinkage than the locked-wheel mode.
Although the measured slippage/sinkage is large on this medium, the accuracy of our CNN estimation network remains very high as Table III shows. Our net shows more predicting accuracy for the planar foot mode than the other two modes. The reason is that the planner foot mode has a large contact area and low contact pressure, which leads to smaller slippage and sinkage (with little fluctuation) than the other modes. The excellent performance (low sinkage and slippage) of the planar foot mode indicates that we should select the planar foot mode over other motion modes when traveling over the extreme granular medium.
Table IV. The average contact parameters for three motion modes in extreme granular medium. Case: slope angle is
![]() $0^\circ$
.
$0^\circ$
.

5.3. Evaluation results
In order to evaluate the generalization capability of our model, we designed a test experiment for new terrain. The new terrain consists of a mixture of quartz sand and garnet sand, the mixture ratio is 2:3. One of the main characteristics of deformable granular terrains is the distribution of particle sizes in the medium, and this is the criteria for selecting the type of medium when designing experiments. Thus, the property of this new terrain is different from the four terrains in our dataset.
We collect 10 impacts for each motion mode on this terrain with three slope angles, that is,
![]() $0^\circ$
,
$0^\circ$
,
![]() $-5^\circ$
, and
$-5^\circ$
, and
![]() $5^\circ$
. The total contact numbers are
$5^\circ$
. The total contact numbers are
![]() $3\times 1\times 3\times 10=90$
(modes
$3\times 1\times 3\times 10=90$
(modes
![]() $\times$
terrain
$\times$
terrain
![]() $\times$
slopes
$\times$
slopes
![]() $\times$
impacts). We use our pre-trained network to estimate contact parameters and compare with ground truth. The results are shown in Table III. The average prediction accuracy for mixed terrain (unknown terrain) is higher, indicating the efficient generalization ability of our model. Therefore, our method can be applied to real-world environments and is applicable to other unfamiliar granular material terrains.
$\times$
impacts). We use our pre-trained network to estimate contact parameters and compare with ground truth. The results are shown in Table III. The average prediction accuracy for mixed terrain (unknown terrain) is higher, indicating the efficient generalization ability of our model. Therefore, our method can be applied to real-world environments and is applicable to other unfamiliar granular material terrains.
5.4. Comparisons
In this subsection, we provide three comparisons to show the efficiency of our definitions and method. We compared our definition with the others’ definition of slippage for wheeled robot (in Section 5.4.1) and footed robot (in Section 5.4.2). We also compared our method with other’s work which is used to estimate the slippage of the wheeled robot and show the result in Section 5.4.3.
5.4.1. Comparison of wheeled robot
We compare the difference of slip ratios calculated using two definitions: the standard slip ratio definition (see ref. [Reference Reina15]) in the automotive area and our proposed slippage definition, as shown in Fig. 13. The results show that our method is robust enough to estimate the contact parameters for driving vehicles. For the three types of sands, the differences between these two slippage definitions are limited; in particular, the difference is negligible for small slope angles. For extreme granular medium (millet), there will be some differences (less than
![]() $0.05$
). The reason is that the strong fluidity of the millet medium will affect parameter measurement accuracy.
$0.05$
). The reason is that the strong fluidity of the millet medium will affect parameter measurement accuracy.

Figure 13. Comparison of slip ratios under two different definitions (driving vehicle field). The red marks and line indicate that the slip ratios are calculated by measuring the parameters required for the definition (Eq. (2)). The blue marks and line are the slip ratio calculated by Eq. (3), and the necessary parameters are measured based on our definition (Eq. (1)).
5.4.2. Comparison of footed robot
We also compare our method with the slippage estimation method for quadruped robots (see ref. [Reference Nisticò, Fahmi, Pallottino, Semini and Fink25]). The reference is a kinematic method. In order to get along with the reference, we use our method to estimate the slippage which equals to “
![]() $d_1-d_2$
” and is different from Fig. 12. Fig. 14 shows the prediction accuracy of the two methods. In the sandy terrain, our method performs better than the reference. Furthermore, our method can not only detect the transitional slippage and stable slippage but also be sensitive to the small slippage, which cannot be handled by the reference.
$d_1-d_2$
” and is different from Fig. 12. Fig. 14 shows the prediction accuracy of the two methods. In the sandy terrain, our method performs better than the reference. Furthermore, our method can not only detect the transitional slippage and stable slippage but also be sensitive to the small slippage, which cannot be handled by the reference.

Figure 14. Comparison of slip ratios under two different definitions (walking robot field). For the Miller dataset, we lack the data in terrain when the slope angles are
![]() $-10^\circ$
and
$-10^\circ$
and
![]() $10^\circ$
, and assume its prediction accuracy equals 1.
$10^\circ$
, and assume its prediction accuracy equals 1.
5.4.3. Comparison of estimation method
To evaluate the efficiency of our method for contact parameter estimation, we compared our method with ref. [Reference Marotta, Ivanov, Strano, Terzo and Tordela27]. For the network used in ref. [Reference Marotta, Ivanov, Strano, Terzo and Tordela27], the input of its network are longitudinal velocity, slip angle, steering angle, vertical force, and wheel rotation speed, and the output is the longitudinal slippage. To train this network using our dataset, we set the longitudinal velocity as the linear velocity. The slip angle equals our heading angle, and the steering angle equals zero. The vertical force is the force calculated by F/T sensor’s data. We provide an evaluation standard called L2 distance (Dist) in this comparison, and Dist is Euclidean distance between the predicted parameter and ground truth.
We only used the wheeled mode data to train and test both networks (ours and references) as ref. [Reference Marotta, Ivanov, Strano, Terzo and Tordela27] is designed for wheeled robots only. The comparison results are listed in Table V. The results in this table are average values of Dist during testing process. Our method can achieve better performance than ref. [Reference Marotta, Ivanov, Strano, Terzo and Tordela27], which means that our method can estimate the contact parameters with smaller errors than ref. [Reference Marotta, Ivanov, Strano, Terzo and Tordela27] (even double the performance for transitional slippage).
Table V. The results of Dist for two methods.

6. Conclusion and future work
In this paper, to describe the contact events in a unified framework for hybrid wheel-leg robots, we propose a unified description of contact parameters for multi-modal locomotion. We use DWT to process sensor signals and feed them into a CNN, which is trained using data acquired from a customized test bench, to estimate the unified contact parameters. We achieve more than
![]() $96\%$
accuracy in parameter estimation, validating the effectiveness of our method. In the future, we plan to predict the complete motion trajectory of the wheel/foot with our estimated contact parameters (slippage and sinkage) and use them for robot state estimation tasks.
$96\%$
accuracy in parameter estimation, validating the effectiveness of our method. In the future, we plan to predict the complete motion trajectory of the wheel/foot with our estimated contact parameters (slippage and sinkage) and use them for robot state estimation tasks.
Acknowledgment
Thanks to Qiaowen Wang and Longteng Hu for their help in implementing the experiment.
Author contributions
Conceptualization, S. L., W. Z., and Z. J.; methodology, S. L., W. Z., and C. Y.; validation and analysis, S. L., W. Z., and C. Y.; data curation, Z. L. and Y. S.; writing, review, and editing, S. L., Z. L., and Z. Z.; supervision, Z. J. All authors have read and agreed to the published version of the manuscript.
Financial support
This work was supported in part by the Science, Technology and Innovation Commission of Shenzhen Municipality under Grant No.ZDSYS20200811143601004, and the National Science Foundation of China #U1913603.
Competing interests
The authors declare no competing interests.