Laser piston-induced relativistic shock wave

The shock wave induced by the laser piston is described by the relativistic Rankine–Hugoniot equations, relating the shock pressure P, energy density e, mass density ρ, particle (piston) velocity u _p and shock velocity u _s. The quantities with subscript zero are the corresponding material parameters before the shock arrival:

(1a)$$\displaystyle{{u_{\rm p}} \over c} = \sqrt {\displaystyle{{\lpar {P-P_0} \rpar \lpar {e-e_0} \rpar } \over {\lpar {e_0 + P} \rpar \lpar {e + P_0} \rpar }}} $$

(1b)$$\displaystyle{{u_{\rm s}} \over c} = \sqrt {\displaystyle{{\lpar {P-P_0} \rpar \lpar {e + P_0} \rpar } \over {\lpar {e-e_0} \rpar \lpar {e_0 + P} \rpar }}} $$

(1c)$$\displaystyle{{{\lpar {e + P} \rpar }^2} \over {\rho ^2}}-\displaystyle{{{\lpar {e_0 + P_0} \rpar }^2} \over {\rho _0^2}} = \lpar {P-P_0} \rpar \left[ {\displaystyle{{\lpar {e_0 + P_0} \rpar } \over {\rho_0^2}} + \displaystyle{{\lpar {e + P} \rpar } \over {\rho^2}}} \right]$$

where c is the speed of light. The velocities u _p and u _s are given in the laboratory frame of reference.

The relativistic shock wave of Eq. (1) yields the following non-relativistic well known Hugoniot equations, when the velocities v satisfy v/c ≪ 1, and e = ρc ² + ρE, where P and ρE are much smaller than ρc ²:

(2a)$$u_{\rm p} = \left( {\displaystyle{1 \over {\rho_0}}-\displaystyle{1 \over \rho}} \right)^{1/2}\lpar {P-P_0} \rpar ^{1/2}$$

(2b)$$u_{\rm s} = \displaystyle{1 \over {\rho _0}}\left( {\displaystyle{1 \over {\rho_0}}-\displaystyle{1 \over \rho}} \right)^{-1/2}\lpar {P-P_0} \rpar ^{1/2}$$

(2c)$$E-E_0 = \displaystyle{1 \over 2}\left( {\displaystyle{1 \over {\rho_0}}-\displaystyle{1 \over \rho}} \right)\lpar {P + P_0} \rpar $$

We assume an ideal equation of state (EOS)

(3)$$e\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3}}} \right] = \; \rho c^2 + \displaystyle{P \over {{\rm \Gamma} -1}}$$

Γ = (c _p/c _v) is the specific heat ratio related to the number of degrees of freedom per particle f by Γ = 1 + (2/f). We assume Γ = (5/3), f = 3. In the non-relativistic limit the above EOS is

$$E\left[ {\displaystyle{{{\rm erg}} \over g}} \right] = \displaystyle{P \over {{\rm \rho} \lpar {{\rm \Gamma} -1} \rpar }}.$$

The laser piston velocity u _p, or β_p = (u _p/c), as a function of the laser intensity I _L can be obtained by solving the relativistic Rankine–Hugoniot equation (1) together with the piston model equation:

(4)$$P = \displaystyle{{2I_{\rm L}} \over c}\displaystyle{{1-\beta _{\rm p}} \over {1 + \beta _{\rm p}}}$$

where P is the radiation pressure equal to the shock pressure. The relativistic Rankine–Hugoniot equations are solved below for dimensionless variables: compression κ = (ρ/ρ₀), dimensionless pressure Π = (P/ρ₀c ²) and dimensionless laser intensity Π_L = (I _L/ρ₀c ³) (Eliezer et al., Reference Eliezer, Nissim, Raicher and Martinez Val2014).

Substituting the ideal EOS [Eq. (3)] with the Rankine–Hugoniot equation (1), we obtain the relativistic Hugoniot equation for dimensionless variables:

(5)$${\rm \Pi} ^2 + B{\rm \Pi} + C = 0$$

(6)$${\rm \Pi} = \displaystyle{{-B + \sqrt {B^2-4C}} \over 2}$$

(7)$$B = \displaystyle{{{\lpar {{\rm \Gamma} -1} \rpar }^2} \over {\rm \Gamma}} \lpar {\kappa_0\kappa -\kappa^2} \rpar + {\rm \Pi} _0\lpar {{\rm \Gamma} -1} \rpar \lpar {1-\kappa^2} \rpar $$

(8)$$C = \displaystyle{{{\lpar {{\rm \Gamma} -1} \rpar }^2} \over {\rm \Gamma}} \lpar {\kappa -\kappa_0\kappa^2} \rpar {\rm \Pi} _0-\kappa ^2{\rm \Pi} _0^2 $$

In Eqs. (7, 8) κ ₀ = (Γ + 1/Γ − 1) is the non-relativistic asymptotic compression in the limit of infinite shock pressure and Π₀ = (P ₀/ρ₀c ²). The solution of the Hugoniot equations for dimensionless variables is material and initial density independent.

We consider here the dimensionless pressure regime:

(9)$$10^{-6} \le {\rm \Pi} \le 10^{-2}$$

This regime corresponds to piston velocities in the range of 0.001–0.1c. The compression as a function of the dimensionless pressure, obtained from solving Eqs. (1, 3) is shown in Figure 1a and a zoom displaying the range considered here is shown in Figure 1b. The non-relativistic shock wave regime corresponds to compressions less than four, followed by an intermediate regime where the compression increases very slowly, while the pressure increases by about 10 orders of magnitude and a relativistic regime where there is no upper limit to the compression, unlike for the non-relativistic Hugoniot Eq. (2). The laser intensities generating the pressures considered here are from several times 10¹⁷ W/cm² to 10²² W/cm², depending on the material initial density. Figure 2 shows the piston/particle and the shock velocity as a function of laser intensity, obtained from the solution of the relativistic Hugoniot equation (1) coupled to the laser piston relation (4), for material initial density ρ₀ = 1 g/cm³. Increasing the initial density shifts the laser intensities linearly to higher values for the same piston velocity.

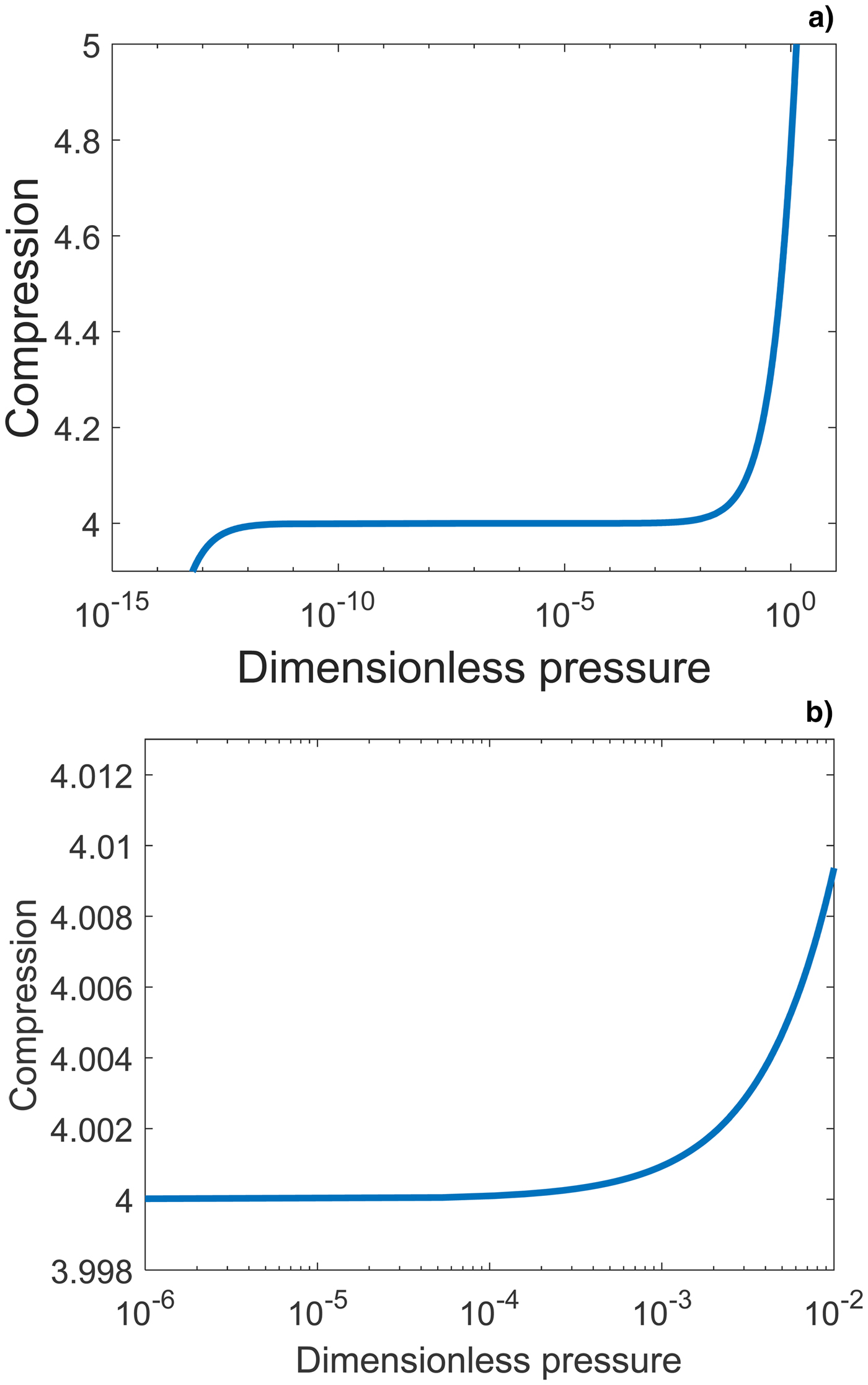
Fig. 1. (a) The compression κ = (ρ/ρ₀) as a function of the normalized, dimensionless pressure, Π = (P/ρ₀c ²)., for Γ = (5/3). (b) Zoom of (a), displaying the compression as a function of the normalized pressure in the pressure regime considered here.

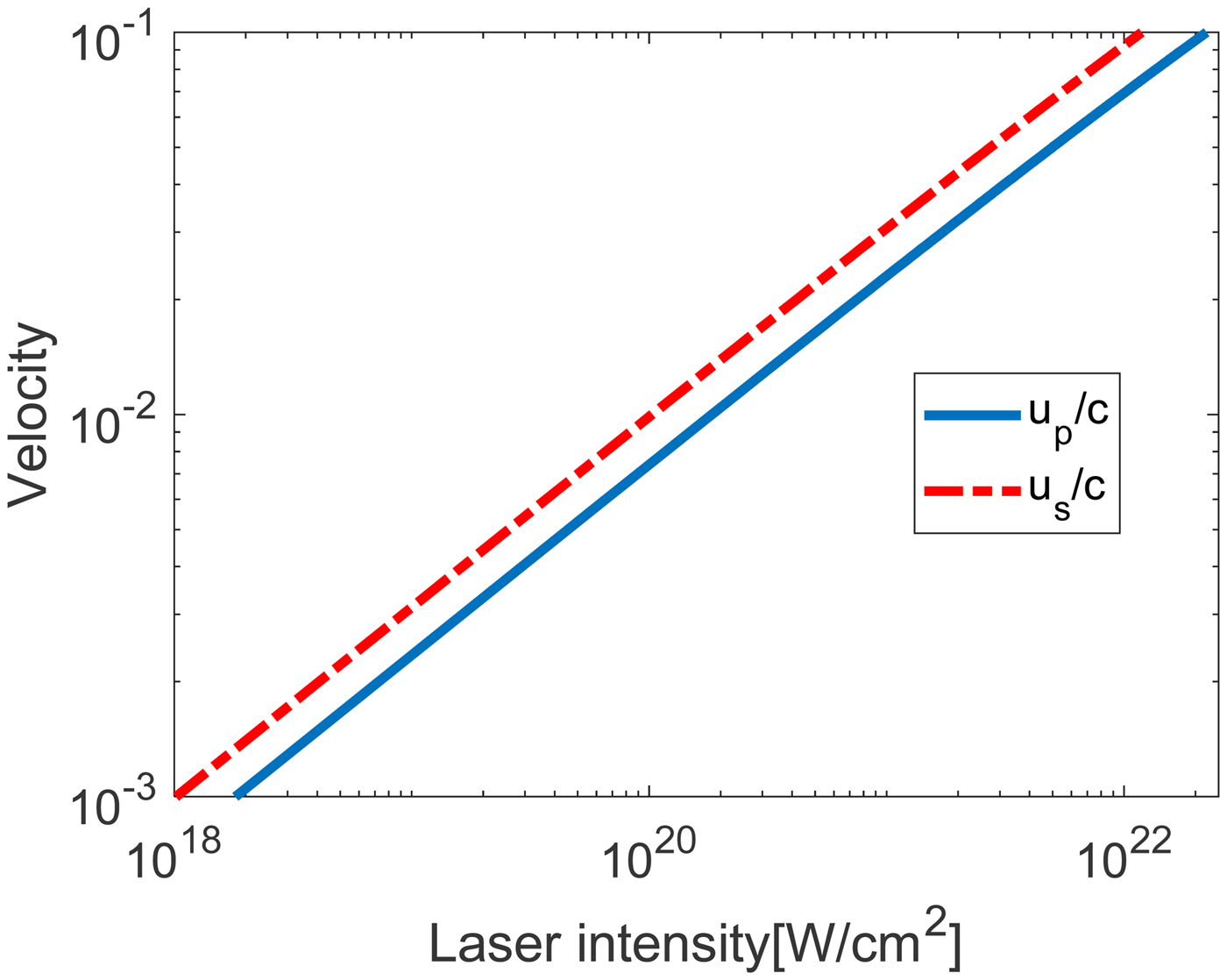
Fig. 2. The particle and shock velocities in units of the velocity of light given by the laser piston model as a function of the laser intensity for initial density ρ₀ = 1 g/cm³, for Γ = (5/3).

Thermalization in laser-induced shock waves

Due to the shock wave formation in the material, the ions and the electrons behind the shock front are moving with the piston velocity u _p. For non-relativistic, and/or nanosecond or longer time duration shock waves the piston work is divided equally to kinetic energy $\int \lpar {\rho u_{\rm p}^2 /2} \rpar dV$ and an increase in internal/thermal energy $\displaystyle \int {3 \over 2}k_{\rm B}\lpar {n_{\rm e}T_{\rm e} + n_{\rm i}T_{\rm i}} \rpar dV $ (Zeldovich and Raizer Reference Zeldovich and Raizer1966). For relativistic and semi-relativistic regimes or shorter laser pulse duration the shocked plasma may have in general different ion and electron shock temperatures, T _i and T _e (Eliezer et al., Reference Eliezer, Henis, Nissim, Pinhasi and Martinez Val2015). Moreover, for extremely short-laser pulse duration and high-laser intensity, the ions might not have enough time to achieve thermalization among themselves during the shock duration. The electrons reach thermalization at time shorter than the time scales considered here. Therefore, the laser piston work may be partitioned differently between kinetic and internal energy. In this paper we address this issue, estimating the time of temperature equilibration among the ions and the time of temperature equilibration between the electrons and the ions. It is shown that for given laser intensity there is a threshold pulse duration for the formation of a shock wave. In addition, dependent on the laser intensity, the electron and ion temperatures at the end of the pulse duration may be different.

The time-dependent equations for the electron and ion temperatures T _e and T _i are obtained from the energy conservation of the electrons and the ions:

(10)$$\displaystyle{d \over {dt}}\left( {\displaystyle{3 \over 2}n_{\rm e}k_{\rm B}T_{\rm e}} \right) = W_{{\rm ie}}-W_{\rm B} + W_{\rm d}^{\rm e} \cdot \nu _\varepsilon ^{{\rm e}/{\rm e}} + W_{\rm d}^{\rm i} \cdot \nu _\varepsilon ^{{\rm i}/{\rm e}} $$

(11)$$\displaystyle{d \over {dt}}\left( {\displaystyle{3 \over 2}n_{\rm i}k_{\rm B}T_{\rm i}} \right) = -W_{{\rm ie}} + W_{\rm d}^{\rm e} \cdot \nu _\varepsilon ^{{\rm e}/{\rm i}} + W_{\rm d}^{\rm i} \cdot \nu _\varepsilon ^{{\rm i}/{\rm i}} $$

The electron and ion densities are n _e and n _i, and k _B is the Boltzmann constant. W _ie (erg/cm³ s) is the rate of the electron–ion exchange energy density and W _B (erg/cm³ s) is the appropriate bremsstrahlung losses of the electron energy density. The energy deposition into the ions $W_{\rm d}^{\rm i} $(erg/cm³) and the electrons $W_{\rm d}^{\rm e} $(erg/cm³) is obtained from the piston work. It is important to point out that the upper limit of $W_{\rm d}^{\rm i} + W_{\rm d}^{\rm e} $ equals 50% of the piston energy density. $\nu _\epsilon ^{\alpha /\beta} $ is the rate of energy loss of test particles α in a background of field particles β. α, β = e, i. These rates are density, temperature, and velocity dependent.

The bremsstrahlung power loss term is:

(12)$$W_{\rm B}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3{\rm s}}}} \right] = 1.2510^{-25}n_{\rm e}n_{\rm i}Z_{{\rm av}}^2 T_{\rm e}^{0.5} \left( {1 + \displaystyle{{2T_{\rm e}} \over {0.511\cdot {10}^6}}} \right)$$

Here the electron temperature is in eV units and Z _av is the average ionization in the material.

The temperature equilibration term between the electrons and the ions is:

(13)$$W_{{\rm ie}}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3{\rm s}}}} \right] = \displaystyle{3 \over 2}n_{\rm e}k_B\displaystyle{{\lpar {T_{\rm i}-T_{\rm e}} \rpar } \over {\tau _{{\rm eq}}}}$$

The electron ion thermal equilibration time τ_eq is given by:

(14)$$\tau _{{\rm eq}} = \displaystyle{{3m_{\rm e}m_{\rm i}} \over {8{\lpar {2\pi} \rpar }^{1/2}}}\displaystyle{1 \over {n_{\rm i}Z_{{\rm av}}^2}} \displaystyle{1 \over {e^4{\rm ln\Lambda}}} \left( {\displaystyle{{k_{\rm B}T_{\rm e}} \over {m_{\rm e}}} + \displaystyle{{k_{\rm B}T_{\rm i}} \over {m_{\rm i}}}} \right)^{3/2}$$

where m _e and m _i are the electron and ion masses and e is the electron charge.

From the fact that 50% of the piston work can contribute to thermal energy and other losses we obtain

(15)$$W_{\rm d}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3}}} \right] = W_{\rm d}^{\rm i} + W_{\rm d}^{\rm e} = \displaystyle{{Pu_{\rm p}} \over {2\lpar {u_{\rm s}-u_{\rm p}} \rpar }} = \displaystyle{{\rho u_{\rm p}^2} \over 2}$$

The last part of Eq. (15) results from the non-relativistic Hugoniot conservation equations.

The deposited energy W _d is calculated after solving the Hugoniot relativistic equations for the pressure and the particle and shock velocities as a function of the laser intensity.

We consider the energy deposition to the electrons and the ions, as test particles and as field particles, separately. The energy deposition is distributed according to the electron and ion masses.

(16)$$W_{\rm d}^{\rm i} = \displaystyle{{W_{\rm d}} \over {\lpar {1 + (n_{\rm e}m_{\rm e}/n_{\rm i}m_{\rm i})} \rpar }}$$

(17)$$W_{\rm d}^{\rm e} = W_{\rm d}-W_{\rm d}^{\rm i} $$

(18)$$W_{\rm d}\left[ {\displaystyle{{{\rm erg}} \over {{\rm c}{\rm m}^3}}} \right] = \displaystyle{{\rho u_{\rm p}^2} \over 2}-\int W_{\rm B}dt$$

Due to the large ion-electron mass ratio $W_{\rm d}^{\rm i} \gg W_{\rm d}^{\rm e} $.

Assuming that the laser pulse rise time is very small in comparison with the laser pulse duration, at the shock wave front the target particle velocity changes instantaneously from zero to a velocity u _p. This is equivalent to a shock wave rise time much shorter than the laser pulse duration. We consider here collisional shock waves, i.e., we assume that the time equilibrations to reach the temperatures T _e(t < τ_L) and T _i(t < τ_L) are obtained by Coulomb binary collisions near the shock wave front. In this model we describe the piston energy deposition of the shocked particles, electrons, and ions into thermal energy using a relaxation rate arising from the interaction of test particles, labeled α, streaming with velocity u _p, through a background of field particles, labeled β with a collision frequency of energy deposition (Huba Reference Huba2011) given by:

(19)$$\nu _\varepsilon ^{\alpha /\beta} = 2\left[ {\displaystyle{{m_\alpha} \over {m_\beta}} \psi \lpar {x^{\alpha /\beta}} \rpar -{\psi}^{\prime}\lpar {x^{\alpha /\beta}} \rpar } \right]\nu _0^{\alpha /\beta} $$

Here α and β stand for the electrons or ions, α/β denotes kinetic energy transferred from test α to field β particles, m _α and m _β stands for the electron and ion mass, $\nu _0^{\alpha /\beta} $, the relaxation rate scale and the function ψ are defined by

(20)$$\nu _0^{\alpha /\beta} = 4\pi q_\alpha ^2 q_\beta ^2 \lambda _{\alpha \beta} n_\beta /m_\alpha ^2 v_\alpha ^3 $$

(21)$$x^{\alpha /\beta} = \displaystyle{{m_\beta v_\alpha ^2} \over {2k_{\rm B}T_\beta}} $$

(22)$$\psi \lpar x \rpar = \displaystyle{2 \over \pi} \mathop \int \limits_0^x dtt^{1/2}e^{-t}\; $$

(23)$${\psi} ^{\prime}\lpar x \rpar = \displaystyle{{d\psi} \over {dx}}$$

T _β denotes the temperature of the field particles, v is the test particle velocity, v = u _p, q _α and q _β are the charges (q equals the electron charge e for the electrons and Z _ave for the ions), and k _B is the Boltzmann constant. λ_αβ = ln Λ_αβ is the Coulomb logarithm. The transfer rate $\nu _\varepsilon ^{\alpha /\beta} $ is positive for $\varepsilon \gt \varepsilon _\alpha ^* $, and negative for $\varepsilon \lt \varepsilon _\alpha ^* $, where $\varepsilon = (1/2)m_\alpha v_\alpha ^2 $ and $x^* = (m_\beta /m_\alpha )(\varepsilon _\alpha ^* /T_\beta )$ are the solution of ψ ^′(x*) = (m _α/m _β)ψ(x*). Eq. (20) indicates that the energy transfer rates increase linearly with the density and the average ionization and decrease with increasing piston velocity.

The timescale for energy dissipation is related to the collision mean free path. For ion–ion collisions the mean free path is (Huba, Reference Huba2011):

(24)$$l_{{\rm ii}} = \displaystyle{{3\sqrt 6} \over 8}\displaystyle{{m_{\rm i}^2 u_{\rm p}^4} \over {\pi Z^4e^4n_{\rm i}{\rm ln\Lambda}}} = \displaystyle{{u_{\rm p}} \over {\nu _0^{{\rm i}/{\rm i}}}} $$

The average ionization Z _av is obtained from the calculation of population of the ionization stages as a function of time:

(25)$$\displaystyle{{dn_z} \over {dt}} = n_{\rm e}(n_{z-1}S_z-n_zS_{z + 1}-n_zR_z + n_{z + 1}R_{z + 1})$$

where S _z is the ionization coefficient for creating an ion with charge z, R _z is the recombination coefficient of an ion with of charge z, $n_{\rm e} = \sum\nolimits_{z = 1}^Z {zn_z} $ is the electron density, and Z is the atomic number.

Analytical expressions for the ionization and recombination rates and values of the ionization potentials of aluminum are given in the Appendix.

The (Z + 1) equations for the ionization states (including the neutral) are solved together with the ion and electron temperatures as a function of time.

The formation of a shock wave requires that the spatial scale of the shocked region is larger than the spatial scale of the shock front width, setting a lower limit on the laser pulse duration τ_L

(26)$$\lpar {u_{\rm s}-u_{\rm p}} \rpar \cdot \tau _L\gg \tau _{\rm R}u_{\rm s}$$

where the relaxation time τ_R is

(27)$$\tau _{\rm R} = \max \lpar {\tau_{\rm e},\tau_{\rm i}} \rpar $$

(28)$$\tau _{\rm e} = \displaystyle{1 \over {\nu _\varepsilon ^{{\rm e}/{\rm e}} + \nu _{\rm e}^{{\rm e}/{\rm i}}}} $$

(29)$$\tau _{\rm i} = \displaystyle{1 \over {\nu _\varepsilon ^{{\rm i}/{\rm e}} + \nu _\varepsilon ^{{\rm i}/{\rm i}}}} $$

Equivalent to Eq. (26), the spatial scale of the shocked region must be larger than the ion–ion mean free path:

(30)$$l_{{\rm ii}} \lt \lpar {u_{\rm s}-u_{\rm p}} \rpar \tau _L.$$

Therefore, a lower limit on the laser pulse duration is:

(31)$$\displaystyle{{\tau _{\rm R}u_{\rm s}} \over {u_{\rm s}-u_{\rm p}}} \lt \tau _{\rm L}$$

Eqs. (10, 11, 24) are numerically integrated up to a time equal to the laser pulse duration.

Numerical results

The following values for the laser piston velocity are considered, 0.001c, 0.01c, and 0.1c. The corresponding shock velocity and compressibility, dimensionless pressure and laser intensity obtained from solving Eqs. 4–8 are given in Table 1.

Table 1. Particle velocity, compressibility and dimensionless pressure, and laser intensity for laser piston-induced shock waves. The shock velocity is u _s = 4/3u _p for Γ = 5/3

The laser intensities, pressure and relaxation rate scales $\nu _0^{{\rm i}/{\rm i}} $ and $\nu _0^{{\rm i}/{\rm e}} $ for deuteron, carbon, and aluminum at normal density are given in Tables 2–4. The relaxation rate scales $\nu _0^{{\rm e}/{\rm e}} $ and $\nu _0^{{\rm e}/{\rm i}} $ are not shown, as $W_{\rm d}^{\rm i} \gg W_{\rm d}^{\rm e} $. The relaxation rate scales were calculated assuming that the plasma is fully ionized.

Table 2. Pressure, laser intensity, ion–ion and ion–electron energy loss rate scales for deuteron at normal liquid density ρ₀ = 0.16 g/cm³

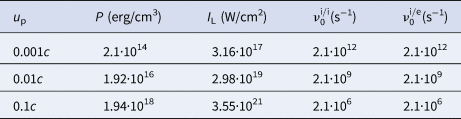
Table 3. Pressure, laser intensity, ion–ion and ion–electron energy loss rate scales for carbon at normal density ρ₀ = 1 g/cm³

Table 4. Pressure, laser intensity, ion–ion and ion–electron energy loss rate scales for aluminum at normal density ρ₀ = 2.7 g/cm³

From Eq. (31) and Tables (2–4) it is seen that the formation of a collisional shock wave during the laser pulse duration is not possible for all the materials and the laser piston velocities considered here. From the energy loss rate scales one may approximate the relaxation time τ_R and obtain an estimate for the lower limit for the laser pulse duration. Table 2 shows that the relaxation time for liquid deuterium at piston velocities of 0.01c and 0.1c is of the order of hundreds of picoseconds and hundreds of nanoseconds, respectively. Therefore, the piston work cannot be transferred into thermal energy of the shocked material on a time scale of few picoseconds. Tables 3 and 4 show that there is no time for piston work deposition in carbon and aluminum at a piston velocity of 0.1c. In other words, the formation of a collisional shock wave is not possible under the above conditions. A lower limit for the laser pulse duration that may allow the formation of a collisional shock wave, resulting from Eq. (31) and estimated with relaxation time scales, is given in Table 5. This estimate is dependent on the material density and atomic number. The temperature-dependent part of the relaxation rates $\nu _\varepsilon ^{{\rm i}/{\rm i}} $ and $\nu _\varepsilon ^{{\rm i}/{\rm e}} $ [Eq. (19)] may shift the value for this lower limit.

Table 5. Estimated range of the laser pulse duration for the formation of a collisional shock wave

The energy loss rates may be increased by the material pre-compression as seen from Eq. (20), and decrease the value of the lower limit for the pulse duration given in Table 5. However, an increase in the initial density will require higher laser intensity.

Solving the electron and the ion temperatures, Eqs. (10, 11) are not dependent on the laser pulse duration. The figures below show the results of the rate equations during a run time of 10 ps.

Figure 3 shows the results of Eqs. (10, 11) for deuterium at liquid normal density at piston velocity u _p = 0.001c. The electron and ion temperatures as a function of time are shown in Figure 3a, the energy transfer rates [Eq. (21)] in Figure 3b, and the available energy for deposition W _d − n _ik _BT _i − n _ek _BT _e in Figure 3c. It is seen that the energy deposition ends after about 40 fs, when the ion temperature is 0.48 keV and then the ions and the electrons reach equilibrium at about 0.35 keV after about 10 ps. Therefore, an equilibrium shock wave can be generated. For a piston velocity u _p = 0.01c, only 13% of the piston work is deposited during a reference time duration of 10 ps, and the ions do not thermalize. Increasing the density to 10 g/cm³ enables thermalization of the ions after 3.6 ps to a temperature T _imax = 43.8 keV, while the electrons are heated to T _emax = 18.4 keV at this time. Therefore, a non-equilibrium shock wave is generated. Figure 4 shows the electron and ion temperatures and the energy transfer rates for initial density 10 g/cm³ and u _p = 0.01c. After the piston work deposition, thermal energy is transferred from the ions to the electrons at a rate of 1/τ_eq [Eq. (14)].

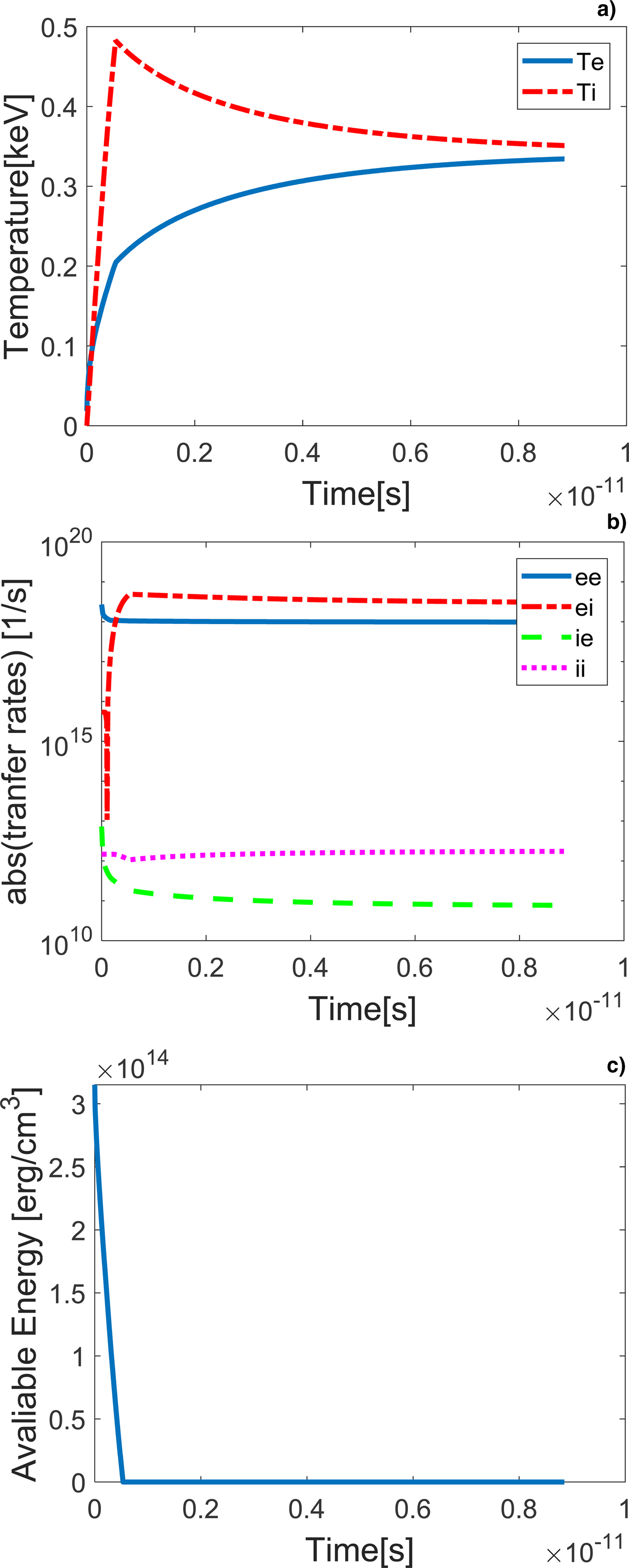
Fig. 3. (a) Numerical results for liquid deuterium, ρ₀ = 0.16 g/cm³, u _p = 0.001c. Electron (solid line) and ion (dashed line) temperatures as a function of time. (b) Absolute value of the energy transfer rates $\nu _\varepsilon ^{\alpha /\beta}, \; $ e/e – solid line, e/i – dash-dotted line, i/e – dashed line, and i/i – dotted line. (c) Available piston work in (erg/cm³) for deposition as a function of time.

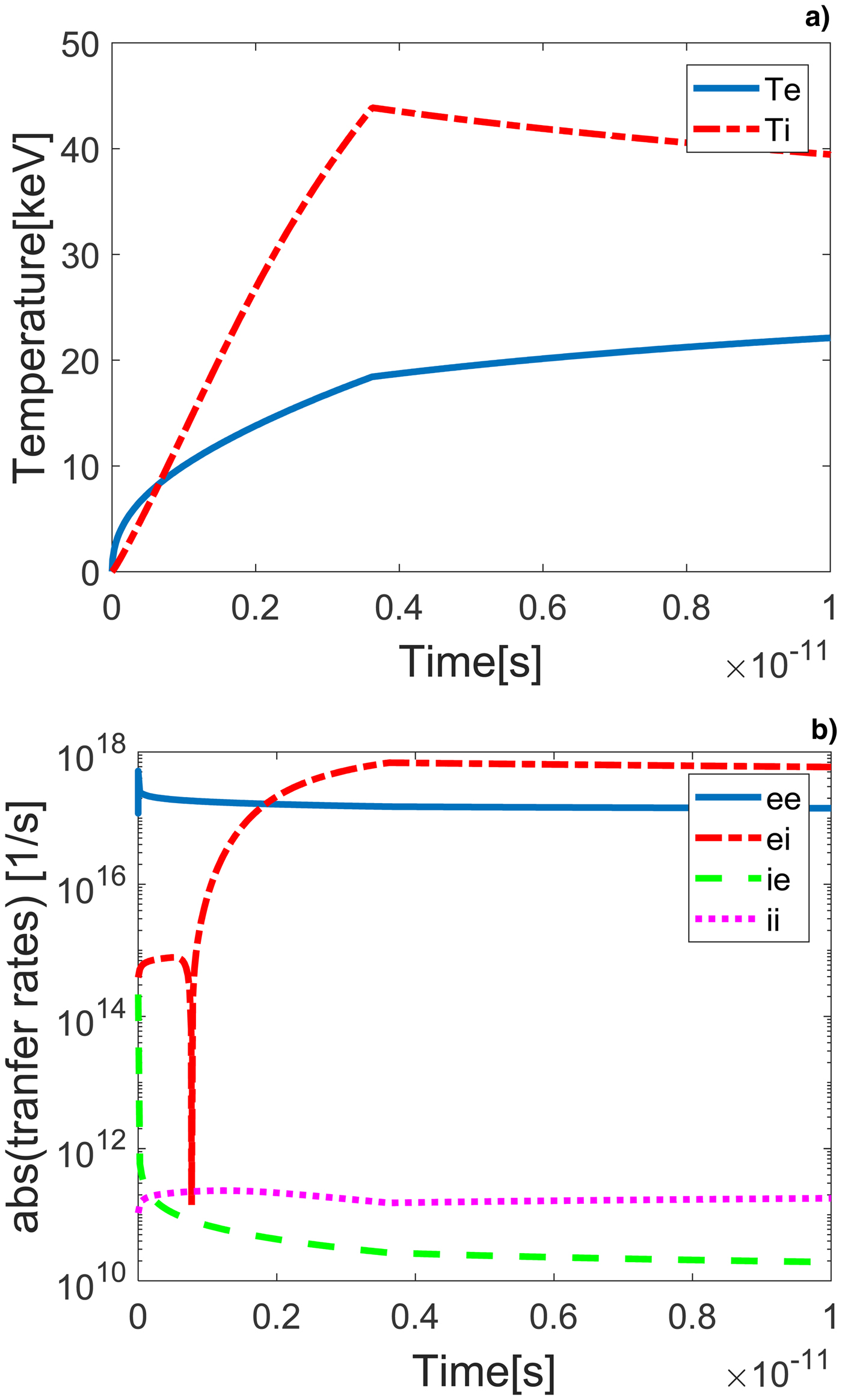
Fig. 4. (a) Numerical results for liquid deuterium, ρ₀ = 10 g/cm³, u _p = 0.01c. Electron (solid line) and ion (dashed line) temperatures as a function of time. (b) Absolute value of the energy transfer rates $\nu _\varepsilon ^{\alpha /\beta}, \; $ e/e – solid line, e/i – dash-dotted line, i/e – dashed line, and i/i – dotted line.

Figure 5 shows the electron and ion temperatures and the energy transfer rates for carbon at initial density ρ₀ = 1 g/cm³ and piston velocity u _p = 0.01c. It is seen that a non-equilibrium shock wave is generated. The maximum ion temperature is about 250 keV at 4.6 ps when the piston work deposition ends. From the energy loss rates displayed in Figure 5b, the relaxation time τ_R is 6.7 ps [Eq. (30)].

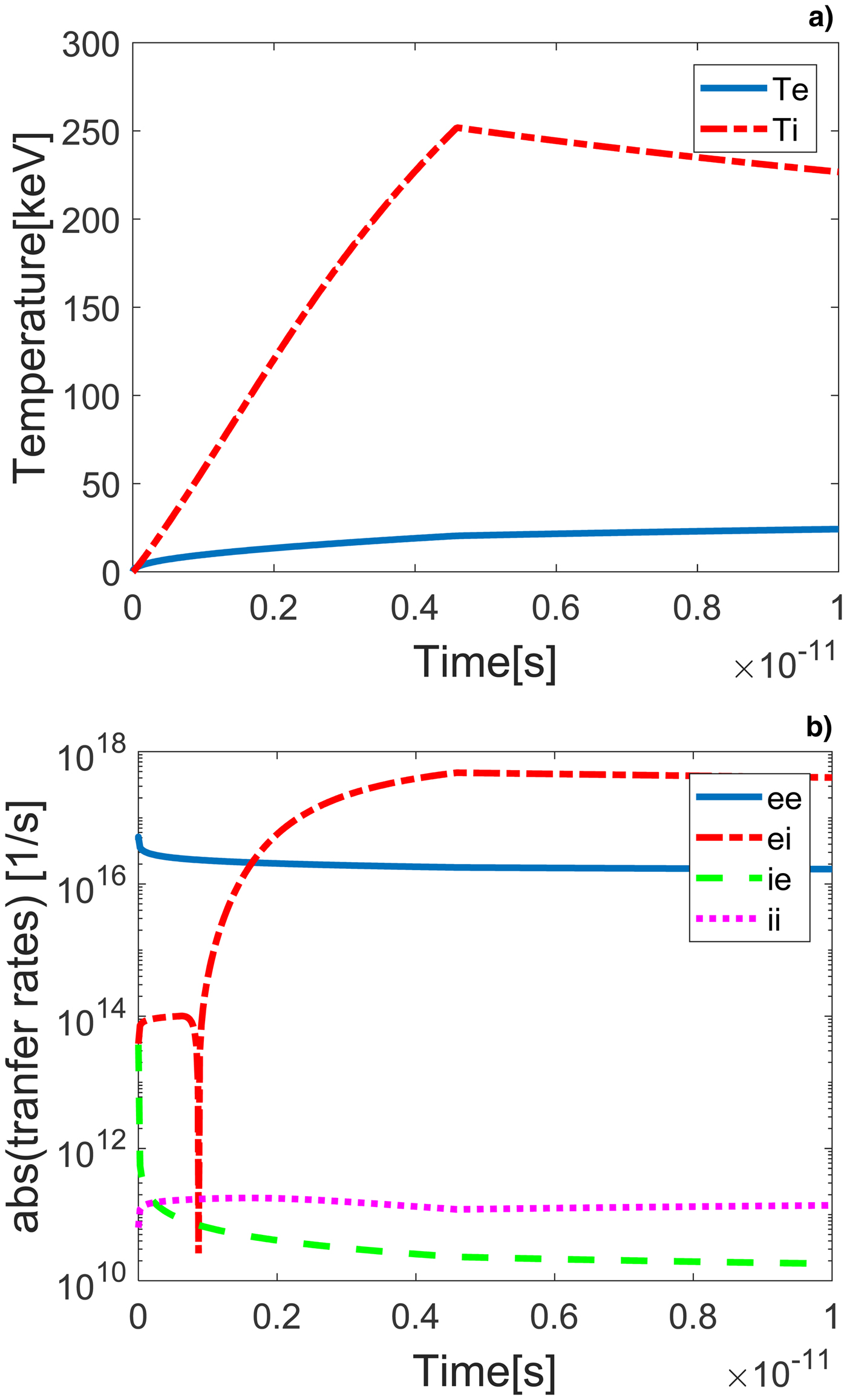
Fig. 5. (a) Numerical results for carbon, ρ₀ = 1 g/cm³, u _p = 0.01c. Electron (solid line) and ion (dashed line) temperatures as a function of time. (b) Absolute value of the energy transfer rates $\nu _\varepsilon ^{\alpha /\beta}, \; $ e/e – solid line, e/i – dash-dotted line, i/e – dashed line, and i/i – dotted line.

Similar calculations for aluminum at normal density show the formation of an equilibrium shock wave at piston velocity u _p = 0.001c, i.e. the electrons and the ions reach temperature equilibration during the shock wave, and a non-equilibrium shock wave at u _p = 0.01c. Figure 6 shows the electron and ion temperatures, energy deposition rates, and piston work deposition as a function of time for normal density and piston velocity u _p = 0.1c. In this case there is no time for collisional shock generation on a time scale of about 10 ps.

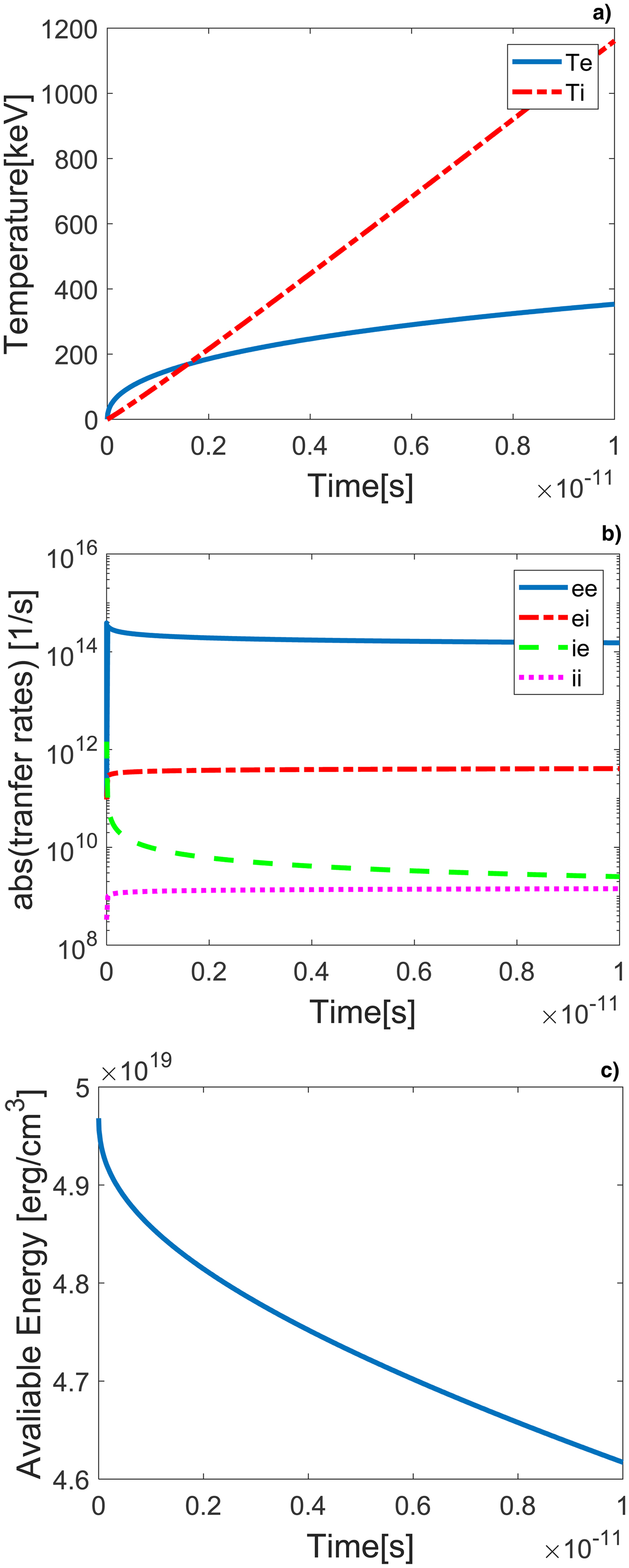
Fig. 6. (a) Numerical results for aluminum, ρ₀ = 2.7 g/cm³, u _p = 0.1c. Electron (solid line) and ion (dashed line) temperatures as a function of time. (b) Absolute value of the energy transfer rates $\nu _\varepsilon ^{\alpha /\beta}, \; $ e/e – solid line, e/i – dash-dotted line, i/e – dashed line, and i/i –dotted line. (c) Available piston work in erg/cm³ for deposition as a function of time.

We note that to obtain a one-dimensional shock wave, the spot size must be larger than l _s the spatial scale of the shocked region:

(32)$$2\cdot r_{\rm L} \gt l_{\rm s} = \lpar {u_{\rm s}-u_{\rm p}} \rpar \cdot \tau _{{\rm L}\;} $$

From Eq. (32) an estimate for the laser pulse energy is $E_{\rm L} = \pi r_{\rm L}^2 \tau _{\rm L}^3 I_{\rm L} \ge (\pi /36)u_{\rm p}^2 \tau _{\rm L}^3 I_{\rm L}$.

Summary

The formation of a collisional shock wave by the light pressure of a short-pulse laser at relativistic intensities and the subsequent heating of a solid layer are considered. The heating model is based on the dissipation of kinetic energy by binary Coulomb collisions at a temperature-dependent rate. We consider laser intensities in the range of 10¹⁸ W/cm² to 10²³ W/cm² for deuterium, carbon, and aluminum targets. It is obtained that the formation of a collisional shock wave is dependent on the laser intensity and the material density. In the framework of the model presented here three cases were distinguished. If the timescale for energy dissipation is shorter than the laser pulse duration a collisional shock wave can be formed, during which the electrons and the ions either may have different temperatures – non-equilibrium shock wave, or may reach equilibrium at equal temperature. In both equilibrium and non-equilibrium shock waves, at early times the electrons are heated by energy transfer from the ions, and eventually the ion temperature overtakes. A third possibility may occur when the timescale for energy dissipation is longer than laser pulse duration, or the ion–ion collision mean free path l _ii is larger than the shock width l _s. In this case a collisional shock wave is not formed. The collisional shock wave described here may serve as a heating mechanism for a fast ignition scheme. In such a scheme deuterium fuel compressed by nanosecond laser pulses to a density by three orders of magnitude higher than normal liquid density can be heated by the a shock wave generated by the radiation pressure of 1 ps duration laser at several times its intensity of 10²³ W/cm².