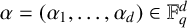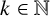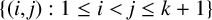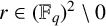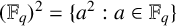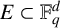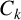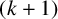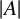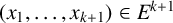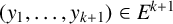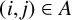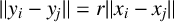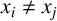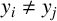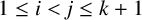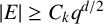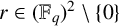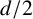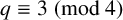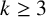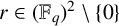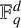1 Introduction
Let
![]() $\mathbb F_q^d$
, where
$\mathbb F_q^d$
, where
![]() $d\ge 2$
, be the d-dimensional vector space over the finite field
$d\ge 2$
, be the d-dimensional vector space over the finite field
![]() $\mathbb F_q$
with q elements. We assume that q is a power of an odd prime p.
$\mathbb F_q$
with q elements. We assume that q is a power of an odd prime p.
Given a set E in
![]() $\mathbb F_q^d$
, the distance set
$\mathbb F_q^d$
, the distance set
![]() $\Delta (E)$
is defined by
$\Delta (E)$
is defined by
where
![]() $\lVert \alpha \rVert = \sum _{i=1}^d \alpha _i^2$
for
$\lVert \alpha \rVert = \sum _{i=1}^d \alpha _i^2$
for
![]() $\alpha = (\alpha _1, \ldots , \alpha _d) \in \mathbb F_q^d$
.
$\alpha = (\alpha _1, \ldots , \alpha _d) \in \mathbb F_q^d$
.
In the finite field setting, the Falconer distance problem asks for the smallest exponent
![]() $\alpha> 0$
such that, for any
$\alpha> 0$
such that, for any
![]() $E \subset \mathbb {F}_q^d$
with
$E \subset \mathbb {F}_q^d$
with
![]() $|E| \geq Cq^\alpha $
, we have
$|E| \geq Cq^\alpha $
, we have
![]() $|\Delta (E)| \geq cq$
, where
$|\Delta (E)| \geq cq$
, where
![]() $C> 1$
represents a sufficiently large constant and
$C> 1$
represents a sufficiently large constant and
![]() $0 < c \leq 1$
represents a constant independent of q and
$0 < c \leq 1$
represents a constant independent of q and
![]() $|E|$
. Here,
$|E|$
. Here,
![]() $|E|$
denotes the cardinality of the set E.
$|E|$
denotes the cardinality of the set E.
This problem was initially proposed by Iosevich and Rudnev in [Reference Iosevich and Rudnev7] as a finite field counterpart of the Falconer distance problem in Euclidean space. The formulation of the finite field Falconer problem was also inspired by the Erdős distinct distances problem over finite fields, as introduced by Bourgain et al. in [Reference Bourgain, Katz and Tao2]. As a result, this problem is often referred to as the Erdős–Falconer distance problem.
One can consider a stronger version of the Erdős–Falconer distance problem known as the Mattila–Sjölin distance problem over finite fields. This problem seeks the smallest threshold
![]() $\beta> 0$
such that, for any
$\beta> 0$
such that, for any
![]() $E \subset \mathbb {F}_q^d$
with
$E \subset \mathbb {F}_q^d$
with
![]() $|E| \geq Cq^\beta $
, we have
$|E| \geq Cq^\beta $
, we have
![]() $\Delta (E) = \mathbb {F}_q$
. Iosevich and Rudnev, using Fourier analytic techniques and Kloosterman sum estimates, successfully determined the threshold to be
$\Delta (E) = \mathbb {F}_q$
. Iosevich and Rudnev, using Fourier analytic techniques and Kloosterman sum estimates, successfully determined the threshold to be
![]() $(d+1)/2$
for all dimensions
$(d+1)/2$
for all dimensions
![]() $d \geq 2$
.
$d \geq 2$
.
Theorem 1.1 (Iosevich and Rudnev, [Reference Iosevich and Rudnev7]).
If
![]() $E\subset \mathbb {F}_q^d \ (d\ge 2)$
and
$E\subset \mathbb {F}_q^d \ (d\ge 2)$
and
![]() $|E|> 2q^{(d+1)/2}$
, then
$|E|> 2q^{(d+1)/2}$
, then
![]() $\Delta (E) = \mathbb {F}_q.$
$\Delta (E) = \mathbb {F}_q.$
The threshold
![]() $(d+1)/2$
in Theorem 1.1 is currently the best-known result for the Mattila–Sjölin distance problem over finite fields in all dimensions
$(d+1)/2$
in Theorem 1.1 is currently the best-known result for the Mattila–Sjölin distance problem over finite fields in all dimensions
![]() $d \geq 2$
. It is considered as a challenging problem to improve the
$d \geq 2$
. It is considered as a challenging problem to improve the
![]() $(d+1)/2$
threshold. In odd dimensions, this threshold is proven to be optimal, as demonstrated in [Reference Hart, Iosevich, Koh and Rudnev4].
$(d+1)/2$
threshold. In odd dimensions, this threshold is proven to be optimal, as demonstrated in [Reference Hart, Iosevich, Koh and Rudnev4].
However, in even dimensions, there is a belief that the exponent
![]() $(d+1)/2$
can potentially be improved, but as of now, there is no reasonable evidence or conjecture stated in the literature. In dimension 2, Murphy and Petridis in [Reference Murphy and Petridis8] have shown that the threshold cannot be lower than
$(d+1)/2$
can potentially be improved, but as of now, there is no reasonable evidence or conjecture stated in the literature. In dimension 2, Murphy and Petridis in [Reference Murphy and Petridis8] have shown that the threshold cannot be lower than
![]() $4/3$
for the Mattila–Sjölin distance problem over finite fields.
$4/3$
for the Mattila–Sjölin distance problem over finite fields.
However, Iosevich and Rudnev in [Reference Iosevich and Rudnev7] conjectured that the threshold
![]() $(d+1)/2$
can be lowered to
$(d+1)/2$
can be lowered to
![]() $d/2$
for the Erdős–Falconer distance problem in even dimensions. In dimension 2, the threshold
$d/2$
for the Erdős–Falconer distance problem in even dimensions. In dimension 2, the threshold
![]() $4/3$
was proven in [Reference Chapman, Burak Erdoğan, Hart, Iosevich and Koh3] (see also [Reference Bennett, Hart, Iosevich, Pakianathan and Rudnev1]). Additionally, if q is a prime number, then the exponent
$4/3$
was proven in [Reference Chapman, Burak Erdoğan, Hart, Iosevich and Koh3] (see also [Reference Bennett, Hart, Iosevich, Pakianathan and Rudnev1]). Additionally, if q is a prime number, then the exponent
![]() $4/3$
was improved to
$4/3$
was improved to
![]() $5/4$
by Murphy et al. in [Reference Murphy, Petridis, Pham, Rudnev and Stevens9]. The threshold
$5/4$
by Murphy et al. in [Reference Murphy, Petridis, Pham, Rudnev and Stevens9]. The threshold
![]() $(d+1)/2$
cannot be improved for the Erdős–Falconer distance problem in odd dimensions (see also [Reference Hart, Iosevich, Koh and Rudnev4]).
$(d+1)/2$
cannot be improved for the Erdős–Falconer distance problem in odd dimensions (see also [Reference Hart, Iosevich, Koh and Rudnev4]).
The distance problems over finite fields have been extended in various directions. Although numerous variants of the distance problems have been extensively studied, the threshold
![]() $d/2$
for the set E in
$d/2$
for the set E in
![]() $\mathbb {F}_q^d$
had not been addressed for any distance-type problems until Iosevich et al. in [Reference Iosevich, Koh and Parshall5] studied the Mattila–Sjölin problem for the quotient set of the distance set over finite fields.
$\mathbb {F}_q^d$
had not been addressed for any distance-type problems until Iosevich et al. in [Reference Iosevich, Koh and Parshall5] studied the Mattila–Sjölin problem for the quotient set of the distance set over finite fields.
1.1 The Mattila–Sjölin problem for the quotient set of the distance set
If E is a subset of
![]() $\mathbb {F}_q^d$
(
$\mathbb {F}_q^d$
(
![]() $d \geq 2$
), then the quotient set of the distance set, denoted by
$d \geq 2$
), then the quotient set of the distance set, denoted by
![]() ${\Delta (E)}/{\Delta (E)}$
, is defined as follows:
${\Delta (E)}/{\Delta (E)}$
, is defined as follows:
One can ask the following question: determine the smallest exponent
![]() $\gamma> 0$
such that for any set
$\gamma> 0$
such that for any set
![]() $E \subset \mathbb {F}_q^d$
with
$E \subset \mathbb {F}_q^d$
with
![]() $|E| \geq Cq^\gamma $
, we have
$|E| \geq Cq^\gamma $
, we have
In [Reference Iosevich, Koh and Parshall5], the authors obtained the threshold
![]() $d/2$
in even dimensions for the Mattila–Sjölin problem for the quotient set of the distance set over finite fields. More precisely, they proved the following result. Here,
$d/2$
in even dimensions for the Mattila–Sjölin problem for the quotient set of the distance set over finite fields. More precisely, they proved the following result. Here,
![]() $(\mathbb F_q)^2 := \{a^2: a\in \mathbb F_q\}.$
$(\mathbb F_q)^2 := \{a^2: a\in \mathbb F_q\}.$
Theorem 1.2 [Reference Iosevich, Koh and Parshall5, Theorems 1.1 and 1.2].
If
![]() $E \subset \mathbb F_q^d \ (d\ge 2)$
, then the following statements hold:
$E \subset \mathbb F_q^d \ (d\ge 2)$
, then the following statements hold:
-
(i) if
 $d\ge 2$
is even and
$d\ge 2$
is even and
 $ |E|\ge 9 q^{d/2},$
then
$ |E|\ge 9 q^{d/2},$
then
 ${\Delta (E)}/{\Delta (E)}=\mathbb F_q;$
${\Delta (E)}/{\Delta (E)}=\mathbb F_q;$
-
(ii) if
 $d\ge 3$
is odd and
$d\ge 3$
is odd and
 $|E|\ge 6 q^{d/2},$
then
$|E|\ge 6 q^{d/2},$
then
 ${\Delta (E)}/{\Delta (E)}\supseteq (\mathbb F_q)^2$
.
${\Delta (E)}/{\Delta (E)}\supseteq (\mathbb F_q)^2$
.
Theorem 1.2 has been extended and generalised with improved constants to general nondegenerate quadratic distances by Iosevich, Koh and the second author (see [Reference Iosevich, Koh and Rakhmonov6]).
For convenience, we will use the notation
![]() $\mathbb F_q^*$
to represent the set of all nonzero elements in
$\mathbb F_q^*$
to represent the set of all nonzero elements in
![]() $\mathbb F_q$
.
$\mathbb F_q$
.
The equality
![]() ${\Delta (E)}/{\Delta (E)}=\mathbb {F}_q$
implies that for each
${\Delta (E)}/{\Delta (E)}=\mathbb {F}_q$
implies that for each
![]() $r\in \mathbb {F}_q^*$
, there exist
$r\in \mathbb {F}_q^*$
, there exist
![]() $(x,y)\in E^2$
and
$(x,y)\in E^2$
and
![]() $(x',y')\in E^2$
such that
$(x',y')\in E^2$
such that
![]() $\lVert x-y\rVert \neq 0$
and
$\lVert x-y\rVert \neq 0$
and
![]() $\lVert x'-y'\rVert = r \lVert x-y\rVert $
. In other words, if
$\lVert x'-y'\rVert = r \lVert x-y\rVert $
. In other words, if
![]() $r\in \mathbb {F}_q^*$
and
$r\in \mathbb {F}_q^*$
and
![]() $E\subseteq \mathbb {F}_q^d$
with
$E\subseteq \mathbb {F}_q^d$
with
![]() $|E|\geq 9q^{d/2}$
, then one can find two pairs
$|E|\geq 9q^{d/2}$
, then one can find two pairs
![]() $(x,y)\in E^2$
and
$(x,y)\in E^2$
and
![]() $(x',y')\in E^2$
such that the length of one of them is r times that of the other.
$(x',y')\in E^2$
such that the length of one of them is r times that of the other.
The following natural question arises: is it possible to generalise this result to other point configurations in
![]() $E\subseteq \mathbb {F}_q^d$
? For example, consider
$E\subseteq \mathbb {F}_q^d$
? For example, consider
![]() $r \in \mathbb {F}_q^{*}$
and
$r \in \mathbb {F}_q^{*}$
and
![]() $E \subset \mathbb {F}_q^2$
. We aim to find the smallest exponent
$E \subset \mathbb {F}_q^2$
. We aim to find the smallest exponent
![]() $\gamma> 0$
such that, for any
$\gamma> 0$
such that, for any
![]() $E \subset \mathbb {F}_q^2$
with
$E \subset \mathbb {F}_q^2$
with
![]() $|E| \geq Cq^{\gamma }$
, there exist 4-tuples
$|E| \geq Cq^{\gamma }$
, there exist 4-tuples
![]() $(x_1, x_2, x_3, x_4) \in E^4$
and
$(x_1, x_2, x_3, x_4) \in E^4$
and
![]() $(y_1, y_2, y_3, y_4) \in E^4$
satisfying the conditions:
$(y_1, y_2, y_3, y_4) \in E^4$
satisfying the conditions:
-
(1)
 $x_i \neq x_j$
and
$x_i \neq x_j$
and
 $y_i \neq y_j$
for
$y_i \neq y_j$
for
 $1 \leq i < j \leq 4$
;
$1 \leq i < j \leq 4$
; -
(2)
 $\lVert y_i - y_j \rVert = r \lVert x_i - x_j \rVert $
if
$\lVert y_i - y_j \rVert = r \lVert x_i - x_j \rVert $
if
 $(i, j) \in A$
, where
$(i, j) \in A$
, where
 $A = \{(1, 2), (2, 3), (3, 4), (1, 4), (1, 3)\}$
(refer to Figure 1).
$A = \{(1, 2), (2, 3), (3, 4), (1, 4), (1, 3)\}$
(refer to Figure 1).
Figure 1 Pair of quadrilaterals with a dilation ratio of
 $r\in \mathbb {F}_q^{*}$
.
$r\in \mathbb {F}_q^{*}$
.
We proceed to formulate the main question. Consider
![]() $r\in \mathbb {F}_q^{*}$
and
$r\in \mathbb {F}_q^{*}$
and
![]() $E\subset \mathbb {F}_q^d$
, and assume that A is a nonempty subset of
$E\subset \mathbb {F}_q^d$
, and assume that A is a nonempty subset of
![]() $\{(i,j): 1 \leq i < j \leq k+1\}$
, where
$\{(i,j): 1 \leq i < j \leq k+1\}$
, where
![]() $k\geq 1$
. How large must E be to ensure the existence of two sets of points,
$k\geq 1$
. How large must E be to ensure the existence of two sets of points,
![]() $(x_1, \ldots , x_{k+1})\in E^{k+1}$
and
$(x_1, \ldots , x_{k+1})\in E^{k+1}$
and
![]() $(y_1, \ldots , y_{k+1})\in E^{k+1}$
, satisfying the conditions:
$(y_1, \ldots , y_{k+1})\in E^{k+1}$
, satisfying the conditions:
-
(1)
 $x_i \neq x_j$
and
$x_i \neq x_j$
and
 $y_i \neq y_j$
for
$y_i \neq y_j$
for
 $1\leq i < j \leq k+1$
;
$1\leq i < j \leq k+1$
; -
(2)
 $\lVert y_i - y_j \rVert = r\lVert x_i - x_j \rVert $
for
$\lVert y_i - y_j \rVert = r\lVert x_i - x_j \rVert $
for
 $(i,j)\in A$
?
$(i,j)\in A$
?
We address this question and provide two proofs. The first proof uses the machinery of group actions and revolves around the investigation of
![]() $L^{k}$
and
$L^{k}$
and
![]() $L^{k+1}$
norms of the counting function:
$L^{k+1}$
norms of the counting function:
Here,
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
,
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
,
![]() $\theta \in \mathrm {O}_d(\mathbb {F}_q)$
and
$\theta \in \mathrm {O}_d(\mathbb {F}_q)$
and
![]() $z\in \mathbb {F}_q^d$
, where
$z\in \mathbb {F}_q^d$
, where
![]() $\mathrm {O}_d(\mathbb {F}_q)$
represents the group of
$\mathrm {O}_d(\mathbb {F}_q)$
represents the group of
![]() $d\times d$
orthogonal matrices with entries in
$d\times d$
orthogonal matrices with entries in
![]() $\mathbb {F}_p$
. We note that
$\mathbb {F}_p$
. We note that
![]() $\sqrt {r}$
is an element of
$\sqrt {r}$
is an element of
![]() $\mathbb {F}_q$
such that its square is r. For
$\mathbb {F}_q$
such that its square is r. For
![]() $r \in (\mathbb {F}_q)^2\setminus \{0\}$
, there are two square roots. However, it does not affect our result, as in the end, we square the element, resulting in the restoration of the original element r. The second proof is elementary and is based on fairly straightforward combinatorial reasoning.
$r \in (\mathbb {F}_q)^2\setminus \{0\}$
, there are two square roots. However, it does not affect our result, as in the end, we square the element, resulting in the restoration of the original element r. The second proof is elementary and is based on fairly straightforward combinatorial reasoning.
Before delving into the details, let us present the main result of this paper.
Theorem 1.3. Suppose
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
and
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
and
![]() $\varnothing \neq A\subset \{(i,j):1\leq i<j\leq k+1\}$
, where
$\varnothing \neq A\subset \{(i,j):1\leq i<j\leq k+1\}$
, where
![]() $k\geq 1$
. If
$k\geq 1$
. If
![]() $E\subset \mathbb {F}_q^d$
with
$E\subset \mathbb {F}_q^d$
with
![]() $|E|\geq 2kq^{d/2}$
, then there exist
$|E|\geq 2kq^{d/2}$
, then there exist
![]() $(x_1,\ldots ,x_{k+1})\in E^{k+1}$
and
$(x_1,\ldots ,x_{k+1})\in E^{k+1}$
and
![]() $(y_1,\ldots ,y_{k+1})\in E^{k+1}$
such that
$(y_1,\ldots ,y_{k+1})\in E^{k+1}$
such that
![]() $\lVert y_i-y_j \rVert =r\lVert x_i-x_j \rVert $
for
$\lVert y_i-y_j \rVert =r\lVert x_i-x_j \rVert $
for
![]() $(i,j)\in A$
, and
$(i,j)\in A$
, and
![]() $x_i\neq x_j$
,
$x_i\neq x_j$
,
![]() $y_i\neq y_j$
for
$y_i\neq y_j$
for
![]() $1\leq i<j\leq k+1$
.
$1\leq i<j\leq k+1$
.
We remark that the second proof gives a stronger result. In particular, we show in Section 4 that the result holds if
![]() $|E| \ge \sqrt {k+1} |E|^{d/2}$
.
$|E| \ge \sqrt {k+1} |E|^{d/2}$
.
As a straightforward corollary, by varying the underlying set A, we can establish thresholds for the existence of dilated k-cycles, k-paths and k-stars (for
![]() $k\geq 3$
) with a dilation ratio of
$k\geq 3$
) with a dilation ratio of
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
(see more details in Section 5).
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
(see more details in Section 5).
Corollary 1.4 (k-paths with a dilation ratio of
 $r \in (\mathbb {F}_q)^2$
).
$r \in (\mathbb {F}_q)^2$
).
Let
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $r \in (\mathbb {F}_q)^2 \setminus \{0\}$
and
$r \in (\mathbb {F}_q)^2 \setminus \{0\}$
and
![]() $E \subset \mathbb {F}_q^d$
such that
$E \subset \mathbb {F}_q^d$
such that
![]() $|E| \geq 2kq^{d/2}$
. Then, there exist two
$|E| \geq 2kq^{d/2}$
. Then, there exist two
![]() $(k+1)$
-point configurations
$(k+1)$
-point configurations
![]() $(x_1, \dots , x_{k+1}) \in E^{k+1}$
and
$(x_1, \dots , x_{k+1}) \in E^{k+1}$
and
![]() $(y_1, \dots , y_{k+1}) \in E^{k+1}$
such that the following conditions hold:
$(y_1, \dots , y_{k+1}) \in E^{k+1}$
such that the following conditions hold:
-
(1)
 $\lVert y_{i+1} - y_i \rVert = r \lVert x_{i+1} - x_i \rVert $
for
$\lVert y_{i+1} - y_i \rVert = r \lVert x_{i+1} - x_i \rVert $
for
 $i\in \{1,\dots ,k\}$
;
$i\in \{1,\dots ,k\}$
; -
(2)
 $x_i \neq x_j$
and
$x_i \neq x_j$
and
 $y_i \neq y_j\kern1pt$
for
$y_i \neq y_j\kern1pt$
for
 $1 \leq i < j \leq k+1$
.
$1 \leq i < j \leq k+1$
.
Corollary 1.4 easily follows from Theorem 1.3 by setting
![]() $A = \{(1, 2), \ldots , (k, k+1)\}$
. Corollary 1.4 generalises [Reference Rakhmonov10, Theorem 1.5]. Xie and Ge [Reference Xie and Ge11, Theorem 1.9] proved similar results, but only for paths of length
$A = \{(1, 2), \ldots , (k, k+1)\}$
. Corollary 1.4 generalises [Reference Rakhmonov10, Theorem 1.5]. Xie and Ge [Reference Xie and Ge11, Theorem 1.9] proved similar results, but only for paths of length
![]() $4$
with exponents
$4$
with exponents
![]() $d/2$
or
$d/2$
or
![]() $(2d+1)/3$
depending on d and q. We obtain the exponent
$(2d+1)/3$
depending on d and q. We obtain the exponent
![]() $d/2$
, which is exponentially better, and we also improve the constants.
$d/2$
, which is exponentially better, and we also improve the constants.
Corollary 1.5 (k-stars with a dilation ratio of
 $r \in (\mathbb {F}_q)^2$
).
$r \in (\mathbb {F}_q)^2$
).
Let
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $r \in (\mathbb {F}_q)^2 \setminus \{0\}$
and
$r \in (\mathbb {F}_q)^2 \setminus \{0\}$
and
![]() $E \subset \mathbb {F}_q^d$
such that
$E \subset \mathbb {F}_q^d$
such that
![]() $|E| \geq 2kq^{d/2}$
. Then, there exist two
$|E| \geq 2kq^{d/2}$
. Then, there exist two
![]() $(k+1)$
-point configurations
$(k+1)$
-point configurations
![]() $(x_1, \dots , x_{k+1}) \in E^{k+1}$
and
$(x_1, \dots , x_{k+1}) \in E^{k+1}$
and
![]() $(y_1, \dots , y_{k+1}) \in E^{k+1}$
such that the following conditions hold:
$(y_1, \dots , y_{k+1}) \in E^{k+1}$
such that the following conditions hold:
-
(1)
 $\lVert y_{i} - y_1 \rVert = r \lVert x_{i} - x_1 \rVert $
for
$\lVert y_{i} - y_1 \rVert = r \lVert x_{i} - x_1 \rVert $
for
 $i\in \{2,\dots ,k+1\}$
;
$i\in \{2,\dots ,k+1\}$
; -
(2)
 $x_i \neq x_j$
and
$x_i \neq x_j$
and
 $y_i \neq y_j$
for
$y_i \neq y_j$
for
 $1 \leq i < j \leq k+1$
.
$1 \leq i < j \leq k+1$
.
Corollary 1.5 easily follows from Theorem 1.3 by setting
![]() $A = \{(1, 2), \ldots , (1, k+1)\}$
. Corollary 1.5 improves the constants of [Reference Xie and Ge11, Theorem 1.8]. There, the constants depend on k quadratically, whereas in our result, the dependence on k is linear.
$A = \{(1, 2), \ldots , (1, k+1)\}$
. Corollary 1.5 improves the constants of [Reference Xie and Ge11, Theorem 1.8]. There, the constants depend on k quadratically, whereas in our result, the dependence on k is linear.
The rest of this paper will focus on proving Theorem 1.3.
2 Notation
We recall some basic notation which we will use throughout the paper.
Let
![]() $\mathrm {O}_d(\mathbb {F}_q)$
denote the group of orthogonal
$\mathrm {O}_d(\mathbb {F}_q)$
denote the group of orthogonal
![]() $d\times d$
matrices with entries in
$d\times d$
matrices with entries in
![]() $\mathbb {F}_q$
.
$\mathbb {F}_q$
.
Let
![]() $\mathbb {F}_q^*$
denote the set of nonzero elements in
$\mathbb {F}_q^*$
denote the set of nonzero elements in
![]() $\mathbb {F}_q$
, that is,
$\mathbb {F}_q$
, that is,
![]() $\mathbb {F}^*_q=\big \{a\in \mathbb {F}_q: a\neq 0 \big \}$
.
$\mathbb {F}^*_q=\big \{a\in \mathbb {F}_q: a\neq 0 \big \}$
.
Let
![]() $(\mathbb {F}_q)^2$
denote the set of quadratic residues in
$(\mathbb {F}_q)^2$
denote the set of quadratic residues in
![]() $\mathbb {F}_q$
, that is,
$\mathbb {F}_q$
, that is,
![]() $(\mathbb {F}_q)^2=\big \{a^2: a\in \mathbb {F}_q \big \}$
.
$(\mathbb {F}_q)^2=\big \{a^2: a\in \mathbb {F}_q \big \}$
.
Define the map
![]() $\lVert \cdot \rVert : \mathbb {F}_q^d \to \mathbb {F}_q$
by
$\lVert \cdot \rVert : \mathbb {F}_q^d \to \mathbb {F}_q$
by ![]() , where
, where
![]() $\alpha = (\alpha _1, \ldots , \alpha _d) \in \mathbb {F}_q^d$
. This map is not a norm, as we do not impose a metric structure on
$\alpha = (\alpha _1, \ldots , \alpha _d) \in \mathbb {F}_q^d$
. This map is not a norm, as we do not impose a metric structure on
![]() $\mathbb {F}_q^d$
. However, it shares an important property with the Euclidean norm: it is invariant under orthogonal transformations.
$\mathbb {F}_q^d$
. However, it shares an important property with the Euclidean norm: it is invariant under orthogonal transformations.
If X is a finite set, let
![]() $|X|$
denote its cardinality.
$|X|$
denote its cardinality.
3 First proof of Theorem 1.3
Let
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $\varnothing \neq A \subset \{(i, j) : 1 \leq i < j \leq k + 1\}$
. For
$\varnothing \neq A \subset \{(i, j) : 1 \leq i < j \leq k + 1\}$
. For
![]() $r \in (\mathbb {F}_q)^2 \setminus \{0\}$
,
$r \in (\mathbb {F}_q)^2 \setminus \{0\}$
,
![]() $z \in \mathbb {F}_q^d$
and
$z \in \mathbb {F}_q^d$
and
![]() $\theta \in \mathrm {O}_d(\mathbb {F}_q)$
, define the counting function:
$\theta \in \mathrm {O}_d(\mathbb {F}_q)$
, define the counting function:
For
![]() $p \geq 1$
, we define the
$p \geq 1$
, we define the
![]() $L^p$
-norm of
$L^p$
-norm of
![]() $\lambda _{r,\theta }(z)$
as follows:
$\lambda _{r,\theta }(z)$
as follows:

From (3.1),
Then, we obtain
 $$ \begin{align*} & \lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1} =\sum_{\theta,z}\lvert\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: u_i-\sqrt{r}\theta v_i=z,\ i\in [k+1]\}\rvert\\ & =\sum_{\theta}\lvert\big\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: u_i-u_j=\sqrt{r}\theta (v_i-v_j),\ 1\leq i< j\leq k+1 \big\}\rvert. \end{align*} $$
$$ \begin{align*} & \lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1} =\sum_{\theta,z}\lvert\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: u_i-\sqrt{r}\theta v_i=z,\ i\in [k+1]\}\rvert\\ & =\sum_{\theta}\lvert\big\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: u_i-u_j=\sqrt{r}\theta (v_i-v_j),\ 1\leq i< j\leq k+1 \big\}\rvert. \end{align*} $$
Let us introduce the notation:
With this notation, one can express the
![]() $L^{k+1}$
-norm of the function
$L^{k+1}$
-norm of the function
![]() $\lambda _{r,\theta }(z)$
in terms of
$\lambda _{r,\theta }(z)$
in terms of
![]() $|\Lambda _{\theta }(r)|$
:
$|\Lambda _{\theta }(r)|$
:
 $$ \begin{align*} \lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1}=\sum_{\theta\in \mathrm{O}_d(\mathbb{F}_q)}|\Lambda_{\theta}(r)|. \end{align*} $$
$$ \begin{align*} \lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1}=\sum_{\theta\in \mathrm{O}_d(\mathbb{F}_q)}|\Lambda_{\theta}(r)|. \end{align*} $$
Let us consider the auxiliary sets:
 $$ \begin{align*} \mathcal{N}_{A,\theta}(r)& :=\bigg\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: \begin{array}{l} u_i-u_{j}=\sqrt{r}\theta(v_i-v_j),\ (i,j)\in A,\\ v_i\neq v_j,\ 1\leq i< j\leq k+1\end{array}\!\!\bigg\}, \\ \mathcal{N}_{\theta}(r)& :=\bigg\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: \begin{array}{l} u_i-u_{j}=\sqrt{r}\theta(v_i-v_j),\\ v_i\neq v_j,\ 1\leq i<j\leq k+1\end{array}\!\!\bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{N}_{A,\theta}(r)& :=\bigg\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: \begin{array}{l} u_i-u_{j}=\sqrt{r}\theta(v_i-v_j),\ (i,j)\in A,\\ v_i\neq v_j,\ 1\leq i< j\leq k+1\end{array}\!\!\bigg\}, \\ \mathcal{N}_{\theta}(r)& :=\bigg\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: \begin{array}{l} u_i-u_{j}=\sqrt{r}\theta(v_i-v_j),\\ v_i\neq v_j,\ 1\leq i<j\leq k+1\end{array}\!\!\bigg\}. \end{align*} $$
To prove Theorem 1.3, we need to show that
![]() $\lvert \mathcal {S}_A\rvert>0$
, where
$\lvert \mathcal {S}_A\rvert>0$
, where
It is easy to verify that
![]() $\mathcal {N}_{A,\theta }(r)\subset \mathcal {S}_A$
for each
$\mathcal {N}_{A,\theta }(r)\subset \mathcal {S}_A$
for each
![]() $\theta \in \mathrm {O}_d(\mathbb {F}_q)$
and hence
$\theta \in \mathrm {O}_d(\mathbb {F}_q)$
and hence
 $$ \begin{align} \lvert \mathcal{S}_A\rvert\geq \frac{1}{\lvert \mathrm{O}_d(\mathbb{F}_q)\rvert}\sum_{\theta\in \mathrm{O}_d(\mathbb{F}_q)}|\mathcal{N}_{A,\theta}(r)|. \end{align} $$
$$ \begin{align} \lvert \mathcal{S}_A\rvert\geq \frac{1}{\lvert \mathrm{O}_d(\mathbb{F}_q)\rvert}\sum_{\theta\in \mathrm{O}_d(\mathbb{F}_q)}|\mathcal{N}_{A,\theta}(r)|. \end{align} $$
Since
![]() $\mathcal {N}_{\theta }(r)\subset \mathcal {N}_{A,\theta }(r)$
for each
$\mathcal {N}_{\theta }(r)\subset \mathcal {N}_{A,\theta }(r)$
for each
![]() $\theta \in \mathrm {O}_d(\mathbb {F}_q)$
, (3.2) yields
$\theta \in \mathrm {O}_d(\mathbb {F}_q)$
, (3.2) yields
 $$ \begin{align} \lvert \mathcal{S}_A\rvert\geq \frac{1}{\lvert \mathrm{O}_d(\mathbb{F}_q)\rvert}\sum_{\theta\in \mathrm{O}_d(\mathbb{F}_q)}|\mathcal{N}_{\theta}(r)|. \end{align} $$
$$ \begin{align} \lvert \mathcal{S}_A\rvert\geq \frac{1}{\lvert \mathrm{O}_d(\mathbb{F}_q)\rvert}\sum_{\theta\in \mathrm{O}_d(\mathbb{F}_q)}|\mathcal{N}_{\theta}(r)|. \end{align} $$
For each pair
![]() $(\alpha ,\beta )$
such that
$(\alpha ,\beta )$
such that
![]() $1\leq \alpha <\beta \leq k+1$
, we define
$1\leq \alpha <\beta \leq k+1$
, we define
 $$ \begin{align*} A_{\alpha,\beta}:=\bigg\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: \begin{array}{l} u_i-u_{j}=\sqrt{r}\theta(v_i-v_j),\\ 1\leq i<j\leq k+1,\ v_{\alpha}=v_{\beta}\end{array}\!\!\bigg\}. \end{align*} $$
$$ \begin{align*} A_{\alpha,\beta}:=\bigg\{(u_1,\dots,u_{k+1},v_1,\dots,v_{k+1})\in E^{2k+2}: \begin{array}{l} u_i-u_{j}=\sqrt{r}\theta(v_i-v_j),\\ 1\leq i<j\leq k+1,\ v_{\alpha}=v_{\beta}\end{array}\!\!\bigg\}. \end{align*} $$
From the set equality
 $$ \begin{align*} \Lambda_{\theta}(r)\setminus \bigcup_{1\leq \alpha<\beta\leq k+1}A_{\alpha,\beta}=\mathcal{N}_{\theta}(r), \end{align*} $$
$$ \begin{align*} \Lambda_{\theta}(r)\setminus \bigcup_{1\leq \alpha<\beta\leq k+1}A_{\alpha,\beta}=\mathcal{N}_{\theta}(r), \end{align*} $$
we obtain
 $$ \begin{align} |\mathcal{N}_{\theta}(r)|\geq |\Lambda_{\theta}(r)|-\sum \limits_{1\leq \alpha<\beta\leq k+1}|A_{\alpha,\beta}|. \end{align} $$
$$ \begin{align} |\mathcal{N}_{\theta}(r)|\geq |\Lambda_{\theta}(r)|-\sum \limits_{1\leq \alpha<\beta\leq k+1}|A_{\alpha,\beta}|. \end{align} $$
One can verify that, for
![]() $(\alpha ,\beta )$
with
$(\alpha ,\beta )$
with
![]() $1\leq \alpha <\beta \leq k+1$
,
$1\leq \alpha <\beta \leq k+1$
,
 $$ \begin{align} |A_{\alpha,\beta}|=\sum \limits_{z\in \mathbb{F}_q^d}\lambda_{r,\theta}(z)^k. \end{align} $$
$$ \begin{align} |A_{\alpha,\beta}|=\sum \limits_{z\in \mathbb{F}_q^d}\lambda_{r,\theta}(z)^k. \end{align} $$
Substituting (3.5) into (3.4}, we obtain
 $$ \begin{align} |\mathcal{N}_{\theta}(r)|\geq |\Lambda_{\theta}(r)|-\binom{k+1}{2}\sum \limits_{z\in \mathbb{F}_q^d}\lambda_{r,\theta}(z)^k. \end{align} $$
$$ \begin{align} |\mathcal{N}_{\theta}(r)|\geq |\Lambda_{\theta}(r)|-\binom{k+1}{2}\sum \limits_{z\in \mathbb{F}_q^d}\lambda_{r,\theta}(z)^k. \end{align} $$
Summing (3.6) over all
![]() $\theta \in \mathrm {O}_d(\mathbb {F}_q)$
yields
$\theta \in \mathrm {O}_d(\mathbb {F}_q)$
yields
 $$ \begin{align} \sum \limits_{\theta}|\mathcal{N}_{\theta}(r)|\geq \sum \limits_{\theta}|\Lambda_{\theta}(r)|-\binom{k+1}{2}\sum \limits_{\theta,z}\lambda_{r,\theta}(z)^k. \end{align} $$
$$ \begin{align} \sum \limits_{\theta}|\mathcal{N}_{\theta}(r)|\geq \sum \limits_{\theta}|\Lambda_{\theta}(r)|-\binom{k+1}{2}\sum \limits_{\theta,z}\lambda_{r,\theta}(z)^k. \end{align} $$
 $$ \begin{align} |\mathcal{S}_A|\geq \frac{1}{|\mathrm{O}_d(\mathbb{F}_q)|}\bigg(\lVert{\lambda_{r,\theta}(z)\rVert}_{k+1}^{k+1}-\binom{k+1}{2}\lVert{\lambda_{r,\theta}(z)\rVert}_{k}^{k}\bigg). \end{align} $$
$$ \begin{align} |\mathcal{S}_A|\geq \frac{1}{|\mathrm{O}_d(\mathbb{F}_q)|}\bigg(\lVert{\lambda_{r,\theta}(z)\rVert}_{k+1}^{k+1}-\binom{k+1}{2}\lVert{\lambda_{r,\theta}(z)\rVert}_{k}^{k}\bigg). \end{align} $$
Note that the lower bound for the size of
![]() $\mathcal {S}_A$
is independent of A. This is a key aspect of the result being proven.
$\mathcal {S}_A$
is independent of A. This is a key aspect of the result being proven.
Now, we will demonstrate that if
![]() $\lvert E\rvert \geq C_k q^{d/2}$
, then
$\lvert E\rvert \geq C_k q^{d/2}$
, then
![]() $\lvert \mathcal {S}_{A}\rvert> 0$
. By applying Hölder’s inequality, we can establish a lower bound for the
$\lvert \mathcal {S}_{A}\rvert> 0$
. By applying Hölder’s inequality, we can establish a lower bound for the
![]() $L^{k+1}$
-norm of
$L^{k+1}$
-norm of
![]() $\lambda _{r,\theta }(z)$
, namely
$\lambda _{r,\theta }(z)$
, namely
 $$ \begin{align} \sum_{\theta,z}\lambda_{r,\theta}(z)^{k+1}\geq \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert\cdot \frac{|E|^{2k+2}}{q^{dk}}. \end{align} $$
$$ \begin{align} \sum_{\theta,z}\lambda_{r,\theta}(z)^{k+1}\geq \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert\cdot \frac{|E|^{2k+2}}{q^{dk}}. \end{align} $$
The second term in (3.8) can be divided into two separate sums, where the terms are categorised as either ‘small’ or ‘large’. More precisely,
where the parameter
![]() $c\in \mathbb {R}_{\geq 0}$
will be chosen later. Combining (3.10) with (3.8), we obtain the lower bound:
$c\in \mathbb {R}_{\geq 0}$
will be chosen later. Combining (3.10) with (3.8), we obtain the lower bound:
 $$ \begin{align} \lvert\mathcal{S}_A\rvert\geq \frac{1}{\lvert \mathrm{O}_d(\mathbb{F}_q)\rvert} \big(\mathcal{S}_1+\mathcal{S}_2\big), \end{align} $$
$$ \begin{align} \lvert\mathcal{S}_A\rvert\geq \frac{1}{\lvert \mathrm{O}_d(\mathbb{F}_q)\rvert} \big(\mathcal{S}_1+\mathcal{S}_2\big), \end{align} $$
where
 $$ \begin{align*} \mathcal{S}_1=\frac{1}{2}\lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1}-\binom{k+1}{2}\sum_{\lambda\geq c}\lambda_{r,\theta}(z)^k, \end{align*} $$
$$ \begin{align*} \mathcal{S}_1=\frac{1}{2}\lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1}-\binom{k+1}{2}\sum_{\lambda\geq c}\lambda_{r,\theta}(z)^k, \end{align*} $$
 $$ \begin{align*} \mathcal{S}_2=\frac{1}{2}\lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1}-\binom{k+1}{2}\sum_{\lambda< c}\lambda_{r,\theta}(z)^k. \end{align*} $$
$$ \begin{align*} \mathcal{S}_2=\frac{1}{2}\lVert \lambda_{r,\theta}(z)\rVert_{k+1}^{k+1}-\binom{k+1}{2}\sum_{\lambda< c}\lambda_{r,\theta}(z)^k. \end{align*} $$
By using the definition of the
![]() $L^{k+1}$
-norm of
$L^{k+1}$
-norm of
![]() $\lambda _{r,\theta }(z)$
, we can establish the following lower bound for
$\lambda _{r,\theta }(z)$
, we can establish the following lower bound for
![]() $\mathcal {S}_1$
:
$\mathcal {S}_1$
:
 $$ \begin{align*} \mathcal{S}_1\geq \frac{1}{2}\bigg(\sum_{\lambda\geq c}\lambda_{r,\theta}(z)^{k+1}-k(k+1)\sum_{\lambda\geq c}\lambda_{r,\theta}(z)^{k}\bigg) =\frac{1}{2}\bigg(\sum_{\lambda \geq c} \lambda_{r,\theta}(z)^k(\lambda_{r,\theta}(z)-k(k+1))\bigg). \end{align*} $$
$$ \begin{align*} \mathcal{S}_1\geq \frac{1}{2}\bigg(\sum_{\lambda\geq c}\lambda_{r,\theta}(z)^{k+1}-k(k+1)\sum_{\lambda\geq c}\lambda_{r,\theta}(z)^{k}\bigg) =\frac{1}{2}\bigg(\sum_{\lambda \geq c} \lambda_{r,\theta}(z)^k(\lambda_{r,\theta}(z)-k(k+1))\bigg). \end{align*} $$
Choosing
![]() $c = k(k+1)$
shows that
$c = k(k+1)$
shows that
![]() $\mathcal {S}_1 \geq 0$
.
$\mathcal {S}_1 \geq 0$
.
Next, we estimate
![]() $\mathcal {S}_2$
: for the first term, we use (3.9), and for the second term, we provide a straightforward estimate. Thus,
$\mathcal {S}_2$
: for the first term, we use (3.9), and for the second term, we provide a straightforward estimate. Thus,
 $$ \begin{align} \mathcal{S}_2&\geq \frac{|E|^{2k+2}}{2q^{dk}}\cdot \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert-\binom{k+1}{2}\sum_{\lambda<c}\lambda_{r,\theta}(z)^k \nonumber\\& \geq \frac{|E|^{2k+2}}{2q^{dk}}\cdot \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert - c^k\binom{k+1}{2}\sum_{\theta, z} 1 \nonumber\\& \geq \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert \bigg(\frac{|E|^{2k+2}}{2q^{dk}}-\frac{(k^2+k)^{k+1}q^d}{2}\bigg). \end{align} $$
$$ \begin{align} \mathcal{S}_2&\geq \frac{|E|^{2k+2}}{2q^{dk}}\cdot \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert-\binom{k+1}{2}\sum_{\lambda<c}\lambda_{r,\theta}(z)^k \nonumber\\& \geq \frac{|E|^{2k+2}}{2q^{dk}}\cdot \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert - c^k\binom{k+1}{2}\sum_{\theta, z} 1 \nonumber\\& \geq \lvert \mathrm{O}_d(\mathbb{F}_q)\rvert \bigg(\frac{|E|^{2k+2}}{2q^{dk}}-\frac{(k^2+k)^{k+1}q^d}{2}\bigg). \end{align} $$
We note that
![]() $\lvert \mathrm {O}_d(\mathbb {F}_q) \rvert> 0$
. By combining this observation with the inequalities
$\lvert \mathrm {O}_d(\mathbb {F}_q) \rvert> 0$
. By combining this observation with the inequalities
![]() $\mathcal {S}_1 \geq 0$
as well as (3.12) and (3.11), we obtain
$\mathcal {S}_1 \geq 0$
as well as (3.12) and (3.11), we obtain
 $$ \begin{align*} \lvert \mathcal{S}_A \rvert \geq \frac{|E|^{2k+2}}{2q^{dk}} - \frac{(k^2+k)^{k+1}q^d}{2}. \end{align*} $$
$$ \begin{align*} \lvert \mathcal{S}_A \rvert \geq \frac{|E|^{2k+2}}{2q^{dk}} - \frac{(k^2+k)^{k+1}q^d}{2}. \end{align*} $$
It is not difficult to verify that if
![]() $\lvert E \rvert \geq 2k q^{d/2}$
, then
$\lvert E \rvert \geq 2k q^{d/2}$
, then
![]() $\lvert \mathcal {S}_A \rvert> 0$
, which completes the proof of Theorem 1.3.
$\lvert \mathcal {S}_A \rvert> 0$
, which completes the proof of Theorem 1.3.
4 Second proof of Theorem 1.3
In this section, we will prove Theorem 1.3 using elementary combinatorial arguments.
Suppose
![]() $E\subset \mathbb {F}_q^d$
and
$E\subset \mathbb {F}_q^d$
and
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
, so
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
, so
![]() $r=t^2$
where
$r=t^2$
where
![]() $t\neq 0$
. For such t, define
$t\neq 0$
. For such t, define
![]() $tE$
as
$tE$
as
![]() $tE = \{tv : v\in E\}$
.
$tE = \{tv : v\in E\}$
.
Now, consider the set:
We will use double counting to determine the cardinality of H. First,
 $$ \begin{align} \lvert H\rvert =\sum_{x\in tE}\sum_{\substack{a\in \mathbb{F}_q^d \\ x\in E+a}}1=\sum_{x\in tE}\sum_{\substack{a\in \mathbb{F}_q^d \\ a\in x-E}}1 =\sum_{x\in tE}\lvert x-E \rvert=\sum_{x\in tE}\lvert E\rvert =\lvert tE\rvert \lvert E\rvert=\lvert E\rvert^2. \end{align} $$
$$ \begin{align} \lvert H\rvert =\sum_{x\in tE}\sum_{\substack{a\in \mathbb{F}_q^d \\ x\in E+a}}1=\sum_{x\in tE}\sum_{\substack{a\in \mathbb{F}_q^d \\ a\in x-E}}1 =\sum_{x\in tE}\lvert x-E \rvert=\sum_{x\in tE}\lvert E\rvert =\lvert tE\rvert \lvert E\rvert=\lvert E\rvert^2. \end{align} $$
However, by changing the order of variables,
 $$ \begin{align} \lvert H\rvert =\sum_{a\in \mathbb{F}_q^d}\sum_{\substack{x\in tE \\ x\in E+a}}1 =\sum_{a\in \mathbb{F}_q^d}\lvert tE\cap (E+a)\rvert. \end{align} $$
$$ \begin{align} \lvert H\rvert =\sum_{a\in \mathbb{F}_q^d}\sum_{\substack{x\in tE \\ x\in E+a}}1 =\sum_{a\in \mathbb{F}_q^d}\lvert tE\cap (E+a)\rvert. \end{align} $$
Comparing (4.1) with (4.2) yields
 $$ \begin{align*} \sum_{a\in \mathbb{F}_q^d}\lvert tE\cap (E+a)\rvert=\lvert E\rvert^2. \end{align*} $$
$$ \begin{align*} \sum_{a\in \mathbb{F}_q^d}\lvert tE\cap (E+a)\rvert=\lvert E\rvert^2. \end{align*} $$
Therefore,
 $$ \begin{align*} \max_{a\in \mathbb{F}_q^d}\lvert tE\cap (E+a)\rvert\geq \frac{\lvert E\rvert^2}{q^d}. \end{align*} $$
$$ \begin{align*} \max_{a\in \mathbb{F}_q^d}\lvert tE\cap (E+a)\rvert\geq \frac{\lvert E\rvert^2}{q^d}. \end{align*} $$
We observe that if
![]() $\lvert E \rvert \geq \sqrt {k+1}q^{d/2}$
, then
$\lvert E \rvert \geq \sqrt {k+1}q^{d/2}$
, then
![]() $\max_{a\in \mathbb{F}_q^d} \lvert tE \cap (E + a) \rvert \geq k + 1$
. Thus, there exists an element
$\max_{a\in \mathbb{F}_q^d} \lvert tE \cap (E + a) \rvert \geq k + 1$
. Thus, there exists an element
![]() $a \in \mathbb {F}_q^d$
such that
$a \in \mathbb {F}_q^d$
such that
![]() $\lvert tE \cap (E + a) \rvert \geq k+1$
. Consequently, we can establish the existence of a sequence
$\lvert tE \cap (E + a) \rvert \geq k+1$
. Consequently, we can establish the existence of a sequence
![]() $\{z_1,\dots ,z_{k+1}\}$
such that
$\{z_1,\dots ,z_{k+1}\}$
such that
![]() $\{z_1,\dots ,z_{k+1}\}\subset tE \cap (E + a)$
. This implies the existence of sequences
$\{z_1,\dots ,z_{k+1}\}\subset tE \cap (E + a)$
. This implies the existence of sequences
![]() $\{x_1,\dots ,x_{k+1}\} \subset E$
and
$\{x_1,\dots ,x_{k+1}\} \subset E$
and
![]() $\{y_1,\dots ,y_{k+1}\} \subset E$
, such that
$\{y_1,\dots ,y_{k+1}\} \subset E$
, such that
![]() $z_i = tx_i$
and
$z_i = tx_i$
and
![]() $z_i = y_i + a$
for
$z_i = y_i + a$
for
![]() $1\leq i\leq k+1$
.
$1\leq i\leq k+1$
.
In summary, we have demonstrated the existence of
![]() $(k+1)$
-tuples
$(k+1)$
-tuples
![]() $(x_1, \ldots , x_{k+1}) \in E^{k+1}$
and
$(x_1, \ldots , x_{k+1}) \in E^{k+1}$
and
![]() $(y_1, \ldots , y_{k+1}) \in E^{k+1}$
satisfying the conditions:
$(y_1, \ldots , y_{k+1}) \in E^{k+1}$
satisfying the conditions:
-
(1)
 $x_i \neq x_j, y_i\neq y_j$
for
$x_i \neq x_j, y_i\neq y_j$
for
 $1 \leq i < j \leq k+1$
;
$1 \leq i < j \leq k+1$
; -
(2)
 $y_i + a = tx_i$
for
$y_i + a = tx_i$
for
 $i \in \{1, \ldots , k+1\}$
.
$i \in \{1, \ldots , k+1\}$
.
Therefore, for
![]() $1\leq i<j\leq k+1$
,
$1\leq i<j\leq k+1$
,
Since A is a nonempty subset of
![]() $\{(i, j) : 1 \leq i < j \leq k+1\}$
, we have demonstrated the existence of two
$\{(i, j) : 1 \leq i < j \leq k+1\}$
, we have demonstrated the existence of two
![]() $(k+1)$
-point configurations:
$(k+1)$
-point configurations:
![]() $(x_1, \ldots , x_{k+1}) \in E^{k+1}$
and
$(x_1, \ldots , x_{k+1}) \in E^{k+1}$
and
![]() $(y_1, \ldots , y_{k+1}) \in E^{k+1}$
satisfying:
$(y_1, \ldots , y_{k+1}) \in E^{k+1}$
satisfying:
-
(1)
 $x_i \neq x_j$
and
$x_i \neq x_j$
and
 $y_i \neq y_j$
for
$y_i \neq y_j$
for
 $1 \leq i < j \leq k+1$
;
$1 \leq i < j \leq k+1$
; -
(2)
 $\lVert y_i - y_j \rVert = r \lVert x_i - x_j \rVert $
for
$\lVert y_i - y_j \rVert = r \lVert x_i - x_j \rVert $
for
 $(i, j) \in A$
.
$(i, j) \in A$
.
This completes the proof of Theorem 1.3.
5 Corollaries
In this section, we will explore some interesting corollaries that follow from Theorem 1.3. For simplicity, we assume a two-dimensional scenario, that is,
![]() $d = 2$
.
$d = 2$
.
5.1 Paths of length k
Let
![]() $k\geq 2$
and fix any element
$k\geq 2$
and fix any element
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
. Taking
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
. Taking
![]() $A=\{(1,2),\dots ,(k,k+1)\}$
, we can see that if
$A=\{(1,2),\dots ,(k,k+1)\}$
, we can see that if
![]() $E\subset \mathbb {F}_q^2$
with
$E\subset \mathbb {F}_q^2$
with
![]() $\lvert E\rvert \geq 2kq$
, then we can find two k-paths in E, that is,
$\lvert E\rvert \geq 2kq$
, then we can find two k-paths in E, that is,
![]() $(x_1,\dots ,x_{k+1})\in E^{k+1}$
and
$(x_1,\dots ,x_{k+1})\in E^{k+1}$
and
![]() $(y_1,\dots ,y_{k+1})\in E^{k+1}$
, such that
$(y_1,\dots ,y_{k+1})\in E^{k+1}$
, such that
![]() $x_i\neq x_j$
and
$x_i\neq x_j$
and
![]() $y_i\neq y_j$
for
$y_i\neq y_j$
for
![]() $1\leq i<j\leq k+1$
, and
$1\leq i<j\leq k+1$
, and
![]() $\lVert y_i-y_{i+1}\rVert =r\lVert x_i-x_{i+1}\rVert $
for
$\lVert y_i-y_{i+1}\rVert =r\lVert x_i-x_{i+1}\rVert $
for
![]() $i\in \{1,\dots ,k\}$
(see Figure 2).
$i\in \{1,\dots ,k\}$
(see Figure 2).
5.2 Cycles of length k
Assuming that
![]() $k\geq 3$
, for k-cycles, one needs to take
$k\geq 3$
, for k-cycles, one needs to take
![]() $A=\{(1,2),\dots ,(k-1,k), (k,1)\}$
. Then, we can see that for
$A=\{(1,2),\dots ,(k-1,k), (k,1)\}$
. Then, we can see that for
![]() $E\subset \mathbb {F}_q^2$
with
$E\subset \mathbb {F}_q^2$
with
![]() $\lvert E\rvert \geq 2kq$
, there exist k-cycles in E. That is, there exist
$\lvert E\rvert \geq 2kq$
, there exist k-cycles in E. That is, there exist
![]() $(x_1,\dots ,x_k)\in E^k$
and
$(x_1,\dots ,x_k)\in E^k$
and
![]() $(y_1,\dots ,y_k)\in E^k$
such that
$(y_1,\dots ,y_k)\in E^k$
such that
![]() $x_i\neq x_j$
and
$x_i\neq x_j$
and
![]() $y_i\neq y_j$
for
$y_i\neq y_j$
for
![]() $1\leq i<j\leq k$
, and
$1\leq i<j\leq k$
, and
![]() $\lVert y_i-y_{i+1}\rVert =r\lVert x_i-x_{i+1}\rVert $
for
$\lVert y_i-y_{i+1}\rVert =r\lVert x_i-x_{i+1}\rVert $
for
![]() $i\in \{1,\dots , k-1\}$
, and
$i\in \{1,\dots , k-1\}$
, and
![]() $\lVert y_k-y_{1}\rVert =r\lVert x_k-x_{1}\rVert $
(see Figure 3).
$\lVert y_k-y_{1}\rVert =r\lVert x_k-x_{1}\rVert $
(see Figure 3).

Figure 2 6-paths with a dilation ratio of
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
.
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
.

Figure 3 6-cycles with a dilation ratio of
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
.
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
.
5.3 Stars with k edges
Assuming that
![]() $k\geq 1$
, for k-stars, one needs to take
$k\geq 1$
, for k-stars, one needs to take
![]() $A=\{(1,2),\dots , (1,k+1)\}$
. Then, for
$A=\{(1,2),\dots , (1,k+1)\}$
. Then, for
![]() $E\subset \mathbb {F}_q^2$
with
$E\subset \mathbb {F}_q^2$
with
![]() $|E|\geq 2k q$
, there exist k-stars in E. That is, there exist
$|E|\geq 2k q$
, there exist k-stars in E. That is, there exist
![]() $(x_1,\dots ,x_{k+1})\in E^{k+1}$
and
$(x_1,\dots ,x_{k+1})\in E^{k+1}$
and
![]() $(y_1,\dots ,y_{k+1})\in E^{k+1}$
such that
$(y_1,\dots ,y_{k+1})\in E^{k+1}$
such that
![]() $x_i\neq x_j$
and
$x_i\neq x_j$
and
![]() $y_i\neq y_j$
for
$y_i\neq y_j$
for
![]() $1\leq i<j\leq k+1$
, and
$1\leq i<j\leq k+1$
, and
![]() $\lVert y_1-y_i\rVert =r\lVert x_1-x_i\rVert $
for
$\lVert y_1-y_i\rVert =r\lVert x_1-x_i\rVert $
for
![]() $i\in \{2,\dots ,k+1\}$
(see Figure 4).
$i\in \{2,\dots ,k+1\}$
(see Figure 4).

Figure 4 5-stars with a dilation ratio of
![]() $r\in (\mathbb {F}_q)^2\setminus \{0\}$
.
$r\in (\mathbb {F}_q)^2\setminus \{0\}$
.
6 Sharp examples
In this section, we will demonstrate that in dimension 2, the exponent
![]() $d/2$
in Theorem 1.3 is optimal under certain mild conditions.
$d/2$
in Theorem 1.3 is optimal under certain mild conditions.
6.1 The case when
 $\lvert A\rvert \geq 1$
$\lvert A\rvert \geq 1$
In this setting, we will demonstrate that if
![]() $q=p^{2\ell }$
with
$q=p^{2\ell }$
with
![]() $p\equiv 3 \pmod 4$
and
$p\equiv 3 \pmod 4$
and
![]() $\ell \equiv 1 \pmod 2$
, the exponent
$\ell \equiv 1 \pmod 2$
, the exponent
![]() $d/2$
in Theorem 1.3 is optimal.
$d/2$
in Theorem 1.3 is optimal.
The ambient space is
![]() $\mathbb {F}_{p^{2\ell }}^{2}$
, a
$\mathbb {F}_{p^{2\ell }}^{2}$
, a
![]() $2$
-dimensional vector space over the finite field
$2$
-dimensional vector space over the finite field
![]() $\mathbb {F}_{p^{2\ell }}$
with
$\mathbb {F}_{p^{2\ell }}$
with
![]() $p^{2\ell }$
elements. The field
$p^{2\ell }$
elements. The field
![]() $\mathbb {F}_{p^{2\ell }}$
contains the subfield
$\mathbb {F}_{p^{2\ell }}$
contains the subfield
![]() $\mathbb {F}_{p^{\ell }}$
with
$\mathbb {F}_{p^{\ell }}$
with
![]() $p^{\ell }$
elements. Consider the subset
$p^{\ell }$
elements. Consider the subset ![]() of
of
![]() $\mathbb {F}_{p^{2\ell }}^{2}$
and observe that
$\mathbb {F}_{p^{2\ell }}^{2}$
and observe that
![]() $\lvert E\rvert =q$
.
$\lvert E\rvert =q$
.
We know that
![]() $\lvert (\mathbb {F}_{p^{2\ell }})^2\setminus \{0\}\rvert =\tfrac 12(p^{2\ell }-1)>p^{\ell }=\lvert \mathbb {F}_{p^{\ell }}\rvert $
, and one can always choose
$\lvert (\mathbb {F}_{p^{2\ell }})^2\setminus \{0\}\rvert =\tfrac 12(p^{2\ell }-1)>p^{\ell }=\lvert \mathbb {F}_{p^{\ell }}\rvert $
, and one can always choose
![]() $r\in (\mathbb {F}_{p^{2\ell }})^2$
such that
$r\in (\mathbb {F}_{p^{2\ell }})^2$
such that
![]() $r\notin \mathbb {F}_{p^{\ell }}$
. Then, for any
$r\notin \mathbb {F}_{p^{\ell }}$
. Then, for any
![]() $x_i,x_j,y_i,y_j\in E$
such that
$x_i,x_j,y_i,y_j\in E$
such that
![]() $x_i\neq x_j$
and
$x_i\neq x_j$
and
![]() $y_i\neq y_j$
, we have
$y_i\neq y_j$
, we have
 $$ \begin{align*} \frac{\lVert y_i-y_j \rVert}{\lVert x_i-x_j\rVert} \in \mathbb{F}_{p^{\ell}}. \end{align*} $$
$$ \begin{align*} \frac{\lVert y_i-y_j \rVert}{\lVert x_i-x_j\rVert} \in \mathbb{F}_{p^{\ell}}. \end{align*} $$
Here, we have used the fact that
![]() $\lVert x\rVert =0$
if and only if
$\lVert x\rVert =0$
if and only if
![]() $x=(0,0)$
, which is true since
$x=(0,0)$
, which is true since
![]() $p\equiv 3 \pmod 4$
and
$p\equiv 3 \pmod 4$
and
![]() $\ell \equiv 1 \pmod 2$
. However, r was chosen such that
$\ell \equiv 1 \pmod 2$
. However, r was chosen such that
![]() $r\notin \mathbb {F}_{p^{\ell }}$
. This observation demonstrates that the exponent
$r\notin \mathbb {F}_{p^{\ell }}$
. This observation demonstrates that the exponent
![]() $d/2$
is optimal in this setting.
$d/2$
is optimal in this setting.
6.2 The case when A contains
 $(a,b),(a,c),(b,c)$
$(a,b),(a,c),(b,c)$
In this scenario, we will establish that if
![]() $q\equiv 3 \pmod {4}$
, then the exponent
$q\equiv 3 \pmod {4}$
, then the exponent
![]() $d/2$
is the optimal exponent in Theorem 1.3.
$d/2$
is the optimal exponent in Theorem 1.3.
Without loss of generality, assume that
![]() $(1,2),(1,3),(2,3)\in A$
, and let
$(1,2),(1,3),(2,3)\in A$
, and let
![]() $r\in (\mathbb {F}_q)^2$
be such that
$r\in (\mathbb {F}_q)^2$
be such that
![]() $r\neq 1$
. Define E as the set:
$r\neq 1$
. Define E as the set:
which represents a sphere of radius
![]() $1$
in
$1$
in
![]() $\mathbb {F}_q^2$
. It can be shown that
$\mathbb {F}_q^2$
. It can be shown that
![]() $\lvert E\rvert =q+1$
. Now, suppose there exist two sets of points
$\lvert E\rvert =q+1$
. Now, suppose there exist two sets of points
![]() $(x_1,\dots ,x_{k+1})\in E^{k+1}$
and
$(x_1,\dots ,x_{k+1})\in E^{k+1}$
and
![]() $(y_1,\dots ,y_{k+1})\in E^{k+1}$
such that
$(y_1,\dots ,y_{k+1})\in E^{k+1}$
such that
![]() $x_i\neq x_j$
and
$x_i\neq x_j$
and
![]() $y_i\neq y_j$
for
$y_i\neq y_j$
for
![]() $1\leq i<j\leq k+1$
, and
$1\leq i<j\leq k+1$
, and
![]() $\lVert y_i-y_j\rVert =r\lVert x_i-x_j\rVert $
for
$\lVert y_i-y_j\rVert =r\lVert x_i-x_j\rVert $
for
![]() $(i,j)\in A$
. In particular, this implies that
$(i,j)\in A$
. In particular, this implies that
![]() $\lVert y_i-y_j\rVert =r\lVert x_i-x_j\rVert $
for
$\lVert y_i-y_j\rVert =r\lVert x_i-x_j\rVert $
for
![]() $(i,j)\in \{(1,2),(1,3),(2,3)\}$
.
$(i,j)\in \{(1,2),(1,3),(2,3)\}$
.
For each
![]() $i\in \{1,2,3\}$
, define
$i\in \{1,2,3\}$
, define ![]() , which implies
, which implies
![]() $z_i-z_j=\sqrt {r}(x_i-x_j)$
. Therefore,
$z_i-z_j=\sqrt {r}(x_i-x_j)$
. Therefore,
![]() $\lVert y_i-y_j\rVert =\lVert z_i-z_j\rVert $
for
$\lVert y_i-y_j\rVert =\lVert z_i-z_j\rVert $
for
![]() $1\leq i<j\leq 3$
. This implies the existence of a transformation
$1\leq i<j\leq 3$
. This implies the existence of a transformation
![]() $T\in \text {ISO}(2)$
such that
$T\in \text {ISO}(2)$
such that
![]() $T(y_i)=z_i$
for
$T(y_i)=z_i$
for
![]() $i\in \{1,2,3\}$
, where
$i\in \{1,2,3\}$
, where
![]() $\text {ISO}(2)$
is the group of rigid motions.
$\text {ISO}(2)$
is the group of rigid motions.
Since
![]() $z_i=\sqrt {r}x_i$
, it follows that
$z_i=\sqrt {r}x_i$
, it follows that
![]() $\lVert z_i \rVert =r\lVert x_i\rVert =r$
. Also, we observe that
$\lVert z_i \rVert =r\lVert x_i\rVert =r$
. Also, we observe that
![]() $\lVert z_i-T(0)\rVert =\lVert y_i\rVert =1$
. Therefore, we have demonstrated that
$\lVert z_i-T(0)\rVert =\lVert y_i\rVert =1$
. Therefore, we have demonstrated that
![]() $\{z_1,z_2,z_3\}\subset S(T(0);1)\cap S(0;r)$
, where
$\{z_1,z_2,z_3\}\subset S(T(0);1)\cap S(0;r)$
, where
![]() $S(a;R)$
denotes the sphere of radius R centred at a. However, the spheres
$S(a;R)$
denotes the sphere of radius R centred at a. However, the spheres
![]() $S(T(0);1)$
and
$S(T(0);1)$
and
![]() $S(0;r)$
are distinct since
$S(0;r)$
are distinct since
![]() $r\neq 1$
. This assumption leads to a contradiction since two distinct spheres in
$r\neq 1$
. This assumption leads to a contradiction since two distinct spheres in
![]() $\mathbb {F}_q^2$
have at most two points in their intersection. Thus, we have established that the exponent
$\mathbb {F}_q^2$
have at most two points in their intersection. Thus, we have established that the exponent
![]() $d/2$
is indeed sharp in this setting.
$d/2$
is indeed sharp in this setting.
Acknowledgements
The authors would like to express their gratitude to Kaave Hosseini and Alexander Iosevich for suggesting this interesting problem and for their valuable discussions.


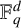
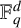
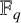
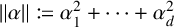 for
for