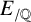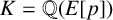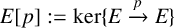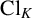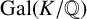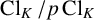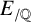1 Introduction
Given a family of number fields, it is natural to study the statistical variation of class groups in the family. Of significant interest is the family of imaginary quadratic extensions
![]() $K/\mathbb {Q}$
. Such investigations go back to the work of Gauss, who was interested in the determination of all imaginary quadratic fields of a given class number h. The problem was solved for
$K/\mathbb {Q}$
. Such investigations go back to the work of Gauss, who was interested in the determination of all imaginary quadratic fields of a given class number h. The problem was solved for
![]() $h=1$
by Baker, Heegner and Stark, for
$h=1$
by Baker, Heegner and Stark, for
![]() $h=2$
by Baker and Stark, and for
$h=2$
by Baker and Stark, and for
![]() $h=3$
by Oesterlé. Watkins in [Reference WatkinsWat04] computed the imaginary quadratic fields for which
$h=3$
by Oesterlé. Watkins in [Reference WatkinsWat04] computed the imaginary quadratic fields for which
![]() $h\leq 100$
. Soundararajan showed that the number of imaginary quadratic fields of class number
$h\leq 100$
. Soundararajan showed that the number of imaginary quadratic fields of class number
![]() $<x$
is asymptotically
$<x$
is asymptotically
![]() ${3\zeta (2)}/{\zeta (3)}x^2$
as
${3\zeta (2)}/{\zeta (3)}x^2$
as
![]() $x\rightarrow \infty $
. The story for real quadratic fields is significantly different. Predictions can be made for the distribution of class groups via Cohen–Lenstra heuristics for all quadratic number fields [Reference Cohen, Lenstra and JagerCL84] and Cohen–Lenstra–Martinet heuristics for general number fields [Reference Martinet and CohenMC90]. We refer to [Reference Wood, Eischen, Long, Pries and StangeWoo16] for a survey of these methods. The study of class numbers on average in families of number fields has notably gained significant momentum in the following works [Reference BhargavaBha05, Reference Davenport and HeilbronnDH71, Reference Ellenberg, Pierce and WoodEPW17, Reference Ellenberg and VenkateshEV07, Reference Fouvry and KlünersFK07, Reference Wong, Gupta and WilliamsWon99]. However, there has been much interest in the study of the p-ranks of class groups of the cyclotomic extension
$x\rightarrow \infty $
. The story for real quadratic fields is significantly different. Predictions can be made for the distribution of class groups via Cohen–Lenstra heuristics for all quadratic number fields [Reference Cohen, Lenstra and JagerCL84] and Cohen–Lenstra–Martinet heuristics for general number fields [Reference Martinet and CohenMC90]. We refer to [Reference Wood, Eischen, Long, Pries and StangeWoo16] for a survey of these methods. The study of class numbers on average in families of number fields has notably gained significant momentum in the following works [Reference BhargavaBha05, Reference Davenport and HeilbronnDH71, Reference Ellenberg, Pierce and WoodEPW17, Reference Ellenberg and VenkateshEV07, Reference Fouvry and KlünersFK07, Reference Wong, Gupta and WilliamsWon99]. However, there has been much interest in the study of the p-ranks of class groups of the cyclotomic extension
![]() $\mathbb {Q}(\mu _p)$
. The Herbrand–Ribet theorem (see [Reference WashingtonWas97]) establishes a precise relationship between generalized Bernoulli numbers and the p-rank of the class group of
$\mathbb {Q}(\mu _p)$
. The Herbrand–Ribet theorem (see [Reference WashingtonWas97]) establishes a precise relationship between generalized Bernoulli numbers and the p-rank of the class group of
![]() $\mathbb {Q}(\mu _p)$
. Ribet’s converse relates congruences between Eisenstein series and cusp forms to the existence of p-cyclic unramified extensions of
$\mathbb {Q}(\mu _p)$
. Ribet’s converse relates congruences between Eisenstein series and cusp forms to the existence of p-cyclic unramified extensions of
![]() $\mathbb {Q}(\mu _p)$
. The rank of the Eisenstein ideal is closely related to the Galois module structure of mod-p class groups that arise from certain families of number fields of the form
$\mathbb {Q}(\mu _p)$
. The rank of the Eisenstein ideal is closely related to the Galois module structure of mod-p class groups that arise from certain families of number fields of the form
![]() $\mathbb {Q}(N^{{1}/{p}})$
, where
$\mathbb {Q}(N^{{1}/{p}})$
, where
![]() $N\equiv 1\, \pmod {\,p}$
is a prime, see [Reference LecouturierLec18, Reference MazurMaz77, Reference Schaefer and StubleySS19, Reference Wake and Wang-EricksonWWE20]. It is however difficult to resolve distribution questions in this context, though there have been some computational experiments done (see [Reference Wake and Wang-EricksonWWE20, Introduction]).
$N\equiv 1\, \pmod {\,p}$
is a prime, see [Reference LecouturierLec18, Reference MazurMaz77, Reference Schaefer and StubleySS19, Reference Wake and Wang-EricksonWWE20]. It is however difficult to resolve distribution questions in this context, though there have been some computational experiments done (see [Reference Wake and Wang-EricksonWWE20, Introduction]).
Motivated by such developments, we consider the family of number field extensions that are generated by the torsion in elliptic curves defined over
![]() $\mathbb {Q}$
. To be specific, given an elliptic curve
$\mathbb {Q}$
. To be specific, given an elliptic curve
![]() $E_{/\mathbb {Q}}$
and a prime p, we let
$E_{/\mathbb {Q}}$
and a prime p, we let
![]() $E[p]$
denote the p-torsion subgroup of
$E[p]$
denote the p-torsion subgroup of
![]() $E(\bar {\mathbb {Q}})$
. Let
$E(\bar {\mathbb {Q}})$
. Let
![]() $K=\mathbb {Q}(E[p])$
be the field generated by
$K=\mathbb {Q}(E[p])$
be the field generated by
![]() $E[p]$
, defined to be the fixed field of the residual representation
$E[p]$
, defined to be the fixed field of the residual representation
on
![]() $E[p]\simeq \mathbb {F}_p\oplus \mathbb {F}_p$
. The extension
$E[p]\simeq \mathbb {F}_p\oplus \mathbb {F}_p$
. The extension
![]() $K/\mathbb {Q}$
in general is a nonabelian extension that contains
$K/\mathbb {Q}$
in general is a nonabelian extension that contains
![]() $\mathbb {Q}(\mu _p)$
. Let
$\mathbb {Q}(\mu _p)$
. Let
![]() $\operatorname {Cl}_K$
be the class group of K. Note that
$\operatorname {Cl}_K$
be the class group of K. Note that
![]() $G=\operatorname {Gal}(K/\mathbb {Q})$
acts on
$G=\operatorname {Gal}(K/\mathbb {Q})$
acts on
![]() $\operatorname {Cl}_K$
and thus on the mod-p class group
$\operatorname {Cl}_K$
and thus on the mod-p class group
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
. We study Galois stable quotients of the
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
. We study Galois stable quotients of the
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
that are isomorphic to
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
that are isomorphic to
![]() $E[p]$
as a G-module. In some sense, such investigations generalize the study of the p-rank of the class group of
$E[p]$
as a G-module. In some sense, such investigations generalize the study of the p-rank of the class group of
![]() $\mathbb {Q}(\mu _p)$
. To be precise, we study the following related questions.
$\mathbb {Q}(\mu _p)$
. To be precise, we study the following related questions.
-
(1) Let p be a fixed odd prime. As E varies over all elliptic curves defined over
 $\mathbb {Q}$
, how often is
$\mathbb {Q}$
, how often is
 $\operatorname {Hom}_{G}(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
nonvanishing?
$\operatorname {Hom}_{G}(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
nonvanishing? -
(2) Let
 $E_{/\mathbb {Q}}$
be a fixed elliptic curve. As p varies over all primes, how does the dimension of
$E_{/\mathbb {Q}}$
be a fixed elliptic curve. As p varies over all primes, how does the dimension of
 $\operatorname {Hom}_{G}(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
vary?
$\operatorname {Hom}_{G}(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
vary?
In the context of the first question above, we order elliptic curves
![]() $E_{/\mathbb {Q}}$
according to height. We assume throughout that the p-primary part of the Tate–Shafarevich group is finite. Our results also rely on heuristics for the statistical behaviour of Tate–Shafarevich groups of elliptic curves. These heuristics were studied by Delaunay [Reference Delaunay, Conrey, Farmer, Mezzadri and SnaithDel07]. Let
$E_{/\mathbb {Q}}$
according to height. We assume throughout that the p-primary part of the Tate–Shafarevich group is finite. Our results also rely on heuristics for the statistical behaviour of Tate–Shafarevich groups of elliptic curves. These heuristics were studied by Delaunay [Reference Delaunay, Conrey, Farmer, Mezzadri and SnaithDel07]. Let
![]() $\mathcal {E}_p$
be the set of elliptic curves
$\mathcal {E}_p$
be the set of elliptic curves
![]() $E_{/\mathbb {Q}}$
such that
$E_{/\mathbb {Q}}$
such that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K, E[p])\neq 0$
. Given
$\operatorname {Hom}_G(\operatorname {Cl}_K, E[p])\neq 0$
. Given
![]() $\Delta \in \mathbb {Z}_{<0}$
with
$\Delta \in \mathbb {Z}_{<0}$
with
![]() $\Delta \equiv 0,1\, \pmod {\ 4}$
, let
$\Delta \equiv 0,1\, \pmod {\ 4}$
, let
![]() $H(\Delta )$
be the Hurwitz class number, see Definition 3.10. Given a set of elliptic curves
$H(\Delta )$
be the Hurwitz class number, see Definition 3.10. Given a set of elliptic curves
![]() $\mathcal {S}$
, we denote by
$\mathcal {S}$
, we denote by
![]() $\underline {\mathfrak {d}}(\mathcal {S})$
the lower density of Weierstrass equations for elliptic curves in
$\underline {\mathfrak {d}}(\mathcal {S})$
the lower density of Weierstrass equations for elliptic curves in
![]() $\mathcal {S}$
(see (3-1) for the definition of
$\mathcal {S}$
(see (3-1) for the definition of
![]() $\underline {\mathfrak {d}}(\mathcal {S})$
).
$\underline {\mathfrak {d}}(\mathcal {S})$
).
Theorem (Theorem 4.4).
Let p be an odd prime and assume that Conjecture 4.2 is satisfied. Then,
where
 $$ \begin{align*}\mathfrak{d}_p=\begin{cases} \zeta(p)-1 & \text{if }p\geq 5,\\ (\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1)& \text{if }p=3,\\ \end{cases}\end{align*} $$
$$ \begin{align*}\mathfrak{d}_p=\begin{cases} \zeta(p)-1 & \text{if }p\geq 5,\\ (\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1)& \text{if }p=3,\\ \end{cases}\end{align*} $$
 $$ \begin{align*}\mathfrak{d}_p'=\begin{cases}\bigg( \dfrac{p-1}{2p^2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ \bigg(\dfrac{p-1}{2p^2}\bigg)(H(1-4p)+H(p^2+1-6p)) & \text{if }p\leq 5.\\ \end{cases}\end{align*} $$
$$ \begin{align*}\mathfrak{d}_p'=\begin{cases}\bigg( \dfrac{p-1}{2p^2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ \bigg(\dfrac{p-1}{2p^2}\bigg)(H(1-4p)+H(p^2+1-6p)) & \text{if }p\leq 5.\\ \end{cases}\end{align*} $$
We obtain the following corollary to the above result.
Corollary (Corollary 4.5).
Let p be an odd prime and assume that Conjecture 4.2 is satisfied. Then,
In other words, for any choice of
![]() $\epsilon>0$
, there is a constant
$\epsilon>0$
, there is a constant
![]() $C>0$
, depending on
$C>0$
, depending on
![]() $\epsilon $
and independent of p, such that
$\epsilon $
and independent of p, such that
Next, we study the second question, where E is fixed and p varies. In this context, we prove two results.
Theorem (Theorem 5.1).
Let
![]() $E_{/\mathbb {Q}}$
be an elliptic curve and assume that the following conditions are satisfied:
$E_{/\mathbb {Q}}$
be an elliptic curve and assume that the following conditions are satisfied:
-
(1)
 is finite;
is finite; -
(2)
 $\operatorname {rank} E(\mathbb {Q})\leq 1$
;
$\operatorname {rank} E(\mathbb {Q})\leq 1$
; -
(3) E does not have complex multiplication.
Then, for
![]() $100\%$
of primes p, we have that
$100\%$
of primes p, we have that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])=0$
.
$\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])=0$
.
Theorem (Theorem 5.2).
Let
![]() $E_{/\mathbb {Q}}$
be an elliptic curve and assume that the following conditions are satisfied:
$E_{/\mathbb {Q}}$
be an elliptic curve and assume that the following conditions are satisfied:
-
(1)
 is finite;
is finite; -
(2)
 $\operatorname {rank} E(\mathbb {Q})\geq 2$
;
$\operatorname {rank} E(\mathbb {Q})\geq 2$
; -
(3) E does not have complex multiplication.
Then, for
![]() $100\%$
(that is, for a Dirichlet density-
$100\%$
(that is, for a Dirichlet density-
![]() $1$
set) of primes p,
$1$
set) of primes p,
Organization: In Section 2, we introduce preliminary notions and also recall results of Prasad and Shekhar [Reference Prasad and ShekharPS21] on the Galois module structure of the class group of the torsion field
![]() $\mathbb {Q}(E[p])$
. In Section 3, we study the density of elliptic curves satisfying local conditions at a possibly infinite set of primes. Such results are crucially used in proving the main results of the article. In Section 4, we fix an odd prime p. The main results are Theorem 4.4 and Corollary 4.5, which establish that
$\mathbb {Q}(E[p])$
. In Section 3, we study the density of elliptic curves satisfying local conditions at a possibly infinite set of primes. Such results are crucially used in proving the main results of the article. In Section 4, we fix an odd prime p. The main results are Theorem 4.4 and Corollary 4.5, which establish that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
is nonvanishing for a positive density set of elliptic curves. Furthermore, we prove a lower bound for this density explicitly. These results are conditional since they rely on the heuristic of Delaunay. In Section 5, we fix an elliptic curve
$\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
is nonvanishing for a positive density set of elliptic curves. Furthermore, we prove a lower bound for this density explicitly. These results are conditional since they rely on the heuristic of Delaunay. In Section 5, we fix an elliptic curve
![]() $E_{/\mathbb {Q}}$
that does not have complex multiplication and study the variation of the dimension of
$E_{/\mathbb {Q}}$
that does not have complex multiplication and study the variation of the dimension of
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
, where p varies over all prime numbers. Finally, in Section 6, we provide explicit computations for the prime
$\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
, where p varies over all prime numbers. Finally, in Section 6, we provide explicit computations for the prime
![]() $p=3$
. These computations do also illustrate cases of interest, when some of the hypotheses on E and p are relaxed.
$p=3$
. These computations do also illustrate cases of interest, when some of the hypotheses on E and p are relaxed.
2 Preliminaries
Fix an algebraic closure
![]() $\bar {\mathbb {Q}}$
of
$\bar {\mathbb {Q}}$
of
![]() $\mathbb {Q}$
and let E be an elliptic curve defined over
$\mathbb {Q}$
and let E be an elliptic curve defined over
![]() $\mathbb {Q}$
. Let p be a prime number and set
$\mathbb {Q}$
. Let p be a prime number and set
![]() $\mathbb {F}_p=\mathbb {Z}/p\mathbb {Z}$
to denote the finite field with p elements. For
$\mathbb {F}_p=\mathbb {Z}/p\mathbb {Z}$
to denote the finite field with p elements. For
![]() $n\geq 1$
, denote by
$n\geq 1$
, denote by
![]() $E[p^n]$
the kernel of the multiplication map
$E[p^n]$
the kernel of the multiplication map
![]() $\times p^n: E(\bar {\mathbb {Q}})\rightarrow E(\bar {\mathbb {Q}})$
and set
$\times p^n: E(\bar {\mathbb {Q}})\rightarrow E(\bar {\mathbb {Q}})$
and set
![]() $E[p^\infty ]:=\bigcup _{n} E[p^n]$
. The absolute Galois group
$E[p^\infty ]:=\bigcup _{n} E[p^n]$
. The absolute Galois group
![]() $\operatorname {G}_{\mathbb {Q}}:=\operatorname {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
acts on
$\operatorname {G}_{\mathbb {Q}}:=\operatorname {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
acts on
![]() $E[p^n]$
. Choosing an isomorphism
$E[p^n]$
. Choosing an isomorphism
![]() $E[p^n]\simeq (\mathbb {Z}/p^n \mathbb {Z})^2$
, let
$E[p^n]\simeq (\mathbb {Z}/p^n \mathbb {Z})^2$
, let
![]() $\rho _n$
be the associated Galois representation on
$\rho _n$
be the associated Galois representation on
![]() $E[p^n]$
,
$E[p^n]$
,
Set
![]() $\rho :=\varprojlim _n \rho _n$
to be the Galois representation on the p-adic Tate-module
$\rho :=\varprojlim _n \rho _n$
to be the Galois representation on the p-adic Tate-module
![]() $\operatorname {T}_p(E):=\varprojlim _n E[p^n]$
. Set
$\operatorname {T}_p(E):=\varprojlim _n E[p^n]$
. Set
![]() $\bar {\rho }$
to denote the mod-p reduction of the characteristic-zero representation
$\bar {\rho }$
to denote the mod-p reduction of the characteristic-zero representation
![]() $\rho :\operatorname {G}_{\mathbb {Q}}\rightarrow \operatorname {GL}_2(\mathbb {Z}_p)$
. We refer to
$\rho :\operatorname {G}_{\mathbb {Q}}\rightarrow \operatorname {GL}_2(\mathbb {Z}_p)$
. We refer to
![]() $\bar {\rho }$
as the residual representation and identify
$\bar {\rho }$
as the residual representation and identify
![]() $\rho _1:\operatorname {G}_{\mathbb {Q}}\rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
with
$\rho _1:\operatorname {G}_{\mathbb {Q}}\rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
with
![]() $\bar {\rho }$
. Let
$\bar {\rho }$
. Let
![]() $\chi :\operatorname {G}_{\mathbb {Q}}\rightarrow \mathbb {Z}_p^\times $
be the p-adic cyclotomic character and
$\chi :\operatorname {G}_{\mathbb {Q}}\rightarrow \mathbb {Z}_p^\times $
be the p-adic cyclotomic character and
![]() $\bar {\chi }:\operatorname {G}_{\mathbb {Q}}\rightarrow \mathbb {F}_p^\times $
its mod-p reduction.
$\bar {\chi }:\operatorname {G}_{\mathbb {Q}}\rightarrow \mathbb {F}_p^\times $
its mod-p reduction.
Given an integer r, set
![]() $\mathbb {Z}_p(r):=\mathbb {Z}_p(\chi ^r)$
and given a
$\mathbb {Z}_p(r):=\mathbb {Z}_p(\chi ^r)$
and given a
![]() $\mathbb {Z}_p[\operatorname {G}_{\mathbb {Q}}]$
-module M, set
$\mathbb {Z}_p[\operatorname {G}_{\mathbb {Q}}]$
-module M, set
![]() $M(r):=M\otimes _{\mathbb {Z}_p} \mathbb {Z}_p(\chi ^r)$
to denote the r th Tate-twist of M. Note that if M is an
$M(r):=M\otimes _{\mathbb {Z}_p} \mathbb {Z}_p(\chi ^r)$
to denote the r th Tate-twist of M. Note that if M is an
![]() $\mathbb {F}_p[\operatorname {G}_{\mathbb {Q}}]$
-module, then,
$\mathbb {F}_p[\operatorname {G}_{\mathbb {Q}}]$
-module, then,
![]() $M(r)=M\otimes _{\mathbb {F}_p} \mathbb {F}_p(r)$
. Let
$M(r)=M\otimes _{\mathbb {F}_p} \mathbb {F}_p(r)$
. Let
![]() $V_{\bar {\rho }}=E[p]$
be the underlying vector space for
$V_{\bar {\rho }}=E[p]$
be the underlying vector space for
![]() $\bar {\rho }$
. Given
$\bar {\rho }$
. Given
![]() $i,j\in \mathbb {Z}$
lying in the range
$i,j\in \mathbb {Z}$
lying in the range
![]() $1\leq i\leq (p-1)$
and
$1\leq i\leq (p-1)$
and
![]() $1\leq j\leq (p-2)$
, we set
$1\leq j\leq (p-2)$
, we set
![]() $V^{i,j}=V^{i,j}_{p,E}$
to denote
$V^{i,j}=V^{i,j}_{p,E}$
to denote
![]() $\operatorname {Sym}^i(V_{\bar {\rho }})(j)$
. Throughout, we assume that
$\operatorname {Sym}^i(V_{\bar {\rho }})(j)$
. Throughout, we assume that
![]() $\bar {\rho }$
is irreducible. However, for the sake of discussion, let us consider the special case when
$\bar {\rho }$
is irreducible. However, for the sake of discussion, let us consider the special case when
![]() $\bar {\rho }$
is surjective. Then, upon choosing a basis of
$\bar {\rho }$
is surjective. Then, upon choosing a basis of
![]() $V_{\bar {\rho }}=E[p]$
, we may identify the image of
$V_{\bar {\rho }}=E[p]$
, we may identify the image of
![]() $\bar {\rho }$
with
$\bar {\rho }$
with
![]() $\operatorname {GL}_2(\mathbb {F}_p)$
and thus the module
$\operatorname {GL}_2(\mathbb {F}_p)$
and thus the module
![]() $V^{i,j}$
is viewed as an irreducible representation of
$V^{i,j}$
is viewed as an irreducible representation of
![]() $\operatorname {GL}_2(\mathbb {F}_p)$
. Note that any irreducible representation of
$\operatorname {GL}_2(\mathbb {F}_p)$
. Note that any irreducible representation of
![]() $\operatorname {GL}_2(\mathbb {F}_p)$
over
$\operatorname {GL}_2(\mathbb {F}_p)$
over
![]() $\mathbb {F}_p$
is of the form
$\mathbb {F}_p$
is of the form
![]() $V^{i,j}$
. A semisimple module M over
$V^{i,j}$
. A semisimple module M over
![]() $\mathbb {F}_p[\operatorname {G}_{\mathbb {Q}}]$
decomposes into a direct sum
$\mathbb {F}_p[\operatorname {G}_{\mathbb {Q}}]$
decomposes into a direct sum
 $$ \begin{align*}M\simeq \bigoplus_{i,j} (V^{i,j})^{r_{i,j}(M)},\end{align*} $$
$$ \begin{align*}M\simeq \bigoplus_{i,j} (V^{i,j})^{r_{i,j}(M)},\end{align*} $$
where
![]() $r_{i,j}(M)\geq 0$
.
$r_{i,j}(M)\geq 0$
.
Let
![]() $K=\mathbb {Q}(E[p])$
be the splitting field of
$K=\mathbb {Q}(E[p])$
be the splitting field of
![]() $\bar {\rho }$
, taken to be the Galois extension of
$\bar {\rho }$
, taken to be the Galois extension of
![]() $\mathbb {Q}$
given by
$\mathbb {Q}$
given by
![]() $K=\bar {\mathbb {Q}}^{\operatorname {ker}\bar {\rho }}$
. Set
$K=\bar {\mathbb {Q}}^{\operatorname {ker}\bar {\rho }}$
. Set
![]() $G:=\operatorname {Gal}(K/\mathbb {Q})$
and identify G with the image of
$G:=\operatorname {Gal}(K/\mathbb {Q})$
and identify G with the image of
![]() $\bar {\rho }$
. Note that when
$\bar {\rho }$
. Note that when
![]() $\bar {\rho }$
is surjective, G is identified with
$\bar {\rho }$
is surjective, G is identified with
![]() $\operatorname {GL}_2(\mathbb {F}_p)$
. There is a natural action of G on the class group
$\operatorname {GL}_2(\mathbb {F}_p)$
. There is a natural action of G on the class group
![]() $\operatorname {Cl}_K$
, and thus on the mod-p class group
$\operatorname {Cl}_K$
, and thus on the mod-p class group
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
. The study of the Galois module structure of
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
. The study of the Galois module structure of
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
is the primary focus of this paper. When
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
is the primary focus of this paper. When
![]() $\bar {\rho }$
is surjective, its semisimplification decomposes into a direct sum of irreducible representations of
$\bar {\rho }$
is surjective, its semisimplification decomposes into a direct sum of irreducible representations of
![]() $\operatorname {GL}_2(\mathbb {F}_p)$
,
$\operatorname {GL}_2(\mathbb {F}_p)$
,
 $$ \begin{align*}(\operatorname{Cl}_K/p \operatorname{Cl}_K)^{\operatorname{ss}}\simeq \bigoplus_{i,j} (V^{i,j})^{n_{i,j}}.\end{align*} $$
$$ \begin{align*}(\operatorname{Cl}_K/p \operatorname{Cl}_K)^{\operatorname{ss}}\simeq \bigoplus_{i,j} (V^{i,j})^{n_{i,j}}.\end{align*} $$
We are specifically interested in the space of homomorphisms
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K{\kern-1.2pt}/{\kern-1.2pt}p\operatorname {Cl}_K, E[p])$
. Note that
$\operatorname {Hom}_G(\operatorname {Cl}_K{\kern-1.2pt}/{\kern-1.2pt}p\operatorname {Cl}_K, E[p])$
. Note that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])\neq 0$
precisely when there is a G-stable quotient of
$\operatorname {Hom}_G(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])\neq 0$
precisely when there is a G-stable quotient of
![]() $\operatorname {Cl}_K/p \operatorname {Cl}_K$
that is isomorphic to
$\operatorname {Cl}_K/p \operatorname {Cl}_K$
that is isomorphic to
![]() $E[p]$
. By class field theory, this corresponds to the existence of an unramified
$E[p]$
. By class field theory, this corresponds to the existence of an unramified
![]() $(\mathbb {Z}/p\mathbb {Z})^2$
-extension L of K that is Galois over
$(\mathbb {Z}/p\mathbb {Z})^2$
-extension L of K that is Galois over
![]() $\mathbb {Q}$
, such that
$\mathbb {Q}$
, such that
![]() $\operatorname {Gal}(L/K)\simeq E[p]$
as a module over
$\operatorname {Gal}(L/K)\simeq E[p]$
as a module over
![]() $G=\operatorname {Gal}(K/\mathbb {Q})$
. We have that
$G=\operatorname {Gal}(K/\mathbb {Q})$
. We have that
with equality in the special case when the representation of G on
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
is semisimple.
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
is semisimple.
Given a prime number
![]() $\ell $
, let
$\ell $
, let
![]() $\mathcal {E}$
be the Néron model of E over
$\mathcal {E}$
be the Néron model of E over
![]() $\mathbb {Z}_\ell $
. Let
$\mathbb {Z}_\ell $
. Let
![]() $E^0(\mathbb {Q}_\ell )$
be the subset of points of
$E^0(\mathbb {Q}_\ell )$
be the subset of points of
![]() $E(\mathbb {Q}_\ell )=\mathcal {E}(\mathbb {Z}_\ell )$
that reduce modulo
$E(\mathbb {Q}_\ell )=\mathcal {E}(\mathbb {Z}_\ell )$
that reduce modulo
![]() $\ell $
to the identity component of
$\ell $
to the identity component of
![]() $E_{/\mathbb {F}_\ell }$
. Fix an absolute value
$E_{/\mathbb {F}_\ell }$
. Fix an absolute value
![]() $|\cdot |_p:\mathbb {Q}_p^\times \rightarrow \mathbb {Q}^\times $
, normalized by
$|\cdot |_p:\mathbb {Q}_p^\times \rightarrow \mathbb {Q}^\times $
, normalized by
![]() $|p|_p^{-1}=p$
. The Tamagawa number at
$|p|_p^{-1}=p$
. The Tamagawa number at
![]() $\ell $
is set to be
$\ell $
is set to be
![]() $c_\ell (E):=[E(\mathbb {Q}_\ell ):E^0(\mathbb {Q}_\ell )]$
, and set
$c_\ell (E):=[E(\mathbb {Q}_\ell ):E^0(\mathbb {Q}_\ell )]$
, and set
![]() $c_\ell ^{(p)}(E):=|c_\ell (E)|_p^{-1}$
. Therefore,
$c_\ell ^{(p)}(E):=|c_\ell (E)|_p^{-1}$
. Therefore,
![]() $c_\ell (E)$
is a unit in
$c_\ell (E)$
is a unit in
![]() $\mathbb {Z}_p$
if and only if
$\mathbb {Z}_p$
if and only if
![]() $c_\ell ^{(p)}(E)=1$
. We denote by
$c_\ell ^{(p)}(E)=1$
. We denote by
![]() $\operatorname {Sel}_p(E/\mathbb {Q})$
the p-Selmer group of E over
$\operatorname {Sel}_p(E/\mathbb {Q})$
the p-Selmer group of E over
![]() $\mathbb {Q}$
defined by
$\mathbb {Q}$
defined by
where the restriction map for the prime
![]() $\ell $
is the composite
$\ell $
is the composite
The Tate–Shafarevich group
fits into an exact sequence
see [Reference Coates and SujathaCoa00, page 8, (1)].
Note that
![]() $\operatorname {dim}_{\mathbb {F}_p} E(\mathbb {Q})/p E(\mathbb {Q})=\operatorname {rank} E(\mathbb {Q})+\operatorname {dim}_{\mathbb {F}_p} E(\mathbb {Q})[p]$
, and since
$\operatorname {dim}_{\mathbb {F}_p} E(\mathbb {Q})/p E(\mathbb {Q})=\operatorname {rank} E(\mathbb {Q})+\operatorname {dim}_{\mathbb {F}_p} E(\mathbb {Q})[p]$
, and since
![]() $\bar {\rho }$
is irreducible,
$\bar {\rho }$
is irreducible,
![]() $E(\mathbb {Q})[p]=0$
, and thus,
$E(\mathbb {Q})[p]=0$
, and thus,
![]() $\operatorname {dim}_{\mathbb {F}_p} E(\mathbb {Q})/p E(\mathbb {Q})=\operatorname {rank} E(\mathbb {Q})$
. Hence, we find that
$\operatorname {dim}_{\mathbb {F}_p} E(\mathbb {Q})/p E(\mathbb {Q})=\operatorname {rank} E(\mathbb {Q})$
. Hence, we find that
Due to the Cassels–Tate pairing, the
![]() $\mathbb {F}_p$
-dimension of
$\mathbb {F}_p$
-dimension of ![]() is even. The following result shows that there is an explicit relationship between
is even. The following result shows that there is an explicit relationship between
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
and the p-torsion in the Tate–Shafarevich group
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
and the p-torsion in the Tate–Shafarevich group ![]() , and is key to constructing quotients of
, and is key to constructing quotients of
![]() $\operatorname {Cl}_K/p\operatorname {Cl}_K$
that are isomorphic to
$\operatorname {Cl}_K/p\operatorname {Cl}_K$
that are isomorphic to
![]() $E[p]$
.
$E[p]$
.
Theorem 2.1 (Prasad and Shekhar).
Let E be an elliptic curve over
![]() $\mathbb {Q}$
and p be an odd prime number at which E has good reduction. With respect to the notation above, suppose that the following assumptions hold:
$\mathbb {Q}$
and p be an odd prime number at which E has good reduction. With respect to the notation above, suppose that the following assumptions hold:
-
(1)
 $c_\ell ^{(p)}(E)=1$
for all primes
$c_\ell ^{(p)}(E)=1$
for all primes
 $\ell \neq p$
;
$\ell \neq p$
; -
(2)
 $E(\mathbb {Q}_p)[p]=0$
.
$E(\mathbb {Q}_p)[p]=0$
.
Then,
In particular, under the above assumptions, if ![]() , or
, or
![]() $\operatorname {rank} E(\mathbb {Q})\geq 2$
, then,
$\operatorname {rank} E(\mathbb {Q})\geq 2$
, then,
![]() $\operatorname {Hom}(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
is nonzero.
$\operatorname {Hom}(\operatorname {Cl}_K/p\operatorname {Cl}_K, E[p])$
is nonzero.
Proof. Equation (2-1) follows from [Reference Prasad and ShekharPS21, Theorem 3.1]. The second assertion follows from Corollary 3.2 of loc. cit.
Definition 2.2. Let
![]() $\mathcal {I}=\mathcal {I}_p(E)$
be the set of primes
$\mathcal {I}=\mathcal {I}_p(E)$
be the set of primes
![]() $\ell \neq p$
such that:
$\ell \neq p$
such that:
-
• E has split multiplicative reduction at
 $\ell $
and
$\ell $
and
 $E(\mathbb {Q}_\ell )[p]$
has rank
$E(\mathbb {Q}_\ell )[p]$
has rank
 $1$
;
$1$
; -
• E has nonsplit multiplicative reduction at
 $\ell $
and
$\ell $
and
 $E(\mathbb {Q}_\ell )[p]$
, and
$E(\mathbb {Q}_\ell )[p]$
, and
 $E(\mathbb {Q}_\ell ^{\operatorname {nr}})[p]$
has rank
$E(\mathbb {Q}_\ell ^{\operatorname {nr}})[p]$
has rank
 $1$
.
$1$
.
Theorem 2.3 (Prasad and Shekhar).
Let
![]() $E_{/\mathbb {Q}}$
be an elliptic curve and p an odd prime at which the conditions of Theorem 2.1 are satisfied. Let
$E_{/\mathbb {Q}}$
be an elliptic curve and p an odd prime at which the conditions of Theorem 2.1 are satisfied. Let
![]() $\mathcal {I}$
be the finite set from Definition 2.2. Then, the following bound is satisfied
$\mathcal {I}$
be the finite set from Definition 2.2. Then, the following bound is satisfied
Proof. The above result is [Reference Prasad and ShekharPS21, Theorem 4.2].
Theorem 2.1 is crucially used in the proof of Theorem 4.4, which is our main result. However, both Theorems 2.1 and 2.3 are applied to prove results in the case when E is a fixed elliptic curve and p varies over all primes at which E has good reduction; see Section 5.
3 Density results for Weierstrass equations with local conditions
In this section, we recall results due to Cremona and Sadek [Reference Cremona and SadekCS23] for the density of elliptic curves
![]() $E_{/\mathbb {Q}}$
satisfying local conditions at a prescribed set of primes. This set of primes may in fact be infinite. The results in this section are used to study the proportion of elliptic curves
$E_{/\mathbb {Q}}$
satisfying local conditions at a prescribed set of primes. This set of primes may in fact be infinite. The results in this section are used to study the proportion of elliptic curves
![]() $E_{/\mathbb {Q}}$
, ordered according to height, that satisfy the conditions of Theorem 2.1. As always, we fix an odd prime p. Given a tuple of integers
$E_{/\mathbb {Q}}$
, ordered according to height, that satisfy the conditions of Theorem 2.1. As always, we fix an odd prime p. Given a tuple of integers
![]() $a=(a_1,a_2,a_3,a_4,a_6)$
, we have an associated elliptic curve
$a=(a_1,a_2,a_3,a_4,a_6)$
, we have an associated elliptic curve
![]() $E_a$
defined by the long Weierstrass equation
$E_a$
defined by the long Weierstrass equation
The height of
![]() $E_a$
is defined as follows:
$E_a$
is defined as follows:
We let
Given a ring R, we let
and let
![]() $\Delta (a)=\Delta (E_a)$
be the associated discriminant. Given a prime
$\Delta (a)=\Delta (E_a)$
be the associated discriminant. Given a prime
![]() $\ell $
, let
$\ell $
, let
![]() $\mathcal {W}_{M}(\mathbb {Z}_\ell )$
be the subset of
$\mathcal {W}_{M}(\mathbb {Z}_\ell )$
be the subset of
![]() $\mathcal {W}(\mathbb {Z}_\ell )$
consisting of equations that are minimal in the sense of [Reference SilvermanSil09, Section VII.1]. Recall that if E is an elliptic curve over
$\mathcal {W}(\mathbb {Z}_\ell )$
consisting of equations that are minimal in the sense of [Reference SilvermanSil09, Section VII.1]. Recall that if E is an elliptic curve over
![]() $\mathbb {Q}_\ell $
, the Kodaira type is one of the following choices:
$\mathbb {Q}_\ell $
, the Kodaira type is one of the following choices:
-
•
 $\operatorname {I}_0$
if E has good reduction;
$\operatorname {I}_0$
if E has good reduction; -
•
 $\operatorname {I}_{\ge 1}$
if E has bad multiplicative reduction, of type
$\operatorname {I}_{\ge 1}$
if E has bad multiplicative reduction, of type
 $\operatorname {I}_m$
for some
$\operatorname {I}_m$
for some
 $m\ge 1$
;
$m\ge 1$
; -
• finally, if E has bad additive reduction, we have the following choices:
 $\mathrm {II}$
,
$\mathrm {II}$
,
 $\mathrm {III}$
,
$\mathrm {III}$
,
 $\mathrm {IV}$
,
$\mathrm {IV}$
,
 $\mathrm {II}^*$
,
$\mathrm {II}^*$
,
 $\mathrm {III}^*$
,
$\mathrm {III}^*$
,
 $\mathrm {IV}^*$
,
$\mathrm {IV}^*$
,
 $\mathrm {I}_0^*$
,
$\mathrm {I}_0^*$
,
 $\mathrm {I}_{\ge 1}^*$
, the latter meaning type
$\mathrm {I}_{\ge 1}^*$
, the latter meaning type
 $\mathrm {I}_m^*$
for some
$\mathrm {I}_m^*$
for some
 $m\geq 1$
.
$m\geq 1$
.
We refer to [Reference SilvermanSil94, IV, Section 9] for a comprehensive study of Kodaira types and how they may be detected via Tate’s algorithm. For
![]() $a\in \mathcal {W}(\mathbb {Z}_\ell )$
, we say that a has Kodaira type T if the associated elliptic curve
$a\in \mathcal {W}(\mathbb {Z}_\ell )$
, we say that a has Kodaira type T if the associated elliptic curve
![]() $E_a$
has Kodaira type T. Note that this definition applies to nonminimal Weierstrass equations as well. Given a Kodaira type T, let
$E_a$
has Kodaira type T. Note that this definition applies to nonminimal Weierstrass equations as well. Given a Kodaira type T, let
![]() $\mathcal {W}^T(\mathbb {Z}_\ell )$
be the subset of
$\mathcal {W}^T(\mathbb {Z}_\ell )$
be the subset of
![]() $\mathcal {W}(\mathbb {Z}_\ell )$
of tuples a of Kodaira type T and set
$\mathcal {W}(\mathbb {Z}_\ell )$
of tuples a of Kodaira type T and set
![]() $\mathcal {W}_{M}^T(\mathbb {Z}_\ell )=\mathcal {W}^T(\mathbb {Z}_\ell )\cap \mathcal {W}_{M}(\mathbb {Z}_\ell )$
. Let
$\mathcal {W}_{M}^T(\mathbb {Z}_\ell )=\mathcal {W}^T(\mathbb {Z}_\ell )\cap \mathcal {W}_{M}(\mathbb {Z}_\ell )$
. Let
![]() $\mu $
be the Haar measure on
$\mu $
be the Haar measure on
![]() $\mathcal {W}(\mathbb {Z}_\ell )\simeq \mathbb {Z}_\ell ^5$
and set
$\mathcal {W}(\mathbb {Z}_\ell )\simeq \mathbb {Z}_\ell ^5$
and set
![]() $\rho ^M(\ell ):=\mu (\mathcal {W}_{M}(\mathbb {Z}_\ell ))$
. Given a Kodaira type T at the prime
$\rho ^M(\ell ):=\mu (\mathcal {W}_{M}(\mathbb {Z}_\ell ))$
. Given a Kodaira type T at the prime
![]() $\ell $
, set
$\ell $
, set
 $$ \begin{align*} \rho^M_T(\ell)& :=\mu(\mathcal{W}_M^T(\mathbb{Z}_\ell)),\\ \rho_T(\ell)& :=\mu(\mathcal{W}^T(\mathbb{Z}_\ell)). \end{align*} $$
$$ \begin{align*} \rho^M_T(\ell)& :=\mu(\mathcal{W}_M^T(\mathbb{Z}_\ell)),\\ \rho_T(\ell)& :=\mu(\mathcal{W}^T(\mathbb{Z}_\ell)). \end{align*} $$
According to [Reference Cremona and SadekCS23, Proposition 2.6], we have that
![]() $\rho _T(\ell )=(1-\ell ^{-10})^{-1}\rho ^M_T(\ell )$
. These local densities are calculated in loc. cit., and these calculations are summarized here.
$\rho _T(\ell )=(1-\ell ^{-10})^{-1}\rho ^M_T(\ell )$
. These local densities are calculated in loc. cit., and these calculations are summarized here.
Theorem 3.1 (Cremona and Sadek).
Let
![]() $\ell $
be a prime, then
$\ell $
be a prime, then
![]() $\rho ^M(\ell )=1-\ell ^{-10}$
. For each Kodaira type T, the local density
$\rho ^M(\ell )=1-\ell ^{-10}$
. For each Kodaira type T, the local density
![]() $\rho _T^M(\ell )$
is given by the values in Table 1.
$\rho _T^M(\ell )$
is given by the values in Table 1.
Table 1 Local densities: Kodaira types.

Proof. The above result follows from [Reference Cremona and SadekCS23, Propositions 2.1(3), 2.2, 2.5].
Let
![]() $\mathcal {S}$
be a subset of
$\mathcal {S}$
be a subset of
![]() $\mathcal {W}(\mathbb {Z})\simeq \mathbb {Z}^5$
, the density of
$\mathcal {W}(\mathbb {Z})\simeq \mathbb {Z}^5$
, the density of
![]() $\mathcal {S}$
is taken to be the following limit
$\mathcal {S}$
is taken to be the following limit
 $$ \begin{align}\mathfrak{d}(\mathcal{S})&:=\lim\limits_{x\rightarrow \infty} \dfrac{\#\{a\in \mathcal{S}\mid \operatorname{ht}(a)<x\}}{\#\{a\in \mathbb{Z}^5\mid \operatorname{ht}(a)<x\}},\nonumber \\&=\lim\limits_{x\rightarrow \infty} 2^{-5}x^{-16}\#\{a\in \mathcal{S}\mid |a_i|<x^i \text{ for }i=1,2,3,4,6\}. \end{align} $$
$$ \begin{align}\mathfrak{d}(\mathcal{S})&:=\lim\limits_{x\rightarrow \infty} \dfrac{\#\{a\in \mathcal{S}\mid \operatorname{ht}(a)<x\}}{\#\{a\in \mathbb{Z}^5\mid \operatorname{ht}(a)<x\}},\nonumber \\&=\lim\limits_{x\rightarrow \infty} 2^{-5}x^{-16}\#\{a\in \mathcal{S}\mid |a_i|<x^i \text{ for }i=1,2,3,4,6\}. \end{align} $$
Note that the above limit may not exist. We let
![]() $\overline {\mathfrak {d}}(\mathcal {S})$
and
$\overline {\mathfrak {d}}(\mathcal {S})$
and
![]() $\underline {\mathfrak {d}}(\mathcal {S})$
be the upper and lower limits, respectively. Note that
$\underline {\mathfrak {d}}(\mathcal {S})$
be the upper and lower limits, respectively. Note that
![]() $\overline {\mathfrak {d}}(\mathcal {S})$
and
$\overline {\mathfrak {d}}(\mathcal {S})$
and
![]() $\underline {\mathfrak {d}}(\mathcal {S})$
are defined by replacing the limit by
$\underline {\mathfrak {d}}(\mathcal {S})$
are defined by replacing the limit by
![]() $\limsup $
and
$\limsup $
and
![]() $\liminf $
, respectively, and that these limits do exist unconditionally. If
$\liminf $
, respectively, and that these limits do exist unconditionally. If
![]() $\mathcal {S}$
is a set of elliptic curves
$\mathcal {S}$
is a set of elliptic curves
![]() $E_{/\mathbb {Q}}$
, we by abuse of notation denote by
$E_{/\mathbb {Q}}$
, we by abuse of notation denote by
![]() $\mathcal {S}$
the subset of
$\mathcal {S}$
the subset of
![]() $\mathcal {W}(\mathbb {Z})$
consisting of all tuples
$\mathcal {W}(\mathbb {Z})$
consisting of all tuples
![]() $a=(a_1,a_2,a_3,a_4,a_6)$
such that
$a=(a_1,a_2,a_3,a_4,a_6)$
such that
![]() $E_a\in \mathcal {S}$
. Note that since we work with long Weierstrass equations, the choice of a for a given isomorphism class of elliptic curves is not unique. According to [Reference Cremona and SadekCS23, Theorem 1.1], the proportion of integral Weierstrass equations that are globally minimal is
$E_a\in \mathcal {S}$
. Note that since we work with long Weierstrass equations, the choice of a for a given isomorphism class of elliptic curves is not unique. According to [Reference Cremona and SadekCS23, Theorem 1.1], the proportion of integral Weierstrass equations that are globally minimal is
![]() $1/\zeta (10)=93\,555/\pi ^{10}\approx 99.99\%$
. Let
$1/\zeta (10)=93\,555/\pi ^{10}\approx 99.99\%$
. Let
![]() $\Phi $
be a possibly infinite set of prime numbers and for each prime
$\Phi $
be a possibly infinite set of prime numbers and for each prime
![]() $\ell \in \Phi $
, let
$\ell \in \Phi $
, let
![]() $U_\ell $
be a subset of
$U_\ell $
be a subset of
![]() $\mathcal {W}(\mathbb {Z}_\ell )$
defined by a set of congruence classes. In other words,
$\mathcal {W}(\mathbb {Z}_\ell )$
defined by a set of congruence classes. In other words,
![]() $U_\ell $
is the inverse image of a subset of
$U_\ell $
is the inverse image of a subset of
![]() $\mathcal {W}(\mathbb {Z}/\ell ^M \mathbb {Z})$
for some integer
$\mathcal {W}(\mathbb {Z}/\ell ^M \mathbb {Z})$
for some integer
![]() $M>0$
. Let U be the family of conditions
$M>0$
. Let U be the family of conditions
![]() $\{U_\ell \mid \ell \in \Phi \}$
. Given
$\{U_\ell \mid \ell \in \Phi \}$
. Given
![]() $N>0$
, let
$N>0$
, let
Definition 3.2. The family
![]() $U=\{U_\ell \mid \ell \in \Phi \}$
is said to be admissible if
$U=\{U_\ell \mid \ell \in \Phi \}$
is said to be admissible if
Let
![]() $\mathcal {W}_U$
be the set of integral Weierstrass equations
$\mathcal {W}_U$
be the set of integral Weierstrass equations
![]() $a\in \mathcal {W}(\mathbb {Z})$
not satisfying
$a\in \mathcal {W}(\mathbb {Z})$
not satisfying
![]() $U_\ell $
at any prime
$U_\ell $
at any prime
![]() $\ell \in \Phi $
.
$\ell \in \Phi $
.
Proposition 3.3. Let U be an admissible family and
![]() $s_\ell =\mu (U_\ell )$
. Then,
$s_\ell =\mu (U_\ell )$
. Then,
![]() $\sum _{\ell \in \Phi } s_\ell $
converges and
$\sum _{\ell \in \Phi } s_\ell $
converges and
Proof. The above result follows from [Reference Cremona and SadekCS23, Proposition 3.4].
Definition 3.4. Given a Kodaira type T, let
![]() $U(T)$
be the family of conditions on the set of primes
$U(T)$
be the family of conditions on the set of primes
![]() $\ell \neq p$
, where
$\ell \neq p$
, where
![]() $U_\ell $
consists of local Weierstrass equations
$U_\ell $
consists of local Weierstrass equations
![]() $a\in \mathcal {W}(\mathbb {Z}_\ell )$
satisfying T. Thus,
$a\in \mathcal {W}(\mathbb {Z}_\ell )$
satisfying T. Thus,
![]() $\mathcal {W}_{U(T)}$
consists of integral Weierstrass equations
$\mathcal {W}_{U(T)}$
consists of integral Weierstrass equations
![]() $a\in \mathcal {W}(\mathbb {Z})$
such that
$a\in \mathcal {W}(\mathbb {Z})$
such that
![]() $E_a$
does not satisfy T at any prime
$E_a$
does not satisfy T at any prime
![]() $\ell \neq p$
.
$\ell \neq p$
.
Lemma 3.5. Let T be a Kodaira type such that
![]() $U(T)$
is admissible, then, the density of
$U(T)$
is admissible, then, the density of
![]() $\mathcal {W}_{U(T)}$
exists and equals
$\mathcal {W}_{U(T)}$
exists and equals
 $$ \begin{align*}\mathfrak{d}(\mathcal{W}_{U(T)})=\prod_{\ell\neq p}(1-\rho_T(\ell))\geq 1-\sum_{\ell\neq p} \rho_T(\ell).\end{align*} $$
$$ \begin{align*}\mathfrak{d}(\mathcal{W}_{U(T)})=\prod_{\ell\neq p}(1-\rho_T(\ell))\geq 1-\sum_{\ell\neq p} \rho_T(\ell).\end{align*} $$
Proof. The result follows directly from Proposition 3.3.
Theorem 3.6. Let p and
![]() $\ell $
be distinct prime numbers, and E an elliptic curve over
$\ell $
be distinct prime numbers, and E an elliptic curve over
![]() $\mathbb {Q}_\ell $
. The following assertions hold.
$\mathbb {Q}_\ell $
. The following assertions hold.
-
(1) Suppose that
 $p\geq 5$
, then,
$p\geq 5$
, then,
 $p|c_{\ell }(E)$
if and only if E has Kodaira type
$p|c_{\ell }(E)$
if and only if E has Kodaira type
 $T=\operatorname {I}_{pm}$
for
$T=\operatorname {I}_{pm}$
for
 $m\in \mathbb {Z}_{\geq 1}$
.
$m\in \mathbb {Z}_{\geq 1}$
. -
(2) Suppose that
 $p=3$
, then,
$p=3$
, then,
 $p|c_{\ell }(E)$
if and only if E has Kodaira type
$p|c_{\ell }(E)$
if and only if E has Kodaira type
 $T=\operatorname {I}_{3m}$
for
$T=\operatorname {I}_{3m}$
for
 $m\in \mathbb {Z}_{\geq 1}$
, or
$m\in \mathbb {Z}_{\geq 1}$
, or
 $T=\operatorname {IV}$
, or
$T=\operatorname {IV}$
, or
 $T=\operatorname {IV}^*$
.
$T=\operatorname {IV}^*$
.
Proof. The result is well known, see [Reference SilvermanSil94, Table 4.1, page 365].
We come to the main result of this section, which is subsequently used in the proof of our main result in the next section.
Definition 3.7. Recall that p is a fixed prime number. Let
![]() $\mathcal {S}_{p}$
be the set of elliptic curves
$\mathcal {S}_{p}$
be the set of elliptic curves
![]() $E_{/\mathbb {Q}}$
such that
$E_{/\mathbb {Q}}$
such that
![]() $p|c_\ell (E)$
for some prime
$p|c_\ell (E)$
for some prime
![]() $\ell \neq p$
.
$\ell \neq p$
.
Theorem 3.8. Let E be an elliptic curve and p an odd prime number. We have the following assertions:
-
(1) if
 $p\geq 5$
, then,
$p\geq 5$
, then,  $$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_{p})< \zeta(p)-1;\end{align*} $$
$$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_{p})< \zeta(p)-1;\end{align*} $$
-
(2) if
 $p=3$
, then,
$p=3$
, then,  $$ \begin{align*}\begin{split}\overline{\mathfrak{d}}(\mathcal{S}_{p}) & <(\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1).\end{split}\end{align*} $$
$$ \begin{align*}\begin{split}\overline{\mathfrak{d}}(\mathcal{S}_{p}) & <(\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1).\end{split}\end{align*} $$
Proof. We prove the result on a case by case basis.
-
(1) First, we consider the case when
 $p\geq 5$
. Then, by Theorem 3.6(1), we have that
$p\geq 5$
. Then, by Theorem 3.6(1), we have that
 $p|c_{\ell }(E)$
if and only if the Kodaira type T is
$p|c_{\ell }(E)$
if and only if the Kodaira type T is
 $\operatorname {I}_{mp}$
for some integer
$\operatorname {I}_{mp}$
for some integer
 ${m\geq 1}$
. Let
${m\geq 1}$
. Let
 $U=U(\operatorname {I}_{\geq p})$
be the datum such that
$U=U(\operatorname {I}_{\geq p})$
be the datum such that
 $U_\ell =I_{\geq p}$
at every prime
$U_\ell =I_{\geq p}$
at every prime
 $\ell \neq p$
. It follows directly from the proof of [Reference Cremona and SadekCS23, Theorem 4.6] that the datum
$\ell \neq p$
. It follows directly from the proof of [Reference Cremona and SadekCS23, Theorem 4.6] that the datum
 $U(\operatorname {I}_{\geq 2})$
is admissible, and hence, so is U. From Lemma 3.5, Since
$U(\operatorname {I}_{\geq 2})$
is admissible, and hence, so is U. From Lemma 3.5, Since $$ \begin{align*}\begin{split}\mathfrak{d}(\mathcal{W}_U)=&\prod_{\ell\neq p} (1-(1-\ell^{-10})^{-1}(1-\ell^{-1})\ell^{-p})\\ \geq & \prod_{\ell\neq p}(1-\ell^{-p})\\ \geq & 1-\sum_{\ell\neq p} \ell^{-p}.\end{split}\end{align*} $$
$$ \begin{align*}\begin{split}\mathfrak{d}(\mathcal{W}_U)=&\prod_{\ell\neq p} (1-(1-\ell^{-10})^{-1}(1-\ell^{-1})\ell^{-p})\\ \geq & \prod_{\ell\neq p}(1-\ell^{-p})\\ \geq & 1-\sum_{\ell\neq p} \ell^{-p}.\end{split}\end{align*} $$
 $\mathcal {S}_p$
is contained in the complement of
$\mathcal {S}_p$
is contained in the complement of
 $\mathcal {W}_U$
, we find that
$\mathcal {W}_U$
, we find that  $$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_p)\leq \sum_{\ell\neq p} \ell^{-p}<\zeta(p)-1.\end{align*} $$
$$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_p)\leq \sum_{\ell\neq p} \ell^{-p}<\zeta(p)-1.\end{align*} $$
-
(2) We now consider the case when
 $p=3$
. By Theorem 3.6(2), we have that
$p=3$
. By Theorem 3.6(2), we have that
 $3|c_{\ell }(E)$
if and only if the Kodaira type T is
$3|c_{\ell }(E)$
if and only if the Kodaira type T is
 $\operatorname {I}_{3m}$
for some integer
$\operatorname {I}_{3m}$
for some integer
 $m\geq 1$
, or,
$m\geq 1$
, or,
 $T=\mathrm {IV}$
or
$T=\mathrm {IV}$
or
 $T=\mathrm {IV}^*$
. Let U be such that
$T=\mathrm {IV}^*$
. Let U be such that
 $U_\ell $
is the subset of
$U_\ell $
is the subset of
 $\mathcal {W}(\mathbb {Z}_\ell )$
with Kodaira type
$\mathcal {W}(\mathbb {Z}_\ell )$
with Kodaira type
 $\operatorname {I}_{\geq 3}$
,
$\operatorname {I}_{\geq 3}$
,
 $\mathrm {IV}$
or
$\mathrm {IV}$
or
 $\mathrm {IV}^*$
, respectively. Note that
$\mathrm {IV}^*$
, respectively. Note that
 $\ell ^2$
divides
$\ell ^2$
divides
 $\Delta $
for such reduction types. Admissibility is a direct consequence of the proof of [Reference Cremona and SadekCS23, Theorem 4.6].
$\Delta $
for such reduction types. Admissibility is a direct consequence of the proof of [Reference Cremona and SadekCS23, Theorem 4.6].We find that
Thus, we find that $$ \begin{align*}\begin{split}\mathfrak{d}(\mathcal{W}_U)&\geq \prod_{\ell\neq p} (1-\rho_{\operatorname{I}_{\geq 3}}(\ell)-\rho_{\mathrm{{IV}}}(\ell)-\rho_{\mathrm{{IV}^*}}(\ell))\\ &\geq \prod_{\ell\neq p} (1-(1-\ell^{-10})^{-1}(1-\ell^{-1})(\ell^{-3}+\ell^{-4}+\ell^{-7}))\\ &\geq \prod_{\ell\neq p} (1-(\ell^{-3}+\ell^{-4}+\ell^{-7}))\\ &\geq 1-\sum_{\ell\neq p} \ell^{-3}-\sum_{\ell\neq p} \ell^{-4}-\sum_{\ell\neq p} \ell^{-7}.\\ &> 1-(\zeta(3)-1)-(\zeta(4)-1)-(\zeta(7)-1). \end{split}\end{align*} $$
$$ \begin{align*}\begin{split}\mathfrak{d}(\mathcal{W}_U)&\geq \prod_{\ell\neq p} (1-\rho_{\operatorname{I}_{\geq 3}}(\ell)-\rho_{\mathrm{{IV}}}(\ell)-\rho_{\mathrm{{IV}^*}}(\ell))\\ &\geq \prod_{\ell\neq p} (1-(1-\ell^{-10})^{-1}(1-\ell^{-1})(\ell^{-3}+\ell^{-4}+\ell^{-7}))\\ &\geq \prod_{\ell\neq p} (1-(\ell^{-3}+\ell^{-4}+\ell^{-7}))\\ &\geq 1-\sum_{\ell\neq p} \ell^{-3}-\sum_{\ell\neq p} \ell^{-4}-\sum_{\ell\neq p} \ell^{-7}.\\ &> 1-(\zeta(3)-1)-(\zeta(4)-1)-(\zeta(7)-1). \end{split}\end{align*} $$
 $$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_p)<(\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1).\\[-35pt] \end{align*} $$
$$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_p)<(\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1).\\[-35pt] \end{align*} $$
Definition 3.9. Denote by
![]() $\mathcal {S}_p'$
the set of elliptic curves E for which
$\mathcal {S}_p'$
the set of elliptic curves E for which
![]() $p\nmid \Delta (E)$
and
$p\nmid \Delta (E)$
and
![]() $E(\mathbb {Q}_p)[p]\neq 0$
. Note that for such elliptic curves and
$E(\mathbb {Q}_p)[p]\neq 0$
. Note that for such elliptic curves and
![]() $p>2$
,
$p>2$
,
![]() $\widetilde {E}(\mathbb {F}_p)[p]\neq 0$
, where
$\widetilde {E}(\mathbb {F}_p)[p]\neq 0$
, where
![]() $\widetilde {E}$
is the reduction of E.
$\widetilde {E}$
is the reduction of E.
Let
![]() $\Delta \in \mathbb {Z}_{<0}$
with
$\Delta \in \mathbb {Z}_{<0}$
with
![]() $\Delta \equiv 0,1\, \pmod {\,4}$
, and set
$\Delta \equiv 0,1\, \pmod {\,4}$
, and set
The group
![]() $\operatorname {SL}_2(\mathbb {Z})$
acts on
$\operatorname {SL}_2(\mathbb {Z})$
acts on
![]() $\mathbb {Z}[x,y]$
, where a matrix
$\mathbb {Z}[x,y]$
, where a matrix
![]() $\sigma = ( {\begin {smallmatrix} p & q \\ r & s \\ \end {smallmatrix} } )$
sends
$\sigma = ( {\begin {smallmatrix} p & q \\ r & s \\ \end {smallmatrix} } )$
sends
![]() $x\mapsto (px+qy)$
and
$x\mapsto (px+qy)$
and
![]() $y\mapsto (rx+sy)$
. Thus, if
$y\mapsto (rx+sy)$
. Thus, if
![]() $f=ax^2+bxy+cy^2$
, the matrix
$f=ax^2+bxy+cy^2$
, the matrix
![]() $\sigma $
acts by
$\sigma $
acts by
We note that
![]() $B(\Delta )$
is stable under the action of
$B(\Delta )$
is stable under the action of
![]() $\operatorname {SL}_2(\mathbb {Z})$
and
$\operatorname {SL}_2(\mathbb {Z})$
and
![]() $B(\Delta )/\operatorname {SL}_2(\mathbb {Z})$
is finite; see [Reference SchoofSch87] for additional details.
$B(\Delta )/\operatorname {SL}_2(\mathbb {Z})$
is finite; see [Reference SchoofSch87] for additional details.
Definition 3.10. The Hurwitz class number
![]() $H(\Delta )$
is the order of
$H(\Delta )$
is the order of
![]() $B(\Delta )/\operatorname {SL}_2(\mathbb {Z})$
.
$B(\Delta )/\operatorname {SL}_2(\mathbb {Z})$
.
Let
![]() $d(p)$
be the number of tuples
$d(p)$
be the number of tuples
![]() $a\in \mathcal {W}(\mathbb {F}_p)$
such that
$a\in \mathcal {W}(\mathbb {F}_p)$
such that
![]() $E_a(\mathbb {F}_p)[p]\neq 0$
. Note that
$E_a(\mathbb {F}_p)[p]\neq 0$
. Note that
 $$ \begin{align*}\frac{d(p)}{\#\mathcal{W}(\mathbb{F}_p)}=\frac{d(p)}{p^5}.\end{align*} $$
$$ \begin{align*}\frac{d(p)}{\#\mathcal{W}(\mathbb{F}_p)}=\frac{d(p)}{p^5}.\end{align*} $$
Lemma 3.11. With respect to the notation above,
![]() $\overline {\mathfrak {d}}(\mathcal {S}_p')\leq {d(p)}/{p^5}$
.
$\overline {\mathfrak {d}}(\mathcal {S}_p')\leq {d(p)}/{p^5}$
.
Proof. Given
![]() $a\in \mathcal {W}(\mathbb {F}_p)$
, let
$a\in \mathcal {W}(\mathbb {F}_p)$
, let
![]() $\mathcal {S}_{a}$
be the set of
$\mathcal {S}_{a}$
be the set of
![]() $\tilde {a}\in \mathcal {W}(\mathbb {Z})$
that reduce to a. It is easy to see that
$\tilde {a}\in \mathcal {W}(\mathbb {Z})$
that reduce to a. It is easy to see that
![]() $\mathfrak {d}(\mathcal {S}_{a})= {1}/{p^5}$
. Note that
$\mathfrak {d}(\mathcal {S}_{a})= {1}/{p^5}$
. Note that
![]() $\mathcal {S}_p'$
is contained in the disjoint union
$\mathcal {S}_p'$
is contained in the disjoint union
![]() $\bigsqcup _{a}\mathcal {S}_{a}$
, where a ranges over the tuples in
$\bigsqcup _{a}\mathcal {S}_{a}$
, where a ranges over the tuples in
![]() $\mathcal {W}(\mathbb {F}_p)$
such that
$\mathcal {W}(\mathbb {F}_p)$
such that
![]() $E_{a}(\mathbb {F}_p)[p]\neq 0$
. The result follows from this.
$E_{a}(\mathbb {F}_p)[p]\neq 0$
. The result follows from this.
Proposition 3.12. With respect to the notation above,
 $$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_p')\leq \begin{cases}\bigg( \dfrac{p-1}{2p^2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ \bigg(\dfrac{p-1}{2p^2}\bigg)(H(1-4p)+H(p^2+1-6p)) & \text{if }p\leq 5. \end{cases} \end{align*} $$
$$ \begin{align*}\overline{\mathfrak{d}}(\mathcal{S}_p')\leq \begin{cases}\bigg( \dfrac{p-1}{2p^2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ \bigg(\dfrac{p-1}{2p^2}\bigg)(H(1-4p)+H(p^2+1-6p)) & \text{if }p\leq 5. \end{cases} \end{align*} $$
Proof. The number of isomorphism classes of elliptic curves E over
![]() $\mathbb {F}_p$
such that
$\mathbb {F}_p$
such that
![]() $E(\mathbb {F}_p)[p]\neq 0$
is
$E(\mathbb {F}_p)[p]\neq 0$
is
 $$ \begin{align*} \begin{cases}H(1-4p) & \text{if }p\geq 7,\\ H(1-4p)+H(p^2+1-6p) & \text{if }p\leq 5; \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases}H(1-4p) & \text{if }p\geq 7,\\ H(1-4p)+H(p^2+1-6p) & \text{if }p\leq 5; \end{cases} \end{align*} $$
see [Reference Ray and SujathaRS23, Corollary 3.11] for additional details. Given
![]() $a\in \mathcal {W}(\mathbb {F}_p)$
and associated integral Weierstrass model
$a\in \mathcal {W}(\mathbb {F}_p)$
and associated integral Weierstrass model
![]() $E_a$
, then, after a transformation
$E_a$
, then, after a transformation
![]() $(X,Y){\kern-1.2pt}\mapsto{\kern-1.2pt} (X+r, Y+sX+t)$
, we obtain an elliptic curve with a short Weierstrass equation. Note that two elliptic curves
$(X,Y){\kern-1.2pt}\mapsto{\kern-1.2pt} (X+r, Y+sX+t)$
, we obtain an elliptic curve with a short Weierstrass equation. Note that two elliptic curves
 $$ \begin{align*} E_{c,d}& : Y^2=X^3+cX+d\\ E_{c',d'}& : Y^2=X^3+c'X+d' \end{align*} $$
$$ \begin{align*} E_{c,d}& : Y^2=X^3+cX+d\\ E_{c',d'}& : Y^2=X^3+c'X+d' \end{align*} $$
are isomorphic over
![]() $\mathbb {F}_p$
if there exists
$\mathbb {F}_p$
if there exists
![]() $s\in \mathbb {F}_p^\times $
such that
$s\in \mathbb {F}_p^\times $
such that
It is thus easy to see that the number of Weierstrass equations in a given isomorphism class is at most
![]() $p^3(({p-1})/{2})$
. Thus, we find that
$p^3(({p-1})/{2})$
. Thus, we find that
 $$ \begin{align*} d(p)\leq \begin{cases}p^3\bigg(\dfrac{p-1}{2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ p^3\bigg(\dfrac{p-1}{2}\bigg)(H(1-4p)+H(p^2+1-6p) ) & \text{if }p\leq 5. \end{cases}\\[-41pt] \end{align*} $$
$$ \begin{align*} d(p)\leq \begin{cases}p^3\bigg(\dfrac{p-1}{2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ p^3\bigg(\dfrac{p-1}{2}\bigg)(H(1-4p)+H(p^2+1-6p) ) & \text{if }p\leq 5. \end{cases}\\[-41pt] \end{align*} $$
4 Results for a fixed prime and varying elliptic curve
In this section, we prove our main results. Throughout, we fix an odd prime number p. Given a set of rational elliptic curves
![]() $\mathcal {S}$
, we obtain a subset of
$\mathcal {S}$
, we obtain a subset of
![]() $\mathcal {W}(\mathbb {Z})$
consisting of all a such that
$\mathcal {W}(\mathbb {Z})$
consisting of all a such that
![]() $E_a\in \mathcal {S}$
. By abuse of notation, we refer to this set as
$E_a\in \mathcal {S}$
. By abuse of notation, we refer to this set as
![]() $\mathcal {S}$
as well. The density
$\mathcal {S}$
as well. The density
![]() $\mathfrak {d}(\mathcal {S})$
is defined as in (3-1). Recall that the upper and lower densities, denoted
$\mathfrak {d}(\mathcal {S})$
is defined as in (3-1). Recall that the upper and lower densities, denoted
![]() $\overline {\mathfrak {d}}(\mathcal {S})$
and
$\overline {\mathfrak {d}}(\mathcal {S})$
and
![]() $\underline {\mathfrak {d}}(\mathcal {S})$
, are always defined even if
$\underline {\mathfrak {d}}(\mathcal {S})$
, are always defined even if
![]() $\mathfrak {d}(\mathcal {S})$
need not be. Let
$\mathfrak {d}(\mathcal {S})$
need not be. Let
![]() $\mathcal {E}_p$
be the set of elliptic curves
$\mathcal {E}_p$
be the set of elliptic curves
![]() $E_{/\mathbb {Q}}$
such that
$E_{/\mathbb {Q}}$
such that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K, E[p])\neq 0$
. Note that for
$\operatorname {Hom}_G(\operatorname {Cl}_K, E[p])\neq 0$
. Note that for
![]() $E\in \mathcal {E}_p$
, we have in particular that
$E\in \mathcal {E}_p$
, we have in particular that
![]() $p\,|\,\#\operatorname {Cl}_K$
.
$p\,|\,\#\operatorname {Cl}_K$
.
Recall from Definition 3.7 that
![]() $\mathcal {S}_{p}$
is the set of elliptic curves
$\mathcal {S}_{p}$
is the set of elliptic curves
![]() $E_{/\mathbb {Q}}$
such that
$E_{/\mathbb {Q}}$
such that
![]() $p|c_\ell (E)$
for some prime
$p|c_\ell (E)$
for some prime
![]() $\ell \neq p$
. Recall from Definition 3.9 that
$\ell \neq p$
. Recall from Definition 3.9 that
![]() $\mathcal {S}_p'$
is the set of elliptic curves E for which
$\mathcal {S}_p'$
is the set of elliptic curves E for which
![]() $p\nmid \Delta (E)$
and
$p\nmid \Delta (E)$
and
![]() $E(\mathbb {Q}_p)[p]\neq 0$
. Denote by
$E(\mathbb {Q}_p)[p]\neq 0$
. Denote by
![]() $\mathcal {S}_p"$
the set of elliptic curves
$\mathcal {S}_p"$
the set of elliptic curves
![]() $E_{/\mathbb {Q}}$
with bad reduction at p. Let
$E_{/\mathbb {Q}}$
with bad reduction at p. Let
![]() $\mathfrak {T}_p$
be the elliptic curves E such that
$\mathfrak {T}_p$
be the elliptic curves E such that ![]() is finite and
is finite and ![]() .
.
Proposition 4.1. Let p be an odd prime. Then,
Proof. Suppose E is an elliptic curve in
![]() $\mathfrak {T}_p\backslash (\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p")$
, then, since
$\mathfrak {T}_p\backslash (\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p")$
, then, since
![]() $E\in \mathfrak {T}_p$
, we have that
$E\in \mathfrak {T}_p$
, we have that ![]() , and since
, and since
![]() $E\notin \mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"$
, we have that
$E\notin \mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"$
, we have that
![]() $p\nmid c_\ell (E)$
for all primes
$p\nmid c_\ell (E)$
for all primes
![]() $\ell \neq p$
, and
$\ell \neq p$
, and
![]() $E(\mathbb {Q}_p)[p]=0$
. So long as the residual representation on
$E(\mathbb {Q}_p)[p]=0$
. So long as the residual representation on
![]() $E[p]$
is irreducible, it follows from Theorem 2.1 that
$E[p]$
is irreducible, it follows from Theorem 2.1 that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_K, E[p])\neq 0$
. As a result, E is contained in
$\operatorname {Hom}_G(\operatorname {Cl}_K, E[p])\neq 0$
. As a result, E is contained in
![]() $\mathcal {E}_p$
. By a well-known result of Duke [Reference DukeDuk97], the residual representation on
$\mathcal {E}_p$
. By a well-known result of Duke [Reference DukeDuk97], the residual representation on
![]() $E[p]$
is irreducible for
$E[p]$
is irreducible for
![]() $100\%$
of elliptic curves, and the result follows.
$100\%$
of elliptic curves, and the result follows.
Throughout, we assume that for any elliptic curve
![]() $E_{/\mathbb {Q}}$
, the p-primary part of the Tate–Shafarevich group
$E_{/\mathbb {Q}}$
, the p-primary part of the Tate–Shafarevich group ![]() is finite. The density of elliptic curves
is finite. The density of elliptic curves
![]() $E_{/\mathbb {Q}}$
such that
$E_{/\mathbb {Q}}$
such that ![]() was studied by Delaunay [Reference Delaunay, Conrey, Farmer, Mezzadri and SnaithDel07].
was studied by Delaunay [Reference Delaunay, Conrey, Farmer, Mezzadri and SnaithDel07].
Conjecture 4.2 (Delaunay).
With respect to the notation above,
Moreover, given a set
![]() $\mathcal {E}$
of elliptic curves defined by local congruence conditions,
$\mathcal {E}$
of elliptic curves defined by local congruence conditions,
Remark 4.3. For the purposes of this article, we use only the second lower bound predicted by the above conjecture: that is, we assume that
where
![]() $\mathcal {E}$
is taken to be the complement of
$\mathcal {E}$
is taken to be the complement of
![]() $\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"$
.
$\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"$
.
Theorem 4.4. Let p be an odd prime and assume the above conjecture. Then,
where
 $$ \begin{align*}\mathfrak{d}_p=\begin{cases} \zeta(p)-1 & \text{if }p\geq 5,\\ (\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1)& \text{if }p=3,\\ \end{cases}\end{align*} $$
$$ \begin{align*}\mathfrak{d}_p=\begin{cases} \zeta(p)-1 & \text{if }p\geq 5,\\ (\zeta(3)-1)+(\zeta(4)-1)+(\zeta(7)-1)& \text{if }p=3,\\ \end{cases}\end{align*} $$
 $$ \begin{align*}\mathfrak{d}_p'=\begin{cases}\bigg( \dfrac{p-1}{2p^2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ \bigg(\dfrac{p-1}{2p^2}\bigg)(H(1-4p)+H(p^2+1-6p)) & \text{if }p\leq 5.\\ \end{cases}\end{align*} $$
$$ \begin{align*}\mathfrak{d}_p'=\begin{cases}\bigg( \dfrac{p-1}{2p^2}\bigg)H(1-4p) & \text{if }p\geq 7,\\ \bigg(\dfrac{p-1}{2p^2}\bigg)(H(1-4p)+H(p^2+1-6p)) & \text{if }p\leq 5.\\ \end{cases}\end{align*} $$
Proof. Let
![]() $\mathcal {E}$
be the set of elliptic curves in the complement of
$\mathcal {E}$
be the set of elliptic curves in the complement of
![]() $\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"$
. We have from Theorem 3.8 (respectively Proposition 3.12) that
$\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"$
. We have from Theorem 3.8 (respectively Proposition 3.12) that
![]() $\mathfrak {d}(\mathcal {S}_p)=\mathfrak {d}_p$
(respectively
$\mathfrak {d}(\mathcal {S}_p)=\mathfrak {d}_p$
(respectively
![]() $\mathfrak {d}(\mathcal {S}_p')=\mathfrak {d}_p'$
). Furthermore, we have from Theorem 3.1 and Proposition 3.3 that
$\mathfrak {d}(\mathcal {S}_p')=\mathfrak {d}_p'$
). Furthermore, we have from Theorem 3.1 and Proposition 3.3 that
![]() $\mathfrak {d}(\mathcal {S}_p")={1}/{p}$
. From Proposition 4.1, we have that
$\mathfrak {d}(\mathcal {S}_p")={1}/{p}$
. From Proposition 4.1, we have that
![]() $\underline {\mathfrak {d}}(\mathcal {E}_p)\geq \underline {\mathfrak {d}}(\mathfrak {T}_p\backslash (\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"))$
. According to our assumption,
$\underline {\mathfrak {d}}(\mathcal {E}_p)\geq \underline {\mathfrak {d}}(\mathfrak {T}_p\backslash (\mathcal {S}_p\cup \mathcal {S}_p'\cup \mathcal {S}_p"))$
. According to our assumption,
 $$ \begin{align*} &\underline{\mathfrak{d}}(\mathfrak{T}_p\backslash (\mathcal{S}_p\cup \mathcal{S}_p'\cup \mathcal{S}_p"))=\underline{\mathfrak{d}}(\mathfrak{T}_p\cap \mathcal{E})\\ &\quad\geq \bigg(1-\prod_{i\geq 1}(1-p^{-(2i-1)})\bigg)\mathfrak{d}(\mathcal{E})\\ &\quad> ( p^{-1}+p^{-3}-p^{-4} )\mathfrak{d}(\mathcal{E})\\ &\quad= ( p^{-1}+p^{-3}-p^{-4} ) (1-p^{-1}-\mathfrak{d}_p-\mathfrak{d}_p'),\end{align*} $$
$$ \begin{align*} &\underline{\mathfrak{d}}(\mathfrak{T}_p\backslash (\mathcal{S}_p\cup \mathcal{S}_p'\cup \mathcal{S}_p"))=\underline{\mathfrak{d}}(\mathfrak{T}_p\cap \mathcal{E})\\ &\quad\geq \bigg(1-\prod_{i\geq 1}(1-p^{-(2i-1)})\bigg)\mathfrak{d}(\mathcal{E})\\ &\quad> ( p^{-1}+p^{-3}-p^{-4} )\mathfrak{d}(\mathcal{E})\\ &\quad= ( p^{-1}+p^{-3}-p^{-4} ) (1-p^{-1}-\mathfrak{d}_p-\mathfrak{d}_p'),\end{align*} $$
and the result follows.
Corollary 4.5. Assume Conjecture 4.2. Then,
In other words, for any choice of
![]() $\epsilon>0$
, there is a constant
$\epsilon>0$
, there is a constant
![]() $C>0$
, depending on
$C>0$
, depending on
![]() $\epsilon $
and independent of p, such that
$\epsilon $
and independent of p, such that
Proof. According to Theorem 4.4,
 $$ \begin{align*}\begin{split} \underline{\mathfrak{d}}(\mathcal{E}_p)&> (p^{-1}+p^{-3}-p^{-4})(1-p^{-1}-\mathfrak{d}_p-\mathfrak{d}_p')\\ &> p^{-1}-p^{-1}(p^{-1}+\mathfrak{d}_p+\mathfrak{d}_p'). \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} \underline{\mathfrak{d}}(\mathcal{E}_p)&> (p^{-1}+p^{-3}-p^{-4})(1-p^{-1}-\mathfrak{d}_p-\mathfrak{d}_p')\\ &> p^{-1}-p^{-1}(p^{-1}+\mathfrak{d}_p+\mathfrak{d}_p'). \end{split}\end{align*} $$
We have that
 $$ \begin{align*}\zeta(p)-1=2^{-p}+\sum_{n\geq 3} n^{-p}< 2^{-p}+\int_{2}^\infty x^{-p}dx=2^{-p}\bigg(\dfrac{p+1}{p-1}\bigg),\end{align*} $$
$$ \begin{align*}\zeta(p)-1=2^{-p}+\sum_{n\geq 3} n^{-p}< 2^{-p}+\int_{2}^\infty x^{-p}dx=2^{-p}\bigg(\dfrac{p+1}{p-1}\bigg),\end{align*} $$
and hence,
However, it follows from known results that
(see [Reference LenstraLJ87, Proposition 1.9]) and the result follows.
5 Results for a fixed elliptic curve and varying prime
In this section, we prove results for a fixed elliptic curve
![]() $E_{/\mathbb {Q}}$
and varying prime p. We assume throughout that E does not have complex multiplication, and that the Tate–Shafarevich group
$E_{/\mathbb {Q}}$
and varying prime p. We assume throughout that E does not have complex multiplication, and that the Tate–Shafarevich group ![]() is finite. Given a prime p, we let
is finite. Given a prime p, we let
![]() $K_p=\mathbb {Q}(E[p])$
. We make a number of observations with regards to the variation of
$K_p=\mathbb {Q}(E[p])$
. We make a number of observations with regards to the variation of
![]() $\operatorname {Cl}_{K_p}/p\operatorname {Cl}_{K_p}$
, where p varies over all primes p.
$\operatorname {Cl}_{K_p}/p\operatorname {Cl}_{K_p}$
, where p varies over all primes p.
Theorem 5.1. Let
![]() $E_{/\mathbb {Q}}$
be an elliptic curve; assume that the following conditions are satisfied:
$E_{/\mathbb {Q}}$
be an elliptic curve; assume that the following conditions are satisfied:
-
(1)
 is finite;
is finite; -
(2)
 $\operatorname {rank} E(\mathbb {Q})\leq 1$
;
$\operatorname {rank} E(\mathbb {Q})\leq 1$
; -
(3) E does not have complex multiplication.
Then, for
![]() $100\%$
of primes p, we have that
$100\%$
of primes p, we have that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_{K_p}\!/p\operatorname {Cl}_{K_p}, E[p])=0$
.
$\operatorname {Hom}_G(\operatorname {Cl}_{K_p}\!/p\operatorname {Cl}_{K_p}, E[p])=0$
.
Proof. Note that for all but finitely many primes p:
-
(1) E has good reduction at p;
-
(2)
 $E(\mathbb {Q}_\ell )[p]=0$
for all primes
$E(\mathbb {Q}_\ell )[p]=0$
for all primes
 $\ell $
at which E has bad reduction;
$\ell $
at which E has bad reduction; -
(3)
 ;
; -
(4) the representation on
 $E[p]$
is irreducible;
$E[p]$
is irreducible; -
(5)
 $c_\ell ^{(p)}(E)=1$
for all primes
$c_\ell ^{(p)}(E)=1$
for all primes
 $\ell $
at which E has bad reduction.
$\ell $
at which E has bad reduction.
Thus, it follows from Theorem 2.3 that we have that
![]() $\operatorname {Hom}_G(\operatorname {Cl}_{K_p}/p\operatorname {Cl}_{K_p}, E[p])=0$
provided
$\operatorname {Hom}_G(\operatorname {Cl}_{K_p}/p\operatorname {Cl}_{K_p}, E[p])=0$
provided
![]() $E(\mathbb {Q}_p)[p]=0$
. Let
$E(\mathbb {Q}_p)[p]=0$
. Let
![]() $\widetilde {E}$
be the reduction of E over
$\widetilde {E}$
be the reduction of E over
![]() $\mathbb {F}_p$
. The formal group
$\mathbb {F}_p$
. The formal group
![]() $\widehat {E}(\mathbb {Z}_p)$
of E at p has no nontrivial p-torsion. Thus, if p is a prime of good reduction, the natural map
$\widehat {E}(\mathbb {Z}_p)$
of E at p has no nontrivial p-torsion. Thus, if p is a prime of good reduction, the natural map
![]() $E(\mathbb {Q}_p)\rightarrow \widetilde {E}(\mathbb {F}_p)$
induces an injection
$E(\mathbb {Q}_p)\rightarrow \widetilde {E}(\mathbb {F}_p)$
induces an injection
A prime p at which E has good reduction is called an anomalous prime if
![]() $\widetilde {E}(\mathbb {F}_p)[p]\neq 0$
. It is well known that for a non-CM elliptic curve,
$\widetilde {E}(\mathbb {F}_p)[p]\neq 0$
. It is well known that for a non-CM elliptic curve,
![]() $100\%$
of primes are nonanomalous (see for instance [Reference Murty and MotohashiMur97]). Thus,
$100\%$
of primes are nonanomalous (see for instance [Reference Murty and MotohashiMur97]). Thus,
![]() $E(\mathbb {Q}_p)[p]=0$
for
$E(\mathbb {Q}_p)[p]=0$
for
![]() $100\%$
of primes p, and thus the result follows.
$100\%$
of primes p, and thus the result follows.
Theorem 5.2. Let
![]() $E_{/\mathbb {Q}}$
be an elliptic curve and assume that the following conditions are satisfied:
$E_{/\mathbb {Q}}$
be an elliptic curve and assume that the following conditions are satisfied:
-
(1)
 is finite;
is finite; -
(2)
 $\operatorname {rank} E(\mathbb {Q})\geq 2$
;
$\operatorname {rank} E(\mathbb {Q})\geq 2$
; -
(3) E does not have complex multiplication.
Then, for
![]() $100\%$
of primes p,
$100\%$
of primes p,
Proof. It follows from the proof of Theorem 5.1 that for
![]() $100\%$
of primes p, all of the following conditions are satisfied:
$100\%$
of primes p, all of the following conditions are satisfied:
-
(1) E has good reduction at p;
-
(2) the representation on
 $E[p]$
is irreducible;
$E[p]$
is irreducible; -
(3)
 $c_\ell ^{(p)}(E)=1$
for all primes
$c_\ell ^{(p)}(E)=1$
for all primes
 $\ell $
at which E has bad reduction;
$\ell $
at which E has bad reduction; -
(4)
 $E(\mathbb {Q}_p)[p]=0$
.
$E(\mathbb {Q}_p)[p]=0$
.
It follows from Theorem 2.1 that
6 Computational results
In this section, we present some computations of
![]() $\operatorname {Cl}_{K}/3\operatorname {Cl}_K$
, where
$\operatorname {Cl}_{K}/3\operatorname {Cl}_K$
, where
![]() $K=\mathbb {Q}(E[3])$
, for certain families of elliptic curves E. Due to the difficulty of computing statistics for larger extensions, we primarily restrict ourselves to the case where
$K=\mathbb {Q}(E[3])$
, for certain families of elliptic curves E. Due to the difficulty of computing statistics for larger extensions, we primarily restrict ourselves to the case where
![]() $\operatorname {Gal}(K/\mathbb {Q})\subset \operatorname {GL}_2(\mathbb {F}_3)$
is the normalizer of a split Cartan subgroup. This is the smallest irreducible subgroup of
$\operatorname {Gal}(K/\mathbb {Q})\subset \operatorname {GL}_2(\mathbb {F}_3)$
is the normalizer of a split Cartan subgroup. This is the smallest irreducible subgroup of
![]() $\operatorname {GL}_2(\mathbb {F}_3)$
. We include also a few additional calculations where the Galois group is the normalizer of a nonsplit Cartan subgroup.
$\operatorname {GL}_2(\mathbb {F}_3)$
. We include also a few additional calculations where the Galois group is the normalizer of a nonsplit Cartan subgroup.
We note that the hypotheses of [Reference Prasad and ShekharPS21] are often violated in these cases. Specifically, a majority of such E has bad reduction at
![]() $3$
. In addition, all ramification at
$3$
. In addition, all ramification at
![]() $3$
is tame as the Galois group has order prime to
$3$
is tame as the Galois group has order prime to
![]() $3$
: thus, any such E for which
$3$
: thus, any such E for which
![]() $a_3(E) \equiv 1\, \pmod {\,3}$
has
$a_3(E) \equiv 1\, \pmod {\,3}$
has
![]() $3$
as a local torsion prime. We computed our examples without regard to these considerations. We have verified that every computation violating the lower bound of [Reference Prasad and ShekharPS21] does not satisfy their hypotheses.
$3$
as a local torsion prime. We computed our examples without regard to these considerations. We have verified that every computation violating the lower bound of [Reference Prasad and ShekharPS21] does not satisfy their hypotheses.
6.1 Normalizer of a split Cartan: varying j-invariants
We use the formula of Zywina [Reference ZywinaZyw15, Theorem 1.2],
 $$ \begin{align*}j_2(t) = 27\frac{(t+1)^3(t-3)^3}{t^3}\end{align*} $$
$$ \begin{align*}j_2(t) = 27\frac{(t+1)^3(t-3)^3}{t^3}\end{align*} $$
such that any elliptic curve with such a j-invariant has
![]() $\operatorname {Gal}(\mathbb {Q}(E[3])/\mathbb {Q})$
contained in the normalizer of a split Cartan subgroup. For any t, let
$\operatorname {Gal}(\mathbb {Q}(E[3])/\mathbb {Q})$
contained in the normalizer of a split Cartan subgroup. For any t, let
![]() $E_t$
denote the elliptic curve of smallest conductor with j-invariant
$E_t$
denote the elliptic curve of smallest conductor with j-invariant
![]() $j_2(t)$
and let
$j_2(t)$
and let
![]() $K_t$
denote the field
$K_t$
denote the field
![]() $\mathbb {Q}(E_t[3])$
. We computed
$\mathbb {Q}(E_t[3])$
. We computed
![]() $\operatorname {Sel}_3(E_t/\mathbb {Q})$
as well as the Galois module structure of
$\operatorname {Sel}_3(E_t/\mathbb {Q})$
as well as the Galois module structure of
![]() $\operatorname {Cl}_{K_t}/3$
for the 599 elliptic curves in the set
$\operatorname {Cl}_{K_t}/3$
for the 599 elliptic curves in the set
Let
![]() $L_t$
denote the unique biquadratic subfield of
$L_t$
denote the unique biquadratic subfield of
![]() $K_t$
; note that
$K_t$
; note that
![]() $L_t$
necessarily contains
$L_t$
necessarily contains
![]() $\mathbb {Q}(\!\sqrt {-3})$
. In each case, there was
$\mathbb {Q}(\!\sqrt {-3})$
. In each case, there was
![]() $d_t \geq 0$
such that there was an isomorphism
$d_t \geq 0$
such that there was an isomorphism
as
![]() $\operatorname {Gal}(K_t/\mathbb {Q})$
-modules. Note that
$\operatorname {Gal}(K_t/\mathbb {Q})$
-modules. Note that
![]() $\operatorname {Gal}(K_t/\mathbb {Q})$
acts on
$\operatorname {Gal}(K_t/\mathbb {Q})$
acts on
![]() $\operatorname {Cl}_{L_t}\!/3$
via its abelianization.
$\operatorname {Cl}_{L_t}\!/3$
via its abelianization.
Our interest here is primarily in comparing
![]() $\operatorname {Sel}_3(E_t/\mathbb {Q})$
and
$\operatorname {Sel}_3(E_t/\mathbb {Q})$
and
![]() $d_t$
. We briefly report the data for
$d_t$
. We briefly report the data for
![]() $\operatorname {Cl}_{L_t}\!/3$
in Table 2. The only curve in our sample with
$\operatorname {Cl}_{L_t}\!/3$
in Table 2. The only curve in our sample with
![]() $\dim \operatorname {Cl}_{L_t}\!/3 = 3$
was
$\dim \operatorname {Cl}_{L_t}\!/3 = 3$
was
![]() $E_{-46/3}$
with
$E_{-46/3}$
with
![]() $L_t = \mathbb {Q}(\!\sqrt {-3}, \sqrt {2917})$
.
$L_t = \mathbb {Q}(\!\sqrt {-3}, \sqrt {2917})$
.
Table 2 Mod 3 class group data.

Please see Table 3 for the other quantities.
Table 3 3 Selmer group data (i).

We remark that the restriction to E with specified
![]() $3$
-torsion fields obviously biases the distribution of
$3$
-torsion fields obviously biases the distribution of
![]() $3$
-Selmer groups. Although it is unwise to extrapolate too much from this limited data, we note that for t with
$3$
-Selmer groups. Although it is unwise to extrapolate too much from this limited data, we note that for t with
![]() $\dim \operatorname {Sel}_3(E_t/\mathbb {Q}) \leq 1$
, the dimension of
$\dim \operatorname {Sel}_3(E_t/\mathbb {Q}) \leq 1$
, the dimension of
![]() $\operatorname {Cl}_{K_t}\!/3$
appears to be roughly the same (being nonzero around
$\operatorname {Cl}_{K_t}\!/3$
appears to be roughly the same (being nonzero around
![]() $19\%$
of the time) whether the Selmer group has dimension zero or one. By contrast, for Selmer groups of dimension two, the proportion having
$19\%$
of the time) whether the Selmer group has dimension zero or one. By contrast, for Selmer groups of dimension two, the proportion having
![]() $d_t \geq 1$
is much larger at
$d_t \geq 1$
is much larger at
![]() $44\%$
. For Selmer groups of dimension three, it is much larger than that in this limited sample.
$44\%$
. For Selmer groups of dimension three, it is much larger than that in this limited sample.
Granting the limits of this data set, it certainly appears that
![]() $\operatorname {Sel}_3(E_t/\mathbb {Q})$
has a significant effect on
$\operatorname {Sel}_3(E_t/\mathbb {Q})$
has a significant effect on
![]() $d_t$
, but there are additional influences as well that are not currently clear.
$d_t$
, but there are additional influences as well that are not currently clear.
6.2 Normalizer of a split Cartan: fixed j-invariants
We also investigated two quadratic twist families. Let
![]() $E_1$
denote the elliptic curve
$E_1$
denote the elliptic curve
with
![]() $j(E_1) = 857\,375/8$
and conductor
$j(E_1) = 857\,375/8$
and conductor
![]() $10\,082=2 \cdot 71^2$
. For any squarefree t, let
$10\,082=2 \cdot 71^2$
. For any squarefree t, let
![]() $E_{1,t}$
denote the quadratic twist of
$E_{1,t}$
denote the quadratic twist of
![]() $E_1$
by t and let
$E_1$
by t and let
![]() $K_{1,t}$
denote the field
$K_{1,t}$
denote the field
![]() $\mathbb {Q}(E_{1,t}[3])$
. Then,
$\mathbb {Q}(E_{1,t}[3])$
. Then,
![]() $\operatorname {Gal}(K_{1,t}/\mathbb {Q})$
is the normalizer of a split Cartan subgroup of
$\operatorname {Gal}(K_{1,t}/\mathbb {Q})$
is the normalizer of a split Cartan subgroup of
![]() $\operatorname {GL}_2(\mathbb {F}_3)$
. We note that each
$\operatorname {GL}_2(\mathbb {F}_3)$
. We note that each
![]() $K_{1,t}$
contains the biquadratic field
$K_{1,t}$
contains the biquadratic field
![]() $L_1=\mathbb {Q}(\!\sqrt {-3},\sqrt {-71})$
, which has trivial
$L_1=\mathbb {Q}(\!\sqrt {-3},\sqrt {-71})$
, which has trivial
![]() $3$
-class group.
$3$
-class group.
Consider the set of 608 elliptic curves
In each case, we computed a
![]() $\operatorname {Gal}(K_{1,t}/\mathbb {Q})$
-isomorphism
$\operatorname {Gal}(K_{1,t}/\mathbb {Q})$
-isomorphism
for some
![]() $d_{1,t}$
. We computed the data as seen in Table 4.
$d_{1,t}$
. We computed the data as seen in Table 4.
Table 4 3 Selmer group data (ii).

We note here that the dependence of
![]() $d_{1,t}$
on
$d_{1,t}$
on
![]() $\mathrm {Sel}_3(E_{1,t}/\mathbb {Q})$
is more clear than in the case of varying j-invariants: the lower bound of [Reference Prasad and ShekharPS21] (although, as noted, the hypotheses are often violated in this data set) appears to control most of the behaviour of
$\mathrm {Sel}_3(E_{1,t}/\mathbb {Q})$
is more clear than in the case of varying j-invariants: the lower bound of [Reference Prasad and ShekharPS21] (although, as noted, the hypotheses are often violated in this data set) appears to control most of the behaviour of
![]() $d_{1,t}$
.
$d_{1,t}$
.
We computed analogous data for the elliptic curve
![]() $E_2$
given by
$E_2$
given by
with
![]() $j(E_2)= -42\,875/8$
and conductor
$j(E_2)= -42\,875/8$
and conductor
![]() $6962 = 2 \cdot 59^2$
. With notation as above, we consider the set of 608 quadratic twists
$6962 = 2 \cdot 59^2$
. With notation as above, we consider the set of 608 quadratic twists
Each
![]() $3$
-division field field
$3$
-division field field
![]() $K_{2,t}$
has Galois group the normalizer of a split Cartan subgroup and contains the biquadratic field
$K_{2,t}$
has Galois group the normalizer of a split Cartan subgroup and contains the biquadratic field
![]() $L_2=\mathbb {Q}(\sqrt {-3},\sqrt {-59}).$
This field has class group
$L_2=\mathbb {Q}(\sqrt {-3},\sqrt {-59}).$
This field has class group
![]() $\mathbb {Z}/3$
, and for each t, we computed a
$\mathbb {Z}/3$
, and for each t, we computed a
![]() $\operatorname {Gal}(K_{2,t}/\mathbb {Q})$
-isomorphism
$\operatorname {Gal}(K_{2,t}/\mathbb {Q})$
-isomorphism
for some
![]() $d_{2,t}$
(see Table 5).
$d_{2,t}$
(see Table 5).
Table 5 3 Selmer group data (iii).

This behaviour appears somewhat less straightforward than for
![]() $S_1$
. The distribution of
$S_1$
. The distribution of
![]() $\mathrm {Sel}_3(E_{2,t}/\mathbb {Q})$
is obviously quite different from that of
$\mathrm {Sel}_3(E_{2,t}/\mathbb {Q})$
is obviously quite different from that of
![]() $\mathrm {Sel}_3(E_{1,t}/\mathbb {Q})$
and the effect on
$\mathrm {Sel}_3(E_{1,t}/\mathbb {Q})$
and the effect on
![]() $d_{2,t}$
is less clear. We do note that the distributions of
$d_{2,t}$
is less clear. We do note that the distributions of
![]() $d_{1,t}$
and
$d_{1,t}$
and
![]() $d_{2,t}$
ignoring Selmer groups are similar, which is somewhat curious.
$d_{2,t}$
ignoring Selmer groups are similar, which is somewhat curious.
6.3 Normalizer of a nonsplit Cartan: fixed j-invariant
We compiled very limited data in one case where the mod
![]() $3$
Galois image is the normalizer of a nonsplit Cartan subgroup. Consider the elliptic curve
$3$
Galois image is the normalizer of a nonsplit Cartan subgroup. Consider the elliptic curve
![]() $E_3$
given by
$E_3$
given by
with
![]() $j(E_3)=-64$
and conductor
$j(E_3)=-64$
and conductor
![]() $1568=2^5 \cdot 7^2$
. We consider its set of 61 twists
$1568=2^5 \cdot 7^2$
. We consider its set of 61 twists
For each t, we have an isomorphism of
![]() $\operatorname {Gal}(K_{3,t}/\mathbb {Q})$
-modules
$\operatorname {Gal}(K_{3,t}/\mathbb {Q})$
-modules
for some
![]() $d_{3,t}$
(see Table 6).
$d_{3,t}$
(see Table 6).
Table 6 3 Selmer group data (iv).

There is too little data here to provide anything more than wild speculations; unfortunately the computations rapidly became very time consuming beyond this point.