Introduction
Sea-ice deformation is a fascinating component of the Arctic geophysical environment which is of critical importance in climate modeling. the deformation of dense pack ice is accommodated by a network of quasi-linear fractures and faults, occurring over a wide range of scales, up to several hundred kilometers, resulting in a heterogeneous and intermittent strain field (Reference Marsan, Stern, Lindsay and WeissMarsan and others, 2004; Reference Weiss, Schulson and SternWeiss and others, 2007; Reference Rampal, Weiss, Lindsay and SternRampal and others, 2008; Reference Stern and LindsayStern and Lindsay, 2009). Opening of new leads in the sea-ice cover is a source of rapid heat exchange between the ocean and the atmosphere, new ice growth and brine rejection to the ocean. Seasonal ice growth in fractures accounts for 25– 40% of the total ice production of the Arctic Ocean (Reference KwokKwok, 2006). For these reasons, global climate models all include a relatively sophisticated description of the dynamics and thermodynamics of the sea-ice cover. It is therefore important that these models capture the properties of sea-ice fracturing and deformation.
Sea-ice rheology describes the relationship between the ice stress (or internal ice forces), the deformation of the ice cover and the material properties of sea ice. the determination of suitable constitutive continuous relations to describe sea-ice rheology has guided research into sea-ice dynamics since it began, and it remains an outstanding problem that limits the success of sea-ice models (Reference FelthamFeltham, 2008). Most models of sea ice currently used in climate models stem from the seminal work of Reference HiblerHibler (1979), who described the ice cover in terms of viscous–plastic (VP) mechanics associated with a rate- and scale-independent failure envelope. This modeling framework, based on a fluid-like mechanics approach, where ice flows as a Newtonian fluid for small deformation rates and plastically for high deformation rates, is not suited to describe the multiscale fracturing processes that accommodate sea-ice deformation. As shown below, the main drawback of this framework is that it does not consider long-range elastic interactions which are at the root of strain localization, intermittency and scaling.
In the Arctic, two major datasets can be used to evaluate sea-ice models in terms of ice deformation. Strain rates can be derived from drifting-buoy trajectories (Reference Rampal, Weiss, Lindsay and SternRampal and others, 2008) or from the sea-ice kinematics produced by the RADARSAT geophysical processor system (RGPS) (Reference Kwok, Tsatsoulis and KwokKwok, 1998) which provides strain-rate estimates down to 10 km resolution. Based on comparisons with these two datasets, poor correlations between the strain rates simulated by the VP rheology and observations have been reported from regional scales (∼300km) to small scales (∼10 km) (Reference ThomasThomas, 1999; Reference Lindsay, Zhang and RothrockLindsay and others, 2003; Reference Kwok, Hunke, Maslowski, Menemenlis and ZhangKwok and others, 2008).
However, the main difficulty in the evaluation of sea-ice rheological models is the definition of an appropriate metric. A high correlation between model and observed ice strain rates is desirable, but it cannot be expected at small spatial and temporal scales (e.g. <100 km and <1month), since sea-ice velocity is mostly stochastic at such scales (Reference Rampal, Weiss and MarsanRampal and others, 2009). Correlation coefficients are thus not the best metric to evaluate models. However, sea-ice deformation exhibits specific statistical and scaling properties that provide an alternative validation metric as they are the signature of the underlying fracturing and faulting processes.
These properties are expressed by a power-law scaling of ice strain rate, a relationship of the form 〈⋵〉 = aL−b , that relates the mean deformation rate to the spatial scale, L, over which it is measured, a and b being constants. the scaling relationship has been extensively analyzed from buoy observations (Reference Rampal, Weiss, Lindsay and SternRampal and others, 2008) and RGPS observations (Reference Marsan, Stern, Lindsay and WeissMarsan and others, 2004; Reference Stern and LindsayStern and Lindsay, 2009). It also extends to the other moments of the strain rate, 〈⋵q〉 ∼ L−b ( q ) , expressing the dependence of the strain-rate distribution upon the spatial scale of observation (Reference Marsan, Stern, Lindsay and WeissMarsan and others, 2004).
Reference Girard, Weiss, Molines, Barnier and BouillonGirard and others (2009) applied this validation metric to high-resolution coupled ocean/sea-ice simulations performed with the VP rheology or its elastic–viscous–plastic (EVP) derivative. They showed that the statistical properties characterizing sea-ice deformation were not reproduced by the simulations, even at large spatial scales. As these properties emanate from the ice mechanical behavior (Reference WeissWeiss, 2008; Reference Rampal, Weiss and MarsanRampal and others, 2009), this suggests that the mechanical framework of the VP rheology is inappropriate.
The aim of this paper is to introduce a new mechanical framework for sea-ice modeling, based on an elasto-brittle (EB) constitutive law. This framework is intended to be able to reproduce the statistical and scaling properties that characterize sea-ice deformation. It is based on continuum mechanics and is simple enough to be implemented in climate models. the main characteristics of the rheology are progressive damage, which models how cracks and faults affect the ice mechanical properties, and long-range elastic interactions. Basin-scale simulations over short timescales (72 hours) are performed with an idealized finite-element application of the model at 10 km resolution. the simulations presented are forced by the wind stress and the drag exerted by an ocean at rest; the thermodynamics and advection of ice are not considered here. These simplified simulations aim to investigate the ice response to the main forcing terms over short time periods. We show that heterogeneous deformation fields are obtained with the EB rheology and that complexity arises from elastic interactions at a wide range of scales.
For comparison purposes, simulations with a similar set-up and forcing are performed with the VP rheology. Observations of sea-ice deformation from the RGPS database are also considered. the statistical and scaling properties of ice deformation are used as the validation metric. We show that the EB rheology gives a much better representation of these properties than the VP rheology.
Models and Observations
EB mechanical framework
The EB framework is built on continuum mechanics in order to be suitable for inclusion within a regional or global climate model. Sea ice is considered as a continuous two-dimensional elastic plate. the ice thickness is not considered explicitly, though it is taken into account in the formulation of the elastic stiffness (in Equation (6)). the model physics accounts for the elastic interactions that can propagate over long distances in the ice cover, as well as for fracturing processes (Reference Weiss, Schulson and SternWeiss and others, 2007). Fracturing processes are considered to play an essential role in sea-ice deformation and dynamics (Reference Schulson and HiblerSchulson and Hibler, 1991; Reference Marsan, Stern, Lindsay and WeissMarsan and others, 2004; Reference SchulsonSchulson, 2004; Reference Weiss, Marsan, Rampal and BorodichWeiss and others, 2009). In the EB model, the effect of fracturing is represented through progressive damage, expressed by a reduction of the local-/gridscale elastic stiffness:
where K and K 0 are, respectively, the effective and initial elastic stiffnesses, expressed in units of force per meter as detailed below, and d ≤ 1 is a scalar indicating the damage level (Reference KachanovKachanov, 1986). This formulation implies that the effect of sub-gridscale fracturing is represented by a scalar damage parameter at the gridscale. the damage parameter thus represents the density of cracks and leads within the ice cover. A similar framework was used in theoretical studies investigating the statistical properties of fracture in brittle materials (Reference Amitrano, Grasso and HantzAmitrano and others, 1999; Reference Girard, Amitrano and WeissGirard and others, 2010).
The model considers a quasi-static ice cover (no advection) driven by wind and ocean stress terms, as well as the internal ice stress term computed by the mechanical framework presented in this section. the model is applied to the Arctic sea-ice cover using a finite-element method with a continuous and linear discretization. This simplified application aims to investigate the ice response, in terms of deformation, to the main forcing terms on short timescales (3 days). the other terms of the momentum balance are neglected in this study as they are less significant on short timescales (Reference Hibler and UntersteinerHibler, 1986). For the timescale considered here, ice advection and thickness variations are thus assumed negligible. With these assumptions, the momentum balance simply reads (forces per unit area):
where ![]() is the ice internal stress tensor,
is the ice internal stress tensor, ![]() is the wind stress and
is the wind stress and ![]() is the water drag. the wind stress is calculated with an air-turning angle of zero as we use 10 mwind fields (Reference McPheeMcPhee, 1975):
is the water drag. the wind stress is calculated with an air-turning angle of zero as we use 10 mwind fields (Reference McPheeMcPhee, 1975):
where ρ
a is the air density, C
a the air drag coefficient and ![]() the wind velocity. the water drag term is calculated considering an ocean at rest, using
the wind velocity. the water drag term is calculated considering an ocean at rest, using
where ρ
w is the water density, C
w the water drag coefficient and ![]() the ice velocity. Sea ice is treated as an isotropic elastic material, and the constitutive equation considered is Hooke’s law under plane-stress hypothesis,
the ice velocity. Sea ice is treated as an isotropic elastic material, and the constitutive equation considered is Hooke’s law under plane-stress hypothesis,
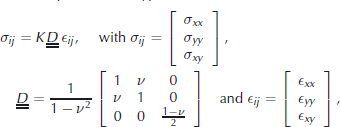
where K is the elastic stiffness, ![]() is the unit elasticity tensor, ϵij is the strain tensor and ν is Poisson’s ratio. the use of an elastic constitutive law requires the elastic strains to be computed from a distinguished stress-free configuration. For the idealized simulations presented in this paper, the quasi-static approximation of state equilibrium is considered (Equation (2)), allowing the displacement and strain fields to be easily computed. In Eulerian models (e.g. with a fixed grid, considering the full momentum equation), computing the elastic strains is more problematic (Reference Coon, Maykut, Pritchard, Rothrock and ThorndikeCoon and others, 1974).
is the unit elasticity tensor, ϵij is the strain tensor and ν is Poisson’s ratio. the use of an elastic constitutive law requires the elastic strains to be computed from a distinguished stress-free configuration. For the idealized simulations presented in this paper, the quasi-static approximation of state equilibrium is considered (Equation (2)), allowing the displacement and strain fields to be easily computed. In Eulerian models (e.g. with a fixed grid, considering the full momentum equation), computing the elastic strains is more problematic (Reference Coon, Maykut, Pritchard, Rothrock and ThorndikeCoon and others, 1974).
The undamaged elastic stiffness of the ice, K 0, is expressed as a function of Young’s modulus, Y, the ice thickness, h, the ice concentration, c, and a constant, υ. the expression of K 0 is inspired from the parameterization of the ice strength used in VP models (see Equation (14)):
The Young’s modulus, Y, refers to an intrinsic sea-ice material property, in units of pressure, while what we define as the stiffness, in units of force per meter, accounts for the ice concentration and thickness over an element. the ice thickness, h, and concentration, c, which determine the initial elastic properties are initialized at the beginning of simulations and are considered to be constant throughout the simulations. the factor exp −υ (1− c ) can be interpreted as the local contact fraction between floes (as suggested by Reference Gray and MorlandGray and Morland, 1994). At each model step, when the stress of an element, i, exceeds a given strength threshold for damage, its elastic stiffness, Ki , is multiplied by a constant damage factor, d 0:
n being the number of damage events of the element i. the constant, d 0, is empirical and should be close enough to one to simulate the small steps of crack growth, but within a given range (e.g. 0.85 ≤ d 0 ≤ 0.95) its value does not significantly affect the simulations (Reference Amitrano, Grasso and HantzAmitrano and others, 1999). After n damage events, the effective stiffness, Ki (n), is given by:
where Ki ,0 is the undamaged elastic stiffness.
After each damage event, the state equilibrium (Equation (2)) is calculated. Since Equation (7) induces locally a decrease of the elastic stiffness of the element i, the stress held by this damaged element decreases as well. This results in a stress redistribution around the damaged element, which mostly affects its nearest neighbors. Because of the stress redistribution, the strength threshold for damage can be exceeded by other elements and this can trigger an avalanche of damage events. an avalanche consists of several cycles of damaging (Equation (7)) and stress redistribution (Equation (2)) which may propagate over long distances across the ice cover. the avalanche stops when the damage criterion is no longer fulfilled by any element. Stress redistribution and induced-damage propagation are key ingredients of this new EB framework, and constitute a major difference with former fluid-like frameworks. the timescale associated with damage propagation and avalanches is considered to be smaller than the duration of a time-step. This means that we consider time as ‘frozen’, i.e. constant, during damage avalanches. Damage avalanches are therefore accounted as sub-iterations during which the external forcing is held constant.
In situ stress measurements (Reference Weiss, Schulson and SternWeiss and others, 2007) and laboratory experiments (Reference Schulson, Fortt, Iliescu and RenshawSchulson and others, 2006) both argue in favor of Coulombic faulting within the sea-ice cover. We therefore choose the Coulomb criterion to define the damage threshold:
where τ and σ N are the shear and the normal stress at the scale of the element, respectively, C is the cohesion and μ is the internal friction coefficient. the internal friction coefficient is set to μ = 0.7. This is within the range of values measured by Reference Fortt and SchulsonFortt and Schulson (2007) from sliding experiments along Coulombic shear faults in laboratory-grown freshwater ice. It is also relevant at geophysical scales for sea ice with a similar internal friction coefficient (Reference Weiss and SchulsonWeiss and Schulson, 2009). To simulate material heterogeneity, which consists of defaults and cracks in the ice at sub-gridscales, the value of the cohesion, C, is randomly drawn from a uniform distribution. In the simulations, we arbitrarily set the range for C between 10 and 20 kPa. This range is close to the values estimated from in situ stress measurements with values of ∼40 kPa for the cohesion (Reference Weiss, Schulson and SternWeiss and others, 2007). As suggested by observations, we apply a tensile strength threshold to the criterion for σ N = −20 kPa (the sign convention chosen is negative for tension).
Field measurements of the sea-ice Young’s modulus report values between 7 and 10GPa depending on the volume fraction of brines and the porosity (Reference Schulson and DuvalSchulson and Duval, 2009). Such values apply for the bulk material, are related to the measurement scale (centimeters to meters) and are performed on crack-free samples. Our model application requires an apparent Young’s modulus, Y, associated with the gridscale, 10 km in this study. This apparent Young’s modulus will be much smaller than the bulk modulus, due to the existence of cracks and faults at sub-gridscales. A decrease in apparent Young’s modulus leads to larger mean ice deformation.
We performed sensitivity tests to determine the apparent Young’s modulus which leads to a simulated mean total deformation at the gridscale comparable to the value estimated by RGPS observations. At 10 km and a temporal scale of 3 days, in March, this value is typically ⋵ tot 〉 = 0.014 d − 1 (Reference Stern and LindsayStern and Lindsay, 2009). the methodology was applied to all simulations and the results were averaged over the different time periods simulated, leading to Y = 0.35GPa. This value should only be taken as an order of magnitude, as the simulations only cover short periods of time. the physical parameters and constants used in this study are summarized in Table 1.
Table 1. Physical parameters and constants

VP simulations
The VP model used for comparison with EB is based on the work of Reference Lietaer, Fichefet and LegatLietaer and others (2008). the ice momentum equation for VP simulations is similar to Equation (2), as is the formulation of the wind forcing and ocean drag terms (Equations (3) and (4)). the ![]() tensor is defined as a function of the strain-rate tensor,
tensor is defined as a function of the strain-rate tensor, ![]() and two of its invariants, the divergence rate, ϵ̇
div, and the shear rate, ϵ̇shear:
and two of its invariants, the divergence rate, ϵ̇
div, and the shear rate, ϵ̇shear:
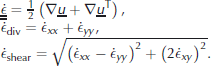
The VP rheology simulates the viscous–plastic behavior with the following constitutive equations:
where tr ![]() is the trace of the strain-rate rate tensor and I is the identity tensor.
is the trace of the strain-rate rate tensor and I is the identity tensor.
These equations ensure that, if the strain rate is greater than γ min, the normal and shear stresses, respectively σ N and τ , will define an elliptical yield curve of size P and with an aspect ratio equal to 1/e. When the strain rate is smaller than γ min, the ice behaves as a viscous fluid. the ice strength, P , is parameterized by
where P ∗ is the ice strength parameter and the other terms are the same as in Equation (6).
The VP simulations are performed on the same mesh as the EB simulations, but, for technical reasons, the computation for VP is made on a sphere (Reference Comblen, Legrand, Deleersnijder and LegatComblen and others, 2009), whereas it is done on a plane projection for EB. This difference does not significantly influence the results. Ice initial conditions and wind forcings are interpolated from the same datasets. the same parameterizations of the wind and ocean stress terms are used. To ensure convergence of the nonlinear system of equations we use the Newton iterative method until the residual norm has been divided by 5 at each time-step (1 hour), in the same way as Reference LemieuxLemieux and others (2010). the finite-element discretization is continuous and linear, and a no-slip boundary condition is imposed on the coast.
Simulations set-up
The simulations are performed on a mesh composed of triangular elements covering the oceans from 50 ˚ N up to the North Pole. the effective resolution of the mesh is 10 km; below 65 ˚ N the resolution coarsens to 150 km.
The ice thickness and concentration are initialized from the outputs of a global ocean/sea-ice numerical model simulation, referred to as ORCA025-G70. This simulation was carried out as part of DRAKKAR, a multiscale ocean modeling project (Reference BarnierBarnier and others, 2006; DRAKKAR Group, 2007). the simulation hindcast compares well with observations in terms of sea-ice extent and concentration in the Arctic (DRAKKAR Group, 2007; Reference Lique, Treguier, Scheinert and PenduffLique and others, 2009). the ice thickness and concentration obtained from ORCA025-G70 for 15 March 2007 are interpolated to the mesh and used as the initial conditions for our simulations (Fig. 1). the simulations are started with an undamaged ice cover. A no-slip boundary condition is imposed on the coast.

Fig. 1. Initial conditions of ice thickness and concentration for the simulations, extracted from the DRAKKAR ORCA025-G70 simulation.
The wind speed used to drive the simulations is obtained from the 6 hourly ECMWF (European Centre for Medium-Range Weather Forecasts) operational analyses (10m wind speed), with an effective resolution of ∼80km in the central Arctic. the wind speed is linearly interpolated in space and time at every model step. the total duration of the simulations is 96 hours. During the first 24 hours, considered as a spin-up, the wind stress is progressively increased to its nominal value, which is then applied during the rest of the simulation (72 hours). the time-step used in all simulations is 20 s. Simulations are performed over three time periods starting on 15, 19 and 27 March 2007.
RGPS observations
RGPS observations of ice deformation from March 2007 are used for statistical comparisons with the simulations. RGPS is based on a cross-correlation technique applied to consecutive SAR (synthetic aperture radar) images (Reference Fily and RothrockFily and Rothrock, 1990), which allows tracking in a Lagrangian fashion of points on the sea-ice cover (http://www-radar.jpl.nasa.gov/rgps/). the tracked points define the corners of cells which are initially squared (10 km ×10 km). the spatial gradients of the velocity field, ∂u/∂x, ∂v/∂x, ∂u/ ∂y and ∂v/∂y, are computed for each cell over the period between two observations (sampled at irregular time intervals within the domain, but typically 3 days) (Reference Kwok, Tsatsoulis and KwokKwok, 1998). Recast in terms of strain-rate tensor components,
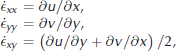
the shear and divergence rates can finally be calculated (Equation (10)), along with the total deformation rate, ͘ϵ
tot = ![]() Henceforth, the term deformation refers to the total deformation rate, ϵ̇
tot. Further details on RGPS observations and their accuracy are presented by Reference Lindsay and SternLindsay and Stern (2003).
Henceforth, the term deformation refers to the total deformation rate, ϵ̇
tot. Further details on RGPS observations and their accuracy are presented by Reference Lindsay and SternLindsay and Stern (2003).
Damage Localization In EB Simulations
In the early stages of EB simulations, the elastic stiffness of the ice cover, set by ice thickness and concentration fields (Fig. 1), varies smoothly over the ocean. During spin-up, the wind stress is progressively increased and damage events start to occur. These damage events are first homogeneously scattered throughout the Arctic Ocean. the reduction of elastic stiffness that occurs when an element is damaged induces a stress redistribution, which can trigger other damage events in the vicinity and onset an avalanche of damage. Later in the simulations, large avalanches occur corresponding to the propagation of the stress relaxation over long distances. This results in linear damage bands, which are the expression of long-range elastic interactions that take place within the ice cover (Fig. 2a). These linear features represent active faults that concentrate shear deformation and divergence (see below). Most of them are very narrow, as observed for real faults (Reference SchulsonSchulson, 2004), with a width set by the spatial resolution (i.e. one element wide).

Fig. 2. Normalized number of damage events at the end of an EB simulation. (a) the usual result, where damage events induce a progressive reduction of the elastic modulus. (b) the result when the reduction of elastic modulus is disabled (d 0 = 1), so damage events are not followed by stress relaxation. the difference between the two fields illustrates the importance of elastic interactions. (Simulation start date 27 March 2007.)
Note that this heterogeneity in the elastic stiffness and damage field is not set as an initial condition in the simulations; rather, it emerges from elastic interactions between the elements. This can be illustrated by performing a simulation without reduction of elastic stiffness (d 0 = 1). In this case, damage events occur only locally, in places where the wind stress is sufficiently large. Damage remains scattered without localization, and linear faults do not appear (Fig. 2b).
Strain-Rate Fields and Linear Kinematic Features
Figure 3 shows an example of the shear and divergence rates from EB and VP simulations, calculated for the 3 day period of the simulation. the RGPS observations available for this time period are also plotted. Similar results are obtained for the other time periods considered. the simulated strain rates are calculated at the gridscale, 10 km, which is also the length scale of the RGPS Lagrangian cells. Considering the high resolution and the idealized settings and forcing, the simulations are not expected to actually predict the observed ice strain field. Faults in the ice cover are initiated at stress concentrators. In EB simulations the stress field is initially nearly homogeneous, as there is no initial damage, but heterogeneities can emerge from the random distribution of the damage thresholds (the cohesion, C). Our simulations start with an undeformed ice cover, though the deformation of the central Arctic ice pack is known to keep a ‘memory’ of large deformation events during the course of a winter season and major faults can be activated several times (Reference Coon, Kwok, Pruis, Schreyer and SulskyCoon and others, 2007).

Fig. 3. Shear and divergence rate from (a) RGPS observations, (b) EB simulation and (c) VP simulation. the RGPS observations represented were obtained between 27 March and 1 April 2007. Strain rates from EB and VP simulations were computed between 27 and 30 March 2007, for a temporal scale of 3 days.
Nevertheless, EB and VP results can be contrasted with each other and with the available observations. the comparison is focused on the central Arctic Ocean (150km away from coastlines and straits), since we have simplified the ice momentum equation. the strain-rate fields obtained with the EB rheology show strong localization of the high strain-rate values, in agreement with observations. As an illustration, in RGPS observations the largest 50% of all shear is accommodated by only 6% of the surface area, a value close to that obtained with the EB simulation, 4%. In contrast, the VP strain field is much less localized, with the largest 50% of all shear accommodated by >20% of theice surface.
Insights into mechanisms driving the ice deformation can be obtained by analyzing the correlations between shear and divergence fields. RGPS observations show a strong correlation between the shear and divergence fields (R 2 = 0.83) that argues for a shear faulting mechanism associated with dilatancy (Reference Weiss and SchulsonWeiss and Schulson, 2009): shearing along rough faults is necessarily accompanied by fault opening, i.e. divergence. A strong correlation between shear and divergence could also result from opening followed by sliding, but this is less likely to occur in the winter ice pack which is confined to the Arctic basin with concentrations close to one. the correlation between shear and divergence is also high in the EB simulation (R 2 = 0.77) but lower in the VP simulation (R 2 = 0.58). It is also interesting that regions of strong shear and divergence rates show conjugate failure lines in EB simulations, such as are seen in satellite images of failure (Reference SchulsonSchulson, 2004) and predicted by the Coulomb theory. This shows that the EB modeling framework captures the physics of shear faulting that accommodates most of the sea-ice deformation. the mechanical framework is thus able to generate the so-called linear kinematic features (Reference Kwok, Dempsey and ShenKwok, 2001).
Strain-Rate Distributions
For many climate applications, it is more important to obtain a good estimate of the ice strain-rate distributions in models than to obtain a good correlation with strain-rate observations, since the strain-rate statistics and the shape of their distribution functions impact winter ice growth rates (Reference Lindsay, Zhang and RothrockLindsay and others, 2003). Reference Hutchings, Roberts, Geiger and Richter-MengeHutchings and others (2011) show that a poor representation of small-scale sea-ice deformation can have an important impact on ice growth estimates. Furthermore, at small spatial and temporal scales, it is impossible to predict in a deterministic sense the ice strain-rate field by considering the stochastic behavior of ice velocity fluctuations. Simulated strain rates are thus evaluated against observations through their probability density functions (PDFs). the PDF of RGPS strain rates is known to exhibit a power-law decay, p( ϵ̇) ∼ ϵ̇ −α , where α depends on the spatial scale considered (Reference Marsan, Stern, Lindsay and WeissMarsan and others, 2004). Such distributions with α ≤ 3 are characterized by ‘wild randomness’ and dominated by extreme values. the PDFs of strain rates simulated by the VP rheology were shown to have a very different shape, with no power-law behavior. Instead, they are in the Gaussian attraction basin and are associated with ‘mild randomness’; the extreme values are not captured (Reference Girard, Weiss, Molines, Barnier and BouillonGirard and others, 2009).
Figure 4 shows the PDFs of shear and absolute divergence rates for EB and VP simulations and RGPS observations. Simulated strain rates are extracted from all simulations, from the central Arctic Ocean (150 km away from the coastlines, the Fram and Bering Straits). In order to obtain a statistically representative number of observations, all RGPS measurements of March 2007 were considered. the PDF obtained with all observations does not vary significantly if only a fraction of them are considered.

Fig. 4. PDFs of shear and absolute divergence rate for EB simulations, VP simulations and RGPS observations. the strain rates are calculated at the spatial scale of 10 km and temporal scale of 3 days. PDFs are normalized by their maximal value. For RGPS and EB, dashed lines indicate the exponents of power-law tails; the blue dashed line is the Gaussian distribution of same mean and standard deviation as the VP distribution.
The PDF of shear rates obtained with EB simulations compares very well with the RGPS observations, with a clear power-law behavior over two orders of magnitude with an exponent of α = 2.2. the fact that these statistical properties are well captured by the EB simulations is a strong argument in favor of the new mechanical framework. Regarding the PDF of divergence rates, the agreement between RGPS observations and the EB rheology is also good since PDFs of both the EB and RGPS show a power-law decay. the PDF exponents show small differences, with an exponent of 2.5 for the RGPS and an exponent of 1.9 for EB simulations. Our results also confirm the strong discrepancy between the PDFs of VP strain rates, which are close to Gaussian distributions, and those of the RGPS. the EB framework successfully captures the statistical properties of strain rates and the power-law tail of the PDFs, while the VP rheology does not.
Scaling Properties of Ice Deformation
The total deformation rate of sea ice is characterized by spatial as well as temporal scaling laws which are the signature of long-range elastic interactions and space/time coupling (Reference Marsan, Stern, Lindsay and WeissMarsan and others, 2004; Reference Rampal, Weiss, Lindsay and SternRampal and others, 2008; Reference Weiss, Marsan, Rampal and BorodichWeiss and others, 2009). These scaling laws are not inherited from the wind forcing; instead they are believed to emanate from the mechanical behavior of ice and thus constitute an interesting metric to evaluate the physics of sea-ice models. the spatial scaling of simulated total deformation rate is analyzed in this study and compared with the scaling law obtained from observations. Seasonal variations of the spatial scaling have been explored (Reference Stern and LindsayStern and Lindsay, 2009); the analysis we perform is intended to be representative of March 2007. Three daily strain rates obtained from the three different time periods of the simulations are thus merged and all RGPS observations from March 2007 are considered for the analysis (a dataset similar to the previous section). A coarse graining procedure is applied to the strain rates in order to compute the total deformation rates on a wide range of scales (10–1000 km) following the methodology presented by Reference Marsan, Stern, Lindsay and WeissMarsan and others (2004). Figure 5 shows the mean total deformation rate as a function of the spatial scale.

Fig. 5. Mean total deformation rate as a function of the spatial scale, L. the dashed lines are power-law fits to the data.
The observations show a power-law scaling of the mean total deformation rate, 〈 ϵ̇ tot 〉 ∼ L−b, with b = 0.17. the last bin shows a small deviation from this power-law behavior, which could be due to a finite-size effect, as the scale reaches the order of magnitude of the width of the Arctic basin. A similar exponent of the scaling law was reported for March by Reference Stern and LindsayStern and Lindsay (2009). Regarding the models, the EB simulated total deformation rate also shows a power-law scaling which is characterized by a slightly shallower exponent, b = 0.1. the last bin also appears to be affected by a finite-size effect. If single EB simulations are considered, the scaling exponent shows variations between b = 0.09 and 0.15. This is slightly lower than the range expected for observations in March (roughly b = 0.12–0.20). the VP simulated strain rate does not vary significantly with the scale, except towards very large scales, again probably an expression of a finite-size effect.
The power-law scaling obtained for EB simulations is another argument in favor of the new mechanical framework. It expresses the heterogeneity of the simulated deformation field that emerges from elastic interactions between elements over a wide range of scales. the limit of this scaling at small scales is only fixed by the model resolution. This means that running simulations at higher resolution would result in increased localization of the deformation and would involve even more extreme strain-rate values.
Discussion and Conclusions
An EB mechanical framework for sea-ice models has been presented. This framework is intended to describe the mechanical behavior of dense pack ice, for ice concentrations typically >95%. In this case, stresses can be transmitted for long distances across the ice cover, resulting in heterogeneous strain-rate fields characterized by specific statistical and scaling properties. These mechanisms are described in the EB framework by progressive damage and long-range elastic interactions. the results presented here demonstrate that such physics allows the emergence of heterogeneity in the simulated ice deformation. the statistics of ice strain rates are well represented by the EB rheology, although the simulations considered here are rather crude and consider only short winter time periods. This is a noteworthy point since no other model of sea-ice mechanics has succeeded in capturing these properties to date. In particular, the VP rheology, currently used in most sea-ice models, has been shown to be unable to capture the properties of ice strain rates (Reference Lindsay, Zhang and RothrockLindsay and others, 2003; Reference Girard, Weiss, Molines, Barnier and BouillonGirard and others, 2009). When ice concentrations are lower, stresses cannot be transmitted as well as in a more continuous ice cover. In this case, the ice cover consists of floes drifting as a granular flow (Reference FelthamFeltham, 2005), or almost freely when ice concentrations are even lower. Physically, the use of the EB rheology at low ice concentrations might be inappropriate. In a global model, it may be necessary to disable the rheology beyond a given concentration threshold (i.e. to switch to free drift).
Our results support the scenario proposed by Reference Weiss, Schulson and SternWeiss and others (2007), that fracture and frictional sliding govern inelastic deformation over a wide range of spatial scales, a viewpoint shared by Reference Hopkins and ThorndikeHopkins and Thorndike’s granular sea-ice model (2006). A similar approach was recently used by Reference Wilchinsky, Feltham and HopkinsWilchinsky and others (2010, Reference Wilchinsky, Feltham and Hopkins2011) to show the importance of shear failure associated with dilatancy for sea-ice deformation. Among the other approaches followed to account for the brittle behavior of sea ice, the elasto decohesive model considers many of the issues addressed in this paper (Reference Schreyer, Sulsky, Munday, Coon and KwokSchreyer and others, 2006; Reference Sulsky, Schreyer, Kwok and CoonSulsky and others, 2007). This model accounts for failure by loss of cohesion rather than damage, and the leads/fractures are represented explicitly, instead of using a continuum damage formulation. the EB rheology offers the advantage of using continuum mechanics which is more suitable for implementation in a global coupled ocean/sea-ice model. At timescales longer than a few days, the effect of refreezing, or ‘healing’, of damaged areas on ice mechanics needs to be considered. Contrary to damage, healing tends to restore the initial ice mechanical properties, when temperature conditions allow refreezing. We are currently working to implement healing into the EB framework, which is a necessary step before the rheology can be used in global sea-ice models over longer time periods.
A justification frequently advanced for the poor quality of the VP simulated ice deformation is the resolution and the quality of the forcing fields (including winds) used to drive sea-ice models. the simulations presented in this study are driven by wind fields derived from reanalysis, similarly to global sea-ice models, with an effective resolution of ∼80 km. In such products, boundary-layer turbulence and small-scale variability of the wind velocity are indeed not captured. Despite this smooth forcing, EB simulated deformation is heterogeneous and the localization of deformation occurs down to the gridscale, 10 km. This provides an interesting insight into the origin of the statistical and scaling properties of the EB sea-ice deformation: they cannot be inherited from the wind forcing since the deformation fields obtained show scaling down to the gridscale, which is much smaller than the wind forcing resolution. This supports the conclusions of Reference Rampal, Weiss and MarsanRampal and others (2009), drawn from statistical analysis of buoy-derived ice deformation. Our results argue that the statistics of sea-ice deformation arise from the elasto-brittle mechanical behavior of the ice. In other words, the limitation of classical sea-ice models is likely to be due, not to the resolution and the quality of the forcing, but rather to the physics of the model itself. Increasing the resolution of these models or of the forcing fields will not suffice to capture the properties of ice deformation.
Acknowledgements
RGPS data were provided by the Polar Remote Sensing Group at the Nasa Jet Propulsion Laboratory, Pasadena, California, USA. ECMWF analyses were provided in the framework of the DRAKKAR cooperation on global ocean/sea-ice modeling. We are grateful to the MEOM– LEGI team and especially J.M. Molines and B. Barnier for providing the DRAKKAR ocean global circulation model simulation. the EB simulations presented in this paper were performed at the Service Commun de Calcul Intensif de l’Observatoire de Grenoble (SCCI–CIMENT). the ice model used for VP simulations is a component of the SLIM project (http://www.climate.be/SLIM), which is funded by the Communauté Française de Belgique, as Actions de Recherche Concertées, under contract ARC 04/09-316. D.A. thanks French program INSU-Catell and EU program TRIGS (Triggering of instabilities in materials and geosystems) for support. L.G. is supported by a grant from Centre National de la Recherche Scientifique, France. P. Rampal is warmly acknowledged for his encouragement. We also thank the scientific editor and the reviewers for their work, which improved the paper.








