Introduction
Information about net accumulation in polar regions may be preserved in layers found in ice sheets. Sources of (information include 10Be (Reference Raisbeck. and Yiou.Raisbeck and Yiou, 1985), dated volcanic-debris and bomb-fallout layers and the thickness of annual ice layers (Reference Paterson and WaddingtonPaterson and Waddington, 1984; Reference Reeh, Bleil and ThiedeReeh, 1990). Dust and other atmospheric constituents are mixed with the precipitation that falls on the ice-sheet surface. When firn compacts to ice, annual variations in these quantities are preserved in the ice, allowing annual layers to be identified. A detailed, continuous record of annual layer thicknesses near the Greenland summit has been obtained from the GISP2 ice core to 50 000 BP (Reference MeeseMeese and others. 1994). Long-term average layer thicknesses for ice older than 50 000 BP can be determined from a depth-age scale based on the Vostok ice-core time scale and sea-sediment records (Reference BenderBender and others, 1994). From this combined layer-thickness record, it is possible to obtain the most detailed, long-term history of accumulation over central Greenland to date.
The thickness of a given annual layer in an ice sheet is determined by the net annual accumulation at the lime of deposition and the amount of strain the layer has experienced from ice flow. The strain-rate pattern in an ice sheet at a given time is in turn determined by the geometry and rheological properties of the ice sheet. Models that have been used to infer accumulation rates from layer thicknesses (e.g. Reference Reeh., Oeschger and LangwayReeh. 1989; Reference AlleyAlley and others, 1993; Reference Dahl-Jensen, Johnsen, Hammer, Clausen, Jouzel. and PeltierDahl-Jensen and others, 1993) assume that the ice sheet maintains a constant thickness over time because the non-linear nature of ice flow makes the ice-sheet thickness rather insensitive to changes in the mass balance (Reference PatersonPaterson, 1981. p. 157). Reference AlleyAlley and others (1993) used this method to analyze the GISP2 layer-thickness record back to 17 000 BP. In this paper, we examine the effect of ice-sheet thickness changes on ice flow and the layer-thickness pattern.
We have developed a non-linear, one-dimensional model to investigate the evolution of ice-sheet thickness, the vertical strain rate and the annual layer thicknesses in response to changing accumulation rates. The model has three key assumptions:
-
(i) The rate of change in ice-sheet thickness can he determined from the accumulation rate and vertical velocity.
-
(ii) As it responds to changes in accumulation, the ice sheet evolves through a series of profiles that correspond to steady-state shapes.
-
(iii) The shape of the depth variation in vertical strain rate is constant over time.
We infer an accumulation history for GISP2 from layer-thickness data using this variable-thickness model.
Theory
Consider the behavior of a large ice sheet at some time. t, with center thickness H at x = 0 and h at x ≠ 0, with an accumulation rate, b, and with ice moving vertically downward and horizontally with velocity components v and u (Fig. 1). We assume that the surface and bed slope near the summit are essentially flat so that  Assumption (i) above can be stated as:
Assumption (i) above can be stated as:
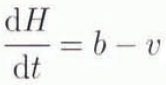
According to this expression of mass conservation, if the accumulation rate increases/decreases with respect to a steady-state value, then the ice sheet gets thicker/thinner.

Fig. 1. Profile of a simple ice sheet. Horizontal and vertical velocity components are represented by u and v, respectively. In steady state, the accumulation rate. b, is independent of position, x, and equal to the surface vertical velocity, v(h).
To relate the geometry of the ice sheet to the surface vertical velocity, we consider the configuration of a two-dimensional ice sheet. Based on the standard assumptions (a) that the ice sheet is frozen to its bed. (b) that shear stress τxy increases linearly with depth from 0 at the surface to τb at the bed, (c) that the surface slope is small, and (d) that there are no horizontal stress gradients, then

In addition, we assume that ice deforms according to Glen’s flow law so that  that n = 3, and that the temperature and structure of the ice are such that the flow-law parameter. A, is independent of depth, y. With these assumptions, the depth-averaged horizontal velocity ū is given by
that n = 3, and that the temperature and structure of the ice are such that the flow-law parameter. A, is independent of depth, y. With these assumptions, the depth-averaged horizontal velocity ū is given by

If we further assume that local variations in the shape of the ice-sheet surface profile caused by transient flow effects diffuse away quickly so that the shape of the ice sheet is smooth and the surface vertical velocity, v(h) = v(H), is independent of position, x, then at any given instant, continuity of ice mass requires that
where h is the thickness at x, and ū is the depth-averaged horizontal velocity.
Combining Equations (3) and (4), and integrating from the edge where h = 0 to the divide where h = H, yields an ice-sheet shape. If the ice sheet were in steady state with v(h) = b then this shape would correspond to the steady-state profile derived by Vialov and described in Reference PatersonPaterson 1981, p. 154-157). Our more general approach allows the ice sheet to change its thickness while maintaining a shape at any given instant that corresponds to a Vialov steady-state profile associated with v(h) rather than b (assumption (ii) above).
At the divide (x = 0), this shape gives the following relationship between H the ice-sheet thickness at the divide, L, the half-width, and v(H), the surface vertical velocity:

where f depends on n and A. for n = 3, the 1/8 power in Equations (5) shows that the thickness is relatively insensitive to changes in mass balance. If the thickness changes, the velocity also changes so as lo oppose the thickness change.
Since the thickness of the Greenland ice sheet at the GISP2 site is essentially the same its the thickness at the divide, we only need to calculate H(t), and the problem is reduced in one dimension. If we further assume that the margins are fixed (L = constant), that the flow law parameter, A, does not change over time, and that the present geometry at GISP2 represents a steady-state geometry, then f is a constant which can be determined by parameterizing Equations (5) for the present conditions at GISP2. The ice thickness there is about 3025 m (ice equivalent), and the surface vertical velocity can be taken to be equal to the present accumulation rate of 0.24 m a−1 ice equivalent (Reference Bolzan and Strobel.Bolzan and Strobel, 1994).
Equations (5) describes how the surface vertical velocity is related to the ice-sheet thickness. To describe the Strain rate at depth, we apply assumption (iii) above: the non-dimensional shape of a given vertical velocity profile that is characteristic of off-divide ice (flank flow) is time-independent. This assumption is based on theoretical and experimental arguments showing that the shapes of velocity profiles in ice sheets with uniform rheological properties are insensitive to small changes in surface geometry (Reference RaymondRaymond, 1983:
Reference HindmarshHindmarsh. 1990). The velocity at depth is then scaled to the vertical velocity at the surface according to a non-dimensional shape, ![]() so that
so that

Equations (1), (5) and (6) together describe the effect of accumulation-rate changes on the ice-sheet thickness and the vertical strain-rate distribution.
However, since the flow law in real ice sheets is not uniform or time-independent, the vertical velocity profile does not actually maintain a given shape over time. To estimate the error from assumption (iii), we compare the model results using three distinct, non-dimensionalized vertical velocity profiles: one generated by a finite-element model of the GRIP-GISP2 flowline Reference Schott., Waddington and RaymondSchott and others, 1992); one calculated analytically for a flow enhancement (ice “softness” caused by impurities and/or development of a c-axis fabric and temperature distribution characteristic of interglacial conditions; and one calculated for an enhancement and temperature distribution characteristic of glacial conditions (Fig. 2). Details of these calculations are provided in a later section.

Fig. 2. Vertical velocity profile shapes used to test sensitivity of model results to possible changes in the strain-rate pattern from temperature and flow enhancement from chemistry and fabric. Corresponding temperature and enhancement distributions used to calculate the velocity profiles are also shown. The dashed-dot line represents the finite-element calculation. The solid and dashed lines represent the velocity calculations for characteristic glacial and interglacial.
Numerical Methods
To run the model forward in time, we take a prescribed accumulation history and calculate a thickness change and a vertical velocity distribution at each (50 a) time step. Horizons are tracked as they move deeper into the ice sheet. This Forward model produces a layer-thickness pattern and an ice-sheet thickness history. The characteristic response time of a glacier or ice sheet to mass-balance changes should be on the order of H/b (Reference Jóhannesson, Raymond and Waddington.Jóhannesson and others, 1989), or about 1Oka for GISP2. Our model, when tested with sinusoidally varying accumulation-rate histories, gives a response time with the correct magnitude, about 6ka.
The inverse problem requires calculation of net-accumulation-rate and thickness histories given a layer-thickness pattern such as the one from the G1SP2 ice core. Simply running the forward model backward and unstraining the layers at each time step is unstable. In the forward model, the thickness response to a mass-balance impulse decays exponentially with time. When the model is run backward, this response to mass balance is expressed as a growing exponential that leads to an unstable thickness prediction. To avoid this instability, we couple the forward and backward calculations and use an iterative method. We start with a constant-thickness history and calculate a corresponding accumulation history by unstraining the layers from the GISP2 core (moving backward in time). This accumulation history is used to calculate a new thickness history by running the model forward in time. This new thickness history ts then used to calculate a new accumulation history from the GISP2 layers by running the model backward in time, and so on. We iterate until a consistent accumulation and thickness history is obtained (about five iterations). Figure 3 illustrates this coupled process. To summarize, model inputs and outputs are the following:
Model inputs
-
1. Annual layer thickness profile from GISP2.
-
2. Non-dimensional vertical velocity profile.
-
3. Reference conditions for thickness, half-width, and surface vertical velocity (to define the parameter f in Equations (5) ).
-
4. Initial thickness history.

Fig. 3. Illustration of the iterative method used in the model. Each rectangular box represents the ice column. Representative interfaces are indicated by horizontal lines. Bold arrows indicate the direction of calculations, and n indicates the time step. A prescribed thickness history, H(t), with an assumed vertical velocity distribution, v(y), is applied to the GISP2 layer-thickness data to calculate an accumulation-rate history, b(t). This accumulation-rate history is then used to calculate a new thickness history. A consistent accumulation-rate and ice-thickness history is achieved after about five iterations.
Model outputs
-
1. Accumulation history.
-
2. Thickness history.
Results and Discussion
We applied this model to layer-thickness data from the GISP2 ice core, from 105 000 to 50 000 BP, the data are based on a 12 point time-scale obtained from the Vostok time-scale and sea-sediment records (Reference BenderBender and others. 1994). More recently than 50 000 BP, the data are based on the identification and counting of annual layers in the core (Reference MeeseMeese and others, 1994). To reduce noise, these annual layer-thickness data were averaged over 2 m.
The solid curve in Figure 4a shows the inferred accumulation rates after five iterations of the model. For this calculation we used the vertical velocity profile from a finite-element calculation along the (GRIP-GISP2 (flow-line (Reference Schott., Waddington and RaymondSchott and others, 1992). The half-width L was fixed at its present value of about 400 km. The dotted curve in the figure is the accumulation-rate history inferred assuming no thickness change. To see the long- time-scale differences between the accumulation histories predicted by the constant-thickness model and the variable-thickness model, both curves shown in Figure 4a have been smoothed with a 500 a running average. Consequently, the amplitude of very high-frequency variations in accumulation rate are somewhat reduced. The sharp peaks In both curves at about 55 000, 81 000 and 86 000 BP are caused by discontinuities in slope of the coarse depth-age curve prior to 50 000 BP. The variable-thickness model predicts accumulation rates about 20-25% lower than the constant-thickness prediction for the pre-Holocene record. The variable-thickness model also preserves the high-frequency variations in accumulation rates. The corresponding ice-sheet thickness histories are shown in Figure 4b.

Fig. 4. (a) Accumulation-rate history in m ice a−1 for GISP2 using this model (solid line) compared to the inferred accumulation history inferred assuming constant thickness (dashed line). These calculations assume the vertical velocity shape given by a finite-element model (Reference Schott., Waddington and RaymondSchott and others, 1992) and a fixed half-width, L. To show long-time scale differences, both curves have been smoothed with a 500 a running average. The sharp peaks in accumulation rates at about 55 000, 81 000 and 86 000 BP are caused by discontinuities in the slope of the coarse depth-age curve prior to 50000 BP. These accumulation-rate histories define the envelope of most plausible accumulation histories at GISP2. (b) Corresponding ice-sheet thickness histories. Maximum thickness reduction for the variable-thickness calculation is about 450 m.
Validity and uniqueness
There are two main sources of uncertainty that become increasingly significant for older ice: (1) over-simplifications in the theory, and (2) errors in the data, first, uncertainties in vertical strain rates become large for deeper and older ice. Secondly, the thickness prediction for the oldest times is suspect because the model ice sheet does not know its accumulation or thickness prior to the time the model begins (105 000 BP), Since it takes several time constants (6 ka) for the ice-sheet thickness to forget its initial conditions, results prior to about 90 000 BP depend on the initial conditions and are not shown in Figure 4. Thirdly, errors in the relative position of measured layer horizons would lead to some artificially thick layers and some corresponding artificially thin layers. The fractional error in these layer thicknesses would be preserved in the model and would lead to higher-amplitude noise in the inferred accumulation history for the older and deeper ice. However, the long-term average would be preserved. Since errors in the vertical strain rate and the data are probably smaller near the upper pail of the ice core, results for the most recent part of the record are the most reliable.
It is not immediately clear that the thickness and accumulation histories recovered by this model are unique. The constant-thickness calculation produces one accumulation history that is consistent with the layer-thickness pattern at GISP2. Our new method, which employs different physical assumptions, produces another accumulation and thickness history that is consistent with the layer-thickness pattern. However, is it plausible that, given the same physical assumptions, this model might give two or more distinct solutions for thickness and accumulation histories that are consistent with the GISP2 layer-thickness data? To test this question, we created synthetic-layer profiles using the forward method with a prescribed periodic (100 ka) accumulation history. We then attempted to reconstruct the accumulation history by our iterative backward calculation. The model recovered the original accumulation history almost exactly. In another test, white noise of a specified maximum amplitude was added to a synthetic-layer thickness profile. The inferred accumulation from the backward iterative calculation preserved the fractional errors introduced by the noise; it did not amplify them. We conclude that high-frequency variations in the inferred accumulation history are recovered with an accuracy controlled by the fractional error of the measured layer thicknesses. We are confident that the solutions calculated by this model are stable and unique given our assumptions.
Comparison with other models
Our calculations, assuming a fixed half-width L, predict a maximum thickness reduction of about 450 m for the last glacial cycle. More complex models of the Greenland ice sheet (Reference Huybrechts, Letréguilly and Reeh.Huybrechts and others, 1991; Reference Letréguilly, Reeh and HuybrechtsLetréguilly and others, 1991) predict more modest values for thickness change. Reference Letréguilly, Reeh and HuybrechtsLetréguilly and others (1991) predict a maximum thickness reduction of about 200 m at the summit, using an accumulation calculated from a temperature history derived from oxygen-isotope measurements at the Pakitsoq margin. Those measurements predict higher temperatures and therefore more precipitation during the last glacial cycle (~ 0.14 m a−1) than the GISP2 layer data seem to indicate. This difference in accumulation history affects the thickness-change prediction. When we used the same accumulation rates as Reference Letréguilly, Reeh and HuybrechtsLetréguilly and others (1991), our model predicted a thickness reduction of 250m, in reasonable agreement with their result. These more complex models also assumed as we did that the margins of the ice sheet were pinned at their present position over time. The discrepancy in the predicted thickness change, then, arises from differences in the accumulation history used in the models rather than fundamental differences in model characteristics and parameterization.
The effect of a non-steady vertical velocity profile
The calculation shown in Figure 4a assumes that the shape of the vertical velocity profile is not altered by evolving temperature and ice-softness (enhancement) distributions in the ice column. We attempted to determine the sensitivity of the inferred accumulation rates to changes in the vertical velocity profile shape by running the model with various distinct velocity profiles. One profile (used in Figure 4a) was generated by a finite-element calculation of ice flow near the Greenland summit (Reference Schott., Waddington and RaymondSchott and others. 1992). Two additional profiles were calculated analytically from simple models of a two-dimensional ice slab. An enhancement factor, E(y), was used to include the effect of flow-law variations caused by the development of a crystal fabric or changes in impurity concentrations. This factor was taken to be 3 for softer glacial ice and 1 for interglacial ice (Reference Paterson.Paterson, 1991), One of the two additional velocity profiles was calculated for a temperature and enhancement-factor distribution, T(y) and E(y), characteristic of interglacial conditions, and the other for a temperature and fabric distribution characteristic of glacial conditions (Fig. 3). The horizontal velocity profile. u(y), can be obtained by integrating the flow-law equation

where y = 0 at the surface and y = H at the bed. The flow-law parameter  , where Q is the activation energy, R is the gas constant, n = 3, and α is the surface slope (Reference PatersonPaterson, 1981). The horizontal velocity, u(x,y), can be approximated as:
, where Q is the activation energy, R is the gas constant, n = 3, and α is the surface slope (Reference PatersonPaterson, 1981). The horizontal velocity, u(x,y), can be approximated as:

Vertical velocity, v(y), can in turn be obtained by continuity:
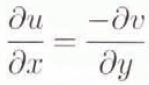
The two parameters, dβ/dx and the constant of integration, are determined by the boundary conditions: v(0) = 0 and v(H) = b. Figure 2 shows the calculated vertical velocity profile shapes and the corresponding temperature and enhancement distributions.
Predicted mass-balance histories calculated using these various vertical velocity profile shapes vary by about 10%. All calculations are within the envelope shown in Figure 4a.
The effect of changing ice-sheet margins
We assumed that the ice-sheet margins were fixed in most of our calculations. However, the margins of the Greenland ice sheet are not fixed; the half-width may have expanded by about 25-100 km from the present position during the last glacial cycle (Reference Reeh.Reeh 1984; Reference Anandakrishnan, Alley and WaddingtonAnandakrishnan and others, 1994). Expanding the margins would decrease the slope of the ice-sheet profile and allow the ice sheet to thicken, even during periods of low accumulation. Assuming that the margin-position, L(t), and mass-balance changes are roughly 180° out of phase, then a changing margin position would make the ice-sheet thickness less sensitive to mass-balance changes and lead to inferred accumulation rates more like those inferred with the constant-thickness assumption. To determine the sensitivity of model results to changing margin position. the model was modified to account for a crude margin position history. Although it is most likely that the margin expansion for Greenland was asymmetric during the last glacial period (Reference Reeh.Reeh 1984; Reference Anandakrishnan, Alley and WaddingtonAnandakrishnan and others 1994). we assumed a symmetric change in margin position, roughly 180° out of phase with the long-term temperature change. We specified L(t) to be constant at 450 km during the last glacial period, decreasing linearly from 12 000 to 50000 BP to the approximate present length of 400 km, and constant to the present. This calculation predicts a thickness change of about 250 m for the Last Glacial Maximum, and the accumulation history inferred is about 10-15% lower than the constant-thickness prediction. When a margin expansion of 100 km is prescribed, the inferred accumulation history closely matches the prediction assuming constant thickness, and the ice-sheet thickness change ranges from +300 to 100 m during the last glacial period.
The effect of flow description
As a final sensitivity test, we used the model to infer an accumulation history for an ice sheet where deformation is concentrated at the base, such that the horizontal velocity, u(y), is independent of depth and proportional to the base stress to a power m = 2 (Reference NyeNye, 1959). This leads to a thickness profile that is more sensitive to changes in mass balance: H ∝ b 1/5. This increased sensitivity predicts a larger ice-sheet thicknessreduction (700 m), lower accumulation rates during the last glacial period (about 30-35% lower than the constant-thickness prediction and a more gradual increase in accumulation rates since the Younger Dryas. However, since it is believed that the Greenland ice sheet is frozen to its bed and does not flow by basal sliding Reference Firestone, Waddington and Cunningham.Firestone and others. 1990, we consider this accumulation history to be outside the envelope of plausible histories for the GISP2 site.
Conclusions
A model that accounts for the effect of ice-sheet thickness change on the vertical straining of ice layers predicts an accumulation history from GISP2 layer-thickness data that is different from that predicted assuming constant ice-sheet thickness. Various tests show that the accumulation history is sensitive to other factors including: (1) the shape of the vertical velocity profile which is affected by the temperature and structure of the ice, (2) the change in margin position over time, and (3) the description of ice flow (e.g. Vialov vs Nye models). These tests are summarized in Table 1. Hence, it is not possible to identify a “true” accumulation history for GISP2 with this model, but an envelope of plausible accumulation histories can be defined (Fig. 4a). The upper bound for this envelope is given by the inferred accumulation rates assuming constant ice-sheet thickness. The lower bound is given by the variable-thickness model assuming (a) that ice flows by internal deformation rather than basal sliding, (b) that the ice-sheet margins remain fixed, and (c) that a vertical velocity shape is given by a finite-element calculation (Reference Schott., Waddington and RaymondSchott and others, 1992). Since the most realistic scenario for the Greenland ice sheet involves an increased half-width during glacial periods, and since the inferred accumulation history considering this change in margin position lies near the upper extreme of the envelope, the envelope of most plausible accumulation histories for the Greenland GISP2 site is probably narrower than the envelope shown in Figure 4a by about 10%.
Table 1. Summary of sensitivity tests (all values are approximate)

The inferred accumulation history for the oldest and deepest ice is uncertain for a variety of reasons. Specifically, the accumulation-rate history inferred from deep ice layers is especially sensitive to changes in the vertical strain-rate pattern. This simple theory may not adequately describe the vertical strain rate for deep ice. Also, decreased accuracy of the data for older ice contributes to errors in the inferred accumulation rate. To further constrain the accumulation history near the Greenland summit) the next step would be to compare these results to the accumulation history inferred from the GRIP core, located about 30 km east of GISP2 (Reference Dahl-Jensen, Johnsen, Hammer, Clausen, Jouzel. and PeltierDahl-Jensen and others. 1993). Perhaps such a comparison would yield information about accumulation variability near the Summit region over time and provide clues about past changes in global circulation patterns.
Acknowledgements
This research was supported by grant No. OPP-9123660 from the U.S. National Science Foundation. We thank the 109th Air National Guard, the Polar Ice Coring Office and the GISP2 Science Management Office for logistical support. We also thank K. M. Cuffey and A.M. Eades for helpful suggestions to improve the manuscript.







