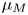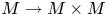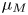1. Introduction
1.1 Poincaré spaces
A distinguishing feature of smooth manifolds is that they carry tangential information: If $M$![]() is a smooth manifold, then at each point $x\in M$
is a smooth manifold, then at each point $x\in M$![]() , one may assign a tangent space $T_xM$
, one may assign a tangent space $T_xM$![]() . The tangent spaces assemble into a vector bundle $\tau _M:\:TM \to M$
. The tangent spaces assemble into a vector bundle $\tau _M:\:TM \to M$![]() . If $M$
. If $M$![]() is compact, then the total space $TM$
is compact, then the total space $TM$![]() is diffeomorphic to a tubular neighbourhood of the diagonal map $M \to M \times M$
is diffeomorphic to a tubular neighbourhood of the diagonal map $M \to M \times M$![]() . The existence of a tubular neighbourhood corresponds to the fact that an $n$
. The existence of a tubular neighbourhood corresponds to the fact that an $n$![]() -manifold is locally diffeomorphic to $\mathbb {R}^n$
-manifold is locally diffeomorphic to $\mathbb {R}^n$![]() in a suitably parametrized way.
in a suitably parametrized way.
Note that a tubular neighbourhood determines a decomposition
where $D(\tau _M)$![]() is the tangent disk bundle of $M$
is the tangent disk bundle of $M$![]() , $S(\tau _M)$
, $S(\tau _M)$![]() is the tangent sphere bundle, and $C$
is the tangent sphere bundle, and $C$![]() is the complement of the tubular neighbourhood.
is the complement of the tubular neighbourhood.
In the 1960s, Browder, Novikov, and Wall developed surgery theory as a tool to classify manifolds up to diffeomorphism in dimensions at least five. A starting point for this theory is that a manifold satisfies Poincaré duality. This led Levitt, Spivak, and Wall to introduce the notion of Poincaré duality space [Reference Spivak26, Reference Wall30]. Such spaces satisfy Poincaré duality globally, however, in contrast with manifolds, duality may fail locally. Nevertheless, Spivak showed that Poincaré spaces can be equipped with stable tangential data: There is a stable spherical fibration, the Spivak tangent fibration, which is unique up to contractible choice, and which can be characterized in a homotopy theoretic way.Footnote 1
One is therefore led to the problem as to what a ‘tubular neighbourhood’ of the diagonal of a Poincaré space should be and how it might relate to the Spivak fibration.
If $M$![]() is a Poincaré duality space formal dimension $n$
is a Poincaré duality space formal dimension $n$![]() , then by analogy with the manifold case, one might define a ‘Poincaré tubular neighbourhood’ of the diagonal $\Delta \colon \! M\to M\times M$
, then by analogy with the manifold case, one might define a ‘Poincaré tubular neighbourhood’ of the diagonal $\Delta \colon \! M\to M\times M$![]() to consist of a homotopy theoretic decomposition of the form
to consist of a homotopy theoretic decomposition of the form
in which $\tau \colon \! S(\tau ) \to M$![]() is an $(n-1)$
is an $(n-1)$![]() -spherical fibration which stabilizes to the Spivak tangent fibration, $D(\tau )$
-spherical fibration which stabilizes to the Spivak tangent fibration, $D(\tau )$![]() is the mapping cylinder of $\tau$
is the mapping cylinder of $\tau$![]() , and $C$
, and $C$![]() is some space such that the pair $(C,S(\tau ))$
is some space such that the pair $(C,S(\tau ))$![]() satisfies Poincaré duality for pairs. The above decomposition amounts to the notion of Poincaré embedding in the special case of the diagonal map [Reference Levitt21], [Reference Wall31, §11], [Reference Klein14].
satisfies Poincaré duality for pairs. The above decomposition amounts to the notion of Poincaré embedding in the special case of the diagonal map [Reference Levitt21], [Reference Wall31, §11], [Reference Klein14].
In this paper, we address the following question: When does $M$![]() possess such a decomposition? Assume in what follows that the formal dimension of $M$
possess such a decomposition? Assume in what follows that the formal dimension of $M$![]() is at least four. In [Reference Klein16], the first author showed that the diagonal admits a Poincaré embedding if $M$
is at least four. In [Reference Klein16], the first author showed that the diagonal admits a Poincaré embedding if $M$![]() is 1-connected. When $M$
is 1-connected. When $M$![]() is not $1$
is not $1$![]() -connected then in [Reference Klein17] the first author defined an obstruction $\mu _M$
-connected then in [Reference Klein17] the first author defined an obstruction $\mu _M$![]() whose vanishing is both necessary and sufficient for the existence of a Poincaré embedding of the diagonal. However, he was unable to determine when the obstruction vanishes.
whose vanishing is both necessary and sufficient for the existence of a Poincaré embedding of the diagonal. However, he was unable to determine when the obstruction vanishes.
Our goal is to relate the obstruction $\mu _M$![]() to other, more well-known ones. We also apply our main results to prove that $\mu _M$
to other, more well-known ones. We also apply our main results to prove that $\mu _M$![]() vanishes in some additional cases.
vanishes in some additional cases.
1.2 The Wall finiteness obstruction
For a group $\pi$![]() , let $K_0(\mathbb {Z}[\pi ])$
, let $K_0(\mathbb {Z}[\pi ])$![]() be the Grothendieck group of finitely generated projective (left) $\mathbb {Z}[\pi ]$
be the Grothendieck group of finitely generated projective (left) $\mathbb {Z}[\pi ]$![]() -modules. According to Wall [Reference Wall29], a connected finitely dominated connected space $X$
-modules. According to Wall [Reference Wall29], a connected finitely dominated connected space $X$![]() with fundamental group $\pi$
with fundamental group $\pi$![]() determines an element
determines an element
called the Wall finiteness obstruction. If we assume that $\pi$![]() is finitely presented, then $X$
is finitely presented, then $X$![]() has the homotopy type of a finite CW complex if and only if $\tilde w(X)= 0$
has the homotopy type of a finite CW complex if and only if $\tilde w(X)= 0$![]() , where $\tilde w(X) \in \widetilde {K}_0(\mathbb {Z}[\pi ])$
, where $\tilde w(X) \in \widetilde {K}_0(\mathbb {Z}[\pi ])$![]() is the image $w(X)$
is the image $w(X)$![]() in the reduced Grothendieck group.
in the reduced Grothendieck group.
1.3 The Reidemeister characteristic
Let $\bar \pi$![]() denote the set of conjugacy classes of $\pi$
denote the set of conjugacy classes of $\pi$![]() , and let $\mathbb {Z}\langle \bar \pi \rangle$
, and let $\mathbb {Z}\langle \bar \pi \rangle$![]() be the free abelian group with basis $\bar \pi$
be the free abelian group with basis $\bar \pi$![]() . The Hattori–Stallings trace [Reference Hattori11, Reference Stallings27] is a homomorphism
. The Hattori–Stallings trace [Reference Hattori11, Reference Stallings27] is a homomorphism
induced by assigning to a finitely generated projective $\mathbb {Z}[\pi ]$![]() -module $P$
-module $P$![]() the trace of the identity map $P \to P$
the trace of the identity map $P \to P$![]() , where the trace is defined by means of the diagram of homomorphisms
, where the trace is defined by means of the diagram of homomorphisms
Here, $\hom _{\mathbb {Z}[\pi ]}(P,\mathbb {Z}[\pi ])$![]() is viewed as a right $\mathbb {Z}[\pi ]$
is viewed as a right $\mathbb {Z}[\pi ]$![]() -module and $\pi^\mathrm{ad} = \pi$
-module and $\pi^\mathrm{ad} = \pi$![]() considered as a $\pi$
considered as a $\pi$![]() -set together with the conjugation action. The second displayed homomorphism in (1.2) is induced by evaluation $f\otimes x\mapsto f(x)$
-set together with the conjugation action. The second displayed homomorphism in (1.2) is induced by evaluation $f\otimes x\mapsto f(x)$![]() .
.
For a connected finitely dominated space $X$![]() with fundamental group $\pi$
with fundamental group $\pi$![]() , the Reidemeister characteristic
, the Reidemeister characteristic
is defined as $r(X) := r(w(X))$![]() .Footnote 2 Let $\widetilde {\mathbb {Z}}\langle \bar \pi \rangle$
.Footnote 2 Let $\widetilde {\mathbb {Z}}\langle \bar \pi \rangle$![]() denote the cokernel of the inclusion $\mathbb {Z}\langle e \rangle \to \mathbb {Z}\langle \bar \pi \rangle$
denote the cokernel of the inclusion $\mathbb {Z}\langle e \rangle \to \mathbb {Z}\langle \bar \pi \rangle$![]() , where $e \in \pi$
, where $e \in \pi$![]() is the trivial element. The reduced Reidemeister characteristic $\tilde r(X)$
is the trivial element. The reduced Reidemeister characteristic $\tilde r(X)$![]() is the image of $r(X)$
is the image of $r(X)$![]() in $\widetilde {\mathbb {Z}}\langle \bar \pi \rangle$
in $\widetilde {\mathbb {Z}}\langle \bar \pi \rangle$![]() .
.
Our first main result is:
Theorem A Suppose that $M$![]() is a connected, finitely dominated Poincaré duality space. If $\tilde r(M) \ne 0$
is a connected, finitely dominated Poincaré duality space. If $\tilde r(M) \ne 0$![]() , then the diagonal map $M \to M^{\times 2}$
, then the diagonal map $M \to M^{\times 2}$![]() does not admit a Poincaré embedding.
does not admit a Poincaré embedding.
Remark 1.1 There is currently no known example in which $\tilde r(M) \ne 0$![]() . In fact, the Bass trace conjecture for a group $\pi$
. In fact, the Bass trace conjecture for a group $\pi$![]() is the statement that the reduced Hattori–Stallings trace
is the statement that the reduced Hattori–Stallings trace
is trivial [Reference Bass3]. Although the conjecture remains open, it has been verified for a large class of groups, including the residually nilpotent ones. See [Reference Berrick and Hesselholt5, §3] for more details.
1.4 The diagonal obstruction
Let $d \ge 0$![]() be an integer. Then the abelian group ${\mathbb {Z}}\langle \bar \pi \rangle$
be an integer. Then the abelian group ${\mathbb {Z}}\langle \bar \pi \rangle$![]() comes equipped with an involution $\alpha \mapsto \bar \alpha$
comes equipped with an involution $\alpha \mapsto \bar \alpha$![]() induced by the operation $x \mapsto (-1)^{-d}x^{-1}$
induced by the operation $x \mapsto (-1)^{-d}x^{-1}$![]() for $x\in \pi$
for $x\in \pi$![]() . We set
. We set
i.e., the coinvariants of the involution. Similarly, one may define a reduced version of $Q_d(\pi )$![]() as the cokernel
as the cokernel
where $e$![]() denotes the trivial group.
denotes the trivial group.
The transfer homomorphism
is defined by $\tilde {\sigma }(\alpha ) = \alpha + \bar \alpha$![]() .
.
Let $M$![]() be a connected, finitely dominated Poincaré duality space of dimension $d$
be a connected, finitely dominated Poincaré duality space of dimension $d$![]() and fundamental group $\pi$
and fundamental group $\pi$![]() . Then as alluded to above, in [Reference Klein17] an obstruction
. Then as alluded to above, in [Reference Klein17] an obstruction
was introduced which vanishes if the diagonal map $M\to M\times M$![]() admits a Poincaré embedding. Conversely, when $d \ge 4$
admits a Poincaré embedding. Conversely, when $d \ge 4$![]() , it was shown that $\mu _M = 0$
, it was shown that $\mu _M = 0$![]() implies that a Poincaré embedding of the diagonal exists. The obstruction $\mu _M$
implies that a Poincaré embedding of the diagonal exists. The obstruction $\mu _M$![]() is an invariant of the homotopy type of $M$
is an invariant of the homotopy type of $M$![]() .
.
Theorem A is an immediate consequence of our second main result, which relates the Reidemeister characteristic $r(M)$![]() to the diagonal obstruction $\mu _M$
to the diagonal obstruction $\mu _M$![]() .
.
Theorem B Let $M$![]() be a connected, finitely dominated Poincaré duality space. Then
be a connected, finitely dominated Poincaré duality space. Then
In particular, if the diagonal $M \to M^{\times 2}$![]() admits a Poincaré embedding, then $\tilde r(M) = 0$
admits a Poincaré embedding, then $\tilde r(M) = 0$![]() .
.
Hypothesis 1.2 $M$![]() is a connected Poincaré duality space of dimension $d$
is a connected Poincaré duality space of dimension $d$![]() such that one of the following conditions hold:
such that one of the following conditions hold:
• $M$
 is homotopy finite, or
is homotopy finite, or• $M$
 is finitely dominated and the Bass trace conjecture holds for $\pi = \pi _1(M)$
is finitely dominated and the Bass trace conjecture holds for $\pi = \pi _1(M)$ .
.
Corollary C Assume $M$![]() satisfies hypothesis 1.2. Then $\tilde \sigma (\mu _M)$
satisfies hypothesis 1.2. Then $\tilde \sigma (\mu _M)$![]() is trivial.
is trivial.
Remark 1.3 As mentioned above, it was known that $\mu _M$![]() vanishes when $M$
vanishes when $M$![]() is simply connected or when $M$
is simply connected or when $M$![]() has the homotopy type of a closed manifold. The only other case that we were aware of occurs when $M$
has the homotopy type of a closed manifold. The only other case that we were aware of occurs when $M$![]() is a ‘two-stage patch space’, i.e., a Poincaré space obtained by gluing together two compact manifolds along a homotopy equivalence of their boundaries. If in addition the fundamental group of the boundary is square root closed, then according to Byun [Reference Byun6] there is a diagonal Poincaré embedding, and we infer $\mu _M = 0$
is a ‘two-stage patch space’, i.e., a Poincaré space obtained by gluing together two compact manifolds along a homotopy equivalence of their boundaries. If in addition the fundamental group of the boundary is square root closed, then according to Byun [Reference Byun6] there is a diagonal Poincaré embedding, and we infer $\mu _M = 0$![]() in this instance.
in this instance.
Using corollary C, we obtain several additional cases:
Corollary D Assume that $M$![]() is a connected, finitely dominated Poincaré space and $d = \dim M \ge 4$
is a connected, finitely dominated Poincaré space and $d = \dim M \ge 4$![]() is even. Additionally, assume that $\pi$
is even. Additionally, assume that $\pi$![]() is abelian and the 2-primary subgroup of $\pi$
is abelian and the 2-primary subgroup of $\pi$![]() is a finite direct product of cyclic groups of order two. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$
is a finite direct product of cyclic groups of order two. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$![]() admits a Poincaré embedding.
admits a Poincaré embedding.
Corollary E Assume that $M$![]() satisfies hypothesis 1.2 with $d \ge 4$
satisfies hypothesis 1.2 with $d \ge 4$![]() . Suppose that every non-trivial element of $\pi$
. Suppose that every non-trivial element of $\pi$![]() has odd order. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$
has odd order. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$![]() admits a Poincaré embedding.
admits a Poincaré embedding.
The above results justify making the following conjecture.
Conjecture F Assume that $M$![]() satisfies hypothesis 1.2 with $d \ge 4$
satisfies hypothesis 1.2 with $d \ge 4$![]() . Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$
. Then the diagonal map $\Delta \colon \! M \to M^{\times 2}$![]() admits a Poincaré embedding.
admits a Poincaré embedding.
Outline. In §2 contains some prerequisites for reading the paper; much of what is contained there is well-known and in the literature. In §3 we introduce the Euler invariant of a Poincaré space equipped with an unstable the Spivak tangent fibration. In §4 we introduce a homotopy-theoretic self-intersection invariant. In §5 is a discussion of the equivariant geometric Hopf invariant as in [Reference Crabb and Ranicki7] but in the more general setting of a topological group. The main results are proved in §6.
2. Preliminaries
Here we develop the minimal foundational scaffolding. All of this material has appeared elsewhere and the exposition is not to be regarded as exhaustive.
2.1 Spaces
Let $\mathrm{Top}$![]() be the Quillen model category of compactly generated weak Hausdorff spaces [Reference Hirschhorn12].Footnote 3 The weak equivalences of $\mathrm{Top}$
be the Quillen model category of compactly generated weak Hausdorff spaces [Reference Hirschhorn12].Footnote 3 The weak equivalences of $\mathrm{Top}$![]() are the weak homotopy equivalences, and the fibrations are the Serre fibrations. The cofibrations are defined using the right lifting property with respect to the trivial fibrations. In particular, every object $\mathrm{Top}$
are the weak homotopy equivalences, and the fibrations are the Serre fibrations. The cofibrations are defined using the right lifting property with respect to the trivial fibrations. In particular, every object $\mathrm{Top}$![]() is fibrant. An object is cofibrant whenever it is a retract of a cell complex. We let $\mathrm{Top}_*$
is fibrant. An object is cofibrant whenever it is a retract of a cell complex. We let $\mathrm{Top}_*$![]() denote the category of based spaces. Then $\mathrm{Top}_*$
denote the category of based spaces. Then $\mathrm{Top}_*$![]() inherits a Quillen model structure from $\mathrm{Top}$
inherits a Quillen model structure from $\mathrm{Top}$![]() by means of the forgetful functor $\mathrm{Top}_\ast \to \mathrm{Top}$
by means of the forgetful functor $\mathrm{Top}_\ast \to \mathrm{Top}$![]() .
.
An object in $\mathrm{Top}$![]() or $\mathrm{Top}_\ast$
or $\mathrm{Top}_\ast$![]() is finite if it is a finite cell complex. It is homotopy finite if it is weakly equivalent to a finite object. A object is $X$
is finite if it is a finite cell complex. It is homotopy finite if it is weakly equivalent to a finite object. A object is $X$![]() is finitely dominated if it is a retract of a homotopy finite object.
is finitely dominated if it is a retract of a homotopy finite object.
We employ the following notation, most of which is standard. For objects $X,Y\in \mathrm{Top}_\ast$![]() , we let $X\vee Y$
, we let $X\vee Y$![]() denote the wedge and we let $X\wedge Y$
denote the wedge and we let $X\wedge Y$![]() denote the smash product. The suspension of $X$
denote the smash product. The suspension of $X$![]() is then $S^1 \wedge X$
is then $S^1 \wedge X$![]() , where $S^1$
, where $S^1$![]() is the circle. When we write $X^{[k]}$
is the circle. When we write $X^{[k]}$![]() , we mean the $k$
, we mean the $k$![]() -fold smash product of $X$
-fold smash product of $X$![]() with itself. When passing to the stable category of based spaces we sometimes write
with itself. When passing to the stable category of based spaces we sometimes write ![]() to indicate a stable map. If $X$
to indicate a stable map. If $X$![]() is an unbased space, we write $X_+$
is an unbased space, we write $X_+$![]() for the based space $X \amalg \ast$
for the based space $X \amalg \ast$![]() given by taking the disjoint union with a basepoint. For a based space $A$
given by taking the disjoint union with a basepoint. For a based space $A$![]() and an unbased space $B$
and an unbased space $B$![]() , our convention will be $A\wedge B_+ := A \wedge (B_+)$
, our convention will be $A\wedge B_+ := A \wedge (B_+)$![]() and $B_+ \wedge A := (B_+) \wedge A$
and $B_+ \wedge A := (B_+) \wedge A$![]() .
.
2.2 Poincaré duality spaces
Recall that an object $M \in \mathrm{Top}$![]() is a Poincaré duality space of (formal) dimension $d$
is a Poincaré duality space of (formal) dimension $d$![]() if there exists a pair
if there exists a pair
in which $\mathscr L$![]() is a rank one local coefficient system (or orientation sheaf) and
is a rank one local coefficient system (or orientation sheaf) and
is a fundamental class such that for all local coefficient systems $\mathscr B$![]() , the cap product homomorphism
, the cap product homomorphism
is an isomorphism in all degrees (cf. [Reference Klein19, Reference Wall30]). The Poincaré spaces considered in this paper are assumed to be connected, finitely dominated and cofibrant. Note that if the pair $(\mathscr L, [M])$![]() exists, then it is determined up to unique isomorphism by the above property. Also note that closed manifolds are homotopy finite Poincaré duality spaces.
exists, then it is determined up to unique isomorphism by the above property. Also note that closed manifolds are homotopy finite Poincaré duality spaces.
Remark 2.1 Let $p$![]() be an odd prime. In [Reference Wall30, cor. 5.4.2], a construction is given of a connected finitely dominated Poincaré duality space $K$
be an odd prime. In [Reference Wall30, cor. 5.4.2], a construction is given of a connected finitely dominated Poincaré duality space $K$![]() of dimension 4 with fundamental group $\pi = \mathbb {Z}/p\mathbb {Z}$
of dimension 4 with fundamental group $\pi = \mathbb {Z}/p\mathbb {Z}$![]() . For a suitable choice of $p$
. For a suitable choice of $p$![]() , the finiteness obstruction $\tilde w(K) \in \tilde K_0(\mathbb {Z}[\pi ])$
, the finiteness obstruction $\tilde w(K) \in \tilde K_0(\mathbb {Z}[\pi ])$![]() has odd order (for example, $p = 97$
has odd order (for example, $p = 97$![]() will do, see [Reference Milnor24, p. 31]). Then if $j \ge 3$
will do, see [Reference Milnor24, p. 31]). Then if $j \ge 3$![]() , the product $K\times S^{2j-4}$
, the product $K\times S^{2j-4}$![]() is a connected finitely dominated Poincaré duality space of dimension $2j$
is a connected finitely dominated Poincaré duality space of dimension $2j$![]() having non-trivial finiteness obstruction (this uses [Reference Gersten10, thm. 0.1]). For other examples see [Reference Klein20].
having non-trivial finiteness obstruction (this uses [Reference Gersten10, thm. 0.1]). For other examples see [Reference Klein20].
More generally, one has the notion of a Poincaré pair $(N,\partial N)$![]() with fundamental class $[N] \in H_d(N,\partial N; \mathscr L)$
with fundamental class $[N] \in H_d(N,\partial N; \mathscr L)$![]() . In this case one assumes that the cap product
. In this case one assumes that the cap product
is an isomorphism and in addition the image of $[N]$![]() with respect to the boundary homomorphism $H_d(N,\partial N; \mathscr L) \to H_{d-1}(\partial N; \mathscr L_{|\partial L})$
with respect to the boundary homomorphism $H_d(N,\partial N; \mathscr L) \to H_{d-1}(\partial N; \mathscr L_{|\partial L})$![]() equips $\partial N$
equips $\partial N$![]() with the structure of a Poincaré space of dimension $d-1$
with the structure of a Poincaré space of dimension $d-1$![]() .
.
Given a spherical fibration $\xi \colon \! S(\xi ) \to M$![]() , we write $D(\xi ) \to M$
, we write $D(\xi ) \to M$![]() for the mapping cylinder. The Thom space is the quotient
for the mapping cylinder. The Thom space is the quotient
Note that the first Stiefel-Whitney class of $\xi$![]() defines an orientation sheaf $\mathscr L^\xi$
defines an orientation sheaf $\mathscr L^\xi$![]() . Moreover, by the Thom isomorphism, $H_\ast (M^\xi ) \cong \tilde H_{\ast -k}(M)$
. Moreover, by the Thom isomorphism, $H_\ast (M^\xi ) \cong \tilde H_{\ast -k}(M)$![]() , where in the latter, the coefficients are taken with respect to the orientation sheaf.
, where in the latter, the coefficients are taken with respect to the orientation sheaf.
A Spivak normal fibration for a Poincaré duality space $M$![]() of dimension $d$
of dimension $d$![]() consists of a pair $(\nu,c)$
consists of a pair $(\nu,c)$![]() in which $\nu$
in which $\nu$![]() is a $(k-1)$
is a $(k-1)$![]() -spherical fibration for some $k$
-spherical fibration for some $k$![]() and
and
is a degree one map in the sense that the image $c_\ast ([S^{d+k}]) \in H_{d+k}(M^\xi ) \cong H_d(M;\mathscr L^\xi )$![]() is a fundamental class for $M$
is a fundamental class for $M$![]() . The pair $(\nu,c)$
. The pair $(\nu,c)$![]() always exists and is unique up to stable fibre homotopy equivalence (see e.g., [Reference Klein15]). The map $c$
always exists and is unique up to stable fibre homotopy equivalence (see e.g., [Reference Klein15]). The map $c$![]() is sometimes called the normal invariant.
is sometimes called the normal invariant.
2.3 Poincaré embeddings of the diagonal
Suppose $M$![]() is a connected finitely dominated Poincaré duality space of dimension $d$
is a connected finitely dominated Poincaré duality space of dimension $d$![]() . If $(\mathscr L,[M])$
. If $(\mathscr L,[M])$![]() is a choice of orientation and fundamental class for $M$
is a choice of orientation and fundamental class for $M$![]() , then $(\mathscr L^{\times 2},[M]^{\times 2})$
, then $(\mathscr L^{\times 2},[M]^{\times 2})$![]() is one for $M\times M$
is one for $M\times M$![]() . In particular $M\times M$
. In particular $M\times M$![]() is a Poincaré duality space of dimension $2d$
is a Poincaré duality space of dimension $2d$![]() .
.
A diagonal Poincaré embedding of $M$![]() consists of a map of (finitely dominated) spaces $S(\xi ) \to C$
consists of a map of (finitely dominated) spaces $S(\xi ) \to C$![]() that fits into a commutative homotopy cocartesian square
that fits into a commutative homotopy cocartesian square

in which
• $\Delta$
 is the diagonal map,
is the diagonal map,• $\xi$
 is a $(d-1)$
is a $(d-1)$ -spherical fibration,
-spherical fibration,• $(C,S(\xi ))$
 is a Poincaré pair of dimension $2d$
is a Poincaré pair of dimension $2d$ with orientation sheaf given by the restriction $\mathscr L^{\times 2}_{|C}$
with orientation sheaf given by the restriction $\mathscr L^{\times 2}_{|C}$ and fundamental class $[C]$
and fundamental class $[C]$ given by taking the image of $[M]^{\times 2}$
given by taking the image of $[M]^{\times 2}$ under the homomorphism
\[ H_{2d}(M\times M; \mathscr L^{{\times} 2}) \to H_{2d}(M\times M, M; \mathscr L^{{\times} 2}) \cong H_{2d}(C,S(\xi);\mathscr L^{{\times} 2}_{|C}), \]where the displayed isomorphism is given by excision.
under the homomorphism
\[ H_{2d}(M\times M; \mathscr L^{{\times} 2}) \to H_{2d}(M\times M, M; \mathscr L^{{\times} 2}) \cong H_{2d}(C,S(\xi);\mathscr L^{{\times} 2}_{|C}), \]where the displayed isomorphism is given by excision.
It follows that the local system associated to $\xi$![]() is $\mathscr L^{-1}$
is $\mathscr L^{-1}$![]() . We refer the reader to [Reference Klein19, §5] or [Reference Klein17, §2] for the definition of Poincaré embeddings in full generality.
. We refer the reader to [Reference Klein19, §5] or [Reference Klein17, §2] for the definition of Poincaré embeddings in full generality.
2.4 $G$ -spaces
-spaces
A topological group object $G$![]() of $\mathrm{Top}$
of $\mathrm{Top}$![]() is said to be cofibrant if its underlying space is. Let $\mathrm{Top}(G)$
is said to be cofibrant if its underlying space is. Let $\mathrm{Top}(G)$![]() and $\mathrm{Top}_\ast (G)$
and $\mathrm{Top}_\ast (G)$![]() denote the category of left $G$
denote the category of left $G$![]() -spaces and based left $G$
-spaces and based left $G$![]() -spaces. We remark here that a right $G$
-spaces. We remark here that a right $G$![]() -space can always be converted to a left $G$
-space can always be converted to a left $G$![]() -space using the involution of $G$
-space using the involution of $G$![]() defined by $g \mapsto g^{-1}$
defined by $g \mapsto g^{-1}$![]() .
.
The categories $\mathrm{Top}(G)$![]() and $\mathrm{Top}_\ast (G)$
and $\mathrm{Top}_\ast (G)$![]() inherit a model structure using the forgetful functor to $\mathrm{Top}$
inherit a model structure using the forgetful functor to $\mathrm{Top}$![]() . In both instances, all objects are fibrant. An object of $\mathrm{Top}(G)$
. In both instances, all objects are fibrant. An object of $\mathrm{Top}(G)$![]() is cofibrant if it is a retract of a free $G$
is cofibrant if it is a retract of a free $G$![]() -cell complex, i.e., a space built up from the empty space by free $G$
-cell complex, i.e., a space built up from the empty space by free $G$![]() -cell attachments, where a free $G$
-cell attachments, where a free $G$![]() -cell is defined to be $D^n \times G$
-cell is defined to be $D^n \times G$![]() for some $n \ge 0$
for some $n \ge 0$![]() . Similarly, an object of $\mathrm{Top}_\ast (G)$
. Similarly, an object of $\mathrm{Top}_\ast (G)$![]() is cofibrant if it is built up from a point by based free $G$
is cofibrant if it is built up from a point by based free $G$![]() -cell attachments. In $\mathrm{Top}(G)$
-cell attachments. In $\mathrm{Top}(G)$![]() and $\mathrm{Top}_\ast (G)$
and $\mathrm{Top}_\ast (G)$![]() one can speak of finite, homotopy finite, and finitely dominated objects.
one can speak of finite, homotopy finite, and finitely dominated objects.
According to Milnor [Reference Milnor23], given a connected based simplicial complex $X$![]() , one may associate a cofibrant topological group $G$
, one may associate a cofibrant topological group $G$![]() and a universal $G$
and a universal $G$![]() -principal fibre bundle $\tilde X \to X$
-principal fibre bundle $\tilde X \to X$![]() . As $\tilde X$
. As $\tilde X$![]() is contractible, it follows that $X$
is contractible, it follows that $X$![]() is identified with $BG$
is identified with $BG$![]() up to homotopy. On the other hand, any connected space $Y$
up to homotopy. On the other hand, any connected space $Y$![]() is weakly equivalent to a simplicial complex $X$
is weakly equivalent to a simplicial complex $X$![]() . It follows that $Y$
. It follows that $Y$![]() is weakly equivalent to $BG$
is weakly equivalent to $BG$![]() .
.
Remark 2.2 In this case, one can identify the homotopy category of $\mathrm{Top}(G)$![]() with $\mathrm{Top}/X$
with $\mathrm{Top}/X$![]() , that is spaces over $X \simeq BG$
, that is spaces over $X \simeq BG$![]() . Concretely, a $G$
. Concretely, a $G$![]() -space $E$
-space $E$![]() is sent to $E_{hG} \to \star _{hG} = BG$
is sent to $E_{hG} \to \star _{hG} = BG$![]() , whereas to a map $f \colon Z \to X$
, whereas to a map $f \colon Z \to X$![]() we assign the $G$
we assign the $G$![]() -space $\tilde X \times _X Z$
-space $\tilde X \times _X Z$![]() which models the homotopy fibre of $f$
which models the homotopy fibre of $f$![]() as a $G$
as a $G$![]() -space.
-space.
If $X, Y\in \mathrm{Top}_\ast (G)$![]() are objects, we write
are objects, we write
for the set of homotopy classes of based $G$![]() -maps $X\to Y$
-maps $X\to Y$![]() . Similarly, we write
. Similarly, we write
for the abelian group of homotopy classes of stable $G$![]() -maps
-maps ![]() .
.
2.5 Naive $G$ -spectra
-spectra
We will also be considering the category $\mathrm{Sp}(G)$![]() of (naive) $G$
of (naive) $G$![]() -spectra formed from objects of $\mathrm{Top}_\ast (G)$
-spectra formed from objects of $\mathrm{Top}_\ast (G)$![]() . A $G$
. A $G$![]() -spectrum $E$
-spectrum $E$![]() in this sense consists of based $G$
in this sense consists of based $G$![]() -spaces $E_n$
-spaces $E_n$![]() for $n \ge 0$
for $n \ge 0$![]() together with based $G$
together with based $G$![]() -maps $\Sigma E_n \to E_{n+1}$
-maps $\Sigma E_n \to E_{n+1}$![]() (structure maps), where $G$
(structure maps), where $G$![]() acts trivially on the suspension coordinate of $\Sigma E_n$
acts trivially on the suspension coordinate of $\Sigma E_n$![]() . A morphism $f\colon \! E\to E'$
. A morphism $f\colon \! E\to E'$![]() of $G$
of $G$![]() -spectra consists of based $G$
-spectra consists of based $G$![]() -maps of $f_n \colon \! E_n \to E_n'$
-maps of $f_n \colon \! E_n \to E_n'$![]() for all $n$
for all $n$![]() which are compatible with the structure maps.
which are compatible with the structure maps.
Then $\mathrm{Sp}(G)$![]() forms a model category in which the fibrant objects are the $\Omega$
forms a model category in which the fibrant objects are the $\Omega$![]() -spectra and the weak equivalences are the maps which induce isomorphisms on homotopy groups after applying fibrant replacement [Reference Schwede25].
-spectra and the weak equivalences are the maps which induce isomorphisms on homotopy groups after applying fibrant replacement [Reference Schwede25].
Notation 2.3 We indicate a weak equivalence $f\colon \! E\to E'$![]() with the decoration $\overset\sim\to$
with the decoration $\overset\sim\to$![]() . If there is a finite chain of weak equivalences connecting $E$
. If there is a finite chain of weak equivalences connecting $E$![]() to $E'$
to $E'$![]() , then by slight notational abuse, we write $E \simeq E'$
, then by slight notational abuse, we write $E \simeq E'$![]() .
.
Let $S$![]() denote the sphere spectrum. Given any $G$
denote the sphere spectrum. Given any $G$![]() -space $X$
-space $X$![]() its suspension spectrum $\Sigma ^\infty (X_+):= S \wedge X_+$
its suspension spectrum $\Sigma ^\infty (X_+):= S \wedge X_+$![]() , is naturally a $G$
, is naturally a $G$![]() -spectrum. We will sometimes denote it by
-spectrum. We will sometimes denote it by
Remark 2.4 It is sometimes convenient to think of a $G$![]() -spectrum as a collection of based $G$
-spectrum as a collection of based $G$![]() -spaces $E_V$
-spaces $E_V$![]() indexed over finite dimensional inner product spaces $V$
indexed over finite dimensional inner product spaces $V$![]() , together with $G$
, together with $G$![]() -maps $S^W \wedge E_V \to E_{V\oplus W}$
-maps $S^W \wedge E_V \to E_{V\oplus W}$![]() .
.
Given a based $G$![]() -space $X$
-space $X$![]() and a $G$
and a $G$![]() -spectrum $E$
-spectrum $E$![]() , we may form the spectrum of equivariant maps from $X$
, we may form the spectrum of equivariant maps from $X$![]() to $E$
to $E$![]() :
:
The $n$![]() -th space of $F_G(X,E)$
-th space of $F_G(X,E)$![]() is given by the function space $F_G(X,E_n)$
is given by the function space $F_G(X,E_n)$![]() consisting of based $G$
consisting of based $G$![]() -maps $X\to E_n$
-maps $X\to E_n$![]() . For $F_G(X,E)$
. For $F_G(X,E)$![]() to have a sensible homotopy type, one should assume that $X$
to have a sensible homotopy type, one should assume that $X$![]() is cofibrant and that $E$
is cofibrant and that $E$![]() is fibrant. Similarly, one may form
is fibrant. Similarly, one may form
which is the spectrum having $n$![]() -space $X\wedge _G E_n$
-space $X\wedge _G E_n$![]() , i.e., the orbits of $G$
, i.e., the orbits of $G$![]() acting diagonally on the smash product $X\wedge E_n$
acting diagonally on the smash product $X\wedge E_n$![]() . For this construction to have a sensible homotopy type, we should assume that $X$
. For this construction to have a sensible homotopy type, we should assume that $X$![]() and $E$
and $E$![]() are cofibrant. We will implicitly apply fibrant/cofibrant replacement to arrange that the above constructions are always homotopy invariant.
are cofibrant. We will implicitly apply fibrant/cofibrant replacement to arrange that the above constructions are always homotopy invariant.
As a special case of the above, let $EG$![]() be a cofibrant free contractible $G$
be a cofibrant free contractible $G$![]() -space. Then the homotopy fixed points and homotopy orbits of $G$
-space. Then the homotopy fixed points and homotopy orbits of $G$![]() acting on $E$
acting on $E$![]() are given by
are given by
2.5.1 Function spectra and smash products
By resorting to one of the standard enriched model categories of spectra [Reference Elmendorf, Kriz, Mandell and May8, Reference Hovey, Shipley and Smith13], we can form internal hom objects
for naive spectra $X$![]() and $Y$
and $Y$![]() .
.
Note that $X$![]() should be cofibrant and $Y$
should be cofibrant and $Y$![]() should be fibrant for the function spectrum to be homotopy invariant. If $X$
should be fibrant for the function spectrum to be homotopy invariant. If $X$![]() and $Y$
and $Y$![]() are naive $G$
are naive $G$![]() -spectra in one of these categories, then $\hom (X,Y)$
-spectra in one of these categories, then $\hom (X,Y)$![]() is equipped with a $(G\times G)$
is equipped with a $(G\times G)$![]() -action and restricting to the $G$
-action and restricting to the $G$![]() -equivariant functions gives the spectrum
-equivariant functions gives the spectrum
When $X = \Sigma ^\infty Z$![]() is a suspension spectrum of a (cofibrant) $G$
is a suspension spectrum of a (cofibrant) $G$![]() -space, then one has an identification
-space, then one has an identification
Similarly, the smash product $X\wedge Y$![]() has the structure of a $(G\times G)$
has the structure of a $(G\times G)$![]() -spectrum and the orbits under the diagonal action of $G$
-spectrum and the orbits under the diagonal action of $G$![]() defines a spectrum $X\wedge _G Y$
defines a spectrum $X\wedge _G Y$![]() . Moreover, $X\wedge _G Y \simeq Z\wedge _G Y$
. Moreover, $X\wedge _G Y \simeq Z\wedge _G Y$![]() when $X= \Sigma ^\infty Z$
when $X= \Sigma ^\infty Z$![]() .
.
2.6 The dualizing spectrum
The main reference for this subsection is [Reference Klein15]. Let $G$![]() be a cofibrant topological group. Let $G^{\ell r}$
be a cofibrant topological group. Let $G^{\ell r}$![]() denote $G$
denote $G$![]() with the left action of $G\times G$
with the left action of $G\times G$![]() given by $(g,h)\cdot x = gxh^{-1}$
given by $(g,h)\cdot x = gxh^{-1}$![]() .
.
Remark 2.5 The $(G \times G)$![]() -spectrum $S[G^{\ell r}]$
-spectrum $S[G^{\ell r}]$![]() has the following useful property: given any $G$
has the following useful property: given any $G$![]() -spectrum $E$
-spectrum $E$![]() , let $E^\ell$
, let $E^\ell$![]() and $E^r$
and $E^r$![]() denote $E$
denote $E$![]() as a $G \times G$
as a $G \times G$![]() -spectrum with trivial right/left action, respectively. Then one has a natural isomorphism of $(G \times G)$
-spectrum with trivial right/left action, respectively. Then one has a natural isomorphism of $(G \times G)$![]() -spectra
-spectra
If we write $G_\ell$![]() in place of $G\times 1$
in place of $G\times 1$![]() and $G_r$
and $G_r$![]() in place of $1\times G$
in place of $1\times G$![]() , then we immediately infer that
, then we immediately infer that
as $G$![]() -spectra and compatible with the above identification. Similarly, if $E$
-spectra and compatible with the above identification. Similarly, if $E$![]() is a $(G \times G)$
is a $(G \times G)$![]() -spectrum, we obtain a $G$
-spectrum, we obtain a $G$![]() -spectrum $E^{\mathrm{ad}}$
-spectrum $E^{\mathrm{ad}}$![]() by restricting to the diagonal action. We then obtain natural equivalences
by restricting to the diagonal action. We then obtain natural equivalences
Example 2.6 Let $G^{\mathrm{ad}}$![]() denote $G$
denote $G$![]() equipped with its conjugation action $g\cdot x= gxg^{-1}$
equipped with its conjugation action $g\cdot x= gxg^{-1}$![]() . We set
. We set
Then $S[G^\mathrm {ad}] = S[G^{{\ell r}}]^{\mathrm {ad}}$![]() .
.
The dualizing spectrum of $G$![]() is the $G$
is the $G$![]() -spectrum
-spectrum
in which $G$![]() acts as $G_r$
acts as $G_r$![]() .
.
For any $G$![]() -spectrum $E$
-spectrum $E$![]() , one has a norm map
, one has a norm map
which is natural in $E$![]() . The map $\eta$
. The map $\eta$![]() arises by noting that composition of functions gives rise to a pairing
arises by noting that composition of functions gives rise to a pairing
which is $G$![]() -invariant, and therefore factors through homotopy orbits. The norm map is then obtained using the evident weak equivalence $E \simeq \hom _{G_\ell }(S[G^{\ell r}],E)$
-invariant, and therefore factors through homotopy orbits. The norm map is then obtained using the evident weak equivalence $E \simeq \hom _{G_\ell }(S[G^{\ell r}],E)$![]() . We recall the following.
. We recall the following.
Theorem 2.7 (Theorem D in [Reference Klein15])
If $BG$![]() is finitely dominated, then the norm map
is finitely dominated, then the norm map
is an equivalence for any $G$![]() -spectrum $E$
-spectrum $E$![]() .
.
Note that the norm map is adjoint to a map of $G$![]() -spectra
-spectra
This map can be obtained from the evaluation map
which is $(G\times G)$![]() -equivariant. The map $\epsilon$
-equivariant. The map $\epsilon$![]() is defined so that it is adjoint to the identity map of $\mathscr D_G$
is defined so that it is adjoint to the identity map of $\mathscr D_G$![]() , i.e., it is given by the evaluating stable maps $EG_+ \to S[G^{\ell r}]$
, i.e., it is given by the evaluating stable maps $EG_+ \to S[G^{\ell r}]$![]() at points of $EG_+$
at points of $EG_+$![]() .
.
Example 2.8 In the case $E = S$![]() , with $G$
, with $G$![]() acting trivially, the norm equivalence is
acting trivially, the norm equivalence is
Hence, the unit $BG_+ \to S$![]() corresponds to a map $S \to ( \mathscr D_G )_{hG}$
corresponds to a map $S \to ( \mathscr D_G )_{hG}$![]() .
.
This relates to the classical normal invariant of the Spivak normal fibration as follows: Suppose that $M$![]() is a (connected, finitely dominated) Poincaré duality space of dimension $d$
is a (connected, finitely dominated) Poincaré duality space of dimension $d$![]() . Let $\tilde M \to M$
. Let $\tilde M \to M$![]() be a universal principal bundle over $M$
be a universal principal bundle over $M$![]() with topological structure group $G$
with topological structure group $G$![]() . Then $\tilde M$
. Then $\tilde M$![]() is a free, contractible $G$
is a free, contractible $G$![]() -space. We may assume that $G$
-space. We may assume that $G$![]() is cofibrant. Then $\tilde M$
is cofibrant. Then $\tilde M$![]() models $EG$
models $EG$![]() and $M$
and $M$![]() models $BG$
models $BG$![]() . In this case $\mathscr D_G$
. In this case $\mathscr D_G$![]() is unequivariantly weakly equivalent to a sphere of dimension $-d$
is unequivariantly weakly equivalent to a sphere of dimension $-d$![]() , and we write
, and we write
in this instance. Then the stable spherical fibration
is the Spivak normal fibration of $M$![]() .Footnote 4 In this context, the Thom spectrum $M^{-\tau }$
.Footnote 4 In this context, the Thom spectrum $M^{-\tau }$![]() is identified with $S^{-\tau }_{hG} = S^{-\tau } \wedge _G (\tilde M_+)$
is identified with $S^{-\tau }_{hG} = S^{-\tau } \wedge _G (\tilde M_+)$![]() , and the norm equivalence in this notation is just Atiyah duality [Reference Atiyah1] for Poincaré duality spaces:
, and the norm equivalence in this notation is just Atiyah duality [Reference Atiyah1] for Poincaré duality spaces:
Summarizing, with respect to $E = S$![]() , the norm equivalence specializes to Atiyah duality and the stable normal invariant $S \to M^{-\tau }$
, the norm equivalence specializes to Atiyah duality and the stable normal invariant $S \to M^{-\tau }$![]() corresponds to the unit $1\colon \! M_+ \to S$
corresponds to the unit $1\colon \! M_+ \to S$![]() .
.
In what follows we set
Then $G=G_\ell$![]() acts on $S^\tau$
acts on $S^\tau$![]() and
and
is the stable Spivak tangent fibration of $M$![]() . In what follows we extend the action of $G = G_\ell$
. In what follows we extend the action of $G = G_\ell$![]() on $S^\tau$
on $S^\tau$![]() to $G\times G$
to $G\times G$![]() by letting $G_r$
by letting $G_r$![]() act trivially.
act trivially.
2.7 The umkehr map $\Delta _!$
To the diagonal map $\Delta \colon \! M \to M\times M$![]() we associate a $(G\times G$
we associate a $(G\times G$![]() )-equivariant umkehr map
)-equivariant umkehr map
where $S^\tau [G^{\ell r}] := S^\tau \wedge G^{\ell r}_+$![]() . The umkehr map is defined as the evaluation map
. The umkehr map is defined as the evaluation map
in conjunction with the observation that the norm map with respect to $E= S^\tau [G^{\ell r}]$![]() defines an equivalence
defines an equivalence
Remark 2.9 If $M$![]() is a closed manifold, then the homotopy orbits of $G\times G$
is a closed manifold, then the homotopy orbits of $G\times G$![]() acting on $\Delta _!$
acting on $\Delta _!$![]() coincides with the map $M_+\wedge M_+ \to M^\tau$
coincides with the map $M_+\wedge M_+ \to M^\tau$![]() given Pontryagin-Thom collapse of the embedding $\Delta$
given Pontryagin-Thom collapse of the embedding $\Delta$![]() .
.
We can now rephrase the norm equivalence in terms of $\Delta _!$![]() . Given any $G$
. Given any $G$![]() -spectrum $E$
-spectrum $E$![]() we obtain a map of $G$
we obtain a map of $G$![]() -spectra
-spectra
The proof of the following is straightforward, but tedious. We leave its verification to the reader.
Lemma 2.10 The map adjoint to $\Delta _! \wedge \operatorname {id}_E$![]() defines a weak equivalence
defines a weak equivalence
that is natural in $E$![]() .
.
3. The tangential Euler invariant
Assume that $M$![]() is a finitely dominated Poincaré duality space of dimension $d$
is a finitely dominated Poincaré duality space of dimension $d$![]() . Suppose in addition that an (unstable) $(d-1)$
. Suppose in addition that an (unstable) $(d-1)$![]() -spherical fibration
-spherical fibration
is specified. We also assume that $\xi$![]() comes equipped with a choice of stable fibre homotopy equivalence to the Spivak tangent fibration of $M$
comes equipped with a choice of stable fibre homotopy equivalence to the Spivak tangent fibration of $M$![]() .
.
Let $D(\xi ) \to M$![]() be the mapping cylinder of $\xi$
be the mapping cylinder of $\xi$![]() . For any space $Y \to M$
. For any space $Y \to M$![]() , let $\tilde Y := \tilde M \times _M Y$
, let $\tilde Y := \tilde M \times _M Y$![]() . Then $\tilde Y$
. Then $\tilde Y$![]() is an unbased $G$
is an unbased $G$![]() -space. Define
-space. Define
Then $S^\xi$![]() is a based $G$
is a based $G$![]() -space which is unequivariantly the homotopy type of a $d$
-space which is unequivariantly the homotopy type of a $d$![]() -sphere (note: $S^\xi$
-sphere (note: $S^\xi$![]() models the fibre of the unreduced fibrewise suspension of $\xi$
models the fibre of the unreduced fibrewise suspension of $\xi$![]() ).
).
In particular, one has a diagonal map
which depends on $\xi$![]() . In view of the stable identification $S^\xi \simeq S^\tau$
. In view of the stable identification $S^\xi \simeq S^\tau$![]() , we resort to the notation
, we resort to the notation
when $\Delta _\xi$![]() is considered as a stable map.
is considered as a stable map.
Definition 3.1 The Euler invariant $\mathfrak e(\xi )$![]() is the $(G\times G)$
is the $(G\times G)$![]() -equivariant composition
-equivariant composition
Lemma 3.2 There is a preferred isomorphism of abelian groups
where $LM := \mathrm{map}(S^1,M)$![]() is the free loop space of $M$
is the free loop space of $M$![]() .
.
Remark 3.3 The group $H_0(LM)$![]() is canonically isomorphic to $\mathbb {Z}\langle \bar \pi \rangle$
is canonically isomorphic to $\mathbb {Z}\langle \bar \pi \rangle$![]() .
.
Proof of lemma 3.2 The norm map applied to the $(G\times G)$![]() -spectrum $S^\tau [G^{\ell r}]\wedge S^\tau [G^{\ell r}]$
-spectrum $S^\tau [G^{\ell r}]\wedge S^\tau [G^{\ell r}]$![]() defines an equivalence
defines an equivalence
As $S\simeq _{G} S^{-\tau } \wedge S^\tau$![]() , the left side of (3.1) coincides up to homotopy with
, the left side of (3.1) coincides up to homotopy with
Consider the map $G^{\ell r} \to G^{\ell r} \times G^{\ell r}$![]() given by the inclusion of $1\times G^{\ell r}$
given by the inclusion of $1\times G^{\ell r}$![]() . It is straightforward to check that the induced map of spectra
. It is straightforward to check that the induced map of spectra
is a weak equivalence. But it is well known that $S[G^{\ell r}]_{hG}$![]() coincides with $\Sigma ^\infty (LM)_+$
coincides with $\Sigma ^\infty (LM)_+$![]() (see e.g., [Reference Klein, Schochet and Smith18, lemma 9.1]). Hence, we have defined a weak equivalence of spectra
(see e.g., [Reference Klein, Schochet and Smith18, lemma 9.1]). Hence, we have defined a weak equivalence of spectra
The conclusion of the Lemma follows by taking $\pi _0$![]() .
.
In view of lemma 3.2, we infer that
Proposition 3.4 For any $\xi$![]() as above, $\mathfrak e(\xi )$
as above, $\mathfrak e(\xi )$![]() lies in the summand defined by the conjugacy class of the trivial element of $\pi$
lies in the summand defined by the conjugacy class of the trivial element of $\pi$![]() .
.
Remark 3.5 The proposition is equivalent to the assertion that $\mathfrak e(\xi ) \in H_0(LM)$![]() factors through $H_0(M)$
factors through $H_0(M)$![]() . Alternatively, the image of $\mathfrak e(\xi )$
. Alternatively, the image of $\mathfrak e(\xi )$![]() in $H_0(LM,M)$
in $H_0(LM,M)$![]() is trivial.
is trivial.
Proof. Consider the homomorphism
induced by assigning to a stable $G$![]() -map $f\colon \! S^\tau \to S^\tau \wedge S^\tau$
-map $f\colon \! S^\tau \to S^\tau \wedge S^\tau$![]() the stable $(G\times G)$
the stable $(G\times G)$![]() -map
-map
Then $\Delta _\xi = \phi (\delta _\xi )$![]() , where $\delta _\xi \colon \! S^\xi \to S^\xi \wedge S^\xi$
, where $\delta _\xi \colon \! S^\xi \to S^\xi \wedge S^\xi$![]() is the diagonal map of $S^\xi$
is the diagonal map of $S^\xi$![]() . Furthermore, smashing with $S^\tau$
. Furthermore, smashing with $S^\tau$![]() defines an isomorphism
defines an isomorphism
On the other hand, the norm map applied to $S^\tau$![]() defines an equivalence
defines an equivalence
where in the above $G$![]() acts trivially on $S$
acts trivially on $S$![]() and recall that $\mathscr D_G \simeq S^{-\tau }$
and recall that $\mathscr D_G \simeq S^{-\tau }$![]() . Taking $\pi _0$
. Taking $\pi _0$![]() , we obtain an isomorphism
, we obtain an isomorphism
With respect the identifications, the homomorphism $\phi$![]() corresponds to inclusion $\mathbb {Z}\langle e\rangle \to \mathbb {Z}\langle \bar \pi \rangle$
corresponds to inclusion $\mathbb {Z}\langle e\rangle \to \mathbb {Z}\langle \bar \pi \rangle$![]() .
.
Remark 3.6 With slightly more effort, it is possible to show that
where $e(\xi ) \in H^d(M, \mathscr L^{-1})$![]() is the (twisted) Euler class of the spherical fibration $\xi$
is the (twisted) Euler class of the spherical fibration $\xi$![]() .
.
4. Self-intersection
Definition 4.1 Let $M$![]() be a finitely dominated Poincaré duality space as above. The self-intersection invariant of $M$
be a finitely dominated Poincaré duality space as above. The self-intersection invariant of $M$![]() is the homology class
is the homology class
given by the $G$![]() -equivariant stable homotopy class of the composition
-equivariant stable homotopy class of the composition
where we use the identification of lemma 3.2.
4.1 The Reidemeister characteristic
The Reidemeister characteristic of $M$![]() is the homology class
is the homology class
which is given by the stable homotopy class of the composition of maps of the form
The first map in this composition is the stable normal invariant and the second map is defined as follows: recall that the evaluation map
is $(G\times G)$![]() -equivariant. We take homotopy orbits of $\epsilon$
-equivariant. We take homotopy orbits of $\epsilon$![]() with respect to the diagonal subgroup $G \subset G\times G$
with respect to the diagonal subgroup $G \subset G\times G$![]() to obtain the map
to obtain the map
(cf. [Reference Berrick, Chatterji and Mislin4, Reference Berrick and Hesselholt5]).
Remark 4.2 As $M$![]() is finitely dominated, there is a homotopy finite space $X$
is finitely dominated, there is a homotopy finite space $X$![]() and a factorization of the identity map
and a factorization of the identity map
Setting $f = s\circ r\colon \! X \to X$![]() , it follows that $f^{\circ 2} = f$
, it follows that $f^{\circ 2} = f$![]() , so $f$
, so $f$![]() is idempotent. Moreover, if $\pi = \pi _1(M)$
is idempotent. Moreover, if $\pi = \pi _1(M)$![]() , and $u \colon \! M \to B\pi$
, and $u \colon \! M \to B\pi$![]() classifies the universal cover, then one has the composition
classifies the universal cover, then one has the composition
Consequently, $v \circ f = v$![]() , i.e., $f$
, i.e., $f$![]() is a map over $B\pi$
is a map over $B\pi$![]() . Then the generalized Lefschetz trace $L(f) \in \mathbb {Z}\langle \bar \pi \rangle = H_0(LM)$
. Then the generalized Lefschetz trace $L(f) \in \mathbb {Z}\langle \bar \pi \rangle = H_0(LM)$![]() is defined (cf.[Reference Berrick, Chatterji and Mislin4, §4], [Reference Geoghegan9]). It is not hard to show that
is defined (cf.[Reference Berrick, Chatterji and Mislin4, §4], [Reference Geoghegan9]). It is not hard to show that
However, we will not make use of this fact.
We next consider the norm equivalence
for the $G$![]() -spectrum $S^\tau [G^\mathrm {ad}]$
-spectrum $S^\tau [G^\mathrm {ad}]$![]() . Recall that $S^\tau [G^\mathrm {ad}]$
. Recall that $S^\tau [G^\mathrm {ad}]$![]() is $S^\tau [G^{{\ell r}}]$
is $S^\tau [G^{{\ell r}}]$![]() when considered as a $G$
when considered as a $G$![]() -spectrum.
-spectrum.
The following result is essentially an unravelling of the definitions. We omit the proof.
Lemma 4.3 With respect to the above norm equivalence, the Reidemeister characteristic $r(M)$![]() is represented by the $G$
is represented by the $G$![]() -equivariant stable composite
-equivariant stable composite
Let $E$![]() be any $(G\times G)$
be any $(G\times G)$![]() -spectrum. smashing $\Delta _!$
-spectrum. smashing $\Delta _!$![]() with $E$
with $E$![]() and taking homotopy fixed points, we obtain a map
and taking homotopy fixed points, we obtain a map
In the above, we have implicitly used the fact that the diagonal map $\Delta _{EG_+ \wedge EG_+} \colon EG_+ \wedge EG_+ \to (EG_+ \wedge EG_+)^{[2]}$![]() is a $(G\times G)$
is a $(G\times G)$![]() -equivariant weak equivalence.
-equivariant weak equivalence.
If we restrict $(G \times G)$![]() -fixed points to $G$
-fixed points to $G$![]() -fixed points along the diagonal inclusion $\Delta \colon G \to G \times G$
-fixed points along the diagonal inclusion $\Delta \colon G \to G \times G$![]() , we obtain a map
, we obtain a map
The following lemma in effect says that the maps $\Delta _! ^E$![]() and $\Delta _E^*$
and $\Delta _E^*$![]() coincide under the norm equivalence:
coincide under the norm equivalence:
Lemma 4.4 Let $E$![]() be any cofibrant $(G{ \times } G)$
be any cofibrant $(G{ \times } G)$![]() -spectrum. Then the following triangle commutes up to homotopy
-spectrum. Then the following triangle commutes up to homotopy

in which the vertical arrow is given by

where $\eta$![]() is the norm equivalence applied to $E \wedge S^\tau [G^{\ell r}]$
is the norm equivalence applied to $E \wedge S^\tau [G^{\ell r}]$![]() .
.
Proof. Note that the diagram is natural in $E$![]() and the functor $E\mapsto E^{h(G \times G)}$
and the functor $E\mapsto E^{h(G \times G)}$![]() is represented by $(EG_+)^{[2]} = EG_+ \wedge EG_+$
is represented by $(EG_+)^{[2]} = EG_+ \wedge EG_+$![]() , where to avoid clutter, we have identified $EG_+$
, where to avoid clutter, we have identified $EG_+$![]() with $S\wedge EG_+$
with $S\wedge EG_+$![]() .
.
Consequently, by the Yoneda lemma, it suffices to show that the two composites

are homotopic. Using that $EG_+$![]() is the unit we can simplify the diagram to
is the unit we can simplify the diagram to

where the upper composite is adjoint to $\Delta _!$![]() . Note that the unit $S \to (EG_+ \wedge EG_+)^{h(G \times G)}$
. Note that the unit $S \to (EG_+ \wedge EG_+)^{h(G \times G)}$![]() is mapped to the unit in $(EG_+)^{hG}$
is mapped to the unit in $(EG_+)^{hG}$![]() under the diagonal map. Thus the lower composite is the unit $S \to (EG_+)^{hG}$
under the diagonal map. Thus the lower composite is the unit $S \to (EG_+)^{hG}$![]() composed with the equivalence
composed with the equivalence

Observe that the last equivalence is obtained from the norm equivalence
by passing to $G$![]() -homotopy fixed points. Thus the lower composite is adjoint to the $(G \times G)$
-homotopy fixed points. Thus the lower composite is adjoint to the $(G \times G)$![]() -equivariant map
-equivariant map
which was the definition of $\Delta _!$![]() (here, the second displayed map is given by evaluation).
(here, the second displayed map is given by evaluation).
Proposition 4.5 For any finitely dominated Poincaré duality space $M$![]() , we have $I(M) = r(M)$
, we have $I(M) = r(M)$![]() .
.
Proof. By definition $I(M)$![]() , is the image under $\Delta _! \wedge -$
, is the image under $\Delta _! \wedge -$![]() of $\Delta _!$
of $\Delta _!$![]() itself, where $E = S^\tau \wedge S[G^{\ell r}]$
itself, where $E = S^\tau \wedge S[G^{\ell r}]$![]() . Lemma 4.4 provides an identification with $r(M)$
. Lemma 4.4 provides an identification with $r(M)$![]() in the form of lemma 4.3 in the previous lemma.
in the form of lemma 4.3 in the previous lemma.
Corollary 4.6 If $M$![]() is homotopy finite, then $I(M) \in H_0(LM)$
is homotopy finite, then $I(M) \in H_0(LM)$![]() lies in summand defined by the conjugacy class of the trivial element of $\pi$
lies in summand defined by the conjugacy class of the trivial element of $\pi$![]() .
.
Proof. By the proposition it is enough to show that $r(M)$![]() lies in the trivial conjugacy class.
lies in the trivial conjugacy class.
It will be convenient to invoke Waldhausen's algebraic $K$![]() -theory of spaces functor $X\mapsto A(X)$
-theory of spaces functor $X\mapsto A(X)$![]() . Here $A(X)$
. Here $A(X)$![]() is the $K$
is the $K$![]() -theory of the category with cofibrations and weak equivalences given by the retractive spaces over $X$
-theory of the category with cofibrations and weak equivalences given by the retractive spaces over $X$![]() which are relatively finitely dominated [Reference Waldhausen28].
which are relatively finitely dominated [Reference Waldhausen28].
As $M$![]() is finitely dominated, $M\times S^0$
is finitely dominated, $M\times S^0$![]() is a relatively finitely dominated retractive space over $M$
is a relatively finitely dominated retractive space over $M$![]() and therefore determines an element of $\pi _0(A(M)) \cong K_0(\mathbb {Z}[\pi _1(M)])$
and therefore determines an element of $\pi _0(A(M)) \cong K_0(\mathbb {Z}[\pi _1(M)])$![]() . With respect to this identification, this element is Wall's finiteness obstruction $w(M)$
. With respect to this identification, this element is Wall's finiteness obstruction $w(M)$![]() . The image of $w(M)$
. The image of $w(M)$![]() in $H_0(LM)$
in $H_0(LM)$![]() under the Bökstedt-Dennis trace map [Reference Bökstedt2] is identified with $r(M)$
under the Bökstedt-Dennis trace map [Reference Bökstedt2] is identified with $r(M)$![]() .
.
If $M$![]() is homotopy finite, then $w(M)$
is homotopy finite, then $w(M)$![]() lies in the image of the homomorphism $\pi _0(A(\ast )) \to \pi _0(A(M))$
lies in the image of the homomorphism $\pi _0(A(\ast )) \to \pi _0(A(M))$![]() . But the composition $\pi _0(A(\ast )) \to \pi _0(A(M)) \to H_0(LM)$
. But the composition $\pi _0(A(\ast )) \to \pi _0(A(M)) \to H_0(LM)$![]() factors through $H_0(L\ast ) =\mathbb {Z}$
factors through $H_0(L\ast ) =\mathbb {Z}$![]() .
.
Corollary 4.7 Assume that $M$![]() is finitely dominated. Suppose that the Bass trace conjecture holds for the group $\pi$
is finitely dominated. Suppose that the Bass trace conjecture holds for the group $\pi$![]() . Then the self-intersection invariant $I(M) \in \mathbb {Z}\langle \bar \pi \rangle$
. Then the self-intersection invariant $I(M) \in \mathbb {Z}\langle \bar \pi \rangle$![]() lies in the summand defined by the conjugacy class of the trivial element of $\pi$
lies in the summand defined by the conjugacy class of the trivial element of $\pi$![]() .
.
5. Hopf invariants
The main reference for this section is the book of Crabb and Ranicki [Reference Crabb and Ranicki7].
Let $Y$![]() be a cofibrant based $G$
be a cofibrant based $G$![]() -space. Then $Y^{[2]}= Y\wedge Y$
-space. Then $Y^{[2]}= Y\wedge Y$![]() is a based $(\mathbb {Z}_2 \times G)$
is a based $(\mathbb {Z}_2 \times G)$![]() -space. We may then form the (not naive) $(\mathbb {Z}_2 \times G)$
-space. We may then form the (not naive) $(\mathbb {Z}_2 \times G)$![]() -spectrum
-spectrum
indexed over the complete $\mathbb {Z}_2$![]() -universe $\mathscr U$
-universe $\mathscr U$![]() (i.e., a countable direct sum of copies of the regular representation $\mathbb {R}[\mathbb {Z}_2]$
(i.e., a countable direct sum of copies of the regular representation $\mathbb {R}[\mathbb {Z}_2]$![]() ).
).
Concretely, the zeroth space of $\Sigma ^\infty _{\mathbb {Z}_2} (Y^{[2]})$![]() is given by the colimit
is given by the colimit
where $S^V$![]() is the one-point compactification of $V$
is the one-point compactification of $V$![]() and $F(S^V,S^V\wedge Y^{[2]})$
and $F(S^V,S^V\wedge Y^{[2]})$![]() denotes the function space of unequivariant based maps $S^V\to S^V \wedge Y^{[2]}$
denotes the function space of unequivariant based maps $S^V\to S^V \wedge Y^{[2]}$![]() .
.
According to [Reference Lewis, May, Steinberger and McClure22, §V.11], one has a tom Dieck fibre sequence of spectra with $G$![]() -action
-action
in which the middle term of (5.1) is the categorical $\mathbb {Z}_2$![]() -fixed point spectrum and $D_2(Y) = Y^{[2]}_{h\mathbb {Z}_2}$
-fixed point spectrum and $D_2(Y) = Y^{[2]}_{h\mathbb {Z}_2}$![]() is the quadratic construction.
is the quadratic construction.
The zeroth space of the middle term of (5.1) will be denoted by
Its points are represented by $\mathbb {Z}_2$![]() -equivariant maps $\alpha \colon \! S^V\to S^V \wedge Y^{[2]}$
-equivariant maps $\alpha \colon \! S^V\to S^V \wedge Y^{[2]}$![]() . The zeroth space of the rightmost term of (5.1) is $QY = \Omega ^\infty \Sigma ^\infty (Y)$
. The zeroth space of the rightmost term of (5.1) is $QY = \Omega ^\infty \Sigma ^\infty (Y)$![]() ; its points are represented by a map $\beta \colon \! S^W\to S^W\wedge Y$
; its points are represented by a map $\beta \colon \! S^W\to S^W\wedge Y$![]() for some finite dimensional inner product space $W$
for some finite dimensional inner product space $W$![]() .
.
The displayed map $\phi$![]() in (5.1) assigns to such an $\alpha$
in (5.1) assigns to such an $\alpha$![]() the induced map of fixed point spaces
the induced map of fixed point spaces
where we have used the fact that $Y$![]() is the fixed point space of $\mathbb {Z}_2$
is the fixed point space of $\mathbb {Z}_2$![]() acting on $Y^{[2]}$
acting on $Y^{[2]}$![]() . Consequently, on the level of zeroth spaces, there is a homotopy fibre sequence of based $G$
. Consequently, on the level of zeroth spaces, there is a homotopy fibre sequence of based $G$![]() -spaces
-spaces
which is $G$![]() -equivariantly split.
-equivariantly split.
The splitting of (5.2) may be defined as follows: a point of $QY$![]() is represented by a map $\beta \colon \! S^W \to S^W\wedge Y$
is represented by a map $\beta \colon \! S^W \to S^W\wedge Y$![]() in which $W$
in which $W$![]() is a trivial $\mathbb {Z}_2$
is a trivial $\mathbb {Z}_2$![]() -representation (i.e., a finite dimensional inner product space). This induces the $\mathbb {Z}_2$
-representation (i.e., a finite dimensional inner product space). This induces the $\mathbb {Z}_2$![]() -equivariant map
-equivariant map
representing a point of $Q_{\mathbb {Z}_2} (Y^{[2]})^{\mathbb {Z}_2}$![]() . This provides a section to the map $\phi$
. This provides a section to the map $\phi$![]() and defines the splitting.
and defines the splitting.
Let $X \in \mathrm{Top}_\ast (G)$![]() be a finite object. Then a stable $G$
be a finite object. Then a stable $G$![]() -map
-map ![]() , is represented by a $G$
, is represented by a $G$![]() -map $f_W\colon \! S^W\wedge X \to S^W\wedge Y$
-map $f_W\colon \! S^W\wedge X \to S^W\wedge Y$![]() . One may associate to $f_W$
. One may associate to $f_W$![]() the $(\mathbb {Z}_2\times G)$
the $(\mathbb {Z}_2\times G)$![]() -equivariant map
-equivariant map
One may also associate to $f_W$![]() the $(\mathbb {Z}_2\times G)$
the $(\mathbb {Z}_2\times G)$![]() -equivariant map
-equivariant map
where it is understood that $W\oplus W$![]() is given the transposition action of $\mathbb {Z}_2$
is given the transposition action of $\mathbb {Z}_2$![]() , and we have implicitly shuffled the factors of the displayed smash product. It follows that $\Delta _Y \circ f_W$
, and we have implicitly shuffled the factors of the displayed smash product. It follows that $\Delta _Y \circ f_W$![]() and $(f_W\wedge f_W)\circ \Delta _X$
and $(f_W\wedge f_W)\circ \Delta _X$![]() represent a pair of $G$
represent a pair of $G$![]() -maps
-maps
Furthermore, it is easily checked that these maps are both coequalized by $\phi$![]() :
:
Set
i.e., the abelian group of homotopy classes of $G$![]() -equivariant maps $X\to Q_{\mathbb {Z}_2}(Y^{[2]})^{\mathbb {Z}_2}$
-equivariant maps $X\to Q_{\mathbb {Z}_2}(Y^{[2]})^{\mathbb {Z}_2}$![]() . Then $\Delta _Y \circ f$
. Then $\Delta _Y \circ f$![]() and $(f\wedge f)\circ \Delta _X$
and $(f\wedge f)\circ \Delta _X$![]() represent elements of $\{X,Y\wedge Y\}_{G}^{\mathbb {Z}_2}$
represent elements of $\{X,Y\wedge Y\}_{G}^{\mathbb {Z}_2}$![]() . Moreover, from (5.2) and the above discussion, one has a canonically split inclusion
. Moreover, from (5.2) and the above discussion, one has a canonically split inclusion
It follows that on the level of homotopy classes, there is a unique $G$![]() -equivariant stable homotopy class
-equivariant stable homotopy class
such that
Then $H(f)$![]() is the ( $G$
is the ( $G$![]() -equivariant geometric) Hopf invariant of the stable $G$
-equivariant geometric) Hopf invariant of the stable $G$![]() -map
-map ![]() .
.
Remark 5.1 In view of the fact that $\iota$![]() is a split injection, we will typically write $H(f)$
is a split injection, we will typically write $H(f)$![]() in place of $\iota \circ H(f)$
in place of $\iota \circ H(f)$![]() in (5.3).
in (5.3).
Remark 5.2 Crabb and Ranicki [Reference Crabb and Ranicki7, §7] only consider the case when $G$![]() is a discrete group. However, the adaptation to cofibrant topological groups $G$
is a discrete group. However, the adaptation to cofibrant topological groups $G$![]() goes through unchanged. In addition, we note that there is a $1$
goes through unchanged. In addition, we note that there is a $1$![]() -connected Hurewicz homomorphism $G\to \pi$
-connected Hurewicz homomorphism $G\to \pi$![]() , where $\pi = \pi _0(G)$
, where $\pi = \pi _0(G)$![]() . Under suitable restrictions on the dimension of $X$
. Under suitable restrictions on the dimension of $X$![]() and the connectivity of $Y$
and the connectivity of $Y$![]() (which are fulfilled in the cases we care about), the evident homomorphism
(which are fulfilled in the cases we care about), the evident homomorphism
which carries $H(f)$![]() to $H(f\wedge _G (\pi _+))$
to $H(f\wedge _G (\pi _+))$![]() is an isomorphism. Consequently, $H(f\wedge _G (\pi _+))$
is an isomorphism. Consequently, $H(f\wedge _G (\pi _+))$![]() will contain the same information as $H(f)$
will contain the same information as $H(f)$![]() . The reason we prefer to work with $G$
. The reason we prefer to work with $G$![]() instead of $\pi$
instead of $\pi$![]() is that it makes some of the proofs more transparent.
is that it makes some of the proofs more transparent.
Definition 5.3 The transfer is the composition
in which the second homomorphism is induced by forgetting that a map is $\mathbb {Z}_2$![]() -equivariant.
-equivariant.
5.1 The diagonal embedding obstruction $\mu _M$
In [Reference Klein17] the first author defines an obstruction to finding a Poincaré embedding of the diagonal as the reduced Hopf invariant of the $(\pi \times \pi )$![]() -equivariant stable map given by inducing $\Delta _!$
-equivariant stable map given by inducing $\Delta _!$![]() along the homomorphism $G\times G \to \pi \times \pi$
along the homomorphism $G\times G \to \pi \times \pi$![]() . After some minor rewriting, takes the form
. After some minor rewriting, takes the form
where $\bar M \to M$![]() is the universal cover, $\hat M = \bar M \times _\pi (\pi \times \pi )$
is the universal cover, $\hat M = \bar M \times _\pi (\pi \times \pi )$![]() and $\hat M^\tau = S^\tau \wedge _{G} ((\pi \times \pi )_+)$
and $\hat M^\tau = S^\tau \wedge _{G} ((\pi \times \pi )_+)$![]() . It is straightforward to check that the Hopf invariants in each case coincide (cf. remark 5.2). Hence,
. It is straightforward to check that the Hopf invariants in each case coincide (cf. remark 5.2). Hence,
It immediately follows that
where $\mu _M$![]() is the complete obstruction to finding a Poincaré embedding of the diagonal.
is the complete obstruction to finding a Poincaré embedding of the diagonal.
Remark 5.4 In the above, we have implicitly used lemma 3.2, remark 3.3 and the proof of proposition 3.4 to define a preferred isomorphism identify $\mathbb {Z}\langle \bar \pi \rangle$![]() with
with
as well as a preferred isomorphism
We refer the reader to [Reference Klein17, §6] for more details (note that the discussion in [Reference Klein17, §6] carries over mutatis mutandis from $\pi$![]() -spectra to $G$
-spectra to $G$![]() -spectra).
-spectra).
6. Proof of the main results
As noted in the introduction theorem A follows immediately from theorem B.
Proof of theorem B From the definition of the Hopf invariant we immediately obtain
By proposition 3.4, $\tilde {\mathfrak e}(M) \in H_0(LM,M)$![]() is trivial, and by proposition 4.5
is trivial, and by proposition 4.5
We thus conclude that
showing the first assertion. The second part follows immediately from [Reference Klein17, theorem A], which states that $\mu _M = 0$![]() if there exists a Poincaré embedding of the diagonal.
if there exists a Poincaré embedding of the diagonal.
Proof of corollary C If $M$![]() is homotopy finite or if the Bass trace conjecture holds for $\pi$
is homotopy finite or if the Bass trace conjecture holds for $\pi$![]() , then $\tilde r(M) = 0$
, then $\tilde r(M) = 0$![]() . The result now follows from theorem B.
. The result now follows from theorem B.
Proof of corollary D In this instance, the Bass trace conjecture holds for $\pi$![]() , so $\tilde \sigma (\mu _M) = \tilde r(M)= 0$
, so $\tilde \sigma (\mu _M) = \tilde r(M)= 0$![]() . The composition
. The composition
is given by multiplication by 2, where $\sigma$![]() is the transfer, and the second displayed map is the projection onto coinvariants. By theorem B, $\tilde \sigma (\mu _M) = 0$
is the transfer, and the second displayed map is the projection onto coinvariants. By theorem B, $\tilde \sigma (\mu _M) = 0$![]() . Consequently, $2\mu _M =0$
. Consequently, $2\mu _M =0$![]() , so by [Reference Klein17, thm. A], it suffices to show that $Q_d(\pi ) = \mathbb {Z} \oplus \tilde Q_d(\pi )$
, so by [Reference Klein17, thm. A], it suffices to show that $Q_d(\pi ) = \mathbb {Z} \oplus \tilde Q_d(\pi )$![]() has no 2-torsion elements (here we have used the fact that $d$
has no 2-torsion elements (here we have used the fact that $d$![]() is even to identify $\tilde Q_d(e) =\mathbb {Z}$
is even to identify $\tilde Q_d(e) =\mathbb {Z}$![]() ).
).
Let use write $\pi$![]() as a direct product of $H \times K$
as a direct product of $H \times K$![]() in which $H\subset \pi$
in which $H\subset \pi$![]() is the $2$
is the $2$![]() -primary subgroup. Denote the involution $x \mapsto x^{-1}$
-primary subgroup. Denote the involution $x \mapsto x^{-1}$![]() of $\pi$
of $\pi$![]() by $\iota$
by $\iota$![]() . Then $\iota$
. Then $\iota$![]() preserves the decomposition of $\pi$
preserves the decomposition of $\pi$![]() , so $Q_d(\pi ) \cong Q_d(H) \otimes Q_d(K)$
, so $Q_d(\pi ) \cong Q_d(H) \otimes Q_d(K)$![]() . It then suffices to show that $Q_d(H)$
. It then suffices to show that $Q_d(H)$![]() and $Q_d(K)$
and $Q_d(K)$![]() are torsion free abelian groups.
are torsion free abelian groups.
Since $d$![]() is even and $\iota$
is even and $\iota$![]() fixes $H$
fixes $H$![]() pointwise, we have $Q_d(H) = \mathbb {Z}\langle H \rangle$
pointwise, we have $Q_d(H) = \mathbb {Z}\langle H \rangle$![]() , so $Q_d(H)$
, so $Q_d(H)$![]() is torsion free.
is torsion free.
Set $K^* = K \setminus \{e\}$![]() . Then $\iota \colon \! K^*\to K^*$
. Then $\iota \colon \! K^*\to K^*$![]() is fixed point free. Consequently, there is a decomposition
is fixed point free. Consequently, there is a decomposition
in which $K_\pm \subset K^*$![]() are subsets, and $\iota \colon \! K_- \to K_+$
are subsets, and $\iota \colon \! K_- \to K_+$![]() is an isomorphism. It follows that $\tilde Q_d(K) \cong \mathbb {Z}\langle K_- \rangle$
is an isomorphism. It follows that $\tilde Q_d(K) \cong \mathbb {Z}\langle K_- \rangle$![]() . We infer that $\tilde Q_d(K)$
. We infer that $\tilde Q_d(K)$![]() is torsion free. Hence, $Q_d(K) = \mathbb {Z} \oplus \tilde Q_d(K)$
is torsion free. Hence, $Q_d(K) = \mathbb {Z} \oplus \tilde Q_d(K)$![]() is also torsion free.
is also torsion free.
Proof of corollary E. The argument is similar to the proof of corollary D. The composition
is multiplication by $2$![]() , where the second displayed map is the projection onto coinvariants. By theorem B, $\tilde \sigma (\mu _M) = 0$
, where the second displayed map is the projection onto coinvariants. By theorem B, $\tilde \sigma (\mu _M) = 0$![]() . Consequently, $2\mu _M = 0$
. Consequently, $2\mu _M = 0$![]() and it will suffice to show that $\tilde Q_d(\pi )$
and it will suffice to show that $\tilde Q_d(\pi )$![]() has no 2-torsion. We will see that $\tilde Q_d(\pi )$
has no 2-torsion. We will see that $\tilde Q_d(\pi )$![]() is torsion free.
is torsion free.
Let $\bar \pi ^* =\bar \pi \setminus \{e\}$![]() . Let $\iota \colon \! \pi ^\ast \to \pi ^\ast$
. Let $\iota \colon \! \pi ^\ast \to \pi ^\ast$![]() be the involution given by $\iota (x) = x^{-1}$
be the involution given by $\iota (x) = x^{-1}$![]() . We claim that $\iota$
. We claim that $\iota$![]() defines a induces a free action of $\mathbb {Z}_2$
defines a induces a free action of $\mathbb {Z}_2$![]() on $\bar \pi ^*$
on $\bar \pi ^*$![]() . We prove this by contradiction: if not, then there are non-trivial elements $g,x\in \pi$
. We prove this by contradiction: if not, then there are non-trivial elements $g,x\in \pi$![]() such that
such that
Inverting both sides (6.1), we obtain $gx^{-1}g^{-1} = x$![]() . Substituting the last expression into (6.1), we infer that $g^2x^{-1}g^{-2} = x^{-1}$
. Substituting the last expression into (6.1), we infer that $g^2x^{-1}g^{-2} = x^{-1}$![]() . Inverting both sides of this last expression, we obtain $g^2xg^{-2} = x$
. Inverting both sides of this last expression, we obtain $g^2xg^{-2} = x$![]() .
.
It follows that $g^2$![]() commutes with $x$
commutes with $x$![]() . Let $2k+1$
. Let $2k+1$![]() be the order of $g$
be the order of $g$![]() . Then $g = (g^2)^{k+1}$
. Then $g = (g^2)^{k+1}$![]() also commutes with $x$
also commutes with $x$![]() . Consequently, $gxg^{-1} = x$
. Consequently, $gxg^{-1} = x$![]() . But by assumption $gxg^{-1} = x^{-1}$
. But by assumption $gxg^{-1} = x^{-1}$![]() , so $x = x^{-1}$
, so $x = x^{-1}$![]() . Hence, $x^2 = e$
. Hence, $x^2 = e$![]() and we obtain a contradiction.
and we obtain a contradiction.
It follows that $\bar \pi ^* = T_- \amalg T_+$![]() where $\iota$
where $\iota$![]() restricts to an isomorphism $T_- \to T_+$
restricts to an isomorphism $T_- \to T_+$![]() . Hence,
. Hence,
is free abelian with basis $T_-$![]() .
.
Acknowledgements
Andrew Ranicki had a profound impact on the first author's mathematical career. He was both a mentor and a friend. The current work was inspired by him. The authors wish to thank Ian Leary for pointing out Wall's examples [Reference Wall30, cor. 5.4.2] of non-homotopy finite Poincaré duality spaces.
This research was supported by the U.S. Department of Energy, Office of Science, under Award Number DE-SC-SC0022134.