For every  $n\geq 2$, Bourgain’s constant
$n\geq 2$, Bourgain’s constant 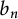 $b_n$ is the largest number such that the (upper) Hausdorff dimension of harmonic measure is at most
$b_n$ is the largest number such that the (upper) Hausdorff dimension of harmonic measure is at most  $n-b_n$ for every domain in
$n-b_n$ for every domain in 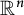 $\mathbb {R}^n$ on which harmonic measure is defined. Jones and Wolff (1988, Acta Mathematica 161, 131–144) proved that
$\mathbb {R}^n$ on which harmonic measure is defined. Jones and Wolff (1988, Acta Mathematica 161, 131–144) proved that  $b_2=1$. When
$b_2=1$. When  $n\geq 3$, Bourgain (1987, Inventiones Mathematicae 87, 477–483) proved that
$n\geq 3$, Bourgain (1987, Inventiones Mathematicae 87, 477–483) proved that  $b_n>0$ and Wolff (1995, Essays on Fourier analysis in honor of Elias M. Stein (Princeton, NJ, 1991), Princeton University Press, Princeton, NJ, 321–384) produced examples showing
$b_n>0$ and Wolff (1995, Essays on Fourier analysis in honor of Elias M. Stein (Princeton, NJ, 1991), Princeton University Press, Princeton, NJ, 321–384) produced examples showing 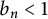 $b_n<1$. Refining Bourgain’s original outline, we prove that
$b_n<1$. Refining Bourgain’s original outline, we prove that 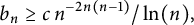 $$\begin{align*}b_n\geq c\,n^{-2n(n-1)}/\ln(n),\end{align*}$$
$$\begin{align*}b_n\geq c\,n^{-2n(n-1)}/\ln(n),\end{align*}$$ $n\geq 3$, where
$n\geq 3$, where 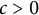 $c>0$ is a constant that is independent of n. We further estimate
$c>0$ is a constant that is independent of n. We further estimate  $b_3\geq 1\times 10^{-15}$ and
$b_3\geq 1\times 10^{-15}$ and  $b_4\geq 2\times 10^{-26}$.
$b_4\geq 2\times 10^{-26}$.