1. Statistics and the Interpretation of Glacier Variability
Climate is defined as the statistics of weather, averaged over some period of interest. The World Meteorological Organization takes 30 years as the time interval over which those statistics should be determined, although other intervals are equally valid depending on the purpose. The statistics of weather includes the average and the standard deviation, as well as higher-order statistical moments. By definition, a constant climate means constant (or stationary) statistics. Variability, as manifest in the standard deviation, is therefore inherent in a constant climate. What does this mean for how glaciers behave in such a climate? Of particular importance are the year-to-year stochastic fluctuations in accumulation and ablation. Glaciers are dynamical systems with a finite memory, and a fundamental property of such systems is that they will integrate such stochastic fluctuations to produce persistent fluctuations on longer timescales (e.g. Reference HasselmannHasselmann, 1976; Reference RoeRoe, 2009).
Reference OerlemansOerlemans (2000) and Reference Reichert, Bengtsson and OerlemansReichert and others (2002) modelled two well-studied glaciers in Scandinavia and the European Alps and concluded that Little Ice Age-scale fluctuations will occur every so often, even in a constant climate. Reference Roe and O’NealRoe and O’Neal (2009) showed that, for the setting of Mount Baker in the Cascade Range of Washington State, USA, glaciers will undergo kilometre-scale, century-scale fluctuations even in a constant climate. Sorting out real climate change from the variability intrinsic to a constant climate is crucial for correctly interpreting the climatic cause of past glacier variations and for the detection and attribution of modern climate change from the modern glacier record.
Reference Burke and RoeBurke and Roe (2009) and Reference RoeRoe (2009) gave a spectral interpretation of this argument, which we review briefly here. The true, physical measure of climatic persistence is whether climate variables are autocorrelated. In other words, does one year’s climate bear any relationship to that of previous years? Consider a climate that has year-to-year variability (drawn randomly from the probability distribution of that climate), but no memory. The time series of such a climate is characterized by a ‘white noise’ power spectrum; that is to say, it has equal power at all frequencies. By construction, a climate that has no persistence nonetheless has power at all frequencies. The reason is that the phase of individual frequencies in the spectrum is random. On average they destructively interfere, leaving no persistence in the time series constructed from that spectrum.
A glacier can be thought of as acting as a low-pass spectral filter: the glacier’s response to this white-noise climate is characterized by a ‘red noise’ power spectrum. Analogous to red light, higher frequencies are damped compared to lower frequencies. Because of this damping, different frequencies will no longer cancel out and the time series of glacier length variations exhibits long-term fluctuations with a timescale related to the spectral filter of the glacier dynamics.
In the above example, the climate was chosen to be white noise (i.e. with no persistence). Weak interannual persistence in sea-surface temperatures does exist because the ocean mixed layer has some thermal intertia (e.g. Reference Deser, Alexander and TimlinDeser and others, 2003). Such weakly red persistence is captured in the 30 year statistics, and so should properly be included in the definition of the climate statistics. The response time of the mixed layer is ∼ 1 year or less, except near sites of deep ocean convection or in the vicinity of the sea-ice margin (e.g. Reference Stouffer, Hegerl and TettStouffer and others, 2000). In other words, it is much less than typical glacier response times and so the above argument is unaffected: the persistence of glacier fluctuations is due to the memory intrinsic to the glacier and not any persistence intrinsic to the climate. Reference Burke and RoeBurke and Roe (2009) analysed the persistence of relevant climate fields and mass-balance records for Europe and, after linearly detrending to account for anthropogenic trends, found no evidence in the instrumental or glacier mass-balance record for decadal-scale persistence.
Lastly, even where such persistence in climate does exist, it is typically only a small fraction of the overall variance. It is always possible to split the time series of climate forcing into a piece that is due to persistence (i.e. what can be related to previous years) and a piece that is a residual without persistence. Reference Burke and RoeBurke and Roe (2009) calculated the relative importance of these two pieces in driving the variance of glacier fluctuations in Europe, and concluded that the residual piece is of greatest importance.
The fundamental and important point is that glaciers can undergo large and persistent fluctuations in a constant climate that has little or no persistence. This fact is often overlooked in the climatic interpretation of past glacier fluctuations. A central goal of palaeoglaciology (and palaeoclimate in general) is to identify glacier fluctuations that are either unusually large or unusually persistent and which are therefore ‘interesting’ to explain. They are interesting because we can then conclude that some definitive change in the climate dynamics or climate forcing has occurred and try to identify the cause. The importance of framing the problem in this way is that the alternative is unsatisfying and violates basic tenets of statistical analysis: if climate is defined as the statistics of weather averaged over some period of choice, and if it is also established that a particular glacier fluctuation is quite likely to occur given those statistics, then it makes no sense to conclude that the glacier fluctuation reflects a climate change.
The interpretation of the climatic cause of glacier fluctuations can therefore be distilled into a classic statistical exercise of correctly identifying changes due to a signal (i.e. the glacier response to a climate change) versus changes due to noise (i.e. the glacier response to interannual variability). What factors control the relative magnitude of this signal and noise? Under the assumption that a glacier is a simple dynamical system relaxing back to equilibrium with a single dynamical response time (e.g. Reference Jóhannesson, Raymond, Waddington and OerlemansJóhannesson and others, 1989a,b), some useful formulae can be derived (e.g. Reference Huybers and RoeHuybers and Roe, 2009; Reference Roe and O’NealRoe and O’Neal, 2009). This study extends these prior analyses to ask two more questions:
-
1. What factors govern the likelihood of a glacier excursion of a given magnitude in a given interval of time?
-
2. How can the statistical significance of a trend in observed or reconstructed glacier length be evaluated?
In both cases, formulae can be derived from the linear equations in which the dependencies on glacier geometry and climate setting can be clearly understood. The value of these formulae is that the parameters involved can be calculated from a glacier’s geometry, and so they give guidance as to which glaciers are likely to be best for detecting past climate change. A second and key part of the present study is to establish whether the formulae successfully predict the behaviour of a flowline glacier model, which obeys a nonlinear rheology.
We find that maximum glacier excursions are governed by high-frequency behaviour of the glacier, and the linear formulae hold provided the short-term lag correlations are used to calculate the response time. The probabilities of a given excursion are, however, very sensitive to the magnitude of the natural variability. We also show that glacier trends can be evaluated using a standard Student’s t test, provided that the correct degrees of freedom are used. These degrees of freedom can be accurately calculated from the linear model equations. Finally, we conclude that the current retreat of glaciers around Mount Baker is consistent with, but not by itself independent proof of, regional warming.
2. Linear and Flowline Models
2.1. Linear model
Reference Roe and O’NealRoe and O’Neal (2009) derived a simple linear model for describing variations in glacier length in response to variations in melt-season temperature and annual accumulation. It is similar in spirit to other earlier models (e.g. Reference Jóhannesson, Raymond, Waddington and OerlemansJóohannesson and others, 1989a,Reference Jóhannesson, Raymond and Waddingtonb; Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others, 2001), all of which are essentially the same first-order ordinary differential equation:
Equation (1) represents a dynamical system in which glacier length L′(t) responds to fluctuations in annual accumulation P′(t) and melt-season temperature T′(t). Primes denote departures from the long-term climatological mean. τ is the e-folding timescale on which the glacier relaxes back to equilibrium or, equivalently, it is the length of time over which the glacier remembers its previous states.
and
are coefficients relating climate forcing to the effect on glacier length. Equation (1) is continuous in time. Its discrete form is
where Δt = 1 year and γ = 1 − Δt/τ and is the lag-1 correlation coefficient. This form of the equation is convenient for deriving expressions for the statistics of glacier length fluctuations. As derived by Reference Roe and O’NealRoe and O’Neal (2009), τ, α and β are functions of the glacier geometry and some mass-balance parameters:
A schematic illustration of the model is given in Figure 1. The geometric parameters for the glacier are: width w; depth H; total area A tot; ablation area A abl; melt area AT> 0; and basal slope tan φ. μ is the melt factor relating melting rates to melt-season temperature and has units m a−1°C−1; Γ is the atmospheric lapse rate, defined as 6.5°C km−1.
Fig. 1. Idealized geometry of the linear glacier model, based on Reference Jóhannesson, Raymond, Waddington and OerlemansJóhannesson and others (1989a). Precipitation falls over the entire surface of the glacier A tot, while melt occurs only on the melt-zone area AT> 0. The ablation zone A abl is the region below the equilibrium-line altitude (ELA). Melt is linearly proportional to the temperature which, in turn, decreases linearly as the tongue of the glacier recedes up the linear slope tan φ and increases as the glacier advances downslope. The height H of the glacier and the width of the ablation area w remain constant (after Reference Roe and O’NealRoe and O’Neal 2009).
2.2. Flowline model
A dynamic flowline model is also used in this study. We follow standard equations for the shallow-ice approximation incorporating glacier sliding (e.g. Reference OerlemansOerlemans, 2001):
H(x) is glacier thickness at position x, F(x) is the vertically integrated flux of ice and dz
s/dx is the surface slope. f
d and f
s are the coefficients governing deformation and sliding, respectively. Following Reference Budd, Keage and BlundyBudd and others (1979) and Reference OerlemansOerlemans (2001), we take f
d = 1.9 × 10−24 Pa3 s−1 and
is the local mass balance. For simplicity we assume a uniform accumulation pattern, and melt-season temperature is calculated as a function of x using the standard lapse rate. Equations (4) were solved using standard numerical techniques on a 50 m grid, although results with 20 and 100 m grid spacing proved very similar.
2.3. Preliminary comparison of linear and flowline models
In order to evaluate and compare the linear and flowline models we use the well-documented setting of Mount Baker, a stratovolcano in Washington State flanked by five typical mid-latitude glaciers. We use the same climate as Reference Roe and O’NealRoe and O’Neal (2009), based on a combination of local station measurements, weather model output and mass-balance measurements. The annual mean accumulation is 5 m a−1 with an interannual standard deviation of 1 m a−1. The interannual standard deviation in melt-season temperature is 0.8°C.
Reference Roe and O’NealRoe and O’Neal (2009) specified parameters and geometry representative of the Mount Baker glaciers, and showed that the linear model was able to simulate historical glacier length variations fairly well. In order to avoid the complex task of deriving this exact geometry and parameter set in the current study, we use a more efficient procedure for the comparison of the linear and flowline models (which is our main purpose). We specify the accumulation and the basal slope and adjust the mean melt-season temperature until the flowline model is approximately correct in terms of total area (which is determined as 23°C at sea level). From the model output, we then diagnose the other geometric factors needed for the linear model (H, A abl and AT> 0). This allows a more exacting comparison between the two models, which is the main aim here. Values for this geometry and standard parameters are listed in Table 1. In particular, the linear timescale calculated from the model geometry ( τ lin) is ∼7 years.
Table 1. Parameters and geometry of a standard-case glacier. The first set of parameters is imposed; the second set is calculated from the flowline model and used for the linear model formulae. Also included is the linear model timescale. The simplified, pseudo one-dimensional geometry means that not every aspect of the typical Mount Baker glacier can be matched at the same time. In particular, the standard glacier has a nominal length of 8 km and the accumulation-area ratio is one-half rather than two-thirds. Compare with values given by Reference Roe and O’NealRoe and O’Neal (2009) for Mount Baker glaciers
In the remainder of this section we perform two preliminary comparisons of the two models. We first calculate the change in length due to step-function changes in mean climate forcing, for which the linear model has analytical solutions (Reference Roe and O’NealRoe and O’Neal, 2009). The flowline model must be integrated until the new equilibrium is reached. There is generally extremely good agreement between the flowline and linear models (Fig. 2), with length changes differing by <5% for climate changes spanning ±6°C in melt-season temperature and ±2 m a−1 in accumulation. There is a suggestion in Figure 2 that the response to precipitation is slightly more linear than the response to temperature. For this range of climate forcing and for this glacier geometry and setting, Figure 2 strongly supports the validity of the assumptions made in deriving the linear model (Reference Roe and O’NealRoe and O’Neal, 2009).
Fig. 2. Response of glacier length to step function changes in accumulation and melt-season temperature. Solid lines show analytic solutions from the linear model, and the symbols show results from the flowline model.
The second comparison is of the models’ response to a linear trend in climate forcing. We pick a warming trend comparable to that experienced in the Pacific Northwest during the 20th century (+0.1°C (10 a)−1; e.g. Reference MoteMote, 2003), and an increasing accumulation trend (0.1 m a−1 (10 a)−1) although the significance of observed accumulation trends is unclear in this region (Reference MoteMote, 2003). Analytical solutions are again available for the linear model, and do a good job of predicting both the rate and magnitude of the response of the flowline model as shown in Figure 3. For both trends, the flowline model lags the predicted linear response slightly. In the case of a temperature trend, the rate of retreat in the flowline model appears slightly greater than predicted from the linear model, consistent with the results in Figure 2.
Fig. 3. Response of glacier length to increasing trends in (a) melt-season temperature (+0.1 m a−1 (10 a)−1) and (b) accumulation (+0.1°C (10 a)−1), imposed beginning in model year 20. There is good agreement between the linear and flowline models.
3. The Response to Climate Variability
In the following we characterize the nature of the glacier response to interannual climate variability in more detail. Equation (2) can be developed further to derive some useful properties of glacier variability, whose dependence on glacier geometry and climate parameters can be clearly understood. As noted in the introduction, a focus of this present study is to evaluate the degree to which these expressions also govern the behaviour of the flowline model.
Reference Roe and O’NealRoe and O’Neal (2009) demonstrated that, after linearly detrending, the observed interannual variability in the Pacific Northwest in both the annual-mean accumulation and the melt-season temperature is consistent with random fluctuations that are Gaussian (i.e. normally distributed) and white (i.e. uncorrelated in time). In other words, after accounting for the trends in climate (presumably anthropogenic), the remaining natural variability has no interannual persistence. The analysis of Reference Roe and O’NealRoe and O’Neal (2009) is sufficient to prove that, even if some interannual persistence in climate does in fact exist for the region, it accounts for a statistically insignificant fraction of the climate variability over the period of the instrumental record.
Two 10 000 year long realizations of white noise were generated to simulate interannual variability in P′ and T′, characteristic of the Pacific Northwest (with standard deviations of 1 m a−1 and 0.8°C, respectively). This is long enough to acquire good statistics on the glacier response. The two climate time series are assumed to be uncorrelated, also consistent with observations for the region (Reference Roe and O’NealRoe and O’Neal, 2009). Both the flowline and the linear models are then integrated forwards in time, using the same realizations of this simulated climate variability.
Figure 4 shows a 500 year segment of the climate and the glacier response. Both the linear and flowline models undergo kilometre-scale, centennial-scale fluctuations in response to a climate that we reiterate has no persistence. The standard deviation of the linear model can be derived from model parameters (Reference Roe and O’NealRoe and O’Neal, 2009) and is 360 m. The standard deviation of the flowline model must be calculated from the numerical integration and is 324 m, a difference of 10%; this is approximately what Reference Roe and O’NealRoe and O’Neal (2009) found for a similar calculation. The smaller standard deviation of the flowline model is evident in Figure 4 as is the fact that the flowline model is noticeably smoother. Finally, it is also clear that the response of the flowline model lags behind the response of the linear model.
Fig. 4. A 500 year segment of a 10 000 year simulation of the glacier response to interannual climate variability. The lower panels are white-noise realizations of interannual fluctuations in melt-season temperature and accumulation, for which a 30 year running mean is also shown. The upper panel shows the response of the two glacier models. Kilometre-scale, century-scale glacier fluctuations occur in this simulated climate that, by construction, has no persistence. Also shown by the thin black curve is a linear fit to the flowline model, using the best-fit τbf of 73 years.
For comparison, Reference OerlemansOerlemans (2001) estimates a 1σ of 660 m for typical glacier parameters, and Reference Reichert, Bengtsson and OerlemansReichert and others (2002) model values of 550 and 290 m for Nigardsbreen, Norway, and Rhonegletscher, Switzerland, respectively. The exact values do, and should, vary with glacier geometry and climate setting. For a particular glacier, the importance of this natural variability relative to past and current changes must be judged on a case-by-case basis.
A linear model such as that of Equation (2) must have a normally distributed response to normally distributed forcing. For the flowline model, one test of its linearity is to calculate the probability density function (PDF) from the histogram of its fluctuations. The PDFs for both models are shown in Figure 5. The smaller standard deviation of the flowline model relative to the linear model is clear in its narrower clustering around zero. Visually, it appears there is a hint of skewness to central and negative values, although the skewness is in fact very slightly positive (0.06). The flowline model PDF is not quite normally distributed, however. A standard Kolmogorov–Smirnov test (e.g. Reference Von Storch and Zwiersvon Storch and Zwiers, 1999) rejects the normal distribution at >95% confidence. The probable reason is that kurtosis of the flowline model is 3.2, implying it is slightly more outlier-prone than a normal distribution for which the kurtosis is 3.0.
Fig. 5. The PDFs of the linear and flowline models. The linear model follows a normal distribution; the flowline model has a slightly non-normal distribution.
Despite some small differences, the response of the linear and flowline models to equilibrium climate changes, climate trends and climate variability has differed by only a few percent. This generally solid agreement between the flowline and linear models in these preliminary tests is a firm basis for proceeding to explore the response to climate variability, using the analytical power of the linear model to understand the reasons for the glacier behaviour.
3.1. The autocorrelation and the spectral response of a glacier
The autocorrelation function and the power spectrum of a time series are powerful tools for revealing the time dependence of a dynamical system. They are of course closely related since the periodogram spectral estimate is simply the Fourier transform of the autocovariance function (e.g. Reference Von Storch and Zwiersvon Storch and Zwiers, 1999). Both were calculated from the 10 000 year integrations, a sample of which is shown in Figure 4.
At low frequencies with periods longer than a few decades, the spectra of the linear and flowline models are identical. These timescales are much longer than the adjustment time of the glacier, and so both linear and flowline models are in near-equilibrium with the forcing. Dynamics are irrelevant and the glacier is simply acting as a reservoir of ice with nearly balanced input and output fluxes. The linear model physics captures exactly this. At higher frequencies, the two spectra differ considerably. Consistent with the time series shown in Figure 4, high frequencies in the flowline model are considerably damped compared to the linear model. In the linear model, any mass imbalance is instantly converted into a tendency on the length (i.e. dL/dt in Equation (1)). In the flowline model however, and in a real glacier, there is some inertia to terminus movement. It takes time for mass to travel to the terminus, and the terminus slope has to steepen to the point it drives a flux of ice forwards.
The autocorrelation curve essentially shows the same information, but in a different light. For a linear model described by a single timescale, the autocorrelation curve decays exponentially with an e-folding timescale of τ. Figure 6b shows that for lags longer than ∼15 years (∼2 × τ lin), the autocorrelations of the linear and flowline models are identical and closely approximate the exponential behaviour. For lags shorter than 15 years, the flowline model has much higher autocorrelations than the linear model. As noted above, the physical reason for this is that the terminus cannot respond immediately to mass-balance changes; its location in one year is strongly related to that of the previous year. This is reflected in the more smoothly varying behaviour of the flowline model, evident in Figure 4. For this setting and geometry, ∼15 years is the true measure of the timescale that separates when dynamics does and does not matter. The power spectrum can be deceptive in this regard. The visual appearance from Figure 6a is that it is only at much longer periods that the behaviours of the flowline and linear models converge. This appearance is because a factor of 2π is included when the exponential decay time is projected onto the sinusoidal components of the power spectrum (e.g. Reference RoeRoe, 2009).
Fig. 6. (a) Power spectral estimate for linear and flowline models, calculated using a windowed periodogram (a 20 ka Hanning window). (b) Autocorrelation function (ACF) for linear and flowline models. Both panels show that the flowline model is damped at higher frequencies compared to the linear model.
There are various ways of characterizing the glacier response time, and there has been substantial discussion in the literature (e.g. Reference NyeNye, 1965; Reference Jóhannesson, Raymond, Waddington and OerlemansJóhannesson and others, 1989a,b; Reference Schwitter and RaymondSchwitter and Raymond, 1993; Reference Van de Wal and OerlemansVan de Wal and Oerlemans, 1995; Reference JóhannessonJóhannesson, 1997; Reference Bahr, Pfeffer, Sassolas and MeierBahr and others, 1998; Reference Raper, Brown and BraithwaiteRaper and others, 2000; Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others, 2001, Reference Harrison, Raymond, Echelmeyer and Krimmel2003; Reference OerlemansOerlemans, 2001, Reference Oerlemans2007; Reference Pelto and HedlundPelto and Hedlund, 2001; Reference Leysinger Vieli and GudmundssonLeysinger Vieli and Gudmundsson, 2004; Reference Raper and BraithwaiteRaper and Braithwaite, 2009). Figure 6b shows that the autocorrelation function of the flowline model cannot be represented by a single timescale. Using the ARfit algorithm of Reference Schneider and NeumaierSchneider and Neumaier (2001), we find that an eighth-order autoregressive process is needed to match it. This suggests that ice dynamics introduces a complicated structure of persistence to the glacier length record.
From Figure 6 it seems that best ‘effective response time’ depends on the timescale and question of interest. Several studies have, however, assumed explicitly or implicitly a single response time in characterizing past and predicting future glacier variations (e.g. Reference HarperHarper, 1992; Reference Pelto and HedlundPelto and Hedlund, 2001; Reference OerlemansOerlemans 2005, Reference Oerlemans2007). We find a single best-fit timescale τ bf for the flowline model by fitting a first-order autoregressive process using the ARfit algorithm. This is equivalent to carrying out a regression analysis of the flowline model to Equation (2) using a least-squares minimization. The high autocorrelations at short lags in the flowline model are weighted heavily in the fitting, and the resulting timescale, τ bf = 73 years, is much longer than predicted from the linear model (τ lin = 7 years). For comparison, Figure 4 shows the output from a linear model driven by the same climate forcing but with τ bf = 73 years. The use of a longer timescale correctly captures much of the low-frequency variability of the flowline model, but cannot capture some of the decadal fluctuations.
4. The Likelihood of a Glacier Excursion
One way of characterizing the expected natural variability of a glacier in a constant climate is to answer questions such as: What is the expected return time, on average, of a particular glacier advance? How long, on average, does the glacier persist above or below its equilibrium length? How likely is an excursion of a given size in a given period?
For linear models of the form Equation (2), answers can be derived using standard formulae for threshold crossings of stochastic processes (first laid out by Reference RiceRice, 1948). Reference VanmarckeVanmarcke (1983) and Reference Leadbetter, Lindgren and RootzenLeadbetter and others (1983) provide good summaries. In the Appendix it is shown that, as long as τ ≫ Δt, the average interval between up-crossings of a particular threshold L 0 is given by
R(L 0) is also the average return time of a glacier advance of size L 0. σL is the standard deviation of natural fluctuations. Reference Roe and O’NealRoe and O’Neal (2009) show that Equation (2) yields
provided that P′ and T′ are neither autocorrelated nor correlated with each other (consistent with climate in the Pacific Northwest). A general expression for σL without these restrictions is also possible (Reference Huybers and RoeHuybers and Roe, 2009).
From Equation (6) the exponent in Equation (5) contains τ; the return time of a given advance is therefore a very sensitive function of the response time. A larger value of τ means that the glacier is slower to return to equilibrium and has a weaker restoring tendency. All else being equal, the shorter the value of τ, the longer the return time will be for a given excursion magnitude (as seen in Fig. 7). Secondly, the
in the exponent in Equation (5) means the average return time lengthens extremely rapidly as the size of the advance increases. For τ = 12 years, for example, an advance of 1 km will happen on average every 250 years. For an advance of 1.5 km, the average return time balloons to 7500 years (Fig. 7).
Fig. 7. The average return time of a glacier advance (i.e. the interval between up-crossings of glacier length beyond a given threshold) calculated from Equation (5). The three curves are for the range of parameters appropriate for a typical glacier on Mount Baker. Note the logarithmic scale on the y-axis and the acute sensitivity of the average return time to changes in glacier properties.
4.1. Return time of zero-crossings
How often does a glacier return to its equilibrium length? For up-crossings across zero, L 0 = 0 in Equation (5) and the average return time is given by
For the linear model with τ = τ lin = 7 years, Equation (7) gives an average up-crossing interval of 12 years which is in excellent agreement with the linear model output in Figure 4. It must be, since it is an exact solution of the linear equations. Using the best-fit response time for the flowline model, τ bf = 73 years, Equation (7) gives a prediction for average up-crossing interval of 38 years. The actual average interval from the flowline model output is 41 years and thus compares well to the prediction.
It can be shown (e.g. Reference VanmarckeVanmarcke, 1983) that the rate of zero-crossings depends only on the first and second statistical moments of the spectrum. Although it is difficult to see from Figure 6a because of the log–log axes, the centroid of the spectrum and its other moments are dominated by the high-frequency part of the spectrum and are consistent with using τ bf.
4.2. Likelihood of maximum glacier excursions
Equation (5) presents the average return time of a particular advance or retreat. It is also possible to calculate the probability distribution of such return times. This is governed by the statistics of a Poisson distribution (e.g. Reference Von Storch and Zwiersvon Storch and Zwiers, 1999), where discrete stochastic events occur at a known rate λ. A requirement of the process is that a time interval between an initial and a final time (t f − t i) can be identified in which the likelihood of one event occurring is proportional to (t f − t i), and that the likelihood of two events occurring in that interval is negligible.
Assuming a Poisson process, the probability of observing zero advances (or retreats) of magnitude L 0 in an interval (t f − t i) is given by
where λ(L 0) is the reciprocal of the up-crossing interval R(L 0) in Equation (7). The probability of at least one occurrence of an L 0 advance (or retreat) is given by the complement of Equation (8):
Equation (9) reveals the dependencies clearly. The probability of seeing an advance or retreat is more sensitive to (t f − t i) than to τ. The probability is also remarkably and acutely sensitive to the ratio of L 0 to σL : the exponent itself has an exponential dependence on the square of this ratio.
The advances or retreats considered so far have been relative to the equilibrium glacier position. In any given glacial valley it is difficult to determine the long-term average position of a glacier, especially in the face of a changing climate. A measure of more practical relevance is the total excursion of the glacier accounting for length changes of both signs (i.e. maximum advance minus maximum retreat). The probability f(L 1) of a total excursion of at least the size of ΔL occurring in a given period is given by the probability density of a maximum advance between L 1 and L 1 + dL multiplied by the probability of the maximum retreat exceeding L 2 ≡ L 1 − ΔL integrated over all possible maximum advances (Fig. 8).
Fig. 8. Schematic illustration for the calculation of the likelihood of exceeding a given total excursion.
The probability density f(L 1) of a maximum advance between L 1 and L 1 + dL is:
The total probability of a maximum excursion exceeding ΔL is therefore
Figure 9 shows the probability distribution of maximum excursions in any 1000 year period calculated from the flowline model output and from Equation (10) using τ bf = 73 years. There is good agreement, demonstrating that the model is closely behaving as a Poisson process with the best-fit timescale. In any 1000 year period, it is very likely (>95%) to undergo an excursion of at least 1.4 km, driven just by interannual variability in a constant climate. On the other hand, it is very unlikely (<5%) to undergo an excursion exceeding 2.2 km. Also shown is the curve for τ = 7 years, which would predict longer excursions. This is because the greater power at higher frequencies and the shorter response time for the linear model (Fig. 6a) makes it more likely to have a short, spiky fluctuation that takes the linear glacier across a given threshold. For the more smoothly varying flowline model, these events are rarer.
Fig. 9. The probability of exceeding a given maximum total excursion (i.e. maximum advance minus maximum retreat) in any 1000 year period. Crosses shows calculations from the flowline model output. The curves are calculated from Equation (10) for two different response times.
Reference Reichert, Bengtsson and OerlemansReichert and others (2002) made some similar calculations for the European Alps and for Scandinavia, but used a different definition of a glacier excursion and determined λ from the output of a numerical model. The results in this paper reinforce their conclusions, however, and also those of Reference Roe and O’NealRoe and O’Neal (2009) for the Cascades: that is, kilometre-scale, centennial-scale variations in glacier length will occur in a constant climate. An advantage of Equation (10) is that the dependency of the excursion probabilities on the underlying glacier properties can be clearly seen. Figure 7 highlights that it is important to identify the correct timescale.
How robust are these excursion probabilities to different assumptions and model parameters? Figure 10a shows how the probabilities change for different time intervals. The change in the curves from a 500 to a 1000 year interval is about the same as that from a 2000 to a 5000 year interval. In other words, for longer intervals the probability of seeing large excursions begins to saturate. However, the super-exponential dependency on σL in Equation (9) makes the excursion probabilities acutely sensitive to glacier properties.
Fig. 10. Probability of maximum excursions for different assumptions. (a) Probability of exceeding a given excursion for different periods of time. Note the uneven time increments. (b) Probability of exceeding a given excursion for different values of σL in Equation (10). All curves use the standard parameters for the flowline model (except where σL is varied).
Figure 10b shows howthe curves change for small changes in σL . It is clear that even ±20% variations have a very large impact. An error in estimating σL of even this small amount may reverse the interpretation of whether an excursion could be caused by interannual climate variability or an actual climate change. It is doubtful that the σL of real glaciers can be known so accurately. It is therefore appropriate to be cautious of studies that use such curves to conclude that modern retreats exceed natural variability (e.g. Reference Reichert, Bengtsson and OerlemansReichert and others, 2002). It is certainly possible, but an exhaustive error analysis is needed to be confident.
5. Trend Detection for Glaciers
How big a trend in glacier length is statistically significant? When does the trend exceed that expected from natural variability? We show here that two factors are of primary importance: (1) the magnitude of the trend relative to the magnitude of the natural variability, and (2) the amount of independent information in the observations. The latter factor depends on the degrees of freedom, which in turn depends on the length of observations and the glacier memory.
Let ρ be the correlation of the observations of glacier length and time at lag Δt, and let ν be the degrees of freedom in the dependent time series (i.e. glacier length in this case). A
statistic (distinct from time t) can be calculated from the following combination of ρ and ν:
Basic textbooks on statistics (e.g. Reference Von Storch and Zwiersvon Storch and Zwiers, 1999) show that, in the absence of a real trend, the probability of finding a given value of
will follow a Student’s
distribution. Standard tables can be used to calculate how often
would occur simply by chance. In general, the larger the absolute value of
, the greater the confidence that the observed trend is significant.
Equation (11) can also be written as:
where b is the regression coefficient between time and glacier length and σt and σ res are the standard deviations of time and of the residuals of glacier length after the time-correlated trend has been subtracted, respectively.
σt is the standard deviation of the independent variables (in this case, time) over a given interval of time (t f − t i), and is given by
Equation (12) therefore becomes
ΔL is equivalent to b(t f − t i) and is the change in glacier length that is attributable to the linear trend.
Equation (14) shows some basic and readily understood dependencies. The first factor on the right-hand side can be regarded as the signal-to-noise ratio; the greater the trend relative to the natural variability, the more significant the trend will be. Glaciers that exist in maritime climates are subject to a high degree of precipitation variability (e.g. Reference Huybers and RoeHuybers and Roe, 2009) and have a muted sensitivity to temperature. As such, a warming trend in melt-season temperature may be obscured by the natural variability. A continental glacier with less precipitation variability and a higher sensitivity to temperature may more directly reflect warming trends.
The second factor on the right-hand side of Equation (14) shows that the degrees of freedom (i.e. the number of independent pieces of information in the glacier record) is critical for assigning statistical confidence to an observed trend. If the glacier position was recorded annually, Δt = 1 year and there would be N = (t f − t i)/Δt observations.
A glacier has a dynamical response time, however, so it has memory of its previous positions. It is therefore autocorrelated and there are fewer than N degrees of freedom. Standard theory (e.g. Reference Von Storch and Zwiersvon Storch and Zwiers, 1999) yields the appropriate formula for the effective degree of freedom as:
where, as noted above, γ is the autocorrelation coefficient at a lag time Δt. Using the approximation that Δt ≪ τ and considering only first-order terms, Equation (3) yields:
For a 100 year glacier record and for τ lin = 7 years, there are about seven effective degrees of freedom.
An important measure of whether the
test can be used for trend detection is to determine whether random realizations of a dynamic glacier that is forced by a climate without a trend does, in fact, follow a Student’s
distribution. In other words, is the glacier variability consistent with the assumptions of the
test? To answer this, the correct number of degrees of freedom needs to be established.
Figure 11 shows the probability distribution of the
statistic (Equation (11)) using 1000 randomly selected 100 year intervals from the flowline model output, assuming that ν = 100/(2τ
lin). Also shown are the theoretical Student’s
distributions calculating ν using both τ = τ
lin = 7 years and τ = τ
bf = 73 years. The close agreement between the distribution derived from the model output assuming τ = 7 years demonstrates the model output has about 7 degrees of freedom per 100 years. We can also conclude that the significance of a trend can be evaluated using a standard
test, using τ
lin to calculate the degrees of freedom.
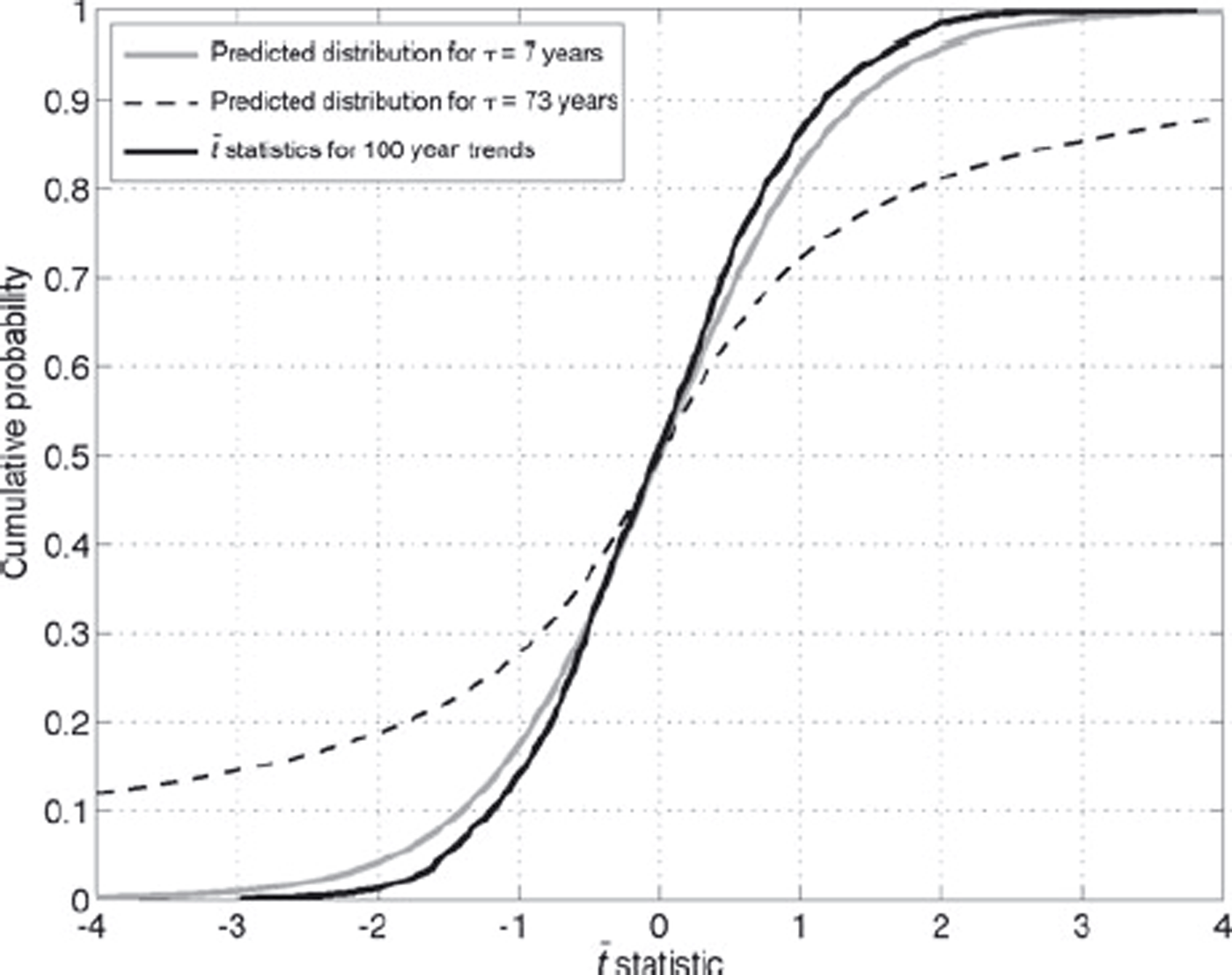
Fig. 11. The distribution of the
statistic calculated from 1000 randomly selected 100 year long periods from the flowline model output, using τ
lin to calculate the degrees of freedom (dof). It agrees very well with the theoretical distributions, meaning the model output has about 7 dof (100 a)−1. For comparison, the theoretical distribution assuming τ
bf is also shown. The
statistic from the model output for τ
bf is imaginary (Equation (14)). In general, though, smaller dofs from assuming larger τs would produce a narrower distribution of the
statistic from the model output (Equation (14)), making it inconsistent with the theoretical distribution.
The
statistic was also calculated for 50, 200 and 1000 year trends, and again using τ
lin for the degrees of freedom. For 50 year trends (just 3.2 effective degrees of freedom) the agreement with the theoretical distribution was slightly worse than that shown in Figure 11, but at no point does the error exceed 5%. For 200 year and 1000 year trends, the
statistic approximated the theoretical distribution even more closely than that in Figure 11. We also note that annual observations of glacier length are not required to estimate trends; providing observations are frequent enough to sample the effective degrees of freedom, there can still be a correct assessment of significance.
The analysis highlights the importance of knowing the correct effective degrees of freedom for evaluating glacier trends in practice. If degrees of freedom were calculated using τ
bf = 73 years, it would formally mean less than one degree of freedom in a 100 year record; Figure 11 shows that significant trends with high
statistics would go unrecognized. One conclusion is that the importance of having degrees of freedom in the observations means that the statistical significance of glacier trends can only be established on multi-decadal or longer timescales.
It is interesting that τ lin is the correct timescale to use for evaluating trends; for the likelihood of large excursions, τ bf works well. The reason seems to be that a trend, like an equilibrium step change, is a low-frequency behaviour of the glacier. It is therefore well described by the linear model, as seen in section 2.3. In contrast, maximum excursions depend on relatively abrupt changes that cause a threshold to be crossed and, for that reason, depend on the high-frequency behaviour of the glacier which is best characterized by τ bf.
5.1. Is the observed trend significant?
Equation (14) provides a way of calculating how large an observed change in glacier length needs to be before the trend can be declared statistically significant:
Consider a 100 year observing period (for which ν = 7.3), a 95% significance level (for which
= 1.88) and let σL
= 324 m, which was what we obtained from the flowline model for typical Mount Baker glaciers. From Equation (17), a change of 900 m would be necessary over that 100 year period in order to declare a significant trend. The actual observed trend over the last 80 years is equivalent to 150 m (100 a)−1 (calculated by linearly detrending the compilation of results of Reference O’NealO’Neal (2005) for Easton, Deming, Boulder, Rainbow and Coleman glaciers in the Cascades). If a shorter period of the last 30 years is considered the observed trend is larger (400 m (30 a)−1), consistent with an anthropogenic climate signal emerging only since that time. The degrees of freedom in the observations are, however, reduced to just 2.2, and so very much larger glacier changes of several kilometres would be required for statistical significance. We therefore conclude that the observed length changes in Mount Baker glaciers, by themselves, cannot be said to reflect a statistically significant trend.
It is important to be clear about the logic here. These results represent the difference between saying that the glaciers by themselves provide independent evidence of climate change versus saying that they are merely consistent with the observed regional warming that is already established to be statistically significant from the instrumental record (e.g. Reference MoteMote, 2003). There is obviously an important distinction between these two statements. The multi-year response time of glaciers means there is much less independent information in their history than in the instrumental record. Moreover, these are maritime glaciers that experience large and largely unrelated interannual accumulation variability (e.g. Reference Bitz and BattistiBitz and Battisti, 1999; Reference Huybers and RoeHuybers and Roe, 2009). It should therefore not be surprising that this variability obscures the effect of warming on the glaciers, and that the glacier record is therefore a less decisive demonstration of regional warming than is provided by thermometers.
5.2. How wrong could σL be?
The results above depend on estimating σL and ν from the flowline model. In general, without long enough records of unforced natural variability, a model must be used. For example, general circulation models are used for estimating the natural variability of global mean climate. It is reasonable to ask whether a model adequately represents this natural variability, and, in the case of global climate, this has been debated extensively.
Alternatively, the question can be turned around to ask what would the value of σL have to be in order for the observed trends ΔL obs to be significant at the 95% level? That is, solve for
For the 100 year and 30 year trends given above, the answer is σL
= 52 m and 20 m, respectively. It seems unlikely that natural variability is as low as this, or that the flowline model is wrong by an order of magnitude. Larger values of σL
could only arise if there were more degrees of freedom coming from a shorter effective response time. The agreement between the
distributions in Figure 11 and the fact that the response time would have to be <7 years also makes this unlikely. The linear timescale is actually a lower bound on the timescale, since it assumes that glacier dynamics are instantaneous (all mass imbalances instantly transferred to the toe). It is hard to imagine, therefore, that there could be more degrees of freedom in the observations. Thus the conclusion – that the retreat of Mount Baker glaciers is consistent with regional warming, but not independent proof of it – is very strong.
5.3. More than one glacier, more than one location
Most glaciers are reported to be retreating around the world. Does this constitute independent evidence of climate change? The
test is a simple and powerful statistical measure that works well, even when the underlying process departs significantly from the test assumptions (e.g. Reference BoneauBoneau, 1960). Rather than detailed modelling of individual glaciers, we could use global datasets of observed glacier length variations (e.g. from the World Glacier Monitoring Service (Reference Haeberli, Haeberli, Hoelzle and SuterHaeberli, 1998)) and use Equation (18) to solve for the combination of σL
and ν required for the observed trend to be significant at the 95% level. Those values could be compared to existing estimates of a glacier’s response time (e.g. Reference OerlemansOerlemans, 2005) and historical or reconstructed estimates of its natural variabilty.
This might provide more rigorous estimates of statistical significance than obtained by varying model parameters (e.g. Reference OerlemansOerlemans, 2005). It would also identify which glaciers are more decisive indicators of climate change than others. The fact that many glaciers within a single region are observed to be retreating or advancing does not necessarily provide much independent information, since they are experiencing essentially the same climate. The independence of individual glaciers can be estimated from the spatial coherence of patterns of natural climate variability (e.g. Reference Bretherton, Widmann, Dymnikov, Wallace and BladéBretherton and others, 1999) of the fields that are most relevant for glaciers (e.g. Reference Burke and RoeBurke and Roe, 2009; Reference Huybers and RoeHuybers and Roe, 2009).
6. Summary and Discussion
Stochastic fluctuations are inherent in a constant climate. Distinguishing between climate records that simply reflect these fluctuations and those that reflect a true climate change is a central challenge in climate science. For the case of global mean temperature, for example, there is widespread agreement that the instrumental record shows a significant warming trend that exceeds the natural variability of the last 30 years. An identical issue arises in interpreting the climatic cause of past glacier fluctuations, which are almost always attributed to climate change. This study expands on earlier work and confirms that interannual variability alone can cause century-scale, kilometre-scale fluctuations in glacier length.
We have presented results for the geometry and setting of the glaciers on Mount Baker in the Pacific Northwest. These are relatively small and steep; to evaluate the impact of glacier geometry we repeated the analyses for a glacier with double the total area and half the basal slope and also for a glacier with quadruple the total area and one-quarter the basal slope (and double the width). For these cases, we obtained comparable agreement between the linear and flowline models to that for the Mount Baker glaciers.
We focused on glacier length because that is typically the clearest signature of past fluctuations. All of the metrics and formulae discussed in this study could instead be applied to glacier volume. The linear model under-predicts the response of glacier volume to climate variability because it does not account for thickness changes. For the spectrum of ice volume fluctuations (i.e. the equivalent of Fig. 6a), the linear and flowline models show very good agreement at high frequencies; however, the linear model under-predicts at low frequencies (by ∼30% for the parameters presented here). At high frequencies, mass-balance fluctuations are simply added to the existing volume and the dynamics have no time to respond. At low frequencies, the linear model does not allow for the thickness changes that amplify the volume fluctuations in the flowline model.
The autocorrelation timescale for volume fluctuations in the flowline model is much shorter than that for length fluctuations (15 years vs 73 years) and so is closer to the predictions of the linear model. Understanding volume fluctuations might find relevance in settings where glacier history is recorded in sediments of proglacial lakes or in trimlines on valley side-walls, or when the impact on sea level is of interest (e.g. Reference Raper and BraithwaiteRaper and Braithwaite, 2009). Another natural metric of glacier response to consider might be the mean thickness of the ice.
The important principle in this study is that stochastic interannual climate variability can cause large and persistent glacier fluctuations that should not be misinterpreted as being driven by a climate change. This principle is fundamental and does not depend in any way upon the details of the models used. These models are sufficient to gauge the magnitude of the effects, and sensitivity to different conditions has been reported here. Glaciers are complicated, and no model can capture all their facets. We note that our linear model does not incorporate the mass-balance (e.g. Reference Harrison, Elsberg, Echelmeyer and KrimmelHarrison and others, 2001) or thickness feedbacks (e.g. Reference Bahr, Meier and PeckhamBahr and others, 1997) that are sometimes included in linear glacier models, although such a modification is easily possible.
Other approaches to estimating the glacier response time have used volume–area scaling ratios that represent some nonlinearities and asymmetries (e.g. Reference Bahr, Pfeffer, Sassolas and MeierBahr and others, 1998; Reference Raper and BraithwaiteRaper and Braithwaite, 2009). For our geometry and setting, and also for the sensitivity experiments, we did not find it necessary to introduce these additional factors in order to successfully emulate a flowline glacier model for our purposes. Further work to establish when such factors or others, such as more complicated geometric settings, cause a breakdown of the relationships derived here will be useful.
One more assumption is that all of the glacier variability is driven by climate variability; in other words, that the glacier physics is fixed. This does not apply to surging or tidewater glaciers, where the physics of glacier flow is itself a function of the glacier state. Such factors will always be difficult to model, however, and it may be best to identify settings where those complications are minimized. Finally, it has also been assumed that climate variability itself does not change during the interval considered. On centennial timescales and longer, we expect greater variability than on interannual timescales (e.g. Reference Huybers and CurryHuybers and Curry, 2006). In general, this will tend to increase in the magnitude of longer-term glacier fluctuations.
The success of the linear model at emulating the flowline model at low frequencies means that, when climate change occurs on timescales longer than a couple of glacier response periods (meaning longer than about 15 years for Mount Baker), the glacier’s response to climate variability (such as the excursion probabilities) can be combined linearly with, and superimposed directly on, the glacier’s response to the climate change.
Extreme events and zero-crossings depend on short rapid advances and retreats, and so are governed by the high-frequency characteristics of the glacier. The flowline model is highly autocorrelated on short timescales (Fig. 6b), and hence the longer decorrelation timescale must be used in the formulae. We also note the extreme sensitivity of threshold-crossing statistics to σL . It may be very hard to determine the value of σL for a real glacier with the accuracy needed to formally establish whether a given glacier advance exceeds that expected from natural variability (cf. Reference OerlemansOerlemans, 2000; Reference Reichert, Bengtsson and OerlemansReichert and others, 2002).
On the other hand, trends,
tests and equilibrium changes depend on the low-frequency characteristics of the glacier, for which it is acting as an essentially passive reservoir of ice. The shorter timescale of the linear model therefore provides excellent agreement; moreover, it can be efficiently estimated from the glacier geometry. Furthermore, the analyses are far less sensitive to parameter uncertainties. Lastly, although not formally as rigorous, by solving for the σL
required for the observed trend to have a nominal confidence level of 95%, the expression for a
statistic can be used to roughly gauge the significance of a trend and so circumvent the need for a comprehensive simulation of the natural variability. Nonparameteric tests that do not rely on the glacier adhering to a particular theoretical PDF might be applied for trend detection (Reference Morell, Fried, Schipp and KrämerMorell and Fried, 2008; Reference CotterCotter, 2009). Such tests are more flexible (although typically less powerful) than parametric tests, and care is needed to account for serial correlations.
Various methods have been used to estimate the glacier response time from observations (e.g. Reference HarperHarper, 1992; Reference OerlemansOerlemans, 2001, Reference Oerlemans2007; Reference Pelto and HedlundPelto and Hedlund, 2001; Reference Harrison, Raymond, Echelmeyer and KrimmelHarrison and others, 2003; Reference Klok and OerlemansKlok and Oerlemans, 2004). A useful exercise would be to repeat those various methods on the output from the flowline model, and see which best captures the correct effective degrees of freedom. A concern is that the results here suggest that short-term lag correlations, which are the most easily estimated from observations, may underestimate the actual degrees of freedom.
Finally, this study evaluated the observed retreat of glaciers around Mount Baker. We conclude there are about seven effective degrees of freedom in a 100 year long record, and that the retreat will have to be much larger than is observed to be considered independent evidence of regional warming. It can certainly be said that the retreat is consistent with the observed warming that is already established to be significant from the instrumental record. It should be made clear that the detection of a trend in glacier length is a different exercise from the detection of a trend in glacier mass balance, which is in many ways more closely related to the instrumental record of climate. Where available, local instrumental and local mass-balance records have more statistical power to resolve climate change than glacier length records. In the case of mass-balance records, changes in glacier area must be factored in (e.g. Reference OerlemansOerlemans, 2001).
Glaciers are consequential and captivating elements of the Earth system. Correctly understanding their dynamics and interpreting their history is a worthwhile challenge. Providing that care is taken to identify the correct timescale, the linear model and the formulae derived from its equations do an excellent job of characterizing some important properties of glacier behaviour. Such formulae can provide guidance as to which glaciers and settings are the most sensitive indicators of warming trends or precipitation trends, and which palaeoreconstructions are likely to be most indicative of past climate changes. Identifying such conditions is an important prerequisite for realizing the fullest potential of glacier records.
Acknowledgements
I am very grateful to M. Baker for discussions and guidance in some of the derivations, to M. Koutnik, E. Steig, E. Waddington, C. Raymond, K. Huybers and E. Burke for insightful conversations and to T. Pfeffer, two anonymous reviewers and the Scientific Editor N. Glasser for helpful reviews.
Appendix: Threshold-Crossing Rates
Let
refer to the rate of change of the glacier. Reference RiceRice (1948) (also Reference VanmarckeVanmarcke, 1983) showed that, for a general random process, the expected rate (λ(L
0)) at which it crosses up over a given threshold L
0 is given by
The term inside the integrand is the joint probability density of the glacier having a length between L
0 and L
0 + dL and, simultaneously, a rate of change which would cause it to cross L
0. The total probability is the integral over all possible rates of change. The primes have been dropped from the Ls for the sake of convenience. If
and L can be considered independent of each other, Rice further showed that the expected rate of up-crossings past L
0 is
where σL
and
are the standard deviations of the glacier length and its rate of change, respectively. We next derive an expression for
, and show that the correlation between
and L can indeed be considered small.
From Equation (1),
which, using Equation (6), becomes
Since we are dealing with typical conditions where τ ≫ Δt, this simplifies to
Next, we determine the correlation coefficient between
and L, which is given by
From Equation (1) it follows directly that
. Equation (A5) therefore implies that the correlation coefficient becomes
For the typical Mount Baker parameters, τ ∼ 12 years giving
. Using a Monte Carlo test (Fig. 7), we show that this correlation is indeed small enough to be neglected and that Equation (A2) therefore provides an accurate description of threshold crossings.
Substituting Equation (A5) into Equation (A2) yields
R(L 0), the average interval between up-crossings across L 0, is the reciprocal of the rate λ(L 0).
