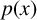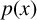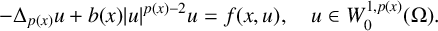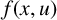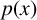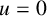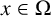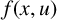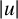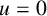1 Introduction
Let
![]() $\Omega \subset \mathbb {R}^{N}$
be a bounded smooth domain,
$\Omega \subset \mathbb {R}^{N}$
be a bounded smooth domain,
![]() $p:\overline {\Omega }\rightarrow \mathbb {R}$
be Lipschitz continuous and
$p:\overline {\Omega }\rightarrow \mathbb {R}$
be Lipschitz continuous and
We consider the Dirichlet problem for the
![]() $p(x)$
-Laplacian equation
$p(x)$
-Laplacian equation
where
![]() $\Delta _{p(x)}u=\operatorname {div}( \vert \nabla u\vert ^{p(x)-2}\nabla u) $
is the
$\Delta _{p(x)}u=\operatorname {div}( \vert \nabla u\vert ^{p(x)-2}\nabla u) $
is the
![]() $p(x)$
-Laplacian of u and
$p(x)$
-Laplacian of u and
![]() $b\in L^{N/p(x)} (\Omega )$
. The definition of the space
$b\in L^{N/p(x)} (\Omega )$
. The definition of the space
![]() $L^{N/p(x)} (\Omega )$
is given in the next section. Note that b can be sign-changing. Let
$L^{N/p(x)} (\Omega )$
is given in the next section. Note that b can be sign-changing. Let
 $$ \begin{align*} p^{\ast}(x)=\frac{Np(x)}{N-p(x)}. \end{align*} $$
$$ \begin{align*} p^{\ast}(x)=\frac{Np(x)}{N-p(x)}. \end{align*} $$
We assume the following conditions on the nonlinearity
![]() $f(x,u)$
:
$f(x,u)$
:
-
(f 1)
 $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$
satisfies the Carathéodory condition and where
$f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$
satisfies the Carathéodory condition and where $$ \begin{align*} \vert f(x,t)\vert \leq C_{1}+C_{2}\vert t\vert ^{q(x)-1}\quad \mbox{for all}\ (x,t) \in\Omega\times \mathbb{R}\text{,} \end{align*} $$
$$ \begin{align*} \vert f(x,t)\vert \leq C_{1}+C_{2}\vert t\vert ^{q(x)-1}\quad \mbox{for all}\ (x,t) \in\Omega\times \mathbb{R}\text{,} \end{align*} $$
 $q\in C(\overline {\Omega })$
and
$q\in C(\overline {\Omega })$
and
 $1< q(x)<p^{*}(x)$
for all
$1< q(x)<p^{*}(x)$
for all
 $x\in \Omega $
;
$x\in \Omega $
;
-
(f 2) there is a ball
 $B_{r}(a)\subset \Omega $
such that (1.3)
$B_{r}(a)\subset \Omega $
such that (1.3) $$ \begin{align} \lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p_{-}}}=+\infty\quad\text{ for almost every (a.e.) }x\in B_{r} (a)\text{, where }F(x,t)=\int_{0}^{t}f(x,\cdot)\text{.} \end{align} $$
$$ \begin{align} \lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p_{-}}}=+\infty\quad\text{ for almost every (a.e.) }x\in B_{r} (a)\text{, where }F(x,t)=\int_{0}^{t}f(x,\cdot)\text{.} \end{align} $$
When
![]() $p(x)\equiv 2$
(thus
$p(x)\equiv 2$
(thus
![]() $p_{-}=2$
) and
$p_{-}=2$
) and
![]() $f(x,\cdot )$
is sublinear at zero, then (1.3) holds with
$f(x,\cdot )$
is sublinear at zero, then (1.3) holds with
![]() $p_{-}=2$
. For this reason, we say that our problem (1.2) is
$p_{-}=2$
. For this reason, we say that our problem (1.2) is
![]() $p(x)$
-sublinear at zero. We emphasise that the limit (1.3) is a pointwise limit, while condition
$p(x)$
-sublinear at zero. We emphasise that the limit (1.3) is a pointwise limit, while condition
![]() $( f_{1}) $
means that the nonlinearity
$( f_{1}) $
means that the nonlinearity
![]() $f(x,u)$
is subcritical. Under these mild conditions, we shall prove the following theorem.
$f(x,u)$
is subcritical. Under these mild conditions, we shall prove the following theorem.
Theorem 1.1. Suppose that the conditions
![]() $( f_{1}) $
and
$( f_{1}) $
and
![]() $( f_{2}) $
hold. If
$( f_{2}) $
hold. If
![]() $f(x,\cdot )$
is odd for all
$f(x,\cdot )$
is odd for all
![]() $x\in \Omega $
, then (1.2) has a sequence of solutions
$x\in \Omega $
, then (1.2) has a sequence of solutions
![]() $u_{n}$
such that
$u_{n}$
such that
![]() $\Phi (u_{n})\leq 0$
,
$\Phi (u_{n})\leq 0$
,
![]() $\Phi (u_{n})\rightarrow 0$
; where
$\Phi (u_{n})\rightarrow 0$
; where
![]() $\Phi $
is the energy functional given in (3.1).
$\Phi $
is the energy functional given in (3.1).
This theorem generalises a recent result of He and Wu [Reference He and Wu5], where the semilinear case
![]() $p(x)\equiv 2$
, namely
$p(x)\equiv 2$
, namely
is considered assuming
![]() $b\in L^{N/2}(\Omega )$
and
$b\in L^{N/2}(\Omega )$
and
![]() $f(x,u)$
is subcritical. In particular, He and Wu assumed the pointwise limit
$f(x,u)$
is subcritical. In particular, He and Wu assumed the pointwise limit
However, in their argument, to verify the condition (1.6) in Proposition 1.2 below, they need the inequality
This could not be true unless the limit (1.5) holds uniformly. In the proof of our Theorem 1.1, we fill this gap (see Lemma 3.4) and generalise their result to the quasilinear variable exponent case. Moreover, the verification of the
![]() $(PS)_{c}$
condition, which is crucial for applying variational methods, has been greatly simplified (see Remark 3.3).
$(PS)_{c}$
condition, which is crucial for applying variational methods, has been greatly simplified (see Remark 3.3).
Both [Reference He and Wu5] and our result are based on a new version of Clark’s theorem recently proved by Liu and Wang [Reference Liu and Wang8]. Our Theorem 1.1 is motivated by [Reference He and Wu5].
Proposition 1.2 [Reference Liu and Wang8, Theorem 1.1].
Let W be a Banach space and
![]() $\Phi \in C^{1}(W,\mathbb {R})$
be an even coercive functional satisfying the
$\Phi \in C^{1}(W,\mathbb {R})$
be an even coercive functional satisfying the
![]() $( PS) _{c}$
condition for
$( PS) _{c}$
condition for
![]() $c\leq 0$
and
$c\leq 0$
and
![]() $\Phi (0)=0$
. If for any
$\Phi (0)=0$
. If for any
![]() $k\in \mathbb {N}$
there are a k-dimensional subspace
$k\in \mathbb {N}$
there are a k-dimensional subspace
![]() $W_{k}$
and
$W_{k}$
and
![]() $\delta _{k}>0$
such that
$\delta _{k}>0$
such that
where
![]() $S_{r}=\{ u\in W : \Vert u\Vert =r\} $
for
$S_{r}=\{ u\in W : \Vert u\Vert =r\} $
for
![]() $r>0$
, then
$r>0$
, then
![]() $\Phi $
has a sequence of critical points
$\Phi $
has a sequence of critical points
![]() $u_{k}\neq 0$
such that
$u_{k}\neq 0$
such that
![]() $\Phi (u_{k})\leq 0$
,
$\Phi (u_{k})\leq 0$
,
![]() $u_{k}\rightarrow 0$
.
$u_{k}\rightarrow 0$
.
Variable exponent variational problems appear in many applications (see [Reference Diening, Harjulehto, Hästö and Růžička2, Reference Jikov, Kozlov and Oleĭnik6, Reference Růžička9]). In particular, there has been great interest in elliptic boundary value problems involving the
![]() $p(x)$
-Laplacian in the last two decades. In [Reference Liang and Zhang7], a sequence of negative energy solutions of the
$p(x)$
-Laplacian in the last two decades. In [Reference Liang and Zhang7], a sequence of negative energy solutions of the
![]() $p(x)$
-Laplacian equation in (1.2) subject to a nonlinear boundary condition is obtained; in addition to
$p(x)$
-Laplacian equation in (1.2) subject to a nonlinear boundary condition is obtained; in addition to
![]() $(f_{1})$
and
$(f_{1})$
and
![]() $(f_{2})$
, it is assumed that (1.3) holds uniformly for
$(f_{2})$
, it is assumed that (1.3) holds uniformly for
![]() $x\in \Omega $
and that the nonlinearity is
$x\in \Omega $
and that the nonlinearity is
![]() $p(x)$
-sublinear at infinity. In [Reference Taarabti10], the existence of positive solutions of (1.2) with concave and convex nonlinearities is studied via Nehari’s method. For other recent results, we refer to [Reference Tavares and Sousa11] for
$p(x)$
-sublinear at infinity. In [Reference Taarabti10], the existence of positive solutions of (1.2) with concave and convex nonlinearities is studied via Nehari’s method. For other recent results, we refer to [Reference Tavares and Sousa11] for
![]() $p(x)$
-Laplacian systems and to [Reference Chinnì, Sciammetta and Tornatore1] for
$p(x)$
-Laplacian systems and to [Reference Chinnì, Sciammetta and Tornatore1] for
![]() $(p(x),q(x))$
-Laplacian problems.
$(p(x),q(x))$
-Laplacian problems.
2 Variable exponent spaces
To study the problem (1.2), we recall the variable exponent Lebesgue space and Sobolev space (see [Reference Fan and Zhao4] for more details). For a Lipschitz continuous function
![]() ${p:\overline {\Omega }\rightarrow \mathbb {R}}$
satisfying (1.1), let
${p:\overline {\Omega }\rightarrow \mathbb {R}}$
satisfying (1.1), let
Here and below, all integrals are taken over
![]() $\Omega $
. Equipped with the Luxemburg norm,
$\Omega $
. Equipped with the Luxemburg norm,
 $$ \begin{align*} \vert u\vert _{p(x)}=\inf\bigg\{ \lambda>0 : \int\bigg\vert \frac{u}{\lambda}\bigg\vert ^{p(x)}\leq1 \bigg\} \text{,} \end{align*} $$
$$ \begin{align*} \vert u\vert _{p(x)}=\inf\bigg\{ \lambda>0 : \int\bigg\vert \frac{u}{\lambda}\bigg\vert ^{p(x)}\leq1 \bigg\} \text{,} \end{align*} $$
![]() $L^{p(x)}(\Omega )$
becomes a separable uniformly convex Banach space.
$L^{p(x)}(\Omega )$
becomes a separable uniformly convex Banach space.
The variable exponent Sobolev space
![]() $W_{0}^{1,p(x)}(\Omega )$
is the completion of
$W_{0}^{1,p(x)}(\Omega )$
is the completion of
![]() $C_{0}^{\infty }(\Omega )$
under the norm
$C_{0}^{\infty }(\Omega )$
under the norm
 $$ \begin{align*} \Vert u\Vert =\vert \nabla u\vert _{p(x)}=\inf\bigg\{ \lambda>0 : \int\bigg\vert \frac{\nabla u}{\lambda}\bigg\vert ^{p(x)}\leq1 \bigg\} \text{,} \end{align*} $$
$$ \begin{align*} \Vert u\Vert =\vert \nabla u\vert _{p(x)}=\inf\bigg\{ \lambda>0 : \int\bigg\vert \frac{\nabla u}{\lambda}\bigg\vert ^{p(x)}\leq1 \bigg\} \text{,} \end{align*} $$
which is also a separable uniformly convex Banach space.
From now on, we denote
![]() $W=W_{0}^{1,p(x)}(\Omega )$
. The functional
$W=W_{0}^{1,p(x)}(\Omega )$
. The functional
![]() $\rho :W\rightarrow \mathbb {R}$
defined by
$\rho :W\rightarrow \mathbb {R}$
defined by
 $$ \begin{align*} \rho(u)=\int\frac{1}{p(x)}\vert \nabla u\vert ^{p(x)} \end{align*} $$
$$ \begin{align*} \rho(u)=\int\frac{1}{p(x)}\vert \nabla u\vert ^{p(x)} \end{align*} $$
is crucial for investigating
![]() $p(x)$
-Laplacian equations like (1.2).
$p(x)$
-Laplacian equations like (1.2).
Lemma 2.1 [Reference Fan and Zhang3, Theorem 3.1].
The functional
![]() $\rho $
is of class
$\rho $
is of class
![]() $C^{1}$
. Moreover, the functional
$C^{1}$
. Moreover, the functional
![]() $\rho ^{\prime }:W\rightarrow W^{\ast }$
is of type
$\rho ^{\prime }:W\rightarrow W^{\ast }$
is of type
![]() $( S_{+}) $
. Thus, if
$( S_{+}) $
. Thus, if
![]() $u_{n}\rightharpoonup u$
in W and
$u_{n}\rightharpoonup u$
in W and
then
![]() $u_{n}\rightarrow u$
in W.
$u_{n}\rightarrow u$
in W.
From the definition of the norm
![]() $\|\cdot \|$
, it is easy to see that:
$\|\cdot \|$
, it is easy to see that:
-
(1) if
 $\Vert u\Vert \geq 1$
, then
$\Vert u\Vert \geq 1$
, then  $$ \begin{align*} \Vert u\Vert ^{p_{-}}\leq\int\vert \nabla u\vert ^{p(x)}\leq\Vert u\Vert ^{p_{+}}\text{;} \end{align*} $$
$$ \begin{align*} \Vert u\Vert ^{p_{-}}\leq\int\vert \nabla u\vert ^{p(x)}\leq\Vert u\Vert ^{p_{+}}\text{;} \end{align*} $$
-
(2) if
 $\Vert u\Vert \leq 1$
, then
$\Vert u\Vert \leq 1$
, then  $$ \begin{align*} \Vert u\Vert ^{p_{+}}\leq\int\vert \nabla u\vert ^{p(x)}\leq\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$
$$ \begin{align*} \Vert u\Vert ^{p_{+}}\leq\int\vert \nabla u\vert ^{p(x)}\leq\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$
The following lemma is an easy consequence because
![]() $p_{-}\le p(x)\le p_{+}$
.
$p_{-}\le p(x)\le p_{+}$
.
Lemma 2.2
-
(1) If
 $\Vert u\Vert \geq 1$
, then
$\Vert u\Vert \geq 1$
, then  $$ \begin{align*} \frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\leq\rho(u)\leq\frac{1}{p_{-} }\Vert u\Vert ^{p_{+}}\text{;} \end{align*} $$
$$ \begin{align*} \frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\leq\rho(u)\leq\frac{1}{p_{-} }\Vert u\Vert ^{p_{+}}\text{;} \end{align*} $$
-
(2) if
 $\Vert u\Vert \leq 1$
, then
$\Vert u\Vert \leq 1$
, then  $$ \begin{align*} \frac{1}{p_{+}}\Vert u\Vert ^{p_{+}}\leq\rho(u)\leq\frac{1}{p_{-} }\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$
$$ \begin{align*} \frac{1}{p_{+}}\Vert u\Vert ^{p_{+}}\leq\rho(u)\leq\frac{1}{p_{-} }\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$
3 Proof of Theorem 1.1
For the variable exponent Sobolev space
![]() $W=W_{0}^{1,p(x)} (\Omega )$
, it is well known that weak solutions of (1.2) are precisely critical points of the
$W=W_{0}^{1,p(x)} (\Omega )$
, it is well known that weak solutions of (1.2) are precisely critical points of the
![]() $C^{1}$
-functional
$C^{1}$
-functional
![]() $\Phi :W\rightarrow \mathbb {R}$
,
$\Phi :W\rightarrow \mathbb {R}$
,
 $$ \begin{align} \Phi(u)=\int\bigg( \frac{1}{p(x)}( \vert \nabla u\vert ^{p(x)}+b(x)\vert u\vert ^{p(x)}) \bigg) -\int F(x,u)\text{.} \end{align} $$
$$ \begin{align} \Phi(u)=\int\bigg( \frac{1}{p(x)}( \vert \nabla u\vert ^{p(x)}+b(x)\vert u\vert ^{p(x)}) \bigg) -\int F(x,u)\text{.} \end{align} $$
At first glance, because b may be sign-changing, the principle part (the first term) of
![]() $\Phi $
appears to be indefinite. We observe that if we set
$\Phi $
appears to be indefinite. We observe that if we set
then the problem (1.2) becomes
in which the new nonlinearity
![]() $\tilde {f}(x,u)$
satisfies the same conditions
$\tilde {f}(x,u)$
satisfies the same conditions
![]() $( f_{1}) $
and
$( f_{1}) $
and
![]() $( f_{2}) $
, and
$( f_{2}) $
, and
 $$ \begin{align*} \lim_{\vert t\vert \rightarrow0}\frac{\tilde{F}(x,t)}{\vert t\vert ^{p_{-}}}=\lim_{\vert t\vert \rightarrow0}\bigg( \frac{F(x,t)}{\vert t\vert ^{p_{-}}}-\frac{b(x)}{p(x)} \frac{\vert t\vert ^{p(x)}}{\vert t\vert ^{p_{-}} }\bigg) =\lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p_{-}}}=+\infty \end{align*} $$
$$ \begin{align*} \lim_{\vert t\vert \rightarrow0}\frac{\tilde{F}(x,t)}{\vert t\vert ^{p_{-}}}=\lim_{\vert t\vert \rightarrow0}\bigg( \frac{F(x,t)}{\vert t\vert ^{p_{-}}}-\frac{b(x)}{p(x)} \frac{\vert t\vert ^{p(x)}}{\vert t\vert ^{p_{-}} }\bigg) =\lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p_{-}}}=+\infty \end{align*} $$
for almost every
![]() $x\in B_{r}(a)$
, because
$x\in B_{r}(a)$
, because
![]() $p(x)\geq p_{-}$
. Here,
$p(x)\geq p_{-}$
. Here,
![]() $\tilde {F}(x,t)=\int _{0}^{t}\tilde {f}(x,\cdot )$
.
$\tilde {F}(x,t)=\int _{0}^{t}\tilde {f}(x,\cdot )$
.
In other words, to prove Theorem 1.1, it suffices to consider the case
![]() $b(x)=0$
. The reason that we state our problem (1.2) with the term
$b(x)=0$
. The reason that we state our problem (1.2) with the term
![]() $b(x)\vert u\vert ^{p(x)-2}u$
is to allow comparison with the results of [Reference He and Wu5, Reference Liang and Zhang7, Reference Taarabti10].
$b(x)\vert u\vert ^{p(x)-2}u$
is to allow comparison with the results of [Reference He and Wu5, Reference Liang and Zhang7, Reference Taarabti10].
Therefore, in what follows, we assume
![]() $b(x)=0$
so that the functional given in (3.1) becomes
$b(x)=0$
so that the functional given in (3.1) becomes
![]() $\Phi :W\rightarrow \mathbb {R}$
,
$\Phi :W\rightarrow \mathbb {R}$
,
 $$ \begin{align*} \Phi(u) =\rho(u)-\int F(x,u) =\int\frac{1}{p(x)}\vert \nabla u\vert ^{p(x)}-\int F(x,u)\text{,} \end{align*} $$
$$ \begin{align*} \Phi(u) =\rho(u)-\int F(x,u) =\int\frac{1}{p(x)}\vert \nabla u\vert ^{p(x)}-\int F(x,u)\text{,} \end{align*} $$
whose critical points are solutions of (1.2) with
![]() $b(x)=0$
. To prove Theorem 1.1, we shall apply Proposition 1.2 to find a sequence
$b(x)=0$
. To prove Theorem 1.1, we shall apply Proposition 1.2 to find a sequence
![]() $\{ u_{n}\} $
of critical points for
$\{ u_{n}\} $
of critical points for
![]() $\Phi $
.
$\Phi $
.
Since we have not assumed any conditions on the nonlinearity
![]() $f(x,t)$
for
$f(x,t)$
for
![]() $|t|$
large (except the subcritical growth condition
$|t|$
large (except the subcritical growth condition
![]() $( f_{1}) $
), it is not possible to verify the
$( f_{1}) $
), it is not possible to verify the
![]() $( PS) _{c}$
condition for
$( PS) _{c}$
condition for
![]() $\Phi $
. To overcome this difficulty, we adopt the truncation method of He and Wu [Reference He and Wu5].
$\Phi $
. To overcome this difficulty, we adopt the truncation method of He and Wu [Reference He and Wu5].
Let
![]() $\phi :[0,\infty )\rightarrow \lbrack 0,1]$
be a decreasing
$\phi :[0,\infty )\rightarrow \lbrack 0,1]$
be a decreasing
![]() $C^{\infty } $
-function such that
$C^{\infty } $
-function such that
![]() $\vert \phi ^{\prime }(t)\vert \leq 2$
,
$\vert \phi ^{\prime }(t)\vert \leq 2$
,
We consider the truncated functional
![]() $\Psi :W\rightarrow \mathbb {R}$
,
$\Psi :W\rightarrow \mathbb {R}$
,
The derivative of
![]() $\Psi $
is given by
$\Psi $
is given by
 $$ \begin{align} \langle\Psi^{\prime}(u),v\rangle & =\langle\rho^{\prime}(u),v\rangle -\phi(\rho(u))\int f(x,u)v-\bigg( \int F(x,u)\bigg) \phi^{\prime} (\rho(u))\langle\rho^{\prime}(u),v\rangle\nonumber\\ & =\bigg( 1-\bigg( \int F(x,u)\bigg) \phi^{\prime}(\rho(u))\bigg) \langle\rho^{\prime}(u),v\rangle-\phi(\rho(u))\int f(x,u)v \end{align} $$
$$ \begin{align} \langle\Psi^{\prime}(u),v\rangle & =\langle\rho^{\prime}(u),v\rangle -\phi(\rho(u))\int f(x,u)v-\bigg( \int F(x,u)\bigg) \phi^{\prime} (\rho(u))\langle\rho^{\prime}(u),v\rangle\nonumber\\ & =\bigg( 1-\bigg( \int F(x,u)\bigg) \phi^{\prime}(\rho(u))\bigg) \langle\rho^{\prime}(u),v\rangle-\phi(\rho(u))\int f(x,u)v \end{align} $$
for
![]() $u,v\in W$
.
$u,v\in W$
.
Lemma 3.1. The functional
![]() $\Psi $
is coercive.
$\Psi $
is coercive.
Proof. We note that by Lemma 2.2, for
![]() $\Vert u\Vert \geq 1+( 2p_{+}) ^{1/p_{-}}$
,
$\Vert u\Vert \geq 1+( 2p_{+}) ^{1/p_{-}}$
,
 $$ \begin{align*} \rho(u)\geq\frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\geq2\text{.} \end{align*} $$
$$ \begin{align*} \rho(u)\geq\frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\geq2\text{.} \end{align*} $$
Hence,
![]() $\phi (\rho (u))=0$
and
$\phi (\rho (u))=0$
and
 $$ \begin{align*} \Psi(u)=\rho(u)\geq\frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$
$$ \begin{align*} \Psi(u)=\rho(u)\geq\frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$
This implies that
![]() $\Psi $
is coercive.
$\Psi $
is coercive.
Lemma 3.2. The functional
![]() $\Psi $
satisfies
$\Psi $
satisfies
![]() $( PS) _{c}$
for
$( PS) _{c}$
for
![]() $c\leq 0$
.
$c\leq 0$
.
Proof. Let
![]() $\{ u_{n}\} $
be a
$\{ u_{n}\} $
be a
![]() $( PS) _{c}$
sequence of
$( PS) _{c}$
sequence of
![]() $\Psi $
with
$\Psi $
with
![]() $c\leq 0$
, that is,
$c\leq 0$
, that is,
![]() $\Psi (u_{n})\rightarrow c$
,
$\Psi (u_{n})\rightarrow c$
,
![]() $\Psi ^{\prime } (u_{n})\rightarrow 0$
. Then for n large,
$\Psi ^{\prime } (u_{n})\rightarrow 0$
. Then for n large,
We claim that
For this purpose, we consider two cases. If
![]() $\rho (u_{n})<1$
, then
$\rho (u_{n})<1$
, then
![]() $\phi ^{\prime }(\rho (u_{n}))=0$
and (3.4) is an equality. If
$\phi ^{\prime }(\rho (u_{n}))=0$
and (3.4) is an equality. If
![]() $\rho (u_{n})\geq 1$
, then the right-hand side of (3.3) is negative. Noting
$\rho (u_{n})\geq 1$
, then the right-hand side of (3.3) is negative. Noting
![]() $\phi (\rho (u_{n}))\geq 0$
, we have
$\phi (\rho (u_{n}))\geq 0$
, we have
So we also have (3.4) because
![]() $\phi ^{\prime }(\rho (u_{n}))\leq 0$
.
$\phi ^{\prime }(\rho (u_{n}))\leq 0$
.
The coerciveness of
![]() $\Psi $
implies that the
$\Psi $
implies that the
![]() $( PS) _{c}$
sequence
$( PS) _{c}$
sequence
![]() $\{ u_{n}\} $
is bounded in W. We may assume that
$\{ u_{n}\} $
is bounded in W. We may assume that
![]() $u_{n}\rightharpoonup u$
in W. Since f is subcritical (condition
$u_{n}\rightharpoonup u$
in W. Since f is subcritical (condition
![]() $(f_{1} )$
), by the compact embedding
$(f_{1} )$
), by the compact embedding
![]() $W\hookrightarrow L^{q(x)}(\Omega )$
, Hölder’s inequality and the boundedness of the Nemytsky operator
$W\hookrightarrow L^{q(x)}(\Omega )$
, Hölder’s inequality and the boundedness of the Nemytsky operator
(as shown in [Reference Fan and Zhao4]), it is well known that up to a subsequence,
Setting
![]() $v=u_{n}-u$
in (3.2), from
$v=u_{n}-u$
in (3.2), from
![]() $\langle \Psi ^{\prime }(u_{n} ),u_{n}-u\rangle \rightarrow 0$
, (3.6) and the boundedness of
$\langle \Psi ^{\prime }(u_{n} ),u_{n}-u\rangle \rightarrow 0$
, (3.6) and the boundedness of
![]() $\phi (\rho (u_{n}))$
, we obtain
$\phi (\rho (u_{n}))$
, we obtain
 $$ \begin{align} \bigg( 1 & -\bigg( \int F(x,u_{n})\bigg) \phi^{\prime} (\rho(u_{n}))\bigg) \langle\rho^{\prime}(u_{n}),u_{n}-u\rangle\nonumber\\ & =\langle\Psi^{\prime}(u_{n}),u_{n}-u\rangle+\phi(\rho(u_{n}))\int f(x,u_{n})( u_{n}-u) \rightarrow0\text{.} \end{align} $$
$$ \begin{align} \bigg( 1 & -\bigg( \int F(x,u_{n})\bigg) \phi^{\prime} (\rho(u_{n}))\bigg) \langle\rho^{\prime}(u_{n}),u_{n}-u\rangle\nonumber\\ & =\langle\Psi^{\prime}(u_{n}),u_{n}-u\rangle+\phi(\rho(u_{n}))\int f(x,u_{n})( u_{n}-u) \rightarrow0\text{.} \end{align} $$
We deduce from this and (3.4) that
It follows from Lemma 2.1 that
![]() $u_{n}\rightarrow u$
in W.
$u_{n}\rightarrow u$
in W.
Remark 3.3. Although our problem (1.2) is much more general than the problem (1.4) considered in [Reference He and Wu5], our verification of the
![]() $( PS) _{c}$
condition is much simpler than in [Reference He and Wu5], where the convergence of
$( PS) _{c}$
condition is much simpler than in [Reference He and Wu5], where the convergence of
![]() $\{u_{n}\}$
is deduced by estimating
$\{u_{n}\}$
is deduced by estimating
![]() $\Vert u_{n}-u\Vert ^{2}$
by the sum of
$\Vert u_{n}-u\Vert ^{2}$
by the sum of
![]() $\langle \Psi ^{\prime }(u_{n})-\Psi ^{\prime }(u),u_{n}-u\rangle $
and four additional complicated terms (see [Reference He and Wu5, (2.20)]). The key points in our proof are the
$\langle \Psi ^{\prime }(u_{n})-\Psi ^{\prime }(u),u_{n}-u\rangle $
and four additional complicated terms (see [Reference He and Wu5, (2.20)]). The key points in our proof are the
![]() $(S_{+})$
property of
$(S_{+})$
property of
![]() $\rho ^{\prime }$
and the observation (3.4).
$\rho ^{\prime }$
and the observation (3.4).
We should also point out that the verification of
![]() $(PS)_c$
for
$(PS)_c$
for
![]() $c=0$
in [Reference He and Wu5] contains a gap. For the
$c=0$
in [Reference He and Wu5] contains a gap. For the
![]() $(PS)_0$
sequence
$(PS)_0$
sequence
![]() $\{u_n\}$
, [Reference He and Wu5, (2.19)] is derived from
$\{u_n\}$
, [Reference He and Wu5, (2.19)] is derived from
![]() ${2\Psi (u_n)-\|u_n\|^2\le 0}$
. However, this may be false because
${2\Psi (u_n)-\|u_n\|^2\le 0}$
. However, this may be false because
![]() $\Psi (u_n)$
may be positive, even though
$\Psi (u_n)$
may be positive, even though
![]() $\Psi (u_n)\to 0$
.
$\Psi (u_n)\to 0$
.
Lemma 3.4. For any
![]() $k\in \mathbb {N}$
, there are a k-dimensional subspace
$k\in \mathbb {N}$
, there are a k-dimensional subspace
![]() $W_{k}$
of W and
$W_{k}$
of W and
![]() $\delta _{k}>0$
, such that
$\delta _{k}>0$
, such that
Proof. Let
![]() $X=\{u\in W : \operatorname {\mathrm {supp}} u\subset B_{r}(a)\}$
,
$X=\{u\in W : \operatorname {\mathrm {supp}} u\subset B_{r}(a)\}$
,
![]() $W_{k}$
be a k-dimensional subspace of X. If the result is not true then, for all
$W_{k}$
be a k-dimensional subspace of X. If the result is not true then, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
This implies that there is a sequence
![]() $\{ u_{n}\} \subset W_{k}\cap S_{1/n}$
, such that
$\{ u_{n}\} \subset W_{k}\cap S_{1/n}$
, such that
Since all norms on
![]() $W_{k}$
are equivalent, from
$W_{k}$
are equivalent, from
![]() $\Vert u_{n}\Vert \rightarrow 0$
, we deduce
$\Vert u_{n}\Vert \rightarrow 0$
, we deduce
![]() $\vert u_{n}\vert _{\infty }\rightarrow 0$
.
$\vert u_{n}\vert _{\infty }\rightarrow 0$
.
Let
![]() $\eta :\Omega \rightarrow [ -\infty ,\infty ] $
be defined by
$\eta :\Omega \rightarrow [ -\infty ,\infty ] $
be defined by
 $$ \begin{align*} \eta(x)=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n}(x))}{\Vert u_{n}\Vert ^{p_{-}}}\text{.} \end{align*} $$
$$ \begin{align*} \eta(x)=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n}(x))}{\Vert u_{n}\Vert ^{p_{-}}}\text{.} \end{align*} $$
Then
![]() $\eta $
is measurable. For
$\eta $
is measurable. For
![]() $x\in B_{r}(a)$
, from the pointwise limit (1.3) in
$x\in B_{r}(a)$
, from the pointwise limit (1.3) in
![]() $( f_{2}) $
, there is
$( f_{2}) $
, there is
![]() $r_{x}>0$
such that
$r_{x}>0$
such that
![]() $F(x,t)\geq 0$
for
$F(x,t)\geq 0$
for
![]() $t\in [ -r_{x},r_{x}] $
. Hence, if
$t\in [ -r_{x},r_{x}] $
. Hence, if
![]() $n\gg 1$
, then
$n\gg 1$
, then
![]() $\vert u_{n}\vert _{\infty }\leq r_{x}$
and
$\vert u_{n}\vert _{\infty }\leq r_{x}$
and
![]() $F(x,u_{n}(x))\geq 0$
, and so
$F(x,u_{n}(x))\geq 0$
, and so
![]() $\eta (x)\ge 0$
for a.e.
$\eta (x)\ge 0$
for a.e.
![]() $x\in B_{r}(a)$
. Consequently,
$x\in B_{r}(a)$
. Consequently,
![]() $\eta (x)\geq 0$
for a.e.
$\eta (x)\geq 0$
for a.e.
![]() $x\in \Omega $
, because
$x\in \Omega $
, because
![]() $\operatorname {\mathrm {supp}} u_{n}\subset B_{r}(a)$
.
$\operatorname {\mathrm {supp}} u_{n}\subset B_{r}(a)$
.
Let
![]() $v_{n}=\Vert u_{n}\Vert ^{-1}u_{n}$
. Since
$v_{n}=\Vert u_{n}\Vert ^{-1}u_{n}$
. Since
![]() $\dim W_{k}<\infty $
, we have
$\dim W_{k}<\infty $
, we have
![]() $v_{n}\rightarrow v$
in
$v_{n}\rightarrow v$
in
![]() $W_{k}$
for some
$W_{k}$
for some
![]() $v\in W_{k}$
, note that
$v\in W_{k}$
, note that
![]() $\|v\|=1$
. For
$\|v\|=1$
. For
![]() $x\in \{ v\neq 0\} $
, using (1.3) again,
$x\in \{ v\neq 0\} $
, using (1.3) again,
 $$ \begin{align*} \eta(x)=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n}(x))}{\Vert u_{n}\Vert ^{p_{-}}}=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n} (x))}{\vert u_{n}(x)\vert ^{p_{-}}}\vert v_{n}(x)\vert ^{p_{-}}=+\infty\text{.} \end{align*} $$
$$ \begin{align*} \eta(x)=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n}(x))}{\Vert u_{n}\Vert ^{p_{-}}}=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n} (x))}{\vert u_{n}(x)\vert ^{p_{-}}}\vert v_{n}(x)\vert ^{p_{-}}=+\infty\text{.} \end{align*} $$
By Fatou’s lemma, since
![]() $\{ v\neq 0\} $
has positive Lebesgue measure,
$\{ v\neq 0\} $
has positive Lebesgue measure,
 $$ \begin{align} \varliminf_{n\rightarrow\infty}\int\frac{F(x,u_{n})}{\Vert u_{n} \Vert ^{p_{-}}}\geq\int\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n} )}{\Vert u_{n}\Vert ^{p_{-}}}=\int\eta\geq\int_{v\neq0}\eta =+\infty\text{.} \end{align} $$
$$ \begin{align} \varliminf_{n\rightarrow\infty}\int\frac{F(x,u_{n})}{\Vert u_{n} \Vert ^{p_{-}}}\geq\int\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n} )}{\Vert u_{n}\Vert ^{p_{-}}}=\int\eta\geq\int_{v\neq0}\eta =+\infty\text{.} \end{align} $$
Because
![]() $\Vert u_{n}\Vert \leq 1$
, we have (see Lemma 2.2)
$\Vert u_{n}\Vert \leq 1$
, we have (see Lemma 2.2)
 $$ \begin{align*} \rho(u_{n})\leq\frac{1}{p_{-}}\Vert u_{n}\Vert ^{p_{-}} \leq1\text{.} \end{align*} $$
$$ \begin{align*} \rho(u_{n})\leq\frac{1}{p_{-}}\Vert u_{n}\Vert ^{p_{-}} \leq1\text{.} \end{align*} $$
Thus,
![]() $\phi (\rho (u_{n}))=1$
and
$\phi (\rho (u_{n}))=1$
and
 $$ \begin{align*} \Psi(u_{n}) =\Phi(u_{n}) & =\rho(u_{n})-\int F(x,u_{n})\\ & \leq\frac{1}{p_{-}}\Vert u_{n}\Vert ^{p_{-}}-\int F(x,u_{n})\\ & =\Vert u_{n}\Vert ^{p_{-}}\bigg( \frac{1}{p_{-}}-\int \frac{F(x,u_{n})}{\Vert u_{n}\Vert ^{p_{-}}}\bigg) =\frac {1}{n^{p_{-}}}\bigg( \frac{1}{p_{-}}-\int\frac{F(x,u_{n})}{\Vert u_{n}\Vert ^{p_{-}}}\bigg) \text{.} \end{align*} $$
$$ \begin{align*} \Psi(u_{n}) =\Phi(u_{n}) & =\rho(u_{n})-\int F(x,u_{n})\\ & \leq\frac{1}{p_{-}}\Vert u_{n}\Vert ^{p_{-}}-\int F(x,u_{n})\\ & =\Vert u_{n}\Vert ^{p_{-}}\bigg( \frac{1}{p_{-}}-\int \frac{F(x,u_{n})}{\Vert u_{n}\Vert ^{p_{-}}}\bigg) =\frac {1}{n^{p_{-}}}\bigg( \frac{1}{p_{-}}-\int\frac{F(x,u_{n})}{\Vert u_{n}\Vert ^{p_{-}}}\bigg) \text{.} \end{align*} $$
Now, from (3.9), we deduce
![]() $n^{p_{-}}\Psi (u_{n})\rightarrow -\infty $
, contradicting (3.8).
$n^{p_{-}}\Psi (u_{n})\rightarrow -\infty $
, contradicting (3.8).
Proof of Theorem 1.1.
Lemmas 3.1, 3.2 and 3.4 permit us to apply Proposition 1.2, and deduce that
![]() $\Psi $
has a sequence of critical points
$\Psi $
has a sequence of critical points
![]() $u_{k}\neq 0$
such that
$u_{k}\neq 0$
such that
![]() $\Psi (u_{k})<0$
and
$\Psi (u_{k})<0$
and
![]() $u_{k}\rightarrow 0$
in W. For some
$u_{k}\rightarrow 0$
in W. For some
![]() $K\in \mathbb {N}$
, if
$K\in \mathbb {N}$
, if
![]() $k\geq K$
,
$k\geq K$
,
 $$ \begin{align*} \rho(u_{k})\leq\frac{1}{p_{-}}\Vert u_{k}\Vert ^{p_{-}}<1\text{.} \end{align*} $$
$$ \begin{align*} \rho(u_{k})\leq\frac{1}{p_{-}}\Vert u_{k}\Vert ^{p_{-}}<1\text{.} \end{align*} $$
Since
![]() $\Psi (u)=\Phi (u)$
for
$\Psi (u)=\Phi (u)$
for
![]() $u\in \rho ^{-1}[0,1)$
, we see that
$u\in \rho ^{-1}[0,1)$
, we see that
![]() $u_{k}$
with
$u_{k}$
with
![]() $k\geq K$
are critical points of
$k\geq K$
are critical points of
![]() $\Phi $
as well, satisfying
$\Phi $
as well, satisfying
![]() $\Phi (u_{k})<0$
and
$\Phi (u_{k})<0$
and
![]() $u_{k}\rightarrow 0$
in W.
$u_{k}\rightarrow 0$
in W.
Remark 3.5. Liu and Wang [Reference Liu and Wang8, Theorem 3.1] treat the case in which
![]() $p(x)$
is a constant
$p(x)$
is a constant
![]() $p>1$
. Assuming that
$p>1$
. Assuming that
![]() $f(x,\cdot )$
is odd only in
$f(x,\cdot )$
is odd only in
![]() $( -\delta ,\delta ) $
for some
$( -\delta ,\delta ) $
for some
![]() $\delta>0$
, and
$\delta>0$
, and
uniformly on some small ball
![]() $B_{r}(x_{0})\subset \Omega $
, a sequence of negative energy solutions approaching zero is obtained. Liu and Wang truncated the nonlinearity
$B_{r}(x_{0})\subset \Omega $
, a sequence of negative energy solutions approaching zero is obtained. Liu and Wang truncated the nonlinearity
![]() $f(x,t)$
for
$f(x,t)$
for
![]() $\vert t\vert>\delta /2$
, resulting in a new nonlinearity
$\vert t\vert>\delta /2$
, resulting in a new nonlinearity
![]() $\hat {f}(x,t)=0$
for
$\hat {f}(x,t)=0$
for
![]() $\vert t\vert>\delta $
. Then Proposition 1.2 is applied to get a sequence of solutions
$\vert t\vert>\delta $
. Then Proposition 1.2 is applied to get a sequence of solutions
![]() $u_{n}$
for the truncated problem. Since
$u_{n}$
for the truncated problem. Since
![]() $u_{n}\rightarrow 0$
in
$u_{n}\rightarrow 0$
in
![]() $W_{0}^{1,p}(\Omega )$
, a regularity argument then yields
$W_{0}^{1,p}(\Omega )$
, a regularity argument then yields
![]() $\vert u_{n}\vert _{\infty }<\delta /2$
for large n. Such
$\vert u_{n}\vert _{\infty }<\delta /2$
for large n. Such
![]() $u_{n}$
are then solutions of the original problem.
$u_{n}$
are then solutions of the original problem.
To the best of our knowledge, a suitable
![]() $L^{\infty }$
-regularity theory is not available for the
$L^{\infty }$
-regularity theory is not available for the
![]() $p(x)$
-Laplacian operator and, at present, we can only deal with the case in which
$p(x)$
-Laplacian operator and, at present, we can only deal with the case in which
![]() $f(x,\cdot )$
is globally odd and subcritical, as we have done in Theorem 1.1. Our argument in proving Lemma 3.4 can be used to slightly improve [Reference Liu and Wang8, Theorem 3.1], requiring only that the limit (3.10) holds pointwise in
$f(x,\cdot )$
is globally odd and subcritical, as we have done in Theorem 1.1. Our argument in proving Lemma 3.4 can be used to slightly improve [Reference Liu and Wang8, Theorem 3.1], requiring only that the limit (3.10) holds pointwise in
![]() $B_{r}(x_{0})$
.
$B_{r}(x_{0})$
.