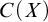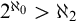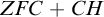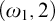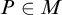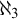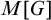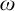1. Introduction
This paper addresses Kaplansky’s conjecture in the theory of Banach algebras concerning the existence of discontinuous homomorphisms of
![]() $C(X)$
, the algebra of continuous real-valued functions with domain X, where X is an infinite compact Hausdorff space. This problem sits squarely in the extensive history of the question of automatic continuity—whether algebraic tameness implies topological tameness. Among the open questions in this area of research is whether the existence of a discontinuous homomorphism of
$C(X)$
, the algebra of continuous real-valued functions with domain X, where X is an infinite compact Hausdorff space. This problem sits squarely in the extensive history of the question of automatic continuity—whether algebraic tameness implies topological tameness. Among the open questions in this area of research is whether the existence of a discontinuous homomorphism of
![]() $C(X)$
implies that the cardinality of the continuum is at most
$C(X)$
implies that the cardinality of the continuum is at most
![]() $\aleph _2$
. We prove in this paper that the existence of a discontinuous homomorphism of
$\aleph _2$
. We prove in this paper that the existence of a discontinuous homomorphism of
![]() $C(X)$
does not imply that
$C(X)$
does not imply that
![]() $2^{\aleph _0} \leq \aleph _2$
.
$2^{\aleph _0} \leq \aleph _2$
.
In [Reference Johnson10], B. Johnson proved that there is a discontinuous homomorphism of
![]() $C(X)$
provided that there is a nontrivial submultiplicative norm on the finite elements of an ultrapower of
$C(X)$
provided that there is a nontrivial submultiplicative norm on the finite elements of an ultrapower of
![]() $\mathbb R$
over
$\mathbb R$
over
![]() $\omega $
. In [Reference Esterle7], J. Esterle constructs an algebra of formal power series,
$\omega $
. In [Reference Esterle7], J. Esterle constructs an algebra of formal power series,
![]() $\mathcal {E}$
, and shows in [Reference Esterle6] that the infinitesimal elements of
$\mathcal {E}$
, and shows in [Reference Esterle6] that the infinitesimal elements of
![]() $\mathcal {E}$
admit a nontrivial submultiplicative norm. By results of Esterle in [Reference Esterle8], it is known that
$\mathcal {E}$
admit a nontrivial submultiplicative norm. By results of Esterle in [Reference Esterle8], it is known that
![]() $\mathcal {E}$
is an
$\mathcal {E}$
is an
![]() $\eta _1$
-ordering of cardinality
$\eta _1$
-ordering of cardinality
![]() $2^{\aleph _0}$
. Furthermore,
$2^{\aleph _0}$
. Furthermore,
![]() $\mathcal {E}$
is a totally ordered field by a result of Hahn in 1907 [Reference Hahn9], and is real-closed by a result of Maclane [Reference Maclane11].
$\mathcal {E}$
is a totally ordered field by a result of Hahn in 1907 [Reference Hahn9], and is real-closed by a result of Maclane [Reference Maclane11].
It is a theorem of P. Erdös, L. Gillman, and M. Henriksen in [Reference Erdös, Gillman and Henriksen5] that any pair of
![]() $\eta _1$
-ordered real-closed fields of cardinality
$\eta _1$
-ordered real-closed fields of cardinality
![]() $\aleph _1$
are isomorphic as ordered fields.Footnote
1
In fact, it is shown using a back-and-forth argument that any order-preserving field isomorphism between countable subsets of
$\aleph _1$
are isomorphic as ordered fields.Footnote
1
In fact, it is shown using a back-and-forth argument that any order-preserving field isomorphism between countable subsets of
![]() $\eta _1$
-ordered real-closed fields may be extended to an order-isomorphism. It is a standard result of model theory that for any non-principal ultrafilter U on
$\eta _1$
-ordered real-closed fields may be extended to an order-isomorphism. It is a standard result of model theory that for any non-principal ultrafilter U on
![]() $\omega $
,
$\omega $
,
![]() ${\mathbb R}^{\omega }/U$
is an
${\mathbb R}^{\omega }/U$
is an
![]() $\aleph _1$
-saturated real-closed field (and hence an
$\aleph _1$
-saturated real-closed field (and hence an
![]() $\eta _1$
-ordering). By a result of Johnson [Reference Johnson10], between any pair of
$\eta _1$
-ordering). By a result of Johnson [Reference Johnson10], between any pair of
![]() $\eta _1$
-ordered real-closed fields of cardinality
$\eta _1$
-ordered real-closed fields of cardinality
![]() $\aleph _1$
there is an
$\aleph _1$
there is an
![]() $\mathbb R$
-linear order-preserving field isomorphism (hereafter
$\mathbb R$
-linear order-preserving field isomorphism (hereafter
![]() $\mathbb R$
-isomorphism). This implies, in a model of the continuum hypothesis (CH), that there is an
$\mathbb R$
-isomorphism). This implies, in a model of the continuum hypothesis (CH), that there is an
![]() $\mathbb R$
-linear order-preserving monomorphism (hereafter
$\mathbb R$
-linear order-preserving monomorphism (hereafter
![]() $\mathbb R$
-monomorphism) from the finite elements of
$\mathbb R$
-monomorphism) from the finite elements of
![]() ${\mathbb R}^{\omega }/U$
to
${\mathbb R}^{\omega }/U$
to
![]() $\mathcal {E}$
, and hence in models of ZFC+CH there exists a discontinuous homomorphism of
$\mathcal {E}$
, and hence in models of ZFC+CH there exists a discontinuous homomorphism of
![]() $C(X)$
. The proof that in a model of ZFC+CH there exists a discontinuous homomorphism of
$C(X)$
. The proof that in a model of ZFC+CH there exists a discontinuous homomorphism of
![]() $C(X)$
is due independently to Dales [Reference Dales1, Reference Dales2] and Esterle [Reference Esterle6].
$C(X)$
is due independently to Dales [Reference Dales1, Reference Dales2] and Esterle [Reference Esterle6].
Shortly thereafter R. Solovay found a model of ZFC+
![]() $\neg $
CH in which all homomorphisms of
$\neg $
CH in which all homomorphisms of
![]() $C(X)$
are continuous. Later, in his Ph.D. thesis, W.H. Woodin constructed a model of ZFC+Martin’s Axiom in which all homomorphisms of
$C(X)$
are continuous. Later, in his Ph.D. thesis, W.H. Woodin constructed a model of ZFC+Martin’s Axiom in which all homomorphisms of
![]() $C(X)$
are continuous. This naturally gave rise to the question of whether there is a model of set theory in which CH fails and there is a discontinuous homomorphism of
$C(X)$
are continuous. This naturally gave rise to the question of whether there is a model of set theory in which CH fails and there is a discontinuous homomorphism of
![]() $C(X)$
. Woodin subsequently showed that in the Cohen extension of a model of ZFC+CH by generic reals indexed by
$C(X)$
. Woodin subsequently showed that in the Cohen extension of a model of ZFC+CH by generic reals indexed by
![]() $\omega _2$
, there is a discontinuous homomorphism of
$\omega _2$
, there is a discontinuous homomorphism of
![]() $C(X)$
[Reference Woodin15]. Woodin shows that in this model the gaps in
$C(X)$
[Reference Woodin15]. Woodin shows that in this model the gaps in
![]() $\mathcal {E}$
that must be witnessed in a classical back-and-forth construction are always countable. He observes that this construction may not be extended to a Cohen extension by more than
$\mathcal {E}$
that must be witnessed in a classical back-and-forth construction are always countable. He observes that this construction may not be extended to a Cohen extension by more than
![]() $\aleph _2$
generic reals. He suggests the plausibility of using morasses to construct an
$\aleph _2$
generic reals. He suggests the plausibility of using morasses to construct an
![]() $\mathbb R$
-monomorphism from the finite elements of an ultrapower of the reals to the Esterle algebra in generic extensions with more than
$\mathbb R$
-monomorphism from the finite elements of an ultrapower of the reals to the Esterle algebra in generic extensions with more than
![]() $\aleph _2$
generic reals. Woodin’s argument does not extend to higher powers of the continuum and leaves open the question of whether there exists a discontinuous homomorphism of
$\aleph _2$
generic reals. Woodin’s argument does not extend to higher powers of the continuum and leaves open the question of whether there exists a discontinuous homomorphism of
![]() $C(X)$
in models of set theory in which
$C(X)$
in models of set theory in which
![]() $2^{\aleph _0}>\aleph _2$
. In this paper we show that the existence of a simplified
$2^{\aleph _0}>\aleph _2$
. In this paper we show that the existence of a simplified
![]() $(\omega _1,2)$
-morass in a model of
$(\omega _1,2)$
-morass in a model of
![]() $ZFC + CH$
is sufficient for the existence of a discontinuous homomorphism of
$ZFC + CH$
is sufficient for the existence of a discontinuous homomorphism of
![]() $C(X)$
in a model in which
$C(X)$
in a model in which
![]() $2^{\aleph _0}=\aleph _3$
.
$2^{\aleph _0}=\aleph _3$
.
We show that in the Cohen extension adding
![]() $\aleph _2$
generic reals to a transitive model of
$\aleph _2$
generic reals to a transitive model of
![]() $ZFC + CH$
containing a simplified
$ZFC + CH$
containing a simplified
![]() $(\omega _1,1)$
-morass, there is a level, morass-commutative term function that, interpreted in the Cohen extension, is an
$(\omega _1,1)$
-morass, there is a level, morass-commutative term function that, interpreted in the Cohen extension, is an
![]() $\mathbb R$
-monomorphism of the finite elements of an ultrapower of
$\mathbb R$
-monomorphism of the finite elements of an ultrapower of
![]() $\mathbb R$
over
$\mathbb R$
over
![]() $\omega $
into the Esterle algebra. This is achieved with a transfinite construction of length
$\omega $
into the Esterle algebra. This is achieved with a transfinite construction of length
![]() $\omega _1$
, utilizing the morass functions from the gap-one morass to complete the construction of size
$\omega _1$
, utilizing the morass functions from the gap-one morass to complete the construction of size
![]() $\aleph _2$
by commutativity with morass maps. Using the techniques of this argument, we construct a term function with a transfinite argument of length
$\aleph _2$
by commutativity with morass maps. Using the techniques of this argument, we construct a term function with a transfinite argument of length
![]() $\omega _1$
and utilize morass-commutativity with the embeddings of a gap-2 morass to complete the construction of an
$\omega _1$
and utilize morass-commutativity with the embeddings of a gap-2 morass to complete the construction of an
![]() $\mathbb R$
-monomorphism from the finite elements of a standard ultrapower of
$\mathbb R$
-monomorphism from the finite elements of a standard ultrapower of
![]() $\mathbb R$
over
$\mathbb R$
over
![]() $\omega $
to the Esterle algebra in the Cohen extension adding
$\omega $
to the Esterle algebra in the Cohen extension adding
![]() $\aleph _3$
generic reals.
$\aleph _3$
generic reals.
The technical obstacles to such a construction may be reduced to conditions we call morass-extendibility. This paper is dependent on the results of [Reference Dumas3] and [Reference Dumas4], in which term functions are constructed that are forced to be order-preserving functions. In this paper we construct a term function that is forced to be order-preserving and is simultaneously an
![]() $\mathbb R$
-linear ring-monomorphism.
$\mathbb R$
-linear ring-monomorphism.
2. Preliminaries
In our initial construction we use a simplified
![]() $(\omega _1,1)$
-morass. We construct a function on terms in the forcing language for adding
$(\omega _1,1)$
-morass. We construct a function on terms in the forcing language for adding
![]() $\aleph _2$
generic reals that is forced, in all generic extensions, to be an
$\aleph _2$
generic reals that is forced, in all generic extensions, to be an
![]() $\mathbb R$
-monomorphism from the finite elements of
$\mathbb R$
-monomorphism from the finite elements of
![]() ${\mathbb R}^{\omega }/U$
, where U is a a non-principal ultrafilter meeting certain technical conditions, into the Esterle algebra,
${\mathbb R}^{\omega }/U$
, where U is a a non-principal ultrafilter meeting certain technical conditions, into the Esterle algebra,
![]() $\mathcal {E}$
. In some sense we follow the classical route to such constructions—extension by transcendental elements in an inductive construction of length
$\mathcal {E}$
. In some sense we follow the classical route to such constructions—extension by transcendental elements in an inductive construction of length
![]() $\omega _1$
. We will require commutativity with morass maps to construct a function on a domain of cardinality
$\omega _1$
. We will require commutativity with morass maps to construct a function on a domain of cardinality
![]() $\aleph _2$
making only
$\aleph _2$
making only
![]() $\aleph _1$
many explicit commitments. However with each commitment of the construction, there are uncountably many future commitments implied by commutativity with morass maps.
$\aleph _1$
many explicit commitments. However with each commitment of the construction, there are uncountably many future commitments implied by commutativity with morass maps.
In [Reference Velleman13] D. Velleman defines a simplified
![]() $(\omega _1,1)$
-morass.
$(\omega _1,1)$
-morass.
Definition 2.1 (Velleman)(Simplified(ω1, 1)-morass)
A simplified
![]() $(\omega ,1)$
-morass is a structure
$(\omega ,1)$
-morass is a structure
that satisfies the following conditions:
(P0) (a)
![]() $\theta _0=1$
,
$\theta _0=1$
,
![]() $\theta _{\omega _1}=\omega _2$
,
$\theta _{\omega _1}=\omega _2$
,
![]() $(\forall \alpha <\omega _1)\ 0<\theta _\alpha <\omega _1$
.
$(\forall \alpha <\omega _1)\ 0<\theta _\alpha <\omega _1$
.
(b)
![]() $\mathcal {F}_{\alpha \beta }$
is a set of order-preserving functions
$\mathcal {F}_{\alpha \beta }$
is a set of order-preserving functions
![]() $f:\theta _\alpha \to \theta _\beta $
.
$f:\theta _\alpha \to \theta _\beta $
.
(P1)
![]() $\left | \mathcal {F_{\alpha \beta }} \right | \leq \omega $
for all
$\left | \mathcal {F_{\alpha \beta }} \right | \leq \omega $
for all
![]() $\alpha <\beta <\omega _1$
.
$\alpha <\beta <\omega _1$
.
![]() $($
P2
$($
P2
![]() $)$
If
$)$
If
![]() $\alpha <\beta <\gamma $
, then
$\alpha <\beta <\gamma $
, then
![]() $\mathcal {F}_{\alpha \gamma }=\{ f\circ g\mid f\in \mathcal {F}_{\beta \gamma }$
,
$\mathcal {F}_{\alpha \gamma }=\{ f\circ g\mid f\in \mathcal {F}_{\beta \gamma }$
,
![]() $g\in \mathcal {F}_{\alpha \beta } \}$
.
$g\in \mathcal {F}_{\alpha \beta } \}$
.
![]() $($
P3
$($
P3
![]() $)$
If
$)$
If
![]() $\alpha <\omega _1$
, then
$\alpha <\omega _1$
, then
![]() $\mathcal {F}_{\alpha (\alpha +1)}=\{ \text {id}\upharpoonright \theta _{\alpha } , f_{\alpha } \}$
where
$\mathcal {F}_{\alpha (\alpha +1)}=\{ \text {id}\upharpoonright \theta _{\alpha } , f_{\alpha } \}$
where
![]() $f_{\alpha }$
satisfies
$f_{\alpha }$
satisfies
![]() $:$
$:$
![]() $($
P4
$($
P4
![]() $)$
If
$)$
If
![]() $\alpha \leq \omega _1$
is a limit ordinal,
$\alpha \leq \omega _1$
is a limit ordinal,
![]() $\beta _1, \beta _2<\alpha $
,
$\beta _1, \beta _2<\alpha $
,
![]() $f_1\in \mathcal {F}_{\beta _1 \alpha }$
and
$f_1\in \mathcal {F}_{\beta _1 \alpha }$
and
![]() $f_2\in \mathcal {F}_{\beta _2 \alpha }$
, then there is
$f_2\in \mathcal {F}_{\beta _2 \alpha }$
, then there is
![]() $\gamma <\alpha $
,
$\gamma <\alpha $
,
![]() $\gamma>\beta _1, \beta _2$
, and there is
$\gamma>\beta _1, \beta _2$
, and there is
![]() $f_1'\in \mathcal {F}_{\beta _1 \gamma }$
,
$f_1'\in \mathcal {F}_{\beta _1 \gamma }$
,
![]() $f_2'\in \mathcal {F}_{\beta _2 \gamma }$
,
$f_2'\in \mathcal {F}_{\beta _2 \gamma }$
,
![]() $g\in \mathcal {F}_{\gamma \alpha }$
such that
$g\in \mathcal {F}_{\gamma \alpha }$
such that
![]() $f_1=g\circ f_1'$
and
$f_1=g\circ f_1'$
and
![]() $f_2=g\circ f_2'$
.
$f_2=g\circ f_2'$
.
![]() $($
P5
$($
P5
![]() $)$
For all
$)$
For all
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\theta _{\alpha }=\bigcup \{ f[\theta _{\beta }] \mid \beta <\alpha $
,
$\theta _{\alpha }=\bigcup \{ f[\theta _{\beta }] \mid \beta <\alpha $
,
![]() $f\in \mathcal {F}_{\beta \alpha } \}$
.
$f\in \mathcal {F}_{\beta \alpha } \}$
.
Simplified gap-1 morasses, as well as higher gap simplified morasses, are known to exist in L.
We will construct, by an inductive argument of length
![]() $\omega _1$
, a function between sets of terms in the forcing language adding
$\omega _1$
, a function between sets of terms in the forcing language adding
![]() $\aleph _2$
generic reals. We interpret the morass functions on ordinals as functions between terms in the forcing language and require that the set of terms under construction satisfy certain commutativity constraints with the morass functions. It is implicit that any commitment to an ordered pair of terms in the construction is de facto a commitment to uncountably many commitments to ordered pairs in mutually generic extensions. In [Reference Dumas3] we worked explicitly with terms in the forcing language. We wish to simplify the details of the construction by working with objects in a forcing extension, where that is possible.
$\aleph _2$
generic reals. We interpret the morass functions on ordinals as functions between terms in the forcing language and require that the set of terms under construction satisfy certain commutativity constraints with the morass functions. It is implicit that any commitment to an ordered pair of terms in the construction is de facto a commitment to uncountably many commitments to ordered pairs in mutually generic extensions. In [Reference Dumas3] we worked explicitly with terms in the forcing language. We wish to simplify the details of the construction by working with objects in a forcing extension, where that is possible.
Notation 2.2 (P(A))
If A is a set of ordinals, we let
![]() $P(A)$
be the poset adding generic reals indexed by the ordinals of A. That is,
$P(A)$
be the poset adding generic reals indexed by the ordinals of A. That is,
the finite partial functions from
![]() $A\times \omega $
to
$A\times \omega $
to
![]() $2$
.
$2$
.
Notation 2.3 (P ν )
If
![]() $\mathcal {M}$
is a simplified
$\mathcal {M}$
is a simplified
![]() $(\omega _1,1)-morass$
, and
$(\omega _1,1)-morass$
, and
![]() $\nu \leq \omega _1$
, we let
$\nu \leq \omega _1$
, we let
![]() $P_{\nu }$
be the poset that adds generic reals indexed by
$P_{\nu }$
be the poset that adds generic reals indexed by
![]() $\theta _{\nu } $
(the ordinal associated with the vertex,
$\theta _{\nu } $
(the ordinal associated with the vertex,
![]() $\nu $
, in
$\nu $
, in
![]() $\mathcal {M}$
).
$\mathcal {M}$
).
Let M be a transitive model of ZFC,
![]() $\beta $
be an ordinal and P be the poset adding generic reals indexed by
$\beta $
be an ordinal and P be the poset adding generic reals indexed by
![]() $\beta $
, then
$\beta $
, then
![]() $P(\beta )=Fn(\beta \times \omega ,2)$
.
$P(\beta )=Fn(\beta \times \omega ,2)$
.
We use the notion of strict level of a term in the forcing language defined in [Reference Dumas3], and apply it to objects in a forcing extension.
Definition 2.4 (Strict level)
Let
![]() $\alpha \leq \beta \leq \omega _2$
be ordinals and
$\alpha \leq \beta \leq \omega _2$
be ordinals and
![]() $\tau \in M^{P(\beta )}$
be a term in the forcing language adding generic reals indexed by
$\tau \in M^{P(\beta )}$
be a term in the forcing language adding generic reals indexed by
![]() $\beta $
. Then
$\beta $
. Then
![]() $\tau $
has strict level
$\tau $
has strict level
![]() $\alpha $
provided that
$\alpha $
provided that
![]() $:$
$:$
-
1. There is a term
 $\bar {\tau }\in M^{P(\alpha )}$
such that
$\bar {\tau }\in M^{P(\alpha )}$
such that
 $\Vdash \bar {\tau }=\tau $
.
$\Vdash \bar {\tau }=\tau $
. -
2. For any
 $\gamma <\alpha $
, and term,
$\gamma <\alpha $
, and term,
 $\bar {\tau }\in M^{P(\gamma )}$
,
$\bar {\tau }\in M^{P(\gamma )}$
,
 $\Vdash \tau \neq \bar {\tau }$
.
$\Vdash \tau \neq \bar {\tau }$
.
Alternatively, for
![]() $\gamma <\alpha <\beta $
, we consider
$\gamma <\alpha <\beta $
, we consider
![]() $P(\beta )$
as the product forcing
$P(\beta )$
as the product forcing
![]() $P(\gamma )\times P(\alpha \setminus \gamma ) \times P(\beta \setminus \alpha )$
. Suppose
$P(\gamma )\times P(\alpha \setminus \gamma ) \times P(\beta \setminus \alpha )$
. Suppose
![]() $G(\gamma )$
is
$G(\gamma )$
is
![]() $P(\gamma )$
-generic over M and G is
$P(\gamma )$
-generic over M and G is
![]() $P(\alpha \setminus \gamma )$
-generic over
$P(\alpha \setminus \gamma )$
-generic over
![]() $M[G(\gamma )]$
, and H is
$M[G(\gamma )]$
, and H is
![]() $P(\beta \setminus \alpha )$
-generic over
$P(\beta \setminus \alpha )$
-generic over
![]() $M[G(\gamma ),G]$
. We say that an object in a forcing extension,
$M[G(\gamma ),G]$
. We say that an object in a forcing extension,
![]() $a\in M[G(\gamma ),G,H]$
, has strict level
$a\in M[G(\gamma ),G,H]$
, has strict level
![]() $\alpha $
if and only if there is a
$\alpha $
if and only if there is a
![]() $\tau \in M^{P(\alpha )}$
with strict level
$\tau \in M^{P(\alpha )}$
with strict level
![]() $\alpha $
, such that
$\alpha $
, such that
![]() $\tau _{G(\gamma ) G}=a$
. If
$\tau _{G(\gamma ) G}=a$
. If
![]() $a \in M[G(\gamma ),G,H]$
has strict level
$a \in M[G(\gamma ),G,H]$
has strict level
![]() $\alpha $
, then for any
$\alpha $
, then for any
![]() $\gamma <\alpha $
,
$\gamma <\alpha $
,
![]() $a \notin M[G(\gamma )]$
.
$a \notin M[G(\gamma )]$
.
Not every term in the forcing language has strict level. However, every object in a forcing extension is the interpretation of a term of strict level. Consequently in our construction we pass freely between objects of strict level
![]() $\alpha $
in a generic extension and terms of
$\alpha $
in a generic extension and terms of
![]() $M^{P(\alpha )}$
.
$M^{P(\alpha )}$
.
Many of the constraints required for commutativity with morass maps are expressed in terms of the strict level of objects in a forcing extension (or correspondingly, terms in a forcing language). For instance, in Section 5 we define a term function to be level if the strict level of any term in the domain equals the strict level of its image under the function. Such maps will commute with morass maps in the manner required by our construction.
3. Constructing an
 $\mathbb R$
-monomorphism on a real-closed field
$\mathbb R$
-monomorphism on a real-closed field
We wish to construct a function between sets of terms in the forcing language for adding
![]() $\aleph _2$
generic reals, that is forced in all generic extensions to be an order-preserving
$\aleph _2$
generic reals, that is forced in all generic extensions to be an order-preserving
![]() $\mathbb R$
-linear monomorphism from the finite elements of an non-principal ultrapower of
$\mathbb R$
-linear monomorphism from the finite elements of an non-principal ultrapower of
![]() $\mathbb R$
,
$\mathbb R$
,
![]() ${\mathbb R}^{\omega }/U$
to
${\mathbb R}^{\omega }/U$
to
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Definition 3.1 (Archimedean valuation)
If x and y are non-zero elements of a real-closed field, they have the same Archimedean valuation,
![]() $x \sim y$
, provided that there are
$x \sim y$
, provided that there are
![]() $m, n \in \mathbb {N}$
such that
$m, n \in \mathbb {N}$
such that
and
If
![]() $\left | x\right | <\left | y\right |$
and
$\left | x\right | <\left | y\right |$
and
![]() $x \nsim y$
, then x has Archimedean valuation greater than y.
$x \nsim y$
, then x has Archimedean valuation greater than y.
Archimedean valuation induces an equivalence relation on the non-zero elements of a real-closed field (RCF). The non-zero real numbers have the same valuation. Elements with the same valuation as a real number are said to have real valuation. In a non-standard real-closed field, elements with valuation greater than a real valuation are infinitesimal. The finite elements of a real closed field are the infinitesimal elements and those with real valuation.
At any stage of the construction, we will have defined a partial function on
![]() ${\mathbb R}^{\omega }/U$
, so we extend the definition of an
${\mathbb R}^{\omega }/U$
, so we extend the definition of an
![]() $\mathbb R$
-monomorphism to include a partial function that may not have all real numbers in its domain.
$\mathbb R$
-monomorphism to include a partial function that may not have all real numbers in its domain.
Definition 3.2 (ℝ-monomorphism)
Let X and Y be subrings of real-closed fields that contain a real-closed subfield of
![]() $\mathbb R$
, and let
$\mathbb R$
, and let
![]() $\mathbb R_0=\mathbb R\cap X=\mathbb R\cap Y$
. A function,
$\mathbb R_0=\mathbb R\cap X=\mathbb R\cap Y$
. A function,
![]() $\phi :X\to Y$
, is an
$\phi :X\to Y$
, is an
![]() $\mathbb R$
-monomorphism if it is an order-preserving ring-monomorphism such that
$\mathbb R$
-monomorphism if it is an order-preserving ring-monomorphism such that
![]() $\phi \upharpoonright _{\mathbb R_0}=id\upharpoonright _{\mathbb R_0}$
.
$\phi \upharpoonright _{\mathbb R_0}=id\upharpoonright _{\mathbb R_0}$
.
It is a result of B. Johnson [Reference Johnson10] that
![]() $\eta _1$
-ordered real-closed fields with cardinality
$\eta _1$
-ordered real-closed fields with cardinality
![]() $\aleph _1$
are
$\aleph _1$
are
![]() $\mathbb R$
-isomorphic in models of ZFC+CH. This result strengthens the classical result that
$\mathbb R$
-isomorphic in models of ZFC+CH. This result strengthens the classical result that
![]() $\aleph _1$
-saturated real closed fields of cardinality
$\aleph _1$
-saturated real closed fields of cardinality
![]() $\aleph _1$
are isomorphic. We review some of the basic results from this work, which we require for extension of these results to higher powers of the continuum.
$\aleph _1$
are isomorphic. We review some of the basic results from this work, which we require for extension of these results to higher powers of the continuum.
Definition 3.3 (Full subfield)
Let
![]() $D^*$
be a field extending
$D^*$
be a field extending
![]() $\mathbb R$
. A subfield
$\mathbb R$
. A subfield
![]() $D\subseteq D^*$
is full iff for every finite element,
$D\subseteq D^*$
is full iff for every finite element,
![]() $r+\delta \in D$
, where
$r+\delta \in D$
, where
![]() $r\in \mathbb R$
and
$r\in \mathbb R$
and
![]() $\delta $
is infinitesimal,
$\delta $
is infinitesimal,
![]() $r\in D$
.
$r\in D$
.
We will need to extend two results due to B. Johnson [Reference Johnson10] to meet the requirement of
![]() $\mathbb R$
-linearity in the context of constructing term functions using a morass.
$\mathbb R$
-linearity in the context of constructing term functions using a morass.
Lemma 3.4 (B. Johnson)
Assume that D and I are full real-closed subfields of
![]() $\eta _1$
-ordered real-closed fields
$\eta _1$
-ordered real-closed fields
![]() $D^*(\supseteq \mathbb R)$
and
$D^*(\supseteq \mathbb R)$
and
![]() $I^*(\supseteq \mathbb R)\ (resp.)$
,
$I^*(\supseteq \mathbb R)\ (resp.)$
,
![]() $\phi :D\to I$
is an
$\phi :D\to I$
is an
![]() $\mathbb R$
-monomorphism, and
$\mathbb R$
-monomorphism, and
![]() $r\in \mathbb R$
. Then there is an extension of
$r\in \mathbb R$
. Then there is an extension of
![]() $\phi $
,
$\phi $
,
![]() $\phi ^*$
, that is an
$\phi ^*$
, that is an
![]() $\mathbb R$
-monomorphism of the real closure of the field generated by D and r,
$\mathbb R$
-monomorphism of the real closure of the field generated by D and r,
![]() $F(D,r)$
, onto the real closure of the field generated by I and r,
$F(D,r)$
, onto the real closure of the field generated by I and r,
![]() $F(I,r)$
. Furthermore
$F(I,r)$
. Furthermore
![]() $F(D,r) (and\ consequently, F(I,r))$
is full.
$F(D,r) (and\ consequently, F(I,r))$
is full.
Lemma 3.5 (B. Johnson)
Let D,
![]() $D^*$
, I,
$D^*$
, I,
![]() $I^*$
and
$I^*$
and
![]() $\phi $
be as in Lemma 3.4,
$\phi $
be as in Lemma 3.4,
![]() $x\in D^*$
and assume that the real closure of the field generated by D and x,
$x\in D^*$
and assume that the real closure of the field generated by D and x,
![]() $F(D,x)$
, is full. Let
$F(D,x)$
, is full. Let
![]() $y\in I^*$
be such that
$y\in I^*$
be such that
Then there is an
![]() $\mathbb R$
-monomorphism extending
$\mathbb R$
-monomorphism extending
![]() $\phi $
,
$\phi $
,
![]() $\phi ^*:F(D,x)\to I^*$
, such that
$\phi ^*:F(D,x)\to I^*$
, such that
![]() $\phi ^*(x)=y$
.
$\phi ^*(x)=y$
.
4. The Esterle algebra
We define the Esterle algebra [Reference Esterle6] and review some basic properties.
Definition 4.1 (S ω 1 )
![]() $S_{\omega _1}$
is the lexicographic linear-ordering with domain
$S_{\omega _1}$
is the lexicographic linear-ordering with domain
![]() $\{s:\omega _1 \to 2 \mid s$
has countable support and the support of s has a largest element
$\{s:\omega _1 \to 2 \mid s$
has countable support and the support of s has a largest element
![]() $\}$
.
$\}$
.
Definition 4.2 (G ω 1 )
![]() $G_{\omega _1}$
is the ordered group with domain
$G_{\omega _1}$
is the ordered group with domain
![]() $\{ g:S_{\omega _1} \to \mathbb R \mid g$
has countable well-ordered support
$\{ g:S_{\omega _1} \to \mathbb R \mid g$
has countable well-ordered support
![]() $ \}$
, lexicographic ordering, and group operation pointwise addition.
$ \}$
, lexicographic ordering, and group operation pointwise addition.
We define an ordered algebra of formal power series,
![]() $\mathcal {E}$
. The universe of
$\mathcal {E}$
. The universe of
![]() $\mathcal {E}$
is the set of formal power series,
$\mathcal {E}$
is the set of formal power series,
![]() $\sum _{\lambda <\gamma } \alpha _{\lambda } x^{a_{\lambda }}$
, where:
$\sum _{\lambda <\gamma } \alpha _{\lambda } x^{a_{\lambda }}$
, where:
-
1.
 $\gamma <\omega _1$
.
$\gamma <\omega _1$
. -
2.
 $(\forall \lambda <\gamma )\, \alpha _{\lambda } \in \mathbb R$
.
$(\forall \lambda <\gamma )\, \alpha _{\lambda } \in \mathbb R$
. -
3.
 $\{a_{\lambda }\mid \lambda <\gamma \}$
is a countable well-ordered subset of
$\{a_{\lambda }\mid \lambda <\gamma \}$
is a countable well-ordered subset of
 $G_{\omega _1}$
and
$G_{\omega _1}$
and
 $\lambda _1<\lambda _2<\gamma \Rightarrow a_{\lambda _1}<a_{\lambda _2}$
.
$\lambda _1<\lambda _2<\gamma \Rightarrow a_{\lambda _1}<a_{\lambda _2}$
.
The ordered algebra,
![]() $\mathcal {E}$
, is isomorphic to the set of functions, with countable well-ordered support, from
$\mathcal {E}$
, is isomorphic to the set of functions, with countable well-ordered support, from
![]() $G_{\omega _1}$
to
$G_{\omega _1}$
to
![]() $\mathbb R$
. The lexicographic order linearly-orders
$\mathbb R$
. The lexicographic order linearly-orders
![]() $\mathcal {E}$
. Addition is pointwise and multiplication is defined as follows: Suppose
$\mathcal {E}$
. Addition is pointwise and multiplication is defined as follows: Suppose
![]() $a=\sum _{\lambda <\gamma _1} \alpha _{\lambda } x^{a_{\lambda }}$
and
$a=\sum _{\lambda <\gamma _1} \alpha _{\lambda } x^{a_{\lambda }}$
and
![]() $b= \sum _{\kappa <\lambda _2} \beta _{\kappa }x^{b_{\kappa }}$
are members of
$b= \sum _{\kappa <\lambda _2} \beta _{\kappa }x^{b_{\kappa }}$
are members of
![]() $\mathcal {E}$
. Let
$\mathcal {E}$
. Let
Then
 $$\begin{align*}a\cdot b= \sum_{c\in C}((\sum_{a_{\lambda}+b_{\kappa}=c} \alpha_{\lambda}\cdot \beta_{\kappa}) \, x^c ). \end{align*}$$
$$\begin{align*}a\cdot b= \sum_{c\in C}((\sum_{a_{\lambda}+b_{\kappa}=c} \alpha_{\lambda}\cdot \beta_{\kappa}) \, x^c ). \end{align*}$$
Definition 4.3 (Esterle algebra, ℰ)
The Esterle algebra,
![]() $\mathcal {E}$
, is
$\mathcal {E}$
, is
![]() $\{ f:G_{\omega _1} \to \mathbb R \mid f$
has countable well-ordered support
$\{ f:G_{\omega _1} \to \mathbb R \mid f$
has countable well-ordered support
![]() $\}$
.
$\}$
.
![]() $\mathcal {E}$
is lexicographically ordered, with pointwise addition, and multiplication defined above.
$\mathcal {E}$
is lexicographically ordered, with pointwise addition, and multiplication defined above.
![]() $\mathbb R$
may be embedded in
$\mathbb R$
may be embedded in
![]() $\mathcal {E}$
by
$\mathcal {E}$
by
![]() $\alpha \longmapsto \alpha x^e$
, where e is the group identity in
$\alpha \longmapsto \alpha x^e$
, where e is the group identity in
![]() $G_{\omega _1}$
. Exponents in
$G_{\omega _1}$
. Exponents in
![]() $G_{\omega _1}$
larger than e (called positive exponents) correspond to infinitesimal Archimedean valuations, and those smaller than e (called negative exponents) correspond to infinite valuations. The finite elements of
$G_{\omega _1}$
larger than e (called positive exponents) correspond to infinitesimal Archimedean valuations, and those smaller than e (called negative exponents) correspond to infinite valuations. The finite elements of
![]() $\mathcal {E}$
are those with leading exponent
$\mathcal {E}$
are those with leading exponent
![]() $\geq e$
. The Archimedean valuations of the Esterle algebra are represented by the group of exponents of
$\geq e$
. The Archimedean valuations of the Esterle algebra are represented by the group of exponents of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Theorem 4.4 (J. Esterle [Reference Esterle6])
![]() $\mathcal {E}$
is an
$\mathcal {E}$
is an
![]() $\eta _1$
-ordered real-closed field.
$\eta _1$
-ordered real-closed field.
A norm,
![]() $\| \, \|$
, on an algebra A is submultiplicative if for any
$\| \, \|$
, on an algebra A is submultiplicative if for any
![]() $a,b \in A$
,
$a,b \in A$
,
Theorem 4.5 (G. Dales [Reference Dales2], J. Esterle [Reference Esterle8])
The set of finite elements of
![]() $\mathcal {E}$
bears a non-trivial submultiplicative norm.
$\mathcal {E}$
bears a non-trivial submultiplicative norm.
It is a standard result of model theory that if U is a non-principal ultrafilter on
![]() $\omega $
, the ultrapower
$\omega $
, the ultrapower
![]() ${\mathbb R}^{\omega }/U$
is an
${\mathbb R}^{\omega }/U$
is an
![]() $\aleph _1$
-saturated real-closed field. Any two
$\aleph _1$
-saturated real-closed field. Any two
![]() $\aleph _1$
-saturated, or
$\aleph _1$
-saturated, or
![]() $\eta _1$
-ordered, real-closed fields with cardinality of the continuum are isomorphic in models of ZFC+CH.
$\eta _1$
-ordered, real-closed fields with cardinality of the continuum are isomorphic in models of ZFC+CH.
Theorem 4.6 (B.Johnson [Reference Johnson10])
![]() $($
CH
$($
CH
![]() $)$
If U is a non-principal ultrafilter, there is an
$)$
If U is a non-principal ultrafilter, there is an
![]() $\mathbb R$
-monomorphism from the finite elements of
$\mathbb R$
-monomorphism from the finite elements of
![]() ${\mathbb R}^{\omega }/U$
into
${\mathbb R}^{\omega }/U$
into
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Hence CH implies that there is a non-trivial submultiplicative norm on the infinitesimal elements of
![]() ${\mathbb R}^{\omega }/U$
.
${\mathbb R}^{\omega }/U$
.
We turn our attention to terms in a forcing language
![]() $M^P$
that are forced to be members of the Esterle algebra. In [Reference Dumas3] and [Reference Dumas4], we found sufficient conditions for morass constructions. The aggregate of these conditions were characterized as morass-definability and gap-2 morass-definability. The central theorem of the papers were that morass-definable
$M^P$
that are forced to be members of the Esterle algebra. In [Reference Dumas3] and [Reference Dumas4], we found sufficient conditions for morass constructions. The aggregate of these conditions were characterized as morass-definability and gap-2 morass-definability. The central theorem of the papers were that morass-definable
![]() $\eta _1$
-orderings are order-isomorphic in the Cohen extension adding
$\eta _1$
-orderings are order-isomorphic in the Cohen extension adding
![]() $\aleph _2$
generic reals of a model of
$\aleph _2$
generic reals of a model of
![]() $ZFC + CH$
containing a simplified
$ZFC + CH$
containing a simplified
![]() $(\omega _1,1)$
-morass; and gap-2 morass definable
$(\omega _1,1)$
-morass; and gap-2 morass definable
![]() $\eta _1$
-orderings are order-isomorphic in the Cohen extension adding
$\eta _1$
-orderings are order-isomorphic in the Cohen extension adding
![]() $\aleph _3$
generic reals of a model of
$\aleph _3$
generic reals of a model of
![]() $ZFC + CH$
containing a simplified
$ZFC + CH$
containing a simplified
![]() $(\omega _1,2)$
-morass.
$(\omega _1,2)$
-morass.
In the definitions that follow, we assume P is the poset adding generic reals indexed by an ordinal,
![]() $\alpha $
.
$\alpha $
.
Definition 4.7 (Countable support)
Let M be a transitive model of ZFC and G be P-generic over M and
![]() $S\subseteq \alpha $
. Then
$S\subseteq \alpha $
. Then
![]() $x\in M[G]$
has support S if there is
$x\in M[G]$
has support S if there is
![]() $\tau \in M^{P(S)}$
such that
$\tau \in M^{P(S)}$
such that
![]() $\tau _G=x$
. If there is a countable
$\tau _G=x$
. If there is a countable
![]() $S\subseteq \alpha $
, and
$S\subseteq \alpha $
, and
![]() $\tau \in M^{P(S)}$
such that
$\tau \in M^{P(S)}$
such that
![]() $\tau _G=x$
, then we say that x has countable support.
$\tau _G=x$
, then we say that x has countable support.
For
![]() $\alpha <\omega _1$
, every element of
$\alpha <\omega _1$
, every element of
![]() $M[G(\alpha )]$
has countable support. The definition may be generalized to posets adding arbitrary sets of ordinals. We note the possibility of confusion with the support of power series in
$M[G(\alpha )]$
has countable support. The definition may be generalized to posets adding arbitrary sets of ordinals. We note the possibility of confusion with the support of power series in
![]() $\mathcal {E}$
treated as functions from
$\mathcal {E}$
treated as functions from
![]() $G_{\omega _1}$
to
$G_{\omega _1}$
to
![]() $\mathbb R$
, exponents in
$\mathbb R$
, exponents in
![]() $G_{\omega _1}$
treated as functions from
$G_{\omega _1}$
treated as functions from
![]() $S_{\omega _1}$
to
$S_{\omega _1}$
to
![]() $\mathbb R$
and transfinite binary sequences of
$\mathbb R$
and transfinite binary sequences of
![]() $S_{\omega _1}$
. Presumably the context will clarify the use of terminology.
$S_{\omega _1}$
. Presumably the context will clarify the use of terminology.
Definition 4.8 (Level-dense)
Let
![]() $\kappa $
be an ordinal,
$\kappa $
be an ordinal,
![]() $P=P(\kappa )$
,
$P=P(\kappa )$
,
![]() $T_X\in M^P$
be forced to be a linear-ordering and
$T_X\in M^P$
be forced to be a linear-ordering and
![]() $X\subseteq M^P$
be a set of terms of strict level for the domain of
$X\subseteq M^P$
be a set of terms of strict level for the domain of
![]() $T_X$
. X is level-dense if for
$T_X$
. X is level-dense if for
![]() $x, y\in X$
, where the support of x and the support of y are disjoint, and G is P-generic over M, there is
$x, y\in X$
, where the support of x and the support of y are disjoint, and G is P-generic over M, there is
![]() $z\in X\cap M$
such that
$z\in X\cap M$
such that
![]() $M[G] \models x<z<y$
.
$M[G] \models x<z<y$
.
Definition 4.9 (Upward level-dense)
Let P be the poset that adds generic reals indexed by an ordinal
![]() $\kappa $
and
$\kappa $
and
![]() $\beta \leq \kappa $
. Let
$\beta \leq \kappa $
. Let
![]() $T_X\in M^P$
be forced to be a linear-ordering, and
$T_X\in M^P$
be forced to be a linear-ordering, and
![]() $X\subseteq M^P$
be a set of terms of strict level for the domain of
$X\subseteq M^P$
be a set of terms of strict level for the domain of
![]() $T_X$
. X is upward level-dense provided that for every
$T_X$
. X is upward level-dense provided that for every
![]() $x,y,z\in X$
and
$x,y,z\in X$
and
![]() $p\in P$
, in which z has strict level
$p\in P$
, in which z has strict level
![]() $\alpha \leq \beta $
with
$\alpha \leq \beta $
with
![]() $p\Vdash x<z<y$
, there is a term
$p\Vdash x<z<y$
, there is a term
![]() $w\in X$
of strict level
$w\in X$
of strict level
![]() $\beta $
such that
$\beta $
such that
![]() $p\Vdash x<w<y$
.
$p\Vdash x<w<y$
.
If
![]() $\zeta <\xi \leq \omega _2$
and
$\zeta <\xi \leq \omega _2$
and
![]() $f\in \mathcal {F}_{\zeta \xi }$
, then f is an order-preserving injection from
$f\in \mathcal {F}_{\zeta \xi }$
, then f is an order-preserving injection from
![]() $\theta _{\zeta }$
to
$\theta _{\zeta }$
to
![]() $\theta _{\xi }$
. We define a function
$\theta _{\xi }$
. We define a function
![]() $g:P(\theta _{\zeta })\to P(\theta _{\xi })$
as follows. If
$g:P(\theta _{\zeta })\to P(\theta _{\xi })$
as follows. If
![]() $x\in P(\theta _{\zeta })$
, then x is a finite partial function from
$x\in P(\theta _{\zeta })$
, then x is a finite partial function from
![]() $\theta _{\zeta } \times \omega \to 2$
. That is, x is composed of finitely many ordered triples,
$\theta _{\zeta } \times \omega \to 2$
. That is, x is composed of finitely many ordered triples,
![]() $\langle \alpha , n ,s \rangle $
where
$\langle \alpha , n ,s \rangle $
where
![]() $\alpha \in \theta _{\zeta }$
,
$\alpha \in \theta _{\zeta }$
,
![]() $n\in \omega $
and s is either
$n\in \omega $
and s is either
![]() $0$
or
$0$
or
![]() $1$
. For
$1$
. For
![]() $x\in P(\theta _{\zeta })$
, let
$x\in P(\theta _{\zeta })$
, let
![]() $g(x)=\{ \langle f(\alpha ),n,s \rangle \mid \langle \alpha ,n,s\rangle \in x \}$
. Then
$g(x)=\{ \langle f(\alpha ),n,s \rangle \mid \langle \alpha ,n,s\rangle \in x \}$
. Then
![]() $g:P(\theta _{\zeta }) \to P(\theta _{\xi })$
replaces forcing conditions of
$g:P(\theta _{\zeta }) \to P(\theta _{\xi })$
replaces forcing conditions of
![]() $P(\theta _{\zeta })$
with forcing conditions of
$P(\theta _{\zeta })$
with forcing conditions of
![]() $P(\theta _{\xi })$
. Finally, we define, by recursion, a function
$P(\theta _{\xi })$
. Finally, we define, by recursion, a function
![]() $h:M^{P(\theta _{\zeta })} \to M^{P(\theta _{\xi })}$
such that for any term,
$h:M^{P(\theta _{\zeta })} \to M^{P(\theta _{\xi })}$
such that for any term,
![]() $\tau \in M^{P(\theta _{\zeta })}$
,
$\tau \in M^{P(\theta _{\zeta })}$
,
![]() $h(\tau )=\{ \langle h(\sigma ), g(q) \rangle \mid \langle \sigma ,q\rangle \in \tau \}$
. We will refer to h as the index replacement function on
$h(\tau )=\{ \langle h(\sigma ), g(q) \rangle \mid \langle \sigma ,q\rangle \in \tau \}$
. We will refer to h as the index replacement function on
![]() $M^{P(\theta _{\zeta })}$
induced by f. For notational convenience we use f for both the order monomorphism on
$M^{P(\theta _{\zeta })}$
induced by f. For notational convenience we use f for both the order monomorphism on
![]() $\theta _{\zeta }$
, and the index replacement function it induces.
$\theta _{\zeta }$
, and the index replacement function it induces.
Definition 4.10 (Morass-closed)
Suppose
![]() $\langle (\theta _\alpha \mid \alpha \leq \omega _1),(\mathcal {F}_{\alpha \beta }\mid \alpha <\beta \leq \omega _1)\rangle $
is a simplified
$\langle (\theta _\alpha \mid \alpha \leq \omega _1),(\mathcal {F}_{\alpha \beta }\mid \alpha <\beta \leq \omega _1)\rangle $
is a simplified
![]() $(\omega _1,1)$
-morass,
$(\omega _1,1)$
-morass,
![]() $\nu < \lambda \leq \omega _1$
and
$\nu < \lambda \leq \omega _1$
and
![]() $X\subseteq M^P$
. We say that X is morass-closed at stage
$X\subseteq M^P$
. We say that X is morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\lambda $
if for any
$\lambda $
if for any ![]() and
and
![]() $x\in X\cap M^{P_{\nu }}$
,
$x\in X\cap M^{P_{\nu }}$
,
![]() $f(x)\in X\cap M^{P_{\lambda }}$
. If for any
$f(x)\in X\cap M^{P_{\lambda }}$
. If for any
![]() $\nu <\lambda $
, X is morass-closed at stage
$\nu <\lambda $
, X is morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\lambda $
, then X is morass-closed beneath
$\lambda $
, then X is morass-closed beneath
![]() $\lambda $
. If X is morass-closed at stage
$\lambda $
. If X is morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\omega _1$
, then X is morass-closed at stage
$\omega _1$
, then X is morass-closed at stage
![]() $\nu $
.
$\nu $
.
Morass-closure extends naturally to structures with operations and relations, with the following useful consequence. Let X be a morass-closed structure at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\lambda $
. Suppose that S is a set of terms for the universe of X that is morass-closed at stage
$\lambda $
. Suppose that S is a set of terms for the universe of X that is morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\lambda $
. If R is a binary relation of X we may consider R as terms in the forcing language that are comprised of ordered pairs of members of S with forcing conditions. That is, for
$\lambda $
. If R is a binary relation of X we may consider R as terms in the forcing language that are comprised of ordered pairs of members of S with forcing conditions. That is, for
![]() $s, t\in S\cap M^{P_{\nu }}$
and
$s, t\in S\cap M^{P_{\nu }}$
and
![]() $p\in P_{\nu }$
, the term
$p\in P_{\nu }$
, the term
![]() $\langle \langle s,t\rangle , p \rangle \in R$
just in case
$\langle \langle s,t\rangle , p \rangle \in R$
just in case
![]() $p\Vdash sRt$
. For the structure to be morass-closed at stage
$p\Vdash sRt$
. For the structure to be morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\lambda $
, the relation R must be morass-closed at stage
$\lambda $
, the relation R must be morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\lambda $
. If
$\lambda $
. If
![]() $p\in P_{\nu }$
,
$p\in P_{\nu }$
, ![]() ,
,
![]() $s, t \in S \cap M^{P_{\nu }}$
and
$s, t \in S \cap M^{P_{\nu }}$
and
![]() $p\Vdash sRt$
, then
$p\Vdash sRt$
, then
![]() $f(p)\Vdash f(s)Rf(t)$
. Similarly for operations. For instance, if
$f(p)\Vdash f(s)Rf(t)$
. Similarly for operations. For instance, if
![]() $+$
is a morass-closed operation of X;
$+$
is a morass-closed operation of X;
![]() $s, t, u\in S\cap M^{P_{\nu }}$
and
$s, t, u\in S\cap M^{P_{\nu }}$
and
![]() $p\Vdash s+t=u$
, then
$p\Vdash s+t=u$
, then
![]() $f(p)\Vdash f(s)+f(t)=f(u)$
.
$f(p)\Vdash f(s)+f(t)=f(u)$
.
Definition 4.11 (Morass-definable)
Let G be P generic over M and
![]() $\langle X,+,\cdot ,<\rangle \in M[G]$
be a linearly-ordered ring. X is morass-definable if there is a set of terms
$\langle X,+,\cdot ,<\rangle \in M[G]$
be a linearly-ordered ring. X is morass-definable if there is a set of terms
![]() $T\subseteq M^P$
satisfying
$T\subseteq M^P$
satisfying
![]() $:$
$:$
-
1. T is a morass-closed set of terms with strict level.
-
2. The linear order is morass-closed.
-
3. The ring operations are morass-closed.
-
4. T is level dense and upward level dense.
-
5. Every term of T has countable support.
The satisfaction of the first three conditions of the definition implies that the structure,
![]() $\langle X,+,\cdot ,<\rangle $
, is morass-closed.
$\langle X,+,\cdot ,<\rangle $
, is morass-closed.
We say that an object in a forcing extension satisfies the definitions above provided that there are terms in the forcing language that satisfy the definitions and that are interpreted as the object of interest. For instance, in any forcing extension of M,
![]() $M[G]$
, the interpretation of
$M[G]$
, the interpretation of
![]() $\langle \mathbb R,+,\cdot ,< \rangle $
is morass-definable. In earlier papers see [Reference Dumas3, Reference Dumas4] we showed that certain ultrapowers of
$\langle \mathbb R,+,\cdot ,< \rangle $
is morass-definable. In earlier papers see [Reference Dumas3, Reference Dumas4] we showed that certain ultrapowers of
![]() $\mathbb R$
over
$\mathbb R$
over
![]() $\omega $
were also morass-definable.
$\omega $
were also morass-definable.
Let
![]() $E\subseteq M^P$
be the set of terms of strict level for elements in the Esterle algebra in the forcing language of the poset P. It is routine to check that
$E\subseteq M^P$
be the set of terms of strict level for elements in the Esterle algebra in the forcing language of the poset P. It is routine to check that
![]() $\mathcal {E}$
is morass-closed and that every element of the Esterle algebra is the interpretation of a term with countable support.
$\mathcal {E}$
is morass-closed and that every element of the Esterle algebra is the interpretation of a term with countable support.
Lemma 4.12. The Esterle algebra is level dense.
Proof Let
![]() $a, b\in M^P$
be terms of strict level for elements of the Esterle algebra bearing disjoint supports. Let G be P-generic over M and
$a, b\in M^P$
be terms of strict level for elements of the Esterle algebra bearing disjoint supports. Let G be P-generic over M and
![]() $M[G]\models a<b$
. We wish to show that a and b are separated in
$M[G]\models a<b$
. We wish to show that a and b are separated in
![]() $M[G]$
by an element of
$M[G]$
by an element of
![]() $\mathcal {E}\cap M$
. We work in
$\mathcal {E}\cap M$
. We work in
![]() $M[G]$
. Let
$M[G]$
. Let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
be countable ordinals and
$\gamma _2$
be countable ordinals and
and
If a and b are equal on a partial sumFootnote 2 then that partial sum is in M so subtracting the largest common partial sum of a and b, we may assume that a and b differ on the first term of the sums, and
If
![]() $a_0=b_0$
, then
$a_0=b_0$
, then
![]() $a_0 \in M$
and there is
$a_0 \in M$
and there is
![]() $q\in \mathbb {Q}$
such that
$q\in \mathbb {Q}$
such that
Then
![]() $q x^{a_0}\in M$
and
$q x^{a_0}\in M$
and
Hence we assume that a and b have distinct Archimedean valuations.
We consider the case
![]() $a_0<b_0$
. Then the sign of
$a_0<b_0$
. Then the sign of
![]() $b-a$
is determined by the sign of
$b-a$
is determined by the sign of
![]() $\alpha _0$
. Hence
$\alpha _0$
. Hence
![]() $\alpha _0<0$
. It is sufficient to prove that there is an element of
$\alpha _0<0$
. It is sufficient to prove that there is an element of
![]() $\mathcal {E} \cap M$
that has valuation between
$\mathcal {E} \cap M$
that has valuation between
![]() $a_0$
and
$a_0$
and
![]() $b_0$
. Let
$b_0$
. Let
and
If
![]() $a_0$
and
$a_0$
and
![]() $b_0$
are equal on an initial segment of their supports, then this initial segment is in the ground model. We can therefore assume that
$b_0$
are equal on an initial segment of their supports, then this initial segment is in the ground model. We can therefore assume that
![]() $a_0$
and
$a_0$
and
![]() $b_0$
either have distinct least members, or have the same least member of their supports,
$b_0$
either have distinct least members, or have the same least member of their supports,
![]() $s\in M$
, and
$s\in M$
, and
In the latter case there is
![]() $q\in \mathbb {Q}$
such that
$q\in \mathbb {Q}$
such that
Then
![]() $\{ (s,q) \} \in M$
and
$\{ (s,q) \} \in M$
and
Hence we have left to consider the case in which
![]() $s_{a_0}$
is the least member of the support of
$s_{a_0}$
is the least member of the support of
![]() $a_0$
,
$a_0$
,
![]() $s_{b_0}$
is the least member of the support of
$s_{b_0}$
is the least member of the support of
![]() $b_0$
and
$b_0$
and
![]() $s_{a_0}\neq s_{b_0}$
. If either
$s_{a_0}\neq s_{b_0}$
. If either
![]() $s_{a_0}$
or
$s_{a_0}$
or
![]() $s_{b_0}$
are in M we can find a member of
$s_{b_0}$
are in M we can find a member of
![]() $G_{\omega _1} \cap M$
that is a valuation between
$G_{\omega _1} \cap M$
that is a valuation between
![]() $a_0$
and
$a_0$
and
![]() $b_0$
. So we may assume that neither
$b_0$
. So we may assume that neither
![]() $s_{a_0}$
nor
$s_{a_0}$
nor
![]() $s_{b_0}$
are in M. As we shall see, it is sufficient to show that between any distinct elements of
$s_{b_0}$
are in M. As we shall see, it is sufficient to show that between any distinct elements of
![]() $S_{\omega _1}$
from mutually generic extensions, there is a member of
$S_{\omega _1}$
from mutually generic extensions, there is a member of
![]() $S_{\omega _1}$
in the ground model. We assume without loss of generality that
$S_{\omega _1}$
in the ground model. We assume without loss of generality that
![]() $s_{b_0}<s_{a_0}$
(the case
$s_{b_0}<s_{a_0}$
(the case
![]() $s_{a_0}<s_{b_0}$
is altogether similar). Treating
$s_{a_0}<s_{b_0}$
is altogether similar). Treating
![]() $s_{b_0}$
and
$s_{b_0}$
and
![]() $s_{a_0}$
as countable subsets of
$s_{a_0}$
as countable subsets of
![]() $\omega _1$
, let
$\omega _1$
, let
![]() $\mu $
be the least element of
$\mu $
be the least element of
![]() $s_{a_0}$
that is not a member of
$s_{a_0}$
that is not a member of
![]() $s_{b_0}$
. Let
$s_{b_0}$
. Let
![]() $\Delta =s_{a_0} \cap \mu $
. Then
$\Delta =s_{a_0} \cap \mu $
. Then
![]() $\Delta =s_{b_0}\cap \mu \in M$
. We note that
$\Delta =s_{b_0}\cap \mu \in M$
. We note that
![]() $b_0(\mu )>0$
, otherwise
$b_0(\mu )>0$
, otherwise
![]() $b_0<a_0$
, contrary to assumption. Let
$b_0<a_0$
, contrary to assumption. Let
Then
![]() $s_{c_0}\in M$
and
$s_{c_0}\in M$
and
Let
![]() $c_0\in M$
be defined so that, for
$c_0\in M$
be defined so that, for
![]() $\rho <\mu $
,
$\rho <\mu $
,
and
Then
![]() $c_0 \in M$
and
$c_0 \in M$
and
Since
![]() $a<b$
, the coefficient of
$a<b$
, the coefficient of
![]() $a_0>0$
. Let
$a_0>0$
. Let
![]() $q\in \mathbb {Q}$
and
$q\in \mathbb {Q}$
and
![]() $0<q<a_0$
. Then
$0<q<a_0$
. Then
![]() $q x^{c_0} \in M$
and
$q x^{c_0} \in M$
and
Therefore
![]() $\mathcal {E}$
is level dense.
$\mathcal {E}$
is level dense.
Lemma 4.13. The Esterle algebra is upward level-dense.
Let
![]() $\alpha \leq \beta \leq \omega _2$
. Suppose
$\alpha \leq \beta \leq \omega _2$
. Suppose
![]() $x, y, z\in M^P$
, with
$x, y, z\in M^P$
, with
![]() $x<z<y$
, and z has strict level
$x<z<y$
, and z has strict level
![]() $\alpha $
. It is sufficient to show that there is an element
$\alpha $
. It is sufficient to show that there is an element
![]() $w\in \mathcal {E}$
of strict level
$w\in \mathcal {E}$
of strict level
![]() $\beta $
such that
$\beta $
such that
Assume that
![]() $G\times H$
is
$G\times H$
is
![]() $P(\alpha )\times P(\beta \setminus \alpha )$
-generic, and work in
$P(\alpha )\times P(\beta \setminus \alpha )$
-generic, and work in
![]() $M[G]$
. Then
$M[G]$
. Then
![]() $z\in M[G]$
. If x and y have an identical partial sums, then z must share that partial sum, and the partial sum is in
$z\in M[G]$
. If x and y have an identical partial sums, then z must share that partial sum, and the partial sum is in
![]() $M[G]$
. We may subtract the largest partial sum shared by x and y and pass to x and y that disagree on the first term of the formal power series. If x and y have the same Archimedean valuation, a, then the first term of z has valuation a. Let
$M[G]$
. We may subtract the largest partial sum shared by x and y and pass to x and y that disagree on the first term of the formal power series. If x and y have the same Archimedean valuation, a, then the first term of z has valuation a. Let
![]() $r\in \mathbb R$
be of strict level
$r\in \mathbb R$
be of strict level
![]() $\beta $
and lie between the initial coefficients of x and y. Let
$\beta $
and lie between the initial coefficients of x and y. Let
![]() $w= r\cdot x^a$
. Then w has strict level
$w= r\cdot x^a$
. Then w has strict level
![]() $\beta $
and
$\beta $
and
So we assume that x and y have distinct valuation. If x and z have the same valuation, a, and the initial coefficient of x is negative, let
![]() $r \in \mathbb R$
be negative and greater than the initial coefficient of x and have strict level
$r \in \mathbb R$
be negative and greater than the initial coefficient of x and have strict level
![]() $\beta $
. If the initial coefficient of x is positive, let r be positive and greater than the initial coefficient of x and have strict level
$\beta $
. If the initial coefficient of x is positive, let r be positive and greater than the initial coefficient of x and have strict level
![]() $\beta $
. In either case, let
$\beta $
. In either case, let
![]() $w=r\cdot x^a$
. Then w has strict level
$w=r\cdot x^a$
. Then w has strict level
![]() $\beta $
and
$\beta $
and
The cases for x and y having the same valuation are similar.
If x and y have distinct valuation, let
![]() $r \in \mathbb R$
be positive and have strict level
$r \in \mathbb R$
be positive and have strict level
![]() $\beta $
. Let
$\beta $
. Let
![]() $w=r \cdot z$
. Then w has strict level
$w=r \cdot z$
. Then w has strict level
![]() $\beta $
and
$\beta $
and
Therefore
![]() $\mathcal {E}$
is upward level dense.
$\mathcal {E}$
is upward level dense.
Theorem 4.14. The Esterle algebra is morass-definable.
Proof Let T be the set of terms of strict level in
![]() $M^{P(\omega _3)}$
for elements of the Esterle algebra. We note that every element of the Esterle algebra in a
$M^{P(\omega _3)}$
for elements of the Esterle algebra. We note that every element of the Esterle algebra in a
![]() $P(\omega _2)$
-generic extension of a transitive model of ZFC has countable support. Hence the interpretation of T in any generic extension will be the Esterle algebra. T is clearly morass-closed. By Lemma 4.12,
$P(\omega _2)$
-generic extension of a transitive model of ZFC has countable support. Hence the interpretation of T in any generic extension will be the Esterle algebra. T is clearly morass-closed. By Lemma 4.12,
![]() $\mathcal {E}$
is level dense. By Lemma 4.13,
$\mathcal {E}$
is level dense. By Lemma 4.13,
![]() $\mathcal {E}$
is upward level dense. Therefore the Esterle algebra is morass-definable.
$\mathcal {E}$
is upward level dense. Therefore the Esterle algebra is morass-definable.
5. Extendible functions
We use a simplified gap-1 morass to construct a function between sets of terms of a forcing language adding Cohen generic reals so that the interpretation of that function in a generic extension will satisfy certain conditions. We require the term function under construction to satisfy properties so that commutativity with morass maps will automatically extend the function on a countable domain to a function on an uncountable domain. Throughout this section we assume M is a transitive model of
![]() $ZFC+CH$
that contains a simplified
$ZFC+CH$
that contains a simplified
![]() $(\omega _1,1)$
-morass.
$(\omega _1,1)$
-morass.
Definition 5.1 (Level term function)
Let
![]() $\theta $
be an ordinal,
$\theta $
be an ordinal,
![]() $X\subseteq M^{P(\theta )}$
a set of terms having strict level and
$X\subseteq M^{P(\theta )}$
a set of terms having strict level and
![]() $\phi :X\to M^{P(\theta )}$
. Then
$\phi :X\to M^{P(\theta )}$
. Then
![]() $\phi $
is a level term function provided that the range of
$\phi $
is a level term function provided that the range of
![]() $\phi $
is a set of terms of strict level, and for any
$\phi $
is a set of terms of strict level, and for any
![]() $x\in X$
, the strict level of x and the strict level of
$x\in X$
, the strict level of x and the strict level of
![]() $\phi (x)$
are equal.
$\phi (x)$
are equal.
Definition 5.2 (Morass-commutative term function)
Assume
![]() $:$
$:$
-
1.
 is a simplified
is a simplified
 $(\omega _1,1)$
-morass.
$(\omega _1,1)$
-morass. -
2.
 $\nu <\bar {\nu } \leq \omega _1$
.
$\nu <\bar {\nu } \leq \omega _1$
. -
3.
 $X\subseteq M^{P_{\bar {\nu }}}$
is morass closed at stage
$X\subseteq M^{P_{\bar {\nu }}}$
is morass closed at stage
 $\nu $
beneath
$\nu $
beneath
 $\bar {\nu }$
.
$\bar {\nu }$
. -
4.
 $\phi :X\to M^{P_{\bar {\nu }}}$
.
$\phi :X\to M^{P_{\bar {\nu }}}$
.
If ![]() , then
, then
![]() $\phi $
commutes with
$\phi $
commutes with
![]() $\sigma $
provided that for every
$\sigma $
provided that for every
![]() $x\in X\cap M^{P_{\nu }}$
,
$x\in X\cap M^{P_{\nu }}$
,
![]() $\sigma [\phi (x)]=\phi (\sigma [x])$
. A function
$\sigma [\phi (x)]=\phi (\sigma [x])$
. A function
![]() $\phi :X\to M^{P_{\bar {\nu }}}$
is morass-commutative at stage
$\phi :X\to M^{P_{\bar {\nu }}}$
is morass-commutative at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\bar {\nu }$
if for every
$\bar {\nu }$
if for every ![]() ,
,
![]() $\phi $
commutes with
$\phi $
commutes with
![]() $\sigma $
. If
$\sigma $
. If
![]() $\phi $
is morass-commutative at stage
$\phi $
is morass-commutative at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\omega _1$
, then
$\omega _1$
, then
![]() $\phi $
is morass-commutative at stage
$\phi $
is morass-commutative at stage
![]() $\nu $
.
$\nu $
.
In order to extend an R-monomorphism by commutativity with a splitting map we must satisfy both algebraic and order constraints.
In the next section we show that the morass-commutative extension of an
![]() $\mathbb R$
-monomorphism, satisfying certain technical constraints (extendibility), may be extended to an
$\mathbb R$
-monomorphism, satisfying certain technical constraints (extendibility), may be extended to an
![]() $\mathbb R$
-monomorphism satisfying those same constraints. The technical constraints are those required for an inductive construction along the vertices of a simplified morass.
$\mathbb R$
-monomorphism satisfying those same constraints. The technical constraints are those required for an inductive construction along the vertices of a simplified morass.
We state the technical conditions that permit the inductive construction of the following sections.
Definition 5.3 (Standard term for a subset of ω)
A standard term for a subset of
![]() $\omega $
,
$\omega $
,
![]() $x\in M^P$
, is a term of strict level such that for each
$x\in M^P$
, is a term of strict level such that for each
![]() $(\tau ,p)\in x$
,
$(\tau ,p)\in x$
,
![]() $\tau $
is a canonical term for a natural number.
$\tau $
is a canonical term for a natural number.
Definition 5.4 (Standard term for an ultrafilter)
Let
![]() $U\subset M^P$
be a morass-closed set of standard terms for subsets of
$U\subset M^P$
be a morass-closed set of standard terms for subsets of
![]() $\omega $
such that, for all
$\omega $
such that, for all
![]() $\alpha \leq \omega _1$
,
$\alpha \leq \omega _1$
,
![]() $U\cap M^{P_{\alpha }}$
is forced to be an ultrafilter in all
$U\cap M^{P_{\alpha }}$
is forced to be an ultrafilter in all
![]() $P(\alpha )$
-generic extensions of M. Then U is a standard term for an ultrafilter.
$P(\alpha )$
-generic extensions of M. Then U is a standard term for an ultrafilter.
We will refer to an ultrapower of
![]() $\mathbb R$
over a standard ultrafilter U as a standard ultrapower. We restrict our attention to functions from terms for a standard ultrapower of
$\mathbb R$
over a standard ultrafilter U as a standard ultrapower. We restrict our attention to functions from terms for a standard ultrapower of
![]() $\mathbb R$
to terms for elements of the Esterle algebra.
$\mathbb R$
to terms for elements of the Esterle algebra.
Definition 5.5 (Extendible function)
Let
![]() $\nu <\omega _1$
,
$\nu <\omega _1$
,
![]() $X, Y\subseteq M^{P_{\nu }}$
have elements of strict level and
$X, Y\subseteq M^{P_{\nu }}$
have elements of strict level and
![]() $\phi :X\to Y\in M^{P_{\nu }}$
be a level term function. Then
$\phi :X\to Y\in M^{P_{\nu }}$
be a level term function. Then
![]() $\phi $
is extendible provided that the following are satisfied
$\phi $
is extendible provided that the following are satisfied
![]() $:$
$:$
-
1. It is forced that X is a subring of a standard ultrapower of
 $\mathbb R$
that has countable transcendence degree over
$\mathbb R$
that has countable transcendence degree over
 $\mathbb R$
.
$\mathbb R$
. -
2. Y is forced to be a subset of the Esterle algebra.
-
3. It is forced that Y is closed under partial sums. That is, every initial series of a power series of Y is a member of Y.
-
4. Y contains canonical forcing terms for every real coefficient appearing in a power series of Y.
-
5.
 $\phi $
is forced to be an
$\phi $
is forced to be an
 $\mathbb R$
-isomorphism.
$\mathbb R$
-isomorphism.
If
![]() $\nu $
is a vertex of a morass,
$\nu $
is a vertex of a morass,
![]() $\theta _{\nu }$
is the ordinal associated with
$\theta _{\nu }$
is the ordinal associated with
![]() $\nu $
and
$\nu $
and
![]() $\sigma \in \mathcal {F}_{\nu \nu +1}$
is the splitting function on
$\sigma \in \mathcal {F}_{\nu \nu +1}$
is the splitting function on
![]() $\theta _{\nu }$
then
$\theta _{\nu }$
then
![]() $X\cup \sigma [X]$
is morass-closed at stage
$X\cup \sigma [X]$
is morass-closed at stage
![]() $\nu $
beneath
$\nu $
beneath
![]() $\nu +1$
. We will show that if
$\nu +1$
. We will show that if
![]() $\phi $
is an extendible term function on X, then
$\phi $
is an extendible term function on X, then
![]() $\phi \cup \sigma [\phi ]$
may be extended to extendible term function.
$\phi \cup \sigma [\phi ]$
may be extended to extendible term function.
6. Commutative extensions of extendible term functions
In the inductive construction of the following sections we will need technical lemmas of two types: those insuring that commutativity with morass maps may be used to extend extendible functions to extendible functions, and those allowing the extension of the domain by a specified element to an extendible function. Throughout this section we assume:
-
1. P is the poset adding generic reals indexed by
 $\omega _2$
.
$\omega _2$
. -
2.
 $\sigma $
is a splitting map on
$\sigma $
is a splitting map on
 $\theta <\omega _1$
with splitting point
$\theta <\omega _1$
with splitting point
 $\delta =0$
. That is,
$\delta =0$
. That is,
 $\sigma :\theta \to \omega _1$
and
$\sigma :\theta \to \omega _1$
and
 $\sigma [\theta ]\cap \theta =\emptyset $
.
$\sigma [\theta ]\cap \theta =\emptyset $
. -
3.
 $G(\theta )$
is
$G(\theta )$
is
 $P(\theta )$
-generic over M.
$P(\theta )$
-generic over M. -
4. H is
 $P[\sigma (\theta )]$
-generic over
$P[\sigma (\theta )]$
-generic over
 $M[G]$
.
$M[G]$
. -
5.
 $\phi :X\to Y\in M^{P(\theta )}$
is an extendible function.
$\phi :X\to Y\in M^{P(\theta )}$
is an extendible function.
We wish to show that the extension of
![]() $\phi \cup \sigma [\phi ]$
to the ring generated by
$\phi \cup \sigma [\phi ]$
to the ring generated by
![]() $X \cup \sigma [X]$
is extendible.
$X \cup \sigma [X]$
is extendible.
6.1. Splitting maps and algebraic independence
The central result of this subsection states, roughly, that a subset of a field in a generic extension that is algebraically independent (AI) over the restriction of the field to the ground model, will be AI over the restriction of an extension field to a mutually generic extension. It will follow that the union of an AI subset of a field in a generic extension with its morass “split” in a mutually generic extension will be AI over the restriction of the field to the ground model. We consider the special case in which a morass-map,
![]() $\sigma $
,“splits” a poset
$\sigma $
,“splits” a poset
![]() $P(\theta )$
, for some ordinal
$P(\theta )$
, for some ordinal
![]() $\theta $
. Then there is
$\theta $
. Then there is
![]() $\delta <\theta $
so that the poset
$\delta <\theta $
so that the poset
![]() $P(\theta ) =P(\delta )\times P(\theta \setminus \delta )$
. Then
$P(\theta ) =P(\delta )\times P(\theta \setminus \delta )$
. Then
![]() $\sigma (\theta )=\delta \cup (\sigma [\theta ]\setminus \delta )$
,
$\sigma (\theta )=\delta \cup (\sigma [\theta ]\setminus \delta )$
,
![]() $\theta \cap \sigma [\theta ]=\delta $
, and
$\theta \cap \sigma [\theta ]=\delta $
, and
![]() $\sigma (P(\theta ))=P(\delta ) \times P(\sigma [\theta ]\setminus \delta )$
. Hence we may consider the case in which
$\sigma (P(\theta ))=P(\delta ) \times P(\sigma [\theta ]\setminus \delta )$
. Hence we may consider the case in which
![]() $G(\delta )$
is
$G(\delta )$
is
![]() $P(\delta )$
-generic over M, and we are forcing over
$P(\delta )$
-generic over M, and we are forcing over
![]() $M[G(\delta )]$
. Then
$M[G(\delta )]$
. Then
Hence, without loss of generality, we may assume that the splitting point is
![]() $\delta =0$
.
$\delta =0$
.
Lemma 6.1. Let P be the poset adding generic reals indexed by
![]() $\omega _2$
, G be P-generic over M and F be a morass-definable field in
$\omega _2$
, G be P-generic over M and F be a morass-definable field in
![]() $M[G]$
. Let
$M[G]$
. Let
![]() $\theta <\omega _1$
,
$\theta <\omega _1$
,
![]() $P_0$
be the poset adding generic reals indexed by
$P_0$
be the poset adding generic reals indexed by
![]() $\theta $
,
$\theta $
,
![]() $G_0$
be the
$G_0$
be the
![]() $P_0$
-generic factor of G, and
$P_0$
-generic factor of G, and
![]() $\sigma $
be a splitting map on
$\sigma $
be a splitting map on
![]() $\theta $
(with splitting point
$\theta $
(with splitting point
![]() $\delta $
). If
$\delta $
). If
![]() $\chi =\{ x_1,\ldots ,x_n\} \subseteq (F\cap M[G_0)])$
is linearly independent
$\chi =\{ x_1,\ldots ,x_n\} \subseteq (F\cap M[G_0)])$
is linearly independent
![]() $($
LI
$($
LI
![]() $)$
over
$)$
over
![]() $M\cap F$
, then
$M\cap F$
, then
![]() $\chi $
is LI over
$\chi $
is LI over
![]() $M[G(\sigma [\theta ])]\cap F$
.
$M[G(\sigma [\theta ])]\cap F$
.
Proof Let M, P, F,
![]() $\chi $
,
$\chi $
,
![]() $\theta $
,
$\theta $
,
![]() $\sigma $
, and G satisfy the hypotheses of the lemma. As discussed at the beginning of this section, without loss of generality, we assume that
$\sigma $
, and G satisfy the hypotheses of the lemma. As discussed at the beginning of this section, without loss of generality, we assume that
![]() $\delta =0$
. Let
$\delta =0$
. Let
![]() $H=G(\sigma [\theta ])$
. So H is
$H=G(\sigma [\theta ])$
. So H is
![]() $P(\sigma [\theta ])$
-generic over
$P(\sigma [\theta ])$
-generic over
![]() $M[G_0]$
. We observe that, since F is morass-definable, it is the interpretation in
$M[G_0]$
. We observe that, since F is morass-definable, it is the interpretation in
![]() $M[G]$
of a set of terms with strict level, T. For any
$M[G]$
of a set of terms with strict level, T. For any
![]() $\alpha <\omega _2$
, the interpretation of
$\alpha <\omega _2$
, the interpretation of
![]() $T\cap M^{P(\alpha )}$
is just
$T\cap M^{P(\alpha )}$
is just
![]() $F\cap M[G(\alpha )]$
, and is a subfield of F. Assume
$F\cap M[G(\alpha )]$
, and is a subfield of F. Assume
![]() $\chi \subseteq (F\cap M[G_0)])$
is linearly dependent over
$\chi \subseteq (F\cap M[G_0)])$
is linearly dependent over
![]() $F\cap M[H]$
and that
$F\cap M[H]$
and that
![]() $\{ y_1,\ldots y_n\} \in M[H]$
(all non-zero) are such that
$\{ y_1,\ldots y_n\} \in M[H]$
(all non-zero) are such that
![]() $\sum _{i=1}^n x_i\cdot y_i=0$
in
$\sum _{i=1}^n x_i\cdot y_i=0$
in
![]() $M[G_0][H]$
. For
$M[G_0][H]$
. For
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $\mathbf {x}_i \in M^{P(\theta )}$
and
$\mathbf {x}_i \in M^{P(\theta )}$
and
![]() $\mathbf {y}_i \in M^{\kern-1pt P(\sigma [\theta ])}$
be terms for
$\mathbf {y}_i \in M^{\kern-1pt P(\sigma [\theta ])}$
be terms for
![]() $x_i$
and
$x_i$
and
![]() $y_i$
, respectively. Then there is
$y_i$
, respectively. Then there is
![]() $(p,q)\in G_0 \times H$
such that, in M,
$(p,q)\in G_0 \times H$
such that, in M,
![]() $(p,q)\Vdash \sum _{i=1}^n \mathbf {x}_i\cdot \mathbf {y}_i = 0$
. We force beneath
$(p,q)\Vdash \sum _{i=1}^n \mathbf {x}_i\cdot \mathbf {y}_i = 0$
. We force beneath
![]() $(p,q)$
.
$(p,q)$
.
Let
![]() $\beta $
be countable,
$\beta $
be countable,
![]() $Q_0$
be a poset for adding countably many generic reals indexed by
$Q_0$
be a poset for adding countably many generic reals indexed by
![]() $\beta \setminus \theta $
and
$\beta \setminus \theta $
and
![]() $H_0$
be
$H_0$
be
![]() $Q_0$
-generic over
$Q_0$
-generic over
![]() $M[G_0]$
such that
$M[G_0]$
such that
![]() $(p,q_0)\in G_0\times H_0$
, and the orthogonal complement of
$(p,q_0)\in G_0\times H_0$
, and the orthogonal complement of
![]() $\mathbf {x}= (x_1,\ldots ,x_n)$
in
$\mathbf {x}= (x_1,\ldots ,x_n)$
in
![]() $F^n \cap M[H_0]$
,
$F^n \cap M[H_0]$
,
![]() $\mathbf {x}_0^{\perp }$
, has maximum possible dimension, m, in
$\mathbf {x}_0^{\perp }$
, has maximum possible dimension, m, in
![]() $F^n\cap M[H_0]$
, where
$F^n\cap M[H_0]$
, where
![]() $0<m<n$
. Let
$0<m<n$
. Let
![]() $q_0 \in H_0$
force that the
$q_0 \in H_0$
force that the
![]() $\mathbf {x}^{\perp }$
has dimension m, where
$\mathbf {x}^{\perp }$
has dimension m, where
![]() $q_0<q$
. Let
$q_0<q$
. Let
![]() $\sigma $
be a splitting map on
$\sigma $
be a splitting map on
![]() $Q_0$
with splitting point
$Q_0$
with splitting point
![]() $\delta =\theta $
. Let
$\delta =\theta $
. Let
![]() $Q_1=\sigma (Q_0)$
,
$Q_1=\sigma (Q_0)$
,
![]() $q_1=\sigma (q_0)<\sigma (q)$
and
$q_1=\sigma (q_0)<\sigma (q)$
and
![]() $\mathbf {x}_1^{\perp }= \sigma (\mathbf {x}_0^{\perp })$
. So
$\mathbf {x}_1^{\perp }= \sigma (\mathbf {x}_0^{\perp })$
. So
![]() $Q_1$
and
$Q_1$
and
![]() $Q_0$
are disjoint. If
$Q_0$
are disjoint. If
![]() $H_1$
is
$H_1$
is
![]() $Q_1$
-generic over
$Q_1$
-generic over
![]() $M[G_0][H_0]$
and
$M[G_0][H_0]$
and
![]() $q_1\in H_1$
, then in
$q_1\in H_1$
, then in
![]() $M[H_1]$
,
$M[H_1]$
,
![]() $\mathbf {x}_1^{\perp }$
has dimension m. Furthermore, in
$\mathbf {x}_1^{\perp }$
has dimension m. Furthermore, in
![]() $M[H_0][H_2]$
,
$M[H_0][H_2]$
,
![]() $\mathbf {x}^{\perp }$
has dimension m. Then
$\mathbf {x}^{\perp }$
has dimension m. Then
![]() $\mathbf {x}_0^{\perp }=\mathbf {x}_1^{\perp }$
are elements of mutually generic extensions of M, and are thereby members of M. Therefore
$\mathbf {x}_0^{\perp }=\mathbf {x}_1^{\perp }$
are elements of mutually generic extensions of M, and are thereby members of M. Therefore
![]() $\mathbf {x}^{\perp }$
, computed in M has dimension
$\mathbf {x}^{\perp }$
, computed in M has dimension
![]() $m>0$
, and the components of x are linearly dependent over
$m>0$
, and the components of x are linearly dependent over
![]() $F\cap M$
.
$F\cap M$
.
Lemma 6.2. Let M, P,F, G,
![]() $\theta $
,
$\theta $
,
![]() $\sigma $
, and
$\sigma $
, and
![]() $\chi $
satisfy the hypotheses of Lemma 6.1, and
$\chi $
satisfy the hypotheses of Lemma 6.1, and
![]() $H=G(\sigma [\theta ])$
. Assume
$H=G(\sigma [\theta ])$
. Assume
![]() $\bar {x}=\langle x_1,\ldots ,x_n\rangle \in M[G(\theta )]$
and
$\bar {x}=\langle x_1,\ldots ,x_n\rangle \in M[G(\theta )]$
and
![]() $\bar {y}=\langle y_1,\ldots ,y_n \rangle \in M[H]$
are such that
$\bar {y}=\langle y_1,\ldots ,y_n \rangle \in M[H]$
are such that
 $$\begin{align*}M[G][H] \models \sum_{i=1}^n x_i\cdot y_i = 0. \end{align*}$$
$$\begin{align*}M[G][H] \models \sum_{i=1}^n x_i\cdot y_i = 0. \end{align*}$$
Then in
![]() $M[H]$
,
$M[H]$
,
![]() $\bar {y}$
is in the span of vectors over
$\bar {y}$
is in the span of vectors over
![]() $F^n\cap M$
, all of which are orthogonal to
$F^n\cap M$
, all of which are orthogonal to
![]() $\bar {x}$
.
$\bar {x}$
.
Proof Let
![]() $M[G][H]\models \sum _{i=1}^n x_i\cdot y_i=0$
. Let
$M[G][H]\models \sum _{i=1}^n x_i\cdot y_i=0$
. Let
![]() $A_0$
be the row-reduced echelon form of the orthogonal complement of
$A_0$
be the row-reduced echelon form of the orthogonal complement of
![]() $\bar {x}, \bar {x}^{\perp }$
, computed in
$\bar {x}, \bar {x}^{\perp }$
, computed in
![]() $M[G]$
. We force over ground model, M. Let
$M[G]$
. We force over ground model, M. Let
![]() $(p,q)\in G\times H$
be such that
$(p,q)\in G\times H$
be such that
![]() $(p,q)\Vdash \sum _{i=1}^n x_i\cdot y_i=0$
. We force below
$(p,q)\Vdash \sum _{i=1}^n x_i\cdot y_i=0$
. We force below
![]() $(p,q)$
. Let
$(p,q)$
. Let
![]() $\theta _1 \geq \sigma (\theta )$
,
$\theta _1 \geq \sigma (\theta )$
,
![]() $Q_1=P(\sigma (\theta _1) \setminus \theta )$
and
$Q_1=P(\sigma (\theta _1) \setminus \theta )$
and
![]() $H_1$
be
$H_1$
be
![]() $Q_1$
-generic over
$Q_1$
-generic over
![]() $M[G]$
be such that the dimension of
$M[G]$
be such that the dimension of
![]() $\bar {x}^{\perp }$
computed in
$\bar {x}^{\perp }$
computed in
![]() $M[H_1]$
,
$M[H_1]$
,
![]() $\bar {x}_1^{\perp }$
, is maximal for all possible choices of
$\bar {x}_1^{\perp }$
, is maximal for all possible choices of
![]() $\theta _1$
and
$\theta _1$
and
![]() $H_1$
(where
$H_1$
(where
![]() $q\in H_1$
). Let
$q\in H_1$
). Let
![]() $A_1\in M[H_1]$
have row space equal to
$A_1\in M[H_1]$
have row space equal to
![]() $\bar {x}_1^{\perp }$
and be in row-reduced echelon form. Since we are forcing below
$\bar {x}_1^{\perp }$
and be in row-reduced echelon form. Since we are forcing below
![]() $(p,q)$
,
$(p,q)$
,
![]() $A_1$
has a non-zero row.
$A_1$
has a non-zero row.
Let the rank of
![]() $A_1$
be m. In any generic extension of
$A_1$
be m. In any generic extension of
![]() $M[G]$
by a poset for adding countably many ordinals, the rank of
$M[G]$
by a poset for adding countably many ordinals, the rank of
![]() $\bar {x}^{\perp }$
computed in that extension is no greater than m. Let
$\bar {x}^{\perp }$
computed in that extension is no greater than m. Let
![]() $q_1\in Q_1$
and
$q_1\in Q_1$
and
![]() $q_1\Vdash (A_1$
is in row-reduced echelon form with row space equal to
$q_1\Vdash (A_1$
is in row-reduced echelon form with row space equal to
![]() $\bar {x}^{\perp }$
and
$\bar {x}^{\perp }$
and
![]() $Rank(A_1)=m)$
.
$Rank(A_1)=m)$
.
Let
![]() $\sigma $
be a splitting function on
$\sigma $
be a splitting function on
![]() $\theta _1$
with splitting point
$\theta _1$
with splitting point
![]() $\theta $
. Let
$\theta $
. Let
![]() $Q_2=P(\sigma (\theta ) \setminus \theta )$
and
$Q_2=P(\sigma (\theta ) \setminus \theta )$
and
![]() $H_2$
be
$H_2$
be
![]() $Q_2$
generic over
$Q_2$
generic over
![]() $M[G][H_1]$
with
$M[G][H_1]$
with
![]() $q_2=\sigma (q_1)\in H_2$
. Let
$q_2=\sigma (q_1)\in H_2$
. Let
![]() $A_2=\sigma (A_1)$
. Then
$A_2=\sigma (A_1)$
. Then
![]() $q_2\Vdash A_2$
is in row-reduced echelon form with row space equal to
$q_2\Vdash A_2$
is in row-reduced echelon form with row space equal to
![]() $\bar {x}^{\perp }$
, and has rank m.
$\bar {x}^{\perp }$
, and has rank m.
Since m is the maximum possible rank for
![]() $\bar {x}^{\perp }$
, and row-reduced echelon form is canonical,
$\bar {x}^{\perp }$
, and row-reduced echelon form is canonical,
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are in mutually generic extensions of
$A_2$
are in mutually generic extensions of
![]() $M[G]$
, so
$M[G]$
, so
But
![]() $A_1\in M[H_1]$
and
$A_1\in M[H_1]$
and
![]() $A_2\in M[H_2]$
, so
$A_2\in M[H_2]$
, so
![]() $A_1\in M$
. Then
$A_1\in M$
. Then
![]() $\bar {y}$
is in the row space of
$\bar {y}$
is in the row space of
![]() $A_1$
. Hence
$A_1$
. Hence
![]() $\bar {y}$
is in the span of vectors in
$\bar {y}$
is in the span of vectors in
![]() $F^n\cap M$
.
$F^n\cap M$
.
Corollary 6.3. Let F,
![]() $G,$
and H satisfy the hypotheses of Lemma 6.1. If
$G,$
and H satisfy the hypotheses of Lemma 6.1. If
![]() $\chi \subseteq M[G] \cap F$
is algebraically independent
$\chi \subseteq M[G] \cap F$
is algebraically independent
![]() $($
AI
$($
AI
![]() $)$
over
$)$
over
![]() $M\cap F$
, then
$M\cap F$
, then
![]() $\chi $
is AI over
$\chi $
is AI over
![]() $M[H]\cap F$
.
$M[H]\cap F$
.
Proof Let
![]() $\chi ^*$
be the multiplicative semi-group generated by the elements of
$\chi ^*$
be the multiplicative semi-group generated by the elements of
![]() $\chi $
. Then
$\chi $
. Then
![]() $\chi ^*$
is LI over
$\chi ^*$
is LI over
![]() $M\cap F$
. By Lemma 6.1,
$M\cap F$
. By Lemma 6.1,
![]() $\chi ^*$
is LI over
$\chi ^*$
is LI over
![]() $M[H]\cap F$
. Therefore
$M[H]\cap F$
. Therefore
![]() $\chi $
is AI over
$\chi $
is AI over
![]() $M[H]\cap F$
.
$M[H]\cap F$
.
Corollary 6.4. Let F, G,
![]() $\sigma $
,
$\sigma $
,
![]() $\theta ,$
and H satisfy the hypotheses of Lemma 6.1. Assume that it is forced in all
$\theta ,$
and H satisfy the hypotheses of Lemma 6.1. Assume that it is forced in all
![]() $P(\theta )$
-generic extensions of M that
$P(\theta )$
-generic extensions of M that
![]() $\chi =\{ \mathbf {x_1},\ldots ,\mathbf {x_n} \} \subseteq M^{P(\theta )}$
is AI over
$\chi =\{ \mathbf {x_1},\ldots ,\mathbf {x_n} \} \subseteq M^{P(\theta )}$
is AI over
![]() $M\cap F$
. Then
$M\cap F$
. Then
![]() $\chi \cup {\sigma [\chi ]}$
is forced in all P-generic extensions of M to be AI over
$\chi \cup {\sigma [\chi ]}$
is forced in all P-generic extensions of M to be AI over
![]() $M\cap F$
. In particular,
$M\cap F$
. In particular,
![]() $val_G(\chi \cup \sigma [\chi ])$
is AI over
$val_G(\chi \cup \sigma [\chi ])$
is AI over
![]() $M\cap F$
.
$M\cap F$
.
Proof F is morass-closed, so in all
![]() $P(\sigma [\theta ])$
-generic extensions of M,
$P(\sigma [\theta ])$
-generic extensions of M,
![]() $\sigma [\mathbf {\chi }]$
is AI over
$\sigma [\mathbf {\chi }]$
is AI over
![]() $M\cap F$
. By Corollary 6.3,
$M\cap F$
. By Corollary 6.3,
![]() $\sigma [\chi ]$
is AI over
$\sigma [\chi ]$
is AI over
![]() $M\cap F$
in
$M\cap F$
in
![]() $M[G]$
. Suppose there is a nontrivial linear combination (over
$M[G]$
. Suppose there is a nontrivial linear combination (over
![]() $M\cap F$
) of distinct elements of the semigroup generated by
$M\cap F$
) of distinct elements of the semigroup generated by
![]() $\chi \cup \sigma [\chi ]$
that equals 0. By Corollary 6.3,
$\chi \cup \sigma [\chi ]$
that equals 0. By Corollary 6.3,
![]() $\chi $
is AI over
$\chi $
is AI over
![]() $M[H]\cap F$
. This implies that there is a nontrivial linear combination (over
$M[H]\cap F$
. This implies that there is a nontrivial linear combination (over
![]() $M\cap F$
) of elements of the semigroup generated by
$M\cap F$
) of elements of the semigroup generated by
![]() $\sigma [\chi ]$
that equals 0. However,
$\sigma [\chi ]$
that equals 0. However,
![]() $\sigma [\chi ]$
is AI over
$\sigma [\chi ]$
is AI over
![]() $M\cap F$
, so
$M\cap F$
, so
![]() $val_G(\mathbf {\chi }\cup \sigma [\mathbf {\chi }])$
is AI over
$val_G(\mathbf {\chi }\cup \sigma [\mathbf {\chi }])$
is AI over
![]() $M\cap F$
.
$M\cap F$
.
Lemma 6.5. Let X be a subring of finite elements of a standard ultrapower of
![]() $\mathbb R$
,
$\mathbb R$
,
![]() ${\mathbb R}^{\omega }/U$
and
${\mathbb R}^{\omega }/U$
and
![]() $Y\subseteq \mathcal {E}$
. Let
$Y\subseteq \mathcal {E}$
. Let
![]() $X^*$
be the ring generated by
$X^*$
be the ring generated by
![]() $X\cup \sigma [X]$
, where
$X\cup \sigma [X]$
, where
![]() $\sigma $
is a splitting function. If
$\sigma $
is a splitting function. If
![]() $\phi :X\to Y$
is an extendible
$\phi :X\to Y$
is an extendible
![]() $\mathbb R$
-monomorphism, then there is an extendible
$\mathbb R$
-monomorphism, then there is an extendible
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi ^*:X^* \to Y^*$
, extending
$\phi ^*:X^* \to Y^*$
, extending
![]() $\phi $
and
$\phi $
and
![]() $\sigma [\phi ]$
.
$\sigma [\phi ]$
.
Proof Without loss of generality we assume that the splitting point of
![]() $\sigma $
,
$\sigma $
,
![]() ${\delta =0}$
. An element of
${\delta =0}$
. An element of
![]() $X^*$
may be expressed as
$X^*$
may be expressed as
![]() $\sum _{i=1}^n x_i\cdot \sigma (y_i)$
, for some
$\sum _{i=1}^n x_i\cdot \sigma (y_i)$
, for some
![]() $n\in \mathbb N$
, and
$n\in \mathbb N$
, and
![]() $x_1,\ldots ,x_n,y_1,\ldots ,y_n \in X$
. Let S be the set of expressions of this form. We define a function
$x_1,\ldots ,x_n,y_1,\ldots ,y_n \in X$
. Let S be the set of expressions of this form. We define a function
![]() $\psi :S\to \mathcal {E}$
where
$\psi :S\to \mathcal {E}$
where
 $$\begin{align*}\psi\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right) = \sum_{i=1}^n \phi(x_i)\cdot \sigma(\phi(y_i)). \end{align*}$$
$$\begin{align*}\psi\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right) = \sum_{i=1}^n \phi(x_i)\cdot \sigma(\phi(y_i)). \end{align*}$$
Let
![]() $\iota :S \to X^*$
be the natural quotient map from the expressions of S to
$\iota :S \to X^*$
be the natural quotient map from the expressions of S to
![]() $X^*$
. The kernel of
$X^*$
. The kernel of
![]() $\iota $
is the set of expressions of S that sum to
$\iota $
is the set of expressions of S that sum to
![]() $0$
in
$0$
in
![]() $X^*$
.
$X^*$
.
![]() $\psi $
defines a ring homomorphism on
$\psi $
defines a ring homomorphism on
![]() $X^*$
if and only if, for any s in the kernel of
$X^*$
if and only if, for any s in the kernel of
![]() $\iota $
,
$\iota $
,
For
![]() $i\leq n$
let
$i\leq n$
let
![]() $z_i=\sigma (y_i)$
and
$z_i=\sigma (y_i)$
and
![]() $s=\sum _{i=1}^n x_i\cdot z_i$
be in the kernel of
$s=\sum _{i=1}^n x_i\cdot z_i$
be in the kernel of
![]() $\iota $
. Then in
$\iota $
. Then in
![]() $X^*$
,
$X^*$
,
 $$\begin{align*}\sum_{i=1}^n x_i\cdot z_i=0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^n x_i\cdot z_i=0. \end{align*}$$
Let
and
By Lemma 6.2,
![]() $\bar {z}$
is in the span of elements of
$\bar {z}$
is in the span of elements of
![]() $X^n\cap M$
that are orthogonal to
$X^n\cap M$
that are orthogonal to
![]() $\bar {x}$
. Let
$\bar {x}$
. Let
![]() $\{ b_1,\ldots ,b_m\}$
be an LI set of vectors of
$\{ b_1,\ldots ,b_m\}$
be an LI set of vectors of
![]() $X^n\cap M$
orthogonal to
$X^n\cap M$
orthogonal to
![]() $\bar {x}$
that contains
$\bar {x}$
that contains
![]() $\bar {z}$
in its span. Let
$\bar {z}$
in its span. Let
![]() $\langle \cdot ,\cdot \rangle $
be the dot product and
$\langle \cdot ,\cdot \rangle $
be the dot product and
![]() $(\alpha _1,\ldots ,\alpha _m)\in \sigma ([X])^n\cap M[H]$
be such that
$(\alpha _1,\ldots ,\alpha _m)\in \sigma ([X])^n\cap M[H]$
be such that
 $$\begin{align*}\sum_{i=1}^m \alpha_i\cdot b_i=\bar{z}. \end{align*}$$
$$\begin{align*}\sum_{i=1}^m \alpha_i\cdot b_i=\bar{z}. \end{align*}$$
Let
![]() $\bar {\phi }:X^n\to \mathcal {E}^n$
be defined by
$\bar {\phi }:X^n\to \mathcal {E}^n$
be defined by
Recall that for a splitting map
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma (\phi ):\sigma [X]\to \mathcal {E}$
is defined so that
$\sigma (\phi ):\sigma [X]\to \mathcal {E}$
is defined so that
![]() $\sigma $
and
$\sigma $
and
![]() $\phi $
commute. Then
$\phi $
commute. Then
 $$\begin{align*}\psi(\langle \bar{x},\bar{z}\rangle) = \left\langle \bar{\phi}(\bar{x}),\sigma(\bar{\phi})\left(\sum_{i=1}^m \alpha_i \cdot b_i\right) \right\rangle = \sum_{i=1}^m \sigma(\alpha_i)\cdot \langle \bar{\phi}(\bar{x}), \sigma(\bar{\phi})(b_i) \rangle. \end{align*}$$
$$\begin{align*}\psi(\langle \bar{x},\bar{z}\rangle) = \left\langle \bar{\phi}(\bar{x}),\sigma(\bar{\phi})\left(\sum_{i=1}^m \alpha_i \cdot b_i\right) \right\rangle = \sum_{i=1}^m \sigma(\alpha_i)\cdot \langle \bar{\phi}(\bar{x}), \sigma(\bar{\phi})(b_i) \rangle. \end{align*}$$
However,
![]() $b_i\in X^n\cap M$
for all
$b_i\in X^n\cap M$
for all
![]() $i\leq n$
, so
$i\leq n$
, so
Hence
 $$\begin{align*}\sum_{i=1}^m \sigma(\alpha_i)\cdot \langle \bar{\phi}(\bar{x}), \sigma(\bar{\phi}) (b_i) \rangle = \sum_{i=1}^m \sigma(\alpha_i)\cdot \langle \bar{\phi}(\bar{x}),\bar{\phi}(b_i) \rangle = \sum_{i=1}^m \sigma(\alpha_i)\cdot \phi(\langle \bar{x},b_i\rangle). \end{align*}$$
$$\begin{align*}\sum_{i=1}^m \sigma(\alpha_i)\cdot \langle \bar{\phi}(\bar{x}), \sigma(\bar{\phi}) (b_i) \rangle = \sum_{i=1}^m \sigma(\alpha_i)\cdot \langle \bar{\phi}(\bar{x}),\bar{\phi}(b_i) \rangle = \sum_{i=1}^m \sigma(\alpha_i)\cdot \phi(\langle \bar{x},b_i\rangle). \end{align*}$$
For all
![]() $i\leq m$
,
$i\leq m$
,
![]() $b_i\perp \bar {x}$
. So for all
$b_i\perp \bar {x}$
. So for all
![]() $i\leq m$
,
$i\leq m$
,
and
![]() $\psi (\langle \bar {x},\bar {z} \rangle )=0$
. Therefore
$\psi (\langle \bar {x},\bar {z} \rangle )=0$
. Therefore
![]() $\psi $
defines a ring homomorphism on
$\psi $
defines a ring homomorphism on
![]() $X^*$
,
$X^*$
,
![]() $\phi ^*$
, that extends
$\phi ^*$
, that extends
![]() $\phi \cup \sigma (\phi )$
to
$\phi \cup \sigma (\phi )$
to
![]() $X^*$
.
$X^*$
.
Assume that
![]() $\bar {x}, \bar {y}\in M[G]\cap X^n$
,
$\bar {x}, \bar {y}\in M[G]\cap X^n$
,
![]() $\bar {z}=\sigma (\bar {y})$
and
$\bar {z}=\sigma (\bar {y})$
and
We consider X as a vector space over
![]() $M\cap X$
. Let B be a basis for X over
$M\cap X$
. Let B be a basis for X over
![]() ${M\cap X}$
. There is a finite subset of basis vectors,
${M\cap X}$
. There is a finite subset of basis vectors,
![]() $X'=\{x_1',\ldots ,x_m'\}\subseteq B$
so that every component of
$X'=\{x_1',\ldots ,x_m'\}\subseteq B$
so that every component of
![]() $\bar {x}$
is in the span of
$\bar {x}$
is in the span of
![]() $X'$
. Hence
$X'$
. Hence
![]() $\langle \bar {x},\bar {y} \rangle $
may be expressed as a linear combination of
$\langle \bar {x},\bar {y} \rangle $
may be expressed as a linear combination of
![]() $X'$
over
$X'$
over
![]() $\sigma [X]$
. For
$\sigma [X]$
. For
![]() $1\leq i\leq m$
, let
$1\leq i\leq m$
, let
![]() $z^{\prime }_i$
be the sum of coefficients of
$z^{\prime }_i$
be the sum of coefficients of
![]() $x_i'$
in the linear combination over
$x_i'$
in the linear combination over
![]() $X'$
. Then
$X'$
. Then
![]() $z_i'\in \sigma [X]$
and
$z_i'\in \sigma [X]$
and
 $$\begin{align*}\sum_{i=1}^m x_i'\cdot z_i'=\sum_{i=1}^n x_i\cdot z_i \neq 0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^m x_i'\cdot z_i'=\sum_{i=1}^n x_i\cdot z_i \neq 0. \end{align*}$$
Then
![]() $\{ \phi (x_1'),\ldots ,\phi (x_m')\}$
is LI over
$\{ \phi (x_1'),\ldots ,\phi (x_m')\}$
is LI over
![]() $\phi [X] \cap M$
. By Lemma 6.1,
$\phi [X] \cap M$
. By Lemma 6.1,
![]() $\{ \phi (x_1'),\ldots ,\phi (x_m')\}$
is LI over
$\{ \phi (x_1'),\ldots ,\phi (x_m')\}$
is LI over
![]() $\mathcal {E} \cap M[H]$
. Therefore
$\mathcal {E} \cap M[H]$
. Therefore
 $$\begin{align*}\sum_{i=1}^n \phi^*(x_i\cdot z_i)=\sum_{i=1}^m \phi^*(x_i'\cdot z_i')\neq 0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^n \phi^*(x_i\cdot z_i)=\sum_{i=1}^m \phi^*(x_i'\cdot z_i')\neq 0. \end{align*}$$
Thus
![]() $\phi ^*$
is a monomorphism.
$\phi ^*$
is a monomorphism.
We show that
![]() $\phi ^*$
is
$\phi ^*$
is
![]() $\mathbb R$
-linear. Let
$\mathbb R$
-linear. Let
![]() $r\in \mathbb R\cap X^*$
. Since X is a subring of finite elements of
$r\in \mathbb R\cap X^*$
. Since X is a subring of finite elements of
![]() ${\mathbb R}^{\omega }/U$
, every element of X may be expressed as the sum of a real number and an infinitesimal.
${\mathbb R}^{\omega }/U$
, every element of X may be expressed as the sum of a real number and an infinitesimal.
Then there are
![]() $x_1\dots ,x_n,y_1, \dots y_n\in X$
such that
$x_1\dots ,x_n,y_1, \dots y_n\in X$
such that
 $$\begin{align*}r=\sum_ {i=1}^n x_i\cdot \sigma(y_i). \end{align*}$$
$$\begin{align*}r=\sum_ {i=1}^n x_i\cdot \sigma(y_i). \end{align*}$$
For
![]() $1\leq i\leq n$
, each
$1\leq i\leq n$
, each
![]() $x_i$
and
$x_i$
and
![]() $y_i$
may be written as
$y_i$
may be written as
![]() $r_i+\delta _i$
and
$r_i+\delta _i$
and
![]() $s_i+\epsilon _i$
, resp., where for
$s_i+\epsilon _i$
, resp., where for
![]() $r_i,s_i\in \mathbb R$
and
$r_i,s_i\in \mathbb R$
and
![]() $\delta _i$
,
$\delta _i$
,
![]() $\epsilon _i$
are infinitesimal. So
$\epsilon _i$
are infinitesimal. So
 $$\begin{align*}\sum_{i=1}^n r_i\cdot \sigma(s_i)=r \end{align*}$$
$$\begin{align*}\sum_{i=1}^n r_i\cdot \sigma(s_i)=r \end{align*}$$
and
 $$\begin{align*}\sum_{i=1}^n r_i\cdot \sigma(\epsilon_i)+\sigma(s_i)\cdot \delta_i+\delta_i\cdot \sigma(\epsilon_i)=0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^n r_i\cdot \sigma(\epsilon_i)+\sigma(s_i)\cdot \delta_i+\delta_i\cdot \sigma(\epsilon_i)=0. \end{align*}$$
Since
![]() $\phi $
is extendible, for
$\phi $
is extendible, for
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $\phi (r_i)=r_i$
and
$\phi (r_i)=r_i$
and
![]() $\phi (\delta _i)$
is infinitesimal in
$\phi (\delta _i)$
is infinitesimal in
![]() $\mathcal {E}$
. Therefore
$\mathcal {E}$
. Therefore
![]() $r_i\in X$
. Similarly,
$r_i\in X$
. Similarly,
![]() $s_i\in X$
. Hence r is in the ring generated by
$s_i\in X$
. Hence r is in the ring generated by
![]() $(\mathbb R\cap X) \cup (\sigma [\mathbb R\cap X])$
. So
$(\mathbb R\cap X) \cup (\sigma [\mathbb R\cap X])$
. So
![]() $\phi ^*(r)=r$
, and
$\phi ^*(r)=r$
, and
![]() $\phi ^*$
is
$\phi ^*$
is
![]() $\mathbb R$
-linear.
$\mathbb R$
-linear.
We show that
![]() $\phi ^*$
is order-preserving. For
$\phi ^*$
is order-preserving. For
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $x_1,\ldots ,x_n,y_1,\ldots ,y_n \in X$
, we show that
$x_1,\ldots ,x_n,y_1,\ldots ,y_n \in X$
, we show that
![]() $\sum _{i=1}^n x_i\cdot \sigma (y_i)>0$
iff
$\sum _{i=1}^n x_i\cdot \sigma (y_i)>0$
iff
![]() $\sum _{i=1}^n \phi ^*(x_i)\cdot \phi ^*(\sigma (y_i))>0$
.
$\sum _{i=1}^n \phi ^*(x_i)\cdot \phi ^*(\sigma (y_i))>0$
.
If
![]() $n=1$
, then the sign of
$n=1$
, then the sign of
![]() $x_1\cdot \sigma (y_1)$
is the sign of the product of the leading coefficients of
$x_1\cdot \sigma (y_1)$
is the sign of the product of the leading coefficients of
![]() $x_1$
and
$x_1$
and
![]() $\sigma (y_1)$
, which are preserved by
$\sigma (y_1)$
, which are preserved by
![]() $\phi ^*$
. So
$\phi ^*$
. So
Assume that
![]() $n \geq 2$
, and
$n \geq 2$
, and
 $$\begin{align*}\sum_{i=1}^n x_i\cdot \sigma(y_i)>0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^n x_i\cdot \sigma(y_i)>0. \end{align*}$$
Let
 $$\begin{align*}y=\phi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)=\sum_{\lambda<\gamma} \alpha_{\lambda}x^{a_{\lambda}}. \end{align*}$$
$$\begin{align*}y=\phi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)=\sum_{\lambda<\gamma} \alpha_{\lambda}x^{a_{\lambda}}. \end{align*}$$
By assumption,
![]() $\phi [X]$
is a ring of finite elements of
$\phi [X]$
is a ring of finite elements of
![]() $\mathcal {E}$
that is closed under partial sums and contains all coefficients that appear in members of the range of
$\mathcal {E}$
that is closed under partial sums and contains all coefficients that appear in members of the range of
![]() $\phi $
. Since
$\phi $
. Since
![]() $\phi $
is extendible, there are
$\phi $
is extendible, there are
![]() $b_0\in M[G]\cap G_{\omega _1}$
and
$b_0\in M[G]\cap G_{\omega _1}$
and
![]() $c_0\in M[H]\cap G_{\omega _1}$
such that
$c_0\in M[H]\cap G_{\omega _1}$
such that
![]() $x^{b_0} \in \phi [X]$
,
$x^{b_0} \in \phi [X]$
,
![]() $x^{c_0}\in \sigma [\phi [X]]$
,
$x^{c_0}\in \sigma [\phi [X]]$
,
![]() $b_0, c_0\geq e$
(in
$b_0, c_0\geq e$
(in
![]() $G_{\omega _1}$
) and
$G_{\omega _1}$
) and
Let
![]() $u,v\in X$
be such that
$u,v\in X$
be such that
and
Let
![]() $\hat {X}$
be the ring generated by X,
$\hat {X}$
be the ring generated by X,
![]() $1/u$
and
$1/u$
and
![]() $1/v$
in
$1/v$
in
![]() ${\mathbb R}^{\omega }/U$
. Let
${\mathbb R}^{\omega }/U$
. Let
![]() $\psi :\hat {X} \to \mathcal {E}$
be the unique ring homomorphism extending
$\psi :\hat {X} \to \mathcal {E}$
be the unique ring homomorphism extending
![]() $\phi $
satisfying
$\phi $
satisfying
![]() $\psi (1/u)=1/\phi (u)=x^{-b_o}\in \mathcal {E}$
and
$\psi (1/u)=1/\phi (u)=x^{-b_o}\in \mathcal {E}$
and
![]() $\psi (\sigma (1/v))=x^{-c_0}\in \mathcal {E}$
. Then
$\psi (\sigma (1/v))=x^{-c_0}\in \mathcal {E}$
. Then
![]() $\psi $
is extendible. Hence the extension of
$\psi $
is extendible. Hence the extension of
![]() $\psi $
to the ring homomorphism,
$\psi $
to the ring homomorphism,
![]() $\psi ^*$
, on the ring generated by
$\psi ^*$
, on the ring generated by
![]() $\hat {X}\cup \sigma [\hat {X}]$
is an
$\hat {X}\cup \sigma [\hat {X}]$
is an
![]() $\mathbb R$
-linear monomorphism. Furthermore, since
$\mathbb R$
-linear monomorphism. Furthermore, since
![]() $\phi $
is an
$\phi $
is an
![]() $\mathbb R$
-linear order-monomorphism,
$\mathbb R$
-linear order-monomorphism,
![]() $\phi $
extends uniquely to an
$\phi $
extends uniquely to an
![]() $\mathbb R$
-linear order-preserving field monomorphism on the field generated by
$\mathbb R$
-linear order-preserving field monomorphism on the field generated by
![]() $\hat {X}$
. Hence
$\hat {X}$
. Hence
![]() $\psi $
and
$\psi $
and
![]() $\sigma [\psi ]$
are
$\sigma [\psi ]$
are
![]() $\mathbb R$
-monomorphisms on
$\mathbb R$
-monomorphisms on
![]() $\hat {X}$
and
$\hat {X}$
and
![]() $\sigma [\hat {X}]$
, resp. Then
$\sigma [\hat {X}]$
, resp. Then
 $$\begin{align*}\psi^*\left((1/u)\cdot (\sigma(1/v))\cdot \left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)\right)= \end{align*}$$
$$\begin{align*}\psi^*\left((1/u)\cdot (\sigma(1/v))\cdot \left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)\right)= \end{align*}$$
 $$\begin{align*}\alpha_0+x^{-a_0}\cdot \phi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right) = \end{align*}$$
$$\begin{align*}\alpha_0+x^{-a_0}\cdot \phi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right) = \end{align*}$$
 $$\begin{align*}\alpha_0+x^{-a_0}\cdot \left(\sum_{\lambda=1}^{\gamma} \alpha_{\lambda} x^{a_{\lambda}}\right) = \end{align*}$$
$$\begin{align*}\alpha_0+x^{-a_0}\cdot \left(\sum_{\lambda=1}^{\gamma} \alpha_{\lambda} x^{a_{\lambda}}\right) = \end{align*}$$
 $$\begin{align*}\alpha_0 + \sum_{\lambda=1}^{\gamma} \alpha_{\lambda} x^{a_{\lambda} - a_0}. \end{align*}$$
$$\begin{align*}\alpha_0 + \sum_{\lambda=1}^{\gamma} \alpha_{\lambda} x^{a_{\lambda} - a_0}. \end{align*}$$
For
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $(1/u)\cdot (\sigma (1/v)) \cdot x_i\cdot \sigma (y_i)$
is finite. Therefore, for
$(1/u)\cdot (\sigma (1/v)) \cdot x_i\cdot \sigma (y_i)$
is finite. Therefore, for
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
where
![]() $r_i, s_i \in \mathbb R\cap X$
and
$r_i, s_i \in \mathbb R\cap X$
and
![]() $(1/u)\cdot \delta _i, \sigma (1/v)\cdot \sigma (\epsilon _i) \in \hat {X}$
are infinitesimal. If the ith term is infinitesimal, then
$(1/u)\cdot \delta _i, \sigma (1/v)\cdot \sigma (\epsilon _i) \in \hat {X}$
are infinitesimal. If the ith term is infinitesimal, then
![]() $r_i=0=s_i$
. Hence,
$r_i=0=s_i$
. Hence,
 $$\begin{align*}\alpha_0=\sum_{i=1}^n r_i\cdot s_i.\end{align*}$$
$$\begin{align*}\alpha_0=\sum_{i=1}^n r_i\cdot s_i.\end{align*}$$
Since
![]() $\psi ^*$
is
$\psi ^*$
is
![]() $\mathbb R$
-linear, the real part of
$\mathbb R$
-linear, the real part of
![]() $(1/u)\cdot (\sigma (1/v))\cdot \sum _{i=1}^n x_i\cdot \sigma (y_i)$
is
$(1/u)\cdot (\sigma (1/v))\cdot \sum _{i=1}^n x_i\cdot \sigma (y_i)$
is
![]() $\alpha _0$
, and therefore
$\alpha _0$
, and therefore
![]() $\alpha _0>0$
. Furthermore,
$\alpha _0>0$
. Furthermore,
![]() $\psi ^*((1/u)\cdot \sigma (1/v))>0$
. Hence
$\psi ^*((1/u)\cdot \sigma (1/v))>0$
. Hence
 $$\begin{align*}\psi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)=\phi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)>0. \end{align*}$$
$$\begin{align*}\psi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)=\phi^*\left(\sum_{i=1}^n x_i\cdot \sigma(y_i)\right)>0. \end{align*}$$
Therefore
![]() $\phi ^*$
is order-preserving and
$\phi ^*$
is order-preserving and
![]() $\phi ^*$
is extendible.
$\phi ^*$
is extendible.
Lemma 6.6. Let:
-
1.
 $\bar {\nu }<\nu \leq \omega _1$
.
$\bar {\nu }<\nu \leq \omega _1$
. -
2.
 $D\in M[G_{\bar {\nu }}]$
be a subring of a standard ultrapower of
$D\in M[G_{\bar {\nu }}]$
be a subring of a standard ultrapower of
 $\mathbb R$
over
$\mathbb R$
over
 $\omega $
.
$\omega $
. -
3.
 $\phi :D\to \mathcal {E} \in M[G_{\bar {\nu }}]$
be an extendible
$\phi :D\to \mathcal {E} \in M[G_{\bar {\nu }}]$
be an extendible
 $\mathbb R$
-monomorphism on D.
$\mathbb R$
-monomorphism on D. -
4.
 $D^*=\bigcup _{\sigma \in \mathcal {F}_{\bar {\nu }, \nu }} \sigma [D]$
.
$D^*=\bigcup _{\sigma \in \mathcal {F}_{\bar {\nu }, \nu }} \sigma [D]$
.
Then there is a unique extendible
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi ^*$
, on the ring generated by
$\phi ^*$
, on the ring generated by
![]() $D^*$
which, for any
$D^*$
which, for any
![]() $\sigma \in \mathcal {F}_{\bar {\nu } \nu }$
, extends
$\sigma \in \mathcal {F}_{\bar {\nu } \nu }$
, extends
![]() $\sigma [\phi ]$
.
$\sigma [\phi ]$
.
Proof If
![]() $\nu =\bar {\nu }+1$
, then the result follows from Lemma 6.5.
$\nu =\bar {\nu }+1$
, then the result follows from Lemma 6.5.
If there is no limit ordinal
![]() $\lambda $
,
$\lambda $
,
![]() $\bar {\nu }<\lambda \leq \nu $
. Then there is
$\bar {\nu }<\lambda \leq \nu $
. Then there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
By Lemma 6.5, for any extendible
![]() $\phi :D\to \mathcal {E}$
and splitting function
$\phi :D\to \mathcal {E}$
and splitting function
![]() $\sigma $
, the ring monomorphism on the ring generated by
$\sigma $
, the ring monomorphism on the ring generated by
![]() $D\cup \sigma [D]$
extending
$D\cup \sigma [D]$
extending
![]() $\phi \cup \sigma [\phi ]$
is extendible. By n iterated applications of Lemma 6.5, there is a unique extendible
$\phi \cup \sigma [\phi ]$
is extendible. By n iterated applications of Lemma 6.5, there is a unique extendible
![]() $\mathbb R$
-monomorphic extension of
$\mathbb R$
-monomorphic extension of
![]() $\phi $
,
$\phi $
,
![]() $\phi ^*\supset \bigcup _{\sigma \in \mathcal {F}_{\bar {\nu } \nu }} \sigma [\phi ]$
, to the ring generated by
$\phi ^*\supset \bigcup _{\sigma \in \mathcal {F}_{\bar {\nu } \nu }} \sigma [\phi ]$
, to the ring generated by
![]() $\bigcup _{\sigma \in \mathcal {F}_{\bar {\nu } \nu }} \sigma [D]$
.
$\bigcup _{\sigma \in \mathcal {F}_{\bar {\nu } \nu }} \sigma [D]$
.
So assume there is a limit ordinal
![]() $\lambda $
,
$\lambda $
,
![]() $\nu _{\bar {\alpha }}<\lambda \leq \nu _{\alpha }$
. Let
$\nu _{\bar {\alpha }}<\lambda \leq \nu _{\alpha }$
. Let
![]() $\lambda $
be the least limit ordinal greater than
$\lambda $
be the least limit ordinal greater than
![]() $\nu _{\bar {\alpha }}$
. Let
$\nu _{\bar {\alpha }}$
. Let
 $$\begin{align*}D_{\lambda}=\bigcup_{\sigma \in \mathcal{F}_{\bar{\nu}, \lambda}} \sigma[D]. \end{align*}$$
$$\begin{align*}D_{\lambda}=\bigcup_{\sigma \in \mathcal{F}_{\bar{\nu}, \lambda}} \sigma[D]. \end{align*}$$
Let
![]() $D^*_{\lambda }$
be the ring generated by
$D^*_{\lambda }$
be the ring generated by
![]() $D_{\lambda }$
, We show that there is an extendible
$D_{\lambda }$
, We show that there is an extendible
![]() $\mathbb R$
-monomorphism of
$\mathbb R$
-monomorphism of
![]() $D^*_{\lambda }$
which, for any
$D^*_{\lambda }$
which, for any
![]() $\sigma \in \mathcal {F}_{\bar {\nu } \lambda }$
, extends
$\sigma \in \mathcal {F}_{\bar {\nu } \lambda }$
, extends
![]() $\sigma [\phi ]$
.
$\sigma [\phi ]$
.
Let F be a finitely generated subring of
![]() $D^*_{\lambda }$
. Let
$D^*_{\lambda }$
. Let
![]() $\{ d_1,\ldots ,d_n\}$
generate F,
$\{ d_1,\ldots ,d_n\}$
generate F,
![]() $\sigma _1, \ldots ,\sigma _n \in \mathcal {F}_{\bar {\nu },\lambda }$
and for all
$\sigma _1, \ldots ,\sigma _n \in \mathcal {F}_{\bar {\nu },\lambda }$
and for all
![]() $i\leq n$
,
$i\leq n$
,
![]() $c_i\in D$
be such that
$c_i\in D$
be such that
By condition P4 in the definition of the simplified morass, there is
![]() $N\in \omega $
,
$N\in \omega $
,
![]() $g\in \mathcal {F}_{\nu _{\bar {\alpha }}+N, \lambda }$
and
$g\in \mathcal {F}_{\nu _{\bar {\alpha }}+N, \lambda }$
and
![]() $f_1,\ldots ,f_n \in \mathcal {F}_{\nu _{\bar {\alpha }}, \nu _{\bar {\alpha }}+N}$
such that, for
$f_1,\ldots ,f_n \in \mathcal {F}_{\nu _{\bar {\alpha }}, \nu _{\bar {\alpha }}+N}$
such that, for
![]() $i\leq n$
,
$i\leq n$
,
For each
![]() $m<n$
, let
$m<n$
, let
![]() $h_m$
be the splitting function of
$h_m$
be the splitting function of
![]() $\mathcal {F}_{\bar {\nu }+m, \bar {\nu }+m+1}$
. By Lemma 6.5,
$\mathcal {F}_{\bar {\nu }+m, \bar {\nu }+m+1}$
. By Lemma 6.5,
![]() $\phi \cup h_1[\phi ]$
may be extended to an extendible
$\phi \cup h_1[\phi ]$
may be extended to an extendible
![]() $\mathbb R$
-monomorphism. Furthermore this ring monomorphism may be extended by the splitting functions
$\mathbb R$
-monomorphism. Furthermore this ring monomorphism may be extended by the splitting functions
![]() $h_2$
through
$h_2$
through
![]() $h_m$
. Let
$h_m$
. Let
![]() $\psi $
be the function on
$\psi $
be the function on
![]() $\bigcup _{\sigma \in \mathcal {F}_{\bar {\nu } \lambda }} \sigma [D]$
resulting after the n splits. Then
$\bigcup _{\sigma \in \mathcal {F}_{\bar {\nu } \lambda }} \sigma [D]$
resulting after the n splits. Then
![]() $\psi $
is extendible and
$\psi $
is extendible and
![]() $f_i(c_i)$
is in the domain of
$f_i(c_i)$
is in the domain of
![]() $\psi $
for all
$\psi $
for all
![]() $i\leq n$
. Therefore
$i\leq n$
. Therefore
![]() $g\circ \psi $
is an
$g\circ \psi $
is an
![]() $\mathbb R$
-linear order monomorphism and is the restriction of
$\mathbb R$
-linear order monomorphism and is the restriction of
![]() $\phi ^*$
to a ring containing F. Thus
$\phi ^*$
to a ring containing F. Thus
is a well-defined extendible
![]() $\mathbb R$
-monomorphism of
$\mathbb R$
-monomorphism of
![]() $D^*_{\lambda }$
.
$D^*_{\lambda }$
.
By an inductive argument on
![]() $\nu $
, invoking condition P2, and the results above at limits and Lemma 6.5 at successor ordinals, it is straightforward to show that
$\nu $
, invoking condition P2, and the results above at limits and Lemma 6.5 at successor ordinals, it is straightforward to show that
![]() $\bigcup _{\sigma \in \mathcal {F}_{\lambda , \nu }} \sigma [\phi ^*_{\lambda }]$
has a unique extension to an extendible
$\bigcup _{\sigma \in \mathcal {F}_{\lambda , \nu }} \sigma [\phi ^*_{\lambda }]$
has a unique extension to an extendible
![]() $\mathbb R$
-monomorphism of the ring generated by
$\mathbb R$
-monomorphism of the ring generated by
![]() $\bigcup _{\sigma \in \mathcal {F}_{\lambda , \nu }} \sigma [D^*_{\lambda }]$
.
$\bigcup _{\sigma \in \mathcal {F}_{\lambda , \nu }} \sigma [D^*_{\lambda }]$
.
6.2. Extensions by a specified element
Because ordered subrings of real closed fields have unique extensions to real closed subfields, we will be able to restrict our attention to extending domains of extendible functions by algebraically independent elements. We wish to prove analogues of Johnson’s theorems that extendible functions may be extended by a specified element. Throughout the arguments of this section, we will commonly use x to represent an element of F, and also to represent the variable in the power series representations of member of
![]() $\mathcal {E}$
. Presumably the context will make clear which use is intended.
$\mathcal {E}$
. Presumably the context will make clear which use is intended.
If X is a subring of a ring R and
![]() $Z\subset R$
, we let
$Z\subset R$
, we let
![]() $X[Z]$
be the subring of R generated by
$X[Z]$
be the subring of R generated by
![]() $X\cup Z$
.
$X\cup Z$
.
Lemma 6.7. Suppose
![]() $\phi :X\to Y$
is an extendible function,
$\phi :X\to Y$
is an extendible function,
![]() $r\in \mathbb R$
and r is transcendental over X. Then there is an extension of
$r\in \mathbb R$
and r is transcendental over X. Then there is an extension of
![]() $\phi $
to an extendible function,
$\phi $
to an extendible function,
![]() $\psi :X[r] \to Y[r]$
.
$\psi :X[r] \to Y[r]$
.
Proof Since
![]() $\phi $
is extendible, X is full and for all
$\phi $
is extendible, X is full and for all
![]() $r_0\in \mathbb R \cap X$
,
$r_0\in \mathbb R \cap X$
,
![]() $\phi (r_0)=r_0\cdot x^e$
(where e is the group identity of
$\phi (r_0)=r_0\cdot x^e$
(where e is the group identity of
![]() $\mathcal {E}$
). Then the real closure of X is full and the set of real numbers of the real-closure of X is the real closure of
$\mathcal {E}$
). Then the real closure of X is full and the set of real numbers of the real-closure of X is the real closure of
![]() $\mathbb R\cap X$
. Let
$\mathbb R\cap X$
. Let
![]() $X^*$
be the real closure of X and
$X^*$
be the real closure of X and
![]() $\phi ^*:X^* \to \mathcal {E}$
be the unique
$\phi ^*:X^* \to \mathcal {E}$
be the unique
![]() $\mathbb R$
-monomorphism extending
$\mathbb R$
-monomorphism extending
![]() $\phi $
to
$\phi $
to
![]() $X^*$
. Then for all
$X^*$
. Then for all
![]() $r_0\in \mathbb R \cap X^*$
,
$r_0\in \mathbb R \cap X^*$
,
![]() $\phi (r_0)=r_0\cdot x^e$
. If r is transcendental over X, then r is transcendental over
$\phi (r_0)=r_0\cdot x^e$
. If r is transcendental over X, then r is transcendental over
![]() $X^*$
. The real closure of Y and
$X^*$
. The real closure of Y and
![]() $X^*$
contain precisely the same real numbers and are full. By Lemma 3.4, there is an
$X^*$
contain precisely the same real numbers and are full. By Lemma 3.4, there is an
![]() $\mathbb R$
-monomorphic extension of
$\mathbb R$
-monomorphic extension of
![]() $\phi ^*$
,
$\phi ^*$
,
![]() $\psi ^*$
, to the real closure of the field generated by
$\psi ^*$
, to the real closure of the field generated by
![]() $X[r]$
. Let
$X[r]$
. Let
![]() $\psi =\psi ^*\upharpoonright _{X[r]}$
. Then
$\psi =\psi ^*\upharpoonright _{X[r]}$
. Then
![]() $\psi $
is extendible.
$\psi $
is extendible.
Lemma 6.8. Suppose
![]() $\phi :X\to Y$
is an extendible function and
$\phi :X\to Y$
is an extendible function and
![]() $x^* \in {\mathbb R}^{\omega }/U$
is transcendental over X. Then there is
$x^* \in {\mathbb R}^{\omega }/U$
is transcendental over X. Then there is
![]() $\bar {X}\supseteq X$
, with
$\bar {X}\supseteq X$
, with
![]() $x^*\in {\mathbb R}^{\omega }/U$
in the real closure of
$x^*\in {\mathbb R}^{\omega }/U$
in the real closure of
![]() $\bar {X}$
, and extendible
$\bar {X}$
, and extendible
![]() $\psi :\bar {X} \to \mathcal {E}$
extending
$\psi :\bar {X} \to \mathcal {E}$
extending
![]() $\phi $
.
$\phi $
.
Proof If
![]() $x^*\in \mathbb R$
, then apply Lemma 6.7. Assume
$x^*\in \mathbb R$
, then apply Lemma 6.7. Assume
![]() $x^*\notin \mathbb R$
. If
$x^*\notin \mathbb R$
. If
![]() $x^*$
is not infinitesimal, then
$x^*$
is not infinitesimal, then
![]() $x^*=r+\delta $
, where
$x^*=r+\delta $
, where
![]() $r\in \mathbb R$
and
$r\in \mathbb R$
and
![]() $\delta $
is infinitesimal. If
$\delta $
is infinitesimal. If
![]() $r\notin X$
, then we may extend
$r\notin X$
, then we may extend
![]() $\phi $
to an extendible function,
$\phi $
to an extendible function,
![]() $\phi ^*:X[r]\to Y[r]$
. We consider the case in which
$\phi ^*:X[r]\to Y[r]$
. We consider the case in which
![]() $r\in X$
. Since X is extendible,
$r\in X$
. Since X is extendible,
![]() $x^*-r=\delta \in X$
. Therefore we may assume that
$x^*-r=\delta \in X$
. Therefore we may assume that
![]() $x^*$
is infinitesimal. Let
$x^*$
is infinitesimal. Let
![]() $(l,u)$
be the gap formed by
$(l,u)$
be the gap formed by
![]() $x^*$
in X,
$x^*$
in X,
![]() $L=\phi [l]$
and
$L=\phi [l]$
and
![]() $U=\phi [u]$
. The Esterle algebra is an
$U=\phi [u]$
. The Esterle algebra is an
![]() $\eta _1$
-ordering, so there is
$\eta _1$
-ordering, so there is
![]() $y\in \mathcal {E}$
that witnesses the gap
$y\in \mathcal {E}$
that witnesses the gap
![]() $(L,U)$
. By application of Johnson’s Lemma 3.5, there is
$(L,U)$
. By application of Johnson’s Lemma 3.5, there is
![]() $y\in \mathcal {E}$
that witnesses the gap
$y\in \mathcal {E}$
that witnesses the gap
![]() $(L,U)$
and such that the real closure of the field extending
$(L,U)$
and such that the real closure of the field extending
![]() $Y[y]$
is full. Although the existence of such an element can be used to advantage, the element y may fail to have some of the properties we require for a morass construction.
$Y[y]$
is full. Although the existence of such an element can be used to advantage, the element y may fail to have some of the properties we require for a morass construction.
Let
![]() $\mu < \omega _1$
be the strict level of
$\mu < \omega _1$
be the strict level of
![]() $x^*$
. We seek an element of
$x^*$
. We seek an element of
![]() $\mathcal {E}$
that witnesses the gap
$\mathcal {E}$
that witnesses the gap
![]() $(L,U)$
and is a candidate for the image of
$(L,U)$
and is a candidate for the image of
![]() $x^*$
. The candidate must have strict level
$x^*$
. The candidate must have strict level
![]() $\mu $
and be transcendental over Y, among other requirements. The Esterle algebra is level dense and upward level dense, so by Lemma 4.5 of [Reference Dumas3] there is
$\mu $
and be transcendental over Y, among other requirements. The Esterle algebra is level dense and upward level dense, so by Lemma 4.5 of [Reference Dumas3] there is
![]() $y\in \mathcal {E}$
, with the strict level
$y\in \mathcal {E}$
, with the strict level
![]() $\mu $
, such that for all
$\mu $
, such that for all
![]() $z\in X$
,
$z\in X$
,
Let Z be the countable set of real coefficients appearing in power series of
![]() $Y[y]$
. Then by iterated applications of Lemma 6.7 there is an extendible extension of
$Y[y]$
. Then by iterated applications of Lemma 6.7 there is an extendible extension of
![]() $\phi $
to
$\phi $
to
![]() $\phi ^*: X[Z] \to Y[Z]$
. Let
$\phi ^*: X[Z] \to Y[Z]$
. Let
![]() $X^*=X[Z]$
and
$X^*=X[Z]$
and
![]() $Y^*=Y[Z]$
. If
$Y^*=Y[Z]$
. If
![]() $x^*$
is in the real-closure of
$x^*$
is in the real-closure of
![]() $X^*$
, let
$X^*$
, let
![]() $\bar {X}=X^*$
and
$\bar {X}=X^*$
and
![]() $\psi :\bar {X} \to \mathcal {E}$
be the unique ring monomorphism extending
$\psi :\bar {X} \to \mathcal {E}$
be the unique ring monomorphism extending
![]() $\phi ^*$
. Then
$\phi ^*$
. Then
![]() $\psi $
is extendible. So we assume that
$\psi $
is extendible. So we assume that
![]() $x^*$
is transcendental over
$x^*$
is transcendental over
![]() $X^*$
.
$X^*$
.
It is possible that
![]() $Y^*[y]$
is not closed under partial sums. We show that there is
$Y^*[y]$
is not closed under partial sums. We show that there is
![]() $y^*\in \mathcal {E}$
that witnesses
$y^*\in \mathcal {E}$
that witnesses
![]() $(L,U)$
and such that
$(L,U)$
and such that
![]() $Y^*[y^*]$
is full and closed under partial sums.
$Y^*[y^*]$
is full and closed under partial sums.
Case 1: There is a largest partial sum of y that is a member of
![]() $Y^*$
.
$Y^*$
.
We include in this case that the first term of y is a monomial not in
![]() $Y^*$
. Let t be the largest partial sum of y that is also a member of
$Y^*$
. Let t be the largest partial sum of y that is also a member of
![]() $Y^*$
and
$Y^*$
and
![]() $s=(\phi ^*)^{-1}(t)\in X^*$
. Then
$s=(\phi ^*)^{-1}(t)\in X^*$
. Then
![]() $y-t \notin Y^*$
and
$y-t \notin Y^*$
and
![]() $x^*-s\notin X^*$
. We shift our attention to the gap formed by
$x^*-s\notin X^*$
. We shift our attention to the gap formed by
![]() $x^*-s$
in
$x^*-s$
in
![]() $X^*$
. Then for all
$X^*$
. Then for all
![]() $z\in X^*$
$z\in X^*$
If
![]() $x^*-s$
were algebraic over
$x^*-s$
were algebraic over
![]() $X^*$
, then it would be in the real-closure of
$X^*$
, then it would be in the real-closure of
![]() $X^*$
. Since
$X^*$
. Since
![]() $X^*$
is a ring, and
$X^*$
is a ring, and
![]() $s\in X^*$
, this would imply that
$s\in X^*$
, this would imply that
![]() $x^*$
is in the real-closure of
$x^*$
is in the real-closure of
![]() $X^*$
, contrary to assumption that
$X^*$
, contrary to assumption that
![]() $x^*$
is transcendental over
$x^*$
is transcendental over
![]() $X^*$
. Therefore
$X^*$
. Therefore
![]() $x^*-s$
is transcendental over
$x^*-s$
is transcendental over
![]() $X^*$
. We claim that
$X^*$
. We claim that
![]() $x^*-s$
must have an Archimedean valuation distinct from the Archimedean valuations of members of
$x^*-s$
must have an Archimedean valuation distinct from the Archimedean valuations of members of
![]() $X^*$
. Let
$X^*$
. Let
![]() $y-t \in \mathcal {E}$
have leading term
$y-t \in \mathcal {E}$
have leading term
![]() $\alpha x^a$
. Then
$\alpha x^a$
. Then
![]() $\alpha \in Z \subseteq Y^*$
. If
$\alpha \in Z \subseteq Y^*$
. If
![]() $x^a$
were in the range of
$x^a$
were in the range of
![]() $\phi ^*$
, then
$\phi ^*$
, then
![]() $t+ \alpha x^a \in Y^*$
would be a partial sum of y, contrary to assumption. So a must be a valuation distinct from the valuations of
$t+ \alpha x^a \in Y^*$
would be a partial sum of y, contrary to assumption. So a must be a valuation distinct from the valuations of
![]() $Y^*$
. Therefore
$Y^*$
. Therefore
![]() $x^*-s$
must have a valuation distinct from the valuations of members of
$x^*-s$
must have a valuation distinct from the valuations of members of
![]() $X^*$
.
$X^*$
.
Let
![]() $(L^*,U^*)$
be the gap formed by
$(L^*,U^*)$
be the gap formed by
![]() $y-t$
in
$y-t$
in
![]() $Y^*$
. If
$Y^*$
. If
![]() $\alpha>0$
, then it is sufficient to show that there is
$\alpha>0$
, then it is sufficient to show that there is
![]() $c\in G_{\omega _1}$
such that
$c\in G_{\omega _1}$
such that
![]() $x^c$
has strict level
$x^c$
has strict level
![]() $\mu $
and witnesses the gap
$\mu $
and witnesses the gap
![]() $(L^*,U^*)$
. The case
$(L^*,U^*)$
. The case
![]() $\alpha <0$
is altogether similar. Let
$\alpha <0$
is altogether similar. Let
![]() $y_0=x^a$
. The strict level of
$y_0=x^a$
. The strict level of
![]() $y_0$
equals the strict level of
$y_0$
equals the strict level of
![]() $a\in G_{\omega _1}$
. It is straightforward to see that there is
$a\in G_{\omega _1}$
. It is straightforward to see that there is
![]() $b\in G_{\omega _1}$
such that:
$b\in G_{\omega _1}$
such that:
-
1. b is positive.
-
2. Any element of the support of b is greater than any element of the support of any exponent occurring in any power series of
 $Y^*$
.
$Y^*$
. -
3. b has strict level
 $\mu $
.
$\mu $
.
The exponent
![]() $b\in G_{\omega _1}$
is greater than
$b\in G_{\omega _1}$
is greater than
![]() $0$
but less than any positive exponent in
$0$
but less than any positive exponent in
![]() $Y^*$
. Furthermore, b is greater than the constant
$Y^*$
. Furthermore, b is greater than the constant
![]() $0$
function, the additive identity of
$0$
function, the additive identity of
![]() $G_{\omega _1}$
(and the valuation of standard reals in
$G_{\omega _1}$
(and the valuation of standard reals in
![]() $\mathcal {E}$
). However b is greater than any positive valuation occurring in
$\mathcal {E}$
). However b is greater than any positive valuation occurring in
![]() $Y^*$
. Consequently
$Y^*$
. Consequently
![]() $x^b$
is less than any infinitesimal of
$x^b$
is less than any infinitesimal of
![]() $Y^*$
. Let
$Y^*$
. Let
![]() $c=a+b$
. Then,
$c=a+b$
. Then,
-
1.
 $x^{c}$
witnesses the gap
$x^{c}$
witnesses the gap
 $(L,U)$
.
$(L,U)$
. -
2.
 $x^{c}$
is transcendental over X.
$x^{c}$
is transcendental over X. -
3.
 $x^{c}$
has strict level
$x^{c}$
has strict level
 $\mu $
.
$\mu $
. -
4. The subring of
 $\mathcal {E}$
generated by
$\mathcal {E}$
generated by
 $Y^*\cup \{ x^{c}\}$
is full and is closed under partial sums.
$Y^*\cup \{ x^{c}\}$
is full and is closed under partial sums.
Let
![]() $\psi :X^*[x^*]\to Y^*[x^{c}]$
be the unique
$\psi :X^*[x^*]\to Y^*[x^{c}]$
be the unique
![]() $\mathbb R$
-monomorphism extending
$\mathbb R$
-monomorphism extending
![]() $\phi $
such that
$\phi $
such that
Then
![]() $\psi $
is extendible.
$\psi $
is extendible.
Case 2: There is no largest partial sum of y that is a member of
![]() $Y^*$
.
$Y^*$
.
Let D be the well-ordering by ascending valuation of the exponents of y. Then D has a countable order-type. Let
![]() $D'$
be the smallest initial segment of D such that
$D'$
be the smallest initial segment of D such that
![]() $y\upharpoonright _{D'}$
(the partial sum of y with exponents from
$y\upharpoonright _{D'}$
(the partial sum of y with exponents from
![]() $D'$
) is not a member of Y. Let
$D'$
) is not a member of Y. Let
![]() $y'=y\upharpoonright _{D'}$
. Then
$y'=y\upharpoonright _{D'}$
. Then
![]() $y'$
witnesses the gap
$y'$
witnesses the gap
![]() $(L,U)$
. The strict level of
$(L,U)$
. The strict level of
![]() $y'$
is no greater than
$y'$
is no greater than
![]() $\mu $
. If the strict level of
$\mu $
. If the strict level of
![]() $y'$
equals
$y'$
equals
![]() $\mu $
, let
$\mu $
, let
![]() $\psi :X^*[x^*]\to Y^*[y']$
be the unique
$\psi :X^*[x^*]\to Y^*[y']$
be the unique
![]() $\mathbb R$
-monomorphism extending
$\mathbb R$
-monomorphism extending
![]() $\phi $
such that
$\phi $
such that
Otherwise, let
![]() $a\in G_{\omega _1}$
be an exponent of
$a\in G_{\omega _1}$
be an exponent of
![]() $\mathcal {E}$
that has strict level
$\mathcal {E}$
that has strict level
![]() $\mu $
and is greater than all exponents occurring in
$\mu $
and is greater than all exponents occurring in
![]() $Y^*$
. Let
$Y^*$
. Let
Then
![]() $y^*$
witnesses the gap
$y^*$
witnesses the gap
![]() $(L,U)$
and has strict level
$(L,U)$
and has strict level
![]() $\mu $
. Let
$\mu $
. Let
![]() $\psi ^*:X^*[x^*]\to Y^*[y^*]$
be the unique
$\psi ^*:X^*[x^*]\to Y^*[y^*]$
be the unique
![]() $\mathbb R$
-monomorphism extending
$\mathbb R$
-monomorphism extending
![]() $\phi $
such that
$\phi $
such that
Then
![]() $\psi ^*$
satisfies the conditions for an extendible function, except closure of the range of
$\psi ^*$
satisfies the conditions for an extendible function, except closure of the range of
![]() $\psi ^*$
under partial sums. In particular
$\psi ^*$
under partial sums. In particular
![]() $y'$
and
$y'$
and
![]() $x^a$
are not in the range of
$x^a$
are not in the range of
![]() $\psi ^*$
. Let
$\psi ^*$
. Let
![]() $(L^*,U^*)$
be the gap formed by
$(L^*,U^*)$
be the gap formed by
![]() $x^a$
in
$x^a$
in
![]() $Y^*[y^*]$
. We observe that
$Y^*[y^*]$
. We observe that
![]() $x^a$
is infinitesimal with respect to every member of
$x^a$
is infinitesimal with respect to every member of
![]() $Y^*[y^*]$
. Since F is level dense and upward level dense, there is a positive element of F,
$Y^*[y^*]$
. Since F is level dense and upward level dense, there is a positive element of F,
![]() $\epsilon $
, with strict level
$\epsilon $
, with strict level
![]() $\mu $
that is infinitesimal with respect to all elements of
$\mu $
that is infinitesimal with respect to all elements of
![]() $X^*[x^*]$
. Therefore there is an
$X^*[x^*]$
. Therefore there is an
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\psi :X^*[x^*,\epsilon ]\to Y^*[y^*, x^a]$
, extending
$\psi :X^*[x^*,\epsilon ]\to Y^*[y^*, x^a]$
, extending
![]() $\psi ^*$
and such that
$\psi ^*$
and such that
We note that
![]() $y'\in Y^*[y^*,x^a]$
and
$y'\in Y^*[y^*,x^a]$
and
Then
![]() $Y^*[y', x^a]$
is closed under coefficients and partial sums, so
$Y^*[y', x^a]$
is closed under coefficients and partial sums, so
![]() $\psi $
is extendible.
$\psi $
is extendible.
These results permit a simplification of the construction. Given an extendible
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi :D\to \mathcal {E}$
, we may extend
$\phi :D\to \mathcal {E}$
, we may extend
![]() $\phi $
to an
$\phi $
to an
![]() $\mathbb R$
-monomorphism of
$\mathbb R$
-monomorphism of
![]() $D[\mathbb R]$
, and then extend by algebraically independent infinitesimals.
$D[\mathbb R]$
, and then extend by algebraically independent infinitesimals.
7. An
 $\mathbb R$
-monomorphism from the finite elements of
$\mathbb R$
-monomorphism from the finite elements of
 ${\mathbb R}^{\omega }/U$
into the Esterle algebra
${\mathbb R}^{\omega }/U$
into the Esterle algebra
In the Cohen extension adding
![]() $\aleph _2$
generic reals, we construct a level
$\aleph _2$
generic reals, we construct a level
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi $
, from the finite elements of a standard ultrapower of
$\phi $
, from the finite elements of a standard ultrapower of
![]() $\mathbb R$
into
$\mathbb R$
into
![]() $\mathcal {E}$
. This construction differs significantly from the construction of Woodin [Reference Woodin15]. The construction of Woodin relies on the fact that in the Cohen extension by
$\mathcal {E}$
. This construction differs significantly from the construction of Woodin [Reference Woodin15]. The construction of Woodin relies on the fact that in the Cohen extension by
![]() $\aleph _2$
-generic reals of a model of
$\aleph _2$
-generic reals of a model of
![]() $ZFC + CH$
, any cut of
$ZFC + CH$
, any cut of
![]() $\mathcal {E}$
has a countable, cofinal subcut. As Woodin observes, this argument is not generalizable to models of ZFC with higher powers of the continuum. Our construction yields a monomorphism that is level, and therefore is sensitive to the “complexity” (with respect to the index of Cohen reals) of the elements of the ultrapower and the Esterle algebra. Consequently, for any
$\mathcal {E}$
has a countable, cofinal subcut. As Woodin observes, this argument is not generalizable to models of ZFC with higher powers of the continuum. Our construction yields a monomorphism that is level, and therefore is sensitive to the “complexity” (with respect to the index of Cohen reals) of the elements of the ultrapower and the Esterle algebra. Consequently, for any
![]() $\mu \leq \omega _2$
,
$\mu \leq \omega _2$
,
![]() $\phi \cap M[G(\mu )]$
is an
$\phi \cap M[G(\mu )]$
is an
![]() $\mathbb R$
-monomorphism of
$\mathbb R$
-monomorphism of
![]() ${\mathbb R}^{\omega }/U \cap M[G(\mu )]$
to
${\mathbb R}^{\omega }/U \cap M[G(\mu )]$
to
![]() $\mathcal {E} \cap M[G(\mu )]$
.
$\mathcal {E} \cap M[G(\mu )]$
.
Theorem 7.1. Suppose M is a transitive model of ZFC+CH containing a simplified
![]() $(\omega _1,1)$
-morass and P is the poset adding generic reals indexed by ordinals less than
$(\omega _1,1)$
-morass and P is the poset adding generic reals indexed by ordinals less than
![]() $\omega _2$
. Let G be P-generic over M,
$\omega _2$
. Let G be P-generic over M,
![]() $F\in M[G]$
be the ring of finite elements of a standard ultrapower of
$F\in M[G]$
be the ring of finite elements of a standard ultrapower of
![]() $\mathbb R$
over
$\mathbb R$
over
![]() $\omega $
, and
$\omega $
, and
![]() $\mathcal {E} \in M[G]$
be the Esterle algebra computed in
$\mathcal {E} \in M[G]$
be the Esterle algebra computed in
![]() $M[G]$
. Then there is a level
$M[G]$
. Then there is a level
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi :F\to \mathcal {E}$
.
$\phi :F\to \mathcal {E}$
.
Proof For each
![]() $\nu $
,
$\nu $
,
![]() $\alpha \leq \omega _1$
, let
$\alpha \leq \omega _1$
, let
![]() $G_{\nu }$
be the factor of G adding generic reals indexed by
$G_{\nu }$
be the factor of G adding generic reals indexed by
![]() $\theta _{\nu }$
(the ordinal associated with the vertex
$\theta _{\nu }$
(the ordinal associated with the vertex
![]() $\nu $
in the morass), and
$\nu $
in the morass), and
![]() $G(\alpha )$
be the factor of G adding generic reals indexed by
$G(\alpha )$
be the factor of G adding generic reals indexed by
![]() $\alpha $
. Let
$\alpha $
. Let
In Lemma 3.3 of [Reference Dumas4], it is proved that, given a simplified
![]() $(\omega _2,1)$
-morass, any countable subset of
$(\omega _2,1)$
-morass, any countable subset of
![]() $\omega _3$
is in the image of a single morass map from a vertex below
$\omega _3$
is in the image of a single morass map from a vertex below
![]() $\omega _2$
. The proof does not depend on
$\omega _2$
. The proof does not depend on
![]() $\omega _2$
and generalizes to simplified
$\omega _2$
and generalizes to simplified
![]() $(\omega _n,1)$
-morasses. Since every element of F has countable support, we observe that
$(\omega _n,1)$
-morasses. Since every element of F has countable support, we observe that
![]() $F(\omega _1)=\bigcup _{\nu <\omega _1} F_{\nu }$
and, since any countable subset of
$F(\omega _1)=\bigcup _{\nu <\omega _1} F_{\nu }$
and, since any countable subset of
![]() $\omega _2$
is a subset of the range of a morass map from
$\omega _2$
is a subset of the range of a morass map from ![]() (
(
![]() $\nu <\omega _1$
),
$\nu <\omega _1$
), ![]() . Any commitment to the construction entails uncountably many subsequent commitments by way of commutativity with morass maps. Terms for members of F are in the image of morass maps from lower vertices of the morass.
. Any commitment to the construction entails uncountably many subsequent commitments by way of commutativity with morass maps. Terms for members of F are in the image of morass maps from lower vertices of the morass.
Definition 7.2 (Morass generator)
If
![]() $\beta < \alpha \leq \omega _1$
,
$\beta < \alpha \leq \omega _1$
,
![]() $\sigma \in \cal {F}_{\beta \alpha }$
,
$\sigma \in \cal {F}_{\beta \alpha }$
,
![]() $x\in M^{P_{\beta }}$
, and
$x\in M^{P_{\beta }}$
, and
![]() $y=\sigma (x)\in M^{P_{\alpha }}$
, then x is a morass ancestor of y and y is a morass descendant of x. If x has no morass ancestors, then we say x is a morass generator.
$y=\sigma (x)\in M^{P_{\alpha }}$
, then x is a morass ancestor of y and y is a morass descendant of x. If x has no morass ancestors, then we say x is a morass generator.
Let X be a a set of strict terms for members of
![]() $F(\omega _1)$
that is forced to be a maximal algebraically independent subset of morass-generators. We may assume that every member of X has Archimedean valuation 0 (is in
$F(\omega _1)$
that is forced to be a maximal algebraically independent subset of morass-generators. We may assume that every member of X has Archimedean valuation 0 (is in
![]() $\mathbb R$
) or is infinitesimal. We note that the morass-closure of X beneath
$\mathbb R$
) or is infinitesimal. We note that the morass-closure of X beneath
![]() $\omega _1$
contains a transcendental basis for F. Although the morass-closure of X has cardinality
$\omega _1$
contains a transcendental basis for F. Although the morass-closure of X has cardinality
![]() $\aleph _2$
in
$\aleph _2$
in
![]() $M[G]$
, X has cardinality
$M[G]$
, X has cardinality
![]() $\aleph _1$
.
$\aleph _1$
.
Let
![]() $\langle x_{\alpha } \mid \alpha <\omega _1 \rangle $
be a well-ordering of X. Let
$\langle x_{\alpha } \mid \alpha <\omega _1 \rangle $
be a well-ordering of X. Let
![]() $\langle \nu _{\alpha } \mid \alpha <\omega _1 \rangle $
be a weakly ascending transfinite sequence of countable ordinals such that
$\langle \nu _{\alpha } \mid \alpha <\omega _1 \rangle $
be a weakly ascending transfinite sequence of countable ordinals such that
![]() $x_{\alpha } \in M[G_{\nu _{\alpha }}]$
. We will construct by transfinite recursion (on
$x_{\alpha } \in M[G_{\nu _{\alpha }}]$
. We will construct by transfinite recursion (on
![]() $\omega _1$
) an ascending sequence of functions (ordered by inclusion),
$\omega _1$
) an ascending sequence of functions (ordered by inclusion),
![]() $\langle \phi _{\alpha }:D_{\alpha } \to \mathcal {E}_{\alpha } \mid \alpha <\omega _1 \rangle $
, such that for all
$\langle \phi _{\alpha }:D_{\alpha } \to \mathcal {E}_{\alpha } \mid \alpha <\omega _1 \rangle $
, such that for all
![]() $\alpha <\omega _1,$
$\alpha <\omega _1,$
-
1.
 $x_\alpha \in D_{\alpha }$
.
$x_\alpha \in D_{\alpha }$
. -
2.
 $D_{\alpha }$
is morass-closed beneath
$D_{\alpha }$
is morass-closed beneath
 $\nu _{\alpha }$
.
$\nu _{\alpha }$
. -
3.
 $\phi _{\alpha }:D_{\alpha }\to E_{\alpha }$
is extendible.
$\phi _{\alpha }:D_{\alpha }\to E_{\alpha }$
is extendible.
At each stage of the construction,
![]() $\alpha <\omega _1$
, the domain of
$\alpha <\omega _1$
, the domain of
![]() $\phi _{\alpha }$
extends
$\phi _{\alpha }$
extends ![]() , so that it contains
, so that it contains
![]() $x_{\alpha }$
and is morass-closed beneath
$x_{\alpha }$
and is morass-closed beneath
![]() $\nu _{\alpha }$
, and
$\nu _{\alpha }$
, and
![]() $\phi _{\alpha }$
is extendible.
$\phi _{\alpha }$
is extendible.
Case:
![]() $\alpha =0$
.
$\alpha =0$
.
Let
![]() $x^*=x_0$
have strict level
$x^*=x_0$
have strict level
![]() $\mu \leq \nu _0$
,
$\mu \leq \nu _0$
,
![]() $\nu $
be the least ordinal such that
$\nu $
be the least ordinal such that
![]() $\mu \in \theta _{\nu }$
, and
$\mu \in \theta _{\nu }$
, and
![]() $X_0=\langle x_{0,n} \rangle $
be a maximal algebraically independent sequence of morass descendents of
$X_0=\langle x_{0,n} \rangle $
be a maximal algebraically independent sequence of morass descendents of
![]() $x^* \in M[G_{\nu _0}]$
. Then
$x^* \in M[G_{\nu _0}]$
. Then
![]() $X_0$
is countable, and possibly finite. If
$X_0$
is countable, and possibly finite. If
![]() $\nu \leq \eta <\nu _{0}$
and
$\nu \leq \eta <\nu _{0}$
and
![]() $x'\in M[G_{\eta }]$
is a morass-descendent of
$x'\in M[G_{\eta }]$
is a morass-descendent of
![]() $x^*$
, then since
$x^*$
, then since ![]() ,
,
![]() $x'$
is a morass-descendent of
$x'$
is a morass-descendent of
![]() $x^*$
in
$x^*$
in
![]() $M[G_{\nu _0}]$
, and
$M[G_{\nu _0}]$
, and
![]() $x'\in X_0$
. Since
$x'\in X_0$
. Since
![]() $x^*$
has strict level
$x^*$
has strict level
![]() $\mu \in \theta _{\nu }$
, for
$\mu \in \theta _{\nu }$
, for ![]() , the strict level of
, the strict level of
![]() $\sigma (x^*)=\sigma (\mu )$
. If
$\sigma (x^*)=\sigma (\mu )$
. If
![]() $y, z\in X_0$
both have the same strict level, then morass functions in
$y, z\in X_0$
both have the same strict level, then morass functions in ![]() that witness that y and z are morass descendents of
that witness that y and z are morass descendents of
![]() $x^*$
, must agree up to
$x^*$
, must agree up to
![]() $\mu \leq \theta _{\nu }$
, and
$\mu \leq \theta _{\nu }$
, and
![]() $y=z$
. Therefore all members of
$y=z$
. Therefore all members of
![]() $X_0$
have pairwise distinct strict levels.
$X_0$
have pairwise distinct strict levels.
We construct a sequence of
![]() $\mathbb R$
-monomorphisms,
$\mathbb R$
-monomorphisms,
![]() $\langle \phi _{0,n} \rangle $
, with the order-type of
$\langle \phi _{0,n} \rangle $
, with the order-type of
![]() $X_0$
, such that, for all n less than the order-type of
$X_0$
, such that, for all n less than the order-type of
![]() $X_0$
,
$X_0$
,
-
1.
 $D_{0,0}=\mathbb {Q}[x_{0,0}]$
.
$D_{0,0}=\mathbb {Q}[x_{0,0}]$
. -
2.
 $D_{0,n}[x_{0, n+1}]\subseteq D_{0, n+1}$
.
$D_{0,n}[x_{0, n+1}]\subseteq D_{0, n+1}$
. -
3.
 $\phi _{0,n}:D_{0,n} \to \mathcal {E} \in M[G_{\nu _0}]$
.
$\phi _{0,n}:D_{0,n} \to \mathcal {E} \in M[G_{\nu _0}]$
. -
4. For all
 $m<n$
,
$m<n$
,
 $\phi _{0,m}\subseteq \phi _{0,n}$
.
$\phi _{0,m}\subseteq \phi _{0,n}$
. -
5.
 $\phi _{0,n}$
is extendible.
$\phi _{0,n}$
is extendible.
Let
![]() $z=x_{0,0}$
, and
$z=x_{0,0}$
, and
![]() $\mu $
be the strict level of z. We may assume that z is positive. If
$\mu $
be the strict level of z. We may assume that z is positive. If
![]() $z\in \mathbb R$
, let
$z\in \mathbb R$
, let
![]() $D_{0,0}=\mathbb {Q}[z]$
and
$D_{0,0}=\mathbb {Q}[z]$
and
![]() $\phi _{0,0}:D_{0,0}\to \mathcal {E}$
be the identity restricted to
$\phi _{0,0}:D_{0,0}\to \mathcal {E}$
be the identity restricted to
![]() $D_{0,0}$
.
$D_{0,0}$
.
If z is infinitesimal, let
![]() $a\in G_{\omega _1}$
be positive and have strict level
$a\in G_{\omega _1}$
be positive and have strict level
![]() $\mu $
, and
$\mu $
, and
Let
![]() $D_{0,0}=\mathbb {Q}[z]$
and
$D_{0,0}=\mathbb {Q}[z]$
and
![]() $\phi _{0,0}:D_{0,0} \to \mathcal {E}$
be the
$\phi _{0,0}:D_{0,0} \to \mathcal {E}$
be the
![]() $\mathbb R$
-linear ring monomorphism such that
$\mathbb R$
-linear ring monomorphism such that
Let
![]() $N\in \omega $
and assume that
$N\in \omega $
and assume that
![]() $\langle \phi _{0,n} \mid n\leq N \rangle $
satisfies conditions 1–5 above (below
$\langle \phi _{0,n} \mid n\leq N \rangle $
satisfies conditions 1–5 above (below
![]() $N+1$
). If
$N+1$
). If
![]() $X_0$
has length
$X_0$
has length
![]() $N+1$
, Then
$N+1$
, Then
![]() $D_0=D_{0,N}$
and
$D_0=D_{0,N}$
and
![]() $\phi _0=\phi _{0,N}$
. Otherwise
$\phi _0=\phi _{0,N}$
. Otherwise
![]() $\phi _{0,N}$
is extendible and Lemmas 6.7 and 6.8 apply. Let
$\phi _{0,N}$
is extendible and Lemmas 6.7 and 6.8 apply. Let
![]() $z=x_{0,N+1}$
. If
$z=x_{0,N+1}$
. If
![]() $z\in \mathbb R$
, let
$z\in \mathbb R$
, let
and
By Lemma 6.7, there is an
![]() $\mathbb R$
-monomorphic extension of
$\mathbb R$
-monomorphic extension of
![]() $\phi ^*$
,
$\phi ^*$
,
![]() $\phi _{0,N+1}:D_{0,N+1}\to \mathcal {E}$
. The sub-ring of
$\phi _{0,N+1}:D_{0,N+1}\to \mathcal {E}$
. The sub-ring of
![]() $\mathcal {E}$
generated by a set closed under partial sums and coefficients is closed under partial sums and coefficients so
$\mathcal {E}$
generated by a set closed under partial sums and coefficients is closed under partial sums and coefficients so
![]() $\phi _{0,N+1}$
is extendible.
$\phi _{0,N+1}$
is extendible.
If z is non-standard, let
![]() $R_0$
be the set of reals contained in the smallest full, real closure of
$R_0$
be the set of reals contained in the smallest full, real closure of
![]() $D_{0,N}\cup \{ z\}$
. By Lemma 6.7 there is an extendible level
$D_{0,N}\cup \{ z\}$
. By Lemma 6.7 there is an extendible level
![]() $\mathbb R$
-monomorphism extending
$\mathbb R$
-monomorphism extending
![]() $\phi _{0,N}$
,
$\phi _{0,N}$
,
![]() $\phi ^*:D_{0,N}[R_0]\to \mathcal {E}$
. Let
$\phi ^*:D_{0,N}[R_0]\to \mathcal {E}$
. Let
Then
![]() $D_{0,N+1}\in M[G_{\nu _0}]$
. By Lemma 6.8 there is an extendible extension of
$D_{0,N+1}\in M[G_{\nu _0}]$
. By Lemma 6.8 there is an extendible extension of
![]() $\phi ^*$
,
$\phi ^*$
,
Let
and
Then the morass descendants of
![]() $x_0$
(in
$x_0$
(in
![]() $M[G_{\nu _0}]$
) are elements of
$M[G_{\nu _0}]$
) are elements of
![]() $D_0$
, and
$D_0$
, and
![]() $\phi _0$
is extendible.
$\phi _0$
is extendible.
Assume
![]() $\alpha $
a successor.
$\alpha $
a successor.
Let
![]() $\alpha =\bar {\alpha }+1$
. Assume that
$\alpha =\bar {\alpha }+1$
. Assume that
![]() $\langle D_{\beta } \mid \beta < \alpha \rangle $
and
$\langle D_{\beta } \mid \beta < \alpha \rangle $
and
![]() $\langle \phi _{\beta } \mid \beta <\alpha \rangle $
have been defined so that for all
$\langle \phi _{\beta } \mid \beta <\alpha \rangle $
have been defined so that for all
![]() $\gamma <\beta \leq \bar {\alpha }$
,
$\gamma <\beta \leq \bar {\alpha }$
,
-
1.
 $x_\gamma \in D_{\gamma }$
.
$x_\gamma \in D_{\gamma }$
. -
2.
 $D_{\gamma }\subseteq D_{\beta }$
and
$D_{\gamma }\subseteq D_{\beta }$
and
 $D_{\beta }$
is morass-closed beneath
$D_{\beta }$
is morass-closed beneath
 $\nu _{\beta }$
.
$\nu _{\beta }$
. -
3.
 $\phi _{\gamma } \subseteq \phi _{\beta }$
.
$\phi _{\gamma } \subseteq \phi _{\beta }$
. -
4.
 $\phi _{\beta }:D_{\beta } \to \mathcal {E}$
is an extendible
$\phi _{\beta }:D_{\beta } \to \mathcal {E}$
is an extendible
 $\mathbb R$
-monomorphism.
$\mathbb R$
-monomorphism.
If
![]() $\nu _{\alpha }=\nu _{\bar {\alpha }}$
, then we may argue as in the previous case. Let
$\nu _{\alpha }=\nu _{\bar {\alpha }}$
, then we may argue as in the previous case. Let
![]() $\langle x_{\alpha ,n} \rangle $
be an enumeration of a maximal AI set of morass descendants of
$\langle x_{\alpha ,n} \rangle $
be an enumeration of a maximal AI set of morass descendants of
![]() $x_{\alpha }$
in
$x_{\alpha }$
in
![]() $M[G_{\nu _{\alpha }}]$
. We may extend
$M[G_{\nu _{\alpha }}]$
. We may extend
![]() $D_{\bar {\alpha }}$
to
$D_{\bar {\alpha }}$
to
![]() $D_{\alpha }$
containing the morass descendants of
$D_{\alpha }$
containing the morass descendants of
![]() $x_{\alpha }$
, and
$x_{\alpha }$
, and
![]() $\phi _{\bar {\alpha }}$
to
$\phi _{\bar {\alpha }}$
to
![]() $\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
so that for all
$\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
so that for all
![]() $\gamma <\beta \leq \alpha ,$
$\gamma <\beta \leq \alpha ,$
-
1.
 $D_{\gamma } \subseteq D_{\beta }$
and
$D_{\gamma } \subseteq D_{\beta }$
and
 $D_{\beta }$
is morass-closed beneath
$D_{\beta }$
is morass-closed beneath
 $\nu _{\beta }$
.
$\nu _{\beta }$
. -
2.
 $\phi _{\gamma }\subseteq \phi _{\beta }$
.
$\phi _{\gamma }\subseteq \phi _{\beta }$
. -
3.
 $\phi _{\beta }$
is extendible.
$\phi _{\beta }$
is extendible.
If
![]() $\nu _{\bar {\alpha }}<\nu _{\alpha }$
, then by Lemma 6.6 there is an extendible
$\nu _{\bar {\alpha }}<\nu _{\alpha }$
, then by Lemma 6.6 there is an extendible
![]() $\mathbb R$
-monomorphism
$\mathbb R$
-monomorphism
![]() $\phi ^*$
extending
$\phi ^*$
extending
![]() $\bigcup _{\sigma \in \mathcal {F}_{\nu _{\bar {\alpha }} \nu _{\alpha }}} \sigma [\phi _{\bar {\alpha }}]$
to the ring generated by
$\bigcup _{\sigma \in \mathcal {F}_{\nu _{\bar {\alpha }} \nu _{\alpha }}} \sigma [\phi _{\bar {\alpha }}]$
to the ring generated by
![]() $\bigcup _{\sigma \in \mathcal {F}_{\nu _{\bar {\alpha }} \nu _{\alpha }}} \sigma [D_{\bar {\alpha }}]$
,
$\bigcup _{\sigma \in \mathcal {F}_{\nu _{\bar {\alpha }} \nu _{\alpha }}} \sigma [D_{\bar {\alpha }}]$
,
![]() $D^*$
. Let
$D^*$
. Let
![]() $D'$
be ring generated by
$D'$
be ring generated by
![]() $D^*$
and the morass descendants of
$D^*$
and the morass descendants of
![]() $x_{\alpha }$
in
$x_{\alpha }$
in
![]() $M[G_{\nu _{\alpha }}]$
. Let
$M[G_{\nu _{\alpha }}]$
. Let
![]() $\mathbb R_0$
be the real numbers of the smallest full extension of the real closure of
$\mathbb R_0$
be the real numbers of the smallest full extension of the real closure of
![]() $D'$
. Then the real closure of
$D'$
. Then the real closure of
![]() $D'[\mathbb R_0]$
is full. Let
$D'[\mathbb R_0]$
is full. Let
By the preceding case, there is an extendible
![]() $\mathbb R$
-monomorphism
$\mathbb R$
-monomorphism
![]() $\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
with
$\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
with
![]() $\phi _{\alpha }\supseteq \phi ^*$
.
$\phi _{\alpha }\supseteq \phi ^*$
.
Finally, assume
![]() $\alpha <\omega _1$
is a limit ordinal.
$\alpha <\omega _1$
is a limit ordinal.
If there is
![]() $\beta <\alpha $
such that
$\beta <\alpha $
such that
![]() $\nu _{\alpha }=\nu _{\beta }$
then we may proceed as in the case
$\nu _{\alpha }=\nu _{\beta }$
then we may proceed as in the case
![]() $\alpha =0$
to define
$\alpha =0$
to define
![]() $D_{\alpha }$
and
$D_{\alpha }$
and
![]() $\phi _{\alpha }$
.
$\phi _{\alpha }$
.
So we assume that
![]() $\nu _{\beta }<\nu _{\alpha }$
for all
$\nu _{\beta }<\nu _{\alpha }$
for all
![]() $\beta <\alpha $
. Let
$\beta <\alpha $
. Let
If
![]() $\lambda =\nu _{\alpha }$
, then let
$\lambda =\nu _{\alpha }$
, then let
 $$\begin{align*}D^*=\bigcup_{\beta<\alpha}( \bigcup_{\sigma \in \mathcal{F}_{\nu_\beta \nu_\alpha}} \sigma[D_{\beta}]). \end{align*}$$
$$\begin{align*}D^*=\bigcup_{\beta<\alpha}( \bigcup_{\sigma \in \mathcal{F}_{\nu_\beta \nu_\alpha}} \sigma[D_{\beta}]). \end{align*}$$
Let D be a finitely generated subring of
![]() $D^*$
with generators
$D^*$
with generators
![]() $\{ d_1,\ldots ,d_n\}$
. Then there is
$\{ d_1,\ldots ,d_n\}$
. Then there is
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
and for,
![]() $i\leq n$
, morass functions
$i\leq n$
, morass functions
![]() $\sigma _i \in \mathcal {F}_{\nu _{\beta } \nu _{\alpha }}$
such that
$\sigma _i \in \mathcal {F}_{\nu _{\beta } \nu _{\alpha }}$
such that
By condition P4 of Definition 2.1, there is
![]() $\nu _{\beta } \leq \gamma <\lambda $
,
$\nu _{\beta } \leq \gamma <\lambda $
,
![]() $f_1, \ldots , f_n \in \mathcal {F}_{\nu _{\beta } \gamma }$
and
$f_1, \ldots , f_n \in \mathcal {F}_{\nu _{\beta } \gamma }$
and
![]() $g\in \mathcal {F}_{\gamma \lambda }$
such that for all
$g\in \mathcal {F}_{\gamma \lambda }$
such that for all
![]() $i\leq n$
,
$i\leq n$
,
By Lemma 6.6 there is an extendible
![]() $\mathbb R$
-monomorphism
$\mathbb R$
-monomorphism
![]() $\phi ^*$
on the ring generated by
$\phi ^*$
on the ring generated by
![]() $\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \lambda }} \sigma [\phi _{\beta }]$
. It follows that there is an extendible
$\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \lambda }} \sigma [\phi _{\beta }]$
. It follows that there is an extendible
![]() $\mathbb R$
-monomorphism on the ring generated by
$\mathbb R$
-monomorphism on the ring generated by
![]() $\bigcup _{\beta <\alpha }(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \nu _{\alpha }}} \sigma [D_{\beta }])$
extending
$\bigcup _{\beta <\alpha }(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \nu _{\alpha }}} \sigma [D_{\beta }])$
extending
![]() $\bigcup _{\beta <\alpha }(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \nu _{\alpha }}} \sigma [\phi _{\beta }])$
. We may then proceed as in earlier cases to define an extendible
$\bigcup _{\beta <\alpha }(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \nu _{\alpha }}} \sigma [\phi _{\beta }])$
. We may then proceed as in earlier cases to define an extendible
![]() $\mathbb R$
-monomorphism
$\mathbb R$
-monomorphism
![]() $\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
, with
$\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
, with
![]() $D_{\alpha }$
containing the morass descendants of
$D_{\alpha }$
containing the morass descendants of
![]() $x_{\alpha }$
in
$x_{\alpha }$
in
![]() $M[G_{\nu _{\alpha }}]$
.
$M[G_{\nu _{\alpha }}]$
.
Finally, assume that
By the previous argument, there is an extendible
![]() $\phi ^*:\bigcup _{\beta <\alpha }(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \lambda }} \sigma [D_{\beta }]) \to \mathcal {E}$
extending the morass images in
$\phi ^*:\bigcup _{\beta <\alpha }(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\beta } \lambda }} \sigma [D_{\beta }]) \to \mathcal {E}$
extending the morass images in
![]() $M[G_{\lambda }]$
of the
$M[G_{\lambda }]$
of the
![]() $\phi _{\beta }$
. By Lemma 6.6 there is an extendible
$\phi _{\beta }$
. By Lemma 6.6 there is an extendible
![]() $\mathbb R$
-monomorphism
$\mathbb R$
-monomorphism
![]() $\phi ^{\prime }_{\alpha }:D^{\prime }_{\alpha } \to \mathcal {E}$
such that
$\phi ^{\prime }_{\alpha }:D^{\prime }_{\alpha } \to \mathcal {E}$
such that
 $$\begin{align*}D^{\prime}_{\alpha} \supseteq \bigcup_{\beta<\alpha}(\bigcup_{\sigma \in \mathcal{F}_{\nu_{\beta} \nu_{\alpha}}} \sigma[D_{\beta}]) \end{align*}$$
$$\begin{align*}D^{\prime}_{\alpha} \supseteq \bigcup_{\beta<\alpha}(\bigcup_{\sigma \in \mathcal{F}_{\nu_{\beta} \nu_{\alpha}}} \sigma[D_{\beta}]) \end{align*}$$
and
 $$\begin{align*}\phi^{\prime}_{\alpha} \supseteq \bigcup_{\beta<\alpha}(\bigcup_{\sigma \in \mathcal{F}_{\nu_{\beta} \nu_{\alpha}}} \sigma[\phi_{\beta}]). \end{align*}$$
$$\begin{align*}\phi^{\prime}_{\alpha} \supseteq \bigcup_{\beta<\alpha}(\bigcup_{\sigma \in \mathcal{F}_{\nu_{\beta} \nu_{\alpha}}} \sigma[\phi_{\beta}]). \end{align*}$$
We proceed as in earlier cases to extend
![]() $\phi ^{\prime }_{\alpha }$
to an extendible
$\phi ^{\prime }_{\alpha }$
to an extendible
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
, where
$\phi _{\alpha }:D_{\alpha } \to \mathcal {E}$
, where
![]() $D_{\alpha }$
extends
$D_{\alpha }$
extends
![]() $D'$
and contains a maximal AI set of morass-descendants of
$D'$
and contains a maximal AI set of morass-descendants of
![]() $x_{\alpha }$
in
$x_{\alpha }$
in
![]() $M[G_{\nu _{\alpha }}]$
.
$M[G_{\nu _{\alpha }}]$
.
Let
![]() $D_{\omega _1}=\bigcup _{\alpha <\omega _1}(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\alpha } \omega _1}} \sigma [D_{\alpha }])$
and
$D_{\omega _1}=\bigcup _{\alpha <\omega _1}(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\alpha } \omega _1}} \sigma [D_{\alpha }])$
and
![]() $\phi _{\omega _1}=\bigcup _{\alpha <\omega _1}(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\alpha } \omega _1}} \sigma [\phi _{\alpha }])$
. Then
$\phi _{\omega _1}=\bigcup _{\alpha <\omega _1}(\bigcup _{\sigma \in \mathcal {F}_{\nu _{\alpha } \omega _1}} \sigma [\phi _{\alpha }])$
. Then
![]() $D_{\omega _1}$
is a subring of F and contains the morass-closure of X (a maximal algebraically independent subset of F). Additionally,
$D_{\omega _1}$
is a subring of F and contains the morass-closure of X (a maximal algebraically independent subset of F). Additionally,
![]() $\phi _{\omega _1}:D_{\omega _1} \to \mathcal {E}$
is an
$\phi _{\omega _1}:D_{\omega _1} \to \mathcal {E}$
is an
![]() $\mathbb R$
-monomorphism on a domain that contains a transcendental basis for F. Therefore
$\mathbb R$
-monomorphism on a domain that contains a transcendental basis for F. Therefore
![]() $\phi _{\omega _1}$
extends uniquely to an
$\phi _{\omega _1}$
extends uniquely to an
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $\phi :F \to \mathcal {E}$
.
$\phi :F \to \mathcal {E}$
.
Theorem 7.3. Suppose M is a transitive model of
![]() $ZFC+CH$
containing a simplified
$ZFC+CH$
containing a simplified
![]() $(\omega _1,1)$
-morass and
$(\omega _1,1)$
-morass and
![]() $M[G]$
is the Cohen extensions adding
$M[G]$
is the Cohen extensions adding
![]() $\aleph _2$
generic reals. Then if X is an infinite compact Hausdorff space in
$\aleph _2$
generic reals. Then if X is an infinite compact Hausdorff space in
![]() $M[G]$
, there is a discontinuous homomorphism of
$M[G]$
, there is a discontinuous homomorphism of
![]() $C(X)$
in
$C(X)$
in
![]() $M[G]$
.
$M[G]$
.
Proof By Corollary 6.9 of [Reference Dumas3], any non-principal ultrafilter on
![]() $\omega $
in M may be extended to a standard ultrafilter in the Cohen extension adding
$\omega $
in M may be extended to a standard ultrafilter in the Cohen extension adding
![]() $\aleph _2$
-generic reals. If U is a standard ultrafilter, then there is a level
$\aleph _2$
-generic reals. If U is a standard ultrafilter, then there is a level
![]() $\mathbb R$
-monomorphism from the finite elements of
$\mathbb R$
-monomorphism from the finite elements of
![]() ${\mathbb R}^{\omega }/U$
into
${\mathbb R}^{\omega }/U$
into
![]() $\mathcal {E}$
. Hence the finite elements of
$\mathcal {E}$
. Hence the finite elements of
![]() ${\mathbb R}^{\omega }/U$
bear a non-trivial submultiplicative norm. The theorem follows from results of B. Johnson [Reference Johnson10].
${\mathbb R}^{\omega }/U$
bear a non-trivial submultiplicative norm. The theorem follows from results of B. Johnson [Reference Johnson10].
8. Discontinuous homomorphisms of
 $C(X)$
in a Cohen extension adding
$C(X)$
in a Cohen extension adding
 $\aleph _3$
-generic reals
$\aleph _3$
-generic reals
We turn to generic extensions adding more than
![]() $\aleph _2$
generic reals. We require a simplified
$\aleph _2$
generic reals. We require a simplified
![]() $(\omega _1,2)$
-morass for the next construction (Velleman [Reference Velleman14]). The simplified
$(\omega _1,2)$
-morass for the next construction (Velleman [Reference Velleman14]). The simplified
![]() $(\omega _1,2)$
-morass will allow us to use morass maps to construct an
$(\omega _1,2)$
-morass will allow us to use morass maps to construct an
![]() $\mathbb R$
-monomorphism from the finite elements of a standard ultrapower to
$\mathbb R$
-monomorphism from the finite elements of a standard ultrapower to
![]() $\mathcal {E}$
in a model with
$\mathcal {E}$
in a model with
![]() $\aleph _3$
generic reals in a manner similar to Theorem 7.1. The construction of a term function on a domain with cardinality
$\aleph _3$
generic reals in a manner similar to Theorem 7.1. The construction of a term function on a domain with cardinality
![]() $\aleph _3$
, requiring only
$\aleph _3$
, requiring only
![]() $\aleph _1$
many explicit commitments, allows us to exploit that standard ultrapowers and
$\aleph _1$
many explicit commitments, allows us to exploit that standard ultrapowers and
![]() $\mathcal {E}$
are
$\mathcal {E}$
are
![]() $\eta _1$
-orderings. We will rely heavily on the definitions and results of D. Velleman [Reference Velleman14] in this section.
$\eta _1$
-orderings. We will rely heavily on the definitions and results of D. Velleman [Reference Velleman14] in this section.
Definition 8.1 (D. Velleman) (Simplified (κ, 2)-morass)
The structure ![]() is a simplified
is a simplified
![]() $(\kappa ,2)$
-morass provided it has the following properties
$(\kappa ,2)$
-morass provided it has the following properties
![]() $:$
$:$
-
1.
 is a neat simplified
is a neat simplified
 $(\kappa ^+,1)$
-morass.
$(\kappa ^+,1)$
-morass. -
2.
 $\forall \alpha <\beta \leq \kappa $
,
$\forall \alpha <\beta \leq \kappa $
,  is a family of embeddings
is a family of embeddings
 $($
see page 172 [Reference Velleman14]
$($
see page 172 [Reference Velleman14]
 $)$
from
$)$
from  to
to  .
. -
3.
 .
. -
4.
 . Here
. Here
 $f\circ g$
is defined by
$f\circ g$
is defined by
 $:$
$:$
 $$\begin{align*}(f\circ g)_{\zeta}=f_{g(\zeta)} \circ g_{\zeta} \; \; \; \; for \; \zeta\leq \theta_{\alpha}, \end{align*}$$
$$\begin{align*}(f\circ g)_{\zeta}=f_{g(\zeta)} \circ g_{\zeta} \; \; \; \; for \; \zeta\leq \theta_{\alpha}, \end{align*}$$
 $$\begin{align*}(f\circ g)_{\zeta \xi}=f_{g(\zeta) g(\xi)} \circ g_{\zeta \xi} \; \; \; \; for \; \zeta<\xi\leq \theta_{\alpha}. \end{align*}$$
$$\begin{align*}(f\circ g)_{\zeta \xi}=f_{g(\zeta) g(\xi)} \circ g_{\zeta \xi} \; \; \; \; for \; \zeta<\xi\leq \theta_{\alpha}. \end{align*}$$
-
5.
 $\forall \alpha <\kappa $
,
$\forall \alpha <\kappa $
,  is an amalgamation
is an amalgamation
 $($
see page 173 [Reference Velleman14]
$($
see page 173 [Reference Velleman14]
 $)$
.
$)$
. -
6. If
 $\beta _1, \beta _2 <\alpha \leq \kappa $
,
$\beta _1, \beta _2 <\alpha \leq \kappa $
,
 $\alpha $
a limit ordinal,
$\alpha $
a limit ordinal,  and
and  , then
, then
 $\exists \beta (\beta _1, \beta _2 < \beta <\alpha $
and
$\exists \beta (\beta _1, \beta _2 < \beta <\alpha $
and  and
and
 $f_2=g\circ f_2'))$
.
$f_2=g\circ f_2'))$
. -
7. If
 $\alpha \leq \kappa $
and
$\alpha \leq \kappa $
and
 $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
 $:$
$:$
-
(a)
 $\theta _{\alpha }=\bigcup \{ f[\theta _{\beta }] \mid \beta <\alpha $
,
$\theta _{\alpha }=\bigcup \{ f[\theta _{\beta }] \mid \beta <\alpha $
,  .
. -
(b)
 $ \forall \zeta \leq \theta _{\alpha }$
,
$ \forall \zeta \leq \theta _{\alpha }$
,  ,
,
 $f(\bar {\zeta })=\zeta ) \}$
.
$f(\bar {\zeta })=\zeta ) \}$
. -
(c)
 $\forall \zeta \kern1.9pt{<}\kern1.9pt\xi \kern1.9pt{\leq}\kern1.9pt \theta _{\alpha }$
,
$\forall \zeta \kern1.9pt{<}\kern1.9pt\xi \kern1.9pt{\leq}\kern1.9pt \theta _{\alpha }$
,  ,
,
 $f(\bar {\zeta })\kern1.9pt{=}\kern1.9pt\zeta $
,
$f(\bar {\zeta })\kern1.9pt{=}\kern1.9pt\zeta $
,
 $f(\bar {\xi })\kern1.9pt{=}\kern1.9pt\xi ) \}$
.
$f(\bar {\xi })\kern1.9pt{=}\kern1.9pt\xi ) \}$
.
-
Theorem 8.2. Let M be a transitive model of
![]() $ZFC+CH$
containing a simplified
$ZFC+CH$
containing a simplified
![]() $(\omega _1,2)$
-morass, and
$(\omega _1,2)$
-morass, and
![]() $M[G]$
be a generic extension of M adding
$M[G]$
be a generic extension of M adding
![]() $\aleph _3$
generic reals. Let X be an infinite compact Haussdorf space in
$\aleph _3$
generic reals. Let X be an infinite compact Haussdorf space in
![]() $M[G]$
, and
$M[G]$
, and
![]() $C(X)$
be the algebra of continuous real-valued functions of X in
$C(X)$
be the algebra of continuous real-valued functions of X in
![]() $M[G]$
. Then there is a discontinuous homomorphism of
$M[G]$
. Then there is a discontinuous homomorphism of
![]() $C(X)$
in
$C(X)$
in
![]() $M[G]$
.
$M[G]$
.
Proof Let M be a transitive model of
![]() $ZFC + CH$
containing a simplified
$ZFC + CH$
containing a simplified
![]() $(\omega _1,2)$
-morass,
$(\omega _1,2)$
-morass, ![]() . Let P be the poset adding generic reals indexed by
. Let P be the poset adding generic reals indexed by
![]() $\omega _3$
, and G be P-generic over M. Then
$\omega _3$
, and G be P-generic over M. Then ![]() is a simplified
is a simplified
![]() $(\omega _2,1)$
-morass, and below
$(\omega _2,1)$
-morass, and below
![]() $\omega _1$
,
$\omega _1$
, ![]() satisfies the axioms of a simplified
satisfies the axioms of a simplified
![]() $(\omega _1,1)$
-morass. Hence, by Lemma 3.3 of [Reference Dumas4], any countable subset of
$(\omega _1,1)$
-morass. Hence, by Lemma 3.3 of [Reference Dumas4], any countable subset of
![]() $\omega _3$
is in the image of a single morass map of
$\omega _3$
is in the image of a single morass map of ![]() . The construction of Theorem 7.1 below
. The construction of Theorem 7.1 below
![]() $\omega _1$
can be completed in M. In particular, if
$\omega _1$
can be completed in M. In particular, if
![]() $U_0\in M$
is a non-principal ultrafilter in M, then by Corollary 6.9 of [Reference Dumas4], there is
$U_0\in M$
is a non-principal ultrafilter in M, then by Corollary 6.9 of [Reference Dumas4], there is
![]() $\overline {U}\subseteq M^{P(\omega _1)}$
, a standard term for an ultrafilter below
$\overline {U}\subseteq M^{P(\omega _1)}$
, a standard term for an ultrafilter below
![]() $\omega _1$
, that is forced to extend
$\omega _1$
, that is forced to extend
![]() $U_0$
. Furthermore, the morass-closure of
$U_0$
. Furthermore, the morass-closure of
![]() $\overline {U}$
, U, is a standard ultrafilter. By Theorem 6.4 of [Reference Dumas4],
$\overline {U}$
, U, is a standard ultrafilter. By Theorem 6.4 of [Reference Dumas4],
![]() ${\mathbb R}^{\omega }/U$
is a gap-2 morass-definable
${\mathbb R}^{\omega }/U$
is a gap-2 morass-definable
![]() $\eta _1$
-ordering.
$\eta _1$
-ordering.
We construct a level term function from the finite elements of a standard ultrapower to the Esterle algebra, that is closed under morass-embeddings and is forced to be an
![]() $\mathbb R$
-monomorphism. For
$\mathbb R$
-monomorphism. For
![]() $\alpha <\omega _1$
, let
$\alpha <\omega _1$
, let
![]() $X_{\alpha }=({\mathbb R}^{\omega }/U) \cap M^{P_{\alpha }}$
and
$X_{\alpha }=({\mathbb R}^{\omega }/U) \cap M^{P_{\alpha }}$
and
![]() $Y_{\alpha }=\mathcal {E} \cap M^{P_{\alpha }}$
. We consider
$Y_{\alpha }=\mathcal {E} \cap M^{P_{\alpha }}$
. We consider
![]() $X_{\alpha }$
and
$X_{\alpha }$
and
![]() $Y_{\alpha }$
as the restrictions of
$Y_{\alpha }$
as the restrictions of
![]() ${\mathbb R}^{\omega }/U$
and
${\mathbb R}^{\omega }/U$
and
![]() $\mathcal {E}$
, resp., to the forcing language adding generic reals indexed by
$\mathcal {E}$
, resp., to the forcing language adding generic reals indexed by
![]() $\varphi _{\theta _{\alpha }}$
. In any P-generic extension of M,
$\varphi _{\theta _{\alpha }}$
. In any P-generic extension of M,
![]() $M[G]$
, the interpretation of
$M[G]$
, the interpretation of
![]() $X_{\alpha }$
in
$X_{\alpha }$
in
![]() $M[G]$
is the interpretation of
$M[G]$
is the interpretation of
![]() $X_{\alpha }$
in
$X_{\alpha }$
in
![]() $M[G_{\alpha }]$
where
$M[G_{\alpha }]$
where
![]() $G_{\alpha }$
is the factor of G that is
$G_{\alpha }$
is the factor of G that is
![]() $P_{\alpha }$
-generic over M.
$P_{\alpha }$
-generic over M.
It is sufficient to construct a level, morass-commutative term injection from
![]() $X_{\omega _1}$
to
$X_{\omega _1}$
to
![]() $Y_{\omega _1}$
that is forced to be an
$Y_{\omega _1}$
that is forced to be an
![]() $\mathbb R$
-monomorphism. The closure under embeddings,
$\mathbb R$
-monomorphism. The closure under embeddings,
![]() $f_{\theta _{\beta }}$
, where
$f_{\theta _{\beta }}$
, where
![]() $\beta <\omega _1$
and
$\beta <\omega _1$
and ![]() , of this term function will be the term function we seek.
, of this term function will be the term function we seek.
Let
![]() $\{ x_{\beta } \mid \beta <\omega _1 \}\subseteq X_{\omega _1}$
be a transfinite sequence of terms of strict level for a maximal algebraically independent set of morass-generators for the infinitesimal elements of
$\{ x_{\beta } \mid \beta <\omega _1 \}\subseteq X_{\omega _1}$
be a transfinite sequence of terms of strict level for a maximal algebraically independent set of morass-generators for the infinitesimal elements of
![]() $X_{\omega _1}$
, such that
$X_{\omega _1}$
, such that
![]() $x_{\alpha }\in X_{\alpha }$
for all
$x_{\alpha }\in X_{\alpha }$
for all
![]() $\alpha <\omega _1$
.
$\alpha <\omega _1$
.
We will inductively construct a transfinite sequence of morass-commutative term functions
![]() $\langle F_{\beta }:D_{\beta }\to E_{\beta } \mid \beta <\omega _1 \rangle $
that satisfies the following for all
$\langle F_{\beta }:D_{\beta }\to E_{\beta } \mid \beta <\omega _1 \rangle $
that satisfies the following for all
![]() $\alpha \leq \beta <\omega _1$
:
$\alpha \leq \beta <\omega _1$
:
-
1.
 $D_{\beta }\subseteq X_{\theta _{\beta }}$
is a subring of finite elements of a standard ultrapower of
$D_{\beta }\subseteq X_{\theta _{\beta }}$
is a subring of finite elements of a standard ultrapower of
 $\mathbb R$
, that is morass-closed beneath
$\mathbb R$
, that is morass-closed beneath
 $\theta _{\beta }$
.
$\theta _{\beta }$
. -
2.
 $E_{\beta }\subseteq Y_{\theta _{\beta }}$
is full and closed under partial sums.
$E_{\beta }\subseteq Y_{\theta _{\beta }}$
is full and closed under partial sums. -
3.
 $D_{\alpha }\subseteq D_{\beta }$
and
$D_{\alpha }\subseteq D_{\beta }$
and
 $E_{\alpha }\subseteq E_{\beta }$
.
$E_{\alpha }\subseteq E_{\beta }$
. -
4.
 $x_{\beta }\in D_{\beta }$
.
$x_{\beta }\in D_{\beta }$
. -
5.
 $F_{\beta }$
is a level term function that is forced to be an
$F_{\beta }$
is a level term function that is forced to be an
 $\mathbb R$
-monomorphism.
$\mathbb R$
-monomorphism. -
6.
 $f_{\theta _{\alpha }}[F_{\alpha }]\subseteq F_{\beta }$
for all
$f_{\theta _{\alpha }}[F_{\alpha }]\subseteq F_{\beta }$
for all  .
.
We call a sequence of term functions satisfying these conditions an extendible sequence beneath
![]() $\beta $
. We argue be induction on
$\beta $
. We argue be induction on
![]() $\gamma <\omega _1$
.
$\gamma <\omega _1$
.
Base Case:
![]() $\gamma =0$
.
$\gamma =0$
.
Let
![]() $y_0$
be a positive infinitesimal monomial of
$y_0$
be a positive infinitesimal monomial of
![]() $Y_0$
having the same strict level as
$Y_0$
having the same strict level as
![]() $x_0$
, and
$x_0$
, and
![]() $\mathbb R_0$
be the reals of the ground model. Let
$\mathbb R_0$
be the reals of the ground model. Let
![]() $D_0$
be the ring generated by
$D_0$
be the ring generated by
![]() $\mathbb R_0 \cup \{ x_0\}$
,
$\mathbb R_0 \cup \{ x_0\}$
,
![]() $\mathbb R_0 [x_0]$
, and
$\mathbb R_0 [x_0]$
, and
![]() $E_0=\mathbb R_0 [y_0]$
. We observe that
$E_0=\mathbb R_0 [y_0]$
. We observe that
![]() $E_0$
is closed under partial sums. Therefore, there is an R-monomorphism,
$E_0$
is closed under partial sums. Therefore, there is an R-monomorphism,
![]() $F_0:D_0 \to E_0$
, with
$F_0:D_0 \to E_0$
, with
![]() $F_0(x_0)=y_0$
.
$F_0(x_0)=y_0$
.
Successor Case:
![]() $\gamma =\beta +1$
. Let
$\gamma =\beta +1$
. Let
![]() $\langle F_{\alpha }:D_{\alpha }\to E_{\alpha } \mid \alpha \leq \beta \rangle $
be an extendible sequence satisfying conditions 1–6 above. Let
$\langle F_{\alpha }:D_{\alpha }\to E_{\alpha } \mid \alpha \leq \beta \rangle $
be an extendible sequence satisfying conditions 1–6 above. Let
![]() $D^*$
be the ring generated by
$D^*$
be the ring generated by ![]() . Then
. Then
![]() $D^*$
is generated by the union of the images of
$D^*$
is generated by the union of the images of
![]() $D_{\beta }$
under the second components of left-branching embeddings of
$D_{\beta }$
under the second components of left-branching embeddings of ![]() . Let h be the right-branching embedding of
. Let h be the right-branching embedding of ![]() and
and
![]() $D'$
be the ring generated by
$D'$
be the ring generated by
![]() $D^*$
and
$D^*$
and
![]() $h_{\theta _{\beta }}[D_{\beta }]$
.
$h_{\theta _{\beta }}[D_{\beta }]$
.
By Lemma 5.2 of [Reference Dumas4], ![]() is a level term function that is forced to be an order-preserving injection. Since
is a level term function that is forced to be an order-preserving injection. Since
![]() $F_{\beta }$
is
$F_{\beta }$
is
![]() $\mathbb R$
-linear, for any
$\mathbb R$
-linear, for any
![]() $f\in \cal {F}_{\beta \gamma }$
,
$f\in \cal {F}_{\beta \gamma }$
,
![]() $f_{\theta _{\beta }}[F_{\beta }]$
is
$f_{\theta _{\beta }}[F_{\beta }]$
is
![]() $\mathbb R$
-linear. Therefore
$\mathbb R$
-linear. Therefore
![]() $\bigcup \{f_{\theta _{\beta }}[F_{\beta \gamma }] \mid f\in \cal {F}_{\beta \gamma } \}$
is
$\bigcup \{f_{\theta _{\beta }}[F_{\beta \gamma }] \mid f\in \cal {F}_{\beta \gamma } \}$
is
![]() $\mathbb R$
-linear. If
$\mathbb R$
-linear. If
![]() $f\in \cal {F}_{\beta \gamma }$
, then
$f\in \cal {F}_{\beta \gamma }$
, then
![]() $f_{\theta _{\beta }}:\theta _{\beta } \to \theta _{\gamma }$
is order-preserving. If f is left-branching, then
$f_{\theta _{\beta }}:\theta _{\beta } \to \theta _{\gamma }$
is order-preserving. If f is left-branching, then
![]() $f_{\theta _{\beta }}\in \cal {G}_{\theta _{\beta } \theta _{\gamma }}$
. If f is right branching, then
$f_{\theta _{\beta }}\in \cal {G}_{\theta _{\beta } \theta _{\gamma }}$
. If f is right branching, then
![]() $f_{\theta }$
is order-preserving. By Lemma 6.6,
$f_{\theta }$
is order-preserving. By Lemma 6.6, ![]() extends to a homomorphism,
extends to a homomorphism,
![]() $F':D'\to \mathcal {E}$
. Therefore there is a unique extendible
$F':D'\to \mathcal {E}$
. Therefore there is a unique extendible
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $F^*:D^* \to \mathcal {E}$
.
$F^*:D^* \to \mathcal {E}$
.
Let B be a transcendental basis of
![]() $D_{\beta }$
over
$D_{\beta }$
over
![]() ${\mathbb R}^{\omega }/U \cap M$
. Let D be the ring generated by B and
${\mathbb R}^{\omega }/U \cap M$
. Let D be the ring generated by B and
![]() $D_{\beta }\cap M$
. Let V be the semigroup generated by B. Because
$D_{\beta }\cap M$
. Let V be the semigroup generated by B. Because ![]() is a set of compatible embeddings, Lemma 6.1 applies and, treating D as a vector space (over the field generated by
is a set of compatible embeddings, Lemma 6.1 applies and, treating D as a vector space (over the field generated by
![]() $D_{\beta } \cap M$
), V is a basis of elements of strict level for D. Therefore, if
$D_{\beta } \cap M$
), V is a basis of elements of strict level for D. Therefore, if
![]() $F:D \to \mathcal {E}$
is the naturally induced
$F:D \to \mathcal {E}$
is the naturally induced
![]() $\mathbb R$
-linear extension of
$\mathbb R$
-linear extension of ![]() , the image of V under F is a linear independent subset of
, the image of V under F is a linear independent subset of
![]() $\mathcal {E}$
over
$\mathcal {E}$
over
![]() $E_{\beta } \cap M$
. Therefore F is a linear transformation and an
$E_{\beta } \cap M$
. Therefore F is a linear transformation and an
![]() $\mathbb R$
-monomorphism of D.
$\mathbb R$
-monomorphism of D.
We argue along the lines of Lemma 6.5 to show that
![]() $F'$
is forced to be order-preserving. By Lemma 6.5,
$F'$
is forced to be order-preserving. By Lemma 6.5,
![]() $F'\upharpoonright _{D^*}$
is forced to be order-preserving. If
$F'\upharpoonright _{D^*}$
is forced to be order-preserving. If
![]() $z\in D'$
, there is
$z\in D'$
, there is
![]() $n\in \mathbb N$
,
$n\in \mathbb N$
,
![]() $x_1,\ldots ,x_n \in D^*$
and
$x_1,\ldots ,x_n \in D^*$
and
![]() $y_1,\ldots ,y_n \in f_{\theta _{\beta }}[D_{\beta }]$
such that
$y_1,\ldots ,y_n \in f_{\theta _{\beta }}[D_{\beta }]$
such that
![]() $z=\sum _{i=1}^n x_i\cdot y_i$
. We show that
$z=\sum _{i=1}^n x_i\cdot y_i$
. We show that
![]() $\sum _{i=1}^n x_i\cdot y_i>0$
iff
$\sum _{i=1}^n x_i\cdot y_i>0$
iff
![]() $\sum _{i=1}^n F'(x_i)\cdot F'(y_i)>0$
.
$\sum _{i=1}^n F'(x_i)\cdot F'(y_i)>0$
.
If
![]() $n=1$
, then the sign of
$n=1$
, then the sign of
![]() $x_1\cdot y_1$
is the sign of the product of the leading coefficients of
$x_1\cdot y_1$
is the sign of the product of the leading coefficients of
![]() $F'(x_1)$
and
$F'(x_1)$
and
![]() $F'(y_1)$
. However,
$F'(y_1)$
. However,
![]() $F'$
is
$F'$
is
![]() $\mathbb R$
-linear. So
$\mathbb R$
-linear. So
Assume that
![]() $n\geq 2$
, and
$n\geq 2$
, and
 $$\begin{align*}\sum_{i=1}^n x_i\cdot y_i>0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^n x_i\cdot y_i>0. \end{align*}$$
Let
 $$\begin{align*}z=F'\left(\sum_{i=1}^n x_i\cdot y_i\right)=\sum_{\lambda<\gamma} \alpha_{\lambda}x^{a_{\lambda}}. \end{align*}$$
$$\begin{align*}z=F'\left(\sum_{i=1}^n x_i\cdot y_i\right)=\sum_{\lambda<\gamma} \alpha_{\lambda}x^{a_{\lambda}}. \end{align*}$$
By assumption, the range of
![]() $F'$
is closed under partial sums, so there are elements
$F'$
is closed under partial sums, so there are elements
![]() $u_1,\ldots , u_j,u_{j+1},\ldots u_k,v_1,\ldots ,v_k \in Y$
such that:
$u_1,\ldots , u_j,u_{j+1},\ldots u_k,v_1,\ldots ,v_k \in Y$
such that:
-
1.
 $z=\sum _{i=1}^k u_i\cdot v_i$
.
$z=\sum _{i=1}^k u_i\cdot v_i$
. -
2. For
 $i\leq j$
, every term in the power series expansion of
$i\leq j$
, every term in the power series expansion of
 $u_i\cdot v_i$
has power less than
$u_i\cdot v_i$
has power less than
 $a_0$
.
$a_0$
. -
3. For
 $j<i\leq k$
, every term of the power series expansion of
$j<i\leq k$
, every term of the power series expansion of
 $u_i\cdot v_i$
has power at least
$u_i\cdot v_i$
has power at least
 $a_0$
.
$a_0$
.
Every term of z, expressed as a power series of
![]() $\mathcal {E}$
, has valuation no less than
$\mathcal {E}$
, has valuation no less than
![]() $a_0$
, therefore
$a_0$
, therefore
 $$\begin{align*}\sum_{i=1}^j u_i\cdot v_i=0 \end{align*}$$
$$\begin{align*}\sum_{i=1}^j u_i\cdot v_i=0 \end{align*}$$
and
 $$\begin{align*}z=\sum_{i=j+1}^k u_i\cdot v_i. \end{align*}$$
$$\begin{align*}z=\sum_{i=j+1}^k u_i\cdot v_i. \end{align*}$$
If
![]() $j<i\leq k$
, then
$j<i\leq k$
, then
![]() $s_i=u_i\cdot v_i$
has valuation no less than
$s_i=u_i\cdot v_i$
has valuation no less than
![]() $a_0$
in
$a_0$
in
![]() $G_{\omega _1}$
. If the leading terms of
$G_{\omega _1}$
. If the leading terms of
![]() $s_i$
has exponent greater than
$s_i$
has exponent greater than
![]() $a_0$
, then
$a_0$
, then
![]() $s_i$
has Archimedean valuation less than z. Let S be the set of all terms of all
$s_i$
has Archimedean valuation less than z. Let S be the set of all terms of all
![]() $s_i$
, for all
$s_i$
, for all
![]() $1\leq j\leq i$
, having exponent
$1\leq j\leq i$
, having exponent
![]() $a_0$
and T be the set of all terms of all
$a_0$
and T be the set of all terms of all
![]() $s_i$
,
$s_i$
,
![]() $1\leq i\leq j$
, with exponent greater than
$1\leq i\leq j$
, with exponent greater than
![]() $a_0$
. S is nonempty and every element of T has Archimedean valuation less than every element of S.
$a_0$
. S is nonempty and every element of T has Archimedean valuation less than every element of S.
There are
![]() $b_0, c_0\in G_{\omega _1}$
such that
$b_0, c_0\in G_{\omega _1}$
such that
![]() $x^{b_0}$
is in the range of
$x^{b_0}$
is in the range of
![]() $F^*$
and
$F^*$
and
![]() $x^{c_0}$
is in the range of
$x^{c_0}$
is in the range of
![]() $f_{\theta _{\beta }}[F_{\beta }]$
and
$f_{\theta _{\beta }}[F_{\beta }]$
and
Let
![]() $u\in D^*$
and
$u\in D^*$
and
![]() $v\in f_{\theta _{\beta }}[D_{\beta }]$
be such that
$v\in f_{\theta _{\beta }}[D_{\beta }]$
be such that
and
We observe that the ordered ring
![]() $D'$
has a unique extension to the field closure of
$D'$
has a unique extension to the field closure of
![]() $D'$
,
$D'$
,
![]() $\bar {D}$
. Treated as a field map, the unique monomorphic extension of
$\bar {D}$
. Treated as a field map, the unique monomorphic extension of
![]() $F'$
,
$F'$
,
![]() $\bar {F}:\bar {D} \to \mathcal {E}$
, is an
$\bar {F}:\bar {D} \to \mathcal {E}$
, is an
![]() $\mathbb R$
-linear field monomorphism of
$\mathbb R$
-linear field monomorphism of
![]() $D'$
. We have previously observed that
$D'$
. We have previously observed that
![]() $F'$
is an
$F'$
is an
![]() $\mathbb R$
-linear monomorphism, and
$\mathbb R$
-linear monomorphism, and
![]() $F^* \cup f_{\theta _{\beta }}[F_{\beta }]$
is an order-preserving injection. So
$F^* \cup f_{\theta _{\beta }}[F_{\beta }]$
is an order-preserving injection. So
 $$\begin{align*}F'\left(\sum_{i=1}^n x_i\cdot y_i\right) =F'\left(\sum_{i=j+1}^k u_i\cdot v_i\right) \end{align*}$$
$$\begin{align*}F'\left(\sum_{i=1}^n x_i\cdot y_i\right) =F'\left(\sum_{i=j+1}^k u_i\cdot v_i\right) \end{align*}$$
and
 $$\begin{align*}\bar{F}\left(\sum_{i=j+1}^k u_i/u\cdot v_i/v\right)=\alpha_0 + \sum_{0<\lambda<\gamma} \alpha_{\lambda}x^{(a_\lambda-a_0)}. \end{align*}$$
$$\begin{align*}\bar{F}\left(\sum_{i=j+1}^k u_i/u\cdot v_i/v\right)=\alpha_0 + \sum_{0<\lambda<\gamma} \alpha_{\lambda}x^{(a_\lambda-a_0)}. \end{align*}$$
The real number,
![]() $\alpha _0$
, is in the domain
$\alpha _0$
, is in the domain
![]() $\bar {F}$
, so
$\bar {F}$
, so
![]() $\bar {F}(\alpha _0)=F'(\alpha _0)=\alpha _0$
. The range of
$\bar {F}(\alpha _0)=F'(\alpha _0)=\alpha _0$
. The range of
![]() $F'$
is closed under partial sums, so both
$F'$
is closed under partial sums, so both
![]() $\sum _{0<\lambda <\gamma } \alpha _{\lambda }x^a_{\lambda }$
and
$\sum _{0<\lambda <\gamma } \alpha _{\lambda }x^a_{\lambda }$
and
![]() $x^{a_0}$
are in the range of
$x^{a_0}$
are in the range of
![]() $F'$
. Thus
$F'$
. Thus
![]() $\sum _{0<\lambda <\gamma } \alpha _{\lambda }x^{a_{\lambda }-a_0}$
is in the range of
$\sum _{0<\lambda <\gamma } \alpha _{\lambda }x^{a_{\lambda }-a_0}$
is in the range of
![]() $\bar {F}$
. Let
$\bar {F}$
. Let
Every term of
![]() $\delta $
is infinitesimal (has Archimedean valuation greater than elements of
$\delta $
is infinitesimal (has Archimedean valuation greater than elements of
![]() $\mathbb R$
).
$\mathbb R$
).
![]() $\bar {F}$
is order preserving on
$\bar {F}$
is order preserving on
![]() $D'$
, so
$D'$
, so
![]() $\bar {F}^{-1}(\delta )$
is infinitesimal. Hence
$\bar {F}^{-1}(\delta )$
is infinitesimal. Hence
 $$\begin{align*}\sum_{i=1}^n (x_i\cdot y_i)/(u\cdot v)=\alpha_0+\bar{F}^{-1}(\delta) \end{align*}$$
$$\begin{align*}\sum_{i=1}^n (x_i\cdot y_i)/(u\cdot v)=\alpha_0+\bar{F}^{-1}(\delta) \end{align*}$$
and the
![]() $\sum _{i=1}^n x_i\cdot y_i>0$
iff
$\sum _{i=1}^n x_i\cdot y_i>0$
iff
![]() $\alpha _0>0$
iff
$\alpha _0>0$
iff
![]() $F'(\sum _{i=1}^n x_i\cdot y_i)>0$
.
$F'(\sum _{i=1}^n x_i\cdot y_i)>0$
.
Therefore
![]() $F':D' \to \mathcal {E}$
is an
$F':D' \to \mathcal {E}$
is an
![]() $\mathbb R$
-monomorphism, in which the range of
$\mathbb R$
-monomorphism, in which the range of
![]() $F'$
is full and contains all partial sums of the range of
$F'$
is full and contains all partial sums of the range of
![]() $F'$
. Let
$F'$
. Let
![]() $\hat {D}=D'[\mathbb R][x_{\gamma }]$
, computed in
$\hat {D}=D'[\mathbb R][x_{\gamma }]$
, computed in
![]() $M[G(\theta _{\gamma })]$
. By application of Lemma 6.7, we may extend
$M[G(\theta _{\gamma })]$
. By application of Lemma 6.7, we may extend
![]() $F'$
to
$F'$
to
![]() $\hat {F}:\hat {D} \to \mathcal {E}$
, to a level
$\hat {F}:\hat {D} \to \mathcal {E}$
, to a level
![]() $\mathbb R$
-monomorphism. Assume that
$\mathbb R$
-monomorphism. Assume that
![]() $x_{\gamma }\notin D'[\mathbb R]$
. By Lemma 6.8, there is
$x_{\gamma }\notin D'[\mathbb R]$
. By Lemma 6.8, there is
![]() $D_{\gamma }\supset D'[\mathbb R]$
, with
$D_{\gamma }\supset D'[\mathbb R]$
, with
![]() $x_{\gamma }\in D_{\gamma }$
, and an extension of
$x_{\gamma }\in D_{\gamma }$
, and an extension of
![]() $\hat {F}$
,
$\hat {F}$
,
![]() $F_{\gamma }:D_{\gamma } \to \mathcal {E}$
, such that
$F_{\gamma }:D_{\gamma } \to \mathcal {E}$
, such that
![]() $F_{\gamma }$
is an extendible function.
$F_{\gamma }$
is an extendible function.
Limit Case: Suppose
![]() $\gamma $
is a limit ordinal. Let
$\gamma $
is a limit ordinal. Let ![]() . Then
. Then
![]() $D'$
is a subring of
$D'$
is a subring of
![]() $D_{\omega _1}$
and has countable transcendence degree over
$D_{\omega _1}$
and has countable transcendence degree over
![]() $\mathbb R$
. By condition 6 of Definition 8.1 it is straightforward to verify that
$\mathbb R$
. By condition 6 of Definition 8.1 it is straightforward to verify that
![]() $F':D' \to \mathcal {E}$
defined by
$F':D' \to \mathcal {E}$
defined by ![]() is an extendible function. Since
is an extendible function. Since
![]() $D'$
is full, we may apply Lemma 6.7 to extend
$D'$
is full, we may apply Lemma 6.7 to extend
![]() $F'$
to an
$F'$
to an
![]() $\mathbb R$
-monomorphism of
$\mathbb R$
-monomorphism of
![]() $D'[\mathbb R]$
(computed in
$D'[\mathbb R]$
(computed in
![]() $M[G_{\theta _{\gamma }}]$
). Let
$M[G_{\theta _{\gamma }}]$
). Let
![]() $D_{\gamma }$
be the ring
$D_{\gamma }$
be the ring
![]() $D'[\mathbb R][x_{\gamma }]$
. Then by Lemma 6.8 there is an extension of
$D'[\mathbb R][x_{\gamma }]$
. Then by Lemma 6.8 there is an extension of
![]() $F'$
,
$F'$
,
![]() $F_{\gamma }:D_{\gamma }\to \mathcal {E}$
that is an extendible function. Let
$F_{\gamma }:D_{\gamma }\to \mathcal {E}$
that is an extendible function. Let ![]() . By Lemma 3.3 of [Reference Dumas4], the domain of F is forced to be the finite elements of
. By Lemma 3.3 of [Reference Dumas4], the domain of F is forced to be the finite elements of
![]() ${\mathbb R}^{\omega }/U$
.
${\mathbb R}^{\omega }/U$
.
Corollary 8.3. Let M be a transitive model of
![]() $ZFC+V=L$
containing a simplified
$ZFC+V=L$
containing a simplified
![]() $(\omega _2,2)$
-morass, and
$(\omega _2,2)$
-morass, and
![]() $M[G]$
be a generic extension of M adding
$M[G]$
be a generic extension of M adding
![]() $\aleph _4$
generic reals. Let X be an infinite compact Haussdorf space in
$\aleph _4$
generic reals. Let X be an infinite compact Haussdorf space in
![]() $M[G]$
. Then there is a discontinuous homomorphism of
$M[G]$
. Then there is a discontinuous homomorphism of
![]() $C(X)$
, the algebra of continuous real-valued functions on X in
$C(X)$
, the algebra of continuous real-valued functions on X in
![]() $M[G]$
.
$M[G]$
.
Proof Let M be a transitive model of
![]() $ZFC + V=L$
containing a simplified
$ZFC + V=L$
containing a simplified
![]() $(\omega _2,2)$
-morass,
$(\omega _2,2)$
-morass, ![]() . Let P be the poset adding generic reals indexed by
. Let P be the poset adding generic reals indexed by
![]() $\omega _4$
, and G be P-generic over M. Then
$\omega _4$
, and G be P-generic over M. Then ![]() is a simplified
is a simplified
![]() $(\omega _3,1)$
-morass, and below
$(\omega _3,1)$
-morass, and below
![]() $\omega _2$
,
$\omega _2$
, ![]() satisfies the axioms of a simplified
satisfies the axioms of a simplified
![]() $(\omega _2,1)$
-morass. Let
$(\omega _2,1)$
-morass. Let
![]() $G_{\omega _2}$
be the factor of G that adds generic reals indexed by
$G_{\omega _2}$
be the factor of G that adds generic reals indexed by
![]() $\omega _2$
. By a routine extension of Theorem 6.4 of [Reference Dumas4] there is
$\omega _2$
. By a routine extension of Theorem 6.4 of [Reference Dumas4] there is
![]() $\overline {U}\subseteq M^{P(\omega _2)}$
, a standard term for an ultrafilter that is morass-closed below
$\overline {U}\subseteq M^{P(\omega _2)}$
, a standard term for an ultrafilter that is morass-closed below
![]() $\omega _2$
. Furthermore, the morass-continuation of
$\omega _2$
. Furthermore, the morass-continuation of
![]() $\overline {U}$
, U, is a standard ultrafilter that is gap-2 morass-closed. By Theorem 6.4 of [Reference Dumas4],
$\overline {U}$
, U, is a standard ultrafilter that is gap-2 morass-closed. By Theorem 6.4 of [Reference Dumas4],
![]() ${\mathbb R}^{\omega }/U\in M^P$
is a gap-2 morass-definable
${\mathbb R}^{\omega }/U\in M^P$
is a gap-2 morass-definable
![]() $\eta _1$
-ordering.
$\eta _1$
-ordering.
We adapt the argument of Theorem 8.2 to the
![]() $(\omega _2,2)$
-morass. The argument is altogether similar except for one detail. The transfinite construction we require will necessarily be of order-type
$(\omega _2,2)$
-morass. The argument is altogether similar except for one detail. The transfinite construction we require will necessarily be of order-type
![]() $\omega _2$
. Hence it is not enough that
$\omega _2$
. Hence it is not enough that
![]() $\mathcal {E}$
is an
$\mathcal {E}$
is an
![]() $\eta _1$
-ordering to extend the term function by
$\eta _1$
-ordering to extend the term function by
![]() $\aleph _2$
many specified terms. Here we use Woodin’s argument [Reference Woodin15], that in the generic extension adding
$\aleph _2$
many specified terms. Here we use Woodin’s argument [Reference Woodin15], that in the generic extension adding
![]() $\aleph _2$
generic reals to L, all cuts of
$\aleph _2$
generic reals to L, all cuts of
![]() $\mathcal {E}$
bear countable cofinal subcuts. We will construct a morass-closed, level term function from the finite elements of a standard ultrapower,
$\mathcal {E}$
bear countable cofinal subcuts. We will construct a morass-closed, level term function from the finite elements of a standard ultrapower,
![]() ${\mathbb R}^{\omega }/U$
, to the Esterle algebra that is forced to be an
${\mathbb R}^{\omega }/U$
, to the Esterle algebra that is forced to be an
![]() $\mathbb R$
-monomorphism.
$\mathbb R$
-monomorphism.
For
![]() $\alpha <\omega _2$
, let
$\alpha <\omega _2$
, let
![]() $X_{\alpha }=({\mathbb R}^{\omega }/U) \cap M^{P_{\alpha }}$
and
$X_{\alpha }=({\mathbb R}^{\omega }/U) \cap M^{P_{\alpha }}$
and
![]() $Y_{\alpha }=\mathcal {E} \cap M^{P_{\alpha }}$
. We consider
$Y_{\alpha }=\mathcal {E} \cap M^{P_{\alpha }}$
. We consider
![]() $X_{\alpha }$
and
$X_{\alpha }$
and
![]() $Y_{\alpha }$
as the restrictions of
$Y_{\alpha }$
as the restrictions of
![]() ${\mathbb R}^{\omega }/U$
and
${\mathbb R}^{\omega }/U$
and
![]() $\mathcal {E}$
, resp., to the forcing language adding generic reals indexed by
$\mathcal {E}$
, resp., to the forcing language adding generic reals indexed by
![]() $\varphi _{\theta _{\alpha }}$
. In any P-generic extension of M,
$\varphi _{\theta _{\alpha }}$
. In any P-generic extension of M,
![]() $M[G]$
, the interpretation of
$M[G]$
, the interpretation of
![]() $X_{\alpha }$
in
$X_{\alpha }$
in
![]() $M[G]$
is the interpretation of
$M[G]$
is the interpretation of
![]() $X_{\alpha }$
in
$X_{\alpha }$
in
![]() $M[G_{\alpha }]$
where
$M[G_{\alpha }]$
where
![]() $G_{\alpha }$
is the factor of G that is
$G_{\alpha }$
is the factor of G that is
![]() $P_{\alpha }$
-generic over M.
$P_{\alpha }$
-generic over M.
We construct a morass-commutative level term injection from
![]() $X_{\omega _2}$
to
$X_{\omega _2}$
to
![]() $Y_{\omega _2}$
that is forced to be an
$Y_{\omega _2}$
that is forced to be an
![]() $\mathbb R$
-monomorphism. The closure under embeddings,
$\mathbb R$
-monomorphism. The closure under embeddings,
![]() $f_{\theta _{\beta }}$
where
$f_{\theta _{\beta }}$
where ![]() , of this function will be the term function we seek.
, of this function will be the term function we seek.
Let
![]() $B=\{ x_{\beta } \mid \beta <\omega _2 \}\subseteq X_{\omega _2}$
be a transfinite sequence of terms of strict level for a maximal algebraically independent set of infinitesimal elements of
$B=\{ x_{\beta } \mid \beta <\omega _2 \}\subseteq X_{\omega _2}$
be a transfinite sequence of terms of strict level for a maximal algebraically independent set of infinitesimal elements of
![]() $X_{\omega _2}$
, such that
$X_{\omega _2}$
, such that
![]() $x_{\alpha }\in X_{\alpha }$
for all
$x_{\alpha }\in X_{\alpha }$
for all
![]() $\alpha <\omega _2$
.
$\alpha <\omega _2$
.
We may inductively construct a transfinite sequence of morass-commutative term functions
![]() $\langle F_{\beta }:D_{\beta }\to E_{\beta } \mid \beta <\omega _2 \rangle $
that satisfies the following for all
$\langle F_{\beta }:D_{\beta }\to E_{\beta } \mid \beta <\omega _2 \rangle $
that satisfies the following for all
![]() $\alpha \leq \beta <\omega _2$
:
$\alpha \leq \beta <\omega _2$
:
-
1.
 $D_{\beta }\subseteq X_{\theta _{\beta }}$
is a subring of finite elements and is morass-closed beneath
$D_{\beta }\subseteq X_{\theta _{\beta }}$
is a subring of finite elements and is morass-closed beneath
 $\theta _{\beta }$
.
$\theta _{\beta }$
. -
2.
 $E_{\beta }\subseteq Y_{\theta _{\beta }}$
is full and closed under partial sums.
$E_{\beta }\subseteq Y_{\theta _{\beta }}$
is full and closed under partial sums. -
3.
 $D_{\alpha }\subseteq D_{\beta }$
and
$D_{\alpha }\subseteq D_{\beta }$
and
 $E_{\alpha }\subseteq E_{\beta }$
.
$E_{\alpha }\subseteq E_{\beta }$
. -
4.
 $x_{\beta }\in D_{\beta }$
.
$x_{\beta }\in D_{\beta }$
. -
5.
 $F_{\beta }$
is a level, morass-commutative term function that is forced to be an
$F_{\beta }$
is a level, morass-commutative term function that is forced to be an
 $\mathbb R$
-monomorphism.
$\mathbb R$
-monomorphism. -
6.
 $f_{\theta _{\alpha }}[F_{\alpha }]\subseteq F_{\beta }$
for all
$f_{\theta _{\alpha }}[F_{\alpha }]\subseteq F_{\beta }$
for all  .
.
The proof is similar to the proof of Theorem 8.2 with only minor modifications. Given an extendible sequence
![]() $\langle F_{\beta }:D_{\beta } \to E_{\beta } \mid \beta <\gamma \rangle $
, where
$\langle F_{\beta }:D_{\beta } \to E_{\beta } \mid \beta <\gamma \rangle $
, where
![]() $\gamma $
is a successor ordinal, we may construct an extendible
$\gamma $
is a successor ordinal, we may construct an extendible
![]() $\mathbb R$
-monomorphism,
$\mathbb R$
-monomorphism,
![]() $F'$
, that extends
$F'$
, that extends
![]() $f_{\theta _{\beta }}[F_{\beta }]$
for all
$f_{\theta _{\beta }}[F_{\beta }]$
for all
![]() $\beta <\gamma $
and
$\beta <\gamma $
and
![]() $f\in \cal {F}_{\beta \gamma }$
. By Lemma 6.7 we may extend
$f\in \cal {F}_{\beta \gamma }$
. By Lemma 6.7 we may extend
![]() $F'$
to
$F'$
to
![]() $\hat {F}$
, a level
$\hat {F}$
, a level
![]() $\mathbb R$
-monomorphism of the ring generated by the domain of
$\mathbb R$
-monomorphism of the ring generated by the domain of
![]() $F'$
and the real numbers of
$F'$
and the real numbers of
![]() $M[G_{\theta _{\gamma }}]$
. If
$M[G_{\theta _{\gamma }}]$
. If
![]() $x_{\gamma }$
is not in the domain of
$x_{\gamma }$
is not in the domain of
![]() $\hat {F}$
, then by Woodin’s argument that all gaps of the Esterle algebra in
$\hat {F}$
, then by Woodin’s argument that all gaps of the Esterle algebra in
![]() $M[G_{\omega _2}]$
are
$M[G_{\omega _2}]$
are
![]() $(\omega ,\omega ^*)$
-gaps, we may apply Johnson’s Lemma 3.5 and Lemma 6.8. Then there is
$(\omega ,\omega ^*)$
-gaps, we may apply Johnson’s Lemma 3.5 and Lemma 6.8. Then there is
![]() $D_{\gamma }$
extending the domain of
$D_{\gamma }$
extending the domain of
![]() $\hat {F}$
, with
$\hat {F}$
, with
![]() $x_{\gamma }\in D_{\gamma }$
, and an extension of
$x_{\gamma }\in D_{\gamma }$
, and an extension of
![]() $\hat {F}$
,
$\hat {F}$
,
![]() $F_{\gamma }:D_{\gamma } \to \mathcal {E}$
such that
$F_{\gamma }:D_{\gamma } \to \mathcal {E}$
such that
![]() $\langle F_{\beta } : D_{\beta } \to E_{\beta } \mid \beta \leq \gamma \rangle $
is an extendible sequence. The argument for
$\langle F_{\beta } : D_{\beta } \to E_{\beta } \mid \beta \leq \gamma \rangle $
is an extendible sequence. The argument for
![]() $\gamma $
a limit is similar.
$\gamma $
a limit is similar.
9. Pressing the continuum
The techniques of this paper, [Reference Dumas3] and [Reference Dumas4] depend on the construction of functions between sets of terms in the forcing language of Cohen extensions, utilizing commutativity with order-preserving injections of indexing ordinals of the Cohen poset. Having presented the details of the construction of level term functions using simplified gap-1 and gap-2 morasses, it is relatively straightforward to see how these constructions extend to simplified higher (finite) gap morasses.
A simplified
![]() $(\kappa ,n+1)$
-morass, for
$(\kappa ,n+1)$
-morass, for
![]() $\kappa $
a regular cardinal and integer n, is a family of embeddings between fake simplified
$\kappa $
a regular cardinal and integer n, is a family of embeddings between fake simplified
![]() $(\kappa , n)$
-morass segments that satisfies properties analogous to those relating a simplified
$(\kappa , n)$
-morass segments that satisfies properties analogous to those relating a simplified
![]() $(\omega _1,2)$
-morass to embeddings between fake simplified
$(\omega _1,2)$
-morass to embeddings between fake simplified
![]() $(\omega _1,1)$
-morass segments. Central to the utility of these constructions is that the embeddings are may be considered as order-preserving injections between ordinals. For a thorough treatment of simplified finite gap morasses, including an inductive definition, see Szalkai [Reference Szalkai12].
$(\omega _1,1)$
-morass segments. Central to the utility of these constructions is that the embeddings are may be considered as order-preserving injections between ordinals. For a thorough treatment of simplified finite gap morasses, including an inductive definition, see Szalkai [Reference Szalkai12].
Higher gap morasses will allow the extension of results of this paper and [Reference Dumas4] to Cohen extensions adding more than
![]() $\aleph _4$
generic reals. The definition of gap-2 morass-definable
$\aleph _4$
generic reals. The definition of gap-2 morass-definable
![]() $\eta _1$
-orderings and
$\eta _1$
-orderings and
![]() $\eta _1$
-ordered real-closed fields (resp.) are easily generalized to gap-n morass-definable
$\eta _1$
-ordered real-closed fields (resp.) are easily generalized to gap-n morass-definable
![]() $\eta _1$
-orderings and
$\eta _1$
-orderings and
![]() $\eta _1$
-ordered real-closed fields (resp.).
$\eta _1$
-ordered real-closed fields (resp.).
Acknowledgments
I would like to thank the referee for many helpful suggestions, particularly a simpler proof of Lemma 6.1.