1 Introduction
The solar wind is a weakly collisional, magnetised plasma characterised by kinetic processes that influence its dynamic evolution in ways that are not fully understood. The expansion of the solar wind into interplanetary space in the presence of a decreasing background magnetic field (Matteini et al. Reference Matteini, Landi, Hellinger, Pantellini, Maksimovic, Velli, Goldstein and Marsch2007, Reference Matteini, Hellinger, Landi, Trávníček and Velli2012) implies that the particle distributions should be highly anisotropic by the time the plasma reaches a distance of ${\sim }1\,\mathrm {au}$
from the Sun (Verscharen et al. Reference Verscharen, Chandran, Klein and Quataert2016). The double-adiabatic (CGL; Chew, Low & Goldberger Reference Chew, Low and Goldberger1956) expansion of the solar wind predicts a decline in $T_\perp /T_\parallel$
with distance from the Sun, where $T_\perp$
($T_\parallel$
) is the proton temperature perpendicular (parallel) to the magnetic field direction (Matteini et al. Reference Matteini, Landi, Hellinger, Pantellini, Maksimovic, Velli, Goldstein and Marsch2007; Cranmer et al. Reference Cranmer, Matthaeus, Breech and Kasper2009). However, observations at $1\,\mathrm {au}$
show that the solar wind is, on average, almost isotropic with respect to the background magnetic field, albeit with significant variability in temperature anisotropy about the isotropic equilibrium (Marsch et al. Reference Marsch, Mühlhäuser, Schwenn, Rosenbauer, Pilipp and Neubauer1982; Kasper, Lazarus & Gary Reference Kasper, Lazarus and Gary2002; Bale et al. Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Maruca, Kasper & Bale Reference Maruca, Kasper and Bale2011; Isenberg, Maruca & Kasper Reference Isenberg, Maruca and Kasper2013; Coburn, Chen & Squire Reference Coburn, Chen and Squire2022).
The presence of temperature anisotropy in the solar wind is also linked to turbulence. Solar-wind turbulence facilitates a nonlinear transfer of energy from larger to smaller scales via a Kolmogorov-like inertial range, leading to the dissipation of energy at kinetic scales (Kolmogorov Reference Kolmogorov1941; Alexandrova et al. Reference Alexandrova, Chen, Sorriso-Valvo, Horbury and Bale2013; Bruno & Carbone Reference Bruno and Carbone2013; Kiyani, Osman & Chapman Reference Kiyani, Osman and Chapman2015; Chen Reference Chen2016; Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023). This nonlinear energy transfer occurs via a cascade which is inherently anisotropic in the distribution of its spectral power with respect to the wavevector of the fluctuations, with $k_\perp \gg k_\parallel$
, where $k_\perp$
($k_\parallel$
) is the component of the wavevector perpendicular (parallel) to the magnetic field direction (Cho & Vishniac Reference Cho and Vishniac2000; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Wicks et al. Reference Wicks, Horbury, Chen and Schekochihin2011; Horbury, Wicks & Chen Reference Horbury, Wicks and Chen2012; Oughton et al. Reference Oughton, Matthaeus, Wan and Osman2015; Chen et al. Reference Chen, Matteini, Schekochihin, Stevens, Salem, Maruca, Kunz and Bale2016; Schekochihin Reference Schekochihin2022). Some solar wind models predict that the turbulent cascade is responsible for the temperature-anisotropic heating of the plasma (Parashar et al. Reference Parashar, Shay, Cassak and Matthaeus2009; Chandran et al. Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Howes Reference Howes2015). Considering the expectations based on CGL expansion and temperature-anisotropic heating models, the observation of, on average, approximately isotropic plasma conditions suggests that additional processes act to restore isotropy through the transfer of energy (Marsch et al. Reference Marsch, Mühlhäuser, Schwenn, Rosenbauer, Pilipp and Neubauer1982). The stability of the solar wind depends on the simultaneous contributions of all species in the plasma to its free energy (Chen et al. Reference Chen, Matteini, Schekochihin, Stevens, Salem, Maruca, Kunz and Bale2016), but here we consider only the protons.
A class of kinetic instabilities is triggered when the proton temperature anisotropy exceeds certain thresholds for the production of plasma waves and non-propagating modes. These instabilities transfer energy from the particles to electromagnetic fields and this transfer restores the proton distribution towards a stable state closer to isotropy (Gary Reference Gary1976, Reference Gary1993; Hellinger et al. Reference Hellinger, Trávníček, Kasper and Lazarus2006). At large scales, compressive fluctuations can drive temperature anisotropy leading to wave-driven instabilities that eventually reduce anisotropy through pitch-angle scattering of protons (Verscharen et al. Reference Verscharen, Chandran, Klein and Quataert2016), while at small scales, kinetic instabilities predicted by linear theory redistribute energy through wave–particle interaction (Gary Reference Gary1993; Kasper et al. Reference Kasper, Lazarus and Gary2002; Hellinger et al. Reference Hellinger, Matteini, Štverák, Trávníček and Marsch2011, Reference Hellinger, Trávníček, Štverák, Matteini and Velli2013; Howes Reference Howes2015).
Proton-kinetic processes, such as temperature-anisotropy-driven instabilities, predominantly occur on scales near the small-scale end of the inertial range of the plasma turbulence (Gary Reference Gary2015). In contrast to the framework of traditional linear theory, kinetic instabilities in the solar wind operate in inhomogeneous and non-constant conditions due to the ubiquitous solar-wind turbulence (Coleman Reference Coleman1968; Frisch, Sulem & Nelkin Reference Frisch, Sulem and Nelkin1978; Tu & Marsch Reference Tu and Marsch1995; Chen Reference Chen2016; Verscharen, Klein & Maruca Reference Verscharen, Klein and Maruca2019; Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022, Reference Opie, Verscharen, Chen, Owen and Isenberg2023). In developing a more robust understanding of where and under what conditions energy transfer takes place, it is therefore important to fully capture the interplay between kinetic and turbulent features at the appropriate scales in the solar wind (Osman et al. Reference Osman, Matthaeus, Hnat and Chapman2012; Chen Reference Chen2016; Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Perri, Greco, Marino and Bruno2018a; Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022, Reference Opie, Verscharen, Chen, Owen and Isenberg2023; Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023).
The solar-wind turbulence is intermittent and consistent with the model of multifractality (Frisch & Kolmogorov Reference Frisch and Kolmogorov1995), meaning that the fluctuations at different scales are not equally space-filling and instead contain coherent structures such as current sheets and velocity shear layers (Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Veltri, Consolini and Bruno1999; Greco et al. Reference Greco, Chuychai, Matthaeus, Servidio and Dmitruk2008; Osman et al. Reference Osman, Matthaeus, Kiyani, Hnat and Chapman2013; Servidio et al. Reference Servidio, Osman, Valentini, Perrone, Califano, Chapman, Matthaeus and Veltri2014; Matthaeus et al. Reference Matthaeus, Wan, Servidio, Greco, Osman, Oughton and Dmitruk2015; Qudsi et al. Reference Qudsi, Maruca, Matthaeus, Parashar, Bandyopadhyay, Chhiber, Chasapis, Goldstein, Bale and Bonnell2020). These structures extend across scales in the inertial range and exhibit a statistical scaling relationship that indicates that they are self-affine (Carbone, Veltri & Bruno Reference Carbone, Veltri and Bruno1995; Carbone, Bruno & Veltri Reference Carbone, Bruno and Veltri1996; Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Veltri, Consolini and Bruno1999; Kiyani, Chapman & Hnat Reference Kiyani, Chapman and Hnat2006; Hnat et al. Reference Hnat, Chapman, Kiyani, Rowlands and Watkins2007).
We hypothesise that the turbulent and intermittent velocity field in the solar wind is dynamically important for driving the temperature anisotropy of the plasma protons. Using a large observational dataset, we localise conditions in the solar wind at and beyond the thresholds for the proton-driven oblique firehose instability when $T_\perp /T_\parallel <1$
(Hellinger & Trávníček Reference Hellinger and Trávníček2008; Markovskii & Vasquez Reference Markovskii and Vasquez2022) and mirror-mode instability when $T_\perp /T_\parallel >1$
(Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Hellinger et al. Reference Hellinger, Landi, Matteini, Verdini and Franci2017), which place effective boundaries for temperature anisotropy in the solar wind (Hellinger et al. Reference Hellinger, Trávníček, Kasper and Lazarus2006; Bale et al. Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Gary Reference Gary2015). Working directly from the dynamical equations, we develop and analyse a quantitative measure for the impact of velocity shears on the temperature anisotropy: the radial rate of strain. We measure the third and fourth statistical moments of the radial rate of strain, the velocity field and the magnetic field, from which we infer where, in terms of turbulent structures in the solar wind, these instabilities are located.
We set out details of our data analysis in § 2. In § 3, we develop and evaluate our novel measure of the radial rate of strain, a one-dimensional proxy for the three-dimensional double-adiabatic strain rate. In § 4, we calculate the skewness and kurtosis of the radial rate of strain, the magnetic field and the velocity field. We discuss the significance of our results in § 5 and conclude with recommendations for further work in § 6.
2 Data analysis
2.1 Dataset
Our dataset, which is a significant extension of that used by Opie et al. (Reference Opie, Verscharen, Chen, Owen and Isenberg2022), comprises ${\approx}1.5\mathrm {M}$
datapoints, as detailed in table 1. Our data are taken from the Solar Orbiter public archive.Footnote 1 We use data from two of the in situ instruments on board the spacecraft which make measurements of the solar wind; namely the magnetic-field vector from the Magnetometer (MAG) at $8\,\mathrm {Hz}$
cadence (Horbury et al. Reference Horbury, O'Brien, Carrasco Blazquez, Bendyk, Brown, Hudson, Evans, Oddy, Carr and Beek2020) and the proton moments from the Proton–Alpha Sensor (PAS). For the periods discussed here, PAS takes a $1\,\mathrm {s}$
sample every $4\,\mathrm {s}$
. PAS is part of the Solar Wind Analyser (SWA) instrument suite (Owen et al. Reference Owen, Bruno, Livi, Louarn, Al Janabi, Allegrini, Amoros, Baruah, Barthe and Berthomier2020). For this study, we work in the $(R,T,N)$
coordinate system, where the axis $R$
points radially outwards from the Sun, $T$
is given by the cross-product between the Sun's rotation vector and $R$
, and $N$
completes the right-handed triad.
Table 1. Data selection from the Solar Orbiter Archive with approximate heliocentric distance (in solar radii, $R_S$
) for each data interval.
The relative error for the PAS data is ${\approx }0.27\,\%$
for the velocity measurements (Louarn et al. Reference Louarn, Fedorov, Prech, Owen, Bruno, Livi, Lavraud, Rouillard, Genot and Andre2021). For our dataset, this represents an average absolute error of ${\approx }1.2\,\mathrm {km}\,\mathrm {s}^{-1}$
.
Since we employ two-point field increments in this analysis, we use continuous data intervals of 4–7 days duration, subject to data availability. We exclude PAS datapoints for which the solar wind bulk velocity ${<}325\,\mathrm {km}\,\mathrm {s}^{-1}$
or when measurements are outside the recommended PAS quality factor $\leq 0.2$
. No attempt is made to eliminate any structures, such as shocks or interplanetary coronal mass ejections (ICMEs), from the dataset. Reference to the Helio4Cast catalogueFootnote 2 for ICMEs observed by Solar Orbiter gives three ICMEs in total within our combined dataset. These occurred on 06 May 2021, 10 May 2021 and 03 November 2021 for an aggregated duration of 79.16 hours of our total observational time frame of 80 days (Möstl et al. Reference Möstl, Isavnin, Boakes, Kilpua, Davies, Harrison, Barnes, Krupar, Eastwood and Good2017, Reference Möstl, Weiss, Bailey, Reiss, Amerstorfer, Hinterreiter, Bauer, McIntosh, Lugaz and Stansby2020).
Solar Orbiter provides a continuous high-resolution dataset of the pristine solar wind for both magnetic and proton velocity field analysis (Louarn et al. Reference Louarn, Fedorov, Prech, Owen, Bruno, Livi, Lavraud, Rouillard, Genot and Andre2021). This enables our two-point field increment method to be statistically robust on time scales that are equivalent to the scales needed to observe unstable intervals (Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022).
2.2 Data processing
We rotate the proton pressure tensor to align with the local associated magnetic field and create a time series for $\beta _{\parallel }\equiv 8{\rm \pi} n_{p}k_{B}T_{\parallel }/B^2$
, where $n_{p}$
is the proton number density, $k_{B}$
is the Boltzmann constant and $B$
is the magnetic field strength averaged over the associated 1 s PAS measurement interval. From the proton pressure tensor, we then calculate the ratio $T_{\perp }/T_{\parallel }$
for each PAS measurement.
To identify intervals in our dataset for which linear theory predicts the growth of kinetic instabilities, we require thresholds for the growth of the specific anisotropy-driven kinetic instabilities of interest. We base our identification of unstable intervals on the parametric approximation for the instability thresholds in the form
where $a$
, $b$
and $c$
are constants with values given for each instability for a range of instability maximum growth rates by Verscharen et al. (Reference Verscharen, Chandran, Klein and Quataert2016). We use the constants given for a maximum growth rate of $\gamma _{m} = 10^{-2} \varOmega _{p}$
, where $\varOmega _{p}$
is the proton gyrofrequency. We evaluate these instability thresholds for the oblique firehose (OF) and for the mirror-mode (M) instabilities. For reference, we also include the instability threshold for the Alfvén/ion-cyclotron (A/IC) instability in part of our analysis.
We analyse data distributed in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space that is bounded by these thresholds. We define the unstable intervals as comprising those data points that lie above the thresholds, while we characterise all data below the thresholds as stable. Consequently, the plasma is considered unstable against M and A/IC instabilities if $T_{\perp }/T_{\parallel }$
is greater than the value given by the right-hand side of (2.1), while it is considered unstable against the OF instability if $T_{\perp }/T_{\parallel }$
is less than the value given by the right-hand side of (2.1) with, in each case, the constants chosen for the respective instability.
3 Radial strain
In this section, we use a single-species (proton) fluid model of space plasma that derives anisotropy directly from the effect of fluid strain on the pressure tensor. We define the radial rate of strain $\varGamma _R$
as a proxy for the strain rate in fully three-dimensional turbulence for this analysis, which we believe to be a novel technique. We then use this measure to test our hypothesis that intermittent velocity shear is dynamically important for the generation of the observed temperature anisotropy in the solar wind.
3.1 Method: determination of the radial strain
We examine the evolution of pressure anisotropy based on the first three moments of the proton distribution function under CGL analysis (Chew et al. Reference Chew, Low and Goldberger1956; Kulsrud Reference Kulsrud1984). We take the form of the equation for pressure anisotropy given by Squire et al. (Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023) which assumes that the pressure tensor is invariant to rotation about the magnetic field direction:
where $p_{\perp }$
and $p_{\parallel }$
are the proton pressure tensor components perpendicular and parallel to the magnetic field, $\boldsymbol {\hat {b}}=\boldsymbol {B}/B$
, $\boldsymbol {v}$
is the proton bulk velocity, $q_\perp$
and $q_\parallel$
are the proton heat fluxes perpendicular and parallel to the magnetic field direction, and $\nu _{c}$
is the proton collisional relaxation frequency for temperature anisotropy. The first two terms on the right-hand side of (3.1) describe how plasma bulk flows directly affect pressure anisotropy through shear and compression. We assume that $\nu _{c}=0$
and $q_\perp = q_\parallel= 0$
following the arguments of Del Sarto & Pegoraro (Reference Del Sarto and Pegoraro2018).
These assumptions allow us to formulate a new proxy measure for the driving of pressure anisotropy by plasma motion based on plasma measurements sampled along the radial direction by a single spacecraft. We use Taylor's hypothesis (Taylor Reference Taylor1938) to transpose spatial partial derivatives to temporal partial derivatives and employ increments to replace $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {v}$
and $\boldsymbol {\nabla }\boldsymbol {v}$
. After these transformations, we define the radial rate of strain as
where $\tau$
is the time increment between measurement points (i.e. the measurement cadence) and $\Delta \phi$
denotes the scale-dependent increment $\Delta \phi =\phi (t)-\phi (t+\tau )$
of any time-dependent observable $\phi$
in the spacecraft reference frame.
Following the interpretation of the first and second terms in (3.1), we decompose (3.2) into proxies for the incompressible ($\varGamma _{R\, I}$
) and compressible ($\varGamma _{R\, C}$
) contributions to $\varGamma _R$
as
and
We set $\tau =8\,\mathrm {s}$
, which results in an average relative value of $\Delta {v}_j/|\boldsymbol {v}|$
for our intervals of $0.48\,\%$
. We check that all data with small $\Delta {v}_j$
values make a negligible contribution to $\varGamma _R$
and so the relevant datapoints are well above the PAS relative error. Any systematic errors due to bias offsets in any quantity $\phi$
are eliminated through the process of calculating the difference $\Delta \phi$
. We exclude any data points for which an increment of $\tau =8\,\mathrm {s}$
cannot be calculated due to data gaps.
3.2 Results: the radial strain of stable and unstable plasma intervals
We calculate $\varGamma _R$
from (3.2) for each datapoint in our dataset after the elimination of data gaps and plot the bin-averaged values in a two-dimensional histogram in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space in figure 1. We also calculate $\varGamma _{R\, I}$
from (3.3) and $\varGamma _{R\, C}$
from (3.4), and plot these separately in two-dimensional histograms in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space in figures 2 and 3, respectively.
Figure 1. Distribution of $\varGamma _R$
as bin averages in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space. We overplot the instability thresholds for the oblique firehose (OF), Alfvén/ion-cyclotron (A/IC) and mirror-mode (M) instabilities.
Figure 2. Distribution of $\varGamma _{R\, I}$
as bin averages in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space. We overplot the instability thresholds for the oblique firehose (OF), Alfvén/ion-cyclotron (A/IC) and mirror-mode (M) instabilities.
Figure 3. Distribution of $\varGamma _{R\mathrm C}$
as bin averages in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space. We overplot the instability thresholds for the oblique firehose (OF), Alfvén/ion-cyclotron (A/IC) and mirror-mode (M) instabilities.
According to figure 1, the unstable intervals show, on average, high absolute values, relative to the stable data, of $\varGamma _R$
, with $\varGamma _R>0$
in the parameter space associated with the M and A/IC instabilities and $\varGamma _R<0$
in the parameter space associated with the OF instability. This relation is equally maintained for both $\varGamma _{R\, I}$
and $\varGamma _{R\mathrm C}$
, as shown in figures 2 and 3, although the signal varies with $\beta _{\parallel }$
and $T_{\perp }/T_{\parallel }$
. The contribution from $\varGamma _{R\, C}$
is important at lower $\beta _{\parallel }$
and higher $T_{\perp }/T_{\parallel }$
for the mirror-mode unstable region of parameter space and at lower values of $T_{\perp }/T_{\parallel }$
for the oblique firehose unstable region. For the stable data, the average value of $\varGamma _R$
is ${\sim }0$
except for the boundary regions of stable parameter space where either $T_{\perp }/T_{\parallel }<0.3$
or $T_{\perp }/T_{\parallel }>2$
. This result is consistent for both $\varGamma _{R\, I}$
and $\varGamma _{R\mathrm C}$
, although we see some variance in the sign of $\varGamma _{R\, I}$
at the boundary to the mirror-mode unstable region.
We verify from the probability density functions (not shown here) of $\varGamma _R$
for each of the stable ($\varGamma _R^S$
), oblique firehose unstable ($\varGamma _R^{OF}$
) and mirror-mode unstable ($\varGamma _R^M$
) regions that the magnitude of the averaged $\varGamma _R$
is consistently larger in the unstable measurement intervals and that the contrast with the stable region is not simply an averaging effect. We find the mean values as $\langle \varGamma _R^S\rangle =-3.76\times 10^{-18}\,\mathrm {J}\,\mathrm {cm}^3\,\mathrm {s}^{-1}$
, $\langle \varGamma _R^{OF}\rangle =-4.95\times 10^{-17}\,\mathrm {J}\,\mathrm {cm}^3\,\mathrm {s}^{-1}$
and $\langle \varGamma _R^M\rangle =3.51\times 10^{-17}\,\mathrm {J}\,\mathrm {cm}^3\,\mathrm {s}^{-1}$
, where $\langle \cdot \rangle$
represents the average over all measurement intervals in the respective category.
4 Intermittency
In this section, we analyse statistical moments, specifically the third (skewness) and fourth (kurtosis) moments, to measure the intermittency of $\varGamma _R$
. We compare this result with the skewness and kurtosis of the background magnetic and velocity fields.
Intermittency of magnetic and electric fields and plasma parameters (velocity, density, temperature) in the inertial range has been extensively studied (Tu & Marsch Reference Tu and Marsch1995; Marsch & Tu Reference Marsch and Tu1997; Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Veltri, Consolini and Bruno1999; Bruno et al. Reference Bruno, Carbone, Veltri, Pietropaolo and Bavassano2001). We examine the statistical measures separately for stable and unstable intervals to understand the dynamics of the driving of anisotropy by the turbulent fluctuations. In particular, we investigate how the intermittency (in the sense of ‘burstiness’) of the pressure strain varies across the relevant scales.
4.1 Method: measuring the skewness and kurtosis across scales
We use the statistical moments of the quantities $\mu _i$
to calculate their skewness $\lambda _i$
and their kurtosis $\kappa _i$
, where $\mu _i$
is the moment about the mean. The skewness and kurtosis are defined as
and
Using (4.1) and (4.2), we calculate $\lambda _i$
and $\kappa _i$
for $\varGamma _R$
, $\boldsymbol {B}$
and $\boldsymbol {v}$
. We calculate $\lambda _i$
and $\kappa _i$
for the whole dataset and for each of the stable, oblique firehose unstable and mirror-mode unstable datasets.
We also calculate $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
across a range of temporal scales. We do this by creating scale-dependent datasets for $\varGamma _R$
using (3.2) with $\tau \in \{8\,\mathrm {s}, 16\,\mathrm {s}, 32\,\mathrm {s}, 64\,\mathrm {s}, 128\,\mathrm {s}, 256\,\mathrm {s}$
, $512\,\mathrm {s}, 1024\,\mathrm {s}, 2048\,\mathrm {s}\}$
. This results in scale-dependent values of $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
from the small-scale end of the inertial range up to the correlation-length scale.
4.2 Results: the intermittency of ${\varGamma }_R$
We show the values obtained for $\lambda _i$
and $\kappa _i$
in table 2. The values of $\lambda _i$
indicate a symmetric distribution in nearly all cases except for $\lambda ^{OF}_{\varGamma _R}$
which is strongly negative and $\lambda ^{M}_{\varGamma _R}$
which is strongly positive, while the overall $\lambda _{\varGamma _R}$
is also strongly negative.
Table 2. Skewness $\lambda _i$
and kurtosis $\kappa _i$
for $\varGamma _R$
, $\boldsymbol {v}$
and $\boldsymbol {B}$
across all data, stable intervals and unstable intervals.
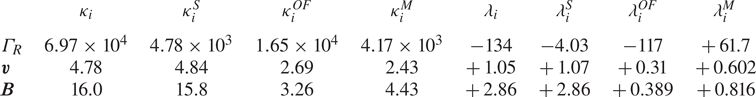
We see that $\kappa _{\varGamma _R} \gg \kappa _{\boldsymbol {v}}$
and $\kappa _{\varGamma _R} \gg \kappa _{\boldsymbol {B}}$
; in both cases, by 2–3 orders of magnitude. This is expected since $\varGamma _R$
is built by multiplying intermittent quantities, and its normalised moments will therefore correspond to higher-order moments when compared with $\boldsymbol {v}$
and $\boldsymbol {B}$
. For the conditioned subsets of $\varGamma _R$
, $\kappa ^{OF}_{\varGamma _R} > \kappa ^{S}_{\varGamma _R} \approx \kappa ^{M}_{\varGamma _R}$
.
We calculate $\lambda _i$
and $\kappa _i$
for $\varGamma _{RI}$
and $\varGamma _{RC}$
. Here, $\lambda _{\varGamma _{RI}}\approx {-}104$
is negative while $\lambda _{\varGamma _{RC}} \approx +46$
is positive. Additionally, $\kappa _{\varGamma _{RI}}\approx 5.1\times 10^{4}$
and $\kappa _{\varGamma _{RC}} \approx 3.05\times 10^{4}$
are consistent with $\kappa _{\varGamma _{R}}$
.
Figure 4 shows the scale-dependent values of $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
as functions of $\tau$
. Both $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
show a power-law scaling which is overlaid as indicated. The values for $\lambda _{\varGamma _R}$
show that the skewness of $\varGamma _R$
increases with decreasing scale from a local minimum at $\tau \approx 512\,\mathrm {s}$
. The sign of all values of $\lambda _{\varGamma _R}$
is negative and has been reversed for visualisation on the logarithmic axis.
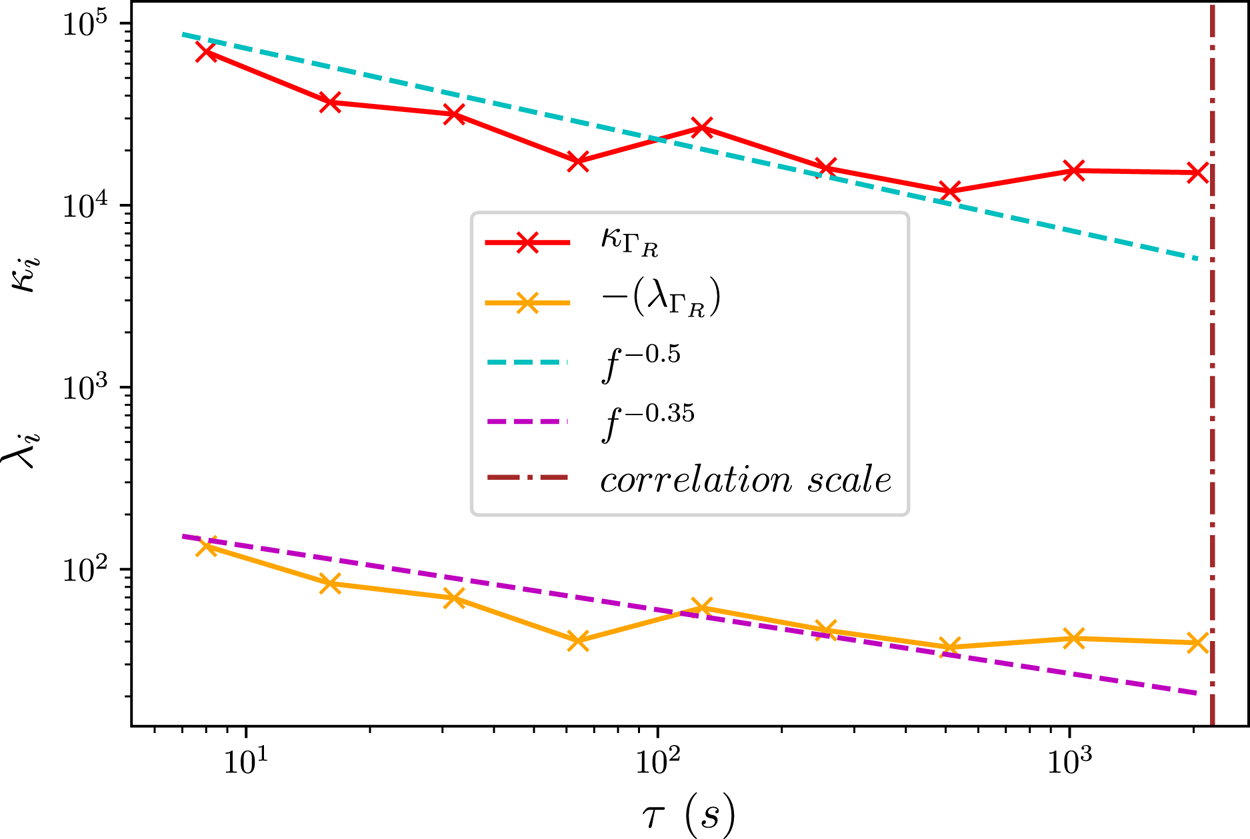
Figure 4. $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
over a range of temporal scales $\tau$
from $8\,\mathrm {s}$
to $2048\,\mathrm {s}$
. The cyan and magenta dashed lines represent a power-law scaling of $-0.5$
and $-0.35$
, respectively. The brown vertical dash-dotted line represents the correlation scale.
The values of $\kappa _{\varGamma _R}$
indicate that the burstiness of the $\varGamma_R$
field increases with decreasing scale, which is the signature of scale-dependent statistics typical of intermittency. Over all $\tau$
in this figure, the $\varGamma _R$
field is evidently intermittent and hence ‘bursty’ due to a heavy-tailed distribution of $\varGamma _R$
. The value of $\kappa _{\varGamma _R}$
reaches a local minimum at $\tau \approx 512\,\mathrm {s}$
.
5 Discussion
Under the assumptions underlying (3.1) in § 3, shear and compression create pressure anisotropy (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), and we interpret our findings as being consistent with that prediction. Relative to the stable data, the absolute values of the bin-averaged $\varGamma _R$
for the unstable data are significantly elevated, on average by a factor of ten. Our interpretation for this observation is that the presence of data in unstable intervals requires the pressure strain from turbulence-driven shears and compressions to compete with the instabilities that act to restore the plasma towards isotropy. In effect, data can only reside in unstable conditions if the time scale associated with the pressure-strain driving of temperature anisotropy is sufficiently small compared with the relaxation time of the relevant instabilities.
Previous work demonstrates that temperature anisotropy and vorticity are well correlated in hybrid simulations of plasma turbulence (Franci et al. Reference Franci, Hellinger, Matteini, Verdini and Landi2016). Hybrid-kinetic simulations also show that oblique firehose and mirror-mode instabilities can be driven by a changing magnetic field in a shear flow (Kunz et al. Reference Kunz, Schekochihin and Stone2014). Our results suggest that the turbulent shears in the velocity field create and modulate temperature anisotropy through a purely dynamical process such as that proposed by Del Sarto & Pegoraro (Reference Del Sarto and Pegoraro2018) and observed in near-Earth space (Servidio et al. Reference Servidio, Osman, Valentini, Perrone, Califano, Chapman, Matthaeus and Veltri2014; Sorriso-Valvo et al. Reference Sorriso-Valvo, Catapano, Retino, Le Contel, Perrone, Roberts, Coburn, Panebianco, Valentini and Perri2019). In this scenario, the non-compressive turbulent fluctuations result in spatially intermittent velocity shears that modulate the frozen-in magnetic field and drive $T_{\perp }/T_{\parallel }\ne 1$
with a corresponding change in magnetic field strength (Del Sarto, Pegoraro & Califano Reference Del Sarto, Pegoraro and Califano2016; Del Sarto & Pegoraro Reference Del Sarto and Pegoraro2018; Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023).
We also see a role for compressive fluctuations in this scenario as per figure 3, where the distribution of $\varGamma _{RC}$
is similar to the distribution of $\varGamma _R$
. Figure 3 also shows that the contribution from compressive fluctuations to $\varGamma _R$
in unstable intervals has the highest absolute average values where $T_{\perp }/T_{\parallel }$
approaches its maximum (M) or minimum (OF) bounds. In particular, we infer from comparison with figure 2 that compressive fluctuations are important in driving temperature anisotropy that creates conditions unstable to the mirror-mode instability. This is consistent with previous findings concerning the distribution of magnetic field fluctuations in unstable intervals (Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2023). We expect the contribution from $\varGamma _{RC}$
to be less significant overall since compressive fluctuations only account for a minor fraction of the solar wind turbulent energy (Tu & Marsch Reference Tu and Marsch1995; Bruno & Carbone Reference Bruno and Carbone2013; Verscharen et al. Reference Verscharen, Klein and Maruca2019; Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023).
The role of $\varGamma _R$
in driving mirror-mode unstable conditions is further supported by the skewness of $\varGamma _R$
and its conditioned subsets where, as set out in § 4, both $\lambda _{\varGamma _{RC}}$
and $\lambda ^M_{\varGamma _R}$
are positive while $\lambda _i$
is negative for the other subsets or close to zero for $\lambda ^S_{\varGamma _R}$
.
In the solar wind, the instabilities, once triggered, act on time scales that rapidly reduce the temperature anisotropy (Bandyopadhyay et al. Reference Bandyopadhyay, Qudsi, Gary, Matthaeus, Parashar, Maruca, Roytershteyn, Chasapis, Giles and Gershman2022; Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022, Reference Opie, Verscharen, Chen, Owen and Isenberg2023). The persistence of unstable intervals is, however, observable over extended spatial and temporal scales (Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022). Although we cannot fully exclude the possibility that $\varGamma _R$
reflects the fluctuations created by the instabilities themselves rather than the anisotropy-driving background turbulence, this persistence time scale argument suggests that the temperature anisotropies are indeed driven by the plasma motions. In addition to the consideration of the magnitude of $\varGamma _R$
, an analysis of the normalised cross-helicity and the Alfvén ratio shows that there are structural differences in the turbulence in the unstable regions (see Appendix A). This analysis suggests that there is an imbalance relative to the stable data whereby, on average, the energy in the velocity field is greater than that in the magnetic field for the unstable intervals. A further discussion of these structural differences would be worthwhile in a future study.
We note that our use of the radial rate of strain is distinct from the pressure strain interaction – the so-called Pi-D formalism – analysis that examines the contribution of turbulent fluctuations to the heating of ions (Yang et al. Reference Yang, Matthaeus, Parashar, Haggerty, Roytershteyn, Daughton, Wan, Shi and Chen2017; Bandyopadhyay et al. Reference Bandyopadhyay, Matthaeus, Parashar, Yang, Chasapis, Giles, Gershman, Pollock, Russell and Strangeway2020; Yang et al. Reference Yang, Pecora, Matthaeus, Roy, Cuesta, Chasapis, Parashar, Bandyopadhyay, Gershman and Giles2023). Nonetheless, our formulation goes some way to explaining the relationship between velocity shears and temperature anisotropy noted as an open question by Yang et al. (Reference Yang, Matthaeus, Parashar, Haggerty, Roytershteyn, Daughton, Wan, Shi and Chen2017).
Similarly, our measure differs from the partial variation of increments (PVI), which is used to locate magnetic (or velocity) field structures in solar-wind turbulence (Greco et al. Reference Greco, Chuychai, Matthaeus, Servidio and Dmitruk2008, Reference Greco, Matthaeus, Perri, Osman, Servidio, Wan and Dmitruk2017). The radial rate of strain $\varGamma _R$
is a dynamical measure that does not involve normalisation by a long-term average and is applied directly to fluctuations in the velocity field. We use $\varGamma _R$
to identify the creation of temperature anisotropy. We calculate the Pearson correlation coefficients between PVI and $\varGamma _R$
for our complete dataset and separately for each of the three conditioned subsets defined by stable, oblique firehose unstable and mirror-mode unstable intervals. We find negligible to no correlation with coefficients that range from ${\approx}0.09$
for the stable data to ${\approx}0.003$
for the whole dataset.
Observations and simulations suggest an important role for turbulent structures in the evolution of plasma conditions in the solar wind (Osman et al. Reference Osman, Matthaeus, Hnat and Chapman2012; Servidio et al. Reference Servidio, Osman, Valentini, Perrone, Califano, Chapman, Matthaeus and Veltri2014; Franci et al. Reference Franci, Landi, Matteini, Verdini and Hellinger2015; Greco et al. Reference Greco, Matthaeus, Perri, Osman, Servidio, Wan and Dmitruk2017; Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Leonardis, Chen, Šafránková and Němeček2017; Hellinger et al. Reference Hellinger, Matteini, Landi, Franci, Verdini and Papini2019; Qudsi et al. Reference Qudsi, Maruca, Matthaeus, Parashar, Bandyopadhyay, Chhiber, Chasapis, Goldstein, Bale and Bonnell2020). In § 4, we use statistical analysis to link the role of $\varGamma _R$
in driving unstable conditions with the skewness and kurtosis of $\varGamma _R$
, $\boldsymbol {B}$
and $\boldsymbol {v}$
. We apply this analysis to the conditioned subsets denoted as stable, oblique firehose unstable and mirror-mode unstable. The large kurtosis of $\varGamma _R$
and its subsets show that $\varGamma _R$
is highly intermittent and exhibits burstiness to a greater degree than either $\boldsymbol {B}$
or $\boldsymbol {v}$
. We see that $\kappa ^{OF}_{\varGamma _R}$
is considerably greater than either $\kappa ^{M}_{\varGamma _R}$
or $\kappa ^{S}_{\varGamma _R}$
, which is not the case for the subsets of $\boldsymbol {B}$
or $\boldsymbol {v}$
.
Coupled with the values for the skewness, we find three distinct subsets of $\varGamma _R$
with positively and negatively skewed subsets being associated with the oblique firehose and mirror-mode instabilities, respectively, whilst for the stable data, the skewness is nearly zero. The fact that the overall magnitudes of the skweness and kurtosis of $\varGamma _R$
are greater than those for the individual subsets implies that additional intermittency comes precisely from the alternation of these three distinct regions of stable data, oblique firehose unstable data and mirror-mode unstable data.
The power-law scalings of $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
, shown in figure 4, follow an exponent that is compatible with standard intermittency in the solar-wind magnetic field (Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Veltri, Consolini and Bruno1999). This correspondence is not unexpected since $\varGamma _R$
is built using various intermittent quantities. However, it implies that the greater magnitudes of $\lambda _{\varGamma _R}$
and $\kappa _{\varGamma _R}$
relative to those of $\boldsymbol {B}$
and $\boldsymbol {v}$
are not scale-dependent. We should therefore expect to see the regions of stable, oblique firehose unstable and mirror-mode unstable data characterised by distinct subsets of $\varGamma _R$
across scales in the inertial range of solar-wind turbulence.
While it has long been known that the turbulence in the solar wind is intermittent and multifractal (Paladin & Vulpiani Reference Paladin and Vulpiani1987; Burlaga Reference Burlaga1991; Frisch & Kolmogorov Reference Frisch and Kolmogorov1995; Tu & Marsch Reference Tu and Marsch1995), the analysis of our statistically robust, large dataset quantifies these characteristics in a novel way, allowing us to treat separately stable and unstable intervals in the data. Calculation from observations of all the quantities in this study requires the use of incremental gradients, and we benefit from Solar Orbiter's in situ instrument suite that provides continuous high-resolution datasets over significant time scales to enable this. The scientific impacts of the efficiency and high resolution of these instruments are by now well documented (Rouillard et al. Reference Rouillard, Pinto, Vourlidas, De Groof, Thompson, Bemporad, Dolei, Indurain, Buchlin and Sasso2020; D'Amicis et al. Reference D'Amicis, Bruno, Panasenco, Telloni, Perrone, Marcucci, Woodham, Velli, De Marco and Jagarlamudi2021; Louarn et al. Reference Louarn, Fedorov, Prech, Owen, Bruno, Livi, Lavraud, Rouillard, Genot and Andre2021; Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022). Nevertheless, our measures are restricted by the use of single-spacecraft data, which confines all analyses in this work to the radial sampling direction. In our view, the most promising route to extend this work lies in the use of high-quality three-dimensional data from a multi-spacecraft mission. This extension would allow the estimation of all relevant three-dimensional gradients rather than sampling along the radial direction via Taylor's hypothesis only. It would also be useful to extend the range of radial distances from the Sun over which these analyses are made using the perihelia data from Solar Orbiter and Parker Solar Probe.
Previous work shows how unstable intervals are statistically spatially and temporally distributed (Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022), and that unstable intervals are ergodicity-breaking and therefore statistically disjoint with respect to the stable regime (Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2023). Our current findings support and extend these previous results and describe more fully the impact of turbulence on kinetic instabilities in the solar wind, and in particular quantify the role of $\varGamma _R$
in driving unstable conditions.
6 Conclusions
In this work, we show that solar-wind intervals with parameters above the thresholds for temperature-anisotropy-driven instabilities are on average characterised by high absolute values of $\varGamma _R$
which is a measure of the extent to which bulk motions in the plasma drive temperature anisotropy. We attribute this observational result to the proposition that strong velocity shears drive temperature anisotropies in the turbulent solar wind through the shearing of the frozen-in magnetic field with a double-adiabatic impact on the particle distributions.
The radial rate of strain $\varGamma _R$
is highly intermittent with a distribution that exhibits greater levels of kurtosis relative to those of $\boldsymbol {B}$
and $\boldsymbol {v}$
, which is not unexpected given the contribution of increments of both $\boldsymbol {B}$
and $\boldsymbol {v}$
in (3.2). Nonetheless, we attribute this observational result to the burstiness of velocity shears in the solar wind with a significant occurrence rate of extreme values leading to a heavy-tailed distribution of $\varGamma _R$
. The conditioned subsets of $\varGamma _R$
that relate to stable, oblique firehose unstable and mirror-mode unstable intervals comprise distributions that are characteristically asymmetric (or symmetric in the case of stable data). The alternation of these distinct subsets contributes to the intermittency of $\varGamma _R$
. We attribute this observational result to the inhomogeneity that distinguishes each of the three regions of $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space represented by the subsets and that are both statistically and physically disjoint. Our observational measures – skewness and kurtosis – exhibit power-law scalings with an exponent that is consistent with the known intermittency in solar-wind turbulence.
Our study opens several areas of extended interest that deserve further exploration. For turbulence studies, our results emphasise the importance of the velocity field for the temperature anisotropy (and potentially other kinetic properties) of the plasma. We suggest that an analysis of the local energy transfer (LET) measure derived from the Politano–Pouquet scaling law (Politano & Pouquet Reference Politano and Pouquet1998; Sorriso-Valvo et al. Reference Sorriso-Valvo, Perrone, Pezzi, Valentini, Servidio, Zouganelis and Veltri2018b), revised to account for pressure-anisotropic magnetohydrodynamic turbulence (Simon & Sahraoui Reference Simon and Sahraoui2022), would be a useful extension of the current study. In addition, the role of $\varGamma _R$
in solar-wind turbulence could be further investigated in the simulation domain, ideally building on the existing work that shows how fluctuations in the velocity field are related to anisotropy (Franci et al. Reference Franci, Landi, Matteini, Verdini and Hellinger2015, Reference Franci, Hellinger, Matteini, Verdini and Landi2016, Reference Franci, Landi, Verdini, Matteini and Hellinger2018; Hellinger et al. Reference Hellinger, Matteini, Landi, Franci, Verdini and Papini2019).
Our work highlights new science opportunities for multi-spacecraft missions such as HelioSwarm (Klein et al. Reference Klein, Spence, Alexandrova, Argall, Arzamasskiy, Bookbinder, Broeren, Caprioli, Case and Chandran2023) and Plasma Observatory (Retinò et al. Reference Retinò, Khotyaintsev, Le Contel, Marcucci, Plaschke, Vaivads, Angelopoulos, Blasi, Burch and De Keyser2022), which will provide a means of measuring fully three-dimensional rates of strain and intermittency. These data will enable a more precise unpicking of the contributions of non-compressive and compressive fluctuations as well as intermittency to the creation and modulation of temperature anisotropy. A mission like HelioSwarm or Plasma Observatory with their complements of fields and plasma instrumentation has thus the potential to create breakthroughs in our understanding of the interplay between turbulence and kinetic instabilities in space plasmas. In particular, our results suggest that accurate and high-resolution measurements of the velocity field will be of fundamental importance to this task.
Our investigation of Solar Orbiter observations reveals a consistent picture of where and under what conditions kinetic instabilities act at the relevant scales in the turbulent solar wind. Unstable intervals are located in regions of strong velocity shear embedded in rapidly changing structures in the intermittent turbulence of the velocity field. The velocity shear and its associated impact on the frozen-in magnetic field drives and modulates the temperature anisotropy necessary to create the unstable conditions. The plasma can only remain above the instability thresholds for as long as the shears are sufficient to overcome the relaxation through the instabilities. This process takes place predominantly at the shear layers of highly intermittent structures whose distribution is strongly non-Gaussian. Accordingly, the presence of instabilities is not evenly distributed either spatially or temporally in the solar wind plasma.
Acknowledgements
Editor T. Passot thanks the referees for their advice in evaluating this article.
Funding
S.O. is supported by NERC grant NE/S007229/1. D.V. and C.J.O. are supported by STFC Consolidated Grant ST/W001004/1. C.H.K.C. is supported by UKRI Future Leaders Fellowship MR/W007657/1 and STFC Consolidated Grants ST/T00018X/1 and ST/X000974/1. P.A.I. is supported by NSF grant AGS2005982. L.F. is supported by the Royal Society University Research Fellowship No. URF/R1/231710 and by UKRI/STFC grant ST/W001071/1. This research was discussed at the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #563 (Ion Kinetic Instabilities in the Solar Wind in Light of Parker Solar Probe and Solar Orbiter Observations) led by L. Ofman and L. Jian. This work was supported by the Royal Society (UK) and the Consiglio Nazionale delle Ricerche (Italy) through the International Exchanges Cost Share scheme/Joint Bilateral Agreement project “Multi-scale electrostatic energisation of plasmas: comparison of collective processes in laboratory and space” (award numbers IEC$\backslash\backslash$
R2$\backslash\backslash$
222050 and SAC.AD002.043.021). Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. Solar Orbiter Solar Wind Analyser (SWA) data are derived from scientific sensors which have been designed, created and are operated under funding provided in numerous contracts from the UK Space Agency (UKSA), STFC, the Agenzia Spaziale Italiana (ASI), the Centre National d’Études Spatiales (CNES), the Centre National de la Recherche Scientifique (CNRS), the Czech contribution to the ESA PRODEX programme and NASA. Solar Orbiter SWA work at UCL/MSSL is currently funded under STFC grants ST/T001356/1 and ST/S000240/1. The Solar Orbiter magnetometer was funded by UKSA grant ST/T001062/1.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Alfvénicity in the solar wind
For this analysis of the Alfvénicity, we consider the fluctuations on the scale of 2 min, which is at the small-scale end of the inertial range and captures the relevant scales for the persistence of unstable intervals (Opie et al. Reference Opie, Verscharen, Chen, Owen and Isenberg2022). We define
and
where $\|\cdot \|$
denotes the time average taken over a 2-minute interval centred on the time of the measurement of $\delta \boldsymbol {b}$
and $\delta \boldsymbol {v}$
.
We define the normalised cross-helicity as
and the Alfvén ratio as
With these definitions, we create point-wise datasets for $\sigma _c$
and $R_A$
that allow us to investigate the correlations of the magnetic field and velocity field fluctuations at the scale of 2 min.
We show $|\sigma _c|$
and $R_A$
as bin-averaged distributions in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space for our whole dataset in figures 5 and 6.
Figure 5. Distribution of $|\sigma _c|$
as bin averages in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space. We overplot the instability thresholds for oblique firehose (OF), Alfvén/ion-cyclotron (A/IC) and mirror-mode (M) instabilities.
Figure 6. Distribution of $R_A$
plotted as bin averages in $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space with instability thresholds shown for oblique firehose (OF), Alfvén/ion-cyclotron (A/IC) and mirror-mode (M) instabilities.
On average, normalised cross-helicity in the solar wind is higher near the core of the stable dataset in this parameter space, and lower in the unstable intervals and at the low-$\beta _{\parallel }$
boundary of the stable data. The distribution of the bin-averaged Alfvén ratio shows that $|\delta {\boldsymbol {v}}|^2\gg |\delta {\boldsymbol {b}}|^2$
in the unstable regions of parameter space when $T_{\perp }/T_{\parallel }\leq 0.6$
or ${T_{\perp }/T_{\parallel }\geq 1.6}$
.
We see that $\sigma _c$
is significantly lower on average in the unstable intervals relative to the stable data, suggesting an imbalance between the velocity and magnetic field fluctuations in the unstable regions of the $T_{\perp }/T_{\parallel }$
–$\beta _{\parallel }$
parameter space. This is consistent with the hypothesis of a restriction on the amplitude of Alfvénic fluctuations in the limit of the oblique firehose instability (Squire, Quataert & Schekochihin Reference Squire, Quataert and Schekochihin2016; Squire, Schekochihin & Quataert Reference Squire, Schekochihin and Quataert2017) and suggests a similar mechanism may apply in the limit of the mirror-mode instability. The distribution of bin-averaged $R_A$
demonstrates that in the unstable intervals, greater temperature anisotropy is associated with the dominance of energy in the velocity field over energy in the magnetic field so that $R_A\gg 1$
.
Open access
