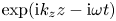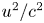Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T14:07:25.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Surface waves in a streaming plasma propagating in a duct: kinetic theory

Published online by Cambridge University Press:  16 May 2022

Hee J. Lee  and
Sang-Hoon Cho Open the ORCID record for Sang-Hoon Cho [Opens in a new window]
Hee J. Lee*
Affiliation:
Korean Physical Society, Division of Plasma Physics, Kangnam-gu, Yuksam-dong, 635-4 Seoul, South Korea
Sang-Hoon Cho
Affiliation:
SK Hynix Inc., Gyeongchung-daero Bubal-eub, Icheon-si Gyeonggi-do 17336, South Korea
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

The dispersion relation of a surface wave generated by a drifting plasma in an infinite duct surrounded by vacuum is derived non-relativistically by means of the Vlasov equation. The kinematic boundary condition imposed on the distribution function, the specular reflection conditions on the four sides of duct, can be satisfied by placing an infinite number of fictitious surface charge sheets spaced by the duct widths. The surface wave mode is specifically the transverse magnetic mode, often called the surface polariton, which propagates with phasor $\exp ({{\rm i}k_zz-{\rm i}\omega t})$. The method of placing appropriate fictitious surface charge sheets enables one to treat the surface waves in semi-infinite, slab and duct plasmas simultaneously on an equal footing, kinetically. The streaming effect manifests itself through the Doppler-shifted frequency and a correction-like term ${u^2}/{c^2}$, where u is the streaming velocity and c is the speed of light.

Keywords

plasma wavesplasma flowsplasma dynamics
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 3 , June 2022 , 905880305
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

1. Introduction

We consider surface waves of wave number $k_z$ and frequency $\omega$, generated by a plasma beam travelling in a duct interfaced with vacuum by using the Vlasov equation. Surface waves are given rise to by satisfying the kinetic and electromagnetic boundary conditions on the interface between the plasma and the vacuum surrounding it. The electric and magnetic fields in the plasma are connected with the vacuum side fields by the appropriate connection formula, and the latter can be deciphered from the basic equations themselves that we adopt. The connection formula can be easily worked out mathematically if the density gradient across the plasma and the other side is very steep. We talk about ‘a sharp interface’ if the density gradient is theoretically infinite. In this case, the connection formula can be obtained by ‘infinitesimal integration’ across the interface, which is the operation performed on a certain relevant equation in the manner $\int _{-\epsilon }^\epsilon (\cdots )\,{{\rm d} x}$. If the quantity $(\cdots )$ is a perfect differential, this operation yields a non-vanishing surface term that contributes to the connection formula. Usually, the surface term is the surface charge or surface current, In this way, the well-known electromagnetic and dynamic boundary conditions on the boundary can be derived (Lee & Cho Reference Lee and Cho1997). In a gross picture, the surface wave and the vacuum side wave are two different manifestations of ‘the same wave’ given rise to in an extreme inhomogeneous plasma.

A cold drifting plasma has a characteristic boundary condition (Lee & Cho Reference Lee and Cho1997,  Reference Lee and Cho1999), which can be expressed in the form

(1.1)\begin{equation} [B_y]=\frac{u}{c}[E_x] \end{equation}

or equivalently,

(1.2)\begin{equation} [D_x]=\frac{ck_z}{\omega}[B_y] \end{equation}

where $[\cdots ]$ signifies the jump across the interface, $D_x$ is the normal to the interface component of ${\boldsymbol D}$, the electric displacement, $u$ is the drift velocity in the $z$-direction, $B_y$ is the tangential component of the magnetic field and $c$ is the speed of light, and the other symbols have the usual meaning. The casual use of $[D_x]=0$ or $[B_y]=0$ in a drifting plasma leads to erroneous results as, discussed in earlier works (Lee & Cho Reference Lee and Cho1997; Lee Reference Lee2005). The physical origin of the boundary relation in (1.1) is due to the surface current formed in a cold drifting plasma, as is evident in the equation.

In a bounded Vlasov plasma, the kinematic boundary condition that is usually referred to as the specular reflection condition is assumed to be satisfied on a sharp boundary (Landau Reference Landau1946). The kinetic theory of surface waves in semi-infinite plasmas is well known (Barr & Boyd Reference Barr and Boyd1972; Alexandrov, Bogdankevich & Rukhadze Reference Alexandrov, Bogdankevich and Rukhadze1984). The kinetic dispersion relation of a surface wave in a slab plasma was worked out earlier (Lee & Lim Reference Lee and Lim2007). In this work, we investigate surface waves of a moving Vlasov plasma in a duct. We consider an infinite duct formed by the intersections of four planes: $x=0,a$ and $y=0,b$, with $-\infty < z<\infty$. Thus the specular reflection condition on the $x=a$ plane, for example, requires for the distribution function $f({\boldsymbol r},{\boldsymbol v},t)$ to satisfy $f(a,y,z, v_x,v_y,v_z,t)=f(a,y,z, -v_x,v_y,v_z,t)$ or, on the $y=b$ plane, $f(x,b,z, v_x,v_y,v_z,t)=f(x,b,z, v_x,-v_y,v_z,t)$, with similar equations for $x=0$ and $y=0$. In our duct-bounded plasma, the kinematic conditions on the four planes are satisfied by introducing an extended electric field in the fashion

(1.3a,b)\begin{gather} E_x({-}x,y,z)={-}E_x(x,y,z),\quad E_x(2a-x,y,z)={-}E_x(x,y,z), \end{gather}
(1.4a,b)\begin{gather} E_y(x,-y,z)={-}E_y(x,y,z),\quad E_y(x,2b-y,z)={-}E_y(x,y,z). \end{gather}

This scheme is workable if $f_0({\boldsymbol v})$, the zero-order distribution function, is invariant with respect to the reflections $v_x\rightarrow -v_x$ and $v_y\rightarrow -v_y$, and clearly this reflectional property is satisfied by the moving Maxwellian, to be introduced later.

The function $E_x(x)$, as defined in (1.3a,b), is a periodic function of a piecewise continuous function of period $'a'$ extending over the range $-\infty < x<\infty$ with discontinuity at $x=\pm 2na$ with a jump of $A_1$ (say) and with discontinuity at $x=\pm (2n-1)a$ with a jump of $A_2$ (say), where $n$ is an integer. The profile of the piecewise function $E_x(x)$ is plotted in Lee (Reference Lee2019). The algebra involved in carrying out the Fourier transform of the piecewise discontinuous functions with the aforementioned discontinuous jumps is quite taxing (Lee & Lim Reference Lee and Lim2007). However, it turns out that, after all the algebraic hard work, the discontinuities that are present in the extended field components $E_x(x,y)$ and $E_y(x,y)$ in (1.3a,b) and (1.4a,b) at the locations $x=\pm 2na$ and $x=\pm (2n-1)a$ and $y=\pm 2nb$ and $y=\pm (2n-1)b$ are mathematically (as well as physically) tantamount to placing fictitious surface charges at the corresponding jump locations in the form

(1.5)\begin{gather} S(x,y,z,t)= A_1\sum_{n=0,1,2,\ldots} \delta(x\pm2na)+A_2\sum_{n=1,2,\ldots} \delta(x\pm(2n-1)a)\nonumber\\ +B_1\sum_{n=0,1,2,\ldots} \delta(y\pm2nb)+B_2\sum_{n=1,2,\ldots} \delta(y\pm(2n-1)b). \end{gather}

This is the vital point of improvement in this work as compared with the earlier work (Lee & Lim Reference Lee and Lim2007). The surface charges are associated with the surface currents by satisfying the charge conservation equation

(1.6)\begin{equation} \frac{\partial S}{\partial t}+\hat{{\boldsymbol z}}\boldsymbol{\cdot} {\boldsymbol J}_s=0. \end{equation}

Therefore, we can assume the presence of the fictitious surface currents

(1.7)\begin{equation} {\boldsymbol J}_s({\boldsymbol r},\omega)=\hat{{\boldsymbol z}}\,{\rm i}\omega S(x,y,z,\omega). \end{equation}

The surface charges in (1.5) and the surface currents in (1.7) should be included in the Maxwell equations for our duct plasma wave analysis.

The basic equations are the linearized Vlasov equation and the Maxwell equations for electrons. Ions are assumed to be stationary and only form the neutralizing background

(1.8)\begin{gather} \frac{\partial}{\partial t} f({\boldsymbol r}, {\boldsymbol v},t)+{\boldsymbol v}\boldsymbol{\cdot}\frac{\partial f}{\partial {\boldsymbol r}}- \frac{e}{m}\left({\boldsymbol E}({\boldsymbol r},t)+\frac{1}{c}{\boldsymbol v}\times{\boldsymbol B}\right)\boldsymbol{\cdot} \frac{\partial f_0(v)}{\partial{\boldsymbol v}}=0, \end{gather}
(1.9)\begin{gather} \boldsymbol{\nabla}\times{\boldsymbol E}={-}\frac{1}{c}\frac{\partial{\boldsymbol B}}{\partial t}, \end{gather}
(1.10)\begin{gather} \boldsymbol{\nabla}\times{\boldsymbol B}=\frac{4{\rm \pi}}{c}{\boldsymbol J}+\frac{1}{c}\frac{\partial{\boldsymbol E}}{\partial t}+\hat{{\boldsymbol z}}J_s, \end{gather}

where

(1.11)\begin{gather} J_s= A_1'\sum_{n=0,1,2,\ldots} \delta(x\pm2na)+A_2'\sum_{n=1,2,\ldots} \delta(x\pm(2n-1)a)\nonumber\\ +B_1'\sum_{n=0,1,2,\ldots} \delta(y\pm2nb)+B_2'\sum_{n=1,2,\ldots} \delta(y\pm(2n-1)b), \end{gather}
(1.12)\begin{gather} {\boldsymbol J}({\boldsymbol r},t)={-}e\int {\boldsymbol v} f({\boldsymbol r}, {\boldsymbol v},t)\,{\rm d}^3v, \end{gather}
(1.13)\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol E}={-}4{\rm \pi} e\int f \,{\rm d}^3v+S(x,y,z), \end{gather}
(1.14)\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol B}=0. \end{gather}

It should be noted that the last term in (1.8) involving the magnetic field vanishes if $f_0$ is isotropic, but in a beam plasma, that term contributes to complexity. The zero-order distribution function is a moving Maxwellian

(1.15)\begin{equation} f_0({\boldsymbol v})=\left(\frac{m}{2{\rm \pi} T}\right)^{3/2}\exp\left[-\frac{m}{2T}({\boldsymbol v}-{\boldsymbol u})^2\right]. \end{equation}

We Fourier transform the above equations by performing $\int _{-\infty }^\infty \,{\rm d}^3r \exp ({{\rm i}{\boldsymbol k}\boldsymbol {\cdot }{\boldsymbol r}})(\cdots )$ and by assuming $\partial /\partial t={\rm i}\omega$. Then, the wave has a phasor $\exp ({{\rm i}k_zz-{\rm i}\omega t})$. The $(k_z,\omega )$ dependency in the Fourier amplitudes will be suppressed. Equation (1.8) is Fourier transformed to give

(1.16)\begin{equation} f({\boldsymbol k},{\boldsymbol v},\omega)=\frac{e}{m}\frac{{\rm i}}{\omega}\frac{E_j}{\omega-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol v}} \left[(\omega-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol v})\delta_{sj}+k_sv_j\right]\frac{\partial f_0}{\partial v_s},\end{equation}

where the repeated indexes are summed over. Here, and in the following, the Fourier-transformed variables are expressed by the argument; for example, $f(t)$ and $f(\omega )$ have different dimensions. If $f_0$ is isotropic, ${\partial f_0}/{\partial v_s}\sim f_0v_s$, and (1.16) reduces to the expression for the isotropic case.

Eliminating ${\boldsymbol B}$ between (1.9) and (1.10) gives

(1.17)\begin{equation} {\boldsymbol k}\times({\boldsymbol k}\times{\boldsymbol E})+\frac{\omega^2}{c^2}\varepsilon_{ij}\boldsymbol{\cdot}{\boldsymbol E}({\boldsymbol k},\omega)=\hat{{\boldsymbol z}}J_s({\boldsymbol k},\omega), \end{equation}

where $\varepsilon _{ij}$ is the dielectric tensor in a moving medium

(1.18)\begin{equation} \varepsilon_{ij}=\left(1-\frac{\omega_p^2}{\omega^2}\right) \delta_{ij}+\frac{\omega_p^2}{\omega^2}\int \,{\rm d}^3v\frac{v_iv_jk_s}{\omega-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol v}} \frac{\partial f_0}{\partial v_s}, \end{equation}

with $\omega _p$ being the plasma frequency. In (1.17), $J_s({\boldsymbol k},\omega )$, the Fourier transform of the surface currents in (1.11), is

(1.19)\begin{gather} J_s({\boldsymbol k},\omega)=\delta(k_y)[A_1\varSigma_0\exp({\pm {\rm i}2nak_x})+A_2\varSigma_1 \exp({\pm {\rm i}(2n-1)ak_x})]\nonumber\\ +\delta(k_x)[B_1\varSigma_0\exp({\pm {\rm i}2nbk_y})+B_2\varSigma_1\exp({\pm {\rm i}(2n-1)bk_y})], \end{gather}

where the $A$ and $B$ values may be functions of $k_z$, the double signs are summed over and the notations $\varSigma _0$ and $\varSigma _1$ are the summations in (1.11).

The foregoing formulation can be applied for simpler boundaries: in a semi-infinite plasma, we can suppose a single surface charge sheet $S(x)=A\delta (x)$, and in a slab geometry $0< x< a$, the surface charges are assumed in the form of (1.5) with $B_1=B_2=0$. The dispersion relation of surface waves in a slab plasma was worked out earlier without introducing the fictitious surface charges by directly Fourier transforming the extended electric field in (1.3a,b) (Lee & Lim Reference Lee and Lim2007).

2. Solutions for plasma fields

First, let us calculate $\varepsilon _{ij}$ in (1.18) by using the moving Maxwellian as given in (1.15). The velocity integral therein can be carried out by transforming ${\boldsymbol w}={\boldsymbol v}-{\boldsymbol u}$, and thus performing the integral over the isotropic Maxwellian distribution $f_0(w)$. Using

(2.1)\begin{equation} \frac{\partial f_0}{\partial v_s}=\frac{m}{T}(u_s-v_s) f_0, \end{equation}

the velocity integral becomes

(2.2)\begin{equation} \int \,{\rm d}^3v\frac{v_iv_jk_s}{\omega-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol v}} \frac{\partial f_0}{\partial v_s}=\delta_{ij}+\frac{m}{T}u_iu_j-\frac{m}{T}\omega'\int_{-\infty}^\infty \,{\rm d}^3v \frac{v_iv_j} {\omega'-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol w}}f_0(v), \end{equation}

where $\omega '=\omega -k_zu$ is the Doppler-shifted frequency. Using (2.1) again for $v_if_0$, eventually (2.2) is integrated to yield

(2.3)\begin{gather} \int \,{\rm d}^3v~\frac{v_iv_jk_s}{\omega-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol v}} \frac{\partial f_0}{\partial v_s}=\delta_{ij}+\frac{m}{T}u_iu_j-\omega' I_1\left(\delta_{ij}+\frac{m}{T}u_iu_j\right)\nonumber\\ -\omega'I_2(u_ik_j+k_iu_j)-2\omega'\frac{T}{m}k_ik_jI_3, \end{gather}
(2.4)\begin{gather} {\rm where}\quad I_n=\int_{-\infty}^\infty \frac{f_0(w)}{(\omega'-{\boldsymbol k}\boldsymbol{\cdot}{\boldsymbol w})^n}\,{\rm d}^3w,\quad (n=1,2,3)\end{gather}

can be written in terms of the plasma dispersion function $Z(\zeta )$

(2.5)\begin{equation} Z(\zeta)=\frac{1}{\sqrt{\rm \pi}}\int_{-\infty}^\infty\frac{{\rm e}^{{-}q^2}\,{\rm d}q}{q-\zeta}\quad \left(\zeta=\frac{\omega'/k}{\sqrt{2T/m}}\right). \end{equation}

We have $I_1=-\zeta Z/\omega '$, $I_2=-2\zeta ^2(1+\zeta Z)/\omega '^2$ and $I_3=\zeta ^2[\zeta Z-2\zeta ^2(1+\zeta Z)]/\omega '^3$. Then, (1.18) can be written in the form

(2.6)\begin{align} \varepsilon_{ij}& =\delta_{ij}+\frac{\omega_p^2}{\omega^2}\left[\left(\delta_{ij}-\frac{k_ik_j}{k^2}\right)\zeta Z(\zeta)+2\zeta^2(1+\zeta Z(\zeta))\right.\nonumber\\ & \left.\quad \times\left(\frac{k_ik_j}{k^2}+\frac{k_iu_j+k_ju_i}{\omega'} +\frac{k^2u_iu_j}{\omega'^2}\right)\right]. \end{align}

Equation (2.6) agrees with the dielectric tensor in a moving medium obtained from Lorentz transform (Alexandrov et al. Reference Alexandrov, Bogdankevich and Rukhadze1984). When the beam velocity ${\boldsymbol u}=0$, the dielectric tensor in (2.6) reduces to the well-known result for an isotropic medium. It is convenient to introduce the longitudinal and transverse dielectric permittivities,

(2.7)\begin{gather} \varepsilon_L=1+2\frac{\omega_p^2}{\omega^2}\zeta^2(1+\zeta Z(\zeta)), \end{gather}
(2.8)\begin{gather} \varepsilon_T=1+\frac{\omega_p^2}{\omega^2}\zeta Z(\zeta)). \end{gather}

In the above expressions, two frequencies are involved: the wave frequency $\omega$ and the Doppler-shifted frequency $\omega '$ hidden in the variable $\zeta$. In terms of $\varepsilon _{L,T}$, we have

(2.9)\begin{equation} \varepsilon_{ij}=\varepsilon_T \delta_{ij}+\frac{k_ik_j}{k^2}(\varepsilon_L-\varepsilon_T)+(\varepsilon_L-1)U_{ij}, \end{equation}

where $U_{ij}$ is the tensor associated with the beam velocity components

(2.10)\begin{equation} U_{ij}=\frac{k_iu_j+k_ju_i}{\omega'}+\frac{k^2u_iu_j}{\omega'^2}, \end{equation}

whose non-zero components are

(2.11a–c)\begin{equation} U_{xz}=U_{zx}=\frac{uk_x}{\omega'},\quad U_{yz}=U_{zy}=\frac{uk_y}{\omega'}, \quad U_{zz}=\frac{2k_zu}{\omega'}+\frac{k^2u^2}{\omega'^2}, \end{equation}

and the other elements are zero.

2.1. Solution for ${E}({k},\omega )$

Using (2.9) in (1.17) gives

(2.12)\begin{equation} \left[\delta_{ij}(\varepsilon_T-n^2)+\frac{k_ik_j}{k^2}(n^2+\varepsilon_L-\varepsilon_T)+U_{ij}(\varepsilon_L-1)\right]E_{j}= \hat{{\boldsymbol z}}~\frac{c^2}{\omega^2}J_s, \end{equation}

where $n^2=c^2k^2/\omega ^2$ is the refractive index.

We inverted the 3$\times$3 matrix in (2.12) to obtain ${\boldsymbol E}$

(2.13)\begin{gather} E_x={-}\frac{J_s}{\varDelta}\left(\frac{k_xk_z}{k^2}\alpha+\gamma U_{xz}\right), \end{gather}
(2.14)\begin{gather} E_y={-}\frac{J_s}{\varDelta}\left(\frac{k_yk_z}{k^2}\alpha+\gamma U_{yz}\right), \end{gather}
(2.15)\begin{gather} E_z=\frac{J_s}{\varDelta}\left(\frac{k_x^2+k_y^2}{k^2}\alpha+\beta\right), \end{gather}
(2.16)\begin{gather} B_x=\frac{c}{\omega}\frac{J_s}{\varDelta}k_y\left(\varepsilon_L+\gamma \frac{uk_z}{\omega'}\right), \end{gather}
(2.17)\begin{gather} B_y={-}\frac{c}{\omega}\frac{J_s}{\varDelta}k_x\left(\varepsilon_L+\gamma \frac{uk_z}{\omega'}\right), \end{gather}
(2.18)\begin{gather} B_z=0, \end{gather}

where

(2.19a–c)\begin{gather} \alpha=\varepsilon_L-\varepsilon_T+n^2,\quad \beta=\varepsilon_T-n^2,\quad \gamma=\varepsilon_L-1, \end{gather}
(2.20)\begin{gather} \varDelta=\beta \left[\varepsilon_L+(\varepsilon_L-1)\left(U_{zz}-\frac{u^2}{\omega'^2}(k_x^2+k_y^2)\right)\right]. \end{gather}

We use (2.18) since we investigate a transverse magnetic mode.

The above expressions for ${\boldsymbol E}({\boldsymbol k})$ need to be Fourier inverted to ${\boldsymbol E}({\boldsymbol r})$ to apply the boundary conditions. To make further development easier and the equations more transparent, we employ the cold plasma approximation. Then we have the cold plasma dielectric permittivities

(2.21)\begin{equation} \varepsilon_L=\varepsilon_T=1-\frac{\omega_p^2}{\omega^2}. \end{equation}

In a cold plasma, $\varDelta$ in (2.20) becomes

(2.22)\begin{equation} \varDelta=\beta\left[\left(1-\frac{\omega_p^2}{\omega^2}\right) -\frac{\omega_p^2}{\omega^2}\left(\frac{u^2k_z^2}{\omega'^2} +\frac{2k_zu}{\omega'} \right)\right]. \end{equation}

The above expression reduces to, for non-relativistic beam velocity ($u^2/c^2<<1)$,

(2.23)\begin{equation} \varDelta=\left(1-\frac{\omega_p^2}{\omega^2} -\frac{c^2k^2}{\omega^2}\right)\left(1-\frac{\omega_p^2}{\omega'^2}\right). \end{equation}

The field components are

(2.24)\begin{gather} E_x({\boldsymbol k},\omega)={-}\frac{J_s}{\varDelta}\frac{c^2}{\omega^2}k_x\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right), \end{gather}
(2.25)\begin{gather} E_y({\boldsymbol k},\omega)={-}\frac{J_s}{\varDelta}\frac{c^2}{\omega^2}k_y\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right), \end{gather}
(2.26)\begin{gather} E_z({\boldsymbol k},\omega)=\frac{J_s}{\varDelta}\left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right), \end{gather}
(2.27)\begin{gather} B_x({\boldsymbol k},\omega)=\frac{J_s}{\varDelta}\frac{c}{\omega}k_y\left(1-\frac{\omega_p^2}{\omega\omega'}\right), \end{gather}
(2.28)\begin{gather} B_y({\boldsymbol k},\omega)={-}\frac{J_s}{\varDelta}\frac{c}{\omega}k_x\left(1-\frac{\omega_p^2}{\omega\omega'}\right), \end{gather}

where $J_s$ is given in (1.19).

The Fourier inversion integrals must be carried out to obtain the plasma fields in ordinary coordinate space before the boundary conditions are applied. The integrals involve infinite series through the surface charge $J_s$, but the infinite series are nicely summed at the particular positions corresponding to $x=0,a$ and $y=0,b$. Thus, we apply the boundary conditions along the two infinite lines $(x,y,z)=(0,0,z)$ and $(a,b,z)$ with $-\infty < z<\infty$. The two lines correspond to the two seams of the duct which are diagonally opposite. When the inversion integrals are performed, the following formulas are useful, which can be verified by a simple change of variable, as is shown in earlier work (Lee & Lim Reference Lee and Lim2007). We have integrals of the type in the inversion integrals

(2.29)\begin{equation} J(x)=\int_{-\infty}^\infty \,{\rm d}k_x k_x \varPhi(k)\,{\rm e}^{{\rm i}k_xx} \left[A_1\varSigma_0\exp({\pm {\rm i}2nak_x})+A_2 \varSigma_1 \exp({\pm {\rm i}(2n-1)ak_x})\right], \end{equation}

where $\varPhi (k)$ is an even function of $k_x$. Then, we have

(2.30)\begin{gather} J(0)=A_1\int_{-\infty}^\infty \,{\rm d}k_xk_x\varPhi(k_x), \end{gather}
(2.31)\begin{gather} J(a)={-}A_2\int_{-\infty}^\infty \,{\rm d}k_xk_x\varPhi(k_x). \end{gather}

When we have integrals of the type

(2.32)\begin{equation} L(x)=\int_{-\infty}^\infty \,{\rm d}k_x \varPhi(k)\,{\rm e}^{{\rm i}k_xx}\left[A_1\varSigma_0 \exp({\pm {\rm i}2nak_x})+A_2 \varSigma_1\exp({\pm {\rm i}(2n-1)ak_x})\right], \end{equation}

we have

(2.33)\begin{gather} L(0)=2\int_{-\infty}^\infty \,{\rm d}k_x\varPhi(k_x)(A_1S_1+A_2S_2), \end{gather}
(2.34)\begin{gather} L(a)=2\int_{-\infty}^\infty \,{\rm d}k_x\varPhi(k_x)(A_1S_2+A_2S_1), \end{gather}

where

(2.35)\begin{gather} S_1=\frac{1}{2}+\exp({2{\rm i}ak_x})+\exp({4{\rm i}ak_x})+\cdots, \end{gather}
(2.36)\begin{gather} S_2=\exp({{\rm i}ak_x})+\exp({3{\rm i}ak_x})+\cdots. \end{gather}

Integrals (2.30), (2.31), (2.33) and (2.34) are useful for evaluating the integrals. We have

(2.37)\begin{align} & E_x(0,0,z)={-}\frac{c^2}{\omega^2}\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right)\int_{-\infty}^\infty \,{\rm d}k_x\int_{-\infty}^\infty \,{\rm d}k_y\times \frac{k_x}{\varDelta}\Big[\delta(k_y)\Big(A_1\varSigma_0\exp({\pm {\rm i}2nak_x})\nonumber\\ & \qquad +\,A_2\varSigma_1 \exp({\pm {\rm i}(2n-1)ak_x})\Big)+\delta(k_x) \Big(B_1\varSigma_0\exp({\pm {\rm i}2nbk_y})\nonumber\\ & \quad\quad +\,B_2\varSigma_1 \exp({\pm {\rm i}(2n-1)bk_y})\Big)\Big]\nonumber\\ & \quad ={-}\frac{c^2}{\omega^2}\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right)\int_{-\infty}^\infty \,{\rm d}k_x \frac{k_x}{\varDelta} \Big(A_1\varSigma_0 \exp({\pm {\rm i}2nak_x})+A_2\varSigma_1 \exp({\pm {\rm i}(2n-1)ak_x})\Big)\nonumber\\ & \quad ={-}\frac{c^2}{\omega^2}\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right)A_1\int_{-\infty}^\infty \,{\rm d}k_x \frac{k_x}{\varDelta}, \end{align}

where we have used (2.30). In the last (also in the later) integral, $k^2$ hidden in $\varDelta$ is $k^2=k_z^2+k_x^2$. We have

(2.38)\begin{align} & E_x(a,b,z)={-}\frac{c^2}{\omega^2}(k_z-\frac{u\omega_p^2}{c^2\omega'})\int_{-\infty}^\infty \,{\rm d}k_x \,{\rm e}^{{\rm i}k_xa}\int_{-\infty}^\infty \,{\rm d}k_y\,{\rm e}^{{\rm i}k_yb}\nonumber\\ & \qquad \times\frac{k_x}{\varDelta}\Big[\delta(k_y)\Big(A_1\varSigma_0\exp({\pm {\rm i}2nak_x})+A_2\varSigma_1 \exp({\pm {\rm i}(2n-1)ak_x})\Big)\nonumber\\ & \qquad +\,\delta(k_x) \Big(B_1\varSigma_0\exp({\pm {\rm i}2nbk_y})+B_2\varSigma_1\exp({\pm {\rm i}(2n-1)bk_y})\Big)\Big]\nonumber\\ & \quad ={-}\frac{c^2}{\omega^2}(k_z-\frac{u\omega_p^2}{c^2\omega'})\int_{-\infty}^\infty \,{\rm d}k_x\, {\rm e}^{{\rm i}k_xa}\frac{k_x}{\varDelta} \Big(A_1\varSigma_0\exp({\pm {\rm i}2nak_x})+A_2\varSigma_1\exp({\pm {\rm i}(2n-1)ak_x})\Big) \nonumber\\ & \quad={-}\frac{c^2}{\omega^2}(k_z-\frac{u\omega_p^2}{c^2\omega'})~({-}A_2)\int_{-\infty}^\infty \,{\rm d}k_x \frac{k_x}{\varDelta}, \end{align}

where we used (2.31). Analogous integrations yield

(2.39)\begin{gather} E_y(0,0,z)={-}\frac{c^2}{\omega^2}\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right)B_1\int_{-\infty}^\infty \,{\rm d}k_y \frac{k_y}{\varDelta}, \end{gather}
(2.40)\begin{gather} E_y(a,b,z)={-}\frac{c^2}{\omega^2}\left(k_z-\frac{u\omega_p^2}{c^2\omega'}\right)({-}B_2)\int_{-\infty}^\infty \,{\rm d}k_y \frac{k_y}{\varDelta}. \end{gather}

In the above (also in the later) $\int \,{\rm d}k_y$ integral, $k^2$ hidden in $\varDelta$ is $k^2=k_z^2+k_y^2$

(2.41)\begin{gather} B_x(0,0,z)=\frac{c}{\omega}\left(1-\frac{\omega_p^2}{\omega\omega'}\right)B_1\int_{-\infty}^\infty \,{\rm d}k_y \frac{k_y}{\varDelta}, \end{gather}
(2.42)\begin{gather} B_x(a,b,z)=\frac{c}{\omega}\left(1-\frac{\omega_p^2}{\omega\omega'}\right)({-}B_2)\int_{-\infty}^\infty \,{\rm d}k_y \frac{k_y}{\varDelta}, \end{gather}
(2.43)\begin{gather} B_y(0,0,z)={-}\frac{c}{\omega}\left(1-\frac{\omega_p^2}{\omega\omega'}\right) A_1\int_{-\infty}^\infty \,{\rm d}k_x \frac{k_x}{\varDelta}, \end{gather}
(2.44)\begin{gather} B_y(a,b,z)={-}\frac{c}{\omega}\left(1-\frac{\omega_p^2}{\omega\omega'}\right) ({-}A_2)\int_{-\infty}^\infty \,{\rm d}k_x \frac{k_x}{\varDelta}. \end{gather}

We encounter a different type of integral in

(2.45)\begin{align} & E_z(0,0,z)=\left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right)\int_{-\infty}^\infty \,{\rm d}k_x \int_{-\infty}^\infty \,{\rm d}k_y \times \frac{1}{\varDelta}\left[\delta(k_y)\left(A_1\varSigma_0\exp({\pm {\rm i}2nak_x})\right.\right.\nonumber\\ & \left.\left.\quad +\,A_2\varSigma_1 \exp({\pm {\rm i}(2n-1)ak_x})\right)+\delta(k_x) \left(B_1\varSigma_0\exp({\pm {\rm i}2nbk_y})\right.\right.\nonumber\\ & \left.\left.\quad\quad +\,B_2\varSigma_1\exp({\pm {\rm i}(2n-1)bk_y})\right)\right], \end{align}

which becomes

(2.46)\begin{align} & E_z(0,0,z)=\left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right)\left[\int_{-\infty}^\infty \frac{{\rm d}k_x}{\varDelta}\left(A_1\varSigma_0 \exp({\pm {\rm i}2nak_x})\right.\right.\nonumber\\ & \left.\left.\quad +\,A_2\varSigma_1\exp({\pm {\rm i}(2n-1)ak_x})\right)\right.\nonumber\\ & \left.\quad +\,\int_{-\infty}^\infty \frac{{\rm d}k_y}{\varDelta}\left(B_1\varSigma_0\exp({\pm {\rm i}2nbk_y}) +B_2\varSigma_1\exp({\pm {\rm i}(2n-1)bk_y})\right)\right], \end{align}

which we write in the form

(2.47)\begin{align} E_z(0,0,z)& =2\left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right)\left[\int_{-\infty}^\infty \frac{{\rm d}k_x}{\varDelta}\left(A_1S_1(ak_x)+A_2 S_2(ak_x)\right)\right.\nonumber\\ & \left.\quad +\int_{-\infty}^\infty \frac{{\rm d}k_y}{\varDelta}\left(B_1S_1(bk_y) +B_2S_2(bk_y)\right)\right], \end{align}

where we have used (2.33), and

(2.48)\begin{equation} S_1(\xi)=\frac{1}{2}+{\rm e}^{2{\rm i}\xi}+{\rm e}^{4{\rm i}\xi}\cdots\quad S_2(\xi)={\rm e}^{{\rm i}\xi}+{\rm e}^{3{\rm i}\xi}+\cdots. \end{equation}

Analogously, we obtain

(2.49)\begin{align} E_z(a,b,z)& =2\left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right)\left[\int_{-\infty}^\infty \frac{{\rm d}k_x}{\varDelta}\left(A_1S_2(ak_x)+A_2 S_1(ak_x)\right)\right.\nonumber\\ & \left.\quad+\int_{-\infty}^\infty \frac{{\rm d}k_y}{\varDelta}\left(B_1S_2(bk_y)+B_2S_1(bk_y)\right)\right], \end{align}

where we have used (2.34).

2.2. Vacuum solution

Vacuum solutions should solve

(2.50)\begin{equation} \left(\boldsymbol{\nabla}^2+\frac{\omega^2}{c^2}\right){\boldsymbol B}=0, \end{equation}

and

(2.51)\begin{equation} {\boldsymbol E}=\frac{{\rm i}c}{\omega}\boldsymbol{\nabla}\times{\boldsymbol B}. \end{equation}

Equation (2.50) is solved by

(2.52)\begin{equation} {\boldsymbol B}\sim {\rm e}^{{\rm i}k_zz}\,{\rm e}^{{\pm} k_xx}\,{\rm e}^{{\pm}~k_yy} \end{equation}

with constraint $k_x^2+k_y^2=k_z^2-{\omega ^2}/{c^2}\equiv \lambda ^2$ and $\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol B}=0$. Furthermore, we assume $B_z=0$ since we consider the transverse magnetic mode.

The vacuum regions corresponding to (or exterior to) the lines $(0,0,z)$ and $(a,b,z)$, which we designate as $(i)$ and $(ii)$, respectively, are:

Vacuum region $(i)$ $~x<0,~y<0$, where we have

(2.53)\begin{gather} B_x^v(i)=H_x\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{k_xx}\,{\rm e}^{k_yy}, \end{gather}
(2.54)\begin{gather} B_y^v(i)=H_y\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{k_xx}\,{\rm e}^{k_yy}, \end{gather}
(2.55)\begin{gather} k_xH_x+k_yH_y=0, \end{gather}
(2.56)\begin{gather} E_z^v(i)= \frac{{\rm i}\,c}{\omega}(H_yk_x-H_xk_y)\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{k_xx}\,{\rm e}^{k_yy}, \end{gather}
(2.57)\begin{gather} E_x^v(i)=\frac{c}{\omega}k_zH_y\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{k_xx}\,{\rm e}^{k_yy}, \end{gather}
(2.58)\begin{gather} E_y^v(i)={-}\frac{c}{\omega}k_zH_x\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{k_xx}\,{\rm e}^{k_yy}. \end{gather}

Vacuum region $(ii)$ $x>a,y>b$, where

(2.59)\begin{gather} B_x^v(ii)=G_x\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{{-}k_xx}\,{\rm e}^{{-}k_yy}, \end{gather}
(2.60)\begin{gather} B_y^v(ii)=G_y\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{{-}k_xx}\,{\rm e}^{{-}k_yy}, \end{gather}
(2.61)\begin{gather} k_xG_x+k_yG_y=0, \end{gather}
(2.62)\begin{gather} E_z^v(ii)= \frac{{\rm i}\,c}{\omega}({-}G_yk_x+G_xk_y)\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{{-}k_xx}\,{\rm e}^{{-}k_yy}, \end{gather}
(2.63)\begin{gather} E_x^v(ii)=\frac{c}{\omega}k_zG_y\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{{-}k_xx}\,{\rm e}^{{-}k_yy}, \end{gather}
(2.64)\begin{gather} E_y^v(ii)={-}\frac{c}{\omega}k_zG_x\,{\rm e}^{{\rm i}k_zz}\,{\rm e}^{{-}k_xx}\,{\rm e}^{{-}k_yy}. \end{gather}

Putting $(x,y)=(0,0)$ or $(a,b)$ in the above equations gives the vacuum side values of the relevant quantities.

3. Dispersion relation

We enforce the following boundary conditions to connect the plasma and the vacuum fields: $[E_z]=0,\ [B_y]=({u}/{c})[E_x],\ [B_x]=-({u}/{c})[E_y]$

Along line $(0,0,z)$

$[E_z]=0$ gives, per (2.47) and (2.56),

(3.1)\begin{gather} \left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right) (A_1I_1+A_2I_2+B_1J_1+B_2J_2) =\frac{{\rm i}c}{\omega}(H_yk_x-H_xk_y), \end{gather}
(3.2)\begin{gather} {\rm where}\quad I_i=2\int_{-\infty}^\infty \frac{{\rm d}k_x}{\varDelta}S_i(ak_x),\quad J_i=2\int_{-\infty}^\infty \frac{{\rm d}k_x}{\varDelta}S_i(bk_y),\quad (i=1,2), \end{gather}

$[B_y]=({u}/{c})[E_x]$ gives

(3.3)\begin{gather} A_1Q\left(1-\frac{\omega_p^2}{\omega'^2}\right)+\frac{\omega}{c}H_y=0, \end{gather}
(3.4)\begin{gather} {\rm where}\quad Q=\int_{-\infty}^\infty \,{\rm d}k_x\frac{k_x}{\varDelta}=\int_{-\infty}^\infty \,{\rm d}k_y\frac{k_y}{\varDelta} \end{gather}

$[B_x]=-({u}/{c})[E_y]$ gives

(3.5)\begin{equation} B_1Q\left(1-\frac{\omega_p^2}{\omega'^2}\right)-\frac{\omega}{c}H_x=0. \end{equation}

Along line $(a,b,z)$

$[E_z]=0$ gives

(3.6)\begin{equation} \left(1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2}\right)(A_1I_2+A_2I_1+B_1J_2+B_2J_1) =\frac{{\rm i}c}{\omega}({-}G_yk_x+G_xk_y)\,{\rm e}^{{-}k_xa}\,{\rm e}^{{-}k_yb}, \end{equation}

$[B_y]=({u}/{c})[E_x]$ gives

(3.7)\begin{equation} A_2Q\left(1-\frac{\omega_p^2}{\omega'^2}\right)-\frac{\omega}{c}G_y\,{\rm e}^{{-}k_xa}\,{\rm e}^{{-}k_yb}=0, \end{equation}

$[B_y]=-({u}/{c})[E_x]$ gives

(3.8)\begin{equation} B_2Q\left(1-\frac{\omega_p^2}{\omega'^2}\right)+\frac{\omega}{c}G_x\,{\rm e}^{{-}k_xa}\,{\rm e}^{{-}k_yb}=0. \end{equation}

In obtaining (3.3), (3.5), (3.7) and (3.8), we neglected $u^2/c^2\ll 1$ as compared with unity. In addition, we have, per $\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol B}=0$ and $B_z=0$,

(3.9)\begin{gather} k_xH_x+k_yH_y=0, \end{gather}
(3.10)\begin{gather} k_xG_x+k_yG_y=0. \end{gather}

Thus, we have 8 equations for 8 unknowns; $A_1,\,A_2,\,B_1,\,B_2,\,H_x,\,H_y,\,G_x,\,G_y$.

Eliminating $H_x$, $H_y$, $G_x$, $G_y$ gives

(3.11)\begin{gather} A_1\left(I_1+{\rm i}\frac{c^2}{\omega^2}\frac{\eta}{\xi}k_xQ\right)+A_2I_2+B_1\left(J_1+{\rm i}\frac{c^2}{\omega^2}\frac{\eta}{\xi}k_yQ\right)+ B_2J_2=0, \end{gather}
(3.12)\begin{gather} A_1I_2+A_2\left(I_1+{\rm i}\frac{c^2}{\omega^2}\frac{\eta}{\xi}k_xQ\right)+B_1J_2+B_2\left(J_1+{\rm i}\frac{c^2}{\omega^2}\frac{\eta}{\xi}k_yQ\right)=0, \end{gather}
(3.13)\begin{gather} k_yA_1=k_xB_1, \end{gather}
(3.14)\begin{gather} k_yA_2=k_xB_2, \end{gather}

where

(3.15)\begin{equation} \xi=1-\frac{\omega_p^2}{\omega^2}-\frac{c^2k_z^2}{\omega^2},\quad \eta=1-\frac{\omega_p^2}{\omega'^2}. \end{equation}

Eliminating $B_1$ and $B_2$ gives

(3.16)\begin{gather} A_1\left[k_xI_1+k_yJ_1+\frac{{\rm i}c^2}{\omega^2}\frac{\eta}{\xi}(k_x^2+k_y^2)Q\right]+A_2(k_xI_2+k_yJ_2)=0, \end{gather}
(3.17)\begin{gather} A_1(k_xI_2+k_yJ_2)+A_2\left[k_xI_1+k_yJ_1+\frac{{\rm i}c^2}{\omega^2}\frac{\eta}{\xi}(k_x^2+k_y^2)Q\right]=0, \end{gather}

and (3.16) and (3.17) yield the dispersion relation in the form

(3.18)\begin{equation} k_x\int_{-\infty}^\infty\frac{{\rm d}k_x}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}ak_x}}{1\mp {\rm e}^{{\rm i}ak_x}}+ k_y\int_{-\infty}^\infty\frac{{\rm d}k_y}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}bk_y}}{1\mp {\rm e}^{{\rm i}bk_y}}+ {{\rm i}\lambda^2}\frac{c^2}{\omega^2}\frac{\eta}{\xi}\int_{-\infty}^\infty k_x\frac{{\rm d}k_x}{\varDelta}=0, \end{equation}

where we used

(3.19)\begin{equation} \int_{-\infty}^\infty \frac{{\rm d}k_x}{\varDelta}\left[S_1(ak_x)\pm S_2(ak_x)\right]= \frac{1}{2}\int_{-\infty}^\infty\frac{{\rm d}k_x}{\varDelta}~\frac{1\pm {\rm e}^{{\rm i}ak_x}}{1\mp {\rm e}^{{\rm i}ak_x}}. \end{equation}

In regard to the Fourier variables $k_x$ and $k_y$ outside the integrals, we imposed the constraint $k_x^2+k_y^2=k_z^2-\omega ^2/c^2\equiv \lambda ^2$. Therefore, it is convenient to transform

(3.20a,b)\begin{equation} k_x=\frac{b\lambda}{\sqrt{a^2+b^2}},\quad k_y=\frac{a\lambda}{\sqrt{a^2+b^2}} \end{equation}

($k_x$, $k_y$ inside the integrals are dummy variables and are left as they are). The transform in (3.20a,b) satisfies the constraint and the relation $ak_x=bk_y$. In fact, it can be derived from the latter and the constraint. Then, the dispersion relation takes the form

(3.21)\begin{equation} \frac{b}{\sqrt{a^2+b^2}}\int_{-\infty}^\infty\frac{{\rm d}k_x}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}ak_x}}{1\mp {\rm e}^{{\rm i}ak_x}}+ \frac{a}{\sqrt{a^2+b^2}}\int_{-\infty}^\infty\frac{{\rm d}k_y}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}bk_y}}{1\mp {\rm e}^{{\rm i}bk_y}}+ {{\rm i}\lambda}\frac{c^2}{\omega^2}~\frac{\eta}{\xi}\int_{-\infty}^\infty k_x~\frac{{\rm d}k_x}{\varDelta}=0. \end{equation}

If either $a$ or $b\rightarrow \infty$, we recover the slab dispersion relation (Lee & Lim Reference Lee and Lim2007)

(3.22)\begin{equation} \int_{-\infty}^\infty\frac{{\rm d}k_x}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}ak_x}}{1\mp {\rm e}^{{\rm i}ak_x}}+ {{\rm i}\lambda}\frac{c^2}{\omega^2}~\frac{\eta}{\xi}\int_{-\infty}^\infty k_x~\frac{{\rm d}k_x}{\varDelta}=0. \end{equation}

It is recalled that the $k^2$ hidden in $\varDelta$ is $k^2=k_z^2+k_x^2$ in $\int \,{\rm d}k_x$-integral and $k^2=k_z^2+k_y^2$ in $\int \,{\rm d}k_y$-integral. Thus, let us change the integration variables, both $k_x$ and $k_y$, in (3.21) to $\kappa$

(3.23)\begin{equation} \frac{b}{\sqrt{a^2+b^2}}\int_{-\infty}^\infty\frac{{\rm d}\kappa}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}a\kappa}}{1\mp {\rm e}^{{\rm i}a\kappa}}+ \frac{a}{\sqrt{a^2+b^2}}\int_{-\infty}^\infty\frac{{\rm d}\kappa}{\varDelta}\frac{1\pm {\rm e}^{{\rm i}b\kappa}}{1\mp {\rm e}^{{\rm i}b\kappa}}+ {{\rm i}\lambda}\frac{c^2}{\omega^2}\frac{\eta}{\xi}\int_{-\infty}^\infty \kappa\frac{{\rm d}\kappa}{\varDelta}=0, \end{equation}

where $k^2=k_z^2+\kappa ^2$. In regard to the double signs in (3.23), the upper (lower) signs correspond to the symmetric (anti-symmetric) mode which also occurs in a slab plasma. For a square duct ($a=b)$, (3.23) reduces to the form identical to the slab dispersion equation (3.22), except for the factor $\sqrt 2$. This reduction is due to the $x$–$y$ symmetry. To recover the slab dispersion relation from (3.18), we take $k_y\rightarrow 0$, $b\rightarrow \infty$, and put $k_x=\lambda$. We can take $k_y\rightarrow 0$ since the $y$-direction has a translational invariance in a slab.

The duct dispersion relation in (3.23) can be contour integrated for a cold plasma, giving

(3.24)\begin{equation} \frac{b\gamma}{\sqrt{a^2+b^2}}\tanh \frac{a\gamma}{2}+\frac{a\gamma}{\sqrt{a^2+b^2}}\tanh \frac{b\gamma}{2} +\sqrt{k_z^2-\frac{\omega^2}{c^2}}\left(1-\frac{\omega_p^2}{\omega'^2}\right)=0, \end{equation}

where $\gamma =\sqrt {k_z^2-({\omega ^2-\omega _p^2})/{c^2}}$. For the anti-symmetric mode, the $\tanh$-function above is replaced by a $\coth$-function.

4. Discussion

In a bounded plasma, one way of solving the Vlasov equation by satisfying the specular reflection condition is to extend the plasma electric field in the manner of (1.3a,b). The job of Fourier transforming such a piecewise continuous periodic function, extending to infinity, is taxing. In this work, we present an alternative way of avoiding the hard labour by placing sheets of fictitious surface charges at the location of discontinuities of the electric field. The magnitudes of the surface charges are undetermined constants, but they can be determined through the connection formula with the vacuum side field – resulting in the dispersion relation of the surface wave. This method enables one to deal with semi-infinite, slab duct plasmas in a common work frame. Taking $b\rightarrow \infty$ in (3.24) gives

(4.1)\begin{equation} \gamma\tanh \frac{a\gamma}{2} +\sqrt{k_z^2-\frac{\omega^2}{c^2}}\left(1-\frac{\omega_p^2}{\omega'^2}\right)=0, \end{equation}

which is the slab ($0< x< a$) dispersion relation. Taking $a\rightarrow \infty$ in (4.1) gives

(4.2)\begin{equation} \gamma +\sqrt{k_z^2-\frac{\omega^2}{c^2}}~\left(1-\frac{\omega_p^2}{\omega'^2}\right)=0. \end{equation}

Equation (4.2) agrees with the semi-infinite dispersion relation obtained by Lee (Reference Lee2005) without introducing the fictitious surface charge sheet. If $u=0$, or $\omega '=\omega$, (4.2) agrees with the slab dispersion relation obtained from the fluid theory worked out by Gradov & Stenflo (Reference Gradov and Stenflo1983).

For a square duct, putting $a=b$ in (3.24) yields

(4.3)\begin{equation} \sqrt2\gamma\tanh \frac{a\gamma}{2} +\sqrt{k_z^2-\frac{\omega^2}{c^2}}\left(1-\frac{\omega_p^2}{\omega'^2}\right)=0, \end{equation}

which is similar to the slab dispersion relation. This is because the complete symmetry between the $x$ and $y$ coordinates makes the three-dimensional problem a two-dimensional problem practically.

The Doppler-shifted frequency $\omega '$ appearing in (3.24) represents the streaming effect. This is the first-order effect of the ratio $u/c$. The second-order effect enters through $U_{zz}$ in (2.11a–c), which produces terms of order $u^2/c^2$. If we chase those terms, we end up with  replacing in (3.24) $(1-{\omega _p^2}/{\omega '^2}) \rightarrow 1-{\omega _p^2}/{\omega '^2}(1-{u^2}/{c^2})$. Relativistic treatment may be desirable to include the higher-order effect of $u^2/c^2$ in a systematic way.

This work may find applications in a laboratory or astrophysical situation where electromagnetic waves propagate through certain channels.

Acknowledgements

Editor P. Helander thanks the referees for their advice in evaluating this article.

Funding

This research received no specific grant from any funding agency, commercial or not-for-profit sectors.

Declaration of interests

The authors report no conflict of interest.

References

REFERENCES

Alexandrov, A.F., Bogdankevich, L.S. & Rukhadze, A.A. 1984 Principles of Plasma Electrodynamics, p. 159, Chapter 6, Springer.CrossRefGoogle Scholar
Barr, H.C. & Boyd, T.J.M. 1972 Surface waves in hot plasmas. J. Phys. A: Gen. Phys. 5 (7), 1108.CrossRefGoogle Scholar
Gradov, O.M. & Stenflo, L. 1983 Linear theory of cold bounded plasma. Phys. Rep. 94, 111–137.CrossRefGoogle Scholar
Landau, L.D. 1946 On the vibrations of the electronic plasma. J. Phys. 10 (1), 25–34.Google Scholar
Lee, H.J. 2005 Comment on “kinetic theory of surface waves in plasma jets”. Phys. Plasmas 12, 094701.CrossRefGoogle Scholar
Lee, H.J. 2019 Fundamentals of Theoretical Plasma Physics: Mathematical Description of Plasma Waves, p. 551. World Scientific.CrossRefGoogle Scholar
Lee, H.J. & Cho, S.H. 1997 Boundary conditions for surface waves propagating along the interface of plasma flow and free space. J. Plasma Phys. 58, 409–419.CrossRefGoogle Scholar
Lee, H.J. & Cho, S.H. 1999 Response to ‘comment on “boundary conditions for surface waves propagating along the interface of plasma flow and free space”’. J. Plasma Phys. 61, 173–174.CrossRefGoogle Scholar
Lee, H.J. & Lim, Y.K. 2007 Kinetic theory of surface waves in a plasma slab. J. Korean Phys. Soc. 50, 1056–1061.CrossRefGoogle Scholar